PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
 2 Термодинамика
2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
-
5.
 3 Фотометрия
3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Лабораторная работа №17 (Определение коэф. трения качения с помощью накл. маятника)
Лабораторная работа № 17
ОПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА ТРЕНИЯ КАЧЕНИЯ С ПОМОЩЬЮ
НАКЛОННОГО МАЯТНИКА.
Цель работы.
Познакомиться с явлением трения, классификацией видов трения.
Рассчитать коэффициент трения качения для заданных пар шарик-подложка.
Теоретическое введение.
При соприкосновении двух тел под некоторым давлением между их поверхностями возникает сила, препятствующая перемещению одного тела относительно другого. Такая сила называется силой трения покоя. Наличие этого вида трения приводит к явлениям застоя и заноса.
Если приложить внешнюю силу, параллельную поверхности соприкосновения тел, то скольжение тел начинается после того, как внешняя сила превзойдет определенное значение. Таким образом, сила трения покоя, направленная противоположно внешней силе и равная ей, изменяется от нуля до некоторого максимального значения.
При скольжении
тел относительно друг друга вдоль
поверхности соприкосновения действует
сила трения скольжения, направленная
противоположно относительной скорости
движения.
FСК = FН, (1)
где: — коэффициент трения скольжения, значение которого находят из опыта.
Данный коэффициент зависит от материала тел, состояния трущихся поверхностей и скорости движения. FН — сила нормального давления.
Когда тело катится по поверхности другого, то появляется сила трения качения:
где: k — коэффициент трения качения; r — радиус катящегося тела.
Обе силы FСК и FТР противодействуют перемещению тел, их
действие приводит к потере механической
энергии.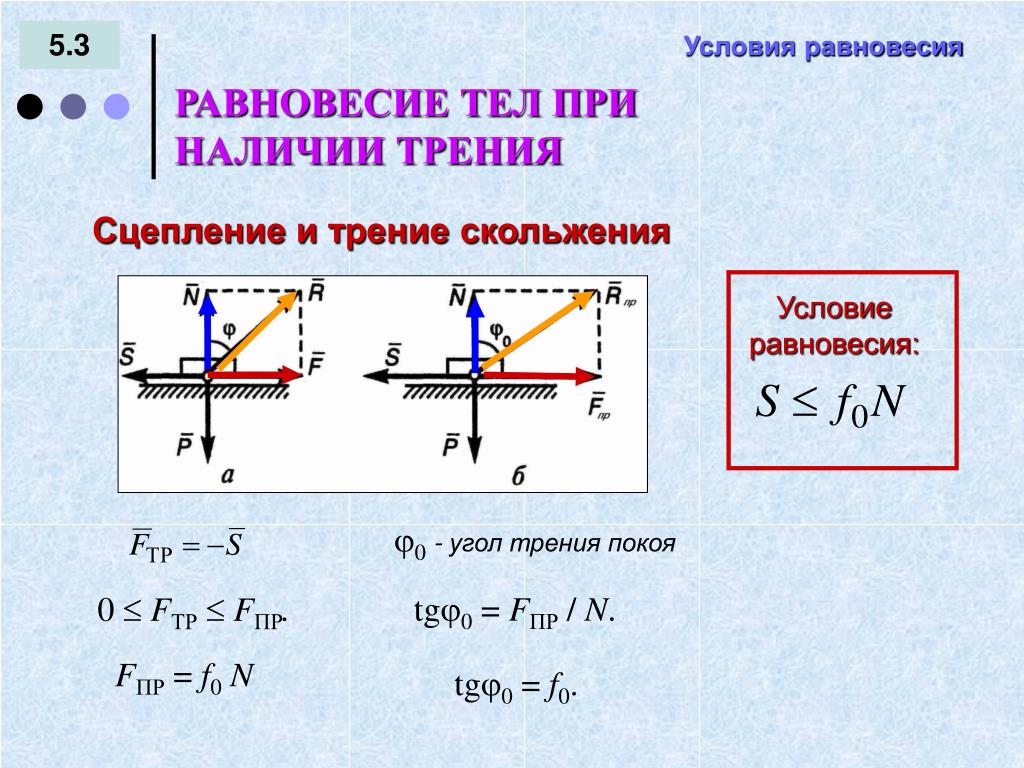 Характерной особенностью
рассмотренных сил является наличие
силы трения покоя; сила трения не
обращается в нуль, когда движение
прекращается. Такое трение называется
сухим. Возникновение сухого трения
обусловлено взаимодействием молекул,
атомов и электронов, находящихся вблизи
поверхности соприкосновения, то есть,
электромагнитным взаимодействием.
Характерной особенностью
рассмотренных сил является наличие
силы трения покоя; сила трения не
обращается в нуль, когда движение
прекращается. Такое трение называется
сухим. Возникновение сухого трения
обусловлено взаимодействием молекул,
атомов и электронов, находящихся вблизи
поверхности соприкосновения, то есть,
электромагнитным взаимодействием.
Если соприкасающиеся поверхности тел хорошо смазать, то тело начинает скользить при очень малых, практически близких к нулю внешних силах. Это объясняется тем, что между собой трутся не твердые поверхности, а тонкие жидкие пленки, которые налипают на поверхности твердых тел. Возникающие при этом силы трения называют силами жидкого трения, так как трение покоя отсутствует.
При сухом трении
движение с ускорением происходит тогда,
когда внешняя сила превосходит силу
трения. В этом случае при постоянной
внешней силе скорость растет неограниченно
( в нерелятивистском смысле). При жидком
трении сила пропорциональна скорости
при небольших скоростях.
Как правило, силы трения качения и жидкого трения меньше: чем силы трения скольжения. Поэтому, когда трение вредно, трение скольжение заменяют трением качения или жидким трением.
Не следует думать, что трение играет только отрицательную роль при движении. Если бы не было трения, не смогли бы двигаться автомобили, поезда, люди не могли бы ходить по ровной поверхности, опасно было бы сидеть на стуле и т.д.
Рассмотрим роль
трения при качении колеса радиусом r.
Если качение происходит без проскальзывания
и тело не деформируется, то вдоль
поверхности соприкасающихся тел
действует только сила трения покоя,
которая и обеспечивает движение. Работа
этой силы равна нулю, следовательно
потери механической энергии нет, если
нет деформации тел.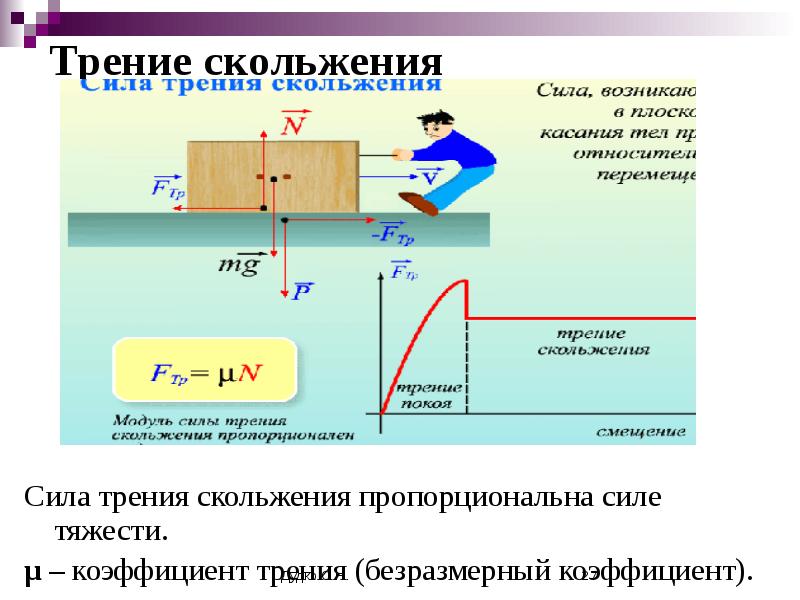
В действительности при качении всегда есть потери механической энергии. Причина этих потерь — сила трения качения, которая не сводится ни к трению покоя, ни к трению скольжения. Возникновение силы трения качения, очевидно, связано с деформацией.
Абсолютно упругие деформации (рис.1а) не приводят к появлению каких-либо сил, тормозящих движение, так как равнодействующая сил F, приложенных к деформированному колесу со стороны участков деформированной плоскости, проходит через центр колеса и имеет только вертикальную составляющую.
Если деформации являются неупругими (рис.1б), то равнодействующая F имеет как вертикальную составляющую FН, так и горизонтальную, направленную против скорости и являющуюся силой трения качения FТР.
Качение — сложное
движение, его можно представить как
сумму двух движений: поступательного
и вращательного относительно мгновенного
центра О’. Сила тяги двигателя F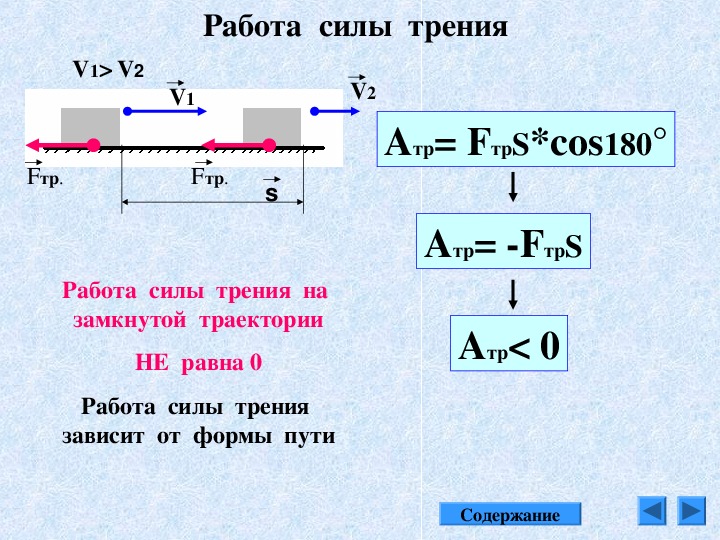 2):
2):
М = FТr
При равномерном вращении сумма моментов сил относительно точки О’ равна нулю:
FТr — FНk — F ТРl = 0, (3)
где: k — плечо силы F Н; l — плечо силы F ТР.
Рис.1 Рис.2
Деформации при качении обычно малы, значит l мало и моментом силы трения качения можно пренебречь. Чтобы колесо катилось с постоянной скоростью V, сила тяги FТ должна уравновешивать силу трения качения FТР: FТ = FТР.
Учитывая это, уравнение (3) можно записать:
F ТРr = F Нk.
Отсюда для силы
трения качения F ТР получим
выражение (2). Таким образом, коэффициент
трения качения k в отличии от
имеет размерность длины, так как является
плечом силы F Н.
ОПИСАНИЕ УСТАНОВКИ И МЕТОДЫ ИЗМЕРЕНИЯ.
Установка представляет собой наклонный маятник (рис.3).
Рис.3
Если шарик отвести от положения равновесия (ось ОО1) на угол 0 и затем отпустить, то он будет совершать колебания, катаясь около положения равновесия. Из-за трения качения амплитуда колебаний будет уменьшаться, колебания будут затухающими. Потери полной механической энергии колебаний равны работе сил трения качения согласно закону сохранения энергии:
E = AТР.
В точках А и В скорость шарика равна нулю, следовательно, полная механическая энергия равна только потенциальной энергии. Так как высота шарика уменьшается на h за половину периода колебаний, потеря механической энергии составит:
E
= mgh. (4)
(4)
Из рис. 3 видно, что потеря высоты h равна:
h = A1B1sin = l(cos — cos 0) sin (5)
где: l — расстояние от точки подвеса до центра тяжести шарика.
Работа силы трения качения на пути s, равном длине дуги АВ, равна:
(6)
где: FН = mgcos (7)
Приравняв выражения (4) и (6), после преобразований с учетом (5) и (7) получим:
k = lrtg (cos — cos ), (8)
Для уменьшения
погрешности определения k рассмотрим
изменение угла отклонения шарика за n
полных колебаний. Если обозначим
амплитудное значение угла отклонения
n через n полных колебаний, то путь, который
при этом проходит центр тяжести маятника
равен:
Если обозначим
амплитудное значение угла отклонения
n через n полных колебаний, то путь, который
при этом проходит центр тяжести маятника
равен:
s = 4lnСР, где:
Выражение (8) в этом случае примет вид:
При небольших углах отклонения можно считать:
Используя это соотношение, для расчета коэффициента трения качения получим формулу:
(9)
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Установить по заданию преподавателя наклон маятника. Определить угол .
Отклонить шарик в крайнее правое положение. Угол не должен превышать 5°.
Определить амплитудное значение угла отклонения n после n полных колебаний.

Определить радиус шарика r.
Повторить опыт не менее 5 раз.
По заданию преподавателя сменить шарик или подложку — пластину, по которой катится шарик. Повторить опыт в новых условиях.
Рассчитать значение k по формуле (9) и его погрешность k.
Записать результат в форме, установленной стандартом.
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯЗначение погрешности коэффициента трения качения k можно определить по формуле:
(10)
КОНТРОЛЬНЫЕ ВОПРОСЫЧто такое “сухое трение” и “жидкое трение”?
Назовите виды трения.
Напишите формулы для силы трения скольжения и силы трения качения.
От чего зависит сила трения скольжения и сила трения качения?
От чего зависит коэффициент трения скольжения? коэффициент трения качения?
В чем отличие коэффициента трения качения от коэффициента трения скольжения?
Что такое наклонный маятник? Выведите формулу для силы нормального давления на наклонной плоскости.

ЛИТЕРАТУРА
[10]-[12]; [8] c. 47-52; [9] c. 765.
Калькулятор формул уравнений статического трения
Научная физика
Решение максимального статического трения.
Ввод:
Преобразование:
коэффициент статического трения (µ статический )
нормальная сила (F нормальный )
= 0
ньютон
Решение:
максимальное трение покоя (f max static )
= НЕ РАСЧЕТНО
Другие единицы:
Изменить уравнение
Выберите, чтобы найти другое неизвестное
трение покоя
| трение покоя | |
| коэффициент трения покоя | |
| 900 48 | нормальная сила |
кинетическое трение
| кинетическое трение | |
| кинетическое коэффициент трения | |
| нормальная сила |
Статическое трение Определение
Статическое трение представляет собой фундаментальную силу в физике и технике, которая препятствует возникновению относительного движения между двумя контактирующими объектами или поверхностями. Мы рассмотрим важность статического трения, приведем примеры, обсудим уравнение и коэффициент, объясним, как решать проблемы, наметим распространенные ошибки, укажем, где оно применяется, и опишем, как его уменьшить или увеличить.
Мы рассмотрим важность статического трения, приведем примеры, обсудим уравнение и коэффициент, объясним, как решать проблемы, наметим распространенные ошибки, укажем, где оно применяется, и опишем, как его уменьшить или увеличить.
Статическое трение имеет решающее значение в различных приложениях и повседневных ситуациях. Например, он обеспечивает необходимое сцепление между предметами и поверхностями, позволяя нам ходить или водить машину, не скользя. В машиностроении статическое трение необходимо для функционирования механических соединений, тормозов, сцеплений и устойчивости конструкций. Кроме того, это помогает предотвратить скольжение или опрокидывание из-за внешних сил, таких как ветер или землетрясения.
Уравнение и коэффициент
Связь между статическим трением и силами, действующими на объект, выражается с помощью следующей формулы:
Fs = мкс * Н
- Fs представляет собой максимальную статическую силу трения. Это также сокращено до статической силы трения.

- мкс обозначает коэффициент статического трения
- Н — нормальная сила, действующая перпендикулярно контактным поверхностям и прижимающая их друг к другу.
Коэффициент статического трения, безразмерное число, представляет собой силу трения между двумя контактирующими поверхностями. Это зависит от материалов и шероховатости поверхностей. Более высокие значения коэффициента указывают на большую силу трения. Коэффициент статического трения имеет диапазон от 0 до 1. Коэффициент 0 означает, что две поверхности совершенно скользкие, а коэффициент 1 означает, что две поверхности совершенно липкие. В реальной жизни коэффициент статического трения обычно находится в пределах от 0,5 до 1,9.0003
Максимальная статическая сила трения
Максимальная статическая сила трения — это наибольшая величина силы трения, которая существует между двумя объектами, находящимися в состоянии покоя относительно друг друга, прежде чем они начнут двигаться. Он действует как сопротивление приложенной силе, предотвращая перемещение или скольжение объектов друг относительно друга. Если приложенная сила превышает максимальную статическую силу трения, объекты начинают скользить, и трение переходит из статического в кинетическое.
Если приложенная сила превышает максимальную статическую силу трения, объекты начинают скользить, и трение переходит из статического в кинетическое.
Как решать проблемы, связанные со статическим трением
При решении проблем, связанных со статическим трением, выполните следующие действия:
- Определите материалы и соответствующий им коэффициент статического трения.
- Рассчитайте нормальную силу (Н), действующую на объект, обычно равную весу объекта для горизонтальных поверхностей.
- Умножьте коэффициент трения покоя (мкс) на нормальную силу (Н), чтобы найти максимальную силу трения покоя (Fs).
- Сравните приложенную силу с силой трения покоя: объект остается неподвижным, если приложенная сила меньше или равна максимальной силе трения покоя (Fs). Однако, если приложенная сила превышает максимальную статическую силу трения, объект начнет двигаться, а силы трения перейдут в кинетические.
Примеры статического трения
- Толкание тяжелой коробки или мебели по полу: При попытке переместить тяжелую коробку по полу трение статического электричества сопротивляется движению.
 Коробка остается неподвижной, если приложенная сила ниже максимальной статической силы трения. Когда сила превышает предел, коробка начинает двигаться.
Коробка остается неподвижной, если приложенная сила ниже максимальной статической силы трения. Когда сила превышает предел, коробка начинает двигаться. - Торможение остановившегося автомобиля: При торможении остановившегося автомобиля статическое трение между тормозными колодками и тормозными дисками удерживает автомобиль на месте.
- Ходьба или бег: статическое трение между обувью и поверхностью обеспечивает сцепление, позволяя нам ходить, не скользя.
- Удержание книги на наклонной поверхности: статическое трение предотвращает скольжение книги по поверхности до тех пор, пока сила тяжести, действующая на книгу, меньше максимальной силы статического трения.
- Лестница у стены: Лестница защищена от скольжения за счет статического трения между ее ножками и землей, а также между ее вершиной и стеной.
- Автомобильные шины сцепляются с дорогой: статическое трение предотвращает скольжение автомобиля или грузовика по дороге.
- Болт и гайка: статическое трение между болтом, гайкой и поверхностью удерживает все на месте.

- Гвоздь в стене: трение между гвоздем и деревом удерживает гвоздь на месте.
Области, в которых используется статическое трение
Статическое трение жизненно важно во многих областях, включая
- Физика
- Автомобилестроение
- Гражданское строительство
- Машиностроение
- Спортивная наука
Распространенные ошибки
- Путают статическое и кинетическое трение.
- Использование неправильного коэффициента трения для данного материала.
- Игнорирование трения в расчетах, когда его следует учитывать.
- Неверный расчет нормальной силы.
- Без учета влияния смазочных материалов или загрязнений на трение.
- Неверная интерпретация направления силы трения.
- Предполагая, что более гладкие поверхности всегда имеют более низкое статическое трение, чем шероховатые поверхности: Хотя шероховатость поверхности влияет на трение, другие факторы, такие как химический состав материалов и наличие смазочных материалов, могут значительно повлиять на коэффициент статического трения.

- Полагая, что трение покоя всегда действует в направлении, противоположном приложенной силе: Хотя в большинстве случаев это верно, бывают ситуации, когда трение покоя может действовать в том же направлении, что и приложенная сила.
- Без учета влияния температуры на трение
Уменьшение или увеличение статического трения
Для уменьшения статического трения можно:
- Использовать смазочные материалы или покрытия для уменьшения коэффициента статического трения между поверхностями.
- Выбирайте материалы с более низким коэффициентом статического трения для контактных поверхностей.
- Используйте более гладкие поверхности, уменьшая шероховатость поверхности.
- Изменить геометрию контакта
- Использовать подшипники или ролики между поверхностями
Чтобы увеличить статическое трение, можно:
- Увеличить нормальную силу, прижимающую поверхности друг к другу.
- Выбирайте материалы с более высоким коэффициентом статического трения для контактных поверхностей.

- Выбирайте более шероховатые поверхности, увеличивая шероховатость поверхности.
Статическое трение, обледенелые дороги и антиблокировочные тормозные системы
Антиблокировочные тормозные системы (ABS) на обледенелых дорогах предотвращают блокировку колес путем регулирования тормозного давления. Статическое трение возникает, когда шины сохраняют контакт с дорогой без скольжения. ABS стремится максимизировать статическое трение, предотвращая блокировку колес. Однако, когда колеса блокируются, кинетическое трение берет верх, вызывая занос и снижая управляемость. ABS обнаруживает неизбежную блокировку колес, быстро регулирует тормозное давление и поддерживает оптимальный баланс между статическим и кинетическим трением. Сохраняя статическое трение и сводя к минимуму кинетическое трение, ABS обеспечивает лучший контроль, позволяя водителям более эффективно управлять автомобилем и останавливаться на скользких поверхностях, таких как лед.
Ссылки — Книги:
Типлер, Пол А. . 1995. Физика для ученых и инженеров. Стоит Издатели. 3-е изд.
. 1995. Физика для ученых и инженеров. Стоит Издатели. 3-е изд.
11.1 Катящееся движение – University Physics Volume 1
11 Угловой момент
Цели обучения
К концу этого раздела вы сможете:
- Описывать физику качения без проскальзывания
- Объясните, как линейные переменные связаны с угловыми переменными для случая качения без проскальзывания
- Найти линейное и угловое ускорения при качении с проскальзыванием и без него
- Расчет статической силы трения, связанной с качением без проскальзывания
- Использование энергосбережения для анализа качения
Движение качения — это обычное сочетание вращательного и поступательного движения, которое мы видим повсюду, каждый день. Подумайте о различных ситуациях, когда колеса движутся по шоссе, или колеса самолета приземляются на взлетно-посадочную полосу, или колеса робота-исследователя на другой планете. Понимание сил и крутящих моментов, участвующих в качающееся движение является решающим фактором во многих различных ситуациях.
Для анализа качения в этой главе обратитесь к рисунку в разделе «Вращение с фиксированной осью», чтобы найти моменты инерции некоторых общих геометрических объектов. Вы также можете найти его полезным в других расчетах, связанных с вращением.
Перекатывание без проскальзывания
Люди наблюдали перекатывание без проскальзывания с момента изобретения колеса. Например, мы можем посмотреть на взаимодействие шин автомобиля и поверхности дороги. Если водитель нажимает педаль акселератора в пол так, что шины крутятся, а автомобиль не движется вперед, между колесами и поверхностью дороги должно быть кинетическое трение. Если водитель медленно нажимает на педаль акселератора, заставляя автомобиль двигаться вперед, то шины катятся без проскальзывания. Для большинства людей удивительно, что на самом деле нижняя часть колеса находится в покое по отношению к земле, что указывает на наличие статического трения между шинами и поверхностью дороги. На рисунке велосипед движется, а всадник остается в вертикальном положении. Шины соприкасаются с дорожным покрытием, и, несмотря на то, что они катятся, нижняя часть шин слегка деформируется, не скользит и находится в состоянии покоя относительно дорожного покрытия в течение измеримого промежутка времени. Для этого между шиной и поверхностью дороги должно быть статическое трение.
Шины соприкасаются с дорожным покрытием, и, несмотря на то, что они катятся, нижняя часть шин слегка деформируется, не скользит и находится в состоянии покоя относительно дорожного покрытия в течение измеримого промежутка времени. Для этого между шиной и поверхностью дороги должно быть статическое трение.
Чтобы проанализировать качение без проскальзывания, мы сначала выводим линейные переменные скорости и ускорения центра масс колеса в терминах угловые переменные, описывающие движение колеса. Ситуация показана на рис.
Рисунок 11. 3 (a) Колесо тянется по горизонтальной поверхности под действием силы [латекс]\mathbf{\overset{\to}}{F}}[/латекс]. Сила статического трения [латекс] {\ mathbf {\ overset {\ to } {f}}} _ {\ text {S}}, | {\ mathbf {\ overset {\ to } {f}}} _ { \text{S}}|\le {\mu }_{\text{S}}N[/latex] достаточно большой, чтобы не скользить. (b) Векторы линейной скорости и ускорения центра масс и соответствующие выражения для [латекс]\омега\,\текст{и}\,\альфа[/латекс]. Точка P покоится относительно поверхности. (c) Относительно системы центра масс (ЦМ) точка P имеет линейную скорость [латекс]\текст{−}R\omega \mathbf{\шляпа{i}}[/латекс].
3 (a) Колесо тянется по горизонтальной поверхности под действием силы [латекс]\mathbf{\overset{\to}}{F}}[/латекс]. Сила статического трения [латекс] {\ mathbf {\ overset {\ to } {f}}} _ {\ text {S}}, | {\ mathbf {\ overset {\ to } {f}}} _ { \text{S}}|\le {\mu }_{\text{S}}N[/latex] достаточно большой, чтобы не скользить. (b) Векторы линейной скорости и ускорения центра масс и соответствующие выражения для [латекс]\омега\,\текст{и}\,\альфа[/латекс]. Точка P покоится относительно поверхности. (c) Относительно системы центра масс (ЦМ) точка P имеет линейную скорость [латекс]\текст{−}R\omega \mathbf{\шляпа{i}}[/латекс]. На рисунке (а) мы видим векторы силы, участвующие в предотвращении проскальзывания колеса. На (b) точка P , касающаяся поверхности, покоится относительно поверхности. Относительно центра масс точка P имеет скорость [латекс]\текст{−}R\omega \mathbf{\hat{i}}[/латекс], где R — радиус колеса, а [ латекс]\омега[/латекс] — угловая скорость колеса относительно своей оси. Поскольку колесо катится, скорость P относительно поверхности равна его скорости относительно центра масс плюс скорость центра масс относительно поверхности:
Поскольку колесо катится, скорость P относительно поверхности равна его скорости относительно центра масс плюс скорость центра масс относительно поверхности:
[латекс] {\ mathbf {\ overset {\ to} {v}}} _ {P} = \ text {−} R \ omega \ mathbf {\ hat {i}} + {v} _ {\ text {CM}}\mathbf{\hat{i}}.[/latex]
Поскольку скорость P относительно поверхности равна нулю, [latex]{v}_{P}=0[/latex] , это говорит о том, что
[латекс]{v}_{\text{CM}}=R\omega .[/латекс]
Таким образом, скорость центра масс колеса равна его радиусу, умноженному на угловую скорость относительно его ось. Покажем соответствие линейной переменной в левой части уравнения угловой переменной в правой части уравнения. Это сделано ниже для линейного ускорения.
Если продифференцировать рисунок в левой части уравнения, то получим выражение для линейного ускорения центра масс. В правой части уравнения R является константой, и поскольку [латекс]\альфа =\фрак{д\омега} {dt},[/латекс] мы имеем
[латекс]{а}_{\ text{CM}}=R\alpha . [/latex]
[/latex]
Кроме того, мы можем найти расстояние, которое проходит колесо, в терминах угловых переменных, обратившись к рис. Когда колесо катится от точки A до точки B , его внешняя поверхность отображается на землю точно на пройденное расстояние, которое составляет [латекс]{d}_{\text{CM}}.[/latex] Из рисунка видно, что длина внешней поверхности, отображает на землю длину дуги [латекс]R\theta \text{}[/латекс]. Приравнивая два расстояния, мы получаем
[латекс]{d}_{\text{СМ}}=R\theta .[/латекс]
Рисунок 11.4 При качении колеса по поверхности длина дуги [латекс ]R\theta[/latex] от A до B отображается на поверхности, что соответствует расстоянию [latex]{d}_{\text{CM}}[/latex], на которое переместился центр масс.Пример
Катится по наклонной плоскости
Твердый цилиндр катится по наклонной плоскости без проскальзывания, начиная с состояния покоя. Он имеет массу m и радиус r . а) Чему равно его ускорение? б) Какому условию должен удовлетворять коэффициент трения покоя [латекс]{\му }_{\текст{S}}[/латекс], чтобы цилиндр не скользил?
Стратегия
Нарисуйте эскиз и диаграмму свободного тела и выберите систему координат. Ставим x в направлении вниз по плоскости и y вверх перпендикулярно плоскости. Определить задействованные силы. Это нормальная сила, сила тяжести и сила трения. Запишите законы Ньютона в направлениях x и y и закон Ньютона для вращения, а затем решите ускорение и силу трения.
Ставим x в направлении вниз по плоскости и y вверх перпендикулярно плоскости. Определить задействованные силы. Это нормальная сила, сила тяжести и сила трения. Запишите законы Ньютона в направлениях x и y и закон Ньютона для вращения, а затем решите ускорение и силу трения.
Решение
- Диаграмма свободного тела и эскиз показаны на рисунке, включая нормальную силу, компоненты веса и силу трения покоя. Трения едва хватает, чтобы цилиндр вращался без проскальзывания. Поскольку проскальзывание отсутствует, величина силы трения меньше или равна [латекс] {\ mu } _ {S} Н [/латекс]. Запись законов Ньютона в x – и y — направления, имеем
[латекс]\сумма {F}_{x}=m{a}_{x};\enspace\sum {F}_{y}=m{a}_{y}.[/latex]
Рис. 11.5 Твердый цилиндр катится по наклонной плоскости, не соскальзывая с места. Система координат имеет x в направлении вниз по наклонной плоскости и y перпендикулярно плоскости. Диаграмма свободного тела показана с нормальной силой, статической силой трения и компонентами веса [латекс] m\mathbf{\overset{\to}}{g}}[/latex]. Трение заставляет цилиндр катиться по плоскости, а не скользить.
Диаграмма свободного тела показана с нормальной силой, статической силой трения и компонентами веса [латекс] m\mathbf{\overset{\to}}{g}}[/latex]. Трение заставляет цилиндр катиться по плоскости, а не скользить.Замена из диаграммы свободного тела,
[латекс]\begin{array}{ccc}\hfill mg\,\text{sin}\,\theta -{f}_{\text{S}}& =\hfill & m{({a}_ {\ text {CM}})} _ {x}, \ hfill \\ \ hfill N-mg \, \ text {cos} \, \ theta & = \ hfill & 0, \ hfill \\ \ hfill {f} _{\text{S}}& \le \hfill & {\mu }_{\text{S}}N,\hfill \end{массив}[/latex]
мы можем тогда найти линейное ускорение центра масс из этих уравнений:
[латекс] {({a} _ {\ text {CM}})} _ {x} = g (\ text {sin} \, \ theta — {\ mu } _ {S} \ text {cos} \ ,\тета).[/латекс]
Однако полезно выразить линейное ускорение через момент инерции. Для этого запишем второй закон Ньютона для вращения:
[латекс]\sum {\tau}_{\text{CM}}={I}_{\text{CM}}\alpha .[/latex]
Крутящие моменты рассчитываются относительно оси, проходящей через центр масс цилиндра.
 Единственный ненулевой крутящий момент обеспечивается силой трения. У нас есть
Единственный ненулевой крутящий момент обеспечивается силой трения. У нас есть[латекс] {f} _ {\ text {S}} r = {I} _ {\ text {CM}} \ alpha .[/latex]
Наконец, линейное ускорение связано с угловым ускорением на
[латекс] {({a}_{\text{CM}})}_{x}=r\alpha .[/latex]
Эти уравнения можно использовать для решения для [латекса] {a} _ {\ text {CM}}, \ alpha , \, \ text {и} \, {f} _ {\ text {S}} [/latex ] с точки зрения момента инерции, где мы опустили индекс x -. Мы записываем [латекс]{а}_{\текст{СМ}}[/латекс] через вертикальную составляющую силы тяжести и силы трения и делаем следующие замены.
[латекс] {a} _ {\ text {CM}} = g \ text {sin} \, \ theta — \ frac {{f} _ {\ text {S}}} {m} [/latex] 9{2})}=\frac{1}{3}\text{tan}\,\theta .[/latex]
Значение
- Линейное ускорение линейно пропорционально [латекс]\текст{sin}\,\тета .[/латекс] Таким образом, чем больше угол наклона, тем больше линейное ускорение, как и следовало ожидать.
 . Угловое ускорение, однако, линейно пропорционально [латекс]\текст{sin}\,\тета[/латекс] и обратно пропорционально радиусу цилиндра. Таким образом, чем больше радиус, тем меньше угловое ускорение. 9{2})}.[/latex]
. Угловое ускорение, однако, линейно пропорционально [латекс]\текст{sin}\,\тета[/латекс] и обратно пропорционально радиусу цилиндра. Таким образом, чем больше радиус, тем меньше угловое ускорение. 9{2})}.[/latex]Это очень полезное уравнение для решения задач, связанных с качением без проскальзывания. Обратите внимание, что ускорение меньше, чем у объекта, скользящего по плоскости без трения без вращения. Ускорение также будет разным для двух вращающихся цилиндров с разной инерцией вращения.
Качение с проскальзыванием
В случае качения с проскальзыванием мы должны использовать коэффициент кинетического трения, который приводит к кинетической силе трения, поскольку статического трения нет. Ситуация показана на рис. В случае проскальзывания [латекс]{v}_{\text{CM}}-R\omega \ne 0[/латекс], поскольку точка P на колесе не покоится на поверхности, а [латекс]{v}_{P}\ne 0[/латекс]. Таким образом, [латекс]\omega \ne \frac{{v}_{\text{CM}}}{R},\alpha \ne \frac{{a}_{\text{CM}}}{R} [/латекс].
Рисунок 11.6 (a) Между колесом и поверхностью возникает кинетическое трение, поскольку колесо проскальзывает. (b) Простые отношения между линейными и угловыми переменными больше не действительны.
Пример
Скатывание по наклонной плоскости с проскальзыванием
Твердый цилиндр скатывается с наклонной плоскости из состояния покоя и испытывает проскальзывание (рис.). имеет массу м и радиус r . а) Чему равно его линейное ускорение? б) Чему равно его угловое ускорение относительно оси, проходящей через центр масс?
Стратегия
Нарисуйте эскиз и диаграмму свободного тела, показывающую действующие силы. Диаграмма свободного тела аналогична случаю отсутствия проскальзывания, за исключением того, что сила трения является кинетической, а не статической. Используйте второй закон Ньютона, чтобы найти ускорение в направлении x . Используйте второй закон вращения Ньютона, чтобы найти угловое ускорение.
Решение
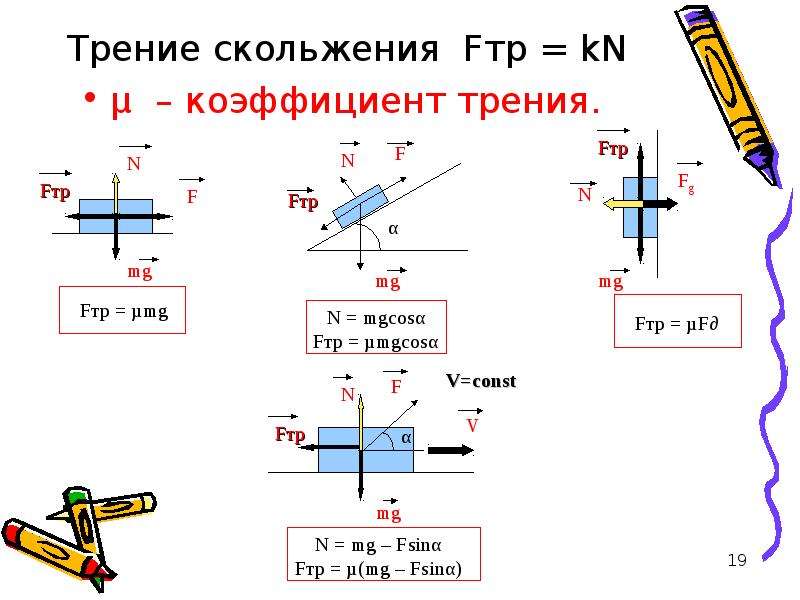
Рис. 11.7 Твердый цилиндр катится по наклонной плоскости из состояния покоя и испытывает скольжение. Система координат имеет x в направлении вниз по наклонной плоскости и y вверх перпендикулярно плоскости. Диаграмма свободного тела показывает нормальную силу, кинетическую силу трения и компоненты веса [латекс]m\mathbf{\overset{\to}}{g}}.[/latex]
11.7 Твердый цилиндр катится по наклонной плоскости из состояния покоя и испытывает скольжение. Система координат имеет x в направлении вниз по наклонной плоскости и y вверх перпендикулярно плоскости. Диаграмма свободного тела показывает нормальную силу, кинетическую силу трения и компоненты веса [латекс]m\mathbf{\overset{\to}}{g}}.[/latex]Сумма сил в y -направление равно нулю, поэтому сила трения теперь равна [латекс] {f} _ {\ text {k}} = {\ mu } _ {\ text {k}} N = {\ mu } _ {\ текст{k}}мг\текст{cos}\,\тета .[/латекс]
Второй закон Ньютона в направлении x становится
[латекс]\сумма {F}_{x}=m{a}_{x},[/latex]
[латекс]мг\,\ текст {sin} \, \ theta — {\ mu} _ {\ text {k}} мг \, \ text {cos} \, \ theta = m {({a} _ {\ text {CM}})} _ {x},[/latex]
или
[латекс] {({a} _ {\ text {CM}})} _ {x} = g (\ text {sin} \, \ theta — { \mu }_{\text{K}}\,\text{cos}\,\theta ).[/latex]
Сила трения обеспечивает единственный крутящий момент относительно оси, проходящей через центр масс, поэтому второй закон Ньютона вращения становится 9{2}\alpha .
 [/latex]
[/latex]Решая для [латекс]\альфа[/латекс], мы получаем
[латекс]\альфа =\фрак{2{f}_{\text{k}}} {mr}=\frac{2{\mu}_{\text{k}}g\,\text{cos}\,\theta}{r}.[/latex]
Значение
Запишем линейную и угловые ускорения через коэффициент кинетического трения. Линейное ускорение такое же, как у тела, скользящего по наклонной плоскости с кинетическим трением. Угловое ускорение относительно оси вращения линейно пропорционально нормальной силе, зависящей от косинуса угла наклона. Как [латекс]\тета\до 9\circ[/latex], эта сила стремится к нулю, и, таким образом, к нулю обращается угловое ускорение.
Сохранение механической энергии при вращении
В предыдущей главе мы ввели кинетическую энергию вращения. Любой катящийся объект несет вращательную кинетическую энергию, а также поступательную кинетическую энергию и потенциальную энергию, если этого требует система. Включая гравитационную потенциальную энергию, полная механическая энергия качения объекта составляет
[латекс] {E} _ {\ text {T}} = \ frac {1} {2} m {v} _ {\ text {CM }}^{2}+\frac{1}{2}{I}_{\text{CM}}{\omega}^{2}+mgh.
 [/latex]
[/latex]В отсутствие каких-либо неконсервативных сил, отнимающих энергию из системы в виде тепла, полная энергия катящегося тела без проскальзывания сохраняется и постоянна на всем протяжении движения. Примерами, когда энергия не сохраняется, являются катящийся объект, который скользит, выделение тепла в результате кинетического трения и катящийся объект, встречающий сопротивление воздуха.
Вы можете спросить, почему катящийся объект, который не скользит, сохраняет энергию, ведь сила трения покоя не является консервативной. Ответ можно найти, вернувшись к рис. Пункт P при контакте с поверхностью находится в состоянии покоя относительно поверхности. Следовательно, его бесконечно малое смещение [латекс]d\mathbf{\overset{\to }{r}}[/латекс] по отношению к поверхности равно нулю, а дополнительная работа, совершаемая силой трения покоя, равна нулю. Мы можем применить закон сохранения энергии к нашему изучению качения, чтобы получить некоторые интересные результаты.

Пример
Марсоход Curiosity
Марсоход Curiosity , показанный на рисунке, был отправлен на Марс 6 августа 2012 года. Колеса марсохода имеют радиус 25 см. Предположим, астронавты прибывают на Марс в 2050 году и обнаруживают ныне недействующий Curiosity на краю бассейна. Пока разбирают марсоход, космонавт случайно теряет сцепление с одним из колес, которое катится, не соскальзывая, на дно котловины на 25 метров ниже. Если колесо имеет массу 5 кг, какова его скорость на дне чаши?
Рис. 11.8 Марсоход «Кьюриосити» из Марсианской научной лаборатории во время испытаний 3 июня 2011 года. Местонахождение находится внутри Цеха сборки космических кораблей в Лаборатории реактивного движения НАСА в Пасадене, Калифорния. (кредит: NASA/JPL-Caltech)Strategy
Мы используем сохранение механической энергии для анализа проблемы. На вершине холма колесо покоится и обладает только потенциальной энергией. На дне бассейна колесо имеет вращательную и поступательную кинетическую энергию, которая должна быть равна начальной потенциальной энергии по закону сохранения энергии.
 Поскольку колесо катится без проскальзывания, мы используем соотношение [латекс]{v}_{\text{CM}}=r\omega[/латекс], чтобы связать поступательные переменные с вращательными переменными в уравнении сохранения энергии. Затем находим скорость. Из рисунка видно, что полый цилиндр является хорошим приближением для колеса, поэтому мы можем использовать этот момент инерции для упрощения расчета. 9{2})25,0\,\text{m}}=9,63\,\text{m}\text{/}\text{s}\text{.}[/latex]
Поскольку колесо катится без проскальзывания, мы используем соотношение [латекс]{v}_{\text{CM}}=r\omega[/латекс], чтобы связать поступательные переменные с вращательными переменными в уравнении сохранения энергии. Затем находим скорость. Из рисунка видно, что полый цилиндр является хорошим приближением для колеса, поэтому мы можем использовать этот момент инерции для упрощения расчета. 9{2})25,0\,\text{m}}=9,63\,\text{m}\text{/}\text{s}\text{.}[/latex]Значение
Это довольно точный результат, учитывая, что на Марсе очень мало атмосферы, и потери энергии из-за сопротивления воздуха будут минимальными. Результат также предполагает, что местность гладкая, так что колесо не будет натыкаться на камни и неровности на своем пути.
Кроме того, в этом примере кинетическая энергия или энергия движения поровну распределяется между линейным и вращательным движением. Если мы посмотрим на моменты инерции на рисунке, то увидим, что полый цилиндр имеет наибольший момент инерции для данного радиуса и массы.
 Если бы колеса вездехода были твердыми и аппроксимировались твердыми цилиндрами, например, кинетическая энергия была бы больше при прямолинейном движении, чем при вращательном. Это дало бы колесу большую линейную скорость, чем приближение полого цилиндра. Таким образом, сплошной цилиндр достигнет дна бассейна быстрее, чем полый цилиндр.
Если бы колеса вездехода были твердыми и аппроксимировались твердыми цилиндрами, например, кинетическая энергия была бы больше при прямолинейном движении, чем при вращательном. Это дало бы колесу большую линейную скорость, чем приближение полого цилиндра. Таким образом, сплошной цилиндр достигнет дна бассейна быстрее, чем полый цилиндр.Резюме
- При качении без проскальзывания между катящимся объектом и поверхностью возникает сила трения покоя. Соотношения [латекс]{v}_{\text{CM}}=R\omega ,{a}_{\text{CM}}=R\alpha ,\,\text{and}\,{d}_ Применяются все {\text{CM}}=R\theta[/latex], так что линейная скорость, ускорение и расстояние до центра масс представляют собой угловые переменные, умноженные на радиус объекта.
- При качении с проскальзыванием между катящимся объектом и поверхностью возникает кинетическая сила трения. В этом случае [латекс] {v} _ {\ text {CM}} \ ne R \ omega , {a} _ {\ text {CM}} \ ne R \ alpha , \, \ text {и} \, {d}_{\text{CM}}\ne R\theta[/latex].

- Энергосбережение можно использовать для анализа движения качения. Энергия сохраняется при качении без проскальзывания. Энергия не сохраняется при качении с проскальзыванием из-за тепла, выделяемого кинетическим трением.
Концептуальные вопросы
Может ли круглый объект, выведенный из состояния покоя на вершине склона без трения, совершить качение?
Показать решениеНет, сила трения покоя равна нулю.
Цилиндрическая банка радиусом R катится по горизонтальной поверхности без скольжения. а) На какое расстояние переместится его центр масс после одного полного оборота банки? б) Будет ли это расстояние больше или меньше, если произойдет скольжение?
Колесо высвобождается сверху на уклоне. Колесо, скорее всего, будет скользить, если уклон будет крутым или пологим?
Показать решениеКолесо с большей вероятностью будет проскальзывать на крутом склоне, так как коэффициент статического трения должен увеличиваться с увеличением угла, чтобы поддерживать качение без проскальзывания.

Что быстрее катится по наклонной плоскости, полый цилиндр или сплошной шар? Оба имеют одинаковую массу и радиус.
Полая сфера и полый цилиндр одинакового радиуса и массы катятся по склону без проскальзывания и имеют одинаковую начальную скорость центра масс. Какой объект достигает большей высоты, прежде чем остановиться?
Показать решениеЦилиндр достигает большей высоты. Судя по рисунку, его ускорение в направлении вниз по склону будет меньше.
Задачи
Какова угловая скорость шины диаметром 75,0 см на автомобиле, движущемся со скоростью 90,0 км/ч?
Показать ответ
[латекс]{v}_{\text{CM}}=R\omega \,\стрелка вправо \omega =66,7\,\text{рад/с}[/latex]
Мальчик едет на велосипеде 2,00 км. Колеса имеют радиус 30,0 см. На какой общий угол поворачиваются шины во время его поездки?
Если мальчик на велосипеде в предыдущей задаче разгоняется из состояния покоя до скорости 10,0 м/с за 10,0 с, каково угловое ускорение шин? 9{2}[/latex]
Шар для боулинга скатывается по пандусу высотой 0,5 м, не соскальзывая при этом на хранение.



 2 Термодинамика
2 Термодинамика
 3 Фотометрия
3 Фотометрия


 Коробка остается неподвижной, если приложенная сила ниже максимальной статической силы трения. Когда сила превышает предел, коробка начинает двигаться.
Коробка остается неподвижной, если приложенная сила ниже максимальной статической силы трения. Когда сила превышает предел, коробка начинает двигаться.
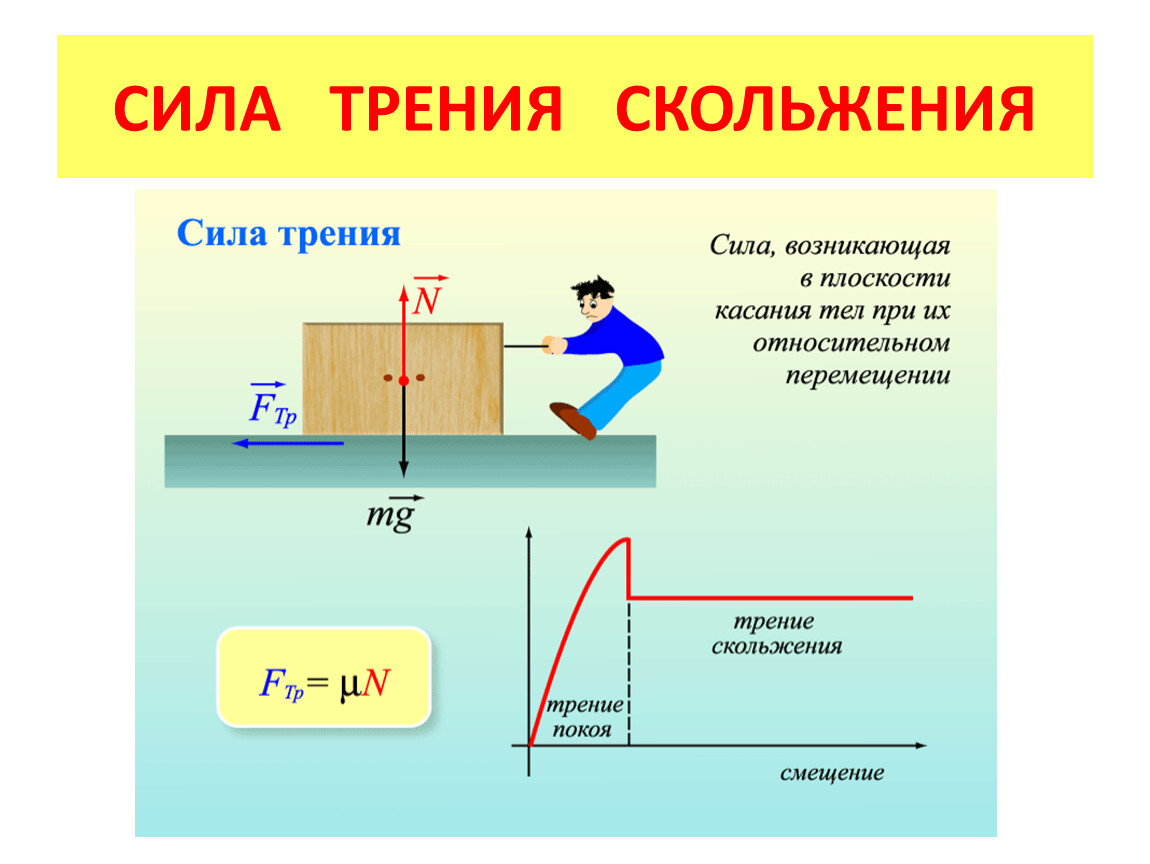

 Диаграмма свободного тела показана с нормальной силой, статической силой трения и компонентами веса [латекс] m\mathbf{\overset{\to}}{g}}[/latex]. Трение заставляет цилиндр катиться по плоскости, а не скользить.
Диаграмма свободного тела показана с нормальной силой, статической силой трения и компонентами веса [латекс] m\mathbf{\overset{\to}}{g}}[/latex]. Трение заставляет цилиндр катиться по плоскости, а не скользить. Единственный ненулевой крутящий момент обеспечивается силой трения. У нас есть
Единственный ненулевой крутящий момент обеспечивается силой трения. У нас есть . Угловое ускорение, однако, линейно пропорционально [латекс]\текст{sin}\,\тета[/латекс] и обратно пропорционально радиусу цилиндра. Таким образом, чем больше радиус, тем меньше угловое ускорение. 9{2})}.[/latex]
. Угловое ускорение, однако, линейно пропорционально [латекс]\текст{sin}\,\тета[/латекс] и обратно пропорционально радиусу цилиндра. Таким образом, чем больше радиус, тем меньше угловое ускорение. 9{2})}.[/latex]
 11.7 Твердый цилиндр катится по наклонной плоскости из состояния покоя и испытывает скольжение. Система координат имеет x в направлении вниз по наклонной плоскости и y вверх перпендикулярно плоскости. Диаграмма свободного тела показывает нормальную силу, кинетическую силу трения и компоненты веса [латекс]m\mathbf{\overset{\to}}{g}}.[/latex]
11.7 Твердый цилиндр катится по наклонной плоскости из состояния покоя и испытывает скольжение. Система координат имеет x в направлении вниз по наклонной плоскости и y вверх перпендикулярно плоскости. Диаграмма свободного тела показывает нормальную силу, кинетическую силу трения и компоненты веса [латекс]m\mathbf{\overset{\to}}{g}}.[/latex] [/latex]
[/latex] [/latex]
[/latex]
 Поскольку колесо катится без проскальзывания, мы используем соотношение [латекс]{v}_{\text{CM}}=r\omega[/латекс], чтобы связать поступательные переменные с вращательными переменными в уравнении сохранения энергии. Затем находим скорость. Из рисунка видно, что полый цилиндр является хорошим приближением для колеса, поэтому мы можем использовать этот момент инерции для упрощения расчета. 9{2})25,0\,\text{m}}=9,63\,\text{m}\text{/}\text{s}\text{.}[/latex]
Поскольку колесо катится без проскальзывания, мы используем соотношение [латекс]{v}_{\text{CM}}=r\omega[/латекс], чтобы связать поступательные переменные с вращательными переменными в уравнении сохранения энергии. Затем находим скорость. Из рисунка видно, что полый цилиндр является хорошим приближением для колеса, поэтому мы можем использовать этот момент инерции для упрощения расчета. 9{2})25,0\,\text{m}}=9,63\,\text{m}\text{/}\text{s}\text{.}[/latex] Если бы колеса вездехода были твердыми и аппроксимировались твердыми цилиндрами, например, кинетическая энергия была бы больше при прямолинейном движении, чем при вращательном. Это дало бы колесу большую линейную скорость, чем приближение полого цилиндра. Таким образом, сплошной цилиндр достигнет дна бассейна быстрее, чем полый цилиндр.
Если бы колеса вездехода были твердыми и аппроксимировались твердыми цилиндрами, например, кинетическая энергия была бы больше при прямолинейном движении, чем при вращательном. Это дало бы колесу большую линейную скорость, чем приближение полого цилиндра. Таким образом, сплошной цилиндр достигнет дна бассейна быстрее, чем полый цилиндр.

