Формулы параллельного, последовательного и смешанного соединения резисторов
Автор Aluarius На чтение 7 мин. Просмотров 6.5k. Опубликовано
Содержание
- 1 Что такое резистор и для чего он нужен
- 2 Понятие параллельного подключения резисторов
- 3 Последовательное подключение
- 4 Смешанное подключение
- 5 Что ещё нужно учитывать при подключении резисторов
- 6 Какая мощность тока при последовательном и параллельном соединении
- 6.1 Мощность при параллельном соединении
- 6.2 Мощность при последовательном соединении
- 7 Как правильно рассчитать сопротивление
- 7.1 При последовательном соединении
- 7.2 При параллельном соединении
- 8 Как рассчитать сложные схемы соединения резисторов
- 8.1 Преобразование «звезда-треугольник»
- 9 Чему равна сила тока в цепи при параллельном соединении резисторов
- 10 Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
Ни одна электрическая схема не обходится без резисторов. Что это такое, для чего он нужен и какими способами их подключают в электрическую цепь рассмотрим подробно.
Что это такое, для чего он нужен и какими способами их подключают в электрическую цепь рассмотрим подробно.
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка:
Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
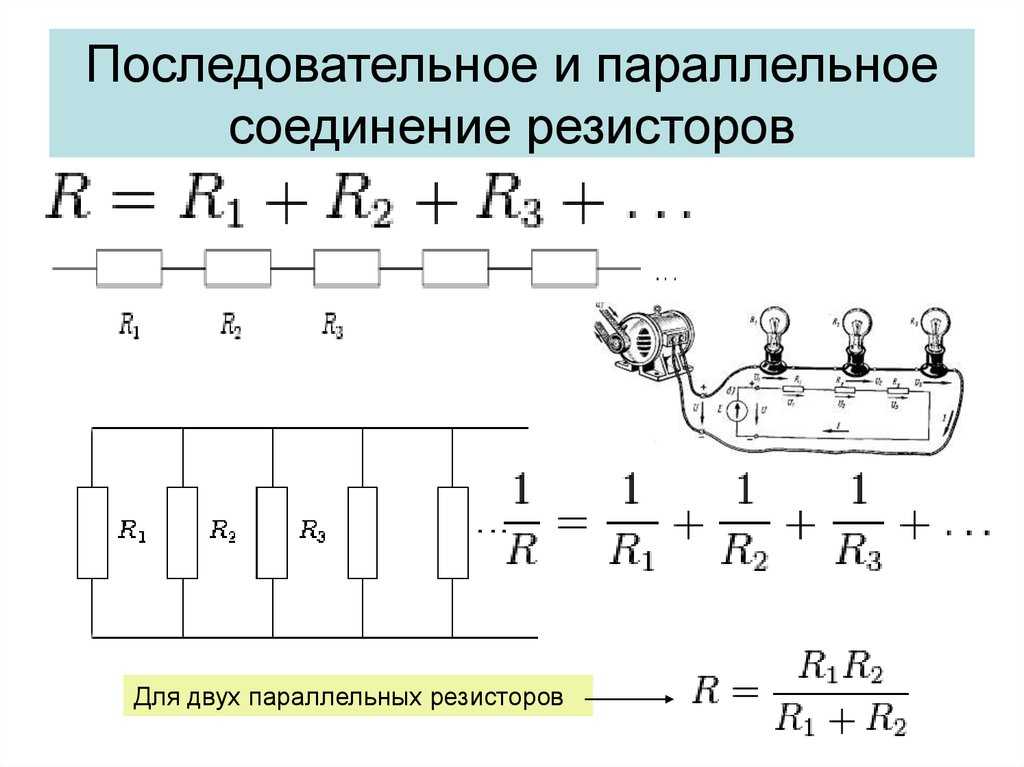
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.

- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.
При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.
Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
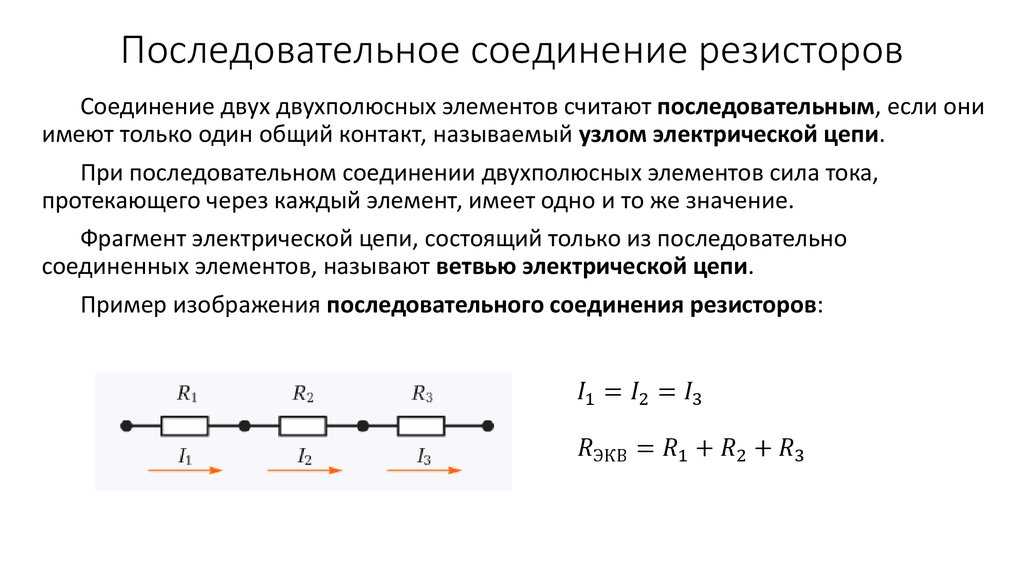
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.
При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.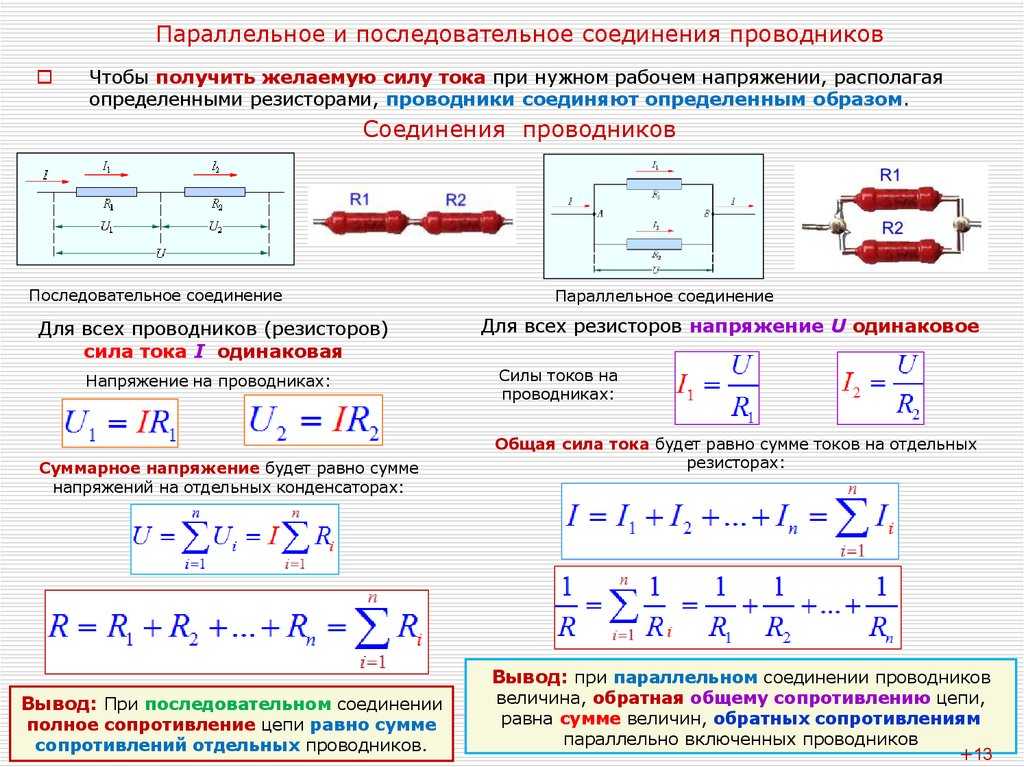
Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.
Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.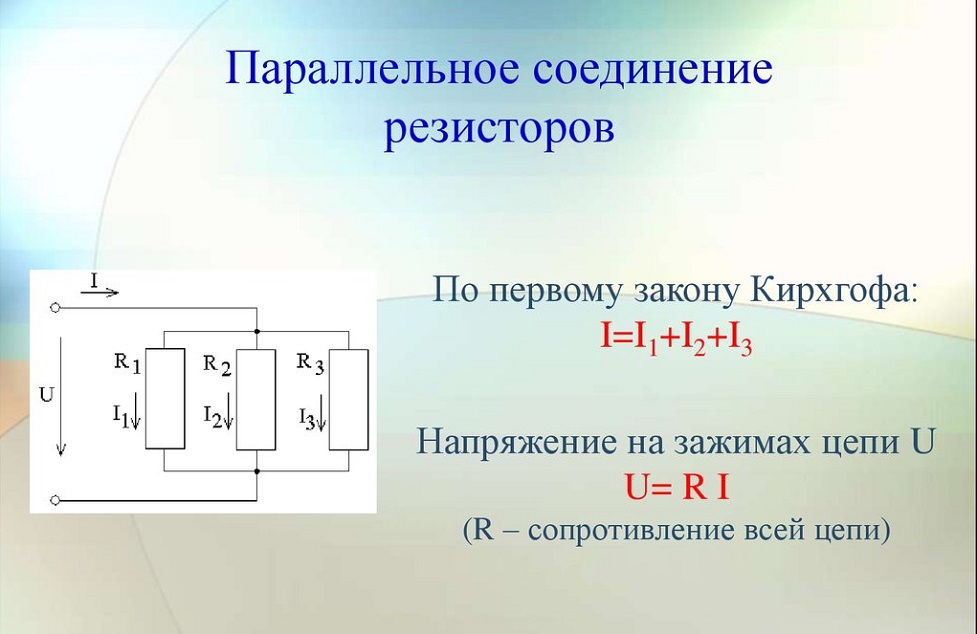
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.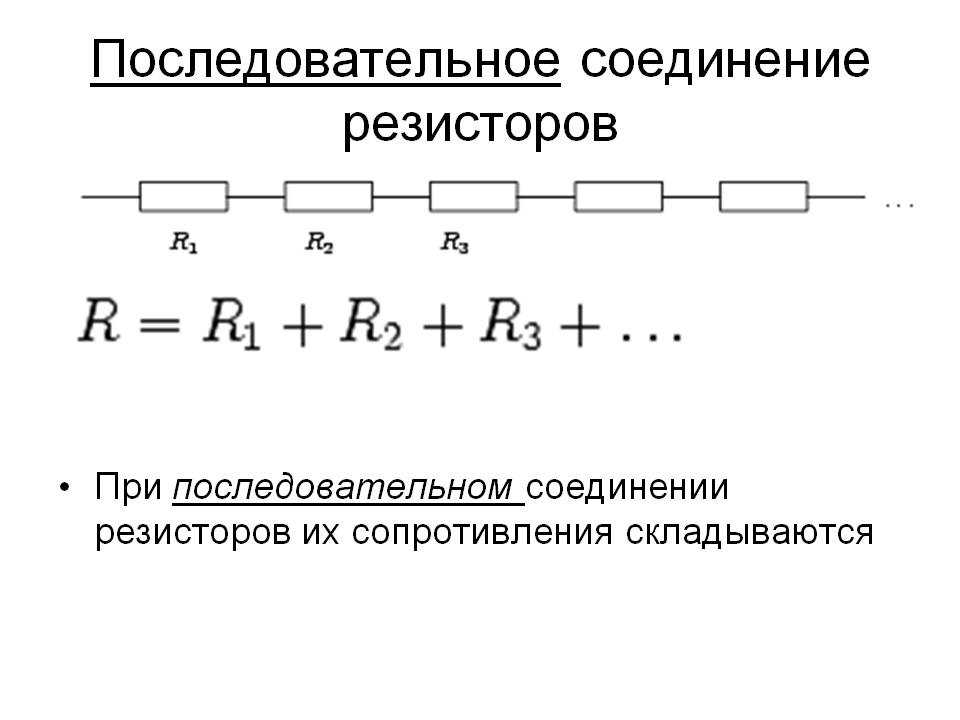
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
Как правильно рассчитать сопротивление
Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где
- U – падение напряжение на конкретном резистивном элементе;
- I – ток, протекающий через него.
При последовательном соединении
Для двух элементов считаем Rобщ = R1+R2.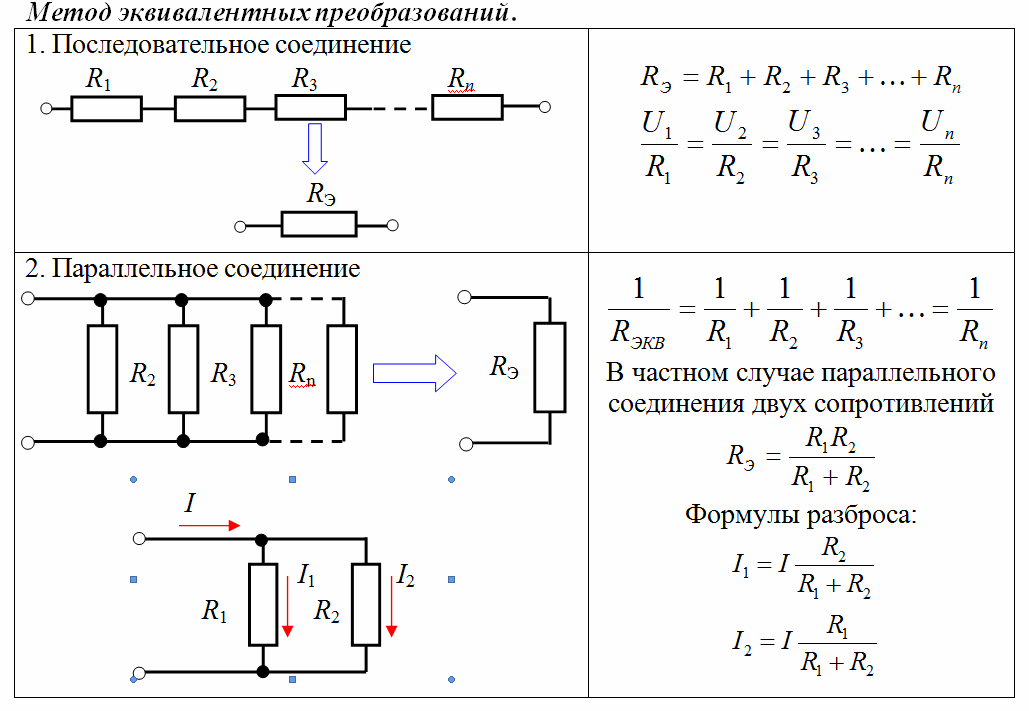
Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.
При параллельном соединении
Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).
Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле
Rобщ = 1/(1/R1+1/R2+1/R3+…+1/Rn).
Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.
Перед нами сложная схема – задача рассчитать общее сопротивление:
- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).

- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R
Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.
Справка: Узел – точка, в которой соединяются три и более проводника электрической цепи.
Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».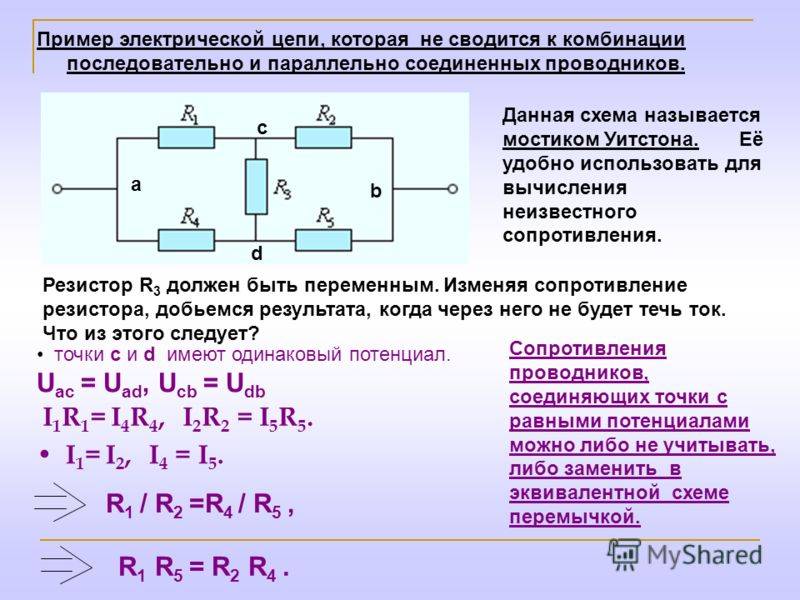
Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
RA = RAB RAC/(RAB+RAC+RDC
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.
RAB=(RARB+RARC+RBRС)/RC
О разнице подключения звезда и треугольник читайте здесь.
Чему равна сила тока в цепи при параллельном соединении резисторов
Согласно правилу Кирхгофа ток, поступающий в узел, равен току, выходящему из узла, – величина тока до группы параллельных резисторов и после нее должна быть неизменной.
Ток в группе параллельных резисторов распределяется по цепи в зависимости от их номинала, после прохождения через сопротивления суммируется в узле и выходит из него неизменным I = I1+I2+I3+…+In.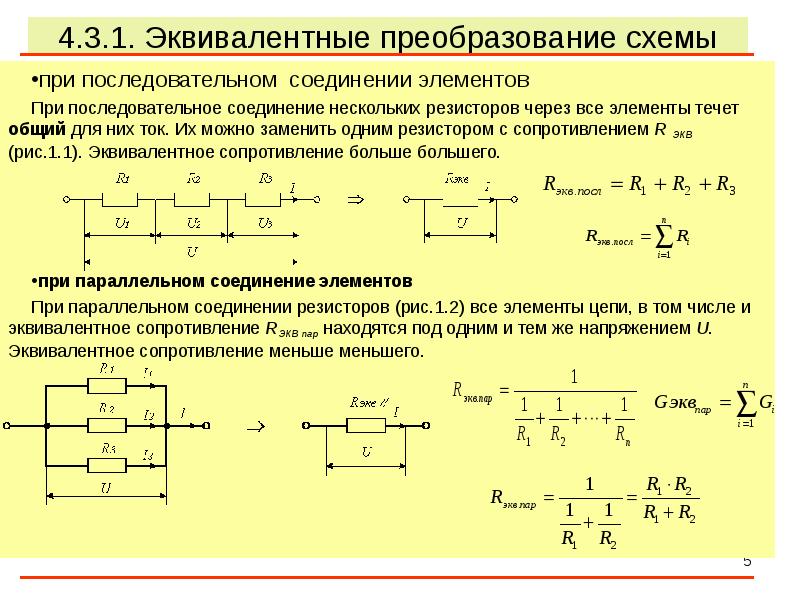
Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
Справка: Эквивалентом сопротивления называется замена части схемы, состоящей из нескольких резистивных элементов, одним элементом.
Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R1+R2+…+Rn.
Например: Нужно посчитать эквивалентное сопротивление данной схемы.
Решение задачи производится путем разделения резистивных элементов на системные группы.
Выделяем первую группу из последовательно соединенных элементов – R2, R3, R4.
Считаем сопротивление Rобщ1 = R2+R3+R4.
Выделяем вторую группу из последовательных элементов R1, R5, R6.
Считаем сопротивление Rобщ2 = R1+R5+R6.
Получаем величину двух эквивалентных сопротивлений Rобщ1 и Rобщ2, соединенных параллельно.
Делаем расчет всей схемы Rэкв= Rобщ1× Rобш2/ (Rобщ1+ Rобщ2).
Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.
Параллельное и смешанное соединение резисторов: разные способы подключения сопротивления
Ни одна операция в электронике или электротехнике не обходится без вычисления сопротивления. В этом случае рассматривают только тот участок цепи, в котором находится смешанное соединение резисторов. Инженерам и физикам необходимо понимать то, как именно происходят расчёты в таких схемах. Всего разделяют несколько видов подключения, которые используются в цепях различной сложности.
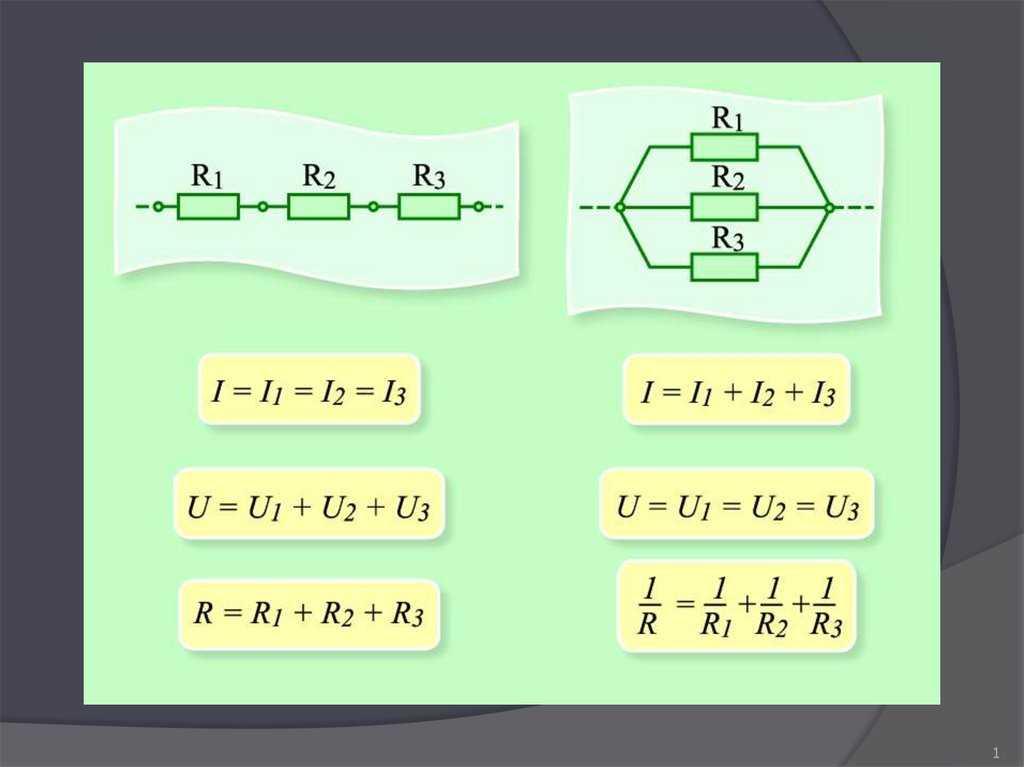
- Последовательное соединение
- Параллельное подключение
- Смешанный вариант
Последовательное соединение
Выделяют такие способы соединения резисторов: последовательное, параллельное и комбинированное. При последовательном подключении конец первого резистора подключают к началу второго, его часть к третьему. Так действуют со всеми составляющими. То есть все компоненты цепи следуют друг за другом. Через них в таком подключении будет проходить один общий электрический ток. Для таких схем физики применяют формулу, в которой между точками А и В есть только один путь протекания заряженных электронов.
При последовательном подключении конец первого резистора подключают к началу второго, его часть к третьему. Так действуют со всеми составляющими. То есть все компоненты цепи следуют друг за другом. Через них в таком подключении будет проходить один общий электрический ток. Для таких схем физики применяют формулу, в которой между точками А и В есть только один путь протекания заряженных электронов.
От количества подключённых резисторов зависит сопротивление протекающему электричеству. Чем больше составляющих, тем оно выше. Его рассчитывают по формуле: R общее = R1+R2+…+Rn, где:
- R общее — это сумма всех сопротивлений;
- R1 — первый резистор;
- R2 — второй компонент;
- Rn — последняя составляющая в цепи.
Параллельное подключение
Параллельное соединение подразумевает подключение начал резисторов к одной точке, а концов к другой.
Из-за того, что в цепи находится несколько компонентов и путей прохода тока, сопротивление значительно меньше, чем при последовательном соединении. То есть общая сумма противодействия уменьшается пропорционально увеличению количества составляющих. Формула для определения общей суммы противостояния электричеству: 1/R общее = 1/R1+1/R2+…+1/Rn.
В расчётах общее сопротивление всегда должно быть меньше любого из составляющих цепи. Способ вычисления суммы противостояния для схемы из двух резисторов немного отличается: 1/R общее = (R1 х R2)/(R1+R2). Если в системе у компонентов одинаковые показатели сопротивления, то общее число будет равно половине одного из составляющих.
Смешанный вариант
В смешанном соединении сопротивлений комбинируют последовательную и параллельную схему подключений.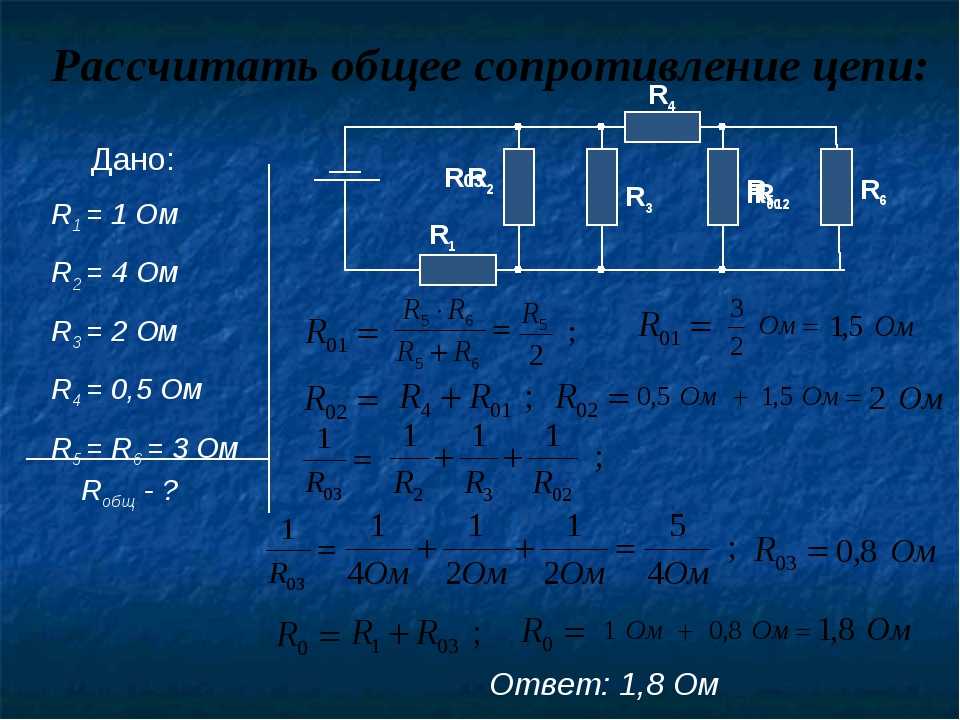 В этом случае несколько компонентов соединяют одним способом, а другие — вторым, но все они включены в одну цепь. В физике такой метод соединения называют последовательно-параллельным.
В этом случае несколько компонентов соединяют одним способом, а другие — вторым, но все они включены в одну цепь. В физике такой метод соединения называют последовательно-параллельным.
Для вычисления суммы противостояния электричеству схему нужно разбить на мелкие участки, в которых резисторы подключены одинаковым способом. Затем расчёты проводят по алгоритму:
- в цепи с параллельно соединёнными компонентами высчитывают эквивалентное сопротивление;
- после этого высчитывают противостояние на последовательно подключённых участках схемы;
- наглядную иллюстрацию нужно перерисовать, обычно получается цепь с последовательным соединением резисторов;
- рассчитывают сопротивление в новой схеме по одной из двух формул.
Лучше понять методы вычислений поможет пример. Если в схеме всего пять компонентов, они могут располагаться по-разному. Начало первого резистора подключено к точке А, конец — к В. От неё идёт отдельная схема с комбинированным соединением. Вторая и третья составляющие находятся на последовательной линии, четвёртый компонент параллелен им. От конечной точки этой цепи — Г — исходит последний резистор.
От неё идёт отдельная схема с комбинированным соединением. Вторая и третья составляющие находятся на последовательной линии, четвёртый компонент параллелен им. От конечной точки этой цепи — Г — исходит последний резистор.
Сначала высчитывают сумму сопротивления последовательного участка внутренней схемы: R2+R3. После этого цепь перерисовывают так, чтобы второй и третий компоненты были соединены в один. В результате внутренняя цепь имеет параллельное подключение. Теперь высчитывают её противостояние: (R2,3xR4)/(R2,3+R4). Можно второй раз изобразить полученную цепь.
В схеме будет три резистора, соединённые последовательным методов. Причём средний включает параметры второго, третьего и четвёртого компонента.
Теперь можно узнать общую сумму сопротивлений. Для этого складывают показатели противостояний электричеству первого, пятого и остальных составляющих. Формула будет иметь вид: R1+(R2,3xR4)/(R2,3+R4)+R5.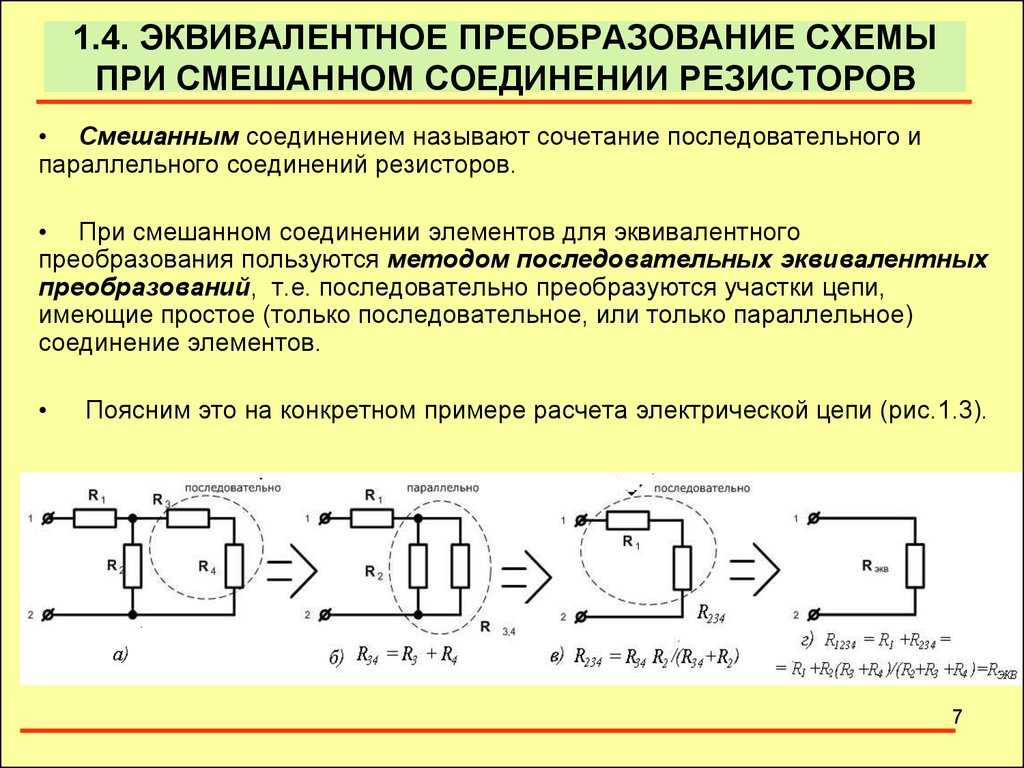 Можно сразу подставить в неё все параметры компонентов.
Можно сразу подставить в неё все параметры компонентов.
На практике последовательный и параллельный метод соединения используются редко, ведь в приборах схемы обычно сложные. Поэтому в цепях резисторы часто соединены комбинированным способом. Сопротивление в таких случаях высчитывают пошагово.
Если сразу выводить числа в общую формулу, то можно ошибиться и получить неверные результаты. А это может отрицательно сказаться на работе электрического прибора.
Формулы для импеданса резистора, конденсатора и индуктора
\(\) Электрический импеданс — это комплексная мера сопротивления, которое цепь представляет изменяющемуся во времени электрическому току при приложении напряжения. В сочетании с преобразованием Лапласа это позволяет нам использовать алгебру для расчета электрических сетей.
\(u\)Вместо \(\Delta v\) мы используем европейский символ разности напряжений: \(u\).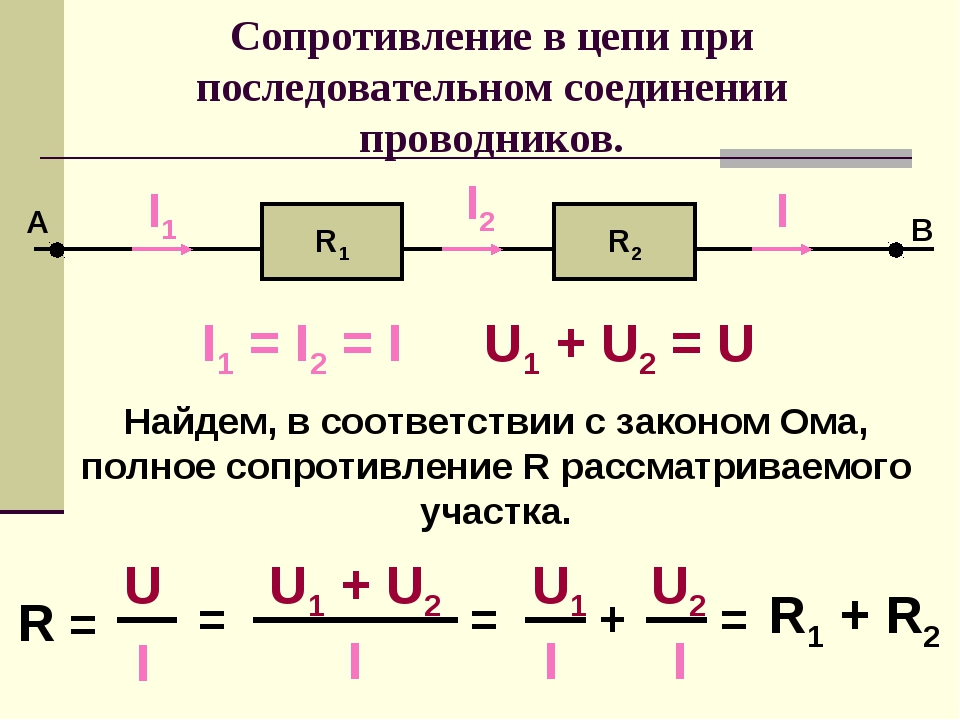 Буква «u» означает «Потенциал 9».0010 у нтершиед».
Буква «u» означает «Потенциал 9».0010 у нтершиед».
Сопротивление конденсатора
Конденсаторы накапливают энергию в электрическом поле. Количество заряда \(q\), хранящегося в конденсаторе, линейно пропорционально напряжению \(u\) на конденсаторе. [МИТ] $$ q(t) = Cu(t)\label{eq:c_equiv} $$ где \(C\) – постоянная, называемая емкостью. Единицей СИ для емкости является фарад со значениями, как правило, в диапазоне от 2,2 пФ до 470 мкФ.
Электрический заряд \(q(t)\) 9{т} \! i(\tau) \, \mathrm{d}\tau = C\,u(t) \\ \ Rightarrow i (t) & = C \ frac {\ mathrm {d} u (t)} {\ mathrm {d} t} \end{выравнивание} $$ Преобразование Лапласа позволяет нам использовать алгебру в комплексной частотной области вместо работы с дифференциальными уравнениями. Используя преобразование Лапласа первой производной
$$
\оставил.
\начать{выравнивать}
I(s) &= \mathfrak{L}i(t)
= \mathfrak{L}\left\{C\frac{\mathrm{d}u(t)}{\mathrm{d}t} \right\}
= C \ mathfrak {L} \ left \ { \ frac {\ mathrm {d}} {\ mathrm {d} t} u (t) \ right \} \ nonumber \\
\mathfrak{L}\left\{\tfrac{\mathrm{d}}{\mathrm{d}t}f(t)\right\}&=
-f(0^-)+s\mathfrak{L}\left\{f(t)\right\} \nonumber \\
f(0^-) &= 0 \номер
\end{выравнивание}
\право\} \стрелка вправо
I(s) = s\,C\,U(s)
\label{eq:c_laplace}
$$
где заглавные буквы используются для обозначения сложных переменных предметной области, таких как \(I(s)=\mathfrak{L}i(t)\) и \(U(s)=\mathfrak{L}u(t)\) .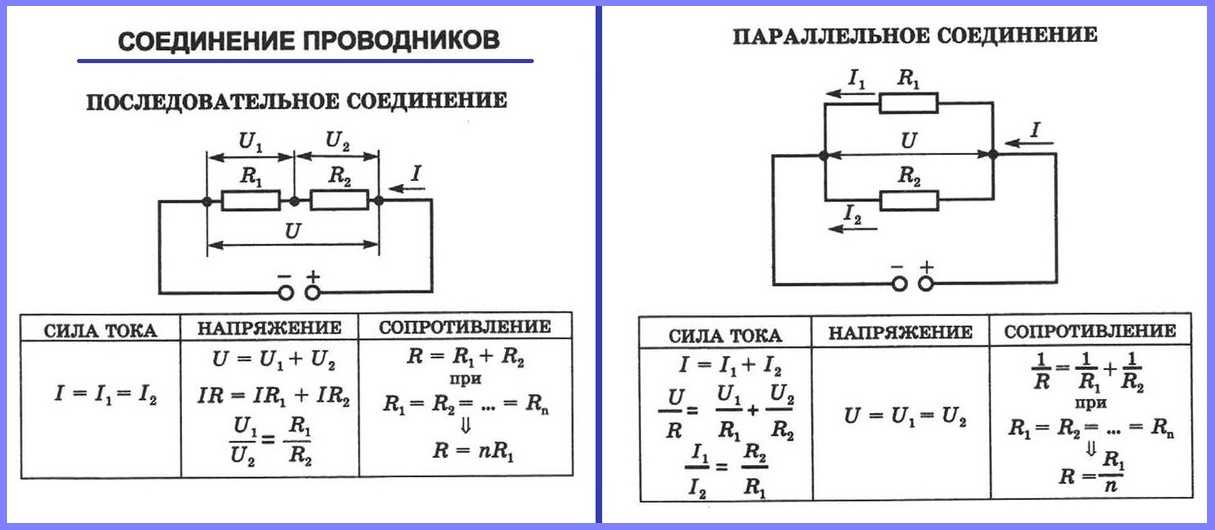
Решая \(\eqref{eq:c_laplace}\) для комплексного импеданса \(Z_{C}(s) \equiv\frac{U(s)}{I(s)}\), мы получаем $$ \затененный{ Z_{C}(s) = \frac{1}{sC} } \label{eq:c_impedance} $$
На приведенном ниже графике показана величина импеданса конденсатора \(Z_C\) в зависимости от частоты, где \(s=\sigma+j\omega\).
\(Z_C(\омега)\)Импеданс индуктора
Катушка индуктивности хранит энергию в магнитном поле. Магнитный поток \(\phi\) в индукторе линейно пропорционален току \(i\) через индуктор. Роль катушки индуктивности в этом магнитном случае аналогична роли конденсатора в электрическом случае. $$ \phi(t) = L i(t) \label{eq:l_equiv} $$ где \(L\) — постоянная, называемая индуктивностью. Единица СИ для индуктивности – Генри со значениями, как правило, в диапазоне от 0,1 мкГн до 1 мГн.
Согласно закону индукции Фарадея [MIT], индуктор противодействует изменениям тока, развивая напряжение \(\varepsilon=-u\), пропорциональное отрицательному значению скорости изменения магнитного потока \(\phi\). $$
\ varepsilon (t) = -u (t) = — \ frac {\ mathrm {d} \ phi (t)} {\ mathrm {d} t}
\метка{экв:l_emf}
$$
$$
\ varepsilon (t) = -u (t) = — \ frac {\ mathrm {d} \ phi (t)} {\ mathrm {d} t}
\метка{экв:l_emf}
$$
Объединение уравнения \(\eqref{eq:l_equiv}\) и \(\eqref{eq:l_emf}\) дает $$ \начать{выравнивать} u(t) = -\varepsilon(t) = + \ frac {\ mathrm {d} \ phi (t)} {\ mathrm {d} t} = L \ гидроразрыва {\ mathrm {d} я (т)} {\ mathrm {d} т} \end{выравнивание} $$
И снова преобразование Лапласа позволяет нам использовать алгебру в комплексной частотной области вместо работы с дифференциальными уравнениями. Используя преобразование Лапласа первой производной
$$
\оставил.
\начать{выравнивать}
U(s) &=\mathfrak{L}u(t)
=\mathfrak{L}\left\{L\tfrac{\mathrm{d}i(t)}{\mathrm{d}t} \right\}
=L\mathfrak{L}\left\{\tfrac{\mathrm{d}}{\mathrm{d}t}i(t) \right\} \nonumber \\
\mathfrak{L}\left\{\tfrac{\mathrm{d}}{\mathrm{d}t}f(t)\right\}
&= -f(0^-)+s\mathfrak{L}\left\{f(t)\right\} \nonumber \\
f(0^-)&=0 \номер
\end{выравнивание}
\право\} \стрелка вправо
U(s) = s\,L\,I(s)
\label{eq:l_laplace}
$$
где заглавные буквы используются для обозначения сложных переменных предметной области, таких как \(I(s)=\mathfrak{L}i(t)\) и \(U(s)=\mathfrak{L}u(t)\) .
Решая \(\eqref{eq:l_laplace}\) для комплексного импеданса \(Z_L(s) \equiv\frac{U(s)}{I(s)}\), мы получаем $$ \затененный{ Z_L(s) = sL } \label{eq:c_inductance} $$
На графике ниже показана величина импеданса индуктора \(Z_L\) в зависимости от частоты
\(Z_L(\омега)\)Импеданс резистора
Для полноты мы показываем импеданс резистора \(Z_r\) как функцию частоты $$ \затененный{ Z_r(s) = R } \label{eq:r_inductance} $$
На графике ниже показана величина импеданса резистора \(Z_r\) в зависимости от частоты
\(Z_R(\омега)\)Обзор
| имя | символ | шт. | импеданс |
|---|---|---|---|
| Напряжение | \(и(т)\) | Вольт | |
| Текущий | \(г(т)\) | Ампер | |
| Сопротивление | \(Р\) | \(и(т)=R\cточка я(т)\) | \(Z_r=R\) |
| Емкость | 9т я (\тау)\,\mathrm{d}\тау\)\(Z_c=\frac{1}{j\omega C}\) | ||
| Индуктивность | \(Л\) | \(u(t)=L\frac{\mathrm{d}i(t)}{\mathrm{d}t}\) | \(Z_l=j\омега L\) |
| \(\сумма и(т)=0\) | \(\сумма i(t)=0\) |
Мои статьи, в которых используются формулы импеданса, включают
- Радиоуправляемый фильтр
- RLC-фильтр
- Резонатор RLC
в параллельной формуле или резисторы.
 Параллельная цепь также известна как делитель тока, поскольку ток цепи в параллельной сети резисторов может проходить более чем по одному каналу, поскольку для него существует несколько путей. В результате ток не одинаков во всех ветвях параллельной сети. С другой стороны, падение напряжения на всех резисторах в параллельной резистивной сети является постоянным.
Параллельная цепь также известна как делитель тока, поскольку ток цепи в параллельной сети резисторов может проходить более чем по одному каналу, поскольку для него существует несколько путей. В результате ток не одинаков во всех ветвях параллельной сети. С другой стороны, падение напряжения на всех резисторах в параллельной резистивной сети является постоянным.
Формула
Общее сопротивление параллельной цепи оценивается путем расчета эквивалентного сопротивления цепи. Его формула гласит, что обратная величина эквивалентного сопротивления равна сумме обратных величин отдельных сопротивлений, соединенных параллельно. Эквивалентное сопротивление обозначается символом R eq . Его единицей измерения СИ является ом (Ом), а размерная формула определяется как [M 1 L 2 А -2 Т -3 ].
1/ REQ = 1/R 1 + 1/R 2 + 1/R 3 +… .
. + 1/R N
. eq — эквивалентное сопротивление,
R 1 — сопротивление первого резистора,
R 2 — сопротивление второго резистора,
R 3 — сопротивление третьего резистора и т. д. на.
Вывод
Примеры задачПредположим, у нас есть цепь напряжения V и тока I. Резисторы R 1 , R 2 и R 3 подключены параллельно цепи.
Известно, что в параллельной цепи ток делится на количество частей, равное количеству резисторов.
Пусть I 1 , I 2 и I 3 будут значениями, на которые делится ток I. Мы знаем,
I = I 1 + I 2 + I 3
Разделив обе части на V, получим, /V
1/(V/I) = 1/(V/I 1 ) + 1/(V/I 2 ) + 1/(V/I 3 )
По Ому закон, V = IR. Итак, приведенное выше уравнение принимает вид:
1/R eq = 1/R 1 + 1/R 2 + 1/R 3
Отсюда выводится формула для эквивалентного сопротивления в параллельной цепи.
Задача 1. Вычислить эквивалентное сопротивление, если три сопротивления 5 Ом, 2 Ом и 7 Ом соединены параллельно.
Solution:
We have,
R 1 = 5 Ω
R 2 = 2 Ω
R 3 = 7 Ω
Using the formula we get,
1/R экв. = 1/R 1 + 1/R 2 + 1/R 3
1/R экв. = 1/5 + 1/2 + 1/7
1/R экв. = 1/1,2
R экв. = 1,2 Ом
2 эквивалентное сопротивление, если три сопротивления 2 Ом, 1 Ом и 3 Ом соединены параллельно.Solution:
We have,
R 1 = 2 Ω
R 2 = 1 Ω
R 3 = 3 Ω
Using the formula we get,
1/р экв. = 1/R 1 + 1/R 2 + 1/R 3
1/R экв.
1/= 1/2 + 1/1 + 1/3
eq = 1/0,55
R eq = 0,55 Ом
Задача 3. Вычислить эквивалентное сопротивление, если три сопротивления 4 Ом, 6 Ом и 10 Ом соединены параллельно.
Решение:
У нас есть,
R 1 = 4 Ом
R 2 = 6 Ом
R 3 = 10 Ом
Используя формулу, получаем, экв. = 1/4 + 1/6 + 1/10
1/R экв. = 1/1,9
R экв. = 1,9 Ом
5 Ом, 3 Ом и 8 Ом соединены параллельно.
Решение:
У нас есть,
R 1 = 5 ω
R 2 = 3 ω
R 3 = 8 ω
Используя формулу. + 1/R 2 + 1/R 3
1/R экв. = 1/5 + 1/3 + 1/8
1/R экв. eq = 1,5 Ом
Задача 5.
Найдите неизвестное сопротивление, если три сопротивления 3 Ом, 8 Ом и x Ом соединены параллельно, чтобы получить эквивалентное сопротивление 1,8 Ом.
Решение:
Мы имеем,
R 1 = 3 Ом
R 2 = 8 ω
R EQ = 1,8 ω
eq = 1,8 ω
r eq = 1,8 ω
r eq . 1/R экв. = 1/R 1 + 1/R 2 + 1/R 3
=> 1/1,8 = 1/3 + 1/8 + 1/R 3 3
=> 1/R 3 = 1/1,8 – 1/3 – 1/8
=> 1/R 3 = 1/11
=> R 3 = 11 Ом
Задача 6. Найдите неизвестное сопротивление, если три сопротивления 2,5 Ом, 1,5 Ом и x Ом соединены параллельно, что дает эквивалентное сопротивление 0,76 Ом.
Решение:
Мы имеем,
R 1 = 2,5 Ом
R 2 = 1,5 Ом
R EQ = 1,566 ω
R EQ = 0,7666
R EQ = 1,5666
R EQ = 1,5666
R EQ = 1,566
R .


 . + 1/R N
. + 1/R N 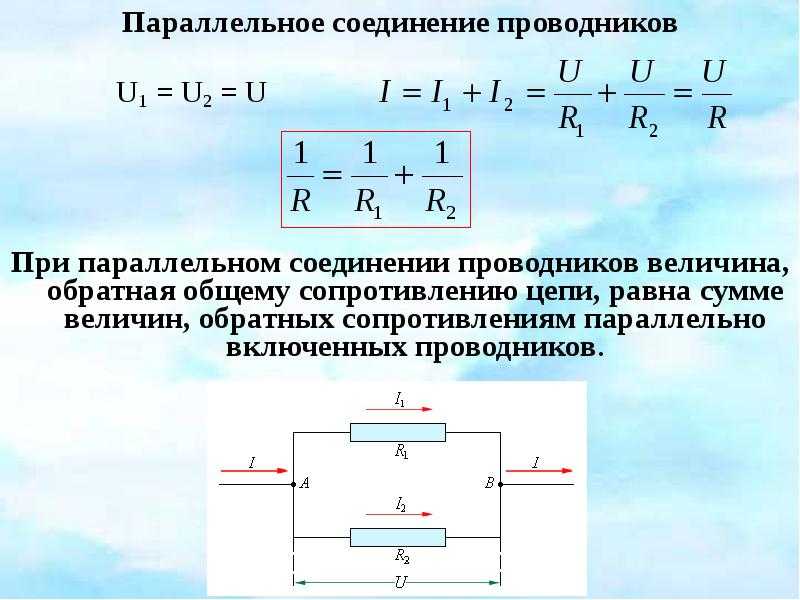
 = 1/2 + 1/1 + 1/3
= 1/2 + 1/1 + 1/3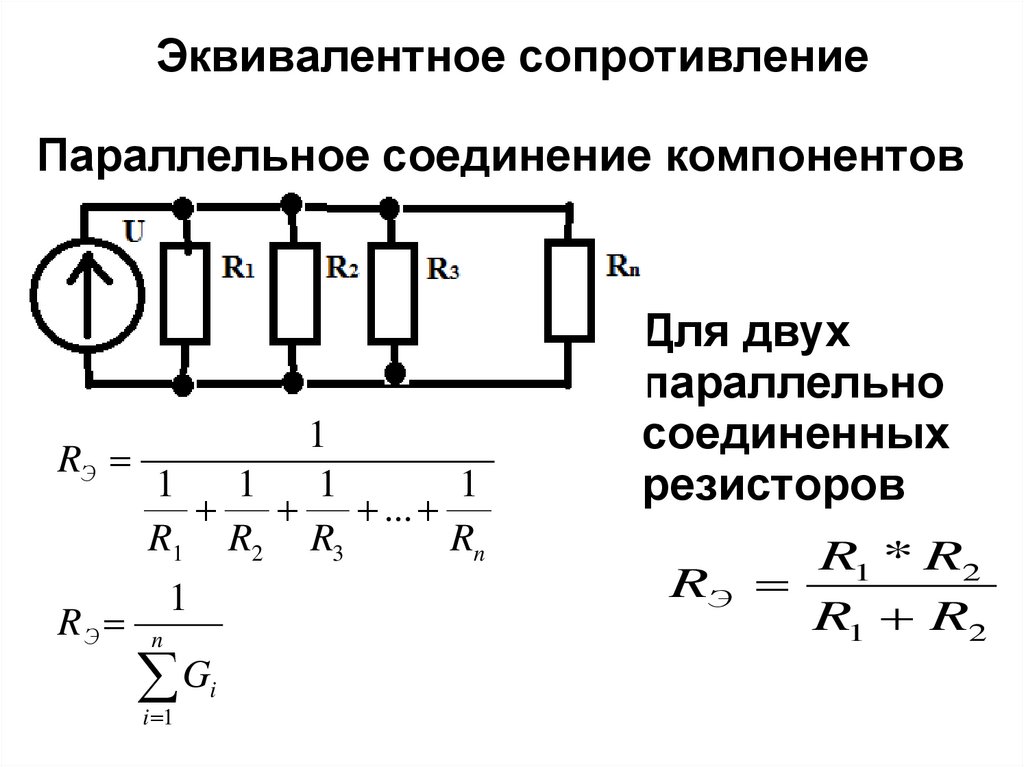 Найдите неизвестное сопротивление, если три сопротивления 3 Ом, 8 Ом и x Ом соединены параллельно, чтобы получить эквивалентное сопротивление 1,8 Ом.
Найдите неизвестное сопротивление, если три сопротивления 3 Ом, 8 Ом и x Ом соединены параллельно, чтобы получить эквивалентное сопротивление 1,8 Ом. 