Электричество — Основные формулы

1. Электростатика

1.1 Закон Кулона

q₁, q₂ — величины точечных зарядов,
r — расстояние между зарядами.

1.2 Напряженность поля уединенного точечного заряда

q — величина уединенного точечного заряда,
r — расстояние от заряда.

1.3 Потенциал точки в поле точечного заряда

q — величина уединенного точечного заряда,
r — расстояние от заряда.

1.4 Потенциальная энергия заряда в электростатическом поле

φ — потенциал,
q₁ — величина заряда.

1.5 Потенциальная энергия заряда q₁ в поле точечного заряда

q — величина уединенного точечного заряда, который создает поле,

r — расстояние между зарядами.

1.6 Теорема Гаусса

N — поток вектора напряженности электрического поля через замкнутую поверхность,
q — полный заряд, находящийся внутри замкнутой поверхности.

1.7 Напряженность электрического поля вблизи от поверхности проводника

σ — поверхностная плотность заряда.

1.8 Емкость плоского кондесатора

q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.

1.9 Энергия плоского кондесатора

q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.

2. Постоянный электрический ток

2.1 Закон Ома для участка однородной цепи

U — напряжение на концах участка,
R — сопротивление участка цепи.

2.2 Закон Ома для замкнутой цепи с источником тока

 — ЭДС (электродвижущая сила),
r — внутреннее сопротивление источника ЭДС.

2.3 Работа постоянного тока

U — напряжение на концах участка цепи,
t — время, за которое совершается работа.

2.4 Закон Джоуля-Ленца

Q — теплота,
R — сопротивление проводника,
t — время, за которое выделяется теплота.

2.5 Полная мощность, развиваемая источником тока

 — ЭДС источника тока,
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.6 Полезная мощность

 — ЭДС источника тока,
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.7 Коэффициент полезного действия источника тока

R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.8 Первое правило Кирхгофа

n — число проводников, сходящихся в узле;
I_k — сила тока в k-м проводнике.

2.9 Второе правило Кирхгофа

n — число неразветвленных участков в контуре;
m — число ЭДС в контуре.

Электричество и магнетизм — основные формулы по физике

Физические законы, формулы, переменные	Формулы электричество и магнетизм
Закон Кулона: где q1 и q2 — величины точечных зарядов, ԑ1 — электрическая постоянная; ε — диэлектрическая проницаемость изотропной среды (для вакуума ε = 1), r — расстояние между зарядами.
Напряженность электрического поля: где Ḟ — сила, действующая на заряд q0 , находящийся в данной точке поля.
Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ: 4) между двумя разноименно заряженными плоскостями
Потенциал электрического поля: где W — потенциальная энергия заряда q0 .
Потенциал поля точечного заряда на расстоянии r от заряда:
По принципу суперпозиции полей, напряженность:
Потенциал: где Ēi и ϕi — напряженность и потенциал в данной точке поля, создаваемый i-м зарядом.
Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ1 в точку с потенциалом ϕ2 :
Связь между напряженностью и потенциалом 1) для неоднородного поля: 2) для однородного поля:	1) 2)
Электроемкость уединенного проводника:
Электроемкость конденсатора: где U = ϕ1 — ϕ2 — напряжение.
Электроемкость плоского конденсатора: где S — площадь пластины (одной) конденсатора, d — расстояние между пластинами.
Энергия заряженного конденсатора:
Сила тока:
Плотность тока: где S — площадь поперечного сечения проводника.
Сопротивление проводника: ρ — удельное сопротивление; l — длина проводника; S — площадь поперечного сечения.
Закон Ома 1) для однородного участка цепи: 2) в дифференциальной форме: 3) для участка цепи, содержащего ЭДС: где ε — ЭДС источника тока, R и r — внешнее и внутреннее сопротивления цепи; 4) для замкнутой цепи:
Закон Джоуля-Ленца 1) для однородного участка цепи постоянного тока: где Q — количество тепла, выделяющееся в проводнике с током, t — время прохождения тока; 2) для участка цепи с изменяющимся со временем током:	1) 2)
Мощность тока:
Связь магнитной индукции и напряженности магнитного поля: где B — вектор магнитной индукции, μ √ магнитная проницаемость изотропной среды, (для вакуума μ = 1), µ0 — магнитная постоянная , H — напряженность магнитного поля.
Магнитная индукция (индукция магнитного поля): 1) в центре кругового тока где R — радиус кругового тока,2) поля бесконечно длинного прямого тока где r — кратчайшее расстояние до оси проводника;3) поля, созданного отрезком проводника с током гдеɑ1 и ɑ2 — углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля; 4) поля бесконечно длинного соленоида где n — число витков на единицу длины соленоида.
Сила Лоренца: по модулю где F — сила, действующая на заряд, движущийся в магнитном поле, v — скорость заряда q, α — угол между векторами v и B.
Поток вектора магнитной индукции (магнитный поток через площадку S): 1) для однородного магнитного поля , где α — угол между вектором B и нормалью к площадке, 2) для неоднородного поля	1) 2)
Потокосцепление (полный поток): где N — число витков катушки.
Закон Фарадея-Ленца: где ԑi — ЭДС индукции.
ЭДС самоиндукции: где L — индуктивность контура.
Индуктивность соленоида: где n — число витков на единицу длины соленоида, V — объем соленоида.
Энергия магнитного поля:
Заряд, протекающий по замкнутому контуру при изменении магнитного потока через контур: где ∆Ф = Ф2 – Ф1 — изменение магнитного потока, R — сопротивление контура.
Работа по перемещению замкнутого контура с током I в магнитном поле:

Формулы — Электричество и магнетизм

Электростатическое поле в вакууме

Закон Кулона: ,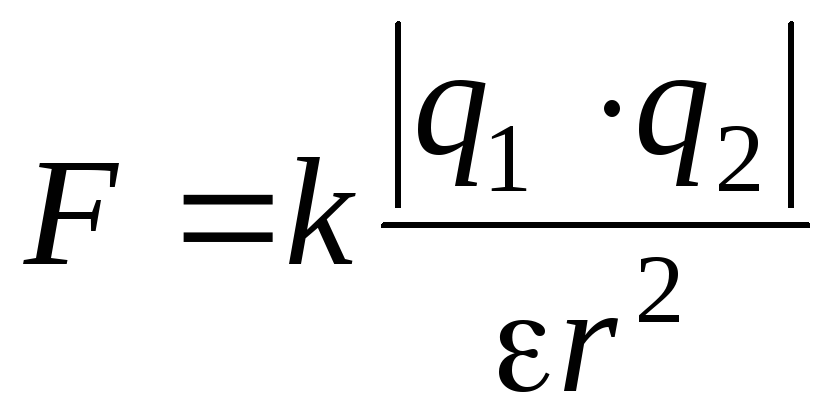

где

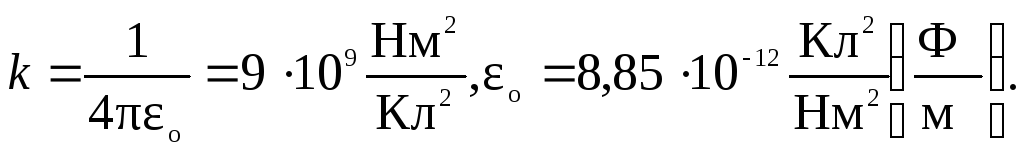
Напряженность электрического поля:

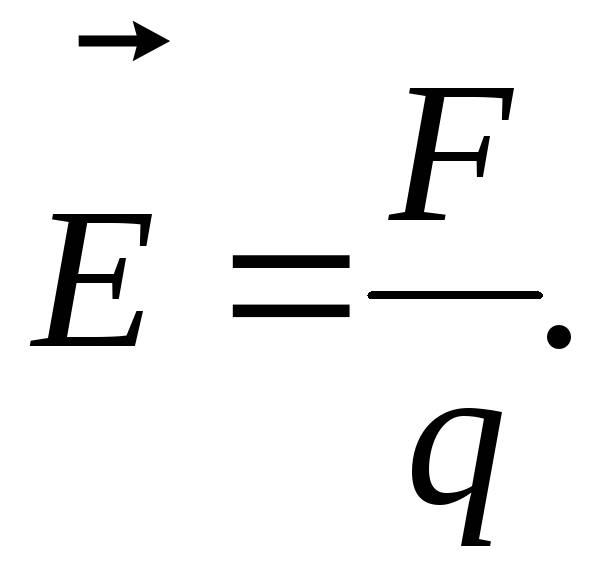
Напряженность поля точечного заряда:

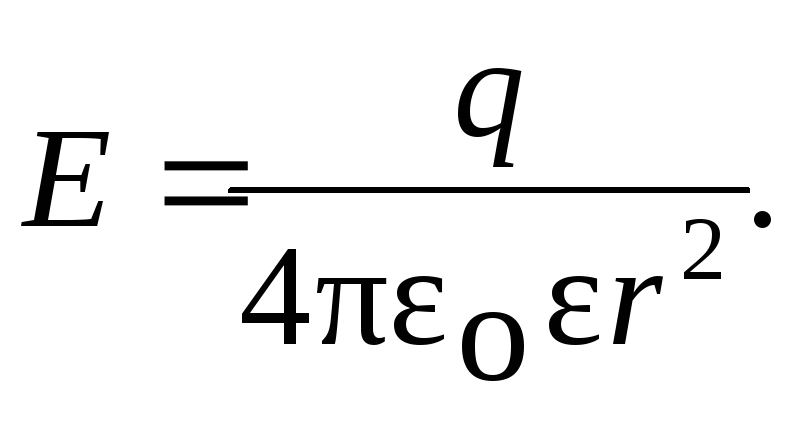
Напряженность поля заряженного шара:

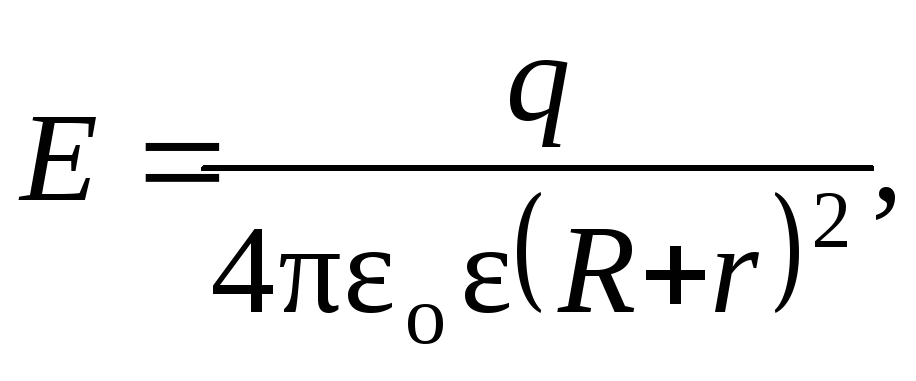
где R — радиус шара.

Принцип суперпозиции электрических полей:

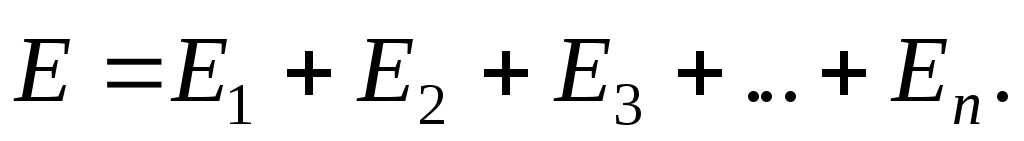
Поток вектора напряженности через поверхность S:

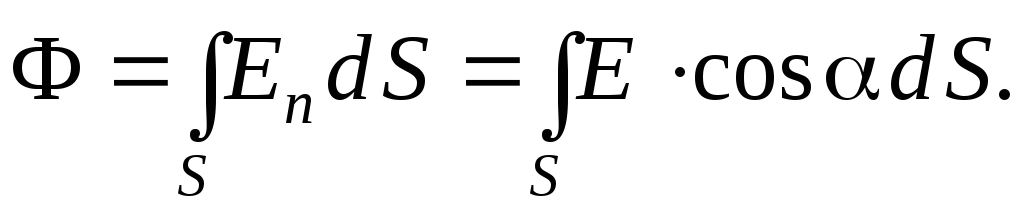
Теорема Гаусса: ,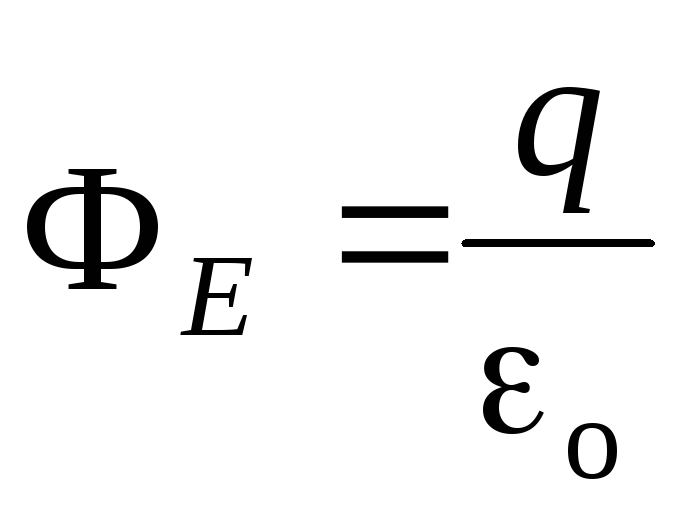

где Ф_Е – поток вектора напряженности через замкнутую поверхность S, q – заряд, заключенный внутри поверхности S.

Линейная плотность заряда: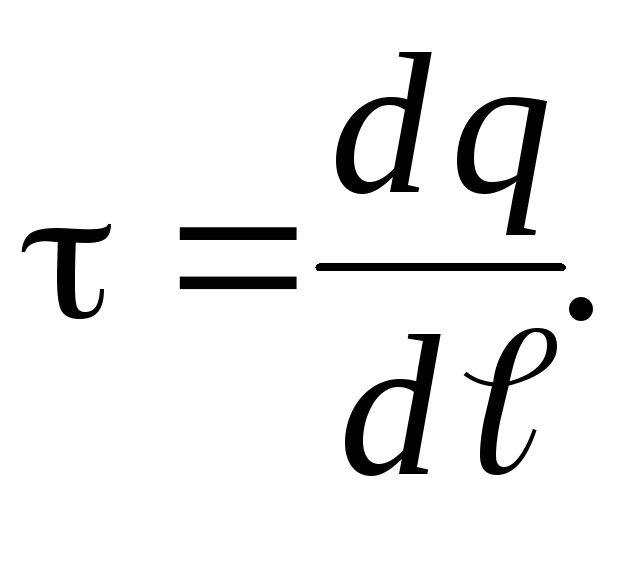

Поверхностная плотность заряда: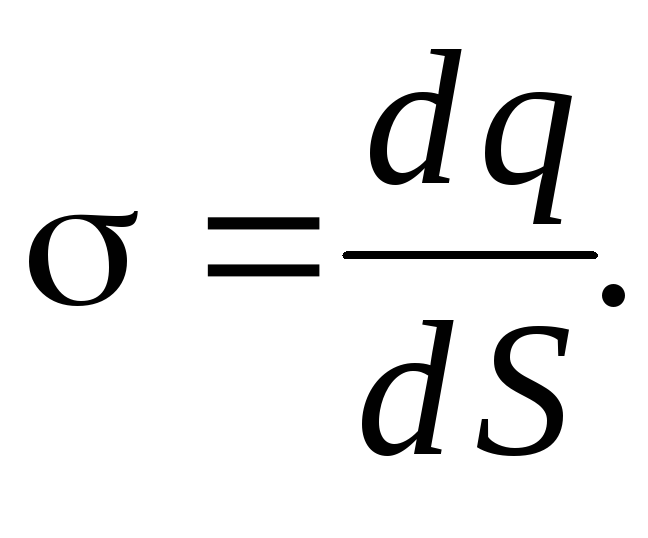

Объемная плотность заряда: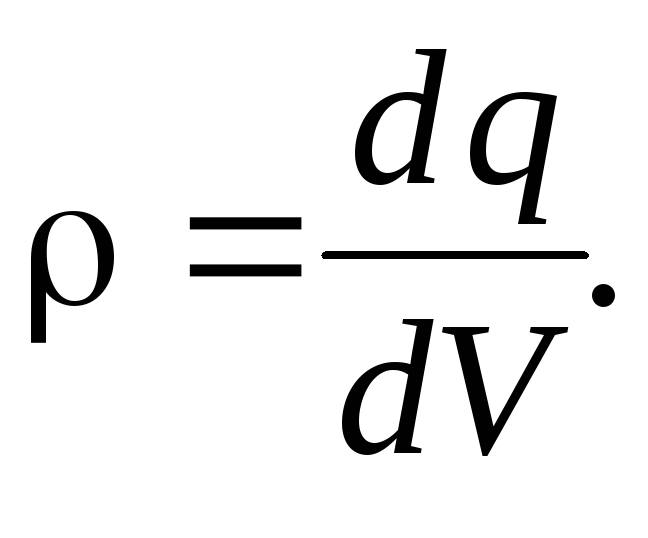

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, нитью:

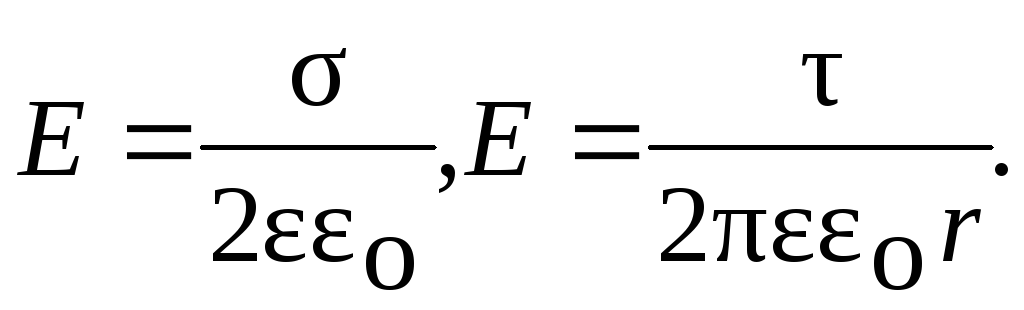
Электрическое смещение:

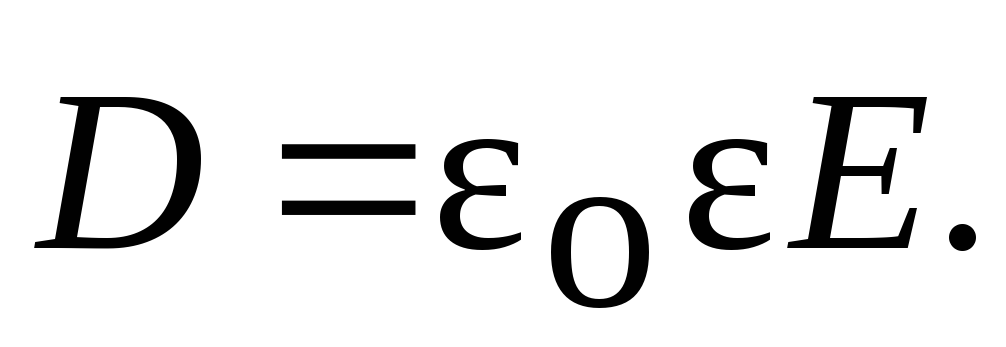
Потенциал электрического поля:

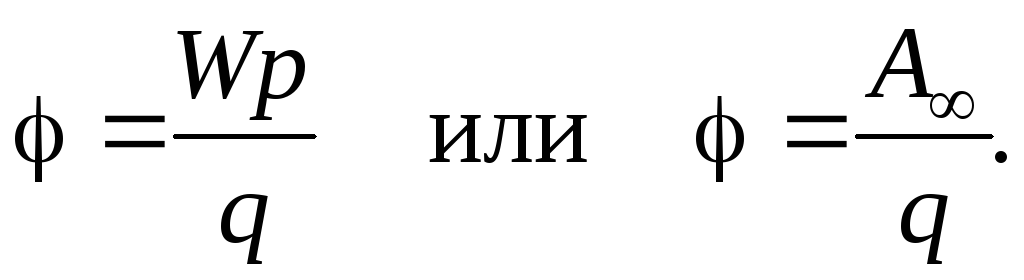
Потенциал поля точечного заряда:

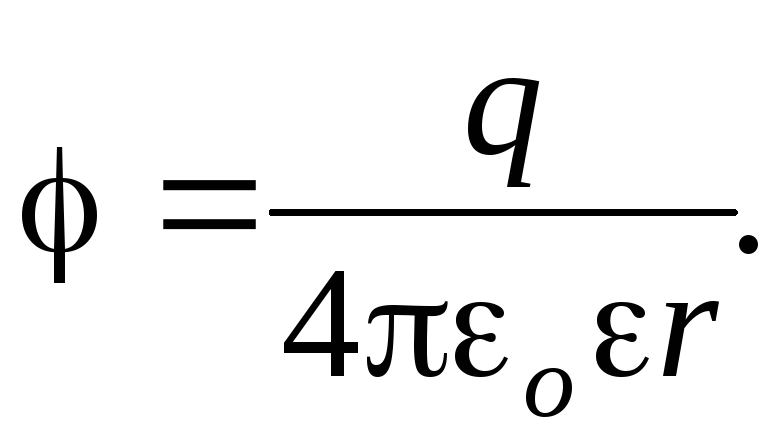
Потенциал поля заряженного шара:

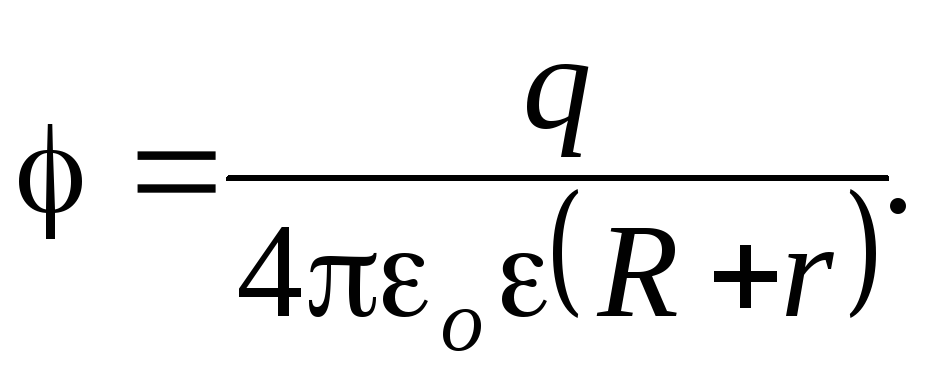
Работа по перемещению заряда в электрическом поле: А = q (__

где (__ — разность потенциалов.

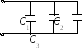
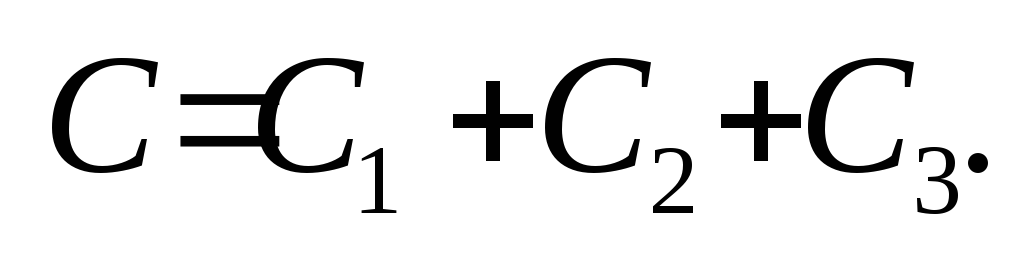
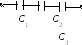
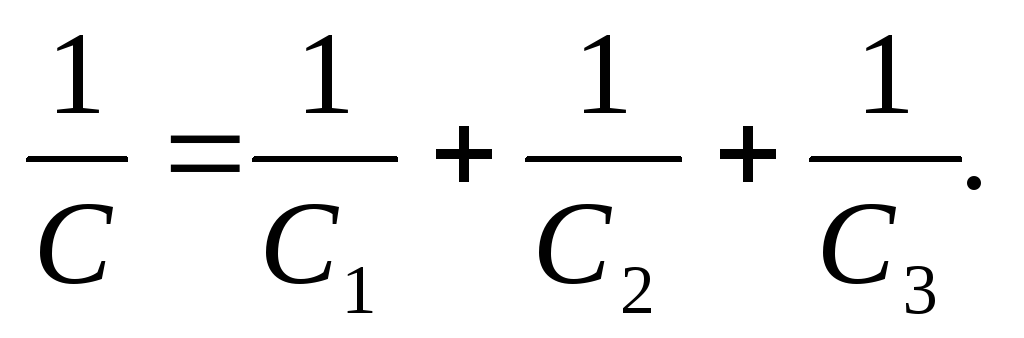
Энергия заряженного конденсатора

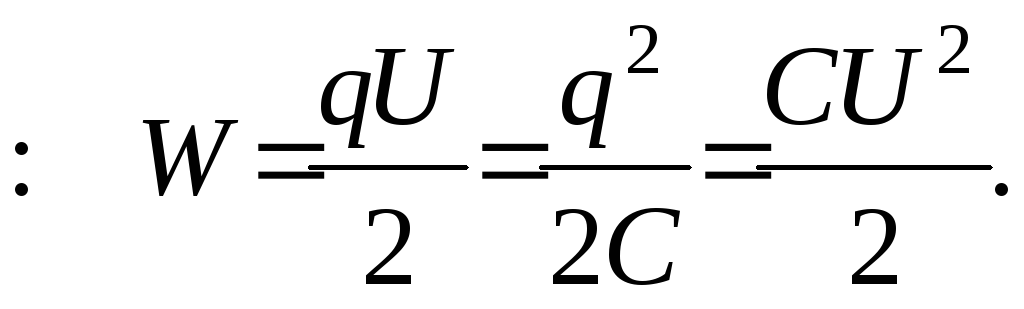
Энергия системы точечных зарядов:

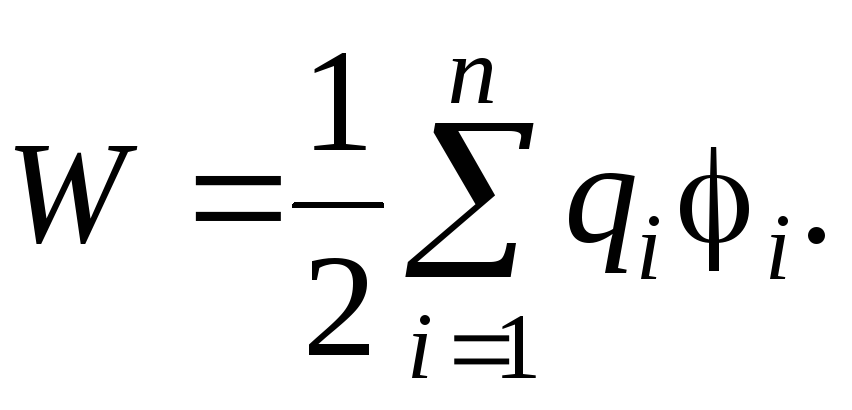
Электрический момент диполя:

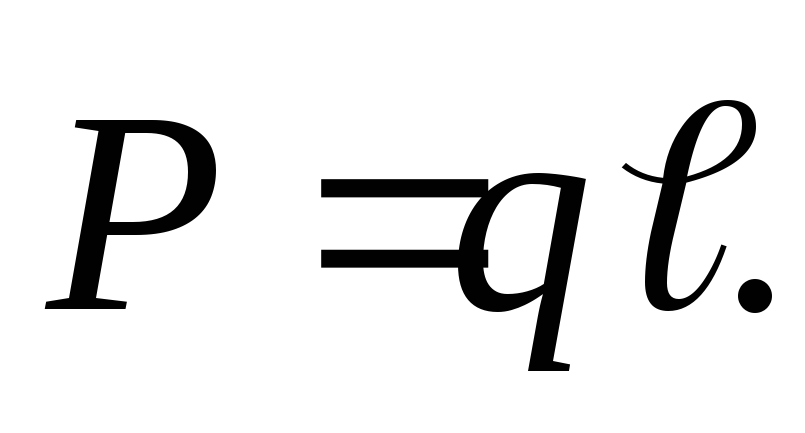
Механический момент, действующий на диполь в электрическом поле:

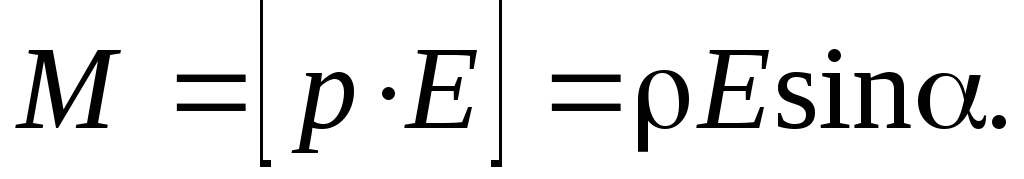
Поляризованность диэлектрика:

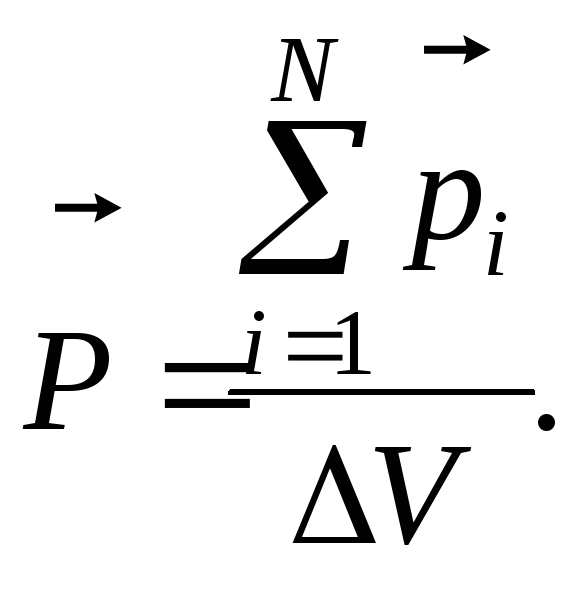
Связь поляризованности и напряженности электрического поля: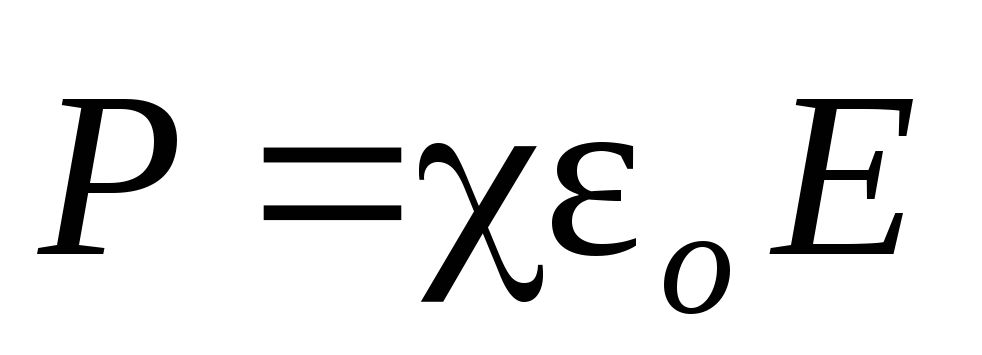, где χ – диэлектрическая восприимчивость.

Постоянный ток

Сила тока: .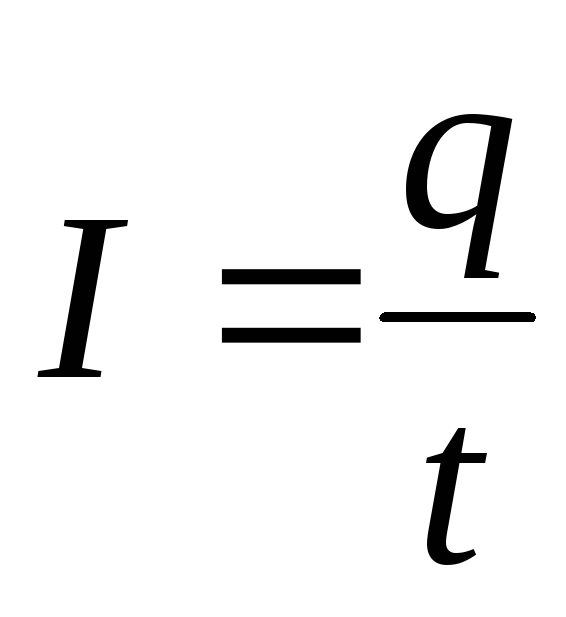

Плотность тока: 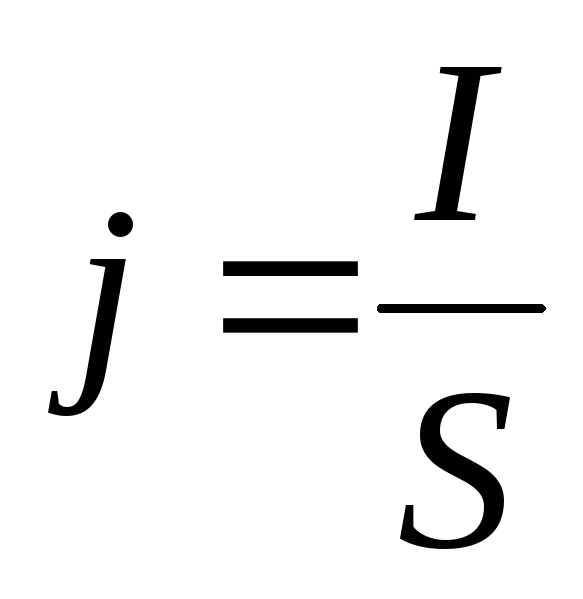, где j=qnV.

Закон Ома для однородного участка цепи:

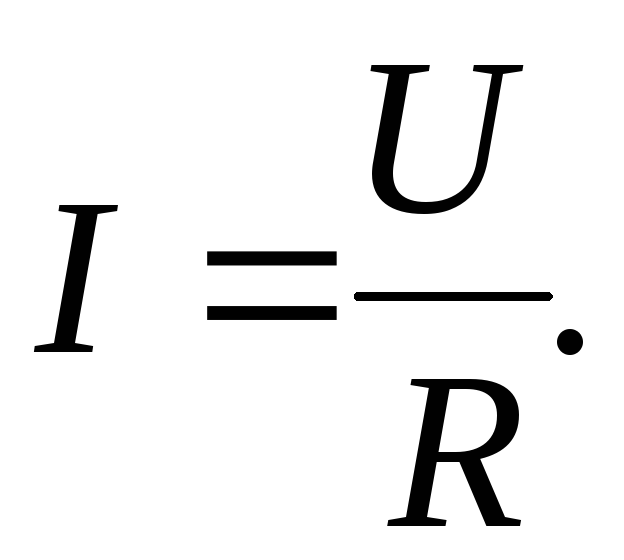
Сопротивление проводника:

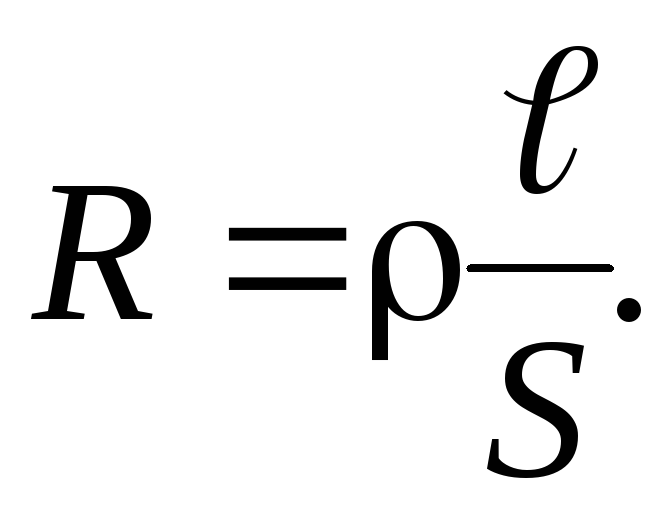
Зависимость удельного сопротивления от температуры:

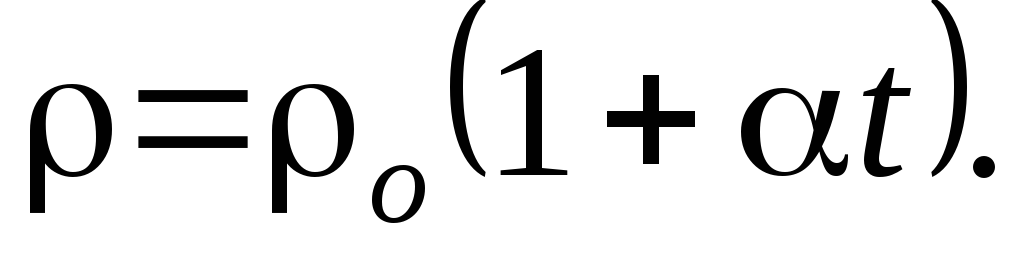
Закон Ома для неоднородного участка цепи:

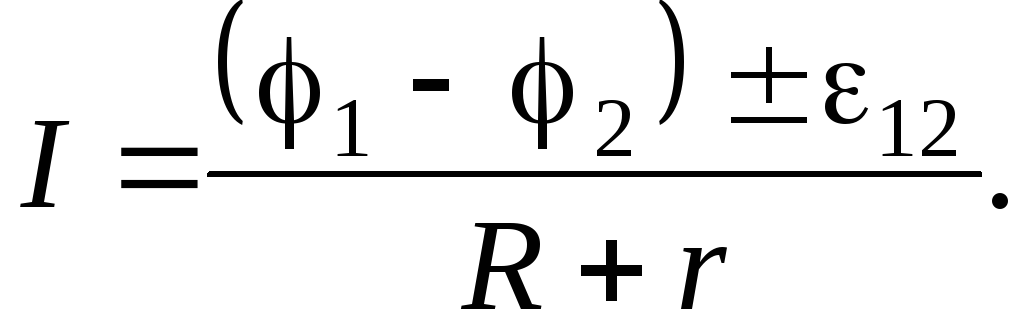
Сила тока короткого замыкания:

.

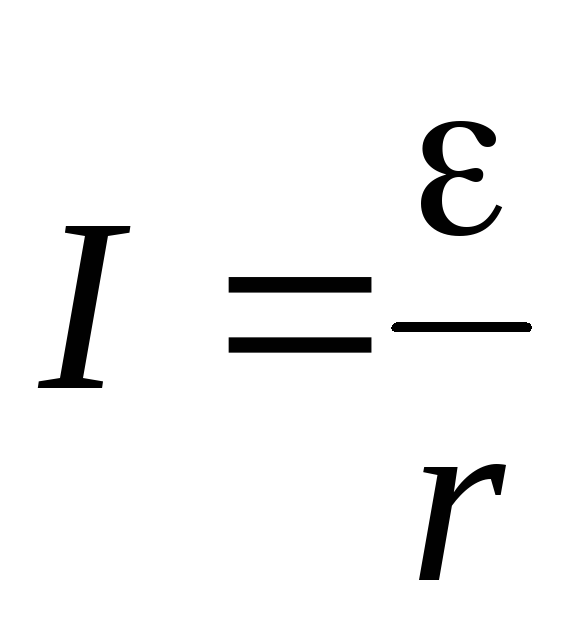Закон Ома для замкнутой цепи: .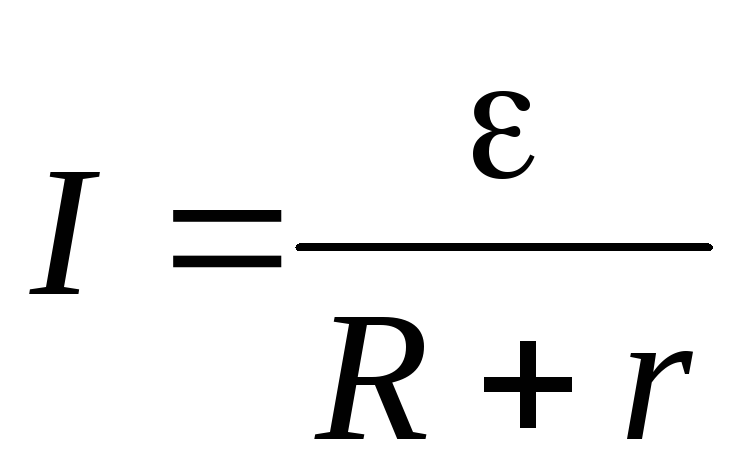

Работа электрического поля на участке цепи:

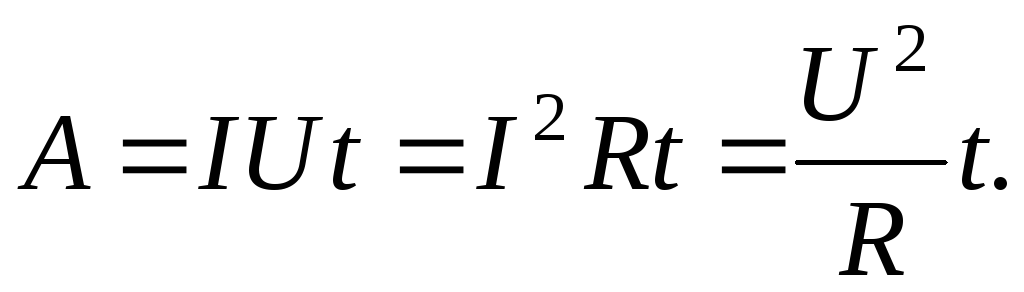
Закон Джоуля-Ленца:

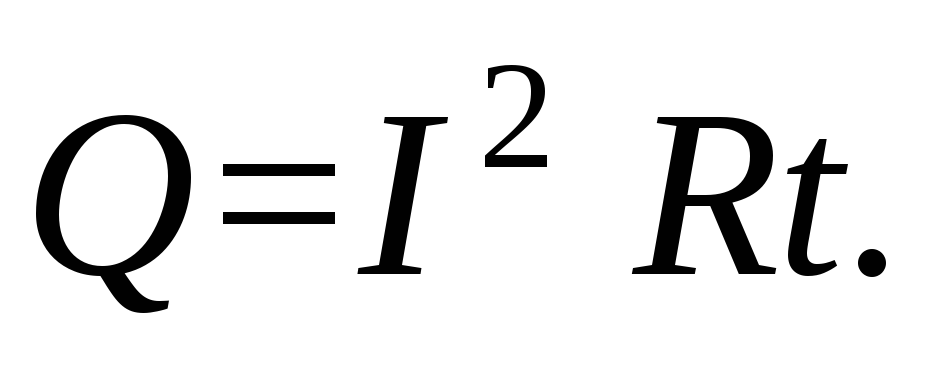
Мощность тока: P=I ^. U .

Полная мощность, выделяемая в цепи: P=I ^.  .

Первый закон Кирхгофа: .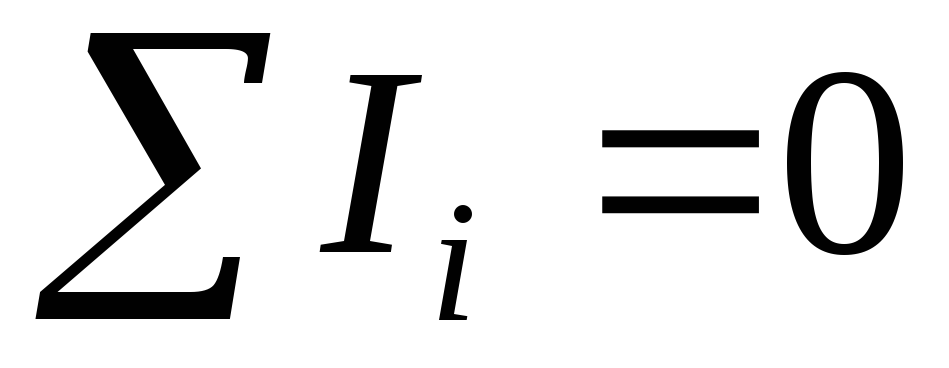

Второй закон Кирхгофа: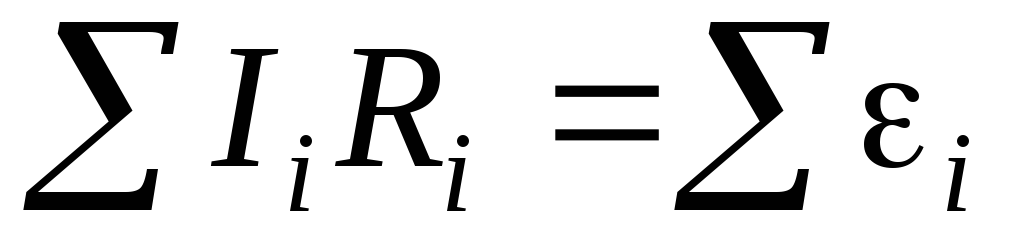

Магнитное поле в вакууме и веществе

Закон Био-Савара-Лапласа:

,

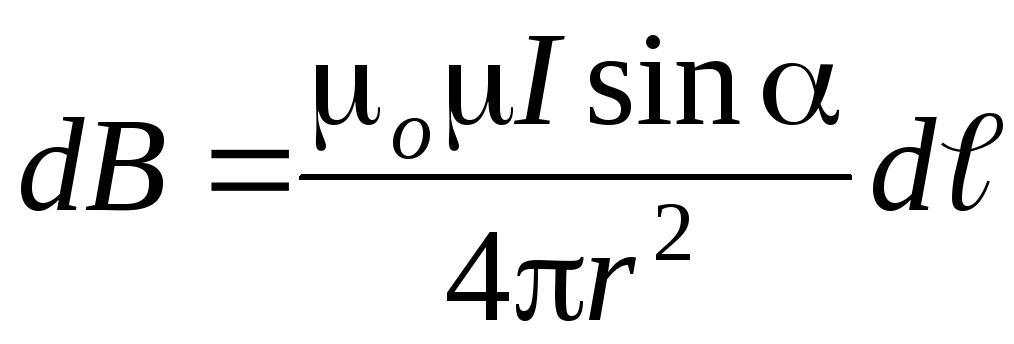где _о=410^-7Гн/м.

Магнитная индукция в центре кругового тока:

.

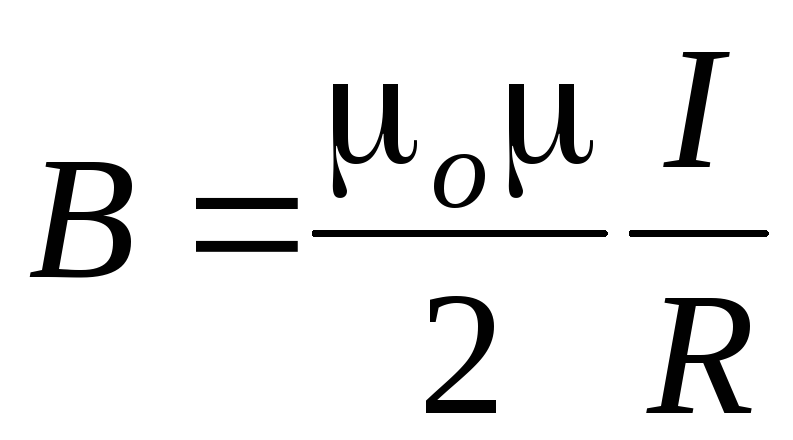Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током:

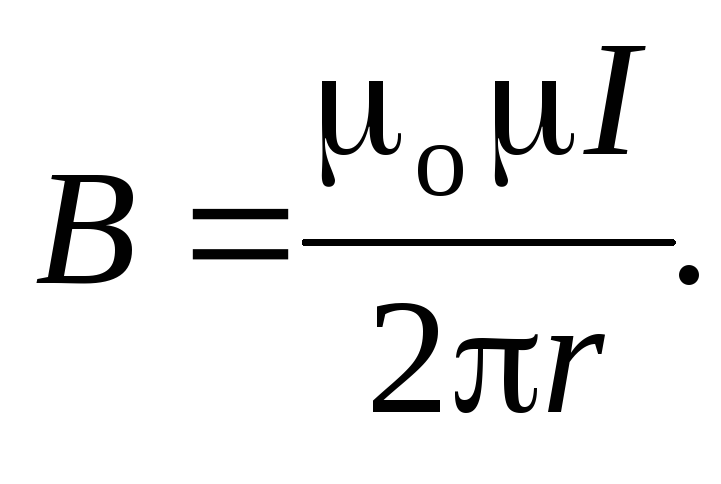
Магнитная индукция поля,

создаваемого отрезком проводника:

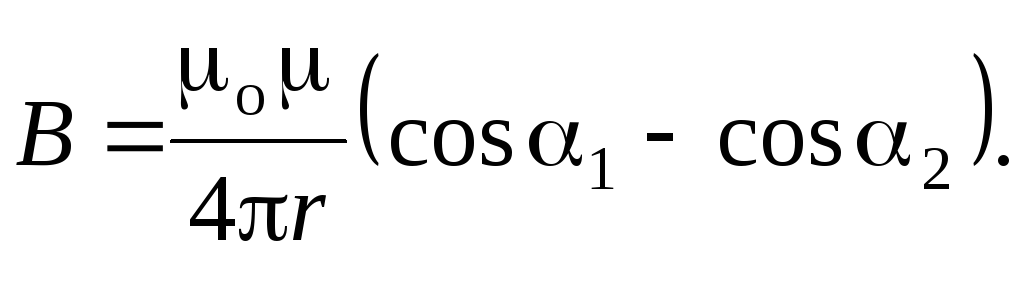
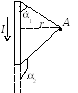
Связь магнитной индукции с напряженностью магнитного поля:

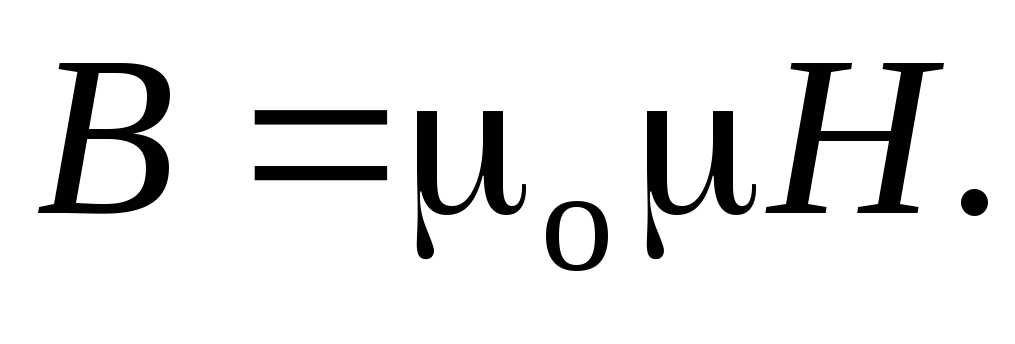
Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси):

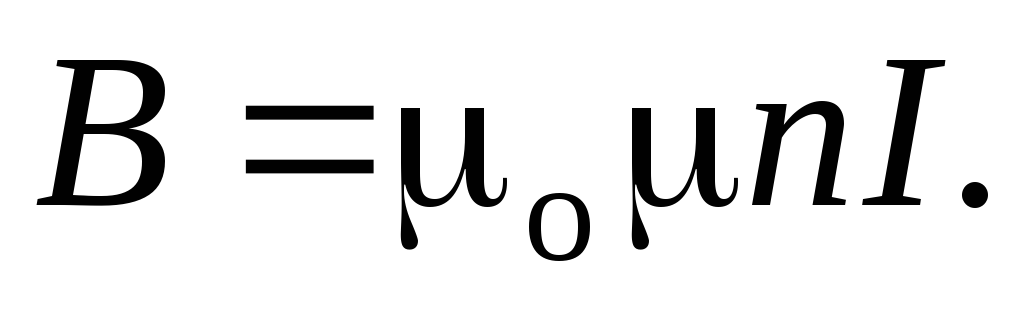
Принцип суперпозиции магнитных полей:

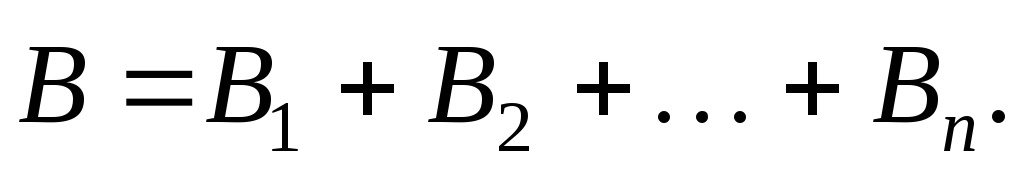
Закон Ампера:

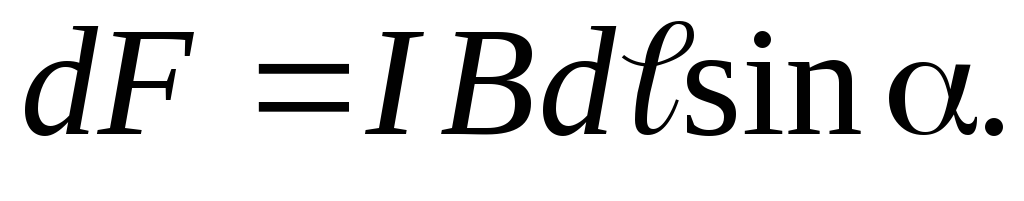
Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами:

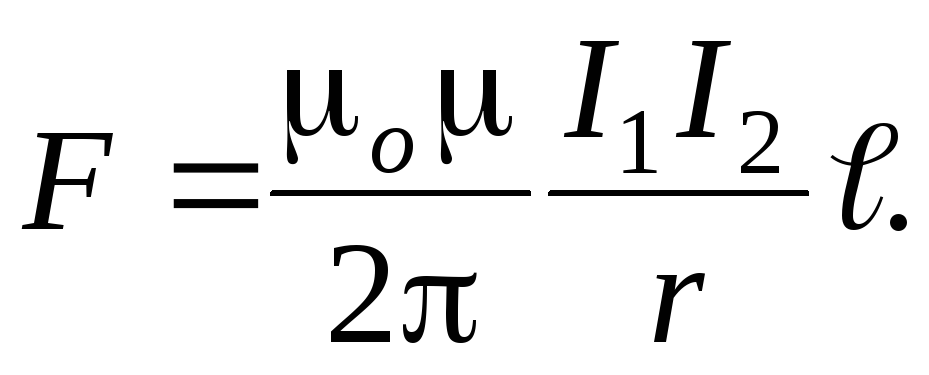
Магнитный момент контура с током:

P_m=I ^. S .

Механический момент, действующий на контур с током, помещенный в однородное магнитное поле:

M = p_m ^. B sin 

Сила, действующая на заряд, движущийся в магнитном поле (сила Лоренца):

F = q V B sin 

Закон полного тока:

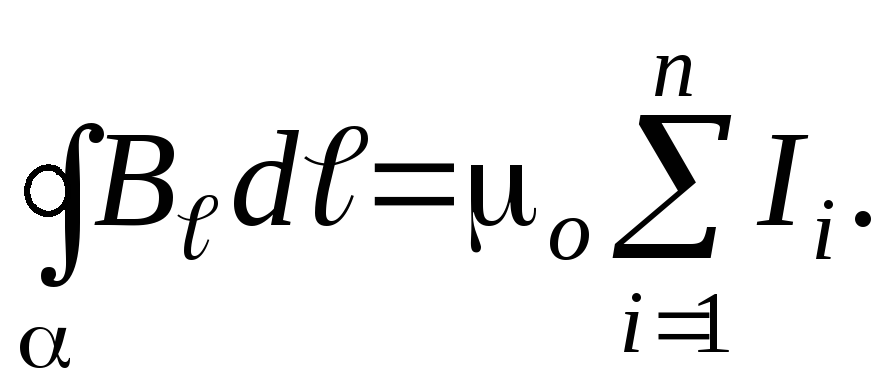
Магнитный поток через плоский контур:

Ф = B S cos  .

Потокосцепление, то есть полный магнитный поток, сцепленный со всеми витками соленоида или тороида:

.

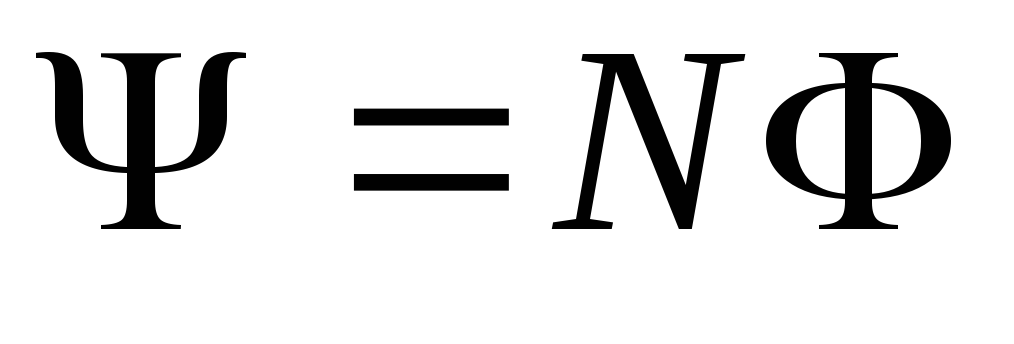М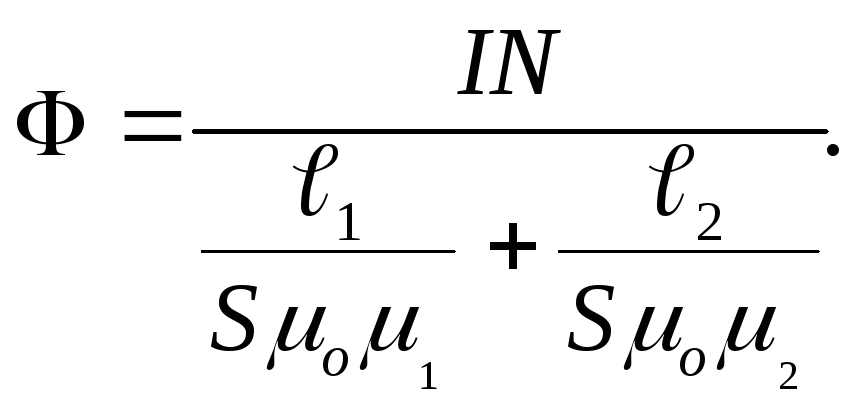агнитный поток сквозь тороид, сердечник которого составлен из двух частей, изготовленных из веществ с различными магнитными проницаемостями:

Made in Russia Made by Miha

Тут физики!: Электричество. Формулы.

Электри́чество — совокупность явлений, обусловленных существованием, взаимодействием и движением электрических зарядов. Термин введён английским естествоиспытателем Уильямом Гилбертом в его сочинении «О магните, магнитных телах и о большом магните — Земле» (1600 год), в котором объясняется действие магнитного компаса и описываются некоторые опыты с наэлектризованными телами. Он установил, что свойством наэлектризовываться обладают и другие вещества Электрический заряд — это свойство тел (количественно характеризуемое физической величиной того же названия), проявляющееся прежде всего в способности создавать вокруг себяэлектрическое поле и посредством него оказывать воздействие на другие заряженные (то есть обладающие электрическим зарядом) тела^[7]. Электрические заряды разделяют на положительные и отрицательные (выбор, какой именно заряд назвать положительным, а какой отрицательным, считается в науке чисто условным, однако этот выбор уже исторически сделан и теперь — хоть и условно — за каждым из зарядов закреплен вполне определенный знак). Тела, заряженные зарядом одного знака, отталкиваются, а противоположно заряженные — притягиваются. При движении заряженных тел (как макроскопических тел, так и микроскопических заряженных частиц, переносящих электрический ток в проводниках) возникает магнитное поле и имеют, таким образом, место явления, позволяющие установить родство электричества и магнетизма (электромагнетизм) (Эрстед, Фарадей, Максвелл). В структуре материи электрический заряд как свойство тел восходит к заряженным элементарным частицам, например, электрон имеет отрицательный заряд, а протон и позитрон — положительный. Наиболее общая фундаментальная наука, имеющая предметом электрические заряды, их взаимодействие и поля, ими порождаемые и действующие на них (то есть практически полностью покрывающая тему электричества, за исключением таких деталей, как электрические свойства конкретных веществ, как то электропроводность итп) — это электродинамика. Квантовые свойства электромагнитных полей, заряженных частиц итп изучаются наиболее глубоко квантовой электродинамикой, хотя часть из них может быть объяснена более простыми квантовыми теориями.

Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.

Цепь постоянного тока (или, строго говоря, цепь без комплексного сопротивления)

Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока.

P = мощность (Ватт)

U = напряжение (Вольт)

I = ток (Ампер)

R = сопротивление (Ом)

r = внутреннее сопротивление источнка ЭДС

ε = ЭДС источника

Тогда для всей цепи:

• I=ε/(R +r) — закон Ома для всей цепи.

И еще ниже куча формулировок закона Ома для участка цепи :

Электрическое напряжение: U = R* I — Закон Ома для участка цепи U = P / I U = (P*R)1/2	Электрическая мощность: P= U* I P= R* I2 P = U 2/ R
Электрический ток: I = U / R I = P/ E I = (P / R)1/2	Электрическое сопротивление: R = U / I R = U 2/ P R = P / I2

НЕ ЗАБЫВАЕМ: Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения.

Цепь переменного синусоидального тока c частотой ω.

Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока и частоты.

Напомним, что любой сигнал, может быть с любой точностью разложен в ряд Фурье, т.е. в предположении, что параметры сети частотнонезависимы — данная формулировка применима ко всем гармоникам любого сигнала.

Закон Ома для цепей переменного тока:

где:

• U = U₀e^iωt  напряжение или разность потенциалов,
• I  сила тока,
• Z = Re^—iφ  комплексное сопротивление (импеданс)
• R = (R_a²+R_r²)^1/2  полное сопротивление,
• R_r = ωL — 1/ωC  реактивное сопротивление (разность индуктивного и емкостного),
• R_а  активное (омическое) сопротивление, не зависящее от частоты,
• φ = arctg R_r/R_a — сдвиг фаз между напряжением и током.
Естественно, применительно к цепям переменного тока можно говорить и об активной/реактивной мощности.

Формулы «Электричество. Магнетизм» — Репетитор физики, математики

15. Электростатика

Значение вектора напряженности [В/м]        

Напряженность точечного заряда                 

Напряженность равномерно заряженной сферы:

1) внутри сферы                                          ;

2) снаружи сферы                                        

Закон Кулона                                               

Для однородного электрического поля:

1) Электрическая сила,
действующая на заряд                                 

2) Потенциальная энергия заряда                

3) Потенциал электрического поля              

4) Напряжение (разность потенциалов)        

5) Напряжение через напряженность            

6) Работа электрического поля                      

                                                                   

                                                                   

                                                                   

Потенциал поля точечного заряда [В]            

Потенциал поля заряженной сферы :

1) внутри сферы равен
потенциалу на поверхности:                         

2) снаружи сферы                                         

Электрическая емкость конденсатора [Ф]      

Электрическая емкость плоского
конденсатора                                                

Энергия конденсатора [Дж]                           

                                                                   

                                                                   

При последовательном соединении конденсаторов:

1) Напряжение батареи конденсаторов         

2) Заряд на всех конденсаторах                    

3) Емкость батареи конденсаторов                

При параллельном соединении конденсаторов:

1) Напряжение на всех конденсаторах          

2) Заряд батареи конденсаторов                   

3) Емкость батареи конденсаторов                

16. Законы постоянного тока

Сила тока [А]                                               

Закон Ома для участка цепи                         

Закон Ома для полной цепи                          

Сопротивление проводника [Ом]                   

При последовательном соединении резисторов:

1) Напряжение между входом
и выходом цепи                                           

2) Сила тока  во всех резисторах                

3) Эквивалентное сопротивление цепи         

При параллельном соединении резисторов:

1) Напряжение на всех резисторах               

2) Сила тока через вход и выход цепи          

3) Эквивалентное сопротивление цепи         

для двух параллельно соединенных резисторов   

Работа тока на однородном
участке цепи [Дж]                                        

                                                                   

                                                                   

Количество теплоты, выделяющееся
на резисторе [Дж]                                        

Мощность тока [Вт]                                      

                                                                   

                                                                   

Первое правило Кирхгофа                            

Второе правило Кирхгофа                            

17. Магнитное поле

Сила Лоренца                                               

Сила Ампера                                               

Магнитный поток [Вб]                                  

ЭДС индукции в замкнутом контуре              

ЭДС индукции в катушке                              

ЭДС индукции в движущемся проводнике      

Индукционный ток                                        

Магнитный поток катушки                             

Индуктивность соленоида                             

ЭДС самоиндукции в катушке                       

Энергия магнитного поля
катушки с током                                          

Колебания — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Гармонические колебания

К оглавлению…

В технике и окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебаниями называют изменения физической величины, происходящие по определенному закону во времени. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.

Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник. Для существования в системе гармонических колебаний необходимо, чтобы у нее было положение устойчивого равновесия, то есть такое положение, при выведении из которого на систему начала бы действовать возвращающая сила.

Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.

Простейшим видом колебательного процесса являются колебания, происходящие по закону синуса или косинуса, называемые гармоническими колебаниями. Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω₀ задаётся следующим образом:

Решение предыдущего уравнения является уравнением движения для гармонических колебаний, которое имеет вид:

где: x – смещение тела от положение равновесия, A – амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний (ω = 2Π/T), t – время. Величина, стоящая под знаком косинуса: φ = ωt + φ₀, называется фазой гармонического процесса. Смысл фазы колебаний: стадия, в которой колебание находится в данный момент времени. При t = 0 получаем, что φ = φ₀, поэтому φ₀ называют начальной фазой (то есть той стадией, из которой начиналось колебание).

Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Если же количество колебаний N, а их время t, то период находится как:

Физическая величина, обратная периоду колебаний, называется частотой колебаний:

Частота колебаний ν показывает, сколько колебаний совершается за 1 с. Единица частоты – Герц (Гц). Частота колебаний связана с циклической частотой ω и периодом колебаний T соотношениями:

Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:

Максимальное значение скорости при гармонических механических колебаниях:

Максимальные по модулю значения скорости υ_m = ωA достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = a_x тела при гармонических колебаниях. Зависимость ускорения от времени при гармонических механических колебаниях:

Максимальное значение ускорения при механических гармонических колебаниях:

Знак минус в предыдущем выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения x(t), и, следовательно, возвращает тело в начальное положение (x = 0), т.е. заставляет тело совершать гармонические колебания.

Следует обратить внимание на то, что:

• физические свойства колебательной системы определяют только собственную частоту колебаний ω₀ или период T.
• Такие параметры процесса колебаний, как амплитуда A = x_m и начальная фаза φ₀, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени, т.е. начальными условиями.
• При колебательном движении тело за время, равное периоду, проходит путь, равный 4 амплитудам. При этом тело возвращается в исходную точку, то есть перемещение тела будет равно нулю. Следовательно, путь равный амплитуде тело пройдет за время равное четверти периода.

Чтобы определить, когда в уравнение колебаний подставлять синус, а когда косинус, нужно обратить внимание на следующие факторы:

• Проще всего, если в условии задачи колебания названы синусоидальными или косинусоидальными.
• Если сказано, что тело толкнули из положения равновесия – берем синус с начальной фазой, равной нулю.
• Если сказано, что тело отклонили и отпустили – косинус с начальной фазой, равной нулю.
• Если тело толкнули из отклоненного от положения равновесия состояния, то начальная фаза не равна нолю, а брать можно и синус и косинус.

 

Математический маятник

К оглавлению…

Математическим маятником называют тело небольших размеров, подвешенное на тонкой, длинной и нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Только в случае малых колебаний математический маятник является гармоническим осциллятором, то есть системой, способной совершать гармонические (по закону sin или cos) колебания. Практически такое приближение справедливо для углов порядка 5–10°. Колебания маятника при больших амплитудах не являются гармоническими.

Циклическая частота колебаний математического маятника рассчитывается по формуле:

Период колебаний математического маятника:

Полученная формула называется формулой Гюйгенса и выполняется, когда точка подвеса маятника неподвижна. Важно запомнить, что период малых колебаний математического маятника не зависит от амплитуды колебаний. Такое свойство маятника называется изохронностью. Как и для любой другой системы, совершающей механические гармонические колебания, для математического маятника выполняются следующие соотношения:

1. Путь от положения равновесия до крайней точки (или обратно) проходится за четверть периода.
2. Путь от крайней точки до половины амплитуды (или обратно) проходится за одну шестую периода.
3. Путь от положения равновесия до половины амплитуды (или обратно) проходится за одну двенадцатую долю периода.

 

Пружинный маятник

К оглавлению…

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению. Таким свойством обладает сила упругости.

Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную совершать в отсутствие трения свободные гармонические колебания. Груз на пружине называют пружинным маятником.

Циклическая частота колебаний пружинного маятника рассчитывается по формуле:

Период колебаний пружинного маятника:

При малых амплитудах период колебаний пружинного маятника не зависит от амплитуды (как и у математического маятника). При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x₀, равную:

А колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты ω₀ и периода колебаний T справедливы и в этом случае. Таким образом, полученная формула для периода колебаний груза на пружине остается справедливой во всех случаях, независимо от направления колебаний, движения опоры, действия внешних постоянных сил.

При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а, следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругой деформации пружины. Для математического маятника – это энергия в поле тяготения Земли.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по инерции. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией (как правило, потенциальную энергию в положении равновесия полагают равной нулю). Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и так далее.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. При этом, максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:

Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:

Взаимосвязь энергетических характеристик механического колебательного процесса (полная механическая энергия равна максимальным значениям кинетической и потенциальной энергий, а также сумме кинетической и потенциальной энергий в произвольный момент времени):

 

Механические волны

К оглавлению…

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной.

Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют немеханические волны, которые способны распространяться и в пустоте (например, световые, т.е. электромагнитные волны могут распространяться в вакууме).

• Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
• Поперечные волны не могут существовать в жидкой или газообразной средах.

Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой ν и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.

Длиной волны λ называют расстояние между двумя соседними точками, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за время равное периоду T, следовательно, длина волны может быть рассчитана по формуле:

где: υ – скорость распространения волны. При переходе волны из одной среды в другую длина волны и скорость ее распространения меняются. Неизменными остаются только частота и период волны.

Разность фаз колебаний двух точек волны, расстояние между которыми l рассчитывается по формуле:

 

Электрический контур

К оглавлению…

В электрических цепях, так же, как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный LC-контур. В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими. Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:

Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:

Циклическая частота колебаний в электрическом колебательном контуре:

Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:

Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:

Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:

Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:

Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:

Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в теплоту, выделяющуюся на резисторе, и колебания становятся затухающими.

 

Переменный ток. Трансформатор

К оглавлению…

Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими синусоидальное напряжение. Они позволяют наиболее просто и экономно осуществлять передачу, распределение и использование электрической энергии.

Устройство, предназначенное для превращения механической энергии в энергию переменного тока, называется генератором переменного тока. Он характеризуется переменным напряжением U(t) (индуцированной ЭДС) на его клеммах. В основу работы генератора переменного тока положено явление электромагнитной индукции.

Переменным током называется электрический ток, который изменяется с течением времени по гармоническому закону. Величины U₀, I₀ = U₀/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.

Переменный ток характеризуется действующими значениями силы тока и напряжения. Действующим (эффективным) значением переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделил бы в единицу времени такое же количество теплоты, что и данный переменный ток. Для переменного тока действующее значение силы тока может быть рассчитано по формуле:

Аналогично можно ввести действующее (эффективное) значение и для напряжения, рассчитываемое по формуле:

Таким образом, выражения для мощности постоянного тока остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

Обратите внимание, что если идет речь о напряжении или силе переменного тока, то (если не сказано иного) имеется в виду именно действующее значение. Так, 220В – это действующее напряжение в домашней электросети.

Конденсатор в цепи переменного тока

Строго говоря, конденсатор ток не проводит (в том смысле, что носители заряда через него не протекают). Поэтому, если конденсатор подключен в цепь постоянного тока, то сила тока в любой момент времени в любой точке цепи равна нулю. При подключении в цепь переменного тока из-за постоянного изменения ЭДС конденсатор перезаряжается. Ток через него по-прежнему не течет, но ток в цепи существует. Поэтому условно говорят, что конденсатор проводит переменный ток. В этом случае вводится понятие сопротивления конденсатора в цепи переменного тока (или емкостного сопротивления). Это сопротивление определяется выражением:

Обратите внимание, что емкостное сопротивление зависит от частоты переменного тока. Оно в корне отличается от привычного нам сопротивления R. Так, на сопротивлении R выделяется теплота (поэтому его часто называют активным), а на емкостном сопротивлении теплота не выделяется. Активное сопротивление связано со взаимодействием носителей заряда при протекании тока, а емкостное – с процессами перезарядки конденсатора.

Катушка индуктивности в цепи переменного тока

При протекании переменного тока в катушке возникает явление самоиндукции, и, следовательно, ЭДС. Из-за этого напряжение и сила тока в катушке не совпадают по фазе (когда сила тока равна нулю, напряжение имеет максимальное значение и наоборот). Из-за такого несовпадения средняя тепловая мощность, выделяющаяся в катушке, равна нулю. В этом случае вводится понятие сопротивления катушки в цепи переменного тока (или индуктивного сопротивления). Это сопротивление определяется выражением:

Обратите внимание, что индуктивное сопротивление зависит от частоты переменного тока. Как и емкостное сопротивление, оно отличается от сопротивления R. Как и на емкостном сопротивлении, на индуктивном сопротивлении теплота не выделяется. Индуктивное сопротивление связано с явлением самоиндукции в катушке.

Трансформаторы

Среди приборов переменного тока, нашедших широкое применение в технике, значительное место занимают трансформаторы. Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении электромагнитной индукции. Простейший трансформатор состоит из сердечника замкнутой формы, на который намотаны две обмотки: первичная и вторичная. Первичная обмотка подсоединяется к источнику переменного тока с некоторым напряжением U₁, а вторичная обмотка подключается к нагрузке, на которой появляется напряжение U₂. При этом, если число витков в первичной обмотке равно n₁, а во вторичной n₂, то выполняется следующее соотношение:

Коэффициент трансформации вычисляется по формуле:

Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):

В неидеальном трансформаторе вводится понятие КПД:

 

Электромагнитные волны

К оглавлению…

Электромагнитные волны – это распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы электрической напряженности и магнитной индукции перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Электромагнитные волны распространяются в веществе с конечной скоростью, которая может быть рассчитана по формуле:

где: ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные: ε₀ = 8,85419·10^–12 Ф/м, μ₀ = 1,25664·10^–6 Гн/м. Скорость электромагнитных волн в вакууме (где ε = μ = 1) постоянна и равна с = 3∙10⁸ м/с, она также может быть вычислена по формуле:

Скорость распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных. Если электромагнитная волна распространяется в какой-либо среде, то скорость ее распространения также выражается следующим соотношением:

где: n – показатель преломления вещества – физическая величина, показывающая во сколько раз скорость света в среде меньше чем в вакууме. Показатель преломления, как видно из предыдущих формул, может быть рассчитан следующим образом:

• Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии.
• Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Цепи постоянного тока, в которых носители заряда движутся с неизменной скоростью, не являются источником электромагнитных волн. А вот цепи, в которых протекает переменный ток, т.е. такие цепи в которых носители заряда постоянно меняют направление своего движения, т.е. двигаются с ускорением – являются источником электромагнитных волн. В современной радиотехнике излучение электромагнитных волн производится с помощью антенн различных конструкций, в которых возбуждаются быстропеременные токи.

Основные формулы по физике. Постоянный электрический ток- ГДЗ, все для учебы на ftechedu.ru

	сила электрического тока
	зависимость силы тока от заряда, концентрации, скорости и площади поперечного сечения проводника
	модуль плотности электрического тока
	закон Ома для участка цепи
	зависимость сопротивления от рода вещества, длины и поперечного сечения проводника
	зависимость сопротивления проводника от температуры
	сопротивление последовательно соединенных резисторов
	величина, обратная сопротивлению параллельно соединенных резисторов
	работа электрического тока
	мощность электрического тока
	закон Джоуля-Ленца