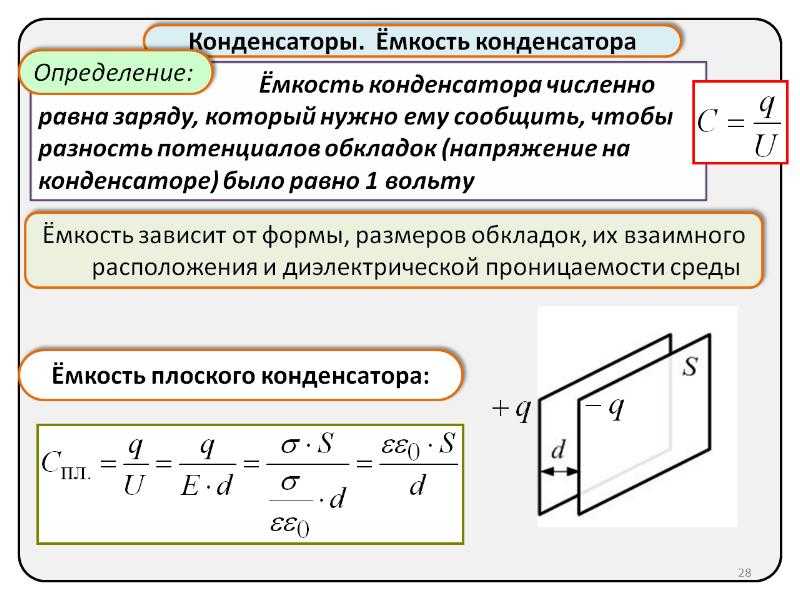
Ёмкость плоского конденсатора.
Плоский конденсатор состоит из двух параллельных пластин, разделённых небольшим зазором шириной , заполненным однородным диэлектриком.
Нам известно, что поле между двумя разноимённо заряженными пластинами с одинаковой по величине поверхностной плотностью равно, где,S– площадь каждой пластины. Напряжение между обкладками:
.
Используя определение емкости конденсатора, получаем:
Отметим, что полученная формула является приближенной, так как выведена без учета искажения поля у краев пластин. Расчет по этой формуле дает завышенное значение ёмкости и тем точнее, чем меньше зазор по сравнению с линейными размерами пластин.
Сферический
конденсатор представляет собой систему
двух концентрических сфер с радиусамии.
Электрическое поле между обкладками
сферического конденсатора согласно
теореме Гаусса определяется зарядом
внутренней сферы.
.
Для ёмкости сферического конденсатора получаем:
.
Это формула точная.
Если , полученная формула переходит в выражение для ёмкости плоского конденсатора.
Ёмкость цилиндрического конденсатора.
Цилиндрический конденсатор составляет систему двух коаксиальных цилиндров с радиусами и, длиной.
Рассуждая аналогично выводу ёмкости сферического конденсатора, получаем:
..
Полученная формула является приближенной и при малом зазоре переходит в формулу емкости плоского конденсатора.
В практике для получения необходимых значений емкости используют соединения конденсаторов: а) последовательное, б) параллельное, в) смешанное (см. рисунок).
Ёмкость последовательного
соединения конденсаторов.
Заряды последовательно соединенных конденсаторов равны , а напряжение на батарее. Из определения емкости следует:
или .
Если , то(ёмкость последовательного соединения меньше наименьшей ёмкости в последовательном соединении).
.
В случае одинаковых конденсаторов: .
Ёмкость параллельного соединения конденсаторов.
Заряд батареи равен сумме зарядов:
,
а напряжение . По определению емкости получаем:
.
Для параллельно соединенных конденсаторов:.
В случае одинаковых конденсаторов: .
Пример.
Оценить емкость батареи (см. рисунок).
.
Ответ:.
Используя свойство бесконечности можно
представить цепь в виде соединения (см.
Для расчета ёмкости батареи получаем:
,
.
Откуда: , так как, то.
Лекция 7.
Диэлектрики в электрическом поле.
Диэлектриками (изоляторами) называют вещества, не проводящие постоянного электрического тока. Это означает, что в диэлектриках отсутствуют «свободные» заряды, способные перемещаться на значительные расстояния.
Диэлектрики состоят либо из нейтральных молекул, либо из ионов, находящихся в узлах кристаллической решетки. Сами же молекулы могут быть
Поляризация.
В электрическом поле диэлектрики
поляризуются. Это явление связано с
появлением в объеме и на поверхности
диэлектрика «связанных» зарядов. При этом конечный объем диэлектрика
приобретает дипольный момент. Механизм
поляризации связан с конкретным строением
диэлектрика. Если диэлектрик состоит
из неполярных молекул, то в пределах
каждой молекулы происходит смещение
зарядов – положительных по полю,
отрицательных против поля, т.е. молекулы,
приобретают дипольный момент. У
диэлектрика с полярными молекулами в
отсутствии внешнего электрического
поля их дипольные моменты ориентированы
хаотично.
При этом конечный объем диэлектрика
приобретает дипольный момент. Механизм
поляризации связан с конкретным строением
диэлектрика. Если диэлектрик состоит
из неполярных молекул, то в пределах
каждой молекулы происходит смещение
зарядов – положительных по полю,
отрицательных против поля, т.е. молекулы,
приобретают дипольный момент. У
диэлектрика с полярными молекулами в
отсутствии внешнего электрического
поля их дипольные моменты ориентированы
хаотично.
Под
действием электрического поля диполи
ориентируются преимущественно в
направлении поля. Рассмотрим подробнее
этот механизм (см. рисунок). Пара силисоздает
вращательный момент равный,
где-
дипольный момент молекулы. Этот момент
стремится ориентировать диполь вдоль
поля. В ионных кристаллах под действием
электрического поля все положительные
ионы смещаются по полю, отрицательные
– против поля. Отметим, что смещение
зарядов очень малы даже по сравнению с
размерами молекул. Это связано с тем,
что напряженность внешнего электрического
поля обычно много меньше напряженности
внутренних электрических полей в
молекулах.
Отметим, что существуют диэлектрики, поляризованные даже при отсутствии внешнего поля (электреты, сегнетоэлектрики). Мы остановимся на рассмотрении только однородных диэлектриков, в которых отсутствует остаточная поляризация, а объемный и «связанный» заряд всегда равен нулю .
Расчёт плоского конденсатора, вывод формулы ёмкости, напряжённость электрического поля конденсатора, напряжение между пластинами
В статье поле плоской пластины была выведена формула напряжённости электрического поля бесконечной плоской пластины. Если эту пластину рассмотреть в разрезе и ввести понятие поверхностной плотности заряда σ, то согласно указанной статьи в любой точке пространства напряжённость электрического поля направлена перпендикулярно плоскости пластины и по величине равно:
E0 здесь жёстко определяется поверхностной плотностью заряда σ:
где σ – поверхностная плотность заряда;
ε0 – диэлектрическая проницаемость для вакуума;
ε – относительная диэлектрическая проницаемость для вещества, которая для вакуума равна 1.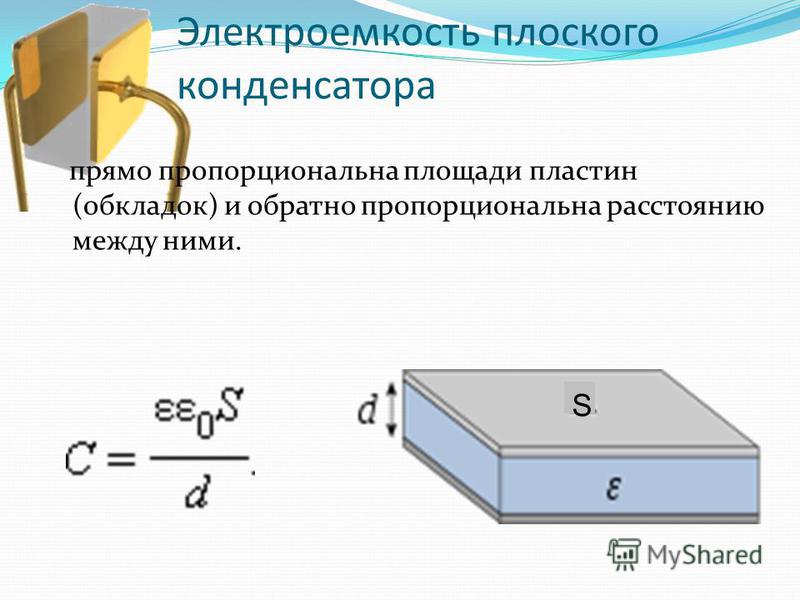
Формулы показывают, что величина напряжённости электрического поля плоской пластины, имеющей бесконечные размеры, не зависит от расстояния до неё.
Если σ положительная, то напряжённость электрического поля будет направлена от пластины и поле отталкивает положительные заряды.
Если σ отрицательная, то напряжённость электрического поля направлена к пластине и поле притягивает положительные заряды.
Плоским конденсатором будем называть пару параллельных плоских пластин с плотностью заряда одинаковой по модулю, но противоположной по знаку.
Напряжённость электрического поля конденсатора
Для расчёта плоского конденсатора расположим две пластины бесконечных размеров параллельно друг другу на некотором расстоянии d. Пусть одна пластина будет иметь поверхностную плотность заряда σ, а другая -σ. По модулю величины поверхностных плотностей зарядов будут равны. В такой ситуации общее поле плоского конденсатора по принципу суперпозиции равно сумме полей.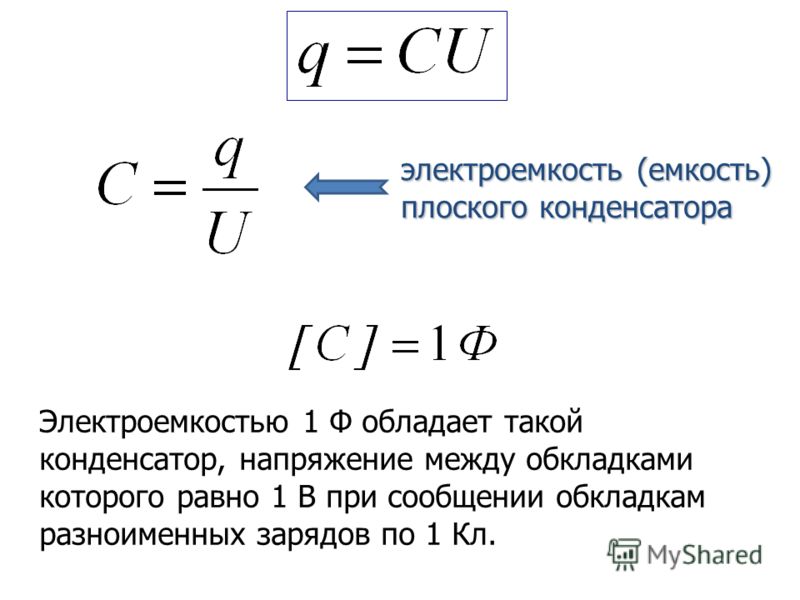
Обозначим напряжённости электрического поля от левой пластины плоского конденсатора как Eл, при этом положительные заряды будут отталкиваться от пластины.
Напряжённость электрического поля от правой пластины плоского конденсатора обозначим как Eп, при этом поле пластины будет притягивать к себе положительные заряды.
При равной плотности заряда напряжённость поля во всех точках пространства и от левой, и от правой пластин конденсатора будут равны по модулю. Это приведёт к тому, что слева и справа от пары пластин поля взаимно компенсируются и их сумма будет равна нулю. При этом поля между пластинами плоского конденсатора будут складываться.
где E0 – напряжённость поля при положительной σ.
Суммарная напряжённость электрического поля плоского конденсатора будет направлена от пластины с положительной σ к пластине с отрицательной σ.
Электрическая энергия плоского конденсатора отсутствует вне его пластин и вся накоплена в пространстве между пластинами.
Работа по перемещению заряда
Для перемещения заряда от отрицательно заряженной пластины в направлении к положительно заряженной придётся совершить работу против электрической силы:
При вычислении этой работы видно, что величина заряда q и напряжённость поля E постоянны, поэтому формула примет вид:
В электрическом поле можно ввести понятие потенциала ϕ и выразить работу по перемещению заряда в точку 2 из точки 1 через разность потенциалов ϕ1-ϕ2.
Напряжение между пластинами плоского конденсатора
Разность электрических потенциалов между двумя точками называют напряжением и обозначают U12:
Таким образом, сравнивая две формулы для работы мы получим:
В реальном конденсаторе площадь пластин ограничена по естественным причинам, поэтому, как правило, мы не имеем возможности знать плотность заряда, а знаем только заряд пластины. В этом случае плотность заряда σ мы можем вычислить по формуле:
где Q – заряд пластины;
S – площадь пластины.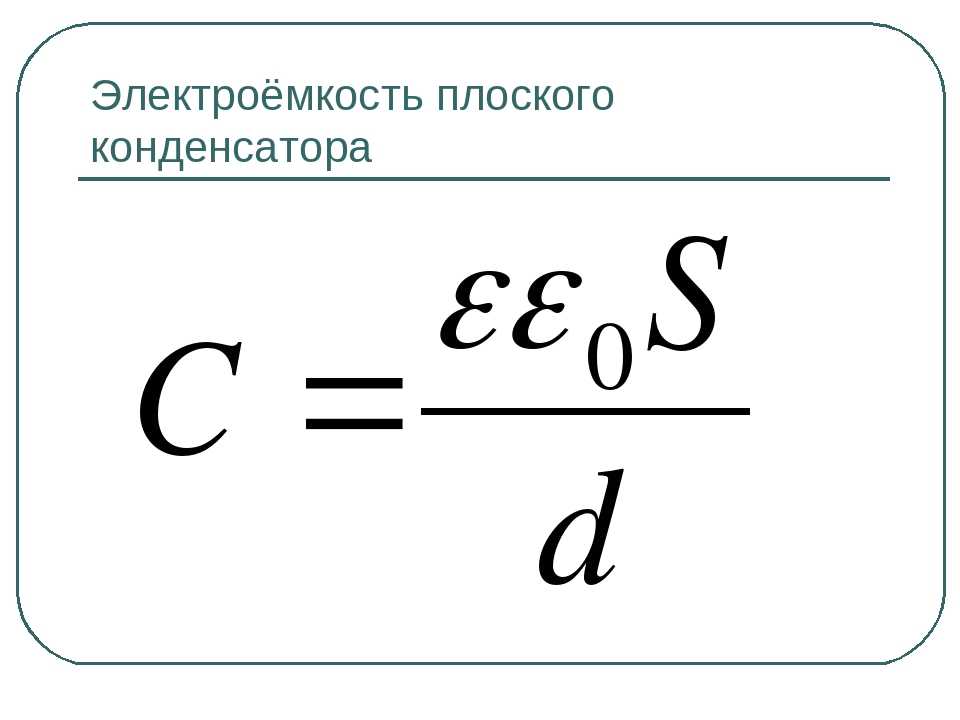
Если пластины плоского конденсатора находятся достаточно близко друг к другу, то краевыми эффектами можно пренебречь и считать, что поле внутри конденсатора реальных размеров подобно полю внутри конденсатора с пластинами бесконечных размеров.
В таком случае имеем следующее выражение:
Напряжение между пластинами пропорционально полному заряду этих пластин:
Электрическая ёмкость плоского конденсатора
Коэффициент пропорциональности между зарядом на обкладках плоского конденсатора и напряжением между ними носит название ёмкости плоского конденсатора и обозначается буквой C:
емкостный калькулятор
, созданный Luciano Mino
Последнее обновление: 04 июля, 2022
- Определение емкостной рассчитайте емкость плоского конденсатора или найдите расстояние между пластинами .
В этой короткой статье ниже мы кратко опишем:
- Что такое и как рассчитать емкость;
- Формула емкости плоского конденсатора; и
- Что такое единицы измерения емкости.

Продолжайте читать, чтобы узнать больше!
Определение емкости
Емкость объекта — это его способность накапливать электрический заряд. Это отношение между накопленным зарядом и разностью потенциалов между двумя проводниками внутри.
Чем выше емкость, тем большее количество заряда можно сохранить при той же разности потенциалов.
Давайте теперь посмотрим, как найти емкость конденсатора и какие единицы измерения емкости.
Как рассчитать емкость
В общем случае емкость определяется как:
C=QVC = \frac{Q}{V}C=VQ
где:
- CCC – емкость в фарадах (Ф) . Конденсатор с зарядом 1 кулон при разности потенциалов 1 вольт имеет емкость 1 фарад.
- QQQ — электрический заряд внутри конденсатора.
- VVV – разность потенциалов.
Для плоского конденсатора мы можем заменить эти переменные другими, с которыми легче работать. Таким образом, формула емкости принимает вид:
C=εAsC = \frac{ε A}{s}C=sεA
, где:
- AAA – площадь пластин в м².
 Наш конвертер площадей может помочь вам с этим шагом, или вы можете изменить единицы измерения, используя встроенный конвертер единиц калькулятора емкости.
Наш конвертер площадей может помочь вам с этим шагом, или вы можете изменить единицы измерения, используя встроенный конвертер единиц калькулятора емкости. - sss — расстояние между пластинами в м.
- εεε — диэлектрическая проницаемость материала между пластинами в фарадах на метр. Диэлектрическая проницаемость вакуума составляет 8,854 пФм8,854\ \frac{\text{пФ}}{\text{м}}8,854 мпФ.
💡 Вы можете ввести любое значение диэлектрической проницаемости, используя расширенный режим
Пример
Допустим, у нас есть плоский конденсатор емкостью 12 пФ12\ \text{пФ}12 пФ с пластинами площадью 10 см²10\ \text{см²}10 см², и мы хотим определить, насколько близко расположены эти пластины. Как мы делаем это?
Во-первых, мы должны изменить формулу емкости, чтобы найти недостающий параметр:
s=εACs = \frac{ε A}{C}s=CεA
диэлектрическая проницаемость вакуума, 8,854 пФм8,854\ \\frac{\text{пФ}}{\text{м}}8,854 мпФ), чтобы получить расстояние между пластинами конденсатора.

Результат:
с≃0,74 мм \simeq 0,74\ \text{мм}с≃0,74 мм
🙋 Не забудьте преобразовать все в м , м² , м² , 90 016 F , 90 015 F , 90 015 F 0,74 мм перед заменой значений в уравнении.
Лучано Мино
Формула цилиндрического конденсатора — GeeksforGeeks
Цилиндрический конденсатор представляет собой устройство, которое накапливает значительное количество электрического тока на небольшой площади. Он состоит из концентрического полого сферического цилиндра, окружающего полый или сплошной цилиндрический проводник. В электродвигателях, зерновых мельницах, электрических соковыжималках и других электроприборах используются цилиндрические конденсаторы. Конденсатор предназначен для ограничения силовых линий электрического поля в ограниченном пространстве. В результате, даже если поле очень сильное, разность потенциалов между двумя проводниками конденсатора весьма мала. Хотя конденсаторы могут быть сгруппированы различными способами для достижения необходимой емкости, наиболее распространенными являются последовательные и параллельные конфигурации.
 Формула для расчета цилиндрической емкости представлена в этой статье.
Формула для расчета цилиндрической емкости представлена в этой статье.Цилиндрический конденсатор
Емкость на единицу длины — это емкость для цилиндрической геометрии.
Разность потенциалов каждого конденсатора уникальна. Существует ряд электрических схем, в которых конденсаторы должны быть расположены в правильном порядке, чтобы получить желаемую емкость. Конденсаторы, соединенные последовательно, и конденсаторы, соединенные параллельно, являются двумя наиболее распространенными конфигурациями. Фарад — стандартная единица измерения емкости (Ф). Для накопления электрического заряда обычно используют цилиндрический конденсатор.
Формула для цилиндрического конденсатора
Емкость цилиндрического конденсатора можно рассчитать по следующей формуле:
- C = Емкость цилиндра,
- ε 0 = Диэлектрическая проницаемость свободного пространства,
- a = Внутренний радиус цилиндра,
- b = Внешний радиус цилиндра,
- L = Длина цилиндра.

Примеры вопросов
Вопрос 1. Почему так много цилиндрических конденсаторов?
Ответ:
Две проводящие пластины разделены изолирующим зазором в общем виде конденсатора. Металлическая фольга, металлизированные полимерные пленки, электролиты и другие материалы могут использоваться для создания изолирующих и проводящих компонентов. Все вышеперечисленные элементы могут быть выполнены в виде плоской прямоугольной формы. Некоторые конденсаторы не имеют сферической формы. Их формируют укладкой слоев изоляционного и проводящего материала поочередно. Многослойные керамические чип-конденсаторы, например, являются хорошим примером.
Вопрос 2: Какие компоненты цилиндрического конденсатора? Дайте несколько применений.
Ответ:
Цилиндрический конденсатор состоит из цилиндрического проводника, окруженного полым сферическим цилиндром.

Вопрос 3: Рассчитайте емкость цилиндрического конденсатора, упакованного в бумагу и состоящего из цилиндров с внутренним и внешним радиусами 2 см и 5 см соответственно.
Ответ:
Подставим диэлектрическую проницаемость, которая равна 3,85 для бумаги, в формулу для емкости цилиндрического конденсатора, получим:
Дано: , L = 3,85, b = 5 см, a = 2 см.
Так как,
C = 2πε
= 2 × 3,14 × 8,85 × 10 -12 × (3,85 / ln(5/2))
= 538,22 × 10 -12 F
Вопрос 4: Цилиндрический конденсатор состоит из двух колец с внутренним радиусом 6 см и внешним радиусом 12 см. Рассчитайте емкость конденсатора, исходя из его длины 16 см.

Ответ:
Дано: A = 6 см, B = 12 см, L = 16 см, ε 0 = 8,85 × 10 -12
С.
C = 2π ЩЕТ. × (L/ln(b/a))
= 2 × 3,14 × 8,85 × 10 -12 × (16 × 10 -2 / ln(12/6))
= 2,954 × 10 -11 F
Вопрос 5. Цилиндрический конденсатор длиной 8 см состоит из двух концентрических колец с внутренним радиусом 3 см и внешним радиусом 6 см. Рассчитайте емкость конденсатора.
Ответ:
Дано: A = 3 см, B = 6 см, L = 8 см, ε 0 = 8,85 × 10 -12
С.
C = 2π ЩЕТ. × (L/ln(b/a))
C = 2 × 3,14 × 8,85 × 10 -12 × (8 × 10 -2 / ln(6/3))
= 1,477 × 10 -11 F
Вопрос 6. Длина цилиндрического конденсатора равна 9 см. . Он состоит из двух концентрических колец с внутренним и внешним радиусами 2 см и 7 см соответственно.




 Наш конвертер площадей может помочь вам с этим шагом, или вы можете изменить единицы измерения, используя встроенный конвертер единиц калькулятора емкости.
Наш конвертер площадей может помочь вам с этим шагом, или вы можете изменить единицы измерения, используя встроенный конвертер единиц калькулятора емкости.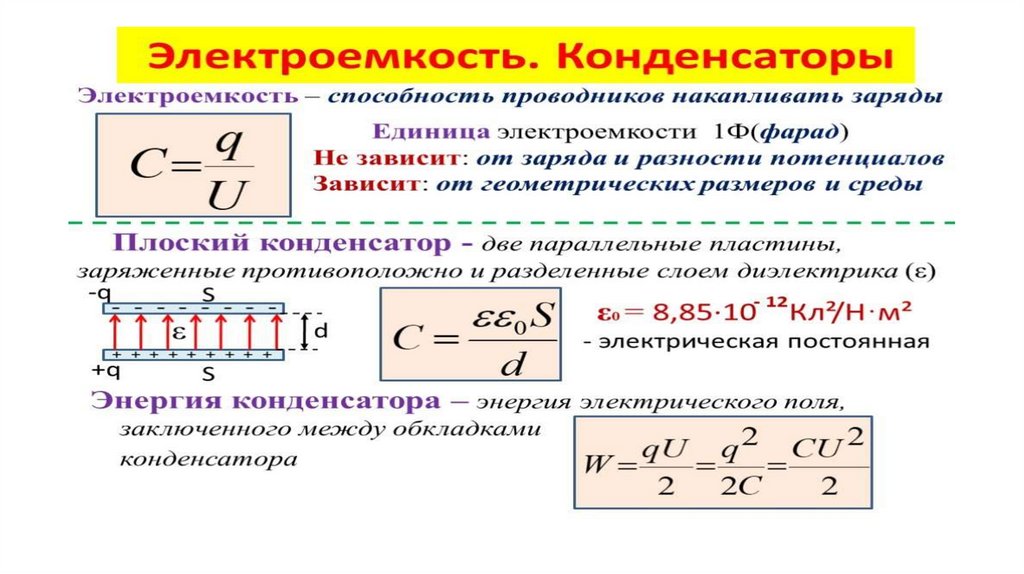
 Формула для расчета цилиндрической емкости представлена в этой статье.
Формула для расчета цилиндрической емкости представлена в этой статье.