Конденсаторы | 8 класс | Физика
Содержание
Если тело обладает некоторым электрическим зарядом, то вокруг него обязательно присутствует электрическое поле. Это поле обладает некоторой энергией — может совершить какую-то работу.
Можно ли как-то накопить эту энергию? Да, такая возможность существует. Для этого используют специальный прибор — конденсатор.
Конденсатор — это устройство, позволяющее накапливать электрические заряды и, соответственно, энергию электрического поля.
На данном уроке вы познакомитесь с устройством этого прибора, его характеристиками и свойствами.
{"questions":[{"content":"Конденсатор — это прибор для[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["накопления энергии электрического поля","измерения энергии электрического поля","регулировки силы тока в цепи"],"explanations":["","","Эту функцию выполняют реостаты."],"answer":[0]}}}]}Простейший конденсатор и его устройство
Устройство простейшего конденсатора представлено на рисунке 1. Он состоит из двух одинаковых металлический пластин. Эти пластины называются обкладками конденсатора.
Он состоит из двух одинаковых металлический пластин. Эти пластины называются обкладками конденсатора.
Обкладки расположены на небольшом расстоянии друг от друга. Этот промежуток между ними обязательно должен быть заполнен слоем диэлектрика. В нашем случае таким диэлектриком является обычный воздух.
Такой конденсатор называется плоским (по форме обкладок).
Конденсатор имеет свой условный знак для обозначения на схеме электрической цепи (рисунок 2).
Рисунок 2. Условный знак для обозначения конденсатора на схеме электрической цепи{"questions":[{"content":"Между обкладками конденсатора обязательно должен присутствовать[[choice-9]]","widgets":{"choice-9":{"type":"choice","options":["слой диэлектрика","проводник","защитный слой"],"answer":[0]}}}]}Зарядка конденсатора и его способность накапливать заряды
Теперь разберемся, каким же образом мы можем накапливать заряды с помощью конденсатора.
Рассмотрим простой опыт. Возьмем конденсатор, состоящий из двух металлических пластин, расположенных параллельно друг другу, и заряженный аккумулятор.
Две обкладки конденсатора подключим к разным полюсам аккумулятора. На обкладках начнут образовываться электрические заряды (рисунок 3). Они будут равны друг другу, но иметь противоположные знаки.
Рисунок 3. Зарядка конденсатора от аккумулятораЭти заряды образуют электрическое поле конденсатора. Оно будет сосредоточено между обкладками.
Отключим аккумулятор от конденсатора. Что мы увидим? Заряды, образованные на обкладках, никуда не деваются. Они сохраняются, как и электрическое поле между пластин. Конденсатор заряжен.
Если мы соединим проводником обкладки конденсатора, то увидим, что по нему некоторое время будет течь ток. Значит, заряженный конденсатор является источником тока в электрической цепи.
{"questions":[{"content":"Какой конденсатор может быть источником тока в электрической цепи?[[choice-12]]","widgets":{"choice-12":{"type":"choice","options":["Заряженный","любой","разряженный","Плоский"],"answer":[0]}}}]}Электроемкость конденсатора
Логично предположить, что разные конденсаторы по-разному будут накапливать заряд. Как охарактеризовать эту способность прибора? Для этого существует специальная величина — электроемкость (или просто емкость) конденсатора.
Как охарактеризовать эту способность прибора? Для этого существует специальная величина — электроемкость (или просто емкость) конденсатора.
Чтобы понять смысл этой величины, рассмотрим опыт. Возьмем две металлические пластины и установим их на изолированных подставках друг напротив друга.
Подключим к пластинам электрометр. Этот прибор (рисунок 4) по своему устройству и принципу действия схож с электроскопом. Он позволит нам зафиксировать значения напряжения, которое возникнет между пластинами.
Рисунок 4. ЭлектрометрИтак, одну из пластин (A) мы соединим проводом со стержнем электрометра, а другую (B) соединим с корпусом прибора (заземлим). Коснемся положительно наэлектризованной стеклянной палочкой внешней стороны пластины A (рисунок 5).
Рисунок 5. Электризация одной пластины конденсатораМы сообщили пластине A положительный заряд $+q$. Вокруг этого заряда (пластины A) теперь существует электрическое поле. Под его действием произойдет перераспределение зарядов в пластине B. Отрицательные заряды перейдут на внутреннюю сторону пластины, а положительные — на внешнюю.
Отрицательные заряды перейдут на внутреннюю сторону пластины, а положительные — на внешнюю.
Помните, что мы заземлили пластину B? За счет этого на пластину пойдут свободные электроны с земли. Они нейтрализуют положительный заряд на внешней стороне пластины. Таким образом, мы получили на пластине B отрицательный заряд $-q$ (рисунок 6). По величине он равен заряду на другой пластине.
Рисунок 6. Результат электризации пластины конденсатораСтрелка электрометра отклонилась. Зафиксируем это значение напряжения между пластинами. Далее мы снова сообщим заряд пластине B, равный по величине первому сообщаемому заряду. Потом сообщим третий и четвертый такие же заряды, наблюдая за стрелкой электрометра.
Вы увидите, что при увеличении заряда в 2, 3, 4 раза, соответственно, в 2, 3, 4 раза увеличиваются показания электрометра — напряжение между пластинами. Важно отметить, что отношение заряда к напряжению при этом будет постоянно:
$\frac{q}{U} = \frac{2q}{2U} = \frac{3q}{3U} = \frac{4q}{4U} = const$.
Теперь мы можем дать определение электроемкости конденсатора.
Электроемкость конденсатора — это величина, измеряемая отношением заряда на одной из пластин конденсатора к напряжению между пластинами:
$C = \frac{q}{U}$.
{"questions":[{"content":"Электроемкость конденсатора определяется отношением[[choice-16]]","widgets":{"choice-16":{"type":"choice","options":["заряда к напряжению между обкладками","напряжения между обкладками к заряду","заряда на одной обкладке к заряду на другой"],"explanations":["","","Эти заряды равны, но противоположны друг другу по знаку. За заряд конденсатора мы принимаем численное значение заряда одной из обкладок."],"answer":[0]}}}]}Единицы измерения электроемкости
В СИ электроемкость измеряется в фарадах ($Ф$).
Электроемкость конденсатора равна единице, если при сообщении ему заряда в $1 \space Кл$ возникает напряжение, равное $1 \space В$ (рисунок 7):
$1 \space Ф = \frac{1 \space Кл}{1 \space В}$.{-12} \space Ф$.
{"questions":[{"content":"Электроемкость измеряется в[[choice-24]]","widgets":{"choice-24":{"type":"choice","options":["фарадах","ньютонах","амперах","ваттах"],"explanations":["","Это единица измерения силы.","Это единица измерения силы тока.","Это единица измерения мощности тока."],"answer":[0]}}}]}Зависимость электроемкости от площади пластин конденсатора
От чего зависит электроемкость? Начнем с размера пластин.
Зафиксируем полученное в первом опыте с электрометром и конденсатором значение напряжения $U_1$. Теперь возьмем пластины, имеющие большую площадь. Сообщим им точно такой же заряд $q$ (рисунок 9).
Рисунок 9. Зависимость емкости конденсатора от площади его пластинМы увидим, что стрелка электрометра отклоняется меньше. Это означает, что напряжение между этими пластинами меньше напряжения между пластинами меньшей площади ($U_1 > U_2$).
Из определения электроемкости:
$C_1 = \frac{q}{U_1}$,
$C_2 = \frac{q}{U_2}$,
$C_2 > C_1$.
Чем больше площадь пластин, тем больше электроемкость конденсатора.
{"questions":[{"content":"Если мы уменьшим площадь обкладок конденсатора, то его электроемкость[[choice-31]]","widgets":{"choice-31":{"type":"choice","options":["уменьшится","увеличится","не изменится"],"answer":[0]}}}]}Зависимость электроемкости от расстояния между пластинами конденсатора
Снова обратимся к опыту. Теперь изменим расстояние между пластинами — уменьшим его (рисунок 10).
Рисунок 10. Зависимость емкости конденсатора от расстояния между пластинамиМы увидим, что напряжение между пластинами уменьшилось: $U_2 < U_1$. Значит,
$C_1 = \frac{q}{U_1}$,
$C_2 = \frac{q}{U_2}$,
$C_2 > C_1$.
При уменьшении расстояния между пластинами конденсатора и при неизменном заряде электроемкость конденсатора увеличивается.
{"questions":[{"content":"Один из способов уменьшить емкость конденсатора — это [[choice-34]]","widgets":{"choice-34":{"type":"choice","options":["увеличить расстояние между его обкладками","уменьшить расстояние между его обкладками","увеличить площадь его обкладок"],"answer":[0]}}}]}Зависимость электроемкости от диэлектрика
Проведем еще один опыт.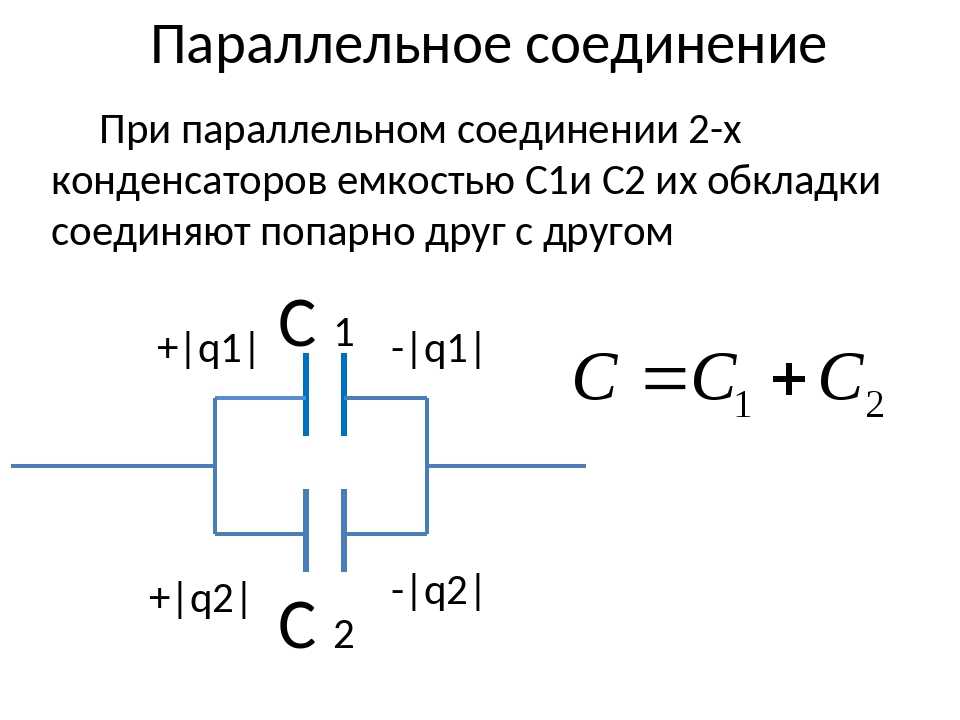 Зафиксируем значение напряжения между пластинами конденсатора. Затем внесем между ними лист из оргстекла (рисунок 11). Он является диэлектриком.
Зафиксируем значение напряжения между пластинами конденсатора. Затем внесем между ними лист из оргстекла (рисунок 11). Он является диэлектриком.
Если раньше диэлектриком между пластинами являлся только воздух, то теперь это и воздух, и лист оргстекла. Напряжение между пластинами уменьшилось: $U_1 > U_2$. Значит,
$C_1 = \frac{q}{U_1}$,
$C_2 = \frac{q}{U_2}$,
$C_2 > C_1$.
При внесении диэлектрика электроемкость конденсатора увеличивается.
{"questions":[{"content":"Если добавить еще один слой диэлектрика между обкладками конденсатора, то его емкость[[choice-37]]","widgets":{"choice-37":{"type":"choice","options":["увеличится","уменьшится","не изменится"],"answer":[0]}}}]}Виды конденсаторов
Между обкладками конденсатора могут быть помещены разнообразные диэлектрики. В зависимости от природы этого диэлектрика конденсаторы разделяют на несколько видов: с твердым, жидким и газообразным диэлектриком.
Также существует классификация и по форме обкладок. Конденсаторы бывают плоские, цилиндрические, сферические (рисунок 12) и др.
Рисунок 12. Виды конденсаторов по форме обкладокКонденсаторы бывают с постоянной емкостью и с переменной емкостью. В последних можно регулировать параметры, от которых зависит емкость — ширину пластин и расстояние между ними.
На данный момент существует огромное разнообразие конденсаторов (рисунок 13). Многие из них носят названия, происходящие от названий материалов, составляющих их: слюдяные, керамические, алюминиевые электролитические, танталовые электролитические, конденсаторы на полимерной пленке.
Рисунок 13. Современные конденсаторы{"questions":[{"content":"Если конденсатор имеет плоские обкладки, параллельные друг другу, его называют[[choice-40]]","widgets":{"choice-40":{"type":"choice","options":["плоским","квадратным","параллельным","прямоугольным"],"answer":[0]}}}]}Энергия конденсатора и работа его электрического поля
Заряженный конденсатор обладает некоторой энергией.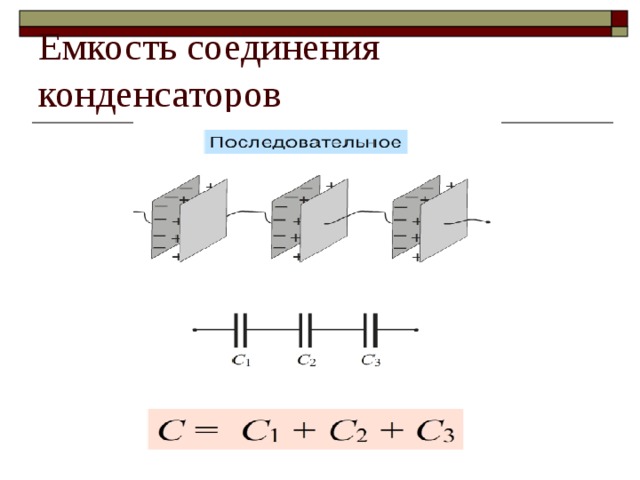 Это легко проверить на опыте. Если мы подключим к конденсатору электрическую лампочку, то она она ярко вспыхнет (рисунок 14). Энергия конденсатора превратилась во внутреннюю энергию нити накаливания лампы и соединительных проводов.
Это легко проверить на опыте. Если мы подключим к конденсатору электрическую лампочку, то она она ярко вспыхнет (рисунок 14). Энергия конденсатора превратилась во внутреннюю энергию нити накаливания лампы и соединительных проводов.
Откуда взялась эта энергия? Конденсатор получает ее при зарядке.
Для того, чтобы зарядить конденсатор, нужно совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии совершенная работа A и будет равна энергии конденсатора E:
$A = E$.
Для расчета такой работы электрического поля конденсатора существует специальная формула.
$A = qU_{ср}$,
где $U_{ср}$ — среднее значение напряжения.
В процессе разрядки напряжение постоянно падает, поэтому нам и необходимо знать для расчетов его среднее значение:
$U_{ср} = \frac{U}{2}$.
Тогда,
$A = qU_{ср} = \frac{qU}{2}$.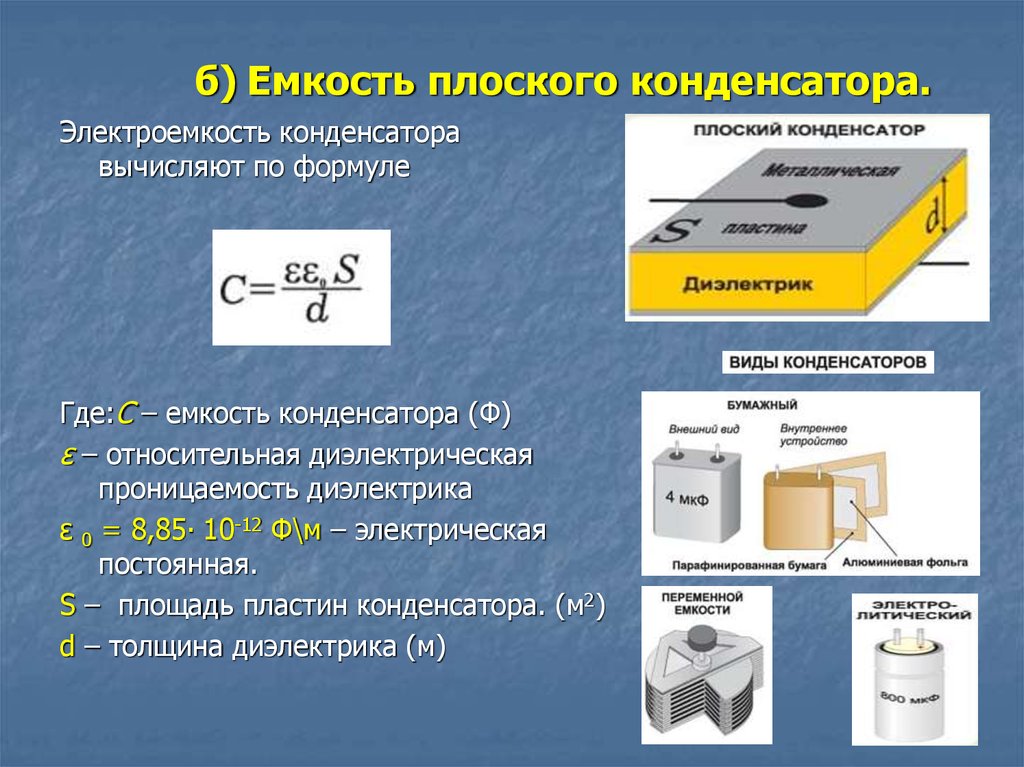 2}{2}$»,»$A = qU$»],»answer»:[0]}}}]}
2}{2}$»,»$A = qU$»],»answer»:[0]}}}]}
Это свойство (накопление энергии и ее быстрая отдача) широко применяется в различных электронных устройствах, в медицинской технике (рентген, устройства для электротерапии), при изготовлении дозиметров, фотосъемке.
Последовательное соединение конденсаторов
В электрической цепи может быть не один, а сразу несколько конденсаторов. Они могут быть соединены как последовательно, так и параллельно.
Рассмотрим первый тип соединения — последовательный (рисунок 15).
Рисунок 15. Последовательное соединение конденсаторовОбкладки 2 и 3, принадлежащие разным конденсаторам, будут являться отдельной деталью. По закону сохранения заряда, заряды на обкладках 2 и 3 будут равны друг другу по модулю, но противоположны по знаку. Из этого следует, что общий заряд конденсаторов численно будет равен заряду на любой из обкладок конденсаторов.
$q = q_1 = q_2 = … = q_n$
Напряжение на концах участка цепи с последовательно соединенными конденсаторами будет складываться из значения напряжений на каждом конденсаторе.
$U = U_1 + U_2 + … + U_n$
Чтобы получить формулу для общей емкости конденсаторов, последнее равенство нужно разделить на заряд q (любой, так как они равны).
$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + … \frac{1}{C_n}$.
{"questions":[{"content":"Общий заряд последовательно соединенных конденсаторов равен[[choice-49]]","widgets":{"choice-49":{"type":"choice","options":["заряду на любой из обкладок конденсаторов","сумме зарядов на всех обкладках конденсаторов","сумме зарядов на двух обкладках одного конденсатора"],"answer":[0]}}}]}Параллельное соединение конденсаторов
Параллельное соединение конденсаторов показано на рисунке 16.
Рисунок 16. Параллельное соединение конденсаторовВ этом случае выходы от источника питания будут соединены с каждой обкладкой конденсаторов. Поэтому напряжение на концах такого участка цепи будет равно напряжению между обкладками любого из конденсаторов.
$U = U_1 = U_2 = … = U_n$
Заряды на обкладках будут суммироваться.
$q = q_1 + q_2 + … + q_n$
Разделим это равенство на значение напряжения и получим формулу для электроемкости параллельно соединенных конденсаторов.
$C = C_1 + C_2 + … + C_n$
{"questions":[{"content":"Напряжение на концах участка цепи с параллельно соединенными конденсаторами равно[[choice-54]]","widgets":{"choice-54":{"type":"choice","options":["напряжению между обкладками любого из конденсаторов","сумме напряжений между обкладками всех конденсаторов","напряжению на полюсах источника тока"],"answer":[0]}}}]}Первый конденсатор — лейденская банка
Лейденская банка официально является первым конденсатором. Изобретение ее относится к 1745 году. Существует множество версий о том, кто же именно должен считаться изобретателем этого прибора, но официально авторство принадлежит Питеру ван Мушенбруку и его студенту Андреасу Кунэусу.
В ранней версии лейденская банка была на часть заполнена водой, которая выступала в роли обкладки (рисунок 17). Второй обкладкой являлась рука, держащая банку. После зарядки этого приспособления Андреас Кунэус испытал сильный удар током, коснувшись до верха металлического стержня.
Рисунок 17. Ранняя версия лейденской банкиБолее поздняя и более распространенная версия этого незамысловатого прибора представляет собой сосуд из стекла с широким горлом, снаружи покрытый листом из фольги (рисунок 18). Фольга также находится и внутри банки. Через пробку в этот сосуд вставляется металлический стержень. Он должен касаться фольги внутри банки.
Рисунок 18. Лейденская банка с обкладками из фольгиТаким образом, фольга внутри и фольга снаружи становятся своеобразными обкладками. При подключении к источнику тока на них накапливается электрический заряд.
Внимание! Лейденская банка не является безопасным инструментом в электротехнике! Разряд такого конденсатора может оказаться смертельным или привести к серьезным физическим повреждениям. Будьте аккуратны при использовании данного прибора: не следует пытаться разрядить лейденскую банку, взявшись за нее голыми руками.
Будьте аккуратны при использовании данного прибора: не следует пытаться разрядить лейденскую банку, взявшись за нее голыми руками.
{"questions":[{"content":"У лейденской банки, изображенной на рисунке 18, обкладками являются[[choice-57]]","widgets":{"choice-57":{"type":"choice","options":["слой фольги снаружи и слой фольги внутри банки","металлический стержень и слой фольги снаружи банки","Пробка и стеклянный сосуд"],"answer":[0]}}}]}Как изготовить лейденскую банку своими руками? Возьмите пластиковую банку с крышкой (из-под кофе, витаминов). Внешнюю сторону банки на $\frac{2}{3}$ обклейте фольгой. Далее или налейте в банку соленую воду, или обклейте изнутри фольгой. Затем закройте крышку и проткните ее достаточно длинным гвоздем, чтобы он касался внутренней обкладки (воды или фольги). После зарядки такая банка представляет собой заряженный конденсатор.
Упражнения
Упражнение №1
Пластины плоского конденсатора подсоединяют к источнику напряжения в $220 \space В$. 6 \space В$.
6 \space В$.
Элеком37, Электрическая емкость. Плоский конденсатор. Соединения конденсаторов. Физика.
Электрическая емкость. Плоский конденсатор. Соединения конденсаторов.
Электрическая емкость. Плоский конденсатор.
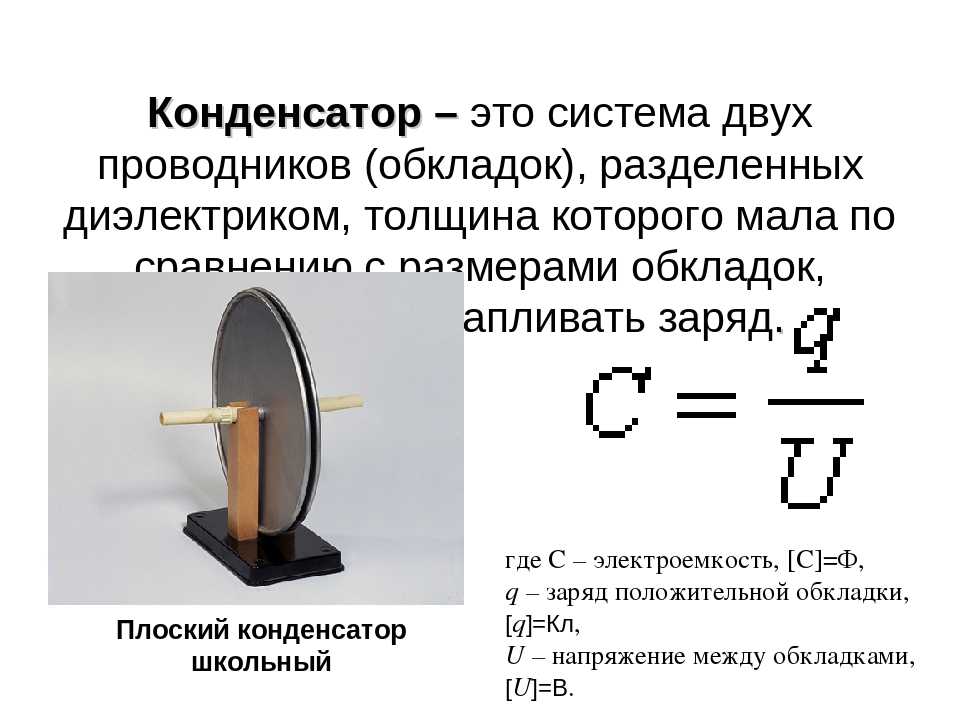
При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:
В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.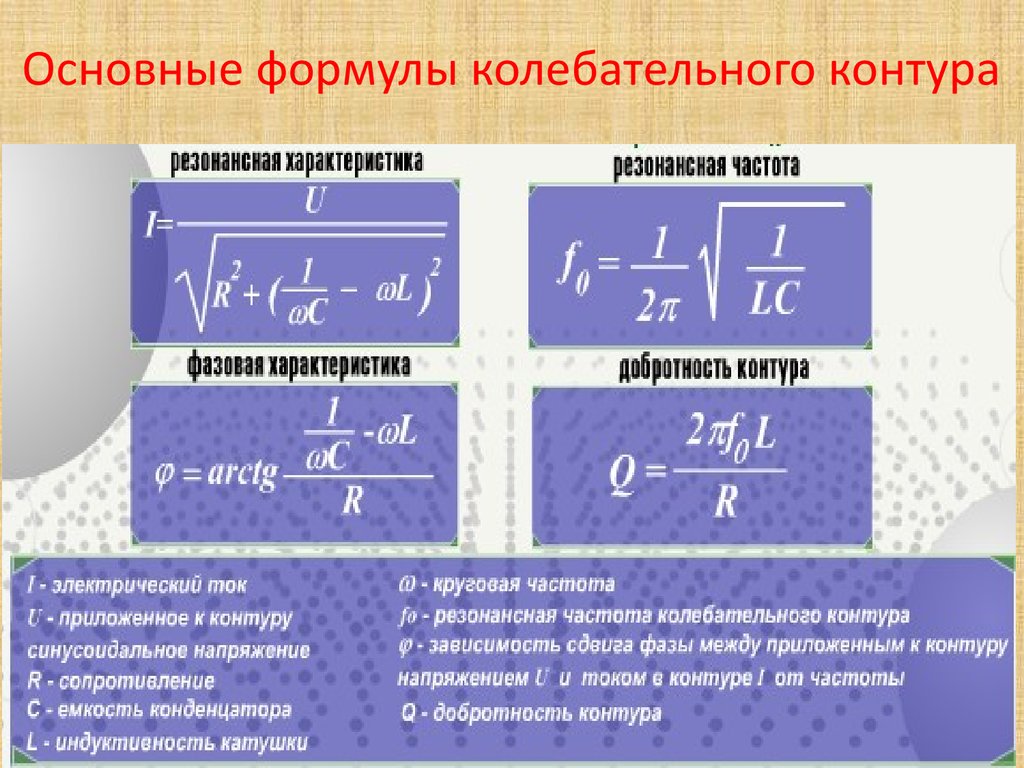
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.
Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:
За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0. Электроёмкость плоского конденсатора может быть рассчитана по формуле:
Электроёмкость плоского конденсатора может быть рассчитана по формуле:
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.
Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:
Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:
Энергия конденсатора.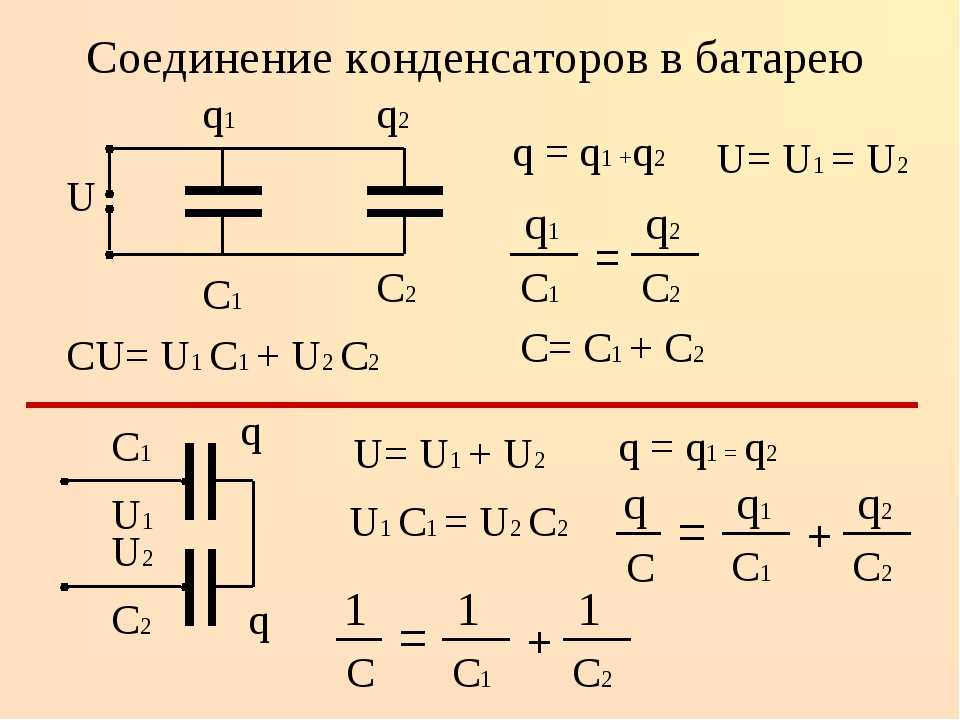 Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):
Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):
Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.
Энергия электрического поля
Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле.
Поэтому ее называют энергией электрического поля.
Соединения конденсаторов
Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:
При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов.
Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:
Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов.
Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:
Из закона сохранения заряда следует, что заряды на соседних обкладках равны:
Напряжение равно сумме напряжений на отдельных конденсаторах.
Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:
Для N одинаковых последовательно соединённых конденсаторов:
Деятельность преподавателя | Деятельность обучающихся | |
3 мин | Приветствие обучающихся Проверка готовности обучающихся к уроку Сообщение темы занятия. Обоснование значения темы и сообщение цели урока. | Показывают наличие учебных принадлежностей Обучающиеся слушают преподавателя, участвуют в обсуждении значения темы и целей урока. |
7 мин | Преподаватель организуют актуализацию материала в виде теста по следующим вопросам:
Обсуждают, осуществляют проверку | В течение 10 минут учащиеся пишут тест. Осуществляют проверку |
30 мин | Объяснение нового материала Преподаватель вводит понятия конденсатора, как системы двух проводников, разделённых слоем диэлектрика; электроемкости конденсатора. Демонстрирует модели конденсаторов. Просит учащихся, используя карточку с изображенным на ней конденсатором определить тип конденсатора, его емкость, напряжение, на которое рассчитан конденсатор. Используя плакат, рассказывает о последовательном и параллельном соединениях конденсаторов в батарею. Записывает формулы на доске. Задает обучающимся вопрос, как следует соединить конденсаторы, чтобы получить наибольшее значение емкости батарее? Записывает формулу для расчета энергии заряженного конденсатора. Просит обучающихся, используя раздаточный материал, рассчитать энергию заряженного конденсатора. Назначение и применение конденсаторов. | Обучающиеся слушают, конспектируют. Используя раздаточный материал, обучающиеся выполняют задание записывают в тетрадь. Обучающиеся слушают, конспектируют. Обучающиеся выполняют задание и делают выводы Рассчитывают, записывают в тетрадь. Слушают, конспектируют |
25 мин | Преподаватель раздает карточки с индивидуальными зданиями (приложение 1) . Организация индивидуальной практической деятельности обучающихся по применению и закреплению первичных умений и навыков (раздаточный материал). Преподаватель консультирует, направляет деятельность обучающихся. | Самостоятельная работа обучающихся. Учащиеся выполняют упражнения по алгоритму. |
13 мин | Преподаватель организует обобщение материала в виде теста. Обсуждение теста, проверка. | Учащиеся выполняют тест. Выполняют взаимопроверку. |
| Выучить конспект | Записывают домашнее задание. | Ответить на вопросы: | Выбрать правильный ответ |
Как называется физическая величина, равная отношению заряда на одной из обкладок конденсатора к напряжению между обкладками? |
| |
Емкость конденсатора зависит | 1) от свойств диэлектрика, площади пластин, расстояния между ними. 2) только от свойств диэлектрика 3) от сопротивления проводника | |
Единица измерения емкости в СИ | 1) 1 микрофарад 2) 1 пикофарад или 1 микрофарад 3) 1 фарад | |
При последовательном соединении конденсаторов емкость батареи … | 1) увеличивается 2) уменьшается 3) остается неизменной | |
При параллельном соединении конденсаторов емкость батареи … | 1) увеличивается 2) уменьшается 3) остается неизменной | |
Конденсаторы применяют для … | 1) накопления электрического заряда и быстрого увеличения напряжения 2) как источник напряжения для лампочек накаливания 3) вместо аккумуляторов |
Электроемкость.
 Конденсаторы. — Физика — Уроки
Конденсаторы. — Физика — УрокиПреподаватель— Гринченко Анастасия Александровна
Предмет— физика
Тема— Электроемкость. Конденсаторы.
Продолжительность занятия— 40 минут.
Класс – 10
Тип урока: изучение нового материала с элементами самостоятельной работы учащихся.
Цель
Формирование понятий электроемкость, единица электроемкости.Конденсатор.
Задачи
Образовательные:
Развивающие :
развить наблюдательность у учащихся
развивать познавательный интерес к физике и технике
продолжить развитие экспериментальных умений, умения делать выводы
закрепить полученные знания через самостоятельное решение задач
Воспитательные:
Оборудование: электрометр, металлические пластины на изолирующих подставках, эбонитовая и пластмассовая палочки, соединительные провода, конденсаторы переменной и постоянной ёмкости, мультимедийный проектор и компьютер для демонстрации презентации изучаемого материала, лист диэлектрика, 2 датчика
Датчик электрического заряда Датчик напряжения
(электрометр) диапазон измерений: ±10В;
диапазон измерений: ±5нКл;±20нКл; точность измерений: 10мв;
±100нКл;
Входная емкость: 10нФ последовательно с
сопротивлением 1МОм
диапазон напряжений: ±150В
постоянная времени: 0,1 с
Демонстрации:
Зависимость электроёмкости от расстояния между пластинами.

Зависимость ёмкости плоского конденсатора от площади пластины.
Зависимость электроёмкости от диэлектрической проницаемости среды.
Зависимость заряда конденсатора от напряжения
План урока.
План урока.
Организационный момент
Повторение изученного материала (Физический диктант).
Изучение нового материала.
Понятие о конденсаторе.
Электроёмкость конденсатора.
Единица электроёмкости
Виды конденсаторов.
Закрепление. Решение задач.Беседа.
Итог
1.Организационный момент
Учитель:Здравствуйте ребята, присаживайтесь!
Эпиграфом урока послужат слова Конфуция:
«Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания — это путь самый легкий, и путь опыта – это путь самый горький».
В ходе урока мы воспользуемся тремя путями, которые ведут к знаниям, по мнению философа. Но какой путь для вас самый приемлемый решать вам.
На сегодняшнем уроке мы с вами узнаем что такое конденсатор, познакомимся стаким понятием как емкость,узнаем от чего она зависит.
2. Повторение изученного материала (Физический диктант).
№ | Вопрос | Ответ |
1 | Cформулируйте и запишите закон Кулона? | Сила взаимодействия электрического заряда прямопропорциональна произведению величин этих зарядов и обратнопропорциональна квадрату расстояния между этими зарядами.F=k |
2 | В каких единицах измеряется напряжённость электрического поля? | |
3 | В каких единицах измеряется электрический заряд? | Кл |
4 | Что такое электрическое поле? | Особая форма материи заполняющая область вокруг заряженных тел и обеспечивающая их взаимодействие |
5 | От чего зависит работа электрического поля? | Не зависит от формы траектории,а только от начального и конечного положения точек |
6 | σ это- | Поверхностная плотность заряда,приходящегося на единицу поверхности |
7 | Ее находят по формуле | |
8 | Потенциалом эл. | Потенциалом эл.ст. поля определяется как отношение потенциальной энергии пробного заряда помещенного в данную точку поля к величине пробного заряда |
3.изучение нового материала
Вода может храниться в ведре,а спомощью чего можно накапливать и сохранять электрическую энергию? Исходя из темы, вы, наверное, догадались, что это устройство называется конденсатором. Немного из истории . В 1745 году в Лейдене голландский физик Питер Ван Мушенбрук совместно с немецким коллегой создали первый накопитель энергии и назвали его лейденской банкой.
Слово »конденсатор» происходит от латинского слова condensare, что означает »сгущение». В учении об электрических явлениях этим словом обозначают устройства, позволяющие сгущать электрические заряды и связанное с этими зарядами электрическое поле.
Простейший конденсатор состоит из двух проводников, разделённых диэлектриком, толщина которого мала по сравнению с размерами проводника.
Свойство конденсатора сгущать (накапливать) электрические заряды и связанное с ним электрическое поле можно наблюдать на опыте.
Опыт 1. Две металлические пластины, укреплённые на изолирующих подставках, располагаем параллельно друг другу и присоединяем к электрометру. Одну из пластин соединяем с землёй.
Одной из пластин сообщаем положительный заряд q. Другая при этом получит через влияние какой заряд?
Ученики:отрицательный заряд- q.
Учитель: Правильно.Электрометр покажет разность потенциалов между пластинами.
Сообщим первой пластине дополнительно заряд q тем же способом, прикоснувшись наэлектризованным шаром. Теперь на пластинах находятся какие заряды?
Ученики: 2 q и -2 q.
Учитель:что произошло с показанием электрометра
Ученики:Показания электрометра увеличились в двое.
Учитель:Не меняя зарядов, начнём сближать пластины. Напряжение между пластинами будет уменьшаться. При некотором расстоянии оно станет таким, каким оно было при зарядах q и –q. Прекратим сближение пластин и вновь первой пластине передадим дополнительный заряд q. Показания электрометра вновь увеличатся. При дальнейшем сближении пластин что замечаем?
При некотором расстоянии оно станет таким, каким оно было при зарядах q и –q. Прекратим сближение пластин и вновь первой пластине передадим дополнительный заряд q. Показания электрометра вновь увеличатся. При дальнейшем сближении пластин что замечаем?
Ученики:что при некотором, ещё меньшем расстоянии между ними электрометр вновь покажет прежнюю разность потенциалов.
Учитель:Следовательнокакой можно сделать вывод?
Ученики: сдвигая пластины конденсатора, можно при одном и том же напряжении накапливать на одной пластине положительные заряды q, 2q, 3q,…, а на другой- равные по модулю отрицательные заряды.
Учитель: т.о, конденсатор накапливает заряды: поверхностная плотность зарядов увеличивается по мере сближения пластин.Свойство конденсатора накапливать и сохранять электрические заряды и связанное с ними электрическое поле характеризуется особой величиной, называемой электроёмкостью.
Чтобы выяснить смысл этой величины, обратимся к исследованиям.
Опыт 2. Касаясь одинаково заряженными палочками внешней стороны пластины конденсатора, передаём этой пластине последовательно по заряду q. При этом заметим, что по мере увеличения заряда что растет?
Ученики: растёт напряжение между пластинами.
Учитель: Причём при зарядах q, 2q, 3q,… напряжение принимает значение U, 2U, 3U,…, возрастая пропорционально заряду. (рис.2) Но отношение заряда к напряжению остаётся постоянным:
рис.2
Проведём такие же опыты с конденсатором, пластины которого имеют большую площадь; при этом расстояние между пластинами сделаем таким же. Увеличивая заряд одной из пластин на q, т.е. делая его равным 2q, 3q,…, заметим, что напряжение между пластинами принимает значения U1, U2, 3U1…, где U1.
Для того чтобы второй конденсатор зарядить до такого же напряжения, как и первый, ему надо сообщить больший заряд. Следовательно, у второго конденсатора, что больше?
Следовательно, у второго конденсатора, что больше?
Ученики: он обладает большей электрической ёмкостью, т.е. второму конденсатору соответствует большее значение отношения заряда к напряжению.
Учитель: Следовательно, величина С что характеризует?
Ученик:характеризует электрическую ёмкость конденсатора.
Учитель:запишите в тетради Электрической ёмкостью конденсатора называется скалярная величина, характеризующая его свойство накапливать и сохранять электрические заряды и связанное с этими зарядами электрическое поле.
Электроёмкость конденсатора равна отношению заряда одной из пластин к напряжению между ними:
За единицу электроёмкости в СИ принимается электроёмкость конденсатора, напряжение между обкладками которого равно 1В, когда на его обкладках имеются разноимённые заряды по 1Кл.
Единица электроемкости в системе СИ названа в честь великого ученого Майкла Фарадея и называется фарад:. На практике применяются:
Из рассмотренных исследований делаем вывод,от чего зависит С ?
Ученики: С конденсатора зависит от площади S пластин и расстояния d между ними: .
Опыт 3. Кроме того, электрическая ёмкость конденсатора зависит от рода диэлектрика, находящегося между пластинами. Внесём в пространство между пластинами заряженного конденсатора лист какого-либо диэлектрика. Мы видим, что напряжение между пластинами уменьшилось.(рис. 3,4) Значит, электрическая ёмкость ,что?
Ученики: увеличилась
Учитель:т.е.
Повторим опыт. Прошу желающего выйти .Итак, еще раз внесем диэлектрик . Получился ли у нас опыт ?
Ученики: да(нет)
Выведем формулу для расчёта электроёмкости плоского конденсатора. По определению . Учитывая, что q = σS , U = Ed, получаем:
Полученная формула согласуется с результатами рассмотренных опытов?
Ученики:да.
рис. 3 | рис.4 |
Для получения нужной электроемкости конденсаторы можно соединять в батареи, используя последовательный и параллельный способ, как в случае с резисторами. Рассмотрим параллельный способ соединения конденсаторов. Если заряд на обкладке первого конденсатора обозначим q1, а на обкладке второго- через q2, то по закону сохранения заряда ,напомните его мне пожалуйста.
Рассмотрим параллельный способ соединения конденсаторов. Если заряд на обкладке первого конденсатора обозначим q1, а на обкладке второго- через q2, то по закону сохранения заряда ,напомните его мне пожалуйста.
Ученики:электрический заряд в замкнутой системе всегда сохраняется.
Учитель: общий заряд будет равен сумме зарядов q1 и q2. Разность потенциалов(напряжение) U между обкладками остается неизменной. Общая емкость конденсаторов при параллельном соединении равна сумме емкостей конденсаторов С1 и С2.
Собщ.=С1+С2
При последовательном соединении конденсаторов, суммарный заряд не меняется. Общая разность потенциалов на обкладках конденсаторов равна сумме разности потенциалов на концах первого и разности потенциалов на обкладках второго конденсатора Uобщ.=U1 +U2. При последовательном соединении складываются обратные величины емкостей :
1/Собщ. = 1/С1+ 1/С2
= 1/С1+ 1/С2
Теперь выясним,как связаны между собой заряд конденсатора и напряжение на его обкладках.
Для этого проведем эксперемент.
В эксперементе будет использоваться специальные датчики: датчики электрического заряда и датчик напряжения. Датчики через блок сбора информации подключен к компьтеру. На экране графическим способом будут отображаться результаты измерений.По значениям оси абсцисс можно будет судить о величине напряжения на обкладках конденсатора, а по оси ординат – о заряде конденсатора. По углу наклона графика будем судить о электроемкости.
Соберем последовательную цепь состоящую из последовательно соедененного источника тока,сопротивления,сопротивление которого составляет 1 МОм, и керамического конденсатора,емкостью 1 нФ.
Подключим датчик электрического заряда красным пружынным контактом к плюсу источника питания,черный к минусу.
Датчик напряжения черным к минусу, красным к плюсу. Теперь мне нужен помощник.
Введем значение емкости выбранного конденсатора в активную ячейку столбца Номинальная емкость Таблицы результатов. Я буду плавно изменяем напряжение регулируемого источника питания в диапозоне от 0В до 10В,а вы нажмете кнопку «измерить». Когда я скажу стоп вы нажмете «остановить».
Итак. Спасибо, присаживайся . На графике отображается зависимость заряда конденсатора от напряжения.
Учитель: что вы можете сказать о характере зависимости?
Ученик:заряд конденсатора прямо пропорционален напряжению на его обкладках.
Учитель: повторим опыт с другими конденсаторами. Что вы можите сказать о результатам предыдущего и проведенного опыта
Ученик:характер зависимости в обоих опытах одинаков,а угол наклона отрезков на графике зависимости различен
Учитель:как можно результаты опытов можно представить аналитически.
Ученик:q ~ U. Переходя к знаку равенства : q=CU
Учитель: Правильно,молодец,присаживайся. теперь давайте выслушаем два сообщения учащихся о различных типах конденсаторов (о конденсаторах переменной ёмкости, технических бумажных и электролитических конденсаторах), их устройстве и применении
теперь давайте выслушаем два сообщения учащихся о различных типах конденсаторов (о конденсаторах переменной ёмкости, технических бумажных и электролитических конденсаторах), их устройстве и применении
1.Сообщение.
В зависимости от назначения конденсаторы имеют различное устройство. Технический бумажный конденсатор состоит из двух полосок алюминиевой фольги, изолированных друг от друга и от металлического корпуса бумажными лентами, пропитанными парафином. Алюминиевая фольга и бумажные ленты туго свёрнуты в пакет небольшого размера. Бумажный конденсатор, имея размеры спичечного коробка, обладает электроёмкостью до 10 мкФ (металлический шар такой же ёмкости имел бы радиус 90 км).
В радиотехнике широко применяют конденсаторы переменной электроёмкости. Такой конденсатор состоит из двух систем металлических пластин, которые при вращении рукоятки могут входить одна в другую. При этом меняется площадь перекрывающейся части пластин и, следовательно, их электроёмкость. Диэлектриком в таких конденсаторах служит воздух.
2.Сообщение.
Значительного увеличения электроёмкости за счёт уменьшения расстояния между обкладками достигают в так называемых электролитических конденсаторах. Диэлектриком в них служит очень тонкая плёнка оксидов, покрывающих одну из обкладок. Второй обкладкой служит бумага, пропитанная раствором специального вещества (электролита). При включении электролитических конденсаторов надо обязательно соблюдать полярность.
В слюдяных конденсаторах в качестве диэлектрика используют слюду, а обкладками служит металлическая фольга или тонкий слой металла, нанесённый непосредственно на слюду. Слюдяные конденсаторы устанавливают, главным образом, в электрических цепях высокой частоты.
В радиотехнике широкое распространение получили керамические конденсаторы, имеющие небольшие размеры, но обладающие хорошими электрическими свойствами. Конструктивно их выполняют в виде трубок или дисков из керамики, а обкладками служит слой металла, нанесённый на керамику.
Назначение конденсаторов:
Накапливать на короткое время заряд или энергию для быстрого изменения потенциала.

В радиотехнике: колебательный контур, выпрямитель
Фотовспышка
в элементах памяти ЭВМ и любимом вами компьютере. Ведь под крышками цифр и символов клавиатуры компьютера стоят конденсаторы.
конденсатор нашел применение при измерении влажности воздуха и древесины,
в системе защиты от короткого замыкания.
4. Закрепление изученного материала.
1.Решение задач с помощью учителя.
При изготовлении конденсатора ёмкостью 200 пФ на пропарафиненную бумагу толщиной 0,2 мм наклеивают с обеих сторон по кружку алюминиевой фольги. Каким должен быть диаметр кружков? Диэлектрическая проницаемость парафина 2,1.
Расстояние между пластинами квадратного плоского конденсатора со стороной 10см равно 1мм. Какова разность потенциалов между пластинами, если заряд конденсатора 1нКл.
Беседа по вопросам.
Что называют ёмкостью двух проводников? (электроёмкостью двух проводников называют физическую величину, характеризующую свойство проводников накапливать электрические заряды; она равна отношению заряда одного из проводников к напряжению между проводниками.
 )
)Назовите единицы ёмкости. (Ф, мкФ, пФ.)
Какая система проводников называется конденсатором?(Конденсатор- эта система двух или более обкладок, разделённых диэлектриком. Заряженный конденсатор содержит на пластинах (обкладках) равные по величине, но противоположные по закону заряды.)
Как зависит электроёмкость плоского конденсатора от его геометрических размеров? (Ёмкость тем больше, чем больше площадь обкладок и чем меньше расстояние между ними.)
5.Итог урока.
Учитель: Таким образом, вы видите насколько прочно вошли в нашу жизнь эти накопители энергии- конденсаторы. Но следует помнить, что заряженный конденсатор опасен для жизни!
На этом наш урок заканчивается, запишите домашнее задание. Всем спасибо, до свидания!
Домашнее задание:§32.подготовиться к самостоятельной работе.
Электроемкость конденсатора. Калькулятор онлайн
| 0 | ||||
| AC | +/- | ÷ | ||
| 8 | 9 | × | ||
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Онлайн калькулятор вычисления емкости конденсатора, позволит найти электроемкость C плоского, цилиндрического и сферического конденсаторов и даст подробное решение.
 Единицы измерения, могут включать любые приставки Си.
Калькулятор автоматически переведет одни единицы в другие.
Единицы измерения, могут включать любые приставки Си.
Калькулятор автоматически переведет одни единицы в другие.Калькулятор вычислит:
Емкость плоского конденсатора.
Емкость цилиндрического конденсатора.
Емкость сферического конденсатора
Емкость плоского конденсатора
Плоский конденсатор представляет собой две параллельные проводящие пластины, разделенные диэлектриком, расположенные на малом расстоянии друг от друга.
Электроемкость C плоского конденсатора равна произведению электрической постоянной ε
Единицей измерения электроемкости является – Фарад (Ф, F).
Электроемкость в 1 Фарад является очень большой емкостью, к примеру емкостью в 1 Фарад обладает сфера в 13 раз, превышающая радиус Солнца, поэтому в основном используют дольные единицы Фарада. -24]
-24]
Емкость цилиндрического конденсатора
Цилиндрический конденсатор представляет собой конденсатор, обкладками, которого являются два цилиндра, внутренний с радиусом R
Электроемкость цилиндрического конденсатора определяется формулой, где
π – число Пи (3.14)
ε0 – электрическая постоянная, ε0 = 8.85418781762039 × 10-12
ε – диэлектрическая проницаемость диэлектрика
l – длина цилиндра
ln – натуральный логарифм
R1 – радиус внутренней обкладки
R2 – радиус внешней обкладки
Единицей измерения электроемкости является – Фарад (Ф, F).
Электроемкость в 1 Фарад является очень большой емкостью, к примеру емкостью в 1 Фарад обладает сфера в 13 раз, превышающая радиус Солнца, поэтому в основном используют дольные единицы Фарада.
Емкость сферического конденсатора
Сферический конденсатор представляет собой конденсатор, обкладками которого являются две концентрические сферы, радиусами R1 и R2, между которыми расположен диэлектрик, с диэлектрической проницаемостью ε.
Электроемкость сферического конденсатора определяется формулой, где
π – число Пи (3.14)
ε0 – электрическая постоянная, ε0 = 8.85418781762039 × 10-12
ε – диэлектрическая проницаемость диэлектрика
R1 – радиус внутренней обкладки
R2 – радиус внешней обкладки
Единицей измерения электроемкости является – Фарад (Ф, F).
Электроемкость в 1 Фарад является очень большой емкостью, к примеру емкостью в 1 Фарад обладает сфера в 13 раз, превышающая радиус Солнца, поэтому в основном используют дольные единицы Фарада.
Диэлектрическая проницаемость ε =
Радиус R1 = Метр (м)Декаметр дам (dam) × [10^1]Гектометр гм (hm) × [10^2]Километр км (km) × [10^3]Мегаметр Мм (Mm) × [10^6]Гигаметр Гм (Gm) × [10^9]Тераметр Тм (Tm) × [10^12]Петаметр Пм (Pm) × [10^15]Эксаметр Эм (Em) × [10^18]Зеттаметр Зм (Zm) × [10^21]Иоттаметр Им (Ym) × [10^24]Дециметр дм (dm) × [10^-1]Сантиметр см (cm) × [10^-2]Миллиметр мм (mm) × [10^-3]Микрометр мкм (µm) × [10^-6]Нанометр нм (nm) × [10^-9]Пикометр пм (pm) × [10^-12]Фемтометр фм (fm) × [10^-15]Аттометр ам (am) × [10^-18]Зептометр зм (zm) × [10^-21]Иоктометр им (ym) × [10^-24]
Радиус R2 = Метр (м)Декаметр дам (dam) × [10^1]Гектометр гм (hm) × [10^2]Километр км (km) × [10^3]Мегаметр Мм (Mm) × [10^6]Гигаметр Гм (Gm) × [10^9]Тераметр Тм (Tm) × [10^12]Петаметр Пм (Pm) × [10^15]Эксаметр Эм (Em) × [10^18]Зеттаметр Зм (Zm) × [10^21]Иоттаметр Им (Ym) × [10^24]Дециметр дм (dm) × [10^-1]Сантиметр см (cm) × [10^-2]Миллиметр мм (mm) × [10^-3]Микрометр мкм (µm) × [10^-6]Нанометр нм (nm) × [10^-9]Пикометр пм (pm) × [10^-12]Фемтометр фм (fm) × [10^-15]Аттометр ам (am) × [10^-18]Зептометр зм (zm) × [10^-21]Иоктометр им (ym) × [10^-24]
Единица измерения электроемкости C Фарад (Ф)Декафарад даФ (daF) × [10^1]Гектофарад гФ (hF) × [10^2]Килофарад кФ (kF) × [10^3]Мегафарад МФ (MF) × [10^6]Гигафарад ГФ (GF) × [10^9]Терафарад ТФ (TF) × [10^12]Петафарад ПФ (PF) × [10^15]Эксафарад ЭФ (EF) × [10^18]Зеттафарад ЗФ (ZF) × [10^21]Иоттафарад ИФ (YF) × [10^24]Децифарад дФ (dF) × [10^-1]Сантифарад сФ (cF) × [10^-2]Миллифарад мФ (mF) × [10^-3]Микрофарад мкФ (µF) × [10^-6]Нанофарад нФ (nF) × [10^-9]Пикофарад пФ (pF) × [10^-12]Фемтофарад фФ (fF) × [10^-15]Аттофарад аФ (aF) × [10^-18]Зептофарад зФ (zF) × [10^-21]Иоктофарад иФ (yF) × [10^-24]
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка.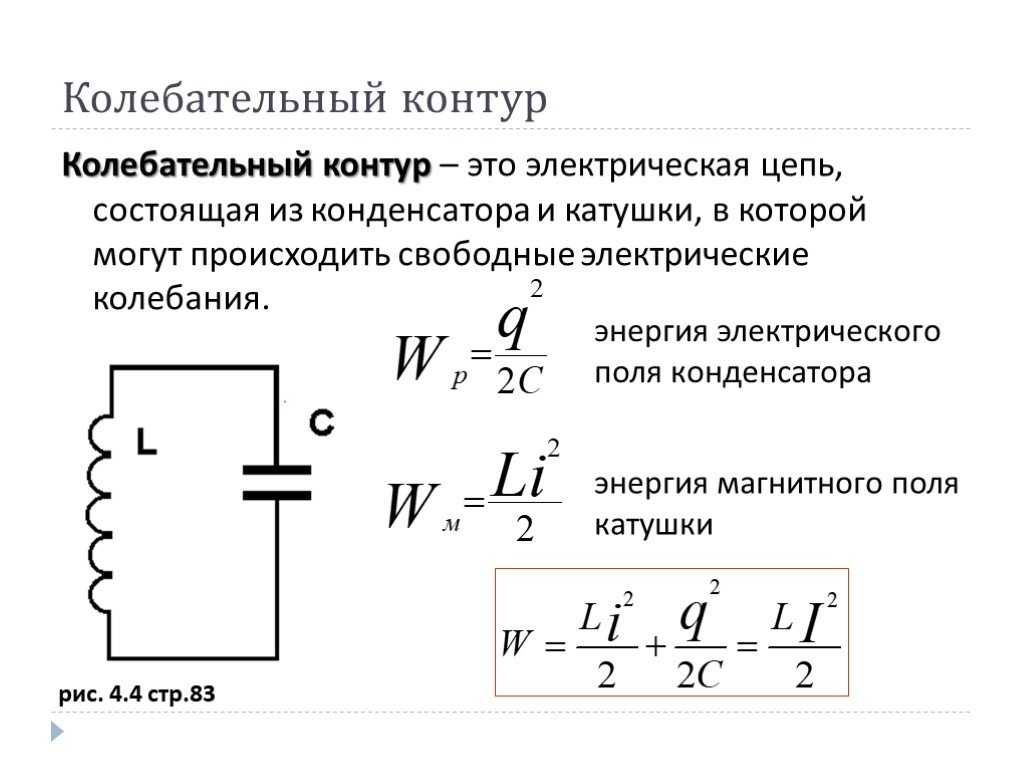 Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Решение задач с конденсаторами — Физика дома
Автор: admin. Рубрики: Это надо знать. Опубликовано: Апрель 24th, 2013
Одной из тем, изучаемых в курсе физики 10-го класса, является тема «Конденсаторы». Сама по себе тема не сложная, но решение задач по этой теме вызывает вопросы. Давайте разберём некоторые задачи и те нюансы, на которые необходимо обращать внимание.
Давайте разберём некоторые задачи и те нюансы, на которые необходимо обращать внимание.
Теорию Вы можете прочитать в учебнике. Поэтому сразу перейдём к задачам — к практике. Рассмотрим несколько задач.
1) Как изменится электроёмкость конденсатора при увеличении заряда на его обкладках в n раз?
Ёмкость конденсатора зависит от геометрических размеров пластин, их взаимного расположения и электрических свойств среды. Ни один из этих параметров здесь не изменяется. Следовательно электроёмкость конденсатора не изменится. При увеличении заряда на пластинах — увеличится напряжение между обкладками.
2) Плоский воздушный конденсатор, площадь каждой пластины которой равна S, а расстояние между ними d1, зарядили до напряжения U и отключили от источника напряжения. После этого увеличили расстояние между пластинами до d2. Как изменится при этом энергия конденсатора ?
При увеличении расстояния между пластинами, электроёмкость конденсатора уменьшается в 2 раза. Это — во-первых. Во-вторых. Для решения этой задачи большинство используют формулу для определения энергии электрического поля заряженного конденсатора. После подстановки получается, что энергия уменьшается в 2 раза. Этот ответ будет не верный.
Это — во-первых. Во-вторых. Для решения этой задачи большинство используют формулу для определения энергии электрического поля заряженного конденсатора. После подстановки получается, что энергия уменьшается в 2 раза. Этот ответ будет не верный.
Для ответа на вопрос этой задачи следует воспользоваться другой формулой для определения энергии. Поскольку после отключения конденсатора от источника напряжения, постоянным остаётся заряд на конденсаторе! Следовательно энергия заряженного конденсатора увеличивается в 2 раза!
3) Тот же самый вопрос, но конденсатор остаётся подключённым к источнику напряжения.
Если конденсатор остаётся подключённым к источнику напряжения, то напряжение между обкладками остаётся неизменным, какие бы изменения не производились с конденсатором. И для ответа на вопрос необходимо воспользоваться первой формулой.
4) Конденсатор ёмкостью С1, заряженный до разности потенциалов U1 соединили одноимённо заряженными обкладками с конденсатором ёмкостью С2, заряженным до напряжения U2. Найдите разность потенциалов между обкладками конденсаторов после их соединения.
Найдите разность потенциалов между обкладками конденсаторов после их соединения.
В основе решения задач подобного типа лежит закон сохранения электрического заряда. Заряд конденсаторов до соединения равен заряду системы после соединения. То есть, записав закон сохранения заряда и расписав заряды конденсаторов, определить неизвестную величину уже не вызывает никаких трудностей.
5) Как изменится ёмкость плоского конденсатора, если между его обкладками поместить стеклянную пластинку, толщина которой равна половине расстояния между обкладками? Какая работа совершается при этом, если конденсатор остаётся подсоединён к источнику напряжения U?
Для начала необходимо понять, а что происходит с конденсатором. Если сделать рисунок, то это выглядит примерно следующим образом:
И если мысленно между воздушным зазором и диэлектриком пометить тонкий проводник, то получившийся конденсатор будет представлять собой два последовательно соединенные конденсатора, с расстояние между пластинами d/2.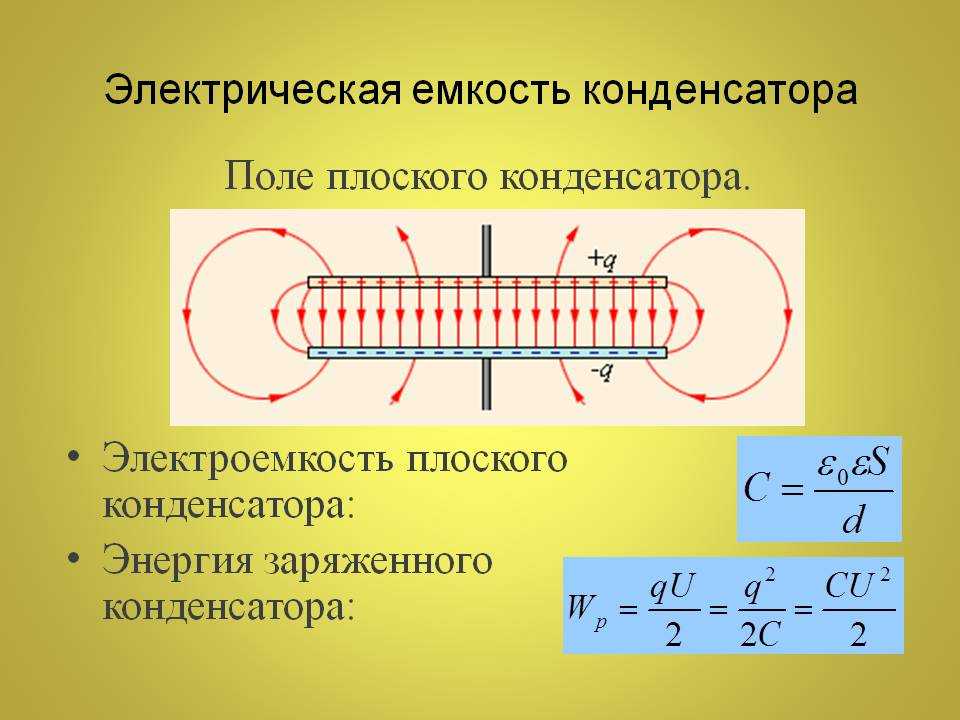 Просчитав ёмкость получившейся системы, отвечаем на первый вопрос задачи.
Просчитав ёмкость получившейся системы, отвечаем на первый вопрос задачи.
Чтобы ответить на вопрос с энергией, рассчитываем энергию системы до и после введения диэлектрика. Разность энергий будет показывать работу, совершённую при этом.
Конденсатор может быть заполнен диэлектриком таким образом, что диэлектрик заполняет конденсатор на половину площади пластин. Тогда конденсатор разрезаем на пополам и решаем задачу, как будто имеем два параллельно соединённых конденсатора с площадью пластин S/2.
6) Конденсатор подключили к источнику тока через резистор сопротивлением 5 кОм. Результаты измерений напряжения между обкладками конденсатора представлены в таблице:
U,B | 0 | 3.8 | 5.2 | 5.7 | 5.9 | 6 | 6 | 6 |
t,c | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Определить силу тока, протекающую через резистор в момент времени 2 с.
Если изобразить схему, то получится следующее:
И здравый смысл подсказывает, что ток через конденсатор не идёт, так как между пластинами диэлектрик.
Но в этой задаче рассматривается именно процесс зарядки конденсатора, который происходит в течение 6 секунд, судя по данным в таблице. Через 6 с после начала наблюдения конденсатор заряжается (ток через резистор протекает!), и, в конечном итоге, напряжение на нём станет равно ЭДС источника — 6 В.
А в момент времени 2 с, напряжение на конденсаторе 5.2 В, а следовательно, напряжение на резисторе 0,8 В. И по закону Ома для участка цепи, определяем силу тока в этот момент времени. Получается — 0,16 мА.
Есть ещё задачи с конденсаторами. И по мере подготовки материала, данная статья будет дополняться.
Вы можете оставить комментарий, или поставить трэкбек со своего сайта.
Написать комментарий
емкость | Определение, формула, единица измерения и факты
- Связанные темы:
- фарада цепь переменного тока электрический проводник
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
емкость , свойство электрического проводника или группы проводников, которое измеряется количеством отделенного электрического заряда, который может храниться на нем на единицу изменения электрического потенциала. Емкость также подразумевает связанное с ней хранение электрической энергии. При переносе электрического заряда между двумя первоначально незаряженными проводниками оба становятся одинаково заряженными, один положительно, другой отрицательно, и между ними устанавливается разность потенциалов. Емкость C представляет собой отношение величины заряда q на любом проводнике к разности потенциалов В между проводниками, или просто C = q / В. метр–килограмм–секунда в научных системах, единицей электрического заряда является кулон, а единицей разности потенциалов – вольт, так что единица измерения емкости, называемая фарад (обозначается символом Ф), равна одному кулону на вольт. Один фарад — очень большая емкость. Удобные в обычном использовании подразделения составляют одну миллионную часть фарада, называемую микрофарадой ( мк Ф) и одна миллионная микрофарад, называемая пикофарад (пФ; более старый термин, микромикрофарад, мкмк Ф).
Емкость также подразумевает связанное с ней хранение электрической энергии. При переносе электрического заряда между двумя первоначально незаряженными проводниками оба становятся одинаково заряженными, один положительно, другой отрицательно, и между ними устанавливается разность потенциалов. Емкость C представляет собой отношение величины заряда q на любом проводнике к разности потенциалов В между проводниками, или просто C = q / В. метр–килограмм–секунда в научных системах, единицей электрического заряда является кулон, а единицей разности потенциалов – вольт, так что единица измерения емкости, называемая фарад (обозначается символом Ф), равна одному кулону на вольт. Один фарад — очень большая емкость. Удобные в обычном использовании подразделения составляют одну миллионную часть фарада, называемую микрофарадой ( мк Ф) и одна миллионная микрофарад, называемая пикофарад (пФ; более старый термин, микромикрофарад, мкмк Ф).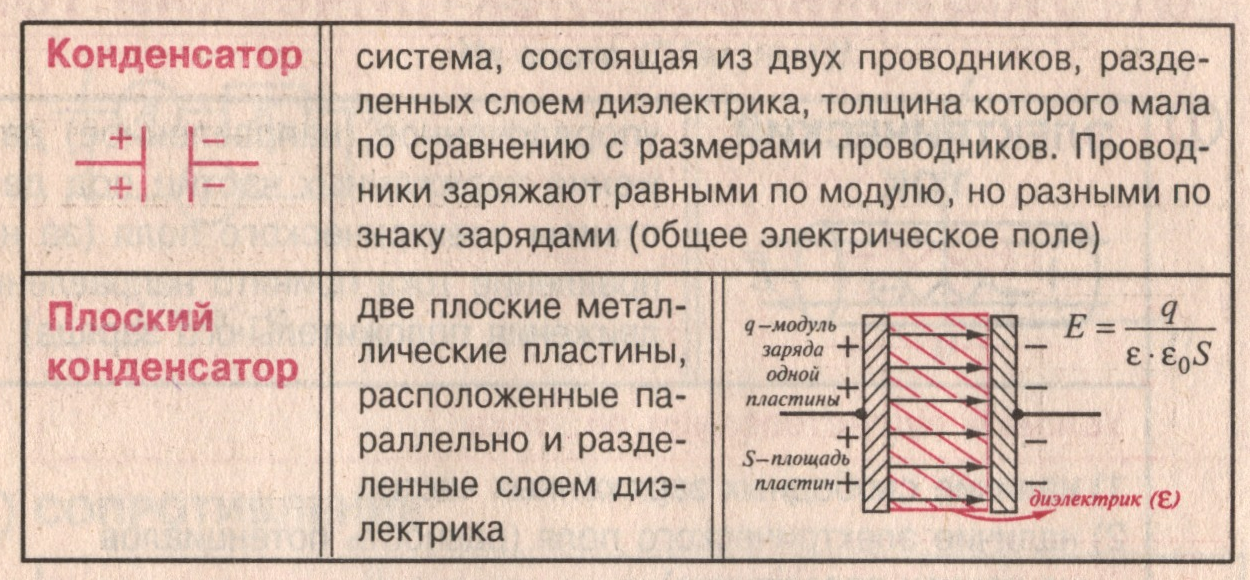 В электростатической системе единиц емкость имеет размерность расстояния.
В электростатической системе единиц емкость имеет размерность расстояния.
Подробнее по этой теме
электричество: емкость
Полезное устройство для хранения электроэнергии состоит из двух проводников, расположенных в непосредственной близости и изолированных друг от друга. Простой пример…
Емкость в электрических цепях преднамеренно вводится устройством, называемым конденсатором. Он был открыт прусским ученым Эвальдом Георгом фон Клейстом в 1745 году и независимо голландским физиком Питером ван Мушенбруком примерно в то же время в процессе исследования электростатических явлений. Они обнаружили, что электричество, полученное от электростатической машины, может накапливаться в течение определенного периода времени, а затем высвобождаться. Устройство, которое стало известно как лейденская банка, состояло из закрытого пробкой стеклянного флакона или банки, наполненной водой, с гвоздем, протыкающим пробку и погружаемым в воду. Держа банку в руке и прикасаясь гвоздем к проводнику электростатической машины, они обнаружили, что от гвоздя можно получить удар после его отсоединения, касаясь его свободной рукой. Эта реакция показала, что часть электричества от машины была сохранена.
Эта реакция показала, что часть электричества от машины была сохранена.
Простой, но фундаментальный шаг в эволюции конденсатора был сделан английским астрономом Джоном Бевисом в 1747 году, когда он заменил воду металлической фольгой, образующей подкладку на внутренней поверхности стекла и другую, покрывающую внешнюю поверхность. Эта форма конденсатора с проводником, выступающим из горлышка банки и касающимся облицовки, имела в качестве основных физических особенностей два проводника протяженной площади, почти одинаково разделенных изолирующим или диэлектрическим слоем, сделанным настолько тонким, насколько это практически возможно. Эти особенности были сохранены в каждой современной форме конденсатора.
Конденсатор, также называемый конденсатором, таким образом, представляет собой сэндвич из двух пластин из проводящего материала, разделенных изолирующим материалом или диэлектриком. Его основная функция заключается в хранении электрической энергии. Конденсаторы различаются размерами и геометрическим расположением пластин, а также видом используемого диэлектрического материала. Отсюда и такие названия, как слюдяные, бумажные, керамические, воздушные и электролитические конденсаторы. Их емкость может быть фиксированной или регулируемой в диапазоне значений для использования в схемах настройки.
Отсюда и такие названия, как слюдяные, бумажные, керамические, воздушные и электролитические конденсаторы. Их емкость может быть фиксированной или регулируемой в диапазоне значений для использования в схемах настройки.
Энергия, накопленная конденсатором, соответствует работе, выполняемой (например, батареей) по созданию противоположных зарядов на двух пластинах при приложенном напряжении. Количество заряда, которое может быть сохранено, зависит от площади пластин, расстояния между ними, диэлектрического материала в пространстве и приложенного напряжения.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Конденсатор, включенный в цепь переменного тока (AC), попеременно заряжается и разряжается каждые полпериода. Таким образом, время, доступное для зарядки или разрядки, зависит от частоты тока, и если требуемое время превышает длину полупериода, поляризация (разделение заряда) не завершена. В таких условиях диэлектрическая проницаемость оказывается меньше, чем наблюдаемая в цепи постоянного тока, и изменяется в зависимости от частоты, становясь ниже на более высоких частотах. При смене полярности пластин заряды должны смещаться через диэлектрик сначала в одну, а затем в другую сторону, и преодоление противодействия, с которым они сталкиваются, приводит к выделению тепла, известному как диэлектрические потери, характеристика, которую необходимо учитывать. следует учитывать при применении конденсаторов в электрических цепях, например, в радио- и телевизионных приемниках. Диэлектрические потери зависят от частоты и материала диэлектрика.
При смене полярности пластин заряды должны смещаться через диэлектрик сначала в одну, а затем в другую сторону, и преодоление противодействия, с которым они сталкиваются, приводит к выделению тепла, известному как диэлектрические потери, характеристика, которую необходимо учитывать. следует учитывать при применении конденсаторов в электрических цепях, например, в радио- и телевизионных приемниках. Диэлектрические потери зависят от частоты и материала диэлектрика.
За исключением утечки (обычно небольшой) через диэлектрик, через конденсатор не протекает ток, когда он находится под постоянным напряжением. Однако переменный ток проходит легко и называется током смещения.
Редакторы Британской энциклопедии Эта статья была недавно пересмотрена и обновлена Адамом Августином.
19.5 Конденсаторы и диэлектрики – Колледж физики главы 1-17
19 Электрический потенциал и электрическое поле
Резюме
- Опишите действие конденсатора и определите емкость.

- Расскажите о конденсаторах с плоскими пластинами и их емкости.
- Обсудите процесс увеличения емкости диэлектрика.
- Определить емкость при данных заряде и напряжении.
Конденсатор — это устройство, используемое для накопления электрического заряда. Применение конденсаторов варьируется от фильтрации статического электричества в радиоприеме до накопления энергии в сердечных дефибрилляторах. Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. 1. (Большую часть времени между двумя пластинами используется изолятор для обеспечения разделения — см. обсуждение диэлектриков ниже.) Когда клеммы батареи подключены к изначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, [латекс]\boldsymbol{+Q}[/латекс] и [латекс]\boldsymbol{-Q}[/латекс], разделены на его две тарелки. Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд [латекс]\boldsymbol{Q}[/латекс].
Конденсатор
Конденсатор — это устройство, используемое для накопления электрического заряда.
Рисунок 1. Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них есть отдельные заряды + Q и – Q на две половины. а) Конденсатор с плоскими пластинами. (b) Свернутый конденсатор с изоляционным материалом между двумя его проводящими листами.Сумма заряда [латекс]\boldsymbol{Q}[/латекс] a , который может хранить конденсатор , зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.
Количество заряда
Q Конденсатор может хранить Количество заряда [латекс]\boldsymbol{Q}[/latex], который может хранить конденсатор , зависит от двух основных факторов: приложенного напряжения и емкости конденсатора. физические характеристики, например размер.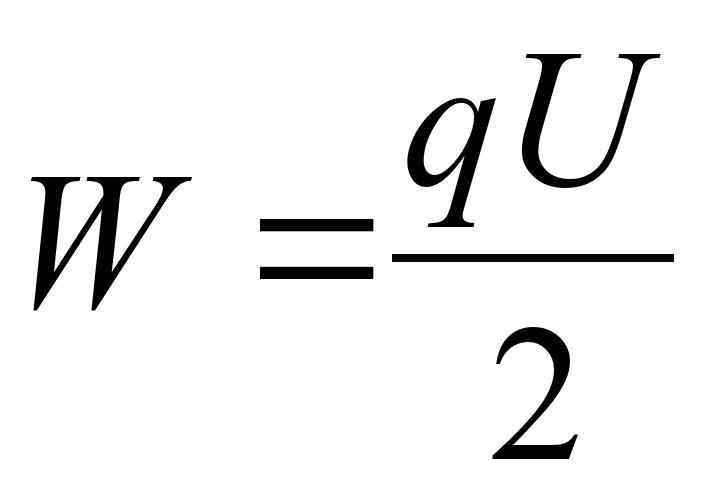
Система, состоящая из двух одинаковых параллельных проводящих пластин, разделенных расстоянием, как показано на рисунке 2, называется конденсатором с параллельными пластинами. Легко увидеть взаимосвязь между напряжением и накопленным зарядом для плоского конденсатора, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поле будет больше. линии, если есть больше заряда. (Рисовать одну силовую линию для каждого заряда — это только для удобства. Мы можем нарисовать много силовых линий для каждого заряда, но их общее число пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна [латексной ]\boldsymbol{Q}[/латекс]
Рисунок 2. Линии электрического поля в этом плоском конденсаторе, как всегда, начинаются с положительных зарядов и заканчиваются с отрицательными зарядами. Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.
Поле пропорционально заряду:
[латекс]\boldsymbol{E \propto Q},[/латекс]
, где символ [латекс]\жирныйсимвол{\пропто}[/латекс] означает «пропорционально». Из обсуждения в главе 19.2 Электрический потенциал в однородном электрическом поле, мы знаем, что напряжение на параллельных пластинах равно [латекс]\boldsymbol{V = Ed}[/латекс]. Таким образом,
[латекс]\boldsymbol{V \propto E}.[/латекс]
Отсюда следует, что [латекс]\boldsymbol{V \propto Q}[/латекс], и наоборот,
[латекс]\boldsymbol{Q \propto V}.[/латекс]
В общем случае это верно: чем больше напряжение, приложенное к любому конденсатору, тем больший заряд в нем хранится.
Различные конденсаторы сохраняют разное количество заряда при одном и том же приложенном напряжении в зависимости от их физических характеристик. Мы определяем их емкость [латекс]\boldsymbol{C}[/latex] так, чтобы заряд [латекс]\boldsymbol{Q}[/латекс], хранящийся в конденсаторе, был пропорционален [латекс]\boldsymbol{C}[ /латекс]. Заряд, хранящийся в конденсаторе, равен 9.0009
Заряд, хранящийся в конденсаторе, равен 9.0009
[латекс]\boldsymbol{Q = CV}.[/латекс]
Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора [латекс]\boldsymbol{C}[/латекс] и напряжение ВВ . Преобразовав уравнение, мы видим, что емкость [латекс]\boldsymbol{C}[/латекс] – это количество накопленного заряда на вольт, или
.[латекс]\boldsymbol{C =}[/латекс] [латекс]\boldsymbol{\frac{Q}{V}}.[/латекс]
Емкость
Емкость [латекс]\boldsymbol{C}[/латекс] — это количество заряда, накопленного на вольт, или
[латекс]\жирный символ{С =}[/латекс] [латекс]\жирныйсимвол{\фракция {Q}{V}}.[/латекс]
Единицей измерения емкости является фарад (Ф), названный в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или
.
[латекс]\boldsymbol{1 \;\textbf{F} =}[/latex] [латекс]\boldsymbol{\frac{1 \;\textbf{C}}{1 \;\textbf{V}}} .[/латекс] 9{-3} \;\textbf{F})}[/latex].
На рис. 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.
Рисунок 3. Некоторые типовые конденсаторы. Размер и значение емкости не обязательно связаны. (кредит: Уинделл Оскей) Конденсатор с плоскими пластинами, показанный на рисунке 4, имеет две одинаковые проводящие пластины, каждая из которых имеет площадь поверхности [латекс]\boldsymbol{A}[/латекс], разделенную расстоянием [латекс]\boldsymbol{d}[/латекс] ( без материала между пластинами). Когда к конденсатору прикладывается напряжение [latex]\boldsymbol{V}[/latex], он накапливает заряд [latex]\boldsymbol{Q}[/latex], как показано на рисунке. Мы можем увидеть, как его емкость зависит от [латекс]\boldsymbol{A}[/латекс] и [латекс]\boldsymbol{d}[/латекс], рассматривая характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, разноименные притягиваются, а сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше. Таким образом, [латекс]\boldsymbol{C}[/latex] должен быть больше для больших [латекс]\boldsymbol{A}[/латекс]. Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Так что [латекс]\boldsymbol{C}[/латекс] должен быть больше для меньшего [латекс]\жирныйсимвол{d}[/латекс].
Мы можем увидеть, как его емкость зависит от [латекс]\boldsymbol{A}[/латекс] и [латекс]\boldsymbol{d}[/латекс], рассматривая характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, разноименные притягиваются, а сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше. Таким образом, [латекс]\boldsymbol{C}[/latex] должен быть больше для больших [латекс]\boldsymbol{A}[/латекс]. Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Так что [латекс]\boldsymbol{C}[/латекс] должен быть больше для меньшего [латекс]\жирныйсимвол{d}[/латекс].
Можно показать, что для конденсатора с плоскими пластинами есть только два фактора ([латекс]\boldsymbol{A}[/латекс] и [латекс]\жирныйсимвол{d}[/латекс]), которые влияют на его емкость [латекс]. 2}[/latex]. Небольшое числовое значение [латекс]\boldsymbol{{\varepsilon}_0}[/латекс] связано с большим размером фарады. Плоский конденсатор должен иметь большую площадь, чтобы иметь емкость, приближающуюся к фарадам. (Обратите внимание, что приведенное выше уравнение справедливо, когда параллельные пластины разделены воздухом или свободным пространством. Когда между пластинами помещается другой материал, уравнение модифицируется, как описано ниже.) 93 \;\textbf{V}}[/latex] применяется к нему?
2}[/latex]. Небольшое числовое значение [латекс]\boldsymbol{{\varepsilon}_0}[/латекс] связано с большим размером фарады. Плоский конденсатор должен иметь большую площадь, чтобы иметь емкость, приближающуюся к фарадам. (Обратите внимание, что приведенное выше уравнение справедливо, когда параллельные пластины разделены воздухом или свободным пространством. Когда между пластинами помещается другой материал, уравнение модифицируется, как описано ниже.) 93 \;\textbf{V}}[/latex] применяется к нему?
Стратегия
Нахождение емкости [латекс]\boldsymbol{C}[/latex] является прямым применением уравнения [латекс]\boldsymbol{C = {\varepsilon}_0 A/d}[/latex] . Как только [латекс]\boldsymbol{C}[/латекс] найден, накопленный заряд можно найти с помощью уравнения [латекс]\жирныйсимвол{Q = CV}[/латекс].
Решение для (a)
Ввод данных значений в уравнение для емкости плоского конденсатора дает 9{-9} \;\textbf{F} = 8,85 \;\textbf{nF}}. \end{array}[/latex]
Обсуждение для (a)
Это маленькое значение емкости показывает, насколько сложно сделать устройство с большой емкостью. Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу.
Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу.
Решение для (b)
Заряд, хранящийся в любом конденсаторе, определяется уравнением [латекс]\boldsymbol{Q = CV}[/латекс]. Ввод известных значений в это уравнение дает 96 \;\textbf{V} / \textbf{m}}[/latex], на этом конденсаторе нельзя накопить больше заряда за счет увеличения напряжения.
Еще один интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам избирательно входить и выходить из клетки. На мембране существует разность потенциалов около -70 мВ. Это связано с наличием в клетке в основном отрицательно заряженных ионов и преобладанием положительно заряженного натрия (Na 96 \;\textbf{V} / \textbf{m}}.[/latex]
Этого электрического поля достаточно, чтобы вызвать пробой воздуха.
Предыдущий пример подчеркивает сложность сохранения большого количества заряда в конденсаторах. Если [латекс]\boldsymbol{d}[/латекс] уменьшить для получения большей емкости, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс]\жирный символ{E = V/d}[/латекс ]). Важное решение этой проблемы состоит в том, чтобы поместить изолирующий материал, называемый диэлектриком, между пластинами конденсатора и позволить [латексу]\boldsymbol{d}[/латексу] быть как можно меньше. Мало того, что меньший [латекс]\boldsymbol{d}[/латекс] увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем разрушиться.
Если [латекс]\boldsymbol{d}[/латекс] уменьшить для получения большей емкости, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс]\жирный символ{E = V/d}[/латекс ]). Важное решение этой проблемы состоит в том, чтобы поместить изолирующий материал, называемый диэлектриком, между пластинами конденсатора и позволить [латексу]\boldsymbol{d}[/латексу] быть как можно меньше. Мало того, что меньший [латекс]\boldsymbol{d}[/латекс] увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем разрушиться.
Использование диэлектрика в конденсаторе имеет еще одно преимущество. В зависимости от используемого материала емкость больше, чем указанная уравнением [латекс]\boldsymbol{C = {\varepsilon}_0 \frac{A}{d}}[/latex], на коэффициент [латекс]\boldsymbol {\kappa}[/latex] , называемая диэлектрической проницаемостью . Емкость плоского конденсатора с диэлектриком между пластинами равна
.
[латекс]\boldsymbol{C = \kappa {\varepsilon}_0}[/latex] [латекс]\boldsymbol{\frac{A}{d}}[/latex] [латекс]\boldsymbol{(\textbf{ плоскопараллельный конденсатор с диэлектриком})}.[/latex]
Значения диэлектрической проницаемости [латекс]\boldsymbol{\kappa}[/латекс] для различных материалов приведены в таблице 1. Обратите внимание, что [латекс]\жирныйсимвол{\каппа}[/латекс] для вакуума ровно 1, а поэтому приведенное выше уравнение справедливо и в этом случае. Если используется диэлектрик, например, путем помещения тефлона между пластинами конденсатора в примере 1, то емкость увеличивается в [латекс]\жирныйсимвол{\каппа}[/латекс], что для тефлона составляет 2,1.
Самостоятельный эксперимент: изготовление конденсатора
Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут алюминиевой фольгой, а перегородка (диэлектрик) между ними будет бумагой.
| Материал | Диэлектрическая проницаемость [латекс]\boldsymbol{\kappa}[/латекс] | Диэлектрическая прочность (В/м) |
|---|---|---|
| Вакуум | 1. 6}[/латекс] 96}[/латекс] 6}[/латекс] 96}[/латекс] | |
| Вода | 80 | — |
| Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC | ||
Также обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, действуют так же, как конденсаторы с вакуумом между пластинами , за исключением , что воздух может стать проводящим, если напряженность электрического поля становится слишком большой . (Напомним, что [латекс]\boldsymbol{E = V/d}[/латекс] для конденсатора с плоскими пластинами.) В таблице 1 также показаны максимальные значения напряженности электрического поля в В/м, называемые диэлектрической прочностью, для нескольких материалов. Это поля, выше которых материал начинает разрушаться и проводить. Диэлектрическая прочность накладывает ограничение на напряжение, которое может быть приложено для данного разделения пластин.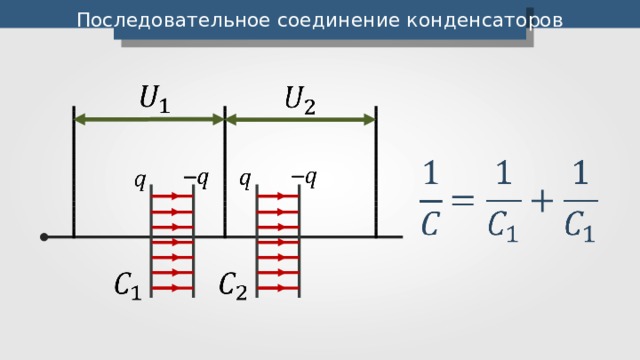 4 \;\textbf{V})} \\[1em] & \boldsymbol{ 1.1 \;\textbf{mC}.} \end{массив}[/latex]
4 \;\textbf{V})} \\[1em] & \boldsymbol{ 1.1 \;\textbf{mC}.} \end{массив}[/latex]
Это в 42 раза больше заряда того же воздушного конденсатора.
Диэлектрическая прочность
Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.
Каким образом диэлектрик увеличивает емкость под микроскопом? В этом виновата поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость [латекс]\boldsymbol{\kappa}[/латекс]. Вода, например, является полярной молекулой, потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды приводит к тому, что она имеет относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации можно лучше всего объяснить с точки зрения характеристик кулоновской силы. На рис. 5 схематично показано разделение заряда в молекулах диэлектрического материала, помещенного между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии [латекс]\boldsymbol{d}[/латекс].
Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии [латекс]\boldsymbol{d}[/латекс].
Другой способ понять, как диэлектрик увеличивает емкость, — рассмотреть его влияние на электрическое поле внутри конденсатора. На рис. 5(b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются на зарядах в диэлектрике, их меньшее количество проходит от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, хотя на пластинах находится тот же заряд. Напряжение между пластинами равно [латекс]\boldsymbol{V = Ed}[/латекс], так что диэлектрик тоже снижает его. Таким образом, существует меньшее напряжение [латекс]\boldsymbol{V}[/латекс] для того же заряда [латекс]\boldsymbol{Q}[/латекс]; поскольку [латекс]\boldsymbol{C = Q/V}[/латекс], емкость [латекс]\boldsymbol{C}[/латекс] больше.
Поскольку силовые линии заканчиваются на зарядах в диэлектрике, их меньшее количество проходит от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, хотя на пластинах находится тот же заряд. Напряжение между пластинами равно [латекс]\boldsymbol{V = Ed}[/латекс], так что диэлектрик тоже снижает его. Таким образом, существует меньшее напряжение [латекс]\boldsymbol{V}[/латекс] для того же заряда [латекс]\boldsymbol{Q}[/латекс]; поскольку [латекс]\boldsymbol{C = Q/V}[/латекс], емкость [латекс]\boldsymbol{C}[/латекс] больше.
Диэлектрическая проницаемость обычно определяется как [латекс]\boldsymbol{\kappa = E_0/E}[/латекс] или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале и тесно связано с поляризуемость материала.
Вещи большие и малые
Субмикроскопическое происхождение поляризации
Поляризация — это разделение зарядов внутри атома или молекулы. Как уже отмечалось, планетарная модель атома изображает его как имеющее положительное ядро, вращающееся вокруг отрицательно заряженных электронов, подобно планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в другом месте, например, в главе 30 «Атомная физика». Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рис. 6.9.0009 Рис. 6. Представление художника о поляризованном атоме. Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.
Как уже отмечалось, планетарная модель атома изображает его как имеющее положительное ядро, вращающееся вокруг отрицательно заряженных электронов, подобно планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в другом месте, например, в главе 30 «Атомная физика». Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рис. 6.9.0009 Рис. 6. Представление художника о поляризованном атоме. Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.
В главе 30 «Атомная физика» мы найдем, что орбиты электронов правильнее рассматривать как электронные облака с плотностью облака, связанной с вероятностью нахождения электрона в этом месте (в отличие от определенных местоположений и путей планет в их орбиты вокруг Солнца).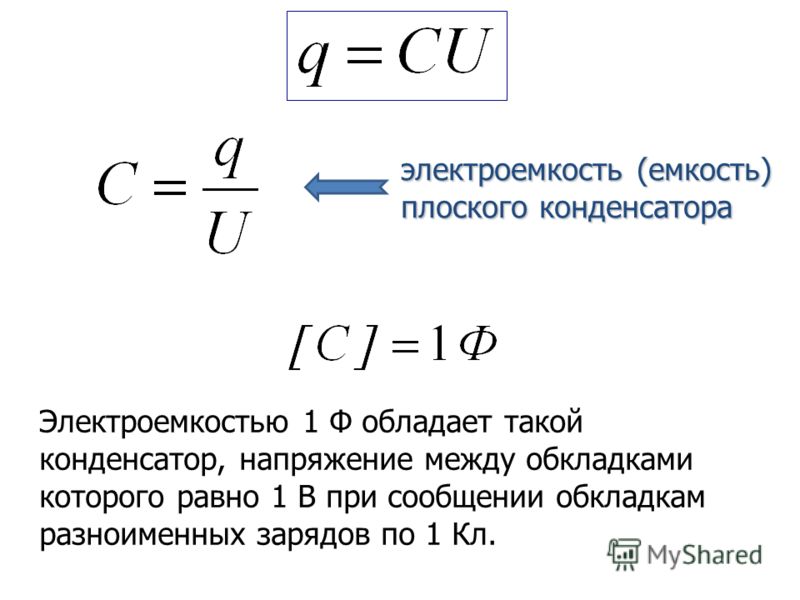 Это облако смещается кулоновской силой так, что атом в среднем имеет разделение заряда. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.
Это облако смещается кулоновской силой так, что атом в среднем имеет разделение заряда. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.
Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому их называют полярными молекулами. На рис. 7 показано разделение заряда в молекуле воды, имеющей два атома водорода и один атом кислорода [латекс]\boldsymbol{\textbf{H}_2 \textbf{O}}[/latex]. Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более сильно заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец оставляет слегка положительным. Присущее полярным молекулам разделение зарядов облегчает их согласование с внешними полями и зарядами. Поэтому полярные молекулы проявляют больший поляризационный эффект и имеют большую диэлектрическую проницаемость.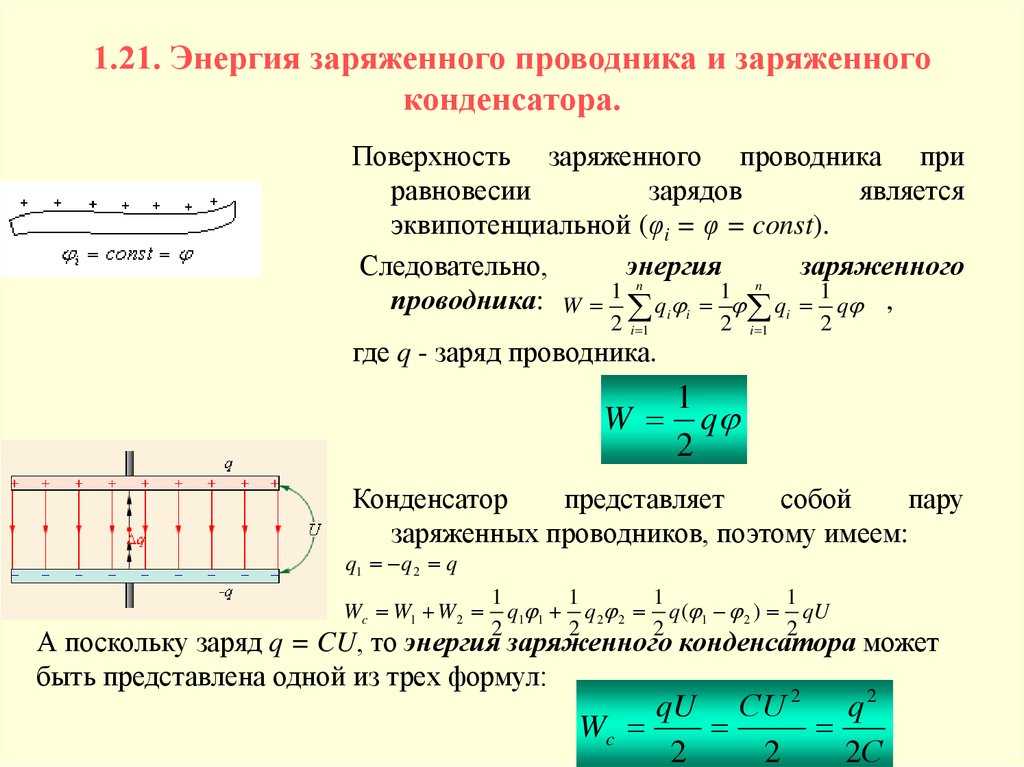 Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.
Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.
PhET Explorations: Capacitor Lab
Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость.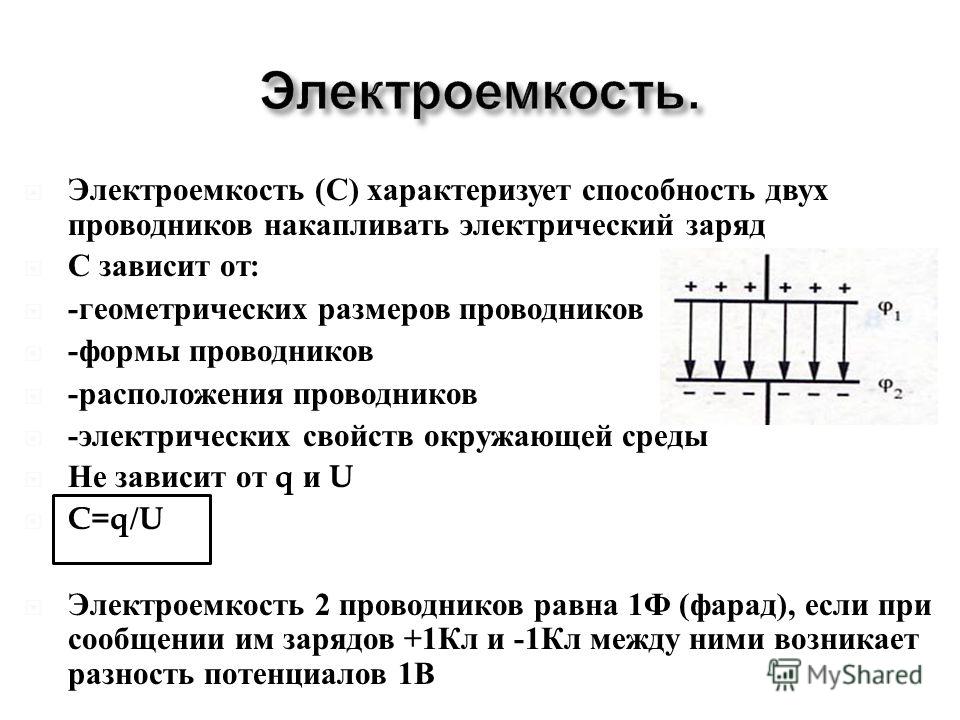 Измените напряжение и увидите заряды на пластинах. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.
Измените напряжение и увидите заряды на пластинах. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.
- Конденсатор — это устройство, используемое для накопления заряда.
- Количество заряда [латекс]\boldsymbol{Q}[/латекс], которое может хранить конденсатор, зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.
- Емкость [латекс]\boldsymbol{C}[/латекс] представляет собой количество накопленного заряда на вольт , или
[латекс]\boldsymbol{C} =[/латекс] [латекс]\boldsymbol{\frac{Q}{V}}. [\латекс]
- Емкость конденсатора с параллельными пластинами равна [латекс]\boldsymbol{C = {\varepsilon}_0 \;\frac{A}{d}}}[/латекс], когда пластины разделены воздухом или свободным пространством. [латекс]\boldsymbol{{\varepsilon}_0}[/латекс] называется диэлектрической проницаемостью свободного пространства.

- Емкость плоского конденсатора с диэлектриком между пластинами определяется выражением
[латекс]\boldsymbol{C = \kappa {\varepsilon}_0}[/latex] [латекс]\boldsymbol{\frac{A}{d}},[/latex]
, где [латекс]\boldsymbol{\kappa}[/латекс] — диэлектрическая проницаемость материала.
- Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.
- конденсатор
- устройство, накапливающее электрический заряд
- емкость
- количество накопленного заряда на единицу вольта
- диэлектрик
- изоляционный материал
- электрическая прочность
- максимальное электрическое поле, при превышении которого изоляционный материал начинает разрушаться и становится проводящим
- Плоский конденсатор
- две одинаковые проводящие пластины, разделенные расстоянием
- полярная молекула
- молекула с присущим разделением зарядов
Физическая формула для класса 12 Глава — Емкость
Физическая формула
- с = кв.

где c = емкость конденсатора (фарад)
Емкость специального проводника C = 4πε 0 R
q-заряд (кулон), V-потенциал (вольт)
- C = ε0 — A/d
Где c 0 = емкость плоского конденсатора (воздух является средой)
A = π r 2 для круглых пластин
d = расстояние между плитами (м)
ε 0 = Диэлектрическая проницаемость свободного пространства (ф/м)
- Если между пластинами поместить среду с диэлектрической проницаемостью k, то ее емкость составит
C = K ε 0 A/K(d — t) + t
- Последовательная комбинация из трех конденсаторов,
(a) Q одинакова для всех конденсаторов
т. е. Q = Q 1 = Q 2 = Q 3
Соотношение зарядов 1 : 1 : 1
(б) Суммарный потенциал, v = v 1 + v 2 + v 3
Отношение потенциалов v 1 :v 2 :v 3 =
V = Q/C 1 + Q/C 2 + Q/C 3
V/Q = 1/C 1 + 1/C 2 + 1/C 3
1/С = 1/С 1 + 1/С 2
V 1 = C 2 /C 1 + C 2 ; V 2 = (C 1 /C 1 + C 2 )V
1/К = 1/К 1 + 1/К 2 + 1/К 3 + 1/К 4 +. ……..
……..
(c) Эффективная емкость
С/Н
Для двух конденсаторов
1/К = 1/К 1 + 1/К 2
Примечание:- Если все одинаковые конденсаторы, то
С/Н
Параллельная комбинация «3» конденсаторов.
(a) «v» одинаково для всех конденсаторов
т. е. v = v 1 = v 2 = v 3
Соотношение потенциалов 1 : 1 : 1
(b) Общий заряд, Q = Q 1 + Q 2 + Q 3 = C 1 : C 2 : C 3
(c) эффективная емкость, C P = C 1 +C 2 +C 3
Примечание. Если все конденсаторы идентичны,
Тогда С 1 = С 2 = С 3 = С и
C P 3C, C P nC [для конденсатора n]
- Энергия, запасенная в конденсаторе
U = 1/2 CV 2 = 1/2 QV = 1/2 Q 2 /С
Где C – емкость конденсатора
V – потенциал, Q – заряд, U – запасенная энергия в Дж
- Если диэлектрик «k» толщиной «t» поместить между пластинами плоского конденсатора, то его емкость составит
C = [ε0 A/(d — t) {1 + 1/t}]
Концептуальные точки:
- Емкость проводника – это отношение заряда (q) на нем к его потенциалу (В).
 с = д/об
с = д/об - Единицей емкости является кулон/вольт или фарад.
- Емкость проводника равна одной фараде, если к проводнику добавить заряд в 1 кулон, чтобы повысить его потенциал на 1 вольт.
Следуйте NCERT Solutions для класса 12 Physics , подготовленным экспертным факультетом физики Wallah. Учащиеся также могут получить важных вопросов для 12 класса CBSE по физике .
Часто задаваемые вопросы (FAQ)
Q1. Какая емкость для 12 класса?
Анс. Емкость (C) конденсатора определяется как отношение заряда (Q) к разности потенциалов (V), приложенной ко всем проводникам, т. е. C = Q / V. Единицей емкости в системе СИ является фарад (Ф).
Q2. Что такое единица измерения емкости в СИ?
Анс. Единицей измерения емкости в системе СИ является фарад.
Q3. Какова формула конденсатора?
Анс.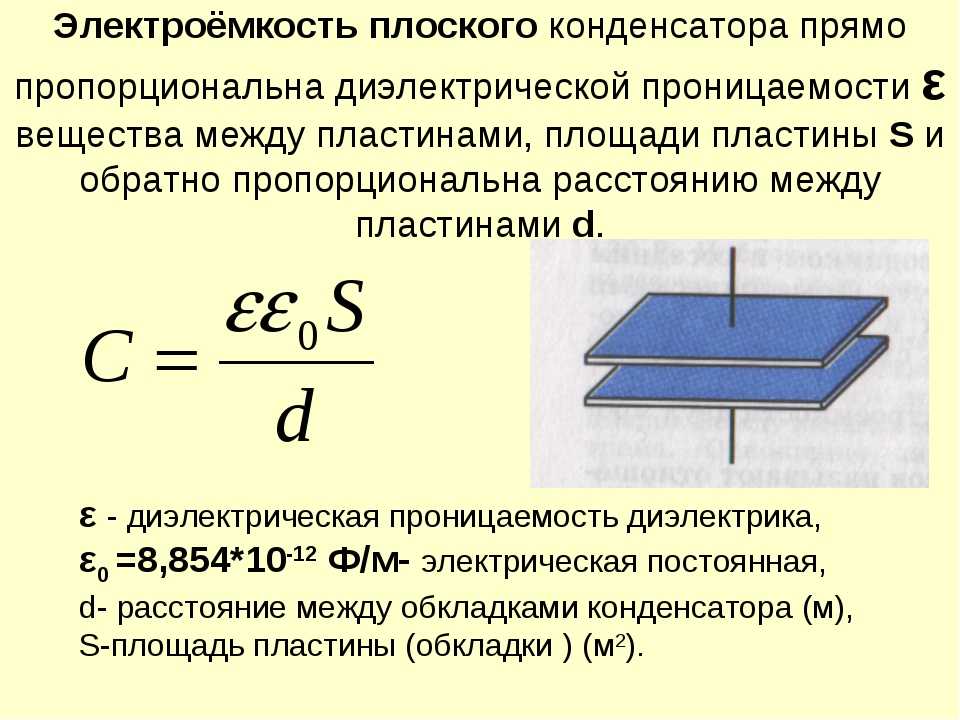 Основное уравнение для расчета конденсатора: C = εA/d. В этом уравнении C — емкость; ε — диэлектрическая проницаемость, показатель того, насколько хорошо диэлектрический материал удерживает электрическое поле; A — площадь параллельной пластины, d — расстояние между двумя проводящими пластинами.
Основное уравнение для расчета конденсатора: C = εA/d. В этом уравнении C — емкость; ε — диэлектрическая проницаемость, показатель того, насколько хорошо диэлектрический материал удерживает электрическое поле; A — площадь параллельной пластины, d — расстояние между двумя проводящими пластинами.
Q4. Какие два типа конденсаторов существуют?
Ответ . Конденсаторы делятся на две механические группы: постоянные конденсаторы с постоянными и переменные конденсаторы с переменными (подстроечными) или регулируемыми (перестраиваемыми) значениями емкости. Наиболее важной группой является фиксированный конденсатор.
В5. Где используются конденсаторы?
Анс. Конденсаторы очень популярны во многих системах, таких как силовые цепи, электронные схемы и блоки питания. Конденсатор называют Большой тройкой пассивных компонентов, а резисторы катушек — основы электрических цепей.
Q6. Что такое кулон?
Что такое кулон?
Анс. Кулон (обозначается буквой C) — стандартная единица электрического заряда в Международной системе единиц (СИ). Это бесконечное число; поделитесь этой особенностью с кротом. Значение 1 C примерно равно 6,24 x 10 18 или квинтиллион 6.24.
Загрузите PDF-файл буклета с формулой для класса 12, главу «Физика» главы «Емкость»
Определение, формула, единицы СИ, измерение
Конденсатор — это устройство, которое может накапливать электрические заряды, а также может использоваться для защиты цепей от нежелательных всплесков. Теперь вы можете подумать, что батарея также делает это.
Однако в этом случае разница заключается в том, что батарея хранит энергию в форме химического потенциала, тогда как конденсаторы хранят энергию в форме электрического потенциала. Кроме того, ток утечки у конденсаторов выше, чем у аккумуляторов, а это означает, что конденсаторы не могут удерживать заряд так же долго, как аккумуляторы.
Рис. 1. Конденсатор A. Источник: Эван-Амос, Wikimedia Commons (общественное достояние).
Быстрое движение электронов между двумя пластинами конденсатора делает его очень полезным в электронных приложениях.
Конденсатор
Внутри конденсатора находятся две металлические пластины из проводящего материала, например алюминия. Эти пластины разделены изоляционным материалом, также известным как диэлектрик.
Прежде чем мы рассмотрим, как работает конденсатор, нам нужно понять концепцию поляризации.
Поляризация – это ориентация полярных молекул внутри диэлектрика по направлению к противоположным электродам.
Диэлектрик состоит из множества полярных молекул, которые имеют как положительный, так и отрицательный конец. Когда конденсатор не накапливает заряд, электрического поля нет, и эти молекулы случайным образом направлены в разные стороны.
Рис. 2. Случайные молекулы (вверху) и молекулы в электрическом поле (внизу). Источник: гиперфизика, Wikimedia Commons (общественное достояние).
Источник: гиперфизика, Wikimedia Commons (общественное достояние).
Когда на конденсатор подается напряжение, создается электрическое поле. Положительные концы молекул притягиваются к отрицательно заряженной пластине и наоборот.
Поскольку диэлектрик является изолятором и молекулы не могут смещаться, поляризованные молекулы ориентируются таким образом, что противоположные заряды на молекулах и пластинах обращены друг к другу.
Рис. 3. Ориентация поляризованных молекул в электрическом поле. Источник: Brews ohare, Wikimedia Commons (CC BY-SA 3.0).
Поскольку электрическое поле поляризованных молекул направлено в противоположную сторону от пластин конденсатора, разность потенциалов уменьшается, а способность конденсатора накапливать заряд на единицу разности потенциалов увеличивается.
Возьмите батарейку и подсоедините отрицательный конец к отрицательному выводу конденсатора (обозначен полосой), а положительный конец к положительному выводу. Однако имейте в виду, что не все конденсаторы имеют маркировку полюсов. Если это так, они могут быть подключены в любом направлении в цепи.
Однако имейте в виду, что не все конденсаторы имеют маркировку полюсов. Если это так, они могут быть подключены в любом направлении в цепи.
Рисунок 4. Символ конденсатора. Источник: Wikimedia Commons (общественное достояние).
Заряды текут от батареи к отрицательной клемме конденсатора и от положительной пластины к положительной клемме батареи.
Рисунок 5. На диаграмме показано, как напряжение на пластинах и ток, протекающий через пластины, изменяются по мере заряда конденсатора. Источник: jjbeard, Wikimedia Commons (общественное достояние).
После того, как заряды перетекли от положительной пластины к батарее и от батареи к отрицательной пластине, дальнейший поток электронов невозможен, и одна сторона конденсатора заряжена отрицательно, а другая сторона заряжена положительно. Конденсатор находится на том же уровне напряжения, что и батарея.
Поскольку электроны накапливаются на одной стороне конденсатора, мы говорим, что он хранит энергию, которую можно высвобождать, когда это необходимо.
Между пластинами конденсатора создается разность потенциалов, так как существует разница в количестве зарядов на пластинах.
Применение конденсатора
Заряженный конденсатор можно использовать для обеспечения непрерывного заряда цепи.
Например, когда мы подключаем светодиод к полностью заряженному конденсатору, заряды от отрицательной пластины конденсатора текут через светодиод к положительной пластине конденсатора до тех пор, пока между двумя клеммами не исчезнет разность потенциалов. В результате светодиод на короткое время мигнет.
Продолжительность вспышки будет очень короткой, так как поток электронов очень быстрый. Однако, если мы подключим батарею к конденсатору в этой цепи, конденсатор будет заряжаться и накапливать энергию и снова разряжаться, если в протекании тока возникнет какое-либо прерывание.
Измерение накопленной энергии
На конденсаторе есть два значения, одно показывает напряжение (В) и емкость в фарадах (Ф).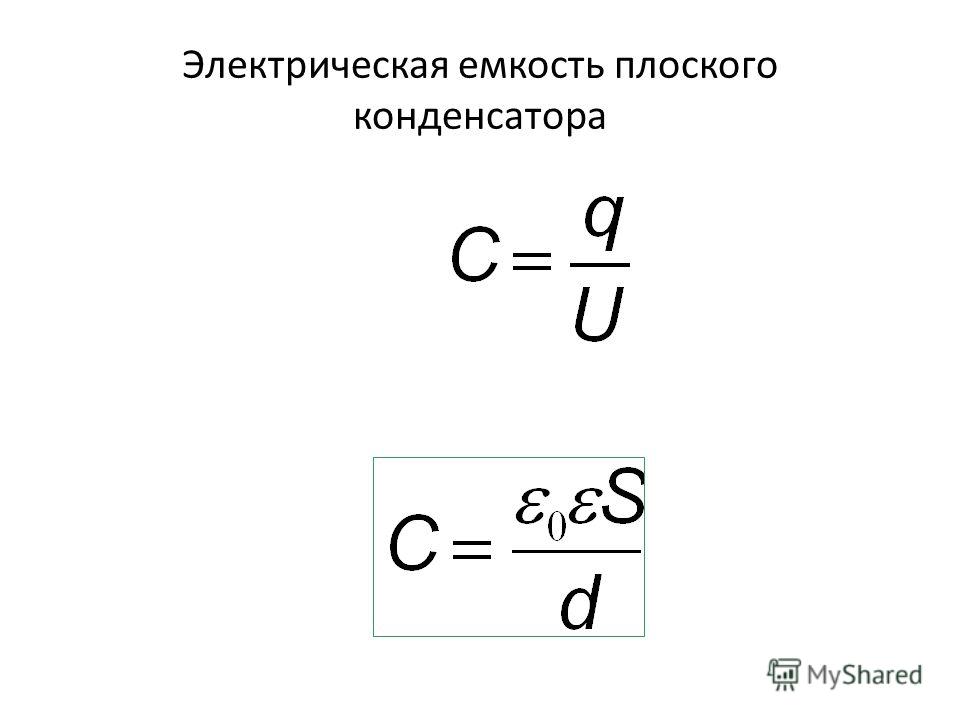
Рисунок 6. Конденсатор с показаниями напряжения и емкости. Источник: Jomegat, Wikimedia Commons (CC BY-SA 3.0).
Показание напряжения на конденсаторе указывает максимальное напряжение, которое он может выдержать. Если это значение превышено, есть вероятность, что конденсатор может сгореть, а иногда даже взорваться.
Емкость конденсатора
Каждый конденсатор имеет емкость, которая представляет собой его способность накапливать электрический заряд. Символом емкости является C, которая измеряется в фарадах. Фарады — это количество кулонов, которое может храниться на вольт:
Таким образом, емкость можно использовать для расчета заряда в кулонах:
- Q = электрический заряд.
- C = емкость.
- В = напряжение.
Формула емкости
Емкость можно рассчитать по следующей формуле:
- C = емкость, измеренная в кулонах на вольт (Ф).

- K = относительная диэлектрическая проницаемость, т. е. диэлектрическая проницаемость материала по отношению к диэлектрической проницаемости свободного пространства. Это выражается как εr/ε0, где εr — диэлектрическая проницаемость материала. Обычно указывается относительная диэлектрическая проницаемость. Например, воздух имеет диэлектрическую проницаемость 1,9.2 и разделены на 2,15 мм.
Поскольку K не указано, мы примем его равным 1. Сложение других значений дает:
Это может показаться очень маленькой емкостью, но на самом деле она огромна.
Емкость (только A2) — основные выводы
- Конденсатор — это проводник, который может накапливать заряд в электрической форме.
Каждый конденсатор имеет емкость, которая представляет собой количество заряда на единицу разности потенциалов.
Конденсатор используется для поддержания тока в цепи в случае прерывания.
Две проводящие пластины с диэлектрическим изолятором между ними образуют конденсатор.

Работа конденсатора заключается в накоплении отрицательных зарядов на одной пластине, что создает разность потенциалов между двумя пластинами.
Единицей измерения емкости являются фарады.
Формула емкости с примерами решения
Шекхар Суман
Куратор контента | Обновлено 18 апреля 2022 г.
Емкость является мерой электрический заряд , который может удерживаться проводником . Он определяется как отношение заряда конденсатора к потенциалу конденсатора. Формула емкости выражается как C = Q / V. Когда конденсаторы соединены последовательно, формула емкости выражается как Cs = 1/C1 + 1/C2. Опять же, формула емкости выражается как Cp = C1 + C2, если конденсаторы соединены параллельно. Где C1, C2, C3…….Cn — это конденсаторы, а емкость выражается в фарадах. Давайте подробнее рассмотрим тему и обсудим некоторые важные вопросы.

Содержание
- Что такое емкость?
- Formula of Capacitance
- Unit of Capacitance
- Potential of a Capacitor
- Solved Examples
- Things to Remember
- Sample Questions
Основные выводы: Емкость, формула емкости, конденсаторы, формула емкости, единица измерения емкости, потенциал конденсатора.
Подробнее: Часть 1 Глава 2 Электростатический потенциал и емкость
Что такое емкость?
[Нажмите здесь, чтобы получить примеры вопросов]
Емкость обычно измеряется в устройстве с параллельными пластинами путем измерения электрического поля между двумя пластинами.
 Это способность объекта накапливать заряд. По мере увеличения электрического поля между пластинами увеличивается и заряд, который может храниться между ними. Это зависит от формы, размера и расстояния между проводниками, а также от типа среды между ними. Любой объект, обладающий способностью накапливать внутри себя заряды, обладает емкостью и называется конденсатором. Конденсаторы есть почти во всех электронных устройств для простой задачи хранения зарядов. Они доступны во всех формах и размерах, в зависимости от количества заряда, которое они должны хранить в себе.
Это способность объекта накапливать заряд. По мере увеличения электрического поля между пластинами увеличивается и заряд, который может храниться между ними. Это зависит от формы, размера и расстояния между проводниками, а также от типа среды между ними. Любой объект, обладающий способностью накапливать внутри себя заряды, обладает емкостью и называется конденсатором. Конденсаторы есть почти во всех электронных устройств для простой задачи хранения зарядов. Они доступны во всех формах и размерах, в зависимости от количества заряда, которое они должны хранить в себе.Емкость
В камере вспышка требует довольно много энергии за короткий промежуток времени, чтобы она могла произвести вспышку с необходимой яркостью. Энергия, необходимая для создания такой яркости, не может быть обеспечена батареей . Вместо этого используется расположение конденсаторов для хранения достаточного количества энергии и быстрого ее высвобождения через нить накала.
 Точно так же во время сбоя питания компьютеры неизбежно потеряют все важные данные или файлы из-за отсутствия конденсатора. Массив конденсаторов, находящихся в компьютере, автоматически заряжается при включении питания. В случае аварийного отключения электроэнергии конденсаторы теряют заряд через цепь , тем самым предоставляя компьютеру достаточно времени для сохранения важных файлов и данных.
Точно так же во время сбоя питания компьютеры неизбежно потеряют все важные данные или файлы из-за отсутствия конденсатора. Массив конденсаторов, находящихся в компьютере, автоматически заряжается при включении питания. В случае аварийного отключения электроэнергии конденсаторы теряют заряд через цепь , тем самым предоставляя компьютеру достаточно времени для сохранения важных файлов и данных.Also Read:
Formula of Capacitance
[Click Here for Sample Questions]
The following is the basic formula of capacitance:
C = QV Где,
C = емкость, измеренная в фарадах,
Q = заряд, измеренный в кулонах,
В = напряжение, измеряемое в вольтах.
Besides this, another formula can also be applied to calculate capacitance which is as follows:
C = kε 0 Ad Where,
C = for capacitance,
К = для относительной диэлектрической проницаемости,
ε0 = для диэлектрической проницаемости свободного пространства,
А = для площади поверхности пластин и
d = для расстояния между пластинами.

If two capacitors are connected in a series connection, the formula becomes as follows:
C s = 1C1 + 1C2 Где
C1 и C2 = соответствующим емкостям конденсаторов и
C s = соответствующей емкости последовательно.
Аналогичным образом, если два конденсатора соединены параллельно, формула для определения емкости всей системы выглядит следующим образом:
C p = C 1 + C 2 Where C p is the capacitance in parallel.

Единица измерения емкости
[Нажмите здесь, чтобы задать пример вопросов]
Единицей измерения емкости является кулон /вольт, которая называется фарад. Фарада (Ф) — это большая единица измерения, и в обычных ситуациях используется микрофарад (мФ).
Подробнее:
Потенциал конденсатора
[Нажмите здесь, чтобы просмотреть примеры вопросов]
В конденсаторе с параллельными пластинами разность потенциалов между двумя пластинами представляет собой потенциал конденсатора. Конденсатор обычно представляет собой устройство из двух металлических пластин, разделенных изолирующей средой. Здесь положительный заряд одной пластины, т. е. положительной пластины, равен отрицательному заряду другой пластины, т. е. отрицательной пластины. Это означает, что суммарный заряд конденсатора будет равен нулю, поскольку обе пластины содержат одинаковые и противоположные заряды.
Емкость и заряд на пластинах конденсатора
Когда конденсатор питается внешним зарядом от батареи или любого другого источника, две пластины накапливают заряд.
 Следовательно, когда этот конденсатор подключается к цепи, начинает течь электрический ток. Отрицательный заряд течет к положительному заряду, и таким образом заряд на конденсаторе нейтрализуется.
Следовательно, когда этот конденсатор подключается к цепи, начинает течь электрический ток. Отрицательный заряд течет к положительному заряду, и таким образом заряд на конденсаторе нейтрализуется.Подробнее:
Что нужно помнить
Ниже приведены некоторые важные моменты:
Примеры вопросов
Вопросы: Найдите емкость конденсатора, через который протекает заряд 10 Кл и к которому приложен потенциал 4 В. (2 балла)
ANS: Заряд (Q) = 10 C
Потенциал (V) = 4 V
C = QV
C = 104
= 2,5 F
QUES. : Человек вошел в большую металлическую клетку, поддерживаемую изолированными столбами. Затем клетку заряжали с помощью мощной электрической машины. Несмотря на то, что человек боялся удара током, внутри клетки он был в безопасности. Как вы думаете, в чем причина этого явления? (2 балла)
Ответ: Поскольку клетка изолирована, подведенный к ней заряд протекает только через внешнюю поверхность клетки.
 Более того, потенциал в каждой точке остается одним и тем же, а это означает, что между любыми двумя точками в клетке нет разности потенциалов. Поэтому человек оставался в клетке в безопасности.
Более того, потенциал в каждой точке остается одним и тем же, а это означает, что между любыми двумя точками в клетке нет разности потенциалов. Поэтому человек оставался в клетке в безопасности.Вопрос: Какова емкость плоского конденсатора с зарядом 100 мкКл и разностью потенциалов 20 мВ? (2 балла)
ANS: Q = 100 мкК
V = 20 мВ
C = QV
= 100 x 10-620 x 10 -3
C = 0,005 F
= 5 MF = 5 MF = 5 MF = 5 мг.
Вопрос: Рассмотрим конденсатор с плоскими пластинами, заряженный батареей с постоянным напряжением. Батарея удаляется из цепи, когда конденсатор достигает максимального заряда. Выясните, какие изменения могут произойти, если параллельные пластины сдвинуть ближе друг к другу. (3 балла)
Ответ: Ниже приведены изменения:
- Заряд: Заряд, нанесенный на пластины, не изменяется при извлечении аккумулятора.
 Следовательно, заряд и плотность заряда остаются неизменными, когда пластины сближаются.
Следовательно, заряд и плотность заряда остаются неизменными, когда пластины сближаются. - Емкость: Поскольку C обратно пропорционально d, при уменьшении расстояния между пластинами емкость увеличивается.
- Напряжение: Поскольку C обратно пропорционально V, при увеличении емкости напряжение уменьшается.
Ques: Calculate the effective capacitance between a and b from the figure given below: C 1 = C 3 = 100 μF, C 2 = С 4 = 200 мкФ. (2 балла)
ANS: Результирующий C 1 и C 2 = C 1 + C 2 = 300 мкф
РЕЗУЛЬТАТ C 3 = 300 мкф
.4 = C 3 + C 4 = 300 мкФ
Эффективная емкость = 1300 + 1300
C = 150 мкФ.

Ques: Calculate the capacitance in a circuit where capacitors 11 F and 2 F are connected: (4 marks)
- In series
- In parallel
Ans: С 1 = 11 Ф
С 2 = 2 Ф
- C s = 1C 1 + 1C 2
= 111 + 12
= 2 + 1111 x 2
= 1322
C S = 0,59 F
- C P = C 1 + C 2
= 11 + 2
CO P = 13 00009
CO PA = 1300009
: CAM489 PA = 1300009
: SAGINAL CAM489: FAPER. 2 площадь поверхности, пластины которой находятся на расстоянии 0,01 м друг от друга.
 Какой заряд могут накопить эти пластины при подключении к батарее 8 В, если между пластинами есть воздух? (4 балла)
Какой заряд могут накопить эти пластины при подключении к батарее 8 В, если между пластинами есть воздух? (4 балла) ANS: A = 0,1 M 2
D = 0,01 м
V = 8 В
K = 1 (так как воздух между пластинами)
ε0 = 8,8544 9
ε0 = 8,8544. -12
C = kε0Ad
= 1 x 8.854 x 10 -12 x 0.1 0.01
= 8.854 x 10 -11 F
Q = C x V
= 8,854 x 10 -11 x 8
Q = 70,8 x 10 -11 C
Вопрос: Если расстояние между пластинами конденсатора равно 2 x 10 -3 м, найдите площадь поверхности пластин. Емкость конденсатора составляет 1 F. (4 балла)
ANS: D = 2 x 10 -3 M
C = 1 F
C = Kε0AD
K = 1
8. ε0 = 8,85 x 10 -12
A = dCk ε0
= 2 x 10 -3 x 11 x 8,85 x 10 -12
A = 2,3 x 10 8 M 2
Связанные ссылки:
CBSE класс 12.

Действие
емкость
Плоский конденсатор
относительная диэлектрическая проницаемость
диэлектрики
Действие
Конденсаторы — это электрические компоненты, используемые для накопления заряда. Их конструкция представляет собой просто две проводящие пластины равной площади с изолятором ( диэлектрик ), зажатым между ними.
При повороте переключателя влево происходит мгновенное протекание тока. Под действием батареи электроны движутся по часовой стрелке. Их снимают с нижней пластины и наносят на верхнюю.
Через очень короткое время все движение прекращается. р.д. поперек пластин теперь такой же, как поперек батареи, но в противоположном направлении. При подключении плюса батареи к плюсу конденсатора нет p.d. существуют. Так что ток не течет.

В этом состоянии конденсатор считается «полностью заряженным». Заряды на верхней и нижней пластинах разнотипны и равны по количеству.
наверх
Емкость
Емкость — это мера емкости конденсатора для накопления заряда. Чем больше конденсатор, тем больше заряда может храниться на вольт p.d. по тарелкам.
где,
Кл емкость в фарадах (Ф)
Ом заряд в кулонах (Кл) между пластинамиЕдиница измерения емкости называется Фарад .
По определению, конденсатор имеет емкость 1 фарад, когда 1 кулон заряда накапливается с p.d. 1 вольт на пластинах.
Следовательно, единицами Фарады являются кулоны на вольт (CV -1 )
Один Фарад слишком велик для обычных цепей.
 Вместо этого используются меньшие производные единицы, например, микрофарады (мкФ) и пикофарады (пФ).
Вместо этого используются меньшие производные единицы, например, микрофарады (мкФ) и пикофарады (пФ).вернуться к началу
Конденсатор с параллельными пластинами
Емкость конденсатора с плоскими пластинами может быть легко получена из первых принципов
.Начиная с нашего основного уравнения для емкости,
(i
Заряд Q равен плотности заряда σ , умноженной на площадь A .
Замена Q в первом уравнении (i ,
(ii
Результаты Теоремы Гаусса* дают напряженность электрического поля E в терминах плотности заряда σ и диэлектрической проницаемости ε : 90 здесь не рассматривается продвинутая теория
Перестановка для получения σ предмет,
Теперь заменяем σ в уравнении (ii
(iii
Для однородного поля внутри конденсатора,
, следовательно,
Подстановка V в уравнение (iii
Примечание: выражение для напряженности электрического поля E из закона Гаусса для бесконечной площади пластины A .
 Таким образом, этот результат является приблизительным.
Таким образом, этот результат является приблизительным.наверх
Относительная диэлектрическая проницаемость
Определение относительной диэлектрической проницаемости – это отношение емкости конденсатора с диэлектриком к емкости конденсатора без диэлектрика (т.е. в свободном пространстве).
Рассматривая емкость, мы можем получить выражение, связывающее относительную диэлектрическую проницаемость ε r , диэлектрическая проницаемость свободного пространства ε o и диэлектрическая проницаемость используемого диэлектрика.
Находим ε r , разделив первое уравнение на второе:
Примечание: поскольку ε r является отношением диэлектрических проницаемостей, оно не имеет единиц
вернуться к началу
Диэлектрики
Чтобы понять действие диэлектрических материалов, важно понимать, что происходит на молекулярном уровне.

Когда к диэлектрику прикладывается электрическое поле, положение компонентов атомов/молекул изменяется.
Положительные атомные ядра перемещаются до своего предела на короткое расстояние и указывают на отрицательную пластину. Электронные облака вокруг атомов деформируются, и основная часть их заряда направлена на положительную пластину. Таким образом, атомы/молекулы становятся поляризованными, и противоположные заряды имеют тенденцию концентрироваться на обоих концах.
В результате поверхности диэлектрика, обращенные к пластинам конденсатора, заряжаются. Положительная пластина противостоит отрицательной стороне диэлектрика, а отрицательная пластина противостоит положительной стороне диэлектрика.Диэлектрик между пластинами конденсатора изменяет емкость в двух конкретных случаях:
Изолированный заряженный конденсатор
Отрицательный заряд на верхней поверхности диэлектрика в сочетании с положительным зарядом на верхней пластине снижает общий потенциал в этой области.
 (Площадь менее положительная.)
(Площадь менее положительная.)Положительный заряд на нижней поверхности диэлектрика в сочетании с отрицательным зарядом на нижней пластине увеличивает там потенциал. (Площадь менее отрицательная.)
В результате разность потенциалов на конденсаторе меньше ( В ). Поскольку Q = CV , Q не изменяется, а V уменьшается, то C увеличивается.
Конденсатор в цепи с аккумулятором
р.д. В между пластинами поддерживается батарея. Поверхностные заряды на диэлектрике заставляют больше электронов оттягиваться от положительной пластины и оседать на отрицательной пластине.
Таким образом, общий заряд Q на пластинах увеличивается. Поскольку В является постоянным и Q = CV , то C увеличивается.
По разным причинам введение диэлектрического вещества между пластинами конденсатора приводит к увеличению емкости.
Ниже приведена таблица общих относительных диэлектрических проницаемостей.
Обратите внимание, что относительная диэлектрическая проницаемость воды намного выше, чем у остальных. Это потому, что вода (наряду со многими другими жидкостями) имеет полярных молекул . Эти поляризованы. То есть у них есть + и — концы. без применения какого-либо поля. Полярные молекулы в жидкостях легко ориентируются в электрическом поле. Таким образом создается больше поверхностных зарядов и эффект больше.
материал
отн. диэлектрическая проницаемость
( ε r )вакуум
1,0
воздух
1.



 {-12} \space Ф$.
{-12} \space Ф$. Иметь представление о применение конденсаторов. Уметь применять имеющиеся знания к различным практическим заданиям.
Иметь представление о применение конденсаторов. Уметь применять имеющиеся знания к различным практическим заданиям.

 Записывает формулу для емкости плоского конденсатора, указывает от чего зависит электроемкость конденсатора.
Записывает формулу для емкости плоского конденсатора, указывает от чего зависит электроемкость конденсатора.
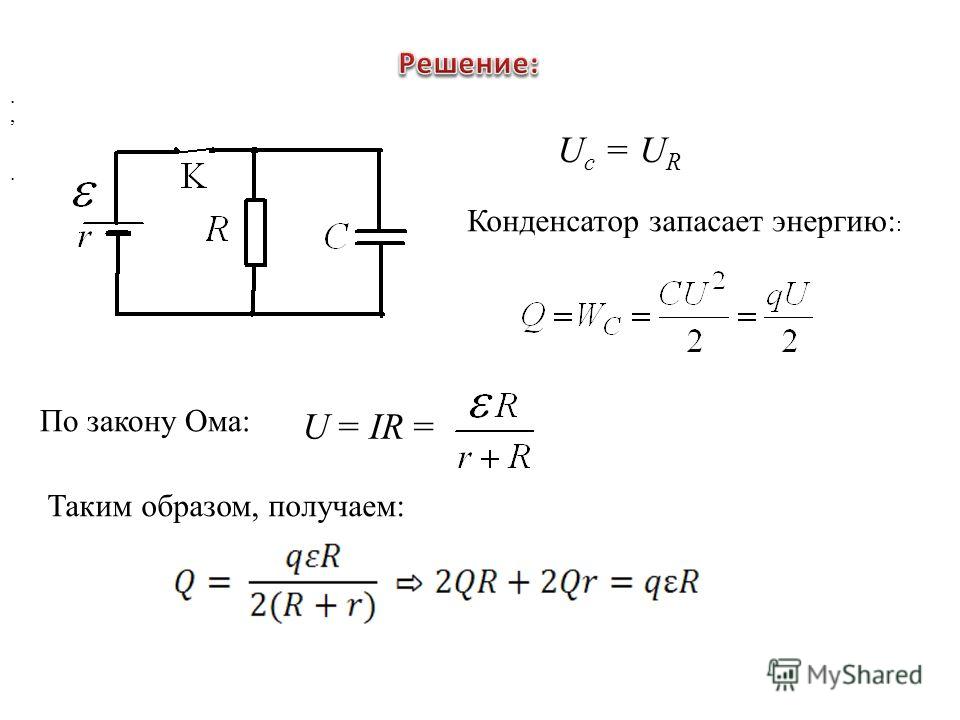 (приложение 2)
(приложение 2)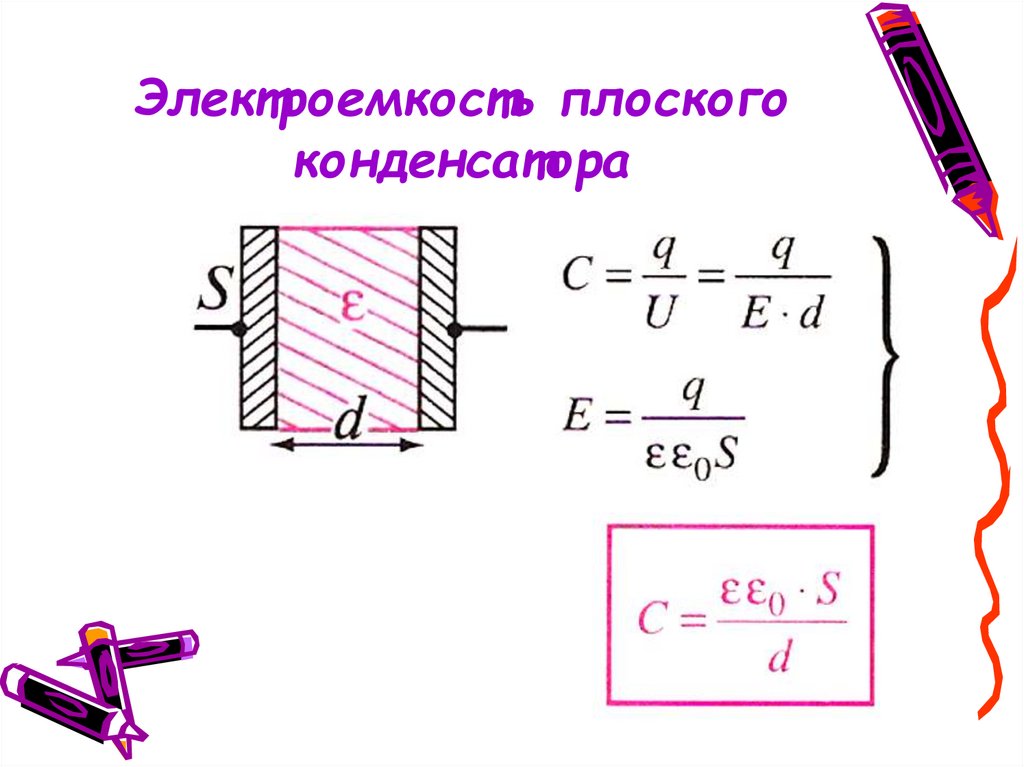


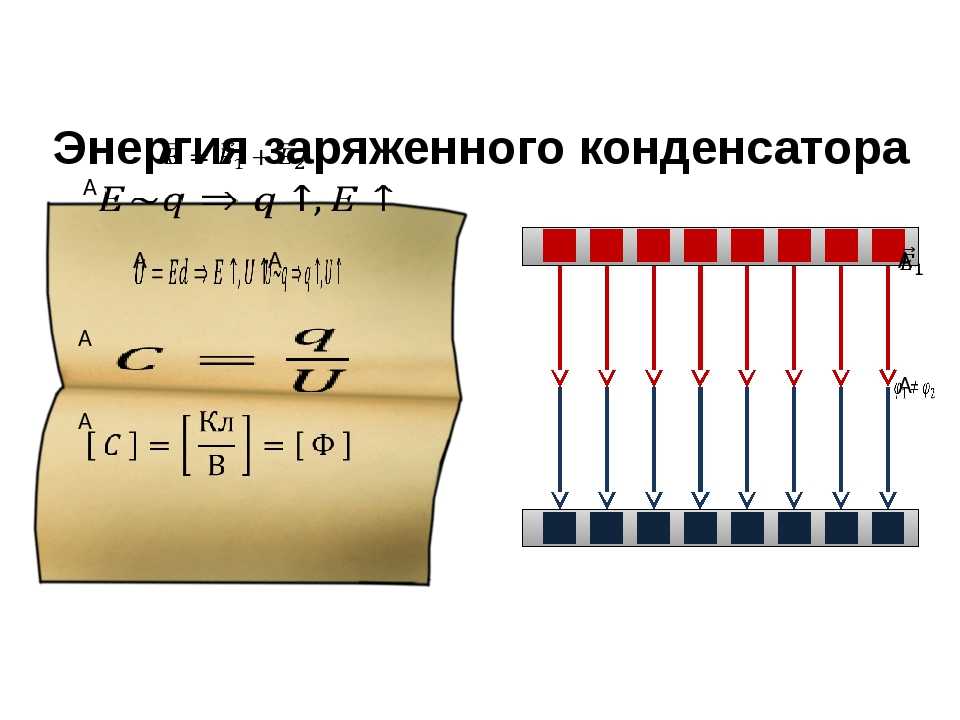 ст. поля определяется как?
ст. поля определяется как?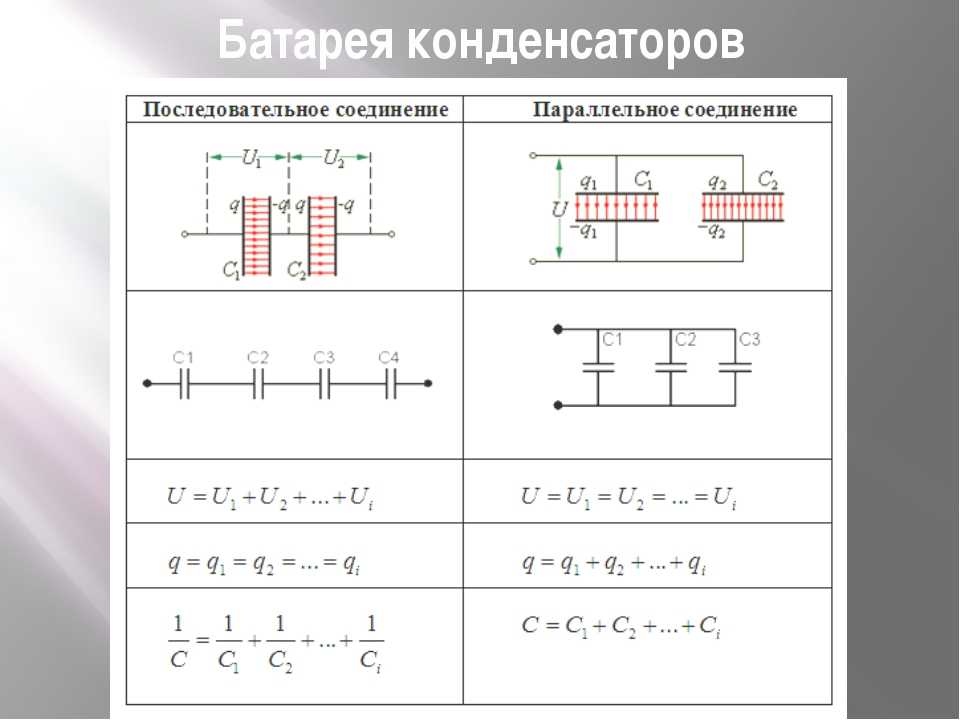
 )
)

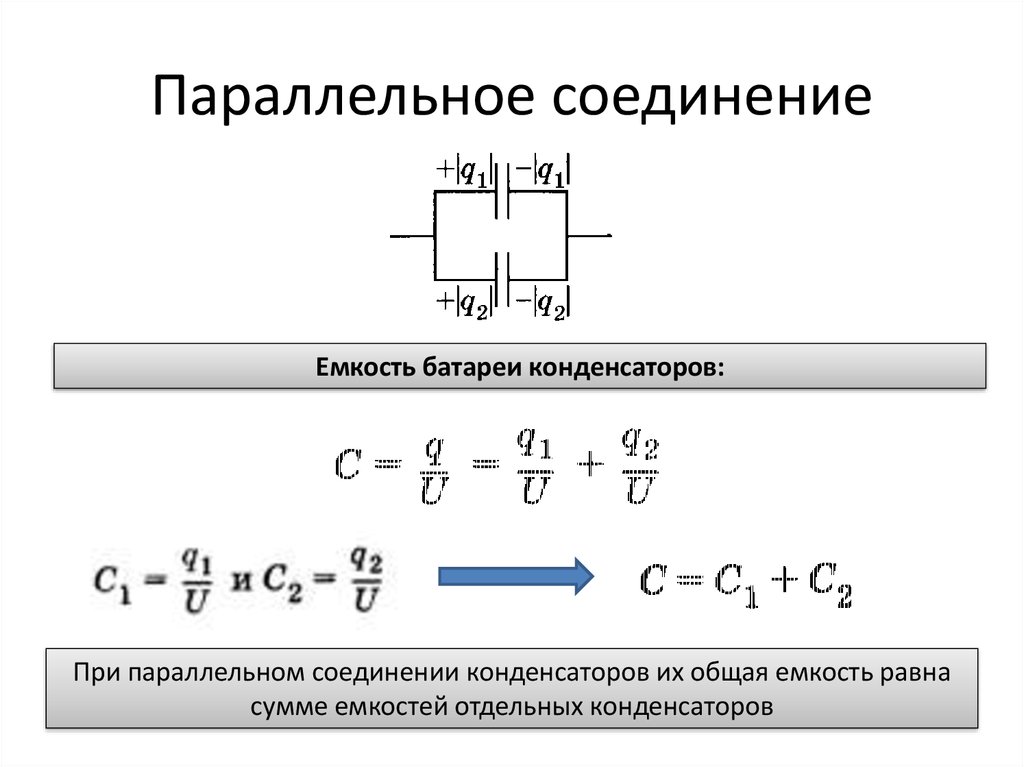
 с = д/об
с = д/об

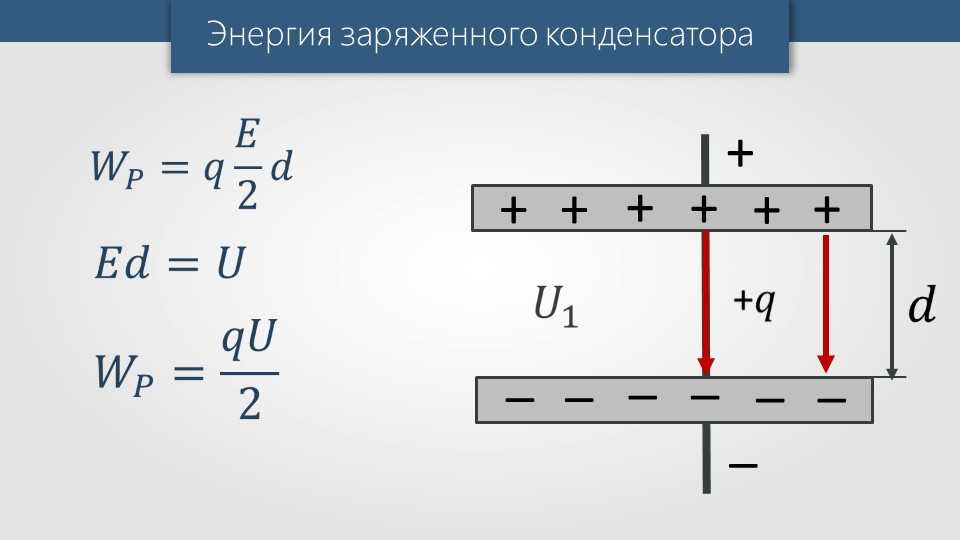
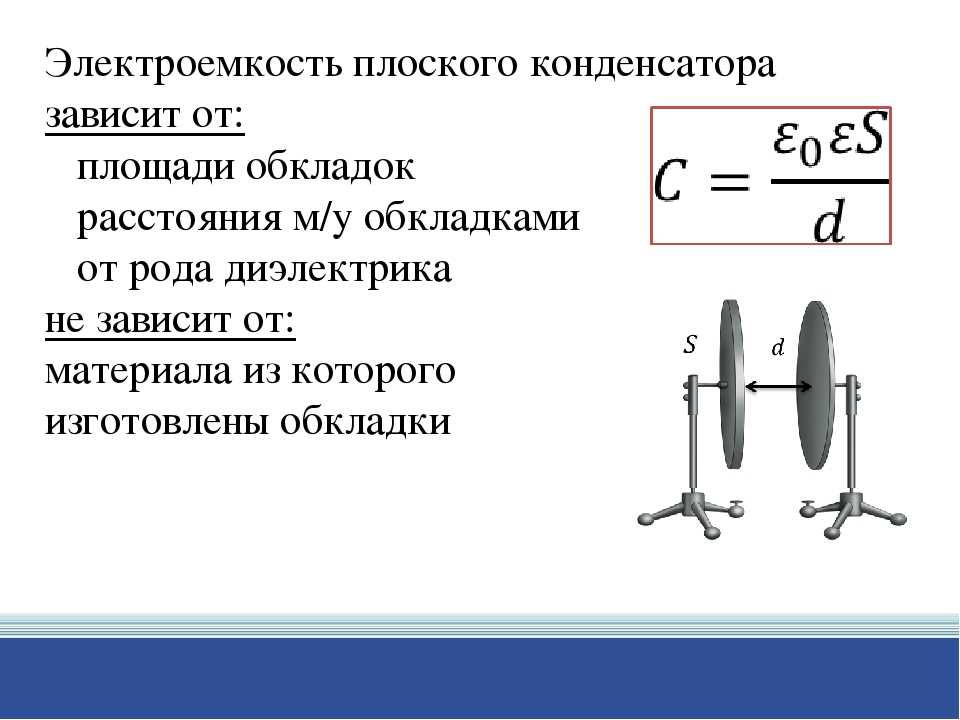 Это способность объекта накапливать заряд. По мере увеличения электрического поля между пластинами увеличивается и заряд, который может храниться между ними. Это зависит от формы, размера и расстояния между проводниками, а также от типа среды между ними. Любой объект, обладающий способностью накапливать внутри себя заряды, обладает емкостью и называется конденсатором. Конденсаторы есть почти во всех электронных устройств для простой задачи хранения зарядов. Они доступны во всех формах и размерах, в зависимости от количества заряда, которое они должны хранить в себе.
Это способность объекта накапливать заряд. По мере увеличения электрического поля между пластинами увеличивается и заряд, который может храниться между ними. Это зависит от формы, размера и расстояния между проводниками, а также от типа среды между ними. Любой объект, обладающий способностью накапливать внутри себя заряды, обладает емкостью и называется конденсатором. Конденсаторы есть почти во всех электронных устройств для простой задачи хранения зарядов. Они доступны во всех формах и размерах, в зависимости от количества заряда, которое они должны хранить в себе. Точно так же во время сбоя питания компьютеры неизбежно потеряют все важные данные или файлы из-за отсутствия конденсатора. Массив конденсаторов, находящихся в компьютере, автоматически заряжается при включении питания. В случае аварийного отключения электроэнергии конденсаторы теряют заряд через цепь , тем самым предоставляя компьютеру достаточно времени для сохранения важных файлов и данных.
Точно так же во время сбоя питания компьютеры неизбежно потеряют все важные данные или файлы из-за отсутствия конденсатора. Массив конденсаторов, находящихся в компьютере, автоматически заряжается при включении питания. В случае аварийного отключения электроэнергии конденсаторы теряют заряд через цепь , тем самым предоставляя компьютеру достаточно времени для сохранения важных файлов и данных.
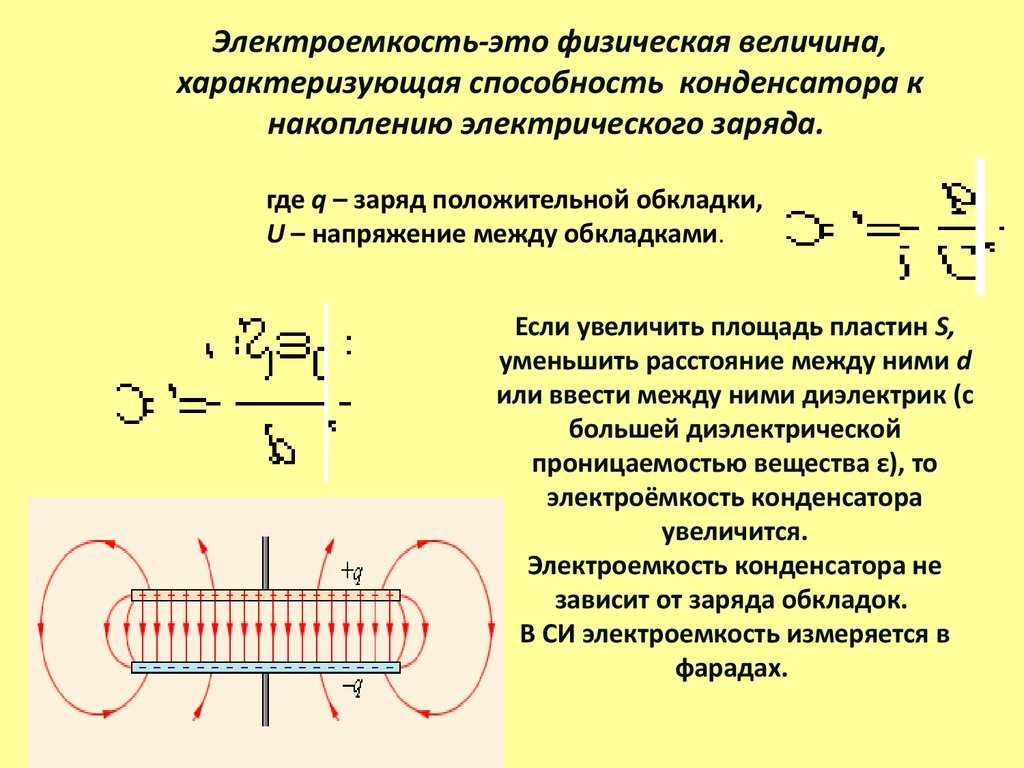
 Следовательно, когда этот конденсатор подключается к цепи, начинает течь электрический ток. Отрицательный заряд течет к положительному заряду, и таким образом заряд на конденсаторе нейтрализуется.
Следовательно, когда этот конденсатор подключается к цепи, начинает течь электрический ток. Отрицательный заряд течет к положительному заряду, и таким образом заряд на конденсаторе нейтрализуется. Более того, потенциал в каждой точке остается одним и тем же, а это означает, что между любыми двумя точками в клетке нет разности потенциалов. Поэтому человек оставался в клетке в безопасности.
Более того, потенциал в каждой точке остается одним и тем же, а это означает, что между любыми двумя точками в клетке нет разности потенциалов. Поэтому человек оставался в клетке в безопасности. Следовательно, заряд и плотность заряда остаются неизменными, когда пластины сближаются.
Следовательно, заряд и плотность заряда остаются неизменными, когда пластины сближаются.
 Какой заряд могут накопить эти пластины при подключении к батарее 8 В, если между пластинами есть воздух? (4 балла)
Какой заряд могут накопить эти пластины при подключении к батарее 8 В, если между пластинами есть воздух? (4 балла) 

 Вместо этого используются меньшие производные единицы, например, микрофарады (мкФ) и пикофарады (пФ).
Вместо этого используются меньшие производные единицы, например, микрофарады (мкФ) и пикофарады (пФ). Таким образом, этот результат является приблизительным.
Таким образом, этот результат является приблизительным.
 (Площадь менее положительная.)
(Площадь менее положительная.)
