Расчеты в электротехнике по первому закону Кирхгофа
Сложно представить любую точную науку без использования соответствующих формул. Они присутствуют в различных основополагающих правилах и канонах.
В электротехнике, которая относится к точным наукам, обязательно применяется первый закон Кирхгофа. Он необходим для проведения грамотных расчетов силы тока на всевозможных участках электрической проводки.
Что собой представляет узел, ветвь и контур
Под электроцепью понимается совокупность нескольких элементов — узлов, ветвей, а также контуров
.
Ветвь — главный элемент электрической цепи
Основным элементом электроцепи считается ветвь. На всей ее протяженности проходит тот же самый ток. Наиболее простой вариант ветви — это некоторый участок провода.
Ветвью называется также электрический прибор, который включен в розетку, и сам кабель, проведенный к данной розетке. На протяжении всей длины каждой ветви могут встречаться узлы, из которых выходят новые разветвления.
На разных участках электропровода эти ветви способны соединяться друг с другом параллельно, последовательно, в том числе образовывать узлы. При последовательном соединении получается новая ветвь, но крупных размеров.
Узел в электрической цепи
Узел — это место, в котором соединяются ветви электросхемы. В законе Кирхгофа подробно описывается прохождение, а также распределение электрического тока в ветвях, которые подключены в одному узлу.
Под узлом в электропроводке понимается подключение разного количества проводов к одной клемме или проводу, в том числе это применительно к двойной розетке либо целому блоку розеток.
Понятие контура в электросхеме
Каждая электрическая сеть имеет источник питания. Например, в электрическом фонарике батарейку и полностью контур можно увидеть, а в случае с жилым зданием системой электрообеспечения выступает трансформаторная подстанция. Причем совсем необязательно, чтобы она находилась близко. Расстояние между домом и подстанцией может составлять несколько километров.
В подобных электросетях мощность источника электрического тока в несколько раз больше мощности проводки в квартире. Исходя из этого, при составлении схемы электрической цепи опускаются значения трансформатора. Расчеты ведутся исключительно для цепи, содержащей несколько узлов.
Что входит в определение закона Кирхгофа
Данный закон, предназначенный для электроцепи, опирается на правило сохранения заряда либо электроэнергии. В соответствии с такими законами, количество электрического тока, поступающего в узел, равняется значению »электричества», выходящего из этого же узла.
На основе такого правила по электроцепи, сделаны следующие выводы:
- Алгебраическая сумма электрических токов в узлах соответствует нулевой отметке. Такой результат получается при складывании положительного значения тока (со знаком »+» ), который направлен в узел, и отрицательного значения тока (со знаком »-»), выходящим из того же узла. Данная формула с подобными расчетами используется при составлении сложных схем.

- Сумма электрических токов, входящих в узел, равняется сумме выходящих из узла токов. Если не учитывать знак величины, то это является арифметической суммой.
Внимание! В электросетях переменного тока высокой частоты наблюдаются потери. Они связаны с емкостью сети. Значение потерь нельзя определить прямыми способами. В такой ситуации кажется, что происходит нарушение первого закона Кирхгофа.
Как записывается правило Кирхгофа
Любое правило электротехники записывается в виде формулы. Первый закон Кирхгофа имеет два способа написания. В качестве образца можно представить узел с парой входящих электропроводов и токами в них — I1 и I2, а также исходящими из узла проводами — I3, I4 и I5.
Здесь следует вычисление:
- Алгебраическая сумма. Суммарное значение выводится на основе преобразования предшествующей формулы k-m=0 или I1+I2-I3-I4-I5=0. Запись получила применение при более сложных расчетах электросхем.
- Арифметическая сумма. Формула записывается как k=m или I1+I2=I3+I4+I5.
 В данном случае k — это приближающиеся к узлу линии, обозначение m — выходящие из узла провода. Предлагаемая форма записи применяется в случае, если необходимо узнать сечение токосодержащих жил для электропроводки с одной фазой либо однолинейной схемы электрообеспечения.
В данном случае k — это приближающиеся к узлу линии, обозначение m — выходящие из узла провода. Предлагаемая форма записи применяется в случае, если необходимо узнать сечение токосодержащих жил для электропроводки с одной фазой либо однолинейной схемы электрообеспечения.
Формула также подходит для определения требуемой мощности блоков электросети.
Внимание! Электрический ток, протекающий в подходящих линиях, является положительным, а в случае исходящих проводов — отрицательным.
Расчеты для трехфазной линии
Для трехфазных линий переменного тока составляется схема, в которой присутствует рабочая нейтраль. В этом случае точкой соединения фазных линий с нулем выступает узел. Здесь используется первый закон Кирхгофа, формула которого записывается в более усложненном виде.
Сложное написание формулы связано с тем, что в электросетях переменного электрического тока помимо активного проходит также другой вид тока — реактивный, емкостной либо индуктивный. Исходя из этого, ток в разнофазных электропроводах оказывается передвинут не на 120 градусов, а другую угловую меру.
Для трехфазной линии ведутся специальные расчеты — строится график с векторами. В процессе определения значения тока в нейтрали суммируется вектор, но никак не величина самого тока.
Подобный расчет имеет свои сложности, поэтому он не проводится. Взамен этому осуществляется равномерное распределение нагрузки по всем фазам с максимальной эффективностью. При этом не требуется выбора профиля нейтрального электропроводника. На практике активно применяется готовая кабельная продукция от различных брендовых компаний.
Как проводятся расчеты электроцепи на основе правила Кирхгофа
Данный закон электроцепи получил применение при определении силы тока, а также профиля электропроводов, мощности блоков питания.
Определение параметра электропроводки
По внешнему виду электропроводка и токопроводящие линии напоминают контуры дерева — это кабель с огромным сечением и силой тока расходится в узле на множество отдельных друг от друга и небольших по сечению ветвей, сравнительно маленькой силой тока.
Запись формулы выглядит таким образом: Iвх=Iвых.
Как найти значение блока питания
Известно, что большая часть электрооборудования, приборов и аппаратов работают при непосредственном их подключении к электросети переменного тока напряжением 220 В. Однако в продаже имеется немалое количество электроустановок, работающих при более низком значении напряжения. С учетом такой разницы в показателях напряжения, подобные приборы подсоединяются к блокам питания.
Закон Кирхгофа — правило, согласно которому выявляется связь между силой электрического тока во входящих и исходящих кабелях одного узла. Под электрическим током следует понимать исключительно направленное движение заряженных частиц.
В соответствии с действующим правилом о сохранении массы и энергии, сколько компонентов подходит к узлу, столько же и выходит из него. Правило Кирхгофа применяется во время расчетов профиля токосодержащих жил, в том числе мощности источника питания.
Закон кирхгофа 1 и 2.
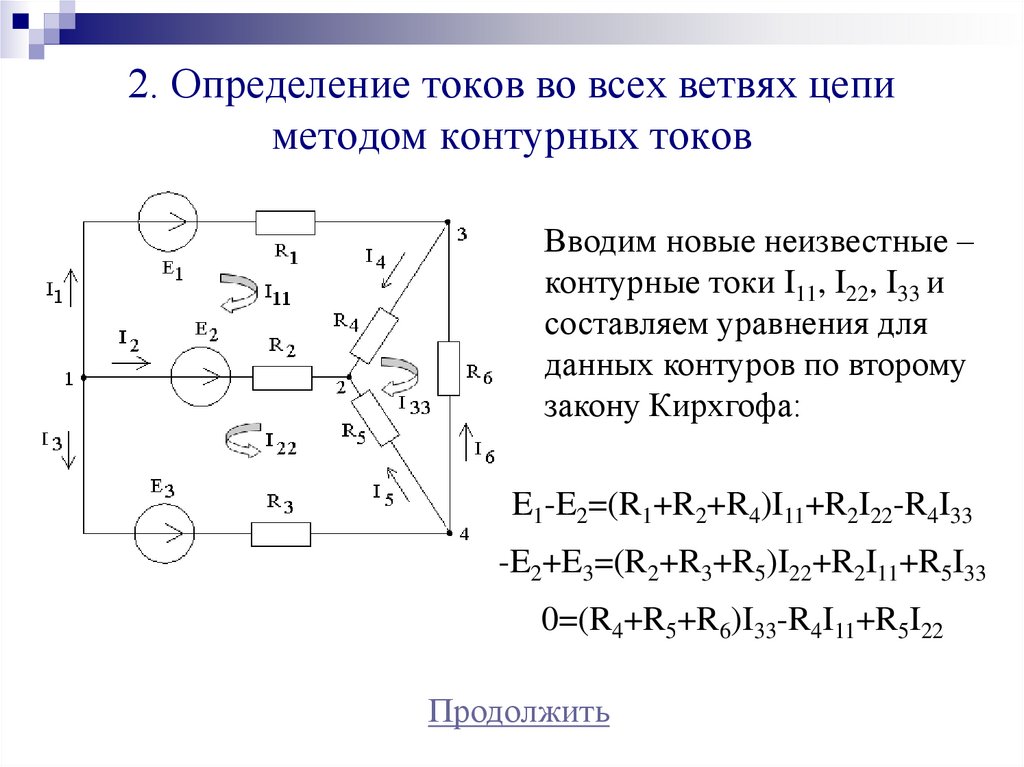 Законы Кирхгофа простыми словами: определение для электрической цепи
Законы Кирхгофа простыми словами: определение для электрической цепиИстория
Пополнил ряды немецких ученых Кирхгоф в девятнадцатом столетии, когда в стране, находившаяся на пороге революции индустриальной, требовались новейших технологии. Ученые занимались поиском решений, которые могли бы ускорить развитие промышленности.
Активно занимались исследованиями в области электричества, поскольку понимали, что в будущем оно будет широко использоваться. Проблема состояла на тот момент не в том, как составлять электрические цепи из возможных элементов, а в проведении математических вычислений. Тут и появились законы, сформулированные физиком. Они очень помогли.
Алгебраическая сумма приходящих к узлам токов и исходящих из него равна нулю. Эта одновременно вытекает из другого закона — постоянства энергии.
К узлу подходят 2 провода, а отходит один. Значение тока, текущего от узла, такое же, как сумма его, протекающего по двум остальным проводникам, т. е. идущим к нему. Правило Кирхгофа объясняет, что, при ином раскладе, накапливался бы заряд, но такого не бывает. Все знают, что всякую сложную цепь легко разделить на отдельные участки.
е. идущим к нему. Правило Кирхгофа объясняет, что, при ином раскладе, накапливался бы заряд, но такого не бывает. Все знают, что всякую сложную цепь легко разделить на отдельные участки.
Но, при этом непросто определить путь, по которому он проходит. Тем более, что на различных участках сопротивления не одинаковы, поэтому и распределение энергии не будет равномерным.
В соответствие со Вторым правилом Кирхгофа, энергия электронов на каждом из замкнутых участков электрической цепи равняется нулю – нулю равняется всегда в таком контуре суммарное значение напряжений. Если бы нарушилось данное правило, энергия электронов при прохождении определенных участков, уменьшалась бы или увеличивалась. Но, этого не наблюдается.
Соединения проводников
Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.
Резисторы и подводящие провода
Проводник, обладающий сопротивлением R, мы называем резистором и изображаем следующим образом (рис. 1):
1):
Рис. 1 Резистор
Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд q перемещается по цепи из точки a в точку b, проходя через резистор R (рис. 2):
Рис.2 U = φa – φb
Стационарное поле совершает при этом положительную работу A = q(φa − φb). Так как q > 0 и A > 0, то и φa − φb > 0, т. е. φa > φb.
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: U = φa − φb.
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если φa − φb = IR и R = 0, то φa = φb (рис. 3):
3):
Рис.3 φa = φb
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора R1 и R2, соединённых последовательно и подключённых к источнику постоянного напряжения U (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере:
- При последовательном соединении проводников сила тока в них одинакова.
 В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне. - Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике. Действительно, напряжение Uab на участке ab — это работа поля по переносу единичного заряда из точки a в точку b; напряжение Ubc на участке bc — это работа поля по переносу единичного заряда из точки b в точку c. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки a в точку c, то есть напряжение U на всём участке: U = Uab + Ubc.
Можно и более формально, без всяких словесных объяснений: U = Uac = φa − φc = (φa − φb) + (φb − φc) = Uab + Ubc.
- Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника. Пусть R — сопротивление участка ac. По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения S, но с разными длинами l1 и l2.
Сопротивления проводников равны:
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения. Доказательство этого даётся с помощью закона Ома, как показано выше. Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).
Резисторы подсоединены к двум точкам: a и b. Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от b к a (по направлению тока) называется неразветвленной частью цепи.
Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от b к a (по направлению тока) называется неразветвленной частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов:
- Напряжение на каждой ветви одинаково и равно напряжению на неразветвленной части цепи. В самом деле, оба напряжения U1 и U2 на резисторах R1 и R2 равны разности потенциалов между точками подключения:
U1 = U2 = φa − φb = U.
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
- Сила тока в неразветвленной части цепи равна сумме сил токов в каждой ветви. Пусть, например, в точку a за время t из неразветвленного участка поступает заряд q. За это же время t из точки a к резистору R1 уходит заряд q1, а к резистору R2 — заряд q2. Ясно, что q = q1 + q2. В противном случае в точке a накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем).
 Тогда имеем:
Тогда имеем:
что и требовалось.
- Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей. Пусть R — сопротивление разветвлённого участка ab. Напряжение на участке ab равно U; ток, текущий через этот участок, равен I. Поэтому:
Сокращая на U, получим:
1/R = 1/R1 + 1/R2 ,
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами l, но разными поперечными сечениями S1 и S2. Тогда это соединение можно рассматривать как проводник той же длины l, но с площадью сечения S = S1 + S2. Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти R:
R = R1R2/(R1 + R2) .
К сожалению, в общем случае n параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
1/R = 1/R1 + 1/R2 + . . . + 1/Rn .
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех n резисторов одинаковы и равны R1. Тогда:
Мы видим, что сопротивление участка из n параллельно соединённых одинаковых проводников в n раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное соединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис. 6).
Рис. 6 Смешанное соединение
Пусть U = 14 В, R1 = 2 Ом, R2 = 3 Ом, R3 = 3 Ом, R4 = 5 Ом, R5 = 2 Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков ab и bc. Сопротивление участка ab:
Сопротивление цепи: R = Rab + Rbc = 1,2 + 1,6 = 2,8 Ом.
Теперь находим силу тока в цепи:
I = U/R = 14/2,8 = 5 A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
Uab = IRab = 5 · 1,2 = 6 B;
Ubc = IRbc = 5 · 1,6 = 8 B.
(Заметим попутно, что сумма этих напряжений равна 14 В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора R1 и R2 находятся под напряжением Uab, поэтому:
Стало быть, через резистор R5 течёт ток I5 = I − I3 = 5 − 1 = 4 A
Законы Кирхгофа
Законы Кирхгофа – правила, которые показывают, как соотносятся токи и напряжения в электрических цепях. Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.
Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.
Первый закон Кирхгофа
Первый закон Кирхгофа говорит, что сумма токов в любом узле электрической цепи равна нулю. Существует и другая, аналогичная по смыслу формулировка: сумма значений токов, входящих в узел, равна сумме значений токов, выходящих из узла.
Давайте разберем сказанное более подробно. Узлом называют место соединения трех и более проводников.
Ток, который втекает в узел, обозначается стрелкой, направленной в сторону узла, а выходящий из узла ток – стрелкой, направленной в сторону от узла.
Согласно первому закону Кирхгофа
Условно присвоили знак «+» всем входящим токам, а «-» ‑ все выходящим. Хотя это не принципиально.
Хотя это не принципиально.
1 закон Кирхгофа согласуется с законом сохранения энергии, поскольку электрические заряды не могут накапливаться в узлах, поэтому, поступающие к узлу заряды покидают его.
Убедиться в справедливости 1-го закона Кирхгофа нам поможет простая схема, состоящая из источника питания, напряжением 3 В (две последовательно соединенные батарейки по 1,5 В), три резистора разного номинала: 1 кОм, 2 кОм, 3,2 кОм (можно применять резисторы любых других номиналов). Токи будем измерять мультиметром в местах, обозначенных амперметром.
Если сложить показания трех амперметров с учетом знаков, то, согласно первому закону Кирхгофа, мы должны получить ноль:
I1 – I2 – I3 = 0.
Или показания первого амперметра А1 будет равняться сумме показаний второго А2 и третьего А3 амперметров.
Второй закон Кирхгофа и его определение
В едином замкнутом контуре алгебраическая сумма ЭДС будет равняться на значение, которое суммирует изменения напряжения на всеобщее количество резистивных элементов данного контура.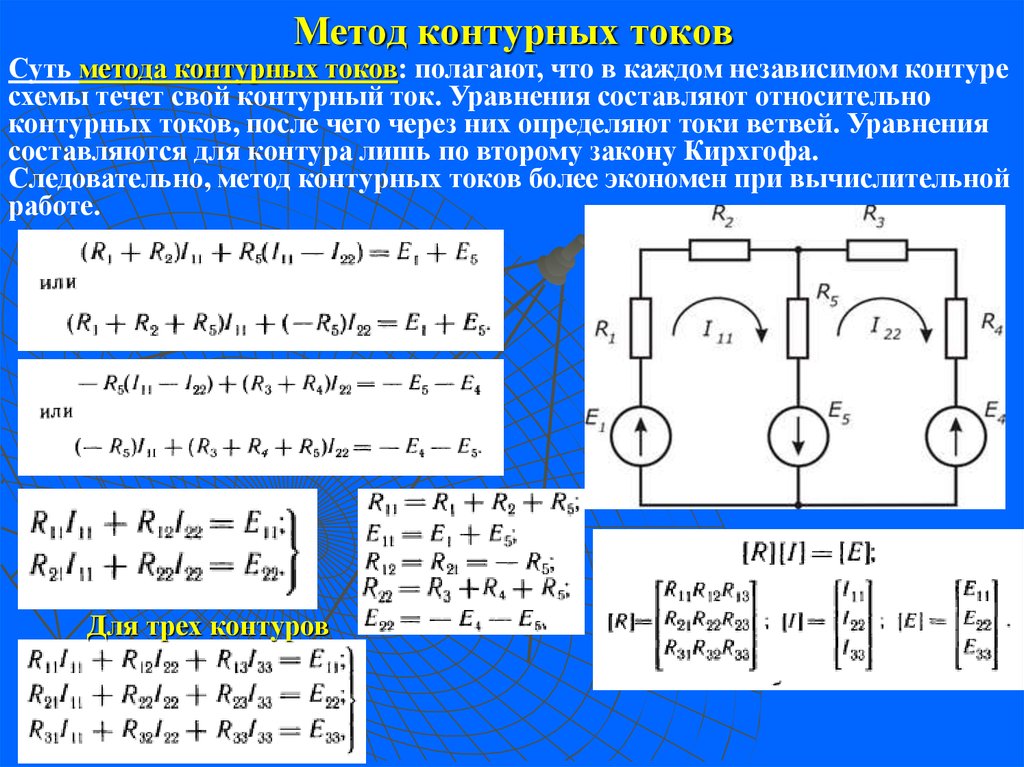
Второе правило Кирхгофа актуально в сетях с постоянным и/или переменным током. В формулировке закона используется именно понятие алгебраическая сумма, так как она может быть указана со знаком плюс или минус. Точное определение возможно в таком случае только посредством простого, но эффективного алгоритма. Для начала надо подобрать какое-то направление для обхода контура, по/против часовой стрелке, на собственное усмотрение. Само направление тока подбирается только через элементы цепи. После следует определить знаки «+» и «-» для напряжениях и ЭДС. Напряжения нужно записывать с отрицательным знаком, когда ток не соответствует обходу контура в плане направления и с плюсом в случае совпадения. То же самое правило нужно использовать и в том случае, когда необходимо отметить ЭДС.
Значение правил Кирхгофа
Законы Кирхгофа выражают фундаментальные принципы физики. Их формулировки кажутся очень простыми и очевидными. Но на самом деле они представляют собой метод, позволяющий рассчитать электрические параметры сетей очень сложной конфигурации.
С помощью законов Кирхгофа можно составить систему независимых уравнений для расчета параметров электрической цепи. Важно, чтобы их количество было не меньше, чем число параметров, которые необходимо определить.
На приведённом рисунке представлена электроцепь, для которой будет проводиться расчёт. Используя первый закон или правило Кирхгофа, для узла A можно записать:
I = I1 + I2.
В этот узел входят два тока, а выходит один. Далее необходимо применить второе правило. Для этого можно выбрать внешний контур. Видно, что здесь имеется два источника тока и два резистора. Поэтому будут получены уравнения:
Здесь приведены 2 эквивалентные формулы. В левой части равенства учтены электродвижущие силы двух источников тока, в правой — падение напряжения на обоих резисторах с учётом направления токов. Ещё одно уравнение можно получить из 2 закона при обходе по правому внутреннему контуру:
В результате получена система, включающая в себя три уравнения с тремя неизвестными:
Используя конкретные данные, можно подставить в систему уравнений численные значения и найти, чему равна сила тока для каждой ветви, относящейся к узлу A.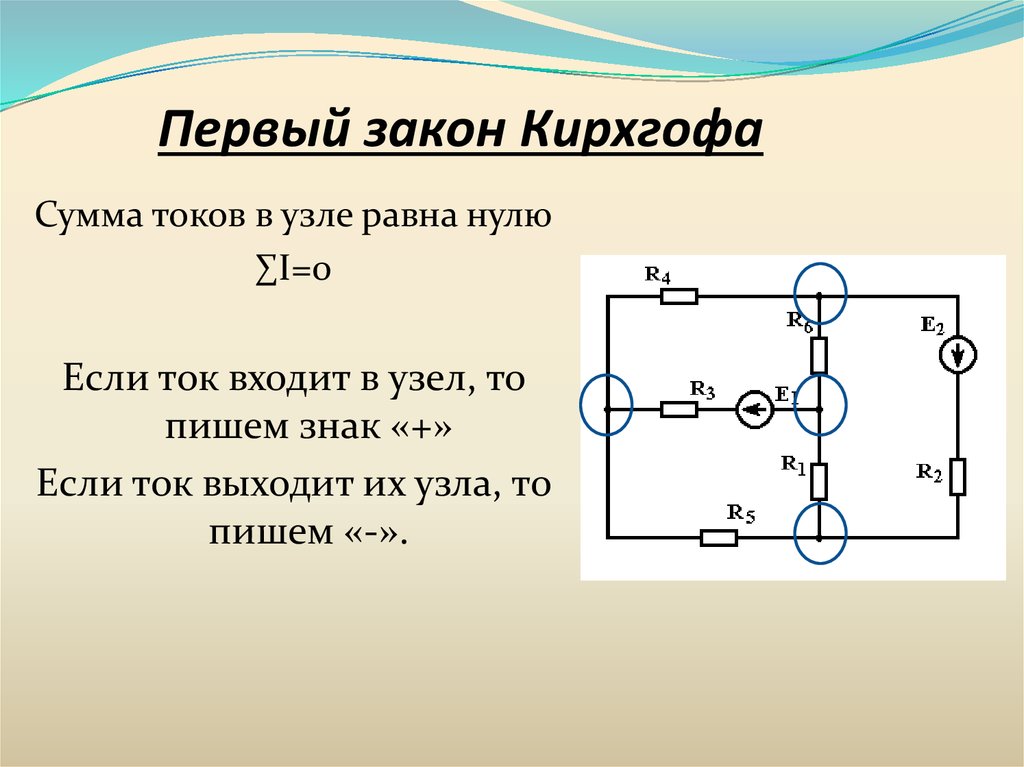 При расчётах важно понимать, что при достаточно сложной конфигурации электроцепи иногда бывает непросто определить направление силы тока для каждой ветви.
При расчётах важно понимать, что при достаточно сложной конфигурации электроцепи иногда бывает непросто определить направление силы тока для каждой ветви.
Первый и второй законы Густава Кирхгофа позволяют точно определить не только величину тока, но и его знак. Если в приведённом примере после вычисления искомых значений с помощью представленной системы уравнений окажется, что ток с индексом 2 принимает отрицательное значение, то это означает, что на самом деле он имеет направление, противоположное указанному на рисунке.
Использование закона Кирхгофа о напряжениях в сложной цепи
Закон Кирхгофа о напряжениях можно использовать для определения неизвестного напряжения в сложной цепи, где известны все другие напряжения вдоль определенного «контура». В качестве примера возьмем следующую сложную схему (на самом деле две последовательные цепи, соединенные одним проводом внизу):
Рисунок 10 – Правило напряжений Кирхгофа в сложной цепи
Чтобы упростить задачу, я опустил значения сопротивлений и просто указал падение напряжения на каждом резисторе.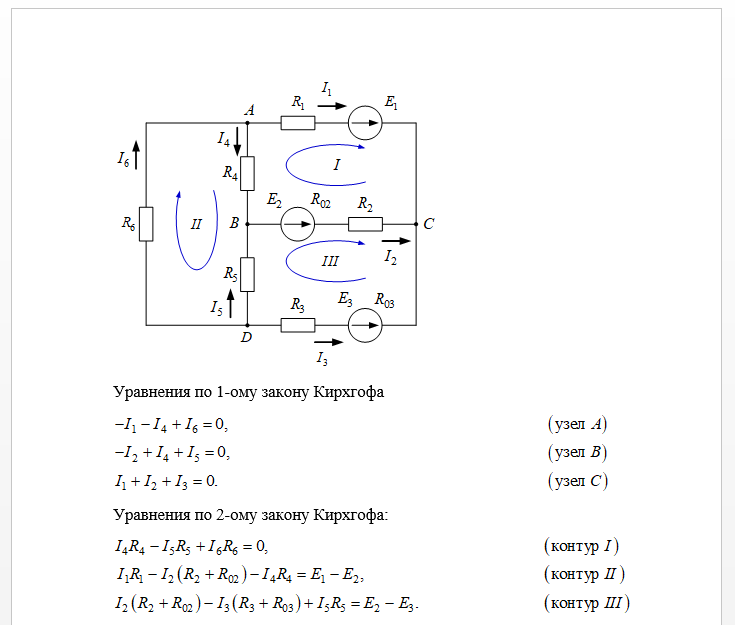 Две последовательные цепи имеют между собой общий провод (провод 7-8-9-10), что делает возможными измерения напряжения между этими двумя цепями. Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение правила напряжений Кирхгофа с напряжением между этими точками как неизвестным:
Две последовательные цепи имеют между собой общий провод (провод 7-8-9-10), что делает возможными измерения напряжения между этими двумя цепями. Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение правила напряжений Кирхгофа с напряжением между этими точками как неизвестным:
E4-3 + E9-4 + E8-9 + E3-8 = 0
E4-3 + 12 + 0 + 20 = 0
E4-3 + 32 = 0
E4-3 = -32 В
Рисунок 11 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3Рисунок 12 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 9 и 4Рисунок 13 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 8 и 9Рисунок 14 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 8
Обойдя контур 3-4-9-8-3, мы записываем значения падений напряжения так, как их регистрировал бы цифровой вольтметр, измеряя с красным измерительным проводом в точке впереди и черным измерительным проводом на точке позади, когда мы продвигаемся вперед по контуру.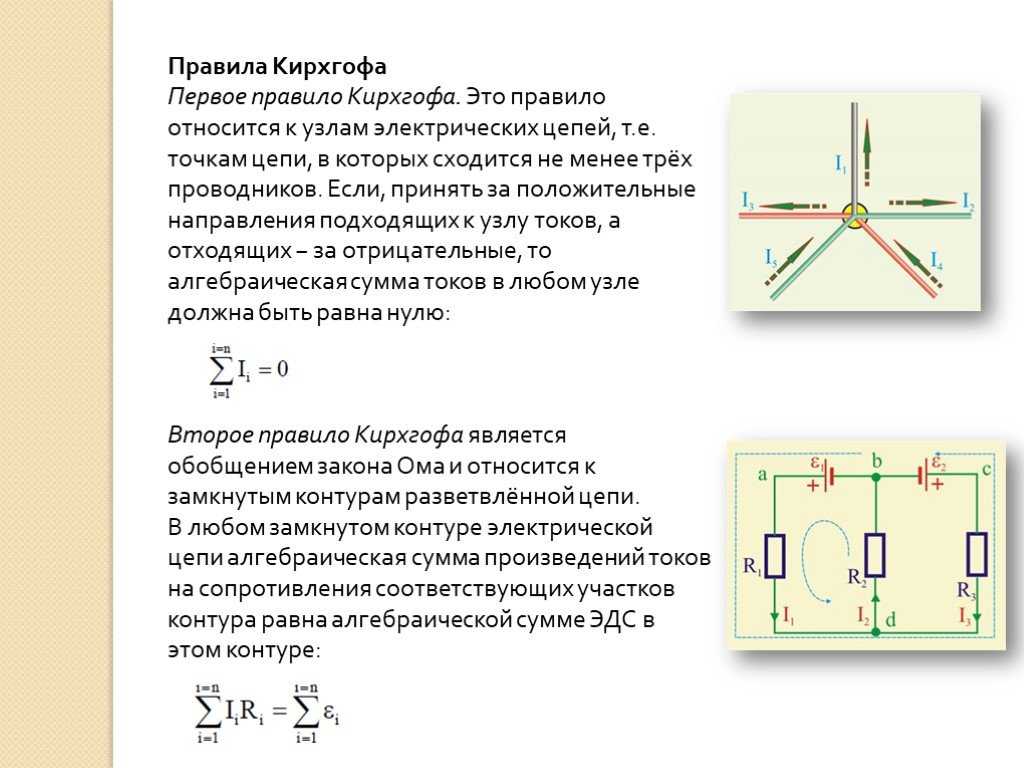 Следовательно, напряжение в точке 9 относительно точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» – в точке 4.
Следовательно, напряжение в точке 9 относительно точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» – в точке 4.
Напряжение в точке 3 относительно точки 8 составляет положительные (+) 20 вольт, потому что «красный провод» находится в точке 3, а «черный провод» – в точке 8. Напряжение в точке 8 относительно точки 9, конечно, равно нулю, потому что эти две точки электрически общие.
Наш окончательный ответ для напряжения в точке 4 относительно точки 3 – это отрицательные (-) 32 вольта, говорящие нам, что точка 3 на самом деле положительна относительно точки 4, именно это цифровой вольтметр показал бы при красном проводе в точке 4 и черном проводе в точке 3:
Рисунок 15 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3
Другими словами, первоначальное размещение наших «измерительных щупов» в этой задаче правила напряжений Кирхгофа было «обратным». Если бы мы сформировали наше уравнение второго закона Кирхгофа, начиная с E3-4, вместо E4-3, обходя тот же контур с противоположной ориентацией измерительных проводов, окончательный ответ был бы E3-4 = +32 вольта:
Рисунок 16 – Правило напряжений Кирхгофа в сложной цепи.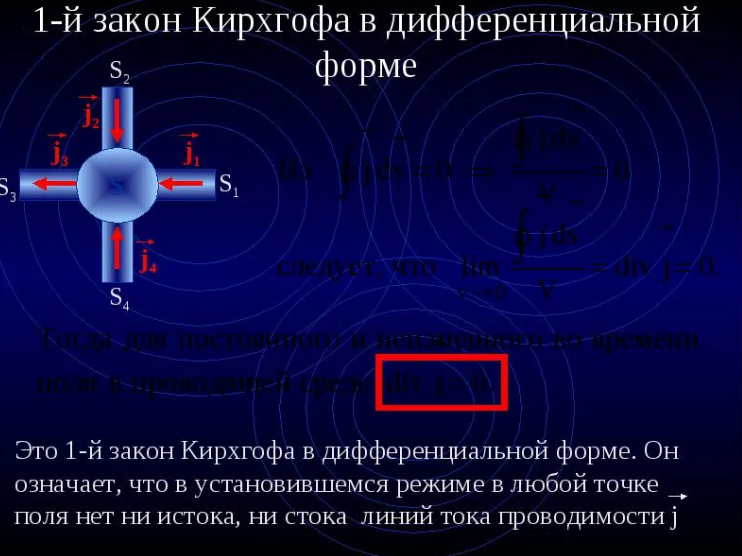 Напряжение между точками 3 и 4
Напряжение между точками 3 и 4
Важно понимать, что ни один из подходов не является «неправильным». В обоих случаях мы приходим к правильной оценке напряжения между двумя точками 3 и 4: точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта.
Правило Кирхгофа применительно к синусоидальным токам
Правила для синусоидального, такие же, как для тока постоянного. Правда, учитываются величины напряжений с комплексными токами.
Первое звучит: «в электрической цепи нулю равна сумма алгебраическая комплексных токов в узле».
Второе правило выглядит так: «алгебраическая сумма ЭДС комплексных в контуре замкнутом равняется сумме алгебраической значений комплексных напряжений, имеющихся на пассивных составляющих данного контура.
Источники
- https://motocarrello.
 ru/jelektrotehnologii/1510-zakon-kirhgofa-dlja-jelektricheskoj-cepi.html
ru/jelektrotehnologii/1510-zakon-kirhgofa-dlja-jelektricheskoj-cepi.html - http://razmishlyajem.ru/o-raznom-vsyakom/prochee/dlya-studentov/zakony-kirxgofa
- https://faultan.ru/simulation/toe/kirchhoffs_laws/
- https://Zaochnik.com/spravochnik/fizika/postojannyj-elektricheskij-tok/pravila-kirhgofa-dlja-razvetvlennyh-tsepej/
- https://diodov.net/zakony-kirhgofa-prostymi-slovami/
- https://reshit.ru/vtoroj-zakon-kirxgofa
- https://ProFazu.ru/knowledge/electrical/zakon-kirhgofa.html
- https://radioprog.ru/post/1005
Как вам статья?
Павел
Бакалавр «210400 Радиотехника» – ТУСУР. Томский государственный университет систем управления и радиоэлектроники
Написать
Пишите свои рекомендации и задавайте вопросы
Законы и правила Кирхгофа для электрических цепей в электротехнике (ТОЭ)
Применение законов Кирхгофа для расчета сложных цепей:
В предыдущих главах рассматривались простейшие схемы электрических цепей — одноконтурные схемы, цепная схема с одним источником электрической энергии и схемы с двумя узлами. Были описаны методы преобразования схем, с помощью которых в ряде случаев удается упростить расчет разветвленной электрической цепи. При этом под расчетом цепи подразумевается вычисление значений электрических величин или их отношений при заданных схеме и параметрах цепи.
Были описаны методы преобразования схем, с помощью которых в ряде случаев удается упростить расчет разветвленной электрической цепи. При этом под расчетом цепи подразумевается вычисление значений электрических величин или их отношений при заданных схеме и параметрах цепи.
В случае, когда схема электрической цепи достаточно сложна и не приводится к схеме одноконтурной цепи или цепи с двумя узлами, пользуются более общими методами расчета.
Описываемые ниже методы и теоремы применимы для цепей постоянного и переменного тока; ради общности изложения они приводятся в комплексной форме.
В общем случае искомые значения электрических величин и их соотношения могут быть найдены в результате совместного решения системы уравнений, выражающих первый и второй законы Кирхгофа для заданной электрической цепи.
Положим, что в схеме, содержащей р ветвей и q-узлов, заданными являются источники э. д. с., а искомыми — токи в ветвях. Следовательно, число неизвестных равно числу ветвей.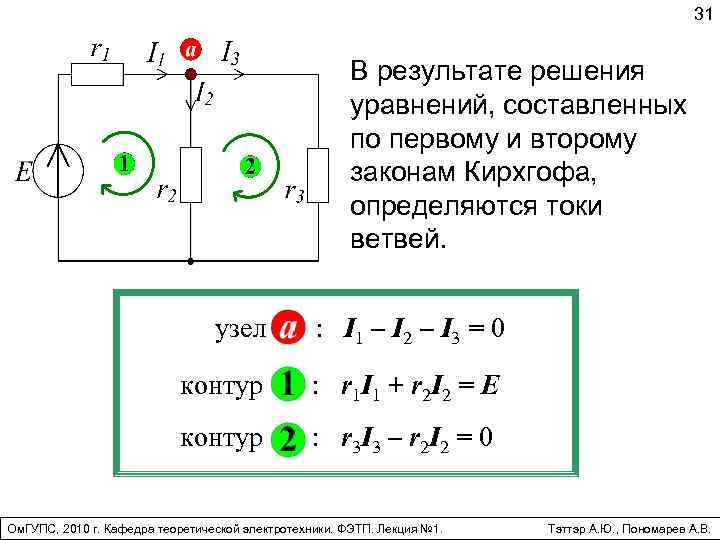
По первому закону Кирхгофа, выражающему равенство нулю алгебраической суммы токов в узле, может быть записано q — 1 независимых уравнений; уравнение для последнего, q-го, узла является следствием предыдущих q — 1 уравнений. Действительно, ввиду того, что каждая ветвь связывает два узла, ток каждой ветви входит дважды с различными знаками в уравнения, записанные для q узлов. Поэтому если просуммировать q уравнений, то получится тождество вида 0 = 0. Следовательно, одно из этих уравнений является зависимым, т. е. вытекающим из всех остальных уравнений.
Узлы, для которых записываются независимые уравнения по первому закону Кирхгофа, можно назвать независимыми узлами. Из сказанного следует, что из общего числа q узлов любые q — 1 узлов являются независимыми, а оставшийся последний узел является зависимым.
По второму закону Кирхгофа, выражающему равенство алгебраической суммы э. д. с. в контуре алгебраической сумме падений напряжения в нем, может быть записано
здесь — комплексное напряжение между узлами i и k; — комплексные э. д. с. источника и Ток в n-й ветви, направленные от узла i к узлу — комплексное сопротивление той же ветви.
д. с. источника и Ток в n-й ветви, направленные от узла i к узлу — комплексное сопротивление той же ветви.
В систему уравнений вида (7-1) входят р неизвестных токов неизвестных потенциалов и т. д. (потенциал одного из узлов принимается равным нулю). Если из имеющейся системы уравнений исключить эти неизвестные потенциалы, останется р — q + 1 уравнений, связывающих комплексные э. д. с. источников с напряжениями на комплексных сопротивлениях; полученные таким путем уравнения выражают второй закон Кирхгофа.
Итак, расчет электрической цепи с помощью первого и второго законов Кирхгофа сводится к решению уравнений — по числу ветвей.
Контуры, для которых уравнения, записанные по второму закону Кирхгофа, являются независимыми, называются независимыми контурами.
На рис, 7-1 в виде примера показана электрическая схема с числом ветвей р — 9 и числом узлов q — 6. Соответственно число уравнений по первому закону Кирхгофа равно 9 — 6 = 3 и по второму закону Кирхгофа 9 — 6 + 1 = 4. В схеме рис. 7-1 независимыми являются четыре контура. На рис. 7-1 показан один из многих возможных вариантов выбора независимых контуров.
В схеме рис. 7-1 независимыми являются четыре контура. На рис. 7-1 показан один из многих возможных вариантов выбора независимых контуров.
Для того чтобы уравнения по второму закону Кирхгофа, а следовательно, и сами контуры были независимыми, достаточно, чтобы каждый последующий контур отличался от предыдущих хотя бы одной новой ветвью. Например, если в схеме рис. 7-1 обходить контур 4 не в последнюю очередь, то каждый последующий контур будет содержать новую ветвь.
Независимый контур в отдельных случаях может не содержать новой ветви схемы, например контур 4 в схеме рис. 7-1, если обходить контуры в порядке их нумерации. При выборе независимых контуров заданную схему цепи удобно изображать в виде г р а ф а, в котором ветви представляются отрезками линий; идеальный источник э. д. с. учитывается как короткозамкнутая ветвь, а идеальный источник тока — как разомкнутая ветвь. На рис. 7-2, а показан граф схемы рис. 7-1.
Граф содержит всю информацию, относящуюся к геометрической структуре соединения ветвей.
Часть графа, содержащая все узлы, но не содержащая ни одного замкнутого контура, называется деревом графа.
Легко показать, что число ветвей дерева на единицу меньше числа узлов схемы, г. е. равно q— 1.
Ветви графа, не входящие в состав дерева, называются главными ветвями дерева или хордами. Подключение к дереву каждой из главных ветвей создает по одному независимому контуру. Совокупность главных ветвей дерева называется дополнением дерева. Так как граф содержит р ветвей, а дерево q — I, то число главных ветвей дерева равно р — (q — I) = р — q + 1, т. е. числу независимых контуров.
На рис. 7-2, б сплошными линиями показано одно из возможных деревьев графа, а пунктиром — главные ветви дерева.
Из сказанного следует способ выбора независимых контуров: чертится дерево схемы и затем поочередно добавляются главные ветви. Любой контур, образуемый добавлением новой ветви, является независимым, так как он отличается от предыдущих контуров новой ветвью. Когда к дереву добавятся все главные ветви, получится граф схемы и число независимых контуров станет достаточным для расчета цепи.
Предлагаем читателям выбрать таким способом независимые контуры в схеме рис. 7-1.
Для получения независимых контуров, достаточных для расчета цепи, можно начать и не с построения дерева, а с самого графа схемы, а затем поочередным размыканием главных ветвей дойти до дерева. В этом случае руководствуются следующим правилом: в заданной схеме выбирается какой-либо контур, размыкается одна из ветвей этого контура и в оставшейся части схемы выбирается новый контур, затем размыкается одна ветвь этого нового контура и т. д. до тех пор, пока в схеме не останется ни одного контура.
Предлагаем читателям применить для выбора независимых контуров и это правило.
Пример 7-1.. В мостовой схеме, представленной на рис. 7-3, заданы все комплекс-, ные сопротивления и э. д. с. Е. Требуется определить ток в ветви (ток в диагонали мостовой схемы).
Схема содержит четыре узла и шесть ветвей. Следовательно, могут быть составлены три уравнения по первому закону Кирхгофа и три уравнения по второму закону Кирхгофа
: для узла А
для узла В
для узла С
для контура ABDA
для контура BCDB
для контура АВС А
В полученной системе из шести уравнений неизвестными являются токи в ветвях. Решая систему уравнений относительно искомого тока, находим:
Решая систему уравнений относительно искомого тока, находим:
где
Полученное выражение показывает, что ток в диагонали равен нулю, если выполнено условие (условие равновесия мостовой схемы).
Рассмотрим применимость данного метода на примере схемы, представленной на рис. 3.1.
Рис. 3.1. Разветвленная цепь с источниками ЭДС
Для составления уравнений зададимся произвольно положительными направлениями токов в ветвях.
Уравнения по первому закону Кирхгофа:
1ый узел:
2ой узел:
4ый узел:
Если просуммировать уравнения то получим
т.е. уравнение для третьего узла. Оно является избыточным, т.к. не содержит новых токов, следовательно, по первому закону Кирхгофа составляем уз. — 1 уравнений, где уз. — число узлов схемы.
Остальные уравнения составляем по второму закону Кирхгофа, где — число независимых контуров, — число ветвей. Направления обхода контуров произвольны:
Для уменьшения объема работ по расчету схемы применяют искусственные методы расчета.
|
⇐ ПредыдущаяСтр 4 из 8Следующая ⇒ <почти полностью совпадает с 42> В основе метода волновой оптики лежат принцип Гюйгенса-Френеля. Согласно этому принципу каждый элемент dS поверхности S, до которого в момент времени t дошла волна из точки N, рассматривается как вторичный источник, излучающий элементарную сферическую ЭМВ с волновой поверхностью ΔS. Огибающая S1этих сферических волн определяет положение волновой поверхности в более поздний момент времени t . В соответствии с принципом Гюйгенса-Френеля поле в точке наблюдения М представляется как результат наложения элементарных вторичных воля, излученных элементами волновой поверхности. При сложении вторичных волн необходимо в точке наблюдения учитывать их фазу и амплитуду, величина которых зависит от угла φS. Строгую математическую формулировку принципа Гюйгенса-Френеля представляет формула Кирхгофа
n – внешняя нормаль к волновому фронту, — может быть любой составляющей ЭМП (ESили HS) на поверхности интегрирования S.
ности S неизвестны, приходится пользоваться приближенными значе- ниями. При равномерном распределении тока на раскрыве излучение будет иметь форму типа sinx/x. 44.Метод геометрической оптики. Геометрическая оптика соответствует тому случаю, когда, отвлекаясь от волнового характера поля, рассматриваются только направления лучей. Применение правил геометрической оптики в качестве приближения при решении дифракционной задачи закономерно в тех случаях, когда кривизна поверхности препятствия мала или размеры объекта дифракции значительно превышают длину волны. В силу приближенности геометрического метода полученные результаты не дают верного представления о характере волн на границе тени. В действительности эта граница не является резкой: в ее области наблюдается сложное колеблющееся распределение интенсивности поля по координате φ. Для весьма коротких волн указанная область становится пренебрежимо малой, а с удлинением волны она быстро увеличивается, видоизменяя поле во всем пространстве. Нормированная ДН рассеянного цилиндром поля в прямоугольной СК (а) и в полярной СК(б): сплошная кривая – ДН, рассчитанная строгим методом, пунктирная кривая – ДН, рассчитанная методом геометрической оптики.
45.Угол Брюстера.
Закон Брюстера — закон оптики, выражающий связь показателей преломления двух диэлектриков с таким углом падения света, при котором свет, отражённый от границы раздела диэлектриков, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения. При этом преломлённый луч частично поляризуется в плоскости падения, и его поляризация достигает наибольшего значения (но не 100 %, поскольку от границы отразится лишь часть света, поляризованного перпендикулярно к плоскости падения, а оставшаяся часть войдёт в состав преломлённого луча). Угол падения, при котором отражённый луч полностью поляризован, называется углом Брюстера.
46.Закон полного внутреннего отражения. Вну́треннее отраже́ние — явление отражения электромагнитных или звуковых волн от границы раздела двух сред при условии, что волна падает из среды, где скорость ее распространения меньше (это соответствует бо́льшему показателю преломления). Неполное внутреннее отражение — внутреннее отражение, при условии, что угол падения меньше критического угла. В этом случае луч раздваивается на преломлённый и отражённый. Полное внутреннее отражение — внутреннее отражение, при условии, что угол падения превосходит некоторый критический угол. При этом падающая волна отражается полностью. Пусть абсолютный показатель преломления первой среды больше, чем абсолютный показатель преломления второй среды , то есть первая среда оптически более плотная.
Тогда, если направить луч света из оптически более плотной среды в оптически менее плотную среду,
⇐ Предыдущая12345678Следующая ⇒ Читайте также: |
Законы теплового излучения — Теплонадзор
Приведенные ниже законы теплового излучения являются основой бесконтактного измерения температуры тепловиорами и пирометрами. Эти законы теплового излучения не применяются термографистами для расчетов в повседневной работе. Вместе с тем, на этих законах излучения основан пересчет температур в программном обеспечении тепловизоров, процедуры калибровки пирометров и тепловизоров, расчет лучистого теплообмена в строительных и промышленных объектах. Знание законов теплового излучения поможет Вам сдать экзамен при аттестации по тепловому контролю на 1 или 2 уровень. Эти законы теплового излучения довольно часто встречаются в вопросах экзаменов по тепловому контролю.
Знание законов теплового излучения поможет Вам сдать экзамен при аттестации по тепловому контролю на 1 или 2 уровень. Эти законы теплового излучения довольно часто встречаются в вопросах экзаменов по тепловому контролю.
Закон Стефана — Больцмана
Австрийский физик и математик Йозеф Стефан (Joseph Stefan) в 1879 году путём измерения теплоотдачи платиновой проволоки при различных температурах установил пропорциональность излучаемой ею энергии четвертой степени абсолютной температуры. Теоретическое обоснование этого закона было дано в 1884 году учеником Стефана Людвигом Больцманом (Ludwig Boltzmann).
Энергетическая светимость (q) абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры (T).
q = σ ⋅ T4
εКонстанта в этой формуле называется постоянной Стефана-Болъцмана, σ = 5.67⋅10-8 (Вт/м2)/К4. Энергетическая светимость — это мощность излучения на всех длинах волн с единицы поверхности (Вт/м2). Из этого следует, что все окружающие нас объекты испускают тепловое излучение, так как всегда имеют температуру выше абсолютного нуля 0 К или выше минус 273ºС. При повышении абсолютной температуры в два раза, мощность излучения увеличится в 16 раз. Но так можно говорить только про температуру в абсолютной шкале Кельвина, в градусах Цельсия температура не меняется в разы или на проценты никогда! Закон теплового излучения справедлив для абсолютно черного тела.
Из этого следует, что все окружающие нас объекты испускают тепловое излучение, так как всегда имеют температуру выше абсолютного нуля 0 К или выше минус 273ºС. При повышении абсолютной температуры в два раза, мощность излучения увеличится в 16 раз. Но так можно говорить только про температуру в абсолютной шкале Кельвина, в градусах Цельсия температура не меняется в разы или на проценты никогда! Закон теплового излучения справедлив для абсолютно черного тела.
Для перехода к реальным объектам (серым телам) необходимо умножить результат на коэффициент излучения (степень черноты) объекта ε, который всегда меньше 1. Важно отметить два момента, о которых часто забывают. Во-первых, этот закон теплового излучения говорит только об общей излучаемой энергии суммарно на всех длинах волн. Тепловизор воспринимает только часть спектра, например, для LWIR камеры рабочий участок 7-14 мкм. Сколько излучения приходится на разные участки длин волн описывается формулой Планка, о которой далее. Во-вторых, приведенная формула показывает только собственное излучение, которое испускает нагретый объект. В случае с поверхностью реального объекта (не АЧТ) к этому излучению добавится некоторое отражение окружающих объектов. Поэтому невозможно узнать фактическую температуру, настраивая только значение коэффициента излучения ε. В некоторых источниках встречается очевидно ошибочная формула для расчета фактической температуры поверхности Tфакт = Tрад / (корень 4 степени из ε).
В случае с поверхностью реального объекта (не АЧТ) к этому излучению добавится некоторое отражение окружающих объектов. Поэтому невозможно узнать фактическую температуру, настраивая только значение коэффициента излучения ε. В некоторых источниках встречается очевидно ошибочная формула для расчета фактической температуры поверхности Tфакт = Tрад / (корень 4 степени из ε).
Закон излучения Кирхгофа
Немецкий физик Густав Кирхгоф (Gustav Kirchhoff), работая работая над основами спектрального анализа, в 1859 году опубликовал статью «О связи между излучением и поглощением света и теплоты», в которой установил общее положение, «что для лучей одной и той же длины волны, при одной и той же температуре, отношение лучеиспускательной способности к поглощательной для всех тел одинаково». В более подробной работе 1861 года Кирхгоф детально и строго обосновал это положение, известное в настоящее время как закон Кирхгофа. Закон получен на основании второго начала термодинамики и затем подтвержден опытным путём.
Отношение излучательной способности (E) к поглощательной способности (A) одинаково для всех тел при данной температуре (T) для данной длины волны (λ) и не зависит от формы тела, его химического состава и проч.
E(λ,T) / A(λ,T) = e(λ,T)
Закон излучения Кирхгофа является одним из основных законов теплового излучения и не распространяется на другие виды излучения. Из закона следует — чем тело больше поглощает при температуре T на длине волны λ, тем оно больше излучает при данных температуре и длине волны. Таким образом, поверхности с высокой степенью черноты (коэффициентом излучения) хорошо поглощают падающее излучение и сами являются хорошими излучателями. Блестящие зеркальные поверхности с низким коэффициентом излучения мало излучают и плохо поглощают падающее на них излучение. Эта связь очень важна в инфракрасной термографии.
Реальные тела имеют поглощательную способность меньше единицы, а значит, и меньше чем у абсолютно чёрного тела излучательную способность. Тела, поглощательная способность которых одинакова для всех длин волн, называются «серыми телами». Их спектр имеет такой же вид, как и у абсолютно чёрного тела. В общем же случае поглощательная способность тел зависит от длины волны и температуры, и их спектр может существенно отличаться от спектра абсолютно чёрного тела. Изучение излучательной способности разных поверхностей впервые было проведено шотландским ученым Лесли при помощи его же изобретения — куба Лесли (Leslie cube).
Их спектр имеет такой же вид, как и у абсолютно чёрного тела. В общем же случае поглощательная способность тел зависит от длины волны и температуры, и их спектр может существенно отличаться от спектра абсолютно чёрного тела. Изучение излучательной способности разных поверхностей впервые было проведено шотландским ученым Лесли при помощи его же изобретения — куба Лесли (Leslie cube).
Формула Планка
Выдающийся немецкий физик Макс Планк (Max Planck), изучая тепловое излучение, открыл его атомный характер. Он рассматривал модель черного тела, представлявшую собой совокупность электромагнитных осцилляторов, излучающих и поглощающих электромагнитную энергию каждый определенной частоты. Планк принял гипотезу, что каждый осциллятор излучает и поглощает энергию конечными порциями — квантами. В 1900 году Планк доложил Берлинскому физическому обществу о своей гипотезе и новой формуле излучения.
Распределение энергии по спектру излучения описывается формулой Планка, в соответствии с которой в спектре имеется единственный максимум, положение которого определяется законом Вина. Площадь под кривой соответствует суммарной мощьности излучения по закону Стефана-Больцмана. Открытие Планка заложило основу развития квантовой физики.
Площадь под кривой соответствует суммарной мощьности излучения по закону Стефана-Больцмана. Открытие Планка заложило основу развития квантовой физики.
Закон Вина
Важные результаты в термодинамике излучения были получены немецким физиком Вильгельмом Вином (Wilhelm Wien). В 1893 году Вин на основе термодинамических соображений впервые вывел закон, определяющий положение максимума в распределении энергии в спектре излучения АЧТ. Закон показывает, как смещается максимум распределения энергии в спектре излучения абсолютно чёрного тела при изменении температуры.
Длина волны (λмакс), на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна абсолютной температуре (Т) абсолютно черного тела.
λмакс = b / T
В приведенной формуле постянная b = 2,897⋅10-3 м·К, чтобы получить результат вычисления λмакс в мкм следует взять значение b = 2897 мкм·К. Например, при температуре 36°С (309 К) максимум излучения приходится на 9,4 мкм. При температуре порядка 6000 К (темература поверхности Солнца) максимум излучения приходится на 0,47 мкм (соответствует желтовато-белому).
При температуре порядка 6000 К (темература поверхности Солнца) максимум излучения приходится на 0,47 мкм (соответствует желтовато-белому).
Законы теплового излучения Планка и Вина объясняют, почему вещество при нагреве начинает светиться в видимом спектре. Как видно из формул, при повышении температуры объекта, все больше излучения испускается с короткими длинами волн. Начиная с температуры около 500°С это излучение уже можно наблюдать невооруженным глазом. Вместе с тем, при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (например, переход белого каления в красное при остывании металла).
17.10.2012 Денис Лездин
Наверх
Search:
Leyes de Kirchhoff 🥇 1º и 2º лей, формулы и образцы
Las leyes de Kirchhoff fueron Formuladas por Gustav Kirchhoff en 1845, mientras aún era estudiante. Tanto la primera como la segunda ley de Kirchhoff son muy utilizadas en ingeniería eléctrica para obtener los valores de la corriente y el potencial en cada punto de un Circuito eléctrico. Surgen де ла aplicación де ла лей де conservación де ла energía .
Surgen де ла aplicación де ла лей де conservación де ла energía .
Индикация
Лейес де Кирхгоф
Для анализа и анализа лейес де Кирхгофа, diremos primeramente que en un Circuito eléctrico , es común que se generen nodos de 0corriente. Un nodo или nudo es el punto del Circuito Donde se unen mas de un terminal de un componente eléctrico.
Primera Ley de Kirchhoff
Se puede generalizar la Primera Ley de Kirchhoff diciendo que la suma de las corrientes entrantes a un nodo son iguales a la suma de las corrientes salientes .
Si se le asigna signos (+ y -) a las corriente del Circuito, positivo las corrientes que entran y negativo las corrientes que salen, entonces, la sumatoria de las corrientes que convergen en un nodo 900 Серо .
Ley de nodos
En un Circuito cerrado:
Σ I = 0
La razón por la cual se cumple esta ley se entiende perfectamente en forma intuitiva si uno considera que la corriente eléctrica es debida a la circulación de electrones de un punto a отро дель цепи.
Piense en una modificación de nuestro Circuito en donde los резисторы tienen un valor mucho más grande que el indicado, de modo que circule una corriente eléctrica muy pequeña , состоит из 10 электронов , состоящих из терминалов положительного заряда батареи.
Los electronices están guiados por el conductor de cobre que los lleva hacia el nodo 1 . Llegados ese punto los electronices se dan cuenta que la Resistance eléctrica hacia ambos резисторы es la misma y entonces sedividen circulando 5 por un резистор y otros 5 por el otro.
Esto es totalmente lógico porque el nodo no puede общие электроны ni retirarlos del Circuito solo puede distribuirlos y lo hase en función de la Resistance de Cada derivación.
En nuestro caso las Resistances son iguales y entonces envía la misma cantidad de electronices para cada lado. Si las Resistances fueran diferentes , podrían циркулярный tal vez 1 electron hacia una y nueve hacia la otra de acuerdo a la aplicación de la лей-де-ом .
Закон о сохранении энергии
Mascientíficamente podríamos decir, que siempre se debe cumplir una ley de la física , a la que suele denonarse Ley de la Conservación de la Energía . Esta dice que la energía no se creani se Consumer , sino que siempre se transforma.
La energía eléctrica que entrega la batería se subdivide en el nodo de modo que se transforma en iguales energías térmicas entregadas al ambiente por cada uno de los резисторы. Си лос резисторы сын iguales у están conectados а-ля неправильное напряжение, deben generar ла misma cantidad de calor y por lo tanto deben estar recorridos por la misma corriente ; que sumadas deben ser iguales a la corriente entregada por la batería, para que se cumpla la ley de conservación de la energía .
Си лос резисторы сын iguales у están conectados а-ля неправильное напряжение, deben generar ла misma cantidad de calor y por lo tanto deben estar recorridos por la misma corriente ; que sumadas deben ser iguales a la corriente entregada por la batería, para que se cumpla la ley de conservación de la energía .
En una palabra, que la energía eléctrica entregada por la batería es igual a la suma de las energías térmicas disipadas por los резисторы.
Aplicación de la Primera Ley de Kirchhoff
En la primera figura se puede observar el mas basico de los Circuitos de corriente continua (CC) que contiene dos nodos .
Обратите внимание на то, какие резисторы 1K ( R1 и R2 ) соединяются с батареей B1 .
Батарея B1 консервация на натяжение фиха и резервирование груза для сопротивления резисторов; esto significa cada резистор tiene aplicada una tensión de 9V эл.
Ла Лей-де-Ом Индикация, которая соединяется с резистором 1K для приложения напряжение 9В для циркуляции корриент 9 мА .
I = E/R = 9/1,000 = 0,009 A = 9 мА
Por lo tanto podemos asegurar que cada резистор va a tomar una corriente de 9 mA vans a o bat tomar 18 мА батареи.
También podríamos decir que desde la batería sale un conductor por el que circulan 18 мА , который соответствует узлу 1 , разделенному на один блок 9 мА , который циркулирует по резистору, по модулю соответствует узлу 2 , который подключается к унитарному ретортеру с батерией с батареей 18 мА .
Primera Ley de Kirchhoff ES decir que en el nodo 1 Podemos decir Que i1 = i2 + i3 y rememplazando valores: que 18 мА = 9 мА + 9 MA y en en el nodo 2 , И4 = И2 + И3 .
Las corriente I1 e I4 son iguales porque lo que egresa de la Batería debe ser igual a lo que ingresa.
https://www.youtube.com/watch?v=W3nK1Pf_Bh0Видео не может быть загружено, так как отключен JavaScript: LEY DE KIRCHOF (https://www.youtube.com/watch?v=W3nK1Pf_Bh0)
Segunda Лей де Кирхгоф
La aplicación de la segunda Лей де Кирхгоф (Густав Кирхгоф 1824-1887) se utiliza cuando un Circuito posee mas de una batería г различные резисторы де карга. En este caso, ya no resulta tan claro como se establecen la corriente por el mismo. En ese caso es de aplicación de esta ley la que nos Allowe Resolver el Circuito con una gran claridad.
Ley de mallas
En un Circuito cerrado:
Σ I * R = 00004 .
Aplicación de la Segunda Ley de Kirchhoff
En la siguiente figura se puede observar un circuito con dos baterías que nos permitirá resolver un ejemplo de aplicación .
Обратите внимание на цепь dos baterías y dos резисторы . Nosotros deseamos saber cual es la tensión de cada punto (или el potencial), con referencia al терминал negativo де B1 al Que le colocamos un símbolo que представляет a una conexión a nuestro planeta y al que llamamos tierra o masa .
Esto es porque podemos al Planeta Tierra como un inmenso conductor de la electricidad .
Лас напряжения де фуэнте , простой сын лас индикации en эль цепи , pero si заявитель aplicar лас caídas де потенциал en lo резисторы , debemos determinar primero cual es la corriente que circula por aquel.
Para determinar la corriente , primero debemos determinar cuál es latension de todas nuestras fuentes sumadas .
Обратите внимание, что dos fuentes están conectadas de modos que sus terminales positivos están galvanicamente conectados entre si por el резистор R1 . Esto significa que la натяжение всего нет es la suma de ambas fuentes sino la resta .
Con ссылка на батарею , батарея B1 повышенный потенциал на 10V для батареи B2 для уменьшения на 1V . Entonces, la fuente que hace circiente es en total de 10 – 1 = 9V .
Los electronices que circulan por ejemplo saliendo de B1 y pasando por R1 , luego pierden potencial en B2 г атрависан R2 . Para calcular la corriente circulante podemos agrupar entonces a los dos резисторы y a las dos fuentes tal como lo indica la siguiente figura.
¿Los dos Circuitos anteriores son iguales?
Нет, este reagrupamiento solo se genera para calcular la corriente del Circuito original.
De acuerdo nuevamente a la Лей де Ом :
I = E / R1 + R2PORQUE LOS ELECTRONES QUE SALEN DE R1 DEBEN PASAR FORZOSAMENTE POR R2 Y ENTONCES ES COMO SI ESSECTIE R1 + R2 = 1100 .
Se dice que los резисторы están conectados en serie cuando están conectados de este modo . De Forma tal que ambos son attravesados por la misma corriente igual a:
I = (10 – 1) / 1000 + 100 = 0,00817 o 8,17 мА.
Cálculo del Circuito Resultsante
Ahora que sabemos cual es la corriente que atraviesa el Circuito podemos calcular la tensión sobre cada резистор .
Выражение лей ома (I = E/R), которое может быть определено как E = R . I y de este modo reemplazando valores se puede obtener que la caída sobre R2 es igual a ER2 = R2. я = 100 . 8,17 мА = 817 мВ с ошибкой ER1 = R1. я = 1000 . 8,17 мА = 8,17 В.
Estos valores recién calculados de caídas detensión pueden ubicarse sobre el Circuito original con el fin de calcular la tensión deseada .
Circuito resulto con la Segunda Ley de Kirchhoff
Circuito resueltoObservando las cuatro flechas de las tensiones de fuente y de las caídas de tensión se puede verificar el cumplimiento de la segunda Ley de Kirchhoff . Ya que comenzando desde la masa de referencia y girando en el sentido de las agujas del reloj podemos decir que:
10 В — 8 17 В — 1 В — 0,817 = 0V
O, реализация Una Transposición de Términos Y Dejando las Fuentes a la derecha y las caídase de tensióna a la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la la derecha d de las voltages de fuente 10V – 1V es igual a la suma de las caídas detension o diferencias de potencial 8,17V + 0,817 = 8,987 приблизительно 9V.
Y además podemos calcular fácilmente que la tensión sobre la salida del Circuito es de 0,817V + 1V = 1,817V con la polaridad indicada en el chaino es decir positiva .
Conclusión
Las dos leyes de Kirchhoff son igualdades que se basan en el principio de la conservación de la energía y la carga en los Circuitos elpunéctricos, y como dijimos al comientos coquiientes coquiientes Hallar izadas de un Circuito Electrico. Ambas leyes de Circuitos pueden derivarse directamente de las ecuaciones de Maxwell, pero Kirchhoff lo hizo primero. Грасиас Георг Ом су trabajo fue generalizado у Actualmente сын ampliamente utilizadas tanto en electricidad como en electronica.
Формула Кирхгофа во временной области для уравнения конвективных акустических волн
. 2016 март; 472 (2187): 20150689.
doi: 10. 1098/rspa.2015.0689.
1098/rspa.2015.0689.
Гадер Горбаниас 1 , Леонидас Сиозос-Русулис 2 , Крис Лакор 2
Принадлежности
- 1 Свободный университет Брюсселя (VUB), Pleinlaan 2, Брюссель 1050, Бельгия; Тегеранский университет, Тегеран, Иран.
- 2 Свободный университет Брюсселя (VUB), Pleinlaan 2, Брюссель 1050, Бельгия.
- PMID: 27118912
- PMCID: PMC4841478
- DOI:
10.
 1098/rspa.2015.0689
1098/rspa.2015.0689
Гадер Горбаниасл и др. Proc Math Phys Eng Sci. 2016 март
. 2016 март; 472 (2187): 20150689.
doi: 10.1098/rspa.2015.0689.
Авторы
Гадер Горбаниас 1 , Леонидас Сиозос-Русулис 2 , Крис Лакор 2
Принадлежности
- 1 Свободный университет Брюсселя (VUB), Pleinlaan 2, Брюссель 1050, Бельгия; Тегеранский университет, Тегеран, Иран.
- 2 Свободный университет Брюсселя (VUB), Pleinlaan 2, Брюссель 1050, Бельгия.

- PMID: 27118912
- PMCID: PMC4841478
- DOI: 10.1098/rspa.2015.0689
Абстрактный
Интегральный метод Кирхгофа позволяет прогнозировать распространение звука на основе давления и его производных во времени и пространстве, полученных на поверхности данных, расположенной в области линейного потока. Формула Кирхгофа для прогнозирования шума от высокоскоростных роторов и гребных винтов страдает ограничением наблюдателя, находящегося в однородном потоке, что требует расширения для произвольно движущихся сред. В данной работе представлена формулировка Кирхгофа для движущихся поверхностей в однородной движущейся среде произвольной конфигурации.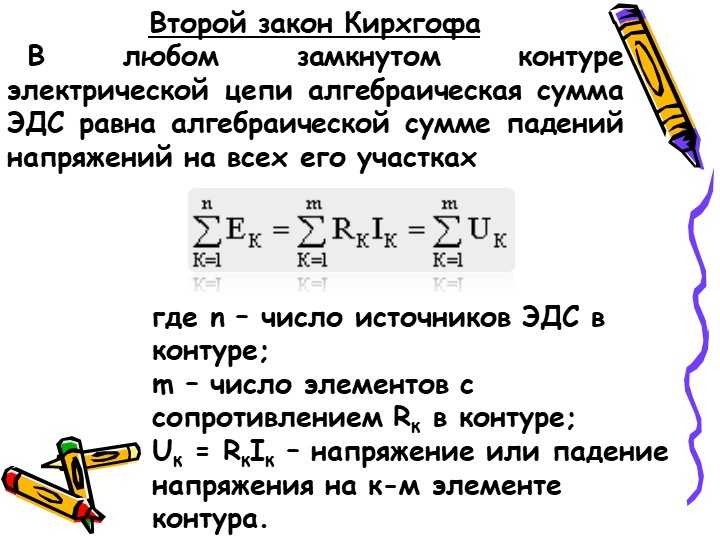 Во-первых, уравнение конвективной волны выводится в подвижной системе отсчета на основе теории обобщенных функций. Затем получается формула Кирхгофа для движущихся поверхностей во временной области. Формула имеет вид, аналогичный формуле Кирхгофа для движущихся поверхностей Фарассата и Майерса, с наличием дополнительных членов из-за эффекта движущейся среды. Уравнение явно учитывает влияние среднего потока и угла атаки на излучаемый шум. Формула проверена аналитическими случаями монопольного источника, находящегося в движущейся среде.
Во-первых, уравнение конвективной волны выводится в подвижной системе отсчета на основе теории обобщенных функций. Затем получается формула Кирхгофа для движущихся поверхностей во временной области. Формула имеет вид, аналогичный формуле Кирхгофа для движущихся поверхностей Фарассата и Майерса, с наличием дополнительных членов из-за эффекта движущейся среды. Уравнение явно учитывает влияние среднего потока и угла атаки на излучаемый шум. Формула проверена аналитическими случаями монопольного источника, находящегося в движущейся среде.
Ключевые слова: формула Кирхгофа; аэроакустика; конвективное волновое уравнение; подвижная среда.
Цифры
Рисунок 1.
Схема данных Кирхгофа…
Рисунок 1.
Схема поверхности данных Кирхгофа во время т .
Фигура 1.Схема поверхности данных Кирхгофа во время t .
Рисунок 2.
Схема сферического Кирхгофа…
Рисунок 2.
Схема сферической поверхности данных Кирхгофа в x − и самолет.
Фигура 2.Схема сферической поверхности данных Кирхгофа в плоскости x − y .
Рисунок 3.
Расчетное акустическое давление…
Рисунок 3.
Расчетное акустическое давление идентично аналитическому решению для трех…
Рисунок 3.The calculated acoustic pressure is identical to the analytical solution for the three observer positions of ( a ) α 1 , ( b ) α 2 and ( c ) α 3 , при среднем числе Маха потока M∞=0,2. (Онлайн-версия в цвете.)
Рис. 4.
Расчетное акустическое давление…
Рисунок 4.
Расчетное акустическое давление идентично аналитическому решению для трех наблюдателей…
Рисунок 4. Расчетное акустическое давление идентично аналитическому решению для трех позиций наблюдателя ( a ) α 1 , ( b ) α 2 и ( c ) α 3 , при среднем числе Маха потока M∞=0,8.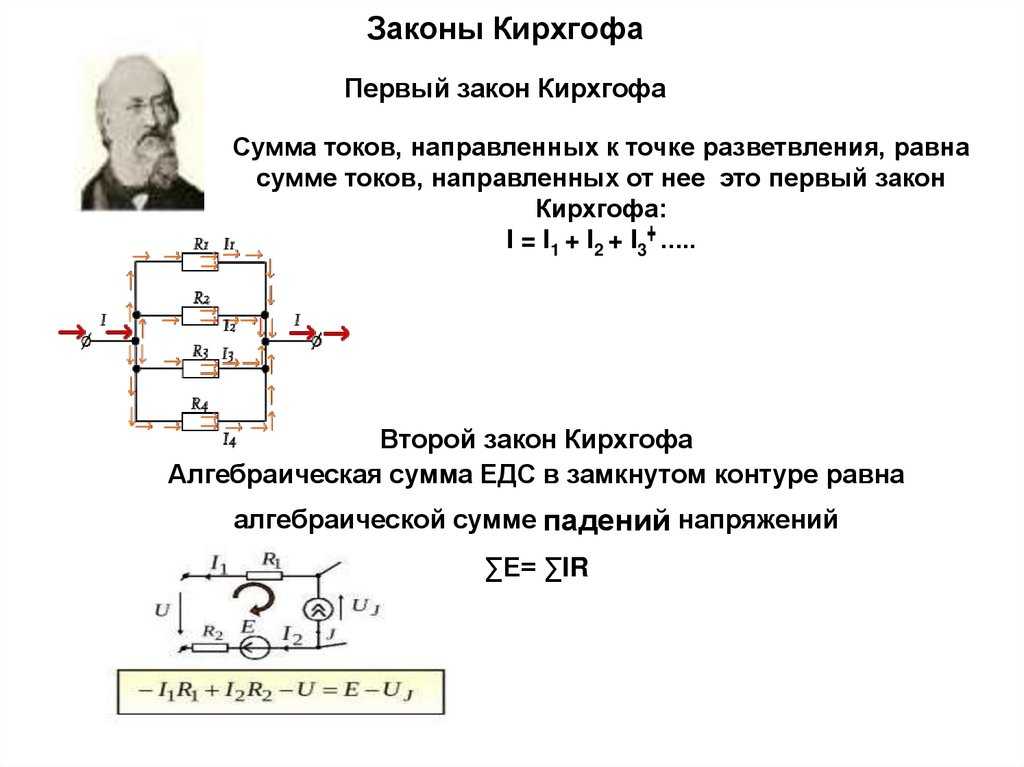 (Онлайн-версия в цвете.)
(Онлайн-версия в цвете.)
Рисунок 5.
Расчетная направленность…
Рисунок 5.
Расчетная направленность акустического давления идентична аналитическому решению…
Рисунок 5.Расчетная направленность акустического давления идентична аналитическому решению для 36 наблюдателей, равномерно распределенных по окружности радиусом 10 м от начала координат, при среднем числе Маха потока M∞=0,2. (Онлайн-версия в цвете.)
Рисунок 6.
Расчетная направленность…
Рисунок 6.
Расчетная направленность акустического давления идентична аналитическому решению…
Рисунок 6.
Расчетная направленность акустического давления идентична аналитическому решению для 36 наблюдателей, равномерно распределенных по окружности радиусом 10 м от начала координат, при среднем числе Маха потока M∞=0,8. (Онлайн-версия в цвете.)
Рисунок 7.
Расчетное акустическое давление…
Рисунок 7.
Расчетное акустическое давление идентично значению, полученному от Фарассата и Майерса…
Рисунок 7. Расчетное акустическое давление идентично полученному по формуле Фарассата и Майерса [20] с использованием метода движущегося наблюдателя для трех положений наблюдателя ( a ) α 1 , ( b ) α 2 и ( c ) α 9 3 . Поверхность данных находится в движении при M =(0,2,0,0) и находится в среднем потоке M∞=0,2. (Онлайн-версия в цвете.)
Поверхность данных находится в движении при M =(0,2,0,0) и находится в среднем потоке M∞=0,2. (Онлайн-версия в цвете.)
Рисунок 8.
Расчетная направленность…
Рис. 8.
Расчетная направленность акустического давления идентична полученному решению…
Рисунок 8.Расчетная направленность акустического давления идентична решению, полученному по формуле Фарассата и Майерса [20] для 36 наблюдателей, равномерно распределенных по окружности радиусом 10 м от начала координат. Поверхность данных находится в движении при M =(0,2,0,0) и находится в среднем потоке M∞=0,2. (Онлайн-версия в цвете.)
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Вывод и реализация граничной интегральной формулы для уравнения конвективных акустических волн во временной области.

Ли Ю.В., Ли Д.Дж. Ли Ю.В. и др. J Acoust Soc Am. 2014 декабрь; 136 (6): 2959. дои: 10.1121/1.4898427. J Acoust Soc Am. 2014. PMID: 25480045
Метод временной области для прогнозирования шума, излучаемого сверхзвуковыми вращающимися источниками в движущейся среде.
Хуанг З., Сиозос-Русулис Л., Де Тройер Т., Горбаниасль Г. Хуан Цзи и др. Proc Math Phys Eng Sci. 2018 Февраль;474(2210):20170089. doi: 10.1098/rspa.2017.0089. Epub 2018 14 февраля. Proc Math Phys Eng Sci. 2018. PMID: 29507507 Бесплатная статья ЧВК.
Неинтрузивная плоская акустическая голография ближнего поля, основанная на скорости, в движущейся жидкой среде.
Паризо-Дюпюи Х., Симон Ф., Пио Э., Мишели Ф. Паризо-Дюпюи Х.
 и др.
J Acoust Soc Am. 2013 г., июнь; 133(6):4087-97. дои: 10.1121/1.4802643.
J Acoust Soc Am. 2013.
PMID: 23742361
и др.
J Acoust Soc Am. 2013 г., июнь; 133(6):4087-97. дои: 10.1121/1.4802643.
J Acoust Soc Am. 2013.
PMID: 23742361Эффективные методы прогнозирования волны микродавления от высокоскоростного поезда, въезжающего в туннель, с использованием формулировки Кирхгофа.
Юн Т, Ли С. Юн Т и др. J Acoust Soc Am. 2001 ноябрь; 110 (5 часть 1): 2379-89. дои: 10.1121/1.1409374. J Acoust Soc Am. 2001. PMID: 11757928
Обзор применения Законов рядов и параллельных потоков Кирхгофа в фармакологии: определение клиренса органов.
Пахтер Дж.А., Дилл К.А., Содхи Дж.К., Бенет Л.З. Пачтер Дж.А. и соавт. Фармакол Тер. 2022, 6 сентября; 239:108278. doi: 10.1016/j.pharmthera.2022.108278. Онлайн перед печатью. Фармакол Тер.
 2022.
PMID: 36075300
Обзор.
2022.
PMID: 36075300
Обзор.
Посмотреть все похожие статьи
Детерминант Кирхгофа и формулы дерева цепей Маркова – Libres pensées d’un mathématicien ordinaire
Густав Роберт Кирхгоф (1824 – 1887)Этот пост посвящен формуле Густава Кирхгофа, выражающей инвариантную меру неприводимой конечной цепи Маркова через пролетные деревья. Многие из нас уже встречали имя Густава Кирхгофа на уроках физики при изучении электричества. 9{tQ}\right)_{i,j}. \]
Недиагональные элементы \( {Q} \) неотрицательны, а строки \( {Q} \) имеют нулевую сумму:
\[ \forall i,j\in V, \ quad i\neq j, \quad Q_{i,j}\geq0, \quad Q_{i,i}=-\sum_{k\neq i}Q_{i,k}. \]
Скелетный граф \( {G=(V,E)} \) of \( {Q} \) является ориентированным графом , определенным
\[ (i,j)\in E \quad\mathrm{iff}\quad Q_{i,j}>0. \]
Предположим, что \( {Q} \) является неприводимым , что означает, что \( {G} \) равно 9{(i,i)})=\sum_{T\in\mathcal{T}_i}\prod_{(j,k)\in T}Q_{j,k} \]
, где сумма пробегает набор \( {\mathcal{T}_i} \) остовных деревьев \({G} \) с корнем в \({i} \). Напомним, что остовное дерево или покрывающее дерево из \( {G} \) с корнем \( {i\in V} \) является подграфом \( {G} \) с набором ребер \( {V} \), которое является деревом с корнем \( {i} \). Обратите внимание, что \( {\mathcal{T}_i} \) непусто, так как \({G} \) связно. Обратите внимание, что \( {\mathcal{T}_1,\ldots,\mathcal{T}_n} \) не обязательно имеют один и тот же кардинал из-за того, что ребра ориентированы: дерево покрытия с корнем в \( {i } \) содержит любой \( {j} \) как вершину, но не обязательно как возможный корень из-за стрелок. 9{(i,s)})\neq0} \).
Напомним, что остовное дерево или покрывающее дерево из \( {G} \) с корнем \( {i\in V} \) является подграфом \( {G} \) с набором ребер \( {V} \), которое является деревом с корнем \( {i} \). Обратите внимание, что \( {\mathcal{T}_i} \) непусто, так как \({G} \) связно. Обратите внимание, что \( {\mathcal{T}_1,\ldots,\mathcal{T}_n} \) не обязательно имеют один и тот же кардинал из-за того, что ребра ориентированы: дерево покрытия с корнем в \( {i } \) содержит любой \( {j} \) как вершину, но не обязательно как возможный корень из-за стрелок. 9{(i,s)})\neq0} \).
Случайное блуждание. Предположим теперь, что \( {Q_{i,j}\in\{0,1\}} \) для каждого \( {i,j\in V} \) с \( {i\neq j} \) . Тогда \( {X} \) — это ближайшие соседи случайных блужданий на \( {G} \), диагональ \( {-Q} \) образована последовательностью степеней из \( {G} \), а \( {Q} \) — это лапласиан \( {\Delta_G} \) из \({G} \). В этом случае \( {Q_{j,k}=1} \) для каждого \( {(j,k)\in G} \) и, таким образом, формула Кирхгофа выше сводится к
\[ \forall i\in V,\quad \mu_i=|\mathcal{T}_i|. \]
\]
Предположим теперь, что \( {Q} \) дополнительно симметрично , что означает, что \( {G} \) не ориентировано в том смысле, что \( {(j,k)\in E} \) тогда и только тогда, когда \( {(k,j)\in E} \). В этом случае инвариантной вероятностной мерой \({Q}\) будет тогда равномерный закон на \({V}\). Из-за отсутствия ориентации множества \( {\mathcal{T}_1,\ldots,\mathcal{T}_n} \) имеют один и тот же кардинал \( {\kappa} \), который является числом остовных деревья \( {G} \) (без укоренения). У нас есть 9{(i,j)}) =|\mathcal{T}|_i=\каппа. \]
Другими словами, матрица кофакторов лапласиана неориентированного графа имеет постоянные элементы, равные количеству остовных деревьев графа.
Соединим \( {\kappa} \) с собственными значениями симметричной матрицы \( {-Q} \), пронумерованными как
\[ 0=\lambda_1<\lambda_2\leq\cdots\leq \ лямбда_н. \]
Здесь \( {\lambda_1} \) просто, так как \( {Q} \) неприводимо. Характеристический многочлен \( {-Q} \) равен 9{n-2}} \).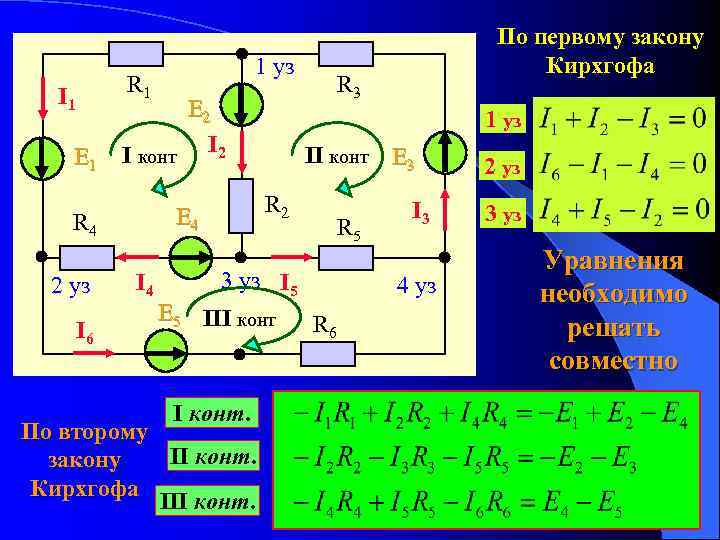
Алгоритм Вильсона. Дэвид Уилсон изобрел точный алгоритм для создания остовного дерева \( {G} \), которое следует равномерному распределению на множестве остовных деревьев \( {G} \). Начиная с вершины \( {1} \), алгоритм состоит в установке \( {A_1=\{1\}} \) и моделировании пути простого случайного блуждания по \( {G} \), начиная с вершине \( {2} \) до тех пор, пока она не достигнет \( {A_1} \). Тогда \( {A_2} \) является объединением \( {A_1} \) и версии этого пути со стертым циклом. Если \( {A_2=V} \), алгоритм останавливается. Если нет, то повторяем то же самое, начиная на этот раз путь из наименьшей вершины не в \({A_2}\), останавливая путь, когда он достигает \({A_2}\), и так далее. Алгоритм Уилсона можно естественным образом связать с функцией Грина случайного блуждания на \({G}\) с граничными условиями Дирихле на подмножестве \({V}\). 9{kQ}\right)_{i,j}. \]
Дополнительная литература.
- Лайонс и Перес, Вероятность на деревьях и сетях (глава 4)
- Лейтон и Ривест, Оценка вероятности с использованием конечной памяти
- Анантарам и Цукас, Доказательство теоремы дерева цепи Маркова конечные цепи Маркова
- Биан и Чапюи, Матрицы Лапласа и остовные деревья древовидных графов
- Розенталь – Примечание о формуле Кирхгофа и алгоритме Уилсона
- Harris and Hirst and Mossinghoff, Комбинаторика и теория графов
Стационарные уравнения Кирхгофа и системы с членами реакции
В этой статье операторный подход, основанный на принципах неподвижной точки Банаха и Шефера, используется для установления существования решений к стационарным уравнениям Кирхгофа с членами реакции. Затем для связанной системы уравнений Кирхгофа доказывается, что при соответствующих предположениях существует единственное решение, которое является равновесием по Нэшу относительно функционалов энергии, связанных с уравнениями системы. Устанавливаются как глобальное равновесие Нэша во всем пространстве, так и локальное равновесие Нэша в шарах. Решение получено с помощью итеративного процесса, основанного на вариационном принципе Экланда и развитие которого имитирует некооперативную игру.
Затем для связанной системы уравнений Кирхгофа доказывается, что при соответствующих предположениях существует единственное решение, которое является равновесием по Нэшу относительно функционалов энергии, связанных с уравнениями системы. Устанавливаются как глобальное равновесие Нэша во всем пространстве, так и локальное равновесие Нэша в шарах. Решение получено с помощью итеративного процесса, основанного на вариационном принципе Экланда и развитие которого имитирует некооперативную игру.
| [1] | Г. Кирхгоф, Vorlesungen über Mechanik , Лейпциг: Teubner, 1883. |
| [2] | Г. Аутуори, П. Пуччи, М. К. Сальватори, Глобальное небытие для нелинейных систем Кирхгофа, Arch. Рациональный мех. Анальный. , 196 (2010), 489–516. https://doi.org/10.1007/s00205-009-0241-x doi: 10.1007/s00205-009-0241-x |
| [3] | М. Дреер, Уравнение Кирхгофа для p -лапласиана, Rend. Сем. Мат. ун-т пол. Турин , 64 (2006), 217–238. Сем. Мат. ун-т пол. Турин , 64 (2006), 217–238. |
| [4] | Дж. Л. Лайонс, О некоторых вопросах краевых задач математической физики, North-Holland Mathematics Studies , 30 (1978), 284–346. https://doi.org/10.1016/S0304-0208(08)70870-3 doi: 10.1016/S0304-0208(08)70870-3 |
| [5] | Т. Ф. Ма, Замечания об эллиптическом уравнении типа Кирхгофа, Nonlinear Anal. Теор. , 63 (2005 г.), e1967-e1977. https://doi.org/10.1016/j.na.2005.03.021 doi: 10.1016/j.na.2005.03.021 |
| [6] | Т. Ф. Ма, Дж. Э. Муньос Ривера, Положительные решения нелинейной нелокальной эллиптической задачи передачи, Заявл. Мат. лат. , 16 (2003), 243–248. https://doi.org/10.1016/S0893-9659(03)80038-1 doi: 10.1016/S0893-9659(03)80038-1 |
| [7] | С. И. Похожаев, Квазилинейное гиперболическое уравнение Кирхгофа, Дифференц.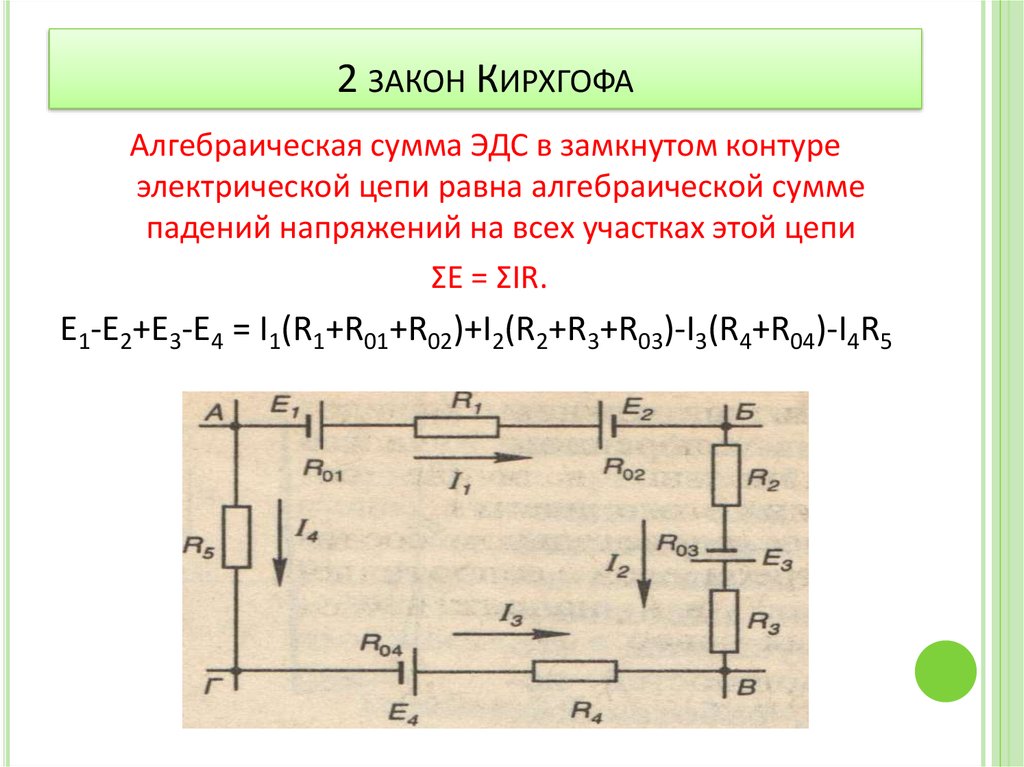 Уравн. , 21 (1985), 101–108. Уравн. , 21 (1985), 101–108. |
| [8] | К. Ф. Васконселлос, О нелинейной стационарной задаче в неограниченных областях, Revista Maemática de la Universidad Complutense de Madrid , 5 (1992), 309–318. |
| [9] | К. О. Алвес, Ф. Дж. С. А. Корреа, Т. Ф. Ма, Положительные решения для квазилинейного эллиптического уравнения типа Кирхгофа, Вычисл. Мат. заявл. , 49 (2005), 85–93. https://doi.org/10.1016/j.camwa.2005.01.008 doi: 10.1016/j.camwa.2005.01.008 |
| [10] | Г. Че, Х. Чен, Бесконечное множество решений систем уравнений типа Кирхгофа с общими потенциалами, Rocky Mountain J. Math. , 48 (2018), 2187–2209. https://doi.org/10.1216/RMJ-2018-48-7-2187 doi: 10.1216/RMJ-2018-48-7-2187 |
| [11] | П. Чен, X. Лю, Положительные решения уравнения Кирхгофа во внешних областях, J. Math. физ. , 62 (2021), 041510. https://doi.org/10.1063/5.0014373 doi: 10.1063/5.0014373 Math. физ. , 62 (2021), 041510. https://doi.org/10.1063/5.0014373 doi: 10.1063/5.0014373 |
| [12] | М. Шипот, В. Валенте, Г. В. Каффарелли, Замечания к нелокальной проблеме, связанной с энергией Дирихле, Rendiconti del Seminario Matematico della Università di Padova , 110 (2003), 199–220. |
| [13] | Н. Т. Чанг, Результат существования класса систем типа Кирхгофа с помощью метода под- и сверхрешений, Appl. Мат. лат. , 35 (2014), 95–101. https://doi.org/10.1016/j.aml.2013.11.005 doi: 10.1016/j.aml.2013.11.005 |
| [14] | К. Перера, З. Чжан, Нетривиальные решения задач типа Кирхгофа с помощью индекса Янга, Ж. Дифференц. Уравнения , 221 (2006), 246–255. http://dx.doi.org/10.1016/j.jde.2005.03.006 doi: 10.1016/j.jde.2005.03.006 |
| [15] | П.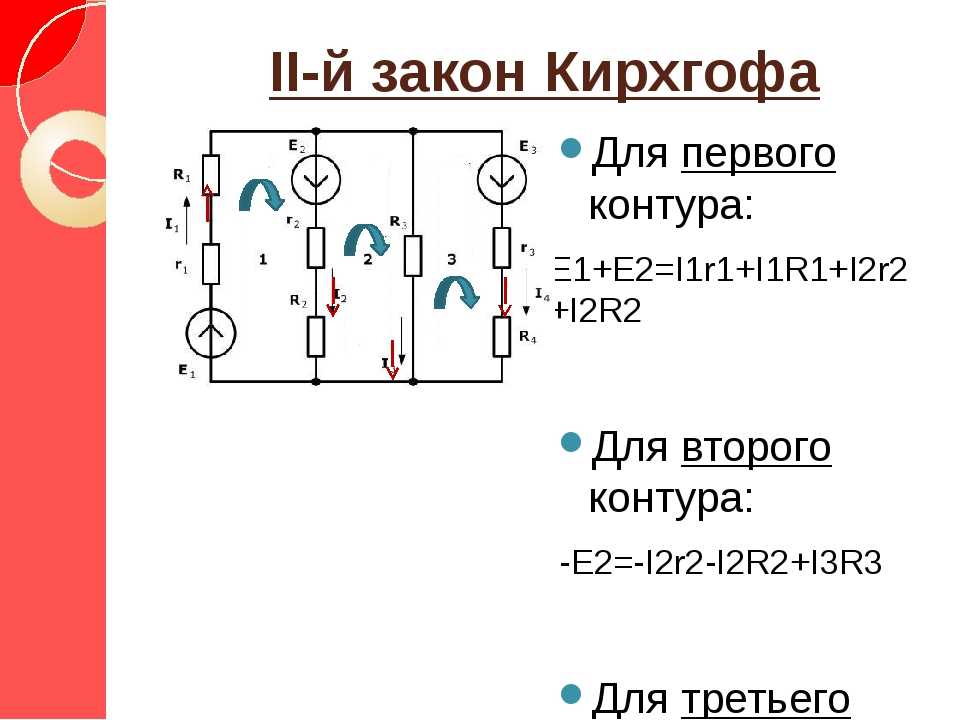 Пуччи, В. Д. Родулеску, Прогресс в решении нелинейных задач Кирхгофа, Нелинейный анализ. , 186 (2019), 1–5. http://dx.doi.org/10.1016/j.na.2019.02.022 doi: 10.1016/j.na.2019.02.022 Пуччи, В. Д. Родулеску, Прогресс в решении нелинейных задач Кирхгофа, Нелинейный анализ. , 186 (2019), 1–5. http://dx.doi.org/10.1016/j.na.2019.02.022 doi: 10.1016/j.na.2019.02.022 |
| [16] | Б. Риччери, Об эллиптической задаче типа Кирхгофа, зависящей от двух параметров, J. Glob. Оптим. , 46 (2010), 543–549. https://doi.org/10.1007/s10898-009-9438-7 doi: 10.1007/s10898-009-9438-7 |
| [17] | З. Т. Чжан, Ю. М. Сунь, Существование и множественность решений для нелокальных систем типа Кирхгофа, Acta Math. заявл. Грех. англ. сер. , 32 (2016), 35–54. https://doi.org/10.1007/s10255-016-0545-1 doi: 10.1007/s10255-016-0545-1 |
| [18] | А. Дип, Дипмала, К. Тунч, О существовании решений некоторых нелинейных функциональных интегральных уравнений в банаховой алгебре с приложениями, Arab J. Basic Appl.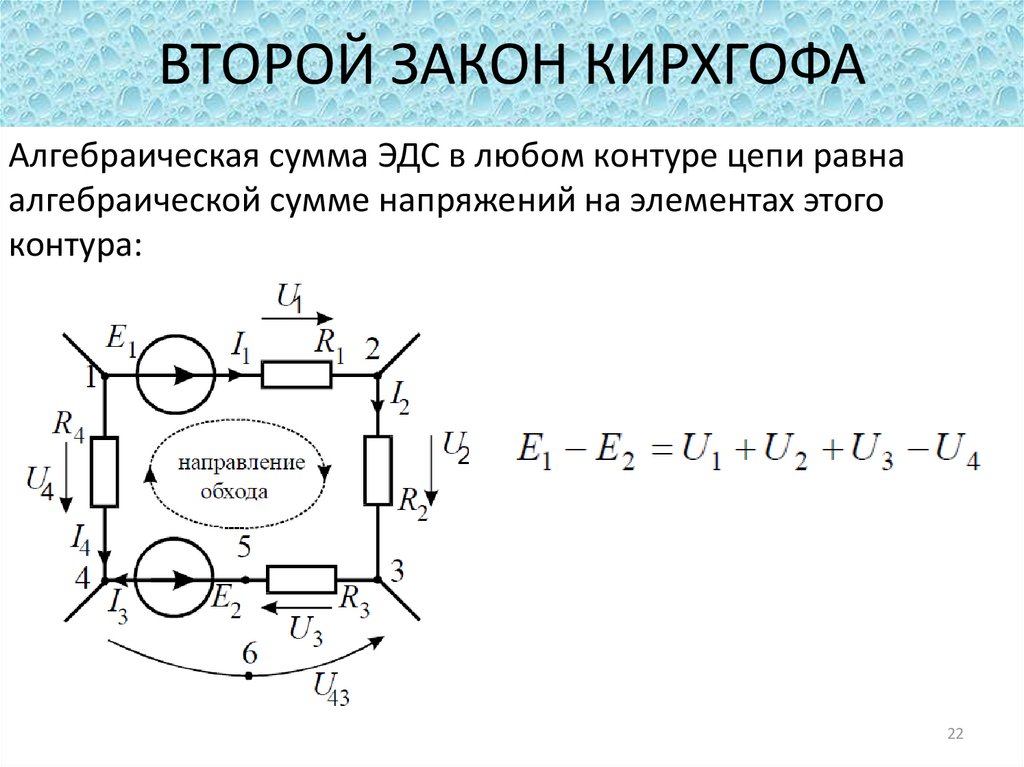 науч. , 27 (2020), 279–286. https://doi.org/10.1080/25765299.2020.1796199 doi: 10.1080/25765299.2020.1796199 науч. , 27 (2020), 279–286. https://doi.org/10.1080/25765299.2020.1796199 doi: 10.1080/25765299.2020.1796199 |
| [19] | С. Ислам, М. Н. Алам, М. Ф. Аль-Асад, К. Тунч, Аналитический метод решения новых вычислительных решений модифицированного уравнения Захарова-Кузнецова, возникающего в электротехнике, J. Appl. вычисл. мех. , 7 (2021), 715–726. https://dx.doi.org/10.22055/jacm.2020.35571.2687 doi: 10.22055/jacm.2020.35571.2687 |
| [20] | М. Н. Алам, К. Тунч, Аналитический метод решения точных решений нелинейного уравнения Богоявленского и нелинейной диффузионной системы хищник-жертва, Alex. англ. J. , 55 (2016), 1855–1865. https://doi.org/10.1016/j.aej.2016.04.024 doi: 10.1016/j.aej.2016.04.024 |
| [21] | Р. Прекап, Равновесия типа Нэша и периодические решения невариационных систем, Adv.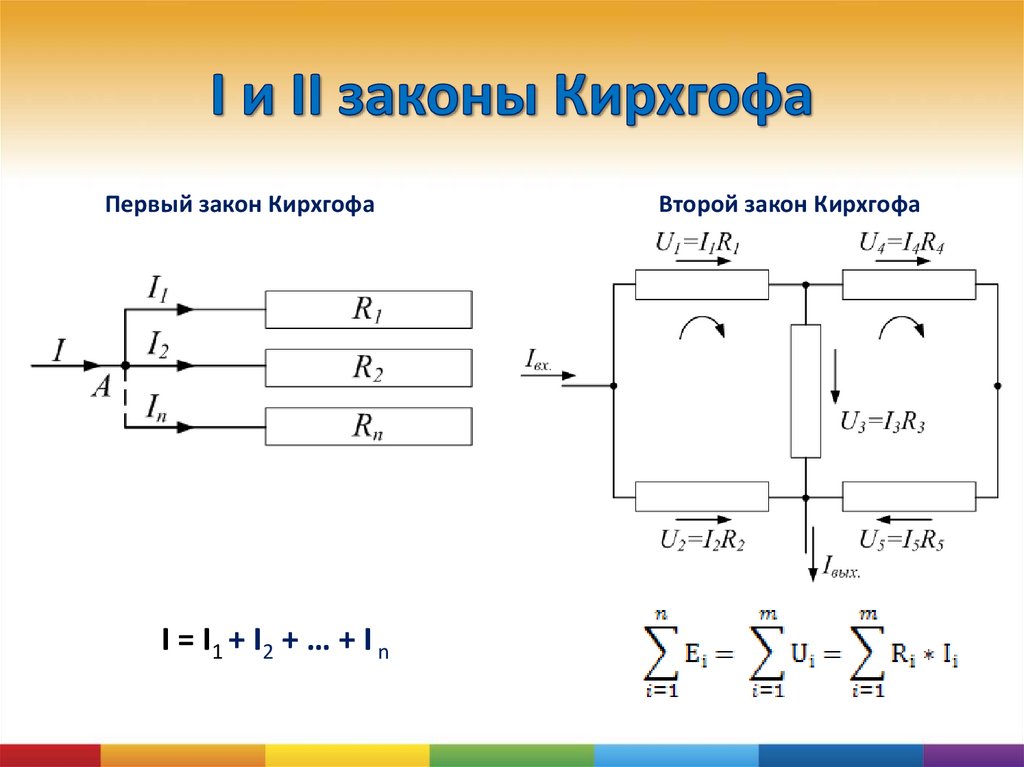 Нелинейный анал. , 4 (2014), 197–207. https://doi.org/10.1515/anona-2014-0006 doi: 10.1515/anona-2014-0006 Нелинейный анал. , 4 (2014), 197–207. https://doi.org/10.1515/anona-2014-0006 doi: 10.1515/anona-2014-0006 |
| [22] | Р. Прекап, Равновесия типа Нэша для систем функционалов Шулкина, Заданное значение Var. Анальный. , 24 (2016), 471–482. https://doi.org/10.1007/s11228-015-0356-1 doi: 10.1007/s11228-015-0356-1 |
| [23] | А. Будеску, Р. Прекап, Вариационные свойства решений сингулярных дифференциальных уравнений и систем второго порядка, J. Прикладная теория фиксированной точки. , 18 (2016), 505–518. https://doi.org/10.1007/s11784-016-0284-1 doi: 10.1007/s11784-016-0284-1 |
| [24] | Р. Прекап, Теорема о критической точке в ограниченных выпуклых множествах и локализация равновесий типа Нэша невариационных систем, J. Math. Анальный. заявл. , 463 (2018), 412–431. https://doi.org/10. 1016/j.jmaa.2018.03.035 doi: 10.1016/j.jmaa.2018.03.035 1016/j.jmaa.2018.03.035 doi: 10.1016/j.jmaa.2018.03.035 |
| [25] | М. Белдински, М. Галевски, Равновесия типа Нэша для систем непотенциальных уравнений, Appl. Мат. вычисл. , 385 (2020), 125456. https://doi.org/10.1016/j.amc.2020.125456 doi: 10.1016/j.amc.2020.125456 |
| [26] | И. Бенедетти, Т. Кардинали, Р. Прекап, Гибридные теоремы о фиксированной точке и критической точке и приложения к системам с частичной вариационной структурой, J. Fixed Point Theory Appl. , 23 (2021), 63. https://doi.org/10.1007/s11784-021-00852-6 doi: 10.1007/s11784-021-00852-6 |
| [27] | А. Стэн, Нелинейные системы с частичным равновесием типа Нэша, Studia Universitatis Babeş-Bolyai Mathematica , 66 (2021), 397–408. https://doi.org/10.24193/subbmath.2021.2.14 doi: 10.24193/subbmath.2021.2.14 |
| [28] | Р. Прекап, Методы нелинейных интегральных уравнений , Дордрехт: Springer, 2002. https://doi.org/10.1007/978-94-015-9986-3 Прекап, Методы нелинейных интегральных уравнений , Дордрехт: Springer, 2002. https://doi.org/10.1007/978-94-015-9986-3 |
| [29] | Р. Прекап, Линейные и полулинейные уравнения в частных производных , Берлин: Де Грюйтер, 2013. https://doi.org/10.1515/9783110269055 |
10.3 Правила Кирхгофа — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Формулировать правило пересечения Кирхгофа
- Правило петли Кирхгофа состояния
- Анализ сложных цепей с использованием правил Кирхгофа
Мы только что видели, что некоторые схемы можно анализировать, сводя схему к одному источнику напряжения и эквивалентному сопротивлению. Многие сложные схемы невозможно проанализировать с помощью последовательно-параллельных методов, разработанных в предыдущих разделах. В этом разделе мы подробно остановимся на использовании правил Кирхгофа для анализа более сложных схем. Например, схема на рис. 10.19.называется многоконтурной схемой, состоящей из соединений. Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы расположены последовательно или параллельно, и их можно уменьшить. Попробуйте. Резисторы R1R1 и R2R2 включены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое и с резисторами R4R4 и R5R5. Но что вы делаете тогда?
Например, схема на рис. 10.19.называется многоконтурной схемой, состоящей из соединений. Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы расположены последовательно или параллельно, и их можно уменьшить. Попробуйте. Резисторы R1R1 и R2R2 включены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое и с резисторами R4R4 и R5R5. Но что вы делаете тогда?
Несмотря на то, что эту цепь нельзя проанализировать с помощью уже изученных методов, для анализа любой цепи, простой или сложной, можно использовать два правила анализа цепей. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).
Рисунок 10.19 Эта схема не может быть сведена к комбинации последовательного и параллельного соединений. Однако мы можем использовать правила Кирхгофа для его анализа.
Правила Кирхгофа
Теперь мы даем объяснения этих двух правил, сопровождаемые советами по решению проблем по их применению и рабочим примером, в котором они используются.
Первое правило Кирхгофа
Первое правило Кирхгофа (правило соединения) применяется к заряду, входящему в соединение и выходящему из него (рис. 10.20). Как указывалось ранее, узел или узел — это соединение трех или более проводов. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу.
Рисунок 10.20 Заряд должен сохраняться, поэтому сумма токов в соединении должна быть равна сумме токов вне соединения.
Хотя это упрощение, можно провести аналогию с водопроводными трубами, соединенными в сантехническом узле. Если бы провода на рис. 10.20 были заменены водопроводными трубами, а вода считалась несжимаемой, то объем воды, поступающей в соединение, должен был бы равняться объему воды, вытекающей из соединения.
Второе правило Кирхгофа
Второе правило Кирхгофа (правило петли) применимо к разности потенциалов. Правило цикла сформулировано в терминах потенциала V , а не потенциальной энергии, но они связаны, поскольку U=qV.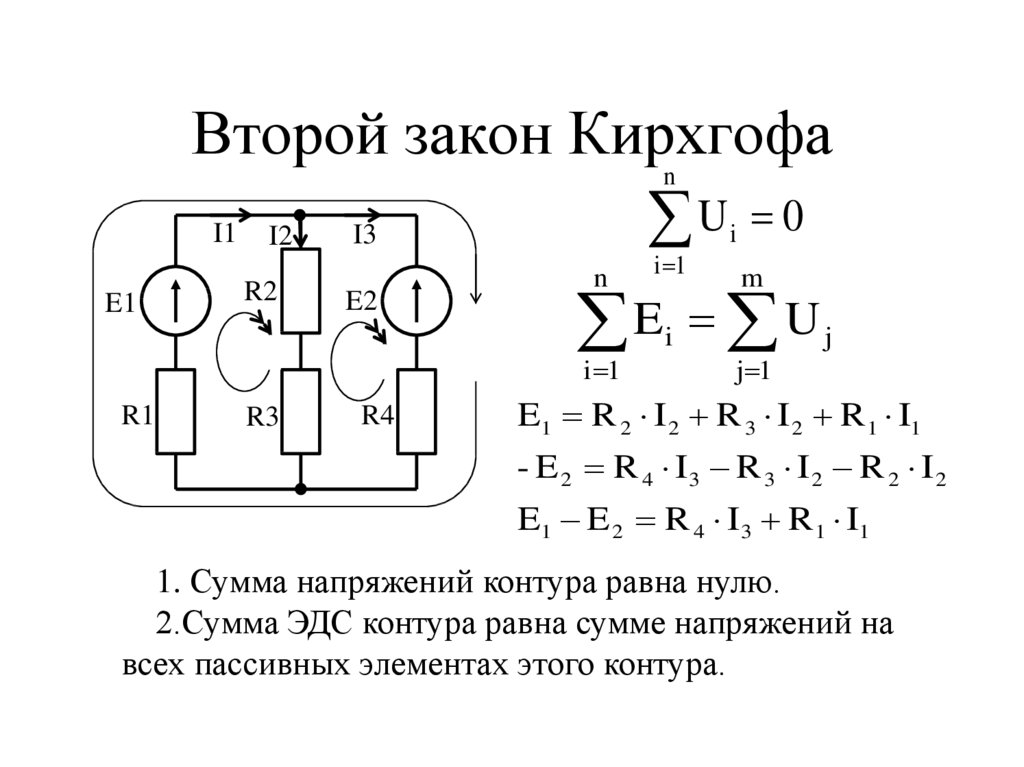 U=qV. В замкнутом контуре, какая бы энергия ни поставлялась источником напряжения, энергия должна передаваться в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжения, подаваемые источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простую петлю без соединений, как на рис. 10.21.
U=qV. В замкнутом контуре, какая бы энергия ни поставлялась источником напряжения, энергия должна передаваться в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжения, подаваемые источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простую петлю без соединений, как на рис. 10.21.
Рисунок 10.21 Простая петля без соединений. Правило цикла Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.
Схема состоит из источника напряжения и трех внешних нагрузочных резисторов. Этикетки a , b , c и d служат в качестве ссылок и не имеют никакого другого значения. Полезность этих ярлыков скоро станет очевидной. Петля обозначена как Loop abcda , а метки помогают отслеживать разность напряжений, когда мы перемещаемся по цепи. Начните с точки a и отправляйтесь в точку b . В уравнение добавляется напряжение источника напряжения и вычитается падение потенциала на резисторе R1R1. От точки b до c вычитается падение потенциала на R2R2. От c до d вычитается падение потенциала на R3R3. От точек d до a ничего не делается, потому что нет компонентов.
Начните с точки a и отправляйтесь в точку b . В уравнение добавляется напряжение источника напряжения и вычитается падение потенциала на резисторе R1R1. От точки b до c вычитается падение потенциала на R2R2. От c до d вычитается падение потенциала на R3R3. От точек d до a ничего не делается, потому что нет компонентов.
На рис. 10.22 показан график изменения напряжения при перемещении по контуру. Напряжение увеличивается, когда мы пересекаем батарею, тогда как напряжение уменьшается, когда мы пересекаем резистор. Падение потенциала или изменение электрического потенциала равно току через резистор, умноженному на сопротивление резистора. Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
Рисунок 10.22 График напряжения при движении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор. Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
Тогда правило цикла Кирхгофа утверждает
В-IR1-IR2-IR3=0.V-IR1-IR2-IR3=0.
Уравнение контура можно использовать для определения тока через контур:
I=VR1+R2+R2=12,00В1,00Ом+2,00Ом+3,00Ом=2,00А.I=VR1+R2+R2=12,00В1,00Ом+2,00Ом+3,00Ом=2,00А.
Эту петлю можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем возможности метода Кирхгофа в следующем разделе.
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы получаем набор линейных уравнений, которые позволяют нам находить неизвестные значения в цепях. Это могут быть токи, напряжения или сопротивления.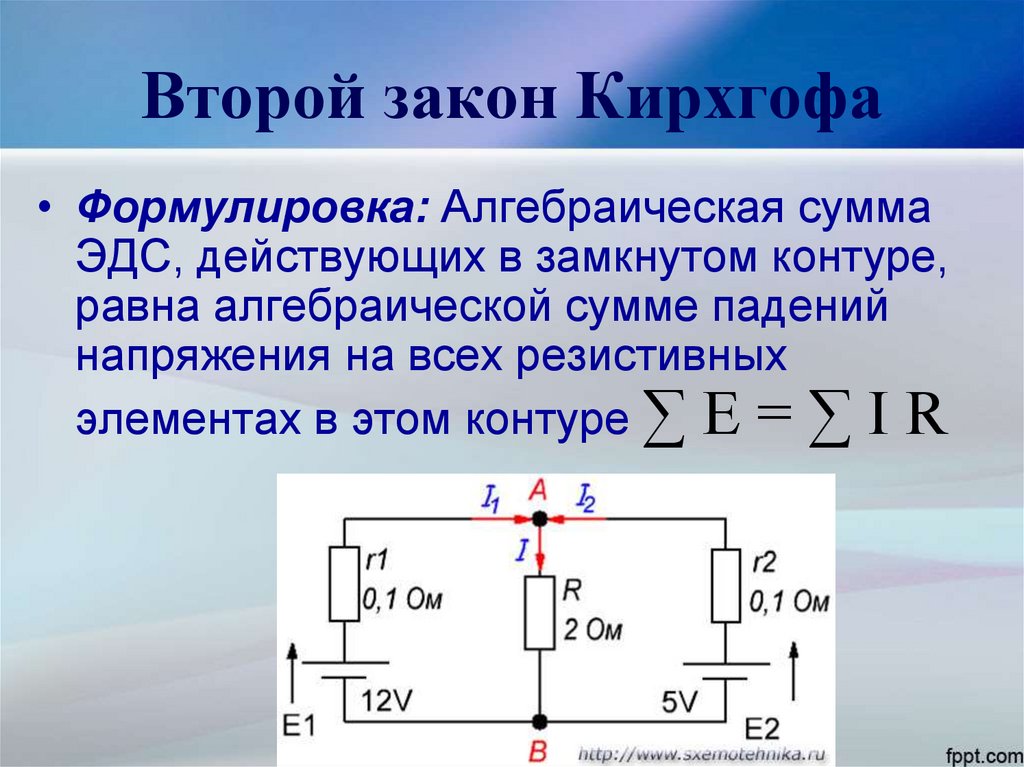 Каждый раз, когда правило применяется, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема.
Каждый раз, когда правило применяется, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема.
Использование метода анализа Кирхгофа требует выполнения нескольких шагов, перечисленных в следующей процедуре.
Стратегия решения проблем
Правила Кирхгофа
- Обозначьте точки на схеме строчными буквами a , b , c , …. Эти метки просто помогают с ориентацией.
- Найдите соединения в цепи. Соединения — это точки, в которых соединяются три или более проводов. Обозначьте каждое соединение токами и направлениями в него и из него. Убедитесь, что по крайней мере один ток указывает на соединение и по крайней мере один ток указывает на соединение.
- Выберите петли в цепи. Каждый компонент должен содержаться по крайней мере в одном цикле, но компонент может содержаться более чем в одном цикле.

- Применить правило соединения. Опять же, некоторые соединения не должны быть включены в анализ. Вам нужно только использовать достаточное количество узлов, чтобы включить каждый текущий.
- Применить правило цикла. Используйте карту на рис. 10.23.
Рисунок 10.23 Каждый из этих резисторов и источников напряжения проходит от до 9от 0055 до б . (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном течению тока, добавьте падение потенциала. (c) При перемещении через источник напряжения от отрицательной клеммы к положительной клемме добавьте падение потенциала. (d) При перемещении через источник напряжения от положительной клеммы к отрицательной клемме вычтите падение потенциала.
Рассмотрим некоторые шаги этой процедуры более подробно. При нахождении соединений в цепи не беспокойтесь о направлении токов. Если направление протекания тока неочевидно, достаточно выбрать любое направление, если хотя бы один ток указывает на соединение, а по крайней мере один ток направлен из соединения. Если стрелка находится в направлении, противоположном обычному течению тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.
Если направление протекания тока неочевидно, достаточно выбрать любое направление, если хотя бы один ток указывает на соединение, а по крайней мере один ток направлен из соединения. Если стрелка находится в направлении, противоположном обычному течению тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.
Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.
См. рис. 10.24. В этой цепи есть два соединения: соединение b и соединение e . Точки a , c , d и f не являются соединениями, поскольку соединение должно иметь три или более соединения. Уравнение для соединения b – это I1=I2+I3I1=I2+I3, а уравнение для перекрестка e – это I2+I3=I1I2+I3=I1. Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.
Уравнение для соединения b – это I1=I2+I3I1=I2+I3, а уравнение для перекрестка e – это I2+I3=I1I2+I3=I1. Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.
Рисунок 10.24 На первый взгляд, эта схема содержит два соединения, соединение b и соединение e , но следует рассматривать только одно, поскольку уравнения их соединения эквивалентны.
При выборе петель в схеме необходимо столько петель, чтобы каждый компонент был покрыт один раз, без повторения петель. На рис. 10.25 показаны четыре варианта циклов для решения примера схемы; варианты (a), (b) и (c) имеют достаточное количество циклов, чтобы полностью решить схему. Вариант (г) отражает больше циклов, чем необходимо для решения схемы.
Рисунок
10.25
Панели (a)–(c) достаточны для анализа схемы. В каждом случае две показанные петли содержат все элементы схемы, необходимые для полного решения схемы. На панели (d) показаны три использованные петли, что больше, чем необходимо. Любые два цикла в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла обеспечивает избыточную информацию.
На панели (d) показаны три использованные петли, что больше, чем необходимо. Любые два цикла в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла обеспечивает избыточную информацию.
Рассмотрим схему на рис. 10.26(а). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала пометьте схему, как показано в части (b).
Рисунок 10.26 а) Многоконтурная схема. (b) Подпишите схему, чтобы помочь с ориентацией.
Далее определите соединения. В этой схеме к точкам b и e подключено по три провода, что делает их соединениями. Начните применять правило соединения Кирхгофа (∑Iin=∑Iout)(∑Iin=∑Iout), нарисовав стрелки, обозначающие токи, и пометив каждую стрелку, как показано на рис. 10.27(b). Развязка b показывает, что I1=I2+I3I1=I2+I3 и развязка e показывает, что I2+I3=I1I2+I3=I1. Поскольку развязка e дает ту же информацию, что и развязка b , ею можно пренебречь. В этой схеме три неизвестных, поэтому для ее анализа нам нужны три линейно независимых уравнения.
Поскольку развязка e дает ту же информацию, что и развязка b , ею можно пренебречь. В этой схеме три неизвестных, поэтому для ее анализа нам нужны три линейно независимых уравнения.
Рисунок 10.27 (a) Эта схема имеет два соединения, обозначенных b и e , но в анализе используется только узел b . (б) Маркированные стрелки представляют токи в и из соединений.
Далее нам нужно выбрать петли. На рис. 10.28 контур до включает в себя источник напряжения V1V1 и резисторы R1R1 и R2R2. Цикл начинается в точке a , затем проходит через точки b , e и f , а затем возвращается к точке a . Второй контур, Loop ebcde , начинается в точке e и включает в себя резисторы R2R2 и R3R3 и источник напряжения V2V2.
Рисунок 10.28 Выберите петли в схеме.
Теперь мы можем применить правило цикла Кирхгофа, используя карту на рис. 10.23. Начиная с точки a и двигаясь к точке b , резистор R1R1 пересекается в том же направлении, что и ток I1I1, поэтому падение потенциала I1R1I1R1 вычитается. При переходе от точки b к точке e резистор R2R2 пересекается в том же направлении, что и ток I2I2, поэтому падение потенциала I2R2I2R2 вычитается. Переход от точки e к точке f источник напряжения V1V1 пересекается с отрицательной клеммы на положительную, поэтому добавляется V1V1. Между точками f и a компонентов нет. Сумма разностей напряжений должна быть равна нулю:
Лупабефа:-I1R1-I2R2+V1=0или V1=I1R1+I2R2. Лупабефа:-I1R1-I2R2+V1=0илиV1=I1R1+I2R2.
Наконец, мы проверяем цикл ebcde . Мы начинаем с точки e и движемся к точке b , пересекая R2R2 в направлении, противоположном текущему течению I2I2. Добавляется падение потенциала I2R2I2R2. Далее пересекаем R3R3 и R4R4 в том же направлении, что и ток I3I3 и вычитаем падения потенциала I3R3I3R3 и I3R4.I3R4. Обратите внимание, что ток через резисторы R3R3 и R4R4 одинаков, потому что они соединены последовательно. Наконец, источник напряжения пересекается с положительной клеммы на отрицательную клемму, а источник напряжения V2V2 вычитается. Сумма этих разностей напряжений равна нулю и дает уравнение контура
Loopebcde:I2R2-I3(R3+R4)-V2=0. Loopebcde:I2R2-I3(R3+R4)-V2=0.
Теперь у нас есть три уравнения, которые мы можем решить для трех неизвестных.
(1) Соединениеb: I1-I2-I3 = 0. (2) Loopabefa: I1R1 + I2R2 = V1. (3) Loopebcde: I2R2-I3 (R3 + R4) = V2. (1) Соединениеb: I1-I2- I3=0;
Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока I2I2. Сначала добавьте уравнение (1) раз R2R2 к уравнению. (2). Результат помечен как уравнение. (4):
Сначала добавьте уравнение (1) раз R2R2 к уравнению. (2). Результат помечен как уравнение. (4):
(R1+R2)I1−R2I3=V1.(4)6ΩI1−3ΩI3=24В.(R1+R2)I1−R2I3=V1.(4)6ΩI1−3ΩI3=24В.
Затем вычтите уравнение (3) из уравнения (2). Результат помечен как уравнение. (5):
I1R1+I3(R3+R4)=V1−V2.(5)3ΩI1+7ΩI3=−5V.I1R1+I3(R3+R4)=V1−V2.(5)3ΩI1+7ΩI3=−5V.
Мы можем решить уравнения. (4) и (5) для тока I1I1. Складывая семь раз уравнение (4) и трижды уравнение. (5) получается 51 Ом I1 = 153 В, 51 Ом I1 = 153 В или I1 = 3,00 А. I1 = 3,00 А. Используя уравнение (4) дает I3=-2,00A.I3=-2,00A. Наконец, уравнение (1) дает I2=I1-I3=5,00 А. I2=I1-I3=5,00 А. Один из способов проверить согласованность решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:
Контакт = I1V1 + I3V2 = 130 Вт, Pвых = I12R1 + I22R2 + I32R3 + I32R4 = 130 Вт. Контакт = I1V1 + I3V2 = 130 Вт, Pвых = I12R1 + I22R2 + I32R3 + I32R4 = 130 Вт.
Обратите внимание, что решение для текущего I3I3 отрицательное. Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединения, указывает направление, противоположное обычному протеканию тока. Мощность, подаваемая вторым источником напряжения, составляет 58 Вт, а не -58 Вт.
Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединения, указывает направление, противоположное обычному протеканию тока. Мощность, подаваемая вторым источником напряжения, составляет 58 Вт, а не -58 Вт.
Пример 10,6
Расчет силы тока с помощью правил Кирхгофа
Найдите токи, протекающие в цепи на рис. 10.29.
Рисунок 10.29 Эта схема представляет собой комбинацию последовательных и параллельных конфигураций резисторов и источников напряжения. Эту цепь нельзя проанализировать с помощью методов, описанных в книге «Электродвижущая сила», но ее можно проанализировать с помощью правил Кирхгофа.
Стратегия
Эта схема достаточно сложна, чтобы токи не могли быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены I1, I1, I2, I2 и I3I3, и были сделаны предположения об их направлениях. Места на схеме обозначены буквами 9.с 1264 а по ч . В решении мы применяем правила соединения и петли, ищем три независимых уравнения, которые позволяют нам найти три неизвестных тока.
Места на схеме обозначены буквами 9.с 1264 а по ч . В решении мы применяем правила соединения и петли, ищем три независимых уравнения, которые позволяют нам найти три неизвестных тока.
Раствор
Применение правил соединения и петли дает следующие три уравнения. У нас есть три неизвестных, поэтому требуется три уравнения.
Junctionc:I1+I2=I3.Loopabcdefa:I1(R1+R4)−I2(R2+R5+R6)=V1−V3.Loopcdefc:I2(R2+R5+R6)+I3R3=V2+V3.Junctionc :I1+I2=I3.Loopabcdefa:I1(R1+R4)−I2(R2+R5+R6)=V1−V3.Loopcdefc:I2(R2+R5+R6)+I3R3=V2+V3.
Упростите уравнения, поместив неизвестные в одну сторону уравнений.
Соединениеc:I1+I2−I3=0.Контур abcdefa:I1(3Ω)−I2(8Ω)=0,5V−2,30V.Контурcdefc:I2(8Ω)+I3(1Ω)=0,6V+2,30V.Соединениеc: I1+I2-I3=0.Определение контура:I1(3Ом)-I2(8Ом)=0,5В-2,30В.Определение контура:I2(8Ом)+I3(1Ом)=0,6В+2,30В.
Упростите уравнения. Уравнение первого контура можно упростить, разделив обе части на 3,00.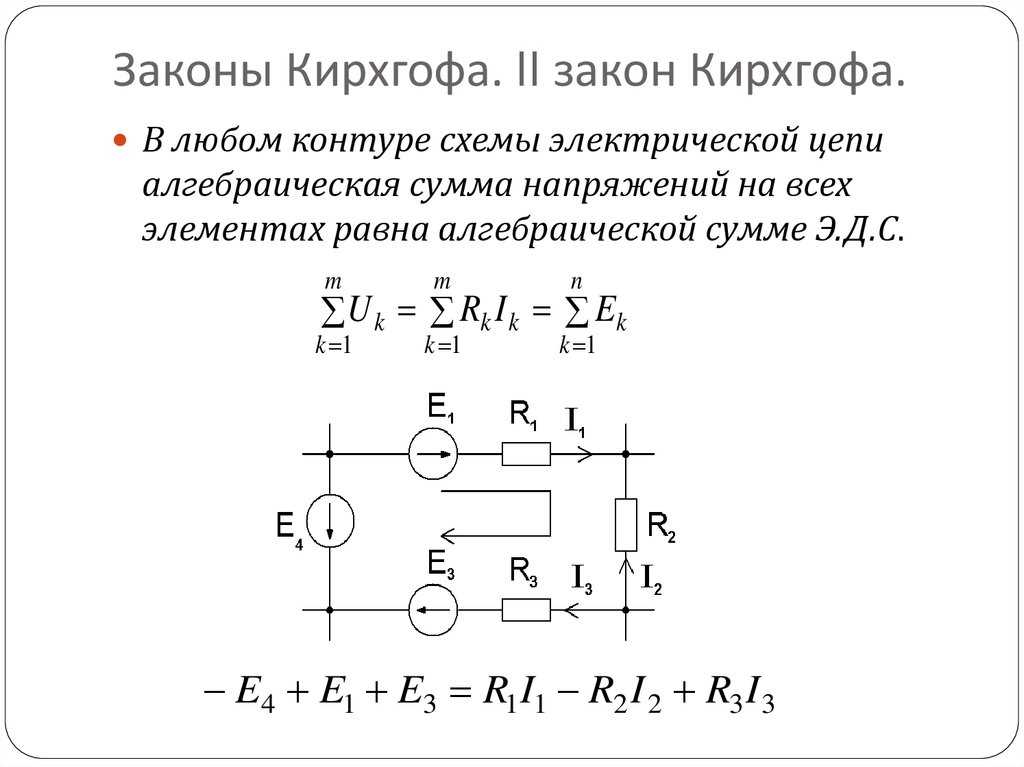 Второе уравнение контура можно упростить, разделив обе части на 6,00.
Второе уравнение контура можно упростить, разделив обе части на 6,00.
Соединениеc:I1+I2−I3=0.Loopabcdefa:I1(3Ω)−I2(8Ω)=−1,8V.Loopcdefc:I2(8Ω)+I3(1Ω)=2,9V.Junctionc: I1+I2−I3=0.Loopabcdefa:I1(3Ω)−I2(8Ω)=−1,8V.Loopcdefc:I2(8Ω)+I3(1Ω)=2,9V.
Результаты:
I1=0,20A,I2=0,30A,I3=0,50A.I1=0,20A,I2=0,30A,I3=0,50A.
Значение
Метод проверки расчетов состоит в том, чтобы вычислить мощность, рассеиваемую резисторами, и мощность, отдаваемую источниками напряжения:
PR1=I12R1=0,04 Вт.PR2=I22R2=0,45 Вт.PR3=I32R3=0,25 Вт.PR4=I12R4=0,08 Вт.PR5=I22R5=0,09 Вт.PR6=I22R6=0,18 Вт.Pрассеиваемая=1,09 Вт.Pисточник =I1V1+I2V3+I3V2=0,10 Вт+0,69W+0,30Вт=1,09Вт.PR1=I12R1=0,04Вт.PR2=I22R2=0,45Вт.PR3=I32R3=0,25Вт.PR4=I12R4=0,08Вт.PR5=I22R5=0,09Вт.PR6=I22R6=0,18Вт. Pрассеиваемая = 1,09 Вт. Pисточник = I1V1 + I2V3 + I3V2 = 0,10 Вт + 0,69 Вт + 0,30 Вт = 1,09 Вт.
Подводимая мощность равна мощности, рассеиваемой резисторами.
Проверьте свое понимание 10,6
Проверьте свое понимание При рассмотрении следующей схемы и мощности, подаваемой и потребляемой цепью, будет ли источник напряжения всегда обеспечивать питание цепи или источник напряжения может потреблять энергию?
Пример 10,7
Расчет тока с использованием правил Кирхгофа
Найдите силу тока в цепи на рис. 10.30.
Рисунок 10.30 Эта схема состоит из трех резисторов и двух батарей, соединенных последовательно. Обратите внимание, что батареи подключены с противоположной полярностью.
Стратегия
Эту схему можно проанализировать с помощью правил Кирхгофа. Есть только одна петля и нет узлов. Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки 9.1264 а до точки б .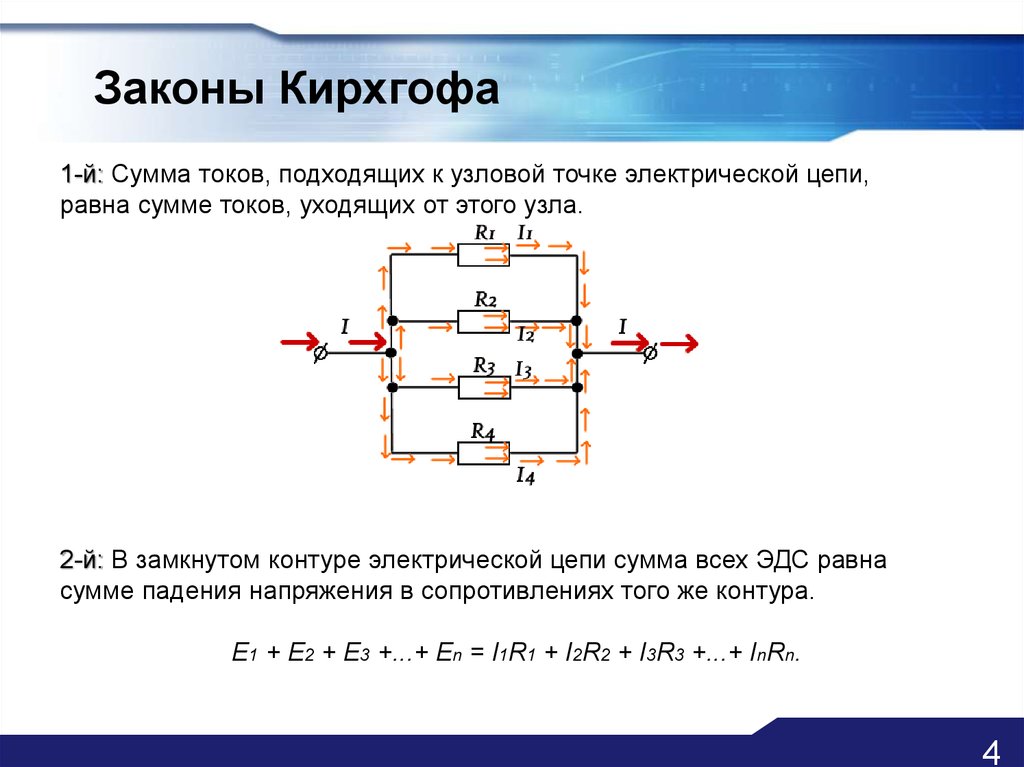 Рассмотрим Loop abcda и используйте рисунок 10.23, чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку 10.23, батарея V1V1 будет добавлена, а батарея V2V2 вычтена.
Рассмотрим Loop abcda и используйте рисунок 10.23, чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку 10.23, батарея V1V1 будет добавлена, а батарея V2V2 вычтена.
Раствор
Применение правила соединения дает следующие три уравнения. У нас есть одно неизвестное, поэтому требуется одно уравнение:
Loopabcda:-IR1-V1-IR2+V2-IR3=0.Loopabcda:-IR1-V1-IR2+V2-IR3=0.
Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.
I(R1+R2+R3)=V2−V1.I=V2−V1R1+R2+R3=24V−12V10,0Ω+30,0Ω+10,0Ω=0,20A.I(R1+R2+R3)=V2−V1 .I=V2-V1R1+R2+R3=24В-12В10,0Ом+30,0Ом+10,0Ом=0,20А.
Значение
Мощность, рассеиваемая или потребляемая схемой, равна мощности, подаваемой в схему, но обратите внимание, что ток в батарее V1V1 протекает через батарею от положительной клеммы к отрицательной клемме и потребляет энергию.
PR1=I2R1=0,40WPR2=I2R2=1,20WPR3=I2R3=0,80WPV1=IV1=2,40WPрассеянное=4,80WPисточник=IV2=4,80WPR1=I2R1=0,40WPR2=I2R2=1,20WPR3=I2R3=0,80W2PV40=IV1=IV1 WPрассеиваемая=4,80WPисходная=IV2=4,80Вт
Подаваемая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей V1.V1.
Проверьте свое понимание 10,7
Проверьте свое понимание При использовании законов Кирхгофа вам необходимо решить, какие петли использовать и направление тока, протекающего через каждую петлю. При анализе схемы в примере 10.7 направление тока было выбрано по часовой стрелке, от точки a до точки b . Как изменились бы результаты, если бы направление тока было выбрано против часовой стрелки, начиная с точки 9?1264 b до точки a ?
Несколько источников напряжения
Для многих устройств требуется более одной батареи. Несколько источников напряжения, таких как батареи, могут быть соединены последовательно, параллельно или в комбинации.
Несколько источников напряжения, таких как батареи, могут быть соединены последовательно, параллельно или в комбинации.
Последовательно положительная клемма одной батареи подключается к отрицательной клемме другой батареи. Любое количество источников напряжения, включая батареи, может быть соединено последовательно. Две батареи, соединенные последовательно, показаны на рис. 10.31. Использование правила цикла Кирхгофа для схемы в части (b) дает результат
ε1-Ir1+ε2-Ir2-IR=0,[(ε1+ε2)-I(r1+r2)]-IR=0,ε1-Ir1+ε2-Ir2-IR=0,[(ε1+ε2) −I(r1+r2)]−IR=0.
Рисунок 10.31 а) Две батареи, соединенные последовательно с нагрузочным резистором. (b) Принципиальная схема двух батарей и нагрузочного резистора, где каждая батарея смоделирована как идеализированный источник ЭДС и внутреннее сопротивление.
Когда источники напряжения соединены последовательно, их внутренние сопротивления могут быть сложены вместе, а их ЭДС могут быть сложены вместе, чтобы получить общие значения. Распространены последовательные соединения источников напряжения, например в фонарях, игрушках и др. приборах. Обычно ячейки соединяют последовательно для получения большей общей ЭДС. На рис. 10.31 напряжение на клеммах равно
Распространены последовательные соединения источников напряжения, например в фонарях, игрушках и др. приборах. Обычно ячейки соединяют последовательно для получения большей общей ЭДС. На рис. 10.31 напряжение на клеммах равно
Vклемма=(ε1−Ir1)+(ε2−Ir2)=[(ε1+ε2)−I(r1+r2)]=(ε1+ε2)+Iтреб.Vтерминал=(ε1−Ir1)+(ε2−Ir2 )=[(ε1+ε2)−I(r1+r2)]=(ε1+ε2)+Iтреб.
Обратите внимание, что в каждой батарее присутствует один и тот же ток I , поскольку они соединены последовательно. Недостатком последовательного соединения ячеек является аддитивность их внутренних сопротивлений.
Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь. Например, светодиодный фонарик может иметь две батарейки типа ААА, каждая с напряжением на клеммах 1,5 В, чтобы обеспечить фонарик напряжением 3,0 В.
Последовательно можно соединить любое количество аккумуляторов. Для последовательно соединенных аккумуляторов N напряжение на клеммах равно
.
Vterminal=(ε1+ε2+⋯+εN−1+εN)−I(r1+r2+⋯+rN−1+rN)=∑i=1Nεi−IreqVterminal=(ε1+ε2+⋯+εN−1+εN)− I(r1+r2+⋯+rN−1+rN)=∑i=1Nεi−Ireq
10,6
, где эквивалентное сопротивление равно req=∑i=1Nrireq=∑i=1Nri.
Когда нагрузка подключена к источникам напряжения последовательно, как показано на рис. 10.32, мы можем найти ток:
(ε1-Ir1)+(ε2-Ir2)=IR,Ir1+Ir2+IR=ε1+ε2,I=ε1+ε2r1+r2+R.(ε1-Ir1)+(ε2-Ir2)=IR,Ir1 +Ir2+IR=ε1+ε2,I=ε1+ε2r1+r2+R.
Как и ожидалось, внутренние сопротивления увеличивают эквивалентное сопротивление.
Рисунок 10.32 Две батареи соединены последовательно со светодиодной лампочкой, как в фонарике.
Источники напряжения, такие как батареи, также могут быть подключены параллельно. На рис. 10.33 показаны две батареи с одинаковыми ЭДС, включенные параллельно и подключенные к нагрузочному сопротивлению. Когда батареи соединены параллельно, положительные клеммы соединены вместе, а отрицательные клеммы соединены вместе, а сопротивление нагрузки подключено к положительной и отрицательной клеммам. Обычно параллельно подключенные источники напряжения имеют одинаковые ЭДС. В этом простом случае, поскольку источники напряжения параллельны, общая ЭДС такая же, как и отдельные ЭДС каждой батареи.
Обычно параллельно подключенные источники напряжения имеют одинаковые ЭДС. В этом простом случае, поскольку источники напряжения параллельны, общая ЭДС такая же, как и отдельные ЭДС каждой батареи.
Рисунок 10.33 а) Две батареи подключены параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея в качестве источника ЭДС и внутреннего резистора. Два источника ЭДС имеют одинаковые ЭДС (обозначенные буквой εε), соединенные параллельно и производящие одинаковую ЭДС.
Рассмотрим анализ Кирхгофа схемы на рис. 10.33(b). Есть две петли и узел в точке b и ε=ε1=ε2ε=ε1=ε2.
Узел b : I1+I2-I=0I1+I2-I=0.
Цикл abcfa : ε−I1r1+I2r2−ε=0,I1r1=I2r2.ε−I1r1+I2r2−ε=0,I1r1=I2r2.
Цикл fcdef : ε2-I2r2-IR=0,ε-I2r2-IR=0,ε2-I2r2-IR=0,ε-I2r2-IR=0.
Решение для тока через нагрузочный резистор дает I=εreq+RI=εreq+R, где req=(1r1+1r2)−1req=(1r1+1r2)−1. Напряжение на клеммах равно падению потенциала на нагрузочном резисторе IR=(εreq+R)IR=(εreq+R). Параллельное соединение снижает внутреннее сопротивление и, таким образом, может производить больший ток.
Напряжение на клеммах равно падению потенциала на нагрузочном резисторе IR=(εreq+R)IR=(εreq+R). Параллельное соединение снижает внутреннее сопротивление и, таким образом, может производить больший ток.
Параллельно можно соединить любое количество аккумуляторов. Для аккумуляторов N , включенных параллельно, напряжение на клеммах равно
.Vterminal=ε−I(1r1+1r2+⋯+1rN−1+1rN)−1=ε−IreqVterminal=ε−I(1r1+1r2+⋯+1rN−1+1rN)−1=ε−Ireq
10,7
, где эквивалентное сопротивление равно req=(∑i=1N1ri)−1req=(∑i=1N1ri)−1.
Например, некоторые дизельные грузовики используют две 12-вольтовые батареи параллельно; они создают общую ЭДС 12 В, но могут обеспечить больший ток, необходимый для запуска дизельного двигателя.
Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме индивидуальных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют одинаковую ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше отдельных внутренних сопротивлений. Батареи соединены последовательно, чтобы увеличить напряжение на клеммах нагрузки. Батареи соединены параллельно для увеличения тока нагрузки.
Батареи соединены последовательно, чтобы увеличить напряжение на клеммах нагрузки. Батареи соединены параллельно для увеличения тока нагрузки.
Солнечные батареи
Другим примером, связанным с несколькими источниками напряжения, является комбинация солнечных элементов, соединенных как последовательно, так и параллельно для получения желаемого напряжения и тока. Фотоэлектрическая генерация, которая представляет собой преобразование солнечного света непосредственно в электричество, основана на фотоэлектрическом эффекте. Фотоэлектрический эффект выходит за рамки этой главы и рассматривается в разделе «Фотоны и волны материи», но в целом фотоны, ударяясь о поверхность солнечного элемента, создают в нем электрический ток.
Большинство солнечных элементов сделаны из чистого кремния. Большинство отдельных элементов имеют выходное напряжение около 0,5 В, а выходной ток зависит от количества солнечного света, падающего на элемент (падающее солнечное излучение, известное как инсоляция). При ярком полуденном солнечном свете типичные монокристаллические клетки производят ток на единицу площади около 100 мА/см2100 мА/см2 площади поверхности клетки.
При ярком полуденном солнечном свете типичные монокристаллические клетки производят ток на единицу площади около 100 мА/см2100 мА/см2 площади поверхности клетки.
Отдельные солнечные элементы электрически соединены в модули для удовлетворения потребностей в электроэнергии. Их можно соединить последовательно или параллельно, как батареи, о которых говорилось ранее. Массив или модуль солнечных элементов обычно состоит из 36–72 элементов с выходной мощностью от 50 до 140 Вт9.0011
Солнечные элементы, как и батареи, обеспечивают напряжение постоянного тока. Ток от источника постоянного напряжения является однонаправленным. Большинству бытовых приборов требуется переменный ток (ac) напряжения.
¿Cuáles son?【 Formulas y Ejercicios 】
¿Qué son las leyes de Kirchhoff?
Estas leyes cuantifican cómo fluye la corriente a través de un Circuito y cómo varia el voltaje alrededor de una malla en un Circuito. Лас-лейес-де-Кирхгоф, сын основных принципов, пункт эль-анализа де Circuitos.
Лас-лейес-де-Кирхгоф, сын основных принципов, пункт эль-анализа де Circuitos.
¿Para qué sirven?
Разрешить распознаватель проблем, определяемых компледжос, определяемых ип конъюнкто де лейес и теоремас де красный базикос пункт лос voltajes у corrientes alrededor де ип Circuito.
¿Cuáles son las leyes de Kirchhoff?
Лас-дос-Лейес-де-Кирхгоф сын: Лей-де-корриентес де Кирхгоф и Лей-де-вольтахес де Кирхгоф.
- Лей-де-Корриентес-де-Кирхгоф (primera ley-de-Kirchhoff)
- Лей-де-вольтахес-де-Кирхгоф (Segunda ley de Kirchhoff)
Estas leyes Surgen de la aplicación de la ley de conservación de la energía.
1 Ley de Corrientes de Kirchhoff
1.1 Primera Ley de Kirchhoff Ejemplos
1,2 LCK ejercicios
2 Ley de Voltajes de Kirchhoff
2. 1. de corrientes de Kirchhoff
1. de corrientes de Kirchhoff
Esta ley axiomática se denomina como Ley de corrientes de Kirchhoff (аббревиатура LCK) , простой юридический адрес, установленный по номеру:
Алгебраическая сумма корриентов, которая входит в общий узел и является основным.
Esta ley представляет ип enunciado matemático del hecho de que la carga no se acumula en un nodo. En consecuencia, las corrientes deben sumar cero.
Primera ley de Kirchhoff ejemplos
Se usará la siguiente ilustración para ejemplificar la aplicación de la LCK. En ella se muestran las direcciones del flujo de corriente en un nodo.
¿Cuál es la corriente i4 в узле распределения?
Esta pregunta pone a pruebatus habilidades con flechas y signos. Las direcciones de las flechas están mezcladas, algunas van hacia adentro, y otras hacia afuera del nodo.
Es recomendable redibujar el nodo con todas las flechas apuntando en la misma dirección. En este caso se dibujan todas hacia afuera.
En este caso se dibujan todas hacia afuera.
Si cambias la dirección de una flecha, deberás también cambiar su signo.
Una Vez Se Cambian Las Direcciones de Las Corriente y Se Realizan Ajustes A Los Signos Numéricos Según Sea Necesario, Se tiene lo Siguiente:
applicando la Lae de kirchhoff yestjando la corpiente 59555 финал де corriente.
-9a+15a+11a+i_4-20a = 0
I_4 =+9A-15A-11A+20A
I_4 = \ BOLD {3A}
LCK eJercicios
EJerciCio 1: a CUál Ejercicios
1: as ejercicios Vuelve a redibujar el Circuito con todas las flechas apuntando hacia la misma dirección (hacia afuera o hacia adentro). En este ejemplo se eligen todas las corrientes apuntando hacia afuera ; haciendo los ajustes necesarios con las flechas y signos se tiene lo siguiente: Ahora simplemente se aplica la Ley de corrientes de Kirchhoff y se despeja la incógnita i6. -100мА-75мА+105мА-210мА+320мА-i_6=0 I_6 = -100MA-75MA+105MA-210MA+320MA I_6 = \ BOLD {40MA} EJERCICIO 2: ENCONTRAR EL VALOR DE LA SUMA DE LAS CORRIENTES IA+IB , SI IC = 37MA IC = 37MA = 37ma IC = 37MA. e iD=33 мА . Алгебраическая сумма las corrientes que entran al nodo debe sercero: i_A+i_B+(-i_C)+(-i_D)=0 Entonces, por obviedad, la manley tambiénera de aplicars per aplicars по алгебраической сумме las corrientes que заброшенный el nodo: (-i_A)+(-i_B)+i_C+i_D=0 Ahora, al igualar la suma de las corrientes que tienen flechas de referencia dirigidas hacia el nodo, con la suma de las dirigidas hacia afuera del mismo , y sustituyendo los valores de iC e iD se tiene lo siguiente: i_A+i_B=i_C+i_D i_A+i_B=37mA+33mA=\bold{70mA}. корриенте
i6 в узле дистрибутива?

Ley de Voltajes de Kirchhoff
La Ley de Voltajes de Kirchhoff (Abreviada lvk) Es la Segunda de las Leyes Fundamentales Queden usar para el Análisis Deose DeoSe DeoSe, LaSeme, LaSeme, LaSeme, LaSeme, LaSeme, LaSemeE, LaSemeE, LaSeme, LaSeme, LaSeme, LaSeme, Lastementee. алгебраическая сумма де лос voltajes alrededor де cualquier Trayectoria cerrada es igual a cero.
En otras palabras, la suma алгебраика de TODAS las voltages alrededor del bucle debe serigual a cero (ΣV = 0) . Ten en cuenta que aquí el término «suma atomicaica» означает рассмотрение лас-поляридадов и сигнос-де-лас-фуэнтес и лас-каидас-де-вольтахе альредедор эль-лазо.
Segunda ley de Kirchhoff ejemplos
Con ayuda de la Ley de Tensiones de Kirchhoff, encuentre el voltaje de la Resistance R2.
Primero elige un nodo para comenzar el análisis. En este ejemplo se inició con el nodo que conecta R4 con la fuente de voltaje. Ahora sigue эль camino en sentido horario alrededor де ла трайектория.
En este ejemplo se inició con el nodo que conecta R4 con la fuente de voltaje. Ahora sigue эль camino en sentido horario alrededor де ла трайектория.
Las flechas de voltaje están mezcladas, no todas apuntan en la misma dirección alrededor de la traceectoria. Entonces, presta mucha atención a la polaridad del voltaje de cada elemento en el bucle. Dependiendo de la dirección de la flecha de voltaje, se define el signo positivo o negativo.
Conseguir los signos correctos para la ecuación es la parte complicada. Esta es la habilidad esencial cuando se aplican las leyes de Kirchhoff. Con ayuda de la LVK se obtiene la siguiente ecuación:
15В+(-5В)+(-V_{R2})+(-3В)+(-1В)=0
15В-5В-V_{R2}-3В-1В=0
6В-V_{R2 }=0
V_{R2}=\bold{6V}
LVK Ejercicios
Ejercicios 1: Расчетное значение напряжения для расчетного сопротивления цепи. Comprobar los resultsados con ayuda de la Ley de Voltajes de Kirchhoff.
El Primer paso para resolver el chaino es calcular la corriente. Luego себе расчет эль voltaje través де лас сопротивления отдельных лиц.
Este Circuito ES Un Circuito en Serie, por lo tanto, solo hay una corriente i que fluye a través de los cinco elementos. Para encontrar la corriente i , las cuatro Resistances en serie se pueden reducir a una sola Resistance эквивалент:
R_{eq}=100\Omega+200\Omega+300\Omega+400\Omega=\bold{1000\ Omega}
Usando la Ley de Ohm, se encuentra la corriente:
I=\frac{V}{R}=\frac{20V}{1000\Omega}=0,020A=\bold{20mA}
Ahora себе conoce эль доблесть де ла corriente. Con este valor es posible encontrar los voltajes de las cuatro Resistances. Regresando al esquema original y agregando etiquetas de voltaje a los cinco elementos se tiene:
Finalmente, se aplica la Ley de Ohm cuatro veces para encontrar el voltaje en cada Resistance:
\begin{aligned} V_{R1}=20mA ⋅100Ω=\bold{+2V} \\ V_{R2}=20mA ⋅200 Ом=\жирный{+4В} \\ V_{R3}=20мА ⋅300Ом=\жирный{+6В} \\ V_{R4}=20мА ⋅400Ом=\жирный{+8В} \end{выровнено}
Пункт comprobar дие лос resultados сын correctos utilice ла LVK.



 В данном случае k — это приближающиеся к узлу линии, обозначение m — выходящие из узла провода. Предлагаемая форма записи применяется в случае, если необходимо узнать сечение токосодержащих жил для электропроводки с одной фазой либо однолинейной схемы электрообеспечения.
В данном случае k — это приближающиеся к узлу линии, обозначение m — выходящие из узла провода. Предлагаемая форма записи применяется в случае, если необходимо узнать сечение токосодержащих жил для электропроводки с одной фазой либо однолинейной схемы электрообеспечения. В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне. Тогда имеем:
Тогда имеем: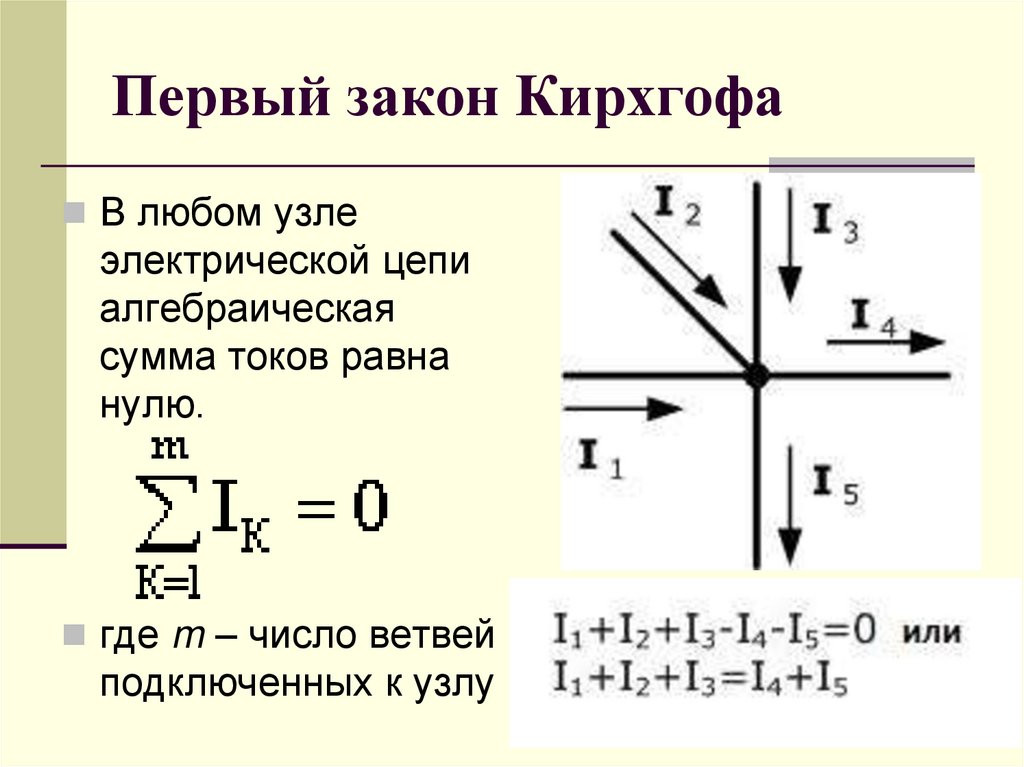 ru/jelektrotehnologii/1510-zakon-kirhgofa-dlja-jelektricheskoj-cepi.html
ru/jelektrotehnologii/1510-zakon-kirhgofa-dlja-jelektricheskoj-cepi.html Т.к. точные значения величин на поверх-
Т.к. точные значения величин на поверх- Тогда диаграмма интенсивности рассеянного препятствием поля, рассчитанная методом геометрической оптики, может резко отличаться от действительной.
Тогда диаграмма интенсивности рассеянного препятствием поля, рассчитанная методом геометрической оптики, может резко отличаться от действительной.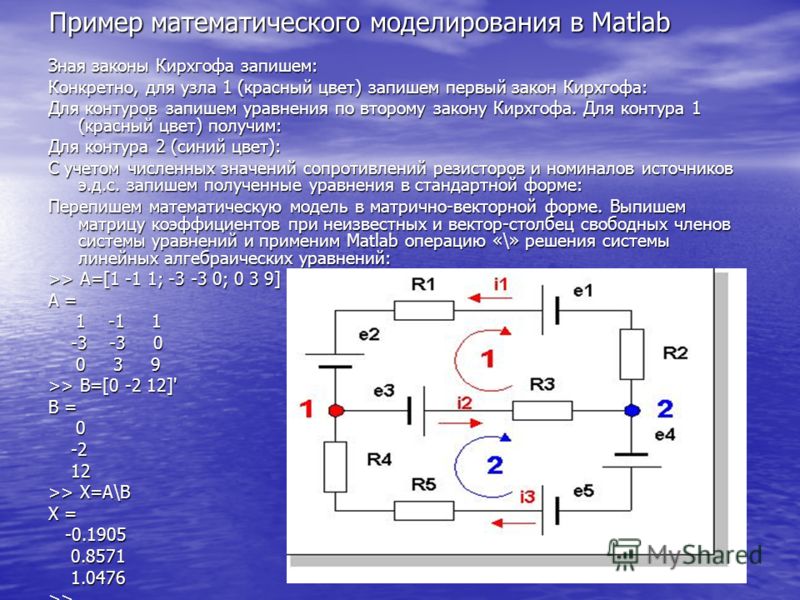 При падении под углом Брюстера отражённый и преломлённый лучи взаимно перпендикулярны.
При падении под углом Брюстера отражённый и преломлённый лучи взаимно перпендикулярны. 1), затем пойдет по границе раздела (рис.2), а при дальнейшем увеличении угла падения преломленный луч исчезнет, т.е. падающий луч будет полностью отражаться границей раздела двух сред (рис.3)).
1), затем пойдет по границе раздела (рис.2), а при дальнейшем увеличении угла падения преломленный луч исчезнет, т.е. падающий луч будет полностью отражаться границей раздела двух сред (рис.3)). 1098/rspa.2015.0689
1098/rspa.2015.0689
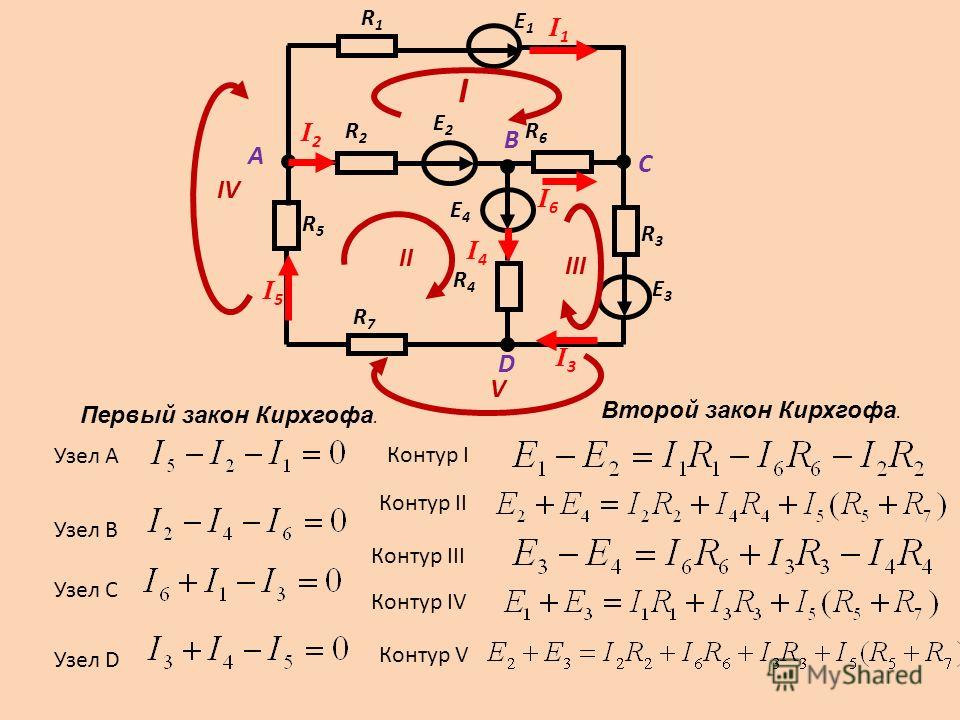
 и др.
J Acoust Soc Am. 2013 г., июнь; 133(6):4087-97. дои: 10.1121/1.4802643.
J Acoust Soc Am. 2013.
PMID: 23742361
и др.
J Acoust Soc Am. 2013 г., июнь; 133(6):4087-97. дои: 10.1121/1.4802643.
J Acoust Soc Am. 2013.
PMID: 23742361 2022.
PMID: 36075300
Обзор.
2022.
PMID: 36075300
Обзор.