физическое обоснование, формулировка, правила знаков; применение для расчета линейных электрических цепей, баланс мощностей.

Правила Кирхгофа— соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.^[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.

Определения

Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U₁, I₁ есть ветвь. Узлом называют точку соединения двух и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый цикл из ветвей. Термин замкнутый цикл

означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило

Сколько тока втекает в узел, столько из него и вытекает. i₂ + i₃ = i₁ + i₄Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:

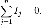
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений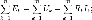

для переменных напряжений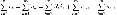

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Баланс мощности – система показателей, характеризующая соответствие суммы значений нагрузок потребителей энергосистемы (ОЭС) и необходимой резервной мощности величине располагаемой мощности энергосистемы.

23. Классическая теория проводимости: природа носителей тока в металлах; постулаты теории, дифференциальная форма законов Ома и Джоуля-Ленца.

Основные положения этой теории сводятся к следующим:

1). Носителями тока в металлах являются электроны, движение которых подчиняется законом классической механики.

2). Поведение электронов подобно поведению молекул идеального газа (электронный газ).

3). При движении электронов в кристаллической решетке можно не учитывать столкновения электронов друг с другом.

4). При упругом столкновении электронов с ионами электроны полностью передают им накопленную в электрическом поле энергию.

При включении электрического поля на хаотическое движение электронов накладывается упорядоченное движение (называемое иногда «дрейфовым»),

происходящее с некоторой средней скоростью ; возникает направленное движение электронов –электрический ток. Плотность тока определяется по формуле.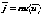

Оценки показывают, что при максимально допустимой плотности тока в металлах j = 10⁷ А/м² и концентрации носителей 10²⁸ – 10²⁹м^-3, . Таким образом, даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов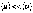

.

закона Ома в дифференциальной форме.

Здесь 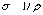–удельная электропроводность.

Размерность σ – [].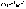

      Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость :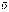

.

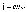      Обозначим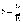

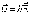, тогда;

Теперь, если удельную электропроводность σ выразить через е, n и b: 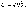то вновь получим выражениезакона Ома в дифференциальной форме: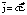

24. Собственная и примесная проводимость полупроводников: механизмы электронной и дырочной проводимости, донорные и акцепторные примеси, зависимость концентрации носителей тока от температуры. Терморезисторы.

Терморезистор — полупроводниковый резистор, в котором используется зависимость электрического сопротивления полупроводникового материала от температуры^[1]. Для терморезистора характерны большой температурный коэффициент сопротивления (ТКС) (в десятки раз превышающий этот коэффициент у металлов), простота устройства, способность работать в различных климатических условиях при значительных механических нагрузках, стабильность характеристик во времени. Терморезистор был изобретён Самюэлем Рубеном (SamuelRuben) в 1930 году. Различают терморезисторы с отрицательным (термисторы) и положительным (позисторы) ТКС. Их ещё называют NTC-термисторы и PTC-термисторы соответственно. У позисторов с ростом температуры растет и сопротивление, а у термисторов —- наоборот: при увеличении температуры сопротивление падает.

Режим работы терморезисторов зависит от того, на каком участке статической вольт-амперной характеристики (ВАХ) выбрана рабочая точка. В свою очередь ВАХ зависит как от конструкции, размеров и основных параметров терморезистора, так и от температуры, теплопроводности окружающей среды, тепловой связи между терморезистором и средой

Виды проводимости полупроводников

Полупроводниковые материалы имеют твердую кристаллическую структуру и по своему удельному сопротивлению, ) занимают промежуточную область между проводниками электрического тока, ) и диэлектриками.

Донорные примеси — атомы химических элементов, внедренные в кристаллическую решетку полупроводника и создающие дополнительную концентрацию электронов. Донорными примесями являются химические элементы, внедренные в полупроводник с меньшей, чем у примеси, валентностью.

Акцепторные примеси — атомы химических элементов, внедренные в кристаллическую решетку полупроводника и создающие дополнительную концентрацию дырок. Акцепторными примесями являются химические элементы, внедренные в полупроводник с большей, чем у примеси, валентностью.

Правила Кирхгофа — Википедия

Пра́вила Кирхго́фа (часто в литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока^[1]. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значения токов на всех ветвях цепи и все межузловые напряжения.

Сформулированы Густавом Кирхгофом в 1845 году^[2].

Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.

Формулировка правил

Определения

Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R

1, I₁ есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило

Сколько тока втекает в узел, столько из него и вытекает.
i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.

∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}

для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Видео по теме

Особенности составления уравнений для расчёта токов и напряжений

Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.

• Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
• Перед тем, как составить уравнения, нужно произвольно выбрать:
  • положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
  • положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
• Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
• При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
• В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.

Пример

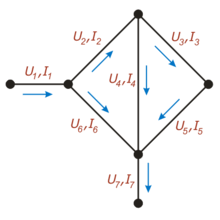На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)

Количество узлов: 3.

p−1=2{\displaystyle p-1=2}

Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.

m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}

Количество контуров: 2.

Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:

{I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.

В соответствии со вторым правилом, справедливы соотношения:

{U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}

Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Закон излучения Кирхгофа

Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Закон Кирхгофа в химии

Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.

Примечания

Литература

• Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
• Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
• Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.

Законы Кирхгофа • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Карьера Густава Кирхгофа во многом типична для немецкого физика XIX столетия. Германия позже своих западных соседей подошла к индустриальной революции и потому сильнее нуждалась в передовых технологиях, которые способствовали бы ускоренному развитию промышленности. В результате ученые, прежде всего естественники, ценились в Германии очень высоко. В год окончания университета Кирхгоф женился на дочери профессора, «соблюдя, тем самым, — как пишет один из его биографов, — два обязательных условия успешной академической карьеры». Но еще до этого, в возрасте двадцати одного года, он сформулировал основные законы для расчета токов и напряжений в электрических цепях, которые теперь носят его имя.

Середина XIX века как раз стала временем активных исследований свойств электрических цепей, и результаты этих исследований быстро находили практические применения. Базовые правила расчета простых цепей, такие как закон Ома, были уже достаточно хорошо проработаны. Проблема состояла в том, что из проводов и различных элементов электрических цепей технически уже можно было изготовлять весьма сложные и разветвленные сети — но никто не знал, как смоделировать их математически, чтобы рассчитать их свойства. Кирхгофу удалось сформулировать правила, позволяющие достаточно просто анализировать самые сложные цепи, и законы Кирхгофа до сих пор остаются важным рабочим инструментом специалистов в области электронной инженерии и электротехники.

Оба закона Кирхгофа формулируются достаточно просто и имеют понятную физическую интерпретацию. Первый закон гласит, что если рассмотреть любой узел цепи (то есть точку разветвления, где сходятся три или более проводов), то сумма поступающих в цепь электрических токов будет равна сумме исходящих, что, вообще говоря, является следствием закона сохранения электрического заряда. Например, если вы имеете Т-образный узел электрической цепи и по двум проводам к нему поступают электрические токи, то по третьему проводу ток потечет в направлении от этого узла, и равен он будет сумме двух поступающих токов. Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит.

Второй закон не менее прост. Если мы имеем сложную, разветвленную цепь, ее можно мысленно разбить на ряд простых замкнутых контуров. Ток в цепи может различным образом распределяться по этим контурам, и сложнее всего определить, по какому именно маршруту потекут токи в сложной цепи. В каждом из контуров электроны могут либо приобретать дополнительную энергию (например, от батареи), либо терять ее (например, на сопротивлении или ином элементе). Второй закон Кирхгофа гласит, что чистое приращение энергии электронов в любом замкнутом контуре цепи равно нулю. Этот закон также имеет простую физическую интерпретацию. Если бы это было не так, всякий раз, проходя через замкнутый контур, электроны приобретали или теряли бы энергию, и ток бы непрерывно возрастал или убывал. В первом случае можно было бы получить вечный двигатель, а это запрещено первым началом термодинамики; во втором — любые токи в электрических цепях неизбежно затухали бы, а этого мы не наблюдаем.

Самое распространенное применение законов Кирхгофа мы наблюдаем в так называемых последовательных и параллельных цепях. В последовательной цепи (яркий пример такой цепи — елочная гирлянда, состоящая из последовательно соединенных между собой лампочек) электроны от источника питания по серии проводов последовательно проходят через все лампочки, и на сопротивлении каждой из них напряжение падает согласно закону Ома.

В параллельной цепи провода, напротив, соединены таким образом, что на каждый элемент цепи подается равное напряжение от источника питания, а это означает, что в каждом элементе цепи сила тока своя, в зависимости от его сопротивления. Примером параллельной цепи является соединение ламп «лесенкой»: напряжение подается на шины, а лампы смонтированы на поперечинах. Токи, проходящие через каждый узел такой цепи, определяются по первому закону Кирхгофа.

Закон кирхгофа с источником постоянного тока решение. Закон кирхгофа простыми словами

В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, ЭДС и сопротивлением всей цепи или, между напряжением и сопротивлением на каком-либо участке цепи определяется законом Ома .

На практике в цепях, токи, от какой-либо точки, идут по разным путям.
Точки, где сходятся несколько проводников, называются узлами, а участки цепи, соединяющие два соседних узла, ветвями.

В замкнутой электрической цепи ни в одной ее точке не могут скапливаться электрические заряды так, как это вызвало бы изменение потенциалов точек цепи. Поэтому электрические заряды притекающие к какому-либо узлу в единицу времени, равны зарядам, утекающим от этого узла за ту же единицу.
Разветвлённая цепь.
В узлеА цепь разветвляется на четыре ветви, которые сходятся в узел В .

Обозначим токи в неразветвленной части цепи —I , а в ветвях соответственно

I1 , I2 , I3 , I4 .

У этих токов в такой цепи будет соотношение:

I = I1+I2+I3+I4;

Cумма токов, подходящих к узловой точке электрической цепи,
равна сумме токов, уходящих от этого узла.

При параллельном соединении резисторов ток проходит по четырем направлениям, что уменьшает общее сопротивление или увеличивает общую проводимость цепи, которая равна сумме проводимостей ветвей.

Обозначим силу тока в неразветвленной ветви буквойI .
Силу тока в отдельных ветвях соответственно I1 , I2 , I3 и I4 .
Напряжение между точками A и B — U .
Общее сопротивление между этими точками — R .

По закону Ома напишем:

I = U/R ; I1 = U/R1 ; I2 = U/R2 ; I3 = U/R3 ; I4 = U/R4 ;

Согласно первому закону Кирхгофа:

I = I1+I2+I3+I4 ; или U/R = U/R1+U/R2+U/R3+U/R4 .

Сократив обе части полученного выражения на U получим:

1/R = 1/R1+1/R2+1/R3+1/R4 , что и требовалось доказать.

Cоотношение для любого числа параллельно соединенных резисторов.
В случае, если в цепи содержится два параллельно соединенных резистора
R1 и R2 , то можно написать равенство:

1/R =1/R1+1/R2 ;

Из этого равенства найдем сопротивление R , которым можно заменить два параллельно соединенных резистора:

Полученное выражение имеет большое практическое применение.
Благодаря этому закону производятся расчёты электрических цепей.

Второй закон Кирхгофа

В замкнутом контуре электрической цепи сумма всех эдс равна
сумме падения напряжения в сопротивлениях того же контура.

E1 + E2 + E3 +…+ En = I1R1 + I2R2 + I3R3 +…+ InRn . При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.

Если в электрической цепи включены два источника энергии, эдс которых совпадают по направлению, т. е. согласно изо1, то эдс всей цепи равна сумме эдс этих источников,
т. е.
E = E1+E2 .

Если же в цепь включено два источника, эдс которых имеют противоположные направления, т. е. включены встречно изо2, то общая эдс цепи равна разности эдс этих источников
Е = Е1-Е2 .

Благодаря этим законам производятся расчёты электрических цепей.
Существует несколько методов расчёта, один из них «Метод узловых напряжений»

Два приема, которые применяют для упрощения процесса составления уравнений, необходимых при расчетах сложных разветвленных цепей постоянного тока называют законами (вернее было бы сказать правилами) Кирхгофа. Прежде чем перейти к самим правила Кирхгофа введем два необходимых определения.

Разветвлёнными цепями названы цепи, которые имеют несколько замкнутых контуров, несколько источников электродвижущей силы (ЭДС).

Узлом разветвлённой цепи называют точку, в которой сходятся три или более проводников с токами.

Первый закон (правило) Кирхгофа, простыми словами

Первое правило Кирхгофа называют правилом узлов, так как оно касается сил токов в узах цепи. Словесно первый закон Кирхгофа формулируют следующим образом: Алгебраическая сумма сил токов в узле равна нулю. В виде формулы это правило запишем как:

С каким знаком сила тока будет входить в сумму (1), зависит от произвольного выбора. Но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Пусть все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными. Если направления токов изначально не заданы,

Законы Кирхгофа — это… Что такое Законы Кирхгофа?

Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока.^[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач теории электрических цепей. Применение правил Кирхгофа к линейной цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи. Сформулированы Густавом Кирхгофом в 1845 году.

Формулировка

Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.

В этом случае законы формулируются следующим образом.

Первый закон

Первый закон Кирхгофа (Закон токов Кирхгофа, ЗТК) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.

Второй закон

Второй закон Кирхгофа (Закон напряжений Кирхгофа, ЗНК) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:

для постоянных напряжений

для переменных напряжений

Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

Пример

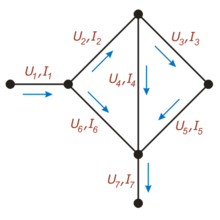На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)

Например, для приведённой на рисунке цепи, в соответствии с первым законом выполняются следующие соотношения:

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

В соответствии со вторым законом, справедливы соотношения:

Особенности составления уравнений для расчёта токов

• Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.
• Перед тем, как составить уравнения, нужно произвольно выбрать:
  • положительные направления токов в ветвях и обозначить их на схеме;
  • положительные направления обхода контуров для составления уравнений по второму закону.
• С целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке)
• Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.
• При записи линейно независимых уравнений по второму закону, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие)

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, метод контурных токов, метод узловых напряжений, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простой формулировке уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Существует мнение, согласно которому «Законы Кирхгофа» следует именовать «Правилами Кирхгофа», ибо они не отражают фундаментальных сущностей природы (и не являются обобщением большого количества опытных данных), а могут быть выведены из других положений и предположений.^{[источник не указан 912 дней]}

Закон излучения

Закон излучения Кирхгофа — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Примечания

Литература

• Матвеев А. Н. Электричество и магнетизм — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
• Калашников С. Г. Электричество — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи — 11-е издание. — М.: Гардарики, 2007.

Формула Кирхгофа — Википедия

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Рассмотрим уравнение

∂2u∂t2−a2△u=f{\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}-a^{2}\triangle u=f}, где функции u=u(x,t){\displaystyle u=u(\mathbf {x} ,t)} и f=f(x,t){\displaystyle f=f(\mathbf {x} ,t)} определены на (x,t)∈Rn×R+{\displaystyle (\mathbf {x} ,t)\in \mathbb {R} ^{n}\times \mathbb {R} ^{+}}, а △{\displaystyle \triangle } — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью a{\displaystyle a} в моменты времени t>0{\displaystyle t>0}.

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени t=0{\displaystyle t=0}:

u|t=0=φ0(x¯),∂u∂t|t=0=φ1(x¯){\displaystyle u|_{t=0}=\varphi _{0}({\bar {x}}),\quad \left.{\frac {\partial u}{\partial t}}\right|_{t=0}=\varphi _{1}({\bar {x}})}

Тогда обобщённая формула Кирхгофа даёт решение этой задачи в трёхмерном случае:

u(x,t)=∂∂t[14πa2t∬Sφ0(y)d2Sn]+14πa2t∬Sφ1(y)d2Sn+14πa2∭|x−y|⩽atf(y,t−|x−y|a)|x−y|d3y{\displaystyle u(\mathbf {x} ,t)={\frac {\partial }{\partial t}}\left[{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{0}(\mathbf {y} )d^{2}S_{n}\right]+{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{1}(\mathbf {y} )d^{2}S_{n}+{\frac {1}{4\pi a^{2}}}\iiint \limits _{\left|\mathbf {x} -\mathbf {y} \right|\leqslant at}{\frac {f\left(\mathbf {y} ,t-{\frac {\left|\mathbf {x} -\mathbf {y} \right|}{a}}\right)}{\left|\mathbf {x} -\mathbf {y} \right|}}d^{3}\mathbf {y} }

где поверхностные интегралы берутся по сфере S:|x−y|=at{\displaystyle S\colon \left|\mathbf {x} -\mathbf {y} \right|=at}.

Сам Кирхгоф рассматривал только трёхмерный случай.

Простой вывод решения основной задачи использует преобразование Фурье.

Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени

Пусть в начальный момент времени t=0{\displaystyle t=0} на некотором компакте M есть локальное возмущение (φ0≠0{\displaystyle \varphi _{0}\neq 0} и/или φ1≠0{\displaystyle \varphi _{1}\neq 0}). Если мы находимся в некоторой точке x¯0∈R3{\displaystyle {\bar {x}}_{0}\in \mathbb {R} ^{3}}, то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время t1=1ainfy¯∈M|y¯−x¯0|{\displaystyle t_{1}={\frac {1}{a}}\inf _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}.

Вне отрезка времени [t1;t2]{\displaystyle \left[t_{1};t_{2}\right]}, где t2=1asupy¯∈M|y¯−x¯0|{\displaystyle t_{2}={\frac {1}{a}}\sup _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}, функция u(x ₀, t) равна нулю.

Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в R2{\displaystyle \mathbb {R} ^{2}}, уже не будет компактным в R3{\displaystyle \mathbb {R} ^{3}}, а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).^[1]

Решение уравнения колебаний мембраны (двумерного пространства)

utt=a2△u+f{\displaystyle u_{tt}=a^{2}\triangle u+f}

(функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

задаётся формулой:

u(x¯,t)=u(x1,x2,t)=12πa∫0t∬r<a(t−τ)f(y1,y2,τ)dy1dy2dτa2(t−τ)2−(y1−x1)2−(y2−x2)2+∂∂t12πa∬r<atφ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2+12πa∬r<atψ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2{\displaystyle u({\bar {x}},t)=u(x_{1},x_{2},t)={\frac {1}{2\pi a}}\int \limits _{0}^{t}\iint \limits _{r<a(t-\tau )}{\frac {f(y_{1},y_{2},\tau )dy_{1}dy_{2}d\tau }{\sqrt {a^{2}(t-\tau )^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {\partial }{\partial t}}{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\varphi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\psi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}}.

Решение одномерного волнового уравнения

utt=a2uxx+f{\displaystyle u_{tt}=a^{2}u_{xx}+f\quad } (функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

имеет вид^[2]

u(x,t)=φ(x+at)+φ(x−at)2+12a∫x−atx+atψ(α)dα+12a∫0t∫x−a(t−τ)x+a(t−τ)f(s,τ)dsdτ{\displaystyle u(x,t)={\frac {\varphi (x+at)+\varphi (x-at)}{2}}+{\frac {1}{2a}}\int \limits _{x-at}^{x+at}{\psi (\alpha )d\alpha }+{\frac {1}{2a}}\int \limits _{0}^{t}\int \limits _{x-a(t-\tau )}^{x+a(t-\tau )}f(s,\tau )dsd\tau }

В область II приходят характеристики только из одного семейства

При пользовании формулой Д’Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области R1×[0,T]{\displaystyle \mathbb {R} ^{1}\times [0,T]}. Решение волнового уравнения представляется в виде суммы двух функций: u(x,t)=f(x+at)+g(x−at){\displaystyle u(x,t)=f(x+at)+g(x-at)}, то есть оно определяется двумя семействами характеристик: x+at=ξ, x−at=η{\displaystyle x+at=\xi ,\ x-at=\eta }. Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д’Аламбера не работает.

В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения ∂2u∂t2=a2△u+f(x¯,t){\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}=a^{2}\triangle u+f({\bar {x}},t)} с начальными условиями u(x¯,0)=φ0(x¯), ut(x¯,0)=φ1(x¯){\displaystyle u({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ u_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}})} и искать решение в виде суммы трех функций: u(x,t)=A(x,t)+B(x,t)+C(x,t){\displaystyle u(x,t)=A(x,t)+B(x,t)+C(x,t)}, которые удовлетворяют следующим условиям:

∂2A∂t2=a2△A+f(x¯,t),A(x¯,0)=0, At(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}A}{\partial t^{2}}}=a^{2}\triangle A+f({\bar {x}},t),\qquad A({\bar {x}},0)=0,\ A_{t}({\bar {x}},0)=0;}

∂2B∂t2=a2△B,B(x¯,0)=φ0(x¯), Bt(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}B}{\partial t^{2}}}=a^{2}\triangle B,\qquad B({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ B_{t}({\bar {x}},0)=0;}

∂2C∂t2=a2△C,C(x¯,0)=0, Ct(x¯,0)=φ1(x¯).{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=a^{2}\triangle C,\qquad C({\bar {x}},0)=0,\ {\mathit {C}}_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}}).}

Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путём замены переменных. Например, пусть φ1(x,y,z)=11+(x+3y−2z)2{\displaystyle \varphi _{1}(x,y,z)={\frac {1}{1+(x+3y-2z)^{2}}}}. Тогда после замены ξ=x+3y−2z{\displaystyle \xi =x+3y-2z} уравнение для задачи «С» примет вид:

∂2C∂t2=14a2∂2C∂ξ2,C(ξ,0)=0, Ct(ξ,0)=11+ξ2.{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=14a^{2}{\frac {\partial ^{2}C}{\partial \xi ^{2}}},\qquad {\mathit {C}}(\xi ,0)=0,\ C_{t}(\xi ,0)={\frac {1}{1+\xi ^{2}}}.}

Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д’Аламбера:

C(ξ,t)=1214a∫ξ−14atξ+14atdη1+η2=1214a(arctg⁡(ξ+14at)−arctg⁡(ξ−14at)).{\displaystyle C(\xi ,t)={\frac {1}{2{\sqrt {14}}a}}\int \limits _{\xi -{\sqrt {14}}at}^{\xi +{\sqrt {14}}at}{\frac {d\eta }{1+\eta ^{2}}}={\frac {1}{2{\sqrt {14}}a}}\left(\operatorname {arctg} (\xi +{\sqrt {14}}at)-\operatorname {arctg} (\xi -{\sqrt {14}}at)\right).}

В силу четности начального условия, решение сохранит свой вид во всей области t>0{\displaystyle t>0}.

• Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6.