Закон электрической индукции. Закон электромагнитной индукции

Закон электрической индукции. Закон электромагнитной индукции

Самый главный закон электротехники – закон Ома

Закон Джоуля — Ленца

Закон Джоуля — Ленца

В словесной формулировке звучит следующим образом – Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля

гдеw — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля, σ — проводимость среды.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах:

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка

В математической форме этот закон имеет вид:
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R

— сопротивление,Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2.

В случае постоянных силы тока и сопротивления:

Законы Кирхгофа

Законы Кирхгофа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Применение правил Кирхгофа к цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи.

Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.
В этом случае законы формулируются следующим образом.

Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит

p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.

Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:

для постоянных напряжений:

для переменных напряжений:

Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)

Например, для приведённой на рисунке цепи, в соответствии с первым законом выполняются следующие соотношения:

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
В соответствии со вторым законом, справедливы соотношения:

Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.

Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.

Существует мнение, согласно которому «Законы Кирхгофа» следует именовать «Правилами Кирхгофа», ибо они не отражают фундаментальных сущностей природы (и не являются обобщением большого количества опытных данных), а могут быть выведены из других положений и предположений.

ЗАКОН ПОЛНОГО ТОКА

ЗАКОН ПОЛНОГО ТОКА один из основных законов электромагнитного поля. Устанавливает взаимосвязь между магнитной силой и величиной тока, проходящего через поверхность. Под полным током понимается алгебраическая сумма токов, пронизывающих поверхность, ограниченную замкнутым контуром.

Намагничивающая сила вдоль контура равна полному току, проходящему сквозь поверхность, ограниченную этим контуром. В общем случае напряженность поля на различных участках магнитной линии может иметь разные значения, и тогда намагничивающая сила будет равна сумме намагничивающих сил каждой линии.

Закон Джоуля — Ленца

Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Открыт в 1840 году независимо Джеймсом Джоулем и Эмилием Ленцом.

В словесной формулировке звучит следующим образом:

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля

Математически может быть выражен в следующей форме:

где

w — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля, σ — проводимость среды.

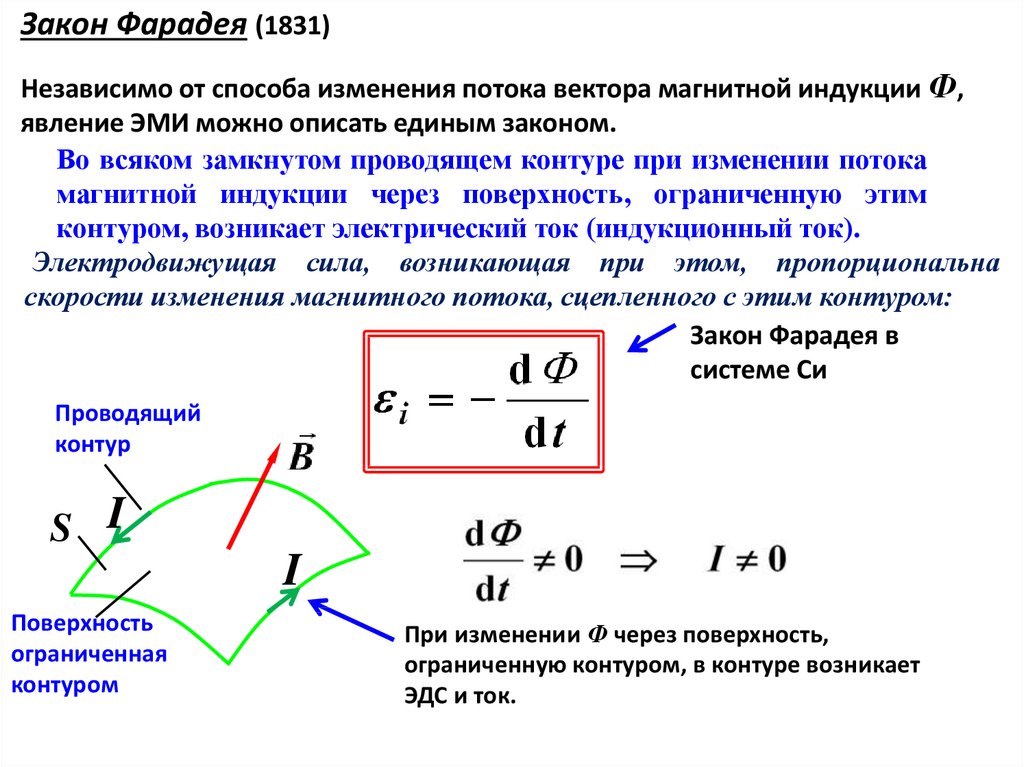
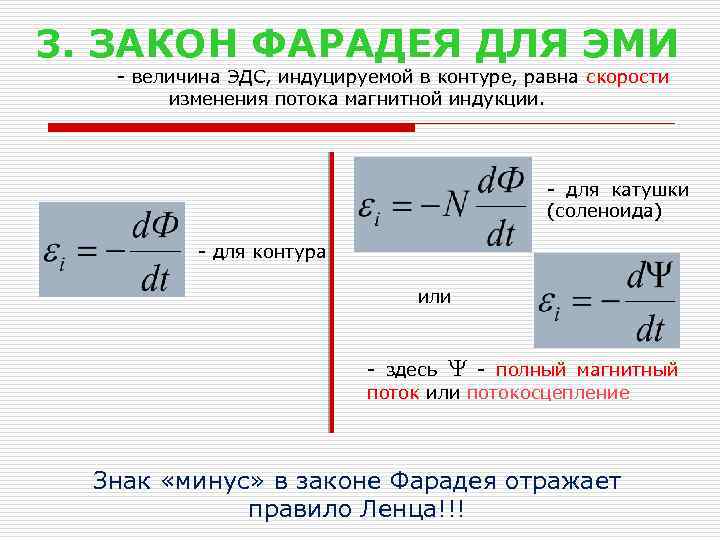
ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ , закон Фарадея – закон, устанавливающий взаимосвязь между магнитными и электрическими явлениями. ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Величина ЭДС поля зависит от скорости изменения магнитного потока.

ЗАКОНЫ ФАРАДЕЯ (по имени английского физика М.Фарадея (1791-1867)) – основные законы электролиза.

Устанавливают взаимосвязь между количеством электричества, проходящего через электропроводящий раствор (электролит), и количеством вещества, выделяющегося на электродах.

При пропускании через электролит постоянного тока I в течение секунды q = It, m = kIt.

Второй закон ФАРАДЕЯ: электрохимические эквиваленты элементов прямо пропорциональны их химическим эквивалентам.

Правило буравчика

Правило Буравчика (также, правило правой руки) — мнемоническое правило для определения направления вектора угловой скорости, характеризующей скорость вращения тела, а также вектора магнитной индукции

B или для определения направления индукционного тока.

Правило правой руки

Правило правой руки

Правило буравчика : «Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции».

Определяет направление индукционного тока в проводнике, движущемся в магнитном поле

Правило правой руки: «Если ладонь правой руки расположить так, чтобы в нее входили силовые линии магнитного поля, а отогнутый большой палец направить по движению проводника, то четыре вытянутых пальца укажут направление индукционного тока».

Для соленоида оно формулируется так: «Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида».

Правило левой руки

Правило левой руки

Если движется заряд, а магнит покоится, то для определения силы действует правило левой руки: «Если левую руку расположить так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно ей, а четыре пальца были направлены по току (по движению положительно заряженной частицы или против движения отрицательно заряженной), то отставленный на 90° большой палец покажет направление действующей силы Лоренца или Ампера.

»

Федун В.И. Конспект лекций по физике Электромагнетизи

Лекция 26.

Электромагнитная индукция. Открытие Фарадея .

В 1831 г. М. Фарадеем было сделано одно из важнейших фундаментальных открытий в электродинамике – обнаружено явлениеэлектромагнитной индукции .

В замкнутом проводящем контуре при изменении магнитного потока (потока вектора ), охватываемого этим контуром, возникает электрический ток

.

Этот ток получил название индукционного .

Появление индукционного тока означает, что при изменении магнитного

	потока в контуре возникает э.д.с. индукции (работа по перенесению единичного заряда по замкнутому контуру). Отметим, что значениесовершенно не зависит от того, каким образом осуществляется изменение магнитного потока, и определяется лишь скоростью его изменения, т. е. величиной . Изменение знака производной приводит к изменению знакаэ.д.с. индукции .
Рисунок 26.1.

Фарадей обнаружил, что индукционный ток можно вызвать двумя различными способами, которые удобно объяснить с помощью рисунка.

1-й способ: перемещение рамки в магнитном поле неподвижной катушки(см. рис.26.1).

2-й способ: изменение магнитного поля , создаваемого катушкой, за счет ее движения или вследствие изменения силы токав ней (или того и другого вместе). Рамкапри этом неподвижна.

В обоих этих случаях гальванометр будет показывать наличие индукционного тока в рамке.

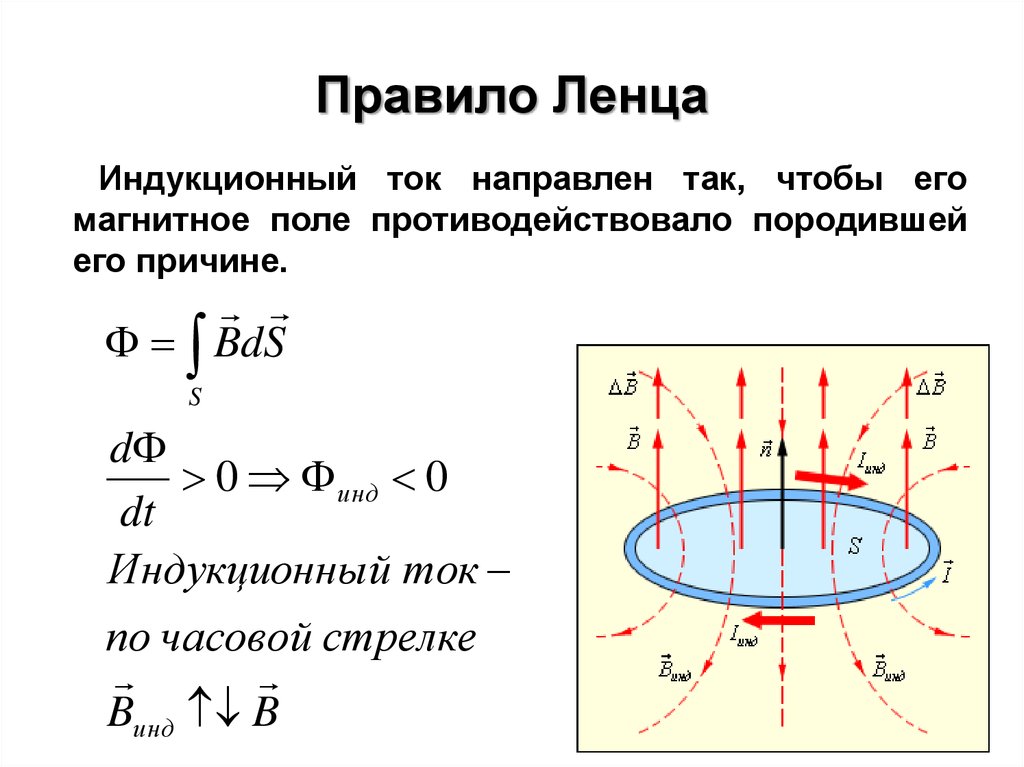
Направление индукционного тока и, соответственно, знак э.д.с. индукции определяются правилом Ленца.

Правило Ленца.

Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей .

Правило Ленца выражает важное физическое свойство – стремление системы противодействовать изменению ее состояния. Это свойство называют электромагнитной инерцией .

Какова бы ни была причина изменения магнитного потока, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с. индукции определяется формулой

Природа электромагнитной индукции .

С целью выяснения физических причин, которые приводят к возникновению э.д.с. индукции, последовательно рассмотрим два случая.

1. Контур движется в постоянном магнитном поле.

действовать сила

Электродвижущая сила, создаваемая этим полем, называется электродвижущей силой индукции . В нашем случае

.

Здесь знак «минус» поставлен потому, что стороннее поле направлено против положительного обхода контура, определяемого правилом правого винта. Произведениеесть скорость приращения площади контура (приращение площади в единицу времени), поэтому

,

где

— приращение магнитного потока сквозь контур.

.

Полученный результат можно обобщить на случай произвольной ориентации вектора индукции магнитного поля относительно плоскости контура и на любой контур, движущийся (и/или деформируемый) произвольным образом в постоянном неоднородном внешнем магнитном поле.

Итак, возбуждение э.д.с. индукции при движении контура в постоянном магнитном поле объясняется действием магнитной составляющей силы Лоренца, пропорциональной

, которая возникает при перемещении проводника.

2. Контур покоится в переменном магнитном поле.

Наблюдаемое на опыте возникновение индукционного тока свидетельствует о том, что и в этом случае в контуре появляются сторонние силы, которые теперь связаны с изменяющимся во времени магнитным полем. Какова же их природа? Ответ на этот принципиальный вопрос был дан Максвеллом.

Поскольку проводник покоится, то скорость упорядоченного движения электрических зарядов

и, следовательно, магнитная сила, пропорциональная

, также равна нулю и уже не может привести заряды в движение. Однако кроме магнитной силы на электрический заряд может действовать только сила со стороны электрического поля, равная. Поэтому остается заключить, чтоиндукционный ток обусловлен электрическим полем , возникающим при изменении во времени внешнего магнитного поля . Именно это электрическое поле и ответственно за появление э.д.с. индукции в неподвижном контуре. Согласно Максвеллу,изменяющееся во времени магнитное поле порождает в окружающем пространстве электрическое поле . Возникновение электрического поля не связано с наличием проводящего контура, который лишь позволяет обнаружить по возникновению в нем индукционного тока существование этого поля.

Формулировка закона электромагнитной индукции , данная Максвеллом, принадлежит к числу наиболее важных обобщений электродинамики.

Всякое изменение магнитного поля во времени возбуждает в окружающем пространстве электрическое поле .

Математическая формулировка закона электромагнитной индукции в понимании Максвелла имеет вид:

Циркуляция вектора напряженности этого поля по любому неподвижному замкнутому контуруопределяется выражением

,

где — магнитный поток, пронизывающий контур.

Используемый для обозначения скорости изменения магнитного потока знак частной производной указывает на то, что контур является неподвижным.

Поток вектора через поверхность, ограниченную контуром, равен

, поэтому выражение закона электромагнитной индукции можно переписать следующим образом:

Это одно из уравнений системы уравнений Максвелла.

Тот факт, что циркуляция электрического поля, возбуждаемого переменным во времени магнитным полем, отлична от нуля, означает, что рассматриваемое электрическое поле не потенциальное .Оно, как и магнитное поле, являетсявихревым .

В общем случае электрическое поле может быть представлено векторной суммой потенциального (поля статических электрических зарядов, циркуляция которого равна нулю) и вихревого (обусловленного изменяющимся во времени магнитным полем) электрических полей.

В основе рассмотренных нами явлений, объясняющих закон электромагнитной индукции, не просматривается общего принципа, позволяющего установить общность их физической природы. Поэтому эти явления следует рассматривать как независимые, а закон электромагнитной индукции — как результат их совместного действия. Тем более удивительным оказывается тот факт, что э.д.с. индукции в контуре всегда равна скорости изменения магнитного потока сквозь контур. В тех случаях, когда меняется и поле и расположение или конфигурация контура в магнитном поле, э.д.с. индукции следует рассчитывать по формуле

Выражение, стоящее в правой части этого равенства, представляет собой полную производную магнитного потока по времени: первое слагаемое связано с изменением магнитного поля во времени, второе – с движением контура.

Можно сказать, что во всех случаях индукционный ток вызывается полной силой Лоренца

.

Какая часть индукционного тока вызывается электрической, а какая магнитной составляющей силы Лоренца — зависит от выбора системы отсчета .

О работе сил Лоренца и Ампера .

Из самого определения работы следует, что сила, действующая в магнитном поле на электрический заряд и перпендикулярная его скорости, не может совершать работы. Однако при движении проводника с током, увлекающего за собой заряды, сила Ампера все же работу совершает. Наглядным подтверждением этого служат электромоторы.

Это противоречие исчезает, если принять во внимание, что движение проводника в магнитном поле неизбежно сопровождается явлением электромагнитной индукции. Поэтому наряду с силой Ампера работу над электрическими зарядами совершает и возникающая в проводнике электродвижущая сила индукции. Т.о., полная работа сил магнитного поля складывается из механической работы, обусловленной силой Ампера, и работы э.д.с., индуцируемой при движении проводника. Обе работы равны по модулю и противоположны по знаку, поэтому их сумма равна нулю. Действительно, работа амперовой силы при элементарном перемещении проводника с током в магнитном поле равна

, за это же время э.д.с. индукции совершает работу

,

тогда полная работа

.

Силы Ампера совершают работу не за счет энергии внешнего магнитного поля, которое может оставаться постоянным, а за счет источника э.д.с., поддерживающего ток в контуре.

В результате многочисленных опытов Фарадей установил основной количественный закон электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток. Возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Фарадей установил, что значение ЭДС электромагнитной индукции E i пропорционально скорости изменения магнитного потока:

E i = -К , (27.1)

где К – коэффициент пропорциональности, зависящий только от выбора единиц измерения.

В системе единиц СИ коэффициент К = 1, т.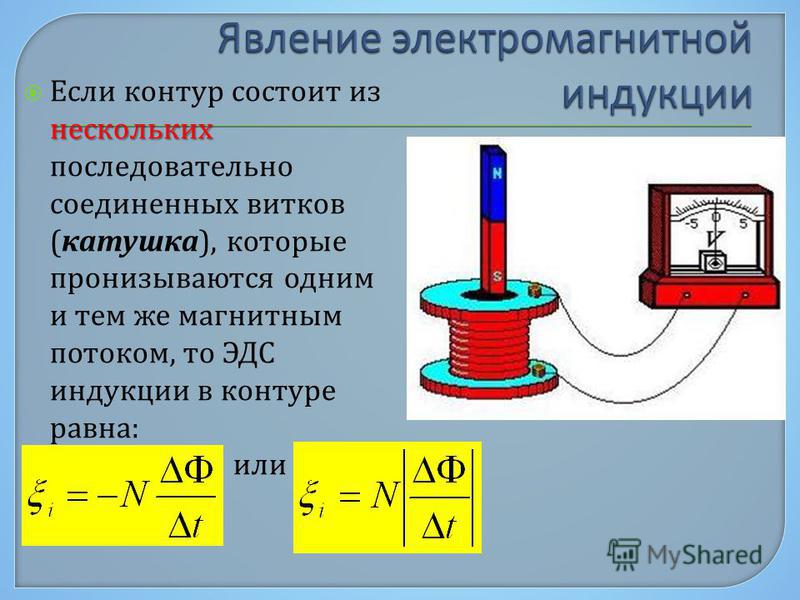 е.

E i = — . (27.2)

Эта формула и представляет собой закон электромагнитной индукции Фарадея. Знак минус в этой формуле соответствует правилу (закону) Ленца.

Закон Фарадея можно сформулировать еще таким образом: ЭДС электромагнитной индукции E i в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: ЭДС E i не зависит от способа изменения магнитного потока.

Знак минус в (27.2) показывает, что увеличение потока ( > 0) вызывает ЭДС E i 0 т. е. направления магнитного потока индукционного тока и потока, вызвавшего его, совпадают. Знак минус в формуле (27.2) является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока (а значит и знака и ЭДС индукции), выведенного в 1833 г. Правило Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Иначе говоря, индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.

ЭДС индукции выражается в вольтах (В). Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим:

Если замкнутый контур, в котором индуцируется ЭДС индукции, состоит из N витков, то E i будет равна сумме ЭДС, индуцируемых в каждом из витков. И если магнитный поток, охватываемый каждым витком, одинаков и равен Ф, то суммарный поток сквозь поверхность N витков, равен (NФ) – полный магнитный поток (потокосцепление). В этом случае ЭДС индукции равна:

E i = -N× , (27.3)

Формула (27.2) выражает закон электромагнитной индукции в общей форме. Она применима как к неподвижным контурам, так и к движущимся проводникам в магнитном поле. Входящая в нее производная от магнитного потока по времени в общем случае состоит из двух частей, одна из которых обусловлена изменением магнитной индукции во времени, а другая – движением контура относительно магнитного поля (или его деформацией). Рассмотрим некоторые примеры применения этого закона.

Пример 1. Прямолинейный проводник длиной l движется параллельно самому себе в однородном магнитном поле (рисунок 38). Этот проводник может входить в состав замкнутой цепи, остальные части которой неподвижны. Найдем ЭДС, возникающую в проводнике.

Если мгновенное значение скорости проводника есть v , то за время dt он опишет площадь dS = l×v ×dt и за это время пересечет все линии магнитной индукции, проходящие через dS. Поэтому изменение магнитного потока через контур, в состав которого входит движущийся проводник, будет dФ = B n ×l×v ×dt. Здесь B n — составляющая магнитной индукции, перпендикулярная к dS. Подставляя это в формулу (27.2) получаем величину ЭДС:

E i = B n ×l×v . (27.4)

Направление индукционного тока и знак ЭДС определяются правилом Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток. В некоторых случаях возможно определение направления индукционного тока (полярности ЭДС индукции) согласно другой формулировке правила Ленца: индукционный ток в движущемся проводнике направлен таким образом, что возникающая при этом сила Ампера противоположна вектору скорости (тормозит движение).

Разберем численный пример. Вертикальный проводник (автомобильная антенна) длиной l = 2 м движется с востока на запад в магнитном поле Земли со скоростью v = 72 км/час = 20 м/с. Вычислим напряжение между концами проводника. Так как проводник разомкнут, то тока в нем не будет и напряжение на концах будет равно ЭДС индукции. Учитывая, что горизонтальная составляющая магнитной индукции поля Земли (т.е. составляющая, перпендикулярная к направлению движения) для средних широт равна 2×10 -5 Тл, по формуле (27.4) находим

U = B n ×l×v = 2×10 -5 ×2×20 = 0,8×10 -3 В,

т.е. около 1 мВ. Магнитное поле Земли направлено с юга на север. Поэтому мы находим, что ЭДС направлена сверху вниз. Это значит, что нижний конец провода будет иметь более высокий потенциал (зарядится положительно), а верхний – более низкий (зарядится отрицательно).

Пример 2. В магнитном поле находится замкнутый проволочный контур, пронизываемый магнитным потоком Ф. Предположим, что этот поток уменьшается до нуля, и вычислим полную величину заряда, прошедшего по цепи. Мгновенное значение ЭДС в процессе исчезновения магнитного потока выражается формулой (27.2). Следовательно, согласно закону Ома мгновенное значение силы тока есть

где R – полное сопротивление цепи.

Величина прошедшего заряда равна

q = = — = . (27.6)

Полученное соотношение выражает закон электромагнитной индукции в форме, найденной Фарадеем, который из своих опытов заключил, что величина заряда, прошедшего по цепи, пропорциональна полному числу линий магнитной индукции, пересеченных проводником (т.е. изменению магнитного потока Ф 1 -Ф 2), и обратно пропорциональна сопротивлению цепи R. Соотношение (27.6) позволяет дать определение единицы магнитного потока в системе СИ: вебер – магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 Ом проходит заряд 1 Кл.

Согласно закону Фарадея, возникновение ЭДС электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае она не может быть причиной возникновения ЭДС индукции. Максвелл для объяснения ЭДС индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора напряженности этого поля по любому неподвижному контуру L проводника представляет собой ЭДС электромагнитной индукции:

E i = = — . (27.7)

Линии напряженности вихревого электрического поля представляют собой замкнутые кривые, поэтому при перемещении заряда в вихревом электрическом поле по замкнутому контуру совершается отличная от нуля работа. В этом заключается отличие вихревого электрического поля от электростатического, линии напряженности которого начинаются и заканчиваются на зарядах.

Явление электромагнитной индукции. Магнитный поток. Закон электромагнитной индукции

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1.

Тема урокаЯвление электромагнитной индукции.
Магнитный поток.
Закон электромагнитной индукции.
Учитель ГБОУ СОШ №1877 «Люблино» Л. Н. Молочко

2. План изложения нового материала

1. История открытия явления
электромагнитной индукции
2. Опыты Фарадея
3. Явление электромагнитной индукции
4. Магнитный поток. Единицы измерения
магнитного потока.
5. Закон электромагнитной индукции

3. В1820 г.Эрстед обнаружил действие электрического тока на магнитную стрелку

М. Фарадей с 1821 по 1831 год проводил опыты и
получил электрический ток с помощью магнитного поля.
Ему удалось « Превратить магнетизм в электричество».
Основоположник учения об
электромагнитном поле; ввел
понятия «электрическое» и
«магнитное поле»;
высказал идею существования
электромагнитных волн.

4. Опыты М. Фарадея

«На деревянную катушку была
29 августа
1831
намотана медная
проволока,
между
года
ее витками была намотана
проволока изолированная от
первой хлопчатобумажной нитью.
Одна из этих спиралей была
соединена с гальванометром,
другая – с батареей.
При замыкании цепи стрелка
гальванометра отклонялась, при
размыкании цепи то же самое.
При непрерывном же прохождении
тока через одну из спиралей не
удалось обнаружить отклонения
стрелки гальванометра…»
Вывод:
электрический
ток возникал
тогда,
когда
проводник
оказывался
в области
действия
переменного
магнитного
Электромагнитная индукция – физическое
явление, заключающееся в возникновении
электрического тока в замкнутом проводящем
контуре при изменении числа линий магнитной
индукции , пронизывающих поверхность,
ограниченную этим контуром.
Возникающий при этом ток называют
индукционным.

7. Поток магнитной индукции

• Потоком магнитной индукции
(магнитным потоком) через
поверхность площадью S называют
величину, равную произведению
модуля вектора магнитной индукции В
на площадь S и косинус угла между
векторами В и n.

8. Математическая формула потока магнитной индукции

• Магнитный поток пропорционален числу
линий магнитной индукции,
пронизывающих поверхность площадью S.
• Магнитный поток характеризует
распределение магнитного поля по
поверхности , ограниченной контуром.

9. Единица магнитного потока

Единицей магнитного потока является
вебер (1 Вб)
1 Вб — магнитный поток, созданный
однородным магнитным полем с
индукцией 1Тл через поверхность
площадью 1м2, расположенную
перпендикулярно вектору магнитной
индукции.
1 Вб=1Тл*1 м2,

10. Явление электромагнитной индукции

• Индукционный ток в замкнутом контуре
возникает при изменении магшнитного
потока через площадь ,ограниченную
контуром

11. Закон электромагнитной индукции — ЭДС индукции прямо пропорциональна скорости изменения магнитного потока

Закон электромагнитной индукции ЭДС индукции прямо пропорциональна
скорости изменения магнитного потока
1. При всяком изменении магнитного
потока через проводящий контур в
этом контуре возникает электрический
ток.
2. ЭДС индукции в замкнутом
контуре равна скорости изменения
магнитного потока через площадь,
ограниченную этим контуром.
3. Ток в контуре имеет положительное
направление при убывании внешнего
магнитного потока.

12. Математическая формула закона электромагнитной индукции

• ε=-ΔΦ/Δt
• ΔΦ/Δt- скорость изменения магнитного
потока ( единицы измерения Вб/с)

13. ЭДС электромагнитной индукции в замкнутом контуре численно равна и противоположна по знаку скорости изменения магнитного потока

через
поверхность, ограниченную этим контуром.
( зависит только от характера изменения
магнитного поля).
ЭДС электромагнитной индукции не
зависит от
материала проводника;
рода носителей тока;
сопротивления проводника;
температуры проводника.

14. Закрепление нового:

1. Какая величина характеризует магнитное
поле в каждой его точке?
2. От чего зависит магнитный поток,
пронизывающий площадь плоского контура,
помещенного в однородное магнитное поле?
3. При какой ориентации контура по
отношению к линиям магнитной индукции
магнитный поток, пронизывающий
площадь этого контура максимален? равен
нулю?
4. В каком случае магнитный поток равен 1 Вб?
5. Как формулируется закон
электромагнитной индукции?
6. Почему в законе электромагнитной
индукции стоит знак «минус»?

15. Задача №1

Магнитный поток через квадратную
проволочную рамку со стороной
5 см, плоскость которой перпендикулярна
линиям индукции однородного магнитного
поля, равен 0,1м Вб.
Каков модуль вектора магнитной индукции
поля? ( Ответ:40 мТл)

16. Задача №2

Какова величина магнитного потока,
пронизывающего плоскую поверхность
площадью 50 см2 при индукции поля
0,4 Тл, если эта поверхность: а)
перпендикулярна вектору индукции
поля; б) расположена под углом 450 к
вектору индукции; в) расположена под
углом 300 к вектору индукции? (Ответ:
2 мВб, 1,4 мВб; 1 мВб)

17.

Задача №3Металлический стержень длиной 0,5 м
равномерно вращается вокруг одного из его
концов в однородном магнитном поле в
плоскости, перпендикулярной к линиям
поля. Какова ЭДС индукции поля, если
магнитная индукция поля 0,2 Тл, а угловая
скорость вращения стержня 50 рад/с?
(Ответ: 1,25 В)

18. Домашнее задание:

§8,9,11,
№№921, 922,928 (Сборник Рымкевича )

English     Русский Правила

Закон Фарадея: определение, уравнение и формула

В 1820 году Ганс Христиан Эрстед понял, что электрический ток создает магнитные поля. Итак, для физиков того времени было естественным задаться вопросом, возможно ли обратное — чтобы магнитное поле создавало электрический ток.

Рис. 1 — Намотка медного провода внутри электродвигателя, использующего электромагнитную индукцию для преобразования электрической энергии в механическую.

Майкл Фарадей, английский ученый, около десяти лет работал над доказательством связи между магнитами и электричеством. Поэтому его именем назван знаменитый закон индукции. Он использовал открытые им свойства электромагнитов, чтобы продемонстрировать электрический эффект, вызванный изменяющимся магнитным полем. В этой статье мы изучим закон индукции Фарадея, его определение, уравнение, примеры и эксперименты, подтверждающие закон.

Закон индукции Фарадея

Майкл Фарадей — один из самых значительных ученых в истории. Он сформулировал закон индукции после своей первой экспериментальной демонстрации электромагнитной индукции. В этом опыте он намотал два провода на противоположную сторону железного кольца, затем подключил один провод к гальванометру , а другой к батарее.

Гальванометр — это инструмент, используемый для измерения малых электрических токов.

Наблюдал отклонение при включении батареи и снова при выключении батареи. Этот эксперимент показал индукцию электрического тока через провод, когда изменение магнитный поток (\(\phi_\mathrm{B}\)) проходит через провод при включении и выключении батареи.

Магнитный поток — это полное магнитное поле, проходящее через определенную область.

Для магнитного поля, которое постоянно по площади, его можно выразить как

\[\phi_\mathrm{B}= \vec{B}\, \mathrm{d} \vec{A},\]

где \(B\) — магнитное поле, а \(A\) — площадь поверхности.

Это выражение можно обобщить для неоднородной площади, применив поверхностный интеграл по дифференциальным сечениям площади поверхности:

\[\phi_\mathrm{B}=\int \vec{B}\, \mathrm{d} \vec{A}.\]

Имея все это в виду, давайте определим закон!

Определение закона Фарадея

Итак, что именно влечет за собой закон Фарадея? Всякий раз, когда происходит изменение магнитного потока (количество силовых линий магнитного поля, проходящих через катушку), связанного с цепью, в цепи индуцируется ЭДС / электрический ток.

Закон индукции Фарадея гласит, что величина индуцированной ЭДС/электрического тока прямо пропорциональна скорости изменения магнитного потока, связанного с цепью.

Давайте рассмотрим пример, чтобы понять его более подробно

Представьте, что у нас есть магнит и катушка. Перемещаем магнит, удерживая катушку в фиксированном положении.

Рис. 2 — Электрический ток индуцируется в катушке из-за изменения проходящих через нее силовых линий магнитного поля.

Приведенная выше установка доказывает нам следующее:

• Количество силовых линий магнитного поля, проходящих через катушку, увеличивается, когда магнит перемещается к катушке. Это изменение магнитного потока индуцирует ЭДС / электрический ток в катушке.
• Точно так же, когда магнит удаляется от катушки, линии магнитного поля, проходящие через катушку, уменьшаются. Это изменение магнитного потока индуцирует ЭДС / электрический ток в катушке.
• Когда магнит быстро перемещается к катушке или от нее, величина ЭДС/электрического тока, индуцируемая в катушке, велика.
• Напротив, когда магнит медленно перемещается к катушке или от нее, величина ЭДС/электрического тока, индуцируемая в катушке, мала.

В приведенном выше примере показано, как силовые линии магнитного поля, проходящие через катушку, связаны с индуцированным электрическим током в катушке. Мы узнаем о законе Фарадея, используя уравнения в следующей части.

Уравнение закона Фарадея

Согласно закону индукции Фарадея, величина ЭДС, индуцированной в катушке в единицах магнитного потока, равна

\[\left|\mathcal{E}\right|=\left|k\frac {\ mathrm {d} \ phi_ \ mathrm {B}} {\ mathrm {d} t} \ right |\], где \ (k \) — константа пропорциональности.

В то время как закон Фарадея дает нам величину ЭДС, индуцированной током, направление определяется с помощью закона Ленца , который преобразует приведенное выше уравнение в \(\mathcal{E}=-k\frac{\mathrm{d }\phi_\mathrm{B}}{\mathrm{d}t}\).

Этот магнитный поток через любую поверхность площадью \(\vec{A}\) измеряется общим числом магнитных силовых линий, пересекающих поверхность нормально:

\[\phi_\mathrm{B}=\vec{ B}\cdot\vec{A}. \]

В случае соленоида, состоящего из \(N\) витков, величина ЭДС, индуцируемой через магнитный поток, проходящий через него, равна

\[\left|\mathcal{E}\right|=N\left|\frac{\mathrm{d}\phi_\mathrm{B}}{\mathrm{d}t}\right|.\]

Рис. 3 – Силовые линии магнитного поля, проходящие через поверхность площади \(\vec{A}\) под углом \(\theta\) к вектору площади.

На приведенной выше диаграмме магнитный поток через поверхность области \(\vec{A}\) равен

\[\phi_\mathrm{B}=\vec{B}\cdot\vec{A}= BA\cos{\theta},\]

где \(\theta\) — угол между силовыми линиями магнитного поля \(\left(\vec{B}\right)\) и вектором площади \(\left (\vec{A}\right)\) катушки. 9\circ\right)}=0,\], что является минимальным значением магнитного потока, проходящего через катушку.

Следовательно, величина ЭДС, индуцируемой в катушке, когда площадь поверхности катушки находится под углом \(\theta\) к силовым линиям магнитного поля, равна

\[\left|\mathcal {E}\right|=\left|\frac{\mathrm{d}}{\mathrm{d}t}\left(\vec{B}\cdot\vec{A}\right)\right|=\ left|\frac{\mathrm{d}}{\mathrm{d}t}BA\cos{\theta}\right|.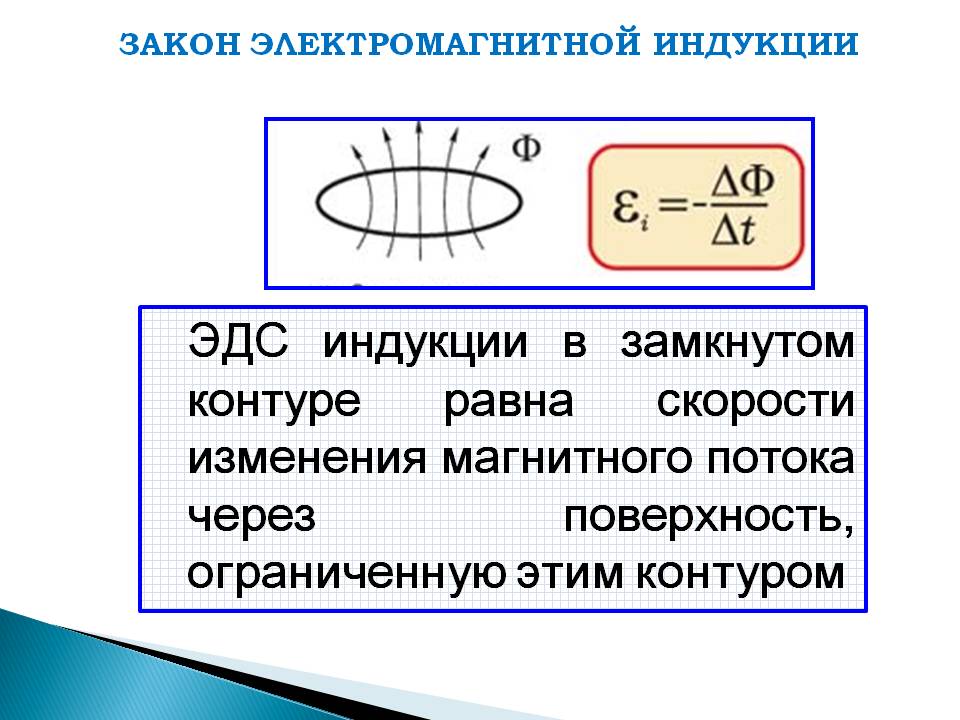 \ circ \ right)} \ right)} {\ mathrm {d} t} \ right | \\\ left | \ mathcal {E }\right|&=\left|\frac{\mathrm{d}\left(BA\right)}{\mathrm{d}t}\right|\\\left|\mathcal{E}\right|& =\left|A\frac{\mathrm{d}B}{\mathrm{d}t}\right|\end{align*}\]

Согласно закону Фарадея, величина ЭДС индукции в катушке равна произведению площади и скорости изменения составляющей магнитного поля во времени, когда катушка с постоянной площадью поверхности расположена перпендикулярно направлению линий магнитного поля.

Если магнитное поле остается постоянным, но площадь поверхности катушки изменяется, то \(\left|\mathcal{E}\right|=\left|B\frac{\mathrm{d}A}{\mathrm{ г}т}\право|\).

В следующей части мы поймем электромагнитную индукцию, используя некоторые эксперименты Фарадея и Джозефа Генри.

Эксперимент с законом Фарадея

Несколько экспериментов могут объяснить закон индукции Фарадея, поэтому в этом разделе мы узнаем о двух из них.

Ток, вызванный током

В этом эксперименте катушка \(\left(\mathrm{C}\right)\), подключенная к гальванометру, помещена рядом с другой катушкой \(\left(\mathrm{C’}\ справа)\) подключен к аккумулятору.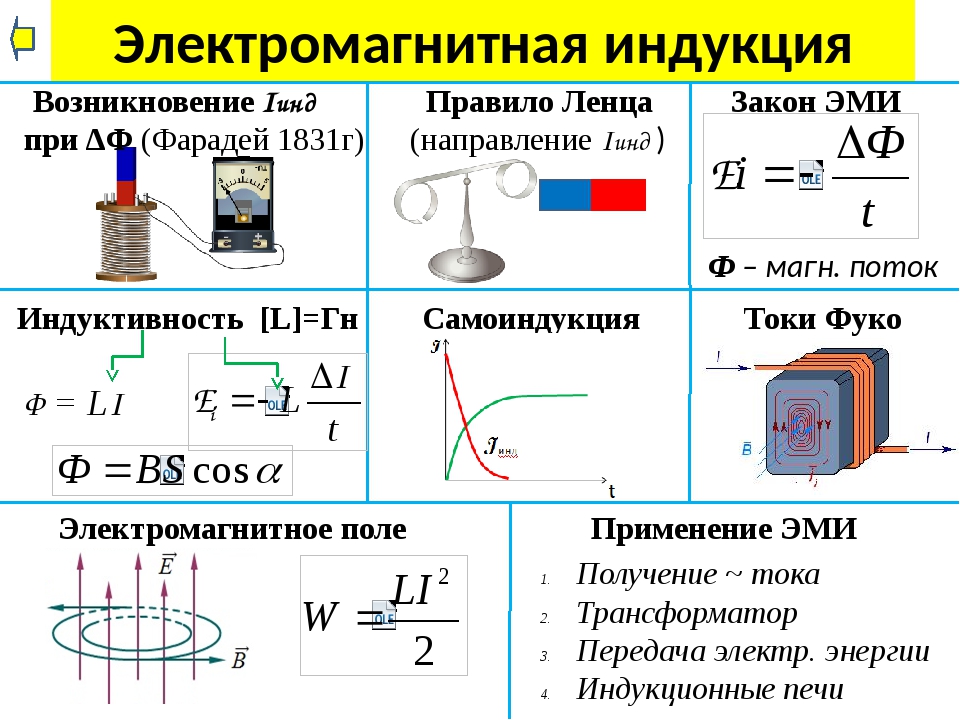

Рис. 4. Из-за движения катушки \(\mathrm{C’}\) по направлению к катушке \(\mathrm{C}\) в катушке индуцируется противодействующая ЭДС \(\mathrm{C’ }\).

На приведенной выше диаграмме видно, что катушка \(\mathrm{C’}\) подключена к батарее, благодаря чему через катушку протекает электрический ток. Этот ток, протекающий через катушку, затем индуцирует магнитное поле, окруженное катушкой. Катушка \(\mathrm{C’}\) затем подключается к гальванометру, который показывает отклонение всякий раз, когда через эту катушку протекает электрический ток.

Когда катушка \(\mathrm{C’}\) движется к катушке \(\mathrm{C}\), магнитный поток, проходящий через катушку \(\mathrm{C}\), увеличивается. Из-за этого изменения магнитного потока в катушке \(\mathrm{C}\) индуцируется противодействующая ЭДС/электрический ток, о чем свидетельствует отклонение гальванометра.

Аналогично, когда катушка \(\mathrm{C’}\) удаляется от катушки \(\mathrm{C}\), магнитный поток, проходящий через катушку, уменьшается. Это уменьшение магнитного потока через катушку \(\mathrm{C}\) индуцирует электрический ток в том же направлении, что и ток в катушке \(\mathrm{C’}\), что показывает отклонение гальванометра в противоположном направлении, как и в предыдущем случае.

Эта индуцированная ЭДС из-за изменения магнитного потока, наблюдаемого в эксперименте, подтверждает закон индукции Фарадея.

Также гальванометр показывает большое отклонение, когда катушка \(\mathrm{C’}\) движется быстрее к катушке или от нее \(\mathrm{C}\), что доказывает, что ЭДС, индуцируемая в катушке \ (\mathrm{C}\) зависит от скорости изменения магнитного потока.

Ток, индуцированный изменением тока

В этом эксперименте вместо перемещения катушки \(\mathrm{C’}\) к катушке или от нее \(\mathrm{C}\) магнитный поток изменяется в катушке \(\mathrm{C}\) из-за изменения электрического тока, проходящего через катушку \(\mathrm{C’}\).

Рис. 5 — При замыкании ключа в цепи, содержащей катушку \(\mathrm{C’}\), в катушке \(\mathrm{C}\) индуцируется ЭДС из-за изменения магнитного потока через это.

На приведенной выше диаграмме видно, что ключ подключен к цепи, содержащей \(\mathrm{C’}\). Когда ключ закрыт, по цепи протекает электрический ток. Благодаря этому току магнитный поток начинает проходить через катушку \(\mathrm{C}\), расположенную рядом с катушкой \(\mathrm{C’}\). Это изменение магнитного потока через катушку \(\mathrm{C}\) от нуля до некоторого значения индуцирует ЭДС/электрический ток в катушке, что показано отклонением в гальванометре.

Как только электрический ток, проходящий через катушку \(\mathrm{C’}\), становится стабильным, гальванометр перестает показывать какое-либо отклонение, что указывает на то, что ЭДС/электрический ток через катушку \(\mathrm{C’}\ ) становится равным нулю. Точно так же, когда мы размыкаем ключ цепи, магнитный поток, проходящий через катушку \(\mathrm{C}\), уменьшается, что индуцирует ЭДС/электрический ток в катушке \(\mathrm{C}\).

Ток в катушке \(\mathrm{C’}\) быстро меняется от нуля до некоторого постоянного тока.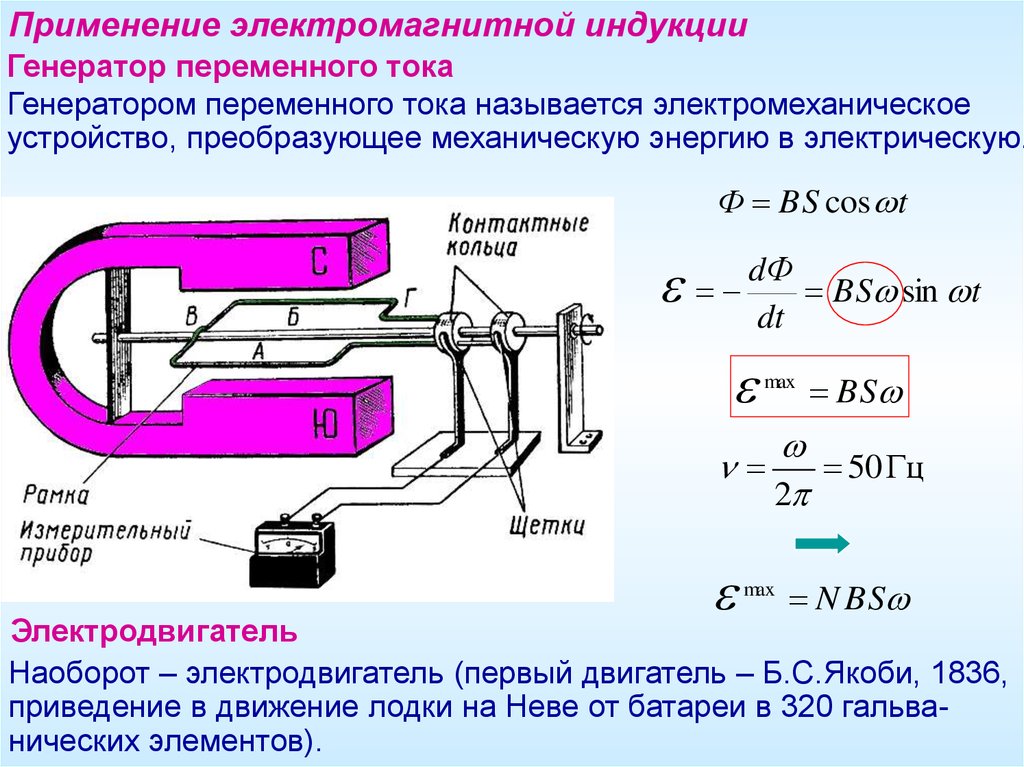 В результате \(\frac{\mathrm{d}\phi_\mathrm{B}}{\mathrm{d}t}\) становится очень большим в катушке \(\mathrm{C}\), поэтому ток через \(\mathrm{C}\) будет огромным в течение очень короткого времени.

Эта индуцированная ЭДС/электрический ток в катушке \(\mathrm{C}\) из-за изменения магнитного потока еще раз доказывает закон индукции Фарадея.

Примеры применения закона индукции Фарадея

Все электрические устройства, в которых индуцируется электрический ток, являются примерами применения закона индукции Фарадея. Некоторые примеры перечислены ниже.

1. Приготовление с использованием индукционной плиты или индукционной плиты, когда посуда нагревается с помощью электрической индукции.

2. Трансформаторы состоят из обмоток, работающих по закону индукции Фарадея.

3. Наушники, в которых изменение электрического тока обусловлено изменением магнитного поля, создаваемого электромагнитами.

4. Электродвигатели используют закон индукции Фарадея для преобразования электрической энергии в механическую.

Закон Фарадея. Основные выводы

---

Ссылки

1. Рис. 1. Электродвигатель со всеми его медными обмотками! (https://unsplash.com/photos/SkUkZ2auN4E) Мика Баумайстер (https://unsplash.com/@mbaumi) по лицензии Unsplash (https://unsplash.com/license).
2. Рис. 2 – Закон индукции Фарадея, StudySmarter Originals.
3. Рис. 3 – Магнитный поток, проходящий через катушку, StudySmarter Originals.
4. Рис. 4. Ток, вызванный текущим экспериментом, StudySmarter Originals.
5. Рис. 5. Ток, индуцированный изменением тока, StudySmarter Originals.

Значение, термины, законы и примеры

Законы термодинамики

Законы термодинамики: Законы термодинамики представляют собой группу физических величин, таких как температура, энергия, работа, теплота и энтропия, которые характеризуют термодинамические системы. в термодинамическом равновесии. Законы также используют различные параметры для термодинамических процессов, чтобы установить отношения между ними. Термодинамика — это раздел физики, который занимается понятиями, касающимися тепла и температуры, а также взаимопревращениями тепла и других форм энергии. Термодинамика является частью макроскопической науки. Он имеет дело только с объемными системами и не вдается в подробности о молекулярном строении материи. В этой статье мы подробно обсудим законы термодинамики.

Термины, относящиеся к законам термодинамики

Существуют некоторые термины, которые часто используются при формулировании законов термодинамики. Поэтому вам необходимо ознакомиться с этим термином. Таким образом, некоторые термины, относящиеся к законам термодинамики, таковы:

Тепловое равновесие: Говорят, что состояние системы находится в тепловом равновесии, когда состояние системы в макроскопических переменных, таких как температура, теплота, работа и энергия не меняется со временем.

Термодинамическая система: Термодинамическая система — это система, в которой материя заключена в стенах, отделяющих систему от окружающей среды. Термодинамические системы могут быть трех типов:

• Изолированная термодинамическая система: В изолированной системе между системой и окружающей средой не происходит обмена энергией или веществом. Изолированный сосуд является примером изолированной системы.
• Замкнутая система термодинамики: В замкнутой системе не происходит обмена веществом, но возможен обмен энергией между системой и окружающей средой. Медь или сталь являются примером закрытой системы.
• Открытая термодинамика Система: В открытой системе происходит перенос массы и энергии между системой и окружающей средой.

Окружение: Включает в себя все, кроме системы. Вселенная вместе включает в себя как системы, так и окружающую среду.

Термодинамический процесс: Процесс, при котором термодинамическое состояние системы изменяется за счет изменения тепла, давления и внутренней энергии. Четыре типа термодинамических процессов:

• Адиабатический процесс – процесс, при котором теплопередача не происходит ни внутрь системы, ни наружу.
• Изохорный процесс – Процесс, при котором не происходит изменения объема, а объем в системе остается неизменным.
• Изобарический процесс – Процесс, при котором не происходит изменения давления и давление в системе остается постоянным.
• Изотермический процесс – Процесс, при котором не происходит изменения температуры и объем в системе остается неизменным.

Четыре закона термодинамики

Термодинамика — это раздел физики, изучающий отношения между теплотой, работой, температурой и энергией. Законы термодинамики описывают, как эти физические переменные ведут себя в различных обстоятельствах. Есть в основном четыре типа законов термодинамики.0003

1. Нулевой закон термодинамики
2. Первый закон термодинамики
3. Второй закон термодинамики
4. Третий закон термодинамики

Нулевой закон термодинамики

Термодинамика в тепловом равновесии друг с другом, а также отдельно в тепловом равновесии с третьей системой, то говорят, что все три находятся в равновесии друг с другом».

Например: Предположим, что две системы А и В разделены адиабатической стенкой, при этом каждая система контактирует с третьей системой С с помощью проводящей стенки. Состояния систем (т. е. их физические переменные) будут изменяться до тех пор, пока А и В не придут к тепловому равновесию с С. После этого представьте, что адиабатическая стенка между А и В заменена проводящей стенкой, а С изолирована от А и В адиабатической стенкой. Можно проанализировать, что состояния A и B больше не меняются. Следовательно, они находятся в равновесии друг с другом.

Первый закон термодинамики

Первый закон термодинамики (обычно называемый законом сохранения энергии) гласит, что «Энергия не может быть ни создана, ни уничтожена, она может быть преобразована из одной формы в другую».

Внутренняя энергия (U) системы может быть изменена двумя способами передачи энергии: теплотой и работой.

Предположим, ∆Q Теплота, поступающая в систему из окружающей среды

∆W — проделанная работа

∆U — изменение внутренней энергии

Итак, общий принцип сохранения энергии: ∆Q = ∆U + ∆W

Второй закон термодинамики

Второй закон термодинамики гласит, что «любой самопроизвольный процесс всегда будет приводить к увеличению энтропии, которая измеряет хаотичность системы во Вселенной.