Что значит электрический заряд квантуется?
На основании большого числа экспериментов установлено, что электрический заряд квантуется, т. е. заряд любого тела кратен целому числу элементарных зарядов, каждый из которых имеет величину, равную 1,60×10-19 Кл. Этот элементарный заряд принято обозначать буквой e.
Что значит электрический заряд квантуется Дискретен?
Дискретность заряда Говорят, что электрический заряд дискретен или квантуется, т. е. существует некоторая минимальная порция заряда, которую дальше разделить нельзя.
Что такое элементарный электрический заряд и чему он равен?
Элемента́рный электри́ческий заря́д — фундаментальная физическая постоянная, минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц. Согласно изменениям определений основных единиц СИ равен точно 1,10−19 Кл в Международной системе единиц (СИ).
Что такое электрический заряд простыми словами?
Электрическим зарядом называется способность тел создавать электромагнитное поле. В физике раздел электростатики изучает взаимодействия неподвижных относительно выбранной инерциальной системы отчета зарядов.
Что такое электрический заряд и его свойства?
Электрический заряд (далее – заряд) – скалярная характеристика тела, обладающая следующими фундаментальными свойствами: Заряд существует в двух видах: положительный и отрицательный. Одноименные заряды отталкиваются, разноименные – притягиваются. … В СИ единица измерения заряда – Кулон: К л .
Как обозначается элементарный заряд?
Самая маленькая частица электрического заряда — называется элементарным зарядом. Заряд всех элементарных частиц (если он не равен нулю) одинаков по абсолютной величине. Положительный элементарный заряд будем обозначать символом (+е), отрицательный – (-е).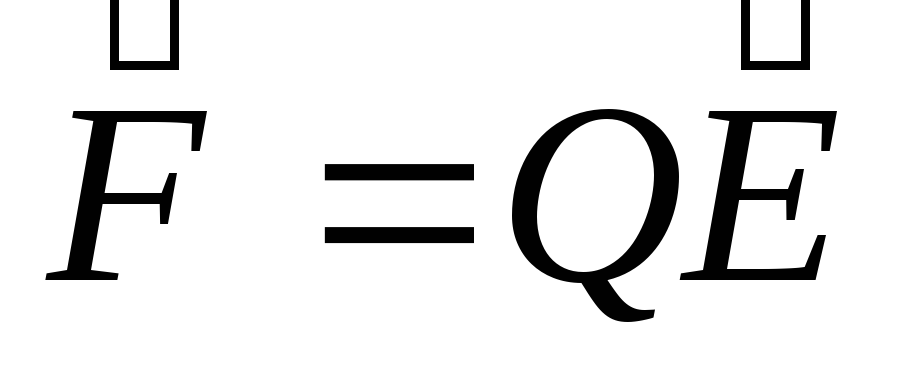 нейтрон обладает элементарным зарядом qнейтр = 0.
нейтрон обладает элементарным зарядом qнейтр = 0.
Как обозначается сила тока в физике?
Для обозначения силы обычно используется символ F — от лат. fortis (сильный). Общепринятое определение силы отсутствует, в современных учебниках физики сила рассматривается как причина ускорения. Важнейший физический закон, в который входит сила, — второй закон Ньютона.
Что характеризует электрический ток?
Когда электроны приходят в движение под действием электрического поля, они становятся движущимся зарядом, то есть электрическим током I. Количество заряда измеряется в кулонах, а ток характеризует скорость перемещения заряда через поперечное сечение проводника (за единицу времени).
Что характеризует напряжение?
Электрическое напряжение характеризует возможность электрического поля совершать работу. … Чем выше электрическое напряжение источника тока, тем большую работу может совершить поток электронов. Электрическое напряжение обозначается буквой U, единицей напряжения является вольт (В). Напряжение измеряется вольтметром.
Электрическое напряжение обозначается буквой U, единицей напряжения является вольт (В). Напряжение измеряется вольтметром.
Какие основные физические величины характеризуют электрический ток?
Электрический ток имеет количественные характеристики: скалярную — силу тока, и векторную — плотность тока. через поперечное сечение проводника, к величине этого промежутка времени. Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А; международное: A).
Формула заряда q. Электрический заряд определение и формула. Основные законы и формулы
ГлавнаяРазноеФормула заряда q
Формула электрического заряда, q
Определение и формула электрического заряда
Фундаментальным свойством электрического заряда является существование двух видов зарядов: положительных и отрицательных. Заряды, имеющие один знак, отталкиваются. Взаимодействие зарядов разного знака определяют как притяжение. Телу можно сообщить заряд любого знака. В макроскопическом теле заряды разных знаков могут взаимно компенсировать друг друга.
Телу можно сообщить заряд любого знака. В макроскопическом теле заряды разных знаков могут взаимно компенсировать друг друга.
Электрический заряд является релятивистски инвариантной величиной. Это значит, что величина заряда не зависит от системы отсчета, не важно, движется заряд (заряженное тело) или покоится.
Электрический заряд тела находят как суммарный заряд его частей.
Разделения электрических зарядов разных знаков можно добиться путем электризации посредством непосредственного контакта тел (например, трением) или без контакта, например посредством электрической индукции. При зарядке тела, мы создаем на нем избыток электронов или недостаток в сравнении с их нормальным количеством, при котором тело не имеет заряда. При этом электроны берутся у другого тела или удаляются из заряжаемого тела, но не уничтожаются или создаются. Важно запомнить, что процесс зарядки и разрядки тел является процедурой перераспределения электронов, при этом общее их число не изменяется.
При соединении заряженного проводника с незаряженным, заряд перераспределяется между обоими телами. Допустим, что одно тело несет отрицательный заряд, его соединяют с незаряженным телом. Электроны заряженного тела под воздействием сил взаимного отталкивания переходят на незаряженное тело. При этом заряд первого тела уменьшается, заряд второго увеличивается, до тех пор, пока не наступит равновесие.
Элементарный заряд
Немецкий физик и физиолог Г. Гельмгольц обратил внимание на то, что заряды, которые переносят ионы при явлении электролиза, являются целыми, кратными некоторой величине, равной Кл. Каждый одновалентный ион переносит такой заряд. Любой двухвалентный ион несет заряд, равный Кл, и так далее. Гельмгольц сделал вывод о том, что заряд Кл является минимальным количеством электричества, которое существует в природе. Данный заряд получил название элементарного заряда.
Закон сохранения заряда
Закон сохранения заряда является фундаментальным законом природы.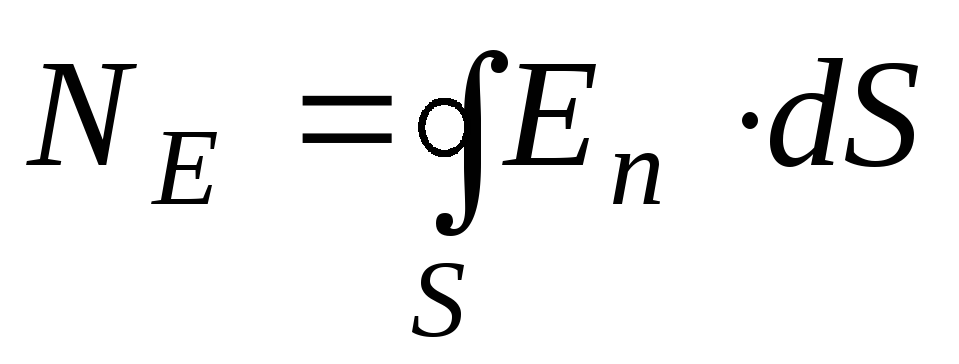 Он был установлен на основании обобщения экспериментальных данных. Подтвержден в 1843 г. английским физиком М. Фарадеем.
Он был установлен на основании обобщения экспериментальных данных. Подтвержден в 1843 г. английским физиком М. Фарадеем.
Формулировка закона: В любой замкнутой системе алгебраическая сумма зарядов – это неизменная величина, и не важно, какие процессы происходят в этой системе:
где N – количество зарядов.
Закон Кулона
На вопрос: С какими силами взаимодействуют неподвижные точечные заряды? Отвечает закон Кулона, который можно записать в виде формулы как:
где – сила, с которой заряд действует на заряд ; – радиус вектор, который проведен от второго заряда к первому; – электрическая постоянная; – диэлектрическая проницаемость вещества в котором находятся заряды. В соответствии с третьим законом Ньютона первый заряд действует на второй с силой равной по модулю и противоположной по направлению силе Обратите внимание, что заряды в формуле (2) точечные.
Примеры решения задач по теме «Электрический заряд»
 com
comФормула заряда конденсатора, q
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
где – радиусы обкладок конденсатора.
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
ru.solverbook.com
Основные законы и формулы
58
ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК
ПОСТОЯННЫЙ ТОК
,
где F – сила взаимодействия двух точечных зарядов q1 и q2; r – расстояние между зарядами; — диэлектрическая проницаемость среды; 0 — электрическая постоянная
.
Закон сохранения заряда:
,
где – алгебраическая сумма зарядов, входящих в изолированную систему;n – число зарядов.
Напряженность и потенциал электростатического поля:
; , или,
где – сила, действующая на точечный положительный зарядq0, помещенный в данную точку поля; П – потенциальная энергия заряда; А∞ — работа, затраченная на перемещение заряда q0 из данной точки поля в бесконечность.
Поток вектора напряженности электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле:
, или ,
где – угол между вектором напряженности и нормальюк элементу поверхности;dS – площадь элемента поверхности; En – проекция вектора напряженности на нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле:
.
Поток вектора напряженности через замкнутую поверхность –
(интегрирование ведется по всей поверхности).
Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –
где – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; n – число зарядов.
Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –
.
Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:
внутри сферы (r R) Е=0;
на поверхности сферы (r=R) ;
вне сферы (r R) .
Принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей, выражается формулой
.
В случае двух электрических полей с напряженностями иабсолютное значение вектора напряженности составляет
,
где — угол между векторами и.
Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –,
где — линейная плотность заряда.
Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):
.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –
,
где — поверхностная плотность заряда.
Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:
.
Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –
.
Электрическое смещение связано с напряженностьюэлектрического поля соотношением
,
которое справедливо только для изотропных диэлектриков.
Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:
.
Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:
.
Потенциал электрического поля в бесконечности условно принят равным нулю.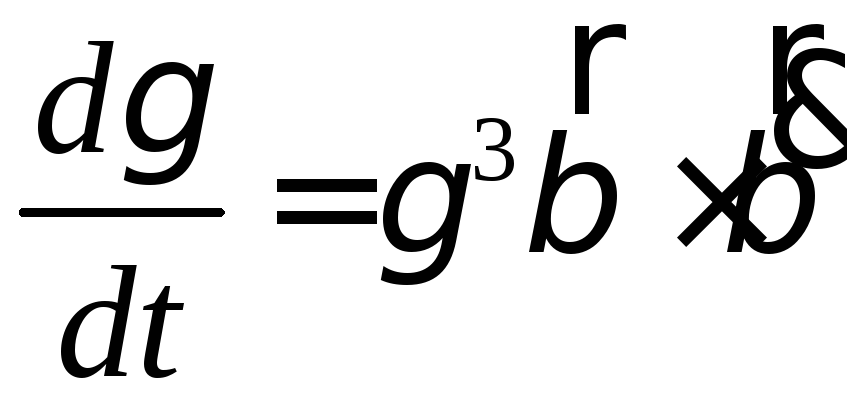
Потенциал электрического поля, создаваемый точечным зарядом q на
расстоянии r от заряда, –
.
внутри сферы (r R) ;
на поверхности сферы (r = R) ;
вне сферы (r R) .
Во всех формулах, приведенных для потенциала заряженной сферы, есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
Потенциал электрического поля, образуемого системой n точечных зарядов в данной точке в соответствии с принципом суперпозиции электрических полей, равен алгебраической сумме потенциалов , создаваемых отдельными точечными зарядами:
.
Энергия W взаимодействия системы точечных зарядов определяется работой, которую эта система может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой
,
где — потенциал поля, создаваемый всеми (n-1) зарядами (за исключением i-го) в точке, где находится заряд .
Потенциал связан с напряженностью электрического поля соотношением
.
В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой
,
или в скалярной форме
.
В случае однородного поля, т.е. поля, напряженность которого в каждой его точке одинакова как по абсолютному значению, так и по направлению, –
,
где 1 и 2 – потенциалы точек двух эквипотенциальных поверхностей; d — расстояние между этими поверхностями вдоль электрической силовой линии.
Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал 1, в другую, имеющую потенциал 2, равна
, или ,
где E – проекция вектора на направление перемещения;- перемещение.
В случае однородного поля последняя формула принимает вид
,
где – перемещение; — угол между направлениями вектора и перемеще-ния.
Диполь есть система двух точечных (равных по абсолютному значению и противоположных по знаку) зарядов, находящихся на некотором расстоянии друг от друга.
Электрический момент диполя есть вектор, направленный от отрицательного заряда к положительному, равный произведению зарядана вектор, проведенный от отрицательного заряда к положительному, и называемый плечом диполя, т.е.
.
Диполь называется точечным, если его плечо намного меньше расстоянияr от центра диполя до точки, в которой нас интересует действие диполя ( r), см. рис. 1.
Рис. 1
Напряженность поля точечного диполя:
,
где р – электрический момент диполя; r – абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; — угол между радиус-вектором и плечомдиполя.
Напряженность поля точечного диполя в точке, лежащей на оси диполя
(=0), находится по формуле
;
в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины , – по формуле
.
Потенциал поля точечного диполя в точке, лежащей на оси диполя (=0), составляет
,
а в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины , –
=0.
Напряженность и потенциал неточечного диполя определяются так же как и для системы зарядов.
Механический момент, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е, –
, или ,
где — угол между направлениями векторов и.
Электроемкость уединенного проводника или конденсатора –
,
где q – заряд, сообщенный проводнику; - изменение потенциала, вызванное этим зарядом.
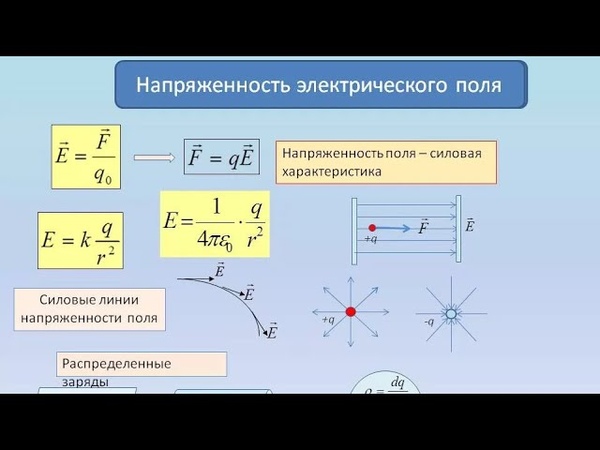
Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью , –
.
Если сфера полая и заполнена диэлектриком, то ее электроемкость при этом не изменяется.
Электроемкость плоского конденсатора:
,
где S – площадь каждой пластины конденсатора; d – расстояние между пластинами; — диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.
Электроемкость плоского конденсатора, заполненного n слоями диэлектрика толщиной di и диэлектрической проницаемостью i каждый (слоистый конденсатор), составляет
.
Электроемкость сферического конденсатора (две концентрические сферы радиусом R1 и R2 , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ) находится так:
.
Электроемкость последовательно соединенных конденсаторов составляет:
в общем случае –
,
где n – число конденсаторов;
в случае двух конденсаторов –
;
в случае n одинаковых конденсаторов с электроемкостью С1 каждый –
.
Электроемкость параллельно соединенных конденсаторов определяется следующим образом:
в общем случае –
С=С1+С2+…+Сn;
в случае двух конденсаторов –
С= С1+С2;
в случае n одинаковых конденсаторов с электроемкостью С1 каждый –
С=nС1.
Энергия заряженного проводника выражается через заряд q, потенциал и электроемкость С проводника следующим образом:
.
Энергия заряженного конденсатора –
,
где q – заряд конденсатора; С – электроемкость конденсатора; U – разность потенциалов на его пластинах.
studfiles.net
Формула напряжённости электрического поля
Здесь – напряжённость электрического поля, – сила, действующая на заряд, – величина заряда.
Единица измерения напряжённости электрического поля – В/м (вольт на метр) или Н/Кл (ньютон на кулон).
Напряжённость – векторная величина, характеризующая интенсивность воздействия электрического поля на заряжённую частицу в конкретной точке. Напряжённость поля в различных точках вообще говоря различна, то есть электрическое поле – это векторное поле, направление векторов которого зависит от того, как было создано это поле. По указанной формуле можно рассчитать не только силу воздействия электрического поля на точечный заряд, но и силу воздействия этого поля на заряжённое тело, если распределение заряда в нём известно.
Примеры решения задач по теме «Напряжённость электрического поля»
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
| Напряженность поля точечного заряда. | |
Обозначим: q — заряд, создающий поле, q0 — заряд, помещенный в поле (внешний заряд). Закон Кулона: . Напряженность поля: . Тогда напряженность поля точечного заряда: | |
Теорема Гаусса. Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке. |
|
Если считать, что напряженность пропорциональна числу силовых линий, приходящихся на единицу площади поверхности (т.е. густоте), то поток напряженности пропорционален полному числу силовых линий, пересекающих данный контур. | |
Поток линий напряженности электростатического поля через произвольную замкнутую поверхность прямо пропорционален величине заряда, находящегося в области пространства, ограниченного данной поверхностью. | |
Применения теоремы Гаусса. |
|
1. Напряженность поля заряженной проводящей сферы радиуса R. Сфера заряжена по поверхности. А) Внутри сферы заряда нет . Е=0 | |
Б) Снаружи сферы. | |
На поверхности сферы: | |
2. Напряженность поля шара заряженного по объему. |
|
Введем понятие объемной плотности заряда: Объемная плотность заряда показывает, какой заряд содержится в единице объема заряженного по всему объему тела. Объем шара произвольного радиуса . Обозначим q — заряд шара, q0 — заряд, находящийся внутри объема произвольного радиуса. | |
Тогда заряд сферы радиуса r , будет: Следовательно: . – напряженность поля внутри шара, равномерно заряженного по объему. Снаружи — см. 1. | |
3. |
|
Введем понятие поверхностной плотности заряда: . Тогда . Коэффициент 2 появляется, т.к. плоскость окружена двумя поверхностями площадью S. Поле бесконечной заряженной плоскости не зависит от расстояния от плоскости! Можно пользоваться, когда расстояние много меньше размеров плоскости. 4. Напряженность поля плоского воздушного конденсатора. Из рисунка видим, что снаружи конденсатора поля пластин взаимно скомпенсированы, и общее поле равно нулю. Внутри конденсатора поля складываются. Используя вывод п.3 получаем: . Формула справедлива при условии, что расстояние между пластинами много меньше размеров самих пластин и вдали от краев пластин. | |
www.eduspb.com
Электрическое поле (к задачнику Рымкевича для 10-11 классов)
Электрическое поле к задачнику по физике за 10-11 классы «Физика. 10-11 класс. Пособие для общеобразовательных учебных заведений» Рымкевич А.П.
10-11 класс. Пособие для общеобразовательных учебных заведений» Рымкевич А.П.
Электрическое поле и электрический заряд — первичные понятия, которые не определяются аналогично понятиям точки и прямой в геометрии. Неподвижный заряд создает вокруг себя электрическое поле. Если замкнутая система обладала зарядом q, то при любых изменениях в ней заряд q сохраняется. Это фундаментальное утверждение носит название закона сохранения заряда.
Точечным зарядом называется заряд исчезающе малых размеров. Из эксперимента известно, что два точечных заряда q1 и q2 на расстоянии r взаимодействуют с силой F, значение которой определяется законом Кулона:
где
— коэффициент пропорциональности. Когда заряды одноименные, то они отталкиваются, когда разноименные — притягиваются.
Силовой характеристикой электрического поля является вектор напряженности E;. Рассмотрим некоторый заряд q, внесенный в электрическое поле E;. Тогда на него будет действовать сила F;, которая определяется формулой: F; = qE;. Это формула может служить определением вектора напряженности электрического поля. Для графического представления электростатического поля пользуются понятием линий напряженности. Эти линии начинаются на положительных зарядах и заканчиваются на отрицательных. Касательная в каждой точке линии напряженности направлена также, как и вектор E; . Если имеется N зарядов, каждый из которых создает свое поле E1;, E2;,…, EN; , то полная напряженность в любой точке пространства E; определяется как векторная сумма этих напряженностей (принцип суперпозиции):
Это формула может служить определением вектора напряженности электрического поля. Для графического представления электростатического поля пользуются понятием линий напряженности. Эти линии начинаются на положительных зарядах и заканчиваются на отрицательных. Касательная в каждой точке линии напряженности направлена также, как и вектор E; . Если имеется N зарядов, каждый из которых создает свое поле E1;, E2;,…, EN; , то полная напряженность в любой точке пространства E; определяется как векторная сумма этих напряженностей (принцип суперпозиции):
Для точечного заряда q значение напряженности E в точке, удаленной от него на расстоянии r, выражается формулой:
Проводником называется тело, содержащее свободные заряды. Если мы сообщим проводнику некоторый заряд q, то он распределится по поверхности, а внутри проводника поле будет равно нулю. Поверхностной плотностью о называется отношение заряда к площади поверхности проводника
Поле заряженного проводящего шара снаружи от него совпадает с полем точечного заряда, а внутри него равно нулю. Поле бесконечной заряженной проводящей плоскости с поверхностной плотностью заряда о определяется формулой:
Поле бесконечной заряженной проводящей плоскости с поверхностной плотностью заряда о определяется формулой:
где ε0 = 8,854⋅10-12 Ф/м — электрическая постоянная.
Диэлектриком называется тело, в котором отсутствуют свободные заряды. При помещении диэлектрика в электрическое поле происходит его поляризация, при этом поле E в диэлектрике уменьшается в ε раз:
где E0 — напряженность поля вне диэлектрика, ε — диэлектрическая проницаемость. При перемещении заряда q в электрическом поле E; на
расстояние
совершается работа A:
Изменение потенциальной энергии ΔWP равно:
Потенциал φ — энергетическая характеристика электрического поля, он определяется формулой:
Эквипотенциальные поверхности — это такие поверхности, в каждой точке которых потенциал постоянен. Потенциал поля φ в некоторой точке пространства, созданный N зарядами, равен алгебраической сумме потенциалов φ1, φ2,…, φN созданных отдельными зарядами (принцип суперпозиции): φ = φ1 + φ2 + … +
φN- Потенциал поля точечного заряда q на расстоянии r от него определяется формулой:
Напряжением U между точками A и B называется разность потенциалов:
где φ1 — потенциал в точке A, φ2 — потенциал в точке B.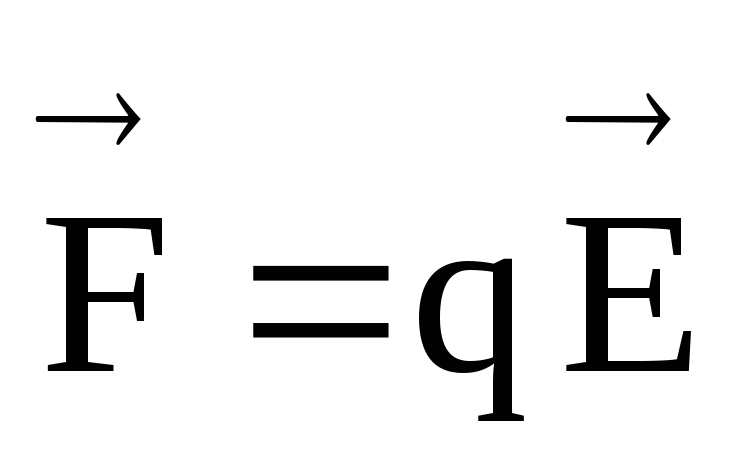 Напряжение U связано с напряженностью E электрического поля следующей формулой:
Напряжение U связано с напряженностью E электрического поля следующей формулой:
Конденсатором называется устройство, способное накапливать заряд. Емкость конденсатора C определяется как отношение заряда q на его обкладках к приложенному напряжению U:
Емкость не зависит от заряда и напряжения на нем, а определяется его геометрическими свойствами (формой и размером) и родом среды. Для плоского конденсатора емкость равна:
где ε — диэлектрическая проницаемость среды между обкладками, S — площадь обкладок, d — расстояние между обкладками. Энергия заряженного конденсатора W определяется формулой:
Плотность энергии ω электрического поля E выражается формулой:
5terka.com
Электрический заряд определение и формула. Основные законы и формулы
Закон Кулона:
где F – сила взаимодействия двух точечных зарядов q 1 и q 2 ; r – расстояние между зарядами; — диэлектрическая проницаемость среды; 0 — электрическая постоянная
.
Закон сохранения заряда:
,
где – алгебраическая сумма зарядов, входящих в изолированную систему;n – число зарядов.
Напряженность и потенциал электростатического поля:
;
, или
,
где – сила, действующая на точечный положительный зарядq 0 , помещенный в данную точку поля; П – потенциальная энергия заряда; А ∞ — работа, затраченная на перемещение заряда q 0 из данной точки поля в бесконечность.
Поток вектора напряженности электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле:
, или
,
где – угол между вектором напряженности и нормальюк элементу поверхности;dS – площадь элемента поверхности; E n – проекция вектора напряженности на нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле:
.
Поток вектора напряженности через замкнутую поверхность –
(интегрирование ведется по всей поверхности).
Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –
,
где – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; n – число зарядов.
Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –
.
Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:
внутри сферы (r R) Е=0;
на поверхности сферы (r=R)
;
вне сферы (r R)
.
Принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей, выражается формулой
В случае двух электрических полей с напряженностями иабсолютное значение вектора напряженности составляет
где — угол между векторами и.
Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –
,
где — линейная плотность заряда.
Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):
ruscos. ru
ru
Электрический заряд — объяснение определения, типов и свойств
Электрический заряд — это фундаментальное понятие в физике, служащее краеугольным камнем для понимания физического мира. В этой статье мы углубимся в сложную природу электрического заряда и сопутствующие ему свойства. Мы раскроем сущность электрического заряда путем тщательного изучения, дав исчерпывающее определение и исследуя его различные типы и принципы управления. Кроме того, наша статья будет включать всесторонний обзор различных методологий, используемых в процессе зарядки, включая трение, проводимость и индукцию.
Содержание
|
Что такое электрический заряд?
В учебной программе CBSE понимание концепции электрического заряда и его различных типов имеет первостепенное значение.
Определение электрического заряда
Электрический заряд можно определить как фундаментальное свойство субатомных частиц, которое приводит к возникновению явления силы в присутствии электрических и магнитных полей.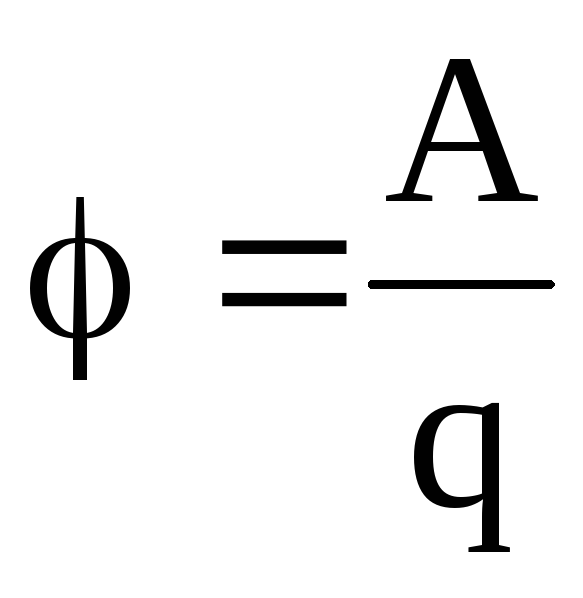 Эти поля воздействуют на заряженные частицы, что приводит к наблюдаемым эффектам.
Эти поля воздействуют на заряженные частицы, что приводит к наблюдаемым эффектам.
Типы электрического заряда
Электрический заряд бывает двух основных типов: положительный и отрицательный заряд . Положительные заряды связаны с протонами, которые являются субатомными частицами, находящимися в ядре атома. Они представлены символом «+». С другой стороны, отрицательные заряды связаны с электронами, которые вращаются вокруг атомного ядра и обозначаются символом «-».
Различие между положительным и отрицательным зарядом играет жизненно важную роль в понимании поведения электрически заряженных объектов. Противоположные заряды, например положительный и отрицательный, притягиваются друг к другу, а одинаковые заряды, например положительный и положительный или отрицательный и отрицательный, отталкивают друг друга. Этот фундаментальный принцип лежит в основе различных концепций электромагнетизма и играет ключевую роль в понимании взаимодействия заряженных частиц.
Когда объект несет отрицательный заряд, он обладает избытком электронов по сравнению с протонами. И наоборот, положительный заряд указывает на избыток протонов по отношению к электронам.
Важно отметить, что когда присутствует равное количество положительных и отрицательных зарядов, они компенсируют друг друга, что приводит к нейтральному состоянию объекта.
Усвоив определение электрического заряда и признав значение положительных и отрицательных зарядов, можно понять фундаментальные принципы, управляющие электричеством и магнетизмом.
Примечание: В контексте электрического заряда термины «притяжение» и «отталкивание» используются для описания того, как заряды взаимодействуют друг с другом.
Является ли электрический заряд векторной величиной?
Нет, электрический заряд не является векторной величиной; это скалярная величина. В то время как векторы имеют как величину, так и направление и подчиняются законам сложения векторов, таким как закон треугольника и закон параллелограмма, электрический заряд не обладает этими свойствами. Когда токи встречаются на стыке, результирующий ток определяется алгебраической суммой отдельных токов, а не их векторной суммой. Таким образом, электрический заряд считается скалярной величиной, несмотря на то, что он имеет величину и направление.
Когда токи встречаются на стыке, результирующий ток определяется алгебраической суммой отдельных токов, а не их векторной суммой. Таким образом, электрический заряд считается скалярной величиной, несмотря на то, что он имеет величину и направление.
Измерение электрического заряда
Колумб — единица измерения электрического заряда.
«Один кулон — это количество заряда, переносимого за одну секунду».
Математически определение колумба представляется как:
Q = I.t
В уравнении Q — электрический заряд, I — электрический ток, t — время.
Свойства электрического заряда
Электрический заряд обладает несколькими важными свойствами, которые помогают нам понять его поведение. Давайте рассмотрим эти свойства:
Аддитивность электрического заряда
Когда заряды объединяются, их величины складываются алгебраически. Например, если у нас есть положительный заряд +3 единицы и отрицательный заряд -2 единицы, результирующий заряд будет +1 единица.
Сохранение электрического заряда:
В изолированной системе сохраняется электрический заряд. Это означает, что общий электрический заряд в системе остается постоянным во времени. Алгебраическая сумма всех зарядов, присутствующих в системе, остается неизменной.
Квантование электрического заряда
Электрический заряд представляет собой дискретные неделимые единицы, называемые элементарными зарядами. Наименьшей единицей электрического заряда является заряд, переносимый электроном, который составляет примерно -1,6 х 10 -19 кулона. Это квантование заряда означает, что электрический заряд нельзя разделить на более мелкие части.
Понимание этих свойств помогает нам понять поведение электрических зарядов и их значение в различных научных явлениях.
Примечание: «Алгебраическая сумма» относится к сложению зарядов с учетом их знаков (+ или -).
Чтобы подробно разобраться в свойствах заряда, прочитайте статью ниже:
Закон Кулона
Мы знаем, что одноименные заряды отталкиваются, а разноименные притягиваются. Однако задумывались ли вы когда-нибудь о величине этих сил, действующих между зарядами? Закон Кулона предлагает нам метод точного расчета этой силы.
Однако задумывались ли вы когда-нибудь о величине этих сил, действующих между зарядами? Закон Кулона предлагает нам метод точного расчета этой силы.
92}\end{array} \)
где F e — электрическая сила, q 1 и q 2 — электрические заряды, k — постоянная Кулона 8,988×10 9 Н⋅ м 2 /C 2 , а r — разделительное расстояние.Применяя закон Кулона, мы можем количественно определить силу электрического взаимодействия между зарядами и получить ценную информацию об их взаимодействии. Этот фундаментальный принцип имеет большое значение в области электромагнетизма и позволяет нам анализировать различные электрические явления.
Благодаря применению Закона Кулона ученые и исследователи смогли раскрыть сложную работу электрических сил и понять их глубокое влияние на мир вокруг нас.
Подробнее: Закон Кулона
Методы зарядки
Процесс подачи электрического заряда к объекту или вызывающий потерю им электрического заряда называется зарядкой.
Существует три различных метода, с помощью которых первоначально незаряженный объект может приобрести заряд:
- Зарядка трением (трибоэлектрическая зарядка)
- Зарядка проводимостью
- Индукционная зарядка
Зарядка трением
Когда два предмета трутся друг о друга, происходит передача заряда. В этом процессе один из объектов теряет электроны, а другой приобретает электроны. Объект, теряющий электроны, становится положительно заряженным, а объект, приобретающий электроны, становится отрицательно заряженным. Это явление, когда оба объекта заряжаются из-за трения, широко известно как электризация от трения.
Зарядка проводимостью
Зарядка за счет проводимости предполагает приближение незаряженного объекта к заряженному объекту. Если заряженный объект имеет неравное количество протонов и электронов, незаряженный объект будет разряжать электроны для достижения стабильности. Эта передача заряда через контакт известна как зарядка за счет проводимости.
Индукционная зарядка
Зарядка с помощью индукции относится к процессу зарядки незаряженного объекта путем простого приближения его к заряженному объекту без какого-либо прямого физического контакта. Посредством индукции заряженный объект вызывает перераспределение зарядов в незаряженном объекте, что приводит к приобретению заряда.
Понимая эти различные методы зарядки, мы можем исследовать захватывающие способы, которыми объекты заряжаются через трение, контакт или близость. Изучение зарядки дает ценную информацию о поведении и взаимодействии электрических зарядов в различных сценариях.
Зарядка с помощью проводимости
Зарядка с помощью индукции
Обзор электрического заряда
Определение
Электрический заряд — это свойство субатомных частиц, которое заставляет их испытывать силу при помещении в электромагнитное поле.
Символ
Q
Формула
Q = I.
t
Единица СИ
Кулон
Другие единицы
Фарадей, Ампер-час
Часто задаваемые вопросы – Часто задаваемые вопросы
Q1
Что такое электрический заряд?
Электрический заряд является фундаментальным свойством материи. Это относится к внутреннему свойству частиц, которое приводит к возникновению электрических сил и взаимодействий.
Q2
Как распределяются электрические заряды внутри атома?
Внутри атома электрические заряды распределены между субатомными частицами. Протоны, находящиеся в ядре, несут положительный заряд, а электроны, вращающиеся вокруг ядра, несут отрицательный заряд. Нейтроны, также присутствующие в ядре, не имеют электрического заряда.
Q3
Как называются положительно заряженные субатомные частицы?
Положительно заряженные субатомные частицы называются протонами.Имеют положительный электрический заряд.
Когда в материи больше протонов, чем электронов, говорят, что она имеет положительный заряд.
Q4
Когда электрический заряд станет отрицательным?
Электрический заряд будет отрицательным, если объект имеет избыток электронов.
Q5
Почему электрический заряд является скалярной величиной?
Когда два тока встречаются на стыке, их результирующий ток будет алгебраической суммой, а не векторной суммой. Следовательно, электрический ток является скалярной величиной.
Q6
Что такое единица измерения электрического заряда?
Единицей измерения электрического заряда является кулон (Кл). Он назван в честь французского физика Шарля-Огюстена де Кулона.
Q7
Один кулон.
Один кулон — это количество заряда, переносимого за одну секунду.
Q8
Какие бывают электрические заряды?
Два типа электрических зарядов — положительные и отрицательные.
Положительные заряды связаны с протонами, а отрицательные — с электронами.
Q9
Как заряжается незаряженный объект?
Незаряженный объект можно зарядить различными способами, такими как зарядка трением (трение двух предметов друг о друга), зарядка проводимостью (контакт с заряженным предметом) или зарядка индукцией (поднесение незаряженного предмета к заряженному предмету без прямой контакт).
Q10
Какие другие единицы измерения электрического заряда?
Фарадей и ампер-час — другие единицы измерения электрического заряда. Помимо кулона, более мелкие единицы электрического заряда включают микрокулон (мкКл), нанокулон (нКл) и пикокулон (пКл). Эти единицы используются для измерения меньших количеств электрического заряда.
Следующее видео служит полезным ресурсом для повторения главы «Электричество» в 10-м классе.
Следите за новостями BYJU’S и влюбитесь в обучение!
Проверьте свое понимание этой концепции, ответив на несколько вопросов MCQ.
Нажмите «Начать викторину», чтобы начать!
Выберите правильный ответ и нажмите кнопку «Готово».
Проверьте свои баллы и ответы в конце викториныПоздравляем!
Посетите BYJU’S для получения всех вопросов, связанных с физикой, и учебных материалов
Ваш результат, как показано ниже Просмотр результатов
Номер мобильного телефона*
Не получили OTP?Запросить OTP на
Войдите для просмотра результатов
Имя*
Идентификатор электронной почты*
Марка* Класс123456789101112
Город*
Пересмотр концепции поля – Колледж Дугласа, физика 1207
Глава 2 Электрический заряд и электрическое поле
Резюме
- Описать силовое поле и рассчитать напряженность электрического поля, создаваемого точечным зарядом.
- Рассчитайте силу, действующую на пробный заряд со стороны электрического поля.
- Объясните взаимосвязь между электрической силой (F) на испытательном заряде и напряженностью электрического поля (E).
Контактные силы, такие как между бейсбольным мячом и битой, объясняются в малом масштабе взаимодействием зарядов в атомах и молекулах в непосредственной близости. Они взаимодействуют через силы, которые включают кулоновскую силу . Действие на расстоянии — это сила между объектами, которые находятся недостаточно близко, чтобы их атомы могли «соприкоснуться». То есть они разделены более чем несколькими атомными диаметрами.
Например, заряженная резиновая расческа притягивает нейтральные кусочки бумаги на расстоянии под действием кулоновской силы. Очень полезно представить объект, окруженный в пространстве силовым полем . Силовое поле переносит силу на другой объект (называемый тестовым объектом) на некотором расстоянии.
Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю (и все другие массы), представляет собой гравитационную силу, которая могла бы возникнуть, если бы в данной точке поля была помещена другая масса.
Точно так же кулоновское силовое поле, окружающее любой заряд, распространяется по всему пространству. Используя закон Кулона, F = k q 1 q 2 /r 2 , его величина определяется уравнением F = k q Q /r 2 , для точечный заряд (частица имеющий заряд Q ), действующий на пробный заряд q на расстоянии r (см. рисунок ниже). Как величина, так и направление кулоновского силового поля зависят от Q и тестовый заряд q .
Рис. 1. Поле кулоновских сил, обусловленное положительным зарядом Q , действует на два разных заряда. Оба заряда находятся на одинаковом расстоянии от Q . (a) Поскольку q 1 положительна, действующая на нее сила F 1 является отталкивающей.(b) Заряд q 2 отрицателен и больше q 1 , и поэтому сила F 2 действующая на него притягательна и сильнее, чем F 1 90 149 . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов q 1 и q 2 , а также от заряда Q .
Для упрощения мы бы предпочли иметь поле, зависящее только от Q и не на испытательном заряде q . Электрическое поле определяется таким образом, что оно представляет собой только создающий его заряд и уникально в каждой точке пространства. В частности, электрическое поле E определяется как отношение кулоновской силы к испытательному заряду:
,, где F — электростатическая сила (или кулоновская сила), действующая на положительный пробный заряд q.
.Понятно, что E находится в том же направлении, что и
Ф . Также предполагается, что q настолько мало, что не меняет распределения заряда, создающего электрическое поле. Единицами электрического поля являются ньютоны на кулон (Н/Кл). Если электрическое поле известно, то электростатическая сила на любом заряде q просто получается путем умножения заряда на электрическое поле, или F = q E . Рассмотрим электрическое поле, создаваемое точечным зарядом Q . По закону Кулона сила, действующая на пробный заряд, равна q равно F = k q Q /r 2 . Таким образом, величина электрического поля E для точечного заряда равнаПоскольку тестовый заряд отменяется, мы видим, что
Таким образом, видно, что электрическое поле зависит только от заряда Q и расстояния r ; он полностью независим от испытательного заряда q.

Пример 1. Расчет электрического поля точечного заряда
Расчет напряженности и направления электрического поля E из-за точечного заряда 2,00 нКл (нанокулоны) на расстоянии 5,00 мм от заряда.
Стратегия
Мы можем найти электрическое поле, создаваемое точечным зарядом, используя уравнение E = kQ/r 2 .
Решение
Здесь Q = 2,00 x 10 -9 C и r = 5,00 x 10 -3 м . Ввод этих значений в приведенное выше уравнение дает
Обсуждение
Эта напряженность электрического поля одинакова в любой точке на расстоянии 5,00 мм от заряда Q , который создает поле. Он положительный, что означает, что он имеет направление, указывающее от заряда Q.
Пример 2. Расчет силы, действующей на точечный заряд электрическим полем
Какую силу электрическое поле, найденное в предыдущем примере, действует на точечный заряд -0,250 мкКл ?
Стратегия
Поскольку мы знаем напряженность электрического поля и заряд в поле, силу, действующую на этот заряд, можно рассчитать, используя определение электрического поля E = F/q преобразованное в F = qE .
Решение
Величина силы, действующей на заряд q = -0,250 мкКл , действующей на поле напряженностью E = 7,20 x 10 5 N/C, таким образом,
9 0002 Поскольку q отрицательно , сила направлена против направления поля.Обсуждение
Сила притяжения, как и ожидалось для разных зарядов. (Поле было создано положительным зарядом, а здесь действует на отрицательный заряд.) Заряды в этом примере типичны для обычного статического электричества, а полученная небольшая сила притяжения аналогична силам, возникающим при статическом прилипании и подобных ситуациях.
PhET Explorations: Electric Field of Dreams
Играй в мяч! Добавьте заряды в Поле Снов и посмотрите, как они реагируют на электрическое поле. Включите фоновое электрическое поле и отрегулируйте направление и величину.
Рисунок 2. Электрическое поле снов. Прямая ссылкаL https://phet.colorado.edu/en/simulation/legacy/efield
Аналогичный PhEt, но использующий HTML 5, который будет работать на большинстве компьютеров, можно найти по прямой ссылке: https://phet.colorado.edu/sims/html/charges-and-fields/latest/charges-and-fields_en.html It откроется ниже автоматически, если вы читаете эту книгу онлайн.
- Поле электростатической силы, окружающее заряженный объект, распространяется в пространстве во всех направлениях.
- Электростатическая сила, действующая точечным зарядом на пробный заряд на расстоянии r , зависит от заряда обоих зарядов, а также от расстояния между ними.
- Электрическое поле E определяется как
, где F – кулоновская или электростатическая сила, действующая на небольшой положительный пробный заряд q . E имеет единицы N/C.
- Величина электрического поля E , создаваемого точечным зарядом Q есть
, где r это расстояние от Q .




 Напряженность поля бесконечной заряженной плоскости.
Напряженность поля бесконечной заряженной плоскости. Существует три различных метода, с помощью которых первоначально незаряженный объект может приобрести заряд:
Существует три различных метода, с помощью которых первоначально незаряженный объект может приобрести заряд: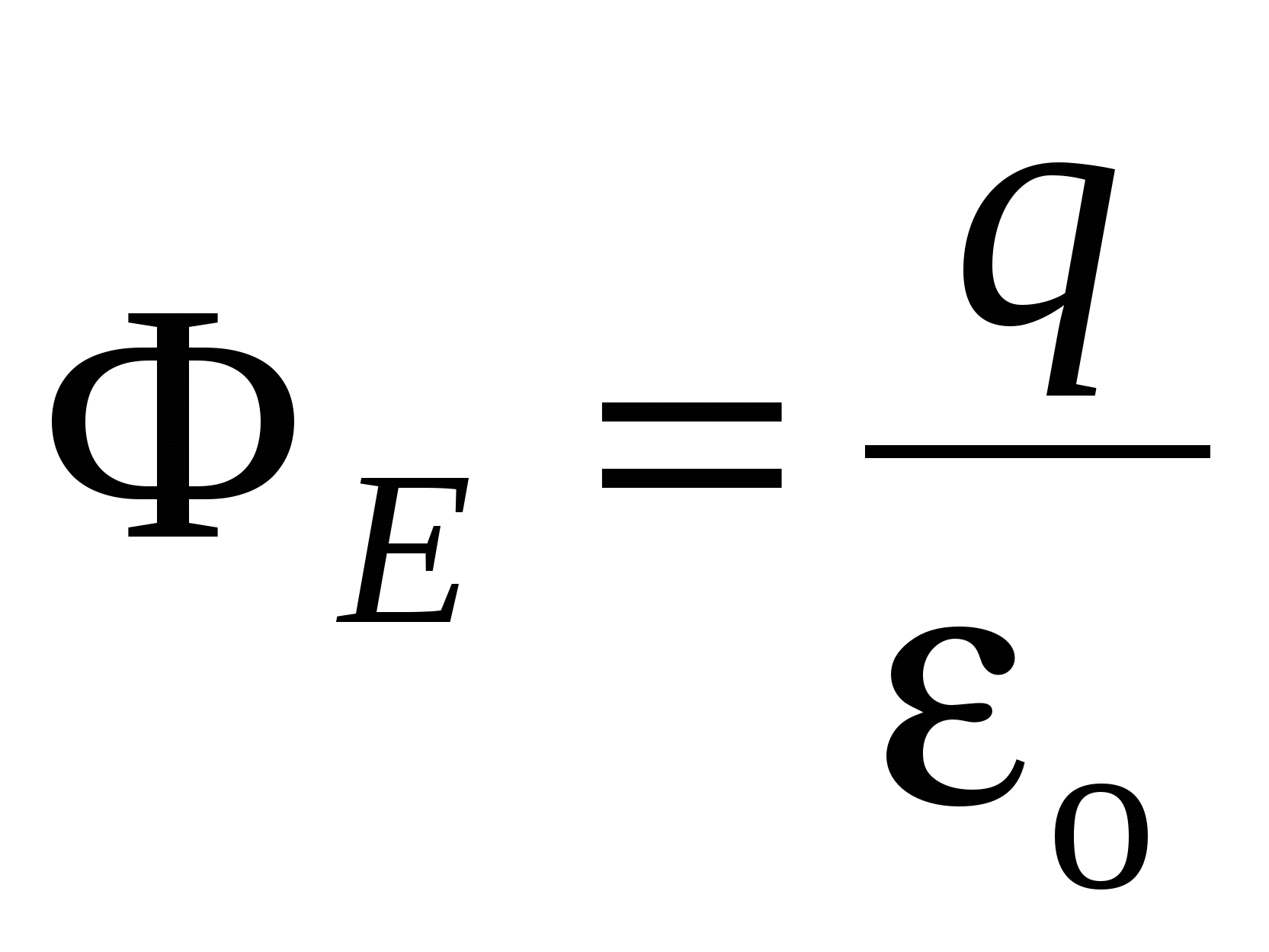
 t
t  Имеют положительный электрический заряд.
Имеют положительный электрический заряд. Положительные заряды связаны с протонами, а отрицательные — с электронами.
Положительные заряды связаны с протонами, а отрицательные — с электронами. Нажмите «Начать викторину», чтобы начать!
Нажмите «Начать викторину», чтобы начать!

 (b) Заряд q 2 отрицателен и больше q 1 , и поэтому сила F 2 действующая на него притягательна и сильнее, чем F 1 90 149 . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов q 1 и q 2 , а также от заряда Q .
(b) Заряд q 2 отрицателен и больше q 1 , и поэтому сила F 2 действующая на него притягательна и сильнее, чем F 1 90 149 . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов q 1 и q 2 , а также от заряда Q . Понятно, что E находится в том же направлении, что и
Понятно, что E находится в том же направлении, что и 

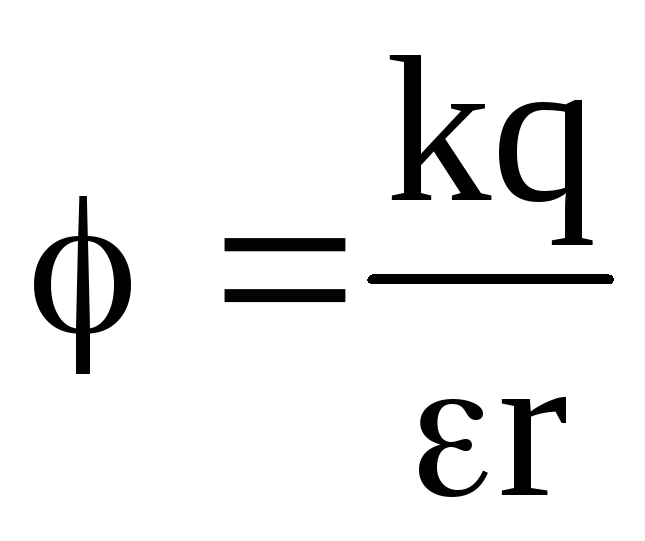 colorado.edu/en/simulation/legacy/efield
colorado.edu/en/simulation/legacy/efield