Закон Кирхгофа (страница 1)
Применение закона Кирхгофа к расчету линейных электрических цепей постоянного тока
1. В цепи (рисунок 10) известны значения токов
; величины сопротивлений . Определить напряжение U на входных зажимах цепи, сопротивление и величину Е источника ЭДС.
Решение:
По закону Ома определим напряжение между узлами 3-2:
Из уравнения, составленного по первому закону Кирхгофа для узла 3:
определим ток
:
Тогда, по закону Ома для ветви с сопротивлением
:
откуда выражаем величину Е источника ЭДС:
Напряжение
можно выразить из уравнения, записанного по II закону Кирхгофа для контура 1-3-2-1:
Зная величины напряжения
и тока , определим величину сопротивления :
Напряжение на входных зажимах цепи определится:
Ток
определим из уравнения, записанного по первому закону Кирхгофа для 1 узла:
тогда
2. В цепи (рисунок 11) известны величины сопротивлений резистивных элементов
В цепи (рисунок 11) известны величины сопротивлений резистивных элементов
; мощность, изменяемая ваттметром Р=320 Вт. Определить токи ветвей, напряжение на зажимах цепи.
Решение:
Из формулы для расчета мощности выражаем ток :
Затем определяем напряжение на зажимах параллельных ветвей:
По закону Ома определяем ток в ветви с сопротивлением
:
Значение тока в неразветвленной части цепи определим из уравнения, записанного по первому закону Кирхгофа для узла 1:
Напряжение на входных зажимах цепи можно представить как сумму падений напряжений на сопротивлениях
:
где
тогда
3. На рисунке 12 показана часть сложной цепи. Задано:
. Найти напряжение .
Решение:
Уравнение по второму закону Кирхгофа для данного контура, при выбранном направлении обхода контура, запишется следующим образом:
откуда выражаем напряжение
:
4. В схеме (рисунок 13) известны:
В схеме (рисунок 13) известны:
. Определить напряжения .
Решение:
Считаем направления обходов контуров совпадающими с направлениям искомых напряжений. Запишем уравнения по второму закону Кирхгофа для каждого контура и выразим напряжения:
контур 1-2-6-5-1
контур 3-4-6-5-3
контур 1-3-5-1
контур 2-4-6-2
контур 1-4-6-5-1
контур 2-3-5-6-2
5. Определить показание амперметра (рисунок 14), если
.
Решение:
По закону Ома определим значения токов в ветвях:
Запишем уравнение по первому закону Кирхгофа для узла b:
откуда
6. На рисунке 15 показана часть сложной цепи. Найти напряжения
, если .
Решение:
По закону Ома определим ток на участке с-d:
Запишем уравнение по второму закону Кирхгофа для контура a-b-c-d:
откуда выразим напряжение
:
7. В схеме электрической цепи, приведенной на рисунке 16, определить токи в ветвях пользуясь законами Кирхгофа. Параметры элементов цени:
В схеме электрической цепи, приведенной на рисунке 16, определить токи в ветвях пользуясь законами Кирхгофа. Параметры элементов цени:
.
Решение:
Выбираем произвольно положительные направления искомых токов ветвей и обозначаем их на схеме. Составляем уравнение по первому закону Кирхгофа для узла 1. Выбрав направления обходов контуров, составляем уравнения по второму закону Кирхгофа. Получаем систему из трех уравнений:
Решаем полученную систему уравнений с помощью определителей:
Находим значения токов:
Для проверки правильности расчета составим уравнение баланса мощностей:
Мощность источников:
Мощность потребителей:
8. Определить токи ветвей цепи (рисунок 17), если:
.
Решение:
Произвольно задаемся положительными направлениями токов в ветвях с сопротивлениями
. В ветви с источником тока направление тока уже определено полярностью источника. Составляем уравнение по первому закону Кирхгофа для узла 1. Количество контурных уравнений зависит от количества ветвей с неизвестными токами, т.е. ветвей, не содержащих источники тока. Для данной цепи количество контурных уравнений равно 1. Составим систему уравнений:
В ветви с источником тока направление тока уже определено полярностью источника. Составляем уравнение по первому закону Кирхгофа для узла 1. Количество контурных уравнений зависит от количества ветвей с неизвестными токами, т.е. ветвей, не содержащих источники тока. Для данной цепи количество контурных уравнений равно 1. Составим систему уравнений:
Решаем систему уравнений с помощью определителей:
Определяем значения токов:
Закон Кирхгофа – энциклопедия VashTehnik.ru
Содержание
- 1 Открытия Густава Кирхгофа
- 2 Законы Киргофа для электрических цепей
- 3 Закон Кирхгофа для термодинамики
- 4 Работы Кирхгофа в области спектроскопии
- 5 Другие работы
Закон Кирхгофа – правило, открытое известным немецким (прусским) учёным.
Открытия Густава Кирхгофа
Чаще под законами Кирхгофа подразумеваются закономерности, сформулированные для замкнутых контуров и узлов электрических цепей. В русскоязычной литературе их предпочитают называть правилами. Закона два. Первый оперирует с токами, второй с напряжениями. Составленная при помощи формул система уравнений позволяет найти параметры сети, удовлетворяющей требованиям применимости к ней данных вычислений. Правила сформулированы в 1845 году, это не единственное открытие Кирхгофа.
Закона два. Первый оперирует с токами, второй с напряжениями. Составленная при помощи формул система уравнений позволяет найти параметры сети, удовлетворяющей требованиям применимости к ней данных вычислений. Правила сформулированы в 1845 году, это не единственное открытие Кирхгофа.
В термодинамике известен другой принцип. Гласит, что соотношение излучательной способности тела и поглощательной постоянно для любых материалов вне зависимости от их природы и определяется двумя внешними параметрами:
- Частотой волны.
- Температурой окружающей среды.
Тесно связан с предыдущим открытием факт из жизни великого учёного. В 17 веке начала развиваться спектроскопия, Кирхгоф не преминул оставить в науке собственный след, открыв три закона:
- Спектр излучения твёрдого тела непрерывный. Кирхгоф ввёл понятие абсолютно-чёрного тела, ставшее сегодня ключевым в изучении вопросов передачи энергии на расстояние.
- Разреженный газ излучает в выделенных волнах спектра, с длинами, зависящими от состояния квантовых переходов электронов вещества.
 На указанной основе работают лазеры.
На указанной основе работают лазеры. - Горячее твёрдое тело, окружённое охлаждённым газом имеет непрерывный спектр излучения за вычетом отдельных частот, поглощённых обволакивающим облаком. Длины волн зависят от квантовых переходов витающего вокруг объекта вещества.
Учёный добрался до термохимии и показал, что тепловой эффект реакции зависит от изменения теплоёмкости системы (до и после процесса). Постулат причислен к основным в разделе науки. В гидродинамике уравнения Кирхгофа описываю движения твёрдого тела в идеальной жидкости.
Первый закон
Законы Киргофа для электрических цепей
- Первый закон Киргофа гласит, что алгебраическая сумма токов в узле цепи равна нулю. Исходящие токи берутся при вычислениях с отрицательным знаком, входящие – с положительным. Хотя в русскоязычной литературе говорится, что допустимо наоборот. Суть неизменна.
- Второй закон Киргофа формулируется для замкнутых контуров. Утверждает, что сумма падений напряжений при обходе по кругу равна всем встречающимся на пути ЭДС.
 Причём контуры любой цепи нужно обходить в едином направлении: по или против часовой стрелки.
Причём контуры любой цепи нужно обходить в едином направлении: по или против часовой стрелки.
Первое уравнение не нуждается в пояснении. Порой сложно понять, в каком направлении течёт ток, с отрицательным или положительным знаком требуется подставить в формулу. Рекомендуется помнить: количество уравнений на единицу меньше, нежели узлов. Если присутствуют сомнения по точке, допустимо исключить её из рассмотрения. В прочих ситуациях анализируется знак разницы потенциалов на концах проблемного участка. Для этого складываются или вычитаются действующие здесь источники питания (в задачках по физике – батарейки).
По общепринятым нормам более длинная черта в графическом обозначении аккумулятора считается положительным полюсом. Ток вытекает отсюда по правилам, принятым в физике, хотя на практике все происходит наоборот – движение образовано отрицательно заряженными электронами. Если ЭДС действуют на участке в разных направлениях, они вычитаются, а направление тока задаётся наибольшей.
Что касается второго закона, знак вхождения в формулу падения напряжения на установленном участке определяется направлением протекания тока. ЭДС берутся с противоположным знаком, либо стоят по другую сторону равенства. Как указано выше, ячейки нужно обходить в одном направлении. Не смущайтесь, что в формулах над напряжением и током стоит точка. Это знак комплексного числа.
Обратите внимание – дана упрощённая запись второго закона. Здесь все ЭДС берутся с обратным реально присутствующему на рисунке знаком. Известна иная форма записи, где падения напряжения отделены от ЭДС знаком равенства. Тогда знаки менять не нужно. Последняя форма записи даётся в школьном курсе физики и приведена на рисунке чуть ниже общей.
Правило Кирхгофа
Закон Кирхгофа для термодинамики
Кирхгоф показал, что соотношение излучательной и поглощательной способности твёрдого тела не зависит от вещества, но считается функцией частоты и температуры при термодинамическом равновесии. Особенно интересной абстракцией в этом плане стало абсолютно-чёрное тело. Это объект, поглощающий падающее на него излучение. Для него формула, представленная на рисунке упрощается. Излучающая способность абсолютно-чёрного тела описывает функцию формулы для прочих тел. Эта ипостась имеет максимум, определяемый законом смещения Вина и амплитуды, определяемую первым законом Вина (частным случаем считается формула Планка).
Это объект, поглощающий падающее на него излучение. Для него формула, представленная на рисунке упрощается. Излучающая способность абсолютно-чёрного тела описывает функцию формулы для прочих тел. Эта ипостась имеет максимум, определяемый законом смещения Вина и амплитуды, определяемую первым законом Вина (частным случаем считается формула Планка).
Отношение излучательной и поглощательной способности любого тела находится по формулам для любых температур и частот. При помощи спектрометра возможно оценить испускаемые волны. Это позволяют теоретически предсказать поглощательную способность любого предмета. На практике подобные исследования приводят к созданию объектов типа самолёт-невидимка, с трудом видимый локаторами.
Из закона сохранения энергии следует, что полное излучение равняется поглощению в термодинамическом равновесии. Значит, по всему спектру их соотношение равняется единице. До признания закона Кирхгофа уже установлено, что – чем лучше тело поглощает энергию, тем оно больше излучает. Обратите внимание, спектральные плотности поглощения и излучения имеют разную форму. В этом и заключается гениальное прозрение Кирхгофа. Взаимодействие определяется законом Вина и на графике выглядит подобно горе с вершиной, смещённой влево относительно центра фигуры.
Обратите внимание, спектральные плотности поглощения и излучения имеют разную форму. В этом и заключается гениальное прозрение Кирхгофа. Взаимодействие определяется законом Вина и на графике выглядит подобно горе с вершиной, смещённой влево относительно центра фигуры.
Это позволяет понять, где находится максимум излучения (на макушке). Во всех участках графика, где линия находится ниже единицы, тело преимущественно поглощает энергию. Благодаря законам возможно предсказать температуру звёзд, к примеру, по цвету, а каждый кузнец знает, что деталь в горне дошла до кондиции лишь по характерному оттенку свечения. Это практические проявления законов Вина и Кирхгофа.
Вторым интересным наблюдением становится температура. Из графиков плотности излучения видно, чем показатель больше, тем активнее идёт излучение. В частности, звезды не поглощают энергию за малым исключением, но преимущественно излучают. У холодных планет преобладает противоположный процесс. Тело излучает, если его температура выше окружающей среды.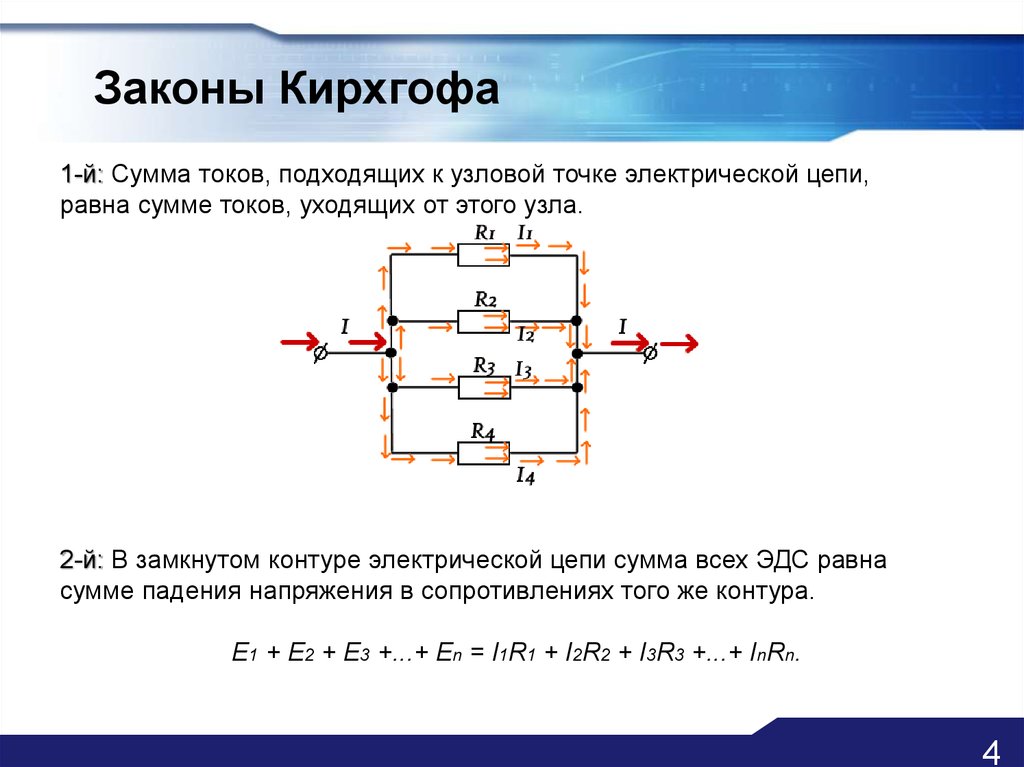 В остальных ситуациях преобладает поглощение энергии.
В остальных ситуациях преобладает поглощение энергии.
Аналогия закона Кирхгофа
Работы Кирхгофа в области спектроскопии
Кирхгоф и Бунзен активно изучали спектры излучения химических элементов, используя изобретения Фраунгофера. При помощи призмы или дифракционной решётки свет раскладывался на спектральные составляющие, и учёные наблюдали эффект. Так установлены индивидуальные частоты ряда элементов таблицы Менделеева. Указанные учёные заложили основы спектроскопии. В 1860 году опубликованы исследования восьми элементов и их уникальных спектров, среди прочих:
- стронций;
- литий;
- калий;
- кальций;
- барий;
- натрий.
Кирхгоф и Бунзен показали, что можно проводить химический анализ веществ при помощи спектроскопии и открыли элементы, прежде неизвестные в науке (цезий – в Древнем Риме «голубой» по спектру свечения и рубидий – в Древнем Риме «темно-красный»). Установили связь между спектрами излучения и поглощения, на основании характеристик солнечного света показали избранные свойства нашего светила (наличие железа, калия, кальция, магния, никеля, хрома и натрия в атмосфере звезды, отсутствие лития). Опыты требовалось проводить в период близости Солнца к зениту: когда звезда клонилась к горизонту, увеличивался итоговый эффект вклада атмосферы Земли. Как результат работы, на свет появился закон Кирхгофа для термодинамики.
Опыты требовалось проводить в период близости Солнца к зениту: когда звезда клонилась к горизонту, увеличивался итоговый эффект вклада атмосферы Земли. Как результат работы, на свет появился закон Кирхгофа для термодинамики.
Применяя устройства, разлагающие спектр на составляющие, учёные открыли ряд прочих законов, упомянутых выше. Учёный применял бунзеновскую горелку (Бунзен), в пламя вводил хлористый натрий или хлористый литий. В результате при помощи дифракционной решётки наблюдал дискретный спектр, причём установлено, что поглощение идёт на прежних частотах. Выводы Кирхгофа:
- Раскалённое газообразное тело, образованное в пламени горелки испускает дискретный спектр излучения.
- Установлено, что в солнечном излучении отсутствуют частоты элемента натрия. Учёный сложил дневной свет с пламенем бунзеновой горелки, дефект изгладился. Излучение натрия в лаборатории дополнило спектр Солнца.
- Если потом для опыта бралась спиртовая горелка, тёмные полосы становились чернее.
 Следовал вывод, что при относительно низкой температуре газообразного тела в пламени горелки оно начинает поглощать. Так установлено, что в более холодной относительно ядра солнечной атмосфере имеется натрий.
Следовал вывод, что при относительно низкой температуре газообразного тела в пламени горелки оно начинает поглощать. Так установлено, что в более холодной относительно ядра солнечной атмосфере имеется натрий.
Опыт с горелкой
Лучшей горелкой для опытов учёный считал газовую. Поскольку светимость её пламени низка и не мешает регистрировать спектр газообразного тела. Соли для опытов брались максимально чистыми, производилось многократное осаждение. Для наблюдения использовался чёрный ящик, в стенки устройства под острым углом вставлялись две подзорные трубы:
- через первую наблюдатель лицезрел зачернённую заднюю стенку;
- через вторую свет концентрировался на выбранном участке.
Вращающаяся призма помогала зафиксировать напротив глаз наблюдателя нужный сегмент спектра. Понятно, что указанная методика годится исключительно для видимого излучения и не затрагивает инфракрасный и ультрафиолетовый диапазоны.
Другие работы
Кирхгоф массу времени посвятил разным отраслям науки. К примеру, нашёл ошибку в постановке граничных условий для решения дифференциальных уравнений по колебаниям мембран, представленных на суд публики в 1811 году Софи Жермен. Не нужно думать, что словосочетание закон Кирхгофа узко ограничено двумя правилами, причём одно прямо приводит к сформулированному ранее закону Ома.
К примеру, нашёл ошибку в постановке граничных условий для решения дифференциальных уравнений по колебаниям мембран, представленных на суд публики в 1811 году Софи Жермен. Не нужно думать, что словосочетание закон Кирхгофа узко ограничено двумя правилами, причём одно прямо приводит к сформулированному ранее закону Ома.
Учёный Г.Кирхгоф
Учёный представлен для получения звания члена-корреспондента Берлинской Академии наук в отделении математики, корреспондента Петербургской Академии наук. Если в первом случае заявители в основном указывали на дар в решении задач механики, наши соотечественники (Ленц и Якоби) немало отметили заслуги Кирхгофа в спектральном анализе.
Учёный преподавал, обладал феноменальной памятью, назубок читал длинные лекции без отступлений от формального текста. Чувство скрупулёзности помогало безукоризненно собирать материалы, и лишь недостаток технической оснастки помешал, вероятно, сделать новые открытия. К примеру, учёный отмечал, что одна из линий спектра кальция совпадает с железом, но не сумел достоверно сказать, кажущееся ли совпадение. Теперь известно, что длины волн отличаются на 5-6 ангстремов, но тогда на глаз сказать оказалось невозможно с полной уверенностью.
Теперь известно, что длины волн отличаются на 5-6 ангстремов, но тогда на глаз сказать оказалось невозможно с полной уверенностью.
Первый и второй законы Кирхгофа для электрической цепи, метод составления уравнений и анализ цепей
Первый закон Кирхгофа для электрической цепи
Любые электрические цепи всегда подчиняются законам Кирхгофа.
Есть для первого закон Кирхгофа два варианта формулировок:
1. Алгебраическая сумма электрических токов ветвей, сходящихся в одном узле, равна нулю.
2. Сумма электрических токов, которые текут в направлении к узлу, равна сумме электрических токов, которые текут из узла.
Токи, направленные к узлам, обычно считают положительными, а выходящие – отрицательными.
Рис. 1. Направление токов в узле.
Для рисунка 1 можно записать по первой формулировке:
По второй формулировке:
Физический смысл для первого закона заключается в том, что заряды в электрической цепи двигаются таким образом, что не скапливаются ни в каком узле.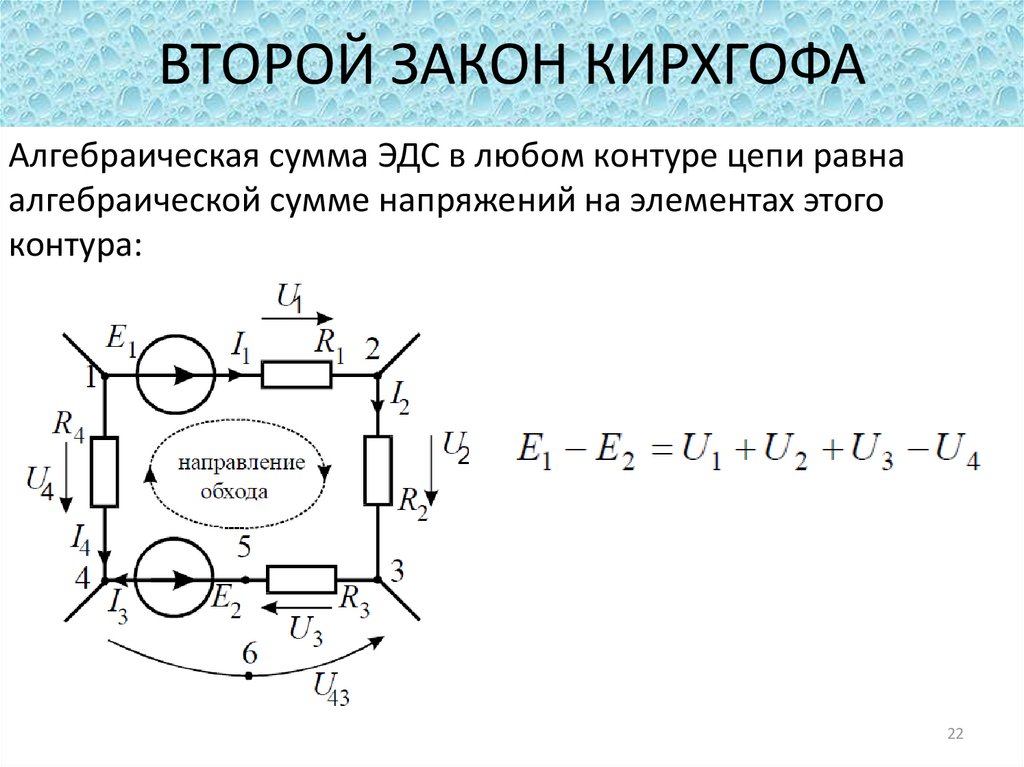
Второй закон Кирхгофа для электрической цепи
Для второго закона тоже есть две формулировки:
1. В замкнутом контуре абсолютно любой электрической цепи алгебраическая сумма существующих падений напряжений равна сумме ЭДС контура.
Если слагаемое совпадает с направление, по которому происходит обход контура цепи, то оно входит в уравнение со знаком «+», если же оно не совпадает – то со знаком «–».
2. Алгебраическая сумма напряжений вдоль какого-либо замкнутого контура цепи равна нулю.
Рис. 2. Электрическая схема.
Для контура на рисунке 2 можно записать:
Оба закона Кирхгофа являются справедливыми как для линейных, так и для нелинейных электрических цепей при любых изменениях напряжений и токов во времени.
Метод составления уравнений по законам Кирхгофа
Оба закона Кирхгофа совместно применяют для поиска электрических токов в ветвях. Давайте обозначим число всех ветвей через b, число ветвей, где есть источник тока через bит, число узлов через y. По каждой из ветвей схемы протекает свой собственный электрический ток. По причине того, что токи, находящиеся в ветвях с источниками электрического тока, известны, число токов, которые неизвестны, равно b–bит.
По каждой из ветвей схемы протекает свой собственный электрический ток. По причине того, что токи, находящиеся в ветвях с источниками электрического тока, известны, число токов, которые неизвестны, равно b–bит.
Перед составление уравнения необходимо выбрать произвольно:
1. Положительное направление электрического тока в каждой из ветви, и затем обозначить их на схеме.
2. Положительные направления для обхода каждого из контуров схемы для записи уравнений по второму закону Кирхгофа.
Для удобства рекомендуется положительные направления для обхода каждого из контуров выбирать одинаковыми, допустим, по часовой стрелке.
С целью получения линейно независимых уравнений, которые были составлены по первому закону Кирхгофа, их количество должно быть равно y–1. Для последнего узла уравнение не составляют, потому что оно совпадало бы с уравнением, которое получено в результате суммирования уравнений для y–1 узлов.
В соответствии со вторым законом Кирхгофа выполняют составление уравнений в количестве, равном количеству ветвей без источника электрического тока (b–bит), вычтя те уравнения, которые были составлены по первому закону:
Во время составления уравнения по второму закону Кирхгофа, нужно охватить все ветви, при этом исключив ветви, где есть источник тока, потому что в этом случае в уравнение были бы включены бесконечно большие слагаемые, в связи с чем оно бы не имело смысла.
Есть рекомендуемое, но не обязательное требование, по которому при составлении в соответствии со 2-м законом Кирхгофа линейно независимых уравнений стремятся к тому, чтобы в каждый новый контур, применительно к которому выполняется составление уравнения, входила как минимум одна новая ветвь, которая не вошла в предыдущие контуры, для которых уравнения по 2-му закону уже составлены. Данные контуры называют независимыми контурами.
Анализ электрических цепей с помощью законов Кирхгофа
Произведём анализ электрических цепей для схемы, изображённой на рисунке 3 и составим для неё уравнения.
Рис. 3. Электрическая схема.
Число неизвестных электрических токов для схемы равно числу ветвей. Обозначим число ветвей через m, число узлов через k. Тогда m=6, k=4.
Теперь зададимся произвольным направлением электрических токов отдельных ветвей цепи. Согласно первого закона Кирхгофа составим независимые уравнения в количестве k–1 штук для узлов a, b и c.
a: I1 + I5 + I6 = 0
b: I2 – I5 – I4 = 0
c: I4 – I3 – I6 = 0
Для определения всех токов ветвей недостающие уравнения, количество которых (m–(k–1)), можно составить, если воспользоваться вторым законом для независимых контуров.
Контур I: I1R1 – I2R2 – I5R5 = E1 – E2
Контур II: I2R2 + I4R4 + I3R3 = E2
Контур III: I5R5 – I6R6 – I4R4 = 0
правил Кирхгофа | безграничная физика |
Введение и значение
Законы цепи Кирхгофа — это два уравнения, которые касаются сохранения энергии и заряда в контексте электрических цепей.
Цели обучения
Описать взаимосвязь между законами Кирхгофа о цепях и энергией и зарядом в электрических цепях
Основные выводы
Ключевые моменты
- Кирхгоф использовал работу Георга Ома в качестве основы для создания закона тока Кирхгофа (KCL) и закона напряжения Кирхгофа ( КВЛ) в 1845 году. Их можно вывести из уравнений Максвелла, появившихся 16-17 лет спустя.
- Невозможно анализировать некоторые замкнутые цепи путем упрощения как суммы и/или ряда компонентов. В этих случаях можно использовать законы Кирхгофа.
- Законы Кирхгофа являются частными случаями сохранения энергии и заряда.
Ключевые термины
- резистор : Электрический компонент, передающий ток прямо пропорционально напряжению на нем.
- электродвижущая сила : (ЭДС) — напряжение, создаваемое батареей или магнитной силой в соответствии с законом Фарадея.
 Измеряется в вольтах (не ньютонах, Н; ЭДС не является силой).
Измеряется в вольтах (не ньютонах, Н; ЭДС не является силой). - конденсатор : Электронный компонент, состоящий из двух проводящих пластин, разделенных пустым пространством (иногда между пластинами зажат диэлектрический материал), и способный накапливать определенное количество заряда.
Введение в законы Кирхгофа
Законы Кирхгофа о цепях — это два уравнения, впервые опубликованные Густавом Кирхгофом в 1845 году. По сути, они касаются сохранения энергии и заряда в контексте электрических цепей.
Хотя законы Кирхгофа можно вывести из уравнений Джеймса Клерка Максвелла, Максвелл не публиковал свой набор дифференциальных уравнений (которые составляют основу классической электродинамики, оптики и электрических цепей) до 1861 и 1862 годов. Кирхгоф, скорее, использовал Работа Георга Ома послужила основой для закона тока Кирхгофа (KCL) и закона напряжения Кирхгофа (KVL) .
Законы Кирхгофа чрезвычайно важны для анализа замкнутых цепей.
Замкнутая цепь : Чтобы определить все переменные (т. е. падение тока и напряжения на различных резисторах) в этой цепи, необходимо применить правила Кирхгофа.
И последнее замечание: законы Кирхгофа зависят от определенных условий. Закон напряжения является упрощением закона индукции Фарадея и основан на предположении, что существует нет флуктуации магнитного поля в замкнутом контуре.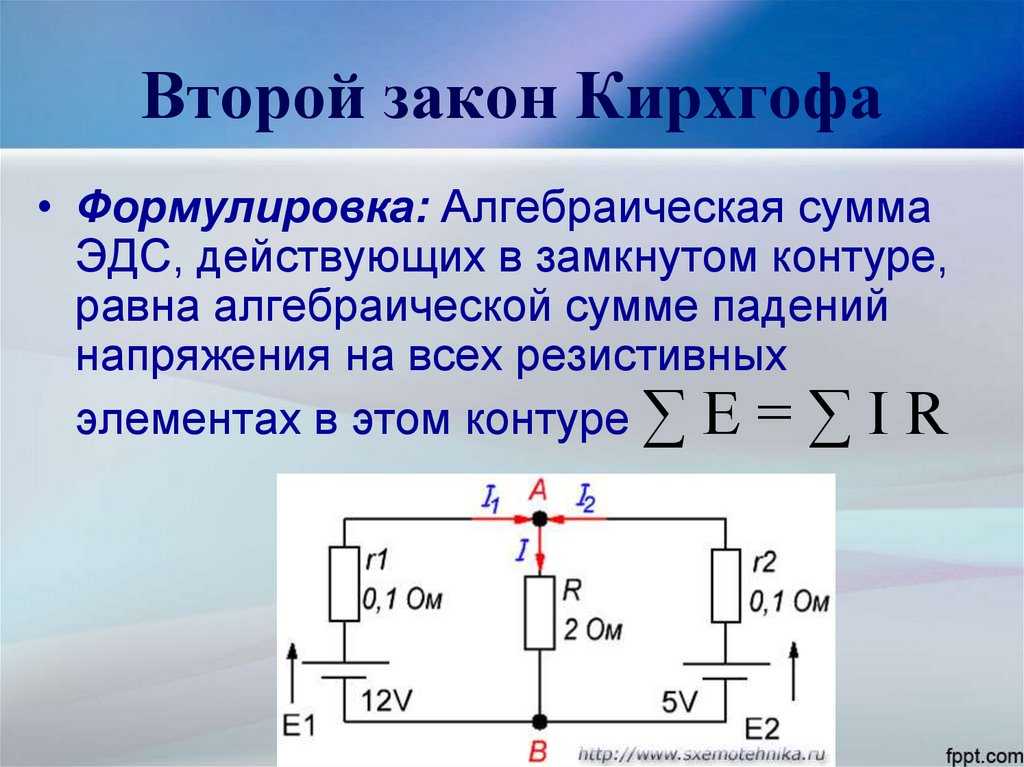 Таким образом, хотя этот закон можно применить к цепям, содержащим резисторы и конденсаторы (а также другие элементы цепи), его можно использовать только как приближение к поведению цепи при изменении тока и, следовательно, магнитного поля.
Таким образом, хотя этот закон можно применить к цепям, содержащим резисторы и конденсаторы (а также другие элементы цепи), его можно использовать только как приближение к поведению цепи при изменении тока и, следовательно, магнитного поля.
Правило соединения
Правило соединения Кирхгофа гласит, что в любом узле цепи сумма токов, втекающих и вытекающих из этого соединения, равна.
Цели обучения
Сформулируйте правило соединения Кирхгофа и опишите его ограничения
Ключевые выводы
Ключевые моменты
Ключевые термины
- электрический заряд : Квантовое число, определяющее электромагнитные взаимодействия некоторых субатомных частиц; по соглашению электрон имеет электрический заряд -1, а протон +1, а кварки имеют дробный заряд.
- ток : Скорость потока электрического заряда во времени.
Правило узлов Кирхгофа, также известное как текущий закон Кирхгофа (KCL), первый закон Кирхгофа, правило точек Кирхгофа и правило узлов Кирхгофа, является применением принципа сохранения электрического заряда.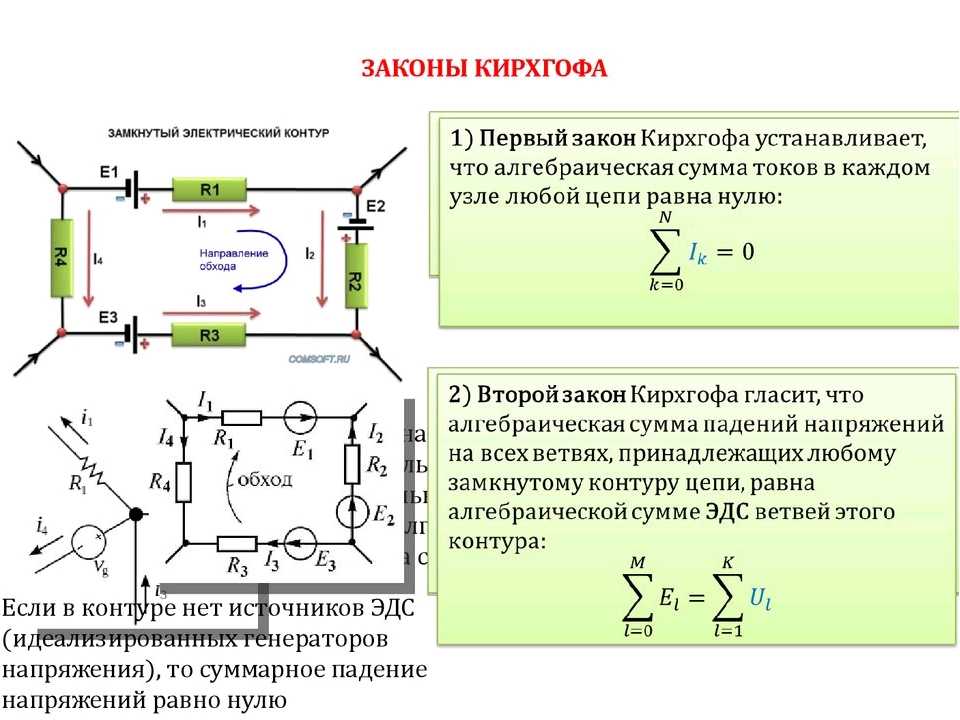
Правило соединения Кирхгофа гласит, что в любом узле (узле) электрической цепи сумма токов, втекающих в это соединение, равна сумме токов, вытекающих из этого соединения. Другими словами, учитывая, что ток будет положительным или отрицательным в зависимости от того, течет ли он к узлу или от него, алгебраическая сумма токов в сети проводников, сходящихся в точке, равна нулю. Визуальное представление можно увидеть в. 9{\text{n}} \text{I}_\text{k}=0∑k=1nIk=0
, где n — общее количество ветвей, несущих ток к узлу или от него.
Этот закон основан на законе сохранения заряда (измеряется в кулонах), который является произведением силы тока (ампер) и времени (секунды).
Ограничение
Применение закона Кирхгофа ограничено. Это верно для всех случаев, когда полный электрический заряд (Q) постоянен в рассматриваемой области. Практически это всегда верно, пока закон применяется для конкретной точки. Однако в области плотность заряда может быть непостоянной.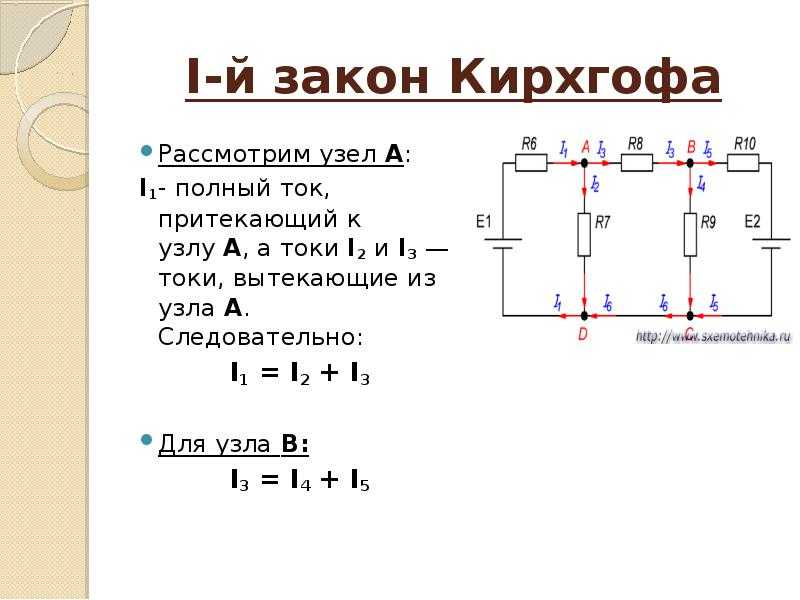
Правило цикла
Правило петли Кирхгофа гласит, что сумма значений ЭДС в любом замкнутом контуре равна сумме падений потенциала в этом контуре.
Цели обучения
Сформулируйте правило петли Кирхгофа, отметив его допущения
Ключевые выводы
Ключевые моменты
Ключевые термины
- электродвижущая сила : (ЭДС) — напряжение, создаваемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.
- Резистор : Электрический компонент, передающий ток прямо пропорционально напряжению на нем.
Правило петли Кирхгофа (также известное как закон напряжения Кирхгофа (KVL), правило сетки Кирхгофа, второй закон Кирхгофа, или второе правило Кирхгофа ) является правилом, относящимся к цепям, и основано на принципе сохранения энергии.
Сохранение энергии — принцип, согласно которому энергия не создается и не уничтожается, — является универсальным принципом во многих исследованиях в области физики, включая электрические цепи. Применительно к схемам подразумевается, что направленная сумма разностей электрических потенциалов (напряжений) вокруг любой замкнутой сети равна нулю. Другими словами, сумма значений электродвижущей силы (ЭДС) в любом замкнутом контуре равна сумме падений потенциала в этом контуре (которые могут исходить от резисторов).
Другое эквивалентное утверждение состоит в том, что алгебраическая сумма произведений сопротивлений проводников (и токов в них) в замкнутом контуре равна полной электродвижущей силе, доступной в этом контуре. Математически правило петли Кирхгофа можно представить как сумму напряжений в цепи, которая приравнивается к нулю:
Теория правил петли и соединения Кирхгофа : Мы обосновываем правила Кирхгофа с точки зрения сохранения энергии. \text{n} \text{V}_\text{k}=0∑k=1nVk=0
\text{n} \text{V}_\text{k}=0∑k=1nVk=0
.
Здесь V k — напряжение на элементе k, а n — общее количество элементов в замкнутой цепи. Иллюстрация такой схемы показана на рис. нуль.
Правило петли Кирхгофа : Правило петли Кирхгофа утверждает, что сумма всех напряжений вокруг петли равна нулю: v1 + v2 + v3 — v4 = 0,
Учитывая, что напряжение является мерой энергии на единицу заряда, правило цикла Кирхгофа основано на законе сохранения энергии, который гласит: общая энергия, полученная на единицу заряда, должна равняться количеству энергии, потерянной на единицу заряда .
Пример
иллюстрирует изменения потенциала в простой петле последовательной цепи. Второе правило Кирхгофа требует ЭДС-Ir-IR 1 -IR 2 =0. Переставлено, это ЭДС=Ir+IR  ЭДС обеспечивает 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, всего 18 В.
ЭДС обеспечивает 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, всего 18 В.
Правило контура : Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) На этой стандартной схеме простой последовательной цепи ЭДС подает напряжение 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В. (b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает ЭДС.)
Ограничение
Правило петли Кирхгофа представляет собой упрощение закона индукции Фарадея и выполняется при условии отсутствия флуктуирующего магнитного поля, связывающего замкнутый контур. В присутствии переменного магнитного поля могут индуцироваться электрические поля и создаваться ЭДС, и в этом случае правило петли Кирхгофа нарушается.
Приложения
Правила Кирхгофа можно использовать для анализа любой цепи и модифицировать для цепей с ЭДС, резисторами, конденсаторами и многим другим.
Цели обучения
Опишите условия, когда полезно применять правила Кирхгофа
Ключевые выводы
Ключевые положения
- Правила Кирхгофа можно применять к любой цепи, независимо от ее состава и структуры.
- Поскольку часто легко комбинировать элементы параллельно и последовательно, применять правила Кирхгофа не всегда удобно.
- Чтобы найти ток в цепи, можно применить правила контура и соединения. Как только все токи связаны правилом соединения, можно использовать правило контура, чтобы получить несколько уравнений, которые можно использовать в качестве системы для нахождения каждого значения тока с точки зрения других токов. Их можно решить как систему.
Ключевые термины
- электродвижущая сила : (ЭДС) — напряжение, создаваемое батареей или магнитной силой в соответствии с законом Фарадея.
 Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.
Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.
Обзор
Правила Кирхгофа можно использовать для анализа любой цепи, изменив их для цепей с электродвижущими силами, резисторами, конденсаторами и т. д. Однако с практической точки зрения правила полезны только для характеристики тех цепей, которые нельзя упростить путем последовательного и параллельного соединения элементов.
Комбинации последовательно и параллельно, как правило, гораздо проще выполнить, чем применить любое из правил Кирхгофа, но правила Кирхгофа более широко применимы и должны использоваться для решения задач, связанных со сложными цепями, которые нельзя упростить путем последовательного или параллельного соединения элементов схемы.
Пример правил Кирхгофа
показывает очень сложную схему, но можно применить правила петли и соединения Кирхгофа. Решить схему для токов I 1 , I 2 и I 3 оба правила необходимы.
Правила Кирхгофа: пример задачи : На этом изображении показана очень сложная схема, которую можно уменьшить и решить с помощью правил Кирхгофа.
Применяя правило соединения Кирхгофа в точке a, находим:
I1=I2+I3\text{I}_1=\text{I}_2+\text{I}_3I1=I2+I3
, потому что I 1 впадает в точку а, а I 2 и I3 вытекают. То же самое можно найти в точке e. Теперь мы должны решить это уравнение для каждой из трех неизвестных переменных, для чего потребуются три разных уравнения.
Рассматривая цикл abcdea, мы можем использовать правило цикла Кирхгофа:
−I2R2+emf1−I2r1−I1R1=−I2(R2)+r1)+emf1−I1R1=0-\text{I}_2\text{R} _2+ \mathrm{\text{ЭДС}}_1-\text{I}_2\text{r}_1-\text{I}_1\text{R}_1=-\text{I}_2(\text{R }_2)+\text{r}_1)+\mathrm{\text{emf}}_1-\text{I}_1\text{R}_1=0−I2R2+emf1-I2r1 −I1R1= −I2(R2)+r1)+ЭДС1-I1R1=0
Подставляя значения сопротивления и ЭДС из диаграммы рисунка и исключая единицу ампер, получаем:
−3I2 +18−6I1=0-3\text{I}_2+18-6\text{I}_1=0−3I2+18−6I1=0
Это вторая часть системы из трех уравнений, которую мы можем использовать для нахождения всех трех текущих значений.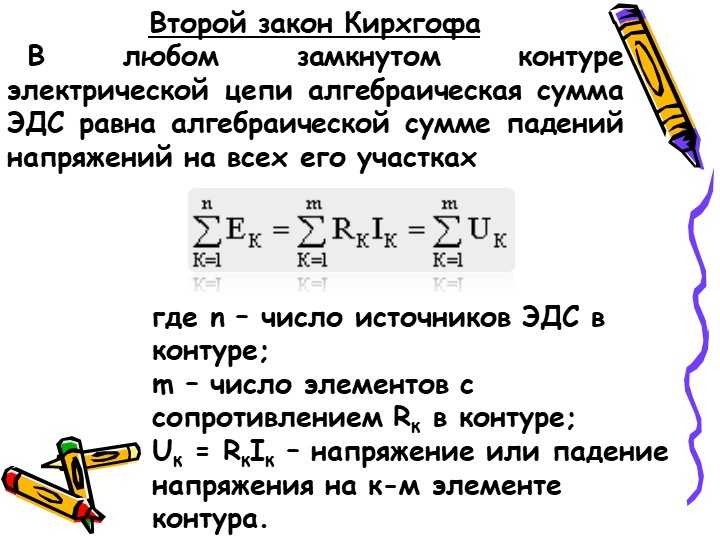 Последнее можно найти, применив правило цикла к циклу aefgha, что дает:
Последнее можно найти, применив правило цикла к циклу aefgha, что дает:
I1R1+I3R3+I3r2−emf2=I1R1+I3(R3+r2)−emf2=0\text{I}_1\text{R} _1+\text{I}_3\text{R}_3+\text{I}_3\text{r}_2-\mathrm{\text{emf}}_2=\text{I}_1\text{R}_1+\ text{I}_3(\text{R}_3+\text{r}_2)-\mathrm{\text{emf}}_2=0I1R1+I3R3+I3r2−emf2=I1 R1+I3(R3+r2)−emf2=0
Используя подстановку и упрощение, получаем:
6I1+2I3−45=06\text{I}_1+2\text{I}_3-45=06I1+2I3−45=0
В этом случае знаки поменялись местами по сравнению с другим циклом , потому что элементы перемещаются в противоположном направлении.
Теперь у нас есть три уравнения, которые можно использовать в системе. Второй будет использоваться для определения I 2 и может быть изменен на:
I2=6-2I1\text{I}_2=6-2\text{I}_1I2=6-2I1
третье уравнение может быть использовано для определения I 3 и может быть преобразовано в:
I3=22,5−3I1\text{I}_3=22,5-3\text{I}_1I3=22,5−3I1
Подставив новые определения I 2 и I 3 (оба в общие члены I 1 ), в первое уравнение (I 1 =I 2 +I 3 ) получаем:
I1=(6−2I1)+(22,5−3I1)=28,5 −5I1\text{I}_1=(6-2\text{I}_1)+(22,5-3\text{I}_1)=28,5-5\text{I}_1I1=(6−2I1) +(22,5−3I1)=28,5−5I1
Упрощая, находим, что I 1 =4,75 А. Подставляя это значение в два других уравнения, находим, что I 2 = -3,50 А и I 3 = 8,25 А.
Подставляя это значение в два других уравнения, находим, что I 2 = -3,50 А и I 3 = 8,25 А.
Лицензии и атрибуты
Лицензионный контент CC, совместно используемый ранее
- Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Контент, лицензированный CC, конкретное указание авторства
- Законы Кирхгофа. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Kirchhoff%27s_circuit_laws. Лицензия : CC BY-SA: Attribution-ShareAlike
- конденсатор. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- резистор. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- электродвижущая сила.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Kirchhoffu2019с Правилами. 14 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Законы Кирхгофа о цепях. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- текущая. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- электрический заряд. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Правила Kirchhoffu2019s. 14 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.
 org/contents/[email protected]. Лицензия : CC BY: Атрибуция
org/contents/[email protected]. Лицензия : CC BY: Атрибуция - KCL — Законы Кирхгофа о цепях. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Теория правил петель и соединений Кирхгофа. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Законодательство Кирхгофа. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Kirchhoff%27s_circuit_laws. Лицензия : CC BY-SA: Attribution-ShareAlike
- электродвижущая сила. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- резистор. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Правила Kirchhoffu2019s.
 14 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
14 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция - KCL — Законы Кирхгофа о цепях. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Теория правил Кирхгофа о петлях и соединениях. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Закон Кирхгофа о напряжении. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Теория правил Кирхгофа о петлях и соединениях. Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, Правила Kirchhoffu2019s.
 15 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
15 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Правила Kirchhoffu2019s. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- электродвижущая сила. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Правила Kirchhoffu2019s. 14 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- KCL — Законы Кирхгофа о цепях. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Теория правил петель и соединений Кирхгофа.
 Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - Закон Кирхгофа о напряжении. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Теория правил Кирхгофа о петлях и соединениях. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, Правила Kirchhoffu2019. 15 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Правила Kirchhoffu2019s. 14 января 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
Закон Кирхгофа о напряжении | Вращающиеся числа
Законы Кирхгофа для тока и напряжения лежат в основе анализа цепей. С этими двумя законами, а также уравнениями $i$-$v$, такими как закон Ома для резисторов, у нас есть базовый набор инструментов, необходимый для анализа цепей.
С этими двумя законами, а также уравнениями $i$-$v$, такими как закон Ома для резисторов, у нас есть базовый набор инструментов, необходимый для анализа цепей.
В этой статье рассматривается закон Кирхгофа о напряжении, также известный как KVL. KVL является компаньоном Текущего закона Кирхгофа.
Вы должны быть знакомы с определениями узла, распределенного узла, ветви и петли.
Содержимое
- Напряжение вокруг петли
- Процедура петли
- Использовать циклическую процедуру
- Закон напряжения Кирхгофа
- Проверка концепции
- Продвинутый уровень: законы Кирхгофа выводятся из уравнений Максвелла
Куда мы движемся
Закон Кирхгофа о напряжении для напряжений вокруг контура,
$\displaystyle \sum_n v_n = 0$
Напряжение вокруг контура
В нашей примерной схеме есть четыре резистора и источник напряжения. Мы решим это с нуля, используя закон Ома. Затем мы посмотрим на результат и сделаем некоторые замечания.
Затем мы посмотрим на результат и сделаем некоторые замечания.
Первым шагом в решении этой схемы является определение тока. Затем найдем напряжения на каждом отдельном резисторе.
Мы распознаем это как последовательную цепь. Через все пять элементов протекает только один ток, $\blueD i$. Чтобы найти $i$, четыре последовательных резистора можно свести к одному эквивалентному резистору,
$R_{серии} = 100 + 200 + 300 + 400 = 1000\,\Omega$
Используя закон Ома, ток равен ,
$i = \dfrac{V}{R_{ряд}} = \dfrac{20\,\text V}{1000\,\Omega} = 0,020\,\text A = 20 \,\text{мА }$
Теперь мы знаем текущий. Это позволяет нам найти напряжения на четырех резисторах. Вернитесь к исходной схеме и добавьте метки напряжения ко всем пяти элементам,
Примените закон Ома четыре раза, чтобы найти напряжение на каждом резисторе,
$v_{\text{R}} \,\,= i\,\text R$
$v_{\text{R1}} = 20\,\text{мА} \cdot 100\,\Omega = +2\,\text{V}$
$v_{\text{R2}} = 20\,\text{мА} \cdot 200\ ,\Omega = +4\,\text{V}$
$v_{\text{R3}} = 20\,\text{мА} \cdot 300\,\Omega = +6\,\text{V} $
$v_{\text{R4}} = 20\,\text{мА} \cdot 400\,\Omega = +8\,\text{V}$
Теперь схема решена. Мы знаем ток и все напряжения.
Мы знаем ток и все напряжения.
Мы можем записать напряжения для резисторов и источника на схеме. Эти пять напряжений называются напряжениями элемента . (Узлы цепи получают имена, от $\greenE{a}$ до $\greenE{e}$, поэтому мы можем говорить о них.)
Давайте быстро проверим. Сложите напряжения на резисторах,
$2\,\text{V} + 4\,\text{V} + 6\,\text{V} + 8\,\text{V} = 20 \,\ text V$
Напряжения отдельных резисторов складываются с напряжением источника. Это имеет смысл и подтверждает наши расчеты.
Циклическая процедура
Теперь мы снова суммируем напряжения, используя немного другую процедуру, «обходя контур». Здесь нет никакой новой науки, мы просто перестраиваем одни и те же вычисления.
Шаг 1. Выберите начальный узел.
Шаг 2. Выберите направление движения по контуру (по часовой стрелке или против часовой стрелки).
Шаг 3. Обойдите петлю. Включите напряжения элементов в растущую сумму. Когда вы сталкиваетесь с каждым новым элементом, смотрите на знак метки напряжения при вводе элемента.
- Если знак $+$, то падение напряжения проходит через элемент. Вычесть напряжение элемента.
- Если знак $-$, то через элемент проходит повышение напряжения. Добавьте напряжение элемента.
Совет от профессионала. Представьте себе крошечную версию себя, стоящую в начальном узле и переходящую по цепи от элемента к элементу.
альтернативное правилоНекоторые учебники преподают другое правило знаков для обхода петли. Правило эквивалентно приведенному выше и дает точно такой же ответ.
Когда вы встречаете новый элемент, смотрите на знак напряжения при вводе элемента.
- Если стоит знак $+$, добавьте напряжение элемента.
- Если знак $-$, вычтите напряжение элемента.
В этом правиле нет понятия подъема/падения напряжения, но его проще запомнить. Вы можете выбрать, как вы хотите думать об этом. Главное — быть последовательным при применении выбранного правила.
Шаг 4. Продолжайте движение по контуру, пока не достигнете начальной точки, включая напряжения элементов по всему периметру.
Используйте циклическую процедуру
Давайте пошагово повторим циклическую процедуру на примере схемы.
Шаг 1. Начните с нижнего левого угла, в узле $\greenE{a}$.
Шаг 2. Идите по часовой стрелке.
Шаг 3. Первый элемент, к которому мы подошли, это источник $20\,\text V$. Первый знак напряжения, с которым мы сталкиваемся, — это знак минус $-$. Это говорит нам о том, что через этот элемент будет происходить повышение напряжения . Итак, мы инициализируем сумму цикла на добавление напряжения источника,
$+20\,\text V \,…$
Следующий элемент, с которым мы сталкиваемся, это резистор $100\,\Omega$. Ближайший знак напряжения $+$. Это говорит нам о том, что через резистор будет происходить падение напряжения . Из растущей суммы вычитаем напряжение элемента,
$+ 20\,\text V — 2\,\text V \,…$
Дальше резистор $200\,\Omega$, и опять сталкиваемся знак $+$, поэтому мы вычитаем это напряжение,
$+ 20\,\text V — 2\,\text V — 4\,\text V \,…$
Завершаем цикл добавлением еще двух напряжений резисторов,
$+ 20\,\text V — 2\,\text V — 4\,\text V — 6\,\text V \,…$
$+ 20\,\text V — 2\,\text V — 4\,\text V — 6\,\text V — 8\,\text V$
(Проверьте принципиальную схему, убедитесь, что я правильно понял два последних знака $-$. )
)
Шаг 4. Готово. Мы вернулись домой к узлу $\greenE{a}$. К чему это приводит?
$+ 20\,\text V — 2\,\text V — 4\,\text V — 6\,\text V — 8\,\text V = 0$
Сумма напряжений, проходящих по контуру, равна $0$.
Мы начали и закончили в одном и том же узле, поэтому вполне понятно, что конечное напряжение такое же, как и начальное. Во время вашей «прогулки» по петле вы поднялись вверх по напряжению и упали вниз по падению напряжения. К тому времени, когда вы вернетесь к тому, с чего начали, все взлеты и падения сводятся на нет. Это как подниматься и спускаться с горы, а в конце дня вернуться в свой кемпинг. Ваше общее изменение высоты за день составляет $0$.
Мы сделаем еще один пример с именами переменных вместо числовых значений. Следующая знакомая схема помечена напряжениями и именами узлов. Посмотрите внимательно, знаки полярности напряжения расположены не так, как вы могли ожидать. Все стрелки напряжения указывают в одном направлении вокруг контура. Это раскроет интересное свойство петель.
Давайте снова пройдемся по петле, складывая напряжения по мере продвижения. Выберите узел $\greenE{a}$ в левом нижнем углу в качестве начальной точки. Пройдите по петле по часовой стрелке (произвольный выбор, в любом случае работает). Начиная с узла $\greenE{a}$ и поднимаясь вверх, мы встречаем знак минус на источнике напряжения. Это означает, что будет напряжение рост $+v_{ab}$, проходящий через источник напряжения. Поскольку это повышение напряжения, напряжение этого элемента получает знак $+$ в сумме цикла,
$+v_{\text{ab}} \, …$
Продолжить по циклу от узла $\greenE{b} от $ до $\greenE{c}$ до $\greenE{d}$ до $\greenE{e}$ и завершается в узле $\greenE{a}$. Добавляйте напряжения резисторов к растущей сумме по пути. Метки полярности на резисторах расположены таким образом, что мы всегда сталкиваемся со знаком $-$ при приближении к каждому резистору. Таким образом, все напряжения резисторов входят в сумму контура со знаком $+$. Окончательная сумма цикла выглядит так:
$+v_{\text{ab}} + v_{\text{R1}} + v_{\text{R2}} + v_{\text{R3}} + v_{\text{R4}}$
Что это дает? Давайте рассуждать.
Цикл начинается и заканчивается в одном и том же узле, поэтому начальное и конечное напряжения идентичны. Мы обошли петлю, добавляя напряжения, и в итоге вернулись к тому же напряжению. Это может быть правдой только в том случае, если сумма всех напряжений равна нулю:
$v_{\text{ab}} + v_{\text{R1}} + v_{\text{R2}} + v_{\ текст{R3}} + v_{\text{R4}} = 0$
Как положительные напряжения могут равняться нулю? Как связка положительных напряжений может равняться нулю? Ответ таков: не все они положительные. Знаки полярности напряжения, которые вы добавляете на схему в начале задачи, являются опорными направлениями . Переменная напряжения с именем $v_1$ может иметь положительное или отрицательное значение. Когда вы комбинируете метку полярности напряжения со знаком переменной напряжения, вы получаете фактическое напряжение. К тому времени, когда вы закончите анализ, одно или несколько напряжений вокруг каждого контура будут отрицательными. Полярность напряжения, которую вы пишете на схеме в начале, не обязательно должна быть «правильной». Они могут указывать в любую сторону. Знаки напряжения разбираются в процессе расчета.
Они могут указывать в любую сторону. Знаки напряжения разбираются в процессе расчета.
Это утверждение может показаться абракадаброй при первом прочтении. В конце концов идея укоренится, так что наберитесь терпения, если у вас кружится голова.
Что произойдет, если вы пройдете петлю в другую сторону?В двух приведенных выше примерах мы прошли цикл по часовой стрелке. Самостоятельно повторите этот пример, но идите в противоположном направлении (против часовой стрелки).
подсказкаИдя против часовой стрелки, когда вы встречаете каждый элемент, вы сначала придете к знаку $+$. Ознакомьтесь с приведенными выше правилами процедуры контура, чтобы узнать, как выбрать знак напряжения каждого элемента в растущей сумме контура.
показать ответЕсли двигаться против часовой стрелки, напряжение каждого элемента входит в сумму контура со знаком $-$.
$ -v_{\text{R4}} — v_{\text{R3}} — v_{\text{R2}} — v_{\text{R1}} — v_{\text{ab}} = 0$
Мы можем разложить это выражение на множители и переупорядочить, чтобы оно выглядело точно так же, как уравнение по часовой стрелке,
$ — (v_{\text{R4}} + v_{\text{R3}} + v_{\text{R2}} + v_{\text{R1}} + v_{\text{ab}}) = 0$
$v_{\text{ab}} + v_{\text{R1}} + v_{\text{R2}} + v_{\text{R3}} + v_{\text{R4}} = 0 $
Неважно, в какую сторону вы ходите по петле. В любом случае вы получите одно и то же уравнение цикла.
В любом случае вы получите одно и то же уравнение цикла.
Закон Кирхгофа о напряжении
Это наблюдение о напряжениях вокруг контура, суммирующихся с нулем, прекрасно отражено в виде закона Кирхгофа о напряжении.
Сумма напряжений вокруг контура равна нулю.
$\large\displaystyle \sum_n v_n = 0$
Индекс $n$ подсчитывает напряжения элементов вокруг контура.
Что такое большой зигзагообразный символ? 9{n=5} v_n = 0$Понятно, что индекс $n$ проходит от нижнего предела $n=1$ до верхнего предела $n=5$ с шагом в $1$. Если символ суммирования не имеет выписанного индекса, предположим, что сумма включает «всех их».
Вы можете выразить закон Кирхгофа о напряжении по-другому:
Сумма повышений напряжения равна сумме падений напряжения на контуре.
$\large \displaystyle \sum v_{rise} = \sum v_{drop}$
Это означает то же самое, что и первая версия закона. Он просто сортирует термины на две группы, повышается и понижается.
Закон Кирхгофа о напряжении имеет несколько замечательных свойств,
- Вы можете проследить петлю, начинающуюся с любого узла. С любой начальной точки сумма напряжений равна нулю, пока вы проходите весь круг.
- Вы можете идти в любом направлении, по часовой стрелке или против часовой стрелки. КВЛ до сих пор работает.
- Если цепь имеет несколько контуров, KVL истинен для каждого контура.
Проверка концепции
Что такое $v_{\text R3}$?
Совет: следите за направлением стрелок напряжения!
$v_{\text R3} = $ _____ $\text V$
показать ответ$v_{\text R3} = +6\,\text V$
Используйте закон Кирхгофа о напряжении, чтобы решить эту проблему.
$\displaystyle \sum_n v_n = 0$
Выберите узел для начала. Узел $\text A$ так же хорош, как и любой другой. Мы будем ходить по часовой стрелке вокруг петли.
Все стрелки напряжения перепутаны. Они не все указывают в одном и том же направлении по кругу. Итак, когда мы напишем это следующее уравнение, мы будем очень осторожно обращайте особое внимание на полярность напряжения каждого элемента. Обратитесь к процедуре контура , чтобы напомнить себе, какое направление стрелки напряжения получает какой знак.
Итак, когда мы напишем это следующее уравнение, мы будем очень осторожно обращайте особое внимание на полярность напряжения каждого элемента. Обратитесь к процедуре контура , чтобы напомнить себе, какое направление стрелки напряжения получает какой знак.
$+15 + (-5) + (-3) + (-v_{\text{R3}}) + (-1) = 0$
Трудно правильно подобрать знаки. Это важный навык при использовании законов Кирхгофа.
$+15 -5 -3 + (-1) = v_{\text{R3}} $
$v_{\text{R3}} = +6 \,\text V$
Проверьте стрелку напряжения для $\text R3$. Он направлен вверх от узла $\greenE{e}$ к узлу $\greenE{d}$. Положительный результат для $v_{\text{R3}}$ означает, что узел $\greenE{d}$ на $6$ выше, чем узел $\greenE{e}$.
Больше практики: повторите эту задачу, но обойдите петлю в противоположном направлении и постройте другое уравнение КВЛ. Вы должны получить такой же ответ.
Сводка
У нас есть два новых друга,
Закон Кирхгофа для токов в узле,
$\large\displaystyle \sum_n i_n = 0$
Закон Кирхгофа для напряжений в контуре,
$ 9004 \large\displaystyle \sum_n v_n = 0$
Наши новые друзья иногда носят инициалы KCL и KVL.
Важно обращать пристальное внимание на знаки напряжения и тока, если вы хотите получить правильные ответы. Это может быть утомительным процессом. Он требует внимания к деталям. Это основной навык каждого хорошего инженера-электрика.
Продвинутый: Законы Кирхгофа выводятся из уравнений Максвелла
Законы Кирхгофа на самом деле являются приближениями, полученными из уравнений Максвелла для электромагнетизма. Законы Кирхгофа применяются, когда размер компонентов в цепи намного меньше, чем длина волны сигналов, проходящих через цепь. Это упрощение применимо практически ко всем схемам, с которыми вы столкнетесь на начальном этапе изучения электротехники.
Если вы хотите узнать больше об этом выводе, хорошие ссылки:
«Основы аналоговых и цифровых электронных схем», Анант Агарвал и Джеффри Х. Ланг, Elsevier Inc, 2005, Приложение 2A.
«Проектирование радиочастотных интегральных схем CMOS, 2-е издание, Томас Х. Ли, издательство Кембриджского университета, глава 6, распределенные системы.
Закон Кирхгофа – закон напряжения, закон тока, расчет
Физика
Учащиеся 11-го класса натолкнутся на схемы и другие связанные темы в главе «Электричество». И чтобы решить большинство задач в этих главах, кандидаты должны сначала понять закон напряжения Кирхгофа и закон тока, а также формулу. Кроме того, закон Кирхгофа играет решающую роль в поиске различных важных принципов, чтобы вычислить различные величины в цепи.
Что такое закон Кирхгофа?Обычно для определения сопротивления и многих других величин внутри двух или более резисторов, соединенных параллельно или последовательно, используется закон Ома. Однако это само по себе нельзя использовать при попытке найти ток и напряжение в сложных цепях, таких как Т-образные сети или мосты. Для расчета этих величин немецкий физик Густав Кирхгоф ввел два закона: напряжение и ток.
Текущий закон Кирхгофа (KCL) Первый закон Кирхгофа или Правило соединения утверждает, что общее количество токов, протекающих через цепь, подобно току, протекающему вне соединения в цепи. При этом согласно этому закону общее количество зарядов, поступающих в узел цепи, будет равно количеству зарядов, покидающих узел. Это, в свою очередь, означает, что при прохождении тока не происходит потери заряда или электричества.
При этом согласно этому закону общее количество зарядов, поступающих в узел цепи, будет равно количеству зарядов, покидающих узел. Это, в свою очередь, означает, что при прохождении тока не происходит потери заряда или электричества.
Итак, из первой диаграммы, как вы можете заметить, входящие в узлы токи I1, I2 и I3, которые обычно положительные, равны отрицательным токам I4, I5 и I6. Что можно указать в уравнении, например
I1 + I2 + I3 – I4 – I5 – I6 = 0
Закон Кирхгофа для напряжения (KVL)Аналогично текущему закону или второму закону Кирхгофа используется для нахождения расчетных напряжений, проходящих через цепь. Например, согласно второму закону Кирхгофа, напряжение, проходящее через контур, должно быть равно падению напряжения, происходящему в том же контуре в замкнутой цепи. Следовательно, при добавлении каждого напряжения внутри замкнутой цепи оно будет равно нулю, этот принцип широко известен как сохранение энергии.
На второй диаграмме вы можете увидеть различные напряжения в замкнутой цепи. Это может быть указано в виде уравнения, например,
Это может быть указано в виде уравнения, например,
V1 + V2 + V3 + V4 + V5 + V6 + V7 – Vs = 0
Применение законов КирхгофаТеперь, когда вы поняли основы закона Кирхгофа Закон тока и напряжения, а также уравнение Кирхгофа. Поговорим о различных применениях этих законов.
- Помогает кандидатам легко определить сопротивление и напряжение в каждой цепи.
- Это также помогает им различать каждое напряжение и сопротивление, проходящее через цепь.

- Учащиеся могут найти уравнения Кирхгофа для каждого узла.
- Используя линейные уравнения из этих принципов, люди смогут находить неизвестные токи и напряжения.

- Их можно использовать для идентификации изменений напряжения или каждого напряжения в замкнутой цепи или независимой цепи.
Вышеупомянутая статья помогла вам найти все ответы на ваши вопросы, например, сформулировать и объяснить закон Кирхгофа, а также его различные приложения. Итак, если вы один из тех людей, которые в настоящее время борются с предметом физики или, в частности, с текущими главами об электричестве, так как существует множество сложных принципов и законов. Тогда вам лучше присоединиться к интерактивный онлайн-класс или получить Home Tutor Online .


 На указанной основе работают лазеры.
На указанной основе работают лазеры.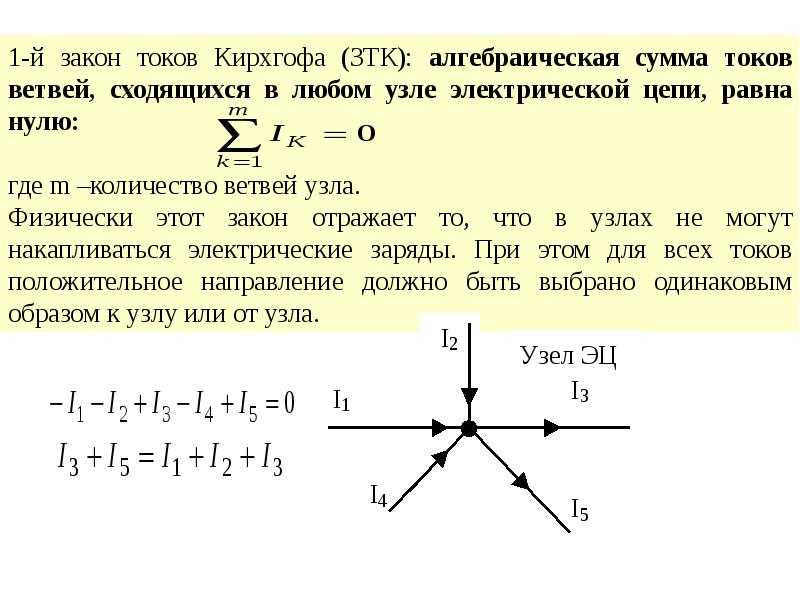 Причём контуры любой цепи нужно обходить в едином направлении: по или против часовой стрелки.
Причём контуры любой цепи нужно обходить в едином направлении: по или против часовой стрелки. Следовал вывод, что при относительно низкой температуре газообразного тела в пламени горелки оно начинает поглощать. Так установлено, что в более холодной относительно ядра солнечной атмосфере имеется натрий.
Следовал вывод, что при относительно низкой температуре газообразного тела в пламени горелки оно начинает поглощать. Так установлено, что в более холодной относительно ядра солнечной атмосфере имеется натрий. Измеряется в вольтах (не ньютонах, Н; ЭДС не является силой).
Измеряется в вольтах (не ньютонах, Н; ЭДС не является силой). Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.
Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  org/contents/[email protected]. Лицензия : CC BY: Атрибуция
org/contents/[email protected]. Лицензия : CC BY: Атрибуция  14 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
14 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция  15 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
15 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция  Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
