Вращающий момент | это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила».
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .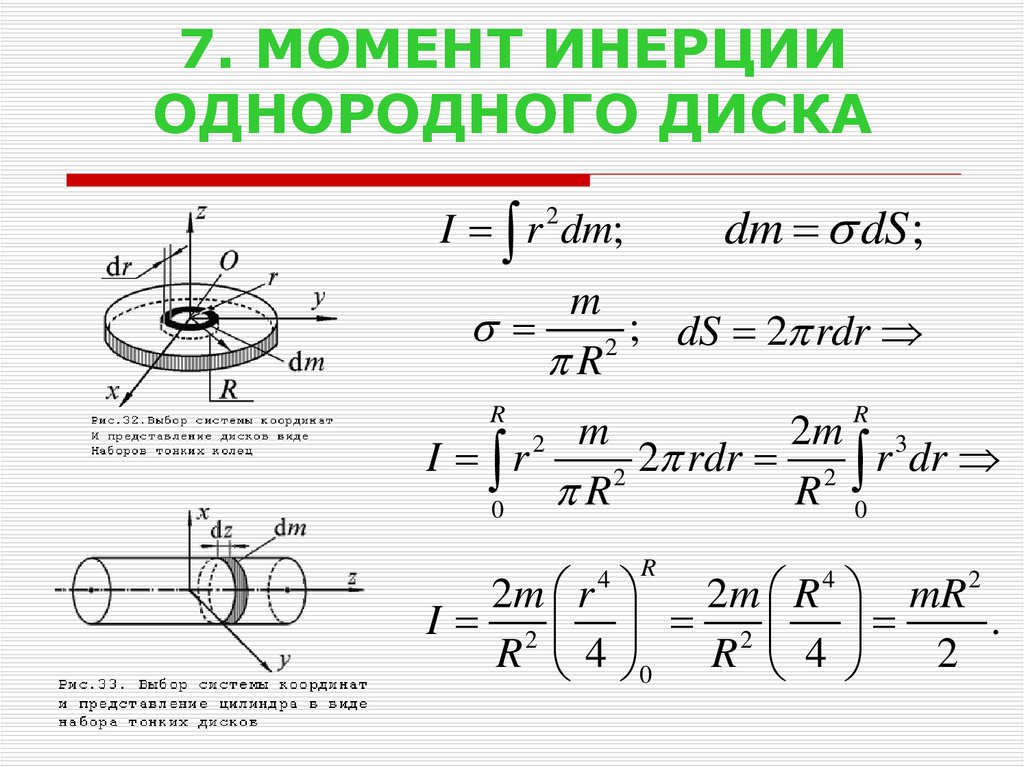
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.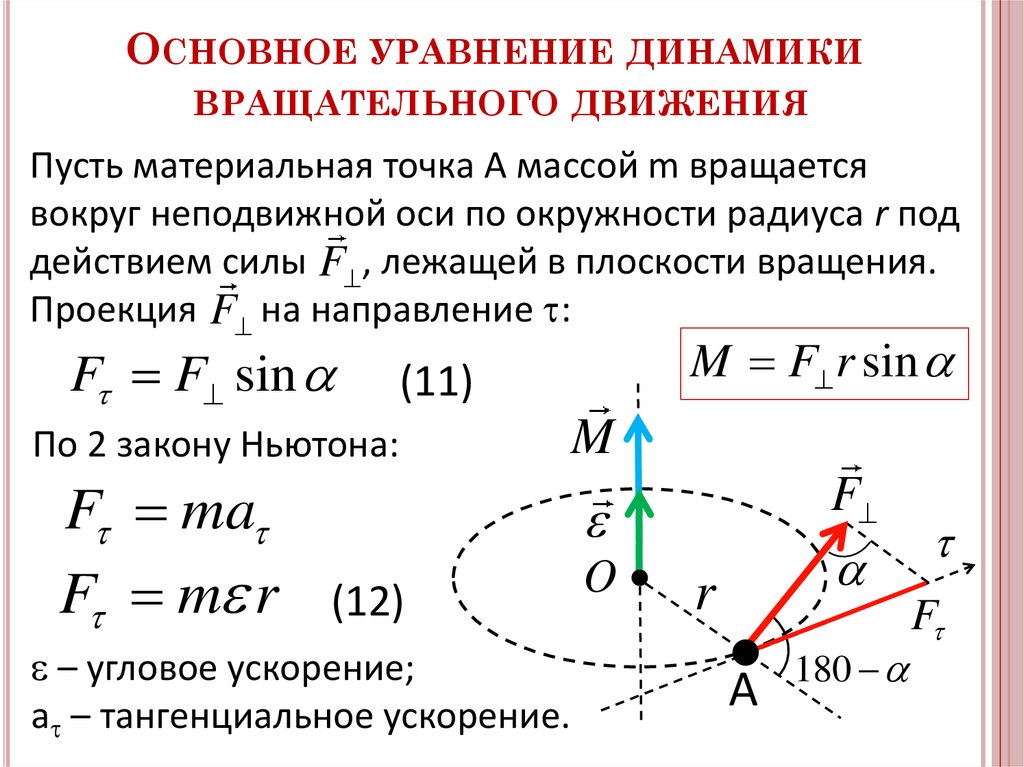
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- =
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Вращающий момент | это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.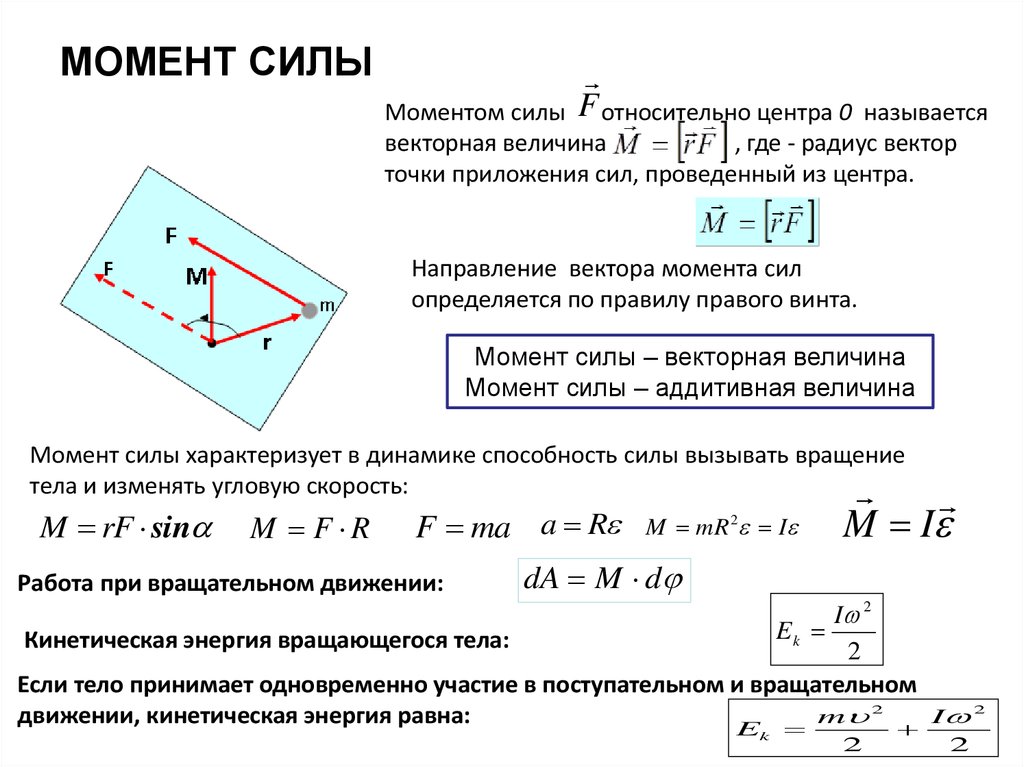
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.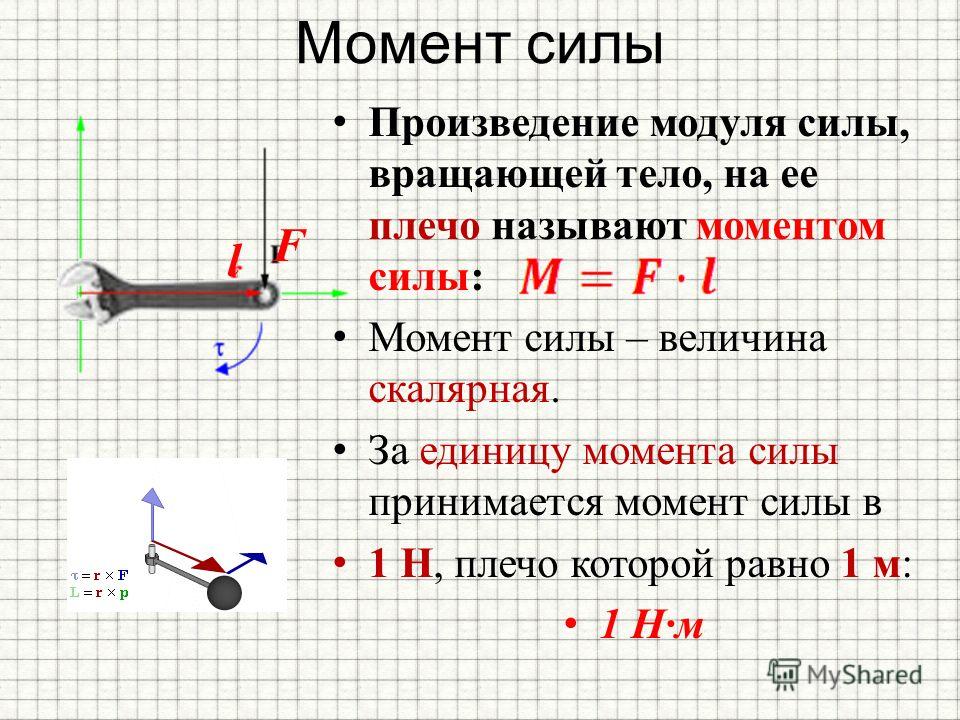
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Вращающий момент | это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.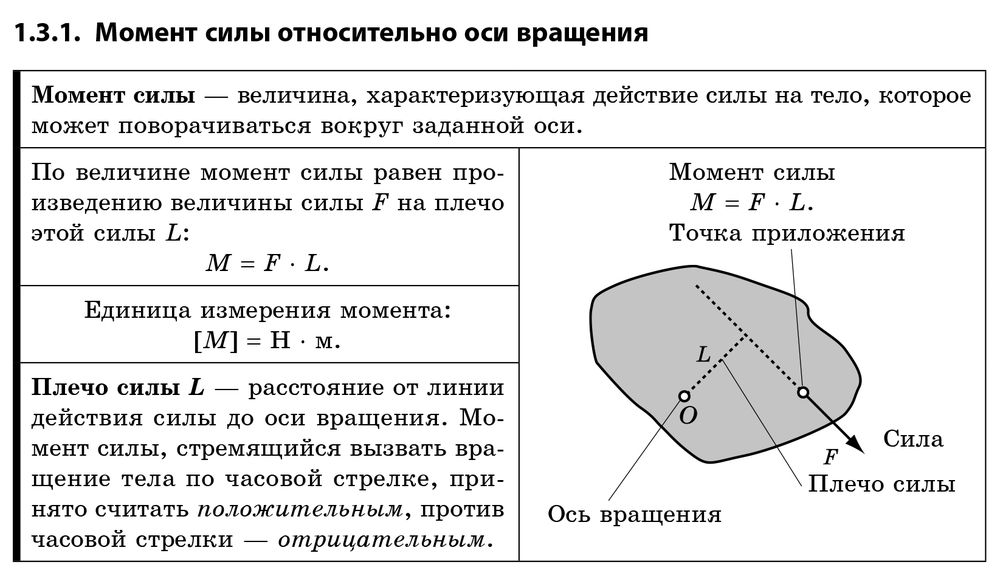
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).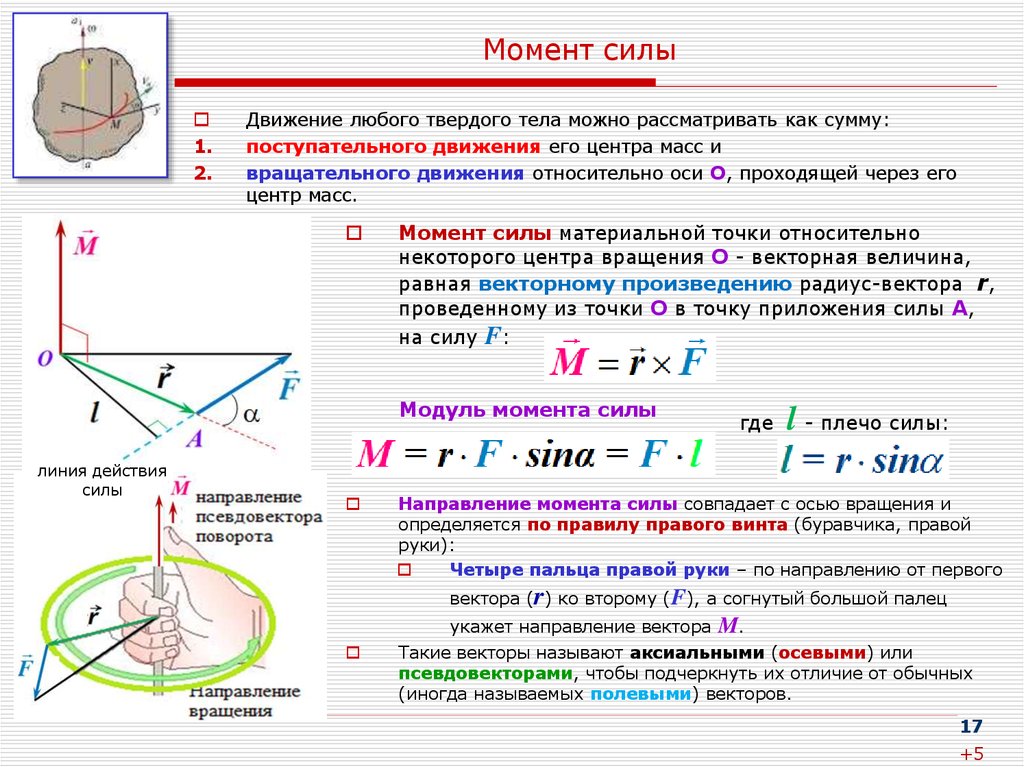
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Какая сила создает вращательный момент. Момент силы. Формула. Понятие. Определение
§ 92. Вращающий момент асинхронного двигателя
Вращающий момент асинхронного двигателя создается при взаимодействии вращающегося магнитного поля статора с токами в проводниках обмотки ротора. Поэтому вращающий момент зависит как от магнитного потока статора Φ, так и от силы тока в обмотке ротора I 2 . Однако в создании вращающего момента участвует только активная мощность, потребляемая машиной из сети. Вследствие этого вращающий момент зависит не от силы тока в обмотке ротора I 2 , а только от его активной составляющей, т. е. I 2 cos φ 2 , где φ 2 — фазный угол между э. д. с. и током в обмотке ротора.
Таким образом, вращающий момент асинхронного двигателя определяется следующим выражением:
M = C ΦI φ 2 cos φ 2 , (122)
где С — конструктивная постоянная машины, зависящая от числа ее полюсов и фаз, числа витков обмотки статора, конструктивного выполнения обмотки и принятой системы единиц.
При условии постоянства приложенного напряжения и изменении нагрузки двигателя магнитный поток остается также почти постоянным.
Таким образом, в выражении вращающего момента величины С и Φ постоянны и вращающий момент пропорционален только активной составляющей тока в обмотке ротора, т. е.
M ~ I 2 cos φ 2 . (123)
Изменение нагрузки или тормозного момента на валу двигателя, как уже известно, изменяет и скорость вращения ротора, и скольжение.
Изменение скольжения вызывает изменение как силы тока в роторе I 2 , так и ее активной составляющей I 2 cos φ 2 .
Можно силу тока в роторе определить отношением э. д. с. к полному сопротивлению, т. е. на основании закона Ома
где Z 2 , r 2 и x 2 — полное, активное и реактивное сопротивления фазы обмотки ротора,
E 2 — э. д. с. фазы обмотки вращающегося ротора.
Изменение скольжения изменяет частоту тока ротора. При неподвижном роторе (n 2 = 0 и S = 1) вращающееся поле с одинаковой скоростью пересекает проводники обмотки статора и ротора и частота тока в роторе равна частоте тока сети (f 2 = f 1). При уменьшении скольжения обмотка ротора пересекается магнитным полем с меньшей частотой, вследствие чего частота тока в роторе уменьшается. Когда ротор вращается синхронно с полем (n 2 = n 1 и S = 0), проводники обмотки ротора не пересекаются магнитным полем, так что частота тока в роторе равна нулю (f 2 = 0). Таким образом, частота тока в обмотке ротора пропорциональна скольжению, т. е.
При уменьшении скольжения обмотка ротора пересекается магнитным полем с меньшей частотой, вследствие чего частота тока в роторе уменьшается. Когда ротор вращается синхронно с полем (n 2 = n 1 и S = 0), проводники обмотки ротора не пересекаются магнитным полем, так что частота тока в роторе равна нулю (f 2 = 0). Таким образом, частота тока в обмотке ротора пропорциональна скольжению, т. е.
f 2 = S f 1 .
Активное сопротивление обмотки ротора почти не зависит от частоты, тогда как э. д. с. и реактивное сопротивление пропорциональны частоте, т. е. изменяются с изменением скольжения и могут быть определены следующими выражениями:
E 2 = S E и X 2 = S X ,
где Е и X — э. д. с. и индуктивное сопротивление фазы обмотки для неподвижного ротора соответственно.
Таким образом, имеем:
и вращающий момент
Следовательно, при небольших скольжениях (примерно до 20%), когда реактивное сопротивление Х 2 = S X мало по сравнению с активным r 2 , увеличение скольжения вызывает увеличение вращающего момента, так как при этом возрастает активная составляющая тока в роторе (I 2 cos φ 2). При больших скольжениях (S X больше, чем r 2) увеличение скольжения будет вызывать уменьшение вращающего момента.
При больших скольжениях (S X больше, чем r 2) увеличение скольжения будет вызывать уменьшение вращающего момента.
Таким образом, при увеличении скольжения (его больших значениях) хотя и повышается сила тока в роторе I 2 , но ее активная составляющая I 2 cos φ 2 и, следовательно, вращающий момент уменьшаются вследствие значительного возрастания реактивного сопротивления обмотки ротора.
На рис. 115 показана зависимость вращающего момента от скольжения. При некотором скольжении S m (примерно 12 — 20%) двигатель развивает максимальный момент, который определяет перегрузочную способность двигателя и обычно в 2 — 3 раза превышает номинальный момент.
Устойчивая работа двигателя возможна только на восходящей ветви кривой зависимости момента от скольжения, т. е. при изменении скольжения в пределах от 0 до S m . Работа двигателя на нисходящей ветви указанной кривой, т. е. при скольжении S > S m , невозможна, так как здесь не обеспечивается устойчивое равновесие моментов.
Если предположить, что вращающий момент был равен тормозному (M вр = M торм) в точках A и Б , то при случайном нарушении равновесия моментов в одном случае оно восстанавливается, а в другом не восстанавливается.
Допустим, что вращающий момент двигателя почему-либо уменьшился (например, при понижении напряжения сети), тогда скольжение начнет увеличиваться. Если равновесие моментов было в точке А , то увеличение скольжения вызовет возрастание вращающего момента двигателя и он станет вновь равным тормозному моменту, т. е. равновесие моментов восстановится при возросшем скольжении. Если же равновесие моментов было в точке Б , то увеличение скольжения вызовет уменьшение вращающего момента, который будет оставаться всегда меньше тормозного, т. е. равновесие моментов не восстановится и скорость вращения ротора будет непрерывно уменьшаться до полной остановки двигателя.
Таким образом, в точке А машина будет работать устойчиво, а в точке Б устойчивая работа невозможна.
Если приложить к валу двигателя тормозной момент, больший максимального, то равновесие моментов не восстановится и ротор двигателя остановится.
Вращающий момент двигателя пропорционален квадрату приложенного напряжения, так как пропорциональны напряжению как магнитный поток, так и сила тока в роторе. Поэтому изменение напряжения в сети вызывает изменение вращающего момента.
Длина и расстояние Масса Меры объема сыпучих продуктов и продуктов питания Площадь Объем и единицы измерения в кулинарных рецептах Температура Давление, механическое напряжение, модуль Юнга Энергия и работа Мощность Сила Время Линейная скорость Плоский угол Тепловая эффективность и топливная экономичность Числа Единицы измерения количества информации Курсы валют Размеры женской одежды и обуви Размеры мужской одежды и обуви Угловая скорость и частота вращения Ускорение Угловое ускорение Плотность Удельный объем Момент инерции Момент силы Вращающий момент Удельная теплота сгорания (по массе) Плотность энергии и удельная теплота сгорания топлива (по объему) Разность температур Коэффициент теплового расширения Термическое сопротивление Удельная теплопроводность Удельная теплоёмкость Энергетическая экспозиция, мощность теплового излучения Плотность теплового потока Коэффициент теплоотдачи Объёмный расход Массовый расход Молярный расход Плотность потока массы Молярная концентрация Массовая концентрация в растворе Динамическая (абсолютная) вязкость Кинематическая вязкость Поверхностное натяжение Паропроницаемость Паропроницаемость, скорость переноса пара Уровень звука Чувствительность микрофонов Уровень звукового давления (SPL) Яркость Сила света Освещённость Разрешение в компьютерной графике Частота и длина волны Оптическая сила в диоптриях и фокусное расстояние Оптическая сила в диоптриях и увеличение линзы (×) Электрический заряд Линейная плотность заряда Поверхностная плотность заряда Объемная плотность заряда Электрический ток Линейная плотность тока Поверхностная плотность тока Напряжённость электрического поля Электростатический потенциал и напряжение Электрическое сопротивление Удельное электрическое сопротивление Электрическая проводимость Удельная электрическая проводимость Электрическая емкость Индуктивность Американский калибр проводов Уровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицах Магнитодвижущая сила Напряженность магнитного поля Магнитный поток Магнитная индукция Мощность поглощенной дозы ионизирующего излучения Радиоактивность. Радиоактивный распад Радиация. Экспозиционная доза Радиация. Поглощённая доза Десятичные приставки Передача данных Типографика и обработка изображений Единицы измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева
единицах Магнитодвижущая сила Напряженность магнитного поля Магнитный поток Магнитная индукция Мощность поглощенной дозы ионизирующего излучения Радиоактивность. Радиоактивный распад Радиация. Экспозиционная доза Радиация. Поглощённая доза Десятичные приставки Передача данных Типографика и обработка изображений Единицы измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева
Исходная величина
Преобразованная величина
ньютон-метр ньютон-сантиметр ньютон-миллиметр килоньютон-метр дина-метр дина-сантиметр дина-миллиметр килограмм-сила-метр килограмм-сила-сантиметр килограмм-сила-миллиметр грамм-сила-метр грамм-сила-сантиметр грамм-сила-миллиметр унция-сила-фут унция-сила-дюйм фунт-сила фут фунт-сила дюйм
Общие сведения
Кода на тело действует сила в определенном направлении — тело поворачивается. Это стремление силы поворачивать тело описывается физической величиной — вращающим моментом или моментом силы.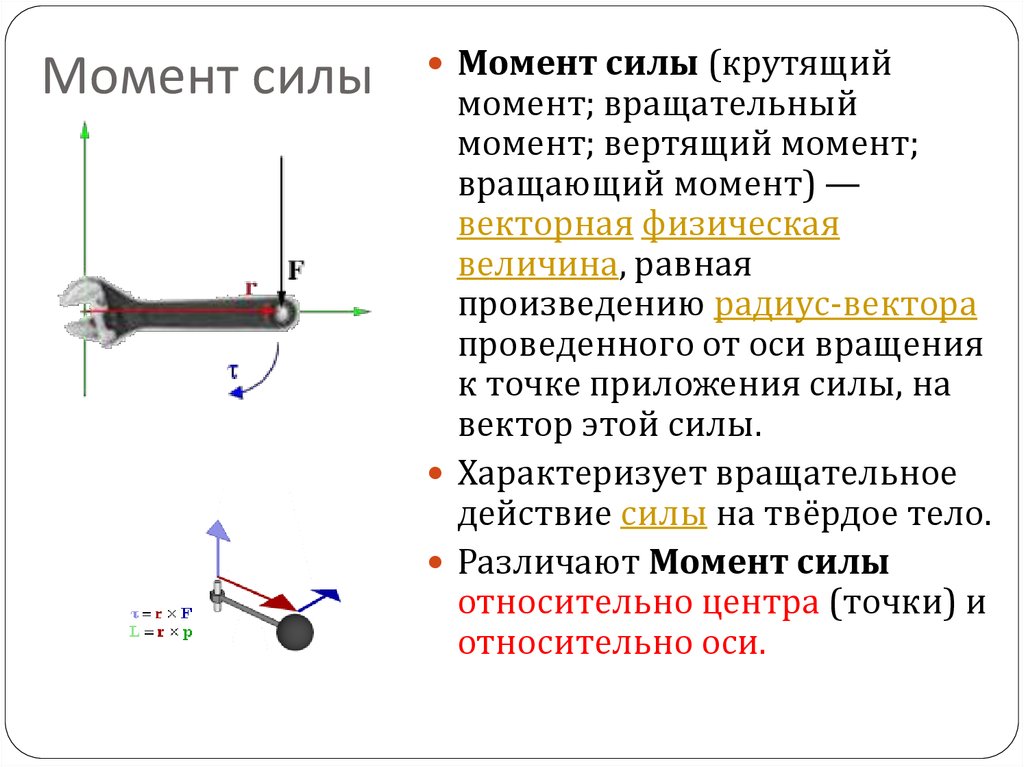 Сама сила, которая вызывает поворот или кручение, а также расстояние между точкой ее приложения и точкой вращения тела влияют на момент силы. В данном случае сила — векторная величина, поэтому важно также и направление силы, то есть угол между направлением силы и отрезком, соединяющим точку приложения силы и центр вращения тела. Если этот угол прямой, то есть сила приложена перпендикулярно отрезку, то момент силы — максимальный. По мере того, как сила становится параллельной отрезку, момент силы уменьшается. То есть, чем ближе угол к 0° или 180°, тем слабее момент силы, пока он не становится равным нулю, когда направление силы параллельно отрезку. Удобно представить момент силы, как комбинацию расстояния, на которое удалена сила от точки вращения, и силы, которая необходима, чтобы заставить тело вращаться с определенной интенсивностью.
Сама сила, которая вызывает поворот или кручение, а также расстояние между точкой ее приложения и точкой вращения тела влияют на момент силы. В данном случае сила — векторная величина, поэтому важно также и направление силы, то есть угол между направлением силы и отрезком, соединяющим точку приложения силы и центр вращения тела. Если этот угол прямой, то есть сила приложена перпендикулярно отрезку, то момент силы — максимальный. По мере того, как сила становится параллельной отрезку, момент силы уменьшается. То есть, чем ближе угол к 0° или 180°, тем слабее момент силы, пока он не становится равным нулю, когда направление силы параллельно отрезку. Удобно представить момент силы, как комбинацию расстояния, на которое удалена сила от точки вращения, и силы, которая необходима, чтобы заставить тело вращаться с определенной интенсивностью.
Давайте посмотрим на эту взаимосвязь на иллюстрации. Здесь силы F2, F3 и F5 перпендикулярны отрезку между осью вращения, обозначенной голубым цветом в центре штурвала, и точкой приложения силы. Создаваемый ими момент силы — максимален. С другой стороны, силы F1 и F4 приложены под углом, отличным от 90°, и создаваемый ими момент силы не максимален. То есть, момент силы этих двух сил отличается от момента силы других трех сил, хотя величина всех сил на рисунке — одинакова.
Создаваемый ими момент силы — максимален. С другой стороны, силы F1 и F4 приложены под углом, отличным от 90°, и создаваемый ими момент силы не максимален. То есть, момент силы этих двух сил отличается от момента силы других трех сил, хотя величина всех сил на рисунке — одинакова.
Чтобы повернуть тело под воздействием силы с заданными условиями, необходимо создать момент силы. Так как эта величина зависит и от расстояния, и от силы, то для получения заданного момента можно изменять либо силу, либо расстояние от точки приложения до точки вращения. Люди используют эту зависимость испокон веков.
Использование момента силы в быту и технике
Обычно легче увеличить расстояние между телом и точкой приложения силы, чем саму силу. Поэтому чаще всего, когда силы человека или животного недостаточно для того или иного задания, которое включает вращение, используют рычаги и другие устройства, чтобы увеличить расстояние между силой и осью вращения, и тем самым увеличить момент силы. Например, чтобы повернуть мельницу или колесо, на которое наматывают цепь, чтобы поднять тяжелый мост, люди или животные вращают устройства с длинными ручками или рычагами. Длинные рычаги и ручки позволяют увеличить приложенное усилие. Это увеличение пропорционально расстоянию между осью вращения тела и точкой приложения силы.
Например, чтобы повернуть мельницу или колесо, на которое наматывают цепь, чтобы поднять тяжелый мост, люди или животные вращают устройства с длинными ручками или рычагами. Длинные рычаги и ручки позволяют увеличить приложенное усилие. Это увеличение пропорционально расстоянию между осью вращения тела и точкой приложения силы.
Велосипедные педали
Момент силы используется также в педалях велосипедов. Чем дальше ступня от центра велосипедного колеса, тем меньше нужно силы, чтобы повернуть это колесо с помощью педали. Длина наших ног ограничивает максимальную длину педалей — если сделать педали длиннее, чем делают их сейчас на современных велосипедах, то крутить их будет неудобно. Несмотря на эти ограничения, педали сильно облегчают передвижение на велосипеде. Конструкция велосипедных педалей настолько удобна, что некоторые люди, особенно в развивающихся странах, где не всегда есть доступ к новейшей технике, используют велосипедные педали в конструкции других устройств, где нужно ножное или ручное управление.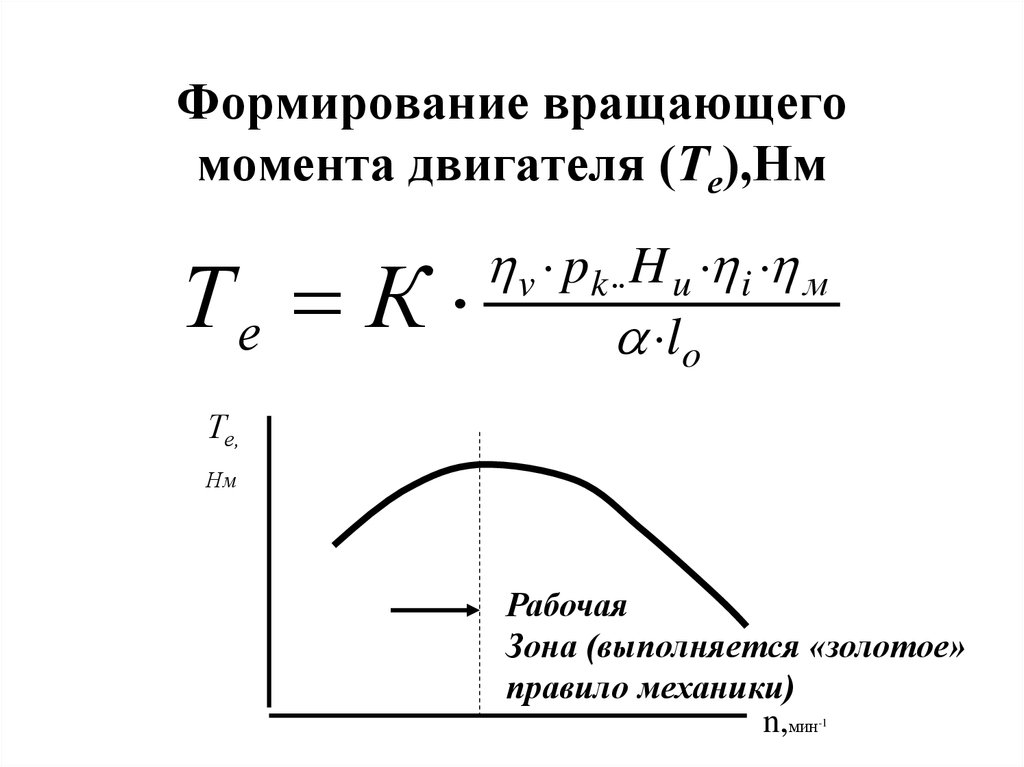 Иногда такие педали устанавливают на инвалидные коляски, чтобы облегчить ручное кручение колес. В этом случае можно немного удлинить педали, чтобы увеличить момент силы, хотя это может несколько затруднить управление коляской.
Иногда такие педали устанавливают на инвалидные коляски, чтобы облегчить ручное кручение колес. В этом случае можно немного удлинить педали, чтобы увеличить момент силы, хотя это может несколько затруднить управление коляской.
Гаечный ключ
Гаечные ключи используют момент силы, чтобы уменьшить силу, необходимую для затягивания или откручивания гайки или болта. Гаечный ключ сделан так, чтобы его удобно было держать, но в то же время его длинная ручка увеличивает силу, к нему приложенную, чтобы затянуть или открутить болт или гайку. Иногда достаточно маленького ключа с короткой ручкой, но в некоторых случаях нужна ручка длиннее, например, если мы пытаемся открутить заржавевшую гайку. Если под рукой не оказалось гаечного ключа, можно использовать плоскогубцы. Их длинные ручки создают достаточно высокий момент силы, хотя иногда они сжимают гайку или винт недостаточно сильно, и могут их повредить.
Удобство гаечного ключа в том, что когда он подобран по размеру к гайке, сила нужна только для того, чтобы повернуть ключ, но не для того, чтобы удерживать его на гайке. Плоскогубцы, наоборот, нужно удерживать вокруг гайки, чтобы они не сорвались, и на это тратится дополнительная сила. Именно поэтому во многих случаях гаечный ключ более экономичен с точки зрения затраченной энергии. С другой стороны, в некоторых случаях плоскогубцы удобнее — например их можно использовать под углом в труднодоступных местах, в то время как гаечный ключ часто работает только в одной плоскости с гайкой. Если откручивать гайку под наклоном, то момент силы уменьшится, но это лучше, чем совсем не иметь возможности ее отвернуть.
Плоскогубцы, наоборот, нужно удерживать вокруг гайки, чтобы они не сорвались, и на это тратится дополнительная сила. Именно поэтому во многих случаях гаечный ключ более экономичен с точки зрения затраченной энергии. С другой стороны, в некоторых случаях плоскогубцы удобнее — например их можно использовать под углом в труднодоступных местах, в то время как гаечный ключ часто работает только в одной плоскости с гайкой. Если откручивать гайку под наклоном, то момент силы уменьшится, но это лучше, чем совсем не иметь возможности ее отвернуть.
Аналогично работают и инструменты, предназначенные для отвинчивания крышек с законсервированных банок. Обычно это резиновый жгут, прикрепленный к ручке так, что жгут образует петлю, диаметр которой регулируется. Сама петля закрепляется на крышке и не влияет на момент силы, а вот ручка как раз помогает создать нужный момент. Чем она больше, тем больше момент силы. Благодаря ему, банку открыть намного легче, чем руками, с использованием полотенца или материала с высоким коэффициентом трения.
Маховик
Хороший пример устройства, которое использует момент силы — маховик. Момент силы приводит его в движение, а также помогает ускорить маховик и, благодаря этому движению, получить энергию. Маховик накапливает и хранит ее для дальнейшего использования. Если эта энергия нужна для других целей, то момент силы, наоборот, замедляет скорость маховика, и вырабатывается энергия, которую потом используют по назначению. Маховики используют в случае, если источник энергии работает в прерывистом режиме, а энергия нужна постоянно. Именно так используют маховики в двигателях автомобилей, где энергия выделяется «вспышками», при сгорании топлива.
В некоторых случаях нужен обратный эффект, то есть необходимо кратковременно подать большое количество энергии, обычно больше, чем источник энергии может выработать в течение заданного промежутка времени. В такой ситуации маховик на протяжении некоторого времени накапливает энергию, поступающую небольшими порциями, чтобы потом отдать нужное количество.
Качели и рычаги
Сила, с которой два ребенка надавливают на качели-балансир, когда сидят по обе стороны от центра, двигает эти качели вверх и вниз. То есть, при этом происходит частичное вращение качелей вокруг своей оси. Если вес обоих детей приблизительно одинаков, то они легко могут качаться на таких качелях. Детям разного веса намного труднее — более тяжелый ребенок тянет качели со своей стороны вниз, а более легкому ребенку не хватает веса, чтобы опустить качели в свою сторону. Это происходит потому, что вес тяжелого ребенка производит больший момент силы. Чтобы решить эту проблему, большому ребенку нужно пересесть ближе к центру настолько, насколько его вес превышает вес второго ребенка. Например, если большой ребенок в три раза тяжелее, то пересесть ему нужно в три раза ближе, и тогда качели придут в равновесие.
Рычаги действуют аналогично: момент силы в них используется для того, чтобы уменьшить силу, нужную для совершения определенной работы. Обычно рычаг — это продолговатый предмет, например ручка или планка, которая вращается вокруг точки, называемой центром вращения или точкой опоры.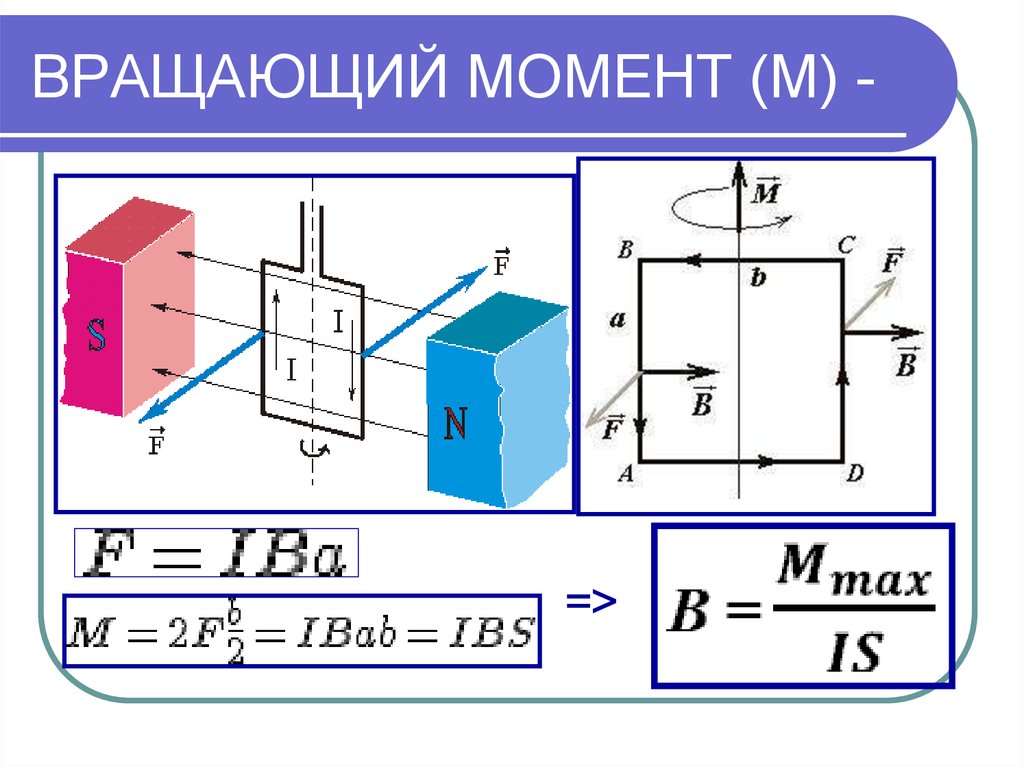 К другой точке рычага прикладывают силу, которая, благодаря длине рычага, увеличивается или уменьшается в зависимости от конструкции рычага и его назначения.
К другой точке рычага прикладывают силу, которая, благодаря длине рычага, увеличивается или уменьшается в зависимости от конструкции рычага и его назначения.
Рычаги делят на три рода, в зависимости от того, где точка опоры, как приложена сила , которая их поворачивает, и где приложена сила сопротивления . Обычно их называют рычагами первого, второго, и третьего рода. Иногда не совсем понятно, при чем тут сила сопротивления, но она действительно есть. Она противодействует силе, которая направлена на то, чтобы повернуть рычаг. Когда приложенная сила больше силы сопротивления, рычаг поворачивается. Мы, а также другие животные, используем эти принципы в организме, и части нашего тела становятся рычагами, как показано на примерах ниже.
Рычаг первого рода похож по конструкции на детские качели-балансир, описанные выше. точка опоры в них посередине, сила приложена на одном конце, а сопротивление возникает на другом конце. Ось вращения в рычаге второго рода находится с одного края рычага, и рядом с ним возникает сопротивление. Сила прилагается к такому рычагу на другом конце. Рычаг третьего рода устроен похоже, но ближе к центру вращения, находящемуся у конца рычага, не сопротивление, а сила, прикладываемая к рычагу. Сопротивление возникает на другом конце рычага.
Сила прилагается к такому рычагу на другом конце. Рычаг третьего рода устроен похоже, но ближе к центру вращения, находящемуся у конца рычага, не сопротивление, а сила, прикладываемая к рычагу. Сопротивление возникает на другом конце рычага.
Рычаги первого рода
Равноплечие весы с чашками — пример рычагов первого рода. Ножницы — тоже, только они состоят из двух рычагов, соединенных между собой. С их помощью намного легче, чем ножом, аккуратно разрезать некоторые материалы, например бумагу или ткань. Чем длиннее ручки, тем более толстые и твердые материалы можно разрезать. С другой стороны, чем дальше поместить от оси вращения материал, который нужно разрезать, тем труднее это сделать.
Чем толще материал, который нужно разрезать, тем больший момент силы необходим для этого, и тем длиннее должны быть ручки ножниц и прочнее материал, из которых они сделаны. В некоторых случаях к ножницам добавляют пружину, которая делает их более удобными в использовании. Так, например, устроен садовый секатор. Кроме этого у специализированных ножниц бывают и другие особенности. В медицине используют ножницы с закругленными, тупыми и острыми концами, в зависимости от их назначения. В отличие от скальпеля, ими удобнее работать и у них механическое преимущество над скальпелем, хотя скальпель тоже широко используется, так как в некоторых случаях он удобнее ножниц. Медицинские ножницы, предназначенные для использования врачами скорой помощи, закруглены на конце, чтобы можно было разрезать ими одежду, не повредив кожи. Некоторые медицинские ножницы — очень маленькие. Например, офтальмологические хирургические ножницы могут быть всего 6 сантиметров длиной, с лезвием до 2 сантиметров, и даже короче.
Так, например, устроен садовый секатор. Кроме этого у специализированных ножниц бывают и другие особенности. В медицине используют ножницы с закругленными, тупыми и острыми концами, в зависимости от их назначения. В отличие от скальпеля, ими удобнее работать и у них механическое преимущество над скальпелем, хотя скальпель тоже широко используется, так как в некоторых случаях он удобнее ножниц. Медицинские ножницы, предназначенные для использования врачами скорой помощи, закруглены на конце, чтобы можно было разрезать ими одежду, не повредив кожи. Некоторые медицинские ножницы — очень маленькие. Например, офтальмологические хирургические ножницы могут быть всего 6 сантиметров длиной, с лезвием до 2 сантиметров, и даже короче.
Лом-монтировку или лом-гвоздодер, называемый также «фомкой» тоже можно считать рычагом первого рода, хотя иногда, в зависимости от использования, он может быть и рычагом второго или третьего рода. Чаще всего его используют, чтобы вынуть забитые гвозди, или разобщить два предмета, соединенных клеем, гвоздями, скрепками, и аналогичными способами. Лом получил дурную репутацию, как инструмент воров, взломщиков, и других преступников, хотя на самом деле преступники используют любые подручные материалы и инструменты, лишь бы они помогли добиться конечного результата.
Лом получил дурную репутацию, как инструмент воров, взломщиков, и других преступников, хотя на самом деле преступники используют любые подручные материалы и инструменты, лишь бы они помогли добиться конечного результата.
Пример рычага первого рода в организме людей и некоторых животных — голова. Она находится в равновесии на шее. Шея — центр вращения, сила мышц прилагается с одной стороны головы, сила сопротивления — с другой. Когда приложенная сила достаточно велика, голова наклоняется в сторону направления этой силы.
Рычаги второго рода
Примеры рычагов второго рода — челюсти людей и животных, и клювы птиц. Являются ими и щипцы для орехов, а также декоративные щелкунчики. Щипцы чаще всего делают из металла, хотя иногда встречаются изделия и из других материалов, например из дерева. Щелкунчики — стилизованные щипцы, сделанные из дерева, и украшенные наподобие кукол. Раньше их использовали по прямому назначению, но сейчас это по большей части украшения. Чаще всего их делают в форме солдат, королей, и других фигурок. В США и Канаде такие фигурки часто используют как новогодние украшения. Считается, что щелкунчиков начали делать в лесистых районах Германии. Их там делают на продажу как сувениры и до сих пор. Сейчас для расщепления орехов чаще всего используют обычные щипцы, а не щелкунчиков. Такие щипцы похожи на щипцы для расщепления клешней крабов и омаров. Кстати, сами крабовые и омаровые клешни — тоже рычаги второго ряда, и работают по тому же принципу, что и щипцы для орехов.
В США и Канаде такие фигурки часто используют как новогодние украшения. Считается, что щелкунчиков начали делать в лесистых районах Германии. Их там делают на продажу как сувениры и до сих пор. Сейчас для расщепления орехов чаще всего используют обычные щипцы, а не щелкунчиков. Такие щипцы похожи на щипцы для расщепления клешней крабов и омаров. Кстати, сами крабовые и омаровые клешни — тоже рычаги второго ряда, и работают по тому же принципу, что и щипцы для орехов.
Чеснокодавилка — еще один пример рычагов второго ряда. По устройству она похожа на щипцы для орехов. Ее часто используют в быту, хотя некоторые повара предпочитают мелко резать чеснок, и считают, что чеснокодавилка портит вкус чеснока. Другие, наоборот, пользуются только чеснокодавилкой, так как вкус чеснока при ее использовании усиливается.
Ступня людей и некоторых животных — тоже рычаг второго типа. Точка опоры в этом случае в районе пальцев, мышцы ноги прикладывают силу около пятки, а сила сопротивления — это наш вес. Этот «рычаг» позволяет нам держать равновесие, а также подниматься и опускаться на пальцах.
Этот «рычаг» позволяет нам держать равновесие, а также подниматься и опускаться на пальцах.
Другие примеры рычагов второго класса — тачки, тормоза в автомобиле и двери. Если толкнуть дверь рядом с осью вращения, то она вряд ли откроется, но если толкать как можно дальше от этой оси, то даже тяжелая дверь легко поддается. Именно поэтому ручки делают со стороны, противоположной расположению петель. Чтобы даже тяжелую дверь было легко открывать, ее можно сделать шире.
Открывалки для бутылок — тоже рычаги второго класса, особенно те, что не прикреплены к стене, как в некоторых барах и ресторанах. В некоторых перочинных ножах имеются маленькие открывалки; также популярны брелки-открывалки. Если под рукой нет открывалки, то иногда получается использовать подручные материалы, например нож или вилку. Сами открывалки можно в некоторых случаях использовать, чтобы поддеть закрученную крышку на банке — если сделать это удачно, то банка легче откроется. Иногда открывалки используют как рычаги первого класса. В этом случае открывалку закрепляют на крышке иначе и давят на нее снизу, а не сверху, как с рычагами второго рода.
В этом случае открывалку закрепляют на крышке иначе и давят на нее снизу, а не сверху, как с рычагами второго рода.
Рычаги третьего рода
Если поднимать рукой тяжелые предметы, сгибая локоть, то рука становится рычагом третьего рода. Во время бега и ходьбы, ноги тоже становятся рычагами. Точка опоры рычага в этом случае — в локтях и коленях. Если «продлить» руку инструментом, например бейсбольной битой или теннисной ракеткой, то опять получится рычаг третьего рода. Чтобы заставить этот рычаг двигаться, силу прикладывают возле центра вращения. При этом сопротивление образуется на другом конце. В случае с ракеткой и битой, сопротивление — в месте, где они соприкасаются с мячом. Удочка — тоже рычаг третьего рода, и сила прикладывается к ней в районе запястья.
Другие примеры рычагов третьего рода — молоток, и аналогичные инструменты, такие как лопаты, грабли, веники, и мухобойки. Некоторые инструменты состоят сразу из двух рычагов, действующих по направлению друг к другу. Так устроены, например, пинцет, степлер и щипцы.
Так устроены, например, пинцет, степлер и щипцы.
Пример
Теперь давайте рассмотрим пример. Представим, что обычный человек среднего телосложения может поднять камень весом в 20 кг. Конечно, это будет нелегко, и придется сильно напрячь мышцы, но поднять такой камень вполне возможно. С другой стороны, маленький ребенок такой камень поднять не в состоянии. Если же дать ребенку достаточно длинный и прочный лом и научить его, как им пользоваться, то он справится с этой задачей, так как сила, нужная для того, чтобы поднять камень, намного уменьшится. Архимед говорил, что он может сдвинуть Землю, если встанет достаточно далеко от нее, и возьмет длинный рычаг. Это утверждение основано на таком же принципе. После того, как мы поднимем наш 20-ти-киллограммовый камень с помощью лома — рычага первого рода — мы можем погрузить его на тачку — рычаг второго рода — и отвезти, куда необходимо, поднимая за ручки руками — рычагами третьего рода.
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь.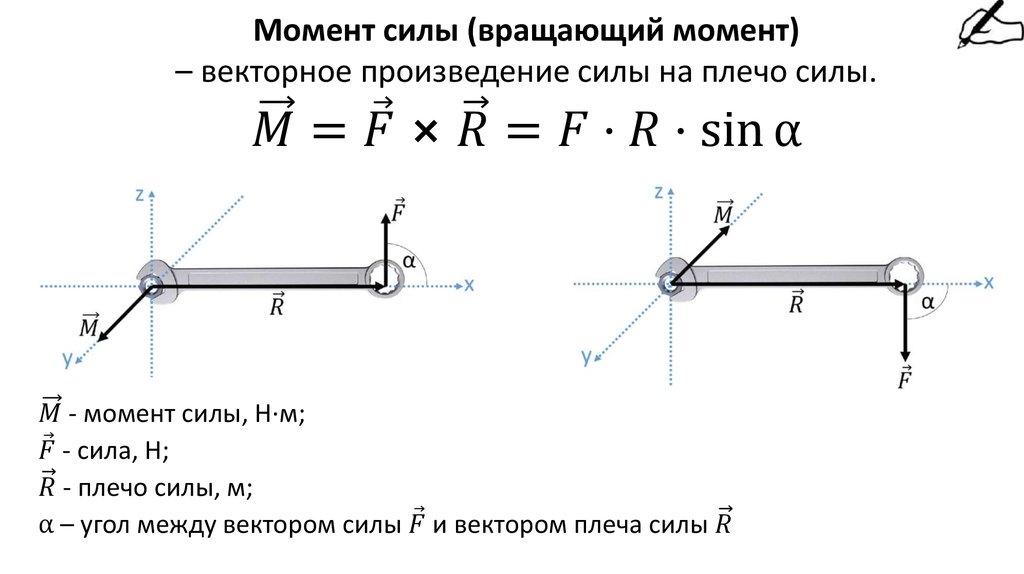 Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Момент силы относительно оси или просто момент силы называется проекция силы на прямую, которая перпендикулярна радиусу и проведена в точке приложения силы умноженная на расстояние от этой точки до оси. Либо произведение силы на плечо ее приложения. Плечо в данном случае это расстояние от оси до точки приложения силы. Момент силы характеризует вращательное действие силы на тело. Ось в данном случае это место крепления тела, относительно которого оно может совершать вращение. Если тело не закреплено, то осью вращения можно считать центр масс.
Формула 1 — Момент силы.
F — Сила действующая на тело.
r — Плечо силы.
Рисунок 1 — Момент силы.
Как видно из рисунка, плечо силы это расстояние от оси до точки приложения силы. Но это в случае если угол между ними равен 90 градусов. Если это не так, то необходимо вдоль действия силы провести линию и из оси опустить на нее перпендикуляр. Длинна этого перпендикуляра и будет равна плечу силы. А перемещение точки приложения силы вдоль направления силы не меняет ее момента.
Длинна этого перпендикуляра и будет равна плечу силы. А перемещение точки приложения силы вдоль направления силы не меняет ее момента.
Принято считать положительным такой момент силы, который вызывает поворот тела по часовой стрелки относительно точки наблюдения. А отрицательным соответственно вызывающий вращение против нее. Измеряется момент силы в Ньютонах на метр. Один Ньютонометр это сила в 1 Ньютон действующая на плечо в 1 метр.
Если сила, действующая на тело, проходит вдоль лини идущей через ось вращения тела, или центр масс, если тело не имеет оси вращения. То момент силы в этом случае будет равен нулю. Так как эта сила не будет вызывать вращения тела, а попросту будет перемещать его поступательно вдоль лини приложения.
Рисунок 2 — Момент силы равен нулю.
В случае если на тело действует несколько сил, то момент силы будет определять их равнодействующая. К примеру, на тело могут действовать две силы равные по модулю и направленные противоположно. При этом суммарный момент силы будет равен нулю. Так как эти силы будут компенсировать друг друга. Если по простому, то представьте себе детскую карусель. Если один мальчик ее толкает по часовой стрелке, а другой с той же силой против, то карусель останется неподвижной.
При этом суммарный момент силы будет равен нулю. Так как эти силы будут компенсировать друг друга. Если по простому, то представьте себе детскую карусель. Если один мальчик ее толкает по часовой стрелке, а другой с той же силой против, то карусель останется неподвижной.
Которая равна произведению силы на ее плечо.
Момент силы вычисляют при помощи формулы:
где F — сила, l — плечо силы.
Плечо силы — это самое короткое расстояние от линии действия силы до оси вращения тела. На рисунке ниже изображено твердое тело, которое может вращаться вокруг оси. Ось вращения этого тела является перпендикулярной к плоскости рисунка и проходит через точку, которая обозначена как буква О. Пле-чом силы F t здесь оказывается расстояние l , от оси вращения до линии действия силы. Определяют его таким образом. Первым шагом проводят линию действия силы, далее из т. О, через которую проходит ось вращения тела, опускают на линию действия силы перпендикуляр.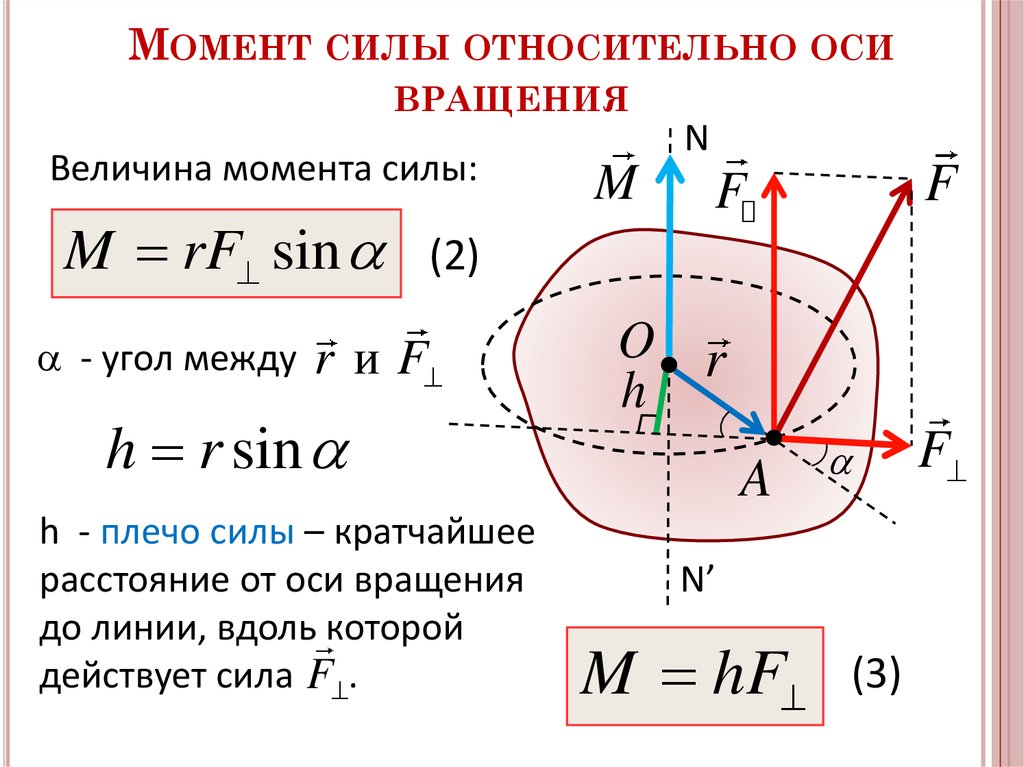 Длина этого перпендикуляра оказывается плечом данной силы.
Длина этого перпендикуляра оказывается плечом данной силы.
Момент силы характеризует вращающее действие силы . Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу необходимо приложить, чтобы получить желаемый результат, то есть один и тот же момент силы (см. рис. выше). Именно поэтому открыть дверь, толкая ее возле петель, намного сложнее, чем берясь за ручку, а гайку отвернуть намного легче длинным, чем коротким гаечным ключом.
За единицу момента силы в СИ принимается момент силы в 1 Н , плечо которой равно 1м — ньютон-метр (Н · м).
Правило моментов.
Твердое тело, которое может вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М 1 вращающей его по часовой стрелке, равняется моменту силы М 2 , которая вращает его против часовой стрелки:
Правило моментов есть следствие одной из теорем механики , которая была сформулирована французским ученым П. Вариньоном в 1687 г.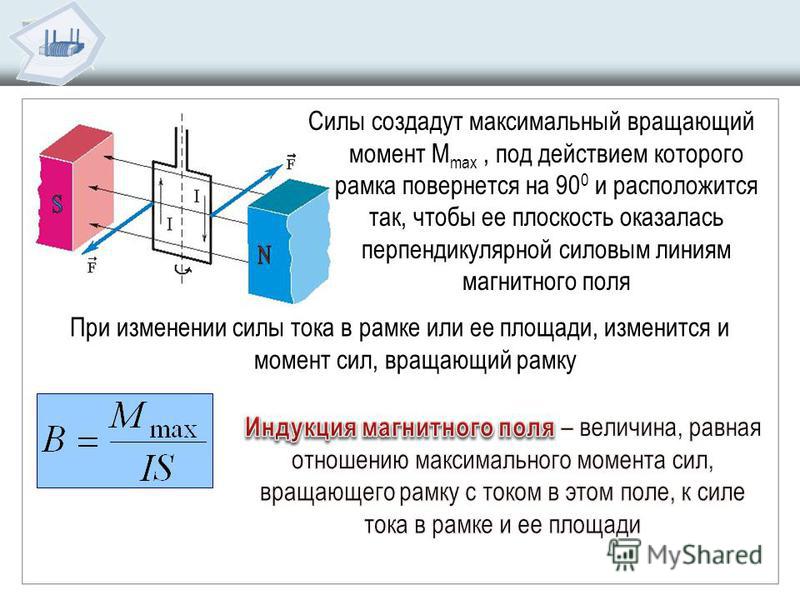
Пара сил.
Если на тело действуют 2 равные и противоположно направленные силы, которые не лежат на одной прямой, то такое тело не находится в равновесии, так как результирующий момент этих сил относительно любой оси не равняется нулю, так как обе силы имеют моменты, направленные в одну сторону. Две такие силы, одновременно действующие на тело, называют парой сил . Если тело закреплено на оси, то под действием пары сил оно будет вращаться. Если пара сил приложена «свободному телу, то оно будет вращаться вокруг оси. проходящей через центр тяжести тела, рисунке б .
Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние l между силами, которое называется плечом пары , независимо от того, на какие отрезки l , и разделяет положение оси плечо пары:
Момент нескольких сил, равнодействующая которых равна нулю, будет одинаковым относи-тельно всех осей, параллельных друг другу, поэтому действие всех этих сил на тело можно заме нить действием одной пары сил с тем же моментом.
Мощность и вращающий момент электродвигателя
Данная глава посвящена вращающему моменту: что это такое, для чего он нужен и др. Мы также разберём типы нагрузок в зависимости от моделей насосов и соответствие между электродвигателем и нагрузкой насоса.
Вы когда-нибудь пробовали провернуть вал пустого насоса руками? Теперь представьте, что вы поворачиваете его, когда насос заполнен водой. Вы почувствуете, что в этом случае, чтобы создать вращающий момент, требуется гораздо большее усилие.
А теперь представьте, что вам надо крутить вал насоса несколько часов подряд. Вы бы устали быстрее, если бы насос был заполнен водой, и почувствовали бы, что потратили намного больше сил за тот же период времени, чем при выполнении тех же манипуляций с пустым насосом. Ваши наблюдения абсолютно верны: требуется большая мощность, которая является мерой работы (потраченной энергии) в единицу времени. Как правило, мощность стандартного электродвигателя выражается в кВт.
Вращающий момент (T) — это произведение силы на плечо силы. В Европе он измеряется в Ньютонах на метр (Нм).
В Европе он измеряется в Ньютонах на метр (Нм).
Как видно из формулы, вращающий момент увеличивается, если возрастает сила или плечо силы — или и то и другое. Например, если мы приложим к валу силу в 10 Н, эквивалентную 1 кг, при длине рычага (плече силы) 1 м, в результате, вращающий момент будет 10 Нм. При увеличении силы до 20 Н или 2 кг, вращающий момент будет 20 Нм. Таким же образом, вращающий момент был бы 20 Нм, если бы рычаг увеличился до 2 м, а сила составляла 10 Н. Или при вращающем моменте в 10 Нм с плечом силы 0,5 м сила должна быть 20 Н.
Работа и мощность
Теперь остановимся на таком понятии как «работа», которое в данном контексте имеет особое значение. Работа совершается всякий раз, когда сила — любая сила — вызывает движение. Работа равна силе, умноженной на расстояние. Для линейного движения мощность выражается как работа в определённый момент времени.
Если мы говорим о вращении, мощность выражается как вращающий момент (T), умноженный на частоту вращения (w).
Частота вращения объекта определяется измерением времени, за которое определённая точка вращающегося объекта совершит полный оборот. Обычно эта величина выражается в оборотах в минуту, т.е. мин-1 или об/мин. Например, если объект совершает 10 полных оборотов в минуту, это означает, что его частота вращения: 10 мин-1 или 10 об/мин.
Итак, частота вращения измеряется в оборотах в минуту, т.е. мин-1.
Приведем единицы измерения к общему виду.
Для наглядности возьмём разные электродвигатели, чтобы более подробно проанализировать соотношение между мощностью, вращающим моментом и частотой вращения. Несмотря на то, что вращающий момент и частота вращения электродвигателей сильно различаются, они могут иметь одинаковую мощность.
Например, предположим, что у нас 2-полюсный электродвигатель (с частотой вращения 3000 мин-1) и 4-полюсной электродвигатель (с частотой вращения 1500 мин-1). Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.
Таким образом, вращающий момент 4-полюсного электродвигателя в два раза больше вращающего момента двухполюсного электродвигателя с той же мощностью.
Как образуется вращающий момент и частота вращения?
Теперь, после того, как мы изучили основы вращающего момента и скорости вращения, следует остановиться на том, как они создаются.
В электродвигателях переменного тока вращающий момент и частота вращения создаются в результате взаимодействия между ротором и вращающимся магнитным полем. Магнитное поле вокруг обмоток ротора будет стремиться к магнитному полю статора. В реальных рабочих условиях частота вращения ротора всегда отстаёт от магнитного поля. Таким образом, магнитное поле ротора пересекает магнитное поле статора и отстает от него и создаёт вращающий момент. Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.
Скольжение является основным параметром электродвигателя, характеризующий его режим работы и нагрузку. Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.
Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.
Помня о том, что было сказано выше, разберём ещё несколько формул. Вращающий момент индукционного электродвигателя зависит от силы магнитных полей ротора и статора, а также от фазового соотношения между этими полями. Это соотношение показано в следующей формуле:
Сила магнитного поля, в первую очередь, зависит от конструкции статора и материалов, из которых статор изготовлен. Однако напряжение и частота тока также играют важную роль. Отношение вращающих моментов пропорционально квадрату отношения напряжений, т.е. если подаваемое напряжение падает на 2%, вращающий момент, следовательно, уменьшается на 4%.
Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.
В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).
Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 0,746) = 14,92 кВт.
И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.
Момент электродвигателя
Мощность [кВт или л.с.] связывает вращающий момент с частотой вращения, чтобы определить общий объём работы, который должен быть выполнен за определённый промежуток времени.
Рассмотрим взаимодействие между вращающим моментом, мощностью и частотой вращения, а также их связь с электрическим напряжением на примере электродвигателей Grundfos. Электродвигатели имеют одну и ту же номинальную мощность как при 50 Гц, так и при 60 Гц.
Это влечёт за собой резкое снижение вращающего момента при 60 Гц: частота 60 Гц вызывает 20%-ное увеличение числа оборотов, что приводит к 20%-ному уменьшению вращающего момента. Большинство производителей предпочитают указывать мощность электродвигателя при 60 Гц, таким образом, при снижении частоты тока в сети до 50 Гц электродвигатели будут обеспечивать меньшую мощность на валу и вращающий момент. Электродвигатели обеспечивают одинаковую мощность при 50 и 60 Гц.
Большинство производителей предпочитают указывать мощность электродвигателя при 60 Гц, таким образом, при снижении частоты тока в сети до 50 Гц электродвигатели будут обеспечивать меньшую мощность на валу и вращающий момент. Электродвигатели обеспечивают одинаковую мощность при 50 и 60 Гц.
Графическое представление вращающего момента электродвигателя изображено на рисунке.
Иллюстрация представляет типичную характеристику вращающий момент/частота вращения. Ниже приведены термины, используемые для характеристики вращающего момента электродвигателя переменного тока.
Пусковой момент (Мп): Механический вращающий момент, развиваемый электродвигателем на валу при пуске, т.е. когда через электродвигатель пропускается ток при полном напряжении, при этом вал застопорен.
Минимальный пусковой момент (Ммин): Этот термин используется для обозначения самой низкой точки на кривой вращающий момент/частота вращения электродвигателя, нагрузка которого увеличивается до полной скорости вращения. Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.
Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.
Блокировочный момент (Мблок): Максимальный вращающий момент — момент, который создаёт электродвигатель переменного тока с номинальным напряжением, подаваемым при номинальной частоте, без резких скачков скорости вращения. Его называют предельным перегрузочным моментом или максимальным вращающим моментом.
Вращающий момент при полной нагрузке (Мп.н.): Вращающий момент, необходимый для создания номинальной мощности при полной нагрузке.
Нагрузка насосов и типы нагрузки электродвигателя
Выделяют следующие типы нагрузок:
Постоянная мощность
Термин «постоянная мощность» используется для определённых типов нагрузки, в которых требуется меньший вращающий момент при увеличении скорости вращения, и наоборот. Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т.п.
Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т.п.
Постоянный вращающий момент
Как видно из названия — «постоянный вращающий момент» — подразумевается, что величина вращающего момента, необходимого для приведения в действие какого- либо механизма, постоянна, независимо от скорости вращения. Примером такого режима работы могут служить конвейеры.
Переменный вращающий момент и мощность
«Переменный вращающий момент» — эта категория представляет для нас наибольший интерес. Этот момент имеет отношение к нагрузкам, для которых требуется низкий вращающий момент при низкой частоте вращения, а при увеличении скорости вращения требуется более высокий вращающий момент. Типичным примером являются центробежные насосы.
Вся остальная часть данного раздела будет посвящена исключительно переменному вращающему моменту и мощности.
Определив, что для центробежных насосов типичным является переменный вращающий момент, мы должны проанализировать и оценить некоторые характеристики центробежного насоса. Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия , которые описывают соотношение между разностями давления и расходами.
Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия , которые описывают соотношение между разностями давления и расходами.
Во-первых, подача насоса прямо пропорциональна частоте вращения. Это означает, что если насос будет работать с частотой вращения на 25% больше, подача увеличится на 25%.
Во-вторых, напор насоса будет меняться пропорционально квадрату изменения скорости вращения. Если частота вращения увеличивается на 25%, напор возрастает на 56%.
В-третьих, что особенно интересно, мощность пропорциональна кубу изменения скорости вращения. Это означает, что если требуемая частота вращения уменьшается на 50%, это равняется 87,5%-ному уменьшению потребляемой мощности.
Итак, законы подобия объясняют, почему использование приводов с переменной частотой вращения более целесообразно в тех областях применения, где требуются переменные значения расхода и давления. Grundfos предлагает ряд электродвигателей со встроенным частотным преобразователем, который регулирует частоту вращения для достижения именно этой цели.
Так же как подача, давление и мощность, потребная величина вращающего момента зависит от скорости вращения.
На рисунке показан центробежный насос в разрезе. Требования к вращающему моменту для такого типа нагрузки почти противоположны требованиям при «постоянной мощности». Для нагрузок при переменном вращающем моменте потребный вращающий момент при низкой частоте вращения — мал, а потребный вращающий момент при высокой частоте вращения — велик. В математическом выражении вращающий момент пропорционален квадрату скорости вращения, а мощность — кубу скорости вращения.
Это можно проиллюстрировать на примере характеристики вращающий момент/частота вращения, которую мы использовали ранее, когда рассказывали о вращающем моменте электродвигателя:
Когда электродвигатель набирает скорость от нуля до номинальной скорости, вращающий момент может значительно меняться. Величина вращающего момента, необходимая при определённой нагрузке, также изменяется с частотой вращения. Чтобы электродвигатель подходил для определённой нагрузки, необходимо чтобы величина вращающего момента электродвигателя всегда превышала вращающий момент, необходимый для данной нагрузки.
Чтобы электродвигатель подходил для определённой нагрузки, необходимо чтобы величина вращающего момента электродвигателя всегда превышала вращающий момент, необходимый для данной нагрузки.
В примере, центробежный насос при номинальной нагрузке имеет вращающий момент, равный 70 Нм, что соответствует 22 кВт при номинальной частоте вращения 3000 мин-1. В данном случае насосу при пуске требуется 20% вращающего момента при номинальной нагрузке, т.е. приблизительно 14 Нм. После пуска вращающий момент немного падает, а затем, по мере того, как насос набирает скорость, увеличивается до величины полной нагрузки.
Очевидно, что нам необходим насос, который будет обеспечивать требуемые значения расход/напор (Q/H). Это значит, что нельзя допускать остановок электродвигателя, кроме того, электродвигатель должен постоянно ускоряться до тех пор, пока не достигнет номинальной скорости. Следовательно, необходимо, чтобы характеристика вращающего момента совпадала или превышала характеристику нагрузки на всём диапазоне от 0% до 100% скорости вращения. Любой «избыточный» момент, т.е. разница между кривой нагрузки и кривой электродвигателя, используется как ускорение вращения.
Любой «избыточный» момент, т.е. разница между кривой нагрузки и кривой электродвигателя, используется как ускорение вращения.
Соответствие электродвигателя нагрузке
Если нужно определить, отвечает ли вращающий момент определённого электродвигателя требованиям нагрузки, Вы можете сравнить характеристики скорости вращения/вращающего момента электродвигателя с характеристикой скорости вращения/ вращающего момента нагрузки. Вращающий момент, создаваемый электродвигателем, должен превышать потребный для нагрузки вращающий момент, включая периоды ускорения и полной скорости вращения.
Характеристика зависимости вращающего момента от скорости вращения стандартного электродвигателя и центробежного насоса.
Если мы посмотрим на характеристику, то увидим, что при ускорении электродвигателя его пуск производится при токе, соответствующем 550% тока полной нагрузки.
Когда двигатель приближается к своему номинальному значению скорости вращения, ток снижается. Как и следовало ожидать, во время начального периода пуска потери на электродвигателе высоки, поэтому этот период не должен быть продолжительным, чтобы не допустить перегрева.
Как и следовало ожидать, во время начального периода пуска потери на электродвигателе высоки, поэтому этот период не должен быть продолжительным, чтобы не допустить перегрева.
Очень важно, чтобы максимальная скорость вращения достигалась как можно точнее. Это связано с потребляемой мощностью: например, увеличение скорости вращения на 1% по сравнению со стандартным максимумом приводит к 3%-ному увеличению потребляемой мощности.
Потребляемая мощность пропорциональна диаметру рабочего колеса насоса в четвертой степени.
Уменьшение диаметра рабочего колеса насоса на 10% приводит к уменьшению потребляемой мощности на (1- (0.9 * 0.9 * 0.9 * 0.9)) * 100 = 34%, что равно 66% номинальной мощности. Эта зависимость определяется исключительно на практике, так как зависит от типа насоса, конструкции рабочего колеса и от того, насколько вы уменьшаете диаметр рабочего колеса.
Время пуска электрдвигателя
Если нам необходимо подобрать типоразмер электродвигателя для определённой нагрузки, например для центробежных насосов, основная наша задача состоит в том, чтобы обеспечить соответствующий вращающий момент и мощность в номинальной рабочей точке, потому что пусковой момент для центробежных насосов довольно низкий. Время пуска достаточно ограниченно, так как вращающий момент довольно высокий.
Время пуска достаточно ограниченно, так как вращающий момент довольно высокий.
Нередко для сложных систем защиты и контроля электродвигателей требуется некоторое время для их пуска, чтобы они могли замерить пусковой ток электродвигателя. Время пуска электродвигателя и насоса рассчитывается с помощью следующей формулы:
tпуск = время, необходимое электродвигателю насоса, чтобы достичь частоты вращения при полной нагрузке
n = частота вращения электродвигателя при полной нагрузке
Iобщ = инерция, которая требует ускорения, т.е. инерция вала электродвигателя, ротора, вала насоса и рабочих колёс.
Момент инерции для насосов и электродвигателей можно найти в соответствующих технических данных.
Мизб = избыточный момент, ускоряющий вращение. Избыточный момент равен вращающему моменту электродвигателя минус вращающий момент насоса при различных частотах вращения.
Как видно из приведённых вычислений, выполненных для данного примера с электродвигателем мощностью 4 кВт насоса CR, время пуска составляет 0,11 секунды.
Число пусков электродвигателя в час
Современные сложные системы управления электродвигателями могут контролировать число пусков в час каждого конкретного насоса и электродвигателя. Необходимость контроля этого параметра состоит в том, что каждый раз, когда осуществляется пуск электродвигателя с последующим ускорением, отмечается высокое потребление пускового тока. Пусковой ток нагревает электродвигатель. Если электродвигатель не остывает, продолжительная нагрузка от пускового тока значительно нагревает обмотки статора электродвигателя, что приводит к выходу из строя электродвигателя или сокращению срока службы изоляции.
Обычно за количество пусков, которое может выполнить электродвигатель в час, отвечает поставщик электродвигателя. Например, Grundfos указывает максимальное число пусков в час в технических данных на насос, так как максимальное количество пусков зависит от момента инерции насоса.
Мощность и КПД (eta) электродвигателя
Существует прямая связь между мощностью, потребляемой электродвигателем от сети, мощностью на валу электродвигателя и гидравлической мощностью, развиваемой насосом.
При производстве насосов используются следующие обозначения этих трёх различных типов мощности.
P1 (кВт) Входная электрическая мощность насосов — это мощность, которую электродвигатель насоса получает от источника электрического питания. Мощность P! равна мощности P2, разделённой на КПД электродвигателя.
P2 (кВт) Мощность на валу электродвигателя — это мощность, которую электродвигатель передает на вал насоса.
Р3 (кВт) Входная мощность насоса = P2, при условии, что соединительная муфта между валами насоса и электродвигателя не рассеивает энергию.
Р4 (кВт) Гидравлическая мощность насоса.
Вращающий момент асинхронного электродвигателя создается, как уже указывалось, за счет взаимодействия между вращающимся магнитным потоком статора и токами в обмотке ротора. Вполне понятно, что при отсутствии тока в обмотке ротора никакого момента создаваться не будет. Скольжение характеризует скорость вращения ротора относительно магнитного поля статора. От величины этой скорости зависит ток в роторе, а от тока—величина вращающего момента электродвигателя, который может быть вычислен по формуле (6). Но выражение (6), несмотря на свою простоту, не дает возможности выяснить влияние различных факторов на величину вращающего момента. Поэтому в курсе электротехники часто используют другое выражение: Но выражение (6), несмотря на свою простоту, не дает возможности выяснить влияние различных факторов на величину вращающего момента. Поэтому в курсе электротехники часто используют другое выражение:где с — постоянная величина, зависящая от конструкции электродвигателя; ?1 —угловая скорость вращающегося магнитного поля. Выражение (90) показывает, что вращающий момент пропорционален квадрату напряжения сети, в связи с чем даже небольшое уменьшение напряжения в питающей сети приводит к резкому снижению вращающего момента, что отрицательно сказывается на работе электродвигателя. Кроме того, выражение (90) учитывает зависимость величины вращающего момента от активных и индуктивных сопротивлений электродвигателя, а также от скольжения. Если обозначить (х1 + сх2) через х и выполнить несложные преобразования в формуле (90), то получим Величинами r1 s и x2 s2 можно пренебречь, ввиду их малости. Тогда, до некоторого предела Таким образом доказано, что с увеличением скольжения возрастает и момент электродвигателя. Более точный анализ выражений (90) и (91) показывает, что момент с увеличением скольжения возрастает лишь до некоторого критического значения Мкрит (так называемый опрокидывающий момент), после чего начинается резкое его снижение. Величина критического скольжения, при которой имеет место опрокидывающий момент, Подставляя это выражение в уравнение (91), получим В последних выражениях знак плюс относится к работе электродвигателя в режимах двигательном и торможения противовключением, а знак минус — к работе в генераторном режиме с отдачей энергии в сеть. Очевидно, что критический момент в двигательном режиме меньше, чем в генераторном. Зависимость М = f (s), построенная по уравнению (91), приведена на рис. 42, который показывает, что при трогании электродвигателя с места, когда скольжение s=1, начальный пусковой момент асинхронного электродвигателя невелик, что является его основным недостатком. Выражения (93) и (94) показывают, что при изменении активного сопротивления роторной цепи величина опрокидывающего момента Мкрит не изменяется, меняется при этом лишь величина критического скольжения sкрит. его роторную цепь. Таким же образом можно регулировать скорость электродвигателя, так как при изменении активного сопротивления роторной цепи меняется величина скольжения (рис. 43), а от скольжения, как показывает выражение (82), зависит число оборотов асинхронного электродвигателя. |
Глава 7.
 Вращательное движение. Кинематика и динамика
Вращательное движение. Кинематика и динамикаКак правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
(7. |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7.3) |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т. е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7.5) |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7. |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7. 5). Имеем
5). Имеем
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7.5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7. 4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7. 2.9 – ответ 1).
2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).
Уравнение крутящего момента и примеры | Что такое крутящий момент? — Видео и стенограмма урока
Научные курсы / Холт Макдугал Физика: онлайн-справка по учебнику Курс / Холт Макдугал Физика Глава 4: Силы и законы движения Глава
Кэтрин Кейлегиан-Старки, Дэмиен Ховард- Автор Кэтрин Кейлегиан-Старки
Кэтрин имеет степень бакалавра в области физики, и она стремится получить степень магистра в области прикладной физики. В настоящее время она преподает учащимся, испытывающим затруднения в области STEM, в муниципальном колледже Лейн.
Посмотреть биографию - Инструктор Дэмиен Ховард
Дэмиен имеет степень магистра физики и преподавал физическую лабораторию студентам колледжа.
Посмотреть биографию
Понять, что такое крутящий момент и как он связан с вращательным движением. Изучите уравнение крутящего момента, способы расчета крутящего момента и повседневные примеры крутящего момента. Обновлено: 07.03.2022
Содержание
- Что такое крутящий момент?
- Уравнение крутящего момента
- Вращательное равновесие
- Как рассчитать крутящий момент
- Краткое содержание урока
Что такое крутящий момент?
Что такое крутящий момент ? Определение крутящего момента в физике состоит в том, что крутящий момент представляет собой крутящую силу, вызывающую вращение. Это не означает, что крутящий момент является круговой силой. В общем, крутящие моменты представляют собой линейные силы, которые приложены к шарнирному плечу рычага таким образом, что заставляют плечо рычага вращаться. Что такое плечо рычага? Рычагом может быть любой шарнирный объект. Например, сиденья на качелях представляют собой рычажные рычаги, потому что они представляют собой твердую вращающуюся массу. При анализе крутящих моментов в системе важно определить плечо рычага и ось вращения плеча рычага. Ось вращения — это точка, вокруг которой вращается плечо рычага, а другой способ представить себе ось вращения — это точка поворота плеча рычага. Для качелей осью вращения является центр качелей, но не все рычаги имеют центральную ось вращения. Многие системы с крутящим моментом, такие как распашная дверь, имеют ось вращения на краю.
При анализе крутящих моментов в системе важно определить плечо рычага и ось вращения плеча рычага. Ось вращения — это точка, вокруг которой вращается плечо рычага, а другой способ представить себе ось вращения — это точка поворота плеча рычага. Для качелей осью вращения является центр качелей, но не все рычаги имеют центральную ось вращения. Многие системы с крутящим моментом, такие как распашная дверь, имеют ось вращения на краю.
Примеры крутящего момента в повседневной жизни
Качели с твердым сиденьем, охватывающим всю игрушку, являются повседневным примером крутящего момента, как и распашная дверь. Существует бесчисленное множество примеров крутящего момента из повседневной жизни, потому что каждый раз, когда приложенная сила заставляет объект вращаться, возникает крутящий момент. В следующем списке приведены различные распространенные примеры крутящих моментов:
- Дверная ручка поворачивается, потому что к ручке приложена линейная сила, направленная вниз.

- Монета вращается, потому что ее толкают с линейной силой, приложенной под некоторым углом к краю монеты.
- Маятник напольных часов качается, потому что сила тяжести действует на маятник и заставляет его качаться по дуге.
- Шестерня в двигателе автомобиля вращается, когда на ее край действует линейная сила.
Крутящий момент в повседневной жизни
Когда мы слышим термин «крутящий момент», чаще всего это относится к автомобилям. Крутящий момент — это один из терминов, обычно используемых для описания мощности автомобиля, но что именно он означает? В автомобиле крутящий момент — это сила, с которой поршни воздействуют на коленчатый вал, заставляя его и колеса вращаться.
Хотя крутящий момент часто считается автомобильным термином, на самом деле это термин общей физики, который имеет множество применений. Крутящий момент определяется как крутящая сила, стремящаяся вызвать вращение. Мы называем точку, в которой объект вращается осью вращения . Вы используете крутящий момент каждый день, не осознавая этого. Вы применяете крутящий момент три раза, когда просто открываете запертую дверь. Поворот ключа, поворот дверной ручки и толкание двери так, чтобы она качалась на петлях, — все это методы приложения крутящего момента.
Вы используете крутящий момент каждый день, не осознавая этого. Вы применяете крутящий момент три раза, когда просто открываете запертую дверь. Поворот ключа, поворот дверной ручки и толкание двери так, чтобы она качалась на петлях, — все это методы приложения крутящего момента.
Произошла ошибка при загрузке этого видео.
Попробуйте обновить страницу или обратитесь в службу поддержки.
Вы должны создать учетную запись, чтобы продолжить просмотр
Зарегистрируйтесь, чтобы просмотреть этот урок
Вы студент или преподаватель?
Создайте свою учетную запись, чтобы продолжить просмотр
Как участник вы также получите неограниченный доступ к уроки математики, английского языка, науки, истории и многое другое. Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам преуспеть.
Получите неограниченный доступ к более чем 84 000 уроков.
Попробуй это сейчас
Настройка занимает всего несколько минут, и вы можете отменить ее в любое время.
Уже зарегистрированы? Войдите здесь для доступ
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Назад
Далее: Трение: определение и типы
пройти викторину Смотреть Следующий урок
Повтор
Просто отмечаюсь. Вы все еще смотрите?
Да! Продолжай играть.Ваш следующий урок будет играть в 10 секунд
- 0:00 Крутящий момент в повседневной жизни
- 0:50 Физика крутящего момента
- 2:10 Вращательное равновесие
- 3:33 Проблема тупика на качелях
- 6:11 Итоги урока
Сохранить Сохранить Сохранить
Хронология
Автовоспроизведение
Автовоспроизведение
Скорость
Скорость
Уравнение крутящего момента
Интересным свойством силы, вызывающей вращение, является то, что результирующее движение плеча рычага перпендикулярно как первоначальной силе, так и плечу рычага. Этот атрибут означает, что крутящий момент равен векторному произведению, а уравнение крутящего момента является векторным произведением плеча рычага и приложенной силы:
Этот атрибут означает, что крутящий момент равен векторному произведению, а уравнение крутящего момента является векторным произведением плеча рычага и приложенной силы:
{экв}\vec \tau = \vec r \times \vec F {/экв}.
В этом уравнении {eq}\vec \tau {/eq} — крутящий момент, {eq}\vec r {/eq} — плечо рычага, а {eq}\vec F {/eq} — сила. Обратите внимание, что каждый компонент уравнения крутящего момента является вектором. Это связано с тем, что векторное произведение является векторной операцией, и при расчете крутящих моментов важно убедиться, что направление плеча рычага и сила определены. Можно выполнить матричные вычисления для определения векторного произведения этих двух векторов. Тем не менее, еще один способ расчета крутящих моментов в системе — использовать определение величины крутящего момента. Магнитуда формула крутящего момента :
{eq}\tau = rFsin(\theta) {/eq}
, где вместо векторов каждая компонента соответствует величине вектора, а угол {eq}\theta { /eq} — угол, который образуется между плечом рычага и приложенной силой. Оба уравнения дадут один и тот же ответ, за исключением того, что один ответ будет направленным и в компонентной форме, а другой будет только величиной крутящего момента. Поскольку крутящий момент представляет собой приложенную силу, единицами крутящего момента в системе СИ являются ньютон-метры, Нм.
Оба уравнения дадут один и тот же ответ, за исключением того, что один ответ будет направленным и в компонентной форме, а другой будет только величиной крутящего момента. Поскольку крутящий момент представляет собой приложенную силу, единицами крутящего момента в системе СИ являются ньютон-метры, Нм.
Вращательное равновесие
Равновесие — это состояние покоя, и для того, чтобы система находилась в равновесии, сумма сил, действующих на систему, должна быть равна нулю. Для системы, которая совершает вращательное движение, вращательное равновесие достигается, когда сумма крутящих моментов в системе равна нулю:
{экв}\сумма\тау = 0 {/экв}.
Как может сумма крутящих моментов в системе равняться нулю? Этот сценарий возникает, когда крутящие моменты, действующие на вращающуюся систему, уравновешиваются, и для этого крутящие моменты должны действовать в противоположных направлениях. {\circ} {/eq}. Эту проблему можно решить, подставив каждое заданное значение в уравнение величины крутящего момента: 9{\circ}) \rightarrow \tau = 3,5 {/eq} Нм
{\circ} {/eq}. Эту проблему можно решить, подставив каждое заданное значение в уравнение величины крутящего момента: 9{\circ}) \rightarrow \tau = 3,5 {/eq} Нм
Крутящий момент в этой системе составляет 3,5 Нм.
Пример 2: Ребенок массой 46 кг идет в школу с тяжелым рюкзаком. Она хочет отдохнуть в парке, и она хотела бы посидеть на качелях. Если ее рюкзак имеет массу 32 кг, где она должна сидеть и куда ей положить рюкзак, чтобы качели были сбалансированы? Используйте рисунок 3.
Эта задача более сложная, чем пример 1, и она будет решаться поэтапно.
1) Для начала поймите, что для того, чтобы качели были сбалансированы, крутящий момент от ребенка должен компенсировать крутящий момент от рюкзака. Начните с балансировки крутящих моментов. Нижний индекс g обозначает девушку, а нижний индекс b — рюкзак.
{eq}\tau_g = \tau_b \rightarrow r_gF_gsin(\theta_g) = r_bF_bsin(\theta_b) {/eq} 9{\ circ} {/eq}. Это означает, что синусоидальные члены сокращаются:
{eq}r_b = \frac{ r_gF_gsin(\theta_g)}{F_bsin(\theta_b)} \rightarrow r_b = \frac{ r_gF_g}{F_b} {/eq}
3) Линейная сила, с которой девушка действует на плечо рычага, равна {eq}F_g = m_gg {/eq}, а сила, с которой рюкзак действует на плечо рычага, равна {eq}F_b = m_bg {/eq}. В обоих случаях g от гравитационного ускорения компенсируется, и результат 2) становится следующим:
{eq}r_b = \frac{ r_gF_g}{F_b} \rightarrow r_b = \frac{ r_gm_g}{m_b} {/eq }
4) Используя результат из 3), девочка могла сесть где угодно и решить, где разместить свой рюкзак, чтобы сбалансировать качели. Чтобы получить численный ответ на задачу, самое простое решение состоит в том, чтобы поместить девочку на один конец качелей так, чтобы расстояние до ее плеча рычага составляло половину расстояния всей качели. Это означает, что {eq}r_g = 2,5 {/eq} м.
5) Подставьте необходимые значения в {eq}r_b = \frac{ r_gm_g}{m_b} {/eq}, чтобы найти численное решение.
{eq}r_b = \frac{ r_gm_g}{m_b} \rightarrow r_b = \frac{ 2,5*46}{32} {/eq}
{eq}r_b = \frac{ 2,5*46}{32} = 3,59 {/экв} м
Девушка должна расположить свой рюкзак на расстоянии 3,59 метра от оси вращения, если она сидит на другом краю качелей.
Резюме урока
Что такое крутящий момент ? В физике определение крутящего момента состоит в том, что крутящий момент — это приложенная сила, вызывающая вращение, а крутящий момент — это линейная сила, приложенная к шарнирному плечу рычага под некоторым углом. Что такое плечо рычага? Плечо рычага представляет собой твердую массу, шарнирно закрепленную и способную вращаться вокруг оси. Другой способ описать ось вращения — это точка поворота системы. Есть бесчисленное множество повседневных примеров крутящего момента, таких как движущиеся качели или крутящаяся дверная ручка.
Когда линейная сила вызывает вращение, результирующее движение перпендикулярно как силе, так и объекту, а формула крутящего момента представляет собой векторное произведение плеча рычага и приложенной силы, {eq}\vec \tau = \ vec r \times \vec F {/eq}, где {eq}\vec \tau {/eq} — крутящий момент, {eq}\vec r {/eq} — плечо рычага, а {eq}\vec F { /eq} — это сила. Можно определить крутящий момент, используя величины вместо векторов, и уравнение крутящего момента с величиной равно {eq}\tau = rFsin(\theta) {/eq}, где {eq}\theta {/eq} – это угол между плечо рычага и усилие. Вращательное равновесие достигается, когда крутящие моменты уравновешены, и в этой ситуации сумма крутящих моментов равна нулю.
Можно определить крутящий момент, используя величины вместо векторов, и уравнение крутящего момента с величиной равно {eq}\tau = rFsin(\theta) {/eq}, где {eq}\theta {/eq} – это угол между плечо рычага и усилие. Вращательное равновесие достигается, когда крутящие моменты уравновешены, и в этой ситуации сумма крутящих моментов равна нулю.
Физика крутящего момента
Чтобы найти линейную силу, нам нужно знать массу и ускорение. Однако крутящий момент немного отличается из-за участия вращения. Подумайте об открытии двери. Куда вы нажимаете на него, когда хотите, чтобы он открылся? Вы нажимаете на ту сторону двери, где нет петель, потому что нажатие на сторону с петлями затруднит открытие. Таким образом, для крутящего момента нам нужно знать не только массу и ускорение линейной силы, но также и то, насколько далеко эта сила находится от оси вращения, поскольку в зависимости от этого мы можем получить разные результаты. Мы можем видеть это на диаграмме и в уравнении для крутящего момента.
T = F * R * SIN ( THETA )
T = Corque
F 903. вращения к месту приложения линейной силы
тета = угол между F и r
В нашем уравнении sin( тета ) не имеет единиц измерения, r имеет единицы измерения в метрах (м), а F имеет единицы измерения в ньютонах (Н). Объединив их вместе, мы видим, что единицей крутящего момента является ньютон-метра (Нм).
Наконец, тета необходима для учета направления приложения линейной силы. Сила не всегда будет толкаться прямо, как дверь. Это может прийти с разных сторон.
Равновесие вращения
Итак, мы видели, как один крутящий момент может воздействовать на объект, но вы легко можете одновременно приложить несколько крутящих моментов. Вспомните двигатель автомобиля. В каждом автомобиле есть более одного поршня, передающего крутящий момент на коленчатый вал. В этом случае имеется общий крутящий момент, который является суммой каждого отдельного крутящего момента.
В этом случае имеется общий крутящий момент, который является суммой каждого отдельного крутящего момента.
Итого T = T {1} + T {2} + … + T {n}
объект. Существует также особый случай этого, называемый вращательным равновесием . Здесь сумма всех крутящих моментов, действующих на объект, равна нулю. Когда это происходит, это может означать, что на объект не действует крутящий момент, или все крутящие моменты, действующие на объект, уравновешивают друг друга. Чтобы визуализировать уравновешивание крутящих моментов, давайте рассмотрим простой случай с двумя крутящими моментами: качели.
В верхней части изображения двое детей сидят на неподвижных качелях. Они уравновешены на оси вращения, которая является точкой опоры в случае качелей. Оба ребенка прилагают вниз силу своего веса, также известную как сила тяжести. Ребенок 1 пытается повернуть качели против часовой стрелки, а ребенок 2 пытается повернуть их по часовой стрелке. Пока величины двух крутящих моментов одинаковы, они компенсируют друг друга, поскольку пытаются двигать качели в противоположных направлениях.
Пока величины двух крутящих моментов одинаковы, они компенсируют друг друга, поскольку пытаются двигать качели в противоположных направлениях.
Проблема тупиковой ситуации на качелях
Давайте рассмотрим пример расчета с использованием вращательного равновесия и уравнения для крутящего момента.
Качели на изображении находятся в равновесии вращения и не двигаются. Мы хотим найти, как далеко дочерний элемент 2 находится справа от оси вращения в точке опоры. Ребенок 1 слева имеет массу 38 кг и находится на расстоянии 4 м от точки опоры. Ребенок 2 имеет массу 25 кг.
Шаг 1: Учет направления
Чтобы математически показать, что два момента движутся в противоположных направлениях, одному из них присваивается отрицательный знак. Стандартной практикой является обозначение крутящего момента, вращающего объект по часовой стрелке, как отрицательное, поэтому мы сделаем T {2} отрицательным. Поскольку качели находятся в равновесии вращения, мы также знаем, что сумма крутящих моментов должна равняться нулю. Это позволяет нам изменить уравнение, чтобы получить один крутящий момент по обе стороны от знака равенства.
Поскольку качели находятся в равновесии вращения, мы также знаем, что сумма крутящих моментов должна равняться нулю. Это позволяет нам изменить уравнение, чтобы получить один крутящий момент по обе стороны от знака равенства.
Т {1} + (- Т {2}) = 0
T {1} — T {2} = 0
T {2} = T {1}
Шаг 2: Вставка уравнений крутящего момента и силы 90
Затем мы подставляем уравнение для крутящего момента в каждую сторону.
F { г 2} * r {2} * sin( тета {2}) = F { г 1} ( r 1} * r 1} {1})
F { г 2} и F { g 1} силы тяжести. Чтобы получить их, мы умножаем массу каждого ребенка на ускорение свободного падения ( г ).
m {2} * g * r {2} * sin( тета {2}) = m {1} * g * r { тета {1})
Шаг 3: Упростим уравнение
Теперь мы можем сделать пару вещей, чтобы упростить это уравнение. Во-первых, поскольку 90 300 г 90 301 одинаково для каждого ребенка и по обе стороны от знака равенства, оно аннулируется. Во-вторых, если мы посмотрим на изображение, то увидим, что силы гравитации перпендикулярны качелям. Это означает, что они перпендикулярны р {1} и р {2}. Таким образом, оба тета имеют значение 90 градусов. Помните, sin(90 градусов) = 1. Теперь у нас осталось следующее:
Во-первых, поскольку 90 300 г 90 301 одинаково для каждого ребенка и по обе стороны от знака равенства, оно аннулируется. Во-вторых, если мы посмотрим на изображение, то увидим, что силы гравитации перпендикулярны качелям. Это означает, что они перпендикулярны р {1} и р {2}. Таким образом, оба тета имеют значение 90 градусов. Помните, sin(90 градусов) = 1. Теперь у нас осталось следующее:
м {2} * r {2} = м {1} * r {1}
Шаг 4: Решите уравнение
Наконец мы можем подставить наши данные, чтобы найти ответ для r {2}.
25 кг * р {2} = 38 кг * 4 м
25 кг * р {2} = 152 кг м
r {2} = 6 м
Ребенок 2 сидит в 6 метрах от точки опоры. Для вращательного равновесия имеет смысл, что более легкий ребенок должен сидеть дальше от точки опоры, чем более тяжелый, чтобы удерживать качели в равновесии.
Резюме урока
Крутящий момент — это крутящая сила, которая стремится вызвать вращение. Точка, в которой вращается объект, называется осью вращения . Математически крутящий момент можно записать как T = F * r * sin( тета ), а единицами измерения являются ньютон-метры. Когда сумма всех крутящих моментов, действующих на объект, равна нулю, это вращательное равновесие . Крутящие моменты, действующие на один объект, компенсируют друг друга, когда они имеют одинаковую величину и противоположные направления. Крутящий момент относится не только к автомобилям; он также позволяет использовать такие объекты, как замки, дверные ручки, петли и даже качели.
Точка, в которой вращается объект, называется осью вращения . Математически крутящий момент можно записать как T = F * r * sin( тета ), а единицами измерения являются ньютон-метры. Когда сумма всех крутящих моментов, действующих на объект, равна нулю, это вращательное равновесие . Крутящие моменты, действующие на один объект, компенсируют друг друга, когда они имеют одинаковую величину и противоположные направления. Крутящий момент относится не только к автомобилям; он также позволяет использовать такие объекты, как замки, дверные ручки, петли и даже качели.
Результаты обучения
Повторите урок и попрактикуйтесь в уравнениях, пока не будете готовы:
- Определение крутящего момента, вращательного равновесия и оси вращения
- Вспомните уравнение для крутящего момента
- Рассчитать крутящий момент
- Рассчитать значение r для объекта в равновесии вращения
- Перечислите несколько примеров крутящего момента в повседневной жизни
Чтобы разблокировать этот урок, вы должны быть участником Study. com.
com.
Создайте свой аккаунт
Крутящий момент в повседневной жизни
Когда мы слышим термин «крутящий момент», чаще всего это относится к автомобилям. Крутящий момент — это один из терминов, обычно используемых для описания мощности автомобиля, но что именно он означает? В автомобиле крутящий момент — это сила, с которой поршни воздействуют на коленчатый вал, заставляя его и колеса вращаться.
Хотя крутящий момент часто считается автомобильным термином, на самом деле это термин общей физики, который имеет множество применений. Крутящий момент определяется как крутящая сила, стремящаяся вызвать вращение. Мы называем точку, в которой объект вращается осью вращения . Вы используете крутящий момент каждый день, не осознавая этого. Вы применяете крутящий момент три раза, когда просто открываете запертую дверь. Поворот ключа, поворот дверной ручки и толкание двери так, чтобы она качалась на петлях, — все это методы приложения крутящего момента.
Физика крутящего момента
Чтобы найти линейную силу, нам нужно знать массу и ускорение. Однако крутящий момент немного отличается из-за участия вращения. Подумайте об открытии двери. Куда вы нажимаете на него, когда хотите, чтобы он открылся? Вы нажимаете на ту сторону двери, где нет петель, потому что нажатие на сторону с петлями затруднит открытие. Таким образом, для крутящего момента нам нужно знать не только массу и ускорение линейной силы, но также и то, насколько далеко эта сила находится от оси вращения, поскольку в зависимости от этого мы можем получить разные результаты. Мы можем видеть это на диаграмме и в уравнении для крутящего момента.
T = F * R * SIN ( THETA )
T = Corque
F 903. вращения к месту приложения линейной силы
тета = угол между F и r
В нашем уравнении sin( тета ) не имеет единиц измерения, r имеет единицы измерения в метрах (м), а F имеет единицы измерения в ньютонах (Н). Объединив их вместе, мы видим, что единицей крутящего момента является ньютон-метра (Нм).
Объединив их вместе, мы видим, что единицей крутящего момента является ньютон-метра (Нм).
Наконец, тета необходима для учета направления приложения линейной силы. Сила не всегда будет толкаться прямо, как дверь. Это может прийти с разных сторон.
Равновесие вращения
Итак, мы видели, как один крутящий момент может воздействовать на объект, но вы легко можете одновременно приложить несколько крутящих моментов. Вспомните двигатель автомобиля. В каждом автомобиле есть более одного поршня, передающего крутящий момент на коленчатый вал. В этом случае имеется общий крутящий момент, который является суммой каждого отдельного крутящего момента.
Итого T = T {1} + T {2} + … + T {n}
объект. Существует также особый случай этого, называемый вращательным равновесием . Здесь сумма всех крутящих моментов, действующих на объект, равна нулю. Когда это происходит, это может означать, что на объект не действует крутящий момент, или все крутящие моменты, действующие на объект, уравновешивают друг друга. Чтобы визуализировать уравновешивание крутящих моментов, давайте рассмотрим простой случай с двумя крутящими моментами: качели.
Чтобы визуализировать уравновешивание крутящих моментов, давайте рассмотрим простой случай с двумя крутящими моментами: качели.
В верхней части изображения двое детей сидят на неподвижных качелях. Они уравновешены на оси вращения, которая является точкой опоры в случае качелей. Оба ребенка прилагают вниз силу своего веса, также известную как сила тяжести. Ребенок 1 пытается повернуть качели против часовой стрелки, а ребенок 2 пытается повернуть их по часовой стрелке. Пока величины двух крутящих моментов одинаковы, они компенсируют друг друга, поскольку пытаются двигать качели в противоположных направлениях.
Проблема тупиковой ситуации на качелях
Давайте рассмотрим пример расчета с использованием вращательного равновесия и уравнения для крутящего момента.
Качели на изображении находятся в равновесии вращения и не двигаются. Мы хотим найти, как далеко дочерний элемент 2 находится справа от оси вращения в точке опоры. Ребенок 1 слева имеет массу 38 кг и находится на расстоянии 4 м от точки опоры. Ребенок 2 имеет массу 25 кг.
Мы хотим найти, как далеко дочерний элемент 2 находится справа от оси вращения в точке опоры. Ребенок 1 слева имеет массу 38 кг и находится на расстоянии 4 м от точки опоры. Ребенок 2 имеет массу 25 кг.
Шаг 1: Учет направления
Чтобы математически показать, что два момента движутся в противоположных направлениях, одному из них присваивается отрицательный знак. Стандартной практикой является обозначение крутящего момента, вращающего объект по часовой стрелке, как отрицательное, поэтому мы сделаем T {2} отрицательным. Поскольку качели находятся в равновесии вращения, мы также знаем, что сумма крутящих моментов должна равняться нулю. Это позволяет нам изменить уравнение, чтобы получить один крутящий момент по обе стороны от знака равенства.
Т {1} + (- Т {2}) = 0
T {1} — T {2} = 0
T {2} = T {1}
Шаг 2: Вставка уравнений крутящего момента и силы 90
Затем мы подставляем уравнение для крутящего момента в каждую сторону.
F { г 2} * r {2} * sin( тета {2}) = F { г 1} ( r 1} * r 1} {1})
F { г 2} и F { g 1} силы тяжести. Чтобы получить их, мы умножаем массу каждого ребенка на ускорение свободного падения ( г ).
m {2} * g * r {2} * sin( тета {2}) = m {1} * g * r { тета {1})
Шаг 3: Упростим уравнение
Теперь мы можем сделать пару вещей, чтобы упростить это уравнение. Во-первых, поскольку 90 300 г 90 301 одинаково для каждого ребенка и по обе стороны от знака равенства, оно аннулируется. Во-вторых, если мы посмотрим на изображение, то увидим, что силы гравитации перпендикулярны качелям. Это означает, что они перпендикулярны р {1} и р {2}. Таким образом, оба тета имеют значение 90 градусов. Помните, sin(90 градусов) = 1. Теперь у нас осталось следующее:
м {2} * r {2} = м {1} * r {1}
Шаг 4: Решите уравнение
Наконец мы можем подставить наши данные, чтобы найти ответ для r {2}.
25 кг * р {2} = 38 кг * 4 м
25 кг * р {2} = 152 кг м
r {2} = 6 м
Ребенок 2 сидит в 6 метрах от точки опоры. Для вращательного равновесия имеет смысл, что более легкий ребенок должен сидеть дальше от точки опоры, чем более тяжелый, чтобы удерживать качели в равновесии.
Резюме урока
Крутящий момент — это крутящая сила, которая стремится вызвать вращение. Точка, в которой вращается объект, называется осью вращения . Математически крутящий момент можно записать как T = F * r * sin( тета ), а единицами измерения являются ньютон-метры. Когда сумма всех крутящих моментов, действующих на объект, равна нулю, это вращательное равновесие . Крутящие моменты, действующие на один объект, компенсируют друг друга, когда они имеют одинаковую величину и противоположные направления. Крутящий момент относится не только к автомобилям; он также позволяет использовать такие объекты, как замки, дверные ручки, петли и даже качели.
Результаты обучения
Повторите урок и попрактикуйтесь в уравнениях, пока не будете готовы:
- Определение крутящего момента, вращательного равновесия и оси вращения
- Вспомните уравнение для крутящего момента
- Рассчитать крутящий момент
- Рассчитать значение r для объекта в равновесии вращения
- Перечислите несколько примеров крутящего момента в повседневной жизни
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свой аккаунт
Чему равен крутящий момент?
Крутящий момент представляет собой векторное произведение плеча рычага и приложенной силы. Это означает, что величина крутящего момента в системе равна величине плеча рычага, умноженной на величину силы, умноженной на синус угла между ними, rFsin(theta).
Что такое крутящий момент в физике?
В физике крутящий момент — это сила, вызывающая вращательное движение. Он определяется как векторное произведение плеча рычага и линейной силы.
Он определяется как векторное произведение плеча рычага и линейной силы.
Зарегистрируйтесь, чтобы просмотреть этот урок
Вы студент или преподаватель?
Разблокируйте свое образование
Убедитесь сами, почему 30 миллионов человек используют Study.com
Станьте участником Study.com и начните учиться прямо сейчас.
Стать участником
Уже являетесь участником? Войти
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Спинка
10.
 7: Крутящий момент — Физика LibreTexts
7: Крутящий момент — Физика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4032
- OpenStax
- OpenStax
Цели обучения
- Описать, как величина крутящего момента зависит от величины плеча рычага и угла, который вектор силы образует с плечом рычага
- Определите знак (положительный или отрицательный) крутящего момента с помощью правила правой руки
- Рассчитайте отдельные крутящие моменты относительно общей оси и просуммируйте их, чтобы найти чистый крутящий момент
Важной величиной для описания динамики вращающегося твердого тела является крутящий момент. Мы видим применение крутящего момента во многих отношениях в нашем мире. У всех нас есть интуитивное представление о крутящем моменте, например, когда мы используем большой гаечный ключ, чтобы открутить упрямый болт. Крутящий момент действует невидимым образом, например, когда мы нажимаем на педаль акселератора в автомобиле, заставляя двигатель передавать дополнительный крутящий момент на трансмиссию. Или каждый раз, когда мы перемещаем свое тело из положения стоя, мы прикладываем крутящий момент к нашим конечностям. В этом разделе мы определяем крутящий момент и аргументируем уравнение для расчета крутящего момента для твердого тела с вращением с фиксированной осью.
Мы видим применение крутящего момента во многих отношениях в нашем мире. У всех нас есть интуитивное представление о крутящем моменте, например, когда мы используем большой гаечный ключ, чтобы открутить упрямый болт. Крутящий момент действует невидимым образом, например, когда мы нажимаем на педаль акселератора в автомобиле, заставляя двигатель передавать дополнительный крутящий момент на трансмиссию. Или каждый раз, когда мы перемещаем свое тело из положения стоя, мы прикладываем крутящий момент к нашим конечностям. В этом разделе мы определяем крутящий момент и аргументируем уравнение для расчета крутящего момента для твердого тела с вращением с фиксированной осью.
Определение крутящего момента
До сих пор мы определили множество переменных, которые являются вращательными эквивалентами своих поступательных аналогов. Рассмотрим, каким должен быть аналог силы. Поскольку силы изменяют поступательное движение объектов, вращательный аналог должен быть связан с изменением вращательного движения объекта вокруг оси. Мы называем этот вращательный аналог крутящим моментом .
Мы называем этот вращательный аналог крутящим моментом .
В повседневной жизни мы постоянно вращаем объекты вокруг оси, поэтому интуитивно мы уже многое знаем о крутящем моменте. Рассмотрим, например, как мы поворачиваем дверь, чтобы открыть ее. Во-первых, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям; более эффективно повернуть дверь, если мы нажмем далеко от петель. Во-вторых, мы знаем, что толкать надо перпендикулярно плоскости двери; если мы нажмем параллельно плоскости двери, мы не сможем ее повернуть. В-третьих, чем больше сила, тем эффективнее она открывает дверь; чем сильнее вы нажимаете, тем быстрее открывается дверь. Первый пункт подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; второй подразумевает, что эффективность зависит от угла приложения силы; третий подразумевает, что величина силы также должна быть частью уравнения. Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. На рисунке \(\PageIndex{1}\) показано вращение против часовой стрелки.
Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. На рисунке \(\PageIndex{1}\) показано вращение против часовой стрелки.

Теперь рассмотрим, как определить крутящие моменты в общем трехмерном случае.
Крутящий момент
Когда сила \(\vec{F}\) приложена к точке P, положение которой равно \(\vec{r}\) относительно точки O (рисунок \(\PageIndex{2}\)) , крутящий момент \(\vec{\tau}\) вокруг O равен
\[\vec{\tau} = \vec{r} \times \vec{F} \ldotp \label{10.22}\]
Рисунок \(\PageIndex{2}\): направление определяется по правилу правой руки.
Из определения векторного произведения крутящий момент \(\vec{\tau}\) перпендикулярен плоскости, содержащей \(\vec{r}\) и \(\vec{F}\), и имеет величина
\[|\vec{\tau}| = |\vec{r} \times \vec{F}| = rF \sin \theta,\]
, где \(\theta\) — угол между векторами \(\vec{r}\) и \(\vec{F}\). Единицей крутящего момента в СИ является ньютон, умноженный на метр, обычно записывается как Н • м. Величина r \(\perp\) = rsin \(\theta\) представляет собой перпендикулярное расстояние от O до линии, определяемой вектором \(\vec{F}\), и называется рычаг . Обратите внимание, что чем больше плечо рычага, тем больше величина крутящего момента. В терминах плеча рычага величина крутящего момента составляет
Обратите внимание, что чем больше плечо рычага, тем больше величина крутящего момента. В терминах плеча рычага величина крутящего момента составляет
\[|\vec{\tau}| = r_{\perp} F \ldotp \label{10.23}\]
Перекрестное произведение \(\vec{r} \times \vec{F}\) также сообщает нам знак крутящего момента. На рисунке \(\PageIndex{2}\) векторное произведение \(\vec{r} \times \vec{F}\) расположено вдоль положительной оси z, что по соглашению представляет собой положительный крутящий момент. Если \(\vec{r} \times \vec{F}\) вдоль отрицательной оси z, это создает отрицательный крутящий момент.
Если мы рассмотрим диск, который может свободно вращаться вокруг оси, проходящей через центр, как показано на рисунке \(\PageIndex{3}\), мы увидим, как угол между радиусом \(\vec{r}\ ), а сила \(\vec{F}\) влияет на величину крутящего момента. Если угол равен нулю, крутящий момент равен нулю; если угол равен 90°, крутящий момент максимальный. Крутящий момент на рисунке \(\PageIndex{3}\) положительный, потому что направление крутящего момента по правилу правой руки выходит за пределы страницы вдоль положительной оси z. Диск вращается против часовой стрелки за счет крутящего момента в том же направлении, что и положительное угловое ускорение.
Диск вращается против часовой стрелки за счет крутящего момента в том же направлении, что и положительное угловое ускорение.
Любое количество крутящих моментов может быть рассчитано относительно данной оси. Отдельные крутящие моменты складываются, чтобы создать чистый крутящий момент вокруг оси. Когда соответствующий знак (положительный или отрицательный) присваивается величинам отдельных крутящих моментов относительно заданной оси, чистый крутящий момент вокруг оси представляет собой сумму отдельных крутящих моментов:
\[\vec{\tau}_{net} = \sum_{i} |\vec{\tau}_{i}| \ldotp \label{10.24}\]
Расчет чистого крутящего момента для твердых тел на неподвижной оси
В следующих примерах мы вычисляем крутящий момент как абстрактно, так и применительно к твердому телу. Сначала мы вводим стратегию решения проблем.
Сначала мы вводим стратегию решения проблем.
Стратегия решения проблем: определение чистого крутящего момента
- Выберите систему координат с точкой вращения или осью вращения в качестве начала выбранной системы координат.
- Определите угол между плечом рычага \(\vec{r}\) и вектором силы.
- Возьмите векторное произведение \(\vec{r}\) и \(\vec{F}\), чтобы определить, является ли крутящий момент положительным или отрицательным относительно точки вращения или оси.
- Оценить величину крутящего момента с помощью r \(\perp\) F.
- Присвойте величине соответствующий знак, положительный или отрицательный.
- Суммируйте крутящие моменты, чтобы найти чистый крутящий момент.
Пример 10.14: Расчет крутящего момента
Четыре силы показаны на рисунке \(\PageIndex{4}\) в определенных местах и ориентациях по отношению к данной системе координат xy. Найдите крутящий момент, вызванный каждой силой относительно начала координат, а затем используйте полученные результаты, чтобы найти чистый крутящий момент вокруг начала координат.
Стратегия
Эта задача требует расчета крутящего момента. Все известные величины — силы с направлениями и плечами рычага — приведены на рисунке. Цель состоит в том, чтобы найти каждый отдельный крутящий момент и чистый крутящий момент путем суммирования отдельных крутящих моментов. Будьте осторожны, чтобы присвоить правильный знак каждому крутящему моменту, используя векторное произведение \(\vec{r}\) и вектора силы \(\vec{F}\).
Решение
Использование |\(\vec{\tau}\)| = r \(\perp\) F = rFsin \(\theta\) для нахождения величины и \(\vec{r} = \vec{r} \times \vec{F}\) для определения знака крутящего момента.
Крутящий момент от силы 40 Н в первом квадранте определяется формулой (4)(40)sin 90° = 160 Н • м.
Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) вне страницы, положительное.
Крутящий момент от силы 20 Н в третьем квадранте определяется выражением −(3)(20)sin 90° = − 60 Н • м.
Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) находится на странице, поэтому оно отрицательно.
Крутящий момент от силы 30 Н в третьем квадранте определяется выражением (5)(30)sin 53° = 120 Н • м.
Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) вне страницы, положительное.
Крутящий момент от силы 20 Н во втором квадранте определяется выражением (1)(20)sin 30° = 10 Н • м.
Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) находится за пределами страницы.
Таким образом, чистый крутящий момент равен \(\tau_{net} = \sum_{i} |\tau_{i}|\) = 160 − 60 + 120 + 10 = 230 Н • м.
Значение
Обратите внимание, что каждая сила, действующая против часовой стрелки, имеет положительный крутящий момент, тогда как каждая сила, действующая по часовой стрелке, имеет отрицательный крутящий момент. Крутящий момент больше, когда расстояние, сила или перпендикулярные компоненты больше.
Пример 10.15: Расчет крутящего момента на твердом теле
На рисунке \(\PageIndex{5}\) показано несколько сил, действующих в разных местах и под разными углами на маховике. Имеем \(|\vec{F}_{1}|\) = 20 Н, \(|\vec{F}_{2}|\) = 30 Н, \(|\vec{F}_{ 3}|\) = 30 Н, r = 0,5 м. Найдите чистый крутящий момент на маховике относительно оси, проходящей через центр.
Имеем \(|\vec{F}_{1}|\) = 20 Н, \(|\vec{F}_{2}|\) = 30 Н, \(|\vec{F}_{ 3}|\) = 30 Н, r = 0,5 м. Найдите чистый крутящий момент на маховике относительно оси, проходящей через центр.
Стратегия
Мы рассчитываем каждый крутящий момент отдельно, используя перекрестное произведение, и определяем знак крутящего момента. Затем мы суммируем крутящие моменты, чтобы найти чистый крутящий момент. Решение Начнем с \(\vec{F}_{1}\). Если мы посмотрим на рисунок \(\PageIndex{5}\), то увидим, что \(\vec{F}_{1}\) составляет угол 90° + 60° с радиус-вектором \(\vec{r }\). Взяв векторное произведение, мы видим, что оно находится вне страницы и, следовательно, является положительным. Мы также видим это из расчета его величины: 9{о} = (-0,5\; m)(30\; N) = -15,0\; Н\; \cdotp m \ldotp\]
Когда мы оцениваем крутящий момент из-за \(\vec{F}_{3}\), мы видим, что угол, который он образует с \(\vec{r}\), равен нулю, поэтому \(\vec{r} \times \vec{F}_{3}\) = 0. Следовательно, \(\vec{F}_{3}\) не создает крутящего момента на маховике.
Следовательно, \(\vec{F}_{3}\) не создает крутящего момента на маховике.
Оцениваем сумму моментов:
\[\tau_{net} = \sum_{i} |\tau_{i}| = 5 — 15 = -10\; Н\; \cdotp m \ldotp\]
Значение
Ось вращения находится в центре масс маховика. Поскольку маховик находится на неподвижной оси, он не может свободно перемещаться. Если бы он находился на поверхности без трения и не был зафиксирован на месте, \(\vec{F}_{3}\) вызвал бы перемещение маховика, а также \(\vec{F}_{1}\). Его движение было бы комбинацией поступательного движения и вращения.
Упражнение 10.6
Большое океанское судно садится на мель у береговой линии, как и Costa Concordia , и лежит под углом, как показано ниже. Спасательные бригады должны приложить крутящий момент, чтобы выровнять судно, чтобы поднять его на воду для транспортировки. Чтобы выровнять судно, необходимо приложить силу 5,0 x 10 5 Н, действующую в точке А. Каков крутящий момент в точке контакта корабля с землей (рис. \(\PageIndex{6}\))?
\(\PageIndex{6}\))?
Эта страница под названием 10.7: Torque распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- рычаг
- источник@https://openstax.
 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1 - крутящий момент
ЧТО Технические статьи и описания продуктов Mechanical Engineering FundamentalsPiston Reference Materials EPI Дополнительные продукты Вещи
Журнал Race Engine Technology ВВЕДЕНИЕ в Race Engine Technology ПОДПИСАТЬСЯ
Последнее обновление: | Последнее обновление: 11 марта 2011 г. ПРИМЕЧАНИЕ. Все наши продукты, конструкции и услуги являются УСТОЙЧИВЫМИ, ОРГАНИЧЕСКИМИ, БЕЗГЛЮТЕНОВЫМИ, НЕ СОДЕРЖАТ ГМО и не будут расстраивать чьи-то драгоценные ЧУВСТВА или тонкие ЧУВСТВАДля более подробного обсуждения силовых установок необходимо понимать понятия МОЩНОСТЬ и КРУТЯЩИЙ МОМЕНТ . ОДНАКО, чтобы понять СИЛА , вы должны сначала понять ЭНЕРГИЯ и РАБОТА . Если вы какое-то время не рассматривали эти концепции, было бы полезно сделать это перед изучением этой статьи. НАЖМИТЕ ЗДЕСЬ, чтобы просмотреть обзор «Энергия и работа». Часто кажется, что люди не понимают отношения между МОЩНОСТЬЮ и КРУТЯЩИМ МОМЕНТОМ. Например, мы слышали двигатель строители , консультанты по распределительным валам и другие «технические эксперты » спрашивают клиентов: «Вы хотите, чтобы ваш двигатель производил ЛОШАДИНУЮ МОЩНОСТЬ или КРУТЯЩИЙ МОМЕНТ?» И вопрос обычно задается тоном, который убедительно свидетельствует о том, что эти «эксперты» считают, что мощность и крутящий момент
как-то взаимоисключающие. На самом деле все наоборот, и вы должны четко понимать следующие факты:
л.с. = крутящий момент x об/мин ÷ 5252(внизу этой страницы для всех, кто интересуется, показан вывод этого уравнения). Двигатель производит МОЩНОСТЬ количество КРУТЯЩИЙ МОМЕНТ на нагрузке при заданных об/мин . Величина КРУТЯЩЕГО МОМЕНТА, который может развить двигатель, обычно зависит от оборотов. КРУТЯЩИЙ МОМЕНТ КРУТЯЩИЙ МОМЕНТ определяется как СИЛА вокруг заданной точки, приложенная на РАДИУС от этой точки. Обратите внимание, что единица
КРУТЯЩИЙ МОМЕНТ равен одному фунт-фут (часто неверно указывается), в то время как единица РАБОТА равна одному фут-фунт . Рисунок 1 Ссылаясь на Рисунок 1 , предположим, что рукоятка прикреплена к кривошипу так, что она параллельна поддерживаемой вала и расположен в радиусе 12 дюймов от центра вала. В этом примере считайте, что вал закреплен на стена. Пусть стрелка представляет собой силу в 100 фунтов, приложенную в направлении, перпендикулярном рукоятке и кривошипу, как показано на рисунке. Поскольку вал прикреплен к стене, вал не вращается, но есть крутящий момент из 100 фунт-фут (100 фунтов раз 1 фут) применяется к валу. ПРИМЕЧАНИЕ о том, что ЕСЛИ кривошип на эскизе был в два раза длиннее (т. е. рукоятка располагалась на расстоянии 24 дюйма от центра вал), то же самое усилие в 100 фунтов, приложенное к рукоятке, создаст крутящий момент 200 фунт-фут (100 фунтов на 2 фута). МОЩНОСТЬ МОЩНОСТЬ является мерой того, сколько РАБОТЫ можно выполнить за указанное ВРЕМЯ. Точно так же, как одна тонна представляет собой большое количество веса (по определению, 2000 фунтов), одна лошадиных сил это большая мощность. Определение одной лошадиной силы: 33 000 футо-фунтов в минуту 9.0082 . Сила, которую произвел парень толкая свою машину через участок (8 250 фут-фунтов в минуту), это равно ¼ лошадиной силы (8 250 ÷ 33 000). Хорошо, все хорошо, но как толкание машины через парковку связано с вращающимся механизмом? Рассмотрим следующее изменение в приведенном выше эскизе с рукояткой и кривошипом . Ручка по-прежнему находится в 12 дюймах от центра
вал, но теперь вместо того, чтобы крепиться к стене, вал теперь проходит сквозь стену, опираясь на подшипники качения, и
прикреплен к генератору за стеной. Предположим, как показано на рис. 2 , что постоянная сила в 100 фунтов. каким-то образом применяется к ручке, так что сила всегда перпендикулярна как рукоятке, так и кривошипу, когда кривошип вращается. Другими словами, «стрелка». вращается вместе с рукояткой и остается в том же положении относительно кривошипа и рукоятки, как показано в приведенной ниже последовательности. (Это называется «тангенциальной силой»). Рисунок 2 Если эта постоянная касательная сила в 100 фунтов, приложенная к 12-дюймовой рукоятке (крутящий момент 100 фунт-фут), заставляет вал вращаться со 2000 об/мин, затем мощность вал передает на генератор за стеной 38 л.с. , рассчитывается следующим образом: 100 фунто-футов крутящего момента (100 фунтов x 1 фут) умножить на 2000 об/мин, разделить на 5252 и получить 38 л.с. Следующие примеры иллюстрируют несколько различных значений КРУТЯЩЕГО МОМЕНТА, которые обеспечивают мощность 300 л. с. с.Пример 1 : Какой КРУТЯЩИЙ МОМЕНТ требуется для создания 300 л.с. при 2700 об/мин? , поскольку HP = КРУТЯЩИЙ МОМЕНТ x ОБ/МИН ÷ 5252 Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 2700 = 584 фунт-фут.Пример 2: Какой КРУТЯЩИЙ МОМЕНТ требуется для создания 300 л.с. при 4600 об/мин? Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 4600 = 343 фунт-фут.Пример 3: Какой КРУТЯЩИЙ МОМЕНТ требуется для создания 300 л.с. при 8000 об/мин? Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 8000 = 197 фунто-футов.Пример 4: Какой КРУТЯЩИЙ МОМЕНТ развивает турбинная секция газотурбинного двигателя мощностью 300 л.с. при 41 000 об/мин? Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 41 000 = 38,4 фунт-фут. Пример 5: Выходной вал редуктора двигателя в Примере 4 вращается со скоростью 1591 об/мин. Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 1591 = 991 фунт-фут.(без учета потерь в редукторе, разумеется). Из этих чисел следует сделать вывод, что заданное количество лошадиных сил может быть получено из бесконечного числа комбинаций крутящего момента и оборотов. Подумайте об этом с другой стороны: в автомобилях одинакового веса 2-литровый двигатель с двумя распредвалами, который развивает мощность 300 л.с. при 8000 об/мин (197 фунт-фут) и 400 л.с.
при 10 000 об/мин (210 фунт-фут) выведет вас из поворота так же, как 5-литровый двигатель, который развивает 300 л.с. при 4000 об/мин (394 фунт-фут)
и 400 л.с. при 5000 об/мин (420 фунт-фут). Фактически, в автомобилях одинакового веса меньший двигатель, вероятно, будет ЛУЧШЕ участвовать в гонках, потому что
он намного легче, поэтому на переднюю часть приходится меньше веса. И в реальности машина с более легким 2-литровым двигателем будет
вероятно, весит меньше, чем большой автомобиль с двигателем V8, поэтому он будет лучшим гоночным автомобилем по нескольким причинам. Измерение мощностиДинамометр определяет МОЩНОСТЬ двигателя путем приложения нагрузки к двигателю выходного вала с помощью водяного тормоза, генератора, вихретокового гасителя или любого другого управляемого устройства, способного поглощать сила. Система управления динамометром заставляет амортизатор точно соответствовать количеству TORQUE , которое производит двигатель. в этот момент, то измеряет , что КРУТЯЩИЙ МОМЕНТ и об/мин вала двигателя, а от тех два измерения, он вычисляет наблюдаемых мощности . Затем применяются различные факторы (температура воздуха, барометрическое давление, относительная влажность) для того, чтобы исправить наблюдаемую мощность до значения, которое было бы, если бы оно было измерено при стандартных атмосферных условиях , вызванная скорректированная мощность . Недавнее изменение на этой странице В этом месте страницы раньше был анализ, показывающий, как определить мощность, потребляемую насосом. Общие замечанияЧтобы спроектировать двигатель для конкретного применения, полезно построить оптимальную кривую мощности для этого конкретного применения, затем из этой информации о конструкции определите кривую крутящего момента, которая требуется для получения желаемой кривой мощности. По оценке крутящего момента требования к реалистичным значениям BMEP, вы можете определить разумность целевая кривая мощности. Как правило, пик крутящего момента возникает при значительно более низких оборотах, чем пик мощности. Причина в том, что в целом кривая крутящего момента
не падает (в %) так же быстро, как увеличивается число оборотов в минуту (в %). Для гоночного двигателя часто выгодно (в пределах границ
условия применения) для работы двигателя далеко за пределами пиковой мощности, чтобы обеспечить максимальную среднюю мощность в течение
необходимый диапазон оборотов. Однако для двигателя, который работает в относительно узком диапазоне оборотов, такого как авиационный двигатель, обычно требуется, чтобы двигатель выдает максимальную мощность при максимальных оборотах. Это требует, чтобы пик крутящего момента был достаточно близок к максимальным оборотам. Для самолета двигатель, вы обычно проектируете кривую крутящего момента так, чтобы она достигла максимума при нормальных настройках круиза и оставалась неизменной до максимальных оборотов. Такое позиционирование кривая крутящего момента позволила бы двигателю производить значительно больше мощности, если бы он мог работать на более высоких оборотах, но цель состоит в том, чтобы оптимизировать производительность в рабочем диапазоне. Пример этой концепции показан на рис. 3 ниже. Три пунктирные линии представляют три различные кривые крутящего момента, каждая из которых имеет точное значение
одинаковая форма и значения крутящего момента, но с пиковыми значениями крутящего момента, расположенными при разных значениях оборотов. Рисунок 3 Обратите внимание, что при пиковом крутящем моменте 587 фунт-футов при 3000 об/мин розовая линия мощности достигает максимума около 375 л.с. между 3500 и 3750 об/мин. С та же кривая крутящего момента сдвинута вправо на 1500 об/мин (черный цвет, пик крутящего момента 587 фунт-фут при 4500 об/мин), пиковая мощность подскакивает примерно до 535 л.с. 5000 об/мин. Опять же, перемещение той же кривой крутящего момента вправо еще на 1500 об/мин (синяя, пик крутящего момента 587 фунт-футов при 6000 об/мин) приводит к тому, что мощность снижается. пик около 696 л.с. при 6500 об/мин Используя черные кривые в качестве примера, обратите внимание, что двигатель развивает мощность 500 л.с. как при 4500, так и при 5400 об/мин, что означает, что двигатель может
такое же количество работы в единицу времени (мощность) на 4500, что и на 5400. ОДНАКО, он будет сжигать меньше топлива для производства 450 л. Диапазон оборотов, в котором двигатель развивает максимальный крутящий момент, ограничен. Вы можете настроить двигатель так, чтобы он имел высокий пиковый крутящий момент с очень узкий диапазон или более низкое значение пикового крутящего момента в более широком диапазоне. Эти характеристики обычно диктуются параметрами область применения, для которой предназначен двигатель. Пример показан на рис. 4 ниже. Это то же самое, что и график на рис. 3 (выше), ЗА ИСКЛЮЧЕНИЕМ, синяя кривая крутящего момента имеет
был изменен (как показано зеленой линией), чтобы он не исчезал так быстро. Обратите внимание, как это приводит к увеличению зеленой линии электропередач.
далеко за пределами пика крутящего момента. Такого рода изменение кривой крутящего момента может быть достигнуто путем изменения различных ключевых компонентов, в том числе
(но не ограничиваясь) профили кулачков, расстояние между кулачками, длина впускных и/или выпускных каналов, поперечное сечение впускных и/или выпускных каналов
раздел. Рис.4 x КРУТЯЩИЙ МОМЕНТ ÷ 5252 , тогда где 5252?» Вот ответ. По определению, МОЩНОСТЬ = СИЛА x РАССТОЯНИЕ ÷ ВРЕМЯ СИЛА рубрика) Используя пример на рисунке 2 выше, где постоянная тангенциальная сила в 100 фунтов была приложена к 12-дюймовой рукоятке, вращающейся со скоростью 2000 об/мин, мы знаем силу задействованную, поэтому для расчета мощности нам нужно расстояние рукоятка перемещения на единицу время , выраженное как: Мощность = 100 фунтов x расстояние в минуту Хорошо, на какое расстояние рукоятка перемещается за одну минуту? Сначала определите расстояние, которое он проходит за один оборот : РАССТОЯНИЕ за оборот = 2 x π x радиус РАССТОЯНИЕ за оборот. Теперь мы знаем, как далеко шатун перемещается за один оборот. Какое расстояние проходит кривошип за одну минуту ? РАССТОЯНИЕ в мин. = 6,283 фута на оборот. х 2000 об. в мин. = 12 566 футов в минуту Теперь мы знаем достаточно, чтобы рассчитать мощность, определяемую как: МОЩНОСТЬ = СИЛА x РАССТОЯНИЕ ÷ ВРЕМЯ Отлично, а как насчет ЛОШАДЕЙ? Помните, что одна ЛОШАДЕЙНАЯ СИЛА определяется как 33000 футо-фунтов работы. в минуту . Следовательно, HP = МОЩНОСТЬ (фут-фунт в минуту) ÷ 33 000. Мы уже подсчитали, что мощность, приложенная к кривошипа выше составляет 1 256 600 футо-фунтов в минуту. Сколько это HP? л.с. = (1 256 600 ÷ 33 000) = 38,1 л.с. Теперь мы объединим уже известные нам вещи, чтобы создать волшебное число 5252. Мы уже это знаем: КРУТЯЩИЙ МОМЕНТ = СИЛА x РАДИУС. Если мы разделим обе части этого уравнения на РАДИУС, мы получим: (a) СИЛА = КРУТЯЩИЙ МОМЕНТ ÷ РАДИУС Теперь, если РАССТОЯНИЕ за оборот = РАДИУС x 2 x π, тогда (b) РАССТОЯНИЕ в минуту = РАДИУС x 2 x π x об/мин Мы уже знаем (c) МОЩНОСТЬ = СИЛА x РАССТОЯНИЕ в минуту Итак, если мы подставим эквивалент СИЛЫ из уравнения (a) и расстояние в минуту из уравнение (б) в уравнение (в), получаем: МОЩНОСТЬ = (МОМЕНТ ÷ РАДИУС) x (ОБ/МИН x РАДИУС x 2 x π) Разделив обе стороны на 33 000, чтобы найти л.с., л.с. Снижение, мы получаем л.с. = крутящий момент x об / мин x 6,28 ÷ 33 000 с 33 000 ÷ 6,2832 = 5252 Следовательно, л.с. . При любых оборотах ниже 5252 значение крутящего момента больше, чем значение HP; Выше 5252 об/мин значение крутящего момента меньше значения л.с. << Вернуться к: Содержание Перейти к началу страницы ↑ Следующая тема: Тепловая эффективность >> |
Что такое уравнение крутящего момента?
Уравнение для крутящего момента можно представить следующим уравнением: τ = F * rsin(θ).
T — вектор крутящего момента, F — заданная сила, r — длина плеча момента, а θ — угол между плечом момента и вектором силы. Это основное уравнение для расчета крутящего момента, но чтобы понять это уравнение, давайте рассмотрим крутящий момент более подробно, чтобы понять, что он собой представляет и как он измеряется.
Что такое крутящий момент?
Крутящий момент — это сила, которая перемещает объект под углом, или сила, которая заставляет данный объект увеличивать угловое ускорение. Иными словами, крутящий момент — это измеряемая сила, которая перемещает объект вокруг оси. Это аналогично тому, как сила является мерой ускорения объекта в линейной кинематике, но вместо этого она измеряет угловое ускорение. Крутящие моменты измеряются в векторах, и направление вектора зависит от направления через ось, в которой распространяется сила.
Фото: susannp4 через Pixabay, CC0
Один из самых простых способов проиллюстрировать крутящий момент на примере изучения движения двери, когда вы ее открываете. Когда вы собираетесь открыть дверь, вы кладете руку на ручку и толкаете/тянете ее, так что это означает, что вы прилагаете силу к двери в точке пространства, наиболее удаленной от петли. Если вы хотите попытаться открыть дверь, нажав на сторону двери, ближайшую к петле, вам потребуется гораздо больше усилий, чтобы сделать это. Таким образом, хотя дверь по-прежнему будет двигаться на ту же величину, одно действие потребует гораздо меньшего усилия, чем другое действие. Сила, которая используется для создания движения открывания двери, называется крутящим моментом.
Когда вы собираетесь открыть дверь, вы кладете руку на ручку и толкаете/тянете ее, так что это означает, что вы прилагаете силу к двери в точке пространства, наиболее удаленной от петли. Если вы хотите попытаться открыть дверь, нажав на сторону двери, ближайшую к петле, вам потребуется гораздо больше усилий, чтобы сделать это. Таким образом, хотя дверь по-прежнему будет двигаться на ту же величину, одно действие потребует гораздо меньшего усилия, чем другое действие. Сила, которая используется для создания движения открывания двери, называется крутящим моментом.
При измерении крутящего момента он может быть динамическим или статическим. Статический крутящий момент — это крутящий момент, который не приводит к ускорению относительно оси, сила, которая не может вызвать угловое ускорение. Если бы дверь, которую вы пытаетесь открыть, была закрыта, а вы нажимали на нее, это был бы статический крутящий момент. В то время как сила будет приложена к двери, дверные петли не вращаются, и, таким образом, крутящий момент является статическим. Между тем, примером динамического крутящего момента является запуск вашего автомобиля и вождение. Когда вы ускоряетесь, это пример динамического крутящего момента, поскольку создается угловое ускорение, и колеса вашего автомобиля перемещают его из одного положения в другое.
Между тем, примером динамического крутящего момента является запуск вашего автомобиля и вождение. Когда вы ускоряетесь, это пример динамического крутящего момента, поскольку создается угловое ускорение, и колеса вашего автомобиля перемещают его из одного положения в другое.
В целях пояснения отметим, что «крутящий момент» — не единственный способ описать силу, вызывающую угловое ускорение. Иногда инженеры могут использовать термин «импульс силы» или просто «импульс» вместо крутящего момента. «Рычаг момента» — это радиус, на который действует приложенная сила, от точки вращения до точки приложения силы.
Как рассчитывается крутящий момент
Фото: Кришнаведала — собственная работа, CC0, https://commons.wikimedia.org/w/index.php?curid=20311913
Теперь, когда мы определили крутящий момент, понять уравнение для расчета крутящего момента стало немного проще. Давайте еще раз взглянем на уравнение для крутящего момента:
τ = F * rsin(θ)
T представляет собой вектор крутящего момента, создаваемого определенной силой, которая представлена F. Переменная r представляет собой длину плеча момента, а Theta заключается в том, что угол, найденный между плечом импульса и вектором силы. Для определения направления вектора крутящего момента можно использовать простую эвристику, получившую название «правило захвата правой рукой». Если вы согните правую руку вокруг оси вращения, сомкнув пальцы вокруг вектора, представляющего направление силы, то вектор крутящего момента будет указывать в направлении вашего большого пальца.
Переменная r представляет собой длину плеча момента, а Theta заключается в том, что угол, найденный между плечом импульса и вектором силы. Для определения направления вектора крутящего момента можно использовать простую эвристику, получившую название «правило захвата правой рукой». Если вы согните правую руку вокруг оси вращения, сомкнув пальцы вокруг вектора, представляющего направление силы, то вектор крутящего момента будет указывать в направлении вашего большого пальца.
Крутящий момент измеряется с помощью ньютонометра, измерения крутящего момента используются в системе единиц СИ. В имперской системе часто используется соотношение фут-фунт, хотя это несколько сложнее интерпретировать, чем систему ньютон-метров, потому что термин «фунт» имеет разговорное значение как единица массы в дополнение к единице силы. . Фунт здесь относится к фунт-силе или силе, действующей на объект весом 1 фунт под действием силы тяжести Земли. Поскольку 1,7 футо-фунта примерно эквивалентны одному ньютон-метру, измерения величины в основном такие же, когда это учитывается.
При измерении статического крутящего момента в стационарной среде без вращения необходимо принять во внимание некоторые дополнительные соображения. Этого можно достичь, взяв длину импульсного плеча и непосредственно найдя крутящий момент, что намного проще, чем измерение крутящего момента во вращающейся системе. Для измерения крутящего момента во вращающейся системе существуют различные методы, но общепринятая система измерения заключается в количественном определении деформации металла внутри приводного вала, который отвечает за передачу крутящего момента.
Как крутящий момент влияет на кинематику вращения
Как упоминалось ранее, крутящий момент можно считать эквивалентным силе в линейной кинематике. Второй закон Ньютона о движении и линейной кинематике представлен уравнением F = ma (сила = масса x ускорение).
В кинематике вращения есть эквивалентное уравнение: r = Ia.
Переменная «а» здесь представляет собой угловое ускорение, а инерция вращения системы представлена переменной «I». Вращательная инерция зависит от того, как распределена масса системы, и по мере увеличения значения I объекту становится все труднее набирать угловое ускорение.
Вращательная инерция зависит от того, как распределена масса системы, и по мере увеличения значения I объекту становится все труднее набирать угловое ускорение.
Понимание вращательного равновесия
Если вращательное равновесие можно считать эквивалентным уравнению силы в линейной кинематике, то отсюда следует, что объект, который неподвижен и не вращается, останется в этом состоянии, если к нему не будет приложен внешний крутящий момент. Отсюда также следует, что только внешний крутящий момент может изменить вращение объекта, который вращается с постоянной угловой скоростью. Равновесие вращения — полезная концепция при попытке определить, как несколько различных крутящих моментов влияют на вращающийся объект. Чтобы выяснить вращение объекта, на который воздействует несколько крутящих моментов, необходимо рассчитать чистый крутящий момент. Объект будет находиться в равновесии вращения, если чистый крутящий момент равен нулю, и объект не может ускоряться.
Разъяснение крутящего момента, мощности и энергии
Людей часто смущает взаимосвязь между энергией, мощностью и крутящим моментом. Например, термин «мощность вращения» часто применяется для описания крутящего момента двигателя, но хотя энергию и крутящий момент можно количественно определить, используя одни и те же основные единицы, они не описывают одно и то же явление. В то время как мощность может быть применена к невращающимся системам, крутящий момент применим только к вращающейся системе. Можно рассчитать мощность по значению крутящего момента, если скорость вращения системы была определена. На самом деле мощность обычно определяется путем расчета скорости вращения и крутящего момента, а не измеряется напрямую.
Например, термин «мощность вращения» часто применяется для описания крутящего момента двигателя, но хотя энергию и крутящий момент можно количественно определить, используя одни и те же основные единицы, они не описывают одно и то же явление. В то время как мощность может быть применена к невращающимся системам, крутящий момент применим только к вращающейся системе. Можно рассчитать мощность по значению крутящего момента, если скорость вращения системы была определена. На самом деле мощность обычно определяется путем расчета скорости вращения и крутящего момента, а не измеряется напрямую.
Чтобы сделать это более понятным, давайте взглянем на уравнения для мощности:
P = (сила x расстояние)/время = (F x 2πr)/t = 2 ππw (оборотов в секунду)
Макс. крутящий момент часто упоминается как важный статистический показатель при предоставлении технических характеристик автомобиля, а также его мощность в лошадиных силах. Максимальный крутящий момент влияет на ускорение автомобиля, а также на его тяговую способность. Максимальная скорость транспортного средства, а не ускорение, больше зависит от мощности, чем от крутящего момента по отношению к весу транспортного средства.
Максимальная скорость транспортного средства, а не ускорение, больше зависит от мощности, чем от крутящего момента по отношению к весу транспортного средства.
Общее движение транспортного средства определяется большим количеством факторов, а не только максимальной мощностью и крутящим моментом транспортного средства, поэтому, хотя знание максимальной мощности и крутящего момента транспортного средства упростит получение определенных спецификаций и расчетов, при определении общего количества транспортных средств необходимо собрать гораздо больше переменных. маневренность. В действительности и мощность, и крутящий момент могут варьироваться в зависимости от скорости вращения, и разные двигатели могут иметь разные отношения между крутящим моментом и скоростью вращения, часто нелинейные отношения.
Изменение уровней крутящего момента
Фото: TheDigitalArtist через Pixabay, CC0
Для различных приложений, использующих угловой момент, часто требуются разные уровни крутящего момента, поэтому уровни крутящего момента должны быть увеличены или уменьшены в соответствии с требованиями проекта. Длина рычага — это то, что уменьшает или увеличивает силу, действующую на объект, по отношению к расстоянию, на которое толкается рычаг. Если вы замечали сходство между крутящим моментом и силой, вы можете догадаться, что крутящий момент, создаваемый двигателем, можно изменить с помощью аналогичного предмета, похожего на рычаг.
Длина рычага — это то, что уменьшает или увеличивает силу, действующую на объект, по отношению к расстоянию, на которое толкается рычаг. Если вы замечали сходство между крутящим моментом и силой, вы можете догадаться, что крутящий момент, создаваемый двигателем, можно изменить с помощью аналогичного предмета, похожего на рычаг.
Использование зубчатой передачи может уменьшить или увеличить крутящий момент двигателя, увеличивая крутящий момент по мере уменьшения скорости вращения. Две шестерни, сталкивающиеся друг с другом, по существу действуют как два рычага, толкающие друг друга. Одним из наиболее наглядных примеров передач, влияющих на крутящий момент объекта, являются передачи велосипеда, позволяющие велосипеду развивать полезную скорость без особых усилий со стороны гонщика.
Использование уравнений крутящего момента — AP Physics C: Mechanics
All AP Physics C: Mechanics Resources
2 диагностических теста 92 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
AP Physics C: Mechanics Help » Экзамен по механике » Движение » Круговое и вращательное движение » Вращательное движение и крутящий момент » Использование уравнений крутящего момента
Объект выходит из состояния покоя и ускоряется до угловой скорости за три секунды при постоянном крутящем моменте . Сколько оборотов сделал объект за это время?
Сколько оборотов сделал объект за это время?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку он испытывает постоянный крутящий момент и постоянное угловое ускорение, угловое смещение можно рассчитать, используя:
Угловое ускорение легко рассчитать, используя угловую скорость и время:
Используя это значение, мы можем найти угловое смещение:
Преобразование углового смещения в обороты путем погружения с помощью :
Сообщить об ошибке
На круговой диск радиусом 0,5 м и массой 3 кг действует сила 25 Н, приложенная перпендикулярно его краю, заставляющая его вращаться. Чему равно угловое ускорение диска?
Возможные ответы:
Правильный ответ:
Пояснение:
Мы можем найти угловое ускорение, используя вращательное движение, эквивалентное второму закону Ньютона. При вращательном движении крутящий момент является произведением момента инерции и углового ускорения:
При вращательном движении крутящий момент является произведением момента инерции и углового ускорения:
Момент инерции для круглого диска:
Крутящий момент — это произведение силы на расстояние (в данном случае на радиус):
. Мы можем подставить их в наше первое уравнение:
Упростите и перекомпонуйте, чтобы вывести уравнение для углового ускорения:
Используйте полученные значения для решения:
Сообщите об ошибке в горизонтальной плоскости, параллельной верхней части стола. На измерительную линейку в разных местах действуют четыре силы одинаковой величины. На рисунке ниже показан вид на измерительную линейку сверху.
Можно предположить, что силы и приложены к центру измерительной палочки, а силы и приложены к концу, противоположному гвоздю.
Какова связь между величинами крутящих моментов на измерительной линейке, вызванных четырьмя различными силами?
Возможные ответы:
Правильный ответ:
Объяснение:
Крутящий момент определяется как,
Поскольку все силы равны по величине, на величину крутящего момента влияет радиус r и угол тета между радиусом и силой.
для,
для,
для,
для,
Объединение этой информации дает отношения,
Сообщение о ошибке
Человек подходит на конце. длинная однородная металлическая балка длиной . Масса человека составляет , а масса балки – .
Какова величина чистого крутящего момента на доске относительно закрепленного конца балки? Используйте гравитацию.
Возможные ответы:
Правильный ответ:
Объяснение:
Чистый крутящий момент на балке получается путем сложения крутящих моментов, вызванных весом человека и весом самой балки, каждый на соответствующем расстоянии от конца балки:
Присвоим направление положительного крутящего момента в направлении крутящих моментов веса человека и балки, отметив, что они будут складываться, поскольку оба они указывают в одном направлении.
Мы можем еще больше упростить, скомбинировав подобные термины:
Используя заданные числовые значения,
Сообщить об ошибке
таким образом, чтобы морская пила балансировала идеально горизонтально. Дочерний элемент слева – это точка опоры.
Какова масса второго ребенка, если он сядет от оси вращения?
Возможные ответы:
Правильный ответ:
Объяснение:
Анализ крутящего момента уместен в этой ситуации из-за включения расстояний от заданной точки поворота. Как правило,
Это статическая ситуация. Есть два крутящих момента вокруг оси, вызванные весом двух детей. Заметим, что эти веса вызывают крутящие моменты в противоположных направлениях относительно оси вращения, так что
Следовательно,
Или проще:
Решение для ,
Сообщить об ошибке Ее масса . Длинная доска имеет массу .
Длинная доска имеет массу .
Рассчитайте силу, которую правая опора оказывает вверх, если она стоит с правого конца. Используйте гравитацию.
Возможные ответы:
Правильный ответ:
Объяснение:
Анализ крутящего момента уместен в этой ситуации из-за включения расстояний от заданной точки поворота. Как правило,
Это статическая ситуация. Таким образом, можно выбрать любую точку разворота, относительно которой можно выполнить анализ крутящего момента. Самый быстрый способ найти неизвестную силу, указанную в вопросе, — это провести анализ крутящего момента относительно левого конца доски. Вокруг этого шарнира действуют три крутящих момента: два по часовой стрелке, вызванные весом гимнаста и самой планки, и один против часовой стрелки, вызванный силой правой опоры. Обозначая по часовой стрелке как положительное,
, следовательно,
Это упрощает до
Решение для,
Решение с численными значениями,
Отчет о ошибке
. Квадратные значения и масса с массой с массой и с массой. возможных осей вращения.
Квадратные значения и масса с массой с массой и с массой. возможных осей вращения.
Какое из утверждений о соотношениях между моментами инерции верно?
Возможные ответы:
Правильный ответ:
Объяснение:
Моменты инерции для обеих осей и равны, поскольку обе эти оси проходят через центр масс.
Согласно теореме о параллельных осях для моментов инерции (), момент инерции для оси больше, чем или
, потому что она расположена на расстоянии
от центра масс.
Сообщить об ошибке
Улавливатель ветра создается путем прикрепления четырех пластиковых чаш с массой к концам четырех легких стержней, которые затем прикрепляются к центральному стержню, который может свободно вращаться на ветру. Четыре легких стержня имеют длину , , и .
Рассчитайте момент инерции четырех чаш относительно центрального стержня. Вы можете считать чаши точечными массами.
Вы можете считать чаши точечными массами.
Возможные ответы:
Правильный ответ:
Пояснение:
Момент инерции точечной массы равен .
Чтобы рассчитать общий момент инерции, мы добавляем момент инерции для каждой части объекта, так что
Массы чашек в этой задаче равны, так что это упрощается до
Подстановка и решение с числовыми значениями,
Сообщить об ошибке
Длинный однородный тонкий стержень длиной имеет массу .
Рассчитайте момент инерции вращения вокруг оси, перпендикулярной ее длине, проходящей через точку с одного из ее концов.
Возможные ответы:
Правильный ответ:
Объяснение:
Для длинного тонкого стержня относительно его центра масс:
Согласно теореме о параллельных осях,
ось параллельна точке, проходящей через центр масс. Для этой задачи является разницей между заданным расстоянием и половиной длины стержня.
Для этой задачи является разницей между заданным расстоянием и половиной длины стержня.
Сочетание вышеуказанного,
Ввод числовых значений,
Сообщить об ошибке
Определен момент инерции длинного тонкого стержня относительно его конца.
Каково новое значение, если и масса, и длина стержня уменьшены в ?
Возможные ответы:
Правильный ответ:
Пояснение:
Момент инерции длинного однородного тонкого стержня относительно его конца равен
При уменьшении массы и длины в четыре раза в уравнение вводятся следующие множители:
Упрощение,
Сообщить об ошибке
All AP Physics C: Ресурсы по механике
2 диагностических теста 92 практических теста Вопрос дня Карточки Учитесь по концепции
Формулы мощности — крутящий момент, скорость, зубчатые редукторы
Предыдущий раздел «Сетевые дроссели и изолирующие трансформаторы привода» • Вернуться к индексу • Далее «Переходные процессы и электрические шумы в приводных устройствах»
л. с. = с. = | ТН 63000 | Где: | T = крутящий момент в (фунт-дюйм) Н = Базовая скорость (об/мин) |
—————————————————————————————
| HP = | ТН 5250 | Где: | T = крутящий момент в (фунт-фут) N = базовая скорость (об/мин) |
РАСЧЕТ МОЩНОСТИ ДЛЯ НАМОТЧИКОВ С ЦЕНТРАЛЬНЫМ ПРИВОДОМ:
| л.с. = | ТВ х Б/У 33000 | Где: | T = натяжение полотна (фунты) В = линейная скорость (фут/мин) Б/У = коэффициент накопления = | полный диаметр рулона диаметр сердцевины |
МОМЕНТ УСКОРЕНИЯ: РАСЧЕТ
Когда машину необходимо разогнать до заданной скорости за определенное время, системе привода HP может потребоваться дополнительный крутящий момент во время ускорения, чтобы компенсировать инерцию нагрузки.


 также
также также
также