Вращающий момент | это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила».
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться.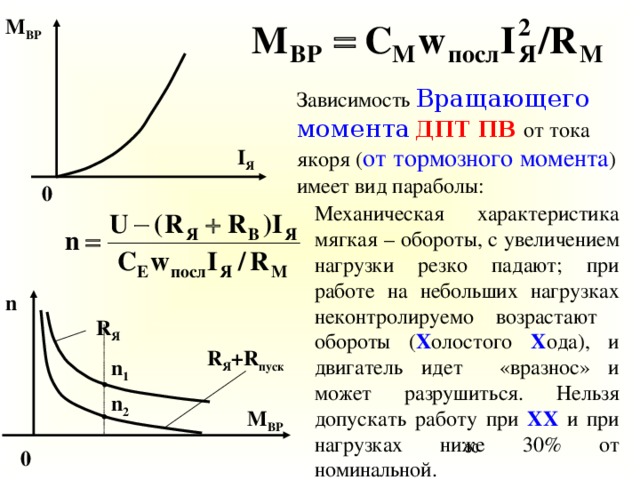 Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- =
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Вращающий момент | это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .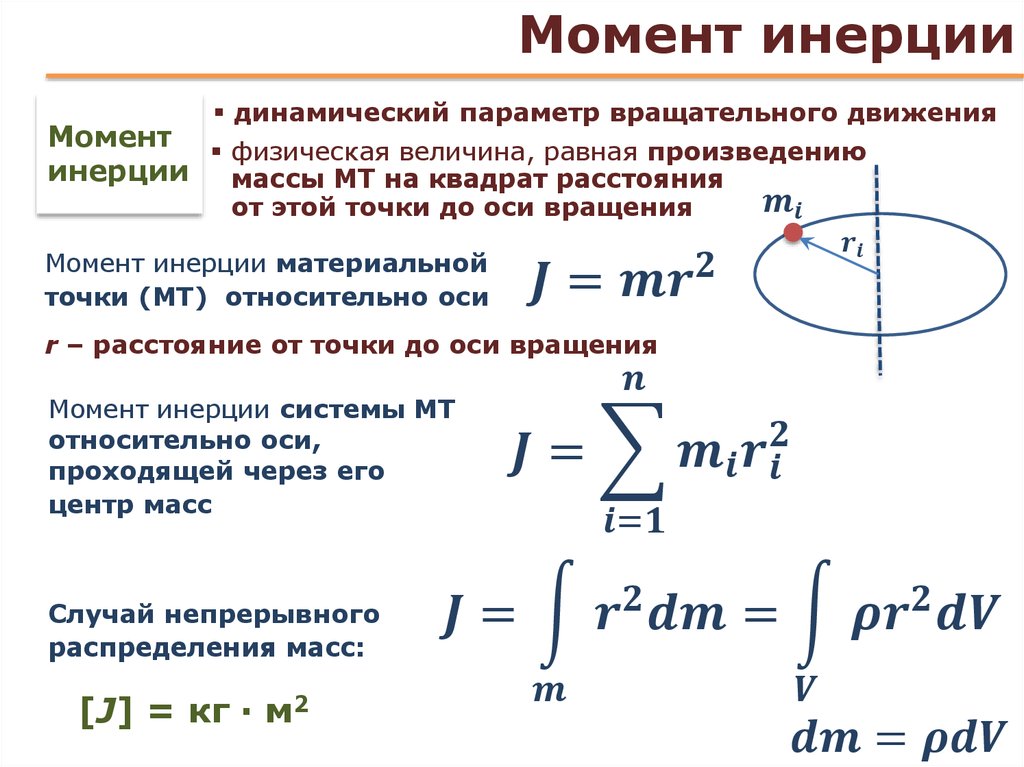
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.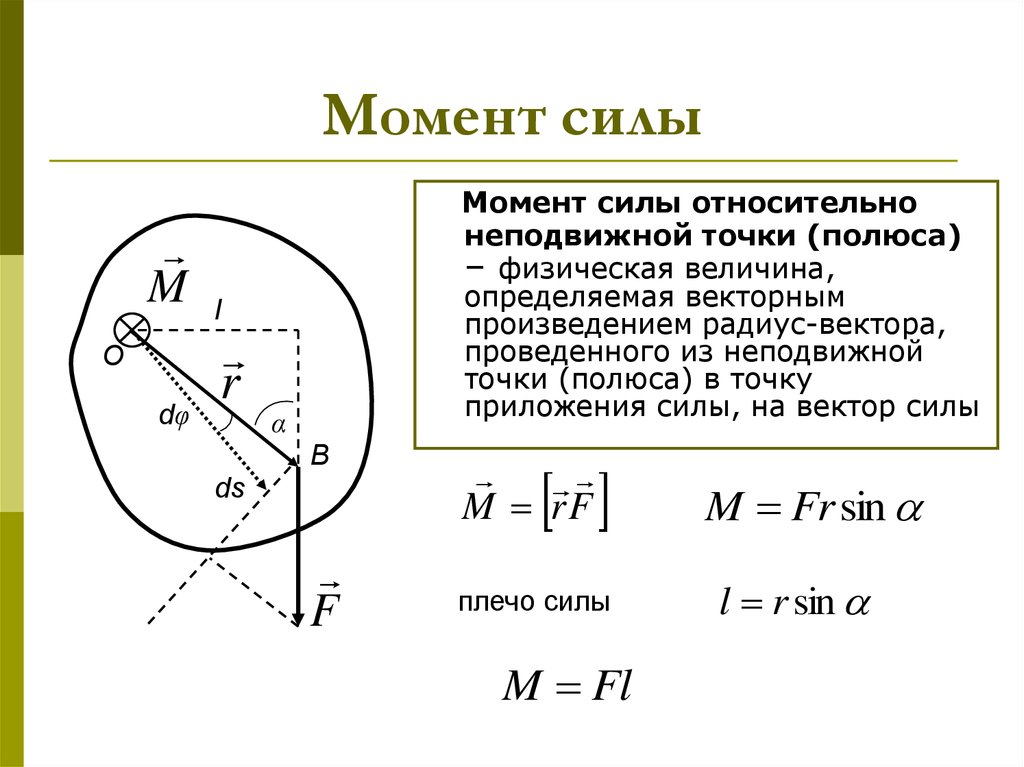
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Вращающий момент | это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.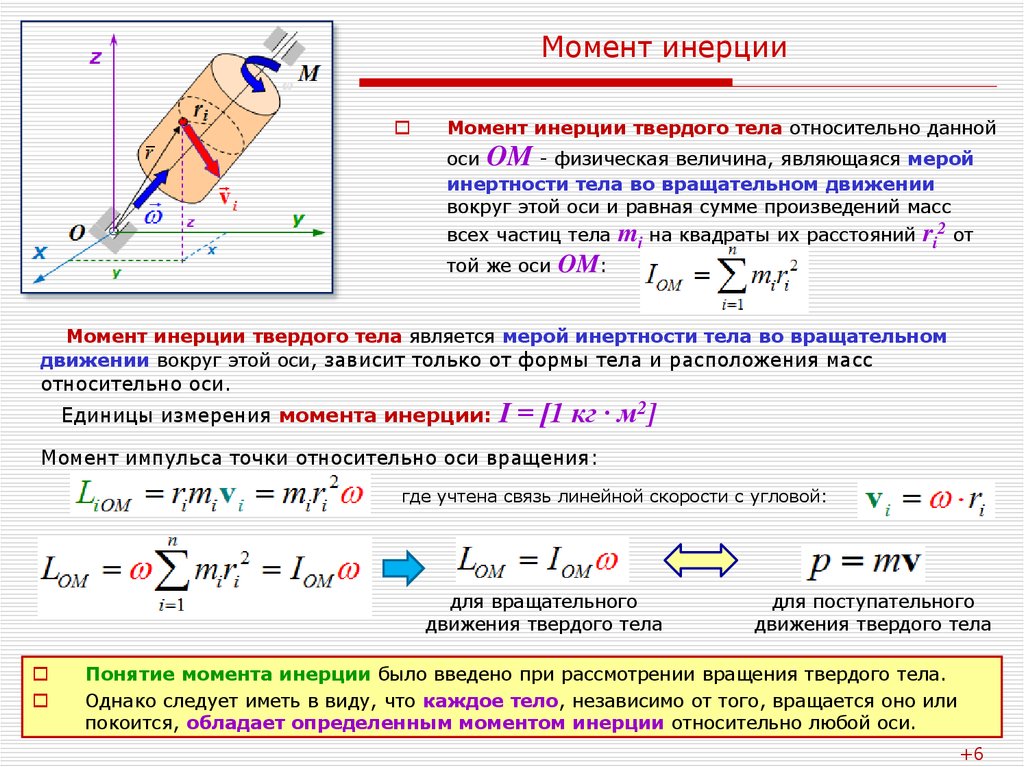
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
7.2: Классическая механика
Область классической механики включает изучение тел в движении, особенно физические законы, касающиеся тел, находящихся под воздействием сил. Большинство механических аспектов проектирования роботов тесно связано с концепциями из этой области. В данном блоке описываются несколько ключевых применяемых концепций классической механики.
СКОРОСТЬ — это мера того, насколько быстро перемещается объект. Обозначает изменение положения во времени (проще говоря, какое расстояние способен преодолеть объект за заданный период времени). Данная мера представлена в единицах расстояния, взятых в единицу времени, например, в количестве миль в час или футов в секунду.
ЧАСТОТА ВРАЩЕНИЯ – Скорость может также выражаться во вращении, то есть насколько быстро объект движется по кругу. Измеряется в единицах углового перемещения во времени (то есть в градусах в секунду), или в циклах вращения в единицу времени (например, в оборотах в минуту). Когда измерения представлены в оборотах в минуту (RPM), речь идет о частоте вращения. Есть речь идет об об/мин автомобильного двигателя, это означает, что измеряется скорость вращения двигателя.
Когда измерения представлены в оборотах в минуту (RPM), речь идет о частоте вращения. Есть речь идет об об/мин автомобильного двигателя, это означает, что измеряется скорость вращения двигателя.
УСКОРЕНИЕ – Изменение скорости во времени представляет собой ускорение. Чем больше ускорение, тем быстрее изменяется скорость. Если автомобиль развивает скорость от 0 до 60 миль в час за две секунды, в этом случае ускорение больше, чем когда он развивает скорость от 0 до 40 миль в час за тот же период времени. Ускорение — это мера изменения скорости. Отсутствие изменения означает отсутствие ускорения. Если объект движется с постоянной скоростью — ускорение отсутствует.
СИЛА — Ускорение является следствием воздействия сил, которые провоцируют изменение в движении, направлении или форме. Если вы нажимаете на объект, это означает, что вы прикладываете к нему силу. Робот ускоряется под воздействием силы, которую его колеса прикладывают к полу. Сила измеряется в фунтах или ньютонах.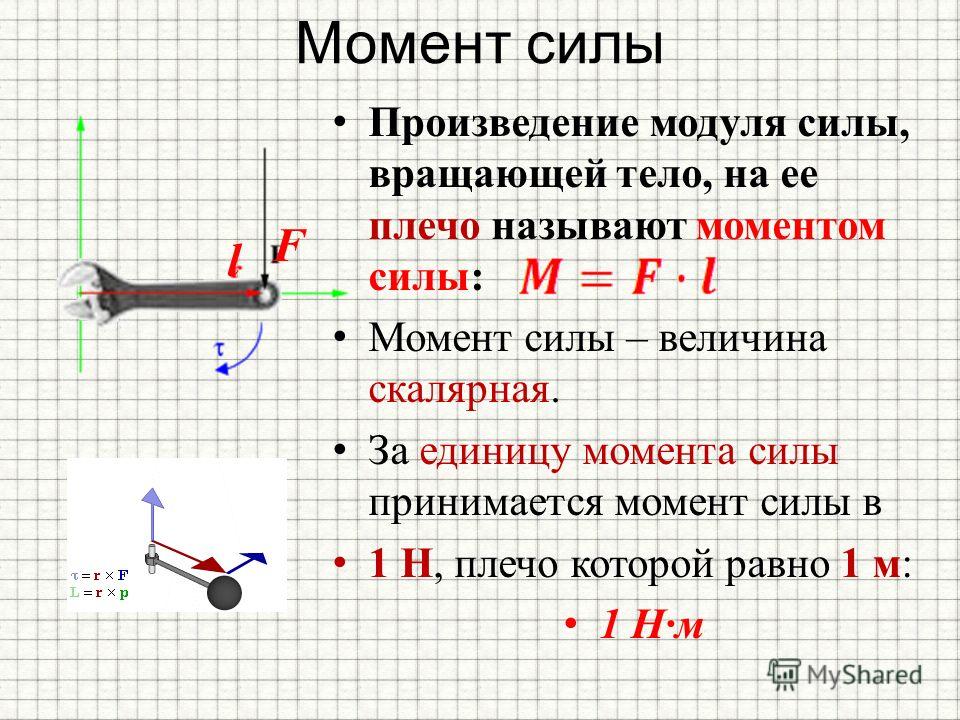
Например, масса объекта воздействует на объект как сила вследствие гравитации (ускорение объекта в направлении центра Земли).
КРУТЯЩИЙ МОМЕНТ – Сила, направленная по кругу (вращение объекта), называется крутящим моментом. Крутящий момент — это вращающая сила. Если к объекту приложен крутящий момент, на границе первого возникает линейная сила. В примере с колесом, катящемся по земле, крутящий момент, приложенный к оси колеса, создает линейную силу на границе покрышки в точке ее контакта с поверхностью земли. Так и определяется крутящий момент — как линейная сила на границе круга. Крутящий момент определяется величиной силы, умноженной на расстояние от центра вращения (Сила х Расстояние = Крутящий момент). Крутящий момент измеряется в единицах силы, умноженной на расстояние, например, фунто-дюймах или ньютон-метрах.
В примере с колесом, катящемся по земле, если известен крутящий момент, приложенный к оси с закрепленным на ней колесом, мы можем рассчитать количество силы, прикладываемой колесом к поверхности. В этом случае, радиус колеса является расстоянием силы от центра вращения.
В этом случае, радиус колеса является расстоянием силы от центра вращения.
Сила = Крутящий момент/Радиус колеса
В примере с рукой робота, удерживающей объект, мы можем рассчитать крутящий момент, требуемый для поднятия объекта. Если объект обладает массой, равной 1 ньютону, а рука имеет длину 0,25 метра (объект располагается на расстоянии 0,25 метра от центра вращения), тогда
Крутящий момент = Сила х Расстояние = 1 ньютон х 0,25 метра = 0,25 ньютон-метров.
Это означает, что для удержания объекта в неподвижном положении, необходимо применить крутящий момент, равный 0,25 ньютон-метров. Чтобы переместить объект вверх, роботу необходимо приложить к нему крутящий момент, значение которого будет превышать 0,25 ньютон-метров, так как необходимо преодолеть силу гравитации. Чем больше крутящий момент робота, тем больше силы он прикладывает к объекту, тем больше ускорение объекта, и тем быстрее рука поднимет объект.
Пример 7.2
Пример 7.3
Для данных примеров, мы можем рассчитать крутящий момент, необходимый для подъем этих объектов.
Пример 7.2 — Крутящий момент = Сила х Расстояние = 1 ньютон х 0,125 метра = 0,125 ньютон-метров.
Для данного примера, длина рука равна половине длины руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза меньше. Значение длины руки пропорционально значению требуемого крутящего момента. При равных исходных характеристиках объекта, чем короче рука, тем меньший крутящий момент необходим для подъема.
Пример 7.3 — Крутящий момент = Сила * Расстояние = 1 ньютон х 0,5 метра = 0,5 ньютон-метров.
Для данного примера, длина рука равна удвоенной длине руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза больше.
Еще одна точка зрения относительно ограниченного крутящего момента в соединении руки робота заключается в следующем: более короткая рука сможет поднять объект большей массы, чем более длинная рука; однако, для первой доступная высота подъема объекта будет меньше, чем для второй.
Пример 7.4
Пример 7. 5
5
Эти примеры иллюстрируют руку робота, поднимающую объекты разной массы. Какова взаимосвязь с требуемым количеством крутящего момента?
Пример 4 — Крутящий момент = Сила х Расстояние = ½ ньютона х 0,25 метра = 0,125 ньютон-метров.
Пример 5 — Крутящий момент = Сила х Расстояние = 2 ньютона х 0,25 метра = 0,5 ньютон-метров.
Эти примеры иллюстрируют уменьшение значения требуемого крутящего момента по мере снижения массы объекта. Масса пропорциональна крутящему моменту, необходимому для ее подъема. Чем тяжелее объект, тем больше крутящий момент, требуемый для его подъема.
Проектировщики роботов должны обратить внимание на ключевые взаимосвязи между значениями крутящего момента, длины руки и массы объекта.
РАБОТА – Мера силы, приложенной на расстоянии, называется работой. Например, для удерживания объекта необходимо 10 фунтов силы. Далее, чтобы поднять этот объект на высоту 10 дюймов, требуется определенное количество работы. Количество работы, требуемое для подъема объекта на высоту 20 дюймов, удваивается. Работа также понимается как изменение энергии.
Работа также понимается как изменение энергии.
МОЩНОСТЬ — Большинство людей полагает, что мощность является термином из области электрики, но мощность также относится и к механике.
Мощность — это количество работы в единицу времени. Насколько быстро кто-то может выполнить работу?
В робототехнике принято понимать мощность как ограничение, так как соревновательные робототехнические системы имеют ограничения в части выходной мощности. Если роботу требуется поднять массу в 2 ньютона (прилагая 2 ньютона силы), скорость подъема будет ограничиваться количеством выходной мощности робота. Если робот способен произвести достаточное количество мощности, он сможет быстро поднять объект. Если он способен произвести лишь малое количество энергии, подъем объекта будет производиться медленно (либо не будет производиться вообще!).
Мощность определяется как Сила, умноженная на Скорость (насколько быстро выполняется толчок при постоянной скорости), и обычно выражается в Ваттах.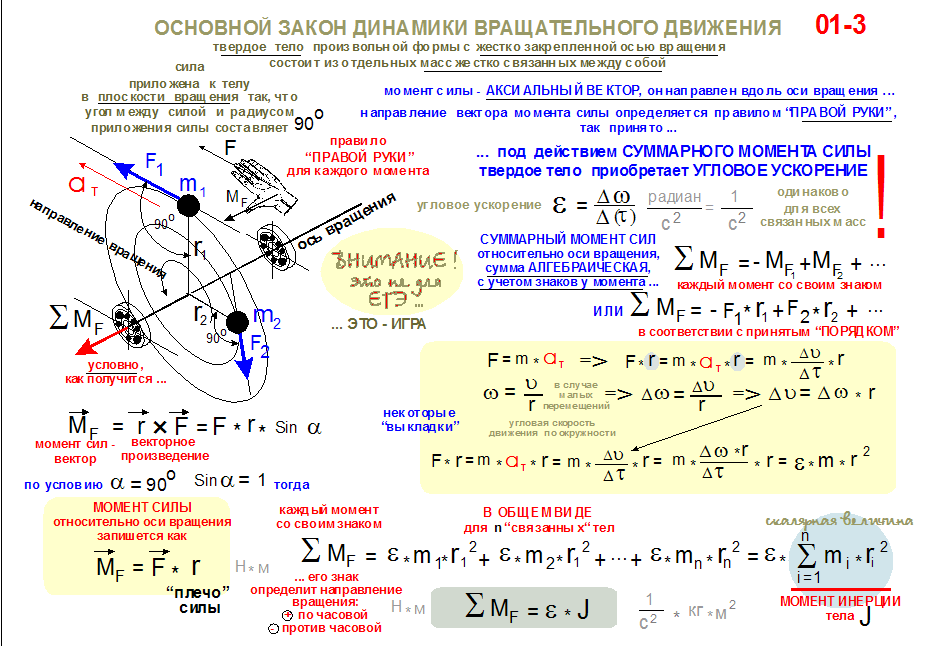
Мощность [Ватты] = Сила [Ньютоны] х Скорость [Метры в секунду]
1 Ватт = 1 (Ньютон х Метр) / Секунда
Как это применяется в соревновательной робототехнике? К проектам роботов применяются определенные ограничения. Проектировщики соревновательных роботов, использующие систему проектирования VEX Robotics Design, также должны учитывать физические ограничения, связанные с применением электромоторов. Электромотор обладает ограниченной мощностью, поэтому он может производить только определенное количество работы с заданной скоростью.
Примечание: все перспективные концепции имеют базовое описание. Более глубоко обсуждать эти физические свойства учащиеся будут в процессе обучения в ВУЗах, если выберут область STEM в качестве направления обучения.
Пусковой момент электродвигателя
В процессе перехода механизма из состояния статики в состояние активности, на обмотки мотора начинает поступать номинальное напряжение, имеющее стандартную частоту. Именно тогда асинхронник может потребить наибольший объем энергии.
Под пусковым крутящим моментом мотора понимается момент его вращения в то время, как ротор остается статичным, а частота и напряжение переменного тока остаются номинальными. ПМ электромотора называется процесс развития повышенного вращающего момента.
Чтобы выявить показатель пускового момента, существует формула, которая предполагает использование кратности пм. Эта величина указывается в паспорте устройства. Чтобы определить величину пм асинхронника, нужно применить формулу:
Повышенных цифр на индикаторах пускового тока лучше не допускать в процессе запуска мотора, поскольку это может способствовать недостатку энергии, требующейся для корректной работы всех прочих систем и механизмов. Чтобы свести к минимуму значение тока пуска рационально применять пм по типу звезда и треугольник. Такие схемы более всего распространены при подключении электрических моторов.
Пусковой момент АЭД с фазным ротором обусловлен показателями по активному сопротивлению регулируемых резисторов, оказавшихся выведенными в роторную цепь. У асинхронников с короткозамкнутым ротором пусковой момент характеризуется наибольшим показателем. Но при этом существенно снижается показатель пускового тока.
У асинхронников с короткозамкнутым ротором пусковой момент характеризуется наибольшим показателем. Но при этом существенно снижается показатель пускового тока.
Проверка электродвигателя по пусковому моменту проводится, учитывая динамическую нагрузку от маховых масс конструкции и дополнительного момента, который создается при помощи силы трения.
Короткозамкнутые асинхронные двигатели с повышенным пм имеют особенную конструкцию ротора. Эти свойства характерны для двигателей, имеющих двухклеточные и глубокопазные роторы.
Пусковой момент АЭД при уменьшении напряжения в 2 раза тоже уменьшается. Это подходит для конструкций, где произвести запуск можно с минимальной нагрузкой.
Что считать пусковым моментом
Многие задаются вопросом о том, как понимать кратность пускового момента АЭД. Ничего сложного здесь нет, поскольку сведения указываются в сертификате, паспорте или другом сопроводительном документе на электронный мотор. Под пусковым моментом понимается вращающий момент, который инициируется механическим способом. Его развивает мотор на валу непосредственно при запуске аккурат в то время, когда ток проходит через двигатель.
Его развивает мотор на валу непосредственно при запуске аккурат в то время, когда ток проходит через двигатель.
Иными словами, ПМ – вращающий момент, проявляющийся на валу, когда ток имеет устоявшееся значение, а скорость вращения нулевая, а обмотки электродвигателя имеют номинальное по частоте и напряжению значение.
Способы определения пускового момента
Чтобы узнать, как определить максимальный пусковой момент АЭД, потребуется воспользоваться специальной формулой:
Она помогает понять, за счет чего удастся повысить показатель. Стоит сказать о том, что пусковой момент обусловлен напряжением, которое подводится к обмотке статора. Чем оно ниже, тем дольше запускается двигатель и, соответственно, пусковой ток увеличивается, как и рабочий.
Расчет пускового момента
Он определяется по определенной формуле. Величина кратности может варьироваться в промежутке от 1.5 до 6. Важно соблюдать правило, в соответствии с которым статический момент всегда должен оказываться меньше пускового. Без этого невозможно добиться корректной работы мотора.
Без этого невозможно добиться корректной работы мотора.
Чтобы понять, как определяется кратность ПМ асинхронника, нужно разобраться в самом механизме работы устройства. Непосредственно при запуске электрический мотор будет потреблять пусковой ток, показатель его существенно выше, чем у рабочего. Именно величина, которая обозначает разницу между указанными токами, обозначается как кратность, ее принято учитывать, как коэффициент. Но номинальный и рабочий токи – это разные обозначения, которые не стоит путать. Кратность тока обусловлена мощностью мотора. Если мощность невелика, то пусковой ток высокий.
Как определить пусковой момент электродвигателя и как определить пусковой момент асинхронного двигателя? Существует формула пусковой момент АЭД для расчета. Можно воспользоваться методом электрических измерений или воспользоваться специальными таблицами.
Увеличение пускового момента
Пусковой момент удастся увеличить за счет частотного преобразователя. Если сменить показатель сопротивления пускового реостата, удастся достичь большего пускового момента.
Но что произойдет, если уменьшить напряжение пускового момента вдвое? Он резко упадет. Изменение первичного тока определяется загрузкой электрического двигателя. При большой нагрузке асинхронного двигателя уменьшение напряжения на его зажимах приводит к перегрузке обмоток двигателя токами со всеми вытекающими отсюда последствиями. Наоборот, пусковой момент асинхронного двигателя при введении реостата в фазный ротор увеличивается.
Существуют правила, в соответствии с которыми должен проводиться запуск асинхронного электродвигателя. При каком способе пуска увеличивается пусковой момент асинхронного двигателя? Соединение ротора с реостатом во время включения подойдет для включения в работу моторов с разным ротором. Если в цепь входит реостат, то уровень сопротивления увеличивается. Это обеспечивает увеличение пускового момента.
Асинхронные моторы, обладающие повышенным пусковым моментом созданы специально для приводов механизмов, характеризующихся высокими нагрузками на момент запуска. А вот моторы с повышенным показателем скольжения используют для оборудования, имеющего неравномерные ударные характеристики нагрузки и высокую частоту запусков и реверсов.
А вот моторы с повышенным показателем скольжения используют для оборудования, имеющего неравномерные ударные характеристики нагрузки и высокую частоту запусков и реверсов.
Как повысить пусковой момент? Нужно использовать АЭД с высоким ПМ. Его дальнейшее увеличение можно произвести, если использовать двигатели с обмоткой ротора по типу двойной «беличьей клетки», паз обязательно должен быть глубоким. У такого АЭД на роторе будет присутствовать пара короткозамкнутых обмоток. Одна из них пусковая, а другая рабочая. Чтобы повысить ПМ обмотка для запуска должна обладать большим активным сопротивлением, нежели рабочая.
Вычисление пускового момента однофазного АЭД при включенной и отключенной обмотке
ПМ для ротора однофазного мотора соответствует нулю, потому что одна обмотка создает два одинаковых по амплитуде магнитных поля только противоположных по направлению, и сумма их векторов будет равна 0.
Пусковым моментом однофазного АЭД называется вращающий момент, развивающийся на валу АЭД, когда ротор статичен, а статор тока закреплен на обмотках.
Ключевыми элементами каждого асинхронника можно по праву считать ротор (вращающийся элемент) и статор (неподвижная часть). За счет статора обеспечивается магнитное поле для вращения ротора.
ПМ однофазного АЭД без пусковой обмотки соответствует 1/2 максимального момента.
подробные объяснения и проблема —
В статье обсуждается как найти крутящий момент из угловой скорости тела вращения и его решаемые задачи.
Крутящий момент на вращающемся теле показывает, насколько сильно приложена сила. Чтобы найти крутящий момент от вращательного движения, мы должны определить, какая работа совершается и сколько энергии передается в единицу времени вращающимся телом при приложении крутящего момента.
Связь между крутящим моментом и угловая скорость находится путем сравнения линейных эквивалентов. В предыдущих статьях, мы понимаем как объект в состоянии покоя или линейного движения ускоряется при приложении силы. Линейный скорость равна угловой скорость.
Таким образом, соотношение между линейной скоростью v и угловой скоростью ω равно v=r * ω ……………….(1)
Компания линейное расстояние d по угловой скорости составляет,
d/t = r * ω……………..2
d=r * ω * t…………………………..3Как найти крутящий момент по угловой скорости
Компания крутящий момент 𝜏 меры что собой представляет приложенная сила F на расстоянии r от его центра вращения, Следовательно, крутящий момент 𝜏 также эквивалентна приложенной силе F.
Как найти крутящий момент𝜏 = г * Ф……………….4
Сила F, приложенная к вращающемуся телу, равна
F = 𝜏/r…………………….5
Компания работа сделана W вращающимся телом – это количество переданной энергии. Это произведение приложенной силы F и линейного пути, пройденного телом.
Ш= Ф * д……………………………6
Количество энергии, передаваемое вращающимся телом в единицу времени, называется его Питания P.
Р = Вт/т………………………. .7
.7
Подставляя работу формулы (6),
P = F*d/t
Подставляя формулу Силы (5) и формулу линейного расстояния (3),
Отменяя условия, мы наконец получаем,
Р = 𝜏 * ω…………………….8
Мгновенная мощность вращающегося тела есть произведение времени действия крутящего момента на его угловую скорость.
Связь между крутящим моментом и угловой скоростью определяется выражением
𝜏 = P/ω
Крутящий момент, действующий на вращающееся тело, есть отношение его мощности или работы, совершаемой в единицу времени, к его угловой скорости.. Отношение между Крутящий момент и угловая скорость
Читать о крутящем моменте против силы
Какой крутящий момент действует на вращающееся тело мощностью 20 Вт, движущееся со скоростью 10 рад/с?Данный:
Р = 20 Вт
ω = 10 рад / с
Найти: 𝜏 = ?
Формула:
𝜏 = P/ω
Решения:
Крутящий момент, действующий на вращающееся тело, равен
𝜏 = P/ω
Подставляя все значения,
𝜏 = 20/10
𝜏 = 2
Действующий крутящий момент на вращающееся тело составляет 2Н.
Данный:
г = 5 м
d = 50м
Вт = 20 Н
t = 5 с
Найти: 𝜏 =?
Формула:
д = г * ш
P=Вт/т
𝜏 = P/ω
Решения:
Угловая скорость рассчитывается по линейному расстоянию, пройденному колесами:
д = г * ш
Перестановка,
ω = d/rt
Подставляя все значения,
ю = 50/25
ω = 2 рад / с
Мощность колес рассчитывается как
Р = вес/т
Подставляя все значения,
Р = 20/5
Р = 4 Вт
Крутящий момент, действующий на колесо, рассчитывается как
𝜏 = P/ω
Подставляя все значения,
𝜏 = 4/2
𝜏 = 2
Крутящий момент, действующий на колесо, движущееся со скоростью 2 рад/с, равен 2 Н.
Крутящий момент относительно углового ускорения по законам Ньютона.
Законы Ньютона связывают силу с ускорением. Первый закон Ньютона выражает момент инерции тела при вращательном движении. Итак, момент инерции и угловое ускорение передает крутящий момент, действующий на вращающееся тело согласно второму закону движения Ньютона.
Крутящий момент на вращающемся теле определяет способность приложенной силы уступить угловое ускорение. Таким образом, когда чистый крутящий момент действует на тело, он изменяет его угловой момент Л. Следовательно,
𝜏 = дл/дт……………9
Для линейного движения импульс р = мв. Точно так же угловой момент определяется выражением
L = Iω…………….10
Когда тело находится во вращательном движении, его масса, противодействующая его угловому ускорению из-за крутящего момента, называетсямомент инерции» обозначен I, который оценивает его вращательную инерцию. Момент инерции основан на распределении масс, сравнимом с его осью вращения.
Момент инерции основан на распределении масс, сравнимом с его осью вращения.
Подставляя формулу углового момента (10) в (9),
𝜏 = dIω/dt
𝜏 = Idω/dt
Член dω/dt представляет собой угловое ускорение α. т. е. α = dω/dt.
Связь между крутящим моментом тела и его угловым ускорением равна
𝜏 =IαСвязь между Крутящий момент и угловое ускорение
Уравнение представляет собой второй закон Ньютона, используемый в системе частиц, находящихся во вращательном движении. Компания соотношение между крутящим моментом и угловое ускорение аналоги второго закона Ньютона. Чем больше приложенный крутящий момент, тем больше его угловое ускорение.
Читать об угловом движении
Вращающееся тело имеет момент инерции около 5 кгм.2. Какой вращающий момент действует на него, если он ускоряется со скоростью 2 рад/с?2?Данный:
я = 5кгм2
α = 2 рад/с2
Найти: 𝜏 = ?
Формула:
𝜏 = Iα
Решения:
Крутящий момент, действующий на вращающееся тело, рассчитывается как
𝜏 =Iα
Подставляя все значения,
𝜏 = 5 * 2
𝜏 = 10
Крутящий момент, действующий на вращающееся тело, имеющее ускорение, равен 10 Н.
Данный:
я = 6 кгм2
я = 6 кгм2
ω2 = 50 рад / с
ω1= 30 рад / с
t2 = 10 с
t2 = 6 с
Найти: 𝜏=?
Формула:
𝜏 = Iα
Решения:
Компания угловое ускорение волчка рассчитывается как,
α = dω/dt
а = ш2-ω1/t2-t1
Подставляя все значения,
α = 50-30/10-6
α = 20/4
α = 5 рад/с2
Крутящий момент, действующий на волчок, рассчитывается как
𝜏 = Iα
Подставляя все значения,
𝜏 = 6*5
𝜏 = 30
Крутящий момент, действующий на волчок, ускоренный со скоростью 5 рад/с2 30N.
Читать о скорости против скорости
Узнайте больше о Является ли угловая скорость отрицательной?
Уравнение крутящего момента и примеры | Что такое крутящий момент? — Видео и стенограмма урока
Научные курсы / Холт Макдугал Физика: онлайн-справка по учебнику Курс / Холт Макдугал Физика Глава 4: Силы и законы движения Глава
Кэтрин Кейлегиан-Старки, Дэмиен Ховард- Автор Кэтрин Кейлегиан-Старки
Кэтрин имеет степень бакалавра в области физики, и она стремится получить степень магистра в области прикладной физики. В настоящее время она преподает учащимся, испытывающим затруднения в области STEM, в муниципальном колледже Лейн.
Посмотреть биографию - Инструктор Дэмиен Ховард
Дэмиен имеет степень магистра физики и преподавал физическую лабораторию студентам колледжа.
Посмотреть биографию
Понять, что такое крутящий момент и как он связан с вращательным движением. Изучите уравнение крутящего момента, способы расчета крутящего момента и повседневные примеры крутящего момента. Обновлено: 07.03.2022
Изучите уравнение крутящего момента, способы расчета крутящего момента и повседневные примеры крутящего момента. Обновлено: 07.03.2022
Содержание
- Что такое крутящий момент?
- Уравнение крутящего момента
- Равновесие вращения
- Как рассчитать крутящий момент
- Краткое содержание урока
Чему равен крутящий момент?
Крутящий момент представляет собой векторное произведение плеча рычага и приложенной силы. Это означает, что величина крутящего момента в системе равна величине плеча рычага, умноженной на величину силы, умноженной на синус угла между ними, rFsin(theta).
Что такое крутящий момент в физике?
В физике крутящий момент — это сила, вызывающая вращательное движение. Он определяется как векторное произведение плеча рычага и линейной силы.
Что такое крутящий момент ? Определение крутящего момента в физике состоит в том, что крутящий момент представляет собой крутящую силу, вызывающую вращение. Это не означает, что крутящий момент является круговой силой. В общем, крутящие моменты представляют собой линейные силы, которые приложены к шарнирному плечу рычага таким образом, что заставляют плечо рычага вращаться. Что такое плечо рычага? Рычагом может быть любой шарнирный объект. Например, сиденья на качелях представляют собой рычажные рычаги, потому что они представляют собой твердую вращающуюся массу. При анализе крутящих моментов в системе важно определить плечо рычага и ось вращения плеча рычага. Ось вращения — это точка, вокруг которой вращается плечо рычага, а другой способ представить себе ось вращения — это точка поворота плеча рычага. Для качелей осью вращения является центр качелей, но не все рычаги имеют центральную ось вращения. Многие системы с крутящим моментом, такие как распашная дверь, имеют ось вращения на краю.
Это не означает, что крутящий момент является круговой силой. В общем, крутящие моменты представляют собой линейные силы, которые приложены к шарнирному плечу рычага таким образом, что заставляют плечо рычага вращаться. Что такое плечо рычага? Рычагом может быть любой шарнирный объект. Например, сиденья на качелях представляют собой рычажные рычаги, потому что они представляют собой твердую вращающуюся массу. При анализе крутящих моментов в системе важно определить плечо рычага и ось вращения плеча рычага. Ось вращения — это точка, вокруг которой вращается плечо рычага, а другой способ представить себе ось вращения — это точка поворота плеча рычага. Для качелей осью вращения является центр качелей, но не все рычаги имеют центральную ось вращения. Многие системы с крутящим моментом, такие как распашная дверь, имеют ось вращения на краю.
Примеры крутящего момента в повседневной жизни
Качели с твердым сиденьем, охватывающим всю игрушку, являются повседневным примером крутящего момента, как и распашная дверь. Существует бесчисленное множество примеров крутящего момента из повседневной жизни, потому что каждый раз, когда приложенная сила заставляет объект вращаться, возникает крутящий момент. В следующем списке приведены различные распространенные примеры крутящих моментов:
Существует бесчисленное множество примеров крутящего момента из повседневной жизни, потому что каждый раз, когда приложенная сила заставляет объект вращаться, возникает крутящий момент. В следующем списке приведены различные распространенные примеры крутящих моментов:
- Дверная ручка поворачивается, потому что к ручке приложена линейная сила, направленная вниз.
- Монета вращается, потому что ее толкают с линейной силой, приложенной под некоторым углом к краю монеты.
- Маятник напольных часов качается, потому что сила тяжести действует на маятник и заставляет его качаться по дуге.
- Шестерня в двигателе автомобиля вращается, когда на ее край действует линейная сила.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свой аккаунт
Крутящий момент в повседневной жизни
Когда мы слышим термин «крутящий момент», чаще всего это относится к автомобилям. Крутящий момент — это один из терминов, обычно используемых для описания мощности автомобиля, но что именно он означает? В автомобиле крутящий момент — это сила, с которой поршни воздействуют на коленчатый вал, заставляя его и колеса вращаться.
Хотя крутящий момент часто считают автомобильным термином, на самом деле это термин из общей физики, который имеет множество применений. Крутящий момент определяется как крутящая сила, стремящаяся вызвать вращение. Мы называем точку, в которой объект вращается осью вращения . Вы используете крутящий момент каждый день, не осознавая этого. Вы применяете крутящий момент три раза, когда просто открываете запертую дверь. Поворот ключа, поворот дверной ручки и толкание двери так, чтобы она качалась на петлях, — все это методы приложения крутящего момента.
Произошла ошибка при загрузке этого видео.
Попробуйте обновить страницу или обратитесь в службу поддержки.
Чтобы продолжить просмотр, необходимо создать учетную запись
Зарегистрируйтесь, чтобы просмотреть этот урок
Вы студент или преподаватель?
Создайте свою учетную запись, чтобы продолжить просмотр
Как участник вы также получите неограниченный доступ к
уроки математики, английского языка, науки, истории и многое другое. Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспевать.
Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспевать.
Получите неограниченный доступ к более чем 88 000 уроков.
Попробуй это сейчас
Настройка занимает всего несколько минут, и вы можете отменить ее в любое время.
Уже зарегистрированы? Войдите здесь для доступ
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Назад
Далее: Трение: определение и типы
пройти викторину Смотреть следующий урок
Повтор
Просто отмечаюсь.
 Вы все еще смотрите? Да! Продолжай играть.
Вы все еще смотрите? Да! Продолжай играть.Ваш следующий урок будет играть в 10 секунд
- 0:00 Крутящий момент в повседневной жизни
- 0:50 Физика крутящего момента
- 2:10 Вращательное равновесие
- 3:33 Проблема тупика на качелях
- 6:11 Итоги урока
Хронология
Автовоспроизведение
Автовоспроизведение
Скорость
Скорость
Интересным свойством силы, вызывающей вращение, является то, что результирующее движение плеча рычага перпендикулярно как исходной силе, так и плечу рычага. Этот атрибут означает, что крутящий момент равен векторному произведению, а уравнение крутящего момента является векторным произведением плеча рычага и приложенной силы:
Этот атрибут означает, что крутящий момент равен векторному произведению, а уравнение крутящего момента является векторным произведением плеча рычага и приложенной силы:
{eq}\vec \tau = \vec r \times \vec F {/eq }.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную запись
Равновесие — это состояние покоя, и для того, чтобы система находилась в равновесии, сумма сил, действующих на систему, должна быть равна нулю. Для системы, которая совершает вращательное движение, вращательное равновесие достигается, когда сумма крутящих моментов в системе равна нулю:
{eq}\sum \tau = 0 {/eq}.
Как может сумма крутящих моментов в системе равняться нулю? Этот сценарий возникает, когда крутящие моменты, действующие на вращающуюся систему, уравновешиваются, и для этого крутящие моменты должны действовать в противоположных направлениях.
Чтобы разблокировать этот урок, вы должны быть участником Study. com.
com.
Создайте свою учетную запись
Чтобы рассчитать крутящий момент в системе, обязательно определите плечо рычага, линейную силу и угол между плечом рычага и силой. В следующих примерах показано, как рассчитать крутящий момент, используя определение величины крутящего момента.
Пример 1: Используйте рис. 2, чтобы найти величину крутящего момента на двери. 9{\circ}) \rightarrow \tau = 3,5 {/eq} Нм
Крутящий момент в этой системе составляет 3,5 Нм.
Пример 2: Ребенок массой 46 кг идет в школу с тяжелым рюкзаком. Она хочет отдохнуть в парке, и она хотела бы посидеть на качелях. Если ее рюкзак имеет массу 32 кг, где она должна сидеть и куда ей положить рюкзак, чтобы качели были сбалансированы? Используйте рисунок 3.
Эта задача более сложная, чем пример 1, и будет решаться поэтапно.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную запись
Что такое крутящий момент ? В физике определение крутящего момента состоит в том, что крутящий момент — это приложенная сила, вызывающая вращение, а крутящий момент — это линейная сила, приложенная к шарнирному плечу рычага под некоторым углом. Что такое плечо рычага? Плечо рычага представляет собой твердую массу, шарнирно закрепленную и способную вращаться вокруг оси. Другой способ описать ось вращения — это точка поворота системы. Есть бесчисленное множество повседневных примеров крутящего момента, таких как движущиеся качели или крутящаяся дверная ручка.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную запись
Физика крутящего момента
Чтобы найти линейную силу, нам нужно знать массу и ускорение. Однако крутящий момент немного отличается из-за участия вращения. Подумайте об открытии двери. Куда вы нажимаете на него, когда хотите, чтобы он открылся? Вы нажимаете на ту сторону двери, где нет петель, потому что нажатие на сторону с петлями затруднит открытие. Таким образом, для крутящего момента нам нужно знать не только массу и ускорение линейной силы, но также и то, насколько далеко эта сила находится от оси вращения, поскольку в зависимости от этого мы можем получить разные результаты. Мы можем видеть это на диаграмме и в уравнении для крутящего момента.
Куда вы нажимаете на него, когда хотите, чтобы он открылся? Вы нажимаете на ту сторону двери, где нет петель, потому что нажатие на сторону с петлями затруднит открытие. Таким образом, для крутящего момента нам нужно знать не только массу и ускорение линейной силы, но также и то, насколько далеко эта сила находится от оси вращения, поскольку в зависимости от этого мы можем получить разные результаты. Мы можем видеть это на диаграмме и в уравнении для крутящего момента.
T = F * R * SIN ( THETA )
T = PORIT
тета = угол между F и r
В нашем уравнении sin( тета ) не имеет единиц измерения, r имеет единицы измерения в метрах (м), а F имеет единицы измерения в ньютонах (Н). Объединив их вместе, мы видим, что единицей крутящего момента является ньютон-метров (Нм).
Объединив их вместе, мы видим, что единицей крутящего момента является ньютон-метров (Нм).
Наконец, тета необходима для учета направления приложения линейной силы. Сила не всегда будет толкаться прямо, как дверь. Это может прийти с разных сторон.
Равновесие вращения
Итак, мы видели, как один крутящий момент может воздействовать на объект, но вы легко можете одновременно приложить несколько крутящих моментов. Вспомните двигатель автомобиля. В каждом автомобиле есть более одного поршня, передающего крутящий момент на коленчатый вал. В этом случае имеется общий крутящий момент, который является суммой каждого отдельного крутящего момента.
Всего T = T {1} + T {2} + … + T {n}
объект. Существует также особый случай этого, называемый вращательным равновесием . Здесь сумма всех крутящих моментов, действующих на объект, равна нулю. Когда это происходит, это может означать, что на объект не действует крутящий момент, или все крутящие моменты, действующие на объект, уравновешивают друг друга. Чтобы визуализировать уравновешивание крутящих моментов, давайте рассмотрим простой случай с двумя крутящими моментами: качели.
Чтобы визуализировать уравновешивание крутящих моментов, давайте рассмотрим простой случай с двумя крутящими моментами: качели.
В верхней части изображения двое детей сидят на неподвижных качелях. Они уравновешены на оси вращения, которая является точкой опоры в случае качелей. Оба ребенка прилагают вниз силу своего веса, также известную как сила тяжести. Ребенок 1 пытается повернуть качели против часовой стрелки, а ребенок 2 пытается повернуть их по часовой стрелке. Пока величины двух крутящих моментов одинаковы, они компенсируют друг друга, поскольку пытаются двигать качели в противоположных направлениях.
Проблема тупиковой ситуации на качелях
Давайте рассмотрим пример расчета с использованием вращательного равновесия и уравнения для крутящего момента.
Качели на изображении находятся в равновесии вращения и не двигаются. Мы хотим найти, как далеко дочерний элемент 2 находится справа от оси вращения в точке опоры. Ребенок 1 слева имеет массу 38 кг и находится на расстоянии 4 м от точки опоры. Ребенок 2 имеет массу 25 кг.
Мы хотим найти, как далеко дочерний элемент 2 находится справа от оси вращения в точке опоры. Ребенок 1 слева имеет массу 38 кг и находится на расстоянии 4 м от точки опоры. Ребенок 2 имеет массу 25 кг.
Шаг 1: Учет направления
Чтобы математически показать, что два крутящих момента движутся в противоположных направлениях, одному из них присваивается отрицательный знак. Стандартной практикой является обозначение крутящего момента, вращающего объект по часовой стрелке, как отрицательное, поэтому мы сделаем T {2} отрицательным. Поскольку качели находятся в равновесии вращения, мы также знаем, что сумма крутящих моментов должна равняться нулю. Это позволяет нам изменить уравнение, чтобы получить один крутящий момент по обе стороны от знака равенства.
Т {1} + (- Т {2}) = 0
T {1} — T {2} = 0
T {2} = T {1}
Шаг 2: Вставка уравнений крутящего момента и силы 90
Затем мы подставляем уравнение для крутящего момента в каждую сторону.
F { g 2} * r {2} * sin( тета {2}) = F { g 1} * r 1}2 * r {1})
F { г 2} и F { g 1} силы тяжести. Чтобы получить их, мы умножаем массу каждого ребенка на ускорение свободного падения ( г ).
m {2} * g * r {2} * sin( тета {2}) = m {1} * g * r { тета {1})
Шаг 3: Упростим уравнение
Теперь мы можем сделать пару вещей, чтобы упростить это уравнение. Во-первых, поскольку 90 257 g 90 258 одинаково для каждого ребенка и по обе стороны от знака равенства, оно аннулируется. Во-вторых, если мы посмотрим на изображение, то увидим, что силы гравитации перпендикулярны качелям. Это означает, что они перпендикулярны р {1} и р {2}. Таким образом, оба тета имеют значение 90 градусов. Помните, sin(90 градусов) = 1. Теперь у нас осталось следующее:
m {2} * r {2} = m {1} * r {1}
Шаг 4: Решите уравнение
Наконец-то мы можем подставить наши данные, чтобы найти ответ для r {2}.
25 кг * r {2} = 38 кг * 4 м
25 кг * r {2} = 152 кг м
r {2} = 6 м
Ребенок 2 сидит в 6 метрах от точки опоры. Для вращательного равновесия имеет смысл, что более легкий ребенок должен сидеть дальше от точки опоры, чем более тяжелый, чтобы удерживать качели в равновесии.
Резюме урока
Крутящий момент — это крутящая сила, которая стремится вызвать вращение. Точка, в которой вращается объект, известна как ось вращения . Математически крутящий момент можно записать как T = F * r * sin( тета ), а единицами измерения являются ньютон-метры. Когда сумма всех крутящих моментов, действующих на объект, равна нулю, это вращательное равновесие . Крутящие моменты, действующие на один объект, компенсируют друг друга, когда они имеют одинаковую величину и противоположные направления. Крутящий момент относится не только к автомобилям; он также позволяет использовать такие объекты, как замки, дверные ручки, петли и даже качели.
Результаты обучения
Повторите урок и попрактикуйтесь в уравнениях, пока не будете готовы:
- Определение крутящего момента, вращательного равновесия и оси вращения
- Вспомните уравнение для крутящего момента
- Рассчитать крутящий момент
- Рассчитать значение r для объекта в равновесии вращения
- Перечислите несколько примеров крутящего момента в повседневной жизни
Крутящий момент в повседневной жизни
Когда мы слышим термин «крутящий момент», чаще всего это относится к автомобилям. Крутящий момент — это один из терминов, обычно используемых для описания мощности автомобиля, но что именно он означает? В автомобиле крутящий момент — это сила, с которой поршни воздействуют на коленчатый вал, заставляя его и колеса вращаться.
Хотя крутящий момент часто считается автомобильным термином, на самом деле это термин общей физики, который имеет множество применений. Крутящий момент определяется как крутящая сила, стремящаяся вызвать вращение. Мы называем точку, в которой объект вращается осью вращения . Вы используете крутящий момент каждый день, не осознавая этого. Вы применяете крутящий момент три раза, когда просто открываете запертую дверь. Поворот ключа, поворот дверной ручки и толкание двери так, чтобы она качалась на петлях, — все это методы приложения крутящего момента.
Мы называем точку, в которой объект вращается осью вращения . Вы используете крутящий момент каждый день, не осознавая этого. Вы применяете крутящий момент три раза, когда просто открываете запертую дверь. Поворот ключа, поворот дверной ручки и толкание двери так, чтобы она качалась на петлях, — все это методы приложения крутящего момента.
Физика крутящего момента
Чтобы найти линейную силу, нам нужно знать массу и ускорение. Однако крутящий момент немного отличается из-за участия вращения. Подумайте об открытии двери. Куда вы нажимаете на него, когда хотите, чтобы он открылся? Вы нажимаете на ту сторону двери, где нет петель, потому что нажатие на сторону с петлями затруднит открытие. Таким образом, для крутящего момента нам нужно знать не только массу и ускорение линейной силы, но также и то, насколько далеко эта сила находится от оси вращения, поскольку в зависимости от этого мы можем получить разные результаты. Мы можем видеть это на диаграмме и в уравнении для крутящего момента.
T = F * R * SIN ( THETA )
T = PORIT
тета = угол между F и r
В нашем уравнении sin( тета ) не имеет единиц измерения, r имеет единицы измерения в метрах (м), а F имеет единицы измерения в ньютонах (Н). Объединив их вместе, мы видим, что единицей крутящего момента является ньютон-метров (Нм).
Наконец, тета необходима для учета направления приложения линейной силы. Сила не всегда будет толкаться прямо, как дверь. Это может прийти с разных сторон.
Равновесие вращения
Итак, мы видели, как один крутящий момент может воздействовать на объект, но вы легко можете одновременно приложить несколько крутящих моментов. Вспомните двигатель автомобиля. В каждом автомобиле есть более одного поршня, передающего крутящий момент на коленчатый вал. В этом случае имеется общий крутящий момент, который является суммой каждого отдельного крутящего момента.
Вспомните двигатель автомобиля. В каждом автомобиле есть более одного поршня, передающего крутящий момент на коленчатый вал. В этом случае имеется общий крутящий момент, который является суммой каждого отдельного крутящего момента.
Всего T = T {1} + T {2} + … + T {n}
объект. Существует также особый случай этого, называемый вращательным равновесием . Здесь сумма всех крутящих моментов, действующих на объект, равна нулю. Когда это происходит, это может означать, что на объект не действует крутящий момент, или все крутящие моменты, действующие на объект, уравновешивают друг друга. Чтобы визуализировать уравновешивание крутящих моментов, давайте рассмотрим простой случай с двумя крутящими моментами: качели.
В верхней части изображения двое детей сидят на неподвижных качелях. Они уравновешены на оси вращения, которая является точкой опоры в случае качелей. Оба ребенка прилагают вниз силу своего веса, также известную как сила тяжести. Ребенок 1 пытается повернуть качели против часовой стрелки, а ребенок 2 пытается повернуть их по часовой стрелке. Пока величины двух крутящих моментов одинаковы, они компенсируют друг друга, поскольку пытаются двигать качели в противоположных направлениях.
Оба ребенка прилагают вниз силу своего веса, также известную как сила тяжести. Ребенок 1 пытается повернуть качели против часовой стрелки, а ребенок 2 пытается повернуть их по часовой стрелке. Пока величины двух крутящих моментов одинаковы, они компенсируют друг друга, поскольку пытаются двигать качели в противоположных направлениях.
Проблема тупиковой ситуации на качелях
Давайте рассмотрим пример расчета с использованием вращательного равновесия и уравнения для крутящего момента.
Качели на изображении находятся в равновесии вращения и не двигаются. Мы хотим найти, как далеко дочерний элемент 2 находится справа от оси вращения в точке опоры. Ребенок 1 слева имеет массу 38 кг и находится на расстоянии 4 м от точки опоры. Ребенок 2 имеет массу 25 кг.
Шаг 1: Учет направления
Чтобы математически показать, что два крутящих момента движутся в противоположных направлениях, одному из них присваивается отрицательный знак. Стандартной практикой является обозначение крутящего момента, вращающего объект по часовой стрелке, как отрицательное, поэтому мы сделаем T {2} отрицательным. Поскольку качели находятся в равновесии вращения, мы также знаем, что сумма крутящих моментов должна равняться нулю. Это позволяет нам изменить уравнение, чтобы получить один крутящий момент по обе стороны от знака равенства.
Стандартной практикой является обозначение крутящего момента, вращающего объект по часовой стрелке, как отрицательное, поэтому мы сделаем T {2} отрицательным. Поскольку качели находятся в равновесии вращения, мы также знаем, что сумма крутящих моментов должна равняться нулю. Это позволяет нам изменить уравнение, чтобы получить один крутящий момент по обе стороны от знака равенства.
Т {1} + (- Т {2}) = 0
T {1} — T {2} = 0
T {2} = T {1}
Шаг 2: Вставка уравнений крутящего момента и силы 90
Затем мы подставляем уравнение для крутящего момента в каждую сторону.
F { g 2} * r {2} * sin( тета {2}) = F { g 1} * r 1}2 * r {1})
F { г 2} и F { g 1} силы тяжести. Чтобы получить их, мы умножаем массу каждого ребенка на ускорение свободного падения ( г ).
m {2} * g * r {2} * sin( тета {2}) = m {1} * g * r { тета {1})
Шаг 3: Упростим уравнение
Теперь мы можем сделать пару вещей, чтобы упростить это уравнение. Во-первых, поскольку 90 257 g 90 258 одинаково для каждого ребенка и по обе стороны от знака равенства, оно аннулируется. Во-вторых, если мы посмотрим на изображение, то увидим, что силы гравитации перпендикулярны качелям. Это означает, что они перпендикулярны р {1} и р {2}. Таким образом, оба тета имеют значение 90 градусов. Помните, sin(90 градусов) = 1. Теперь у нас осталось следующее:
Во-первых, поскольку 90 257 g 90 258 одинаково для каждого ребенка и по обе стороны от знака равенства, оно аннулируется. Во-вторых, если мы посмотрим на изображение, то увидим, что силы гравитации перпендикулярны качелям. Это означает, что они перпендикулярны р {1} и р {2}. Таким образом, оба тета имеют значение 90 градусов. Помните, sin(90 градусов) = 1. Теперь у нас осталось следующее:
m {2} * r {2} = m {1} * r {1}
Шаг 4: Решите уравнение
Наконец-то мы можем подставить наши данные, чтобы найти ответ для r {2}.
25 кг * r {2} = 38 кг * 4 м
25 кг * r {2} = 152 кг м
r {2} = 6 м
Ребенок 2 сидит в 6 метрах от точки опоры. Для вращательного равновесия имеет смысл, что более легкий ребенок должен сидеть дальше от точки опоры, чем более тяжелый, чтобы удерживать качели в равновесии.
Резюме урока
Крутящий момент — это крутящая сила, которая стремится вызвать вращение. Точка, в которой вращается объект, известна как ось вращения . Математически крутящий момент можно записать как T = F * r * sin( тета ), а единицами измерения являются ньютон-метры. Когда сумма всех крутящих моментов, действующих на объект, равна нулю, это вращательное равновесие . Крутящие моменты, действующие на один объект, компенсируют друг друга, когда они имеют одинаковую величину и противоположные направления. Крутящий момент относится не только к автомобилям; он также позволяет использовать такие объекты, как замки, дверные ручки, петли и даже качели.
Точка, в которой вращается объект, известна как ось вращения . Математически крутящий момент можно записать как T = F * r * sin( тета ), а единицами измерения являются ньютон-метры. Когда сумма всех крутящих моментов, действующих на объект, равна нулю, это вращательное равновесие . Крутящие моменты, действующие на один объект, компенсируют друг друга, когда они имеют одинаковую величину и противоположные направления. Крутящий момент относится не только к автомобилям; он также позволяет использовать такие объекты, как замки, дверные ручки, петли и даже качели.
Результаты обучения
Повторите урок и попрактикуйтесь в уравнениях, пока не будете готовы:
- Определение крутящего момента, вращательного равновесия и оси вращения
- Вспомните уравнение для крутящего момента
- Рассчитать крутящий момент
- Рассчитать значение r для объекта в равновесии вращения
- Перечислите несколько примеров крутящего момента в повседневной жизни
Чтобы разблокировать этот урок, вы должны быть участником Study. com.
com.
Создайте свою учетную запись
Зарегистрируйтесь для просмотра этого урока
Вы студент или преподаватель?
Разблокируйте свое образование
Убедитесь сами, почему 30 миллионов человек используют Study.com
Станьте участником Study.com и начните учиться прямо сейчас.
Стать участником
Уже являетесь участником? Войти
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Спинка
Как рассчитать крутящий момент | Физика
Этапы расчета крутящего момента
Шаг 1 : Составьте список известных величин, включая величину силы, величину плеча рычага и угол между векторами силы и плеча рычага.
Шаг 2 : Подставьте эти величины в уравнение {eq}\tau = |r|\ |F| \ грех {\ тета} {/eq} для расчета крутящего момента.
Шаг 3 : Примените правило правой руки, чтобы определить направление крутящего момента.
Формула и словарь для расчета крутящего момента
Крутящий момент : Крутящий момент, {eq}\tau {/eq} — это термин, обозначающий силу, которая заставляет объект изменять свою угловую (вращательную) скорость. Это происходит, когда к объекту прикладывается сила на некотором расстоянии от точки его вращения.
Рычаг : Рычаг, {eq}r {/eq} — вектор расстояния, проведенный от точки вращения объекта до точки приложения приложенной силы.
Формула для крутящего момента : Формула для расчета крутящего момента: {eq}\tau = |r|\ |F| \ грех {\ тета}
{/экв}, где {экв}|r|
{/eq} — величина плеча рычага, {eq}|F|
{/eq} — величина вектора силы, а {eq}\theta
{/eq} — угол, образованный между векторами силы и плеча рычага.
Правило правой руки для крутящего момента : Направление вектора крутящего момента определяется с помощью правила правой руки:
- Начиная с точки вращения, направьте пальцы правой руки к точке приложения силы.
- Согните пальцы в направлении вектора силы и вытяните большой палец наружу из ладони.
- Большой палец указывает в направлении крутящего момента. Обычно, если ваш большой палец направлен за пределы страницы, крутящий момент положительный. Если ваш большой палец указывает на страницу, крутящий момент отрицательный.
В следующих трех примерах показано, как рассчитать крутящий момент.
Пример задачи 1. Расчет крутящего момента
Стержень длиной 1,5 метра ориентирован горизонтально и закреплен так, что вращается вокруг своего левого конца. К точке на расстоянии 0,4 м от левой стороны стержня приложена восходящая сила 20 Н. Какой крутящий момент приложен к стержню? 9\circ} = 8.0\ \rm{N\cdot m} $$
Шаг 3 : Направление (положительное или отрицательное) крутящего момента можно определить с помощью правила правой руки. В этом случае начните с левой стороны перекладины и направьте пальцы правой руки вправо (в направлении точки приложения силы). Согните пальцы в направлении вектора силы. Ваш большой палец должен быть направлен в сторону от страницы, что является положительным направлением.
В этом случае начните с левой стороны перекладины и направьте пальцы правой руки вправо (в направлении точки приложения силы). Согните пальцы в направлении вектора силы. Ваш большой палец должен быть направлен в сторону от страницы, что является положительным направлением.
Крутящий момент в этой задаче равен {eq}\tau = +8.0\ \rm{N\cdot m} {/экв}.
Пример задачи 2. Расчет крутящего момента
Вертикально ориентированный стержень закреплен таким образом, что он вращается вокруг своего верхнего конца. В точке на 0,75 м ниже верхнего штифта к стержню справа под углом 20 градусов ниже горизонтали приложена сила 15 Н. Какой крутящий момент действует на стержень?
Шаг 1 : Сначала составьте список всех известных величин. Углы в этом могут быть немного сложными, поэтому может быть полезно нарисовать картину ситуации: 9\circ}\приблизительно 11\ \rm{N\cdot m} $$
Шаг 3 : Чтобы найти направление крутящего момента, направьте пальцы вниз и согните их вправо. Ваш большой палец указывает за пределы страницы, что указывает на положительный крутящий момент.
Ваш большой палец указывает за пределы страницы, что указывает на положительный крутящий момент.
Крутящий момент на стержне равен {eq}\tau = +11\ \rm{N\cdot m} {/экв}
Пример задачи 3. Расчет крутящего момента
Вертикально ориентированный стержень длиной 0,80 м закреплен так, что он вращается вокруг своего верхнего конца. Сила 120 Н прикладывается непосредственно вверх к нижнему концу стержня. Какой крутящий момент действует на стержень? 9\круг} = 0 $$
Поскольку векторы параллельны, к стержню не приложен крутящий момент.
Шаг 3 : Поскольку крутящий момент отсутствует, с ним не связано и направление.
На этот стержень не действует крутящий момент.
10.7: Torque — Physics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4032
- OpenStax
- OpenStax
Цели обучения
- Описать, как величина крутящего момента зависит от величины плеча рычага и угла, который вектор силы образует с плечом рычага
- Определите знак (положительный или отрицательный) крутящего момента, используя правило правой руки
- Рассчитайте отдельные крутящие моменты относительно общей оси и просуммируйте их, чтобы найти чистый крутящий момент
Важной величиной для описания динамики вращающегося твердого тела является крутящий момент. Мы видим применение крутящего момента во многих отношениях в нашем мире. У всех нас есть интуитивное представление о крутящем моменте, например, когда мы используем большой гаечный ключ, чтобы открутить упрямый болт. Крутящий момент действует невидимым образом, например, когда мы нажимаем на педаль акселератора в автомобиле, заставляя двигатель передавать дополнительный крутящий момент на трансмиссию. Или каждый раз, когда мы перемещаем свое тело из положения стоя, мы прикладываем крутящий момент к нашим конечностям. В этом разделе мы определяем крутящий момент и аргументируем уравнение для расчета крутящего момента для твердого тела с вращением с фиксированной осью.
Мы видим применение крутящего момента во многих отношениях в нашем мире. У всех нас есть интуитивное представление о крутящем моменте, например, когда мы используем большой гаечный ключ, чтобы открутить упрямый болт. Крутящий момент действует невидимым образом, например, когда мы нажимаем на педаль акселератора в автомобиле, заставляя двигатель передавать дополнительный крутящий момент на трансмиссию. Или каждый раз, когда мы перемещаем свое тело из положения стоя, мы прикладываем крутящий момент к нашим конечностям. В этом разделе мы определяем крутящий момент и аргументируем уравнение для расчета крутящего момента для твердого тела с вращением с фиксированной осью.
Определение крутящего момента
До сих пор мы определили множество переменных, которые являются вращательными эквивалентами своих поступательных аналогов. Рассмотрим, каким должен быть аналог силы. Поскольку силы изменяют поступательное движение объектов, вращательный аналог должен быть связан с изменением вращательного движения объекта вокруг оси. Мы называем этот вращательный аналог крутящим моментом .
Мы называем этот вращательный аналог крутящим моментом .
В повседневной жизни мы постоянно вращаем объекты вокруг оси, поэтому интуитивно мы уже многое знаем о крутящем моменте. Рассмотрим, например, как мы поворачиваем дверь, чтобы открыть ее. Во-первых, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям; более эффективно повернуть дверь, если мы нажмем далеко от петель. Во-вторых, мы знаем, что толкать надо перпендикулярно плоскости двери; если мы нажмем параллельно плоскости двери, мы не сможем ее повернуть. В-третьих, чем больше сила, тем эффективнее она открывает дверь; чем сильнее вы нажимаете, тем быстрее открывается дверь. Первый пункт подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; второй подразумевает, что эффективность зависит от угла приложения силы; третий подразумевает, что величина силы также должна быть частью уравнения. Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. На рисунке \(\PageIndex{1}\) показано вращение против часовой стрелки.
Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. На рисунке \(\PageIndex{1}\) показано вращение против часовой стрелки.

Теперь рассмотрим, как определить крутящие моменты в общем трехмерном случае.
Крутящий момент
Когда сила \(\vec{F}\) приложена к точке P, положение которой равно \(\vec{r}\) относительно точки O (рисунок \(\PageIndex{2}\)) , крутящий момент \(\vec{\tau}\) вокруг O равен
\[\vec{\tau} = \vec{r} \times \vec{F} \ldotp \label{10.22}\]
Рисунок \(\PageIndex{2}\): направление определяется по правилу правой руки.
Из определения векторного произведения крутящий момент \(\vec{\tau}\) перпендикулярен плоскости, содержащей \(\vec{r}\) и \(\vec{F}\), и имеет величина
\[|\vec{\tau}| = |\vec{r} \times \vec{F}| = rF \sin \theta,\]
, где \(\theta\) — угол между векторами \(\vec{r}\) и \(\vec{F}\). Единицей крутящего момента в СИ является ньютон, умноженный на метр, обычно записывается как Н • м. Величина r \(\perp\) = rsin \(\theta\) представляет собой перпендикулярное расстояние от O до линии, определяемой вектором \(\vec{F}\), и называется рычаг . Обратите внимание, что чем больше плечо рычага, тем больше величина крутящего момента. В терминах плеча рычага величина крутящего момента составляет
Обратите внимание, что чем больше плечо рычага, тем больше величина крутящего момента. В терминах плеча рычага величина крутящего момента составляет
\[|\vec{\tau}| = r_{\perp} F \ldotp \label{10.23}\]
Перекрестное произведение \(\vec{r} \times \vec{F}\) также сообщает нам знак крутящего момента. На рисунке \(\PageIndex{2}\) векторное произведение \(\vec{r} \times \vec{F}\) расположено вдоль положительной оси z, что по соглашению представляет собой положительный крутящий момент. Если \(\vec{r} \times \vec{F}\) вдоль отрицательной оси z, это создает отрицательный крутящий момент.
Если мы рассмотрим диск, который может свободно вращаться вокруг оси, проходящей через центр, как показано на рисунке \(\PageIndex{3}\), мы увидим, как угол между радиусом \(\vec{r}\ ), а сила \(\vec{F}\) влияет на величину крутящего момента. Если угол равен нулю, крутящий момент равен нулю; если угол равен 90°, крутящий момент максимальный. Крутящий момент на рисунке \(\PageIndex{3}\) положительный, потому что направление крутящего момента по правилу правой руки выходит за пределы страницы вдоль положительной оси z. Диск вращается против часовой стрелки за счет крутящего момента в том же направлении, что и положительное угловое ускорение.
Диск вращается против часовой стрелки за счет крутящего момента в том же направлении, что и положительное угловое ускорение.
Любое количество крутящих моментов может быть рассчитано относительно данной оси. Отдельные крутящие моменты складываются, чтобы создать чистый крутящий момент вокруг оси. Когда соответствующий знак (положительный или отрицательный) присваивается величинам отдельных крутящих моментов относительно указанной оси, чистый крутящий момент вокруг оси представляет собой сумму отдельных крутящих моментов:
\[\vec{\tau}_{net} = \sum_{i} |\vec{\tau}_{i}| \ldotp \label{10.24}\]
Расчет чистого крутящего момента для твердых тел на неподвижной оси
В следующих примерах мы вычисляем крутящий момент как абстрактно, так и применительно к твердому телу. Сначала мы вводим стратегию решения проблем.
Сначала мы вводим стратегию решения проблем.
Стратегия решения проблем: определение чистого крутящего момента
- Выберите систему координат с точкой вращения или осью вращения в качестве начала выбранной системы координат.
- Определите угол между плечом рычага \(\vec{r}\) и вектором силы.
- Возьмите векторное произведение \(\vec{r}\) и \(\vec{F}\), чтобы определить, является ли крутящий момент положительным или отрицательным относительно точки вращения или оси.
- Оценить величину крутящего момента с помощью r \(\perp\) F.
- Присвойте величине соответствующий знак, положительный или отрицательный.
- Суммируйте крутящие моменты, чтобы найти чистый крутящий момент.
Пример 10.14: Расчет крутящего момента
Четыре силы показаны на рисунке \(\PageIndex{4}\) в определенных местах и ориентациях по отношению к данной системе координат xy. Найдите крутящий момент, вызванный каждой силой относительно начала координат, а затем используйте полученные результаты, чтобы найти чистый крутящий момент вокруг начала координат.
Стратегия
Эта задача требует расчета крутящего момента. Все известные величины — силы с направлениями и плечами рычага — приведены на рисунке. Цель состоит в том, чтобы найти каждый отдельный крутящий момент и чистый крутящий момент путем суммирования отдельных крутящих моментов. Будьте осторожны, чтобы присвоить правильный знак каждому крутящему моменту, используя векторное произведение \(\vec{r}\) и вектора силы \(\vec{F}\).
Решение
Использование |\(\vec{\tau}\)| = r \(\perp\) F = rFsin \(\theta\) для нахождения величины и \(\vec{r} = \vec{r} \times \vec{F}\) для определения знака крутящего момента.
Крутящий момент от силы 40 Н в первом квадранте определяется формулой (4)(40)sin 90° = 160 Н • м.
Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) вне страницы, положительное.
Крутящий момент от силы 20 Н в третьем квадранте определяется выражением −(3)(20)sin 90° = − 60 Н • м.
Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) находится на странице, поэтому оно отрицательно.
Крутящий момент от силы 30 Н в третьем квадранте определяется выражением (5)(30)sin 53° = 120 Н • м.
Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) вне страницы, положительное.
Крутящий момент от силы 20 Н во втором квадранте определяется выражением (1)(20)sin 30° = 10 Н • м.
Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) находится за пределами страницы.
Таким образом, чистый крутящий момент равен \(\tau_{net} = \sum_{i} |\tau_{i}|\) = 160 − 60 + 120 + 10 = 230 Н • м.
Значение
Обратите внимание, что каждая сила, действующая против часовой стрелки, имеет положительный крутящий момент, тогда как каждая сила, действующая по часовой стрелке, имеет отрицательный крутящий момент. Крутящий момент больше, когда расстояние, сила или перпендикулярные компоненты больше.
Пример 10.15. Расчет крутящего момента на твердом теле
На рисунке \(\PageIndex{5}\) показано несколько сил, действующих в разных местах и под разными углами на маховике. Имеем \(|\vec{F}_{1}|\) = 20 Н, \(|\vec{F}_{2}|\) = 30 Н, \(|\vec{F}_{ 3}|\) = 30 Н, r = 0,5 м. Найдите чистый крутящий момент на маховике относительно оси, проходящей через центр.
Имеем \(|\vec{F}_{1}|\) = 20 Н, \(|\vec{F}_{2}|\) = 30 Н, \(|\vec{F}_{ 3}|\) = 30 Н, r = 0,5 м. Найдите чистый крутящий момент на маховике относительно оси, проходящей через центр.
Стратегия
Мы рассчитываем каждый крутящий момент отдельно, используя перекрестное произведение, и определяем знак крутящего момента. Затем мы суммируем крутящие моменты, чтобы найти чистый крутящий момент. Решение Начнем с \(\vec{F}_{1}\). Если мы посмотрим на рисунок \(\PageIndex{5}\), то увидим, что \(\vec{F}_{1}\) составляет угол 90° + 60° с радиус-вектором \(\vec{r }\). Взяв векторное произведение, мы видим, что оно находится вне страницы и, следовательно, является положительным. Мы также видим это из расчета его величины: 9{о} = (-0,5\; m)(30\; N) = -15,0\; Н\; \cdotp m \ldotp\]
Когда мы оцениваем крутящий момент из-за \(\vec{F}_{3}\), мы видим, что угол, который он образует с \(\vec{r}\), равен нулю, поэтому \(\vec{r} \times \vec{F}_{3}\) = 0. Следовательно, \(\vec{F}_{3}\) не создает крутящего момента на маховике.
Следовательно, \(\vec{F}_{3}\) не создает крутящего момента на маховике.
Оцениваем сумму моментов:
\[\tau_{net} = \sum_{i} |\tau_{i}| = 5 — 15 = -10\; Н\; \cdotp m \ldotp\]
Значение
Ось вращения находится в центре масс маховика. Поскольку маховик находится на неподвижной оси, он не может свободно перемещаться. Если бы он находился на поверхности без трения и не был зафиксирован на месте, \(\vec{F}_{3}\) вызвал бы перемещение маховика, а также \(\vec{F}_{1}\). Его движение было бы комбинацией поступательного движения и вращения.
Упражнение 10.6
Большое океанское судно садится на мель у береговой линии, как и Costa Concordia , и лежит под углом, как показано ниже. Спасательные бригады должны приложить крутящий момент, чтобы выровнять судно, чтобы поднять его на воду для транспортировки. Чтобы выровнять судно, необходимо приложить силу 5,0 x 10 5 Н, действующую в точке А. Каков крутящий момент в точке контакта корабля с землей (рис. \(\PageIndex{6}\))?
\(\PageIndex{6}\))?
Эта страница под названием 10.7: Torque распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- рычаг
- источник@https://openstax.
 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1 - крутящий момент
Что такое крутящий момент? — Определение, Формула, Типы, Единица измерения, Примеры
Крутящий момент – это эффект вращения силы вокруг оси вращения (точки, в которой вращается объект), который заставляет объект вращаться вокруг оси. Как Сила заставляет объект ускоряться в линейном направлении, так и крутящий момент заставляет объект ускоряться в угловом направлении. Его еще называют моментом силы. Обозначается символом «τ» (тау). Крутящий момент зависит от величины силы и момента рычага (т. е. перпендикулярного расстояния между линией действия силы и осью вращения)
Что такое крутящий момент?
Сила, которая может заставить объект вращаться вокруг оси, измеряется как крутящий момент. В линейной кинематике сила — это то, что управляет ускорением объекта. Подобно этому, угловое ускорение вызывается крутящим моментом.
В результате крутящий момент можно рассматривать как вращательный аналог силы. Ось вращения — это прямая линия, вокруг которой вращается предмет.
Крутящий момент в физике — это всего лишь склонность силы к повороту или скручиванию. Крутящий момент упоминается с использованием различных терминов, включая момент и момент силы. Плечо момента или плечо рычага — это измерение расстояния между точкой приложения силы и осью вращения.
- Для обозначения используется символ τ (тау).
- Единицей крутящего момента в системе СИ является N . м (Ньютон-метр) или кг. м 2. с -2 . А единица измерения крутящего момента СГС — dyne . см.
- Размер крутящего момента [ML 2 T -2 ].
Возможно, вы видели, как механик грузовика использует длинный стержень для ослабления болта колеса. Использование длинной механики увеличило величину крутящего момента, поэтому механики легко теряют болт, прикладывая меньшее усилие. Дверцы с ручками легче открывать или закрывать у внешнего края вдали от петель.
Дверцы с ручками легче открывать или закрывать у внешнего края вдали от петель.
Примечание: Крутящий момент будет прямо пропорционален приложенной силе, а также перпендикулярному расстоянию между линией действия силы и осью вращения (Момент рычага).
Подробнее:
- Момент на электрическом диполе в однородном электрическом поле
- Момент на прямоугольной токовой петле
Типы крутящего момента
- Статический крутящий момент — Любой крутящий момент, который не приводит к угловому ускорению, является статическим. Когда кто-то толкает закрытую дверь, дверь получает статический крутящий момент, потому что, несмотря на приложенную силу, она не крутится на петлях. Поскольку они не ускоряются, кто-то, кто едет на велосипеде с постоянной скоростью, также создает статический крутящий момент.
- Динамический крутящий момент — Когда гоночный автомобиль разгоняется с места, приводной вал должен создавать угловое ускорение колес, учитывая, что автомобиль быстро движется по трассе.

Как рассчитывается крутящий момент?
Как показано на рисунке выше, N обозначает ось вращения, F представляет собой горизонтальную силу, приложенную в точке p для вращения, а d представляет момент рычага (перпендикулярное расстояние между линией действия силы и осью вращения ).
Крутящий момент = Сила × NO × sinθ
τ = F × d × sin90° [θ = 90°, NO = d]
= F × d × 1 [sin90° =1]
= F × d
Или, другими словами,
τ = F × r
Следовательно, крутящий момент = сила × момент рычага
Читайте также: Крутящий момент и угловой момент
Применение крутящего момента
должна иметь точку опоры. Вот некоторые применения крутящего момента:
- Езда на велосипеде,
- Маятник,
- Качели и гаечные ключи,
- Летающий флаг,
- Гироскоп и т. д.
Решенные9 Примеры крутящего момента0017
Пример 1: Механик прикладывает силу 400 Н к гаечному ключу, чтобы ослабить болт. Он приложил силу, перпендикулярную плечу ключа. Расстояние от болта до руки 60см. Узнайте приложенный крутящий момент.
Он приложил силу, перпендикулярную плечу ключа. Расстояние от болта до руки 60см. Узнайте приложенный крутящий момент.
Решение:
Как упоминалось в вопросе, приложенная сила перпендикулярна плечу ключа, поэтому угол будет 90°.
F = 400 Н
r = 60 см = 60/100 = 0,60
Крутящий момент = F × расстояние × угол
τ = F × r × sin90°
τ = 400 × 0,60 × 1 [sin90° = 1]
= 240 Нм
Следовательно, величина крутящего момента будет равна 240 Нм .
Пример 2: Ширина двери 50 см. К его краю (находящемуся от шарнира) приложена сила 3 Н. Определить крутящий момент, при котором дверь открывается.
Решение:
Учитывая, что
F = 3 N
D = 50 см = 50/100 = 0,5 м
Крутящий момент = F × D
τ = 3 × 0,5 нм
= 1,5 нм
Следовательно, образованный крутящий момент будет 1,5 нм
Пример 3: К стержню, который может вращаться вокруг своего центра, приложена сила 50 Н, как показано на рисунке ниже. Сила находится на расстоянии 0,45 м от центра под углом θ=45°. Найдите крутящий момент на стержне.
Сила находится на расстоянии 0,45 м от центра под углом θ=45°. Найдите крутящий момент на стержне.
изображение
Решение:
Учитывая, что
Сила = 50 N
Расстояние (R) = 45M
θ = 45 °
крутящий момент = FRSINθ
τ = 50 × 45 × SIN 45 °
= 50 × 45 7777 = 50 × 45 7777770 [70258 × 7 4587777771010277 гг. sin 45° = 0,7071]
= 15,
Нм
Часто задаваемые вопросы о крутящем моменте
Вопрос 1: Что такое крутящий момент в автомобиле?
Ответ:
Когда двигатель работает, крутящий момент, который представляет собой крутящую силу, говорит о вращательной силе двигателя и количественно определяет доступную часть этой крутящей силы.
Вопрос 2: Является ли крутящий момент формой энергии?
Ответ:
Нет, крутящий момент — это форма силы, а не энергия.
Вопрос 3: В чем разница между крутящим моментом и силой?
Ответ:
Крутящий момент определяется как мера силы, которая приводит к вращению объекта вокруг своей оси. В то время как Сила является причиной, которая заставляет объект ускоряться в линейной кинематике.
Вопрос 4: В чем разница между крутящим моментом и моментом?
Ответ:
Момент — это мера угла между осью вращения и линией действия силы, тогда как крутящий момент — это сила, которая поворачивает тело.
Вопрос 5: Как мы можем увеличить или уменьшить крутящий момент?
Ответ:
Как плечо момента, так и перпендикулярная сила, приложенная к плечу момента, могут быть увеличены для увеличения крутящего момента. Когда крутящий момент уменьшается, все происходит наоборот. Когда объект находится в состоянии покоя, его крутящие моменты уравновешены (они компенсируются), и их сумма равна нулю.
Вопрос 6: Почему трудно открыть дверь, толкнув ее или потянув за петли?
Решение:
Когда сила приложена к петлям, перпендикулярное расстояние между линией действия и осью вращения r = 0, τ = rFsinθ = 0. толкая или дергая его за петли.
WHAT’S Technical Articles and Product Descriptions Mechanical Engineering FundamentalsPiston Справочные материалы EPI Дополнительные продукты Материалы 3
Журнал Race Engine Technology ВВЕДЕНИЕ в Race Engine Technology ПОДПИСАТЬСЯ
Последнее обновление: | Последнее обновление: 11 марта 2011 г. ПРИМЕЧАНИЕ. Все наши продукты, конструкции и услуги являются УСТОЙЧИВЫМИ, ОРГАНИЧЕСКИМИ, БЕЗГЛЮТЕНОВЫМИ, НЕ СОДЕРЖАТ ГМО и не будут расстраивать чьи-либо драгоценные ЧУВСТВА или деликатные ЧУВСТВАЧтобы обсуждать силовые установки в любой степени, важно понимать концепции МОЩНОСТЬ и КРУТЯЩИЙ МОМЕНТ . ОДНАКО, чтобы понять МОЩНОСТЬ , вы должны сначала понять ЭНЕРГИЯ и РАБОТА . Если вы какое-то время не рассматривали эти концепции, было бы полезно сделать это перед изучением этой статьи. НАЖМИТЕ ЗДЕСЬ, чтобы просмотреть обзор «Энергия и работа». Часто кажется, что люди не понимают отношения между МОЩНОСТЬЮ и КРУТЯЩИМ МОМЕНТОМ. Например, мы слышали двигатель строители , консультанты по распределительным валам и другие « технические специалисты» спрашивают клиентов: «Вы хотите, чтобы ваш двигатель производил ЛОШАДИНЫЕ МОЩНОСТИ или КРУТЯЩИЙ МОМЕНТ?» И вопрос обычно задается тоном, который убедительно свидетельствует о том, что эти «эксперты» считают, что мощность и крутящий момент
как-то взаимоисключающие. На самом деле все наоборот, и вы должны четко понимать следующие факты:
л.с. = крутящий момент x об/мин ÷ 5252(в нижней части этой страницы показан вывод этого уравнения для всех, кто интересуется). количество КРУТЯЩИЙ МОМЕНТ на нагрузку при заданных об/мин . Величина КРУТЯЩЕГО МОМЕНТА, который может развить двигатель, обычно зависит от оборотов. МОМЕНТ КРУТЯЩИЙ МОМЕНТ определяется как СИЛА вокруг заданной точки, приложенная на РАДИУС от этой точки. Обратите внимание, что единица
КРУТЯЩИЙ МОМЕНТ равен одному фунт-фут (часто неверно указывается), в то время как единица РАБОТА равна одному фут-фунт . Рисунок 1 Ссылаясь на Рисунок 1 , предположим, что рукоятка прикреплена к кривошипу так, что она параллельна поддерживаемой вала и расположен в радиусе 12 дюймов от центра вала. В этом примере рассмотрим вал равным исправлено в стена. Пусть стрелка представляет собой силу в 100 фунтов, приложенную в направлении, перпендикулярном рукоятке и кривошипу, как показано на рисунке. Поскольку вал прикреплен к стене, вал не вращается, но есть крутящий момент в 100 фунт-фут (100 фунтов раз 1 фут) применяется к валу. ПРИМЕЧАНИЕ о том, что ЕСЛИ кривошип на эскизе был в два раза длиннее (т. е. рукоятка располагалась на расстоянии 24 дюйма от центра вал), то же самое усилие в 100 фунтов, приложенное к рукоятке, произвело бы 200 крутящего момента (100 фунтов на 2 фута). МОЩНОСТЬ МОЩНОСТЬ является мерой того, сколько РАБОТЫ можно выполнить за указанное ВРЕМЯ. Точно так же, как одна тонна представляет собой большое количество веса (по определению, 2000 фунтов), одна лошадиных сил это большая мощность. Определение одной лошадиной силы: 33 000 футо-фунтов в минуту . Сила, которую произвел парень толкая свою машину через участок (8 250 фут-фунтов в минуту), это равно ¼ лошадиной силы (8 250 ÷ 33 000). Хорошо, все хорошо, но как толкание машины через парковку связано с вращающимся механизмом? Рассмотрим следующее изменение в приведенном выше эскизе с ручкой и кривошипом . Ручка по-прежнему находится в 12 дюймах от центра
вал, но теперь вместо того, чтобы крепиться к стене, вал теперь проходит сквозь стену, опираясь на подшипники качения, и
прикреплен к генератору за стеной. Предположим, как показано на рис. 2 , что постоянная сила в 100 фунтов. каким-то образом применяется к ручке, так что сила всегда перпендикулярна как рукоятке, так и кривошипу, когда кривошип вращается. Другими словами, «стрелка». вращается вместе с рукояткой и остается в том же положении относительно кривошипа и рукоятки, как показано в приведенной ниже последовательности. (Это называется «тангенциальной силой»). Рисунок 2 Если эта постоянная тангенциальная сила в 100 фунтов, приложенная к 12-дюймовой рукоятке (крутящий момент 100 фунт-фут), заставляет вал вращаться со скоростью 2000 об/мин, то мощность вал передает на генератор за стеной 38 л.с. , рассчитывается следующим образом: 100 фунто-футов крутящего момента (100 фунтов x 1 фут) умножить на 2000 об/мин, разделить на 5252 и получить 38 л.с. Следующие примеры иллюстрируют несколько различных значений КРУТЯЩЕГО МОМЕНТА, которые обеспечивают мощность 300 л. с. с.Пример 1 : Какой КРУТЯЩИЙ МОМЕНТ требуется для создания 300 л.с. при 2700 об/мин? , так как л.с. = КРУТЯЩИЙ МОМЕНТ x ОБ/мин ÷ 5252 Пример 2: Какой КРУТЯЩИЙ МОМЕНТ требуется для создания 300 л.с. при 4600 об/мин? Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 4600 = 343 фунт-фут.Пример 3: Какой КРУТЯЩИЙ МОМЕНТ требуется для производства 300 л.с. при 8000 об/мин? Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 8000 = 197 фунт-фут.Пример 4: Какой КРУТЯЩИЙ МОМЕНТ развивает турбинная секция газотурбинного двигателя мощностью 300 л.с. при 41 000 об/мин? Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 41 000 = 38,4 фунт-фут.Пример 5: Выходной вал редуктора двигателя в Примере 4 вращается со скоростью 1591 об/мин. Сколько КРУТЯЩИЙ МОМЕНТ доступен на этом валу? Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 1591 = 991 фунт-фут. (без учета потерь в редукторе, разумеется). Из этих чисел следует сделать вывод, что заданное количество лошадиных сил может быть получено из бесконечного числа комбинаций крутящего момента и оборотов. Подумайте об этом с другой стороны: в автомобилях одинакового веса 2-литровый двигатель с двумя распредвалами мощностью 300 л.с. при 8000 об/мин (197 фунт-фут) и 400 л.с. при 10 000 об/мин (210 lb-ft) выведет вас из поворота точно так же, как 5-литровый двигатель мощностью 300 л.с. при 4000 об/мин (394 фунта-фута) и 400 л.с. при 5000 об/мин (420 фунт-фут). Фактически, в автомобилях одинакового веса меньший двигатель, вероятно, будет ЛУЧШЕ участвовать в гонках, потому что он намного легче, поэтому на переднюю часть приходится меньше веса. И в реальности машина с более легким 2-литровым двигателем будет вероятно, весит меньше, чем большой автомобиль с двигателем V8, поэтому он будет лучшим гоночным автомобилем по нескольким причинам. Измерение мощности Динамометр определяет МОЩНОСТЬ двигателя при приложении нагрузки к двигателю
выходного вала с помощью водяного тормоза, генератора, вихретокового гасителя или любого другого управляемого устройства, способного поглощать
власть. Последние изменения на этой страницеВ этом месте страницы раньше был анализ, показывающий, как определить мощность, потребляемую насосом. Это обсуждение имеет была перемещена на более подходящую, недавно обновленную страницу «Системы смазки двигателя». Общие замечания Чтобы спроектировать двигатель для конкретного применения, полезно построить оптимальную кривую мощности для этого конкретного применения,
затем из этой информации о конструкции определите кривую крутящего момента, которая требуется для получения желаемой кривой мощности. Как правило, пик крутящего момента возникает при значительно более низких оборотах, чем пик мощности. Причина в том, что в целом кривая крутящего момента не падает (в %) так же быстро, как увеличивается число оборотов в минуту (в %). Для гоночного двигателя часто выгодно (в пределах границ условия применения) для работы двигателя далеко за пределами пиковой мощности, чтобы обеспечить максимальную среднюю мощность в течение необходимый диапазон оборотов. Однако для двигателя, который работает в относительно узком диапазоне оборотов, такого как авиационный двигатель, обычно требуется, чтобы
двигатель выдает максимальную мощность при максимальных оборотах. Это требует, чтобы пик крутящего момента был достаточно близок к максимальным оборотам. Для самолета
двигатель, вы обычно проектируете кривую крутящего момента так, чтобы она достигла максимума при нормальных настройках круиза и оставалась неизменной до максимальных оборотов. Пример этой концепции показан на рис. 3 ниже. Три пунктирные линии представляют три различные кривые крутящего момента, каждая из которых имеет точное значение одинаковая форма и значения крутящего момента, но с пиковыми значениями крутящего момента, расположенными при разных значениях оборотов. Сплошные линии показывают мощность, вырабатываемую кривыми крутящего момента того же цвета. Рисунок 3 Обратите внимание, что при пиковом крутящем моменте 587 фунт-футов при 3000 об/мин розовая линия мощности достигает максимума около 375 л.с. между 3500 и 3750 об/мин. С
та же кривая крутящего момента сдвинута вправо на 1500 об/мин (черный цвет, пик крутящего момента 587 фунт-фут при 4500 об/мин), пиковая мощность подскакивает примерно до 535 л. Используя черные кривые в качестве примера, обратите внимание, что двигатель развивает мощность 500 л.с. как при 4500, так и при 5400 об/мин, что означает, что двигатель может такое же количество работы в единицу времени (мощность) на 4500, что и на 5400. ОДНАКО, он будет сжигать меньше топлива для производства 450 л.с. при 4500 об / мин. чем при 5400 об/мин, из-за паразитных потерь мощности (мощность, расходуемая на вращение коленчатого вала, возвратно-поступательных узлов, клапанного механизма) увеличивается пропорционально квадрату частоты вращения коленчатого вала. Диапазон оборотов, в котором двигатель развивает максимальный крутящий момент, ограничен. Вы можете настроить двигатель так, чтобы он имел высокий пиковый крутящий момент с
очень узкий диапазон или более низкое значение пикового крутящего момента в более широком диапазоне. Пример показан на рис. 4 ниже. Это то же самое, что и график на рис. 3 (выше), ЗА ИСКЛЮЧЕНИЕМ, синяя кривая крутящего момента имеет был изменен (как показано зеленой линией), чтобы он не исчезал так быстро. Обратите внимание, как это приводит к увеличению зеленой линии электропередач. далеко за пределами пика крутящего момента. Такого рода изменение кривой крутящего момента может быть достигнуто путем изменения различных ключевых компонентов, в том числе (но не ограничиваясь) профили кулачков, расстояние между кулачками, длина впускных и/или выпускных каналов, поперечное сечение впускных и/или выпускных каналов раздел. Изменения, направленные на расширение пикового крутящего момента, неизбежно уменьшат значение пикового крутящего момента, но желательность данное изменение определяется приложением. Рис.4 x КРУТЯЩИЙ МОМЕНТ ÷ 5252 , тогда где 5252?» Вот ответ. По определению, МОЩНОСТЬ = СИЛА x РАССТОЯНИЕ ÷ ВРЕМЯ ПИТАНИЕ рубрика) Используя пример на рисунке 2 выше, где постоянная тангенциальная сила в 100 фунтов была приложена к 12-дюймовой рукоятке, вращающейся со скоростью 2000 об/мин, мы знаем силу задействованную, поэтому для расчета мощности нам нужно расстояние рукоятка перемещения на единицу время , выраженное как: Мощность = 100 фунтов x расстояние в минуту Хорошо, на какое расстояние рукоятка перемещается за одну минуту? Сначала определите расстояние, которое он проходит за один оборот : РАССТОЯНИЕ за оборот = 2 x π x радиус РАССТОЯНИЕ за оборот. = 2 x 3,1416 x 1 фут = 6,283 фута. Теперь мы знаем, как далеко шатун перемещается за один оборот. Какое расстояние проходит кривошип за одну минут ? РАССТОЯНИЕ в мин. = 6,283 фута на оборот. х 2000 об. Теперь мы знаем достаточно, чтобы рассчитать мощность, определяемую как: МОЩНОСТЬ = СИЛА x РАССТОЯНИЕ ÷ ВРЕМЯ Отлично, а как насчет ЛОШАДЕЙ? Помните, что одна ЛОШАДЕЙНАЯ СИЛА определяется как 33000 футо-фунтов работы. в минуту . Следовательно, HP = МОЩНОСТЬ (фут-фунт в минуту) ÷ 33 000. Мы уже подсчитали, что мощность, приложенная к кривошипа выше составляет 1 256 600 футо-фунтов в минуту. Сколько это HP? л.с. = (1 256 600 ÷ 33 000) = 38,1 л.с. Теперь мы объединим уже известные нам вещи, чтобы создать волшебное число 5252. Мы уже это знаем: КРУТЯЩИЙ МОМЕНТ = СИЛА x РАДИУС. Если мы разделим обе части этого уравнения на РАДИУС, мы получим: (a) СИЛА = КРУТЯЩИЙ МОМЕНТ ÷ РАДИУС Теперь, если РАССТОЯНИЕ за оборот = РАДИУС x 2 x π, тогда (b) РАССТОЯНИЕ в минуту = РАДИУС x 2 x π x RPM Мы уже знаем (c) МОЩНОСТЬ = СИЛА x РАССТОЯНИЕ в минуту Итак, если мы подставим эквивалент СИЛЫ из уравнения (a) и расстояние в минуту из уравнение (б) в уравнение (в), получаем: МОЩНОСТЬ = (МОМЕНТ ÷ РАДИУС) x (ОБ/МИН x РАДИУС x 2 x π) Разделив обе стороны на 33 000, чтобы найти л. л.с. Снижение, мы получаем л.с. = крутящий момент x об / мин x 6,28 ÷ 33 000 с 33 000 ÷ 6,2832 = 5252 Следовательно, л.с. . При любых оборотах ниже 5252 значение крутящего момента больше, чем значение HP; Выше 5252 об/мин значение крутящего момента меньше значения л.с. << Вернуться к: Содержание Перейти к началу страницы ↑ Следующая тема: Тепловая эффективность >> |
Крутящий момент
Нагрузка
Мощность — это скорость, с которой совершается работа, то есть скорость, с которой энергия передается силой. Сила вращения, создаваемая двигателем (с помощью которой передается энергия), называется крутящим моментом.
об/мин — это сокращение от «оборотов в минуту». Это скорость, с которой двигатель вращает маховик.
Двигатели внутреннего сгорания (ВС) не производят одинаковую мощность на всех скоростях двигателя, поэтому должна быть частота вращения двигателя (об/мин), при которой двигатель будет генерировать максимальную мощность. То же самое и с крутящим моментом.
То же самое и с крутящим моментом.
В качестве характеристики двигателя внутреннего сгорания максимальный крутящий момент обычно создается при меньшей частоте вращения двигателя, чем при максимальной мощности.
Проще говоря.
Мощность — это количество энергии, которое двигатель может передать за определенное время… (Вот откуда вы берете пикап)
Крутящий момент – это грузоподъемность.
Так что это зависит от ваших потребностей. Чем большее ускорение вы хотите, тем больше мощности вам нужно… в то время как в случае, если вам нужно нести груз, вам нужен больший крутящий момент.
Об/мин указывает, при каких оборотах двигатель может развивать максимальную мощность/крутящий момент.
Бензиновые автомобили лучше развивают мощность, а дизельные двигатели — крутящий момент.
Для ускорения нужны и мощность, и крутящий момент. Проще говоря, крутящий момент — это скорость, с которой двигатель может производить мощность. Помните, что ускорение — это скорость, с которой изменяется скорость, поэтому для поддержания скорости вам нужна мощность для преодоления сопротивления (трение о дорогу, трение о воздух, а также трение в движущихся частях двигателя автомобиля и трансмиссии). Как правило, число оборотов в минуту между максимальным крутящим моментом и максимальной мощностью является диапазоном мощности автомобиля, нижний предел этого диапазона соответствует диапазону, в котором вы будете двигаться, а верхний предел соответствует диапазону, в котором вы участвуете в гонках. 92). Радиус F x станет
более важно позже.
Как правило, число оборотов в минуту между максимальным крутящим моментом и максимальной мощностью является диапазоном мощности автомобиля, нижний предел этого диапазона соответствует диапазону, в котором вы будете двигаться, а верхний предел соответствует диапазону, в котором вы участвуете в гонках. 92). Радиус F x станет
более важно позже.
Крутящий момент — это мера того, какая сила, действующая на объект, заставляет этот объект вращаться. Объект вращается вокруг оси, которую мы назовем точкой вращения и обозначим буквой «О». Мы назовем силу «F». Расстояние от точки вращения до точки, в которой действует сила, называется плечом момента и обозначается буквой «r». Обратите внимание, что это расстояние «r» также является вектором и указывает от оси вращения до точки, где действует сила. (Обратитесь к рисунку 1 для изображения этих определений.)
Вы создаете крутящий момент каждый раз, когда прикладываете усилие с помощью гаечного ключа. Хорошим примером является затяжка гаек на колесах. Когда вы используете гаечный ключ, вы прикладываете усилие к рукоятке. Эта сила создает крутящий момент на гайке, который стремится провернуть гайку.
Когда вы используете гаечный ключ, вы прикладываете усилие к рукоятке. Эта сила создает крутящий момент на гайке, который стремится провернуть гайку.
Единицей СИ для крутящего момента является ньютон-метр (Нм). В имперских и американских единицах измерения он измеряется в футо-фунтах (фут-фунт-сила) (также известный как «фунт-фут»), а для меньшего измерения крутящего момента: дюйм-фунт (дюйм·фунт-сила) или даже дюйм-унция (дюйм·унция). .
Крутящий момент определяется как:
| r X F = r F sin |
Обратите внимание, что единицы крутящего момента содержат расстояние и силу. Чтобы рассчитать крутящий момент в имперских единицах, вы просто умножаете силу на расстояние от центра. В случае с зажимными гайками, если ключ имеет длину в фут и вы прикладываете к нему усилие в 200 фунтов, вы создаете крутящий момент в 200 фунт-футов. Если вы используете 2-футовый ключ, вам нужно приложить к нему всего 100 фунтов силы, чтобы создать такой же крутящий момент.
Если вы используете 2-футовый ключ, вам нужно приложить к нему всего 100 фунтов силы, чтобы создать такой же крутящий момент.
В единицах СИ сила в три ньютона, приложенная в двух метрах от зажимных гаек, например, вызывает тот же крутящий момент, что и один ньютон, приложенный в шести метрах от зажимных гаек. Это предполагает, конечно, в обоих случаях, что сила направлена под прямым углом к прямому рычагу.
Автомобильный двигатель создает крутящий момент и использует его для вращения коленчатого вала. Этот крутящий момент создается точно так же: сила прикладывается на расстоянии. Давайте внимательно посмотрим на некоторые детали двигателя:
Сгорание газа в цилиндре создает давление на поршень. Это давление создает силу на головке поршня, которая толкает ее вниз. Усилие передается от поршня к шатуну, а от шатуна к коленчатому валу. Обратите внимание, что точка крепления шатуна к коленчатому валу находится на некотором расстоянии от центра вала. Горизонтальное расстояние изменяется по мере вращения коленчатого вала, поэтому изменяется и крутящий момент, поскольку крутящий момент равен силе, умноженной на расстояние.
Вам может быть интересно, почему только горизонтальное расстояние важно для определения крутящего момента в этом двигателе. Вы можете видеть, что когда поршень находится в верхней или нижней части своего хода, шатун указывает прямо вниз или вверх в центре коленчатого вала. В этом положении крутящий момент не создается, потому что только сила, действующая на рычаг в направлении, перпендикулярном рычагу, создает крутящий момент.
Таким же образом можно описать работу двигателя Ванкеля Рото. На изображении выше вы можете видеть синий «шатун», соединенный с центральным валом. При изменении угла изменяется крутящий момент, но редко случается, что «синий шатун» указывает прямо на центр коленчатого вала. Точнее, каждое третье вращение. Двигатель Отто делает это дважды за каждый оборот. И, как я объяснял ранее, это момент, когда крутящий момент равен 0. Вот почему двигатель Ванкеля имеет лучший крутящий момент и мощность, чем двигатель Отто.
Крутящий момент в физике — это псевдовектор, который измеряет тенденцию силы вращать объект вокруг некоторой оси (или точки опоры, или оси вращения). Точно так же, как сила представляет собой толчок или тягу, крутящий момент можно рассматривать как крутящий момент. Символом крутящего момента является греческая буква тау.
Точно так же, как сила представляет собой толчок или тягу, крутящий момент можно рассматривать как крутящий момент. Символом крутящего момента является греческая буква тау.
Крутящий момент также называют моментом или моментом силы. Это не следует путать с различными другими определениями «момент» в физике. В контексте машиностроения термины «момент» и «крутящий момент» не обязательно взаимозаменяемы; скорее, тот или иной предпочтительнее в конкретном контексте. Например, «крутящий момент» обычно используется для описания силы вращения на валу, например, с помощью гаечного ключа, тогда как «момент» чаще используется для описания изгибающей силы, действующей на балку.
Величина крутящего момента зависит от трех величин: во-первых, приложенной силы; во-вторых, длина плеча рычага, соединяющего ось с точкой приложения силы; и в-третьих, угол между ними. Опять же условными обозначениями:
Где
| — вектор крутящего момента | |
| — вектор плеча рычага (вектор от оси до точки приложения силы и r длина плеча момента | |
| — вектор силы, а F — величина силы | |
| Х | обозначает векторное произведение |
| — угол между вектором силы и вектором плеча момента | .|
| величина крутящего момента |
Особенно важна длина плеча рычага; Правильный выбор этой длины лежит в основе работы рычагов, шкивов, зубчатых колес и большинства других простых механизмов, требующих механического преимущества
Направление крутящего момента можно определить с помощью правила захвата правой рукой: согните пальцы правой руки, чтобы указать направление вращения, и вытяните большой палец так, чтобы он совпадал с осью вращения. Ваш большой палец указывает в направлении вектора крутящего момента.
Крутящий момент является частью базовой спецификации двигателя: выходная мощность двигателя выражается как его крутящий момент, умноженный на его скорость вращения оси. Двигатели внутреннего сгорания создают полезный крутящий момент только в ограниченном диапазоне скоростей вращения (обычно от 2000 до 5000 об/мин для небольшого автомобиля). Изменение выходного крутящего момента в этом диапазоне можно измерить с помощью динамометра и показать в виде кривой крутящего момента. Пик этой кривой крутящего момента находится несколько ниже общего пика мощности. Пик крутящего момента не может по определению появляться при более высоких оборотах, чем пик мощности.
Изменение выходного крутящего момента в этом диапазоне можно измерить с помощью динамометра и показать в виде кривой крутящего момента. Пик этой кривой крутящего момента находится несколько ниже общего пика мощности. Пик крутящего момента не может по определению появляться при более высоких оборотах, чем пик мощности.
Понимание взаимосвязи между крутящим моментом, мощностью и частотой вращения двигателя имеет жизненно важное значение в автомобилестроении, поскольку оно связано с передачей мощности от двигателя через трансмиссию к колесам. Мощность обычно зависит от крутящего момента и частоты вращения двигателя. Зубчатая передача трансмиссии должна быть выбрана соответствующим образом, чтобы максимально использовать характеристики крутящего момента двигателя.
Обычно кривая крутящего момента двигателя с турбонаддувом представляет собой крутой подъем, а затем пологую почти до максимальных оборотов. Типичный атмосферный двигатель очень отличается, с очень низким крутящим моментом на низких оборотах, а затем быстрым ростом оборотов до пикового крутящего момента, а затем снова быстрым падением. Область под кривой крутящего момента Turbo намного больше у турбодвигателя. И если вы удвоите крутящий момент, вы удвоите ускорение, уберите из него коробку передач. Крутящий момент играет роль в улучшении ускорения именно по тем причинам, которые я изложил в отношении кривой крутящего момента: большее количество передач позволяет разработчику удерживать двигатель в более точном диапазоне оборотов, обеспечивающих максимальный крутящий момент. Атмосферному двигателю нужны обороты для производства мощности.
Область под кривой крутящего момента Turbo намного больше у турбодвигателя. И если вы удвоите крутящий момент, вы удвоите ускорение, уберите из него коробку передач. Крутящий момент играет роль в улучшении ускорения именно по тем причинам, которые я изложил в отношении кривой крутящего момента: большее количество передач позволяет разработчику удерживать двигатель в более точном диапазоне оборотов, обеспечивающих максимальный крутящий момент. Атмосферному двигателю нужны обороты для производства мощности.
Если сила действует на расстоянии, она совершает механическую работу. Точно так же, если крутящему моменту позволено действовать через расстояние вращения, он совершает работу. Мощность — это работа в единицу времени. Однако время и расстояние вращения связаны угловой скоростью, где каждый оборот приводит к тому, что длина окружности проходит под действием силы, создающей крутящий момент.
Мощность, подаваемая приложенным крутящим моментом, может быть рассчитана как:
Мощность = Крутящий момент x Угловая скорость
Как видите, крутящий момент и мощность напрямую связаны. Мощность — это просто приложение X количества крутящего момента в течение Y времени. Необходимо использовать согласованные единицы. Для метрических единиц СИ мощность — это ватты, крутящий момент — это ньютон-метры, а угловая скорость — это радианы в секунду (не об/мин и не обороты в секунду).
Мощность — это просто приложение X количества крутящего момента в течение Y времени. Необходимо использовать согласованные единицы. Для метрических единиц СИ мощность — это ватты, крутящий момент — это ньютон-метры, а угловая скорость — это радианы в секунду (не об/мин и не обороты в секунду).
В правой части это скалярное произведение двух векторов, дающее скаляр в левой части уравнения. Математически уравнение можно изменить, чтобы вычислить крутящий момент для заданной выходной мощности. Обратите внимание, что мощность, подаваемая крутящим моментом, зависит только от мгновенной угловой скорости, а не от того, увеличивается ли угловая скорость, уменьшается или остается постоянной во время приложения крутящего момента (это эквивалентно линейному случаю, когда мощность, подаваемая силой зависит только от мгновенной скорости, а не от результирующего ускорения, если таковое имеется).
Для различных единиц мощности, крутящего момента или угловой скорости в уравнение необходимо ввести коэффициент преобразования. Кроме того, если скорость вращения (оборот за время) используется вместо угловой скорости (радианы за время), необходимо добавить коэффициент преобразования 2Pi, поскольку в одном обороте 2Pi радиан:
Кроме того, если скорость вращения (оборот за время) используется вместо угловой скорости (радианы за время), необходимо добавить коэффициент преобразования 2Pi, поскольку в одном обороте 2Pi радиан:
Мощность = крутящий момент X 2π X скорость вращения
, где скорость вращения выражается в оборотах в единицу времени.
Теперь вы можете рассчитать мощность вашего автомобиля при заданных оборотах. И теперь вы понимаете, почему Формула 1 так жаждет оборотов двигателя. Самый «простой» способ увеличить мощность — увеличить скорость вращения двигателя.
Аа, кстати, Формула 1!
В Формуле-1 инженеры склонны сопоставлять уровень крутящего момента двигателя для отдельных трасс, для разных участков трассы и для разных условий на гоночной трассе. Карты двигателей — одно из темных искусств F1. На мокрой трассе нет смысла использовать высокое значение крутящего момента. Карта крутящего момента двигателя представляет крутящий момент, создаваемый двигателем, в зависимости от частоты вращения двигателя и положения дроссельной заслонки двигателя. В ЭБУ карта крутящего момента двигателя используется для позиционирования дроссельной заслонки двигателя в соответствии с потребностями водителя в крутящем моменте. Карта крутящего момента водителя представляет крутящий момент, запрошенный водителем, в зависимости от частоты вращения двигателя и положения педали акселератора. FIA ввела правила, которые определяют, как вы можете контролировать крутящий момент двигателя, и подпадают под действие статей 5.5 и 5.6 технического регламента.
В ЭБУ карта крутящего момента двигателя используется для позиционирования дроссельной заслонки двигателя в соответствии с потребностями водителя в крутящем моменте. Карта крутящего момента водителя представляет крутящий момент, запрошенный водителем, в зависимости от частоты вращения двигателя и положения педали акселератора. FIA ввела правила, которые определяют, как вы можете контролировать крутящий момент двигателя, и подпадают под действие статей 5.5 и 5.6 технического регламента.
За исключением некоторых особых исключений, крутящий момент двигателя должен контролироваться водителем. Эти исключения включают в себя: переключение на более низкую передачу, ограничитель скорости на пит-лейн, функцию предотвращения заклинивания и стратегию ограничителя конца прямой. Обратите внимание, что здесь перечислены не все исключения. Есть много других.
Водитель может управлять крутящим моментом только с помощью одной педали акселератора.
При педали с нулевым процентом (отключена дроссельная заслонка) требуемый крутящий момент должен быть меньше или равен нулю; при педали на 100% (полный газ) требуемый крутящий момент должен соответствовать или превышать максимальный выходной крутящий момент двигателя в его текущем состоянии (Статья 5. 5.3).
5.3).
Существуют ограничения на форму требуемого крутящего момента в зависимости от положения педали и частоты вращения двигателя (для предотвращения характеристик двигателя, которые могут использоваться в качестве вспомогательных средств для водителя).
При соблюдении этих ограничений требуемый крутящий момент формируется в зависимости от положения дроссельной заслонки и частоты вращения двигателя, чтобы обеспечить желаемую реакцию водителя и автомобиля.
Карты педалей водителя можно менять от цепи к цепи в зависимости от характеристик цепи. Например, водители могут захотеть большей точности при первом нажатии педали в Монако. Точно так же некоторые водители настаивают на карте педали для влажной погоды.
Карты крутящего момента двигателя также корректируются с учетом выходной мощности двигателя в зависимости от условий окружающей среды. Все двигатели будут развивать больший крутящий момент в холодный день в Сильверстоуне, чем в Интерлагосе (низкое давление воздуха) или Малайзии (высокая удельная влажность).


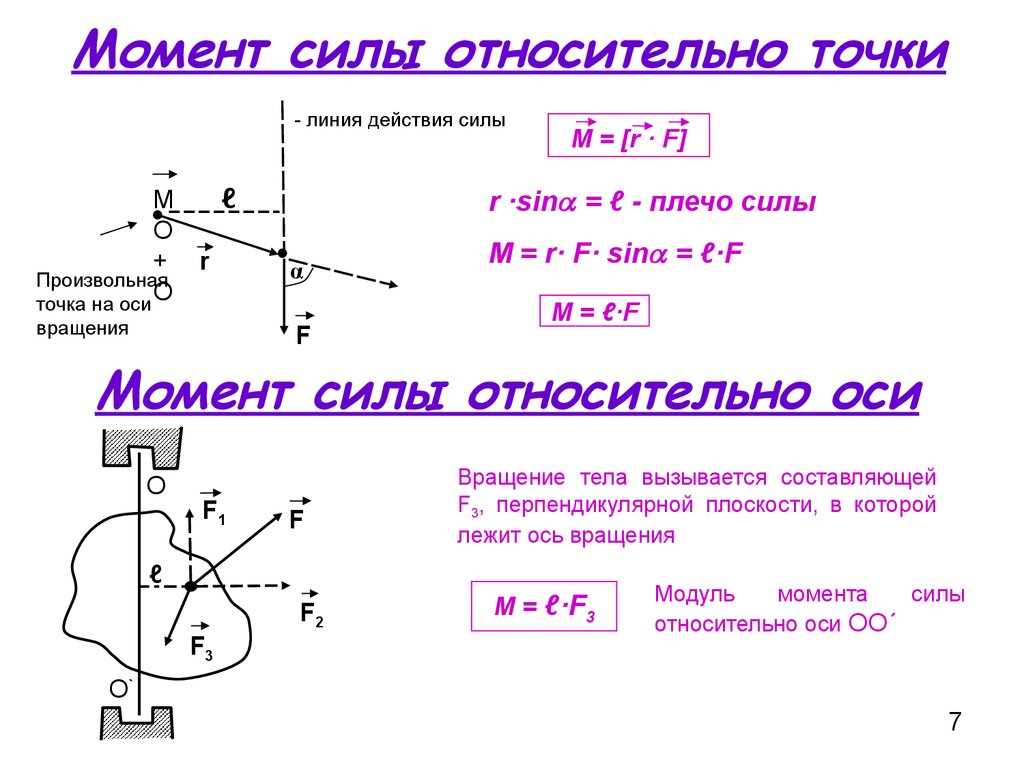 также
также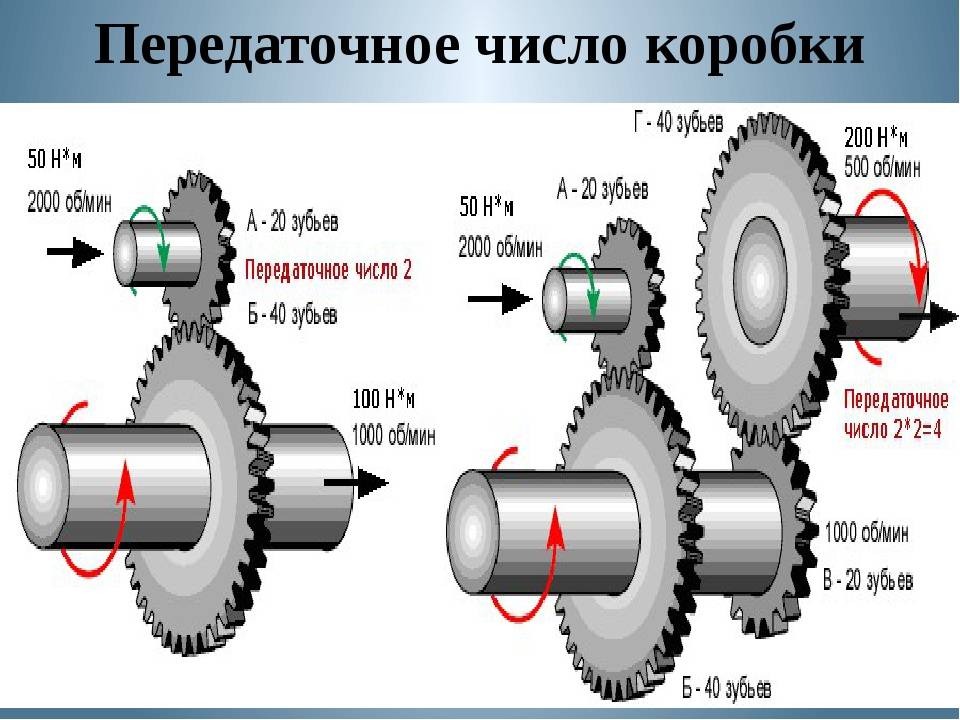 также
также