Формула трение: Сила трения скольжения — Википедия – Трение — Википедия — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Трение — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 января 2019; проверки требуют 9 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 января 2019; проверки требуют 9 правок.

Тре́ние — процесс механического взаимодействия соприкасающихся тел при их относительном смещении в плоскости касания (внешнее трение) либо при относительном смещении параллельных слоёв жидкости, газа или деформируемого твёрдого тела (внутреннее трение, или вязкость). Далее в этой статье под трением понимается лишь внешнее трение. Изучением процессов трения занимается раздел физики, который называется механикой фрикционного взаимодействия, или трибологией.

Трение главным образом имеет электронную природу при условии, что вещество находится в нормальном состоянии. В сверхпроводящем состоянии вдалеке от критической температуры основным «источником» трения являются фононы, а коэффициент трения может уменьшиться в несколько раз

[ссылка 1].

Сила трения — это сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению. Причиной возникновения трения является шероховатость трущихся поверхностей и взаимодействие молекул этих поверхностей. Сила трения зависит от материала трущихся поверхностей и от того, насколько сильно эти поверхности прижаты друг к другу. В простейших моделях трения (закон Кулона для трения) считается, что сила трения прямо пропорциональна силе нормальной реакции между трущимися поверхностями. В целом же, в связи со сложностью физико-химических процессов, протекающих в зоне взаимодействия трущихся тел, процессы трения принципиально не поддаются описанию с помощью простых моделей классической механики.

Разновидности силы трения[править | править код]

При наличии относительного движения двух контактирующих тел силы трения, возникающие при их взаимодействии, можно подразделить на:

Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.
Трение качения — момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого.
Трение покоя — сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения.
Трение верчения — момент силы, возникающий между двумя контактирующими телами при вращении одного из них относительно другого и направленный против вращения. Определяется формулой: M=pN{\displaystyle M=pN}, где N{\displaystyle N} — нормальное давление, p{\displaystyle p} — коэффициент трения верчения, имеющий размерность длины^[1].

Характер фрикционного взаимодействия[править | править код]

В физике взаимодействие трения принято разделять на:

сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками (в том числе и твёрдыми смазочными материалами) — очень редко встречающийся на практике случай, характерная отличительная черта сухого трения — наличие значительной силы трения покоя;
граничное, когда в области контакта могут содержаться слои и участки различной природы (оксидные плёнки, жидкость и так далее) — наиболее распространённый случай при трении скольжения;
смешанное, когда область контакта содержит участки сухого и жидкостного трения;

жидкостное (вязкое), при взаимодействии тел, разделённых слоем твёрдого тела (порошком графита), жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость, величина вязкого трения характеризуется вязкостью среды;
эластогидродинамическое (вязкоупругое), когда решающее значение имеет внутреннее трение в смазывающем материале, возникает при увеличении относительных скоростей перемещения.

Основной характеристикой трения является коэффициент трения μ{\displaystyle \mu }, определяющийся материалами, из которых изготовлены поверхности взаимодействующих тел.

В простейших случаях сила трения F{\displaystyle F} и нормальная нагрузка (или сила нормальной реакции) Nnormal{\displaystyle N_{normal}} связаны неравенством

|F|⩽μNnormal,{\displaystyle |F|\leqslant \mu {N_{normal}},}

Пары материалов	μ{\displaystyle \mu } покоя	μ{\displaystyle \mu } скольжения
Сталь-Сталь	0,5—0,8^[2]	0,15—0,18
Резина-Сухой асфальт	0,95—1	0,5—0,8
Резина-Влажный асфальт		0,25—0,75
Лёд-Лёд	0,05—0,1	0,028
Резина-Лёд	0,3	0,15—0,25
Стекло-Стекло	0,9	0,7
Нейлон-Нейлон	0,15—0,25
Полистирол-Полистирол	0,5
Плексиглас, оргстекло	0,8

Закон Амонтона — Кулона с учетом адгезии[править | править код]

Для большинства пар материалов значение коэффициента трения μ{\displaystyle \mu } не превышает 1 и находится в диапазоне 0,1 — 0,5. Если коэффициент трения превышает 1 (μ>1){\displaystyle (\mu >1)}, это означает, что между контактирующими телами имеется сила адгезии Nadhesion{\displaystyle N_{adhesion}} и формула расчета коэффициента трения меняется на

μ=(Ffriction+Fadhesion)/Nnormal{\displaystyle \mu =(F_{friction}+F_{adhesion})/{N_{normal}}}.

Трение в механизмах и машинах[править | править код]

В большинстве традиционных механизмов (ДВС, автомобили, зубчатые шестерни и пр.) трение играет отрицательную роль, уменьшая КПД механизма. Для уменьшения силы трения используются различные натуральные и синтетические масла и смазки. В современных механизмах для этой цели используется также напыление покрытий (тонких плёнок) на детали. С миниатюризацией механизмов и созданием микроэлектромеханических систем (МЭМС) и наноэлектромеханических систем (НЭМС) величина трения по сравнению с действующими в механизме силами увеличивается и становится весьма значительной (μ⩾1){\displaystyle (\mu \geqslant 1)}, и при этом не может быть уменьшена с помощью обычных смазок, что вызывает значительный теоретический и практический интерес инженеров и учёных к данной области. Для решения проблемы трения создаются новые методы его снижения в рамках трибологии и науки о поверхности (англ.).

Сцепление с поверхностью[править | править код]

Наличие трения обеспечивает возможность перемещаться по поверхности. Так, при ходьбе именно за счёт трения происходит сцепление подошвы с полом, в результате чего происходит отталкивание от пола и движение вперёд. Точно так же обеспечивается сцепление колёс автомобиля (мотоцикла) с поверхностью дороги. В частности, для улучшения этого сцепления разрабатываются новые формы и специальные типы резины для покрышек, а на гоночные болиды устанавливаются антикрылья, сильнее прижимающие машину к трассе.

Трение внутри материалов[править | править код]

Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 1. Трение в машинах. Теория, расчет и конструкция подшипников и подпятников скольжения. Машгиз. М.-Л. — 1947. 256 с.
Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 2. Износ материалов. Классификация видов износа, методов и машин для лабораторного испытания материалов на износ машины и производственные на них исследования. Машгиз. М.-Л. — 1947. 220 с.
Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 3. Износ машин. Износ машин и деталей и способы борьбы с их износом. Машгиз. М.-Л. — 1947. 164 с.
Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 4. Смазка машин. Машгиз. М.-Л. — 1948. 279 с.

Archbutt L., Deeley R.M. Lubrication and Lubicants. London. — 1927
Арчбютт Л., Дилей Р. М. Трение, смазка и смазочные материалы. Руководство по теории и практике смазки и по методам испытания смазочных материалов. Госгоргеолнефтиздат. — Л. — 1934. — 703 с.
Арчбютт Л., Дилей Р. М. Трение, смазка и смазочные материалы — 2-е изд., перераб. и доп. — М.-Л.: Гостоптехиздат. — 1940. — 824 с.
Дерягин Б. В. Что такое трение? М.: Изд. АН СССР, 1963.
Крагельский И. В., Щедров В. С. Развитие науки о трении. Сухое трение. М.: Изд. АН СССР, 1956.
Фролов, К. В. (ред.) Современная трибология: Итоги и перспективы

. ЛКИ, 2008.
Bowden F. P., Tabor D. The Friction and Lubrication of Solids. Oxford University Press, 2001.
Persson Bo N. J.: Sliding Friction. Physical Principles and Applications. Springer, 2002.
Popov V. L. Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation, Springer, 2009.
Rabinowicz E. Friction and Wear of Materials. Wiley-Interscience, 1995.

↑ Зиновьев В. А. Краткий технический справочник. Том 1. — М.: Государственное издательство технико-теоретической литературы, 1949. — С. 296
↑ Friction theory and coefficients of friction for some common materials and materials combinations.

Формула силы трения | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

, где – сила трения, – коэффициент трения, – сила реакции опоры.

Единица измерения силы – Н (ньютон).

Существование силы трения объясняется взаимодействием неровностей на поверхностях тел. Сила трения существует всегда, так как абсолютно гладких тел не бывает.

Сила трения всегда направлена в сторону, противоположную направлению движения, а сила реакции опоры – перпендикулярно поверхности, в сторону, противоположную силе тяжести. зависит от взаимодействующих материалов и гладкости трущихся поверхностей, но не зависит от площади соприкосновения трущихся тел. Это безразмерная величина.

Различают силу трения покоя и силу трения движения. Сила трения покоя – минимальная сила, которую нужно приложить для того, чтобы тело начало движение. Сила трения движения – сила, препятствующая движению, если движущая сила станет меньше её, то тело остановится. Если движущая сила равна силе трения, то тело будет двигаться прямолинейно и равномерно.

Примеры решения задач по теме «Сила трения»

Конспект «Трение покоя и трение скольжения»

Трение покоя и трение скольжения

Код ОГЭ 1.11. Трение покоя и трение скольжения. Формула для вычисления модуля силы трения скольжения.

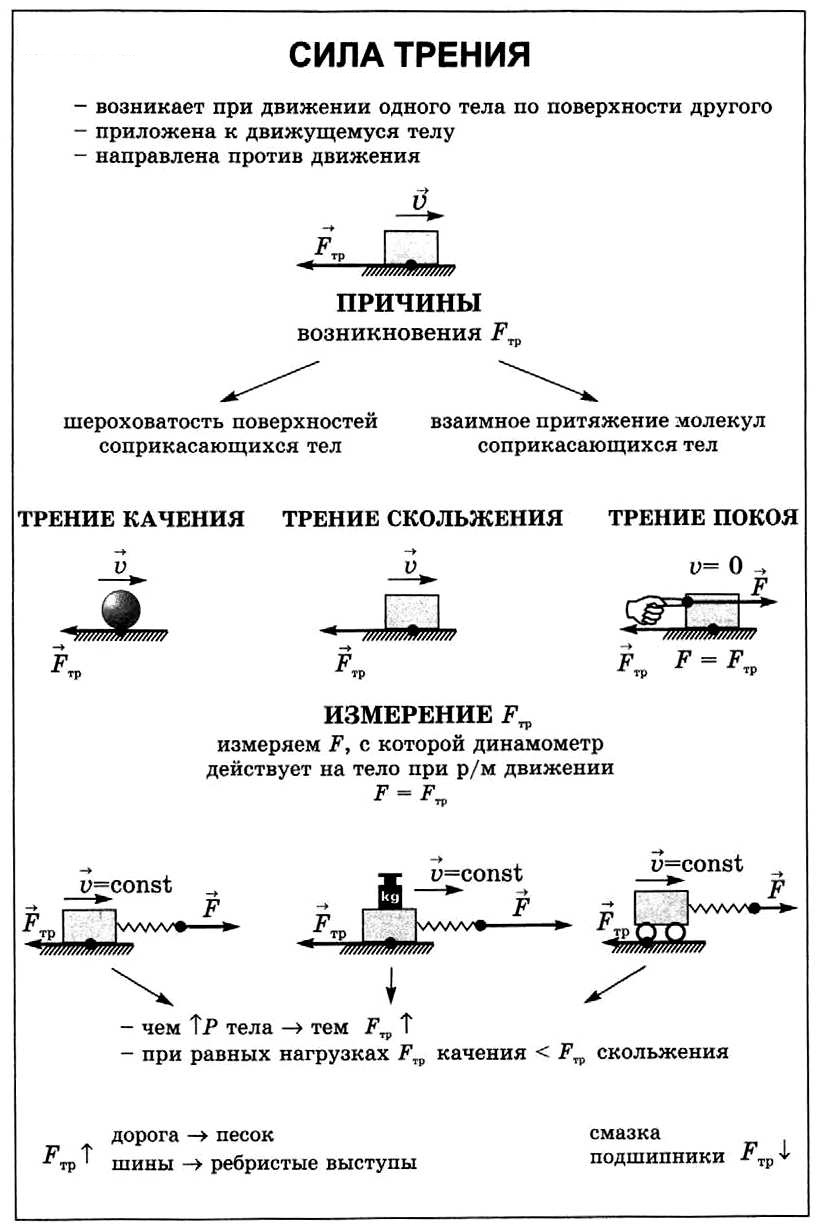
Сила трения возникает при движении одного тела по поверхности другого. Существуют следующие виды сил трения:

Сила трения покоя. Возникает в ситуации возможного движения одного тела по поверхности другого и направлена вдоль поверхности соприкосновения, против направления возможного движения. Сила трения покоя саморегулирующаяся – может принимать любые значения от 0 до максимального: .

Внимание! Сила трения покоя имеет важную особенность – она может не только препятствовать возможному движению, но и обеспечивать это движение. Например, при ходьбе поверхность обуви взаимодействует с поверхностью дороги – они «отталкиваются» друг от друга. При этом в соответствии с третьим законом Ньютона возникают две силы взаимодействия – силы трения покоя. Одна из них действует на поверхность дороги, другая – на поверхность обуви, обеспечивая тем самым движение пешехода.

Сила трения скольжения. Возникает при движении тела по поверхности другого тела, направлена в сторону, противоположную направлению вектора скорости движущегося тела.

Внимание! При решении стандартных физических задач принимается, что максимальная сила трения покоя равна силе трения скольжения и рассчитывается по формуле F_тр= μN, где N–сила реакции опоры; μ – коэффициент трения.

Коэффициент трения – это безразмерная величина. Он зависит от свойств соприкасающихся поверхностей и не зависит от силы давления (соответственно, и от силы реакции опоры, так как это силы, описываемые третьим законом Ньютона) и от площади соприкасающихся поверхностей.

Конспект урока «Трение покоя и трение скольжения».

Следующая тема: «Деформация тела».

Трение покоя — Википедия

Материал из Википедии — свободной энциклопедии

Тре́ние поко́я, трение сцепления — сила, возникающая между двумя неподвижными контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Трение покоя наблюдается до перехода к движению на макроуровне, когда начинает действовать сила трения качения или скольжения. Действует в направлении, противоположном направлению возможного относительного движения. Максимальная сила трения покоя обычно несколько выше, чем сила трения скольжения.

В 1779 году французский физик Кулон установил, от чего зависит максимальная сила трения покоя. Оказалось, что сила трения покоя зависит от того, с какой силой прижимаются друг к другу соприкасающиеся предметы. Также было установлено, что трение покоя зависит от материала соприкасающихся поверхностей.

Примером силы трения покоя может служить эскалатор со стоящим на нем человеком. Также эта сила проявляется в забитом в доску гвозде, завязанном банте или шнурке и т.д.

Максимальная сила трения покоя в простейшем приближении^[1]: F≈k0N{\displaystyle F\approx k_{0}N}, где k0{\displaystyle k_{0}} — коэффициент трения покоя, N{\displaystyle N} — сила нормальной реакции опоры.

↑ Кабардин О. Ф. Физика. — М., Просвещение, 1985. — Тираж 754000 экз. — с. 31

Сила трения скольжения — урок. Физика, 9 класс.

Сила трения скольжения возникает, если одно тело скользит по поверхности другого тела. Трение скольжения характеризуется силой трения, которая тормозит движение скольжения.

Сила трения скольжения прямо пропорциональна силе реакции опоры и коэффициенту трения скольжения.

Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры и вычисляется по формуле: Fтр=μ⋅Fр.

При увеличении веса тела и коэффициента трения увеличивается сила трения. Сила трения скольжения действует в тех случаях, когда тело движется или его пытаются сдвинуть с места.

Сила реакции опоры — сила, при помощи которой опора действует на тело. Сила реакции опоры — сила, при помощи которой опора давит на тело, которое находится на ней. Из третьего закона Ньютона следует, что сила реакции опоры всегда равна силе, при помощи которой тело воздействует на опору. На неподвижной горизонтальной поверхности сила реакции опоры всегда равна весу тела или силе тяжести: Fр=Fт. На наклонной плоскости сила тяжести и сила, при помощи которой тело воздействует на опору, различаются.

Обрати внимание!

Сила реакции опоры всегда направлена перпендикулярно поверхности опоры.

Коэффициент трения скольжения — отношение силы трения к силе реакции опоры. Коэффициент трения между двумя любыми материалами легко определить, если возможно измерить силу трения, которая равна силе тяги, при которой тело перемещается равномерно, и силу тяжести, которая на горизонтальной поверхности равна силе реакции опоры. В таблице представлены различные коэффициенты трения скольжения.

Пары материалов	Коэффициент трения скольжения
Сталь — лёд (коньки)	$0,015$
Древесина — древесина	$0,2$–$0,5$
Покрышка — мокрый асфальт	$0,35$–$0,45$
Покрышка — сухой асфальт	$0,50$–$0,75$

Обрати внимание!

Коэффициент трения скольжения не имеет размерности.

Если сравнивать коэффициенты трения покрышки на сухом и мокром асфальте, то на мокром асфальте у одной и той же машины коэффициент трения, а также сила трения почти в $2$ раза меньше, чем на сухом асфальте. В результате также увеличивается замедление торможения почти в $2$ раза, поэтому тормозной путь может увеличиться почти в $4$ раза.

У силы трения имеются как положительные, так и отрицательные свойства. Если бы не было силы трения, то мы не могли бы оттолкнуться при ходьбе от земли, а машина не могла бы «оттолкнуться» от поверхности дороги. Но в технике трение между различными вращающимися и скользящими поверхностями весьма нежелательно, поэтому такое оборудование смазывают, чтобы снизить влияние силы трения.

Сила трения скольжения | Все формулы

Сообщение от администратора:

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении

Вектор силы трения скольжения всегда направлен противоположно вектору скорости движения тела относительно соприкасающегося с ним тела. Поэтому действие силы трения скольжения всегда приводит к уменьшению модуля относительной скорости тел.

Если проделать некоторые опыты с бруском и динамометром можно придти к выводу, что сила трения скольжения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. Это можно объяснить тем, что увеличивая площадь соприкосновения, мы уменьшаем удельное давление тел друг на друга.

Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой μ. Обычно коэффициент трения меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки поверхностей. При скольжении сила трения направлена по касательной к соприкасающимся поверхностям в сторону, противоположную относительной скорости

В формуле мы использовали :

— Сила трения скольжения

— Коэффициент трения скольжения

— Сила нормальной реакции опоры

— Масса тела

— Ускорение свободного падения

Сила трения — ЗФТШ, МФТИ

Сила трения – сила механического сопротивления, возникающая в плоскости соприкосновения двух прижатых друг к другу тел при их относительном перемещении.

Сила сопротивления, действующая на тело, направлена противоположено относительному перемещению данного тела.

Сила трения возникает по двум причинам: 1) первая и основная причина заключается в том, что в местах соприкосновения молекулы веществ притягиваются друг к другу, и для преодоления их притяжения требуется совершить работу. Соприкасающиеся поверхности касаются друг друга лишь в очень небольших по площади местах. Их суммарная площадь составляет 0,01÷0,0010,01 \div 0,001 от общей (кажущейся) площади соприкосновения. При скольжении площадь реального соприкосновения не остается неизменной. Сила трения (скольжения) будет изменяться в процессе движения. Если тело, которое скользит, прижать сильнее к телу, по которому происходит скольжение, то вследствие деформации тел площадь пятен соприкосновения (и сила трения) увеличится пропорционально прижимающей силе.

$$F_\text{тр} \sim F_\text{приж}$$

2) вторая причина возникнове ния силы трения – это наличие шероховатостей (неровностей) поверхностей, и деформация их при движении одного тела по поверхности другого. Глубина проникновения (зацепления) шероховатостей зависит от прижимающей силы, а от этого зависит и величина деформаций. Последние, в свою очередь, определяют величину силы трения: Fтр∼FприжF_\mathrm{тр} \sim F_\mathrm{приж}.

При относительном скольжении обе причины имеют место, потому характер взаимодействия имеет вид простого соотношения:

Fтр=μN -\boxed{F_\mathrm{тр} =\mu N}\ -сила трения скольжения (формула Кулона — Амонтона), где

μ -\mu\ — коэффициент трения скольжения,

N -N\ — сила реакции опоры, равная прижимающей силе.

Величина коэффициента трения различна для разных комбинаций трущихся веществ даже при одинаковой их обработке (силы притяжения и упругие свойства зависят от рода вещества).

Если между трущимися поверхностями будет находится смазка, то сила притяжения изменится заметным образом (будут притягиваться другие молекулы, и сила трения скольжения частично заменится силой вязкого трения, которую мы рассмотрим ниже).

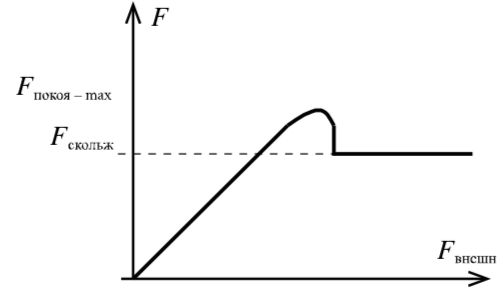
Если на тело, лежащее на горизонтальной поверхности, действует горизонтальная сила F→\vec F, то движение будет вызвано этой силой только в том случае, когда она станет больше некоторого значения (μN)(\mu N). До начала движения внешняя сила скомпенсирована силой трения покоя.

Рис. 13

Сила трения покоя всегда равна внешней силе, параллельной поверхности, и возникает по причине притяжения между молекулами в областях пятен соприкосновения и деформации шероховатостей.

Сила трения покоя различна в разных участках поверхности по которой будет происходить движение. Если тело долго лежит на поверхности, то вследствие вибраций (они всегда присутствуют на поверхности Земли) площадь пятен соприкосновения незначительно увеличится. Поэтому для начала движения придётся преодолеть немного большую силу трения, чем сила трения скольжения. Данное явление называется явлением застоя. С этим явлением мы сталкиваемся, например передвигая мебель в комнате. (На рисунке 13 превосходство трения покоя над трением скольжения сильно преувеличено).

Силой трения покоя мы пользуемся для перемещения на лыжах или просто при ходьбе.

Рассмотренные виды силы трения относятся к сухому трению или внешнему. Но есть еще один вид силы трения – вязкое трение.

При движении тела в жидкости или газе происходят достаточно сложные процессы обмена молекулами между слоями обтекающей жидкости или газа. Эти процессы называют процессами переноса.

При небольших скоростях движения тела относительно газа или жидкости сила сопротивления будет определяться выражением:

Fтр=6πηrv -\boxed{F_\mathrm{тр} = 6\pi \eta r v}\ — закон Стокса для шара, где

η -\eta\ — вязкость вещества, в котором движется тело;

r -r\ — средний поперечный размер (радиус) тела;

v -v\ — относительная скорость тела;

6π -6\pi\ — коэффициент, соответствующей сферической форме тела.

Вывод о величине скорости (большая она или маленькая) можно сделать, определив безразмерный коэффициент, называемый числом Рейнольдса:

Re=ρrvη -\boxed{Re = \frac{\rho r v}{\eta}}\ — число Рейнольдса, где

ρ -\rho\ — плотность вещества, в которой движется тело.

Если Re<1700Re , то движение газа (жидкости) вокруг тела ламинарное (слоистое), и скорости можно считать малыми.

Если Re>1700Re > 1700, то движение газа (жидкости) вокруг тела турбулентное (с завихрениями), и скорости можно считать большими.

В последнем случае на образование вихрей тратится большая часть кинетической энергии тела, а значит, сила трения становится большей, а зависимость перестаёт быть линейной.

Fтр=kv2ρS -\boxed{F_\mathrm{тр} = kv^2\rho S}\ — сила вязкого трения при больших скоростях, где

S -S\ — площадь поперечного сечения тела,

k -k\ — постоянная величина, зависящая от поперечных размеров тела.

Часто последнюю формулу можно видеть в виде:

\[F_\text{тр} = \beta v^2.\]

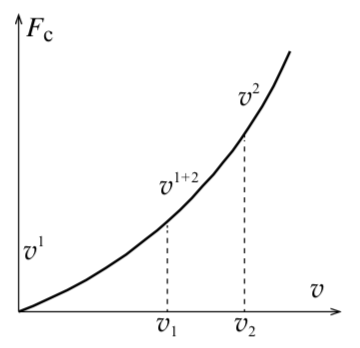
Число Рейнольдса, выбранное равным 17001700, в действительности определяется конкретной задачей (условиями) и может принимать другие значения того же порядка. Объясняется это тем, что зависимость силы вязкого трения от скорости носит сложный характер: при некотором значении скорости линейная зависимость начинает нарушаться, а при некотором значении скорости эта зависимость становится квадратичной.

Рис. 14

В промежутке от v1v_1 до v2v_2 степень принимает дробные значения (рис. 14) . Число Рейнольдса характеризует состояние динамической системы, при котором движение слоёв остаётся ламинарным, и сильно зависит от внешних условий. К примеру: стальной шар, двигаясь в воде вдали от границ жидкости (в океане, озере) сохраняет ламинарным движение слоёв при Re=1700Re = 1700, а тот же шар, движущийся в вертикальной трубе немного большего, чем шар, радиуса, заполненной водой, уже при Re=2Re=2 вызовет появление завихрений воды вокруг шара. (Отметим, что число Рейнольдса не единственное, применяемое для описания подобного движения. Например, применяют ещё числа Фруда и Маха.)

Из-за такой сложной зависимости силы сопротивления от размеров, формы тела и его скорости рассчитать с необходимой точностью силу сопротивления невозможно. Потому приходится создавать макеты летательных аппаратов и измерять силу сопротивления опытным путём, продувая воздух в аэродинамических трубах.

Пример 7. Сила сопротивления воздуха, действующая на капли тумана, пропорциональна произведению скорости на радиус капель: F=krvF = krv. Капли радиуса 0,1 мм0,1\ \text{мм}, падая с большой высоты, у земли имеют скорость около 1 м/с1\ \mathrm{м}/\mathrm{с}. Какую скорость будут иметь капли, радиус которых в два раза меньше? В десять раз меньше?

Решение: Капля падает с постоянной скоростью, т. к. сила тяжести скомпенсирована силой вязкого трения о воздух: krv=mgkrv = mg или krv=ρ43πr3gkrv = \rho \frac 43 \pi r^3 g, откуда v=4ρπg3kr2v = \frac{4\rho\pi g}{3k}r^2.

Из полученного результата следует, что скорость капли прямо пропорциональна квадрату радиуса. Если радиус капли уменьшится в два раза, то скорость её падения уменьшится в четыре раза, и составит v1≈0,25 м/сv_1 \approx 0,25\ \text{м}/\text{с}; а если радиус окажется в десять раз меньше, то скорость будет в сто раз меньше, т. е. v2≈0,01 м/сv_2 \approx 0,01\ \mathrm{м}/\mathrm{с}.

Задача любопытна тем, что может объяснить почему облака не падают. Ведь облака – это туман, который не падает из-за наличия восходящих потоков воздуха. На нижней границе облака находятся наиболее крупные капли. Поднимаясь, скорость потока уменьшается, т. к. он совершает работу над встретившимся воздухом и увеличивает свою потенциальную энергию. Раз скорость потока в верхней части облака меньше, то и размер капель там тоже меньше. Капли «висят» над поверхностью земли на постоянной высоте.