Формула силы притяжения

ОПРЕДЕЛЕНИЕ

Сила гравитационного притяжения между телами равна произведению гравитационной постоянной и масс обоих объектов, делённому на квадрат расстояния между ними.

   

Здесь – сила притяжения, – гравитационная постоянная, — массы объектов, – расстояние между центрами масс объектов.

Единица измерения силы – Н (ньютон).

Сила гравитации возникает между любыми объектами в Вселенной, обладающими массой. Будучи приложенной к каждому объекту, она направлена на другой, причём модуль этой силы равен для обоих объектов:

Для тела, находящегося на поверхности Земли, формула упрощается, так как масса Земли и расстояние от центра Земли до поверхности известно:

   

Где м/с. называют ускорением свободного падения.

Примеры решения задач по теме «Сила притяжения»

ПРИМЕР 1

Задание	Найти силу притяжения между объектами, массами 100т и 1000т, находящимися на расстоянии 3 км.
Решение	Напомним, что 1 т = 1000 кг, а 1 км = 1000 м. Подставим исходные данные в формулу:
Ответ	Сила гравитации равна .

Понравился сайт? Расскажи друзьям!

точная формула силы всемирного притяжения, определение гравитации

Самым главным явлением, постоянно изучаемым физиками, является движение. Электромагнитные явления, законы механики, термодинамические и квантовые процессы – все это широкий спектр изучаемых физикой фрагментов мироздания. И все эти процессы сводятся, так или иначе, к одному – к движению тел.

…

Вконтакте

Facebook

Twitter

Мой мир

Все во Вселенной движется. Гравитация – привычное явление для всех людей с самого детства, мы родились в гравитационном поле нашей планеты, это физическое явление воспринимается нами на самом глубоком интуитивном уровне и, казалось бы, даже не требует изучения.

Но, увы, вопрос, почему и каким образом все тела притягиваются друг к другу, остается и на сегодняшний день не до конца раскрытым, хотя и изучен вдоль и поперек.

В этой статье мы рассмотрим, что такое всемирное притяжение по Ньютону – классическую теорию гравитации. Однако прежде чем перейти к формулам и примерам, расскажем о сути проблемы притяжения и дадим ему определение.

Быть может, изучение гравитации стало началом натуральной философии (науки о понимании сути вещей), быть может, натуральная философия породила вопрос о сущности гравитации, но, так или иначе, вопросом тяготения тел заинтересовались еще в Древней Греции

.

Движение понималось как суть чувственной характеристики тела, а точнее, тело двигалось, пока наблюдатель это видит. Если мы не можем явление измерить, взвесить, ощутить, значит ли это, что этого явления не существует? Естественно, не значит. И с тех пор, как Аристотель понял это, начались размышления о сути гравитации.

Как оказалось в наши дни, спустя многие десятки веков, гравитация является основой не только земного притяжения и притяжения нашей планеты к Солнцу, но и основой зарождения Вселенной и почти всех имеющихся элементарных частиц.

Задача движения

Проведем мысленный эксперимент. Возьмем в левую руку небольшой шарик. В правую возьмем такой же. Отпустим правый шарик, и он начнет падать вниз. Левый при этом остается в руке, он по-прежнему недвижим.

Остановим мысленно ход времени. Падающий правый шарик «зависает» в воздухе, левый все также остается в руке. Правый шарик наделен «энергией» движения, левый – нет. Но в чем глубокая, осмысленная разница между ними?

Где, в какой части падающего шарика прописано, что он должен двигаться? У него такая же масса, такой же объем. Он обладает такими же атомами, и они ничем не отличаются от атомов покоящегося шарика. Шарик обладает потенциальной энергией? Да, это правильный ответ, но откуда шарику известно, что обладает потенциальной энергией, где это зафиксировано в нем?

Именно эту задачу ставили перед собой Аристотель, Ньютон и Альберт Эйнштейн. И все три гениальных мыслителя отчасти решили для себя эту проблему, но на сегодняшний день существует ряд вопросов, требующих разрешения.

Гравитация Ньютона

В 1666 году величайшим английским физиком и механиком И. Ньютоном открыт закон, способный количественно посчитать силу, благодаря которой вся материя во Вселенной стремится друг к другу. Это явление получило название всемирное тяготение. Когда вас просят: «Сформулируйте закон всемирного тяготения», ваш ответ должен звучать так:

Сила гравитационного взаимодействия, способствующая притяжению двух тел, находится в прямой пропорциональной связи с массами этих тел и в обратной пропорциональной связи с расстоянием между ними.

Важно! В законе притяжения Ньютона используется термин «расстояние». Под этим термином следует понимать не дистанцию между поверхностями тел, а расстояние между их центрами тяжести. К примеру, если два шара радиусами r1 и r2 лежат друг на друге, то дистанция между их поверхностями равна нулю, однако сила притяжения есть. Все дело в том, что расстояние между их центрами r1+r2 отлично от нуля. В космических масштабах это уточнение не суть важно, но для спутника на орбите данная дистанция равна высоте над поверхностью плюс радиус нашей планеты. Расстояние между Землей и Луной также измеряется как расстояние между их центрами, а не поверхностями.

Для закона тяготения формула выглядит следующим образом:

,

где:

• F – сила притяжения,
• – массы,
• r – расстояние,
• G – гравитационная постоянная, равная 6,67·10−11 м³/(кг·с²).

Что же представляет собой вес, если только что мы рассмотрели силу притяжения?

Сила является векторной величиной, однако в законе всемирного тяготения она традиционно записана как скаляр. В векторной картине закон будет выглядеть таким образом:

.

Но это не означает, что сила обратно пропорциональна кубу дистанции между центрами. Отношение следует воспринимать как единичный вектор, направленный от одного центра к другому:

.

Закон гравитационного взаимодействия

Вес и гравитация

Рассмотрев закон гравитации, можно понять, что нет ничего удивительного в том, что лично мы ощущаем притяжение Солнца намного слабее, чем земное. Массивное Солнце хоть и имеет большую массу, однако оно очень далеко от нас. Земля тоже далеко от Солнца, однако она притягивается к нему, так как обладает большой массой. Каким образом найти силу притяжения двух тел, а именно как вычислить силу тяготения Солнца, Земли и нас с вами – с этим вопросом мы разберемся чуть позже.

Насколько нам известно, сила тяжести равна:

P = mg,

где m – наша масса, а g – ускорение свободного падения Земли (9,81 м/с²).

Важно!

Не бывает двух, трех, десяти видов сил притяжения. Гравитация – единственная сила, дающая количественную характеристику притяжения. Вес (P = mg) и сила гравитации – одно и то же.

Если m – наша масса, M – масса земного шара, R – его радиус, то гравитационная сила, действующая на нас, равна:

.

Таким образом, поскольку F = mg:

.

Массы m сокращаются, и остается выражение для ускорения свободного падения:

.

Как видим, ускорение свободного падения – действительно постоянная величина, поскольку в ее формулу входят величины постоянные — радиус, масса Земли и гравитационная постоянная. Подставив значения этих констант, мы убедимся, что ускорение свободного падения равно 9,81 м/с ².

На разных широтах радиус планеты несколько отличается, поскольку Земля все-таки не идеальный шар. Из-за этого ускорение свободного падения в отдельных точках земного шара разное.

Вернемся к притяжению Земли и Солнца. Постараемся на примере доказать, что земной шар притягивает нас с вами сильнее, чем Солнце.

Примем для удобства массу человека: m = 100 кг. Тогда:

• Расстояние между человеком и земным шаром равно радиусу планеты: R = 6,4∙10⁶ м.
• Масса Земли равна: M ≈ 6∙10²⁴ кг.
• Масса Солнца равна: Mc ≈ 2∙10³⁰ кг.
• Дистанция между нашей планетой и Солнцем (между Солнцем и человеком): r=15∙10¹⁰ м.

Гравитационное притяжение между человеком и Землей:

.

Данный результат довольно очевиден из более простого выражения для веса (P = mg).

Сила гравитационного притяжения между человеком и Солнцем:

.

Как видим, наша планета притягивает нас почти в 2000 раз сильнее.

Как найти силу притяжения между Землей и Солнцем? Следующим образом:

.

Теперь мы видим, что Солнце притягивает нашу планету более чем в миллиард миллиардов раз сильнее, чем планета притягивает нас с вами.

Первая космическая скорость

После того как Исаак Ньютон открыл закон всемирного тяготения, ему стало интересно, с какой скоростью нужно бросить тело, чтобы оно, преодолев гравитационное поле, навсегда покинуло земной шар.

Правда, он представлял себе это несколько иначе, в его понимании была не вертикально стоящая ракета, устремленная в небо, а тело, которое горизонтально совершает прыжок с вершины горы. Это была логичная иллюстрация, поскольку на вершине горы сила притяжения немного меньше.

Так, на вершине Эвереста ускорение свободного падения будет равно не привычные 9,8 м/с², а почти м/с². Именно по этой причине там настолько разряженный воздух, частицы воздуха уже не так привязаны к гравитации, как те, которые «упали» к поверхности.

Постараемся узнать, что такое космическая скорость.

Первая космическая скорость v1 – это такая скорость, при которой тело покинет поверхность Земли (или другой планеты) и перейдет на круговую орбиту.

Постараемся узнать численной значение этой величины для нашей планеты.

Запишем второй закон Ньютона для тела, которое вращается вокруг планеты по круговой орбите:

,

где h — высота тела над поверхностью, R — радиус Земли.

На орбите на тело действует центробежное ускорение

, таким образом:

.

Массы сокращаются, получаем:

,

.

Данная скорость называется первой космической скоростью:

Как можно заметить, космическая скорость абсолютно не зависит от массы тела. Таким образом, любой предмет, разогнанный до скорости 7,9 км/с, покинет нашу планету и перейдет на ее орбиту.

Первая космическая скорость

Вторая космическая скорость

Однако, даже разогнав тело до первой космической скорости, нам не удастся полностью разорвать его гравитационную связь с Землей. Для этого и нужна вторая космическая скорость. При достижении этой скорости тело покидает гравитационное поле планеты и все возможные замкнутые орбиты.

Важно! По ошибке часто считается, что для того чтобы попасть на Луну, космонавтам приходилось достигать второй космической скорости, ведь нужно было сперва «разъединиться» с гравитационным полем планеты. Это не так: пара «Земля — Луна» находятся в гравитационном поле Земли. Их общий центр тяжести находится внутри земного шара.

Для того чтобы найти эту скорость, поставим задачу немного иначе. Допустим, тело летит из бесконечности на планету. Вопрос: какая скорость будет достигнута на поверхности при приземлении (без учета атмосферы, разумеется)? Именно такая скорость и потребуется телу, чтобы покинуть планету.

Вторая космическая скорость

Запишем закон сохранения энергии:

,

где в правой части равенства стоит работа силы тяжести: A = Fs.

Отсюда получаем, что вторая космическая скорость равна:

Таким образом, вторая космическая скорость в 

 раз больше первой:

.

Закон всемирного тяготения. Физика 9 класс

 

Закон Всемирного тяготения.

Вывод

Мы с вами узнали, что хотя гравитация является основной силой во Вселенной, многие причины этого явления до сих пор остались загадкой. Мы узнали, что такое сила всемирного тяготения Ньютона, научились считать ее для различных тел, а также изучили некоторые полезные следствия, которые вытекают из такого явления, как всемирный закон тяготения.

Формула силы притяжения

История проблемы гравитации

Уже древнегреческие философы задумывались над причинами притяжения тел к земной поверхности и закономерностями свободного падения. Аристотель, например, утверждал, что если бросить вниз с одинаковой высоты два камня, то более тяжелый достигнет поверхности первым. В IV в. до н.э., когда жил этот мыслитель, единственным приемлемым методом познания считалось наблюдение и размышление, поэтому проверить опытом свое утверждение Аристотель не потрудился. Лишь спустя века итальянский физик Галилео Галилей (1564 – 1642 гг.) решил подвергнуть утверждение античного философа испытанию практикой. Результаты своих опытов он опубликовал в трактате «Беседы и математические доказательства, касающиеся двух новых наук», где писал от имени персонажа Сагредо: «пушечное ядро не опередит мушкетной пули при падении с высоты двухсот локтей».

Теоретически закрепить наблюдения Галилея о том, что тела разной массы падают на землю с равными ускорениями, смог Исаак Ньютон, сформулировавший около 1666 г. закон всемирного тяготения. Согласно ему сила, с которой взаимно притягиваются друг к другу два тела, прямопропорциональна их массами и обратнопропорциональна расстоянию между ними. Гравитацию Ньютон считал всеобщим свойством тел, обладающих массой, притягиваться друг к другу.

Достоверность открытия Ньютона была многократно подтверждена практикой. Однако к началу XX в. в физике появились задачи, связанные с крупными астрономическими объектами, такими, как планетарные системы, галактики. Ньютоновский закон давал недостаточно точные результаты при наблюдениях за ними. Новую теорию, позволяющую устранить эти погрешности, разработал в начале XX в. Альберт Эйнштейн (1879 — 1955 гг.). В своей Общей теории относительности он предложил считать гравитацию не силой, а зависящим от массы искривлением четырехмерного пространства-времени. При этом нельзя сказать, что открытие Эйнштейна отменило теорию гравитации Ньютона. Закон всемирного тяготения является частным случаем Общей теории относительности, действующим на сравнительно небольших расстояниях. Он по-прежнему широко применяется при решении практических задач.

Закон всемирного тяготения

Определение 1

Гравитацией называется способность тел, обладающих массой, притягиваться друг к другу. Ее можно представить как поле, способное дистанционно воздействовать на объекты, которые не связаны никакими другими способами.

Гравитационную закономерность, найденную Ньютоном, математически можно сформулировать как

$F = G \cdot \frac{m_1 \cdot m_2}{r^2}$,

где $m_1, m_2$ — массы притягивающихся с силой $F$ тел, $r$ — расстояние между ними, $G$ — т.н. гравитационная постоянная, констнта, равная 6,67.

Важно отметить, что

1. сила гравитационного взаимодействия ослабевает по мере удаления тел друг от друга пропорционально не просто расстаянию, а расстоянию в квадрате;
2. под расстоянием понимается не расстояние между поверхностями, а расстояние между центрами тяжести тел.

Замечание 1

Зависимость интенсивности от квадрата расстояния роднит гравитацию с другими фундаментальными физическими взаимодействиями: электромагнитным, сильным и слабым.

Квадратичная зависимость силы притяжения от расстояния позволяет понять, почему Солнце, масса которого в миллион раз больше земной, практически не притягивает нас, когда мы находимся на поверхности нашей планеты. Расстояние от Земли до центра Солнечной системы составляет около 150 млн. км. На такой большой дистанции солнечная гравитация практически не ощущается, хотя с помощью высокоточных приборов ее можно зарегистрировать.

В условиях планеты Земля силу, с которой она притягивает к себе близлежащие предметы (иными словами, их вес) можно подсчитать как

$P = mg$,

где $m$ – масса притягиваемого объекта, $g$ – ускорение свободного падения близ Земли (для других планет значение будет отличаться). Ускорение свободного падения несколько колеблется в зависимости от географической широты, но в среднем его можно принимать как константу, равную $9,81 \frac{м}{с^2}$.

Замечание 2

В физике вес и масса — разные понятия. Вес — сила, с которой притягивается тело к планете (не обязательно к Земле). Масса — мера инертности вещества и не зависит от находящихся рядом других тел. Однако в некоторых системах единиц измерения сила измеряется не в ньютонах, а в килограмм-силах. Для них утверждение «человек весит 80 кг» может оказаться справедливым.

Первая и вторая космические скорости

Гравитационную силу можно преодолеть с помощью противодействия других сил (например, реактивной), что делает возможными авиационные и космические полеты.

Можно провести мысленный эксперимент, представив пушку, стреляющую горизонтально с вершины высокой горы. Такую систему удобно выбрать еще и потому, что воздух тоже подчиняется законам гравитации, и вблизи поверхности планеты он плотнее, чем, скажем, на высоте 8000 м. над уровнем моря. Таким образом, снаряду, вылетающему из «высокогорной» пушки, вязкость атмосферы будет оказывать меньшее сопротивление.

Если выстрел из такой пушки будет относительно слабым, вылетевшее из нее тело упадет где-нибудь неподалеку под действием гравитации Земли, совершив полет по искривленной гравитацией траектории. Чем больше будет начальная скорость снаряда, тем дальше он пролетит, огибая земной шар. Наконец, сила выстрела может достигнуть такого значения, что кривизна траектории снаряда совпадет с окружностью радиусом от центра Земли до пушки, и снаряд начнет вращаться вокруг планеты по круговой орбите. Скорость, на которой это произойдет, называется первой космической. Ее можно вычислить как

$V_1 = \sqrt{G \cdot \frac{M}{R}}$,

где $G$ – гравитационная постоянная, $M$ – масса планеты, $R$ – ее радиус.

Пример 1

Масса Земли равна $ 5,97 \cdot 10^{24}$ кг, радиус — $6371$ км. Подставив эти значения в формулу, получим, что первая космическая скорость здесь равна $7,9$ км/с.

Продолжая наращивать интенсивность выстрела, мы можем превратить траекторию сначала в эллиптическую (снаряд будет вращаться вокруг Земли по вытянутой орбите), а затем и в гиперболическую (он начнет удаляться от планеты, не возвращаясь к ней). Последнее будет означать, что снаряд достиг второй космической скорости, которую можно посчитать как

$V_2 = \sqrt{2 \cdot G \frac{M}{R}} = \sqrt{2} \cdot V_1 = 1,41 \cdot 7,9 \approx 11,17 км/с $

Сила гравитационного притяжения | LAMPA

Итак, модуль силы гравитационного притяжения дается выражением

F=GM1⋅M2R2.F=G\frac{M_1\cdot M_2}{R^2}{.}F=GR2M1​⋅M2​​.

Сила гравитационного притяжения направлена по линии, соединяющей центры масс притягивающихся тел.

Надо отметить, что по 3-му закону Ньютона не только первое тело притягивает второе, но и второе тело притягивает первое. Причем притягивает с точно такой же по модулю силой.

Осталось последнее — выяснить: а что же такое GGG? GGG — это гравитационная постоянная. G=6,67⋅10−11Н⋅м2кг2G=6,67\cdot 10^{-11}\frac{Н\cdot м^2}{кг^2}G=6,67⋅10−11кг2Н⋅м2​. Это просто константа. Запоминать ее вовсе не обязательно. Достаточно просто знать, что она присутствует в формуле. Ее значение есть в справочниках, а на ЕГЭ — в начале экзаменационных листов в списке физических констант.

Множитель 10−1110^{-11}10−11, который содержится в константе GGG, — это очень маленькое число. Именно из-за этого множителя сила гравитационного притяжения очень мала. Сидя за одной партой, два ученика тоже притягиваются друг к другу, но сила этого притяжения настолько мала, что почувствовать ее невозможно.

Земля притягивает все тела (в частности, каждого из нас) как раз таки по закону всемирного тяготения:

Fтяготения=Gm⋅MЗемли(RЗемли)2F_{тяготения}=G\frac{m\cdot M_{Земли}}{(R_{Земли})^2}Fтяготения​=G(RЗемли​)2m⋅MЗемли​​,

где mmm — масса тела, притягиваемого Землей. Масса Земли MЗемлиM_{Земли}MЗемли​, радиус Земли RЗемлиR_{Земли}RЗемли​ — это постоянные величины, которые не изменяются уже много-много лет. Поэтому можно переписать силу тяготения на Земле в виде:

Fтяготения=m⋅[GMЗемли(RЗемли)2]F_{тяготения}=m\cdot [G\frac{M_{Земли}}{(R_{Земли})^2}]Fтяготения​=m⋅[G(RЗемли​)2MЗемли​​].

Представим себе ситуацию, когда тело находится в свободном падении. Единственная сила, которая действует на тело, — это сила гравитационного притяжения Земли. По 2-му закону Ньютона можно записать:

Fтяготения=m⋅aF_{тяготения}=m\cdot aFтяготения​=m⋅a.

При этом Fтяготения=m⋅[GMЗемли(RЗемли)2]F_{тяготения}=m\cdot [G\frac{M_{Земли}}{(R_{Земли})^2}]Fтяготения​=m⋅[G(RЗемли​)2MЗемли​​]. Из этих двух уравнений следует, что

m⋅[GMЗемли(RЗемли)2]=m⋅a⇒a=GMЗемли(RЗемли)2=gm\cdot [G\frac{M_{Земли}}{(R_{Земли})^2}]=m\cdot a\,\,\Rightarrow\,\, a=G\frac{M_{Земли}}{(R_{Земли})^2}=gm⋅[G(RЗемли​)2MЗемли​​]=m⋅a⇒a=G(RЗемли​)2MЗемли​​=g.

ggg — это ускорение свободного падения, с которым двигаются все тела, подброшенные на Земле (в отсутсвие силы сопротивления воздуха, силы трения). С ускорением свободного падения мы познакомились ранее — в теме «Движение тела, брошенного вертикально вверх». Теперь понятно, почему все тела на Земле двигаются в свободном падении с одним и тем же ускорением g=GMЗемли(RЗемли)2=9,8мс2≈10мс2g=G\frac{M_{Земли}}{(R_{Земли})^2}=9,8\frac{м}{с^2}\approx 10\frac{м}{с^2}g=G(RЗемли​)2MЗемли​​=9,8с2м​≈10с2м​. Так происходит оттого, что масса Земли MЗемлиM_{Земли}MЗемли​ и радиус Земли RЗемлиR_{Земли}RЗемли​, а также гравитационная постоянная GGG — неизменные величины. Их значения можно всегда найти в справочных данных задачников или же прямо в заданиях ЕГЭ.

Сила гравитации — урок. Физика, 7 класс.

Одна из имеющихся в природе сил — сила гравитации. Она действует на любые тела. Сила гравитации проявляется как взаимное притяжение.

Всемирное гравитационное взаимодействие проявляется в том, что все тела взаимно притягиваются с силой, которая зависит от масс тел и расстояния между телами.

 

Fгр=Gm1⋅m2R2,

 

где G=6,67⋅10−11Н⋅м2кг2 — гравитационная постоянная,

 

R — расстояние между центрами тел,

 

m1,m2 — массы тел.

Обрати внимание!

Чем больше масса тел, тем сильнее притяжение.

Сила притяжения действует также между нами и яблоком, которое находится на столе, однако эта сила столь ничтожна, что её невозможно ощутить. Для того чтобы ощутить силу гравитации, хотя бы одно из тел должно быть большой массы. У Земли масса велика — 6⋅1024кг, поэтому она сильно притягивает всё, что находится на Земле и вблизи неё, она удерживает воды океана, не позволяет Луне улететь в космос.

Силу гравитации, с которой Земля притягивает находящееся вблизи неё тело, называют силой тяжести.

В Солнечной системе самую большую силу гравитации создаёт Солнце, масса которого в \(300 000\) раз больше массы Земли. Солнце удерживает на орбитах все планеты Солнечной системы.

 

 

Обрати внимание!

Чем больше взаимное расстояние тел, тем меньше сила гравитации.

Приливами называют повышение уровня моря, которое вызывается движением и взаимным положением Земли, Луны и Солнца. Это движение и взаимное положение влияет на силу притяжения между данными небесными телами. 

 

При воздействии на Землю сил гравитации Солнца и Луны возникает приливная волна. Приливы возникают в открытых водоёмах, однако их можно заметить, и эффект от них ощущается только в прибрежных районах. Максимальный прилив происходит тогда, когда Земля, Луна и Солнце находятся на одной прямой. Наибольшие приливы наблюдаются в Атлантическом океане в заливе Фанди (у побережья США) — \(18\) метров.

 

 

Несмотря на то, что масса Луны во много раз меньше массы Солнца, она находится гораздо ближе к Земле, и в связи с этим сила притяжения Луны гораздо больше, и, соответственно, приливы в основном вызываются Луной. Сила гравитации Луны два раза в сутки «тянет за собой» огромную массу воды.

определение, формула, виды :: SYL.ru

На вопрос «Что такое сила?» физика отвечает так: «Сила есть мера взаимодействия вещественных тел между собой или между телами и другими материальными объектами – физическими полями». Все силы в природе могут быть отнесены к четырем фундаментальным видам взаимодействий: сильному, слабому, электромагнитному и гравитационному. Наша статья рассказывает о том, что представляют собой гравитационные силы – мера последнего и, пожалуй, наиболее широко распространенного в природе вида этих взаимодействий.

Начнем с притяжения земли

Всем живущим известно, что существует сила, которая притягивает объекты к земле. Она обычно именуется гравитацией, силой тяжести или земным притяжением. Благодаря ее наличию у человека возникли понятия «верх» и «низ», определяющие направление движения или расположения чего-либо относительно земной поверхности. Так в частном случае, на поверхности земли или вблизи нее, проявляют себя гравитационные силы, которые притягивают объекты, обладающие массой, друг к другу, проявляя свое действие на любых как самых малых, так и очень больших, даже по космическим меркам, расстояниях.

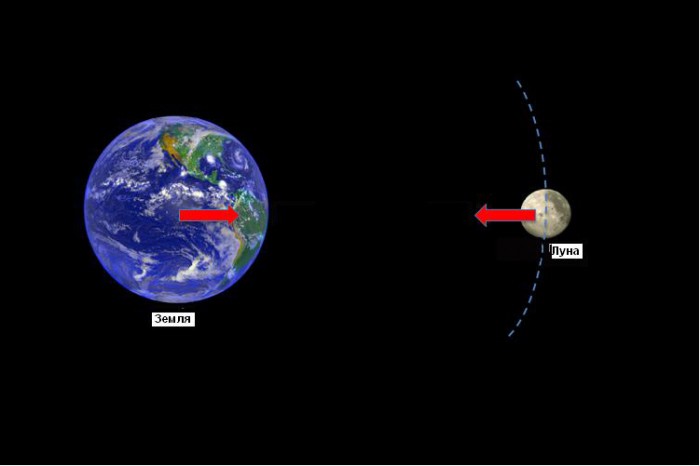
Сила тяжести и третий закон Ньютона

Как известно, любая сила, если она рассматривается как мера взаимодействия физических тел, всегда приложена к какому-нибудь из них. Так и в гравитационном взаимодействии тел друг с другом, каждое из них испытывает такие виды гравитационных сил, которые вызваны влиянием каждого из них. Если тел всего два (предполагается, что действием всех других можно пренебречь), то каждое из них по третьему закону Ньютона будет притягивать другое тело с одинаковой силой. Так Луна и Земля притягивают друг друга, следствием чего являются приливы и отливы земных морей.

Каждая планета в Солнечной системе испытывает сразу несколько сил притяжения со стороны Солнца и других планет. Конечно, определяет форму и размеры ее орбиты именно сила притяжения Солнца, но и влияние остальных небесных тел астрономы учитывают в своих расчетах траекторий их движения.

Что быстрее упадет на землю с высоты?

Главной особенностью этой силы является то, что все объекты падают на землю с одной скоростью, независимо от их массы. Когда-то, вплоть до 16-го ст., считалось, что все наоборот – более тяжелые тела должны падать быстрее, чем легкие. Чтобы развеять это заблуждение Галилео Галилею пришлось выполнить свой знаменитый опыт по одновременному сбрасыванию двух пушечных ядер разного веса с наклонной Пизанской башни. Вопреки ожиданиям свидетелей эксперимента оба ядра достигли поверхности одновременно. Сегодня каждый школьник знает, что это произошло благодаря тому, что сила тяжести сообщает любому телу одно и то же ускорение свободного падения g = 9,81 м/с² независимо от массы m этого тела, а величина ее по второму закону Ньютона равна F = mg.

Гравитационные силы на Луне и на других планетах имеют разные значения этого ускорения. Однако характер действия силы тяжести на них такой же.

Сила тяжести и вес тела

Если первая сила приложена непосредственно к самому телу, то вторая к его опоре или подвесу. В этой ситуации на тела со стороны опор и подвесов всегда действуют силы упругости. Гравитационные силы, приложенные к тем же телам, действуют им навстречу.

Представьте себе груз, подвешенный над землей на пружине. К нему приложены две силы: сила упругости растянутой пружины и сила тяжести. Согласно третьему закону Ньютона груз действует на пружину с силой, равной и противоположной силе упругости. Эта сила и будет его весом. У груза массой 1 кг вес равен Р = 1 кг ∙ 9,81 м/с² = 9,81 Н (ньютон).

Гравитационные силы: определение

Первая количественная теория гравитации, основанная на наблюдениях движения планет, была сформулирована Исааком Ньютоном в 1687 году в его знаменитых «Началах натуральной философии». Он писал, что силы притяжения, которые действуют на Солнце и планеты, зависят от количества вещества, которое они содержат. Они распространяются на большие расстояния и всегда уменьшаются как величины, обратные квадрату расстояния. Как же можно вычислить эти гравитационные силы? Формула для силы F между двумя объектами с массами m₁ и m₂, находящимися на расстоянии r, такова:

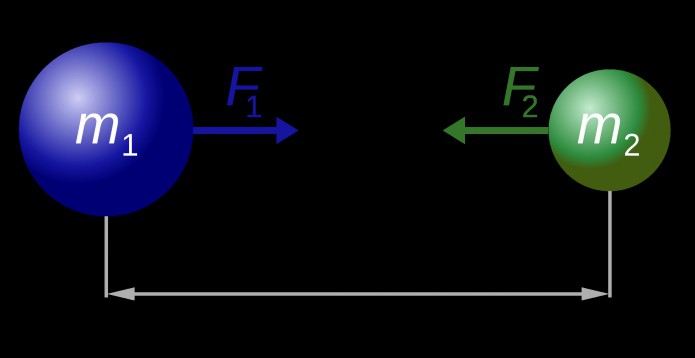
Физический механизм гравитации

Ньютон был не полностью удовлетворен своей теорией, поскольку она предполагала взаимодействие между притягивающимися телами на расстоянии. Сам великий англичанин был уверен, что должен существовать некий физический агент, ответственный за передачу действия одного тела на другое, о чем он вполне ясно высказался в одном из своих писем. Но время, когда было введено понятие гравитационного поля, которое пронизывает все пространство, наступило лишь через четыре столетия. Сегодня, говоря о гравитации, мы можем говорить о взаимодействии любого (космического) тела с гравитационным полем других тел, мерой которого и служат возникающие между каждой парой тел гравитационные силы. Закон всемирного тяготения, сформулированный Ньютоном в вышеприведенной форме, остается верным и подтверждается множеством фактов.

Теория гравитации и астрономия

Она была очень успешно применена к решению задач небесной механики во время XVIII и начале XIX века. К примеру, математики Д. Адамс и У. Леверье, анализируя нарушения орбиты Урана, предположили, что на него действуют гравитационные силы взаимодействия с еще неизвестной планетой. Ими было указано ее предполагаемое положение, и вскоре астрономом И. Галле там был обнаружен Нептун.

Хотя оставалась одна проблема. Леверье в 1845 году рассчитал, что орбита Меркурия прецессирует на 35» за столетие, в отличие от нулевого значения этой прецессии, получаемого по теории Ньютона. Последующие измерения дали более точное значение 43». (Наблюдаемая прецессия равна действительно 570»/век, но кропотливый расчет, позволяющий вычесть влияние от всех других планет, дает значение 43».)

Только в 1915 г. Альберт Эйнштейн смог объяснить это несоответствие в рамках созданной им теории гравитации. Оказалось, что массивное Солнце, как и любое другое массивное тело, искривляет пространство-время в своей окрестности. Эти эффекты вызывают отклонения в орбитах планет, но у Меркурия, как самой малой и ближайшей к нашей звезде планете, они проявляются сильнее всего.

Инерционная и гравитационная массы

Как уже отмечалось выше, Галилей был первым, кто наблюдал, что объекты падают на землю с одинаковой скоростью, независимо от их массы. В формулах Ньютона понятие массы происходит от двух разных уравнений. Второй его закон говорит, что сила F, приложенная к телу с массой m, дает ускорение по уравнению F = ma.

Однако сила тяжести F, приложенная к телу, удовлетворяет формуле F = mg, где g зависит от другого тела, взаимодействующего с рассматриваемым (земли обычно, когда мы говорим о силе тяжести). В обоих уравнений m есть коэффициент пропорциональности, но в первом случае это инерционная масса, а во втором – гравитационная, и нет никакой очевидной причины, что они должны быть одинаковыми для любого физического объекта.

Однако все эксперименты показывают, что это действительно так.

Теория гравитации Эйнштейна

Он взял факт равенства инерционной и гравитационной масс как отправную точку для своей теории. Ему удалось построить уравнения гравитационного поля, знаменитые уравнения Эйнштейна, и с их помощью вычислить правильное значение для прецессии орбиты Меркурия. Они также дают измеренное значение отклонения световых лучей, которые проходят вблизи Солнца, и нет никаких сомнений в том, что из них следуют правильные результаты для макроскопической гравитации. Теория гравитации Эйнштейна, или общая теория относительности (ОТО), как он сам ее назвал, является одним из величайших триумфов современной науки.

Гравитационные силы – это ускорение?

Если вы не можете отличить инерционную массу от гравитационной, то вы не можете отличить и гравитацию от ускорения. Эксперимент в гравитационном поле вместо этого может быть выполнен в ускоренно движущемся лифте в отсутствии гравитации. Когда космонавт в ракете ускоряется, удаляясь от земли, он испытывает силу тяжести, которая в несколько раз больше земной, причем подавляющая ее часть приходит от ускорения.

Если никто не может отличить гравитацию от ускорения, то первую всегда можно воспроизвести путем ускорения. Система, в которой ускорение заменяет силу тяжести, называется инерциальной. Поэтому Луну на околоземной орбите также можно рассматривать как инерциальную систему. Однако эта система будет отличаться от точки к точке, поскольку изменяется гравитационное поле. (В примере с Луной гравитационное поле изменяет направление из одной точки в другую.) Принцип, согласно которому всегда можно найти инерциальную систему в любой точке пространства и времени, в которой физика подчиняется законам в отсутствии гравитации, называется принципом эквивалентности.

Гравитация как проявление геометрических свойств пространства-времени

Тот факт, что гравитационные силы можно рассматривать как ускорения в инерциальных системах координат, которые отличаются от точки к точке, означает, что гравитация – это геометрическое понятие.

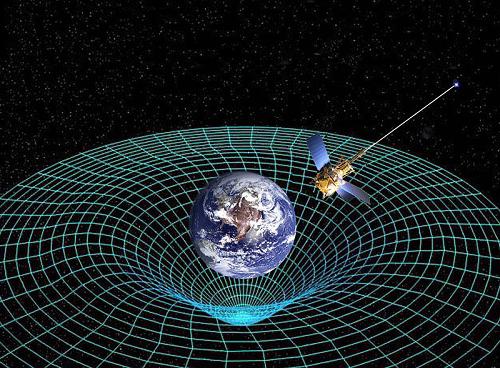
Мы говорим, что пространство-время искривляется. Рассмотрим мяч на плоской поверхности. Он будет покоиться или, если нет никакого трения, равномерно двигаться при отсутствии действия каких-либо сил на него. Если поверхность искривляется, мяч ускорится и будет двигаться до самой низкой точки, выбирая кратчайший путь. Аналогичным образом теория Эйнштейна утверждает, что четырехмерное пространство-время искривлено, и тело движется в этом искривленном пространстве по геодезической линии, которой соответствует кратчайший путь. Поэтому гравитационное поле и действующие в нем на физические тела гравитационные силы – это геометрические величины, зависящие от свойств пространства-времени, которые наиболее сильно изменяются вблизи массивных тел.

Закон всемирного тяготения. Движение тел под действием силы тяжести

Исходя из трактовки второго закона Ньютона, можно сделать вывод, что изменение движения происходит посредствам силы. Механика рассматривает силы различной физической природы. Многие из них определяются с помощью действия сил тяготения.

Закон всемирного тяготения. Формулы

В 1862 году был открыт закон всемирного тяготения И. Ньютоном. Он предположил, что силы, удерживающие Луну, той же природы, что и силы, заставляющие яблоко падать на Землю. Смысл гипотезы состоит в наличии действия сил притяжения, направленных по линии и соединяющих центры масс, как изображено на рисунке 1.10.1. Шаровидное тело имеет центр массы, совпадающий с центром шара.

Рисунок 1.10.1. Гравитационные силы притяжения между телами. F1→=-F2→.

Далее, Ньютон искал физическое объяснение законам движения планет, которые открыл И. Кеплер в начале XVII века, и давал количественное выражение для гравитационных сил.

Определение 1

При известных направлениях движений планет Ньютон пытался выяснить, какие силы действуют на них. Этот процесс получил название обратной задачи механики.

Основная задача механики – определение координат тела известной массы с его скоростью в любой момент времени при помощи известных сил, действующих на тело, и заданным условием (прямая задача). Обратная же выполняется с определением действующих сил на тело с известным его направлением. Такие задачи привели ученого к открытию определения закона всемирного тяготения.

Ускорение свободного падения

Определение 2

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.

F=Gm1m2r2.

Значение G определяет коэффициент пропорциональности всех тел в природе, называемое гравитационной постоянной и обозначаемое по формуле G=6,67·10-11 Н·м2/кг2 (СИ).

Большинство явлений в природе объясняются наличием действия силы всемирного тяготения. Движение планет, искусственных спутников