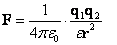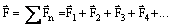Глава 17. Взаимодействие электрических зарядов. Закон Кулона, принцип суперпозиции
Взаимодействие электрических зарядов описывается законом Кулона, который утверждает, что сила взаимодействия двух покоящихся точечных зарядов в вакууме равна
(17.1) |
где и — модули зарядов, — расстояние между ними. Коэффициент пропорциональности в формуле (17.1) зависит от системы единиц. В международной системе единиц СИ этот коэффициент принято записывать в виде
(17.2) |
где величина называется электрической постоянной, размерность величины сводится к отношению размерности длины к размерности электрической емкости (Фарада). Электрические заряды бывают двух типов, которые условно принято называть положительным и отрицательным. Как показывает опыт, заряды притягиваются, если они разноименные и отталкиваются, если одноименные.
В любом макроскопическом теле содержится огромное количество электрических зарядов, поскольку они входят в состав всех атомов: электроны заряжены отрицательно, протоны, входящие в состав атомных ядер — положительно. Однако большинство тел, с которыми мы имеем дело, не заряжены, поскольку количество электронов и протонов, входящих в состав атомов, одинаково, а их заряды по абсолютной величине в точности совпадают. Тем не менее, тела можно зарядить, если создать в них избыток или недостаток электронов по сравнению с протонами. Для этого нужно передать электроны, входящие в состав какого-нибудь тела, другому телу. Тогда у первого возникнет недостаток электронов и соответственно положительный заряд, у второго — отрицательный. Такого рода процессы происходят, в частности, при трении тел друг о друга.
Если заряды находятся в некоторой среде, которая занимает все пространство, то сила их взаимодействия ослабляется по сравнению с силой их взаимодействия в вакууме, причем это ослабление не зависит от величин зарядов и расстояния между ними, а зависит только от свойств среды. Характеристика среды, которая показывает, во сколько раз ослабляется сила взаимодействия зарядов в этой среде по сравнению с силой их взаимодействия в вакууме, называется диэлектрической проницаемостью этой среды и, как правило, обозначается буквой . Формула Кулона в среде с диэлектрической проницаемостью принимает вид
(17.3) |
Если имеется не два, а большее количество точечных зарядов для нахождения сил, действующих в этой системе, используется закон, который называется принципомсуперпозиции1. Принцип суперпозиции утверждает, что для нахождения силы, действующей на один из зарядов (например, на заряд ) в системе из трех точечных зарядов , и надо сделать следующее. Сначала надо мысленно убрать заряд и по закону Кулона найти силу, действующую на заряд со стороны оставшегося заряда . Затем следует убрать заряд и найти силу, действующую на заряд со стороны заряда . Векторная сумма полученных сил и даст искомую силу.
Кроме того, школьник должен знать (без вывода) формулы для силы, действующей на точечный заряд со стороны равномерно заряженной сферы и бесконечной плоскости. Если имеется сфера радиуса , равномерно заряженная зарядом , и точечный заряд , расположенный на расстоянии от центра сферы, то величина силы взаимодействия равна
(17.4) |
если точечный заряд находится снаружи сферы, и
(17.5) |
если заряд находится внутри (причем не обязательно в центре). Из формул (17.4), (17.5) следует, что сфера снаружи создает такое же электрическое поле как весь ее заряд, помещенный в центре, а внутри — нулевое.
Если имеется очень большая плоскость с площадью , равномерно заряженная зарядом , и точечный заряд , то сила их взаимодействия равна
(17.6) |
где величина имеет смысл поверхностной плотности заряда плоскости. Как следует из формулы (17.6) сила взаимодействия точечного заряда и плоскости не зависит от расстояния между ними. Обратим внимание читателя на то, что формула (17.6) является приближенной и «работает» тем точнее, чем дальше точечный заряд находится от ее краев. Поэтому при использовании формулы (17.6) часто говорят, что она справедлива в рамках пренебрежения «краевыми эффектами», т.е. когда плоскость считается бесконечной.
Рассмотрим теперь решение данных в первой части книги задач.
Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов из задачи 17.1.1 выражается формулой
Заряды отталкиваются (ответ 2).
Поскольку капелька воды из задачи 17.1.2 имеет заряд ( – заряд протона), то она имеет в избытке электронов по сравнению с протонами. Значит при потере трех электронов их избыток уменьшится, и заряд капельки станет равен (ответ
Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов при увеличении в раз расстояния между ними уменьшится в раз (задача 17.1.3 — ответ 4).
Если заряды двух точечных тел увеличить в раз при неизменном расстоянии между ними, то сила их взаимодействия, как это следует из закона Кулона (17.1), увеличится в раз (задача 17.1.4 — ответ 3).
При увеличении одного заряда в 2 раза, а второго в 4, числитель закона Кулона (17.1) увеличивается в 8 раз, а при увеличении расстояния между зарядами в 8 раз — знаменатель увеличивается в 64 раза. Поэтому сила взаимодействия зарядов из
При заполнении пространства диэлектрической средой с диэлектрической проницаемостью = 10, сила взаимодействия зарядов согласно закону Кулона в среде (17.3) уменьшится в 10 раз (задача 17.1.6 — ответ 2).
Сила кулоновского взаимодействия (17.1) действует как на первый, так и на второй заряд, а поскольку их массы одинаковы, то ускорения зарядов, как это следует из второго закона Ньютона, в любой момент времени одинаковы (задача 17.1.7 — ответ 3).
Похожая задача, но массы шариков разные. Поэтому при одинаковой силе ускорение шарика с меньшей массой в 2 раза больше ускорения шарика с меньшей массой , причем этот результат не зависит от величин зарядов шариков (
Поскольку электрон заряжен отрицательно, он будет отталкиваться от шара (задача 17.1.9). Но поскольку начальная скорость электрона направлена к шару, он будет двигаться в этом направлении, но его скорость будет уменьшаться. В какой-то момент он на мгновение остановится, а потом будет двигаться от шара с увеличивающейся скоростью (ответ 4).
В системе двух заряженных шариков, связанных нитью (задача 17.1.10), действуют только внутренние силы. Поэтому система будет покоиться и для нахождения силы натяжения нити можно использовать условия равновесия шариков. Поскольку на каждый из них действуют только кулоновская сила и сила натяжения нити, то из условия равновесия заключаем, что эти силы равны по величине.
Отсюда
где (ответ 1).
Система трех шариков в задаче 17.2.1 покоится, поэтому силы натяжения должны компенсировать силы кулоновского отталкивания крайних зарядов. Последние найдем по закону Кулона и принципу суперпозиции. Каждый крайний заряд отталкивается от центрального заряда и другого крайнего. Для суммы этих сил получаем
Этой величине и будет равна сила натяжения нитей (ответ 4). Отметим, что рассмотрение условия равновесия центрального заряда не помогло бы найти силу натяжения, а привело бы к заключению, что силы натяжения нитей одинаковы (впрочем, это заключение и так очевидно благодаря симметрии задачи).
Для нахождения силы, действующей на заряд — в задаче 17.2.2, используем принцип суперпозиции. На заряд — действуют силы притяжения к левому и правому зарядам (см. рисунок). Поскольку расстояния от заряда — до зарядов одинаковы, модули этих сил равны друг другу и они направлены под одинаковыми углами к прямой, соединяющей заряд — с серединой отрезка — . Поэтому сила, действующая на заряд — направлена вертикально вниз (вектор результирующей силы выделен жирным на рисунке; ответ
Задача 17.2.3 похожа на предыдущую, но изменен знак одного из зарядов. Поэтому сила, действующая на заряд — со стороны правого заряда, не изменившись по величине, изменится по направлению (см. рисунок). Поэтому вектор результирующей силы будет направлен влево (вектор результирующей силы выделен жирным на рисунке; ответ 1). |
|
На каждый заряд в задаче 17.2.4 действуют силы отталкивания со стороны двух других зарядов (см. рисунок), причем значения этих сил одинаковы (из-за равенства величин всех зарядов и расстояний между ними) и равны |
Из-за равенства значений сил-слагаемых параллелограмм сложения сил представляет собой ромб, и, следовательно, вектор результирующей силы направлен вдоль биссектрисы треугольника из зарядов (выделен жирным на рисунке). Поэтому угол, отмеченный на рисунке дугой равен 30°, а значение результирующей силы равно
(ответ 3).
Из формулы (17.6) заключаем, что правильный ответ в задаче 17.2.5 — 4. В задаче 17.2.6 нужно использовать формулу для силы взаимодействия точечного заряда и сферы (формулы (17.4), (17.5)). Имеем = 0 (ответ 3).
В задаче 17.2.7 необходимо применить принцип суперпозиции к двум сферам. Принцип суперпозиции утверждает, что взаимодействие каждой пары зарядов не зависит от наличия других зарядов. Поэтому каждая сфера действует на точечный заряд независимо от другой сферы, и для нахождения результирующей силы нужно сложить силы со стороны первой и второй сфер. Поскольку точечный заряд расположен внутри внешней сферы, она не действует на него (см. формулу (17.5)), внутренняя действует с силой
где . Поэтому и результирующая сила равна этому выражению (ответ 2)
В задаче 17.2.8 также следует использовать принцип суперпозиции. Если заряд поместить в точку , то силы, действующие на него со стороны зарядов и , направлены влево. Поэтому по принципу суперпозиции имеем для равнодействующей силы
где — расстояния от зарядов до исследуемых точек. Если поместить положительный заряд в точку , то силы будут направлены противоположно, и на основании принципа суперпозиции находим результирующую силу
В точке на заряд будут действовать силы, направленные направо, и потому
Из этих формул следует, что наибольшей сила будет в точке — ответ 1.
Пусть, для определенности, заряды шариков и в задаче 17.2.9 положительны. Так как шарики одинаковы, заряды после их соединения распределяться между ними равномерно и для сравнения сил, нужно сравнить друг с другом величины
(1) |
которые представляют собой произведения зарядов шариков до и после их соединения. После извлечения квадратного корня сравнение (1) сводится к сравнению среднего геометрического и среднего арифметического двух чисел. А поскольку среднее арифметическое любых двух чисел больше их среднего геометрического, то сила взаимодействия шариков возрастет независимо от величин их зарядов (ответ 1).
Задача 17.2.10 очень похожа на предыдущую, а ответ — другой. Непосредственной поверкой легко убедиться, что сила может как увеличиться, так и уменьшиться в зависимости от величин зарядов. Например, если заряды равны по величине, то после соединения шариков их заряды станут равны нулю, поэтому нулевой будет и сила их взаимодействия, которая, следовательно, уменьшится. Если один из первоначальных зарядов равен нулю, то после соприкосновения шариков заряд одного из них распределится между шариками поровну, и сила их взаимодействия увеличится. Таким образом, правильный ответ в этой задаче — 3.
Закон Кулона. Точечный заряд. | Физика для всех
Силы электростатического взаимодействия зависят от формы и размеров наэлектризованных тел, а также от характера распределения заряда на этих телах. В некоторых случаях можно пренебречь формой и размерами заряженных тел и считать, что каждый заряд сосредоточен в одной точке.
Точечный заряд – это электрический заряд, когда размер тела, на котором этот заряд сосредоточен, намного меньше расстояния между заряженными телами. Приближённо точечные заряды можно получить на опыте, заряжая, например, достаточно маленькие шарики.
Взаимодействие двух покоящихся точечных зарядов определяет основной закон электростатики – закон Кулона. Этот закон экспериментально установил в 1785 году французский физик Шарль Огюстен Кулон (1736 – 1806). Формулировка закона Кулона следующая:
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональная произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Эта сила взаимодействия называется кулоновская сила, и формула закона Кулона будет следующая:
F = k · (|q1| · |q2|) / r2
где |q1|, |q2| – модули зарядов, r – расстояния между зарядами, k – коэффициент пропорциональности.
Коэффициент k в СИ принято записывать в форме:
k = 1 / (4πε0ε)
где ε0 = 8,85 * 10-12 Кл/Н*м2 – электрическая постоянная, ε – диэлектрическая проницаемость среды.
Для вакуума ε = 1, k = 9 * 109 Н*м/Кл2.
Сила взаимодействия неподвижных точечных зарядов в вакууме:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2]
Если два точечных заряда помещены в диэлектрик и расстояние от этих зарядов до границ диэлектрика значительно больше расстояния между зарядами, то сила взаимодействия между ними равна:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2] = k · (1 /π) · [(|q1| · |q2|) / r2]
Диэлектрическая проницаемость среды всегда больше единицы (π > 1), поэтому сила, с которой взаимодействуют заряды в диэлектрике, меньше силы взаимодействия их на том же расстоянии в вакууме.
Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела (рис. 1.8).
Рис. 1.8. Силы взаимодействия двух неподвижных точечных заряженных тел.
Кулоновские силы, как и гравитационные силы, подчиняются третьему закону Ньютона:
F1,2 = -F2,1
Кулоновская сила является центральной силой. Как показывает опыт, одноимённые заряженные тела отталкиваются, разноимённо заряженные тела притягиваются.
Вектор силы F2,1, действующей со стороны второго заряда на первый, направлен в сторону второго заряда, если заряды разных знаков, и в противоположную, если заряды одного знака (рис. 1.9).
Рис. 1.9. Взаимодействие разноименных и одноименных электрических зарядов.
Электростатические силы отталкивания принято считать положительными, силы притяжения – отрицательными. Знаки сил взаимодействия соответствуют закону Кулона: произведение одноимённых зарядов является положительным числом, и сила отталкивания имеет положительный знак. Произведение разноимённых зарядов является отрицательным числом, что соответствует знаку силы притяжения.
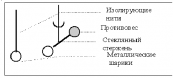
В опытах Кулона измерялись силы взаимодействия заряженных шаров, для чего применялись крутильные весы (рис. 1.10). На тонкой серебряной нити подвешена лёгкая стеклянная палочка с, на одном конце которой закреплён металлический шарик а, а на другом противовес d. Верхний конец нити закреплён на вращающейся головке прибора е, угол поворота которой можно точно отсчитывать. Внутри прибора имеется такого же размера металлический шарик b, неподвижно закреплённый на крышке весов. Все части прибора помещены в стеклянный цилиндр, на поверхности которого нанесена шкала, позволяющая определить расстояние между шариками a и b при различных их положениях.
Рис. 1.10. Опыт Кулона (крутильные весы).
При сообщении шарикам одноимённых зарядов они отталкиваются друг от друга. При этом упругую нить закручивают на некоторый угол, чтобы удержать шарики на фиксированном расстоянии. По углу закручивания нити и определяют силу взаимодействия шариков в зависимости от расстояния между ними. Зависимость силы взаимодействия от величины зарядов можно установить так: сообщить каждому из шариков некоторый заряд, установить их на определённом расстоянии и измерить угол закручивания нити. Затем надо коснуться одного из шариков таким же по величине заряженным шариком, изменяя при этом его заряд, так как при соприкосновении равных по величине тел заряд распределяется между ними поровну. Для сохранения между шариками прежнего расстояния необходимо изменить угол закручивания нити, а следовательно, и определить новое значение силы взаимодействия при новом заряде.
Сила электростатического взаимодействия двух точечных зарядов
\(F\) — сила, действующая на заряд 2 со стороны заряда 1 \((Н)\)
\(r\) — расстояние от заряда 1 до заряда 2 \((м)\)
\(q_1\) — электрический заряд \((Кл)\)
\(q_2\) — электрический заряд \((Кл)\)
\(k = \frac{1}{4 \pi \varepsilon_0}\) — коэффициент пропорциональности в электричестве \(\approx 8.99 * 10^{9}\) \(\frac{Н*м^2}{Кл^2}\)
\(\varepsilon_0\) — диэлектрическая постоянная \(\approx 8.85 * 10^{-12}\) \(\frac{Ф}{м}\)
\(\pi\) — число Пи \(\approx 3.14\)
Закон Кулона. | |
З-н Кулона — основной закон электростатики, позволяющий рассчитать силу взаимодействия между двумя точечными неподвижными зарядами в вакууме.Открыт в 1785 г. французским физиком Шарлем Огюстеном Кулоном (раньше и более точно закономерности установлены Г. Кавендишем, но не опубликованы). |
|
Опыт Кулона. Металлические шарики заряжаются и взаимодействуют. Заряд измеряется в относительных единицах. Нить закручивается. Сила упругости нити уравновешивает электрическую силу. По углу закручивания нити определяют силу взаимодействия. 1.
2.
3. |
|
Вывод: Сила взаимодействия двух точечных неподвижных зарядов в вакууме прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между ними. |
|
Сила центральна. Направлена по прямой, соединяющей заряды. Если знаки зарядов одинаковы, то направление силы и радиус-вектора совпадают, если знаки зарядов разные, то направление силы и радиус-вектора противоположны. Силы взаимодействия между зарядами равны по величине и противоположны по направлению по 3-ему з-ну Ньютона. |
Пример: сила взаимодействия между двумя ионами в кристалле поваренной соли F=2.10-9 Н. |
Коэффициент k зависит от выбора системы единиц. Коэффициент k численно равен силе взаимодействия между двумя точечными неподвижными зарядами по единице заряда каждый, находящимися в вакууме на расстоянии, равном единице длины друг от друга. |
|
В СИ удобно представить |
|
Диэлектрическая проницаемость среды ( e ). Характеризует электрические свойства среды. Для любой среды e >1. Зависит только от свойств среды. Диэлектрическая проницаемость показывает во сколько раз сила взаимодействия двух точечных неподвижных зарядов в вакууме больше их сил взаимодействия в среде.
| Примеры:
|
Полная форма записи закона Кулона.
|
|
Если заряды не точечные или их больше двух, то силы складываются по правилу сложения векторов:
|
|
1.2. Взаимодействие электрических зарядов. Закон Кулона.
В 1785 г. Кулон экспериментально установил зависимость силы взаимодействия зарядов от их величины, знака и расстояния между ними.
Сила взаимодействия двух точечных зарядов, находящихся в вакууме, прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними, направлена вдоль прямой линии, соединяющей эти заряды (рис. 1.1)..
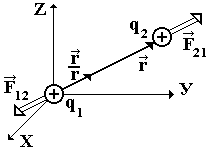
Рис. 1.1
В СИ закон Кулона запишем в виде 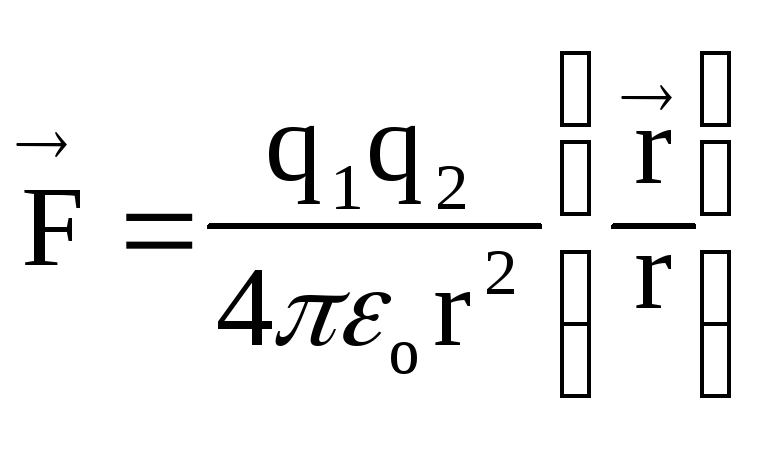 ,
(1.2)
,
(1.2)
где
о = 8,851012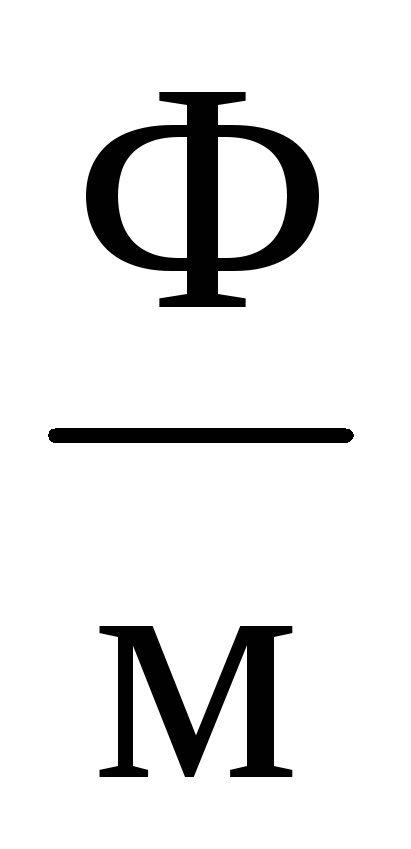
электрическая постоянная;
электрическая постоянная; 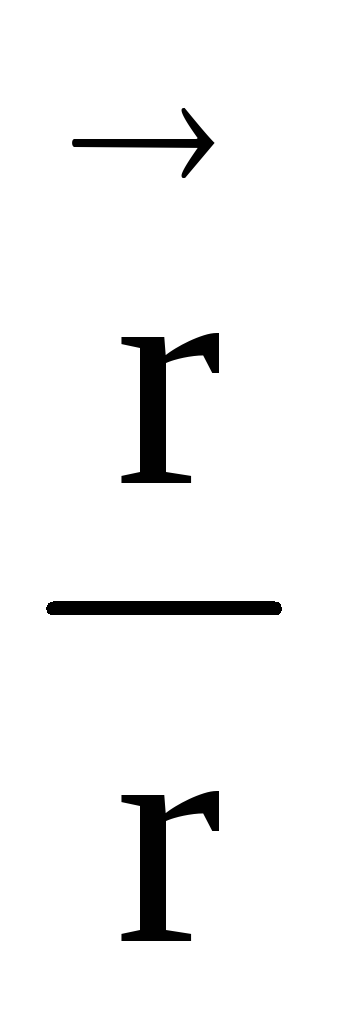
единичный вектор.
единичный вектор.
При решении задач удобно использовать величину
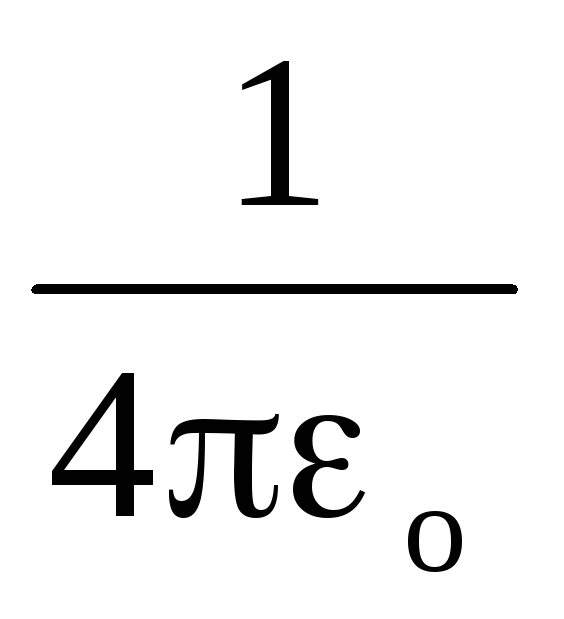 = 9109
= 9109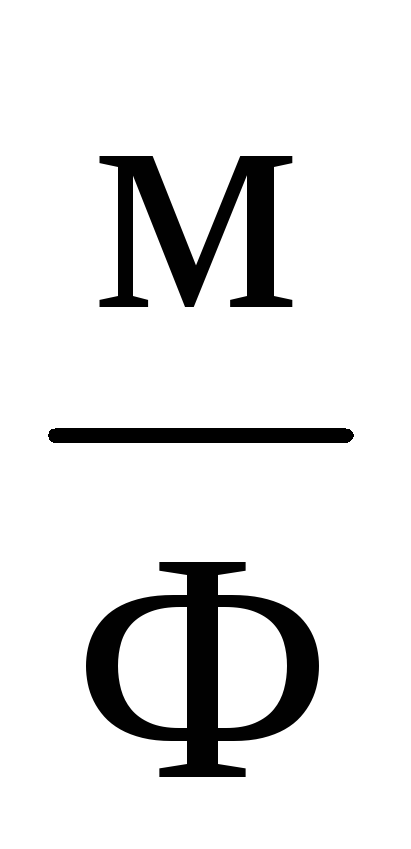 .
.
Согласно третьего закона Ньютона
F12 =F21= F.
Знак силы взаимодействия зарядов зависит от знака этих зарядов. Притяжению соответствует знак « », разноименные заряды притягиваются, отталкиванию « + », одноименные заряды отталкиваются (рис. 1.2, а, б).
По абсолютной величине закон Кулона
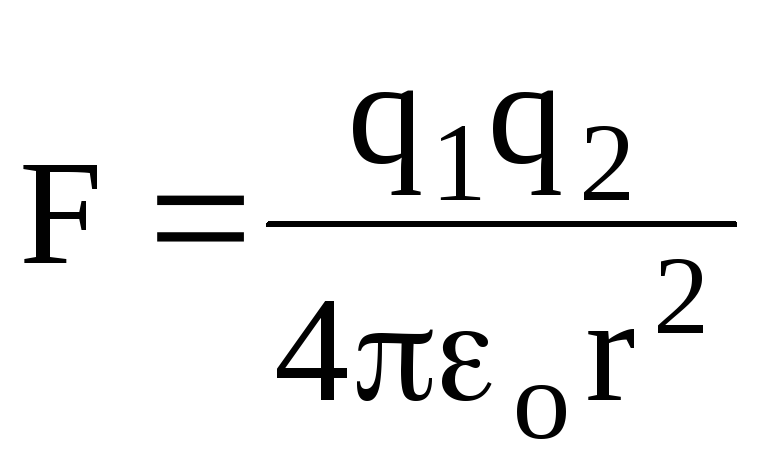 .
(1.3)
.
(1.3)
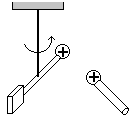
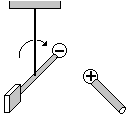
а б
Рис. 1.2
Если заряды находятся в диэлектрической среде, то 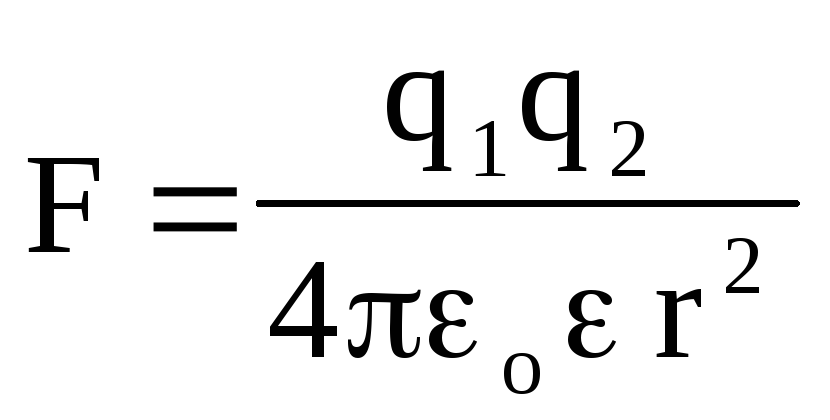 ,
(1.4)
,
(1.4)
где диэлектрическая проницаемость среды,
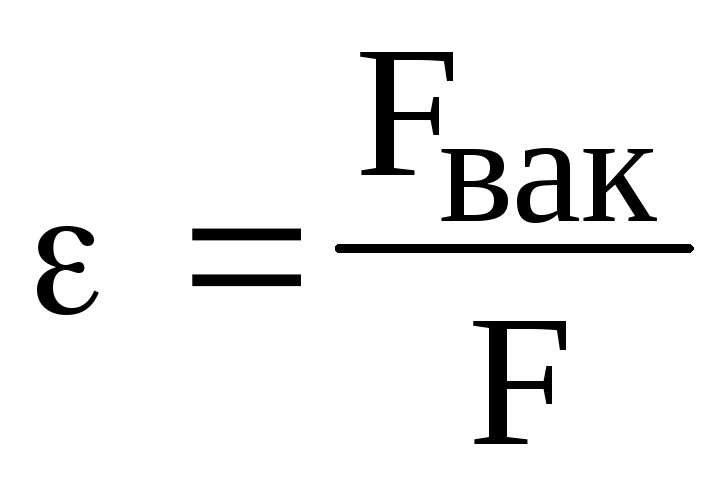 .
(1.5)
.
(1.5)
В СИ заряд измеряют в кулонах (Кл).
На основании экспериментальных данных установлено, что закон Кулона справедлив для расстояний от 1015 м до нескольких километров, а возможно и до бесконечности.
1.3. Электрическое поле
Взаимодействие между зарядами (согласно современным представлениям) осуществляется посредством электрического поля. Если заряды неподвижны, то поле называют электростатическим.
Любой
электрический заряд q
создает в окружающем его пространстве
электрическое поле (изменяет свойства
этого пространства). Электрическое поле
проявляет себя в том, что помещенный в
любую точку этого поля «пробный» заряд
испытывает действие кулоновской силы
со стороны этого поля. Основной
количественной характеристикой
электрического поля является вектор
напряженности 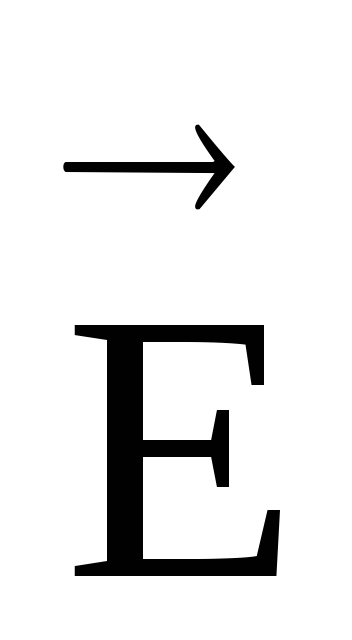 .
.
Напряженность электростатического поля сила, действующая на единичный, положительный точечный неподвижный пробный заряд.
Замечание: пробный заряд qo должен быть достаточно малым, чтобы его внесение в электрическое поле не вызывало заметного искажения его.
На основании опытов установлено, что напряженность электрического поля и кулоновская сила, действующая на внесенный в это поле пробный заряд, связаны соотношением
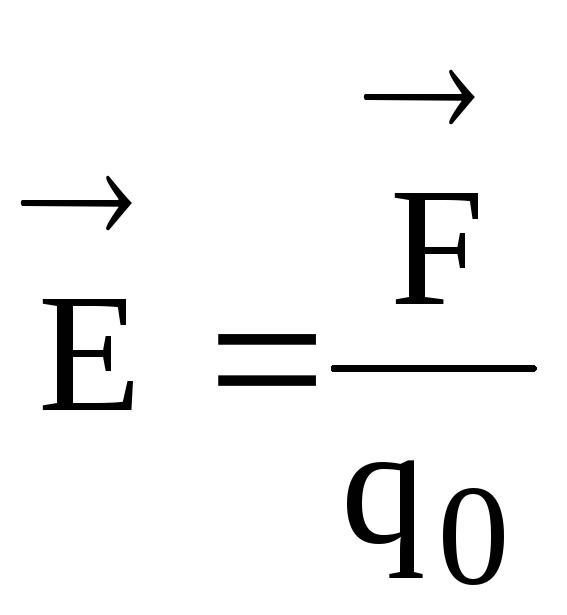 ,
(1.6)
,
(1.6)
где 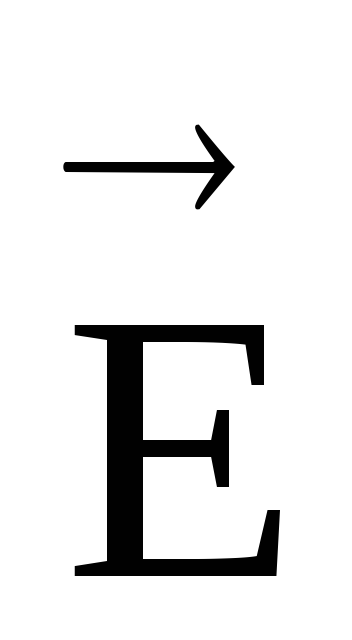
вектор напряженности электростатического
поля в данной точке.
вектор напряженности электростатического
поля в данной точке.
Напряженность
поля 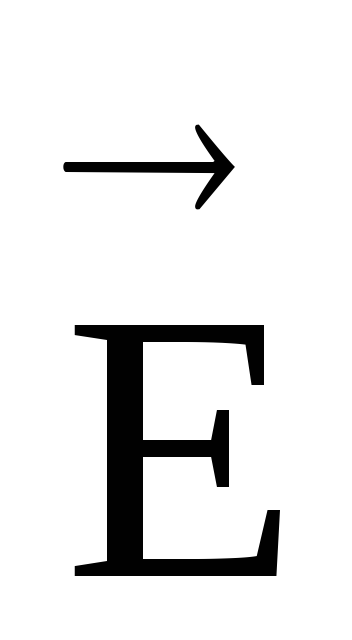 неподвижного точечного заряда q
в вакууме на расстоянии r
от него
неподвижного точечного заряда q
в вакууме на расстоянии r
от него
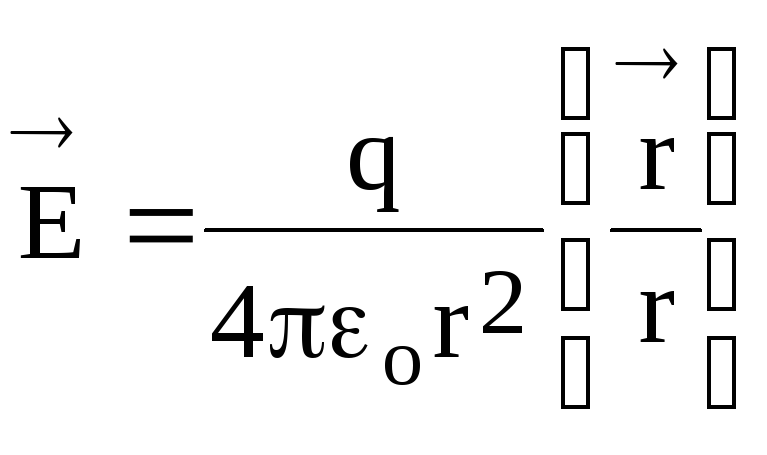 (1.7)
(1.7)
или по модулю
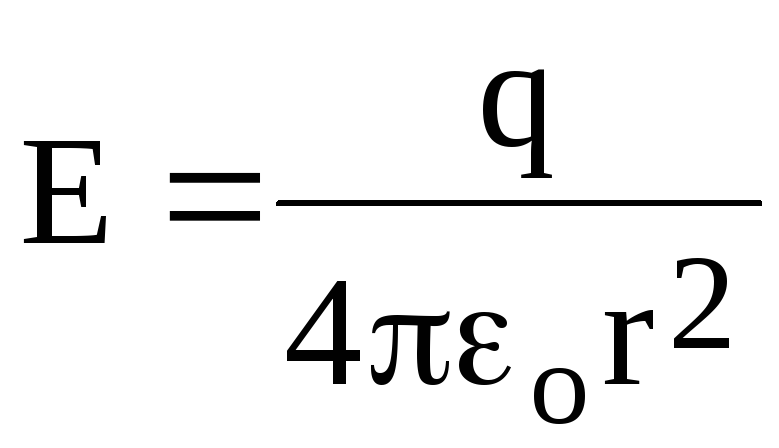 ,
(1.8)
,
(1.8)
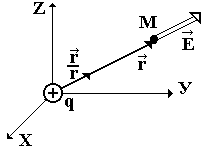
Рис. 1.3
где r расстояние от заряда q, создающего электрическое поле, до точки пространства, в которой определяется напряженность этого поля (рис. 1.3).Если заряд находится в безграничной среде с диэлектрической проницаемостью , то
. (1.9)
В электрическом поле, создаваемом неподвижным точечным зарядом, сила, действующая на внесенный пробный заряд, не зависит от того, покоится пробный заряд или движется. Это относится и к системе неподвижных зарядов.
Напряженность в СИ измеряется в вольтах на метр (В/м).
Если
мы имеем систему точечных неподвижных
зарядов, то можно определить напряженность 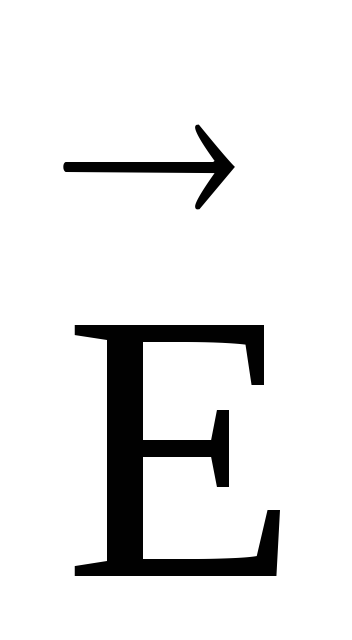 результирующего электрического поля в произвольной точке этого поля (принцип
суперпозиции).
результирующего электрического поля в произвольной точке этого поля (принцип
суперпозиции).
Вектор напряженности поля системы точечных неподвижных зарядов равен векторной сумме напряженности полей, созданной каждым из зарядов в отдельности, т. е.
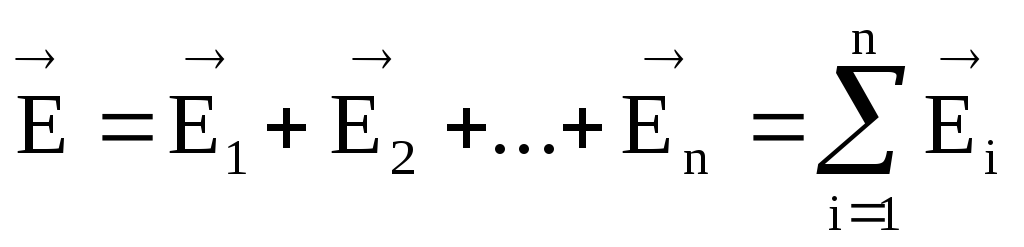 (1.10)
(1.10)
или 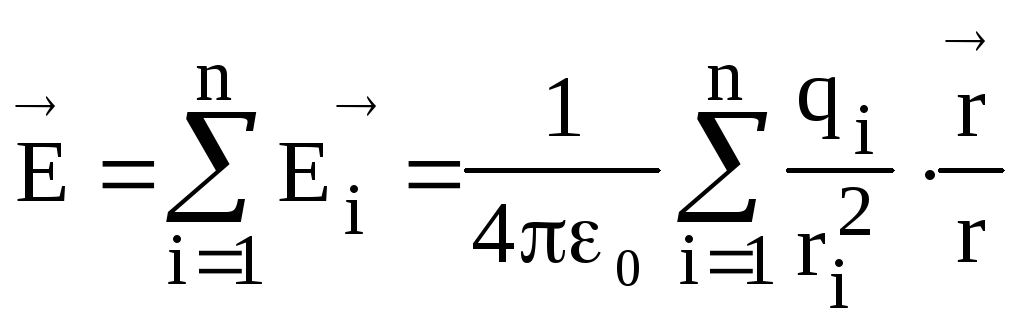 ,
(1.11)
,
(1.11)
где  i
вектор напряженность поля, созданного
i
м
точечным зарядом на расстоянии ri от него.
i
вектор напряженность поля, созданного
i
м
точечным зарядом на расстоянии ri от него.
Взаимодействие зарядов. закон кулона — fiziku5.ru
· Атом меди содержит 29 электронов и такое же количество протонов. Электроны атомов меди расположены вокруг ядра на четырех оболочках. На первой находятся два электрона, на второй — восемь, на третьей — восемнадцать, на четвертой, наиболее удаленной от ядра, — один электрон. Число электронов, расположенных на наиболее удаленной от ядра оболочке, совпадает с номером группы данного элемента в периодической системе Д. И. Менделеева, а общий отрицательный заряд электронов атома равен положительному заряду протонов, содержащихся в ядре. Равные по величине положительные и отрицательные заряды по отношению к внешней среде электрически уравновешиваются — взаимно нейтрализуются. В результате этого атомы вещества в обычном состоянии электрически нейтральны.
·
·
·
· [1] Электронная оболочка – область, внутри которой движутся электроны.
· §2. ВЗАИМОДЕЙСТВИЕ ЗАРЯДОВ. ЗАКОН КУЛОНА
· Электрические заряды взаимодействуют между собой, т. е. одноименные заряды взаимно отталкиваются, а разноименные притягиваются. Силы взаимодействия электрических зарядов определяются законом Кулона и направлены по прямой линии, соединяющей точки, в которых сосредоточены заряды.
· Согласно закону Кулона, сила взаимодействия двух точечных электрических зарядов прямо пропорциональна произведению количеств электричества в этих зарядах, обратно пропорциональна квадрату расстояния между ними и зависит от среды, в которой находятся заряды:
·
· где F — сила взаимодействия зарядов, н (ньютон[2]),
· q1, q2, — количество электричества каждого заряда, к (кулон[3]),
· r — расстояние между зарядами, м,
· a— абсолютная диэлектрическая проницаемость среды (материала) ; эта величина характеризует электрические свойства той среды, в которой находятся взаимодействующие заряды.
· В Международной системе единиц (СИ) a измеряется в (ф/м). Абсолютная диэлектрическая проницаемость среды
·
· где 0 — электрическая постоянная, равная абсолютной диэлектрической проницаемости вакуума (пустоты). Она равна 8,86•10-12 ф/м.
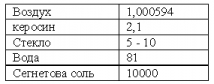
· Величина , показывающая, во сколько раз в данной среде электрические заряды взаимодействуют между собой слабее, чем в вакууме (табл. 1), называется диэлектрической проницаемостью.
· Величина есть отношение абсолютной диэлектрической проницаемости данного материала к диэлектрической проницаемости вакуума:
·
· Для вакуума =1. Диэлектрическая проницаемость воздуха практически равна единице.
· На основании закона Кулона можно сделать вывод, что большие электрические заряды взаимодействуют сильнее, чем малые. С увеличением расстояния между зарядами сила их взаимодействия значительно слабее. Так, с увеличением расстояния между зарядами в 6 раз уменьшается сила их взаимодействия в 36 раз. При сокращении расстояния между зарядами в 9 раз увеличивается сила их взаимодействия в 81 раз. Взаимодействие зарядов также зависит от материала, находящегося между зарядами.
· Пример. Между электрическими зарядами Q1=2 • 10-6 к и Q2=4, • 10-6 к, расположенными на расстоянии 0,5 м, помещена слюда (=6). Вычислить силу взаимодействия указанных зарядов.
· Решение. Подставляя в формулу значения известных величин, получим:
·
· Если в вакууме электрические заряды взаимодействуют с силой Fв, то, поместив между этими зарядами, например, фарфор, их взаимодействие можно ослабить в 6,5 раз, т. е. в раз. Это значит, что сила взаимодействия между зарядами может быть определена как отношение
·
·
· Пример. Одноименные электрические заряды взаимодействуют в вакууме с силой Fв =0,25 н. С какой силой будут отталкиваться два заряда, если пространство между ними заполнено бакелитом? Диэлектрическая проницаемость этого материала равна 5.
· Решение. Сила взаимодействия электрических зарядов
·
· Так как один ньютон 102 г силы, то 0,05 н составляет 5,1 г.
·
·
· [2] Один ньютон содержит 102 г силы
· [3] Один кулон содержит 6,3• 1018 зарядов электрона
· § 3. ЭЛЕКТРИЗАЦИЯ ТЕЛ
·
· Известно, что электроны находятся на разном расстоянии от ядра атома. В связи с этим, согласно закону Кулона, взаимодействие положительно заряженных протонов ядра с электронами, расположенными в слое, ближайшем к ядру, значительно сильнее взаимодействия протонов с электронами, находящимися в наиболее удаленном слое.
· Если от атомов того или иного вещества «оторвать» один или несколько таких слабо связанных (свободных) с ядром электронов, то нарушится электрическое равновесие в атомах и вещество будет заряжено положительным электричеством.
· Наоборот, если у атомов вещества количество электронов больше количества протонов, то тело приобретает отрицательный заряд. Атом с отрицательным зарядом называют отрицательным ионом.
· Изменить количество электронов в атомах различных твердых материалов (наэлектризовать тела) можно, например, воздействием световой энергии, нагреванием, использованием химических процессов, деформацией кристаллов.
· Электризация световой энергией. Профессор А. Г. Столетов в 1888 г. установил, что под действием света из таких материалов, как цинк, алюминий, цезий, натрий, свинец, калий и т. п., вылетают электроны и эти материалы заряжаются положительным электричеством. В этом можно убедиться на опыте.
· На стержне электроскопа укрепим полированный диск из цинка. При отсутствии электрического заряда на цинке лепестки электроскопа будут опущены.
· Если на диск направить световой поток (рис. 2, а), лепестки электроскопа оттолкнутся и разойдутся на некоторый угол. Это показывает, что диск электроскопа и листочки, прикрепленные к его стержню, зарядились одноименными электрическими зарядами. По углу отклонения листочков можно судить о величине заряда.
·
· Рис.2 Приборы, определяющие электризацию тел:
· а — под действием светового потока, б – при нагревании нити.
· в – под действием химической реакции, г – под давлением кристалла
· Явление, при котором под воздействием света из материалов вырываются электроны, называется фотоэффектом. На использовании его основано действие фотоэлементов (см. гл. XIV).
· Электризация нагреванием. При сильном нагревании металлов электроны приобретают такую энергию, что вылетают за пределы нагретого металла. В результате этого металл «теряет» электроны и заряжается положительно.
· Если к металлической пластинке 1, помещенной в вакууме (рис. 2, б), присоединить электроскоп и нагреть нить 2, то лепестки электроскопа, отталкиваясь друг от друга, разойдутся на некоторый угол. Это объясняется тем, что из накаленной нити вылетают электроны. Через пластинку 1 они попадают на электроскоп и заряжают его.
Электричество, заряд, Кулон, поле, напряженность, потенциал, диэлектрики, проводники. Формулы, примеры, тесты
Skip navigation- ФизикаМатематикаАстрономия
- Элементы математики
- Физические величины
- Единицы измерения
- Постоянные величины в физике
- Формулы
- I. Механика
- Кинематика
- Динамика
- Законы сохранения
- Статика
- Колебания и волны
- II. Молекулярная физика
- Молекулярная физика
- Термодинамика
- III. Основы электродинамики
- Электричество
- электрический заряд
- закон Кулона
- напряженность поля
- потенциал и работа поля
- диэлектрики, проводники
- электроемкость, конденсаторы
- энергия конденсатора
- Электрический ток
- Магнетизм
- Электромагнетизм
- IV. Оптика
- Волновая оптика
- Геометрическая оптика
- V. Теория относительности
- Теория относительности
- VI. Квантовая физика
- Световые кванты
- Атомное ядро
- Современная физика*
- Меню
Логин
Пароль



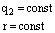 → F ~ q1
→ F ~ q1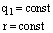 → F ~ q2
→ F ~ q2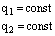 → F ~
→ F ~ 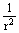
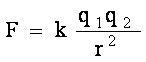
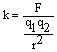
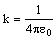 , где e0=8,85.10-12 Кл2/(Н.м2) — электрическая постоянная вакуума.
, где e0=8,85.10-12 Кл2/(Н.м2) — электрическая постоянная вакуума.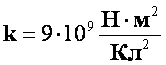
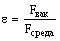 — безразмерная величина!
— безразмерная величина!