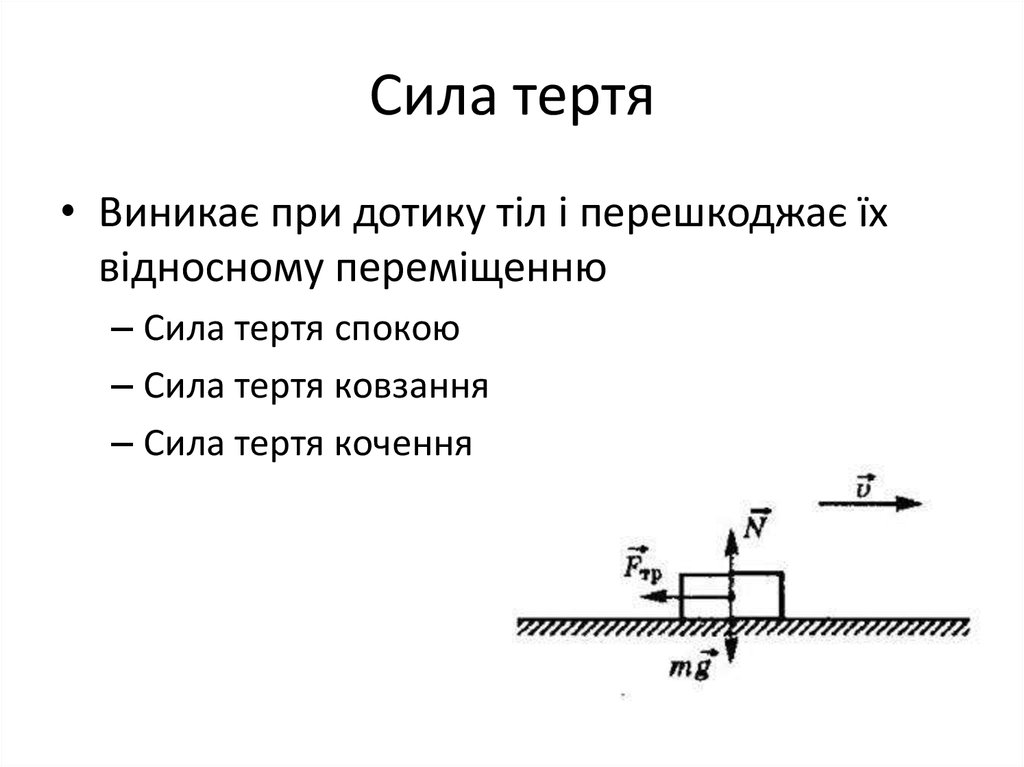
Сила тертя ковзання — Фізика: Класична механіка
Пiсля того, як ви зрушили тiло, тобто приклали потрiбну силу
F=μcNF = \mu_c NF=μcN
, тiло починає ковзати по поверхнi. Тепер у дiю вступає сила тертя ковзання .
Щоб тiло ковзало з рiвномiрною швидкiстю, за другим законом Ньютона:
$$F = F_T = \mu_k N$$ |
Сила тертя ковзання на вiдмiну вiд сили тертя спокою – постiйна. Вона не залежить вiд прикладеної сили. Якщо прикладена сила буде бiльшою за силу тертя ковзання – тiло буде рухатися з прискоренням, якщо рiвною – з постiйною швидкiстю.
Важливо$$\Large!$$ Якщо самостiйно провести аналiз, не важко пересвiдчитися, що зсунути тiло важче, нiж потiм штовхати його з рiвномiрною швидкiстю.
$$\mu_c > \mu_k$$ |
Поверхні |
| Коефіцієнт тертя ковзання |
Дерево/дерево | $$0. | $$0.2$$ |
$$0.1$$ | $$0.03$$ | |
Метал/метал (з лубрикантом) | $$0.15$$ | $$0.07$$ |
Метал/метал (без лубриканта) | $$0.7$$ | $$0.6$$ |
У ЗНО та шкiльнiй фiзицi часто використовують лише коефiцiєнт тертя ковзання. Отже, коли не сказано, який саме коефiцiєнт дано, то це означає, що мають на увазi коефiцiєнт тертя ковзання.
Отже, коли не сказано, який саме коефiцiєнт дано, то це означає, що мають на увазi коефiцiєнт тертя ковзання.
Побудуймо графiк залежностi сили тертя вiд прикладеної сили.
1.
Поки тiло у спокої, збiльшення прикладеної сили $$\vec{F}$$ викликає пропорцiйне збiльшення сили тертя спокою i при цьому $$F_T = F$$.
2.
Коли прикладена сила стає рiвною $$F = \mu_c N$$, тiло зрушиться з мiсця.
3.
Під час руху тіла дiє постiйна сила тертя ковзання $$F_T = \mu_k N
Шкала графiка зображена для випадку з коефiцiєнтом тертя спокою $$\mu_c = 0.39$$, коефiцiєнтом тертя ковзання $$\mu_k = 0.3$$ та масою тiла $$10$$ кг на горизонтальнiй площинi.
Задача 1 ШТОВХАТИ ЧИ ТЯГТИ?
Уявiть ситуацiю: вам потрiбно покатати на санчатах маленького Петра (iм’я не впливає на розв’язок задачi).
Розв’язання Вiдповiдь ПриховатиРозв’язок.
Зобразімо всi сили, які діють на санчата у двох випадках.
Другий закон Ньютона: $$\vec{F} + \vec{F_T} +\vec{N} + m \vec{g} = 0$$.Проекцiя на вiсь $$y: -mg + N — F \sin \alpha = 0 \Rightarrow$$$$ N = mg + F \sin \alpha $$.Проекцiя на вiсь $$x: F \cos \alpha — F_T = 0 \Rightarrow$$$$ F = \dfrac{F_T}{\cos \alpha}$$ – прикладена сила.Сила тертя ковзання: $$F_T = \mu N$$.Пiдставимо отриману силу $$N$$. $$F_T = \mu N =$$$$ \mu (mg + F \sin \alpha) \Rightarrow$$$$ F = \dfrac{\mu (mg + F \sin \alpha)}{\cos \alpha}$$Другий закон Ньютона: $$\vec{F} + \vec{F_T} +\vec{N} + m \vec{g} = 0$$.Проекцiя на вiсь $$y: -mg + N + F \sin \alpha = 0 \Rightarrow$$$$ N =$$$$ mg — F \sin \alpha $$.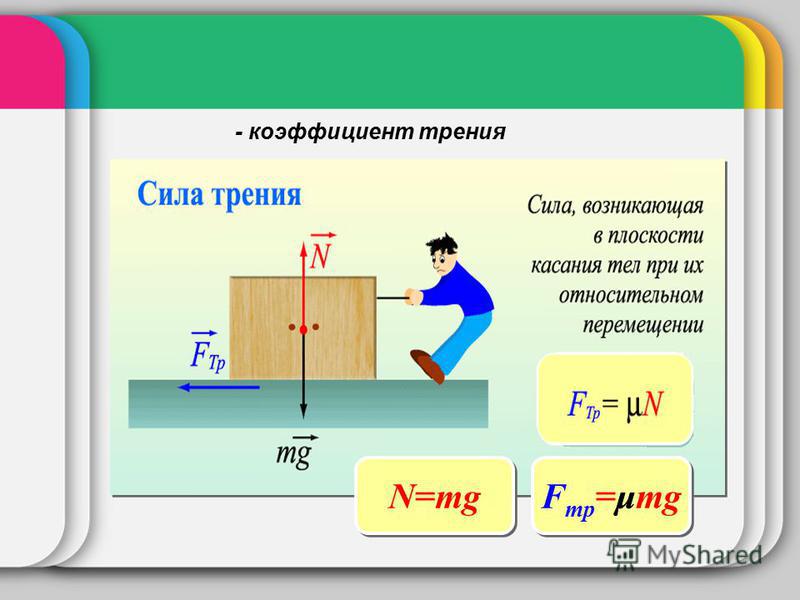
Брусок масою $$15$$ кг лежить на поверхні з коефіцієнтом тертя спокою $$\mu_c=0,5$$ і коефіцієнтом тертя ковзання $$\mu_к=0,3$$. Чи вистачить сили $$55$$ Н, щоб рухати брусок? Ні Так Вага бруска: $$N = mg = 150 \thinspace H$$
Сила тертя ковзання: $$F_{к} = \mu_к N = 0,3 \cdot 150 = 45 \thinspace H$$
Отже сила тертя ковзання менша за прикладені $$55$$ Н, і брусок може рухатись під дією цієї сили.
Сила тертя кочення: опис, формула
Тертя – фізичне явище, з яким людина бореться з метою його зменшення в будь-яких обертаються і ковзних частинах механізмів, без якого, проте, неможливо рух ні одного з цих механізмів. У цій статті розглянемо з точки зору фізики, що таке сила тертя кочення.
Які види сил тертя існують в природі?
В першу чергу розглянемо, яке місце тертя кочення займає серед інших сил тертя. Ці сили виникають в результаті контакту двох різних тел. Це можуть бути тіла тверді, рідкі або газоподібні. Наприклад, політ літака в тропосфері супроводжується наявністю тертя між його корпусом і молекулами повітря.
Розглядаючи виключно тверді тіла, виділяють сили тертя спокою, ковзання і кочення. Кожен з нас помічав: щоб зрушити з місця коробок, що знаходиться на підлозі, необхідно вздовж поверхні підлоги прикласти певну силу. Значення сили, яка виведе коробок із стану спокою, буде за модулем дорівнює силі тертя спокою. Остання діє між дном коробка і поверхнею підлоги.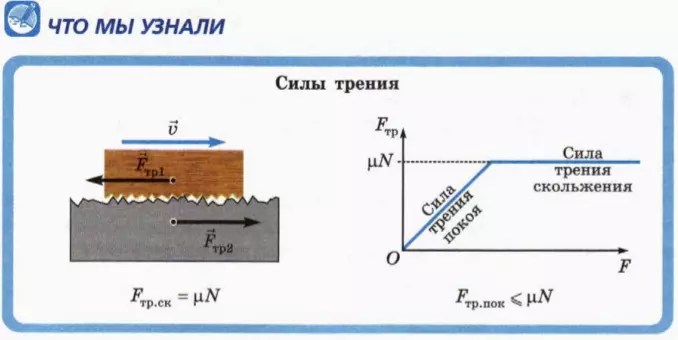
Як тільки коробок почав свій рух, необхідно докладати постійну силу, щоб зберігати цей рух рівномірним. Цей факт пов’язаний з тим, що між контактом підлоги і коробкою на останній діє сила тертя ковзання. Як правило, вона на кілька десятків відсотків менше, ніж тертя спокою.
Якщо під коробок покласти круглі циліндри з твердого матеріалу, то переміщати його стане набагато легше. На що обертаються в процесі руху циліндри під коробкою буде діяти сила тертя кочення. Вона зазвичай набагато менше попередніх двох сил. Саме тому винахід людством колеса стало величезним стрибком у бік прогресу, адже люди отримали можливість переміщати набагато більші вантажі з допомогою невеликої прикладеної сили.
Фізична природа тертя кочення
Чому виникає сила тертя кочення? Це питання є непростим. Для відповіді на нього слід детально розглянути, що відбувається з колесом і поверхнею в процесі кочення. В першу чергу вони не є ідеально гладкими – ні поверхня колеса, ні поверхня, по якій воно котиться.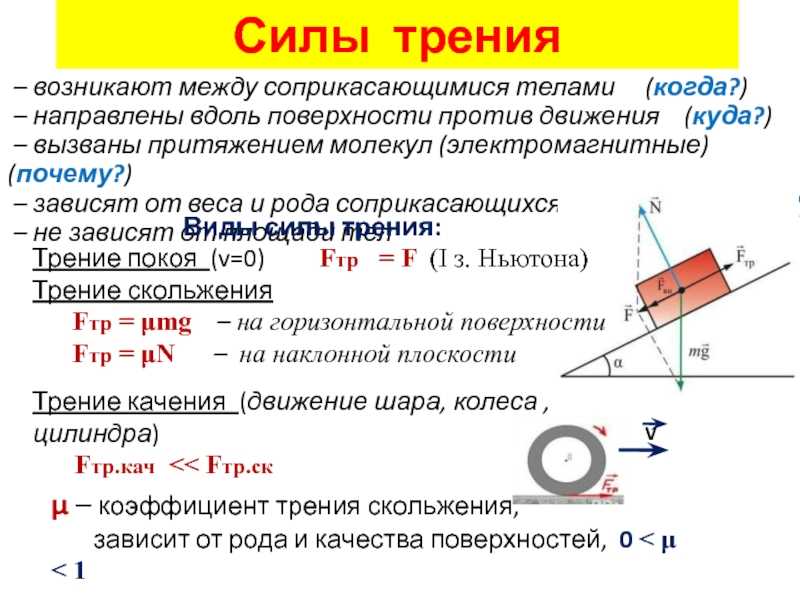 Тим не менш, це не основна причина появи тертя. Головною ж причиною є деформація одного або обох тел.
Тим не менш, це не основна причина появи тертя. Головною ж причиною є деформація одного або обох тел.
Будь-які тіла, з будь-якого твердого матеріалу вони не складалися, деформуються. Чим більше вага тіла, тим більше воно чинить тиск на поверхню, а значить, деформується саме в точці контакту і деформує поверхню. Ця деформація в ряді випадків настільки мала, що не перевищує межі пружності.
В процесі кочення колеса деформовані ділянки після припинення контакту з поверхнею відновлюють вихідну форму. Тим не менше ці деформації циклічно повторюються з новим обертом колеса. Будь-яка циклічна деформація, навіть якщо вона лежить в межі пружності, супроводжується гістерезисом. Іншими словами, на мікроскопічному рівні форма тіла до і після деформації відрізняється. Гістерезис циклів деформації в процесі кочення колеса призводить до “розпорошення” енергії, що виявляється на практиці у вигляді появи сили тертя кочення.
Рух ідеального тіла
Під ідеальним тілом в даному випадку мається на увазі те, що воно є недеформованих.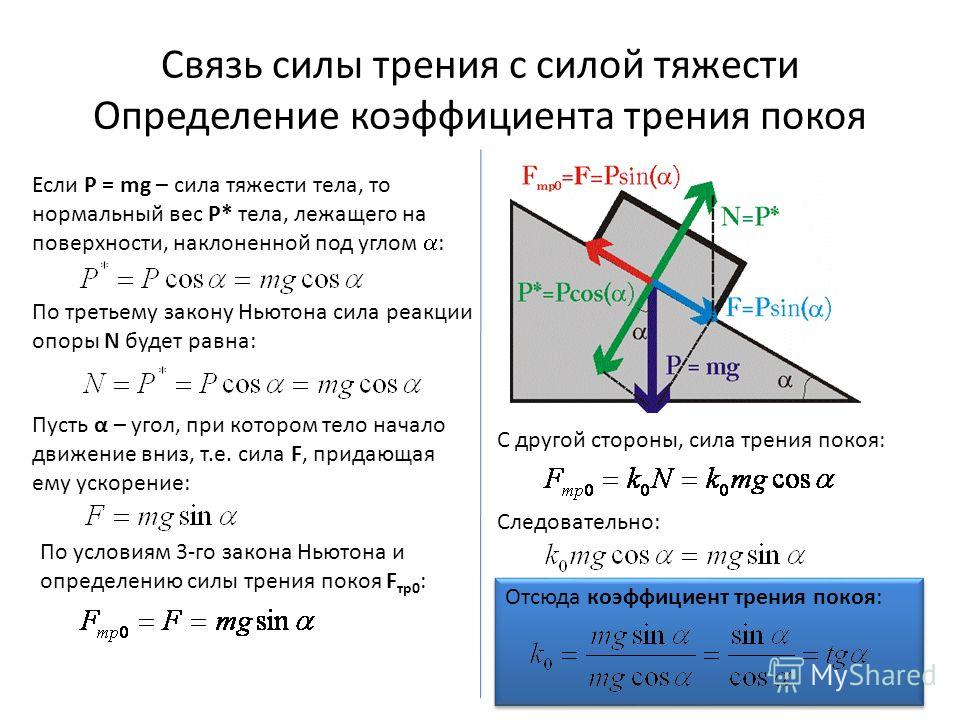 У разі ідеального колеса площа його контакту з поверхнею дорівнює нулю (воно стосується поверхні вздовж лінії).
У разі ідеального колеса площа його контакту з поверхнею дорівнює нулю (воно стосується поверхні вздовж лінії).
Охарактеризуємо сили, які діють на недеформируемое колесо. По-перше, це дві вертикальні сили: вага тіла P і сила реакції опори N. Обидві сили проходять через центр мас (вісь колеса), тому у створенні крутного моменту не приймають участі. Для них можна записати:
P = N
По-друге, це дві горизонтальні сили: зовнішня сила F, яка штовхає колесо вперед (вона проходить через центр мас, і сила тертя кочення fr. Остання створює крутний момент M. Для них можна записати такі рівності:
M = fr*r;
F = fr
Тут r – радіус колеса. Ці рівності містять дуже важливий висновок. Якщо сила тертя fr буде нескінченно малою, то вона все одно створить крутний момент, який призведе до руху колеса. Оскільки зовнішня сила F дорівнює величині fr, то будь-нескінченно мале значення F призведе до коченню колеса. Це означає, що якщо тіло кочення є ідеальним і не зазнає деформації в процесі руху, то ні про яку силу тертя кочення говорити не доводиться.
Всі існуючі тіла є реальними, тобто відчувають деформацію.
Кочення реального тіла
Тепер розглянемо описану вище ситуацію тільки для випадку реальних (деформованих) тел. Площу дотику колеса і поверхні вже не буде дорівнює нулю, вона буде мати деяке кінцеве значення.
Проведемо аналіз сил. Почнемо з дії вертикальних сил, тобто ваги і реакції опори. Вони як і раніше рівні один одному, тобто:
N = P
Однак сила N тепер діє вертикально вгору не через вісь колеса, а дещо зміщена від неї на відстань d. Якщо уявити площу контакту колеса з поверхнею у вигляді площі прямокутника, то завдовжки цього прямокутника буде товщина колеса, а ширина дорівнює 2*d.
Тепер перейдемо до розгляду горизонтальних сил. Зовнішня сила F, як і раніше, не створює моменту обертання і дорівнює силі тертя fr по абсолютній величині, тобто:
F = fr.
Момент сил, що приводить до обертання, буде створювати тертя fr і реакцію опори N.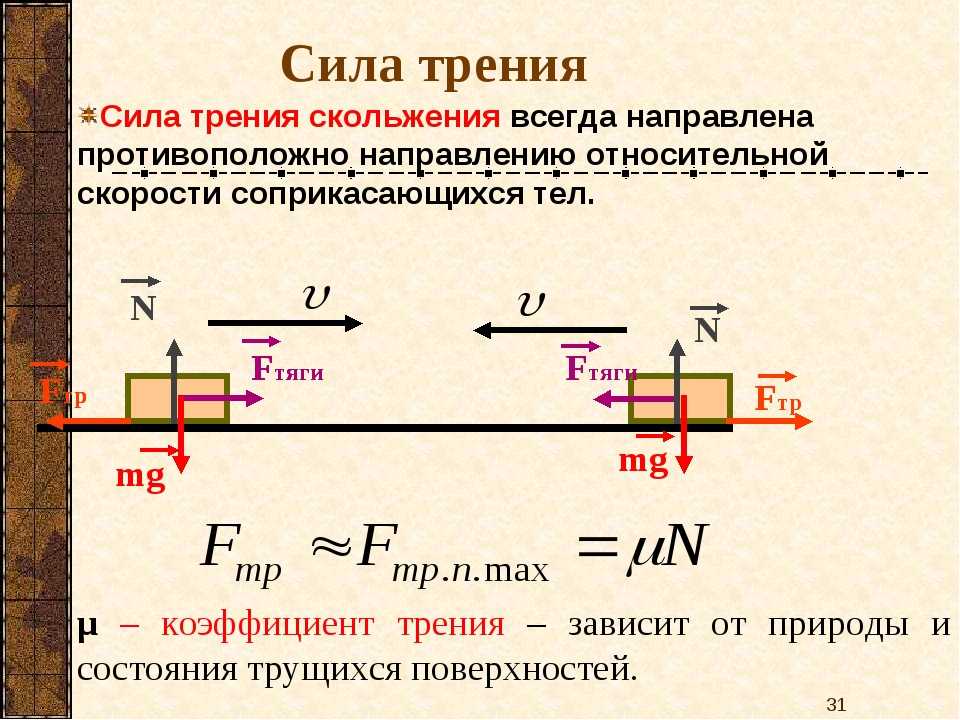 Причому ці моменти будуть спрямовані в різні сторони. Відповідний вираз має вигляд:
Причому ці моменти будуть спрямовані в різні сторони. Відповідний вираз має вигляд:
M = N*d – fr*r
В випадку рівномірного руху момент M дорівнюватиме нулю, тому отримуємо:
N*d – fr*r = 0 =>
fr = d/r*N
Останнє рівність з урахуванням записаних вище формул можна переписати так:
F = d/r*P
По суті, ми отримали головну для розуміння сили тертя кочення формулу. Далі в статті проведемо її аналіз.
Коефіцієнт опору коченню
Цей коефіцієнт вже був введений вище. Також було дано геометричне його пояснення. Мова йде про величину d. Очевидно, що чим більше ця величина, тим більший момент створює сила реакції опори, який перешкоджає руху колеса.
Коефіцієнт опору коченню d, на відміну від коефіцієнтів тертя спокою, ковзання, величина розмірна. Вимірюється він в одиницях довжини. У таблицях його приводять зазвичай в міліметрах. Наприклад, для коліс поїзда, катящихся по сталевих рейках, d = 0,5 мм Величина d залежить від твердості двох матеріалів, від навантаження на колесо, від температури і деяких інших факторів.
Коефіцієнт тертя кочення
Не потрібно його плутати з попереднім коефіцієнтом d. Коефіцієнт тертя кочення позначають символом Cr і обчислюють за наступною формулою:
Cr = d/r
Це рівність означає, що величина Cr є безрозмірною. Саме вона приводиться в ряді таблиць, що містять інформацію про розглянутому виді тертя. Цей коефіцієнт зручно використовувати для практичних розрахунків, оскільки він не припускає знання радіуса колеса.
Величина Cr в переважній більшості випадків менше, ніж коефіцієнти тертя і спокою. Наприклад, для автомобільних шин, що рухаються по асфальту, величина Cr знаходиться в межах декількох сотих (0,01 – 0,06). Проте вона значно зростає при русі спущених коліс по траві і піску (≈0,4).
Аналіз отриманої формули для сили fr
Запишемо ще раз отриману вище формулу сили тертя кочення:
F = d/r*P = fr
З рівності випливає, що чим більше діаметр колеса, тим меншу силу F слід докласти, щоб воно почало рух. Тепер запишемо цю рівність через коефіцієнт Cr, маємо:
Тепер запишемо цю рівність через коефіцієнт Cr, маємо:
fr = Cr*P
Як видно, сила тертя прямо пропорційна вазі тіла. Крім того, при значному збільшенні ваги P змінюється сам коефіцієнт Cr (він зростає на увазі збільшення d). У більшості практичних випадків Cr лежить в межах кількох сотих. У свою чергу, значення коефіцієнта тертя ковзання лежить в межах декількох десятих. Оскільки для сил тертя кочення і ковзання формули однакові, то кочення виявляється вигідним з енергетичної точки зору (сила fr менше на порядок сили ковзання у більшості практичних ситуацій).
Умова кочення
Багато з нас зустрічалися з проблемою проковзування коліс автомобіля при русі по льоду або по бруду. Чому це відбувається? Ключ до відповіді на це питання лежить в співвідношенні абсолютних значень сил тертя кочення і спокою. Ще раз випишемо формулу для кочення:
F ≥ Cr*P
Коли сила F буде більше або дорівнює тертя кочення, тоді колесо почне котитися. Однак якщо ця сила раніше перевершить величину тертя спокою, то раніше настане прослизання колеса, ніж його кочення.
Однак якщо ця сила раніше перевершить величину тертя спокою, то раніше настане прослизання колеса, ніж його кочення.
Таким чином, ефект прослизання визначається співвідношенням коефіцієнтів тертя спокою, тертя кочення.
Способи протидії прослизання колеса автомобіля
Тертя кочення колеса автомобіля, що знаходиться на слизькій поверхні (наприклад, на льоду) характеризується коефіцієнтом Cr = 0,01-0,06. Однак значення такого ж порядку характерні для коефіцієнта тертя спокою.
Щоб уникнути ризику прослизання колеса, використовують спеціальну “зимову” гуму, яку вкручені металеві шипи. Останні, врізаючись у крижану поверхню, збільшують коефіцієнт тертя спокою.
Інший спосіб збільшення тертя спокою полягає в модифікації поверхні, по якій рухається колесо. Наприклад, з допомогою посипання її піском або сіллю.
Скольжение – Физика тела 2.0
Перейти к содержимому
Соскальзывание происходит, когда пространство между ступнями и поверхностью для ходьбы недостаточно велико, чтобы предотвратить соскальзывание задней ступни при отталкивании или соскальзывание передней ступни, когда она пытается замедлить движение вперед.
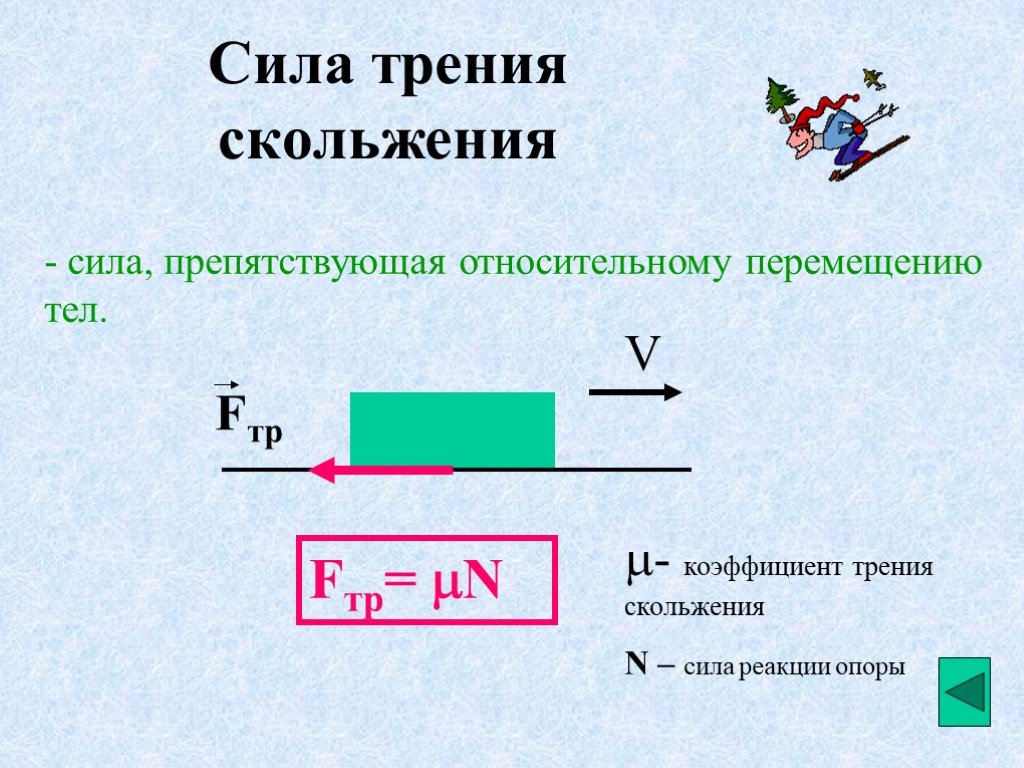
Трение () — это сила, противодействующая скольжению поверхностей друг относительно друга. Потрите ладони друг о друга, сопротивление, которое вы почувствуете, и есть трение. В дополнение к , который указывает только на поверхности, трение указывает только на поверхности. Две поверхности должны соприкасаться, чтобы возникло трение, поэтому вы также не можете получить трение без нормальной силы. На самом деле сила трения пропорциональна нормальной силе.
Упражнение с подкреплением
Потрите ладони друг о друга. Теперь сильно сожмите ладони вместе и попытайтесь скользить ими одновременно.
Теперь нормальная сила больше, что пропорционально увеличивает силу трения.
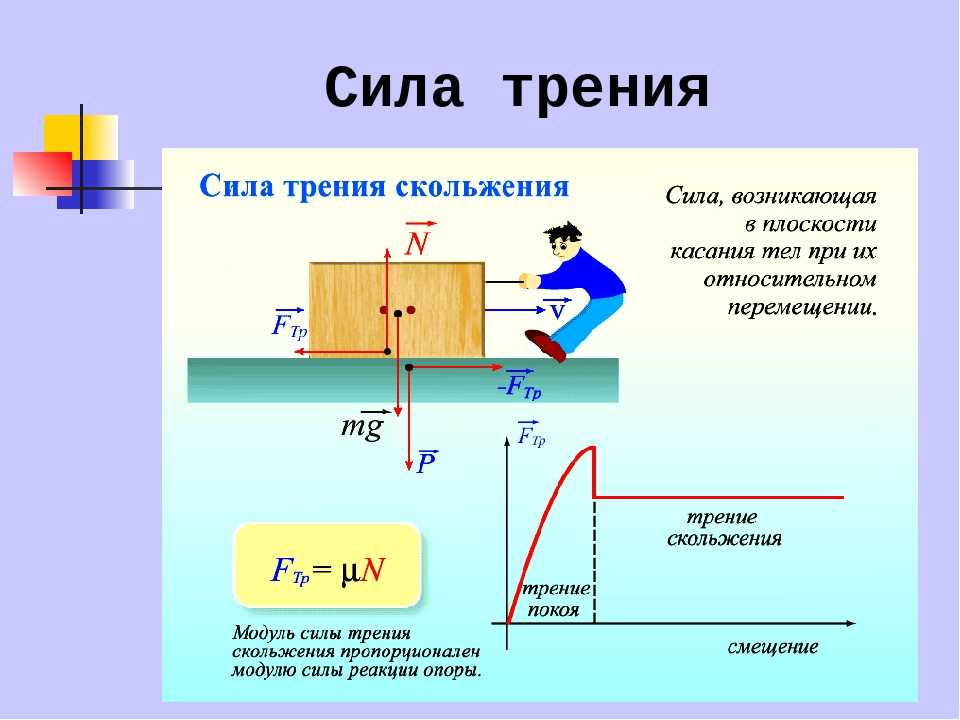 Для того чтобы объект двигался, он должен подняться туда, где пики могут проскакивать по нижней поверхности. Таким образом, сила требуется только для того, чтобы привести объект в движение. Некоторые из пиков будут сломаны, что также потребует силы для поддержания движения. На самом деле большая часть трения возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже гладкие поверхности не лишены трения. Шероховатость и сцепление поверхностей определяют коэффициенты трения (μ).
Для того чтобы объект двигался, он должен подняться туда, где пики могут проскакивать по нижней поверхности. Таким образом, сила требуется только для того, чтобы привести объект в движение. Некоторые из пиков будут сломаны, что также потребует силы для поддержания движения. На самом деле большая часть трения возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже гладкие поверхности не лишены трения. Шероховатость и сцепление поверхностей определяют коэффициенты трения (μ).
Кинетическое трение
() действует всякий раз, когда две поверхности скользят относительно друг друга, и обычно размер кинетического трения не зависит от относительной скорости между скользящими поверхностями. Если объект скользит, но нет другой силы, толкающей объект, чтобы поддерживать его скольжение, то кинетическое трение в конечном итоге остановит скользящий объект. (Толкните объект так, чтобы он скользил по полу и в конце концов остановился. Это кинетическое трение в действии).
Статическое трение
В отличие от кинетического трения, статическое трение не имеет постоянной величины. Вместо этого статическое трение регулируется, чтобы предотвратить скольжение поверхностей, но оно может делать это только до максимального значения. Если сила, необходимая для предотвращения скольжения, больше, чем максимальное значение статического трения, объект будет скользить, и преобладает кинетическое трение. больше, чем . Следующий график зависимости силы от времени демонстрирует процесс «освобождения» статического трения между двумя поверхностями. График был построен путем измерения силы, которую ученики прикладывали к коробке, стоящей на столе, потянув за веревку, привязанную к коробке.
Сила тяги, приложенная к ящику на столе. Студенты сначала тянули слегка, затем все сильнее, пока коробка не начала скользить, а затем тянули точно так, чтобы коробка двигалась с постоянной скоростью. Обратите внимание, что по мере того, как ученики тянут сильнее, коробка еще не двигается, а это означает, что статическое трение реагирует и увеличивается, чтобы предотвратить скольжение.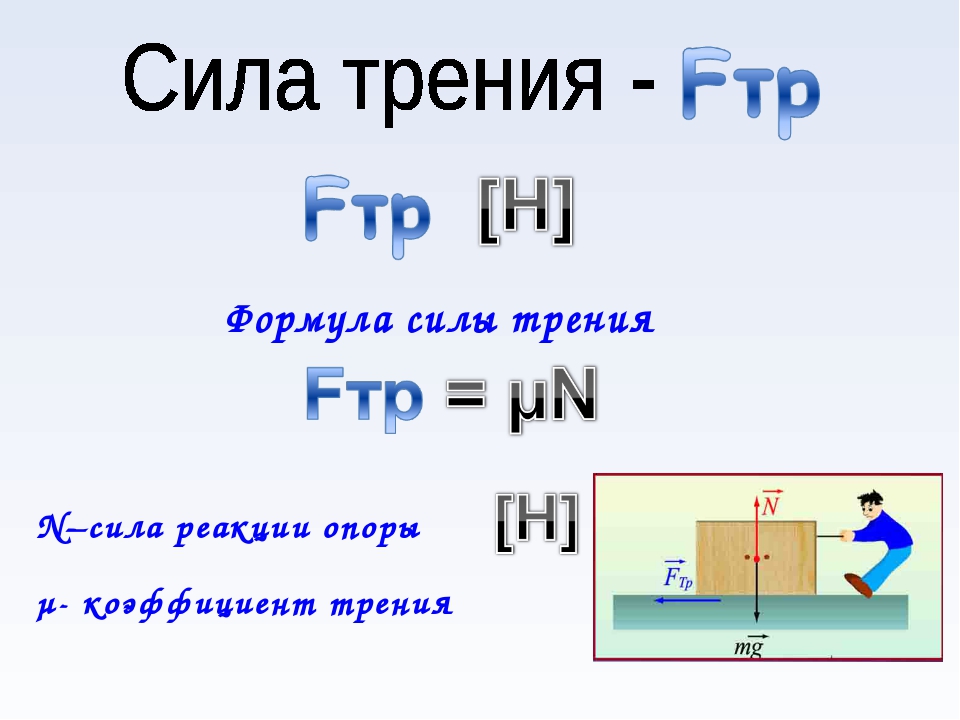 Максимальная статическая сила трения 6,4 Н достигается до того, как коробка начинает скользить и начинает действовать кинетическое трение. Мы видим, что в этой точке сила падает, а это означает, что студенты должны были уменьшить силу тяги до 5,5 9 .0032 N , чтобы сбалансировать кинетическое трение и поддерживать постоянную скорость. Это показывает, что кинетическое трение меньше, чем статическое трение. Эти данные были получены студентами-физиками муниципального колледжа Ампкуа Либби Фрегосо и Маккензи Кэрриер.
Максимальная статическая сила трения 6,4 Н достигается до того, как коробка начинает скользить и начинает действовать кинетическое трение. Мы видим, что в этой точке сила падает, а это означает, что студенты должны были уменьшить силу тяги до 5,5 9 .0032 N , чтобы сбалансировать кинетическое трение и поддерживать постоянную скорость. Это показывает, что кинетическое трение меньше, чем статическое трение. Эти данные были получены студентами-физиками муниципального колледжа Ампкуа Либби Фрегосо и Маккензи Кэрриер.Выберите симуляцию трения из набора симуляций, чтобы увидеть, как ведет себя статическое и кинетическое трение.
Деятельность по усилению
Коэффициент трения
Теперь мы знаем, что сила пропорциональна и что существует два типа трения: статическое и кинетическое. Последним понятием, влияющим на трение, является шероховатость или, альтернативно, гладкость двух поверхностей. () — это безразмерное число, которое оценивает шероховатость и обычно определяется экспериментально.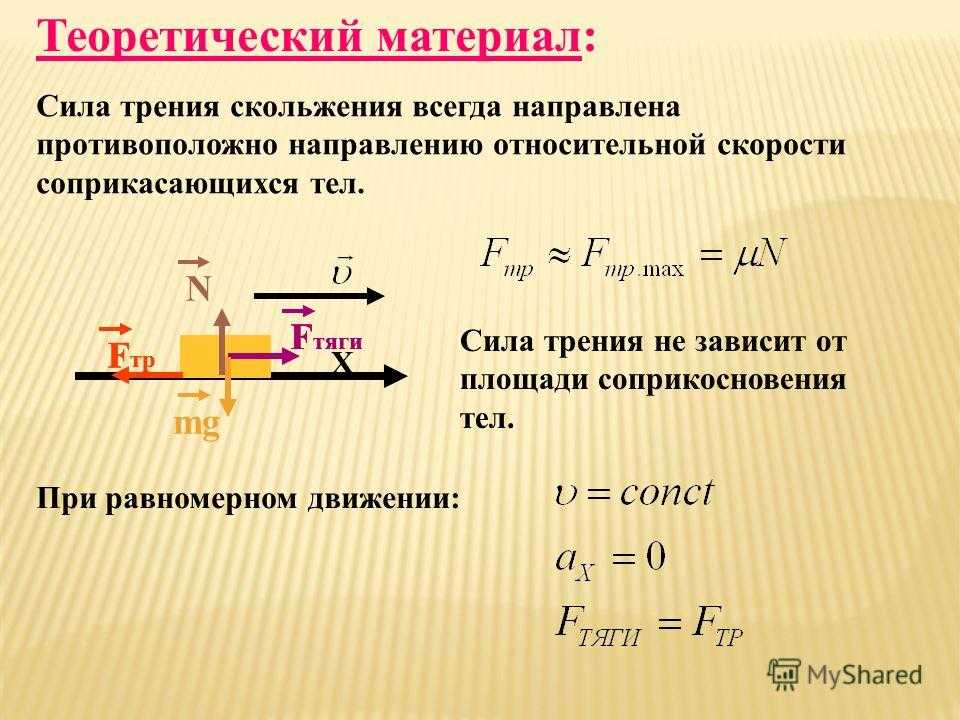 Статическая сила трения больше кинетической силы трения, потому что она больше . Взгляните на таблицу коэффициентов статического и кинетического трения, приведенную ниже. Вы можете найти больше значений в этой массивной таблице коэффициентов статического трения.
Статическая сила трения больше кинетической силы трения, потому что она больше . Взгляните на таблицу коэффициентов статического и кинетического трения, приведенную ниже. Вы можете найти больше значений в этой массивной таблице коэффициентов статического трения.
| Резина на сухом бетоне | 1,0 | 0,7 |
|---|---|---|
| Резина на мокром бетоне | 0,7 | 0,5 |
| Дерево на дереве | 0,5 | 0,3 |
| Вощеная древесина на мокром снегу | 0,14 | 0,1 |
| Металл на дереве | 0,5 | 0,3 |
| Сталь по стали (сухая) | 0,6 | 0,3 |
| Сталь по стали (промасленный) | 0,05 | 0,03 |
| Тефлон на стали | 0,04 | 0,04 |
| Кость, смазанная синовиальной жидкостью | 0,016 | 0,015 |
| Туфли на дереве | 0,9 | 0,7 |
| Обувь на льду | 0,1 | 0,05 |
| Лед на льду | 0,1 | 0,03 |
| Сталь на льду | 0,4 | 0,02 |
Обратите внимание, что в таблице всегда указаны две поверхности; у вас должно быть две поверхности, чтобы определить файл . Когда кто-то задает вопрос типа «Что такое лед?» они обычно имеют в виду между льдом и льдом, но лучше не задавать такие вопросы и всегда ссылаться на две поверхности.
Когда кто-то задает вопрос типа «Что такое лед?» они обычно имеют в виду между льдом и льдом, но лучше не задавать такие вопросы и всегда ссылаться на две поверхности.
Расчет сил трения
Мы можем суммировать все, о чем мы узнали, в двух уравнениях, связывающих силы трения с коэффициентом трения для двух поверхностей и действующими на них поверхностями:
Максимальное статическое трение перед выпуском:
(1)
Кинетическое трение при движении:
(2)
Повседневный пример: тест на физические способности пожарного
Кандидаты в пожарные должны пройти тест на физические способности (PAT), который включает перетаскивание манекена по полу. В PAT города Линкольн, штат Небраска, указано, что кандидаты должны тащить манекен в человеческом обличии весом 170 9 .0032 lbs на 25 футов вокруг бочки, а затем обратно через начальную точку на общее расстояние 50 футов за шесть минут или меньше. Кандидаты могут тащить манекен только с помощью ремня безопасности, прикрепленного к манекену, и не могут нести манекен [5] .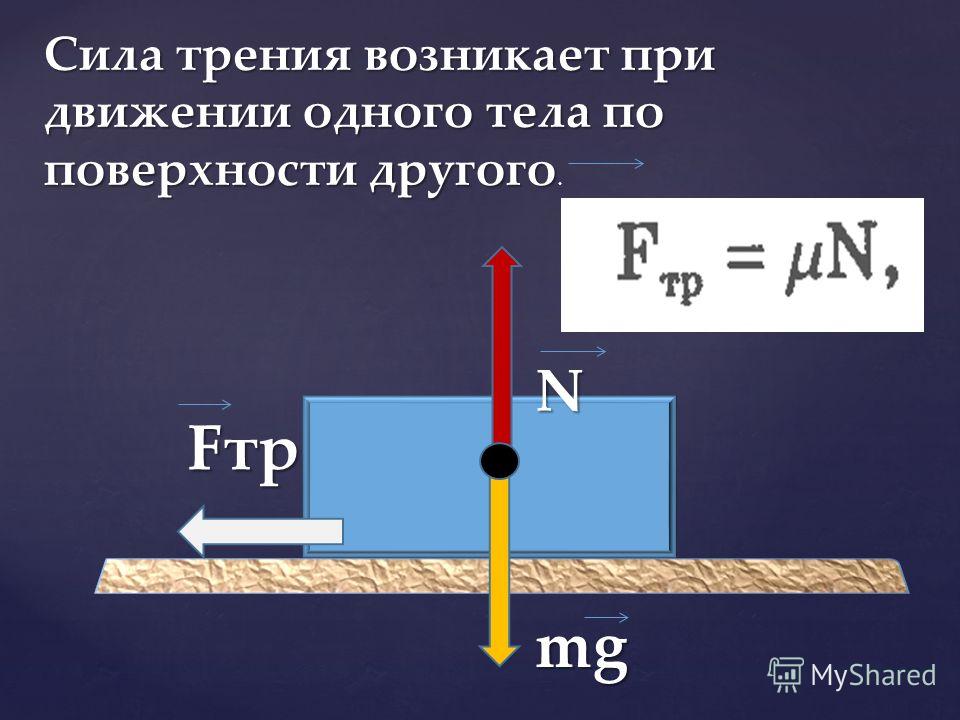
Испытание проводится на полированном бетонном полу. Коэффициент статического трения между хлопчатобумажной одеждой и полированным бетоном составляет 0,5. Если кандидат потянет ремни вертикально вверх с силой 70 фунтов , какое горизонтальное тяговое усилие должен приложить кандидат, чтобы заставить манекен двигаться?
Манекен начинает движение, поэтому мы знаем, что результирующая сила должна быть равна нулю как в вертикальном, так и в горизонтальном направлениях. Во-первых, давайте проанализируем вертикальное направление: если кандидат тянет ремни вертикально вверх с усилием 70 фунтов , то пол должен обеспечивать силу 100 фунтов , чтобы поддерживать манекен.
Теперь давайте проанализируем горизонтальное направление: статическое трение будет соответствовать любому горизонтальному натяжению, которое обеспечивает кандидат, но в противоположном направлении, так что манекен остается внутри до тех пор, пока натяжение не превысит максимальную силу статического трения. Это сила, которую кандидат должен приложить, чтобы заставить манекен двигаться, так что давайте найдем ее. У нас есть коэффициент трения, и мы уже нашли его, так что мы готовы:
Это сила, которую кандидат должен приложить, чтобы заставить манекен двигаться, так что давайте найдем ее. У нас есть коэффициент трения, и мы уже нашли его, так что мы готовы:
После того, как манекен начинает двигаться, начинает действовать кинетическое трение, которое мы можем использовать для расчета кинетической силы трения. Эта сила меньше, чем максимальная статическая сила трения, поэтому для удержания манекена в движении потребуется меньшее усилие, чем для его запуска.
Упражнения с подкреплением
Человек цепляется за пожарный столб детской площадки. «Firepole» от Donkeysforever, через Wikimedia Commons находится в общественном достоянии
Уравнения, данные для статического и кинетического трения, описывают поведение сил трения. Хотя эти формулы очень полезны для практических целей, они не имеют статуса или . На самом деле, есть случаи, для которых эти уравнения даже не годятся. Например, ни одна из формул не является точной для поверхностей, которые хорошо смазаны или скользят на высоких скоростях. Если не указано иное, мы не будем касаться этих исключений. [6]
Если не указано иное, мы не будем касаться этих исключений. [6]
- «Фото» Фрица Хенле, Библиотека Конгресса, находится в общественном достоянии. Университетская физика, Университетская физика, том 1. OpenStax CNX. 2 августа 2018 г. http://cnx.org/contents/[email protected]. ↵
- «Руководство для кандидатов на проверку физических способностей пожарных» от Industrial/Organizational Solutions, Inc. ↵
- OpenStax University Physics, University Physics Volume 1. OpenStax CNX. 2 августа 2018 г. http://cnx.org/contents/[email protected]. ↵
License
Body Physics 2.0 от Lawrence Davis находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, если не указано иное.
Поделиться этой книгой
Поделиться в Твиттере
Сил и Движений — Неуравновешенные Силы
Как мы узнали во введении ко второму закону Ньютона и убедились в орбитальном движении и законе всемирного тяготения, неуравновешенная сила приводит к ускорению. И, как мы видели при движении снаряда, иногда эта сила и ускорение проявляются только в одном из двух измерений движения.
И, как мы видели при движении снаряда, иногда эта сила и ускорение проявляются только в одном из двух измерений движения.
В предыдущих изученных случаях мы прикладывали силы только в одном направлении. Пришло время сложить многомерные силы. Но не волнуйтесь: мы будем делать это по одному двумерному шагу за раз.
Трение
Прежде чем мы начнем серьезно изучать двухмерное движение, нам нужно узнать о трении, как действительно знают о нем.
Трение — это сила, противодействующая движению и действующая на любой объект, скользящий или катящийся по поверхности другого объекта. Даже сопротивление воздуха является разновидностью трения. Он существует из-за молекулярных различий двух поверхностей на микроскопическом уровне. Если бы у нас было идеально отполированное стекло, скользящее по другой пластине идеально отполированного стекла, они могли бы скользить друг относительно друга без какого-либо трения, отбирая энергию у их общей канавки.
«Без трения» возможен только теоретически, потому что «идеально отполированный» возможен только теоретически. На самом деле на поверхности нашего стекла всегда будут крошечные выпуклости, которые будут цепляться за другие крошечные выпуклости, препятствующие общему движению объекта.
На самом деле на поверхности нашего стекла всегда будут крошечные выпуклости, которые будут цепляться за другие крошечные выпуклости, препятствующие общему движению объекта.
Как и нормальная сила, трение является контактной силой. В отличие от нормальной силы, ее величина определяется тем, насколько устойчивы две поверхности к трению друг о друга. На самом деле, это связано с величиной нормальной силы: F f = мкН , где мкН — коэффициент трения , определяемый двумя присутствующими материалами. Существуют таблицы этих коэффициентов, но их также можно рассчитать, зная величину нормальной силы, Н , и величину силы трения, F f .
Чтобы еще больше усложнить ситуацию, трение имеет два подтипа: статическое трение и кинетическое трение.
Статическое трение — трение, противодействующее движению скольжения или трения. Чтобы преодолеть статическое трение, должна присутствовать сила, превышающая силу статического трения. Однако, как только два объекта начинают двигаться , появляется кинетическое трение . Если подумать, трение воздушного шара о волосы требует наличия кинетического трения.
Однако, как только два объекта начинают двигаться , появляется кинетическое трение . Если подумать, трение воздушного шара о волосы требует наличия кинетического трения.
Статическое трение и кинетическое трение имеют разные коэффициенты для одних и тех же двух материалов. Например, для стекла по стеклу коэффициент статического трения может быть равен 9.0253 μ с = 0,9, а коэффициент кинетического (подвижного) трения равен μ k = 0,3. Эти коэффициенты не имеют единиц измерения и могут быть рассчитаны для любой комбинации поверхностей, таких как резина на асфальте, с использованием диаграмм сил.
Даже без вычислений мы можем почувствовать размер статического трения по сравнению с кинетическим трением, замедляя увеличение силы, которую мы прикладываем к объекту. Как только мы преодолеем статическое трение, толкать станет легче, потому что сила, поддерживающая постоянную скорость, меньше, чем раньше. Давай, попробуй, мы знаем, что ты этого хочешь.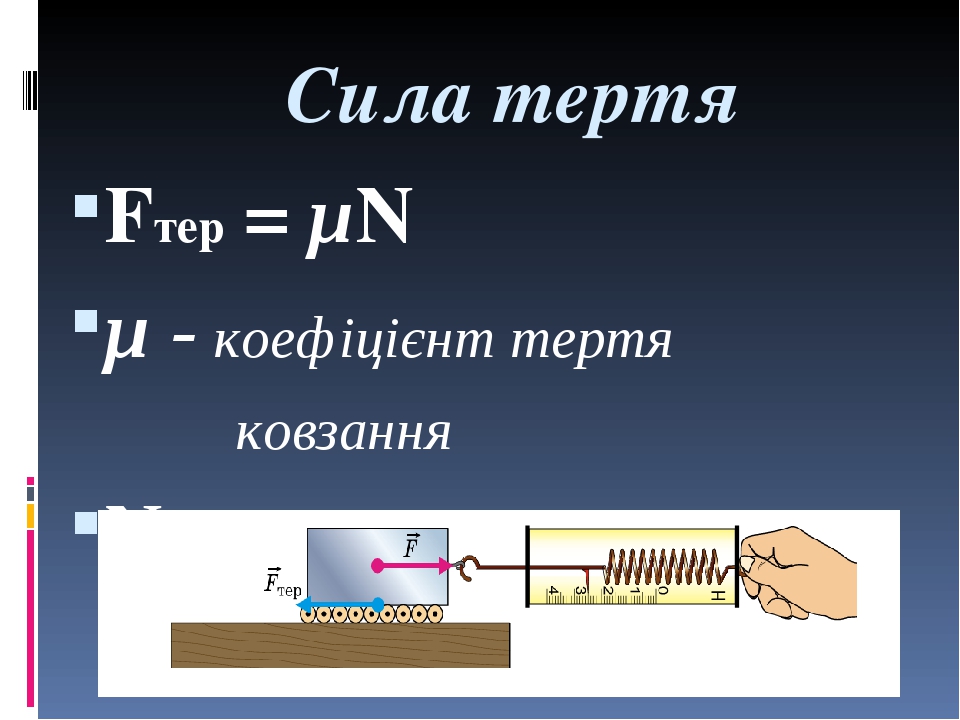
Задумайтесь на минутку: автомобиль зависит от статического или кинетического трения между шинами и дорогой?
Правильный ответ: статическое трение: резина на дороге не скользит, а цепляется. Когда шина вращается, резина не скользит, но если бы она скользила, у нас были бы следы заноса и кинетическое трение.
Теперь давайте посмотрим на силовую диаграмму, включающую статическое трение. Эти особые силы уравновешены таким образом, что , какое уравнение означает, что сумма всех сил равна силам, добавленным в x и y направления по отдельности, а затем объединены с теоремой Пифагора. Однако сумма любых уравновешенных сил по-прежнему равна нулю.
Здесь у нас есть блок, стоящий на шероховатой поверхности, хотя кто-то толкает его, что создает статическое трение между блоком и самой поверхностью. Трение всегда действует в направлении, противоположном движению. В этом случае нормальная сила и вес уравновешивают друг друга, а толчок является направлением предполагаемого движения.
Обратите внимание, что движение не происходит, потому что W = N и F статическое = F толчок . Все силы уравновешены. Статическое трение не требует движения, помните?
В качестве аргумента предположим, что толчок равен максимально возможной силе статического трения до того, как объект начнет скользить, хотя, если толчок был меньше максимальной силы статического трения, силы все равно были бы уравновешены , потому что сила трения покоя будет противостоять ей в равной степени. Если бы мы знали величину толкающей силы, мы могли бы рассчитать коэффициент через F статическая = F толкающая = μ с N = μ с Вт 90
Если толкающая сила возрастает сверх максимально возможного значения статического трения, F = μ с Н , то сила статического трения превращается в силу кинетического трения, которая представляет собой меньший вектор силы , что приводит к меньшему коэффициенту.
Теперь, когда мы суммируем все наши силы, силы уравновешены только по вертикали с W = N или F y = N – W = 0. Та же разница. В направлении x у нас есть F x = F толчок – F кинетика = ma . Мы можем сделать больше замен, превратив уравнение в F push – μ k N = ma , затем в F μ 9 253 – – – 0262 к Вт = мА . Мы можем сократить это далее до F push – μ k mg = ma . Как правило, полезно указывать силы в пересчете на вес 90 253 мг 90 254. Все знают, как найти вес.
Зная вес, можно найти трение. Это может быть правдой в отношении большего количества «взвешиваний», чем один, поскольку вес является липкой темой. Сделайте как Филеас Фогг из Вокруг света за восемьдесят дней , и цитируем:
Он жил один и, так сказать, вне всяких социальных отношений; а так как он знал, что в этом мире нужно принимать во внимание трение, а трение замедляет, он никогда ни с кем не терся.
Уклоны
Говоря языком физики, уклон — это пандус. В отличие от эксперимента Галилея с минимальным трением, мы продолжим говорить о силе, когда объекты скользят, а не катятся. Сила тяжести тоже присутствует, как обычно, и нормальная сила тоже, но они не компенсируют друг друга на наклонной поверхности: нормальная сила не будет направлена против силы тяжести, когда поверхность наклоняется.
Это будет легче увидеть, если мы нарисуем другую диаграмму свободного тела. Для задачи наклонной плоскости нам нравится устанавливать начало декартовых координат в центре масс, чтобы оси были выровнены по углу наклона. Давайте посмотрим на диаграмму ниже:
На приведенной выше диаграмме мы наклонили ось координат с наклоном, так как большая часть действующих сил параллельна или перпендикулярна наклону. Это означает, что единственный вектор, о котором нам нужно беспокоиться, разделяется на наши новые, не горизонтальные и не вертикальные 9Компоненты 0253 x — и y — это сила W , которая падает вертикально вниз под углом θ к новой системе координат. С помощью этого трюка мы также можем сказать, что у нас есть движение только в направлении x . Верь нам; вот так проще.
С помощью этого трюка мы также можем сказать, что у нас есть движение только в направлении x . Верь нам; вот так проще.
Диаграмма уже разбила W на новые компоненты: в нашем x -направлении у нас есть W sin θ , а в y -направлении, уравновешивающем нормальную силу, мы имеем W cos θ . Тригонометрия — лучший друг наклона.
Давай попробуем, а?
Пишем , а в направлении y имеем . Обратите внимание, что в любом случае не имеет значения, какое направление мы называем положительным. Здесь мы выбрали направление, в котором блок будет ускоряться вниз по рампе, как положительное.
Пока все хорошо. Казалось бы, мы создаем отличный рецепт решения этих печально известных проблем с наклонной плоскостью. Далее мы можем сделать замены, зная, что Ш x , Ш y и F f ар. Эта сила трения является кинетической, потому что пандус уже скользит вниз, поэтому F f = μ k N .
Находя N из y -направления, получаем N = W y = W cos θ 2 093 cos Если бы мы знали значения массы и угла, мы могли бы получить числовое значение для N , но оставим это символично, просто так. Это что-то из физики.
Имея под рукой нормальную силу, мы готовы сделать дополнительную замену внутри . Follow along: ma x = W x – F f = W sin θ – μ k N = mg sin θ – μ k mg cos θ . Вау!
Перепишем это: мА x = мг sin θ – μ k мг cos θ . Посмотрите, что мы можем сделать сейчас? Все слагаемые имеют m , так что это аннулирует оставшееся a x = g sin θ – μ k g 2 cos 902 9. 9. Если бы мы действительно хотели максимально упростить математически, мы могли бы записать как x = 9.0253 г (sin θ – μ k cos θ ).
9. Если бы мы действительно хотели максимально упростить математически, мы могли бы записать как x = 9.0253 г (sin θ – μ k cos θ ).
Представьте, если бы мы оставили оси x — и y на их обычных местах, что бы произошло? Нам пришлось бы иметь дело с компонентами ускорения и трения в обоих направлениях x и y ! Выбрав определение осей, которые мы сделали, ускорение и трение были ограничены одним измерением. Поэтому у нас были уравновешенные силы в другом измерении. Это позволило найти соотношения между силами и решить задачу. Вот так мы и нашли ускорение блока. Или что означает этот прямоугольник.
Когда мы говорим о наклонах, есть несколько возможных ситуаций: мы можем попытаться выяснить, как трение уравновешивает силу тяжести и заставляет блок стоять на месте, или нам может быть интересно выяснить, насколько сильно мы должны толкнуть блок, чтобы сдвинуть его. вверх по холму, или мы можем попытаться рассчитать, как быстро блок соскользнет вниз по склону и будет ли у нас достаточно времени, чтобы убраться с дороги, если наш друг отпустит его. Возможности безграничны, но диаграмма свободного тела всегда является отправной точкой.
вверх по холму, или мы можем попытаться рассчитать, как быстро блок соскользнет вниз по склону и будет ли у нас достаточно времени, чтобы убраться с дороги, если наш друг отпустит его. Возможности безграничны, но диаграмма свободного тела всегда является отправной точкой.
В другом варианте вместо толчка используется натяжение веревки или проволоки. Просто назовите его T и продолжайте как обычно. Проблема в системе шкивов? Напряжение есть. Вот пример диаграммы «два в одном», связанной натяжением, потому что натяжение одинаково по всей струне или проволоке. В остальном эта проблема очень похожа на ту, что мы уже делали. Попробуйте!
Распространенные ошибки
Всегда, нет, никогда опускайте трение на диаграмме свободного тела. Если есть ускорение и контактная сила, под которой мы подразумеваем нормальную силу, то есть трение.
Следите за тем, чтобы на диаграмме отображался правильный вид трения: «Статическое» для стационарного, «кинетическое» для движения.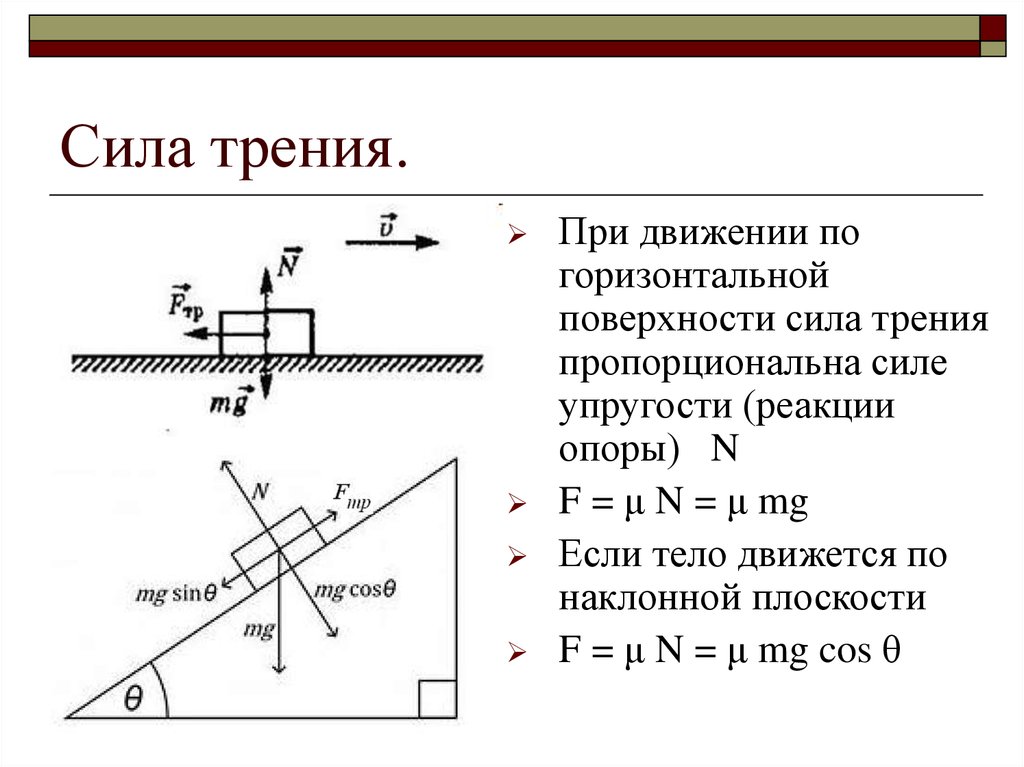


 4$$
4$$