Формула расчета катушки индуктивности
Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при этом низкими емкостью и активным сопротивлением. Их используют:. Катушка представляет собой намотанную на каркасе проволоку в виде спирали, а намотка может быть однослойной или многослойной, виток к витку или с расстоянием. Они бывают различных типов и форм, например, без сердечника обладают небольшой индуктивностью, а с сердечником она значительно увеличивается.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- В помощь изучающему электронику
- Расчет катушек индуктивности для фильтров и схем
Калькулятор для расчета катушки индуктивности - Расчет катушек индуктивности без сердечника
- Онлайн калькулятор расчета индуктивности катушки с воздушным сердечником
- Расчет индуктивности катушек (однослойных)
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Расчёт катушки индуктивности
youtube.com/embed/kTKwbPUi0e4″ frameborder=»0″ allowfullscreen=»»/>В помощь изучающему электронику
Катушка индуктивности является неотъемлемым элементом большинства современных приборов. При этом она используется для различных целей в работе электрических цепей. В случае необходимости замены можно использовать как заводскую, так и изготовленную самостоятельно катушку. Но при этом необходимо учитывать ее основной параметр — индуктивность. Для того чтобы рассчитать индуктивность катушки без сердечника можно воспользоваться универсальной формулой:.
Такой способ является универсальным и может использоваться, как для полых катушек, так и для имеющих сердечник. Если рассматривать частный вариант — катушку с воздушным сердечником, то для расчета ее индуктивности можно использовать формулу:. Где D — диаметр катушки, n — количество витков, а l — длина ее намотки. Такой способ расчета будет справедливым для катушек, имеющих однослойную структуру, набираемых в один уровень.
В случае если катушка наматывается в несколько слоев, то их толщина вносит дополнительные изменения в расчет. При этом формула расчета преобразится к виду:. Где D — диаметр катушки, n — количество витков, h — высота самой катушки, g — толщина слоя намотки.
Для упрощения процесса расчета индуктивности катушки без сердечника можно воспользоваться онлайн калькулятором. Понравилась статья? Поделиться с друзьями:. Вам также может быть интересно. Комментарии и отзывы Добавить комментарий Отменить ответ. Политика конфиденциальности Пользовательское соглашение О нас.
Расчет катушек индуктивности для фильтров и схем
Индуктивность катушки зависит от ее размеров, количества витков и способа намотки. Чем больше эти параметры, тем выше индуктивность. Если катушка наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется изготовить катушку по заданным размерам и нет провода нужного диаметра, то при использовании более толстого провода надо сделать больше витков, а тонкого — уменьшить их количество, чтобы получить необходимую индуктивность. Все приведенные выше рекомендации справедливы при намотке катушек без ферритовых сердечников. То есть намотать катушку определенной индуктивности, что часто скажем надо для фильтров. В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.
Все приведенные выше рекомендации справедливы при намотке катушек без ферритовых сердечников. То есть намотать катушку определенной индуктивности, что часто скажем надо для фильтров. В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.
Калькулятор для расчета катушки индуктивности. Катушкой Воспользовавшись формулой для расчёта, зная индуктивность катушки: Здесь.
Калькулятор для расчета катушки индуктивности
Данный справочник собран из разных источников. Кронегера в ГДР в году. Не смотря на такую ее древность, она является моей настольной книгой наряду с несколькими другими справочниками. Думаю время над такими книгами не властно, потому что основы физики, электро и радиотехники электроники незыблемы и вечны. В настоящее время в технике принята величина, обратная. Относительная магнитная проницаемость является безразмерной величиной. Е на рис. Для случая параллельного соединения двух катушек Знак плюс ставится при одинаковом, а знак минус при встречном направлении магнитных полей.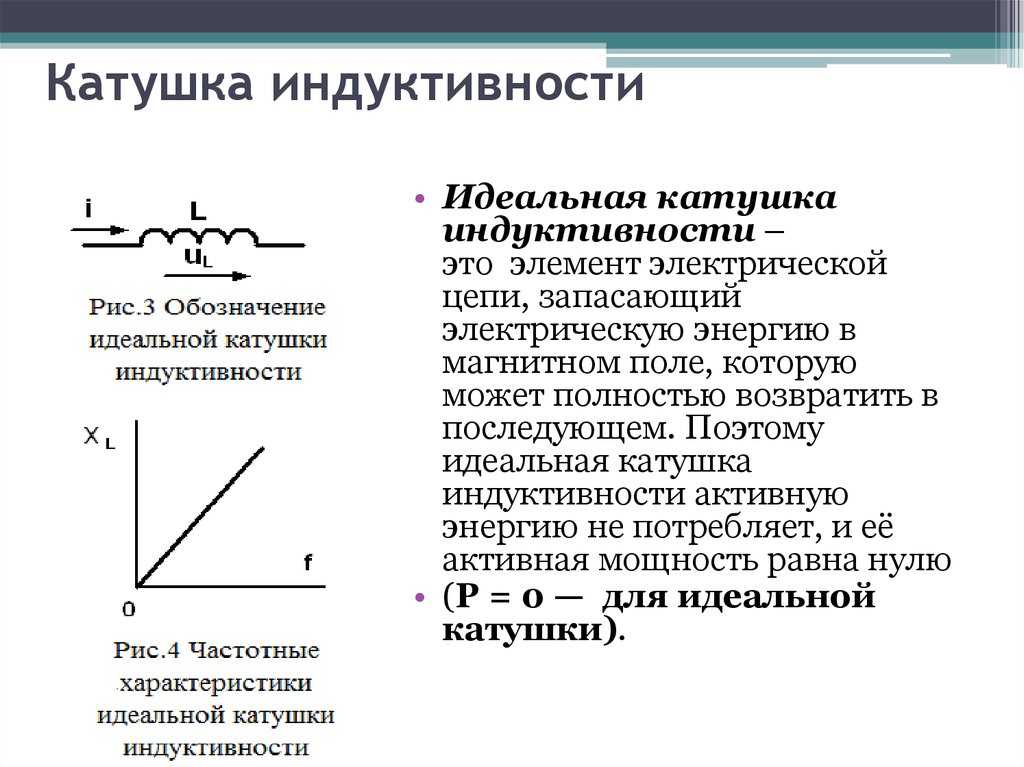 Взаимная индуктивность определяется формулой где буквой k обозначен коэффициент связи, который всегда меньше единицы, Определение коэффициента связи производится следующимобразом рис.
Взаимная индуктивность определяется формулой где буквой k обозначен коэффициент связи, который всегда меньше единицы, Определение коэффициента связи производится следующимобразом рис.
Расчет катушек индуктивности без сердечника
Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки. Чем больше диаметр, длина намотки и число витков тем больше индуктивность. При плотной намотке витков катушки, ее индуктивность будет больше чем катушка намотанная не плотно. Если необходимо намотать катушку индуктивность которой известна, а так же дано число витков и диаметр провода, но нет провода нужного диаметра, то при более толстом проводе можно увеличить число витков, а при меньшем диаметре провода уменьшить кол-во витков, в итоге можно получить примерно заданную индуктивность катушки.
Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при этом низкими емкостью и активным сопротивлением.
Онлайн калькулятор расчета индуктивности катушки с воздушным сердечником
Русский: English:. Бесплатный архив статей статей в Архиве. Справочник бесплатно. Параметры радиодеталей бесплатно. Даташиты бесплатно. Прошивки бесплатно.
Бесплатный архив статей статей в Архиве. Справочник бесплатно. Параметры радиодеталей бесплатно. Даташиты бесплатно. Прошивки бесплатно.
Расчет индуктивности катушек (однослойных)
Катушкой индуктивности — это элемент электрической цепи с высоким значением индуктивности, при этом низкими емкостью и активным сопротивлением. Их используют:. Катушка представляет собой намотанную на каркасе проволоку в виде спирали, а намотка может быть однослойной или многослойной, виток к витку или с расстоянием. Они бывают различных типов и форм, например, без сердечника обладают небольшой индуктивностью, а с сердечником она значительно увеличивается. Это обусловлено магнитной проницаемостью материала. Форма сердечника может быть разной, выделяют броневые, стержневые и тороидальные. Для улучшения массогабаритных параметров катушки наматывают на ферритовом кольце — такой вариант называется тороидальным способом намотки.
Калькулятор для расчета катушки индуктивности. Катушкой Воспользовавшись формулой для расчёта, зная индуктивность катушки: Здесь.
Очень полезная программа. Жалъ, что толко на соленоида. Я иногда потребовал бы и разчёт тороида.
Основные положения электромагнетизма, в том числе определение понятия индуктивность — здесь. Формулы и численные методы расчета катушек индуктивности, которые использует Coil32 , вы можете посмотреть в справочном разделе сайта, а именно:. Здесь приведены простые эмпирические формулы расчета индуктивностей, которые Coil32 не использует, но которые могут быть полезны и радиолюбителям и студентам. Во всех расчетных формулах таблицы все размеры в метрах, индуктивность в Генри. Имя обязательное.
Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки.
Катушка индуктивности является неотъемлемым элементом большинства современных приборов. При этом она используется для различных целей в работе электрических цепей. В случае необходимости замены можно использовать как заводскую, так и изготовленную самостоятельно катушку. Но при этом необходимо учитывать ее основной параметр — индуктивность.
Онлайн расчет многослойной катушки. Калькулятор считает по алгоритму с применением эллиптических интегралов Максвелла. Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении.
Как рассчитать сердечник и витки самодельных катушек индуктивности
Содержание
- Как определить эффективную магнитную проницаемость сердечника с зазором
- Самоиндукция
- Что такое электрический дроссель?
- Особенности применения дросселей в схемах
- Изготовление дросселя
- Реактивное сопротивление катушки индуктивности.
- Расчёт катушки с броневым сердечником
- Изготовление дросселя
- Плагин Ferrite: Расчет индуктивности на ферритовом стержне
Как определить эффективную магнитную проницаемость сердечника с зазором
Эффективная магнитная проницаемость сердечника с зазором μе связанная c таким понятием, как сопротивление магнитному потоку R Сопротивление магнитному потоку определяется следующим выражением
Сопротивление магнитному потоку определяется следующим выражением
Из данного выражения можно сделать вывод, что чем меньше магнитная проницаемость материала, тем выше магнитное сопротивление. Не трудно заметить, что с учетом относительной магнитной проницаемости вещества сердечника (порядка нескольких тысяч) и воздуха (примерно равно единице), магнитное сопротивление сердечника с зазором будет, в значительной степени, определятся размерами воздушного зазора.
Таким образом, полное магнитное сопротивление сердечника с зазором RO будет состоять из последовательных магнитных сопротивлений сердечника RC и магнитного сопротивления зазора RЗ. С учётом того что относительная магнитная проницаемость воздуха примерно равна единице μr = 1, то получим следующее выражение
где μ – магнитная постоянная, μ0 = 4π*10-7,
μе – эквивалентная магнитная проницаемость сердечника с зазором,
μr – абсолютная магнитная проницаемость вещества сердечника,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника,
l – длина магнитной силовой линии сердечника с зазором,
δ – длина воздушного зазора.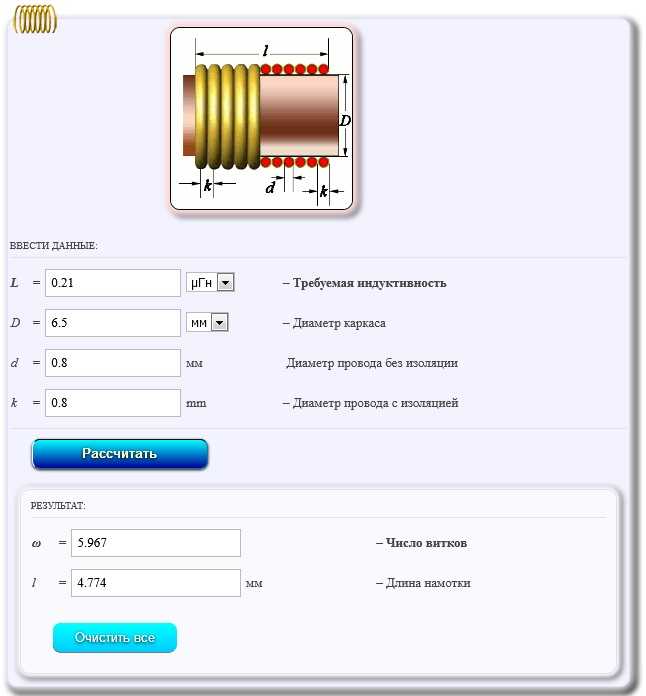
После преобразования получим
Так как длина зазора меньше чем длина магнитной линии сердечника (δ << le), то из данного выражения можно получить выражение для эффективной магнитной проницаемости сердечника с зазором
где μе – эквивалентная магнитная проницаемость сердечника с зазором,
μr – абсолютная магнитная проницаемость вещества сердечника,
le – эффективный путь магнитной линии сердечника,
δ – длина воздушного зазора.
Данное выражение показывает, что эффективная магнитная проницаемость сердечника с зазором, а, следовательно, и индуктивность катушки про прочих постоянных параметрах уменьшается при увеличении величины зазора.
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
где
I – сила тока в катушке , А
U – напряжение в катушке, В
R – сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Что такое электрический дроссель?
Дросселем, в общем случае, называют катушку индуктивности, чаще всего с сердечником, которая служит для устранения или уменьшения переменного (импульсного) тока, разделения или ограничения сигналов различной частоты. Исходя из этого, дроссели условно можно разделить на следующие типы:
— сглаживающие дроссели, предназначены для ослабления переменной составляющей постоянного тока или напряжения различной частоты, то есть сглаживания пульсаций, на выходе и входе силовых преобразователей или выпрямителей;
— дроссели переменного тока, предназначены для ограничения электрического тока, при резких изменениях нагрузки, например, при пуске электродвигателей или источников питания;
— дроссели насыщения, или управляемые дроссели, предназначенные для регулирования индуктивного сопротивления за счёт изменения тока подмагничивания.
Дроссели, как и любая другая катушка индуктивности, может быть без сердечника, с замкнутым сердечником, с сердечником, имеющим малый зазор и с сердечником, имеющим большой зазор или разомкнутым сердечником. Поэтому в независимости от назначения дросселя его принцип действия основан на электромагнитных свойствах катушки индуктивности и сердечника, на котором она выполнена.
Особенности применения дросселей в схемах
Дроссели можно соединять последовательно и параллельно.
[Индуктивность последовательно соединенных дросселей] = [Индуктивность первого дросселя] + [Индуктивность второго дросселя]
[Индуктивность параллельно соединенных дросселей] = 1 / (1 / [Индуктивность первого дросселя] + 1 / [Индуктивность второго дросселя])
На рисунке приведены типовые схемы на катушках индуктивности. (А) — Индуктивный делитель переменного напряжения. [Напряжение на нижнем дросселе] = [Входное напряжение] * [индуктивность нижнего дросселя] / ([индуктивность нижнего дросселя] + [индуктивность верхнего дросселя]) (Б) — Фильтр высших частот. (В) — Фильтр низших частот.
(В) — Фильтр низших частот.
(читать дальше…) :: (в начало статьи)
| 1 | 2 | 3 |
:: ПоискТехника безопасности :: Помощь
К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.
Если что-то непонятно, обязательно спросите!Задать вопрос. Обсуждение статьи. сообщений.
Вот одна формула = * * / / , по которой получается, что чем больше ток через дроссель, тем больше получается число витков — что в корне противоречит теории — чем нужен больший ток, тем должно быть меньше число витков (ЭТО Читать ответ…
А что такое E в первой формуле, прямо таки получается огромная величина индуктивности.
В первой формуле правдоподобно, если индуктивность в микрогенри
Если я правильно понял, то, например, E-3 означает 0.001? Читать ответ…
Как рассчитать и изготовить самому дроссель ВЧ, индуктивностью 5мкГн, на ток 3-4А ? Читать ответ…
Еще статьи
Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить…
Намотка. Изготовить…
Приемы намотки импульсного дросселя / трансформатора….
Инвертор, преобразователь, чистая синусоида, синус…
Как получить чистую синусоиду 220 вольт от автомобильного аккумулятора, чтобы за…
Преобразователь однофазного в трехфазное. Конвертер одной фазы в три. …
Схема преобразователя однофазного напряжения в трехфазное….
Резонансный инвертор, преобразователь напряжения повышающий. Схема, ко…
Инвертор 12/24 в 300. Резонансная схема….
Простой импульсный прямоходовый преобразователь напряжения. 5 — 12 вол…
Схема простого преобразователя напряжения для питания операционного усилителя….
Диодные схемы. Схемные решения. Схемотехника. Частота, мощность, шумы….
Классификация, типы полупроводниковых диодов. Схемы, схемные решения на диодах. …
Понижающий импульсный источник питания. Онлайн расчет. Форма. Подавлен…
Как рассчитать понижающий импульсный преобразователь напряжения. Как подавить пу…
Проверка электронных элементов, радиодеталей. Проверить исправность, р…
Проверить исправность, р…
Как проверить исправность детали. Методика испытаний. Какие детали можно использ…
Изготовление дросселя
Для изготовления дросселя нужно выбрать подходящий каркас — в нашем случае это резистор определенной мощности и соответственно габаритов. Ниже приведены фото отечественных и зарубежных резисторов с обозначением их мощности.
Рис. 2. Резисторы МЛТ и зарубежные резисторы по мощности.
Рис. 3. Пример намотки дросселя на резисторе МЛТ-0,5.
Для намотки дросселя подойдут резисторы с высоким сопротивлением, например: 100кОм, 200кОм и т.д
Важно чтобы сопротивление резистора было большим, иначе добротность вашего самодельного дросселя может получиться плохой
Пример намотки равномерными слоями приведен на рисунке 3.
Для намотки можно использовать тонкий эмалированный провод (ПЭТВ) или же провод в шелковой изоляции (ПЭЛШО) диаметром 0,1-0,2мм, важно чтобы все витки намотанные таким проводом вместились на нашем каркасе из резистора. После намотки каждый из концов провода припаивают к выводам резистора, а на катушку сверху можно капнуть немножко клея чтобы витки потом не расползались
После намотки каждый из концов провода припаивают к выводам резистора, а на катушку сверху можно капнуть немножко клея чтобы витки потом не расползались
После намотки каждый из концов провода припаивают к выводам резистора, а на катушку сверху можно капнуть немножко клея чтобы витки потом не расползались.
Реактивное сопротивление катушки индуктивности.
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию,
оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС,
равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения,
что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС,
равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая
пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со
сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома,
где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
Расчёт катушки с броневым сердечником
Броневые сердечники представляют собой сборную конструкцию, состоящую из двух чашеобразных частей. В центре каждой чашки имеется центральный керн, в большинстве случаев имеющий осевое отверстие, используемое для подстройки величины индуктивности.
Такие сердечники имеют универсальное применение благодаря высокой добротности в заданной полосе частот, низким искажениям, отсутствие полей рассеяния и небольшими габаритами.
Расчёт постоянных С1 и С2 данного типа сердечника выполняется по аналогии с предыдущими типами, но в связи с формой броневого сердечника имеются свои особенности. Рассмотрим сечение броневого сердечника
Разделим данный сердечник на простейшие линейные и угловые участки с различным сечением: линейные – l1, l2, l3 и угловые – l4, l5, так же выделим соответствующие им поперечные сечения: S1, S2, S3, S4, S5. Длины линейных участков достаточно просто определить, для нахождения длины угловых участков и сечений на всех участках можно используя следующие выражения
Длины линейных участков достаточно просто определить, для нахождения длины угловых участков и сечений на всех участках можно используя следующие выражения
Таким образом, вычислив длину и площадь поперечного сечения отдельных участков, можно вычислить постоянные для данного типа сердечников
Данные выражения определяют параметры сердечника без технологических пазов и вырезов. При желании их учитывать необходимо, внести следующие поправки
где n – число пазов,
g – ширина паза.
Пример. В качестве примера рассчитаем индуктивность дросселя выполненного на броневом сердечнике, состоящем из двух чашек типа Ч22 из феррита марки 50ВН (μr = 50), количество витков ω = 100.
123412
С учётом конструктивных особенностей выразим величины заложенные в требуемые нам выражения:
Найдем длины и сечение участков магнитопровода. Расчёт будем вести без учёта технологических пазов и вырезов.
С учётом рассчитанных выше значений определим индуктивность исходного дросселя
На этом можно и остановиться с расчётами индуктивных элементов с замкнутыми сердечниками. В следующей статье я рассмотрю индуктивные элементы на разомкнутых сердечниках.
Изготовление дросселя
Для изготовления дросселя нужно выбрать подходящий каркас — в нашем случае это резистор определенной мощности и соответственно габаритов. Ниже приведены фото отечественных и зарубежных резисторов с обозначением их мощности.
Рис. 2. Резисторы МЛТ и зарубежные резисторы по мощности.
Рис. 3. Пример намотки дросселя на резисторе МЛТ-0,5.
Для намотки дросселя подойдут резисторы с высоким сопротивлением, например: 100кОм, 200кОм и т.д
Важно чтобы сопротивление резистора было большим, иначе добротность вашего самодельного дросселя может получиться плохой
Пример намотки равномерными слоями приведен на рисунке 3.
Для намотки можно использовать тонкий эмалированный провод (ПЭТВ) или же провод в шелковой изоляции (ПЭЛШО) диаметром 0,1-0,2мм, важно чтобы все витки намотанные таким проводом вместились на нашем каркасе из резистора. После намотки каждый из концов провода припаивают к выводам резистора, а на катушку сверху можно капнуть немножко клея чтобы витки потом не расползались
После намотки каждый из концов провода припаивают к выводам резистора, а на катушку сверху можно капнуть немножко клея чтобы витки потом не расползались
После намотки каждый из концов провода припаивают к выводам резистора, а на катушку сверху можно капнуть немножко клея чтобы витки потом не расползались.
Плагин Ferrite: Расчет индуктивности на ферритовом стержне
В отличии от тороидальной индуктивности на ферритовом кольце, магнитный поток катушки на ферритовом стержне не замкнут целиком внутри феррита и каждая силовая линия проходит и по ферритовому стержню и по воздуху, поэтому расчет такой катушки представляет довольно сложную задачу. Индуктивность зависит от:
- магнитной проницаемости ферритового стержня и его размеров;
- размеров самой катушки;
- взаимного соотношения размеров катушки и стержня;
- положения катушки относительно центра стержня.
Расчет индуктивности катушки на ферритовом стержне основан на определении относительной эффективной проницаемости стержня.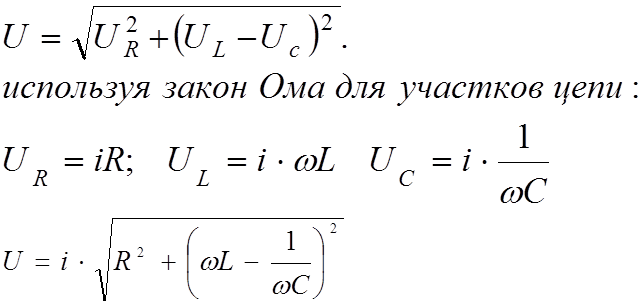 Другими словами, нам нужно определить насколько возрастет индуктивность катушки с «воздушным сердечником» если внутрь нее вставить ферритовый стержень. Основная формула выглядит вот так:
Другими словами, нам нужно определить насколько возрастет индуктивность катушки с «воздушным сердечником» если внутрь нее вставить ферритовый стержень. Основная формула выглядит вот так:
,где Lf / Lair — отношение индуктивности катушки с ферритом к индуктивности той же катушки без феррита, а коэффициенты x, k и μfe вычисляются по следующему алгоритму:
- l’ = lc + 0.45 dc;
- φ_φmax ≈ 1 / [ 1 + { ( ( lf — lc ) / df )1.4 } / ( 5 μ ) ];
- Canf = 0.5 π ε ( lf — lc ) / [ ln { 2 ( lf + df) / df } — 1 ];
- k = [ (φ_φmax Canf / ε ) + 2 df ] / 2 dc
- x = 5.1 [ l’ / dc ] / [1+ 2.8 ( dc / l’ )];
- μfe = ( μ -1) ( df /dc)2 +1;
где ε = 8,8542*10-12 Ф/м — электрическая постоянная, μ — начальная магнитная проницаемость материала стержня. Основные размеры в метрах, обозначения понятны из рисунка:
Основные размеры в метрах, обозначения понятны из рисунка:
Немного теории обосновывающей этот алгоритм.
- Можно считать что воздушная катушка имеет магнитную цепь состоящую из двух частей. Снаружи катушки и внутри нее. Они отличаются плотностью силовых линий и . Если магнитное сопротивление внутренней части магнитной цепи выше, чем наружной части (а это так, поскольку ее площадь поперечного сечения намного меньше), тогда применение феррита уменьшает это сопротивление и имеет эффект увеличения индуктивности. Это отношение двух частей магнитных сопротивлений магнитной цепи воздушной катушки обозначено в основной формуле как x и вычисляется на 5-ом шагу алгоритма.
- Параметр μfe учитывает случай, когда обмотка не плотно прилегает к стержню, т.е. между стержнем и обмоткой существует радиальный зазор.
- Параметр Canf учитывает влияние частей стержня, которые выступают за пределы катушки. Эти части уменьшают магнитное сопротивление внешней части магнитной цепи и также увеличивают индуктивность.

- Параметр φ_φmax учитывает конечное магнитное сопротивление феррита. Этот параметр, наряду с параметром Canf используется для расчета коэффициента k из основного уравнения
При смещении катушки относительно стержня индуктивность катушки уменьшается, это обстоятельство учитывается с помощью поправочного коэффициента K:
,где
sh — относительное смещение = смещение s деленное на половину длины сердечника [sh = s / ( lf / 2 )].
Эта формула получена методом регрессионного анализа и справедлива при s = 0,05 — 0,75
В итоге индуктивность катушки на ферритовом стержне определяется по следующей формуле:
Индуктивность катушки «воздушным» сердечником Lair рассчитывается по алгоритму расчета однослойной катушки с учетом шага намотки. Длину намотки можно определить по следующей формуле:
,где
- N — число витков.
- dw — диаметр провода.
- p — шаг намотки.
Алгоритм имеет следующие ограничения в расчетах:
- шаг намотки не может превышать удвоенного диаметра провода;
- диаметр катушки не может быть больше удвоенного диаметра стержня;
- длина намотки должна быть меньше 3/4 длины стержня;
- длина стержня должна быть не менее чем в 12 раз больше его диаметра;
- при смещении катушки она не должна доходить до края стержня на 1/8 его длины;
- начальная магнитная проницаемость стержня должна быть больше 100;
Также как и в дросселе на ферритовом кольце с немагнитным зазором, при больших значениях начальной магнитной проницаемости стержня его эффективная магнитная проницаемость слабо зависит от начальной и составляет величину не более нескольких десятков.
Кроме того, вы можете воспользоваться онлайн-калькулятором катушки на ферритовом стержне.
Особая благодарность за конструктивную помощь и соавторство в разработке методики расчета.
Tags: амплитуда, бра, вид, дом, е, знак, импульсный, как, кт, магнит, магнитный, мощность, напряжение, принцип, провод, пуск, р, размер, расчет, резистор, ряд, сопротивление, схема, тип, ток, трансформатор, ук, фото, эффект
Катушка индуктивности. Дроссель ДроссельВозьмем отрезок медного провода и намотаем его на карандаш, а затем снимем с карандаша полученную спираль. У нас получился очень необходимой в радиоэлектронике элемент под названием катушка индуктивности. В дальнейшем такую спираль будем называть катушкой. Полученная нами катушка в электронике называется «однослойная цилиндрическая катушка без сердечника». В промышленности катушки наматывают проводами с низким удельным сопротивлением — медь, алюминий, серебро и т.д. Провода покрывают электротехническим лаком для проедотвращения замыкания между витками катушки. В цепях постоянного тока и в цепях переменного тока катушка обладает различными свойствами, о чем в дальнейшем и будет идти речь. Вспомним, из физики, что вокруг всякого проводника, по которому протекает электрический ток, образуется магнитное поле. Так как катушка — это проводник скрученный в спираль, то вокруг катушки также образуется магнитное поле. При протекании через катушку постоянного тока iL силовые линии магнитного поля направлены так, как показано на рисунке.  Чем больше количество витков и чем больше сила тока через катушку, тем больше величина магнитного поля. Параметры катушки характеризуются величиной L которая называется: «индуктивность». Индуктивность зависит от геометрических размеров катушки и количества витков намотки. Следовательно, чем больше ток через катушку и больше индуктивность, тем сильнее магнитное поле. Если в катушку ввести сердечник из магнитного материала (например сталь), то индуктивность катушки возрастет во много раз. Сам сердечник введенный в катушку, при подаче на катушку постоянного напряжения, намагнитится. Из сказанного следует, что мы можем рассматривать катушку с сердечником как электрический магнит. Электромагниты широко используются как в промышленности, так и в быту. Свойства электромагнита используются в электродвигателях постоянного тока. Более всего электромагниты распространены в таких приборах, как электромагнитные реле. Реле, это такие приборы, при подаче напряжения на которые включается электромагнит и происходит замыкание или размыкание мощных контактов. Чем больше количество витков и чем больше сила тока через катушку, тем больше величина магнитного поля. Параметры катушки характеризуются величиной L которая называется: «индуктивность». Индуктивность зависит от геометрических размеров катушки и количества витков намотки. Следовательно, чем больше ток через катушку и больше индуктивность, тем сильнее магнитное поле. Если в катушку ввести сердечник из магнитного материала (например сталь), то индуктивность катушки возрастет во много раз. Сам сердечник введенный в катушку, при подаче на катушку постоянного напряжения, намагнитится. Из сказанного следует, что мы можем рассматривать катушку с сердечником как электрический магнит. Электромагниты широко используются как в промышленности, так и в быту. Свойства электромагнита используются в электродвигателях постоянного тока. Более всего электромагниты распространены в таких приборах, как электромагнитные реле. Реле, это такие приборы, при подаче напряжения на которые включается электромагнит и происходит замыкание или размыкание мощных контактов. Реле, следовательно могут коммутировать большие токи и напряжения. Реле, так же, широко используют в системах автоматики. При определенном включении реле могут выполнять логические функции. Несмотря на простоту конструкции, расчёт индуктивности катушки весьма сложен. Приходится учитывать геометрические размеры, форму, количество витков, тип сердечника и т.д. Для примера приведём формулу расчета индуктивности L простой однослойной цилиндрической катушки диаметром D, длиной намотки l, числом витков W, без сердечника: L(мкГн) = W2 * D * 10-3 *l / (D + 0,45). Индуктивность катушки измеряется в единицах — генри (Гн). Величина в 1 генри очень большая единица, поэтому на практике часто применяют кратные единицы: миллигенри (мГн), 1мГн = 1*10-3 Гн; микрогенри (мкГн), 1мкГн = 1*10-6 Гн. Вернемся к катушке в цепи постоянного тока. Если катушку из нескольких витков, с сердечником, использовать в качестве электромагнита, т.е. подключить ее к источнику тока, то она перегорит (если мощность источника достаточно велика). Произойдет это потому, что сопротивление катушки постоянному току очень мало, и соответственно ток через катушку и мощность будут максимальны. В связи с этим, для катушек в цепи постоянного тока, важна не индуктивность, а сопротивление катушки постоянному току. У электромагнитных реле, например, в справочниках указывается сопротивление обмотки и рабочее напряжение. Как получить высокое сопротивление обмотки катушки, если провод которым они наматываются имеет низкое удельное сопротивление? Для этого используют провод с малой площадью поперечного сечения и наматывают большое количество витков в несколько слоев, например распространенное реле РЭС-9 имеет обмотку проводом диаметром 0,1мм и числом витков порядка 2000. Иначе обстоит дело, когда катушка включена в цепь переменного тока. Так как ток переменный, то и магнитное поле создаваемое катушкой, тоже будет переменным. Переменное магнитное поле будет создавать сопротивление прохождению тока через катушку. Причем, чем больше частота переменного тока, при неизменной индуктивности катушки, тем больше получается сопротивление. Это сопротивление называется — индуктивным (или реактивным) сопротивлением Rl. Рассчитывается Rl по формуле Rl = 2 * pi * f *L, где частота f в герцах, индуктивность L в генри и сопротивление Rl в омах. Свойство катушки, когда с увеличением частоты увеличивается ее сопротивление, широко используется на практике. Например, если подключить радиоприемник (РП) к бортовой сети автомобиля, то прием радиостанций будет затруднен из за сильных помех от приборов автомобиля. Помехи, это паразитные сигналы переменного тока (не синусоидального) распространяющиеся по цепям питания автомобиля. Избавиться от помех можно если в цепи питания поставить фильтр состоящий из катушки и конденсаторов. Так как катушка имеет низкое сопротивление постоянному току, то постоянное напряжение питания проходит через катушку без затухания, а для помехи сопротивление катушки велико и сигнал помехи ослабляется. Сопротивление конденсатора для помехи наоборот мало и помеха заземляется. Назначение индуктивно-емкостного фильтра не только защита от помех. В связи с тем, что конструктивный расчет катушек индуктивности очень сложен, на практике, в основном, применяют готовые (стандартные) катушки индуктивности. Для фильтров применяют катушки которые называют «дроссель». В радиоаппаратуре применяют катушки с изменяемой индуктивностью — сердечник такой катушки делается подвижным и может перемещаться внутри катушки. В зависимости от применяемого сердечника индуктивность может возрастать или наоборот уменьшаться. Через определенный промежуток времени конденсатор зарядится. Как только конденсатор зарядится переключим переключатель SA на катушку L (Рис.2). Конденсатор С разрядится через низкое сопротивление катушки L, но на этом процесс в цепи параллельно включенных катушки и конденсатора не закончится. Вспомним, что при прохождении тока через катушку индуктивности вокруг нее образуется магнитное поле. Как только конденсатор разрядился магнитное поле катушки создает в катушке ЭДС, которая создает ток заряда конденсатора (В данном случае I2. Как видно из рисунка направление тока I2 противоположно току I1. За счет ЭДС катушки конденсатор заряжается. Как только конденсатор зарядился он тут же начинает разряжаться через низкое сопротивление катушки и процесс повторяется. В связи с потерями энергии в катушке и конденсаторе ток заряда — разряда постепенно уменьшается и процесс затухает. На графике этот процесс выглядит так, как показано но рисунке. Параллельное включение катушки и конденсатора называется: «параллельный колебательный контур» или просто «колебательный контур». Колебательный контур обладает замечательными свойствами. Одно из свойств колебательного контура, это равенство периодов (Т) колебательного процесса, то есть частота колебаний (f) является постоянной величиной (смотрите график на рисунке). Частота колебаний зависит от емкости конденсатора и индуктивности катушки. Частота колебательного контура называется «резонансной частотой» (fр). На рисунке показана математическая запись расчета резонансной частоты колебательного контура. Здесь к генератору (G) переменного тока подключен колебательный контур (LC). Ток I проходящий через контур измеряет амперметр переменного тока (А). Мы можем плавно изменять частоту генератора от f1 (см. график) которая меньше резонансной частоты колебательного контура до f2 которая больше резонансной частоты. На этих частотах величина тока максимальна. На частоте резонанса контура fp ток через контур резко падает. Это еще одно замечательное свойство колебательного контура. Мы знаем, что чем больше сопротивление цепи, тем меньше ток в этой цепи. Тогда резонансное сопротивление колебательного контура Rp, будет максимальным именно на частоте резонанса. Свойство колебательного контура, когда резонансное сопротивление контура на частоте резонанса стремится к бесконечности, широко используется на практике. Например, рассмотрим как работает простой радиоприемник. В нашем примере (см. рисунок) радиостанция имеет частоту передающего сигнала 1200 KHz (килогерц). Приемник принимает через антенну радиосигналы. Радиосигналов в эфире очень много и все они имеют разные частоты. Как нам выделить сигнал нужной радиостанции (в нашем примере с частотой 1200 KHz)? Для настройки радиоприемника на нужную частоту воспользуемся свойствами колебательного контура. Рассмотрим схему показанную на рисунке. Антенна (А) принимает радиосигналы различных частот. Предположим, что колебательный контур (LC) имеет частоту резонанса равную 1200 KHz, именно ту частоту которая нам нужна. Тогда радиосигналы у которых частоты не равны 1200 KHz практически без помех пройдут через колебательный контур на землю. Для сигнала с частотой 1200 KHz сопротивление колебательного контура велико, поэтому сигнал пойдет не на землю, а на преобразователь радиосигнала высокой частоты в сигнал звуковой частоты (называется «детектор») и далее на усилитель и динамик. В простых приёмниках (например рассмотренного нами) возникает такое явление, как наравне с основной радиостанцией, на частоту которой настроен колебательный контур, прослушивается и другая радиостанция (с меньшей громкостью) имеющая частоту близкую к частоте основной радиостанции. Это явление возникает потому, что частота (fp1) мешающей радиостанции близка к частоте основной радиостанции и резонансное (Rp1) сопротивление колебательного контура велико (Рис. 2). Относительно высокое сопротивление колебательного контура, не на частоте резонанса, позволяет мешающему сигналу проходить на детектор и соответственно на усилитель и динамик. Поэтому для колебательного контура существует такое понятие как добротность контура. На графике представлены две кривые зависимости (А и Б) сопротивления контура от частоты сигнала. |
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров. История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному… Интересное: Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 11 из 14Следующая ⇒ При расчете основных параметров КИ используются геометрические размеры их обмоток: диаметр D, длина l и толщина t (последнее только для многослойных обмоток) (рисунок 3). В однослойной катушке диаметр D представляет собой диаметр окружности, образуемой центром тяжести активного сечения провода. На высоких частотах диаметр D можно принять равным внутреннему диаметру витков. Длина катушки представляет собой расстояние между осевыми линиями крайних витков. Расстояние между осевыми линиями смежных витков называется шагом намотки . Величины и связаны между собой простым соотношением
где N −число витков; При сплошной намотке расстояние между смежными витками определяется диаметром провода в изоляции и неплотностью прилегания витков друг к другу. Последнее может быть учтено коэффициентом неплотности , который зависит в основном от диаметра провода (таблица 3).
Таблица 3 − Значения коэффициента неплотности
Размеры многослойной катушки определяются наружным D и внутренним D 0 диаметрами и длиной намотки. Расчет индуктивности. Из теоретической электротехники известно следующее выражение для расчета индуктивности длинного соленоида круглого сечения (без сердечника):
Здесь индуктивность L получается выраженной в мкГн, если длину намотки выразить в см, а площадь сечения S — в см2. В реальных катушках длина обычно соизмерима с диаметром, вследствие чего сильнее сказывается уменьшение магнитного сцепления крайних витков и фактическая индуктивность оказывается меньше расчетной. Точный учет этого явления приводит к громоздким и неудобным формулам. На практике используют простые полуэмпирические формулы с поправочными коэффициентами, зависящими от относительных размеров катушки. Для расчета индуктивности сплошной однослойной обмотки применяется следующая формула, обеспечивающая погрешность расчета не более 2-3 %:
где − индуктивность, мкГн; − диаметр катушки (каркаса), см; − поправочный коэффициент, величина которого зависит от отношения , а значения приведены в таблице 4. Таблица 4 − Значения коэффициента
При намотке с шагом происходит дополнительное уменьшение потокосцепления и индуктивности.
где − фактическая индуктивность, мкГн; − индуктивность, рассчитанная для сплошной обмотки по формуле (3), мкГн; − диаметр катушки, см; А и В − поправочные коэффициенты, зависящие соответственно от отноше- ния диаметра провода без изоляции к шагу намотки и числа витков (рисунок 4). Формула (4) может использоваться и для расчета индуктивности многослойных катушек. В этом случае в формулу в качестве подставляется средний диаметр а для более точного расчета необходимо учитывать зависимость коэффициента не только от отношения но и от отношения . Рисунок 4− Значения коэффициентов А и В для расчета индуктивности катушек, намотанных с шагом
Расчет числа витков. Формулу для расчета числа витков можно получить из уравнения (3), решив его относительно :
Вследствие того, что коэффициент сложным образом зависит от размеров катушки, формула дает возможность определения требуемого числа витков, если известны все размеры катушки. Обычно хотя бы один из размеров является неизвестным. Поэтому расчет числа виттов должен производиться методом последовательного приближения. Расчет собственной емкости. Величина собственной емкости С0 зависит от размеров катушки, конструкции обмотки, диэлектрической проницаемости изоляции провода и каркаса, близости экрана или деталей корпуса прибора и ряда других факторов. Для однослойной неэкранированной КИ расчет С0 производится по выражению
где , −диаметр провода без изоляции. Наименьшей собственной емкостью (1…2 пф) обладают однослойные катушки, намотанные с шагом. Собственная емкость многослойных катушек зависит от способа и плотности намотки, толщины и диэлектрической проницаемости изоляции провода. Для простых многослойных обмоток собственную емкость приближенно можно определить по формуле
где −средний диаметр обмотки, см; −относительнаядиэлектрическая проницаемость изоляции провода. Собственная емкость катушек с универсальной намоткой обычно составляет 5-10 пф.
⇐ Предыдущая567891011121314Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… |
Катушка индуктивности. описание, характеристики, формула расчета
Фильтр для низкочастотного динамика
Фильтр нижних частот из дросселя и конденсатора большой ёмкости называется схемой Баттерворта второго порядка. Он обеспечивает спад частот выше частоты среза до 12 dBна октаву. Схема работает следующим образом. Индуктивность в LC контуре выполняет функцию переменного резистора. Его сопротивление прямо пропорционально частоте ивозрастает с увеличением диапазона. Поэтому высокие частоты практически не попадают на НЧ динамик. Такую же функцию выполняет и конденсатор. Его сопротивление обратно пропорционально частоте и он включается параллельно громкоговорителю.
Он обеспечивает спад частот выше частоты среза до 12 dBна октаву. Схема работает следующим образом. Индуктивность в LC контуре выполняет функцию переменного резистора. Его сопротивление прямо пропорционально частоте ивозрастает с увеличением диапазона. Поэтому высокие частоты практически не попадают на НЧ динамик. Такую же функцию выполняет и конденсатор. Его сопротивление обратно пропорционально частоте и он включается параллельно громкоговорителю.
Поскольку схема устройства должна хорошо пропускать низкие частоты и обрезать высокие, то конденсаторы такого устройства имеют большую ёмкость.Пассивный фильтр для динамика может быть выполнен по более сложной схеме. Если соединить две схемы Баттерворта последовательно, то получится устройство четвёртого порядка из двух индуктивностей и двух конденсаторов. Оно обеспечивает спад частотной характеристики низкочастотного громкоговорителя в 24 децибела на октаву.
Для того чтобы выровнять частотную характеристику и более точно согласовать схему Баттерворта и динамик, между катушкой индуктивности и конденсатором, включается резистор с небольшим сопротивлением. Для этой цели лучше использовать проволочные резисторы.
Для этой цели лучше использовать проволочные резисторы.
Основные технические параметры
Катушки индуктивности имеют следующие характеристики:
- добротность отклонения;
- эффективность;
- начальная индуктивность;
- температура;
- стабильность;
- предельная емкость;
- номинальная индуктивность.
Стабильность демонстрирует свойства устройства при изменении условий использования. Температура фиксируется вследствие различных причин. Многое зависит от размера каркаса. Когда температура уменьшается, индуктивность также снижается. Современные параметры — это цикличность, которая является отношением температуры к линейному расширению. Учитывается изменение в керамической основе плюс показатель плотности.
Вам это будет интересно Установка импульсного разрядника УЗИП
Температура отслеживается на горячей намотке. В этом плане хорошо себя показали многослойные дроссели с сердечником, которые сделаны из карбонильного железа. Ёмкость отображает количество витков катушки, берется в расчет количество секций и контуров. Высокочастотные модели считаются более емкостными и стабильными.
Ёмкость отображает количество витков катушки, берется в расчет количество секций и контуров. Высокочастотные модели считаются более емкостными и стабильными.
Емкостные катушки
Номинальная индуктивность — это параметр, который учитывает изменение размеров волны. Измерение происходит в микрогенрах. Если смотреть на формулу, учитывается количество витков, длина намотки, плюс диаметр катушки.
Постоянная времени индуктора
Теперь мы знаем, что ток не может изменяться мгновенно в индуктивности, потому что для этого ток должен измениться на конечную величину за нулевое время, что приведет к тому, что скорость изменения тока будет бесконечной di / dt = ∞ , делая индуцированную ЭДС бесконечной, а бесконечного напряжения не существует. Однако, если ток, протекающий через индуктор, изменяется очень быстро, например, при работе переключателя, на катушке индуктивности могут возникать высокие напряжения.
Рассмотрим схему индуктора выше. Когда переключатель ( S1 ) разомкнут, ток через катушку индуктивности не течет. Поскольку через индуктор ток не течет, скорость изменения тока ( di / dt ) в катушке будет равна нулю. Если скорость изменения тока равна нулю, то в катушке индуктивности нет ЭДС самоиндукции ( V L= 0 ).
Поскольку через индуктор ток не течет, скорость изменения тока ( di / dt ) в катушке будет равна нулю. Если скорость изменения тока равна нулю, то в катушке индуктивности нет ЭДС самоиндукции ( V L= 0 ).
Если мы теперь закроем переключатель (t = 0), ток будет проходить через цепь и медленно подниматься до своего максимального значения со скоростью, определяемой индуктивностью индуктора. Эта скорость тока, протекающего через катушку индуктивности, умноженная на индуктивность по Генри, приводит к тому, что на катушке образуется некоторая самоиндуцированная ЭДС с фиксированным значением, определенная уравнением Фарадея V L = Ldi / dt.
Эта самоиндуцированная ЭДС на катушке индуктивности ( V L ) борется с приложенным напряжением до тех пор, пока ток не достигнет своего максимального значения и не будет достигнуто устойчивое состояние. Ток, который сейчас течет через катушку, определяется только постоянным или «чистым» сопротивлением обмоток катушек, поскольку значение реактивного сопротивления катушки уменьшилось до нуля, поскольку скорость изменения тока (di / dt) равна нулю в устойчивом состоянии. Другими словами, теперь существует только сопротивление катушек постоянного тока, чтобы противостоять потоку тока.
Другими словами, теперь существует только сопротивление катушек постоянного тока, чтобы противостоять потоку тока.
Аналогичным образом, если переключатель ( S1 ) разомкнут, ток, протекающий через катушку, начнет падать, но индуктор снова будет бороться с этим изменением и попытается удержать ток в своем прежнем значении, индуцируя напряжение в другом направлении. Наклон падения будет отрицательным и связан с индуктивностью катушки, как показано ниже.
Опыт с катушкой индуктивности с замкнутым сердечником
Во второй серии опытов не
замкнутый сердечник катушки (стержень) заменён на замкнутый сердечник (кольцо).
Увеличен диаметр провода в катушке и снижено число витков.
Замена катушки индуктивности
позволила качественно оценить разницу обратной ЭДС двух различных по исполнению
и по принципу работы катушек индуктивности
Ниже приведены две осциллограммы,
снятые у двух разных катушек индуктивности при неизменных остальных параметрах
– настройке осциллографа, частоте следования импульсов, их скважности и
напряжении источника питания
Как видно, что характер
накопления и отдачи энергии практически не изменился – как говорится, сколько
дал, столько и взял, хотя длительности процессов немного изменились.
Смотрим видеофрагмент:
Чем обычно заняты исследователи,
собирающие подобные схемы? Как правило, после предварительного анализа, они
стараются снять с катушки индуктивности наибольшее напряжение. Сделаем это и
мы.
Ниже представлена схема зарядки
конденсатора через диод за счёт тока, возникающего при обратной ЭДС в катушке
индуктивности. Таким образом, будучи заряженным, конденсатор не может обратно
разрядиться через схему, длительно сохраняя в себе электрическую энергию.
По этой схеме конденсатор
заряжался до напряжения около 600 Вольт. Высокое напряжение на конденсаторе –
это главный признак обратной ЭДС в катушке индуктивности.
Некоторые посетители канала задавали
мне вопрос о том, что такое рекуперация
электрической энергиии, какова
её схема? Ниже на схеме я привожу две фазы рекуперации, тем более, что они являются
прямым доказательством переполюсовки напряжения, возникающей на концах катушки
индуктивности во время самоиндукции ЭДС и обратной ЭДС.
На рисунке видно, что в первой
фазе, что когда ключ открыт, ток идёт по катушке и за счёт ЭДС самоиндукции происходит
накопление энергии в сердечнике катушки индуктивности. Здесь катушка вместе с
сердечником временно является потребителем энергии и запасает её. Полярность
напряжения на катушке в первой фазе указана на её концах.
Во второй фазе, когда ключ заперт,
и ток в цепи отсутствует, катушка индуктивности, накопив энергию в первой фазе,
сама временно становится источником энергии. При этом обратная ЭДС приводит к
появлению в катушке тока, который через диод заряжает конденсатор. Полярность
напряжения на катушке во второй фазе также указана на её концах.
Видно, что в момент запирания
ключа, скачком меняется напряжение на концах катушки. Если в катушке индуктивности
не возникало бы переполюсовки, то, конечно, ни о какой зарядке конденсатора не
могло бы быть речи, а по-другому в этой схеме зарядить конденсатор невозможно.
И так, в схеме рекуперации ток в
катушке индуктивности направления не меняет, а напряжение на её концах меняется
на обратное. Все приведённые выше рассуждения и опыты показаны в
видеофрагменте.На
этом, как правило, у многих исследователей работа заканчивается. Но, я полагаю,
что на этом ещё рано ставить точку.
Индуктивность (катушка) или влияние индуктивности на диапазон пропускания частот при изготовлении многополосных АС
Для начала описания принципов работы катушки индуктивности необходимо еще раз освежить наши знания по физики о процессах связанных с магнитным полем. Что за физическая субстанция магнитное поле до настоящего времени является неразрешимым определением, но что вызывает магнитное поле и что оно вызывает собой, поддается объяснению и логическому анализу.Магнитное поле образуется вокруг проводника, по которому течет ток. Также верно и обратное утверждение, когда ток образуется в проводнике движущемся в магнитном поле, например постоянного магнита. При этом магнитное поле в зависимости от характера возбуждения постоянный ток или переменный ток также является постоянным или переменным. При этом наблюдается интересная зависимость, когда сила магнитного поля зависит от времени изменения тока в проводнике. То есть при мгновенном изменении тока (например, замыкание контура через выключатель) магнитное поле стремится к бесконечности, тем самым наводя обратно на проводник гораздо более сильный ток, относительно первоначального. Такой ток называется индукционным. Магнитное поле и ток неотделимы друг от друга, изменение одного из этих параметров влечет за собой пропорциональное изменение другого. На основании аксиом предыдущего абзаца можно понять и принцип пропускания частот катушкой индуктивности. В частности получается следующая ситуация. Катушка является проводником и при прохождении тока (переменного тока от усилителя) вокруг проводника наводится магнитное поле, при этом это же магнитное поле влияет и на ток в проводнике. Чем более быстро будет меняться ток в проводнике, тем более существенное влияние на него окажет магнитное поле, так как оно фактически является «памятью» предыдущего уровня тока.
При этом магнитное поле в зависимости от характера возбуждения постоянный ток или переменный ток также является постоянным или переменным. При этом наблюдается интересная зависимость, когда сила магнитного поля зависит от времени изменения тока в проводнике. То есть при мгновенном изменении тока (например, замыкание контура через выключатель) магнитное поле стремится к бесконечности, тем самым наводя обратно на проводник гораздо более сильный ток, относительно первоначального. Такой ток называется индукционным. Магнитное поле и ток неотделимы друг от друга, изменение одного из этих параметров влечет за собой пропорциональное изменение другого. На основании аксиом предыдущего абзаца можно понять и принцип пропускания частот катушкой индуктивности. В частности получается следующая ситуация. Катушка является проводником и при прохождении тока (переменного тока от усилителя) вокруг проводника наводится магнитное поле, при этом это же магнитное поле влияет и на ток в проводнике. Чем более быстро будет меняться ток в проводнике, тем более существенное влияние на него окажет магнитное поле, так как оно фактически является «памятью» предыдущего уровня тока. В этой ситуации получается минимальное сопротивление для тока с незначительным изменением уровня относительно промежутка времени, то есть фактически с низкой частотой. Катушка индуктивности пропускает низкие частоты и соответственно является сопротивлением для высоких частот, именно это свойство и используется в фильтрах акустических систем для ограничения полосы пропускаемости. Естественно данной полосой пропускаемости можно управлять, устанавливая определенные параметры для катушки индуктивности (плотность намотки витков, количество витков, сердечник и т.д.)
В этой ситуации получается минимальное сопротивление для тока с незначительным изменением уровня относительно промежутка времени, то есть фактически с низкой частотой. Катушка индуктивности пропускает низкие частоты и соответственно является сопротивлением для высоких частот, именно это свойство и используется в фильтрах акустических систем для ограничения полосы пропускаемости. Естественно данной полосой пропускаемости можно управлять, устанавливая определенные параметры для катушки индуктивности (плотность намотки витков, количество витков, сердечник и т.д.)
ЗВУКОСНИМАТЕЛЬ КАК ЦЕПЬ
С точки зрения схемотехники, магнитный звукосниматель соответствует цепи, показанной на рис.1.
Катушку звукоснимателя можно описать как идеальную катушку с индуктивностью L в последовательном подключении к сопротивлению R и в параллельном подключении к конденсатору C. Самым важным качеством является индуктивность, которая зависит от количества витков, от магнитного материала катушки и её геометрии. Сопротивление и емкость не оказывают особого влияния и ими можно пренебречь. Когда струны колеблятся, в катушке возникает напряжение переменного тока. Поэтому датчик действует как источник переменного тока с электрическими компонентами (рис.2).
Сопротивление и емкость не оказывают особого влияния и ими можно пренебречь. Когда струны колеблятся, в катушке возникает напряжение переменного тока. Поэтому датчик действует как источник переменного тока с электрическими компонентами (рис.2).
Внешняя нагрузка состоит из сопротивления (потенциометры громкости и тембра и любое сопротивление заземления на входе усилителя) и конденсатора (из-за ёмкости между проводником и экранирующей оплеткой в гитарном кабеле). Емкость кабеля играет немалую роль и ею нельзя пренебрегать. Эти пассивные компоненты образуют так называемый фильтр высоких частот второго порядка (рис.3).
Таким образом, как любой другой подобный фильтр, этот обладает частотой среза fg; на этой частоте амплитуда падает на 3дБ (то есть, вполовину). После fg происходит спад 12 дБ на октаву, а до fg звук не меняется никак. Спада на низких частотах не наблюдается, однако, немного ниже fg существует электрический резонанс между индукцией катушки и ёмкостью кабеля. На этой частоте, называемой fmax, наблюдается пик амплитуды. Пассивный фильтр ВЧ выступает здесь в роли усилителя напряжения (но не усилителя мощности, так как выходное сопротивление соответственно повышается). На рис.4 указан типичный контур частотной характеристики звукоснимателя.
На этой частоте, называемой fmax, наблюдается пик амплитуды. Пассивный фильтр ВЧ выступает здесь в роли усилителя напряжения (но не усилителя мощности, так как выходное сопротивление соответственно повышается). На рис.4 указан типичный контур частотной характеристики звукоснимателя.
Если мы знаем резонансную частоту и высоту резонансного пика, можно сказать, что нам известно 90% информации о передающих характеристиках датчика; эти два параметра являются своего рода ключом к «секрету» звука датчика (в рамках данной модели нельзя описать некоторые другие свойства, но их значение гораздо меньше).
Всё это означает, что обертоны в области резонансной частоты усиливаются, за этой частотой уменьшаются, а основная вибрация и обертоны до резонансной частоты воспроиводятся без изменений.
ИЗМЕРЕНИЕ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
Чтобы точно измерить частотную характеристику датчика, теоретически важно измерить вибрацию струны и сравнить её с выходным напряжением на каждой частоте. Осуществить это на практике очень трудно
Осуществить это на практике очень трудно
В качестве альтернативы предлагается поместить звукосниматель во внешнее магнитное поле, создаваемое передающей катушкой. Поток заряженных частиц меняет направление, создавая напряжение в датчике. Это напряжение прямо пропорционально изменениям магнитного поля в единицу времени, а возбуждающий ток, проходящий через катушку, должен быть обратно пропорционален частоте.
Синусоидное напряжение проходит в цепь интегратора, производя выходное напряжение, обратно пропорциональное частоте. Этот сигнал затем поступает в усилитель, а затем на передающую катушку, которая удваивает сигнал и передаёт его в датчик. Катушка эта может состоять из 50 витков эмалированой медной проволоки (диаметром около 0,5 мм). Точное количество витков не имеет большого значения. Катушка устанавливается у звукоснимателя так, чтобы излучать в него как можно большую часть своего магнитного поля. Если мы проверяем однокатушечный звукосниматель, то магнитные оси должны быть параллельны, если хамбаккер — то перпендикулярны.
Чтобы выяснить частотную характеристику, подавайте синусоиды с частотами в пределах от 100 до 10кГц и измеряйте выходное напряжение звукоснимателя широкополосным мультиметром или осциллографом. Абсолютные значения не важны: самое главное — это положение резонансного пика над общей амплитудой низких частот. Таким же образом легко определить влияние на звук различных ёмкостей (например, шнуров) и резисторов. Одно из главных достоинств этого способа в том, что не требуется изменять устройство гитары или вытаскивать из неё звукосниматели.
Полученный результат по-настоящему точен только при проверке однокатушечных датчиков. Дело в том, что в хамбакерах звук снимается со струны сразу в двух точках. Высокие обертоны, где на одном полюсе одной и той же волны оказывается пик, а на другом провал, могут частично взаимовычитаться. В результате пики находятся на разных частотах для каждой струны. Например, при стандартном размере хамбаккера, для шестой струны пик находится на частоте 3000 Гц, а для пятой — на 4000 Гц. Для высоких же струн этот пик находится за пределом частоты среза и его почти не слышно.
Для высоких же струн этот пик находится за пределом частоты среза и его почти не слышно.
Разница между звучанием одной катушки и двух часто переоценивается. Главная причина большего количества высоких частот при одной катушке в том, что резонансная частота повышается в результате уменьшения индуктивности вдвое. Влияние оказывает и то, что звук со струны снимается только в одной точке, но это влияние намного меньше.
Данный метод измерения также не учитывает нелинейных искажений датчика, которые также влияют на звук. Но тем не менее, проверка звукоснимателя данным образом даёт полезную информацию о его характеристиках. Зная её, можно определить, какие звуки подходят Вам больше всего, и изменить частотную характеристику посредством внешних конденсаторов и резисторов, настраивая звукосниматель по своему вкусу (а также в наилучшем соответствии с корпусом и струнами).
Размышлизмы о катушках индуктивности в фильтрах акустических систем
Все верно. Сказанное ниже относится не только к железу, но к любому ферромагнитному материалу. Слово «железо» употребляется для простоты. 1. Железо нелинейное. Причем на самом деле нелинейное и на малых амплитудах тока намотанной на нем катушки. Причем сами параметры нелинейности железа меняются с амплитудой тока катушки. Что вносит совершенно противоестественные гармонические и интермодуляционные составляющие. Хоть они и малы (при малых токах), но как раз забивают собой «воздух». 2. Магнитные свойства железа (и его нелинейность) зависят от частоты. То есть для разных составляющих спектра (например основного тона и его первого — самого сильного — обертона инструмента) свойства катушки будут разными и изменяться по-разному от уровня сигнала (например атака и затухание). 3. Нелинейность железа не только создает собственные нелинейные искажения. Изменение магнитной проницаемости, вызванное изменением тока катушки, изменяет (модулирует) ее индуктивность. В результате динамически изменяются параметры фильтра — не только частота среза, но и характеристическое сопротивление, ответственное за взаимодействие фильтра с нагрузкой (динамиком).
Слово «железо» употребляется для простоты. 1. Железо нелинейное. Причем на самом деле нелинейное и на малых амплитудах тока намотанной на нем катушки. Причем сами параметры нелинейности железа меняются с амплитудой тока катушки. Что вносит совершенно противоестественные гармонические и интермодуляционные составляющие. Хоть они и малы (при малых токах), но как раз забивают собой «воздух». 2. Магнитные свойства железа (и его нелинейность) зависят от частоты. То есть для разных составляющих спектра (например основного тона и его первого — самого сильного — обертона инструмента) свойства катушки будут разными и изменяться по-разному от уровня сигнала (например атака и затухание). 3. Нелинейность железа не только создает собственные нелинейные искажения. Изменение магнитной проницаемости, вызванное изменением тока катушки, изменяет (модулирует) ее индуктивность. В результате динамически изменяются параметры фильтра — не только частота среза, но и характеристическое сопротивление, ответственное за взаимодействие фильтра с нагрузкой (динамиком). И появляется параметрическая модуляция тока катушки самой катушкой — дополнительные искажения. 4. Железо имеет хоть и небольшой, но гистеререзис. Это вообще катастрофа — нелинейные искажения и модуляция индуктивности происходят «хаотично» (эффект «памяти» — начинает иметь значение в какую сторону изменяется ток: например, уменьшается после того, как увеличивался, или продолжает увеличиваться) и с некоторым переменным запаздыванием — величина тока должна измениться на определенную величину, а для этого требуется время, обратно пропорциональное скорости изменения тока. Есть мнение, что на «тонкие моменты» звука (вроде «воздуха»), гистерезис влияет даже сильнее, чем нелинейность магнитной проницаемости. 5. Феррит в этом плане хуже железа — у него все эти вещи выражены сильнее. Но у железа есть еще беда — вихревые токи в пластинах. С точки зрения сетевых трансформаторов ими можно пренебречь (железо и делают ради сетевых трансформаторов). А для гораздо более высокочастотного звука, тем более в котором изменения сигнала на «жалкие» 0,1% на самом деле хорошо слышны, влияние вихревых токов тоже сказывается неприятно (хоть и малозаметно).
И появляется параметрическая модуляция тока катушки самой катушкой — дополнительные искажения. 4. Железо имеет хоть и небольшой, но гистеререзис. Это вообще катастрофа — нелинейные искажения и модуляция индуктивности происходят «хаотично» (эффект «памяти» — начинает иметь значение в какую сторону изменяется ток: например, уменьшается после того, как увеличивался, или продолжает увеличиваться) и с некоторым переменным запаздыванием — величина тока должна измениться на определенную величину, а для этого требуется время, обратно пропорциональное скорости изменения тока. Есть мнение, что на «тонкие моменты» звука (вроде «воздуха»), гистерезис влияет даже сильнее, чем нелинейность магнитной проницаемости. 5. Феррит в этом плане хуже железа — у него все эти вещи выражены сильнее. Но у железа есть еще беда — вихревые токи в пластинах. С точки зрения сетевых трансформаторов ими можно пренебречь (железо и делают ради сетевых трансформаторов). А для гораздо более высокочастотного звука, тем более в котором изменения сигнала на «жалкие» 0,1% на самом деле хорошо слышны, влияние вихревых токов тоже сказывается неприятно (хоть и малозаметно). 6. А еще бывает, что пластины сердечника сложены недостаточно аккуратно, некоторые пластины «выпирают» из общей стопки. Таким пластинам достается больше всего, и они могут даже сильно насыщаться при работе. 7. Если катушка не пропускает через себя ток сигнала, а «уводит его в землю», как в ФВЧ через которые работают ВЧ динамики, эти негативные эффекты снижены (ток катушки не проходит через динамик), но все равно есть. В этом случае есть шанс, что искажения, вызванные влиянием железа, будут незаметны. Но это выясняется только экспериментально. Жаль, что катушки с сердечником используются даже в дорогих Hi-End колонках (видел такие на MHES-2017). 5+
6. А еще бывает, что пластины сердечника сложены недостаточно аккуратно, некоторые пластины «выпирают» из общей стопки. Таким пластинам достается больше всего, и они могут даже сильно насыщаться при работе. 7. Если катушка не пропускает через себя ток сигнала, а «уводит его в землю», как в ФВЧ через которые работают ВЧ динамики, эти негативные эффекты снижены (ток катушки не проходит через динамик), но все равно есть. В этом случае есть шанс, что искажения, вызванные влиянием железа, будут незаметны. Но это выясняется только экспериментально. Жаль, что катушки с сердечником используются даже в дорогих Hi-End колонках (видел такие на MHES-2017). 5+
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:
Давайте рассмотрим цепь:
Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь.
Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку будет равен 0.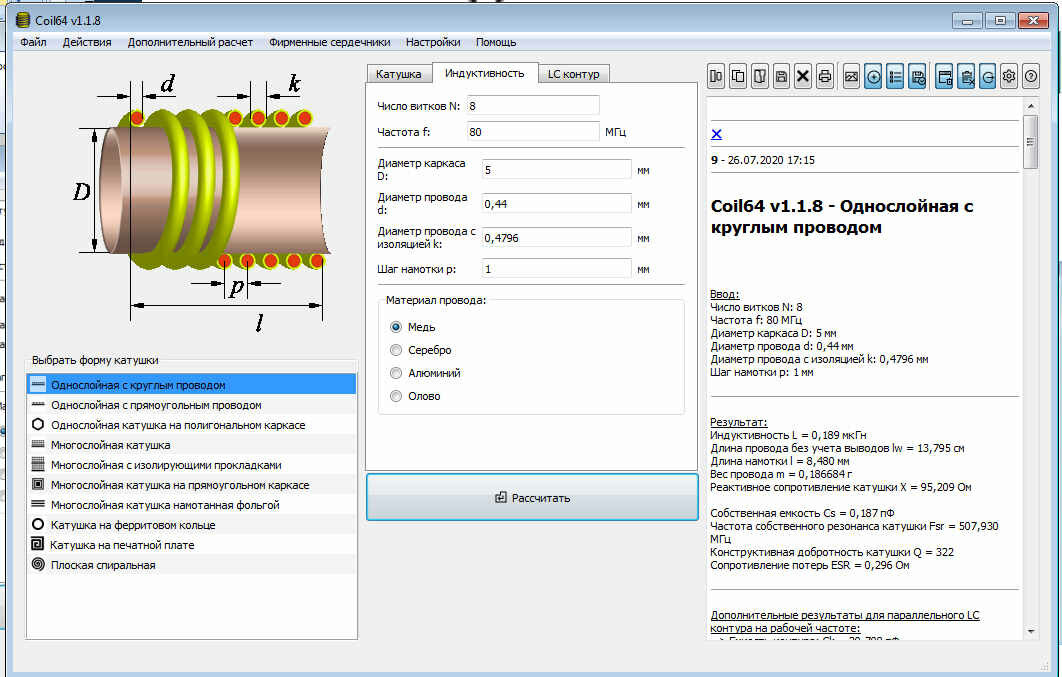 В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать. Напряжения на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).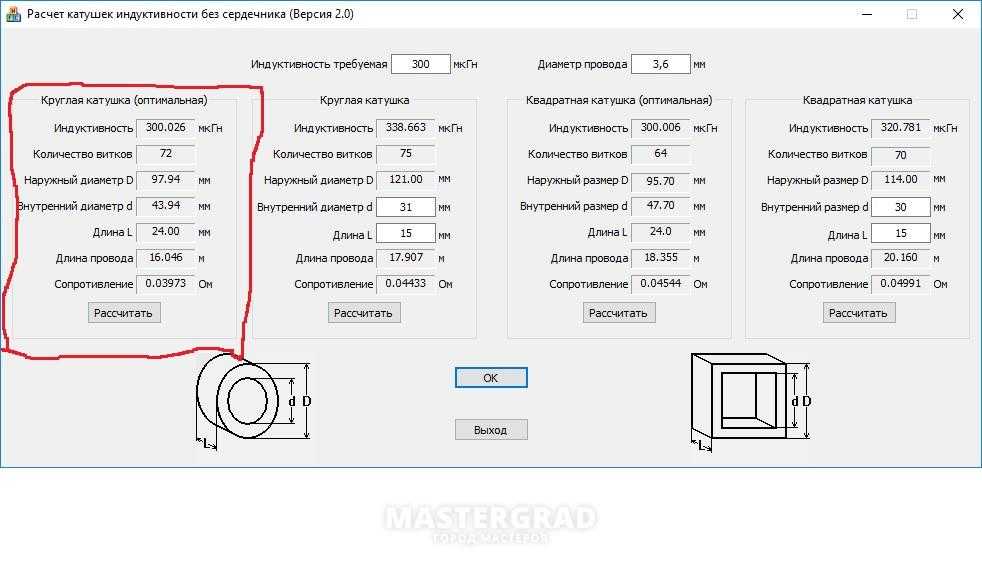
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:
На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Мощность в индукторе
Мы знаем, что индуктор в цепи противостоит потоку тока I через него, потому что поток этого тока индуцирует ЭДС, которая противостоит ему, закон Ленца. Затем необходимо выполнить работу от внешнего источника батареи, чтобы ток протекал против этой индуцированной ЭДС. Мгновенная мощность, используемая для форсирования тока I по отношению к этой самоиндуцированной ЭДС (V L), определяется как:
Мощность в цепи задается как P = V * I, поэтому:
Идеальный индуктор не имеет сопротивления, только индуктивность, поэтому R = 0 Ом, и поэтому мощность в катушке не рассеивается, поэтому можно сказать, что идеальный индуктор имеет нулевую потерю мощности.
Что такое индуктивность?
Как известно, вокруг каждого проводника, по которому протекает электрический ток, возникают силовые линии. Число этих линий зависит от силы тока. Чем сильнее ток, тем больше силовых линий появляется вокруг провода.
При прохождении по проводнику постоянного тока количество силовых линий не меняется; при прохождении по проводу переменного тока или при изменении силы постоянного тока, число силовых линий возрастает при увеличении силы тока и уменьшается при ослаблении его.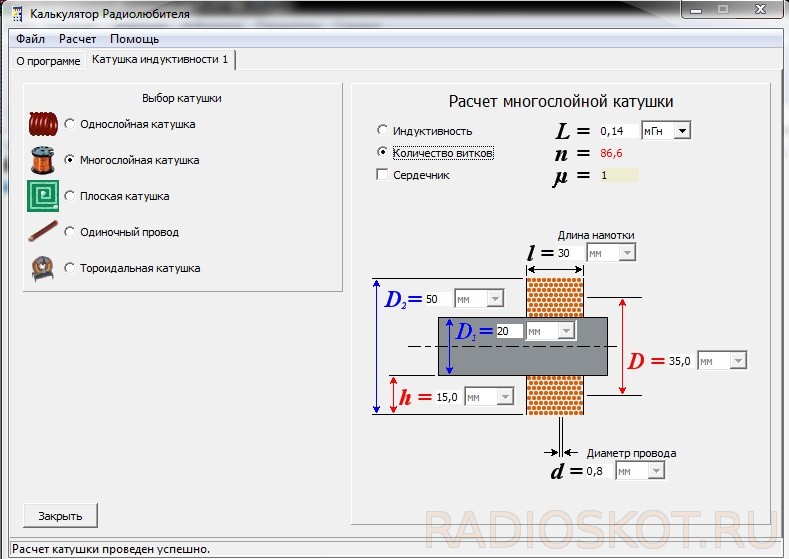
Мы можем себе представить, что при увеличении силы тока силовые линии как бы “разворачиваются” из провода, выходят из него всё в большем количестве, а при ослаблении тока как бы сжимаются, сворачиваются в провод.
Из теории электротехники известно, что в тех случаях, когда какой-либо проводник пересекается силовыми линиями, то в этом проводнике возникает электрический ток.
Это явление носит название индукции. Но возникновение в проводнике тока имеет место не только тогда, когда проводник пересекается силовыми линиями “чужого поля”, т. е. поля, созданного соседним проводником, а также и тогда, когда провод пересекается собственными силовыми линиями, т. е. теми линиями, которые созданы в нём тем током, который протекает по нему от какого-либо источника.
Совершенно естественно, что в том случае, когда по проводнику протекает постоянный ток -никакого пересечения провода силовыми линиями происходить не будет.
Если же сила тока увеличивается или уменьшается, то вокруг провода разворачиваются силовые линии или, наоборот, сворачиваются и при этом они пересекают провод, вследствие чего в последнем будет возникать дополнительное напряжение.
Появление в проводе дополнительного напряжения, вызванного своими же собственными силовыми линиями, носит название индуктивности. Индуктированный ток имеет направление, обратное начальному току в том случае, когда сила начального тока увеличивается и совпадает с ним по направлению, когда сила начального тока уменьшается.
Следовательно, можно сказать, что индуктированный ток как бы стремится противодействовать всем изменениям начального тока, так как если начальный ток усиливается, то индуктированный направляется в противоположную сторону и как бы ослабляет его, когда же первичный ток ослабляется, то индуктированный ток течёт в направлении начального, складывается с ним.
Явление индуктивности наблюдается во всех проводниках любых форм, но в прямолинейных проводниках оно сравнительно слабо; в прямолинейных проводниках, свитых в катушку, явление индуктивности заметно чрезвычайно резко.
Это объясняется тем, что силовые линии, возникающие вокруг каждого витка катушки, пересекают не только свой виток, но и соседние витки, индуктируя в них также напряжение; вследствие этого токи индуктивности в проводниках, свитых в катушку, получаются значительно более сильными.
Рис. 1. Магнитное поле и проводник, катушка.
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.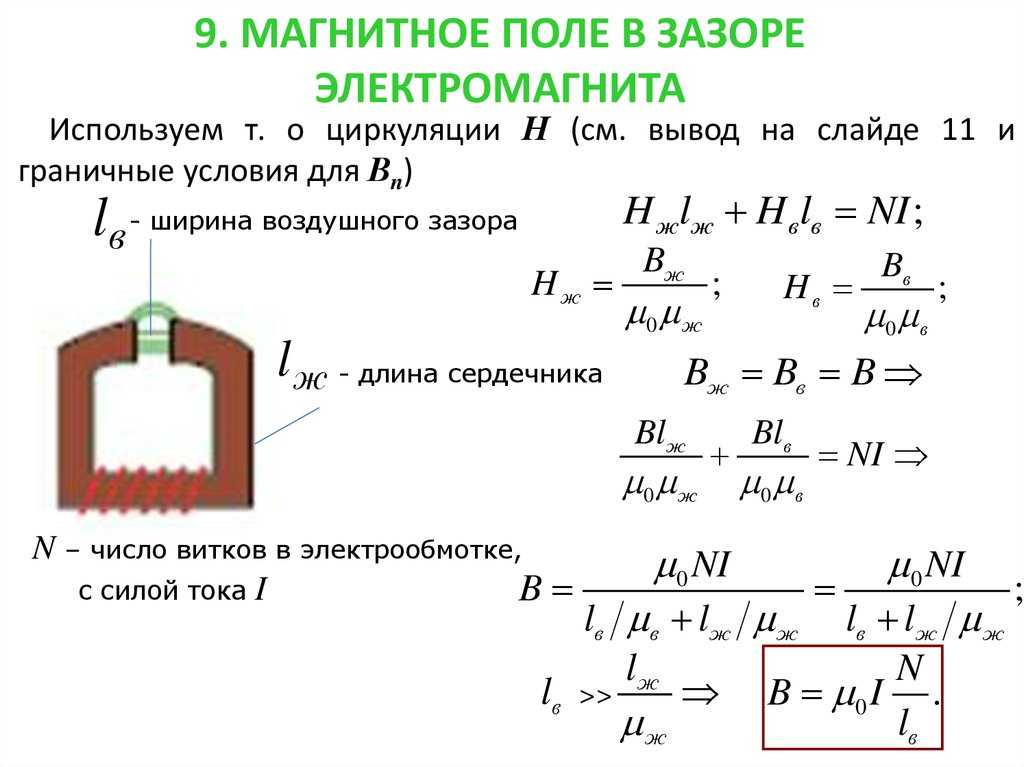
Что влияет на индуктивность?
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
где
1 – это каркас катушки
2 – это витки катушки
3 – сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо “виток к витку”.
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков – тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.
Замеряем индуктивность
15 микрогенри
Отдалим витки катушки друг от друга
Замеряем снова
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Замеряем
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от “витков в квадрате”. Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Gale Apps — Технические трудности
Приложение, к которому вы пытаетесь получить доступ, в настоящее время недоступно. Приносим свои извинения за доставленные неудобства. Повторите попытку через несколько секунд.
Если проблемы с доступом сохраняются, обратитесь за помощью в наш отдел технической поддержки по телефону 1-800-877-4253. Еще раз спасибо, что выбрали Gale, обучающую компанию Cengage.
org.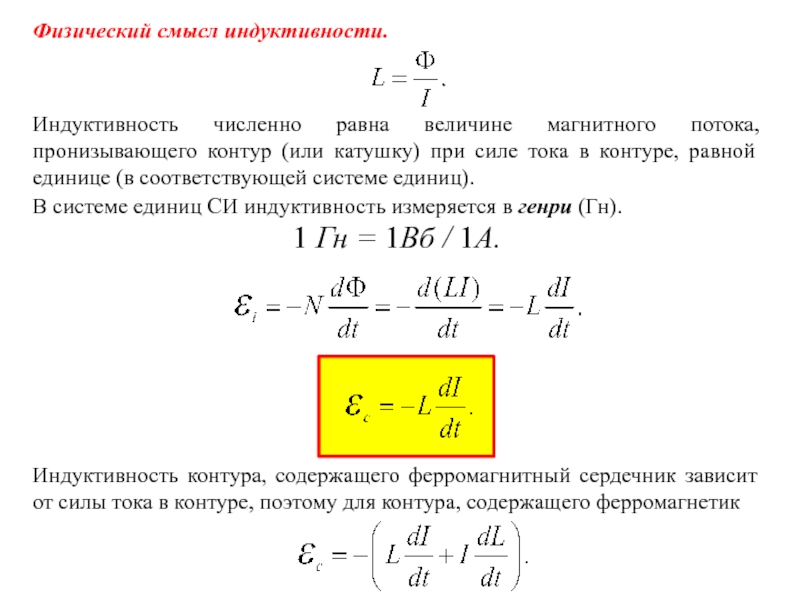 springframework.remoting.RemoteAccessException: невозможно получить доступ к удаленной службе [authorizationService@theBLISAuthorizationService]; вложенным исключением является com.zeroc.Ice.UnknownException
unknown = «java.lang.IndexOutOfBoundsException: индекс 0 выходит за границы для длины 0
в java.base/jdk.internal.util.Preconditions.outOfBounds(Preconditions.java:64)
в java.base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.
springframework.remoting.RemoteAccessException: невозможно получить доступ к удаленной службе [authorizationService@theBLISAuthorizationService]; вложенным исключением является com.zeroc.Ice.UnknownException
unknown = «java.lang.IndexOutOfBoundsException: индекс 0 выходит за границы для длины 0
в java.base/jdk.internal.util.Preconditions.outOfBounds(Preconditions.java:64)
в java.base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure. reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.
reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer. getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.
getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com. gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool.access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.
gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool.access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.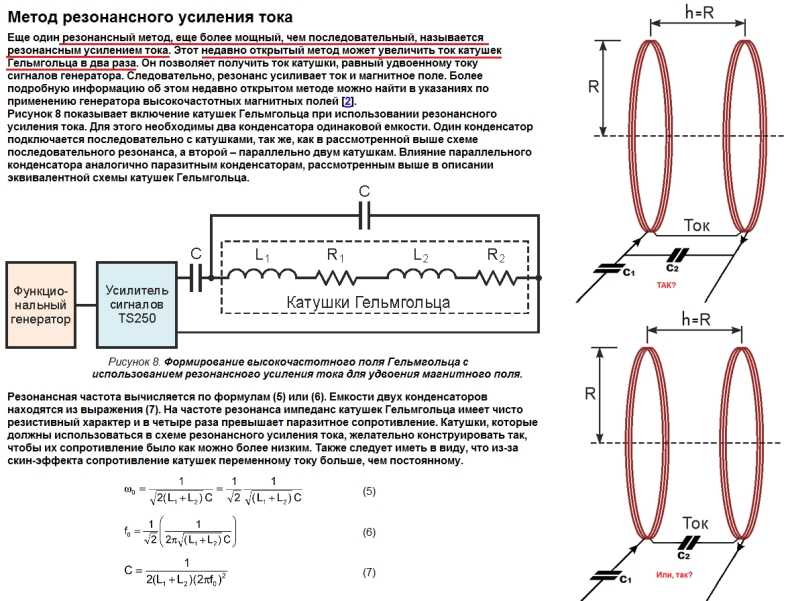 remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)
org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.
remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)
org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com. gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22)
jdk.internal.reflect.GeneratedMethodAccessor246.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.base/java.lang.reflect.Method.invoke(Method.java:566)
org.
gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22)
jdk.internal.reflect.GeneratedMethodAccessor246.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.base/java.lang.reflect.Method.invoke(Method.java:566)
org. springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.
springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org. springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.servlet.http.HttpServlet.service(HttpServlet.java:626)
org.
springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.servlet.http.HttpServlet.service(HttpServlet.java:626)
org. springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.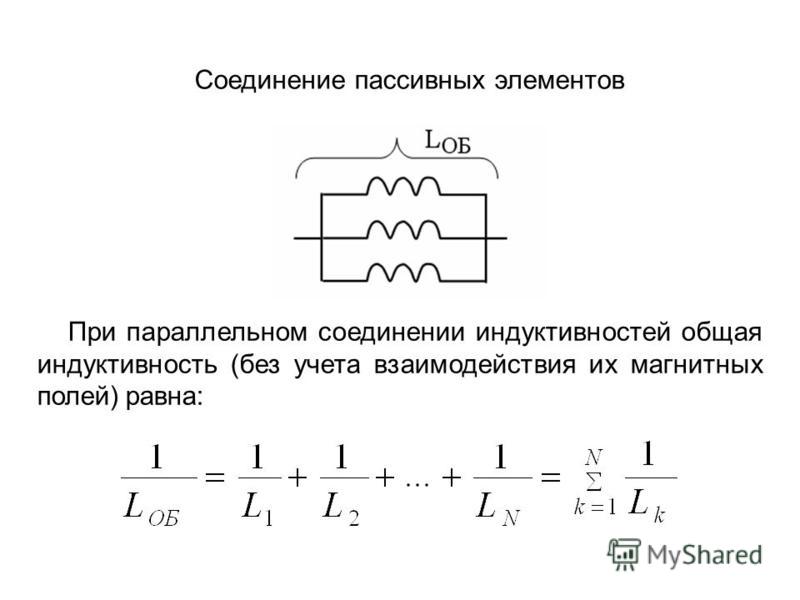 apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.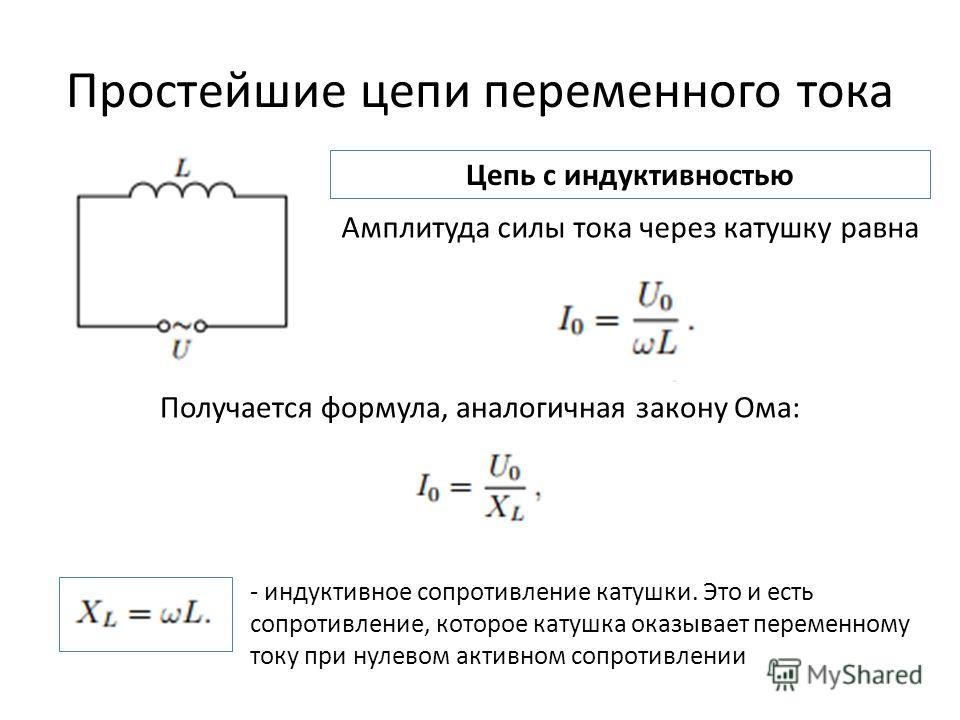 apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.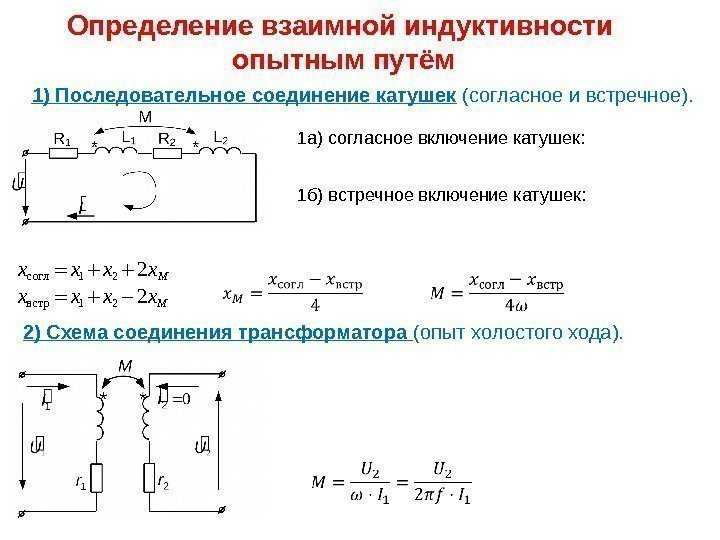 springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.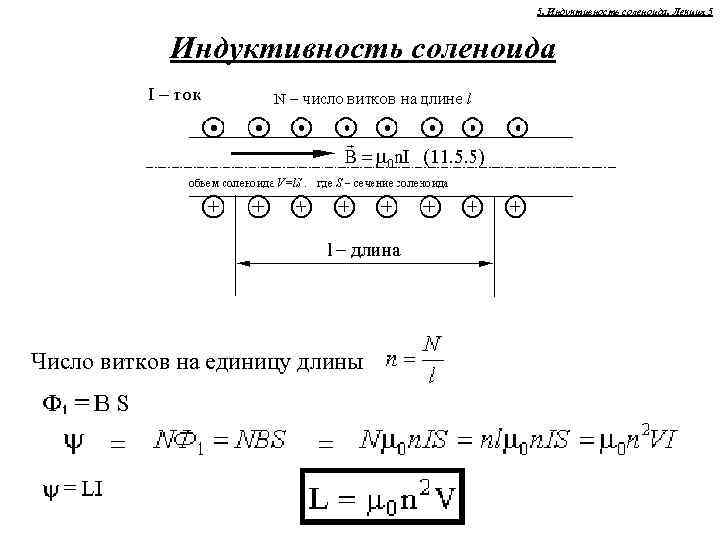 apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.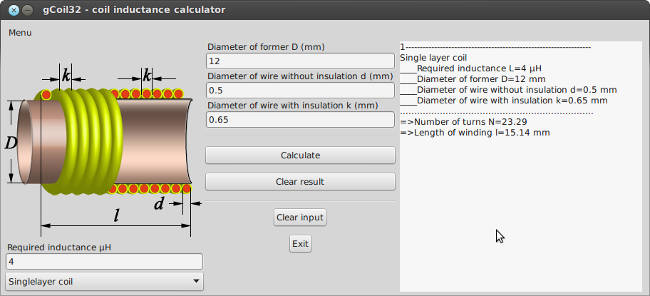 apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org. springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.
springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter. java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.
java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve. invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.
invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight. java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707)
org.apache.tomcat.util.net.SocketProcessorBase.run(SocketProcessorBase.java:49)
java.base/java.util.concurrent.ThreadPoolExecutor.runWorker(ThreadPoolExecutor.java:1128)
java.base/java.util.concurrent.ThreadPoolExecutor$Worker.run(ThreadPoolExecutor.java:628)
org.apache.tomcat.util.threads.TaskThread$WrappingRunnable.
java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707)
org.apache.tomcat.util.net.SocketProcessorBase.run(SocketProcessorBase.java:49)
java.base/java.util.concurrent.ThreadPoolExecutor.runWorker(ThreadPoolExecutor.java:1128)
java.base/java.util.concurrent.ThreadPoolExecutor$Worker.run(ThreadPoolExecutor.java:628)
org.apache.tomcat.util.threads.TaskThread$WrappingRunnable. run(TaskThread.java:61)
java.base/java.lang.Thread.run(Thread.java:834)
run(TaskThread.java:61)
java.base/java.lang.Thread.run(Thread.java:834)
Описание формулы расчета индуктивности полой катушки
Характеристики и использование катушек с воздушным сердечником: простая конструкция, высокая точность индуктивности, малая распределенная емкость, высокая частота собственного резонанса, малый температурный коэффициент, стабильность
.
Он обладает хорошими свойствами и сильной помехоустойчивостью. Это индуктор, который можно применять на высоких частотах.
Катушки с воздушным сердечником обычно можно использовать в качестве трансформаторов тока, с полосой частот, малыми размерами, легким весом, удобными для цифровых измерений и микрокомпьютером 9.0011
защита. Широкий спектр приложений для телевизионной техники, аудиотехники, передачи связи, приема и фильтрации питания, радиоголовок VCD, антенных усилителей,
Записывающие машины, антенные микрофоны и другие области.
Основные продукты Fuying Electronics включают в себя:
1) Акустические изделия (катушки для слуховых аппаратов, катушки индуктивности для слуховых аппаратов)
2) Бытовая электроника (катушки индуктивности, электронные катушки, катушки с воздушным сердечником, катушки с жестким диском компьютера, самоклеящиеся катушки, каркасные катушки, катушки с магнитным стержнем, катушки с солнечными игрушками, 9)0011
Катушки для монет и др.
3) Автозапчасти (датчик ABS, катушка мультимедийной антенны, катушка автосигнализации, катушка зажигания автомобиля и т.д.)
4) ID, RFID (карта ISO ~ контактная и бесконтактная, сенсорная катушка, катушка для отслеживания животных, армейская идентификационная катушка, катушка IC для метро,
Электронные замки, индукционные катушки и т.п.
5) Вставная сборка электронной печатной платы, сборка различных электронных деталей
6) Предметы торговли (соединительные линии, соединительные кабели, скобяные изделия, металлические детали, детали для цветной печати, электронные игрушки, электронные небольшие машины и т. д.)
д.)
Формула расчета катушки с воздушным сердечником выглядит следующим образом:
Нагрузите его индуктивность следующим образом: формула катушки
Импеданс (Ом) = 2 * 3,14159 * F (рабочая частота) * Индуктивность (мГн), установка требует импеданса 360 Ом, поэтому:
Индуктивность (мГн) = импеданс (Ом) ÷ (2*3,14159) ÷ F (рабочая частота) = 360 ÷ (2*3,14159) ÷ 7,06 = 8,116 мГн
По этому можно рассчитать количество обмоток:
Количество витков = [индуктивность * { ( 18 * диаметр окружности (吋)) + ( 40 * длина окружности (吋))}] ÷ диаметр окружности (吋)
Количество оборотов = [8,116 * {(18*2,047) + (40*3,74)}] ÷ 2,047 = 19 кругов
Формула расчета индуктивности катушки с воздушным сердечником: L (мГн) = (0,08D.D.N.N) / (3D + 9W + 10H)
D —— диаметр катушки
N——витков катушки
D —— диаметр провода
H—-высота катушки
W —- ширина рулона
Единицы мм и мГн соответственно. .
.
Формула расчета индуктивности воздушного сердечника:
л=(0,01*Д*Н*Н)/(Д/Д+0,44)
Индуктивность катушки л Единица измерения: Wei Heng
Диаметр рулона D блока: см
Количество витков в катушке N блока: 匝
Длина катушки L единица: см
Формула расчета емкости частотной индуктивности:
l=25330,3/[(f0*f0)*c]
Рабочая частота: f0 Единица измерения: МГц Этот вопрос f0=125 кГц=0,125
Резонансный конденсатор: c Единица: PF Этот вопрос определяется как c=500…1000pf, что может быть определено само по себе или по величине добротности.
Резонансная индуктивность: l Единица измерения: Weiheng
Формула расчета индуктивности катушки
1. Для круглого СЕРДЕЧНИКА доступна следующая формула: (ЖЕЛЕЗО)
Л=N2. AL L= значение индуктивности (Гн)
H-DC=0,4πNI / l N= витков катушки (круг)
AL= индуктивность
H-DC=сила намагничивания постоянного тока I=проходящий ток (А)
l= длина магнитной цепи (см)
l и размер значения AL см. в сравнительной таблице Microl. Например: возьмите материал T50-52, катушка состоит из 5 витков и половины, а ее значение L равно T50-52 (указывает, что внешний диаметр составляет 0,5 дюйма). После проверки таблицы его значение AL составляет около 33 нГн.
в сравнительной таблице Microl. Например: возьмите материал T50-52, катушка состоит из 5 витков и половины, а ее значение L равно T50-52 (указывает, что внешний диаметр составляет 0,5 дюйма). После проверки таблицы его значение AL составляет около 33 нГн.
Л=33. (5.5) 2 = 998,25 нГн ≒ 1 мкГн
При протекании тока 10 А его значение L можно изменить на l=3,74 (см. таблицу)
H-DC=0,4πNI / l = 0,4×3,14×5,5×10/3,74 = 18,47 (после поиска)
Вы можете увидеть степень снижения значения L (мкi%)
2. Ввести эмпирическую формулу
L=(k*µ0*µs*N2*S)/л
из них
00 — проницаемость вакуума = 4π * 10 (-7). (10 минус семь степеней)
Ss — относительная магнитная проницаемость внутреннего сердечника катушки, мкс=1 для катушки с воздушным сердечником
.
N2 — квадрат числа витков катушки
S Площадь поперечного сечения рулона в квадратных метрах
l Длина бухты, в метрах
Коэффициент k зависит от отношения радиуса (R) катушки к длине (l).
Единицей расчетной индуктивности является Генри.
таблица значений k
2р/л к
0,1 0,96
0,2 0,92
0,3 0,88
0,4 0,85
0,6 0,79
0,8 0,74
1,0 0,69
1,5 0,6
2,0 0,52
3,0 0,43
4,0 0,37
5,0 0,32
10 0,2
20 0,12
ПРЕДЫДУЩАЯ:Разница между магнитным кольцом и промышленным ДАЛЕЕ:Определение эмалированной электромагнитной катушки w
Индуктивность катушки с параметрами
Добро пожаловать на EDAboard.com
Добро пожаловать на наш сайт! EDAboard.com — это международный дискуссионный форум по электронике, посвященный программному обеспечению EDA, схемам, схемам, книгам, теории, документам, asic, pld, 8051, DSP, сети, радиочастотам, аналоговому дизайну, печатным платам, руководствам по обслуживанию… и многому другому. более! Для участия необходимо зарегистрироваться. Регистрация бесплатна.
 Нажмите здесь для регистрации.
Нажмите здесь для регистрации.Регистрация Авторизоваться
JavaScript отключен. Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.
- Автор темы Шера
- Дата начала
- Статус
- Закрыто для дальнейших ответов.
шера
Младший член уровня 3
Здравствуйте,
Я создал катушку с сердечником, и мне нужно смоделировать ее, чтобы найти индуктивность с помощью HFSS. Я смоделировал это и получил некоторые параметры (S, Y и Z), может ли кто-нибудь помочь мне, как я могу рассчитать индуктивность катушки, используя параметры. Заранее спасибо.
Заранее спасибо.
Дарктракс
Полноправный член уровня 5
Полное сопротивление катушки индуктивности зависит от частоты, с которой она сталкивается, но значение индуктивности в идеале не зависит от частоты. Это не всегда верно, потому что проницаемость некоторых материалов сердечника может зависеть от частоты, а некоторые структуры катушек могут иметь паразитную емкость, что делает модель немного более сложной.
Все это говорит о том, что если катушка находилась по существу в воздухе, и вы смоделировали ее в HFSS и получили значение Z или значение Y, то вы почти у цели.
Z = |jωL| = где ω=2*pi*частота, L — индуктивность и j=SQRT(-1)
Таким образом, мы имеем Z=2*pi*частота*L
. Тогда можно получить L = Z/(2*pi* частота)
Вы можете обнаружить, что если вы поместите маркеры на несколько значений Z на разных частотах, отображаемых либо на прямоугольном дисплее, либо на диаграмме Смита, и попробуете их в столбце электронной таблицы, с частотами в следующем столбце. к ним, а затем сгенерируйте третий столбец расчетных значений индуктивности, вы увидите, насколько постоянной является ваша индуктивность. Извините, я потерял небольшой пример электронной таблицы, который использовал, но его легко воссоздать. 99 множитель.
к ним, а затем сгенерируйте третий столбец расчетных значений индуктивности, вы увидите, насколько постоянной является ваша индуктивность. Извините, я потерял небольшой пример электронной таблицы, который использовал, но его легко воссоздать. 99 множитель.
шера
Младший член уровня 3
Привет Darktrax,
спасибо за ответ, что если внутри катушки есть материал сердечника, обладающий некоторой относительной проницаемостью. Тогда как мы можем рассчитать индуктивность????
Дарктракс
Полноправный член уровня 5
Роль проницаемости достаточно проста — константа для материала.
Индуктивность, хотя и связана с количеством витков в катушке и физическими размерами объекта, на самом деле определяется напряжениями, которые будут появляться на (катушке, опоре, конструкции и т. д.) из-за скорости поменять тока через него.
д.) из-за скорости поменять тока через него.
Это v=L*dI/dT, хотя вы обнаружите, что ему нужен знак минус, чтобы заставить его работать по закону Ленца. Но это не показывает вам зависимости от проницаемости.. 9-7 называют проницаемостью свободного пространства.
и µr — относительная проницаемость, значение 1 в вакууме, 2000 для мягкой стали, 7000 для кремнистого железа, 200 000 для очищенного железа, 1E+6 для супермагнитного сплава.
Вы можете видеть, что ферритовый тороид, например, представляет собой магнитную цепь, полностью состоящую из феррита, и магнитный поток может легко достичь очень высоких значений, возможно, даже насыщая его. В сердечнике горшка с крошечным воздушным зазором, даже доли миллиметра, часть воздушного зазора будет иметь проницаемость около 4 * пи * 1,0E-7, что предотвращает насыщение.
Если вы введете в поиск Google «индуктивность» и, возможно, «калькулятор индуктивности», вы получите гораздо больше информации, чем когда-либо хотели. Многие из них очень сложные, нацелены на специальные структуры, такие как многослойные или спиральные с воздушным сердечником.
Многие из них очень сложные, нацелены на специальные структуры, такие как многослойные или спиральные с воздушным сердечником.
—> https://hamwaves.com/antennas/inductance.html
—> https://www.g3ynh.info/zdocs/ Magnetics/part_1.html
—> https://www.qsl .net/in3otd/indcalc.html
бигмао
Уровень новичка 1
Привет, Darktrax
, если катушка находилась по существу в воздухе и необходимо учитывать паразитную емкость, то есть Z=|jωL+1/jωC|, то как я могу получить L с помощью HFSS?
Кроме того, существуют ли какие-либо методы чтобы получить добротность катушки? на любой частоте? просто с точки зрения Q = (мощность ЭМ ближнего поля) / (мощность рассеяния)?
Заранее спасибо.
nvt088
Членский уровень 4
Привет всем, вы можете мне помочь?
У меня спиральная катушка с открытым концом и коротким концом, как показано ниже.
Для спиральной катушки необходимо учитывать паразитную емкость катушки.
Итак, как я могу получить значение L и C отдельно, используя HFSS
Дарктракс
Полноправный член уровня 5
Хотя я уверен, что есть много элегантных способов сделать это, мой разум всегда придумывает «быстро и грязно»!
Моей первой мыслью было…
Вы можете смоделировать это на определенной частоте и найти импеданс точки подачи. Проблема в том, что вы не знаете, какая часть реактивной части (т.е. комплексного числа) состоит из (отрицательного) вклада C, а какая из положительной части L.
Диаграмма Смита движется по кругу? Хорошо, я знаю, что вы можете просто выбрать две точки с разными частотами на графике и поиграть с комплексными числами, но я люблю более легкую жизнь. Ставим маркер на резонанс и находим Z. 92)*C
На данный момент, вероятно, есть целая куча вещей, которые можно сделать.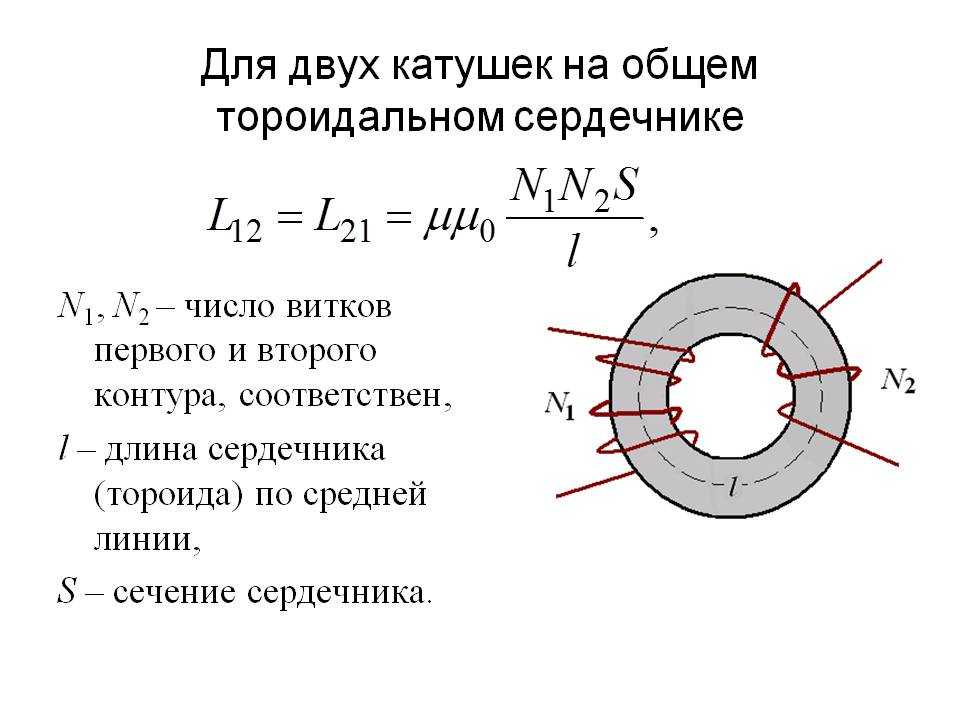 Может быть, даже есть какой-то симпатичный способ заставить HFSS тянуть это за вас. Если вы не против манипулировать комплексными числами, просто получите импеданс на какой-то новой частоте.
Может быть, даже есть какой-то симпатичный способ заставить HFSS тянуть это за вас. Если вы не против манипулировать комплексными числами, просто получите импеданс на какой-то новой частоте.
В моем случае я бы использовал тот же прием, который обычно применяется в ВЧ Q-метрах. Просто временно добавьте немного искусственного (идеального) Cx через катушку в точках подачи и снова проведите сканирование, чтобы найти новый низкочастотный резонанс.
Теперь у вас есть два уравнения для двух неизвестных, которые легко решить. 92)/[(частота1-частота2)*(частота1+частота2)]
Легко! Две резонансные частоты, и вы все знаете на правой стороне.
Это C будет эквивалентным C для межвитковой емкости, распределенной между всеми витками.
Может получить полную модель просто (временно) за два хода??
Действительно правдивая модель может быть немного более сложной, с некоторой емкостью между витками, а другой частью С запасенной энергии в ближнем поле. Будет некоторый L, который хранится аналогичным образом. Открытая катушка, подобная этой, в какой-то степени является излучающим антенным объектом. Поднесение руки, экрана или чего-либо еще к нему повлияет на это. Я не очень хочу туда идти.
Открытая катушка, подобная этой, в какой-то степени является излучающим антенным объектом. Поднесение руки, экрана или чего-либо еще к нему повлияет на это. Я не очень хочу туда идти.
или… может быть, мы можем использовать один из многих онлайн-калькуляторов — очень заманчиво…
https://www.deepfriedneon.com/tesla_f_calchelix.html
https://hamwaves.com/antennas/inductance.html
MrElec
Расширенный член уровня 4
Как по ВЧСС найти частотный резонанс индуктивности и ее добротность?
Последнее редактирование:
@Darktrax
Спасибо за долгое обсуждение. Ваши методы выглядят хорошо. Я попробую.
Ваши методы выглядят хорошо. Я попробую.
У меня есть еще одна идея. Для бака серии LC: Z= j(wL-1/w*C) . Две переменные L & C.
Итак, мы моделируем эту катушку в HFSS с разверткой частоты. Возьмите мнимую часть Z(1,1) на двух разных частотах и найдите L и C. 92*Л-З1*ш1).
Что вы думаете об этом методе?
Однако, когда я применил этот метод на частотах 10 МГц и 15 МГц, решения равны L = 2,71E-4 H и C = 3,35e-11 F.
На разных парах частот L, C отличается!
Что вы думаете об этом результате?
Цель моих катушек — выполнить Беспроводную систему передачи энергии на частоте 13,56 МГц. И эти катушки саморезонансные.
Ниже приведен график мнимой части Z(1,1)
@MrElec: Вы просто делаете развертку по частоте и моделируете в HFSS, чтобы найти резонансную частоту. Чтобы найти Q, Q = wL/R .
Итак, вам нужно рассчитать L и R индуктора, катушек… Я тоже изучаю этот вопрос.
Большое спасибо
Последнее редактирование:
MrElec
Расширенный член уровня 4
@nvt088 спасибо за ответ. Резонансная частота вашего индуктора находится на уровне 15,6 МГц?. У вас есть идея, как получить добротность из HFSS? Некоторые используют эту формулу: Q=-Im(Y(1,1))/re(Y(1,1)) (почему параметр Y, а не параметр Z?). Однако это соотношение не учитывает емкость катушки, а для сопротивления оно связано с re(Y(1,1)).
nvt088
Членский уровень 4
@MrElec
Моя спиральная катушка резонировала на частоте 13,2 МГц.
На самом деле, Y(1,1) = 1/Z(1,1), верно? Но ImY(1,1) отличается от 1/ImZ(1,1). То же самое для реальной части.
Думаю, в этом случае лучше использовать Z-параметры.
В этой формуле в самый раз, если емкость = 0. Например: Один контур.
В спиральной катушке или спиральной катушке мы не можем использовать эту формулу.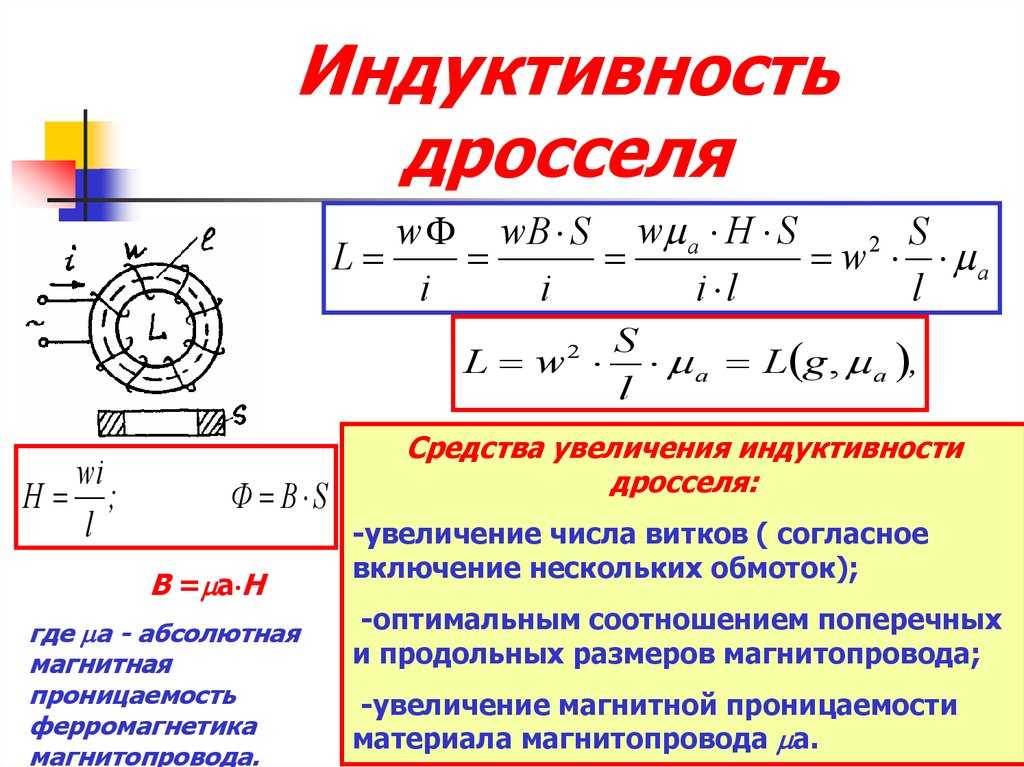 Поэтому нам нужно рассчитать R, L, C отдельно и использовать общую формулу Q=wL/R.
Поэтому нам нужно рассчитать R, L, C отдельно и использовать общую формулу Q=wL/R.
Вам нужно найти способ их вычислить.
volker@muehlhaus
Расширенный член уровня 5
nvt088 сказал:
На самом деле, Y(1,1) = 1/Z(1,1), верно?
Нажмите, чтобы развернуть…
Только для 1-портовых данных.
Для многопортовых данных Z11 — входной импеданс при открытых всех других портах, а 1/Y11 — входной импеданс при всех других закороченных портах.
nvt088 сказал:
Но ImY(1,1) отличается от 1/ImZ(1,1). То же самое для реальной части.
Нажмите, чтобы развернуть…
Оба должны быть разными.
Я думаю, вы хотели сравнить Im{Y11} и Im{1/Z11}
Im{1/Z11} не то же самое, что 1/Im{Z11}.
MrElec
Расширенный член уровня 4
@nvt088
Судя по изображению Im(Z(1,1)), я думаю, что собственная резонансная частота (SRF) спиральной катушки составляет около 15 МГц. Я ошибаюсь?
nvt088
Членский уровень 4
volker@muehlhaus сказал:
Только для 1-портовых данных.
Для многопортовых данных Z11 — входной импеданс при открытых всех других портах, а 1/Y11 — входной импеданс при всех других закороченных портах.Нажмите, чтобы развернуть…
В чем разница между коротким и открытым входным сопротивлением. Можете ли вы объяснить более четко? Потому что когда я анализирую Z-матрицу, я вижу, что можно использовать Z(1,1).
Можете ли вы объяснить более четко? Потому что когда я анализирую Z-матрицу, я вижу, что можно использовать Z(1,1).
@MrElec
Собственный резонанс этой катушки составляет около 12 МГц, когда Im(Z(1,1))=0.
На частоте 15 МГц Im(Z(1,1)) велико, кажется, это называется «антирезонанс». Верно?
MrElec
Расширенный член уровня 4
nvt088 сказал:
@MrElec
Собственный резонанс этой катушки составляет около 12 МГц, когда Im (Z (1,1)) = 0.
На частоте 15 МГц Im(Z(1,1)) велико, кажется, это называется «антирезонанс». Верно?
Нажмите, чтобы развернуть…
@nvt088, да, ты прав, извини, я перепутал с антирезонансным.
volker@muehlhaus
Расширенный член уровня 5
nvt088 сказал:
В чем разница между коротким и открытым входным сопротивлением.
Можете ли вы объяснить более четко? Потому что когда я анализирую Z-матрицу, я вижу, что можно использовать Z(1,1).
Нажмите, чтобы развернуть…
Если ваша схема имеет только один порт, то Z11 = 1/Y11.
Если ваша схема имеет более одного порта, входное сопротивление порта 1 также зависит от нагрузки на другие порты.
По определению, Z11 — входной импеданс при токе i=0 на других портах => Z11 — входной импеданс при всех других открытых портах (i=0A)
По определению, Y11 — входной импеданс полной проводимости при напряжении u =0 на других портах => 1/Y11 — входное сопротивление при закороченных всех остальных портах (u=0В).
Но, как вы выяснили, для схем только с одним портом Z11=1/Y11.
FvM
Супер модератор
Собственный резонанс этой катушки составляет около 12 МГц, когда Im(Z(1,1))=0.
На частоте 15 МГц Im(Z(1,1)) велико, кажется, это называется «антирезонанс». Верно?
Нажмите, чтобы развернуть…
Две резонансные частоты можно объяснить только комбинацией последовательного и параллельного резонанса. У вас больше параметров, чем одиночные L и C.
nvt088
Членский уровень 4
volker@muehlhaus сказал:
Если ваша схема имеет только один порт, то Z11 = 1/Y11.
Если ваша схема имеет более одного порта, входное сопротивление порта 1 также зависит от нагрузки на другие порты.По определению, Z11 — входное сопротивление при токе i=0 на других портах => Z11 — входное сопротивление при всех открытых других портах (i=0A)
По определению, Y11 — входное полное сопротивление при напряжении u=0 на других портах => 1/Y11 — входное сопротивление при закороченных всех других портах (u=0 В).
Но, как вы выяснили, для схем только с одним портом Z11=1/Y11.
Нажмите, чтобы развернуть…
Спасибо за ваше объяснение. Я понял это.
Но не могли бы вы объяснить для многопортовой системы при расчете значения L, должны ли мы использовать L=Im(Z(1,1))/(2*pi*Freq) или использовать L=Im(1/Y( 1,1))/(2*pi*Freq) или другие формулы? и почему?
Я читал на этом форуме, что многим нравится использовать второй формуляр. В моем случае, я думаю, что первый формуляр тоже подходит?
Большое спасибо
volker@muehlhaus
Расширенный член уровня 5
nvt088 сказал:
Но не могли бы вы объяснить для многопортовой системы при расчете значения L, должны ли мы использовать L=Im(Z(1,1))/(2*pi*Freq) или использовать L=Im(1/Y(1 ,1))/(2*pi*Freq) или другие формулы? и почему?
Нажмите, чтобы развернуть.
..
Если вы моделируете индуктор с одним портом, где (+) и (-) клеммы порта подключены между обоими концами катушки, оба уравнения эквивалентны.
Часто индуктор моделируется с двумя портами, где порт 1 (+) находится на одном конце катушки, а порт 2 (+) — на другом конце катушки, а номера портов 1(-) и 2( -) подключены к некоторому общему заземляющему проводнику. В этом случае вы не можете использовать Z11, потому что это означает, что один конец индуктора открыт (плавающий). Никакой ток не может течь. Вы увидите разомкнутую цепь, если посмотрите на порт 1 при открытом порте 2.
В этом случае вместо этого вы используете 1/Y11, что означает, что порт 2 закорочен на общую землю. Теперь по проводнику будет течь ток, и можно будет измерить индуктивность.
Таким образом, простой причиной использования 1/Y11 является то, что он работает в обоих случаях: он работает для моделей с 1 и 2 портами.
nvt088
Членский уровень 4
volker@muehlhaus сказал:
Если вы моделируете индуктор с одним портом, где (+) и (-) клеммы порта подключены между обоими концами катушки, оба уравнения эквивалентны.
Часто индуктор моделируется с двумя портами, где порт 1 (+) находится на одном конце катушки, а порт 2 (+) — на другом конце катушки, а номера портов 1(-) и 2( -) подключены к некоторому общему заземляющему проводнику. В этом случае вы не можете использовать Z11, потому что это означает, что один конец индуктора открыт (плавающий). Никакой ток не может течь. Вы увидите разомкнутую цепь, если посмотрите на порт 1 при открытом порте 2.
В этом случае вместо этого вы используете 1/Y11, что означает, что порт 2 закорочен на общую землю. Теперь по проводнику будет течь ток, и можно будет измерить индуктивность.
Таким образом, простой причиной использования 1/Y11 является то, что он работает в обоих случаях: он работает для моделей с 1 и 2 портами.
Нажмите, чтобы развернуть…
Большое спасибо за ваше объяснение.
Я проверю ваш метод на своей симуляции и позже опубликую результаты здесь.
Большое спасибо!
- Статус
- Закрыто для дальнейших ответов.

Икс
Собственная индуктивность и емкость каждого витка катушки
- Автор Xeeshan143
- Ответов: 0
Электромагнитное проектирование и моделирование
р
Катушка цилиндра с использованием CST
- Инициировано Rafraf
- Ответов: 0
Электромагнитное проектирование и моделирование
А
Моделирование согласования импеданса катушки из HFSS
- Автор Alfie_Guo
- Ответов: 2
Электромагнитное проектирование и моделирование
Икс
Нахождение собственной индуктивности и коэффициента связи в HFSS
- Автор: Xeeshan143
- Ответов: 0
Электромагнитное проектирование и моделирование
К
Мне нужна помощь в разработке квадратной катушки с помощью ANSYS
- Автор Khatandeee
- Ответов: 0
Электромагнитное проектирование и моделирование
Делиться:
Фейсбук Твиттер Реддит Пинтерест Тамблер WhatsApp Эл. адрес Делиться Ссылка на сайт
адрес Делиться Ссылка на сайт
Верх
РАДИО РАСЧЕТЫ
РАДИО РАСЧЕТЫВот несколько калькуляторов для электронных/радиосхем. Они довольно грубо, но они работают. Обратите внимание, что эти формулы теперь принимают «с плавающей запятой». переменные (значение индуктивности 0,01 является допустимым числом).
Резисторы последовательно (или конденсаторы параллельно)
Просто добавьте их вместе!
Параллельные резисторы (или последовательные конденсаторы)
Формула: Эффективное сопротивление = (R1 x R2) / (R1 + R2)
(все единицы одинаковы, Ом/Фарады и т. д.)
Реактивное сопротивление конденсатора
Формула: реактивное сопротивление = 1 / (2 * Pi * F * C)
| Частота (Гц) [F] | Цоколь (пФ) [C] |
| Реактивное сопротивление (Ом) |
Инструкции для калькулятора
Я включил сюда несколько калькуляторов. Каждый раз, когда вы видите текст [Enter] вас спрашивают
для ввода данных в поле. Если вы ранее использовали другой калькулятор
то для вас уже будут введены начальные значения по умолчанию. Это
результаты предыдущего расчета. Конечно, вы можете ввести новые значения.
Каждый раз, когда вы видите текст [Enter] вас спрашивают
для ввода данных в поле. Если вы ранее использовали другой калькулятор
то для вас уже будут введены начальные значения по умолчанию. Это
результаты предыдущего расчета. Конечно, вы можете ввести новые значения.
Конденсаторы (C1, C2 и C3)
С1, С2 и С3 соединены последовательно и образуют один подстроечный конденсатор около 60 пф. Отношения C2:C3 определяют коэффициент усиления, и их значения могут варьироваться. достаточно много. В общем, C2 = 3-кратная длина волны, C3 = 9-кратная длина волны. С1 может быть любое значение от длины волны 1x до длины волны 10x и обычно выбирается для точной настройки частота осциллятора. Сделайте начальное значение C1 примерно таким же, как C2. фактические значения могут варьироваться в довольно широком диапазоне. Этот калькулятор рассчитает общая емкость настройки для выбранных вами значений.
В приведенном выше калькуляторе введите частоту и нажмите «ПОКАЗАТЬ C1, C2 и C3». и значения C1, C2 и C3 будут отображаться. Если вы затем нажмете кнопку
Кнопка «SHOW CAPACITANCE», вы увидите значение эффективного настроечного конденсатора.
это будет резонировать с L1. Вы также можете ввести свои собственные значения C1, C2 и C3.
найти эффективный подстроечный конденсатор, который будет резонировать с L1.
и значения C1, C2 и C3 будут отображаться. Если вы затем нажмете кнопку
Кнопка «SHOW CAPACITANCE», вы увидите значение эффективного настроечного конденсатора.
это будет резонировать с L1. Вы также можете ввести свои собственные значения C1, C2 и C3.
найти эффективный подстроечный конденсатор, который будет резонировать с L1.
Индуктор (L1)
Катушка индуктивности L1 резонирует с общей емкостью выше, чтобы определить рабочая частота. Если вы знаете емкость, только что прочитав предыдущую главу, затем используйте свою базовую частоту (транспонированную), чтобы дать индуктивности, или введите свои значения в этот маленький калькулятор:
Обмотка катушки
Теперь вы знаете индуктивность и емкость, это просто купить и
вставьте эти значения в схему. Но если вы действительно хотите накрутить
катушки самостоятельно, то вы, вероятно, будете использовать либо катушку с воздушным сердечником диаметром 6 мм.
шпангоуты или использовать шпангоуты с ферритовым сердечником. Существуют точные формулы для
использовать, но мне нравится этот метод. Вставьте требуемую индуктивность и нажмите кнопку
кнопка.
Существуют точные формулы для
использовать, но мне нравится этот метод. Вставьте требуемую индуктивность и нажмите кнопку
кнопка.
Пожалуйста, помните, что это последнее «вычисление» очень приблизительный так как многое зависит от индивидуального бывшего. Предполагается «ферритовый сердечник». быть перемотанным ЕСЛИ может.
Реактивное сопротивление катушки индуктивности
Формула: реактивное сопротивление = 2 * Pi * F * L
| Частота (Гц) [F] | Индуктивность (мкГн) [л] |
| Реактивное сопротивление (Ом) |
Основная частота
Формула: Частота (F) = 1 / (2 * Pi * Sqrt(LC))
Однослойная катушка
| Формула: |
Многослойная катушка
| Формула: |
Оценка радиатора
Рассчитывает эффективный коэффициент повышения температуры
мерный радиатор. ОТКРЫТАЯ площадь поверхности радиатора
в квадратных сантиметрах.
ОТКРЫТАЯ площадь поверхности радиатора
в квадратных сантиметрах.
| Формула: | градусов по Цельсию на ватт = 50 / Sqrt (площадь кв-см) |
| Площадь (кв. см) [A] | Только открытые участки. |
| Градусов C/Ватт |
Расчет радиатора
Вычисляет площадь поверхности радиатора, необходимую для данного радиатора температурный коэффициент.
| Формула: | Требуемая площадь (кв. см) = кв. м (50/C-ватт) |
Аттенюаторы — тип «T» и «H»
| Формулы: |
Входные/выходные мощности могут быть в любых электрических единицах, которые вы предпочитаете, например:
Мегаватты, пиковатты, джоули, обороты беговой дорожки для хомяков в час и т.







 Фильтры широко используют для частотной селекции (разделения, выделения) сигналов. Например частота звукового сигнала (частота которую в состоянии услышать человеческое ухо) лежит в диапазоне от 20 Гц до 20000 Гц. Для качественного воспроизведения звуковых сигналов в акустических системах применяют 3 динамика — для воспроизведения низких (НЧ), средних (СЧ) и высоких (ВЧ) частот звукового диапазона. Динамики включаются через фильтры которые выделяют именно тот диапазон частот, какой должен воспроизводить конкретный динамик.
Фильтры широко используют для частотной селекции (разделения, выделения) сигналов. Например частота звукового сигнала (частота которую в состоянии услышать человеческое ухо) лежит в диапазоне от 20 Гц до 20000 Гц. Для качественного воспроизведения звуковых сигналов в акустических системах применяют 3 динамика — для воспроизведения низких (НЧ), средних (СЧ) и высоких (ВЧ) частот звукового диапазона. Динамики включаются через фильтры которые выделяют именно тот диапазон частот, какой должен воспроизводить конкретный динамик. Если применен сердечник из магнитного материала — сталь, феррит…, то индуктивность катушки увеличивается; если сердечник из диамагнитного материала — латунь, алюминий…, то индуктивность катушки уменьшается. Катушки индуктивности, так же, как резисторы и конденсаторы, для получения заданной индуктивности, можно включать как последовательно, так и параллельно. Формулы расчета результирующей индуктивности Lr аналогичны формулам расчета результирующего сопротивления, а именно: для параллельного включения катушек: 1/Lr = 1/L1 + 1/L2 + … + 1/Ln; для последовательного включения — Lr = L1 + L2 + … + Ln.
Если применен сердечник из магнитного материала — сталь, феррит…, то индуктивность катушки увеличивается; если сердечник из диамагнитного материала — латунь, алюминий…, то индуктивность катушки уменьшается. Катушки индуктивности, так же, как резисторы и конденсаторы, для получения заданной индуктивности, можно включать как последовательно, так и параллельно. Формулы расчета результирующей индуктивности Lr аналогичны формулам расчета результирующего сопротивления, а именно: для параллельного включения катушек: 1/Lr = 1/L1 + 1/L2 + … + 1/Ln; для последовательного включения — Lr = L1 + L2 + … + Ln. Трансформаторы широко используются в радио и электронике для преобразования одного напряжения в другое той же частоты. Для усиления индуктивной связи катушки (в трансформаторах они называются «обмотки») размещаются на одном общем сердечнике. Обмотка подключенная к источнику питания называется первичной, а обмотка к которой подключена нагрузка называется вторичной. Трансформаторы предназначенные для питания радио и электронной аппаратуры называются силовыми. Силовые трансформаторы, обычно, используют для понижения высокого (220V) напряжения осветительной сети в низкое напряжение порядка 9 … 80V. В радиоаппаратуре применяют, обычно, стандартные трансформаторы. Кроме вторичного напряжения, для силовых трансформаторов обязательно указывается мощность которую трансформатор может отдавать в нагрузку. Показанный на рисунке трансформатор типа ТП-200 имеет мощность 200 Ватт. Отношение (k) числа витков первичной обмотки (W1) к числу витков (W2) вторичной обмотки трансформатора называется коэффициентом трансформации k = W1 / W2.
Трансформаторы широко используются в радио и электронике для преобразования одного напряжения в другое той же частоты. Для усиления индуктивной связи катушки (в трансформаторах они называются «обмотки») размещаются на одном общем сердечнике. Обмотка подключенная к источнику питания называется первичной, а обмотка к которой подключена нагрузка называется вторичной. Трансформаторы предназначенные для питания радио и электронной аппаратуры называются силовыми. Силовые трансформаторы, обычно, используют для понижения высокого (220V) напряжения осветительной сети в низкое напряжение порядка 9 … 80V. В радиоаппаратуре применяют, обычно, стандартные трансформаторы. Кроме вторичного напряжения, для силовых трансформаторов обязательно указывается мощность которую трансформатор может отдавать в нагрузку. Показанный на рисунке трансформатор типа ТП-200 имеет мощность 200 Ватт. Отношение (k) числа витков первичной обмотки (W1) к числу витков (W2) вторичной обмотки трансформатора называется коэффициентом трансформации k = W1 / W2. Если k больше 1 то трансформатор является понижающим, т.е. напряжение на вторичной обмотке будет меньше напряжения на первичной обмотке в k раз. Если k меньше 1 то трансформатор является повышающим и напряжение на вторичной обмотке будет больше напряжения на первичной обмотке в k раз. В общем случае напряжение на вторичной обмотке (U2) будет: U2 = U1/k, где U1 — напряжение на первичной обмотке.
Если k больше 1 то трансформатор является понижающим, т.е. напряжение на вторичной обмотке будет меньше напряжения на первичной обмотке в k раз. Если k меньше 1 то трансформатор является повышающим и напряжение на вторичной обмотке будет больше напряжения на первичной обмотке в k раз. В общем случае напряжение на вторичной обмотке (U2) будет: U2 = U1/k, где U1 — напряжение на первичной обмотке. Смотрите рисунок.).
Смотрите рисунок.). Компьютернаязапись той же формулы выглядит так: fp = 1 / (2 * pi * sqrt(L * C)), где sqrt означает — корень квадратный. Рассмотрим схему показанную на рисунке.
Компьютернаязапись той же формулы выглядит так: fp = 1 / (2 * pi * sqrt(L * C)), где sqrt означает — корень квадратный. Рассмотрим схему показанную на рисунке. Радиостанции передают радиосигнал в эфир на определенной частоте. За каждой радиостанцией закреплены определенные частоты.
Радиостанции передают радиосигнал в эфир на определенной частоте. За каждой радиостанцией закреплены определенные частоты. Для настройки на другую частоту, обычно, в колебательном контуре применяют конденсатор переменной ёмкости (рис.1) С изменением емкости конденсатора изменяется и резонансная частота контура fp, то есть изменяется настройка на другую частоту.
Для настройки на другую частоту, обычно, в колебательном контуре применяют конденсатор переменной ёмкости (рис.1) С изменением емкости конденсатора изменяется и резонансная частота контура fp, то есть изменяется настройка на другую частоту. Очевидно, что сопротивление Rp1 кривой А, на частоте fp1, больше сопротивления Rp2 кривой Б. Из этого следует, что ослабление мешающего сигнала лучше у контура имеющего кривую Б. В радио и электронике принято говорить, что чем острей кривая, тем лучше добротность контура. Добротность контура зависит от качества изготовления катушки индуктивности и качества применяемого конденсатора переменной ёмкости. Колебательные контуры, в радиоэлектронике применяются не только для настройки на радиостанции. Широкое применение колебательные контуры нашли в радиоэлектронике как фильтры различных сигналов, а так же в качестве стабилизаторов частоты генераторов переменного тока применяемых в передатчиках и других приборах.
Очевидно, что сопротивление Rp1 кривой А, на частоте fp1, больше сопротивления Rp2 кривой Б. Из этого следует, что ослабление мешающего сигнала лучше у контура имеющего кривую Б. В радио и электронике принято говорить, что чем острей кривая, тем лучше добротность контура. Добротность контура зависит от качества изготовления катушки индуктивности и качества применяемого конденсатора переменной ёмкости. Колебательные контуры, в радиоэлектронике применяются не только для настройки на радиостанции. Широкое применение колебательные контуры нашли в радиоэлектронике как фильтры различных сигналов, а так же в качестве стабилизаторов частоты генераторов переменного тока применяемых в передатчиках и других приборах. Индуктивные катушки бывают разных форм и размеров.
Индуктивные катушки бывают разных форм и размеров. Когда температура уменьшается, индуктивность также снижается. Современные параметры — это цикличность, которая является отношением температуры к линейному расширению. Учитывается изменение в керамической основе плюс показатель плотности.
Когда температура уменьшается, индуктивность также снижается. Современные параметры — это цикличность, которая является отношением температуры к линейному расширению. Учитывается изменение в керамической основе плюс показатель плотности.

 ..
..

 Часто в расчетах используются толщина намотки и средний диаметр
Часто в расчетах используются толщина намотки и средний диаметр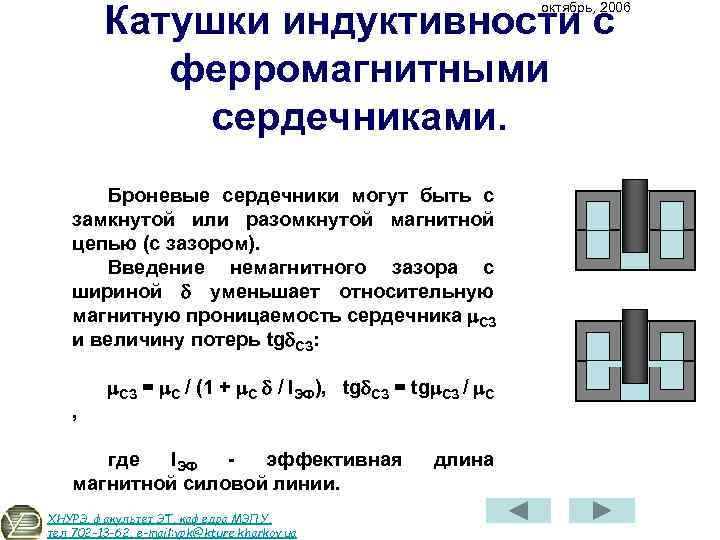
 Поэтому для более точного расчета индуктивности КИ, намотанной с шагом проводом круглого сечения, при числе витков не менее 4…5 следует использовать формулу:
Поэтому для более точного расчета индуктивности КИ, намотанной с шагом проводом круглого сечения, при числе витков не менее 4…5 следует использовать формулу: При проектировании КИ величина индуктивности, как правило, является исходной величиной. Может быть задан также один из размеров катушки, чаще всего− диаметр обмотки. Необходимо найти число витков и остальные размеры катушки, предварительно выбрав, если не заданы, конструкцию и тип намотки.
При проектировании КИ величина индуктивности, как правило, является исходной величиной. Может быть задан также один из размеров катушки, чаще всего− диаметр обмотки. Необходимо найти число витков и остальные размеры катушки, предварительно выбрав, если не заданы, конструкцию и тип намотки. Чем больше диаметр катушки, ближе друг к другу расположены витки, выше диэлектрическая проницаемость изоляции провода и материала каркаса, тем больше собственная емкость катушки индуктивности.
Чем больше диаметр катушки, ближе друг к другу расположены витки, выше диэлектрическая проницаемость изоляции провода и материала каркаса, тем больше собственная емкость катушки индуктивности. Для значительного уменьшения собственной емкости многослойных катушек применяют секционирование.
Для значительного уменьшения собственной емкости многослойных катушек применяют секционирование. Можете ли вы объяснить более четко? Потому что когда я анализирую Z-матрицу, я вижу, что можно использовать Z(1,1).
Можете ли вы объяснить более четко? Потому что когда я анализирую Z-матрицу, я вижу, что можно использовать Z(1,1).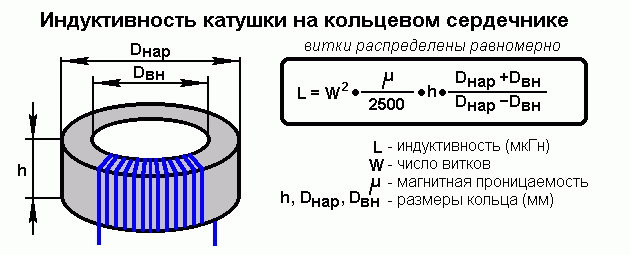

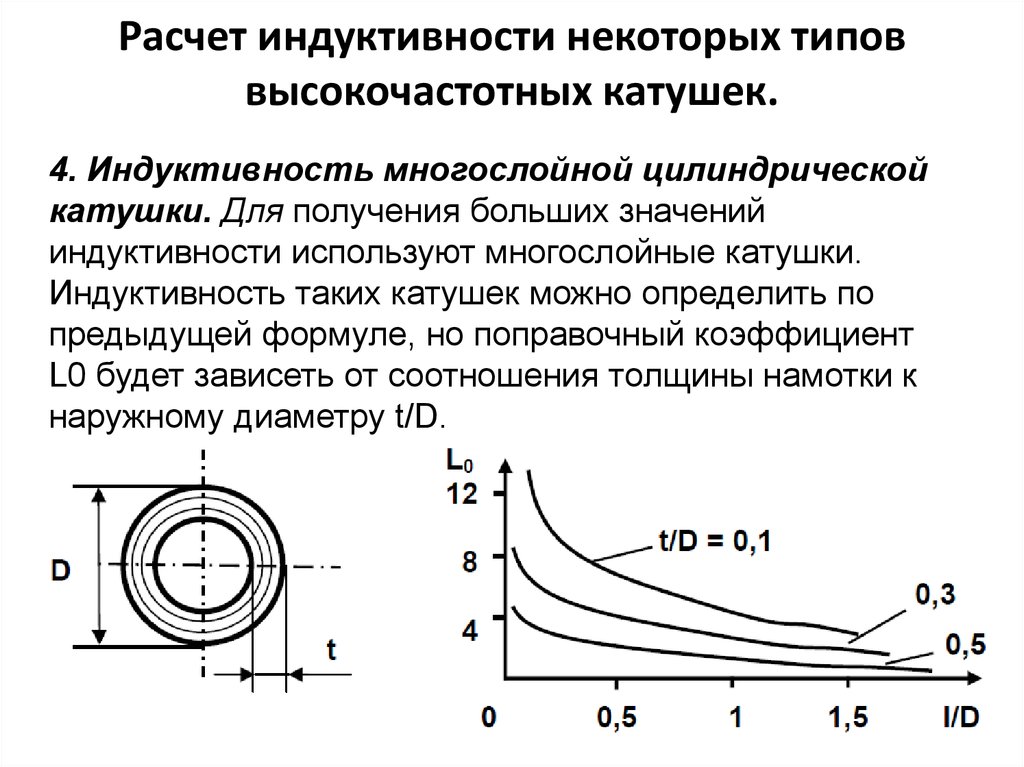 ..
..
