Момент силы: формула расчета

В физике рассмотрение задач с вращающимися телами или системами, которые находятся в равновесии, осуществляется с использованием концепции «момент силы». В этой статье будет рассмотрена формула момента силы, а также ее использование для решения указанного типа задач.

Момент силы в физике

Как было отмечено во введении, в данной статье пойдет речь о системах, которые могут вращаться либо вокруг оси, либо вокруг точки. Рассмотрим пример такой модели, изображенной на рисунке ниже.

Мы видим, что рычаг серого цвета закреплен на оси вращения. На конце рычага имеется черный кубик некоторой массы, на который действует сила (красная стрелка). Интуитивно понятно, что результатом воздействия этой силы будет вращение рычага вокруг оси против часовой стрелки.

Момент сил относительно оси вращения: основные понятия,…

Когда решают задачи на перемещение объектов, то в ряде случаев пренебрегают их пространственными…

Моментом силы называется величина в физике, которая равна векторному произведению радиуса, соединяющего ось вращения и точку приложения силы (зеленый вектор на рисунке), и самой внешней силе. То есть формула момента силы относительно оси записывается следующим образом:

M¯ = r¯ * F¯

Результатом этого произведения будет вектор M¯. Направление его определяют, исходя из знания векторов-множителей, то есть r¯ и F¯. Согласно определению векторного произведения, M¯ должен быть перпендикулярен плоскости, образованной векторами r¯ и F¯, и направлен в соответствии с правилом правой руки (если четыре пальца правой руки расположить вдоль первого умножаемого вектора в направлении к концу второго, то отставленный вверх большой палец укажет, куда направлен искомый вектор). На рисунке можно видеть, куда направлен вектор M¯ (синяя стрелка).

Импульс и момент импульса в физике: формулы, описывающие…

Задачи с движущимися телами в физике, когда скорость много меньше световой, решаются с помощью…

Скалярная форма записи M¯

На рисунке в предыдущем пункте сила (красная стрелка) действует на рычаг под углом 90^o. В общем же случае она может быть приложена под совершенно любым углом. Рассмотрим изображение ниже.

Здесь мы видим, что на рычаг L сила F уже действует под некоторым углом Φ. Для этой системы формула момента силы относительно точки (показана стрелкой) в скалярном виде примет форму:

M = L * F * sin(Φ)

Из выражения следует, что момент силы M будет тем больше, чем ближе направление действия силы F к углу 90^o по отношению к L. Наоборот, если F действует вдоль L, то sin(0) = 0, и сила не создает никакого момента (M = 0).

При рассмотрении момента силы в скалярной форме часто пользуются понятием «рычага силы». Эта величина представляет собой расстояние между осью (точкой вращения) и вектором F. Применяя это определение к рисунку выше, можно сказать, что d = L * sin(Φ) — это рычаг силы (равенство следует из определения тригонометрической функции «синус»). Через рычаг силы формулу для момента M можно переписать так:

M = d * F

Физический смысл величины M

Рассматриваемая физическая величина определяет способность внешней силы F оказывать вращательное воздействие на систему.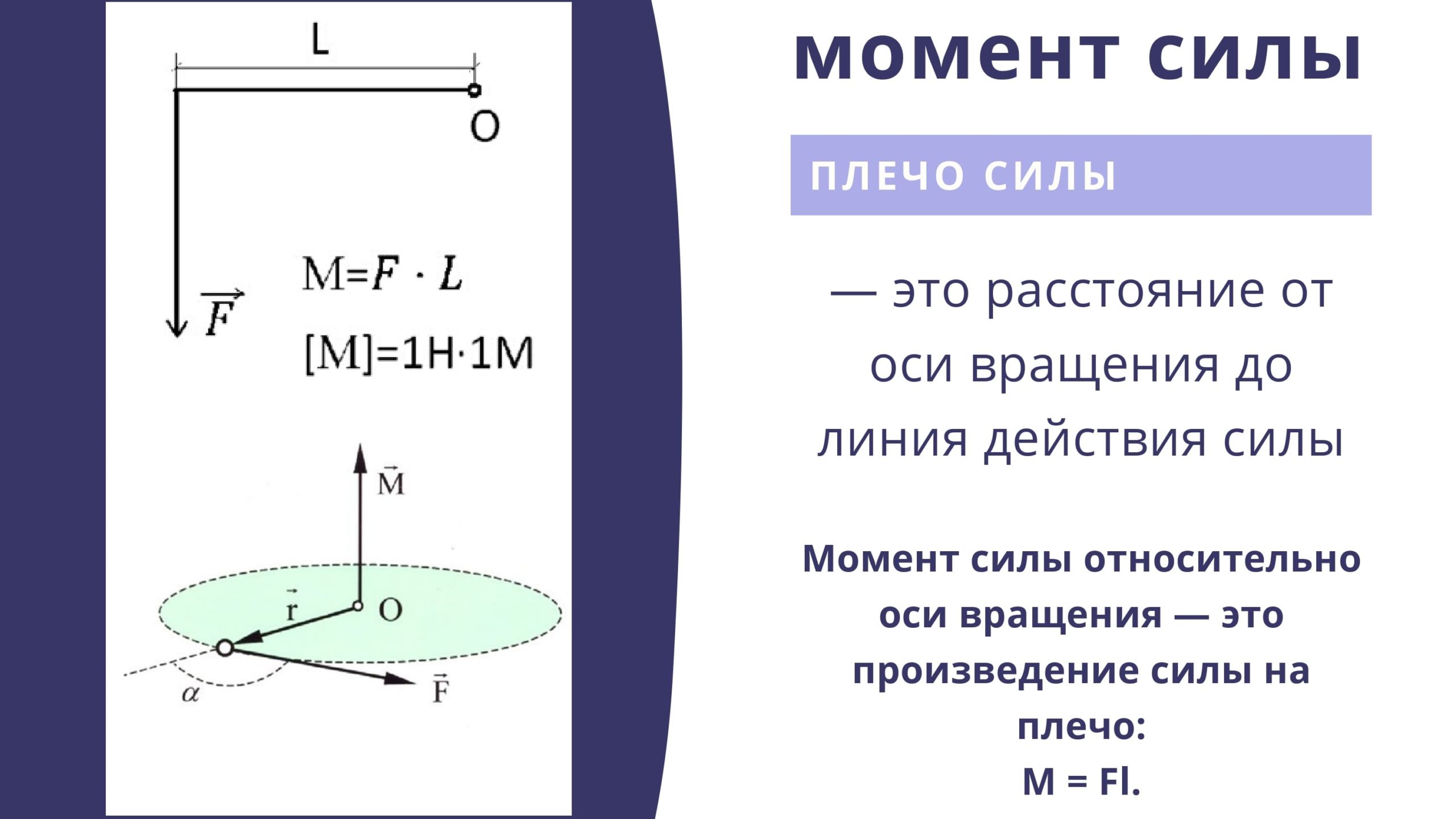 Чтобы привести тело во вращательное движение, ему необходимо сообщить некоторый момент M.

Ярким примером этого процесса является открывание или закрывание двери в комнату. Взявшись за ручку, человек прикладывает усилие и поворачивает дверь на петлях. Каждый сможет это сделать. Если же попытаться открыть дверь, воздействуя на нее вблизи петель, то потребуется приложить большие усилия, чтобы сдвинуть ее с места.

Момент инерции маятника: определение, специфические…

При решении уравнений вращательного или колебательного (осциллирующего) движения необходимо знать…

Другим примером является откручивание гайки ключом. Чем короче будет этот ключ, тем труднее выполнить поставленную задачу.

Указанные особенности демонстрирует формула момента силы через плечо, которая была приведена в предыдущем пункте. Если M считать постоянной величиной, то чем меньше d, тем большую F следует приложить для создания заданного момента силы.

Несколько действующих сил в системе

Выше были рассмотрены случаи, когда на систему, способную к вращению, действует всего одна сила F, но как быть, когда таких сил несколько? Действительно, эта ситуация является более частой, поскольку на систему могут действовать силы различной природы (гравитационная, электрическая, трение, механическая и другие). Во всех этих случаях результирующий момент силы M¯ может быть получен с помощью векторной суммы всех моментов M_i¯, то есть:

M¯ = ∑_i(M_i¯), где i — номер силы F_i

Из свойства аддитивности моментов следует важный вывод, который получил название теоремы Вариньона, названной так по фамилии математика конца XVII — начала XVIII века — француза Пьера Вариньона. Она гласит: «Сумма моментов всех сил, оказывающих воздействие на рассматриваемую систему, может быть представлена в виде момента одной силы, которая равна сумме всех остальных и приложена к некоторой точке». Математически теорему можно записать так:

∑_i(M_i¯) = M¯ = d * ∑_i(F_i¯)

Эта важная теорема часто используется на практике для решения задач на вращение и равновесие тел.

Совершает ли работу момент силы?

Анализируя приведенные формулы в скалярном или векторном виде, можно прийти к выводу, что величина M — это некоторая работа. Действительно, ее размерность равна Н*м, что в СИ соответствует джоулю (Дж). На самом деле момент силы — это не работа, а лишь величина, которая способна ее совершить. Чтобы это произошло, необходимо наличие кругового движения в системе и продолжительного во времени действия M. Поэтому формула работы момента силы записывается в следующем виде:

A = M * θ

В этом выражении θ — это угол, на который было произведено вращение моментом силы M. В итоге единицу работы можно записать как Н*м*рад или же Дж*рад. Например, значение 60 Дж*рад говорит о том, что при повороте на 1 радиан (приблизительно 1/3 окружности) создающая момент M сила F совершила работу в 60 джоулей. Эту формулу часто используют при решении задач в системах, где действуют силы трения, что будет показано ниже.

Момент силы и момент импульса

Как было показано, воздействие на систему момента M приводит к появлению в ней вращательного движения. Последнее характеризуется величиной, которая получила название «момент импульса».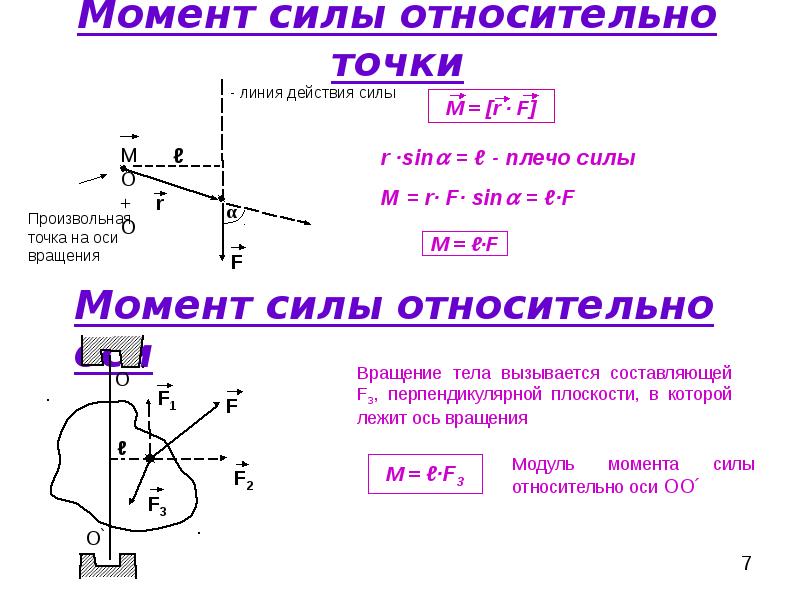 Его можно вычислить, применяя формулу:

L = I * ω

Здесь I — это момент инерции (величина, которая играет такую же роль при вращении, что и масса при линейном движении тела), ω — угловая скорость, она связана с линейной скоростью формулой ω = v/r.

Оба момента (импульса и силы) связаны друг с другом следующим выражением:

M = I * α, где α = dω / dt — угловое ускорение.

Приведем еще одну формулу, которая важна для решения задач на работу моментов сил. С помощью этой формулы можно вычислить кинетическую энергию вращающегося тела. Она выглядит так:

E_k = 1/2 * I * ω²

Далее приведем две задачи с решениями, где покажем, как пользоваться рассмотренными физическими формулами.

Равновесие нескольких тел

Первая задача связана с равновесием системы, в которой действуют несколько сил. На рисунке ниже приведена система, на которую действуют три силы. Необходимо рассчитать, какой массы предмет необходимо подвесить к этому рычагу и в какой точке это следует сделать, чтобы данная система находилась в равновесии.

Из условия задачи можно понять, что для ее решения следует воспользоваться теоремой Вариньона. На первую часть задачи можно ответить сразу, поскольку вес предмета, которые следует подвесить к рычагу, будет равен:

P = F₁ — F₂ + F₃ = 20 — 10 + 25 = 35 Н

Знаки здесь выбраны с учетом того, что сила, вращающая рычаг против часовой стрелки, создает отрицательный момент.

Положение точки d, куда следует подвесить этот вес, вычисляется по формуле:

M₁ — M₂ + M₃ = d * P = 7 * 20 — 5 * 10 + 3 * 25 = d * 35 => d = 165/35 = 4,714 м

Отметим, что с помощью формулы момента силы тяжести мы вычислили эквивалентную величину M той, которую создают три силы. Чтобы система находилась в равновесии, необходимо подвесить тело весом 35 Н в точке 4,714 м от оси с другой стороны рычага.

Задача с движущимся диском

Решение следующей задачи основано на использовании формулы момента силы трения и кинетической энергии тела вращения. Задача: дан диск радиуса r = 0,3 метра, который вращается со скоростью ω = 1 рад/с. Необходимо рассчитать, какое расстояние способен он пройти по поверхности, если коэффициент трения качения равен μ = 0,001.

Эту задачу легче всего решить, если воспользоваться законом сохранения энергии. Мы располагаем начальной кинетической энергией диска. Когда он начнет катиться, то вся эта энергия расходуется на нагрев поверхности за счет действия силы трения. Приравнивая обе величины, получим выражение:

I * ω²/2 = μ * N/r * r * θ

Первая часть формулы — это кинетическая энергия диска. Вторая часть — это работа момента силы трения F = μ * N/r, приложенной к краю диска (M=F * r).

Учитывая, что N = m * g и I = 1/2m * r², вычисляем θ:

θ = m * r² * ω²/(4 * μ * m * g) = r² * ω²/(4 * μ *g) = 0,3² * 1²/(4 * 0,001 * 9,81) = 2,29358 рад

Поскольку 2pi радиан соответствуют длине 2pi * r, тогда получаем, что искомое расстояние, которое пройдет диск, равно:

s = θ * r = 2,29358 * 0,3 = 0,688 м или около 69 см

Отметим, что на данный результат масса диска никак не влияет.

Момент силы. Формула момента силы

В физике рассмотрение задач с вращающимися телами или системами, которые находятся в равновесии, осуществляется с использованием концепции «момент силы». В этой статье будет рассмотрена формула момента силы, а также ее использование для решения указанного типа задач.

Как было отмечено во введении, в данной статье пойдет речь о системах, которые могут вращаться либо вокруг оси, либо вокруг точки. Рассмотрим пример такой модели, изображенной на рисунке ниже.

Мы видим, что рычаг серого цвета закреплен на оси вращения. На конце рычага имеется черный кубик некоторой массы, на который действует сила (красная стрелка). Интуитивно понятно, что результатом воздействия этой силы будет вращение рычага вокруг оси против часовой стрелки.

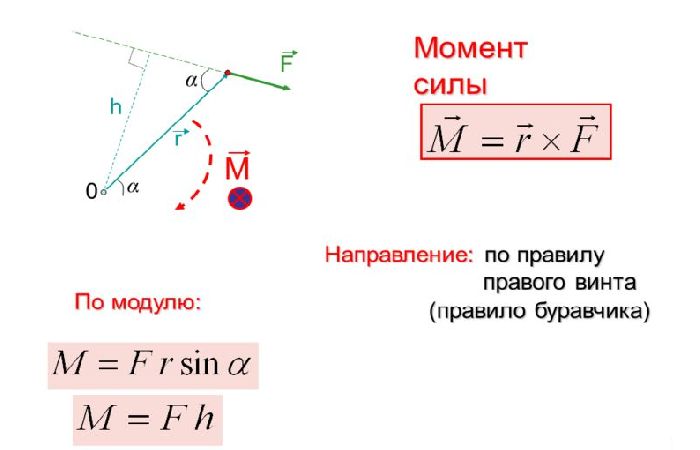
Моментом силы называется величина в физике, которая равна векторному произведению радиуса, соединяющего ось вращения и точку приложения силы (зеленый вектор на рисунке), и самой внешней силе. То есть формула момента силы относительно оси записывается следующим образом:

M¯ = r¯ * F¯

Результатом этого произведения будет вектор M¯. Направление его определяют, исходя из знания векторов-множителей, то есть r¯ и F¯. Согласно определению векторного произведения, M¯ должен быть перпендикулярен плоскости, образованной векторами r¯ и F¯, и направлен в соответствии с правилом правой руки (если четыре пальца правой руки расположить вдоль первого умножаемого вектора в направлении к концу второго, то отставленный вверх большой палец укажет, куда направлен искомый вектор). На рисунке можно видеть, куда направлен вектор M¯ (синяя стрелка).

Скалярная форма записи M¯

На рисунке в предыдущем пункте сила (красная стрелка) действует на рычаг под углом 90^o. В общем же случае она может быть приложена под совершенно любым углом. Рассмотрим изображение ниже.

Здесь мы видим, что на рычаг L сила F уже действует под некоторым углом Φ. Для этой системы формула момента силы относительно точки (показана стрелкой) в скалярном виде примет форму:

M = L * F * sin(Φ)

Из выражения следует, что момент силы M будет тем больше, чем ближе направление действия силы F к углу 90^o по отношению к L. Наоборот, если F действует вдоль L, то sin(0) = 0, и сила не создает никакого момента (M = 0).

При рассмотрении момента силы в скалярной форме часто пользуются понятием «рычага силы». Эта величина представляет собой расстояние между осью (точкой вращения) и вектором F. Применяя это определение к рисунку выше, можно сказать, что d = L * sin(Φ) — это рычаг силы (равенство следует из определения тригонометрической функции «синус»). Через рычаг силы формулу для момента M можно переписать так:

M = d * F

Физический смысл величины M

Рассматриваемая физическая величина определяет способность внешней силы F оказывать вращательное воздействие на систему. Чтобы привести тело во вращательное движение, ему необходимо сообщить некоторый момент M.

Ярким примером этого процесса является открывание или закрывание двери в комнату. Взявшись за ручку, человек прикладывает усилие и поворачивает дверь на петлях. Каждый сможет это сделать. Если же попытаться открыть дверь, воздействуя на нее вблизи петель, то потребуется приложить большие усилия, чтобы сдвинуть ее с места.

Другим примером является откручивание гайки ключом. Чем короче будет этот ключ, тем труднее выполнить поставленную задачу.

Указанные особенности демонстрирует формула момента силы через плечо, которая была приведена в предыдущем пункте. Если M считать постоянной величиной, то чем меньше d, тем большую F следует приложить для создания заданного момента силы.

Несколько действующих сил в системе

Выше были рассмотрены случаи, когда на систему, способную к вращению, действует всего одна сила F, но как быть, когда таких сил несколько? Действительно, эта ситуация является более частой, поскольку на систему могут действовать силы различной природы (гравитационная, электрическая, трение, механическая и другие). Во всех этих случаях результирующий момент силы M¯ может быть получен с помощью векторной суммы всех моментов M_i¯, то есть:

M¯ = ∑_i(M_i¯), где i — номер силы F_i

Из свойства аддитивности моментов следует важный вывод, который получил название теоремы Вариньона, названной так по фамилии математика конца XVII — начала XVIII века — француза Пьера Вариньона. Она гласит: «Сумма моментов всех сил, оказывающих воздействие на рассматриваемую систему, может быть представлена в виде момента одной силы, которая равна сумме всех остальных и приложена к некоторой точке». Математически теорему можно записать так:

∑_i(M_i¯) = M¯ = d * ∑_i(F_i¯)

Эта важная теорема часто используется на практике для решения задач на вращение и равновесие тел.

Совершает ли работу момент силы?

Анализируя приведенные формулы в скалярном или векторном виде, можно прийти к выводу, что величина M — это некоторая работа. Действительно, ее размерность равна Н*м, что в СИ соответствует джоулю (Дж). На самом деле момент силы — это не работа, а лишь величина, которая способна ее совершить. Чтобы это произошло, необходимо наличие кругового движения в системе и продолжительного во времени действия M. Поэтому формула работы момента силы записывается в следующем виде:

A = M * θ

В этом выражении θ — это угол, на который было произведено вращение моментом силы M. В итоге единицу работы можно записать как Н*м*рад или же Дж*рад. Например, значение 60 Дж*рад говорит о том, что при повороте на 1 радиан (приблизительно 1/3 окружности) создающая момент M сила F совершила работу в 60 джоулей. Эту формулу часто используют при решении задач в системах, где действуют силы трения, что будет показано ниже.

Момент силы и момент импульса

Как было показано, воздействие на систему момента M приводит к появлению в ней вращательного движения. Последнее характеризуется величиной, которая получила название «момент импульса». Его можно вычислить, применяя формулу:

L = I * ω

Здесь I — это момент инерции (величина, которая играет такую же роль при вращении, что и масса при линейном движении тела), ω — угловая скорость, она связана с линейной скоростью формулой ω = v/r.

Оба момента (импульса и силы) связаны друг с другом следующим выражением:

M = I * α, где α = dω / dt — угловое ускорение.

Приведем еще одну формулу, которая важна для решения задач на работу моментов сил.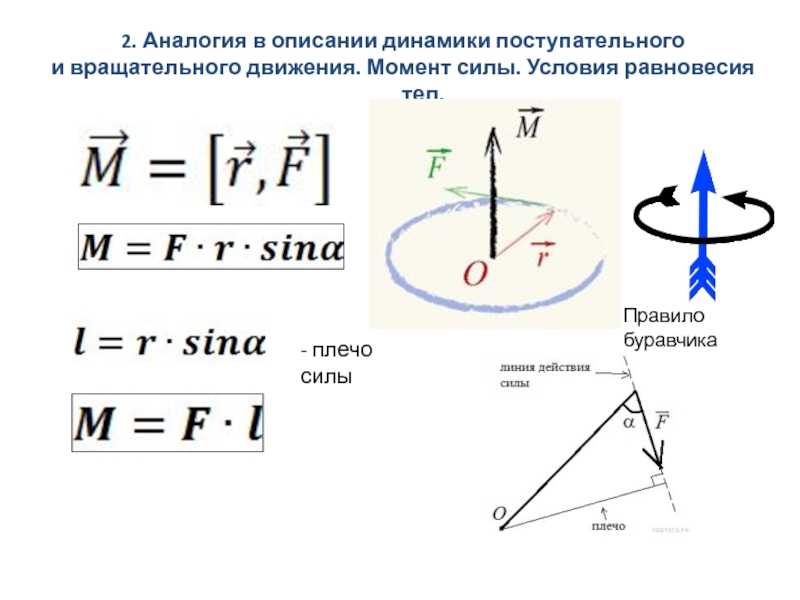 С помощью этой формулы можно вычислить кинетическую энергию вращающегося тела. Она выглядит так:

E_k = 1/2 * I * ω²

Далее приведем две задачи с решениями, где покажем, как пользоваться рассмотренными физическими формулами.

Равновесие нескольких тел

Первая задача связана с равновесием системы, в которой действуют несколько сил. На рисунке ниже приведена система, на которую действуют три силы. Необходимо рассчитать, какой массы предмет необходимо подвесить к этому рычагу и в какой точке это следует сделать, чтобы данная система находилась в равновесии.

Из условия задачи можно понять, что для ее решения следует воспользоваться теоремой Вариньона. На первую часть задачи можно ответить сразу, поскольку вес предмета, которые следует подвесить к рычагу, будет равен:

P = F₁ — F₂ + F₃ = 20 — 10 + 25 = 35 Н

Знаки здесь выбраны с учетом того, что сила, вращающая рычаг против часовой стрелки, создает отрицательный момент.

Положение точки d, куда следует подвесить этот вес, вычисляется по формуле:

M₁ — M₂ + M₃ = d * P = 7 * 20 — 5 * 10 + 3 * 25 = d * 35 => d = 165/35 = 4,714 м

Отметим, что с помощью формулы момента силы тяжести мы вычислили эквивалентную величину M той, которую создают три силы. Чтобы система находилась в равновесии, необходимо подвесить тело весом 35 Н в точке 4,714 м от оси с другой стороны рычага.

Задача с движущимся диском

Решение следующей задачи основано на использовании формулы момента силы трения и кинетической энергии тела вращения. Задача: дан диск радиуса r = 0,3 метра, который вращается со скоростью ω = 1 рад/с. Необходимо рассчитать, какое расстояние способен он пройти по поверхности, если коэффициент трения качения равен μ = 0,001.

Эту задачу легче всего решить, если воспользоваться законом сохранения энергии. Мы располагаем начальной кинетической энергией диска. Когда он начнет катиться, то вся эта энергия расходуется на нагрев поверхности за счет действия силы трения. Приравнивая обе величины, получим выражение:

I * ω²/2 = μ * N/r * r * θ

Первая часть формулы — это кинетическая энергия диска. Вторая часть — это работа момента силы трения F = μ * N/r, приложенной к краю диска (M=F * r).

Учитывая, что N = m * g и I = 1/2m * r², вычисляем θ:

θ = m * r² * ω²/(4 * μ * m * g) = r² * ω²/(4 * μ *g) = 0,3² * 1²/(4 * 0,001 * 9,81) = 2,29358 рад

Поскольку 2pi радиан соответствуют длине 2pi * r, тогда получаем, что искомое расстояние, которое пройдет диск, равно:

s = θ * r = 2,29358 * 0,3 = 0,688 м или около 69 см

Отметим, что на данный результат масса диска никак не влияет.

Вращательная инерция – Физика Колледжа Дугласа 1104 Индивидуальный учебник – Зима и лето 2020

Глава 9 Вращательное движение и угловой момент

Резюме

• Понять взаимосвязь между силой, массой и ускорением.
• Изучите вращающее действие силы.
• Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, линейным ускорением и угловым ускорением.

Если вы когда-нибудь крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 1. На самом деле ваша интуиция надежно предсказывает многие из задействованных факторов . Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.

Рисунок 1. Для вращения велосипедного колеса требуется сила. Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если надавить на спицу ближе к оси, угловое ускорение будет меньше.

Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу

F к точке массой m , находящейся на расстоянии r от точки вращения, как показано на рисунке 2. Поскольку сила перпендикулярна r , ускорение [латекс]\boldsymbol{a=\frac{F}{m}}[/latex ] получается по направлению F . Мы можем изменить это уравнение так, что F = ma , а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что a = r ω , и подставим это выражение в F = мА , что дает

[латекс]\boldsymbol{F=г-н\альфа}. 2\alpha}[/латекс] 92\альфа}.[/латекс]

Это последнее уравнение является вращательным аналогом второго закона Ньютона ( F = ma ), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению и mr ² аналогичен к массе (или инерции). Количество mr ² называется

инерцией вращения или моментом инерции точечной массы м расстояние r от центра вращения.

Рис. 2. Объект поддерживается горизонтальным столом без трения и прикреплен к точке поворота шнуром, создающим центростремительную силу. Сила F приложена к объекту перпендикулярно радиусу r , заставляя его ускоряться относительно точки вращения. Сила удерживается перпендикулярно r .

ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.

Прежде чем мы сможем рассмотреть вращение чего-либо, кроме точечной массы, подобной той, что изображена на рис. 2, мы должны распространить идею инерции вращения на все типы объектов. Чтобы расширить наше понятие инерции вращения, мы определяем момент инерции I объекта должен быть суммой mr ² для всех точечных масс, из которых он состоит. То есть

I =∑ мр ² . Здесь I аналогично m в поступательном движении. Из-за расстояния r момент инерции любого объекта зависит от выбранной оси. На самом деле, вычисляя I выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одинаковом расстоянии от его оси. Следовательно, момент инерции обруча вокруг своей оси равен MR ² , где

M — его полная масса, а R — его радиус. (Мы используем M и R для всего объекта, чтобы отличить их от m и r для точечных масс.) Во всех других случаях мы должны обращаться к рисунку 3 (обратите внимание, что таблица представляет собой произведение искусства, имеющее формы, а также формулы) для формул для I , которые имеют получена интегрированием по непрерывному телу. Обратите внимание, что I имеет единицы массы, умноженные на квадрат расстояния ( кг⋅м ² ), как и следовало ожидать из его определения.

Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением составляет

[латекс] \boldsymbol{\textbf{net}\tau=I\alpha}[/латекс]

или

[латекс]\boldsymbol{\alpha\:=}[/латекс][латекс]\boldsymbol{\frac{\textbf{net}\tau}{I}},[/latex]

, где net τ — это суммарный крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в [латекс]\boldsymbol{\tau=I\alpha},\:\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}}[/latex] является аналогом вращения Ньютона. второй закон и очень широко применимы. Это уравнение действительно справедливо для

любой крутящий момент, примененный к любому объекту относительно любой оси .

Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение.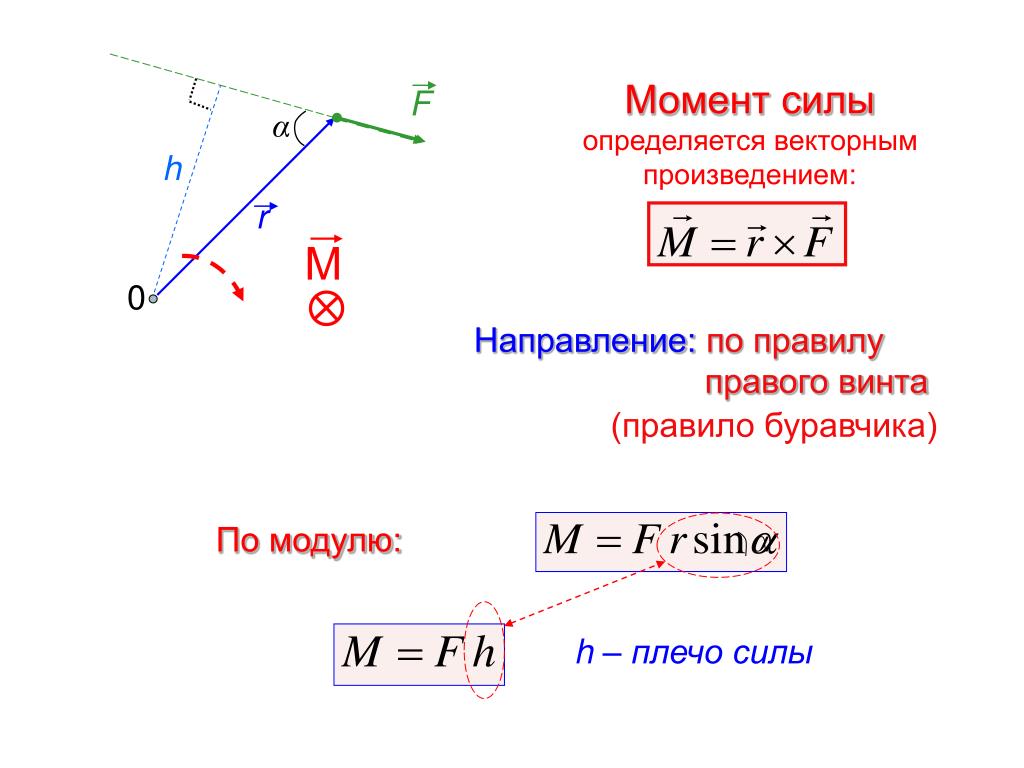 Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его

распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.

ЭКСПЕРИМЕНТ ДЛЯ ДОМА

Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо.

(Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.

СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ ДЛЯ ДИНАМИКИ ВРАЩЕНИЯ

1. Изучите ситуацию, чтобы определить, что крутящий момент и масса участвуют во вращении . Нарисуйте тщательный набросок ситуации.
2. Определить интересующую систему .
3. Нарисуйте диаграмму свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
4. Применить [латекс]\boldsymbol{\textbf{net}\tau=I\alpha},\:\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}},[/latex ] вращательный эквивалент второго закона Ньютона для решения задачи . Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
5. Как всегда, проверьте решение, чтобы убедиться, что оно разумно .

ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ

В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.

Рисунок 3. Некоторые инерции вращения.

Пример 1. Расчет влияния распределения массы на карусель

Рассмотрим отца, толкающего игровую карусель на рис. 4. Он прикладывает силу 250 Н к краю карусели весом 50,0 кг. круговой, который имеет радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.

Рис. 4. Отец толкает игровую карусель за ее край и перпендикулярно ее радиусу для достижения максимального крутящего момента.

Стратегия

Угловое ускорение задается непосредственно выражением [латекс]\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}}:[/latex]

[латекс]\boldsymbol {\alpha\:=}[/latex][latex]\boldsymbol{\frac{\tau}{I}}.[/latex]

Чтобы найти [латекс]\boldsymbol{\alpha},[/latex ] мы должны сначала рассчитать крутящий момент  τ (одинаковый в обоих случаях) и момент инерции I (во втором случае больше). Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трение незначительно, так что

[латекс]\boldsymbol{\tau=rF\:\sin\:\theta=(1,50\textbf{ m })(250\textbf{ N})=375\textbf{ N}\cdotp\textbf{m}.}[/latex]

Решение задачи (a)

Момент инерции твердого диска около эта ось указана на рисунке 3 как 92}}. 2}.[/латекс] 92}}.[/latex]

Обсуждение

Угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если бы, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, и только 8,89 рад/с, когда на ней находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.

• Чем дальше приложена сила от оси вращения, тем больше угловое ускорение; угловое ускорение обратно пропорционально массе.
• Если мы приложим силу F к точке массой m , которая находится на расстоянии r от точки вращения и потому что сила перпендикулярна r , ускорение a = F / m получается в направлении Ф . Мы можем изменить это уравнение так, что

  [латекс]\boldsymbol{F = ma},[/латекс]

  , а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что [latex]\boldsymbol{a = r\alpha},[/latex] и подставим это выражение в F = ma , что даст

  [латекс]\boldsymbol{F=г-н\альфа}[/латекс]

• Крутящий момент — это вращающая способность силы. В данном случае, потому что 92}.[/латекс]

• Общая взаимосвязь между крутящим моментом, моментом инерции и угловым ускорением такова:

  [латекс]\boldsymbol{\tau=I\alpha}[/латекс]

  или

  [латекс]\boldsymbol{\alpha=}[/латекс][латекс]\boldsymbol{\frac{\textbf{net}\tau}{I}}[/latex]

крутящий момент

поворотная эффективность силы

инерция вращения

сопротивление изменению вращения. Чем больше инерция вращения у объекта, тем труднее его вращать

момент инерции

масса, умноженная на квадрат перпендикулярного расстояния от оси вращения; для точечной массы это I = mr ² и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции

Моменты балансировки (физика GCSE) — Study Mind

Чтение за 5 мин.

Силы и вращение

Мы можем заставить объект вращаться, приложив к объекту одну силу или систему сил. Например, когда вы толкаете дверь, она поворачивается на петлях.

Эффект поворота силы заставляет объект вращаться.

 

Примеры сил, вызывающих вращение

Уравновешивающие моменты

 

Моменты

• Вращающее действие силы называется моментом. Моменты используются для описания поворотного действия силы. Ранее мы упоминали, что эффект поворота вызывает вращение объекта. Теперь мы можем сказать, что моменты вызывают вращение объекта.
• Моменты различаются по размеру. Размер на данный момент повлияет на количество производимого вращения. Если момент больше, то объект будет сильно вращаться. Если момент мал, то объект будет испытывать очень малую вращающую силу. В следующем разделе мы обсудим, как изменить размер момента.

Уравновешивающие моменты

 

Расчет моментов

Это уравнение для расчета величины момента:

Где:

• момент силы , М, в ньютон-метрах, Нм
• сила , Ф, в ньютонах, Н
• расстояние , d, — расстояние по перпендикуляру от центра вращения до линии действия силы, в метрах, м .

Когда мы вычисляем величину момента, очень важно помнить, что сила всегда действует под прямым углом к ​​измеряемому расстоянию (рис. 2).

Уравновешивающие моменты

 

Вопрос: Чему равен момент силы 4 Н, направленной вниз на расстоянии 0,4 м от оси вращения?

1. Нарисуйте схему.
Чтобы ответить на этот вопрос, мы должны начать с рисования диаграммы.

Уравновешивающие моменты

 

2. Посмотрите на формулу.
Теперь, когда у нас есть визуальное представление, мы можем видеть, что наша сила перпендикулярна заданному расстоянию. Теперь мы можем использовать нашу формулу:

М = Fd

 

3. Подставьте цифры.
Как только мы подставим числа в уравнение, мы должны получить ответ.

М = 4 х 0,4

М = 1,6 Н·м

 

Изменение размера момента

• Моменты можно увеличить. Мы можем увеличить величину момента либо увеличив приложенную силу, либо увеличив перпендикулярное расстояние от оси вращения.
• Моменты можно уменьшить. Мы можем уменьшить величину момента, либо уменьшая приложенную силу, либо уменьшая перпендикулярное расстояние от оси вращения.

 

Моменты по часовой и против часовой стрелки

Поскольку моменты заставляют объекты вращаться, мы можем классифицировать их по направлению. Два термина, которые мы используем для описания направления момента, — по часовой стрелке и против часовой стрелки, как на рис. 3.

Балансирующие моменты

 

Балансирующие моменты

В определенных ситуациях моменты могут уравновесить друг друга, и объект останется неподвижным (вместо того, чтобы вращаться). Чтобы это было так, общий момент по часовой стрелке будет равен общему моменту против часовой стрелки относительно оси вращения.

Если общий момент по часовой стрелке не равен общему моменту против часовой стрелки, объект будет вращаться:

Уравновешивающие моменты

 

Расчет силы и расстояния по моментам

Ранее мы рассматривали расчет момента по силе и расстоянию. Теперь мы собираемся работать в обратном направлении, используя момент, чтобы найти силу или расстояние.

В этих ситуациях мы будем использовать тот факт, что система сбалансирована . Как мы упоминали ранее, в сбалансированной системе общий момент по часовой стрелке будет равен общему моменту против часовой стрелки. Используя этот принцип, мы можем составить уравнение, которое поможет нам решить вопросы:

 

Вопрос: Сэм и Джесс сидят на противоположных концах качелей. Джесс весит 300 Н и сидит в 3 метрах от центра оси. Сэм весит 450 Н. Пока они сидят на своих текущих позициях, качели уравновешены. На каком расстоянии от центра оси находится Сэм?

1. Нам нужно нарисовать схему.
Очень важно нарисовать четкую диаграмму, чтобы точно видеть, что происходит. Добавьте все значения весов и расстояний, которые мы знаем. Мы просто обозначим расстояние, которое мы пытаемся найти, как «d».

Уравновешивающие моменты

 

2. Назначение моментов направления.
В этом случае из диаграммы видно, что Сэм создает момент против часовой стрелки, тогда как Джесс создает момент по часовой стрелке.

3. Рассчитайте момент, для которого у нас есть информация.
В этом вопросе мы можем вычислить момент Джесс.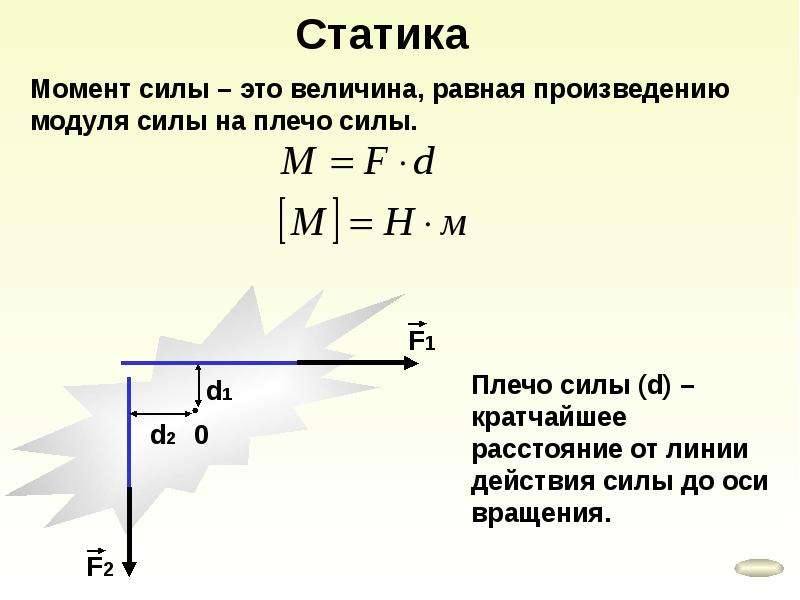 Мы можем сделать это, используя уравнение

M = Fd
M = 300 x 3
M = 900 Н·м

4. Помните, что моменты против часовой стрелки = моменты по часовой стрелке.
Качели уравновешены, поэтому мы знаем, что моменты против часовой стрелки равны моментам по часовой стрелке.

5. Подставьте числа в уравнение.
Мы уже рассчитали момент Джесс, поэтому нам просто нужно ввести недостающую информацию для Сэма.

Мы можем использовать эту информацию, чтобы составить сбалансированное уравнение:

момент против часовой стрелки = момент по часовой стрелке
момент Сэма = момент Джесса
Fd = Fd (поскольку M = Fd)
450 x d = 300 x 3
450 x d = 900
d = 900 / 450
d = 2 м

Следовательно, мы можем сказать, что Сэм сидит на расстоянии 2 м от центра оси.

 

Несколько сил

Вопрос: (продолжение предыдущего вопроса)… Сэм меняет свое положение на качелях и передвигает свою сумку с земли на свою сторону качелей. Расстояние между стержнем и Сэмом в два раза больше расстояния между стержнем и мешком. Мешок весит 100 Н, а Сэм весит 450 Н. Джесс не двигалась — она находится в 300 Н и на расстоянии 3 м от оси вращения с другой стороны. На каком расстоянии мешок от оси? Качели все еще сбалансированы.

1. Нам нужно нарисовать еще одну схему.
Нарисуйте обновленную схему. Расстояние от точки вращения до мешка можно обозначить как d, поэтому расстояние от точки вращения до Сэма равно 2d.

Уравновешивающие моменты

 

2. Назначение моментов направления.
В этом случае из диаграммы видно, что Сэм и мешок создают момент против часовой стрелки, тогда как Джесс создает момент по часовой стрелке.

3. Рассчитайте момент, для которого у нас есть информация.
В этом вопросе мы можем рассчитать момент Джесс. Мы знаем, что это 900 Нм из предыдущего вопроса.

4. Помните, что моменты против часовой стрелки = моменты по часовой стрелке.
Качели уравновешены, поэтому мы знаем, что моменты против часовой стрелки равны моментам по часовой стрелке.

5. Подставьте числа в уравнение.
Мы уже рассчитали момент Джесс. Мы знаем

момент против часовой стрелки = момент по часовой стрелке

Сэм + момент сумки = момент Джесс = 900
Момент Сэма = 450 x 2d = 900d
Момент мешка = 100 x d = 100d
Сэм + Момент мешка = 1000d
1000d = 900
d = 0,9

Следовательно, мы можем сказать, что мешок находится на расстоянии 0,9 м от центра оси, а Сэм — на расстоянии 1,8 м.

 

Объекты в равновесии

Метод

1. Соберите свое снаряжение. Вам понадобится балка, линейка, два ньютона метра, опора для балки и предмет, чтобы повесить на балку. Балансирующие моменты
2. Настройка оборудования. Сбалансируйте балку с помощью опор и прикрепите объект к балке.
3. Замените опоры. Когда балка придет в равновесие, замените опоры на два ньютон-метра с каждой стороны балки.
4. Найти силы. С помощью ньютонометра снимите показания сил, действующих на балку.
5. Найдите расстояния. Используя линейку, измерьте перпендикулярное расстояние каждой силы, действующей на балку.
6. Найдите моменты против и по часовой стрелке. Используя силы и расстояния, найдите моменты. Момент против часовой стрелки должен равняться моменту по часовой стрелке.

Часто задаваемые вопросы

→Что такое уравновешивающие моменты в физике?

Уравновешивающие моменты, также известные как крутящий момент, относятся к силе, которая заставляет объект вращаться вокруг фиксированной точки. В физике уравновешивающие моменты важны при рассмотрении устойчивости объекта и того, опрокинется ли он или останется в вертикальном положении.

→Какие факторы влияют на уравновешивающий момент?

Факторы, влияющие на уравновешивающие моменты, включают положение центра масс объекта, длину плеча рычага и величину приложенной силы. Более длинное плечо рычага или большее усилие создадут больший крутящий момент, из-за чего объекту будет труднее ба

→Как можно сбалансировать объект?

Вы можете сбалансировать объект, убедившись, что вес равномерно распределен, а центр масс расположен над точкой опоры. Таким образом, приложенные силы будут создавать равные и противоположные крутящие моменты, предотвращая опрокидывание объекта.

→Какова связь между силой и крутящим моментом?

Сила и крутящий момент связаны тем, что сила может создавать крутящий момент в зависимости от своего положения относительно точки, вокруг которой вращается объект. Чем больше сила, тем больший крутящий момент она создаст, и наоборот.

→Как рассчитывается крутящий момент в физике?

Крутящий момент можно рассчитать по следующей формуле: крутящий момент = усилие x плечо рычага. Плечо рычага — это расстояние от точки вращения до точки приложения силы.

→Какие примеры уравновешивания моментов есть в реальной жизни?

Примеры уравновешивающих моментов из реальной жизни включают качели, дверную петлю и вращающийся конькобежец.