формулы и примеры определения емкости

Мы все знаем об электрическом токе, проводимости и сопротивлении. Но емкость является еще одной важной частью понимания концепции электричества. Возможно, вы слышали, что ничто не может хранить электричество. Однако это не так — конденсаторы способны накапливать электрический заряд. Давайте подробнее рассмотрим концепцию конденсаторов и емкости. Начнем с конденсатора.

Конденсатор образован двумя обращенными друг к другу проводниками, между которыми вставлен диэлектрик, то есть изолирующий материал. Эти два проводника называются обкладками конденсатора.

Главной характеристикой конденсаторов является величина емкости.

Емкость конденсатора — формула

Определение

Емкость конденсатора — это ничто иное, как умение конденсатора накапливать энергию в виде электрического заряда. Другими словами, емкость — это запоминающая способность конденсатора. Измеряется емкость в фарадах.

Емкость может быть рассчитана, когда известны заряд Q и напряжение V конденсатора:

Емкость используется для описания того, сколько заряда может удерживать любой проводник.  Он представляет собой отношение заряда к приложенному потенциалу. 

Любой объект, который может быть электрически заряжен, показывает емкость. Конденсатор с двумя параллельными пластинами — это обычная форма накопителя энергии. Емкость отображается параллельным расположением пластин и определяется с точки зрения накопления заряда. Когда конденсатор заряжен полностью, между его пластинами имеется разность потенциалов, и чем больше площадь пластин и чем меньше расстояние между ними, тем больше будет заряд конденсатора и тем больше будет его Емкость.

Если конденсаторы соединены последовательно, формула емкости выражается следующим образом:

Если конденсаторы подключены параллельно, формула емкости выражается следующим образом:

Где C1, C2, C3 ……. Cn — конденсаторы, а емкость выражается в фарадах.

Примеры решения:

Пример 1

Определите емкость конденсатора, если течет 5 кулонов заряда и приложен потенциал 2 В.

Решение

Приведенные параметры

Заряд Q составляет 5 C,

Приложенное напряжение V равно 2 В.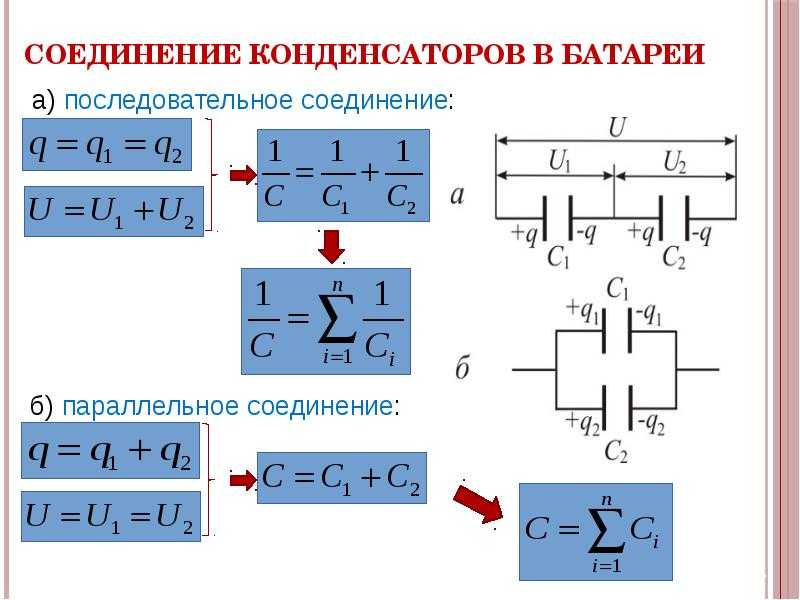

Формула емкости определяется как

C=Q/V

= 5/2

= 2,5 F

Пример 2

Определите емкость, если подключены конденсаторы 6 Ф и 5 Ф.

a) последовательно;

b) параллельно

Решение

Формула последовательной емкости определяется как

Cs = 1 / C1 + 1 / C2

= C1 + C2 / C1C2

= 6 + 5/30

Cs = 0,367 F

Емкость в параллельной формуле определяется как

Ср = С1 + С2

= 6 + 5

Cp = 11 F

Различают три вида конденсаторов:

1. Конденсатор плоский;
2. Конденсатор цилиндрический
3. Конденсатор сферический.

Конденсатор плоский

Данный конденсатор образован двумя металлическими пластинами, которые мы называем A и B, расположенными на расстоянии d.

Две проводящие пластины A и B являются пластинами конденсатора, d — их расстояние, более того, поскольку две пластины параллельны, их поверхности равны.

Мы знаем, что внутри двух поверхностей электрическое поле однородно, а снаружи равно нулю

Рассчитываем разность потенциалов между двумя пластинами

Как только разность потенциалов известна, мы можем рассчитать емкость плоского конденсатора.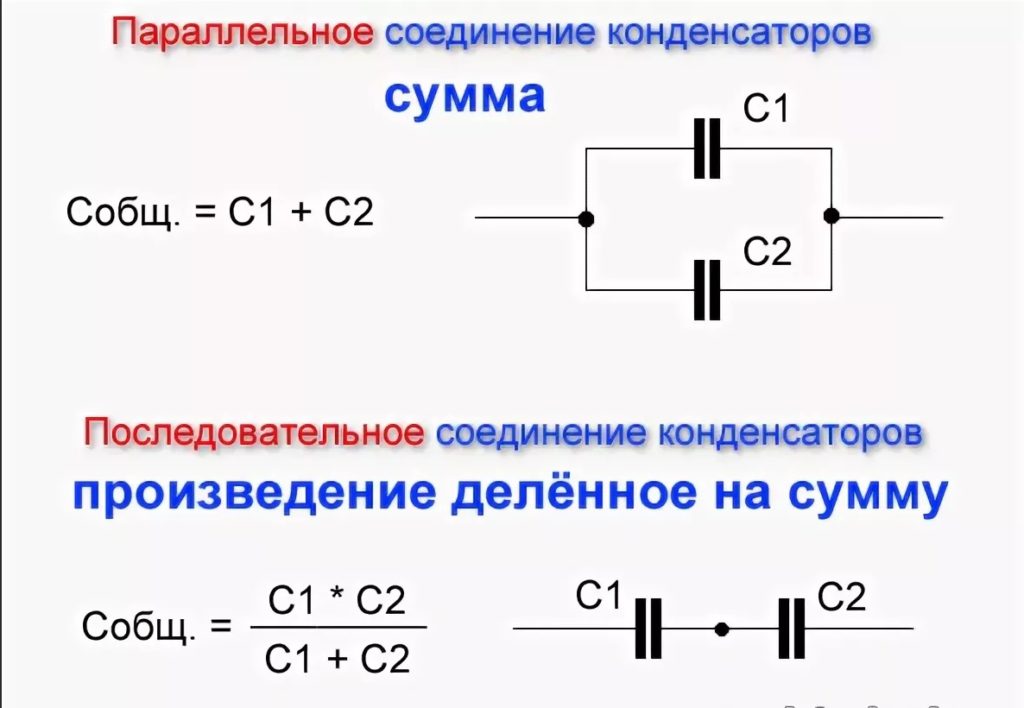

Заменим найденную ранее разность потенциалов

Конденсатор цилиндрический

Конденсатор используется для хранения большого количества электрического тока в небольшом пространстве. Цилиндрический конденсатор включает полый или сплошной цилиндрический проводник, окруженный концентрическим полым сферическим цилиндром. Конденсаторы широко используются в электродвигателях, мельницах, электрических соковыжималках и других электрических инструментах. Разность потенциалов между конденсаторами различна. Существует множество электрических цепей, в которых конденсаторы должны быть сгруппированы соответствующим образом, чтобы получить желаемую емкость. Есть два общих режима, включая конденсаторы, включенные последовательно, и конденсаторы, подключенные параллельно. Единица измерения емкости — Фарад (Ф).

Его часто используют для хранения электрического заряда. Цилиндрический конденсатор — это тип конденсатора, который имеет форму цилиндра, имеющую внутренний радиус как a и внешний радиус как b.

Формула для цилиндрического конденсатора:

C = емкость цилиндра
L = длина цилиндра
a = внутренний радиус цилиндра,
b = внешний радиус
εₒ= диэлектрическая проницаемость свободного пространства (8.85×10ˉ¹²)

Пример

Цилиндрический конденсатор длиной 8 см состоит из двух колец с внутренним радиусом 3 см и внешним радиусом 6 см. Найдите емкость конденсатора.

Дано:

Длина L = 8 см

внутренний радиус a = 3 см

внешний радиус b = 6 см

Решение

Формула для конденсатора цилиндрического:

Конденсатор сферический

Данный конденсатор состоит из сплошного или полого сферического проводника, окруженного другой полой концентрической сферической формой другого радиуса.

Формула для определения емкости сферического конденсатора

Где,

C = емкость

Q = заряд

V = напряжение

r ₁ = внутренний радиус

r ₂ = внешний радиус

ε ₀ = диэлектрический потенциал (8,85 x ^10-12 Ф / м)

Значение емкости двух разных конденсаторов может быть одинаковым, а номинальное напряжение двух конденсаторов может быть разным.  Возьмем два конденсатора — один с малым номинальным напряжением, а другой с высоким. Если мы заменим конденсатор с меньшим номинальным напряжением на конденсатор с более высоким номинальным напряжением, то получится конденсатор меньшего размера. Это может произойти из-за неожиданного повышения напряжения.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Влияние диэлектрика на емкость

Плотности поверхностного заряда равны σ _p  и — σ _p. Когда мы полностью помещаем диэлектрик между двумя пластинами конденсатора, его диэлектрическая проницаемость увеличивается по сравнению с вакуумным значением.

Внутри конденсатора следующее электрическое поле:

Следовательно, мы имеем:

а именно:

Ɛ — диэлектрическая проницаемость. Разность потенциалов между пластинами задаются

Для линейных диэлектриков:

Где k — диэлектрическая проницаемость вещества, K = 1.

Электрическое поле между пластинами конденсатора прямо пропорционально емкости конденсатора. Напряжение электрического поля снижается из-за наличия диэлектрика. Если общий заряд на пластинах поддерживается постоянным, то уменьшается разность потенциалов на пластинах конденсатора. Таким образом, диэлектрик увеличивает емкость конденсатора.

Электроемкость. Емкость конденсатора

Главная → Примеры решения задач ТОЭ → Электроемкость. Емкость конденсатора

Электроемкость. Емкость конденсатора

Основные положения и соотношения

1. Закон Кулона

F=Q1⋅Q24π⋅εa⋅R2,  (1)

здесь

F — сила взаимодействия между зарядами;

Q₁ и Q₂ — точечные заряды;

R — расстояние между ними;

ε_a — абсолютная диэлектрическая проницаемость среды, равная ε₀·ε_r;

ε_r — относительная диэлектрическая проницаемость;

ε0=14π⋅с2⋅10−7≈8,85418782⋅10−12  Фм  – электрическая постоянная.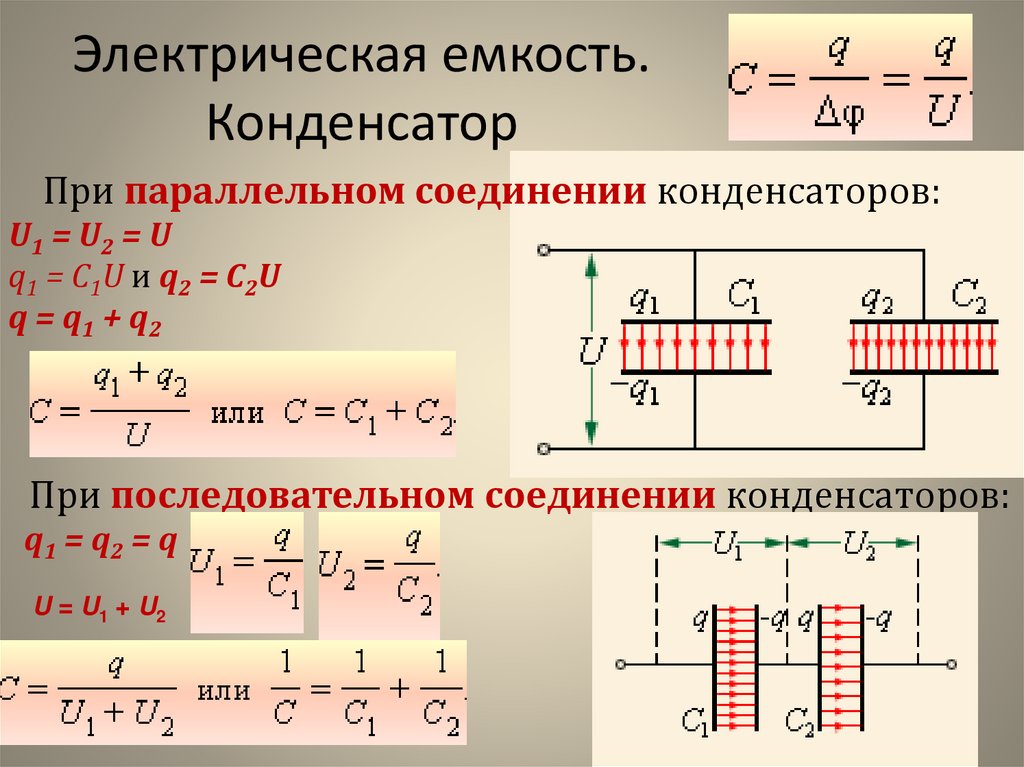

2. Напряженность электростатического поля точечного заряда Q

на расстоянии R от него

E=Q4π⋅εa⋅R2.  (2)

Напряженность поля в любой точке между пластинами плоского конденсатора вдалеке от краев

E=Ud,  (3)

здесь d — расстояние между пластинами конденсатора, U — напряжение.

Напряженность поля в точке, отстоящей на расстоянии r от бесконечно длинной заряженной оси с линейной плотностью τ

E=τ2π⋅εa⋅r.  (4)

Напряженность поля в точке, отстоящей на расстоянии r от оси цилиндрического конденсатора (r₁ <r < r₂)

E=Ur⋅lnr2r1,  (5)

здесь U — напряжение конденсатора, r

1 и r₂ — соответственно внутренний и внешний радиусы конденсатора.

Напряженность поля в точке, отстоящей на расстоянии R от центра сферического конденсатора (R₁ < R < R₂)

E=U⋅R1⋅R2R2⋅(R2−R1),  (6)

здесь U — напряжение конденсатора, R₁ и R₂ — соответственно внутренний и внешний радиусы конденсатора.

3. Вектор электрического смещения

D→=εa⋅E→.  (7)

4. Общее выражение емкости конденсатора

C=QU.  (8)

Емкость плоского конденсатора

C=εa⋅Sd=εr⋅ε0⋅Sd,  (9)

здесь S — поверхность каждой пластины конденсатора; d — расстояние между ними.
Скачать статью Вывод формулы емкости плоского конденсатора

Емкость цилиндрического конденсатора

C=2π⋅εa⋅llnr2r1,  (10)

здесь l — длина конденсатора, r₁ и r₂ — соответственно внутренний и внешний радиусы конденсатора.
Скачать статью Вывод формулы емкости коаксиального кабеля

Емкость сферического конденсатора

C=4π⋅εa⋅R1⋅R2R2−R1,  (11)

здесь R₁ и R₂ — соответственно внутренний и внешний радиусы конденсатора.
Скачать статью Вывод формулы емкости сферического конденсатора

Емкость двухпроводной линии

C=π⋅εa⋅lln[D2a+(D2a)2−1],  (12)

здесь l — длина линии, D — расстояние между осями проводов, a — радиус проводов.

Емкость однопроводной линии

C=2π⋅εa⋅lln[ha+(ha)2−1],  (13)

здесь

l — длина линии, h — высота подвеса провода над землей, a — радиус провода.

5. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

C=C1+C2+…+Cn=∑k=1nCk.  (14)

При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

1C=1C1+1C2+…+1Cn=∑k=1n1Ck.  (15)

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет

C=C1⋅C2C1+C2,  (16)

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям

U1=U⋅C2C1+C2;   U2=U⋅C1C1+C2.  (17)

6. Энергия электростатического поля конденсатора

W=C⋅U22=Q⋅U2=Q22C.  (18)

Удельная энергия электростатического поля (на единицу объема диэлектрика) выражается следующим образом

w=dWdV=E⋅D2=εa⋅E22.  (19)

Общая величина энергии электростатического поля выражается интегралом величины удельной энергии по всему объему диэлектрика конденсатора

W=∫Vεa⋅E22dV.  (20)

7. Расчет распределения зарядов в сложных цепях, содержащих источники э. д. с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

ΣQ=ΣQ′.  (21)

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:

∑k=1nEk=∑k=1nUC k=∑k=1nQkCk.  (22)

---

Упражнения и задачи

Задача 1.

Имеется конденсатор переменной емкости от 500 до 1500 пФ. Указать, какой добавочный конденсатор с минимальным диапазоном переменной емкости следует взять и как его включить, чтобы эквивалентная емкость изменялась от 100 до 250 пФ.

Ответ: 125 — 300 пФ, включить параллельно.

---

Задача 2. Емкость плоского конденсатора, имеющего слюдяной диэлектрик, равна 44,3 пФ. Площадь каждой пластины конденсатора составляет 25 см², расстояние между пластинами равно 3 мм.

Чему равна относительная диэлектрическая проницаемость слюды? Принимая пробивное напряжение слюды равным 80 кВ/мм, определить, при каком максимальном напряжении может работать этот конденсатор, чтобы он имел трехкратный запас прочности.

Начертить график изменения потенциала между пластинами конденсатора.

Ответ: ε_r = 6; U_max = 80 кВ; график падения потенциала вычерчивается по уравнению φ = U·(1 — x/d), здесь U — потенциал положительно заряженной обкладки, принятый равным напряжению конденсатора, d — расстояние между пластинами, x — переменное расстояние до положительной обкладки конденсатора.

---

Задача 3. Доказать, что многопластинчатый конденсатор (рис. 1), состоящий из n одинаковых пластин, площадью S каждая, с рас стоянием между двумя соседними пластинами d, с диэлектриком, абсолютная диэлектрическая проницаемость которого ε, имеет емкость, равную

C=εa⋅S⋅(n−1)d.

Рис. 1

Подсчитать, сколько надо взять листов станиоля, каждый площадью S = 40 см², чтобы получить многопластинчатый конденсатор емкостью 0,5 мкФ при условии, что диэлектриком является парафинированная бумага (ε_r = 1,8) толщиною 0,05 мм.

Ответ: 393 листа.

---

Задача 4. Плоский слоистый конденсатор (рис. 2), поверхность каждой пластины которого S = 12 см², имеет диэлектрик, состоящий из слюды (ε_r1 = 6) толщиною d₁ = 0,3 мм и стекла (ε_r2 = 7) толщиною d₂ =0,4 мм.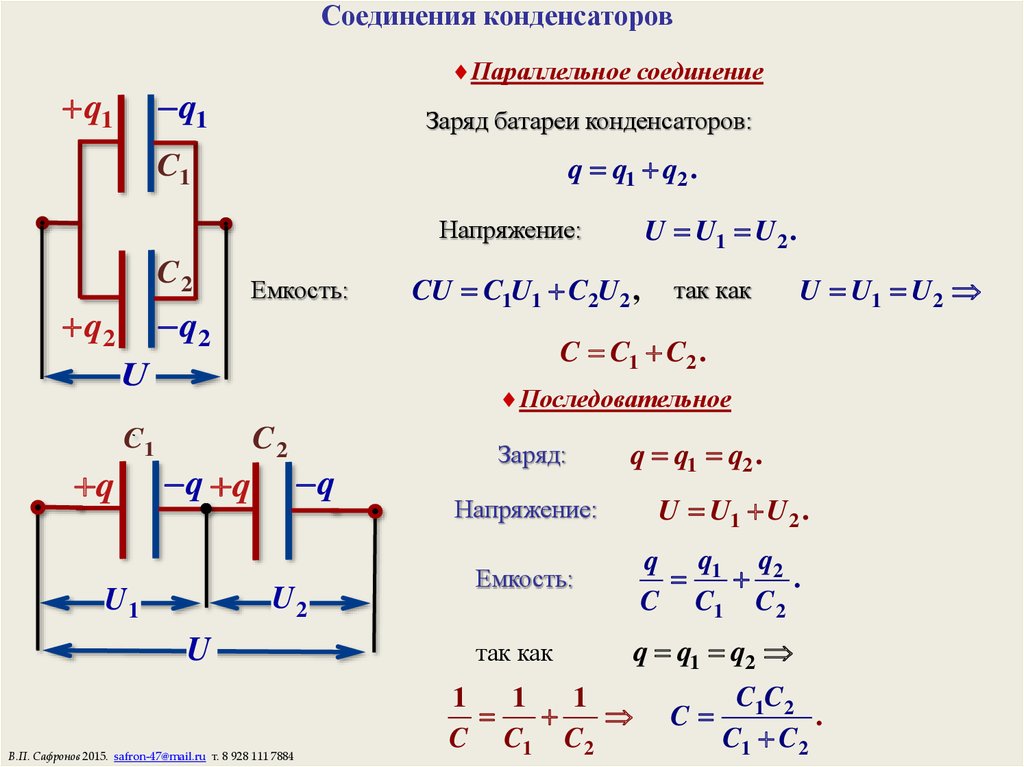

Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

Рис. 2

Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.

Решение

Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов

C=C1⋅C2C1+C2=εa1⋅Sd1⋅εa2⋅Sd2εa1⋅Sd1+εa2⋅Sd2=εa1⋅εa2⋅Sεa1⋅d2+εa2⋅d1.

Подставляя сюда числовые значения, предварительно заменив ε_a1 = ε₀ε_r1 и ε_a2 = ε₀ε_r2, получим

C=ε0⋅εr1⋅εr2⋅Sεr1⋅d2+εr2⋅d1=8,85⋅10−12⋅6⋅7⋅12⋅10−46⋅0,4⋅10−3+7⋅0,3⋅10−3=99⋅10−12  Ф.

Обозначим общее напряжение, подключаемое к слоистому конденсатору, через

U_пр, при этом заряд конденсатора будет равен

Q = C·U_пр.

Напряжения на каждом слое будут равны

U1=QC1=C⋅Uпрεa1⋅Sd1=εa2⋅d1εa1⋅d2+εa2⋅d1⋅Uпр;U2=QC2=C⋅Uпрεa2⋅Sd2=εa1⋅d2εa1⋅d2+εa2⋅d1⋅Uпр.

Напряженности электростатического поля в каждом слое

E1=U1d1=εa2εa1⋅d2+εa2⋅d1⋅U′пр;E2=U2d2=εa1εa1⋅d2+εa2⋅d1⋅U″пр.

Здесь U’_np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U»_np — общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

U′пр=E1⋅εa1⋅d2+εa2⋅d1εa2=49,5  кВ;U″пр=E2⋅εa1⋅d2+εa2⋅d1εa1=27,0  кВ.

Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

27,0 кВ / 2 = 13,5 кВ.

---

Задача 5. Вычислить емкость 1 км коаксиального кабеля типа 2,6/9,4. В этом кабеле изоляция осуществлена с помощью полиэтиленовых шайб (ε_r = 2,2) толщиною a = 2,2 мм, размещенных через равные промежутки b = 25 мм, остальное пространство между шайбами заполнено воздухом (рис. 3). Диаметр жилы d = 2,6 мм, внутренний диаметр наружного провода D = 9,4 мм.

Рис. 3

Указание. Емкость кабеля может быть подсчитана, исходя из того, что отдельные его участки соединены параллельно.

Ответ: 48·10^–9 Ф/км = 48 нФ/км.

---

Задача 6. Силовой одножильный кабель с резиновой изоляцией в свинцовой оболочке марки СРГ имеет сечение жилы 25 мм². Известно, что наибольшая напряженность электростатического поля в изоляции кабеля не должна превышать 6 кВ/мм. Определить толщину слоя резиновой изоляции, если при испытании кабеля между жилой и оболочкой включают напряжение, равное 10 кВ.

Принимая потенциал жилы кабеля равным U = 10 кВ, построить график падения потенциала в диэлектрике кабеля в зависимости от расстояния до центра кабеля.

Ответ: 2,25 мм. График строится по уравнению φ(r)=U⋅lnr2rlnr2r1.

---

Задача 7. Цилиндрический конденсатор длиною l = 5 см имеет двухслойный диэлектрик (рис. 4).

Рис. 4

Внутренний радиус r₁ = 1 см, внешний — r₂ = 3 см, радиус разграничения слоев диэлектриков r₃ = 1.5 см. Относительные диэлектрические проницаемости: внутреннего слоя изоляции ε_r1 = 2, наружного ε_r2 = 4.

Вычислить емкость конденсатора и начертить кривые изменения напряженностей и потенциалов в каждом из слоев, если конденсатор находится под напряжением U = 2 кВ.

Указание. При помощи теоремы Гаусса находятся напряженности электростатического поля в каждом из слоев

E1=τ2π⋅εa1⋅r;   E2=τ2π⋅εa2⋅r,

где τ — линейная плотность заряда (заряд на единицу длины конденсатора). Затем вычисляется напряжение между обкладками конденсатора по формуле

U=∫r1r3E1dr+∫r3r2E2dr.

Отсюда определяется линейная плотность заряда

τ=2π⋅U1εa1lnr3r1+1εa2lnr2r3.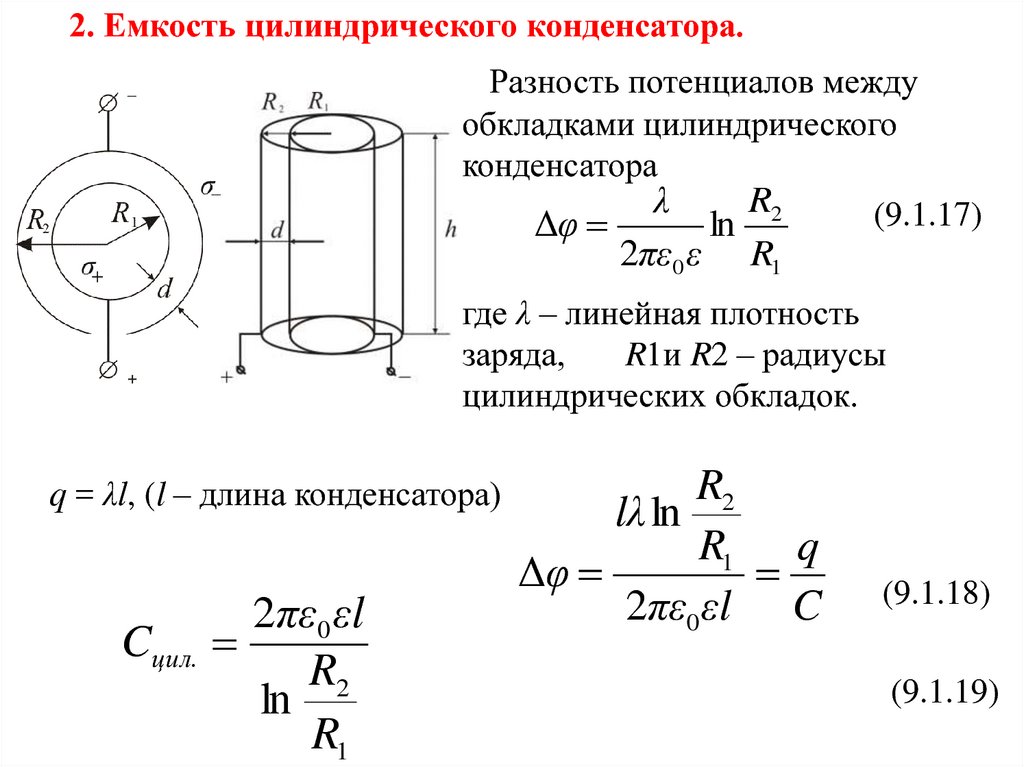

Емкость конденсатора вычисляется по формуле (8). Потенциал φ₁ в любой точке области первого слоя диэлектрика (r₃ > r > r₁) определяется из выражения

φr1−φ1=∫r1rE1dr,

а потенциал φ₂ в любой точке области второго слоя (r₂ > r > r₃) диэлектрика вычисляется из выражения

φr2−φ2=∫r2rE2dr.

В последних формулах φ_r1 = U — потенциал внутренней обкладки конденсатора, φ_r2 — потенциал на границе раздела диэлектриков. Внешняя оболочка заземлена: φ₂(r₂) = 0.

Ответ:

C=2π⋅l1εa1lnr3r1+1εa2lnr2r3;E1(r)=Ur⋅(lnr3r1+εa1εa2lnr2r3);   E2(r)=Ur⋅(εa2εa1lnr3r1+lnr2r3);φ1(r)=U⋅(1−lnrr1lnr3r1+εa1εa2lnr2r3);    φ2(r)=U⋅εa1εa2lnr2rlnr3r1+εa1εa2lnr2r3.

Пример вывода формулы емкости двухслойного цилиндрического конденсатора при помощи теоремы Гаусса

---

Задача 8. Чему равен внешний радиус сферического конденсатора емкостью 20 пФ, внутренний радиус которого 2 см. а относительная Диэлектрическая проницаемость изоляции ε_r = 3. При каком напряжении конденсатор будет пробит, если пробивное напряжение изоляции равно 15 кВ/мм?

Ответ: 3 см, 100 кВ.

---

Задача 9. Найти емкость сферического конденсатора, изображенного на рис. 5.

Рис. 5

Даны радиусы R₁, R₂ и R₃; изоляция однородная, ее абсолютная диэлектрическая проницаемость равна ε.

Указание. Данный конденсатор может быть рассмотрен как два Параллельно соединенных конденсатора.

Ответ: C=4π⋅εa⋅R22⋅(R3−R1)(R3−R2)(R2−R1).

---

Задача 10. К пластинам плоского двухслойного конденсатора приложено напряжение 3 кВ. Площадь пластины равна 5 см². Толщины первого и второго слоев конденсатора равны соответственно 4 и 6 мм, а диэлектрические проницаемости — 6 и 1.

Построить графики изменения напряженности и потенциала между пластинами в зависимости от расстояния до положительной пластины, потенциал которой принять равным + 3 кв.

---

Задача 11. Имеется два одинаковых конденсатора переменной емкости. Емкость каждого конденсатора можно плавно изменять от 20 до 200 пФ.

Какие границы изменения емкости можно получить при различном соединении этих конденсаторов между собой?

Ответ: от 10 до 400 пФ.

---

Задача 12. Определить емкость воздушной двухпроводной линии длиной 2 км, если диаметр проводов равен 3 мм и расстояние между осями проводов составляет 30 см.

---

Задача 13. Определить емкость однопроводной телеграфной линии длиною 180 км, если диаметр провода равен 3 мм, а средняя высота подвеса провода над землей составляет 7 м.

Начертить кривую зависимости емкости этого провода в функции расстояния от земли.

Ответ: 1,1 мкФ.

---

Задача 14. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d₁ = 1 см друг от друга. Площадь обкладок S = 50 см². Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.

Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.

Решение

Энергия заряженного плоского конденсатора равна

W1=C1⋅U22=ε0⋅Sd1⋅U22,

где С₁ — емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения

Q = C₂·U₂,

где C₂ — емкость конденсатора после раздвижения обкладок, следует, что, так как C2=ε0⋅Sd2  стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d₂ будет больше первоначальной

W2=ε0⋅Sd2⋅U222=ε0⋅S10d1⋅(10U)22=10⋅ε0⋅Sd1⋅U22=10⋅W1.

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

W2−W1=9⋅W1=9⋅ε0⋅Sd1⋅U22=2,86⋅10−7  Дж.

---

Задача 15. Плоский конденсатор с воздушным диэлектриком заряжается от источника электрической энергии с напряжением U.

Определить, как изменится энергия конденсатора, если после отключения его от источника энергии расстояние между обкладками увеличить вдвое.

Ответ: энергия увеличится в два раза.

---

Задача 16. Плоский конденсатор с диэлектриком из эбонита (ε_r = 2,5) в виде пластинки толщиной d = 5 см присоединен к полюсам батареи. После зарядки эбонитовая пластинка вынимается.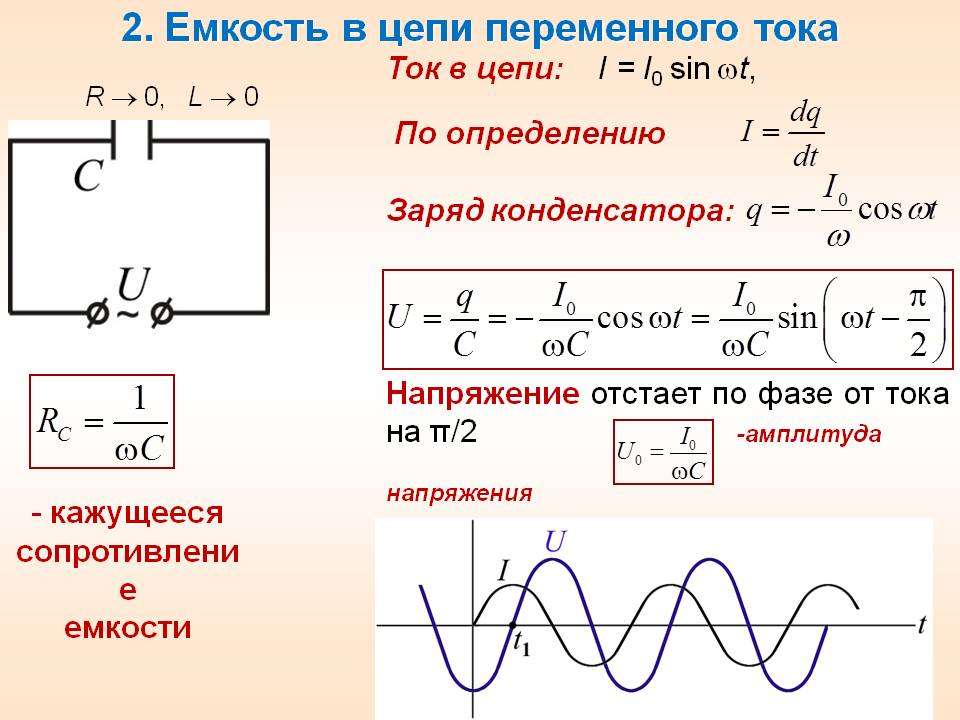 Как нужно изменить расстояние между обкладками конденсатора, чтобы энергия конденсатора осталась без изменения?

Задачу решить в двух случаях: 1) если конденсатор остается присоединенным к батарее и 2) если конденсатор отключить от батареи.

Ответ: в обоих случаях пластины должны отстоять друг от друга на расстоянии 2 см.

---

Задача 17. Конденсатор емкостью C₁ = 40 мкФ заряжен от сети до напряжения U₁ = 220 В; другой конденсатор емкостью C₂ = 10 мкФ заряжен от другой сети до напряжения U₂ = 110 В.

Положительные зажимы конденсаторов после отсоединения от источников соединяются вместе:

а) Чему равна разность потенциалов между отрицательными зажимами конденсаторов?

б) Чему равны заряды до и после последующего соединения друг с другом отрицательных зажимов конденсаторов?

в) Чему равны напряжения на конденсаторах после соединения их отрицательных зажимов?

г) Чему равна энергия каждого конденсатора до. и после соединения отрицательных зажимов?

Ответ: а) 110 В, б) до соединения: Q₁ = 8800 мкКл, Q₂ = 1100 мкКл; после соединения: Q′₁ = 7920 мкКл, Q′₂ = 1980 мкКл, в) 198 В, г) до соединения: W₁ = 0,97 Дж, W₂ = 0,06 Дж; после соединения: W′₁ = 0,784 Дж, W′₂ = 0,196 Дж.

---

Задача 18. Три последовательно соединенных конденсатора, емкости которых 2, 10 и 15 мкФ, заряжаются от сети с напряжением 120 В. После отключения от сети конденсаторы разъединяются друг от друга без потери заряда. Если затем конденсаторы соединить параллельно, то чему будет равно напряжение на их зажимах?

Ответ: 20 В.

---

Список литературы

1. Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле. — М.: Гардарики, 2001.– 317 с.

2. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники: в 3-х тт.: Учебник для вузов. Том 3. –4-е изд. — СПб.: Питер, 2003. — 377 с.

3. Купалян С.Д. Теоретические основы электротехники / Под ред. Г.И. Атабекова. — М.-Л.: Госэнергоиздат, 1963. — ч. 3. Электромагнитное поле. — 112 с.

4. Теоретические основы электротехники. т. 2. Нелинейные цепи и основы теории электромагнитного поля. Под ред. П.А. Ионкина. Учебник для электротехн. вузов. Изд. 2-е, перераб. и доп. — М.: Высш. шк., 1976. — 383 с.

5. Поливанов, К.М. Теоретические основы электротехники: в 3-х ч. / К.М. Поливанов. ч. 3: Теория электромагнитного поля. — М.: Энергия, 1969. — 352 с.

6. Бессонов Л.А. Сборник задач по теоретическим основам электротехники: Учебное пособие для вузов / Бессонов Л.А., Демидова И.Г. и др.; Под ред. Л.А. Бессонова. — М., Высшая школа, 2000. — 528с.: ил.

7. Колли Я.Н. и др. Задачник по теоретическим основам электротехники (теория поля). Уч. пособие для вузов. Под ред. Поливанова К.М. — М., «Энергия», 1972.

8. Ионкин П.А. Сборник задач и упражнений по теоретическим основам электротехники: Учебное пособие. — М., Энергоиздат, 1982. — 768с.

9. Татур Т.А. Основы теории электромагнитного поля: Справочное пособие. — М.: Высш. шк., 1989 . — 270 с.

электрическая постоянная, емкость конденсатора, электроемкость, емкость плоского конденсатора, емкость цилиндрического конденсатора, сферический конденсатор, емкость двухпроводной линии, емкость однопроводной линии, емкость коаксиального кабеля

домашнее задание и упражнения — Уравнение емкости конденсатора

спросил 1 год, 4 месяца назад

Изменено 1 год, 4 месяца назад

Просмотрено 898 раз

$\begingroup$

Представьте себе две клеммы плоского конденсатора подключены к двум выводам батареи с разностью электрических потенциалов $V$. Если емкость конденсатора $C$, а площадь каждой пластины $A$, то как я могу выразить заряд, накопленный на каждой пластине ($\pm Q$), только через $C$, $V $ и $А$?

Моя попытка:

Мы знаем, что напряжение на конденсаторе равно $V=\frac{Qd}{\epsilon A}$, где $d$ — расстояние между пластинами (поскольку имеется только один конденсатор подключен к батарее электрического потенциала $V$), а емкость равна $C=\frac{\epsilon A}{d}$. Мы можем изменить это, чтобы получить $d=\frac{\epsilon A}{C}$; затем подставив его в первое уравнение, мы получим: $V=\frac{Q}{\epsilon A}\cdot \frac{\epsilon A}{C}= \frac{Q}{C}$, так что накопленный заряд это $Q=CV$. К сожалению, это элементарная формула, которая связывает только $C$ и $V$ с $Q$, но не с площадью пластин $A$.

Мне нужна формула, связывающая $C$, $V$ и $A$ с $Q$.

• домашние задания и упражнения
• электростатика
• заряд
• напряжение
• емкость

$\endgroup$

0

$\begingroup$

Ответ: $$Q(C,V,A)=CV,$$, вот почему у вас проблемы.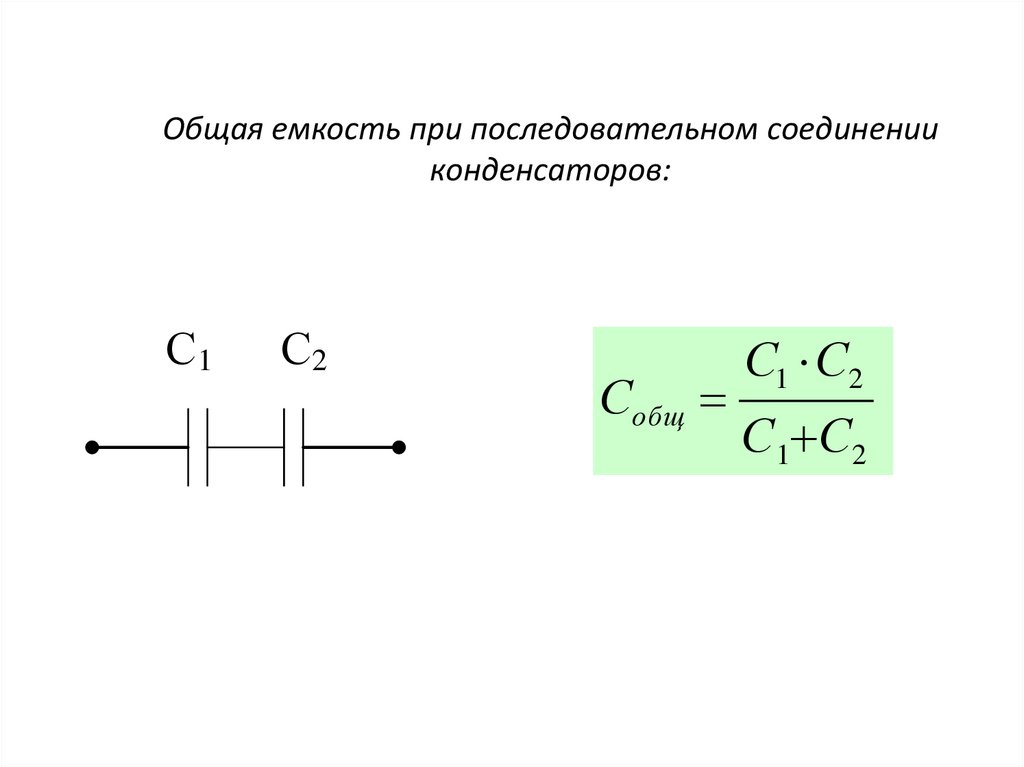

Это похоже на уравнение для горизонтальной линии: $$y=f(x)=2$$

В уравнении нет $x$.

$\endgroup$

$\begingroup$

Отдельные величины в $\frac d {\epsilon A}$ могут свободно изменяться, пока общая величина остается неизменной. Например, если вы удвоите и расстояние, и площадь, то $\frac d {\epsilon A}$ останется постоянной, и, таким образом, $Q$, $V$ и $C$ могут остаться постоянными. Это показывает, что вы можете иметь два разных конденсатора с одинаковыми $Q,V,C$, но с разными $A$. 90$, если хотите. Если вы выполняли логарифмическую линейную регрессию для $\log Q = \beta_1\log C+\beta_2\log V+\beta_3 \log A$, вы обнаружите, что $\beta_3=0$. Это значение $\beta$. Никакая дальнейшая перестановка терминов не приведет к получению другого $\beta$. Это единственный правильный ответ. Величина влияния $A$ на $Q$ после учета $C$ и $V$ равна нулю.

$\endgroup$

2

$\begingroup$

В вопросе есть формула: $Q=CV$ (справедливая для любого конденсатора, а не только для конденсатора с параллельными пластинами).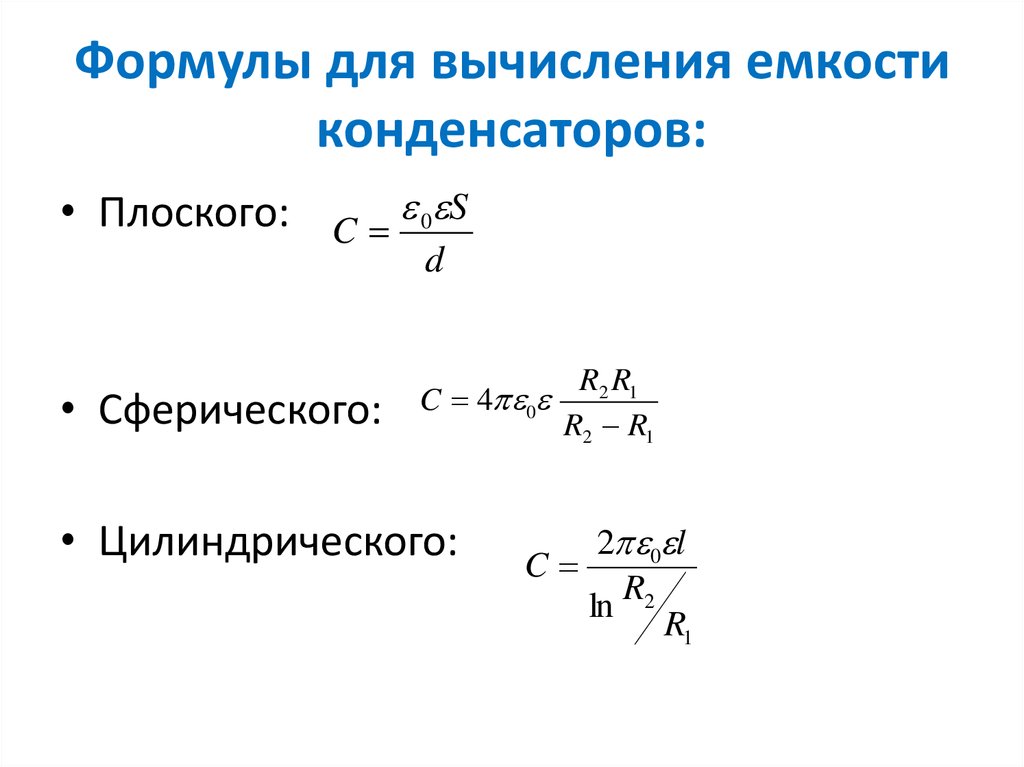 Невозможно включить какую-либо дополнительную зависимость от площади пластин $A$, потому что, как только вы знаете $C$ и $V$, $Q$ уже полностью определено. Таким образом, при записи в виде функции от $C$, $V$ и $A$ зависимость $Q(C,V,A)=CV$ от $A$ тривиальна.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Что такое емкость | Определение и формула

Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.

Определение: Емкость – это свойство, противодействующее любому изменению напряжения. Конденсатор — это устройство, временно хранящее электрический заряд.

Конденсатор принимает или возвращает этот заряд для поддержания постоянного напряжения. Схематические символы, используемые для обозначения конденсатора, показаны на рис. 1 .

Рисунок 1. Схематические обозначения конденсатора.

Конденсатор изготовлен из двух пластин из проводящего материала, разделенных изоляцией. Эта изоляция называется диэлектриком, Рисунок 2 .

 На рисунке пластины подключены к источнику постоянного напряжения. Цепь выглядит разомкнутой, потому что пластины не соприкасаются друг с другом. Однако счетчик в цепи будет показывать некоторый ток в течение короткого периода времени после замыкания переключателя.

Рисунок 2. Основная форма конденсатора.

В Рисунок 3 , когда переключатель замкнут, электроны с отрицательной клеммы источника перетекают на одну пластину конденсатора. Эти электроны отталкивают электроны от второй пластины (как отталкиваются заряды), которые затем притягиваются к положительному выводу источника. Конденсатор теперь заряжен до того же потенциала, что и источник, и противостоит напряжению источника.

Если конденсатор удалить из цепи, он останется заряженным. Энергия накапливается в электрическом поле конденсатора. Как только конденсатор полностью зарядится, ток в цепи перестанет течь.

Рис. 3. Конденсатор заряжается до напряжения источника.

Важно помнить, что в схеме на рис. 3 через конденсатор не проходят электроны. Это связано с тем, что конденсатор блокирует постоянный ток. Однако одна пластина стала отрицательно заряженной, а другая положительно заряженной. Между ними существует сильное электрическое поле.

Изоляционные или диэлектрические материалы различаются по своей способности поддерживать электрическое поле. Эта способность известна как диэлектрическая проницаемость материала.

 Константы различных материалов показаны на рис. 4 . Эти цифры основаны на сравнении с диэлектрической проницаемостью сухого воздуха. Константа для сухого воздуха была установлена ​​как 1.

Рисунок 4. Диэлектрические постоянные. Большие числа лучше способны поддерживать электрические поля.

Рабочее напряжение конденсатора

Диэлектрики, используемые для конденсаторов, могут выдерживать только определенные напряжения. Если это напряжение будет превышено, диэлектрик разрушится и возникнет дуга. Это максимальное напряжение известно как рабочее напряжение (ВВ).

Превышение рабочего напряжения может вызвать короткое замыкание и вывести из строя другие части цепи, соединенные с диэлектриком.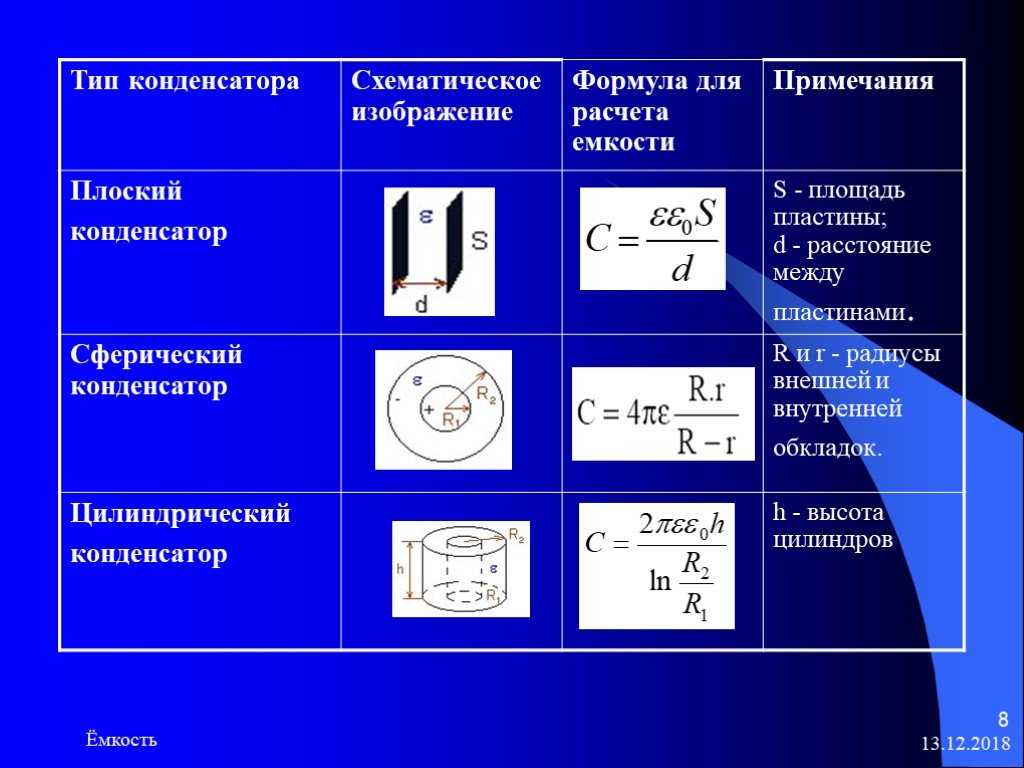

Для повышенных номинальных напряжений требуются специальные материалы и более толстые диэлектрики. При замене конденсатора проверьте его емкость и рабочее напряжение постоянного тока.

Когда конденсатор используется в цепи переменного тока, рабочее напряжение должно безопасно превышать пиковое напряжение переменного тока. Например, эффективное переменное напряжение 120 В имеет пиковое напряжение 120 В × 1,414 = 169.7 вольт. Любые используемые конденсаторы должны выдерживать напряжение 169,7 вольт.

Формула расчета емкости

Емкость определяется количеством электронов, которые могут храниться в конденсаторе на каждый вольт приложенного напряжения. Емкость измеряется в фарадах (Ф). Фарад представляет собой заряд в один кулон, повышающий потенциал на один вольт. Это уравнение записывается так:

\[C=\frac{Q}{E}\]

Где C — емкость в фарадах, Q — заряд в кулонах, а E — напряжение в вольтах.

Емкость конденсаторов, используемых в электронике, измеряется в микрофарадах (1/1 000 000 Ф) и пикофарадах (1/1 000 000 от 1/1 000 000 Ф).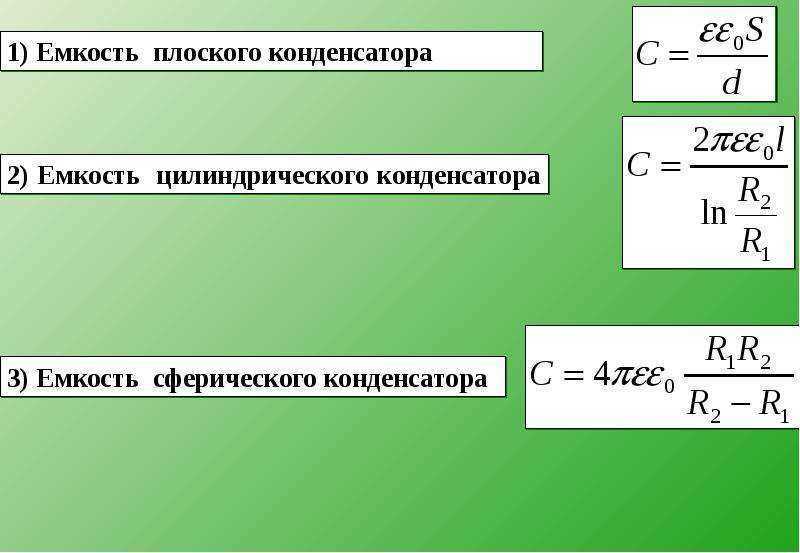 Микрофарада обычно записывается как мкФ или иногда записывается как мкФ. Пикофарад записывается как пФ. Нанофарад не является обычным измерением емкости.

Таблица преобразования этих единиц показана на рис. 5 .

Рисунок 5. Префиксы, используемые с фарадами. Обратите особое внимание на то, что префикс nano отсутствует. Нанофарад не является стандартным номиналом для конденсатора.

Емкость определяется:

• Материалом, используемым в качестве диэлектрика. (Чем больше диэлектрическая проницаемость, тем больше емкость.)
• Площадь пластин. (Чем больше площадь пластины, тем больше емкость.)
• Расстояние между пластинами. (Чем меньше расстояние, тем больше емкость.)
• Эти коэффициенты связаны математической формулой:

\[C=0,225\times \frac{KA\left( n-1 \right)}{d} \]

Где C — емкость в пикофарадах, K — диэлектрическая проницаемость, A — площадь одной стороны одной пластины в квадратных дюймах, d — расстояние между пластинами в дюймах, n — количество пластин.