Коефіцієнт тертя — Вікіпедія

Матеріал з Вікіпедії — вільної енциклопедії.

Схема дії сил при терті ковзання: W — сила притискання (наприклад, сила ваги), N — нормальна сила реакції опори, F — прикладена сила, що заставляє тіло ковзати по поверхні, F_f — сила тертя ковзання.

Коефіціє́нт тертя́ — це величина, що характеризує силу опору від тертя між взаємодіючими тілами і зазвичай позначається μ, k або f. У залежності від виду тертя відрізняють і відповідний коефіцієнт тертя.

Коефіцієнт тертя — характеристика, яка застосовується при виконанні технічних розрахунків, що характеризують фрикційні взаємодії двох тіл. У залежності від виду переміщення одного тіла по іншому розрізняють: коефіцієнт тертя при зсуві — ковзання і коефіцієнт тертя при коченні. У свою чергу, при ковзанні залежно від величини тангенціальної сили розрізняють коефіцієнт неповного тертя ковзання, коефіцієнт тертя спокою і коефіцієнт тертя ковзання. Всі ці коефіцієнти тертя можуть змінюватися в широких межах залежно від шорсткості і хвилястості поверхонь, характеру плівок, що покривають поверхні.

Коефіціє́нт тертя́ ковзання — відношення сили тертя ковзання Ff{\displaystyle F_{f}} до нормальної сили N, що притискує тіла одне до одного^[1].

Перші наукові міркування на тему тертя твердих тіл були виявлені в записах Леонардо да Вінчі. У них багато правильних тверджень, підкріплених розрахунками, наприклад, вказано на пропорційність опору тертя навантаженню на поверхні тіл, що труться і на те, що тіла з шорсткою поверхнею мають більший опір тертя. Таким чином, закон, згідно з яким сила тертя прямо пропорційна навантаженню, тобто

Ff=μ⋅N{\displaystyle F_{f}=\mu \cdot N}

був відкритий Леонардо да Вінчі, який вважав, що коефіцієнт тертя зазвичай дорівнює 0,25.

У 1699 році оригінальні роботи на тему тертя в щорічниках Французької королівської академії наук опублікував Г. Амонтон. Він знову відкрив забутий закон тертя Леонардо да Вінчі: сила тертя пропорційна навантаженню на поверхні, що труться, не залежить від розмірів тіл, а коефіцієнт тертя не змінюється і є рівним 0,3.

Вперше поняття про коефіцієнт тертя застосував Леонардо да Вінчі, пізніше Г. Амонтон, запропонувавши формулу

μ=FfN{\displaystyle \mu ={\frac {F_{f}}{N}}}

Інколи цю формулу помилково називають законом Кулона. Кулон запропонував абсолютно іншу формулу

f=k+A0N,{\displaystyle f=k+{\frac {{\mathrm {A} }_{0}}{N}},}

де k — коефіцієнт, залежний від властивостей поверхонь тіл; A0{\displaystyle {{\mathrm {A} }_{0}}} — коефіцієнт зчеплення цих поверхонь.

Під поверхнею тертя розуміють номінальну поверхню твердого тіла, на якій здійснюється взаємодія твердих тіл при зовнішньому терті. Визначення сил і коефіцієнтів тертя має великий практичний і теоретичний інтерес. Відомо, наприклад, що значення коефіцієнта тертя із збільшенням гладкості поверхні зменшується, але при дуже високому ступені гладкості починає різко зростати. Із збільшенням гладкості зменшується значення когезійного компоненту (когезія — зчеплення молекул (атомів, іонів) у фізичному тілі. Це зумовлене міжмолекулярною взаємодією і (або) хімічним зв’язком), тому що зменшується кількість нерівностей, які деформуються або зрізуються, але поступово починають зростати фактична площа контакту та коефіцієнт тертя.

Для тертя кочення коефіцієнт тертя кочення дорівнює відношенню моменту тертя кочення M_t до притискової сили N. Цей коефіцієнт має розмірність в одиницях довжини (метр).

f=MtN{\displaystyle f={\frac {M_{t}}{N}}}

Коефіцієнти тертя ковзання частинок деяких мінералів у повітряному середовищі[ред. | ред. код]

1. ↑ ДСТУ 2823-94 Зносостійкість виробів тертя, зношування та мащення. Терміни та визначення.

• Кореняко А. С. Теорія механізмів і машин/ Під ред. М. К. Афанасьєва. — К.: Вища школа: Головне вид-во, 1987. — 206 с.
• Попов С.В., Бучинський М.Я., Гнітько С.М., Чернявcький А.М. Теорія механізмів технологічних машин: підручник для студентів механічних спеціальностей закладів вищої освіти. Харків: НТМТ, 2019. 268 с.

Тертя ковзання — Вікіпедія

Матеріал з Вікіпедії — вільної енциклопедії.

Сила тертя ковзання Fr протидіє ковзанню тіла вниз по похилій площині Тертя ковзання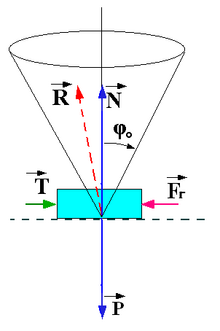 Кут тертя та конус тертя

Тертя́ ко́взання — зовнішнє тертя руху, під час якого швидкості тіл в точках дотику відрізняються за величиною і (чи) напрямком^[1] і діє на тіло у напрямку, протилежному до напрямку проковзування.

Негативними наслідками тертя ковзання в механізмах є не тільки зменшення ККД, а й знос механізмів.

Основною причиною тертя ковзання є те, що поверхні тіл, котрі дотикаються є шорсткими; внаслідок цього під час переміщення одного тіла по поверхні іншого потрібна сила для подолання опору мікроскопічних нерівностей цих поверхонь. Крім шорсткості поверхонь на явища тертя певний вплив роблять і сили міжмолекулярної взаємодії між двома тілами.

Сила тертя виникає в тій чи іншій мірі між усякими реальними поверхнями, якими б гладкими вони не були. Якщо два тіла взаємодіють одне з одним в умовах тертя, то реакцію

R, що діє з боку одного тіла на інше тіло, котре ковзає по ньому можна розкласти на дві складові: N, спрямовану по спільній нормалі до поверхні тіл що дотикаються, і F_r, що лежить в дотичній площині. Сила F_r називається силою тертя ковзання — вона перешкоджає ковзанню тіла по поверхні іншого тіла.

Якщо до тіла прикласти дві активні сили — силу тяжіння P й силу тяги або штовхаючу силу F, то відносне переміщення тіла починається тільки при деякому значенні сили F > F_rmax. При цьому, сила тертя, яка з’являється при відносному спокої тіла, називається силою тертя спокою, сила тертя, що діє при ковзанні тіла, відноситься до тертя руху.

Максимальна сила тертя спокою F_rmax є пропорційною до нормального тиску N тіла на площину (закон Амонтона — Кулона):

Frmax=μmax⋅N,{\displaystyle F_{r}max=\mu _{max}\cdot N,}

де μmax{\displaystyle \mu _{max}} — безрозмірна величина, яка називається коефіцієнтом тертя спокою або статичним коефіцієнтом тертя.

Сила тертя під час руху менша від сили тертя спокою і коефіцієнт тертя руху (динамічний коефіцієнт тертя) менший ніж статичний коефіцієнт тертя:

μ<μmax.{\displaystyle \mu <\mu _{max}.}

Часто під час інженерних розрахунків не роблять різниці між статичним і динамічним коефіцієнтами тертя і їх значення визначають для відповідних матеріалів за таблицями тангенсів кута φ₀, утвореного реакцією R шорсткої поверхні з нормаллю N до поверхні, так як μ = tg φ.

Кут φ₀ називається кутом тертя.

Розглянемо тіло, що перебуває в стані граничної рівноваги на шорсткій поверхні. В залежності від дії заданих сил напрям граничної реакції F₀ може змінюватися. Геометричне місце всіх можливих напрямків реакції F₀ в граничних умовах утворює конусну поверхню —

конус тертя. Приведемо усі активні сили, що діють на тіло, до однієї рівнодійної R, яка утворює кут α з нормаллю до поверхні. Така сила робить подвійну дію — її нормальна складова визначає реакцію поверхні N і, як наслідок, граничну силу тертя Frmax=μ⋅N{\displaystyle F_{r}max=\mu \cdot N}, дотична складова сили R намагається цю силу перебороти. При збільшенні сили R будуть пропорційно зростати обидві складові. Отже стан спокою або руху тіла не залежить від модуля сили R і визначається тільки кутом її прикладання α.

При рівновазі тіла α≤ϕ0{\displaystyle \alpha \leq \phi _{0}}, і для того, щоб тіло почало рухатися, необхідно і достатньо, щоб рівнодійна активних сил

R знаходилась поза конусом тертя.

1. ↑ ДСТУ 2823-94 Зносостійкість виробів тертя, зношування та мащення. Терміни та визначення.

• Кіндрачук М. В., Лабунець В. Ф., Пашечко М. І., Корбут Є. В. Трибологія: підручник/ МОН. — Київ: НАУ-друк, 2009. — 392 с. ISBN 978-966-598-609-6
• Теорія механізмів і машин / А. С. Кореняко; Під ред. М. К. Афанасьєва. — К.: Вища школа Головне вид-во, 1987. — 206 с.
• Сивухин Д. В. Общий курс физики — М.: Наука, 1979. — Т. I. Механика. — С. 101—102. — 520 с.

• Експлуатаційне зміцнення поверхонь тертя ковзання в активному середовищі / В. М. Гайдучок; Львів. держ. аграр. ун-т. — Л., 1998. — 112 c. — Бібліогр.: 111 назв.

Тертя кочення — Вікіпедія

Матеріал з Вікіпедії — вільної енциклопедії.

Тертя́ ко́чення — опір рухові, що виникає при перекочуванні тіла одне по одному. За ДСТУ 2823-94^[1] тертя кочення — тертя руху, під час якого швидкості тіл однакові за величиною і напрямком, принаймні, в одній точці зони контакту. Проявляється, наприклад, між елементами підшипників кочення, між шиною колеса автомобіля і дорожнім полотном. Як правило, зусилля тертя кочення набагато менші від зусиль тертя ковзання і тому, кочення є поширеним видом руху в техніці.

Тертя кочення виникає на межі двох тіл, і тому воно класифікується як вид зовнішнього тертя.

Динаміка тертя кочення[ред. | ред. код]

Сила тертя кочення[ред. | ред. код]

На тіло, що котиться по поверхні діють сили:

• P — тягнуча сила, що прикладена до середини тіла;
• N — сила притискування тіла до поверхні кочення;
• R_p — асиметрична сила реакції поверхні кочення.

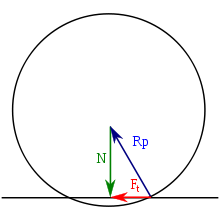
Якщо векторна сума цих сил дорівнює нулю, то середина тіла кочення рухається рівномірно прямолінійно (див. рис.1).

N→+P→+R→p=0{\displaystyle {\vec {N}}+{\vec {P}}+{\vec {R}}_{p}=0\,}

Це означає що вертикальна складова сили реакції зрівноважується притискною силою, а горизонтальна складова Ft{\displaystyle F_{t}} зрівноважується тягнучою силою, протидіючи рухові тіла кочення і за аналогією до тертя ковзання називається силою тертя кочення: F→t=−P→{\displaystyle {\vec {F}}_{t}=-{\vec {P}}\,}.

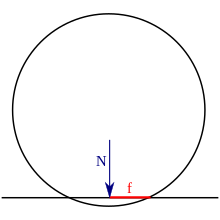
Рівномірне кочення означає, також, що сума моментів сил відносно довільної точки дорівнює нулю. З рівноваги моментів сил зображених на рис.2 і 3 відносно середини тіла кочення випливає:

Ft⋅R=N⋅f{\displaystyle F_{t}\cdot R=N\cdot f}

Звідки випливає:

Ft=fR⋅N{\displaystyle F_{t}={\frac {f}{R}}\cdot N\,}

де:

• Ft{\displaystyle F_{t}} — сила тертя кочення;
• f — коефіцієнт тертя кочення, одиниці вимірювання метр;
• R — радіус тіла кочення;
• N — притискна сила тіла до поверхні.

Ця залежність підтверджується експериментально. Для малої швидкості кочення сила тертя кочення не залежить від цієї швидкості. Коли швидкість кочення досягає значень, коли швидкість утворення деформації стає порівняльною із швидкістю поширення деформації в матеріалі, тертя кочення різко зростає і навіть може перевищити тертя ковзання за аналогічних умов.

Момент сил тертя кочення[ред. | ред. код]

Визначимо для рухомого циліндра гальмівний момент обертального руху тіла. Якщо розглянути цей момент відносно центру обертового колеса (наприклад, колеса автомобіля) то він дорівнюватиме добутку гальмівного зусилля на осі на радіус колеса. Відносно точки контакту рухомого тіла з землею момент буде рівний добутку тягового зусилля, що врівноважує сили тертя, на радіус колеса (рис.2).

Mt=Ft⋅R=P⋅R{\displaystyle M_{t}=F_{t}\cdot R=P\cdot R\,}.

З іншого боку, момент тертя дорівнює моменту притискної сили (N) на плече довжиною, що дорівнює коефіцієнту тертя кочення (f):

Mt=f⋅N{\displaystyle M_{t}=f\cdot N\,},

де

Коефіцієнт тертя кочення[ред. | ред. код]

Із записаного вище рівняння випливає, що коефіцієнт тертя може бути визначений як відношення моменту тертя кочення (Mt{\displaystyle M_{t}}) до притискної сили (N):

f=MtN{\displaystyle f={\frac {M_{t}}{N}}}

Графічна інтерпретація коефіцієнта тертя кочення f подана на рис.3. і рис.4.

Коефіцієнт тертя кочення має наступні фізичні інтерпретації:

• Якщо тіло знаходиться у спокої і тягнуча сила відсутня, сила реакції поверхні кочення лежить на тій же лінії, що і притискна сила. Коли тіло котиться, з умови рівноваги випливає, що перпендикулярна складова сили реакції поверхні кочення є паралельною до притискної сили і не збігається з нею. Коефіцієнт тертя кочення дорівнює відстані між прямими, вздовж яких діють притискна сила і нормальна до поверхні кочення складова сили реакції поверхні (рис. 4).
• Тіло, що котиться можна розглядати як тіло, що обертається навколо миттєвої осі обертання (рис.4 — точка прикладання вектора Rp{\displaystyle Rp}), котра для ідеально твердих матеріалів є точкою, що лежить на прямій, котра проходить через центр кола і перпендикулярна до поверхні кочення. Для випадку реальних матеріалів, точка миттєвого центру обертання є зміщеною у напрямку кочення тіла а відстань рівну значенню коефіцієнта тертя кочення.

Орієнтовні значення коефіцієнта тертя для різних пар кочення.

Тіло кочення	Поверхня кочення	Коефіцієнт тертя в мм
деревина м’яка	деревина м’яка	1,5
деревина м’яка	сталь	0,8
деревина тверда	деревина тверда	0,8
ебоніт	бетон	10-20
ебоніт	сталь	7,7
гума	бетон	15-35
загартована сталь	загартована сталь	0,01
полімер	сталь	2
сталь	асфальт	6
сталь	тротуарна плитка	1,5
сталь	сталь	0,5
залізо	деревина м’яка	5,6
залізо	граніт	2,1
залізо	залізо	0,51
чавунне литво	чавунне литво	0,8

1. ↑ ДСТУ 2823-94 Зносостійкість виробів тертя, зношування та мащення. Терміни та визначення.

• Онищенко О. Г., Коробко Б. О., Ващенко К. М. Структура, кінематика та динаміка механізмів. ПолтНТУ, 2010. — 274 с. ISBN 978-966-616-078-5

§ 29. Тертя. Сили тертя. Коефіцієнт тертя ковзання » Народна Освіта

Спостереження 1. Автомобіль, вимкнувши двигун, через певний час зупиняється. Шайба, рухаючись по льоду, також згодом зупиниться. Зупиняється і велосипед, якщо припинити крутити педалі.

Що ж є причиною зменшення швидкості руху тіл?

З раніше вивченого ви знаєте, що причиною зміни швидкості руху тіл є дія одного тіла на інше. Отже, у випадках, які розглядали, на кожне рухоме тіло діяла сила. Тіла зупинилися, тому що на них діяла сила, яка напрямлена протилежно їх руху — сила тертя ^_тер.

Сила тертя виникає під час взаємодії між твердими тілами в місцях їх дотику і перешкоджає їх відносному переміщенню.

Однією з причин виникнення сили тертя є шорсткість стичних поверхонь тіл. Навіть гладенькі на вигляд поверхні тіл мають нерівності, горбики і подряпини. На малюнку 135 ці нерівності зображено у збільшеному вигляді. Коли одне тіло ковзає по поверхні іншого, ці нерівності зачіплюються одна за одну, що створює силу, яка заважає руху.

Друга причина тертя — взаємне притягання молекул стичних поверхонь тіл. Якщо поверхні тіл дуже добре відполіровано, то їх молекули розміщуються так близько одна до одної, що помітно починає проявлятися притягання між ними.

Розрізняють кілька видів тертя залежно від того, як взаємодіють тертьові тіла: тертя спокою, тертя ковзання, тертя кочення.

Дослід 1. Покладемо брусок на похилу дошку. Брусок перебуває в стані спокою. Що утримує його від зісковзування вниз? Тертя спокою забезпечує зчеплення бруска й дошки.

Дослід 2. Притисніть свою руку до зошита, що лежить на столі, і пересуньте його. Зошит буде рухатися відносно стола, але перебуває у спокої відносно вашої долоні. За допомогою чого ви примусили цей зошит рухатися? За допомогою тертя спокою зошита об руку.

Тертя спокою переміщує вантажі, що розміщуються на рухомій стрічці транспортера, запобігає розв’язуванню шнурків, утримує шурупи і цвяхи в дошці тощо.

Якщо одне тіло ковзає по іншому, то тертя, що виникає при цьому, називають тертям ковзання. Таке тертя виникає під час руху саней або лиж по снігу, підошв по землі.

Якщо одне тіло котиться по іншому, то говорять про тертя кочення. Під час кочення коліс вагона, автомобіля, воза, під час перекочування бочок по землі проявляється тертя.

А від чого залежить сила тертя?

Дослід 3. Прикріпимо до бруска динамометр і будемо тягнути його, надаючи бруску рівномір-

ного руху (мал. 136). При цьому динамометр буде показувати силу, з якою ми тягнемо брусок, а отже, і силу тертя, яка виникає під час руху бруска по поверхні стола. Покладемо на брусок тягарці й повторимо дослід. Динамометр зафіксує більшу силу тертя.

Що більша сила притискає тіло до поверхні, то більша сила тертя виникає при цьому.

Виконаємо попередній дослід, але тіло будемо рухати по поверхні скла, по бетону. З’ясуємо, що сила тертя залежить від якості поверхні, по якій рухається тіло.

Сила тертя залежить від матеріалу і якості обробки поверхні, по якій рухається тіло.

Силу тертя ковзання визначають за формулою:

де F — сила тертя ковзання; N — сила реакції опори, що за значенням дорівнює силі тиску тіла на поверхню ковзання; ц — коефіцієнт тертя ковзання. Якщо поверхня ковзання горизонтальна, то сила тиску на неї дорівнює вазі тіла, тобто N = P = gm, а ^_тер = ^gm, де g = 9,81 Н/кг; т -маса тіла.

У таблиці 5 вказано коефіцієнти тертя ковзання для деяких матеріалів.

Таблиця 5

Матеріал	Коефіцієнт тертя
Сталь по сталі	0,17
Залізо по залізу	0,3

Визначення коефіцієнта тертя ковзання різними способами

МЕТА РОБОТИ. Навчитися визначати коефіцієнт тертя ковзання різними способами.

При підготовці до роботи використовуйте підручники 8 класу .

Дайте відповідь на наступні питання.

1. Як розраховується робота сили тертя ковзання?

2. Чому дорівнює потенційна енергія розтягнутої пружини?

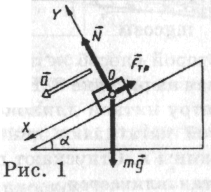
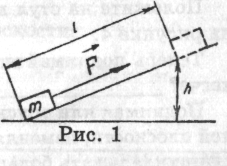
3. Які сили діють на вантаж, що зісковзує

з похилої площини? Покажіть їх на мал. 1.

4. Брусок ковзає по похилій площині, чому дорівнює реакція опори?

Чому дорівнює сила тертя в цьому випадку?

1 спосіб

УСТАТКУВАННЯ: динамометр, мірна стрічка, дерев’яна лінійка, штатив, брусок, нитка.

ПІДГОТОВКА ДО РОБОТИ

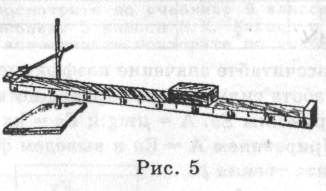
1. В якості похилої площини використовуйте дерев’яну лінійку, що встановлюється одним кінцем на штативі (дивися малюнок 5).

2. Встановите лінійку з вантажем і поступово, піднімайте один кінець до тих пір, поки брусок не почне ковзати рівномірно.

ПОРЯДОК ВИКОНАННЯ РОБОТИ

1. Повільно піднімаючи і опускаючи лінійку, домагайтеся, щоб вантаж ковзав по лінійці рівномірно вниз.

2. Точно вимірять довжину і висоту похилої площини.

3. По формулі розрахуйте коефіцієнт тертя.

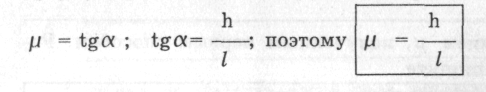
2 спосіб

ПІДГОТОВКА ДО РОБОТИ

1. Розташуєте дерев’яну лінійку горизонтально.

2. На неї покладете дерев’яний брусок, сполучений ниткою завдовжки 25-30 см з динамометром.

ПОРЯДОК ВИКОНАННЯ РОБОТИ

1. Динамометром вимірять масу бруска.

2. Однією рукою тримаєте брусок, а інший натягуйте динамометр. Виміряйте силу F і розтягування пружини х.

3. Відпустите брусок. Він проїде деяку відстань S і зупиниться.

4. Експеримент повторите кілька разів, записуючи значення F, x, S.

5. Розрахуйте значення коефіцієнта тертя.

Робота сили тертя А дорівнює потенційній енергії розтягнутої пружини

Прирівняємо А = Е_п і виведемо формулу для розрахунку коефіцієнта тертя μ.

6. Розрахуйте середнє значення_μ

7. Порівняєте зі значенням μ отриманим першим способом. Результати дослідів запишіть.

Контрольні питання.

1. Який спосіб визначення коефіцієнта тертя точніший?

2. Чи виконується в процесі виміру к-та тертя іншим способом закон збереження енергії (за результатами роботи)?

ВИЗНАЧЕННЯ КОЕФІЦІЄНТА КОРИСНОЇ ДІЇ ПОХИЛОЇ ПЛОЩИНИ

МЕТА РОБОТИ. Навчитися визначати коефіцієнт корисної дії похилої площини

При підготовці до роботи використовуйте підручники 8 класу .

Дайте відповідь на наступні питання.

1. Як розрахувати роботу по підйому тіла на висоту

2. Як розрахувати роботу сили F, на шляху П

3. По якій формулі розраховується коефіцієнт корисної дії — ККД?

4. Прикладаючи силу F, тіло масою m піднімають по похилій площині, на висоту h (як показано на мал. 1). Довжина похилої площини l. Визначите: Ап — корисну роботу, Аз — витрачену роботу, ККД.

УСТАТКУВАННЯ: динамометр, мірна стрічка, дерев’яна лінійка, штатив, брусок, три вантажі вагою в 1 Н.

ПІДГОТОВКА ДО РОБОТИ

1. В якості похилої площин використовуйте дерев’яну лінійку, закріплену в штативі.

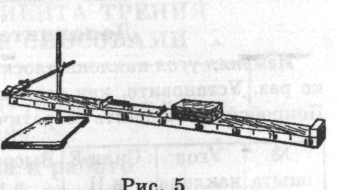
2. Закріпите лінійку, як показано на малюнку 5.

3. Встановите кут похилої площини близько 30 градусів.

4. Розташуєте на лінійці вантаж.

5. Прикріпите до вантажу динамометр, яким можна тягнути вантаж по лінійці.

ПОРЯДОК ВИКОНАННЯ РОБОТИ

1. Динамометром визначите вагу бруска. Усі результати записуйте в таблицю.

2. Рівномірно піднімаючи брусок по похилій площині, визначите силу тяги.

3. Покладіть на брусок один вантаж вагою в 1 Н (у наступних дослідах два, три вантажі), і повторите досвід, записуючи масу бруска, що рухається, з вантажами і силу, що додається.

4. Виміряйте висоту і довжину похилої площини.

5. Розрахуйте ККД похилій площині по формулі ККД = 100%ˑ mgh/Fl

6. Розрахуйте середнє значення ККД і запишіть в таблицю результати роботи.

27

ЛР «Вимірювання коефіцієнта тертя ковзання»

Лабораторна робота  «Вимірювання коефіцієнта тертя ковзання»

Мета уроку:   виміряти коефіцієнт тертя ковзання дерева по дереву, розвивати уважність,спостережливість, виховувати кмітливість.

Тип уроку:   урок контролю й оцінювання знань.

Обладнання:  дерев’яний брусок, дерев’яна лінійка, набір тягарців відомої маси, динамометр.

РЕКОМЕНДАЦІЇ ЩОДО ПРОВЕДЕННЯ ЛАБОРАТОРНОЇ РОБОТИ

1.        Виміряйте динамометром вагу бруска.

2.        Покладіть брусок на горизонтально розташовану дерев’яну лі­нійку. На брусок поставте тягарець.

3.        Тягніть брусок рівномірно по горизонтальній лінійці, як пока­зано на рисунку. Запишіть показання динамометра.

4.        Повторіть дослід, поставивши на брусок 2 й 3 тягарці. 5.   Заповніть у зошиті для лабораторних робіт таблицю.

Кількість тягарців	Сила нормальної реакції   N, H	Сила тертя  Fтер H
1
2
3

5.        Накресліть у зошиті осі координат N й F_Tep, виберіть зруч­ний масштаб і нанесіть отримані вами три експерименталь­ні точки.

6.        Оцініть (якісно), чи підтверджується на досліді, що сила тертя прямо пропорційна силі нормального тиску; чи перебувають всі експериментальні точки поблизу однієї прямої, що проходить через початок координат.

7.        Візьміть на проведеній прямій точку,  розташовану не дуже близько від початку координат, і визначте значення F   й  N, що відповідають цій точці. За формулою      визначте коефіцієнт тертя ковзання дерева по дереву.

Домашнє завдання

1.        Підготуватися до самостійної роботи №  «Сили тертя».

Тертя. Сила тертя. Коефіцієнт тертя ковзання

Дата _____________

Тема. Тертя. Сила тертя. Коефіцієнт тертя ковзання

Мета уроку:

• Навчальна: формувати в учнів знання про явище тертя, силу тертя, причину виникнення сили тертя, способи збільшенні і зменшення сили тертя ковзання.

• Виховна: виховувати самостійність, наполегливість.

• Розвиваюча: розвивати вміння розв’язувати фізичні задачі, застосовуючи формули сили.

Основні поняття: тертя, сила тертя, коефіцієнт тертя, тертя ковзання, тертя кочення, тертя спокою, в’язке тертя.

Обладнання: таблиця «Сила тертя. Види тертя.», динамометр, дерев’яний брусок, тягарці.

Тип уроку: урок вивчення нового матеріалу.

Хід уроку

І. Організаційний момент

ІІ. Актуалізація опорних знань

Методом фронтального опитування з’ясувати уміння учнів пояснювати причину зміни швидкості та деформації тіл внаслідок дії одного тіла на інше, знання про фізичну величину, яка є мірою такого впливу; позначення, одиниці вимірювання та графічне зображення сили, пошук рівнодійної; розуміння умов виникнення сили пружності, формулювання та пояснення закону Гука; розкривати зміст понять «тяжіння», «вага», «невагомість», «перевантаження», вміння встановити залежність між силою тяжіння (вагою) та масою тіла; вміння застосовувати свої знання для пояснень явищ природи.

ІІІ. Оголошення теми та мети уроку

Окрім сил, які ми з вами пригадали, існує сила, з якою ми зіштовхуємося на кожному кроці. Та, вірніше було б сказати, сила без якої мий кроку не ступили б. Можливо, ви здогадалися що це за сила? (відповіді учнів) Так, вірно – це сила тертя.

Тертя може бути як корисним так і шкідливим, цю аксіому людина опанувала ще на зорі цивілізації. Адже два найголовніші винаходи – колесо і добування вогню – пов’язані із прагненням зменшити, або збільшити ефекти тертя.

Сьогодні на уроці ми познайомимося із тертям, силою тертя, видами тертя, способами зменшення, або збільшення тертя, методами визначення сили тертя.

ІV. Формування нових знань

Спостереження. Ми не раз спостерігали з вами, що в реальних умовах рух не може тривати нескінченно довго (автомобіль чи потяг зупиняються після вимикання двигуна; кулька, що скотилась з похилої площини – зупиняється, зупиниться ще швидше брусок, який лежить на горизонтальній площині, якщо його штовхнути)

Що є причиною зменшення швидкості руху і зупинки тіла?

Ми з вами вивчаючи взаємодії між тілами говорили, що причиною зміни швидкості тіла є взаємодія між ними, а мірою цієї взаємодії є сила. Тому, логічно припустити, що на тіла що рухалися діяла сила, яка і призвела до їх зупинки. Причому ця сила повинна була діяти протилежно напрямку руху тіла. Таку силу називають силою тертя.

Сила тертя виникає під час взаємодії між твердими тілами в місцях їх дотику і перешкоджає їх відносному переміщенню.

Причин виникнення сили тертя є декілька:

• Шорсткість стичних поверхонь. Навіть гладенькі на вигляд поверхні мають нерівності, подряпини. Тому, коли одне тіло ковзає по поверхні іншого, ці нерівності зачіплюються одна за одну.

• Взаємне притягання молекул стичних поверхонь. Якщо поверхні надто гладенькі – «відполіровані до блиску», то їх молекули розміщуються дуже близько одна до одної. А як відомо молекулам властиве притягання, в результаті якого і зменшується рух тіла.

Сила тертя проявляється не лише під час руху тіла, а й під час його спокою. Тай рухи тіл можуть бути різними: брусок ковзати по похилій площині, м’яч котитись по футбольному полі, ковзаняр кататись на ковзанах по льоду. Тому розрізняють тертя спокою, тертя ковзання, тертя кочення, в’язке тертя.

Кожен знає, що шафу зрушити з місця не просто. Яка ж сила, зрівноважує силу, прикладену нами? Це – сила тертя спокою, яка виникає при спробі зрушити одне тіло з дотичних тіл відносно іншого і напрямлена вздовж поверхонь дотику тіл мак, що перешкоджає відносному рухові тіл.

Покладемо книжку на стіл, сядемо на стілець, покладемо брусок на похилу площину – ці тіла перебуватимуть у спокої тому, що їх утримує сила тертя спокою. Тертя спокою перемішує вантажі, що розміщуються на рухомій стрічці транспортера, пасажирів, що піднімаються нагору за допомогою ескалатора, запобігає розв’язуванню шнурків і розстібуваню ґудзиків, утримує гвіздки у дошках та стінах. Максимальна сила тертя спокою дорівнює тій силі, яка виводить тіло із стану спокою.

Якщо брусок, покладений на горизонтальну площину, рухається із сталою швидкістю, значить, рівнодійна всіх сил, прикладених до бруска дорівнює нулю. Яка сила компенсує силу, прикладену нами? Це – сила тертя ковзання. Сили тертя ковзання діють між дотичними тілами, які рухаються одне відносно одного, причому сила тертя, що діє на кожне з тіл, напрямлена протилежно швидкості руху цього тіла відносно іншого тіла. (коефіцієнт тертя ковзання є трохи меншим від коефіцієнта тертя спокою, тому в разі збільшення сили, що «зрушує» тіло зсувається з місця ривком).

Сила тертя кочення – це сила, що виникає, коли одне тіло котиться по поверхні іншого.

Сила в’язкого тертя виникає під час руху тіла в рідині або газі. При невеликих швидкостях сила в’язкого тертя пропорційна швидкості руху (чим більша швидкість, тим більше тертя).

Чим більша сила притискає тіло до поверхні, тим більша сила тертя виникає при цьому.

Сила тертя залежить від матеріалу і якості обробки поверхонь, по якій рухається тіло; від швидкості руху тіл одне відносно одного.

Силу тертя ковзання визначають за формулою , де сила тертя ковзання, N – сила реакції опори – дорівнює силі тиску тіла на поверхню, — коефіцієнт тертя ковзання.

Якщо поверхня горизонтальна то сила тиску на неї дорівнює вазі тіла.

m – маса тіла.

При однакових навантаженнях сила тертя кочення завжди менша за силу тертя ковзання.

Тертя, як і будь яке фізичне явище може бути і шкідливим і корисним. Коли тертя є шкідливим його намагаються зменшити. Для цього використовують мастило, замінюють ковзання коченням, застосовують підшипники.

Коли тертя є корисним його намагаються збільшити: в ожеледь посипають тротуари і переходи піском, використовують шипи на взутті й автомобільних шинах.

Про наявність сили тертя т їх види вперше було вказано французьким фізиком Г. Амонтоном у 1699р. і незалежно від нього Ш. Кулоном у 1785р. (хоча строгої теорії сил тертя спокою, як сили сухого тертя ще не створено).

V. Закріплення вивченого матеріалу

Робота з підручником. Оформлення конспекту. Ознайомлення з таблицею коефіцієнт тертя.

Контактуючі поверхні	Коефіцієнт тертя
Сталь по сталі	0,2
Сталь по льоду	0,015
Гума по бетону	0,75
Гума по ґрунту	0,3 – 0,5
Дерево по льоду	0,035

Розв’язування задач:

1. Що змінюється зі збільшенням ваги автомобіля: сила тертя чи коефіцієнт тертя?

2. Чому головку сиру легше розрізати на шматки міцною ниткою, ніж ножем?

3. Яку силу треба прикласти до шафи масою 150кг у горизонтальному напрямку, щоб зрушити її з місця? Коефіцієнт тертя рівний 0,8.

4. Контейнер масою 800кг стоїть на горизонтальній площині. Чи рухатиметься контейнер, якщо до нього прикласти горизонтальну силу 1,2кН? Коефіцієнт тертя дорівнює 0,3.

5. Під час тривалої роботи кінь розвиває сталу силу 600Н. Який вантаж він може везти на санях масою 100кг, якщо коефіцієнт тертя становить 0,05?

6. Брусок масою 1,6кг рівномірно тягнуть по столу за допомогою пружини жорсткістю 40Н/м. Яке видовження пружини, якщо коефіцієнт тертя рівний 0,3.

VІ. Підсумок уроку

Інтерактивна вправа «Мікрофон».

Сьогодні на уроці мені сподобалося…

Я зрозумів (зрозуміла) …

VІІ. Домашнє завдання

Розв’язати:

Брусок тягнуть по столу,прикладаючи горизонтальну силу 1Н. яка аса бруска, якщо він рухається рівномірно й коефіцієнт тертя дорівнює 0,2?