Формула Кирхгофа | это… Что такое Формула Кирхгофа?

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Содержание 1 Полная формулировка задачи и ответа 2 Физические следствия 3 Формула Пуассона-Парсеваля 4 Формула Д’Аламбера 5 Применение формул 6 Примечания 7 Литература 8 Ссылки

Полная формулировка задачи и ответа

Рассмотрим уравнение

, где функции и определены на , а  — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью в моменты времени .

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени :

Тогда обобщённая формула Кирхгофа даёт решение этой задачи в трёхмерном случае:

где поверхностные интегралы берутся по сфере .

Сам Кирхгоф рассматривал только трёхмерный случай.

Простой вывод решения основной задачи использует преобразование Фурье.

Физические следствия

Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени

Пусть в начальный момент времени на некотором компакте M есть локальное возмущение ( и/или ). Если мы находимся в некоторой точке , то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время .

Вне отрезка времени , где , функция u(x ₀, t) равна нулю.

Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в , уже не будет компактным в , а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).

[1]

Решение уравнения колебаний мембраны (двумерного пространства)

(функция соответствует вынуждающей внешней силе)

с начальными условиями

задаётся формулой:

.

Решение одномерного волнового уравнения

(функция соответствует вынуждающей внешней силе)

с начальными условиями

имеет вид^[2]

В область II приходят характеристики только из одного семейства

При пользовании формулой Д’Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области . Решение волнового уравнения представляется в виде суммы двух функций: , то есть оно определяется двумя семействами характеристик: . Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области

II формула Д’Аламбера не работает.

Применение формул

В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения с начальными условиями и искать решение в виде суммы трех функций: , которые удовлетворяют следующим условиям:

Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путем замены переменных. Например, пусть .

Тогда, сделав замену , уравнение для задачи «С» примет вид:

Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д’Аламбера:

В силу четности начального условия, решение сохранит свой вид во всей области .

Примечания

1. ↑ КИРХГОФА ФОРМУЛА // Физическая энциклопедия / Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов, Б. К. Вайнштейн, С. В. Вонсовский, А. В. Гапонов-Грехов, С. С. Герштейн, И. И. Гуревич, А. А. Гусев, М. А. Ельяшевич, М. Е. Жаботинский, Д. Н. Зубарев, Б. Б. Кадомцев, И. С. Шапиро, Д. В. Ширков; под общ. ред. А. М. Прохорова. — М.: Советская энциклопедия, 1988—1998.
2. ↑ Формула Д’Аламбера в Физической энциклопедии

Литература

• Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6

Ссылки

• Раздел о формуле Д’Аламбера

6.

11. Какая формула выражает первое правило Кирхгофа?

Ответ:

1) ; 2) ; 3) ; 4) .

Согласно первому правилу Кирхгофа алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла – отрицательным.

Запишем первый закон Кирхгофа в комплексной форме:

Первый закон Кирхгофа гласит, что алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла. То есть, сколько тока втекает в узел, столько же вытекает (как следствие закона сохранения электрического заряда). Алгебраическая сумма — это сумма, в которую входят слагаемые со знаком плюс и со знаком минус.

7.11. Какая формула выражает второе правило Кирхгофа?

Ответ:

1) ; 2) 3) ; 4)

8.11.Отношение работы, совершаемой сторонними силами при перемещении электрического заряда по замкнутой электрической цепи, к величине этого заряда определяет:

Ответ:

1) напряжение в цепи; 2) сила тока в цепи;

3) электродвижущая сила источника тока;

4) сопротивление полной цепи.

Отношение работы, совершаемой сторонними силами при перемещении положительного заряда по всей замкнутой цепи, к значению этого заряда называется электродвижущей силой источника (сокращенно ЭДС): Участок электрической цепи, не содержащей источников ЭДС, называется однородным.

9.11. При последовательном соединении n одинаковых источников тока с одинаковыми  каждый и одинаковыми внутренними сопротивлениями

r каждый, полный ток в цепи с внешним сопротивлением R будет равен:

Ответ:

1) , 2) , 3) , 4) .

10.11. Зависимость тока I, протекающего через сопротивление R, от напряжения U, дана на рисунке. Чему равна мощность, выделяемая на сопротивлении R, при U=40В?

Ответ:

1) 0,8 Вт; 2) 1,6 Вт; 3) 2,4 Вт; 4) 3,2 Вт.

11.11. Найти общее сопротивление участка цепи, если R=3 Ом.

Ответ:

1) (15/8) Ом; 2) (13/5) Ом; 3) 7 Ом; 4) (3/4)Ом.

12.11. Найти общее сопротивление участка цепи, если R=3Ом, сопротивлением проводов пренебречь.

Ответ:

1) 9Ом; 2) 13Ом; 3) 5Ом; 4) 3Ом.

13.11. Найти общее сопротивление участка цепи, если R₁ =2 Ом, R₂ =2 Ом, R₃ =2 Ом, R₄ =2 Ом, R₅=2 Ом.

Ответ:

1) 0,5Ом; 2) 0,8Ом; 3) 1Ом; 4) 2Ом.

14.11.Найти общее сопротивление участка цепи, если R₁ =2 Ом, R₂ =2 Ом, R₃ =2 Ом, R₄ =2 Ом,

R₅ =2 Ом.

Ответ:

1) 0,5Ом; 2) 0,75Ом; 3) 1Ом; 4) 2Ом.

15.11. На рисунке представлена зависимость силы тока в двух параллельно соединенных проводниках от приложенного напряжения. Во сколько раз отличаются сопротивления проводников R₂/ R₁?

Ответ:

1) в 2 раза; 2) в 4 раза; 3) в 6 раз; 4) в 8 раз.

12.Магнитное поле тока. Действие магнитного поля на токи и заряды.

1.12. Вектор магнитной индукции поля, созданного двумя параллельными одинаковыми (I₁ = I₂) прямолинейными токами, но текущими в противоположных направлениях, как показано на рисунке, в точке Д направлен:

Ответ:

1) направлен вверх; 2) направлен вниз; 3) равен нулю; 4) направлен влево.

2.12. В магнитное поле, изменяющееся вдоль оси ОХ по закону В = В₀ – кх, где к = 2 мТл/м, помещен круглый проволочный виток диаметром d=2м так, что его плоскость перпендикулярна линиям индукции магнитного поля. Определить изменение магнитного потока через виток при его перемещении из точки с координатой Х₁ = 3м в точку с координатой Х₂ = 8м.

Ответ:

1) 3,14 мВб; 2) 6,28 мВб; 3) 31,4 мВб; 4) 62,8 мВб.

3.12. По проводнику AB протекает постоянный ток. Проводник помещен в однородное магнитное поле, линии индукции которого перпендикулярны проводнику (см. рис.). Если потенциал точки A больше потенциала точки B, то сила Ампера, действующая на проводник, имеет направление:

Ответ:

1) вниз; 2) вверх; 3) влево; 4) вправо.

Использование формулы Кирхгофа для расчета объемных волн в Земле | Международный геофизический журнал

Фильтр поиска панели навигации Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic Введите поисковый запрос

Расширенный поиск

Журнальная статья

Р. А. В. Хэддон,

Р. А. В. Хэддон

Ищите другие работы этого автора на:

Оксфордский академический

Google Scholar

ОБЪЯВЛЕНИЯ

П. В. Бухен

П. В. Бухен

Ищите другие работы этого автора на:

Оксфордский академический

Google Scholar

ОБЪЯВЛЕНИЯ

Geophysical Journal International , том 67, выпуск 3, декабрь 1981 г., страницы 587–598, https://doi.org/10.1111/j.1365-246X.1981.tb06939.x

Опубликовано:

9 0002 01 Декабрь 1981 г.

История статьи

Получено:

3 февраля 1981 г.

Опубликовано:

01 декабря 1981 г.

Фильтр поиска панели навигации Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic Введите поисковый запрос

Advanced Search

Резюме

Зависящее от времени поверхностное интегральное представление скалярного волнового поля Кирхгофа применяется к задаче вычисления синтетических сейсмограмм для P -волн в Земле. С помощью соответствующей параметризации интеграл Кирхгофа преобразуется в свертку весовой функции с производной исходной функции во временной области. Весовая функция рассчитывается с использованием простой теории лучей. Этот метод расширяет применимость теории простых лучей к каустикам и другим явлениям дифракции и позволяет учитывать определенные виды отклонений от сферической симметрии. Метод подробно проиллюстрирован приложением к ПКП -волновое поле Земли.

Ссылки

Baker

B.B.

Copson

E. T.

,

1939

.

Математическая теория принципа Гюйгена

,

Clarendon Press

, Оксфорд.

Буллен

К. Е.

,

1963

.

Введение в теорию сейсмологии

,

Cambridge University Press

.

Берридж

Р.

,

1963

.

Отражение импульса в твердой сфере

,

Proc. Р. Соц. А

,

276

,

367

–

400

.

Чепмен

Ч. Х.

,

1974

.

Точка поворота упругодинамических волн

,

Геофиз. Дж. Р. астр. соц.

,

39

,

613

–

621

.

Чепмен

Ч. Х.

,

1978

.

Новый метод расчета синтетических сейсмограмм

,

Геофиз. Дж. Р. астр. соц.

,

54

,

481

–

518

.

Чепмен

Ч. Х.

Финни

Р. А.

,

1972

.

Дифрагированные сейсмические сигналы и их численное решение

,

Мет. комп. физ.

,

12

,

165

–

230

.

Чой

Г. Л.

Кормье

В. Ф.

Кинд

Р.

Мюллер

Г. 900 03

Ричардс

П. Г.

,

1980

.

Сравнение синтетических сейсмограмм керновых фаз, полученных с помощью полноволновой теории и метода отражательной способности

,

Геофиз. Дж. Р. астр. соц.

,

61

,

21

–

39

.

Фукс

К.

Мюллер

Г.

,

1971

.

Расчет синтетических сейсмограмм методом отражательной способности и сравнение с наблюдениями

,

Геофиз. Дж. Р. астр. соц.

,

23

,

417

–

433

.

Гилберт

Ф.

Хельмбергер

Д. В.

,

1972

.

Обобщенная лучевая теория для слоистой сферы

,

Геофиз. Дж. Р. астр. соц.

,

27

,

57

–

80

.

Хильтерман

Ф. Дж.

,

1970

.

Трехмерное сейсмическое моделирование

,

Геофизика

,

35 0003

1037

.

Хильтерман

Ф. Дж.

,

1975

.

Амплитуды сейсмических волн — краткий обзор

,

Геофизика

,

40

,

745

–

762

.

Кеннет

Б.Л.Н.

,

1980

.

Сейсмические волны в стратифицированном полупространстве — II. Теоретическая сейсмология

,

Геофиз. Дж. Р. Астр. соц.

,

61

,

1

–

10

.

Финни

Р. А.

Кэтлз

Л. М.

,

1969

.

Дифракция P на ядре: исследование длиннопериодных амплитуд вблизи края тени

,

J. geophys. Рез.

,

74

,

1556

–

1574

.

Ричардс

П. Г.

,

1971

.

Теорема упругости для неоднородных сред на примере дисперсии объемных волн в Земле

,

Геофиз. Дж. Р. астр. соц.

,

22

,

453

–

472

.

Ричардс

П. Г.

,

1973

.

Расчет объемных волн для каустик и туннелирующих ядерных фаз

,

Геофиз. Дж. Р. астр. соц.

,

35

,

243

–

264

.

Трори

А. В.

,

1970

.

Простая теория сейсмической дифракции

,

Геофизика

,

35

,

762

900 04 –

784

.

Трори

А. В.

,

1977

.

Дифракции для произвольного расположения источника-приемника

,

Геофизика

,

42

,

1177

–

1182

.

Виггинс

Р. А.

,

1975

.

Расчеты синтетических сейсмограмм объемных волн с помощью теории квантованных лучей

,

Bull Can. Жопа. физ.

,

31

,

47

.

Виггинс

Р. А.

,

1976

.

Расчеты амплитуд объемных волн — II

,

Геофиз. Дж. Р. астр. соц.

,

46

,

1

–

10

.

Этот контент доступен только в формате PDF.

Раздел выпуска:

Статьи

Скачать все слайды

Реклама

Цитаты

Альтметрика

Дополнительная информация о метриках

Оповещения по электронной почте

Оповещение об активности статьи

Предварительные уведомления о статьях

Оповещение о новой проблеме

Оповещение о текущей проблеме

Оповещение о теме

Получайте эксклюзивные предложения и обновления от Oxford Academic

Система астрофизических данных

Резюме объявлений

Ссылки на статьи по телефону

• Последний

• Самые читаемые

• Самые цитируемые

Эффективный алгебраический подход к выборке с несколькими разрешениями для трехмерного магнитотеллурического моделирования

Геодезические ограничения землетрясения в Алоре силой 6,5 балла в 2015 г. , Восточная Индонезия: сдвиговый разлом на сходящейся границе

Средне-краткосрочный прогноз движения полюсов, сочетающий разность между сериями с разницей внутри серии

Deep-pre-trained-FWI: где контролируемое обучение встречается с нейронными сетями, основанными на физике

Преобразование волнового числа по частоте с двойным источником для точного извлечения дисперсии двумерной среды

Реклама

Стационарные уравнения Кирхгофа и системы с членами реакции

В этой статье операторный подход, основанный на принципах неподвижной точки Банаха и Шефера, используется для установления существования решений стационарных уравнений Кирхгофа с членами реакции. Затем для связанной системы уравнений Кирхгофа доказывается, что при соответствующих предположениях существует единственное решение, которое является равновесием по Нэшу относительно функционалов энергии, связанных с уравнениями системы. Устанавливаются как глобальное равновесие Нэша во всем пространстве, так и локальное равновесие Нэша в шарах. Решение получено с помощью итеративного процесса, основанного на вариационном принципе Экланда и развитие которого имитирует некооперативную игру.

[1]	Г. Кирхгоф, Vorlesungen über Mechanik , Лейпциг: Teubner, 1883.
[2]	Г. Аутуори, П. Пуччи, М. К. Сальватори, Глобальное небытие для нелинейных систем Кирхгофа, Arch. Рациональный мех. Анальный. , 196 (2010), 489–516. https://doi.org/10.1007/s00205-009-0241-x doi: 10.1007/s00205-009-0241-x
[3]	М. Дреер, Уравнение Кирхгофа для p -лапласиана, Rend. Сем. Мат. ун-т пол. Турин , 64 (2006), 217–238.
[4]	Дж. Л. Лайонс, О некоторых вопросах краевых задач математической физики, North-Holland Mathematics Studies , 30 (1978), 284–346. https://doi.org/10.1016/S0304-0208(08)70870-3 doi: 10.1016/S0304-0208(08)70870-3
[5]	Т. Ф. Ма, Замечания об эллиптическом уравнении типа Кирхгофа, Nonlinear Anal. Теор. , 63 (2005 г.), e1967-e1977. https://doi.org/10.1016/j.na.2005.03.021 doi: 10.1016/j.na.2005.03.021
[6]	Т. Ф. Ма, Х. Э. Муньос Ривера, Положительные решения нелинейной нелокальной эллиптической задачи передачи, заявл. Мат. лат. , 16 (2003), 243–248. https://doi.org/10.1016/S0893-9659(03)80038-1 doi: 10.1016/S0893-9659(03)80038-1
[7]	С. И. Похожаев, Квазилинейное гиперболическое уравнение Кирхгофа, Дифференц. Уравн. , 21 (1985), 101–108.
[8]	К. Ф. Васконселлос, О нелинейной стационарной задаче в неограниченных областях, Revista Maemática de la Universidad Complutense de Madrid , 5 (1992), 309–318.
[9]	К. О. Алвес, Ф. Дж. С. А. Корреа, Т. Ф. Ма, Положительные решения для квазилинейного эллиптического уравнения типа Кирхгофа, Вычисл. Мат. заявл. , 49 (2005), 85–93. https://doi.org/10.1016/j.camwa.2005.01.008 doi: 10.1016/j.camwa.2005.01.008
[10]	Г. Че, Х. Чен, Бесконечное множество решений систем уравнений типа Кирхгофа с общими потенциалами, Rocky Mountain J. Math. , 48 (2018), 2187–2209. https://doi.org/10.1216/RMJ-2018-48-7-2187 doi: 10.1216/RMJ-2018-48-7-2187
[11]	П. Чен, X. Лю, Положительные решения уравнения Кирхгофа во внешних областях, J. Math. физ. , 62 (2021), 041510. https://doi.org/10.1063/5.0014373 doi: 10.1063/5.0014373
[12]	М. Шипот, В. Валенте, Г. В. Каффарелли, Замечания к нелокальной проблеме, связанной с энергией Дирихле, Rendiconti del Seminario Matematico della Università di Padova , 110 (2003), 199–220.
[13]	Н. Т. Чанг, Результат существования класса систем типа Кирхгофа с помощью метода под- и сверхрешений, Appl. Мат. лат. , 35 (2014), 95–101. https://doi.org/10.1016/j.aml.2013.11.005 doi: 10.1016/j.aml.2013.11.005
[14]	К. Перера, З. Чжан, Нетривиальные решения задач типа Кирхгофа с помощью индекса Янга, Ж. Дифференц. Уравнения , 221 (2006), 246–255. http://dx.doi.org/10.1016/j.jde.2005.03.006 doi: 10.1016/j.jde.2005.03.006
[15]	П. Пуччи, В. Д. Родулеску, Прогресс в решении нелинейных задач Кирхгофа, Нелинейный анализ. , 186 (2019), 1–5. http://dx.doi.org/10.1016/j.na.2019.02.022 doi: 10.1016/j.na.2019.02.022
[16]	Б. Риччери, Об эллиптической задаче типа Кирхгофа, зависящей от двух параметров, J. Glob. Оптим. , 46 (2010), 543–549. https://doi.org/10.1007/s10898-009-9438-7 doi: 10.1007/s10898-009-9438-7
[17]	З. Т. Чжан, Ю. М. Сунь, Существование и множественность решений для нелокальных систем типа Кирхгофа, Acta Math. заявл. Грех. англ. сер. , 32 (2016), 35–54. https://doi.org/10.1007/s10255-016-0545-1 doi: 10.1007/s10255-016-0545-1
[18]	А. Дип, Дипмала, К. Тунч, О существовании решений некоторых нелинейных функциональных интегральных уравнений в банаховой алгебре с приложениями, Arab J. Basic Appl. науч. , 27 (2020), 279–286. https://doi.org/10.1080/25765299.2020.1796199 doi: 10.1080/25765299.2020.1796199
[19]	С. Ислам, М. Н. Алам, М. Ф. Аль-Асад, К. Тунч, Аналитический метод решения новых вычислительных решений модифицированного уравнения Захарова-Кузнецова, возникающего в электротехнике, J. Appl. вычисл. мех. , 7 (2021), 715–726. https://dx.doi.org/10.22055/jacm.2020.35571.2687 doi: 10.22055/jacm.2020.35571.2687
[20]	М. Н. Алам, К. Тунч, Аналитический метод решения точных решений нелинейного уравнения Богоявленского и нелинейной диффузионной системы хищник-жертва, Alex. англ. J. , 55 (2016), 1855–1865. https://doi.org/10.1016/j.aej.2016.04.024 doi: 10.1016/j.aej.2016.04.024
[21]	Р. Прекап, Равновесия типа Нэша и периодические решения невариационных систем, Adv. Нелинейный анал. , 4 (2014), 197–207. https://doi.org/10.1515/anona-2014-0006 doi: 10.1515/anona-2014-0006
[22]	Р. Прекап, Равновесия типа Нэша для систем функционалов Шулкина, Заданное значение Var. Анальный. , 24 (2016), 471–482. https://doi.org/10.1007/s11228-015-0356-1 doi: 10.1007/s11228-015-0356-1
[23]	А.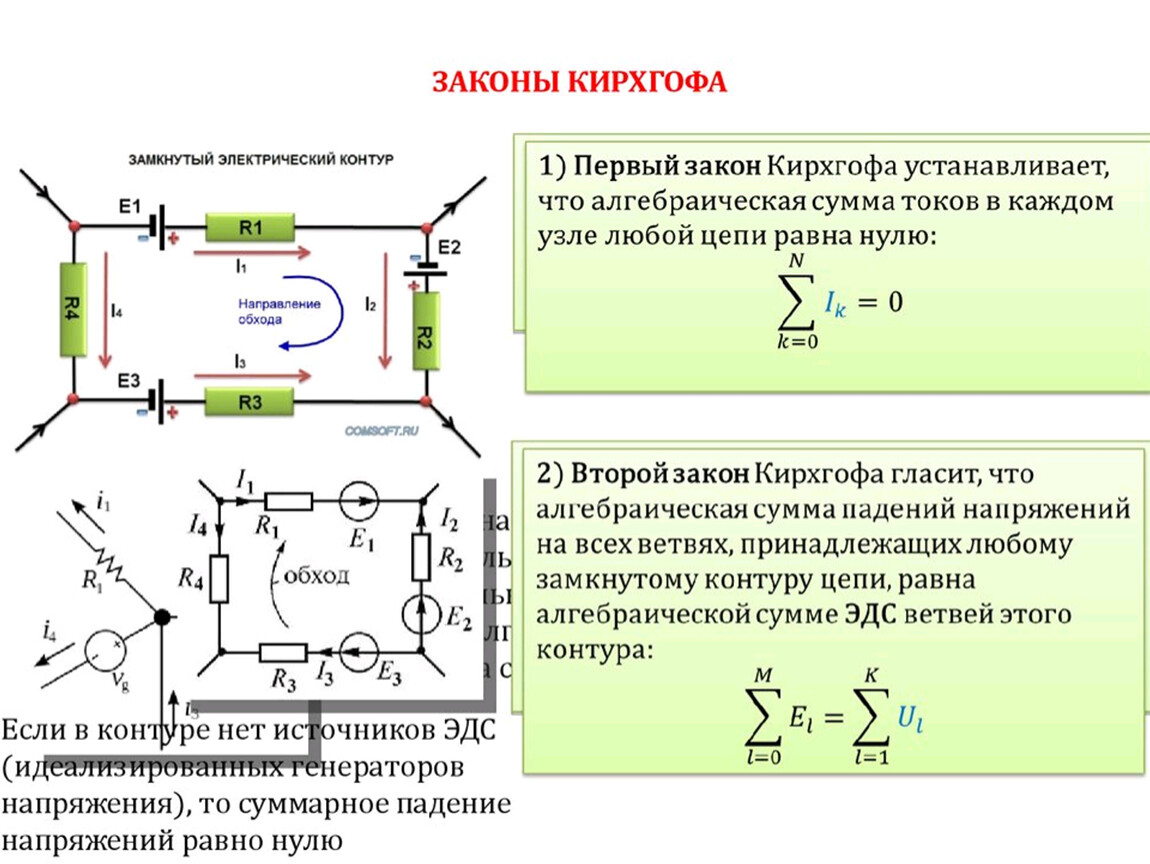 Будеску, Р. Прекап, Вариационные свойства решений сингулярных дифференциальных уравнений и систем второго порядка, J. Прикладная теория фиксированной точки. , 18 (2016), 505–518. https://doi.org/10.1007/s11784-016-0284-1 doi: 10.1007/s11784-016-0284-1
[24]	Р. Прекап, Теорема о критической точке в ограниченных выпуклых множествах и локализация равновесий типа Нэша невариационных систем, J. Math. Анальный. заявл. , 463 (2018), 412–431. https://doi.org/10.1016/j.jmaa.2018.03.035 doi: 10.1016/j.jmaa.2018.03.035
[25]	М. Белдински, М. Галевски, Равновесия типа Нэша для систем непотенциальных уравнений, Appl. Мат. вычисл. , 385 (2020), 125456. https://doi.org/10.1016/j.amc.2020.125456 doi: 10.1016/j.amc.2020.125456
[26]	И. Бенедетти, Т. Кардинали, Р. Прекап, Гибридные теоремы о фиксированной точке и критической точке и приложения к системам с частичной вариационной структурой, J. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника