Физика — 11
Из вышесказанного становится ясно, что возникающий в контуре собственный магнитный поток прямо пропорционален силе проходящего через контур тока — Ф~I или:
Ф = LI. (1)
Здесь L является коэффициентом пропорциональности (между Ф и I) и называется индуктивностью контура (катушки).
Индуктивность зависит от геометрических размеров контура (катушки), от магнитной проницаемости среды внутри него, от числа витков. Она не зависит от силы тока в контуре и магнитного потока.
Индуктивность — скалярная величина, единица ее измерения в СИ названа генри (1 Гн), в честь американского ученого Джозефа Генри:
[L] = [Ф]I
[ ] = 1 Вб
A = 1 Гн.
• 1 Гн — индуктивность такого контура (катушки), в которой при силе тока 1А через контур проходит собственный магнитный поток 1 Вб.
Если учесть выражение (1) в законе электромагнитной индукции, то получим, что ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, проходящего через контур:
εis = — ΔФt
Δ = — Δ(LI)
Δt = —L ΔI
Δt.
(2)
Здесь εis — ЭДС самоиндукции, ΔI
Δt — скорость изменения силы тока в контуре.
Энергия магнитного поля. Согласно закону сохранения энергии, работа, совершенная при создании ЭДС индукции, будет равна энергии магнитного поля, создавшего его. Для определения этой энергии удобно воспользоваться схожестью явления самоиндукции с явлением инерции. Так, индуктивность 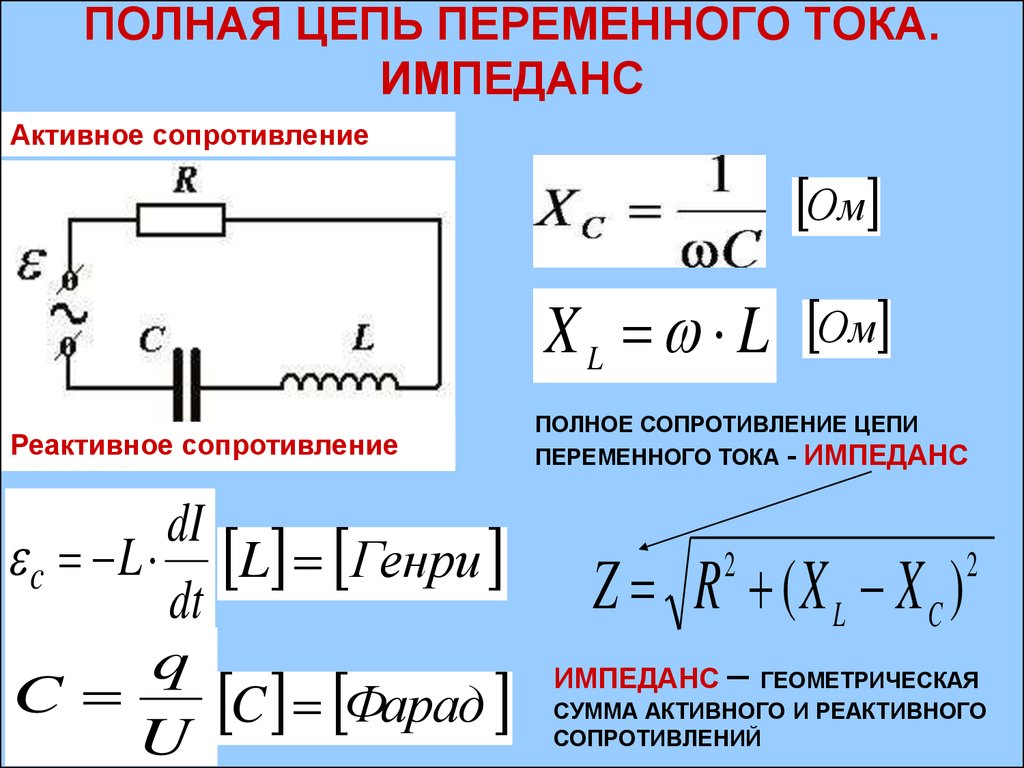 Тогда для энергии магнитного поля, создаваемого контуром в электромагнитных явлениях, можно принять выражение, аналогичное выражению кинетической энергии тела в механических явлениях:
Тогда для энергии магнитного поля, создаваемого контуром в электромагнитных явлениях, можно принять выражение, аналогичное выражению кинетической энергии тела в механических явлениях:
2. (3)
Если в этом выражении учесть формулу (1), получим ещё две формулы для энергии магнитного поля:
Wm = Ф2L
2
= ФI
2. (4)
Из теоретических вычислений получено, что плотность энергии магнитного поля прямо пропорциональна квадрату магнитной индукции и обратно пропорциональна магнитным свойствам среды:
Wm = B2 μ0 μ
2 .
(5)
Здесь μ0 — магнитная постоянная: μ0 = 4π • 10-7 Гн
м.
Лабораторная работа №4. Исследование параметров катушек индуктивности — Учись Как На Парах!
Цель работы
Ознакомление с основными параметрами катушек индуктивности и методами их измерений.
4.1. Основные сведения об индуктивностях
Движущиеся заряды (токи) порождают магнитное поле. Магнитное поле имеет направленный характер и характеризуется векторной величиной В, называемой электромагнитной индукцией. Было бы логично присвоить величине В, по аналогии с напряженностью электрического поля Е, название напряженность магнитного поля. Однако по историческим причинам это название носит вспомогательная величина Н, аналогичная вектору электрического смещения D. Связь между В и Н определяется следующей формулой:
В = μ0 μ Н, (4.1)
Где μ0 = 4π ∙ 10-7 [Гн/м] — магнитная проницаемость вакуума (воздуха), μ – относительная магнитная проницаемость вещества по отношению к вакууму.
Магнитное поле удается сконцентрировать внутри катушки, образованной множеством близко расположенных витков с током I. Если принять, что все составляющие индукции по сечению катушки S равны некоторому среднему значению В, что справедливо для катушек с сердечником, то отдельные значения В суммируются в полный поток электромагнитной индукции или, просто, Магнитный поток F:
F = ВS = LI, (4.2)
Где L – коэффициент пропорциональности между током и полным магнитным потоком катушки, называемый Индуктивностью Катушки. Индуктивность зависит от геометрии катушки, от магнитной проницаемости сердечника и от магнитных свойств окружающей среды. Единицей индуктивности является генри [Гн]. Одному генри соответствует индуктивность катушки без сердечника, которая развивает поток электромагнитной индукции в 1 вебер [Вб] в результате протекания в ней тока 1А.
В соответствии с законом Ленца, изменение магнитного потока Ф, пронизывающего замкнутый контур, порождает в нем возникновение индуцированной э. д.с. Е. Это относится как к катушкам, находящимся во внешнем поле, так и к катушкам в собственном магнитном поле:
д.с. Е. Это относится как к катушкам, находящимся во внешнем поле, так и к катушкам в собственном магнитном поле:
(4.3)
С учетом (4.2) из (4.3) получаем очень важное для практики выражение для э. д.с. катушки индуктивности при изменении протекающего через нее тока:
(4.4)
Из (4.4) следует, что включение индуктивности последовательно с цепью нагрузки, питаемой от пульсирующего источника тока, снижает пульсации тока за счет возникающей э. д.с. самоиндукции. Благодаря этому свойству индуктивности нашли широкое применение в качестве фильтров источников питания. Другим важным выводом, вытекающим из (4.4), является то, что резкие перепады тока в цепях, содержащих индуктивности, приводят к появлению больших перенапряжений. В ряде случаев с перенапряжениями приходится бороться, но часто они эффективно используются, например, в импульсных источниках питания радиоаппаратуры.
Если предположить, что ток в катушке изменяется от некоторого значения I до нуля, то работа, совершаемая этим током за время Dt, равна:
DA = EI∙Dt = – LI ∙ DI
Примем, что индуктивность L не зависит от тока, тогда работа, затрачиваемая на исчезновение магнитного потока равна:
Поскольку нигде в других элементах цепи никаких изменений не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается данная работа. Таким образом, катушка с индуктивностью L, через которую протекает ток I, запасает энергию WL, равную:
Таким образом, катушка с индуктивностью L, через которую протекает ток I, запасает энергию WL, равную:
(4.5)
Катушка не может запасти энергию мгновенно. Ее нужно зарядить аналогично тому, как заряжают конденсатор. Если индуктивность подключается к источнику постоянного напряжения U, то ее зарядка происходит по экспоненциальному закону:
, (4.6)
Где R – полное активное сопротивление, ограничивающее ток индуктивности; τ = L/R – постоянная времени зарядки индуктивности.
Цепь, состоящую из катушки индуктивности и параллельно подключенного ей конденсатора, называют Колебательным контуром. При работе индуктивности L в составе колебательного контура, ее периодическая зарядка и разрядка происходят на резонансной частоте контура F:
, (4.7)
Где С – емкость конденсатора, входящего в колебательный контур.
В колебательном контуре происходит периодическое превращение энергии, запасенной в индуктивности, в энергию заряженного конденсатора:
(4.8)
Шунтирование конденсаторами позволяет снизить выброс напряжения на индуктивностях схемы до предусмотренных разработчиком значений. Используя формулу (4.5) можно вначале рассчитать энергию, запасаемую в индуктивности при известном значении тока, а затем, с помощью равенства (4.8) найти необходимую емкость конденсатора, обеспечивающего заданную амплитуду броска напряжения.
Основными параметрами катушек индуктивности (дросселей) являются: индуктивность L при заданном максимальном значении тока Im и внутреннее сопротивление R. К числу дополнительных параметров относят диапазон рабочих частот, собственную резонансную частоту, температурный коэффициент индуктивности (ТКИ) и добротность (Q = ωL/R).
Активное сопротивление катушек индуктивности легко измеряется с помощью омметра. Реактивное сопротивление катушек, обладающих значительной индуктивностью, может быть измерено на промышленной частоте F = 50 Гц. Для этого катушку подключают к источнику переменного напряжения и с помощью амперметра переменного тока измеряют эффективное (действующее) значение тока. Полученный ток обусловлен совместным влиянием активного и реактивного сопротивлений цепи:
Реактивное сопротивление катушек, обладающих значительной индуктивностью, может быть измерено на промышленной частоте F = 50 Гц. Для этого катушку подключают к источнику переменного напряжения и с помощью амперметра переменного тока измеряют эффективное (действующее) значение тока. Полученный ток обусловлен совместным влиянием активного и реактивного сопротивлений цепи:
, (4.9)
Где ω = 2πF – угловая частота.
При известных значениях U, I, R и F с помощью формулы (4.9) несложно вычислить индуктивность катушки L.
Если индуктивность катушки невелика, то измерения на низкой частоте затруднительны или невозможны. Требуется более высокая частота. Однако измерения токов и напряжений в высокочастотных цепях представляют значительные трудности. В этом случае используется резонансный метод, в котором параллельно индуктивности устанавливают конденсатор с известной емкостью и измеряют частоту резонанса образованного колебательного контура. Далее с помощью формулы (4.7) вычисляют индуктивность L.
Далее с помощью формулы (4.7) вычисляют индуктивность L.
4.2. Порядок выполнения исследований
В лабораторной работе исследуются 2 катушки индуктивности: низкочастотный дроссель с сердечником из трансформаторной стали и высокочастотная катушка индуктивности с броневым ферритовым сердечником.
4.2.1. Измерение индуктивности низкочастотного дросселя
1. Перед началом сборки схемы измерьте с помощью мультиметра сопротивление дросселя L1, установленного на сборочном поле лабораторного стенда.
2. Используя в качестве амперметра и вольтметра переменного тока мультиметры 1 и 2, соберите схему, изображенную на рис. 4.1 (элементы сборочного поля, не используемые при измерении индуктивности дросселя L1, на рисунке не показаны).
Рис. 4.1. Схема измерений индуктивности низкочастотного дросселя
3. Включите питание стенда и измерьте переменный ток и переменное напряжение на дросселе для двух вариантов подключения измерительной цепи к выходам трансформатора:
1) при подаче напряжения с выходов СОМ и Uac1;
2) при подаче напряжения с выходов Uac1 и Uac2.
4. Рассчитайте с помощью формулы (4.9) индуктивность дросселя L1 для двух напряжений его питания и сравните полученные результаты. Постройте векторную диаграмму напряжений для одного из вариантов питания дросселя.
4.2.2. Измерение индуктивности и энергии, запасаемой в высокочастотном дросселе
1. Получите у преподавателя высокочастотный дроссель L с параллельно включенным конденсатором C = 0,047 мкФ. Перед началом сборки схемы измерьте с помощью мультиметра сопротивление дросселя.
2. Соберите схему, изображенную на рис. 4.2. Слева (рис. 4.2а) изображена принципиальная схема, в которой исследуется высокочастотный дроссель. Короткие импульсы длительностью 20…30 мкс поступают на затвор ключа на полевом N-канальном транзисторе VT. В моменты воздействия импульсов транзистор отпирается (ключ замыкается) и происходит зарядка индуктивности L от регулируемого источника напряжения 0 … 28 В с постоянной времени L/(RL + RS3). После окончания импульса транзистор резко запирается (ключ размыкается) и вся энергия, накопленная в индуктивности, идет на зарядку конденсатора С. В контуре возникает затухающий колебательный процесс, по частоте и амплитуде которого можно вычислить индуктивность дросселя и накопленную в нем энергию.
После окончания импульса транзистор резко запирается (ключ размыкается) и вся энергия, накопленная в индуктивности, идет на зарядку конденсатора С. В контуре возникает затухающий колебательный процесс, по частоте и амплитуде которого можно вычислить индуктивность дросселя и накопленную в нем энергию.
Рис. 4.2. Принципиальная схема (a) и монтажная схема (b) исследований высокочастотного дросселя
3. Подключите осциллограф между общей точкой схемы и выводом модулятора. Установите потенциометр R1 в положение, обеспечивающее подачу на контур минимального напряжения питания. Включите питание стенда и, увеличивая напряжение на выходе 0… +28 В, убедитесь в появлении на входе осциллографа периодических затухающих колебаний. Увеличьте входное постоянное напряжение до уровня, при котором амплитуда сигнала на стоке транзистора (клемма Mod) будет около 50 … 70 В. Измерьте с помощью осциллографа период и амплитуду колебаний напряжения на колебательном контуре. Зарисуйте осциллограмму.
4. Не изменяя напряжения питания схемы, подключите осциллограф к шунту RS3 и измерьте амплитуду тока индуктивности в конце стадии ее зарядки и продолжительность зарядки. Пользуясь формулами (4.5) – (4.7) рассчитайте индуктивность дросселя, амплитуду тока дросселя в конце стадии зарядки и запасенную им энергию. Сравните расчетное и экспериментальное значения энергии, полученные через ток дросселя в конце зарядки, с энергией, сообщаемой от дросселя конденсатору в колебательном контуре (формула (4.8)).
Содержание отчета
Схемы исследований.
Расчет индуктивности низкочастотного дросселя для двух исследованных режимов и векторная диаграмма.
Осциллограммы токов и напряжений при исследованиях высокочастотного дросселя.
Расчеты индуктивности высокочастотного дросселя, тока в конце зарядки дросселя, запасенной в нем энергии для расчетного и экспериментального значений тока, энергии, сообщаемой конденсатору контура.
Выводы по результатам исследований.
Энергия, запасенная в индукторе
Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.
Если мы подключим идеальную катушку индуктивности к источнику напряжения, не имеющему внутреннего сопротивления, напряжение на индуктивности должно оставаться равным приложенному напряжению. Следовательно, ток увеличивается с постоянной скоростью, как показано на рис. 1(b) . Источник подает электрическую энергию идеальному индуктору со скоростью p = Ei.
В отличие от сопротивления, индуктивность не может преобразовывать эту энергию в тепло или свет. Вместо этого энергия накапливается в магнитном поле, поскольку нарастающий ток заставляет магнитные силовые линии расширяться вопреки их стремлению стать как можно короче — что-то вроде того, как резиновая лента накапливает энергию, когда ее растягивают.
. VIт.
Хотя напряжение в цепи остается постоянным Рис. 1(a) , ток постоянно увеличивается с течением времени. Однако, поскольку скорость изменения тока постоянна, среднее значение тока I при повышении от нуля до I м это 1/2 I м . Следовательно, энергия, накопленная катушкой индуктивности при увеличении тока от нуля до I м , равна
Однако, поскольку скорость изменения тока постоянна, среднее значение тока I при повышении от нуля до I м это 1/2 I м . Следовательно, энергия, накопленная катушкой индуктивности при увеличении тока от нуля до I м , равна
\[W=V\times \frac{1}{2}{{\operatorname{I}}_{m}} \times t\]
Поскольку скорость изменения тока постоянна, напряжение на дросселе становится равным
\[V=L\frac{di}{dt}=\frac{L{{\operatorname{I}}_{ m}}}{t}\]
Замена V в уравнении для W дает
\[W=L\times \frac{{{\operatorname{I}}_{m}}}{t}\ раз \ гидроразрыва {1} {2} {{\ operatorname {I}} _ {м}} \ раз t \] 9{2} & {} & \left( 1 \right) \\\end{matrix}\]
С практической катушкой индуктивности мгновенное напряжение и ток изменяются, и скорость их изменения непостоянна. Если мы найдем напряжение на индуктивности и ток через индуктивность в данный момент, мы можем использовать соотношение p = vi для расчета скорости, с которой индуктивность цепи накапливает энергию в этот момент. {2} }=36J \\\конец{выравнивание}\]
{2} }=36J \\\конец{выравнивание}\]
Вы нашли apk для Android? Вы можете найти новые бесплатные игры и приложения для Android.
Калькулятор накопления энергии в индукторах
Создано Luciano Mino
Последнее обновление: 27 ноября 2022 г.
Содержание:- Как индукторы хранят энергию?
- Как рассчитать энергию, запасенную в катушке индуктивности
- Как использовать калькулятор накопления энергии в катушке индуктивности
Наш калькулятор накопления энергии в катушке индуктивности является идеальным инструментом для расчета энергии, запасенной в катушке индуктивности/соленоиде
Продолжайте читать, чтобы узнать больше о:
- Что такое индуктор и как он работает;
- Как рассчитать энергию, запасенную в катушке индуктивности;
- Какова формула энергии, запасенной в соленоиде; и
- Подробнее о катушках индуктивности!
Как катушки индуктивности хранят энергию?
Одним из основных электронных компонентов является катушка индуктивности. Индуктор представляет собой катушку из проволоки, которая используется для хранения энергии в виде магнитного поля 9.0006 , похожие на конденсаторы, которые накапливают энергию в электрическом поле между своими пластинами (см. наш калькулятор энергии конденсатора).
Индуктор представляет собой катушку из проволоки, которая используется для хранения энергии в виде магнитного поля 9.0006 , похожие на конденсаторы, которые накапливают энергию в электрическом поле между своими пластинами (см. наш калькулятор энергии конденсатора).
Когда ток протекает через индуктор, он создает магнитное поле вокруг индуктора . Это магнитное поле накапливает энергию, и по мере увеличения тока увеличивается и количество запасенной энергии.
Энергия высвобождается обратно в цепь, когда ток перестает течь. Эта способность накапливать энергию делает катушки индуктивности невероятно полезными во многих электронных схемах! 9{2}E=21LI2
, где:
- LLL — индуктивность катушки индуктивности;
- III — ток, протекающий через него; и
- EEE — это энергия, запасенная в магнитном поле, создаваемом катушкой индуктивности.
🔎 Проверьте наш калькулятор цепи rlc, чтобы узнать, как работают катушки индуктивности, резисторы и конденсаторы, когда они помещены в одну цепь.