сопротивление и удельное сопротивление | Физика II |

Цели обучения

К концу этого раздела вы сможете:

• Объяснить понятие удельного сопротивления.
• Используйте удельное сопротивление для расчета сопротивления определенных конфигураций материала.
• Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.

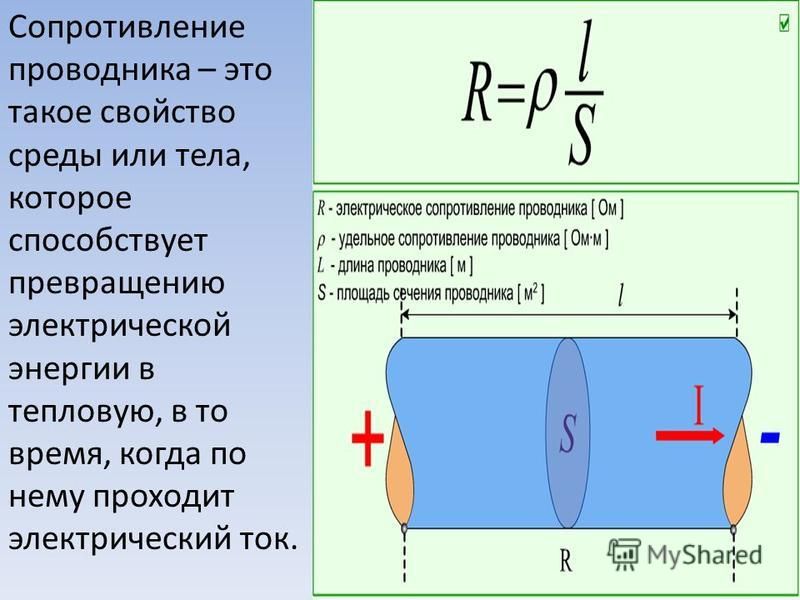
Зависимость сопротивления от материала и формы

Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор на рисунке 1 легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорционально его длине L , аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет. Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же аналогично потоку жидкости по трубе). На самом деле

R обратно пропорциональна площади поперечного сечения цилиндра A .

Рис. 1. Однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А, тем меньше его сопротивление.

Для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы оказывают различное сопротивление потоку заряда. Мы определяем удельное сопротивление ρ вещества, так что

сопротивление R объекта прямо пропорционально ρ . Удельное сопротивление ρ является внутренним свойством материала, не зависящим от его формы или размера. Сопротивление R однородного цилиндра длиной L , площадью поперечного сечения A , изготовленного из материала с удельным сопротивлением ρ , равно

R=ρLAR=\frac{\rho L}{ A}\\R=AρL​

.

В таблице 1 приведены репрезентативные значения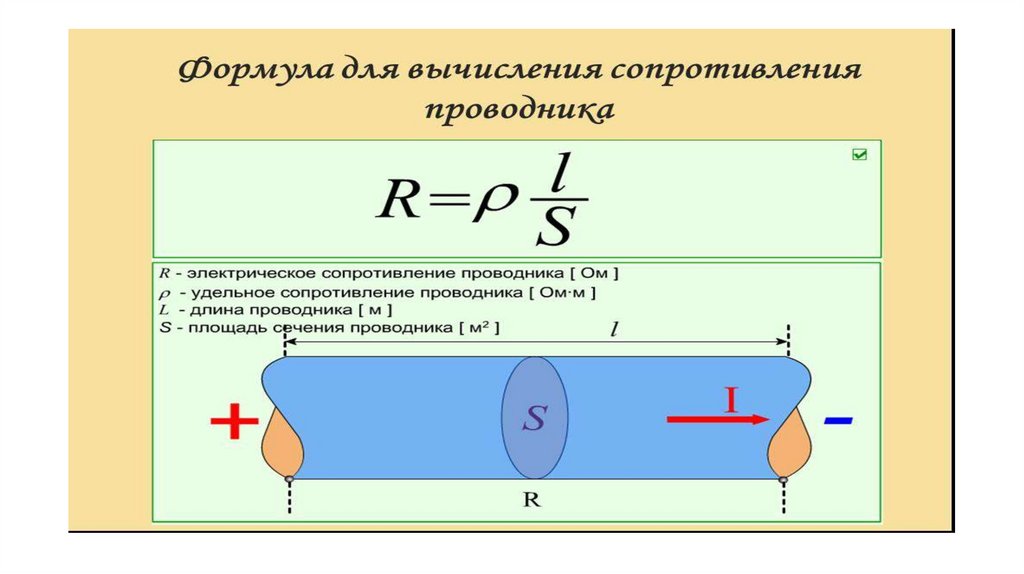

ρ . Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления. Проводники имеют наименьшее удельное сопротивление, а изоляторы — наибольшее; полупроводники имеют промежуточное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться. Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что будет рассмотрено в последующих главах.

Таблица 1. Удельные сопротивления ρ различных материалов при 20ºC

Материал	Удельное сопротивление ρ ( Ом ⋅ м )
Проводники
Серебро	1. 59 × 10 −8
Медь	1. 72 × 10 −8
Золото	2. 44 × 10 −8
Алюминий	2. 65 × 10 −8
Вольфрам	5. 6 × 10 −8
Железо	9. 71 × 10 −8
Платина	10. 6 × 10 −8
Сталь	20 × 10 −8
Свинец	22 × 10 −8
Манганин (сплав меди, марганца, никеля)	44 × 10 −8
Константан (сплав Cu, Ni)	49 × 10 −8
Меркурий	96 × 10 −8
Нихром (сплав Ni, Fe, Cr)	100 × 10 −8
Полупроводники [3]
Углерод (чистый)	3,5 × 10 5
Углерод	(3,5 − 60) × 10 5
Германий (чистый)	600 × 10 −3
Германий	(1−600) × 10 −3
Кремний (чистый)	2300
Кремний	0,1–2300
Изоляторы
Янтарный	5 × 10 14
Стекло	10 9 − 10 14
Люцит	>10 13
Слюда	10 11 − 10 15
Кварц (плавленый)	75 × 10 16
Резина (твердая)	10 13 − 10 16
Сера	10 15
Тефлон	>10 13
Дерево	10 8 − 10 11

Пример 1.

Расчет диаметра резистора: нить накала фары

Нить накала автомобильной фары изготовлена ​​из вольфрама и имеет холодное сопротивление 0,350 Ом. Если нить представляет собой цилиндр длиной 4,00 см (можно свернуть в спираль для экономии места), то каков ее диаметр?

Стратегия

Мы можем изменить уравнение

R=ρLAR=\frac{\rho L}{A}\\R=AρL​

 найти площадь поперечного сечения A нити накала по данной информации. Тогда его диаметр можно найти, предполагая, что он имеет круглое поперечное сечение.

Раствор

Площадь поперечного сечения, найденная перестановкой выражения для сопротивления цилиндра, приведенного в

R=ρLAR=\frac{\rho L}{A}\\R=AρL​

, равна

A=ρLRA =\frac{\rho L}{R}\\A=RρL​

. Подставляя данные значения и принимая 9{-5}\text{м}\end{массив}\\D​==​2(pA​)21​=2(3.146.40×10−9м2​)21​9.0×10−5м​

.

Обсуждение

Диаметр чуть меньше десятой доли миллиметра. Оно приводится только с двумя цифрами, потому что ρ известно только с двумя цифрами.

Изменение сопротивления в зависимости от температуры

Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. рис. 2.)

Рис. 2. Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры его сопротивление делает резкий скачок, а затем увеличивается почти линейно с температурой.

И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы вибрируют быстрее и преодолевают большие расстояния при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, что фактически увеличивает удельное сопротивление. При относительно небольших изменениях температуры (около 100ºC и менее) удельное сопротивление

ρ изменяется с изменением температуры Δ T , что выражается в следующем уравнении где ρ ₀ — исходное удельное сопротивление, а α — температурный коэффициент удельного сопротивления . (См. значения α в Таблице 2 ниже.) Для больших изменений температуры α может варьироваться, или может потребоваться нелинейное уравнение, чтобы найти р . Обратите внимание, что α положительно для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Манганин (состоящий из меди, марганца и никеля), например, имеет

α , близкое к нулю (трем цифрам на шкале в таблице 2), и поэтому его удельное сопротивление лишь незначительно зависит от температуры. Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.

Таблица 2. Температурные коэффициенты сопротивления α

Материал	Коэффициент (1/°C) [4]
Проводники
Серебро	3,8 × 10 −3
Медь	3,9 × 10 −3
Золото	3,4 × 10 −3
Алюминий	3,9 × 10 −3
Вольфрам	4,5 × 10 −3
Железо	5,0 × 10 −3
Платина	3,93 × 10 −3
Свинец	3,9 × 10 −3
Манганин (сплав Cu, Mn, Ni)	0,000 × 10 −3
Константан (сплав Cu, Ni)	0,002 × 10 −3
Меркурий	0,89 × 10 −3
Нихром (сплав Ni, Fe, Cr)	0,4 × 10 −3
Полупроводники
Углерод (чистый)	−0,5 × 10 −3
Германий (чистый)	−50 × 10 −3
Кремний (чистый)	−70 × 10 −3

Отметим также, что α является отрицательным для полупроводников, перечисленных в таблице 2, что означает, что их удельное сопротивление уменьшается с повышением температуры.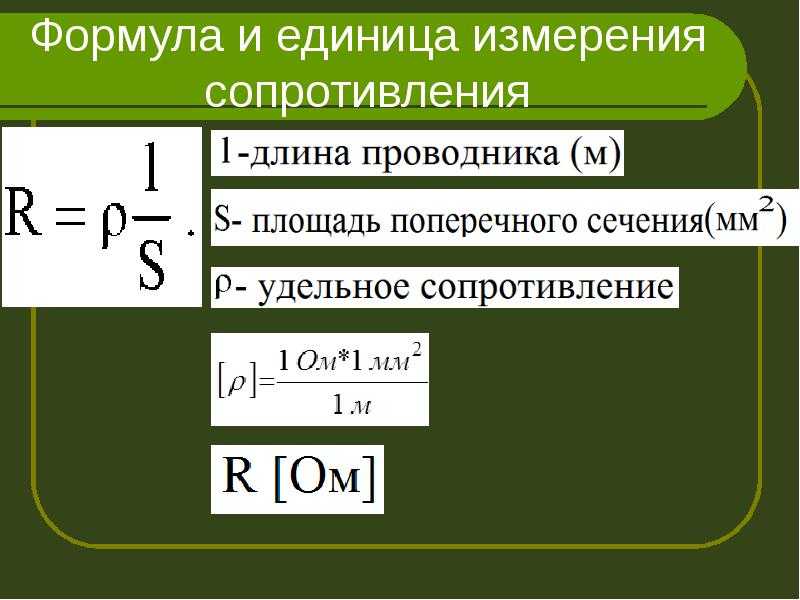 Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. Сопротивление объекта также зависит от температуры, так как R ₀ прямо пропорционально ρ . Для цилиндра мы знаем, что R = ρL / A , и поэтому, если L и A не сильно меняются с температурой, то R будет иметь такую ​​же зависимость от температуры, как ρ . (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L и A составляет примерно два порядка меньше, чем на ρ .) Таким образом,

R = R ₀ (1 + α Δ T )

400044 – температурная зависимость сопротивления объекта, где R ₀ – исходное сопротивление, а R – сопротивление после изменения температуры Δ T .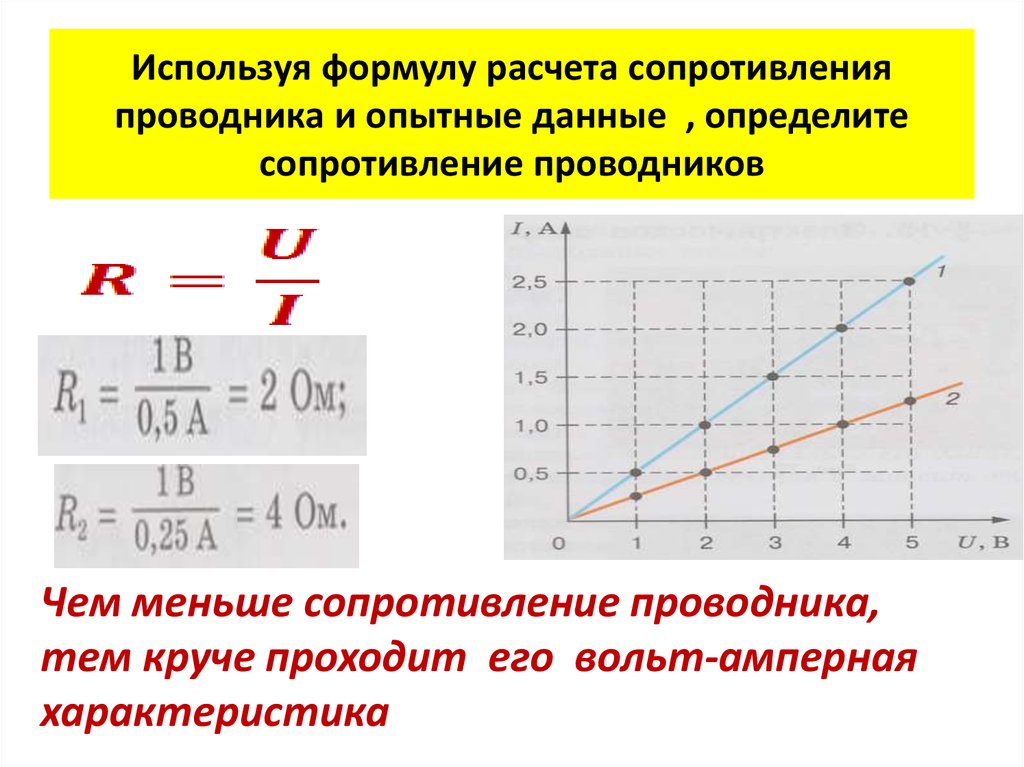 Многие термометры основаны на влиянии температуры на сопротивление. (См. рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.

Рисунок 3. Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры. (кредит: Biol, Wikimedia Commons)

Пример 2. Расчет сопротивления: сопротивление горячей нити

Хотя предупреждение должно использоваться при применении ρ = ρ ₀ (1 + α Δ T ) и R = R ₀ (1 + α 2020202020202020202020202019 ₀ (1 + α 20202020202020202020202020202019 _{. для изменений температуры более 100ºC, для вольфрама уравнения работают достаточно хорошо при очень больших изменениях температуры. {-3}/º\текст{C}\вправо)\влево(2830°\текст{C}\вправо)\вправо]\\ & =& {4,8\Omega }\end{массив}\\R​===​R0​(1+αΔT)(0.350Ω)[1+(4.5×10−3/ºC)(2830ºC)]4.8Ω​}

.

Обсуждение

Это значение согласуется с примером сопротивления фары в Законе Ома: сопротивление и простые схемы.

Исследования PhET: сопротивление в проводе

Узнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.

Нажмите, чтобы запустить симуляцию.

Резюме сечения

• Сопротивление R цилиндра длиной L и площадью поперечного сечения A равно

  R=ρLAR=\frac{\rho L}{A}\\R=AρL​

  , где ρ — удельное сопротивление материала.
• Значения ρ в таблице 1 показывают, что материалы делятся на три группы: проводники, полупроводники и изоляторы .
• Температура влияет на удельное сопротивление; для относительно небольших изменений температуры Δ T , удельное сопротивление

  ρ=ρ0(1+αΔT)\rho ={\rho }_{0}\left(\text{1}+\alpha \Delta T\right)\\ρ=ρ0​( 1+αΔT)

  , где ρ ₀  – исходное удельное сопротивление, а

  α\alpha α

  – температурный коэффициент удельного сопротивления.
• В таблице 2 приведены значения для α , температурного коэффициента удельного сопротивления.
• Сопротивление R объекта также зависит от температуры:

  R=R0(1+αΔT)R={R}_{0}\left(\text{1}+\alpha \Delta T\right)\ \R=R0​(1+αΔT)

  , где R ₀ — исходное сопротивление, а R — сопротивление после изменения температуры.

Концептуальные вопросы

1. В каком из трех полупроводниковых материалов, перечисленных в таблице 1, примеси создают свободные заряды? (Подсказка: изучите диапазон удельного сопротивления для каждого и определите, имеет ли чистый полупроводник более высокую или более низкую проводимость.)

2. Зависит ли сопротивление объекта от пути прохождения тока через него? Рассмотрим, например, прямоугольный стержень — одинаково ли его сопротивление по длине и по ширине? (См. рис. 5.)

Рис. 5. Встречает ли ток, проходящий двумя разными путями через один и тот же объект, разное сопротивление?

3. Если алюминиевый и медный провода одинаковой длины имеют одинаковое сопротивление, какой из них имеет больший диаметр? Почему?

4. Объясните, почему

R=R0(1+αΔT)R={R}_{0}\left(1+\alpha\Delta T\right)\\R=R0​(1+αΔT)

для температурное изменение сопротивления R  объекта не так точно, как

ρ=ρ0(1+αΔT)\rho ={\rho }_{0}\left({1}+\alpha \Delta T \справа)\\ρ=ρ0​(1+αΔT)

, что дает температурное изменение удельного сопротивления ρ .

Задачи и упражнения

1. Чему равно сопротивление отрезка медной проволоки 12-го калибра диаметром 2,053 мм длиной 20,0 м?

2. Диаметр медной проволоки нулевого калибра составляет 8,252 мм. Найти сопротивление такого провода длиной 1,00 км, по которому осуществляется передача электроэнергии.

3. Если вольфрамовая нить накаливания диаметром 0,100 мм в электрической лампочке должна иметь сопротивление 0,200 Ом при 20°С, какой длины она должна быть?

4. Найдите отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление на единицу длины (как это могло бы быть в бытовой электропроводке).

5. Какой ток протекает через стержень из чистого кремния диаметром 2,54 см и длиной 20,0 см, если к нему приложено напряжение 1,00 × 10 ³ В? (Такой стержень можно использовать, например, для изготовления детекторов ядерных частиц. )

6. (а) До какой температуры вы должны нагреть медный провод, первоначально равный 20,0 °С, чтобы удвоить его сопротивление, не принимая во внимание изменение размеров? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?

7. Резистор из нихромовой проволоки используется в приложениях, где его сопротивление не может измениться более чем на 1,00% от его значения при 20,0ºC. В каком диапазоне температур его можно использовать?

8. Из какого материала изготовлен резистор, если его сопротивление при 100°С на 40,0% больше, чем при 20,0°С?

9. Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0ºC до 55,0ºC, содержит чисто углеродные резисторы. Во сколько раз увеличивается их сопротивление в этом диапазоне?

10. а) Из какого материала сделан провод, если он имеет длину 25,0 м, диаметр 0,100 мм и сопротивление 77,7 Ом при 20,0°С? б) Каково его сопротивление при 150°С?

11. Предполагая постоянный температурный коэффициент удельного сопротивления, каково максимальное процентное уменьшение сопротивления константановой проволоки, начиная с 20,0ºC?

12. Проволоку протягивают через матрицу, растягивая ее в четыре раза по сравнению с первоначальной длиной. Во сколько раз увеличивается его сопротивление?

13. Медный провод имеет сопротивление 0,500 Ом при 20,0°С, а железный провод имеет сопротивление 0,525 Ом при той же температуре. При какой температуре их сопротивления равны?

14. (a) Цифровые медицинские термометры определяют температуру путем измерения сопротивления полупроводникового устройства, называемого термистором (которое имеет α  = –0,0600/ºC), когда оно имеет ту же температуру, что и пациент. Какова температура тела пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0°С (нормальная температура тела)? (б) Отрицательное значение для α нельзя эксплуатировать при очень низких температурах. Обсудите, почему и так ли это, здесь. (Подсказка: сопротивление не может стать отрицательным.)

15. Интегрированные концепции  (a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити. Вы можете принять коэффициент теплового расширения равным 12 × 10 ⁻⁶ /ºC. б) На сколько процентов ваш ответ отличается от ответа в примере?

16. Необоснованные результаты  (a) До какой температуры вы должны нагреть резистор, сделанный из константана, чтобы удвоить его сопротивление, предполагая постоянный температурный коэффициент удельного сопротивления? б) Разрезать пополам? в) Что неразумного в этих результатах? (d) Какие предположения неразумны, а какие предпосылки противоречивы?

Сноски

1. 1 Значения сильно зависят от количества и типов примесей
2. 2 Значения при 20°C.

Глоссарий

удельное сопротивление:

внутреннее свойство материала, не зависящее от его формы или размера, прямо пропорциональное сопротивлению, обозначаемое ρ

температурный коэффициент удельного сопротивления:

обозначается α , что описывает изменение сопротивления или удельного сопротивления материала при температуре

Избранные решения задач и упражнений

1. 0,104 Ом

3. 2,8 × 10 ⁻² м

5. 1,10 × 10 ⁻³ А 7. -5ºC до 45ºC

9. 1.03

11. 0.06%

13. -17ºC

15. (a) 4,7 Ом (всего) (b) 3,0% уменьшение

5

5 Значения «сильно зависят от количества и типов примесей» ↵

Значения «при 20°С». ↵

Значения «сильно зависят от количества и типов примесей» ↵

Значения «при 20°С». ↵

Лицензии и ссылки

Контент по лицензии CC, совместно используемый ранее

• College Physics. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Лицензия
• Интерактивное моделирование PhET . Предоставлено : Университет Колорадо в Боулдере. Расположен по адресу : https://phet.colorado.edu/. Лицензия : CC BY: Атрибуция

Электрическое сопротивление и проводимость — Расчеты и формула

«Сопротивление» перенаправляется сюда. Термин, используемый применительно к сенсорным экранам, см. в резистивном сенсорном экране .

Электрическое сопротивление электрического проводника является мерой трудности прохождения электрического тока через этот проводник. Обратная величина — электрическая проводимость и представляет собой легкость, с которой проходит электрический ток. Электрическое сопротивление имеет некоторые концептуальные параллели с понятием механического трения. Единицей электрического сопротивления в системе СИ является ом (Ом), а электрическая проводимость измеряется в сименсах (См).

Объект с однородным поперечным сечением имеет сопротивление, пропорциональное его удельному сопротивлению и длине и обратно пропорциональное площади его поперечного сечения. Все материалы обладают некоторым сопротивлением, за исключением сверхпроводников, сопротивление которых равно нулю.

Сопротивление (R) объекта определяется как отношение напряжения на нем ( В ) к току через него ( I ), а проводимость (G) обратно пропорциональна:

R = VI, G = IV = 1R {\ displaystyle R = {V \ over I}, \ qquad G = {I \ over V} = {\ frac {1} {R}}}

Для широкий спектр материалов и условий, V и I прямо пропорциональны друг другу, и поэтому R и G постоянны (хотя они могут зависеть от других факторов, таких как температура или деформация). Эта пропорциональность называется законом Ома, а материалы, удовлетворяющие ему, называются омические материалы.

В других случаях, таких как диод или батарея, В и I прямо пропорциональны , а не . Отношение V/I иногда все еще полезно, и его называют «сопротивлением хорды» или «статическим сопротивлением», ^{[1] [2]} , поскольку оно соответствует обратному наклону хорды между началом координат и кривая ВАХ . В других ситуациях производная может быть наиболее полезной; это называется «дифференциальным сопротивлением».

Содержание

• 1 Введение
• 2 Провода и резисторы
• 3 Закон Ома
• 4 Отношение к удельному сопротивлению и проводимости
  • 4.1 Что определяет удельное сопротивление?
• 5 Измерение сопротивления
• 6 Типовые сопротивления
• 7 Статическое и дифференциальное сопротивление
• 8 цепей переменного тока
  • 8.1 Полное сопротивление и проводимость
  • 8.2 Зависимость сопротивления от частоты
• 9 Рассеяние энергии и Джоулев нагрев
• 10 Зависимость сопротивления от других условий
  • 10. 1 Температурная зависимость
  • 10.2 Зависимость от деформации
  • 10.3 Зависимость от освещенности
• 11 Сверхпроводимость
• 12 См. также
• 14 Внешние ссылки

Введение

В гидравлической аналогии ток, протекающий по проводу (или резистору), подобен воде, протекающей по трубе, а падение напряжения на проводе подобно перепаду давления, толкающему воду по трубе. Проводимость пропорциональна тому, какой поток возникает при данном давлении, а сопротивление пропорционально тому, какое давление требуется для достижения данного потока. (Проводимость и сопротивление обратны.)

Падение напряжения (т. е. разница между напряжениями на одной и другой сторонах резистора), а не само напряжение, обеспечивает движущую силу, проталкивающую ток через резистор. В гидравлике аналогично: давление разница между двумя сторонами трубы, а не само давление определяет поток через нее. Например, над трубой может быть большое давление воды, которое пытается протолкнуть воду вниз по трубе. Но под трубой может быть такое же большое давление воды, которое пытается вытолкнуть воду обратно через трубу. Если эти давления равны, вода не течет. (На изображении справа давление воды под трубой равно нулю.)

Сопротивление и проводимость провода, резистора или другого элемента в основном определяются двумя свойствами:

• геометрия (форма) и
• материал

Геометрия важна, потому что по длинной узкой трубе труднее протолкнуть воду, чем по широкой и короткой трубе. Точно так же длинный тонкий медный провод имеет более высокое сопротивление (более низкую проводимость), чем короткий толстый медный провод.

Материалы также важны. Труба, заполненная волосами, ограничивает поток воды больше, чем чистая труба той же формы и размера. Точно так же электроны могут свободно и легко течь по медному проводу, но не могут так же легко течь по стальному проводу той же формы и размера, и они, по сути, вообще не могут течь через изолятор, такой как резина, независимо от его формы. Разница между медью, сталью и резиной связана с их микроскопической структурой и электронной конфигурацией и количественно определяется свойством, называемым удельным сопротивлением.

Помимо геометрии и материала, существуют различные другие факторы, влияющие на сопротивление и проводимость, такие как температура; Смотри ниже.

Проводники и резисторы

Вещества, в которых может течь электричество, называются проводниками. Кусок проводящего материала определенного сопротивления, предназначенный для использования в цепи, называется резистором. Проводники изготавливаются из материалов с высокой проводимостью, таких как металлы, в частности медь и алюминий. Резисторы, с другой стороны, изготавливаются из самых разных материалов в зависимости от таких факторов, как желаемое сопротивление, количество энергии, необходимое для рассеивания, точность и стоимость.

Закон Ома

Основная статья: Закон Ома

Закон Ома представляет собой эмпирический закон, связывающий напряжение В на элементе с током I через него:

I ∝ V {\ displaystyle I \ propto V}

( I прямо пропорционально V ). Этот закон не всегда верен: например, он неверен для диодов, аккумуляторов и других устройств, проводимость которых непостоянна. Однако это верно для очень хорошего приближения для проводов и резисторов (при условии, что другие условия, включая температуру, остаются постоянными). Материалы или предметы, для которых выполняется закон Ома, называются омические , тогда как объекты, не подчиняющиеся закону Ома, неомические .

Отношение к удельному сопротивлению и проводимости

Основная статья: Удельное электрическое сопротивление и проводимость

Сопротивление данного объекта зависит главным образом от двух факторов: материала, из которого он сделан, и его формы. Для данного материала сопротивление обратно пропорционально площади поперечного сечения; например, толстый медный провод имеет меньшее сопротивление, чем такой же тонкий медный провод. Кроме того, для данного материала сопротивление пропорционально длине; например, длинный медный провод имеет более высокое сопротивление, чем такой же короткий медный провод. Следовательно, сопротивление R и проводимость G проводника с однородным поперечным сечением можно вычислить как

R = ρℓA, G = σAℓ. {\ displaystyle {\ begin {align} R & = \ rho {\ frac {\ ell} {A}}, \\ G & = \ sigma {\ frac {A} {\ ell }}.\end{align}}}

где ℓ{\displaystyle \ell } – длина проводника, измеренная в метрах [м], A  – площадь поперечного сечения проводника, измеренная в квадратных метров [м²], σ (сигма) — электрическая проводимость, измеренная в сименсах на метр (С·м ⁻¹ ), а ρ (rho) — удельное электрическое сопротивление (также называемое удельным электрическим сопротивлением 9 ).0943 ) материала, измеренное в ом-метрах (Ом·м). Удельное сопротивление и проводимость являются константами пропорциональности и, следовательно, зависят только от материала, из которого сделана проволока, а не от геометрии проволоки. Удельное сопротивление и проводимость обратны: ρ = 1 / σ {\ displaystyle \ rho = 1 / \ sigma}. Удельное сопротивление является мерой способности материала противостоять электрическому току.

Эта формула не является точной, так как предполагает, что плотность тока в проводнике полностью однородна, что не всегда верно в практических ситуациях. Однако эта формула по-прежнему дает хорошее приближение для длинных тонких проводников, таких как провода.

Другая ситуация, для которой эта формула не является точной, связана с переменным током (AC), поскольку скин-эффект препятствует протеканию тока вблизи центра проводника. По этой причине геометрическое поперечное сечение отличается от эффективного поперечного сечения , в котором фактически протекает ток, поэтому сопротивление выше ожидаемого. Точно так же, если два проводника рядом друг с другом несут переменный ток, их сопротивления увеличиваются из-за эффекта близости. На промышленной частоте эти эффекты существенны для больших проводников, несущих большие токи, таких как шины на электрической подстанции, ^[3] или большие силовые кабели с током более нескольких сотен ампер.

Что определяет удельное сопротивление?

Основная статья: Удельное электрическое сопротивление и проводимость

Удельное сопротивление различных материалов сильно различается: например, проводимость тефлона примерно в 10 ³⁰ раз ниже, чем проводимость меди. Почему такая разница? Грубо говоря, металл имеет большое количество «делокализованных» электронов, которые не застревают ни в одном месте, а свободно перемещаются на большие расстояния, тогда как в изоляторе (например, в тефлоне) каждый электрон прочно связан с одной молекулой и требуется большая сила, чтобы вытащить его. Полупроводники находятся между этими двумя крайностями. Подробнее можно прочитать в статье: Удельное электрическое сопротивление и проводимость. О растворах электролитов см. статью: Электропроводность (электролитическая).

Удельное сопротивление зависит от температуры. В полупроводниках удельное сопротивление также изменяется при воздействии света. Смотри ниже.

Измерение сопротивления

Основная статья: омметр

Прибор для измерения сопротивления называется омметром. Простые омметры не могут точно измерить низкое сопротивление, потому что сопротивление их измерительных проводов вызывает падение напряжения, которое мешает измерению, поэтому в более точных устройствах используется измерение с четырьмя клеммами.

Типовые сопротивления

См. также: Удельное электрическое сопротивление элементов (страница данных) и Удельное электрическое сопротивление и проводимость

Компонент	Сопротивление (Ом)
1 метр медной проволоки диаметром 1 мм	0,02 [4]
1 км ВЛ ( типовой )	0,03 [5]
Батарейка типа АА (типичное внутреннее сопротивление )	0,1 [6]
Нить накала лампы накаливания ( тип. )	200–1000 [7]
Тело человека	от 1000 до 100 000 [8]

Статическое и дифференциальное сопротивление

См. также: Модель слабого сигнала

Многие электрические элементы, такие как диоды и батареи, удовлетворяют , а не закону Ома. Они называются неомическими или нелинейные , а их I – V кривые представляют собой , а не прямые линии, проходящие через начало координат.

Сопротивление и проводимость можно определить для неомических элементов. Однако, в отличие от омического сопротивления, нелинейное сопротивление не является постоянным, а зависит от напряжения или тока, проходящего через устройство; т. е. его рабочая точка. Существует два типа сопротивления: ^{[1] [2]}

• Статическое сопротивление (также называемое хорда или сопротивление постоянному току ) — это соответствует обычному определению сопротивления; напряжение, деленное на ток

Rstatic=VI{\displaystyle R_{\mathrm {static}}={\frac {V}{I}}\,}.

Это наклон линии (хорды) от начала координат до точки на кривой. Статическое сопротивление определяет рассеиваемую мощность в электрическом компоненте. Точки на кривой IV , расположенные во 2-м или 4-м квадранте, для которых наклон хордовой линии отрицателен, имеют отрицательное статическое сопротивление . Пассивные устройства, не имеющие источника энергии, не могут иметь отрицательное статическое сопротивление. Однако активные устройства, такие как транзисторы или операционные усилители, могут синтезировать отрицательное статическое сопротивление с обратной связью, и это используется в некоторых схемах, таких как гираторы.

• Дифференциальное сопротивление (также называемое динамическим , инкрементным или малым сигнальным сопротивлением ) — Дифференциальное сопротивление является производной напряжения по отношению к току; склон IV кривая в точке

Rdiff=dVdI{\displaystyle R _{\mathrm {diff}}={\frac {dV}{dI}}\,}.

Если кривая IV немонотонна (с пиками и впадинами), кривая имеет отрицательный наклон в некоторых областях, поэтому в этих областях устройство имеет отрицательное дифференциальное сопротивление . Устройства с отрицательным дифференциальным сопротивлением могут усиливать подаваемый на них сигнал и используются для изготовления усилителей и генераторов. К ним относятся туннельные диоды, диоды Ганна, диоды IMPATT, магнетронные трубки и однопереходные транзисторы.

Цепи переменного тока

Полное сопротивление и полная проводимость

Основные статьи: Электрический импеданс и полная проводимость

При протекании переменного тока по цепи соотношение между током и напряжением на элементе цепи характеризуется не только отношением их величин , но и различие их фаз. Например, в идеальном резисторе в момент, когда напряжение достигает своего максимума, ток также достигает своего максимума (ток и напряжение колеблются в фазе). Но для конденсатора или катушки индуктивности максимальный ток возникает, когда напряжение проходит через ноль и наоборот (ток и напряжение колеблются 9{j \ omega t}), \ quad Z = {\ frac {V_ {0}} {I_ {0}}}, \ quad Y = {\ frac {I_ {0}} {V_ {0}}}}

где:

• т время,
• V ( t ) и I ( t ) — соответственно напряжение и ток как функция времени,
• V ₀ , I ₀ , Z и Y комплексные числа,
• Z называется импедансом,
• Д называется допуском,
• Re указывает на действительную часть,
• — угловая частота переменного тока,
• j=−1{\displaystyle j={\sqrt {-1}}} — мнимая единица измерения.

Полное сопротивление и полная проводимость могут быть выражены в виде комплексных чисел, которые можно разбить на действительную и мнимую части:

Z=R+jX,Y=G+jB{\displaystyle Z=R+jX,\quad Y=G+jB}

где R и G — сопротивление и проводимость соответственно, X — это реактивное сопротивление, а B — это реактивная проводимость. Для идеальных резисторов Z и Y уменьшаются до R и G соответственно, но для сетей переменного тока, содержащих конденсаторы и катушки индуктивности, X и B отличны от нуля.

Z=1/Y{\displaystyle Z=1/Y} для цепей переменного тока, так же, как R=1/G{\displaystyle R=1/G} для цепей постоянного тока.

Зависимость сопротивления от частоты

Другая сложность цепей переменного тока заключается в том, что сопротивление и проводимость могут зависеть от частоты. Одной из причин, упомянутых выше, является скин-эффект (и связанный с ним эффект близости).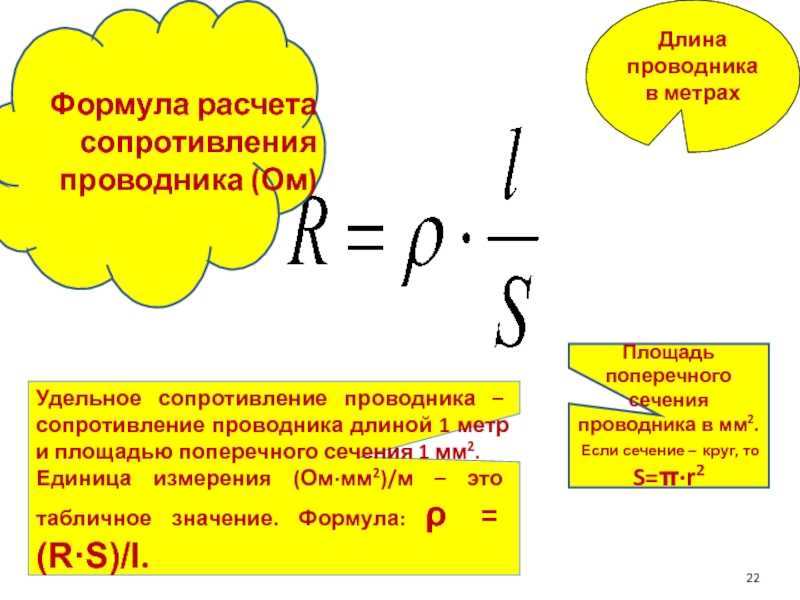 Другая причина заключается в том, что само удельное сопротивление может зависеть от частоты (см. модель Друде, ловушки глубоких уровней, резонансная частота, соотношения Крамерса-Кронига и т. д.).

Рассеивание энергии и джоулев нагрев

Основная статья: Джоулев нагрев

Резисторы (и другие элементы с сопротивлением) препятствуют протеканию электрического тока; поэтому для проталкивания тока через сопротивление требуется электрическая энергия. Эта электрическая энергия рассеивается, нагревая при этом резистор. Это называется джоулевым нагревом (в честь Джеймса Прескотта Джоуля), также называемым омическим нагревом или резистивным нагревом .

Рассеивание электрической энергии часто нежелательно, особенно в случае потерь при передаче в линиях электропередач. Передача высокого напряжения помогает уменьшить потери за счет уменьшения тока для заданной мощности.

С другой стороны, Джоулев нагрев иногда полезен, например, в электрических плитах и ​​других электрических нагревателях (также называемых резистивными нагревателями ). В качестве другого примера, лампы накаливания основаны на джоулевом нагреве: нить накаливания нагревается до такой высокой температуры, что она раскаляется до белого каления тепловым излучением (также называемым накалом). 9{2}R}

, где P — мощность (энергия в единицу времени), преобразованная из электрической энергии в тепловую, R — сопротивление, а I — ток через резистор.

Зависимость сопротивления от других условий.

Зависимость от температуры. увеличена. Удельное сопротивление изоляторов и электролитов может увеличиваться или уменьшаться в зависимости от системы. Подробное описание поведения и объяснение см. в разделе Удельное электрическое сопротивление и проводимость.

Как следствие, сопротивление проводов, резисторов и других компонентов часто меняется в зависимости от температуры. Этот эффект может быть нежелательным, вызывая сбои в работе электронной схемы при экстремальных температурах. Однако в некоторых случаях этот эффект используется с пользой. Когда температурно-зависимое сопротивление компонента используется целенаправленно, этот компонент называется термометром сопротивления или термистором. (Термометр сопротивления изготавливается из металла, обычно из платины, а термистор из керамики или полимера.)

Термометры сопротивления и термисторы обычно используются двумя способами. Во-первых, их можно использовать в качестве термометров: измеряя сопротивление, можно определить температуру окружающей среды. Во-вторых, их можно использовать в сочетании с джоулевым нагревом (также называемым самонагревом): если через резистор протекает большой ток, температура резистора повышается, и, следовательно, изменяется его сопротивление. Следовательно, эти компоненты можно использовать для защиты цепей, как и предохранители, или для обратной связи в цепях, или для многих других целей. В общем, самонагревание может превратить резистор в нелинейный и гистерезисный элемент цепи. Для получения дополнительной информации см. Термистор#Эффекты самонагрева.

Если температура T не изменяется слишком сильно, обычно используется линейное приближение: где α {\ displaystyle \ alpha} называется температурным коэффициентом сопротивления , T0 {\ displaystyle T_ {0}} — это фиксированная эталонная температура (обычно комнатная температура), а R 0 {\ displaystyle R_ {0}} — это сопротивление. при температуре T0{\displaystyle T_{0}}. Параметр представляет собой эмпирический параметр, подобранный на основе данных измерений. Поскольку линейное приближение является всего лишь приближением, оно отличается для разных эталонных температур. По этой причине обычно указывается температура, при которой было измерено α {\ displaystyle \ alpha}, с суффиксом, например α 15 {\ displaystyle \ alpha _ {15}}, и соотношение сохраняется только в диапазоне температур около ссылка. ^[9]

Температурный коэффициент α{\displaystyle \alpha} обычно составляет от +3×10 ⁻³ K ⁻¹ до +6×10 ⁻³ K ⁻¹ для металлов вблизи помещения температура. Обычно он отрицательный для полупроводников и изоляторов с сильно изменчивой величиной. ^[10]

Зависимость от деформации

Основная статья: Тензодатчик

Так же, как сопротивление проводника зависит от температуры, сопротивление проводника зависит от деформации. При помещении проводника на растяжение (форма напряжения, приводящая к деформации в виде растяжения проводника) длина участка натяжения проводника увеличивается, а площадь его поперечного сечения уменьшается. Оба эти эффекта способствуют увеличению сопротивления натянутого участка проводника. При сжатии (деформации в обратном направлении) сопротивление натянутого участка проводника уменьшается. См. обсуждение тензорезисторов для получения подробной информации об устройствах, сконструированных для использования этого эффекта.

Зависимость от освещения

Основные статьи: Фоторезистор и фотопроводимость

Некоторые резисторы, особенно сделанные из полупроводников, проявляют фотопроводимость , что означает, что их сопротивление изменяется, когда на них падает свет.