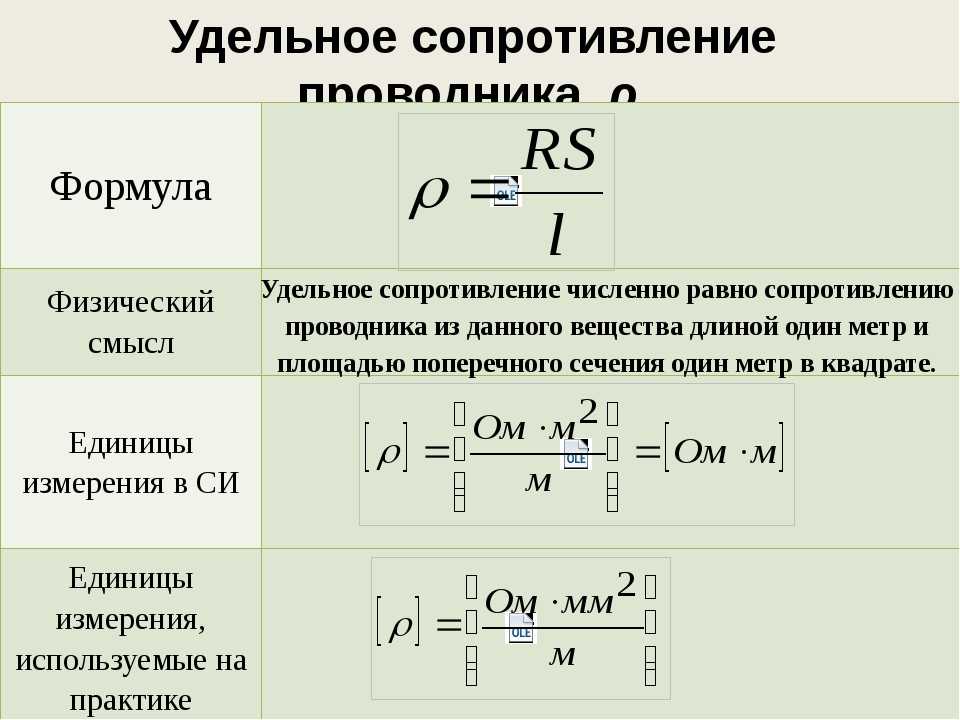
Расчет сопротивления проводника – формула

4.6

Средняя оценка: 4.6

Всего получено оценок: 97.

4.6

Средняя оценка: 4.6

Всего получено оценок: 97.

Сопротивление проводника ограничивает величину тока в электрической цепи. Чем больше величина сопротивление, тем меньше ток. Расчет сопротивления проводника можно произвести двумя способами: первый способ заключается в использовании формулы закона Ома, а второй вариант расчета подразумевает знание геометрических размеров проводника и удельного сопротивления вещества, из которого он сделан.

Почему проводник “сопротивляется”?

Напряжение U, поданное на концы проводника, создает внутри него электрическое поле, которое приводит в движение свободные электроны вещества. Электроны, получив дополнительную кинетическую энергию, начинают двигаться упорядоченно в одном направлении, создавая тем самым электрический ток цепи.

В процессе движения электроны сталкиваются с нейтральными и заряженными атомами, из которых стоит проводник, теряют энергию.

Масса атома превосходит массу электрона в тысячи раз, поэтому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).

Таким образом возникает сопротивление протеканию (нарастанию) тока. Рис. 1. Электрический ток в проводнике ограничивается столкновением электронов с атомами.

Расчет сопротивления с помощью закона Ома

Немецкий физик Георг Ом в 1826 г. обнаружил, что отношение напряжения U между концами металлического проводника, являющегося участком электрической цепи, к силе тока I есть величина постоянная:

$ R={U \over I}=const $ (1),

где:

U — напряжение, В;

I — сила тока, А;

R — сопротивление, Ом.

Эту величину стали называть электрическим сопротивлением. Пользуясь этой формулой, можно экспериментально определить величину неизвестного сопротивления.

Рис. 2. Схема измерения напряжения и тока для определения сопротивления участка цепи.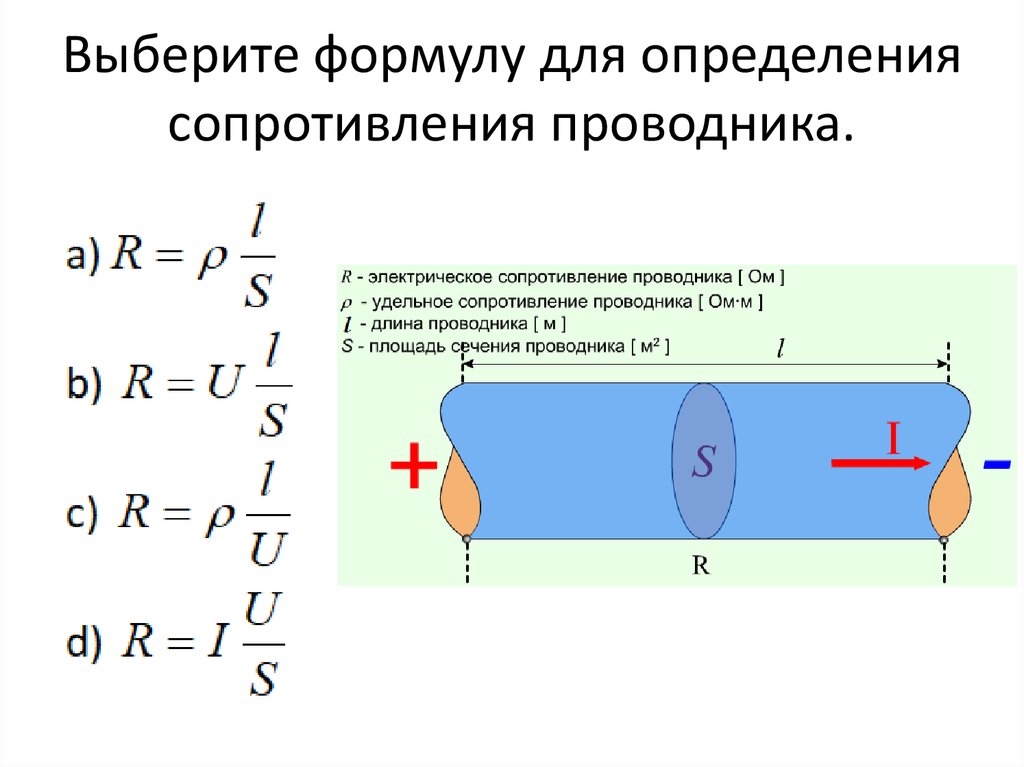

Для этого амперметром измеряется величина электрического тока через сопротивление, а вольтметром — напряжение на участке цепи. Далее, применяя формулу (1), вычисляется значение R.

Единица измерения названа в честь Георга Ома. Электрическим сопротивлением 1 Ом обладает участок цепи, на котором при силе тока 1 А напряжение равно 1 В:

$$ 1 Ом = { 1 В\over 1 A} $$

Расчет с помощью удельного сопротивления

Расчет сопротивления проводника можно произвести без измерения величин напряжения и тока. Но для этого необходимо знать дополнительную информацию о проводнике.

Рис. 3. Проводник с поперечным сечением S и длиной L, через который течет ток I.

Георг Ом и другие исследователи опытным путем определили, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S. Эту закономерность можно описать формулой расчета сопротивления проводника:

$ R = ρ *{ L\over S} $ (2)

Коэффициент ρ был назван удельным сопротивлением.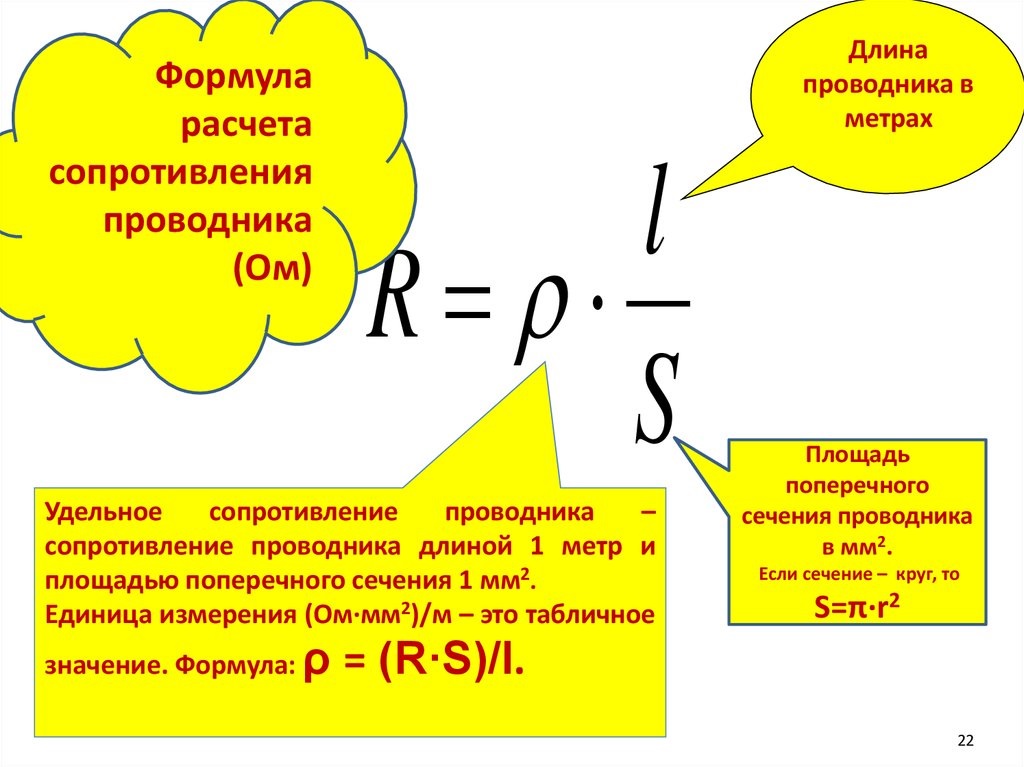 2\over м} $. Этим объясняется использование такого довольно дорогого металла для пайки особенно важных радиодеталей (микросхем, микропроцессоров, электронных плат), которые должны как можно меньше нагреваться в процессе работы.

Что мы узнали?

Итак, мы узнали, что расчет сопротивления проводника можно произвести двумя способами. Первый расчет проводится с помощью формулы закона Ома после измерения величин напряжения и тока. Для второго расчета необходима информация о геометрических размерах проводника и его удельном сопротивлении.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 97.

---

А какая ваша оценка?

Рациональная формула для определения тягового сопротивления плуга — тезисы доклада

Рациональная формула для определения тягового сопротивления плугатезисы доклада Исследовательская статья

• Автор: Чиненова В. Н.
• Сборник: Институт истории естествознания и техники им. С.И.Вавилова. Годичная научная конференция, посвященная 85-летию ИИЕТ РАН
• Том: 23
• Тезисы
• Год издания: 2017
• Место издания: Янус-К Москва
• Первая страница: 169
• Последняя страница: 172
• Аннотация: В. П.Горячкину принадлежит открытие рациональной формулы для тягового сопротивления плуга. Горизонтальную составляющую Rx сопротивления плуга при вспашке В. П. Горячкин назвал тяговым сопротивлением и выразил ее трехчленом: Rx=fПG + kПabn+εabnV2. (1) Первое слагаемое — fПG- сопротивление перекатыванию опорных колес плуга и трению о дно и стенку борозды, пропорциональное весу G плуга. Коэффициент пропорциональности fП назван коэффициентом сопротивления протаскиванию. Силу fПG определяют протаскиванием плуга в открытой борозде. Значение коэффициента fП, зависит от типа почв, их агрофона, конструкции плугов и находится в пределах 0,4… 1,0. Второе слагаемое — kПabn- вызвано сопротивлением подрезанию, разрушению и укладыванию пласта в борозду. Действие этой составляющей общего сопротивления считается полезным. Коэффициент kП оценивает удельное сопротивление почвы, определяемое из соотношения kП=RX / abn, где RX- горизонтальная составляющая силы сопротивления почвы при вспашке плугом; а— глубина вспашки; b— ширина захвата корпуса; n— число корпусов. Силу RX находят при динамометрировании (осциллографировании) без учета первого и третьего слагаемых формулы (1). Величина kП зависит от типа почв и степени их освоенности. Так, для глинистых и дерново-подзолистых почв значение kП в 2,3…2,6 раза больше, чем для легкосуглинистых и супесчаных. При вспашке после уборки зерновых значение kП на 10…20 % меньше в сравнении с обработкой травяного пласта. Третье слагаемое — εabnV2- скоростное сопротивление, зависящее от кинематической энергии, сообщаемой почвенным пластом. Эта составляющая не оказывает существенного влияния на полезное деформирование почвы. Коэффициентεскоростного сопротивления зависит от типа почв, геометрических форм рабочих поверхностей плужных корпусов. При скоростях вспашки до 5 км/ч коэффициентεнезначительно (2…3 %) изменяет общую силу RX С увеличением скорости движения до 12 км/ч сопротивление плугов с традиционными корпусами существенно возрастает. Для пахоты на скоростях 12… 15 км/ч применяют скоростные рабочие поверхности плужных корпусов, в которых уменьшено значение коэффициента ε. Формула Горячкина (1) выражает физическую сущность взаимодействия плуга с почвой, но определение силы RX и ее составляющих требует многочисленных трудоемких экспериментов, поэтому в практических расчетах широко применяют упрощенное выражение для тягового сопротивления плуга Rx= kabn, где k— удельное сопротивление плуга. Значение к рассчитывают по формуле k = Rx/abn, замерив среднее тяговое сопротивление Rx, глубину а пахоты и ширину bn захвата плуга. Коэффициент k отражает все три составляющие тягового сопротивления плуга, входящие в выражение (3.9). На величину k влияют технологические свойства почвы, конструктивные параметры плуга и скорость его движения. В зависимости от коэффициента k почвы разделяют на легкие — k< 30 кН/м2, средние — 30…50, среднетяжелые — 50…70, тяжелые — 70…120 и очень тяжелые — k> 120 кН/м2.
• Добавил в систему: Чиненова Вера Николаевна

Прикрепленные файлы

---

№	Имя	Описание	Имя файла	Размер	Добавлен
1.	Краткий текст		Kratkoe_soderzh_k_rats-formule.doc	50,5 КБ	17 декабря 2017 [Chinenova]

Калькулятор сопротивления провода

Создано Luciano Mino

Последнее обновление: 04 июля 2022 г.

Содержание:

• Сопротивление провода и удельное сопротивление
• Формула сопротивления провода и его связь с проводимостью
• Как рассчитать длину провода используя сопротивление

С помощью калькулятора сопротивления проводов вы сможете легко найти сопротивление и проводимость различных проводов в зависимости от их длины, материала и площади поперечного сечения.

Мы объединили этот калькулятор с объяснением различных областей, связанных с этой темой, таких как:

• Как найти сопротивление провода;
• Как рассчитать сопротивление медного провода по формуле сопротивления провода; и
• Как рассчитать длину провода по сопротивлению.

Продолжайте читать, чтобы узнать больше!

Сопротивление провода и удельное сопротивление

Сопротивление и удельное сопротивление — это два сходных свойства объекта. Однако они не совсем одинаковы.

Удельное сопротивление ρ описывает сопротивление потоку заряженных частиц через объект и является внутренним свойством материала, не зависящим от размеров провода.

Аналогично, сопротивление σ относится к тому, насколько сильно провод определенных размеров (длины и площади) сопротивляется потоку электронов.

Калькулятор сопротивления проводов также имеет поле для проводимости , которая является обратной величиной сопротивления.

Не волнуйся. Эти концепции станут ясны, как только вы поймете их формулы.

🙋 С помощью этого инструмента вы можете рассчитать сопротивление медного провода или любого другого материала. Наш калькулятор сопротивления проводов позволяет выбирать различные материалы проводов с соответствующим удельным сопротивлением. Не стесняйтесь экспериментировать с ним!

Формула сопротивления провода и его связь с проводимостью

Сопротивление прямого провода можно рассчитать по следующей формуле:

R=ρLAR = \frac{\rho L}{A}R=AρL​

где:

• ρ\rhoρ – удельное сопротивление материала, в ом-метрах Ом⋅мОм \cdot мОм⋅м; 9{2} м2; и
• RRR — сопротивление в омах ΩΩΩ.

Другое понятие, проводимость , является обратной величиной удельного сопротивления и мерой того, насколько легко току течь через материал:

σ=1ρ\sigma = \frac{1}{\rho}σ =ρ1​

Аналогично, проводимость обратно пропорциональна сопротивлению:

G=1R=AρLG = \frac{1}{R} = \frac{A}{\rho L}G=R1​=ρLA​

и их единицы сименс на метр и сименс 9{-8}\ \Omega \cdot \text{м}1,68×10−8 Ом⋅м. Теперь мы можем просто заменить каждый параметр нашими данными в приведенном выше уравнении, чтобы получить:

L=119,05 мл = 119,05\ \text{м}L=119,05 м

🙋 Не забывайте соблюдать единицы площади и длины. Вы можете попробовать конвертер площади или конвертер длины, если у вас есть сомнения по поводу этих преобразований.

Или вы можете ввести информацию в калькулятор сопротивления проводов, и наш инструмент автоматически найдет любой отсутствующий параметр !

Лучано Мино

Видео с вопросами: Определение правильной формулы, связывающей сопротивление и удельное сопротивление

Стенограмма видео

Какая из следующих формул правильно связывает удельное сопротивление 𝜌 вещества с сопротивлением объекта длиной 𝑙, который состоит из вещество, если объект имеет площадь поперечного сечения 𝐴 и сопротивление 𝑅? (A) 𝜌 равно 𝑅, умноженному на 𝑙, деленному на 𝐴. (B) 𝑅 равно произведению 𝜌 на 𝑙, деленному на 𝐴. (C) 𝑅 равно произведению 𝜌 на 𝐴, деленному на 𝑙.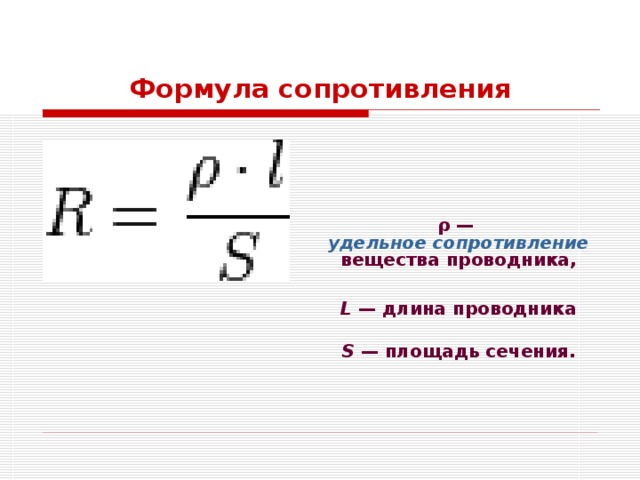 (D) 𝑅 равно 𝜌 умножить на 𝐴 умножить на 𝑙.

Каждое из этих четырех уравнений претендует на то, чтобы математически правильно связать удельное сопротивление вещества 𝜌 с сопротивлением объекта, сделанного из этого вещества 𝑅. Даже если мы не вспомним навскидку соотношение, связывающее эти величины, мы все равно сможем работать над нашим ответом, признав, что для того, чтобы любое из этих уравнений было истинным, единицы в левой части должны быть равны единицам в левой части. правая сторона.

Относительно единиц, напомним, что в системе СИ единицами электрического сопротивления являются омы. Так, например, если бы у нас был провод такой длины, и мы должны были бы пропускать ток через этот провод, у этого провода было бы некоторое электрическое сопротивление, и мы записываем его в омах. Но тогда представьте это. Скажем, у нас есть провод из того же материала и того же сечения, что и предыдущий, но только теперь его длина короче. Если мы еще раз пропустим ток через этот меньший отрезок провода, мы получим сопротивление, но оно будет меньше, чем сопротивление по длине этого провода. Это говорит нам о том, что сопротивление — это величина, которая зависит не только от материала, из которого сделан объект, но и от его размеров.

В отличие от этого удельное сопротивление 𝜌 материала. Для двух объектов, сделанных из одного и того же материала, таких как эти две проволоки, удельное сопротивление одного объекта равно удельному сопротивлению другого. В отличие от сопротивления, удельное сопротивление не зависит от размеров объекта, а только от материала, из которого он сделан. Мы можем увидеть как сходство удельного сопротивления с сопротивлением, так и разницу между ними, взглянув на единицы удельного сопротивления. И удельное сопротивление, и сопротивление включают единицы Ом. Но в удельном сопротивлении это дополнительное, мы могли бы назвать это измерение длины, делает так, что удельное сопротивление этого провода такое же, как у этого, даже если два провода имеют разную длину.

Знание единиц измерения этих двух величин поможет нам выбрать правильный вариант ответа. Обратите внимание, что если мы останемся в системе СИ, то основными единицами длины будут метры, а единицами площади — метры в квадрате. Зная все это, давайте теперь изучим единицы по обе стороны этих уравнений, начиная с варианта ответа (А). Чтобы это уравнение было правильным, должно быть так, что единицы удельного сопротивления, омы, умноженные на метры, равны единицам сопротивления, омам, умноженным на единицу длины, метры, деленные на единицу площади, метры в квадрате. Тем не менее, мы видим, что в правой части числитель и знаменатель сокращаются на один множитель в метрах, в результате чего у нас остаются общие единицы измерения в омах, деленные на метры. Тогда это равенство не выполняется. Поэтому мы не будем выбирать вариант ответа (А).

Переходим к варианту ответа (B), здесь слева у нас есть сопротивление, измеряемое в омах. И это, как утверждается, равно единицам удельного сопротивления, омам, умноженным на метры, умноженные на единицы длины, метры, все поделенные на метры в квадрате, единицы площади. В этом случае мы видим, что два множителя метров в нашем числителе уравновешиваются двумя множителями метров в нашем знаменателе. Упрощенными единицами справа являются омы. Это говорит нам о том, что для варианта ответа (В) единицы по обе стороны уравнения согласуются друг с другом.

Чтобы подтвердить, что это наш правильный ответ, давайте перейдем к вариантам (C) и (D). В варианте ответа (C) в левой части у нас есть единицы измерения сопротивления, омы, и говорят, что они равны омам, умноженным на метры, умноженные на метры в квадрате, все деленные на метры. В правой части этого выражения уравновешивается один множитель метров. Это оставляет нам омы, умноженные на метры в квадрате, которые, как мы знаем, не равны омам. Единицы в выборе ответа (С) не согласуются друг с другом.

Наконец, мы рассмотрим вариант ответа (D). Здесь говорят, что сопротивление в единицах Ом равно удельному сопротивлению в единицах Ом, умноженному на метры, умноженному на площадь в единицах метров в квадрате, умноженному на длину в единицах метров.