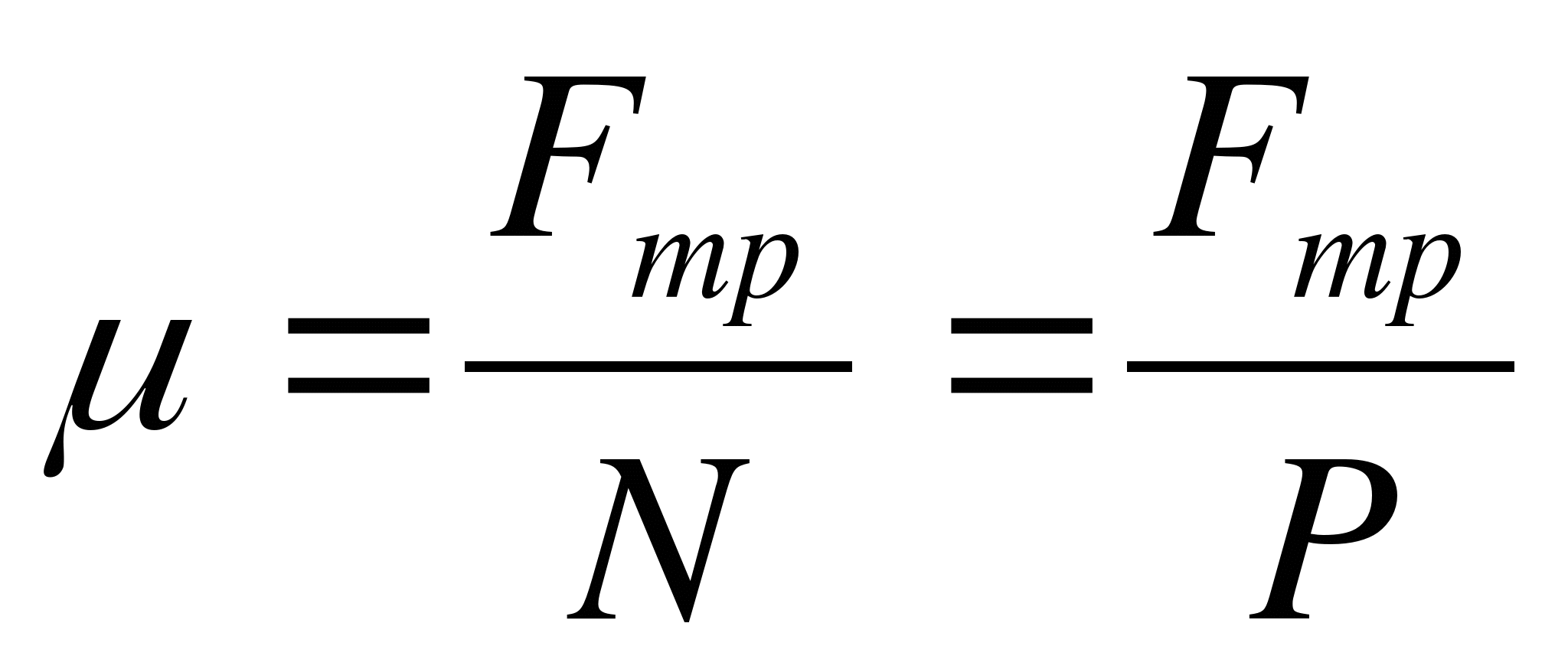Сила трения: сложная тема простым языком
Добавлено: 7 августа 2022 в 10:33
Содержание
Физика – великая наука, выводящая и объясняющая принципы работы нашего запутанного мира. А знали ли вы, какая из ее тем является одной из самых часто встречающихся и в то же время самых прикладных?
Она вокруг нас, и именно благодаря ней летят самолеты, двигаются поезда, бегут марафонцы, крутятся шестеренки, а без нее невозможно никакое движение. Знакомьтесь, перед вами сила трения.
Сила трения: сложная тема простым языком
Согласно классической формулировке, сила трения — это величина, которая дает характеристику процессу механического трения объектов по величине и направлению.
Поводами к ее появлению становятся шероховатости на соприкасающихся поверхностях, создающие сопротивление при передвижении, и притяжения и отталкивания на атомарном уровне.
Зависит ее значение от:
- Массы
- Степени шлифовки
- Материала, использованного при изготовлении
- Давления (реакции опоры)
- Смазки
Обратите внимание на то, что площадь соприкосновения поверхностей при прочих равных влияния не оказывает.
Сила трения ЕГЭ по физике — одна из интереснейших тем. Давайте остановимся на ней поподробнее.
Как измерить силу трения
Сила трения: сложная тема простым языком
Для нахождения данной силы используется закон Амонтона-Кулона.
Его формула: Fтр= μ • N, где N – сила реакции опоры, которая равна силе тяжести, следовательно, массе, умноженной на ускорение (m • g), а μ – коэффициент, зависящий от материала и имеющий постоянные значения для определенных веществ.
Классификация
У рассматриваемого явления есть множество разновидностей. Оно может быть:
- внешним (взаимодействуют два отдельных тела)
- внутренним (происходит между частями определенного вещества, в школьном курсе физики практически не рассматривается)
- смешанным (имеющее участки и вязкого, и сухого)
- жидкостным или вязким (возникает при перемещении жидкостей или газов, значение зависит от степени вязкости среды)
- сухим (имеются в виду твердые вещества)
В свою очередь, последнее делится на скольжение, качение и покой.
Давайте поговорим о них поподробнее.
Скольжение
Перед нами трение в классическом его виде. Возникает при перемещении чего-либо по поверхности и тормозит этот процесс.
Примером этого явления могут послужить подошвы кроссовок бегуна, как бы отталкивающиеся от асфальта. В этом им помогает именно скольжение. Его направление всегда противоположно движению тела.
Сила трения: сложная тема простым языком
Качение
Возникает, когда объект (чаще всего шаровидной формы) перекатывается по определенной поверхности. Направлено всегда по катящемуся телу в сторону, обратную его вращению.
Примером может послужить передвижение колес транспортного средства или шариков в подшипнике. Это явление гораздо слабее, чем скольжение, и именно поэтому любую вещь легче катить, чем тащить.
Сила трения: сложная тема простым языком
Покой
Самый необычный подвид, сильнее остальных разновидностей. Появляется между двумя касающимися неподвижными предметами и препятствует их движению относительно друг друга.
Именно это явление помогает вещам не выскальзывать из наших рук, узлам не развязываться и тому подобное.
Направлено всегда противоположно стороне, в которую могли бы перемещаться объекты, если бы не имели никаких шероховатостей.
Сила трения: сложная тема простым языком
Кратко о том, что такое сила трения
- Сила трения – величина, характеризующая процесс механического трения тел по величине и направлению.
- Зависит от массы, гладкости, вещества, давления и смазки.
- Находится по формуле: Fтр= μ • N
- Делится на разновидности. Самые часто встречаемые из них – скольжение, качение и покой.
- Скольжение – классическое взаимодействие между двумя предметами. Направлено в сторону, обратную их передвижению.
- Качение – сопротивление при перемещении объекта по поверхности, сопровождаемое его кручением по своей оси. Направлено обратно ему.
- Покой – сопротивление, мешающее объекту сдвинуться. Направлено обратно стороне, в которую передвигалось бы тело.
Теперь вы знаете об этой теме больше, и это здорово!
Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:
Владислав Барышников
Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР
Задать вопрос
Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Магистр физико-математических наук. Преподавательский стаж более 13 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.
Читайте также:
Силы трения — Вопросы к экзмену
Силы трения
Абсолютно гладких поверхностей опоры практически не существует. Между телом человека и опорой при движении по ней всегда возникает трение.
Сила трения — это мера противодействия движущемуся телу, направленного по касательной к соприкасающимся поверхностям. Сила трения считается равной произведению нормального давления на коэффициент трения:
Т= N * k ; [Т] = ML * ( T в -2 степени)
где ктр — коэффициент трения
Как видно из формулы, коэффициент трения — это отношение силы трения к силе нормального давления (прижимающей силе), которая прижимает трущиеся тела друг к другу:
k (трения)= T/N
Это справедливо для трения скольжения, когда одно тело перемещается относительно другого, не теряя контакта с ним, скользит по нему.
Предел, до которого может увеличиваться статическая сила трения, называется предельной силой трения скольжения покоя. Она равна произведению нормального давления на статический коэффициент трения скольжения:
T=N*k
Следовательно, статический коэффициент трения скольжения равен отношению статической силы трения скольжения (предельной) к силе нормального
давления; можно сказать иначе: это отношение сдвигающей силы к прижимающей.
Механизм трения скольжения объясняют зацеплением неровностей поверхностей скользящих тел друг за друга (механическая теория), а также молекулярным сцеплением, когда гладкие поверхности обеспечивают плотный контакт тел (молекулярная теория).
При смазке неровности поверхности «сглаживаются».
Второй вид трения, отличающийся от трения скольжения, проявляется при качении, когда точки соприкосновения тел все время сменяются (точки покрышки велосипеда и места его опоры на дорожке). Механизм трения качения объясняют деформацией соприкасающихся тел. Колесо как бы вдавливается в опору, образуя ямку, через край которой колесу все время приходится перекатываться . Коэффициент трения качения вычисляют как отношение момента движущей силы к моменту трения ( N сила нормального давления, умноженная на ее плечо относительно края ямки — к к ). Плечо силы
Третий вид трения проявляется, когда между трущимися поверхностями имеется неподвижная точка. Это трение верчения — движение происходит вокруг этой точки. Так, стопа при отталкивании от опоры, если на подошве обуви нет шипов, вращается относительно грунта. У метателя молота на подошве обуви имеется один шип, верчение происходит при повороте вокруг шипа.
Силы трения, направленные навстречу движению, тормозят его. Они вызывают отрицательное ускорение, совершают отрицательную работу. Силы трения, направленные одинаково с движением, не создают положительного ускорения, не совершают положительной работы, а только не дают точке контакта движущегося тела «проскальзывать» назад.
Еще статьи в этом разделе
Биомеханика как наука о движениях человека.
Биомеханическая характеристика силовых качеств
Биомеханическая характеристика скоростных качеств
Биомеханическая характеристика выносливости
Биомеханическая характеристика гибкости
Биомеханические методы изучения движения.
Временные характеристики.
Пространственно — временные характеристики.
Геометрия масс тела
Движения в биокинематических цепях
Задачи биомеханики спорта
Звенья тела как рычаги и маятники
Импульс силы и импульс момента силы
Инерционные характеристики
Кинематические характеристики
Динамические характеристики тела человека.
Механические свойства мышц
Развитие биомеханики спорта и связи ее с другими науками.
Разновидности работы мышц
Сила и момент силы
Силы действия среды
Силы тяжести и вес
Соединение звеньев тела
Степени свободы и связи движений в биомеханических цепях
Выносливость и способы ее измерения
Строение биомеханической системы.
Разновидности работы мышц
Механизм отталкивания от опоры
Биодинамика прыжка
Онтогенез моторики
Телосложение и моторика человека
Эффективность владения спортивной техникой
Показатели технического мастерства
Калькулятор трения | Определение | Пример
Трение — это сила , которая противодействует относительному движению материальных текстур, жидких слоев и элементов материала , скользящих друг относительно друга. Трение является одной из фундаментальных физических сил в природе , и понимание того, как оно работает, является ключом к пониманию многих природных и искусственных явлений.
Мы сделали этот калькулятор, который поможет вам рассчитать силу трения.
Если вы хотите найти силу объекта, вы можете использовать наш калькулятор силы.
Определение тренияТрение возникает в результате контакта между двумя поверхностями , которые обычно соприкасаются только в точках их контакта. Трение — это также термин, используемый для описания сопротивления одного объекта другому. Например, вы можете найти трение в связи с тем, что по земле трудно ходить из-за песка или камней. Песок или камни заставляют человека сильнее нажимать на ноги, чтобы двигаться.
Как найти силу трения Силу трения легко найти с помощью нашего калькулятора. Она пропорциональна силе, приложенной к поверхности, и нормальной силе. Коэффициент трения 
Если вы пытаетесь найти силу трения, вы можете использовать следующую формулу:
F = \mu \cdot Н Где F — сила трения, μ — коэффициент трения, а N — нормальная сила. Коэффициент трения
Второй закон движения Ньютона описывает, что результирующая сила, действующая на объект, равна его массе, умноженной на его ускорение. Когда предмет находится в состоянии покоя, на него действует только сила трения. Влияние трения зависит от двух соприкасающихся поверхностей и величины прилагаемого давления. Когда объект движется , результирующая сила, действующая на него, представляет собой силу трения и силы тяжести.
Чистая сила эквивалентна массе объекта, умноженной на его ускорение.
Если вам нужно найти силу тяжести объекта, вы можете использовать наш калькулятор гравитационной силы.
Вы можете использовать уравнение в случае двух поверхностей , но вы можете применить его к любому количеству поверхностей. Вы можете часто использовать его в тех случаях, когда нет большого трения. Коэффициент трения — это эмпирическое число, которое изменяется в зависимости от типа поверхности, температуры и относительной скорости.
Виды силы трения В литературе можно найти три основных типа силы трения: статическая, кинетическая и скользящая . Статическая сила трения — это сила, противодействующая движению объекта, когда объект не движется. С другой стороны, кинетическая сила трения — это сила, противодействующая движению объекта, когда он движется. Когда мы говорим о трении скольжения, это сила, которая сопротивляется движению, когда две поверхности скользят друг относительно друга.
Если вы изучаете физику трения , этот резиновый материал идеально вам подойдет. Вы можете использовать его для проведения экспериментов по трению в своей лаборатории или дома. Он изготовлен из высококачественной резины, которая отличается прочностью и долговечностью.
Вы также можете воспользоваться нашим калькулятором, чтобы убедиться, что вы правильно рассчитали силу трения.
Вот два примера для лучшего понимания силы трения:
Когда автобус едет по мокрой дороге, шина скользит по поверхности дороги. Это движение стало возможным благодаря смазывающей пленке воды между шиной и дорогой. Вода на поверхности дороги действует как смазка, уменьшая силу трения на шине.
Типичным примером коэффициента трения является коэффициент трения между двумя деревянными брусками на столе. Коэффициент трения более значителен для резины на стеклянном столе, чем для дерева на деревянном столе.
Статическое трение — это один из видов силы трения, который сопротивляется относительному движению двух поверхностей, соприкасающихся друг с другом. Она не зависит от направления приложенной силы, но зависит от соприкасающихся поверхностей.
Кинетическое трение — это один из видов силы трения, который сопротивляется относительному движению двух поверхностей, соприкасающихся друг с другом. Он зависит от направления приложенной силы, но не зависит от контактирующих поверхностей.
Часто задаваемые вопросы?
1. Является ли трение контактной силой?Да. Это контактная сила, которая сопротивляется относительному движению двух контактирующих поверхностей.
2. Сила трения двух тел?Это сила между двумя объектами , которые соприкасаются друг с другом и стремятся двигаться в противоположных направлениях.
3.
Как рассчитать силу трения? Формула расчета силы трения F = µN , где F – сила трения, µ – коэффициент трения, N – нормальная сила.
4. Как рассчитать коэффициент трения? Чтобы найти коэффициент трения, вы можете использовать формулу: μ=μs*μn .
Где μs — статический коэффициент трения, а μn — кинетический коэффициент трения.
Если вам нужна помощь, проверьте наш калькулятор!
Вы можете рассчитать силу без учета коэффициента трения, если он неизвестен. Вы можете сделать это, используя уравнение F=μN, где F — величина силы, μ — коэффициент трения, а N — нормальная сила.
Единицей измерения коэффициента трения является единица (1). Коэффициент трения можно определить по склону с переменным наклоном, выбрав угол α, при котором тело начинает двигаться вниз по склону, где μ = tg α .
Во-первых, вы должны знать, что статическое трение — это сила, которая сопротивляется движению объекта, когда он находится в состоянии покоя. Его также называют кинетическим трением. Уравнение для расчета статического трения: Fs = мкс*N.
Fs — сила трения покоя, µs — коэффициент трения покоя, N — нормальная сила.
Работа трения равна потере кинетической энергии. Общее определение работы — это количество энергии, переданной объекту под действием силы. В случае трения количество работы, совершаемой трением, равно 9.0003 энергия передана объекту силой . Затем сила трения рассчитывается путем умножения чистой силы трения на вес объекта.
Усовершенствованный алгоритм расчета силы трения и крутящего момента в эвольвентных косозубых передачах
На этой странице
РезюмеВведениеРезультаты и обсуждениеЗаключениеСсылкиАвторское правоСтатьи по теме Изменяющиеся во времени сила трения и крутящий момент являются одним из основных возбуждающих источников вибрации в косозубых передачах.
В статье представлен подход к определению силы трения и крутящего момента в эвольвентных косозубых передачах с учетом неравномерного распределения нагрузки вдоль контактных линий. Аналитическая модель распределения нагрузки используется и расширяется для получения нагрузки на единицу длины вдоль контактных линий. Выведены модели силы трения и крутящего момента в неравномерном предположении. Проведено сравнение полученных значений силы трения и крутящего момента с результатами из однородного предположения. Кроме того, выявлены различия между постоянным коэффициентом трения и переменным коэффициентом. Кроме того, изучены два типовых расчетных случая косозубых передач. Результаты показывают, что колебания силы трения и крутящего момента при однородном предположении более значительны, чем при неравномерном предположении в образце I для одного зуба, но менее значительны для суммы этих трех зубьев, в то время как в образце II колебания при равномерное допущение менее значимо, чем при неоднородном допущении.
Разница, вызванная коэффициентом трения, незначительна по сравнению с разницей, вызванной предположениями о распределении нагрузки.
1. Введение
Шестерни широко используются во многих областях, таких как тяжелые машины, вертолеты, морские суда и станки. Шум и вибрация существенно влияют на эффективность и надежность в этих приложениях. Помимо изменяющихся во времени жесткости зацепления, демпфирования, статической ошибки передачи и люфта, изменяющиеся во времени сила трения и крутящий момент между зацепляющимися парами зубьев также являются важными возбуждающими источниками шума и вибрации в зубчатых парах.
Можно найти ряд литературных работ, посвященных влиянию трения на динамику цилиндрических зубчатых колес. Метод конечных элементов применялся в [1] для моделирования упругих свойств пары цилиндрических зубчатых колес и для анализа эффектов трения. Был сделан вывод о том, что входной и выходной крутящий момент не остаются постоянными при учете эффектов трения, и возникает изменяющаяся во времени ошибка динамической передачи.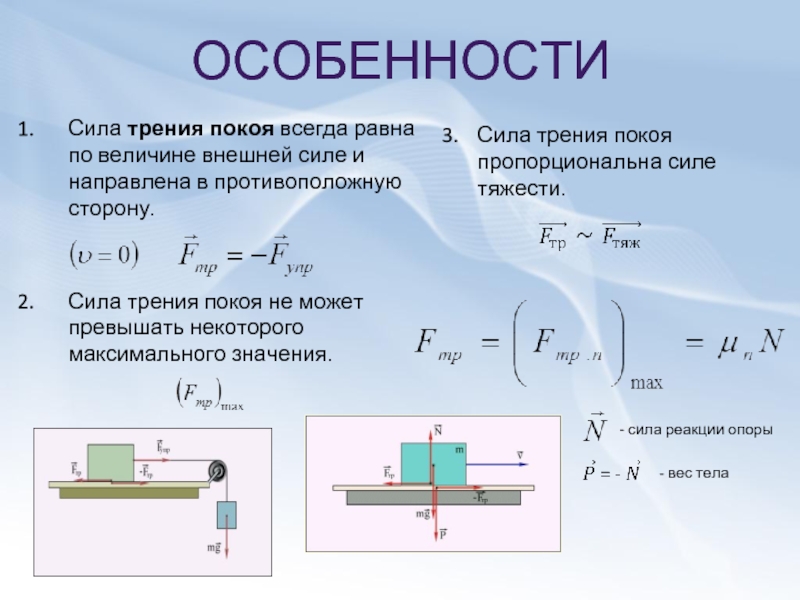
Было исследовано влияние трения зубьев на динамику зубчатых колес, где предполагалась средняя жесткость зацепления на единицу контактной длины, равномерное распределение нормальной нагрузки и постоянный коэффициент трения, и результаты показали потенциально значительный вклад трения зубьев в вибрацию зубчатого колеса. и шум. На трение скольжения приходится большая часть потерь при низких-средних скоростях, в то время как трение качения становится более значительным при высоких скоростях [2, 3].
Авторами работ [4, 5] представлена процедура получения силы трения и крутящего момента. Автор [4] представил динамическую модель с 16 степенями свободы для цилиндрической зубчатой пары, включив эффекты трения между зацепляющимися зубьями. Предполагалось, что коэффициент трения изменяется линейно в зависимости от угла наклона вала, а сила трения рассчитывается по нормальной силе зацепления, включающей значения как жесткости сетки, так и значений демпфирования. Линейная изменяющаяся во времени и нелинейная изменяющаяся во времени динамика для систем цилиндрических зубчатых колес были смоделированы для исследования эффектов, вносимых трением, с различными соображениями коэффициента трения.
А затем авторы дали полуаналитическое решение и численное решение соответственно [5]. Авторы [6, 7] представили улучшенную модель цилиндрической зубчатой пары MDOF с альтернативными формулами трения скольжения, и моделирование показало небольшие различия при использовании разных формулировок трения скольжения.
По сравнению с прямозубым зубчатым колесом длина линии контакта зуба в косозубом колесе зависит от различных положений зацепления шестерни и шестерни, что вызывает вибрации, особенно в косозубом зубчатом колесе [8]; распределение нагрузки по линии контакта неравномерно, в отличие от пар цилиндрических зубчатых колес. В [9] показано, что флуктуации силы трения и крутящего момента вызывают более значительные эффекты, чем эффекты, вносимые значениями силы трения и крутящего момента в зубчатой передаче. Автор [10] предложил новую аналитическую модель для косозубых передач, которая характеризовала динамику плоскости контакта и учитывала изменение направления скорости на делительной линии из-за трения скольжения, при допущении постоянной жесткости сетки на единицу длины вдоль линии контакта.
Была создана динамическая модель с 12 степенями свободы с учетом силы трения и крутящего момента, а для анализа динамики была предложена упрощенная модель с 6 степенями свободы. Кар и Моханти [11, 12] представили алгоритм определения изменяющихся во времени силы трения и крутящего момента на зацеплении зубьев и подшипников в системе косозубых зубчатых колес, который является расширением метода, предложенного в [4] для прямозубых зубчатых колес. Одним из допущений в их работе является равномерное распределение нагрузки по линиям контакта.
Целью данной статьи является выявление различий между равномерным и неравномерным распределением нагрузки по линиям контакта при расчете силы трения и крутящего момента для косозубых передач. Подход является расширением работы, представленной в [11] для косозубых передач. Во-первых, представлен вариант контактной линии. Затем аналитическая модель распределения нагрузки для эвольвентных косозубых передач, предложенная Pedrero et al. [13] используется и расширяется для получения нормальной нагрузки вдоль контактных линий.
При допущении о постоянном коэффициенте трения рассчитываются как сила трения, так и крутящий момент в каждой точке контакта, и сравниваются с результатами, полученными при допущении о равномерном распределении нагрузки. Кроме того, исследуется еще один образец типовой конструкции и приводятся результаты. Также исследуется влияние различных моделей коэффициента трения на результирующую силу и крутящий момент.
2. Математическая модель
2.1. Изменяющаяся во времени длина контактных линий
На рис. 1 показана схема зацепления пары эвольвентных винтовых зубчатых колес. Линии контакта образованы сцепленными зубьями шестерни и шестерни, и все они лежат во внутренней общей касательной плоскости двух основных цилиндрических поверхностей шестерни и шестерни. Угол между осью шестерни и линией мгновенного контакта равен . Как правило, общее передаточное отношение косозубых зубчатых колес составляет , что означает, что два или три зуба находятся в одновременном контакте.
Обозначаются следующие обозначения: где функция означает десятичную долю поперечного коэффициента контакта и означает десятичную долю осевого коэффициента контакта. Два типовых образца конструкции будут исследованы следующим образом: : сумма невязок поперечных и осевых коэффициентов контакта меньше единицы; : сумма невязок поперечного и осевого коэффициентов контакта больше единицы.
Варианты линий контакта для обоих образцов показаны на рис. 2.
Для одного зуба линия контакта постепенно увеличивается, прежде чем достигнет максимума. Затем длина контактной линии некоторое время остается постоянной, после чего контактная линия постепенно уменьшается по мере дальнейшего вращения шестерни до окончательного зацепления. На рис. 2(а) длина достигает своего максимального значения в точке С и сохраняет значение до точки D. На рис. 2(б) линия контакта сохраняет максимальное значение в течение периода сетки от точки D до точки С.
Индивидуальная и общая длины контактных линий для трех зубьев при одном поперечном шаге выражаются следующим образом.
(1) Образец I (2) Образец II, где
2.2. Нагрузка на единицу длины вдоль контактных линий
Хотя в большей части литературы предполагается равномерное распределение нагрузки, нагрузка на единицу длины варьируется вдоль контактных линий. В данной работе для получения реального распределения нагрузки в эвольвентных косозубых передачах используется аналитическая модель распределения нагрузки.
Выражение определяется выражением где функция представляет собой нагрузку на единицу длины, приложенную к точке линии контакта, соответствующей моменту, когда эталонное поперечное сечение находится в контакте с точкой, и представляет собой приложенную нагрузку. Более подробную информацию можно найти в [13].
В этой статье, чтобы получить нагрузку на единицу длины вдоль линий контакта, каждая линия контакта делится на сегменты вдоль оси зубчатого колеса, и выражение для нормальной нагрузки, приложенной к сегменту th зуба в th момент зацепления, имеет вид написано здесь как Что касается изменяющейся во времени длины контактных линий, то это количество сегментов для каждого контактного зуба, которое зависит от положения зацепления.
Параметры в (6) определяются как обозначает параметр профиля, соответствующий внутренней точке контакта шестерни, и представляет собой расстояние от точки приложения силы до центра шестерни или шестерни в поперечной плоскости, показанной на рисунке 3.
Выражения для параметров и для трех зубьев в сеточном цикле задаются выражением соответственно, где — радиусы кривизны, указанные в следующем разделе.
2.3. Сила трения
Направление силы трения перпендикулярно линии действия в поперечной плоскости параллельно поперечному сечению шестерни и шестерни и перпендикулярно линиям контакта в плоскости действия. Предполагается, что сила положительна, когда точка контакта на линии контакта находится выше линии шага, и отрицательна в противном случае. Следовательно, сила трения th-го сегмента th-го зуба шестерни в th-й момент зацепления может быть определена как где – постоянный коэффициент трения, – длина сегмента. Сила трения зуба th в момент зацепления выражается как где функция round() получает целое число, ближайшее к .
2.4. Момент трения
Формулы для момента трения образца I при равномерной нагрузке можно найти в [14], а формулы для каждого зуба в образце II при равномерной нагрузке получены как
Ниже приведены расчеты момента трения при неравномерной нагрузке. Плечо момента трения равно радиусу кривизны в направлении захвата в каждой точке контакта, как показано пунктирными линиями на рисунке 5. Согласно эвольвентному профилю зуба, радиусы кривизны i -й сегмент k -я пара зубьев шестерни в j -й момент зацепления в поперечной плоскости можно записать как Соответственно, фрикционный рычаг крутящего момента для шестерни определяется выражением
Знаки момента трения считаются положительными, если они способствуют вращению, и отрицательными в противном случае.
Момент трения на i -м сегменте k -й зубчатой пары шестерни в момент j -го зацепления рассчитывается как Следовательно, общий момент трения в трех зубьях для одного поперечного шага определяется выражением
3. Результаты и обсуждение
3.1. Проверка модели
Модель распределения нагрузки, используемая в этой статье, проверяется путем сравнения результатов из [13] с текущим моделированием. Нормализованная нагрузка на единицу длины, полученная из анализа методом конечных элементов, интегрирования упругой потенциальной энергии и текущей модели, показана на рисунке 6 соответственно. Опорное поперечное сечение выбрано при .
Как видно из рисунка 6, получено хорошее совпадение.
3.2. Изменяющаяся во времени длина контактных линий
Параметры моделирования, использованные в образцах I и II, показаны в таблицах 1 и 2 соответственно. Цикл сетки для одного поперечного шага разбивается на 50 шагов по времени, и . Максимальное значение равно 62 в образце I и 60 в образце II, что соответствует максимальной длине линии контакта в обоих случаях.
Изменяющаяся во времени длина контактной линии для одного зуба в образце I показана на рис. 7(а). Имеется хорошее согласие с функцией, сформулированной Велексом и Сенсо [3].
Максимальное значение линии контакта составляет , а максимальная длина линии контакта в образце II составляет , как показано на рисунке 7(c). Изменения общей длины контакта для одного поперечного шага в обоих случаях показаны на рисунках 7(b) и 7(d) соответственно. Как видно из рисунка, временные интервалы минимальной суммарной длины контактных линий отличаются друг от друга.
3.3. Распределение нагрузки
В [10] предполагается равномерное распределение нагрузки, а нагрузка на единицу длины меняется в зависимости от положения вдоль линии контакта.
Распределение нагрузки на один зуб обоих образцов в полном цикле показано на рисунках 8(а) и 8(б). Как видно из рисунка, ось x представляет собой координату вдоль линии мгновенного контакта, а ось y представляет время зацепления для одного зуба в трех поперечных шагах.
А z -ось означает нагрузку на единицу длины вдоль линии контакта. Очевидно, что распределения в двух расчетных случаях различны. Чтобы прояснить разницу, также представлены распределения нагрузки в течение интервала времени, когда линии контакта достигают максимальных значений и остаются постоянными, как показано на рисунках 8(c) и 8(d). Указано, что максимальная нагрузка на единицу длины в образце I приходится на среднюю часть контактной линии, а в образце II — на одну из граней зубчатого колеса.
3.4. Сила трения и крутящий момент
Сила трения и крутящий момент как для одного зуба, так и для трех зубьев показаны на рис. 9. Как видно из рисунка, сила трения не синусоидальна, а периодична, как и в цилиндрическом зубчатом колесе [15]. ]. Пунктирные линии представляют силы трения, полученные при допущении равномерного распределения нагрузки, а сплошные линии представляют результаты при неравномерном допущении.
Для одиночного зуба разница сил при двух допущениях незначительна до момента, когда линия контакта достигает своего максимального значения.
Однако разница становится существенной в оставшееся время всего цикла построения сетки. В отличие от одиночного зуба, всегда существует значительная разница между общими силами трения при двух допущениях для поперечного шага. Статистические значения рисунка 9показаны в таблице 3. Из нее видно, что флуктуация при однородном допущении более значительна, чем при неоднородном допущении.
Моменты трения для одного и трех зубьев показаны на рисунках 9(c) и 9(d) соответственно. Подобно силе трения, флуктуация крутящего момента при однородном допущении более значительна, чем при неоднородном допущении. Следует отметить, как видно из рисунка 9(d), пиковое значение момента трения при неравномерном допущении является положительным, а при равномерном допущении — отрицательным. Эти различия могут привести к разным динамическим характеристикам винтовых зубчатых передач.
Результаты показаны на рисунке 10, а статистические значения рисунка показаны в таблице 4. Очевидно, что колебания как силы трения, так и крутящего момента при однородном допущении менее значительны, чем при неоднородном допущении, что противоречит образцу I.
короткий интервал постоянной силы, появившийся в первом примере, в этом не выходит.
3.5. Результаты из изменяющегося во времени коэффициента трения
Для исследования влияния изменяющегося во времени коэффициента трения на результирующую силу трения и крутящий момент используется формула коэффициента трения, предложенная в [14] как где – усредненная шероховатость поверхности, – динамическая вязкость масла, поступающего в контакт шестерни. и представляют собой скорость скольжения и скорость захвата
Как видно из рисунков 11(a) и 11(b), силы трения в предположениях NV и NC очень близки друг к другу; аналогично, разница в силе между предположением UV и предположением UC незначительна. Однако очевидно, что существует незначительная разница между предположением о равномерном и неравномерном распределении нагрузки, что означает, что флуктуация силы при неравномерном предположении более значительна, чем при равномерном предположении. Аналогичный вывод можно сделать по моменту трения, как показано на рисунках 11(c) и 11(d).
4. Заключение
В статье предложен усовершенствованный алгоритм расчета силы трения и крутящего момента в косозубых зубчатых парах с учетом неравномерного распределения нагрузки вдоль контактных линий. Исследуются два образца конструкции. В образце I максимальная нагрузка на единицу длины приходится на середину контактной линии, а в образце II — на одну из граней зубчатого колеса.
Колебания силы трения и крутящего момента при однородном предположении в первом образце для одного зуба более значительны, чем при неравномерном предположении, а сумма силы трения и крутящего момента для трех зубьев менее значительна. Напротив, колебания как силы трения, так и крутящего момента при однородном предположении во втором образце менее значительны, чем при неравномерном предположении как для одного зуба, так и для суммы трех зубьев. По сравнению с разницей, вызванной предположениями о равномерном и неравномерном распределении нагрузки, разница, вызванная различными моделями коэффициента трения, незначительна. Эти различия могут привести к разным динамическим характеристикам в редукторной системе. Кроме того, как коэффициент трения, так и приложенная нагрузка линейно пропорциональны разнице между колебаниями силы трения и крутящего момента, полученными при двух допущениях. Представленная здесь работа дает возможность для дальнейшего анализа динамики зубчатых передач.
Номенклатура
| : | Ширина зубчатого колеса |
| : | Вспомогательный параметр |
| : | Десятичная дробь |
| : | Десятичная дробь |
| : | Целое число часть ε |
| : | Длина зоны контакта |
| : | Параметры длины в зоне контакта показаны на рисунке 2 |
| : | Нагрузка на единицу длины |
| : | Приложенная нагрузка |
| : | Сила трения k -го зуба |
| : | Суммарная сила трения трех зубьев |
| : | Сила из однородного предположения |
| : | Сила из неравномерного предположения |
| : | Сумма стих унитарный потенциал |
| : | Общая длина трех контактных линий |
| : | Фрикционный рычаг |
| : | 902 95 Длина контактной линии|
| : | й сегмент контактной линии |
| : | Длина каждого сегмента |
| : | Количество сегментов th зуба в th момент |
| : | Всего шагов по времени |
| : | Количество сегментов на линейных сегментах |
| : | Шаг в поперечной плоскости |
| : | 902 95 Базовый шаг в поперечной плоскости|
| : | Базовый радиус показан на рис. 3 |
| : | Радиус дополнительной окружности |
| : | Радиус основной окружности |
| : | Радиус базовой окружности шестерни |
| : | Радиус кривизны на каждом сегменте |
| : | Время создания сетки |
| : | 9 0295 Момент времени, соответствующий позиции зацепления|
| : | Период зацепления для шагового перемещения |
| : | Момент трения трех зубьев |
| : | Момент трения 1-го зуба |
| : | Линейная скорость вдоль линии действия |
| : | Обратный унитарный потенциал угол наклона винтовой линии |
| : | Общее передаточное отношение косозубых колес |
| : | Поперечный коэффициент контакта |
| : | Осевой коэффициент контакта |
| : | Вспомогательный параметр |
| : | Вспомогательный параметр |
| : | Коэффициент трения |
| : | Параметр профиля |
| : | Параметр профиля, соответствующий внутренняя точка контакта шестерни |
| : | Частота вращения шестерни |
| : | Скорость вращения шестерни. |
Благодарность
Эта работа была поддержана Национальными научными и технологическими крупными проектами Китая (грант № 2012ZX04012-031).
Ссылки
О. Лундвалл, Н. Стромберг и А. Кларбринг, «Гибкий подход с несколькими телами для фрикционного контакта в цилиндрических зубчатых колесах», Journal of Sound and Vibration , vol. 278, нет. 3, стр. 479–499, 2004.
Посмотреть по адресу: Сайт издателя | Google ScholarП. Велекс и В. Кауэ, «Экспериментальные и численные исследования влияния трения зубьев в динамике цилиндрических и косозубых зубчатых колес», Journal of Mechanical Design , том. 122, нет. 4, стр. 515–522, 2000.
Просмотр по адресу: Google ScholarП. Велекс и П. Сенсо, «Аналитическое исследование возбуждения трения зубьев в безошибочных цилиндрических и косозубых передачах», Механизм и Теория машин , том. 37, нет. 7, стр. 641–658, 2002.
Посмотреть по адресу: Сайт издателя | Google ScholarИ. Ховард, С. Цзя и Дж. Ван, «Динамическое моделирование цилиндрического зубчатого колеса в зацеплении, включая трение и трещину», Механические системы и обработка сигналов , том. 15, нет. 5, стр. 831–853, 2001.
Посмотреть по адресу: Сайт издателя | Google ScholarМ. Вайшья и Р. Сингх, «Нелинейность и параметрические эффекты, вызванные трением скольжения, в динамике зубчатых передач», Journal of Sound and Vibration , vol. 248, нет. 4, стр. 671–694, 2001.
Посмотреть по адресу: Сайт издателя | Google ScholarС. Хе, Р. Гунда и Р. Сингх, «Влияние трения скольжения на динамику пары цилиндрических зубчатых колес с реалистичной изменяющейся во времени жесткостью», Журнал звука и вибрации , том. 301, нет. 3–5, стр. 927–949, 2007 г.
Посмотреть по адресу: Сайт издателя | Google ScholarС. Хе, С.
Посмотреть по адресу: Сайт издателя | Google Scholar Чо и Р. Сингх, «Прогнозирование сил динамического трения в цилиндрических зубчатых колесах с использованием альтернативных формул трения скольжения», Journal of Sound and Vibration , vol. 309, нет. 3–5, стр. 843–851, 2008 г.М. Маатар и П. Велекс, «Аналитическое выражение для изменяющейся во времени контактной длины в идеальных цилиндрических зубчатых колесах: некоторые возможные приложения в динамике зубчатых колес», Журнал механического проектирования , том. 118, нет. 4, стр. 586–589, 1996.
Посмотреть по адресу: Google ScholarМ. Вайшья и Р. Сингх, «Стратегии моделирования трения в динамике зубчатых передач», Journal of Mechanical Design , vol. 125, нет. 2, стр. 383–393, 2003 г.
Посмотреть по адресу: Сайт издателя | Google ScholarС. Хе, Р. Гунда и Р. Сингх, «Включение трения скольжения в модель контактной динамики для винтовых зубчатых колес», Журнал механического проектирования , том.
Посмотреть по адресу: Сайт издателя | Google Scholar 129, нет. 1, стр. 48–57, 2007 г.К. Кар и А. Р. Моханти, «Алгоритм определения изменяющихся во времени силы трения и крутящего момента в системе косозубых передач», Механизм и теория машин, , том. 42, нет. 4, стр. 482–496, 2007 г.
Посмотреть по адресу: Сайт издателя | Google ScholarC. Kar и A.R. Mohanty, «Определение изменяющихся во времени контактной длины, силы трения, крутящего момента и усилий в подшипниках в системе косозубых передач», Журнал звука и вибрации , том. 309, нет. 1–2, стр. 307–319, 2008 г.
Посмотреть по адресу: Сайт издателя | Google ScholarДж. И. Педреро, М. Плегесуэлос, М. Артес и Дж. А. Антона, «Модель распределения нагрузки вдоль линии контакта для эвольвентных внешних зубчатых колес», Механизм и теория машин , том. 45, нет. 5, стр. 780–794, 2010.
Посмотреть по адресу: Сайт издателя | Google ScholarГ.
Чо и Р. Сингх, «Прогнозирование сил динамического трения в цилиндрических зубчатых колесах с использованием альтернативных формул трения скольжения», Journal of Sound and Vibration , vol. 309, нет. 3–5, стр. 843–851, 2008 г.
129, нет. 1, стр. 48–57, 2007 г.
