Site Loader
Posted on 09.09.2018

Содержание

Урок 31. закон ома для полной цепи — Физика — 10 класс

Физика, 10 класс

Урок 31. Закон Ома для полной цепи

Перечень вопросов, рассматриваемых на уроке:

1) закон Ома для полной цепи;

2) связь ЭДС с внутренним сопротивлением;

3) короткое замыкание;

4) различие между ЭДС, напряжением и разностью потенциалов.

Глоссарий по теме

Электрическая цепь – набор устройств, которые соединены проводниками, предназначенный для протекания тока.

Электродвижущая сила – это отношение работы сторонних сил при перемещении заряда по замкнутому контуру к абсолютной величине этого заряда.

Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению:

Основная и дополнительная литература по теме урока:

1. Мякишев Г. Я., Буховцев Б. Б., Сотский Н.Н. Физика. 10 класс. Учебник для общеобразовательных организаций М.

: Просвещение, 2017. С. 348 – 354.

2.Рымкевич А. П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009. С. 106-108.

Теоретический материал для самостоятельного изучения

Любые силы, которые действуют на электрически заряженные частицы, кроме сил электростатического происхождения (т.е. кулоновских), называют сторонними силами. Сторонние силы приводят в движение заряженные частицы внутри всех источников тока.

Действие сторонних сил характеризуется важной физической величиной электродвижущей силой (ЭДС). Электродвижущая сила в замкнутом контуре — отношение работы сторонних сил при перемещении заряда вдоль контура к заряду.

В источнике тока из-за действием сторонних сил происходит разделение зарядов. Так как они движутся, они взаимодействуют с ионами кристаллов и электролитов и отдают им часть своей энергии. Это приводит к уменьшению силы тока, таким образом, источник тока обладает сопротивлением, которое называют

внутренним r.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи:

Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению

Короткое замыкание

При коротком замыкании, когда внешнее сопротивление стремится к нулю , сила тока в цепи определяется именно внутренним сопротивлением и может оказаться очень большой . И тогда провода могут расплавиться, что может привести к опасным последствиям.

Примеры и разбор решения заданий:

1. К каждой позиции первого столбца подберите соответствующую позицию второго:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

ФОРМУЛЫ

Электродвижущая сила

Сила тока

Сопротивление

Разность потенциалов

Решение.

Электродвижущая сила гальванического элемента есть величина, численно равная работе сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому.

Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории перемещения зарядов.

ЭДС определяется по формуле:

Сила тока определяется по формуле:

Сопротивление определяется по формуле:

Разность потенциалов определяется по формуле:

Правильный ответ:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

ФОРМУЛЫ

Электродвижущая сила

Сила тока

Сопротивление

Разность потенциалов

2. ЭДС батарейки карманного фонарика — 3,7 В, внутреннее сопротивление 1,5 Ом. Батарейка замкнута на сопротивление 11,7 Ом. Каково напряжение на зажимах батарейки?

Решение:

Напряжение рассчитывается по формуле:

Чтобы найти силу тока применим закон Ома для полной цепи:

Делаем расчёт:

Ответ: U = 3,28 В.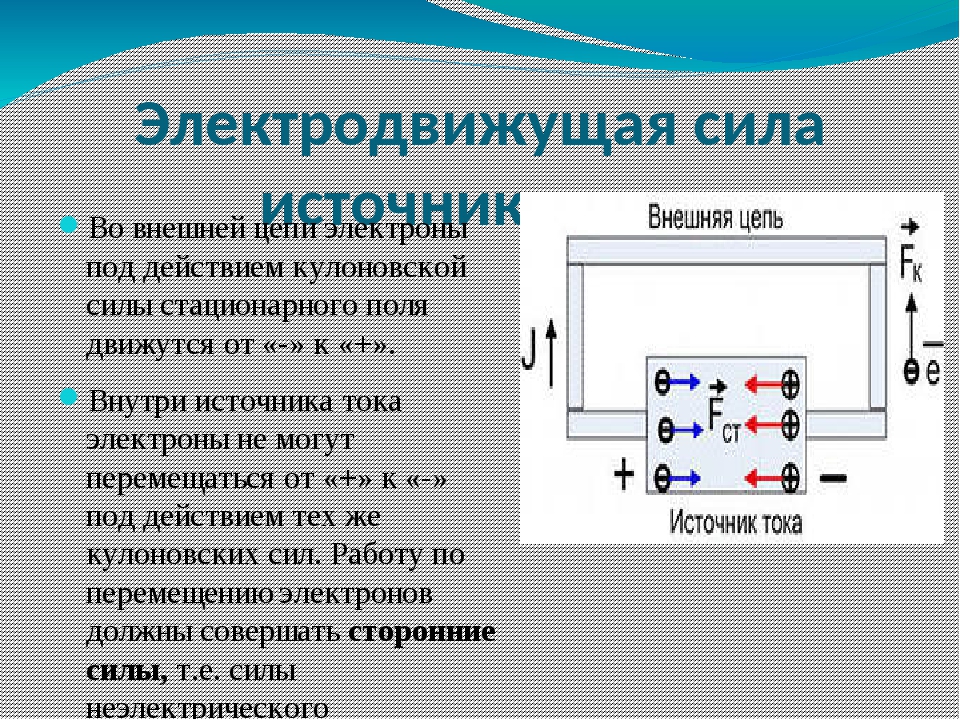

ЭДС. Закон Ома для полной цепи.

Если свободные заряды перемещаются в электрической цепи по замкнутой траектории, то такую цепь называют полной или замкнутой.

При этом на каждом из участков такой цепи работа электростатических сил переходит в тепловую, механическую или энергию химических связей. Так как работа электростатических сил, перемещающих заряд по замкнутой траектории, всегда равна нулю, то только силы электростатического поля не могут обеспечить постоянное движение зарядов по замкнутой траектории.

Чтобы электрический ток в замкнутой цепи не прекращался, необходимо включить в неё источник тока (см. рис. а), внутри которого перемещение свободных зарядов происходило бы не под действием электростатических сил, а при участии любых других сил, называемых

сторонними. Сторонние силы — силы неэлектростатического происхождения, действующих на заряды со стороны источника тока. Природа сторонних сил может быть различной (кроме неподвижных зарядов):

1) химические реакции – в гальванических элементах (батарейках), аккумуляторах (сторонние силы возникают в результате химических реакций между электродами и жидким электролитом),

2) электромагнитной – в генераторах. При этом генераторы могут использовать а) механическую энергию – ГЭС, б) ядерную – АЭС, в) тепловую – ТЭС, г) приливов и отливов – ПЭС, д) ветровую – ВЭС и т.д. (силы, действующие на свободные заряды, перемещающиеся в магнитном поле).

3) использование фотоэффекта – фото-ЭДС в калькуляторах и солнечных батареях (в фотоэлементах сторонние силы возникают при действии света на электроны атомов, входящих в состав некоторых веществ),

4) пьезоэффект – пьезо-ЭДС, например, в пьезозажигалках,

5) контактная разность потенциалов – термо-ЭДС в термопарах и т.д.

Например, в цепи на рис. а, свободные заряды, перемещаются от тела А к телу Б под действием электростатических сил, а сторонние силы источника питания заставляют их возвращаться обратно – от Б к А

.

Сторонние силы в источнике тока разделяют разноимённые электрические заряды друг от друга, совершая работу против электростатических (кулоновских сил). Контакт (полюс) источника тока, где в результате действия сторонних сил накапливается положительный заряд, называют положительным, а противоположно заряженный полюс – отрицательным, обозначая их так, как изображено на рис. б. Очевидно, что чем больший заряд накопится на полюсе источника тока, тем больше работы совершили сторонние силы по разделению зарядов, т.к. работа против кулоновских сил прямо пропорциональна величине заряда. Поэтому  отношение работы,

Аст, сторонних сил, перемещающих заряд q внутри источника тока от отрицательного полюса к положительному, не зависит от величины заряда и служит характеристикой источника тока, называемой электродвижущей силой (ЭДС) источника,

.

 

Как и разность потенциалов, ЭДС в СИ измеряют в вольтах.

Сопротивление источника тока или внутреннее сопротивление тоже является его важной характеристикой. Внутренним сопротивлением гальванического элемента, например, является сопротивление электродов и электролита, находящегося между ними. Внешним участком замкнутой цепи называют её участок, подсоединённый снаружи к источнику тока (см. рис. а).

Чтобы определить, как зависит сила тока от ЭДС источника в цепи, изображённой на рис.

а, нарисуем эквивалентную схему (см. рис. в), где R соответствует сопротивлению проводника между А и Б, (внешняя цепь), а r – внутреннему сопротивлению источника тока. Согласно закону Джоуля-Ленца работа  Аполн тока, протекающего по замкнутой цепи, за интервал времени t равна: Аполн = I2.R.t + I2.r.t .  Из закона сохранения энергии следует, что работа тока должна быть равна работе сторонних сил Астор
 = Ɛ.q = Ɛ.It . Приравняв Аполн и Астор, получаем следующее выражение для 

которое называют законом Ома для полной цепи.

1) Напряжение на зажимах источника, а соответственно и во внешней цепи

где величина Ir— падение напряжения внутри источника тока.

2) Если внешнее сопротивление замкнутой цепи равно нулю, то такой режим источника тока называется коротким замыканием.

3) Для полной цепи закон Джоуля-Ленца

Легко показать, что, если полная цепь содержит несколько последовательно соединённых источников тока, то для вычисления силы тока следует вместо Ɛ взять алгебраическую сумму ЭДС всех этих источников, выбрав какое-нибудь направление обхода цепи, например, по часовой стрелке (рис.

г). Если при таком обходе мы идём от положительного полюса источника тока к отрицательному, то ЭДС данного источника следует суммировать со знаком минус.  

  Более подробную информацию смотри ЗДЕСЬ.

Закон Ома для участка цепи с источником ЭДС. (Лекция N 5)


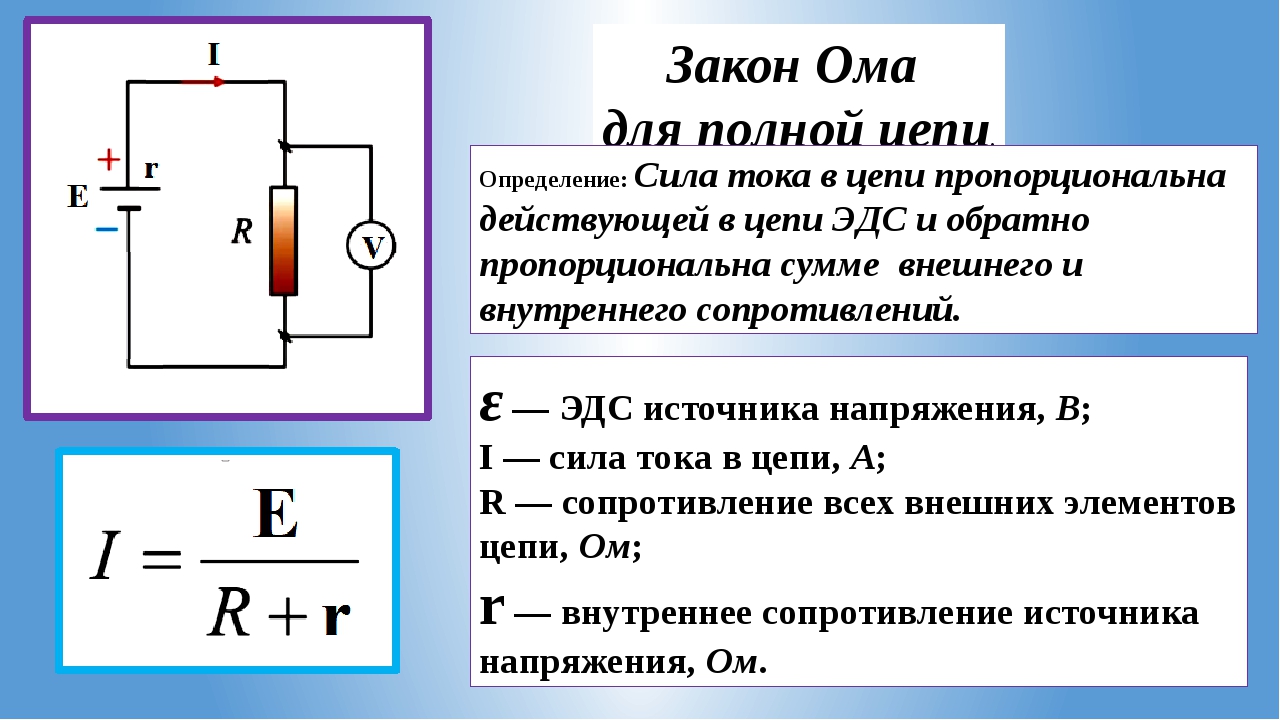
Возьмем два участка цепи a—bи c—d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.

Объединяя оба случая, получим

(1)

или для постоянного тока

. (2)

Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.

Основы символического метода расчета цепей
синусоидального тока

Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности.

Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме.

Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.

1.     Первый закон Кирхгофа в комплексной форме:

. (3)

2.     Второй закон Кирхгофа в комплексной форме:

(4)

или применительно к схемам замещения с источниками ЭДС

.   (5)

3.     Соответственно матричная запись законов Кирхгофа в комплексной форме имеет вид:

§         первый закон Кирхгофа:

. ; (6)

§         второй закон Кирхгофа

. (7)

Пример.

Дано:

Рис. 2

Решение:

1.     .

2.     .

3.    

.

4.     Принимая начальную фазу напряжения за нуль, запишем:

.

Тогда

.

5.     Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то

6.      .

7.     Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме

или после подстановки численных значений параметров схемы

Специальные методы расчета

Режим работы любой цепи полностью характеризуется уравнениями, составленными на основании законов Кирхгофа. При этом необходимо составить и решить систему с n неизвестными, что может оказаться весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может быть сокращено, если воспользоваться специальными методами расчета, к которым относятся методы контурных токов и узловых потенциалов.

Метод контурных токов

Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т. е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа . Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми. Их выбор облегчает использование топологических понятий дерева и ветвей связи.

Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.

Пусть имеем схему по рис. 3.

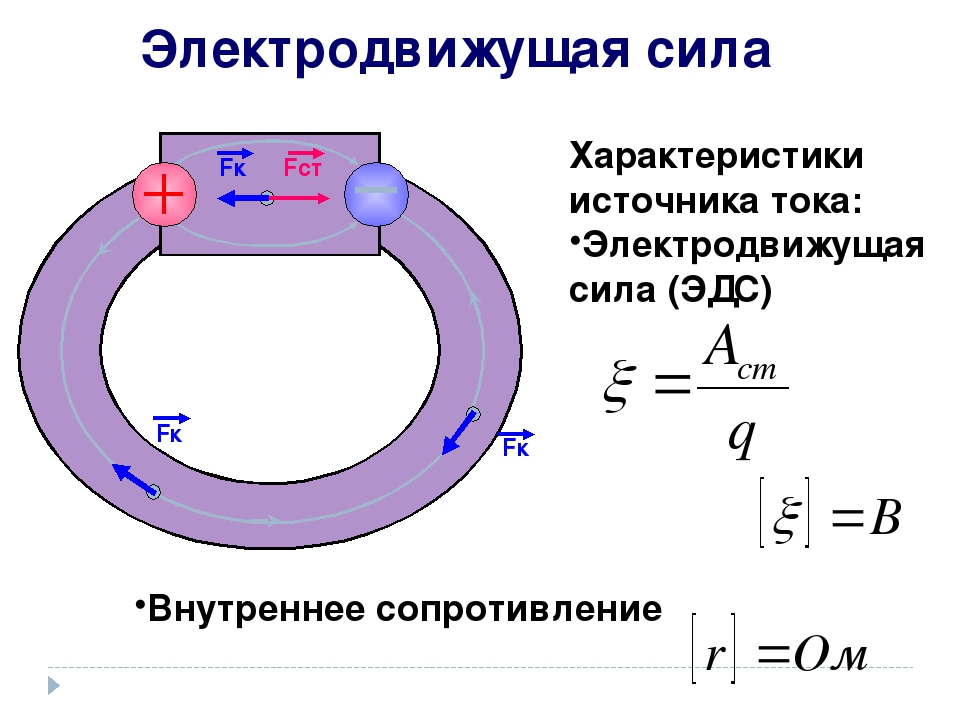
Выразим токи ветвей через контурные токи:

;

; ;

; .

Обойдя контур aeda, по второму закону Кирхгофа имеем

.

Поскольку ,

то

.

Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров:

совместно с первым решить их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найти последние.

Однако данная система уравнений может быть составлена формальным путем:

При составлении уравнений необходимо помнить следующее:

— сумма сопротивлений, входящих в i-й контур;

— сумма сопротивлений, общих для i-го и k-го контуров, причем ;

члены на главной диагонали всегда пишутся со знаком “+”;

знак “+” перед остальными членами ставится в случае, если через общее сопротивление i-й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;

если i-й и k- й контуры не имеют общих сопротивлений, то ;

в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает.

В нашем случае, для первого уравнения системы, имеем:

Следует обратить внимание на то, что, поскольку , коэффициенты контурных уравнений всегда симметричны относительно главной диагонали.

Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются в левых частях уравнений как известные контурные токи: k- й контурный ток, проходящий через ветвь с k- м источником тока равен этому току .

Метод узловых потенциалов

Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно , т.е. числу ветвей дерева .

Пусть имеем схему по рис. 4, в которой примем .

Допустим, что и известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС

Запишем уравнение по первому закону Кирхгофа для узла а:

и подставим значения входящих в него токов, определенных выше:

.

Сгруппировав соответствующие члены, получим:

.

Аналогично можно записать для узла b:

.

Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:

1.      В левой части i-го уравнения записывается со знаком “+”потенциал i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциал соседних узлов, каждый из которых умножен на сумму проводимостей ветвей, присоединенных к i-му и k-му узлам.

Из сказанного следует, что все члены , стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем . Последнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.

2.      В правой части i-го уравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “-”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.

В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.

 

Литература

1.     Основы теории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2.     Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с

.

Контрольные вопросы и задачи

1.      В ветви на рис. 1 . Определить ток .

Ответ: .

2.      В чем заключается сущность символического метода расчета цепей синусоидального тока?

3.      В чем состоит сущность метода контурных токов?

4.      В чем состоит сущность метода узловых потенциалов?

5.      В цепи на рис. 5 ; ;

; . Методом контурных токов определить комплексы действующих значений токов ветвей.

Ответ: ; ; .

6.      В цепи на рис. 6 . Рассчитать токи в ветвях, используя метод узловых потенциалов.

Ответ: ; ; ; ; ; ; .

Закон Ома для полной цепи

1. Источник тока

При прохождении тока в проводнике выделяется некоторое количество теплоты. Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.

Может ли источником этой энергии быть электростатическое поле? Нет, не может, потому что при перемещении заряда вдоль всей цепи, то есть по замкнутой траектории, работа электростатического поля равна кулю.

Следовательно, для существования тока в замкнутой цепи в ней должен быть участок, на котором свободные заряды движутся против сил электростатического поля. Таким участком цепи является источник тока (рис. 59.1).

В источнике тока на свободные заряды действуют силы, которые имеют не электростатическую природу. Их называют сторонними силами. В результате действия сторонних сил происходит разделение зарядов: на одном полюсе источника тока накапливается положительный заряд, а на другом – отрицательный. Вследствие этого возникает электростатическое поле, которое движет свободные заряды в электрической цепи вне источника тока, то есть во внешней цепи.

В химических источниках тока сторонние силы имеют химическую природу. Например, если погрузить цинковый и медный электроды в серную кислоту, то положительные ионы цинка будут чаще покидать электрод, чем положительные ионы меди. В результате между медным и цинковым электродами возникнет разность потенциалов: потенциал медного электрода будет больше, чем цинкового. Медный электрод станет положительным полюсом источника тока, а цинковый – отрицательным.

В генераторах электростанций сторонними силами являются силы, действующие на свободные электроны в металле со стороны вихревого электрического поля, порождаемого переменным магнитным полем. Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.

Электродвижущая сила источника тока

В источнике тока сторонние силы, перемещая свободные заряды против действия сил электростатического поля, совершают работу, которую мы обозначим Aстор.

Эта работа пропорциональна заряду q, который перемещается вдоль цепи за данный промежуток времени. Поэтому отношение работы сторонних сил к величине заряда не зависит ни от Aстор, ни от q. Следовательно, оно является характеристикой источника тока. Это отношение называют электродвижущей силой источника (ЭДС) и обозначают ξ:

ξ = Aстор/q.     (1)

(Это название не совсем удачно, потому что ЭДС – не «сила» в механическом смысле, а энергетическая характеристика источника.)

ЭДС, как и напряжение, измеряют в вольтах. Например, ЭДС батарейки составляет несколько вольт.

2. Закон Ома для полной цепи

Если сила тока в цепи равна I, то за время t по цепи проходит заряд q = It. Поэтому формулу (1) можно записать в виде

Aстор = ξIt.     (2)

При этом во внешней цепи сопротивлением R выделяется количество теплоты

Qвнеш = I2Rt,     (3)

а внутри источника тока выделяется количество теплоты

Qвнутр = I2rt,     (4)

где r – сопротивление источника, которое называют его внутренним сопротивлением.

Из закона сохранения энергии следует, что

Qвнеш + Qвнутр = Aстор.     (5)

? 1. Докажите, что из формул (2) – (5) следует:

I = ξ / (R + r).     (6)

Это соотношение называют законом Ома для полной цепи.

Сумму сопротивлений R + r называют полным сопротивлением цепи.

? 2. ЭДС источника тока 12 В, а его внутреннее сопротивление равно 2 Ом.
а) Чему равна сила тока в цепи, если сопротивление внешней цепи равно 4 Ом?
б) Какова максимально возможная сила тока в цепи? При каком сопротивлении внешней цепи это имеет место?

? 3. При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А.
а) Чему равно внутреннее сопротивление источника?
б) Чему равна ЭДС источника?

Напряжение на полюсах источника

Закон Ома для полной цепи можно записать в виде

ξ = IR + Ir.     (7)

Первое слагаемое в этой формуле согласно закону Ома для участка цепи равно напряжению U на полюсах источника тока:

IR = U.

Поэтому формулу (7) можно записать в виде

U = ξ – Ir.     (8)

Формула (8) выражает зависимость напряжения U на полюсах источника тока от силы тока I в цепи.

Поставим опыт
Зависимость U(I) можно измерить на опыте, изменяя силу тока в цепи с помощью реостата (рис. 59.2, а, б). Красная пунктирная линия на схеме 59.2, б показывает, как идет ток в реостате. Например, если ползунок реостата, изображенного на рисунке 59,2, а, сдвинуть вправо, то сопротивление реостата увеличится, потому что увеличится длина обмотки, по которой идет ток.

? 4. На рисунке 59.3 изображен график зависимости U(I) для некоторого источника тока.

а) Чему равна ЭДС этого источника тока?
б) Чему равна наибольшая сила тока?
в) Чему равно внутреннее сопротивление источника тока?
г) Чему равно внешнее сопротивление, когда сила тока равна нулю?
д) Чему равно внешнее сопротивление, когда сила тока максимальна?
е) Чему равно внешнее сопротивление при I = 1,5 А?

Максимальное напряжение на полюсах источника равно ξ. Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).

Следовательно, напряжение между разомкнутыми полюсами источника тока равно ЭДС этого источника.

Минимальное же напряжение между полюсами источника равно нулю. Это имеет место при коротком замыкании, когда внешнее сопротивление R = 0. В этом случае сила тока максимальна. Ее называют силой тока короткого замыкания.

? 5. Покажите, что сила тока короткого замыкания выражается формулой

Iка = ξ/r.     (9)

Подсказка. Воспользуйтесь законом Ома для полной цепи.

Из формулы (9) видно, что при очень малом внутреннем сопротивлении источника (как, например, у автомобильного аккумулятора) сила тока короткого замыкания будет очень большой, что может вывести источник тока из строя.

? 6. Сила тока при коротком замыкании батарейки равна 2 А. Когда к батарейке подключили резистор сопротивлением 4 Ом, сила тока стала равной 1 А.
а) Как изменилось полное сопротивление цепи?
б) Чему равно внутреннее сопротивление батарейки?

Измерив напряжение на полюсах источника и силу тока в цепи при двух различных значениях сопротивления внешней цепи, можно найти ЭДС ξ и внутреннее сопротивление r источника тока. Это можно сделать графически и аналитически.

? 7. При силе тока в цепи 2 А напряжение на полюсах источника равно 8 В, а при силе тока 4 А напряжение на полюсах равно 4 В.
а) Постройте систему координат I, U и нанесите две точки графика зависимости U(I) согласно приведенным данным.
б) Проведите прямую через эти точки и отметьте точки пересечения этой прямой с осями координат. Используя этот график, найдите, чему равны ЭДС, сила тока короткого замыкания и внутреннее сопротивление источника тока.
в) Используя уравнение (8), составьте систему двух уравнений с двумя неизвестными ξ и r и решите ее.

3. КПД источника тока

Работу тока во внешней цепи называют полезной работой. Обозначим ее Aпол. Используя формулу для работы тока, получаем:

Aпол = I2Rt.

Поскольку источник обладает внутренним сопротивлением, полезная работа меньше работы сторонних сил, потому что часть работы сторонних сил расходуется на выделение в источнике тока количества теплоты I2rt. Поскольку

Aстор = I2Rt + I2rt,

получаем для отношения полезной работы к работе сторонних сил:

η = Aпол / Aстор = (I2Rt) / (I2Rt + I2rt) = R / (R + r).

Это отношение, выраженное в процентах, называют КПД источника тока.

? 8. При каком отношении внешнего сопротивления к внутреннему сопротивлению КПД источника тока равен: 50 %; 80 %? Почему случай, когда КПД источника тока равен 100 %, не представляет практического интереса?


Дополнительные вопросы и задания

9. На рисунке 59.4 изображена схема измерения зависимости напряжения U на полюсах источника тока от силы тока I. Амперметр и вольтметр считайте идеальными. Сопротивление всей обмотки реостата 16 Ом. При первом положении ползунка реостата показания приборов 3 А и 8 В, а при втором положении – 2 А и 12 В.

а) Как сдвинули ползунок реостата между первым и вторым измерениями – влево или вправо?
б) Чему равны ЭДС источника тока и его внутреннее сопротивление?
в) Каковы будут показания приборов, если ползунок реостата передвинуть в крайнее левое положение? в крайнее правое?

10. При силе тока 6 А мощность тока во внешней цепи равна 90 Вт, а при силе тока 2 А она равна 60 Вт.
а) Чему равна ЭДС источника тока?
б) Чему равно внутреннее сопротивление источника тока?
в) Чему равно напряжение на полюсах источника в первом и втором случаях?
г) Чему равен КПД источника тока в первом и втором случаях?

Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.


 Навигация по справочнику TehTab.ru:  главная страница  / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Понятия и формулы для электричества и магнетизма.  / / Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.

Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.

Цепь постоянного тока (или, строго говоря, цепь без комплексного сопротивления)

Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока.

P = мощность (Ватт)

U = напряжение (Вольт)

I = ток (Ампер)

R = сопротивление (Ом)

r = внутреннее сопротивление источнка ЭДС

ε = ЭДС источника

Тогда для всей цепи:

  • I=ε/(R +r) — закон Ома для всей цепи.

И еще ниже куча формулировок закона Ома для участка цепи :

Электрическое напряжение:

  • U = R* I — Закон Ома для участка цепи
  • U = P / I
  • U = (P*R)1/2

Электрическая мощность:

  • P= U* I
  • P= R* I2
  • P = U 2/ R

Электрический ток:

  • I = U / R
  • I = P/ E
  • I = (P / R)1/2

Электрическое сопротивление:

  • R = U / I
  • R = U 2/ P
  • R = P / I2

НЕ ЗАБЫВАЕМ: Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения.

Цепь переменного синусоидального тока c частотой ω.

Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока и частоты.

Напомним, что любой сигнал, может быть с любой точностью разложен в ряд Фурье, т.е. в предположении, что параметры сети частотнонезависимы — данная формулировка применима ко всем гармоникам любого сигнала.

Закон Ома для цепей переменного тока:

где:

Естественно, применительно к цепям переменного тока можно говорить и об активной/реактивной мощности.

  • U = U0eiωt  напряжение или разность потенциалов,
  • I  сила тока,
  • Z = Re—iφ  комплексное сопротивление (импеданс)
  • R = (Ra2+Rr2)1/2  полное сопротивление,
  • Rr = ωL — 1/ωC  реактивное сопротивление (разность индуктивного и емкостного),
  • Rа  активное (омическое) сопротивление, не зависящее от частоты,
  • φ = arctg Rr/Ra — сдвиг фаз между напряжением и током.
 Дополнительная информация:
  1. Электростатика.
  2. Закон Ома.
  3. Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения.
  4. Формулы. Электрическое сопротивление проводника при постоянном токе, зависимость сопротивления проводника от температуры, индуктивное и ёмкостное (реактивное) сопротивление, полное реактивное сопротивление, полное сопротивление цепи при переменном токе
  5. Коэффициент мощности (cos φ, косинус фи ), Полная (кажущаяся), активная и реактивная мощность электродвигателя=электромотора и не только его. Коэффициент мощности для трехфазного электродвигателя.



Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.
TehTab.ru

Реклама, сотрудничество: [email protected]

 Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями.

формулы и определения / Блог / Справочник :: Бингоскул

Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.

 

Закон Ома для участка цепи:

Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

  1. I — сила тока (в системе СИ измеряется — Ампер)
    • Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
    • Формула: I=\frac{U}{R}
  2. U — напряжение (в системе СИ измеряется — Вольт)
    • Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
    • Формула: U=IR
  3. R — электрическое сопротивление (в системе СИ измеряется — Ом).
    • Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
    • Формула R=\frac{U}{I}

 

    Определение единицы сопротивления — Ом

    1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).

     

    Закон Ома для полной цепи

    Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

     

    Формула I=\frac{\varepsilon}{R+r}

    • \varepsilon — ЭДС источника напряжения, В;
    • I — сила тока в цепи, А;
    • R — сопротивление всех внешних элементов цепи, Ом;
    • r — внутреннее сопротивление источника напряжения, Ом.

     

    Как запомнить формулы закона Ома

    Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

    .

     

    • U — электрическое напряжение;
    • I — сила тока;
    • P — электрическая мощность;
    • R — электрическое сопротивление

     

    Смотри также:

     

    Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.

    Полная цепь 🐲 СПАДИЛО.РУ

    Полная цепь содержит источник тока — элемент электрической цепи, который поддерживают энергию с заданными параметрами. При этом энергоснабжение цепи не зависит от характеристик элементов, входящих в её состав, в частности, сопротивления.

    Определения

    В полной цепи действует электродвижущая сила, или ЭДС — скалярная физическая величина, которая характеризует работу сторонних сил, действующих в электрических цепях постоянного и переменного тока.

    Сторонние силы — это силы любой природы (кроме электрической), которые разделяют заряды внутри источника тока. Виды сторонний сил:

    • механические;
    • магнитные;
    • химические;
    • световые;
    • тепловые.

    Принято считать, что сторонние силы переносят положительные заряды в направлении от «–» к «+».

    Электродвижущая сила обозначается как ε. Единица измерения — Вольт (В). Численно ЭДС равна отношению работы сторонних сил по перемещению заряда к величине этого заряда:

    ε=Aстq..

    Aст (Дж) — работа сторонних сил по перемещению заряда q (Кл).

    Не следует путать напряжение и ЭДС. Напряжение характеризует работу электрического поля, а ЭДС — работу сторонних сил.

    Закон Ома для полной цепи

    Определение

    Сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи:

    I=εR+r..

    R (Ом) — полное сопротивление внешней цепи, r (Ом) — внутреннее сопротивление источника тока.

    Пример №1. Рассчитайте силу тока в замкнутой цепи, состоящей из источника тока, у которого ЭДС равна 10 В, а внутреннее сопротивление равно 1 Ом. Сопротивление резистора равно 4 Ом.

    I=εR+r..=101+4..=2 (А)

    Напряжение на внешней цепи

    Напряжение на внешней цепи — это напряжение на клеммах источника, или падение напряжения на внешней цепи. Оно равно:

    U=IR

    Выразим сопротивление через ЭДС:

    R=εI..−r

    Следовательно, напряжение на внешней цепи равно:

    U=I(εI..−r)=ε−Ir

    КПД источника тока

    Не вся работа сторонних сил идет непосредственно на перемещение зарядов. Для выражения доли, которая идет именно на перемещение зарядов, вводится понятие КПД (коэффициента полезного действия).

    КПД источника тока равен:

    η=Uε..100%=RR+r..100%

    Пример №2. Напряжение на внешней цепи равно 6 В, ЭДС источника тока равно 12 В. Определить КПД источника тока.

    η=Uε..100%=612..=50%

    Короткое замыкание

    Рассмотрим простую электрическую цепь:

    Она состоит из источника тока (1), ключа (2) и потребителя (3). Теперь поговорим о том, что же произойдет, если цепь замкнуть проводником так, как показано на рисунке ниже.

    Соединив точки А и В напрямую, мы заставим течь ток, минуя потребитель тока, поскольку сопротивление проводника АВ много меньше сопротивления потребителя. А ток всегда течет по пути наименьшего сопротивления.

    В результате соединения точек А и В сопротивление в электрической цепи резко упадет, что приведет к резкому скачку силы тока. Такое явление называется коротким замыканием.

    Определение

    Короткое замыкание — соединение концов участка цепи проводником, сопротивление которого очень мало по сравнению с сопротивлением участка цепи.

    Если полное сопротивление внешней цепи R стремится к нулю, то сила тока при коротком замыкании равна:

    Iк.з.=εr

     

    .

    Задание EF22543 В цепи, изображённой на рисунке, идеальный амперметр показывает 1 А. Найдите ЭДС источника, если его внутреннее сопротивление 1 Ом.

    Ответ:

    а) 23 В

    б) 25 В

    в) 27 В

    г) 29 В

    Алгоритм решения

    1.Записать исходные данные.

    2.Записать закон Ома для полной цепи.

    3.Выполнить решение в общем виде.

    4.Подставить известные данные и вычислить искомую величину.

    Решение

    Запишем исходные данные:

    • Сила то на первом резисторе: I1 = 1 А.

    • Внутреннее сопротивление источника тока: r = 1 Ом.

    • Сопротивление первого резистора: R1= 3 Ом.

    • Сопротивление первого резистора: R2= 1 Ом.

    • Сопротивление первого резистора: R3= 5 Ом.

    Закон Ома для полной цепи:

    I=εR+r..

    R — полное сопротивление внешней цепи. Цепь состоит из последовательно соединенного третьего резистора с параллельным участком цепи, состоящим из первого и второго резисторов. Вычислим сопротивление параллельного участка цепи:

    1R12..=1R1..+1R2..

    R12=R1R2R1+R2..

    Полное сопротивление внешней цепи равно:

    R=R12+R3=R1R2R1+R2..+R3

    Следовательно, ЭДС источника тока равен:

    ε=I(R+r)=I(R1R2R1+R2..+R3+r)

    Полная сила тока равна силе тока параллельного участка цепи, так как I = I3 = I12. А сила тока параллельного участка цепи равна сумме силы тока на первом и втором резисторе:

    I12=I1+I2=I

    Сначала найдем напряжение на первом резисторе, используя закон Ома для участка цепи:

    U1=I1R1

    Так как это параллельный участок, то:

    U1=U2=U12

    Следовательно, сила тока на втором резисторе равна:

    I2=U2R2..=I1R1R2..

    Сила тока на всем участке цепи равна:

    I=I12=I1+I1R1R2..=I1(1+R1R2..)

    Теперь можем вычислить ЭДС источника тока:

    ε=I1(1+R1R2..)(R1R2R1+R2..+R3+r)

    ε=1(1+31..)(3·13+1..+5+1)=6,75·4=27 (В)

    Ответ: в

    pазбирался: Алиса Никитина | обсудить разбор | оценить

    Задание EF17511 Конденсатор ёмкостью С = 2 мкФ присоединён к батарее с ЭДС ε = 10 В и внутренним сопротивлением r = 1 Ом. В начальный момент времени ключ К был замкнут (см. рисунок). Какой станет энергия конденсатора через длительное время (не менее 1 с) после размыкания ключа К, если сопротивление резистора R = 10 Ом? Ответ округлите до сотен.

    Ответ:

    а) 100 нДж

    б) 200 нДж

    в) 100 мкДж

    г) 200 мкДж

    Алгоритм решения

    1.Записать исходные данные и перевести единицы измерения в СИ.

    2.Записать закон Ома для полной цепи и формулу для нахождения энергии конденсатора.

    3.Выполнить решение задачи в общем виде.

    4.Подставить исходные данные и вычислить искомую величину.

    Решение

    Запишем исходные данные:

    • Емкость конденсатора: C = 2 мкФ.

    • ЭДС батареи: ε = 10 В.

    • Внутреннее сопротивление источника тока: r = 1 Ом.

    • Сопротивление резистора: R = 10 Ом.

    2 мкФ = 2∙10–6 Ф

    Запишем закон Ома для полной цепи:

    I=εR+r..

    Энергия конденсатора определяется формулой:

    W=CU22..

    Напряжение внешней цепи связано с ЭЛС источника формулой:

    U=ε−Ir

    Используя закон Ома для полной цепи, получаем:

    U=ε−εrR+r..=εR+εr−εrR+r..=εRR+r..

    Тогда энергия конденсатора через длительное время станет равной:

    W=12..C(εRR+r..)2

    Округлим ответ до сотен и получим 100 мкДж.

    Ответ: в

    pазбирался: Алиса Никитина | обсудить разбор | оценить

    Задание EF17550 Реостат R подключен к источнику тока с ЭДС E и внутренним сопротивлением r (см. рисунок). Зависимость силы тока в цепи от сопротивления реостата представлена на графике. Найдите сопротивление реостата, при котором мощность тока, выделяемая на внутреннем сопротивлении источника, равна 8 Вт.

    Алгоритм решения

    1.Записать исходные данные.

    2.Записать формулу для определения мощности тока, выделяемой на внутреннем сопротивлении источника, и выразить из нее сопротивление.

    3.С помощью закона Ома для полной цепи найти неизвестные величины.

    4.Выполнить решение в общем виде.

    5.Выполнить вычисления, подставив известные и найденные данные.

    Решение

    Запишем исходные данные:

    • Внутренне сопротивление источника тока: r.

    • ЭДС источника тока: ε.

    • Мощность тока, выделяемая на внутреннем сопротивлении источника: Pвнутр = 8 Вт.

    Мощность тока, выделяемая на внутреннем сопротивлении источника, определяется формулой:

    Pвнутр=(εR+r..)2r

    Выразим отсюда сопротивление реостата:

    R=ε√rPвнутр..−r

    Запишем закон Ома для полной цепи:

    I=εR+r..

    Согласно графику, при нулевом сопротивлении реостата, сила тока, равна 6 Амперам. Следовательно:

    I(0 Ом)=εr..=6

    Но при сопротивлении реостата в 4 Ом сила тока равна 2 Амперам. Следовательно:

    I(4 Ом)=ε4+r..=2

    Получили систему уравнений:

    {.εr..=6..ε4+r..=2.)

    ε=6r

    6r4+r..=2

    6r=8+2r

    4r=8

    r=2 (Ом)

    ε=6·2=12 (В)

    Теперь можем вычислить искомое сопротивление:

    R=12√28..−2=4 (Ом)

    Ответ: 4

    pазбирался: Алиса Никитина | обсудить разбор | оценить

    Задание EF18414 Конденсатор подключён к источнику тока последовательно с резистором R=20 кОм (см. рисунок). В момент времени t=0 ключ замыкают. В этот момент конденсатор полностью разряжен. Результаты измерений силы тока в цепи представлены в таблице.

    Внутренним сопротивлением источника и сопротивлением проводов пренебречь. Выберите два верных утверждения о процессах, наблюдаемых в опыте.

    Ответ:

    а) Ток через резистор в процессе наблюдения увеличивается.

    б) Через 6 с после замыкания ключа конденсатор полностью зарядился.

    в) ЭДС источника тока составляет 6 В.

    г) В момент времени  t = 3 с напряжение на резисторе равно 0,6 В.

    д) В момент времени t = 3 с напряжение на конденсаторе равно 5,7 В.

    Алгоритм решения

    1.Проверить истинность каждого утверждения.

    2.Записать в ответе только истинные утверждения.

    Решение

    Согласно утверждению «а», ток через резистор в процессе наблюдения увеличивается. Но это не так, поскольку в таблице с течением времени сила тока уменьшается. Утверждение «а» неверно.

    Согласно утверждению «б», через 6 с после замыкания ключа конденсатор полностью зарядился. Если это было бы так, то сила тока была бы равна 0. Но в момент времени t = 6 с она равна 1 мкА. Следовательно, утверждение «б» неверно.

    Согласно утверждению «в», ЭДС источника тока составляет 6 В. Напряжение в цепи в начальный момент времени равно ЭДС источника. Следовательно:

    ε=U(при t=0 c)=IR=300 мкА ·20 кОм=0,3·10−3А·20·103Ом=6 (В)

    Вывод: утверждение «в» верное.

    Согласно утверждению «г», в момент времени t = 3 с напряжение на резисторе равно 0,6 В. Чтобы проверить это, нужно умножить соответствующую силу тока на сопротивление резистора:

    U=IR=15 мкА ·20 кОм=0,015·10−3А·20·103Ом=0,3 (В)

    Вывод: утверждение «г» неверное.

    Согласно утверждению «д», в момент времени t = 3 с напряжение на конденсаторе равно 5,7 В. Чтобы проверить это, нужно из ЭДС в этот момент времени вычесть напряжение на внешней цепи. Его мы уже нашли. Оно равно 0,3 В. ЭДС мы тоже нашли. Она равна 6 В. Их разность равна 5,7 В. Следовательно, утверждение «д» верно.

    Ответ: вд

    pазбирался: Алиса Никитина | обсудить разбор | оценить

    Задание EF18453

    На рис. 1 изображена зависимость силы тока через светодиод D от приложенного к нему напряжения, а на рис. 2 – схема его включения. Напряжение на светодиоде практически не зависит от силы тока через него в интервале значений 0,05 А<I<0,2 А. Этот светодиод соединён последовательно с резистором R и подключён к источнику с ЭДС E1=6 В. При этом сила тока в цепи равна 0,1 А. Какова сила тока, текущего через светодиод, при замене источника на другой с ЭДС E2=4,5 В? Внутренним сопротивлением источников пренебречь.

    Алгоритм решения

    1.Записать исходные данные.

    2.С помощью закона Ома для участка и для полной цепи определить сопротивление на светодиоде.

    3.Выполнить решение задачи в общем виде.

    4.Подставить известные данные и вычислить искомую величину.

    Решение

    Запишем исходные данные:

    • ЭДС первого источника тока: ε1=6 В.

    • Сила тока, проходящая через светодиод, подключенный к первому источнику тока: I1 = 0,1 А.

    • ЭДС второго источника тока: ε2=4,5 В.

    Из рисунка 1 следует, что при силе тока, равной I1= 0,1 А напряжение на светодиоде равно UD = 3 В. По закону Ома для участка цепи напряжение на резисторе, будет равно:

    U1=I1R

    По закону Ома для полной (замкнутой) цепи, имеем:

    ε1=U1+UD

    Следовательно:

    U1=ε1−UD

    Тогда сопротивление резистора равно:

    R=ε1−UDI1..

    Напряжение на светодиоде не зависит от силы тока, проходящего через него в интервале значений (это следует из графика рис. 1), поэтому U2=ε2−UDдля любой силы тока из этого интервала значений, следовательно, сила тока в цепи при изменении ЭДС источника:

    I2=U2R..=ε2−UDR..=I1ε2−UDε1−UD..

    I2=0,14,5−36−3..=0,05 (А)

    Ответ: 0,05

    pазбирался: Алиса Никитина | обсудить разбор | оценить

    Как рассчитать ЭДС | Sciencing

    Обновлено 2 ноября 2020 г.

    Ли Джонсон

    Электродвижущая сила (ЭДС) — понятие незнакомое для большинства людей, но оно тесно связано с более знакомым понятием напряжения. Понимание разницы между ними и того, что означает ЭДС, дает вам инструменты, необходимые для решения многих проблем в физике и электронике, а также знакомит с концепцией внутреннего сопротивления батареи. ЭДС сообщает вам напряжение батареи без уменьшения внутреннего сопротивления, как это происходит при обычных измерениях разности потенциалов.Вы можете рассчитать его несколькими способами, в зависимости от того, какая информация у вас есть.

    TL; DR (слишком долго; не читал)

    Рассчитайте ЭДС по формуле:

    ε = V + Ir

    Здесь (В) означает напряжение элемента, (I) означает ток в цепи, а (r) означает внутреннее сопротивление ячейки.

    Что такое ЭДС?

    Электродвижущая сила — это разность потенциалов (т. Е. Напряжение) на клеммах батареи при отсутствии тока.Может показаться, что это не имеет значения, но каждая батарея имеет «внутреннее сопротивление». Это похоже на обычное сопротивление, которое снижает ток в цепи, но оно существует внутри самой батареи. Это связано с тем, что материалы, из которых состоят элементы в батарее, имеют собственное сопротивление (так как практически все материалы имеют).

    Когда через элемент не течет ток, это внутреннее сопротивление ничего не меняет, потому что нет тока для его замедления.В некотором смысле, ЭДС можно рассматривать как максимальную разность потенциалов на клеммах в идеальной ситуации, и на практике она всегда больше, чем напряжение батареи.

    Уравнения для расчета ЭДС

    Есть два основных уравнения для расчета ЭДС. Наиболее фундаментальное определение — это количество джоулей энергии (E), которое набирает каждый кулон заряда (Q) при прохождении через ячейку:

    Где (ε) — символ электродвижущей силы, (E) — энергия в цепи, а (Q) — заряд цепи.Если вы знаете результирующую энергию и количество заряда, проходящего через ячейку, это самый простой способ рассчитать ЭДС, но в большинстве случаев у вас нет этой информации.

    Вместо этого вы можете использовать определение, больше похожее на закон Ома (V = IR). Это может быть выражено как:

    \ epsilon = I (R + r)

    , где (I) означает ток, (R) — сопротивление рассматриваемой цепи, а (r) — внутреннее сопротивление ячейки. Расширение этого показывает тесную связь с законом Ома:

    \ epsilon = IR + Ir = V + Ir

    Это показывает, что вы можете рассчитать ЭДС, если вы знаете напряжение на клеммах (напряжение, используемое в реальных ситуациях) , протекающий ток и внутреннее сопротивление ячейки.

    Как рассчитать ЭДС: пример

    В качестве примера представьте, что у вас есть цепь с разностью потенциалов 3,2 В, протекающим током 0,6 А и внутренним сопротивлением батареи 0,5 Ом. Используя формулу выше:

    \ epsilon = V + Ir = 3.2 \ text {V} + (0.6 \ text {A}) (0.5 \ text {} \ Omega) = 3.5 \ text {V}

    Итак, ЭДС этой цепи составляет 3,5 В.

    Емкость цепи 15 А

    Обновлено 26 сентября 2019 г.

    Автор Винченцо Джамбанко

    Поток электричества проходит через человеческое тело.Электрические сигналы производятся в человеческом мозге между нейронами и нейротрансмиттерами (дофамин, норэпинефрин, серотонин), все из которых требуют тока или потока электричества для нормального функционирования человеческого тела и человеческого мозга.

    Без электричества человеческое тело не могло бы работать. Сотовые телефоны, компьютеры, планшеты и многие другие приложения не могут работать без тока. Математическое представление тока определяется как изменение заряда за изменение в единицу времени.Ток, используемый в этой статье, будет составлять 15 ампер.

    Текущее определение

    Где I — ток, Дельта (Q) (измеряется в кулонах) — изменение заряда, Дельта (t) (измеряется в секундах) — изменение во времени на единицу заряжать.

    Фундаментальная единица заряда на электрон составляет 1,6021765 × 10 — 19 кулонов или Q

    Другой способ определения тока связан с законом Ома, который выглядит следующим образом:

    Где I — ток, В, — потенциал напряжения, а R — сопротивление.

    Мощность по отношению к току

    Мощность — это количество энергии, передаваемой за единицу времени. Математически мощность определяется следующим образом:

    где P — мощность (измеряется в ваттах или джоулях / сек) Delta (E) (измеряется в джоулях или при любом другом измерении энергии) — это изменение энергии, а Delta (t) (измеряется в секундах) — это изменение времени.

    Где В, — потенциал напряжения (измеряется в вольтах), I — ток (измеряется в амперах), а R — это сопротивление (измеряется в Ом).

    Электрический потенциал определяется как U = qV

    Где V i — электрический потенциал, Q — заряд, и, поскольку электрический потенциал является формой потенциальной энергии, его можно заменить на Delta (E)

    P = qV / Delta (t) = qV / Delta (t)

    Замените I in на q / Delta (t)

    Напряжение и мощность для 15-амперного выключателя

    Максимальное напряжение для обычное домашнее хозяйство составляет 120 вольт, и это всего лишь общие характеристики.Чтобы найти максимальную мощность для выключателя на 15 А, используйте уравнение мощности, полученное выше.

    P = IV = (15 ампер) (120 В) = 1800 Вт

    Все, что выходит за рамки этой спецификации, схема на 15 ампер не сможет обработать, поскольку максимальное напряжение для обычного домашнего хозяйства составляет 120 вольт.

    Чтобы найти максимальную допустимую нагрузку по току, перепишите приведенное выше уравнение следующим образом и подключите 1800 Вт для мощности и 120 В для напряжения.

    Обсуждение емкости цепи на 15 ампер

    Ток протекает в сотовых телефонах, компьютерах, автомобилях, самолетах или во всем, что имеет какое-либо электронное применение.Электричество проходит даже через человеческое тело. Без энергии не было бы ничего. Энергия является источником жизни и пронизывает всю вселенную.

    Даже мультиметр можно использовать для измерения электрического тока, проходящего через человеческое тело. Ток можно рассчитать по закону Ома. Мощность можно рассчитать по закону Ома. Вся физика связана математическими соотношениями.

    Электричество во всем

    Все во Вселенной связано с помощью математики.Итак, каждый раз, когда открывается учебник физики или решается физическая проблема, человеческое существо выходит за пределы языковых мер Вселенной.

    Математика связывает человечество со вселенной точно так же, как каждый раз, когда решается проблема с током или законом Ома. Подумайте обо всем электричестве, протекающем через человеческое тело, компьютеры, сотовые телефоны и большинство электронных устройств. Физика приближает человека к пониманию Вселенной.

    Детали батареи | Sciencing

    Состав батареи различается в зависимости от типа — щелочная, литиевая или хлорид цинка.Батареи бывают всех форм и размеров и доступны в широком диапазоне мощности с точки зрения мощности. Батареи любого типа объединяет то, как они работают. Батареи перемещают энергию от одного конца элемента к другому, создавая ток, который можно использовать для питания многих устройств.

    Области применения

    Батареи имеют много применений. Они могут приводить в действие слуховые аппараты, сотовые телефоны, проигрыватели компакт-дисков, детекторы дыма, компьютеры и даже автомобили. Возможность получать электричество, не будучи «подключенным к розетке», — невероятно полезная идея, имеющая бесчисленное множество применений.

    Как это работает

    Батарея или элемент состоит из катода, анода и электролита. Внутри клетки происходит химическая реакция, при которой электроны перемещаются из одного места в другое и образуется электрический ток. Половина ячейки содержит электролит и анод. Другая половина содержит электролит и катод. Электроны собираются на отрицательном конце батареи (аноде). Когда провод подсоединяется от положительного конца (катода) к отрицательному концу, электроны перемещаются через ячейку от анода к катоду.

    Анод

    Анод — это часть батареи, которая отдает электроны. При разряде энергии анод является отрицательным электродом. При зарядке элемента анод становится положительным электродом. В щелочных батареях анод обычно состоит из цинкового порошка. Чтобы ограничить коррозию, в анод обычно добавляют оксид цинка.

    Катод

    Катод — это часть батареи, которая поглощает электроны. При разряде энергии катод является положительным электродом.При зарядке элемента катод становится отрицательным электродом. В щелочных батареях катод обычно состоит из диоксида марганца. Для улучшения проводимости в катоде традиционно используется графит.

    Электролит

    Электролит — это проводящее вещество, которое передает энергию через элемент. Анод и катод никогда не соприкасаются; они связаны друг с другом через электролит. Электролиты могут быть в твердой или жидкой форме. Материалы, обычно используемые для электролитов, — это гидроксид калия, хлорид аммония или хлорид цинка.

    10.2: Электродвижущая сила — Physics LibreTexts

    Цели обучения

    К концу раздела вы сможете:

    • Опишите электродвижущую силу (ЭДС) и внутреннее сопротивление батареи
    • Объясните основную работу аккумулятора

    Если вы забудете выключить автомобильные фары, они будут медленно тускнеть по мере разрядки аккумулятора. Почему они не мигают внезапно, когда батарея разряжена? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разряда батареи.Причина снижения выходного напряжения для разряженных батарей заключается в том, что все источники напряжения состоят из двух основных частей — источника электрической энергии и внутреннего сопротивления. В этом разделе мы исследуем источник энергии и внутреннее сопротивление.

    Введение в электродвижущую силу

    Voltage имеет множество источников, некоторые из которых показаны на рисунке \ (\ PageIndex {2} \). Все такие устройства создают разность потенциалов и могут подавать ток, если подключены к цепи.Особый тип разности потенциалов известен как электродвижущая сила (ЭДС) . ЭДС — это вовсе не сила, но термин «электродвижущая сила» используется по историческим причинам. Он был изобретен Алессандро Вольта в 1800-х годах, когда он изобрел первую батарею, также известную как вольтовую батарею . Поскольку электродвижущая сила не является силой, принято называть эти источники просто источниками ЭДС (произносимыми буквами «ee-em-eff»), а не источниками электродвижущей силы.

    Рисунок \ (\ PageIndex {1} \): различные источники напряжения. а) ветряная электростанция Бразос в Флуванна, штат Техас; (б) Красноярская плотина в России; (c) солнечная ферма; (d) группа никель-металлогидридных батарей. Выходное напряжение каждого устройства зависит от его конструкции и нагрузки. Выходное напряжение равно ЭДС только при отсутствии нагрузки. (кредит a: модификация работы «Leaflet» / Wikimedia Commons; кредит b: модификация работы Алекса Полежаева; кредит c: модификация работы Министерства энергетики США; кредит d: модификация работы Тиаа Монто)

    Если Электродвижущая сила — это вообще не сила, тогда что такое ЭДС и что является источником ЭДС? Чтобы ответить на эти вопросы, рассмотрим простую схему лампы 12 В, подключенной к батарее 12 В, как показано на рисунке \ (\ PageIndex {2} \).Батарея может быть смоделирована как устройство с двумя выводами, которое поддерживает один вывод с более высоким электрическим потенциалом, чем второй вывод. Более высокий электрический потенциал иногда называют положительной клеммой и обозначают знаком плюс. Клемму с более низким потенциалом иногда называют отрицательной клеммой и обозначают знаком минус. Это источник ЭДС.

    Рисунок \ (\ PageIndex {2} \): Источник ЭДС поддерживает на одном выводе более высокий электрический потенциал, чем на другом выводе, действуя как источник тока в цепи.

    Когда источник ЭДС не подключен к лампе, нет чистого потока заряда внутри источника ЭДС. Как только батарея подключена к лампе, заряды перетекают от одной клеммы батареи через лампу (в результате чего лампа загорается) и обратно к другой клемме батареи. Если мы рассмотрим протекание положительного (обычного) тока, положительные заряды покидают положительный вывод, проходят через лампу и попадают в отрицательный вывод.

    Положительный поток тока полезен для большей части анализа схем в этой главе, но в металлических проводах и резисторах наибольший вклад в ток вносят электроны, протекающие в направлении, противоположном положительному потоку тока.Поэтому более реалистично рассматривать движение электронов для анализа схемы на рисунке \ (\ PageIndex {2} \). Электроны покидают отрицательную клемму, проходят через лампу и возвращаются к положительной клемме. Чтобы источник ЭДС поддерживал разность потенциалов между двумя выводами, отрицательные заряды (электроны) должны быть перемещены с положительного вывода на отрицательный. Источник ЭДС действует как накачка заряда, перемещая отрицательные заряды от положительного вывода к отрицательному для поддержания разности потенциалов.Это увеличивает потенциальную энергию зарядов и, следовательно, электрический потенциал зарядов.

    Сила, действующая на отрицательный заряд электрического поля, действует в направлении, противоположном электрическому полю, как показано на рисунке \ (\ PageIndex {2} \). Чтобы отрицательные заряды переместились на отрицательную клемму, необходимо провести работу с отрицательными зарядами. Для этого требуется энергия, которая возникает в результате химических реакций в батарее. Потенциал поддерживается высоким на положительной клемме и низким на отрицательной клемме, чтобы поддерживать разность потенциалов между двумя клеммами.ЭДС равна работе, выполняемой над зарядом на единицу заряда \ (\ left (\ epsilon = \ frac {dW} {dq} \ right) \) при отсутствии тока. Поскольку единицей работы является джоуль, а единицей заряда — кулон, единицей измерения ЭДС является вольт \ ((1 \, V = 1 \, J / C) \).

    Напряжение на клеммах \ (V_ {клемма} \) батареи — это напряжение, измеренное на клеммах батареи, когда к клемме не подключена нагрузка. Идеальная батарея — это источник ЭДС, который поддерживает постоянное напряжение на клеммах, независимо от тока между двумя клеммами.Идеальная батарея не имеет внутреннего сопротивления, а напряжение на клеммах равно ЭДС батареи. В следующем разделе мы покажем, что у реальной батареи есть внутреннее сопротивление, а напряжение на клеммах всегда меньше, чем ЭДС батареи.

    Источник потенциала батареи

    ЭДС батареи определяется комбинацией химических веществ и составом выводов батареи. Свинцово-кислотный аккумулятор , используемый в автомобилях и других транспортных средствах, является одним из наиболее распространенных сочетаний химикатов.На рисунке \ (\ PageIndex {3} \) показана одна ячейка (одна из шести) этой батареи. Катодная (положительная) клемма ячейки соединена с пластиной из оксида свинца, а анодная (отрицательная) клемма подключена к свинцовой пластине. Обе пластины погружены в серную кислоту, электролит для системы.

    Рисунок \ (\ PageIndex {3} \): Химические реакции в свинцово-кислотном элементе разделяют заряд, отправляя отрицательный заряд на анод, который соединен со свинцовыми пластинами. Пластины из оксида свинца подключаются к положительному или катодному выводу ячейки.Серная кислота проводит заряд, а также участвует в химической реакции.

    Небольшое знание того, как взаимодействуют химические вещества в свинцово-кислотной батарее, помогает понять потенциал, создаваемый батареей. На рисунке \ (\ PageIndex {4} \) показан результат одной химической реакции. Два электрона помещаются на анод , что делает его отрицательным, при условии, что катод подает два электрона. Это оставляет катод положительно заряженным, потому что он потерял два электрона.Короче говоря, разделение заряда было вызвано химической реакцией.

    Обратите внимание, что реакция не происходит, если нет замкнутой цепи, позволяющей подавать два электрона на катод. Во многих случаях эти электроны выходят из анода, проходят через сопротивление и возвращаются на катод. Также обратите внимание, что, поскольку в химических реакциях участвуют вещества, обладающие сопротивлением, невозможно создать ЭДС без внутреннего сопротивления.

    Рисунок \ (\ PageIndex {4} \): В свинцово-кислотной батарее два электрона прижимаются к аноду элемента, а два электрона удаляются с катода элемента.В результате химической реакции в свинцово-кислотной батарее два электрона помещаются на анод и два электрона удаляются с катода. Для работы требуется замкнутая цепь, так как два электрона должны быть доставлены на катод.

    Внутреннее сопротивление и напряжение на клеммах

    Величина сопротивления прохождению тока внутри источника напряжения называется внутренним сопротивлением . Внутреннее сопротивление r батареи может вести себя сложным образом. Обычно она увеличивается по мере разряда батареи из-за окисления пластин или снижения кислотности электролита.Однако внутреннее сопротивление может также зависеть от величины и направления тока через источник напряжения, его температуры и даже его предыстории. Внутреннее сопротивление никель-кадмиевых аккумуляторов, например, зависит от того, сколько раз и насколько глубоко они были разряжены. Простая модель батареи состоит из идеализированного источника ЭДС \ (\ epsilon \) и внутреннего сопротивления r (рисунок \ (\ PageIndex {5} \)).

    Рисунок \ (\ PageIndex {5} \): Батарею можно смоделировать как идеализированную ЭДС \ ((\ epsilon) \) с внутренним сопротивлением ( r ).Напряжение на клеммах аккумулятора равно \ (V_ {terminal} = \ epsilon — Ir \).

    Предположим, что внешний резистор, известный как сопротивление нагрузки R , подключен к источнику напряжения, например батарее, как показано на рисунке \ (\ PageIndex {6} \). На рисунке показана модель аккумулятора с ЭДС ε, внутренним сопротивлением r и нагрузочным резистором R , подключенным к его клеммам. При обычном протекании тока положительные заряды покидают положительную клемму батареи, проходят через резистор и возвращаются к отрицательной клемме батареи.Напряжение на клеммах аккумулятора зависит от ЭДС, внутреннего сопротивления и силы тока и равно

    .

    Примечание

    \ [V_ {терминал} = \ epsilon — Ir \]

    При заданной ЭДС и внутреннем сопротивлении напряжение на клеммах уменьшается по мере увеличения тока из-за падения потенциала Ir внутреннего сопротивления.

    Рисунок \ (\ PageIndex {6} \): Схема источника напряжения и его нагрузочного резистора R . Поскольку внутреннее сопротивление – последовательно с нагрузкой, оно может значительно повлиять на напряжение на клеммах и ток, подаваемый на нагрузку.

    График разности потенциалов на каждом элементе цепи показан на рисунке \ (\ PageIndex {7} \). По цепи проходит ток I , а падение потенциала на внутреннем резисторе равно Ir . Напряжение на клеммах равно \ (\ epsilon — Ir \), что равно падению потенциала на нагрузочном резисторе \ (IR = \ epsilon — Ir \). Как и в случае с потенциальной энергией, важно изменение напряжения. Когда используется термин «напряжение», мы предполагаем, что это на самом деле изменение потенциала, или \ (\ Delta V \).Однако \ (\ Delta \) часто для удобства опускается.

    Рисунок \ (\ PageIndex {7} \): график напряжения в цепи батареи и сопротивления нагрузки. Электрический потенциал увеличивает ЭДС батареи из-за химических реакций, выполняющих работу с зарядами. В аккумуляторе происходит снижение электрического потенциала из-за внутреннего сопротивления. Потенциал уменьшается из-за внутреннего сопротивления \ (- Ir \), в результате чего напряжение на клеммах батареи равно \ ((\ epsilon — Ir) \).Затем напряжение уменьшается на ( IR ). Ток равен \ (I = \ frac {\ epsilon} {r + R} \).

    Ток через нагрузочный резистор равен \ (I = \ frac {\ epsilon} {r + R} \). Из этого выражения видно, что чем меньше внутреннее сопротивление r , тем больший ток подает источник напряжения на свою нагрузку R . По мере разряда батарей r увеличивается. Если r становится значительной частью сопротивления нагрузки, то ток значительно снижается, как показано в следующем примере.

    Пример \ (\ PageIndex {1} \): анализ цепи с батареей и нагрузкой

    Данная батарея имеет ЭДС 12,00 В и внутреннее сопротивление \ (0,100 \, \ Omega \). (a) Рассчитайте напряжение на его клеммах при подключении к нагрузке с \ (10.00 \, \ Omega \). (b) Какое напряжение на клеммах при подключении к нагрузке \ (0.500 \, \ Omega \)? (c) Какая мощность рассеивается при нагрузке \ (0.500 \, \ Omega \)? (d) Если внутреннее сопротивление увеличивается до \ (0.500 \, \ Omega \), найдите ток, напряжение на клеммах и мощность, рассеиваемую элементом \ (0.500 \, \ Omega \) загрузка.

    Стратегия

    Приведенный выше анализ дал выражение для тока с учетом внутреннего сопротивления. Как только ток будет найден, напряжение на клеммах можно рассчитать с помощью уравнения \ (V_ {terminal} = \ epsilon — Ir \). Как только ток будет найден, мы также сможем найти мощность, рассеиваемую резистором.

    Решение

    1. Ввод заданных значений ЭДС, сопротивления нагрузки и внутреннего сопротивления в выражение выше дает \ [I = \ frac {\ epsilon} {R + r} = \ frac {12.00 \, V} {10.10 \, \ Omega} = 1.188 \, A. \] Введите известные значения в уравнение \ (V_ {terminal} = \ epsilon — Ir \), чтобы получить напряжение на клеммах: \ [V_ { клемма} = \ epsilon — Ir = 12.00 \, V — (1.188 \, A) (0.100 \, \ Omega) = 11.90 \, V. \] Напряжение на клеммах здесь лишь немного ниже, чем ЭДС, что означает, что ток втягивается этой легкой нагрузкой незначительно.
    2. Аналогично, с \ (R_ {load} = 0.500 \, \ Omega \), ток равен \ [I = \ frac {\ epsilon} {R + r} = \ frac {12.00 \, V} {0.2} {R} \) или \ (IV \), где В, — напряжение на клеммах (в данном случае 10,0 В).
    3. Здесь внутреннее сопротивление увеличилось, возможно, из-за разряда батареи, до точки, в которой оно равно сопротивлению нагрузки. Как и раньше, мы сначала находим ток, вводя известные значения в выражение, получая \ [I = \ frac {\ epsilon} {R + r} = \ frac {12.00 \, V} {1.00 \, \ Omega} = 12.00 \, A. \] Теперь напряжение на клеммах равно \ [V_ {terminal} = \ epsilon — Ir = 12.00 \, V — (12.2 (0.500 \, \ Omega) = 72.00 \, W. \] Мы видим, что повышенное внутреннее сопротивление значительно снизило напряжение на клеммах, ток и мощность, подаваемую на нагрузку.

    Значение

    Внутреннее сопротивление батареи может увеличиваться по многим причинам. Например, внутреннее сопротивление перезаряжаемой батареи увеличивается с увеличением количества раз, когда батарея перезаряжается. Повышенное внутреннее сопротивление может иметь двоякое влияние на аккумулятор.Сначала снизится напряжение на клеммах. Во-вторых, аккумулятор может перегреться из-за повышенной мощности, рассеиваемой внутренним сопротивлением.

    Упражнение \ (\ PageIndex {1} \)

    Если вы поместите провод прямо между двумя выводами батареи, эффективно закоротив клеммы, батарея начнет нагреваться. Как вы думаете, почему это происходит?

    Решение

    Если к клеммам подключен провод, сопротивление нагрузки близко к нулю или, по крайней мере, значительно меньше внутреннего сопротивления батареи.2р) \). Мощность рассеивается в виде тепла.

    Тестеры батарей

    Тестеры батарей, такие как те, что показаны на рисунке \ (\ PageIndex {8} \), используют малые нагрузочные резисторы, чтобы намеренно потреблять ток, чтобы определить, падает ли потенциал клемм ниже допустимого уровня. Хотя измерить внутреннее сопротивление батареи сложно, тестеры батареи могут обеспечить измерение внутреннего сопротивления батареи. Если внутреннее сопротивление высокое, батарея разряжена, о чем свидетельствует низкое напряжение на клеммах.

    Рисунок \ (\ PageIndex {8} \): Тестеры батарей измеряют напряжение на клеммах под нагрузкой, чтобы определить состояние батареи. (a) Техник-электронщик ВМС США использует тестер аккумуляторов для проверки больших аккумуляторов на борту авианосца USS Nimitz . Тестер батарей, который она использует, имеет небольшое сопротивление, которое может рассеивать большое количество энергии. (b) Показанное небольшое устройство используется на небольших батареях и имеет цифровой дисплей для индикации допустимого напряжения на клеммах. (кредит А: модификация работы Джейсона А.Джонстон; кредит b: модификация работы Кейта Уильямсона)

    Некоторые батареи можно перезарядить, пропустив через них ток в направлении, противоположном току, который они подают в прибор. Это обычно делается в автомобилях и батареях для небольших электроприборов и электронных устройств (Рисунок \ (\ PageIndex {9} \)). Выходное напряжение зарядного устройства аккумулятора должно быть больше, чем ЭДС аккумулятора, чтобы ток через него реверсировал. Это приводит к тому, что напряжение на клеммах аккумулятора превышает ЭДС, так как \ (V = \ epsilon — Ir \) и I теперь отрицательны.

    Рисунок \ (\ PageIndex {9} \): автомобильное зарядное устройство меняет нормальное направление тока через аккумулятор, обращая вспять его химическую реакцию и пополняя ее химический потенциал.

    Важно понимать последствия внутреннего сопротивления источников ЭДС, таких как батареи и солнечные элементы, но часто анализ цепей выполняется с помощью напряжения на клеммах батареи, как мы делали в предыдущих разделах. Напряжение на клеммах обозначается просто как В , без индекса «клемма».Это связано с тем, что внутреннее сопротивление батареи трудно измерить напрямую, и оно может со временем измениться.

    Авторы и ссылки

    Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

    Физика — Электродвижущая сила — Бирмингемский университет

    Электродвижущая сила (ЭДС) равна разности потенциалов на клеммах при отсутствии тока.ЭДС и разность потенциалов на клеммах ( В, ) измеряются в вольтах, но это не одно и то же. ЭДС ( ϵ ) — это количество энергии ( E ), обеспечиваемое батареей на каждый проходящий кулон заряда ( Q ).

    Как рассчитать ЭДС?

    ЭДС можно записать через внутреннее сопротивление батареи ( r ) где: ϵ = I (r + R )

    Что из закона Ома, мы можем затем изменить это с точки зрения оконечного сопротивления: ϵ = В + Ir

    ЭДС ячейки может быть определена путем измерения напряжения на ячейке с помощью вольтметра и тока в цепи с помощью амперметра для различных сопротивлений.Затем мы можем настроить схему для определения ЭДС, как показано ниже.

    ЭДС и внутреннее сопротивление электрических элементов и батарей

    Исследование ЭМП

    Как закон Фарадея соотносится с ЭМП?

    Закон Фарадея гласит, что любое изменение магнитного поля катушки будет индуцировать в катушке ЭДС (а следовательно, и ток). Он пропорционален минус скорости изменения магнитного потока ( ϕ ) (примечание: N — количество витков в катушке).

    Используя закон Фарадея, общество извлекло выгоду из таких важных технологий, как трансформаторы, которые используются для передачи электроэнергии в национальной энергосистеме Великобритании, которая теперь является необходимостью в наших домах. Также он используется в электрических генераторах и двигателях, таких как плотины гидроэлектростанций, которые производят электричество, которое сейчас является неотъемлемой частью наших современных технологических потребностей. Текущий исследовательский проект MAG-DRIVE в Бирмингеме направлен на поиск способов разработки и улучшения материалов с постоянными магнитами, которые можно использовать в электромобилях следующего поколения.ЭМП также генерируется солнечными батареями, поэтому он важен для исследований в области возобновляемых источников энергии.

    Лабораторные признания

    Исследователи подкаста In the Laboratory Confessions рассказывают о своем лабораторном опыте в контексте практических экзаменов A Level. Эпизоды, которые касаются надлежащего использования цифровых инструментов (простое гармоническое движение), правильного построения принципиальных схем (удельное сопротивление в проводе) и использования источников питания постоянного тока (конденсаторов), имеют отношение к эксперименту по ЭДС, ниже вы можете услышать удельное сопротивление. в проводном подкасте.

    Как мы интерпретируем наши данные?

    По мере увеличения сопротивления переменного резистора величина тока будет уменьшаться. График зависимости напряжения от тока должен давать линейную зависимость, где градиент линии дает отрицательное внутреннее сопротивление ячейки ( -r ), а точка пересечения дает ЭДС (напряжение, при котором ток равен 0).

    Выполнение нескольких измерений при разных значениях сопротивления даст больше точек на графике V-I, что сделает подбор более надежным.Также рекомендуется повторить измерения, так как ячейка будет постепенно стекать, что повлияет на показания. Во избежание разряда элемента / батареи ее следует отключать между измерениями. В качестве альтернативы в схему можно включить выключатель. Также не рекомендуется использовать перезаряжаемые батареи, поскольку они имеют низкое внутреннее сопротивление.

    Хотя этот эксперимент довольно прост, он поможет вам отличить конечную разницу от ЭДС, что может быть сложной концепцией для понимания учащимися.Поскольку люди становятся все более зависимыми от электричества, исследования, связанные с ЭМП, важны для развития и технического прогресса электричества.

    Следующие шаги

    Эти ссылки предоставлены только для удобства и в информационных целях; они не означают одобрения или одобрения Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте. Бирмингемский университет не несет ответственности за точность, законность или содержание внешнего сайта или последующих ссылок.Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы относительно его содержания.

    Электродвижущая сила и внутреннее сопротивление

    Электродвижущая сила (э) или э.д.с. это энергия, обеспечиваемая элементом или батареей на один кулон заряда, проходящего через них, она равна , измеренная в вольтах (В). Это равно разности потенциалов на выводах ячейки, когда ток не течет.

    • e = электродвижущая сила в вольтах, В
    • E = энергия в джоулях, Дж
    • Q = заряд в кулонах, Кл

    Батареи и элементы имеют внутреннее сопротивление (r) , которое составляет единиц измерения в омах (Вт). Когда электричество течет по цепи, внутреннее сопротивление самого элемента сопротивляется прохождению тока, поэтому тепловая (тепловая) энергия расходуется в самом элементе.

    • e = электродвижущая сила в вольтах, В
    • I = ток в амперах, А
    • R = сопротивление нагрузки в цепи в Ом, Вт
    • r = внутреннее сопротивление ячейки в Ом, Вт

    Мы можем изменить приведенное выше уравнение;

    , а затем на

    В этом уравнении ( В, ) появляется разность потенциалов на клеммах, измеренная в вольтах (В).Это разность потенциалов на выводах ячейки при протекании тока в цепи, она всегда меньше ЭДС. ячейки.

    Пример;

    Q1) p.d. на выводах элемента составляет 3,0 В, когда он не подключен к цепи и не течет ток. Когда ячейка подключена к цепи и течет ток 0,37 А, клемма p.d. падает до 2,8 В. Какое внутреннее сопротивление ячейки?

    График терминала п.d. против нынешних

    Если мы построим график зависимости разности потенциалов на клеммах (V) от тока в цепи (I), мы получим прямую линию с отрицательным градиентом.

    Мы можем им переставить э.д.с. уравнение сверху для соответствия общему выражению для прямой линии y = mx + c.

    Из красных прямоугольников выше видно;

    • пересечение по оси Y равно ЭДС. ячейки
    • градиент графика равен -r, где r — внутреннее сопротивление ячейки.

    Электрические свойства цепей RC:

    В простейшем виде цепь R-C содержит сопротивление R, конденсатор C и электродвижущую силу ЭДС (обычно аккумулятор). Принципиальная схема RC-цепи выглядит так:

    Когда тумблер находится в разомкнутом положении, показанном на схеме, конденсатор не подключен к электродвижущей силе, ЭДС, и, если конденсатор не был ранее заряжен, в конденсаторе не будет никаких зарядов (т.е., q = 0) и разность потенциалов между обкладками конденсатора, соответственно, также будет равна нулю.
    Если переключатель переключен так, что он соединяет конденсатор с электродвижущей силой, заряды будут накапливаться на пластинах конденсатора, + на одной пластине, _ на другой. Это будет продолжаться до тех пор, пока накопленный заряд не создаст разность потенциалов (V c ) между двумя пластинами, которая численно равна электродвижущей силе.То есть, когда:

    V c = e,

    ток через соединительные провода прекратится (т. Е. I = 0).
    Когда переключатель переведен в свое альтернативное положение, (i) ЭДС обходится, (ii) две пластины конденсатора соединены, и (iii) заряды, накопленные на конденсаторе, будут стремиться пройти через соединительный провод к противоположная пластина. Другими словами, заряженный конденсатор разрядится.
    Об электрических свойствах цепей R-C следует помнить две важные вещи:

    1.Когда конденсатор (C) полностью заряжен, сохраняется следующее соотношение:

    q = Ce Уравнение 1a

    где q — общее количество заряда, накопленного конденсатором, C — емкость конденсатора, а e — электродвижущая сила, которая фактически заряжает конденсатор.Обратите внимание, что q = 0, когда конденсатор разряжен. Также обратите внимание, что уравнение можно переставить так:

    q / C = e = V c Уравнение 1b

    Это означает, что размещение избытка + на одной пластине конденсатора и избытка на другой пластине создаст разность потенциалов между пластинами.

    2. Из-за наличия сопротивления (R) в цепи ток через цепь замедляется. В результате для изменения количества заряда, хранящегося на пластинах конденсатора, требуется время. Например, если вы начнете с полностью разряженного конденсатора (т.е. q = 0 и V c = 0) и подключите его к батарее, зарядка конденсатора будет описана экспоненциальным уравнением ,

    q t = Ce (1 e -t / RC ) Уравнение 2a

    и если C = 1, e = 10 и R = 1 график зависимости q t отвремя будет выглядеть так:

    Аналогично, если бы вы начали с того же конденсатора в полностью заряженном состоянии (т.е. q = Ce и V c = e ) и соедините две его пластины друг с другом, разряд конденсатора будет описан экспоненциальным уравнением:

    q t = Ce e -t / RC Уравнение 2b

    и график q t vs.время будет выглядеть так:

    Упражнения:

    1. Имея в виду уравнения 1b, 2a и 2b и определение тока, можете ли вы предсказать внешний вид графиков V c и тока (I) в зависимости от времени для той же цепи R-C?

    2. Запустите моделирование электрических свойств RC-цепи и получите качественное представление о влиянии изменения e на электрическое поведение RC-цепи.

    3. Величина RC называется постоянной времени цепи R-C и иногда обозначается как t (= RC).Исследуйте влияние изменения t на электрическое «поведение» RC-цепи, повторяя упражнение 2, на этот раз изменяя R и / или C.

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *