Электродвижущая сила — Википедия
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил (то есть любых сил, кроме электростатических и диссипативных) действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура[1][2].
По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил E→ex{\displaystyle {\vec {E}}_{ex}}, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре L{\displaystyle L} ЭДС будет равна:
- E=∮LE→ex⋅dl→,{\displaystyle {\mathcal {E}}=\oint \limits _{L}{\vec {E}}_{ex}\cdot {\vec {dl}},}
где dl→{\displaystyle {\vec {dl}}} — элемент контура.
ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.
Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи
- φ1−φ2+E=IR,{\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}
где φ1−φ2{\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I{\displaystyle I} — сила тока, текущего по участку, а R{\displaystyle R} — сопротивление участка.
Если точки 1 и 2 совпадают (цепь замкнута), то φ1−φ2=0{\displaystyle \varphi _{1}-\varphi _{2}=0} и предыдущая формула переходит в формулу закона Ома для замкнутой цепи[1]:
- E=IR,{\displaystyle {\mathcal {E}}=IR,}
где теперь R{\displaystyle R} — полное сопротивление всей цепи.
В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи (Re{\displaystyle R_{e}}) и внутреннего сопротивления самого́ источника тока (r{\displaystyle r}). С учётом этого следует:
- E=IRe+Ir.{\displaystyle {\mathcal {E}}=IR_{e}+Ir.}
Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:
- φ1−φ2=IR.{\displaystyle \varphi _{1}-\varphi _{2}=IR.}
Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода φa{\displaystyle \varphi _{a}} и катода φk{\displaystyle \varphi _{k}} можно записать:
- φa−φk=IRe,{\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}
где как и ранее Re{\displaystyle R_{e}} — сопротивление внешнего участка цепи.
Из этого соотношения и закона Ома для замкнутой цепи, записанного в виде E=IRe+Ir{\displaystyle {\mathcal {E}}=IR_{e}+Ir} нетрудно получить
- φa−φkE=ReRe+r{\displaystyle {\frac {\varphi _{a}-\varphi _{k}}{\mathcal {E}}}={\frac {R_{e}}{R_{e}+r}}} и затем φa−φk=ReRe+rE.{\displaystyle \varphi _{a}-\varphi _{k}={\frac {R_{e}}{R_{e}+r}}{\mathcal {E}}.}
Из полученного соотношения следуют два вывода:
- Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φa−φk{\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
- В предельном случае, когда Re{\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E=φa−φk.{\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}
Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи[1].
Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
- E=−dΦdt,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi }{dt}},}
где Φ{\displaystyle \Phi } — поток магнитного поля через замкнутую поверхность, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.
Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектростатической природы, преодолевающей силу электрического отталкиванияСторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца[3].
Формула ЭДС
Здесь – ЭДС, – работа сторонних сил, – величина заряда.
Единица измерения напряжения – В (вольт).
ЭДС – скалярная величина. В замкнутом контуре ЭДС равна работе сил по перемещению аналогичного заряда по всему контуру. При этом ток в контуре и внутри источника тока будут течь в противоположных направлениях. Внешняя работа, которая создаёт ЭДС, должна быть не электрического происхождения (сила Лоренца, электромагнитная индукция, центробежная сила, сила, возникающая в ходе химических реакций). Эта работа нужна для преодоления сил отталкивания носителей тока внутри источника.
Если в цепи идёт ток, то ЭДС равна сумме падений напряжений во всей цепи.
Примеры решения задач по теме «Электродвижущая сила»
| Понравился сайт? Расскажи друзьям! | |||
определение и формула, в чём измеряется, работа источника электродвижущей силы
 Электрический ток не протекает в медном проводе по той же причине, по которой остаётся неподвижной вода в горизонтальной трубе. Если один конец трубы соединить с резервуаром таким образом, чтобы образовалась разность давлений, жидкость будет вытекать из одного конца. Аналогичным образом, для поддержания постоянного тока необходимо внешнее воздействие, перемещающее заряды. Это воздействие называется электродвижущая сила или ЭДС.
Электрический ток не протекает в медном проводе по той же причине, по которой остаётся неподвижной вода в горизонтальной трубе. Если один конец трубы соединить с резервуаром таким образом, чтобы образовалась разность давлений, жидкость будет вытекать из одного конца. Аналогичным образом, для поддержания постоянного тока необходимо внешнее воздействие, перемещающее заряды. Это воздействие называется электродвижущая сила или ЭДС.
От электростатики к электрокинетике
Между концом XVIII и началом XIX века работы таких учёных, как Кулон, Лагранж и Пуассон, заложили математические основы определения электростатических величин. Прогресс в понимании электричества на этом историческом этапе очевиден. Франклин уже ввёл понятие «количество электрической субстанции», но пока ещё и он, ни его преемники не смогли его измерить.
Следуя за экспериментами Гальвани, Вольта пытался найти подтверждения того, что «гальванические жидкости» животного были одной природы со статическим электричеством. В поисках истины он обнаружил, что когда два электрода из разных металлов контактируют через электролит, оба заряжаются и остаются заряженными несмотря на замыкание контура нагрузкой. Это явление не соответствовало существующим представлениям об электричестве потому, что электростатические заряды в подобном случае должны были рекомбинировать.
Вольта ввёл новое определение силы, действующей в направлении разделения зарядов и поддержании их в таком состоянии. Он назвал её электродвижущей. Подобное объяснение описания работы батареи не вписывалось в теоретические основы физики того времени. В Кулоновской парадигме первой трети XIX века э. д. с. Вольта определялась способностью одних тел вырабатывать электричество в других.
Важнейший вклад в объяснение работы электрических цепей внёс Ом. Результаты ряда экспериментов привели его к построению теории электропроводности. Он ввёл величину «напряжение» и определил её как разность потенциалов на контактах. Подобно Фурье, который в своей теории различал количество тепла и температуру в теплопередаче, Ом создал модель по аналогии, связывающую количество перемещаемого заряда, напряжение и электропроводность. Закон Ома не противоречил накопленным знаниям об электростатическом электричестве.
Затем, благодаря Максвеллу и Фарадею, пояснительные модели тока получили новую теорию поля. Это позволило разработать связанную с полем концепцию энергии как для статических потенциалов, так и для электродвижущей силы. Основные даты эволюции понятия ЭДС:
- 1800 г. — создание Вольтой гальванической батареи;
- 1826 г. — Ом формулирует свой закон для полной цепи;
- 1831 г. — обнаружение электромагнитной индукции Фарадеем.
Определение и физический смысл
 Приложение некоторой разности потенциалов между двумя концами проводника создаст перетекание электронов от одного конца к другому. Но этого недостаточно для поддержания потока зарядов в проводнике. Дрейф электронов приводит к уменьшению потенциала до момента его уравновешивания (прекращение тока). Таким образом, для создания постоянного тока необходимы механизмы, непрерывно возвращающие описанную систему в первоначальную конфигурацию, то есть, препятствующие агрегации зарядов в результате их движения. Для этой цели используются специальные устройства, называемые источники питания.
Приложение некоторой разности потенциалов между двумя концами проводника создаст перетекание электронов от одного конца к другому. Но этого недостаточно для поддержания потока зарядов в проводнике. Дрейф электронов приводит к уменьшению потенциала до момента его уравновешивания (прекращение тока). Таким образом, для создания постоянного тока необходимы механизмы, непрерывно возвращающие описанную систему в первоначальную конфигурацию, то есть, препятствующие агрегации зарядов в результате их движения. Для этой цели используются специальные устройства, называемые источники питания.
В качестве иллюстрации их работы удобно рассматривать замкнутый контур из сопротивления и гальванического источника питания (батареи). Если предположить, что внутри батареи тока нет, то описанная проблема объединения зарядов остаётся неразрешённой. Но в цепи с реальным источником питания электроны перемещаются постоянно. Это происходит благодаря тому, что поток ионов протекает и внутри батареи от отрицательного электрода к положительному. Источник энергии, перемещающий эти заряды в батарее — химические реакции. Такая энергия называется электродвижущей силой.
ЭДС является характеристикой любого источника энергии, способного управлять движением электрических зарядов в цепи. В аналогии с замкнутым гидравлическим контуром работа источника э. д. с. соответствует работе насоса для создания давления воды. Поэтому значок, обозначающий эти устройства, неотличим на гидравлических и электрических схемах.
Несмотря на название, электродвижущая сила на самом деле не является силой и измеряется в вольтах. Её численное значение равно работе по перемещению заряда по замкнутой цепи. ЭДС источника выражается формулой E=A/q, в которой:
- E — электродвижущая сила в вольтах;
- A — работа сторонних сил по перемещению заряда в джоулях;
- q — перемещённый заряд в кулонах.
Из этой формулы ЭДС следует, что электродвижущая сила не является свойством цепи или нагрузки, а есть способность генератора электроэнергии к разделению зарядов.
Сравнение с разностью потенциалов
 Электродвижущая сила и разность потенциалов в цепи очень похожие физические величины, так как оба измеряются в вольтах и определяются работой по перемещению заряда. Одно из основных смысловых различий заключается в том, что э. д. с. (E) вызывается путём преобразования какой-либо энергии в электрическую, тогда как разность потенциалов (U) реализует электрическую энергию в другие виды. Другие различия выглядят так:
Электродвижущая сила и разность потенциалов в цепи очень похожие физические величины, так как оба измеряются в вольтах и определяются работой по перемещению заряда. Одно из основных смысловых различий заключается в том, что э. д. с. (E) вызывается путём преобразования какой-либо энергии в электрическую, тогда как разность потенциалов (U) реализует электрическую энергию в другие виды. Другие различия выглядят так:
- E передаёт энергию всей цепи. U является мерой энергии между двумя точками на схеме.
- Е является причиной U, но не наоборот.
- Е индуцируется в электрическом, магнитном и гравитационном поле.
- Концепция э. д. с. применима только к электрическому полю, в то время как разность потенциалов применима к магнитным, гравитационным и электрическим полям.
Напряжение на клеммах источника питания, как правило, отличается от ЭДС источника. Это происходит из-за наличия внутреннего сопротивления источника (электролита и электродов, обмоток генератора). Связывающая разность потенциалов и ЭДС источника тока формула выглядит как U=E-Ir. В этом выражении:
- U — напряжение на клеммах источника;
- r — внутреннее сопротивление источника;
- I — ток в цепи.
Из этой формулы электродвижущей силы следует, что э. д. с. равна напряжению когда ток в цепи не течёт. Идеальный источник ЭДС создаёт разность потенциалов независимо от нагрузки (протекающего тока) и не обладает внутренним сопротивлением.
В природе не может существовать источника с бесконечной мощностью при замыкании на клеммах, как и материала с бесконечной проводимостью. Идеальный источник используется как абстрактная математическая модель.
Источники электродвижущей силы
Суть источника ЭДС заключается в преобразовании других видов энергии в электрическую с помощью сторонних сил. С точки зрения физики обеспечения э. д. с различают следующие два основных вида источников:
- гальванические;
- электромагнитные.

Первые представляют собой электрохимические источники, основанные на вовлечение в химическую реакцию процесса переноса электронов. В обычных условиях химические взаимодействия сопровождаются выделением или поглощением тепла, но существует немало реакций, в результате которых генерируется электрическая энергия.
Электрохимические процессы в большинстве случаев обратимы, поскольку энергия электрического тока может быть использована, чтобы заставить реагировать вещества между собой. Эта возможность позволяет создавать возобновляемые гальванические источники — аккумуляторы.
В генераторах тока э. д. с. создаётся другим способом. Разделение зарядов происходит с помощью явления электромагнитной индукции, которое заключается в том, что изменение величины или направления магнитного поля создаёт ЭДС. Согласно закону Фарадея, нахождение э. д. с. индукции возможно из выражения E=—dФ/dt. В этой формуле:
- Ф — магнитный поток;
- t — время.
ЭДС индукции измеряется также в вольтах. В зависимости от того, каким способом вызываются изменения магнитного потока, различают:
- Динамически индуцированную. Когда в стационарном магнитном поле перемещается проводник. Характерен для генераторов.
- Статически индуцированную. Когда изменения потока возникают из-за изменений магнитного поля вокруг неподвижного проводника. Так работают трансформаторы.
Существуют также источники э. д. с, не основанные на электрохимии или магнитной индукции. К таким устройствам можно отнести полупроводниковые фотоэлементы, контактные потенциалы и пьезокристаллы. Понятие ЭДС имеет практическое применение прежде всего как параметр выбора источников питания для тех или иных целей. Чтобы получить максимальный эффект от работы устройств в цепи, нужно согласовывать их возможности и характеристики. Прежде всего внутреннее сопротивление источника ЭДС силы с характеристиками подключаемой нагрузки.
Электротехника. Основы. Закон Ома — Всё об энергетике
Электротехника. Основы. Закон Ома
В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.
Закон Ома
Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.
Закон Ома для участка цепи без ЭДС
Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:
\begin{equation} I = {U_{ab}\over R}; \end{equation}Где:
- I — ток через участок ab электрической цепи;
- Uab — напряжение на участке ab электрической цепи;
- R — сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation} I = U_{ab} × G; \end{equation}Где:
- G — проводимость участка ab электрической цепи.
Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.
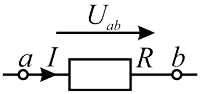
Рисунок 1 — Участок цепи без ЭДС
Закон Ома для участка цепи содержащего ЭДС
Или обобщённый закон Ома. Формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation} I = {U_{ab} + E\over R}; \end{equation}Где:
- I — ток через участок ac электрической цепи;
- Uab — напряжение на участке ab электрической цепи;
- E — ЭДС на участке bс электрической цепи;
- R — сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation} I = {(U_{ab} + E) × G}; \end{equation}Где:
- G — проводимость участка ab электрической цепи.
Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.
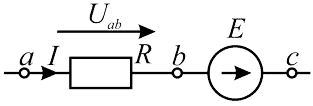
Рисунок 2 — Участок цепи содержащий ЭДС
Закон Ома для полной цепи
Закон формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation} I = {E\over {R + r}}; \end{equation}Где:
- I — ток в электрической цепи;
- E — ЭДС электрической цепи;
- R — сопротивление электрической цепи;
- r — внутреннее сопротивление источника ЭДС.
Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).
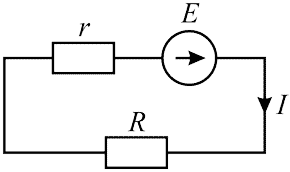
Рисунок 3 — Полная цепь
На схеме видно, что R и r соединены последовательно, а в формуле это отражено как сумма R (сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на Rп
\begin{equation} I = {E\over R_п}; \end{equation}Где:
- Rп — полное сопротивление электрической цепи (включая сопротивление источника ЭДС).
Закон Ома в дифференциальной форме
Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].
\begin{equation} \vec E = {ρ × \vec\jmath}; \end{equation}Где:
- \(\vec\jmath\) — плотность тока;
- ρ — удельное сопротивление;
- \(\vec E\) — напряжённость электрического поля.
Примеры применения
Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.
Пример 1
Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.
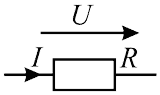
Рисунок 4 — Схема к 1 и 2-му примеру
Для решения задания воспользуемся выражением (1):
\begin{equation} I = {U\over R} = {26\over 5,2} = {5 \ А;} \end{equation}Пример 2
Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.
Для решения задания преобразуем выражение (2) относительно G:
\begin{equation} I = {U × G} \ \Rightarrow \ G = {I\over U} = {1,5\over 24} = {0,0625 \ См;} \end{equation}Пример 3
Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.
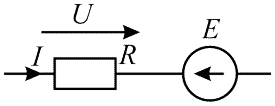
Рисунок 5 — Схема к 3-му примеру
Для решения задания преобразуем выражение (3) относительно E:
\begin{equation} I = {U — E\over R} \ \Rightarrow \ {I × R} = {U — E} \ \Rightarrow \ E = {U — I × R}; \end{equation}Подставим в выражение (10) известные величины:
\begin{equation} E = {U — I × R} = {220 — 0,5 × 140} = {150 \ В;} \end{equation}
Пример 4
Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь — 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.
Преобразуем выражение (5) относительно r:
\begin{equation} I = {E\over {R + r}} \ \Rightarrow \ {I × (R + r)} = E \ \Rightarrow \ {I × r} = {E — I × R} \ \Rightarrow \ r = {E — I × R\over I}; \end{equation}Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:
\begin{equation} r = {E — I × R\over I} = {9 — 0,72 × 12\over 0,72} = {0,36\over 0,72} = {0,5 \ Ом;} \end{equation}
Использованные термины
Электрический потенциал точки:
Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.
Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.
Электрическое напряжение:
Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: Uab = φa — φb.
Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение — скалярная величина, но на электрических схемах указывают его положительное направление.
Электродвижущая сила (ЭДС):
Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.
ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС — скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.
Электрическое ток:
Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление — направленное движение заряженных частиц.
Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11].
Плотность тока:
Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.
Плотность тока обозначается буквой \(\vec\jmath\) латинского алфавита и измеряется в амперах на метр квадратный (А/м2). Плотность тока — векторная величина [4].
Электрическое сопротивление:
Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.
Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление — скалярная величина.
Электрическая проводимость:
Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.
Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость — скалярная величина.
Удельное сопротивление:
Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м2.
Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].
В дальнейшем при использовании вышеперечисленных терминов слово «электрический» будет упускаться.
Список использованных источников
- Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов — Москва: Высшая школа, 1996. — 623 с.
- Иванова, С.Г. Теоретические основы электротехники: Версия 1.0 [Электронный ресурс] : учеб. пособие / С. Г. Иванова, В. В. Новиков – Красноярск: ИПК СФУ, 2008. — 318 с.
- Википедия — Удельное электрическое сопротивление [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление
- Википедия — Плотность тока [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Плотность_тока
Формула связи между ЭДС (электродвижущей силой) и напряжением.
В задачах на электрический ток в качестве дано или найти присутствуют напряжение и ЭДС (электродвижущая сила). Есть достаточно простая связь между этими параметрами. Введём любую цепь (рис. 1).
Рис. 1. Связь между ЭДС и напряжением
Пусть дан источник с ЭДС
, напряжение во внешней цепи . Внутреннее сопротивление источника — , а сопротивление внешней цепи — . В данной системе течёт электрический ток . Тогда: (1) (2)Логично предположить, что количество электронов, сгенерированных источником, равно количеству электронов, ушедших в цепь, тогда приравниваем (1) и (2):
Откуда:
(3)Соотношение (3) — связь между ЭДС и напряжением в полной цепи постоянного тока.
В условиях идеальной цепи (внутреннее сопротивление источника равно нулю
), ЭДС численно равно напряжению.Вывод: приведенные соотношения помогают в ряде задач, в которых даны параметры источника тока/напряжения, а необходимо найти силу тока или напряжения на каком-либо элементе цепи (резистор, катушка, лампа и т.д.), и наоборот.
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
| Электродвижущая сила. | |
Роль источника тока: разделить заряды за счет совершения работы сторонними силами. Любые силы, действующие на заряд, за исключением потенциальных сил электростатического происхождения (т. е. кулоновских) называютсторонними силами. (Сторонние силы объясняются электромагнитным взаимодействием между электронами и ядрами) |
|
ЭДС — энергетическая характеристика источника. Это физическая величина, равная отношению работы, совершенной сторонними силами при перемещении электрического заряда по замкнутой цепи, к этому заряду: Измеряется в вольтах (В). |
|
Еще одна характеристика источника — внутреннее сопротивление источника тока: r. |
|
Закон Ома для полной цепи. | |
Энергетические преобразования в цепи:
(А — работа сторонних сил; Авнеш.— работа тока на внешнем участке цепи сопротивлением R; Авнутр.— работа тока на внутреннем сопротивлении источникаr.) |
|
|
|
Закон Ома: Сила тока в цепи постоянного тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению электрической цепи. |
|
Следствия: |
|
1. Если R>>r, то ε=U. Измеряют e высокоомным вольтметром при разомкнутой внешней цепи. |
|
2.Если R<<r, то ток | e= U1+U2 |
3. На внутреннем участке цепи: Aвнутр=U1q , на внешнем участке цепи: Aвнеш=U2q. A=Aвнутр+ Aвнеш. Тогда: εq=U1q+U2q. Следовательно: ε= U1+U2 ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем участках цепи. |
|
4. Если R растет, то I уменьшается. |
|
5. Мощность: а) Полная.. б) Полезная. в) Теряемая. г) КПД |
|
Соединение источников тока. | |
1. Последовательное соединение источников: полная ЭДС цепи равнаалгебраической сумме ЭДС отдельных источников, полное внутреннее сопротивление равно сумме внутренних сопротивлений всех источников тока. Если все источники одинаковы и включены в одном направлении, то Тогда з-н Ома запишется в виде: |
|
2. Параллельное соединение источников: один из источников (с наибольшейЭДС) работает как источник, остальные — как потребители (на этом принципе основана зарядка аккумулятора). Расчет по правилам Кирхгофа (см.). Если все источники одинаковы , то закон Ома запишется в виде:. |
|
Закон Ома для неоднородного участка цепи . | |
|
|
Правила Кирхгофа. | |
1. Алгебраическая сумма сил токов в каждом узле (точке разветвления) равна 0. |
|
2. В любом замкнутом контуре цепи алгебраическая сумма произведений сил токов в отдельных участках на их сопротивления равна алгебраической сумме ЭДС источников в этих контурах. |
|
Направление токов выбирают произвольно. Если после вычислений значение силы тока отрицательно, то направление противоположно. Замкнутый контур обходят в одном направлении. Если направление обхода совпадает с направлением тока, то IR>0. Если при обходе приходят к «+» источника, то его ЭДС отрицательна. В полученную систему уравнений должны входить все ЭДС и все сопротивления. Т.о. система должна состоять из одного уравнения для токов и k-1 — го уравнения для ЭДС (k — количество замкнутых контуров). |
|
схема, расчет, рисунок, как вычислить?
В разгар учебного года многим ученым деятелям требуется эдс формула для разных расчетов. Эксперименты, связанные с гальваническим элементом, так же нуждаются в информации об электродвижущей силе. Но для начинающих не так-то просто понять, что же это такое.
Формула нахождения эдс
Первым делом разберемся с определением. Что означает эта аббревиатура?
ЭДС или электродвижущая сила – это параметр характеризующий работу любых сил не электрической природы, работающих в цепях где сила тока как постоянного, так и переменного одинакова по всей длине. В сцепленном токопроводящем контуре ЭДС приравнивается работе данных сил по перемещению единого плюсового (положительного) заряда вдоль всего контура.
Ниже на рисунке представлена эдс формула.

Аст – означает работу сторонних сил в джоулях.
q – это переносимый заряд в кулонах.
Сторонние силы – это силы которые выполняют разделение зарядов в источнике и в итоге образуют на его полюсах разность потенциалов.
Для этой силы единицей измерения является вольт. Обозначается в формулах она буквой «E».
Только в момент отсутствия тока в батареи, электродвижущая си-а будет равна напряжению на полюсах.
ЭДС индукции:

ЭДС индукции в контуре, имеющем N витков:

При движении:

Электродвижущая сила индукции в контуре, крутящемся в магнитном поле со скоростью w:

Таблица значений

Простое объяснение электродвижущей силы
Предположим, что в нашей деревне имеется водонапорная башня. Она полностью наполнена водой. Будем думать, что это обычная батарейка. Башня — это батарейка!
Вся вода будет оказывать сильное давление на дно нашей башенки. Но сильным оно будет только тогда, когда это строение полностью наполнено H2O.
В итоге чем меньше воды, тем слабее будет давление и напор струи будет меньше. Открыв кран, заметим, что каждую минуту дальность струи будет сокращаться.
В результате этого:
- Напряжение – это сила с которой вода давит на дно. То есть давление.
- Нулевое напряжение — это дно башни.
С батареей все аналогично.
Первым делом подключаем источник с энергией в цепь. И соответственно замыкаем ее. Например, вставляем батарею в фонарик и включаем его. Изначально заметим, что устройство горит ярко. Через некоторое время его яркость заметно понизится. То есть электродвижущая сила уменьшилась (вытекла если сравнивать с водой в башне).
Если брать в пример водонапорную башню, то ЭДС это насос качающие воду в башню постоянно. И она там никогда не заканчивается.
Эдс гальванического элемента – формула
Электродвижущую силу батарейки можно вычислить двумя способами:
- Выполнить расчет с применением уравнения Нернста. Нужно будет рассчитать электродные потенциалы каждого электрода, входящего в ГЭ. Затем вычислить ЭДС по формуле .
- Посчитать ЭДС формуле Нернста для суммарной ток образующей реакции, протекающей при работе ГЭ.

Таким образом вооружившись данными формулами рассчитать электродвижущую силу батарейки будет проще.
Где используются разные виды ЭДС?
- Пьезоэлектрическая применяется при растяжении или сжатии материала. С помощью нее изготавливают кварцевые генераторы энергии и разные датчики.
- Химическая используется в гальванических элементах и аккумуляторах.
- Индукционная появляется в момент пересечения проводником магнитного поля. Ее свойства применяют в трансформаторах, электрических двигателях, генераторах.
- Термоэлектрическая образуется в момент нагрева контактов разнотипных металлов. Свое применение она нашла в холодильных установках и термопарах.
- Фото электрическая используется для продуцирования фотоэлементов.
Batareykaa.ru


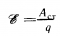
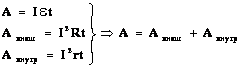 — закон сохранения энергии
— закон сохранения энергии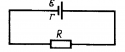
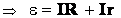
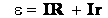
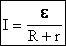

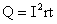 — возрастает
— возрастает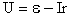 — при уменьшении силы тока в цепи напряжение увеличивается!
— при уменьшении силы тока в цепи напряжение увеличивается!
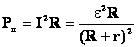 .
.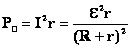 .
.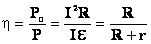 .
.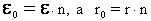 .
. 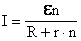
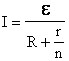
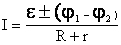 — знаки «+» или «-« выбираются в зависимости от того, в одну или в противоположные стороны направлены токи создаваемые источником ЭДС и электрическим полем.
— знаки «+» или «-« выбираются в зависимости от того, в одну или в противоположные стороны направлены токи создаваемые источником ЭДС и электрическим полем.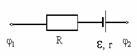
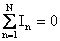 — следствие закона сохранения электрического заряда.
— следствие закона сохранения электрического заряда.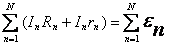 — следствие закона Ома для неоднородного участка цепи.
— следствие закона Ома для неоднородного участка цепи.