Мощности в цепях переменного тока

Расчетные формулы для цепей однофазного тока

1. Мгновенное значение мощности в цепи с активным сопротивлением r, Вт:

 

 

 

Среднее значение активной мощности в цепи с активным сопротивлением г, Вт:

2. Цепи с чисто индуктивным сопротивлением: ток в цепи i=Im sinωt, тогда ЭДС самоиндукции

 

т.е. ЭДС отстает от тока, ее вызвавшего, на угол

 

 

 

 

Падение напряжения на катушке

Мгновенная мощность катушки

Средняя за период мощность идеальной катушки:

 

Это означает, что в течение периода идеальная катушка дважды получает от источника энергию, преобразуя ее в магнитное поле, и дважды возвращает ее.

.

Емкостное сопротивление, Ом,

ействующее значение тока, А,

Мгновенная мощность

Средняя мощность

В течение периода конденсатор дважды получает от ис­точника энергию для заряда (создания электрического поля в диэлектрике) и дважды возвращает ее источнику (разряжа­ется).

Реактивная мощность конденсатора, вар,

Из изложенного следует важный для практики вывод:

токи индуктивности и емкости в цепи переменного тока в каждый момент времени направлены в противоположные стороны. Другими словами, в каждый момент времени, когда катушка получает от источника электромагнитную энергию, конденсатор возвращает ее источнику и наоборот.

4. Цепь, содержащая последовательно включенные

ак­тивное, индуктивное и емкостное сопротивления (рис. 1.9).

 

Реактивное сопротивление цепи, Ом,

Полное сопротивление цепи, Ом,

Угол сдвига фаз между векторами напряжения и тока

Коэффициент мощности цепи

Мгновенное значение приложенного напряжения равно сум­ме мгновенных значений падений напряжений на участках цепи:

Мгновенное значение мощности для этой цепи, Вт,

Среднее значение мощности равно активной мощности, Вт:

 

Реактивная мощность, вар,

Полная мощность, В-А,

При xL = xc имеет место резонанс напряжения, цепь ведет себя как чисто активная, а ток имеет наибольшее (при U = const) значение.

 

5. Цепь, содержащая параллельно включенные активное, индуктивное и емкостное сопротивления (рис. 1.10).

В такой цепи все элементы находятся под одинаковым напряжением источника

Проводимости элементов цепи:

активная, См,

емкостная,См, 

индуктивная, См,

 

Угол сдвига фаз тока и напряжения

Токи в ветвях

Полная проводимость цепи, содержащей элементы R, L, С, См:

Значения мощностей рассчитываются по приведенным выше формулам.

При вс= Bl имеет место резонанс токов. Общий ток в цепи имеет минимальное значение и активный характер.

На практике параллельное включение конденсаторов в однофазной и трехфазной цепях широко используется для разгрузки питающих линий (проводов, кабелей, шин) от реактивной (индуктивной) составляющей тока. Это позволяет уменьшить потери электроэнергии в передающих линиях, и тем самым экономить ее, выбирать меньшие сечения про­водов и кабелей для питания тех же самых электроприем­ников.

← Предыдущая | Следующая →
… содержание …

§57. Мощность переменного тока и коэффициент мощности

Мгновенное значение мощности. В цепи, содержащей активное, индуктивное и емкостное сопротивления, в которой ток I и напряжение u в общем случае сдвинуты по фазе на некоторый угол ?, мгновенное значение мощности р равно произведению мгновенных значений силы тока i и напряжения u. Кривую мгновенной мощности р можно получить перемножением мгновенных значений тока i и напряжения u при различных углах ?t (рис. 199, а. Из этого рисунка видно, что в некоторые моменты времени, когда ток и напряжение направлены навстречу друг другу, мощность имеет отрицательное значение. Возникновение в электрической цепи отрицательных значений мощности является вредным. Это означает, что в такие периоды времени приемник возвращает часть полученной электроэнергии обратно источнику; в результате уменьшается мощность, передаваемая от источника к приемнику. Очевидно, что чем больше угол сдвига фаз ?, тем больше время, в течение которого часть электроэнергии возвращается обратно к источнику, и тем больше возвращаемая обратно энергия и мощность.

Активная и реактивная мощности. Мгновенная мощность может быть представлена в виде суммы двух составляющих 1 и 2 (рис. 199,б). Составляющая 1 соответствует изменению мощности в цепи с активным сопротивлением (см. рис. 175,б).

Среднее ее значение, которое называют активной мощностью,

P = UI cos ? (75)

Она представляет собой среднюю мощность, которая поступает от источника к электрическим установкам при переменном токе.

Составляющая 2 изменяется подобно изменению мощности в цепи с реактивным сопротивлением (индуктивным или емкостным, см. рис. 179, а и б). Среднее ее значение равно нулю, поэтому для оценки этой составляющей пользуются ее амплитудным значением, которое называют реактивной мощностью:

Q = UI sin ? (76)

Рассматривая кривые мощности (см. рис. 199,б), можно установить, что только активная мощность может обеспечить преобразование в приемнике электрической энергии в другие виды энергии. Эта мощность в течение всего периода имеет положительный знак, т. е. соответствующая ей электрическая энергия 2, называемая активной, непрерывно переходит от источника 1 к приемнику 4 (рис. 200, а). Реактивная мощность никакой полезной работы создать не может, так как среднее значение ее в течение одного периода равно нулю. Как видно из рис. 199,б, эта мощность становится то положительной, то отрицательной, т. е. соответствующая ей электрическая энергия ,3, называемая реактивной,

Рис. 199. Зависимость мгновенной мощности р (а) и ее составляющих (б) от угла ?t

Рис. 200. Диаграмма, иллюстрирующая передачу электрической энергии между источником и приемником, содержащим активное и реактивное сопротивления, при отсутствии компенсатора (а) и при наличии его (б): 1 — источник; 2,3 — условные изображения активной и реактивной энергии; 4 — приемник; 5 — компенсатор

непрерывно циркулирует по электрической цепи от источника электрической энергии 1 к приемнику 4 и обратно (см. рис. 200, а).

Возникновение реактивной мощности в цепи переменного тока возможно только при включении в эту цепь накопителей энергии, таких как катушка индуктивности или конденсатор. В первом случае электрическая энергия, поступающая от источника, накапливается в электромагнитном поле катушки индуктивности, а затем отдается обратно; во втором случае она накапливается в электрическом поле конденсатора, а затем возвращается обратно к источнику. Постоянная циркуляция реактивной мощности от источника к приемникам загружает генераторы переменного тока и электрические сети реактивными токами, не создающими полезной работы, и тем самым не дает возможности использовать их по прямому назначению для выработки и передачи потребителям активной мощности. Поэтому в производственных условиях стараются по возможности уменьшить реактивную мощность, потребляемую электрическими установками.

Полная мощность. Источники электрической энергии переменного тока (генераторы и трансформаторы) рассчитаны на определенный номинальный ток I_ном и определенное номинальное напряжение U_ном, которые зависят от конструкции машины, размеров ее основных частей и пр. Увеличить значительно номинальный ток или номинальное напряжение нельзя, так как это может привести к недопустимому нагреву обмоток машины или пробою их изоляции. Поэтому каждый генератор или трансформатор может длительно отдавать без опасности аварии только вполне определенную мощность, равную произведению его номинального тока на номинальное напряжение. Произведение действующих значений тока и напряжения называется полной мощностью,

S = UI

Следовательно, полная мощность представляет собой наибольшее значение активной мощности при заданных значениях тока и напряжения. Она характеризует ту наибольшую мощность, которую можно получить от источника переменного тока при условии, что между проходящим по нему током и напряжением отсутствует сдвиг фаз. Полную мощность измеряют в вольт-амперах (В*А) или киловольт-амперах (кВ*А).

Связь между мощностями Р, Q и S можно определить из векторной диаграммы напряжений (рис. 201, а). Если умножить на ток I все стороны треугольника ABC, то получим треугольник мощностей А’В’С’ (рис. 201,б), стороны которого равны Р, Q и S. Из треугольника мощностей имеем:

S = ?(P² + Q²)

Из этого выражения следует, что при заданной полной мощности S (т. е. напряжении U и токе I) чем больше реактивная мощность Q, которая проходит через генератор переменного тока или трансформатор, тем меньше активная мощность Р, которую он может отдать приемнику. Иными словами, реактивная мощность не позволяет полностью использовать всю расчетную мощность источников переменного тока для выработки полезно используемой электрической энергии. То же самое относится и к электрическим сетям. Ток I = ?(I_a²+I_p²), который можно безопасно пропускать по данной электрической сети, определяется, главным образом, поперечным сечением ее проводов. Поэтому если часть I_р проходящего по сети тока (см. рис. 194,б) идет на создание реактивной мощности, то должен быть уменьшен активный ток I_а, обеспечивающий создание активной мощности, которую можно пропустить по данной сети.

Рис. 201. Векторная диаграмма напряжений (а) и треугольник мощностей (б) для цепи переменного тока

Если задана активная мощность Р, то при увеличении реактивной мощности Q возрастут реактивный ток I_р и общий ток I, проходящий по проводам генераторов переменного тока, трансформаторов, электрических сетей и приемников электрической энергии. При этом увеличиваются и потери мощности ?Р = I²R_пp в активном сопротивлении R_пp этих проводов.

Таким образом, бесполезная циркуляция электрической энергии между источником переменного тока и приемником, обусловленная наличием в нем реактивных сопротивлений, требует также затраты определенного количества энергии, которая теряется в проводах всей электрической цепи.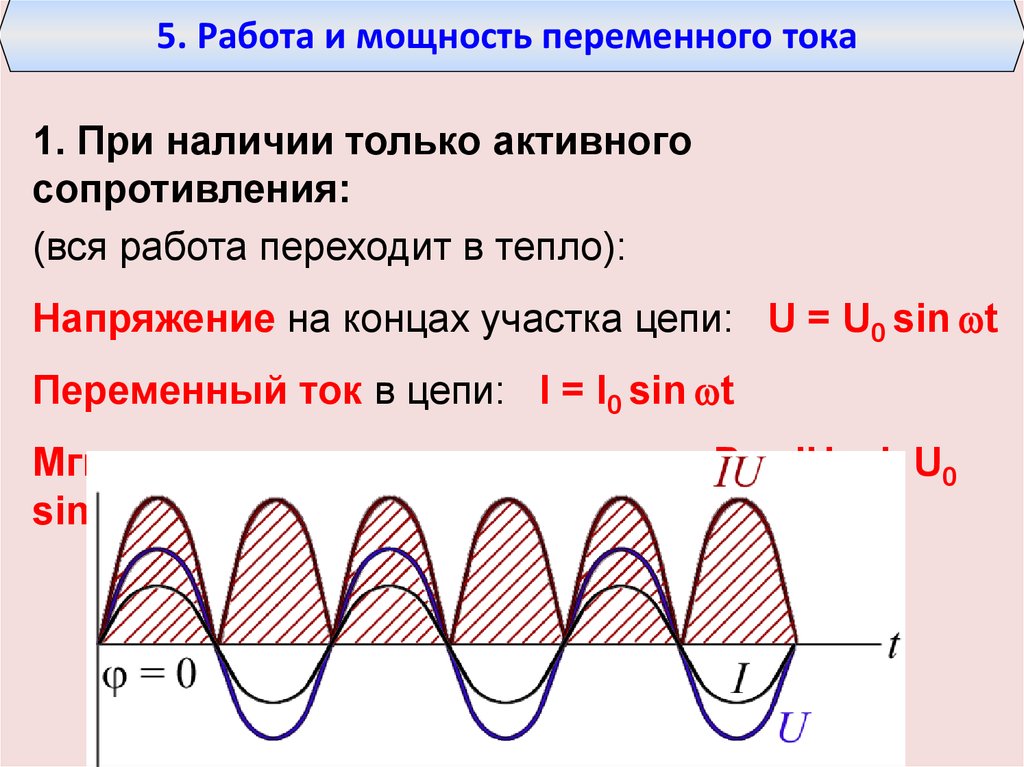

Коэффициент мощности. Из формулы (75) следует, что активная мощность Р зависит не только от тока I и напряжения U, но и от величины cos?, называемой коэффициентом мощности:

cos ? = P/(UI) = P/S = P/?(P² + Q²)

По значению cos ? можно судить, как использует мощность источника данный приемник или электрическая цепь. Чем больше cos ?, тем меньше sin ?, следовательно, согласно формулам (75) и (76) при заданных U и I, т. е. S, тем больше активная и меньше реактивная мощности, отдаваемые источником. При повышении cos ? и постоянной активной мощности Р, поступающей в приемник, уменьшается ток в цепи I = P/(U cos ?). При этом уменьшаются потери мощности ?P = I²R_пp в проводах и обеспечивается возможность дополнительной загрузки источника и электрической сети, т. е. лучшего их использования. Если приемник питается от источника при неизменном токе нагрузки, то повышение cos ? ведет к возрастанию активной мощности Р, используемой приемником. При cos?=1 реактивная мощность равна нулю, и вся мощность, отдаваемая источником, является активной. Поэтому на всех предприятиях и во всех отраслях народного хозяйства стремятся всемерно повышать коэффициент мощности и доводить его по возможности до единицы.

Значения коэффициента мощности электрических установок переменного тока различны. Электрические лампы обладают, главным образом, активным сопротивлением, поэтому при их включении сдвиг фаз между током и напряжением практически отсутствует. Следовательно, для осветительной нагрузки коэффициент мощности можно считать равным единице. Коэффициент мощности для двигателей переменного тока зависит от нагрузки. При номинальной расчетной нагрузке двигателя cos? = 0,8-0,9, а у крупных двигателей даже выше. При недогрузке двигателей коэффициент мощности их резко снижается (при холостом ходе cos ? = 0,25-0,3).

Повышение коэффициента мощности. Cos ? повышают различными способами. Основной из них — включение параллельно приемникам электрической энергии специальных устройств, называемых компенсаторами. В качестве последних чаще всего используют батареи конденсаторов (статические компенсаторы), но могут быть применены также и синхронные электрические машины (вращающиеся компенсаторы).

Способ повышения cos ? с помощью статического компенсатора (рис. 202, а) называют компенсацией сдвига фаз, или компенсацией реактивной мощности. При отсутствии компенсатора от источника к приемнику, содержащему активное и индуктивное сопротивления, поступает ток i₁ который отстает от напряжения и на некоторый угол сдвига фаз ?₁. При включении компенсатора Х_с по нему проходит ток i_c, опережающий напряжение и на 90°. Как видно из векторной диаграммы (рис. 202,б), при этом в цепи источника будет проходить ток i<i₁ и угол сдвига фаз его ? относительно напряжения также будет меньше ?₁.

Для полной компенсации угла сдвига фаз ?, т. е. для получения cos ? =1 и минимального значения тока I_min, необходимо, чтобы ток компенсатора I_с был равен реактивной составляющей I_1p = I₁ sin ?₁ тока I₁.
При включении компенсатора 5 (см. рис. 200,б) источник 1 и электрическая сеть разгружаются от реактивной энергии 3, так как она циркулирует уже по цепи «приемник — компенсатор». Благодаря этому достигаются существенное повышение использования генераторов переменного тока и электрических сетей и уменьшение потерь энергии, возникающих при бесполезной циркуляции реактивной энергии между источником 1 и приемником 4. Компен-

Рис. 202. Схема, иллюстрирующая способ повышения cos ? с помощью компенсатора (а), и векторная диаграмма (б)

сатор в этом случае выполняет роль генератора реактивной энергии, так как токи I_св конденсаторе и I_1р в катушке индуктивности (см, рис. 202,б) направлены навстречу один другому (первый опережает по фазе напряжение на 90°, второй отстает от него на 90°), вследствие чего включение компенсатора уменьшает общий реактивный ток I_р и сдвиг фаз между током I и напряжением U. При надлежащем подборе реактивной мощности компенсатора можно добиться, что вся реактивная энергия 3 (см. рис. 200,б), поступающая в приемник 4, будет циркулировать внутри контура «приемник — компенсатор», а генератор и сеть не будут участвовать в ее передаче. При этих условиях от источника 1 к приемнику 4 будет передаваться только активная мощность 2, т. е. cos ? будет равен единице.

В большинстве случаев по экономическим соображениям в электрических установках осуществляют неполную компенсацию угла сдвига фаз и ограничиваются значением cos ? = 0,95.

Переменный ток, мощность переменного тока

В свое время Эдисон и Тесла были противниками в вопросе использования электрического тока в энергетике. Тесла считал, что необходимо использовать переменный ток, а Эдисон – что нужно применять постоянный ток. У второго ученого было больше возможностей, так как он занимался бизнесом, однако Тесла в конечном итоге удалось победить, так как он был попросту прав.

Вступление

Переменный ток значительно эффективнее использовать для передачи энергии. Обсудим, как вычисляется мощность переменного тока, ведь переменный ток — это мощность, которая передается на расстоянии.

Вычисление мощности

Допустим, у нас имеется генератор переменного напряжения, который подключен к нагрузке. На выходе генератора, между двумя точками на клеммах, напряжение меняется по гармоническому закону, а нагрузка взята произвольная: катушки, активное сопротивление, конденсаторы, электромотор.

В цепи нагрузки течет ток, который меняется по гармоническому закону. Наша задача – установить, чему равна мощность потребляемой нагрузки от генератора. В распоряжении имеем генератор. В качестве исходных данных представлено направление на входе, которое будет меняться по гармоничному правилу:

(U(t) = U(m) cos w t)

Нагрузка – самое произвольное понятие.

Сила тока в нагрузке и, соответственно, в проводах, которые подводят мощность к нагрузке, будет меняться. Частота колебаний тока выйдет такая же, как частота колебаний напряжения, но существует также понятие сдвига фазы в промежутках колебаний тока и напряжения:

(I (t) = I (m) cos w t)

Дальнейшие вычисления

Показатели мощность будут равны произведению:

P (t) = I (t) U (t)

Этот закон остаётся справедливым как для переменного тока с мощностью, которую необходимо было вычислить, так и для постоянного.

(I (t) = I (m) cos (wt + J)

Мощность переменного тока при переменном токе вычисляется при помощи трех формул. Представленные выше расчеты относятся к основной формуле, которая вытекает из определения силы тока и напряжения.

Если участок цепи однородный и можно пользоваться законом Ома для этого участка цепи, здесь такие вычисления использовать нельзя, так как нам неизвестен характер нагрузки.

Определяем результат

Подставим показатели силы тока и напряжения в данную формулу, и тут нам на помощь придет знание тригонометрических формул:

cosa cosb = cos(a +b) + cos(a — b) / 2

Воспользуемся этой формулой и получим вычисления:

P(t) = I(m) U (m) cos (wt + J) cos wt

После упрощения результатов получим:

P(t) = I(m) U (m)/2 cos (wt + J) + I(m) U (m) cosJ

Посмотрим на эту формулу. Здесь первое слагаемое зависит от времени, меняясь по гармоническому закону, а второе является величиной постоянной. Мощность переменного тока при переменном токе складывается из постоянной и переменной составляющей.

Если мощность положительна, значит, нагрузка потребляет энергию от генератора. При отрицательной мощности, наоборот, нагрузка раскручивает генератор.

Найдем среднее значение мощности за период времени. Для этого работу, совершенную электрическим током, поделим на величину этого периода.

Мощность трехфазной цепи переменного тока– это сумма переменной и постоянной составляющих.

Активная и реактивная мощность

Многие физические процессы можно представить аналогиями друг друга. На этой базе постараемся раскрыть суть понятий активной мощности цепи переменного тока и реактивной мощности цепи переменного тока.

Стакан представляет собой электростанцию, вода – электроэнергию, трубочка – кабель или провод. Чем выше поднимается стакан, тем больше напряжение или давление.

Параметры мощности в сети переменного тока активного или реактивного типа зависят от тех элементов, которые потребляют такую энергию. Активная – энергия индуктивности и ёмкости.

Покажем это на конденсаторе, ёмкости и стакане. Активными называются те элементы, которые способны преобразовывать энергию в другой вид. К примеру, в тепло (утюг), свет (лампочка), движение (мотор).

Реактивная энергия

При имитации реактивной энергии напряжение увеличивается, и ёмкость заполняется. При уменьшении напряжения накопленная энергия возвращается по проводу обратно в электростанцию. Так повторяется циклически.

Сам смысл реактивных элементов заключается в накоплении энергии, которая потом обратно возвращается или используется для других функций. Но никуда не тратится. Основной минус этой производной в том, что виртуальный трубопровод, по которому как-бы идет энергия, имеет сопротивление, и на нем тратится процент экономии.

Полной мощности цепи переменного тока требуются затраты определенного процента усилий. По этой причине на крупных предприятиях идет борьба с реактивной составляющей полной мощности.

Активная мощность – это та энергия, которая потребляется или преобразуется в другие виды – свет, тепло, движение, то есть в какую-либо работу.

Опыт

Для опыта возьмем стакан, которые служит активной составляющей мощности. Он представляет часть энергии, которую необходимо потребить или преобразовать в другой вид.

Часть энергии воды можно выпить. Полная мощность переменного тока коэффициент мощности — это показатель, который складывается из реактивной и активной составляющих: энергии, текущей по водопроводу и той, которая преобразуется.

Как выглядит полная мощность в нашей аналогии? Часть воды выпиваем, а оставшаяся будет продолжать бежать по трубке. Так как у нас есть реактивный ёмкостной элемент – конденсатор или ёмкость, воду опускаем и начинаем имитировать увеличение и уменьшение напряжения. При этом видно, как вода перетекает в двух направлениях. Следовательно, в этом процессе применяется и активная, и реактивная составляющая. Вместе это – полная мощность.

Преобразование мощности

Активная мощность преобразовывается в другой вид энергии, к примеру, в механическое движение или нагрев. Реактивная мощность, которая накапливается в реактивном элементе, позднее возвращается назад.

Полная мощность – это геометрическая сумма активной и реактивной мощности.

Для произведения вычислений используем тригонометрические функции. Физический смысл расчетов такой. Возьмем прямоугольный треугольник, в котором одна из сторон равна 90 градусов. Одна из сторон – это его гипотенуза. Есть прилежащий и противолежащий относительно прямого угла катеты.

Косинус представлен отношением, которое предопределяет длина прилегающего катета относительно длины гипотенузы.

Синусом угла является вид отношения, которое составляет длина противолежащего катета относительно гипотенузы. Зная угол и длину любой из сторон, можно вычислить все остальные углы и длину.

В данном треугольнике можно взять длину гипотенузы и прилежащего катета и вычислить этот угол с помощью тригонометрической функции косинусов. Мощность постоянного и переменного тока вычисляется с применением таких знаний.

Для вычисления угла можно применять обратную функцию от косинуса. Получим необходимый результат вычислений. Чтобы вычислить длину противолежащего катета, можно вычислить синус и получить соотношение противолежащего катета к гипотенузе.

Вычисление мощности цепи переменного тока по формуле предложено в этом описании.

В цепях постоянного тока мощность равна произведению напряжения на ток. В цепях переменного тока также работает это правило, но его трактовка будет не совсем правильной.

Индуктивность

Помимо активных элементов, действуют реактивные элементы – индуктивность и ёмкость. В цепях постоянного тока, где амплитудное значение напряжения токов не меняется во времени, работа данного сопротивления будет происходить только во времени. Индуктивность и ёмкость могут негативным образом влиять на сеть.

Активная мощность, которую имеет трехфазная цепь переменного тока, может выполнять полезную работу, а реактивная не выполняет никакой полезной работы, а только расходуется на преодоление реактивных сопротивлений индуктивности и ёмкости.

Попытаемся выполнить опыт. Возьмем источник переменного напряжения на 220 Вт с частотой 50Гц, датчик напряжения и тока источника, нагрузка, которая составляет активное 1Ом и индуктивное 1ОМ сопротивление.

Также есть выключатель, который подключится в определенный момент, активно-ёмкостная нагрузка. Запустим такую систему. Для удобства рассмотрения введем коэффициенты поправки напряжения.

Запускаем устройство

При запуске устройства видно, что напряжение и ток сети не совпадают по фазе. Наблюдается переход через 0, при котором существует угол – коэффициент мощности сети. Чем меньше этот угол, тем выше коэффициент мощности, который указывается на всех устройствах переменного тока, к примеру, электрических машинах или сварочных трансформаторах.

Угол зависит от величины индуктивного сопротивления нагрузки. Когда сдвиг уменьшается, увеличивается ток сети. Представим, что сопротивление катушки уменьшить нельзя, но надо улучшить косинус сети. Для этого и нужны конденсаторы, которые, в отличие от индуктивности, опережают напряжение и могут взаимно компенсировать реактивную мощность.

В момент подключения конденсаторной батареи за 0,05 с происходит резкое снижение косинуса, практически до 0. Также идет резкое снижение тока, который без конденсаторной батареи имел амплитудное значение намного ниже, чем при включении конденсаторной батареи.

Фактически подключением конденсаторной батареи удалось снизить мощность тока, потребляемого из сети. Это является положительным моментом и позволяет снижать ток сети и экономить на сечение кабелей, трансформаторах, силовом оборудовании.

Если произойдет отключение индуктивной нагрузки и останется активное сопротивление, произойдет процесс, когда косинус сети после подключения конденсаторной батареи приведет к фазовому сдвигу и большому скачку тока, который идёт в сеть, а не потребляется из неё, что происходит в генераторном режиме реактивной мощности.

Итоги

Активная мощность опять остается постоянной и равна нулю, так как нет индуктивного сопротивления. Начался процесс генерации реактивной мощности в сеть.

Следовательно, компенсировать реактивную мощность на крупных предприятий, потребляемых колоссальные её объёмы из энергосистем, — это приоритетная задача, так как это позволяет экономить не только на электрооборудовании, но и на затратах по оплате самой реактивной мощности.

Такое понятие регламентируется, и предприятие оплачивает и потребляемую, и генерируемую мощность. Здесь устанавливаются автоматические компенсаторы, обеспечивающие поддержку баланса мощности на заданном уровне.

При отключении мощной нагрузки, если не выключить из сети компенсирующее устройство, будет происходить генерация реактивной мощности в сеть, что создаст проблемы в энергосистеме.

В быту компенсация реактивной мощности не имеет смысла, так как потребление мощности здесь значительно ниже.

Активная и реактивная мощность – понятия школьного курса физики.

Реальная, реактивная и активная мощность — интеллектуальные сети

Цепь пост. . Единицами мощности постоянного тока являются ватты [названы в честь Джеймса Ватта (1736-1819)].

Мощность постоянного тока можно рассматривать как мощность, потребляемую резистором.

Цепь переменного тока
В цепи переменного тока питание становится намного сложнее. В США мощность переменного тока вырабатывается по стандарту 60 Гц, 120 вольт. Гц означает количество циклов в секунду. Следовательно, 60 раз в секунду генерируется синусоидальная волна с пиковой амплитудой приблизительно 170 вольт. Эта циклическая синусоида переменного тока может создавать три типа мощности: 1) активная мощность, 2) реактивная мощность и 3) полная мощность.

1.  Реальная, активная или средняя мощность — это мощность, потребляемая резистором. Обозначается буквой «П». Как и в цепях постоянного тока, реальная мощность измеряется в ваттах. Для расчета активной мощности можно использовать только две формулы мощности:
   P = I ² R или P = V ² /R.
   Примеры 
   #1    Рассчитайте мощность, потребляемую резистором 1 кОм, через который протекает ток 5 мА.
   P = I ² R = (5 мА) ² *1 кОм = 25 мВт
   #2 Рассчитайте мощность, потребляемую резистором 1 кОм при падении напряжения на нем 15 В.
   P = V ² /R = (15 В) ² /1 кОм = 225 мВт
   Примерами электрических устройств, которые потребляют только реальную мощность, являются электрические плиты, фены, электрические водонагреватели и тостеры.
2. Реактивная мощность — это мощность, потребляемая катушками индуктивности и конденсаторами. Обозначается буквой «Q». Реактивная мощность измеряется в варах (реактивных вольтамперах). Следовательно, в катушках индуктивности и конденсаторах сохраняется и высвобождается в 60 раз больше энергии, чем в секунду. Индуктивное сопротивление чистых катушек индуктивности +jX _л . Это означает, что индуктор на +90 градусов не совпадает по фазе с резистором (который находится на 0 градусов). Емкостное сопротивление чистого конденсатора -jX _C . Это означает, что конденсатор на -90 градусов не совпадает по фазе с резистором (который находится на 0 градусов). Чистое реактивное сопротивление в цепи равно X = +jX _L -jX _C . Следовательно, реактивное сопротивление всегда будет либо чистым емкостным, либо чистым индуктивным. Для расчета реактивной мощности можно использовать только две формулы мощности:
   Q = I ² X или Q = V ² /X. Если чистое реактивное сопротивление индуктивное, Q положительное, а если чистое реактивное сопротивление емкостное, Q отрицательное.
   
   Примеры 
   #1    Рассчитайте мощность, потребляемую индуктивным сопротивлением 2 кОм при протекании через него тока 4 мА.
   Q = I ² R = (4 мА) ² *2 кОм = 32 мВАР
   #2 Рассчитайте мощность, потребляемую катушкой индуктивности 1 кОм при падении напряжения на ней 15 В.
   P = V ² /XL = (15v) ² /1 кОм = 225 мВАР
   Примерами электрических устройств, генерирующих некоторую реактивную мощность, являются микроволновые печи, стиральные машины, вентиляторы и кондиционеры.
3. Полная мощность представляет собой гипотенузу активной и реактивной мощности (см. рисунок ниже). Обозначается буквой «С». Полная мощность измеряется в ВА (Вольт-Ампер). Полная мощность полезна, поскольку она показывает общий ток, используемый комбинацией резистивных, индуктивных и емкостных компонентов. Полная мощность = V*I. S = sqrt(R ² + Q ² ).
   изображение автора
4. Коэффициент мощности
   Коэффициент мощности определяется как Fp = cos Θ. Где Θ — угол в треугольнике мощности, показанном выше (угол между кажущейся мощностью и реальной мощностью). Если Fp = 1 (единица), то реальная и кажущаяся мощности совпадают; следовательно, реактивная мощность будет равна нулю. В идеале коммунальные предприятия хотели бы, чтобы все потребители электроэнергии просто использовали только реальную мощность, чтобы коэффициент мощности оставался равным единице. Дома в среднем имеют коэффициент мощности 0,9.5, рестораны 0,88 и промышленное производство 0,77 (Кутитас 15).
   ПРИМЕРЫ
   Вот несколько примеров. В таблице ниже предполагается источник переменного тока 120 В и R _L = 5 Ом для всех катушек индуктивности.

   Значение	Общее сопротивление = RL + R	Импеданс прямоугольный	Текущий	Реальная мощность	Реактивная мощность	Полная мощность	Коэффициент мощности
   1 мкФ + 47 мГн f = 100 Гц	5 Ом	5 + j29 -j 1592 Ом = 5 -j1562 Ом	76,8 мА	29,5 мВт	-9,2 ВАР	9,2 ВА	приблизительно 0
   1 мкФ + 47 мГн f = 1 кГц	5 Ом	5 + j295 -j 159 Ом = 5 +j139 Ом	863 мА	3,74 Вт	+104 ВАР	104 ВА	приблизительно 0
   1 мкФ + 47 мГн f = 10 кГц	5 Ом	5 + j2953 -j 16 Ом = 5 +j2938 Ом	40,8 мА	8,3 мВт	+4,9 ВАР	4,9 ВА	приблизительно 0
   300 Ом + 47 мГн + 1 мкФ f = 100 Гц	305 Ом	305 + j29 -j 1592 Ом = 305 -j1562 Ом	75,4 мА	1,73 Вт	-8,88 ВАР	9,04 ВА	0,191
   300 Ом + 47 мГн + 1 мкФ f = 1 кГц	305 Ом	305 + j295 -j 159 Ом = 305 + j139 Ом	358 мА	39,1 Вт	+17,8 ВАР	43 ВА	0,909
   300 Ом + 47 мГн + 1 мкФ f = 10 кГц	305 Ом	305 + j2953 -j 16 Ом = 305 +j2938 Ом	40,63 мА	503 мВт	+4,84 ВАР	4,87 ВА	0,1
   3,3 кОм + 22 нФ + 470 мГн    f = 100 Гц	3305 Ом	3305 + j29 -j 1592 Ом = 3305 -j1562 Ом	32,83 мА	3,56 Вт	-1,68 ВАР	3,94 ВА	0,904
   3,3 кОм + 22 нФ + 470 мГн    f = 1 кГц	3305 Ом	3305 + j295 -j 159 Ом = 3305 +j139 Ом	36,3 мА	4,34 Вт	+183 мВАр	4,34 ВА	приблизительно 1
   3,3 кОм + 22 нФ + 470 мГн    f = 10 кГц	3305 Ом	3305 + j2953 -j 16 Ом = 3305 +j2938 Ом	27,13 мА	2,43 Вт	+2,16 ВАР	3,256 ВА	0,746

   Выполните прилагаемый рабочий лист https://kirkwood. pressbooks.pub/app/uploads/sites/13/2022/01/Real-Reactive-and-Apparent-Power-2.docx

    

   Процитированные работы
   Кутитас, Джордж и Стэн Макклеллан. Smart Grid как платформа для разработки приложений . Дом Артех, 2017.

Формула коэффициента мощности и полная мощность для цепей переменного тока – Wira Electrical

Коэффициент мощности – это отношение рабочей мощности.

Этот термин часто упоминается в электротехнической промышленности, но знаете ли вы, что он означает?

Сначала обязательно прочитайте, что такое цепь переменного тока.

Существует несколько типов мощности в цепи переменного тока:

1. Максимальная средняя передаваемая мощность
2. Среднеквадратичное значение напряжения и тока
3. Коэффициент мощности и полная мощность
4. Треугольник мощности и комплекс мощности
5. Сохранение мощности переменного тока
903 и Коэффициент мощности

Мы видели, что если напряжение и ток на клеммах цепи равны

(1)

or, in phasor form, V =  V _m ∠θ _v  and  I  =  I _m ∠θ _i , the average power is

(2)

. 0098 (4)

Средняя мощность является произведением двух членов. Произведение В _{действующее значение} I _{действующее значение} известно как полная мощность S .

Коэффициент cos(θ _v  – θ _i ) называется коэффициентом мощности (пФ).

Полная мощность (в ВА) является произведением среднеквадратичных значений напряжения и тока.

Полная мощность названа так потому, что кажется очевидным, что мощность должна быть произведением напряжения на ток по аналогии с резистивными цепями постоянного тока.

Измеряется в вольт-амперах или ВА, чтобы отличить ее от средней или реальной мощности, которая измеряется в ваттах.

Коэффициент мощности является безразмерным, поскольку он является соотношением средней мощности к кажущейся мощности,

(5)

IS _V – θ _{I I I I I I I I I I I I I I I I I I I I I I . называется углом коэффициента мощности , поскольку это угол, косинус которого является коэффициентом мощности.}

Угол коэффициента мощности равен импедансу нагрузки, если V — напряжение на нагрузке, а I — ток через нее. Это видно из того, что

(6)

Alternatively, since

(7a)

and

(7b)

Импеданс составляет

(8)

. Париф. Это также косинус угла импеданса нагрузки.

Из уравнения (5) коэффициент мощности можно рассматривать как коэффициент, на который необходимо умножить кажущуюся мощность, чтобы получить реальную или среднюю мощность.

Значение pf находится в диапазоне от нуля до единицы.

Для чисто резистивной нагрузки напряжение и ток совпадают по фазе, так что θ _v  – θ _i = 0 и pf = 1.

Это означает, что кажущаяся мощность равна средней мощности.

Для чисто реактивной нагрузки θ _v  – θ _i  = ± 90 ^o  и pf = 0. В этом случае средняя мощность равна нулю. Между этими двумя крайними случаями говорят, что pf опережает или отстает от .

Опережающий коэффициент мощности означает, что ток опережает напряжение, что подразумевает емкостную нагрузку.

Отстающий коэффициент мощности означает, что ток отстает от напряжения, что подразумевает наличие индуктивной нагрузки.

Коэффициент мощности влияет на счета за электроэнергию, которые потребители платят электроэнергетическим компаниям. Мы узнаем, как исправить коэффициент мощности, используя коррекцию коэффициента мощности.

См. также: последовательный резонансный контур

Примеры полной мощности и коэффициента мощности

Для лучшего понимания рассмотрим примеры ниже:
t + 10 ^o ) А при приложенном напряжении v(t) = 120 cos(100π t – 20 ^o ) В.

Найдите полную мощность и коэффициент мощности нагрузки. Определить номиналы элементов, образующих последовательно включенную нагрузку.

Решение:

Полная мощность равна

Коэффициент мощности равен

Коэффициент мощности опережает, поскольку ток опережает напряжение. Коэффициент мощности можно также получить из импеданса нагрузки.

Полное сопротивление нагрузки Z может быть смоделировано с помощью резистора 25,98 Ом, включенного последовательно с конденсатором

или

2. Определите коэффициент мощности всей цепи на рисунке (1) с точки зрения источника. Рассчитайте среднюю мощность, отдаваемую источником.

Рисунок 1

Решение:
Общее сопротивление —

. Коэффициент мощности

2

С. Среднеквадратичное значение тока равно

. Средняя мощность, подаваемая источником, равна

или

, где R — резистивная часть Z.

 

Мощность в цепи переменного тока — уравнение, коэффициент мощности и примеры решений0001

В зависимости от направления тока, протекающего по цепи, различают два типа. Один переменного тока, а другой постоянного тока. Когда электрический ток периодически меняет свое направление, протекая по электрической цепи, называется переменным током (AC). С другой стороны, когда ток течет только в одном направлении, это называется постоянным током (DC).

Основное преимущество переменного тока заключается в том, что напряжение переменного тока можно легко преобразовать с более высокого на более низкое напряжение и наоборот. Благодаря этому достоинству, мощность высокого напряжения от электростанций может быть снижена до более безопасного напряжения для бытового использования. Только переменный ток совместим с конденсаторами и катушками индуктивности. Используя их в цепях переменного тока, можно повернуть поток электричества. Это свойство помогает настроить радиостанции. По этим причинам электричество переменного тока является наиболее предпочтительным для бытовой техники.

 

Мощность, потребляемая в цепи переменного тока

Электрическая цепь производит мощность, которая определяется выражением P= I В.

Где I – ток, протекающий по цепи, а

В – напряжение на ней.

Цепи переменного тока всегда имеют реактивное сопротивление, поэтому есть две составляющие мощности: силовая составляющая из-за магнитного поля и другая из-за электрического поля. Средняя мощность, поглощаемая цепью, становится суммой мощности, сохраненной и возвращенной за один полный цикл. Таким образом, средняя мощность, потребляемая схемой, будет равна мгновенной мощности за один цикл.

 

Коэффициент мощности

Коэффициент мощности = \[\frac{ \text {Истинная мощность}}{\text{Полная мощность}}\]

Кроме того, cosΦ = \[\frac{R}{Z}\ ]

R- сопротивление в цепи

Z- полное сопротивление в цепи.

Определение мощности в цепи переменного тока

Скорость выполнения работы или количество энергии, передаваемой цепью в единицу времени, называется мощностью в цепях переменного тока. Он используется для расчета общей мощности, необходимой для питания нагрузки. Коэффициент мощности: в цепи переменного тока коэффициент мощности (PF) определяется как отношение активной мощности (P) к полной мощности (S). PF может быть выражен в процентах или десятичной форме.

Значение мощности в цепи переменного тока 

Мощность в цепи переменного тока очень важна, поскольку она определяет количество тока, протекающего через цепь, и, следовательно, размер требуемого провода. На формы сигналов напряжения и тока также влияет коэффициент мощности. Низкий коэффициент мощности означает, что большое количество энергии тратится впустую в виде тепла из-за плохого использования электричества. Это может привести к перегреву и выходу из строя электрооборудования.

Значение коэффициента мощности

Коэффициент мощности очень важен, поскольку он определяет количество тока, протекающего по цепи, и, следовательно, размер требуемого провода. Этот фактор также влияет на формы сигналов напряжения и тока. Низкий коэффициент мощности означает, что большое количество энергии теряется в виде тепла из-за плохого использования электроэнергии, что может привести к перегреву и выходу из строя электрооборудования.

Вот несколько советов по изучению мощности в цепи переменного тока

1. Знание того, как решать простые проблемы с цепью переменного тока, поможет вам больше узнать о коэффициенте мощности и его применении в реальных жизненных ситуациях. Некоторые примеры включают определение реактивной мощности, общей мощности, тока и напряжения для заданного коэффициента мощности. Эти примеры могут помочь вам узнать больше о PF и его применении в реальных ситуациях. Вот несколько советов по изучению Power Factor:

2. Знать основы. Перед изучением коэффициента мощности важно знать основы цепи переменного тока. Таким образом, вы можете легко понять важность и применение коэффициента мощности. Решение простых проблем. Знание того, как решать простые проблемы с цепями переменного тока, поможет вам больше узнать о коэффициенте мощности и его применении в реальных ситуациях. Некоторые примеры включают определение реактивной мощности, общей мощности тока или напряжения для заданного коэффициента мощности. Учитесь по учебникам. Учебники содержат подробную информацию о формулах вместе с решенными примерами.

3. Практикуйте больше задач. Практика на множестве примеров является одним из наиболее эффективных способов изучения и понимания концепции коэффициента мощности, который поможет вам использовать коэффициент мощности в реальных задачах.