Физика u r i: Закон Ома — Википедия – Закон Ома. Формула Закона Ома — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Закон Ома. Формула Закона Ома

Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.

Георг Симон Ом

Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.

Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.

Формула закона Ома записывается в следующем виде:

где

I – сила тока в проводнике, единица измерения силы тока — ампер [А];

U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];

R – электрическое сопротивление проводника, единица измерения электрического сопротивления — ом [Ом].

Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза

И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.

Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:

Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.

Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.

Где и когда можно применять закон Ома?

Нужна помощь в написании работы?

Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.

Значение Закона Ома

Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.

Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.

Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.

Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:

Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

формулы и определения / Блог :: Бингоскул

Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.

Закон Ома для участка цепи:

Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=\frac{U}{R}
U — напряжение (в системе СИ измеряется — Вольт)
R — электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=\frac{U}{I}

Определение единицы сопротивления — Ом

1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1(Вольт) протекает ток 1 (Ампер).

Закон Ома для полной цепи

Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

Формула I=\frac{\varepsilon}{R+r}

\varepsilon — ЭДС источника напряжения, В;
I — сила тока в цепи, А;
R — сопротивление всех внешних элементов цепи, Ом;
r — внутреннее сопротивление источника напряжения, Ом.

Как запомнить формулы закона Ома

Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

U — электрическое напряжение;
I — сила тока;
P — электрическая мощность;
R — электрическое сопротивление

Смотри также:

Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.

Закон Джоуля-Ленца: определение, формула, применение

Мы ежедневно пользуемся электронагревательными приборами, не задумываясь, откуда берётся тепло. Разумеется, вы знаете, что тепловую энергию вырабатывает электричество. Но как это происходит, а тем более, как оценить количество выделяемого тепла, знают не все. На данный вопрос отвечает закон Джоуля-Ленца, обнародованный в позапрошлом столетии.

В 1841 году усилия английского физика Джоуля, а в 1842 г. исследования русского учёного Ленца увенчались открытием закона, применение которого позволяет количественно оценить результаты теплового действия электрического тока [ 1 ]. С тех пор изобретено множество приборов, в основе которых лежит тепловое действие тока. Некоторые из них, изображены на рис. 1.

Определение и формула

Тепловой закон можно сформулировать и записать в следующей редакции: «Количество тепла, выработанного током, прямо пропорционально квадрату приложенного к данному участку цепи тока, сопротивления проводника и промежутка времени, в течение которого электричество действовало на проводник».

Обозначим символом Q количество выделяемого тепла, а символами I, R и Δt – силу тока, сопротивление и промежуток времени, соответственно. Тогда формула закона Джоуля-Ленца будет иметь вид: Q = I²*R*Δt

Согласно законам Ома I=U/R, откуда R = U/I. Подставляя выражения в формулу Джоуля-Ленца получим: Q = U²/R * Δt ⇒ Q = U*I*Δt.

Выведенные нами формулы – различные формы записи закона Джоуля-Ленца. Зная такие параметры как напряжение или силу тока, можно легко рассчитать количество тепла, выделяемого на участке цепи, обладающем сопротивлением R.

Дифференциальная форма

Чтобы перейти к дифференциальной форме закона, проанализируем утверждение Джоуля-Ленца применительно к электронной теории. Приращение энергии электрона ΔW за счёт работы электрических сил поля равно разности энергий электрона в конце пробега (m/2)*(u=υ_max)² и в начале пробега (mu²)/2 , то есть

Здесь u – скорость хаотического движение (векторная величина), а υ_max– максимальная скорость электрического заряда в данный момент времени.

Поскольку установлено, что скорость хаотического движения с одинаковой вероятностью совпадает с максимальной (по направлению и в противоположном направлении), то выражение 2*u*υ_max в среднем равно нулю. Тогда полная энергия, выделяющаяся при столкновениях электронов с атомами, образующими узлы кристаллической решётки, составляет:

Это и есть закон Джоуля-Ленца, записанный в дифференциальной форме. Здесь γ – согласующий коэффициент, E – напряжённость поля.

Интегральная форма

Предположим, что проводник имеет цилиндрическую форму с сечением S. Пусть длина этого проводника составляет l. Тогда мощность P, выделяемая в объёме V= lS составляет:

гдеR – полное сопротивление проводника.

Учитывая, что

U = I×R,

P = U×I;
P = I²R;
P = U²/R.

Если величина тока со временем меняется, то количество теплоты вычисляется по формуле:

Данное выражение, а также вышеперечисленные формулы, которые можно переписать в таком же виде, принято называть интегральной формой закона Джоуля-Ленца.

Формулы очень удобны при вычислении мощности тока в нагревательных элементах. Если известно сопротивление такого элемента, то зная напряжение бытовой сети легко определить мощность прибора, например, электрочайника или паяльника.

Физический смысл

Вспомним, как электрический ток протекает по металлическому проводнику. Как только электрическая цепь замкнётся, то под действием ЭДС движение свободных электронов упорядочивается, и они устремляются к положительному полюсу источника питания. Однако на их пути встречаются стройные ряды кристаллических решёток, атомы которых создают препятствия упорядоченному движению, то есть оказывают сопротивление.

На преодоление сопротивления уходит часть энергии движущихся электронов. В соответствии с фундаментальным законом сохранения энергии, она не может бесследно исчезнуть. Она-то и превращается в тепло, вызывающее нагревание проводника. Накапливаемая тепловая энергия излучается в окружающее пространство или нагревает другие предметы, соприкасающиеся с проводником.

На рисунке 2 изображёна схема опыта, демонстрирующего закон теплового действия тока, разогревающего участок провода в электрической цепи.

Явление нагревания проводников было известно практически с момента получения электротока, но исследователи не могли тогда объяснить его природу, и тем более, предложить способ оценки количества выделяемого тепла. Эту проблему решает закон Джоуля-Ленца, которым мы пользуемся по сегодняшний день.

Практическая польза закона Джоуля-Ленца

При сильном нагревании можно наблюдать излучение видимого спектра света, что происходит, например, в лампочке накаливания. Слабо нагретые тела тоже излучают тепловую энергию, но в диапазоне инфракрасного излучения, которого мы не видим, но можем ощутить своими тепловыми рецепторами.

Допускать сильное нагревание проводников нельзя, так как чрезмерная температура разрушает структуру металла, проще говоря – плавит его. Это может привести к выводу из строя электрооборудования, а также стать причиной пожара. Для того, чтобы не допустить критических параметров нагревания необходимо делать расчёты тепловых элементов, пользуясь формулами, описывающими закон Джоуля-Ленца.

Проанализировав выражение U²/R убеждаемся, что когда сопротивление стремится к нулю, то количество выделенного тепла стремится к бесконечности. Такая ситуация возникает при коротких замыканиях. В это основная опасность КЗ.

В борьбе с короткими замыканиями используют:

автоматические выключатели:
электронные защитные блоки;
плавкие предохранители;
другие защитные устройства.

Применение и практический смысл

Непосредственное превращение электричества в тепловую энергию нельзя назвать экономически выгодным. Однако, с точки зрения удобства и доступности современного человечества к источникам электроэнергии различные нагревательные приборы продолжают массово применяться как в быту, так и на производстве.

Перечислим некоторые из них:

электрочайники;
утюги;
фены;
варочные плиты;
паяльники;
сварочные аппараты и многое другое.

На рисунке 3 изображены бытовые нагревательные приборы, которыми мы часто пользуемся.

Использование тепловых мощностей в химической, металлургической и в других промышленных отраслях тесно связно с использованием электрической энергии.

Без знания физического закона Джоуля-Ленца было бы невозможно сконструировать безопасный нагревательный прибор. Для этого нужны расчёты, которые невозможно сделать без применения рассмотренных нами формул. На основе расчётов происходит выбор материалов с нужным удельным сопротивлением, влияющим на нагревательную способность устройств.

Закон Джоуля-Ленца без преувеличения можно назвать гениальным. Это один из тех законов, которые повлияли на развитие электротехники.

10 формул по физике

Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“

Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.

Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.

В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.

Соотношения закона Ома

Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:

Искомая величина	Формула
Напряжение, В	U=I*R
Ток, А	I=U/R
Сопротивление, Ом	R=U/I
Мощность, Вт	P=U*I

В этой таблице используются следующие общепринятые обозначения физических величин:

U — напряжение (В),

I — ток (А),

Р — мощность (Вт),

R — сопротивление (Ом),

Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.

А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:

I = U / R

Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.

Что же в этой формуле есть что? Рассмотрим переменные подробнее.

> U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.

> I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.

> R: искомое сопротивление токоограничивающего резистора, в омах.

В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:

R = U/I = 8,5 В / 0,050 А= 170 Ом

Расчёты сопротивления

Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.

Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.

> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.

> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.

Расчет сопротивления последовательных резисторов

Формула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:

Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)

В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.

Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.

Расчет сопротивления параллельных резисторов

Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид:

R общ = R1 * R2 / (R1 + R2)

где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим

776,47 = 2640000 / 3400

Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:

Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина.

Расчёты ёмкости

Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.

Расчет емкости параллельных конденсаторов

Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:

Собщ = CI + С2 + СЗ + …

В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.

Расчет емкости последовательных конденсаторов

Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:

Собщ = С1 * С2 /( С1+С2)

где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи

Расчет емкости трех и более последовательно соединенных конденсаторов

В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:

И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина.

Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.

Расчёт энергетических уравнений

Наиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:

ватт-часы = Р х Т

В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.

Расчёт постоянной ёмкости RC-цепочки

В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).

Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.

Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.

T = RC

В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.

Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.

Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:

Значение емкости конденсатора, мкФ	Емкость конденсатора для расчета
10	0,000 01
1	0,000 001
0,1	0,000 000 1
0,01	0,000 000 01

Расчёты частоты и длины волны

Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.

Расчет частоты сигнала

Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны:

Частота = 300000 / длина волны

Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.

Расчет длины волны сигнала

Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:

Длина волны = 300000 / Частота

Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.

Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:

6000 миллиметров = 300000 / 50 МГц

Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!

Открытая Физика. Электрический ток. Закон Ома

Если изолированный проводник поместить в электрическое поле E→, то на свободные заряды q в проводнике будет действовать сила F→=qE→. В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю (см. § 1.5).

Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.

Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени Δt, к этому интервалу времени: I=ΔqΔt.

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.

В Международной системе единиц СИ сила тока измеряется в амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током (см. § 1.16).

Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю (см. § 1.4). Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.

Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.

При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.

Физическая величина, равная отношению работы A_ст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС): ЭДС=ℰ=Aстq.

Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.

Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными.

При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δφ₁₂ = φ₁ – φ₂ между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе ℰ₁₂, действующей на данном участке. Поэтому полная работа равна U₁₂ = φ₁ – φ₂ + ℰ₁₂.

Величину U₁₂ принято называть напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов: U₁₂ = φ₁ – φ₂.

Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника: I=1RU или RI=U, где R = const.

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.

Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме: IR = U₁₂ = φ₁ – φ₂ + ℰ = Δφ₁₂ + ℰ.

Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи.

На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.

По закону Ома IR = Δφ_cd.

Участок (ab) содержит источник тока с ЭДС, равной ℰ.

По закону Ома для неоднородного участка, Ir = Δφ_ab + ℰ.

Сложив оба равенства, получим: I (R + r) = Δφ_cd + Δφ_ab + ℰ.

Но Δφ_cd = Δφ_ba = – Δφ_ab. Поэтому I=ℰR+r.

Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.

Сопротивление r неоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 1.8.2 является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R << r), тогда в цепи потечет ток короткого замыкания Iкз=ℰr.

Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой ℰ и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.

В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику последовательно подсоединяется некоторое внешнее сопротивление. Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего сопротивления, и при коротком замыкании сила тока не окажется чрезмерно большой.

Если внешняя цепь разомкнута, то Δφ_ba = – Δφ_ab = ℰ, т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.

Если внешнее нагрузочное сопротивление R включено и через батарею протекает ток I, разность потенциалов на ее полюсах становится равной Δφ_ba = ℰ – Ir.

На рис. 1.8.3 дано схематическое изображение источника постоянного тока с ЭДС равной ℰ и внутренним сопротивлением r в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность E→ электрического поля внутри батареи и силы, действующие на положительные заряды: F→э – электрическая сила и F→ст – сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.

Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.

Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением R_B. Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1.8.4, это условие записывается в виде: R_B >> R₁. Это условие означает, что ток I_B = Δφ_cd / R_B, протекающий через вольтметр, много меньше тока I = Δφ_cd / R₁, который протекает по тестируемому участку цепи.

Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.

Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением R_A. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию R_A << (r + R₁ + R₂), чтобы при включении амперметра ток в цепи не изменялся.

Измерительные приборы – вольтметры и амперметры – бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений.

Формулы по физике для ЕГЭ и 7-11 класса

Рубрика: Подготовка к ЕГЭ по физике

Шпаргалка с формулами по физике для ЕГЭ

и не только (может понадобиться 7, 8, 9, 10 и 11 классам).

Для начала картинка, которую можно распечатать в компактном виде.

Механика

Давление Р=F/S
Плотность ρ=m/V
Давление на глубине жидкости P=ρ∙g∙h
Сила тяжести Fт=mg
5. Архимедова сила Fa=ρ_ж∙g∙Vт
Уравнение движения при равноускоренном движении

X=X₀+υ₀∙t+(a∙t²)/2 S= (υ²—υ₀²)^{/2а S= (υ+υ₀) ∙t /2}

Уравнение скорости при равноускоренном движении υ=υ₀+a∙t
Ускорение a=(υ—υ₀)/t
Скорость при движении по окружности υ=2πR/Т
Центростремительное ускорение a=υ²/R
Связь периода с частотой ν=1/T=ω/2π
II закон Ньютона F=ma
Закон Гука Fy=-kx
Закон Всемирного тяготения F=G∙M∙m/R²
Вес тела, движущегося с ускорением а↑ Р=m(g+a)
Вес тела, движущегося с ускорением а↓ Р=m(g-a)
Сила трения Fтр=µN
Импульс тела p=mυ
Импульс силы Ft=∆p
Момент силы M=F∙ℓ
Потенциальная энергия тела, поднятого над землей Eп=mgh
Потенциальная энергия упруго деформированного тела Eп=kx²/2
Кинетическая энергия тела Ek=mυ²/2
Работа A=F∙S∙cosα
Мощность N=A/t=F∙υ
Коэффициент полезного действия η=Aп/Аз
Период колебаний математического маятника T=2π√ℓ/g
Период колебаний пружинного маятника T=2 π √m/k
Уравнение гармонических колебаний Х=Хmax∙cos ωt
Связь длины волны, ее скорости и периода λ= υТ

Молекулярная физика и термодинамика

Количество вещества ν=N/ Na
Молярная масса М=m/ν
Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT
Основное уравнение МКТ P=nkT=1/3nm₀υ²
Закон Гей – Люссака (изобарный процесс) V/T =const
Закон Шарля (изохорный процесс) P/T =const
Относительная влажность φ=P/P₀∙100%
Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
Работа газа A=P∙ΔV
Закон Бойля – Мариотта (изотермический процесс) PV=const
Количество теплоты при нагревании Q=Cm(T₂-T₁)
Количество теплоты при плавлении Q=λm
Количество теплоты при парообразовании Q=Lm
Количество теплоты при сгорании топлива Q=qm
Уравнение состояния идеального газа PV=m/M∙RT
Первый закон термодинамики ΔU=A+Q
КПД тепловых двигателей η= (Q₁— Q₂)/ Q₁
КПД идеал. двигателей (цикл Карно) η= (Т₁— Т₂)/ Т₁

https://5-ege.ru/formuly-po-fizike-dlya-ege/

Электростатика и электродинамика – формулы по физике

Закон Кулона F=k∙q₁∙q₂/R²
Напряженность электрического поля E=F/q
Напряженность эл. поля точечного заряда E=k∙q/R²
Поверхностная плотность зарядов σ = q/S
Напряженность эл. поля бесконечной плоскости E=2πkσ
Диэлектрическая проницаемость ε=E₀/E
Потенциальная энергия взаимод. зарядов W= k∙q₁q₂/R
Потенциал φ=W/q
Потенциал точечного заряда φ=k∙q/R
Напряжение U=A/q
Для однородного электрического поля U=E∙d
Электроемкость C=q/U
Электроемкость плоского конденсатора C=S∙ε∙ε₀/d
Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
Сила тока I=q/t
Сопротивление проводника R=ρ∙ℓ/S
Закон Ома для участка цепи I=U/R
Законы послед. соединения I₁=I₂=I, U₁+U₂=U, R₁+R₂=R
Законы паралл. соед. U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R
Мощность электрического тока P=I∙U
Закон Джоуля-Ленца Q=I²Rt
Закон Ома для полной цепи I=ε/(R+r)
Ток короткого замыкания (R=0) I=ε/r
Вектор магнитной индукции B=Fmax/ℓ∙I
Сила Ампера Fa=IBℓsin α
Сила Лоренца Fл=Bqυsin α
Магнитный поток Ф=BSсos α Ф=LI
Закон электромагнитной индукции Ei=ΔФ/Δt
ЭДС индукции в движ проводнике Ei=Вℓυsinα
ЭДС самоиндукции Esi=-L∙ΔI/Δt
Энергия магнитного поля катушки Wм=LI²/2
Период колебаний кол. контура T=2π ∙√LC
Индуктивное сопротивление X_L=ωL=2πLν
Емкостное сопротивление Xc=1/ωC
Действующее значение силы тока Iд=Imax/√2,
Действующее значение напряжения Uд=Umax/√2
Полное сопротивление Z=√(Xc-X_L)²+R²

Оптика

Закон преломления света n₂₁=n₂/n₁= υ₁/ υ₂
Показатель преломления n₂₁=sin α/sin γ
Формула тонкой линзы 1/F=1/d + 1/f
Оптическая сила линзы D=1/F
max интерференции: Δd=kλ,
min интерференции: Δd=(2k+1)λ/2
Диф.решетка d∙sin φ=k λ

Квантовая физика

Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U_зе
Красная граница фотоэффекта ν_к = Aвых/h
Импульс фотона P=mc=h/ λ=Е/с

Физика атомного ядра

Закон радиоактивного распада N=N₀∙2^—^t^/^T
Энергия связи атомных ядер

E_CB=(Zm_p+Nm_n-Mя)∙c²

СТО

t=t₁/√1-υ²/c²
ℓ=ℓ₀∙√1-υ²/c²
υ₂=(υ₁+υ)/1+ υ₁∙υ/c²
Е = mс²

Скачать эти формулы в doc: formuly-po-fizike-5-ege.ru (файл расположен на 5-ege.ru).

Рекомендуем:

Формулы по физике для ЕГЭ

Источник: http://5-ege.ru/formuly-po-fizike-dlya-ege/

Шпаргалка с формулами по физике для ЕГЭ

Источник: http://5-ege.ru/formuly-po-fizike-dlya-ege/

и не только (может понадобиться 7, 8, 9, 10 и 11 классам).

Записаться на занятия к репетитору.

Для начала картинка, которую можно распечатать в компактном виде.

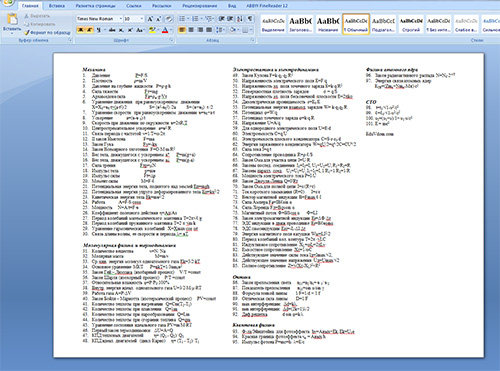
А потом вордовский файл, который содержит все формулы чтобы их распечатать, которые находятся внизу статьи.

Механика

Давление Р=F/S
Плотность ρ=m/V
Давление на глубине жидкости P=ρ∙g∙h
Сила тяжести Fт=mg
5. Архимедова сила Fa=ρ_ж∙g∙Vт
Уравнение движения при равноускоренном движении

X=X₀+υ₀∙t+(a∙t²)/2 S= (υ²—υ₀²)^{/2а S= (υ+υ₀) ∙t /2}

Уравнение скорости при равноускоренном движении υ=υ₀+a∙t
Ускорение a=(υ—υ₀)/t
Скорость при движении по окружности υ=2πR/Т
Центростремительное ускорение a=υ²/R
Связь периода с частотой ν=1/T=ω/2π
II закон Ньютона F=ma
Закон Гука Fy=-kx
Закон Всемирного тяготения F=G∙M∙m/R²
Вес тела, движущегося с ускорением а↑ Р=m(g+a)
Вес тела, движущегося с ускорением а↓ Р=m(g-a)
Сила трения Fтр=µN
Импульс тела p=mυ
Импульс силы Ft=∆p
Момент силы M=F∙ℓ
Потенциальная энергия тела, поднятого над землей Eп=mgh
Потенциальная энергия упруго деформированного тела Eп=kx²/2
Кинетическая энергия тела Ek=mυ²/2
Работа A=F∙S∙cosα
Мощность N=A/t=F∙υ
Коэффициент полезного действия η=Aп/Аз
Период колебаний математического маятника T=2π√ℓ/g
Период колебаний пружинного маятника T=2 π √m/k
Уравнение гармонических колебаний Х=Хmax∙cos ωt
Связь длины волны, ее скорости и периода λ= υТ

Молекулярная физика и термодинамика

Количество вещества ν=N/ Na
Молярная масса М=m/ν
Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT
Основное уравнение МКТ P=nkT=1/3nm₀υ²
Закон Гей – Люссака (изобарный процесс) V/T =const
Закон Шарля (изохорный процесс) P/T =const
Относительная влажность φ=P/P₀∙100%
Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
Работа газа A=P∙ΔV
Закон Бойля – Мариотта (изотермический процесс) PV=const
Количество теплоты при нагревании Q=Cm(T₂-T₁)
Количество теплоты при плавлении Q=λm
Количество теплоты при парообразовании Q=Lm
Количество теплоты при сгорании топлива Q=qm
Уравнение состояния идеального газа PV=m/M∙RT
Первый закон термодинамики ΔU=A+Q
КПД тепловых двигателей η= (Q₁— Q₂)/ Q₁
КПД идеал. двигателей (цикл Карно) η= (Т₁— Т₂)/ Т₁

Электростатика и электродинамика – формулы по физике

Закон Кулона F=k∙q₁∙q₂/R²
Напряженность электрического поля E=F/q
Напряженность эл. поля точечного заряда E=k∙q/R²
Поверхностная плотность зарядов σ = q/S
Напряженность эл. поля бесконечной плоскости E=2πkσ
Диэлектрическая проницаемость ε=E₀/E
Потенциальная энергия взаимод. зарядов W= k∙q₁q₂/R
Потенциал φ=W/q
Потенциал точечного заряда φ=k∙q/R
Напряжение U=A/q
Для однородного электрического поля U=E∙d
Электроемкость C=q/U
Электроемкость плоского конденсатора C=S∙ε∙ε₀/d
Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
Сила тока I=q/t
Сопротивление проводника R=ρ∙ℓ/S
Закон Ома для участка цепи I=U/R
Законы послед. соединения I₁=I₂=I, U₁+U₂=U, R₁+R₂=R
Законы паралл. соед. U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R
Мощность электрического тока P=I∙U
Закон Джоуля-Ленца Q=I²Rt
Закон Ома для полной цепи I=ε/(R+r)
Ток короткого замыкания (R=0) I=ε/r
Вектор магнитной индукции B=Fmax/ℓ∙I
Сила Ампера Fa=IBℓsin α
Сила Лоренца Fл=Bqυsin α
Магнитный поток Ф=BSсos α Ф=LI
Закон электромагнитной индукции Ei=ΔФ/Δt
ЭДС индукции в движ проводнике Ei=Вℓυsinα
ЭДС самоиндукции Esi=-L∙ΔI/Δt
Энергия магнитного поля катушки Wм=LI²/2
Период колебаний кол. контура T=2π ∙√LC
Индуктивное сопротивление X_L=ωL=2πLν
Емкостное сопротивление Xc=1/ωC
Действующее значение силы тока Iд=Imax/√2,
Действующее значение напряжения Uд=Umax/√2
Полное сопротивление Z=√(Xc-X_L)²+R²

Оптика

Закон преломления света n₂₁=n₂/n₁= υ₁/ υ₂
Показатель преломления n₂₁=sin α/sin γ
Формула тонкой линзы 1/F=1/d + 1/f
Оптическая сила линзы D=1/F
max интерференции: Δd=kλ,
min интерференции: Δd=(2k+1)λ/2
Диф.решетка d∙sin φ=k λ

Квантовая физика

Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U_зе
Красная граница фотоэффекта ν_к = Aвых/h
Импульс фотона P=mc=h/ λ=Е/с

Физика атомного ядра

Закон радиоактивного распада N=N₀∙2^—^t^/^T
Энергия связи атомных ядер

E_CB=(Zm_p+Nm_n-Mя)∙c²

СТО

t=t₁/√1-υ²/c²
ℓ=ℓ₀∙√1-υ²/c²
υ₂=(υ₁+υ)/1+ υ₁∙υ/c²
Е = mс²

Закон Ома. Формула Закона Ома

Где и когда можно применять закон Ома?

Значение Закона Ома

формулы и определения / Блог :: Бингоскул

Закон Ома для участка цепи:

Определение единицы сопротивления — Ом

Закон Ома для полной цепи

Как запомнить формулы закона Ома

Закон Джоуля-Ленца: определение, формула, применение

Определение и формула

Дифференциальная форма

Интегральная форма

Физический смысл

Практическая польза закона Джоуля-Ленца

Применение и практический смысл

10 формул по физике

Соотношения закона Ома

Расчёты сопротивления

Расчет сопротивления последовательных резисторов

Расчет сопротивления параллельных резисторов

Расчёты ёмкости

Расчет емкости параллельных конденсаторов

Расчет емкости последовательных конденсаторов

Расчет емкости трех и более последовательно соединенных конденсаторов

Расчёт энергетических уравнений

Расчёт постоянной ёмкости RC-цепочки

Расчёты частоты и длины волны

Расчет частоты сигнала

Расчет длины волны сигнала

Открытая Физика. Электрический ток. Закон Ома

Формулы по физике для ЕГЭ и 7-11 класса

Электростатика и электродинамика – формулы по физике

Формулы по физике для ЕГЭ

Формулы по физике для ЕГЭ

Электростатика и электродинамика – формулы по физике

alexxlab

Добавить комментарий Отменить ответ

Рубрики