Какой буквой обозначают частоту — MOREREMONTA
частота обозначение
Автор Ёветлана Тула задал вопрос в разделе Домашние задания
какой буквой обозначается частота? и получил лучший ответ
Ответ от Lmn[гуру]
Стандартные обозначения в формулах —
F. Единицей частоты в Международной системе единиц (СИ) в общем случае является Герц (Гц, Hz)
30 МГц = 10 метров
Около 2,9 метра
Длина волны измеряется в метрах, и каждому
подробнее.
F. Единицей частоты в Международной системе единиц (СИ) в общем случае является Герц (Гц, Hz). Величина, обратная частоте, называется периодом.
Вопрос по физике:
Какой буквой обозначается частота в физике?
Ответы и объяснения 2
оно обозначается в и измеряется в герцах
Единицей измерения частоты в Международной системе единиц (СИ) является герц (русское обозначение: Гц; международное: Hz), названный в честь немецкого физика Генриха Герца.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.
Частота — это физический параметр, которые используют для характеристики периодических процессов. Частота равна количеству повторений или свершения событий в единицу времени.
Чаще всего в физике частоту обозначают буквой $
Частота (наряду со временем) является самой точно измеряемой величиной.
Формула частоты колебаний
При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$
Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:
где $Delta t$ — время за которое происходят $N$ колебаний.
Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:
Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами ($<
u >_1 и <
u >_2$) равна:
Еще одно величиной характеризующей колебательный процесс является циклическая частота ($<omega >_0$), связанная с частотой как:
Циклическая частота измеряется в радианах, деленных на секунду:
Частота колебаний тела, имеющего массу$ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:
Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.
Для математического маятника частоту колебаний вычисляют как: длина нити:
где $g$ — ускорение свободного падения; $ l$ — длина нити (длина подвеса) маятника.
Физический маятник совершает колебания с частотой:
где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.
Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.
Формулы для вычисления частоты дискретных событий, частота вращения
дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $ au $, то частота дискретных событий равна:
Единицей измерения частоты дискретных событий является обратная секунда:
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $ au $ — время, затрачиваемое на один полный оборот, то:
Примеры задач с решением
Задание. Колебательная система совершила за время равное одной минуте ($Delta t=1 мин$) 600 колебаний. Какова частота этих колебаний?
Решение.
Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $Delta t=1 мин=60 с$. Вычислим частоту:
Ответ. $
u =10Гц$
Задание. На рис.1 изображен график колебаний некоторого параметра $xi (t)$, Какова амплитуда и частота колебаний этой величины?
Решение. Из рис.1 видно, что амплитуда величины $xi left(t
ight)=<xi >_=5 (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:
Частота — величина обратная периоду колебаний, значит:
Ответ. 1) $<xi >_=5 (м)$. 2) $
u =0,5$ Гц
Угловая частота — Википедия
Материал из Википедии — свободной энциклопедии
Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).
Угловая частота является производной по времени от фазы колебания:
- ω=∂φ/∂t.{\displaystyle \omega =\partial \varphi /\partial t.}
Другое распространённое обозначение ω=φ˙.{\displaystyle \omega ={\dot {\varphi }}.}
Угловая частота связана с частотой ν соотношением[1]
- ω=2πν.{\displaystyle \omega ={2\pi \nu }.}
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
- ω=360∘ν.{\displaystyle \omega ={360^{\circ }\nu }.}
В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2π единиц времени.
Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна ωLC=1/LC,{\displaystyle \omega _{LC}=1/{\sqrt {LC}},} тогда как обычная резонансная частота νLC=1/(2πLC).{\displaystyle \nu _{LC}=1/(2\pi {\sqrt {LC}}).}
В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.
- ↑ Угловая частота (неопр.). Большой энциклопедический политехнический словарь. Дата обращения 27 октября 2016.
Герц (единица измерения) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Герц.Герц (русское обозначение: Гц, международное обозначение: Hz) — единица частоты периодических процессов (например, колебаний) в Международной системе единиц (СИ) а также в системах единиц СГС и МКГСС[1]. Герц — производная единица, имеющая специальные наименование и обозначение. Через основные единицы СИ герц выражается следующим образом:
- 1 Гц = 1 с−1.
1 Гц означает одно исполнение (реализацию) такого процесса за одну секунду, другими словами — одно колебание в секунду, 10 Гц — десять исполнений такого процесса, или десять колебаний за одну секунду.
В соответствии с общими правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы герц пишется со строчной буквы, а её обозначение — с заглавной.
Единица названа в честь немецкого учёного-физика XIX века Генриха Герца, который внёс важный вклад в развитие электродинамики. Название было учреждено Международной электротехнической комиссией (МЭК) в 1930 году[2]. В 1960 году XI Генеральной конференцией по мерам и весам вместе с учреждением СИ это название было принято для единицы частоты в СИ.
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Гц | декагерц | даГц | daHz | 10−1 Гц | децигерц | дГц | dHz |
| 102 Гц | гектогерц | гГц | hHz | 10−2 Гц | сантигерц | сГц | cHz |
| 103 Гц | килогерц | кГц | kHz | 10−3 Гц | миллигерц | мГц | mHz |
| 106 Гц | мегагерц | МГц | MHz | 10−6 Гц | микрогерц | мкГц | µHz |
| 109 Гц | гигагерц | ГГц | GHz | 10−9 Гц | наногерц | нГц | nHz |
| 1012 Гц | терагерц | ТГц | THz | 10−12 Гц | пикогерц | пГц | pHz |
| 1015 Гц | петагерц | ПГц | PHz | 10−15 Гц | фемтогерц | фГц | fHz |
| 1018 Гц | эксагерц | ЭГц | EHz | 10−18 Гц | аттогерц | аГц | aHz |
| 1021 Гц | зеттагерц | ЗГц | ZHz | 10−21 Гц | зептогерц | зГц | zHz |
| 1024 Гц | иоттагерц | ИГц | YHz | 10−24 Гц | иоктогерц | иГц | yHz |
| применять не рекомендуется не применяются или редко применяются на практике | |||||||
Кроме герца в СИ существует ещё одна производная единица, равная секунде в минус первой степени (1/с): таким же соотношением с секундой связан беккерель. Существование двух равных, но имеющих различные названия единиц, связано с различием сфер их применения: герц используется только для периодических процессов, а беккерель — только для случайных процессов распада радионуклидов[3]. Хотя использовать обратные секунды в обоих случаях было бы формально правильно, рекомендуется использовать единицы с различными названиями, поскольку различие названий единиц подчёркивает различие природы соответствующих физических величин.
| Обозначения в Юникоде.[4] | ||
|---|---|---|
| Символ | Название | Номер Юникода |
| ㎐ | Герц (Square HZ) | U+3390 |
| ㎑ | Килогерц (Square KHZ) | U+3391 |
| ㎒ | Мегагерц (Square MHZ) | U+3392 |
| ㎓ | Гигагерц (Square GHZ) | U+3393 |
| ㎔ | Терагерц (Square THZ) | U+3394 |
- Диапазон частот звуковых колебаний, которые способен слышать человек, лежит в пределах от 20 Гц до 20 кГц.
- Сердце человека в спокойном состоянии бьётся с частотой приблизительно 1 Гц (Примечательно, что Herz в переводе с немецкого означает «сердце». Однако фамилия великого физика пишется Hertz).
- Частота ноты ля первой октавы по стандарту настройки, принятому в настоящее время, составляет 440 Гц. Является стандартной частотой камертона (нота ля первой октавы является эталонной для настройки музыкальных инструментов). В концертных залах применяется настройка в 442 Гц, иногда выше.
- Частоты колебаний электромагнитного поля, воспринимаемого человеком как видимое излучение (свет), лежат в диапазоне от 3,9⋅1014 до 7,9⋅1014 Гц.
- Частота электромагнитного излучения, используемого в микроволновых печах для нагрева продуктов, обычно равна 2,45 ГГц.
Формула частоты в физике
ОпределениеЧастота — это физический параметр, которые используют для характеристики периодических процессов. Частота равна количеству повторений или свершения событий в единицу времени.
Чаще всего в физике частоту обозначают буквой $\nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.
Частота (наряду со временем) является самой точно измеряемой величиной.
Формула частоты колебаний
При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$
\[\nu =\frac{1}{T}\left(1\right).\]Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:
\[\nu =\frac{N}{\Delta t}\left(2\right),\]где $\Delta t$ — время за которое происходят $N$ колебаний.
Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:
\[\left[\nu \right]=с^{-1}=Гц.\]Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${\nu }_1\ и\ {\nu }_2$) равна:
\[{\nu =\nu }_1-\ {\nu }_2\left(3\right).\]Еще одно величиной характеризующей колебательный процесс является циклическая частота (${\omega }_0$), связанная с частотой как:
\[{\omega }_0=2\pi \nu \left(4\right).\]Циклическая частота измеряется в радианах, деленных на секунду:
\[\left[{\omega }_0\right]=\frac{рад}{с}.\]Частота колебаний тела, имеющего массу$\ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:
\[\nu =\frac{1}{2\pi \sqrt{{m}/{k}}}\left(5\right).\]Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.
Для математического маятника частоту колебаний вычисляют как: длина нити:
\[\nu =\frac{1}{2\pi \sqrt{{l}/{g}}}\left(6\right),\]где $g$ — ускорение свободного падения; $\ l$ — длина нити (длина подвеса) маятника.
Физический маятник совершает колебания с частотой:
\[\nu =\frac{1}{2\pi \sqrt{{J}/{mgd}}}\left(7\right),\]где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.
Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.
Формулы для вычисления частоты дискретных событий, частота вращения
дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:
\[n=\frac{1}{\tau }\left(8\right).\]Един
Единица измерения частоты, теория и онлайн калькуляторы
Прежде чем перейти к единицам измерения частоты, скажем о том, что следует выделить: частоту периодических процессов (колебаний, излучений и т.д.), частоту дискретных событий (импульсов и т.д. ) и частоту вращения.
Герц — единица измерения частоты периодического процесса в системе СИ
ОпределениеЧастота периодических процессов ($\nu$) — это физическая величина, которая равна количеству циклов, которые происходят в единицу времени. Это определение говорит о том, что:
\[\nu =\frac{1}{T}\left(1\right),\]где $T$ — период процесса.
Из выражения (1) очевидно, что единицей измерения частоты служит обратная секунда:
\[\left[\nu \right]=с^{-1}.\]В Международной системе единиц (СИ) эта единица измерения имеет специальное название, ее называют герцем (Гц) с 1960 г (начала существования системы). Герц — единица измерения частоты периодического процесса, при которой за время в одну секунду протекает один цикл процесса.
Единица измерения частоты периодического процесса называется в честь немецкого ученого Г. Герца, который много и успешно занимался электродинамикой.
Герц, как единица измерения частоты может использоваться со стандартными приставками системы СИ для обозначения десятичных кратных и дольных единиц. Например, гГц (гектогерц): $1г\ Гц=100\ Гц$; мкГц (микрогерц): $1мкГц={10}^{-6}Гц.$ Биения здорового человеческого сердца в спокойном состоянии происходят с частотой 1Гц.
Иногда частоту периодических колебаний обозначают буквой $f$.
Часто в расчётах используют циклическую частоту (угловую частоту, радиальную частоту, круговая частота) ($\omega $), которая равна:
\[\omega =2\pi {\mathbf \nu }\left(2\right).\]Угловая частота измеряется в радианах, деленных на секунду:
\[\left[\omega \right]=\frac{рад}{с}.\]В системах СИ и СГС единицы измерения круговой частоты одинаковы.
Секунда в минус первой степени — единица измерения частоты дискретных событий
Частота дискретных колебаний ($n$) — это физическая величина, которая равна количеству действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:
\[n=\frac{1}{\tau }\left(3\right).\]Из определения (3) следует, что обратная секунда (секунда в минус первой степени) — единица измерения частоты дискретных событий:
\[\left[n\right]=\frac{1}{с}.\]Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Секунда в минус первой степени — единица измерения частоты вращения
Частота вращения ($n$) — это величина, равная количеству полных оборотов в единицу времени. Если $\tau $ — время, затрачиваемое на один полный оборот, то:
\[n=\frac{1}{\tau }\left(4\right).\]Секунда в минус пе
Частота — Циклопедия
Период и частота механических колебаний. Урок 116 // EduLibNet [3:28] Период и частота колебаний [Радиолюбитель TV 11] [3:51]Частота — физическая величина, характеристика всяких процессов, которые повторяются (периодических процессов или колебаний). Частота показывает, сколько периодов процесса происходит за единицу времени. Измеряется в герцах.
Различают линейную частоту и циклическую частоту.
Линейная частота — это количество периодических процессов в секунду. Линейная частота обычно обозначается греческой буквой ν или латинской буквой f.
- [math] \nu = \frac{1}{T} [/math]
где T — это период
Циклическая или угловая частота — это количество колебаний за 2π секунд. Циклическая частота обычно обозначается греческой буквой ω.
Циклическая частота обозначается в формулах для того, чтобы не писать множитель 2π, но численные значения приводятся для линейной частоты.
Когда говорят, что тактовая частота компьютера 1,8 ГГц, или, что человек слышит звуки частот от 20 Гц до 20000 Гц, имеется в виду именно линейная частота ν.
Самый простой способ измерения малых частот — подсчет числа колебаний за определенный промежуток времени. Для измерения высоких частот используют стробоскоп.
В области высокочастотных электрических колебаний частоту можно измерять благодаря резонансу.
Лучше частота определена для гармонических колебаний. Временную зависимость других периодических, но не гармонических, колебаний можно разложить в ряд Фурье, то есть выразить через сумму гармонических колебаний. В этой сумме будет составляющая с наименьшей, основной частотой, соответствующей периоду, и другие составляющие с частотами, кратными основной, обертоны. Совокупность этих частот называют частотным спектром периодического процесса.
Временную зависимость характеристик непериодических процессов можно представить в виде совокупности гармонических колебаний с помощью преобразования Фурье. В отличие от периодических процессов, частотный спектр непериодических процессов непрерывный, то есть непериодический процесс, является совокупностью бесчисленных гармонических колебаний.
В случае, когда в непрерывном спектре нельзя выделить отдельных сильных гармонических составляющих, процесс называют шумом. Тогда, когда амплитуды всех составляющих спектра примерно одинаковые, возникает белый шум.
Что такое частота колебаний? :: SYL.ru
Всё на планете имеет свою частоту. Согласно одной из версий, она даже положена в основу нашего мира. Увы, теория весьма сложна, чтобы излагать её в рамках одной публикации, поэтому нами будет рассмотрена исключительно частота колебаний как самостоятельное действие. В рамках статьи будет дано определения этому физическому процессу, его единицам измерений и метрологической составляющей. И под конец будет рассмотрен пример важности в обычной жизни обыкновенного звука. Мы узнаем, что он собой представляет и какова его природа.
Что называют частотой колебаний?
Под этим подразумевают физическую величину, которая используется для характеристики периодического процесса, что равен количеству повторений или возникновений определённых событий за одну единицу времени. Этот показатель рассчитывается как отношение числа данных происшествий к промежутку времени, за который они были совершены. Собственная частота колебаний есть у каждого элемента мира. Тело, атом, дорожный мост, поезд, самолёт – все они совершают определённые движения, которые так называются. Пускай эти процессы не видны глазу, они есть. Единицами измерений, в которых считается частота колебаний, являются герцы. Своё название они получили в честь физика немецкого происхождения Генриха Герца.Мгновенная частота
Периодический сигнал можно охарактеризовать мгновенной частотой, которая с точностью до коэффициента является скоростью изменения фазы. Его можно представить как сумму гармонических спектральных составляющих, обладающих своими постоянными колебаниями.
Циклическая частота колебаний
Её удобно применять в теоретической физике, особенно в разделе про электромагнетизм. Циклическая частота (её также называют радиальной, круговой, угловой) – это физическая величина, которая используется для обозначения интенсивности происхождения колебательного или вращательного движения. Первая выражается в оборотах или колебаниях на секунду. При вращательном движении частота равняется модулю вектора угловой скорости.Выражение этого показателя осуществляется в радианах на одну секунду. Размерность циклической частоты является обратной времени. В числовом выражении она равняется числу колебаний или оборотов, что произошли за количество секунд 2π. Её введения для использования позволяет значительно упрощать различный спектр формул в электронике и теоретической физике. Самый популярный пример использования – это обсчёт резонансной циклической частоты колебательного LC-контура. Другие формулы могут значительно усложняться.
Частота дискретных событий
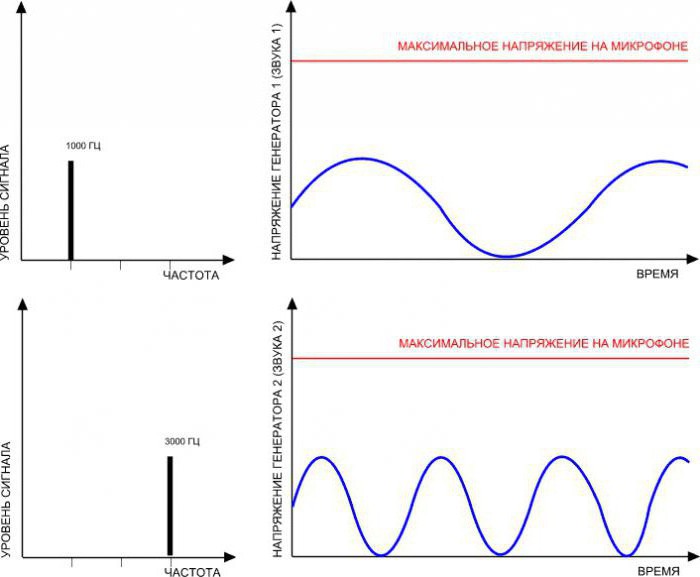Под этой величиной подразумевают значение, что равно числу дискретных событий, которые происходят за одну единицу времени. В теории обычно используется показатель – секунда в минус первой степени. На практике, чтобы выразить частоту импульсов, обычно применяют герц.Частота вращения
Под нею понимают физическую величину, которая равняется числу полных оборотов, что происходят за одну единицу времени. Здесь также применяется показатель – секунда в минус первой степени. Для обозначения сделанной работы могут использовать такие словосочетания, как оборот в минуту, час, день, месяц, год и другие.
Единицы измерения
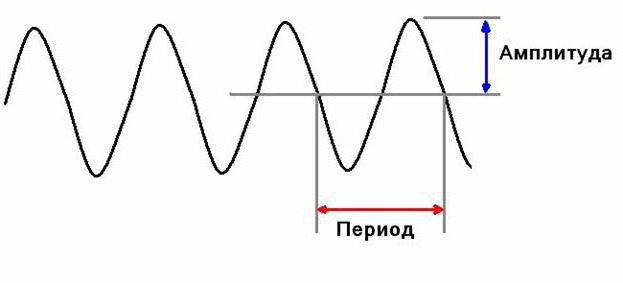В чём же измеряется частота колебаний? Если брать во внимание систему СИ, то здесь единица измерения – это герц. Первоначально она была введена международной электротехнической комиссией ещё в 1930 году. А 11-я генеральная конференция по весам и мерам в 1960-м закрепила употребление этого показателя как единицы СИ. Что было выдвинуто в качестве «идеала»? Им выступила частота, когда один цикл совершается за одну секунду.Но что делать с производством? Для них были закреплены произвольные значения: килоцикл, мегацикл в секунду и так далее. Поэтому беря в руки устройство, которое работает с показателем в ГГц (как процессор компьютера), можете примерно представить, сколько действий оно совершает. Казалось бы, как медленно для человека тянется время. Но техника за тот же промежуток успевает выполнять миллионы и даже миллиарды операций в секунду. За один час компьютер делает уже столько действий, что большинство людей даже не смогут представить их в численном выражении.
Метрологические аспекты
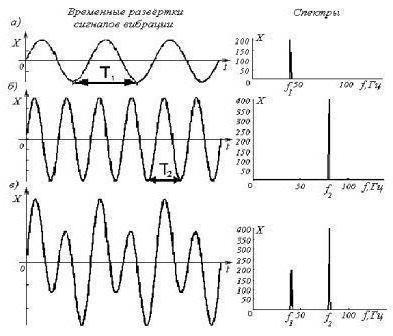Частота колебаний нашла своё применение даже в метрологии. Различные устройства имеют много функций:- Измеряют частоту импульсов. Они представлены электронно-счётными и конденсаторными типами.
- Определяют частоту спектральных составляющих. Существуют гетеродинные и резонансные типы.
- Производят анализ спектра.
- Воспроизводят необходимую частоту с заданной точностью. При этом могут применяться различные меры: стандарты, синтезаторы, генераторы сигналов и другая техника этого направления.
- Сравнивают показатели полученных колебаний, в этих целях используют компаратор или осциллограф.
Пример работы: звук
Всё выше написанное может быть довольно сложным для понимания, поскольку нами использовался сухой язык физики. Чтобы осознать приведённую информацию, можно привести пример. В нём всё будет детально расписано, основываясь на анализе случаев из современной жизни. Для этого рассмотрим самый известный пример колебаний – звук. Его свойства, а также особенности осуществления механических упругих колебаний в среде, находятся в прямой зависимости от частоты.
Человеческие органы слуха могут улавливать колебания, которые находятся в рамках от 20 Гц до 20 кГц. Причём с возрастом верхняя граница будет постепенно снижаться. Если частота колебаний звука упадёт ниже показателя в 20 Гц (что соответствует ми субконтроктавы), то будет создаваться инфразвук. Этот тип, который в большинстве случаев не слышен нам, люди всё же могут ощущать осязательно. При превышении границы в 20 килогерц генерируются колебания, которые называются ультразвуком. Если частота превысит 1 ГГц, то в этом случае мы будем иметь дело с гиперзвуком. Если рассматривать такой музыкальный инструмент, как фортепиано, то он может создавать колебания в диапазоне от 27,5 Гц до 4186 Гц. При этом следует учитывать, что музыкальный звук не состоит только из основной частоты – к нему ещё примешиваются обертоны, гармоники. Это всё вместе определяет тембр.
Заключение
Как вы имели возможность узнать, частота колебаний является чрезвычайно важной составляющей, которая позволяет функционировать нашему миру. Благодаря ей мы можем слышать, с её содействия работают компьютеры и осуществляется множество других полезных вещей. Но если частота колебаний превысит оптимальный предел, то могут начаться определённые разрушения. Так, если повлиять на процессор, чтобы его кристалл работал с вдвое большими показателями, то он быстро выйдет из строя.
Подобное можно привести и с человеческой жизнью, когда при высокой частотности у него лопнут барабанные перепонки. Также произойдут другие негативные изменения с телом, которые повлекут за собой определённые проблемы, вплоть до смертельного исхода. Причём из-за особенности физической природы этот процесс растянется на довольно длительный промежуток времени. Кстати, беря во внимание этот фактор, военные рассматривают новые возможности для разработки вооружения будущего.
