Сложение сил – правило для системы
4.7
Средняя оценка: 4.7
Всего получено оценок: 118.
4.7
Средняя оценка: 4.7
Всего получено оценок: 118.
Если на тело действует несколько сил, то для определения результата их действия необходимо учитывать их все. Это возможно с помощью правил сложения сил. Познакомимся с этими правилами поближе.
Равнодействующая сила
Ситуации, когда на тело действует только одна сила, в Природе сравнительно редки. Практически всегда на любое тело действует сила тяжести, а кроме того, присутствуют силы трения.
Поэтому встает задача определения результата совместного действия всех сил, действующих на тело. Сколько бы таких сил не было – тело либо останется в покое, либо начнет совершать движение. Причем, это всегда будет происходить так, как будто на тело действует только одна сила. Сколько бы сил не действовало на тело, всегда можно подобрать одну такую силу, результат действия которой будет равен действую всех сил, приложенных к телу.
Сила, которая производит то же действие, как и несколько других сил, называется равнодействующей.
Рис. 1. Равнодействующая сила.Равнодействующая сила используется при решении задач. Заменив силы, действующие на тело, равнодействующей, дальше для определения результата считают, что на тело действует только она.
Правила сложения сил
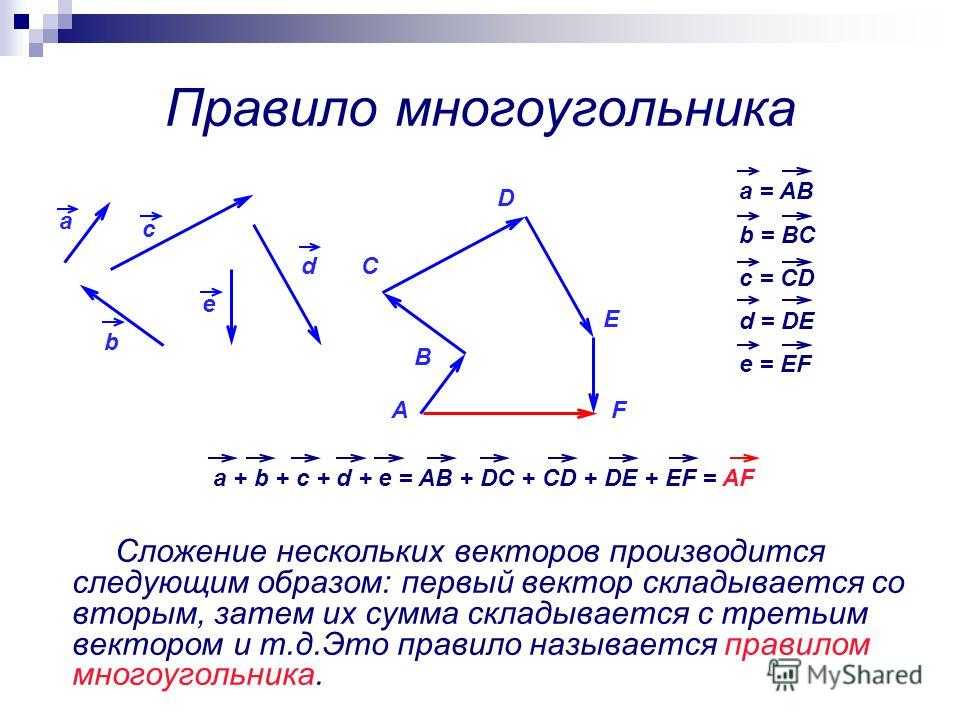
Действие по нахождению равнодействующей нескольких сил называется сложением сил. Для сложения сил существует переместительный и сочетательный законы. Поэтому, если на тело действует более двух сил, сперва складывают две из них, потом к результату прибавляют третью, потом четвертую – и так до последней силы.
Само сложение пары сил отличается от простого арифметического сложения.
В первую очередь, надо убедиться, что силы приложены к одной точке. Силы, приложенные к разным точкам складывать нельзя.
Во-вторых, необходимо учесть, что сила – величина векторная, а значит, для сложения двух сил необходимо пользоваться не обычным арифметическим сложением, а сложением по векторным правилам.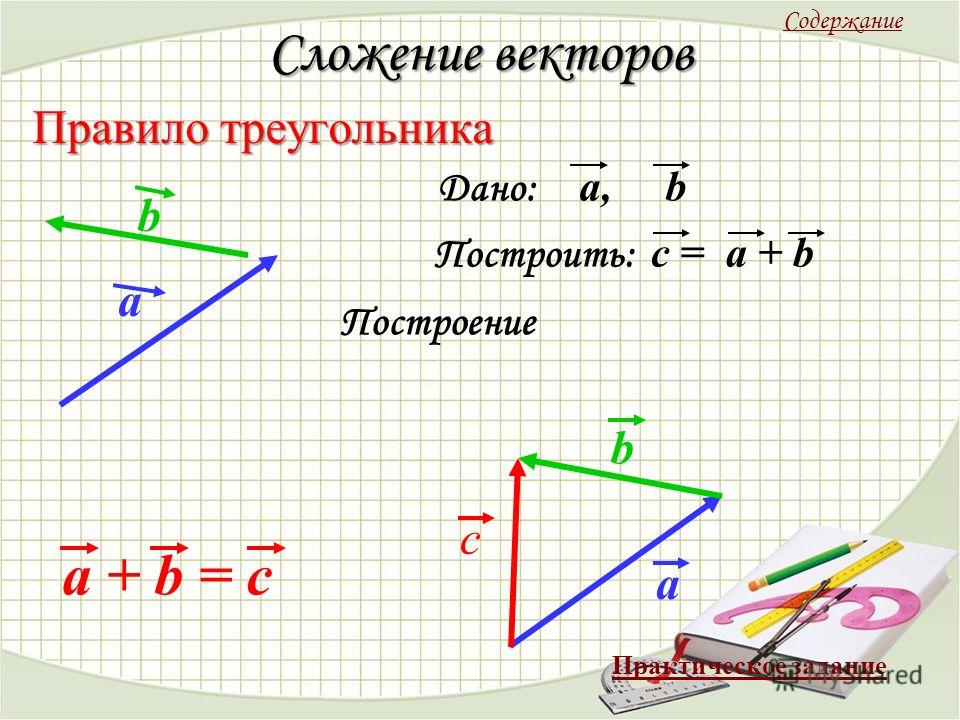
Для сложения сил необходимо найти их проекции на оси системы координат, сложить эти проекции, а потом по проекциям найти результирующую силу.
В простейшем случае, когда координатная ось одна – модули проекций равны модулям самих сил, и их знак совпадает с их направлением. В результате, равнодействующая сил, направленных в одну сторону, направлена в ту же сторону, а ее модуль равен сумме модулей сил. Если силы направлены в разные стороны, равнодействующая их будет направлена в сторону большей по модулю силы, а ее модуль будет равен разности модулей большей и меньшей силы.
Если координатных осей две или три – необходимо определять проекции на все оси, складывать или вычитать их, в зависимости от направления, а затем, по полученным суммам определять модуль и направление равнодействующей.
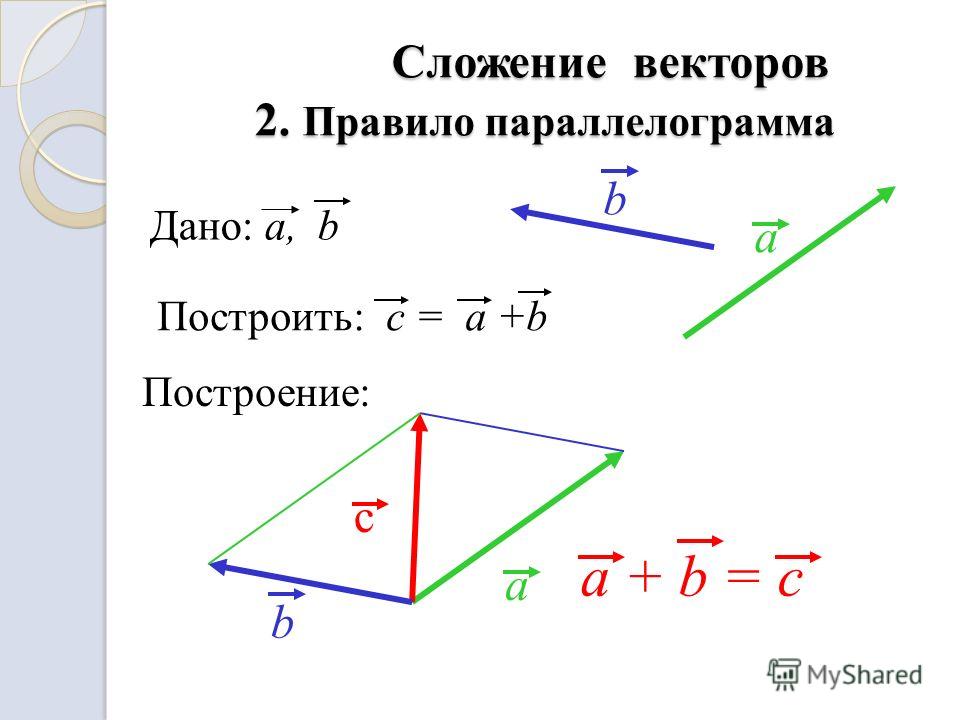
Для двух координатных осей при сложении сил нередко удобно использовать правила параллелограмма или треугольника – это приводит к нахождению равнодействующей быстрее.
Что мы узнали?
Сила, производящая такой же результат, как несколько других, называется равнодействующей. Для ее нахождения необходимо убедиться, что исходные силы приложены к одной точке, а потом сложить их по правилам сложения векторов.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 118.
А какая ваша оценка?
Сложение векторов. Геопсихология в шаманизме, физике и даосизме
Сложение векторов. Геопсихология в шаманизме, физике и даосизмеВикиЧтение
Геопсихология в шаманизме, физике и даосизме
Минделл Арнольд
Содержание
Сложение векторов
«Дао» данного момента — это сумма триграмм, так что конечное Дао, «направление», или путь, которым мы должны следовать в данный момент, в принципе, представляет собой сумму направлений.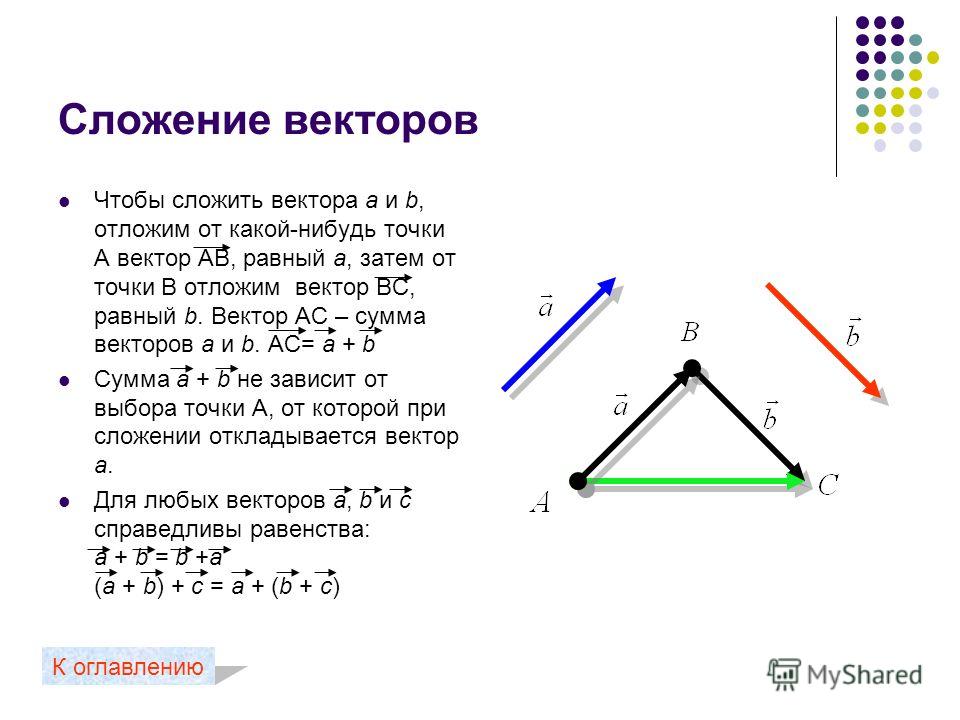
На рис. 8.6А показано сложение двух векторов направлений, связанных с триграммами рис. 8.5А, дающее общий вектор направления — жирную линию.
Таким образом, Дао — наиболее вероятный исход, курс, или путь данной ситуации — подобен квантово-волновой функции, представляющей собой сумму различных векторов. В квантовой физике, конечная жирная линия соответствовала бы наиболее вероятному исходу ситуации с двумя возможными состояниями.
(Рисунок 8.6А. Гексаграмма И-Цзин, направления триграмм, и сложение векторов)
Следовательно, Дао — это еще одно название для большого U данной ситуации. Поэтому данная книга — «Гео-психология» — в некотором смысле, обновляет гадательный подход древнего даосизма. Книга И-Цзин тысячелетия назад предполагала, что общий гештальт гексаграммы, ее форму суперпозиции, можно использовать для понимания отдельных линий. Точно так же, я полагаю, что большое U можно использовать для понимания значения отдельных субвекторов. В известном смысле, гексаграмма представляет собой своего рода «пилот-волну» или вектор большого U, которое заключает в себе все ее параллельные миры.
Сложение
Сложение Софизм сложения возникает, когда утверждается, что нечто, верное для отдельных членов какого-либо класса, справедливо и для всего класса как единого целого. Некоторые существительные можно употреблять относительно либо всего явления в целом, либо составляющих
От издателя: о системе векторов
От издателя: о системе векторов В 1908 году Зигмунд Фрейд опубликовал статью «Характер и анальная эротика», ставшую началом психоаналитического учения о характерах. Кратко описав в этой статье психологические особенности людей с высокой чувствительностью ануса, Фрейд
Глава 2. Значение и принятие векторов
Глава 2. Значение и принятие векторов
Как вы уже знаете из первой главы, чувствительность наших отверстий закладывается генетически.
§ 2. Определения и понятия у детей. Логическое сложение и умножение
§ 2. Определения и понятия у детей. Логическое сложение и умножение Мы не намерены заниматься здесь проблемой детских определений ради нее самой. Мы удовольствуемся обсуждением ее в той мере, в какой она касается вопроса, поставленного в предыдущем параграфе, и в
Сложение стрел или векторов
Сложение векторов
Сложение векторов
«Дао» данного момента — это сумма триграмм, так что конечное Дао, «направление», или путь, которым мы должны следовать в данный момент, в принципе, представляет собой сумму направлений.
На рис. 8.6А показано сложение двух векторов направлений, связанных с
9. О сложении векторов
9. О сложении векторов Первоначальное значение термина «вектор» происходит от латинского слова vectus, или «носитель».[165]* В психологии векторы соответствуют ощущению человека, что телесно-ориентированный и связанный с землей опыт ведет его в определенном реальном или
Сложение
Сложение Это более сложная загадка, представленная учителем танцев Алехандро для его студентов (см. задачу П9). Как и в стандартной головоломке судоку, сетка состоит из девяти квадратов, внутри которых находятся обведенные точками участки, сумма чисел в которых
3.2 Сложение и вычитание векторов: графические методы — College Physics 2e
Цели обучения
К концу этого раздела вы сможете:
- Понимать правила сложения, вычитания и умножения векторов.
- Применение графических методов сложения и вычитания векторов для определения перемещения движущихся объектов.
Рисунок 3,7 Смещение можно определить графически, используя масштабную карту, например, карту Гавайских островов. Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (кредит: Геологическая служба США)
Векторы в двух измерениях
Вектор – это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.
На рис. 3.8 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассматриваемого в книге «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный символ, такой как DD, обозначает вектор. Его величина представлена курсивным символом DD, а его направление — θθ.
Векторы в этом тексте
В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором FF, который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например FF, а направление переменной будет задано углом θθ.
Рисунок 3,8 Человек проходит 9 кварталов на восток и 5 кварталов на север. Смещение 10,3 блока под углом 29,1º29,1º к северу от востока.
Рисунок
3,9
Чтобы графически описать результирующий вектор для человека, идущего по городу, изображенному на рис.
3.8, нарисуйте стрелку, обозначающую вектор полного смещения DD. Используя транспортир, начертите линию под углом θθ относительно оси восток-запад. Длина DD стрелки пропорциональна модулю вектора и измеряется вдоль линии линейкой. В этом примере величина DD вектора составляет 10,3 единицы, а направление θθ равно 29.1º29,1º к северу от востока.
Сложение векторов: метод «голова к хвосту»
Метод «голова к хвосту» — это графический способ добавления векторов, описанный на рис. 3.10 ниже и в следующих шагах. Хвост вектора — это начальная точка вектора, а начало (или кончик) вектора — это конечный заостренный конец стрелки.
Рисунок
3.10 Метод «голова к хвосту»: Метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рис. 3.8. (a) Нарисуйте вектор, представляющий смещение на восток. (b) Нарисуйте вектор, представляющий смещение на север.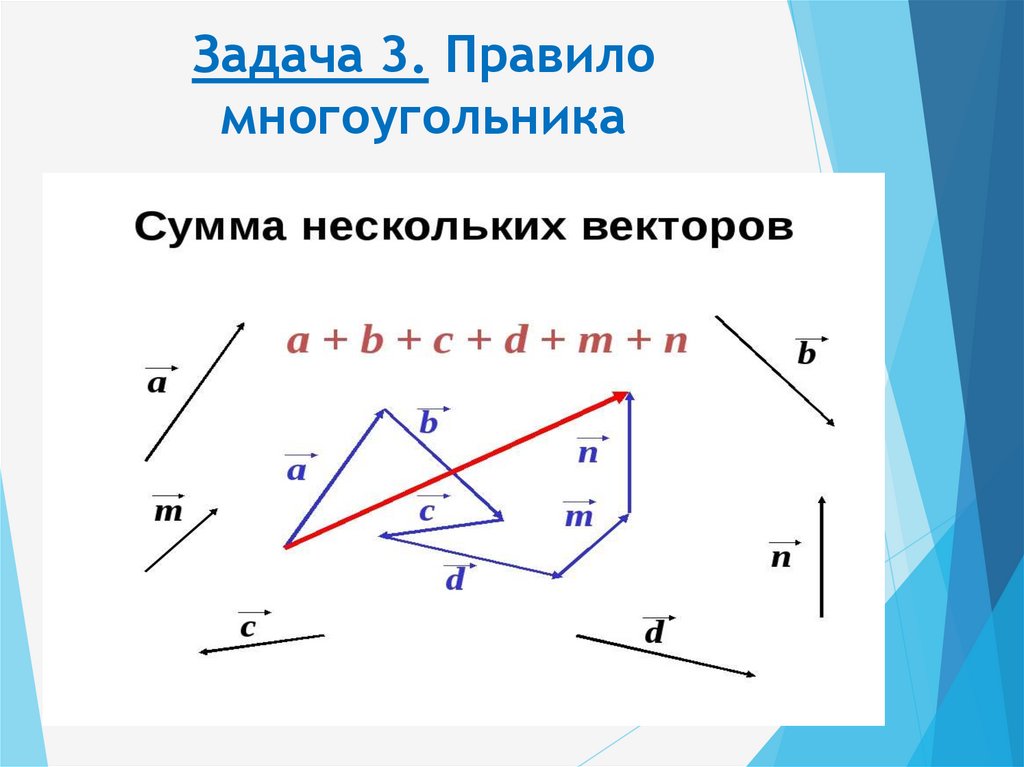
Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, к началу вектора, указывающего на север, чтобы сформировать сумму или результирующий вектор DD. Длина стрелки DD пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θθ, измеряется транспортиром и составляет 29°..1º29,1º.
Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Рисунок 3.11
Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 блоков на север). Поместите конец второго вектора в начало первого вектора .
Рисунок 3.12
Шаг 3.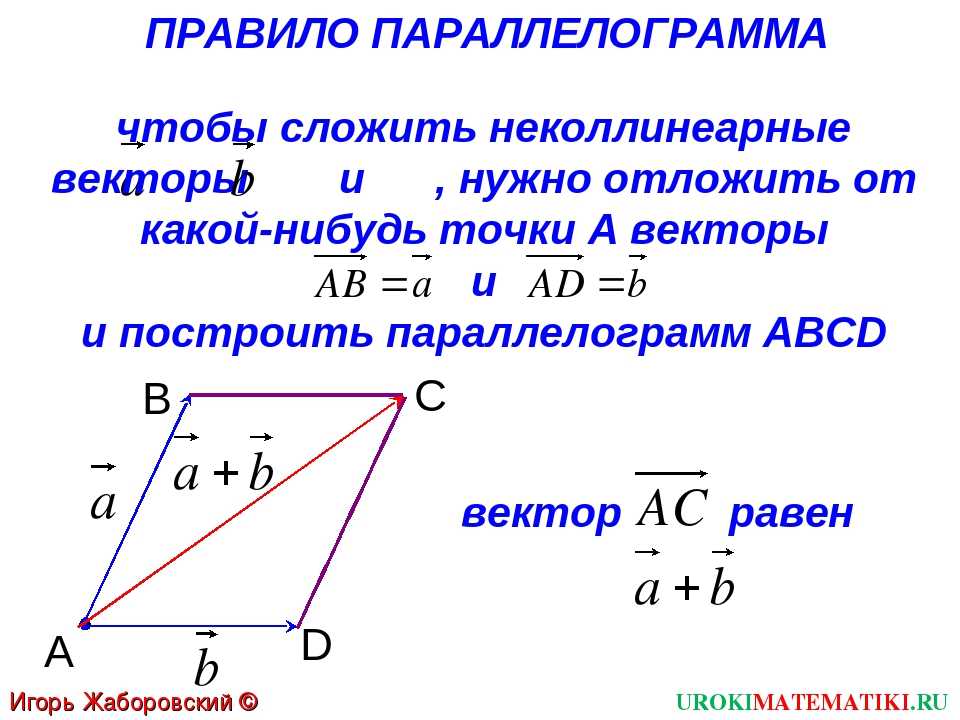
Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от кончика до хвоста 9.0020 .
Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Рисунок 3.13
Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве расчетов мы будем использовать теорему Пифагора для определения этой длины.)
Шаг 6. Чтобы определить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир.
(Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)
Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Пример 3.1
Графическое сложение векторов с использованием метода «голова к хвосту»: женщина на прогулке
Используйте графический метод сложения векторов, чтобы найти полное перемещение человека, который проходит следующие три пути (перемещения) по плоскому полю. Сначала она проходит 25,0 м в направлении 49,0º49,0º к северу от востока. Затем она проходит 23,0 м в направлении 15,0º15,0º к северо-востоку. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
Стратегия
Представьте каждый вектор смещения графически со стрелкой, обозначив первую AA, вторую BB и третью CC, сделав длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад.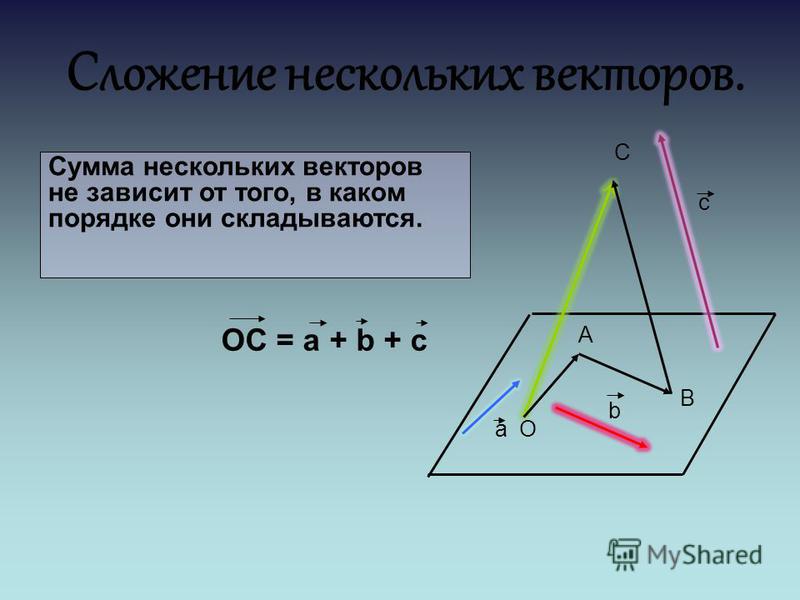
Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого RR.
Решение
(1) Нарисуйте три вектора смещения.
Рисунок 3.14
(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рисунок 3.15
(3) Нарисуйте результирующий вектор RR.
Рисунок 3.16
(4) Используйте линейку для измерения величины RR и транспортир для измерения направления RR. Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.
Рисунок 3.17
В этом случае видно, что полное смещение RR имеет величину 50,8 м и направлено в направлении 5,47º5,47º к югу от востока.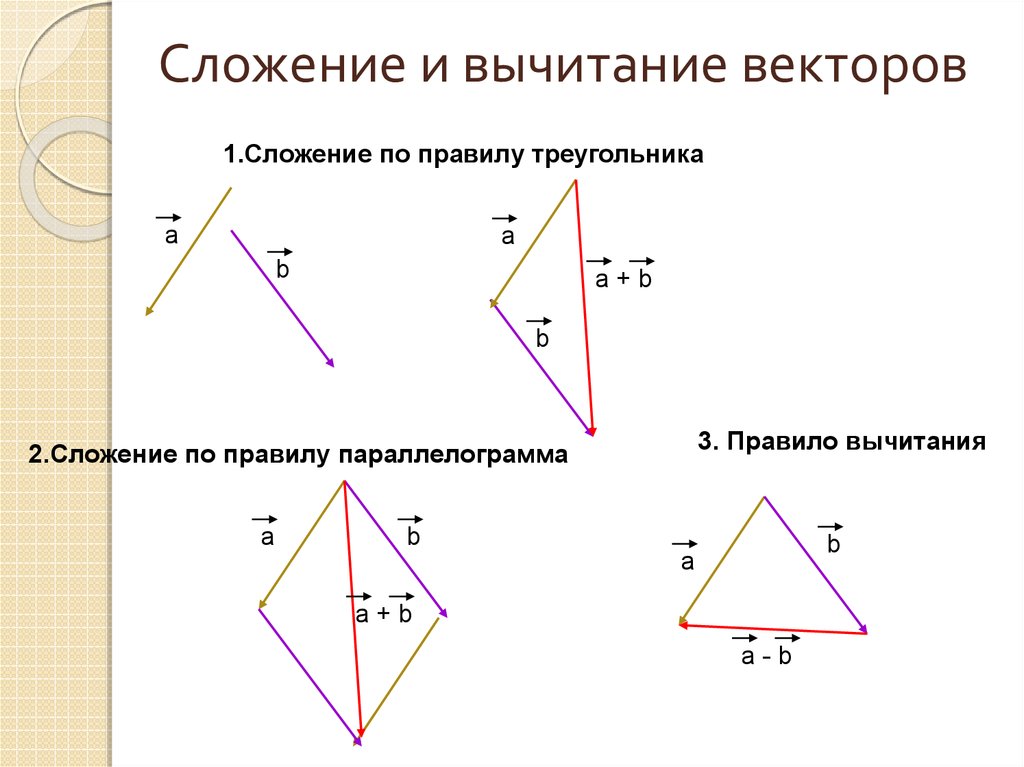
Используя его величину и направление, этот вектор можно выразить как R=50,8 м, R=50,8 м и θ=5,47ºθ=5,47º к югу от востока.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем складывать векторы в любом порядке, как показано на рис. 3.18, и все равно получим то же решение.
Рисунок 3.18
Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно. Векторы можно добавлять в любом порядке.
А+В=В+А.А+В=В+А.
3.1
(Это верно и для сложения обычных чисел — вы получите тот же результат, если сложите 2+32+3 или 3+23+2, например).
Вычитание векторов
Вычитание векторов — это прямое расширение сложения векторов.
Чтобы определить вычитание (скажем, мы хотим вычесть BB из
АА
, пишется А-ВА-Б
, мы должны сначала определить, что мы подразумеваем под вычитанием. минус вектора BB
определяется как –B–B; то есть графически отрицательное значение любого вектора имеет ту же величину, но противоположное направление , как показано на рис. 3.19. Другими словами, BB имеет ту же длину, что и –B–B, но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Рисунок 3.19 Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Таким образом, BB является отрицательным значением –B–B; он имеет ту же длину, но противоположное направление.
Затем вычитание вектора BB из вектора AA просто определяется как добавление –B–B к AA. Обратите внимание, что вычитание вектора — это добавление отрицательного вектора.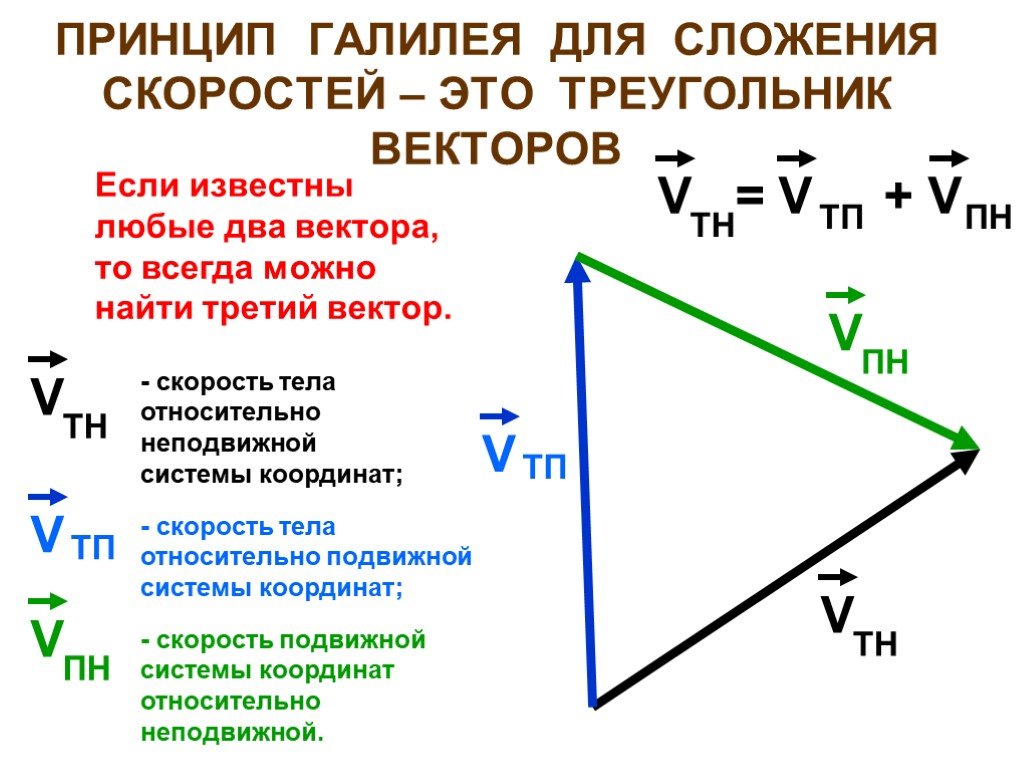
Порядок вычитания не влияет на результат.
A – B = A + (–B).A – B = A + (–B).
3.2
Это аналогично вычитанию скаляров (где, например, 5 – 2 = 5 + (–2)5 – 2 = 5 + (–2)). Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.
Пример 3.2
Графическое вычитание векторов: женщина, плывущая на лодке
Женщина, плывущая на лодке ночью, следует указаниям к пристани. Инструкции гласили: сначала пройти 27,5 м в направлении 66,0º66,0º к северу от востока от ее текущего местоположения, а затем пройти 30,0 м в направлении 112º112º к северу от востока (или 22,0º22,0º к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.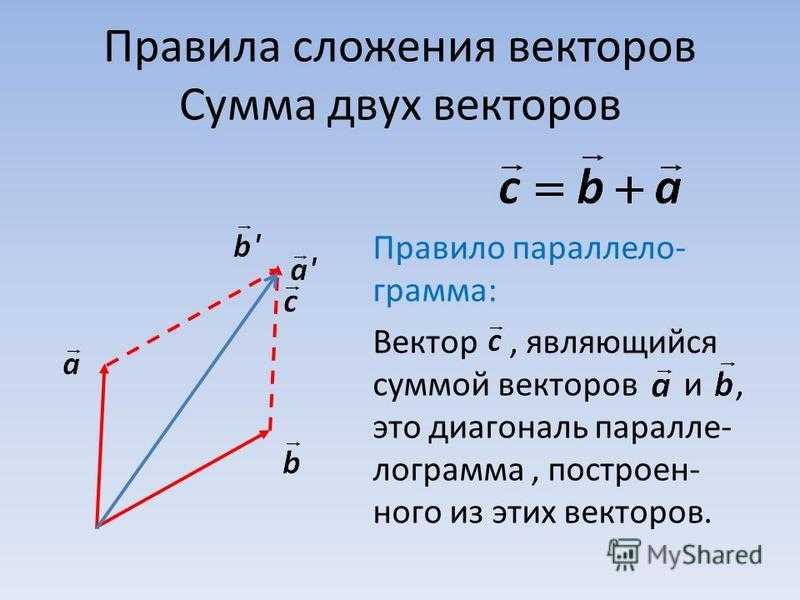
Рисунок 3.20
Стратегия
Мы можем представить первый отрезок пути вектором AA, а второй отрезок пути вектором ББ. Пристань находится в точке A + BA + B. Если женщина по ошибке едет в направлении , противоположном , для второго этапа путешествия, она проедет расстояние BB (30,0 м) в направлении 180º–112º=68º180º –112º=68º к югу от востока. Мы представляем это как –B–B, как показано ниже. Вектор –B–B имеет ту же величину, что и BB, но направлен в противоположную сторону. Таким образом, она окажется в точке A+(–B)A+(–B) или A–BA–B.
Рисунок 3.21
Мы выполним сложение векторов, чтобы сравнить местоположение причала, A + BA + B, с местом, в которое по ошибке прибыла женщина, A + (–B)A + (–B).
Решение
(1) Чтобы определить место, куда случайно попала женщина, начертите векторы AA и –B–B.
(2) Разместите векторы лицом к хвосту.
(3) Нарисуйте результирующий вектор RR.
(4) С помощью линейки и транспортира измерьте величину и направление RR.
Рисунок 3.22
В данном случае R=23,0 мR=23,0 м и θ=7,5ºθ=7,5º к югу от востока.
(5) Чтобы определить местоположение дока, мы повторяем этот метод, добавляя векторы AA и BB. Получаем результирующий вектор R’R’:
Рисунок 3,23
В этом случае R = 52,9 мR = 52,9 м и θ=90,1ºθ=90,1º к северу от востока.
Мы видим, что женщина окажется на значительном расстоянии от пристани, если она отправится в противоположном направлении на второй этап поездки.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Умножение векторов и скаляров
Если бы мы решили пройти в три раза большее расстояние на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м3 × 27,5 м, или 82,5 м, в направлении 66,0º66,0º к северу от востока.
Это пример умножения вектора на положительную скалярную величину. Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору направление , противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор AA умножается на скаляр cc,
- , модуль вектора становится абсолютным значением ccAA, .
- , если cc положителен, направление вектора не меняется,
- , если cc отрицательное, направление меняется на противоположное.
В нашем случае c=3c=3 и A=27,5 мА=27,5 м. Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр от 0 до 1.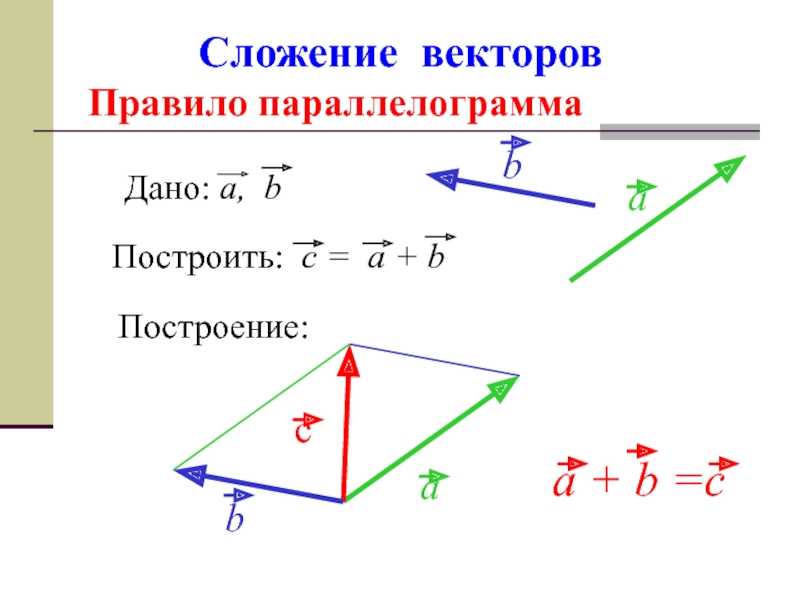
Разложение вектора на компоненты
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает определение перпендикулярных компонентов одного вектора, например компонентов x — и y , или компонентов север-юг и восток-запад.
Например, мы можем знать, что общее перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29.0º29.0º к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и на север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, применяемому для нахождения полного смещения.
Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.
Исследования ФЕТ
игра лабиринт
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Нажмите, чтобы просмотреть содержимое.
Аналитические методы – Колледж физики главы 1-17
3 Двумерная кинематика
Резюме
- Понимание правил сложения и вычитания векторов с использованием аналитических методов.
- Применение аналитических методов для определения векторов вертикальной и горизонтальной составляющих.
- Применение аналитических методов для определения величины и направления результирующего вектора.
Аналитические методы сложения и вычитания векторов используют геометрию и простую тригонометрию, а не линейку и транспортир графических методов. Часть графической техники сохранена, потому что векторы по-прежнему представлены стрелками для облегчения визуализации. Однако аналитические методы более лаконичны, точны и точны, чем графические методы, которые ограничены точностью, с которой может быть выполнен чертеж. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины.
Аналитические методы и прямоугольные треугольники идут рука об руку в физике, потому что (среди прочего) движения вдоль перпендикулярных направлений независимы. Нам очень часто нужно разделить вектор на перпендикулярные компоненты.
Например, имея такой вектор, как [latex]\textbf{A}[/latex] на рисунке 1, мы можем захотеть найти, какие два перпендикулярных вектора, [latex]\boldsymbol{\textbf{A}_x}[/latex] и [латекс]\boldsymbol{\textbf{A}_y}[/латекс], добавьте, чтобы создать его.
[латекс]\boldsymbol{\textbf{A}_x}[/latex] и [латекс]\boldsymbol{\textbf{A}_y}[/latex] определены как компоненты [латекс]\textbf{A }[/latex]оси x и y. Три вектора[latex]\textbf{A},\:\boldsymbol{\textbf{A}_x},[/latex]и[latex]\boldsymbol{\textbf{A}_y}[/latex] образуют правый треугольник:
[латекс]\boldsymbol{\textbf{A}_x +\textbf{A}_y =\textbf{A}.}[/latex]
Обратите внимание, что эта связь между компонентами вектора и результирующим вектором сохраняется только для векторных величин (которые включают как величину, так и направление).
Отношения не применимы только к величинам. Например, если [латекс]\boldsymbol{\textbf{A}_x=3\textbf{м}}[/латекс]восток,[латекс]\boldsymbol{\textbf{A}_y=4\textbf{м}} [/latex]север и [latex]\boldsymbol{\textbf{A}=5\textbf{ m}}[/latex]северо-восток, то верно, что векторы[latex]\boldsymbol{\textbf{ A}_x+\textbf{A}_y=\textbf{A}}.[/latex]Тем не менее, это не правда, что сумма модулей векторов тоже равна. То есть
[латекс]\boldsymbol{3\textbf{м}+4\textbf{м}\neq 5\textbf{м}}[/латекс]
Таким образом,
[латекс]\boldsymbol{\textbf{A}_x+\textbf{A}_y\neq\textbf{A}}[/latex]
Если известен вектор[latex]\textbf{A}[/latex], то его величина[latex]\textbf{A}[/latex]и угол[latex]\boldsymbol{\theta}[/latex] (его направление) известны. Чтобы найти[latex]\boldsymbol{\textbf{A}_x}[/latex]и[latex]\boldsymbol{A_y},[/latex] его x- и y-компоненты, мы используем следующие соотношения для прямоугольного треугольника .
[латекс]\boldsymbol{\textbf{A}_x=\textbf{A cos}\:\theta}[/latex]
и
[латекс]\boldsymbol{\textbf{A}_y=\textbf{A sin}\:\theta}.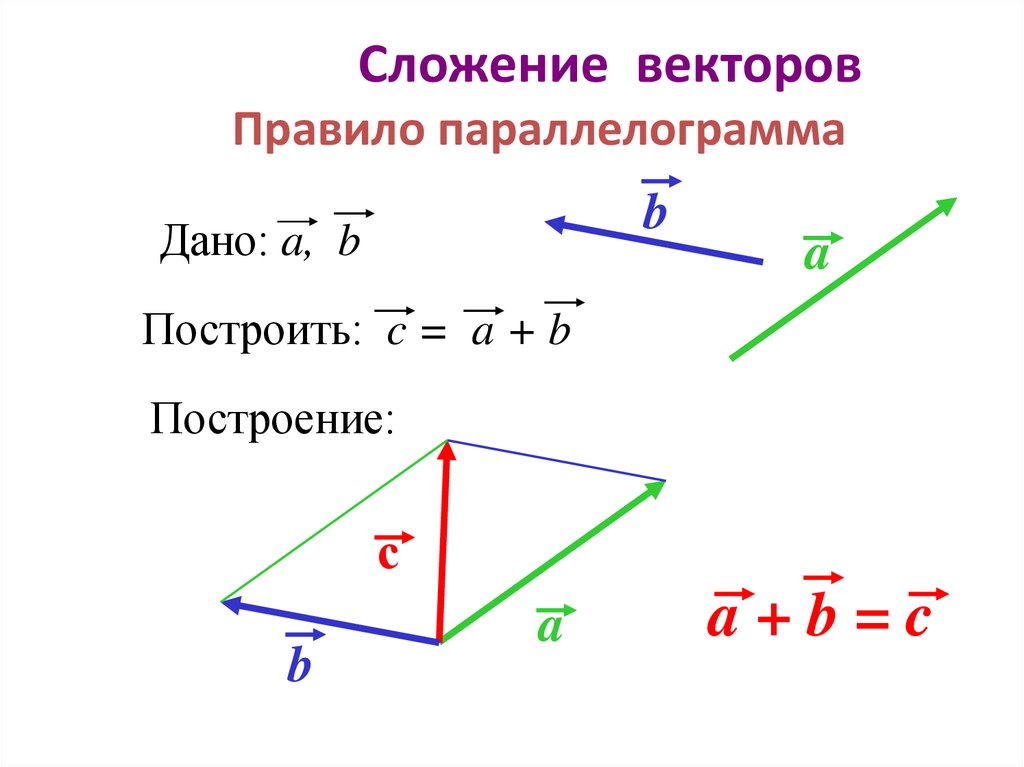
[/latex]
Предположим, например, что [latex]\textbf{A}[/latex] является вектором, представляющим полное перемещение человека, идущего по городу, рассмотренному в главе 3.1 «Кинематика в двух измерениях: введение» и главе 3.2 «Сложение векторов» и Вычитание: графические методы.
Рисунок 3. Мы можем использовать соотношения A x =A cos θ и A y =A sinθ 9о)=5.0\textbf{ блоков}.}[/latex] Если перпендикулярные компоненты [латекс]\boldsymbol{\textbf{A}_x}[/latex]и[латекс]\boldsymbol{\textbf{A}_y}[/latex]вектора[латекс]\textbf{A }[/latex] известны, то[latex]\textbf{A}[/latex]можно найти и аналитически. Чтобы найти величину[latex]\textbf{A}[/latex]и направление[latex]\boldsymbol{\theta}[/latex]вектора по его перпендикулярным компонентам[latex]\boldsymbol{\textbf{A}_x }[/latex]и[latex]\boldsymbol{\textbf{A}_y},[/latex]используем следующие соотношения: 9о},[/latex]как и раньше.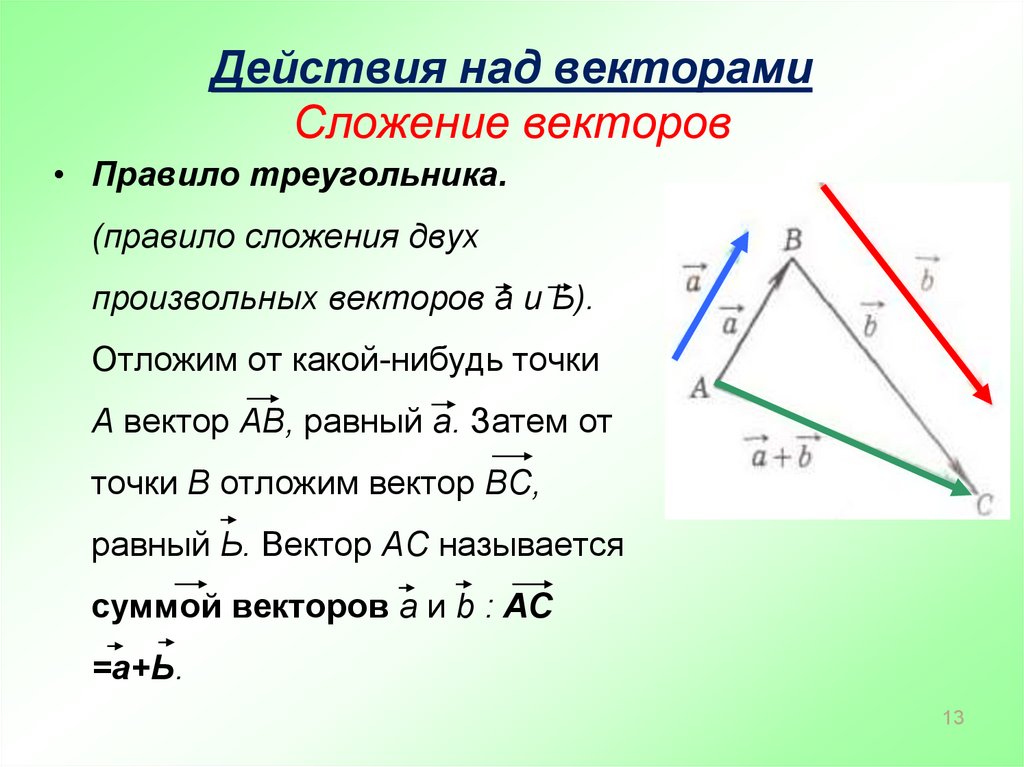
{-1}(\textbf{A}_y\:/\:\textbf{A}_x)}[/latex] используются для нахождения вектора по его перпендикулярным компонентам — то есть перейти от [латекс]\boldsymbol{\textbf{A}_x}[/latex]и[латекс]\boldsymbol{\textbf{A}_y}[/latex]к[латекс]\textbf{A }[/latex] и [latex]\boldsymbol{\theta}.[/latex] Оба процесса имеют решающее значение для аналитических методов сложения и вычитания векторов.
Чтобы увидеть, как складывать векторы, используя перпендикулярные компоненты, рассмотрите рисунок 5, на котором векторы[latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex]добавляются для получения результирующего [латекс]\textbf{R}.[/латекс]
Рис. 5. Векторы A и B — два участка пути, а R — равнодействующее или полное перемещение. Вы можете использовать аналитические методы для определения величины и направления R . Если[latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex]представляют два этапа ходьбы (два смещения), то[latex]\textbf{R}[/latex] ] — полное водоизмещение.
Человек, совершающий прогулку, оказывается на кончике[latex]\textbf{R}.[/latex]Есть много способов попасть в одну и ту же точку. В частности, человек мог ходить первым в 9{-1}(\textbf{A}_y\:/\:\textbf{A}_x)}.[/latex]При использовании аналитического метода сложения векторов можно определить компоненты или величину и направление вектор.
Шаг 1. Определите оси X и Y, которые будут использоваться в задаче. Затем найдите компоненты каждого вектора, которые должны быть добавлены вдоль выбранных перпендикулярных осей . Используйте уравнения [латекс]\boldsymbol{\textbf{A}_x=\textbf{A cos}\:\theta}[/latex]и[латекс]\boldsymbol{\textbf{A}_y=\textbf{A sin}\:\theta}[/latex], чтобы найти компоненты. На рисунке 6 этими компонентами являются [латекс]\boldsymbol{\textbf{A}_x},\boldsymbol{\textbf{A}_x},\boldsymbol{\textbf{B}_x},[/latex]и[латекс ]\boldsymbol{\textbf{B}_y}.[/latex]Углы, которые векторы[latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex]составляют с x -ось [латекс]\жирныйсимвол{\тета_{А}}[/латекс] и [латекс]\жирныйсимвол{\тета_{В}},[/латекс] соответственно.
Шаг 2. Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси . То есть, как показано на рисунке 7,
[латекс]\boldsymbol{\textbf{R}_x=\textbf{A}_x+\textbf{B}_x}[/latex]
и
[латекс]\boldsymbol{\textbf{R}_y=\textbf{A}_y+\textbf{B}_y.}[/latex]
Рисунок 7. Величина векторов A x и B x добавьте, чтобы получить величину R x результирующего вектора в горизонтальном направлении.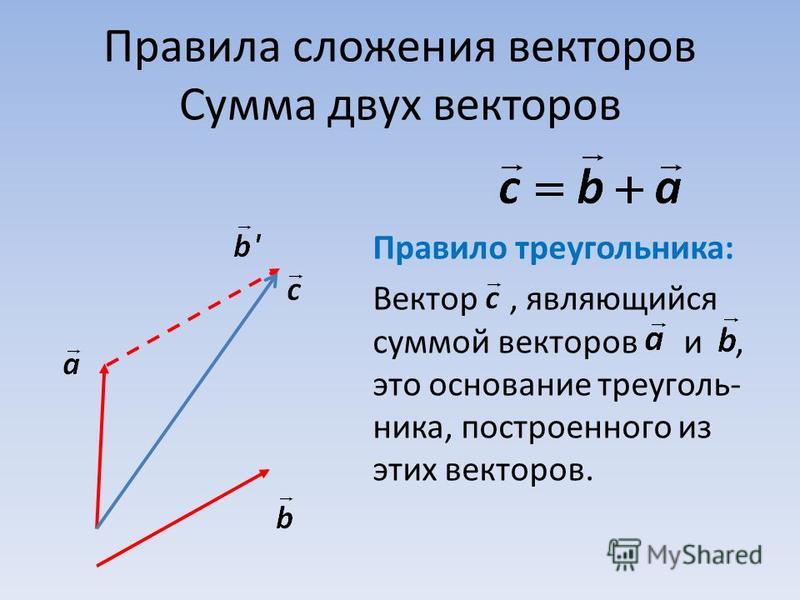
Точно так же величины векторов A y и B y складываются, чтобы получить величину R y 0 в вертикальном направлении результирующего вектора.Компоненты вдоль одной и той же оси, скажем, оси x , являются векторами вдоль одной и той же прямой и, таким образом, могут складываться друг с другом, как обычные числа. То же самое верно для компонентов вдоль y -ось. (Например, пройти 9 кварталов на восток можно двумя этапами: первые 3 квартала на восток и вторые 6 кварталов на восток, всего 9, потому что они идут в одном направлении.) Таким образом, разложение векторов на компоненты вдоль общие оси облегчают их добавление. Теперь, когда компоненты [латекса]\textbf{R}[/латекс] известны, можно найти его величину и направление.
Шаг 3. Чтобы получить величину[latex]\textbf{R}[/latex]результата, используйте теорему Пифагора: 9{-1}(\textbf{R}_y\:/\:\textbf{R}_x).
o} [/latex]северо-восток.
Стратегия
Компоненты [latex]\textbf{A}[/latex]и [latex]\textbf{B}[/latex] вдоль x 9о)}[/латекс]
[латекс]\жирныйсимвол{=(34,0\textbf{м})(0,891)=30,3\текстбф{м}.}\:\:\:\:\:[/латекс]
x — и y -компоненты равнодействующей, таким образом, равны
[латекс]\boldsymbol{\textbf{R}_x=\textbf{A}_x\:+\:\textbf{B}_x =49,8\textbf{м}\:+\:15,4\textbf{м}=65,2\textbf{м}}[/латекс]
и
[латекс]\boldsymbol{\textbf{R}_y=\textbf {A}_y\:+\:\textbf{B}_y=18.1\textbf{ m}\:+\:30.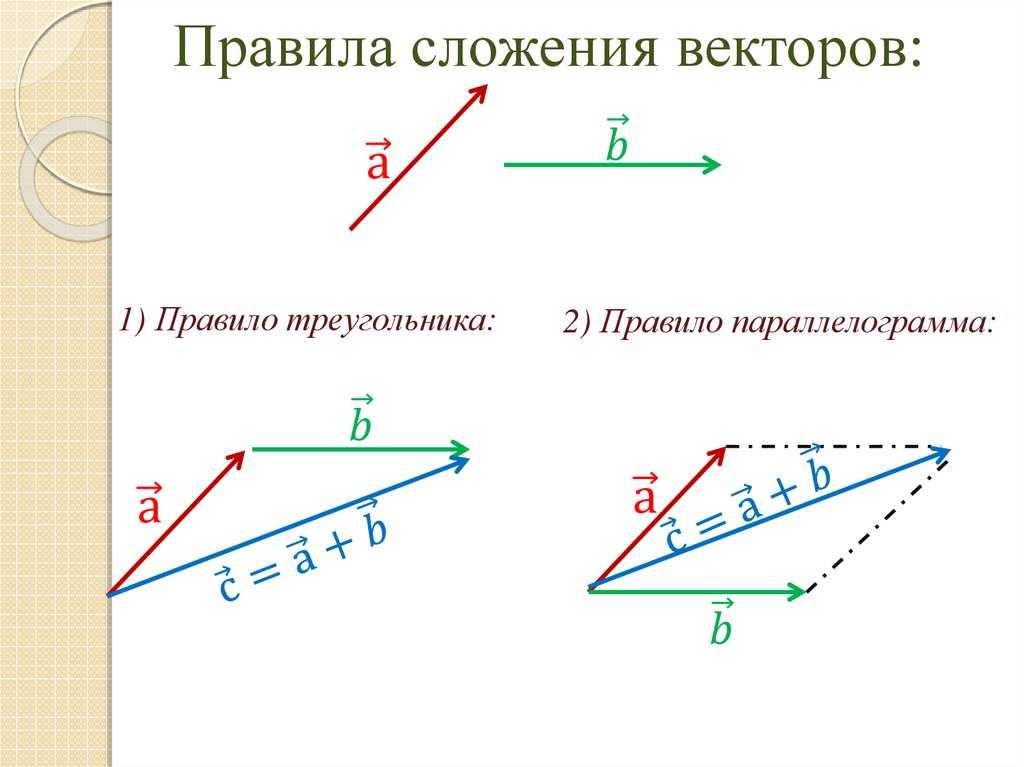
3\textbf{ m}=48.4\textbf{ m}.}[/latex]
Теперь мы можно найти величину равнодействующей, используя теорему Пифагора: 9o.}[/latex]
Рисунок 9. Используя аналитические методы, мы видим, что звездная величина R равна 81,2 м , а ее направление 36,6 0 к северу от востока.Обсуждение
Этот пример иллюстрирует сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание векторов осуществляется добавлением отрицательного вектора. То есть [латекс]\boldsymbol{\textbf{A}-\textbf{B}\equiv\textbf{A}+(-\textbf{B})}.[/latex] Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты [латекс]\boldsymbol{-\textbf{B}}[/latex]являются негативами компонентов [латекс]\textbf{B}.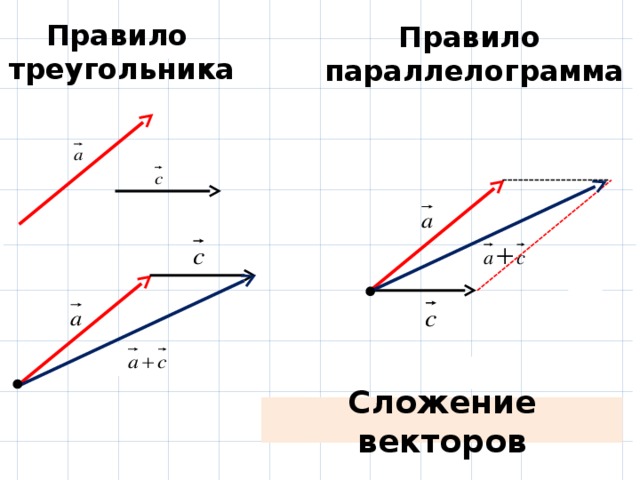
[/latex] x – и y – Таким образом, компоненты результирующего [латекса]\boldsymbol{\textbf{A}-\textbf{B}=\textbf{R}}[/latex] равны
[латекс]\boldsymbol{\textbf{R}_x=\ textbf{A}_x\:+\:(-\textbf{B}_x)}[/latex]
и
[латекс]\boldsymbol{\textbf{R}_y=\textbf{A}_y\: +\:(-\textbf{B}_y)}[/латекс]
, а в остальном метод, описанный выше, идентичен методу добавления. (См. рис. 10.)
Анализ векторов с использованием перпендикулярных компонент очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга. Следующий модуль, Глава 3.4 Движение снаряда, является одним из многих, в которых использование перпендикулярных компонентов помогает сделать картинку более ясной и упростить физику.
Рисунок 10. Вычитание двух векторов, показанных на рисунке 5. Компоненты -B являются минусами компонентов B . Метод вычитания такой же, как и для сложения.
ИССЛЕДОВАНИЯ PHET: ДОБАВЛЕНИЕ ВЕКТОРОВ
Узнайте, как добавлять векторы. Перетащите векторы на график, измените их длину и угол и суммируйте их вместе. Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах.
Рис. 11. Сложение векторов- Аналитический метод сложения и вычитания векторов включает использование теоремы Пифагора и тригонометрических тождеств для определения величины и направления результирующего вектора.
- Шаги для добавления векторов[latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex]с использованием аналитического метода следующие:
Шаг 1: Определите систему координат для векторов. Затем определите горизонтальную и вертикальную составляющие каждого вектора, используя уравнения
[латекс]\boldsymbol{\textbf{A}_x=\textbf{A cos}\:\theta}[/latex]
[латекс]\boldsymbol{\textbf{B}_x=\textbf{B cos}\:\theta}[/latex]
и
[латекс]\boldsymbol{\textbf{A}_y=\textbf{A sin}\:\theta}[/latex]
[латекс]\boldsymbol{\textbf{B}_y=\textbf{B sin}\:\theta}.
