| Осциллограмма | Fiziku5

Все биологические объекты Природы потребляют электрическую энергию, питающую, например, сердце, импульсами. Это самый экономный процесс её потребления. Все источники электрической энергии, изобретённые человеком, производят её непрерывно. Абсолютное большинство этой энергии также потребляется непрерывно и все приборы, учитывающие её расход, настроены на непрерывное напряжение, генерируемое первичными источниками энергии: генераторами электростанций, аккумуляторами и батареями. Так как напряжение и ток являются функциями изменения электрической энергии, то математики первые взялись за решение задачи правильного учёта её расхода. Сейчас мы увидим, как дорого обходится человечеству стремление носителей математических знаний присваивать себе роль судей в достоверности физических знаний. Ниже информация о том, как авторитет математики закрывает возможность выявления физических ошибок с глобальными последствиями.

В системе СИ энергия выражается в Джоулях (Дж).

Количество электрической энергии зависит от напряжения , тока и времени их действия и определяется зависимостью

. (25)

Чтобы иметь представление о величине энергии, генерируемой в одну секунду, введено понятие мощность. Она определяется по формуле

. (26)

Когда напряжение и ток непрерывны (рис. 46), то отдельное интегрирование функций напряжения и тока даёт их средние величины:

; (27)

(28)

и формула для расчёта средней мощности принимает простой вид

. (29)

На рис. 46. Постоянное напряжение, средняя величина которого обозначена , а средняя величина тока — . Они непрерывны и мощность, генерируемая ими, определяется по зависимости (26).

Если изменения напряжения и тока имеют более сложный вид и эти изменения можно выразить аналитическими функциями напряжения и тока , то средняя электрическая мощность рассчитывается по формуле (26). Она позволяет получить аналитический результат, если функции напряжения и тока изменяются непрерывно и выражаются аналитическими зависимостями, например, синусоидами.

При производстве или потреблении электроэнергии импульсами напряжения и тока формула (26) исключает возможность получения аналитического результата, так как аналитические функции напряжения и тока теряют непрерывность и превращаются в периодические или хаотические импульсы (рис. 47).

Рис. 46. Осциллограмма напряжения и тока на клеммах аккумулятора и лампочки

а)

b)

Рис. 47. а) периодические импульсы тока; b) хаотические импульсы тока

Вполне естественно, что невозможно составить аналитические функции изменения импульсов тока, представленных на осциллограммах (рис. 47). Поэтому в таких случаях используется эмпирический метод графического интегрирования уже не функций, а экспериментальных зависимостей изменения тока или напряжения во времени (рис. 47). Проанализируем этот метод на примере осциллограммы импульсного питания лампочки, подключённой к аккумулятору (рис.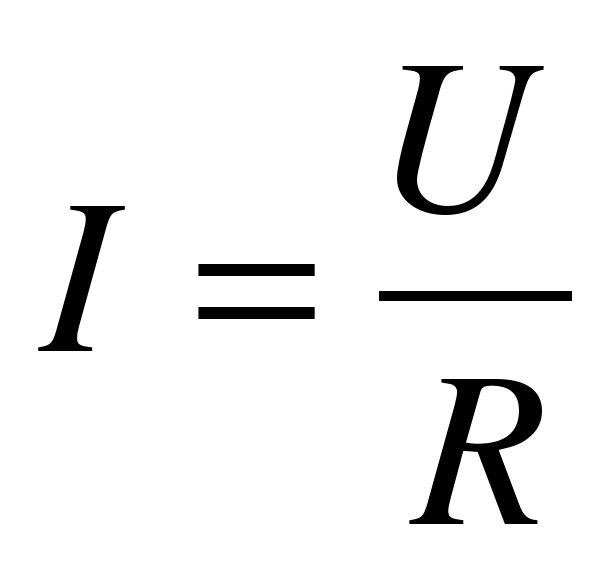

48).

Известно, что при подключении нагрузки к аккумулятору его номинальное напряжение уменьшается или, как говорят, падает. Если нагрузку подключать импульсно, то и напряжение будет падать импульсами. Ток тоже будет появляться импульсами (рис. 48). Для характеристики этих импульсов введены понятия амплитуда и длительность импульса. На рис. 48 амплитуда напряжения, упавшего после подключения нагрузки, обозначена символом , а амплитуда тока – символом . Как видно, импульсы напряжения и тока прямоугольные. Их длительность обозначена символом . Импульсы напряжения и тока появляются периодически. Длительность периода обозначена символом .

Математическая программа, заложенная в осциллограф, базируется на формуле (26) и позволяет определять средние значения напряжения , тока и мощности . Проанализируем процесс её работы. Предварительно отметим, что программа составлена так, что она может измерять десятки тысяч ординат, меняющейся величины в секунду.

Рис. 48. Осциллограмма импульсной разрядки аккумулятора

Итак, математическая программа графического интегрирования, составленная на основе уравнения (26), начинает измерять ординаты напряжения и тока с начала формирования импульсов (рис.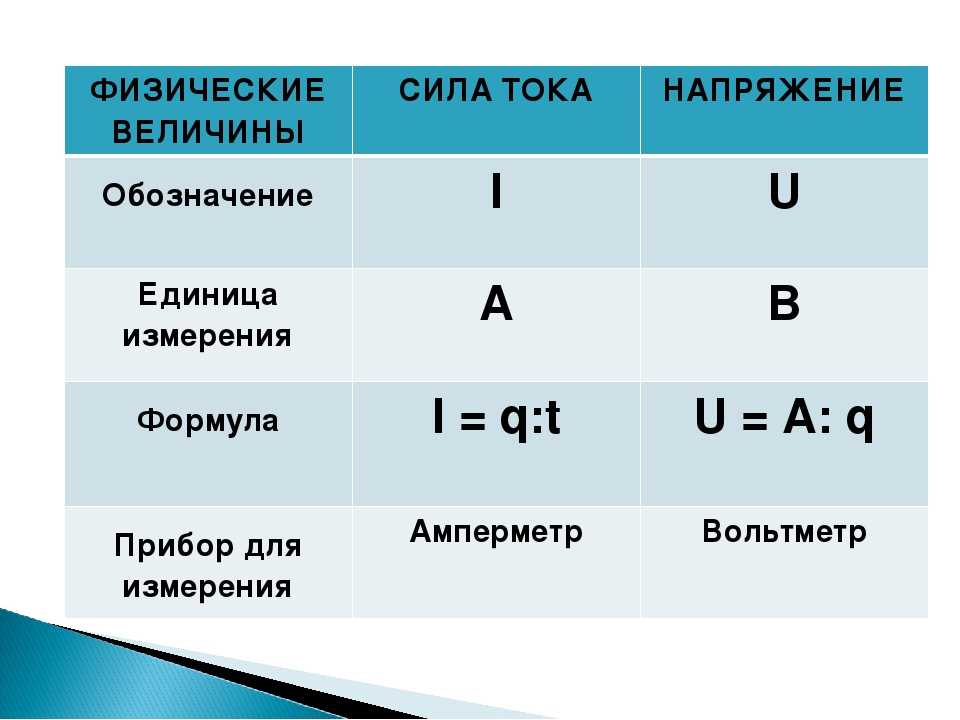

48, точка А). Измерив первые ординаты напряжения и тока , она перемножает их. Затем измеряет вторые, третьи и т. д. ординаты, перемножает их и складывает произведения. В интервале нет тока, его ординаты равны нулю, а напряжение есть, поэтому произведения реальных ординат напряжения на нулевые ординаты тока, в этом интервале, дают нулевой результат. Однако программа учитывает количество произведений нулевых ординат тока и реальных ординат напряжения в интервале . Зачем она это делает? Затем, чтобы в общую сумму произведений ординат вошло и количество произведений с нулевыми значениями. Эта процедура эквивалентна делению суммы произведений ординат напряжения и тока на скважность импульсов, равную . Параллельно с описанным процессом программа делит суммы ординат напряжения на количество их ординат и суммы ординат тока на количество ординат тока в интервале периода с учетом нулевых значений его ординат. Так как у напряжения нет ординат с нулевым значением, то в результате его средняя величина оказывается достаточно большой.

Обозначим её символом и назовём эту величину фиктивной средней величиной напряжения. Причину придания этой величине среднего напряжения фиктивного значения проясним ниже. Поскольку количество ординат у напряжения и тока, снятых в интервале периода одинаковое и поскольку у тока большая часть ординат равна нулю, то деление суммы ординат тока, снятых в интервале периода на количество ординат значительно уменьшает среднюю величину. Это реальная средняя величина тока в интервале периода, поэтому обозначим её символом . В результате описанной процедуры определения средней величины тока в интервале периода узкий импульс тока с амплитудой превратился в продольный прямоугольник с ординатой , заполняющий интервал всего периода. Эта операция эквивалентна делению амплитуды импульса тока на скважность импульсов.

. (30)

Теперь мы видим (рис. 48), что величина тока действует непрерывно в интервале всего периода . Это соответствует определению понятия Ватт в системе СИ. Величина среднего напряжения тоже действует непрерывно в интервале всего периода и создаётся впечатление, что она тоже соответствует определению Ватт системы СИ, требующей непрерывного действия напряжения и тока в течение одной секунды.

Так как секунды складываются из периодов, то значит и — в течение периода. Из этого следует, что средняя мощность должна определяться по формуле

. (31)

Так как описанная процедура графического интегрирования экспериментальных зависимостей напряжения и тока, представленных на рис. 48, аналогична аналитическому интегрированию непрерывных аналитических функций изменения напряжения и тока, то у нас есть основание показать стрелкой переход уравнения (26) к результату графического интегрирования экспериментальных зависимостей напряжения и тока, представленных на рис. 48.

. (32)

Обратим внимание на то, что в конце этой формулы величину средней мощности мы обозначили символом , и показали, что скважности импульсов принадлежит импульсам тока, так как напряжение вошло в эту формулу своей средней величиной , которую мы назвали фиктивной.

Отметим, что конечная часть формулы (32) встречается в учебниках [3]. Посмотрим, отражает ли она реальность? Для этого внимательно присмотримся к рис.

48. Мы видим явные импульсы напряжения и тока с одинаковой длительностью . Мы видим также, что в интервале ток явно равен нулю, а напряжение не равно нулю. Это четко отражено и в конечном результате формулы (32). Кажется, всё логично и соответствует реальности [6]. И, тем не менее, у нас возникает вопрос: как понимать физику процесса падения напряжения аккумулятора только в интервале длительности импульса и восстановления его номинального значения сразу после импульса, в интервале (рис. 48, точки С и D)?

Ответ очевиден. Напряжение участвует в процессе формирования средней величины импульсной мощности только в интервале длительности импульса и не участвует в интервале остальной части периода . Следующий вопрос: как понимать присутствие в формулах (31) и (32) полной средней величины напряжения , которую мы назвали фиктивной? Ответ очевиден. Присутствие полной средней величины напряжения в указанных формулах означает, что напряжение всей своей средней величиной участвует в формировании средней импульсной мощности не в интервале только длительности импульса , а в интервале всего периода .

Но ведь это противоречит осциллограмме (рис. 48). Там явно видно, что напряжение всей своей средней величиной участвует в формировании средней импульсной мощности , которую мы также назвали фиктивной, только в интервале длительности импульса . Что делать?

Ответ простой. Мы явно видим (рис. 48), что для учета неучастия средней величины напряжения в интервале надо её среднюю импульсную величину , которая в этом случае близка к её амплитудному значению , растянуть на длительность всего периода , то есть разделить на скважность импульсов. Вполне естественно, что для удобства практического использования конечной части формулы среднюю импульсную величину тока надо также заменить её амплитудным значением Тогда формула (32) приобретает вид

. (33)

Как проверить экспериментально достоверность формулы (33), уже названной новым законом формирования средней импульсной электрической мощности? [5], [6]. Ответ на этот вопрос следует из осциллограммы на рис. 48. Надо взять импульсный потребитель электрической энергии и подключить его к аккумулятору. Записать осциллограмму на клеммах аккумулятора и потребителя, рассчитать величину средней мощности, следующую из этой осциллограммы по формулам (32) и (33) и проследить за скоростью падения напряжения аккумулятора. При этом желательно не выходить за рекомендуемый интервал максимальной разрядки аккумулятора. Если это 12-ти вольтовый аккумулятор, то указанный интервал 12,5-11,0В.

В качестве доказательства достоверности нового закона формирования электрической мощности (33) проследим за скоростью падения напряжения на клеммах аккумулятора, питающего мотор – генератор МГ-2 импульсами напрямую, без каких либо промежуточных электронных устройств. Роль мотора у него выполняет ротор, а роль генератора – статор (рис. 49) [5], [6].

Электричество — подробное содержание

Дом >> Электричество, мощность и энергия

энергия

мощность

кВтч

Переменный ток

 

 

Энергия

 

Чтобы понять, как преобразуется энергия, рассмотрим простую схему с «нагрузочным» * резистором и источником постоянного тока.
* это может быть нагревательный элемент, двигатель или любой компонент с сопротивлением

 

 

 

 

Заряд теряет потенциальную энергию (PE) при прохождении через резистор. Этот электрический PE преобразуется в основном в тепловую энергию, рассеиваемую в резисторе.

PE определяется как*:

 

работа = заряд x разность потенциалов

 

Вт = QV

 

(Джоули) = (Кулоны) x (Вольты)

 

 

*дополнительную информацию об этом уравнении см. в определении вольта

 

 

С,

 

заряд = (ток) x (время прохождения тока)

 

Q = Это

 

(Кулоны) = (Ампер) x (секунды)

 

 

поэтому, заменив Q в уравнении работы,

 

Вт = (Ит)В

 

перестановка,

 

Вт = Вит

 

 

вернуться к началу

 

 

Мощность

 

По определению, «мощность» — это скорость работы, равная выполненной работе, деленной на затраченное время.

 

 

 

вместо W

 

отмена т

 

 

 

(Ватт) = (Вольт) x (Ампер)

 

 

примечание: 1 ватт — это скорость работы 1 джоуль в секунду.

 

 

 

Уравнение для мощности можно изменить, если мы сделаем замены, используя Закон Ома .

 

 

 

 

подставляя в уравнение мощности В ,

 

 

подставляя в уравнение степени I ,

 

 

 

вернуться к началу

 

 

Киловатт-час (кВтч)

 

Киловатт-час — единица энергии.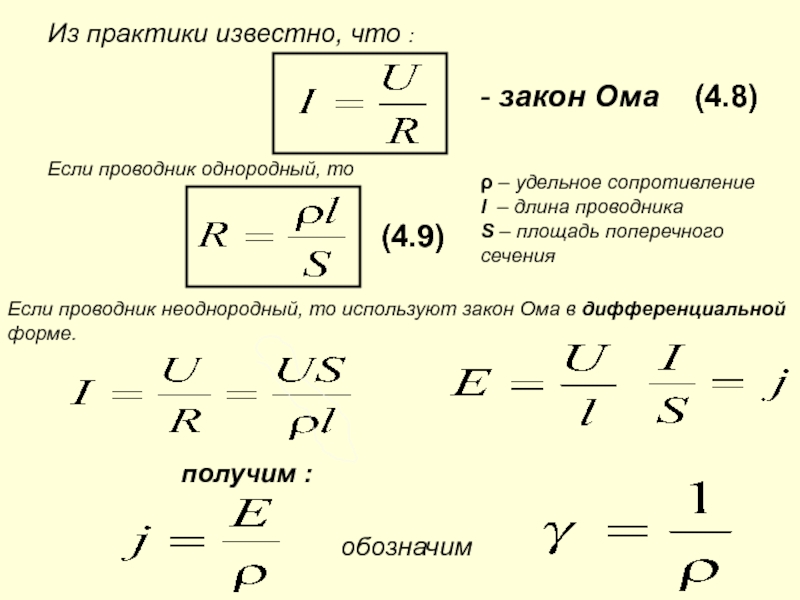

 

По определению, киловатт-час – это количество энергии, потребляемой при «рабочей скорости» (мощности) 1 киловатт в течение 1 часа.

 

преобразование 1 кВтч в джоули:

 

1 кВтч = 1 кВт x 1 ч = 1000 Вт x 3600 с = 3600000 Дж

 

1 кВтч = 3,6 x 10 ⁶ Дж

 

 

вернуться к началу

 

 

Энергия постоянного тока (D.C.) и переменного тока (AC)

 

Постоянный ток не меняется со временем и всегда в одном направлении.

 

На графике зависимости мощности от времени постоянный ток представляет собой горизонтальную линию.

 

Площадь под графиком показывает общую проделанную работу/затраченную энергию.

Это просто произведение постоянной мощности ( P _const. ) и интервала времени, в течение которого мощность используется ( t ^‘ ).

 

 

 

 

 

 

Однако для А.С. ситуация более сложная.

 

Здесь меняется не только значение тока, но и его направление.

 

Мощность через резистор определяется как:

 

 

Но мы должны взять среднее значение этой мощности за время t, чтобы рассчитать энергию/работу.

 

Таким образом, энергия/работа определяется выражением

.

 

 

 

Среднеквадратичное значение ( RMS ) ток определяется как:

 

 

I _RMS — квадратный корень из среднего значения тока в квадрате.

 

Следовательно, энергия/работа определяется как

.

 

 

I _{Среднеквадратичное значение} — эквивалентный постоянный ток, оказывающий такое же воздействие на резистор, как и переменный ток

Вот график синусоидального сигнала переменного тока:

 

 

 

где,

 

I o максимальный ток

ω – угловая частота, ω = 2πf ( π pi , f частота)

 

 

 

 

 

 

 

 

 

 

 

 

 

Вызов уравнения энергии переменного тока/совершенной работы,

 

 

и заменяющий I _RMS

 

 

 

 

 

Следовательно, в момент времени t ^‘ энергия W, рассеиваемая на резисторе R, определяется выражением:

 

 

 

примечание : во избежание путаницы между W в уравнениях и W на графике

 

 

P (Вт) на графике означает мощность P в ваттах.

Вт в уравнениях — это энергия/совершенная работа

 

 

 

вернуться к началу

 

Лист формул — V(Напряжение)=I(Ток)×R(Сопротивление). Кроме того, P(мощность)=V(напряжение)×I(ток)

V(напряжение)=I(ток)×R(сопротивление). Кроме того, P (мощность) = V (напряжение) × I (ток). Гальванометр в вольтметр — последовательное внешнее сопротивление Гальванометр в амперметр – внешнее сопротивление параллельно

Серия: Rtotal=R 1 +R 2 +R 3 +… Ток тот же.

Параллельный:

1

Rtotal

= 1

R 1

+ 1

R 2

+ 1

R 3

+… Напряжение одинаковое.

В 2 =Vэлектропитание( 1 −e

−t RC) Удельное сопротивление, ρ=RA L, где L – длина.

q=Qoe

−t

RC Q=CV – Определение емкости – C=

ε 0 A г τ=RC – C – емкость, R – сопротивление V=Ed

q=ne – q – заряд, n – количество протонов, e – заряд протона/электрона

F=k¿q 1 q 2 ∨¿ r 2

¿ – Электростатическая сила между двумя точечными зарядами, разделенными расстоянием (r)

F=k¿q 1 q 2 ∨¿ r 2

+k¿q 3 q 2 ∨¿ r 2

¿ ¿ – Сила действия обоих зарядов q 1 и q 3 на заряд q 2

E=kq r 2

– электрическое поле заряда, E.

Также E=

kQr 1 R 3

, если r 1

F=qE a=qE/m

Ex= 2 πkσ( 1 −

х √x 2 +R 2 )

– Электрическое поле, создаваемое заряженным диском в точке на его осевой линии

τ=p× E – Максимальный крутящий момент, где p – электрический дипольный момент, а E – электрическое поле

φ=EA – Электрический поток – φ=¿E∙ A∨¿

φ=q

ε 0 – Электрический поток через замкнутую поверхность

V=

кЭкв r

– Уравнение для электрического потенциала

Потенциал в третьей точке от двухточечных зарядов: V(r)=

ккал 1 |r−r 1 |

+

ккв 2 ¿r−r 2 ∨¿ ¿

Общий электрический потенциал: V=∑kq r

=

k q 1 г

+

к кв 2 r

U=

кэкв 1 q 2 r

– Уравнение для электрической потенциальной энергии. Кроме того, U=Vq.

Изменение потенциала, ∆V=Ed E∙dl=ElCos(θ)ЭДС:ε=IT×RTобщ.