| Общий взгляд на интегральный закон Ома
Видно, что уравнения (1) и (1’) не являются линейно независимыми: (1’) получается из (1) почленным умножением на -1. Поэтому мы имеем три линейно независимых уравнения:
относительно трёх неизвестных:
§17.8. Общий взгляд на интегральный закон Ома.
Рис.17.11
Вы заметили, что I-я и III-я формы закона Ома получаются из II-ой обнулением соответствующих членов равенства? Точно так же и формула практического определения ЭДС. Значит, II-я форма закона Ома является центральной для теории тока. Всю теорию можно изобразить в виде «конверта» с центральной печатью и с печатями по углам (рис.17.11). На четвёртый угол «обнулений» уже не хватает. Четвёртая печать получается через почленное умножение закона Ома на силу тока. А каков физический смысл этого математического действия, Вы узнаете из следующего параграфа.
§17.9. Закон Джоуля-Ленца в интегральной форме
Этот параграф наиболее важный из всей лекции, поскольку он касается вопроса: «для чего нам нужен электрический ток?».
Умножим закон Ома для неоднородного участка цепи на силу тока на участке:
® ,
и рассмотрим физический смысл каждого полученного члена.
. Но тепло, выделяемое при протекании единицы заряда , следовательно, — тепловая мощность участка, или количество тепла, выделяемое на участке в единицу времени, благодаря протеканию по участку электрического тока.
. Но сброс механической энергии единицы заряда на участке , следовательно, — электрическая мощность участка, или количество механической энергии носителей заряда (электроэнергии), приносимой ими на данный участок и сбрасываемой на нём в единицу времени. С этим членом как раз и связан ответ на вопрос, заданный в начале параграфа.
Смысл последнего слагаемого мы будем раскрывать для каждого знака по отдельности, и начнём со знака минус, то есть с участка потребителя.
, где Nпотр — мощность потребителя, то есть количество энергии, которое электроприбор выделяет в единицу времени в том виде, в каком нужно нам. Здесь становится ясен «потребительский» смысл отрицательных ЭДС. Это такое свойство различных технических устройств, благодаря которому на устройстве происходит обмен электроэнергии на другие виды энергии, нужной потребителю (кроме тепловой). Отрицательная ЭДС в электродвигателях связана с обменом электроэнергии на механическую энергию; в лампах дневного света, светодиодах — на световую; в динамиках — на акустическую; в заряжающихся аккумуляторах — на электрохимическую.
Теперь подставим выявленные физические смыслы в закон Ома для участка потребителя, почленно умноженный на силу тока:
Þ
Þ .
Полученное соотношение означает, что количество энергии, получаемое потребителем в единицу времени, равно электроэнергии, получаемой участком потребителя, за вычетом тепла, выделяемого на участке.
Частным случаем участка потребителя является нагреватель, то есть однородный участок цепи. Поскольку на нём отсутствует ЭДС, то закон Джоуля-Ленца примет вид:
.
Домножив и разделив правую сторону равенства на R получим: с учётом закона Ома для однородного участка. Тогда получаем три эквивалентных выражения мощности участка нагревателя: электрической и двух тепловых:
.
При этом выражение тепловой мощности справедливо только на участке нагревателя.
В случае участка источника произведение называется мощностью источника.
Теперь мы можем легко записать соотношение мощностей на участке источника:
Þ
Þ .
Если электрическая мощность участка Nэл равна скорости потребления участком механической энергии носителей, то , наоборот, равна скорости передачи энергии от участка носителям. Значит, энергия, вырабатываемая источником положительной ЭДС в единицу времени, частично поглощается на самом участке источника и выделяется в виде тепла, а её остаток в виде механической энергии носителей уходит за пределы участка.
Законом Джоуля-Ленца можно назвать всю совокупность выражений мощностей, связанных с электрическим током: тепловой, электрической, потребителя и источника. Таким образом, умножая почленно закон Ома на силу тока, мы приходим к закону Джоуля-Ленца. Этот закон является самым важным с практической точки зрения законом теории тока. Ведь из него понятно, зачем нужен электрический ток: для того, чтобы донести энергию от источников потребителям.
§17.10. Закон Джоуля-Ленца в дифференциальной форме
Рассмотрим скалярное произведение плотности тока на напряжённость движущей силы:
Выражение , стоящее в числителе, представляет собой мощность электрических и сторонних сил, имеющую место в элементарном объёме проводника dV. Следовательно, скалярное произведение представляет собой объёмную плотность мощности этих сил.
В стационарном случае заряд dq находится в равновесии, а значит, элементарная работа и мощность его равнодействующей равна 0.
Следовательно, мощность движущей силы по модулю равна мощности силы сопротивления, то есть тепловой мощности. Итак, объёмная плотность движущей силы равна объёмной плотности тепловой мощности
Вспомним закон Ома в дифференциальной форме: . Умножим скалярно обе части этого равенства на вектор :
.
Поскольку, в левой части стоит объёмная плотность мощности движущей силы, то правая часть представляет собой объёмную плотность тепловой мощности. Её можно выразить также через плотность тока и удельное сопротивление, используя выражение напряжённости из дифференциального закона Ома: Итак, мы получили выражение объёмной плотности тепловой мощности в случае стационарного поля плотности тока:
Каков физический смысл 2-го закона Ньютона? : Дискуссионные темы (Ф)
Munin писал(а):
Ещё сложение физического смысла не имеет.
Величин разной размерности — нет.
Munin писал(а):
И вообще цифры.
Так что если вам линейка или вольтметр показывают 12, не верьте глазам своим.
Не цифры, а числа.
Вольтметром мы сравниваем значение измеряемой величины с эталоном.
Сравнивать удобнее всего с помощью чисел: ставим в соответствие значениям числа, а потом сравниваем числа.
Представьте, что чисел и математики вообще нет; вопрос: перестанет ли от этого существовать физика?
Если перестанет, то она есть только раздел математики, разве не так?
Munin писал(а):
Это не закон, а принцип наименьшего действия.
Если указан конкретный вид функционала действия, запись его совершенно эквивалентна записи уравнений движения.
Это просто одно и то же.
Чем-то иным оно станет, если добавить правило выбора конкретного вида функционала действия.
Тогда же всё сведётся опять к физическому смыслу того правила.
Одних соображений инвариантности относительно группы Галилея не хватит (уже физический смысл массы явно неясен).
Munin писал(а):
Тогда это уравнение движения, которое можно использовать либо для решения основной задачи механики, либо для решения обратной задачи механики.
Разумеется, только чуть наоборот: из законов физики следуют уравнения движения.
Интересует именно то, что именно утверждают те законы…
Munin писал(а):
Не бывает физического смысла без расчёта.
Это очень и очень жаль…
Добавлено спустя 25 минут 53 секунды:
chiba писал(а):
Потому что слева стоит не сила, а производная импульса по времени.
Почему производная от импульса не может быть силой в том же смысле как это сила Гука?
chiba писал(а):
II закон Ньютона только устанавливает между этими физическими величинами равенство (причем только в строго определенных случаях)
Измеримые величины тут импульс и сила.
Чтобы размерность совпала в левой части стоит производная (считай — отношение).
Отношение двух физических величин имеет смысл, только как новая физвеличина — нужно изготовить новый эталон.
Ситуация аналогична оной с площадью: чтобы измерять площадь потребуется два прибора, а не один — линейка и угольник, например, — одной линейки не достаточно.
Говоря «устанавливает между этими физическими величинами равенство» Вы утверждаете, по сути, то же, что площадь можно измерять одной линейкой — просто умножая стороны квадрата.
chiba писал(а):
Думаю, что в этом случае надо быть конкретнее.
Не возражаю быть конкретнее, но принципиальную разницу между этими двумя частными случаями вижу слабо.
chiba писал(а):
Скорость изменения импульса (есть такая физическая величина, у которой есть свой физический смысл).
Если бы был отдельный эталон для скорости изменения импульса.
Но есть набор фундаментальных величин, по которым мы строим, например, систему единиц.
Здесь такие величины сила и импульс, а физический смысл скорости изменения импульса мы уже выводим из второго закона.
Можно взять вместо импульса скорость импульса (строго говоря, как раз и нельзя, если силу не заменить чем-то другим), но тогда всё переформулируется по отношению к другому набору фундаментальных величин…
chiba писал(а):
Во-первых, я не пойму в чем неточность? Я где-то сказал, что у меня справа стоит одна только сила?
Вы говорите, что второй закон — это правило, по которому, например, можно найти изменение импульса, зная силу и интервал времени.
Проблема только в том, как именно найти: для того придётся умножить на , а умножение величин разной размерности — это что такое физически?
chiba писал(а):
Во-вторых, не пойму причем здесь рассуждения о смысле операций? Вы хотите сепарировать силу от времени?
Нет.
Я не понимаю физсмысла умножения величин разной размерности.
chiba писал(а):
Munin уже ответил. Я только поясню, что у него записан принцип экстремального (минимального) действия.
Здесь термин «действие» это строго определяемая в физике величина, которая имеет размерность и часто обозначается буквой ,
Это так, но, чтобы получить уравнения движения одного измерения действия не достаточно: нужо ещё задать конкретный вид функционала действия.
Поэтому принцип наименьшего действия — это лишь иная форма записи уравнений движения.
chiba писал(а):
Вы хотите вернуться в доньютоновские времена и порассуждать о божественной природе импульса?
Божественная сила тут больше подходит…
Но, если серьёзно, то в какой-то степени да: представим, что математики нет совсем — сможет ли в таких условиях функционироать физика?
tolstopuz писал(а):
Может быть, закон Ома утверждает нечто вроде: цепь сопротивляется току с напряжением, равным приложенному напряжению?
Если природа этих законов действительно одна, то — разумеется.
Что такое закон Ома? (с картинками)
`;
Наука
Факт проверен
Каризе Уй
Закон Ома — это закон, используемый в физике, который в основном объясняет, как электричество работает должным образом в простой цепи. Чтобы объяснить электрический процесс, закон показывает, как три элемента электричества — ампер, сопротивление и напряжение — работают вместе, чтобы создать функционирующую электрическую цепь. Закон гласит, что количество электрического тока, измеряемого в амперах, протекающего через проводник, пропорционально или равно напряжению, но обратно пропорционально сопротивлению в проводнике.
Работая профессором в иезуитской гимназии Кельна в Германии, он экспериментировал и наблюдал за поведением электричества в простых цепях с проводами разной длины. Он описал и задокументировал все результаты в книге «Гальваническая цепь, исследованная математически», которая сначала была отвергнута, но позже признана, что привело к установлению закона Ома.0003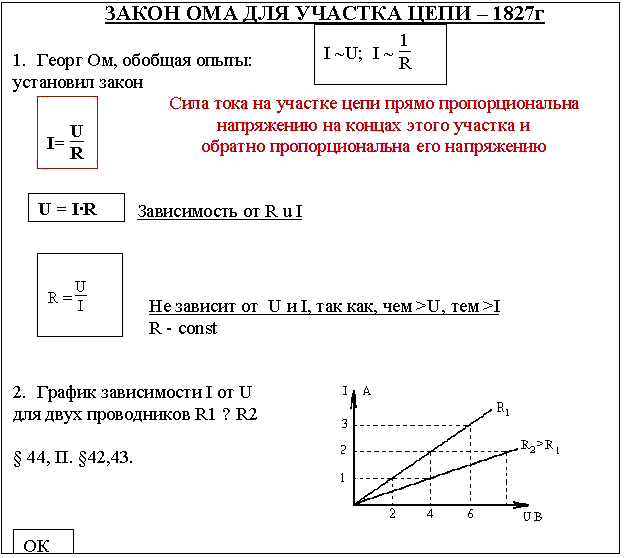
Есть по существу три «истинных» утверждения, которые следует помнить в отношении закона Ома. Первое утверждение состоит в том, что значение I будет увеличиваться или уменьшаться, если значение V соответственно увеличивается или уменьшается. Второе утверждение состоит в том, что значение I уменьшится, если значение R увеличится, а значение V не изменится.
Третье утверждение состоит в том, что значение I увеличится, если значение R уменьшится, а значение V останется прежним.
Принцип закона Ома может быть практически применен в приборах и любом оборудовании, работающем от электричества или батареи. Например, простому светоизлучающему диоду (LED) требуется всего 2 вольта и 0,02 ампера, чтобы загореться, но он подключен к 6-вольтовой батарее. Это может привести к короткому замыканию светодиода, и для уменьшения тока необходим резистор. Используя формулу R = V/I, можно определить, что резистор, содержащий 200 Ом, необходим для управления током, поступающим в светодиод.
Вам также может понравиться
Рекомендуется
КАК ПОКАЗАНО НА:
Что такое закон Ома?
by Veerendra
Что такое закон Ома?
- Пропорциональная зависимость разности потенциалов между концами идеального проводника и протекающего по нему тока известна как закон Ома .
- Закон Ома утверждает , что ток, проходящий через идеальный проводник, прямо пропорционален разности потенциалов между его концами при условии, что температура и другие физические факторы проводника остаются постоянными.
- Определение: В соответствии с законом Ома при постоянной температуре ток, протекающий через проводник, прямо пропорционален разности потенциалов на проводнике.
- Таким образом, если I — ток, протекающий по проводнику, а V — разность потенциалов (или напряжение) на проводнике, то по закону Ома.
I ∝ V (когда T постоянна)
\(I=\frac{V}{R}\text{ }…..\text{ (i)}\)
где R — константа, называемая сопротивлением проводник.
Уравнение (i) может быть записано как
V = I × R …… (ii) - Единица сопротивления:
Единицей сопротивления в системе СИ (R) является ом. Ом обозначается греческой буквой омега (Ω).
\( \text{Из закона Ома, }R=\frac{V}{I} \) - Теперь, если V = 1 вольт и I = 1 ампер
\( \text{Тогда, }R=\ frac{\text{1}\,\text{вольт}}{\text{1}\,\text{ампер}} \)
Таким образом, 1 Ом определяется как сопротивление проводника, по которому может протекать ток силой 1 ампер, когда на нем поддерживается разность потенциалов 1 вольт. - Результаты закона Ома
Ток, протекающий через проводник, прямо пропорционален разности потенциалов на проводнике. - Когда разность потенциалов в цепи поддерживается постоянной, ток обратно пропорционален сопротивлению проводника.
\( I\propto \frac{1}{R} \) - Отношение разности потенциалов к току постоянно. Значение константы равно сопротивлению проводника (или резистора).
\( \frac{V}{I}=R \)
Люди также спрашивают
- Как длина провода влияет на сопротивление?
- Как площадь поперечного сечения влияет на сопротивление?
- Какое определение сопротивления в физике?
- Как температура влияет на сопротивление провода?
- Когда к проводнику приложена разность потенциалов 12 В, сила тока, проходящего через проводник, равна 0,2 А. Чему равно сопротивление проводника?
Решение:
\( R = \frac{V}{I} \)
= 12/0,2
= 60 Ом - Чему равна разность потенциалов на лампочке сопротивлением 5 Ом при протекании тока через это 0,5А?
Решение:
В = I × R
= 0,5 × 5 = 2,5 В - К электрическому нагревателю приложена разность потенциалов 230 В. Через нагревательный элемент нагревателя протекает ток силой 5 А.
(а) Каково сопротивление нагревательного элемента?
(b) Можно ли использовать этот электронагреватель в стране, где напряжение сети составляет 110 В? Поясните свой ответ.
Решение:
(a) \( R = \frac{V}{I} \)
= 230/5
= 46 Ом
(b) Нагреватель все еще можно использовать, но эффект нагрева будет очень сильным меньше, поскольку ток, проходящий через нагреватель, намного меньше. Ток, проходящий через нагреватель, равен:
\( I = \frac{V}{R} \)
= 110/46
= 2,4 А
Это значение меньше 5 А. - Электродвигатель с внутренним сопротивлением 10 Ом может работать при определенной скорости при протекании через него тока силой 0,5 А. Скорость двигателя увеличивается, когда к нему прикладывается разность потенциалов, в два раза превышающая прежнюю. Какой новый ток проходит через двигатель?
Решение:
Разность потенциалов на двигателе при прохождении через него тока 0,5 А:
В = IR = 0,5 x 10 = 5 В
При удвоении разности потенциалов
2 x 5 = I x 10
I = 1 А
Через нагревательный элемент нагревателя протекает ток силой 5 А. Из чего состоит сверхпроводник?
- Большинство материалов имеют электрическое сопротивление, что приводит к потере мощности и нагреву.
