Импульс силы — Википедия

Материал из Википедии — свободной энциклопедии

И́мпульс си́лы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени (в поступательном движении).

За конечный промежуток времени эта величина равна определённому интегралу от элементарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы. В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время.

N→=∫t0tF→(t)dt{\displaystyle {\vec {N}}=\int \limits _{t_{0}}^{t}{\vec {F}}(t)\;\mathrm {d} \,t}

Во вращательном движении момент силы, действуя в течение определённого времени, создаёт импульс момента силы. Импульс момента силы — это мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении):

M→=∫t0t[r→;F→(t)]dt{\displaystyle {\vec {M}}=\int \limits _{t_{0}}^{t}[{\vec {r}};{\vec {F}}(t)]\;\mathrm {d} \,t}

где [⋅;⋅]{\displaystyle [\cdot ;\cdot ]} — векторное произведение.

Теорема об изменении количества движения системы[править | править код]

Понятие импульса силы позволяет сформулировать теорему об изменении количества движения системы для произвольных систем:

p→2−p→1=N→,{\displaystyle {\vec {p}}_{2}-{\vec {p}}_{1}={\vec {N}},}

где p→1{\displaystyle {\vec {p}}_{1}} — начальный, а p→2{\displaystyle {\vec {p}}_{2}} — конечный импульс изолированной системы, взаимодействующей с другими системами лишь посредством сил. Фактически, в этой формулировке закон сохранения импульса эквивалентен второму закону Ньютона и является его интегралом по времени, так как

dp→dt=∑iF→i.{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i}{\vec {F}}_{i}.}

Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы также является векторной величиной.

Раздел 1 «Механика»

Лекция 3. Тема «Импульс тела. Работа и энергия. Законы сохранения.»

1. Импульс. Закон сохранения импульса.

2. Центр масс. Уравнение движения тела переменной массы.

3. Энергия, работа, мощность.

4. Кинетическая и потенциальная энергии.

5. Закон сохранения механической энергии.

Импульс тела

Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.

Силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренниминазываются силы, действующие на точки системы со стороны других точек или тел этой же системы.

 

Пусть на тело массой m в течение некоторого малого промежутка времени Δt действовала сила Под действием этой силы скорость тела изменилась на Следовательно, в течение времени Δt тело двигалось с ускорением

Из основного закона динамики (второго закона Ньютона) следует:

Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с).

Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы также является векторной величиной.

В новых терминах второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы.

Обозначив импульс тела буквой второй закон Ньютона можно записать в виде

Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси:

Fx Δt = Δpx; Fy Δt = Δpy; Fz Δt = Δpz.

Таким образом, изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось. Рассмотрим в качестве примера одномерное движение, т. е. движение тела по одной из координатных осей (например, оси OY). Пусть тело свободно падает с начальной скоростью υ₀ под действием силы тяжести; время падения равно t. Направим ось OY вертикально вниз. Импульс силы тяжести F

т = mg за время t равен mgt. Этот импульс равен изменению импульса тела

Fтt = mgt = Δp = m (υ – υ0), откуда υ = υ0 + gt.

Этот простой результат совпадает с кинематической формулой для скорости равноускоренного движения.

 

Если движение тела во время действия силы происходило по некоторой криволинейной траектории, то начальный и конечный импульсы тела могут отличаться не только по модулю, но и по направлению. В этом случае для определения изменения импульса удобно использовать диаграмму импульсов, на которой изображаются вектора и , а также вектор построенный по правилу параллелограмма. В качестве примера на рис. 1 изображена диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой m налетел на стенку со скоростью под углом α к нормали (ось OX) и отскочил от нее со скоростью под углом β. Во время контакта со стеной на мяч действовала некоторая сила направление которой совпадает с направлением вектора

Рисунок 1. Отскок мяча от шероховатой стенки и диаграмма импульсов

При нормальном падении мяча массой m на упругую стенку со скоростью после отскока мяч будет иметь скорость Следовательно, изменение импульса мяча за время отскока равно В проекциях на ось OX этот результат можно записать в скалярной форме Δp

x = –2mυ_x. Ось OX направлена от стенки (как на рис. 2), поэтому υ_x < 0 и Δp_x > 0. Следовательно, модуль Δp изменения импульса связан с модулем υ скорости мяча соотношением Δp = 2mυ.

Читайте также:

Рекомендуемые страницы:

Поиск по сайту

Импульс

В динамике процесс взаимодействия тел описывается третьим законом Ньютона, согласно которому всегда можно выделить пары взаимодействующих тел, для которых «действие равно противодействию»:

Знание силы, действующей на каждое тело в данный момент времени, позволяет находить его мгновенное ускорение, а далее, по мере необходимости, скорость, перемещение, координаты.

Но, во-первых, существует целый класс задач, в которых требуется знание только конечного результата взаимодействия тел. Для постоянных сил решение таких задач, как правило, не вызывает особых трудностей, но требует предварительного выполнения одних и тех же преобразований уравнений динамики.

Во-вторых, решение подобных задач посредством применения второго закона Ньютона существенно усложняется в случае изменяющихся в процессе взаимодействия сил.

Таким образом, имеет смысл предварительно выполнить для обозначенного класса задач преобразования законов Ньютона и полученный результат далее применять в готовом виде.

Действие одного тела на другое характеризуется понятием сила.

Второй закон Ньютона гласит, что сумма сил, действующих на тело, равна произведению массы этого тела на сообщаемое силами ускорение.

Ускорение же – это физическая величина, равная отношению изменения скорости тела ко времени, в течение которого это изменение произошло.

Таким образом, можно записать: или

Физическая величина, равная произведению силы, действующей на тело, на время ее действия, называется импульсом силы: Чтобы получить единицу импульса силы, надо в его определяющее уравнение подставить единицы силы 1 Н и времени 1 с. Получаем: [K] = 1 Н∙с.

Физическая величина, равная произведению массы тела на его скорость, называется импульсом (или количеством движения) тела:

Чтобы получить единицу импульса тела, надо в его определяющее уравнение подставить единицы массы 1 кг и скорости 1 м/с. Получаем: [p] = 1 кг∙м/с.

Импульс сил и импульс тела – величины векторные.

Направление импульса тела совпадает с направлением вектора скорости. Импульс силы сонаправлен с вектором силы.

С учетом введенных понятий, второй закон Ньютона получает новые формулировки.

Сумма сил, действующих на тело, равна скорости изменения его импульса:

Импульс результирующей силы, действующей на тело, равен изменению импульса тела:

Механическая работа. Мощность – FIZI4KA

1. Механическая работа ​\( A \)​ — физическая величина, равная произведению вектора силы, действующей на тело, и вектора его перемещения: ​\( A=\vec{F}\vec{S} \)​. Работа — скалярная величина, характеризуется числовым значением и единицей.

За единицу работы принимают 1 джоуль (1 Дж). Это такая работа, которую совершает сила 1 Н на пути 1 м.

\[ [\,A\,]=[\,F\,][\,S\,]; [\,A\,]=1Н\cdot1м=1Дж \]

2. Если сила, действующая на тело, составляет некоторый угол ​\( \alpha \)​ с перемещением, то проекция силы ​\( F \)​ на ось X равна ​\( F_x \)​ (рис. 42).

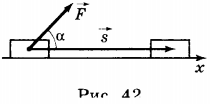
Поскольку ​\( F_x=F\cdot\cos\alpha \)​, то \( A=FS\cos\alpha \).

Таким образом, работа постоянной силы равна произведению модулей векторов силы и перемещения и косинуса угла между этими векторами.

3. Если сила ​\( F \)​ = 0 или перемещение ​\( S \)​ = 0, то механическая работа равна нулю ​\( A \)​ = 0. Работа равна нулю, если вектор силы перпендикулярен вектору перемещения, т.е. ​\( \cos90^\circ \)​ = 0. Так, нулю равна работа силы, сообщающей телу центростремительное ускорение при его равномерном движении по окружности, так как эта сила перпендикулярна направлению движения тела в любой точке траектории.

4. Работа силы можетбыть как положительной, так и отрицательной. Работа положительная ​\( A \)​ > 0, если угол 90° > ​\( \alpha \)​ ≥ 0°; если угол 180° > ​\( \alpha \)​ ≥ 90°, то работа отрицательная ​\( A \)​ < 0.

Если угол ​\( \alpha \)​ = 0°, то ​\( \cos\alpha \)​ = 1, ​\( A=FS \)​. Если угол ​\( \alpha \)​ = 180°, то ​\( \cos\alpha \)​ = -1, ​\( A=-FS \)​.

5. При свободном падении с высоты ​\( h \)​ тело массой ​\( m \)​ перемещается из положения 1 в положение 2 (рис. 43). При этом сила тяжести совершает работу, равную:

​

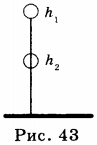
\[ A=F_тh=mg(h_1-h_2)=mgh \]

​При движении тела вертикально вниз сила и перемещение направлены в одну сторону, и сила тяжести совершает положительную работу.

Если тело поднимается вверх, то сила тяжести направлена вниз, а перемещение вверх, то сила тяжести совершает отрицательную работу, т.е.

\[ A=-F_тh=-mg(h_1-h_2)=-mgh \]

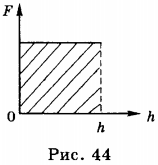
6. Работу можно представить графически. На рисунке изображён график зависимости силы тяжести от высоты тела относительно поверхности Земли (рис. 44). Графически работа силы тяжести равна площади фигуры (прямоугольника), ограниченного графиком, координатными осями и перпендикуляром, восставленным к оси абсцисс
в точке ​\( h \)​.

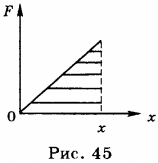
Графиком зависимости силы упругости от удлинения пружины является прямая, проходящая через начало координат (рис. 45). По аналогии с работой силы тяжести работа силы упругости равна площади треугольника, ограниченного графиком, координатными осями и перпендикуляром, восставленным к оси абсцисс в точке ​\( x \)​.
​\( A=Fx/2=kx\cdot x/2 \)​.

\[ F=kx^2/2 \]

7. Работа силы тяжести не зависит от формы траектории, по которой перемещается тело; она зависит от начального и конечного положений тела. Пусть тело сначала перемещается из точки А в точку В по траектории АВ (рис. 46). Работа силы тяжести в этом случае

\[ A_{AB}=mgh \]

Пусть теперь тело движется из точки А в точку В сначала вдоль наклонной плоскости АС, затем вдоль основания наклонной плоскости ВС. Работа силы тяжести при перемещении по ВС равна нулю. Работа силы тяжести при перемещении по АС равна произведению проекции силы тяжести на наклонную плоскость ​\( mg\sin\alpha \)​ и длины наклонной плоскости, т.е. ​\( A_{AC}=mg\sin\alpha\cdot l \)​. Произведение ​\( l\cdot\sin\alpha=h \)​. Тогда \( A_{AC}=mgh \). Работа силы тяжести при перемещении тела по двум различным траекториям не зависит от формы траектории, а зависит от начального и конечного положений тела.

Работа силы упругости также не зависит от формы траектории.

Предположим, что тело перемещается из точки А в точку В по траектории АСВ, а затем из точки В в точку А по траектории ВА. При движении по траектории АСВ сила тяжести совершает положительную работу, при движении по траектории В А работа силы тяжести отрицательна, равная по модулю работе при движении по траектории АСВ. Следовательно работа силы тяжести по замкнутой траектории равна нулю. То же относится и к работе силы упругости.

Силы, работа которых не зависит от формы траектории и по замкнутой траектории равна нулю, называют консервативными. К консервативным силам относятся сила тяжести и сила упругости.

8. Силы, работа которых зависит от формы пути, называют неконсервативными. Неконсервативной является сила трения. Если тело перемещается из точки А в точку В (рис. 47) сначала по прямой, а затем по ломаной линии АСВ, то в первом случае работа силы трения ​\( A_{AB}=-Fl_{AB} \)​, а во втором ​\( A_{ABC}=A_{AC}+A_{CB} \)​, \( A_{ABC}=-Fl_{AC}-Fl_{CB} \).

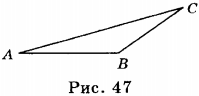
Следовательно, работа ​\( A_{AB} \)​ не равна работе ​\( A_{ABC} \)​.

9. Мощностью называется физическая величина, равная отношению работы к промежутку времени, за который она совершена. Мощность характеризует быстроту совершения работы.

Мощность обозначается буквой ​\( N \)​.

\[ N = A/t \]

Единица мощности: ​\( [N]=[A]/[t] \)​. ​\( [N] \)​ = 1 Дж/1 с = 1 Дж/с. Эта единица называется ватт (Вт). Один ватт — такая мощность, при которой работа 1 Дж совершается за 1 с.

10. Мощность, развиваемая двигателем, равна: ​\( N = A/t \)​, ​\( A=F\cdot S \)​, откуда ​\( N=FS/t \)​. Отношение перемещения ко времени представляет собой скорость движения: ​\( S/t = v \)​. Откуда ​\( N = Fv \)​.

Из полученной формулы видно, что при постоянной силе сопротивления скорость движения прямо пропорциональна мощности двигателя.

В различных машинах и механизмах происходит преобразование механической энергии. За счёт энергии при её преобразовании совершается работа. При этом на совершение полезной работы расходуется только часть энергии. Некоторая часть энергии тратится на совершение работы против сил трения. Таким образом, любая машина характеризуется величиной, показывающей, какая часть передаваемой ей энергии используется полезно. Эта величина называется коэффициентом полезного действия (КПД).

Коэффициентом полезного действия называют величину, равную отношению полезной работы ​\( (A_п) \)​ ко всей совершённой работе \( (A_с) \): ​\( \eta=A_п/A_с \)​. Выражают КПД в процентах.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Работа определяется по формуле

1) ​\( A=Fv \)​
2) \( A=N/t \)​
3) \( A=mv \)​
4) \( A=FS \)​

2. Груз равномерно поднимают вертикально вверх за привязанную к нему верёвку. Работа силы тяжести в этом случае

1) равна нулю
2) положительная
3) отрицательная
4) больше работы силы упругости

3. Ящик тянут за привязанную к нему верёвку, составляющую угол 60° с горизонтом, прикладывая силу 30 Н. Какова работа этой силы, если модуль перемещения равен 10 м?

1) 300 Дж
2) 150 Дж
3) 3 Дж
4) 1,5 Дж

4. Искусственный спутник Земли, масса которого равна ​\( m \)​, равномерно движется по круговой орбите радиусом ​\( R \)​. Работа, совершаемая силой тяжести за время, равное периоду обращения, равна

1) ​\( mgR \)​
2) ​\( \pi mgR \)​
3) \( 2\pi mgR \)​
4) ​\( 0 \)​

5. Автомобиль массой 1,2 т проехал 800 м по горизонтальной дороге. Какая работа была совершена при этом силой трения, если коэффициент трения 0,1?

1) -960 кДж
2) -96 кДж
3) 960 кДж
4) 96 кДж

6. Пружину жёсткостью 200 Н/м растянули на 5 см. Какую работу совершит сила упругости при возвращении пружины в состояние равновесия?

1) 0,25 Дж
2) 5 Дж
3) 250 Дж
4) 500 Дж

7. Шарики одинаковой массы скатываются с горки по трём разным желобам, как показано на рисунке. В каком случае работа силы тяжести будет наибольшей?

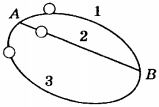
1) 1
2) 2
3) 3
4) работа во всех случаях одинакова

8. Работа по замкнутой траектории равна нулю

А. Силы трения
Б. Силы упругости

Верным является ответ

1) и А, и Б
2) только А
3) только Б
4) ни А, ни Б

9. Единицей мощности в СИ является

1) Дж
2) Вт
3) Дж·с
4) Н·м

10. Чему равна полезная работа, если совершённая работа составляет 1000 Дж, а КПД двигателя 40 %?

1) 40000 Дж
2) 1000 Дж
3) 400 Дж
4) 25 Дж

11. Установите соответствие между работой силы (в левом столбце таблицы) и знаком работы (в правом столбце таблицы). В ответе запишите выбранные цифры под соответствующими буквами.

РАБОТА СИЛЫ
A. Работа силы упругости при растяжении пружины
Б. Работа силы трения
B. Работа силы тяжести при падении тела

ЗНАК РАБОТЫ
1) положительная
2) отрицательная
3) равна нулю

12. Из приведённых ниже утверждений выберите два правильных и запишите их номера в таблицу.

1) Работа силы тяжести не зависит от формы траектории.
2) Работа совершается при любом перемещении тела.
3) Работа силы трения скольжения всегда отрицательна.
4) Работа силы упругости по замкнутому контуру не равна нулю.
5) Работа силы трения не зависит от формы траектории.

Часть 2

13. Лебёдка равномерно поднимает груз массой 300 кг на высоту 3 м за 10 с. Какова мощность лебёдки?

Ответы

Механическая работа. Мощность

Оценка

Помогите решить задачу по физике? срочно.

Решение. N=(Fc^2+(m*g)^2)^0,5; Fc=(m*v^2)/R; m=60; v=10; R=12; g=9,8; Для решения необходим рисунок!

Импульс силы. Покой и движение тела относительны, скорость движения тела зависит от выбора системы отсчета. По второму закону Ньютона независимо от того, находилось ли тело в покое или двигалось, изменение скорости его движения может происходить только при действии силы, т. е. в результате взаимодействия с другими телами. Если на тело массой т в течение времени t действует сила F и скорость его движения изменяется от и0 до v, то ускорение а движения тела равно t На основании второго закона Ньютона для силы F можно написать выражение F=ma=m(v~Vo) . A6.1) Из равенства A6.1) следует Ft = mv — mv0. A6.2) Физическая величина, равная произведению силы F на время t ее действия, называется импульсом силы. Импульс тела. Выражение A6.2) показывает, что имеется физическая величина, одинаково изменяющаяся у всех тел под действием одинаковых сил, если время действия силы одинаково. Эта физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела или количеством движения. Изменение импульса тела равно импульсу силы, вызывающей это изменение. Импульс тела является количественной характеристикой поступательного движения тел. За единицу импульса в СИ принят импульс тела массой 1 кг, движущегося поступательно со скоростью 1 м/с. Единицей импульса является килограмм-метр в секунду (кг-м/с) . Закон сохранения импульса. Выясним, как изменяются импульсы двух тел при их взаимодействии. Обозначим скорости тел массами гп\\ и rtiz до взаимодействия через v\\ и v2, а после взаимодействия — через i&gt;i и v’2. По третьему закону Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; ^поэтому их можно обозначить F и —F. Для изменений импульсов тел при их взаимодействии на основании равенства A6.2) можно записать Ft = m\\v\\ — — Ft = WI2V2 — где t — время взаимодействия тел. Из этих выражений получаем 2. A6.3) Таким образом, векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия. Экспериментальные исследования взаимодействий различных тел — от планет и звезд до атомов и элементарных частиц — показали, что в любой системе взаимодействующих между собой тел

Тест по физике по теме: контрольное тестирование

I вариант

Часть А.

1. Тело массой  m  движется со скоростью V. Каков импульс тела?

А.  mV². Б.  mV². В.  mV . Г. mV . Д.  mV . Е.  mV .

        2             2                               2                           2

2. Тело массой  m  движется со скоростью V. Какова кинетическая энергия тела?

А.  mV². Б.  mV². В.  mV . Г. mV . Д.  mV . Е.  mV .

        2             2                               2                           2

3. Тело массой m поднято над поверхностью Земли на высоту h. Какова потенциальная  

    энергия тела?

А. mg. Б. mgh . В. mh . Г gh . Д. mg .

                                       h

4. Пружина жескостью k под действием силы F растянута на x м. Какова потенциальная

     энергия упругой деформации пружины?        

А. kx. Б. kx². В. kx. Г. kx². Д. mgh .                      

          2          2

5. Мяч был брошен с поверхности Земли вертикально вверх. Он достиг высшей точки

    траектории и затем упал на Землю. В какой момент времени движения полная

    механическая энергия мяча имела максимальное значение? Сопротивлением воздуха

    пренебречь.

А. В момент начала движения вверх. Б. В момент достижения верхней точки траектории. В. В момент прохождения половины расстояния до верхней точки траектории. Г. В

     момент падения на Землю. Д. В течение всего времени полёта полная механическая

     энергия была одинакова.

6. Два шара с одинаковыми массами m двигались навстречу друг другу с одинаковыми по

    модулю скоростями V. После неупругого столкновения оба шара остановились. Каково

    изменение суммы импульсов двух шаров в результате столкновения?

А. mV . Б. 2mV . В. 0 . Г.- mV . Д. — 2mV .                      

7. Камень брошен вертикально вверх. На пути 1 м его кинетическая энергия уменьшилась

    на 16 Дж. Какую работу совершила сила тяжести на этом пути?

А. — 16 Дж. Б.- 4 Дж.  В. 16 Дж. Г. 4 Дж. Д. 0 Дж.         

8. Какова кинетическая энергия автомобиля массой 1000 кг, движущегося со скоростью 36

    км/ч?

А. 36 · 10³ Дж. Б. 648 · 10³ Дж.  В. 10 Дж. Г. 5· 10 Дж.

Часть В.      

1. Тело поднимается вертикально вверх под действием силы F = 10Н. В начальный момент

    времени тело находилось на высоте, равной 1м, от поверхности Земли. Найдите

    положение тела в тот момент, когда сила, поднимающая груз, совершила работу,

    равную 200 Дж.

2. Недеформированную пружину растягивают на ∆l = 10см. Найдите работу

    деформирующей пружину силы, если при растяжении пружины на ∆l˳ = 1см требуется

    сила F˳= 4Н. Чему равна работа силы упругости пружины?

II вариант

Часть А.

1. Как называется физическая величина, равная произведению массы тела на вектор его

    мгновенной скорости?

А. Импульс тела. Б. Импульс силы. В. Кинетическая энергия. Г. Потенциальная энергия. Д. Двойная кинетическая энергия.

2. Как называется физическая величина, равная половине произведения массы тела на

    квадрат его мгновенной скорости?

А. Импульс тела. Б. Импульс силы. В. Кинетическая энергия. Г. Потенциальная энергия. Д. Двойная кинетическая энергия.

3. Как называется физическая величина, равная произведению массы тела m на ускорение

    свободного падения и на расстояние h  от тела до поверхности Земли?

А. Импульс тела. Б. Импульс силы. В. Кинетическая энергия. Г. Потенциальная энергия. Д. Двойная кинетическая энергия.

4. Растяжение пружины жесткостью k увеличено на ∆x. Как изменилась при этом

    потенциальная энергия упругой деформации пружины?

А. Увеличилась на k∆x. Б. Увеличилась на  k∆x². В. Увеличилась на  k∆x² .

        2

Г. Уменьшилась на k∆x. Д. Уменьшилась на  k∆x² . Е. Уменьшилась на  k∆x² .

                                                                                                                                 2

5. Мяч был брошен с поверхности Земли вертикально вверх. Он достиг высшей точки

    траектории и затем упал на Землю. В какой момент времени движения полная

    механическая энергия мяча имела минимальное значение? Сопротивлением воздуха

    пренебречь.

А. В момент достижения верхней точки траектории. Б. В течение всего времени полёта

     полная механическая энергия была одинакова.  В. В момент падения на Землю. Г. В

     момент прохождения половины расстояния до верхней точки траектории. Д. В момент

     начала движения вверх.

6. Два шара с одинаковыми массами m двигались навстречу друг другу с одинаковыми по

    модулю скоростями V. После упругого столкновения каждый шар стал двигаться в

    обратном направлении с прежней по модулю скоростью. Каково

    изменение суммы импульсов двух шаров в результате столкновения?

А. mV . Б. — 2mV . В. 4mV . Г.- 4mV . Д. 0 .                      

7.. Камень брошен вертикально вверх. На пути 1 м его кинетическая энергия увеличилась

    на 16 Дж. Какую работу совершила сила тяжести на этом пути?

А. — 16 Дж. Б.- 4 Дж.  В. 16 Дж. Г. 4 Дж. Д. 0 Дж. 

8. Какова кинетическая энергия ракеты массой 100 кг, движущегося со скоростью 60

    км/мин?

А. 10⁸ Дж. Б. 5 · 10⁷ Дж.  В. 1,8 · 10 Дж. Г. 6 · 10³ Дж. Д. 50 Дж.

         

Часть В.

1. Тело поднимается вертикально вверх под действием силы F = 10Н. В начальный момент

    времени тело находилось на высоте, равной 1м, от поверхности Земли. Найдите

    положение тела в тот момент, когда сила, поднимающая груз, совершила работу,

    равную 300 Дж.

2. Недеформированную пружину растягивают на ∆l = 10см. Найдите работу

    деформирующей пружину силы, если при растяжении пружины на ∆l˳ = 1см требуется

    сила F˳= 6Н. Чему равна работа силы упругости пружины?

Контрольное тестирование

по дисциплине физика

Коды правильных ответов:

	Часть А								Часть В
	1	2	3	4	5	6	7	8	1	2
1 вариант	Д	Б	Б	Г	Д	В	А	Г	21	2
2 вариант	А	В	Г	В	Б	Д	В	Б	31	3

Шкала оценки знаний обучающихся по итогам выполнения теста:

        

Число правильных ответов	0-2	3-4	5-6	7-8	9-10
Оценка в баллах	1	2	3	4	5

Механическая работа — Википедия

Механическая работа

A=F⋅S=F⋅S⋅cos⁡φ{\displaystyle A={\mathbf {F}}\cdot {\mathbf {S}}=F\cdot S\cdot \cos \varphi } Работа силы

Ключевые статьи

Работа в физике

Известные учёные

См. также: Портал:Физика

Механическая работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)^[1].

Работа обычно обозначается буквой A (от нем. Arbeit — работа, труд) или буквой W (от англ. work — работа, труд).

Работа силы, приложенной к материальной точке[править | править код]

Суммарная работа по перемещению одной материальной точки, совершаемая несколькими силами, приложенными к этой точке, определяется как работа равнодействующей этих сил (их векторной суммой). Поэтому дальше будем говорить об одной силе, приложенной к материальной точке.

При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:

A=Fss=Fs cos(F,s)=F→⋅s→{\displaystyle A=F_{s}s=Fs\ \mathrm {cos} (F,s)={\vec {F}}\cdot {\vec {s}}}

Здесь точкой обозначено скалярное произведение, s→{\displaystyle {\vec {s}}} — вектор перемещения; подразумевается, что действующая сила F→{\displaystyle {\vec {F}}} постоянна в течение времени, за которое вычисляется работа.

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки^[2]:

A=∫F→⋅ds→.{\displaystyle A=\int {\vec {F}}\cdot {\vec {ds}}.}

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений ds→,{\displaystyle {\vec {ds}},} если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[3], интеграл определяется^[4] следующим образом:

A=∫r→0r→1F→(r→)⋅dr→{\displaystyle A=\int \limits _{{\vec {r}}_{0}}^{{\vec {r}}_{1}}{\vec {F}}\left({\vec {r}}\right)\cdot {\vec {dr}}},

где r→0{\displaystyle {\vec {r}}_{0}} и r→1{\displaystyle {\vec {r}}_{1}} — радиус-векторы начального и конечного положения тела соответственно.

• Следствие. Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа (этой силы) равна нулю.

Работа сил, приложенных к системе материальных точек[править | править код]

Работа сил по перемещению системы материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой).

Даже если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

• Эти определения могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаемся выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если Atotal{\displaystyle A_{total}} — полная работа, совершённая над частицей, определяемая как сумма работ, совершенных приложенными к частице силами, то она выражается как:

Atotal=Δ(mv22)=ΔEk,{\displaystyle A_{total}=\Delta \left({\frac {mv^{2}}{2}}\right)=\Delta E_{k},}

где Ek{\displaystyle E_{k}} называется кинетической энергией. Для материальной точки кинетическая энергия определяется как половина произведения массы этой точки на квадрат её скорости и выражается как^[5]:

Ek=12mv2.{\displaystyle E_{k}={\frac {1}{2}}mv^{2}.}

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая Ep{\displaystyle E_{p}}, такая, что

F→=−∇Ep.{\displaystyle {\vec {F}}=-\nabla E_{p}.}

Если все силы, действующие на частицу, консервативны, и Ep{\displaystyle E_{p}} является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, тогда:

F→⋅Δs→=−∇→Ep⋅Δs→=−ΔEp⇒−ΔEp=ΔEk⇒Δ(Ek+Ep)=0{\displaystyle {\vec {F}}\cdot \Delta {\vec {s}}=-{\vec {\nabla }}E_{p}\cdot \Delta {\vec {s}}=-\Delta E_{p}\Rightarrow -\Delta E_{p}=\Delta E_{k}\Rightarrow \Delta (E_{k}+E_{p})=0}.

Этот результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы,

∑E=Ek+Ep{\displaystyle \sum E=E_{k}+E_{p}},

является постоянной во времени. Этот закон широко используется при решении задач классической механики.

В термодинамике работа, совершённая газом при расширении^[6], рассчитывается как интеграл давления по объёму:

A1→2=∫V1V2PdV.{\displaystyle A_{1\rightarrow 2}=\int \limits _{V_{1}}^{V_{2}}PdV.}

Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

• Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
• В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет

dA=PdSh.{\displaystyle dA=PdSh.}

Видно, что это и есть произведение давления на приращение объёма вблизи данной элементарной площадкой. А просуммировав по всем dS, получим конечный результат, где будет уже полное приращение объёма, как и в главной формуле раздела.

Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.

Пусть материальная точка M{\displaystyle M} движется по непрерывно дифференцируемой кривой G={r=r(s)}{\displaystyle G=\{r=r(s)\}}, где s — переменная длина дуги, 0≤s≤S{\displaystyle 0\leq s\leq S}, и на неё действует сила F(s){\displaystyle F(s)}, направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под F(s){\displaystyle F(s)} проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина F(ξi)△si,△si=si−si−1,i=1,2,…,iτ{\displaystyle F(\xi _{i})\triangle s_{i},\triangle s_{i}=s_{i}-s_{i-1},i=1,2,…,i_{\tau }}, называется элементарной работой силы F{\displaystyle F} на участке Gi{\displaystyle G_{i}} и принимается за приближённое значение работы, которую производит сила F{\displaystyle F}, воздействующая на материальную точку, когда последняя проходит кривую Gi{\displaystyle G_{i}}. Сумма всех элементарных работ ∑i=1iτF(ξi)△si{\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} является интегральной суммой Римана функции F(s){\displaystyle F(s)}.

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма ∑i=1iτF(ξi)△si{\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} всех элементарных работ, когда мелкость |τ|{\displaystyle |\tau |} разбиения τ{\displaystyle \tau } стремится к нулю, называется работой силы F{\displaystyle F} вдоль кривой G{\displaystyle G}.

Таким образом, если обозначить эту работу буквой W{\displaystyle W}, то, в силу данного определения,

W=lim|τ|→0∑i=1iτF(ξi)△si{\displaystyle W=\lim _{|\tau |\rightarrow 0}\sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}},

следовательно,

W=∫0sF(s)ds{\displaystyle W=\int \limits _{0}^{s}F(s)ds} (1).

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра t{\displaystyle t} (например, времени) и если величина пройденного пути s=s(t){\displaystyle s=s(t)}, a≤t≤b{\displaystyle a\leq t\leq b} является непрерывно дифференцируемой функцией, то из формулы (1) получим

W=∫abF[s(t)]s′(t)dt.{\displaystyle W=\int \limits _{a}^{b}F[s(t)]s'(t)dt.}

Единицей измерения работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг

1 Дж = 1 кг·м²/с² = 1 Н·м

1 эрг = 1 г·см²/с² = 1 дин·см

1 эрг = 10⁻⁷Дж

1. ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
2. ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения ds→{\displaystyle {\vec {ds}}}, на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях ds→{\displaystyle {\vec {ds}}} суммируется, что и дает в результате интеграл.
3. ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
4. ↑ По сути через предыдущий, поскольку здесь F→(t)=F→(r→(t)){\displaystyle {\vec {F}}(t)={\vec {F}}({\vec {r}}(t))}; вектор же малого перемещения ds→{\displaystyle {\vec {ds}}} совпадает с dr→{\displaystyle d{\vec {r}}}.
5. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
6. ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле ∫PdV{\displaystyle \int PdV} давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

• История механики с древнейших времен до конца XVIII в. В 2 т. М.: Наука, 1972.
• Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
• Льоцци М. История физики. М.: Мир, 1970.
• Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
• Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
• Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.