Полосовой фильтр — frwiki.wiki

Изображение, к которому был применен полосовой фильтр (результат справа)

Полосовой фильтр представляет собой фильтр, позволяя только полосу или интервал частот, чтобы пройти между низким отсечения частоты и высокой частоты среза фильтра.

Концепция полосового фильтра — это математическое преобразование, применяемое к данным (сигналу). Полосовой фильтр можно реализовать в цифровом виде или с помощью электронных компонентов. Функция этого преобразования заключается в ослаблении частот за пределами полосы пропускания, интервала частот между частотами среза. Таким образом, только частоты, включенные в этот интервал, остаются нетронутыми или с небольшим затуханием.

Резюме

• 1 Идеальный фильтр
• 2 Аналоговый полосовой фильтр
  • 2.1 Полосовой фильтр второго порядка
• 3 Пропускная способность
• 4 Использование в электронике
  • 4.1 Схема RLC и диаграмма Боде
• 5 Использование с механическими волнами
• 6 Статьи по теме

Идеальный фильтр

Идеальный полосовой фильтр имеет постоянное усиление в полосе пропускания и нулевое усиление в полосе среза. Переход между двумя состояниями происходит мгновенно. В действительности, фильтр имеет на своей частоте среза усиление Gmax -3  дБ, а затем уменьшает усиление на -20  дБ на декаду (т. Е. -6  дБ на октаву) (фильтр

1- ^го  порядка).

Аналоговый полосовой фильтр

Полосовой фильтр может быть реализован аналогично электронным компонентам. Следовательно, этот вид фильтра применяется к непрерывным сигналам в реальном времени. Компоненты и конфигурация схемы будут фиксировать различные характеристики фильтра, такие как порядок, частоты среза и его диаграмма Боде . Обычные аналоговые фильтры бывают первого или второго порядка. Существует несколько семейств аналоговых фильтров: Баттерворта, Чебышева, Бесселя, эллиптические и др.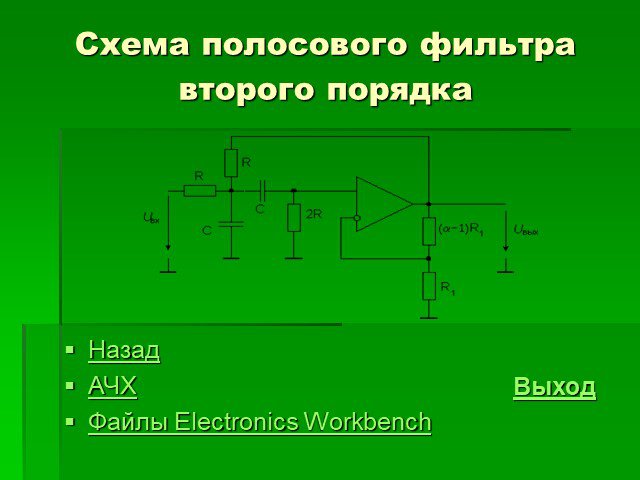 Реализация фильтров одного и того же семейства обычно выполняется с использованием одной и той же конфигурации схемы, и они имеют одинаковую форму передаточной функции, но изменяются ее параметры, следовательно, значение компонентов передаточной функции. .

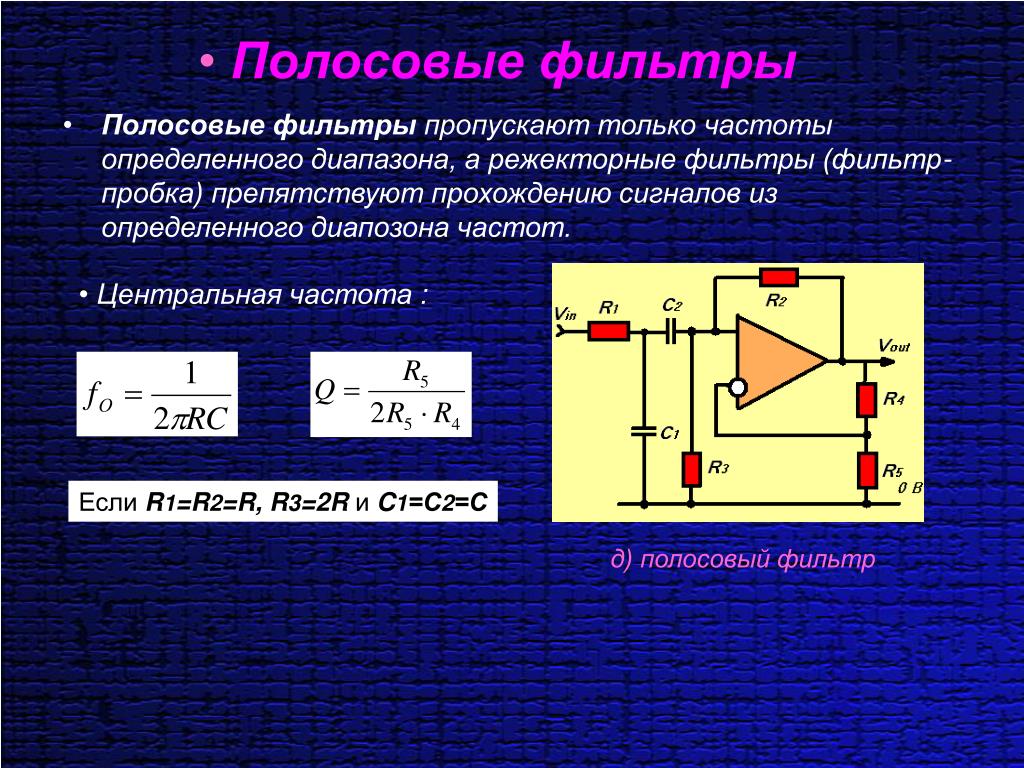
Полосовой фильтр второго порядка

Передаточная функция второго порядка полосового фильтра записывается в виде :, с A ₀ коэффициент усиления; и ( сокращенная переменная ). А Q — добротность. час(jш)знак равноВ01+j⋅Q⋅(Икс-1Икс){\ displaystyle h (jw) = {\ frac {A_ {0}} {1 + j \ cdot Q \ cdot (x — {\ frac {1} {x}})}}}Иксзнак равноωω0{\ displaystyle x = {\ frac {\ omega} {\ omega _ {0}}}}

Пропускная способность

Полоса пропускания BP полосового фильтра — это интервал импульсов [ω

c1, ω _c2 ], который соответствует таким импульсам, что коэффициент усиления не более чем на 3 децибела ниже максимального усиления (здесь 0 дБ).

G (ω _ci ) = G (ω ₀ ) -3,

а также

BP = [ω _c1, ω _c2 ]

Эти импульсы отсечки таковы, что

|час(jωпротив1)|знак равно|час(jωпротив2)|знак равночасмвИкс2{\ displaystyle | час (j \ omega _ {c1}) | = | h (j \ omega _ {c2}) | = {\ frac {h _ {\ mathrm {max}}} {\ sqrt {2}} }}

(так как20бревно⁡12≈-3){\ displaystyle \ left ({\ text {car}} \ quad 20 \ log {\ frac {1} {\ sqrt {2}}} \ приблизительно -3 \ right)}

Использование в электронике

Есть много приложений в электронике . Полосовая схема может использоваться для удаления шума из сигнала, если известно, что сигнал имеет частоты в пределах указанного диапазона частот. Это также полосовая схема, которая позволяет при радиосвязи выбирать радиочастоту для прослушивания.

Схема RLC и диаграмма Боде

Схема полосового фильтра RLC

Пассивный полосовой фильтр можно получить с помощью схемы RLC, описанной на диаграмме напротив. Затем мы находим следующую передаточную функцию:

час(jш)знак равно11+j(Lрω-1рПРОТИВω){\ displaystyle h (jw) = {\ frac {1} {1 + j \ left ({\ frac {L} {R}} \ omega — {\ frac {1} {RC \ omega}} \ right)} }}

который имеет вид: час(jИкс)знак равно11+jQ(Икс-1Икс){\ displaystyle h (jx) = {\ frac {1} {1 + jQ \ left (x — {\ frac {1} {x}} \ right)}}}

с участием:

Иксзнак равноωω0{\ displaystyle x = {\ frac {\ omega} {\ omega _ {0}}}}

ω0знак равно1LПРОТИВ{\ displaystyle \ omega _ {0} = {\ frac {1} {\ sqrt {LC}}}}

Qзнак равно1рLПРОТИВ{\ displaystyle Q = {\ frac {1} {R}} {\ sqrt {\ frac {L} {C}}}}

Таким образом, мы имеем:

час(jω)знак равно11+jQ(ωω0-ω0ω){\ displaystyle h (j \ omega) = {\ frac {1} {1 + jQ \ left ({\ frac {\ omega} {\ omega _ {0}}} — {\ frac {\ omega _ {0}) } {\ omega}} \ right)}}}

Мы делаем вывод, что:

|час(jω)|знак равно11+Q2(ωω0-ω0ω)2{\ displaystyle | час (j \ omega) | = {\ frac {1} {\ sqrt {1 + Q ^ {2} \ left ({\ frac {\ omega} {\ omega _ {0}}} — { \ frac {\ omega _ {0}} {\ omega}} \ right) ^ {2}}}}}

аргумент⁡(час(jω))знак равно-арктан⁡(Q(Икс-1Икс)){\ displaystyle \ arg (час (j \ omega)) = — \ arctan \ left (Q \ left (x — {\ frac {1} {x}} \ right) \ right)}

Использование с механическими волнами

В акустике можно использовать полосовой фильтр, чтобы ослабить некоторые неприятные или даже вредные звуки, пропуская при этом «полезные» звуки (голос, предупреждающий сигнал).

В механике полосовой фильтр может позволить ослабить мешающие или даже вредные вибрации или колебания, сохраняя при этом определенную гибкость системы: система может деформироваться и, следовательно, адаптироваться к условиям, она имеет возвратную силу. до исходных размеров, но он не очень чувствителен к внешним воздействиям, имеющим быструю или медленную частоту. В случае измерения ( микрофон, сейсмограф и т. Д.) Такой фильтр также позволяет выбрать диапазон регистрируемых волн.

Статьи по Теме

• Режекторный фильтр, фильтр, принцип действия которого противоположен принципу полосового фильтра.
• Фильтр высоких частот
• Фильтр низких частот
• Фильтр (электронный)

Фильтры
Типы фильтров	Фильтр низких частот  · High Pass Filter  · полосовой фильтр  · режекторный фильтр
линейные фильтры	Фильтр Бесселя  · Фильтр Баттерворта  · Фильтр Чебышева  · Фильтр эллиптический
цифровые фильтры	Конечная импульсная характеристика  · фильтр бесконечной импульсной характеристики

<img src=»https://fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Электрические фильтры (Лекция №15)

Электрическим фильтром называется четырехполюсник, устанавливаемый между источником питания и нагрузкой и служащий для беспрепятственного (с малым затуханием) пропускания токов одних частот и задержки (или пропускания с большим затуханием) токов других частот.

Диапазон частот, пропускаемых фильтром без затухания (с малым затуханием), называется полосой пропускания или полосой прозрачности; диапазон частот, пропускаемых с большим затуханием, называется полосой затухания или полосой задерживания. Качество фильтра считается тем выше, чем ярче выражены его фильтрующие свойства, т.е. чем сильнее возрастает затухание в полосе задерживания.

В качестве пассивных фильтров обычно применяются четырехполюсники на основе катушек индуктивности и конденсаторов. Возможно также применение пассивных RC-фильтров, используемых при больших сопротивлениях нагрузки.

Фильтры применяются как в радиотехнике и технике связи, где имеют место токи достаточно высоких частот, так и в силовой электронике и электротехнике.

Для упрощения анализа будем считать, что фильтры составлены из идеальных катушек индуктивности и конденсаторов, т.е. элементов соответственно с нулевыми активными сопротивлением и проводимостью. Это допущение достаточно корректно при высоких частотах, когда индуктивные сопротивления катушек много больше их активных сопротивлений ( ), а емкостные проводимости конденсаторов много больше их активных проводимостей ( ).

Фильтрующие свойства четырехполюсников обусловлены возникающими в них резонансными режимами – резонансами токов и напряжений. Фильтры обычно собираются по симметричной Т- или П-образной схеме, т.е. при или (см. лекцию №14). В этой связи при изучении фильтров будем использовать введенные в предыдущей лекции понятия коэффициентов затухания и фазы.

Классификация фильтров в зависимости от диапазона пропускаемых частот приведена в табл. 1.

Таблица 1. Классификация фильтров

Название фильтра	Диапазон пропускаемых частот
Низкочастотный фильтр (фильтр нижних частот)
Высокочастотный фильтр (фильтр верхних частот)
Полосовой фильтр (полосно-пропускающий фильтр)
Режекторный фильтр (полосно-задерживающий фильтр)	и , где

В соответствии с материалом, изложенным в предыдущей лекции, если фильтр имеет нагрузку, сопротивление которой при всех частотах равно характеристическому, то напряжения и соответственно токи на его входе и выходе связаны соотношением

.  .

(1)

В идеальном случае в полосе пропускания (прозрачности) , т.е. в соответствии с (1) , и . Следовательно, справедливо и равенство , которое указывает на отсутствие потерь в идеальном фильтре, а значит, идеальный фильтр должен быть реализован на основе идеальных катушек индуктивности и конденсаторов. Вне области пропускания (в полосе затухания) в идеальном случае , т.е. и .

Рассмотрим схему простейшего низкочастотного фильтра, представленную на рис. 1,а.

Связь коэффициентов четырехполюсника с параметрами элементов Т-образной схемы замещения определяется соотношениями (см. лекцию № 14)

или конкретно для фильтра на рис. 1,а

;

(2)

;

(3)

.

(4)

Из уравнений четырехполюсника, записанных с использованием гиперболических функций (см. лекцию № 14), вытекает, что

.

Однако в соответствии с (2) — вещественная переменная, а следовательно,

.

(5)

Поскольку в полосе пропускания частот коэффициент затухания , то на основании (5)

.

Так как пределы изменения : , — то границы полосы пропускания определяются неравенством

,

которому удовлетворяют частоты, лежащие в диапазоне

.

(6)

Для характеристического сопротивления фильтра на основании (3) и (4) имеем

.

(7)

Анализ соотношения (7) показывает, что с ростом частоты w в пределах, определяемых неравенством (6), характеристическое сопротивление фильтра уменьшается до нуля, оставаясь активным.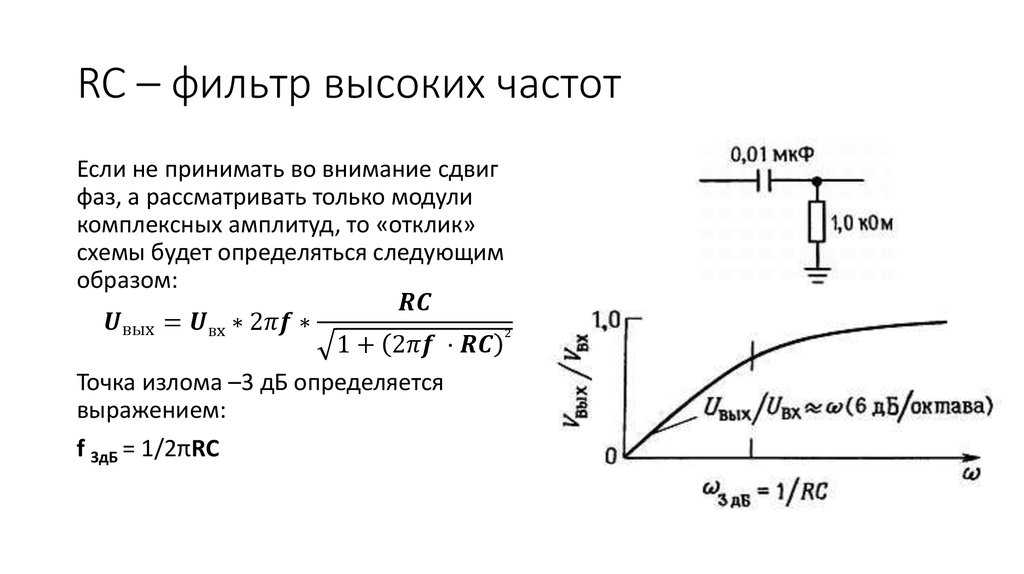

Поскольку, при нагрузке фильтра сопротивлением, равным характеристическому, его входное сопротивление также будет равно , то, вследствие вещественности , можно сделать заключение, что фильтр работает в режиме резонанса, что было отмечено ранее. При частотах, больших , как это следует из (7), характеристическое сопротивление приобретает индуктивный характер.

На рис. 2 приведены качественные зависимости и .

Следует отметить, что вне полосы пропускания . Действительно, поскольку коэффициент А – вещественный, то всегда должно удовлетворяться равенство

.

(8)

Так как вне полосы прозрачности , то соотношение (8) может выполняться только при .

В полосе задерживания коэффициент затухания определяется из уравнения (5) при . Существенным при этом является факт постепенного нарастания , т.

е. в полосе затухания фильтр не является идеальным. Аналогичный вывод о неидеальности реального фильтра можно сделать и для полосы прозрачности, поскольку обеспечить практически согласованный режим работы фильтра во всей полосе прозрачности невозможно, а следовательно, в полосе пропускания коэффициент затухания будет отличен от нуля.

Другим вариантом простейшего низкочастотного фильтра может служить четырехполюсник по схеме на рис. 1,б.

Схема простейшего высокочастотного фильтра приведена на рис. 3,а.

Для данного фильтра коэффициенты четырехполюсника определяются выражениями

;

(9)

;

(10)

.

(11)

Как и для рассмотренного выше случая, А – вещественная переменная. Поэтому на основании (9)

.

Данному неравенству удовлетворяет диапазон изменения частот

.

(12)

Характеристическое сопротивление фильтра

,

(13)

изменяясь в пределах от нуля до с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с в ограниченном диапазоне частот.

Вне области пропускания частот определяется из уравнения

(14)

при .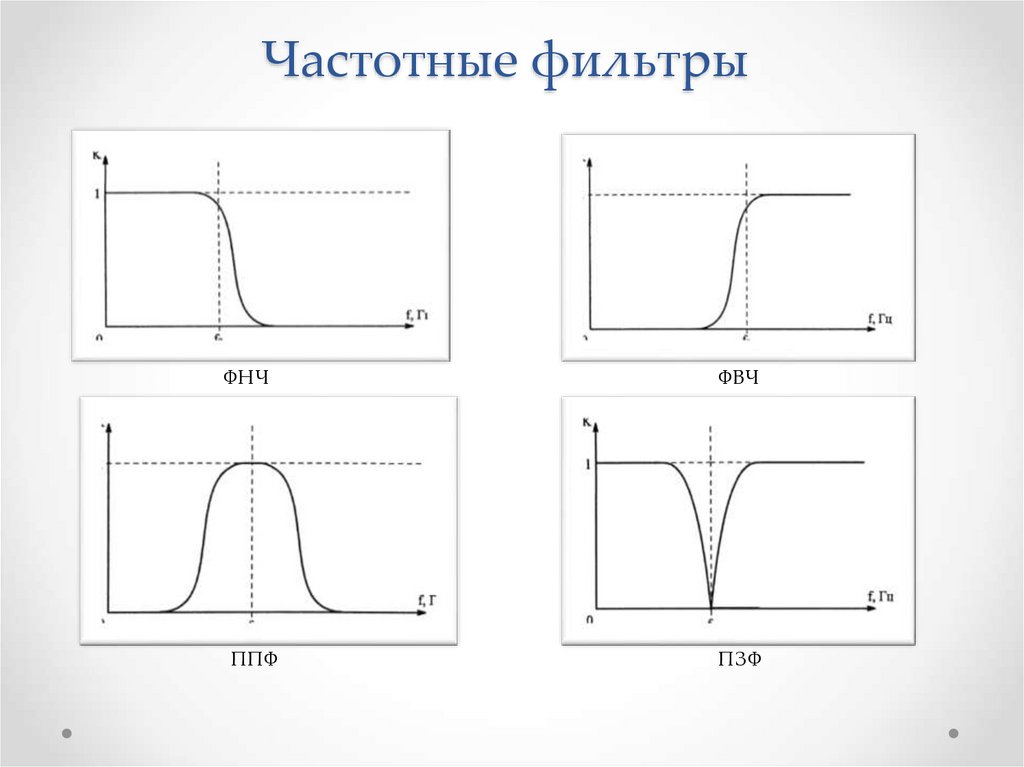 Плавное изменение коэффициента затухания в соответствии с (14) показывает, что в полосе задерживания фильтр не является идеальным.

Качественный вид зависимостей и для низкочастотного фильтра представлен на рис. 4.

Следует отметить, что другим примером простейшего высокочастотного фильтра может служить П-образный четырехполюсник на рис. 3,б.

Полосовой фильтр формально получается путем последовательного соединения низкочастотного фильтра с полосой пропускания и высокочастотного с полосой пропускания , причем . Схема простейшего полосового фильтра

приведена на рис. 5,а, а на рис. 5,б представлены качественные зависимости для него.

У режекторного фильтра полоса прозрачности разделена на две части полосой затухания. Схема простейшего режекторного фильтра и качественные зависимости для него приведены на рис.6.

В заключение необходимо отметить, что для улучшения характеристик фильтров всех типов их целесообразно выполнять в виде цепной схемы, представляющей собой каскадно включенные четырехполюсники.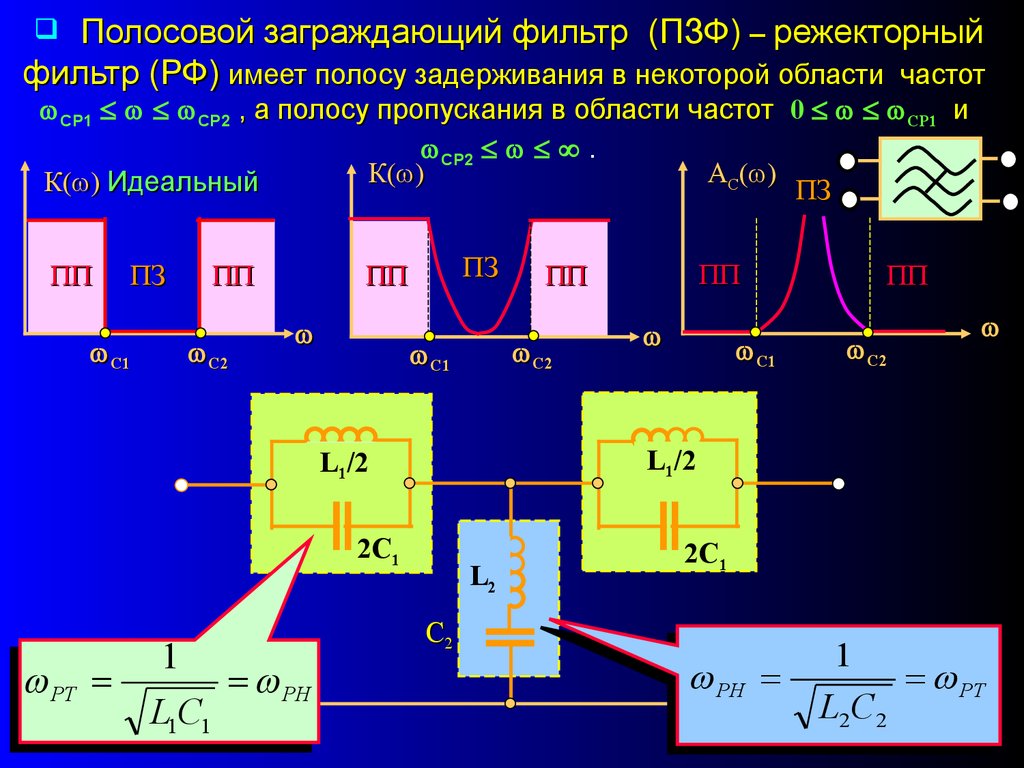 При обеспечении согласованного режима работы всех n звеньев схемы коэффициент затухания такого фильтра возрастает в соответствии с выражением , что приближает фильтр к идеальному.

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Каплянский А. Е. и др. Электрические основы электротехники. Изд. 2-е. Учеб. пособие для электротехнических и энергетических специальностей вузов. -М.: Высш. шк., 1972. -448с.

Контрольные вопросы и задачи

1. Для чего служат фильтры?
2. Что такое полосы прозрачности и затухания?
3. Как классифицируются фильтры в зависимости от диапазона пропускаемых частот?
4. В каком режиме работают фильтры в полосе пропускания частот?
5. Почему рассмотренные фильтры нельзя считать идеальными?
6. Как можно улучшить характеристики фильтра?
7. Определить границы полосы прозрачности фильтров на рис. 1,а и 3,а, если L=10 мГн, а С=10 мкФ.

Ответ: , .

Что такое полосовой фильтр и стоит ли его использовать?

Комбинация фильтра верхних частот и фильтра нижних частот может использоваться для установления узкой полосы пропускания, что может помочь в изучении поведения поверхности в определенном масштабе. Старший эксперт Digital Surf по метрологии поверхности Франсуа Блатейрон дает дополнительные пояснения по этому типу фильтрации, инструмент для которого выпущен с Mountains® 9.2.

 

Концепция полосы пропускания в поверхностном анализе

Шероховатость и волнистость — два удобных названия для обозначения профилей с ограниченным масштабом.

Профиль волнистости фильтруется с помощью фильтра нижних частот, что означает пропускание низких частот (длинных волн) и ослабление высоких частот (коротких волн).

Профиль шероховатости получается обратным процессом с использованием фильтра верхних частот, который ослабляет длинные волны. Каждый профиль получает подмножество частот, содержащихся в исходном профиле. В этом смысле они ограничены полосой или масштабом.

Когда оба фильтра нижних и верхних частот применяются последовательно с одним и тем же значением отсечки, длины волн ниже и выше отсечки ослабляются, и передаются только длины волн вокруг значения отсечки.

Оба типа фильтров имеют коэффициент затухания 50 % на границе отсечки, поэтому передаваемая длина волны умножается на ¼. По конструкции этот фактор можно компенсировать, умножив результат на 4, чтобы получить передачу 100 % при отсечке. Это то, что сделано в стандарте VDA2007 для обнаружения доминирующих длин волн.

Этот тип фильтра известен как полосовой фильтр . Он изолирует узкую полосу пропускания при определенной границе отсечки и позволяет нам анализировать поведение поверхности в этом масштабе. Изменение значения центральной границы отсечки от наименьшей до наибольшей длины волны позволяет выполнять многомасштабный анализ .

Из-за формы гауссовой характеристики передачи кривая полосы пропускания несимметрична. Это связано с тем, что шероховатость фактически получается путем вычитания волнистости из исходного профиля. Однако при обработке сигналов и звука фильтры нижних и верхних частот имеют симметричную конструкцию. Те же принципы можно применить к анализу поверхности и получить симметричный фильтр.

Выше. Классические характеристики передачи Гаусса для отсечки 800 мкм (синяя кривая для шероховатости, красная для волнистости).

 

Выше. Комбинированные характеристики передачи, компенсированные с коэффициентом 4, образуют элементарный полосовой фильтр. Пропускание отложено по вертикальной оси, длины волн по горизонтальной оси в мкм.

 

Набор фильтров

Многомасштабный анализ с использованием полосовых фильтров может генерировать ряд профилей или ряд поверхностей, каждый из которых отфильтрован по разным пороговым значениям. Это иллюстрирует концепцию «банка фильтров», который разлагает спектр на отдельные полосы, подобно аудиографическому эквалайзеру. Количество гамм может быть определено количеством полос на октаву, причем октава представляет собой интервал между длиной волны и ее удвоением или половиной.

Симметричные фильтры можно каскадировать для получения второго, четвертого или восьмого порядка, которые имеют более избирательные кривые передачи с меньшим перекрытием. Их можно использовать для разложения спектра на большее количество полос.

Выше. Характеристики передачи симметричного полосового фильтра Гаусса.

Выше. Четыре симметричных полосовых фильтра с центром в каждой октаве.

 

Оператор New Mountains®

Новый банк Bandpass-фильтров Operator, выпущенный вместе с Mountains® 9.2, разлагает профиль или поверхность на ряд полос, которые затем можно анализировать с использованием параметров текстуры поверхности.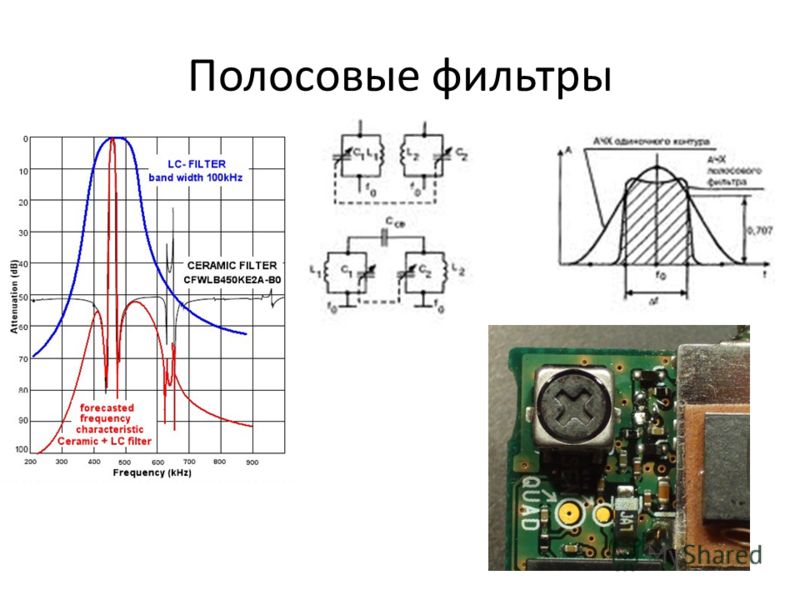 Функциональная корреляция может быть выполнена для идентификации активных полос, где корреляция выше. Это может помочь в определении диапазона шкал, которые будут использоваться для управления конкретной функцией на заготовке.

Выше. Mountains® версии 9.2 предлагает новый оператор банка полосовых фильтров для поверхностей

Выше. Оператор банка полосовых фильтров для профилей

 

Инструмент также предоставляет новый способ выполнения многомасштабного анализа в качестве альтернативы вейвлет-анализу или чувствительному к масштабу фрактальному анализу, которые уже доступны в Mountains®. Преимущество банков полосовых фильтров заключается в использовании более простых для понимания инструментов, основанных на хорошо известном фильтре Гаусса.

Физические явления обычно многомасштабны по своей природе, поэтому сложные поверхности должны быть проанализированы с использованием многомасштабных инструментов, чтобы уловить эту сложность, и программное обеспечение Mountains® теперь предлагает полный набор таких инструментов.

Выше. Пример многомасштабного анализа профиля с использованием банка фильтров Гаусса. Полосовые фильтры | Фильтры BP

Полосовые фильтры (также называемые полосовыми фильтрами, фильтрами BP или полосовыми фильтрами) были основой бизнеса Omega с первых дней, когда мы выпустили одни из первых полосовых фильтров для сканеров супермаркетов еще в середине 19-го века.70-е годы. Они предназначены для обеспечения высокой передачи в определенном диапазоне длин волн, блокируя свет с других длин волн, чтобы обеспечить хорошее соотношение сигнал-шум в области передачи.

 

Просмотр полосовых фильтров

 

Перейти к-

• Требуемые характеристики полосовых фильтров
• Типы полосовых фильтров
• Специальные полосовые фильтры

Пиковая передача — максимальная передача фильтра (%).
Центральная длина волны (CWL) — средняя точка области передачи (нм).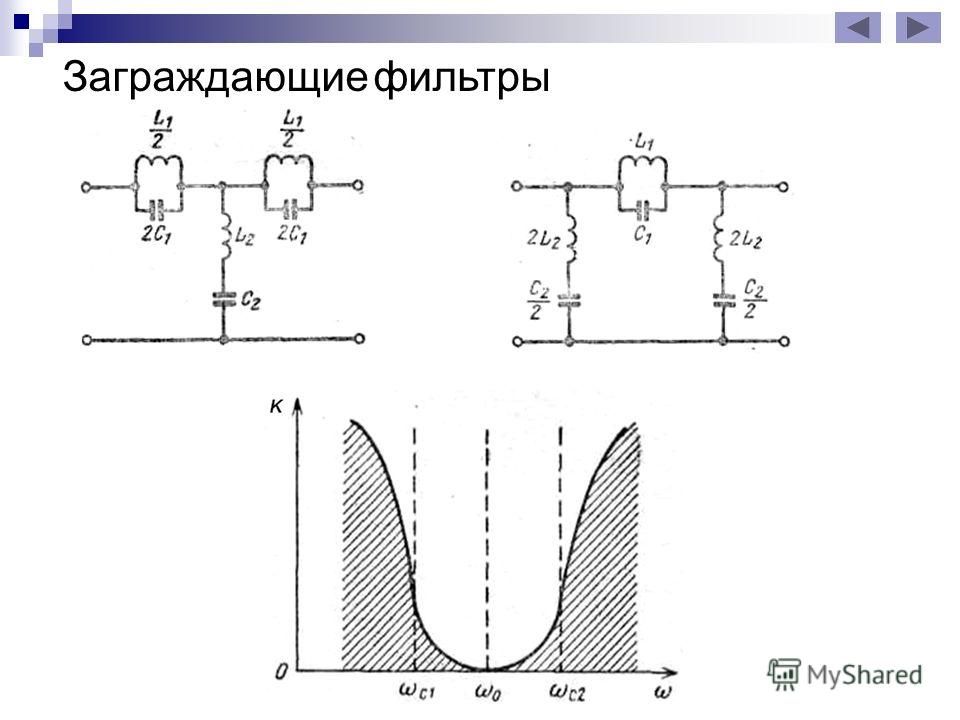
Полуширина-полумакс (FWHM) описывает ширину области передачи на половине максимального значения передачи (нм). Из-за физических свойств тонкопленочных интерференционных фильтров ширина на полувысоте обычно увеличивается с увеличением длины волны. Его можно рассчитать, используя процент от центральной длины волны.

 

 

Длина волны отсечки и отсечки можно использовать вместо FWHM и CWL для обозначения краев передающей области фильтра (нм).
Пульсация полосы пропускания описывает неравномерность передающей области (%). Некоторые узкополосные фильтры и более старые конструкции имеют остроконечную форму полосы пропускания вместо плоской вершины. Это зависит от конструкции фильтра. Как правило, конструкции с плоским верхом требуют большего количества слоев и большей стоимости.

 

 

Кромка Крутизна более подробно описывает переход от блокировки к передаче (нм).

 

 

Блокирование   Технические характеристики определяют диапазон длин волн (нм) и блокирование (ОП) нежелательного света. Обычно диапазон длин волн определяется характеристикой вашего детектора. Однако для некоторых приложений (например, лазерная очистка или рамановские фильтры) расширенная блокировка не требуется, когда нежелательные сигналы присутствуют только в ограниченном диапазоне длин волн. Оптическая плотность (ОП) представляет собой логарифмическую шкалу отношения прошедшего и падающего света.

OD=2-log(%T)

 

 

• Стандартный полосовой фильтр

  • Основная часть бизнеса Omega связана с полосовыми фильтрами в диапазоне 400–1100 нм.
  • FWHM, начиная с 10 морских миль
  • Размер 2–90 мм 

• Фильтры RapidBand

  • Фильтры Rapidband состоят из короткопроходных и длиннопроходных фильтров, спрессованных в узел с воздушным зазором, что обеспечивает быстрое и экономичное решение.
  • Доступны для видимых длин волн (отстоящих друг от друга на 10 нм) от 400 до 700 нм. Также доступны выбранные другие длины волн.
  • Размер патронов 25 мм, с кольцевым креплением.
  • Подходит для большинства кубов флуоресцентных микроскопов.

• Многополосные фильтры

  • Многополосные фильтры имеют ряд полос пропускания и заблокированных областей. Они используются для визуализации нескольких цветов одновременно, для объединения лучей, трехмерных движущихся изображений и коррекции дальтонизма.
  • Размер 2–50 мм

• Узкополосный

  • Часто используется в высокомультиплексных экспериментах (проточная цитометрия, флуоресцентная гибридизация in situ и т. д.) для уменьшения спектральных перекрестных помех между сигналами. Также используется в качестве очищающих фильтров для лазеров или светодиодов.
  • FWHM 1–10 морских миль
  • Размер 2–50 мм

• Узкополосный с плоским верхом

  • Клиентам, которых беспокоит спектральный дрейф из-за циклического изменения температуры или нестабильности длины волны лазера, требуется узкополосный датчик с низкочастотными пульсациями, чтобы сигнал не изменялся по интенсивности при изменении длины волны.