Фильтр низких частот — frwiki.wiki
Изображение, к которому был применен фильтр нижних частот (результат справа)
Фильтр низких частот представляет собой фильтр , который проходит низкие частоты и ослабляет высокие частоты , то есть частоты выше частоты среза . Его также можно было бы назвать фильтром высоких частот. Фильтр нижних частот является инверсией фильтра верхних частот, и эти два фильтра вместе образуют полосовой фильтр .
Концепция фильтра нижних частот — это математическое преобразование, применяемое к данным (сигналу). Фильтр нижних частот можно реализовать в цифровом виде или с помощью электронных компонентов. Функция этого преобразования состоит в том, чтобы ослабить частоты выше его частоты среза , чтобы сохранить только низкие частоты. Частота среза фильтра — это частота, разделяющая два идеальных режима работы фильтра: прохождение или блокирование. жпротив{\ displaystyle f_ {c}}
Резюме
- 1 Идеальный фильтр
- 2 Аналоговый фильтр нижних частот
- 2.
 1 Фильтр нижних частот первого порядка
1 Фильтр нижних частот первого порядка- 2.1.1 Пассивная схема
- 2.1.2 Активная цепь
- 2.2 Фильтр нижних частот второго порядка
- 2.2.1 Пассивная схема
- 2.2.2 Активная цепь
- 2.3 Фильтр высшего порядка
- 2.
- 3 Цифровой фильтр нижних частот
- 4 См. Также
- 4.1 Связанные статьи
Идеальный фильтр
Идеальный фильтр нижних частот имеет постоянное усиление в полосе пропускания и нулевое усиление в полосе среза. Переход между двумя состояниями происходит мгновенно. Математически это может быть достигнуто путем умножения сигнала на прямоугольное окно в частотной области или путем свертки с кардинальным синусом (sinc) во временной области. Этот тип фильтра на инженерном жаргоне называется «кирпичной стеной».
Конечно, идеальный фильтр вряд ли возможен, поскольку кардинальный синус — бесконечная функция. Таким образом, фильтр должен предсказывать будущее и иметь бесконечное знание прошлого, чтобы выполнить свертку и достичь желаемого эффекта. Этот фильтр можно очень точно аппроксимировать в цифровом виде, когда есть предварительно записанный сигнал (путем добавления нулей на обоих концах серии выборок) или для периодического сигнала.
Этот фильтр можно очень точно аппроксимировать в цифровом виде, когда есть предварительно записанный сигнал (путем добавления нулей на обоих концах серии выборок) или для периодического сигнала.
В реальном времени цифровые фильтры могут аппроксимировать этот фильтр, вставляя преднамеренную задержку в сигнал, что позволяет «узнать будущее сигнала». Эта операция создает фазовый сдвиг между выходом и входом, и, естественно, чем дольше вставленная задержка, тем больше фильтр будет приближаться к идеальному фильтру.
Аналоговый фильтр нижних частот
Фильтр нижних частот может быть реализован аналогично электронным компонентам. Таким образом, этот вид фильтра применяется к непрерывным сигналам в реальном времени. Компоненты и конфигурация схемы фиксируют различные характеристики фильтра , такие как порядок, частота среза и его диаграмма Боде . Обычные аналоговые фильтры бывают первого или второго порядка. Существует несколько семейств аналоговых фильтров: Баттерворта , Чебышева , Бесселя , эллиптические и др.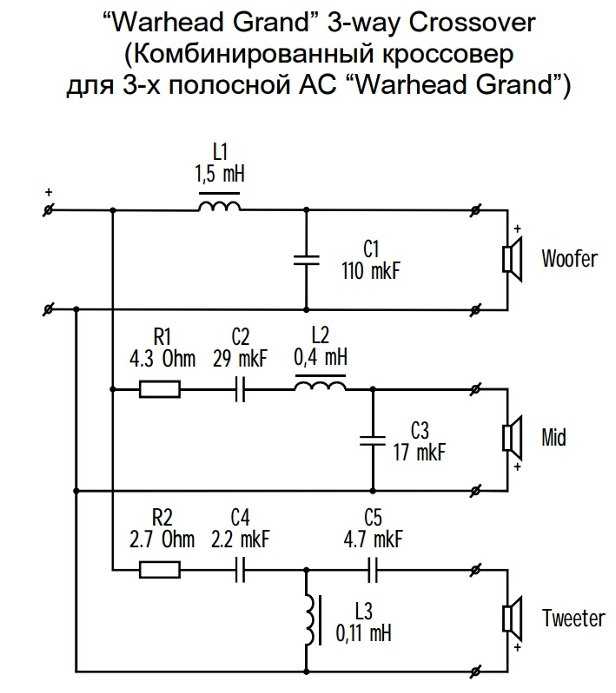
Фильтр нижних частот первого порядка
Фильтр нижних частот первого порядка характеризуется частотой среза . Передаточная функция фильтра получается денормализацией нормализованного фильтра нижних частот путем замены на , что дает следующую передаточную функцию : жпротив{\ displaystyle f_ {c}}ωнет{\ displaystyle \ omega _ {n}}ω/ωпротив{\ displaystyle \ omega / \ omega _ {c}}
или же
Модуль и фаза передаточной функции равны:
Есть несколько способов реализовать этот фильтр.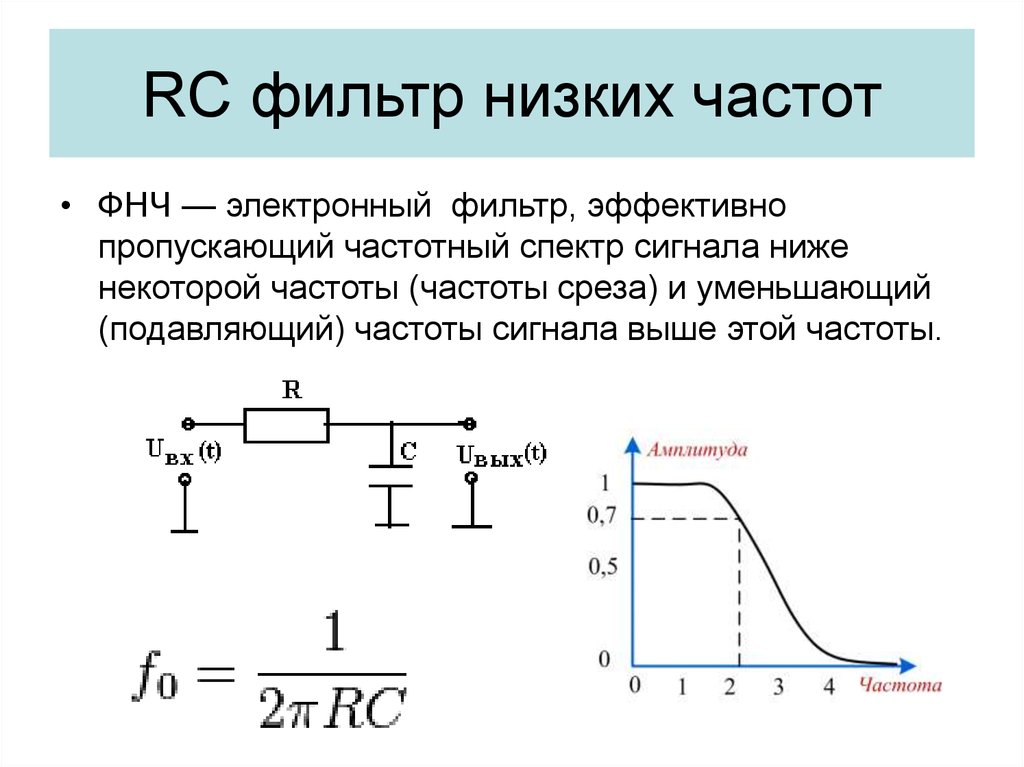 Здесь представлены активная реализация и пассивная реализация. K — коэффициент усиления фильтра.
Здесь представлены активная реализация и пассивная реализация. K — коэффициент усиления фильтра.
Пассивная схема
Самый простой способ получить этот фильтр физически — использовать RC-цепь . Как следует из названия, эта схема состоит из резистора и конденсаторного конденсатора . Эти два элемента размещены последовательно с источником сигнала. Выходной сигнал восстанавливается на выводах конденсатора. Несмотря на то, что сопротивление постоянно независимо от частоты, оно не одинаково для конденсатора; чем выше частота, тем меньше времени у конденсатора для заряда / разряда. Когда частота стремится к бесконечности, конденсатор ведет себя как короткое замыкание (шунт). Когда частота стремится к 0, это ведет себя как разомкнутая цепь. В каком-то смысле это переменный резистор, зависящий от частоты. Чтобы найти передаточную функцию этого фильтра, необходимо работать в области Лапласа, используя импедансы элементов. С помощью этой техники схема становится простым делителем напряжения , и мы получаем: р{\ displaystyle R}ПРОТИВ{\ displaystyle C}vя{\ displaystyle v_ {i}}vо{\ displaystyle v_ {o}}
В этом уравнении — комплексное число (j такое, что j² = -1) и представляет собой пульсацию цепи или радиальную частоту, выраженную в рад / с. Поскольку частота среза RC-цепи равна:
j{\ displaystyle j}ω{\ displaystyle \ omega}
Поскольку частота среза RC-цепи равна:
j{\ displaystyle j}ω{\ displaystyle \ omega}
Аналоговый фильтр нижних частот первого порядка на RC-цепи.
Здесь пульсация отсечки также является собственной пульсацией контура. Это также величина, обратная постоянной времени цепи (увеличенной на константу ). Таким образом, действительно получается типичная передаточная функция фильтра нижних частот первого порядка. ωпротив{\ displaystyle \ omega _ {c}}ωо{\ displaystyle \ omega _ {o}}τ{\ Displaystyle \ тау}2π{\ displaystyle 2 \ pi}
С помощью этой передаточной функции мы можем получить диаграммы Боде :
- Прирост в децибелах :
- Фаза в радианах :
Тогда мы можем выделить две идеальные ситуации:
Расположение Боде пассивного фильтра нижних частот первого порядка
- Когда у нас есть:ω≪ωпротив{\ displaystyle \ omega \ ll \ omega _ {c}}
- Когда у нас есть:ω≫ωпротив{\ displaystyle \ omega \ gg \ omega _ {c}}
Обратите внимание, что для , у нас = -3 дБ. ωзнак равноωпротив{\ displaystyle \ omega = \ omega _ {c}}граммdB{\ displaystyle G_ {дБ}}
ωзнак равноωпротив{\ displaystyle \ omega = \ omega _ {c}}граммdB{\ displaystyle G_ {дБ}}
Активная схема
Также возможно реализовать фильтр нижних частот с активной схемой. Эта опция позволяет добавить усиление к выходному сигналу, то есть получить амплитуду более 0 дБ в полосе пропускания. Несколько конфигураций позволяют реализовать этот вид фильтра.
Активный фильтр нижних частот
В представленной здесь конфигурации частота среза определяется следующим образом:
Используя свойства операционных усилителей и импедансы элементов, мы получаем следующую передаточную функцию:
На низкой частоте конденсатор действует как разомкнутая цепь , что подтверждается тем фактом, что правый член предыдущего уравнения стремится к 1.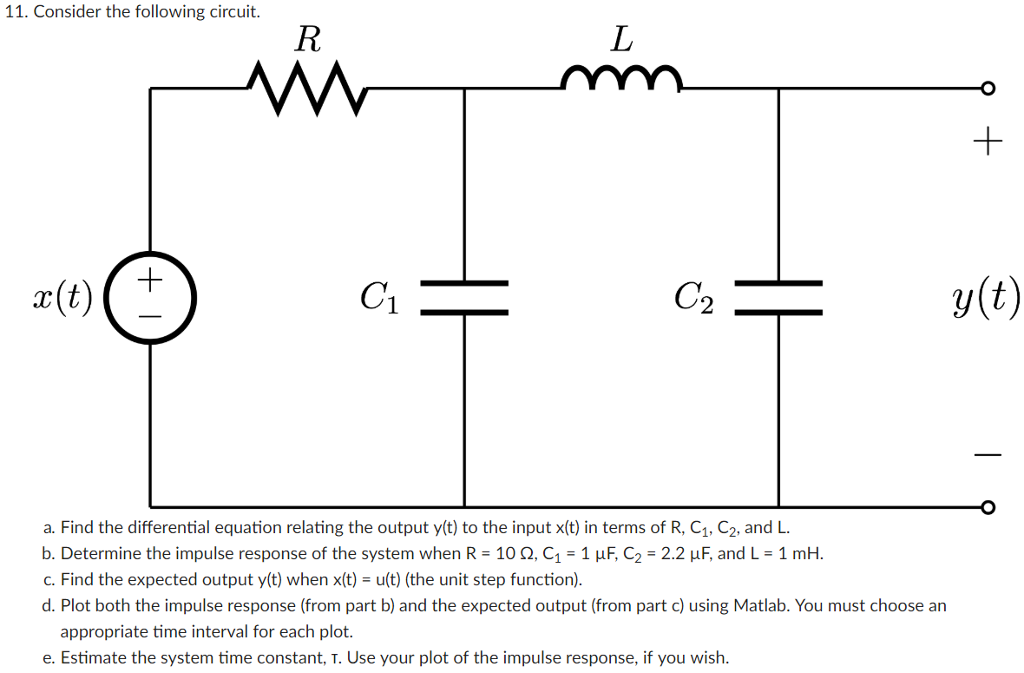 Полученная таким образом упрощенная формула дает нам коэффициент усиления в полосе пропускания:
Полученная таким образом упрощенная формула дает нам коэффициент усиления в полосе пропускания:
На высокой частоте конденсатор действует как замкнутая цепь, и член справа стремится к нулю, что заставляет формулу стремиться к нулю.
С помощью передаточной функции можно продемонстрировать, что затухание в отклоненной полосе составляет 20 дБ / декаду или 6 дБ на октаву, как ожидается для фильтра первого порядка.
Часто можно увидеть схему усиления или ослабления, преобразованную в фильтр нижних частот путем добавления конденсатора C. Это уменьшает отклик высокочастотной схемы и помогает уменьшить колебания в усилителе. Например, аудиоусилитель может быть активным фильтром нижних частот с частотой среза порядка 100 кГц для уменьшения усиления на частотах, которые в противном случае будут колебаться.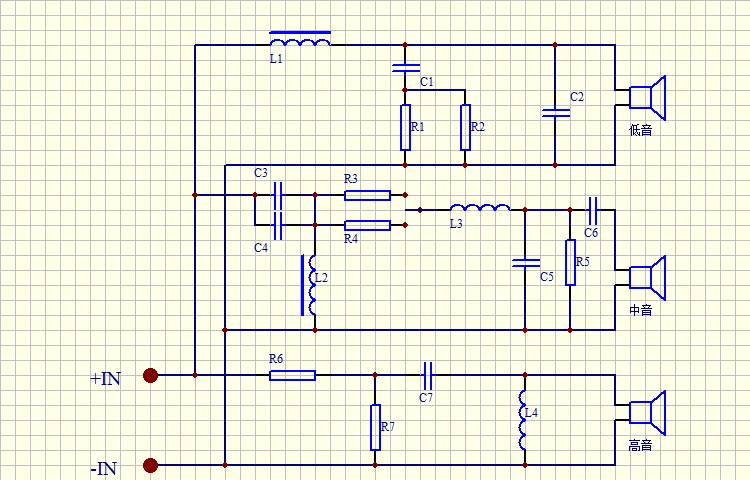 {2}}} \ right)}
{2}}} \ right)}
Активная схема
Для создания активного фильтра второго порядка существует несколько типов фильтров. Наиболее популярны конструкции MFB и VCVS.
Фильтр высшего порядка
Фильтры более высокого порядка обычно состоят из фильтров первого и второго порядка в каскаде. Например, реализация фильтра 5-го порядка осуществляется путем размещения двух фильтров 2-го порядка и фильтра 1-го порядка. Можно было бы напрямую реализовать фильтр 5-го порядка, но сложность конструкции значительно возрастет. Также следует знать, что любой фильтр порядка больше 2 может быть разложен на продукт (каскад) фильтров порядка 1 и 2, благодаря свойствам полиномов (любой полином порядка больше 2 может быть разложен на произведение многочленов степени меньше или равной 2). Это объясняет, почему бесполезно напрямую разрабатывать фильтр 5-го порядка, когда мы можем получить точно такой же результат с каскадом из двух фильтров 2-го и 1-го порядка. Однако концепция фильтра более высокого порядка является ошибкой. Практика, которая существовала, в основном, на заре электроники, когда активные компоненты были относительно дорогими. Фильтр пятого порядка, разработанный как таковой, действительно требует только одного активного компонента, тогда как каскад из трех фильтров потребует трех.
Практика, которая существовала, в основном, на заре электроники, когда активные компоненты были относительно дорогими. Фильтр пятого порядка, разработанный как таковой, действительно требует только одного активного компонента, тогда как каскад из трех фильтров потребует трех.
Цифровой фильтр нижних частот
См. Цифровой фильтр .
Смотрите также
Статьи по Теме
- Режекторный фильтр
- Полосовой фильтр
- Фильтр высоких частот
- Фильтр (электронный)
- Пространственная фильтрация с помощью оптической , более конкретно к очистке лазера .
Фильтры | |
|---|---|
| Типы фильтров | Фильтр низких частот · High Pass Filter · полосовой фильтр · режекторный фильтр |
| линейные фильтры | Фильтр Бесселя · Фильтр Баттерворта · Фильтр Чебышева · Фильтр эллиптический |
| цифровые фильтры | Конечная импульсная характеристика · фильтр бесконечной импульсной характеристики |
<img src=»https://fr.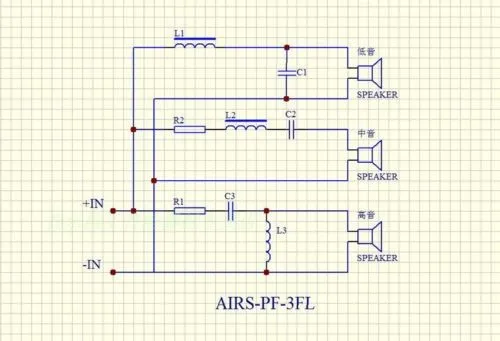 wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Фильтры. Вновь. По порядку… | журнал АвтоЗвук
Профессиональный рецепт Огюста Родена наилучшим образом подходит для нашей темы. А тема была давно обещана читателям. Вновь (поскольку «вспомнить всё») разобраться с электрическими фильтрами во всех формах, в которых они применяются в нашей узкой отрасли.
…взять глыбу мрамора и отсечь от нее всё лишнее…
Огюст Роден
Любой фильтр, в сущности, делает со спектром сигнала то же, что Роден с мрамором. Но в отличие от творчества скульптора замысел принадлежит не фильтру, а нам с вами.
Нам с вами по понятным причинам больше всего знакома одна сфера применения фильтров — разделение спектра звуковых сигналов для последующего воспроизведения их динамическими головками (нередко мы говорим «динамиками», но сегодня материал серьёзный, поэтому к терминам будем тоже подходить со всей строгостью).
Конечно, первые фильтры были пассивными, состояли они из катушек и конденсаторов, а с помощью резисторов удавалось получить нормированные характеристики.
Изначально предполагалось посвятить этот материал целиком и полностью пассивным фильтрам, их в практике инсталляторов приходится рассчитывать и изготавливать своими силами несравнимо чаще, чем активные. Но логика потребовала, чтобы мы всё же начали с активных. Как ни странно, потому что они проще, что бы ни казалось при первом взгляде на приводимые иллюстрации.
Хочу быть понятым верно: сведения об активных фильтрах не призваны служить исключительно руководством по их изготовлению, такая надобность появляется далеко не всегда.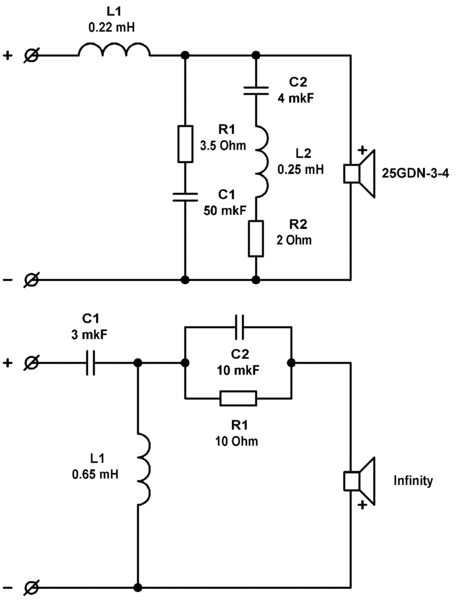 Гораздо чаще возникает нужда понять, как работают уже имеющиеся фильтры (главным образом — в составе усилителей) и почему они не всегда работают так, как нам бы хотелось. И здесь, действительно, может прийти мысль о ручной работе.
Гораздо чаще возникает нужда понять, как работают уже имеющиеся фильтры (главным образом — в составе усилителей) и почему они не всегда работают так, как нам бы хотелось. И здесь, действительно, может прийти мысль о ручной работе.

Для фильтров первого порядка (рис. 1) я приведу два варианта схемной реализации активных фильтров — с ОУ и с эмиттерным повторителем на транзисторе n-p-n типа, а вы уж сами при случае выберете, с чем вам проще будет работать. Почему n-p-n? Потому, что их больше, и потому, что при прочих равных условиях в производстве они получаются несколько «лучше». Моделирование проводилось для транзистора КТ315Г — единственного, наверное, полупроводникового прибора, цена на который до последнего времени была точно такая же, как и четверть века назад — 40 копеек. Фактически вы можете использовать любой n-p-n транзистор, коэффициент усиления которого (h31э) не намного ниже 100.
Рис. 1. Фильтры ВЧ первого порядка
Резистор в цепи эмиттера (R1 на рис.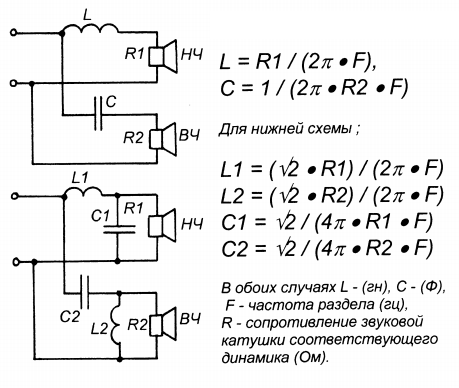 1) задаёт ток коллектора, для большинства транзисторов его рекомендуют выбирать примерно равным 1 мА или немного меньше. Частоту среза фильтра определяет ёмкость входного конденсатора C2 и общее сопротивление параллельно включённых резисторов R2 и R3. В нашем случае это сопротивление составляет 105 кОм. Надо только следить, чтобы оно было значительно меньше, нежели сопротивление в цепи эмиттера (R1), умноженное на показатель h31э — в нашем случае это примерно 1200 кОм (в действительности при разбросе значений h31э от 50 до 250 — от 600 кОм до 4 МОм). Выходной конденсатор добавлен, что называется, «для порядка» — если нагрузкой фильтра будет входной каскад усилителя, там, как правило, уже стоит конденсатор для развязки входа по постоянному напряжению.
1) задаёт ток коллектора, для большинства транзисторов его рекомендуют выбирать примерно равным 1 мА или немного меньше. Частоту среза фильтра определяет ёмкость входного конденсатора C2 и общее сопротивление параллельно включённых резисторов R2 и R3. В нашем случае это сопротивление составляет 105 кОм. Надо только следить, чтобы оно было значительно меньше, нежели сопротивление в цепи эмиттера (R1), умноженное на показатель h31э — в нашем случае это примерно 1200 кОм (в действительности при разбросе значений h31э от 50 до 250 — от 600 кОм до 4 МОм). Выходной конденсатор добавлен, что называется, «для порядка» — если нагрузкой фильтра будет входной каскад усилителя, там, как правило, уже стоит конденсатор для развязки входа по постоянному напряжению.
В схеме фильтра на ОУ здесь (как и в последующем) использована модель TL082C, поскольку этот операционный усилитель очень часто применяется для построения фильтров. Впрочем, можно брать едва ли не любой ОУ из тех, что нормально работают с однополярным питанием, предпочтительнее с входом на полевых транзисторах.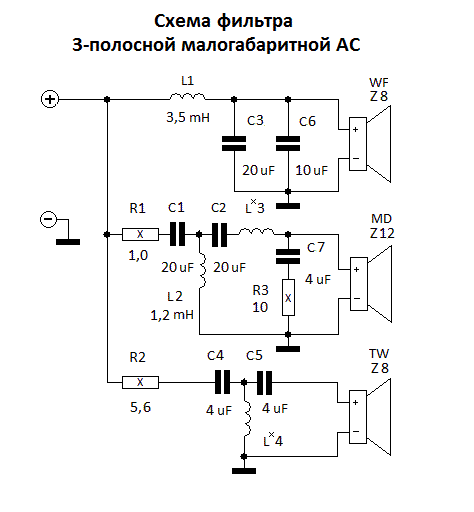 Здесь также частота среза определяется соотношением ёмкости входного конденсатора C2 и сопротивлением параллельно включённых резисторов R3, R4. (Почему параллельно включённых? Потому, что с точки зрения переменного тока плюс питания и минус — одно и то же.) Соотношение резисторов R3, R4 определяет среднюю точку, если они будут немного различаться, это не трагедия, это лишь означает, что сигнал максимальной амплитуды начнёт ограничиваться с одной стороны несколько раньше. Фильтр рассчитан на частоту среза 100 Гц. Чтобы её понизить, надо увеличить либо номинал резисторов R3, R4, либо емкость C2. То есть номинал изменяется обратно пропорционально первой степени частоты.
Здесь также частота среза определяется соотношением ёмкости входного конденсатора C2 и сопротивлением параллельно включённых резисторов R3, R4. (Почему параллельно включённых? Потому, что с точки зрения переменного тока плюс питания и минус — одно и то же.) Соотношение резисторов R3, R4 определяет среднюю точку, если они будут немного различаться, это не трагедия, это лишь означает, что сигнал максимальной амплитуды начнёт ограничиваться с одной стороны несколько раньше. Фильтр рассчитан на частоту среза 100 Гц. Чтобы её понизить, надо увеличить либо номинал резисторов R3, R4, либо емкость C2. То есть номинал изменяется обратно пропорционально первой степени частоты.
В схемах фильтра НЧ (рис. 2) на пару деталей больше, поскольку входной делитель напряжения не используется как элемент частотно-зависимой цепи и добавляется разделительная ёмкость. Для понижения частоты среза фильтра надо увеличивать входной резистор (R5).
Рис. 2. Фильтры НЧ первого порядка
Разделительная ёмкость имеет нешуточный номинал, так что без электролита обойтись будет трудно (хотя можно ограничиться плёночным конденсатором 4,7 мкФ). Следует учитывать, что разделительная ёмкость совместно с C2 образуют делитель, и чем она меньше, тем выше ослабление сигнала. Как следствие, несколько смещается и частота среза. В некоторых случаях можно обойтись без разделительного конденсатора — если, к примеру, источником является выход другого каскада фильтра. А вообще стремление избавиться от громоздких разделительных конденсаторов и явилось, наверное, основной причиной перехода от однополярного питания к двухполярному.
Следует учитывать, что разделительная ёмкость совместно с C2 образуют делитель, и чем она меньше, тем выше ослабление сигнала. Как следствие, несколько смещается и частота среза. В некоторых случаях можно обойтись без разделительного конденсатора — если, к примеру, источником является выход другого каскада фильтра. А вообще стремление избавиться от громоздких разделительных конденсаторов и явилось, наверное, основной причиной перехода от однополярного питания к двухполярному.
На рис. 3 и 4 показаны частотные характеристики фильтров ВЧ и НЧ, схемы которых мы только что рассмотрели.
Рис. 3. Характеристики фильтров ВЧ первого порядка
Рис. 4. Характеристики фильтров НЧ первого порядка
Весьма вероятно, что у вас уже возникли два вопроса. Первый: а что это мы так плотно занялись изучением фильтров первого порядка, когда для сабвуферов они не годятся вовсе, да и для разделения полос фронтальной акустики, если верить высказываниям автора, они применимы, мягко говоря, не часто? И второй: а почему автор не упомянул ни Баттерворта, ни его однофамильцев — Линквица, Бесселя, Чебышева, в конце концов? На первый вопрос я пока отвечать не буду, чуть позже вам всё станет ясно. Сразу перехожу ко второму. Баттервортом со товарищи были определены характеристики фильтров от второго порядка и выше, а частотная и фазовая характеристика фильтров первого порядка всегда одна и та же.
Сразу перехожу ко второму. Баттервортом со товарищи были определены характеристики фильтров от второго порядка и выше, а частотная и фазовая характеристика фильтров первого порядка всегда одна и та же.
Итак, фильтры второго порядка, с номинальной крутизной спада 12 дБ/окт. Такие фильтры повсеместно делаются с использованием ОУ. Можно, конечно, обойтись и транзисторами, но для того, чтобы схема работала точно, приходится учитывать много всего, и в результате простота оказывается чисто мнимой. Известно энное количество вариантов схемной реализации таких фильтров. Я даже не скажу какое, поскольку любое перечисление всегда может оказаться неполным. Да и нам оно мало что даст, поскольку по-настоящему углубляться в теорию активных фильтров нам вряд ли имеет смысл. Тем более что в построении фильтров усилителей участвуют по большей части лишь две схемные реализации, можно даже сказать, что полторы. Начнём с той, которая «целая». Это так называемый фильтр Саллена — Ки (Sallen — Key).
Рис. 5. Фильтр ВЧ второго порядка
5. Фильтр ВЧ второго порядка
Здесь, как и всегда, частота среза определяется номиналами конденсаторов и резисторов, в данном случае — C1, C2, R3, R4, R5. Обратите внимание, для фильтра Баттерворта (ну наконец-то!) номинал резистора в цепи обратной связи (R5) должен быть вдвое меньше номинала резистора, включённого в «землю». Как обычно, в «землю» получаются включенными резисторы R3 и R4 параллельно, и суммарный номинал их 50 кОм.
Теперь несколько слов как бы в сторону. Если у вас фильтр не перестраиваемый, проблем с подбором резисторов не будет. Но если вам надо плавно менять частоту среза фильтра, нужно одновременно изменять два резистора (у нас их три, но в усилителях питание двухполярное, и там один резистор R3, номинала такого же, как наши два R3, R4, включённые параллельно). Специально для таких целей выпускаются сдвоенные переменные резисторы разного номинала, но они и дороже, и не так их много. Кроме того, можно разработать фильтр с очень близкими характеристиками, но у которого оба резистора будут одинаковыми, а ёмкости C1 и C2 — разными. Но это хлопотно. А теперь давайте посмотрим, что будет, если взять фильтр, рассчитанный на среднюю частоту (330 Гц) и начать менять лишь один резистор — тот, который в «землю». (Рис. 6).
Но это хлопотно. А теперь давайте посмотрим, что будет, если взять фильтр, рассчитанный на среднюю частоту (330 Гц) и начать менять лишь один резистор — тот, который в «землю». (Рис. 6).
Рис. 6. Перестройка фильтра ВЧ
Согласитесь, нечто подобное мы многократно видели на графиках в тестах усилителей.
Схема фильтра НЧ похожа на зеркальное отображение фильтра ВЧ: в обратной связи стоит конденсатор, а в горизонтальной полке буквы «Т» — резисторы. (Рис. 7).
Рис. 7. Фильтр НЧ второго порядка
Как и в случае с фильтром НЧ первого порядка, добавляется разделительный конденсатор (C3). Величина резисторов в цепи создания локальной «земли» (R3, R4) влияет на величину затухания, вносимого фильтром. При указанном на схеме номинале аттенюация около 1,3 дБ, думаю, с этим можно мириться. Как всегда, частота среза обратно пропорциональна номиналу резисторов (R5, R6). Для фильтра Баттерворта номинал конденсатора в обратной связи (C2) должен быть вдвое больше, чем ёмкость C1.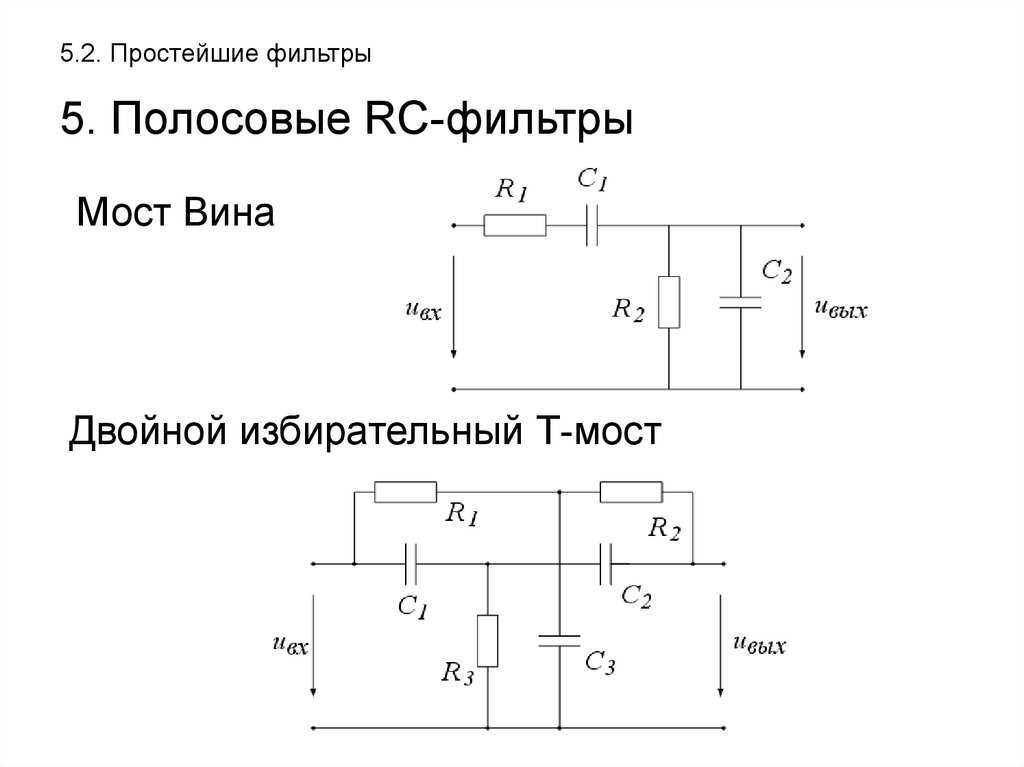 Поскольку номинал резисторов R5, R6 один и тот же, для плавной перестройки частоты среза подходит почти любой сдвоенный подстроечный резистор — именно поэтому во многих усилителях характеристики фильтров НЧ более стабильны, нежели характеристики фильтров ВЧ.
Поскольку номинал резисторов R5, R6 один и тот же, для плавной перестройки частоты среза подходит почти любой сдвоенный подстроечный резистор — именно поэтому во многих усилителях характеристики фильтров НЧ более стабильны, нежели характеристики фильтров ВЧ.
На рис. 8 показаны амплитудно-частотные характеристики фильтров второго порядка.
Рис. 8. Характеристики фильтров второго порядка
Вот теперь можно вернуться к тому вопросу, который остался без ответа. Схему фильтра первого порядка мы «проходили» потому, что активные фильтры создаются в основном путём каскадирования базовых звеньев. Так что последовательное соединение фильтров первого и второго порядка даст третий порядок, цепочка из двух фильтров второго порядка даст четвёртый и так далее. Поэтому я приведу лишь два варианта схем: фильтр ВЧ третьего порядка и фильтр НЧ — четвёртого. Тип характеристики — Баттерворт, частота среза — те же 100 Гц. (Рис. 9).
Рис. 9. Фильтр ВЧ третьего порядка
Предвижу вопрос: отчего вдруг изменились номиналы резисторов R3, R4, R5? А отчего бы им не измениться? Если в каждой «половинке» схемы уровню -3 дБ соответствовала частота 100 Гц, значит, совместное действие обеих частей схемы приведёт к тому, что спад на частоте 100 Гц составит уже 6 дБ. А мы так не договаривались. Так что самое привести методику выбора номиналов — пока только для фильтров Баттерворта.
А мы так не договаривались. Так что самое привести методику выбора номиналов — пока только для фильтров Баттерворта.
1. По известной частоте среза фильтра задаться одним из характерных номиналов (R или C) и вычислить второй номинал, используя зависимость:
Fc = 1/(2πRC) (1.1)
Поскольку ассортимент номиналов конденсаторов, как правило, более узкий, разумнее всего задаться базовым значением ёмкости C (в фарадах), а по нему определить базовое значение R (Ом). Но если у вас, к примеру, есть пара конденсаторов 22 nF и несколько штук на 47 nF, никто не мешает вам брать и те, и эти — но в разных частях фильтра, если он составной.
2. Для фильтра первого порядка формула (1.1) даёт сразу значение резистора. (В нашем конкретном случае получаем 72,4 кОм, округляем до ближайшего стандартного значения, получаем 75 кОм.) Для базового фильтра второго порядка вы точно так же определяете стартовое значение R, но для того, чтобы получить действительные значения резисторов, надо будет воспользоваться таблицей.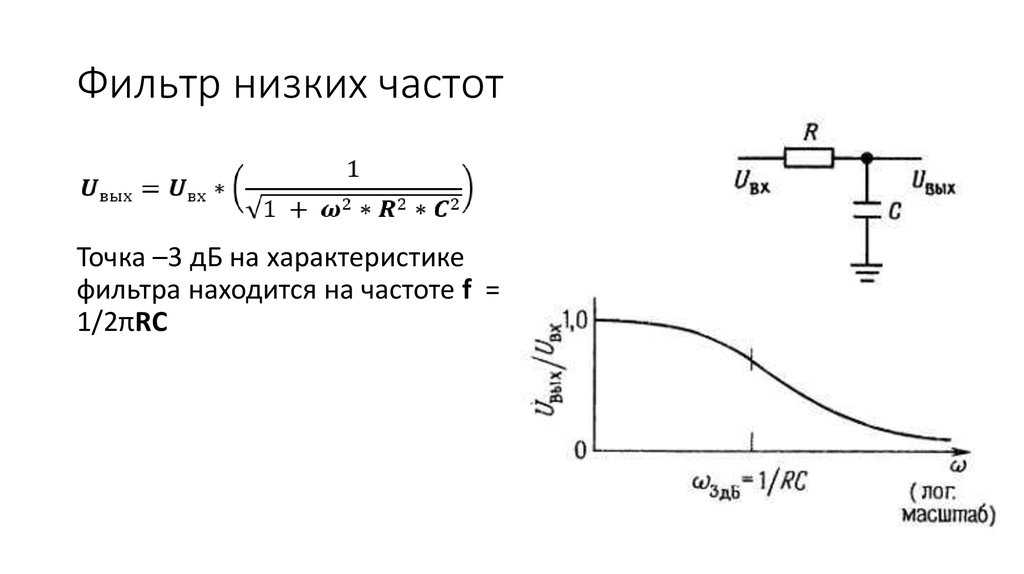 Тогда номинал резистора в цепи обратной связи определится как
Тогда номинал резистора в цепи обратной связи определится как
Rp = KpR (1.2)
а номинал резистора, идущего в «землю», будет равен
Rs = KsR (1.3)
| Порядок фильтра | Kp | Ks |
| 2 | 0,7070 | 1,414 |
| 3 | 0,5000 | 2,000 |
| 4 (1) | 0,3827 | 2,613 |
| 4 (2) | 0,9240 | 1,082 |
Единичкой и двойкой в скобках обозначены строки, относящиеся к первому и второму каскадам фильтра четвёртого порядка. Можете проверить: произведение двух коэффициентов в одной строке равно единице — это, действительно, обратные величины. Впрочем, мы договорились в теорию фильтров не лезть.
Расчёт номиналов определяющих компонентов фильтра НЧ осуществляется сходным образом и по той же таблице. С той только разницей, что в общем случае вам придётся танцевать от удобного номинала резистора, а номиналы конденсаторов подбирать по таблице.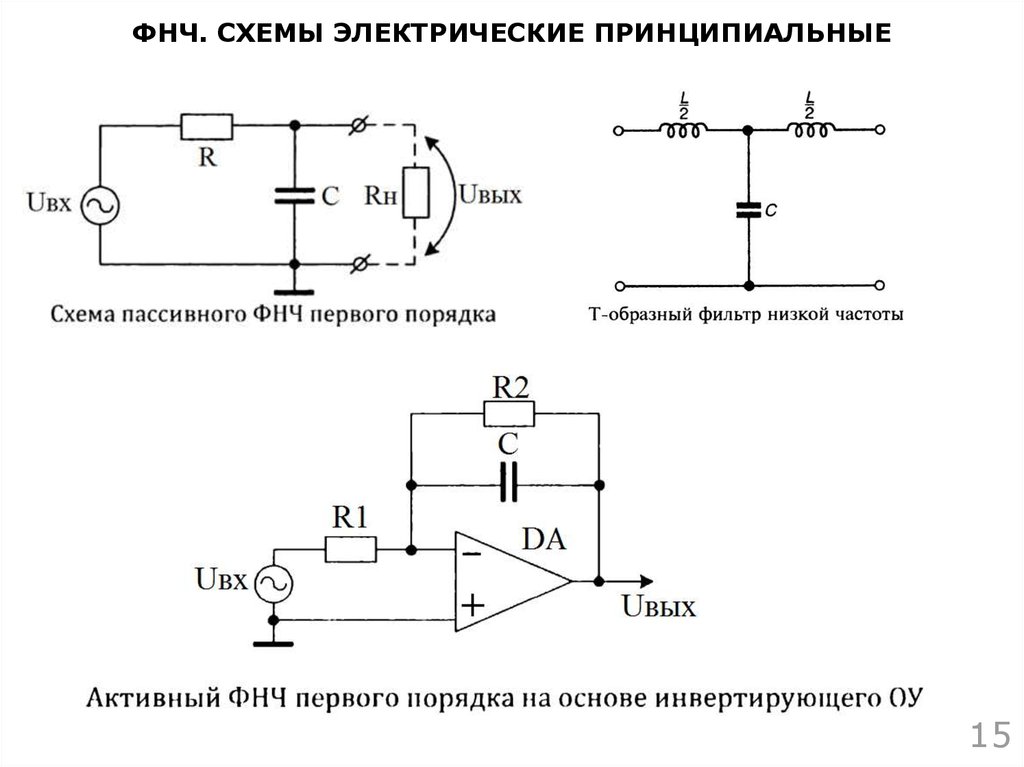 Конденсатор в цепи обратной связи определится как
Конденсатор в цепи обратной связи определится как
Cp = KsC, (1.4)
а конденсатор, соединяющий вход ОУ с «землёй», как
Cs = KpC (1.5)
Пользуясь вновь приобретёнными знаниями, рисуем фильтр НЧ четвёртого порядка, который уже вполне можно применить для работы с сабвуфером (рис. 10). На схеме я на этот раз привожу расчётные значения емкостей, без округления до стандартного номинала. Это чтобы вы могли себя проверить при желании.
Рис. 10. Фильтр НЧ четвёртого порядка
Я до сих пор ни слова не сказал о фазовых характеристиках, и правильно сделал — вопрос этот отдельный, отдельно им и займёмся. В следующий раз, вы же поняли, мы только начинаем…
Рис. 11. Характеристики фильтров третьего и четвёртого порядка
Теги: Фильтры
Фильтр 1 порядка схема
А не фильтрануть ли нам широким махом входной сигнал на предмет подавления помехи относительно единичного уровня на требуемой частоте, в заданное число раз отличающейся от границы полосы пропускания? А как насчёт расчёта активных полиномиальных фильтров второго порядка на звеньях Рауха, Сален-Ки и биквадратного звена? А кривую изменения реактивного сопротивления ёмкости в зависимости от частоты — не изобразить ли? И действительно.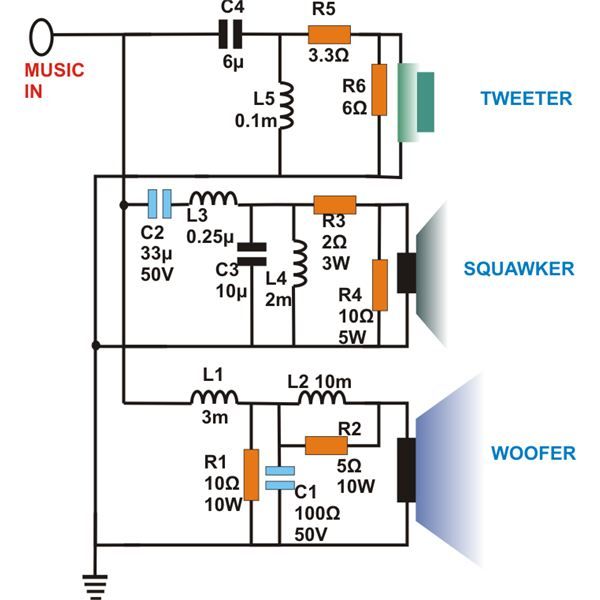
Поиск данных по Вашему запросу:
Фильтр 1 порядка схема
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Активный фильтр низких частот первого порядка
- Фильтры 1-го порядка
- Аналоговые измерительные устройства
- Расчет пассивных разделительных фильтров в акустических системах
- Фильтр Саллена — Ки
- На сайте радиочипи представлены принципиальные схемы сабвуферов, собранные своими руками
- 4 Пример расчета элементов схемы аналогового фильтра нижних частот (афнч)
- Электрические пассивные фильтры
- Фильтр (электроника)
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Лекция 66. Фильтр низкой частоты
Фильтр низкой частоты
Активный фильтр низких частот первого порядка
При дифференцировании входного сигнала ФВЧ подчеркивает шумы и высокочастотные сигналы, поэтому в дифференциаторе для исключения насыщения ОУ ВЧ сигналом его усиление на ВЧ ограничивают с помощью дополнительного резистора на входе R 1 , что ограничивает диапазон дифференцирования. Фильтры более высоких порядков 2 и выше в принципе могут быть построены при каскадном соединении фильтров 1го порядка, но при этом на каждый порядок необходим ОУ.
Таким образом, например, в фильтрах 2-го порядка, требуются 2 ОУ. Известны схемы и структуры, которые позволяют реализовать фильтр 2-го порядка на одном ОУ. В основе построения фильтра 2-го порядка широко используются свойства ОУ, которые позволяют рассматривать его как:. ИНУН — источник напряжения управляемый напряжением. В простейшем случае — не инвертирующий усилитель, у которого.
В простейшем случае — не инвертирующий усилитель, у которого.
ИТУТ — источник тока, управляемый током. Это источник тока на ОУ в не инвертирующем включении. Используется не инвертирующее включение ОУ, в результате ОУ не нагружает фильтр. Поэтому существуют ограничения на выбор R 3 и R 4 , т. Фильтр Чебышева имеет колебания в пределах полосы пропускания, но более крутую характеристику в переходной полосе. Чем круче переходная полоса, тем больше выбросы. Имеет более нелинейную ФЧХ, чем фильтр Баттерворта.
Нелинейность ФЧХ для этих фильтров приводит к тому, что при прохождении импульсных сигналов появляются выбросы на них. Это эквивалентно тому, что все сигналы задерживаются линейно в полосе пропускания.
Эти фильтры не искажают импульсные сигналы. Также используются эллиптические фильтры, которые имеют неравномерную характеристику, как в полосе пропускания, так и в полосе заграждения, и более крутую характеристику в переходной области, чем фильтр Чебышева.
Файловый архив студентов. Логин: Пароль: Забыли пароль? Email: Логин: Пароль: Принимаю пользовательское соглашение. FAQ Обратная связь Вопросы и предложения. Добавил: Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Логин: Пароль: Забыли пароль? Email: Логин: Пароль: Принимаю пользовательское соглашение. FAQ Обратная связь Вопросы и предложения. Добавил: Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Уфимский Государственный Авиационный Технический Университет. Скачиваний: Параметры усилителя оэ в области средних частот. Эквивалентная схема оэ на вч. Например, стабилитроны. Фильтры Фильтры электрических сигналов. Исходные положения. Фильтры 1-го порядка ФНЧ пассивным является интегрирующая цепочка. Достоинства фильтров на ОУ: Усиление входного сигнала в выбранном диапазоне частот Фильтры более высоких порядков 2 и выше в принципе могут быть построены при каскадном соединении фильтров 1го порядка, но при этом на каждый порядок необходим ОУ.
Фильтры 2-го порядка на оу В основе построения фильтра 2-го порядка широко используются свойства ОУ, которые позволяют рассматривать его как: ИНУН — источник напряжения управляемый напряжением. Это источник тока на ОУ.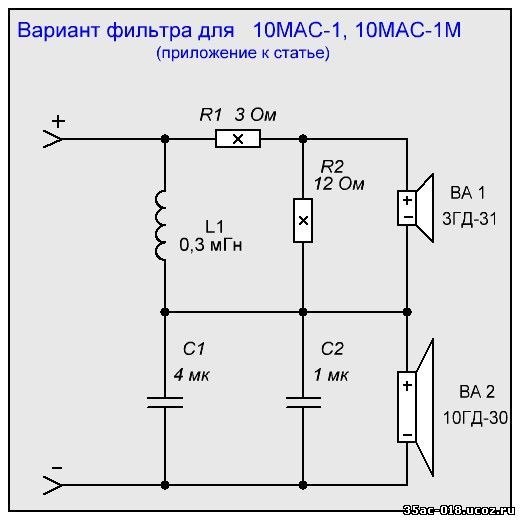 ИНУТ — источник напряжения, управляемый током. Это инвертирующий усилитель. Наиболее простая — ИНУН. Фильтры используются для выравнивания и компенсации задержек, возникающих в линиях связи. Соседние файлы в предмете Электроника Как травить платы.
ИНУТ — источник напряжения, управляемый током. Это инвертирующий усилитель. Наиболее простая — ИНУН. Фильтры используются для выравнивания и компенсации задержек, возникающих в линиях связи. Соседние файлы в предмете Электроника Как травить платы.
Транзисторная преобразовательная техника
Фильтры 1-го порядка
В воздушном, водяном, масляном и других видах фильтров происходит очистка от посторонних частиц и примесей. Но что же фильтрует электрический фильтр? Ответ простой: частоту. Для остальных частот, которые не входят в полосу пропускания , фильтр создает большое затухание, вплоть до полного их исчезновения. Ниже пример идеального фильтра, который пропускает частоты до какого-то определенного значения частоты среза. На практике такой фильтр реализовать нереально. При проектировании фильтров стараются как можно ближе приблизиться к идеальной характеристике.
I-фильтр Баттерворта четвертого порядка; 2-фильтр Чебышева четвертого ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ; СХЕМА С ОБЩИМ ИСТОКОМ.
Аналоговые измерительные устройства
Обычно активные фильтры формируются в виде каскадного соединителя четырехполюсников, обладающих относительно простой структурой и называемых звеньями ARC— фильтра рисунок 8. При этом степень передаточной функции отдельного звена не превышает числа 2. Поэтому при нечетном числе звеньев в фильтре N, одно звено фильтра будет первого порядка. Фильтр нижних частот первого порядка может быть реализован, если в цепи обратной связи операционного усилителя использовать пассивный RC-фильтра первого порядка рисунок 9. На рисунке 10 представлена схема ARC— фильтра нижних частот второго порядка с отрицательной обратной связью. Рисунок 10 — Активный фильтр нижних частот второго порядка с отрицательной обратной связью. Реализация передаточных функций фильтров на активных RC-цепях осуществляется следующим образом [2]. Каждую передаточную функциюH i p реализуют в видеARC-звена первого или второго порядка.
Расчет пассивных разделительных фильтров в акустических системах
При дифференцировании входного сигнала ФВЧ подчеркивает шумы и высокочастотные сигналы, поэтому в дифференциаторе для исключения насыщения ОУ ВЧ сигналом его усиление на ВЧ ограничивают с помощью дополнительного резистора на входе R 1 , что ограничивает диапазон дифференцирования.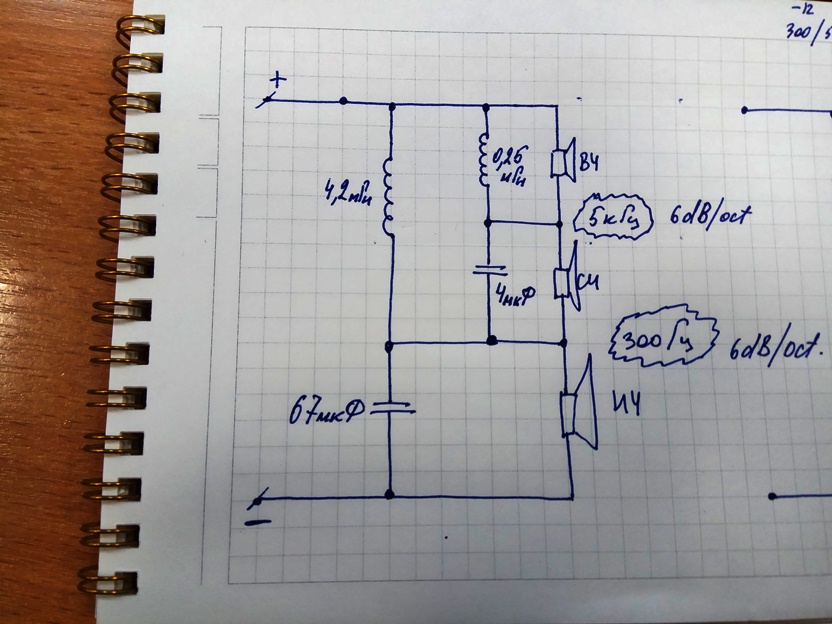 Фильтры более высоких порядков 2 и выше в принципе могут быть построены при каскадном соединении фильтров 1го порядка, но при этом на каждый порядок необходим ОУ. Таким образом, например, в фильтрах 2-го порядка, требуются 2 ОУ. Известны схемы и структуры, которые позволяют реализовать фильтр 2-го порядка на одном ОУ. В основе построения фильтра 2-го порядка широко используются свойства ОУ, которые позволяют рассматривать его как:.
Фильтры более высоких порядков 2 и выше в принципе могут быть построены при каскадном соединении фильтров 1го порядка, но при этом на каждый порядок необходим ОУ. Таким образом, например, в фильтрах 2-го порядка, требуются 2 ОУ. Известны схемы и структуры, которые позволяют реализовать фильтр 2-го порядка на одном ОУ. В основе построения фильтра 2-го порядка широко используются свойства ОУ, которые позволяют рассматривать его как:.
Реализуется в виде электронной схемы с двумя резисторами , двумя конденсаторами и активным элементом например, с операционным усилителем , в совокупности образующих фильтр с передаточной функцией второго порядка. Фильтры более высокого порядка могут быть реализованы включением нескольких фильтров последовательно, причем для реализации фильтра с нечетным порядком в цепочку фильтров включают по крайней мере один фильтр 1-го порядка.
Фильтр Саллена — Ки
На рис. Коэффициент передачи в комплексном виде может быть выражен формулой:. При увеличении частоты в 10 раз коэффициент усиления уменьшается в 10 раз, т. Произведем расчет коэффициента передачи по формуле 9. Будем принимать частоту от 0, Гц до кГц с шагом
Произведем расчет коэффициента передачи по формуле 9. Будем принимать частоту от 0, Гц до кГц с шагом
На сайте радиочипи представлены принципиальные схемы сабвуферов, собранные своими руками
Активные RC-фильтры ARCF в зависимости от полос пропускания и задержания подразделяются на фильтры нижних и верхних частот, а также полосовые и режекторные. Микросхемы представляют собой активные RC-фильтры верхних частот. Микросхемы представляют собой активные RC-фильтры нижних частот. Разновидностью таких цепей являются генераторы и активные RC-фильтры с управляемыми параметрами. Темброблок состоит из двух каскадов: эмиттерного повторителя и активного RC-фильтра. Кроме того, в эмиттерной цепи транзистора VTI через резистор R IK контакт б предусмотрен выход для подключения магнитофона на запись.
I-фильтр Баттерворта четвертого порядка; 2-фильтр Чебышева четвертого ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ; СХЕМА С ОБЩИМ ИСТОКОМ.
4 Пример расчета элементов схемы аналогового фильтра нижних частот (афнч)
Фильтр 1 порядка схема
Расчет аналогового фильтра.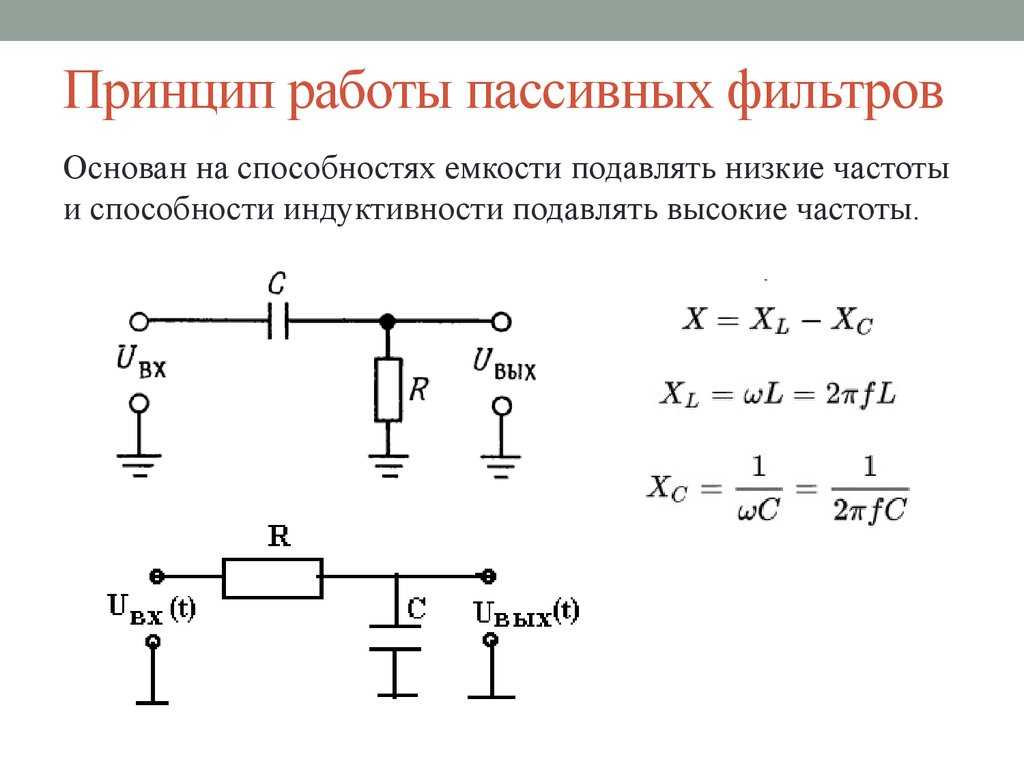 Типы фильтров. Параметры аппроксимации амплитудно-частотной характеристики фильтра нижних частот.
Типы фильтров. Параметры аппроксимации амплитудно-частотной характеристики фильтра нижних частот.
Электрические пассивные фильтры
ВИДЕО ПО ТЕМЕ: Фильтр ВЧ — 1й порядок. Схема
Активный фильтр низких частот усиливает низкие частоты. Схема простейшего фильтра низких частот представлена на рис. При объединении фильтров низких и высоких частот получается полосовой фильтр рис. Полосовой фильтр пропускает сигнал в определенной области частот.
Полезные ссылки. Гостевая книга.
Фильтр (электроника)
Например, пресловутая керамика Н90 — из-за пьезоэлектрического эффекта. А как другие типы, скажем, пленочные? Тут можно написать целую поэму. Но можно ли строить частотнозависимые цепи без них, только с помощью дросселей индуктивностей? Оказывается, можно. И не только можно, но и нужно! Мои старые акустические колонки постройки до г.
Среди множества рекурсивных фильтров отдельно выделяют следующие фильтры по виду передаточной функции :. По порядку степени уравнения передаточной функции см. В конструкциях пассивных аналоговых фильтров используют сосредоточенные или распределённые реактивные элементы , такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя их, можно добиться усиления или ослабления гармоник с нужными частотами.
: видеоуроки | Поддержка LG США
Перейти к содержанию Перейти к справке по специальным возможностям
- ДОМ
- ПОДДЕРЖКА org/ListItem»> Зарегистрировать продукт
- Видеоуроки
Найдите полезные видео о вашем продукте LG
Найдите ключевое слово или выберите категорию продукта, а затем выберите тему.
searchFieldВведите ключевое слово и выполните поиск. Открыто окно слоя предиктивного поиска.
Содержимое Продукт
Нет связанного содержимого.
Ваши недавние поиски
Нет истории недавних поисков.
Предлагаемые поиски
- Регистрация
- смартшар
- LG-мост
- Пакет ПК
- руководства
Выберите категорию КатегорияМобильныйТВ/ВидеоКухняПрачечнаяДругая бытовая техникаКомпьютерыСолнечная энергияКоммерческий дисплейAUDIO
Выберите продукт Товар
Выберите тему Тема
Выберите подтему Подтема
Выберите категорию и продукт ниже.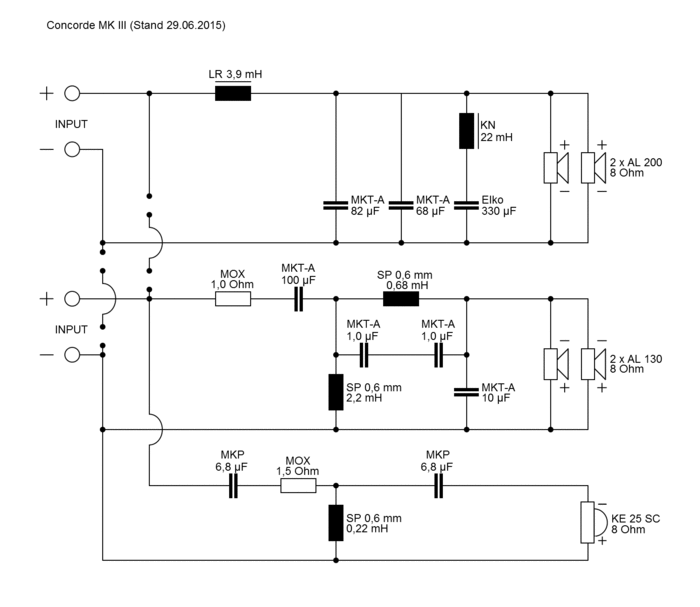
Выберите категорию КатегорияМобильныйТВ/ВидеоКухняПрачечнаяДругая бытовая техникаКомпьютерыСолнечная энергияКоммерческий дисплейМалый бизнесАУДИО
Выберите продукт Товар
Выберите категорию продукта
309 результатов сопоставления для Очистить условие поиска Очистить ключевое слово поиска
- Популярные видео
- Новейшие видео
Популярные видео
00:41
- УстановкаХолодильники
- Преимущества использования оригинальных фильтров для воды холодильника LG
01:54
- Устранение неисправностейХолодильники
- Начало работы с LG Craft Ice
02:22
- Операционные сушилки
- LG Dryer — причины, по которым ваша сушилка не сушит
01:04
- Рабочие шайбы
- Стиральная машина LG — опция «Только отжим»
01:45
- ЭксплуатацияПриборы для приготовления пищи
- Микроволновая печь LG Over The Range — замена лампы
Новые видео
01:39
- Ремонт осушителей
- Сушильная машина для белья — коды ошибок d90 и d95
01:52
- Рабочие шайбы
- Стиральная машина и сушилка LG с фронтальной загрузкой — штабелирование
02:27
- Поиск и устранение неисправностей Осушители
- Установка осушителя
01:14
- Рабочие шайбы
- Стиральная машина LG — обслуживание диспенсера
01:20
- ЭксплуатацияПриборы для приготовления пищи
- Микроволновая печь LG Over The Range — Замена угольного фильтра
Фильтр для воды LG | Фильтры для воды холодильника
- Нижняя морозильная камера
- Французский 3-дверный
- Французский 4-дверный
- Бок о бок
- Бок о бок 4-дверный
- Верхняя морозильная камера
- Под прилавком
- Столбец
- Французский 3-дверный
- Нижняя морозильная камера
- Бок о бок
- Французский 5-дверный
- Бок о бок 3-дверный
- Бок о бок 4-дверный
- Бок о бок 3-дверный вид
- Одна дверь
- решетка
- Верхний правый интерьер
- решетка
- Нижний правый интерьер
- Верхний левый интерьер
- Верхний правый интерьер
- Нижний центральный интерьер
- Верхний левый интерьер
- Верхний правый интерьер
- Верхний правый интерьер
- решетка
- Нижний правый интерьер
- Верхний правый интерьер
- решетка
- Верхний правый интерьер
- решетка
- Нижний центральный интерьер
- Нижний левый интерьер
- задняя часть холодильника
- Нижний центральный интерьер
- Вне холодильника
- Верхний средний интерьер
- Верхняя решетка
- Верхняя решетка
- Верхняя решетка
- Верхняя решетка
- Верхняя левая внутренняя стена
- Левая дверь утоплена
- Верхний правый
- Нижний центральный интерьер
- Панель левой двери
- Верхний левый за кувшином
- Нижний левый интерьер
- Панель левой двери
- Средний левый
- Выпадающий лоток, поверните, чтобы удалить
- Нажмите фильтр, чтобы извлечь
- Поверните фильтр, чтобы удалить
- Фильтр с коротким воротником, поверните, чтобы снять
- Фильтр с коротким стержнем, поверните, чтобы удалить
- Съемная чашка
- Нажмите кнопку для извлечения, слайд-аут для удаления
- Выпадающий лоток, потяните, чтобы снять
- Откиньте дверь, потяните, чтобы снять
- Нажмите вкладку, чтобы извлечь
- Фильтр с длинным воротником, поверните, чтобы снять
- Утопленный монтаж, нажмите, чтобы извлечь
- Встроенный фильтр, подключение на обоих концах
- Внешний фильтр, поверните, чтобы удалить
- Поверните, чтобы удалить, белый фильтр
- Поверните, чтобы удалить, темно-синий фильтр
- Поверните, чтобы удалить
- Поверните от стены, потяните, чтобы удалить
- Карманная дверь, наклон, потяните, чтобы удалить
- Панельная дверь, наклон, потяните, чтобы снять
- Поверните против часовой стрелки вниз, чтобы снять
- Квадратное основание, поворотный фильтр для удаления
- Поверните из углубления, поверните, чтобы удалить
Обратите внимание:
Поскольку эти фильтры устанавливаются в одном и том же месте на холодильниках, их часто путают друг с другом. Если вы не уверены, какой фильтр используется в вашем холодильнике, извлеките устройство из холодильника и осмотрите фильтр. Сравните внешний вид вашего фильтра с изображениями выше, прежде чем перейти к следующему шагу нашего поиска фильтров.
Если вы не уверены, какой фильтр используется в вашем холодильнике, извлеките устройство из холодильника и осмотрите фильтр. Сравните внешний вид вашего фильтра с изображениями выше, прежде чем перейти к следующему шагу нашего поиска фильтров.
- Длинный разъем
- Короткий разъем
- Соединитель воротника
- Большой овальный соединитель
- Низ закруглен
- Нижний зубчатый
- Два штока 9,25 дюйма
- Два штока 11,25 дюйма
- Бирка безопасности на спине
- Без бирки на спине
- 1 маленькое/1 большое резиновое уплотнение
- Средний коннектор с ошейником
- Два разъема — слайды прямо назад
- Одинарный разъем — выкручивается наружу
- 2 больших резиновых уплотнения
- Короткий коннектор с ошейником
- Средний соединитель
- Короткий, широкий картридж с одним отверстием в центре
- Нижняя квартира
- Длинный, тонкий картридж с одинарным креплением в центре.

- Тонкий картридж с 2 отверстиями разного размера
- Короткий картридж с патрубком (металлическая канистра)
Не можете найти свой фильтр? Не беспокойтесь, у нас есть специалисты.
Выберите предпочтительный вид связи ниже и поговорите со специалистом.Хотите сохранить место в поисковике?
Позвоните нам по бесплатному номеру (888) 407-5688
(Пн–Пт, 9:00–16:00 по восточному поясному времени)LG Фильтры для воды в холодильнике
LG (Lucky Goldstar) является одним из двух крупнейших конгломератов Южной Кореи наряду с Samsung.
LG была первой корейской компанией, которая начала заниматься пластиком. По мере того, как бизнес по производству пластмасс расширялся, они в конечном итоге диверсифицировались в сторону бытовой электроники и произвели первый в Южной Корее радиоприемник под маркой Goldstar, согласно данным www.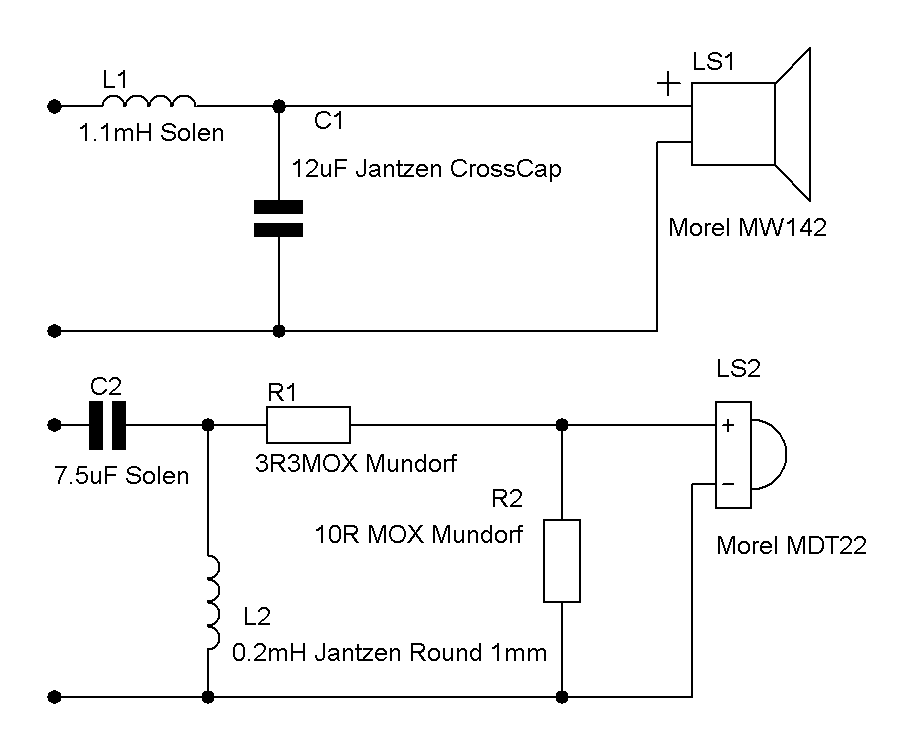 lg.com. Сегодня LG производит электронику (LG Electronics), телекоммуникационную продукцию (LG Telecom) и химикаты (LG Chem).
lg.com. Сегодня LG производит электронику (LG Electronics), телекоммуникационную продукцию (LG Telecom) и химикаты (LG Chem).
Компания LG зарекомендовала себя как один из самых надежных брендов бытовой техники в мире. Компания также занялась производством аксессуаров, таких как фильтры для воды для холодильников. LG 5231JA2006A модели LG 5231JA2002A соответствуют стандартам NSF/ANSI (Национальный фонд санитарии/Американский национальный институт стандартов) 42. Обе модели были протестированы на уменьшение вкуса и запаха хлора и твердый. LG также предлагает фильтры, сертифицированные по стандартам NSF/ANSI Standard 42 и 53. Таким образом, в отличие от моделей LG 5231JA2006A и LG 5231JA2002A, LG 5231JA2006B и LT 700P способны удалять кисты, вредные элементы (ртуть и свинец), химикаты (2,4 D, атразин, бензол и линдан), мутность и другие патогенные микроорганизмы, передающиеся через воду.
Производители фильтров для воды, такие как LG, рекомендуют потребителям регулярно менять свои фильтры.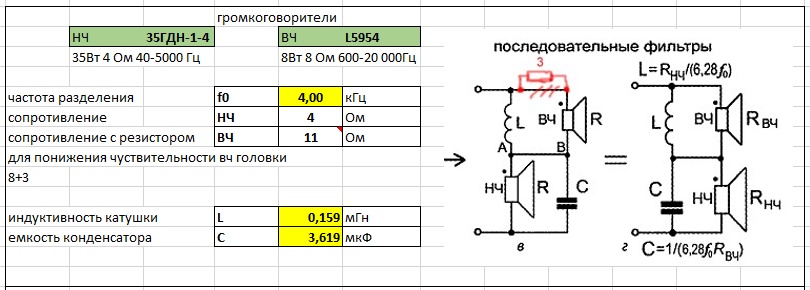 Если фильтры не будут заменены вовремя, они уже не смогут эффективно отфильтровывать патогены.
Если фильтры не будут заменены вовремя, они уже не смогут эффективно отфильтровывать патогены.
Фильтры LG со скидкой
Сменные фильтры для воды LG от DiscountFilters.com помогут улучшить качество, вкус и запах воды и льда в холодильнике. Эти фильтры используют активированный уголь для улавливания минералов и загрязняющих веществ, которые могут придать воде и льду странный вкус или запах. Очистите воду и пейте здоровее с заменой фильтра для воды LG от DiscountFilters.com.
1 BarryB BondsBonds LF | 2986 | 9847 | 2227 | 2935 | 601 | 77 | 762 | 1996 | 2558 | 1539 | 514 | 141 | .3298 | 12364 | 2174 | 3771 | 624 | 98 | 755 | 2297 | 1402 | 1383 | 240 | 73 | . 305 305 | .374 | .555 | .929 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
3 BabeB RuthRuth RF | 2504 | 8399 | 2174 | 2873 | 506 | 136 | 714 | 2213 | 2062 | 1330 | 123 | 117 | . 342 342 | .474 | .690 | 1.164 | |||||||||||||
4 AlbertA PujolsPujols DH | 3080 | 11421 | 1914 | 3384 | 686 | 16 | 703 | 2218 | 1373 | 1404 | 117 | 43 | .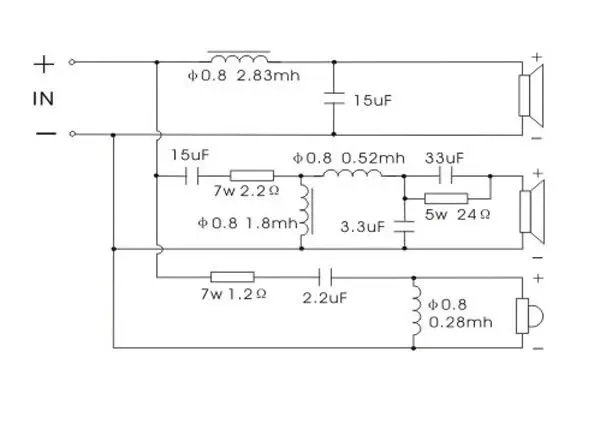 296 296 | .374 | .544 | .918 | |||||||||||||
5 AlexA RodriguezRodriguez SS | 2784 | 10566 | 2021 | 3115 | 548 | 31 | 696 | 2086 | 1338 | 2287 | 329 | 76 | .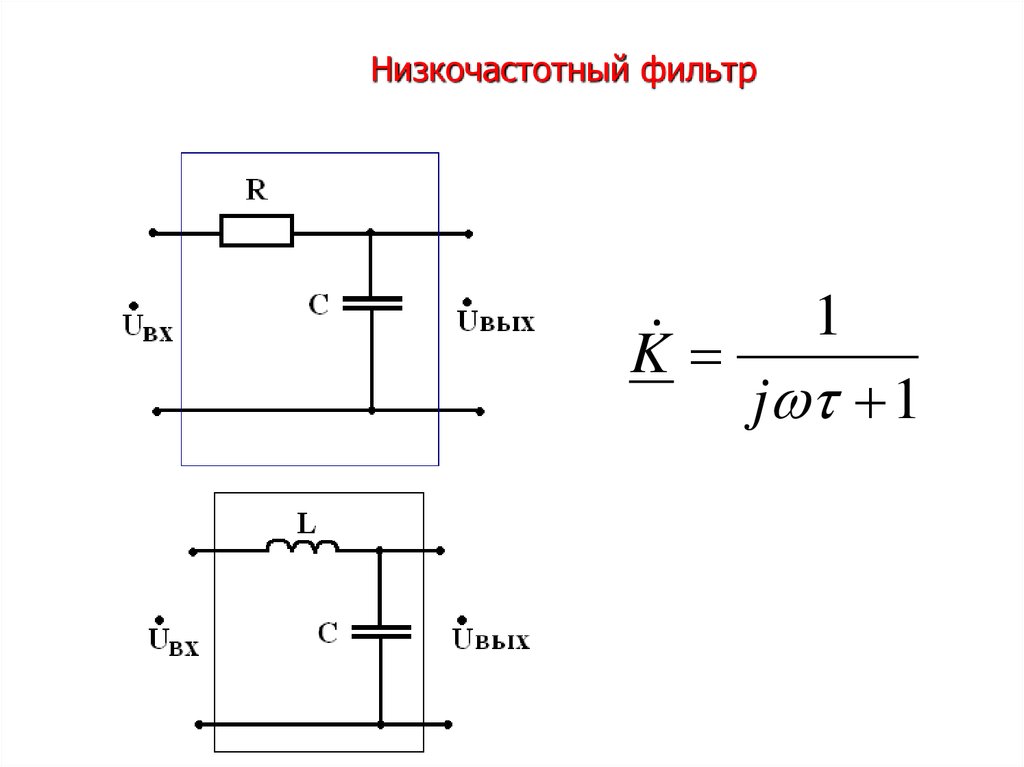 295 295 | .380 | .550 | .930 | |||||||||||||
6 WillieW MaysMays CF | 2992 | 10881 | 2062 | 3283 | 523 | 140 | 660 | 1903 | 1464 | 1526 | 338 | 103 | . 302 302 | .384 | .557 | . 941 | |||||||||||||
7 KenK GriffeyGriffey CF | 2671 | 9801 | 1662 | 2781 | 524 | 38 | 630 | 1836 | 1312 | 1779 | 184 | 69 | .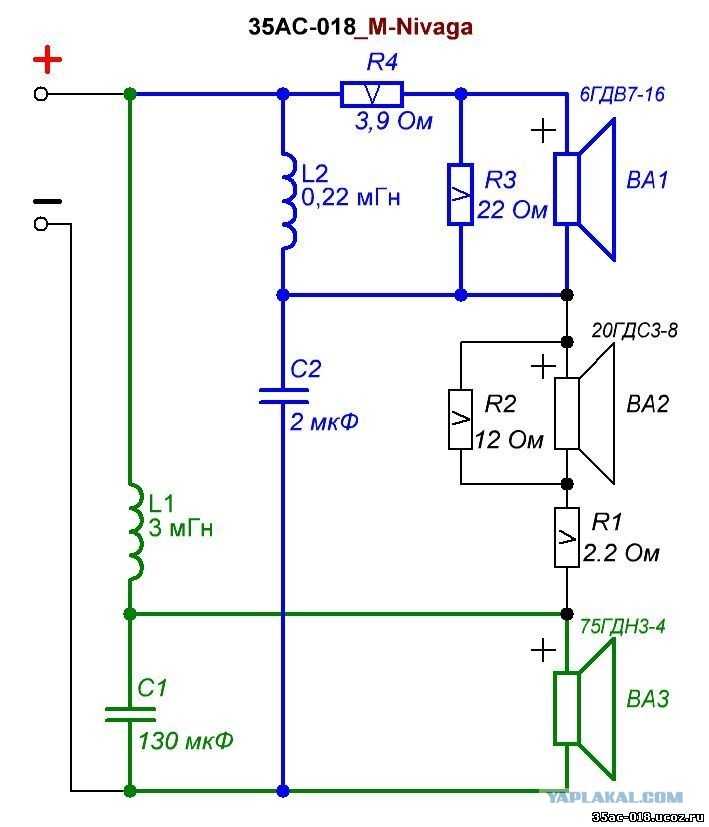 284 284 | .370 | .538 | .908 | |||||||||||||
8 JimJ ThomeThome 1B | 2543 | 8422 | 1583 | 2328 | 451 | 26 | 612 | 1699 | 1747 | 2548 | 19 | 20 | .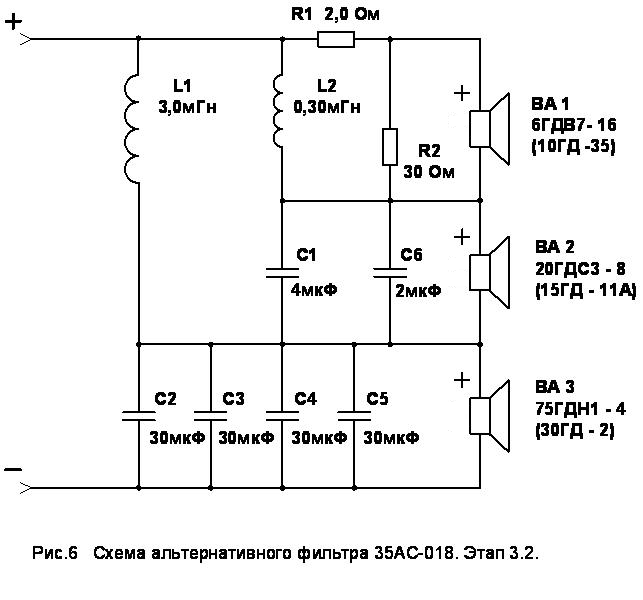 276 276 | .402 | .554 | .956 | |||||||||||||
9 SammyS SosaSosa RF | 2354 | 8813 | 1475 | 2408 | 379 | 45 | 609 | 1667 | 929 | 2306 | 234 | 107 | .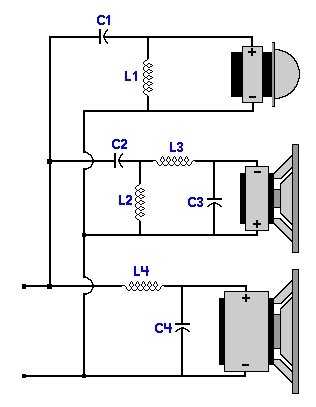 273 273 | .344 | .0445 | 1829 | 2943 | 528 | 72 | 586 | 1812 | 1420 | 1532 | 204 | 77 | .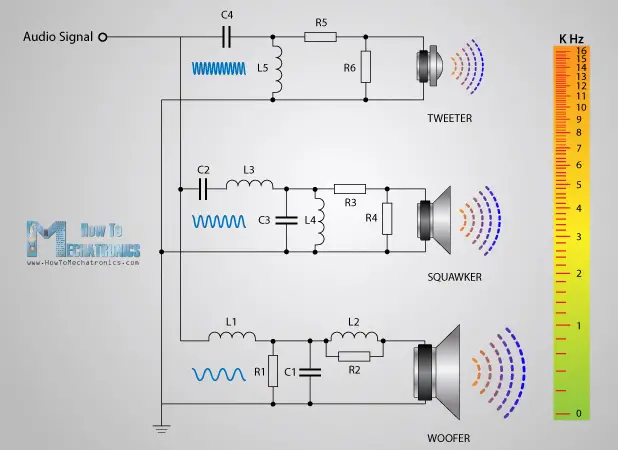 294 294 | .389 | .537 | .926 |
11 MarkM McGwireMcGwire 1B | 1874 | 6187 | 1167 | 1626 | 252 | 6 | 583 | 1414 | 1317 | 1596 | 12 | 8 | .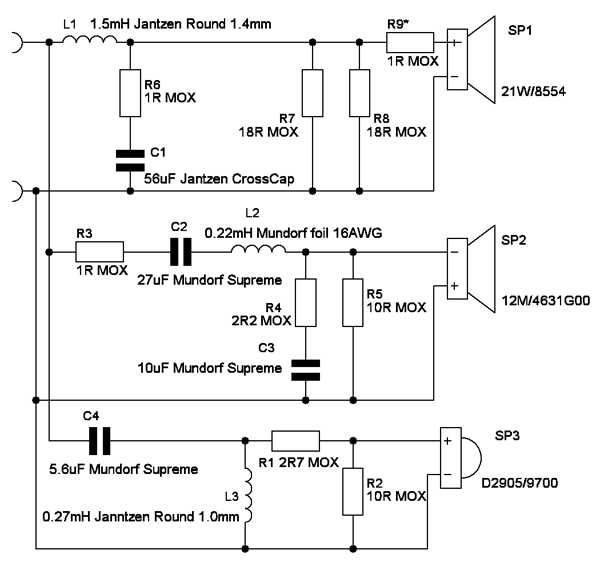 263 263 | .394 | .588 | .982 | |||||||||||||
12 HarmonH KillebrewKillebrew 1B | 2435 | 8147 | 1283 | 2086 | 290 | 24 | 573 | 1584 | 1559 | 1699 | 19 | 18 | . 256 256 | .376 | .509 | .885 | |||||||||||||
13 RafaelR PalmeiroPalmeiro 1B | 2831 | 10472 | 1663 | 3020 | 585 | 38 | 569 | 1834 | 1353 | 1348 | 97 | 40 | . 288 288 | .371 | .515 | .886 | |||||||||||||
14 ReggieR JacksonJackson RF | 2820 | 9864 | 1551 | 2584 | 463 | 49 | 563 | 1702 | 1375 | 2597 | 228 | 115 | . 262 262 | .356 | .490 | .846 | |||||||||||||
15 MannyM RamirezRamirez LF | 2302 | 8244 | 1544 | 2574 | 547 | 20 | 555 | 1831 | 1329 | 1813 | 38 | 33 | .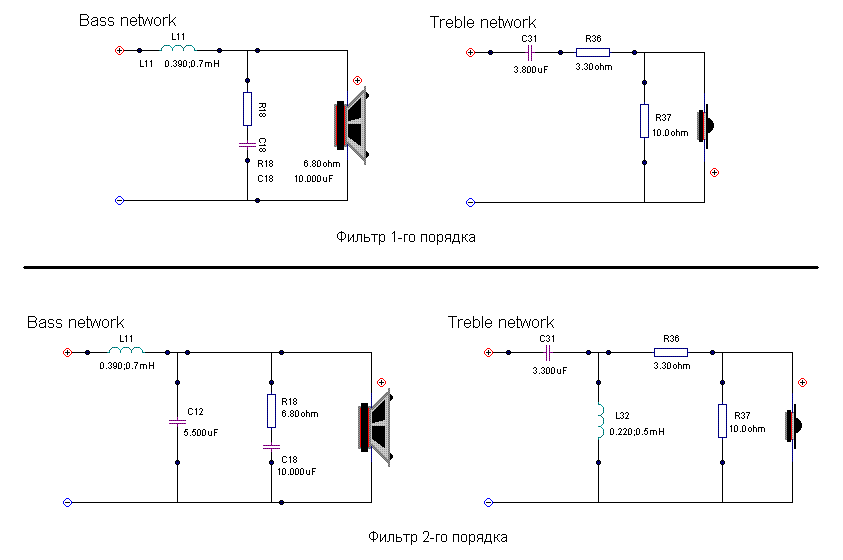 312 312 | .411 | .585 | .996 | |||||||||||||
16 MikeM SchmidtSchmidt 3B | 2404 | 8352 | 1506 | 2234 | 408 | 59 | 548 | 1595 | 1507 | 1883 | 174 | 91 | .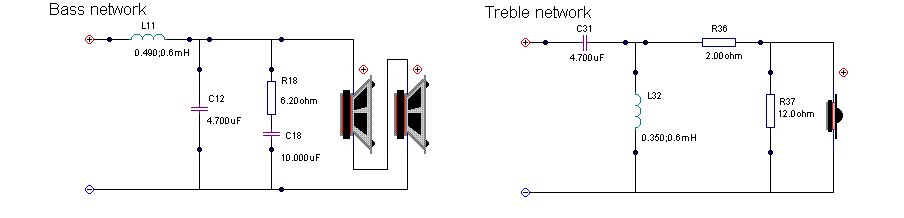 267 267 | .380 | .527 | .907 | |||||||||||||
17 DavidD OrtizOrtiz DH | 2408 | 8640 | 1419 | 2472 | 632 | 19 | 541 | 1768 | 1319 | 1750 | 17 | 9 | .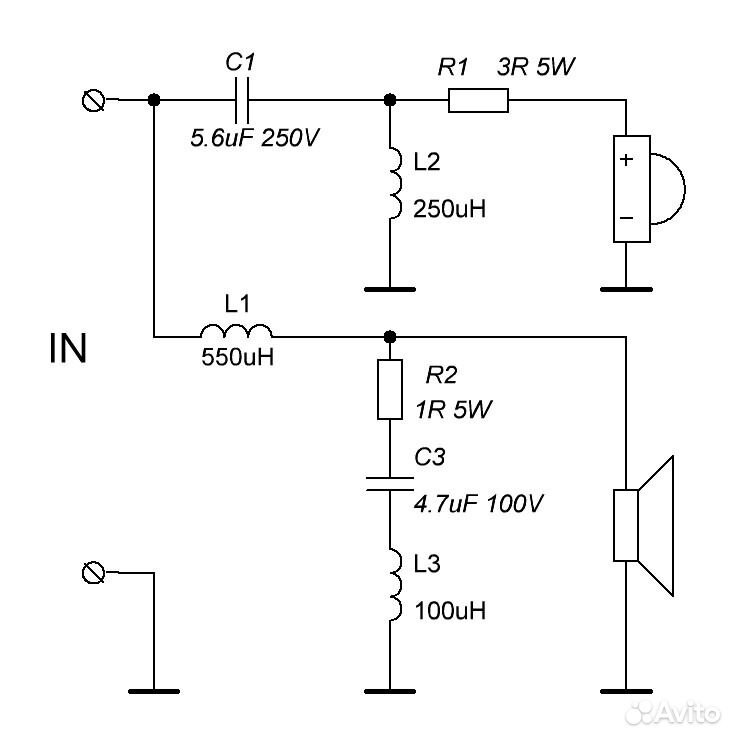 286 286 | .380 | .552 | .932 | |||||||||||||
18 MickeyM MantleMantle CF | 2401 | 8102 | 1677 | 2415 | 344 | 72 | 536 | 1509 | 1733 | 1710 | 153 | 38 | . 298 298 | .421 | .557 | .978 | |||||||||||||
19 JimmieJ FoxxFoxx 1B | 2317 | 8134 | 1751 | 2646 | 458 | 125 | 534 | 1922 | 1452 | 1311 | 87 | 72 | .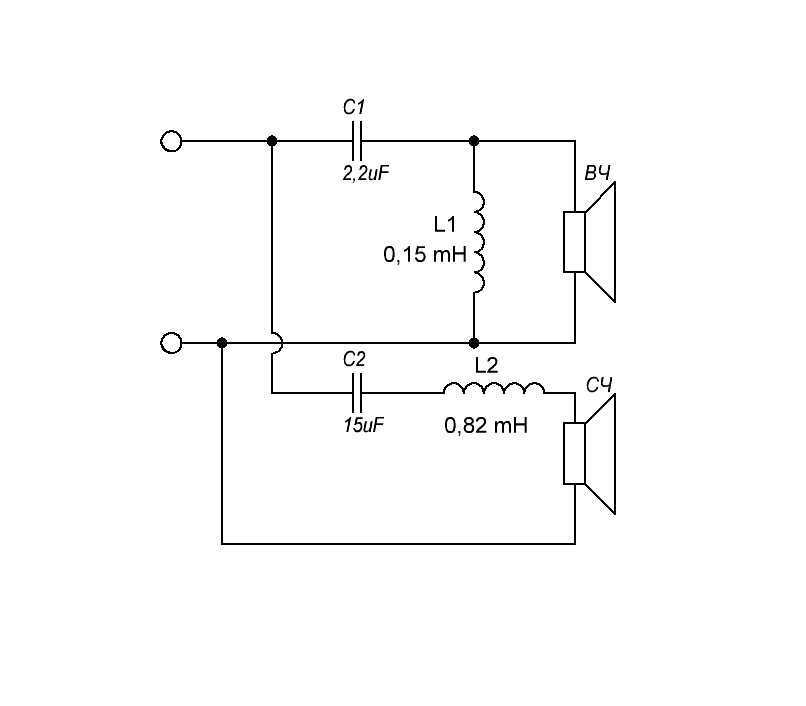 325 325 | .428 | .609 | 1.037 | |||||||||||||
20 WillieW McCoveyMcCovey 1B | 2588 | 8197 | 1229 | 2211 | 353 | 46 | 521 | 1555 | 1345 | 1550 | 26 | 22 | .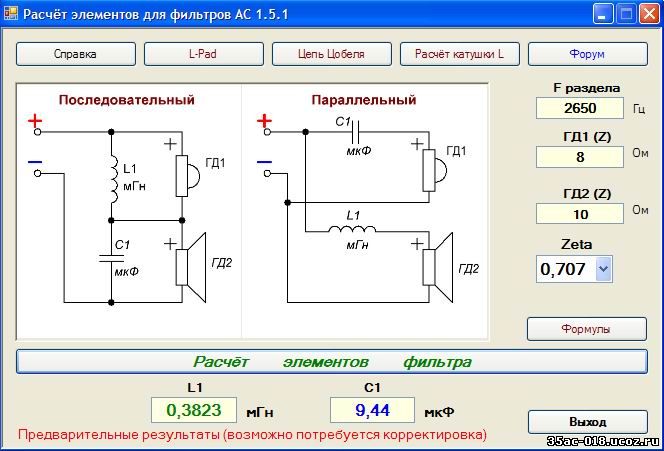 270 270 | .374 | .515 | .889 | |||||||||||||
20 FrankF ThomasThomas DH | 2322 | 8199 | 1494 | 2468 | 495 | 12 | 521 | 1704 | 1667 | 1397 | 32 | 23 | .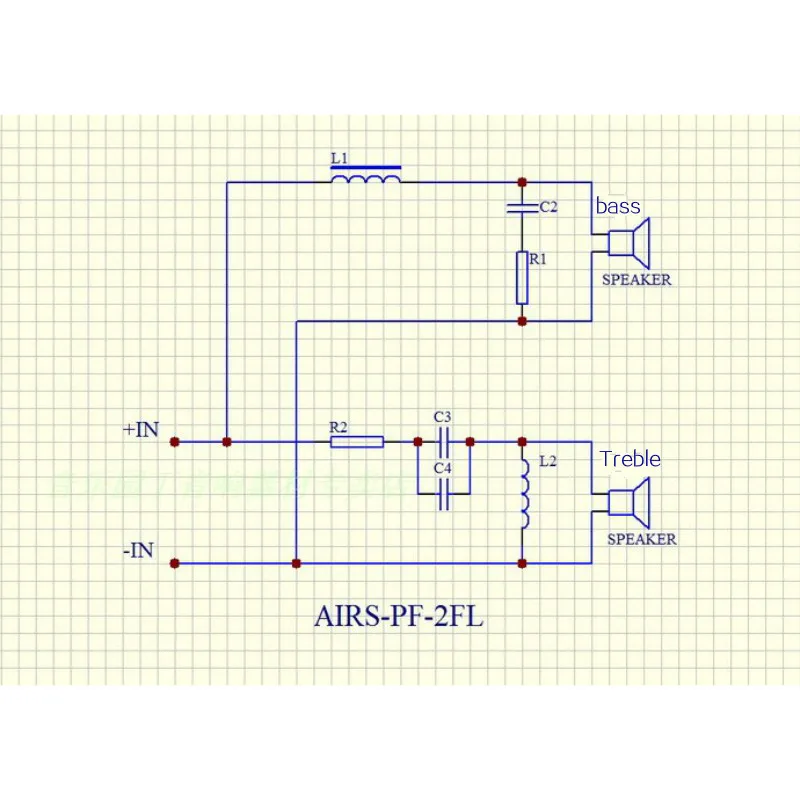 301 301 | .419 | .555 | .974 | |||||||||||||
20 TEDT WILLIAMSWILLIAMS LF | 2292 | 4444444444444444444444444444444444444444444444444444444444444444444444444444449н | 44444444444444444444444444444444444444444444444444444444444444444449н.1332 2654 | 525 | 71 | 521 | 1839 | 2019 | 709 | 24 | 17 | . 344 344 | .482 | .634 | 1.116 | ||||||||||||||
23 ErnieE BanksBanks 1B | 2528 | 9421 | 1305 | 2583 | 407 | 90 | 512 | 1636 | 763 | 1236 | 50 | 53 | .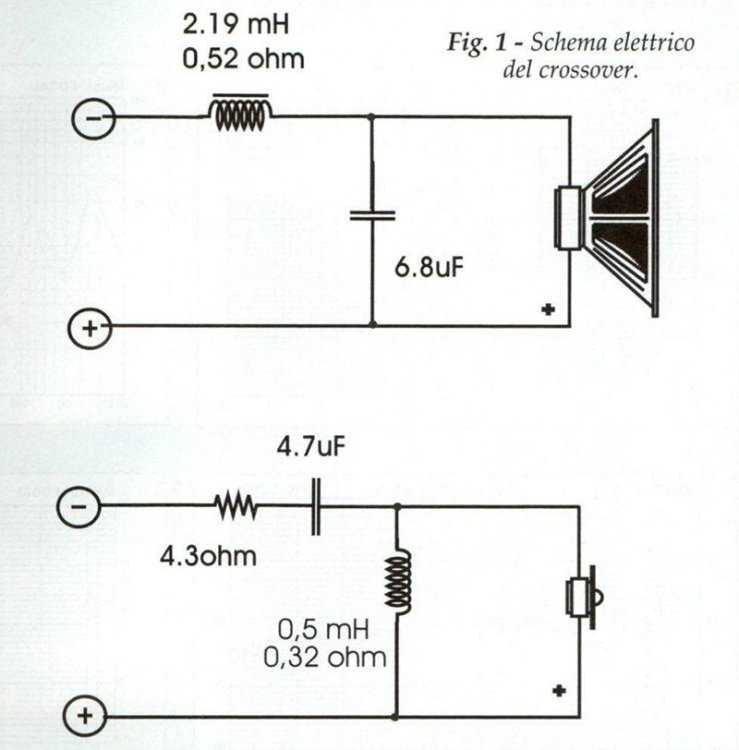 274 274 | .330 | .500 | .830 | |||||||||||||
23 EddieE MathewsMathews 3B | 2391 | 8537 | 1509 | 2315 | 354 | 72 | 512 | 1453 | 1444 | 1487 | 68 | 39 | .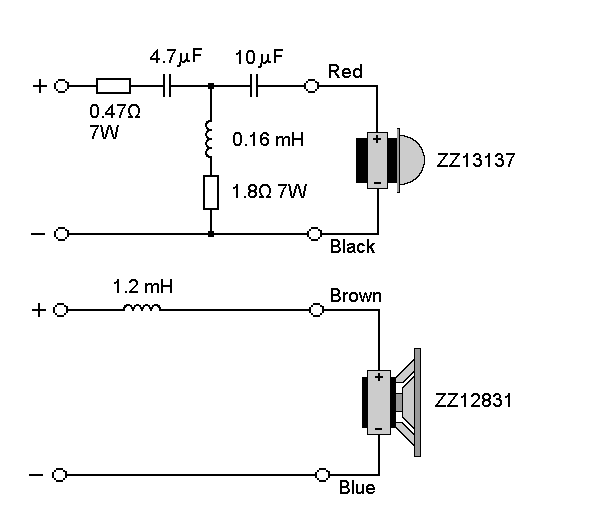 |


 1 Фильтр нижних частот первого порядка
1 Фильтр нижних частот первого порядка
 0003
0003