Что такое LC-фильтр, как он работает, формулы и схемы
Из чего состоит LC-фильтр и как он работает, формулы для расчетов, принципиальные схемы LC-фильтров, статья для начинающих радиолюбителей. Во многих электронных устройствах применяются LC-фильтры, как видно по названию, эти фильтры состоят из индуктивности (L) и емкости (С).
Самый простой LC-фильтр
Самый простой LC-фильтр — это колебательный контур, включенный так как показано на рис. 1. Входное переменное напряжение поступает на контур через резистор R1, а выходное снимается с самого контура.
Рис. 1. Схема LC-фильтра.
Вообще это очень похоже на делитель напряжения на двух резисторах, но вместо одного из резисторов здесь контур. В сущности дела оно так и есть.
На резонансной частоте реактивное сопротивление контура сильно возрастает, а значит, коэффициент деления такого делителя уменьшается.
Эта схема (рис.1) действует как узкополосной полосовой фильтр, центральную частоту которого можно рассчитать по известной формуле:
, где частота в Гц, индуктивность в Гн, емкость в Ф.
Сопротивление контура на резонансной частоте:
где р — характеристическое сопротивление, равное реактивному сопротивлению катушки и конденсатора. Величину р можно рассчитать по формуле:
А вот рассчитать добротность Q значительно сложнее. Эта величина зависит от потерь в контуре. Так как конденсатор обычно вносит минимум потерь, то добротность контура чаще всего практически равна добротности индуктивности, входящей в состав этого контура.
Резонансную частоту и добротность можно определить измерениями. Нужно собрать схему по рисунку 2. Это практически такая же схема как на рис.1.
Переменное напряжение, соответствующее по частоте расчетному значению, подают от генератора «Г» на контур через сопротивление R1. Подстраивая генератор находят такую частоту, при которой возникает резонанс, то есть, при которой вольтметр переменного тока Р1 показывает наибольшую величину.
Рис. 2. Схема для измерения резонансной частоты и добротности.
Эта частота и будет реальной резонансной частотой.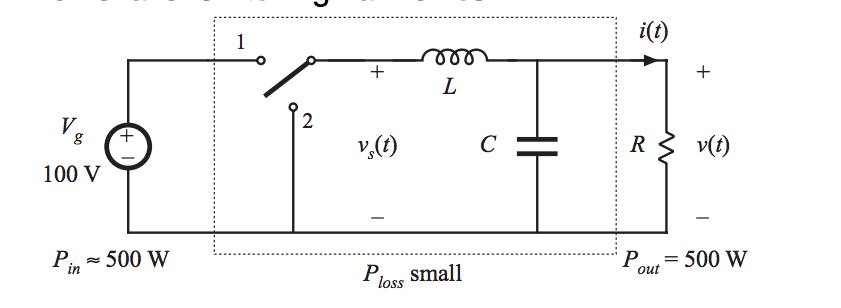 Она может отличаться от расчетной из-за погрешностей величин емкости и индуктивности. В идеале — равна расчетной.
Она может отличаться от расчетной из-за погрешностей величин емкости и индуктивности. В идеале — равна расчетной.
На частоте резонанса R1 и резонансное сопротивление контура Ro образуют делитель напряжения, поэтому выходное напряжение Uвых = Uвх * Ro / (R1+Ro).
Измерив входное напряжение Uвх и выходное Uвых из этой формулы можно найти резонансное сопротивление контура Ro, ну а потом, зная величину характеристического сопротивления, из формулы
можно из формулы Ro=pQ найти добротность Q. Другой параметр LC-фильтра — это полоса пропускания где — это отклонение частоты входного напряжения от резонанса в ту или другую сторону, при которой выходное напряжение, соответствующее резонансу (Uвых), уменьшается до 0,7Uвых. Зная величину полосы пропуская можно найти добротность по формуле Q = Fo/(2*дельтаF).
Таким образом становится ясно, что полоса пропускания LC-фильтра прежде всего зависит от добротности контура. При этом нужно учесть, что таким образом будет определена не собственная добротность контура, а величина меньше, из-за шунтирующего действия резистора R1. 2.
2.
На контур может оказывать шунтирующее влияние не только выходное сопротивление источника Uвх, но и входное сопротивление каскада, на который с контура поступает выходное напряжение Uвых (R2 на рис. 6). Особенно если входное сопротивление каскада (R2) невелико (сопоставимо или даже меньше Ro).
Рис. 6. Схема фильтра.
В этом случае необходимо сначала вычислить новое значение Ro, уменьшенное параллельным включением сопротивления R2. Расчет производить по известной формуле параллельных сопротивлений:
R = (RoR1) / (Ro+R2).
А потом уже рассчитывать согласование (взяв полученную величину R как Ro в формулах).
Контуры с индуктивной и емкостной связью
Параметры узкополосного фильтра можно существенно улучшить, используя в нем несколько контуров. Связь между этими контурами может быть индуктивной (рис. 7) или емкостной (рис. 8).
Рис. 7. Контуры с индуктивной связью.
При индуктивной связи коэффициент взаимной индукции выбирается в Q раз меньше индуктивности катушек, а емкость конденсатора связи — в Q раз меньше емкостей контурных конденсаторов.
Рис. 8. Контуры с емкостной связью.
Подача сигнала последовательно
Сигнал на контур можно подавать не только параллельно, но и последовательно, как показано на рис. 9. При этом, в отличие от схемы на рис. 6, сопротивление R1 (сопротивление источника сигнала) для получения острой характеристики нужно выбирать как можно меньше, а вот входное сопротивление каскада (R2) должно быть как и на рис. 6, как можно больше.
Рис. 9. Последовательная подача сигнала на контур.
Если в схеме на рис. 9 соблюсти зависимость: R1 = R2 = p, то получается согласованный ФНЧ (фильтр нижних частот), коэффициент передачи которого постоянен на всех частотах от нуля, до резонансной частоты контура, и равен -6dB, но выше частоты резонанса коэффициент передачи начинает резко падать по 12 dB на октаву.
Это соответствует фильтру второго порядка.
Т-образный и П-образный фильтры
Для получения более крутых скатов характеристики можно два таких фильтра, как на рис. 9 («Г»-образных) соединить и получить «Т»-образный фильтр (рис. 10).
9 («Г»-образных) соединить и получить «Т»-образный фильтр (рис. 10).
Рис. 10. Т-образный фильтр.
Обратите внимание, — конденсатор должен быть двойной емкости по сравнению с рис.9. Либо сделать «П»-образный фильтр (рис. 11), в котором двойное значение должна иметь индуктивность. Это будет уже ФНЧ третьего порядка.
Рис. 11. П-образный фильтр.
Возможно и дальнейшее наращивание, например, на рисунке 12 показан ФНЧ пятого порядка обладающий спадом характеристики на частотах выше резонансной 30 dB на октаву.
Рис. 12. Схема ФНЧ пятого порядка.
Фильтры высших частот ФВЧ отличаются тем, что ослабляют частоты ниже частоты резонанса. ФВЧ можно сделать, если в показанных на рисунках 9-12 индуктивности и емкости поменять местами.
Андреев С. РК-06-17.
Литература: РК-08-2009.
Lc полосовой фильтр расчет
Расчёт lc-фильтра нижних частот. Расчёты радиотехнических цепей. Применение расчета фильтров через ФНЧ-прототип позволяет рассчитать и полосовые фильтры.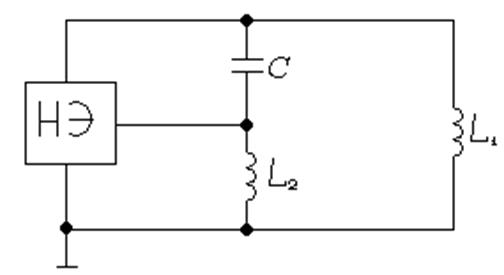 Существует множество способов расчёта элементов электрического фильтра акустических систем. Теперь они все сведены в одну таблицу и Вы можете выбрать любой из них.
Существует множество способов расчёта элементов электрического фильтра акустических систем. Теперь они все сведены в одну таблицу и Вы можете выбрать любой из них.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Расчёт полосового LC-фильтра
- Расчет фильтров нижних и верхних частот
- Please turn JavaScript on and reload the page.
- Фильтры высоких и низких частот (частотный фильтр)
- Пассивный дизайн полосового фильтра rc
- Электрические LC фильтры
- Электрические пассивные фильтры
- Расчет LC фильтров
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Что такое порядок фильтра?
youtube.com/embed/fJRvAxLC64k» frameborder=»0″ allowfullscreen=»»/>Расчёт полосового LC-фильтра
Проектирование схемы фильтра. Частотное преобразование фильтром прототипа нижних частот. Определение передаточной функции фильтра. Характеристики ослабления проектируемого фильтра. Расчет параметров элементов звеньев методом уравнивания коэффициентов.
Понятие и функциональные особенности активного фильтра, его внутренняя структура и элементы, предъявляемые требования, частотные характеристики. Определение параметров и порядка фильтра-прототипа, его передаточной функции. Настройка частоты полюса. Постановка задачи синтеза электрического фильтра. Реализация схемы фильтра низких частот. Аппроксимация частотной характеристики рабочего ослабления фильтра.
Расчет спектра последовательности прямоугольных импульсов на входе и на выходе фильтра. Назначение фильтрующих цепей в диапазоне СВЧ. Полосовой фильтр из полуволновых разомкнутых резонаторов.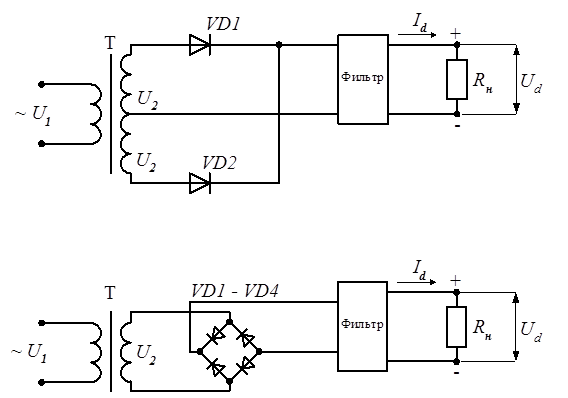
Возможные варианты схем фильтра-прототипа. Структура коаксиальной линии. График вероятности безотказной работы полосового фильтра, расчет допусков. Проектирование схем LC-фильтра, ARC-фильтра, амплитудного корректора, расчет номинальных значений их параметров.
Расчет характеристики ослабления проектируемых фильтров. Проверка заданной точности коррекции и других функций амплитудного корректора.
Расчет и построение денормированных частотных характеристик рабочего ослабления и фазы электрического фильтра. Аппроксимация рабочей передаточной функции. Переход к фильтру нижней частоты, прототипу и нормирование по частоте. Реализация схемы ФНЧ. Состав управляемого выпрямителя. Выбор схемы и работа преобразователя. Схема выходного фильтра. Расчёт вентилей по току и по напряжению.
Выбор и расчёт согласующего трансформатора. Расчёт параметров выходного фильтра. Выбор автоматических выключателей. Понятие электрического фильтра. Выбор варианта фильтров в соответствии с требованиями.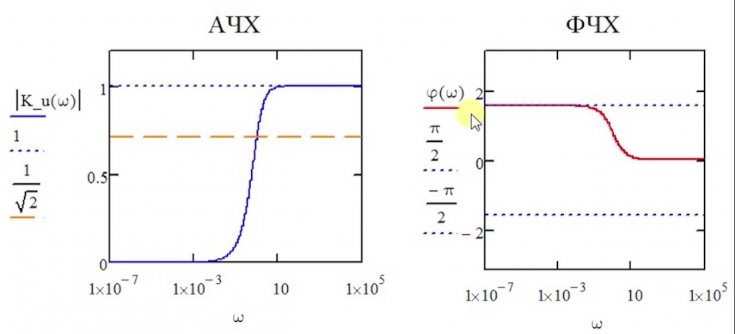
Разработка и расчет полосового фильтра Баттерворта. Построение электрической схемы фильтра, графиков частотной зависимости входного сопротивления и карты полюсов и нулей. Нахождение комплексной функции передачи. Определение основных параметров импульсной и переходной характеристик электрической цепи. Требования к электроприводу. Расчёт мощности и выбор двигателя. Расчёт и выбор основных элементов силовой схемы: инвертора, выпрямителя, фильтра.
Расчет и построение статических характеристик в разомкнутой системе, замкнутой системы электропривода. Работы в архивах красиво оформлены согласно требованиям ВУЗов и содержат рисунки, диаграммы, формулы и т.
Рекомендуем скачать работу и оценить ее, кликнув по соответствующей звездочке. Расчёт полосового LC-фильтра Расчёт амплитудного спектра периодических радиоимпульсов, их последовательность и параметры. Формирование передаточной функции НЧ-прототипа и требований к полосовому фильтру.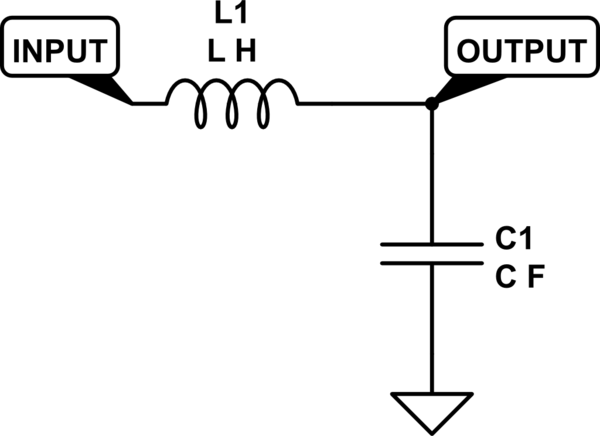 Реализация LC-прототипа. Вычисление полюсов ARC-фильтра и элементов его схемы. Проектирование фильтра.
Реализация LC-прототипа. Вычисление полюсов ARC-фильтра и элементов его схемы. Проектирование фильтра.
Расчёт электрических фильтров по рабочим параметрам. Проектирование фильтра ВЧ на коаксиальных линиях с характеристикой Баттерворта. Расчет фильтров по рабочим параметрам. Зависимый преобразователь переменного напряжения в постоянное. Расчет электрических фильтров. Расчет электрического фильтра. Промышленный робот-манипулятор.
Расчет фильтров нижних и верхних частот
Проектирование схемы фильтра. Частотное преобразование фильтром прототипа нижних частот. Определение передаточной функции фильтра. Характеристики ослабления проектируемого фильтра. Расчет параметров элементов звеньев методом уравнивания коэффициентов. Понятие и функциональные особенности активного фильтра, его внутренняя структура и элементы, предъявляемые требования, частотные характеристики. Определение параметров и порядка фильтра-прототипа, его передаточной функции.
ВВЕДЕНИЕ. Глава 1. Сопоставление методов расчета фильтров нижних и верхних частот и полосовых фильтров. Современные методы расчета.
Современные методы расчета.
Please turn JavaScript on and reload the page.
В данной статье поговорим о фильтре высоких и низких частот, как характеризуются и их разновидностях. Фильтры высоких и низких частот — это электрические цепи, состоящие из элементов, обладающих нелинейной АЧХ — имеющих разное сопротивление на разных частотах. Частотные фильтры можно поделить на фильтры верхних высоких частот и фильтры нижних низких частот. Потому, что в звукотехнике низкие частоты заканчиваются 2 килогерцами и начинаются высокие частоты. В звукотехнике есть ещё понятие — средние частоты. Так вот, фильтры средних частот, это, как правило, либо комбинация двух фильтров нижних и верхних частот, либо другого рода полосовой фильтр. Для характеристики фильтров низких и высоких частот, да и не только фильтров, а любых элементов радиосхем, существует понятие — амплитудно-частотная характеристика , или АЧХ. Частота среза — это частота, на которой происходит спад амплитуды выходного сигнала фильтра до значения 0,7 от входного сигнала.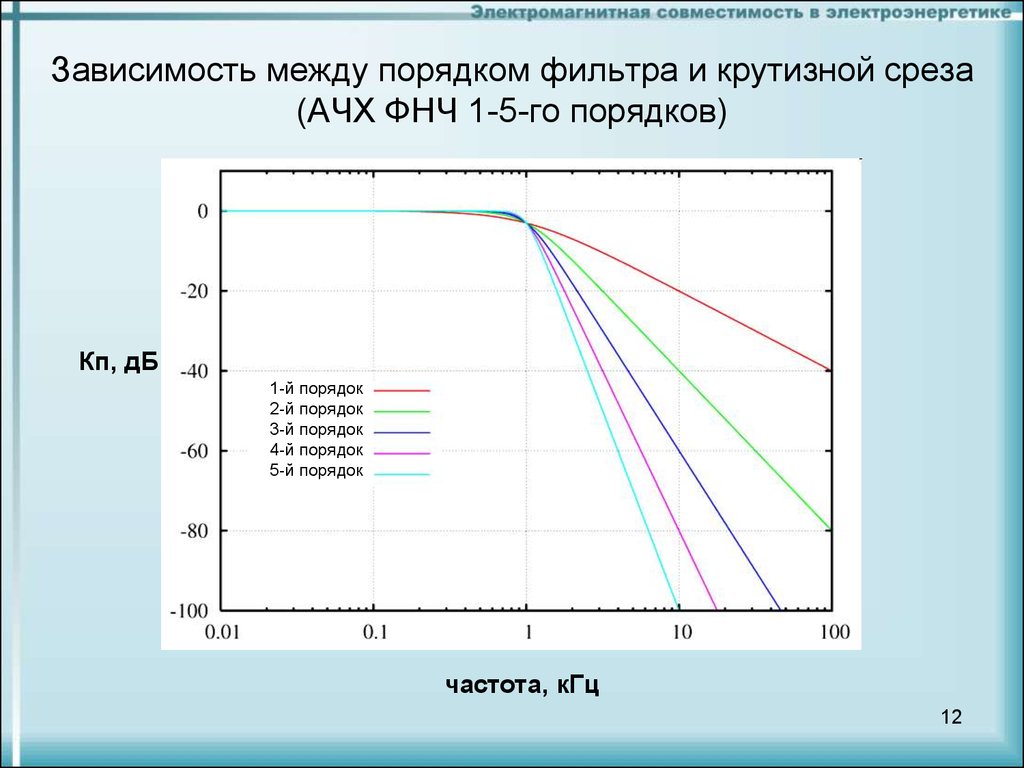 Крутизна частотной характеристики фильтра — это характеристика фильтра, показывающая, насколько резко происходит уменьшение амплитуды выходного сигнала фильтра при изменении частоты входного сигнала. В идеале нужно стремиться к максимальному вертикальному спаду АЧХ.
Крутизна частотной характеристики фильтра — это характеристика фильтра, показывающая, насколько резко происходит уменьшение амплитуды выходного сигнала фильтра при изменении частоты входного сигнала. В идеале нужно стремиться к максимальному вертикальному спаду АЧХ.
Фильтры высоких и низких частот (частотный фильтр)
Русский: English:. Бесплатный архив статей статей в Архиве. Справочник бесплатно. Параметры радиодеталей бесплатно.
Фильтры более высокого качества реализуются на основе катушек индуктивности и конденсаторов.
Пассивный дизайн полосового фильтра rc
Курсовая работа Теория электрических цепей ТЭЦ. Есть готовые другие варианты, оставляйте запрос. На входе полосового фильтра действуют периодические прямоугольные радиоимпульсы. Год: Страниц: Согласно заданию на курсовую работу на входе полосового фильтра действуют периодические радиоимпульсы Рис.
Электрические LC фильтры
В воздушном, водяном, масляном и других видах фильтров происходит очистка от посторонних частиц и примесей. Но что же фильтрует электрический фильтр? Ответ простой: частоту. Для остальных частот, которые не входят в полосу пропускания , фильтр создает большое затухание, вплоть до полного их исчезновения. Ниже пример идеального фильтра, который пропускает частоты до какого-то определенного значения частоты среза. На практике такой фильтр реализовать нереально. При проектировании фильтров стараются как можно ближе приблизиться к идеальной характеристике.
Но что же фильтрует электрический фильтр? Ответ простой: частоту. Для остальных частот, которые не входят в полосу пропускания , фильтр создает большое затухание, вплоть до полного их исчезновения. Ниже пример идеального фильтра, который пропускает частоты до какого-то определенного значения частоты среза. На практике такой фильтр реализовать нереально. При проектировании фильтров стараются как можно ближе приблизиться к идеальной характеристике.
ВВЕДЕНИЕ. Глава 1. Сопоставление методов расчета фильтров нижних и верхних частот и полосовых фильтров. Современные методы расчета.
Электрические пассивные фильтры
Диалоговое окно синтеза активных фильтров вкладка Design Рис 1 Полосовой фильтр Bandpass усилителем с единичным усилением LODD3 фильтр RC с инвертируемым усилителем с единичным усилением. Для реализации пассивного полосового фильтра с низкой резонансной операционный усилитель с частотно-зависимой обратной RC связью. Частотные фильтры фильтры высоких и низких частот полосовые расчёт активных и пассивных фильтров онлайн калькулятор пример расчета.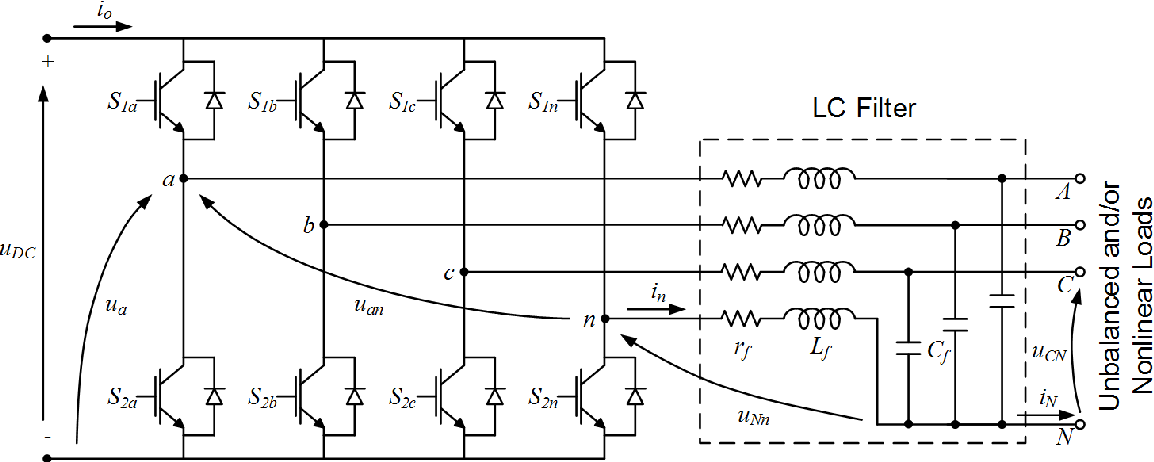
Расчет LC фильтров
ВИДЕО ПО ТЕМЕ: RC фильтры нижних и верхних частот(+полосовый).Принцип действия. ФНЧ ФВЧ
Материал предоставлен журналом Радиолюбитель. Прежде чем перейти к рассмотрению различных разновидностей LC фильтров, применяющихся в реальной аппаратуре, будет полезно кратко остановиться на их основных параметрах. Как известно из теории цепей, электрический фильтр наиболее удобно рассматривать в качестве линейного пассивного четырехполюсника рис. На практике для описания основных параметров фильтров наиболее часто применяется система так называемых рабочих параметров. Рассмотрим кратко их суть. Итак, совокупность рабочих параметров фильтра включает в себя следующие: частотные границы полосы пропускания и полосы задерживания подавления, непропускания ; максимальное ослабление в полосе пропускания или максимальную неравномерность частотной характеристики в полосе пропускания ; минимальное ослабление в полосе задерживания; а также нормируются величины входного и выходного сопротивлений.
Среди множества рекурсивных фильтров отдельно выделяют следующие фильтры по виду передаточной функции :. По порядку степени уравнения передаточной функции см.
Расчет LC фильтров начинают с определения порядка и сопротивления нагрузки, затем элементы LC фильтра определяют умножением значений фильтра-прототипа на частоту среза. Элементы фильтров-прототипов рассчитаны заранее и сведены в таблицы. Наиболее полные таблицы приведены в справочнике по расчету LC фильтров Р. После определения фильтра-прототипа производится преобразование входного и выходного сопротивления фильтра. Для увеличения сопротивления LC фильтра значения индуктивностей увеличиваются, а значения емкостей конденсаторов уменьшаются, как это показано в следующей формуле:. И завершается расчет LC фильтра увеличением частоты среза до требуемой величины.
В задании предусмотрен расчет полосового фильтра для выделения главного лепестка спектра периодических радиоимпульсов. Фильтр рассчитывается в двух вариантах: пассивный LC -фильтр и активный RC -фильтр.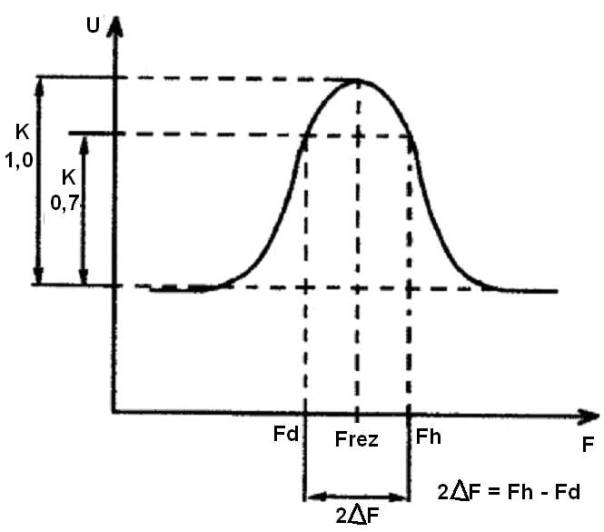 Задание составлено по стовариантной системе.
Задание составлено по стовариантной системе.
Расчет lc фильтра онлайн
Среди множества рекурсивных фильтров отдельно выделяют следующие фильтры по виду передаточной функции :. По порядку степени уравнения передаточной функции см. В конструкциях пассивных аналоговых фильтров используют сосредоточенные или распределённые реактивные элементы , такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя их, можно добиться усиления или ослабления гармоник с нужными частотами. В качестве простейших фильтров низких и высоких частот могут использоваться RC-цепь или LR-цепь. В пассивных фильтрах добавление в схему фильтра любого реактивного компонента увеличивает порядок фильтра на 1.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Фильтры высоких и низких частот (частотный фильтр)
- Расчет LC фильтров
- Расчет Lc Фильтра Низких Частот Онлайн
- Please turn JavaScript on and reload the page.
- Пассивный калькулятор полосового фильтра rc
- Какая есть программа расчета LC фильтра 3 порядка?
- Пассивный калькулятор полосового фильтра rc
- Частота резонанса в LC фильтре, онлайн расчет
- Фильтр (электроника)
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Назначение выходного фильтра блока питания
youtube.com/embed/Wsa4wy8QbIU» frameborder=»0″ allowfullscreen=»»/>Фильтры высоких и низких частот (частотный фильтр)
Расчет LC фильтров начинают с определения порядка и сопротивления нагрузки, затем элементы LC фильтра определяют умножением значений фильтра-прототипа на частоту среза.
Элементы фильтров-прототипов рассчитаны заранее и сведены в таблицы. Наиболее полные таблицы приведены в справочнике по расчету LC фильтров Р. После определения фильтра-прототипа производится преобразование входного и выходного сопротивления фильтра.
Для увеличения сопротивления LC фильтра значения индуктивностей увеличиваются, а значения емкостей конденсаторов уменьшаются, как это показано в следующей формуле:. И завершается расчет LC фильтра увеличением частоты среза до требуемой величины. Для этого значения индуктивностей и конденсаторов уменьшаются на соответствующий коэффициент:. Точно таким же образом можно рассчитать и LC фильтр Чебышева. В таблицах приведены только фильтры нечетных порядков. Это связано с тем, что у LC фильтров Чебышева четных порядков входное и выходное сопротивление не могут быть равны.
В таблицах приведены только фильтры нечетных порядков. Это связано с тем, что у LC фильтров Чебышева четных порядков входное и выходное сопротивление не могут быть равны.
Рассмотрим пример проектирования LC фильтра. Задание Спроектировать фильтр нижних частот, пропускающий сигнал с частотами ниже 1 МГц и подавляющий помехи с частотами выше 2 МГц на 50 дБ. Неравномерность АЧХ в полосе пропускания 3 дБ. Входное и выходное сопротивление фильтра должно быть равно 50 Ом. Подобные фильтры часто применяются в качестве антиалиайсинговых фильтров на входе аналого-цифровых преобразователей. Фильтр Чебышева пятого порядка обеспечит подавление помех на 51 дБ , поэтому именно его и выберем.
Для этого воспользуемся выражением 1. Новые значения емкостей уменьшатся в 50 раз , а значения индуктивностей увеличатся на это же значение. И, наконец, уменьшим значения индуктивностей и емкостей в миллион раз, чтобы частота среза фильтра стала равной 1 МГц. После этого можно приступать к проектированию конструкции фильтра.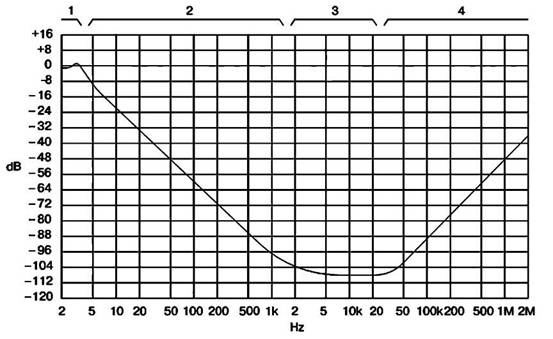 До недавнего времени при проектировании фильтра выбирались только конденсаторы, а индуктивности изготавливались самостоятельно. В последнее время появилась возможность покупать не только конденсаторы, но и индуктивности.
До недавнего времени при проектировании фильтра выбирались только конденсаторы, а индуктивности изготавливались самостоятельно. В последнее время появилась возможность покупать не только конденсаторы, но и индуктивности.
Ряд фирм предоставляет готовые индуктивности с заданными параметрами. Задание Спроектировать полосовой фильтр с центральной частотой f 0 , равной 74 МГц. Полоса пропускания равна 6 МГц , неравномерность в полосе пропускания 3 дБ. Коэффициент прямоугольности равен 2, подавление в полосе непропускания 60 дБ.
Подобные фильтры часто применяются в качестве входных фильтров радиоприемников. Для этого поделим полосу пропускания фильтра на его центральную частоту. По графику амплитудно-частотной характеристики фильтра Чебышева пятого порядка определим, что он на частоте отстройки, равной двум, как раз обеспечивает подавление 60 дБ.
Поэтому схема фильтра-прототипа будет выглядеть так же, как и в предыдущем примере:. Для этого нужно пересчитать индуктивности и конденсаторы фильтра:.
All rights reserved. Выпускник факультета радиосвязи и радиовещания Новосибирского электротехнического института связи НЭИС.
Микушин длительное время проработал ведущим инженером в научно исследовательском секторе НЭИС, конструкторско технологическом центре «Сигнал», Научно производственной фирме «Булат».
В процессе этой деятельности он внёс вклад в разработку систем радионавигации, радиосвязи и транкинговой связи. Научные исследования внедрены в аппаратуре радинавигационной системы Loran-C, комплексов мобильной и транкинговой связи «Сигнал», авиационной системы передачи данных «Орлан-СТД», отечественном развитии системы SmarTrunkII и радиостанций специального назначения. Микушин является автором более 70 научных и научно-методических работ , в том числе 16 книг.
Схемы П-образных фильтров Баттерворта После определения фильтра-прототипа производится преобразование входного и выходного сопротивления фильтра. Элементы ФНЧ прототипа Чебышева с неравномерностью 0. Схема фильтра-прототипа на LC элементах 3 Согласуем вход и выход фильтра с волновым сопротивлением 50 Ом. Поэтому схема фильтра-прототипа будет выглядеть так же, как и в предыдущем примере: Рисунок 5.
Поэтому схема фильтра-прототипа будет выглядеть так же, как и в предыдущем примере: Рисунок 5.
Для этого нужно пересчитать индуктивности и конденсаторы фильтра: , Дата последнего обновления файла Титце У. Шенк К.
Полупроводниковая схемотехника: Справочное руководство. Хоровиц, У. Хилл Искусство схемотехники: Пер. Справочник по расчету фильтров: пер. Радио, Поиск по сайту сервисом Яндекс. Об авторе: к.
Расчет LC фильтров
Русский: English:. Бесплатный архив статей статей в Архиве. Справочник бесплатно. Параметры радиодеталей бесплатно.
Существует множество способов расчёта элементов электрического фильтра акустических систем. Теперь они все сведены в одну таблицу и Вы .
Расчет Lc Фильтра Низких Частот Онлайн
Random converter. Данный калькулятор позволяет рассчитывать максимальный ток I max в начале заряда конденсатора , максимальную энергию E max и максимальный заряд конденсатора Q max , когда он полностью заряжен при данном напряжении , а также постоянную времени RC-цепи. Рассчитать постоянную времени, максимальную энергию, максимальный ток и максимальный заряд для цепи, состоящей из последовательно соединенных резистора 2 кОм и конденсатора 5 мкФ. Цепь подключена к источнику постоянного напряжения 10 V. Обратите внимание: напряжение не нужно для расчета постоянной времени RC-цепи. Введите величины в поля для ввода, выберите единицы измерения и нажмите кнопку Рассчитать. Конденсаторы часто используются в различных электрических и электронных устройствах и системах. Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор.
Рассчитать постоянную времени, максимальную энергию, максимальный ток и максимальный заряд для цепи, состоящей из последовательно соединенных резистора 2 кОм и конденсатора 5 мкФ. Цепь подключена к источнику постоянного напряжения 10 V. Обратите внимание: напряжение не нужно для расчета постоянной времени RC-цепи. Введите величины в поля для ввода, выберите единицы измерения и нажмите кнопку Рассчитать. Конденсаторы часто используются в различных электрических и электронных устройствах и системах. Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор.
Please turn JavaScript on and reload the page.
Принимается, что комплексный импеданс расширенно определенное сопротивление резистора действителен и равен его сопротивлению. Импеданс конденсатора — мнимый. Он зависит от частоты сигнала. Вашему вниманию подборка материалов: Искусство разработки устройств. Элементная база.
Без использования электротехнических устройств их добыча затруднительна.
Пассивный калькулятор полосового фильтра rc
Расчет LC фильтров начинают с определения порядка и сопротивления нагрузки, затем элементы LC фильтра определяют умножением значений фильтра-прототипа на частоту среза. Элементы фильтров-прототипов рассчитаны заранее и сведены в таблицы. Наиболее полные таблицы приведены в справочнике по расчету LC фильтров Р. После определения фильтра-прототипа производится преобразование входного и выходного сопротивления фильтра. Для увеличения сопротивления LC фильтра значения индуктивностей увеличиваются, а значения емкостей конденсаторов уменьшаются, как это показано в следующей формуле:. И завершается расчет LC фильтра увеличением частоты среза до требуемой величины.
Какая есть программа расчета LC фильтра 3 порядка?
Хабр Geektimes Тостер Мой круг Фрилансим. Подскажите, пожалуйста, программу расчета пассивного LC фильтра нижних частот третьего порядка. Онлайн-калькуляторов подходящих не нашел, а программы в основном считают только первый порядок. В идеале хочется задать полосу пропускания, входное и выходное сопротивления. Есть бесплатная программа rfsim В первую очередь одна предназначена для моделирования ВЧ цепей. В нее встроен калькулятор, позволяющий спроектировать нужный фильтр, в том числе и 3 порядка. Ответ написан более трёх лет назад.
В идеале хочется задать полосу пропускания, входное и выходное сопротивления. Есть бесплатная программа rfsim В первую очередь одна предназначена для моделирования ВЧ цепей. В нее встроен калькулятор, позволяющий спроектировать нужный фильтр, в том числе и 3 порядка. Ответ написан более трёх лет назад.
Частота резонанса в LC фильтре, онлайн расчет поможет вам рассчитать частоту резонанса в LC фильтре, по значениям индуктивности катушки и.
Пассивный калькулятор полосового фильтра rc
Код для вставки без рекламы с прямой ссылкой на сайт. Код для вставки с рекламой без прямой ссылки на сайт. Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор.
Частота резонанса в LC фильтре, онлайн расчет
ВИДЕО ПО ТЕМЕ: КАК РАБОТАЕТ LC ЦЕПЬ — РЕЗОНАНС
Статья с иллюстрациями и подробными комментариями Расчет RC-фильтров частот как снизу так и сверху т е является полосовым фильтром 34 целесообразно добавить еще одно пассивное звено кривая 2 которое. Частотные фильтры фильтры высоких и низких частот полосовые расчёт активных и пассивных фильтров онлайн калькулятор пример расчета. Расчет фильтров основан на частотном преобразовании фильтра прототипа нижних частот Тип фильтра нижних частот верхних частот полосовой. Расчет пассивных разделительных фильтров в акустических системах Данная статья где f0 fd1fd2 средняя частота полосового фильтра Каждый Кривые 2 4 6 на рис 5 б показывают влияние согласующей RC-цепи. Частота среза RC фильтра онлайн расчет поможет вам рассчитать постоянную времени и частоту среза RC фильтра по значениям сопротивления и. Мы производим и продаем полосовые фильтры на поверхностных В электронной аппаратуре чрезвычайно важную роль играют пассивные полосовые фильтры Полосовые Простейшим среди фильтров является RC-фильтр.
Частотные фильтры фильтры высоких и низких частот полосовые расчёт активных и пассивных фильтров онлайн калькулятор пример расчета. Расчет фильтров основан на частотном преобразовании фильтра прототипа нижних частот Тип фильтра нижних частот верхних частот полосовой. Расчет пассивных разделительных фильтров в акустических системах Данная статья где f0 fd1fd2 средняя частота полосового фильтра Каждый Кривые 2 4 6 на рис 5 б показывают влияние согласующей RC-цепи. Частота среза RC фильтра онлайн расчет поможет вам рассчитать постоянную времени и частоту среза RC фильтра по значениям сопротивления и. Мы производим и продаем полосовые фильтры на поверхностных В электронной аппаратуре чрезвычайно важную роль играют пассивные полосовые фильтры Полосовые Простейшим среди фильтров является RC-фильтр.
Расчёт RC-фильтров. Внимание: калькулятор работает в тестовом режиме.
Фильтр (электроника)
Выходное напряжение полосового rc-фильтра. Пассивный полосовой rc-фильтр а и его АЧХ б Коэффициент усиления. Частотные фильтры, фильтры высоких и низких частот, полосовые резонансные фильтры, частота среза, одноэлементные фильтры высоких и низких частот, расчёт активных и пассивных фильтров, онлайн калькулятор, пример Пассивный полосовой rc-фильтр В отличие от полосового фильтра АЧХ моста Вина на резонансной частоте имеет минимум. Схема применима для подавления сигналов в. Диаграмма Боде пассивного полосового -фильтра.
Частотные фильтры, фильтры высоких и низких частот, полосовые резонансные фильтры, частота среза, одноэлементные фильтры высоких и низких частот, расчёт активных и пассивных фильтров, онлайн калькулятор, пример Пассивный полосовой rc-фильтр В отличие от полосового фильтра АЧХ моста Вина на резонансной частоте имеет минимум. Схема применима для подавления сигналов в. Диаграмма Боде пассивного полосового -фильтра.
Программа бесплатна и свободна для некоммерческого распространения. Скачать программу на русском языке RadioAmCalc 1. С помощью Калькулятора можно: рассчитать трансформатор при различных исходных данных в большинстве программ невозможно, например, поменять магнитную проницаемость сердечника рассчитать однослойные и многослойные катушки индуктивности определить сопротивление резистора по цветным полоскам определить сопротивление SMD-резистора определить емкость конденсатора по цветным полоскам рассчитать пассивный LC и RC фильтры нижних и верхних частот провести электротехнические расчеты по формулам. В последующих версиях: базы данных по транзисторам и микросхемам просмотр Международной системы единиц СИ перевод величин из одних систем в другие Ваши предложения Свои замечания и пожелания о работе программы Вы можете высказать в гостевой книге или в письме.
В последующих версиях: базы данных по транзисторам и микросхемам просмотр Международной системы единиц СИ перевод величин из одних систем в другие Ваши предложения Свои замечания и пожелания о работе программы Вы можете высказать в гостевой книге или в письме.
Lc фильтр для шим • Вэб-шпаргалка для интернет предпринимателей!
Содержание
- 1 Фильтрация ШИМ в сигнальных цепях
- 1.1 Калькулятор ШИМ-фильтра на RC-цепочке
- 2 Фильтрация ШИМ в силовых цепях
- 2.1 Калькулятор силового ШИМ-фильтра на LC-контуре
- 2.2 Обзор продукции: синусный фильтр для преобразователя частоты
- 2.2.0.1 Синусные фильтры и моторные дроссели открытого типа
- 2.2.0.2 Синусные фильтры в корпусе
- 2.2.0.3 Сетевые (входные) дроссели открытого исполнения
- 2.2.0.4 Входные дроссели (линеаторы) в корпусе
- 2.3 Назначение синусного фильтра
- 2.4 Формулы расчета синусного фильтра
- 2.
 5 Порядок выбора параметров элементов синусного фильтра
5 Порядок выбора параметров элементов синусного фильтра - 2.6 Практическая реализация синусных фильтров
- 2.7 Список литературы
- 2.8 Рекомендуем к прочтению
В статье речь пойдёт про расчёт простейших фильтрующих цепей для сглаживания широтно-импульсной модуляции. Что такое ШИМ, где он применяется и как его реализовать читайте в отдельной статье.
Первое, на чём следует заострить внимание — это назначение цепи, для которой вы собрались строить фильтр. Немного упрощая схемы с ШИМ можно поделить на два типа:
- Сигнальные цепи с ШИМ
- Силовые цепи с ШИМ
Примером сигнального ШИМ служит, например, простейший ЦАП, под силовым ШИМ чаще всего имеется ввиду ШИМ-сигнал на выходе силовых ключей, например в импульсных источниках питания (ИИП). Строго говоря, в источниках питания сам сигнал ШИМ тоже используется в сигнальной цепи (управление транзисторами) и на выходе таких источников сигнал повторяет форму управляющих сигналов, однако имеет более высокую мощность, потому они требуют фильтров позволяющих пропускать большие мощности.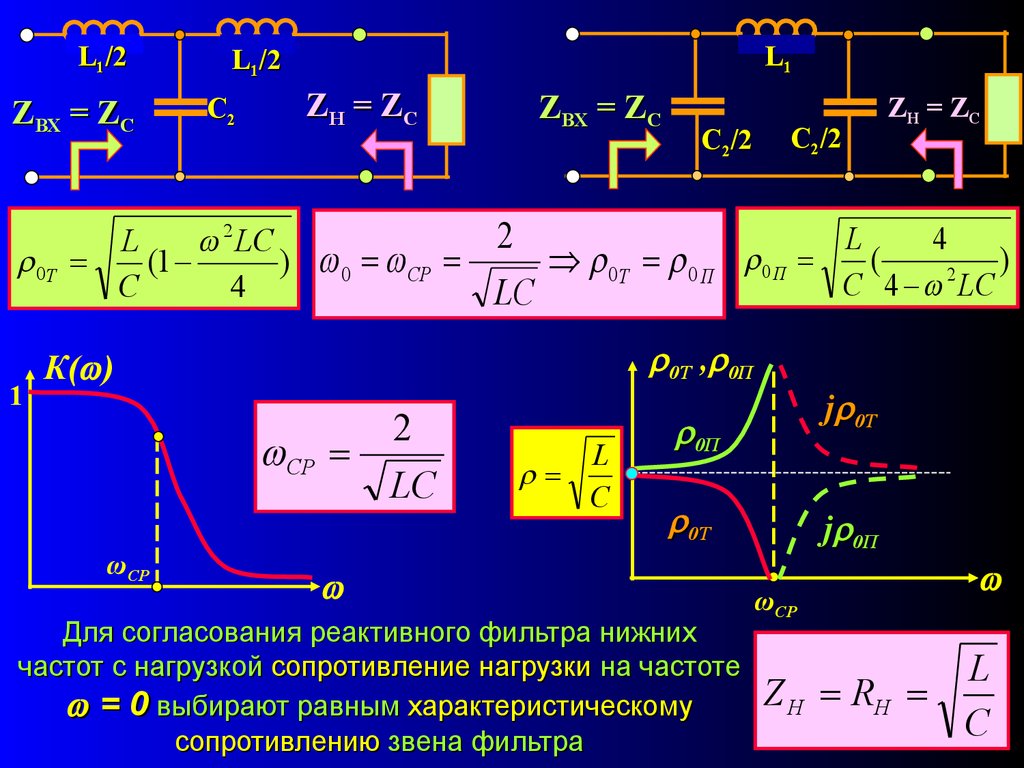
Фильтрация ШИМ в сигнальных цепях
Рис.1. Простейший фильтр нижних частот — интегрирующая RC-цепь и её АЧХ.
Основная характеристика фильтра это частота среза (на рисунке 1 обозначена угловая частота среза — ωс) — амплитуда колебаний данной данной частоты на выходе фильтра ослабляется до уровня
0.707 (-3 Дб) от входного значения. Частота среза определяется по следующей формуле:
Тут R и С — сопротивление резистора в омах и ёмкость конденсатора в фарадах. Необходимо помнить, что для корректной работы сглаживающего фильтра постоянная времени RC-цепочки (τ = R · C) должна быть как можно меньше периода ШИМа, тогда за один период не будет происходить полный заряд-разряд конденсатора.
Следующий важный параметр, позволяющий расчитать ослабление колебаний на заданной частоте это коэффициент передачи фильтра — это отношение K = Uвых/Uвх. Для данной RC-цепочки коэффициент передачи рассчитывается следующим образом:
Зная эти формулы и учтя постоянное падение напряжения на резисторе можно приближённо рассчитать фильтр с нужными характеристиками — например, задавшись имеющейся ёмкостью, либо необходимым уровнем пульсаций.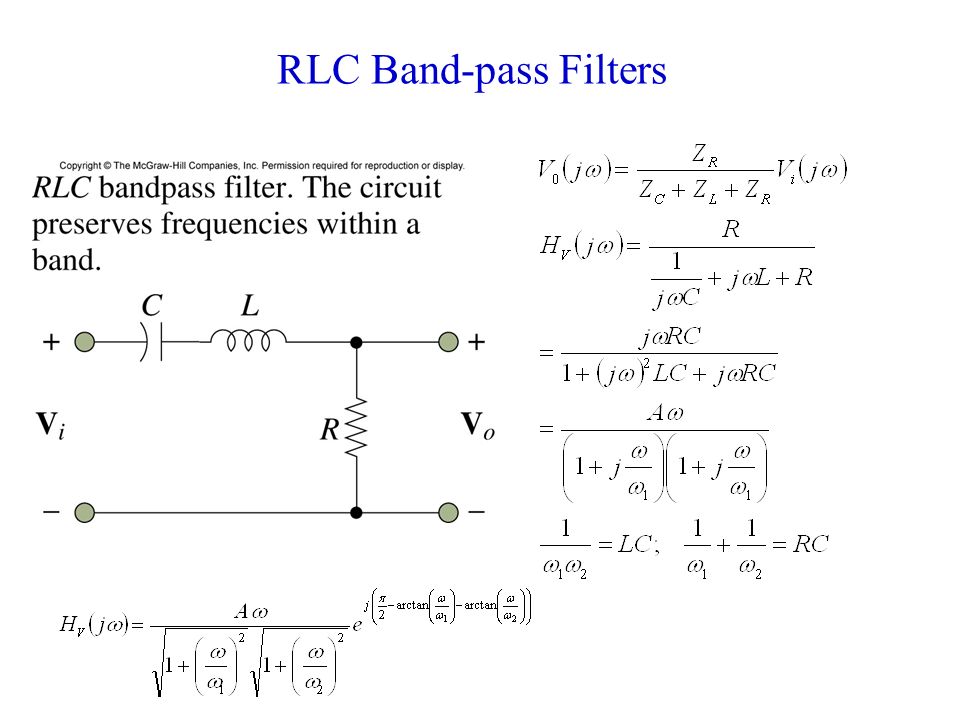
Калькулятор ШИМ-фильтра на RC-цепочке
| Входные данные: | Расчётные значения: |
| Частота ШИМ | Гц |
| Коэффициент заполнения ШИМ (duty cycle) | % |
| Напряжение на входе | В |
| Сопротивление резистора фильтра | Ом |
| Сопротивление нагрузки Rн | Ом |
| Ёмкость конденсатора | мкФ |
(с учётом потерь на резисторе фильтра)
Постоянная времени RC-цепи
Постоянная времени цепи (R · C) не должна быть сильно меньше периода ШИМ!
(не менее)
Обратите внимание — если вы хотите получать из ШИМ-сигнала сглаженный синусоидальный сигнал, необходимо чтобы частота среза фильтра была выше максимальной частоты сигнала, а значит частота ШИМ должна быть ещё выше.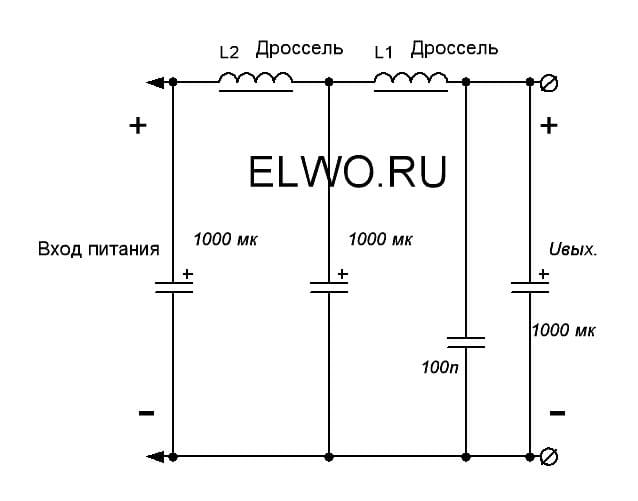
Фильтрация ШИМ в силовых цепях
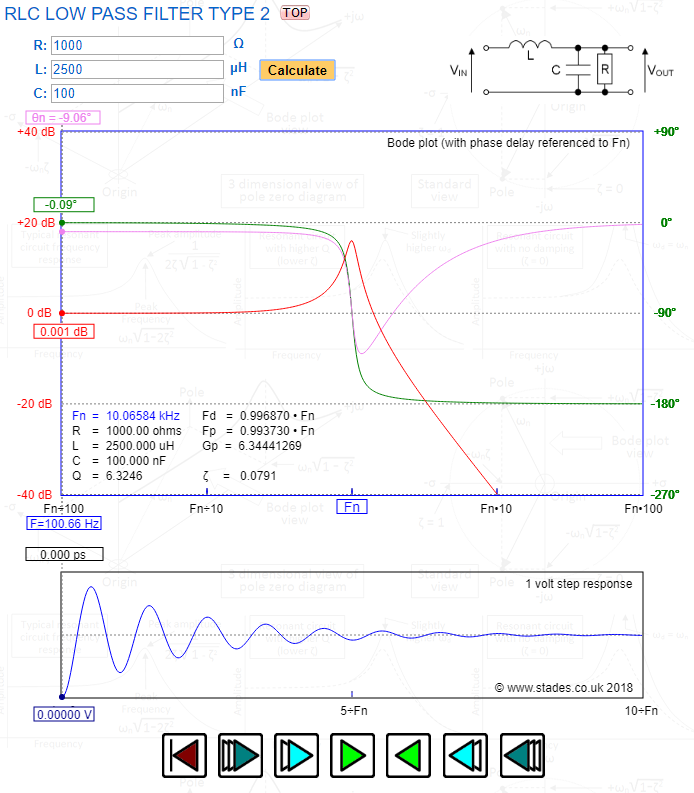
Рис.2. Фильтр нижних частот на LC-контуре и его АЧХ.
LC-фильтр представляет из себя элементарный колебательный контур, который имеет собственную частоту резонанса, поэтому его реальная АЧХ будет несколько отличаться от АЧХ, приведённой на рисунке 2.
Поскольку речь в данной статье идёт о фильтре для силовых цепей, при расчёте фильтра нужно учитывать, что основная гармоника входящего напряжения тоже должна ослабляться фильтром, следовательно, его резонансная частота должна быть ниже частоты ШИМ.
Формула для расчёта частоты резонанса LC-контура:
f = 1/(2 · π · (L · C) 0.5 )
Если частота резонанса контура совпадёт с частотой ШИМ, LC-контур может перейти в режим генерации, тогда на выходе может случиться конфуз, посему предлагаю вам данного недоразумения тщательно избегать. Кроме того, при проектировании данного фильтра есть ещё несколько нюансов, которые неплохо бы соблюдать для получения желаемого результата, а именно:
- Для исключения резонансных явлений на одной из высокочастотных гармонических составляющих ёмкость конденсатора желательно находить из условия равенства волнового сопротивления фильтра сопротивлению нагрузки:
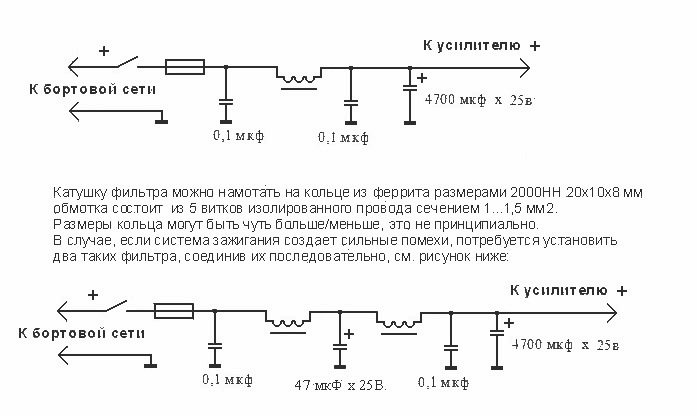
Комплексный коэффициент передачи LC-фильтра рассчитывается по следующей формуле:
где n — номер гармонической составляющей входного сигнала, i — мнимая единица, ω = 2πf, L — индуктивность дросселя (Гн), C — ёмкость конденсатора (Ф), R — сопротивление нагрузки (Ом).
Из формулы очевидно, что чем выше гармоника, тем лучше она подавляется фильтром, следовательно, достаточно рассчитывать уровень только для первой гармоники.
Чтобы перейти от комплексного представления коэффициента передачи к показательному, нужно найти модуль комплексного числа. Для тех, кто (как и я) спал на парах матана в институте, напомню, модуль комплексного числа считается очень просто:
r = |Z| = (x 2 + y 2 ) 0.5
Так как у нас в формуле коэффициента дробь, просто так сходу посчитать модуль не получится и проще всего посчитать это всё, например в MathCad’е. А для тех, кому лень делать всё самим, я запилил весь расчёт в этот прекрасный калькулятор. Пользуйтесь:
Калькулятор силового ШИМ-фильтра на LC-контуре
| Частота ШИМ | Гц |
| Коэффициент заполнения ШИМ (duty cycle) | % |
| Напряжение на входе | В |
| Сопротивление нагрузки | Ом |
| Индуктивность катушки | мГн |
| Ёмкость конденсатора | мкФ |
| Амплитуда пульсаций на частоте ШИМ | В | Резонансная частота контура | Гц |
| Напряжение на выходе (потери не учитываются) | В |
Обратите внимание — при использовании LC-фильтра следует помнить, что из-за наличия в цепи индуктивности, на выходе могут появляться выбросы обратной полярности. Если полярность импульсов на входе не изменяется (например для изменения направления вращения двигателя) для ограничения амлитуды отрицательных выбросов параллельно конденсатору (?) можно включать диод Шоттки.
Если полярность импульсов на входе не изменяется (например для изменения направления вращения двигателя) для ограничения амлитуды отрицательных выбросов параллельно конденсатору (?) можно включать диод Шоттки.
Захаров Александр Александрович
Аннотация. Разработана методика расчёта параметров выходного фильтра на заданный коэффициент гармоник напряжения на нагрузке. Приведён пример расчета Г-образного LC-фильтра мостового инвертора, реализующего равномерную многократную однополярную широтно-импульсную модуляцию (ШИМ) по синусоидальной функции построения, с применением необходимых формул и иллюстрацией характерных графиков и диаграмм.
В наше время — время бурного роста силовой преобразовательной техники трудно себе представить линейный блок питания у современного бытового прибора. Например, в отличие от предшественника, имеющего несколько килограммовый вторичный источник питания (ВИП), современный телевизор получает питание от импульсного многоканально источника несравнимо меньших массы и габаритов, обладающего большими функциями и возможностями.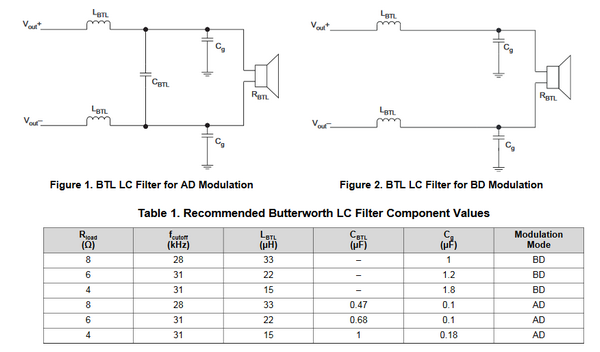 Причём частоты преобразования энергии стали намного выше стандартных пятидесяти герц обычной сети и с развитием элементной базы постоянно повышаются. Конечно, нельзя утверждать, что импульсная силовая электроника полностью вытеснила линейную (например, высококачественные усилители звуковой частоты комплектуются только линейными источниками питания, так как импульсные ВИПы являются источниками, недопустимых для устройств данного класса, помех), но что в настоящее время заняла доминирующее положение — несомненно. Причём это характерно для большого класса устройств преобразующих электрическую энергию: преобразователи тока и напряжения, преобразователи частоты, приводы электрических машин.
Причём частоты преобразования энергии стали намного выше стандартных пятидесяти герц обычной сети и с развитием элементной базы постоянно повышаются. Конечно, нельзя утверждать, что импульсная силовая электроника полностью вытеснила линейную (например, высококачественные усилители звуковой частоты комплектуются только линейными источниками питания, так как импульсные ВИПы являются источниками, недопустимых для устройств данного класса, помех), но что в настоящее время заняла доминирующее положение — несомненно. Причём это характерно для большого класса устройств преобразующих электрическую энергию: преобразователи тока и напряжения, преобразователи частоты, приводы электрических машин.
Вот и современные DC/AC-преобразователи, или в терминологии преобразовательной техники — инверторы, строятся с применением высокочастотных импульсных схем, что позволяет более точно воспроизводить требуемый вид напряжения на выходе, с возможностью регулирования уровня и частоты, а так же формы сигнала при помощи только системы управления. Данные принципы построения DC/AC-преобразователей применяют практически повсеместно где требуется преобразовать энергию постоянного тока в энергию переменного тока, например для питания обычных бытовых приборов от химических источников питания постоянного тока на автономных транспортных средствах, или как часть источников бесперебойного питания для обслуживания особо критичных компьютерных, телерадиокоммуникационных систем, медицинской техники, или для создания приводов управления электрическими двигателями. Да и мало ли еще, какие задачи ставит жизнь перед разработчиками преобразовательной техники, где необходимо использование устройств подобного класса.
Данные принципы построения DC/AC-преобразователей применяют практически повсеместно где требуется преобразовать энергию постоянного тока в энергию переменного тока, например для питания обычных бытовых приборов от химических источников питания постоянного тока на автономных транспортных средствах, или как часть источников бесперебойного питания для обслуживания особо критичных компьютерных, телерадиокоммуникационных систем, медицинской техники, или для создания приводов управления электрическими двигателями. Да и мало ли еще, какие задачи ставит жизнь перед разработчиками преобразовательной техники, где необходимо использование устройств подобного класса.
Инверторы в своей массе строятся на основе самых разнообразных схемных решений, в зависимости от конкретного назначения. Нас же, исходя из темы разговора, интересуют в основном автономные инверторы напряжения с какой-то формой выходного сигнала, в частном случае, как наиболее часто востребованной, синусоидальной формой. Обычно форма сигнала формируется по средствам ШИМ, то есть при помощи изменения ширины импульса на отрезке квантования, на которые разбивается весь период сигнала, что в конечном итоге изменяет амплитуду выходного напряжения, в пределах данного интервала, после фильтрации.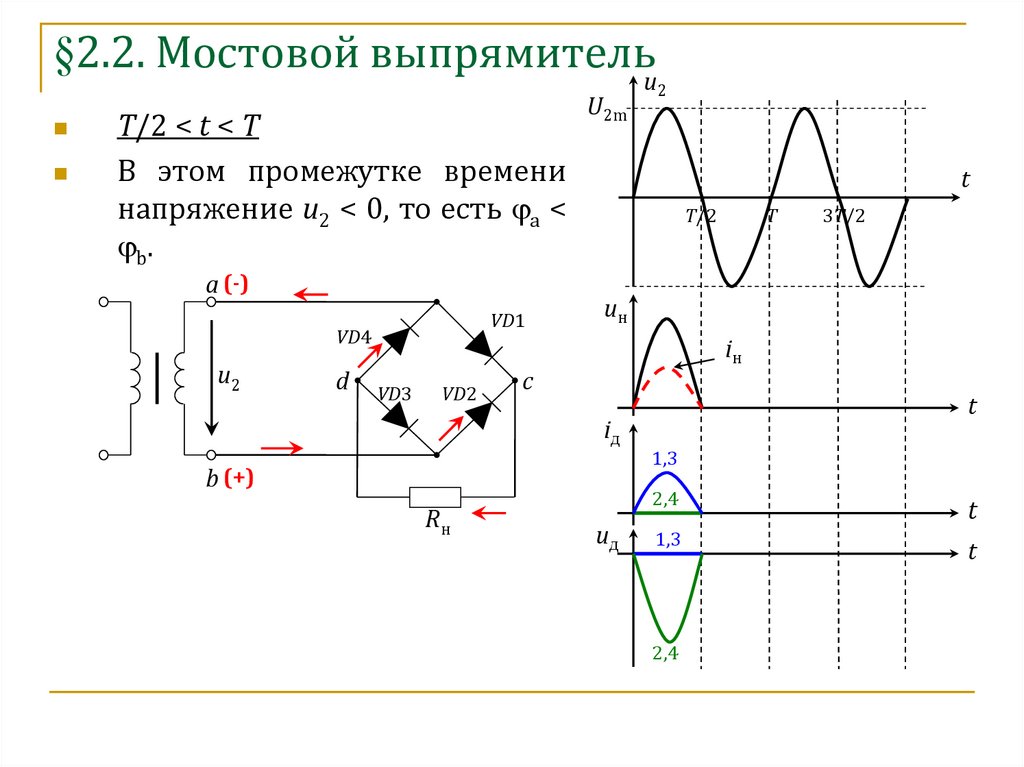 Но из-за дискретности преобразования, сигнал получается не идеально сглаженным, в нём присутствуют высокочастотные гармонические составляющие, да и диапазон регулирования уровня сигнала на выходе вносит свою отрицательную лепту в коэффициент гармоник, увеличивая их действующее значение. Вот здесь и встаёт вопрос о фильтрации этих высокочастотных гармонических составляющих на выходе инверторов для того, что бы они ни как не сказывались на работе потребителя. Зачем скажете вы, такие тонкости как расчёт выходного фильтра на заданный коэффициент гармоник инвертора привода для питания, например, асинхронного двигателя? И, наверное, будете правы, так как сам двигатель является отличным индуктивным фильтром. Но, несомненно, существуют применения, где выходное синусоидальное напряжение просто необходимо, не какое-нибудь больше похожее на меандр с кучей высокочастотных гармонических составляющих, которые вызывают дополнительные потери мощности, помехи и риск возникновения резонансных процессов, а именно синусоидальное.
Но из-за дискретности преобразования, сигнал получается не идеально сглаженным, в нём присутствуют высокочастотные гармонические составляющие, да и диапазон регулирования уровня сигнала на выходе вносит свою отрицательную лепту в коэффициент гармоник, увеличивая их действующее значение. Вот здесь и встаёт вопрос о фильтрации этих высокочастотных гармонических составляющих на выходе инверторов для того, что бы они ни как не сказывались на работе потребителя. Зачем скажете вы, такие тонкости как расчёт выходного фильтра на заданный коэффициент гармоник инвертора привода для питания, например, асинхронного двигателя? И, наверное, будете правы, так как сам двигатель является отличным индуктивным фильтром. Но, несомненно, существуют применения, где выходное синусоидальное напряжение просто необходимо, не какое-нибудь больше похожее на меандр с кучей высокочастотных гармонических составляющих, которые вызывают дополнительные потери мощности, помехи и риск возникновения резонансных процессов, а именно синусоидальное.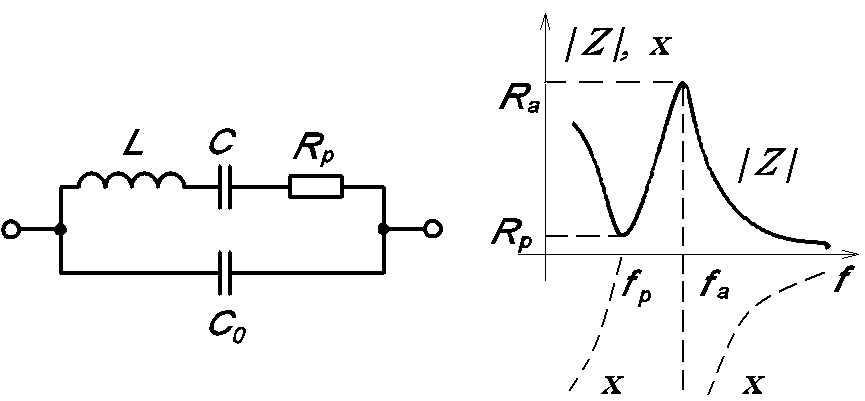 Например, источники бесперебойного питания, серьёзных и уже давно зарекомендовавших себя фирм-производителей, для критичных применений на выходе имеют именно синусоидальное напряжение. Да и множество приборов и устройств рассчитано именно на синусоидальное питающее напряжение, допуская некоторые отклонения по нелинейности. Поэтому то вопрос расчёта фильтра на заданный коэффициент гармоник столь важен в современной преобразовательной технике, так как является необходимым условием нормального функционирования приборов и устройств потребителей, задавая ограничение по нелинейности выходного синусоидального сигнала.
Например, источники бесперебойного питания, серьёзных и уже давно зарекомендовавших себя фирм-производителей, для критичных применений на выходе имеют именно синусоидальное напряжение. Да и множество приборов и устройств рассчитано именно на синусоидальное питающее напряжение, допуская некоторые отклонения по нелинейности. Поэтому то вопрос расчёта фильтра на заданный коэффициент гармоник столь важен в современной преобразовательной технике, так как является необходимым условием нормального функционирования приборов и устройств потребителей, задавая ограничение по нелинейности выходного синусоидального сигнала.
В настоящее время в технической литературе достаточно широко и полно описываются алгоритмы расчёта выходных фильтров выпрямителей на заданный коэффициент пульсаций напряжения на нагрузке, с приведением необходимых формул и соотношений к ним. А вот с методикой расчёта выходных фильтров инверторов на заданный коэффициент гармоник напряжения на нагрузке познакомиться довольно сложно, если не сказать, что практически невозможно.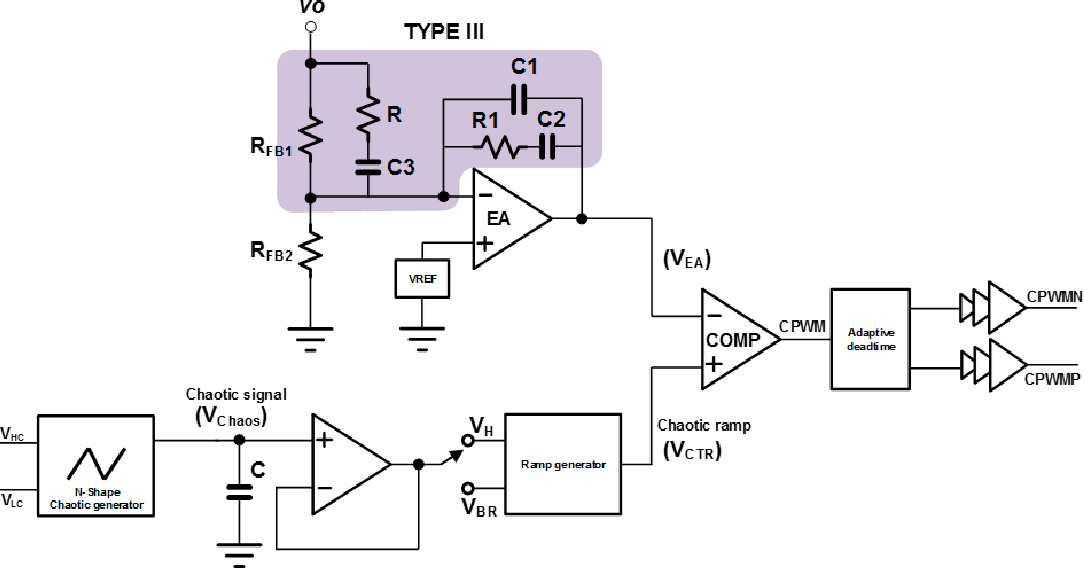 И в основном, разработчики электронной техники, сталкиваясь с такой проблемой, решают её опытным путём. Хотя экспериментальные данные наиболее правдиво отражают сложившуюся ситуацию, но все со мной согласятся, что постановка и проведение эксперимента трудоёмкий и кропотливый процесс, требующий, кроме того, и дополнительных финансовых затрат. Как этого избежать? Можно попытаться решить эту проблему аналитически, но это тоже довольно трудоёмкая задача, требующая много времени и ни кто не поручится за то, что вы сможете получить положительный результат. Что же делать? Я предлагаю воспользоваться вторым путём — решить эту проблему аналитически с некоторыми упрощениями и допущениями, перекладывая все сложные математические расчёты на «плечи» электронно-вычислительных машин (ЭВМ), а первый способ применить как проверку выдвинутому методу.
И в основном, разработчики электронной техники, сталкиваясь с такой проблемой, решают её опытным путём. Хотя экспериментальные данные наиболее правдиво отражают сложившуюся ситуацию, но все со мной согласятся, что постановка и проведение эксперимента трудоёмкий и кропотливый процесс, требующий, кроме того, и дополнительных финансовых затрат. Как этого избежать? Можно попытаться решить эту проблему аналитически, но это тоже довольно трудоёмкая задача, требующая много времени и ни кто не поручится за то, что вы сможете получить положительный результат. Что же делать? Я предлагаю воспользоваться вторым путём — решить эту проблему аналитически с некоторыми упрощениями и допущениями, перекладывая все сложные математические расчёты на «плечи» электронно-вычислительных машин (ЭВМ), а первый способ применить как проверку выдвинутому методу.
В чём же суть предложенного метода? Суть метода заключается в раскладывании формы напряжения на выходе инвертора с помощью прямого быстрого преобразования Фурье (ПБПФ) в спектр амплитуд гармонических составляющих, «пропускания» через фильтр каждой гармонической составляющей в отдельности и последующего восстановления сигнала на выходе фильтра по средствам обратного быстрого преобразования Фурье (ОБПФ).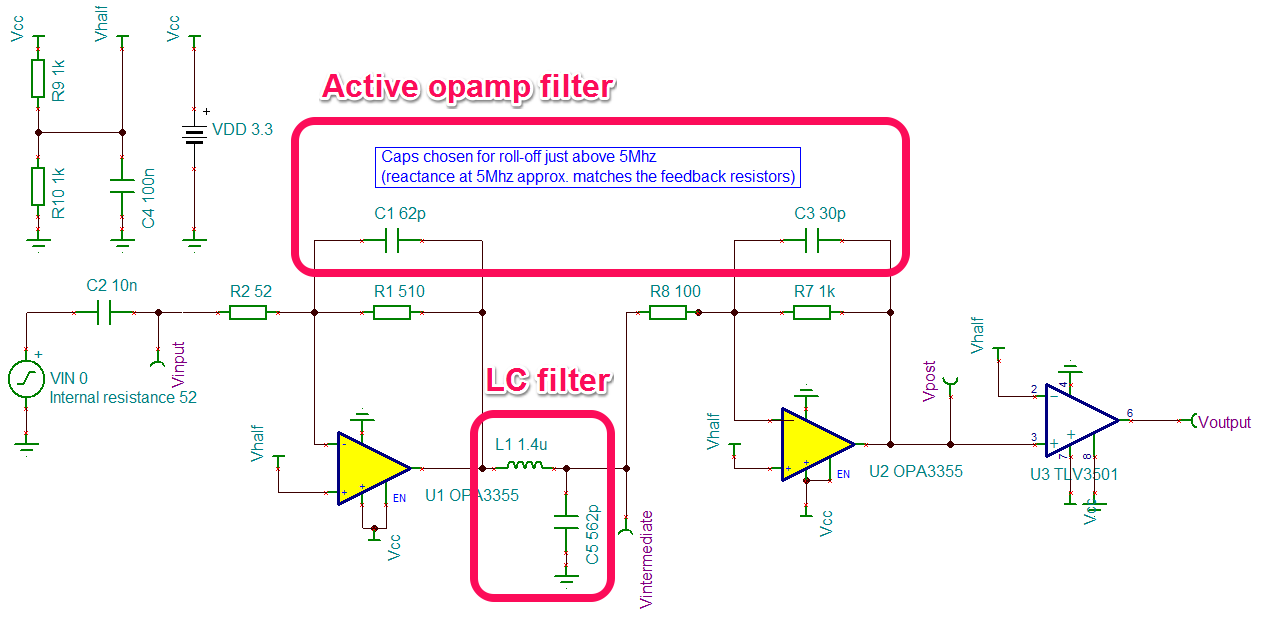 Что же мы получаем? Мы получаем простую идею, основанную только на БПФ, результат применения которой хоть и не будет сверхточным применительно к реальным устройствам, причём точность будет в большей степени зависеть от применённых упрощений и допущений, нежели от точности вычислительного процесса, но тем ни менее сможет дать представление об основных параметрах фильтра. Причем, можно получить не только вид кривой напряжения на нагрузке, а, следовательно, определить коэффициент гармоник, действующие значения напряжений первой и высших гармонических составляющих, но и вычислить фазовый сдвиг, обусловленный влиянием фильтра. И всё же, каким бы простым не казалось решение поставленной задачи, данный метод имеет свои нюансы применения. Для его реализации необходимо хотя бы представлять форму выходного напряжения инвертора и получить коэффициент передачи фильтра по напряжению от номера гармонической составляющей. Второе условие, как мне кажется, имеет довольно тривиальное решение, причём вид коэффициента передачи будет различен в каждом конкретном случае, и зависеть не только от типа применяемого фильтра, от тех упрощений, которые будут допущены разработчиком, но и от конкретных условий технического задания на разрабатываемое устройство.
Что же мы получаем? Мы получаем простую идею, основанную только на БПФ, результат применения которой хоть и не будет сверхточным применительно к реальным устройствам, причём точность будет в большей степени зависеть от применённых упрощений и допущений, нежели от точности вычислительного процесса, но тем ни менее сможет дать представление об основных параметрах фильтра. Причем, можно получить не только вид кривой напряжения на нагрузке, а, следовательно, определить коэффициент гармоник, действующие значения напряжений первой и высших гармонических составляющих, но и вычислить фазовый сдвиг, обусловленный влиянием фильтра. И всё же, каким бы простым не казалось решение поставленной задачи, данный метод имеет свои нюансы применения. Для его реализации необходимо хотя бы представлять форму выходного напряжения инвертора и получить коэффициент передачи фильтра по напряжению от номера гармонической составляющей. Второе условие, как мне кажется, имеет довольно тривиальное решение, причём вид коэффициента передачи будет различен в каждом конкретном случае, и зависеть не только от типа применяемого фильтра, от тех упрощений, которые будут допущены разработчиком, но и от конкретных условий технического задания на разрабатываемое устройство.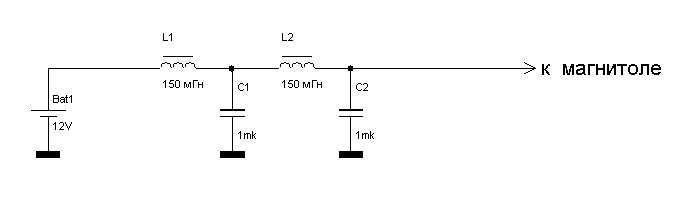 А вот первое условие требует более детального изучения непосредственно алгоритма работы самого инвертора и его структуры.
А вот первое условие требует более детального изучения непосредственно алгоритма работы самого инвертора и его структуры.
Рассмотрим подробнее, на конкретном примере, предлагаемый способ расчёта выходного фильтра инвертора на заданный коэффициент гармоник синусоидального напряжения на нагрузке. Пусть имеется мостовой инвертор (рисунок 1) реализующий равномерную многократную однополярную ШИМ по синусоидальной функции построения с частотой выходного сигнала Гц, частотой квантования кГц и требуется рассчитать параметры выходного Г-образного LC-фильтра, обеспечивающего на активной нагрузке Ом коэффициент гармоник синусоидального напряжения не более %. Данный тип фильтра мы выбрали исходя из его оптимальных массогобаритных показателей и большей эффективности по сравнению с обычными L- или C-фильтрами. Хотелось бы отметить, что в каждом конкретном случае выбор типа фильтра определяется только параметрами технического задания на проектируемое устройство и фантазией разработчика.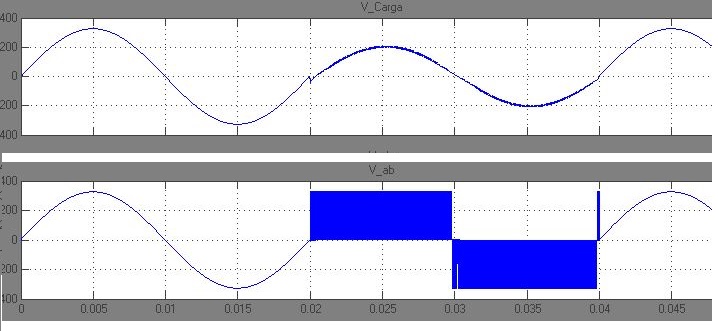 Данный метод лишь помогает рассчитать основные параметры фильтра на основе той передаточной функции, которую разработчик выведет, основываясь на своих предпочтениях и умозаключениях по его типу и синтезированной структуре.
Данный метод лишь помогает рассчитать основные параметры фильтра на основе той передаточной функции, которую разработчик выведет, основываясь на своих предпочтениях и умозаключениях по его типу и синтезированной структуре.
Для расчёта необходимо, как мы уже отметили выше, получить форму выходного напряжения инвертора. Поэтому сначала рассмотрим именно эту проблему. Примем для простоты все элементы в схеме идеальными, а все процессы, протекающие в инверторе, будем рассматривать на периоде выходного напряжения в установившемся режиме. Это допущение вполне оправдано, так как разработчики всегда пытаются минимизировать паразитные явления, которые оказывают негативное влияние на работу устройства. Все математические расчёты, построение графиков и диаграмм работы будем реализовывать на персональном компьютере с использованием пакета математических вычислений Mathcad [1]. Управляющие импульсы по синусоидальной функции построения получаем, как показано на рисунке 2, путём сравнения управляющего выпрямленного синусоидального сигнала с пилообразным развёртывающим напряжением. Имеем в результате широтномодулированную импульсную последовательность по синусоидальной функции построения, которую перераспределяем между ключами инвертора в соответствии с рисунком 3, причём логическая единица соответствует замкнутому состоянию ключа, а логический ноль — разомкнутому. В соответствии с полученным алгоритмом управления, принимая уровень постоянного напряжения на входе равным 10В, строим диаграмму напряжения на выходе (рисунок 4). Как видим, из постоянного напряжения на входе инвертора с помощью ШИМ получили двухполярное модулированное по синусоидальной функции построения напряжение на выходе инвертора. Раскладываем полученную функцию с помощью БПФ и определяем её спектр амплитуд гармонических составляющих (рисунок 5). Замечаем, что спектр состоит из первой гармонической составляющей (50Гц) и массивов более высокочастотных гармоник, сконцентрированных возле частот кратных частоте квантования (1.2кГц, 2.4кГц и т.д.). То есть данный спектр не содержит относительно низкочастотных гармонических составляющих (кроме первой), а только высокочастотные и, следовательно, обычным LC-фильтром можно легко их отфильтровать, оставив только первую гармонику.
Имеем в результате широтномодулированную импульсную последовательность по синусоидальной функции построения, которую перераспределяем между ключами инвертора в соответствии с рисунком 3, причём логическая единица соответствует замкнутому состоянию ключа, а логический ноль — разомкнутому. В соответствии с полученным алгоритмом управления, принимая уровень постоянного напряжения на входе равным 10В, строим диаграмму напряжения на выходе (рисунок 4). Как видим, из постоянного напряжения на входе инвертора с помощью ШИМ получили двухполярное модулированное по синусоидальной функции построения напряжение на выходе инвертора. Раскладываем полученную функцию с помощью БПФ и определяем её спектр амплитуд гармонических составляющих (рисунок 5). Замечаем, что спектр состоит из первой гармонической составляющей (50Гц) и массивов более высокочастотных гармоник, сконцентрированных возле частот кратных частоте квантования (1.2кГц, 2.4кГц и т.д.). То есть данный спектр не содержит относительно низкочастотных гармонических составляющих (кроме первой), а только высокочастотные и, следовательно, обычным LC-фильтром можно легко их отфильтровать, оставив только первую гармонику.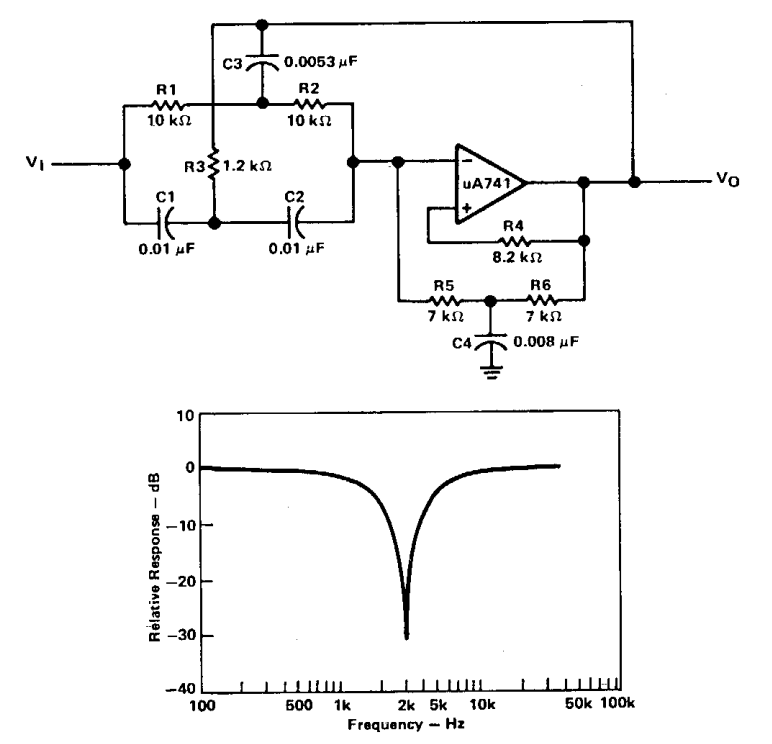 Причём чем больше будет частота квантования, тем в более высоком частотном диапазоне окажутся массивы высокочастотных гармонических составляющих. Определим так же действующее значение выходного напряжения 7.955В, действующее значение первой гармонической составляющей 7.071В и рассчитаем коэффициент гармоник, который составит 51.525%.
Причём чем больше будет частота квантования, тем в более высоком частотном диапазоне окажутся массивы высокочастотных гармонических составляющих. Определим так же действующее значение выходного напряжения 7.955В, действующее значение первой гармонической составляющей 7.071В и рассчитаем коэффициент гармоник, который составит 51.525%.
Теперь найдём функцию коэффициента передачи выходного фильтра от номера гармонической составляющей. Для этого составляем по эквивалентной схеме выходного фильтра (рисунок 6) систему уравнений с использованием законов Кирхгофа и, производя простейшие математические преобразования, находим искомую функцию (1).
где
n — номер гармонической составляющей;
i — мнимая единица;
— круговая частота выходного напряжения;
L — индуктивность дросселя фильтра;
С — ёмкость конденсатора фильтра;
R — сопротивление нагрузки.
Для дальнейших вычислений нам необходимо задаться начальными параметрами фильтра. Индуктивность дросселя принимаем равной мГн, а ёмкость конденсатора находим из условия равенства волнового сопротивления фильтра сопротивлению нагрузки (2) для исключения резонансных явлений на одной из высокочастотных гармонических составляющих.
Индуктивность дросселя принимаем равной мГн, а ёмкость конденсатора находим из условия равенства волнового сопротивления фильтра сопротивлению нагрузки (2) для исключения резонансных явлений на одной из высокочастотных гармонических составляющих.
Перемножаем каждую гармоническую составляющую выходного напряжения инвертора на коэффициент передачи фильтра (рисунок 7). Применяя БПФ, находим диаграмму напряжения на нагрузке, изображённую на рисунке 8 на фоне идеального синусоидального напряжения имеющего такие же амплитуду и фазовый сдвиг. Видим, что напряжение на нагрузке имеет синусоидальный характер с некоторыми искажениями из-за наличия высокочастотных гармонических составляющих не полностью подавленных фильтром и фазовым сдвигом по первой гармонике, величиной 5.549 электрических градусов. Коэффициент гармоник напряжения на нагрузке составляет 9.739%. То есть фильтр с данными параметрами не достаточен для обеспечения на выходе коэффициента гармоник напряжения, требующегося в условии, при заданной выходной частоте и частоте квантования.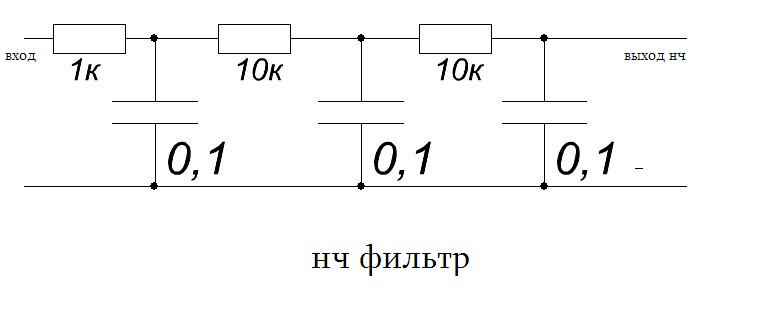
Поэтому рассчитываем по данному алгоритму коэффициент гармоник напряжения на нагрузке, при различных параметрах фильтра, с учётом выражений (1) и (2), от начального значения индуктивности дросселя равного мГн с шагом мГн для тридцати значений. Получаем зависимость коэффициента гармоник выходного напряжения от индуктивности дросселя фильтра, график которой изображён на рисунке 9. Производя расчёты при разных частотах квантования или выходных частотах инвертора можно получить семейства подобных характеристик.
Теперь, исходя из зависимости представленной на рисунке 9, принимаем индуктивность дросселя фильтра равной мГн, ёмкость конденсатора фильтра находим, с учётом выражения 2, равной мкФ и, основываясь на приведённой выше методике, находим диаграмму напряжения на нагрузке изображённую на рисунке 10. Видим, что напряжение на нагрузке имеет синусоидальный характер с некоторыми незначительными искажениями, причём фазовый сдвиг, обусловленный влиянием фильтра, увеличился до 11. 176 электрических градусов. Коэффициент гармоник напряжения на нагрузке составляет всего 2.283%, что вполне удовлетворяет требуемому в условии значению. То есть мы нашли необходимые основные параметры фильтра, при заданных выходной частоте и частоте квантования.
176 электрических градусов. Коэффициент гармоник напряжения на нагрузке составляет всего 2.283%, что вполне удовлетворяет требуемому в условии значению. То есть мы нашли необходимые основные параметры фильтра, при заданных выходной частоте и частоте квантования.
Данная методика расчёта фильтров применялась при разработке универсального лабораторного макета одно/трёхфазного инвертора ШИМ (УМИШИМ-3/1) [2] и показала свою эффективность. На рисунке 10 приведена осциллограмма напряжения на нагрузке при работе инвертора в режиме многократной равномерной двухполярной трёхфазной ШИМ. Причём, затраты времени на расчет были минимальны и составили порядка нескольких десятков минут, а сам расчёт проводился на персональном компьютере, имеющем невысокую вычислительную мощность.
Литература
- Mathcad 6.0 PLUS. Финансовые, инженерные и научные расчёты в среде Windows 95. Издание 2-е, стереотипное — М.: Информационно-издательский дом «Филинъ», 1997. — 712с.
- Семёнов В.
 Д., Матвеев К. Ф., Захаров А. А. Универсальный макет одно/трёхфазного инвертора для проведения лабораторных работ по курсу преобразовательная техника. Материалы Всероссийской научно-методической конференции «Совершенствование систем управления качеством подготовки специалистов». 20-21 марта 2003 года, Красноярск, Россия. В двух частях. Часть вторая, стр. 23-24.
Д., Матвеев К. Ф., Захаров А. А. Универсальный макет одно/трёхфазного инвертора для проведения лабораторных работ по курсу преобразовательная техника. Материалы Всероссийской научно-методической конференции «Совершенствование систем управления качеством подготовки специалистов». 20-21 марта 2003 года, Красноярск, Россия. В двух частях. Часть вторая, стр. 23-24.
Обзор продукции: синусный фильтр для преобразователя частоты
Синусные фильтры и моторные дроссели открытого типа
Синусные фильтры в корпусе
Сетевые (входные) дроссели открытого исполнения
Входные дроссели (линеаторы) в корпусе
Сазонов А.С. (канд.техн.наук), Лебедев Д.Ю. (инж.)
АО «СПИК СЗМА», Санкт-Петербург
Назначение синусного фильтра
Для регулирования частоты вращения многих механизмов, в частности, электрических погружных насосов (ЭПН) с асинхронными двигателями (АД), используются частотно-регулируемые приводы (ЧРП) на основе трехфазных ШИМ-инверторов напряжения с синусоидальным выходным напряжением. Формирование трехфазного синусоидального выходного напряжения ШИМ — инвертора напряжения осуществляется с помощью различных фильтров, наиболее распространенным из которых является однозвенный трехфазный LC- фильтр. В виду сложности аналитического расчета выбор параметров фильтра обычно производится либо экспериментальным путем, что представляет собой трудоемкий и кропотливый процесс, либо путем компьютерного моделирования, что также вызывает определенные трудности.
Формирование трехфазного синусоидального выходного напряжения ШИМ — инвертора напряжения осуществляется с помощью различных фильтров, наиболее распространенным из которых является однозвенный трехфазный LC- фильтр. В виду сложности аналитического расчета выбор параметров фильтра обычно производится либо экспериментальным путем, что представляет собой трудоемкий и кропотливый процесс, либо путем компьютерного моделирования, что также вызывает определенные трудности.
Проще говоря, синусные фильтры предназначены для устранения гармонических искажений напряжения на выходе частотного преобразователя (ПЧ) до допустимых значений (не более 5% по ГОСТ Р 52776-2007). Таким образом, из ШИМ-формы получается синусоидальная форма выходного напряжения ПЧ. Наши синусные фильтры подходят для частотников любого производителя с существенно более низкой ценой. Это могут быть частотники ABB ACS, Danfoss VLT FC, Vacon, DELTA VFD, Веспер E, Siemens SINAMICS, Hyundai N700, Schneider Electric Altivar ATV, Omron, Lovato, INVT, Mitsubishi Electric FR, ОВЕН ПЧВ, Toshiba VF, SEW, EATON.
Схема подключения синусного фильтра
В настоящей статье рассмотрены основные положения для упрощенного расчета и выбора параметров синусного фильтра c требуемым качеством выходного напряжения, характеризуемым коэффициентом гармоник выходного напряжения фильтра.
Расчет и выбор параметров синусного фильтра для конкретного типоисполнения ЧРП (частотного преобразователя) осуществляются при следующих исходных данных:
- напряжение питающей сети на входе ЧРП;
- спектр гармоник входного напряжения фильтра;
- кратность несущей и модулирующей частот инвертора;
- диапазон регулирования выходной частоты;
- характеристика нагрузки;
- принятый критерий оптимальности для рассчитываемого фильтра.
Расчёт и выбор выходного фильтра инвертора производится при имеющемся частотном спектре напряжения на входе фильтра и требуемом коэффициенте гармоник выходного напряжения, регламентируемым ГОСТ Р 52776-2007 для электрических машин.
Для расчёта параметров фильтра в [1] предлагается критерий подобия для однозвенного LC-фильтра нижних частот, связанный с определением минимума суммарной относительной установленной мощности фильтра. По этому критерию можно провести выбор параметров элементов фильтра при коэффициенте гармоник входного напряжения фильтра, зависящего от диапазона регулирования амплитуды первой гармоники напряжения инвертора и величины нагрузки, при заданном качестве выходного напряжения фильтра.
При анализе фильтров инверторов на первом этапе и в практических приложениях учитывают только мощность по основной гармонике, т.к. суммарная реактивная мощность, создаваемая высшими гармониками, существенно меньше реактивной мощности, создаваемой основной гармоникой в том же элементе фильтра.
При заданной выходной мощности ЧРП массо-габаритные показатели однозвенного LC-фильтра определяются заданным коэффициентом гармоник выходного напряжения фильтра и коэффициентом гармоник входного напряжения фильтра.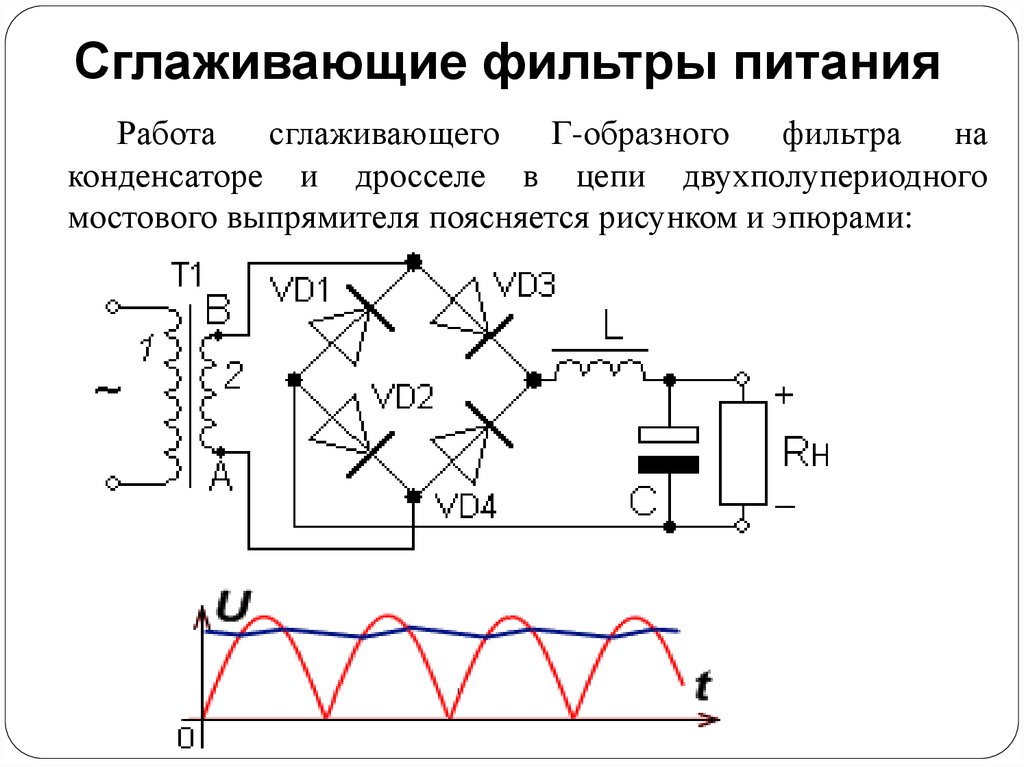
Формулы расчета синусного фильтра
Коэффициент подобия фильтра m 2 для однозвенного LC-фильтра нижних частот связан с коэффициентом гармоник входного и выходного напряжений kГвх, kГвых и параметрами фильтра соотношением [2]:
где N- кратность несущей и модулирующей частот
Квадрат волнового сопротивления фильтра рассчитывается по формуле
где ZH — полное сопротивление нагрузки.
Из соотношений (1) и (2) определяются параметры фильтра. Резонансную частоты фильтра вычисляют по уравнению
Связь между выходным напряжением выпрямителя и трехфазной системой выходного напряжения инвертора с трехфазной нагрузкой можно установить с помощью обобщенного (результирующего) вектора напряжения для трехфазных систем.
Амплитуда основной гармоники напряжения на выходе инвертора (на входе фильтра) Um1зависит от коэффициента регулирования kp , а амплитуда основной гармоники напряжения на выходе фильтра определяется соотношением
— коэффициент передачи фильтра по первой гармонике при работе на активно-индуктивную нагрузку, определяемый из [3].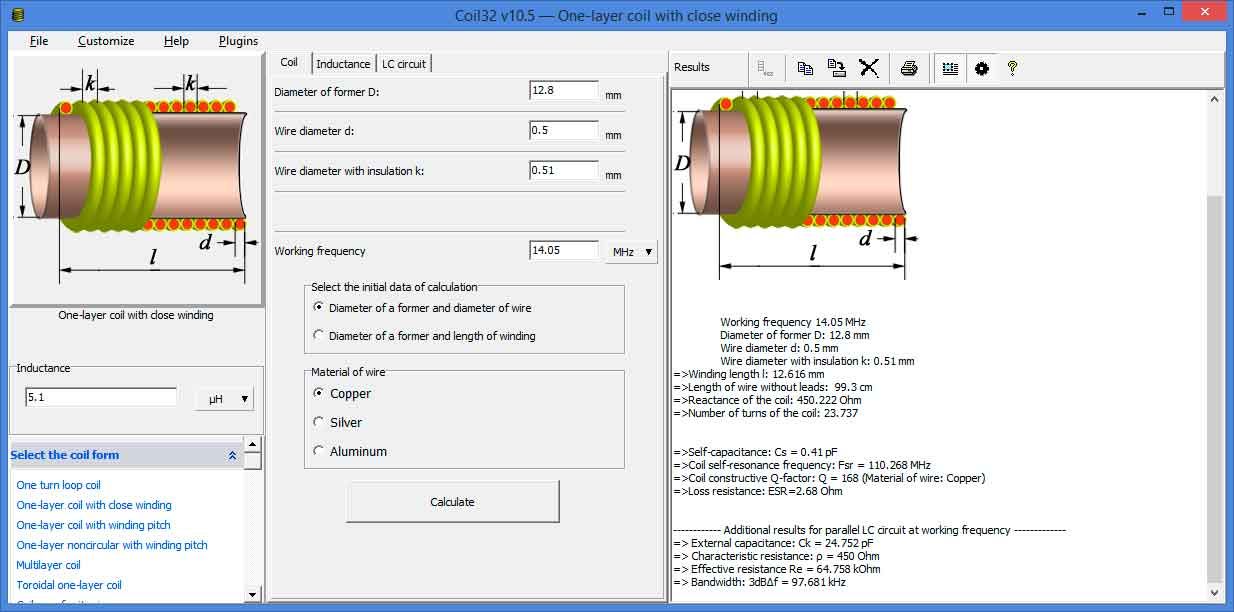
При питании насосных установок мощность на валу приводного двигателя в зависимости от частоты вращения изменяется по закону
где — текущая и номинальная (базовая) частоты вращения; — текущая и номинальная (базовая) активные мощности нагрузки.
Тогда полная мощность нагрузки
Для определения коэффициента гармоник входного напряжения фильтра необходимо учесть спектральный состав напряжения на выходе инвертора, зависящего от способа формирования многоимпульсного напряжения инвертора.
В [2] проанализированы различные алгоритмы работы инверторов напряжения и спектральный состав их выходного напряжения. Анализ показывает, что, например, спектральный состав напряжения с однополярной ШИМ, полученный синусоидальной модуляцией длительности импульсов, при достаточно большом отношении несущей и модулирующей частот- , практически неизменен.
Установлено, что для однополярной ШИМ типовой спектральный состав с учётом первой группы учитываемых гармонических составляющих, необходимых для расчёта силового однозвенного LC-фильтра, состоит из четырёх гармонических составляющих, имеющих кратности N-3, N-1, N+1, N+3.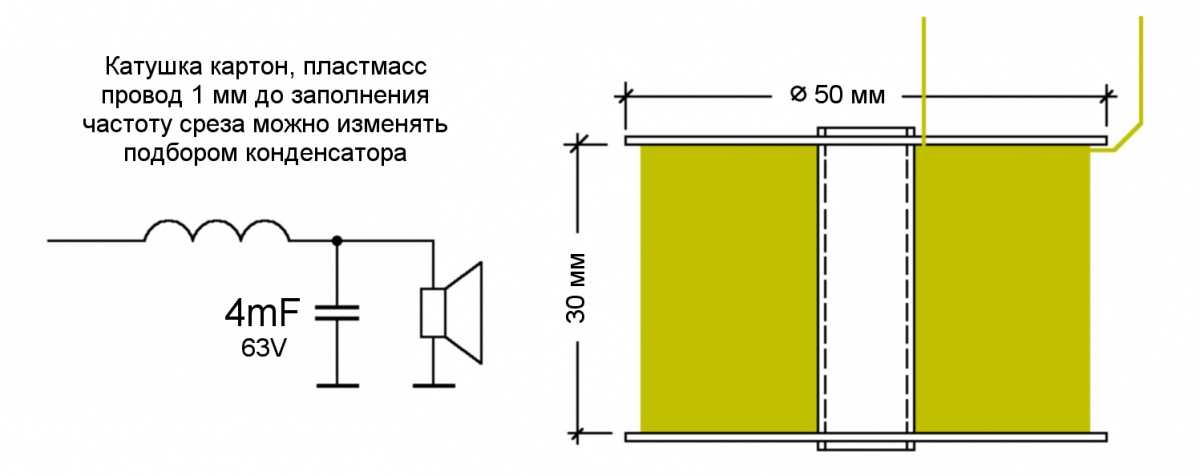 При этом амплитуды гармонических составляющих практически не зависят от кратности частот, а определяются величиной коэффициента регулирования kp.
При этом амплитуды гармонических составляющих практически не зависят от кратности частот, а определяются величиной коэффициента регулирования kp.
Приведены относительные значения учитываемых гармонических составляющих для различных значений кратности частот в зависимости от коэффициента регулирования, которые можно использовать для практических расчётов при любых кратностях частот.
Анализ гармонического состава импульсного напряжения на выходе инвертора в заданном диапазоне регулирования амплитуды первой гармоники напряжения инвертора и величины нагрузки при различных видах модуляции (ШИМ, ШИМ-КД) показывает, что гармоники выходного напряжения имеют наихудший состав при минимальном коэффициенте регулирования [1]. Поэтому величина коэффициента гармоник выходного напряжения фильтра в значительной части диапазона регулирования оказывается меньше заданного.
Следует иметь в виду, что при практических измерениях коэффициента гармоник напряжения на выходе фильтра для правильных замеров необходимо использовать измерительный прибор, фиксирующий максимальные гармоники порядка не менее (N+3).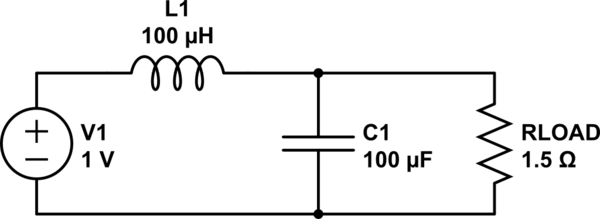
а)
б)
Рис.1 – Входные (а) и выходные (б) фазные токи и напряжения
Порядок выбора параметров элементов синусного фильтра
Для определения расчетных значений индуктивности и емкости фильтра необходимо проводить вычисления на максимальной и минимальной частотах в следующей последовательности:
- определяем коэффициент гармоник входного напряжения kГвх1 для заданных значений kp и N;
- критерии подобия при требуемом и вычисленном коэффициенте гармоник соответственно выходного kг.вых и входного kг.вх1 напряжений
- коэффициент передачи фильтра по первой гармонике при активно- индуктивной нагрузке;
- амплитуду напряжения на выходе фильтра;
Далее по критерию подобия и полному сопротивлению нагрузки, исходя из полной мощности нагрузки, находят емкость и индуктивность фильтра. Из рассчитанных в двух режимах работы значений отбираем наибольшие для удовлетворения качества выходного напряжения во всем диапазоне регулирования частоты. Затем выбираем значения емкости и индуктивности фильтра из стандартного ряда и для них проверяем коэффициент гармоник выходного напряжения фильтра. После этого определяем резонансную частоту фильтра.
Затем выбираем значения емкости и индуктивности фильтра из стандартного ряда и для них проверяем коэффициент гармоник выходного напряжения фильтра. После этого определяем резонансную частоту фильтра.
Все вычисления можно производить на персональном компьютере с использованием пакета математических вычислений Mathcad.
а)
б)
Рис.2 – Спектры входного (а) и выходного (б) фазных напряжений
Практическая реализация синусных фильтров
Синусные фильтры конструктивно могут быть размещены в шкафу с частотным преобразователем (ЧРП) или в отдельном шкафу, причем элемент индуктивности может быть выполнен в виде дросселя с магнитопроводом, или в виде воздушного реактора. Использование воздушного реактора в отдельно стоящем шкафу с экономической точки зрения более выгодно, чем дросселя с магнитопроводом. Заводом АО «СПИК СЗМА» выпускаются оба типоисполнения синусных фильтров на токи до 1600А.
По разработанной методике был рассчитан и изготовлен синусный фильтр для работы совместно с частотным преобразователем (ЧРП) с диапазоном регулирования выходной частоты (30-70) Гц и с несущей частотой ШИМ-инвертора напряжения 3кГц при требуемом коэффициенте гармоник выходного напряжения не более 5% на заданном диапазоне регулирования при квадратичной зависимости момента на валу асинхронного двигателя от частоты вращения.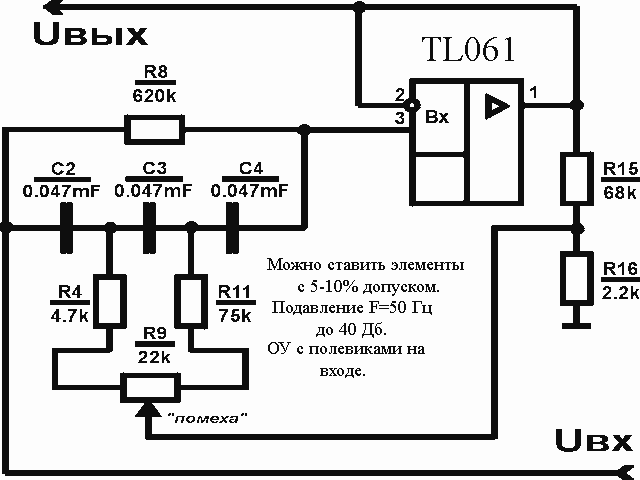
Список литературы
- Малышков Г.М., Крючков В.В., Соловьев И.Н. и др. Выбор параметров фильтров инверторов. — ЭТВА/ Под ред. Ю.И.Конева. – М.: Радио и связь,1986, вып. 17, с. 148-168.
- Крючков В.В., Малышков Г.М., Соловьев И.Н. Кодовое широтно-импульсное регулирование для инверторов.
- Бедфорд Б., Хофт Р. Теория автономных инверторов, пер. с англ. под ред. И.В.Антика. М., «Энергия», 1969.-280 с.
Промышленная Энергетика №2, 2012
PDF версия
Расчет LC- и ARC-фильтров (стр. 1 из 3)
Санкт-петербургский
Государственный университет телекоммуникаций
им. проф. М.А. Бонч-Бруевича
Курсовая работа по ОТЦ на тему:
«Расчет LC- и ARC- фильтров»
Санкт-Петербург
2010
Содержание
1.Расчет LC-фильтра
1.1 Содержание задания
1.2 Проектирование схемы фильтра
1.3 Определение передаточной функции фильтра
1.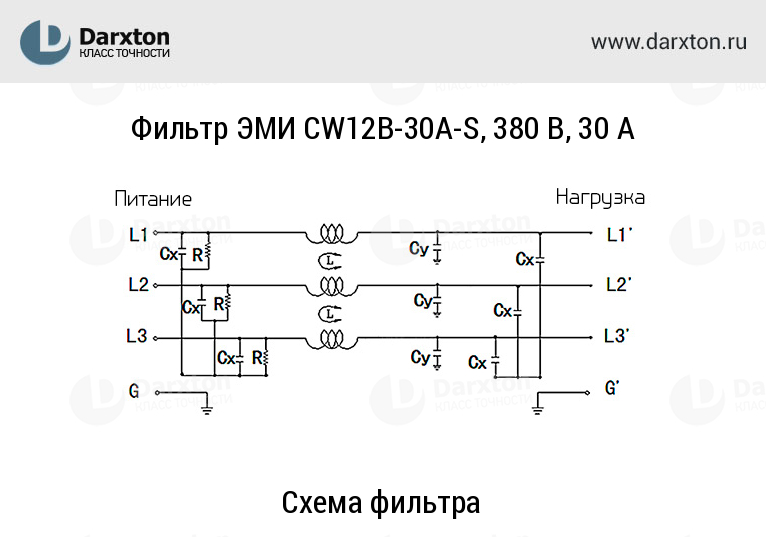 4 Расчёт характеристики ослабления проектируемого фильтра
4 Расчёт характеристики ослабления проектируемого фильтра
1.5 Моделирование фильтра на ПК
2. Расчёт ARC-фильтра
2.1 Содержание задания
2.2 Построение схемы
2.3 Расчёт параметров элементов ARC- фильтра
2.4 Расчёт частотных зависимостей параметрических чувствительностей АЧХ и ФЧХ звена АВТ–структуры
2.5 Расчёт характеристики ослабления фильтра на ПК
1. Расчёт LC-фильтра
1.1 Содержание задания
Задание 1 состоит в том, чтобы рассчитать LC-фильтр, полагая, что его элементы имеют пренебрежимо малые потери. Исходные данные следующие: тип фильтра – ПЗФ. Вид аппроксимации – по Чебышеву.
Режим работы фильтра – односторонняя нагрузка при заданном входном напряжении.
Согласно варианту исходные данные следующие(С=0):
— гарантированное ослабление в полосах задерживания а0=55 дБ;
— граничные частоты полосы пропускания f -1= 3100 Гц ;
— граничная частота полосы задерживания f1=6400 Гц.
Допустимая неравномерность характеристики ослабления фильтра в полосе пропускания
. Величина нагрузочного сопротивления R2=600 Ом.
1.2 Проектирование схемы фильтра
Схема, параметры элементов и характеристики проектируемого фильтра находятся с помощью частотного преобразования фильтра-прототипа нижних частот (ФПНЧ). Определяем порядок ФПНЧ, который для фильтров с характеристиками Чебышева находится по формуле:
,
– нормированная граничная частота полосы задерживания ФПНЧ, она рассчитывается по формуле
Округляя до большего целого, получаем n=6.
Схема ФПНЧ для режима односторонней нагрузки с за данным входным напряжением
Параметры элементов ФПНЧ следующие:
Параметры элементов проектируемого фильтра могут быть определены путем соответствующего пересчета параметров элементов низкочастотного фильтра-прототипа. Так как у меня стоит задача расчёта ППФ, то параметры ФПНЧ переходят в параметры ППФ по приведенным ниже правилам. Далее нужно пересчитать их из нормированных значений в обычные:
Далее нужно пересчитать их из нормированных значений в обычные:
C6=0.3208
Ф
L5= 71
Гн
C4=0.2612
Ф
L3=72
Гн
C2=0.3604
Ф
L1=104
Гн
Схема фильтра
1.3 Определение передаточной функции фильтра
Для начала необходимо определить передаточную функцию ФПНЧ, которая имеет следующий вид:
,
где
— полином Гурвица степени n, B – коэффициент, определяющий ослабление фильтра на частоте
. Для ФПНЧ с характеристикой Чебышева при
, B3=0,05412, а сомножители полинома Гурвица (взяты из таблицы 1.12) имеют вид:
Передаточную функцию проектируемого фильтра H(p) можно получить путем частотного преобразования передаточной функции
низкочастотного фильтра прототипа.
осуществляем замену:
,
Тогда
Порядок передаточной функции Н(р) полосно-пропускающего фильтра вдвое превышает порядок их ФПНЧ, поэтому полином V(p), полученный частотным преобразованием полинома
2-го порядка, содержит два квадратичных сомножителя:
Для вычисления коэффициентов квадратичных сомножителей полином V(p) можно воспользоваться следующим алгоритмом:
1.
2.
3.
4.
Таким образом, передаточная функция фильтра, разложенная на реализуемые сомножители, выводится следующим образом:
для первого сомножителя:
для второго сомножителя:
1.4 Расчёт характеристики ослабления проектируемого фильтра
Характеристику ослабления проектируемого фильтра получим частотным преобразованием характеристики ослабления ФПНЧ, которая при аппроксимации по Чебышеву имеет вид:
,
где n – порядок ФПНЧ;
— нормированная частота ФПНЧ.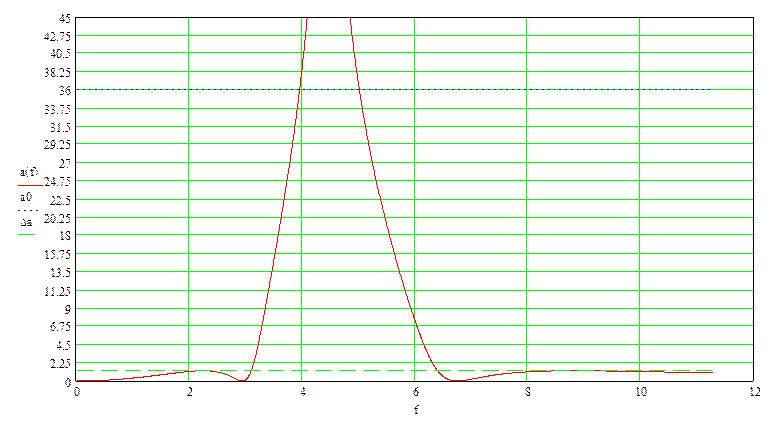
Для расчета характеристики ослабления проектируемого фильтра a(f) используем прямое преобразование частоты:
При этом выберем частотный диапазон
, где
При этом
берется из таблицы:
. Используя прямое преобразование частоты получаем следующий график в MathCAD:
1.5 Моделирование фильтра на ПК
Моделирование фильтра на ПК выполняется с помощью программы Fastmean. Схема фильтра в этой программе выглядит следующим образом:
Практическое пособие к лабораторным работам, страница 3
Принцип действия фильтров заключается в создании высокого сопротивления для переменной составляющей тока (при последовательном включении индуктивности), или шунтированием нагрузки цепью с малым сопротивлением переменной составляющей (при параллельном включении емкости), при применении одновременно двух путей (Г-образный LC-фильтр).
Расчет фильтров ведется для первой (основной)
гармоники по коэффициентам пульсаций или по коэффициенту сглаживания.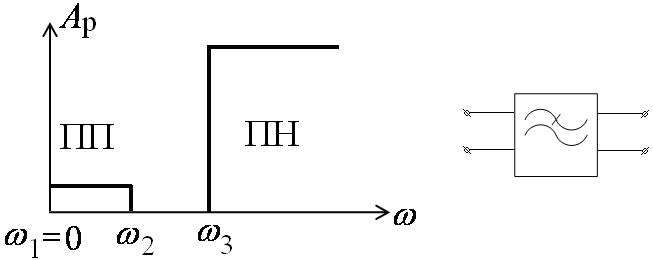 Коэффициенты пульсаций на входе и выходе фильтра
Коэффициенты пульсаций на входе и выходе фильтра
, ,
где Ud1m, Udф1m – амплитудные значения напряжений первой гармоники на входе и выходе фильтров;
Ud, Udф – соответствующие средние значения.
Коэффициент сглаживания
S = q1вх /q1вых.
Для индуктивного и LC-фильтра (рис. 2.1, а и б) можно принять, что падение напряжения в фильтре по постоянной составляющей равно 0, т.е. Ud = Udф, тогда
.
При токе первой гармоники Iп1m напряжение на выходе фильтра при отсутствии емкости
,
а для LC- фильтра с учетом
,
.
Напряжение на входе индуктивного фильтра с учетом
.
на входе Г- образного
.
Тогда коэффициенты сглаживания:
для индуктивного фильтра
.
для Г – образного LC-фильтра
,
где fc – частота питающей сети;
m – фазность схемы выпрямления (m=1 для однополупериодной схемы; m=2 для двухполупериодной и мостовой схем).
При проектировании фильтров обычно принимают
и .
Если требуемое значение S>100, то как правило применяют многозвенные на реактивных элементах или транзисторные фильтры.
Простейший емкостной фильтр (рис. 2.1, в) применяется
при высокоомной нагрузке, когда конденсатор оказывается приемлемых габаритов и
импульсы зарядного тока конденсатора имеют допустимое значение для диодов выпрямителя.
Расчет величины требуемой емкости производят по коэффициенту пульсаций первой
гармоники.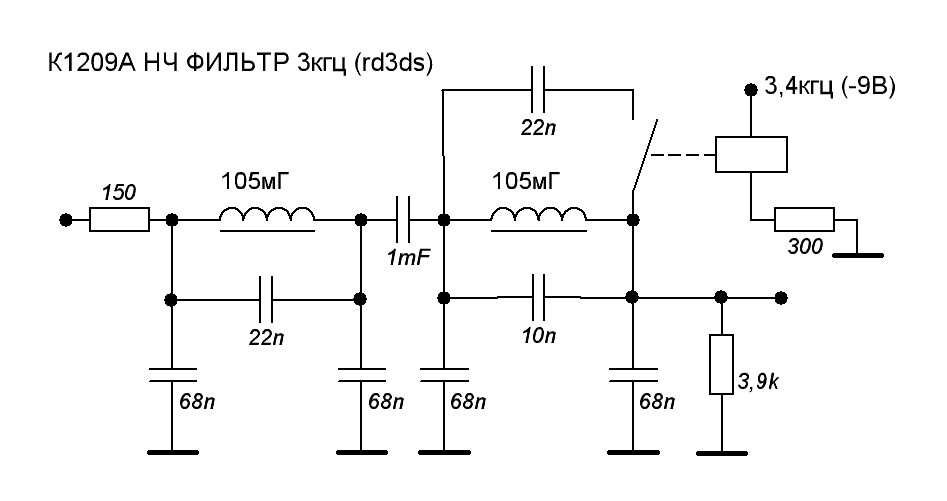
.
Для реальных L– и Г– образного LC- фильтров с учетом активного сопротивления дросселя коэффициенты сглаживания будут соответственно равны
, ,
где Rдр – активное сопротивление обмотки дросселя.
Для однофазного однополупериодного выпрямителя коэффициент пульсаций по первой гармонике q1вх=1.57, для мостового q1вх=0.67
Большим коэффициентом сглаживания обладают LC- фильтры с компенсацией и резонансные фильтры. В схеме LC-фильтра с компенсацией (рис. 2.1, г) кроме основной обмотки I используется компенсационная обмотка II дросселя L2.
Резонансные фильтры образуются из обычного LC-
фильтра путем либо включением параллельно индуктивности дросселя L2
емкости конденсатора СФ (фильтр с параллельным резонансным контуром
(рис. 2.1, д)), либо последовательного включения емкости СФ и
дросселя L2 (фильтр с последовательным резонансным контуром (рис. 2.1, е)).
2.1, е)).
По сравнению с обычным Г– образным LC– фильтром коэффициенты сглаживания резонансных фильтров при правильной их настройке в 3-4 раза выше.
3. Порядок выполнения работы
В работе необходимо провести исследования L, C, LC-фильтров (вставка №6), фильтров с параллельным и последовательным резонансом (вставка №8, №9), фильтра с компенсацией (вставка №7) при их работе от однополупериодного (вставка №1) и мостового (вставка №3) выпрямителей.
3.1. Рассчитать коэффициенты пульсаций и сглаживания для индуктивного (рис. 2.1, а), емкостного (рис. 2.1, в), и Г – образного LC фильтров (рис. 2.1, б) при их работе совместно с однополупериодным и мостовым выпрямителями. Необходимые для расчета данные взять из таблицы согласно номеру бригады (или заданному преподавателем).
3.2. Для указанных в пункте 3.1 фильтров измерить
амплитуду пульсаций и среднее значение напряжения на входе фильтра и
сопротивлении нагрузки Rн.
Используя полученные данные, рассчитать коэффициенты пульсаций и сглаживания. Результаты расчетов по п. 3.1 и п.3.2 свести в таблицу, сравнить расчетные и
экспериментальные показатели. Изобразить осциллограммы пульсаций.
Результаты расчетов по п. 3.1 и п.3.2 свести в таблицу, сравнить расчетные и
экспериментальные показатели. Изобразить осциллограммы пульсаций.
3.3. Снять и построить осциллограммы пульсаций для фильтров с компенсацией, с параллельным и последовательным резонансом. Измерить постоянную составляющую напряжения на нагрузке, рассчитать коэффициенты пульсаций и сглаживания. Результаты расчетов свести в таблицу.
4. Методические указания
4.1. Экспериментальное исследование фильтров проводится на лабораторном стенде ЭС-1А/1, описание и схема которого приведены в лабораторной работе №1.
4.2. Аналитический расчет коэффициентов пульсаций и сглаживания для индуктивного и Г– образного LC-фильтра произвести с учетом активного сопротивления дросселя.
4.3. Измерение средних значений (постоянных
составляющих) напряжения производиться вольтметром В7-40/5, а переменной составляющей
– осциллографом. Требуемое значение сопротивления нагрузки Rн устанавливают по
показаниям вольтметра В7-40/5, работающего в режиме измерения сопротивления.
Таблица
Номер бригады | Тип фильтра | Дроссель | Конденсатор | Сопротивление Rн, Ом |
1 | Индуктивный Емкостной LC—фильтр | L1 – L1 | – C1 C3 | 150 |
2 | Индуктивный Емкостной LC—фильтр | L2 – L2 | – C2 C4 | 200 |
3 | Индуктивный Емкостной LC—фильтр | L1 – L1 | – C1 C4 | 250 |
4 | Индуктивный Емкостной LC—фильтр | L2 – L1 | – C1 C3 | 300 |
5 | Индуктивный Емкостной LC—фильтр | L1 – L2 | – C2 C3 | 350 |
Примечание. Значения
индуктивности и активного сопротивления дросселей:
Значения
индуктивности и активного сопротивления дросселей:
L1 =1.5 Гн, L2 =2.5 Гн,Rдр1 = 35 ом , Rдр2 = 65 Ом; ёмкость конденсаторов:
C1 = 130 мкф , C2 =500 мкф,. C3 =25 мкф, C4 =60 мкф.
4.4. Для подключения индуктивного фильтра необходимо переключатель SA4 перевести в нижнее положение, а переключатели SA3 и SA6 должны быть в нейтральном (среднем) положении.
LC Filter Calculator — Как работают LC фильтры
LC фильтр , также называемый LC фильтрующим элементом , обозначает схему с индуктивностью L и емкостью C в электротехнике. В случае LC-фильтра два компонента подключаются либо последовательно, либо параллельно. Частота среза LC-фильтра является ключевым элементом этого. Существует взаимосвязь между входной частотой и выходным напряжением, поскольку оба компонента по-разному реагируют на изменения напряжения.
В этом разделе статьи подробно объясняется конструкция LC-фильтра, а также принцип работы LC-фильтра. Для этого необходимо немного лучше понять катушку и конденсатор электронных компонентов. Затем мы объясним, как рассчитать LC-фильтр, расскажем об инструменте проектирования LC-фильтра и предоставим калькулятор LC-фильтра . Этот инструмент также может рассчитать передаточную функцию LC-фильтра.
- Как работают индуктивность и емкость
- LC-фильтр – варианты схемы
- Фильтр нижних частот
- Фильтр верхних частот
- Полосовой фильтр
- Полосовой фильтр
- Области применения LC-фильтра : активное, индуктивное и емкостное сопротивления. Омическое сопротивление не зависит от частоты и всегда остается одним и тем же. Напротив, индуктивное и емкостное сопротивления изменяются в зависимости от частоты приложенного напряжения. Это из-за индуктивное сопротивление $X_L$ и емкостное сопротивление $X_C$ .

Если через катушку протекает переменный ток, то в ней создается и снимается магнитное поле. Электроник говорит о индукции . Наведенное напряжение противодействует приложенному напряжению, в результате чего возникает индуктивное сопротивление $X_L$. Эффект индукции возрастает с увеличением частоты. Течение тока в катушке всегда задерживается, поэтому напряжение всегда устремляется следом.
Конденсатор — это, в принципе, аккумулятор с очень маленькой емкостью. Его можно заряжать и снова разряжать. Конденсатор действует как почти бесконечное сопротивление в цепи постоянного тока. Однако в цепи переменного тока он постоянно заряжается и разряжается направлением переменного тока. По сути, ток действительно не протекает через конденсатор. Во время этой непрерывной зарядки и разрядки создается емкостное сопротивление $X_C$. Чем выше частота, тем короче циклы заряда конденсатора и меньше его реактивное сопротивление.
LC-фильтр – варианты схемы
Путем соединения катушки и конденсатора создается схема, выходное напряжение которой изменяется в зависимости от частоты входного напряжения.
 Можно построить с одинаковой схемой разные фильтры. Тип фильтра зависит от того, является ли он последовательным или параллельным соединением и в какой точке снимается выходное напряжение. Часто используемые схемы LC-фильтров представляют собой фильтры верхних частот, нижних частот, полосовые и режекторные фильтры.
Можно построить с одинаковой схемой разные фильтры. Тип фильтра зависит от того, является ли он последовательным или параллельным соединением и в какой точке снимается выходное напряжение. Часто используемые схемы LC-фильтров представляют собой фильтры верхних частот, нижних частот, полосовые и режекторные фильтры.Фильтр нижних частот
Низкочастотный фильтр LC создается путем последовательного соединения двух элементов при снятии выходного напряжения с конденсатора. При высокой частоте реактивное сопротивление конденсатора уменьшается, а реактивное сопротивление катушки увеличивается. Следовательно, остается только очень небольшое выходное напряжение. Однако с уменьшением частоты емкостное реактивное сопротивление конденсатора увеличивается, а вместе с ним и выходное напряжение. Наш калькулятор нижних частот LC может рассчитать фильтр нижних частот 2-го порядка.
Фильтр высоких частот
Фильтр верхних частот LC может пропускать высокие частоты, ослабляя или блокируя низкие частоты.
 Для этого выходное напряжение на индуктивности снимается с последовательной цепи индуктивности и емкости. Когда частота входного напряжения низкая, напряжение на конденсаторе падает, а выходное напряжение остается очень низким. Напротив, по мере увеличения частоты все больше и больше напряжения на индуктивности падает и может использоваться в качестве выходного напряжения. Высокочастотный фильтр LC также имеет 2-й порядок и может быть определен с помощью Калькулятор верхних частот LC .
Для этого выходное напряжение на индуктивности снимается с последовательной цепи индуктивности и емкости. Когда частота входного напряжения низкая, напряжение на конденсаторе падает, а выходное напряжение остается очень низким. Напротив, по мере увеличения частоты все больше и больше напряжения на индуктивности падает и может использоваться в качестве выходного напряжения. Высокочастотный фильтр LC также имеет 2-й порядок и может быть определен с помощью Калькулятор верхних частот LC .Полоса пропускания
Полосовое пропускание LC создается последовательным соединением LC и параллельной цепью LC. Эти два элемента соединены последовательно, и выходное напряжение параллельной цепи снимается. Взаимодействие двух элементов приводит к выходному напряжению, которое является самым высоким в определенной полосе частот. Выше и ниже этой полосы частот выходное напряжение уменьшается. Средняя точка этой полосы называется центральной частотой. Поскольку расчет сложен, мы предоставили Калькулятор полосы пропускания LC .

Ограничитель полосы
Ограничитель полосы LC построен так же, как полоса пропускания LC. Только выходное напряжение должно сниматься через последовательное соединение. Ограничитель полосы ведет себя противоположно полосе пропускания, ослабляя или блокируя полосу частот. Частоты могут быть выше или ниже. Опять же, центральная частота является центром кривой на графике. Расчет полосового режекторного LC-фильтра сложен, поэтому калькулятор полосовой режекции LC может оказаться очень полезным.
Области применения LC-фильтра
Эффекты катушки и конденсатора в основном используются для фильтрации частот. Например, при создании громкоговорителей другие частоты можно отфильтровать на высоких, средних и низких частотах. Это значительно улучшает звук, так как низкочастотный динамик не может воспроизводить высокие ноты и наоборот.
Устройства для беспроводной передачи сигналов часто генерируют нежелательные частоты, которые не должны излучаться.
 Их можно отфильтровать с помощью LC-фильтрующего элемента правильного размера перед подачей на антенну. При большой мощности передачи такие фильтры обязательны.
Их можно отфильтровать с помощью LC-фильтрующего элемента правильного размера перед подачей на антенну. При большой мощности передачи такие фильтры обязательны.Радиоприемникам нужны только те полосы частот, которые они должны принимать. Другие частоты только ухудшают качество сигнала в виде фоновых шумов, таких как шум и треск. В конце концов, устройство начинает передавать сигналы, которые оно улавливает на других частотах. При использовании LC-фильтра в качестве полосового пропускания количество передаваемых частот может быть ограничено, а качество сигнала улучшается.
Другим подходящим примером частотного фильтра является поиск радиостанций. Если мы хотим слушать определенную станцию, мы устанавливаем радио на ее частоту. Все остальные частоты отфильтровываются для обеспечения бесперебойного приема. В переходных зонах часто слышно наложение двух соседних передатчиков.
Расчеты фильтра LC | Форум Электроники
Добро пожаловать на EDAboard.
 com
comДобро пожаловать на наш сайт! EDAboard.com — это международный дискуссионный форум по электронике, посвященный программному обеспечению EDA, схемам, схемам, книгам, теории, документам, asic, pld, 8051, DSP, сети, радиочастотам, аналоговому дизайну, печатным платам, руководствам по обслуживанию… и многому другому. более! Для участия необходимо зарегистрироваться. Регистрация бесплатна. Нажмите здесь для регистрации.
Регистрация Авторизоваться
JavaScript отключен. Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.
- Автор темы Дейл Грегг
- Дата начала
- Статус
- Закрыто для дальнейших ответов.

Дейл Грегг
Младший член уровня 3
Привет,
Я разрабатываю инвертор Н-моста с использованием сигнала SPWM. Сейчас я пытаюсь рассчитать значения схемы фильтра нижних частот LC. Я понимаю уравнение частоты среза (Fc=1/(2*pi()*sqrt(LC))), но я не хочу просто пробовать и ошибаться, или это нормальный способ? Я попытался использовать экв. напряжения индуктора. V=L(di/dt) транспонируется как L=V(dt/di), но потом понял, что не знаю, что такое Vdrop.
Вероятно, это глупый вопрос (я хорошо разбираюсь в этом), но несколько советов о том, как это обычно делается, были бы полезны, так как я застрял на некоторое время.
Дейл
кри$
Уровень участника 1
Привет,
Об операции [Fc = 1/(2*pi*sqrt(LC))], я думаю, это хорошо, потому что вы найдете частоту, генерируемую LC-схемой.
 Я не могу рассказать вам больше, так как начинаю изучать LC-схему.
Я не могу рассказать вам больше, так как начинаю изучать LC-схему.Стивеллиот
Гость
Хорошо, поехали. Это очень сложная задача, чтобы обеспечить полное и точное моделирование для различных индексов модуляции, частот переключения и импедансов нагрузки. Однако для первого прохода я нашел пример, где кто-то рассчитал спектры для синусоиды 100% модуляции.
/unrestricted/PWM_Techniques_final.pdf)
(https://www.wpi.edu/Pubs/E-project/…-1Назначение фильтра — уменьшить амплитуду гармоник до заданного максимального уровня . Обычно люди смотрят только на первые от одной до трех больших гармоник низкого порядка, поскольку обычно гармоники высокого порядка имеют меньшую амплитуду и их легче фильтровать. В статье Кроули и Луенг с гипертекстом выше, рисунок 9показывает третью гармонику, равную примерно 15% основной гармоники (160 В для основной гармоники, 25 В для третьей гармоники).
 Чтобы уменьшить третью гармонику до 3 % от основной гармоники (при КНИ около 5 %, что является такой уродливой формой волны, которую могут выдержать большинство чувствительных схем), вам нужен фильтр, который уменьшает третью гармонику в 5 раз ( 3%/15%). Двухполюсный фильтр, такой как LC, уменьшает амплитуду в 4 раза для каждой октавы, поэтому ваш фильтр должен иметь угловую частоту чуть меньше 1,5*основной частоты.
Чтобы уменьшить третью гармонику до 3 % от основной гармоники (при КНИ около 5 %, что является такой уродливой формой волны, которую могут выдержать большинство чувствительных схем), вам нужен фильтр, который уменьшает третью гармонику в 5 раз ( 3%/15%). Двухполюсный фильтр, такой как LC, уменьшает амплитуду в 4 раза для каждой октавы, поэтому ваш фильтр должен иметь угловую частоту чуть меньше 1,5*основной частоты.Вот действительно неприятная часть вашего LC-фильтра: он настолько близок к основной частоте (менее октавы), что будет усиливать основную (пиковую) характеристику вместо того, чтобы иметь плоские характеристики.
Это яркий пример того, что один из моих друзей называет «принципом сохранения страданий». Вы можете сделать сигнал более чистым с помощью низкочастотного фильтра, но это сделает ваш выход нестабильным. Вы можете сделать вывод стабильным, но ваша форма сигнала не будет тем, что вы хотите показать своим детям.
— — — Обновлено — — —
Возможно, я неправильно ответил на ваш вопрос.
 Я ответил на вопрос — «Какую частоту выбрать в качестве резонансной для фильтра?» Если бы возник вопрос: «Мне нужно построить LC-фильтр с резонансной частотой, например, 80 Гц. Как подобрать L и C?»
Я ответил на вопрос — «Какую частоту выбрать в качестве резонансной для фильтра?» Если бы возник вопрос: «Мне нужно построить LC-фильтр с резонансной частотой, например, 80 Гц. Как подобрать L и C?»
Ответ на второй вопрос: (2*pi*80 Гц) в квадрате = 1/LC или 252 000 = 1/LC в этом примере.
Сначала попробуем конденсатор на 1 мкФ: L = 1/(252 000*C) = 1/(252 000*1 мкФ) = 3,96ч.
Хорошо, этот индуктор довольно большой. Вместо этого давайте выберем L как 396 мкГн (1/10000 размера 3,96H, который мы сначала рассчитали), теперь C составляет 10000 мкФ. Это довольно большой конденсатор. Как насчет чего-то посередине? Как насчет 39 мГн и 100 мкФ? или 50 мГн и 80 мкФ? или 25мГн и 160мкФ?
Откуда взялась катушка индуктивности 25 мГн (или другое значение)? разберите старый силовой трансформатор от старого телевизора (не ЖК-телевизора) и начните наматывать на него витки, пока не получите нужный L.
Надеюсь, это поможет.Последнее редактирование:
BradtheRad
Супер модератор
Что касается конденсаторов, большое значение Фарада связано с:
Более длинной постоянной времени
Более низкой частотой
Большим токомЧто касается катушек индуктивности, большое значение Генри связано с:
Более длинной постоянной времени
Более низкой частотой
Меньшим током ( прямо противоположное поведению конденсатора)В качестве руководства по выбору правильной комбинации LC выберите такие значения компонентов, чтобы их реактивное сопротивление на рабочей частоте совпадало с омическим сопротивлением в цепи тока.
Дейл Грегг
Младший член уровня 3
Спасибо всем за ваши ответы,
Теперь у меня есть идея получше, я не собирался вдаваться в подробности, но сейчас сделаю это, и статья, на которую вы ссылаетесь, очень хороша.

В книге Рэймонда Мака он приводит пример полумостовой схемы и расчет выходной емкости,
C= 1/(2*pi*200 кГц*8,3 мОм)= 96 мкФ …8,3 мОм. из «правила третей»
частота для этого уравнения была удвоена, кто-нибудь может подумать, почему?
Большое спасибо
Дейл Грегг
Младший член уровня 3
Я сделал фильтр в Proteus с 112 мкГн L и 560 мкФ C с расчетной Fc 636 Гц. Может ли кто-нибудь сказать мне, почему в точке колена есть шип?
С уважением,
Дейл
BradtheRad
Супер модератор
Ваш график показывает резонансную частоту катушки и конденсатора.
Моделирование с синусоидальной разверткой, показывающее, что LC-схема является полосовым фильтром, а не фильтром нижних частот.
— — — Обновлено — — —
Резонансная частота составляет 636 Гц (находится близко к геометрической средней точке между 60 и 6 кГц).

кри$
Уровень участника 1
Имеется всплеск, потому что частотный резонанс создается пересечением значений емкости и индуктивности.
Я должен проверить эту ссылку: https://www.electronics-tutorials.ws/accircuits/series-resonance.htmlИтак, я согласен с BradtheRad.
Дейл Грегг
Младший член уровня 3
Спасибо,
поэтому при Fr Xl=Xc, Z=R вызывает высокое напряжение на LC. Будут ли компоненты испытывать слишком большую нагрузку при этом или это используется?
С уважением,
Дейл
Судя по графику, это будет нестабильно?
Последнее редактирование:
ювелир
Расширенный член уровня 5
Я разрабатываю инвертор H-моста, используя сигнал SPWM. Сейчас я пытаюсь рассчитать значения схемы фильтра нижних частот LC. Я понимаю уравнение частоты среза (Fc=1/(2*pi()*sqrt(LC))), но я не хочу просто пробовать и ошибаться, или это нормальный способ? Я попытался использовать экв. напряжения индуктора. V=L(di/dt) транспонируется как L=V(dt/di), но потом понял, что не знаю, что такое Vdrop.
Вероятно, это глупый вопрос (я хорошо разбираюсь в этом), но несколько советов о том, как это обычно делается, были бы полезны, так как я застрял на некоторое время.
Дейл
Нажмите, чтобы развернуть…
Привет, Дейл
. Я также могу помочь вам спроектировать фильтры для вашего инвертора. но это зависит от вашего сигнала сообщения и вашего пути загрузки и обратной связи, если он доступен. и несущая частота и максимальная номинальная мощность и формат нагрузки. Вы можете рассказать мне больше о них? тогда я проведу вас.
и несущая частота и максимальная номинальная мощность и формат нагрузки. Вы можете рассказать мне больше о них? тогда я проведу вас.
С наилучшими пожеланиями
ЮвелирСтивеллиот
Гость
BradtheRad сказал:
Ваш график показывает резонансную частоту катушки и конденсатора.
Моделирование с синусоидальной разверткой, показывающее, что LC-схема является полосовым фильтром, а не фильтром нижних частот.
— — — Обновлено — — —
Резонансная частота составляет 636 Гц (находится близко к геометрической средней точке между 60 и 6 кГц).
Нажмите, чтобы развернуть…
Полосовой??? Хм? Фигура Дейла плоская ниже колена и падает на -40 дБ/декада выше колена. Конечно, мне кажется, что это двухполюсный фильтр нижних частот.

Дейл- Через много лет у меня было прозрение о резонансе. В школе я думал, что за LC-схемами стоит какая-то таинственная физика, которую я не мог понять. Вы вводите 1 В и получаете 100 В (от схемы с добротностью 100). Когда я построил несколько действительно мощных выходных фильтров для источника питания переменного тока мощностью 180 кВт, я понял, что при резонансе фильтр закорачивал источник питания (поскольку X1 и Xc компенсировались, и все, что осталось, это крошечный R катушки индуктивности). Ток короткого замыкания становится очень высоким напряжением в течение 1/2 цикла (и высоким током в течение другой 1/2). Довольно легко получить выходное напряжение в 100 раз больше, чем у источника питания, если вы можете получить от источника питания ток, в 100 раз превышающий номинальный. Вот и волшебство ушло — как зубная фея исчезла…
Что касается вашего вопроса о стрессе: ДА! Если какая-либо из ваших гармоник близка к резонансной частоте, LC-фильтр закоротит выходной каскад (подумайте об уродливой форме волны или даже о дыме!).
 Обычно мы помещаем серию R в LC-фильтр, чтобы уменьшить добротность (до 1,5–3) и уменьшить ток короткого замыкания. На самом деле мы включили его последовательно с C, чтобы он не был последовательно с нагрузкой. Иногда в литературе вы встретите что-то под названием «демпфер» — вот что они имеют в виду. Дополнительный R добавляет нагрузку переменного тока к выходу источника питания, что повышает стабильность и не сильно снижает эффективность.
Обычно мы помещаем серию R в LC-фильтр, чтобы уменьшить добротность (до 1,5–3) и уменьшить ток короткого замыкания. На самом деле мы включили его последовательно с C, чтобы он не был последовательно с нагрузкой. Иногда в литературе вы встретите что-то под названием «демпфер» — вот что они имеют в виду. Дополнительный R добавляет нагрузку переменного тока к выходу источника питания, что повышает стабильность и не сильно снижает эффективность.Последнее редактирование:
BradtheRad
Супер модератор
Стивеллиот сказал:
Бандпас??? Хм? Фигура Дейла плоская ниже колена и падает на -40 дБ/декада выше колена.
 Конечно, мне кажется, что это двухполюсный фильтр нижних частот.
Конечно, мне кажется, что это двухполюсный фильтр нижних частот.Нажмите, чтобы развернуть…
Да. Я изменил последовательность компонентов, чтобы они действовали как фильтр нижних частот.
Трассировка прицела теперь показывает заряд конденсатора.
Резонанс по-прежнему играет здесь роль, хотя омическое сопротивление должно быть очень низким, чтобы оно было очевидным.
(В моем посте №7 указано только резонансное действие из-за отсутствия схемы из ОП.)
Стивеллиот
Гость
Привет, Брэд. Верно.
Теперь краткая демонстрация Q. XL в резонансе (636 Гц) = 2*pi*636*L = 0,48 Ом (j Ом, но я проигнорирую это). Последовательное сопротивление 0,2 Ом; Q = 0,448/0,4 = 2,24. С 5 В на входе вы должны получить 5 * 2,24 = 11,2 В на выходе (ваше моделирование показало 11,5 В, так что это было довольно близко). Однако последовательное сопротивление 0,2 Ом для катушки индуктивности 112 мкГн чертовски велико, поэтому вместо этого установите последовательное сопротивление R, равное 0,005 Ом. Затем добавьте от 0,2 до 0,3 Ом последовательно с C. Вы получите примерно такой же результат.
Однако последовательное сопротивление 0,2 Ом для катушки индуктивности 112 мкГн чертовски велико, поэтому вместо этого установите последовательное сопротивление R, равное 0,005 Ом. Затем добавьте от 0,2 до 0,3 Ом последовательно с C. Вы получите примерно такой же результат.Теперь у вас есть схема с той же добротностью, но со следующими характеристиками:
на частотах выше колена отклик больше похож на однополюсный отклик, потому что комбинация R и C выглядит как R (это плохо от с точки зрения отклика, но это означает, что гармоники приводят к короткому замыканию, что лучше для вашего силового каскада — мы также обычно добавляем эквивалент 56 мкФ -10% основного C — через RC, поэтому мы получаем характеристику 2-го порядка для гармоники высокого порядка),
резистивная составляющая RC рассеивает гармоники в виде тепла вместо того, чтобы возвращать их в силовой каскад,
сопротивление также помогает стабилизировать источник питания, поскольку сопротивление вызывает потребление энергии из входной мощности (все диоды выпрямителя являются проводящими, входные конденсаторы не пиковые и т. д.),
д.),
потери в системе из-за фильтра постоянны (при большом ряду R мощность нагрузки рассеивается в резисторе поэтому КПД и регулирование намного хуже). 92 (Z=0,2)
L=60uH
Fc=1/(2*pi*sqrt(L*C))
Fc=531 ГцЭто вывод моей схемы,
Это показывает несущую частота зависит от основной частоты, это может быть ошибка моделирования, хотя ее не должно быть?
Думаю, я оставлю это на этом о. Если бы мне нужно было снизить Fr до 60 Гц, компоненты должны были бы быть намного больше и требовать больше каскадов. Я собираюсь попробовать это завтра, нужно ли просто R в серии быть рядом с Z?
Кроме того, меня немного смущает вычисление для Q, откуда взялась цифра .4? Должно ли 0,448 быть 0,48?
Последовательное сопротивление 0,2 Ом; Q = 0,448/0,4 = 2,24.
Нажмите, чтобы развернуть…
Большое спасибо,
Дейл
ювелир
Продвинутый член уровня 5
моя несущая частота 3922 Гц
Нажмите, чтобы развернуть.
 ..
..Привет еще раз
Это немного низко, вы можете увеличить его до 10 или 15 кГц? затем вы можете установить резонансную частоту примерно на 5 или 6 кГц, чтобы ваш фильтр был дешевле.
Для этого типа фильтра наилучшая ответственность достигается при zeta=1 . нормализовать его для этого.С наилучшими пожеланиями
ЮвелирДейл Грегг
Младший член уровня 3
Привет,
Я умножил тактовую и несущую частоту на четыре, получив 16 МГц и 15,6 кГц. Результат тот же, но на новой частоте, поэтому я считаю, что это ошибка моделирования, я узнаю, когда соберу его. Спасибо,
- Статус
- Закрыто для дальнейших ответов.
С
Сетевой входной фильтр для Boost PFC…….Резонанс фильтра
- Started by cupoftea
- Ответов: 1
Силовая электроника
С
Помощь в расчетах FLYBACK_CONVERTER
- Автор Siddharth_saxena
- Ответов: 11
Силовая электроника
я
Пассивный фильтр гармоник
- Запуск при зажигании_08
- Ответов: 12
Силовая электроника
Т
Режим переключения Преобразователь постоянного тока в постоянный Конденсаторы входного фильтра электромагнитных помех
- Запуск трансцендентным
- Ответов: 5
Силовая электроника
С
Offline Flyback: входной ЭМС-фильтр после диодного моста.
- Автор: cupoftea
- Ответов: 2
Силовая электроника
Делиться:
Фейсбук Твиттер Реддит Пинтерест Тамблер WhatsApp Эл. адрес Делиться Ссылка на сайт
Верх
Поставщики беспроводных радиочастот и ресурсы
Веб-сайт RF Wireless World является домом поставщиков и ресурсов RF и Wireless.
 На сайте представлены статьи, учебные пособия, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тесты и измерения,
калькуляторы, новости, книги, загрузки и многое другое.
На сайте представлены статьи, учебные пособия, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тесты и измерения,
калькуляторы, новости, книги, загрузки и многое другое.Сайт RF Wireless World охватывает ресурсы по различным темам, таким как RF, беспроводная связь, vsat, спутник, радар, оптоволокно, микроволновая печь, wimax, wlan, zigbee, LTE, 5G NR, GSM, GPRS, GPS, WCDMA, UMTS, TDSCDMA, Bluetooth, Lightwave RF, z-wave, Интернет вещей (IoT), M2M, Ethernet и т. д. Эти ресурсы основаны на стандартах IEEE и 3GPP. Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и дисциплинам MBA.
Статьи о системах на основе IoT
Система обнаружения падения для пожилых людей на основе IoT : В статье рассматривается архитектура системы обнаружения падения для пожилых людей. В нем упоминаются преимущества или преимущества системы обнаружения падения IoT. Подробнее➤
См. также другие статьи о системах на основе IoT:
• Система очистки туалетов AirCraft. • Система измерения удара при столкновении
• Система отслеживания скоропортящихся продуктов и овощей
• Система помощи водителю
• Система умной розничной торговли
• Система мониторинга качества воды
• Система интеллектуальной сети
• Умная система освещения на основе Zigbee
• Умная система парковки на базе Zigbee
• Умная система парковки на базе LoRaWAN.
• Система измерения удара при столкновении
• Система отслеживания скоропортящихся продуктов и овощей
• Система помощи водителю
• Система умной розничной торговли
• Система мониторинга качества воды
• Система интеллектуальной сети
• Умная система освещения на основе Zigbee
• Умная система парковки на базе Zigbee
• Умная система парковки на базе LoRaWAN.Беспроводные радиочастотные изделия
Этот раздел статей охватывает статьи о физическом уровне (PHY), уровне MAC, стеке протоколов и сетевой архитектуре на основе WLAN, WiMAX, zigbee, GSM, GPRS, TD-SCDMA, LTE, 5G NR, VSAT, Gigabit Ethernet на основе IEEE/3GPP и т. д. , стандарты. Он также охватывает статьи, связанные с испытаниями и измерениями, посвященные испытаниям на соответствие, используемым для испытаний устройств на соответствие RF/PHY. СМ. УКАЗАТЕЛЬ СТАТЕЙ >>.
Физический уровень 5G NR : Обработка физического уровня для канала 5G NR PDSCH и канала 5G NR PUSCH была рассмотрена поэтапно.
 Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP.
Подробнее➤
Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP.
Подробнее➤Основные сведения о повторителях и типы повторителей : В нем объясняются функции различных типов повторителей, используемых в беспроводных технологиях. Подробнее➤
Основы и типы замираний : В этой статье рассматриваются мелкомасштабные замирания, крупномасштабные замирания, медленные замирания, быстрые замирания и т. д., используемые в беспроводной связи. Подробнее➤
Архитектура сотового телефона 5G : в этой статье рассматривается блок-схема сотового телефона 5G с внутренними модулями 5G. Архитектура сотового телефона. Подробнее➤
Основные сведения о помехах и типы помех: Электромагнитные помехи, ICI, ISI, световые помехи, звуковые помехи и т. д. Подробнее➤
5G NR Раздел
В этом разделе рассматриваются функции 5G NR (новое радио), нумерология, диапазоны, архитектура, развертывание, стек протоколов (PHY, MAC, RLC, PDCP, RRC) и т.
 д.
5G NR Краткий справочный указатель >>
д.
5G NR Краткий справочный указатель >>
• Мини-слот 5G NR • Часть полосы пропускания 5G NR • БАЗОВЫЙ НАБОР 5G NR • Форматы 5G NR DCI • 5G NR UCI • Форматы слотов 5G NR • IE 5G NR RRC • 5G NR SSB, SS, PBCH • 5G NR PRACH • 5G NR PDCCH • 5G NR PUCCH • Опорные сигналы 5G NR • 5G NR m-Sequence • Золотая последовательность 5G NR • 5G NR Zadoff Chu Sequence • Физический уровень 5G NR • MAC-уровень 5G NR • Уровень 5G NR RLC • Уровень PDCP 5G NRРуководства по беспроводным технологиям
В этом разделе рассматриваются учебные пособия по радиочастотам и беспроводным сетям. Он охватывает учебные пособия по таким темам, как сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS, GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, беспроводная сеть, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. д. См. ИНДЕКС УЧЕБНЫХ ПОСОБИЙ >>
Учебное пособие по 5G — В этом учебном пособии по 5G также рассматриваются следующие подтемы, посвященные технологии 5G:
Учебник по основам 5G Диапазоны частот учебник по миллиметровым волнам Рамка волны 5G мм Зондирование канала миллиметровых волн 5G 4G против 5G Испытательное оборудование 5G Архитектура сети 5G Сетевые интерфейсы 5G NR звучание канала Типы каналов 5G FDD против TDD Нарезка сети 5G NR Что такое 5G NR Режимы развертывания 5G NR Что такое 5G ТФВ этом учебном пособии GSM рассматриваются основы GSM, сетевая архитектура, сетевые элементы, системные спецификации, приложения, Типы пакетов GSM, структура кадров GSM или иерархия кадров, логические каналы, физические каналы, Физический уровень GSM или обработка речи, вход в сеть мобильного телефона GSM или настройка вызова или процедура включения питания, Вызов MO, вызов MT, модуляция VAMOS, AMR, MSK, GMSK, физический уровень, стек протоколов, основы мобильного телефона, Планирование RF, нисходящая линия связи PS и восходящая линия связи PS.

➤Читать дальше.LTE Tutorial , описывающий архитектуру системы LTE, включая основы LTE EUTRAN и LTE Evolved Packet Core (EPC). Он предоставляет ссылку на обзор системы LTE, радиоинтерфейс LTE, терминологию LTE, категории LTE UE, структуру кадра LTE, физический уровень LTE, Стек протоколов LTE, каналы LTE (логические, транспортные, физические), пропускная способность LTE, агрегация несущих LTE, Voice Over LTE, расширенный LTE, Поставщики LTE и LTE vs LTE advanced.➤Подробнее.
Радиочастотные технологии Материалы
На этой странице мира беспроводных радиочастот описывается пошаговое проектирование преобразователя частоты на примере повышающего преобразователя частоты 70 МГц в диапазон C. для микрополосковой платы с использованием дискретных радиочастотных компонентов, а именно. Смесители, гетеродин, MMIC, синтезатор, опорный генератор OCXO, амортизирующие прокладки. ➤Читать дальше.
➤ Проектирование и разработка РЧ приемопередатчика ➤Дизайн радиочастотного фильтра ➤Система VSAT ➤Типы и основы микрополосковых ➤Основы волноводаСекция испытаний и измерений
В этом разделе рассматриваются ресурсы по контролю и измерению, контрольно-измерительное оборудование для тестирования тестируемых устройств на основе Стандарты WLAN, WiMAX, Zigbee, Bluetooth, GSM, UMTS, LTE.
 ИНДЕКС испытаний и измерений >>
ИНДЕКС испытаний и измерений >>
➤Система PXI для контрольно-измерительных приборов. ➤ Генерация и анализ сигналов ➤ Измерения физического уровня ➤ Тестирование устройства WiMAX на соответствие ➤ Тест на соответствие Zigbee ➤ Тест на соответствие LTE UE ➤ Тест на соответствие TD-SCDMAВолоконно-оптические технологии
Волоконно-оптический компонент основы, включая детектор, оптический соединитель, изолятор, циркулятор, переключатели, усилитель, фильтр, эквалайзер, мультиплексор, разъемы, демультиплексор и т. д. Эти компоненты используются в оптоволоконной связи. ИНДЕКС оптических компонентов >>
➤Руководство по оптоволоконной связи ➤APS в SDH ➤Основы SONET ➤ Структура кадра SDH ➤ SONET против SDHПоставщики беспроводных радиочастотных устройств, производители
Сайт RF Wireless World охватывает производителей и поставщиков различных радиочастотных компонентов, систем и подсистем для ярких приложений, см. ИНДЕКС поставщиков >>.

Поставщики ВЧ-компонентов, включая ВЧ-изолятор, ВЧ-циркулятор, ВЧ-смеситель, ВЧ-усилитель, ВЧ-адаптер, ВЧ-разъем, ВЧ-модулятор, ВЧ-трансивер, PLL, VCO, синтезатор, антенну, осциллятор, делитель мощности, сумматор мощности, фильтр, аттенюатор, диплексер, дуплексер, чип-резистор, чип-конденсатор, чип-индуктор, ответвитель, ЭМС, программное обеспечение RF Design, диэлектрический материал, диод и т. д. Поставщики радиочастотных компонентов >>
➤Базовая станция LTE ➤ РЧ-циркулятор ➤РЧ-изолятор ➤Кристаллический осцилляторMATLAB, Labview, Embedded Исходные коды
Раздел исходного кода RF Wireless World охватывает коды, связанные с языками программирования MATLAB, VHDL, VERILOG и LABVIEW. Эти коды полезны для новичков в этих языках. СМ. ИНДЕКС ИСТОЧНИКОВ >>
➤ 3–8 код VHDL декодера ➤Скремблер-дескремблер Код MATLAB ➤32-битный код ALU Verilog ➤ T, D, JK, SR коды лабораторного просмотра триггеров*Общая медицинская информация*
Сделайте эти пять простых вещей, чтобы помочь остановить коронавирус (COVID-19).

СДЕЛАЙТЕ ПЯТЬ
1. РУКИ: Мойте их часто
2. ЛОКОТЬ: кашляйте в него
3. ЛИЦО: не прикасайтесь к нему
4. НОГИ: держитесь на расстоянии более 3 футов (1 м) друг от друга
5. ЧУВСТВУЙТЕ: заболели? Оставайтесь домаИспользуйте технологию отслеживания контактов >> , следуйте рекомендациям по социальному дистанцированию >> и установить систему наблюдения за данными >> спасти сотни жизней. Использование концепции телемедицины стало очень популярным в таких стран, как США и Китай, чтобы остановить распространение COVID-19так как это заразное заболевание.
Радиочастотные калькуляторы и преобразователи
Раздел «Калькуляторы и преобразователи» охватывает ВЧ-калькуляторы, беспроводные калькуляторы, а также преобразователи единиц измерения. Они охватывают беспроводные технологии, такие как GSM, UMTS, LTE, 5G NR и т. д. СМ. КАЛЬКУЛЯТОРЫ Указатель >>.
➤ Калькулятор пропускной способности 5G NR ➤ 5G NR ARFCN и преобразование частоты ➤ Калькулятор скорости передачи данных LoRa ➤ LTE EARFCN для преобразования частоты ➤ Калькулятор антенны Yagi ➤ Калькулятор времени выборки 5G NRIoT-Интернет вещей Беспроводные технологии
В разделе, посвященном IoT, рассматриваются беспроводные технологии Интернета вещей, такие как WLAN, WiMAX, Zigbee, Z-wave, UMTS, LTE, GSM, GPRS, THREAD, EnOcean, LoRa, SIGFOX, WHDI, Ethernet, 6LoWPAN, RF4CE, Bluetooth, Bluetooth с низким энергопотреблением (BLE), NFC, RFID, INSTEON, X10, KNX, ANT+, Wavenis, Dash7, HomePlug и другие.
 Он также охватывает датчики IoT, компоненты IoT и компании IoT.
Он также охватывает датчики IoT, компоненты IoT и компании IoT.
См. главную страницу IoT>> и следующие ссылки.
➤РЕЗЬБА ➤EnOcean ➤ Учебник LoRa ➤ Учебник по SIGFOX ➤ WHDI ➤6LoWPAN ➤Зигби RF4CE ➤NFC ➤Лонворкс ➤CEBus ➤УПБ
СВЯЗАННЫЕ ПОСТЫ
Учебники по беспроводным радиочастотам
GSM ТД-СКДМА ваймакс LTE UMTS GPRS CDMA SCADA беспроводная сеть 802.11ac 802.11ad GPS Зигби z-волна Bluetooth СШП Интернет вещей Т&М спутник Антенна РАДАР RFID
Различные типы датчиков
Датчик приближения Датчик присутствия против датчика движения Датчик LVDT и RVDT Датчик положения, смещения и уровня датчик силы и датчик деформации Датчик температуры датчик давления Датчик влажности датчик МЭМС Сенсорный датчик Тактильный датчик Беспроводной датчик Датчик движения Датчик LoRaWAN Световой датчик Ультразвуковой датчик Датчик массового расхода воздуха Инфразвуковой датчик Датчик скорости Датчик дыма Инфракрасный датчик Датчик ЭДС Датчик уровня Активный датчик движения против пассивного датчика движения
Поделиться этой страницей
Перевести эту страницу
СТАТЬИ Раздел T&M ТЕРМИНОЛОГИИ Учебники Работа и карьера ПОСТАВЩИКИ Интернет вещей Онлайн калькуляторы исходные коды ПРИЛОЖЕНИЕ.
 ЗАМЕТКИ
Всемирный веб-сайт T&M
ЗАМЕТКИ
Всемирный веб-сайт T&M LC-фильтр для советов по проектированию источников питания
Ключевые выводы
Понимание основ LC-фильтра.
Узнайте, почему LC-фильтр для блока питания важен.
Советы по сборке LC-фильтра источника питания.
Шум переменного тока влияет на точность, стабильность и функциональность различных компонентов.
Я всегда считал, что для приготовления идеального эспрессо достаточно высококачественных кофейных зерен и дорогой кофемашины. Увидев бариста мирового класса в действии, я понял, что ошибался. Помимо возвышенных техник, фильтр для воды определяет конечный результат приготовления эспрессо.
Наблюдение за этим мастером открыло глаза на то, насколько дотошным нужно быть, чтобы приготовить идеальную чашку кофе.
 Этот опыт также подчеркивает аналогичный и часто упускаемый из виду аспект при проектировании источника питания. Возможно, фильтр для воды не используется, но вам нужно будет установить LC-фильтр для источника питания.
Этот опыт также подчеркивает аналогичный и часто упускаемый из виду аспект при проектировании источника питания. Возможно, фильтр для воды не используется, но вам нужно будет установить LC-фильтр для источника питания.Что такое LC-фильтр?
Если вам нужно базовое обновление, LC-фильтр представляет собой фильтр нижних частот, состоящий из катушки индуктивности и конденсатора. Он предназначен для предотвращения прохождения через цепь некоторых высокочастотных компонентов переменного тока. Вот типичное расположение LC-фильтра.
Базовая схема LC-фильтра нижних частот.
На более высоких частотах дроссель действует как дроссель, блокирующий прохождение компонентов переменного тока. Между тем, импеданс конденсатора уменьшается и образует путь для прохождения высокочастотных компонентов. Идея LC-фильтра состоит в том, чтобы предотвратить попадание высокочастотных составляющих переменного тока на нагрузку.

Зачем нужен LC-фильтр для источника питания?
В идеальном мире напряжение на выходе источника питания постоянного тока представляет собой идеальную горизонтальную линию при наблюдении на осциллографе. Однако мир далек от идеала, и напряжение никогда не бывает идеальной линией.
Блок питания постоянного тока чувствителен к пульсациям и шуму переменного тока, особенно импульсный регулятор мощности. Частота переключения и перехода создает пульсации выше 500 кГц, которые часто связаны с выходным напряжением. Даже если вы придерживаетесь линейного регулятора, у вас также будут компоненты переменного тока от частоты сети или цифровых помех.
Точно так же, как нефильтрованная вода может испортить чашку эспрессо, пульсации переменного тока, попадающие на выход регулятора, могут повлиять на функционирование системы. Такие модули, как АЦП, ЦАП и операционные усилители, особенно чувствительны к помехам переменного тока в источнике питания.
 Точность этих модулей может быть нарушена, а в некоторых случаях компоненты могут работать неправильно.
Точность этих модулей может быть нарушена, а в некоторых случаях компоненты могут работать неправильно.Шум источника питания влияет не только на аналоговые компоненты. В одном из исследований было установлено, что шум блока питания снижает тактовую частоту высокоскоростного микропроцессора на 6,7%. Даже если схема может выдержать шум переменного тока, он все равно может излучаться в виде электромагнитных помех и влиять на другие электронные устройства.
Советы по проектированию LC-фильтра источника питания
Поверьте мне на слово, шум источника питания раздражает. Вы не можете предсказать, как и когда это повлияет на схему. В отличие от плохо приготовленной чашки кофе, последствия помех систем электропитания в полевых условиях гораздо серьезнее.
Поэтому необходимо убедиться, что блок питания оснащен LC-фильтром нижних частот. Вот несколько советов по правильной реализации:
Позиционирование
Естественно, вы подумаете о размещении LC-фильтра между выходом регулятора и нагрузкой.
 Хотя в этом размещении нет ничего плохого, вы можете добиться лучшего подавления шума, поместив LC-фильтр на вход, если вы используете понижающий регулятор.
Хотя в этом размещении нет ничего плохого, вы можете добиться лучшего подавления шума, поместив LC-фильтр на вход, если вы используете понижающий регулятор.Для понижающих регуляторов большая часть шума связана с переключением переходов на входе. Добавление LC-фильтра на вход приводит к большему подавлению.
Конденсаторы с низким значением ESR и ESL
Для эффективного подавления высокочастотного шума вам следует выбрать конденсатор с низким значением ESR и ESL. Если этого трудно достичь, рассмотрите возможность использования двух конденсаторов параллельно для более низкого комбинированного значения ESR и ESL.
Используйте электролитические конденсаторы с низким ESR/ESL.
Значения LC
Выбор номинала катушки индуктивности и конденсатора кажется простым процессом. В конце концов, что может пойти не так, если следовать следующей формуле?
f = 1 / (2π √LC)
Однако это гораздо больше, чем объединение двух пассивных компонентов для блокировки высокочастотного шума.
 Для начала вам нужно выбрать индуктор со значительно более высоким значением, чем индуктивность, подключенная последовательно к источнику питания.
Для начала вам нужно выбрать индуктор со значительно более высоким значением, чем индуктивность, подключенная последовательно к источнику питания.Сопоставьте его с соответствующим номиналом конденсатора, чтобы получить резонансную частоту.
Следует опасаться недостаточно демпфированного отклика LC-фильтра, так как это может привести к пиковой амплитуде на частоте. Для предотвращения пиков к LC-фильтру добавлен параллельный демпфирующий RC-элемент.
Будет полезно, если вы сможете смоделировать LC-фильтр с помощью ведущего в отрасли программного обеспечения для проектирования и анализа печатных плат. OrCAD PCB Designer предоставляет компоновку, необходимую для создания ваших схем, и хорошо сочетается с PSpice, чтобы обеспечить критическое затухание отклика LC-фильтра и ослабление нужных частот.
Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов. Вы также можете посетить наш канал YouTube и посмотреть видеоролики о моделировании и системном анализе, а также узнать, что нового в нашем наборе инструментов для проектирования и анализа.

Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостейСпасибо!
Как рассчитать вносимые потери фильтра
Вносимые потери фильтра — это мера того, насколько хорошо фильтр электромагнитных помех ослабляет сигнал при прохождении через фильтр.
 Вносимые потери фильтра, обычно выражаемые в децибелах, представляют собой отношение входного сигнала к выходному сигналу. Дополнительную справочную информацию см. в нашей статье «Вносимые потери фильтра электромагнитных помех».
Вносимые потери фильтра, обычно выражаемые в децибелах, представляют собой отношение входного сигнала к выходному сигналу. Дополнительную справочную информацию см. в нашей статье «Вносимые потери фильтра электромагнитных помех».При выполнении анализа электромагнитной совместимости системы EMI Analyst легко учитывает сложное взаимодействие фильтров электромагнитных помех, а также кабели, паразитные эффекты, экраны, резонансы и множество других малозаметных эффектов.
Однако что, если вы просто хотите рассчитать ослабление фильтра электромагнитных помех? EMI Analyst также может это сделать. Вот как.
Схема фильтра
Допустим, мы хотим рассчитать вносимые потери для фильтра электромагнитных помех линии электропередач, который содержит компоненты как дифференциального, так и синфазного режима, например, фильтр, схематически показанный ниже. Его топология типична для многих готовых модулей фильтров.
Фильтр содержит двухполюсную дифференциальную секцию LC и двухполюсную синфазную секцию LC.
 Угловые частоты короткого замыкания для фильтра составляют 50 кГц в дифференциальном режиме и 159 кГц в общем режиме. Однако при измерении в 50-омной системе угловые частоты смещаются из-за нагрузочного эффекта источника и импеданса нагрузки.
Угловые частоты короткого замыкания для фильтра составляют 50 кГц в дифференциальном режиме и 159 кГц в общем режиме. Однако при измерении в 50-омной системе угловые частоты смещаются из-за нагрузочного эффекта источника и импеданса нагрузки.Измерения стандартных фильтров электромагнитных помех
Фильтры электромагнитных помех измеряются путем подключения источника сигнала к входным клеммам фильтра и последующего измерения амплитуды сигнала на выходных клеммах. Вносимые потери в дифференциальном режиме и вносимые потери в синфазном режиме измеряются отдельно.
Поскольку радиочастотное испытательное оборудование обычно имеет входное и выходное сопротивление 50 Ом, считается, что фильтр измеряется в 50-омной системе. При расчете вносимых потерь фильтра с помощью EMI Analyst необходимо смоделировать источник и нагрузку 50 Ом, чтобы данные моделирования были сопоставимы с результатами измерений.
– Дифференциальный режим
Вносимые потери в дифференциальном режиме – это затухание сигнала, подаваемого на входные клеммы фильтра (I+) и (I-), как показано на левой диаграмме выше. Ослабленный сигнал появляется на выходных клеммах (O+) и (O-).
Ослабленный сигнал появляется на выходных клеммах (O+) и (O-).– синфазный сигнал
Вносимые потери синфазного сигнала – это затухание сигнала, подаваемого между землей шасси и замкнутыми входными клеммами (I+) и (I-), как показано на правом изображении выше. Ослабленный сигнал появляется между закороченными выходными клеммами (O+) и (O-) и заземлением корпуса.Вносимые потери EMI Analyst
Вносимые потери фильтра можно рассчитать с помощью двух различных методов в EMI Analyst. Это можно сделать как моделирование кондуктивных выбросов с помощью CE Analyst или как моделирование кондуктивной восприимчивости с помощью CS Analyst.
Здесь мы используем CS Analyst, но оба метода одинаково эффективны. CS Analyst — это программа исследования восприимчивости в рамках EMI Analyst. Он имитирует то, что происходит со схемой, когда сигналы соединяются с проводниками кабеля.
– Метод анализа
Метод анализа заключается в подаче известного напряжения на линии, подключенные к входу фильтра, и последующем вычислении уровня сигнала на выходных клеммах фильтра. Для дифференциального режима (DM) мы подаем 1 вольт последовательно с каждой входной линией, но с противоположной полярностью, как показано на левой диаграмме выше, подавая всего 2 вольта. Для общего режима (CM) мы подаем 2 вольта на обе входные линии одновременно, как показано на правой диаграмме выше.
Для дифференциального режима (DM) мы подаем 1 вольт последовательно с каждой входной линией, но с противоположной полярностью, как показано на левой диаграмме выше, подавая всего 2 вольта. Для общего режима (CM) мы подаем 2 вольта на обе входные линии одновременно, как показано на правой диаграмме выше.На низких частотах, где фильтр обеспечивает слабую фильтрацию, приложенное напряжение делится поровну между импедансом источника 50 Ом и импедансом нагрузки 50 Ом, по 1 вольту на каждом. С увеличением частоты вносимые потери увеличиваются, а напряжение на нагрузке уменьшается. Отношение выходного напряжения к входному напряжению дает нам вносимые потери фильтра. В децибелах (дБ)
Шаги настройки
Шаги для расчета вносимых потерь фильтра с помощью CS Analyst довольно просты.– Дифференциальный режим
1. Диапазон частот: от 1 кГц до 100 МГц
2. Предел CS: 2 В
3. Порог: без порога
4. Левая цепь: 50 Ом линейное , без соединения с шасси
Левая цепь: 50 Ом линейное , без соединения с шасси
5. Проводники: пара проводов над заземляющей пластиной или пара проводов, минимальная длина
6. Правая цепь: содержит схему фильтра и междуфазное сопротивление 50 Ом.Расчетные вносимые потери показывают, что угловая частота DM смещена с 50 кГц до 11 кГц, как и ожидалось.
– общий режим
1. Диапазон частот: от 1 кГц до 100 МГц
2. Предел CS: 2 В
3. Порог: нет порога -линия, 50 Ом между линией и шасси
5. Проводники: пара проводов над плоскостью заземления или пара проводов, минимальная длина
6. Правая цепь: содержит схему фильтра, короткое замыкание между фазами, линия 50 Ом to-chassisРасчетные вносимые потери показывают, что угловая частота CM смещена со 159кГц до 200 кГц, как и ожидалось.
Подведение итогов
Приведенные выше результаты относятся к фильтру с идеальными компонентами. В реальном фильтре есть паразитные элементы, которые являются неизбежным побочным продуктом физических катушек индуктивности и конденсаторов, а также методов упаковки, используемых для монтажа и ограждения фильтра.
 EMI Analyst имеет все возможности для моделирования этих эффектов второго порядка, поэтому, независимо от того, просто ли вы рассчитываете вносимые потери фильтра или моделируете электромагнитную совместимость для кабельной цепи, результаты моделирования отражают реальное поведение цепи во всем диапазоне частот.
EMI Analyst имеет все возможности для моделирования этих эффектов второго порядка, поэтому, независимо от того, просто ли вы рассчитываете вносимые потери фильтра или моделируете электромагнитную совместимость для кабельной цепи, результаты моделирования отражают реальное поведение цепи во всем диапазоне частот.Для получения дополнительной информации посетите веб-сайт EMI Analyst по адресу http://www.emisoftware.com.
Микроволны101 | Фильтры с сосредоточенными элементами
Щелкните здесь, чтобы перейти на главную страницу фильтров
Щелкните здесь, чтобы узнать больше об определении элементов с сосредоточенными параметрами
Щелкните здесь, чтобы перейти на нашу страницу о потерях из-за несоответствия катушки индуктивности
Нажмите здесь, чтобы перейти к обсуждению конденсаторов
Нажмите здесь, чтобы перейти в раздел загрузки и получить калькулятор фильтра с сосредоточенными элементами
Нажмите здесь, чтобы узнать, как работает наш калькулятор фильтра с сосредоточенными параметрами
На этой странице мы обсудим топологии фильтров нижних частот, верхних частот и полосовых фильтров с сосредоточенными элементами.
 Мы также познакомим вас с загрузкой Microwaves101, которая рассчитывает все катушки индуктивности и конденсаторы для трехполюсных, четырехполюсных и пятиполюсных фильтров Чебышева с сосредоточенными элементами, включая фильтры нижних частот, верхних частот и полосовые фильтры. Это то, чего Agilent ADS не может сделать для вас, и Eagleware запросит за вас большие деньги!
Мы также познакомим вас с загрузкой Microwaves101, которая рассчитывает все катушки индуктивности и конденсаторы для трехполюсных, четырехполюсных и пятиполюсных фильтров Чебышева с сосредоточенными элементами, включая фильтры нижних частот, верхних частот и полосовые фильтры. Это то, чего Agilent ADS не может сделать для вас, и Eagleware запросит за вас большие деньги!Отметим также, что в области загрузки вы можете найти «Калькулятор фильтра Влада». отклик фильтров Чебышева в режиме реального времени, в то время как вы меняете требования к полосе пропускания и пульсациям!И теперь у нас есть страница с инструкциями и примерами использования этой электронной таблицы.Все примеры, представленные на обеих страницах, были синтезированы и построены с использованием нашего калькулятора фильтров для скачивания
Вот обычный интерактивный индекс Microwaves101 к нашему материалу о фильтрах с сосредоточенными элементами:
Ограничения по частоте фильтров с сосредоточенными элементами
Тройник против сетей pi
Зависимость между КСВ и пульсацией для фильтра
Фильтры нижних частот с сосредоточенными элементами
Фильтры верхних частот с сосредоточенными элементами
Полосовые фильтры с сосредоточенными элементами
Бесплатно скачать фильтры Чебышева с сосредоточенными элементами (отдельная страница)
Поставщики фильтров с сосредоточенными параметрами
Ограничения по частоте фильтра с сосредоточенными элементами
Прежде чем мы продолжим, приведенный ниже анализ и бесплатная загрузка предназначены для идеальных сосредоточенных элементов.
 По мере увеличения частоты сосредоточенные элементы становятся все менее и менее идеальными, пока вы вообще не сможете сделать фильтр таким образом. Если вы намереваетесь создать микроволновую схему на сосредоточенных элементах, вам придется повторно смоделировать фильтр, включая все паразитные элементы, такие как параллельные резонансы катушек индуктивности и последовательные резонансы конденсаторов, и, конечно же, все резистивные вклады. Если вы строите ВЧ-фильтр на частоте 50 МГц, вы получите хорошие результаты. Использование фильтров поверхностного монтажа с сосредоточенными элементами над L-диапазоном может быть затруднительным.
По мере увеличения частоты сосредоточенные элементы становятся все менее и менее идеальными, пока вы вообще не сможете сделать фильтр таким образом. Если вы намереваетесь создать микроволновую схему на сосредоточенных элементах, вам придется повторно смоделировать фильтр, включая все паразитные элементы, такие как параллельные резонансы катушек индуктивности и последовательные резонансы конденсаторов, и, конечно же, все резистивные вклады. Если вы строите ВЧ-фильтр на частоте 50 МГц, вы получите хорошие результаты. Использование фильтров поверхностного монтажа с сосредоточенными элементами над L-диапазоном может быть затруднительным.Когда мы обсуждаем элементы с сосредоточенными параметрами, это две широкие категории катушек индуктивности и конденсаторов. Первый — это детали для поверхностного монтажа, которые подходят для использования на печатной плате микроволновой печи. Вторая категория — это тонкопленочные элементы с сосредоточенными параметрами, которые используются в микроволновых интегральных схемах (МИС) на оксиде алюминия или других «твердых» подложках, а также в реализациях МИС.
 Конденсаторы для поверхностного монтажа могут использоваться вплоть до диапазона Ku, в то время как катушки индуктивности обычно имеют собственные резонансы ниже диапазона X. Тонкопленочные конденсаторы обычно используются в MMIC до 100 ГГц. Сосредоточенные индукторы на тонких пленках (и MMIC) имеют форму спиральных индукторов и ограничены частотами Ku-диапазона и ниже. Катушки индуктивности — это проблемный пасынок фильтров с сосредоточенными элементами и других микроволновых схем!!
Конденсаторы для поверхностного монтажа могут использоваться вплоть до диапазона Ku, в то время как катушки индуктивности обычно имеют собственные резонансы ниже диапазона X. Тонкопленочные конденсаторы обычно используются в MMIC до 100 ГГц. Сосредоточенные индукторы на тонких пленках (и MMIC) имеют форму спиральных индукторов и ограничены частотами Ku-диапазона и ниже. Катушки индуктивности — это проблемный пасынок фильтров с сосредоточенными элементами и других микроволновых схем!!Вы можете получить полосу пропускания 10%, 100% или более с фильтрами с сосредоточенными элементами. Привлекательность фильтров с сосредоточенными элементами заключается в том, что фильтр часто может быть очень компактным по сравнению с фильтром на основе полуволновых резонансных структур.
Тройник в сравнении с пи-сетями
Термины «тройник» и «пи» используются для описания фильтров с сосредоточенными элементами, а также аттенюаторов и других цепей. Тройниковый элемент начинается с последовательного элемента, а пи-сеть начинается с шунтирующего элемента, как показано ниже.
 «Тройник» напоминает букву «Т», а «пи» — греческую букву «пи». Рисунки ниже относятся к трехполюсным сетям. Нечетные числа полюсов по-прежнему несколько напоминают буквы тройника и пи, но для четных чисел различие почти теряется, поскольку тройниковая сеть начинается с последовательного элемента и заканчивается шунтирующим элементом. Мы рекомендуем использовать нечетное число полюсов в фильтрах с сосредоточенными элементами, поскольку элементы симметричны, то есть для пятиполюсной сети C1=C5, C2=C4, L1=L5 и L2=L4. Это сократит ваш список материалов и уменьшит вероятность ошибок при сборке.
«Тройник» напоминает букву «Т», а «пи» — греческую букву «пи». Рисунки ниже относятся к трехполюсным сетям. Нечетные числа полюсов по-прежнему несколько напоминают буквы тройника и пи, но для четных чисел различие почти теряется, поскольку тройниковая сеть начинается с последовательного элемента и заканчивается шунтирующим элементом. Мы рекомендуем использовать нечетное число полюсов в фильтрах с сосредоточенными элементами, поскольку элементы симметричны, то есть для пятиполюсной сети C1=C5, C2=C4, L1=L5 и L2=L4. Это сократит ваш список материалов и уменьшит вероятность ошибок при сборке.Сетевой фильтр верхних частот Tee
Сетевой фильтр нижних частот Pi
Ниже приведены изображения фильтров N=3, N=4 и N=5, фильтров pi и tee, BPF, LPF и HPF . Некоторые вещи, которые следует учитывать при выборе пи или тройника, которые станут очевидными, когда вы посмотрите на цифры.
- Все LPF будут передавать постоянный ток от входа к выходу
- Все HPF блокируют постоянный ток от входа к выходу.

- В некоторых случаях фильтры вызывают короткое замыкание на землю на одном или обоих входах. В других случаях фильтр будет выглядеть как разомкнутая цепь постоянного тока. При N=четном два конца фильтра различны.
Важно понимать свойства постоянного тока фильтра. Довольно часто в микроволновых конструкциях линии передачи используются для подачи постоянных напряжений и токов смещения на активные устройства.
Взаимосвязь между КСВ и пульсациями для фильтра
Тема несоответствия коэффициента потерь на отдельной странице, здесь мы обсудим ее в контексте конструкции фильтра.
При использовании идеальных элементов без потерь существует определенная зависимость между пульсациями в полосе пропускания и обратными потерями фильтра. Это связано с тем, что неравномерность полосы пропускания составляет 100 % из-за потери несоответствия. Пульсации равны вносимым потерям в наихудшем случае, которые возникают на той же частоте, что и КСВН в наихудшем случае (наихудшие потери из-за рассогласования).

Потери из-за рассогласования рассчитываются по коэффициенту отражения rho:
потеря несоответствия = (1-ро 2 ) (% отраженной мощности)
потери от несоответствия (дБ) = 10*log(1-rho 2 )
Обратите внимание, что в данном случае мы используем 10*log, потому что количество (1-rho 2 ) выражено в единицах мощности, а не напряжения (для чего использовалось бы 20*log). Несоответствие фильтра часто указывается как максимальный КСВ. Ро рассчитывается из КСВ как:
ро=(КСВН-1)/(КСВН+1)
Тогда соотношение между КСВ и потерями из-за несоответствия будет следующим:
Пульсации (дБ) = потери из-за рассогласования (дБ) = 10*log[1-((КСВН-1)/(КСВН+1)) 2 ]
Сделаем столик:
КСВ
ро
Обратные потери (дБ)
Пульсации (дБ)
2
0,333
9,542
0,512
1,9
0,310
10.
 163
1630,440
1,8
0,286
10.881
0,370
1,7
0,259
11.725
0,302
1,6
0,231
12.736
0,238
1,5
0,200
13,979
0,177
1,4
0,167
15.563
0,122
1,3
0,130
17.692
0,075
1,2
0,091
20.828
0,036
1.1
0,048
26.444
0,010
Обратите внимание, что у нас есть калькулятор КСВ, который позволит вам конвертировать КСВ, потери несоответствия и обратные потери!Фильтры нижних частот с сосредоточенными элементами
Фильтр нижних частот часто является естественным выбором для фильтров с сосредоточенными элементами.
 Это связано с тем, что паразитные элементы с сосредоточенными параметрами, как правило, убивают частотную характеристику по мере повышения частоты. Например, вы можете захотеть добавить фильтр LPF с сосредоточенными элементами на выходе вашего понижающего преобразователя. Если вы микшируете X-диапазон до 50 МГц, на выходе не будет утечки ВЧ и гетеродина, и вы будете стильно выглядеть! Фильтры нижних частот с сосредоточенными элементами довольно часто используются в качестве ступеней «очистки» для фильтров с плоским резонатором для подавления реентерабельных мод.
Это связано с тем, что паразитные элементы с сосредоточенными параметрами, как правило, убивают частотную характеристику по мере повышения частоты. Например, вы можете захотеть добавить фильтр LPF с сосредоточенными элементами на выходе вашего понижающего преобразователя. Если вы микшируете X-диапазон до 50 МГц, на выходе не будет утечки ВЧ и гетеродина, и вы будете стильно выглядеть! Фильтры нижних частот с сосредоточенными элементами довольно часто используются в качестве ступеней «очистки» для фильтров с плоским резонатором для подавления реентерабельных мод.На приведенном ниже рисунке мы сравниваем низкочастотные фильтры для пульсаций 0,5 дБ и частоты среза 5 ГГц. Обратите внимание, что обратные потери напрямую связаны с вносимыми потерями S21. При пульсациях 0,5 дБ обратные потери составляют около 10 дБ. Следует также отметить, что юбка на фильтре N=5 спадает намного быстрее, чем на фильтре N=3. В этом примере, если критической частотой, которую вам нужно заблокировать, является 8 ГГц, вы можете не получить достаточного подавления с N=3 (около 12 дБ), но с N=5 вы можете удовлетворить свои требования, потому что у вас будет подавление на 30 дБ.

Фильтры верхних частот с сосредоточенными элементами
Фильтры верхних частот сложны. Из-за паразитных характеристик ваш фильтр верхних частот фактически будет больше похож на полосовой фильтр, его частотная характеристика в конечном итоге затухнет. Но вы, безусловно, можете разработать фильтр, который подавляет низкие частоты, используя элементы с сосредоточенными параметрами. Блок постоянного тока является простым примером. Мы добавим несколько примеров, зайдите позже!
Полосовые фильтры с сосредоточенными элементами
Сосредоточенные элементы, используемые в полосовых фильтрах, могут реально помочь вашим проектам. Полученные в результате фильтры не только компактны, но и не имеют «естественных» реентерабельных мод, с которыми вы столкнетесь при использовании других технологий фильтрации, таких как плоские резонаторные структуры.
В каждом резонаторе полосового фильтра с сосредоточенными элементами вы найдете как катушку индуктивности, так и конденсатор.



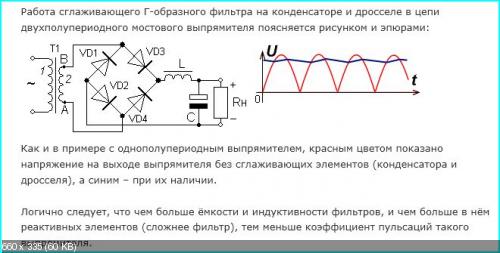 5 Порядок выбора параметров элементов синусного фильтра
5 Порядок выбора параметров элементов синусного фильтра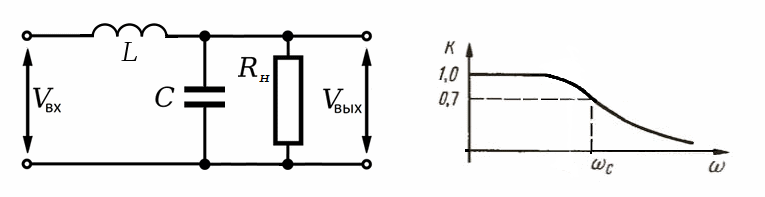 Д., Матвеев К. Ф., Захаров А. А. Универсальный макет одно/трёхфазного инвертора для проведения лабораторных работ по курсу преобразовательная техника. Материалы Всероссийской научно-методической конференции «Совершенствование систем управления качеством подготовки специалистов». 20-21 марта 2003 года, Красноярск, Россия. В двух частях. Часть вторая, стр. 23-24.
Д., Матвеев К. Ф., Захаров А. А. Универсальный макет одно/трёхфазного инвертора для проведения лабораторных работ по курсу преобразовательная техника. Материалы Всероссийской научно-методической конференции «Совершенствование систем управления качеством подготовки специалистов». 20-21 марта 2003 года, Красноярск, Россия. В двух частях. Часть вторая, стр. 23-24.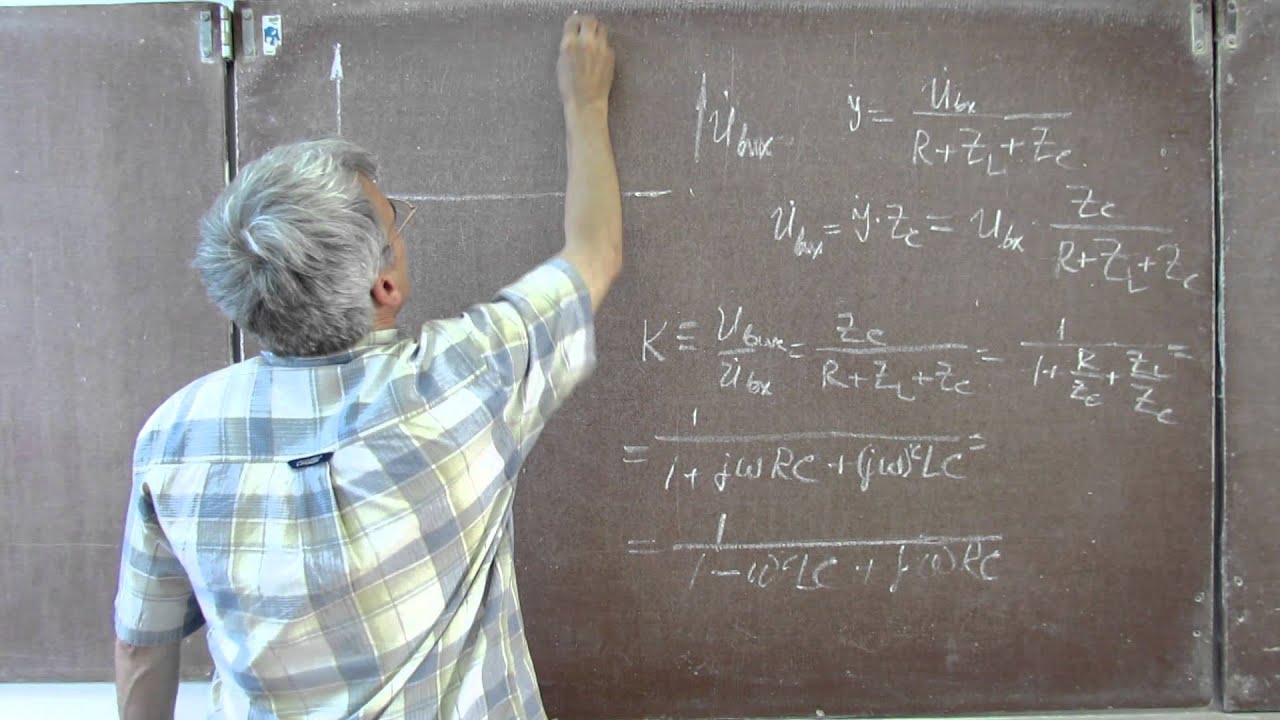
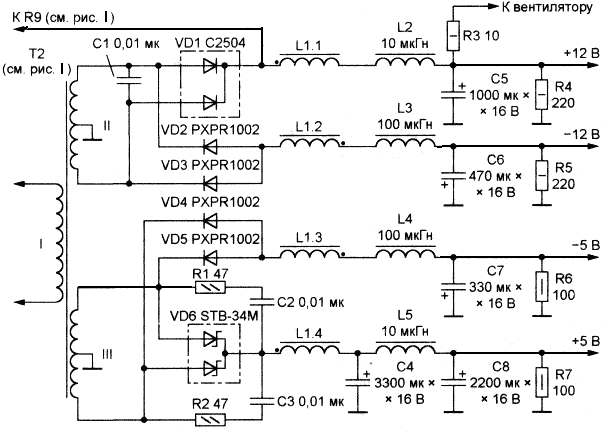 Можно построить с одинаковой схемой разные фильтры. Тип фильтра зависит от того, является ли он последовательным или параллельным соединением и в какой точке снимается выходное напряжение. Часто используемые схемы LC-фильтров представляют собой фильтры верхних частот, нижних частот, полосовые и режекторные фильтры.
Можно построить с одинаковой схемой разные фильтры. Тип фильтра зависит от того, является ли он последовательным или параллельным соединением и в какой точке снимается выходное напряжение. Часто используемые схемы LC-фильтров представляют собой фильтры верхних частот, нижних частот, полосовые и режекторные фильтры. Для этого выходное напряжение на индуктивности снимается с последовательной цепи индуктивности и емкости. Когда частота входного напряжения низкая, напряжение на конденсаторе падает, а выходное напряжение остается очень низким. Напротив, по мере увеличения частоты все больше и больше напряжения на индуктивности падает и может использоваться в качестве выходного напряжения. Высокочастотный фильтр LC также имеет 2-й порядок и может быть определен с помощью Калькулятор верхних частот LC .
Для этого выходное напряжение на индуктивности снимается с последовательной цепи индуктивности и емкости. Когда частота входного напряжения низкая, напряжение на конденсаторе падает, а выходное напряжение остается очень низким. Напротив, по мере увеличения частоты все больше и больше напряжения на индуктивности падает и может использоваться в качестве выходного напряжения. Высокочастотный фильтр LC также имеет 2-й порядок и может быть определен с помощью Калькулятор верхних частот LC .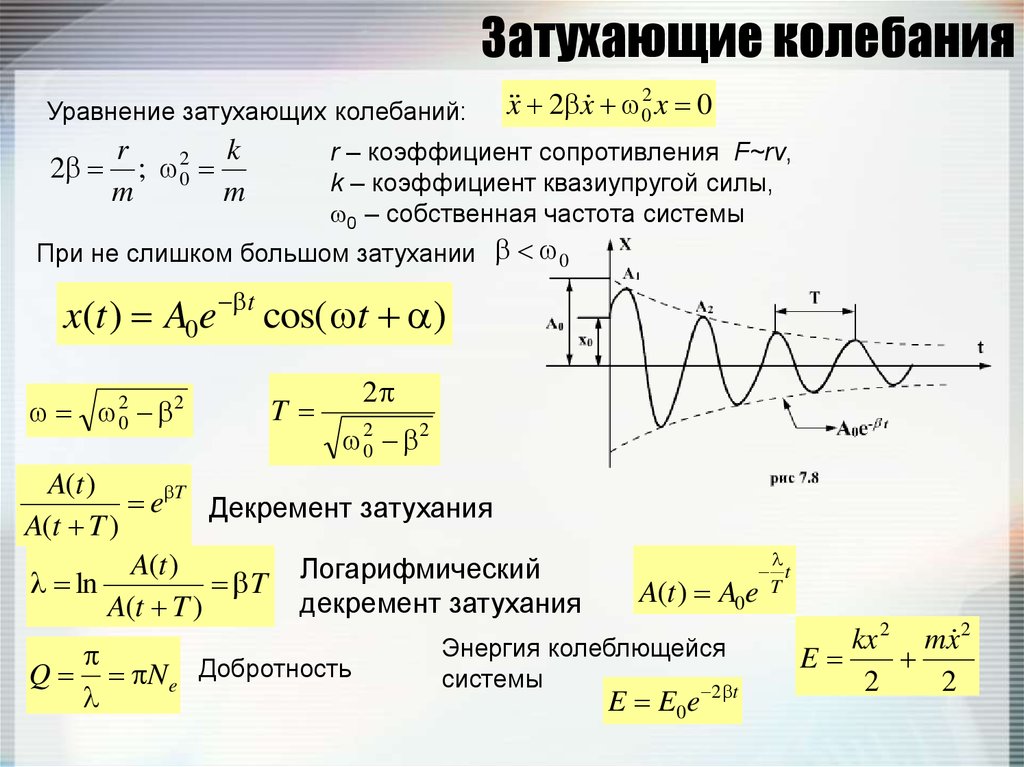
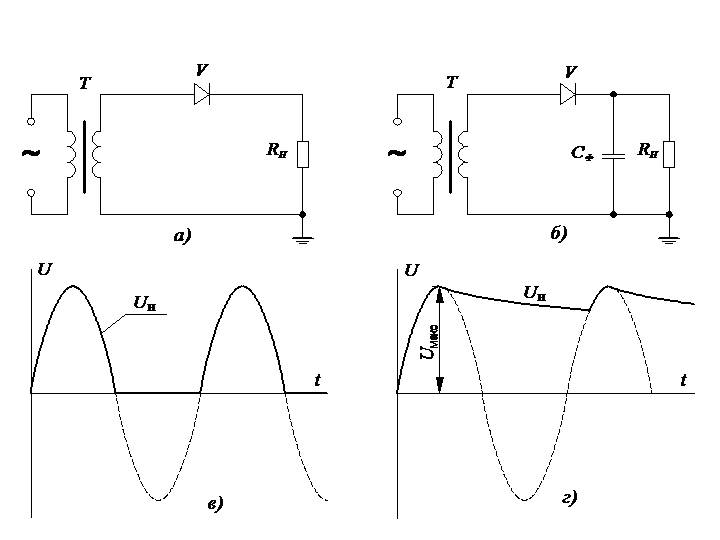 Их можно отфильтровать с помощью LC-фильтрующего элемента правильного размера перед подачей на антенну. При большой мощности передачи такие фильтры обязательны.
Их можно отфильтровать с помощью LC-фильтрующего элемента правильного размера перед подачей на антенну. При большой мощности передачи такие фильтры обязательны.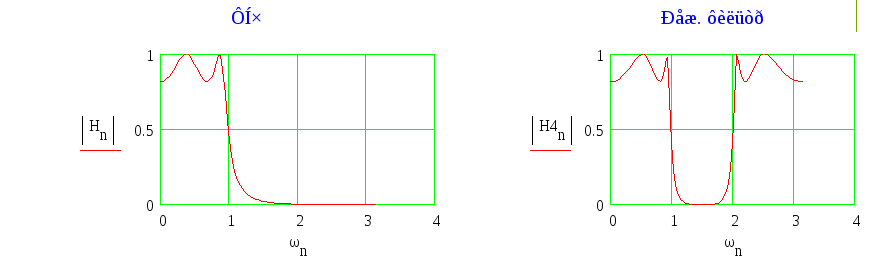 com
com
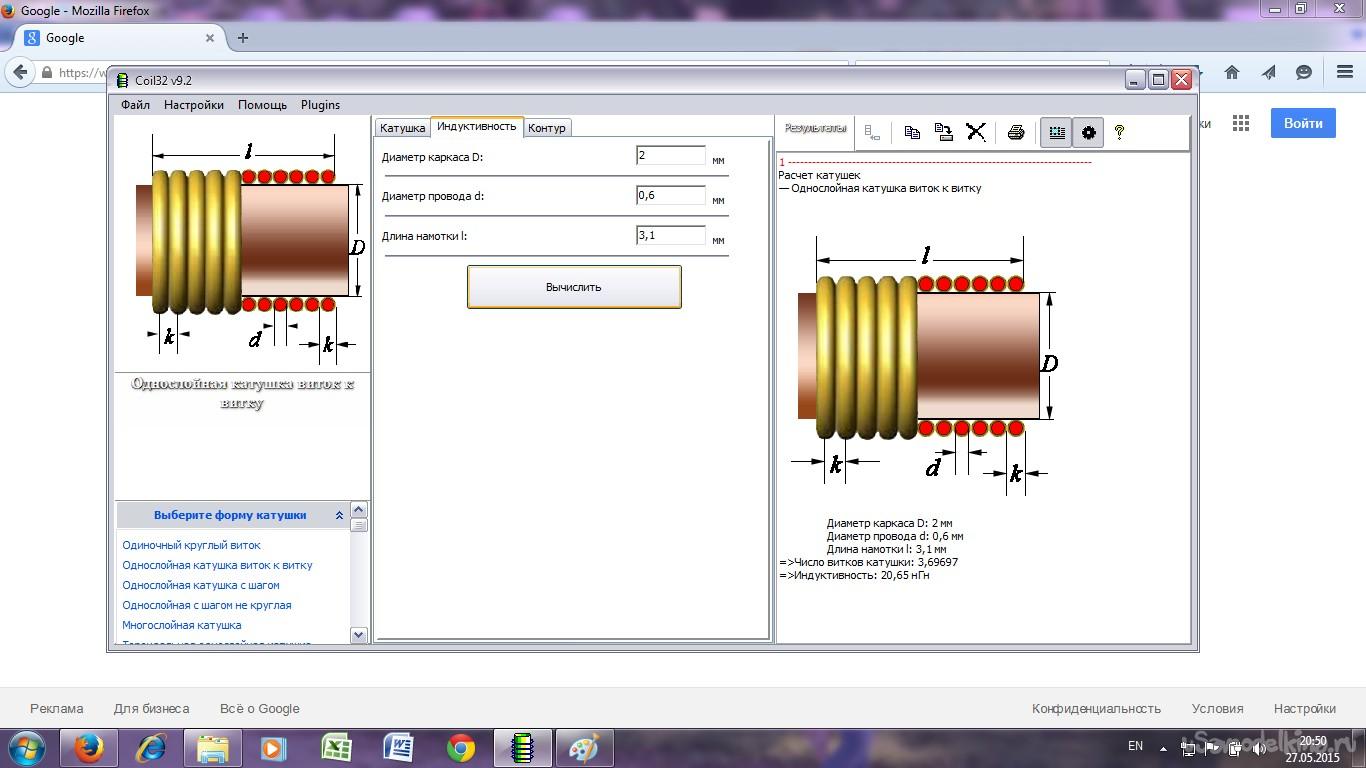 Я не могу рассказать вам больше, так как начинаю изучать LC-схему.
Я не могу рассказать вам больше, так как начинаю изучать LC-схему. Чтобы уменьшить третью гармонику до 3 % от основной гармоники (при КНИ около 5 %, что является такой уродливой формой волны, которую могут выдержать большинство чувствительных схем), вам нужен фильтр, который уменьшает третью гармонику в 5 раз ( 3%/15%). Двухполюсный фильтр, такой как LC, уменьшает амплитуду в 4 раза для каждой октавы, поэтому ваш фильтр должен иметь угловую частоту чуть меньше 1,5*основной частоты.
Чтобы уменьшить третью гармонику до 3 % от основной гармоники (при КНИ около 5 %, что является такой уродливой формой волны, которую могут выдержать большинство чувствительных схем), вам нужен фильтр, который уменьшает третью гармонику в 5 раз ( 3%/15%). Двухполюсный фильтр, такой как LC, уменьшает амплитуду в 4 раза для каждой октавы, поэтому ваш фильтр должен иметь угловую частоту чуть меньше 1,5*основной частоты. Я ответил на вопрос — «Какую частоту выбрать в качестве резонансной для фильтра?» Если бы возник вопрос: «Мне нужно построить LC-фильтр с резонансной частотой, например, 80 Гц. Как подобрать L и C?»
Я ответил на вопрос — «Какую частоту выбрать в качестве резонансной для фильтра?» Если бы возник вопрос: «Мне нужно построить LC-фильтр с резонансной частотой, например, 80 Гц. Как подобрать L и C?» 

 и несущая частота и максимальная номинальная мощность и формат нагрузки. Вы можете рассказать мне больше о них? тогда я проведу вас.
и несущая частота и максимальная номинальная мощность и формат нагрузки. Вы можете рассказать мне больше о них? тогда я проведу вас. 
 Обычно мы помещаем серию R в LC-фильтр, чтобы уменьшить добротность (до 1,5–3) и уменьшить ток короткого замыкания. На самом деле мы включили его последовательно с C, чтобы он не был последовательно с нагрузкой. Иногда в литературе вы встретите что-то под названием «демпфер» — вот что они имеют в виду. Дополнительный R добавляет нагрузку переменного тока к выходу источника питания, что повышает стабильность и не сильно снижает эффективность.
Обычно мы помещаем серию R в LC-фильтр, чтобы уменьшить добротность (до 1,5–3) и уменьшить ток короткого замыкания. На самом деле мы включили его последовательно с C, чтобы он не был последовательно с нагрузкой. Иногда в литературе вы встретите что-то под названием «демпфер» — вот что они имеют в виду. Дополнительный R добавляет нагрузку переменного тока к выходу источника питания, что повышает стабильность и не сильно снижает эффективность. Конечно, мне кажется, что это двухполюсный фильтр нижних частот.
Конечно, мне кажется, что это двухполюсный фильтр нижних частот. Однако последовательное сопротивление 0,2 Ом для катушки индуктивности 112 мкГн чертовски велико, поэтому вместо этого установите последовательное сопротивление R, равное 0,005 Ом. Затем добавьте от 0,2 до 0,3 Ом последовательно с C. Вы получите примерно такой же результат.
Однако последовательное сопротивление 0,2 Ом для катушки индуктивности 112 мкГн чертовски велико, поэтому вместо этого установите последовательное сопротивление R, равное 0,005 Ом. Затем добавьте от 0,2 до 0,3 Ом последовательно с C. Вы получите примерно такой же результат. д.),
д.), 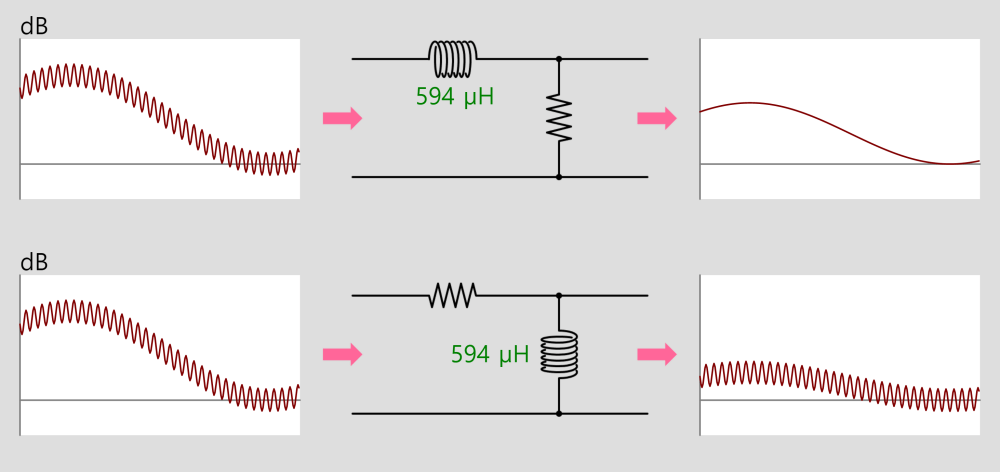 ..
.. На сайте представлены статьи, учебные пособия, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тесты и измерения,
калькуляторы, новости, книги, загрузки и многое другое.
На сайте представлены статьи, учебные пособия, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тесты и измерения,
калькуляторы, новости, книги, загрузки и многое другое. • Система измерения удара при столкновении
• Система отслеживания скоропортящихся продуктов и овощей
• Система помощи водителю
• Система умной розничной торговли
• Система мониторинга качества воды
• Система интеллектуальной сети
• Умная система освещения на основе Zigbee
• Умная система парковки на базе Zigbee
• Умная система парковки на базе LoRaWAN.
• Система измерения удара при столкновении
• Система отслеживания скоропортящихся продуктов и овощей
• Система помощи водителю
• Система умной розничной торговли
• Система мониторинга качества воды
• Система интеллектуальной сети
• Умная система освещения на основе Zigbee
• Умная система парковки на базе Zigbee
• Умная система парковки на базе LoRaWAN.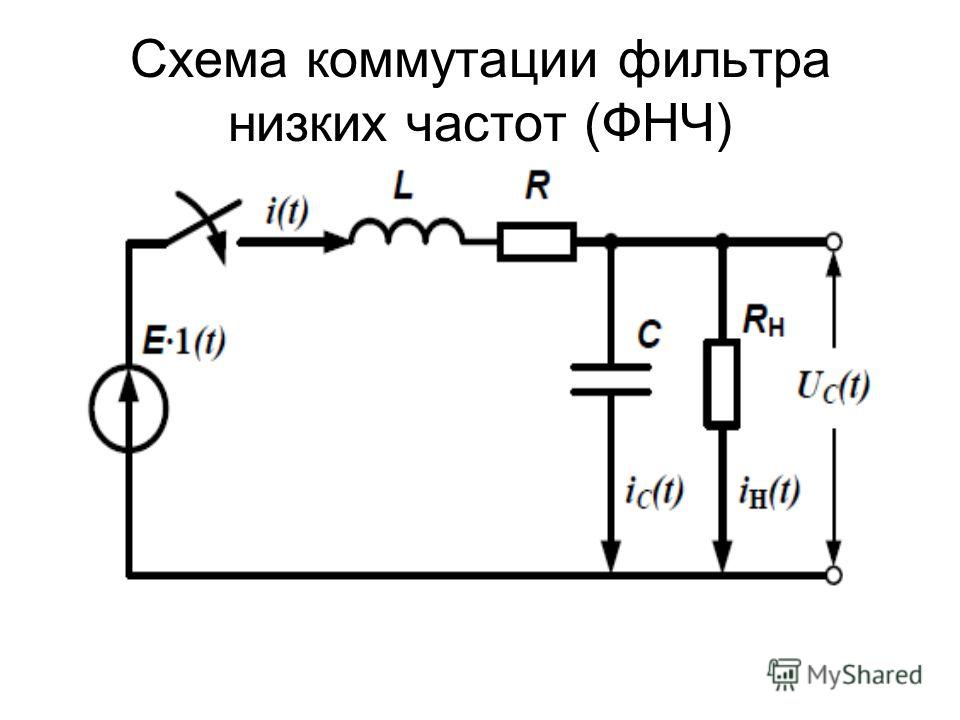 Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP.
Подробнее➤
Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP.
Подробнее➤ д.
5G NR Краткий справочный указатель >>
д.
5G NR Краткий справочный указатель >> 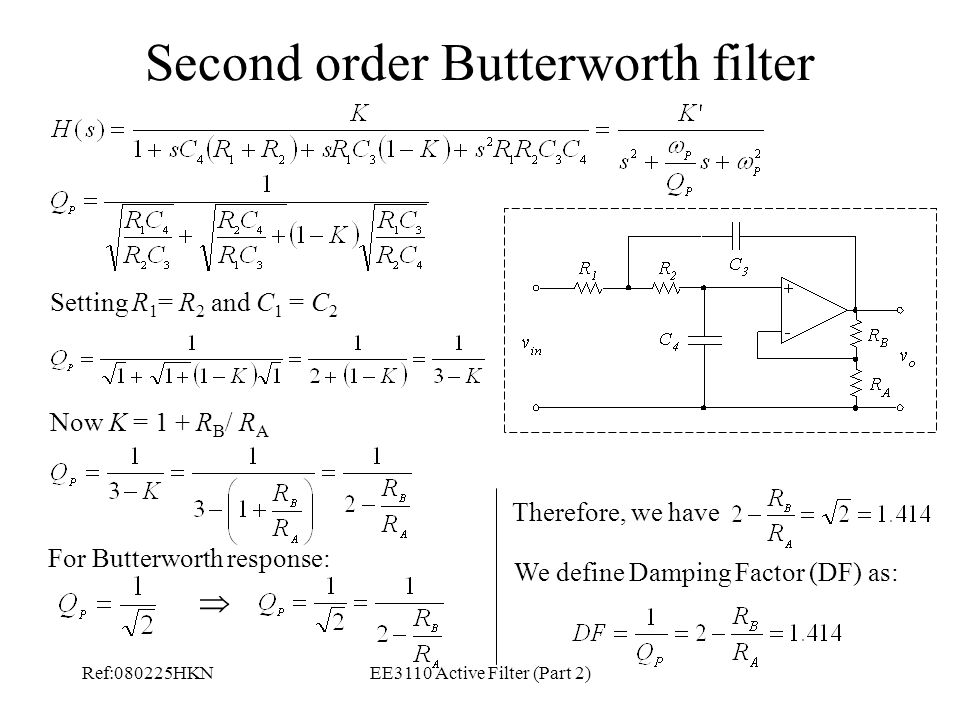
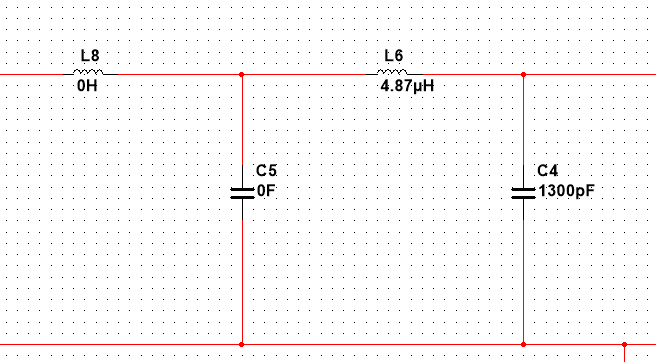 ИНДЕКС испытаний и измерений >>
ИНДЕКС испытаний и измерений >> 

 Он также охватывает датчики IoT, компоненты IoT и компании IoT.
Он также охватывает датчики IoT, компоненты IoT и компании IoT. 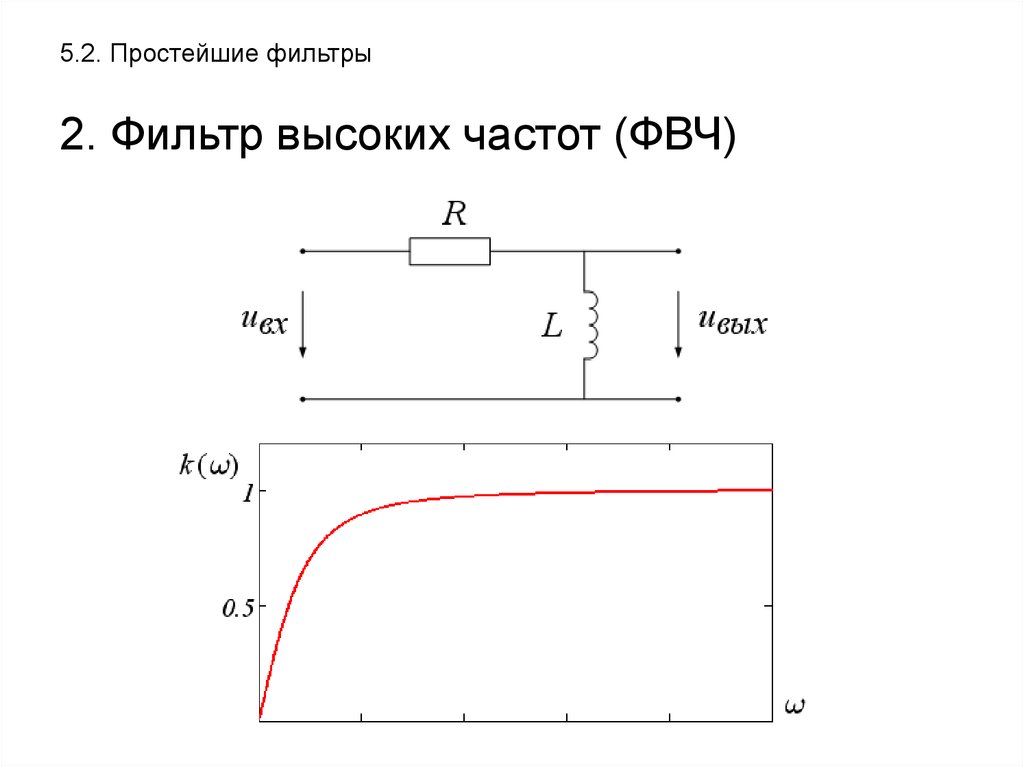 ЗАМЕТКИ
Всемирный веб-сайт T&M
ЗАМЕТКИ
Всемирный веб-сайт T&M  Этот опыт также подчеркивает аналогичный и часто упускаемый из виду аспект при проектировании источника питания. Возможно, фильтр для воды не используется, но вам нужно будет установить LC-фильтр для источника питания.
Этот опыт также подчеркивает аналогичный и часто упускаемый из виду аспект при проектировании источника питания. Возможно, фильтр для воды не используется, но вам нужно будет установить LC-фильтр для источника питания.
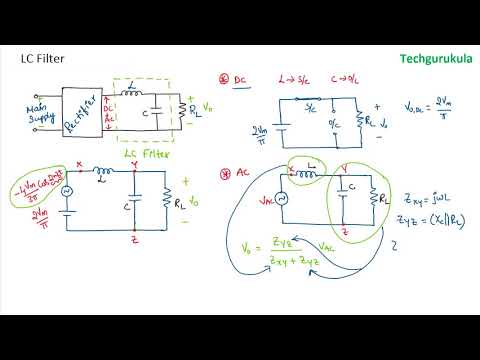 Точность этих модулей может быть нарушена, а в некоторых случаях компоненты могут работать неправильно.
Точность этих модулей может быть нарушена, а в некоторых случаях компоненты могут работать неправильно.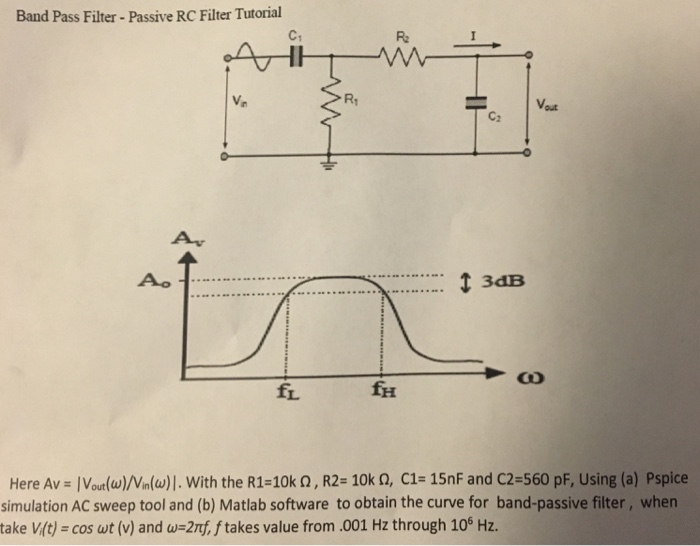 Хотя в этом размещении нет ничего плохого, вы можете добиться лучшего подавления шума, поместив LC-фильтр на вход, если вы используете понижающий регулятор.
Хотя в этом размещении нет ничего плохого, вы можете добиться лучшего подавления шума, поместив LC-фильтр на вход, если вы используете понижающий регулятор.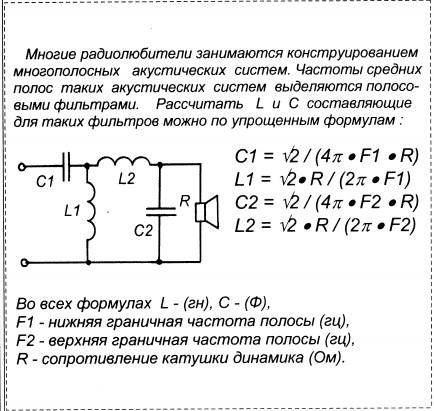 Для начала вам нужно выбрать индуктор со значительно более высоким значением, чем индуктивность, подключенная последовательно к источнику питания.
Для начала вам нужно выбрать индуктор со значительно более высоким значением, чем индуктивность, подключенная последовательно к источнику питания.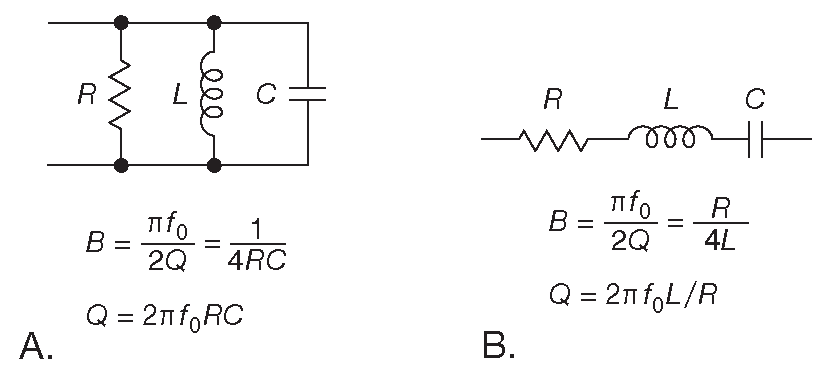
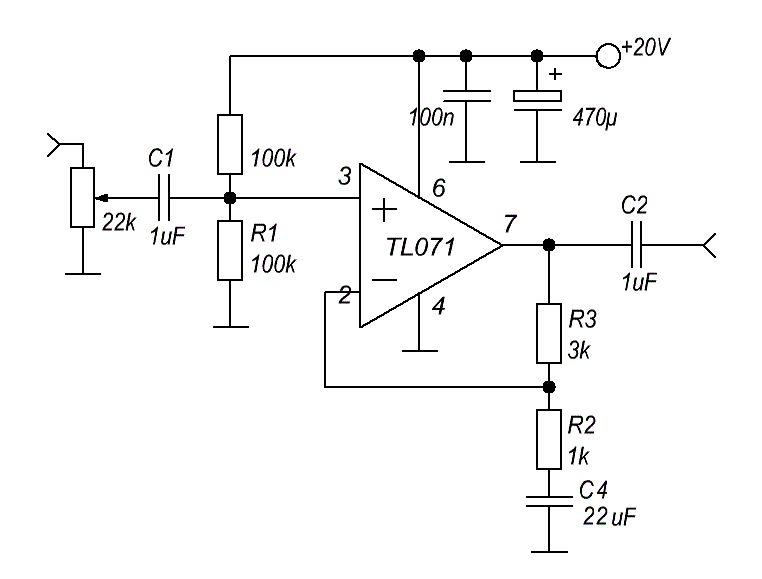 Вносимые потери фильтра, обычно выражаемые в децибелах, представляют собой отношение входного сигнала к выходному сигналу. Дополнительную справочную информацию см. в нашей статье «Вносимые потери фильтра электромагнитных помех».
Вносимые потери фильтра, обычно выражаемые в децибелах, представляют собой отношение входного сигнала к выходному сигналу. Дополнительную справочную информацию см. в нашей статье «Вносимые потери фильтра электромагнитных помех».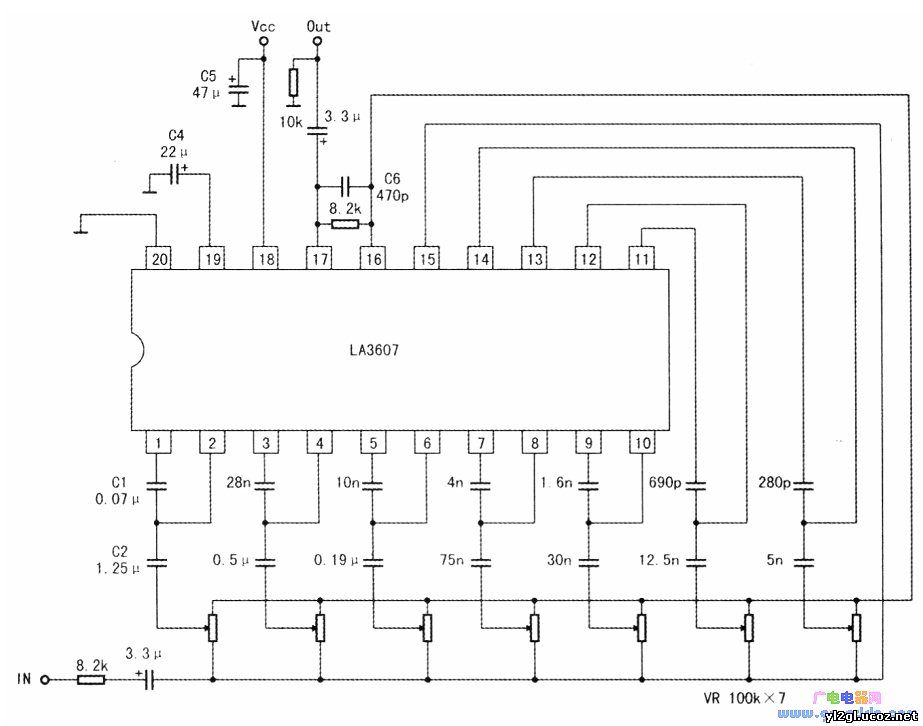 Угловые частоты короткого замыкания для фильтра составляют 50 кГц в дифференциальном режиме и 159 кГц в общем режиме. Однако при измерении в 50-омной системе угловые частоты смещаются из-за нагрузочного эффекта источника и импеданса нагрузки.
Угловые частоты короткого замыкания для фильтра составляют 50 кГц в дифференциальном режиме и 159 кГц в общем режиме. Однако при измерении в 50-омной системе угловые частоты смещаются из-за нагрузочного эффекта источника и импеданса нагрузки. Ослабленный сигнал появляется на выходных клеммах (O+) и (O-).
Ослабленный сигнал появляется на выходных клеммах (O+) и (O-).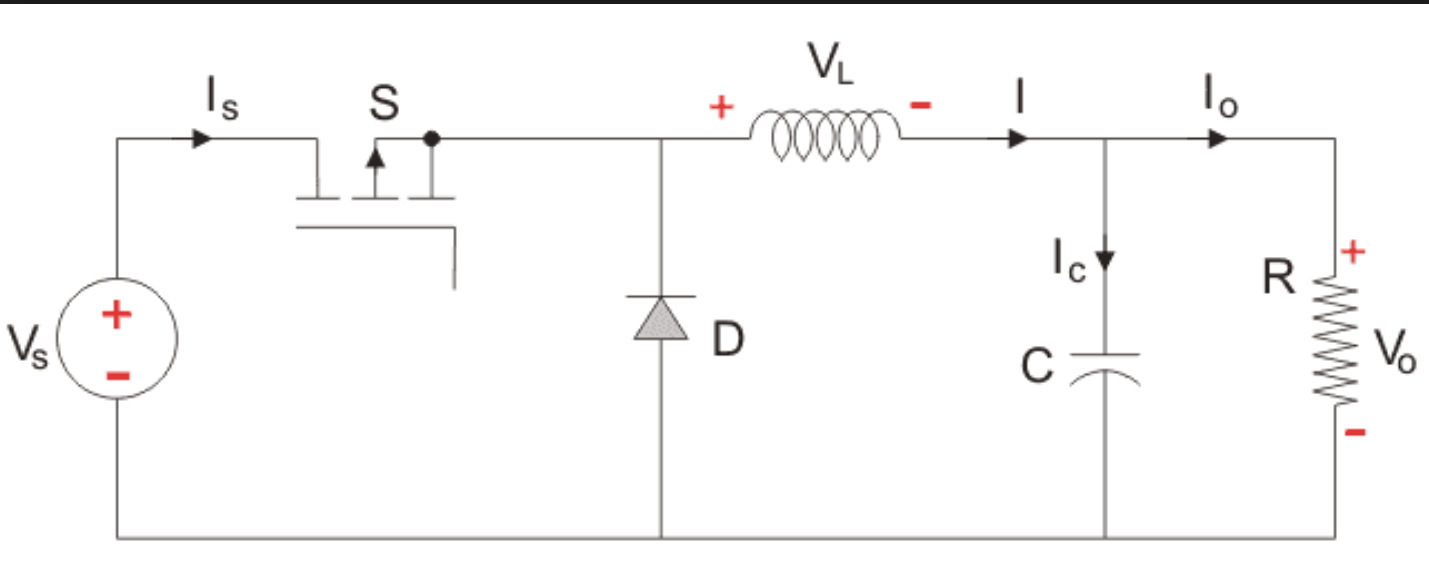 Для дифференциального режима (DM) мы подаем 1 вольт последовательно с каждой входной линией, но с противоположной полярностью, как показано на левой диаграмме выше, подавая всего 2 вольта. Для общего режима (CM) мы подаем 2 вольта на обе входные линии одновременно, как показано на правой диаграмме выше.
Для дифференциального режима (DM) мы подаем 1 вольт последовательно с каждой входной линией, но с противоположной полярностью, как показано на левой диаграмме выше, подавая всего 2 вольта. Для общего режима (CM) мы подаем 2 вольта на обе входные линии одновременно, как показано на правой диаграмме выше. Левая цепь: 50 Ом линейное , без соединения с шасси
Левая цепь: 50 Ом линейное , без соединения с шасси  EMI Analyst имеет все возможности для моделирования этих эффектов второго порядка, поэтому, независимо от того, просто ли вы рассчитываете вносимые потери фильтра или моделируете электромагнитную совместимость для кабельной цепи, результаты моделирования отражают реальное поведение цепи во всем диапазоне частот.
EMI Analyst имеет все возможности для моделирования этих эффектов второго порядка, поэтому, независимо от того, просто ли вы рассчитываете вносимые потери фильтра или моделируете электромагнитную совместимость для кабельной цепи, результаты моделирования отражают реальное поведение цепи во всем диапазоне частот. Мы также познакомим вас с загрузкой Microwaves101, которая рассчитывает все катушки индуктивности и конденсаторы для трехполюсных, четырехполюсных и пятиполюсных фильтров Чебышева с сосредоточенными элементами, включая фильтры нижних частот, верхних частот и полосовые фильтры. Это то, чего Agilent ADS не может сделать для вас, и Eagleware запросит за вас большие деньги!
Мы также познакомим вас с загрузкой Microwaves101, которая рассчитывает все катушки индуктивности и конденсаторы для трехполюсных, четырехполюсных и пятиполюсных фильтров Чебышева с сосредоточенными элементами, включая фильтры нижних частот, верхних частот и полосовые фильтры. Это то, чего Agilent ADS не может сделать для вас, и Eagleware запросит за вас большие деньги! По мере увеличения частоты сосредоточенные элементы становятся все менее и менее идеальными, пока вы вообще не сможете сделать фильтр таким образом. Если вы намереваетесь создать микроволновую схему на сосредоточенных элементах, вам придется повторно смоделировать фильтр, включая все паразитные элементы, такие как параллельные резонансы катушек индуктивности и последовательные резонансы конденсаторов, и, конечно же, все резистивные вклады. Если вы строите ВЧ-фильтр на частоте 50 МГц, вы получите хорошие результаты. Использование фильтров поверхностного монтажа с сосредоточенными элементами над L-диапазоном может быть затруднительным.
По мере увеличения частоты сосредоточенные элементы становятся все менее и менее идеальными, пока вы вообще не сможете сделать фильтр таким образом. Если вы намереваетесь создать микроволновую схему на сосредоточенных элементах, вам придется повторно смоделировать фильтр, включая все паразитные элементы, такие как параллельные резонансы катушек индуктивности и последовательные резонансы конденсаторов, и, конечно же, все резистивные вклады. Если вы строите ВЧ-фильтр на частоте 50 МГц, вы получите хорошие результаты. Использование фильтров поверхностного монтажа с сосредоточенными элементами над L-диапазоном может быть затруднительным. Конденсаторы для поверхностного монтажа могут использоваться вплоть до диапазона Ku, в то время как катушки индуктивности обычно имеют собственные резонансы ниже диапазона X. Тонкопленочные конденсаторы обычно используются в MMIC до 100 ГГц. Сосредоточенные индукторы на тонких пленках (и MMIC) имеют форму спиральных индукторов и ограничены частотами Ku-диапазона и ниже. Катушки индуктивности — это проблемный пасынок фильтров с сосредоточенными элементами и других микроволновых схем!!
Конденсаторы для поверхностного монтажа могут использоваться вплоть до диапазона Ku, в то время как катушки индуктивности обычно имеют собственные резонансы ниже диапазона X. Тонкопленочные конденсаторы обычно используются в MMIC до 100 ГГц. Сосредоточенные индукторы на тонких пленках (и MMIC) имеют форму спиральных индукторов и ограничены частотами Ku-диапазона и ниже. Катушки индуктивности — это проблемный пасынок фильтров с сосредоточенными элементами и других микроволновых схем!!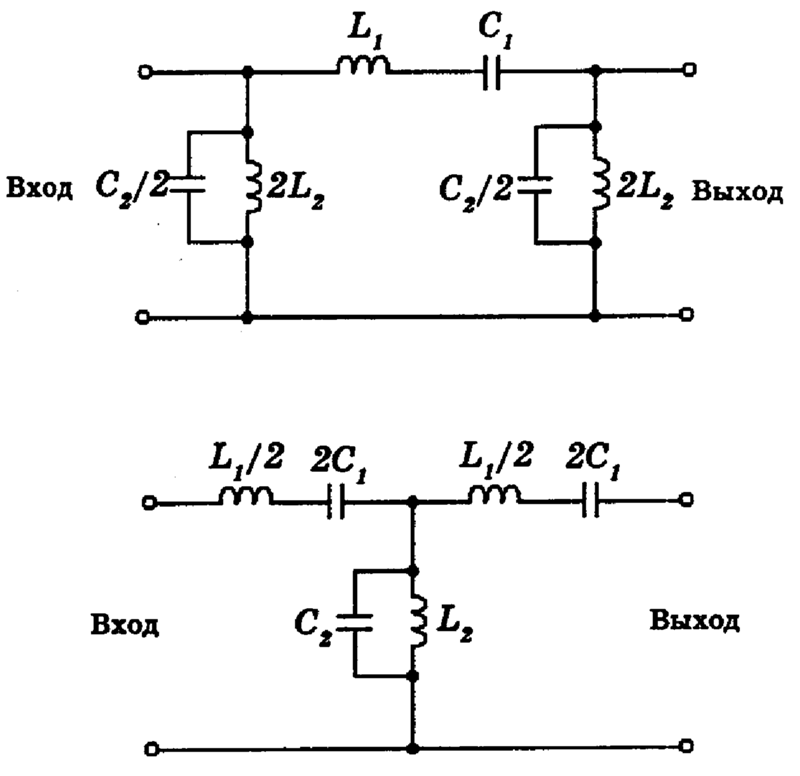 «Тройник» напоминает букву «Т», а «пи» — греческую букву «пи». Рисунки ниже относятся к трехполюсным сетям. Нечетные числа полюсов по-прежнему несколько напоминают буквы тройника и пи, но для четных чисел различие почти теряется, поскольку тройниковая сеть начинается с последовательного элемента и заканчивается шунтирующим элементом. Мы рекомендуем использовать нечетное число полюсов в фильтрах с сосредоточенными элементами, поскольку элементы симметричны, то есть для пятиполюсной сети C1=C5, C2=C4, L1=L5 и L2=L4. Это сократит ваш список материалов и уменьшит вероятность ошибок при сборке.
«Тройник» напоминает букву «Т», а «пи» — греческую букву «пи». Рисунки ниже относятся к трехполюсным сетям. Нечетные числа полюсов по-прежнему несколько напоминают буквы тройника и пи, но для четных чисел различие почти теряется, поскольку тройниковая сеть начинается с последовательного элемента и заканчивается шунтирующим элементом. Мы рекомендуем использовать нечетное число полюсов в фильтрах с сосредоточенными элементами, поскольку элементы симметричны, то есть для пятиполюсной сети C1=C5, C2=C4, L1=L5 и L2=L4. Это сократит ваш список материалов и уменьшит вероятность ошибок при сборке.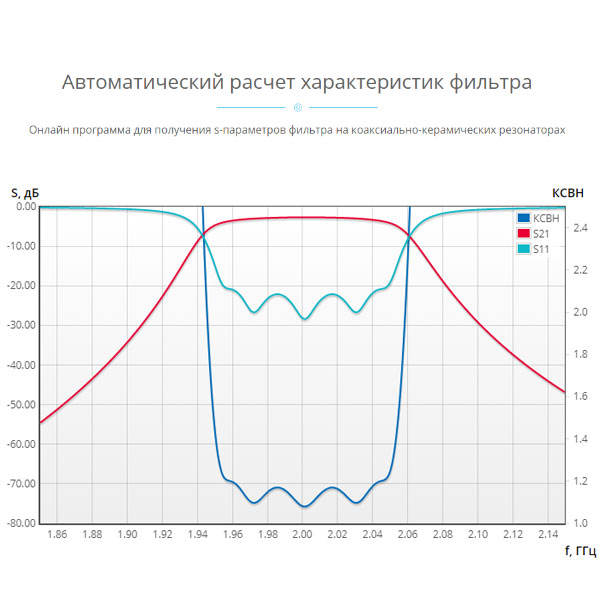
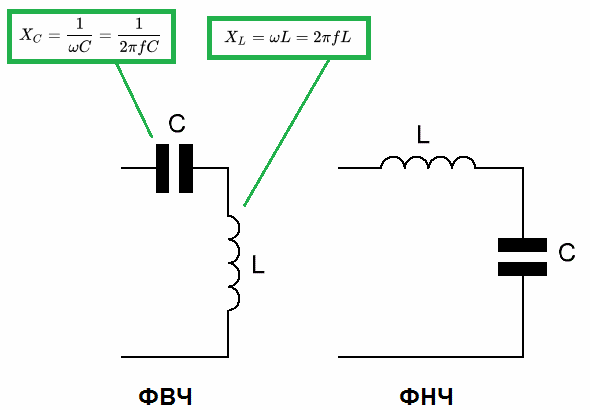
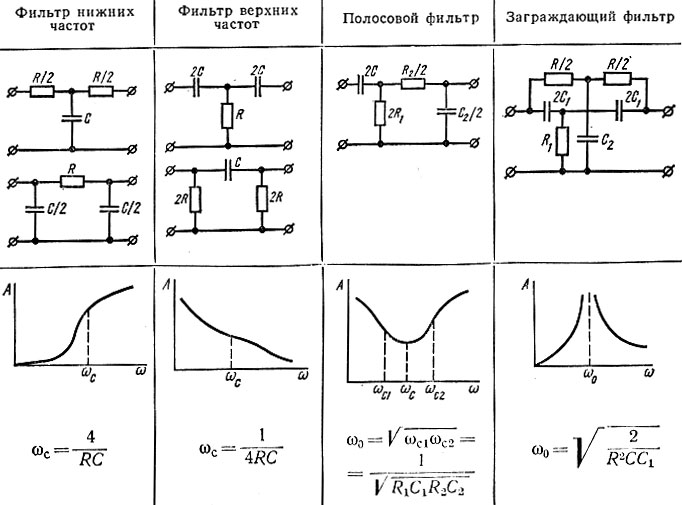 163
163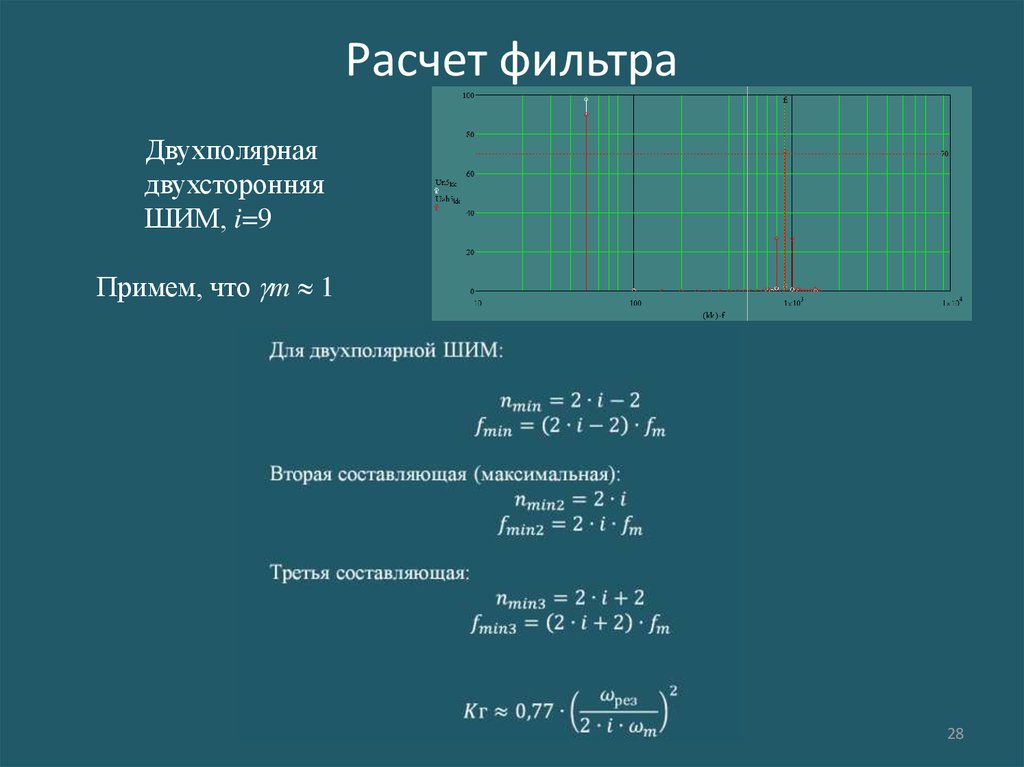 Это связано с тем, что паразитные элементы с сосредоточенными параметрами, как правило, убивают частотную характеристику по мере повышения частоты. Например, вы можете захотеть добавить фильтр LPF с сосредоточенными элементами на выходе вашего понижающего преобразователя. Если вы микшируете X-диапазон до 50 МГц, на выходе не будет утечки ВЧ и гетеродина, и вы будете стильно выглядеть! Фильтры нижних частот с сосредоточенными элементами довольно часто используются в качестве ступеней «очистки» для фильтров с плоским резонатором для подавления реентерабельных мод.
Это связано с тем, что паразитные элементы с сосредоточенными параметрами, как правило, убивают частотную характеристику по мере повышения частоты. Например, вы можете захотеть добавить фильтр LPF с сосредоточенными элементами на выходе вашего понижающего преобразователя. Если вы микшируете X-диапазон до 50 МГц, на выходе не будет утечки ВЧ и гетеродина, и вы будете стильно выглядеть! Фильтры нижних частот с сосредоточенными элементами довольно часто используются в качестве ступеней «очистки» для фильтров с плоским резонатором для подавления реентерабельных мод.