Фильтр Баттерворта
АЧХ фильтра Баттерворта описывается уравнением
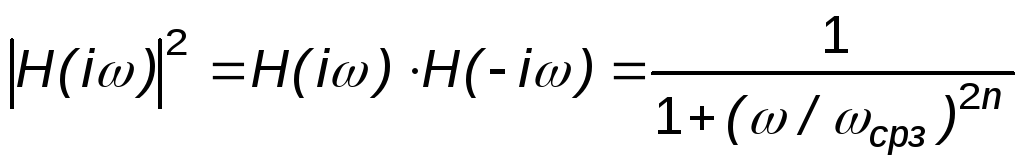 .
.
Особенности фильтра Баттерворта: нелинейная ФЧХ; частота среза не зависящая от числа полюсов; колебательный характер переходной характеристики при ступенчатом входном сигнале. С увеличением порядка фильтра колебательный характер усиливается.
Фильтр Чебышева
АЧХ фильтра Чебышева описывается уравнением
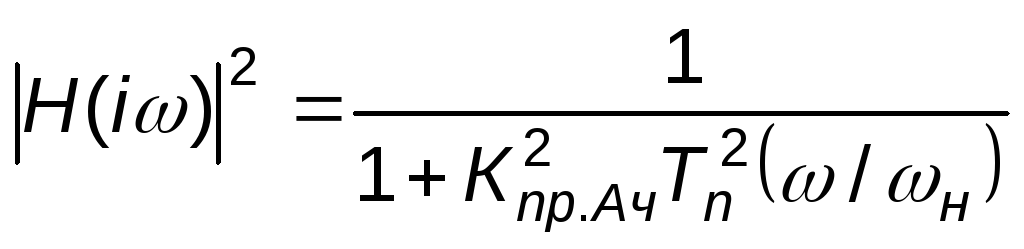 ,
,
где Tn2(ω/ωн) – полином Чебышева n–го порядка.
Полином Чебышева вычисляется по рекуррентной формуле
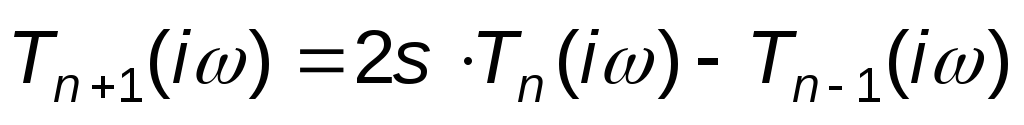 .
.
Особенности фильтра Чебышева: повышенная неравномерность ФЧХ; волнообразная характеристика в полосе пропускания. Чем выше коэффициент неравномерности АЧХ фильтра в полосе пропускания, тем более резкий спад в переходной области при одном и том же порядке. Колебания переходного процесса при ступенчатом входном сигнале сильнее, чем у фильтра Баттерворта. Добротность полюсов фильтра Чебышева выше, чем у фильтра Баттерворта.
Фильтр Бесселя
АЧХ фильтра Бесселя описывается уравнением
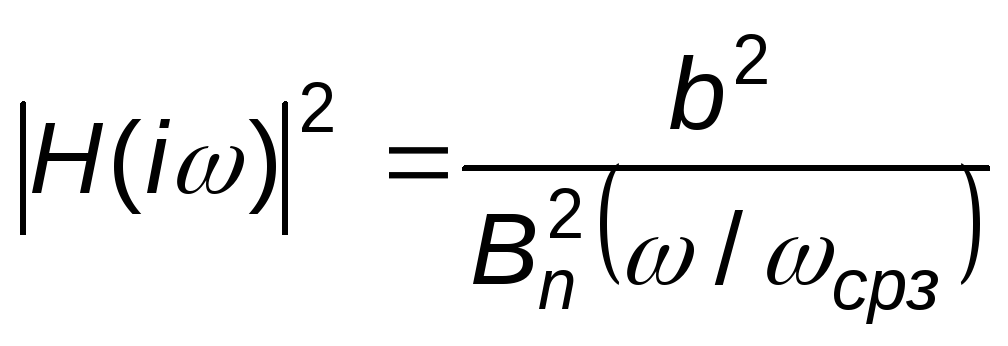
где 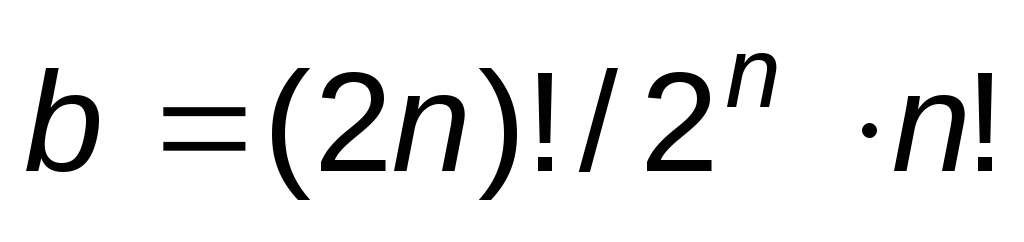 ;Bn2(ω/ωcpз) – полином Бесселя n-го
порядка.
;Bn2(ω/ωcpз) – полином Бесселя n-го
порядка.
Полином Бесселя вычисляется по рекуррентной формуле
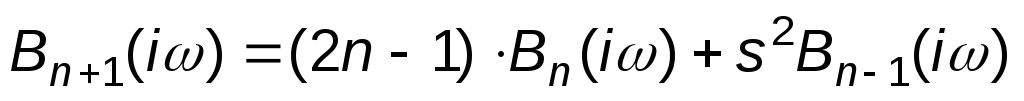 .
.
Особенности фильтра Бесселя: достаточно равномерные АЧХ и ФЧХ, аппроксимируемые функцией Гаусса; фазовый сдвиг фильтра пропорционален частоте, т.е. фильтр обладает частотно-независимым групповым временем задержки. Частота среза изменяется при изменении количества полюсов фильтра. Спад АЧХ фильтра обычно более пологий, чем у Баттерворта и Чебышева. Особенно хорошо этот фильтр подходит для импульсных цепей и фазочувствительной обработки сигнала.
Фильтр Кауэра (эллиптический фильтр)
Общий вид передаточной функции фильтра Кауэра
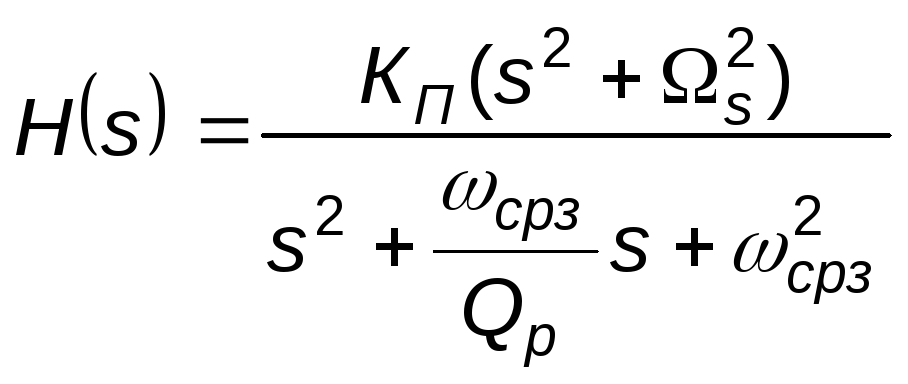 .
.
Особенности фильтра Кауэра: неравномерная АЧХ в полосе пропускания и в полосе задерживания; самый резкий спад АЧХ из всех приведенных фильтров; реализует требуемые передаточные функции при меньшем порядке фильтра, чем при использовании фильтров других типов.
Определение порядка фильтра
Требуемый порядок фильтра определяется по приведенным ниже формулам и округляется в сторону ближайшего целого значения. Порядк фильтра Баттерворта
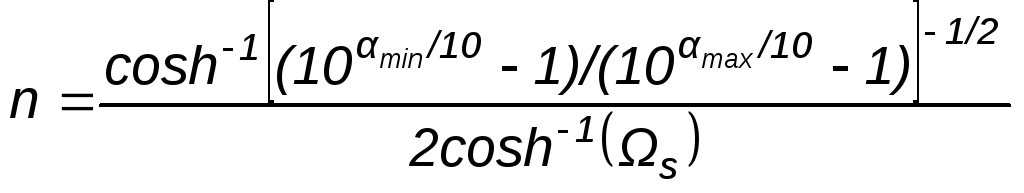 .
.
Порядка фильтра Чебышева
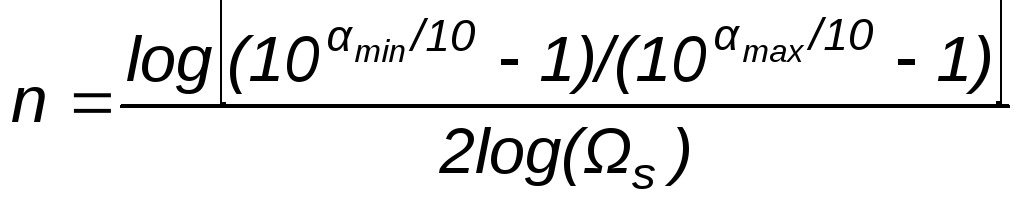 .
.
Для фильтра Бесселя не существует формулы расчета порядка, вместо этого приводятся таблицы соответствия порядка фильтра минимально необходимым на заданной частоте отклонению времени задержки от единичной величины и уровню потерь в дБ).
При расчете порядка фильтра Бесселя задаются следующие параметры:
Допустимое процентное отклонение группового времени задержки на заданной частоте ω, нормированной относительно ωcpз;
Может быть задан уровень ослабления коэффициента передачи фильтра в дБ на частоте ω, нормированной относительно ωcpз.
На основании этих данных определяется требуемый порядок фильтра Бесселя.
Схемы каскадов фнч 1–го и 2–го порядка
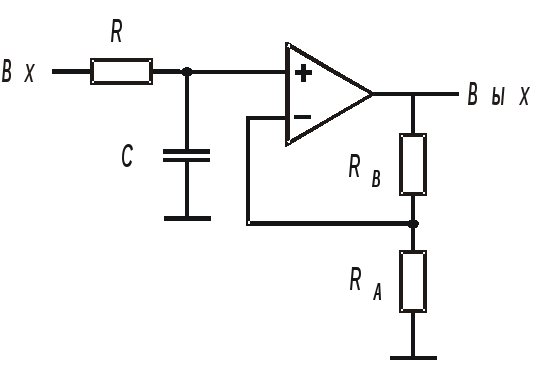
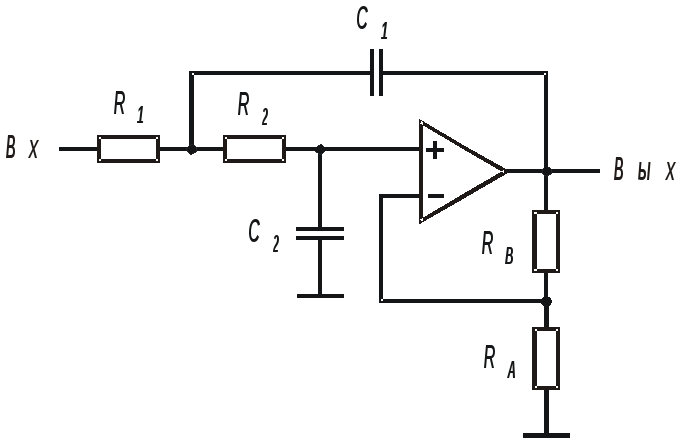
а) б)
Рис. 12.4. Каскады ФНЧ Баттерворта, Чебышева и Бесселя: а – 1–го порядка; б – 2–го порядка
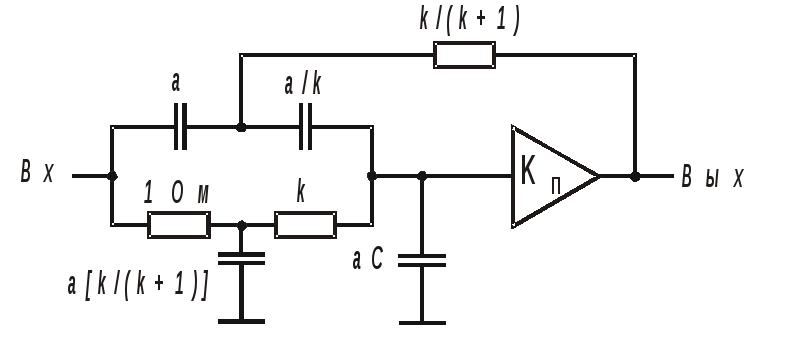
а) б)
Рис. 12.5. Каскады ФНЧ Кауэра:
Общий вид передаточных функций ФНЧ Баттерворта, Чебышева и Бесселя 1–го и 2–го порядка
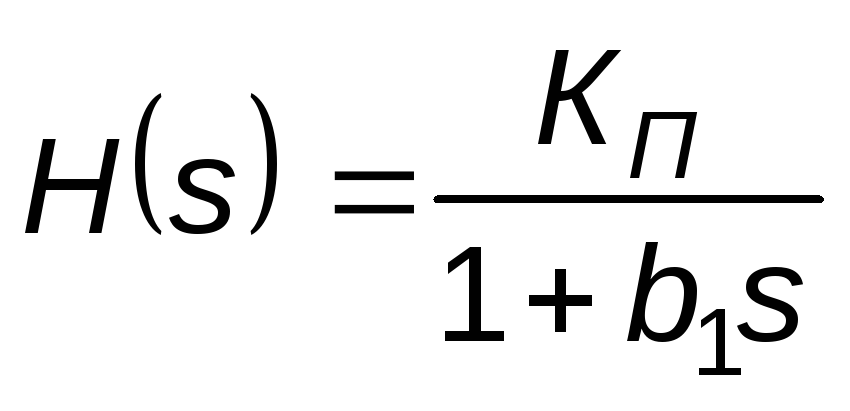 ,
,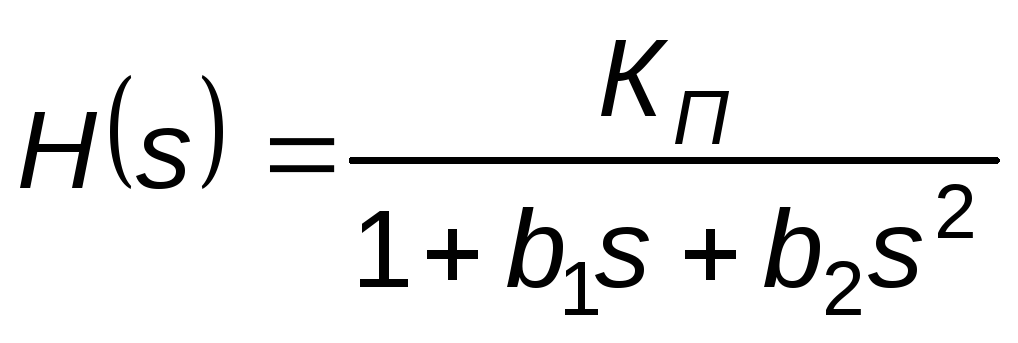 .
.
Общий вид передаточных функций ФНЧ Кауэра 1–го и 2–го порядка
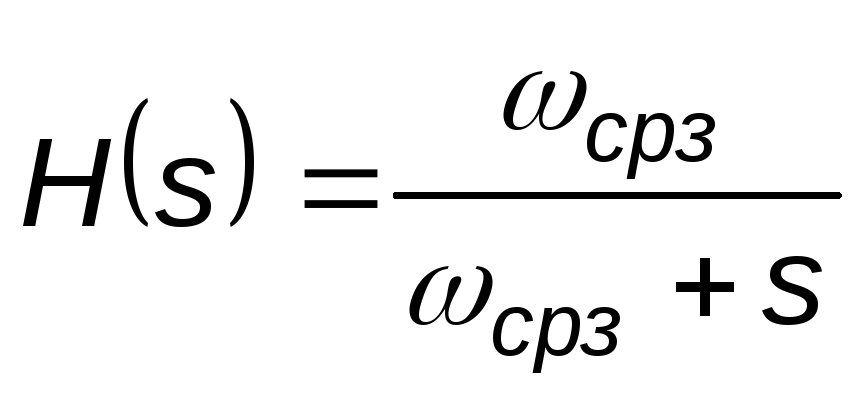 ,
, 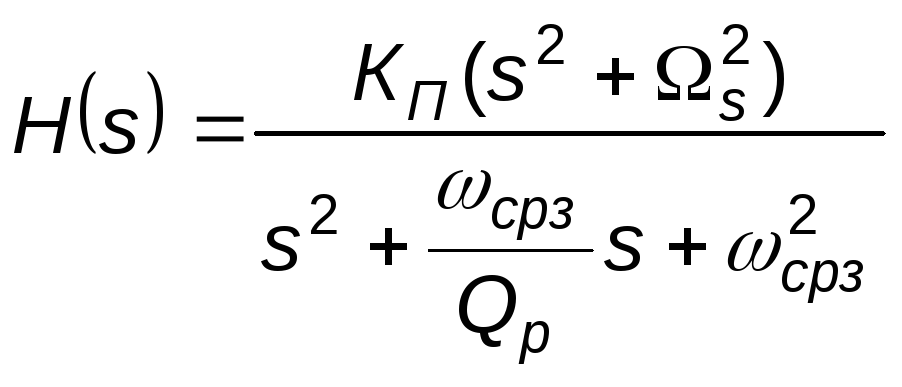 .
.
Ключевым отличием фильтра Кауэра 2–го порядка от заграждающего фильтра является то, что в передаточной функции фильтра Кауэра отношение частот
Методика расчета ФНЧ Баттерворта, Чебышева и Бесселя
Данная методика построена на основе коэффициентов, приведенных в таблицах и справедлива для фильтров Баттерворта, Чебышева и Бесселя. Методика расчета фильтров Кауэра приводится отдельно. Расчет ФНЧ Баттерворта, Чебышева и Бесселя начинается с определения их порядка. Для всех фильтров задаются параметры минимального и максимального ослабления и частота среза. Для фильтров Чебышева дополнительно определяется коэффициент неравномерности АЧХ в полосе пропускания, а для фильтров Бесселя – групповое время задержки. Далее определяется передаточная функция фильтра, которая может быть взята из таблиц, и рассчитываются его каскады 1–го и 2–го порядка, соблюдается следующий порядок расчета:
В зависимости от порядка и типа фильтра выбираются схемы его каскадов, при этом фильтр четного порядка состоит из n/2 каскадов 2–го порядка, а фильтр нечетного порядка – из одного каскада 1–го порядка и (n–1)/2 каскадов 2–го порядка;
Для расчета каскада 1–го порядка:
По выбранному типу и
порядку фильтра определяется значение b
Уменьшая занимаемую площадь, выбирается номинал емкости C и рассчитывается R по формуле (можно выбрать и R, но рекомендуется выбирать C, из соображения точности)
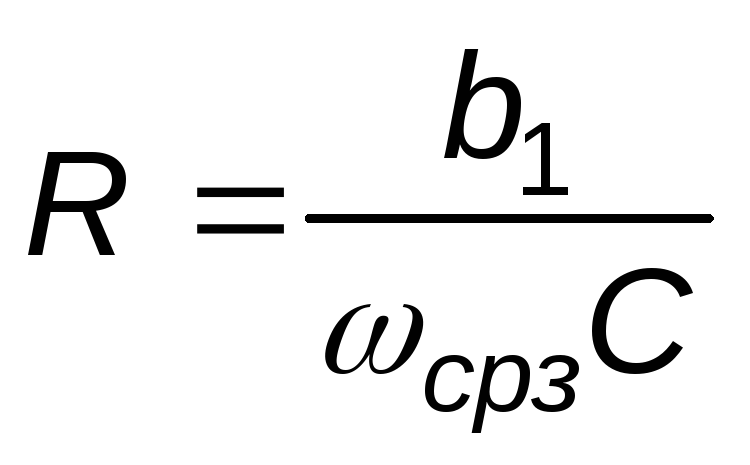 ;
;
Вычисляется коэффициента усиления КуU1 каскада 1–го порядка, который определяется из соотношения
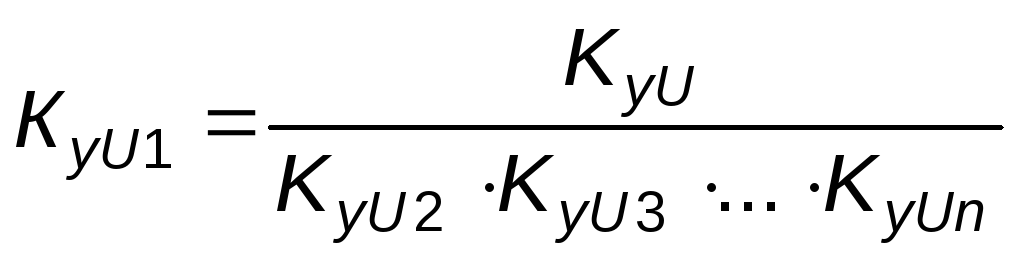 ,
,
где КуU – коэффициент усиления фильтра в целом; КуU2, …, КуUn – коэффициенты усиления каскадов 2–го порядка;
Для реализации усиления КуU1 необходимо задать резисторы, исходя из следующего соотношения
RB = RAּ(КуU1 –1) .
Для расчета каскада 2–го порядка:
Уменьшая занимаемую площадь выбраются номиналы емкостей C1 = C2 = C;
Выбраются по таблицам коэффициенты b1i и Qpi для каскадов 2–го порядка;
По заданному номиналу конденсаторов C рассчитываются резисторы R по формуле
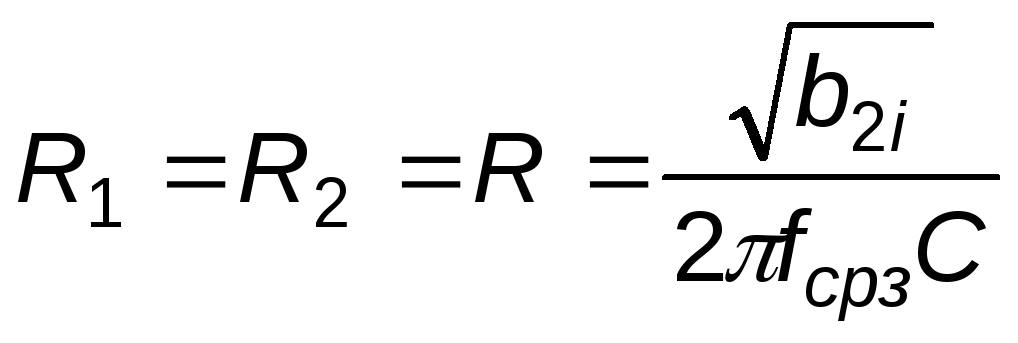 ;
;
Для выбранного типа фильтра необходимо задать соответствующий коэффициент усиления КуUi= 3 – (1/Qpi) каждого каскада 2-го порядка, посредством задания резисторов, исходя из следующего соотношения
RB = RAּ(КуUi –1) ;
Для фильтров Бесселя необходимо умножить номиналы всех емкостей на требуемое групповое время задержки.
28.1 Определения.
 Тема
занятия 28: Классификация электрических
фильтров.
Тема
занятия 28: Классификация электрических
фильтров.
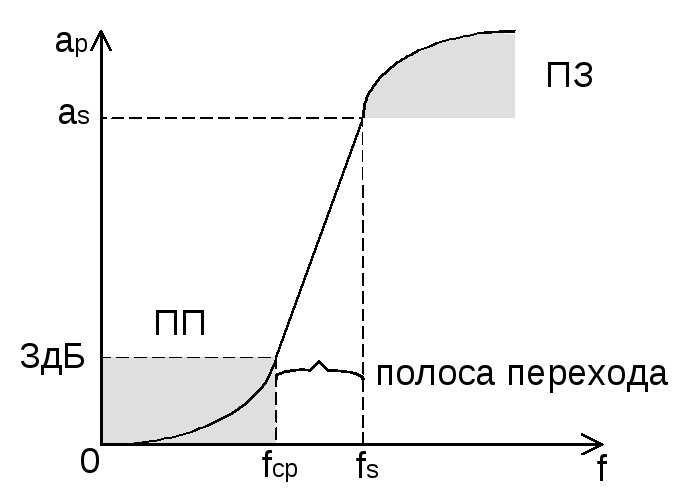
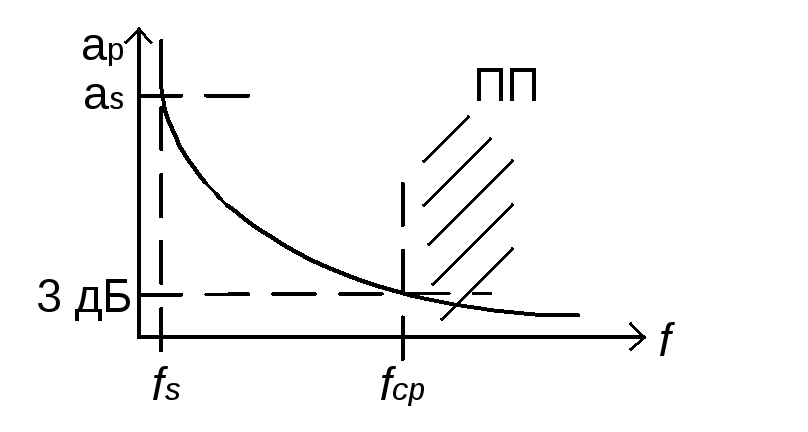
Электрическим частотным фильтром называется четырехполюсник, который токи одних частот пропускает хорошо с малым затуханием (ослаблением 3 дБ), а токи других частот плохо с большим затуханием (30 дБ).
Диапазон частот, в которых ослабление мало называется полосой пропускания.
Диапазон частот , в которых ослабление велико называется полосой задерживания.
Между этими полосами вводят полосу перехода.
Основной характеристикой электрических фильтров является зависимость рабочего затухания от частоты.
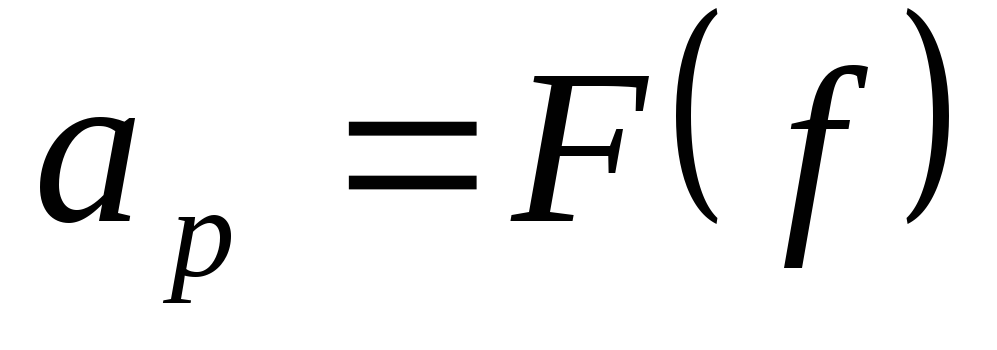
Эта характеристика называется частотной характеристикой затухания.
рис
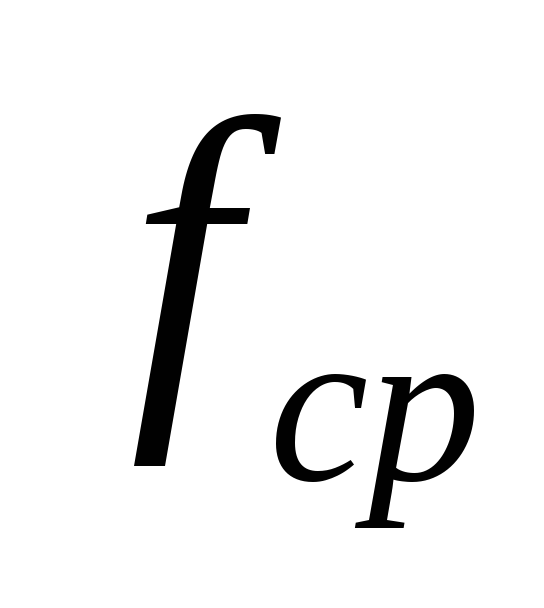
 —
частота среза, на которой рабочее
затухание составляет 3 дБ.
—
частота среза, на которой рабочее
затухание составляет 3 дБ.
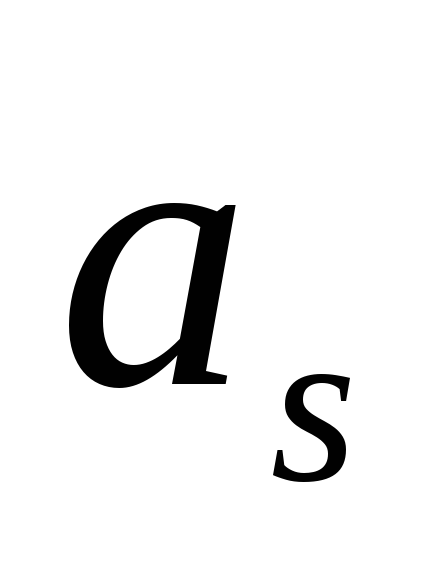 —
допустимое затухание , задается
механическими параметрами фильтра.
—
допустимое затухание , задается
механическими параметрами фильтра.
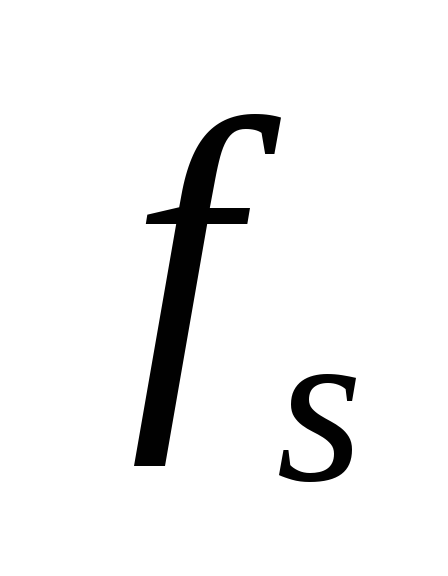 —
допустимая частота, соответствующая
допустимому затуханию.
—
допустимая частота, соответствующая
допустимому затуханию.
ПП- полоса пропускания – область частот,
в которых 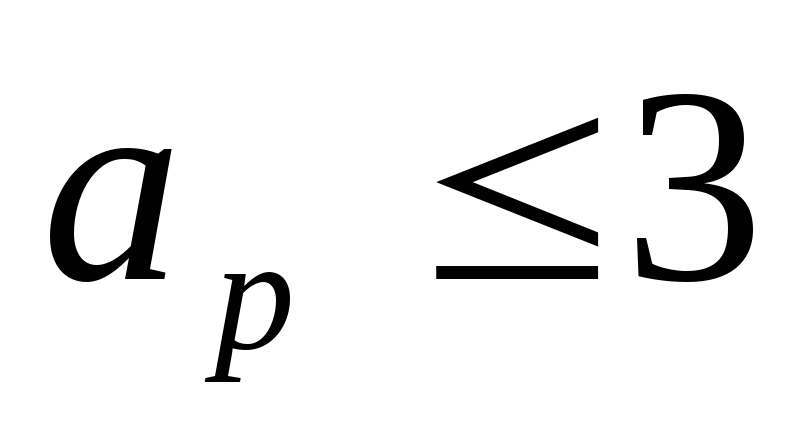 дБ.
дБ.
ПЗ – полоса задерживания – область частот, в которых рабочее затухание больше допустимого.
28.2 Классификация
1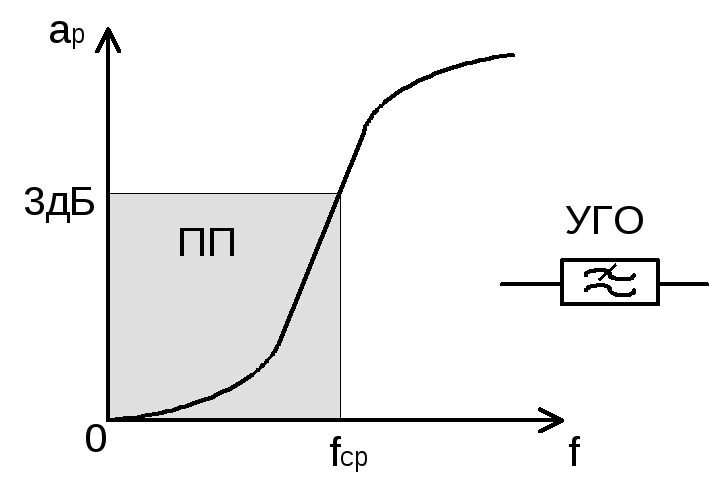 По расположению полосы пропускания:
По расположению полосы пропускания:
а) ФНЧ – фильтр нижних частот – пропускает низкие частоты и задерживает верхние.
Применяется в аппаратуре связи(телевизионные приемники).
б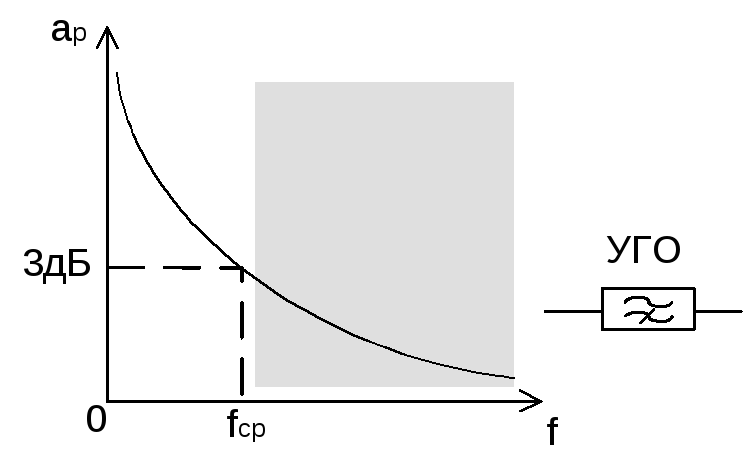 )
ФВЧ – фильтр верхних частот – пропускает
высокие частоты и задерживает низкие.
)
ФВЧ – фильтр верхних частот – пропускает
высокие частоты и задерживает низкие.
в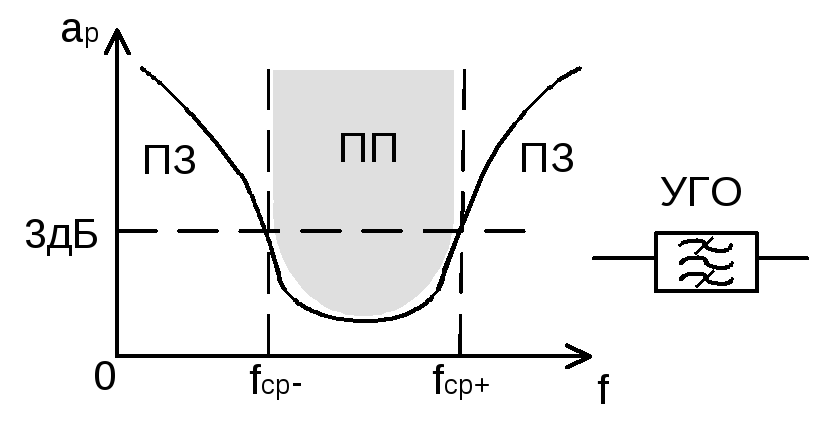 )
ПФ – полосовые фильтры – пропускают
только определенную полосу частот.
)
ПФ – полосовые фильтры – пропускают
только определенную полосу частот.
г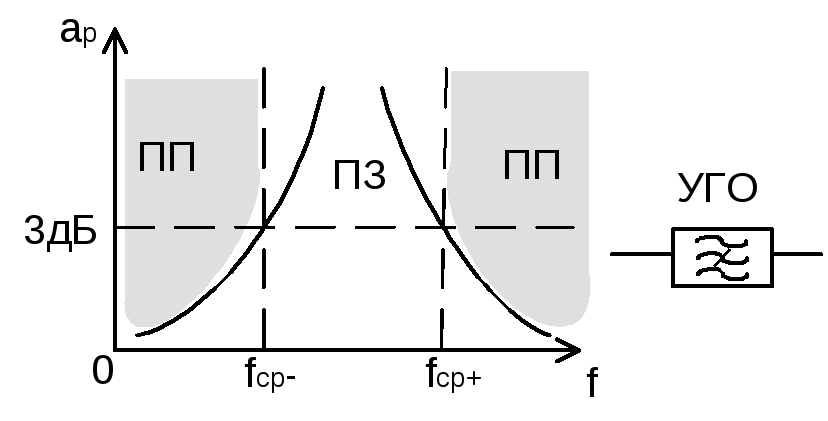 )
ЗФ — режекторные или заграждающие фильтры
– не пропускают только определенную
полосу частот, а остальные пропускают.
)
ЗФ — режекторные или заграждающие фильтры
– не пропускают только определенную
полосу частот, а остальные пропускают.
2 По элементной базе:
а) фильтры LC(пассивные)
б) фильтры RC(пассивные)
в) активные фильтры ARC
г) специальные типы фильтров:
-пьезоэлектрические
-магнитострикционные
3 По математическому обеспечению:
а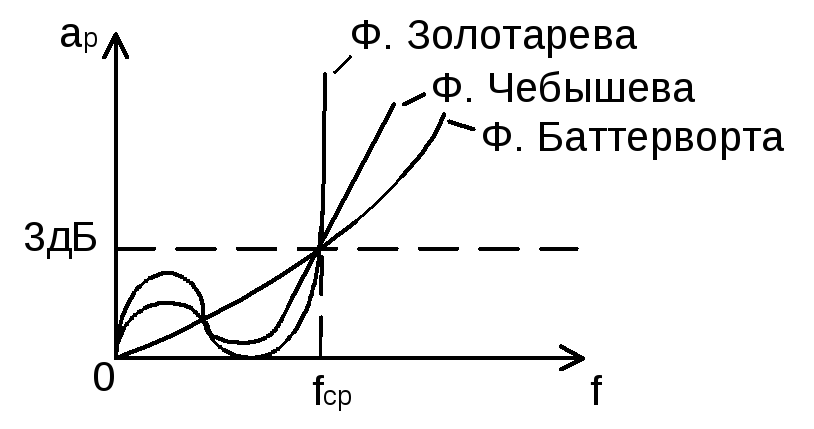 )
фильтры Баттерворта. Характеристика
рабочего затухания
)
фильтры Баттерворта. Характеристика
рабочего затухания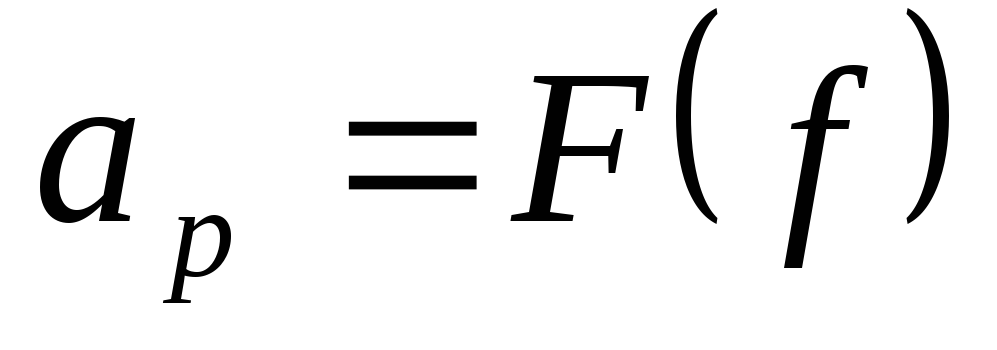 имеет
на частотеf=0 значение 0
, а затем монотонно увеличивается. В
полосе пропускания имеет плоскую
характеристику – это достоинство, но
в полосе задерживания идет не круто –
это недостаток.
имеет
на частотеf=0 значение 0
, а затем монотонно увеличивается. В
полосе пропускания имеет плоскую
характеристику – это достоинство, но
в полосе задерживания идет не круто –
это недостаток.
б) фильтры Чебышева. Чтобы получить более крутую характеристику используют фильтры Чебышева, но у них в полосе пропускания появляется «волнистость», что является недостатком.
в) фильтры Золотарева. Характеристика
рабочего затухания 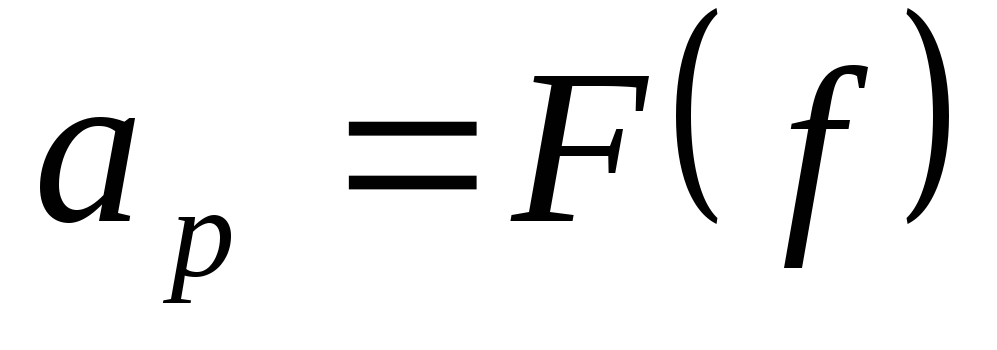 в полосе пропускания имеет волнистость,
а в полосе задерживания провал
характеристик.
в полосе пропускания имеет волнистость,
а в полосе задерживания провал
характеристик.
Тема занятия 29: Фильтры НЧ и ВЧ Баттерворта.
29.1 Фнч Баттерворта.
Баттерворт предложил следующую формулу затухания:
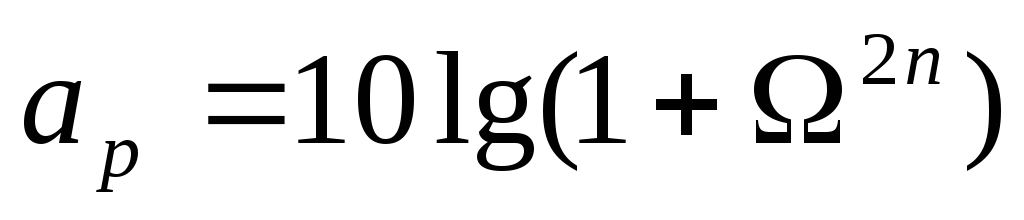 ,дБ
,дБ
где 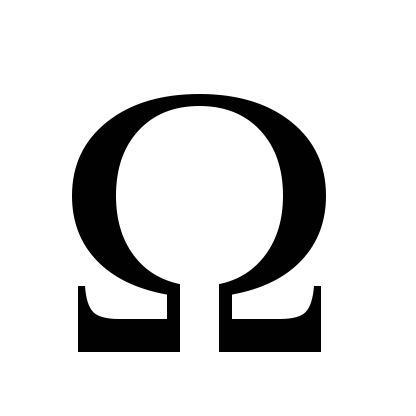 —
функция Баттерворта (нормированная
частота)
—
функция Баттерворта (нормированная
частота)
n– порядок фильтра
Для ФНЧ 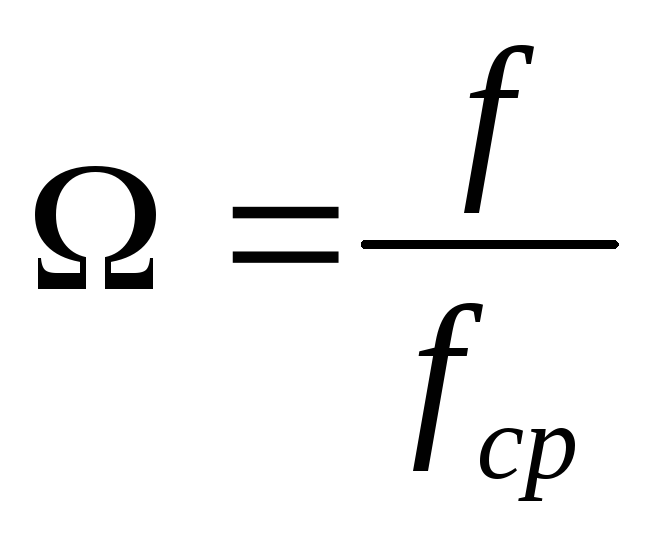 ,
где
,
где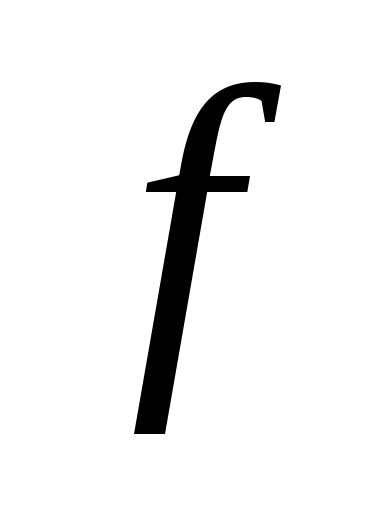 —
любая нужная частота
—
любая нужная частота
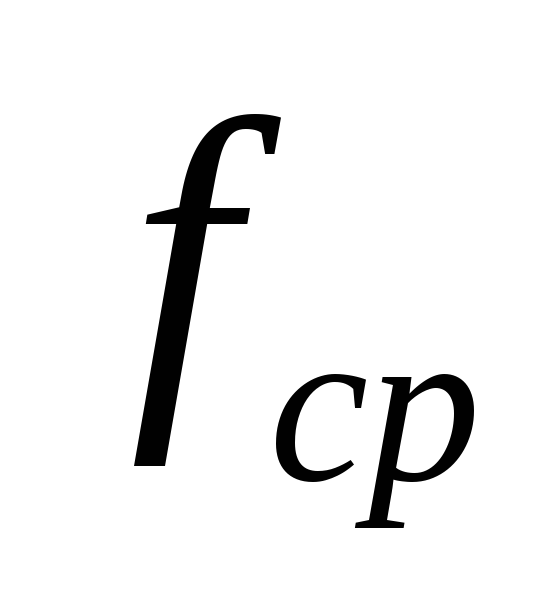 —
частота среза, которая равна
—
частота среза, которая равна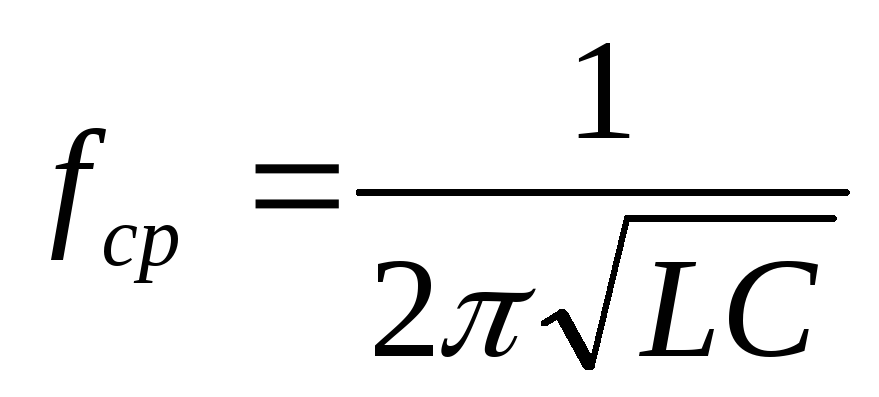
Чтобы реализовать такую характеристику используются фильтры LиC.
И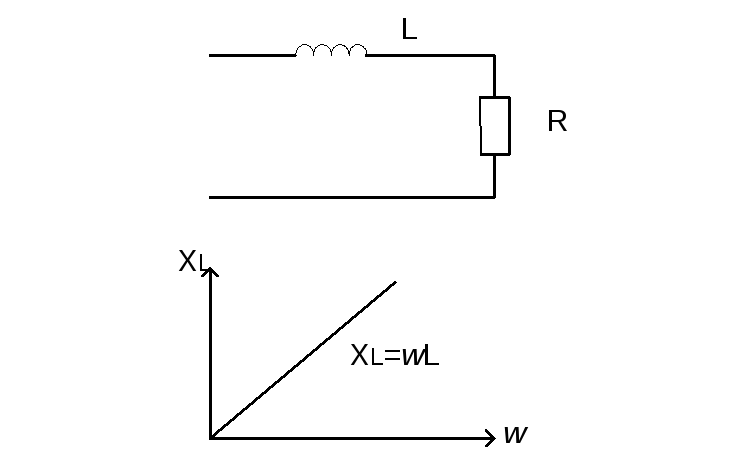
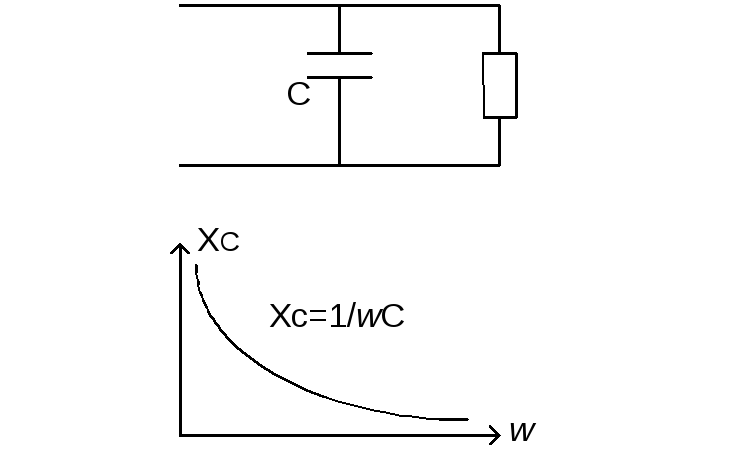 ндуктивность
ставят последовательно нагрузке, так
как
ндуктивность
ставят последовательно нагрузке, так
как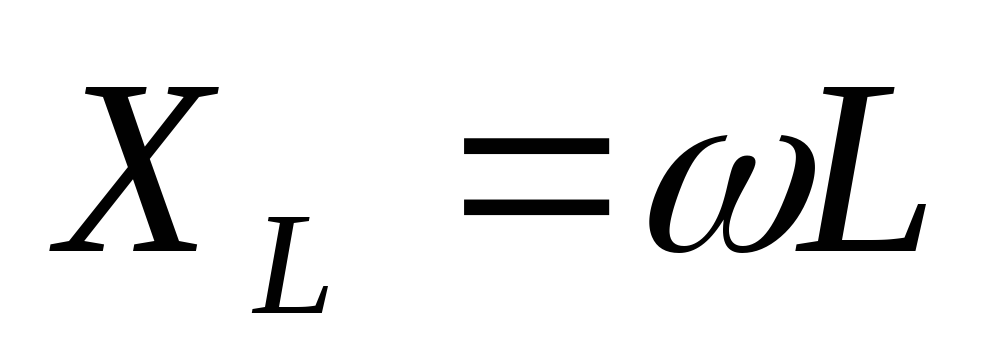 и с ростом
и с ростом увеличивается
увеличивается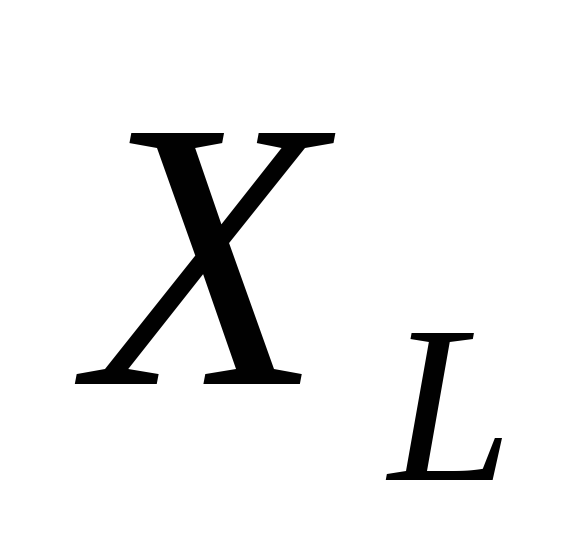 .Поэтому
токи низких частот легко пройдут через
сопротивление индуктивности, а токи
высоких частот задержатся и в нагрузку
не попадут.
.Поэтому
токи низких частот легко пройдут через
сопротивление индуктивности, а токи
высоких частот задержатся и в нагрузку
не попадут.
Конденсатор ставят параллельно нагрузке,
так как 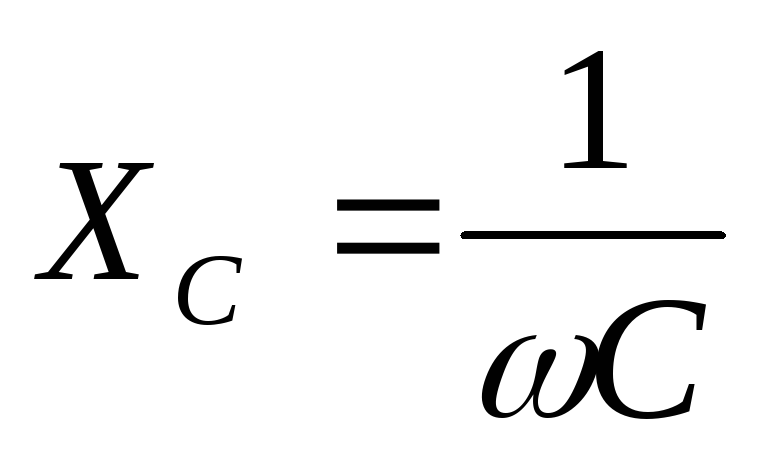 ,
поэтому конденсатор хорошо пропускает
токи верхних частот и плохо нижних. Токи
верхних частот замкнутся через конденсатор
, а токи низких частот пройдут в нагрузку.
,
поэтому конденсатор хорошо пропускает
токи верхних частот и плохо нижних. Токи
верхних частот замкнутся через конденсатор
, а токи низких частот пройдут в нагрузку.
Схема фильтра состоит из чередующихся LиC.
 ФНЧ
Баттерворта 3-го порядка Т-образный
ФНЧ
Баттерворта 3-го порядка Т-образный
ФНЧ Баттерворта. 3-го порядка П-образный.
фильтр Баттерворта — Butterworth filter
 Частотная характеристика участка от 1930 бумаги Баттеруорса.
Частотная характеристика участка от 1930 бумаги Баттеруорса.Фильтр Баттерворта представляет собой тип обработки сигнала фильтра разработан , чтобы иметь частотную характеристику , как плоские , как это возможно в полосе пропускания . Он также упоминается как максимально плоской величины фильтра . Впервые он был описан в 1930 году британским инженером и физиком Стивеном Баттерворта в своей статье , озаглавленной «О теории фильтров усилителей».
Оригинальная статья
Баттерворта имел репутацию решения «невозможные» математические задачи. В то время, конструкция фильтра требуется значительное количество дизайнерского опыта из — за ограничения теории затем в использовании . Фильтр не был в общем пользовании в течение более чем 30 лет после его опубликования. Баттерворта заявил , что:
«Идеальный электрический фильтр должен не только полностью отказаться от нежелательных частот, но также должен иметь равномерную чувствительность пожелавших частот».
Такой идеальный фильтр не может быть достигнута , но Баттерворта показал , что последовательно более близкие приближения были получены с увеличением числа фильтрующих элементов правых значений. В то время, фильтры генерируются существенные пульсации в полосе пропускания, и выбор значений компонентов был очень интерактивным. Баттерворта показал , что фильтр нижних частот может быть спроектирован частота среза которого была нормирована на 1 радиан в секунду , и чьи частотной характеристики ( коэффициент усиления ) был
- г(ω)знак равно11+ω2N,{\ Displaystyle G (\ Omega) = {\ гидроразрыва {1} {\ SQRT {1 + {\ Omega} ^ {2n}}}}}
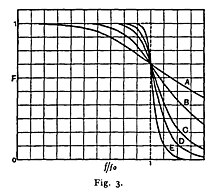
где ω является угловой частотой в радианах в секунду и п есть число полюсов в фильтре-равно число реактивных элементов в пассивном фильтре. Если со = 1, то амплитуда отклика такого типа фильтра в полосе пропускания составляет 1 / √ 2 ≈ 0,707, которая составляет половину мощности или -3 дБ . Баттерворта имел дело только с помощью фильтров с четным числом полюсов в его работе. Он может не знать , что такие фильтры могут быть разработаны с нечетным числом полюсов. Он построил свои фильтры более высокого порядка от 2-полюсных фильтров , разделенных ламповых усилителях. Его график частотной характеристики 2, 4, 6, 8, 10 и полюсные фильтры показан как A, B, C, D, и Е в его исходном графе.
Баттерворта решил уравнение для двух- и четыре-полюсных фильтров, показывая , как последний может быть каскадно , когда отделены друг от ламповых усилителей и так позволяя конструкцию фильтров более высокого порядка , несмотря на индукторных потери. В 1930 году, с низким уровнем потерь в сердечнике материалы , такие как molypermalloy не были обнаружены и с воздушным сердечником аудио индукторы были довольно потерями. Баттерворта обнаружил , что можно было скорректировать значение компонентов фильтра для компенсации сопротивления обмотки индукторов.
Он использовал форму катушки «диаметра и 3» 1,25 длины с разъемными клеммами. Ассоциированные конденсаторы и резисторы содержатся в виде спиральных. Катушка сформирована часть резистора нагрузки пластины. Два полюса были использованы в вакуумной трубке и RC-муфта была использована на сетку следующей трубы.
Баттерворта также показало , что основной фильтр нижних частот может быть модифицирован , чтобы дать низкий проход , высокий проход , полосовой и полосовой стоп функциональность.
обзор
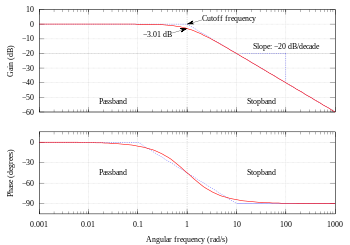 Боде из первого порядка фильтра Баттерворта нижних частот
Боде из первого порядка фильтра Баттерворта нижних частотЧастотная характеристика фильтра Баттерворта является максимально плоской (т.е. не имеет пульсации ) в полосе пропускания и скатывается к нулю в режекции. При взгляде на логарифмической Боде , реакция наклонена от линейно в сторону отрицательной бесконечности. Ответ первого порядка фильтра скатывается при -6 дБ на октаву (-20 дБ на десятилетие ) (все фильтры нижних частот первого порядка имеют тот же нормализованный частотный отклик). Фильтр второго порядка уменьшается при -12 дБ на октаву, третий порядок при -18 дБ и так далее. Баттерворта фильтры имеют монотонно меняющуюся функцию величины с ш, в отличии от других типов фильтров , которые имеют немонотонные пульсации в полосе пропускания и / или задерживании.
По сравнению с Чебышева типа I / II типа фильтра или эллиптического фильтра , фильтр Баттерворта имеет более медленный спад , и , таким образом , будет требовать более высокого порядка для реализации конкретного задерживания спецификации, но Баттерворта фильтры имеют более линейную фазовую характеристику в полоса пропускания , чем Чебышева типа I / II типа и эллиптические фильтры могут достичь.
пример
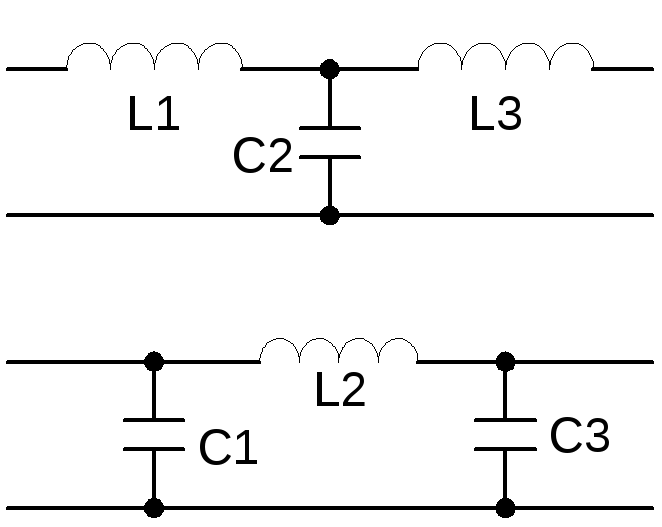
Функция передачи низких частот конструкции фильтра Баттерворта третьего порядка, показанного на рисунке справа выглядит следующим образом:
- Во(s)Вя(s)знак равнорs3(L1С2L3)+s2(L1С2р)+s(L1+L3)+р,{\ Displaystyle {\ гидроразрыва {V_ {O} (ы)} {V_ {я} (ы)}} = {\ гидроразрыва {R}, {s ^ {3} (L_ {1} C_ {2} L_ {3 }) + s ^ {2} (L_ {1} C_ {2} r) + s (L_ {1} + L_ {3}) + R}}.}
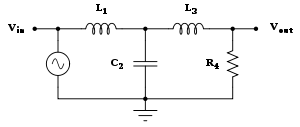 Фильтр нижних частот третьего порядка ( Кауэр топология ). Фильтр становится фильтр Баттерворта с частотой среза & omega с = 1 , когда (например) C 2 = 4/3 фарад, R 4 = 1 Ом, L 1 = 3/2 и L генри 3 = 1/2 генри.
Фильтр нижних частот третьего порядка ( Кауэр топология ). Фильтр становится фильтр Баттерворта с частотой среза & omega с = 1 , когда (например) C 2 = 4/3 фарад, R 4 = 1 Ом, L 1 = 3/2 и L генри 3 = 1/2 генри.Простой пример фильтра Баттерворта является конструкция нижних частот третьего порядка показано на рисунке справа, с C 2 = 4/3 F, R 4 = 1 Ом, L 1 = 3/2 H, и L 3 = 1/2 Х. Принимая сопротивление конденсаторов C , чтобы быть 1 / (Cs) , и полное сопротивление индуктивности L , чтобы быть Ls , где S = σ + J ω является комплексной частотой, уравнение цепи дают функцию передачи для этого устройства:
- ЧАС(s)знак равноВо(s)Вя(s)знак равно11+2s+2s2+s3,{\ Displaystyle Н (з) = {\ гидроразрыва {V_ {O} (ы)} {V_ {я} (ы)}} = {\ гидроразрыва {1} {1 + 2s + 2s ^ {2} + s ^ {3}}}.}
Величина частотной характеристики (усиление) G (со) задается
- г(ω)знак равно|ЧАС(Jω)|знак равно11+ω6,{\ Displaystyle G (\ Omega) = | H (J \ омега) | = {\ гидроразрыва {1} {\ SQRT {1+ \ Omega ^ {6}}}}}
получен из
- г2(ω)знак равно|ЧАС(Jω)|2знак равноЧАС(Jω)⋅ЧАС*(Jω)знак равно11+ω6,{\ Displaystyle G ^ {2} (\ Omega) = | H (J \ омега) | ^ {2} = H (J \ Omega) \ CDOT H ^ {*} (J \ Omega) = {\ гидроразрыва {1 } {1+ \ Omega ^ {6}}}}
и фазы задается
- Φ(ω)знак равноArg(ЧАС(Jω)),{\ Displaystyle \ Phi (\ Omega) = \ аг (H (J \ омега)). \!}
Групповая задержка определяется как производная фаза по отношению к угловой частоте и является мерой искажения в сигнале , введенный разностью фаз для разных частот. Усиления и задержка для этого фильтра приведены на графике слева. Можно видеть , что нет ряби на кривой усиления в каждой полосе пропускания или стоп — зоны.
Логарифм абсолютного значения передаточной функции Н (з) строится в комплексном частотном пространстве во втором графике справа. Функция определяется тремя полюсами в левой половине плоскости комплексной частоты.
Вход график плотности передаточной функции H (ы) в комплексном частотном пространстве для третьего порядка фильтра Баттерворта с & omega с = 1. Эти три полюса лежат на окружности единичного радиуса в левой полуплоскости.Они расположены на окружности радиуса единицы , симметричной относительно вещественной сек оси. Функция усиления будет иметь еще три полюса на правой полуплоскости , чтобы завершить круг.
Путем замены каждого индуктора с конденсатором и конденсатором с каждым индуктором, верхних частот фильтра Баттерворта получается.
Полосовой фильтр Баттерворта получается путем размещения конденсатора последовательно с каждым индуктором и индуктором параллельно с каждым конденсатором с образованием резонансных контуров. Значение каждого нового компонента должно быть выбрано, чтобы резонировать со старой составляющей на частоте интереса.
Полоса остановка фильтр Баттерворт получается путем размещения конденсатора параллельно с каждым индуктором и индуктором последовательно с каждым конденсатором с образованием резонансных контуров. Значение каждого нового компонента должно быть выбрано, чтобы резонировать со старой составляющей на частоте быть отвергнуто.
Функция передачи
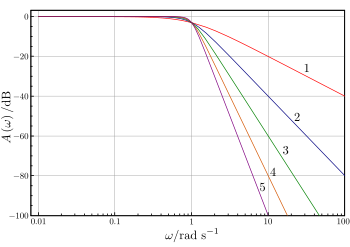 Участок усиления Баттерворта нижних частот фильтров заказов от 1 до 5, с частотой среза . Обратите внимание , что наклон 20 п дБ / декада , где п есть порядок фильтра.ω0знак равно1{\ Displaystyle \ омега _ {0} = 1}
Участок усиления Баттерворта нижних частот фильтров заказов от 1 до 5, с частотой среза . Обратите внимание , что наклон 20 п дБ / декада , где п есть порядок фильтра.ω0знак равно1{\ Displaystyle \ омега _ {0} = 1}Как и все фильтры, типичный прототип является низкочастотным фильтром, который может быть изменен в фильтр высоких частот, или помещен в серии с другими , чтобы сформировать полосовые и полосовую стоп — фильтры и более поздние версии порядка этих.
Усиления из п -ого обобщенного фильтра Баттерворт нижних частот даются в терминах передаточной функции H (ы) как г(ω){\ Displaystyle G (\ Omega)}
- г2(ω)знак равно|ЧАС(Jω)|2знак равног021+(Jωωс)2N{\ Displaystyle G ^ {2} (\ Omega) = \ влево | H (J \ Omega) \ право | ^ {2} = {\ гидроразрыва {{G_ {0}} ^ {2}} {1+ \ влево ({\ гидроразрыва {J \ Omega} {\ омега _ {с}}} \ справа) ^ {2n}}}}
где
- п = порядок фильтра
- ω с = частота среза (примерно частота -3 дБ)
- г0{\ Displaystyle G_ {0}} коэффициент усиления постоянного тока (коэффициент усиления на нулевой частоте)
Можно видеть , что , как п стремится к бесконечности, коэффициент усиления становится функцией прямоугольника и частот ниже & omega с будут переданы с усилением , в то время как частоты выше & omega с будут подавлены. При меньших значениях п , отсечка будет менее резким. г0{\ Displaystyle G_ {0}}
Мы хотим , чтобы определить передаточную функцию H (ы) , где (от преобразования Лапласа ). Потому и, как общее свойство преобразования Лапласа на , если мы выбираем H (ы) таким образом, что: sзнак равноσ+Jω{\ Displaystyle s = \ сигма + J, \ Omega}|ЧАС(s)|2знак равноЧАС(s)ЧАС(s)¯{\ Displaystyle влево \ | H (s) \ право | ^ {2} = H (s) {\ Overline {H (s)}}}sзнак равноJω{\ Displaystyle з = J \ Omega}ЧАС(-Jω)знак равноЧАС(Jω)¯{\ Displaystyle Н (-j \ Omega) = {\ Overline {Н (J \ Omega)}}}
- ЧАС(s)ЧАС(-s)знак равног021+(-s2ωс2)N,{\ Displaystyle Н (с) H (-s) = {\ гидроразрыва {{G_ {0}} ^ {2}} {1+ \ влево ({\ гидроразрыва {-s ^ {2}} {\ Omega _ { с} ^ {2}}} \ справа) ^ {п}}}}
затем, мы имеем частотную характеристику фильтра Баттерворта. sзнак равноJω{\ Displaystyle з = J \ Omega}
В п полюсы этого выражения происходят на окружности радиуса & omega с на одинаковом расстоянии друг от друга точках, симметричных и вокруг отрицательной действительной оси. Для устойчивости, передаточная функция H (s), поэтому выбирают таким образом, что она содержит только полюсов в отрицательной действительной полуплоскости с . К -м полюс задается
- -sК2ωс2знак равно(-1)1Nзнак равноеJ(2К-1)πNКзнак равно1,2,3,…,N{\ Displaystyle — {\ гидроразрыва {S_ {к} ^ {2}} {\ омега _ {C} ^ {2}}} = (- 1) ^ {\ гидроразрыва {1} {п}} = е ^ { \ гидроразрыва {J (2k-1) \ Pi} {п}} \ qquad к = 1,2,3, \ ldots, п}
и поэтому;
- sКзнак равноωсеJ(2К+N-1)π2NКзнак равно1,2,3,…,N,{\ Displaystyle S_ {к} = \ омега _ {с} е ^ {\ гидроразрыва {J (2k + п-1) \ пи} {2n}} \ qquad к = 1,2,3, \ ldots, п. }
Передаточная функция (или система) может быть записана в терминах этих полюсов, как
- ЧАС(s)знак равног0ΠКзнак равно1N(s-sК)/ωс,{\ Displaystyle Н (з) = {\ гидроразрыва {G_ {0}} {\ прод _ {к = 1} ^ {п} (S-S_ {к}) / \ омега _ {C}}}.}
Где это произведение последовательности оператора. Знаменатель является полиномом Баттерворта в с . Π{\ Displaystyle \ прод}
Нормированные полиномы Баттерворта
Полиномы Баттерворта может быть записана в комплексной форме , как указано выше, но, как правило , написаны с вещественными коэффициентами путем умножения пар полюсов , которые являются сложные конъюгаты, такие как и . Многочлены нормированы путем установки . Нормированные полиномы Баттерворта , то есть общий вид s1{\ Displaystyle s_ {1}}sN{\ Displaystyle S_ {п}}ωсзнак равно1{\ Displaystyle \ омега _ {C} = 1}
- ВN(s)знак равноΠКзнак равно1N2[s2-2sсоз(2К+N-12Nπ)+1]Nзнак равночетное{\ Displaystyle B_ {п} (з) = \ прод _ {к = 1} ^ {\ гидроразрыва {N} {2}} \ влево [с ^ {2} -2s \ \ соз левой ({\ гидроразрыва {2k + п-1} {2n}} \, \ р \ справа) +1 \ вправо] \ qquad п = {\ текст {даже}}}
- ВN(s)знак равно(s+1)ΠКзнак равно1N-12[s2-2sсоз(2К+N-12Nπ)+1]Nзнак равностранный,{\ Displaystyle B_ {п} (з) = (S + 1) \ прод _ {к = 1} ^ {\ гидроразрыва {п-1} {2}} \ влево [с ^ {2} -2s \ соз \ левый ({\ гидроразрыва {2k + п-1} {2n}} \, \ р \ справа) +1 \ вправо] \ qquad п = {\ текст {нечетным}}.}
Для четырех знаков после запятой, они
|
Нормированные полиномы Баттерворта могут быть использованы для определения функции передачи для любого фильтра нижних частот частоту среза , как показано ниже ωс{\ Displaystyle \ омега _ {с}}
- ЧАС(s)знак равног0ВN(a){\ Displaystyle Н (з) = {\ гидроразрыва {G_ {0}} {B_ {п} (а)}}} , где aзнак равноsωс,{\ Displaystyle а = {\ гидроразрыва {s} {\ Omega _ {с}}}.}
Преобразование в другую bandforms также возможно, см прототипа фильтра .
Максимальная плоскостность
Предполагая , и , производная от коэффициента усиления по отношению к частоте , может быть показана ωсзнак равно1{\ Displaystyle \ омега _ {C} = 1}г0знак равно1{\ Displaystyle G_ {0} = 1}
- dгdωзнак равно-Nг3ω2N-1{\ Displaystyle {\ гидроразрыва {дО} {d \ Omega}} = — ^ НГ {3} \ Omega ^ {2n-1}}
которая монотонно убывает для всех , так как усиление G всегда положительно. Таким образом, функция усиления фильтра Баттерворта не имеет пульсаций. Расширение серии усиления задается ω{\ Displaystyle \ Omega}
- г(ω)знак равно1-12ω2N+38ω4N+…{\ Displaystyle G (\ Omega) = 1 — {\ гидроразрыва {1} {2}} \ Omega ^ {2n} + {\ гидроразрыва {3} {8}} \ Omega ^ {4n} + \ ldots}
Другими словами, все производные усиления до , но не включая 2 п -й производной равны нулю на , что приводит к «максимальной плоскостности». Если требование монотонный ограничиваются только полосой пропускания и пульсации разрешены в режекции, то можно спроектировать фильтр тех же порядка, такие , как обратный фильтр Чебышева , то есть в полосе пропускания более плоский , чем «максимально плоский»Баттерворта. ωзнак равно0{\ Displaystyle \ омега = 0}
Высокочастотный спадание
Опять же при условии , наклон логарифма коэффициента усиления при больших со является ωсзнак равно1{\ Displaystyle \ омега _ {C} = 1}
- Итω→∞dжурнал(г)dжурнал(ω)знак равно-N,{\ Displaystyle \ Нт _ {\ Omega \ RightArrow \ infty} {\ гидроразрыва {d \ лог (G)} {d \ лог (\ Omega)}} = -. П}
В децибелах , высокочастотное спадание Поэтому 20 п дБ / декада, или 6 н дБ / октава (коэффициент 20 используются потому , что мощность пропорциональна квадрату коэффициента усиления по напряжению, см 20 правила журнала .)
Реализация фильтра и дизайн
Есть несколько различных топологий фильтров , доступных для реализации линейного аналогового фильтра. Наиболее часто используется топология для пассивной реализации является Кауэра топологии и наиболее часто используется топология для активной реализации является Sallen-Key топологии.
Кауэра топология
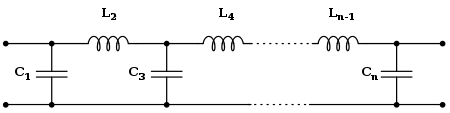
Топология Кауэра использует пассивные компоненты (шунтирующие конденсаторы и катушки индуктивности серии) осуществлять линейный аналоговый фильтр. Фильтр Баттерворта , имеющий заданную функцию передачи может быть реализована с использованием Кауэра 1-форму. К -й элемент задается
- СКзнак равно2грех[(2К-1)2Nπ]Кзнак равностранный{\ Displaystyle C_ {к} = 2 \ грех \ влево [{\ гидроразрыва {(2k-1)} {2n}} \ пи \ вправо] \ qquad к = {\ текст {нечетным}}}
- LКзнак равно2грех[(2К-1)2Nπ]Кзнак равночетное,{\ Displaystyle L_ {к} = 2 \ грех \ левой [{\ гидроразрыва {(2k-1)} {2n}} \ пи \ вправо] \ qquad к = {\ текст {даже}}.}
Фильтр может начать с последовательным индуктором , если это желательно, в этом случае L K являются K нечетными и C к являются к даже. Эти формулы могут быть объединены с пользой, сделав как L K и C K , равный г к . То есть, например к является иммитанс делится с .
- гКзнак равно2грех[(2К-1)2Nπ]Кзнак равно1,2,3,…,N,{\ Displaystyle g_ {к} = 2 \ грех \ влево [{\ гидроразрыва {(2k-1)} {2n}} \ пи \ вправо] \ qquad к = 1,2,3, \ ldots, п.}
Эти формулы применимы к двукратно с концевыми фильтра (то есть, источник и импеданс нагрузки оба равны единице) с & omega с = 1. Этот фильтр — прототип может быть масштабируется для других значений импеданса и частоты. Для однократно с концевым фильтром (то есть, один с приводом от идеального напряжения или источником тока) значение элементов задаются
- гJзнак равноaJaJ-1сJ-1гJ-1Jзнак равно2,3,…,N{\ Displaystyle g_ {J} = {\ гидроразрыва {а_ {J} а_ {J-1}} {C_ {J-1} {g_ J-1}}} \ qquad J = 2,3, \ ldots, п }
где
- г1знак равноa1{\ displaystyle g_ {1} = а_ {1}}
а также
- aJзнак равногрехπ2[(2J-1)N]Jзнак равно1,2,3,…,N{\ Displaystyle а_ {J} = \ грех {\ гидроразрыва {\ Pi} {2}} \ влево [{\ гидроразрыва {(2j-1)} {п}} \ право] \ qquad J = 1,2,3 , \ ldots, N}
- сJзнак равносоз2[πJ2N]Jзнак равно1,2,3,…,N,{\ Displaystyle C_ {J} = \ сов ^ {2} \ влево [{\ гидроразрыва {\ Pi J} {2n}} \ вправо] \ qquad J = 1,2,3, \ ldots, п.}
Напряжения привода фильтры должны начинаться с элементом серии и током управляемых фильтрами должны начинаться с шунтирующим элементом. Эти формы могут быть использованы при проектировании диплексеров и мультиплексоров .
Sallen-Key топологии
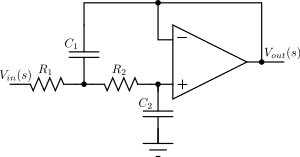
Саллен-Key топология использует активные и пассивные компоненты (неинвертирующие буфера, как правило , операционные усилители , резисторы и конденсаторы) осуществлять линейный аналоговый фильтр. Каждый этап Sallen-Key реализует сопряженную пару полюсов; общий фильтр реализован путем каскадного все этапы последо
29.2 Порядок расчета фнч Баттерворта.
1 Определим порядок фильтра. Порядок фильтра это число реактивных элементов в ФНЧ и ФВЧ.
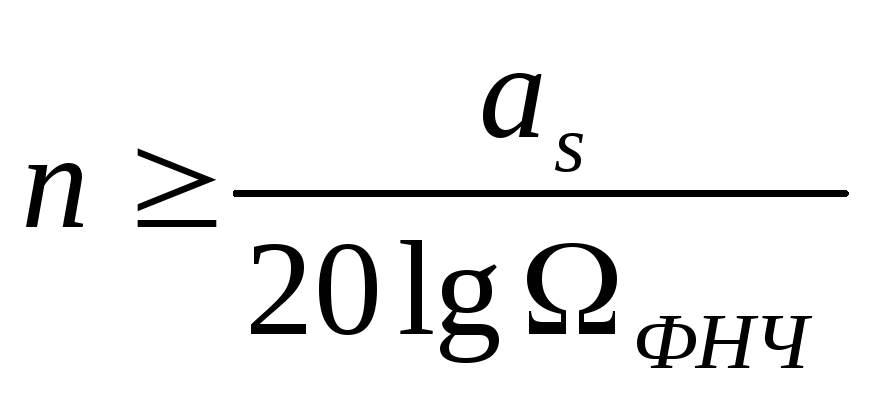 ;
;
где 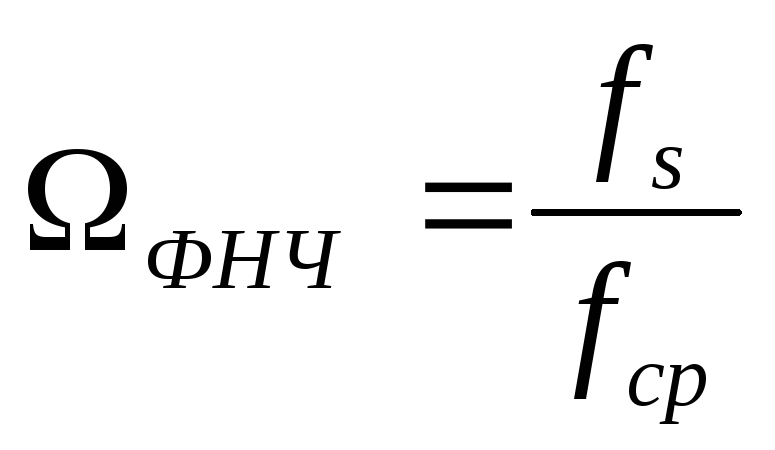 —
функция Баттерворта , соответствующая
допустимой частоте
—
функция Баттерворта , соответствующая
допустимой частоте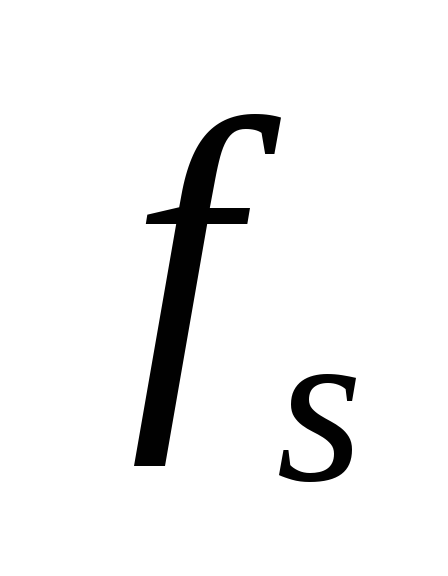 .
.
 —
допустимое затухание.
—
допустимое затухание.
2 Чертим схему фильтра полученного порядка. При практической реализации предпочтительны схемы с меньшим количеством индуктивностей.
3 Рассчитываем постоянные преобразования фильтра.
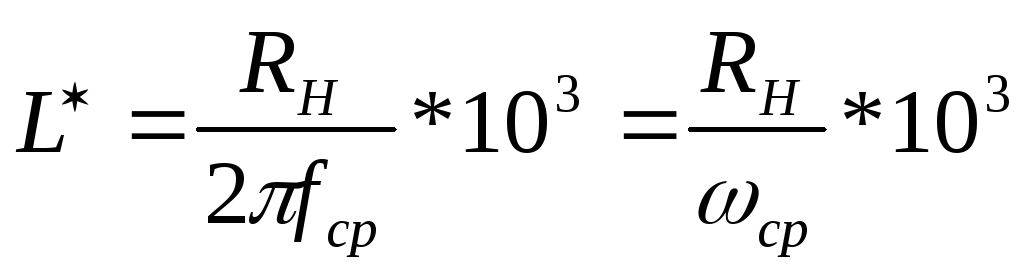 ,
мГн
,
мГн
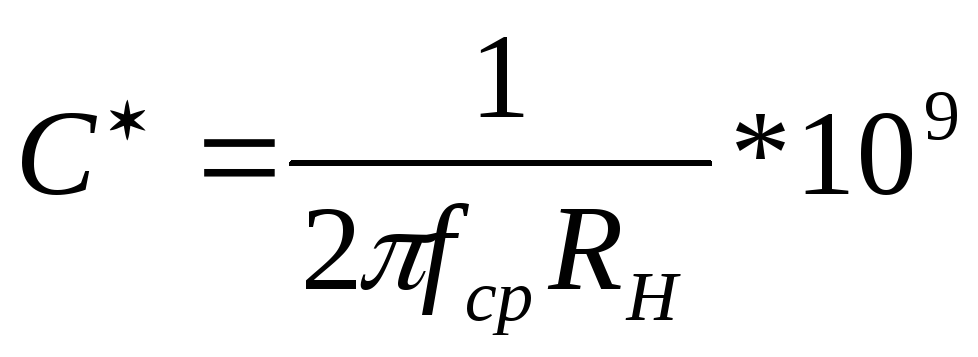 ,
нФ
,
нФ
4 Для идеального фильтра с сопротивлением
генератора 1 Ом, сопротивление нагрузки
1 Ом, 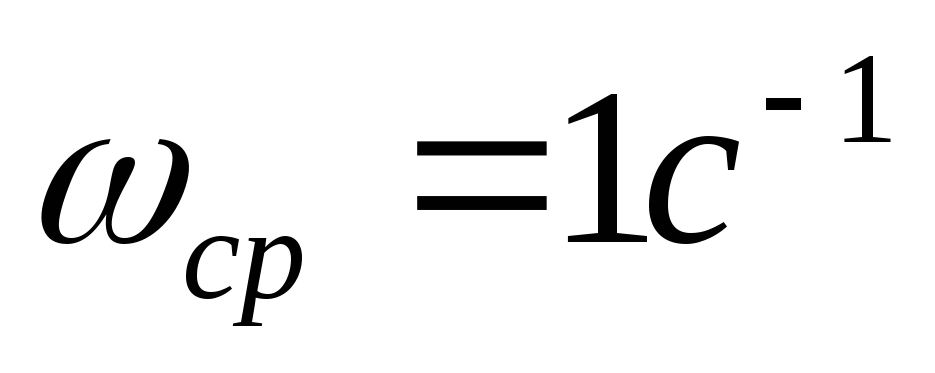 составлена
таблица нормированных коэффициентов
фильтра Баттерворта. В каждой строке
таблицы коэффициенты симметричны, к
середине увеличиваются, а затем
уменьшаются.
составлена
таблица нормированных коэффициентов
фильтра Баттерворта. В каждой строке
таблицы коэффициенты симметричны, к
середине увеличиваются, а затем
уменьшаются.
5 Чтобы найти элементы схемы, необходимо постоянные преобразования умножить на коэффициент из таблицы.
Порядок фильтра | Порядковые номера фильтра m | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 2 | |||||||||
2 | 1,414 | 1,414 | ||||||||
3 | 1 | 2 | 1 | |||||||
4 | 0,765 | 1,848 | 1,848 | 0,765 | ||||||
5 | 0,618 | 1,618 | 2 | 1,618 | 0,618 | |||||
6 | 0,518 | 1,414 | 1,932 | 1,932 | 1,414 | 0,518 | ||||
7 | 0,445 | 1,247 | 1,802 | 2 | 1,802 | 1,247 | 0,445 | |||
8 | 0,390 | 1,111 | 1,663 | 1,962 | 1,962 | 1,663 | 1,111 | 0,390 | ||
9 | 0,347 | 1 | 1,532 | 1,879 | 2 | 1,879 | 1,532 | 1 | 0,347 | |
10 | 0,313 | 0,907 | 1,414 | 1.782 | 1,975 | 1,975 | 1,782 | 1,414 | 0,907 | 0,313 |
Задача 1.
Рассчитать параметры фильтра низких
частот Баттерворта , если ПП=0,15 кГц, 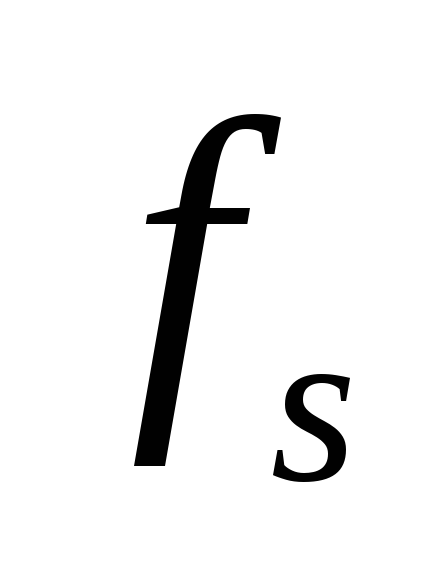 =25
кГц,
=25
кГц,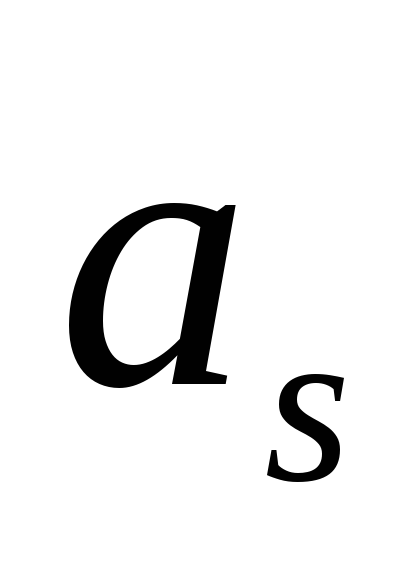 =30
дБ,
=30
дБ,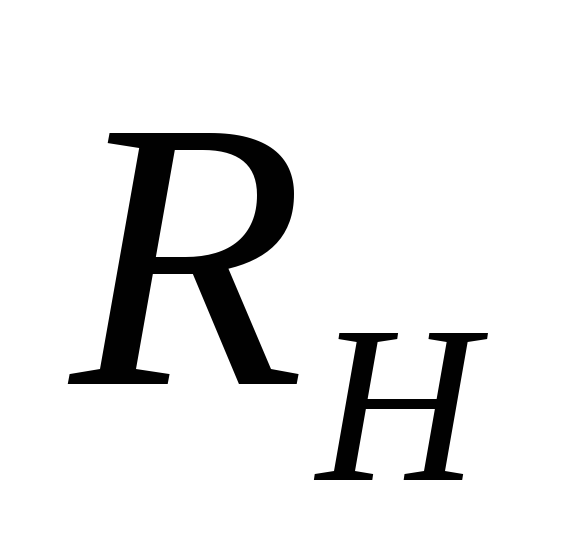 =75
Ом. Найти
=75
Ом. Найти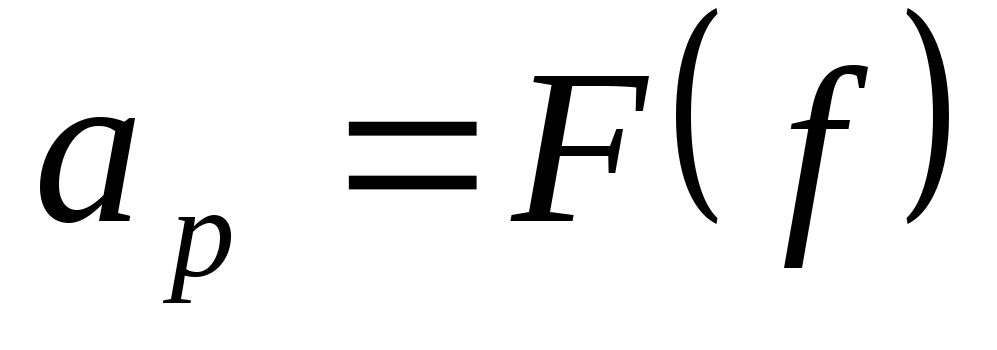 для трех точек.
для трех точек.
29.3 Фвч Баттерворта.
Фильтры ФВЧ – это четырехполюсники, у
кторых в диапазоне (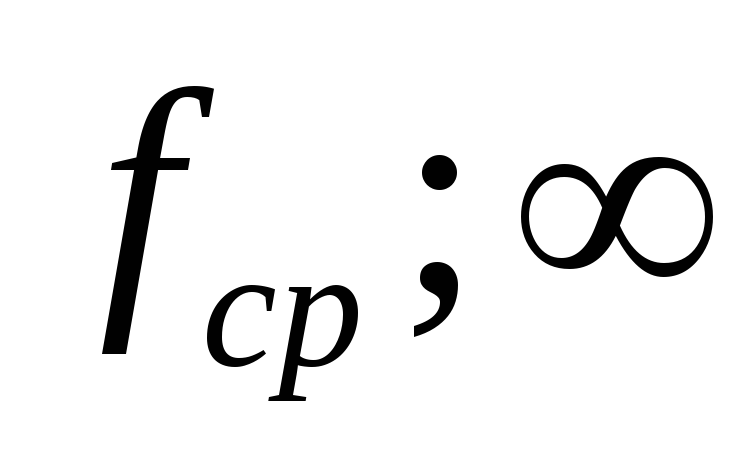 )
затухание мало, а в диапазоне (
)
затухание мало, а в диапазоне (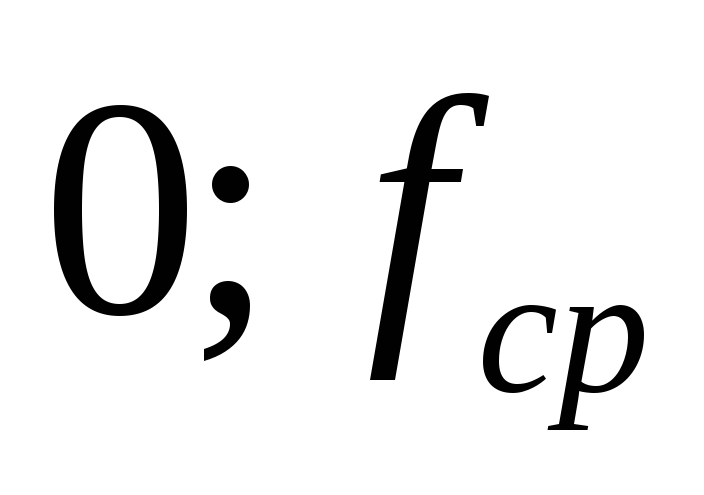 )
– велико, то есть фильтр должен пропускать
в нагрузку токи верхних частот.
)
– велико, то есть фильтр должен пропускать
в нагрузку токи верхних частот.
Так как ФВЧ должен пропускать токи высоких частот, то на пути тока, идущего в нагрузку, должен стоять частотно зависимый элемент, который хорошо пропускает токи высоких частот и плохо токи низких частот. Таким элементом является конденсатор.
Ф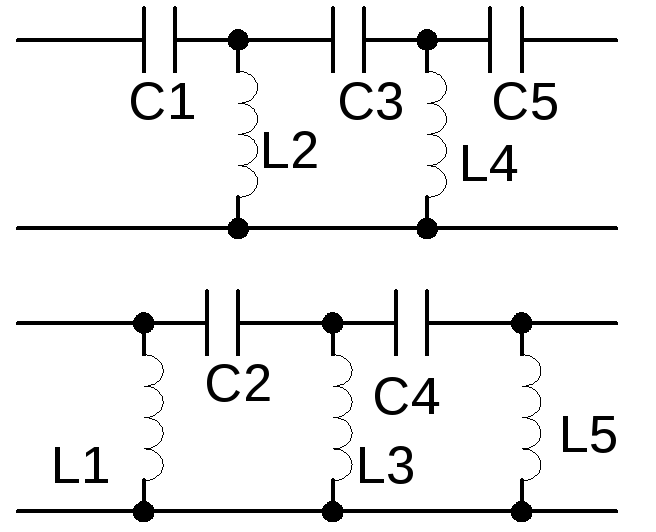 ВЧ
Т-образный
ВЧ
Т-образный
ФВЧ П-образный
Конденсатор ставят последовательно с
нагрузкой, так как 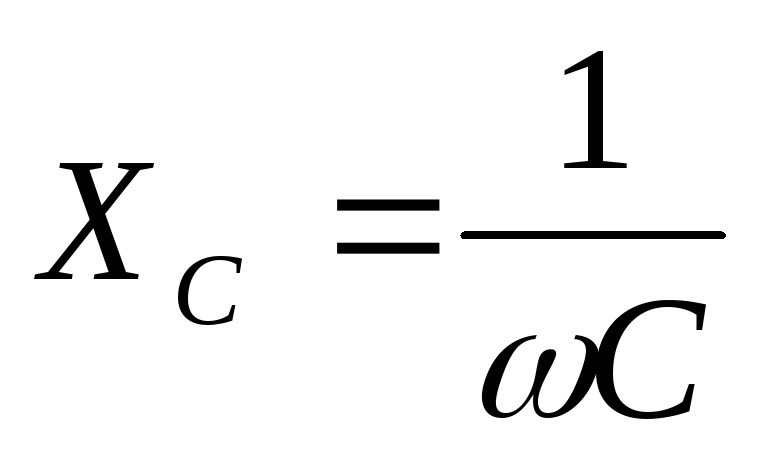 и с ростом частоты
и с ростом частоты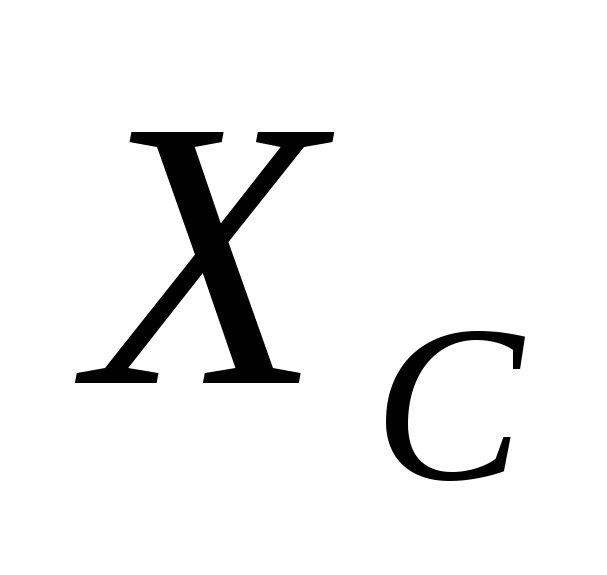 уменьшается, следовательно токи высоких
частот легко проходят в нагрузку через
конденсатор. Катушку индуктивности
ставят параллельно нагрузке, так как
уменьшается, следовательно токи высоких
частот легко проходят в нагрузку через
конденсатор. Катушку индуктивности
ставят параллельно нагрузке, так как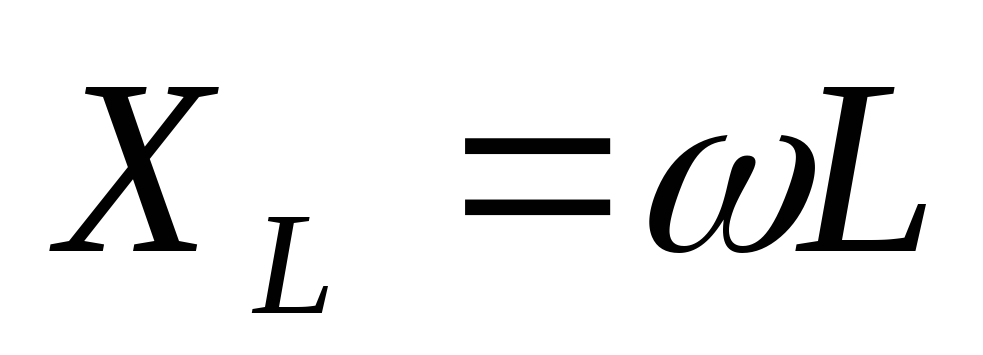 и с увеличением частоты увеличивается
и с увеличением частоты увеличивается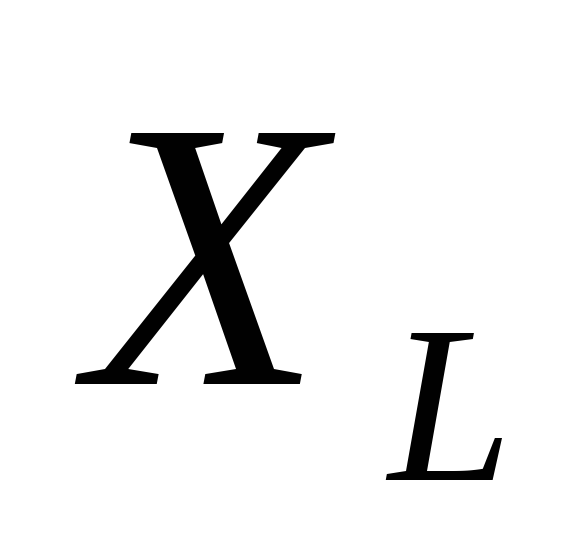 ,
поэтому токи низких частот замыкаются
через индуктивности и не попадут в
нагрузку.
,
поэтому токи низких частот замыкаются
через индуктивности и не попадут в
нагрузку.
Расчет ФВЧ Баттерворта аналогичен расчету ФНЧ Баттерворта, проводится по тем же формулам, только
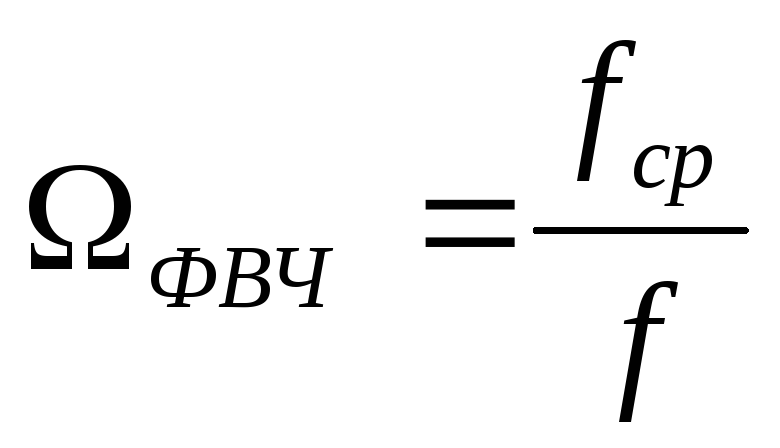
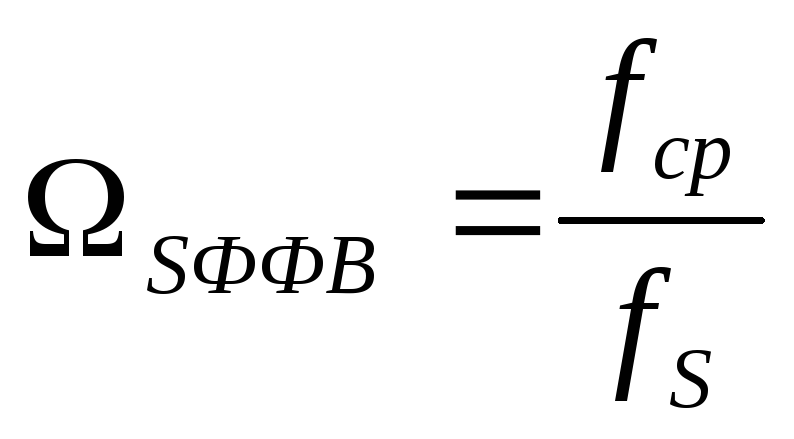
Чтобы рассчитать элементы фильтра, необходимо постоянные преобразования разделить на коэффициент из таблицы.
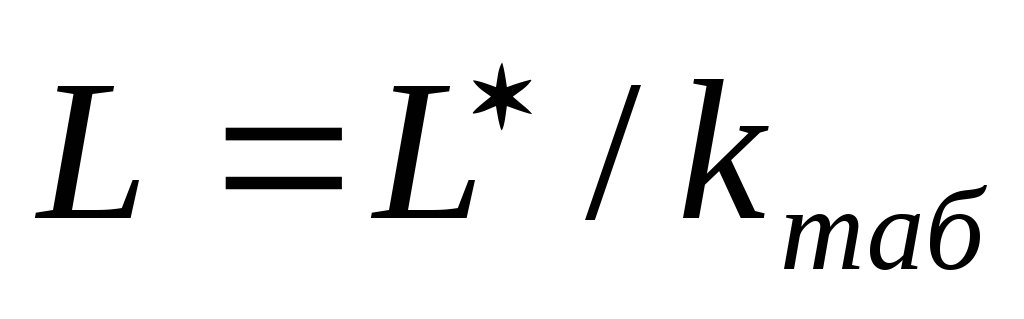
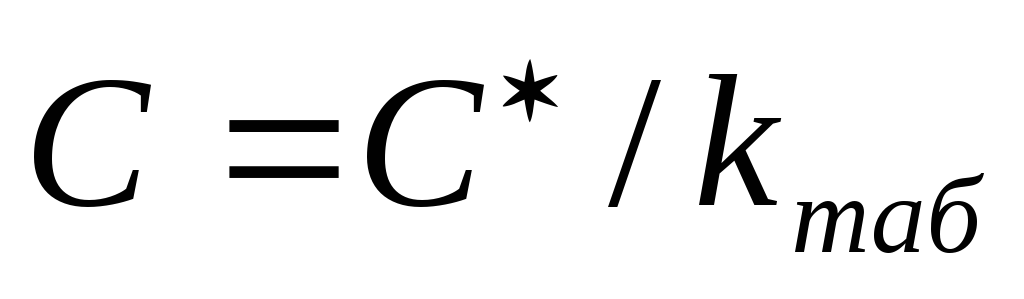 .
.
Задача.
Рассчитать фильтр верхних частот ФВЧ
Баттерворта, если 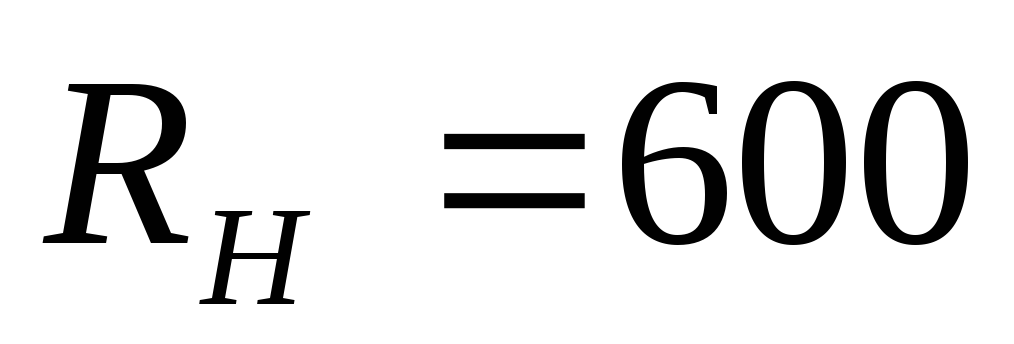 Ом,
Ом,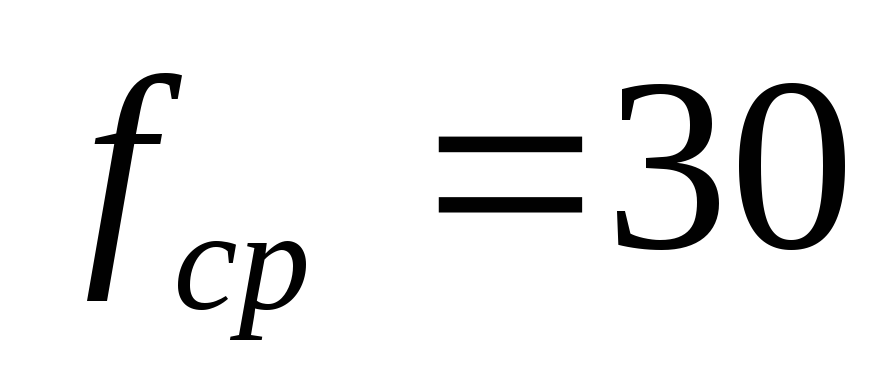 кГц,
кГц,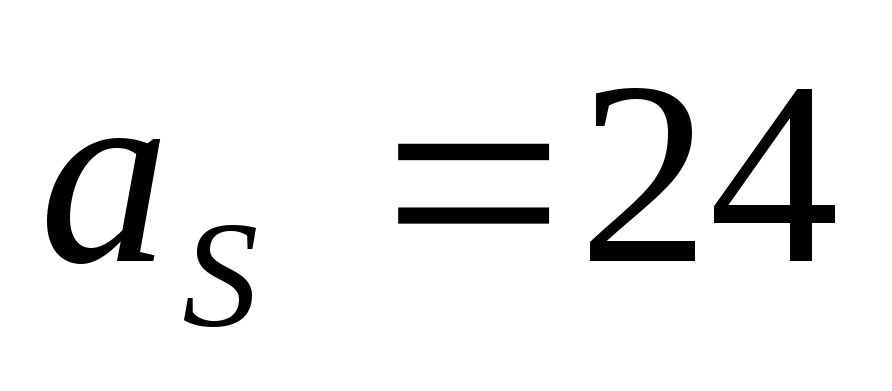 дБ,
дБ,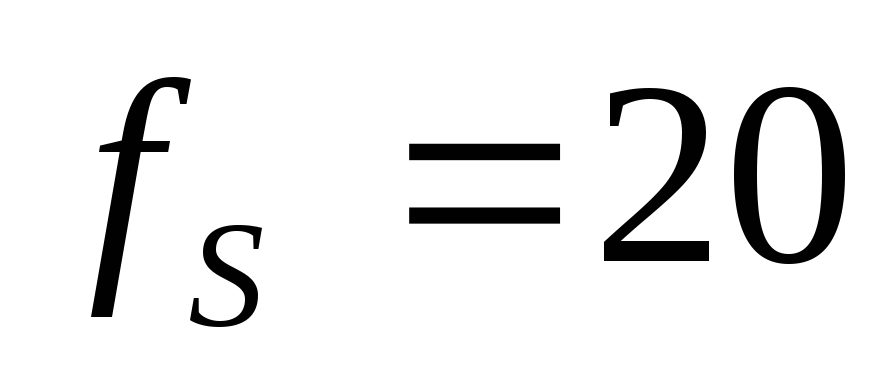 кГц.
Найти:
кГц.
Найти: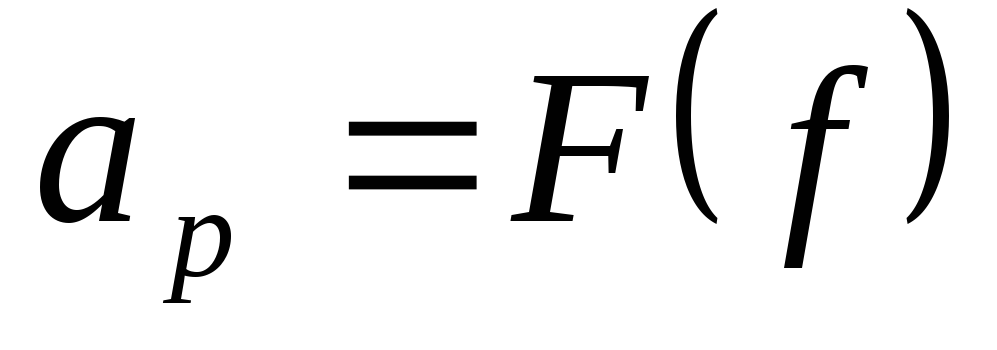 .
.
Тема занятия 30: Полосовые и режекторные фильтры Баттерворта.
Схема ФНЧ 2-го порядка по Баттерворду
В радиотехнике регулярно возникает необходимость в использовании различных фильтров. Чаще других возникает необходимость в построении Фильтра Низких Частот (ФНЧ). Зачастую обходятся обычной RC-цепочкой. Но в некоторых случаях требуется более крутой спад частотной характеристики. Довольно универсальным можно назвать фильтр Баттерворда. Рассмотрим схему ФНЧ 2-го порядка.
Схема ФНЧ 2-го порядка
В даташите на AD823 была найдена удобная для повторения схема ФНЧ второго порядка. С приведенными в даташите номиналами деталей R1, R2, C1 и C2 частота среза фильтра равна 200кГц.
АЧХ сигнала после фильтра приведена на следующей картинке:
Формулы для расчета ФНЧ 2-го порядка
Ребята из Analog Devices рекомендуют выбрать величину номинала резисторов, в пределах от 10 до 100кОм, а затем по приводимым формулам рассчитать емкости конденсаторов.
Стоящее в числителе число 1.414 это √2, а число 0.707, это 1/√2. Если поделить одно на второе получим, что емкость С1 в два раза больше емкости С2.
Это видно и из самих формул. Не знаю почему нельзя было привести формулу только для С2 и написать что С1=С2*2. Выглядело бы это следующим образом.
В процессе углубления в тему фильтров было замечено, что большинство авторов начинают рассчет с того, что выбирают величину резистора, а затем рассчитывают величины емкостей.
Не знаю как у Вас, но у меня прецизионные конденсаторы не такое частое явление. По этой причине, на мой взгляд, проще взять за основу емкость имеющегося в наличии конденсатора и уже под него подобрать резисторы.
Для расчетов достаточно просто поменять местами R и C в формуле для C2.
Расчет элементов ФНЧ 2-го порядка
В закромах родины были найдены конденсаторы на 82 пФ точностью 1%. Требовалась частота среза в 27 кГц. При расчетах величину конденсатора следует брать в фарадах, тогда величину резистора мы получим в Омах.
Подставляя нужные значения в переделанную формулу для С2 находим нужную величину сопротивления.
Итак, получилось, что нужен резистор номиналом в 50849Ом. Отлично, это укладывается в рекомендуемый диапазон 10-100кОм. Самая близка величина резистора в стандартном ряду — 51кОм.
Теперь подсчитаем какой будет частота среза получившейся цепи с учетом выбора близкого резистора. Для подсчета fcutoff наша формула будет выглядеть следующим образом:
Подставляем величины в формулу и проводим несложные расчеты.
Отлично! Думаю что ошибка в 0.3% и не ошибка вовсе. Тут точность номиналов элементов то +-1%.
А что же делать с конденсатором C1, где взять 162пФ? Для этого просто припаиваем два таких же конденсатора по 82 пФ параллельно.
Последний конденсатор
Обратите внимание, что на схеме так же присутствует конденсатор в 50пФ, включенный с выхода на землю. Можно считать, что этот конденсатор включен к инвертирующему входу усилителя и обеспечивает его привязку к земле по переменке. Его я так же установил 82 пФ.
Отсутствие этого конденсатора может приводить к самовозбуждению ОУ. Особенно это актуально, если вы используете скоростные ОУ, например тот же AD823.
Вместо заключения
По хорошему, до и после фильтра желательно установить повторители, для развязки и согласованию по сопротивлениям. Это касается любого фильтра. Вопросу повторителей посвящена отдельная статья: Схема повторителя напряжение на ОУ. Мощный повторитель напряжения на TDA2030.
Расчет аналогового нормированного фильтра нижних частот Баттерворта
Исходные данные для расчета нормированного ФНЧ Баттерворта
В предыдущем разделе был рассмотрена постановка задачи расчета передаточной характеристики аналогового фильтра, и проанализированы основные виды аппроксимирующих полиномов АЧХ фильтра. В данном разделе мы рассмотрим расчет передаточной характеристики аналогового нормированного фильтра нижних частот (ФНЧ) Баттерворта по заданым праметрам квадрата АЧХ , показанным на рисунке 1.Рисунок 1. Квадрат АЧХ аналогового нормированного ФНЧ Баттерворта
Мы называем этот фильтр нормированным, потому что частота среза рад/c. Нормированный ФНЧ является прототипом из которого можно получить любой другой фильтр: ФНЧ, ФВЧ, полосовой или режекторный, путем частотных преобразований передаточной функции .Приведем основные соотношения связывающие параметры аппроксимации АЧХ:
(1)
Аппроксимация квадрата АЧХ нормированного ФНЧ Баттерворта представляется в виде:(2)
Порядок фильтра Баттерворта рассчитывается из уравнения:
(3)
Прологарифмируем правую и левую части уравнения (3) и получим:
(4)
Все вышеприведенные соотношения уже были рассмотрены в предыдущем разделе. Мы привели их еще раз без пояснений, и они нам будут необходимы при расчете фильтра Баттерворта. Исходными данными для расчета нормированного ФНЧ Баттерворта служат: частота среза рад/c, переходная полоса, задаваемая частотой , допустимое искажение в полосе пропускания (дБ) и требуемое подавление в полосе заграждения (дБ). На основе исходных данных, мы можем рассчитать параметры , согласно (1), а также требуемый порядок фильтра согласно (4). Для расчета передаточной характеристики мы должны получить выражения для нулей и полюсов нормированного ФНЧ Баттерворта.Нули и полюса аналогового нормированного ФНЧ Баттерворта
(5)
Очевидно, что ни при каких конечных комплексных выражение (5) не равно нулю, значит передаточная характеристика нормированного ФНЧ Баттерворта не имеет конечных нулей. Для расчета полюсов нормированного ФНЧ Баттерворта приравняем знаменатель к нулю:(6)
Рассмотрим отдельно четные и нечетные порядки фильтра . При четных имеем:(7)
Представим в правой части через комплексную экспоненту , , тогда(8)
Прологарифмируем левую и правую части уравнения (8) и получим:
(9)
Преобразуем:
(10)
тогда
(11)
и окончательно можно записать выражения для полюсов квадрата модуля передаточной функции при четных :(12)
При нечетных из выражения (6) имеем:(13)
Представим в правой части через комплексную экспоненту , , тогда(14)
Прологарифмируем левую и правую части уравнения (14) и получим:
(15)
Преобразуем (15):
(16)
тогда:
(17)
И окончательно можно записать выражения для полюсов квадрата модуля предаточной функции при нечетных :(18)
На рисунке 2 показано расположение полюсов квадрата модуля передаточной функции, заданной выражением (5) при четном (слева) и нечетном (справа) порядках фильтра Баттерворта. Рисунок 2: Расположение полюсов квадрата модуля передаточной функции при четном и нечетном порядках фильтра БаттервортаПередаточная характеристика аналогового нормированного ФНЧ Баттерворта
В предыдущем параграфе мы получили выражения для полюсов квадрата модуля . Мы получили, что фильтра Баттерворта имеет полюсов, расположенных как в левой, так и в правой половинах комплексной плоскости . Для получения устойчивого и физически реализуемого фильтра необходимо, чтобы все нули и полюса располагались в левой полуплоскости комплексной плоскости, или на мнимой оси . Тогда для расчета передаточной функции фильтра Баттерворта необходимо из всех полюсов квадрата ее модуля выбрать только те, что лежат в левой полуплоскости. Все полюса расположенные в левой полуплоскости могут быть записаны как для четного, так и для нечетного порядка (смотри рисунок 2):(19)
Или перепишем (19) в тригонометрической форме:
(20)
Таким образом мы задали все полюса передаточной функции нормированного ФНЧ Баттерворта порядка , расположенные в левой полуплоскости комплексной плоскости . Тогда передаточная функция нормированного ФНЧ Баттерворта может быть представлена:(21)
Обратим внимание, что все полюса передаточной функции фильтра Баттерворта четного порядка (смотри рисунок 2) представляют собой комплексно-сопряженные пары, а у фильтра нечетного порядка есть один вещественный полюс. Тогда можно представить передаточную функцию нормированного ФНЧ Баттерворта при помощи биквадратной формы. Для четного :(22)
Тогда окончательно можно записать:
(23)
В случае нечетного имеем дополнительный вещественный полюс . Тогда для нечетного можно представить передаточную функцию нормированного ФНЧ Баттерворта при помощи биквадратной формы как:(24)
Окончательно можно объединить выражения (23) и (24). Для любого целого ( может принимать значения 0 или 1) передаточную функцию нормированного ФНЧ Баттерворта можно представить в виде:(25)
Коэффициент передачи фильтра Баттерворта на нулевой частоте равен:(26)
Для нормировки коэффициента передачи на нулевой частоте необходимо передаточную функцию нормированного ФНЧ Баттерворта (25) разделить на . Тогда получим:(27)
(28)
Такая форма записи (28) передаточной характеристики получила широкое распространение ввиду того, что не требуется нормировки. Однако выражение (27) позволяет регулировать коэффициент передачи фильтра на частоте среза и является более общей.Пример расчета аналогового нормированного ФНЧ Баттерворта
Рассчитаем нормированный ФНЧ Баттерворта при следующих параметрах:
(29)
Шаг 1
Рассчитываем все необходимые параметры исходя из выражения (1):
(30)
Шаг 2
Рассчитываем порядок фильтра согласно выражению (4):
(31)
Округляем в большую сторону и получаем порядок фильтра .Шаг 3
(32)
Рассчитываем значения . В нашем случае , поэтому будет только одно значение равное :(33)
Тогда передаточную характеристику нормированного ФНЧ Баттерворта можно записать:(34)
На этом расчет фильтра Баттерворта окончен. Комплексный коэффициент передачи полученного фильтра равен:(35)
На рисунке 3 показаны квадрат АЧХ , ФЧХ , групповая задержка и импульсная характеристика рассчитанного фильтра Баттерворта.Рисунок 3: Квадрат АЧХ, ФЧХ, групповая задержка и импульсная характеристика полученного фильтра
Обратите внимание, что по оси абсцисс частота представлена в логарифмическом масштабе.Выводы
Таким образом, в данном разделе мы рассмотрели порядок расчета передаточной функции аналогового нормированного ФНЧ Баттерворта и привели пример расчета фильтра по заданным параметрам АЧХ.
Список литературы
[1] Лем Г. Аналоговые и цифровые фильтры Москва, Мир, 1982.
[2] Sophocles J. Orfanidis Introduction to Signal Processing Rutgers University, 2010. [PDF]
[3] Sophocles J. Orfanidis Lecture notes on elliptic filter design Rutgers University, 2006. [PDF]
[4] Оппенгейм А., Шафер Р. Цифровая обработка сигналов Пер. с англ., Москва, Техносфера, 2006.
[5] Сергиенко А.Б. Цифровая обработка сигналов Санкт-Петербург, Питер, 2002.
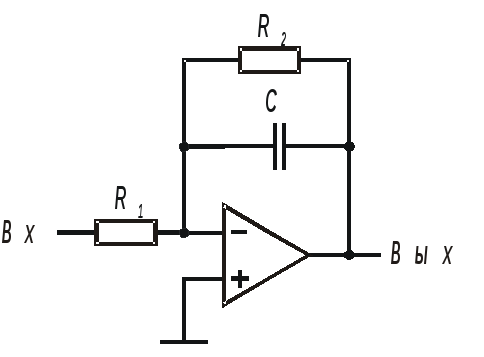
Низкочастотный фильтр Баттерворта второго порядка
Низкочастотный фильтр Баттерворта второго порядка
Воспользуемся таблицами нормированных многочленов Баттерворта, чтобы найти коэффициенты для фильтра второго порядка:
s? + 1,414s + 1.
Фильтр второго порядка показан на рис. 5.24. Для вводного примера найдем элементы R1, R2, R и С для фильтра Баттерворта с частотой среза fc=5 кГц. Как обычно, в качестве частоты среза принимается частота, при которой характеристика снижается на 3 дБ. Согласно теории, низкочастотный коэффициент усиления задается выражением:
Avo = 3 – 2k,
где k представляет собой коэффициент затухания, определенный как половина коэффициента при s? из таблицы полиномов Баттерворта (см. Hillburn and Johnson. Manual of Active Filter Designs, McGraw-Hill, 1973). Для этого примера k=0,707 и
Av0 = 3 — 1,414 = 1,586.

Рис. 5.24. Низкочастотный фильтр Баттерворта второго порядка
Допустим, что R1=10 кОм. Из выражения

получаем R2=5,86 кОм. Если положить R=1 кОм, из выражения fc=1/(2?RC) найдем С=31,83 нФ. Чтобы проверить теорию Баттерворта, используем идеальную модель ОУ в качестве подсхемы, как показано на рис. 5.25. Для этого создайте следующий входной файл:
Second-Order Butterworth Filter
V1 1 0 AC 1mV
R3 1 2 1k
R4 2 3 1k
R1 4 0 10k
R2 5 4 5.86k
C1 2 5 31.83nF
C2 3 0 31.83nF
X 4 3 5 iop
.AC DEC 40 1 100kHz
.PROBE
.subckt iop m p vo
e vo 0 p m 2e5
rin m p 1meg
.ends
.END

Рис. 5.25. Подсхема для идеального ОУ
Проведите анализ и получите график V(5)V(1). Выясните, что Аv0=1,586, что соответствует нашему расчету. Затем удалите этот график и получите график зависимости
20·lg(V(5)/(V(1)·1,587В)).
Убедитесь, что fc=5 кГц. Этот фильтр второго порядка должен иметь вдвое большую крутизну спада, чем фильтр первого порядка. Вспомним, что фильтр первого порядка имеет скорость спада 20 дБ/дек. Убедитесь, что при f=10 кГц Av=12,31 дБ, а при f=100 кГц Av=52,05 дБ, что составляет приблизительно 40 дБ/дек. Этот график показан на рис. 5.26.

Рис. 5.26. График Боде для низкочастотного фильтра Баттерворта второго порядка
Данный текст является ознакомительным фрагментом.Читать книгу целиком
Поделитесь на страничкеСледующая глава >

