Основные физические величины, их буквенные обозначения в физике.
Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Физика и основные физические величины
Благодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения — законы Вселенной, конкретнее — то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.
Знак дельта и его значение. Знак дельта в Ворде
Достаточно часто приходится в процессе набора различных документов вводить нам знак дельта.
Именно…
Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого — первого в России учебника по физике.
Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд — их всего 7:
- длина,
- масса,
- время,
- сила тока,
- температура,
- количество вещества,
- сила света.
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры — Т. Также у всех величин есть своя единица измерения: у силы света — кандела (кд), а у количества вещества единицей измерения является моль.
Узнаем что измеряет физическая величина
В природе существует большое количество самых разнообразных сил, влияющих на предметы и окружающую…
Производные физические величины
Производных физических величин значительно больше, чем основных.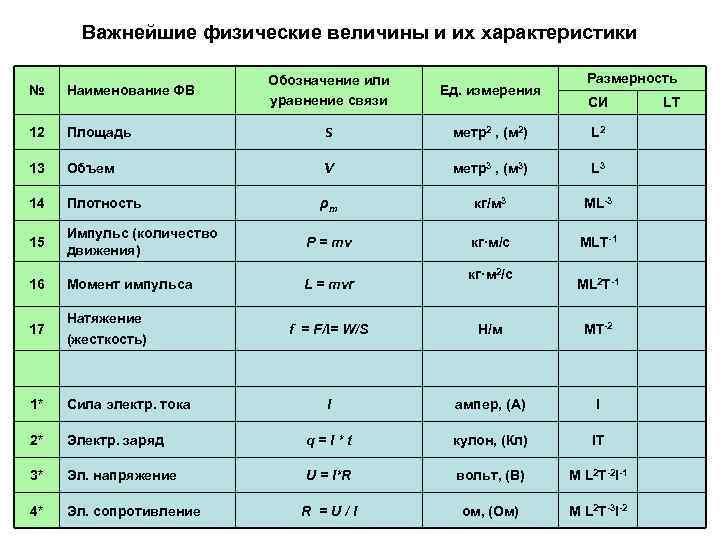
Их насчитывается 26, причем часто некоторые из них приписывают к основным.
Итак, площадь является производной от длины, объем — также от длины, скорость — от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила — произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы — все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
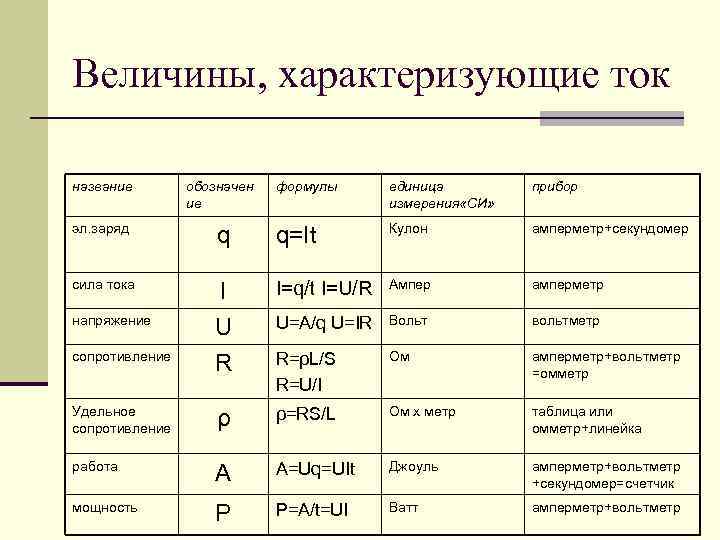
Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы — А, а для энергии — Е.
Электрический заряд принято обозначать буквой q, а магнитный поток — Ф.
СИ: общие сведения
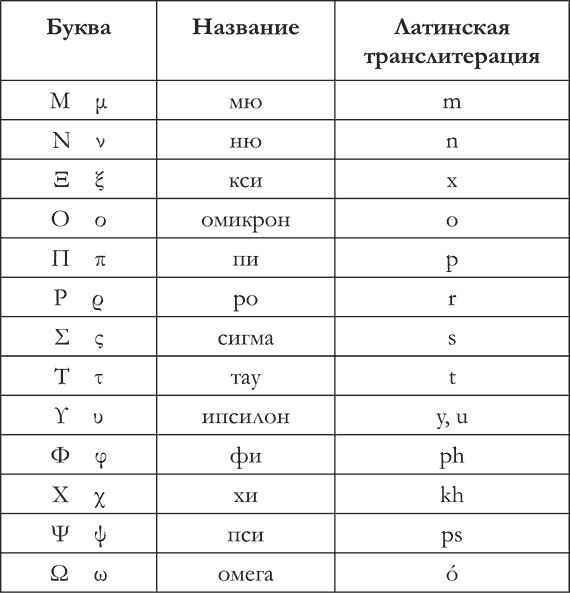
Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях — греческого. Также возможно в качестве обозначения использование специальных символов.
Заключение
Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других.
Производные же величины получают при помощи умножения и деления из основных.
Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки
Шпаргалки по физике за 7 класс
В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачать шпаргалку со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).
Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Измерение физических величин
Измерением называют определение с помощью инструментов и технических средств числового значения физической величины. Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения. |
В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:
ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.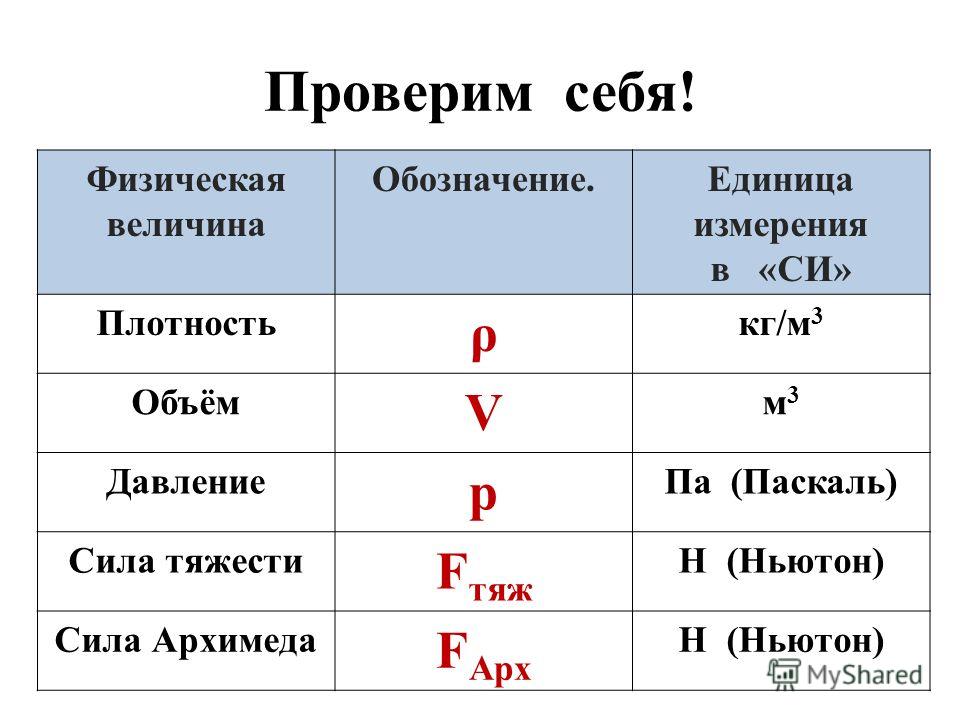
Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.
Выделяют прямое и косвенное измерение:
при прямом измерении результат можно увидеть непосредственно на шкале инструмента;
при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).
Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.
Механическое движение: формулы за 7 класс
Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. |
Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики.Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.
Изучение механического движения в курсе по физике за 7 класс включает следующие термины:
Перемещение тела — минимальное расстояние, которое соединяет две выбранные точки траектории движения.
Траектория движения — мысленная линия, вдоль которой перемещается тело.
Путь — длина траектории тела от начальной до конечной точки.
Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.
Ускорение — быстрота изменения скорости, с которой движется тело.
Равномерное движение — механическое движение, при котором тело за любые равные промежутки времени проходит одно и то же расстояние. |
Формула скорости равномерного прямолинейного движения:
V = S / t, где S — путь тела, t — время, за которое этот путь пройден.
Формула скорости равномерного криволинейного движения:
где S1 и S2 — отрезки пути, а t1 и t2 — время, за которое был пройден каждый из них.
Единица измерения скорости в СИ: метр в секунду (м/с).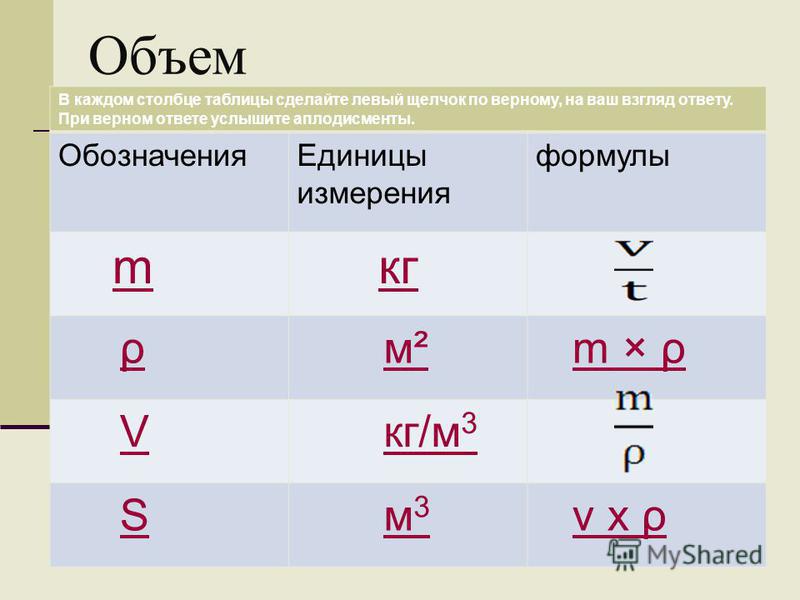
Формула скорости равноускоренного движения:
V = V0 + at, где V0— начальная скорость, а — ускорение.
Единица измерения ускорения в СИ: м/с2.
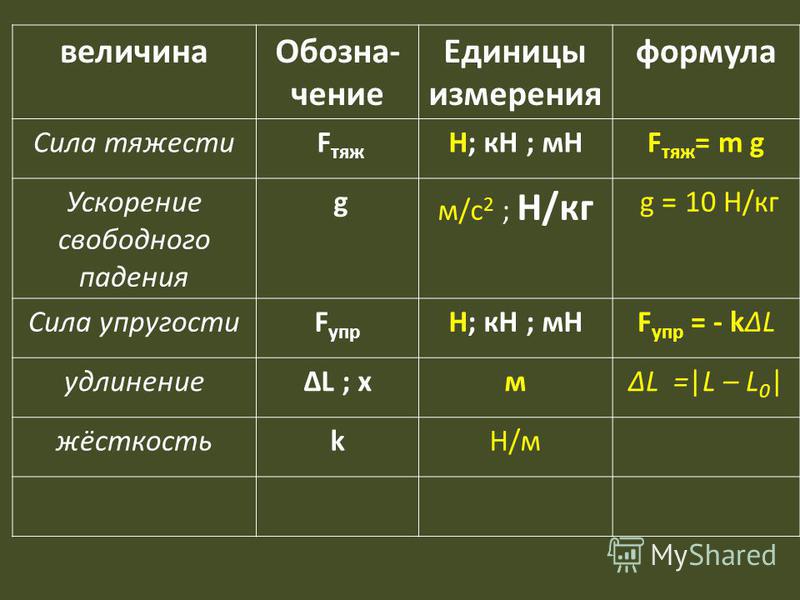
Сила тяжести, вес, масса, плотность
Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.
Вес тела или вещества — это физическая величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес. |
Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.
Формула веса:
P = mg, где m — масса тела, g — ускорение свободного падения.
Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.
g = 9,806 65 м/с2 или 9,8 Н/кг
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.
Fтяж = mg
Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.
Плотность тела или вещества — величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему. |
Формула плотности:
ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.
Единица измерения плотности в СИ: кг/м3.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Механический рычаг, момент силы
О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз. Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы. |
Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.
Уравнение равновесия рычага:
F1 × l1 = F2 × l2
Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.
Момент силы — это физическая величина, равная произведению модуля силы F на ее плечо l. |
Формула момента силы:
M = F × l, где F — модуль силы, l — длина плеча.
Единица измерения момента силы в СИ: ньютон-метр (Н·м).
Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении. |
Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.
М1 + М2 + Мn + … = 0
Давление, сила давления
Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности. Сила давления направлена перпендикулярно поверхности. |
Формула давления:
p = F / S, где F — модуль силы, S — площадь поверхности.
Единица измерения давления в СИ: паскаль (Па).
1 Па = 1 Н/м2
Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.
Формулу для расчета силы давления вывести несложно:
F = p × S
В задачах по физике за 7 класс сила давления, как правило, равна весу тела.
Давление газов и жидкостей
Жидкости и газы, заполняющие сосуд, давят во всех направлениях: на стенки и дно сосуда. Это давление зависит от высоты столба данного вещества и от его плотности.
Формула гидростатического давления:
р = ρ × g × h, где ρ — плотность вещества, g — ускорение свободного падения, h — высота столба.
g = 9,8 м/с2
Единица измерения давления жидкости или газа в СИ: паскаль (Па).
Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.
Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления. |
Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:
p = F / S, где F — модуль силы, S — площадь поверхности.
Сообщающиеся сосуды
Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. |
Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.Если ρ1 = ρ2, то h1 = h2 и ρ1gh1 = ρ2gh2, где:
p — плотность жидкости,
h — высота столба жидкости,
g = 9,8 м/с2.
Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.
Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.
Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. |
д.).Если под поршнем 1 образуется давление p1 = f1/s1, а под поршнем 2 будет давление p2 = f2/s2, то, согласно закону Паскаля, p1 = p2
Следовательно,
Силы, действующие на поршни гидравлического пресса F1 и F2, прямо пропорциональны площадям этих поршней S1 и S2.
Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.
Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ. |
Формула архимедовой силы:
Fa = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с2.
Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:
если плотность тела выше плотности среды, оно уйдет на дно;
если плотность тела ниже, оно всплывет на поверхность.
Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.
Работа, энергия, мощность
Механическая работа — это физическая величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение. |
Формула работы в курсе физики за 7 класс:
A = F × S, где F — действующая сила, S — пройденный телом путь.
Единица измерения работы в СИ: джоуль (Дж).
Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.
Мощность — это физическая величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения. |
Формула мощности:
N = A / t, где A — работа, t — время ее совершения.
Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.
N = F × v, где F — сила, v — средняя скорость тела.
Единица измерения мощности в СИ: ватт (Вт).
Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.
Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.
Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.
Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:
Кинетическая энергия | Пропорциональна массе тела и квадрату его скорости. | Ek = mv2/2 |
Потенциальная энергия | Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания. | Ep= mgh |
Полная механическая энергия | Складывается из кинетической и потенциальной энергии. | E = Ek+Ep |
Сохранение и превращение энергии | Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу. | Ek+ Ep= const |
Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.
Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии. |
Формула для расчета КПД:
где Ап— полезная работа, Аз— затраченная работа.
КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т.
д.
Удачи на экзаменах!
Орбитальный | химия и физика
электронные орбитали в атомах
Смотреть все СМИ
- Ключевые люди:
- Роберт Бернс Вудворд Мария Митчел Роальд Хоффманн Фукуи Кеничи Арнольд Зоммерфельд
- Похожие темы:
- электронное продвижение перекрывать энергия сопряжения узловая плоскость молекулярная орбиталь
См. все связанное содержимое →
орбитальный , в химии и физике математическое выражение, называемое волновой функцией, которое описывает свойства, характерные не более чем для двух электронов вблизи атомного ядра или системы ядер, как в молекула. Орбиталь часто изображают как трехмерную область, внутри которой существует 95-процентная вероятность обнаружения электрона ( см. иллюстрацию ).
Понимание концепции различных форм и размеров орбит
Просмотреть все видео к этой статье Атомные орбитали обычно обозначаются комбинацией цифр и букв, которые представляют определенные свойства электронов, связанных с орбиталями, например, 1 s , 2 p , 3 d , 4 ф .
Цифры, называемые главными квантовыми числами, указывают уровни энергии, а также относительное расстояние от ядра. Электрон 1 с занимает ближайший к ядру энергетический уровень. Менее прочно связанный 2 s электрон проводит большую часть своего времени дальше от ядра. Буквы, s , p , d и f обозначают форму орбитали. (Форма является следствием величины углового момента электрона, возникающего в результате его углового движения.) Орбиталь s имеет сферическую форму с центром в ядре. Таким образом, 1 s электрон почти полностью ограничен сферической областью, близкой к ядру; 2 s электрон ограничен несколько большей сферой. Орбиталь p имеет приблизительную форму пары долей на противоположных сторонах ядра или несколько форму гантели. Электрон в p орбиталь имеет одинаковую вероятность оказаться в любой половине. Формы других орбиталей более сложны. Буквы s , p , d , f первоначально использовались для описательной классификации спектров на серии, называемые острыми, основными, диффузными и фундаментальными, до того, как стала известна связь между спектрами и конфигурацией атомных электронов.
Викторина «Британника»
Физика и естественное право
Узнайте о расположении электронных орбиталей и энергетических уровней в атомах
Просмотреть все видео к этой статье№ p орбитали существуют на первом энергетическом уровне, но есть набор из трех на каждом из более высоких уровней. Эти тройки ориентированы в пространстве так, как если бы они находились по трем осям под прямым углом друг к другу, и их можно различить нижними индексами, например, 2 p x , 2 p y , 2 р z . На всех основных уровнях, кроме первых двух, имеется набор из пяти орбиталей d , а на всех основных уровнях, кроме первых трех, — набор из семи орбиталей f , все со сложной ориентацией.
Только два электрона из-за их спина могут быть связаны с каждой орбиталью. Можно представить, что электрон вращается вокруг своей оси по или против часовой стрелки, что делает каждый электрон крошечным магнитом.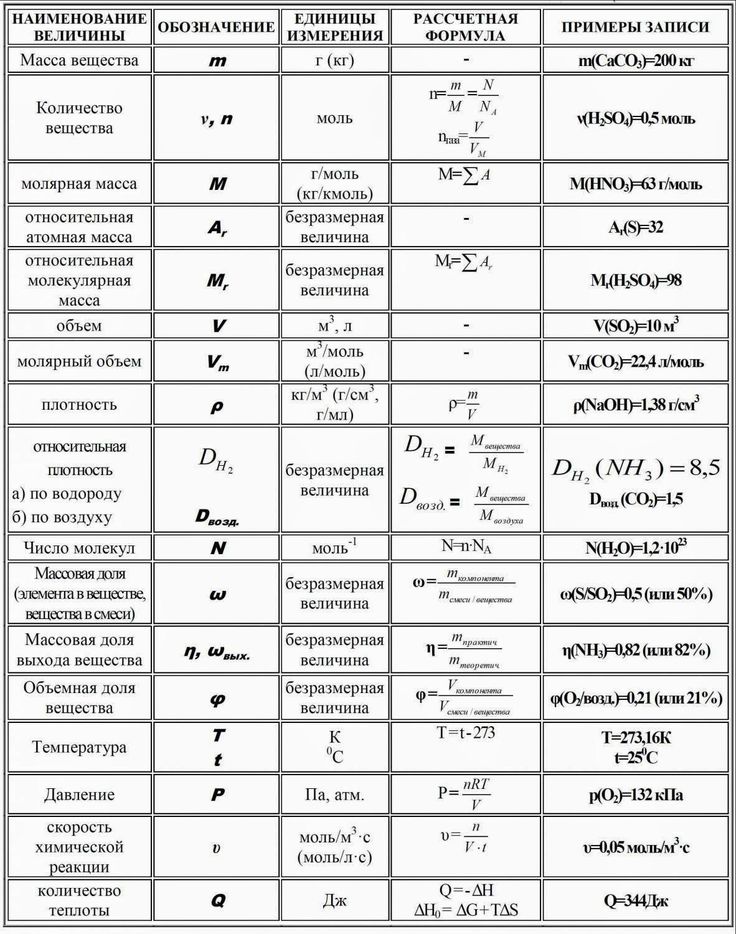
Электроны на полных орбиталях образуют пары с противоположными спинами или противоположными магнитными полярностями.
The Editors of Encyclopaedia Britannica
Несколько параллельно с маркировкой атомных энергетических состояний метки ядерных состояний определяются их угловыми моментами. Для одночастичных состояний вы знаете, что спиновая часть равна S=1/2, а затем орбитальный угловой момент используется для определения буквенного обозначения в соответствии со спектроскопическими обозначениями. Если L=2, то состояние обозначается буквой «d», и тогда полный угловой момент может быть либо L-S=3/2, либо L+S=5/2. Затем два состояния будут помечены: 1d 3/2 и 1d 5/2 Число n, предшествующее буквенному обозначению, аналогично главному квантовому числу в атоме водорода в том смысле, что оно указывает порядок энергетических состояний. Для легких ядер предполагается, что нуклоны будут заполнять уровни в соответствии с последовательностью оболочечной модели. Предполагается, что нуклоны в закрытых оболочках не вносят вклад в общий ядерный спин, поэтому конфигурация ядра будет обозначаться символами для нуклонов вне закрытых оболочек. Например, 17 O имеет один нейтрон вне замкнутой оболочки (Z=N=8=магическое число), и его основное состояние будет обозначено (1d 5/2 ) 1 . 17 О: [(1с 1/2 ) 2 (1п 3/2 ) 4 (1п 1/2 ) 2]. Четность ядерного состояния также является важной характеристикой и часто указывается как часть обозначения состояния. По корреляции с моделью одночастичной оболочки значение L может быть связано с данным нечетным нуклоном, а четность состояния равна (-1) л . Для случая 17 O соответствующий L равен 2 (состояние d), поэтому можно предсказать, что четность будет четной. Для 15 O нечетный нейтрон находится в p-состоянии (L=1), поэтому четность этого состояния нечетна. Состояние 15 O иногда записывают как 1p 1/2 — , а состояние 17 O как 1d 5/2 + , чтобы указать как спин, так и четность этих ядер в их основные состояния. Четность, как и ядерный спин, считается характеристикой всего ядра, но четность будет четной для замкнутых оболочек, поэтому обычно достаточно учитывать четность нечетного нуклона.  |
Но на это число n не распространяются те же ограничения, что и в атомарном случае, — это просто параметр индексации. Таким образом, самые низкие энергии с L=2 помечены 1d (1d 3/2 ,1d 5/2 ), но есть более высокие уровни с L=2, которые будут помечены как 2d 3/2 , 2d 5/2 , 3d 3/2 , 3d 5/2 и т. д.
….. 1d 5/2 ) 1 