Как определить частоту по фигуре Лиссажу. » Хабстаб

В одной из прошлых статей описывалось как определить разность фаз двух сигналов по фигуре Лиссажу. Но у фигур Лиссажу есть ещё одно интересное свойство и заключается оно в следующем: если известна частота одного из колебаний, то по виду фигуры Лиссажу можно определить частоту другого.

Для определения соотношения частот проведём горизонтальную и вертикальную прямые, пересекающие фигуру. При этом через точки пере­сечения линий самой фигуры эти прямые проходить не должны.

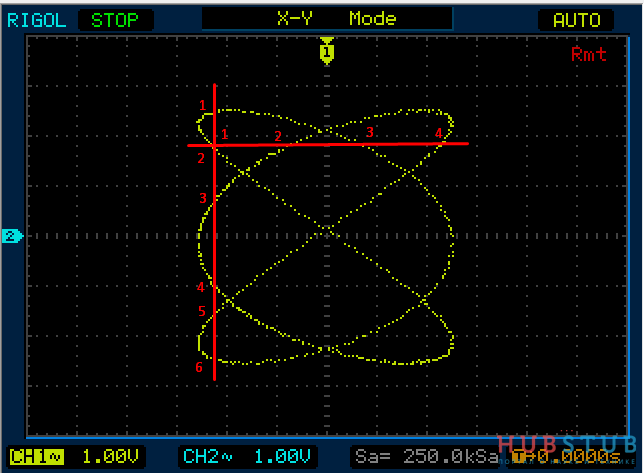
Тогда количество пересечений фигуры с горизонтальной прямой соответствует количеству изменений напряжения одного сигнала, а с вертикальной – количеству изменений напряжения другого сигнала. А из соотношения количества изменений сигналов можно найти соотношение частот колебаний.
А теперь тоже самое простыми словами, если синус с частотой 10KHz два раза пересекает горизонтальную прямую, а синус с неизвестной нам частотой пересекает четыре раза вертикальную прямую, то ясно что их частоты относятся как один к двум и частота неизвестного сигнала в два раза больше, то есть 20KHz. Кстати на осциллограмме выше частоты относятся как 6/4 или 3/2.
Почему мы один раз считаем пересечения с горизонтальной прямой, а второй с вертикальной?
Ответ на этот вопрос можно найти в определении фигуры Лиссажу:
Фигуры, получаемые при сложении взаимно перпендикулярных колебаний разных частот, называются фигурами Лиссажу.

Давайте на подадим на оба входа осциллографа синус с частотой 1KHz и посмотрим как будут выглядеть фигура Лиссажу в зависимости от разности фаз между каналами.

Разность фаз равна 0 °.

Разность фаз равна 45°.

Разность фаз равна 90°.

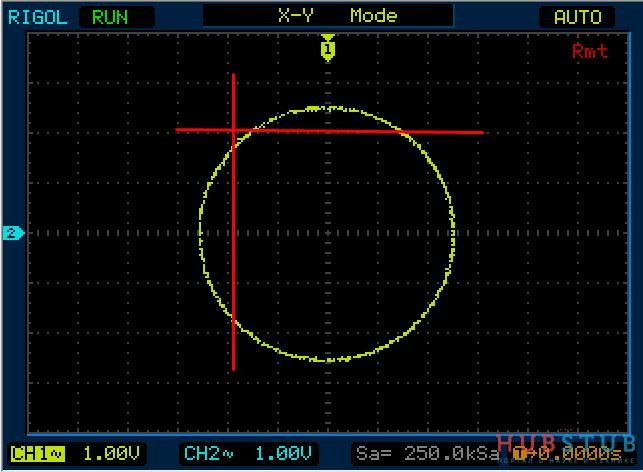
На осциллограммах видно, что количество пересечений с вертикальной и горизонтальной прямой одинаковое.

Теперь проделаем тоже самое но для частот 1KHz и 2KHz.
Разность фаз равна 0 °.

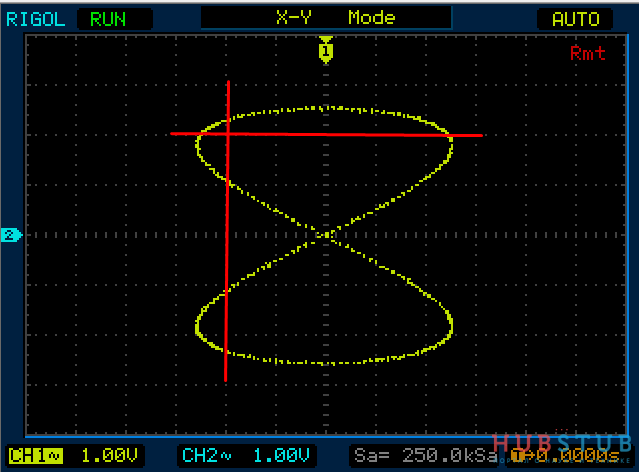
Разность фаз равна 45 °.

Разность фаз равна 90 °.

На осциллограммах видно, что количество пересечений с вертикальной прямой в два раза больше чем с горизонтальной.

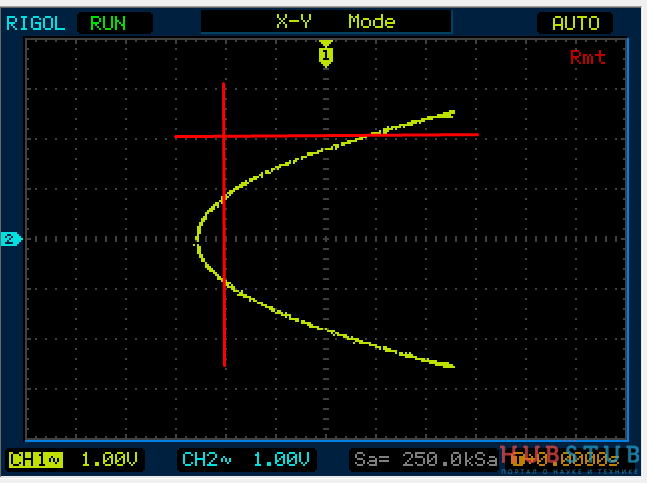
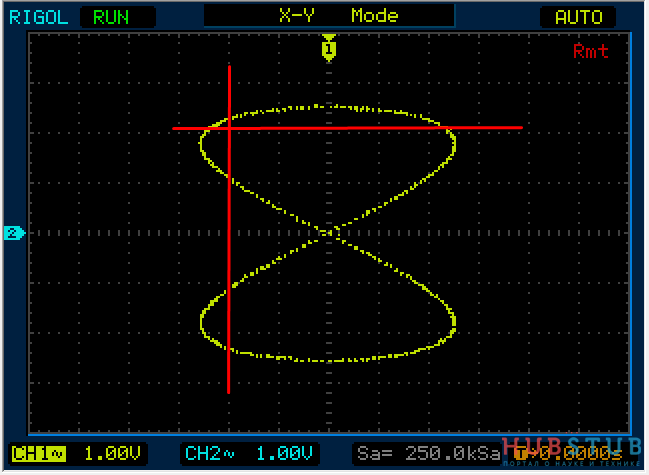
Теперь на один вход подадим 1Khz, а на второй 3Khz и проделаем тоже самое.
Разность фаз равна 0 °.

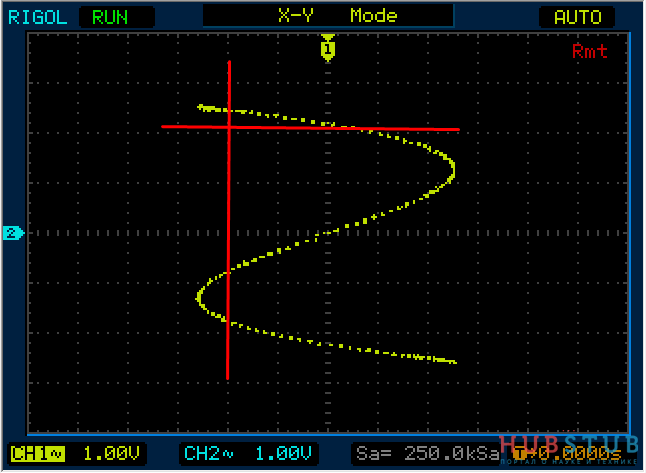
Разность фаз равна 45 °.

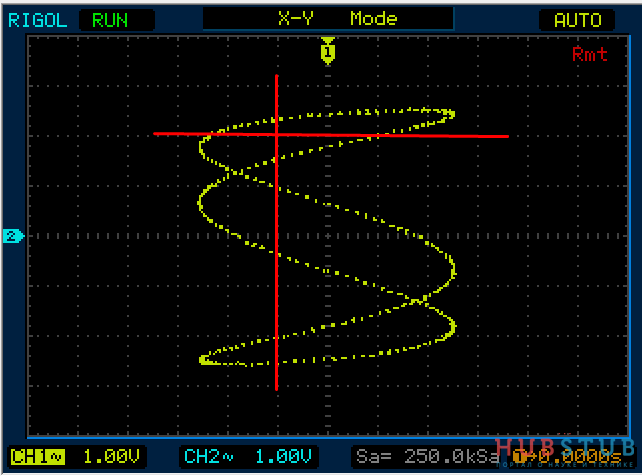
Разность фаз равна 90 °.

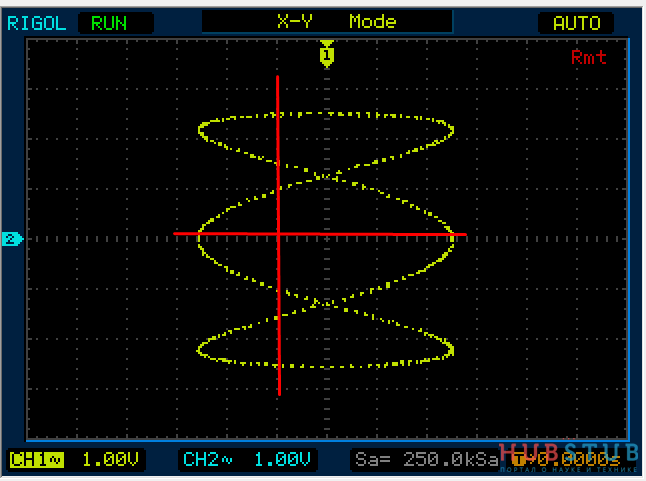
На осциллограммах видно, что количество пересечений с вертикальной прямой в три раза больше чем с горизонтальной.

Оказывается определить частоту неизвестного сигнала очень просто, если знать это замечательно свойство фигур Лиссажу.

Источник: hubstub.ru

Как рассчитать разность фаз по фигуре Лиссажу. » Хабстаб

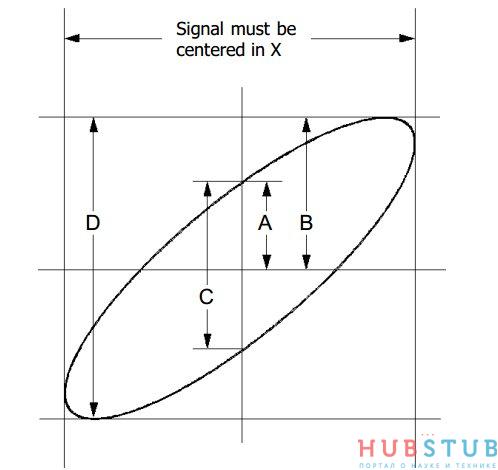
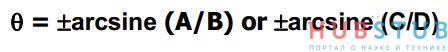
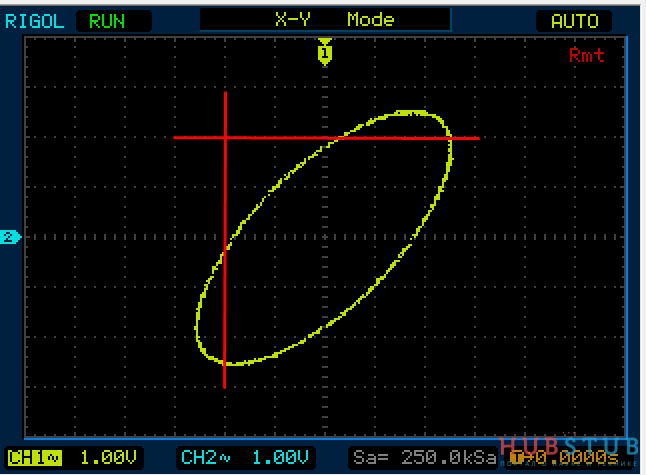
Давно было интересно как использовать на практике фигуры Лиссажу. На днях, листая документацию на осциллографы Rigol серии DS,  нашёл как использовать фигуры Лиссажу для измерения разности фаз двух исследуемых сигналов. Описанный в документации метод называется методом эллипса и состоит он в следующем, в режиме X-Y сигналы  равные по частоте, но сдвинутые по фазе, представляют собой эллипс. От сдвига фаз между сигналами и отношения амплитуд, зависят геометрические размеры эллипса. Произведя определённые замеры можно посчитать разность фаз между сигналами. Если главная ось эллипса расположена в первом и третьем квадранте, то сдвиг фаз между сигналами лежит в диапазоне от 0° до 90° или от 270° до 360°, если она располагается во втором и четвёртом квадранте, то сдвиг фаз лежит в диапазоне от 90° до 180° или от 180° до 270°. На рисунке ниже изображены расстояния, которые необходимо измерить и формула для расчёта, взятые из документации.

Современные цифровые осциллографы имеют функцию измерения сдвига фазы между сигналами. Давайте измерим расстояния A и B,  вычислим сдвиг фазы и сравним его с тем, что покажет осциллограф.

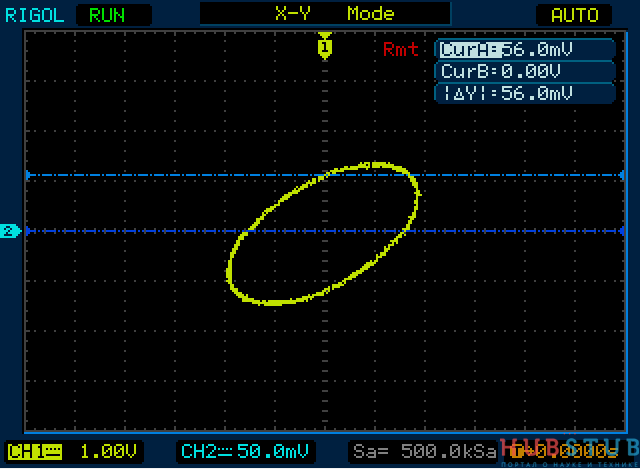
Расстояние A равно 56.

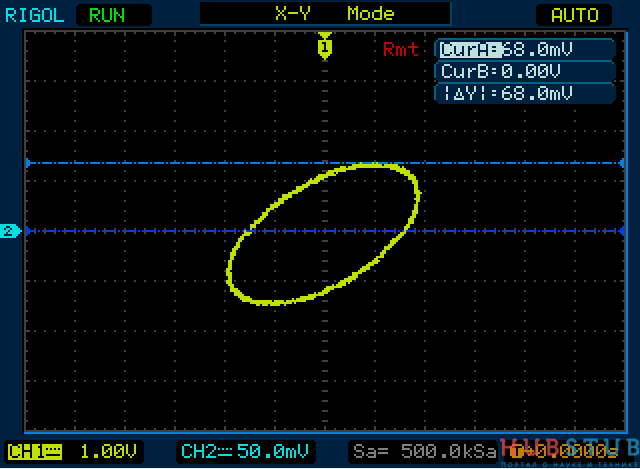
Расстояние В равно 68. Разделим 56 на 68 и посчитаем арксинус.

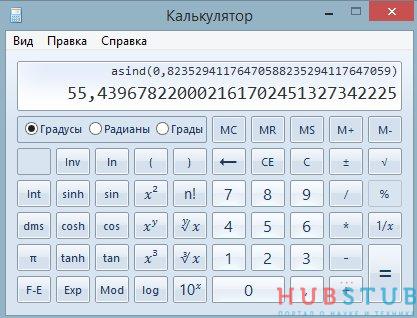
Получилось 55,44°, результат  почти сходится с тем, что измерил осциллограф.

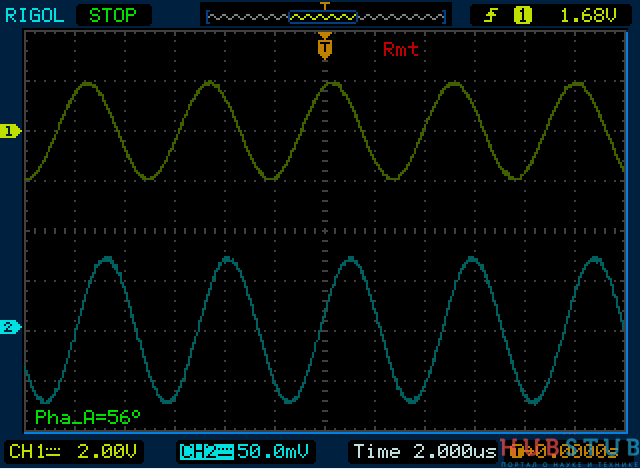
Дело в том, что из-за джиттера измеряемых сигналов значение сдвига фаз, колебалось в районе нескольких градусов, поэтому результат можно считать положительным.
Давайте посмотрим какую информацию ещё можно получить, анализируя фигуры Лиссажу.
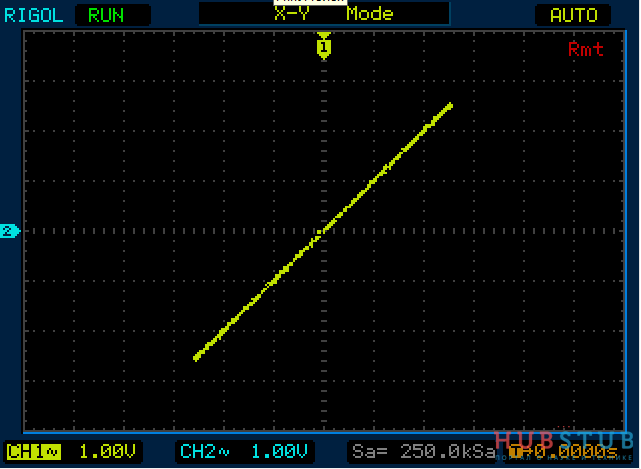
Если частоты и фазы сигналов равны, то эллипс вырождается в прямую, то же самое происходит если разность фаз равна 180°. Если разность фаз равна 90°,  то эллипс превратится в окружность.

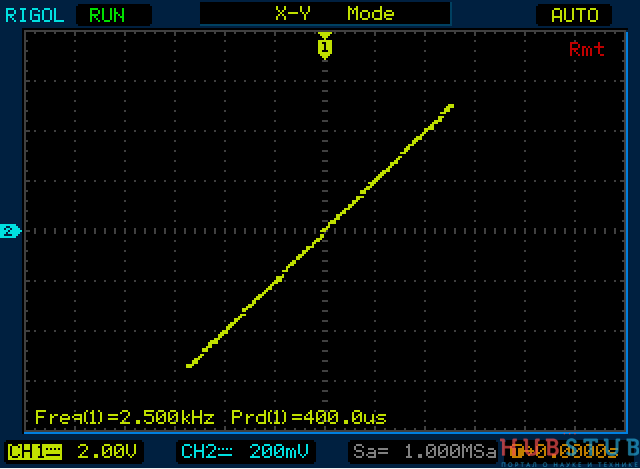
Угол наклона эллипса или прямой зависит от амплитуд измеряемых сигналов.
Интересный случай представляют собой вращающиеся фигуры. Вращаются они потому, что их частоты отличаются на малую величину и это приводит к постоянному изменению фазового сдвига. Причём период вращения это величина обратная разности частот, исследуемых сигналов.
Теперь мы знаем как измерить разность фаз, анализируя фигуры Лиссажу, а в следующей статье мы узнаем как определить частоту неизвестного сигнала по фигуре Лиссажу.

Источник: hubstub.ru

Фигуры Лиссажу — Lissajous curve

Не следует путать с спирографами , которые , как правило , окруженными круговой границей, тогда как кривые Лиссаж заключены в прямоугольных границах.

В математике , А Лиссаж кривого л ɪ с ə ʒ ¯u / , также известный как Лиссаж фигуры или кривой Bowditch б aʊ д ɪ tʃ / , является графиком системы параметрических уравнений

Иксзнак равноAгрех⁡(aT+δ),Yзнак равноВгрех⁡(бT),{\ Displaystyle х = А \ Sin (при + \ дельта), \ четырехъядерных у = В \ Sin (Ь),}

которые описывают сложное гармоническое движение . Это семейство кривых было исследовано Боудичем в 1815 году, а затем более подробно Ейся Antoine Lissajous в 1857 году.

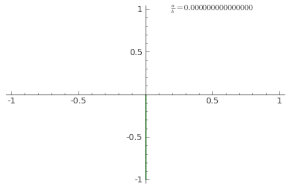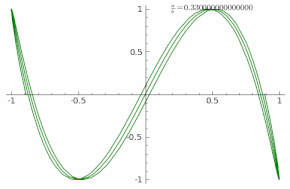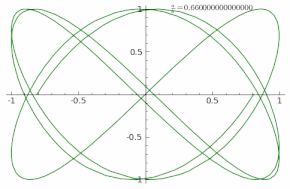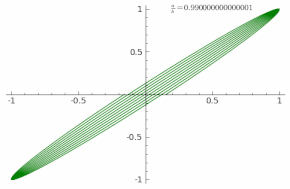
Внешний вид фигуры очень чувствителен к отношению к / б . Для получения соотношении 1, эта цифра является эллипс , со специальными случаями , включая круги ( A = B , δ = & pi ; / 2 радиана ) и линии ( δ = 0 ). Другой простой Лиссажу показатель является параболой ( б / = 2 , δ = π / 4 ). Другие коэффициенты производить более сложные кривые, которые закрыты , только если / б является рациональным . Визуальная форма этих кривых часто наводит на мысли о трехмерном узле , и действительно много видов узлов, в том числе тех , которые известно , как Лиссаж узлы , проект самолета , как фигуры Лиссажа.

Визуально, отношение / б определяет количество «доля» фигуры. Например, соотношение 3 / 1 или 1 / 3 создает фигуру с тремя основными лопастями (см рисунок). Аналогичным образом , отношение 5 / 4 производит фигуру с пятью горизонтальными лопастями и четырьмя вертикальными лопастями. Рациональное соотношение производит закрытый (подключено) или «еще» цифра, а иррациональные отношения производят цифры , которые появляются вращаться. Соотношение / B определяет относительное соотношение ширины к высоте кривой. Например, отношение 2 / 1 производит фигуру, вдвое шире, чем это высоко. Наконец, значение б определяет видимый «вращение» угол на чертеж, рассматриваются как если бы он был на самом деле трехмерный кривым. Например, δ = 0 производит й и Y компоненты, которые точно в фазе, так что в результате фигура как очевидная трехмерная фигура если смотреть прямо (0 °). В отличие от этого , любой ненулевой δ производит фигуру , которая появляется с возможностью поворота, либо как влево-вправо или вверх-вниз вращения ( в зависимости от соотношения в / б ).

Фигура Лиссажу на осциллографе , отображение 1: 3 соотношение между частотами вертикальных и горизонтальных синусоидальных входов, соответственно.

Фигуры Лиссажу , где = 1 , Ь = N ( N является натуральным числом ) , и

δзнак равноN-1Nπ2{\ Displaystyle \ дельта = {\ гидроразрыва {N-1} {N}} {\ гидроразрыва {\ Pi} {2}}}

являются многочлены Чебышева первого рода степени N . Это свойство используется для получения набора точек, называемого PADUA точек , в которых функция может быть дискретизированной для того , чтобы вычислить либо двухмерную интерполяцию или квадратурную функции по области [-1,1] × [-1,1 ] .

Отношение некоторых Лиссажа кривых Чебышева многочленов яснее понять, если кривой Лиссаж, который генерирует каждый из них выражаются с помощью функции косинуса, а не синусоидальных функций.

Иксзнак равносоз⁡(T),Yзнак равносоз⁡(NT){\ Displaystyle х = \ сов (т), \ четырехъядерных у = \ сов (Nt)}

Примеры

Анимация показывает кривые адаптации как соотношение / б возрастает от 0 до 1

Анимация показывает адаптацию кривой с непрерывно возрастает в / б фракции от 0 до 1 с шагом 0,01 ( δ = 0 ).

Ниже приведены примеры фигур Лиссажу с б = π / 2 , нечетное натуральное число , даже натуральное число б , а | — б | = 1 .

• 
• 
• 
• 

поколение

До современную электронной аппаратуры, Лиссаж кривые могут быть сгенерированы механически с помощью harmonograph .

Практическое применение

Лиссажу кривые также могут быть получены с помощью осциллографа (как показано). Схема осьминога может использоваться для демонстрации осциллограмм изображения на экране осциллографа. Две сдвинутых по фазе синусоиды входов применяются к осциллографу в режиме XY , и фазовое соотношение между сигналами представлены в виде фигуры Лиссажа.

В мире профессионального аудио, этот метод используется для анализа в реальном времени фазовые соотношения между левым и правым каналами стереофонического звукового сигнала. На более крупные, более сложные микширование утешает осциллограф может быть встроен для этой цели.

На осциллографе, мы предполагаем , х являются СН1 и у представл ет собой Ch3, амплитуда Ch2 и B является амплитудой Ch3, частота Ch2 и б является частота Ch3, поэтому / б этого отношения частоты этих двух каналов, и δ является фазовый сдвиг Ch2.

Чисто механическое применение Лиссажа кривого с в = 1 , Ь = 2 находится в приводном механизме Марс свет типа колеблющегося луч лампа популярности у железных дорог в середине 1900-х года. Пучок в некоторых версиях прослеживает криво рисунок фигура-8 на его стороне.

Применение для случая с = Ь

На этом рисунке оба входных частоты одинаковы, но дисперсия фазы между ними создает форму с эллипсом . 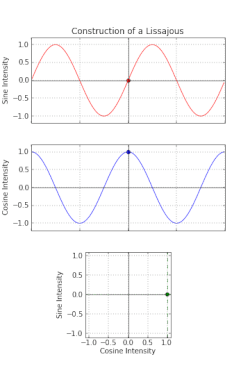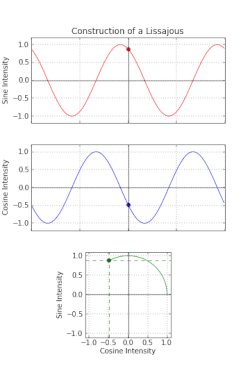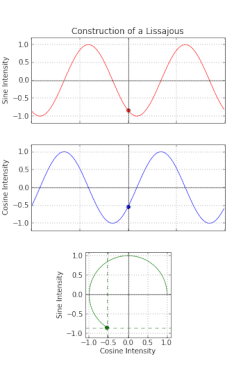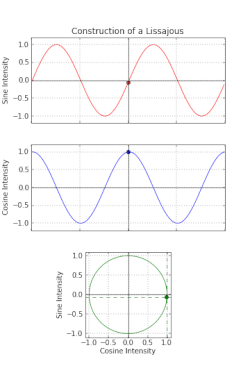Вверху: Выходной сигнал в зависимости от времени.
Средний: Входной сигнал как функция времени.
Внизу: Результирующая кривая Лиссажу при выходе на графике как функцию от входных данных.
В этом конкретном примере, потому что выход составляет 90 градусов по фазе от входа, кривая Лиссажу представляет собой окружность, и вращаются против часовой стрелки.

Когда входной сигнал к системе LTI синусоидальный выходной сигнал синусоидальный с той же частотой, но он может иметь различную амплитуду и некоторые фазовый сдвиг . С помощью осциллографа , что можно построить один сигнал против другого (в отличии от одного сигнала в зависимости от времени) , чтобы построить выход системы LTI против входа в систему LTI производит эллипс , который является фигурой Лиссажа для специального случая с = Ь , Соотношение сторон результирующего эллипса является функцией фазового сдвига между входом и выходом, с соотношением сторон 1 (идеального круга) , соответствующее фазовым сдвигом ± 90 ° и соотношение сторон ∞ (линия) , соответствующими с фазовым сдвигом 0 ° или 180 °.

На приведенном ниже рисунке показано , как Лиссаж фигура изменяется в течение различных фазовых сдвигов. Фазовые сдвиги все отрицательные , так что задержки семантика может быть использована с причинной системой LTI (обратите внимание , что -270 ° эквивалентно + 90 °). Стрелки показывают направление вращения фигуры Лиссажу.

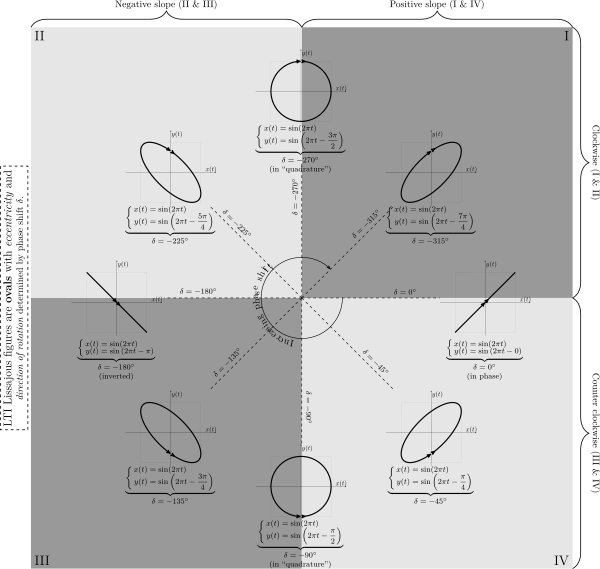Чистый сдвиг фаз влияет на эксцентричность в Лиссажу овала. Анализ овала позволяет фазовый сдвиг от системы LTI , подлежащий измерению ..

В машиностроении

Лиссаж кривой используются в экспериментальных испытаниях , чтобы определить , является ли устройство может быть надлежащим образом классифицировано как мемристор .

В культуре

В фильме

Наука стиль фантастика Lissajous анимация

Фигуры Лиссажа иногда отображаются на осциллографах, предназначенных для имитации высокотехнологичного оборудования в научно-фантастических телевизионных шоу и фильмах в 1960-х и 1970-х годах.

Название последовательность по Джону Уитне для Альфреда Хичкока «s 1958 фильма Головокружения основана на фигурах Лиссажа.

В последовательности к концу эпизода Коламба под названием «Сделайте мне Идеальное убийство», детектив сидит смотрит Лиссаж кривые отображаются музыка на мониторах в телевизоре за пределами широковещательного фургона.

логотип компании

Фигуры Лиссажа иногда используется в области графического дизайна в качестве логотипов . Примеры включают в себя:

В современном искусстве

Смотрите также

Заметки

внешняя ссылка

Интерактивные демонстрации

Лиссажу Фигуры — CoderLessons.com

Фигура Лиссажу – это рисунок, который отображается на экране, когда синусоидальные сигналы подаются как на горизонтальные, так и на вертикальные отклоняющие пластины CRO. Эти шаблоны будут варьироваться в зависимости от амплитуд, частот и разностей фаз синусоидальных сигналов, которые применяются как к горизонтальным, так и к вертикальным отклоняющим пластинам CRO.

На следующем рисунке показан пример фигуры Лиссажу.

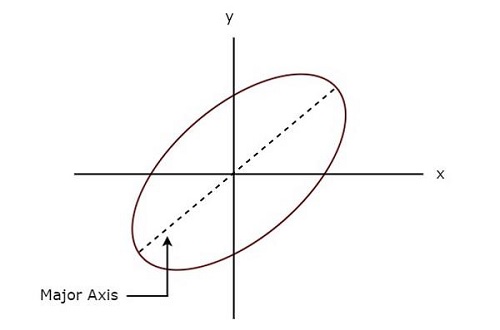
Вышеуказанная фигура Лиссажу имеет эллиптическую форму, а ее главная ось имеет некоторый угол наклона с положительной осью х.

Измерения с использованием фигур Лиссажу

Мы можем сделать следующие два измерения из фигуры Лиссажу.

• Частота синусоидального сигнала
• Разность фаз между двумя синусоидальными сигналами

Теперь давайте поговорим об этих двух измерениях по одному.

Измерение частоты

Фигура Лиссажу будет отображаться на экране, когда синусоидальные сигналы подаются как на горизонтальные, так и на вертикальные отклоняющие пластины CRO. Следовательно, подайте синусоидальный сигнал, который имеет стандартную известную частоту, на пластины горизонтального отклонения CRO. Аналогичным образом применяется синусоидальный сигнал, частота которого неизвестна вертикальным отклоняющим пластинам CRO

Пусть fH и fV – частоты синусоидальных сигналов, которые применяются к горизонтальным и вертикальным отклоняющим пластинам CRO соответственно. Соотношение между fH и fV можно математически представить, как показано ниже.

 гидроразрываFVFH= гидроразрываП−HП−V

Из приведенного выше соотношения мы получим частоту синусоидального сигнала, которая применяется к пластинам вертикального отклонения CRO как

fV= left( fracnHnV right)fH(уравнение 1)

Куда,

nH – количество горизонтальных касаний

nV – количество вертикальных касаний

Мы можем найти значения nH и nV по фигуре Лиссажу. Таким образом, подставив в уравнение 1 значения nH, nV и fH, мы получим значение fV , то есть частоту синусоидального сигнала. это применяется к вертикальным отклоняющим пластинам CRO.

Измерение разности фаз

Фигура Лиссажу отображается на экране, когда синусоидальные сигналы подаются как на горизонтальные, так и на вертикальные отклоняющие пластины CRO. Следовательно, применяйте синусоидальные сигналы, которые имеют одинаковую амплитуду и частоту, к горизонтальным и вертикальным отклоняющим пластинам CRO.

Для нескольких фигур Лиссажу, основанных на их форме, мы можем прямо сказать разность фаз между двумя синусоидальными сигналами.

• Если фигура Лиссажу представляет собой прямую линию с наклоном 45 circ с положительной осью x, то разность фаз между двумя синусоидальными сигналами составит 0 circ. Это означает, что между этими двумя синусоидальными сигналами нет разности фаз.

• Если фигура Лиссажу представляет собой прямую линию с наклоном 135 circ с положительной осью x, то разность фаз между двумя синусоидальными сигналами составит 180 circ. Это означает, что эти два синусоидальных сигнала находятся в противофазе.

• Если фигура Лиссажу имеет круглую форму , то разность фаз между двумя синусоидальными сигналами будет составлять 90 circ или 270 circ.

Если фигура Лиссажу представляет собой прямую линию с наклоном 45 circ с положительной осью x, то разность фаз между двумя синусоидальными сигналами составит 0 circ. Это означает, что между этими двумя синусоидальными сигналами нет разности фаз.

Если фигура Лиссажу представляет собой прямую линию с наклоном 135 circ с положительной осью x, то разность фаз между двумя синусоидальными сигналами составит 180 circ. Это означает, что эти два синусоидальных сигнала находятся в противофазе.

Если фигура Лиссажу имеет круглую форму , то разность фаз между двумя синусоидальными сигналами будет составлять 90 circ или 270 circ.

Мы можем рассчитать разность фаз между двумя синусоидальными сигналами, используя формулы, когда фигуры Лиссажу имеют эллиптическую форму .

• Если главная ось фигуры Лиссажу эллиптической формы, имеющая угол наклона, лежит между 0 circ и 90 circ с положительной осью x, то разность фаз между двумя синусоидальными сигналами будет.

Если главная ось фигуры Лиссажу эллиптической формы, имеющая угол наклона, лежит между 0 circ и 90 circ с положительной осью x, то разность фаз между двумя синусоидальными сигналами будет.

 phi= sin−1 left( fracx1x2 right)= sin−1 left( fracy1y2 right)

• Если главная ось фигуры Лиссажу эллиптической формы, имеющая угол наклона, лежит между 90 circ и 180 circ с положительной осью x, то разность фаз между двумя синусоидальными сигналами будет.

Если главная ось фигуры Лиссажу эллиптической формы, имеющая угол наклона, лежит между 90 circ и 180 circ с положительной осью x, то разность фаз между двумя синусоидальными сигналами будет.

 phi=180− sin−1 left( fracx1x2 right)=180− sin−1 left( fracy1y2 right)

Куда,

x1 – расстояние от начала координат до точки на оси х, где пересекается фигура Лиссажу эллиптической формы

x2 – расстояние от начала координат до вертикальной касательной эллиптической формы фигуры Лиссажу

y1 – расстояние от начала координат до точки на оси y, где пересекается фигура Лиссажу эллиптической формы

y2 – расстояние от начала координат до горизонтальной касательной эллиптической формы фигуры Лиссажу

В этой главе мы узнаем, как найти частоту неизвестного синусоидального сигнала и разность фаз между двумя синусоидальными сигналами из фигур Лиссажу, используя формулы.

Орбита Лиссажу — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 июля 2019; проверки требуют 4 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 июля 2019; проверки требуют 4 правки.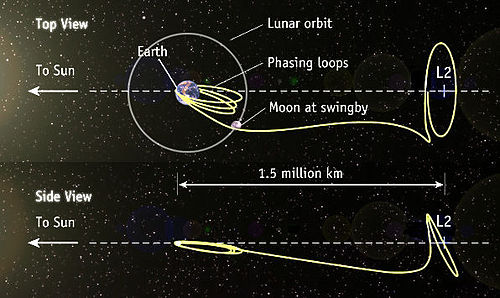 Пример траектории от Земли к орбите Лиссажу вокруг точки Лагранжа L₂ в системе Солнце-Земля. На нижней части иллюстрации, представляющей вид сбоку, Земля и Луна убраны для лучшего обзора траектории.

Орбита Лиссажу — квазипериодическая орбитальная траектория, по которой тело может двигаться вокруг точки Лагранжа в рамках задачи трёх тел без включения двигателей. Орбиты Ляпунова вокруг точек Лагранжа являются кривыми, лежащими в одной плоскости с двумя главными телами в системе трёх тел. Орбиты Лиссажу, напротив, включают участки как в этой плоскости, так и в перпендикулярной к ней, и следуют кривым Лиссажу. Гало-орбиты также включают компоненты в перпендикулярной плоскости, но гало-орбиты, в отличие от орбит Лиссажу, являются периодическими.^[1]

На практике, любая орбита вокруг точек Лагранжа L₁, L₂, L₃ динамически неустойчива, и малые возмущения орбиты со временем возрастают.^[2] В результате космический аппарат должен включать двигатели для коррекции орбиты. В отсутствие других воздействий орбиты вокруг точек L₄ и L₅ (при отношении масс главных тел более 25) устойчивы, причём в случае возникновения отклонений от траектории возникает сила, возвращающая тело на орбиту вблизи точки Лагранжа.^[3] Такие орбиты могут всё же быть выведены из состояния устойчивости при наличии поблизости других массивных тел. Было выявлено, что точки L₄ и L₅ в системе Земля-Луна будут устойчивы в течение миллиардов лет даже при учёте возмущений от Солнца; но при учёте возмущений от планет орбиты вокруг этих точек могут существовать только в течение нескольких миллионов лет.^[4]

Космические аппараты, использующие орбиты Лиссажу[править | править код]

Несколько космических миссий используют орбиты Лиссажу: ACE в точке Лагранжа L₁ системы Солнце-Земля,^[5]SOHO в точке Лагранжа L₁ системы Солнце-Земля, DSCOVR в точке Лагранжа L₁ системы Солнце-Земля,^[6]WMAP в точке Лагранжа L₂ системы Солнце-Земля^[7] и миссия Genesis, исследующая солнечные частицы, в точке Лагранжа L₁.^[8] 14 мая 2009 года Европейское космическое агентство (ЕКА) осуществило запуск обсерваторий Herschel и Planck, находящихся на орбитах Лиссажу вокруг точки L₂ системы Солнце-Земля.^[9] Миссия Gaia также использует орбиту Лиссажу вокруг точки L₂ системы Солнце-Земля.^[10] В 2011 году НАСА перевело два из аппаратов THEMIS с орбиты вокруг Земли на орбиту вокруг Луны через две орбиты Лиссажу вокруг точек L₁ и L₂ системы Земля-Луна.^[11] Китайский лунный модуль Чанъэ-2 8 июня 2011 года покинул лунную орбиту и был переведён на орбиту Лиссажу вокруг точки L₂ системы Солнце-Земля до середины 2012 года, когда модуль должен был отправиться к астероиду Тутатис.^[12]

В научно-фантастическом романе 2005 года «Солнечная Буря» Артура Кларка и Стивена Бакстера в космосе построен огромный щит для защиты Земли от смертельной солнечной бури. Там описано, что щит находился на орбите Лиссажу на L₁. В этой истории группа богатых и могущественных людей прячется напротив щита на L₂, чтобы быть защищенным от солнечной бури щитом, Землей и Луной.

1. ↑ Koon, Wang Sang (2000). «Dynamical Systems, the Three-Body Problem, and Space Mission Design». International Conference on Differential Equations: 1167–1181, Berlin: World Scientific. 
2. ↑ ESA Science & Technology: Orbit/Navigation (неопр.). European Space Agency (14 июня 2009). Дата обращения 12 июня 2009.
3. ↑ Vallado, David A. Fundamentals of Astrodynamics and Applications (англ.). — 3. — Springer New York, 2007. — ISBN 978-1-881883-14-2.
4. ↑ «Solar and planetary destabilization of the Earth-Moon triangular Lagrangian points» by Jack Lissauer and John Chambers, Icarus, vol. 195, issue 1, May 2008, pp. 16-27.
5. ↑ Advanced Composition Explorer (ACE) Mission Overview, Caltech, retrieved 2014-09-06.
6. ↑ SpaceX Falcon 9 successfully launches the DSCOVR spacecraft, NASA, retrieved 2015-08-05.
7. ↑ WMAP Trajectory and Orbit, NASA, retrieved 2014-09-06.
8. ↑ Genesis: Lissajous Orbit Insertion, NASA, retrieved 2014-09-06.
9. ↑ Herschel: Orbit/Navigation (неопр.). ESA. Дата обращения 15 мая 2006.
10. ↑ Gaia’s Lissajous Type Orbit (неопр.) (недоступная ссылка). ESA. Дата обращения 15 мая 2006. Архивировано 18 марта 2017 года.
11. ↑ ARTEMIS: The First Mission to the Lunar Libration Orbits
12. ↑ 嫦娥二号有望探索»拉格朗日点»-科技-人民网

Сложение взаимно перпендикулярных гармонических колебаний (фигуры Лиссажу)

Для наблюдения фигур Лиссажу на входы Х и У осциллографа необходимо подать гармоническое напряжение. Форма фигур зависит от соотношения частот и фаз колебаний. При небольшом различии частот форма фигур медленно меняется, а при большом картина сливается в виде прямоугольника.

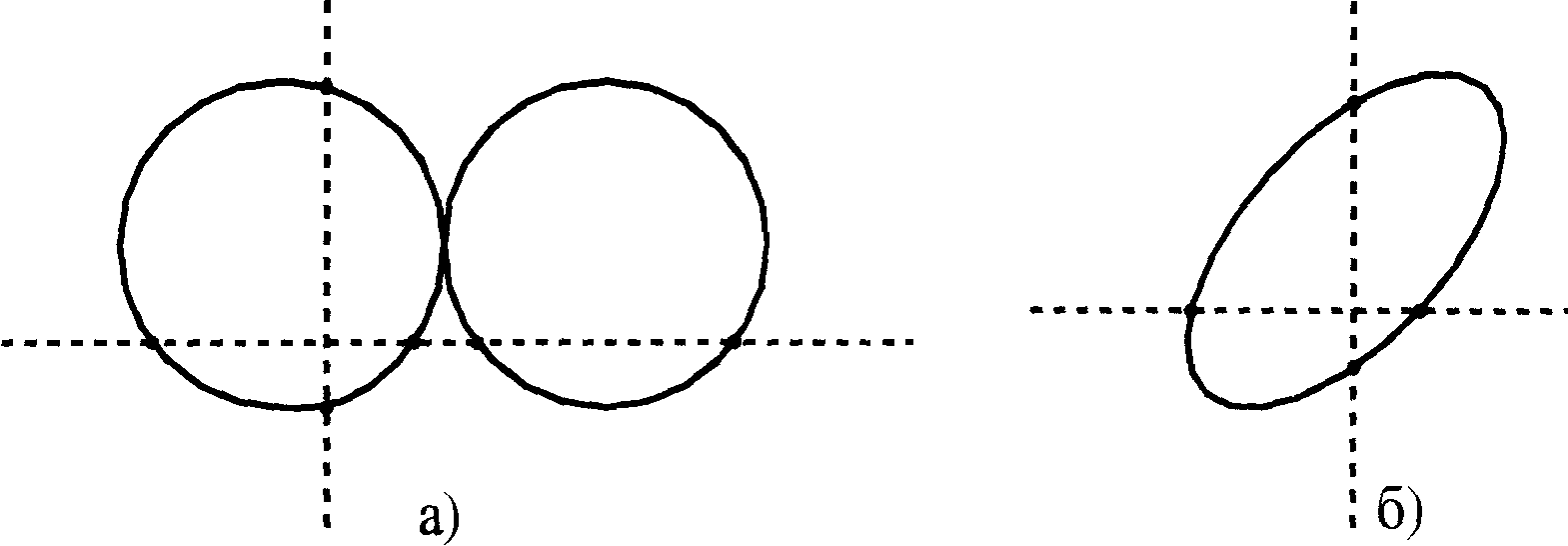
Рис 4

Пусть от генератора на вход Х подается напряжение х = Acos(t + ₁) от генератора звуковой частоты, а на вход У напряжение той же частоты от другого генератора или от сети переменного тока у = Bcos(t + ₂). Уравнение траектории движения луча можно получить, исключив время t из этих уравнений:

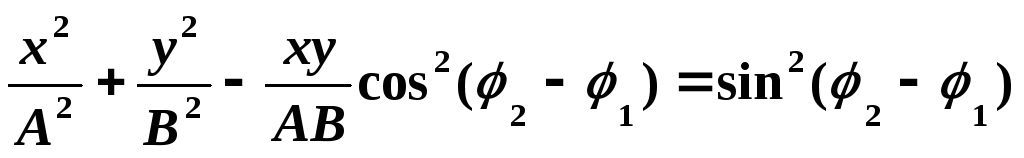. (3)

Таким образом, фигура, которую описывает луч при сложении колебаний одинаковой частоты, представляет собой эллипс. Ориентация этого эллипса зависит от разности фаз колебаний.

В общем случае вид фигуры Лиссажу зависит от соотношений между

-6-

частотами, фазами и амплитудами колебаний.

Для определения частоты одного из складываемых колебаний необходимо знать частоту другого, и число пересечений п₁ и п₂ фигуры с условными линиями параллельными осям Х и У не проходящими через особые точки. Соотношение между частотами и соответствующим числом пересечений имеет вид обратной пропорции:

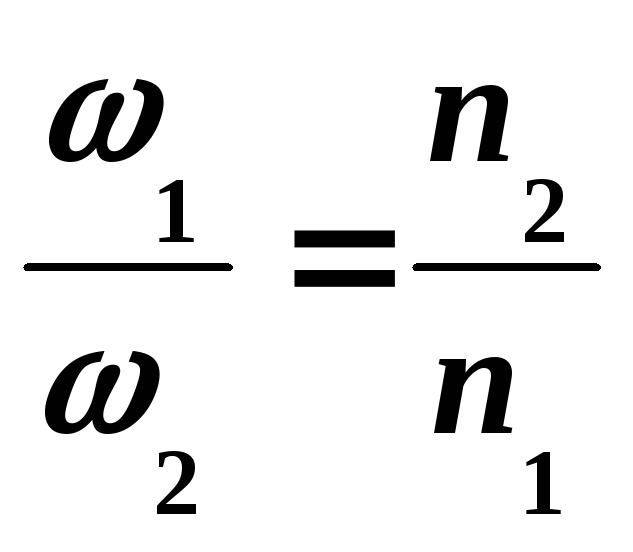(4)

В первом случае (Рис. 4, а) n₂/n₁ = 2/4, а во втором (Рис. 4, б) n₂/n₁ = 2/2. При этом, если частота первого из сигналов равна, например, 50 Гц, то частота второго сигнала — 25Гц. Во втором случае частоты равны.

Выполнение работы. Органы управления осциллографа.

На передней панели осциллографа расположены следующие регуляторы и переключатели:

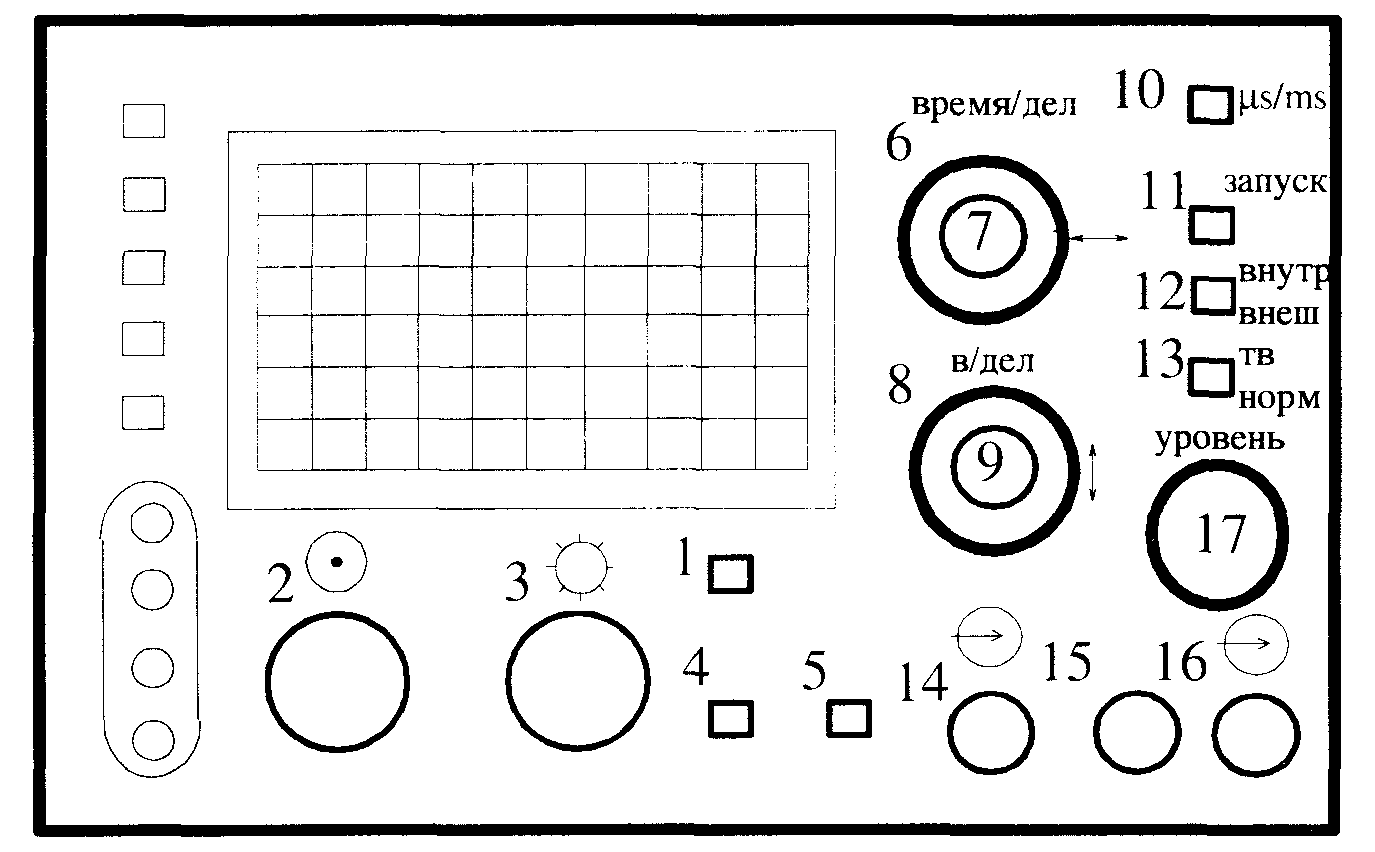
Рис. 5

1. — «Сеть» — кнопка включения.

2. «Фокус» — регулятор фокусировки луча.

3. — «Яркость» — регулятор яркости.

4. Кнопка переключения осциллографа в режим мультиметра (в данной работе не используется).

5. Переключатель входа осциллографа «открытый — закрытый». Закрытый вход используется для исследования переменной составляющей входного сигнала. В этом случае сигнал подается на вход через разделительный

-7-

конденсатор.

6. Переключатель «время/дел» — выбор длительности развертки.

7. — Совмещенный с переключателем (5) регулятор положения луча по горизонтали.

8. «V/дел» — Переключатель делителя напряжения канала У — регулятор чувствительности осциллографа.

9. — Совмещенный с переключателем (7) регулятор положения луча по вертикали.

10. «s/ms» — Переключатель множителя частоты генератора развертки.

11. «ЗАПУСК» — Переключатель полярности запускающего импульса синхронизации.

12. «ВНУТР/ВНЕШ» — Переключатель вида синхронизации.

13. «ТВ/НОРМ» — Выключатель генератора развертки.

14. — Вход У.

15. -Общий.

16. -ВходХ.

17. — Регулятор уровня сигнала синхронизации.

Упражнение 1 Наблюдение формы сигнала звукового генератора, измерение его частоты

1. Изучите назначение и расположение органов управления осциллографом.

2. Подключите ко входу У выход звукового генератора (ЗГ). Включите электропитание ЗГ (выключатель расположен на задней стенке генератора). Установите величину сигнала 5В, частоту 100Гц. Отрегулируйте чувствительность осциллографа так, чтобы сигнал не выходил за пределы экрана по вертикали.

3. Подберите частоту генератора развертки и уровень синхронизации осциллографа. Добейтесь устойчивого изображения сигнала на экране.

4. Изменяя форму и частоту f_z сигнала ЗГ наблюдайте изменения на экране.

5. Измеряя время одного или нескольких периодов сигнала ЗГ т рассчитайте частоту f_о по формуле (1). Сравните полученный результат с показаниями ЗГ.

6. Повторите измерения для разных частот и формы сигнала, результаты измерений запишите в табл. 1.

-8-

Таблица 1

N	f,(Гц)	m	 (мс/дел)	l (дел)	t = l (мс)	fo = m/t
Номер измерения	(частота по шкале звукового генератора)	число периодов осциллограммы	цена одного деления шкалы генератора развертки	длина измеряемого участка осциллограммы	время измеряемого участка колебаний	(Гц) (по осциллографу)
1-5

7. Сделайте выводы относительно точности измерения частоты с помощью осциллографа.

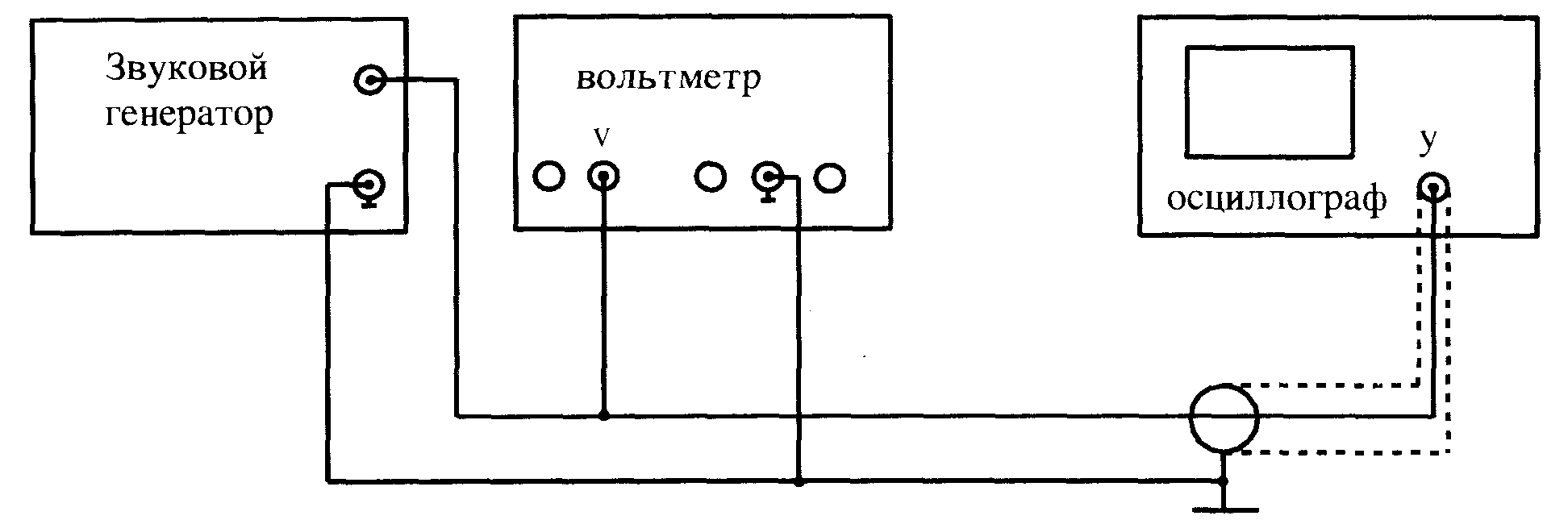
Рис.6

Выводы к работе:

Задача 1. При сложении двух колебаний, происходящих вдоль одного направления, согласно уравнениям

U  U

01

cos

 t 

,

(6а)

1



101

U

2

 U

02

cos

 t 





202

(6б)

(при условии ₁ ₂ ), получается результирующее колебание с той же частотой .Биения возникают вследствие того, что разность фаз складываемых колебаний (6а), (6б) с близкими частотами все время изменяется так, что оба колебания в какой-то момент оказываются в фазе, а через некоторое время – в противофазе, затем снова в фазе и снова в противофазе и т. д. В итоге возникают периодические изменения амплитуды результирующего колебания. Изучение биений представляет практический интерес, поскольку это один из вариантов осуществления амплитудной модуляции колебаний.

Задача 2. Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или  вырождаются в отрезки прямых, а при разности фаз  и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.

Контрольные вопросы

1. Какая электрическая цепь называется колебательным контуром? Какие процессы в ней происходят? Почему эта цепь так называется?

Колебательный контур. Электрическая цепь, изображенная на

2. рис. 1, называется колебательным контуром.

   Основными элементами в ней являются: катушка

   индуктивности L, конденсатор C и

   активное C

   L

   сопротивление R. Пусть в начальный момент

   конденсатор заряжен. Напомним, что в этой цепи

   происходит

   периодический

   обмен

   энергией

   между электрическим полем конденсатора и

   R

   магнитным полем катушки.

   Дважды за период

   колебаний

   электрическая энергия WE 

   q 2

   ,

   Рис. 1. Колебательный

   2C

   контур

   где q – заряд, сосредоточенный на

   обкладках

конденсатора, полностью (идеальный контур) или частично (реальный контур)

переходит в энергию магнитного поля катушки (W_B  ^LI2₂ , где I – разрядный

ток, протекающий через катушку). В реальном контуре собственные колебания являются затухающими.

2. Запишите уравнения изменения заряда, тока и напряжения в идеальном колебательном контуре.

Заряд — q  q

cos

 t 



Напряжение — U  U ₀ cos ₀t ₀ 

Электрический ток — I  I ₀ cos ₀t ₀ 

3. Что такое биения? Как можно наблюдать картину биений? Как определить частоту биений?

При сложении колебаний одного направления с близкими частотами возникает колебание, которое называется биением Частота биений обратнопропорциональна периоду биений. Период биений можно определить по графику биений. Период биений – это период изменения амплитуды колебаний.

4. Как получить на экране осциллографа фигуры Лиссажу? От чего зависит форма фигуры? Как по форме фигуры Лиссажу определить отношение частот складываемых колебаний?

Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причем период цикла вращения является величиной, обратной разности частот, например, период оборота равен 2 с — разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счет кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.

Вид фигур Лиссажу зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры Лиссажу представляют собой эллипсы, которые при разности фаз φ=0 или φ=π вырождаются в отрезки прямых, а при φ=π/2 и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний не совпадают точно, то φ всё время меняется, вследствие чего эллипс непрерывно деформируется. При существенно различных периодах эллипс деформируется быстро, картина размывается, и фигуры Лиссажу не наблюдаются. Однако если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. При этом число касаний фигуры Лиссажу со сторонами прямоугольника, в который она вписывается, даёт отношение периодов обоих колебаний.  Вид фигур Лиссажу при различных соотношениях периодов (1 : 1, 1 : 2 и т. д.) и разностях фаз. Фигуры Лиссажу можно наблюдать, например, на экране электронно-лучевого осциллографа, если к двум парам отклоняющих пластин подведены переменные напряжения с равными или кратными периодами. Вид фигур Лиссажу позволяет определить соотношения между периодами и фазами обоих колебаний. Если колебания, которые совершает точка, происходят не по гармоническому, а по более сложному закону, но с одинаковым периодом, то получаются замкнутые траектории, аналогичные фигурам Лиссажу, но искажённой формы. По виду этих фигур можно судить о форме колебаний. Таким образом, наблюдение фигур Лиссажу- удобный метод исследования соотношений между периодами и фазами колебаний, а также и формы колебаний.

5. Изменяется ли частота промышленной электрической сети, и от чего она зависит? Частота промышленной электрической сети – величина постоянная, равная 50 Гц. Зависит она от принципа работы генератора.