| ||||||||||||||
| Специальный поиск | ||||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
|||||||||||||
энергии магнитного поля катушки Задача 13709 Колебательный контур содержит катушку индуктивностью L = 6 мкГн, конденсатор емкостью С = 10 нФ и резистор сопротивлением R = 10 Ом. Определите для случая максимума тока отношение энергии магнитного поля катушки к энергии электрического поля.
Задача 70064 Определить энергию магнитного поля катушки, состоящей из 200 витков, если при силе тока 4 А в ней возникает магнитный поток, равный 0,01 Вб.
Задача 70227 Определить энергию магнитного поля катушки индуктивностью 25 мГн при протекании в ней тока 40 мА.
Задача 21807 Заряженный конденсатор емкостью C = 0,2 мкФ подключили к катушке индуктивностью L = 8 мГн. Через какое время от момента подключения энергия электрического поля конденсатора станет равной энергии магнитного поля катушки?
Задача 60528 В колебательном контуре, состоящем из индуктивности и емкости ток, изменяется по закону , А. Индуктивность контура 0,6 Гн.
Задача 11303 Энергия магнитного поля катушки с индуктивностью L = 0,2 Гн составляет W = 5 Дж. Определите, чему равна ЭДС самоиндукции в катушке при равномерном уменьшении силы тока до нуля в течение промежутка времени Δt = 0,1 с.
Задача 13389 Энергия магнитного поля в катушке уменьшилась за счет изменения тока в ней в п = 4 раза в течение Δt = 0,2 с. Индуктивность катушки L = 0,16 Гн, первоначальный ток в катушке I0 = 8 А. определите ЭДС самоиндукции εs в катушке, считая, что сила тока зависит от времени линейно.
Задача 14029 Конденсатор колебательного контура подключен к источнику постоянного напряжения (см. рисунок). Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре после переведения переключателя К в положение 2. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) заряд левой обкладки конденсатора 2) энергия электрического поля конденсатора 3) сила тока в катушке 4) энергия магнитного поля катушки
Задача 14568 Какое преобразование энергии происходит в контуре в промежутке от 2·10–3 с до 3·10–3 с? 1) Энергия магнитного поля катушки уменьшается от максимального значения до нуля 2) Энергия магнитного поля катушки преобразуется в энергию электрического поля конденсатора 3) Энергия электрического поля конденсатора увеличивается до максимального значения 4) Энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки
Задача 21092 На рисунке приведен график зависимости заряда q от времени t в идеальном колебательном контуре.
Задача 22001 Записать уравнение колебаний силы тока в цепи идеального электрического контура с индуктивностью L = 0,33 Гн и емкостью С = 0,46 мкФ, если колебания заряда происходят по закону синуса с амплитудой qm = 2,3·107 Кл и с начальной фазой π/6. Найти значение энергии магнитного поля катушки в начальный момент времени и для t = Т/12, где Т — период колебаний. Чему равна полная энергия электромагнитных колебаний в системе?
Задача 22482 Чему равно отношение энергии магнитного поля катушки к энергии электрического поля конденсатора, спустя время T/8 после того, как сила тока в контуре была равна нулю?
Задача 23055 Тороидальная катушка квадратного сечения имеет в своей обмотке N = 1000 витков.
| ||||||||||||||
Беспроводная передача энергии через магнитно-связанные индуктивные катушки / Хабр
Введение
Думаю, что многие из читателей видели хотя бы один ролик на популярных видеосервисах, где электричество передается через пустое пространство при помощи индуктивных катушек.
В этой статье мы хотим обратиться к первоосновам процесса беспроводной передачи энергии с помощью магнитного поля. Начав с рассмотрения простейшей индуктивной катушки, и вычисления ее индуктивности, мы постепенно перейдем к теории электрических цепей, в рамках которой, будет показан и обоснован способ
Магнитное поле одиночного витка с током
Рассмотрим магнитное поле одиночного витка с током. Найдем магнитное поле витка в любой точке пространства. Почему необходимо подобное рассмотрение? Потому что почти во всех книгах, по крайней мере в тех, которые удалось отыскать автору статьи, решение данной задачи ограничивается нахождением лишь одной компоненты магнитного поля и лишь вдоль оси витка — , в то время как мы отыщем закон для магнитного поля во всем пространстве.
Найдем магнитное поле витка в любой точке пространства. Почему необходимо подобное рассмотрение? Потому что почти во всех книгах, по крайней мере в тех, которые удалось отыскать автору статьи, решение данной задачи ограничивается нахождением лишь одной компоненты магнитного поля и лишь вдоль оси витка — , в то время как мы отыщем закон для магнитного поля во всем пространстве.
Иллюстрация к закону Био-Савара-Лапласа
Для нахождения магнитного поля, воспользуемся законом Био-Савара-Лапласа (смотри Википедия — Закон Био-Савара-Лапласа). На рисунке видно, что центр системы координат совпадает с центром витка. Контур окружности витка обозначен как , а радиус окружности — как .По витку течет ток . — это переменная-радиус-вектор из начала координат в произвольную точку витка. — это радиус-вектор в точку наблюдения. Еще нам понадобится полярный угол — угол между радиус-вектором и осью . Расстояние от оси витка до точки наблюдения обозначим за . И наконец, — элементарное приращение радиус-вектора .
Согласно закону Био-Савара-Лапласа, элемент контура с током создает элементарный вклад в магнитное поле, который дается формулой
Теперь остановимся подробнее на переменных и выражениях, входящих в формулу. С учетом аксиальной симметрии задачи можем записать
Для того чтобы найти результирующее магнитное поле, нужно проинтегрировать по всему контуру витка, то есть
После подстановки всех выражений и некоторых тождественных преобразований получаем выражения для аксиальной и радиальной компоненты магнитного поля соответственно
Для нахождения абсолютного значения магнитного поля необходимо просуммировать компоненты по теореме Пифагора .
Продемонстрируем полученное решение на примере витка радиуса (м) и (А).
Амплитуда аксиальной компоненты магнитного поля
Амплитуда радиальной компоненты магнитного поля
Абсолютная амплитуда магнитного поля
Заметим, что для витка произвольной формы, на больших расстояниях , т. е. много больше характерного размера витка, поведение магнитного поля будет стремиться к найденному решению.
е. много больше характерного размера витка, поведение магнитного поля будет стремиться к найденному решению.
Подсказка…
Для подобных вычислений и построения графиков удобно использовать MathCad 15
Катушка индуктивности. Магнитно-связанные катушки
Теперь, когда мы знаем решение для магнитного поля одного витка, можем найти индуктивность катушки, состоящей из витков. По определению индуктивность — это коэффициент пропорциональности между током в витке и магнитным потоком через площадь сечения витка. Мы пользуемся здесь идеальной моделью катушки, которая безразмерна по направлению своей оси симметрии. Конечно же, на практике такого не бывает. Однако, как приближенные, полученные формулы будут достаточно хороши. Хотя катушки и считаются безразмерными вдоль , необходимо задаться ненулевым радиусом сечения провода. Обозначим его , и пример равным (мм). Иначе при интегрировании магнитного потока подынтегральное выражение обратится в бесконечность.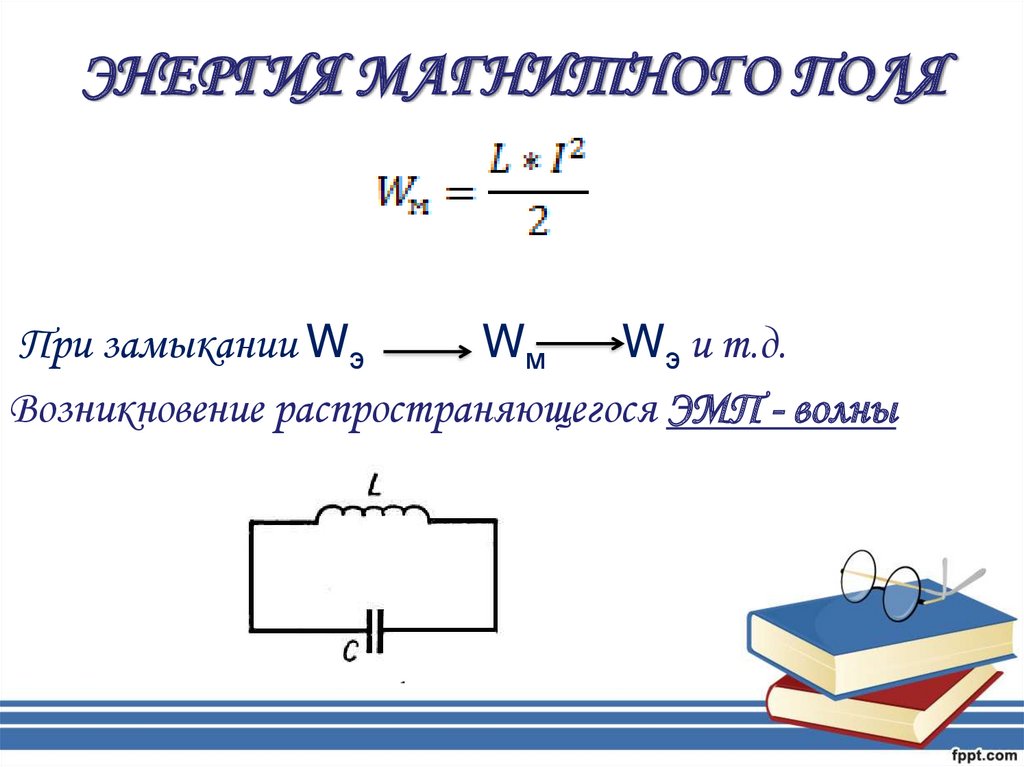
Индуктивно связанные катушки
На рисунке изображены две магнитно связанные катушки. Пусть первая катушка имеет радиус и содержит витков, а вторая — и соответственно. Тогда для нахождения собственных индуктивностей необходимо вычислить магнитный поток каждой катушки через свое собственное сечение.
Поскольку в катушке много витков, найдем величину, называемую потокосцепление, дважды умножив на количество витков
По определению, индуктивность это коэффициент пропорциональности в формуле . Таким образом, получим собственные индуктивности катушек
Пусть центры катушек разделены расстоянием , лежат на одной оси, и их плоскости витков сориентированы параллельно. Для нахождения взаимной индуктивности, нужно вычислить потокосцепление, образуемое одной катушкой через сечение другой, то есть
Тогда взаимная индуктивность катушек дается выражением
Насколько известно автору, такие интегралы можно взять только численно.
Заметим, что как правило и . Коэффициентом связи катушек называется величина
Исследуем зависимость коэффициента связи катушек от расстояния. Для этого рассмотрим две одинаковые катушки с радиусом витков (м) и количеством витков . При этом собственная индуктивность каждой из катушек составит (мГн).
Коэффициент связи катушек от расстояния между ними
График не изменится, если одинаково изменить число витков в обеих катушках, либо одинаково изменить радиус обеих катушек. Коэффициент связи удобно выражать в процентах. Из графика видно, что даже при расстоянии между катушками в 1 (мм) коэффицент связи меньше 100%. Коэффициент падает до 10% на расстоянии порядка 60 (мм), и до 1% на 250 (мм).
Беспроводная передача энергии
Итак, нам известны индуктивности и коэффициент связи. Теперь воспользуемся теорией электрических цепей переменного тока для поиска оптимальных параметров, при которых передаваемая мощность оказалась бы максимальной. Для понимания этого параграфа читатель должен быть знаком с понятием электрического импеданса, а также с законами Кирхгофа и законом Ома. Как известно из теории цепей, две индуктивно-связанные катушки образуют воздушный трансформатор. Для анализа трансформаторов удобна Т-образная схема замещения.
Для понимания этого параграфа читатель должен быть знаком с понятием электрического импеданса, а также с законами Кирхгофа и законом Ома. Как известно из теории цепей, две индуктивно-связанные катушки образуют воздушный трансформатор. Для анализа трансформаторов удобна Т-образная схема замещения.
Воздушный трансформатор и его эквивалентная схема
Передающую катушку слева будем условно называть «трасмиттер», а принимающую катушку справа — «ресивер». Между катушками коэффициент связи . На стороне ресивера находится потребитель, представленный нагрузкой . Нагрузка в общем случае может быть комплексной. Входное напряжение на стороне трансмиттера , а входной ток — . Напряжение, передаваемое на ресивер — , и передаваемый ток . Полный импеданс на стороне трансмиттера обозначим как , а полный импеданс на стороне ресивера .
Предполагается, что на вход схемы подается синусоидальное напряжение .
Обозначим — сопротивления и индуктивности катушек (две собственные и одна взаимная) соответственно. Тогда, согласно теории трансформатора
Тогда, согласно теории трансформатора
С другой стороны, согласно нашим обозначениям
где — полные
активныесопротивления на стороне трансмиттера и ресивера соответственно, и — полные
реактивныесопротивления.
Импеданс связи равен .
Найдем входной ток цепи
где знак обозначает параллельное соединение сопротивлений. Тогда напряжение, переданное на ресивер
И наведенный ток
Можем найти комплексную мощность, переданную в ресивер
Таким образом имеем выражение для комплексной мощности
Выражение для
активнойкомпоненты мощности
Выражение для
реактивнойкомпоненты мощности
В большинстве практических задач требуется передать максимальную активную мощность, поэтому
Либо, что то же самое
Для удобства введем функцию
и исследуем ее на наличие экстремумов
Откуда получаем систему из двух уравнений
Эта система имеет пять решений, два из которых нефизичны, так как приводят к мнимым значениям величин, которым полагается быть действительными. Три других
Три других
решения приведены ниже вместе с соответствующими формулами для мощности
Решение 1Мощность
Решение 2 и 3
Мощность для решений 2 и 3
Решение 2 и 3 нужно использовать, когда реактивное сопротивление связи достаточно велико
Когда же это не так, нужно использовать решение 1. Чаще всего в реальных ситуациях окажется мало, поэтому рассмотрим решение 1 несколько подробнее.
Решение 1: . И соответствующая ему активная мощность дается формулой
Из формулы мощности видно, что мощность зависит от реактивного сопротивления связи , а значит и от частоты передачи , и от геометрии взаимного расположения катушек, которая учитывается коэффициентом связи .
Как заметили внимательные читатели, зависимость — нелинейная. Функция достигает максимума при .
Исследование формулы мощности на экстремумы
Максимальная активная мощность при равна
Таким образом, вышеозначенная формула представляет
абсолютный теоретический пределпереданной активной мощности при любых условиях. При этом для реактивной мощности, переданной в ресивер, имеем
Численное моделирование
Продемонстрировать работу всей вышеизложенной теории можно, выполнив симуляцию SPICE модели нашего устройства из двух связанных катушек.
SPICE модель двух индуктивно-связанных катушек
Симуляция выполнена для коэффициента связи %, что соответствует 25 см удаления между катушками. Параметры катушек те же, что и в предыдущем параграфе, принятые для построения графика .
Получается, что реактивные сопротивления каждой из катушек необходимо скомпенсировать конденсаторами и . То есть настроить каждый из контуров (передающий и принимающий) в резонанс на заданной частоте. Если предположить, что величина нагрузки действительная, то величины емкостей могут быть найдены из формул
То есть настроить каждый из контуров (передающий и принимающий) в резонанс на заданной частоте. Если предположить, что величина нагрузки действительная, то величины емкостей могут быть найдены из формул
Ниже приведены два графика для переданного напряжения и переданной мощности во времени на частоте (кГц).
Переданное напряжение
Переданная мощность
Из рисунков видно, что на расстоянии 25 (см) переданное напряжение оказалось приблизительно в 2.5 меньше входного, а переданная пиковая мощность — приблизительно в 4 раза меньше мощности, потребляемой от входа, что согласуется с полученными формулами.
В заключении опишем, какие меры можно предпринять для увеличения передаваемой мощности:
- увеличить количество витков в катушках
- увеличить радиус витков
- увеличить частоту передачи
- уменьшить расстояние между катушками
- ввести магнитный сердечник, принадлежащий обеим катушкам (замкнутый либо открытый)
- ввести незамкнутый магнитный сердечник, принадлежащий лишь катушке-ресиверу
Пожалуй, написание этой статьи накладывает на автора обязательство изготовить и протестировать такую систему из двух катушек в лабораторных условиях, но это уже совсем другая история. Благодарю за внимание.
Благодарю за внимание.
Литература
- Сивухин, Д. В. «Общий курс физики. Т. 3: Электричество и магнетизм.» (1990).
- Бессонов, Лев Алексеевич. Теоретические основы электротехники. Электромагнитное поле. Общество с ограниченной ответственностью Издательство ЮРАЙТ, 2012.
- Лаврентьев, М. А., and Б. В. Шабат. «Теория функций комплексной переменной.» (1972).
фильтрация помех и энергия для ВЧ DC/DC
24 августа 2011
Производители стараются уменьшить размер, увеличить частоту переключений и мощность DC/DC-преобразователей. Сложные условия работы (в особенности это касается автомобильной электроники) и весьма строгий контроль качества бросают серьезный вызов разработчикам устройств.
Современные требования подразумевают все большее использование электроники при уменьшении пригодного для ее размещения пространства. Именно для таких случаев и разработаны малоразмерные, предназначенные для поверхностного монтажа, полностью защищенные катушки индуктивности серии IHLP производства компании Vishay. Эта серия была создана для решения двух основных задач — фильтрации электромагнитных помех в сетях большой мощности и накопления энергии для высокочастотных DC/DC-преобразователей.
Эта серия была создана для решения двух основных задач — фильтрации электромагнитных помех в сетях большой мощности и накопления энергии для высокочастотных DC/DC-преобразователей.
Для соответствия заданным в современных компьютерах типоразмерам разработчикам необходимы высоковольтные катушки индуктивности, минимальные по размерам и полностью защищенные. Катушки серии IHLP от Vishay отвечают этим требованиям. На рынке автомобильной электроники они широко используются с 2002 года.
Устройство IHLP
Катушка IHLP собрана из медной обмотки и выводной рамки, соединенных методом ультразвуковой сварки (рис. 1). Окончательную форму катушке придает опрессованный корпус из эпоксидного наполнителя с металлическим порошком.
Рис. 1. Устройство катушки IHLP
Медная обмотка внутри катушки, покрытая лаком и изоляцией, выдерживает рабочую температуру до 200°С.
Использованные порошковые материалы позволяют катушке стабильно работать на высоких нагрузках при температуре до 125°С. Данная температура определяется как температура саморазогрева катушки плюс температура окружающей среды. В настоящее время катушки серии IHLP могут стабильно работать при температуре до 125°С и соответствуют стандарту AEC-Q200. Они могут эксплуатироваться и при большей температуре, впрочем, в данном случае необходимо принимать во внимание эффект теплового старения (см. ниже). В настоящее время Vishay разрабатывает материал, способный выдерживать рабочую температуру в 155°С без эффекта старения.
Фильтрация электромагнитных помех (ЭМП)
ЭМП-фильтр предназначен для уменьшения воздействия электромагнитных помех, создаваемых силовыми цепями. Этот элемент особенно важен в автомобилях, так как электромагнитное излучение (ЭМИ) может негативно сказаться на работе многих схем. Для разработчиков ЭМП-фильтров важны такие характеристики, как потеря мощности сигнала, падение напряжения, вносимые потери и количество необходимых каскадов. Преимуществом ILHP является низкое для таких размеров активное сопротивление, так как все проблемы, связанные с фильтрацией ЭМП, в той или иной форме зависят именно от него. При применении многокаскадных фильтров снижение падения напряжения в каскадах будет складываться.
Преимуществом ILHP является низкое для таких размеров активное сопротивление, так как все проблемы, связанные с фильтрацией ЭМП, в той или иной форме зависят именно от него. При применении многокаскадных фильтров снижение падения напряжения в каскадах будет складываться.
Ключевыми требованиями в автомобильной электронике являются избавление от (или существенное снижение) ЭМП, ЭМИ и их негативного влияния на электрические цепи без заметных потерь напряжения. Провода, по которым передается ток между электронными узлами управления, имеют достаточную длину, так что вопрос падения напряжения встает достаточно остро. ЭМП-фильтр и кабель с суммарным сопротивлением 200 мОм при токе в 10 А дадут падение напряжения в 2 В.
DC/DC-преобразователи
Основное применение катушки индуктивности, выполненные по технологии IHLP, находят в неизолированных DC/DC-преобразователях. Для современных и перспективных источников питания двумя определяющими факторами являются максимальное значение напряжения питания и минимальный размер. Для достижения поставленных целей разработчики должны повышать рабочую частоту, что позволит использовать компоненты меньшего размера, однако обратной стороной медали является увеличение потерь.
Для достижения поставленных целей разработчики должны повышать рабочую частоту, что позволит использовать компоненты меньшего размера, однако обратной стороной медали является увеличение потерь.
DC/DC-преобразователи также должны работать при постоянно увеличивающейся температуре окружающей среды. При таких условиях повышается собственная температура катушки индуктивности, дополнительно разогреваемой ввиду тепловых потерь на ней. Известно, что признаком теплового старения катушек с металлическим порошком при повышении рабочих температур является эффект потерь в сердечнике. Эти потери должны быть приняты во внимание во время проектирования схем с использованием композитных катушек для рабочих температур, превышающих 125°С. Эффект теплового старения может быть минимизирован простым ограничением верхней планки рабочих температур до 125°С. Это не означает, что катушки перестанут работать при большей температуре, однако в этом случаи разработчикам придется более тщательно подходить к созданию схем.
Тепловое старение
По результатам исследований Vishay тепловое старение, выраженное в форме потерь в сердечнике, возникает при температурах свыше 125°С и определяется как функция времени и температуры. Чем сильнее температура превышает 125°С, тем быстрее потери в сердечнике достигают определенного уровня. Эффект старения обусловлен тем, что изоляция между металлическими частицами начинает проводить ток. Исследования показали, что катушка без корпуса и изоляции имеет примерно такое же сопротивление, как и катушка с композитным корпусом, подверженная тепловому старению. Продукция IHLP демонстрирует плато величины потерь в сердечнике (рис. 2) между 2500 и 9000 часами работы при повышенных температурах. Чем больше рабочая температура, тем быстрее достигается это плато.
Рис. 2. График зависимости потерь в сердечнике от часов работы при различных рабочих температурах
Подтверждено, что изолирующий слой между частицами металла при повышении температуры вступает в реакцию с кислородом, снижая свое сопротивление, что в результате приводит к повышению индукционных токов и неоправданно высоким потерям в сердечнике.
После того как все покрытие вступило в реакцию, темпы увеличения проводимости снижаются, что приводит к появлению плато на кривой старения, как показано на рис. 2.
На рисунке 3 показан тепловой пробой, в случаи возникновения которого потери в сердечнике окажут самое серьезное влияние на всю схему целиком.
Рис. 3. График зависимости потерь в сердечнике от времени
Vishay рекомендует следить за тем, чтобы величина потерь в сердечнике не превышала приблизительно трети от общих потерь, а также чтобы сумма температуры окружающей среды и температуры катушки, повышающаяся из-за них, не превышала 125°С. Если необходимо, чтобы катушка работала при больших температурах, значение потерь в сердечнике должно быть в пределах одной шестой от общих потерь для уменьшения эффекта теплового старения. Vishay предполагает, что общее повышение температуры катушки, связанное со всеми факторами (потери в сердечнике, тепловые потери, наведенные потери, поверхностный эффект), составит 40°С или менее вне зависимости от температуры окружающей среды. Если потери в сердечнике составляют лишь малую часть от общих потерь в катушке, повышение первых в связи с тепловым старением незначительно скажется на окончательной температуре катушки. Для определения потерь в сердечнике вы можете воспользоваться документом Vishay №34250, Selecting IHLP Composite Inductors for Non-Isolated Converters Utilizing Vishay’s Application Sheet.
Если потери в сердечнике составляют лишь малую часть от общих потерь в катушке, повышение первых в связи с тепловым старением незначительно скажется на окончательной температуре катушки. Для определения потерь в сердечнике вы можете воспользоваться документом Vishay №34250, Selecting IHLP Composite Inductors for Non-Isolated Converters Utilizing Vishay’s Application Sheet.
Как отмечалось ранее, тепловой пробой случится при следующих условиях: если потери в сердечнике превосходят все остальные, и если импеданс катушки является ограничителем тока через нее. При увеличении потерь в сердечнике эффективная индуктивность и энергия магнитного поля катушки (1/2LI2) уменьшаются. Вероятность возникновения теплового пробоя повышается, если ширина импульса преобразователя увеличивается, чтобы компенсировать возросшую нагрузку. Это приводит к увеличению тока через катушку. Чем больше ток, тем выше температура, и так до тех пор, пока не произойдет тепловой пробой.
Тем не менее, если в схеме предусмотрено ограничение тока переключающим транзистором, регулятор отключится, и тепловой пробой не произойдет. Энергия магнитного поля на катушке будет невелика в связи с эффектом теплового старения, но перегрева не произойдет, если величина тока будет ограничена. Помимо этого, потери в материале, содержащем металлический порошок, не могут увеличиваться по экспоненте бесконечно, как предполагает график. Рост потерь остановится в тот момент, когда магнитные характеристики материала уже не будут зависеть от температуры.
Энергия магнитного поля на катушке будет невелика в связи с эффектом теплового старения, но перегрева не произойдет, если величина тока будет ограничена. Помимо этого, потери в материале, содержащем металлический порошок, не могут увеличиваться по экспоненте бесконечно, как предполагает график. Рост потерь остановится в тот момент, когда магнитные характеристики материала уже не будут зависеть от температуры.
К вопросу о печатных платах
В 1956 году Национальное бюро стандартов предприняло попытку определить токопроводящую способность дорожек печатных плат (PCB). Попытка окончилась неудачей в связи с неспособностью точно рассчитать изменение температуры этих дорожек. Далее последовали документ MILSTD-275 1973 года и измененный в 1999 году IPC-2221, они также окончательно не определили стандарт дорожек печатных плат. В этих документах определяется токопроводимость дорожек, тогда как случаи поверхностного монтажа элементов, использующих дорожки в качестве радиаторов, не рассматриваются.
Чтобы соответствовать требованиям современного рынка, разработчики постоянно должны создавать все более дешевые и меньшие по размерам мощные источники питания. Для достижения этой цели конструкторы зачастую уменьшают толщину и/или ширину дорожек печатных плат. В результате это оканчивается перегревом и снижением эффективности, а навесные элементы, в данном случае катушки индуктивности, использующие дорожки в качестве радиаторов, вносят свой вклад в общие потери.
Каждый производитель силовых катушек индуктивности предоставляет рассчитанную заранее величину тока для каждой катушки. Эти расчеты обычно основываются на увеличении температуры или достижении режима насыщения. Во многих случаях увеличение температуры является главным фактором для расчетов величины силы тока. Чаще всего расчетный ток — это величина постоянного тока, приводящая к увеличению температуры катушки на 40°С из-за активного сопротивления катушки и сопротивления материала обмотки. Эта расчетная величина не принимает во внимание нагрев из-за потерь в сердечнике, что является темой для отдельного разговора. Тем не менее при использовании величины расчетного тока подразумевается, что выводы деталей и дорожки печатных плат способны выдержать проводимый ток и рассеять тепло, выделяемое обмоткой. Многие разработчики не принимают во внимание тот факт, что количества меди в обмотке, призванной справляться с достаточно большими токами в катушке, достаточно, чтобы повышением своей температуры вывести катушку в тепловой режим, не предусмотренный документацией производителя. Несмотря на то, что количество факторов, определяющих способность дорожек печатных плат проводить тепло, достаточно велико, были сформулированы основные требования к размерам дорожек, предназначенных для проведения больших токов.
Эта расчетная величина не принимает во внимание нагрев из-за потерь в сердечнике, что является темой для отдельного разговора. Тем не менее при использовании величины расчетного тока подразумевается, что выводы деталей и дорожки печатных плат способны выдержать проводимый ток и рассеять тепло, выделяемое обмоткой. Многие разработчики не принимают во внимание тот факт, что количества меди в обмотке, призванной справляться с достаточно большими токами в катушке, достаточно, чтобы повышением своей температуры вывести катушку в тепловой режим, не предусмотренный документацией производителя. Несмотря на то, что количество факторов, определяющих способность дорожек печатных плат проводить тепло, достаточно велико, были сформулированы основные требования к размерам дорожек, предназначенных для проведения больших токов.
Таблица 1 сводит воедино рекомендуемые максимальные токи для дорожек указанных размеров.
Таблица 1. Рекомендованные соотношения размеров внешних дорожек и их проводимости на основе повышения температуры
| Повышение температуры | 30°C | 40°C | 50°C | 60°C | 70°C | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Толщина дорожки, мм | 0,0175 | 0,035 | 0,07 | 0,0175 | 0,035 | 0,07 | 0,0175 | 0,035 | 0,07 | 0,0175 | 0,035 | 0,07 | 0,0175 | 0,035 | 0,07 |
| Ширина дорожки, мм | Максимальный ток, А | ||||||||||||||
| 0,250 | 0,6 | 0,8 | 1,2 | 0,7 | 0,9 | 1,4 | 0,7 | 1,0 | 1,5 | 0,8 | 1,1 | 1,6 | 0,8 | 1,2 | 1,8 |
| 0,500 | 1,0 | 1,4 | 2,1 | 1,0 | 1,6 | 2,4 | 1,3 | 1,8 | 2,6 | 1,4 | 2,0 | 2,8 | 1,5 | 2,1 | 3,0 |
| 0,750 | 1,4 | 2,0 | 2,9 | 1,6 | 2,3 | 3,3 | 1,7 | 2,5 | 3,6 | 1,9 | 2,7 | 3,9 | 2,0 | 2,9 | 4,2 |
| 1,000 | 1,7 | 2,5 | 3,6 | 2,0 | 2,8 | 4,1 | 2,2 | 3,1 | 4,5 | 2,4 | 3,4 | 4,9 | 2,5 | 3,6 | 5,3 |
| 1,250 | 2,1 | 3,0 | 4,3 | 2,3 | 3,0 | 4,9 | 2,6 | 3,7 | 5,4 | 2,8 | 4,1 | 5,9 | 3,0 | 4,4 | 6,3 |
| 1,500 | 2,4 | 3,4 | 5,0 | 2,7 | 3,9 | 5,6 | 3,0 | 4,3 | 6,2 | 3,2 | 4,7 | 6,8 | 3,5 | 5,0 | 7,3 |
| 1,750 | 2,7 | 3,9 | 5,6 | 3,1 | 4,4 | 6,4 | 3,4 | 4,9 | 7,0 | 3,7 | 5,3 | 7,6 | 3,9 | 5,7 | 8,2 |
| 2,000 | 3,0 | 4,3 | 6,2 | 3,0 | 4,9 | 7,1 | 3,8 | 5,4 | 7,8 | 4,1 | 5,9 | 8,5 | 4,4 | 6,3 | 9,1 |
| 2,250 | 3,3 | 4,7 | 6,8 | 3,7 | 5,4 | 7,8 | 4,1 | 6,0 | 8,6 | 4,5 | 6,5 | 9,3 | 4,8 | 6,9 | 10,0 |
| 2,500 | 3,6 | 5,1 | 7,4 | 4,1 | 5,9 | 8,4 | 4,5 | 6,5 | 9,3 | 4,9 | 7,0 | 10,1 | 5,2 | 7,5 | 10,9 |
| 2,750 | 3,8 | 5,5 | 8,0 | 4,4 | 6,3 | 9,1 | 4,8 | 7,0 | 10,1 | 5,2 | 7,6 | 10,9 | 5,6 | 8,1 | 11,7 |
| 3,000 | 4,1 | 5,9 | 8,6 | 4,7 | 6,8 | 9,8 | 5,2 | 7,5 | 10,8 | 5,6 | 8,1 | 11,7 | 6,0 | 8,7 | 12,5 |
| 3,250 | 4,4 | 6,3 | 9,1 | 5,0 | 7,2 | 10,4 | 5,5 | 8,0 | 11,5 | 6,0 | 8,6 | 12,5 | 6,4 | 9,3 | 13,4 |
| 3,500 | 4,6 | 6,7 | 9,7 | 5,3 | 7,6 | 11,0 | 5,8 | 8,4 | 12,2 | 6,3 | 9,2 | 13,2 | 6,8 | 9,8 | 14,2 |
| 3,750 | 4,9 | 7,2 | 10,2 | 5,6 | 8,1 | 11,6 | 6,2 | 8,9 | 12,9 | 6,7 | 9,7 | 14,0 | 7,2 | 10,4 | 15,0 |
| 4,000 | 5,2 | 7,5 | 10,8 | 5,9 | 8,5 | 12,2 | 6,5 | 9,4 | 13,5 | 7,0 | 10,2 | 14,7 | 7,6 | 10,9 | 15,8 |
| 4,250 | 5,4 | 7,8 | 11,3 | 6,2 | 8,9 | 12,8 | 6,8 | 9,8 | 14,2 | 7,4 | 10,7 | 15,4 | 7,9 | 11,4 | 16,5 |
| 4,500 | 5,7 | 8,2 | 11,8 | 6,4 | 9,3 | 13,4 | 78,2 | 10,3 | 14,9 | 7,7 | 11,2 | 16,1 | 8,3 | 12,0 | 17,3 |
| 4,750 | 5,9 | 8,5 | 12,3 | 6,7 | 4,1 | 14,0 | 7,4 | 10,7 | 15,5 | 8,5 | 11,7 | 16,8 | 8,7 | 12,5 | 18,0 |
| 5,000 | 6,2 | 8,9 | 12,8 | 7,0 | 10,1 | 14,6 | 7,7 | 11,2 | 16,1 | 8,4 | 12,1 | 15,5 | 9,0 | 13,0 | 18,8 |
| Примечание: Для внутренних дорожек величина тока уменьшается на 50% | |||||||||||||||
Расчеты были выполнены по формуле:
I = 3,188х∆Т0,45х W0,79 x Th0,53,
где повышение температуры измеряется в 40°С; ширина и толщина дорожек в мм; 3,188 — константа, взятая из общей термодинамической модели и переведенная в единицы СИ.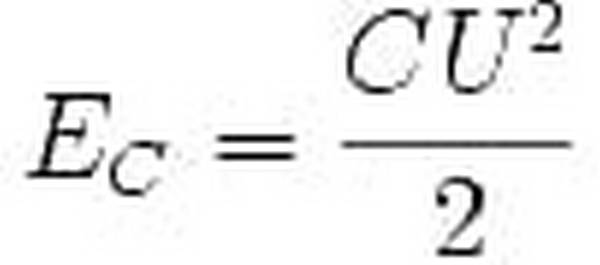 При выполнении этих рекомендаций разработчик может рассчитывать на температуры, близкие к описанным в документации по продукции IHLP.
При выполнении этих рекомендаций разработчик может рассчитывать на температуры, близкие к описанным в документации по продукции IHLP.
Получение технической информации, заказ образцов, поставка — e-mail: [email protected]
•••
19)Энергия магнитного поля катушки с током. Плотность энергии магнитного поля.
Посмотрим, как влияет э.д.с. самоиндукции на процесс установления тока в цепи, содержащей индуктивность. Отключим источник , разомкнув в момент времени t = 0 ключ К. Ток в катушке начинает убывать, но при этом возникает э.д.с. самоиндукции, поддерживающая убывающий ток.
Закон изменения тока в цепи приобретает вид:
Оказывается, ток в цепи, после выключения источника, будет убывать по экспоненциальному закону и станет равным нулю только спустя t = .
Вы и сами теперь легко покажете, что при включении источника (после замыкания ключа К) ток будет нарастать тоже по экспоненциальному закону, асимптотически приближаясь к значению I0
.
Но вернёмся к первоначальной задаче размыкания цепи.
Мы отключили в цепи источник питания (разомкнули ключ К), но ток — теперь в цепи продолжает течь. Где черпается энергия, обеспечивающая бесконечное течение этого убывающего тока? Ток поддерживается электродвижущей силой самоиндукции = . За время dt убывающий ток совершит работу: dA = СИIdt = –LIdI.
Ток будет убывать от начального значения I0 до нуля. Проинтегрировав последнее выражение в этих пределах, получим полную работу убывающего тока:
.
Совершение этой работы сопровождается двумя процессами: исчезновением тока в цепи и исчезновением магнитного поля катушки индуктивности.
Опыт даёт ответ на эти вопросы: энергия электрического тока связана с его магнитным полем и распределена в пространстве, занятом этим полем.
Несколько изменим
выражение, учтя, что для длинного
соленоида справедливы следующие
утверждения: L = 0n2Sl—
индуктивность; B0 = 0nI0 — поле соленоида.
Эти выражения используем в (10.9) и получим новое уравнение для полной работы экстратока размыкания, или — начального запаса энергии магнитного поля: .
Здесь V = Sl — объём соленоида (магнитного поля!).
Энергия катушки с током пропорциональна квадрату вектора магнитной индукции.
Разделив эту энергию на объём магнитного поля, получим среднюю плотность энергии:
[].
Локальная плотность энергии в заданной точке поля:
.
20)Собственные электрические колебания в колебательном контуре. Логарифмический декремент затухания и добротность колебания
Колебания электрических величин — заряда, напряжения, тока — можно наблюдать в цепи, состоящей из последовательно соединённых сопротивления (R), ёмкости (C) и катушки индуктивности (L)
Колебания,
происходящие только за счёт внутренних
энергетических ресурсов системы,
называются собственными. Первоначально энергия была сообщена
конденсатору и локализована в
электростатическом поле. При замыкании
конденсатора на катушку, в цепи появляется
разрядный ток, а в катушке — магнитное
поле. Э.д.с. самоиндукции катушки будет
препятствовать мгновенной разрядке
конденсатора. Через четверть периода
конденсатор полностью разрядится, но
ток будет продолжать течь, поддерживаемый
электродвижущей силой самоиндукции. К
моменту эта э.д.с. перезарядит конденсатор. Ток
в контуре и магнитное поле уменьшатся
до нуля, заряд на обкладках конденсатора
достигнет максимального значения.
Первоначально энергия была сообщена
конденсатору и локализована в
электростатическом поле. При замыкании
конденсатора на катушку, в цепи появляется
разрядный ток, а в катушке — магнитное
поле. Э.д.с. самоиндукции катушки будет
препятствовать мгновенной разрядке
конденсатора. Через четверть периода
конденсатор полностью разрядится, но
ток будет продолжать течь, поддерживаемый
электродвижущей силой самоиндукции. К
моменту эта э.д.с. перезарядит конденсатор. Ток
в контуре и магнитное поле уменьшатся
до нуля, заряд на обкладках конденсатора
достигнет максимального значения.
Эти колебания электрических величин в контуре будут происходить неограниченно долго, если сопротивление контура R = 0. Такой процесс называют собственные незатухающие колебания.
Если сопротивлением резистора R (силой сопротивления в механическом осцилляторе) пренебречь нельзя, то в подобных системах будут происходить собственные затухающие колебания.
Характер затухающих
колебаний меняется с увеличением
сопротивления резистора R. Когда сопротивление превысит определённое критическое значение Rк,
колебания в системе не возникают.
Происходит монотонный апериодический разряд конденсатора
Когда сопротивление превысит определённое критическое значение Rк,
колебания в системе не возникают.
Происходит монотонный апериодический разряд конденсатора
. Это линейное дифференциальное уравнение второго порядка — дифференциальное уравнение собственных незатухающих электрических колебаний. Решением этого уравнения является следующая гармоническая функция: q = Acos(0t + ). частота собственных незатухающих колебаний гармонического осциллятора: .
Окончательно закон изменения заряда конденсатора во времени принимает следующий вид:
q = q0cos(0t). Ток в цепи при этом меняется так:
Собственные затухающие колебания происходят в колебательном контуре RLC
Эти колебания можно
описать следующим дифференциальным
уравнением (правило напряжений Кирхгофа): IR – UC = СИ. Здесь
по-прежнему: I =
; UC =
;
СИ = = =
.
Здесь
по-прежнему: I =
; UC =
;
СИ = = =
.
Учитывая эти соотношения, уравнению придадим следующий вид:
;(11.7). есь = — коэффициент затухания; = — частота собственных незатухающих колебаний. Уравнение 11.7— дифференциальное уравнение собственных затухающих электрических колебаний.
Важной характеристикой затухающего процесса является логарифмический декремент затухания — логарифм отношения амплитуд двух соседних колебаний : . Логарифмический декремент затухания равен произведению коэффициента затухания на время одного полного колебания (период) Т. Процесс затухания колебания до нуля продолжается бесконечное время, поэтому условно принято считать, что процесс затух, если амплитуда колебаний уменьшилась в е раз.
и .
Логарифмический
декремент затухания d обратен числу колебаний, по истечению
которых амплитуда падает в е раз.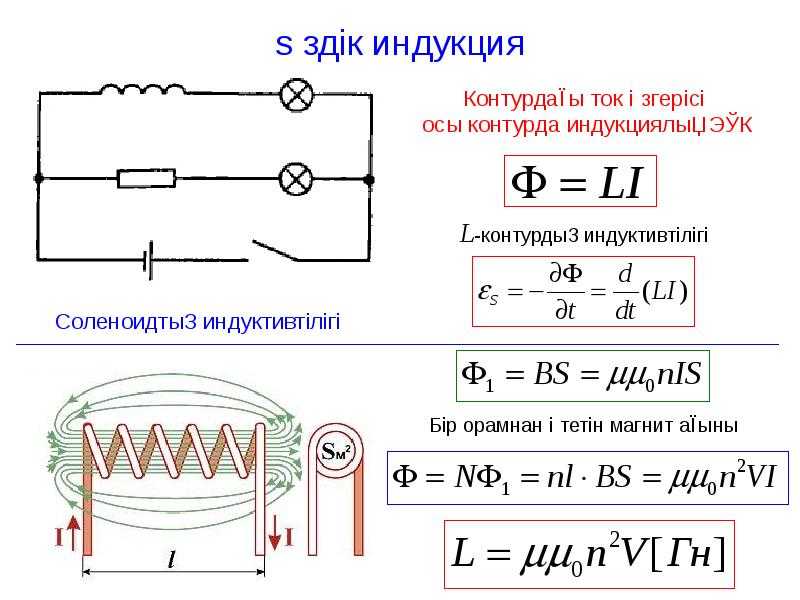 В радиотехнике для энергетической
характеристики затухания часто используют
величину, которая получила название
добротность контура:
.
В радиотехнике для энергетической
характеристики затухания часто используют
величину, которая получила название
добротность контура:
.
Энергия магнитного поля тока | СПАДИЛО
теория по физике 🧲 магнетизм
Согласно закону сохранения энергии энергия магнитного поля, созданного током, равна той энергии, которую должен затратить источник тока (гальванический элемент, генератор на электростанции и др.) на создание тока. При размыкании цепи эта энергия переходит в другие виды энергии.
То, что для создания тока необходимо затратить энергию, т. е. необходимо совершить работу, объясняется тем, что при замыкании цепи, когда ток начинает нарастать, в проводнике появляется вихревое электрическое поле, действующее против того электрического поля, которое создается в проводнике благодаря источнику тока. Для того чтобы сила тока стала равной I, источник тока должен совершить работу против сил вихревого поля. Эта работа идет на увеличение энергии магнитного поля тока.
При размыкании цепи ток исчезает, и вихревое поле совершает положительную работу. Запасенная током энергия выделяется. Это обнаруживается, например, по мощной искре, возникающей при размыкании цепи с большой индуктивностью.
Записать выражение для энергии тока I, текущего по цепи с индуктивностью L (т.е. для энергии магнитного поля тока), можно на основании аналогии между инерцией и самоиндукцией, о которой мы говорили в прошлой теме.
Если самоиндукция аналогична инерции, то индуктивность в процессе создания тока должна играть ту же роль, что и масса при увеличении скорости тела в механике. Роль скорости тела в электродинамике играет сила тока I как величина, характеризующая движение электрических зарядов.
Если это так, то энергия магнитного поля тока WМ будет подобна кинетической энергии тела в механике. Поэтому ее можно определить формулой:
Энергия магнитного поля токаWМ=LI22..
Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока.
Пример №1. В катушке индуктивностью 0,15 Гн и очень малым сопротивлением r сила тока равна 4 А. Параллельно катушке присоединили резистор сопротивлением R>> r. Какое количество теплоты выделится в катушке и в резисторе после быстрого отключения силы тока?
При параллельном подключении к катушке большого сопротивления R>> r, сила тока, идущая через катушку, почти не изменяется. Энергия в катушке равна:
WМ=LI22..
При отключении источника тока система катушка–сопротивление станет изолированной. Для изолированной системы справедлив закон сохранения энергии. В данном случае это означает, что вся энергия, запасенная в катушке, выделится в виде тепла в катушке и резисторе:
WМ=0,15·422..=1,2 (Дж)
Задание EF17636Катушка индуктивности подключена к источнику постоянного тока. Как изменится энергия магнитного поля катушки при увеличении силы тока через катушку в 3 раза?
Ответ:
а) уменьшится в 3 раза
б) увеличится в 9 раз
в) увеличится в 3 раза
г) уменьшится в 9 раз
Алгоритм решения
1. Записать формулу, определяющую энергию магнитного поля тока.
Записать формулу, определяющую энергию магнитного поля тока.
2.Установить, как изменится энергия магнитного поля тока при увеличении силы тока через катушку в 3 раза.
Решение
Энергия магнитного поля тока определяется формулой:
WМ=LI22..
Видно, что энергия магнитного поля тока прямо пропорционально зависит от квадрата силы тока в катушке. Следовательно, если сила тока увеличится втрое, то энергия магнитного поля увеличится в 32, то есть в 9 раз.
Ответ: бpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22688Энергия магнитного поля катушки с током равна 0,64 Дж. Индуктивность катушки равна 20 мГн. Какова сила тока в катушке?
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу, определяющую энергию магнитного поля тока.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
- Индуктивность катушки: L = 20 мГн.
- Энергия магнитного поля катушки с током: WM = 0,64 Дж.
20 мГн = 0,02 Гн
- Формула для нахождения энергии магнитного поля тока:
WМ=LI22..
Отсюда сила тока равна:
I=√2WМL..=√2·0,640,02..=8 ⎛⎝А⎞⎠
Ответ: 8pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22800На рисунке показана схема электрической цепи, состоящей из источника тока с ЭДС ε = 12 В и внутренним сопротивлением r = 1 Ом, двух резисторов с сопротивлениями R1 = 7 Ом и R2 = 4 Ом, конденсатора электроёмкостью С = 3 мкФ и катушки с индуктивностью L = 32 мкГн. Какое количество теплоты выделится на резисторе R2 после размыкания ключа К? Сопротивлением провода катушки пренебречь.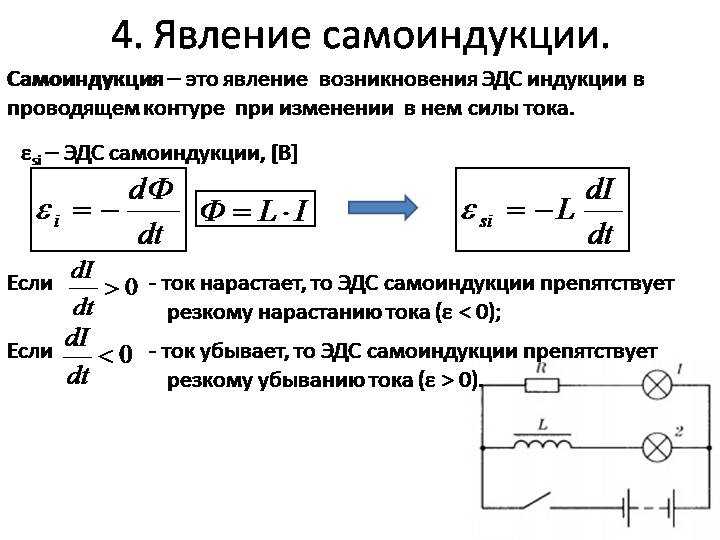 Ответ запишите в мкДж.
Ответ запишите в мкДж.
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать закон электромагнитной индукции для двигающихся стержней.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 12 В.
• Сопротивление источника тока: R = 1 Ом.
• Сопротивление первого резистора: R1 = 7 Ом.
• Сопротивление второго резистора: R2 = 4 Ом.
• Электроемкость конденсатора: C = 3 мкФ.
• Индуктивность катушки: L = 32 мкГн.
3 мкФ = 3∙10–6 Ф
32 мкГн = 32∙10–6 Гн
До размыкания ключа электрический ток протекает через последовательно соединённые резисторы R1, R2 и катушку L. После размыкания ключа вся накопленная в элементах цепи энергия выделится в виде тепла на резисторе R2:
E=Wкон+Wкат
Энергия электрического поля в конденсаторе определяется формулой:
Wкон=CU22. .
.
Напряжение U на конденсаторе можно выразит из закона Ома для участка цепи:
U=IR2
Чтобы выразить силу тока, потребуется записать закон Ома для полной цепи:
I=εR+r..
Так как в цепи есть два последовательно соединенных резистора, общее сопротивление цепи будет равно сумме их сопротивлений:
R=R1+R2
Тогда закон Ома для полной цепи примет вид:
I=εR1+R2+r..
Тогда напряжение на конденсаторе равно:
U=εR2R1+R2+r..
.
Следовательно, энергия электрического поля в конденсаторе будет равна:
Wкон=C2..(εR2R1+R2+r..)2
Энергия электромагнитного поля в катушке определяется формулой:
Wкат=LI22..=L2..(εR1+R2+r..)2
Следовательно, на втором резисторе выделится энергия, равная:
E=C2..(εR2R1+R2+r..)2+L2..(εR1+R2+r..)2
Ответ: 40pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 1. 7k | Оценить:
7k | Оценить:
1
Первый слайд презентации: Магнитное поле Самоиндукция. Индуктивность. Катушка индуктивности
Энергия катушки
Изображение слайда
2
Слайд 2: Магнитное поле Самоиндукция. Индуктивность. Катушка индуктивности
Энергия магнитного поля катушки с током равна 0,64 Дж. Индуктивность катушки равна 20 мГн. Какова сила тока в катушке? На рисунке приведён график зависимости силы тока от времени в электрической цепи, содержащей катушку, индуктивность которой 2 мГн. Определите модуль ЭДС самоиндукции в катушке в интервале времени от 15 до 20 с.
Изображение слайда
3
Слайд 3: Магнитное поле Самоиндукция.
 Индуктивность. Катушка индуктивности
Индуктивность. Катушка индуктивности
Изображение слайда
4
Слайд 4: Магнитное поле Самоиндукция. Индуктивность. Катушка индуктивности
Параллельно катушке индуктивности L включена лампочка (см. рис. а). Яркость свечения лампочки прямо пропорциональна напряжению на ней. На рис. б представлен график зависимости силы тока I в катушке от времени t. Сопротивлением катушки пренебречь. Опираясь на законы физики, изобразите график зависимости яркости свечения лампочки от времени.
Изображение слайда
5
Слайд 5: Магнитное поле Самоиндукция. Индуктивность. Катушка индуктивности
На рисунке показана схема электрической цепи, состоящей из источника тока с ЭДС = 12В и внутренним сопротивлением, двух резисторов с сопротивлениями и, конденсатора электроёмкостью С = 3 мкФ и катушки с индуктивностью L. Определите индуктивность катушки L, если известно, что после размыкания ключа К на резисторе выделилось количество теплоты, равное 40 мкДж. Сопротивлением провода катушки пренебречь.
Определите индуктивность катушки L, если известно, что после размыкания ключа К на резисторе выделилось количество теплоты, равное 40 мкДж. Сопротивлением провода катушки пренебречь.
Изображение слайда
6
Слайд 6: Колебания в LC- контуре Вывод уравнения колебаний из закона сохранения энергии
Изображение слайда
7
Слайд 7: Колебания в LC- контуре Задачи
На рисунке приведена зависимость силы тока от времени в колебательном контуре при свободных электромагнитных колебаниях. Какой станет частота свободных колебаний в контуре, если катушку в этом контуре заменить на другую катушку, индуктивность которой в 4 раза меньше?
Изображение слайда
8
Слайд 8: Колебания в LC- контуре Задачи
Конденсатор колебательного контура длительное время подключён к источнику постоянного напряжения (см.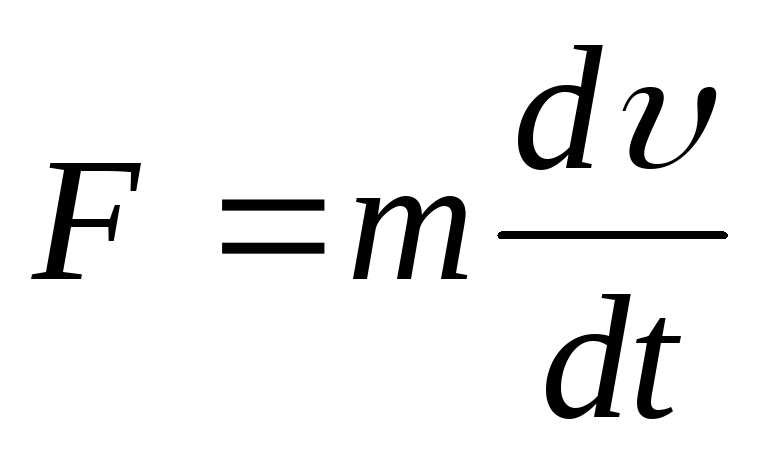 рисунок). В момент t = О переключатель К переводят из положения 1 в положение 2. Графики А и Б представляют изменения физических величин, характеризующих электромагнитные колебания в контуре после этого (Т — период колебаний).
Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
Сила тока в контуре
Энергия магнитного поля катушки
Энергия эл- го поля конденсатора
Заряд левой обкладки конденсатора
рисунок). В момент t = О переключатель К переводят из положения 1 в положение 2. Графики А и Б представляют изменения физических величин, характеризующих электромагнитные колебания в контуре после этого (Т — период колебаний).
Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
Сила тока в контуре
Энергия магнитного поля катушки
Энергия эл- го поля конденсатора
Заряд левой обкладки конденсатора
Изображение слайда
9
Слайд 9: Колебания в LC- контуре Задачи
Идеальный колебательный контур состоит из конденсатора и катушки индуктивностью 4 мГн. Заряд на пластинах конденсатора изменяется во времени в соответствии с формулой ( все величины выражены в СИ).
Установите соответствие между физическими величинами и формулами, выражающими их зависимость от времени в условиях данной задачи. А) сила тока в колебательном контуре
Б) энергия магнитного поля катушки
А) сила тока в колебательном контуре
Б) энергия магнитного поля катушки
Изображение слайда
10
Слайд 10: Колебания в LC- контуре Резонанс в LC- контуре
Изображение слайда
11
Слайд 11: Колебания в LC- контуре Использование LC- контура в радиоприёмнике
При настройке колебательного контура генератора, задающего частоту излучения радиопередатчика, электроёмкость его конденсатора увеличили. Как при этом изменились частота излучаемых волн и длина волны излучения? Для каждой величины определите соответствующий характер изменения: 1 ) увеличилась 2 ) уменьшилась 3) не изменилась
Изображение слайда
12
Слайд 12: Колебания в LC- контуре Использование LC- контура в радиоприёмнике
Колебательный контур радиоприёмника настроен на длину волны м. Индуктивность катушки контура, максимальный ток в ней. В контуре используется плоский воздушный конденсатор, расстояние между пластинами которого. Чему равно максимальное значение напряжённости электрического поля в конденсаторе в процессе колебаний?
Индуктивность катушки контура, максимальный ток в ней. В контуре используется плоский воздушный конденсатор, расстояние между пластинами которого. Чему равно максимальное значение напряжённости электрического поля в конденсаторе в процессе колебаний?
Изображение слайда
13
Последний слайд презентации: Магнитное поле Самоиндукция. Индуктивность. Катушка индуктивности: Катушка индуктивности. LC- контур Задачи для самостоятельного решения
17-15, 59-28, 92-15, 98-31, 272-15, 113-16, 18-17, 56-18, 74-15, 79-31, 98-32, 113-15, 134-17, 155-18, 157-23, 174-15, 179-32!, 195-18, 198-27, 213-15, 252-18, 292-18, 296-31
Изображение слайда
power — Можно ли хранить энергию в индукторе и использовать ее позже?
\$\начало группы\$
Моя компания использует суперконденсаторы для питания устройства в случае отключения электроэнергии. Мне было интересно, можно ли сделать то же самое с катушкой индуктивности. Если нельзя, то почему?
Мне было интересно, можно ли сделать то же самое с катушкой индуктивности. Если нельзя, то почему?
- мощность
- конденсатор
- дроссель
\$\конечная группа\$
2
\$\начало группы\$
Магнитное поле, хранящее энергию, является функцией тока через индуктор: нет тока, нет поля, нет энергии. Вам понадобится активная цепь, чтобы поддерживать этот ток, как только вы отключите ток, индуктор выделит энергию магнитного поля также в виде тока, а индуктор станет источником тока (тогда как его двойной конденсатор является источником напряжения) .
Аспекты дуальности конденсатор-индуктор с точки зрения накопления энергии:
\begin{array}{ll} \mbox{Конденсатор} и \mbox{Дроссель} \\ \mbox{* сохраняет энергию в электрическом поле} & \mbox{* сохраняет энергию в магнитном поле} \\ \mbox{* должен быть разомкнутым контуром (бесконечное сопротивление) } & \mbox{* должен быть замкнутым контуром (нулевое сопротивление)} \\ \mbox{* теряет энергию из-за параллельного сопротивления} & \mbox{* теряет энергию из-за последовательного сопротивления} \end{array}
A сверхпроводник 9Однако 0028 может поддерживать магнитное поле в токовой петле с нулевым сопротивлением. 2R. Это можно преодолеть, используя сверхпроводники, которые вообще не имеют сопротивления, но проблема в том, что все известные в настоящее время сверхпроводники должны охлаждаться до криогенных температур. Кроме того, в то время как идеальный сверхпроводник оставался бы сверхпроводящим при любом произвольном токе, все известные сверхпроводники (на самом деле) имеют некоторый верхний предел плотности тока, который они могут поддерживать, прежде чем эффект исчезнет.
2R. Это можно преодолеть, используя сверхпроводники, которые вообще не имеют сопротивления, но проблема в том, что все известные в настоящее время сверхпроводники должны охлаждаться до криогенных температур. Кроме того, в то время как идеальный сверхпроводник оставался бы сверхпроводящим при любом произвольном токе, все известные сверхпроводники (на самом деле) имеют некоторый верхний предел плотности тока, который они могут поддерживать, прежде чем эффект исчезнет.
\$\конечная группа\$
0
\$\начало группы\$
\$\begin{массив}{lcl}
\textbf{Емкостное хранилище} & & \textbf{Индуктивное хранилище} \\
\mbox{Должно иметь бесконечное внутреннее сопротивление} & | & \mbox{Должен иметь нулевое внутреннее сопротивление} \\
\mbox{Напряжение должно оставаться в нем навсегда} & | & \mbox{Ток должен течь через него вечно} \\
\mbox{Вы имеете дело с напряжением} & | & \mbox{Вы имеете дело с текущим} \\
\mbox{Саморазряд может занять годы} & | & \mbox{Саморазряд за очень короткое время} \\
\mbox{Электрическое поле практически не выходит наружу} & | & \mbox{Магнитное поле может мешать другим компонентам} \\
\mbox{Легче} & | & \mbox{Очень тяжелый (железо, медь и т. д.)} \\
\mbox{Может быть дешевле} & | & \mbox{В некоторых странах Fe и Cu могут быть очень дорогими} \\
\конец{массив}\$
д.)} \\
\mbox{Может быть дешевле} & | & \mbox{В некоторых странах Fe и Cu могут быть очень дорогими} \\
\конец{массив}\$
\$\конечная группа\$
0
\$\начало группы\$
Да, люди могут накапливать энергию в индукторе и использовать ее позже.
Люди построили несколько сверхпроводящих магнитных накопителей энергии, которые хранят мегаджоуль энергии в течение дня или около того с довольно высокой эффективностью, в катушке индуктивности, сформированной из сверхпроводящего «провода». Мне сказали, что несколько электроэнергетических компаний купили несколько таких блоков и используют их для улучшения качества электроэнергии.
Большинство людей в США имеют десятки импульсных преобразователей напряжения.
Большинство этих импульсных преобразователей напряжения постепенно накапливают энергию при одном напряжении в катушке индуктивности или трансформаторе, а затем «позже» постепенно извлекают эту энергию из катушки индуктивности или трансформатора при более желаемом напряжении, снова и снова, часто 40 000 или миллион раз в секунду. второй.
второй.
Многие популярные поставщики электронных компонентов позволяют сортировать катушки индуктивности по их добротности. Коэффициент добротности показывает, насколько хорошо катушка индуктивности или конденсатор хранит энергию. В импульсных стабилизаторах напряжения и других приложениях для накопления энергии чем больше добротность, тем лучше.
Лучшие готовые катушки индуктивности (все несверхпроводящие) популярных поставщиков имеют добротность 150 при 25 кГц. Большинство конденсаторов имеют на порядок лучшее накопление энергии (более высокую добротность), чем это.
Люди могут сохранять и сохраняют некоторое количество энергии в индукторах для последующего использования. Но почти во всех ситуациях с накоплением энергии мы используем что-то другое, потому что это что-то другое либо (а) имеет более низкие первоначальные затраты, либо (б) более эффективно, либо (в) требует меньше места, либо (г) какое-то сочетание вышеперечисленного.
\$\конечная группа\$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
электромагнитный — Как индуктор хранит энергию?
Задавать вопрос
Спросил
Изменено 3 месяца назад
Просмотрено 37 тысяч раз
\$\начало группы\$
Я знаю, что конденсаторы хранят энергию, накапливая заряды на своих пластинах, так же люди говорят, что катушка индуктивности накапливает энергию в своем магнитном поле. Я не могу понять это утверждение. Я не могу понять, как индуктор накапливает энергию в своем магнитном поле, то есть я не могу это визуализировать.
Обычно, когда электроны движутся через индуктор, что происходит с электронами и как они блокируются магнитным полем? Может ли кто-нибудь объяснить мне это концептуально?
А также, пожалуйста, объясните это:
Если электроны текут по проводу, как они преобразуются в энергию в магнитном поле?
Как возникает обратная ЭДС?
- индуктор
- электромагнитный
- противо-ЭДС
\$\конечная группа\$
9
\$\начало группы\$
Это более глубокий вопрос, чем кажется. Даже физики расходятся во мнениях относительно точного смысла хранения энергии в поле и даже того, является ли это хорошим описанием того, что происходит. Не помогает и то, что магнитные поля — это релятивистский эффект, а значит, по своей сути странный.
Даже физики расходятся во мнениях относительно точного смысла хранения энергии в поле и даже того, является ли это хорошим описанием того, что происходит. Не помогает и то, что магнитные поля — это релятивистский эффект, а значит, по своей сути странный.
Я не физик твердого тела, но постараюсь ответить на ваш вопрос об электронах. Давайте посмотрим на эту схему:
смоделируйте эту схему – Схема создана с помощью CircuitLab
Начнем с того, что на катушке индуктивности нет ни напряжения, ни тока. Когда переключатель замыкается, ток начинает течь. Когда ток течет, он создает магнитное поле. Это требует энергии, которая исходит от электронов. Есть два взгляда на это:
Теория цепей: в катушке индуктивности изменяющийся ток создает напряжение на катушке индуктивности \$(V = L\frac{di}{dt})\$. Напряжение, умноженное на ток, равно мощности. Таким образом, изменение тока индуктора требует энергии.
Физика: изменяющееся магнитное поле создает электрическое поле.
 Это электрическое поле отталкивает электроны, поглощая при этом энергию. Таким образом, ускорение электронов требует энергии сверх того, что вы ожидаете от одной только инерционной массы электрона.
Это электрическое поле отталкивает электроны, поглощая при этом энергию. Таким образом, ускорение электронов требует энергии сверх того, что вы ожидаете от одной только инерционной массы электрона.
В конце концов, ток достигает 1 ампера и остается на этом уровне из-за резистора. При постоянном токе на катушке индуктивности нет напряжения \$(V = L\frac{di}{dt} = 0)\$. В постоянном магнитном поле нет индуцированного электрического поля.
А что, если мы уменьшим напряжение источника до 0 вольт? Электроны теряют энергию в резисторе и начинают замедляться. При этом магнитное поле начинает разрушаться. Это снова создает электрическое поле в индукторе, но на этот раз оно толкает электроны, чтобы поддерживать их движение, давая им энергию. Ток, наконец, прекращается, когда магнитное поле исчезает.
Что, если мы попытаемся разомкнуть выключатель, пока течет ток? Все электроны пытаются мгновенно остановиться. Это приводит к тому, что магнитное поле сразу разрушается, что создает массивное электрическое поле. Это поле часто достаточно велико, чтобы выталкивать электроны из металла через воздушный зазор в переключателе, создавая искру. (Энергия конечна, но мощность очень велика.)
Это поле часто достаточно велико, чтобы выталкивать электроны из металла через воздушный зазор в переключателе, создавая искру. (Энергия конечна, но мощность очень велика.)
Обратная ЭДС — это напряжение, создаваемое индуцированным электрическим полем при изменении магнитного поля.
Вам может быть интересно, почему этого не происходит в резисторе или проводе. Ответ таков: любой ток создает магнитное поле. Однако индуктивность этих компонентов невелика — например, обычная оценка составляет 20 нГн/дюйм для дорожек на печатной плате. Это не станет серьезной проблемой, пока вы не доберетесь до мегагерцового диапазона, и в этот момент вам придется использовать специальные методы проектирования для минимизации индуктивности.
\$\конечная группа\$
8
\$\начало группы\$
Это мой способ визуализации концепции катушки индуктивности и конденсатора. 2\$.
Итак, емкость \$C\$ аналогична жесткости пружины \$k\$.
Емкостное напряжение, \$V\$, аналогично смещению пружины, \$x\$.
Электрическое поле на емкости аналогично силе, создаваемой на пружине. Происходит следующее: кинетическая энергия электронов запасается в конденсаторе в виде потенциальной энергии. Результирующая разность потенциалов представляет собой напряжение, представляющее собой своего рода давление в виде электрического поля. Итак, конденсатор всегда отталкивает электроны назад из-за своей потенциальной энергии. 92\$, где \$i\$ — текущий. Таким образом, ток аналогичен скорости, которая равна \$i = \frac{dq}{dt}\$.
2\$.
Итак, емкость \$C\$ аналогична жесткости пружины \$k\$.
Емкостное напряжение, \$V\$, аналогично смещению пружины, \$x\$.
Электрическое поле на емкости аналогично силе, создаваемой на пружине. Происходит следующее: кинетическая энергия электронов запасается в конденсаторе в виде потенциальной энергии. Результирующая разность потенциалов представляет собой напряжение, представляющее собой своего рода давление в виде электрического поля. Итак, конденсатор всегда отталкивает электроны назад из-за своей потенциальной энергии. 92\$, где \$i\$ — текущий. Таким образом, ток аналогичен скорости, которая равна \$i = \frac{dq}{dt}\$.
Когда по проводу течет ток, движущиеся электроны создают магнитное поле вокруг провода. Для прямого провода генерируемое магнитное поле не будет воздействовать на электроны в этом проводе или, по крайней мере, в большинстве случаев им можно пренебречь. Однако если мы намотаем провода несколько тысяч раз так, что генерируемое магнитное поле воздействует на сами электроны провода, то любому изменению скорости будет противодействовать сила магнитного поля.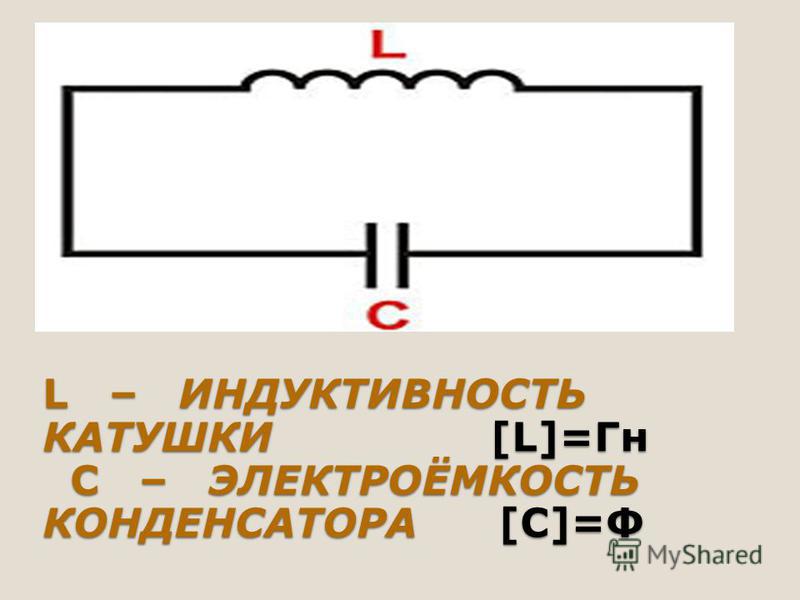 Таким образом, общая сила, \$F\$, с которой сталкиваются электроны, выражается как \$\mathbf{F} = q\mathbf{E} + q\mathbf{v} \times \mathbf{B}\$.
Потенциальная энергия в конденсаторе запасается в виде электрического поля, а кинетическая энергия в катушке индуктивности запасается в виде магнитного поля.
Таким образом, общая сила, \$F\$, с которой сталкиваются электроны, выражается как \$\mathbf{F} = q\mathbf{E} + q\mathbf{v} \times \mathbf{B}\$.
Потенциальная энергия в конденсаторе запасается в виде электрического поля, а кинетическая энергия в катушке индуктивности запасается в виде магнитного поля.
Таким образом, индуктор действует как инерция, реагирующая на изменение скорости электронов, а конденсатор действует как пружина, реагирующая на приложенную силу.
Используя приведенные выше аналогии, вы можете легко найти, почему соотношение фаз между напряжением и током различно для катушек индуктивности и конденсаторов. Эта аналогия также помогает понять механизм обмена энергией между конденсатором и катушкой индуктивности, например, в LC-генераторе.
Для дальнейшего размышления задайте следующие вопросы. Как запасается кинетическая энергия в механической системе? Когда мы бежим, где и как запасается кинетическая энергия? Когда мы бежим, создаем ли мы поле, которое взаимодействует с нашим движущимся телом?
\$\конечная группа\$
\$\начало группы\$
Один из способов осмыслить это — представить, что это похоже на инерцию тока через индуктор. Хороший способ проиллюстрировать это с помощью гидравлического поршневого насоса:
Хороший способ проиллюстрировать это с помощью гидравлического поршневого насоса:
В гидравлическом поршневом насосе вода течет по большой трубе в быстродействующий клапан. Когда клапан закрывается, инерция тяжелой текущей массы воды вызывает внезапное резкое увеличение давления воды на клапане. Затем это давление заставляет воду подниматься вверх через односторонний клапан. По мере того, как энергия водяного тарана рассеивается, главный быстродействующий клапан открывается, и вода набирает некоторый импульс в основной трубе, и цикл повторяется снова. См. иллюстрацию на вики-странице. 92}{2}\$, где L — индуктивность, а I — текущий ток.
В частности, у меня всегда были проблемы с визуализацией заряда и напряжения, но у меня никогда не было проблем с визуализацией тока (за исключением случаев, когда нужно понять, что ток — это поток заряда). Я принимаю, что напряжение такое, какое оно есть, и просто живу с этим. Может быть, я слишком много думаю. Может быть, вы тоже?
В конце концов я вернусь к основам, и это для меня, насколько я хочу вернуться, потому что я не физик.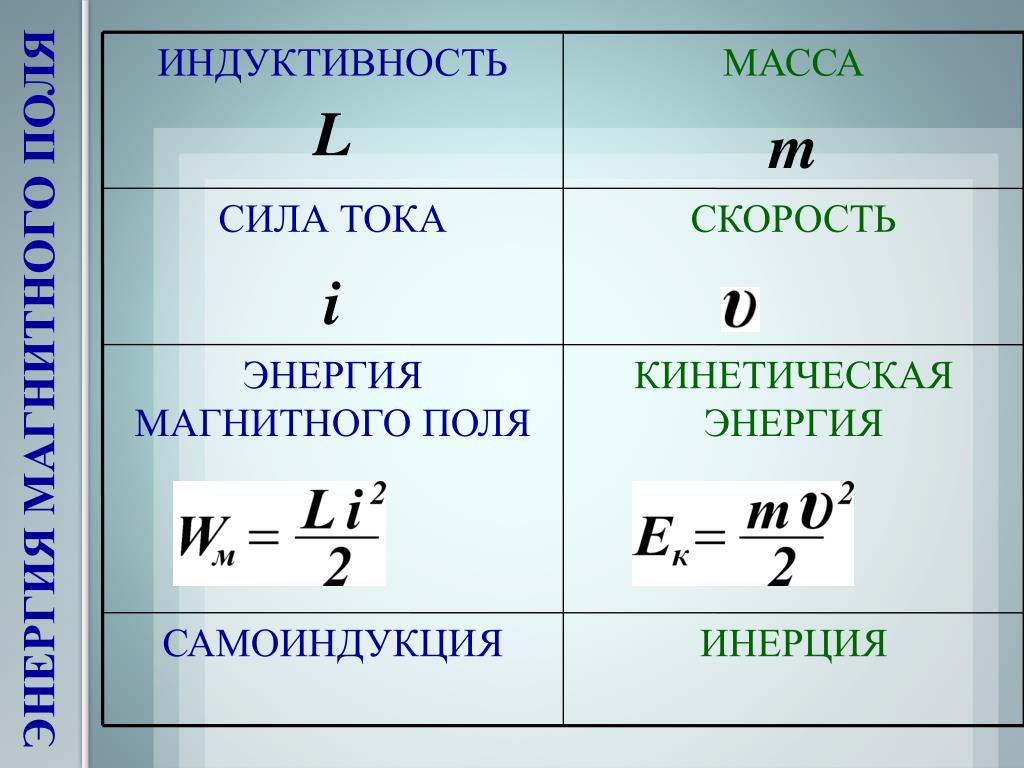 Основы: —
Основы: —
Q = CV или \$\dfrac{dQ}{dt} = C\cdot\dfrac{dV}{dt}\$ = ток, I
Это говорит мне о том, что для заданной скорости изменения напряжения на конденсаторе существует ток ИЛИ, если вы форсируете ток через конденсатор, будет линейное напряжение.
Существует аналогичная формула для катушки индуктивности, которая в основном говорит вам, что при заданном напряжении, приложенном к клеммам, ток будет возрастать пропорционально: —
В = \$L\dfrac{di}{dt}\$, когда V подается на клеммы и
V = \$-L\dfrac{di}{dt}\$ при вычислении противо-ЭДС из-за схлопывания внешнего потока или изменения потока от другой катушки.
Эти две формулы объясняют мне, что происходит.
\$\конечная группа\$
0
\$\начало группы\$
Может быть, мы можем представить это таким образом. Катушки индуктивности изготавливаются путем витков проводника над магнитным сердечником или просто воздухом. В отличие от конденсатора, в котором между пластинами проводников зажато диэлектрическое вещество.
каждый атом действует как петля с током. Это так, потому что электрон вращается по круговой траектории. Это приводит к возникновению магнитных диполей (атомов) внутри веществ. Изначально все магнитные диполи хаотично направлены внутрь вещества, что делает результирующее направление силовых линий магнитного поля нулевым.
Ток течет из-за потока электронов. В цепи, состоящей из индуктора, существует определенное направление протекания тока (или потока электронов) через индуктор. как таковой, этот ток пытается выровнять магнитные диполи в определенном направлении.
В отличие от конденсатора, в котором между пластинами проводников зажато диэлектрическое вещество.
каждый атом действует как петля с током. Это так, потому что электрон вращается по круговой траектории. Это приводит к возникновению магнитных диполей (атомов) внутри веществ. Изначально все магнитные диполи хаотично направлены внутрь вещества, что делает результирующее направление силовых линий магнитного поля нулевым.
Ток течет из-за потока электронов. В цепи, состоящей из индуктора, существует определенное направление протекания тока (или потока электронов) через индуктор. как таковой, этот ток пытается выровнять магнитные диполи в определенном направлении.
Нежелание магнитных диполей выровняться в определенном направлении отвечает за противодействие тока. противодействие можно назвать обратной ЭДС.
Предлагаемая оппозиция отличается для разных материалов. следовательно, у нас разные значения сопротивления. индуктор считается насыщенным, когда все магнитные диполи выровнены в определенном направлении, которое определяется правилом большого пальца правой руки Флеминга . направление противодействия определяется законом Ленца (направление противодействия).
направление противодействия определяется законом Ленца (направление противодействия).
Эти магнитные диполи отвечают только за накопление магнитной энергии. Предположим, что эта катушка индуктивности подключена к замкнутой цепи без подачи тока. теперь выровненные магнитные диполи пытаются сохранить свое исходное положение из-за отсутствия тока. Это приводит к протеканию тока. можно сказать, что энергия, накопленная в катушке индуктивности, обусловлена временным выравниванием этих диполей. но немногие магнитные диполи не могут достичь своей начальной конфигурации. следовательно, мы говорим, что чистая катушка индуктивности практически отсутствует.
Ученые знают, что электрические и магнитные поля взаимосвязаны . Впервые это подтвердил Эрстед в своем эксперименте с магнитным компасом. даже ученые считают, что магнитное поведение проявляют и отдельные электроны из-за их вращения вокруг собственной оси.
\$\конечная группа\$
1
\$\начало группы\$
Представьте последовательную цепь, состоящую из идеального конденсатора C, идеальной катушки индуктивности L и переключателя. Индуктор имеет магнитомягкий сердечник, так что сила его магнитного поля пропорциональна току, протекающему через него. Диэлектрик конденсатора идеальный, поэтому потерь нет.
Сначала предположим, что переключатель разомкнут и все начальные условия равны нулю. То есть на конденсаторе нет заряда, ток через катушку индуктивности равен нулю и, следовательно, магнитное поле в сердечнике равно нулю. Придаем конденсатору первоначальный заряд до В вольт с помощью батарейки.
Переключатель теперь замкнут, при t=0, а L и C образуют простую последовательную цепь. При всех значениях времени после замыкания ключа напряжение на конденсаторе должно быть равно напряжению на индукторе (закон Кирхгофа о напряжении). Так что же происходит????
Так что же происходит????
При t=o напряжение на C равно V, поэтому напряжение на L также должно быть V. Следовательно, скорость изменения тока di/dt от C к L должна быть такой, чтобы Ldi/dt = V. Таким образом, скорость изменения тока достаточно велика, но сам ток в момент t=0 равен i=0, и di/dt = V/L
С течением времени напряжение на C уменьшается (по мере вытекания заряда) и скорость изменения тока, необходимая для поддержания напряжения катушки индуктивности на том же уровне, что и напряжение конденсатора, уменьшается. Ток все еще увеличивается, но его градиент уменьшается.
По мере увеличения тока увеличивается напряженность магнитного поля в сердечнике индуктора (напряженность поля пропорциональна току).
В точке, где конденсатор потерял весь свой заряд, напряжение на конденсаторе равно нулю, ток достигает своего максимального значения (он увеличивается с момента t=0), но скорость изменения di/dt теперь равна нулю поскольку катушке индуктивности не нужно генерировать напряжение, чтобы уравновесить напряжение конденсатора.
 2/2
2/2Теперь в конденсаторе больше нет энергии, поэтому он не может подавать ток для поддержания магнитного поля индуктора. Магнитное поле начинает разрушаться, но при этом создается ток, который стремится противодействовать разрушающемуся магнитному полю (закон Ленца). Этот ток имеет то же направление, что и первоначальный ток, протекающий в цепи, но теперь он заряжает конденсатор в противоположном направлении (то есть, если верхняя пластина изначально могла быть положительной, теперь нижняя пластина заряжается положительно).
Индуктор теперь на месте водителя. Он генерирует ток i в ответ на разрушающееся магнитное поле, и, поскольку этот ток уменьшается по сравнению с его первоначальным значением (I), генерируется напряжение с величиной Ldi/dt (полярность, противоположная предыдущей).
Этот режим продолжается до тех пор, пока магнитное поле полностью не рассеется, передав свою энергию обратно конденсатору, хотя и с противоположной полярностью, и вся операция начнется снова, но на этот раз конденсатор нагнетает ток по цепи в направлении, противоположном предыдущему.

Вышеприведенное представляет собой положительный полупериод текущего сигнала, а шаг 7 является началом отрицательного полупериода. Один полный сигнал разряда-заряда представляет собой один цикл синусоидального сигнала. Если компоненты L и C идеальны или «идеальны», потерь энергии нет, а синусоиды напряжения и тока продолжаются до бесконечности.
Итак, я думаю, ясно, что магнитное поле обладает способностью накапливать энергию. Однако он не способен к долговременному хранению, как конденсатор, поскольку возможности и механизмы утечки энергии разнообразны. Интересно отметить, что ранняя компьютерная память была сделана из катушек индуктивности, намотанных на ферритовые тороидальные сердечники (один тороид на бит!!), но они нуждались в частом электронном обновлении для сохранения сохраненных данных.
\$\конечная группа\$
\$\начало группы\$
О полях вообще не будем. Давайте сначала поговорим о том, что такое напряжение. Электроны очень не любят находиться рядом друг с другом. Электрическая сила невероятно сильная. Позвольте мне привести вам пример этого. Если бы через провод прошло 1 ампер тока, это означало бы, что 1 колумб электрического заряда прошел по этому проводу за 1 секунду . Предположим, что вы смогли сохранить все эти электроны, прошедшие за одну секунду, на электрически изолированной металлической сфере. Затем вы подождали еще секунду и сохранили такое же количество электронов на другой изолированной металлической сфере. Теперь у вас есть 98 кг в земной гравитации. Это вес очень большого здания. Это показывает, что лишние электроны вообще не любят находиться рядом друг с другом.
Давайте сначала поговорим о том, что такое напряжение. Электроны очень не любят находиться рядом друг с другом. Электрическая сила невероятно сильная. Позвольте мне привести вам пример этого. Если бы через провод прошло 1 ампер тока, это означало бы, что 1 колумб электрического заряда прошел по этому проводу за 1 секунду . Предположим, что вы смогли сохранить все эти электроны, прошедшие за одну секунду, на электрически изолированной металлической сфере. Затем вы подождали еще секунду и сохранили такое же количество электронов на другой изолированной металлической сфере. Теперь у вас есть 98 кг в земной гравитации. Это вес очень большого здания. Это показывает, что лишние электроны вообще не любят находиться рядом друг с другом.
Напряжение — это энергия, которую имеет избыточный электрон, когда он добавляется к объекту. И вам вообще не нужно много электронов, чтобы существенно увеличить напряжение. Это означает, что объекты, в том числе металлические провода, имеют очень низкую емкость для избыточных электронов. Что же такое конденсатор? Конденсатор обладает высокой емкостью для электронов, поэтому, когда батарея добавляет электроны к куску провода с конденсатором на конце, напряжение не увеличивается так сильно на каждый электрон. это , а не из-за того, что у конденсатора есть пластина (независимо от того, насколько она велика): одна пластина имеет очень-очень НИЗКУЮ емкость для дополнительных электронов. Секрет конденсатора в пластине , расположенной напротив пластины , которая находится очень близко к нему. Что происходит, так это то, что любые избыточные электроны на пластине притягиваются к противоположной пластине, из которой электроны были удалены батареей. Это означает, что общая энергия на избыточный электрон уменьшается, и вы можете разместить больше электронов на единицу увеличения напряжения. Следовательно, между конденсаторами не может быть воздушного зазора, потому что силы очень велики. Между ними должно быть твердое тело, чтобы пластины не врезались друг в друга.
Что же такое конденсатор? Конденсатор обладает высокой емкостью для электронов, поэтому, когда батарея добавляет электроны к куску провода с конденсатором на конце, напряжение не увеличивается так сильно на каждый электрон. это , а не из-за того, что у конденсатора есть пластина (независимо от того, насколько она велика): одна пластина имеет очень-очень НИЗКУЮ емкость для дополнительных электронов. Секрет конденсатора в пластине , расположенной напротив пластины , которая находится очень близко к нему. Что происходит, так это то, что любые избыточные электроны на пластине притягиваются к противоположной пластине, из которой электроны были удалены батареей. Это означает, что общая энергия на избыточный электрон уменьшается, и вы можете разместить больше электронов на единицу увеличения напряжения. Следовательно, между конденсаторами не может быть воздушного зазора, потому что силы очень велики. Между ними должно быть твердое тело, чтобы пластины не врезались друг в друга.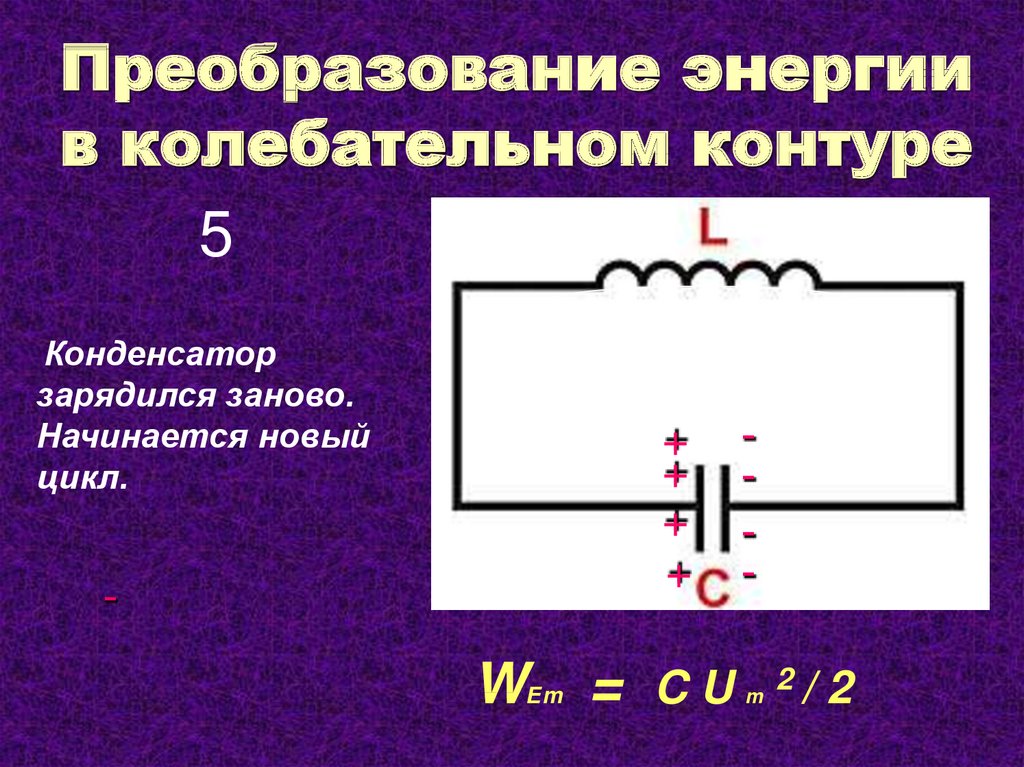
Теперь переходим к индуктору. Это безумие. Нет такой вещи, как магнитное поле. Это просто притяжение Кулона. Но в данном случае это кулоновское притяжение возникает только при протекании тока. Как это может произойти? Хорошо помните, что кулоновская сила невероятно велика, поэтому ее эффекты можно увидеть по довольно тонким едва заметным изменениям электронной плотности, которые мы не можем видеть. А теперь о сути дела. Тонкие изменения на самом деле связаны с относительностью Эйнштейна. Электроны имеют среднее расстояние в проводе, и это среднее расстояние такое же, как среднее расстояние положительных зарядов. Когда течет ток, вы можете подумать, что среднее расстояние остается прежним, но теперь вы должны учитывать сокращение длины . Стороннему наблюдателю любой движущийся объект будет казаться короче, и именно это происходит с (пространством между) электронами. С катушкой проволоки на противоположных сторонах круга электроны текут в противоположном направлении. Одна сторона видит другую как имеющую большую плотность электронов, чем положительные заряды из-за относительности. Это создает отталкивание между электронами в проводах с противоположными направлениями тока и увеличивает их энергия (т.е. напряжение). Поэтому напряжение нарастает гораздо быстрее, чем на обычном проводе. Поэтому люди думают о катушках индуктивности как о , противостоящих току. Но что на самом деле происходит, так это то, что напряжение увеличивается очень быстро и тем более, если протекает больший ток. Вы могли заметить, что во всех учебниках по магнетизму трактуются математически и никогда не указывают, какая именно частица ответственна за это. Ну, это электрон, а сила обусловлена теорией относительности, и эта сила определенно кулонова. Это верно даже для постоянно намагниченных материалов (но это другой разговор). Забудьте о полях, это математическая конструкция для людей, которые не хотят понимать мир.
Одна сторона видит другую как имеющую большую плотность электронов, чем положительные заряды из-за относительности. Это создает отталкивание между электронами в проводах с противоположными направлениями тока и увеличивает их энергия (т.е. напряжение). Поэтому напряжение нарастает гораздо быстрее, чем на обычном проводе. Поэтому люди думают о катушках индуктивности как о , противостоящих току. Но что на самом деле происходит, так это то, что напряжение увеличивается очень быстро и тем более, если протекает больший ток. Вы могли заметить, что во всех учебниках по магнетизму трактуются математически и никогда не указывают, какая именно частица ответственна за это. Ну, это электрон, а сила обусловлена теорией относительности, и эта сила определенно кулонова. Это верно даже для постоянно намагниченных материалов (но это другой разговор). Забудьте о полях, это математическая конструкция для людей, которые не хотят понимать мир.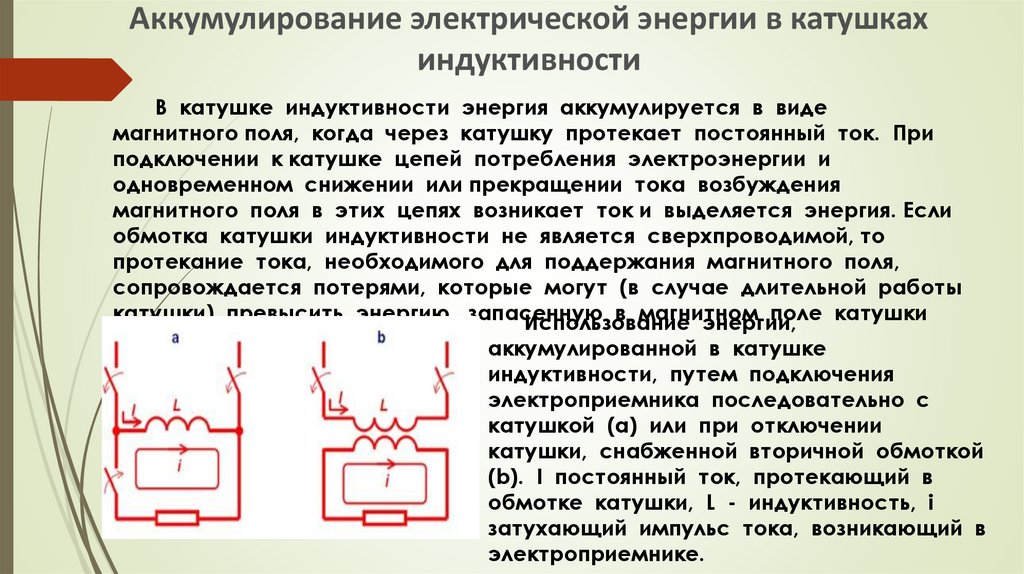
\$\конечная группа\$
2
\$\начало группы\$
Визуализация b-полей и катушек индуктивности? Нравится это видео?
https://youtu.be/1elpVmpkBh5
Найдите видео профессора Дж. Белчера из курса MIT e&m «TEAL project» с анимированными визуализациями EM. Каждая катушка подобна набору металлических маховиков, где электроны внутри витков проволоки подобны атомам в движущихся маховиках.
- Внезапно включилась катушка: https://youtu.be/1elpVmpkBh5
- Отключение катушки: https://youtu.be/iesoHVfIg6I Супермагнит
- проваливается сквозь медное кольцо с потоком электронов наведенные поля https://youtu.be/YywaJkGKOaY
- то же со сверхпроводящим кольцом https://youtu.be/c3kxyqbsERI также https://youtu.be/uL4pfisCX14
- Зарядка конденсатора с двумя сферами: https://youtu.be/O5fHvc4Edvg
Также: Экскурсия по классическому электромагнетизму (с анимацией MPG)
http://web. mit.edu/8.02t/www/802TEAL3D/visualizations/guidedtour/Tour.htm
mit.edu/8.02t/www/802TEAL3D/visualizations/guidedtour/Tour.htm
Попробуйте эти коллекции MPEG:
- http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/magnetostatics/
- http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/faraday/
обнаружил, что нет возможности визуализировать то, что происходит в индукторе
НЕПРАВДА! Вместо этого авторы-инженеры никогда не пытаются этого делать, отчасти потому, что анимированные диаграммы не работают в бумажных учебниках. Но также я неоднократно обнаруживал, что анимированные диаграммы рассматриваются как метод «для чайников» и вызывают насмешки, поскольку они делают вещи слишком простыми для понимания. Никакой математической строгости, слишком много «физики для поэтов». Ожидается, что работа инженерного курса будет сложной и трудной: мы должны изучать только математические модели, никогда не видя простых прямых анимаций, основанных на тех же уравнениях. (Хех, если нам НУЖНА нематематическая визуальная версия, то, может быть, мы ошибаемся в программе обучения и должны брать более простые предметы? К черту: вместо этого я хочу преподавать этот материал всем, маленьким детям и дедушкам.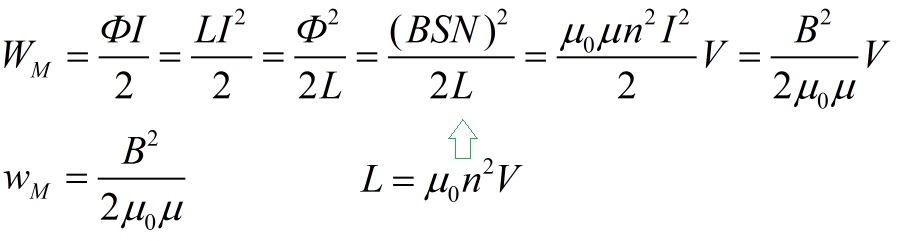 Используйте математические модели для создания 3D-анимации, интерактивные визуальные симуляции, где мы можем ВИДЕТЬ токи внутри проводов и т. д.)
Используйте математические модели для создания 3D-анимации, интерактивные визуальные симуляции, где мы можем ВИДЕТЬ токи внутри проводов и т. д.)
\$\конечная группа\$
\$\начало группы\$
Все эти ответы замечательны, но чтобы ответить на вопрос об обратной ЭДС, необходимо помнить о ключевых моментах:
Изменение поля B индуцирует поле E.
E связан с ε (ЭДС) через: ε = W/q -> W = ∮F⋅ds -> W/q = -∮(F/q)⋅ds -> E = F/q -> W/q = -∮E⋅ds (где s — бесконечно малое расстояние в направлении движения)
Итак, когда есть изменяющееся магнитное поле, возникает индуцированное поле E, а значит, будет индуцированное напряжение (ЭДС).
- ε = -∮(E_ind)⋅ds = -∂(Φ_B)/∂t = -(d/dt)(∫B⋅dA) Помните, здесь меняется поле B, поэтому: = -(∂B /∂т)А
Причина того, что он противостоит источнику постоянного напряжения (например, батарее), заключается в том, что F (пропорционально E) указывает перпендикулярно B и I:
- F = Ids × B.
 (Текущие времена ds, бесконечно малая часть провода в направлении I — ток может течь только по проводу)
(Текущие времена ds, бесконечно малая часть провода в направлении I — ток может течь только по проводу)
(Направление определяется правилом правой руки)
Эта сила добавляет компонент скорости к зарядам в потоке в направлении F. В свою очередь, этот новый компонент скорости теперь создает компонент силы, взаимно ортогональный новому компоненту и полю B, который находится в направлении, противоположном первоначальному потоку тока или противоположно исходному напряжению питания, и поэтому это называется «противоэдс».
Именно эта противо-ЭДС замедляет заряд (а не блокирует их).
\$\конечная группа\$
\$\начало группы\$
Мне нравится думать об этом так.
Это аналогично тому, почему требуется работа, чтобы остановить движущееся тело;
почему тело движется бесконечно с неизменной скоростью, когда на него не действует результирующая сила.
➡️ Электроны делают то же самое.
Ток аналогичен этой кинетической энергии тела, и, соответственно, электроны, загоняемые в конденсатор, аналогичны подъему тела вверх (потенциальная энергия). (Электроны или тело загоняются туда, куда они «не хотят» идти сами, а они «хотят» уйти.)
Примечание: Это не физическое рассуждение. Сообщение ОП требует рабочей ментальной модели, а не глубокого объяснения.
Но мне нравится думать об этом и объяснять так. Нам нужны хорошие ментальные модели, чтобы иметь возможность проектировать. Это хорошая модель IMO, потому что поведение одинаково в обоих случаях — даже дифференциальные уравнения одинаковы.
\$\конечная группа\$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
ток — Нарушают ли кинетическая энергия и энергия индуктора закон сохранения энергии?
Задавать вопрос
Спросил
92\$. Таким образом, кажется, что мы создали энергию в этом процессе.Единственный способ обойти эту проблему — предположить, что кинетическая энергия уже каким-то образом учтена в энергии магнитного поля, но я не уверен.
- ток
- индуктор
- электромагнетизм
- энергия
\$\конечная группа\$
2
\$\начало группы\$
Напряжение и ток являются приблизительными значениями, а не фундаментальными вещами. Если вы хотите принять во внимание скорости электронов, вам нужно понять, что происходит на квантово-механическом уровне. Это тяжелая работа.
Это тяжелая работа.
Работа с I и V требует игнорирования поведения электрона, точно так же, как работа с давлением, которое также является эмерджентным приближением, требует игнорирования скоростей и размеров отдельных атомов. В то время как давление и объем хорошо аппроксимируются в широком диапазоне значений, конечный размер атомов заставляет давление отклоняться от простых линейных законов при очень высоком давлении, а конечные скорости приводят (например) к ограничению дульной скорости в пушках, которые использовать расширяющиеся газы в качестве драйвера.
Оказывается, использование I и V, как если бы они были фундаментальными, очень хорошо работает на гораздо большем количестве порядков, чем газовые законы, аппроксимирующие поведение газов.
На практике L выводится из измерений энергии, так что вы можете считать, что любой небольшой электронный вклад в энергию уже учтен.
\$\конечная группа\$
1
\$\начало группы\$
В дополнение к другим ответам, я хотел бы добавить, что есть два разных вида индуктивности.
— обычная индуктивность, описывающая энергию, запасенную в магнитном поле.
— кинетическая индуктивность. Это происходит всякий раз, когда длина свободного пробега электронов становится заметной, например. при пересечении вакуума, в сверхпроводниках или некоторых других материалах, которые имеют топологическое усиление проводящих состояний, приводящее к баллистическому переносу. Этот вклад в индуктивность приходится на инерцию носителей заряда. Впечатляющая демонстрация этого — попытка изменить ток через сверхпроводник.
Оба являются индуктивностями, потому что они описывают желание, чтобы ток продолжал течь. При использовании компонента с индуктивностью L в электротехнике не раскрывается происхождение его индуктивности.
\$\конечная группа\$
Твой ответ
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Индуктивность— интуитивный способ «визуализации» того, как энергия хранится в индукторе?
Я начну с обсуждения конденсаторов, а затем перейду к катушкам индуктивности. Я буду избегать сложных уравнений (чтобы спасти себя, а также это обсуждение). Я могу даже обсудить двойственность между емкостью и индуктивностью и то, как это связано с физическими идеями, такими как масса, сила, скорость и импульс. (Это будет рассматривать их изолированно с целью обеспечения некоторой интуиции, только.) Но когда у меня будет время для этого. Я думаю, что важно начать с той области, где каждый из нас может чувствовать себя более комфортно.
Я буду избегать сложных уравнений (чтобы спасти себя, а также это обсуждение). Я могу даже обсудить двойственность между емкостью и индуктивностью и то, как это связано с физическими идеями, такими как масса, сила, скорость и импульс. (Это будет рассматривать их изолированно с целью обеспечения некоторой интуиции, только.) Но когда у меня будет время для этого. Я думаю, что важно начать с той области, где каждый из нас может чувствовать себя более комфортно.
Нижеследующее будет более качественным и обсудит идеи, которых нет в учебниках. Я делаю это, потому что это может помочь вам визуализировать, несмотря на риск использования нестандартного подхода.
Конденсаторы
Для конденсаторов вы, вероятно, уже знаете, что площадь пластины (при условии, что обе пластины имеют одинаковую площадь), расстояние, разделяющее пластины, и физическая материя (вставленная вместо вакуума или воздуха), используемая между пластинами. напрямую связаны с его емкостью. Эти идеи о площади пластины, разделении пластины и вставленной среде (если есть) нетрудно понять. Формула тоже довольно проста:
Формула тоже довольно проста:
$$C=\epsilon_{_0}\frac{A}{d}$$
Важно, чтобы вы думали о том, что вышеизложенное подразумевает наличие вакуума между пластинами. Можно, конечно, и между ними просунуть кусочки материи. А кто знает? Может случиться что-то другое. Оказывается, для некоторых типов материи приведенное выше уравнение действительно требует дополнительного фактора — относительной диэлектрической проницаемости. Это всего лишь условный коэффициент, который должен быть либо равен 1, либо больше 1 и кое-что говорит вам о способности вставленного материала реагировать на разницу зарядов между пластинами.
Новое уравнение с его причудливым новым вымышленным коэффициентом:
$$C=\epsilon_{_r}\epsilon_{_0}\frac{A}{d}$$
И оно отлично работает, если вы знаете \$\эпсилон_{_r}\$. Если вы заполните весь объем между пластинами (без промежутков и т. д.), вы можете просто использовать \$\epsilon_{_r}\$ материала. Конечно, если вы делаете что-то странное, например, заполняете странные части тома, тогда все не так просто.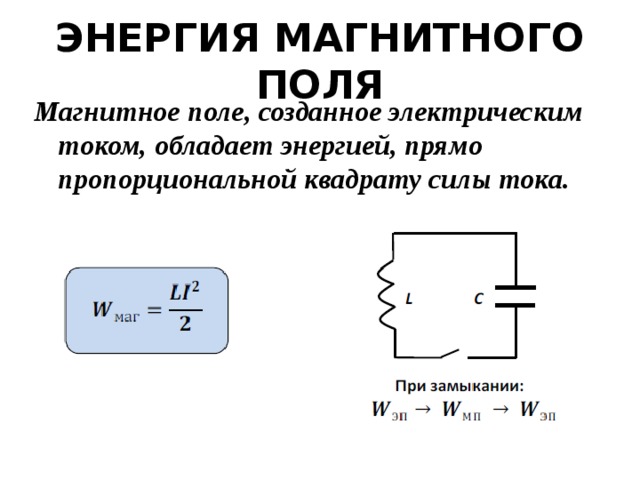 (Но люди в основном не делают таких вещей. Они стараются сделать все просто и дешево.)
(Но люди в основном не делают таких вещей. Они стараются сделать все просто и дешево.)
Что делает фактор выдумки? Что это значит? С чем это связано, физически?
Ну, заряды разделены промежутком, который не дает им пересечься и нейтрализоваться. Они хотят, но не могут. Это создает поле между пластинами, при этом линии поля перпендикулярны поверхности пластины и проходят прямо от одной пластины к другой. В другом месте также есть поле, окружающее конденсатор в воздухе вокруг него, и эти линии поля указывают повсюду, в зависимости от того, где вы находитесь (и / или время, когда вы находитесь там для изменения ситуации), как вращающиеся векторы, когда вы двигаетесь. через это пространство. Но интеграл по пути туда и обратно требует, чтобы линии между пластинами указывали прямо от одной пластины к другой, и это важный момент, который имеет значение для диэлектрической среды, которая может быть помещена в этот объем.
Когда туда что-то вставляется, вещество внутри материала может образовывать диполи. Молекулы немного сложнее, чем диполь. Я должен признать, что использование идеи идеализированного диполя является некоторым упрощением. Но упрощение довольно близкое и достаточно хорошее для большинства применений.
Молекулы немного сложнее, чем диполь. Я должен признать, что использование идеи идеализированного диполя является некоторым упрощением. Но упрощение довольно близкое и достаточно хорошее для большинства применений.
Теперь, прежде чем идти дальше, давайте вернемся к случаю, когда между пластинами находится только вакуум или воздух. При зарядке конденсатора сохраняется определенное количество полезной энергии где-то . Где? Ну, в вакууме между пластинами. Я хочу, чтобы вы твердо зафиксировали это в своем уме. Он не хранится в пластинах, где вообще нет электрического поля (если бы оно было, вокруг двигались бы электроны, а мы знаем, что этого не происходит). тарелки.
Теперь давайте вернемся к идее диполя, где мы вставили какой-то волшебный материал, который может образовывать диполи под воздействием силовых линий электрического поля между пластинами. Некоторые молекулы или группы молекул в диэлектрике могут вращаться и выстраиваться вдоль силовых линий электрического поля. Это ответ на поле. При вращении для выравнивания эти диполи можно рассматривать как образующие своего рода «короткое замыкание» или «сокращение», которое «перекрывает» (если хотите) часть вакуума. Вакуум, в котором хранится энергия, тоже имеет, скажем, сопротивление. И молекулы образуют короткое замыкание, которое обходит это сопротивление вакуума и уменьшает эффективный зазор.
Это ответ на поле. При вращении для выравнивания эти диполи можно рассматривать как образующие своего рода «короткое замыкание» или «сокращение», которое «перекрывает» (если хотите) часть вакуума. Вакуум, в котором хранится энергия, тоже имеет, скажем, сопротивление. И молекулы образуют короткое замыкание, которое обходит это сопротивление вакуума и уменьшает эффективный зазор.
Теперь, согласно приведенным выше уравнениям, если расстояние между пластинами меньше, то значение емкости увеличивается, при прочих равных условиях. Итак, если вы примете такой способ мышления, это может объяснить, почему диэлектрик увеличивает емкость.
Однако некоторые материалы не поляризуются и не образуют диполи. Таким образом, они не считаются диэлектриками. И я ничего не знаю о формах диполей, противоположно направленных против направления линии электрического поля, поэтому, если кто-то не знает что-то, что я упускаю, мы не можем уменьшить емкость конденсатора с вакуумным зазором, вставив антидиэлектрический .
Отсюда дело не столько в самих зарядках, сколько в полях . Поля, которые существуют при наличии разницы зарядов между пластинами. Кроме того, здесь полезно представить, что энергия не может храниться в материи, а только в вакууме. И что, если вы заполните этот вакуум чем-то, что может образовывать диполи, тогда будет меньше вакуума, в котором может храниться энергия, или, по сути, меньший эффективный зазор .
Итак, есть зазор, который можно измерить рулеткой. Это один номер. Но есть также зазор, который вы не можете измерить напрямую, это эффективный зазор, в котором хранится энергия. Значение \$\epsilon_{_r}\$ — это просто величина, говорящая вам, насколько укорачивается измеримый зазор, чтобы получить оставшийся истинный вакуумный зазор, который является единственным зазором, о котором заботится конденсатор.
Обратите внимание, что это тоже не совсем так. Это упрощение. Материя, которая вращается в выравнивании, может также повернуться обратно из выравнивания. И для достижения вращения требуется некоторая энергия, и она высвобождается, когда силовые линии уменьшаются и молекулы могут немного «раскручиваться». Для конденсаторов этот эффект может привести к некоторому нагреву, поскольку движение молекул — это в значительной степени определение тепловой энергии. И если вы сбиваете их с толку, осциллируя полем, то часть этой энергии превращается в дополнительную вибрационную энергию в конденсаторе. Кроме того, есть вопрос о том, сколько «памяти» могут иметь эти молекулы — возможно, они не полностью возвращаются туда, где были до зарядки конденсатора, после разрядки. Они могут что-то «помнить». Но для большинства конденсаторов этот эффект довольно незначителен, поэтому обычно считается, что конденсаторы не имеют гистерезиса.
И для достижения вращения требуется некоторая энергия, и она высвобождается, когда силовые линии уменьшаются и молекулы могут немного «раскручиваться». Для конденсаторов этот эффект может привести к некоторому нагреву, поскольку движение молекул — это в значительной степени определение тепловой энергии. И если вы сбиваете их с толку, осциллируя полем, то часть этой энергии превращается в дополнительную вибрационную энергию в конденсаторе. Кроме того, есть вопрос о том, сколько «памяти» могут иметь эти молекулы — возможно, они не полностью возвращаются туда, где были до зарядки конденсатора, после разрядки. Они могут что-то «помнить». Но для большинства конденсаторов этот эффект довольно незначителен, поэтому обычно считается, что конденсаторы не имеют гистерезиса.
(Эта деталь гистерезиса не соответствует действительности для материалов сердечника, используемых в катушках индуктивности, где гистерезис является важной деталью, которую вы часто не можете игнорировать.) физический дизайн конденсатора. Но обычно они не важны.
Но обычно они не важны.
Катушки индуктивности
Что касается катушек индуктивности, вы, вероятно, уже знаете, что проволочная катушка и физическая материя (снова вставленная вместо вакуума или воздуха), которую окружает проволочная катушка, напрямую связаны со значением ее индуктивности. Здесь все несколько сложнее для понимания. Эквивалентом разделения пластин, но для индуктора, является длина магнитного пути.
Проблема с катушками индуктивности заключается в том, что в них нет монопольных магнитных зарядов. Таким образом, вы не можете просто прикрепить магнитные заряды к какой-либо поверхности. Итак, здесь у вас не может быть этих силовых линий магнитного поля между двумя пластинами.
Говоря о корпусе конденсатора, я упомянул, что снаружи конденсатора тоже есть дорожка, но в целом мы можем просто сфокусироваться на силовых линиях между пластинами и игнорировать все остальное. Но с индуктором мы должны сосредоточиться на всем магнитном пути, а не только на его небольшом сегменте.
Это означает, что простейшая катушка индуктивности представляет собой тороид. Это потому, что весь магнитный путь представляет собой простой круг — среднюю окружность вокруг тороида. (Эта штука с \$2\pi\,r\$.)
(Хорошо, позвольте мне взять это обратно. Простейшая катушка индуктивности — это соленоид, простирающийся до бесконечности. Но поскольку бесконечно длинные катушки индуктивности трудно найти, а короткие добавляют некоторая сложность, которую я не хочу здесь затрагивать, вернемся к тому тороиду.)
Формула тороида здесь тоже довольно проста: 92\$ фактор. Вы, вероятно, можете себе представить, почему количество циклов будет иметь значение. Однако причина, по которой значение возведено в квадрат, немного выходит за рамки того, куда я хочу пойти. Так что давайте просто назовем это небольшой дополнительной сложностью. Но это не так много.
Еще раз, имейте в виду, что энергия катушки индуктивности не хранится в проводе. Он хранится в вакуумном объеме, в котором находится магнитное поле. Вот это внутренняя часть тороида.
Вот это внутренняя часть тороида.
Итак, что происходит, когда материал с проницаемостью помещается в вакуумный объем? Что ж, в некоторых случаях все снова «выстраивается», как те диполи раньше. В данном случае все сложнее. Итак, термин домен используется для представления совокупности небольших частиц материи, которые могут выравниваться с магнитным полем. Электроны, вращающиеся вокруг отдельных атомов, также могут выстроиться в линию (и они в некоторой степени так и делают). Но достаточно того, что остается основная идея. Некоторые магнитные домены выстраиваются в линию с линиями магнитного поля и образуют «кратчайшие пути» через вакуум вдоль линий магнитного поля, что заставляет их выравниваться. Это сокращает эффективную длину магнитного пути и, следовательно, увеличивает индуктивность. 92\frac{A}{2\pi\,r}$$
Здесь \$\mu_{_r}\$ — это просто число, указывающее, насколько укорачивается длина вакуумного пути. Это может быть в 1000 раз и более.
Итак, снова есть магнитная дорожка, которую можно измерить рулеткой. Это один номер. Но есть также длина магнитного пути, которую вы не можете измерить напрямую, это эффективная длина, в пределах которой хранится энергия. (Общий объем вакуума, в котором хранится энергия, будет равен укороченной длине, умноженной на площадь поперечного сечения тороида.)
Это один номер. Но есть также длина магнитного пути, которую вы не можете измерить напрямую, это эффективная длина, в пределах которой хранится энергия. (Общий объем вакуума, в котором хранится энергия, будет равен укороченной длине, умноженной на площадь поперечного сечения тороида.)
С материалами, которые мы можем использовать для увеличения индуктивности, с выровненными доменами возникает гистерезис. Если вы начнете с такого материала с доменами, выровненными в случайных направлениях, затем приложите магнитное поле, которое вынуждает их выровняться, а затем уберете это магнитное поле, они частично вернутся в свое прежнее состояние (или что-то достаточно близкое на данный момент), но они не вернутся полностью в свое рандомизированное состояние. Некоторая «память» о предыдущем поле выравнивания все еще будет висеть.
Если вы перевернете поле, вам придется сначала преодолеть эту память, а затем перестроить их противоположно. Удаление поля также оставит некоторую память об этом поле, которое было противоположным. Этот процесс продолжается снова и снова, когда переменный ток подается на индуктор.
Этот процесс продолжается снова и снова, когда переменный ток подается на индуктор.
Как и в случае с любым другим материалом, вращение доменов оставляет в материале некоторую колебательную энергию — тепло.
Изменяющееся магнитное поле индуцирует некулоновское электрическое поле. Это означает, что токи могут протекать в условиях переменного тока. Поскольку некоторые материалы, которые мы используем (железо), являются проводящими, эти токи на самом деле текут и также выделяют тепло. Некулоновский эффект первого порядка называется вихревым током. Это не то, о чем вам нужно беспокоиться в конденсаторе, потому что по определению диэлектрик является изолятором, и токи просто не текут в них. Но для катушек индуктивности и на более высоких частотах это проблема. Ферриты помогают в этом, потому что проводящие частицы смешиваются с непроводящими частицами, которые помогают блокировать эти токи.
Наконец, существуют практические ограничения на силу магнитного поля (количество тесла), которое можно поддерживать. Различные материалы также будут накладывать здесь разные ограничения. Как только он исчерпан (т. е. все магнитные домены выполнили все «выстраивания», которые они могут сделать, и больше ничего не осталось), тогда индуктор начинает вести себя так, как будто материала сердечника вообще не было. Больше похоже на индуктор с воздушным сердечником. Процесс часто постепенный, так что эффект не будет внезапным. Некоторые колебательные схемы фактически зависят от этой «функции», чтобы работать.
Различные материалы также будут накладывать здесь разные ограничения. Как только он исчерпан (т. е. все магнитные домены выполнили все «выстраивания», которые они могут сделать, и больше ничего не осталось), тогда индуктор начинает вести себя так, как будто материала сердечника вообще не было. Больше похоже на индуктор с воздушным сердечником. Процесс часто постепенный, так что эффект не будет внезапным. Некоторые колебательные схемы фактически зависят от этой «функции», чтобы работать.
Упрощение
Прежде чем я продолжу, я хочу вернуться к конденсатору и копать на один уровень ниже моего качественного ручного подметания выше. Причина в том , что я хочу указать на новую концепцию , которую вы должны включить в каждую свою мысль об окружающем вас мире — идею возникающих явлений .
Иногда теории, хорошо описывающие один уровень опыта и хорошо проверенные экспериментально, не имеют никакого смысла на более глубоком уровне. Вместо этого эти идеи срочный вызов — как правило, в результате большого количества статистических данных о населении.
Понятия температуры и энтропии из статистической термодинамики хорошо известны и чрезвычайно важны. Они просто работают. Но идеи температуры и энтропии не имеют никакого значения на атомном уровне. Их просто не существует. Есть энергия. А энергия — важное понятие как на атомном уровне, так и в термодинамике. Так что есть что-то общее. Просто отдельные частицы не имеют представления о температуре. У них может быть скорость, импульс, энергия и т. д. Но не температура и не энтропия. Эти два возникают из статистики квадриллионов (и более) частиц, которые взаимодействуют с чем-то другим, что также включает такое же большое количество частиц.
Например, чашка с водой и термометр. В них обоих содержится огромное, невообразимое количество отдельных частиц. И когда вы помещаете термометр в чашку с водой, чтобы измерить ее температуру, вы спрашиваете, «что происходит с квинтиллионами частиц в термометре, когда он погружен в септиллионы частиц воды, которые все будут случайным образом подпрыгивать и влиять друг на друга? » Это имеет значение из-за большого количества возможных начальных состояний и множества возможных результатов, почти все из которых будут давать «показания» термометра, которые вы ожидаете увидеть в пределах погрешности. Есть несколько исключительных начальных состояний, которые дадут разные результаты. Но вероятность того, что это произойдет, настолько мала, что время жизни всей Вселенной истекло бы до того, как это произошло. Так что правильно говорить о температуре и энтропии, как если бы они существовали на этом эмерджентном уровне. (Поскольку необычное поведение встречается крайне редко.)
Есть несколько исключительных начальных состояний, которые дадут разные результаты. Но вероятность того, что это произойдет, настолько мала, что время жизни всей Вселенной истекло бы до того, как это произошло. Так что правильно говорить о температуре и энтропии, как если бы они существовали на этом эмерджентном уровне. (Поскольку необычное поведение встречается крайне редко.)
(Примечание: здесь тоже стоит упомянуть 0-й закон термодинамики). и из которого, как вы думаете, вы знаете, получается !
Конденсатор — как раз такой пример. Я выше махнул рукой про диэлектрические диполи и прочее. Но в глубине, конечно, намного интереснее и сложнее. И еще ниже, еще более захватывающим и сложным. Позвольте мне дать вам представление о следующем уровне ниже, основанном главным образом на идеях, изложенных в превосходной книге Чабея и Шервуда для изучения физики под названием «9».0166 Материя и взаимодействия ».
Вот моя интерпретация того, о чем они пишут:
всего несколько дополнительных электронов у поверхности (и чуть меньше электронов у поверхностей с правой стороны. ) Между ними я показываю поляризованные диэлектрические диполи. вектора направления поля при перемещении снаружи конденсатора по некоторой кривой.0003
) Между ними я показываю поляризованные диэлектрические диполи. вектора направления поля при перемещении снаружи конденсатора по некоторой кривой.0003
(Имейте в виду, что из очень, очень большого количества электронов зоны проводимости, присутствующих на обеих пластинах, на левой пластине их немного меньше, чем на правой пластине.)
Я также добавил зеленый и оранжевая точка в двух интересных местах внутри диэлектрика. Зеленая точка находится прямо посередине одного из этих диполей. С его точки зрения вектор указывает, как указано выше. Оранжевая точка находится между двумя диполями, и с ее точки зрения вектор указывает в другую сторону, как указано выше. Как вы можете себе представить, когда вы перемещаетесь внутри диэлектрика, существуют очень сложные направления электронного поля. Я проиллюстрировал только два более простых.
Вопрос в том, каково направление электронного поля внутри диэлектрика? Кажется, это очень сложно вычислить. Но если вы посмотрите на векторы направления и представите, что суммируете их, когда вы двигаетесь по замкнутому пути, огибающему внешнюю сторону конденсатора, а затем проходите через его середину, чтобы закончить там, где вы начали, мы знаем, что эта сумма должна быть равна нулю. (Он не может быть ненулевым.)
(Он не может быть ненулевым.)
Но вы можете видеть, что два внешних вектора (крайний левый и крайний правый) указывают в одном и том же направлении. Таким образом, сумма вокруг внешнего вида и на мгновение игнорируя диэлектрик, должна быть отличной от нуля, а сеть должна указывать вправо. Следовательно, чистое направление самого диэлектрика должно быть направлено влево ровно на столько, сколько нужно, чтобы компенсировать сумму внешних путей. 92\$. Кажется интересным, что есть некоторые сходства, просто одинаковые.
$$\begin{выравнивание*} \begin{массив}[t]{r} {\ текст {импульс:}} \ vphantom {q = C \: V} \\\\ {\ text {импульс:}} \ vphantom {\ text {d} \, q = C \: \ text {d} \, V} \\\\ {\ text {force:}} \ vphantom {\ frac {\ text {d} q} {\ text {d} t} = C \: \ frac {\ text {d} \, V} {\ text {d }т}}\\\\ {\ text {масса:}} \ vphantom {C = \ frac {\ text {d} q} {\ text {d} V}} \\\\ {\ текст {скорость:}} \ vphantom {q = C \: V} \\\\ {\ текст {ускорение:}} \ vphantom {q = C \: V} \\\\ {\ текст {энергия:}} \ vphantom {\ frac12 C \, V ^ 2} \конец{массив} && \overbrace{ \begin{массив}[т]{с} д=С\:В\\\\ \text{d}q=C\:\text{d}V\\\\ I = \ frac {\ text {d} q} {\ text {d} t} = C \: \ frac {\ text {d} \, V} {\ text {d} t} \\\\ C = \ frac {\ text {d} q} {\ text {d} V} \\\\ В\\\\ \ гидроразрыв {\ текст {d} V} {\ текст {d} т} \\\\ \frac12 C \,V^2 \конец{массив} } ^ {\ текст {конденсатор}} && \overbrace{ \begin{массив}[т]{с} p=m\:v\vphantom{q=C\:V}\\\\ \text{d}p=m\:\text{d}v\vphantom{q=C\:V}\\\\ F = \ frac {\ text {d} p} {\ text {d} t} = m \: \ frac {\ text {d} \, v} {\ text {d} t} = m \: a \ \\\ m = \ frac {\ text {d} p} {\ text {d} v} \ vphantom {C = \ frac {\ text {d} q} {\ text {d} V}} \\\\ в\\\\ а = \ frac {\ text {d} v} {\ text {d} t} \\\\ \frac12 м\,v^2\vphantom{\frac12 C \,V^2} \конец{массив} } ^ {\ текст {частица}} && \overbrace{ \begin{массив}[т]{с} \phi=L\:I\vphantom{q=C\:V}\\\\ \text{d}\phi=L\:\text{d}I\\\\ V = \ frac {\ text {d} \ phi} {\ text {d} t} = L \: \ frac {\ text {d} \, I} {\ text {d} t} \\\\ L = \ frac {\ text {d} \ phi} {\ text {d} I} \ vphantom {C = \ frac {\ text {d} q} {\ text {d} V}} \\\\ Я\\\\ \ гидроразрыва {\ текст {d} \, I} {\ текст {d} т} \\\\ \frac12 L\,I^2\vphantom{\frac12 C \,V^2} \конец{массив} } ^ {\ текст {индуктор}} \end{выравнивание*}$$
Также поищите Лагранжевую механику и принцип наименьшего действия . (Я не зря начал с импульса.)
(Я не зря начал с импульса.)
Уверен, вы знаете, что заряд конденсатора сохраняется. Вы можете думать о заряде конденсатора как о связанном с потенциальной энергией в физической системе и думать о Вебере катушки индуктивности как о связанном кинетической энергии в физической системе. (Вы можете выбрать другой путь, если хотите.)
Как бы то ни было, мне нравится думать о веберах (или вольт-секундах) в катушке индуктивности как о магнитном двойнике электрического заряда конденсатора. Поначалу это немного странно, потому что заряд исчисляем (в нашем воображении), но вольт-секунды, кажется, зависят от времени (и это так) и не поддаются исчислению таким же образом. Но во всех смыслах \$L I\$ — это магнитный заряд, а \$C V\$ — электрический заряд. Эти вещи сохраняются точно так же, как сохраняется импульс в физической системе.
Точно так же ток в конденсаторе является силой. Когда вы прикладываете эту силу к конденсатору, он ускоряет , изменяя напряжение. Напряжение на катушке индуктивности является силой. Когда вы прикладываете напряжение к катушке индуктивности, она также ускоряет , изменяя ток.
Напряжение на катушке индуктивности является силой. Когда вы прикладываете напряжение к катушке индуктивности, она также ускоряет , изменяя ток.
Также полезно (особенно при рассмотрении LC-бака) рассматривать энергию индуктора как кинетическую, а энергию конденсатора как потенциальную. Танк LC представляет собой простую систему, которая преобразует одно в другое, а затем обратно. Это, возможно, очень похоже на идею кометы на очень высокоэллиптической орбите. В апоапсисе почти вся кинетическая энергия преобразуется в потенциальную энергию. Затем, когда комета ускоряется обратно к Солнцу, эта потенциальная энергия преобразуется в кинетическую энергию. Таким образом, в перицентре почти вся потенциальная энергия преобразуется в кинетическую энергию. И комета затем продолжается, снова и снова. LC-танк похож на этот, за исключением того, что полярности меняются так, что есть четыре состояния вместо двух, если вы включаете полярность. Если просто энергия, то два состояния, как у кометы.
Очень хорошая статья для чтения — Введение в квантовые электромагнитные цепи , Вул и Деворет, где авторы обсуждают своего рода рецепт для нахождения лагранжианов без необходимости догадываться об этом. Там много классической физики, так что не слишком беспокойтесь о слове в заголовке статьи, которое предполагает обратное.
Где-то в этой статье они выбирают иначе, чем я сделал выше, говоря, что энергия индуктора представляет собой потенциальную, а не кинетическую энергию. Но, как я уже сказал, вам выбирать. Поэтому я предпочитаю думать о кулонах конденсатора как о координатах положения, а о веберах катушки индуктивности — как о координатах импульса, которые меняются местами. (Но авторы намного умнее меня. Так что, возможно, вам следует слушать их, а не меня.)
Как работают ферритовые бусины? Ключевые факторы для рассмотрения | Блог Advanced PCB Design
Большинство детей школьного возраста читали о таких исследователях, как американцы Льюис и Кларк, которые торговали безделушками с коренными американцами в обмен на еду и безопасный проход. Отмечается, что многие из этих безделушек включали стеклянные бусины. Я был свидетелем того, как ученик за учеником задавался вопросом: «Что кому-то нужно со стеклянными бусинами?»
Отмечается, что многие из этих безделушек включали стеклянные бусины. Я был свидетелем того, как ученик за учеником задавался вопросом: «Что кому-то нужно со стеклянными бусинами?»
Хотя я не могу ответить, зачем нужны стеклянные бусины, я знаю, что сталкивался с очень похожим вопросом, связанным с ферритовыми бусами в производстве и электронике. Хотя я сторонник того, что ферритовые бусины действительно ценны, многие могут вернуться к одному и тому же вопросу: «Зачем им ферритовые бусины?»
Подавление электромагнитных помех, фильтр электромагнитных помех и кондуктивные электромагнитные помехи в электронных схемах могут выиграть от знаний о технологиях ферритовых колец, ферритовых сердечников и ферритовых дросселей. В частности, в аналоговых устройствах или при работе с такими объектами, как смещение постоянного тока, подавление шума или высокочастотные сигналы, ферритовый шарик или ферритовые шарики в некоторых случаях могут использовать ферритовый материал для минимизации подавления электромагнитных помех.
В частности, в аналоговых устройствах или при работе с такими объектами, как смещение постоянного тока, подавление шума или высокочастотные сигналы, ферритовый шарик или ферритовые шарики в некоторых случаях могут использовать ферритовый материал для минимизации подавления электромагнитных помех.
Ферритовые бусины: наши невоспетые электронные герои
Ответ на этот животрепещущий вопрос заключается в нашем бесконечном стремлении устранить электромагнитные помехи. Этот поиск становится особенно важным для тех из нас, кто пользуется мобильными телефонами, телевизорами, DVD-дисками, игровыми системами и компьютерами.
Когда мы углубимся в технологии с высокой скоростью передачи данных, мы обнаружим, что конструкции печатных плат часто требуют нескольких, но отдельных цифровых и аналоговых шин питания. Высокоскоростные тактовые сигналы, данные и скорости переключения ввода-вывода создают частоты и гармоники, которые могут перегрузить шины питания. В результате цепь может испытывать пульсации напряжения и выходной джиттер. Использование ферритовых колец между шинами позволяет разработчикам печатных плат упростить схемы питания и минимизировать пространство на плате, сохраняя при этом высокочастотное разделение между шинами.
В результате цепь может испытывать пульсации напряжения и выходной джиттер. Использование ферритовых колец между шинами позволяет разработчикам печатных плат упростить схемы питания и минимизировать пространство на плате, сохраняя при этом высокочастотное разделение между шинами.
Взаимосвязь между характеристиками этих устройств и ферритовыми шариками становится яснее, когда мы исследуем электромагнитные свойства феррита. Поскольку ферритовые шарики состоят из проводника, вставленного в полый цилиндр из высокопроницаемого керамического материала на основе оксида железа, электромагнитные свойства влияют на протекание тока. Проницаемость оксидов железа, содержащихся в керамическом материале, поддерживает формирование магнитного поля при протекании тока через проводник.
Вы можете найти никель-цинковые (NiZn) или марганцево-цинковые (MnZn) ферритовые шарики. Каждый из них имеет разные электромагнитные свойства, которые могут быть улучшены в процессе производства. Эти процессы изменяют импеданс ферритового шарика за счет изменения химического состава и физической длины ферритов. В результате бусины оптимизируются для подавления частот в определенных полосах пропускания.
Эти процессы изменяют импеданс ферритового шарика за счет изменения химического состава и физической длины ферритов. В результате бусины оптимизируются для подавления частот в определенных полосах пропускания.
Никель-цинковые ферритовые шарики лучше всего подходят для маломощных цепей с высокой индуктивностью, работающих в диапазоне частот от 500 кГц до 100 МГц, благодаря низкой магнитной проницаемости, высокому объемному удельному сопротивлению, хорошей температурной стабильности и высокой добротности. Имея диапазон проницаемости от 20 до 850 мкм, никель-цинковые шарики могут использоваться в широкополосных трансформаторах. Высокое сопротивление ферритовых бусинок NiZn позволяет конструкторам использовать бусины на частотах от 2 МГц до 500 сот МГц.
В отличие от никель-цинковых шариков, шарики из марганцево-цинкового феррита обладают высокой проницаемостью, превышающей 800 мкм, низким объемным сопротивлением и низкой добротностью. Ферритовые сердечники из MnZn работают с импульсными силовыми трансформаторами, работающими в диапазоне частот от 20 до 100 кГц. Поскольку ферритовые сердечники из MnZn могут ослаблять ВЧ-сигналы в диапазоне от 2 до 250 МГц, разработчики печатных плат используют эти устройства в индукторах с низкими рабочими частотами.
Поскольку ферритовые сердечники из MnZn могут ослаблять ВЧ-сигналы в диапазоне от 2 до 250 МГц, разработчики печатных плат используют эти устройства в индукторах с низкими рабочими частотами.
Подавление ЭМС может быть достигнуто с помощью феррита
Wallflowers of the Electronic Component Society
Когда мы проектируем печатные платы, редко упоминаются ферритовые бусины. Ведь это пассивные устройства. И… ферритовые шарики не могут претендовать на роль конденсаторов, катушек индуктивности или резисторов. Однако красота ферритовых бусинок заключается в их емкостных, индуктивных и резистивных характеристиках. Ферритовые шарики обладают резистивными характеристиками в диапазоне от одной до двух декад частоты. В то время как ферритовые бусины являются индуктивными на более низких частотах, ферриты являются емкостными на более высоких частотах.
В отличие от своих пассивных собратьев, ферритовые бусины рассеивают, а не накапливают высокочастотную энергию. Вместо того, чтобы отражаться обратно в систему, энергия рассеивается в виде тепла. Как мы уже видели, ферритовые шарики с низкой добротностью не влияют на цепь на низких частотах, но сопротивляются высокочастотной энергии.
Вместо того, чтобы отражаться обратно в систему, энергия рассеивается в виде тепла. Как мы уже видели, ферритовые шарики с низкой добротностью не влияют на цепь на низких частотах, но сопротивляются высокочастотной энергии.
Ферритовые шарики с низкой добротностью предлагают наилучшее решение для фильтрации источников питания за счет ослабления высокочастотных помех источника питания в тонкой полосе. Поскольку катушки индуктивности накапливают энергию, высокочастотная энергия может сочетаться с емкостью в цепи и вызывать звон. В конструкциях высокоскоростных цифровых схем часто используются ферритовые бусины с низкой добротностью для изоляции высоких частот между общими шинами питания и для достижения целевых импедансов. Соединение ферритовой шайбы последовательно с шиной питания и как часть сети фильтров нижних частот также помогает снизить высокочастотный шум источника питания.
Высокодобротные ферритовые бусины используются для приложений с высоким уровнем резонанса, таких как фильтрация сигналов в телекоммуникациях, и предотвращают передачу помех от устройства или к устройству. Бусины High-Q хорошо подходят для создания схем ВЧ-генераторов и фильтров, требующих высокорезонансных элементов и малых потерь.
Бусины High-Q хорошо подходят для создания схем ВЧ-генераторов и фильтров, требующих высокорезонансных элементов и малых потерь.
С точки зрения конструкции следует использовать ферритовые кольца с четко определенными температурными факторами, которые остаются стабильными с течением времени. Эти характеристики позволяют комбинации LC работать при изменении температуры. Когда дорожки на печатной плате действуют как радиочастотные антенны, ферритовые бусины с высокой добротностью помогают уменьшить электромагнитные помехи, излучаемые платой. Бусины также предотвращают попадание помех в схему через дорожки.
Использование ферритовых бусинок в конструкции вашей печатной платы
Как и в случае с любым электронным компонентом, вы должны выбрать феррит, характеристики которого соответствуют вашему применению. Например, вы не можете использовать ферритовые бусины высокой добротности в силовых цепях изоляции из-за нежелательного резонанса. Поскольку нежелательный высокочастотный шум, требующий ослабления, должен совпадать с полосой сопротивления феррита, необходимо также определить источник электромагнитных помех и диапазон нежелательных частот. Когда вы выполняете проектирование и анализ схемы фильтрации шума, вы можете найти приблизительное значение индуктивности шарика и определить резонансную частоту среза.
Когда вы выполняете проектирование и анализ схемы фильтрации шума, вы можете найти приблизительное значение индуктивности шарика и определить резонансную частоту среза.
Кроме того, вы можете проверить технические характеристики ферритовых колец в зависимости от частотной характеристики. Большинство производителей также включают модели эквивалентных схем для ферритовых колец, которые подходят для системного моделирования.
Правильное использование инструментов SPICE также может сэкономить время, повысить производительность и определить точность при работе с ферритовыми кольцами. Развязка мощности, имитация высокочастотного затухания и представление эффекта ферритовой шайбы с помощью RLC особенно легко достижимы при одновременном повышении безопасности и наглядности вашей схемы.
Производственные проверки будут проще, если вы будете знать, что отправляете своим производителям
пик может произойти. Благодаря индуктивности ферритового шарика и развязывающей емкости с высокой добротностью, образующим сеть фильтров нижних частот, на частотах переключения преобразователей могут возникать резонансные пики, что создает перекрестные помехи. Добавление большого конденсатора с последовательным демпфирующим резистором в цепь развязывающего конденсатора может погасить резонанс, не влияя на характеристики затухания ферритового кольца.
Благодаря индуктивности ферритового шарика и развязывающей емкости с высокой добротностью, образующим сеть фильтров нижних частот, на частотах переключения преобразователей могут возникать резонансные пики, что создает перекрестные помехи. Добавление большого конденсатора с последовательным демпфирующим резистором в цепь развязывающего конденсатора может погасить резонанс, не влияя на характеристики затухания ферритового кольца.
Производители оценивают ферритовые шарики в зависимости от удельного тока. Любая сила тока, превышающая номинальный ток, может повредить ферритовый шарик. Когда смещение по постоянному току в цепи питания превышает 30-40% номинального тока, ферритовые кольца насыщаются и теряют способность подавлять электромагнитные помехи. При этом эффективная индуктивность ферритовых колец может уменьшиться на 50 %. Дополнительное увеличение смещения постоянного тока может снизить импеданс на 90%. Вы можете использовать предоставленные производителем кривые импеданса в зависимости от тока нагрузки, чтобы найти ферритовые кольца, которые выдерживают постоянный ток без достижения насыщения или потери импеданса.
Имея в виду резистивные характеристики ферритовых колец, вы также должны предусмотреть падение напряжения в вашей цепи. Кроме того, вам также необходимо предусмотреть нагрев, который происходит, когда феррит рассеивает высокочастотную энергию. Всегда проверяйте спецификации производителя по максимальному постоянному току и номинальному сопротивлению постоянному току. Выбранная ферритовая бусина должна иметь номинальный постоянный ток, более чем в два раза превышающий значение требуемого тока для шины.
Принимая все это во внимание, ваша электронная схема имеет множество конструктивных особенностей, которые могут повлиять на работу ферритового кольца, ферритового зажима или бусинок с ферритовыми чипами. Контролируйте свою радиочастотную энергию, падение напряжения и различные магнитные материалы и минимизируйте энергию высокочастотного шума, чтобы максимизировать эффективность вашей технологии.
Контролируйте свою радиочастотную энергию, падение напряжения и различные магнитные материалы и минимизируйте энергию высокочастотного шума, чтобы максимизировать эффективность вашей технологии.
Независимо от того, что вы проектируете, если вы планируете использовать ферритовую бусину, убедитесь, что с вашей платой проведено моделирование и анализ, прежде чем отправлять ее в производство. Симулятор OrCAD PSpice от Cadence обязательно предоставит вам необходимый анализ до и во время процесса проектирования.
Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостей
Спасибо!
Катушки индуктивности — Часть 2 Основы индукторов ②|Азбука электроники|Журнал TDK Techno
Катушки индуктивности — Часть 2 Основы индукторов ②
- фейсбук
- твиттер
- Линкедин
Эта статья переиздана. Прошлые статьи были реорганизованы и переписаны. Он включает информацию о прошлых технологиях и продуктах, которая в настоящее время не обрабатывается TDK.
Поведение катушки индуктивности при постоянном токе
Переходная характеристика катушки
Благодаря эффекту самоиндукции катушки (индукторы) создают электродвижущую силу (индуктивная электродвижущая сила), которая направлена таким образом, чтобы противодействовать изменению тока. Следовательно, при подаче напряжения на катушку ток не сразу начинает течь, а при снятии напряжения ток не сразу прекращается. Неравномерное изменение тока или напряжения, которое происходит, например, в точке включения или выключения, называется переходной характеристикой (переходным явлением) катушки. Например, в схеме, показанной ниже, где катушка и неоновая лампа (напряжение начала разряда не менее нескольких десятков вольт) соединены параллельно, простое замыкание выключателя батареи (напряжение всего несколько вольт) не даст результата. вызвать загорание неоновой лампы. Но если переключатель разомкнуть, когда через катушку течет ток, неоновая лампа загорится. Электродвижущая сила (V), создаваемая катушкой из-за эффекта самоиндукции, пропорциональна коэффициенту изменения тока (ΔI/Δt). Когда переключатель установлен в положение ON, ток постепенно увеличивается, поэтому электродвижущая сила не превышает напряжения источника питания. Но когда переключатель установлен в положение OFF, протекающий ток мгновенно отключается, что означает, что коэффициент изменения тока велик, вызывая создание большой электродвижущей силы, достаточной для зажигания неоновой лампы.
Следовательно, при подаче напряжения на катушку ток не сразу начинает течь, а при снятии напряжения ток не сразу прекращается. Неравномерное изменение тока или напряжения, которое происходит, например, в точке включения или выключения, называется переходной характеристикой (переходным явлением) катушки. Например, в схеме, показанной ниже, где катушка и неоновая лампа (напряжение начала разряда не менее нескольких десятков вольт) соединены параллельно, простое замыкание выключателя батареи (напряжение всего несколько вольт) не даст результата. вызвать загорание неоновой лампы. Но если переключатель разомкнуть, когда через катушку течет ток, неоновая лампа загорится. Электродвижущая сила (V), создаваемая катушкой из-за эффекта самоиндукции, пропорциональна коэффициенту изменения тока (ΔI/Δt). Когда переключатель установлен в положение ON, ток постепенно увеличивается, поэтому электродвижущая сила не превышает напряжения источника питания. Но когда переключатель установлен в положение OFF, протекающий ток мгновенно отключается, что означает, что коэффициент изменения тока велик, вызывая создание большой электродвижущей силы, достаточной для зажигания неоновой лампы.
Энергия, накопленная катушкой
В приведенной выше схеме неоновая лампа может загореться, потому что катушка накапливает энергию. Эта энергия пропорциональна индуктивности катушки и квадрату тока. Когда переключатель установлен в положение OFF, накопленная энергия мгновенно высвобождается, создавая высокую электродвижущую силу.
Поведение катушки с переменным током
Индуктивное реактивное сопротивление (XL)
Катушка (индуктор) плавно пропускает постоянный ток, но оказывает сопротивление переменному току. Сопротивление увеличивается в сторону более высоких частот. Этот эффект называется индуктивным сопротивлением (XL) катушки. Между частотой переменного тока (f) и индуктивностью (L) существует следующая зависимость.
Сопротивление увеличивается в сторону более высоких частот. Этот эффект называется индуктивным сопротивлением (XL) катушки. Между частотой переменного тока (f) и индуктивностью (L) существует следующая зависимость.
Осциллограмма напряжения и осциллограмма тока цепи переменного тока с катушкой
Переменный ток от промышленной розетки переменного тока имеет синусоидальную форму. Когда катушка подключена к источнику переменного тока, эффект самоиндукции будет создавать электродвижущую силу, направленную таким образом, чтобы противодействовать изменению тока. Таким образом, изменение тока задерживается на 90 градусов (1/4 цикла) по отношению к изменению напряжения.
Намагниченность сердечника и магнитная проницаемость
Кривая намагничивания и магнитное насыщение
Магнитный поток (Φ), создаваемый в катушке, пропорционален индуктивности (L) и протекающему току (I). Поскольку индуктивность пропорциональна магнитной проницаемости, использование магнитного материала с высокой магнитной проницаемостью и применение большого тока приведет к созданию более сильного магнитного потока. Однако существуют пределы способности магнитного материала собирать магнитный поток, и когда ток увеличивается до определенной точки, сердечник достигает магнитного насыщения. Плотность магнитного потока (B) в этой точке называется максимальной плотностью магнитного потока (Bm).
Поскольку индуктивность пропорциональна магнитной проницаемости, использование магнитного материала с высокой магнитной проницаемостью и применение большого тока приведет к созданию более сильного магнитного потока. Однако существуют пределы способности магнитного материала собирать магнитный поток, и когда ток увеличивается до определенной точки, сердечник достигает магнитного насыщения. Плотность магнитного потока (B) в этой точке называется максимальной плотностью магнитного потока (Bm).
Процесс намагничивания сердечника и изменение магнитной проницаемости
По мере намагничивания сердечника магнитная проницаемость сердечника изменяется. Как показано на графике ниже, магнитная проницаемость (μ) выражается градиентом кривой намагничивания сердечника (θ). Начальный градиент вблизи начала кривой представляет собой начальную магнитную проницаемость (µ0). Эта начальная магнитная проницаемость обычно называется магнитной проницаемостью, и это также значение, которое указывается в каталогах ферритовых материалов. Увеличение тока в катушке и, следовательно, увеличение намагниченности в конечном итоге приведет к тому, что магнитная проницаемость достигнет максимально возможного значения. Это называется максимальной магнитной проницаемостью (мкм), за пределами которой значение снова падает.
Увеличение тока в катушке и, следовательно, увеличение намагниченности в конечном итоге приведет к тому, что магнитная проницаемость достигнет максимально возможного значения. Это называется максимальной магнитной проницаемостью (мкм), за пределами которой значение снова падает.
Потери на вихревые токи в сердечнике
При подаче на катушку переменного тока создается электродвижущая сила, противодействующая изменению магнитного потока, и в сердечнике течет концентрический ток. Это называется вихревым током, и он лишает систему мощности RI2 (R: сопротивление, I: ток), которая выделяется в виде джоулева тепла. Это называется потерями на вихревые токи. В металлических сердечниках с низким электрическим сопротивлением потери на вихревые токи более выражены. Многослойные сердечники, используемые для силовых трансформаторов, представляют собой попытку уменьшить потери на вихревые токи.


 Определить емкость конденсатора и максимальную энергию магнитного поля катушки.
Определить емкость конденсатора и максимальную энергию магнитного поля катушки.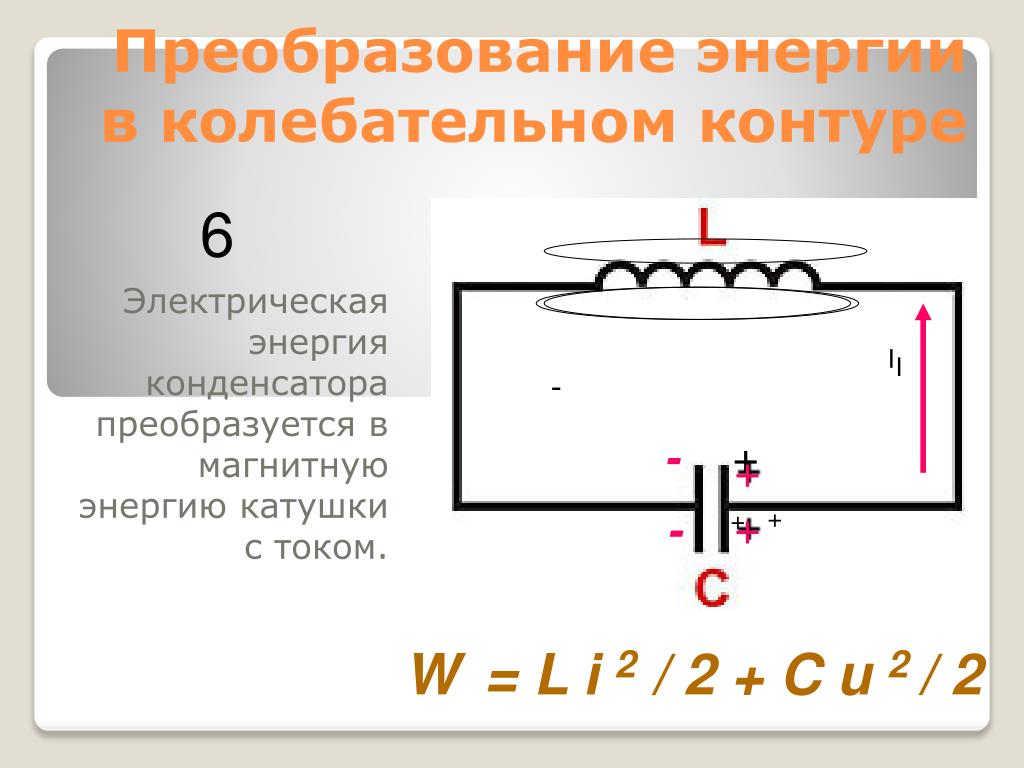

 Наружный диаметр тороида d
Наружный диаметр тороида d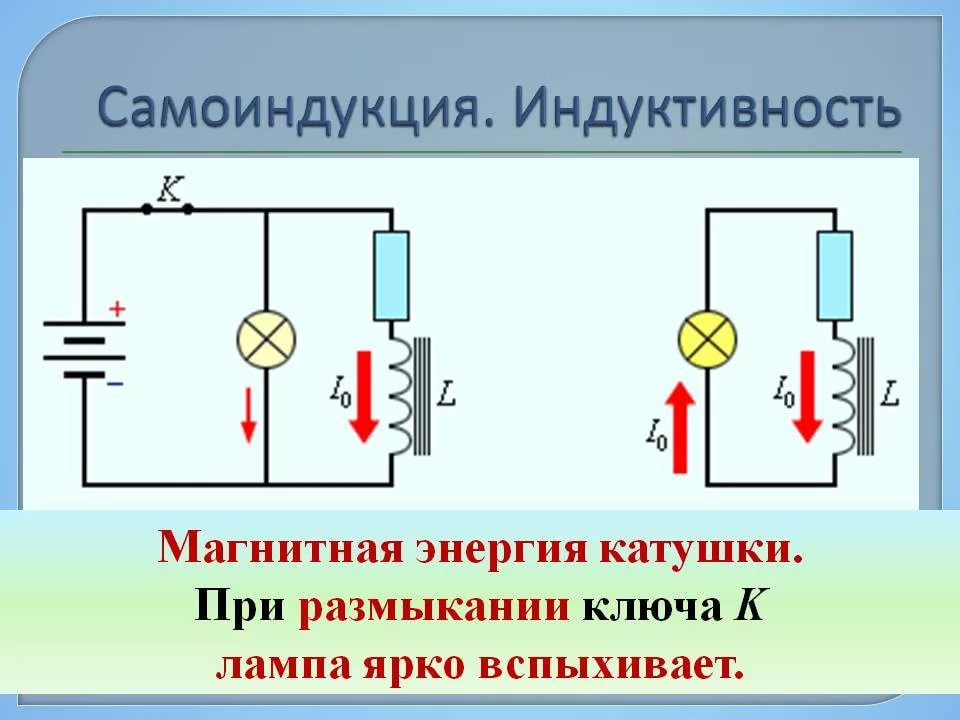 Это электрическое поле отталкивает электроны, поглощая при этом энергию. Таким образом, ускорение электронов требует энергии сверх того, что вы ожидаете от одной только инерционной массы электрона.
Это электрическое поле отталкивает электроны, поглощая при этом энергию. Таким образом, ускорение электронов требует энергии сверх того, что вы ожидаете от одной только инерционной массы электрона. 2/2
2/2
 (Текущие времена ds, бесконечно малая часть провода в направлении I — ток может течь только по проводу)
(Текущие времена ds, бесконечно малая часть провода в направлении I — ток может течь только по проводу)