| ||||||||||||||
| Специальный поиск | ||||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
|||||||||||||
энергии магнитного поля катушки Задача 13709 Колебательный контур содержит катушку индуктивностью L = 6 мкГн, конденсатор емкостью С = 10 нФ и резистор сопротивлением R = 10 Ом. Определите для случая максимума тока отношение энергии магнитного поля катушки к энергии электрического поля.
Задача 70064 Определить энергию магнитного поля катушки, состоящей из 200 витков, если при силе тока 4 А в ней возникает магнитный поток, равный 0,01 Вб.
Задача 70227 Определить энергию магнитного поля катушки индуктивностью 25 мГн при протекании в ней тока 40 мА.
Задача 21807 Заряженный конденсатор емкостью C = 0,2 мкФ подключили к катушке индуктивностью L = 8 мГн. Через какое время от момента подключения энергия электрического поля конденсатора станет равной энергии магнитного поля катушки?
Задача 60528 В колебательном контуре, состоящем из индуктивности и емкости ток, изменяется по закону , А. Индуктивность контура 0,6 Гн.
Задача 11303 Энергия магнитного поля катушки с индуктивностью L = 0,2 Гн составляет W = 5 Дж. Определите, чему равна ЭДС самоиндукции в катушке при равномерном уменьшении силы тока до нуля в течение промежутка времени Δt = 0,1 с.
Задача 13389 Энергия магнитного поля в катушке уменьшилась за счет изменения тока в ней в п = 4 раза в течение Δt = 0,2 с. Индуктивность катушки L = 0,16 Гн, первоначальный ток в катушке I0 = 8 А. определите ЭДС самоиндукции εs в катушке, считая, что сила тока зависит от времени линейно.
Задача 14029 Конденсатор колебательного контура подключен к источнику постоянного напряжения (см. рисунок). Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре после переведения переключателя К в положение 2. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) заряд левой обкладки конденсатора 2) энергия электрического поля конденсатора 3) сила тока в катушке 4) энергия магнитного поля катушки
Напряжение на клеммах конденсатора в колебательном контуре меняется с течением времени согласно графику на рисунке.
Задача 21092 На рисунке приведен график зависимости заряда q от времени t в идеальном колебательном контуре.
Задача 22001 Записать уравнение колебаний силы тока в цепи идеального электрического контура с индуктивностью L = 0,33 Гн и емкостью С = 0,46 мкФ, если колебания заряда происходят по закону синуса с амплитудой qm = 2,3·107 Кл и с начальной фазой π/6. Найти значение энергии магнитного поля катушки в начальный момент времени и для t = Т/12, где Т — период колебаний. Чему равна полная энергия электромагнитных колебаний в системе?
Задача 22482 Чему равно отношение энергии магнитного поля катушки к энергии электрического поля конденсатора, спустя время T/8 после того, как сила тока в контуре была равна нулю?
Задача 23055 Тороидальная катушка квадратного сечения имеет в своей обмотке N = 1000 витков.
| ||||||||||||||
Энергия магнитного поля тока | СПАДИЛО
Согласно закону сохранения энергии энергия магнитного поля, созданного током, равна той энергии, которую должен затратить источник тока (гальванический элемент, генератор на электростанции и др.) на создание тока. При размыкании цепи эта энергия переходит в другие виды энергии.
То, что для создания тока необходимо затратить энергию, т. е. необходимо совершить работу, объясняется тем, что при замыкании цепи, когда ток начинает нарастать, в проводнике появляется вихревое электрическое поле, действующее против того электрического поля, которое создается в проводнике благодаря источнику тока. Для того чтобы сила тока стала равной  Эта работа идет на увеличение энергии магнитного поля тока.
Эта работа идет на увеличение энергии магнитного поля тока.
При размыкании цепи ток исчезает, и вихревое поле совершает положительную работу. Запасенная током энергия выделяется. Это обнаруживается, например, по мощной искре, возникающей при размыкании цепи с большой индуктивностью.
Записать выражение для энергии тока
Если самоиндукция аналогична инерции, то индуктивность в процессе создания тока должна играть ту же роль, что и масса при увеличении скорости тела в механике. Роль скорости тела в электродинамике играет сила тока I как величина, характеризующая движение электрических зарядов.
Если это так, то энергия магнитного поля тока WМ будет подобна кинетической энергии тела в механике. Поэтому ее можно определить формулой:
Энергия магнитного поля токаWМ=LI22.
Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока.
Пример №1. В катушке индуктивностью 0,15 Гн и очень малым сопротивлением r сила тока равна 4 А. Параллельно катушке присоединили резистор сопротивлением R>> r. Какое количество теплоты выделится в катушке и в резисторе после быстрого отключения силы тока?
При параллельном подключении к катушке большого сопротивления R>> r, сила тока, идущая через катушку, почти не изменяется. Энергия в катушке равна:
WМ=LI22..
При отключении источника тока система катушка–сопротивление станет изолированной. Для изолированной системы справедлив закон сохранения энергии. В данном случае это означает, что вся энергия, запасенная в катушке, выделится в виде тепла в катушке и резисторе:
WМ=0,15·422..=1,2 (Дж)
Задание EF17636Катушка индуктивности подключена к источнику постоянного тока.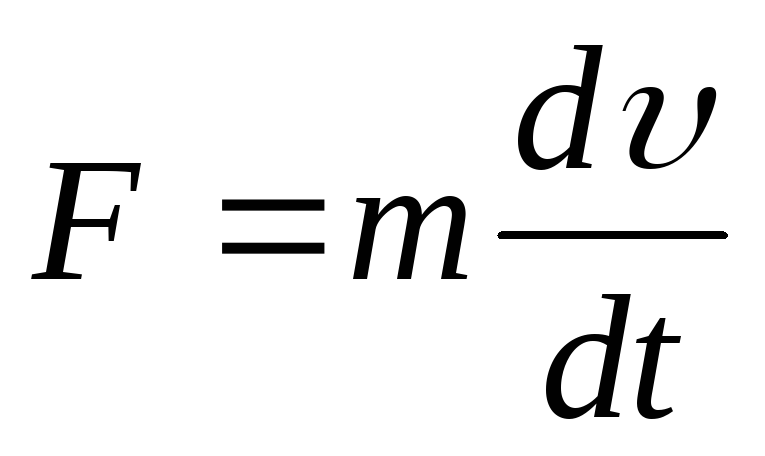 Как изменится энергия магнитного поля катушки при увеличении силы тока через катушку в 3 раза?
Как изменится энергия магнитного поля катушки при увеличении силы тока через катушку в 3 раза?
Ответ:
а) уменьшится в 3 раза
б) увеличится в 9 раз
в) увеличится в 3 раза
г) уменьшится в 9 раз
Алгоритм решения
1.Записать формулу, определяющую энергию магнитного поля тока.
2.Установить, как изменится энергия магнитного поля тока при увеличении силы тока через катушку в 3 раза.
Решение
Энергия магнитного поля тока определяется формулой:
WМ=LI22..
Видно, что энергия магнитного поля тока прямо пропорционально зависит от квадрата силы тока в катушке. Следовательно, если сила тока увеличится втрое, то энергия магнитного поля увеличится в 32, то есть в 9 раз.
Ответ: бpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22688Энергия магнитного поля катушки с током равна 0,64 Дж. Индуктивность катушки равна 20 мГн. Какова сила тока в катушке?
Индуктивность катушки равна 20 мГн. Какова сила тока в катушке?
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу, определяющую энергию магнитного поля тока.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
- Индуктивность катушки: L = 20 мГн.
- Энергия магнитного поля катушки с током: WM = 0,64 Дж.
20 мГн = 0,02 Гн
- Формула для нахождения энергии магнитного поля тока:
WМ=LI22..
Отсюда сила тока равна:
I=√2WМL..=√2·0,640,02..=8 ⎛⎝А⎞⎠
Ответ: 8pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22800На рисунке показана схема электрической цепи, состоящей из источника тока с ЭДС ε = 12 В и внутренним сопротивлением r = 1 Ом, двух резисторов с сопротивлениями R1 = 7 Ом и R2 = 4 Ом, конденсатора электроёмкостью С = 3 мкФ и катушки с индуктивностью L = 32 мкГн. Какое количество теплоты выделится на резисторе R2 после размыкания ключа К? Сопротивлением провода катушки пренебречь. Ответ запишите в мкДж.
Какое количество теплоты выделится на резисторе R2 после размыкания ключа К? Сопротивлением провода катушки пренебречь. Ответ запишите в мкДж.
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать закон электромагнитной индукции для двигающихся стержней.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 12 В.
• Сопротивление источника тока: R = 1 Ом.
• Сопротивление первого резистора: R1 = 7 Ом.
• Сопротивление второго резистора: R2 = 4 Ом.
• Электроемкость конденсатора: C = 3 мкФ.
• Индуктивность катушки: L = 32 мкГн.
3 мкФ = 3∙10–6 Ф
32 мкГн = 32∙10–6 Гн
До размыкания ключа электрический ток протекает через последовательно соединённые резисторы R1, R2 и катушку L. После размыкания ключа вся накопленная в элементах цепи энергия выделится в виде тепла на резисторе R2:
E=Wкон+Wкат
Энергия электрического поля в конденсаторе определяется формулой:
Wкон=CU22. .
.
Напряжение U на конденсаторе можно выразит из закона Ома для участка цепи:
U=IR2
Чтобы выразить силу тока, потребуется записать закон Ома для полной цепи:
I=εR+r..
Так как в цепи есть два последовательно соединенных резистора, общее сопротивление цепи будет равно сумме их сопротивлений:
R=R1+R2
Тогда закон Ома для полной цепи примет вид:
I=εR1+R2+r..
Тогда напряжение на конденсаторе равно:
U=εR2R1+R2+r..
.
Следовательно, энергия электрического поля в конденсаторе будет равна:
Wкон=C2..(εR2R1+R2+r..)2
Энергия электромагнитного поля в катушке определяется формулой:
Wкат=LI22..=L2..(εR1+R2+r..)2
Следовательно, на втором резисторе выделится энергия, равная:
E=C2..(εR2R1+R2+r..)2+L2..(εR1+R2+r..)2
Ответ: 40pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 2. 5k
5k
power — Можно ли хранить энергию в индукторе и использовать ее позже?
спросил
Изменено 5 лет, 7 месяцев назад
Просмотрено 13 тысяч раз
\$\начало группы\$
Моя компания использует суперконденсаторы для питания устройства в случае отключения электроэнергии. Мне было интересно, можно ли сделать то же самое с катушкой индуктивности. Если нельзя, то почему?
- мощность
- конденсатор
- дроссель
\$\конечная группа\$
2
\$\начало группы\$
Магнитное поле, хранящее энергию, является функцией тока через индуктор: нет тока, нет поля, нет энергии. Вам понадобится активная цепь, чтобы поддерживать этот ток, как только вы отключите ток, индуктор выделит энергию магнитного поля также в виде тока, а индуктор станет источником тока (тогда как его двойной конденсатор является источником напряжения) .
Вам понадобится активная цепь, чтобы поддерживать этот ток, как только вы отключите ток, индуктор выделит энергию магнитного поля также в виде тока, а индуктор станет источником тока (тогда как его двойной конденсатор является источником напряжения) .
Аспекты дуальности конденсатор-индуктор с точки зрения накопления энергии:
\begin{array}{ll} \mbox{Конденсатор} и \mbox{Дроссель} \\ \mbox{* сохраняет энергию в электрическом поле} & \mbox{* сохраняет энергию в магнитном поле} \\ \mbox{* должен быть разомкнутым контуром (бесконечное сопротивление) } & \mbox{* должен быть замкнутым контуром (нулевое сопротивление)} \\ \mbox{* теряет энергию из-за параллельного сопротивления} & \mbox{* теряет энергию из-за последовательного сопротивления} \end{array}
A сверхпроводник 9Однако 0036 может поддерживать магнитное поле в токовой петле с нулевым сопротивлением.
К сожалению, на подобных фотографиях вы всегда будете видеть пары водяного пара, вызванные жидким азотом, что означает температуру ниже -183 °C. 2R. Это можно преодолеть, используя сверхпроводники, которые вообще не имеют сопротивления, но проблема в том, что все известные в настоящее время сверхпроводники должны охлаждаться до криогенных температур. Кроме того, в то время как идеальный сверхпроводник оставался бы сверхпроводящим при любом произвольном токе, все известные сверхпроводники (на самом деле) имеют некоторый верхний предел плотности тока, который они могут поддерживать, прежде чем эффект исчезнет.
2R. Это можно преодолеть, используя сверхпроводники, которые вообще не имеют сопротивления, но проблема в том, что все известные в настоящее время сверхпроводники должны охлаждаться до криогенных температур. Кроме того, в то время как идеальный сверхпроводник оставался бы сверхпроводящим при любом произвольном токе, все известные сверхпроводники (на самом деле) имеют некоторый верхний предел плотности тока, который они могут поддерживать, прежде чем эффект исчезнет.
\$\конечная группа\$
0
\$\начало группы\$
\$\begin{массив}{lcl}
\textbf{Емкостное хранилище} & & \textbf{Индуктивное хранилище} \\
\mbox{Должно иметь бесконечное внутреннее сопротивление} & | & \mbox{Должен иметь нулевое внутреннее сопротивление} \\
\mbox{Напряжение должно оставаться в нем навсегда} & | & \mbox{Ток должен течь через него вечно} \\
\mbox{Вы имеете дело с напряжением} & | & \mbox{Вы имеете дело с текущим} \\
\mbox{Саморазряд может занять годы} & | & \mbox{Саморазряд за очень короткое время} \\
\mbox{Электрическое поле практически не выходит наружу} & | & \mbox{Магнитное поле может мешать другим компонентам} \\
\mbox{Легче} & | & \mbox{Очень тяжелый (железо, медь и т. д.)} \\
\mbox{Может быть дешевле} & | & \mbox{В некоторых странах Fe и Cu могут быть очень дорогими} \\
\конец{массив}\$
д.)} \\
\mbox{Может быть дешевле} & | & \mbox{В некоторых странах Fe и Cu могут быть очень дорогими} \\
\конец{массив}\$
\$\конечная группа\$
0
\$\начало группы\$
Да, люди могут накапливать энергию в индукторе и использовать ее позже.
Люди построили несколько сверхпроводящих магнитных накопителей энергии, которые хранят мегаджоуль энергии в течение дня или около того с довольно высокой эффективностью в катушке индуктивности, сформированной из сверхпроводящего «провода». Мне сказали, что несколько электроэнергетических компаний купили несколько таких блоков и используют их для улучшения качества электроэнергии.
Большинство людей в США имеют десятки импульсных преобразователей напряжения.
Большинство этих импульсных преобразователей напряжения постепенно накапливают энергию при одном напряжении в катушке индуктивности или трансформаторе, а затем «позже» постепенно вытягивают эту энергию из катушки индуктивности или трансформатора при более желаемом напряжении, снова и снова, часто 40 000 или миллион раз в секунду. второй.
второй.
Многие популярные поставщики электронных компонентов позволяют сортировать катушки индуктивности по их добротности. Коэффициент добротности показывает, насколько хорошо катушка индуктивности или конденсатор хранит энергию. В импульсных стабилизаторах напряжения и других приложениях для накопления энергии чем больше добротность, тем лучше.
Лучшие готовые катушки индуктивности (все несверхпроводящие) популярных поставщиков имеют добротность 150 при 25 кГц. Большинство конденсаторов имеют на порядок лучшее накопление энергии (более высокую добротность), чем это.
Люди могут накапливать энергию в катушках индуктивности для последующего использования. Но почти во всех ситуациях с накоплением энергии мы используем что-то другое, потому что это что-то другое либо (а) имеет меньшие первоначальные затраты, либо (б) более эффективно, либо (в) требует меньше места, либо (г) какое-то сочетание вышеперечисленного.
\$\конечная группа\$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
inductance — интуитивный способ «визуализации» того, как энергия хранится в индукторе?
Я начну с обсуждения конденсаторов, а затем перейду к катушкам индуктивности. Я буду избегать сложных уравнений (чтобы спасти себя, а также это обсуждение). Я могу даже обсудить двойственность между емкостью и индуктивностью и то, как это связано с физическими идеями, такими как масса, сила, скорость и импульс. (Это будет рассматривать их изолированно с целью обеспечения некоторой интуиции, только.) Но когда у меня будет время для этого. Я думаю, что важно начать с той области, где каждый из нас может чувствовать себя более комфортно.
Далее будет более качественно и будут обсуждаться идеи, которых нет в учебниках. Я делаю это, потому что это может помочь вам визуализировать, несмотря на риск использования нестандартного подхода.
Конденсаторы
Для конденсаторов вы, вероятно, уже знаете, что площадь пластины (при условии, что обе пластины имеют одинаковую площадь), расстояние, разделяющее пластины, и физическое вещество (вставленное вместо вакуума или воздуха), используемое между пластинами. напрямую связаны с его емкостью. Эти идеи о площади пластины, разделении пластины и вставленной среде (если есть) нетрудно понять. Формула тоже довольно проста:
напрямую связаны с его емкостью. Эти идеи о площади пластины, разделении пластины и вставленной среде (если есть) нетрудно понять. Формула тоже довольно проста:
$$C=\epsilon_{_0}\frac{A}{d}$$
Важно, чтобы вы думали о том, что вышеизложенное подразумевает наличие вакуума между пластинами. Можно, конечно, и между ними просунуть кусочки материи. А кто знает? Может случиться что-то другое. Оказывается, для некоторых типов материи приведенное выше уравнение действительно требует дополнительного фактора — относительной диэлектрической проницаемости. Это всего лишь условный коэффициент, который должен быть либо равен 1, либо больше 1 и кое-что говорит вам о способности вставленного материала реагировать на разницу зарядов между пластинами.
Новое уравнение с его причудливым новым вымышленным коэффициентом:
$$C=\epsilon_{_r}\epsilon_{_0}\frac{A}{d}$$
И оно отлично работает, если вы знаете \$\эпсилон_{_r}\$. Если вы заполните весь объем между пластинами (без промежутков и т. д.), вы можете просто использовать \$\epsilon_{_r}\$ материала. Конечно, если вы делаете что-то странное, например, заполняете странные части тома, тогда все не так просто. (Но люди в основном не делают таких вещей. Они стараются сделать все просто и дешево.)
д.), вы можете просто использовать \$\epsilon_{_r}\$ материала. Конечно, если вы делаете что-то странное, например, заполняете странные части тома, тогда все не так просто. (Но люди в основном не делают таких вещей. Они стараются сделать все просто и дешево.)
Что делает фактор выдумки? Что это значит? С чем это связано, физически?
Ну, заряды разделены промежутком, который не дает им пересечься и нейтрализоваться. Они хотят, но не могут. Это создает поле между пластинами, при этом линии поля перпендикулярны поверхности пластины и проходят прямо от одной пластины к другой. В другом месте также есть поле, окружающее конденсатор в воздухе вокруг него, и эти линии поля указывают повсюду, в зависимости от того, где вы находитесь (и / или время, когда вы находитесь там для изменения ситуации), как вращающиеся векторы, когда вы двигаетесь. через это пространство. Но интеграл по пути туда и обратно требует, чтобы линии между пластинами указывали прямо от одной пластины к другой, и это важный момент, который имеет значение для диэлектрической среды, которая может быть помещена в этот объем.
Когда туда что-то вставляется, вещество внутри материала может образовывать диполи. Молекулы немного сложнее, чем диполь. Я должен признать, что использование идеи идеализированного диполя является некоторым упрощением. Но упрощение довольно близкое и достаточно хорошее для большинства применений.
Теперь, прежде чем идти дальше, давайте вернемся к случаю, когда между пластинами находится только вакуум или воздух. При зарядке конденсатора сохраняется определенное количество полезной энергии где-то . Где? Ну, в вакууме между пластинами. Я хочу, чтобы вы твердо зафиксировали это в своем уме. Он не хранится в пластинах, где вообще нет электрического поля (если бы оно было, вокруг двигались бы электроны, а мы знаем, что этого не происходит). тарелки.
Теперь давайте вернемся к идее диполя, где мы вставили какой-то волшебный материал, который может образовывать диполи под воздействием силовых линий электрического поля между пластинами. Некоторые молекулы или группы молекул в диэлектрике могут вращаться и выстраиваться вдоль силовых линий электрического поля. Это ответ на поле. При вращении для выравнивания эти диполи можно рассматривать как образующие своего рода «короткое замыкание» или «сокращение», которое «перекрывает» (если хотите) часть вакуума. Вакуум, в котором хранится энергия, тоже имеет, скажем, сопротивление. И молекулы образуют короткое замыкание, которое обходит это сопротивление вакуума и уменьшает эффективный зазор.
Это ответ на поле. При вращении для выравнивания эти диполи можно рассматривать как образующие своего рода «короткое замыкание» или «сокращение», которое «перекрывает» (если хотите) часть вакуума. Вакуум, в котором хранится энергия, тоже имеет, скажем, сопротивление. И молекулы образуют короткое замыкание, которое обходит это сопротивление вакуума и уменьшает эффективный зазор.
Теперь, согласно приведенным выше уравнениям, если расстояние между пластинами меньше, то значение емкости увеличивается, при прочих равных условиях. Итак, если вы примете такой способ мышления, это может объяснить, почему диэлектрик увеличивает емкость.
Однако некоторые материалы не поляризуются и не образуют диполи. Таким образом, они не считаются диэлектриками. И я ничего не знаю о формах диполей, противоположно направленных против направления линии электрического поля, поэтому, если кто-то не знает что-то, что я упускаю, мы не можем уменьшить емкость конденсатора с вакуумным зазором, вставив антидиэлектрический .
Отсюда дело не столько в самих зарядках, сколько в полях . Поля, которые существуют при наличии разницы зарядов между пластинами. Кроме того, здесь полезно представить, что энергия не может храниться в материи, а только в вакууме. И что, если вы заполните этот вакуум чем-то, что может образовывать диполи, тогда будет меньше вакуума, в котором может храниться энергия, или, по сути, меньший эффективный зазор 9.0130 .
Итак, есть зазор, который можно измерить рулеткой. Это один номер. Но есть также зазор, который вы не можете измерить напрямую, это эффективный зазор, в котором хранится энергия. Значение \$\epsilon_{_r}\$ — это просто величина, говорящая вам, насколько укорачивается измеримый зазор, чтобы получить оставшийся истинный вакуумный зазор, который является единственным зазором, о котором заботится конденсатор.
Обратите внимание, что это тоже не совсем так. Это упрощение. Материя, которая вращается в выравнивании, может также повернуться обратно из выравнивания. И для достижения вращения требуется некоторая энергия, и она высвобождается, когда силовые линии уменьшаются и молекулы могут немного «раскручиваться». Для конденсаторов этот эффект может привести к некоторому нагреву, поскольку движение молекул — это в значительной степени определение тепловой энергии. И если вы сбиваете их с толку, осциллируя полем, то часть этой энергии превращается в дополнительную вибрационную энергию в конденсаторе. Кроме того, есть вопрос о том, сколько «памяти» могут иметь эти молекулы — возможно, они не полностью возвращаются туда, где были до зарядки конденсатора, после разрядки. Они могут что-то «помнить». Но для большинства конденсаторов этот эффект довольно незначителен, поэтому обычно считается, что конденсаторы не имеют гистерезиса.
И для достижения вращения требуется некоторая энергия, и она высвобождается, когда силовые линии уменьшаются и молекулы могут немного «раскручиваться». Для конденсаторов этот эффект может привести к некоторому нагреву, поскольку движение молекул — это в значительной степени определение тепловой энергии. И если вы сбиваете их с толку, осциллируя полем, то часть этой энергии превращается в дополнительную вибрационную энергию в конденсаторе. Кроме того, есть вопрос о том, сколько «памяти» могут иметь эти молекулы — возможно, они не полностью возвращаются туда, где были до зарядки конденсатора, после разрядки. Они могут что-то «помнить». Но для большинства конденсаторов этот эффект довольно незначителен, поэтому обычно считается, что конденсаторы не имеют гистерезиса.
(Эта деталь гистерезиса не соответствует действительности для материалов сердечника, используемых в индукторах, где гистерезис является важной деталью, которую вы часто не можете игнорировать.) физический дизайн конденсатора. Но обычно они не важны.
Но обычно они не важны.
Катушки индуктивности
Что касается катушек индуктивности, вы, вероятно, уже знаете, что проволочная катушка и физическая материя (снова вставленная вместо вакуума или воздуха), которую окружает проволочная катушка, непосредственно связаны со значением ее индуктивности. Здесь все несколько сложнее для понимания. Эквивалентом разделения пластин, но для индуктора, является длина магнитного пути.
Проблема с катушками индуктивности заключается в том, что в них нет монопольных магнитных зарядов. Таким образом, вы не можете просто прикрепить магнитные заряды к какой-либо поверхности. Итак, здесь у вас не может быть этих силовых линий магнитного поля между двумя пластинами.
Говоря о корпусе конденсатора, я упомянул, что снаружи конденсатора тоже есть дорожка, но в целом мы можем просто сфокусироваться на силовых линиях между пластинами и игнорировать все остальное. Но с индуктором мы должны сосредоточиться на всем магнитном пути, а не только на его небольшом сегменте.
Это означает, что простейшая катушка индуктивности представляет собой тороид. Это потому, что весь магнитный путь представляет собой простой круг — среднюю окружность вокруг тороида. (Эта штука с \$2\pi\,r\$.)
(Хорошо, позвольте мне взять это обратно. Простейшая катушка индуктивности — это соленоид, простирающийся до бесконечности. Но поскольку бесконечно длинные катушки индуктивности трудно найти, а короткие добавляют некоторая сложность, которую я не хочу здесь затрагивать, вернемся к тому тороиду.)
Формула тороида здесь тоже довольно проста: 92\$ фактор. Вы, вероятно, можете себе представить, почему количество циклов будет иметь значение. Однако причина, по которой значение возведено в квадрат, немного выходит за рамки того, куда я хочу пойти. Так что давайте просто назовем это небольшой дополнительной сложностью. Но это не так много.
Опять же, имейте в виду, что энергия катушки индуктивности не сохраняется в проводе. Он хранится в вакуумном объеме, в котором находится магнитное поле. Вот это внутренняя часть тороида.
Вот это внутренняя часть тороида.
Итак, что происходит, когда материал с проницаемостью помещается в вакуумный объем? Что ж, в некоторых случаях все снова «выстраивается», как те диполи раньше. В данном случае все сложнее. Итак, термин домен используется для представления совокупности небольших частиц материи, которые могут выравниваться с магнитным полем. Электроны, вращающиеся вокруг отдельных атомов, также могут выстроиться в линию (и они в некоторой степени так и делают). Но достаточно того, что остается основная идея. Некоторые магнитные домены выстраиваются в линию с линиями магнитного поля и образуют «кратчайшие пути» через вакуум вдоль линий магнитного поля, что заставляет их выравниваться. Это сокращает эффективную длину магнитного пути и, следовательно, увеличивает индуктивность. 92\frac{A}{2\pi\,r}$$
Здесь \$\mu_{_r}\$ — это просто число, указывающее, насколько укорачивается длина вакуумного пути. Это может быть в 1000 раз и более.
Итак, снова есть магнитная дорожка, которую можно измерить рулеткой. Это один номер. Но есть также длина магнитного пути, которую вы не можете измерить напрямую, это эффективная длина, в пределах которой хранится энергия. (Общий объем вакуума, в котором хранится энергия, будет равен укороченной длине, умноженной на площадь поперечного сечения тороида.)
Это один номер. Но есть также длина магнитного пути, которую вы не можете измерить напрямую, это эффективная длина, в пределах которой хранится энергия. (Общий объем вакуума, в котором хранится энергия, будет равен укороченной длине, умноженной на площадь поперечного сечения тороида.)
С материалами, которые мы можем использовать для увеличения индуктивности, с выровненными доменами возникает гистерезис. Если вы начнете с такого материала с доменами, выровненными в случайных направлениях, затем приложите магнитное поле, которое вынуждает их выровняться, а затем уберете это магнитное поле, они частично вернутся в свое прежнее состояние (или что-то достаточно близкое на данный момент), но они не вернутся полностью в свое рандомизированное состояние. Некоторая «память» о предыдущем поле выравнивания все еще будет висеть.
Если вы перевернете поле, вам придется сначала преодолеть эту память, а затем перестроить их противоположно. Удаление поля также оставит некоторую память об этом поле, которое было противоположным. Этот процесс продолжается снова и снова, когда переменный ток подается на индуктор.
Этот процесс продолжается снова и снова, когда переменный ток подается на индуктор.
Как и в случае с любым другим материалом, вращение доменов оставляет в материале некоторую колебательную энергию — тепло.
Изменяющееся магнитное поле индуцирует некулоновское электрическое поле. Это означает, что токи могут протекать в условиях переменного тока. Поскольку некоторые материалы, которые мы используем (железо), являются проводящими, эти токи на самом деле текут и также выделяют тепло. Некулоновский эффект первого порядка называется вихревым током. Это не то, о чем вам нужно беспокоиться в конденсаторе, потому что по определению диэлектрик является изолятором, и токи просто не текут в них. Но для катушек индуктивности и на более высоких частотах это проблема. Ферриты помогают в этом, потому что проводящие частицы смешиваются с непроводящими частицами, которые помогают блокировать эти токи.
Наконец, существуют практические ограничения на силу магнитного поля (количество Тесла), которое можно поддерживать. Различные материалы также будут накладывать здесь разные ограничения. Как только это исчерпано (т. Е. Все магнитные домены выполнили все «выстраивания», которые они могут сделать, и больше ничего не осталось), тогда индуктор начинает вести себя так, как будто материала сердечника вообще не было. Больше похоже на индуктор с воздушным сердечником. Процесс часто постепенный, так что эффект не будет внезапным. Некоторые колебательные схемы фактически зависят от этой «функции», чтобы работать.
Различные материалы также будут накладывать здесь разные ограничения. Как только это исчерпано (т. Е. Все магнитные домены выполнили все «выстраивания», которые они могут сделать, и больше ничего не осталось), тогда индуктор начинает вести себя так, как будто материала сердечника вообще не было. Больше похоже на индуктор с воздушным сердечником. Процесс часто постепенный, так что эффект не будет внезапным. Некоторые колебательные схемы фактически зависят от этой «функции», чтобы работать.
Упрощение
Прежде чем продолжить, я хочу вернуться к конденсатору и копнуть на один уровень ниже моего качественного ручного подметания выше. Причина в том , что я хочу указать на новую концепцию , которую вы должны включить в каждую свою мысль об окружающем вас мире — идею возникающих явлений .
Иногда теории, хорошо описывающие один уровень опыта и хорошо проверенные экспериментально, не имеют никакого смысла на более глубоком уровне. Вместо этого эти идеи срочный вызов — обычно в связи с большим количеством статистических данных о населении.
Понятия температуры и энтропии из статистической термодинамики хорошо известны и чрезвычайно важны. Они просто работают. Но идеи температуры и энтропии не имеют никакого значения на атомном уровне. Их просто не существует. Есть энергия. А энергия — важное понятие как на атомном уровне, так и в термодинамике. Так что есть что-то общее. Просто отдельные частицы не имеют представления о температуре. У них может быть скорость, импульс, энергия и т. д. Но не температура и не энтропия. Эти два возникают из статистики квадриллионов (и более) частиц, которые взаимодействуют с чем-то другим, что также включает такое же большое количество частиц.
Например, чашка с водой и термометр. В них обоих содержится огромное, невообразимое количество отдельных частиц. И когда вы помещаете термометр в чашку с водой, чтобы измерить ее температуру, вы спрашиваете: «Что происходит с квинтиллионами частиц в термометре, когда он погружен в септиллионы частиц воды, которые все будут случайным образом подпрыгивать и влиять друг на друга? » Это имеет значение из-за большого количества возможных начальных состояний и множества возможных результатов, почти все из которых будут давать «показания» термометра, которые вы ожидаете увидеть в пределах погрешности. Есть несколько исключительных начальных состояний, которые дадут разные результаты. Но вероятность того, что это произойдет, настолько мала, что время жизни всей Вселенной истекло бы до того, как это произошло. Так что правильно говорить о температуре и энтропии, как если бы они существовали на этом эмерджентном уровне. (Поскольку необычное поведение встречается крайне редко.)
Есть несколько исключительных начальных состояний, которые дадут разные результаты. Но вероятность того, что это произойдет, настолько мала, что время жизни всей Вселенной истекло бы до того, как это произошло. Так что правильно говорить о температуре и энтропии, как если бы они существовали на этом эмерджентном уровне. (Поскольку необычное поведение встречается крайне редко.)
(Примечание: здесь тоже стоит упомянуть 0-й закон термодинамики). и из которого, как вы думаете, вы знаете !
Конденсатор — как раз такой пример. Я выше махнул рукой про диэлектрические диполи и прочее. Но в глубине, конечно, намного интереснее и сложнее. И еще ниже, еще более захватывающим и сложным. Позвольте мне дать вам представление о том, что находится на следующем уровне ниже, основанном главным образом на идеях, изложенных в превосходной книге Чабея и Шервуда для изучения физики под названием «9».0129 Материя и взаимодействия ».
Вот моя интерпретация того, о чем они пишут:
всего несколько дополнительных электронов у поверхности (и чуть меньше электронов у поверхностей с правой стороны. ) Между ними я показываю поляризованные диэлектрические диполи. вектора направления поля при перемещении снаружи конденсатора по некоторой кривой.0005
) Между ними я показываю поляризованные диэлектрические диполи. вектора направления поля при перемещении снаружи конденсатора по некоторой кривой.0005
(Имейте в виду, что из очень, очень большого количества электронов зоны проводимости, присутствующих на обеих пластинах, на левой пластине их немного меньше, чем на правой пластине.)
Я также добавил зеленый и оранжевая точка в двух интересных местах внутри диэлектрика. Зеленая точка находится прямо посередине одного из этих диполей. С его точки зрения вектор указывает, как указано выше. Оранжевая точка находится между двумя диполями, и с ее точки зрения вектор указывает в другую сторону, как указано выше. Как вы можете себе представить, когда вы перемещаетесь внутри диэлектрика, существуют очень сложные направления электронного поля. Я проиллюстрировал только два более простых.
Вопрос в том, каково направление электронного поля внутри диэлектрика? Кажется, это очень сложно вычислить. Но если вы посмотрите на векторы направления и представите, что суммируете их, когда вы двигаетесь по замкнутому пути, огибающему внешнюю сторону конденсатора, а затем проходите через его середину, чтобы закончить там, где вы начали, мы знаем, что эта сумма должна быть равна нулю. (Он не может быть ненулевым.)
(Он не может быть ненулевым.)
Но вы можете видеть, что два внешних вектора (крайний левый и крайний правый) указывают в одном направлении. Таким образом, сумма вокруг внешнего вида и на мгновение игнорируя диэлектрик, должна быть отличной от нуля, а сеть должна указывать вправо. Следовательно, чистое направление самого диэлектрика должно быть направлено влево ровно на столько, сколько нужно, чтобы компенсировать сумму внешних путей. 92\$. Кажется интересным, что есть некоторые сходства, просто одинаковые.
$$\begin{выравнивание*} \begin{массив}[t]{r} {\ текст {импульс:}} \ vphantom {q = C \: V} \\\\ {\ text {импульс:}} \ vphantom {\ text {d} \, q = C \: \ text {d} \, V} \\\\ {\ text {force:}} \ vphantom {\ frac {\ text {d} q} {\ text {d} t} = C \: \ frac {\ text {d} \, V} {\ text {d }т}}\\\\ {\ text {масса:}} \ vphantom {C = \ frac {\ text {d} q} {\ text {d} V}} \\\\ {\ текст {скорость:}} \ vphantom {q = C \: V} \\\\ {\ текст {ускорение:}} \ vphantom {q = C \: V} \\\\ {\ текст {энергия:}} \ vphantom {\ frac12 C \, V ^ 2} \конец{массив} && \overbrace{ \begin{массив}[т]{с} д=С\:В\\\\ \text{d}q=C\:\text{d}V\\\\ I = \ frac {\ text {d} q} {\ text {d} t} = C \: \ frac {\ text {d} \, V} {\ text {d} t} \\\\ C = \ frac {\ text {d} q} {\ text {d} V} \\\\ В\\\\ \ гидроразрыв {\ текст {d} V} {\ текст {d} т} \\\\ \frac12 C \,V^2 \конец{массив} } ^ {\ текст {конденсатор}} && \overbrace{ \begin{массив}[т]{с} p=m\:v\vphantom{q=C\:V}\\\\ \text{d}p=m\:\text{d}v\vphantom{q=C\:V}\\\\ F = \ frac {\ text {d} p} {\ text {d} t} = m \: \ frac {\ text {d} \, v} {\ text {d} t} = m \: a \ \\\ m = \ frac {\ text {d} p} {\ text {d} v} \ vphantom {C = \ frac {\ text {d} q} {\ text {d} V}} \\\\ в\\\\ а = \ frac {\ text {d} v} {\ text {d} t} \\\\ \frac12 м\,v^2\vphantom{\frac12 C \,V^2} \конец{массив} } ^ {\ текст {частица}} && \overbrace{ \begin{массив}[т]{с} \phi=L\:I\vphantom{q=C\:V}\\\\ \text{d}\phi=L\:\text{d}I\\\\ V = \ frac {\ text {d} \ phi} {\ text {d} t} = L \: \ frac {\ text {d} \, I} {\ text {d} t} \\\\ L = \ frac {\ text {d} \ phi} {\ text {d} I} \ vphantom {C = \ frac {\ text {d} q} {\ text {d} V}} \\\\ Я\\\\ \ гидроразрыва {\ текст {d} \, I} {\ текст {d} т} \\\\ \frac12 L\,I^2\vphantom{\frac12 C \,V^2} \конец{массив} } ^ {\ текст {индуктор}} \end{выравнивание*}$$
Также поищите Лагранжевую механику и принцип наименьшего действия . (Я не зря начал с импульса.)
(Я не зря начал с импульса.)
Уверен, вы знаете, что заряд конденсатора сохраняется. Вы можете рассматривать заряд конденсатора как связанный с потенциальной энергией в физической системе и думать о Вебере катушки индуктивности как связанном с кинетической энергией в физической системе. (Вы можете выбрать другой путь, если хотите.)
Как бы то ни было, мне нравится думать о веберах (или вольт-секундах) в катушке индуктивности как о магнитном двойнике электрического заряда конденсатора. Поначалу это немного странно, потому что заряд исчисляем (в нашем воображении), но вольт-секунды, кажется, зависят от времени (и это так) и не поддаются исчислению таким же образом. Но во всех смыслах \$L I\$ — это магнитный заряд, а \$C V\$ — электрический заряд. Эти вещи сохраняются точно так же, как сохраняется импульс в физической системе.
Точно так же ток в конденсаторе является силой. Когда вы прикладываете эту силу к конденсатору, он ускоряет , изменяя напряжение. Напряжение на катушке индуктивности является силой. Когда вы прикладываете напряжение к катушке индуктивности, она также ускоряет , изменяя ток.
Напряжение на катушке индуктивности является силой. Когда вы прикладываете напряжение к катушке индуктивности, она также ускоряет , изменяя ток.
Также полезно (особенно при рассмотрении LC-бака) рассматривать энергию катушки индуктивности как кинетическую, а энергию конденсатора как потенциальную. Танк LC представляет собой простую систему, которая преобразует одно в другое, а затем обратно. Это, возможно, очень похоже на идею кометы на очень высокоэллиптической орбите. В апоапсисе почти вся кинетическая энергия преобразуется в потенциальную энергию. Затем, когда комета ускоряется обратно к Солнцу, эта потенциальная энергия преобразуется в кинетическую энергию. Таким образом, в перицентре почти вся потенциальная энергия преобразуется в кинетическую энергию. И комета затем продолжается, снова и снова. LC-танк похож на этот, за исключением того, что полярности меняются так, что есть четыре состояния вместо двух, если вы включаете полярность. Если просто энергия, то два состояния, как у кометы.



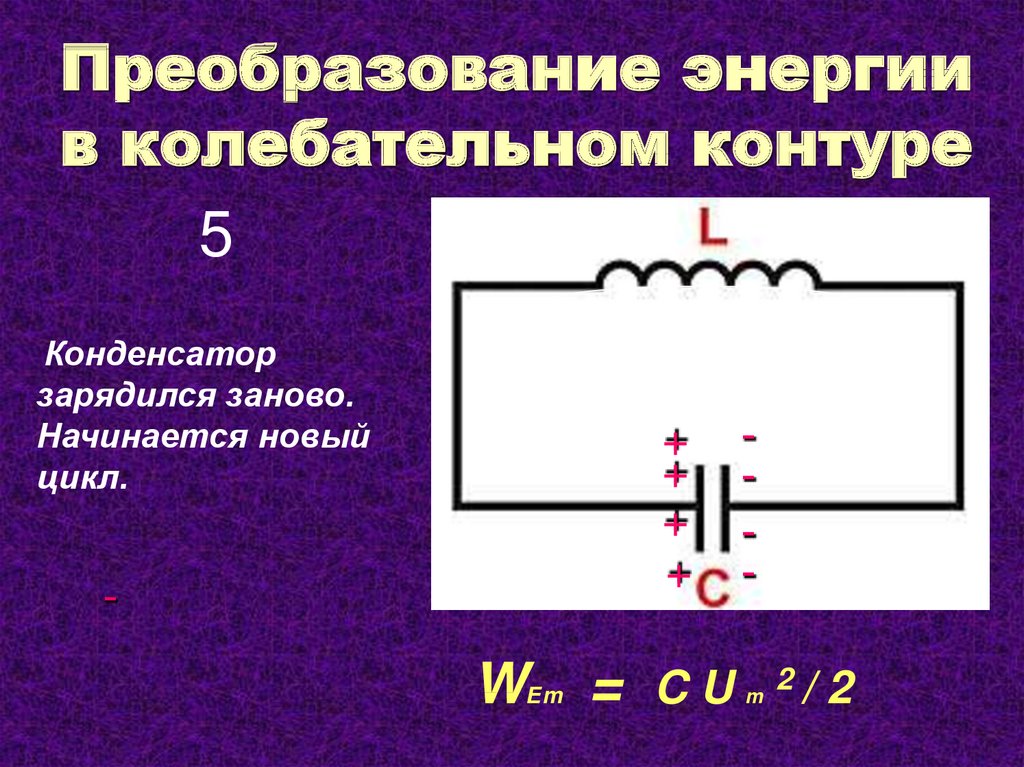 Определить емкость конденсатора и максимальную энергию магнитного поля катушки.
Определить емкость конденсатора и максимальную энергию магнитного поля катушки.

 Наружный диаметр тороида d
Наружный диаметр тороида d