Влияние развязывающих конденсаторов на качество электропитания и целостность сигнала
Влияние развязывающих конденсаторов на качество электропитания и целостность сигнала
Чанг Фей Йи (Chang Fei Yee) KEYSIGHT TECHNOLOGIES
В статье обсуждается влияние развязывающих конденсаторов на печатной плате на качество электропитания и целостность сигнала. Исследование было выполнено путем совместного моделирования качества электропитания и целостности сигнала в созданной топологии для анализа импеданса цепи питания, шума коммутации и глазковых диаграмм.
Введение
Разработчикам оборудования крайне важно определить резонансную частоту каждого элемента (например, блокировочного/развязывающего конденсатора, планарного конденсатора и индуктивности межсоединения) цепи питания на печатной плате и ее влияние на качество электропитания. Низкое качество электропитания печатной платы – например, из-за более высокого, чем планировалось, импеданса цепи питания в широком диапазоне частот – приводит к одновременному появлению шума коммутации (SSN) и сужению глазковой диаграммы сигнала, передаваемого интегральной схемой, которая подключена к этой цепи питания.
Анализ и результаты
Исследовалась печатная плата, содержащая систему на кристалле (SoC) с интерфейсом памяти DDR4. На рис. 1а показана цепь питания 1,2 В, расположенная на слое 4, которая подает питание на интерфейс памяти, состоящей из одной ИС (выводы выделены синим цветом). При этом цепь заземления или опорная земля, выделенная зеленым цветом, располагается на слое 5. ИС памяти имеет 13 выводов питания BGA. Места, занимаемые развязывающими конденсаторами 0,22 мкФ (выделены коричневым цветом) в корпусе типа 0201, находятся между выводами каждого контакта питания и заземления. Кроме того, между цепью 1,2 В и заземлением включены шунтирующие конденсаторы 10 мкФ и 1 мкФ (выделены коричневым цветом). Восемь информационных сигналов этого интерфейса показаны на рис.
Для изучения влияния развязывающих конденсаторов на импеданс цепи питания, SSN и глазковые диаграммы, совместное моделирование качества электропитания и целостности сигнала в созданной топологии выполняется с помощью ПО HyperLynx для нескольких конфигураций цепи питания, перечисленных в таблице 1. Каждая конфигурация цепи питания имеет одинаковые топологии печатной платы и слои, показанные на рисунке 1a и 1б, нагруженные одним шунтирующим конденсатором 10 мкФ и одним шунтирующим конденсатором 1 мкФ.
Рис. 1а. Шина питания 1,2 В для интерфейса памяти DDR4, вид сверху.
1 – ИС памяти
Рис. 1б. Восемь сигналов данных интерфейса памяти DDR4.
В конфигурации А конденсаторы 0,22 мкФ отсутствуют. В конфигурации Б имеются четыре конденсатора 0,22 мкФ. В конфигурации В количество конденсаторов 0,22 мкФ увеличивается до восьми. В конфигурации Г количество конденсаторов 0,22 мкФ увеличивается ещё больше, до тринадцати.
Затем в программный инструмент импортируются модели питания ИС памяти и системы на кристалле в формате IBIS v5.
0. Операция чтения памяти со скоростью 1 Гбит/с и частотой Найквиста 500 МГц установлена для режима совместного моделирования, в котором шиной данных управляет ИС памяти, а SoC служит приемником (Rx).
Во-первых, было проведено сравнение импедансов цепи питания в диапазоне от 1000 Гц до 2 ГГц для четырех конфигураций цепи питания. В теории резонансная частота обратно пропорциональна емкости. Как видно на рис. 2, все четыре конфигурации цепи питания имеют одинаковый профиль импеданса в диапазоне от 1000 Гц до 10 МГц из-за размещения одинакового количества шунтирующих конденсаторов 10 мкФ и 1 мкФ. Конфигурация А (без развязывающих конденсаторов 0,22 мкФ) отличается от конфигураций Б, В и Г (в каждом из них присутствует не менее четырех развязывающих конденсаторов 0,22 мкФ). Обратите внимание на уменьшение импеданса цепи питания как минимум на 0,9 Ом на частотах более 10 МГц.
Табл. 1. Исследуемые конфигурации цепи питания.
| Конфигурация цепи питания | Шунтирующий/развязывающий конденсатор | Количество |
| 10 мкФ | 1 | |
| 1 мкФ | 1 | |
| 0,22 мкФ | 0 | |
| Б | 10 мкФ | 1 |
| 1 мкФ | 1 | |
| 0,22 мкФ | 4 | |
| В | 10 мкФ | 1 |
| 1 мкФ | 1 | |
| 0,22 мкФ | 8 | |
| Г | 10 мкФ | 1 |
| 1 мкФ | 1 | |
| 0,22 мкФ | 13 |
1 – Импеданс цепи питания, Ом
2 –
— конфигурация А
— конфигурация Б
— конфигурация В
— конфигурация Г
3 – 1000 Гц
4 – 100 кГц
5 – 10 МГц
6 – 1000 МГц
7 – Частота
Рис.
2. Смоделированная зависимость импеданса цепи питания от частоты.
1 – Напряжение, В
2 – Время, с
3 –
I. В конфигурации А переключаются 8 буферов передачи.
II. В конфигурации Б переключается только 1 буфер передачи.
III. В конфигурации Б переключаются 8 буферов передачи.
IV. В конфигурации В переключаются 8 буферов передачи.
V. В конфигурации Г переключаются 8 буферов передачи.
Рис. 3. Смоделированная зависимость шума коммутации от времени для конфигураций цепи питания, перечисленных в табл. 1.
Во-вторых, были построены графики зависимости SSN от времени для всех конфигураций цепи питания, см. рис. 3. SSN возникает в результате прохождения через полное сопротивление цепи питания переходного тока в буфере передачи (Tx) интегральной схемы во время передачи сигнала. Переходной ток возрастает при увеличении числа буферов Tx в интегральной схеме, которые одновременно переключаются для передачи информационного сигнала.
На рис. 3 видно, что в конфигурации Б амплитуда SSN (III) в два раза больше амплитуды (II) из-за большего переходного тока в ИС, поскольку переключается больше буферов Tx.
С другой стороны, при одновременном переключении восьми буферов Tx на скорости 1 Гбит/с наибольшая амплитуда SSN наблюдается у цепи питания в конфигурации A с наименьшей развязкой и наибольшим импедансом (в диапазоне, составляющем сотни МГц): 505 мВ пик-пик, см. рис. 3 (I). Напротив, цепь питания в конфигурации Г с наилучшей развязкой (13 конденсаторов 0,22 мкФ) и наименьшим импедансом демонстрирует наименьшую амплитуду SSN – 95 мВ пик-пик, см. рис. 3 (V) – что соответствует допуску ±5 % для источника питания 1,2 В, указанному в таблице технических характеристик ИС памяти.
В-третьих, глазковые диаграммы информационных сигналов DDR4 со скоростью 1 Гбит/с с последовательностью битов PRBS-7 (наблюдаемой при Rx или в SoC) были сравнены для конфигураций А и Г, см. рис. 4a и 4б соответственно.
Гораздо большая высота и ширина глазка для информационных сигналов данных в конфигурации Г указывает на то, что подавление SSN за счет лучшего качества электропитания помогает уменьшить джиттер в сигналах, передаваемых интегральной схемой памяти. Закрытие глазка в конфигурации А указывает на увеличение риска битовых ошибок и неустойчивости приема. Подавление SSN достигается путем правильного размещения достаточного количества развязывающих конденсаторов на шине питания относительно земли.
Рис. 4а. Смоделированные глазковые диаграммы информационных сигналов DDR4 для конфигурации А.
Рис. 4б. Смоделированные глазковые диаграммы информационных сигналов DDR4 для конфигурации Г.
Выводы
Описанное в данной статье совместное моделирование качества электропитания и целостности сигнала в созданной топологии продемонстрировало, что правильное размещение достаточного количества развязывающих конденсаторов в цепи питания относительно земли положительно влияет на импеданс цепи питания, SSN и глазковые диаграммы.
Литература
1. B. Olney, “Power Distribution Network Planning,” The PCB Magazine, May 2012.
2. F. Carrio, V. Gonzalez, and E. Sanchis, “Basic Concepts of Power Distribution Network Design for High-Speed Transmission,” The Open Optics Journal, 5, (Suppl 1-M8) pp. 51– 61, 2011.
3. E. Bogatin, Signal and Power Integrity—Simplified: 2nd Edition, Prentice Hall, 2009.
4. Mentor HyperLynx, “Power-Aware Signal Integrity Analysis.”
5. Micron, “Power Integrity Simulation With IBIS 5.0 Models Technical Note.”
Об авторе
Чанг Фей Йи является инженером-разработчиком аппаратной части в компании Keysight Technologies.
Сфера его деятельности включает в себя разработку системного аппаратного обеспечения, а также анализ качества электропитания и целостности сигнала.
Конденсаторы и электроемкость | Электричество
Пришло время поговорить еще об одной штуке, которая часто вызывает вопросы у студентов, изучающих физику электричества. Она называется конденсатор.
Конденсатор – это устройство, которое способно запасать электрический заряд. В простейшим случае оно представляет собой две проводящие электрический ток пластины, находящиеся на некотором расстоянии друг от друга.
Пластины конденсатора иногда называют обкладками. На представленном выше рисунке от них отходят выводы, при помощи которых конденсатор можно присоединить к источнику тока, чтобы он зарядился. Давайте рассмотрим схематичное изображение такой электрической цепи.
Итак, на конденсаторе начнет накапливаться электрический заряд. Дело в том, что электроны, находящиеся на правой обкладке, будут притягиваться положительным полюсом источника тока, поэтому вся эта пластина начнет приобретать положительный заряд.
А с левой стороны все будет наоборот: отрицательно заряженные электроны будут двигаться от минуса к плюсу, то есть от отрицательного полюса источника тока к положительно заряженной правой пластине конденсатора. Но так как пластины не соединены друг с другом, на левой обкладке начнет создаваться переизбыток электронов.
Отметим, что по модулю заряд на обоих обкладках конденсатора будет одинаковым.
Процесс зарядки конденсатора будет происходить до тех пор, пока напряжение на нем не станет равным напряжению на источнике тока. Когда это произойдет, электроны будут притягиваться положительно заряженной пластиной конденсатора точно так же, как они будут притягиваться положительным полюсом источника тока. В связи с этим их движение в электрической цепи прекратится.
Что интересно, так это то, что разные конденсаторы по-разному запасают электрический заряд. На некоторых из них можно накопить очень большой заряд, а на других – нет. Величина, которая характеризует такое различие между изучаемыми нами сейчас устройствами, называется электроемкостью.
Она обозначается буквой C и измеряется в фарадах (Ф) – единицах, названных так в честь Майкла Фарадея.
С точки зрения физики, электроемкость – это отношение заряда, накопленного на какой-либо пластине конденсатора, к напряжению между его обкладками:
\boxed{C=\dfrac{q}{U}}
Чем больше заряда будет на пластинах конденсатора, тем больше будет напряженность создаваемого электрического поля, то есть тем больше будет напряжение. Электроемкость же является коэффициентом пропорциональности между ними:
q\thicksim{U}
q=CU
Здесь мы подходим к интересному вопросу. Как уже было сказано выше, заряд на конденсаторе тесно связан с напряжением на нем. Получается, что, изменяя какую-либо из этих величин, мы никак не будем влиять на емкость конденсатора:
C=\dfrac{q\Uparrow}{U\Uparrow}
C=\dfrac{q\Downarrow}{U\Downarrow}
От чего же зависит ее значение в такое случае?
Прежде всего, логично предположить, что большую роль будет играть размер обкладок, точнее площадь их перекрытия S (то есть площадь области, в которой пластины накладываются друг на друга, в простейшем случае – это площадь одной из пластин конденсатора).
Чем больше будет размер обкладок, тем больше на них сможет накопиться электрического заряда, тем больше будет электроемкость:
C\thicksim{S}
Конечно, можно предположить, что расстояние d между обкладками конденсатора также будет иметь определенное значение.
Мы уже знаем, как связаны между собой заряд и напряжение на конденсаторе:
q=CU
При этом напряжение – это работа по перемещению пробного положительного заряда силами электрического поля:
U=Ed
Мы можем объединить два этих выражения и немного перегруппировать то, что получится в итоге:
q=C×Ed
q=Cd×E
При уменьшении или, наоборот, увеличении расстояния между обкладками конденсатора заряд на нем никак не будет меняться, значит, не будет меняться и напряженность электрического поля. Поэтому произведение электроемкости и расстояния между пластинами конденсатора можно считать константой:
Cd=const
Это можно записать в виде обратной пропорциональности:
C\thicksim\dfrac{1}{d}
Оказывается, что это не все, и есть еще один очень интересный способ изменить емкость конденсатора: если поместить между пластинами устройства какое-то вещество, не проводящее электрический ток, электроемкость конденсатора вырастет.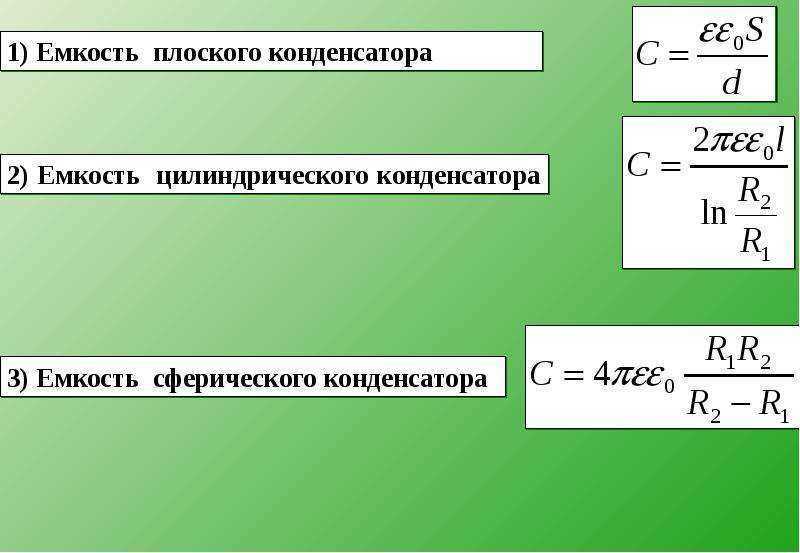
Рассмотрим пример с заряженным конденсатором, уже отключенным от источника тока, между пластинами которого помещен некоторый непроводник.
Электрическое поле, создаваемое пластинами конденсатора, будет заставлять молекулы диэлектрика поляризоваться – менять свою ориентацию в пространстве таким образом, что положительно заряженные ядра будут смещаться ближе к отрицательно заряженной пластине, а вот отрицательно заряженные электроны будут смещаться ближе к положительно заряженной обкладке. Это приведет к тому, что поверхности диэлектрика начнут приобретать электрический заряд, и внутри него появится свое электрическое поле.
Из рисунка видно, что это поле ослабляет поле, создаваемое зарядами на обкладках конденсатора. Напряженность падает, а вместе с ней падает и напряжение. А вот емкость будет расти, так как заряд на конденсаторе никак не будет меняться в данном случае:
\Uparrow{C}=\dfrac{q}{U\Downarrow}
Если бы мы держали конденсатор, подключенным к источнику тока, и тогда бы поместили в него диэлектрик, емкость всего равно стала бы больше.
2.
электростатика — Как определяется емкость конденсатора?
спросил
Изменено 2 года, 8 месяцев назад
Просмотрено 249 раз
$\begingroup$
Мы знаем, что емкость проводника есть отношение накопленного в нем заряда к потенциалу на поверхности проводника, $C=q/V$. Но как определяется емкость конденсатора, состоящего из $2$ проводников ($\mathrm{C = q/(p.d)}$ между проводниками). Я хочу увидеть вывод, который привел к этому заключению.
- электростатика
- заряд
- напряжение
- емкость
- определение
$\endgroup$
12
$\begingroup$
Для конденсатора важна разность потенциалов В между двумя проводниками.
Затем емкость определяется, как и раньше, как Кл = Ом / В .
Можно представить отдельный проводник как имеющий потенциал и емкость относительно некоторого эталонного или окружающего потенциала 0 В, т. е. мы берем разность потенциалов между 0 В и проводником. Если вы измените свой опорный потенциал, то кажущаяся емкость также изменится.
$\endgroup$
1
$\begingroup$
Рассмотрим конденсатор q, состоящий из двух параллельных пластин с поверхностью $A$ и расстоянием $d$, разделенных средой с относительной диэлектрической проницаемостью $\epsilon_r$. Поле каждой пластины будет равно $$E = \frac{Q}{2 \epsilon_0 \epsilon A}$$ без учета краевых эффектов. Между пластинами поля складываются в $$E = \frac{Q}{\epsilon_0 \epsilon_r A}$$, а за пределами пластин они сокращаются. Разность потенциалов равна $$V=Ed=\frac{Qd}{\epsilon_0 \epsilon_r A}$$, поэтому емкость $$C = \frac{\epsilon_0 \epsilon_r A}{d} ~.
$$
$\endgroup$
$\begingroup$
Физическая емкость определяется как
$$C=\frac{εA}{d}$$
Где $A$ = площадь пластины, $ε$ = диэлектрическая проницаемость пространства между пластин и $d$ = расстояние между пластинами.
Разность потенциалов $V$ между пластинами конденсатора равна
$$V=Ed$$
Где $E$ — однородное электрическое поле между пластинами. Или
$$d=\frac{V}{E}$$
Подставляя в первое уравнение
$$C=\frac{εAE}{V}$$
Электрическое поле между бесконечными параллельными пластинами (или пластины с размерами намного большими, чем расстояние $d$) равно
$$E=\frac{ρ_{s}}{ε}=\frac{q}{εA}$$
Подставляя в предыдущее уравнение
$$C=\frac{q}{V}$$
Надеюсь, это поможет.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Имеет ли планета емкость?
You are here: Home / Новые статьи / Есть ли у планеты емкость?
Автор: Дэвид Херрес Оставить комментарий
Собственная емкость Земли составляет примерно 710 мкФ, если предположить, что диэлектриком в свободном пространстве является вакуум. Емкость Марса 378 мкФ. На первый взгляд может быть неясно, откуда берутся эти цифры или как планета может иметь емкость. А если у планеты есть емкость, может ли она иметь и индуктивность, а если да, то может ли она иметь и резонансную частоту? На эти вопросы ответ положительный. Интересно, что, возможно, именно Никола Тесла первым задумался над этими вопросами.
Емкость планеты определяется уравнением емкости сферы. Емкость C сферы радиуса R определяется выражением C=4πεR . Здесь ε — диэлектрическая проницаемость диэлектрической среды. Учитывая, что в большинстве конденсаторов используется разность потенциалов между двумя пластинами, вы можете задаться вопросом, где находится другая пластина, когда мы говорим о сфере.
Ответ: Другой проводник считается удаленным на бесконечность. Таким образом, диэлектрическая проницаемость в уравнении становится ε 0 , диэлектрическая проницаемость свободного пространства. (Вероятно, хорошая оценка, потому что большая часть пространства между Землей и бесконечностью действительно занята свободным пространством.) Радиус Земли = 6378 км. Таким образом, емкость земли C= 4π×8,854×10 -12 ×6,378×10 3 = 7,096×10 -4 фарад, или 710 мкФ. Поскольку Марс имеет радиус 3400 км, его емкость меньше. Вы можете использовать уравнение для емкости между двумя сферами и сделать несколько предположений, чтобы получить оценку емкости между Землей и Луной как 159мкФ.
Лаборатория Теслы в Колорадо-Спрингс (Википедия). Тесла заинтересовался электрическими свойствами Земли благодаря своим экспериментам по беспроводной передаче энергии на своей экспериментальной станции Шорхэм в Лонг-Айленде, штат Нью-Йорк, и в Колорадо-Спрингс, полковник.
полость. Понятно, что Тесла в какой-то мере разобрался с концепцией полости Шумана, хотя формально она не была задумана до 1950-х годов. Вот идея: на самом деле атмосфера — слабый проводник. Имеется полость, определяемая поверхностью Земли и внутренним краем ионосферы на высоте 55 км. Резонансы Шумана представляют собой квазистоячие электромагнитные волны, существующие в этой полости. Но чтобы их увидеть, их нужно «возбудить» электрической активностью в атмосфере, как от сильной молнии. Они бывают на частотах 7,8, 14, 20, 26, 33, 39.и 45 Гц, с суточными колебаниями около ± 0,5 Гц.
Стоячие волны (модоподобные) образуются в полости, которая функционирует как волновод. Решая классические уравнения Максвелла, можно прийти к выводу, что в полости присутствуют как продольные (пропорциональные среднему радиусу полости), так и поперечные (пропорциональные высоте полости) моды (или стоячие волны). Помимо частот ELF (0-100 Гц) Шумана, существуют также резонансы VLF (0-10 кГц). Грозовые (или техногенные) разряды могут возбудить эти моды, особенно моду 7,83 Гц.
Тесла сделал первые задокументированные наблюдения глобального электромагнитного резонанса в своей лаборатории в Колорадо-Спрингс в 1899 году. Наблюдения привели его к идее беспроводной передачи энергии. Расчеты, основанные на его экспериментах, привели Теслу к выводу, что резонансная частота Земли составляет около 8 Гц, то есть резонансная частота Шумана.
Оказывается, беспроводная передача с использованием резонансов Шумана не очень практична. Одна из причин заключается в том, что полость между землей и ионосферой имеет малую добротность (отношение энергии электрического поля, хранящейся в полости за цикл, к средней подводимой мощности). Тем не менее, Тесла в Колорадо-Спрингс возмущал электрическое поле Земли (или одеяло) сильными электрическими разрядами, пытаясь возбудить земно-ионосферную полость. Он определил, что время, необходимое переданному импульсу для прохождения от точки передачи до антипода (точки на поверхности Земли, диаметрально противоположной) и обратно, составляет 0,08484 секунды, что дает частоту фундаментального земного резонанса 11,78689.
2 Гц.
Завод Теслы в Уорденклиффе на Лонг-Айленде в 1904 году (Википедия). Для дальнейшей проверки своих теорий Тесла переехал на Шорхэмскую экспериментальную станцию, где располагалась культовая 187-футовая башня, часто связанная с его именем. Башня на самом деле была конденсатором. Идея Теслы состояла в том, чтобы электрически соединить два отдаленных поднятых терминала таким образом, чтобы это напоминало передачу электрической энергии между двумя близко расположенными пластинами конденсатора. Но задействованные расстояния значительно превышали одну шестую или половину длины волны передаваемых частот, типичных для обычных конденсаторных пластин.
Тесла придерживался двух разных принципов работы беспроводной передачи. Один из них назывался методом разомкнутой цепи или земного резонанса. Здесь передатчик катушки Тесла создает локальное возмущение заряда земли. Источник работает на некоторой гармонике резонанса поля Земли 11,78 Гц. Приемная катушка Теслы является пассивной и симпатически активируется способом, аналогичным камертону, вибрирующему в соответствии с другой соседней вилкой на той же частоте, по которой ударили молотком.
Вторым методом Теслы была атмосферная или замкнутая проводимость. электростатическая индукция вместо истинной проводимости. В нем использовался передатчик катушки Тесла, создающий ионизированный путь, соединяющий верхнюю атмосферу передатчика, и ионизированный путь, соединяющий верхние слои атмосферы обратно вниз с принимающей катушкой Теслы. Цепь замыкается за счет тока, протекающего обратно к передатчику через землю.
В частности, колеблющееся электрическое поле RF формирует состояние плазмы в пластине конденсатора высокого напряжения (от 10 до 12 МВ). Ионизирующий пучок ультрафиолетового излучения должен был также использоваться для формирования высоковольтной плазменной линии передачи в верхней тропосфере для создания токопроводящей дорожки. В основе процесса лежали плазменные волны, развивающиеся в ионизированной области между двумя терминалами (электростатические волны или магнито-гидродинамические волны). Ионизация пространства между двумя «конденсаторными» пластинами, в свою очередь, позволит волнам ELF и VLF проходить между двумя точками.
