1. Явление эми. Закон Фарадея. Вихревые токи.
8
Лекция 11. Электромагнитная индукция (ЭМИ).
Уравнения Максвелла.
[1] гл. 15, 16
План лекции
Явление ЭМИ. Закон Фарадея. Вихревые токи.
Индуктивность. Самоиндукция и взаимная индукция. Энергия магнитного поля.
Ток смещения.
Система уравнений Максвелла.
В 1821 году Эрстед обнаружил, что любой ток создает вокруг себя магнитное поле. Возник вопрос: способно ли магнитное поле порождать электрический ток? Само сочетание слов «ЭМИ» означает создание электричества с помощью магнетизма.
Фарадей обнаружил, что в проводящем
контуре возникает электрический ток
при изменении магнитного потока через
контур (рис. 1). Он показал, что величина
индукционного тока зависит не от
,
а от(вводя в соленоид с током железный
сердечник,).
ЭМИ— явление возникновения индукционного тока в замкнутом проводящем контуре при изменении магнитного потока через площадь, ограниченную этим контуром.
Экспериментально было установлено, что величинаIiне зависит от способа изменения Ф, а определяется лишь скоростью его изменения. Максвелл обобщил результаты экспериментов Фарадея и сформулировал закон ЭМИ в математическом виде.
Если в контуре протекает , значит, в нем действует э.д.с., которая получила название э.д.с. ЭМИ.
Закон Фарадея для ЭМИ:
.
Э.д.с. ЭМИ в замкнутом контуре равна скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром, взятой со знаком «минус».
деформация изменение В вращение
контура
При экспериментах можно наблюдать
эффект, который дает каждое из слагаемых.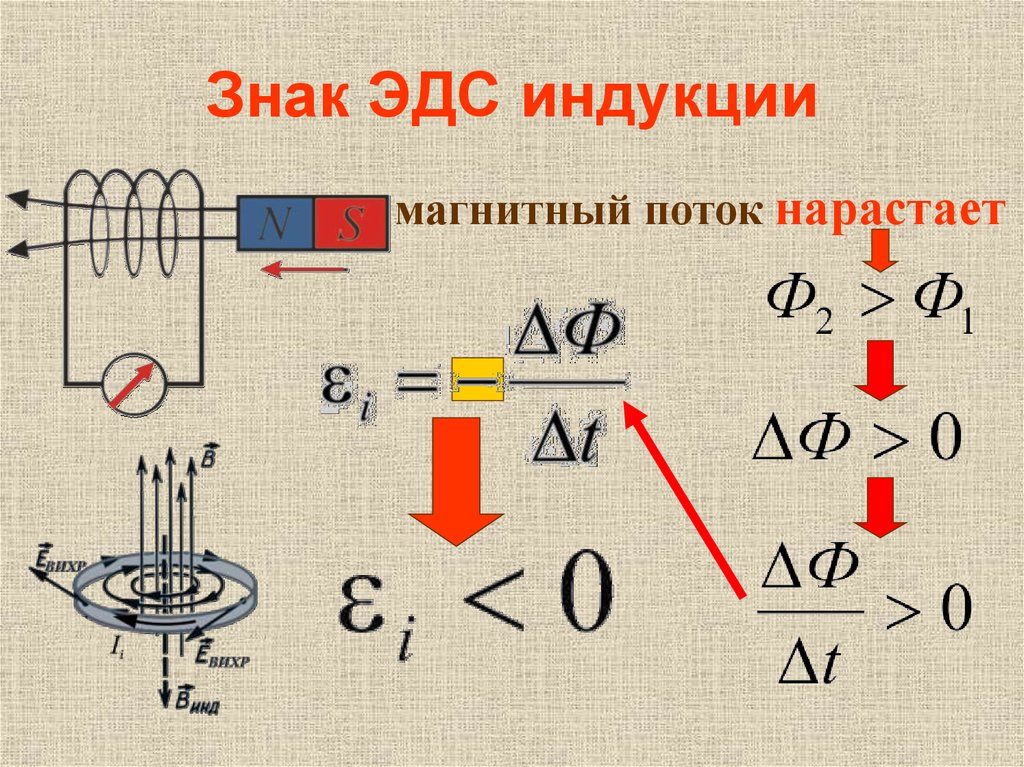 Знак «минус» имеет принципиальное
значение и отражает закон сохранения
энергии. Вначале он был установлен
экспериментально профессором
Петербургского университета Э.Х. Ленцем
в 1834 году.
Знак «минус» имеет принципиальное
значение и отражает закон сохранения
энергии. Вначале он был установлен
экспериментально профессором
Петербургского университета Э.Х. Ленцем
в 1834 году.
Немецкий физик Г. Гельмгольц показал, что основной закон ЭМИ является следствием закона сохранения энергии.
Природа ЭМИ.
1. Если проводник движется в постоянном магнитном поле, возникновение ЭМИ объясняется действием силы Лоренца на заряды внутри проводника (свободные электроны). Между концами проводника возникает разность потенциалов(рис. 2).
Если проводник замкнуть, в нем возникнет :
сопротивление проводника.

2. Если неподвижный замкнутый проводник находится в переменном магнитном поле, сила Лоренца не действует на неподвижные заряды. Максвелл предположил, что переменное магнитное поле возбуждает в окружающем пространстве переменное вихревое электрическе поле, которое является причиной возникновения в неподвижном проводнике.
Вихревые токи (токи Фуко)
Индукционные токи могут возбуждаться и в сплошных массивных проводниках, при этом замкнутая цепь индуктивного тока образуется в толще самого проводника, и они носят вихревой характер. Вихревые токи вызывают сильное нагревание проводников. Впервые на это обратил внимание французский физик Л. Фуко.
Применение.
Тепловое действие токов Фуко используют в индукционных печах.

Прогрев внутренних металлических частей вакуумных установок для их обезгазживания.
Для успокоения (демпфирования) подвижных частей различных приборов. Токи Фуко, как индукционные токи, подчиняются правилу Ленца. Если между полюсами не включенного электромагнита массивный медный маятник совершает практически незатухающие колебания, то при включении тока он испытывает сильное торможение и очень быстро останавливается. Это объясняется тем, что возникающие токи Фуко направлены так, что действующая на них со стороны магнитного поля сила Ампера тормозит движение маятника.
Во многих случаях токи Фуко нежелательны.
Так сердечники трансформаторов набирают
из тонких пластин, разделенных изолирующими
прослойками, для предотвращения потерь
энергии на нагревание.
Явление ЭМИ применяется для преобразования
механической энергии в энергию
электрического тока. Для этого используются
генераторы переменного тока, принцип
действия которых основан на возникновении
Закон электромагнитной индукции Фарадея при изменении магнитного поля
Similar presentations:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
Работу выполнила учитель физики
МБОУ «Кингисеппская средняя
общеобразовательная школа №4»
Васильева Ольга Владимировна
Кингисепп 2019
Электромагнитную индукцию обнаружили
независимо друг от друга в 1831 году
Майкл Фарадей
Джозеф Генри
Однако Фарадей первым опубликовал
результаты своих экспериментов
Ученые того времени отклонили
теоретические идеи Фарадея,
так как они не были
сформулированы математически.
Исключение составил Максвелл,
который использовал идеи Фарадея в
качестве основы для своей
теории.
В работе Максвелла аспект
изменения во времени
электромагнитной индукции
выражен в виде
дифференциальных уравнений.
Оливер Хевисайд
назвал это законом Фарадея.
Джеймс Клерк Максвелл
Эмилий Христианович Ленц сформулировал в
1834 году закон (правило Ленца), который
описывает «поток через цепь» и дает
направление индуцированной ЭДС и тока в
результате электромагнитной индукции
Закон ЭМИ Фарадея является основным законом
электродинамики, касающимся принципов работы
трансформаторов, дросселей, многих видов
электродвигателей и генераторов.
Это послужило огромным толчкам в развитии
промышленности и транспорта, что привело к
развитию капитализации и изменению классового
состава общества.
Так открытия в физике меняют жизнь человечества!
Φ = B · S · cos α
возникает при:
1) изменении величины магнитного поля;
2) изменении площади, ограниченной контуром;
3) изменении ориентации контура относительно
магнитных линий.

В работе приведены примеры для первого
случая
По круговому витку идет возрастающий ток.
Найти силу, действующую на заряд q, расположенный
вблизи витка.
R
q
r
F
На заряд q не действует сила электростатического
тоже увеличивается, что порождает вихревое
электрическое поле, которое будет действовать на
заряд q
Маг. поток, возникающий в витке:
Φ=LI
ε=-L∆I/ ∆ t;
Ε равно по определению работе силы по перемещению
заряда q по замкнутому контуру.
qₒ ∑Εₒ∆r=- qₒ L ∆I/∆t
Eₒ-напряженность вихревого электрического поля
Eₒ*2πR= -L ∆I/∆t
Eₒ= -L ∆I/∆t*2πR
F=qEₒ-сила со стороны вихревого электрического поля
F=qL ∆I/∆t*2πR
Как эта сила направлена?
Если ток возрастает, должна возникать сила, которая
препятствует этому возрастанию.
Это и есть сила вихревого электрического поля. Эта
сила действует на заряды в проводнике и рядом с

Эта сила будет направлена близко к касательной,
против силы тока.
Контур в виде квадрата со стороной a помещен в магнитное поле,
магнитная индукция которого линейно возрастает со временем. В
контур включен конденсатор ёмкостью C.
Найти заряд на конденсаторе как функцию времени.
1
2
Β=αtn Запишем закон Ома:
ε=∆φ+I(R+r)
∆φ=φ2-φ1
Работа поля по перемещению заряда в
цепи:∆qε=∆q(φ2-φ1)+I²(R+r)*∆t
ε= φ2-φ1=ε1-2
Работа ЭДС идет на приращение
потенциала
εi=-∆Ф/∆t -если контур замкнутый
В нашем случае
εi=-∆Ф/∆t=ε1-2+ε2-1
Но расстояние между обкладками конденсатора
маленькое, поэтому│ε │<< │ε │
1
2
ε=-∆Ф/∆t
По определению φ -φ =q/C
B
q=-C∆Ф/∆t
B
Ф=nBS=-SB=-Sαt=-a²αt
Заряд q=-C∆(-a²αt)/∆t=Ca²α
Внешнее магнитное поле увеличивается, значит B ↑↓B
Определим направление I =>против часовой стрелки.
Значит пластинка 2 заряжена положительно.
1-2
2-1
2
1
i
i
i
Параллельно
соединенные катушка
индуктивности и
резистор подключены к
источнику тока с ε и r.
Во время размыкания
цепи определить
1) заряд, который
пройдет через резистор;
2) количество теплоты,
выделившееся на
резисторе.
Катушка идеальная, значит R=0. В замкнутой
цепи ток идет через катушку и не идет через
резистор. Катушка обладает энергией:W=LI²/2,
которая при размыкании цепи перейдет в тепло.
В замкнутой цепи I=ε/r
Когда цепи разомкнули, ток в цепи стал
уменьшаться, магнитное поле катушки стало
уменьшаться, и в ней начал возникать
индукционный ток I =ε /R, который пойдет через
резистор.
Заряд, который пройдет через резистор:
q=∑I∆t=∑-L∆I∆t/R∆t=-(L/R)∑∆I=L(I -I )/R
I =0
I =ε/r
q=Lε/Rr
i
i
нач
кон
нач
кон
В работе использованы материалы Википедии,
видеолекции «Математика и физика с Асхатом
Башаровым»
Башаров Асхат Масхудович – кандидат физикоматематических наук, старший научный сотрудник
НИЦ «Курчатовский институт»,
доцент МФТИ(кафедра математики и
математических методов физики).

English Русский Rules
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.
 1 Электростатика
1 Электростатика - 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 4.
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.
 6 СТО
6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
«Двуликая» индукция | Электродинамика: взгляд физика
Кратко:
Механизм электромагнитной индукции в замкнутом контуре и в движущемся проводнике один и тот же — механизм «пересечения». Причина «парадоксов» в ошибочной трактовке физики явления электромагнитной индукции.
Причина «парадоксов» в ошибочной трактовке физики явления электромагнитной индукции.
Подмена экспериментальной зависимости Фарадея «Основным законом электромагнитной индукции» Максвелла стала поворотным пунктом в развитии электродинамики. Из процесса взаимодействия магнитного поля с электрическими зарядами электромагнитная индукция (ЭМИ) превратилась в процесс взаимодействия полей. Это было самой большой мистификацией в электродинамике, определившей всё её развитие в XX веке. В частности, исследования ЭМИ пошли по двум принципиально отличным путям.
Электромагнитная индукция в движущемся проводнике
ЭДС в деформируемом контуреЭксперименты показывают, что ЭДС индукции возникает в любом отрезке проводника, движущемся в магнитном поле и пересекающем линии магнитной индукции. ЭДС индукции в таком «микрогенераторе» можно рассчитать с помощью схемы, представленной на Рис. 1. По параллельным металлическим «рельсам», замкнутым с одной стороны проводящей перемычкой AB, в однородном поле с магнитной индукцией B с постоянной скоростью v скользит проводящий «мостик» CD длиной l .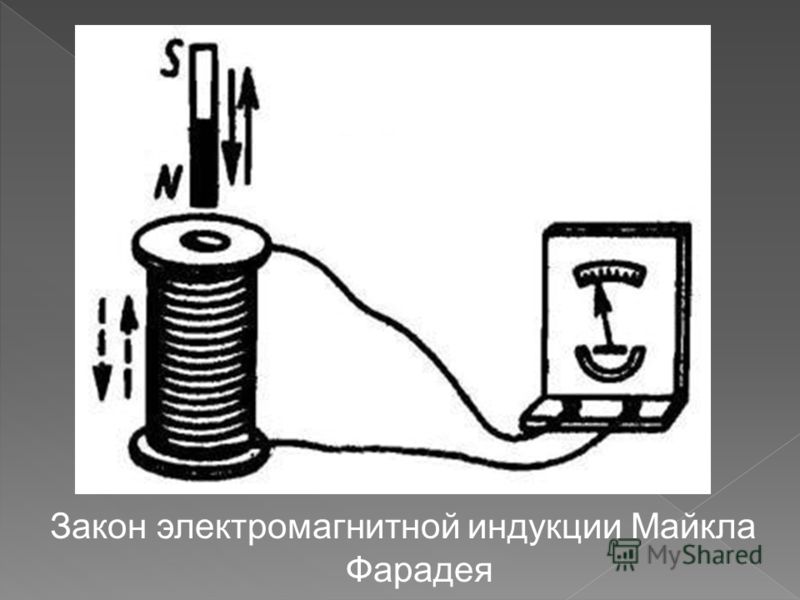 За время dt магнитный поток, пронизывающий контур ABCD, возрастает на величину dФ = Bvl·dt , откуда
За время dt магнитный поток, пронизывающий контур ABCD, возрастает на величину dФ = Bvl·dt , откуда
Согласно основному закону электромагнитной индукции ЭДС, индуцируемая в контуре, определяется соотношением
(2) ЭДС в движущемся проводникеТак как все элементы контура, кроме «мостика», неподвижны относительно магнитного поля, то (2) — это и есть ЭДС, возникающая в движущемся проводнике.
Эта же ЭДС возникает и в незамкнутом проводящем отрезке, движущемся в магнитном поле (Рис. 2). Считается, что при перемещении проводящего отрезка в магнитном поле силой, «разделяющей» заряды q в проводнике и создающей на концах такого «микрогенератора» индукционную ЭДС, является магнитная составляющая силы Лоренца:
(3)Если скорость движения проводника постоянна, то и ЭДС индукции остаётся постоянной. В момент остановки заряды в проводнике под действием кулоновских сил «схлопываются» и микрогенератор практически мгновенно разряжается.
ЭДС в таком индукционном микрогенераторе возникает вследствие того, что проводник пересекает линии магнитного поля с некоторой скоростью v . Назовем (для краткости) такой способ генерации ЭДС электромагнитной индукции «способом пересечения». Процесс электромагнитной индукции «с пересечением» можно схематически представить так:
Назовем (для краткости) такой способ генерации ЭДС электромагнитной индукции «способом пересечения». Процесс электромагнитной индукции «с пересечением» можно схематически представить так:
пересечение → возникновение силы Лоренца → перемещение зарядов → образование ЭДС
Электромагнитная индукция в замкнутом контуре
В неподвижном недеформируемом контуре пересечение линий магнитного поля проводниками отсутствует. Изменение магнитного потока, пронизывающего контур, происходит вследствие изменения магнитной индукции В . Как же возникает индукционная ЭДС в этом случае? Вот как описан этот процесс в учебнике1:
В этом случае объяснение возникновения ЭДС оказывается в принципе (выделение моё — К.К.) другим. Изменяющееся со временем магнитное поле порождает вихревое электрическое поле Е… Под действием поля Е носители тока в проводнике приходят в движение — возникает индуцированный ток.
Назовем такой способ генерация ЭДС «способом индукции».
Сравнивая «способ индукции» со «способом пересечения», автор2 замечает, что «в результате изменения индукции на элементе проводника dl появляется ЭДС индукции Фарадея, которая не зависит от индукции B и скорости v движения этого элемента, а зависит только от dB/dt . Это и доказывает, что физическая природа ЭДС индукции в этих двух случаях различна». И даже так: «… оба эти явления (два механизма генерации ЭДС индукции — К.К.) … независимы друг от друга, и, тем не менее — что удивительно — ЭДС индукции в контуре всегда равна скорости изменения магнитного потока сквозь контур»3.
Индукционный процесс по «способу индукции» можно представить так:
изменение магнитного потока → возникновение ЭДС → перемещение зарядов (индукционный ток)
Таким образом, сегодня электромагнитная индукция имеет «два лица», абсолютно непохожие друг на друга. Сравнив схематическое представление обоих процессов, можно заметить, что они в чём-то даже смотрятся шиворот-навыворот: в «способе пересечения» движение зарядов предшествует возникновению индукционной ЭДС, а по «способу индукции» — наоборот. Если вдуматься, то в «двуличии» индукционного процесса просматривается извечная проблема: что первично — яйцо или курица, то есть — заряды или поля. Попробуем решить эту вечную проблему в одном частном случае.
Сравнив схематическое представление обоих процессов, можно заметить, что они в чём-то даже смотрятся шиворот-навыворот: в «способе пересечения» движение зарядов предшествует возникновению индукционной ЭДС, а по «способу индукции» — наоборот. Если вдуматься, то в «двуличии» индукционного процесса просматривается извечная проблема: что первично — яйцо или курица, то есть — заряды или поля. Попробуем решить эту вечную проблему в одном частном случае.
Многочисленные эксперименты показывают, что ЭДС индукции в замкнутом контуре не зависит от того, каким способом изменяется пронизывающий его магнитный поток. Поскольку движение относительно, то во многих случаях возникновение ЭДС в замкнутом контуре можно свести к механизму пересечения проводниками магнитного потока. Этим механизмом можно объяснить возникновение в контуре индукционной ЭДС при приближении или удалении постоянного магнита, при вращении контура в однородном (или его поступательном движении — в неоднородном) магнитном поле, при деформации контура, приводящей к изменению его площади и/или ориентации, и во многих других случаях. И только один случай не удаётся описать этим механизмом: возникновение ЭДС в замкнутом неподвижном и недеформируемом контуре вследствие изменения магнитной индукции в потоке, пронизывающем контур.
И только один случай не удаётся описать этим механизмом: возникновение ЭДС в замкнутом неподвижном и недеформируемом контуре вследствие изменения магнитной индукции в потоке, пронизывающем контур.
Уже то обстоятельство, что только один экспериментальный факт не удаётся объяснить механизмом, безотказно работающим во всех остальных случаях (в том числе — и в замкнутом контуре), заставляет поискать другой способ описания процесса генерации ЭДС по «способу индукции».
Большинство авторов, по-видимому, представляет себе механизм изменения магнитного потока так: по мере увеличения магнитной индукции вновь появляющиеся линии магнитного поля как бы «расталкивают» уже существующие линии, увеличивая их плотность. Кстати, именно так представлял себе процесс возрастания магнитного потока в замкнутом контуре Максвелл:
… по мере возрастания… тока [в индукционной катушке] появляются новые линии и постепенно распространяются вовне, так что вся система развертывается изнутри4.
Представление магнитного поля совокупностью линий поля — это лишь модель непростого физического объекта, позволяющая дать его математическое описание. Предполагаемый механизм изменения магнитного поля — не единственный. Среди множества других вариантов описания этого процесса можно поискать и такой, который примирил бы оба способа генерации индукционной ЭДС.
Индукция по «способу пересечения» в замкнутом контуреНа Рис. 3 показан замкнутый проводящий контур в бесконечном однородном магнитном поле. Процесс увеличения магнитной индукции можно представить себе, как сгущение поля за счет поступления в поток, пронизывающий контур, новых линий поля извне — из окружающего пространства. При этом «вновь прибывающие» линии в своем движении «проникают» в контур, создавая в нём ЭДС индукции по «механизму пересечения». Такая модель сводит все случаи электромагнитной индукции к одному механизму — процессу пересечения магнитного потока проводником. Если, конечно, она не противоречит основному закону электромагнитной индукции. В этом ещё нужно убедиться…
В этом ещё нужно убедиться…
Разобьём замкнутый контур, представленный на рисунке 3, на n участков, изолированных друг от друга. При возрастании индукции в магнитном потоке по предлагаемому механизму магнитные линии, «проникая» в контур, пересекают его со скоростью v по направлению к центру. При этом выделенный на рисунке участок контура находится в тех же условиях, что и одиночный участок на рисунке 2. На каждый заряд в проводнике действует сила Лоренца FL (3), с той лишь разницей, что скорость v — это скорость движения линий поля относительно неподвижного проводника. Как и на рисунке 2, сторонние силы «разносят» электрические заряды на концы участка, создавая на нём разность потенциалов Δφk = φ1-φ2 . При этом на каждый заряд q действует кулоновская сила
(4)где Ek — напряжённость электрического поля на k -том участке контура. Эта сила равна по модулю и направлена навстречу силе Лоренца:
Эта сила равна по модулю и направлена навстречу силе Лоренца:
Полагая, что векторы v , B и элемент длины контура Δlk взаимно перпендикулярны, соотношение (3) можно записать в скалярной форме:
(6)Подставив (4) и (6) в (5), получаем
(7)Если теперь соединить все участки в замкнутый контур, получим результирующую ЭДС в контуре
(8)Разность потенциалов на участке определяется зависимостью
(9)Подставляя (7) в (9) и далее в (8), получаем
(10)В пределе (при n → ∞ и Δlk → 0 ) эта сумма переходит в интеграл
(11)«Приток» линий магнитного поля в контур за время dt составляет, очевидно,
(12)Сравнивая (12) и (2), получаем основной закон электромагнитной индукции.
Таким образом, предлагаемый механизм не противоречит основному закону электромагнитной индукции. Но он позволяет убрать «исключения» и свести все индукционные процессы к механизму пересечения.
Должен, однако, признаться, что идея описывать процесс возникновения индукционной ЭДС в замкнутом контуре способом пересечения принадлежит не мне.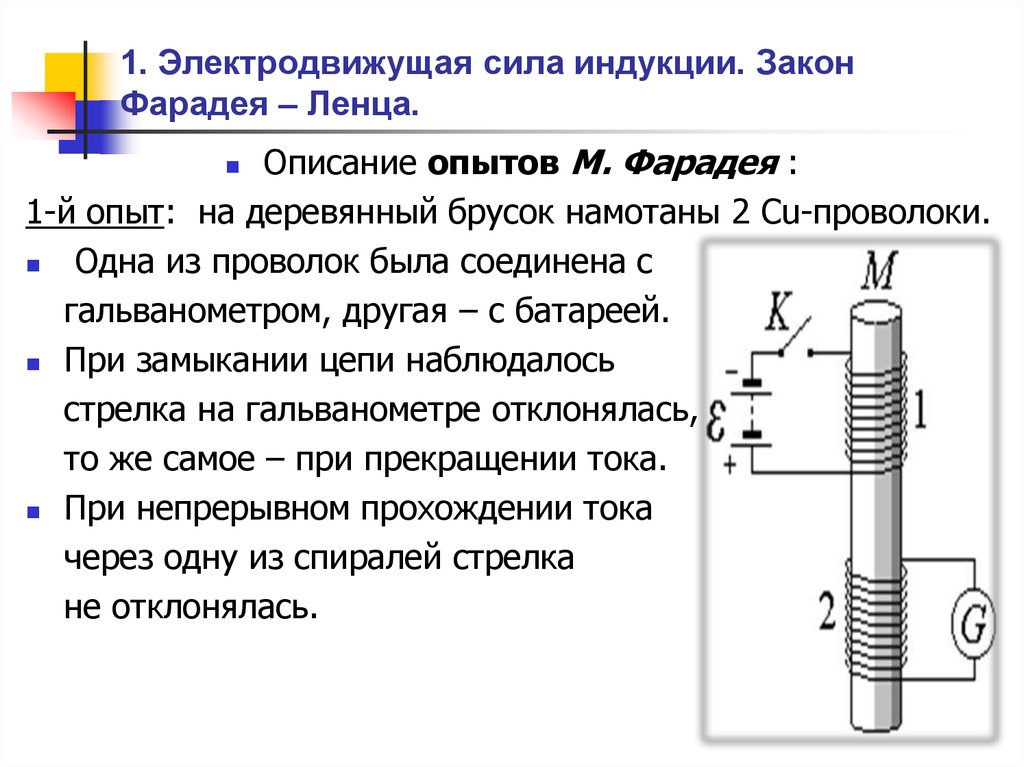 Меня опередил… Майкл Фарадей! Вот что писал по этому поводу ветеран электротехнического образования профессор МГУ С. Г. Калашников:
Меня опередил… Майкл Фарадей! Вот что писал по этому поводу ветеран электротехнического образования профессор МГУ С. Г. Калашников:
… если проводник находится в покое, но изменяется магнитная индукция, то, при усилении поля густота линий индукции будет увеличиваться, и они будут стягиваться друг к другу, а при ослаблении поля — расходиться друг от друга. И в этом случае произойдет пересечение некоторого числа линий индукции проводником. Поэтому Фарадей заключил, что индукционный ток возникает в проводнике в том случае, если проводник или какая-либо его часть пересекает линии магнитной индукции5.
Разрешение «парадоксов»
Таким образом, физическая природа электромагнитной индукции («способ пересечения») — едина:
Индукционная ЭДС возникает лишь в том случае, когда электрические заряды (проводник) пересекают линии магнитного поля.
Теперь можно вернуться к «парадоксам» электромагнитной индукции.
Расчёт, приведенный выше, сделан для того, чтобы показать, что возникновение индукционной ЭДС в замкнутом контуре по методу пересечения не противоречит и максвелловской формулировке закона электромагнитной индукции. Но «парадоксальные» схемы, приведенные здесь, ведут себя парадоксально лишь по отношению к максвелловской формулировке закона. Если же оценивать результаты этих экспериментов с точки зрения закона электромагнитной индукции Фарадея, то никаких парадоксов не возникает.
Но «парадоксальные» схемы, приведенные здесь, ведут себя парадоксально лишь по отношению к максвелловской формулировке закона. Если же оценивать результаты этих экспериментов с точки зрения закона электромагнитной индукции Фарадея, то никаких парадоксов не возникает.
Начнём с того, что только при пересечении проводником линий поля на электрические заряды действует сила (сила Лоренца), способная совершить работу (создать ЭДС) (см. далее). Когда такое пересечение отсутствует, работа не совершается, не возникает индукционный ток и не создаётся ЭДС индукции.
Если обратиться к тем экспериментам (схемам), которые дают «парадоксальные» результаты, то во всех этих случаях пересечение проводниками линий магнитного поля отсутствует, в чём читатель может убедиться самостоятельно.
Наиболее трудным для понимания является сам Парадокс Геринга. Хотя цепь гальванометра остаётся замкнутой, магнитное поле всё-таки из неё «выскальзывает». Почему же гальванометр «молчит»? Причина в том, что магнитное поле «выскальзывает» из контура… вместе с электронами на этом участке цепи (металлическом «мостике» через магнитопровод).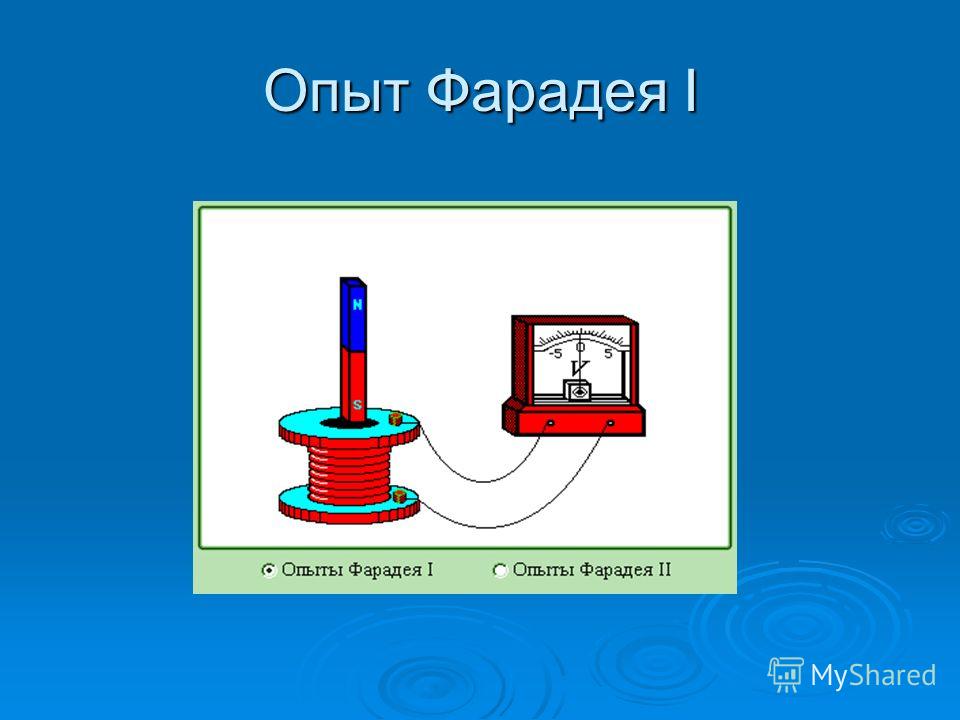 То есть и в этом случае электроны не пересекают линии магнитного поля. Поэтому ток в цепи и не возникает.
То есть и в этом случае электроны не пересекают линии магнитного поля. Поэтому ток в цепи и не возникает.
И ещё один «парадокс»
В заключение этого раздела рассмотрим ещё один — классический — пример, который называют «Парадоксом Фарадея». Речь идёт о так называемых униполярных генераторах, которые уже много десятилетий используются в качестве сильноточных низковольтных электрогенераторов.
После открытия электромагнитной индукции М. Фарадей предложил несколько устройств с использованием этого явления. Одним из таких устройств был индукционный генератор, получивший название «Диск Фарадея». Устройство представляло вращающийся металлический диск 1 (см. Рис. 4), который пронизывал магнитный поток от постоянного магнита 2. Электрический контур, содержавший электроизмерительный прибор (3), подключался к диску двумя скользящими контактами — на оси диска (4) и на ободе (5). При вращении диска прибор показывал в цепи постоянный ток, зависящий от скорости вращения. Возникновение индукционной ЭДС в контуре объяснялось воздействием силы Лоренца на свободные электроны вращающегося диска при пересечении ими линий магнитного поля.
Возникновение индукционной ЭДС в контуре объяснялось воздействием силы Лоренца на свободные электроны вращающегося диска при пересечении ими линий магнитного поля.
В XIX веке было опробовано много вариантов машины Фарадея. Один из них озадачил исследователей. Оказалось, что ЭДС индукции возникает в контуре и в том случае, если магнит… вращается вместе с диском. Казалось бы, при этом сила Лоренца на электроны не действует, но прибор показывал ток в контуре. На рисунке 5 схематически представлен вариант такой модификация машины Фарадея. Конструкция отличается от «Диска Фарадея» тем, что вместо диска вращается сам цилиндрический магнит.
Этот парадоксальный результат вызвал в XIX веке оживлённую дискуссию по странному вопросу: а вращается ли магнитное поле вместе с его материальным носителем — магнитом? За полтора века ученые так и не пришли к единому мнению по этому вопросу. Сегодня эта тема активно обсуждается на Интернет-форумах. Один из участников этого форума привел простой аргумент, который (по моему мнению) даёт логичный и исчерпывающий ответ на этот вопрос: «Ведь никто … не сомневается, что когда мы переносим магнит из комнаты в комнату, то с ним вместе перемещается и его магнитное поле. Почему же при вращении должно быть не так?!»6.
Почему же при вращении должно быть не так?!»6.
Согласиться с этим простым и очевидным заключением, диктуемым здравым смыслом, мешает лишь… закон ЭМИ в максвелловской формулировке. Круг замкнулся.
История науки в XX веке изобилует примерами, когда, зайдя в тупик, научная мысль прибегала к услугам палочки-выручалочки — представлениям релятивизма. В 1929 году академик И. Е. Тамм, обсуждая принцип работы униполярного генератора, писал:
В движении силовых линий [магнитного поля — К. К.], пересекающих неподвижный проводник … усматривалась причина возникновения в этом проводнике электродвижущих сил индукции. Нечего и говорить, что такая интерпретация не выдерживает никакой критики…7
Но если магнитное поле неподвижно, как возникает ЭДС в контуре? Объяснить работу униполярного генератора удалось лишь с помощью… представлений теории относительности. Такое объяснение уже тогда не встретило у специалистов ни восторга, ни понимания, ни согласия.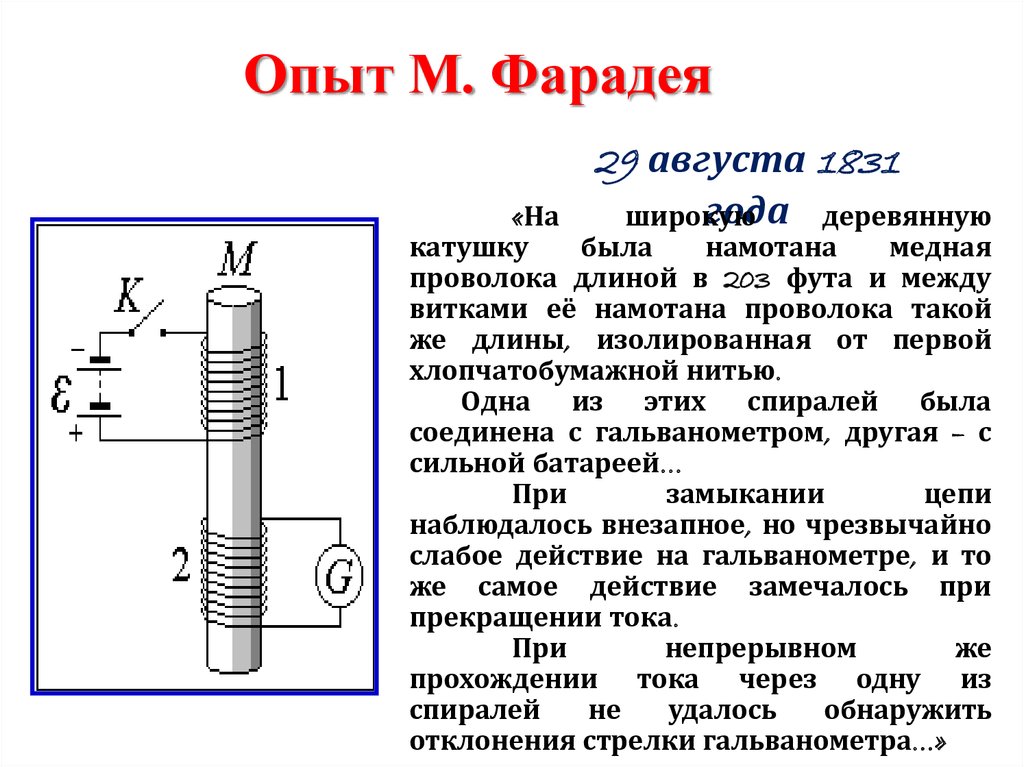
В 1956 году С. Г. Калашников снова привел описание работы униполярного генератора5. В отличие от варианта, рассмотренного И. Е. Таммом, автор считал линии магнитной индукции вращающегося магнита направленными не вдоль оси магнита, а радиально (наподобие жестких спиц). Но магнитное поле по-прежнему предполагалось неподвижным в пространстве. И хотя это — принципиально другая конструкция, тем не менее, теория относительности объяснила работу и такого устройства! Ну чем не палочка-выручалочка! Такое объяснение «униполярной индукции» сегодня доказательно оспаривается участниками Интернет-форумов.
Как же работает униполярный генератор? Если признать, что магнитное поле связано с магнитом, то очевидно, что в объёме магнита никакая ЭДС возникнуть не может. Это тот же механизм, который отвечает за Парадокс Геринга: в обоих случаях электроны магнита движутся вместе с его магнитным полем, отсутствует пересечение линий поля электрическими зарядами, а, следовательно, и индукционная ЭДС.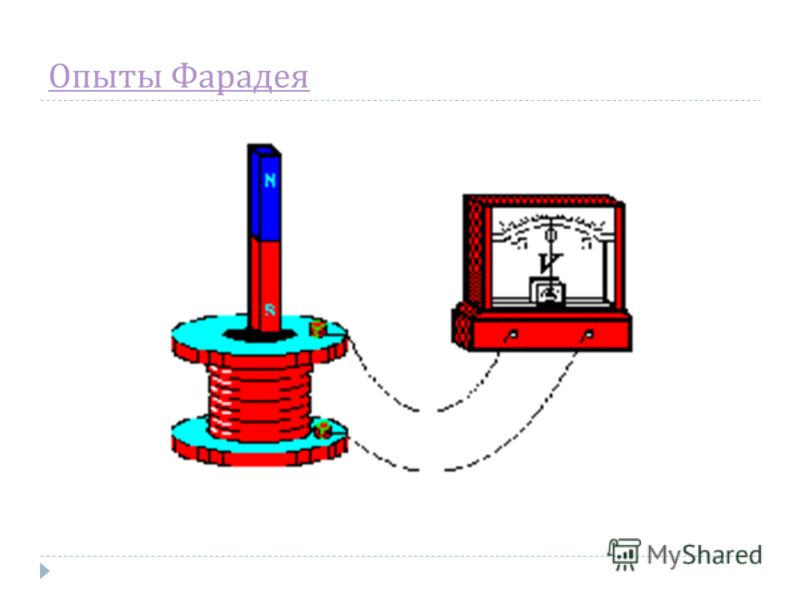 Где же генерируется ток в контуре? Ответ очевиден: там, где линии поля пересекают контур, то есть в проводах на участке контура АС (см. рис. 5).
Где же генерируется ток в контуре? Ответ очевиден: там, где линии поля пересекают контур, то есть в проводах на участке контура АС (см. рис. 5).
Так представления о механизме электромагнитной индукции по «способу пересечения» позволяют разрешить многие «парадоксы» электромагнитного взаимодействия, в том числе и классический «Парадокс Фарадея».
Таким образом, «парадокс» в том, что уже более 100 лет ошибочно трактуется физическая природа самого процесса электромагнитной индукции. Экспериментальная зависимость Фарадея заменена её математически тождественным выражением Максвелла, из которого исчезли главные участники процесса — электрические заряды. Почему так произошло, почему этот «парадокс» больше века оставался не замеченным? На эти вопросы отвечать не физикам, а психологам…
Чтобы понять природу электромагнитных взаимодействий, познакомимся поближе с участниками этих взаимодействий — магнитным и электрическим полем.
- Назад: «Парадоксы» электромагнитной индукции
- Далее: Магнитное поле: свойства и «парадоксы»
Савельев И.
 В. Курс общей физики. Т. 2. М.: Наука, 1978. С. 178. ↩︎
В. Курс общей физики. Т. 2. М.: Наука, 1978. С. 178. ↩︎Матвеев А. Н. Электричество и магнетизм. М.: Высш. школа, 1956. С. 317. ↩︎
Иродов И. Е. Электромагнетизм. Основные законы. М.: Лаб. Базовых Знаний, 2001. С. 248. ↩︎
Максвелл Д. К. Статьи и речи. М.: Наука, 1968. С. 59. ↩︎
Калашников С. К. Электричество. М.: Физматлит, 2004. С. 194. ↩︎
Мисюченко И. Последняя тайна Бога. СПб.: 2009. С. 106. ↩︎
Тамм И. Е. Основы теории электричества, §112. М.: Гос. изд-во техн.-теорет. лит., 1956. ↩︎
формулировка закона Фарадея, физическая формула
Содержание
- История открытия
- Закон Фарадея
- Применение явления
- Опыт Фарадея
- ЭДС индукции. Закон электромагнитной индукции
- Закон Фарадея-Максвелла
- Примечания
- Труды в области электролиза
- Закон Максвелла
- Магнитный поток
- ЭДС индукции в движущемся проводнике
- Закон электромагнитной индукции
- Что мы узнали?
- История развития и опыты Фарадея
- Литература
- Открытие ЭИ
- История
- Энергия магнитного поля
- Открытие электромагнитной индукции
- Явление ЭИ
- Закон
История открытия
Явление электромагнитной индукции было открыто сразу двумя учеными. Это были Майкл Фарадей и Джозеф Генри, сделавшие свое открытие в 1831 году. Публикация Фарадеем результатов проведенных экспериментов была сделана раньше его коллеги, поэтому индукцию связывают именно с этим ученым. В дальнейшем это понятие было включено в систему СГС.
Это были Майкл Фарадей и Джозеф Генри, сделавшие свое открытие в 1831 году. Публикация Фарадеем результатов проведенных экспериментов была сделана раньше его коллеги, поэтому индукцию связывают именно с этим ученым. В дальнейшем это понятие было включено в систему СГС.
Для демонстрации явления использовался железный тор, напоминающий конфигурацию современного трансформатора. Противоположные стороны его были обмотаны двумя проводниками с целью использования электромагнитных свойств.
К одному из проводов подключался ток, вызывающий своеобразную электрическую волну при прохождении сквозь тор, и некоторый электрический всплеск с противоположной стороны. Наличие тока было зафиксировано гальванометром. Точно такой же всплеск электричества наблюдался и в момент отключения провода.
Постепенно были обнаружены и другие формы проявления электромагнитной индукции. Кратковременное возникновение тока наблюдалось во время генерации его на медном диске, вращающемся возле магнита. На самом диске был установлен скользящий электропровод.
Когда обе катушки находятся в неподвижном положении относительно друг друга, никаких явлений не происходит. Когда небольшая катушка начинает двигаться, то есть выходить из большой катушки или входить в нее, наступает изменение магнитного потока. В результате, в большой катушке наблюдается появление электродвижущей силы.
Открытие Фарадея доработал другой ученый – Максвелл, который обосновал его математически, отображая данное физическое явление дифференциальными уравнениями. Еще одному ученому-физику – Ленцу удалось определить направление электротока и ЭДС, полученных под действием электромагнитной индукции.
Закон Фарадея
Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.
Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.
Формула закона электромагнитной индукции Фарадея выглядит следующим образом:
Рис. 2. Формула закона электромагнитной индукции
2. Формула закона электромагнитной индукции
И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея. По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.
Напряжение электрического тока – виды, формула, единица измерения
Применение явления
Значение закона Фарадея трудно недооценить, понимая, в каких целях он используется на практике. Вся электрическая промышленность построена на реализации открытия учёного. Одним из устройств использующего принцип возникновения ЭДС за счёт движения замкнутого проводника в магнитном поле является электрический генератор.
Его работа заключается в том, что если постоянный магнит перемещать относительно контура, то возникнет электродвижущая сила. Соответственно подключив проводник к нагрузке, можно получить ток. А это значит, что механическая энергия превратится в электрическую. При этом различают два принципиально разных механизма работы:
Соответственно подключив проводник к нагрузке, можно получить ток. А это значит, что механическая энергия превратится в электрическую. При этом различают два принципиально разных механизма работы:
- Индуцированный — вращение магнита, вокруг не изменяющего своё положение проводника. В этом случае электрическое поле двигает заряды через проводник.
- Двигательный — магнит неподвижен, а проводник вращается. Появляется сила Лоренца, и магнитное поле толкает заряды.
Второе, но не менее важное устройство, электродвигатель. По сути, это генератор работающий «задом наперёд»
На заряд действует магнитная сила, вращающая диск в обратном направлении, определить которое можно по правилу левой руки. Если будут потери небольшие, например, связанные с трением или выделением тепла, то подключённый диск будет вращаться с такой скоростью, чтобы отношение dF / dt сравнялось с разностью потенциалов вызывающего ток.
На использовании ЭДС построена работа и трансформатора.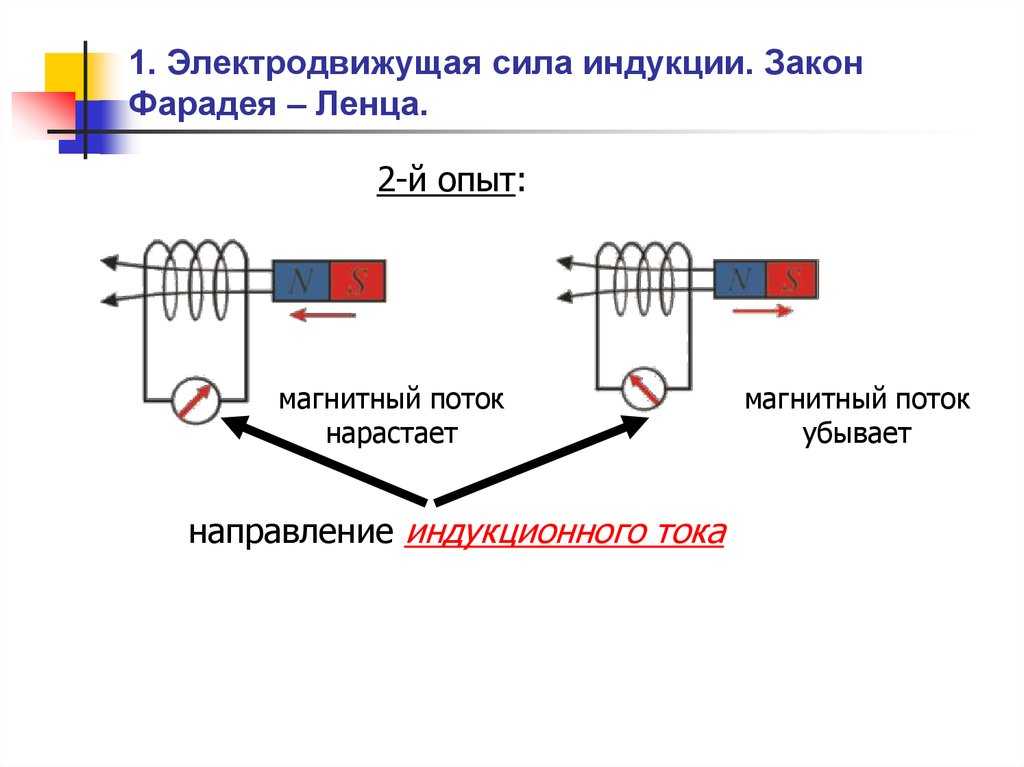 Проходящий по первичным виткам переменный электрический ток приводит к возникновению магнитного поля. Последнее и наводит во вторичной обмотке электродвижущую силу. Если только концы катушки подключить к нагрузке, то через неё сразу же потечёт ток.
Проходящий по первичным виткам переменный электрический ток приводит к возникновению магнитного поля. Последнее и наводит во вторичной обмотке электродвижущую силу. Если только концы катушки подключить к нагрузке, то через неё сразу же потечёт ток.
Опыт Фарадея
Вначале XIX века пришёлся бум на открытия в области электричества и магнетизма. Установленные в это время законы служат базисами и в современных исследованиях. Так, одним из важных открытий стала взаимосвязь между магнитными и электрическими полями. Фарадею удалось сделать то, что не получилось у Эрстеда и Ампера. Он смог превратить магнетизм в электричество.
Для открытия своего закона учёному понадобилось подготовить:
- магнит;
- две проволочные катушки;
- гальванометр;
- источник тока.

Фарадей провёл два разных опыта. Для первого он собрал цепь, содержащую одну катушку. Вокруг неё он передвигал магнит и смотрел за поведением гальванометра. Физик наблюдал как при внесении намагниченного тела в катушку, стрелка в измерительном устройстве откланялась. При выведении же из проводника указатель изменял направление. Если же магнит оставался неподвижным, то гальванометр ток не обнаруживал.
Во втором эксперименте Фарадей использовал две катушки. К одной он подключил источник переменного тока, а ко второй измерительный прибор. При этом он опять же наблюдал ток, возникающий во вторичном проводнике. Фактически Фарадей сам того не зная изобрёл трансформатор.
Открытия позволили сформулировать определение, после названное именем учёного. Звучит закон Фарадея в современной трактовке так: когда поток вектора индукции, пронизывающий замкнутый, контур проводника, изменяется, то в замкнутой цепи возникает упорядоченное движение электрических зарядов. Другими словами, возникает ток. Природное же явление называют электромагнитной индукцией, а возникший ток — индукционным.
Природное же явление называют электромагнитной индукцией, а возникший ток — индукционным.
Описывается закон Фарадея формулой: E = — ΔФ / Δt. Как видно из выражения электродвижущая сила зависит от скорости, с которой изменяется магнитный поток. При этом знак минус показывает направление индукционного тока. Определяется он по правилу Лоренца. Таким образом, идея Фарадея описывает как двигательную ЭДС, так и трансформаторную, то есть генерируемую магнитной и электрической силами
Впервые на это обратил внимание Максвелл, который в своих трудах дал подробное физическое объяснение для каждого из этих двух явлений
ЭДС индукции. Закон электромагнитной индукции
Выше рассмотренные опыты показали, что в замкнутом контуре возникает индукционный ток при изменении магнитного потока, пронизывающего поверхность, ограниченную контуром. Как известно, ток в проводнике возникает в том случае, если на свободные заряды проводника действуют сторонние силы. Работу этих сил при перемещении единичного заряда вдоль замкнутого проводника называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром, в нем появляются сторонние силы (природу их выясним ниже: ЭДС индукции в движущихся проводниках), действие которых характеризуется ЭДС, называемой ЭДС индукции.
Как известно, ток в проводнике возникает в том случае, если на свободные заряды проводника действуют сторонние силы. Работу этих сил при перемещении единичного заряда вдоль замкнутого проводника называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром, в нем появляются сторонние силы (природу их выясним ниже: ЭДС индукции в движущихся проводниках), действие которых характеризуется ЭДС, называемой ЭДС индукции.
Как показывает опыт, значение индукционного тока (а значит, и \(~\varepsilon_i\)) не зависит от причины изменения магнитного потока (изменяется ли площадь, ограниченная контуром, или его ориентация в пространстве, изменяется ли индукция магнитного поля при перемещении его источников или за счет изменения среды и т.д.). Существенное значение имеет лишь скорость изменения магнитного потока \(~\frac {\Delta \Phi}{\Delta t}\) (так, стрелка гальванометра в опытах Фарадея отклоняется тем больше, чем быстрее вдвигается магнит в катушку).
Эта формула выражает закон Фарадея для электромагнитной индукции:
среднее значение ЭДС индукции в проводящем контуре пропорционально скорости изменения магнитного потока через поверхность, ограничен ную контуром. Мгновенное значение ЭДС индукции равно взятой с противоположным знаком первой производной от магнитного потока по времени, т.е. \(~\mathcal h \varepsilon_i \mathcal i = {\Phi}'(t)\).
Знак “-” учитывает правило Ленца, согласно которому при увеличении магнитного потока \(~(\frac {\Delta \Phi}{\Delta t} > 0)\) ЭДС индукции отрицательная \(~(\varepsilon_i 0)\).
Сила индукционного тока в замкнутом контуре рассчитывается по закону Ома\ где R — сопротивление контура.
Индукционный ток возникает не только в линейных проводниках, но и в массивных сплошных проводниках, помещенных в переменное магнитное поле. В соответствии с законом электромагнитной индукции любые изменения магнитного потока, пронизывающего проводящее тело, сопровождаются возникновением в нем индукционных токов. Эти токи оказываются замкнутыми в толще проводника и поэтому называются вихревыми (а также токами Фуко). Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующего вихревые токи. Токи Фуко можно обнаружить на опыте с маятником (проводящей пластиной), колеблющемся в зазоре между полюсами электромагнита. До включения маятник совершает практически незатухающие колебания. При пропускании тока через катушку электромагнита маятник испытывает сильное торможение и очень быстро останавливается. Торможение маятника объясняется действием магнитного поля на индукционные токи, возникающие в пластине при ее движении в магнитном поле. Если в пластине сделать разрезы, то вихревые токи ослабляются и торможение почти отсутствует. Этот факт торможения используется для успокоения подвижных частей различных приборов.
Эти токи оказываются замкнутыми в толще проводника и поэтому называются вихревыми (а также токами Фуко). Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующего вихревые токи. Токи Фуко можно обнаружить на опыте с маятником (проводящей пластиной), колеблющемся в зазоре между полюсами электромагнита. До включения маятник совершает практически незатухающие колебания. При пропускании тока через катушку электромагнита маятник испытывает сильное торможение и очень быстро останавливается. Торможение маятника объясняется действием магнитного поля на индукционные токи, возникающие в пластине при ее движении в магнитном поле. Если в пластине сделать разрезы, то вихревые токи ослабляются и торможение почти отсутствует. Этот факт торможения используется для успокоения подвижных частей различных приборов.
Токи Фуко вызывают нагревание проводников (якоря генераторов и сердечников трансформаторов), выделяемая токами Фуко теплота используется в индукционных металлургических печах и в других случаях.
По закону Фарадея (1) определяется ЭДС индукции, возникающая и в движущемся проводнике, и в неподвижном (см. опыты, описанные в разделе Электромагнитная индукция). Но механизм происхождения ЭДС индукции в этих случаях различен.
Закон Фарадея-Максвелла
В 1873 Дж.К.Максвелл по-новому изложил теорию электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:
- Edl = -dФ/dt – уравнение электродвижущей силы
- Hdl = -dN/dt – уравнение магнитодвижущей силы.
Где E – напряженность электрического поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток электрической индукции, t – время.
Симметричный характер данных уравнений устанавливает связь электрических и магнитных явлений, а также магнитных с электрическими. физический смысл, которым определяются эти уравнения, можно выразить следующими положениями:
- если электрическое поле изменяется, то это изменение всегда сопровождается магнитным полем.

- если магнитное поле изменяется, то это изменение всегда сопровождается электрическим полем.
Рис. 3. Возникновение вихревого магнитного поля
Примечания
- Миллер М. А., Пермитин Г. В. // Физическая энциклопедия : / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 537—538. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
Это уравнение Максвелла может быть переписано в эквивалентном виде
- ∮∂SE→⋅dl→=−∫S∂B→∂t⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-\int _{S}{\frac {\partial {\vec {B}}}{\partial t}}\cdot {\vec {ds}}}
(здесь просто производная по t внесена под знак интеграла). В таком виде уравнение также может быть включено в систему уравнений Максвелла, причем оговорка о неподвижности контура интегрирования теряет актуальность, так как производная теперь не действует на границу области (на пределы интегрирования), а само интегрирование в любом случае полагается «мгновенным».
 В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).
В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).- Такой отказ объясняется тем, что, в отличие от закона для циркуляции электрического поля, выполняющегося всегда, «правило» корректно работает лишь для случаев, когда контур, в котором вычисляется ЭДС, совпадает физически с проводником (то есть совпадает их движение; в противном же случае правило может не работать (самый известный пример — униполярная машина Фарадея; контур, который в этом случае трудно определить, но кажется довольно очевидным, что он не меняется; во всяком случае, довольно затруднительно указать разумное определение для контура, который бы в этом случае менялся), то есть проявляется парадокс, что для «закона природы» недопустимо.
Труды в области электролиза
При использовании законов Фарадея описываются закономерности, которые существуют при электролизе. Этот процесс заключается в превращении веществ с разнообразными характеристиками. Это происходит при движении электричества сквозь электролит.
Этот процесс заключается в превращении веществ с разнообразными характеристиками. Это происходит при движении электричества сквозь электролит.
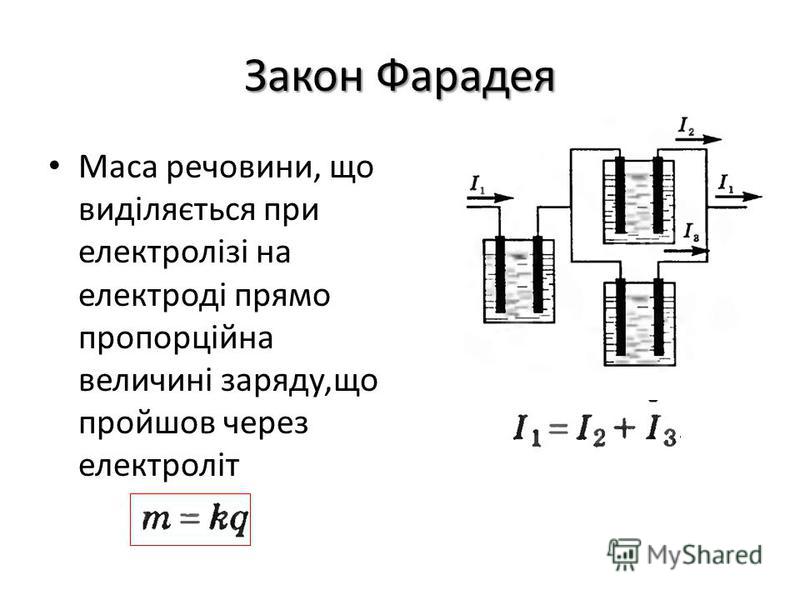
Эти закономерности были доказаны М. Фарадеем в 1834 году. Первое утверждение гласит, что масса вещества, которое образуется на электроде, меняется соответственно заряду, перемещенному сквозь электролит.
Второе утверждение гласит, что эквиваленты компонентов с разными характеристиками пропорциональны химическим эквивалентам этих компонентов.
Оба представленных утверждения совмещаются в объединенный закон Фарадея. Из него следует, что число Фарадея будет равняться электричеству, способному выделить на электролите 1 моль вещества. Ее рассчитывают на единицу валентности. Именно по объединенной формуле в далеком 1874 году был вычислен заряд электрона.
Законы электролиза, установленные Фарадеем, тестировались при различном значении тока, температуры, давления, а также при одновременном выделении двух и более веществ. Электролиз также проводился в разных расплавах и растворителях. Концентрация электролита также отличалась в разных опытах. При этом иногда наблюдались небольшие отклонения от закона Фарадея. Они объясняются электронной проводимостью электролитов, которая определяется наравне с ионной проводимостью.
Концентрация электролита также отличалась в разных опытах. При этом иногда наблюдались небольшие отклонения от закона Фарадея. Они объясняются электронной проводимостью электролитов, которая определяется наравне с ионной проводимостью.
Открытия, сделанные английским физиком М. Фарадеем, позволили описать множество явлений. Его законы являются основой современной электродинамики. По этому принципу функционирует различное современное оборудование.
Закон Максвелла
В 1873 году Джон Максвелл теоретически изложил действие электромагнитного поля. Его уравнения составили основу для создания электротехники. Уравнения, полученные им устанавливают взаимосвязь магнитных явлений с электрическими и наоборот. Вместе с тем физик обнаружил, что значение распространения электромагнитной волны совпадает со скоростью света.
Физический смысл уравнений заключается в следующем:
- изменение электрического поля приводит к возникновению магнитного: Edl = -dФ/dt;
- если существует магнитное поле, то оно вызывает появление электрического: Hdl = -dN/dt.

В формулах: E — это напряжение электрополя на участке цепи; H — напряжённость; N — поток индукции; t — время. В том случае, когда контур замкнут при изменении магнитного потока возникает электродвижущая сила (ЭДС). Проявляется она в виде индукционного тока: I = e * i / R, где R — сопротивление цепи. Если контур будет незамкнутым, то в месте обрыва возникнет разность потенциалов.
Направление движения индукционного тока определяется по правилу Ленца. Формулироваться оно будет так: возникающее движение носителей зарядов направлено таким образом, чтобы магнитное поле противодействовало потоку им вызывающимся. На практике же сторону движения индукционного тока можно определить следующим образом:
- выяснить направление внешнего магнитного поля;
- узнать возрастает или спадает поток вектора магнитной индукции;
- используя правило Ленца, определить направление вектора;
- воспользовавшись методом правого винта найти направление индукционного тока в контуре.

Таким образом, если имеется N витков в контуре, то сила индукции равна: E = — N * (dФ / dt). Отсюда сила тока в цепи будет следующей: I = E / R. Если же длина проводника равна L, а скорость V, то в однородном постоянном поле электромагнитную индукцию (ЭМИ) можно найти как E = B * V * L * sin (a), где альфа-угол между векторами.
Кратко объяснить природу ЭДС самоиндукции можно так. Пусть имеется проводник длиной L вокруг которого изменяется магнитное поле со скоростью V. На заряд двигающийся под действием намагниченности оказывает влияние сила Лоренца: F = q * (E + v * B). Отрицательные заряды собираются возле одного края проводника, а некомпенсированные положительные у другого. В итоге возникает напряжение. Представляет оно собой ЭДС индукции (e * i). Найти её значение можно, определив работу, которая совершается силой Лоренца при движении заряда по проводнику: ei = A / q = F * L / q = B·V·L·sin (a).
youtube.com/embed/2vGT5YlCEtk?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Магнитный поток
Вектор магнитной индукции \(~\vec B\) характеризует силовые свойства магнитного поля в данной точке пространства. Введем еще одну величину, зависящую от значения вектора магнитной индукции не в одной точке, а во всех точках произвольно выбранной поверхности. Эту величина называется магнитным потоком и обозначается греческой буквой Φ (фи).
Магнитный поток Φ однородного поля через плоскую поверхность — это скалярная физическая величина, численно равная произведению модуля индукции B магнитного поля, площади поверхности S и косинуса угла α между нормалью \(~\vec n\) к поверхности и вектором индукции \(~\vec B\) (рис. 1):
В СИ единицей магнитного потока является вебер (Вб):

Магнитный поток в 1 Вб — это магнитный поток однородного магнитного поля с индукцией 1 Тл через перпендикулярную ему плоскую поверхность площадью 1 м2.
- Поток может быть как положительным, так и отрицательным в зависимости от значения угла α.
- Поток магнитной индукции наглядно может быть истолкован как величина, пропорциональная числу линий вектора индукции \(~\vec B\), пронизывающих данную площадку поверхности.
Из формулы (1) следует, что магнитные поток может изменяться:
- или только за счет изменения модуля вектора индукции B магнитного поля, тогда
\(~\Delta \Phi = (B_2 – B_1) \cdot S \cdot \cos \alpha\) ;
- или только за счет изменения площади контура S, тогда
\(~\Delta \Phi = B \cdot (S_2 – S_1) \cdot \cos \alpha\) ;
- или только за счет поворота контура в магнитном поле, тогда
\(~\Delta \Phi = B \cdot S \cdot (\cos \alpha_2 – \cos \alpha_1)\) ;
- или одновременно за счет изменения нескольких параметров, тогда
\(~\Delta \Phi = B_2 \cdot S_2 \cdot \cos \alpha_2 – B_1 \cdot S_1 \cdot \cos \alpha_1\) . 
ЭДС индукции в движущемся проводнике
При движении проводника длиной l со скоростью \(\vec{\upsilon}\) в постоянном магнитном поле с вектором индукции \(\vec{B}\) в нем возникает ЭДС индукции
где α – угол между направлением скорости \(\vec{\upsilon}\) проводника и вектором магнитной индукции \(\vec{B}\).
Причиной появления этой ЭДС является сила Лоренца, действующая на свободные заряды в движущемся проводнике. Поэтому направление индукционного тока в проводнике будет совпадать с направлением составляющей силы Лоренца на этот проводник.
С учетом этого можно сформулировать следующее для определения направления индукционного тока в движущемся проводнике (правило левой руки):
нужно расположить левую руку так, чтобы вектор магнитной индукции \(\vec{B}\) входил в ладонь, четыре пальца совпадали с направлением скорости \(\vec{\upsilon}\)проводника, тогда отставленный на 90° большой палец укажет направление индукционного тока (рис. 5).
5).
- Если проводник движется вдоль вектора магнитной индукции, то индукционного тока не будет (сила Лоренца равна нулю).
Закон электромагнитной индукции
М. Фарадей провел многочисленные опыты, записывая результаты, и из этих опытных таблиц электромагнитной индукции установил, что ток в проводящем контуре возникает только при изменении магнитного поля, пронизывающего этот контур.
Для количественного описания этого явления используется понятие магнитного потока. Если индукция характеризует силу магнитного поля в точке, то магнитный поток характеризует плотность линий магнитной индукции. Магнитный поток через контур площадью S равен произведению модуля индукции B на площадь S и на косинус угла между вектором индукции и нормалью к контуру:
$$Ф=BScosα$$
Рис. 3. Ф=BScosa.
Явление электромагнитной индукции состоит в том, что при изменении за время Δt магнитного потока через контур на величину ΔФ, в нем возникают сторонние силы, создающие разность потенциалов, называемую ЭДС (электродвижущей силой):
$$ε= -{ΔФ\over Δt}$$
Знак минус в данной формуле электромагнитной индукции означает, что возникающая ЭДС, в соответствии с правилом Э. Ленца, направлена так, чтобы создавать ток, противодействующий создавшей его причине.
Ленца, направлена так, чтобы создавать ток, противодействующий создавшей его причине.
Что мы узнали?
Кратко и понятно явление электромагнитной индукции можно описать, как возникновение электрического тока в проводящем контуре при изменении магнитного потока, проходящего через этот контур. При этом возникающий ток направлен так, чтобы противодействовать причине, его создавшей.
История развития и опыты Фарадея
До середины XIX века считалось, что электрическое и магнитное поле не имеют никакой связи, и природа их существования различна. Но М. Фарадей был уверен в единой природе этих полей и их свойств. Явление электромагнитной индукции, обнаруженное им, впоследствии стало фундаментом для устройства генераторов всех электростанций. Благодаря этому открытию знания человечества о электромагнетизме шагнули далеко вперед.
Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг нее возрастало магнитное поле. Далее линии индукции данного магнитного поля пересекали катушку II, в которой возникал индукционный ток.
Рис. 1. Схема опыта Фарадея
Сколько бы экспериментов не проводил Фарадей, неизменным оставалось одно условие: для образования индукционного тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).
Литература
- Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C.344- 351.
- Жилко В.В. Физика: учеб. пособие для 11-го кл. общеобразоват. учрежде-ний с рус. яз. Обучения с 12-летним сроком обучения (базовый и повышенный уровни) / В.В. Жилко, Л.Г. Маркович. — Мн.: Нар. асвета, 2008. — С. 170-182.
- Мякишев, Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. — М.: Дрофа, 2005. — С. 399-408, 412-414.
Открытие ЭИ
электроток «окружает» себя магнитным полем.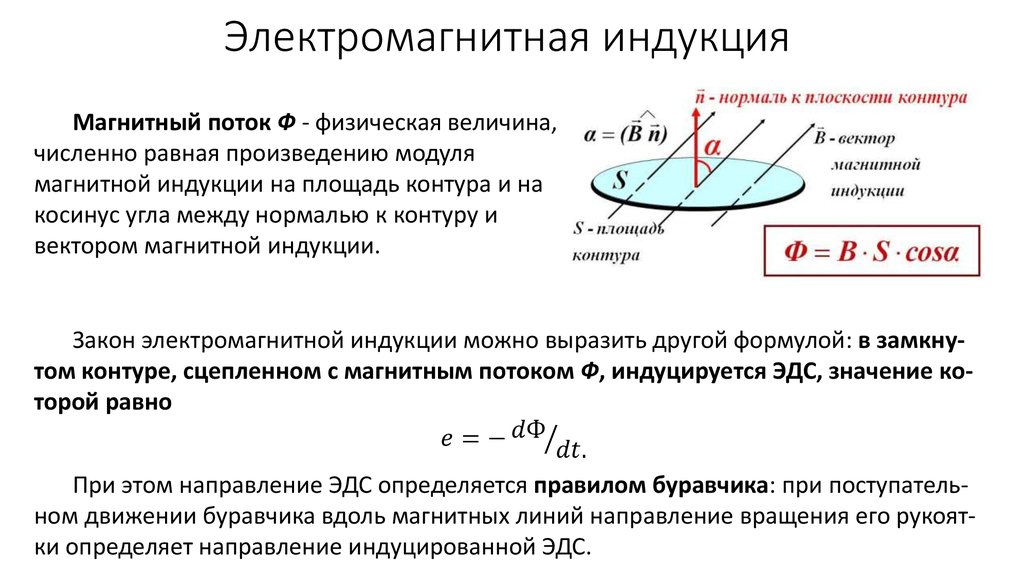
Так нельзя ли добиться его возникновения посредством магнитного поля — подобную задачу поставил Майкл Фарадей. В 1821 году он отметил это свойство в своем дневнике о превращении магнетизма в электричество.
Успех к ученому пришел не сразу. Лишь глубокая уверенность в единстве природных сил и упорный труд привели его через десять лет к новому великому открытию.
Решение задачи долго не давалось Фарадею и другим его коллегам, потому как они пытались получить электричество в неподвижной катушке, используя действие постоянного магнитного поля. Между тем, впоследствии выяснилось: изменяется количество силовых линий, пронизывающих провода, и возникает электроэнергия.
История
В 1820 году Ганс Христиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 году в своём дневнике. Многие годы настойчиво ставил он различные опыты, но безуспешно, и только 29 августа 1831 года наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, состояла из кольца из мягкого железа примерно 2 см шириной и 15 см диаметром. На каждой половине кольца было намотано много витков медной проволоки. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.
Многие годы настойчиво ставил он различные опыты, но безуспешно, и только 29 августа 1831 года наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, состояла из кольца из мягкого железа примерно 2 см шириной и 15 см диаметром. На каждой половине кольца было намотано много витков медной проволоки. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.
В это же время американский физик Джозеф Генри также успешно проводил опыты по индукции токов, но пока он собирался опубликовать результаты своих опытов, в печати появилось сообщение М. Фарадея об открытии им электромагнитной индукции.
Фарадея об открытии им электромагнитной индукции.
М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.
Энергия магнитного поля
Вспомним второй опыт с лампочкой, которая не горит при замкнутом ключе и ярко вспыхивает при размыкании цепи. Мы непосредственно наблюдаем, что после размыкания ключа в лампочке выделяется энергия. Но откуда эта энергия берётся?
Берётся она, ясное дело, из катушки — больше неоткуда. Но что за энергия была запасена в катушке и как вычислить эту энергию? Чтобы понять это, продолжим нашу электромеханическую аналогию между индуктивностью и массой.
Чтобы разогнать тело массы из состояния покоя до скорости , внешняя сила должна совершить работу . Тело приобретает кинетическую энергию, которая равна затраченной работе: .
Чтобы после замыкания цепи ток в катушке индуктивности достиг величины , источник тока должен совершить работу по преодолению вихревого электрического поля, направленного против тока. Работа источника идёт на создание тока и превращается в энергию магнитного поля созданного тока. Эта энергия запасается в катушке; именно эта энергия и выделяется потом в лампочке после размыкания ключа (во втором опыте).
Работа источника идёт на создание тока и превращается в энергию магнитного поля созданного тока. Эта энергия запасается в катушке; именно эта энергия и выделяется потом в лампочке после размыкания ключа (во втором опыте).
Индуктивность служит аналогом массы ; сила тока является очевидным аналогом скорости . Поэтому естественно предположить, что для энергии магнитного поля катушки может иметь место формула, аналогичная выражению для кинетической энергии:
(3)
(тем более, что правая часть данной формулы имеет размерность энергии — проверьте!).
Формула (3) действительно оказывается справедливой. Уметь её выводить пока не обязательно, но если вы знаете, что такое интеграл, то вам не составит труда понять следующие рассуждения.
Пусть в данный момент сила тока через катушку равна . Возьмём малый промежуток времени . В течение этого промежутка приращение силы тока равно ; величина считается настолько малой, что много меньше, чем .
За время по цепи проходит заряд .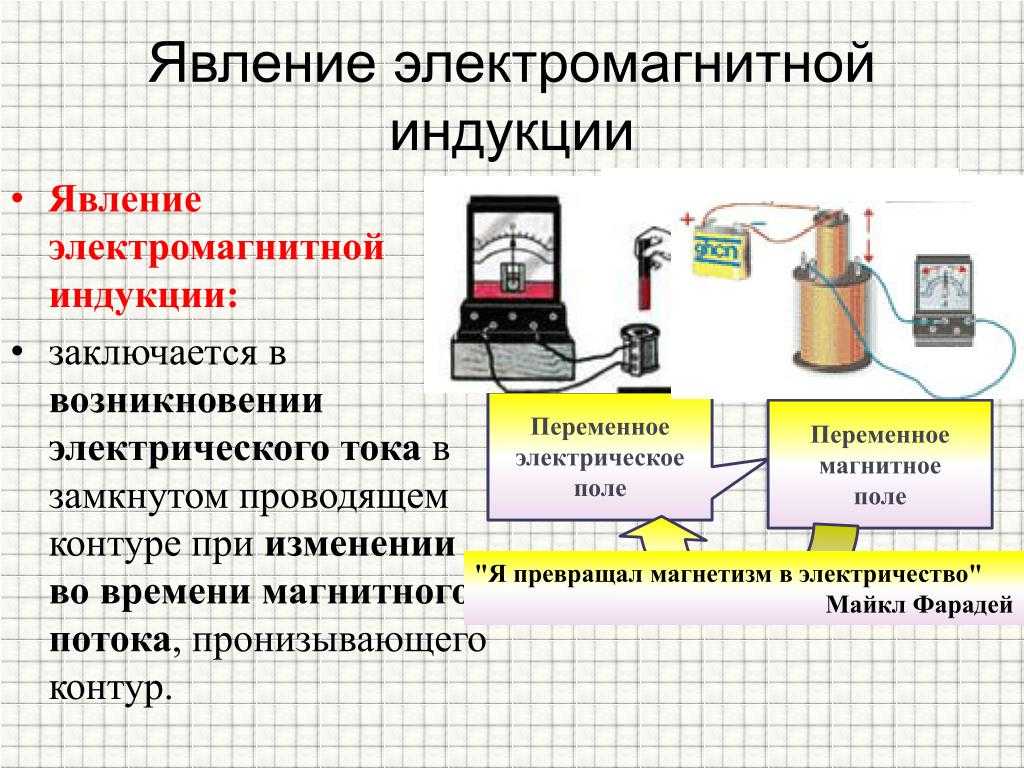 Вихревое электрическое поле совершает при этом отрицательную работу:
Вихревое электрическое поле совершает при этом отрицательную работу:
Источник тока совершает такую же по модулю положительную работу (сопротивлением катушки, напомним, мы пренебрегаем, так что вся работа источника совершается против вихревого поля):
Интегрируя это от нуля до , найдем работу источника , которая затрачивается на создание тока :
Открытие электромагнитной индукции
Практически сразу с момента открытия электрического тока было выявлено, что ток, проходящий по проводнику, создает магнитное поле.
Логично было предположить, что магнитное поле тоже может создать движение электрических зарядов в проводнике. Многие ученые безуспешно бились над этой задачей. Однако, электрические заряды, помещенные в постоянное магнитное поле, никак на него не реагировали.
Открытие было сделано М. Фарадеем 29 августа 1831 года (редкий случай, когда точно известна дата открытия).
Рис. 1. М. Фарадей.
В опыте использовались две катушки – одна создавала магнитное поле, вторая была расположена рядом, так, чтобы сквозь нее проходили магнитные линии первой катушки.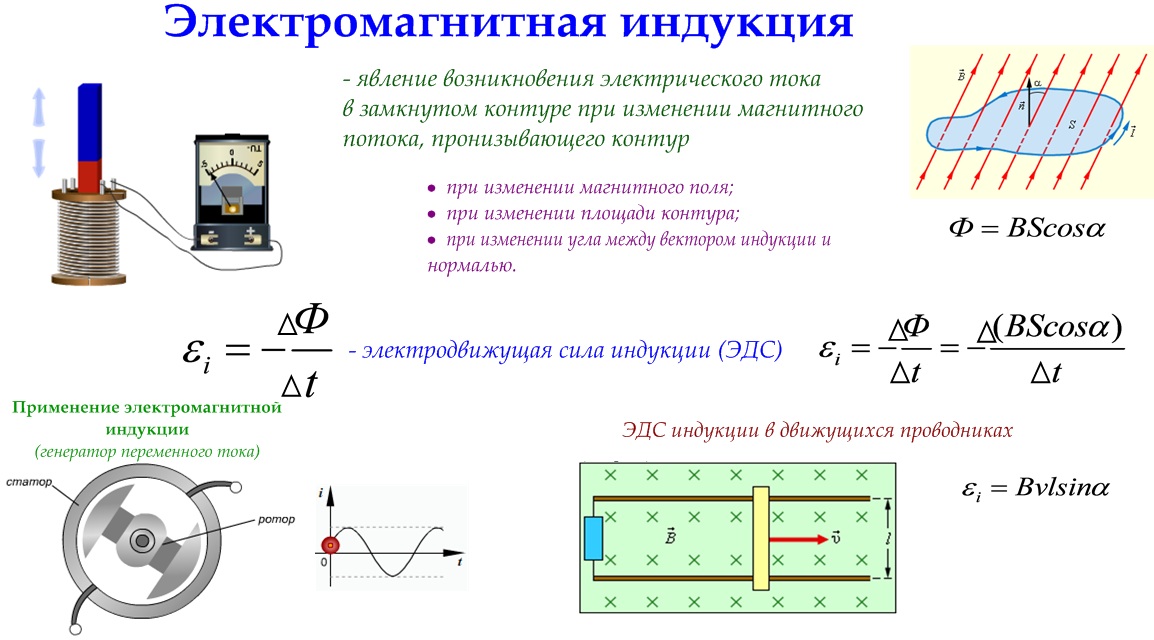 Вторая катушка была подключена к гальванометру, который был предназначен для определения возникающего в ней электрического тока.
Вторая катушка была подключена к гальванометру, который был предназначен для определения возникающего в ней электрического тока.
Рис. 2. Опыт Фарадея с двумя катушками.
Опыт давал отрицательный результат, постоянное поле, пронизывающее вторую катушку, не создавало в ней электрического тока, сколько бы времени не прошло. Но, Фарадей заметил, что перед самым опытом, в момент пуска электрического тока через первую катушку, стрелка гальванометра давала слабое колебание
Порядок опыта был перестроен – теперь главное внимание было уделено моменту включения. И выяснилось, что включение и выключение тока через первую катушку вызывает возникновение импульса тока во второй катушке
В дальнейшем было определено, что для появления импульса можно не только включать и выключать магнитное поле другой катушкой, а, к примеру, приближать и удалять обычный постоянный магнит.
Причем, возникающий ток (как и любой ток в проводнике) создает свое магнитное поле, а направлен он так, чтобы возникающее магнитное поле препятствовало причине, создавшей ток в контуре. Данное правило было позже открыто русским физиком Э.Ленцем.
Данное правило было позже открыто русским физиком Э.Ленцем.
Многие исследователи, разрабатывавшие теорию электричества, такие, как Х.Эрстед, Ж.Колладон, Дж.Генри, были близки к открытию. Но колебание стрелки в момент запуска или выключения установки они либо вообще не замечали, либо расценивали, как результат случайных внешних сотрясений и не придавали ему значения.
Явление ЭИ
Процесс появления в катушке электричества в результате изменения магнитного поля характерен для электромагнитной индукции и определяет это понятие. Вполне закономерно, что разновидность тока, возникающего в ходе данного процесса, называется индукционным. Эффект сохранится, если саму катушку оставить без движения, но перемещать при этом магнит. С использованием второй катушки можно и вовсе обойтись без магнита.
Если пропустить электричество через одну из катушек, то при их взаимном перемещении во второй возникнет индукционный ток. Можно надеть одну катушку на другую и менять величину напряжения одной из них, замыкая и размыкая ключ. При этом магнитное поле, пронизывающее катушку, на которую воздействуют ключом, меняется, и это становится причиной возникновения индукционного тока во второй.
При этом магнитное поле, пронизывающее катушку, на которую воздействуют ключом, меняется, и это становится причиной возникновения индукционного тока во второй.
Закон
Во время опытов легко обнаружить, что увеличивается число пронизывающих катушку силовых линий — стрелка используемого прибора (гальванометр) смещается в одну сторону, уменьшается – в иную. Более тщательное исследование показывает, что сила индукционного тока прямо пропорциональна скорости изменения числа силовых линий. В этом заключен основной закон электромагнитной индукции.
Данный закон выражает формула:
Она применяется, если за период времени t магнитный поток изменяется на одну и ту же величину, когда скорость изменения магнитного потока Ф/t постоянна.
Важно! Для индукционных токов справедлив закон Ома: I=/R, где — это ЭДС индукции, которую находят по закону ЭИ.
Замечательные опыты, проведенные когда-то знаменитым английским физиком и ставшие основой открытого им закона, сегодня без особого труда способен проделать любой школьник. Для этих целей используются:
Для этих целей используются:
- магнит,
- две проволочные катушки,
- источник электроэнергии,
- гальванометр.
Поворачивая, наклоняя и перемещая ее вверх и вниз, мы меняем число силовых линий магнитного поля, пронизывающих ее витки.
Гальванометр регистрирует возникновение электричества с постоянно меняющимися в ходе опыта величиной и направлением.
Находящиеся же относительно друг друга в покое катушка и магнит не создадут условий и для возникновения электричества.
| Электромагнитная индукция Электромагнитная индукция
Магнитный поток Магнитный поток Магнитный поток Майкл Фарадей Майкл Фарадей ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ Электромагнитная индукция Электромагнитная индукция
Электромагнитная индукция Направление индукционного тока Направление индукционного тока
Правило Ленца Направление индукционного тока Направление индукционного тока Сила индукционного тока Сила индукционного тока Джозеф Генри Катушки Закон электромагнитной индукции. Вихревое электрическое поле Электрическое поле Электрическое поле Электрическое поле ЭДС индукции в движущихся проводниках Самоиндукция Самоиндукция Энергия магнитного поля тока Электромагнитное поле Электромагнитное поле Электромагнитное поле
Вопросы и задания Вопросы и задания Электромагнитная индукция
Электромагнитная индукция Электромагнитная индукция Электромагнитная индукция Электромагнитная индукция Электромагнитная индукция Каталог: public -> prezent жүктеу/скачать 445 b. Достарыңызбен бөлісу: |
Дорожно-транспортные происшествия Адвокаты в Карловы Вары | Адвокаты по семейному праву в Карлсбаде, Калифорния
Сострадательный адвокат по семейным делам в округе Сан-Диего
Даже при самых благоприятных обстоятельствах развод является трудным, эмоциональным и событие, изменившее жизнь. Столкнувшись с распадом брака, вы вероятная борьба с эмоциями вины, гнева, одиночества и/или печали, и идея проведения бракоразводного процесса в разгар таких эмоций может быть подавляющим, мягко говоря.
Или адвокаты по разводам в Карловых Варах уверяют вас, что вы не
придется пережить этот опыт самостоятельно.
Как ваша команда по бракоразводным процессам, мы должны гарантировать, что вы примете соответствующие меры. шаги, чтобы обеспечить комфортное будущее для себя и своей семьи, как финансово и эмоционально. Для этого мы предлагаем экспертные услуги по семейному праву. в Сан-Диего, опираясь на опыт целой команды талантливых, новаторских профессиональные юристы, которые хотят помочь вам выйти на другую сторону чувство уверенности в завтрашнем дне.
Наши адвокаты по разводам в Карловых Варах готовы помочь вам на протяжении всего Сан Диего бракоразводного процесса, от первоначальной подачи до посредничество в переговорах опека над детьми и супружеская поддержка.
Стратегическая траектория дела, которую мы используем в Griffith, Young & Lass, разработана
чтобы дать вам наилучшие шансы на успех по самой разумной цене.
Под руководством опытного юриста по семейному праву наша команда начнет с обсуждения
ваши конкретные цели, определяя результаты, наиболее важные для вас в
процесс, а затем принять необходимые меры для защиты ваших прав
и наилучшие интересы на каждом этапе процесса.
Каждый член нашей команды пришел в бизнес по одной и той же причине: помогать людям.
Мы добиваемся успеха, берясь за дела, которые другие бюро разводов не берут, и достижения результатов, которые помогут вам чувствовать себя уверенно в новой жизни впереди ты. Сострадательный в нашем подходе и решительный в нашей стратегии, наш Карловы Вары Адвокаты по разводам разрабатывают веские дела, которые помогают нашим клиентам установить твердая основа, на которой можно начать новую жизнь. Мы более чем готовы сделать то же самое для вас.
Как компания Griffith, Young & Lass может вам помочь
Когда вы становитесь клиентом GYL, вы становитесь нашим приоритетом.
Учитывая эмоциональные, финансовые и юридические последствия развода для вас и вашей семьи, мы стремимся тесно сотрудничать с вами на каждом этапе шаг процесса, чтобы убедиться, что вы получаете поддержку, в которой вы нуждаетесь и которую заслуживаете.
Под руководством нашей команды вы можете рассчитывать на исключительный сервис, открытые
и доступные линии связи, конфиденциальность, уважение и вежливость. Мы знаем, что у каждой истории есть две стороны, и мы здесь, чтобы убедиться,
твое слышно.
Мы знаем, что у каждой истории есть две стороны, и мы здесь, чтобы убедиться,
твое слышно.
Узнайте больше о нашем подходе к разводу и семейному праву, особенно это относится к вашей ситуации. Свяжитесь с адвокатом по семейным делам через наш форму обратной связи или по телефону (858) 371-5569 сегодня! Мы обслуживаем весь Сан-Диего из нашего офиса в Карлсбаде.
Обеспечение спокойствия через юридическую бурю
Вопросы семейного права сложны для всех участников. Наша цель — дать вам свежий взгляд и плавный переход к следующему этапу вашей жизни.
Узнайте больше о нас
«Я очень рекомендую компанию Griffith, Young & Lass всем, кто ищет этичных, честных, трудолюбивых и опытных юристов (подчеркну, что это на самом деле редкие качества в юридической отрасли и…»
— Скотт Г.
«Я не могу сказать достаточно хороших слов о Джоне Гриффите и этой юридической фирме. Каждый человек, с которым я общался, был отзывчивым, умным, вдумчивым и профессиональным. Адвокат Гриффит очень много работал, чтобы…»
— Мишель П.«Она ни перед кем не отступает. Это было лучшее решение, которое я когда-либо принимал, и, надеюсь, оно будет и вашим».
— Ян Р.«С нами легко работать, открыто рассказывает о процессе, устанавливает реалистичные ожидания и всегда помнит о затратах».
— Дженнифер П.«Команда GYL всегда оперативно отвечает на звонки и электронные письма.
— Келси Л. По личному опыту могу сказать, что они не откажутся от вашего дела, пока оно не будет завершено».
По личному опыту могу сказать, что они не откажутся от вашего дела, пока оно не будет завершено».«GYL оказала невероятную поддержку и поддержку в моем разводе. Поскольку мужчина служит в армии, процесс развода и опеки сложен. GYL была чрезвычайно полезна, и я смогла полностью взять на себя опеку над своими детьми. Уже одно это является таким монументальным подвигом».
— Фрэнки С.«Я ненавижу смотреть, как кто-то проходит через битвы за опеку, но если вы находитесь в такой ситуации и нуждаетесь в ком-то, кто заслуживает доверия и отлично разбирается в том, что он делает, то я клянусь, что это место, где можно получить помощь!»
— Эмили Б.«С кем бы я ни переписывался, они всегда были в курсе моего дела и быстро реагировали».
— Кимберли Ф.
«Мой допуск был предоставлен без каких-либо дополнительных вопросов. Я бы порекомендовал эту юридическую команду любому солдату, которому нужна помощь с допуском».
— К. Брукс«Сострадательный и добрый, однако, он будет бороться за вас и ваши интересы. Он спокоен, расчетлив и чрезвычайно умен».
— Энн М.«Она и ее команда были чрезвычайно сострадательны и деликатны со мной, одновременно активно защищая меня».
— Джереми Р.«Профессиональная и краткая помощь была столь необходимым глотком свежего воздуха в лабиринте препятствий и осложнений нашего дела по семейному праву».
— Дэвид Р.
/
Подробнее Отзывы
- Джон Н. Гриффит, эсквайр, CFLS
- Кэти Э. Янг, эсквайр, CFLS
- Эми Дж. Ласс, эсквайр, CFLS
- Ширин Асгари, эсквайр, CFLS
- Ноэль Дж. Слэттери, эсквайр.
- Эрик Каудери, эсквайр.
- Джошуа Йи, эсквайр.
- Шауди Малекзаде, эсквайр.
- Леа Трояновски, эсквайр.
- Грейсон Шарп, эсквайр.
Джон Н.
 Гриффит, эсквайр, CFLS Джон Н. Гриффит, эсквайр, CFLS
Гриффит, эсквайр, CFLS Джон Н. Гриффит, эсквайр, CFLS Партнер
Джон Гриффит занимается исключительно семейным правом с 2009 года. Джон является сертифицированным специалистом по семейному праву, получившим сертификат эксперта в области семейного права Калифорнийским советом по юридической специализации. До открытия Griffith, Young & Lass он работал управляющим партнером одной из крупнейших семейных юридических фирм в Северном округе Сан-Диего.
Просмотр профиля
Кэти Э. Янг, эсквайр, CFLS Кэти Э. Янг, эсквайр, CFLS
Партнер
Кэти Э. Янг преуспевает в делах об опеке над детьми и судебных процессах о переезде. У нее уникальный подход к делам об опеке над детьми, и клиенты Griffith, Young & Lass, как правило, тяготеют к ней в этих делах. С момента прихода в фирму она постоянно проявляла свое усердие и сострадание, представляя клиентов в делах об опеке над детьми и насилии в семье, а в декабре 2011 года она стала партнером Griffith, Young & Lass.

Просмотр профиля
Эми Дж. Ласс, эсквайр, CFLS Эми Дж. Ласс, эсквайр, CFLS
Партнер
Эми Ласс, сертифицированный специалист по семейному праву, родилась в Нью-Йорке и выросла в Сан-Диего, Калифорния. Эми окончила Калифорнийский политехнический университет в Сан-Луис-Обиспо в 2003 году со степенью бакалавра искусств. по экономике со специализацией в области бухгалтерского учета предприятий. Эми получила степень юриста в Юридической школе Томаса Джефферсона и закончила ее с отличием в 2006 году.0005
Просмотр профиля
Ширин Асгари, эсквайр, CFLS Ширин Асгари, эсквайр, CFLS
Ассоциированный
Адвокат Ширин Асгари обладает широким юридическим опытом и занималась вопросами семейного права, уголовного права, коммерческого права и права национальной безопасности.
 В настоящее время она занимается вопросами семейного права и активно защищает права своих клиентов. Она уделяет время и внимание потребностям каждого клиента и уникальным обстоятельствам их дела.
В настоящее время она занимается вопросами семейного права и активно защищает права своих клиентов. Она уделяет время и внимание потребностям каждого клиента и уникальным обстоятельствам их дела.Просмотр профиля
Ноэль Дж. Слэттери, эсквайр. Ноэль Дж. Слэттери, эсквайр.
Ассоциированный
Ноэль Дж. Слэттери, эсквайр. имеет степень бакалавра исполнительских искусств/актерского мастерства в Колледже Эмерсон в Бостоне и степень доктора юридических …
Просмотр профиля
Эрик Каудери, эсквайр. Эрик Каудери, эсквайр.
Ассоциированный
Эрик Каудери получил степень бакалавра и магистра, а затем получил степень доктора права в Университете Золотых Ворот в рамках программы юристов с отличием. Он был принят в Калифорнийскую коллегию адвокатов в 2013 году и с тех пор усердно работает в этой области.
 Применяя индивидуальный подход к каждому делу, Эрик Каудери стремится работать с клиентами, чтобы помочь им пройти часто запутанный и сложный юридический процесс развода.
Применяя индивидуальный подход к каждому делу, Эрик Каудери стремится работать с клиентами, чтобы помочь им пройти часто запутанный и сложный юридический процесс развода.Просмотр профиля
Джошуа Йи, эсквайр. Джошуа Йи, эсквайр.
Ассоциированный
Адвокат Джошуа Йир получил степень бакалавра политических наук в Калифорнийском университете в Сан-Диего. Джошуа получил степень доктора юридических наук в Университете Сан-Франциско. Его опыт работы с местным сертифицированным специалистом по семейному праву укрепил его желание стать адвокатом по семейному праву. Став адвокатом, Джош занимается исключительно семейным правом.
Просмотр профиля
Шауди Малекзаде, эсквайр. Шауди Малекзаде, эсквайр.
Ассоциированный
Шауди Малекзаде — адвокат по семейным делам в Карловых Варах в Griffith, Young & Lass, защищающий права и интересы семей Южной Калифорнии в различных делах по семейному праву, таких как опекунство над детьми, алименты, супружеская поддержка и разделение сообщества.
 имущество. Она стремится обеспечить эффективное юридическое представительство наших клиентов, активно отстаивая их законные права и предлагая сострадательные юридические консультации.
имущество. Она стремится обеспечить эффективное юридическое представительство наших клиентов, активно отстаивая их законные права и предлагая сострадательные юридические консультации.Просмотр профиля
Леа Трояновски, эсквайр. Леа Трояновски, эсквайр.
Ассоциированный
Леа Трояновски — адвокат Гриффита, Янга и Ласса, присоединившаяся к фирме в марте 2021 года. Ее прагматичный и уравновешенный подход к семейному праву позволил ей добиться успеха даже в самых эмоциональных делах по семейному праву. Леа эффективно представляла интересы клиентов в широком спектре разбирательств по семейным делам, но ее особенно привлекали дела о применении запретительного судебного приказа о домашнем насилии.
Просмотр профиля
Грейсон Шарп, эсквайр. Грейсон Шарп, эсквайр.

Ассоциированный
Грейсон Шарп получил степень бакалавра искусств в области коммуникаций в Калифорнийском государственном университете во Фресно. После …
Просмотр профиля
Познакомьтесь с нашей командой
- Развод
- Семейное право
- Посредничество
- Соглашения
- Планирование недвижимости
О наших услугах по бракоразводным и семейным делам
Сертифицированные специалисты по семейному праву
Благодаря многолетнему опыту и таланту, наши адвокаты по бракоразводным процессам иметь опыт работы со всеми типами дел по семейному праву и бракоразводным процессам. Области нашей практики включают, но не ограничиваются:
- Развод с крупными активами
- Насилие в семье и чрезвычайные запретительные судебные приказы
- Борьба за права отцов и родителей, не являющихся опекунами
- Права бабушек и дедушек и предоставление временной родительской опеки (например, parte) в чрезвычайных ситуациях
- Разводы, затронутые иммиграционными, добрачными соглашениями и исками о разделе имущества
Для вашего удобства, мы предлагаем встречи в нерабочее время и в выходные дни по мере необходимости .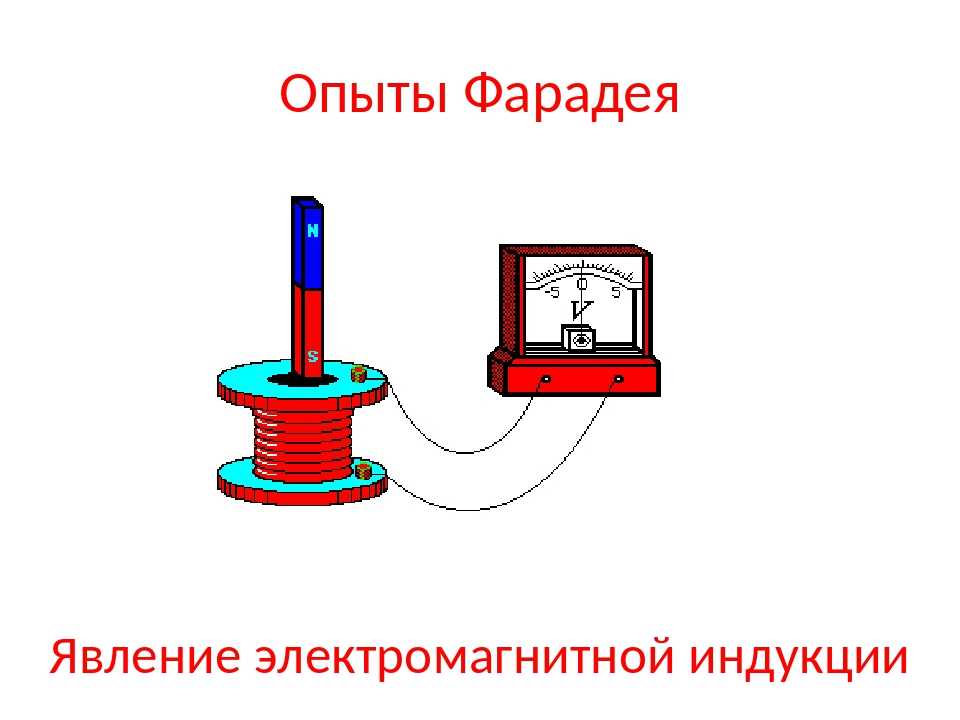 В некоторых случаях мы может даже включать встречи в тот же день и планы платежей для тех,
чьи ситуации оправдывают это. Как мы уже говорили ранее, вы наш приоритет, и мы
готовы помочь в случае возникновения проблемы, требующей немедленного внимания.
В некоторых случаях мы может даже включать встречи в тот же день и планы платежей для тех,
чьи ситуации оправдывают это. Как мы уже говорили ранее, вы наш приоритет, и мы
готовы помочь в случае возникновения проблемы, требующей немедленного внимания.
Во время первой консультации ваш адвокат по семейным делам объяснит детали процесса развода в Калифорнии и помочь вам подготовиться к ваше предстоящее дело. Мы, конечно, будем вести переговоры об урегулировании, но будет готов предстать перед судом в случае необходимости.
В GYL мы стремимся вести нашу юридическую практику ответственно и этично. Наши услуги заслуживают доверия, а наши адвокаты честны — у нас по-другому нельзя.
Свяжитесь с нами для консультации с юристом по семейным делам рядом с вами! Позвоните (858) 371-5569 или отправьте онлайн контактная форма здесь!
Связаться
В GYL важна ваша история — помощь клиентам — это то, что помогает нам добиваться успеха. Мы не торопимся, чтобы узнать наших клиентов и понять их обстоятельства. Это позволяет нам разработать уникальное и индивидуальное решение, которое наилучшим образом соответствует потребностям наших клиентов.
Мы не торопимся, чтобы узнать наших клиентов и понять их обстоятельства. Это позволяет нам разработать уникальное и индивидуальное решение, которое наилучшим образом соответствует потребностям наших клиентов.
СВЯЖИТЕСЬ С НАМИ
Избранные статьи
Оставайтесь в курсеВопросы для размышления при рассмотрении вопроса о разводе
Посмотреть статью
- Развод
Чего ожидать от консультации по разводу
Посмотреть статью
- Развод
Вопросы, которые следует задать потенциальному адвокату по разводам
Посмотреть статью
- Развод
Подробнее
Ресурсы для клиентов
Мы здесь, чтобы провести вас через этот процесс- Приглашаем юриста по разводам
- Ваша первая встреча с GYL
- Часто задаваемые вопросы
Майкл Фарадей — Super Mario Wiki, энциклопедия Mario
Из Super Mario Wiki, энциклопедия Mario
Перейти к навигацииПерейти к поиску
Майкл Фарадей был английским ученым, изучавшим области физики и химии, в частности идентификацией бензола. Согласно Машина времени Марио , Фарадей находился в своей лаборатории в Лондоне примерно в 1831 году, когда Баузер украл его Магнит. Затем он встречает Марио после того, как последний сам путешествует во времени, чтобы вернуть Магнит. Поскольку Марио не знает, что Магнит принадлежит Фарадею, если он все равно разговаривает с Фарадеем, он спрашивает, открыл ли он Фарадея, и Фарадей отвечает, что открыл.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Авиатрикс Эми Джонсон и полет в Австралию пролетев 18 000 км, она стала первой женщиной-пилотом, совершившей в одиночку перелет из Англии в Австралию.
Эми Джонсон – Ранние годы
Эми Джонсон была увлеченной спортсменкой, которая играла в хоккей и крикет. В 14 лет она потеряла несколько передних зубов из-за крикетного мяча. Поскольку она происходила из небедной семьи — ее отец был преуспевающим рыбным торговцем, — семья могла позволить себе дорогих дантистов, и Эми получила хорошие искусственные зубы. Тем не менее, она чувствовала себя изуродованной, и ее уверенность в себе страдала. Это часто рассматривается как причина депрессии и гиперчувствительности, от которых она позже страдала. Эми Джонсон училась в Шеффилдском университете. После получения степени бакалавра искусств она уехала в Лондон, где застенчивая молодая женщина устроилась секретаршей, а затем в рекламное агентство. Зимой 1928/29 она начала свои уроки пилотирования в Лондонском авиаклубе. Один час стоил 5 фунтов, что составляло ее недельную зарплату.
Зимой 1928/29 она начала свои уроки пилотирования в Лондонском авиаклубе. Один час стоил 5 фунтов, что составляло ее недельную зарплату.
Первый самостоятельный полет
9 июня 1929 года совершила свой первый самостоятельный полет, а в августе получила лицензию пилота. В отличие от других женщин-пилотов своего времени, Эми Джонсон также интересовалась механикой и сама обслуживала и ремонтировала свой самолет. Поскольку работа секретарем ее не удовлетворяла, она сразу же согласилась, когда начальник механиков аэропорта захотел нанять ее в качестве подмастерья механика. Она была первой женщиной в Великобритании, сдавшей экзамен на авиамеханика 19 декабря.29. Ее мечтой было стать профессиональным пилотом, но в то время летным навыкам женщины никто не доверял.
Что-то зрелищное
Благодаря финансовой поддержке отца она смогла бросить работу секретаря и уделять все необходимое время сдаче экзаменов на сертификат B (частный пилот). Чтобы добиться признания, она запланировала нечто впечатляющее: она хотела полететь в одиночку в Австралию и побить рекорд Берта Хинклера в 1928 дней в 15½. На деньги своего отца она купила Gypsy Moth с одним двигателем у de Havilland, покрасила его в зеленый цвет и окрестила машину. , сейчас выставленная в лондонском Музее науки, по названию компании ее отца Джейсон . В конце 1920-х и начале 1930-х годов конкуренция за спонсоров смелых полетов была чрезвычайно жесткой. После многих усилий и неудач британский нефтяной предприниматель лорд Уэйкфилд наконец проявил готовность взять на себя половину расходов и предоставить топливо во время остановок этапа. Эми Джонсон тщательно готовилась к полету. 5 мая 1930 года она вылетела из аэропорта Кройдон на своем Gypsy Moth. Поскольку в то время она была еще совершенно неизвестна, на взлете присутствовали только ее отец и несколько товарищей-пилотов — пресса ничего не хотела знать о неопытном пилоте, чье самое большое расстояние на сегодняшний день составляло 237 км от Лондона. в Кингстон-апон-Халл.
На деньги своего отца она купила Gypsy Moth с одним двигателем у de Havilland, покрасила его в зеленый цвет и окрестила машину. , сейчас выставленная в лондонском Музее науки, по названию компании ее отца Джейсон . В конце 1920-х и начале 1930-х годов конкуренция за спонсоров смелых полетов была чрезвычайно жесткой. После многих усилий и неудач британский нефтяной предприниматель лорд Уэйкфилд наконец проявил готовность взять на себя половину расходов и предоставить топливо во время остановок этапа. Эми Джонсон тщательно готовилась к полету. 5 мая 1930 года она вылетела из аэропорта Кройдон на своем Gypsy Moth. Поскольку в то время она была еще совершенно неизвестна, на взлете присутствовали только ее отец и несколько товарищей-пилотов — пресса ничего не хотела знать о неопытном пилоте, чье самое большое расстояние на сегодняшний день составляло 237 км от Лондона. в Кингстон-апон-Халл.
Горы Таурус
Оглядываясь назад, Джонсон писала, что была очень наивна и недооценивала опасности приключений.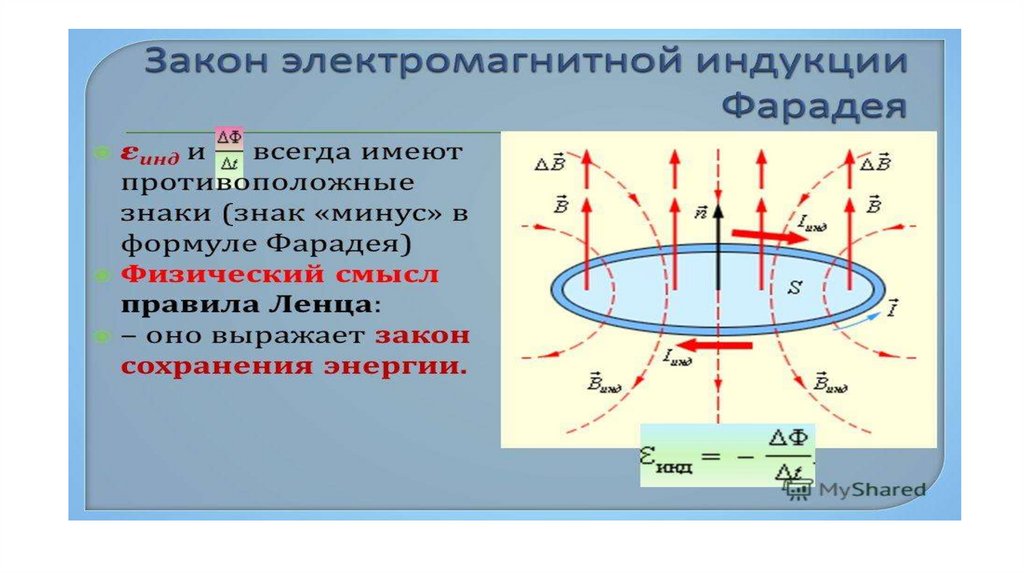 Из Лондона в Стамбул проблем не было. В бортовом журнале Эми Джонсон пожаловалась лишь на выхлопные газы из дополнительных баков, установленных вместо пассажирского сиденья. На третий день после старта она столкнулась с первым серьезным испытанием: горы Тавр были высотой 3600 м, а ее тяжело нагруженный самолет мог безопасно подняться только до 3300 м. Горы Таурус были самыми высокими горами в мире. После тщательных поисков в тумане она наконец нашла железнодорожную ветку Багдадской железной дороги, по которой летел, прежде чем, наконец, с облегчением приземлилась в Алеппо, Сирия.
Из Лондона в Стамбул проблем не было. В бортовом журнале Эми Джонсон пожаловалась лишь на выхлопные газы из дополнительных баков, установленных вместо пассажирского сиденья. На третий день после старта она столкнулась с первым серьезным испытанием: горы Тавр были высотой 3600 м, а ее тяжело нагруженный самолет мог безопасно подняться только до 3300 м. Горы Таурус были самыми высокими горами в мире. После тщательных поисков в тумане она наконец нашла железнодорожную ветку Багдадской железной дороги, по которой летел, прежде чем, наконец, с облегчением приземлилась в Алеппо, Сирия.
Из Багдада в Аллахабад – Летающий секретарь
Следующим этапом она должна была доставить ее в Багдад, но незадолго до финиша она попала в песчаную бурю. Джонсон ничего не видел, а ее непарный шелкопряд не был оборудован для слепого полета. Ветер унес ее в пустыню. Наконец, из соображений безопасности она приземлилась посреди пустыни, надеясь не попасть в глубокий песок. После трех часов ожидания шторм утих, и она смогла лететь дальше. В Багдаде у нее не было больше сил, чтобы самостоятельно выполнять работы по техническому обслуживанию, и она была вне себя от радости, когда ее взял на себя механик Imperial Airways. Когда она прибыла в Карачи на следующий день, она уже на два дня опередила пионера австралийской авиации Берта Хинклера. Внезапно о «Летучем секретаре» стало известно, и пресса запестрела сообщениями о ее полете. Она была очень удивлена, когда приехала в Аллахабад и была принята группой журналистов.
В Багдаде у нее не было больше сил, чтобы самостоятельно выполнять работы по техническому обслуживанию, и она была вне себя от радости, когда ее взял на себя механик Imperial Airways. Когда она прибыла в Карачи на следующий день, она уже на два дня опередила пионера австралийской авиации Берта Хинклера. Внезапно о «Летучем секретаре» стало известно, и пресса запестрела сообщениями о ее полете. Она была очень удивлена, когда приехала в Аллахабад и была принята группой журналистов.
Из Рангуна в Дарвин
Из Рангуна маршрут шел в Сингапур. Над морем между Сингапуром и Явой ее снова застал шторм, из которого она не могла выбраться в течение шести часов. Когда она прибыла на Яву, ей снова пришлось совершить аварийную посадку из-за поврежденных штормом крыльев. За неимением другого материала она заделала порванную ткань липкими полосками. После Явы перед ней лежало Тиморское море, которого боялись все лоцманы: 800 км над водой. Чтобы не уснуть, она пела, пока не достигла острова Мелвилл у австралийского континента.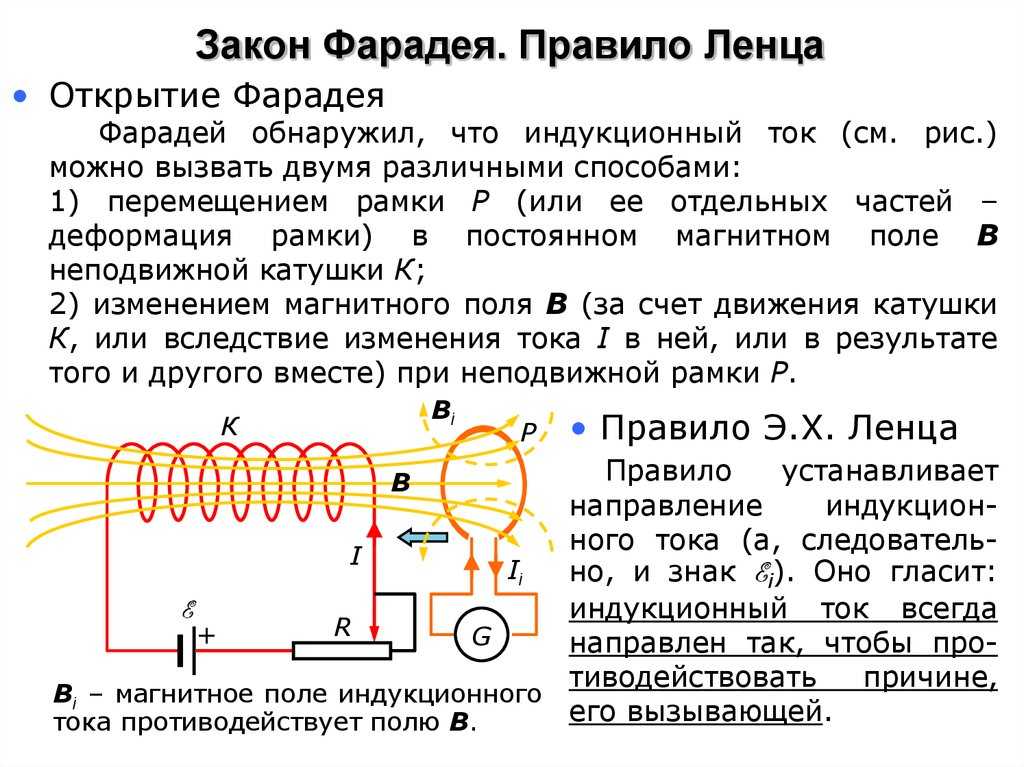 Эми Джонсон без проблем приземлилась в Дарвине 24 мая. Ей потребовалось на четыре дня больше полета, чем Берту Хинклеру. Тем не менее, этот полет сделал ее звездой среди летчиц. В ее честь даже сочинили две эстрадные песни. Застенчивую Эми Джонсон передавали из рук в руки, чтобы получать подарки и почести, читать лекции и писать отчеты. Вскоре суета стала для нее невыносимой. Когда она узнала от отца, что он подписал эксклюзивный контракт от ее имени с Daily Mail , у нее случился нервный срыв.
Эми Джонсон без проблем приземлилась в Дарвине 24 мая. Ей потребовалось на четыре дня больше полета, чем Берту Хинклеру. Тем не менее, этот полет сделал ее звездой среди летчиц. В ее честь даже сочинили две эстрадные песни. Застенчивую Эми Джонсон передавали из рук в руки, чтобы получать подарки и почести, читать лекции и писать отчеты. Вскоре суета стала для нее невыносимой. Когда она узнала от отца, что он подписал эксклюзивный контракт от ее имени с Daily Mail , у нее случился нервный срыв.
Дальнейшие достижения
Эми Джонсон поднялась в воздух. В июле 1931 года Джонсон и ее второй пилот Джек Хамфрис стали первыми пилотами, совершившими перелет из Лондона в Москву всего за один день. Они преодолели 2830-километровое путешествие примерно за 21 час, а оттуда продолжили свой путь через Сибирь и в Токио, установив рекордное время полета из Великобритании в Японию. Полет был совершен на самолете G-AAZV de Havilland DH.80 Puss Moth, получившем имя «9».0730 Джейсон II ». Всего через год пилот установил рекорд одиночного перелета из Лондона в Кейптаун, Южная Африка, на мотыльке G-ACAB под номером Desert Cloud. Ее следующие полеты были в составе дуэта. Она вылетела без пересадок из Пендин-Сэндс, Южный Уэльс, в Соединенные Штаты. Однако у их самолета закончилось топливо, и он совершил аварийную посадку в Бриджпорте, Коннектикут. В результате аварии оба пилота были ранены, но получили парад бегущей строки на Уолл-стрит.
Всего через год пилот установил рекорд одиночного перелета из Лондона в Кейптаун, Южная Африка, на мотыльке G-ACAB под номером Desert Cloud. Ее следующие полеты были в составе дуэта. Она вылетела без пересадок из Пендин-Сэндс, Южный Уэльс, в Соединенные Штаты. Однако у их самолета закончилось топливо, и он совершил аварийную посадку в Бриджпорте, Коннектикут. В результате аварии оба пилота были ранены, но получили парад бегущей строки на Уолл-стрит.
Эми Джонсон в Индии Изображение пользователя Wikimedia Dabbler
«Летающие любовники»
В Англии вокруг Эми Джонсон было необычно тихо. Ранее неизвестный шотландский пилот по имени Джеймс «Джим» Аллан Моллисон преодолел «ее» австралийский маршрут всего за 9 дней и, таким образом, опередил ее в рейтинге. Она познакомилась с Джимом Моллисоном лично в июне 1932 года в Южной Африке, где восстановилась после одиночного перелета из Лондона в Кейптаун. Джим пролетел по тому же маршруту, побив существующий рекорд. Два удачливых пилота уже были сведены друг с другом при первой встрече, а уже при следующей встрече в Лондоне через несколько недель Джим сделал Эми предложение руки и сердца. Британская пресса отметила свадьбу двух своих любимцев 19 июля.32. Сразу после свадьбы Эми Джонсон-Моллисон побила рекорд мужа на маршруте Лондон-Кейптаун.
Два удачливых пилота уже были сведены друг с другом при первой встрече, а уже при следующей встрече в Лондоне через несколько недель Джим сделал Эми предложение руки и сердца. Британская пресса отметила свадьбу двух своих любимцев 19 июля.32. Сразу после свадьбы Эми Джонсон-Моллисон побила рекорд мужа на маршруте Лондон-Кейптаун.
29 июля 1932 года Эми Джонсон и Джим Моллисон поженились.
Последний полет Эми Джонсон
Джонсон была повышена до первого офицера примерно в 1940 году, когда она присоединилась к вспомогательному авиатранспортному подразделению, которое отвечало за транспортировку самолетов Королевских ВВС по стране. Всего год спустя отважный пилот совершил перелет на самолете Airspeed Oxford для ATA из Блэкпула в Королевские ВВС Кидлингтон недалеко от Оксфорда. Она сбилась с курса в неблагоприятных погодных условиях, и предполагается, что у нее закончилось топливо. Джонсон выручила, когда ее самолет врезался в устье Темзы. Ее парашют был замечен, когда она спускалась в воду, и известно, что в тот момент она была еще жива. Однако условия были плохими, и женщина столкнулась с очень сильным морем и сильным приливом. К тому же шел снег и было очень холодно. Во время попытки ближайшей команды лодки спасти ее, она умерла, и ее тело так и не удалось найти.
Однако условия были плохими, и женщина столкнулась с очень сильным морем и сильным приливом. К тому же шел снег и было очень холодно. Во время попытки ближайшей команды лодки спасти ее, она умерла, и ее тело так и не удалось найти.
Обстоятельства, при которых погибла женщина, до сих пор остаются загадкой. Точная причина полета до сих пор является государственной тайной, и есть некоторые свидетельства того, что помимо Джонсона и Флетчера, пытавшихся ее спасти, в воде был замечен еще третий человек, который также погиб. Кто был третьим лицом, пока неизвестно. В 1999 году официально сообщалось, что Эми Джонсон могла быть сбита. Том Митчелл из Кроуборо, Суссекс, заявил, что «причина, по которой Эми была сбита, заключалась в том, что она дала неправильный цвет дня (сигнал для идентификации самолета, известный всем британским силам) по радио».0474». По-видимому, стало ясно, что это была Эми Джонсон, которая управляла самолетом только на следующий день, и Митчелл сказал, что « офицеры сказали нам никогда никому не рассказывать о том, что произошло ».
Ссылки и дополнительная литература:
- [1] Эми Джонсон в Музее науки
- [2] Эми Джонсон на BBC
- [3] Эми Джонсон в Викиданных
- [4] Кто такая Эми Джонсон? (тур Amy Aviation по Великобритании), Amy’s Aviation @ youtube
- [5] «На случай, если вы никогда не слышали об Эми Джонсон». Ассоциация экспериментальных самолетов.
- [6] Несбитт, Рой. «Что случилось с Эми Джонсон? » Airplane Monthly (Часть 1), Vol. 16, нет. 1, январь 1988 г., (Часть 2) Том. 16, нет. 2 февраля 1988 г.
- [7] «Мисс Эми Джонсон». Канберра Таймс . Том. 4, нет. 813. Австралийская столичная территория, Австралия. 30 мая 1930 г.
- [8] Хронология женщин-пионеров авиации, родившихся до 19 лет.05, через Викиданные
Глава 15.
 Электромагнитные машины. Карточки Эми Паквуд
Электромагнитные машины. Карточки Эми ПаквудЧто такое магнитное поле?
Область приложения силы к магнитному материалу
Как можно представить магнитные поля?
полевых линий?
В каком направлении движутся линии поля?
С севера на юг
Как напряженность магнитного поля представлена силовыми линиями?
Чем сильнее поле, тем ближе друг к другу будут линии поля
Что такое нейтральная точка?
Точка, в которой магнитные поля нейтрализуются
Что будет генерироваться вокруг провода, по которому течет электрический ток?
Магнитное поле
Для чего используется правило хвата правой рукой?
Определение направления магнитного поля вокруг провода с током
Что такое правило хвата правой рукой?
Направление большого пальца = ток
Изгиб пальцев = магнитное поле
Что такое соленоид?
Форма электромагнита — катушка/несколько катушек проволоки, которые действуют как стержневой магнит при прохождении тока
Что происходит, когда провод с током находится во внешнем магнитном поле?
На провод действует сила
(поскольку магнитные поля вокруг провода и внешнее магнитное поле взаимодействуют, поэтому силовые линии вокруг магнита сжимаются)
Что происходит, когда проводник с током находится во внешнем магнитном поле, но ток идет параллельно силовым линиям магнитного поля?
Сила не действует
Когда провод находится во внешнем магнитном поле, в каком направлении будет действовать сила, действующая на провод?
перпендикулярно магнитному полю и направлению тока
Для чего используется правило левой руки Флеминга?
Определение направления силы на проводе с током в магнитном поле
Что такое правило левой руки Флеминга?
большой палец = сила
указательный палец = поле
второй палец = текущий
По какому уравнению находят величину силы, действующей на провод с током во внешнем магнитном поле?
F = сила BIL
= напряженность магнитного поля x сила тока x длина провода
Каким символом обозначается напряженность магнитного поля?
Что такое определение напряженности магнитного поля?
Сила, действующая на один метр провода, по которому течет ток в один ампер под прямым углом к магнитному полю
Как иначе называется напряженность магнитного поля? 9-2
Веберов на квадратный метр
Что такое плотность магнитного потока?
Количество силовых линий на единицу площади
(напряженность магнитного поля)
Является ли напряженность магнитного поля векторной или скалярной величиной?
вектор
Как работает двигатель?
Контур с током помещен во внешнее магнитное поле, которое заставляет его вращаться
Коммутатор с разъемным кольцом меняет направление тока каждые пол-оборота, чтобы двигатель вращался в постоянном направлении
Что делает коммутатор с разъемным кольцом?
Изменяет направление тока в контуре двигателя каждые пол-оборота, чтобы поддерживать его вращение в постоянном направлении
Как работает асинхронный двигатель?
Магнитное поле изменяется вокруг катушки с проводом, который может свободно двигаться, индуцируя ток и заставляя провод вращаться
Что такое плотность магнитного потока?
Напряженность магнитного поля на единицу площади
Какое уравнение для нахождения магнитного потока?
Φ = магнитный поток BA
= напряженность магнитного поля x площадь
Какой символ обозначает магнитный поток?
Что такое потокосцепление?
Поток в ряде связанных катушек (например, в соленоиде0
Какое уравнение для потокосцепления?
поток x число витков
ΦN
Что происходит, когда проводник проходит через внешнее магнитное поле?
Электродвижущая сила (ЭДС) ИНДУЦИРОВАНА по проводнику
Если он является частью полной цепи, то будет протекать ток
Почему в проводнике с током, движущемся во внешнем магнитном поле, возникает ЭДС?
На электроны действует сила, заставляющая их накапливаться на одном конце провода
Это вызывает разность потенциалов -ЭДС- на проводе
Что такое электромагнитная индукция?
Когда индуцируется электродвижущая сила (проводником, движущимся через магнитное поле) и течет ток (если цепь замкнута)
Что вызывает появление электродвижущей силы?
Изменения потока
Там, где имеется относительное движение между проводником и магнитом
Что происходит, когда линии потока «перерезаются»?
Наводится ЭДС
(и ток будет течь, если цепь замкнута)
Что такое закон Фарадея?
ЭДС индукции прямо пропорциональна скорости изменения потокосцепления
Какое уравнение для ЭДС индукции?
(закон Фарадея)
ЭДС = изменение потока/затраченное время
ЭДС = Δ(ΦN)/Δt
Как графически определить величину ЭДС?
График зависимости градиента потокосцепления от времени
ΦN/t
Как графически определить изменение потока?
Площадь под графиком зависимости ЭДС от времени
ЭДС/т
Почему ЭДС индукции может быть задана Blv?
Поток определяется формулой Φ = BA
A = xl, которая представляет собой длину x пройденное расстояние
Φ = Blx
ЭДС = Φ/t = Blx/t
v = x/t
ЭДС = Blv
Что такое закон Ленца?
ЭДС индукции всегда имеет такое направление, чтобы противодействовать вызвавшему ее изменению
Как можно объединить закон Ленца и закон Фарадея, чтобы получить уравнение для ЭДС индукции?
ЭДС = -d(ΦN)/dt
(знак минус только для того, чтобы показать, что направление ЭДС противоположно вызвавшим ее изменениям)
В каком направлении будет течь ток, если в полной цепи индуцируется ЭДС?
То же направление, что и ЭДС
При использовании правила левой руки Флеминга для ЭДС индукции, в каком направлении указывает большой палец?
Направление, противоположное движению проводника, поскольку сила сопротивления противоположна направлению движения
Для чего используются трансформаторы?
Изменение напряжения на переменный ток
Как в трансформаторах возникает переменный ток во второй катушке?
Переменный ток в первой катушке создает изменяющееся магнитное поле. Он проходит через железный сердечник. Изменение потока, испытываемого второй катушкой, вызывает переменную ЭДС индукции, которая вызывает протекание переменного тока
Он проходит через железный сердечник. Изменение потока, испытываемого второй катушкой, вызывает переменную ЭДС индукции, которая вызывает протекание переменного тока
Какое уравнение идеального трансформатора?
Vp/Vs = Np/Ns
(N = количество витков в катушке)
Что делают повышающие трансформаторы?
Как?
Увеличить напряжение
За счет большего количества витков вторичной обмотки
Что делают понижающие трансформаторы?
Как?
Уменьшить напряжение
За счет меньшего количества витков вторичной обмотки
Что такое символ постоянства?
Какое уравнение для перманентности?
Λ = мкА/л
проницаемость = (проницаемость x площадь поперечного сечения)/длина
Что означает более высокая проницаемость материала?
Более высокий поток, индуцируемый в нем при заданном числе витков тока
Как бы вы увеличили проницаемость сердечника трансформатора?
— Большая площадь поперечного сечения
— Меньшая длина
— Изготовлен из материала с большей проницаемостью (например, железа)
Будет ли магнитная цепь работать в вакууме/на воздухе?
да
(но проницаемость намного ниже, поэтому величина потока резко уменьшится)
Какие проблемы может вызвать увеличение толщины сердечника трансформатора (для увеличения проводимости)?
Проводимость катушек из медного провода уменьшится, что приведет к большим потерям энергии
Медные катушки имеют наибольшую проводимость, когда есть наибольшее количество витков с наименьшей длиной провода, т.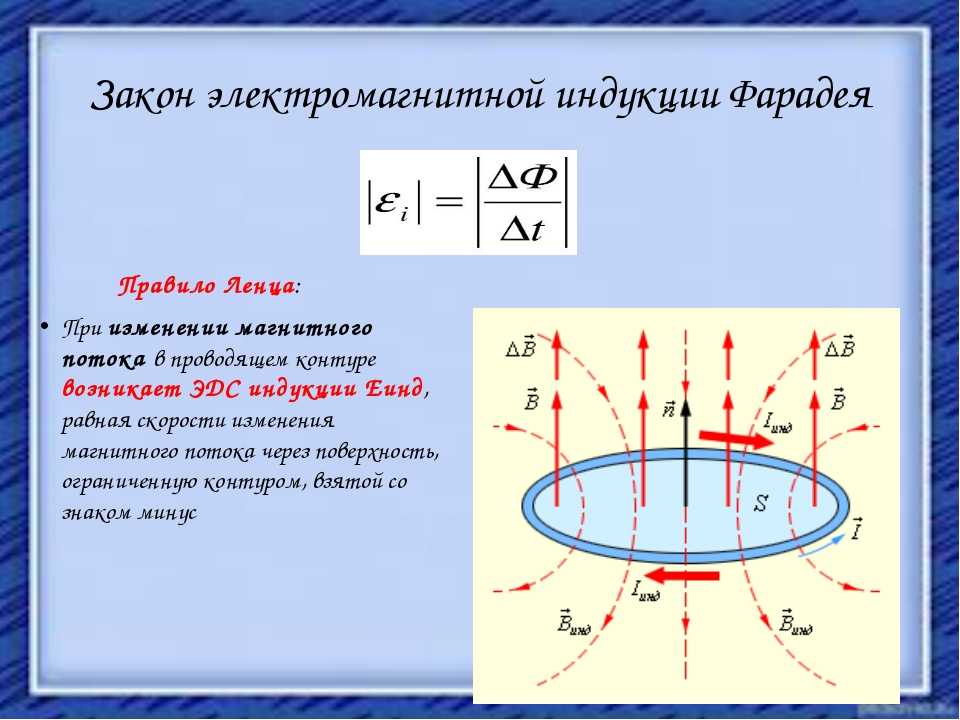 е. плотные катушки с малым радиусом
е. плотные катушки с малым радиусом
КПД трансформаторов 100%?
Что происходит с потерями энергии в трансформаторах?
В основном теряется в виде тепла от вихревых токов/токов в медных проводах, проходящих через сопротивление
Что такое вихревые токи в трансформаторах?
Токи индуцируются изменением потока в железном сердечнике в направлении, противоположном первоначальному току
Как минимизировать вихревые токи в трансформаторах?
Сердечник ламинирован слоями изолятора. Магнитная цепь не будет разорвана, так как она может проходить через изоляторы, но электрическая цепь для вихревых токов будет разорвана, то есть они не смогут протекать должным образом 92R, поэтому меньший ток означает меньшие тепловые потери при прохождении тока через сопротивление
Это более эффективно
Какое напряжение электричества используется в домах?
Какое примерно напряжение используется для передачи по национальной сети?
400, 000В
Что такое генератор?
Генератор переменного тока
Что делают генераторы/динамо?
Преобразование кинетической энергии в электрическую
Как работают генераторы/динамо?
Электрический ток возникает при вращении проводящей катушки в магнитном поле
Что у генераторов вместо коллектора с разрезным кольцом?
контактные кольца и щетки
Для генератора переменного тока, как часто меняется направление выходного напряжения и тока?
Каждые пол-оборота
Быстрое зондирование с электропереносом для повышения чувствительности обнаружения в иммуноанализах в геле
- Список журналов
- Рукописи авторов HHS
- PMC7552878
Анальные методы.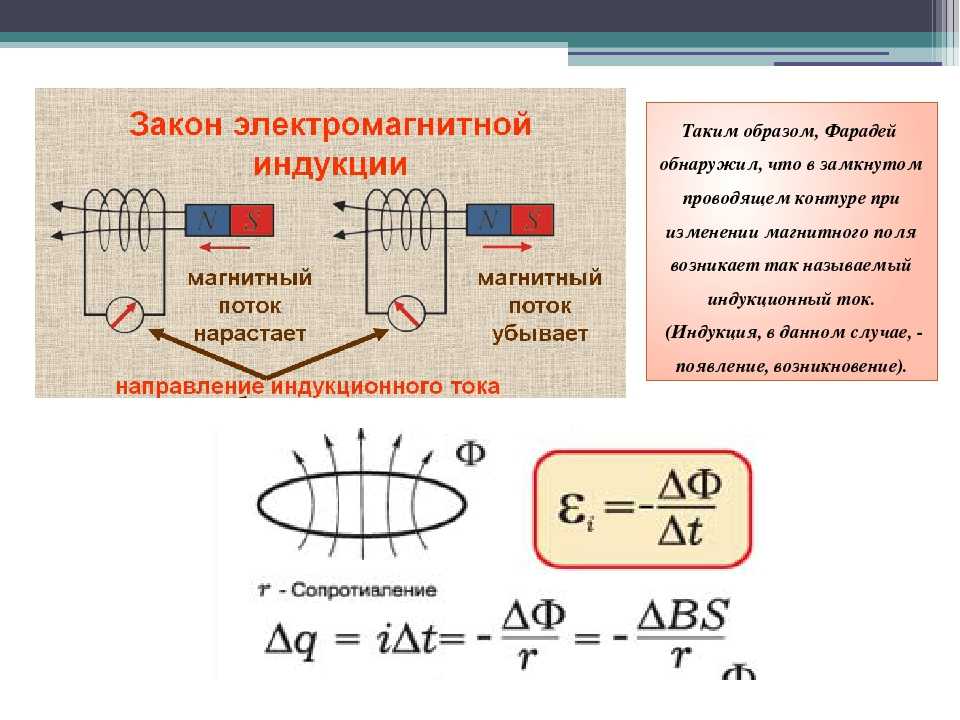 Авторская рукопись; доступно в PMC 2021 8 октября.
Авторская рукопись; доступно в PMC 2021 8 октября.
Опубликовано в окончательной редакции как:
Анальные методы. 2020 8 октября; 12(38): 4638–4648.
doi: 10.1039/d0ay01203c
PMCID: PMC7552878
NIHMSID: NIHMS1626807
PMID: 33030469
, a , b and a, b, c, *
Author information Copyright and License information Disclaimer
- Дополнительные материалы
Электроперенос белков в обычном вестерн-блоттинге облегчает обнаружение белков с разделением по размеру с помощью диффузионного иммунозондирования, поскольку аналиты переносятся из геля для определения размера пор на блоттинговую мембрану для обнаружения. Однако этот дополнительный этап переноса может ухудшить чувствительность обнаружения из-за потери белка и неправильной локализации белка. Чтобы решить проблемы, связанные с переносом белка, иммуноанализы в геле иммобилизуют целевые белки на матрице гидрогеля для последующего иммунозондирования в геле. Тем не менее, чувствительность обнаружения при диффузионном иммунозондировании гидрогелей определяется размером пор геля по отношению к размеру зонда, а иммунозондирование в геле приводит к (i) снижению концентрации зонда в геле по сравнению с окружающим свободным раствором и (ii) замедлению перенос зонда в гель по сравнению с диссоциацией иммунокомплекса. Здесь мы демонстрируем электротрансферное зондирование для эффективного и быстрого иммунозондирования иммуноанализов в геле. Важно отметить, что зонд (а не целевой белок) электропереносится из инертного крупнопористого «загрузочного геля» в мелкопористый гель для определения размера белка. Электрическое поле используется в качестве настраиваемого параметра скорости электромиграции, обеспечивая электропереносное зондирование фундаментальным преимуществом перед диффузионным зондированием. Используя зондирование с электропереносом, мы наблюдаем увеличение концентрации зонда, загруженного в гель, в 6,5 ± 0,1 раза при сокращении времени примерно в 82 раза и уменьшение концентрации зонда, оставшейся в геле после выгрузки, в 2,7 ± 0,4 раза при сокращении времени примерно в 180 раз (по сравнению с диффузионным зондированием).
Тем не менее, чувствительность обнаружения при диффузионном иммунозондировании гидрогелей определяется размером пор геля по отношению к размеру зонда, а иммунозондирование в геле приводит к (i) снижению концентрации зонда в геле по сравнению с окружающим свободным раствором и (ii) замедлению перенос зонда в гель по сравнению с диссоциацией иммунокомплекса. Здесь мы демонстрируем электротрансферное зондирование для эффективного и быстрого иммунозондирования иммуноанализов в геле. Важно отметить, что зонд (а не целевой белок) электропереносится из инертного крупнопористого «загрузочного геля» в мелкопористый гель для определения размера белка. Электрическое поле используется в качестве настраиваемого параметра скорости электромиграции, обеспечивая электропереносное зондирование фундаментальным преимуществом перед диффузионным зондированием. Используя зондирование с электропереносом, мы наблюдаем увеличение концентрации зонда, загруженного в гель, в 6,5 ± 0,1 раза при сокращении времени примерно в 82 раза и уменьшение концентрации зонда, оставшейся в геле после выгрузки, в 2,7 ± 0,4 раза при сокращении времени примерно в 180 раз (по сравнению с диффузионным зондированием). Затем мы применяем зондирование с электропереносом для обнаружения OVA, иммобилизованного в геле, и добиваемся увеличения отношения сигнал/шум в 4,1 ± 3,4 раза и сокращения общей продолжительности иммунозондирования в 30 раз по сравнению с диффузионным зондированием. Мы демонстрируем зондирование с электропереносом как значительно более быстрый метод иммунозондирования для повышения чувствительности определения размера белка в иммуноанализе в геле.
Затем мы применяем зондирование с электропереносом для обнаружения OVA, иммобилизованного в геле, и добиваемся увеличения отношения сигнал/шум в 4,1 ± 3,4 раза и сокращения общей продолжительности иммунозондирования в 30 раз по сравнению с диффузионным зондированием. Мы демонстрируем зондирование с электропереносом как значительно более быстрый метод иммунозондирования для повышения чувствительности определения размера белка в иммуноанализе в геле.
Белки являются ключевыми движущими силами целого ряда биологических процессов, 1 и количественный анализ белков из биологических образцов является важным показателем для понимания состояния клеток и тканей. 2 Обнаружение белков можно проводить с помощью иммуноанализа в геле, при котором белки иммобилизуют на гидрогелевой матрице для последующего иммунозондирования. Иммобилизация белка в геле также может обеспечить структурную целостность биологического образца, оценить локализацию белка и определить размер белка. 3,4,5,6,7 Зондирование иммуноанализа в геле включает (i) загрузку зонда в гель для иммуноанализа, (ii) инкубацию зонда в геле для образования равновесного иммунокомплекса и (iii) выгрузку несвязавшегося зонда из гель для иммуноанализа (–). 8 Концентрация иммунокомплекса, остающегося во время считывания результатов анализа, зависит от концентрации зонда, загруженного в гель ([ Ab ] гель ; моль·м -3 ) и диссоциации иммунокомплекса в несвязанном состоянии. разгрузка зонда. В бимолекулярной системе образование равновесного иммунокомплекса ([ AbAg ] макс ; моль·м -3 ) на стадии (ii) зависит от [ Ab ] гель по 9
3,4,5,6,7 Зондирование иммуноанализа в геле включает (i) загрузку зонда в гель для иммуноанализа, (ii) инкубацию зонда в геле для образования равновесного иммунокомплекса и (iii) выгрузку несвязавшегося зонда из гель для иммуноанализа (–). 8 Концентрация иммунокомплекса, остающегося во время считывания результатов анализа, зависит от концентрации зонда, загруженного в гель ([ Ab ] гель ; моль·м -3 ) и диссоциации иммунокомплекса в несвязанном состоянии. разгрузка зонда. В бимолекулярной системе образование равновесного иммунокомплекса ([ AbAg ] макс ; моль·м -3 ) на стадии (ii) зависит от [ Ab ] гель по 9
[AbAg]max[Ag]gel=11+KD[Ab]gel
5 (1)
где [ Ag ] гель — концентрация целевого белка, K D (м 3 ·моль −1 ) — константа диссоциации (равновесная диссоциация).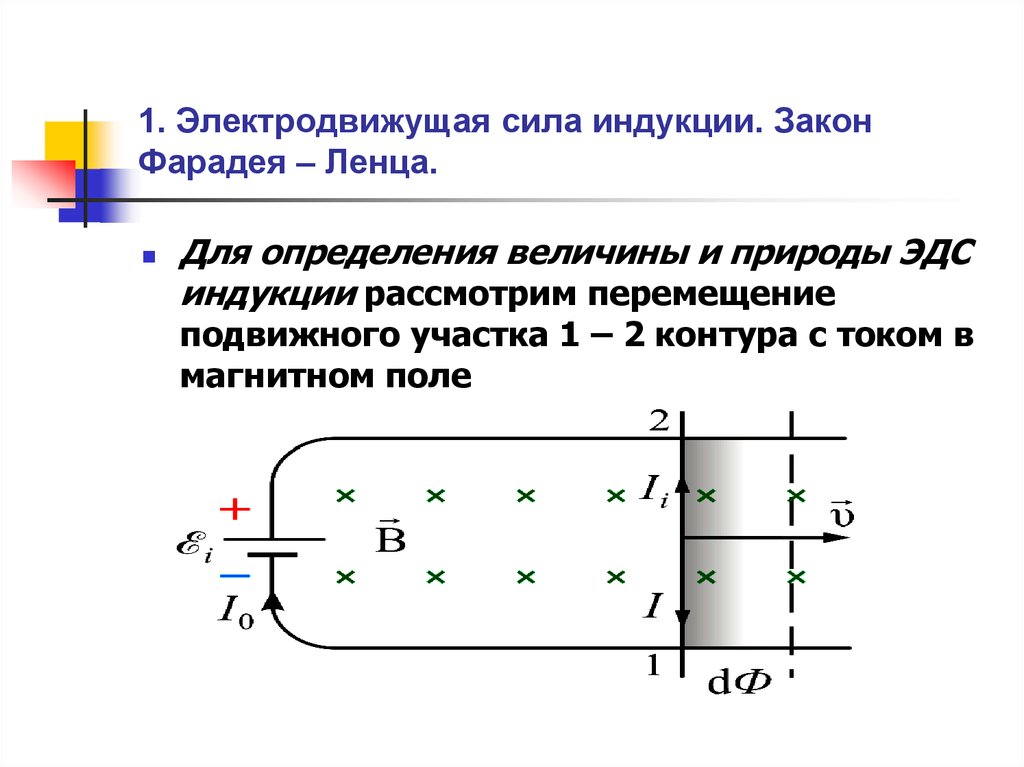 В отсутствие новых событий связывания [ AbAg ] max dissociates during step (iii) according to the dissociation rate constant ( k off ; s −1 ) 9
В отсутствие новых событий связывания [ AbAg ] max dissociates during step (iii) according to the dissociation rate constant ( k off ; s −1 ) 9
[AbAg]t[AbAg]max =1-exp(-kofft)
(2)
где [ AbAg ] t (моль·м -3 ) — иммунокомплекс, остающийся в момент времени t (с) ().
Открыть в отдельном окне
Иммунокомплекс, остающийся во время считывания результатов анализа, уменьшается за счет больших расстояний диффузии зонда и малого соотношения размеров пор и геля. ( A ) Загрузка зонда в гель для иммуноанализа (показан голубым цветом). ( B ) Инкубация зонда в геле для образования равновесного иммунокомплекса. ( C ) Выгрузка несвязанного зонда из геля для иммуноанализа. ( D ) Образование равновесного иммунокомплекса, [ AbAg ] max , максимизируется за счет увеличения концентрации зонда антитела в геле, [ Ab ] гель . ( E ) Значительная диссоциация иммунокомплекса происходит в течение нескольких часов при средней константе скорости диссоциации, k off ( F ) Коэффициент распределения зонда антител, K часть , снижен ниже 0,25 для полиакриламидных белковых проклеивающих гелей (7–2,12% T). ( G ) Значительная диссоциация иммунокомплекса происходит в диапазоне значений 90 730 k 90 731 91 164 90 730 от 90 731 91 167 значений в течение времени, необходимого для диффузионной разгрузки зонда гелей для определения размера белка в миллиметровом масштабе (7% T, 2,7% C).
( E ) Значительная диссоциация иммунокомплекса происходит в течение нескольких часов при средней константе скорости диссоциации, k off ( F ) Коэффициент распределения зонда антител, K часть , снижен ниже 0,25 для полиакриламидных белковых проклеивающих гелей (7–2,12% T). ( G ) Значительная диссоциация иммунокомплекса происходит в диапазоне значений 90 730 k 90 731 91 164 90 730 от 90 731 91 167 значений в течение времени, необходимого для диффузионной разгрузки зонда гелей для определения размера белка в миллиметровом масштабе (7% T, 2,7% C).
При диффузионной загрузке зонда из свободного раствора в гидрогель концентрация зонда в геле сильно зависит от размера пор геля по сравнению с размером зонда. 10,11 Небольшие поры относительно размера зонда препятствуют диффузионному нанесению зонда на гидрогель. В равновесии диффузионно загруженный [ Ab ] гель меньше, чем концентрация зонда в свободном растворе ([ Ab ] золь ) из-за эксклюзионного разделения. Отношение [ Ab ] гель к [ Ab ] золь в равновесии представляет собой коэффициент распределения зонда ( К часть ). В гидрогелях, которые используют маленькие гелевые поры (10–100 нм) для разделения белков по размеру, наблюдалось K часть < 0,2 3,12 для больших зондов антител (гидродинамический радиус ~5 нм) 13 диффузионно загружается в гидрогель.
Отношение [ Ab ] гель к [ Ab ] золь в равновесии представляет собой коэффициент распределения зонда ( К часть ). В гидрогелях, которые используют маленькие гелевые поры (10–100 нм) для разделения белков по размеру, наблюдалось K часть < 0,2 3,12 для больших зондов антител (гидродинамический радиус ~5 нм) 13 диффузионно загружается в гидрогель.
Чтобы отделить требования к размеру пор геля для определения размера белка от требований геля для эффективной загрузки зонда ( K часть ~1), целевые белки в вестерн-блоттинге электропереносят из геля для определения размера белков с малыми порами в блоттинговая мембрана с большими порами (например, нитроцеллюлоза или ПВДФ, поры 200–450 нм). 14,15,16,17,18 Однако, хотя определение размера белка и иммунозондирование в отдельных материалах позволяет независимо оптимизировать размеры пор для каждого этапа, целевой белок может быть потерян из анализа из-за неполного гель-мембранного электропереноса (всего масса белка, захваченная мембраной, меньше, чем масса белка в геле). 14 Степень потери массы белка при гель-мембранном электропереносе также зависит от мишени, что усложняет количественную оценку аналита. 14 Кроме того, разрешение разделения белков по размеру снижается из-за диффузионного уширения разделенных полос белков во время электропереноса. 14,17 Благодаря минимизации временных масштабов диффузионного уширения и потери белка характеристики размера белка из одиночных клеток были выполнены с использованием иммобилизации белка в геле. 3 Иммобилизация белка в геле также сделала возможной трехмерную локализацию белка в ткани с помощью гибридных иммуноанализов гидрогель-ткань. 4,5
14 Степень потери массы белка при гель-мембранном электропереносе также зависит от мишени, что усложняет количественную оценку аналита. 14 Кроме того, разрешение разделения белков по размеру снижается из-за диффузионного уширения разделенных полос белков во время электропереноса. 14,17 Благодаря минимизации временных масштабов диффузионного уширения и потери белка характеристики размера белка из одиночных клеток были выполнены с использованием иммобилизации белка в геле. 3 Иммобилизация белка в геле также сделала возможной трехмерную локализацию белка в ткани с помощью гибридных иммуноанализов гидрогель-ткань. 4,5
Чтобы сохранить преимущества проведения иммуноанализа в геле, класс методов диффузионной загрузки зонда увеличивает равновесную концентрацию зонда в геле и, таким образом, K , часть , за счет использования электростатических взаимодействий между заряженными молекулами и заряженными гидрогелями, 19 дегидратации иммуноанализа в геле перед загрузкой зонда, 8 и формирования двухфазных систем с использованием солей и ПЭГ. 20 Хотя эти методы существенно смещают равновесие разделения зонда в сторону гидрогеля, они не ускоряют разгрузку несвязанного зонда. Таким образом, время диссоциации иммунокомплекса при выгрузке зонда остается неизменным.
20 Хотя эти методы существенно смещают равновесие разделения зонда в сторону гидрогеля, они не ускоряют разгрузку несвязанного зонда. Таким образом, время диссоциации иммунокомплекса при выгрузке зонда остается неизменным.
Электрофоретическое зондирование было продемонстрировано в микрокапиллярных гелевых системах как метод преодоления эксклюзионного разделения и быстрой загрузки и выгрузки зонда по сравнению с диффузионным переносом зонда. 21,22 Было показано, что эти важные демонстрации электрофоретического зондирования улучшают чувствительность иммуноанализа, в том числе в иммуноанализах с малыми порами и определением размера белка в геле. 21 Однако применимые дизайны анализов были ограничены закрытыми микроканалами и капиллярами, что усложняло дизайн анализов, ограничивало пропускную способность образцов и требовало уникального дизайна резервуара для микрочипового зонда для каждого микроканального иммуноанализа. В отличие от инкапсулированных микроканалов, «открытые» микрожидкостные системы снимают ограничения для биологических образцов и этапов предварительной обработки, устраняя по крайней мере одну ограничивающую границу образца жидкости.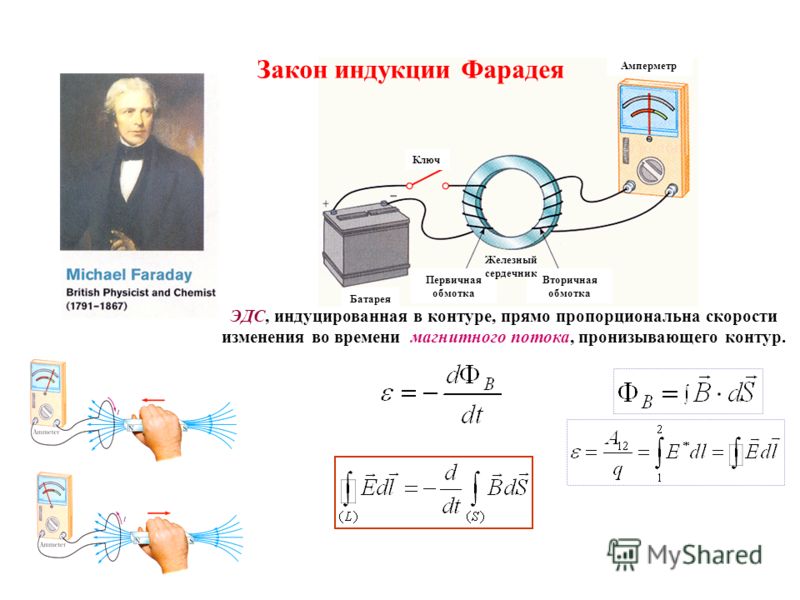 23,24,25 Доступность пробы жидкости также облегчается в открытых устройствах благодаря как минимум одному интерфейсу жидкость-жидкость или жидкость-пар. Обобщенная система электрофоретического зондирования, которая может широко применяться в иммуноанализах 7 для определения размера белка в открытом плоском формате в миллиметровом масштабе, еще не была продемонстрирована.
23,24,25 Доступность пробы жидкости также облегчается в открытых устройствах благодаря как минимум одному интерфейсу жидкость-жидкость или жидкость-пар. Обобщенная система электрофоретического зондирования, которая может широко применяться в иммуноанализах 7 для определения размера белка в открытом плоском формате в миллиметровом масштабе, еще не была продемонстрирована.
Здесь мы представляем обобщенную платформу электротрансферного зондирования для повышения чувствительности обнаружения открытых, миллиметровых, мелкопористых иммуноанализов в геле по сравнению с диффузионным зондированием. Платформа построена на принципах гель-мембранного электропереноса, используемого в обычном вестерн-блоттинге, но с критически важным электропереносом зонда (вместо целевого белка) из инертного крупнопористого геля в иммуноанализ в геле. Мы оценили нашу конструкцию по сравнению с диффузионным зондированием, исследуя максимальную загрузку и разгрузку зонда, а также временные рамки для достижения максимальной загрузки и разгрузки зонда в геле для определения размера белка. Наконец, мы демонстрируем зондирование электропереносом для значительного улучшения отношения сигнал-шум (SNR) иммуноанализа в геле за значительно меньшее время (по сравнению с диффузионным зондированием) с использованием обнаружения OVA, иммобилизованного в геле для определения размера белка, в качестве модельной системы.
Наконец, мы демонстрируем зондирование электропереносом для значительного улучшения отношения сигнал-шум (SNR) иммуноанализа в геле за значительно меньшее время (по сравнению с диффузионным зондированием) с использованием обнаружения OVA, иммобилизованного в геле для определения размера белка, в качестве модельной системы.
Изготовление полиакриламидного геля
Полиакриламидный (ПА) гель использовали в качестве матрицы для молекулярного сита, гели 20%ТПА (использовали в экспериментах по определению характеристик электрофоретической подвижности зонда) и 4%ТПА-загрузочный гель. Проклеивающие гели изготавливали в формах, состоящих из предметного стекла (VWR), кремниевой пластины с фотолитографически-микроузорчатыми элементами SU-8 3050 (Microchem) и двух прокладок толщиной 1 мм (C.B.S. Scientific Gel Wrap). Предметное стекло и кремниевая пластина были разделены прокладками толщиной 1 мм. Чтобы нанести рисунок на поверхность проклеивающего геля с элементами микролунок, элементы SU-8 были нанесены на кремниевую пластину с помощью фотолитографии, как описано ранее. 26 Элементы SU-8 представляли собой цилиндрические микроштифты высотой 40 мкм и диаметром 32 мкм, расположенные на расстоянии 100 мкм друг от друга (расстояние между центральными элементами). Для уменьшения адгезии геля слой SU-8 покрывали дихлордиметилсиланом (№ 440272, Sigma-Aldrich), а предметное стекло обрабатывали гелем Slick® (№ 50640, Lonza). Гели 20% TPA готовили между предметным стеклом и стеклянной пластиной (McCormick). Гели 20% TPA и нагрузочные гели 4% TPA были изготовлены в формах, состоящих из предметного стекла, стеклянной пластины (McCormick) и двух прокладок толщиной 1 мм. Предметное стекло и стеклянная пластинка были разделены прокладками толщиной 1 мм. Предметное стекло и стеклянная пластина были обработаны Gel Slick®. На гелях с 20% T PA или 4 % T PA нагрузочные гели не формировались.
26 Элементы SU-8 представляли собой цилиндрические микроштифты высотой 40 мкм и диаметром 32 мкм, расположенные на расстоянии 100 мкм друг от друга (расстояние между центральными элементами). Для уменьшения адгезии геля слой SU-8 покрывали дихлордиметилсиланом (№ 440272, Sigma-Aldrich), а предметное стекло обрабатывали гелем Slick® (№ 50640, Lonza). Гели 20% TPA готовили между предметным стеклом и стеклянной пластиной (McCormick). Гели 20% TPA и нагрузочные гели 4% TPA были изготовлены в формах, состоящих из предметного стекла, стеклянной пластины (McCormick) и двух прокладок толщиной 1 мм. Предметное стекло и стеклянная пластинка были разделены прокладками толщиной 1 мм. Предметное стекло и стеклянная пластина были обработаны Gel Slick®. На гелях с 20% T PA или 4 % T PA нагрузочные гели не формировались.
Условия изготовления гелей PA описаны в таблице S1. Проклеивающие гели сополимеризовали с N-[3-[(3-бензоилфенил)формамидо]пропил]метакриламидом (BPMA) для иммобилизации белка в геле. 3,26 BPMA может иммобилизовать белки на гелевой матрице путем ковалентного связывания с белками в геле под воздействием ультрафиолетового света. 27 Все гели PA подвергали химической полимеризации в течение 60 минут с использованием персульфата аммония (APS; № A36778, Sigma-Aldrich) и TEMED (№ T9281, Sigma-Aldrich). Растворы прекурсоров геля PA дегазировали и обрабатывали ультразвуком в течение 5 минут перед добавлением химических инициаторов. Чтобы отлить калибровочный гель в форму для изготовления, сначала к кремниевой пластине с покрытием SU-8 прикрепили прокладки толщиной 1 мм с помощью клейкой ленты. Затем раствор предшественника ПА наносили пипеткой на форму SU-8 в зазор между прокладками (рис. S1A). Затем поверх прокладок поместили предметное стекло, чтобы раствор прекурсора геля PA образовался между предметным стеклом, кремниевой пластиной с покрытием SU-8 и прокладками (рис. S1B). После полимеризации геля ПА (60 мин) гели высвобождали из форм для изготовления путем скольжения бритвы между предметным стеклом и кремниевой пластиной (при изготовлении проклеивающего геля) или стеклянной пластиной (в геле 20% ТПА и 4% Изготовление загрузочного геля T PA) (рис.
3,26 BPMA может иммобилизовать белки на гелевой матрице путем ковалентного связывания с белками в геле под воздействием ультрафиолетового света. 27 Все гели PA подвергали химической полимеризации в течение 60 минут с использованием персульфата аммония (APS; № A36778, Sigma-Aldrich) и TEMED (№ T9281, Sigma-Aldrich). Растворы прекурсоров геля PA дегазировали и обрабатывали ультразвуком в течение 5 минут перед добавлением химических инициаторов. Чтобы отлить калибровочный гель в форму для изготовления, сначала к кремниевой пластине с покрытием SU-8 прикрепили прокладки толщиной 1 мм с помощью клейкой ленты. Затем раствор предшественника ПА наносили пипеткой на форму SU-8 в зазор между прокладками (рис. S1A). Затем поверх прокладок поместили предметное стекло, чтобы раствор прекурсора геля PA образовался между предметным стеклом, кремниевой пластиной с покрытием SU-8 и прокладками (рис. S1B). После полимеризации геля ПА (60 мин) гели высвобождали из форм для изготовления путем скольжения бритвы между предметным стеклом и кремниевой пластиной (при изготовлении проклеивающего геля) или стеклянной пластиной (в геле 20% ТПА и 4% Изготовление загрузочного геля T PA) (рис. S1C) и используется в качестве рычага для подъема предметного стекла из формы. Наконец, полимеризованные гели PA толщиной 1 мм затем обрезали бритвой до размеров, описанных в таблице S1 (рис. S1D). Гели PA уравновешивали в буфере для электропереноса (таблица S2) при 4 °C в течение не менее 12 часов и до 4 дней перед использованием.
S1C) и используется в качестве рычага для подъема предметного стекла из формы. Наконец, полимеризованные гели PA толщиной 1 мм затем обрезали бритвой до размеров, описанных в таблице S1 (рис. S1D). Гели PA уравновешивали в буфере для электропереноса (таблица S2) при 4 °C в течение не менее 12 часов и до 4 дней перед использованием.
Изготовление геля для нанесения зонда
Гель для нанесения отливали из смеси расплавленной 1,5% масс./об. сверхчистой агарозы с низкой температурой плавления (№ 16520050, Invitrogen), растворенной в 1X трис-глицине (№ 1610734, Bio-Rad). и зонд с флуоресцентно-меченым антителом (Ab). Проклеивающие гели изготавливали в формах, состоящих из предметного стекла, стеклянной пластины и двух прокладок толщиной 1 мм. Предметное стекло и стеклянная пластинка были разделены прокладками толщиной 1 мм.
Условия изготовления загрузочных гелей описаны в таблице S3. Чтобы отлить загрузочный гель в форму для изготовления, сначала была собрана форма для изготовления: (i) прокладки толщиной 1 мм были прикреплены клейкой лентой к стеклянной пластине, (ii) предметное стекло было прикреплено клейкой лентой поверх стеклянной пластины. прокладки и (iii) стеклянную пластину помещали на плиту и нагревали до ~ 35–40 ° C (рис. S2A). Измерения температуры проводились с помощью инфракрасной термометрии. Затем приготовили расплавленную смесь агарозы с концентрацией 1,5 % масс./об. и зонда: (i) раствор зонда добавили в пробирку Эппендорфа объемом 1,5 мл, которую нагрели до ~35–40 °C на горячей плите (рис. S2B), и (ii) расплавленную агарозу при температуре ~40–50 °C добавляли к раствору зонда антитела и смешивали с помощью пипетки (рис. S2C). Температуры были оптимизированы для поддержания расплавленного состояния агарозы без превышения максимальной температуры в диапазоне термостабильности зонда. Сверхчистая агароза с низкой температурой плавления остается жидкой при 37 °C и быстро затвердевает при температуре ниже 25 °C. Антитела IgG проявляют конформационную стабильность при температуре <55 °C. 28 Затем загрузочный гель отливали путем пипетирования расплавленной смеси агарозного геля и зонда в форму для изготовления (рис.
прокладки и (iii) стеклянную пластину помещали на плиту и нагревали до ~ 35–40 ° C (рис. S2A). Измерения температуры проводились с помощью инфракрасной термометрии. Затем приготовили расплавленную смесь агарозы с концентрацией 1,5 % масс./об. и зонда: (i) раствор зонда добавили в пробирку Эппендорфа объемом 1,5 мл, которую нагрели до ~35–40 °C на горячей плите (рис. S2B), и (ii) расплавленную агарозу при температуре ~40–50 °C добавляли к раствору зонда антитела и смешивали с помощью пипетки (рис. S2C). Температуры были оптимизированы для поддержания расплавленного состояния агарозы без превышения максимальной температуры в диапазоне термостабильности зонда. Сверхчистая агароза с низкой температурой плавления остается жидкой при 37 °C и быстро затвердевает при температуре ниже 25 °C. Антитела IgG проявляют конформационную стабильность при температуре <55 °C. 28 Затем загрузочный гель отливали путем пипетирования расплавленной смеси агарозного геля и зонда в форму для изготовления (рис. S2D). После отливки загрузочного геля загрузочный гель охлаждали до образования геля путем переноса формы для изготовления в пакет со льдом (рис. S2E). После гелеобразования производственная форма была перенесена на плоскую поверхность при ~ 20 ° C, а загрузочный гель был высвобожден из производственной формы и обрезан с помощью того же процесса, который использовался для высвобождения и обрезки геля PA (рис. S2F, G). Наконец, загружающие гели погружали в буфер для электропереноса и сразу же использовали.
S2D). После отливки загрузочного геля загрузочный гель охлаждали до образования геля путем переноса формы для изготовления в пакет со льдом (рис. S2E). После гелеобразования производственная форма была перенесена на плоскую поверхность при ~ 20 ° C, а загрузочный гель был высвобожден из производственной формы и обрезан с помощью того же процесса, который использовался для высвобождения и обрезки геля PA (рис. S2F, G). Наконец, загружающие гели погружали в буфер для электропереноса и сразу же использовали.
Сэндвич-гелевая сборка для зондирования с электропереносом
Для загрузки зонда с помощью электропереноса в калибровочный гель был изготовлен гель-гель-сэндвич с использованием нагрузочного геля, калибровочного геля, двух кусочков фильтровальной бумаги для вестерн-блоттинга (толщиной 1 мм; № 84783, Thermo Fisher Scientific), изготовленный на заказ акриловый зажим и пластиковые эластомеры. Изготовление хомута описано ниже в подразделе Изготовление акрилового хомута. Кусочки фильтровальной бумаги нарезали до размеров 55 мм в ширину и 85 мм в высоту, чтобы они соответствовали размерам зажима, и уравновешивали в буфере для электропереноса в течение 5 минут перед сборкой сэндвича.
Для сборки сэндвича гель-гель, используемого при загрузке зонда, сначала на кусок фильтровальной бумаги был помещен проклеивающий гель (рис. S3A). Затем загрузочный гель был помещен поверх проклеивающего геля без захвата пузырьков воздуха в слое жидкости между гелями (грани x-y геля соприкасаются; рис. S3B). Затем второй кусок фильтровальной бумаги был помещен поверх загрузочного геля (края двух кусочков фильтровальной бумаги были выровнены при размещении второй фильтровальной бумаги; рисунок S3C). Пакет фильтровальная бумага-гели-фильтровальная бумага затем был перенесен в акриловый зажим (рис. S4), и сборка была сжата вместе с помощью полимерных эластичных лент (Scünci Polybands).
Для выгрузки зонда с помощью электропереноса из проклеивающего геля выполняли тот же процесс сборки сэндвичей, который выполнялся для загрузки зонда, но без геля для нанесения. Таким образом, проклеивающий гель помещали на кусок фильтровальной бумаги, а второй кусок фильтровальной бумаги помещали поверх проклеивающего геля. Сборка фильтровальная бумага — проклеивающий гель — фильтровальная бумага помещалась в зажим и сжималась с использованием пластиковых эластомеров.
Сборка фильтровальная бумага — проклеивающий гель — фильтровальная бумага помещалась в зажим и сжималась с использованием пластиковых эластомеров.
Изготовление акриловых зажимов
Для сжатия гелевых сэндвичей, используемых для зондирования электропереносом, и подвешивания гелевых сэндвичей в буферной камере системы электропереноса плиты-геля был разработан и изготовлен акриловый зажим. Отдельные компоненты зажима были разработаны в Adobe® Illustrator® и вырезаны из акриловых листов (прозрачные акриловые листы толщиной 3,175 мм; № FJ-639).61240, Astari) с помощью лазерного резака (программное обеспечение для лазерной резки: RetinaEngrave3D; лазерный резак: № HL40–5G-110, Full Spectrum Laser). Отдельные компоненты хомута были скреплены между собой суперклеем. Собранный хомут состоял из двух одинаковых половинок, сжатых пластиковыми эластомерами (рис. S4A,B). Зажим был разработан для размещения до 6 сэндвичей с гелем в центре буферной камеры системы электропереноса пластинчатого геля путем подвешивания (и самовыравнивания) к верхнему краю камеры (система электрофореза мини-клеток XCell SureLock™, № EI0001, Invitrogen; Блот-модуль XCell II™, № EI0002, Invitrogen; рис. S4C).
S4C).
Условия электропереноса зонда
Для выполнения загрузки или разгрузки зонда электропереноса собирали гелевый сэндвич (описанный в подразделе Сборка гелевого сэндвича для зондирования электропереносом), закрепляли зажимом и подвешивали в буферной камере пластинчато-гелевой системы электропереноса. . При загрузке зонда электропереносом загрузочный гель располагался по направлению к катоду (-), а проклеивающий гель располагался рядом с анодом (+), так что отрицательно заряженные молекулы зонда мигрировали в проклеивающий гель и через него при приложении поля. Буферная камера была заполнена буфером для электропереноса, а внешняя камера была заполнена ледяной водой (рис. S4C). Всю систему электропереноса slab-gel помещали на лед. Система электропереноса пластин-гелей была подключена к источнику питания (PowerPac High-Voltage Power Supply; № 1645056, Bio-Rad). Источник питания устанавливали на постоянное напряжение и прикладывали электрическое поле. Напряженность и время приложенного электрического поля описаны в таблице S4. По завершении загрузки или разгрузки зонда электропереноса питание отключалось, а зажим снимался с системы электропереноса пластины-геля. Полимерные эластики были сняты с зажима, а гели извлечены. Фильтровальную бумагу выбрасывали после каждого использования, а акриловый зажим и полимерные резинки промывали водой и сушили перед повторным использованием.
По завершении загрузки или разгрузки зонда электропереноса питание отключалось, а зажим снимался с системы электропереноса пластины-геля. Полимерные эластики были сняты с зажима, а гели извлечены. Фильтровальную бумагу выбрасывали после каждого использования, а акриловый зажим и полимерные резинки промывали водой и сушили перед повторным использованием.
Система полусухого электропереноса
Анодная и катодная пластины (обе анодные пластины Bio-Rad Criterion с пластиковыми корпусами, модифицированными таким образом, чтобы электроды располагались в непосредственной близости) были прикреплены к вырезанным лазером пластиковым корпусам для выравнивания (рис. S5A). . 29 Электродные пластины были разделены 3-миллиметровыми прокладками, расположенными по обеим сторонам поверхности электрода и приведенными в контакт с помощью магнита (рис. S5B). Система полусухого электропереноса была подключена к источнику питания (Bio-Rad PowerPac Basic).
Характеристика электрофоретической подвижности зонда
Чтобы охарактеризовать зонд мк гель в проклеивающем геле, электромиграцию дискретной полосы зонда отслеживали с использованием системы электропереноса slab-gel. Полусухая система электропереноса была впервые использована для электрофоретического введения зонда из слоя свободного раствора между проклеивающим гелем и гелем с 20% TPA в проклеивающий гель (рис. S5D-F). Система полусухого электропереноса была подключена к источнику питания. Источник питания устанавливали на постоянное напряжение и прикладывали электрическое поле 100 В/см в течение 30 с. После отключения питания систему полусухого электропереноса разобрали и извлекли проклеивающий гель. Затем собирали сэндвич из фильтровальной бумаги, проклеивающего геля и фильтровальной бумаги и переносили в акриловый зажим, как описано в подразделе Сборка сэндвича из геля для электротрансферного зондирования. Наконец, сэндвич с зажатым гелем был вставлен в систему электропереноса пластины-геля и зонд 9.0730 x E (проклеивающая гелевая микролунка, направленная к катоду; электрическое поле = 12 В/см, время приложения = 30 с, 60 с, 120 с, 180 с, 240 с, 300 с). Расстояние электромиграции зонда регистрировали для каждого времени электропереноса, и для определения электрофоретической подвижности зонда в геле применяли аппроксимацию линейной регрессии методом наименьших квадратов.
Полусухая система электропереноса была впервые использована для электрофоретического введения зонда из слоя свободного раствора между проклеивающим гелем и гелем с 20% TPA в проклеивающий гель (рис. S5D-F). Система полусухого электропереноса была подключена к источнику питания. Источник питания устанавливали на постоянное напряжение и прикладывали электрическое поле 100 В/см в течение 30 с. После отключения питания систему полусухого электропереноса разобрали и извлекли проклеивающий гель. Затем собирали сэндвич из фильтровальной бумаги, проклеивающего геля и фильтровальной бумаги и переносили в акриловый зажим, как описано в подразделе Сборка сэндвича из геля для электротрансферного зондирования. Наконец, сэндвич с зажатым гелем был вставлен в систему электропереноса пластины-геля и зонд 9.0730 x E (проклеивающая гелевая микролунка, направленная к катоду; электрическое поле = 12 В/см, время приложения = 30 с, 60 с, 120 с, 180 с, 240 с, 300 с). Расстояние электромиграции зонда регистрировали для каждого времени электропереноса, и для определения электрофоретической подвижности зонда в геле применяли аппроксимацию линейной регрессии методом наименьших квадратов.
Сборка многослойного геля для зондирования методом диффузионного переноса
Для загрузки зонда путем диффузионного переноса в калибровочный гель был изготовлен гелевый сэндвич с использованием двух нагрузочных гелей и калибровочного геля. Сначала калибровочный гель был обрезан до окончательных размеров x-y-z: 5–5–1 мм. Затем загрузочные гели обрезали до окончательных размеров x-y-z: 7–7–1 мм. Затем поверх нагрузочного геля помещали проклеивающий гель (грани x-y соприкасаются). Затем поверх проклеивающего геля наносили второй загрузочный гель. Сэндвич с тремя гелями затем хранили в темной влажной камере (одна лунка 96-луночный планшет) при 4 ° C. Во время сборки сэндвича между слоями геля не было пузырьков воздуха. Чтобы разгрузить зонд путем диффузионного переноса, гель с зондом помещали в одну лунку 96-луночного планшета. Лунку заполняли буфером для электропереноса (~300 мкл), и буфер обновляли каждые 6 часов. 96-луночный планшет хранили в темноте при 4°С. Время диффузионного переноса зонда описано в таблице S5.
Иммобилизация OVA в геле и зондирование
Раствор овальбумина, меченного AlexaFluor® 488 (OVA, разбавленный до 5 мкМ в 1X трис-глицине; № 034783, Thermo Fisher Scientific), электрофоретически вводили в калибровочный гель и иммобилизовали. в геле. Для электрофоретического введения OVA использовали индивидуальную полусухую систему электропереноса (система и образец в сборе описаны в подразделе «Характеристика электрофоретической подвижности зонда»). Все гели уравновешивали в буфере 1X RIPA (вместо буфера для электропереноса; таблица S2) сразу после изготовления при 4 °C в течение не менее 12 часов и до 4 дней перед использованием. Фильтровальную бумагу также уравновешивали в буфере 1XRIPA (вместо буфера для электропереноса). После сборки системы полусухого электропереноса к ней подавали постоянный ток силой 35 мА в течение 15 с. После отключения питания система была разобрана, и проклеивающий гель подвергался воздействию УФ-излучения в течение 45 с для фотозахвата OVA на проклеивающий гель, функционализированный BPMA, как описано ранее. 27 Затем проклеивающий гель инкубировали в буфере для электропереноса при 4 °C в течение не менее 12 часов для замены буферов и выгрузки несвязанного OVA (темный, 4 °C). OVA, иммобилизованный в геле, исследовали с помощью электропереноса и диффузионного переноса с использованием Ab-зондов 1° и 2° (зонды описаны в таблице S3; условия переноса зонда описаны в таблицах S4 и S5). Между каждой стадией загрузки и выгрузки зонда проклеивающий гель инкубировали во влажной камере для образования равновесного иммунокомплекса (темнота, ~20 °C). Время инкубации для зондирования с электропереносом определяли с помощью существующих устройств для иммуноанализа гидрогеля (инкубация 1°Ab: 2 ч; инкубация 2°Ab: 1 ч). 3 Таким образом, полная последовательность зондирования антител 1° и 2° включала: (i) загрузку зонда 1°Ab, (ii) образование равновесного иммунокомплекса зонда OVA-1°Ab (2 ч), (iii) 1°Ab выгрузка зонда, (iv) загрузка зонда 2°Ab, (v) образование равновесного иммунокомплекса зонда 1°Ab-2°Ab (1 ч) и (vi) выгрузка зонда 2°Ab.
27 Затем проклеивающий гель инкубировали в буфере для электропереноса при 4 °C в течение не менее 12 часов для замены буферов и выгрузки несвязанного OVA (темный, 4 °C). OVA, иммобилизованный в геле, исследовали с помощью электропереноса и диффузионного переноса с использованием Ab-зондов 1° и 2° (зонды описаны в таблице S3; условия переноса зонда описаны в таблицах S4 и S5). Между каждой стадией загрузки и выгрузки зонда проклеивающий гель инкубировали во влажной камере для образования равновесного иммунокомплекса (темнота, ~20 °C). Время инкубации для зондирования с электропереносом определяли с помощью существующих устройств для иммуноанализа гидрогеля (инкубация 1°Ab: 2 ч; инкубация 2°Ab: 1 ч). 3 Таким образом, полная последовательность зондирования антител 1° и 2° включала: (i) загрузку зонда 1°Ab, (ii) образование равновесного иммунокомплекса зонда OVA-1°Ab (2 ч), (iii) 1°Ab выгрузка зонда, (iv) загрузка зонда 2°Ab, (v) образование равновесного иммунокомплекса зонда 1°Ab-2°Ab (1 ч) и (vi) выгрузка зонда 2°Ab.
Визуализация и анализ
Захват изображения был выполнен с помощью программного обеспечения для визуализации MetaMorph® (Molecular Devices) с использованием инвертированного широкопольного флуоресцентного микроскопа Olympus IX51, оснащенного объективом Olympus UPlanFLN 4X (№ UPLFLN4X) и источником освещения X-Cite® (Excelitas). технологий), ПЗС-камера CoolSNAP™ HQ2 (Teledyne Photometrics), набор фильтров GFP (Chroma 49011 ET), набор фильтров DAPI (Chroma 4900) и набор фильтров TRITC (Chroma 41002c).
Получение изображения флуоресценции в геле, возникающей в результате загрузки и выгрузки зонда, выполняли путем помещения калибровочного геля на чашку Петри диаметром 65 мм (грань x-y геля размером 10–10 мм контактирует с чашкой Петри). Плоскость фокуса микроскопа была отрегулирована на среднюю глубину проклеивающего геля толщиной 1 мм. Рассчитывали среднюю флуоресценцию в геле. Вычитание фона выполняли путем вычитания средней флуоресценции гелей в геле без воздействия молекул флуоресцентного зонда из средней флуоресценции в геле гелей испытуемой группы. Эффективные коэффициенты распределения рассчитывали как отношение средней флуоресценции проклеивающего геля в геле после загрузки к средней флуоресценции геля в геле после изготовления (эффективный коэффициент распределения определяли после этого расчета как для электропереноса, так и для диффузионной загрузки зонда). . Для загрузки зонда диффузионным переносом используется степенной закон 9.Модель 1132 30,31 для общей загрузки массы зонда соответствовала измерениям временной точки флуоресценции в геле с использованием MATLAB®. В MATLAB использовалась функция fit() и пользовательское уравнение для моделирования нагрузки зонда по степенному закону ()
Эффективные коэффициенты распределения рассчитывали как отношение средней флуоресценции проклеивающего геля в геле после загрузки к средней флуоресценции геля в геле после изготовления (эффективный коэффициент распределения определяли после этого расчета как для электропереноса, так и для диффузионной загрузки зонда). . Для загрузки зонда диффузионным переносом используется степенной закон 9.Модель 1132 30,31 для общей загрузки массы зонда соответствовала измерениям временной точки флуоресценции в геле с использованием MATLAB®. В MATLAB использовалась функция fit() и пользовательское уравнение для моделирования нагрузки зонда по степенному закону ()
Флуоресцентный гель=[Ab]t[Ab]∞=a∗tb
(3)
где [ Ab ] t – масса зонда в геле в момент времени t , [ Ab ] ∞ – масса зонда в геле в состоянии равновесия, a – структурная константа геля, и b — экспонент выпуска. 30,31 Параметры подгонки модели: a = 104,1, b = 0,1992, r 2 = 0,9321‡.
Открыть в отдельном окне
( A ) Загрузка зонда электропереносом приводит к большему коэффициенту распределения, чем диффузионная нагрузка зонда. Электротрансферная нагрузка n=4. Диффузионная нагрузка n=4. ( * указывает статистическую разницу по U-критерию Манна-Уитни, p = 0,0286 ) ( B ) Диффузионная нагрузка зонда на проклеивающий гель происходит в течение нескольких часов (n = 4, отдельные гели имеют цветное покрытие).
Для расчета выгрузки зонда среднюю флуоресценцию в геле после выгрузки нормализовали к средней флуоресценции в геле после загрузки. Для разгрузки зонда путем диффузионного переноса модель степенного закона 30,31 была приспособлена к временным измерениям флуоресценции в геле с использованием MATLAB®. В MATLAB использовалась функция fit() и пользовательское уравнение для моделирования разгрузки зонда по степенному закону ()
Флуоресценция=[Ab]t[Ab]∞=1−a∗tb
(4)
где [ Аб ] t – масса зонда в геле в момент времени t , [ Ab ] ∞ – масса зонда в геле в состоянии равновесия, a – структурная константа геля 301 b 9073 9073 является показателем выпуска. 30,31 Параметры подгонки модели: a = 0,1766, b = 0,4236, r 2 = 0,9812.
30,31 Параметры подгонки модели: a = 0,1766, b = 0,4236, r 2 = 0,9812.
Открыть в отдельном окне
( A ) Электротрансферная разгрузка несвязанного зонда приводит к меньшему захвату зонда гелем, чем диффузионная разгрузка. E: электротрансферная разгрузка, n=5. D: диффузная разгрузка, n=6. ( * указывает статистическую разницу по U-критерию Манна-Уитни, p<0,05 ) ( B ) Диффузионная разгрузка зонда из проклеивающего геля происходит в течение нескольких часов (n=3, отдельные гели имеют цветное покрытие).
Для визуализации положения пика зонда при характеристике электрофоретической подвижности зонда, а также положения пиков иммобилизованного OVA и зондируемого сигнала в экспериментах по иммунозондированию OVA бритвой отрезали 0,5 мм полоску проклеивающего геля (10 мм x ~0,5 мм x 1 мм по осям x-y-z; рисунок S6A). Полоса проклеивающего геля была уложена на чашку Петри диаметром 65 мм (полоска размером 10 мм x 1 мм x-z соприкасается с чашкой Петри (рис. S6B). Профили флуоресценции по оси z рассчитывались путем усреднения интенсивности флуоресценции на изображении размером ~ 2 мм. область по оси x на каждой глубине по оси z (рисунок S6B для ориентации оси).Усредненные профили флуоресценции были сопоставлены с гауссовыми кривыми для определения местоположения пика (MATLAB®, функция fit(), модель соответствия ‘gauss1’, анализируемая область: положение пика ± 3σ). Вычитание фона, выполняемое путем вычитания среднего значения пикселя в диапазоне от 3σ до 4σ (определяемого как фон) из значений пикселей в области положения пика ± 3σ (определяемого как сигнал). Фоновый шум для определения значений ОСШ зондируемый сигнал рассчитывали, взяв стандартное отклонение интенсивности флуоресценции между границами 3σ и 4σ профилей флуоресценции.Положение пика определяли по положению пика аппроксимации Гаусса.
S6B). Профили флуоресценции по оси z рассчитывались путем усреднения интенсивности флуоресценции на изображении размером ~ 2 мм. область по оси x на каждой глубине по оси z (рисунок S6B для ориентации оси).Усредненные профили флуоресценции были сопоставлены с гауссовыми кривыми для определения местоположения пика (MATLAB®, функция fit(), модель соответствия ‘gauss1’, анализируемая область: положение пика ± 3σ). Вычитание фона, выполняемое путем вычитания среднего значения пикселя в диапазоне от 3σ до 4σ (определяемого как фон) из значений пикселей в области положения пика ± 3σ (определяемого как сигнал). Фоновый шум для определения значений ОСШ зондируемый сигнал рассчитывали, взяв стандартное отклонение интенсивности флуоресценции между границами 3σ и 4σ профилей флуоресценции.Положение пика определяли по положению пика аппроксимации Гаусса.
Конструкция электролитической ячейки для зондирования с электропереносом
Чтобы улучшить чувствительность обнаружения иммуноанализа в геле, определяемую диффузионным переносом зонда, мы стремились учесть следующие критерии дизайна иммунозондирования: (i) почти полная загрузка зонда ( K часть ~1) и выгрузку в гидрогеле, и (ii) быструю загрузку и разгрузку зонда в гидрогеле по сравнению с временными шкалами диссоциации иммунокомплекса. Гели для определения размера белка PA, разработанные со средним радиусом пор 10–100 нм, используются для разделения белков с молекулярной массой ~ 10–9.0 кДа, 32 , соответствующие гидродинамическим радиусам ( R h ) ~ 1,5–4,0 нм. 33 Эксклюзивное разделение диффузионно нагруженного зонда на гидрогели снижает равновесие K части зонда и может быть аппроксимировано с помощью модели Огстона 10,11
Гели для определения размера белка PA, разработанные со средним радиусом пор 10–100 нм, используются для разделения белков с молекулярной массой ~ 10–9.0 кДа, 32 , соответствующие гидродинамическим радиусам ( R h ) ~ 1,5–4,0 нм. 33 Эксклюзивное разделение диффузионно нагруженного зонда на гидрогели снижает равновесие K части зонда и может быть аппроксимировано с помощью модели Огстона 10,11
Kpart=[Abgel[Abgel] ]sol=exp(−ϕ(1+Rhaf)2)
(5)
где ϕ — объемная доля полимера в геле, a f (нм) – радиус полимерного волокна геля. Средний размер пор геля связан с ϕ отрицательной экспоненциальной зависимостью. 34 Таким образом, увеличение ϕ вызывает экспоненциальное уменьшение среднего размера пор геля и K часть . Для изготовления геля ϕ линейно связано с общей плотностью акриламидного мономера (% T ), а гель % T можно настроить для контроля размера пор геля (для фиксированного процента бис-акриламидного сшивающего агента, % С ). При использовании больших зондов антител (150 кДа, R h ~5 нм) 13 для диффузионного зондирования гидрогеля для определения размера белка (7–12 %T, 2–5 %C), [ Ab ] gel может быть на порядок ниже [ Ab ] sol (). 3,6,7,35
При использовании больших зондов антител (150 кДа, R h ~5 нм) 13 для диффузионного зондирования гидрогеля для определения размера белка (7–12 %T, 2–5 %C), [ Ab ] gel может быть на порядок ниже [ Ab ] sol (). 3,6,7,35
Длительные временные рамки разгрузки диффузионного зонда по сравнению с диссоциацией иммунокомплекса снижают концентрацию иммунокомплекса, остающегося во время считывания результатов анализа. 36 Ожидаемое расстояние диффузии одномерного зонда, 〈 x Diff 〉 (мкм), линейно связано с квадратным корнем из времени, определяемым выражением 34,37
〉xDiff〈 %Tt
(6)
D%T=Dsolexp(−3,03Rh0,59%T0,94)
(7)
где D % T (мкм 2 · с −1 ) — коэффициент диффузии зонда в геле, D золь — коэффициент диффузии свободного раствора зонд. Аналитическая модель показывает, что за время, необходимое для диффузии антител через 1,2 мм геля 7% T, 2,7% C PA (~ 53 ч), <50% исходного иммунокомплекса останется интактным для антител с k выкл > 10 −6 с −1 ().
Аналитическая модель показывает, что за время, необходимое для диффузии антител через 1,2 мм геля 7% T, 2,7% C PA (~ 53 ч), <50% исходного иммунокомплекса останется интактным для антител с k выкл > 10 −6 с −1 ().
В отличие от диффузионной миграции зонда, скорость электромиграции зонда ( ν ; мкм·с −1 ) линейно пропорциональна напряженности приложенного электрического поля ( E ; В·см −1 )
v=мкгE
(8)
мкг=q6πηRh20−Kr%T
(9)
где q (Кл) — суммарный заряд молекулы, η (Па·с −1 ) is the solution viscosity, K r is the gel retardation coefficient, and μ gel (cm 2 ·V −1 ·s −1 ) is the электрофоретическая подвижность зонда в геле. Таким образом, E обеспечивает настраиваемый параметр для ускорения электромиграции зонда и увеличения K части (по сравнению с диффузионным зондированием) без изменения размера пор геля. 38 Кроме того, расстояние электромиграции зонда ( x E ; мкм) линейно связано с t , тогда как 〈 x Diff 〉 линейно связано с квадратным корнем из t (xE~t;〈xDiff〉~t). 39
38 Кроме того, расстояние электромиграции зонда ( x E ; мкм) линейно связано с t , тогда как 〈 x Diff 〉 линейно связано с квадратным корнем из t (xE~t;〈xDiff〉~t). 39
xE=мкгEt
(10)
Таким образом, мы разработали платформу зондирования с электропереносом, чтобы удовлетворить конструктивным критериям увеличения K часть и ускорить перенос зонда по сравнению с диффузионным зондированием. При электротрансферном зондировании: (i) зонд загружается в гель для проклеивания пор (гель ПА 7%T, 3,5%C, радиус пор ~40–87 нм 9 ).1132 40 ) с помощью электропереноса из инертного геля с большими порами для загрузки зонда (1,5% масс./об. агарозы, радиус пор ~100–150 нм 41 ), (ii) зонд инкубируют в калибровочном геле для достижения равновесия иммунокомплекса, и (iii) зонд выгружается электропереносом из калибровочного геля (-). Наша система включает в себя сэндвич между загрузочным гелем и проклеивающим гелем и выполнение электропереноса зонда в электролитической ячейке с использованием обычной системы электропереноса с пластинчатым гелем для создания однородного электрического поля поперек геля. Мы разработали инертный загрузочный гель с большими порами для облегчения электропереноса почти всей массы зонда антитела из загрузочного геля в калибровочный гель. Мы оценили временные рамки загрузки и выгрузки зонда электропереноса, а также массу зонда, загруженного и выгруженного в проклеивающем геле. Наконец, мы исследовали влияние зондирования с электропереносом на чувствительность обнаружения иммуноанализа в геле для определения размера белка в демонстрации концепции с помощью иммунозондирования для OVA, иммобилизованного в геле.
Наша система включает в себя сэндвич между загрузочным гелем и проклеивающим гелем и выполнение электропереноса зонда в электролитической ячейке с использованием обычной системы электропереноса с пластинчатым гелем для создания однородного электрического поля поперек геля. Мы разработали инертный загрузочный гель с большими порами для облегчения электропереноса почти всей массы зонда антитела из загрузочного геля в калибровочный гель. Мы оценили временные рамки загрузки и выгрузки зонда электропереноса, а также массу зонда, загруженного и выгруженного в проклеивающем геле. Наконец, мы исследовали влияние зондирования с электропереносом на чувствительность обнаружения иммуноанализа в геле для определения размера белка в демонстрации концепции с помощью иммунозондирования для OVA, иммобилизованного в геле.
Открыть в отдельном окне
Электротрансферное зондирование обеспечивает предсказуемую электромиграцию зонда без прямой визуализации. ( A ) Загрузка зонда: Бутерброд из фильтровальной бумаги, загрузочный гель и гель для определения размера белка погружают в объем буфера. Зонд загружают в калибровочный гель электропереносом. ( B ) Формирование равновесного иммунокомплекса: Нагруженный зондом проклеивающий гель удаляют из объема буфера для образования равновесного иммунокомплекса. ( С ) Выгрузка зонда: Бутерброд из фильтровальной бумаги и калибровочного геля погружают в буферный объем, и несвязанный зонд выгружают из калибровочного геля с помощью электропереноса. ( D ) Стабильность pH в центре электролитической ячейки прогнозируется путем моделирования анализа pH в результате подачи тока на систему электропереноса зонда. Гелевые бутерброды расположены в центре электролизера шириной 2,5 см (12,5 мм от каждого электрода). ( E ) Расстояние электромиграции зонда линейно связано со временем (r2 = 0,9888, модель линейной регрессии методом наименьших квадратов). Было проведено пять испытаний с различным временем электромиграции (t = 30 с, 60 с, 120 с, 180 с, 240 с, 300 с) с использованием двух гелей на испытание (отдельные гели имеют цветовую кодировку).
Зонд загружают в калибровочный гель электропереносом. ( B ) Формирование равновесного иммунокомплекса: Нагруженный зондом проклеивающий гель удаляют из объема буфера для образования равновесного иммунокомплекса. ( С ) Выгрузка зонда: Бутерброд из фильтровальной бумаги и калибровочного геля погружают в буферный объем, и несвязанный зонд выгружают из калибровочного геля с помощью электропереноса. ( D ) Стабильность pH в центре электролитической ячейки прогнозируется путем моделирования анализа pH в результате подачи тока на систему электропереноса зонда. Гелевые бутерброды расположены в центре электролизера шириной 2,5 см (12,5 мм от каждого электрода). ( E ) Расстояние электромиграции зонда линейно связано со временем (r2 = 0,9888, модель линейной регрессии методом наименьших квадратов). Было проведено пять испытаний с различным временем электромиграции (t = 30 с, 60 с, 120 с, 180 с, 240 с, 300 с) с использованием двух гелей на испытание (отдельные гели имеют цветовую кодировку). Между отдельными гелями, использованными в каждом испытании, не наблюдалось существенной разницы (p > 0,22, U-критерий Манна-Уитни).
Между отдельными гелями, использованными в каждом испытании, не наблюдалось существенной разницы (p > 0,22, U-критерий Манна-Уитни).
Конструкция зонда с электропереносом снижает негативное влияние продуктов электролиза на характеристики электромиграции0730 x
E , E и t , заданные уравнением 10, можно использовать до тех пор, пока ключевые параметры, такие как q и E , остаются постоянными. При разработке зондовой системы электрогранфера мы исходили из того, что непредсказуемая или плохо воспроизводимая внутригелевая электромиграция внутри электролитической ячейки (не соблюдая уравнение 10) может быть результатом газообразных и ионных продуктов реакций электролиза, происходящих на поверхности электродов: 42Катод: 2h3O(ж)+2e-↔2OH-(водн.)+h3(г)
(11)
Анод:h3O(ж)↔2e-+2H+(водн.)+12O2(г)
(12)
В частности, продукты электролиза с газовыми пузырьками могут препятствовать прохождению электрического поля и вызывать переменные во времени падения напряжения (и, следовательно, E ) в гелях. 43 Для удаления пузырьков электролизного газа с пути нанесенного E обычная камера для электропереноса с пластинчатым гелем была оснащена зажимом для акрилового геля (рис. SI1). Зажим облегчил удаление пузырей из E путем включения открытой границы буферного раствора с воздухом, что позволяет пузырькам всплывать на поверхность буферного объема по мере их образования.
43 Для удаления пузырьков электролизного газа с пути нанесенного E обычная камера для электропереноса с пластинчатым гелем была оснащена зажимом для акрилового геля (рис. SI1). Зажим облегчил удаление пузырей из E путем включения открытой границы буферного раствора с воздухом, что позволяет пузырькам всплывать на поверхность буферного объема по мере их образования.
Отклонения от теоретического поведения электромиграции (уравнение 10) также могут быть результатом сильного основания (ОН-) и сильной кислоты (Н+) продуктов электролиза. Сильные основания и кислоты могут вызывать резкие изменения рН вблизи поверхностей электродов, в частности делая раствор возле катода более щелочным, а раствор возле анода более кислым. 42,44 Это явление хорошо описано в аналогичных системах, особенно для капиллярного электрофореза 42 , и даже применялось для формирования естественных градиентов pH в изоэлектрофокусирующих системах. 44 Такое изменение pH может вызвать изменения в геле μ за счет замены зонда q (уравнение 9). 45
45
Предварительно установленная модель моделирования 42 предсказанный рН в буферном растворе в результате применения E и t (общая загрузка). Вкратце, общий заряд, переданный от электродов раствору, рассчитывали с использованием закона электролиза Фарадея на основе силы и продолжительности приложенного электрического тока. Общий доставленный заряд использовали для расчета изменения [H+] или [OH-] (от поверхности анода или катода соответственно) в растворе, а изменение концентрации ионов использовали вместе с начальными концентрациями ионов в буфере и pKa в буфере для расчета рН системы. Затем регистрировали рН системы как функцию расстояния от поверхности каждого электрода (где общее количество буферных веществ, доступных для смягчения изменения рН, является функцией увеличения объема буфера). Результаты этого модельного анализа включены в , который показывает ожидаемый pH как функцию расстояния от поверхности каждого электрода в этой системе. Для 1X-трис-глицинового буфера с размерами 10 см x 10 см x 2,5 см (ширина x высота x глубина, 250 см 3 общий объем) центр 1 мм между электродами (расстояние между противоположными поверхностями проклеивающего геля) испытывает минимальные изменения pH (разница pH 0,031, в пределах вариабельности 1X трис-глицина, изготовленного из имеющегося в продаже маточного раствора 46 и ниже разрешимой разницы pI, продемонстрированной в технологиях изоэлектрической фокусировки отдельных клеток 47 ). Таким образом, мы разработали систему, в которой газообразные продукты электролиза могут быть пассивно удалены, а ионные продукты будут вызывать незначительные изменения pH (как предполагает модельный анализ).
Для 1X-трис-глицинового буфера с размерами 10 см x 10 см x 2,5 см (ширина x высота x глубина, 250 см 3 общий объем) центр 1 мм между электродами (расстояние между противоположными поверхностями проклеивающего геля) испытывает минимальные изменения pH (разница pH 0,031, в пределах вариабельности 1X трис-глицина, изготовленного из имеющегося в продаже маточного раствора 46 и ниже разрешимой разницы pI, продемонстрированной в технологиях изоэлектрической фокусировки отдельных клеток 47 ). Таким образом, мы разработали систему, в которой газообразные продукты электролиза могут быть пассивно удалены, а ионные продукты будут вызывать незначительные изменения pH (как предполагает модельный анализ).
Probe electromigration distance is linearly dependent on time in electrotransfer system
We next sought to experimentally demonstrate that probe x E responds linearly with t , and calculate the probe μ gel в нашей системе. Для мониторинга зонда x E зонд электрофоретически вводили в гель из свободного раствора с использованием изготовленной на заказ системы полусухого электропереноса (рис. S5). Образец зонда подвергся электрофоретическому штабелированию образца (нижний зонд мк гель чем электрофоретическая подвижность зонда в свободном растворе, уравнение 9). Поскольку раствор зонда изначально образовывал тонкий слой и подвергался укладке образцов, ширина полосы зонда в геле (подгонка по Гауссу, ± 3σ) была меньше толщины геля. Местоположение мигрирующей полосы зонда отслеживали путем подгонки кривой Гаусса для определения местоположения пика зонда. Затем полосу зонда в системе электропереноса зонда в геле характеризовали в течение т .
Для мониторинга зонда x E зонд электрофоретически вводили в гель из свободного раствора с использованием изготовленной на заказ системы полусухого электропереноса (рис. S5). Образец зонда подвергся электрофоретическому штабелированию образца (нижний зонд мк гель чем электрофоретическая подвижность зонда в свободном растворе, уравнение 9). Поскольку раствор зонда изначально образовывал тонкий слой и подвергался укладке образцов, ширина полосы зонда в геле (подгонка по Гауссу, ± 3σ) была меньше толщины геля. Местоположение мигрирующей полосы зонда отслеживали путем подгонки кривой Гаусса для определения местоположения пика зонда. Затем полосу зонда в системе электропереноса зонда в геле характеризовали в течение т .
Линейная зависимость между зондом x E и t в электромиграции была определена с использованием модели линейной регрессии наименьших квадратов (r 2 = 0,9888, ). Зонд ν для примененного E был извлечен из наклона линейной аппроксимации ( ν = 2,17 мкм/с) и определено используя уравнение 8; мкм 7% T = 1,81 × 10 −5 см 2 /(В·с). Не наблюдалось существенной разницы в x E между гелями, что облегчало прогнозирование местоположения зонда в геле без визуализации местоположения зонда в реальном времени (p > 0,22, U-критерий Манна-Уитни; ). Как описано уравнением 9, μ 7% T может варьироваться в зависимости от вида молекулы в естественных условиях электропереноса на r ч и q зонда. Однако в случае зондов антител одного и того же класса антител (изотипа) больших различий в электрофоретической подвижности не ожидается из-за минимальной вариации r h и q . Здесь использовались антитела изотипа IgG, которые преимущественно используются в качестве первичных и вторичных зондов в вестерн-блоттинге и других иммуноанализах.
Зонд ν для примененного E был извлечен из наклона линейной аппроксимации ( ν = 2,17 мкм/с) и определено используя уравнение 8; мкм 7% T = 1,81 × 10 −5 см 2 /(В·с). Не наблюдалось существенной разницы в x E между гелями, что облегчало прогнозирование местоположения зонда в геле без визуализации местоположения зонда в реальном времени (p > 0,22, U-критерий Манна-Уитни; ). Как описано уравнением 9, μ 7% T может варьироваться в зависимости от вида молекулы в естественных условиях электропереноса на r ч и q зонда. Однако в случае зондов антител одного и того же класса антител (изотипа) больших различий в электрофоретической подвижности не ожидается из-за минимальной вариации r h и q . Здесь использовались антитела изотипа IgG, которые преимущественно используются в качестве первичных и вторичных зондов в вестерн-блоттинге и других иммуноанализах. Повторная характеристика зонда μ 7% T потребовалась бы, если бы использовались антитела разных классов (например, IgM вместо IgG), так как можно ожидать, что разные изотипы будут существенно различаться в r h и q . Кроме того, конъюгация зонда с метками с различным зарядом может повлиять на q конъюгированного с меткой зонда и, таким образом, также потребовать повторной характеристики µ 7% T .
Повторная характеристика зонда μ 7% T потребовалась бы, если бы использовались антитела разных классов (например, IgM вместо IgG), так как можно ожидать, что разные изотипы будут существенно различаться в r h и q . Кроме того, конъюгация зонда с метками с различным зарядом может повлиять на q конъюгированного с меткой зонда и, таким образом, также потребовать повторной характеристики µ 7% T .
Электроперенос обеспечивает почти полное высвобождение зонда из агарозного геля для загрузки
Чтобы максимизировать полезность ряда внутригельных иммуноанализов, мы разработали гель для загрузки зонда с двумя ключевыми характеристиками: (i) быстрое изготовление и сборка с минимальными трудозатратами, и (ii) эффективное высвобождение зонда (минимальное попадание зонда в загрузочный гель) для максимального увеличения количества зонда, доступного для загрузки в гель для иммуноанализа. Мы предположили, что инертный гидрогель с большими порами (радиус пор 100–1000 нм) можно использовать в качестве геля для загрузки зонда, чтобы удовлетворить этим двум критериям дизайна. Таким образом, мы использовали 1,5% агарозный гель с низкой температурой плавления в качестве модельного геля для загрузки зонда (рис. S2). 48 Чтобы оценить эффективность высвобождения зонда, мы сравнили высвобождение зонда из агарозного загрузочного геля с высвобождением зонда из загрузочного геля с 4% T PA. Параметры электропереноса были выбраны для рассчитанного зонда x E > 1500 мкм, тогда как толщина загрузочного геля составляла 1000 мкм (уравнение 10; ).
Мы предположили, что инертный гидрогель с большими порами (радиус пор 100–1000 нм) можно использовать в качестве геля для загрузки зонда, чтобы удовлетворить этим двум критериям дизайна. Таким образом, мы использовали 1,5% агарозный гель с низкой температурой плавления в качестве модельного геля для загрузки зонда (рис. S2). 48 Чтобы оценить эффективность высвобождения зонда, мы сравнили высвобождение зонда из агарозного загрузочного геля с высвобождением зонда из загрузочного геля с 4% T PA. Параметры электропереноса были выбраны для рассчитанного зонда x E > 1500 мкм, тогда как толщина загрузочного геля составляла 1000 мкм (уравнение 10; ).
После разгрузки флуоресценция, оставшаяся в геле для загрузки агарозы, составляла 3,93% ± 1,76% от исходной флуоресценции в геле (ошибка выражена как стандартное отклонение, n=3, ). Флуоресценция, оставшаяся в геле с 4% TPA, составляла 75,8% ± 12,3% от исходной флуоресценции в геле (ошибка выражена как стандартное отклонение, n=6, ). Таким образом, гель для загрузки агарозы сохранил ~19X меньше зонда, чем загрузочный гель PA после разгрузки электропереносом (p = 0,0238, U-критерий Манна-Уитни).
Таким образом, гель для загрузки агарозы сохранил ~19X меньше зонда, чем загрузочный гель PA после разгрузки электропереносом (p = 0,0238, U-критерий Манна-Уитни).
Открыть в отдельном окне
Захват несвязанного зонда в загрузочных гелях после выгрузки с помощью электропереноса (12 В/см, 12 минут). Загрузочные гели были изготовлены с 0,2 мг/мл ослиного антикроличьего антитела AF647 в расплавленном (1,5% масс./об. гель агарозы) или неполимеризованном (4%T, 3,5%C PA гель) состояниях. Предварительная разгрузка: n=9. Гель ПА После разгрузки: n=6. Агароза после выгрузки: n=3. Столбики погрешностей указывают на стандартное отклонение. ( * указывает статистическую разницу по U-критерию Манна-Уитни, p<0,0238 )
Интересно, что большая часть зонда в растворе предшественника загружающего геля 4% T PA оставалась в геле после выгрузки с помощью электропереноса. Из расчетов зонда x E для применения E и T (уравнение 10), мы ожидаем, что срезов до Unload от 4%T . x E > 1500 мкм в геле с 7% TPA и, следовательно, также в геле с 4% TPA). Поэтому мы не приписываем наблюдаемый сигнал недостаточному приложению E или t . Однако известно, что свободнорадикальный каскад, возникающий в результате химически инициированной (APS и TEMED) полимеризации геля ПА, взаимодействует с белками, включенными в растворы предшественников геля ПА. Было показано, что это взаимодействие вызывает денатурацию белка в гелях ПА во время полимеризации, о чем свидетельствует вестерн-блоттинг. 49 Кроме того, неполное высвобождение макромолекул из устройств для доставки лекарств из гидрогеля наблюдалось для устройств из гидрогеля, полимеризованных с лекарством, включенным в раствор предшественника геля. 31,50 Зонд, остающийся в геле 4% TPA после разгрузки электропереноса, может быть вызван аналогичными взаимодействиями, приводящими к энтропийному захвату денатурированного зонда в порах или иммобилизации зонда на матрице гидрогеля.
x E > 1500 мкм в геле с 7% TPA и, следовательно, также в геле с 4% TPA). Поэтому мы не приписываем наблюдаемый сигнал недостаточному приложению E или t . Однако известно, что свободнорадикальный каскад, возникающий в результате химически инициированной (APS и TEMED) полимеризации геля ПА, взаимодействует с белками, включенными в растворы предшественников геля ПА. Было показано, что это взаимодействие вызывает денатурацию белка в гелях ПА во время полимеризации, о чем свидетельствует вестерн-блоттинг. 49 Кроме того, неполное высвобождение макромолекул из устройств для доставки лекарств из гидрогеля наблюдалось для устройств из гидрогеля, полимеризованных с лекарством, включенным в раствор предшественника геля. 31,50 Зонд, остающийся в геле 4% TPA после разгрузки электропереноса, может быть вызван аналогичными взаимодействиями, приводящими к энтропийному захвату денатурированного зонда в порах или иммобилизации зонда на матрице гидрогеля. 50 Гелеобразование в агарозе не подвергается такому же процессу полимеризации и относительно инертно по отношению к белкам при переходе из расплавленного состояния в затвердевшее 51 . Инертная природа крупнопористого геля для загрузки агарозы удовлетворяет критериям дизайна как минимального захвата зонда в геле, так и быстрого и простого изготовления.
50 Гелеобразование в агарозе не подвергается такому же процессу полимеризации и относительно инертно по отношению к белкам при переходе из расплавленного состояния в затвердевшее 51 . Инертная природа крупнопористого геля для загрузки агарозы удовлетворяет критериям дизайна как минимального захвата зонда в геле, так и быстрого и простого изготовления.
Зонд быстро загружается с повышенным коэффициентом распределения при электропереносе зонда
После разработки системы для контролируемой электромиграции зонда с постоянной скоростью (r 2 = 0,9888, ) и минимального захвата зонда в агарозном загрузочном геле (96,07% ± 1,76% датчик удален, ), мы стремились продемонстрировать эту систему для увеличенного K , часть , и быстрый перенос зонда из геля для нанесения на калибровочный гель при загрузке зонда электропереносом (по сравнению с диффузионным зондированием; критерии проектирования системы диффузионного зондирования были получены в предыдущей работе 52 и описаны в примечании. С1). Для определения ожидаемого зонда x E в системе для нанесенного E снова использовался зонд μ 7% T , рассчитанный из. В E = 8 В/см, ожидаемое ν = 1,45 мкм/с, а расчетное значение t , необходимое для электромиграции зонда на 1000 мкм (толщина проклеивающего геля), составило ~11,5 мин. Зонд μ гель в геле с 1,5% агарозной загрузкой, как ожидается, будет больше, чем в проклеивающем геле с 7% TPA, на основании предыдущих сравнений электрофоретического переноса макромолекул в двух материалах (больший размер пор в агарозном геле позволяет более быстрый транспорт макромолекул). 48 Из-за этой разницы в μ гель ожидается, что электроперенос зонда из загрузочного геля в калибровочный гель будет подвергаться электрофоретическому стэкингу, становясь более концентрированным при входе в калибровочный гель в соотношении двух μ гель значений.
С1). Для определения ожидаемого зонда x E в системе для нанесенного E снова использовался зонд μ 7% T , рассчитанный из. В E = 8 В/см, ожидаемое ν = 1,45 мкм/с, а расчетное значение t , необходимое для электромиграции зонда на 1000 мкм (толщина проклеивающего геля), составило ~11,5 мин. Зонд μ гель в геле с 1,5% агарозной загрузкой, как ожидается, будет больше, чем в проклеивающем геле с 7% TPA, на основании предыдущих сравнений электрофоретического переноса макромолекул в двух материалах (больший размер пор в агарозном геле позволяет более быстрый транспорт макромолекул). 48 Из-за этой разницы в μ гель ожидается, что электроперенос зонда из загрузочного геля в калибровочный гель будет подвергаться электрофоретическому стэкингу, становясь более концентрированным при входе в калибровочный гель в соотношении двух μ гель значений. 53 Поскольку загрузочный гель и проклеивающий гель имеют одинаковую толщину (1 мм), мы предположили, что такое электрофоретическое наложение минимизирует степень потери зонда из геля в окружающий буферный раствор за счет диффузионного расширения во время электромиграции зонда. Среднее эффективное K , часть , для нагрузки зонда электропереноса была K , часть , E = 0,87 ± 0,05 (n = 4, ошибка выражена как стандартное отклонение; ).
53 Поскольку загрузочный гель и проклеивающий гель имеют одинаковую толщину (1 мм), мы предположили, что такое электрофоретическое наложение минимизирует степень потери зонда из геля в окружающий буферный раствор за счет диффузионного расширения во время электромиграции зонда. Среднее эффективное K , часть , для нагрузки зонда электропереноса была K , часть , E = 0,87 ± 0,05 (n = 4, ошибка выражена как стандартное отклонение; ).
Продолжительность мониторинга диффузионной загрузки зонда определялась уравнениями 6 и 7. Диффузия зонда на расстояние более 0,5 мм в геле 7% T PA (минимальная характеристическая длина диффузии, так как зонд загружается с обеих противоположных сторон проклеивающего геля толщиной 1 мм) ожидается, что это произойдет через ~ 4,8 ч (τ). Измерения флуоресценции в геле регистрировали в течение 28 часов (>5,8 τ) при диффузионной загрузке зонда. среднее K часть после 28 часов нагрузки зонда диффузионного переноса составляла часть K , diff = 0,13 ± 0,01 (n = 4, ошибка выражена как стандартное отклонение; ). Таким образом, средняя эффективная концентрация K части в проклеивающем геле была увеличена при нагрузке зонда электропереноса по сравнению с нагрузкой зонда диффузионного переноса в 6,5 ± 0,1 раза (p = 0,0286, U-критерий Манна-Уитни).
Таким образом, средняя эффективная концентрация K части в проклеивающем геле была увеличена при нагрузке зонда электропереноса по сравнению с нагрузкой зонда диффузионного переноса в 6,5 ± 0,1 раза (p = 0,0286, U-критерий Манна-Уитни).
Чтобы охарактеризовать загрузку зонда более t с помощью диффузионного переноса, флуоресценцию в геле в течение 28 часов диффузионной загрузки зонда использовали для создания подгонки модели по степенному закону 30,31 (r 2 = 0,9321‡; ). По степенному закону было определено, что 90% флуоресценции в геле, измеренной через 28 часов, происходит через ~ 16 часов. Таким образом, загрузка зонда электропереносом не только привела к эффективному зонду K part , который был в 6,5 ± 0,1 X больше, чем при диффузионном переносе, но также было продемонстрировано, что он более чем в 82 раза быстрее, чем диффузионный перенос. (время загрузки электротрансфера = 11,5 мин).
(время загрузки электротрансфера = 11,5 мин).
Электроперенос способствует быстрой и эффективной разгрузке зонда
Далее мы рассмотрели флуоресценцию зонда, сохраняющуюся в калибровочном геле после разгрузки с помощью электропереноса зонда, по сравнению с диффузионным переносом. Для этого проклеивающие гели с зондами разгружали либо электропереносом зонда, либо диффузионным переносом зонда. E и t (12 В/см, 15 мин) для удаления несвязанного зонда определяли из мк 7% T рассчитано в . Расчеты оценочного зонда x E ≈ 2000 мкм, что обеспечивает полную разгрузку проклеивающего геля (1000 мкм). После снятия зонда с помощью электропереноса флуоресценция, оставшаяся в проклеивающем геле, составляла 5,54% ± 1,16% (n=5, ) от исходной флуоресценции проклеивающего геля, загруженного зондом. Разгрузка зонда за счет диффузионного переноса должна была произойти через ~4,8 ч (τ; ). Через 45 часов диффузионного вымывания (>9,7τ) мы наблюдали среднюю флуоресценцию в геле, равную 15,09% ± 4,62% (n=6, ) от исходного проклеивающего геля с зондом в геле.
Интересно, что флуоресценция в геле во время разгрузки зонда путем диффузионного переноса продолжала снижаться в течение 45 ч (n=3, ). Чтобы охарактеризовать разгрузку зонда посредством диффузионного переноса, данные флуоресценции в геле t во время удаления зонда согласовывали с моделью степенной зависимости 30,31 диффузионной разгрузки зонда (r 2 = 0,9812; ). Согласно степенному закону, 90% несвязанного зонда было удалено примерно через 45 часов. Скорость удаления зонда может быть потенциально увеличена за счет более регулярной замены буферной ванны (например, два раза в час, как это делается для аналогичных этапов удаления зонда антитела из аналогичных плотных иммуноанализов в геле PA 9).1132 3 вместо каждых 12 часов, как здесь) или хранение в более теплой среде (>4 °C). Такие меры не принимались в этих экспериментальных процедурах, поскольку 30-минутные замены буфера в течение > 24 часов не считались экспериментально практичными, а также для предотвращения загрязнения образца или денатурации антител путем дополнительных этапов обработки и хранения в теплой среде. В конечном счете, остаточная фоновая флуоресценция в геле, возникающая в результате разгрузки зонда электропереносом, была на 2,7 ± 0,4 Х меньше, чем разгрузка зонда диффузионным переносом, и происходила более чем в 180 раз быстрее, чем разгрузка диффузионным переносом.
В конечном счете, остаточная фоновая флуоресценция в геле, возникающая в результате разгрузки зонда электропереносом, была на 2,7 ± 0,4 Х меньше, чем разгрузка зонда диффузионным переносом, и происходила более чем в 180 раз быстрее, чем разгрузка диффузионным переносом.
Зондирование с электропереносом повышает эффективность иммунологического анализа по сравнению с диффузионным зондированием
Наконец, мы оценили влияние зондирования с электропереносом на чувствительность детектирования иммуноанализа в геле по сравнению с зондированием с диффузионным переносом. Мы предположили, что применение зондирования с электропереносом для обнаружения OVA, иммобилизованного в геле для определения размера белка, приведет к большему SNR и потребует меньшего времени иммунозондирования, чем обнаружение OVA с помощью зондирования с диффузионным переносом. Микрофотографии флуоресценции полос OVA и зонда показаны на рис. Мы заметили, что среднее отношение сигнал-шум при электропереносном зондировании составило 20,56 ± 15,60 (n = 6), а при диффузном зондировании — 5,02 ± 1,70 (n = 4, p = 0,009). 5, U-критерий Манна-Уитни). Изменчивость SNR электротрансферного зондирования могла быть завышена за счет различной концентрации зонда в загрузочных гелях, как описано в таблице S3 (зонд 1° Ab: 0,1–0,0075 мг/мл, зонд 2° Ab: 0,2–0,015 мг/мл). Загрузочные гели, используемые при диффузионном зондировании, не различались по концентрации зонда (зонд 1° Ab: 0,1 мг/мл, зонд 2° Ab: 0,2 мг/мл). Необходимы дальнейшие эксперименты для изучения влияния концентрации зонда в загрузочных гелях на ОСШ. Оценку местоположения пика целевого белка и обнаруженного местоположения пика зонда при электропереносе и диффузионном зондировании выполняли, чтобы убедиться, что измеренный сигнал зонда соответствует фактическому местоположению целевого белка (p > 0,17 для обоих методов, U-критерий Манна-Уитни, ). Примечательно, что общее время, необходимое для завершения этапов зондирования при электропереносе и зондировании с диффузионным переносом, сильно различается: зондирование с диффузионным переносом было завершено за 120 часов, а зондирование с электропереносом было завершено менее чем за 4 часа ().
5, U-критерий Манна-Уитни). Изменчивость SNR электротрансферного зондирования могла быть завышена за счет различной концентрации зонда в загрузочных гелях, как описано в таблице S3 (зонд 1° Ab: 0,1–0,0075 мг/мл, зонд 2° Ab: 0,2–0,015 мг/мл). Загрузочные гели, используемые при диффузионном зондировании, не различались по концентрации зонда (зонд 1° Ab: 0,1 мг/мл, зонд 2° Ab: 0,2 мг/мл). Необходимы дальнейшие эксперименты для изучения влияния концентрации зонда в загрузочных гелях на ОСШ. Оценку местоположения пика целевого белка и обнаруженного местоположения пика зонда при электропереносе и диффузионном зондировании выполняли, чтобы убедиться, что измеренный сигнал зонда соответствует фактическому местоположению целевого белка (p > 0,17 для обоих методов, U-критерий Манна-Уитни, ). Примечательно, что общее время, необходимое для завершения этапов зондирования при электропереносе и зондировании с диффузионным переносом, сильно различается: зондирование с диффузионным переносом было завершено за 120 часов, а зондирование с электропереносом было завершено менее чем за 4 часа (). Таким образом, по сравнению с зондированием с диффузионным переносом, зондирование с электропереносом улучшило чувствительность обнаружения иммуноанализа в геле, отмеченное в 4,1 ± 3,4 X большим SNR, и потребовало в 30 раз меньше времени иммунозондирования.
Таким образом, по сравнению с зондированием с диффузионным переносом, зондирование с электропереносом улучшило чувствительность обнаружения иммуноанализа в геле, отмеченное в 4,1 ± 3,4 X большим SNR, и потребовало в 30 раз меньше времени иммунозондирования.
Открыть в отдельном окне
Электротрансферное зондирование выявляет иммобилизованный в геле OVA с более высоким SNR и меньшей продолжительностью иммунозондирования, чем диффузионное зондирование. ( A ) Микрофотографии флуоресценции иммобилизованного OVA и зонда для обнаружения электропереноса в проклеивающем геле. ( B ) SNR зонда обнаружения OVA при электропереносном зондировании больше, чем при диффузионном зондировании. Электроперенос: n=6. Диффузный: n=4. (* указывает статистическую разницу по U-критерию Манна-Уитни, p=0,0095) . ( C,D ) Расположение пиков целевого белка OVA и детектирующего зонда не показывает статистической разницы в условиях электропереноса ( C ) и диффузионного зондирования ( D ) (p>0,17, U-критерий Манна-Уитни ). ( E ) Продолжительность иммунозондирования при электротрансферном зондировании в 30 раз меньше, чем при диффузионном зондировании. E: электротрансферное зондирование. D: диффузионное зондирование.
( E ) Продолжительность иммунозондирования при электротрансферном зондировании в 30 раз меньше, чем при диффузионном зондировании. E: электротрансферное зондирование. D: диффузионное зондирование.
Мы представили гель-гелевую систему зондирования с электропереносом для быстрой и эффективной загрузки и выгрузки зонда в миллиметровом масштабе, плотных, открытых иммуноанализах в геле. Наша конструкция включает (i) электролитическую ячейку, которая была разработана и охарактеризована для предсказуемой миграции зонда, и (ii) гель для загрузки агарозы для доставки зонда в гель для определения размера белка с низкими потерями. Мы продемонстрировали эту систему для более быстрой и эффективной загрузки и выгрузки зонда в большой, плотный, открытый гидрогель, чем это возможно при обычном зондировании с диффузионным переносом. Мы дополнительно оценили влияние электротрансферного зондирования на чувствительность обнаружения иммуноанализа в геле, используя обнаружение OVA из геля для определения размера белка в качестве примера проверки концепции. По сравнению с зондированием с диффузным переносом мы наблюдали повышенное SNR зондируемого сигнала при существенно более короткой общей продолжительности иммунозондирования. Электротрансферное зондирование повышает SNR измерения исследуемого белка и требует в 30 раз меньше времени иммунозондирования, чем диффузионное зондирование переноса. Учитывая преобладающее использование иммуноанализов в геле для обнаружения целевого белка в биологических образцах, мы ожидаем, что электротрансферное зондирование повысит чувствительность обнаружения в широком диапазоне иммуноанализов в геле. Открытые вопросы включают исследования электротрансферного зондирования с использованием альтернативных зондовых меток (например, флуоресцентных меток с переменным зарядом). Кроме того, устраняя проблемы, связанные с иммунозондированием гидрогелей для измерения белков в миллиметровом масштабе, мы ожидаем, что зондирование с помощью электропереноса облегчит разработку новых гелевых иммуноанализов с расширенными форм-факторами и улучшенными возможностями точного определения характеристик белков.
По сравнению с зондированием с диффузным переносом мы наблюдали повышенное SNR зондируемого сигнала при существенно более короткой общей продолжительности иммунозондирования. Электротрансферное зондирование повышает SNR измерения исследуемого белка и требует в 30 раз меньше времени иммунозондирования, чем диффузионное зондирование переноса. Учитывая преобладающее использование иммуноанализов в геле для обнаружения целевого белка в биологических образцах, мы ожидаем, что электротрансферное зондирование повысит чувствительность обнаружения в широком диапазоне иммуноанализов в геле. Открытые вопросы включают исследования электротрансферного зондирования с использованием альтернативных зондовых меток (например, флуоресцентных меток с переменным зарядом). Кроме того, устраняя проблемы, связанные с иммунозондированием гидрогелей для измерения белков в миллиметровом масштабе, мы ожидаем, что зондирование с помощью электропереноса облегчит разработку новых гелевых иммуноанализов с расширенными форм-факторами и улучшенными возможностями точного определения характеристик белков.
esi
Нажмите здесь для просмотра. (5.6M, pdf)
Эта работа была поддержана Национальным институтом рака Национальных институтов здравоохранения, наградой Cancer Moonshot (R33CA225296, A.E.H.). С.М.Г. был поддержан постдокторской стипендией Канадского совета по естественным наукам и инженерным исследованиям (NSERC). APM был поддержан грантом на обучение Национального института здравоохранения (T32GM008155) и стипендией Национального научного фонда для выпускников (1106400). Фотолитографию проводили в Центре биомолекулярных нанотехнологий QB3. Авторы благодарны за обсуждения со всеми членами Herr Lab.
Конфликт интересов
Авторы заявляют об отсутствии конкурирующих финансовых интересов.
Доступна электронная дополнительная информация (ESI): [здесь следует указать подробную информацию о любой доступной дополнительной информации]. См. DOI: 10.1039/x0xx00000x
‡ . Соответствие этой модели оценивали с помощью r-квадрата. Были выявлены два выброса для этого набора данных, которые были исключены из данных, включенных в подбор модели (1 в момент времени 10 ч и 1 в момент времени 12,5 ч). Измеренная флуоресценция в идентифицированных выбросах была выше, чем ожидалось, потому что одна сторона проклеивающего геля была усеяна массивом микролунок (диаметр 32 мкм, глубина 40 мкм, расстояние между центрами 100 мкм), и эта поверхность была непреднамеренно обращена вверх во время визуализация флуоресценции геля в размер. Таким образом, раствор флуоресцентно меченого антитела мог скапливаться в микролунках, искусственно увеличивая измеренную флуоресценцию зонда антитела в калибровочном геле для двух измерений выбросов. Все остальные измерения флуоресценции (во всех гелях и во все моменты времени) проводились микролунками вниз. Включая выбросы, параметры подгонки модели, использующие тот же процесс степенного закона, следующие: а = 108,9, б = 0,2046, г 2 = 0,7886.
Были выявлены два выброса для этого набора данных, которые были исключены из данных, включенных в подбор модели (1 в момент времени 10 ч и 1 в момент времени 12,5 ч). Измеренная флуоресценция в идентифицированных выбросах была выше, чем ожидалось, потому что одна сторона проклеивающего геля была усеяна массивом микролунок (диаметр 32 мкм, глубина 40 мкм, расстояние между центрами 100 мкм), и эта поверхность была непреднамеренно обращена вверх во время визуализация флуоресценции геля в размер. Таким образом, раствор флуоресцентно меченого антитела мог скапливаться в микролунках, искусственно увеличивая измеренную флуоресценцию зонда антитела в калибровочном геле для двух измерений выбросов. Все остальные измерения флуоресценции (во всех гелях и во все моменты времени) проводились микролунками вниз. Включая выбросы, параметры подгонки модели, использующие тот же процесс степенного закона, следующие: а = 108,9, б = 0,2046, г 2 = 0,7886.
Заявление об ограничении ответственности издателя: Принятые рукописи публикуются в Интернете вскоре после принятия, перед техническим редактированием, форматированием и чтением корректуры. Используя этот бесплатный сервис, авторы могут сделать свои результаты доступными для сообщества в форме для цитирования, прежде чем мы опубликуем отредактированную статью. Мы заменим эту принятую рукопись отредактированной и отформатированной предварительной статьей, как только она будет доступна.
Используя этот бесплатный сервис, авторы могут сделать свои результаты доступными для сообщества в форме для цитирования, прежде чем мы опубликуем отредактированную статью. Мы заменим эту принятую рукопись отредактированной и отформатированной предварительной статьей, как только она будет доступна.
1. Берг Дж., Дж. Л. Т. и С. Л., Биохимия, 5-е изд. [Google Scholar]
2. Vogel C, Abreu RDS, Ko D, Le S, Shapiro BA, Burns SC, Sandhu D, Boutz DR, Marcotte EM and Penalva LO, Mol. Сист. биол, 2010, 6, 1–9. [Google Scholar]
3. Hughes AJ, Spelke DP, Xu Z, Kang C-C, V Schaffer D and Herr AE, Nat. Методы, 2014, 11, 455–464. [Google Scholar]
4. Chen F, Tillberg PW и Boyden ES, Science (80-.), 2015, 347, 543–548. [Бесплатная статья PMC] [PubMed] [Google Scholar]
5. Costantini I, Ghobril JP, Di Giovanna AP, Allegra Mascaro AL, Silvestri L, Müllenbroich MC, Onofri L, Conti V, Vanzi F, Sacconi L, Guerrini R, Markram H, Iannello G and Pavone FS, Sci. Rep, 2015, 5, 9808. [Бесплатная статья PMC] [PubMed] [Google Scholar]
[Бесплатная статья PMC] [PubMed] [Google Scholar]
6. Theisen MJ, Chu ML and Laboratories A, Иммунохимическое обнаружение белков в геле, которые плохо переносятся в мембраны, 2004.
7. Desai S, Dworecki B и Cichon E, Anal. Биохим, 2001, 297, 94–98. [PubMed] [Академия Google]
8. Влассакис Дж. и Герр А.Е., Anal Chem, 2015, 87, 11030–11038. [Статья бесплатно PMC] [PubMed] [Google Scholar]
9. Goodrich JA and Kugel JF, Binding and Kinetics for Molecular Biologist, Cold Spring Harbour Laboratories Press, Cold Spring Harbour, 2007. [Google Scholar]
10. Ogston АГ, пер. Фарадей Сок, 1958, 54, 1754–1757. [Google Scholar]
11. Tong J and Anderson JL, Biophys. Дж., 1996, 70, 1505–1513. [Бесплатная статья PMC] [PubMed] [Google Scholar]
12. Su A, Smith BE и Herr AE, Anal Chem, 2020, 875–883. [Бесплатная статья PMC] [PubMed] [Google Scholar]
13. Jøssang T, Feder J and Rosenqvist E, J. Protein Chem, 1988, 7, 165–171. [PubMed] [Google Scholar]
14. MacPhee DJ, J. Pharmacol. Токсикол. Методы, 2010, 61, 171–177. [PubMed] [Google Scholar]
MacPhee DJ, J. Pharmacol. Токсикол. Методы, 2010, 61, 171–177. [PubMed] [Google Scholar]
15. Burnette WN, Anal. Биохим, 1981, 112, 195–203. [PubMed] [Google Scholar]
16. Towbin H, Staehelin T and Gordon J, Proc. Натл. акад. наук, 1979, 76, 4350–4354. [Бесплатная статья PMC] [PubMed] [Google Scholar]
17. Anderson GJ, Cipolla CM и Kennedy RT, Anal. Chem, 2011, 83, 17. [Бесплатная статья PMC] [PubMed] [Google Scholar]
18. Jin S, Furtaw MD, Chen H, Lamb DT, Ferguson SA, Arvin NE, Dawod M and Kennedy RT, Anal. хим., 2016, 88, 6703–10. [Бесплатная статья PMC] [PubMed] [Google Scholar]
19. Kotsmar C, Sells T, Taylor N, Liu DE, Prausnitz JM and Radke CJ, Macromolecules, 2012, 45, 9177–9187. [Google Scholar]
20. Герке С.Х., Уден Л.Х., Макбрайд Дж.Ф., Дж. Контроль. Релиз, 1998, 55, 21–33. [PubMed] [Google Scholar]
21. Gerver RE и Herr AE, Anal. хим., 2014, 86, 10625–10632. [PMC free article] [PubMed] [Google Scholar]
22. Крылов С. Н., Электрофорез, 2007, 28, 69–88. [PubMed] [Google Scholar]
Н., Электрофорез, 2007, 28, 69–88. [PubMed] [Google Scholar]
23. Berthier J, Brakke KA и Berthier E, Open Microfluidics, Wiley, 2016. [Google Scholar]
24. Pfohl T, Mugele F, Seemann R and Herminghaus S, ChemPhysChem, 2003 , 4, 1291–1298. [PubMed] [Google Scholar]
25. Kaigala GV, Lovchik RD and Delamarche E, Angew. Чеми Инт. Эд, 2012, 51, 11224–11240. [PubMed] [Академия Google]
26. Kang C-CC, Yamauchi KA, Vlassakis J, Sinkala E, Duncombe TA and Herr AE, Nat Protoc, 2016, 11, 1508–1530. [Бесплатная статья PMC] [PubMed] [Google Scholar]
27. Dormán G, Nakamura H, Pulsipher A and Prestwich GD, Chem. Рев., 2016, 116, 15284–15398. [PubMed] [Google Scholar]
28. Vermeer AWP and Norde W, Biophys. Дж., 2000, 78, 394–404. [Бесплатная статья PMC] [PubMed] [Google Scholar]
29. Grist SM, Mourdoukoutas AP and Herr AE, bioRxiv, 2019, doi: 10.1101/805770. [Перекрестная ссылка]
30. Siepmann J и Peppas NA, Adv. Наркотик Делив. Рев., 2001, 48, 139–157. [PubMed] [Google Scholar]
[PubMed] [Google Scholar]
31. Lin CC и Metsters AT, Adv. Наркотик Делив. Рев., 2006, 58, 1379–1408. [PubMed] [Google Scholar]
32. Shapiro AL, Viñuela E and Maizel JV Jr., Biochem. Биофиз. Рез. Коммун, 1967, 28, 815–820. [PubMed] [Google Scholar]
33. Erickson HP, Biol. Обработано Онлайн, 2009, 11, 32–51. [Бесплатная статья PMC] [PubMed] [Google Scholar]
34. Парк Х, Джонсон К.С. и Габриэль Д.А., Макромолекулы, 1990, 23, 1548–1553. [Google Scholar]
35. Yamauchi KA and Herr AE, Microsystems Nanoeng, 2017, 3, 16079. [бесплатная статья PMC] [PubMed] [Google Scholar]
36. Shapiro SJ, Dendukuri D and Doyle PS, Anal. хим., 2018, 90, 13572–13579. [PubMed] [Google Scholar]
37. Berg H. Случайные блуждания в биологии, 1993. [Google Scholar]
38. Ferguson K, Metab., Clin. Опыт, 1964, 13, 985–1002. [PubMed] [Google Scholar]
39. Squires TM, Messinger RJ and Manalis SR, Nat. Биотехнология, 2008, 26, 417–426. [PubMed] [Академия Google]
40. Холмс Д.Л. и Стеллваген Н.К., Электрофорез, 1991, 12, 612–619. [PubMed] [Google Scholar]
Холмс Д.Л. и Стеллваген Н.К., Электрофорез, 1991, 12, 612–619. [PubMed] [Google Scholar]
41. Narayanan J, Xiong J-Y and Liu X-Y, J. Phys. конф. Сер, 2006, 28, 83–86. [Google Scholar]
42. Corstjens H, Billiet HAH, Frank J and Luyben KCAM, Electrophoresis, 1996, 17, 137–143. [PubMed] [Google Scholar]
43. Sillen CWMP, Barendrecht E, Janssen LJJ и van Stralen SJD, Int. J. Hydrogen Energy, 1982, 7, 577–587. [Google Scholar]
44. Macounova K, Cabrera CR, Holl MR and Yager P, Anal Chem, 2000, 72, 3745–3751. [PubMed] [Академия Google]
45. Bjellqvist B, Ek K, Giorgio Righetti P, Gianazza E, Görg A, Westermeier R and Postel W, J. Biochem. Биофиз. Методы, 1982, 6, 317–339. [PubMed] [Google Scholar]
46. Тентори А.М., Ямаути К.А. и Герр А.Е., Angew Chem Int Ed Engl, 2016, 55, 12431–12435. [Бесплатная статья PMC] [PubMed] [Google Scholar]
/buffers/tris-glycine-buffer-tg-buffer-ph-8-3-0-2-10x-concentrate/ (по состоянию на 26 января 2020 г.



 1 Электростатика
1 Электростатика 6 СТО
6 СТО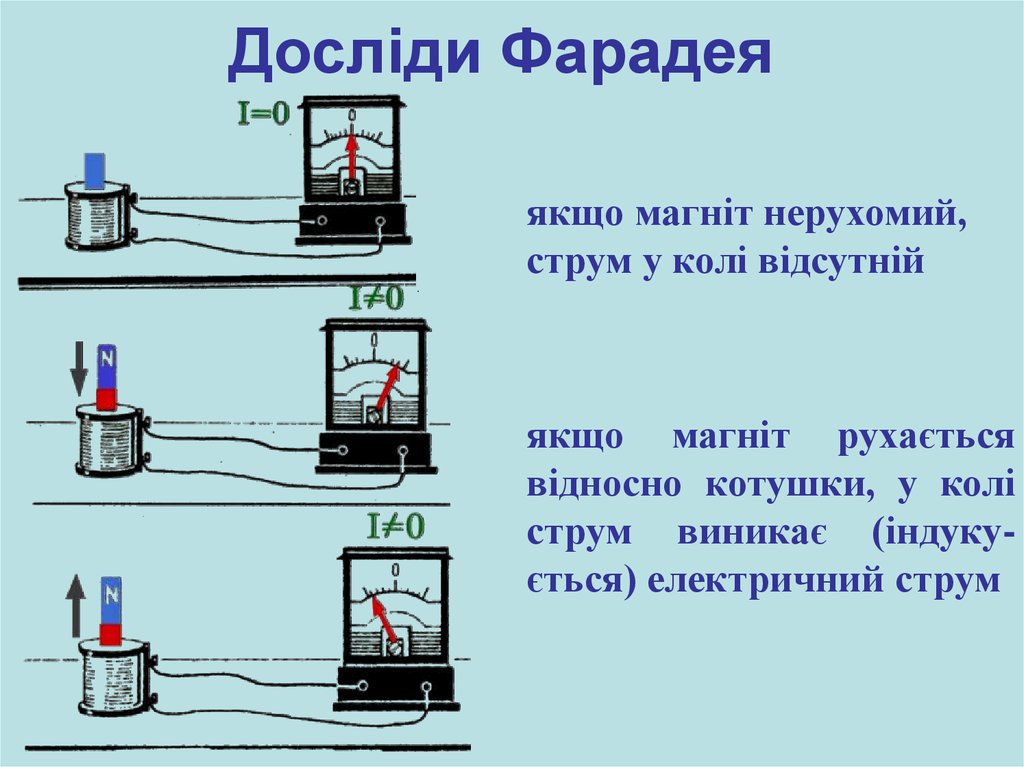

 В. Курс общей физики. Т. 2. М.: Наука, 1978. С. 178. ↩︎
В. Курс общей физики. Т. 2. М.: Наука, 1978. С. 178. ↩︎

 В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).
В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).




 А. Тобы: 103 фк
А. Тобы: 103 фк
 По личному опыту могу сказать, что они не откажутся от вашего дела, пока оно не будет завершено».
По личному опыту могу сказать, что они не откажутся от вашего дела, пока оно не будет завершено».

 Гриффит, эсквайр, CFLS Джон Н. Гриффит, эсквайр, CFLS
Гриффит, эсквайр, CFLS Джон Н. Гриффит, эсквайр, CFLS 
 В настоящее время она занимается вопросами семейного права и активно защищает права своих клиентов. Она уделяет время и внимание потребностям каждого клиента и уникальным обстоятельствам их дела.
В настоящее время она занимается вопросами семейного права и активно защищает права своих клиентов. Она уделяет время и внимание потребностям каждого клиента и уникальным обстоятельствам их дела. Применяя индивидуальный подход к каждому делу, Эрик Каудери стремится работать с клиентами, чтобы помочь им пройти часто запутанный и сложный юридический процесс развода.
Применяя индивидуальный подход к каждому делу, Эрик Каудери стремится работать с клиентами, чтобы помочь им пройти часто запутанный и сложный юридический процесс развода. имущество. Она стремится обеспечить эффективное юридическое представительство наших клиентов, активно отстаивая их законные права и предлагая сострадательные юридические консультации.
имущество. Она стремится обеспечить эффективное юридическое представительство наших клиентов, активно отстаивая их законные права и предлагая сострадательные юридические консультации.
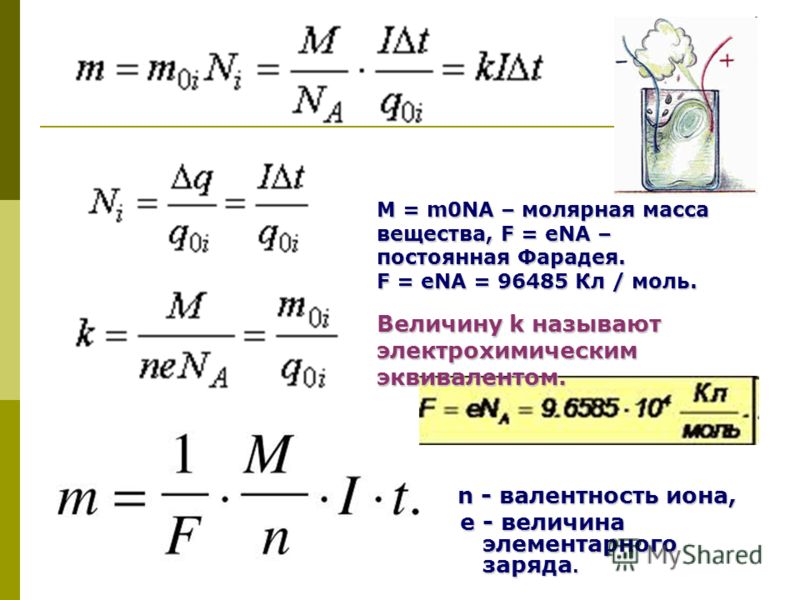 Он родился в семье бедного кузнеца и в молодом возрасте стал учеником переплетчика. Он увлекся наукой и в юном возрасте посещал лекции Хамфри Дэви. Он был самоучкой и представил Дэви кучу сделанных им заметок, и вскоре он стал учеником Дэви. При нем Фарадей стал превосходным ученым, став самостоятельным лектором, что сделало научные лекции интересными для среднего человека, особенно детей, и, в первую очередь, открыло связь между магнитными полями и электричеством (позже названную законом индукции Фарадея). В Машина времени Марио , Магнит, который Фарадей использовал для своих экспериментов, украден путешествующим во времени Боузером, что мешает ему завершить свои открытия.
Он родился в семье бедного кузнеца и в молодом возрасте стал учеником переплетчика. Он увлекся наукой и в юном возрасте посещал лекции Хамфри Дэви. Он был самоучкой и представил Дэви кучу сделанных им заметок, и вскоре он стал учеником Дэви. При нем Фарадей стал превосходным ученым, став самостоятельным лектором, что сделало научные лекции интересными для среднего человека, особенно детей, и, в первую очередь, открыло связь между магнитными полями и электричеством (позже названную законом индукции Фарадея). В Машина времени Марио , Магнит, который Фарадей использовал для своих экспериментов, украден путешествующим во времени Боузером, что мешает ему завершить свои открытия. Фарадей говорит, что он на пороге «захватывающего» открытия, и он не хочет, чтобы Марио беспокоил его. Затем Марио спрашивает разных людей, в том числе жену Фарадея, Сару Барнард, о Фарадее и Магните. Полностью убедившись, что Магнит принадлежит Фарадею, он возвращается в лабораторию и сообщает Фарадею, что нашел свой Магнит. Фарадей взволнованно берет его у Марио и сразу же использует в своем эксперименте. Затем он объясняет Марио, как работает эксперимент, в том числе как генерируется электрический ток, когда он пропускает Магнит через катушку провода. Марио замечает, что Фарадей теперь может приводить в действие большие машины, и Фарадей удивлен дерзкими комментариями Марио. Он не уверен, какое практическое применение могут иметь его открытия, но уверен, что правительство планирует обложить их налогом.
Фарадей говорит, что он на пороге «захватывающего» открытия, и он не хочет, чтобы Марио беспокоил его. Затем Марио спрашивает разных людей, в том числе жену Фарадея, Сару Барнард, о Фарадее и Магните. Полностью убедившись, что Магнит принадлежит Фарадею, он возвращается в лабораторию и сообщает Фарадею, что нашел свой Магнит. Фарадей взволнованно берет его у Марио и сразу же использует в своем эксперименте. Затем он объясняет Марио, как работает эксперимент, в том числе как генерируется электрический ток, когда он пропускает Магнит через катушку провода. Марио замечает, что Фарадей теперь может приводить в действие большие машины, и Фарадей удивлен дерзкими комментариями Марио. Он не уверен, какое практическое применение могут иметь его открытия, но уверен, что правительство планирует обложить их налогом. Коз • Эйс • Алекс • Элли • Азалия • Б. Коз • Барб • Бин • Бет • Билли • Бёрд • Боб • Брайан • Базз • Чад • Чарли • Чес • Чет • Крис • Клэй • Курт • Дуизил • Элден • Элла • Элрой • Эми • Эмили • Фэй • Флит • Гэри • Джин • Грейс • Грэмми • Грэмпи • Гарри ( Марио Гольф ) • Гарри ( Марио Теннис серия) • Директор школы • Хелен • Джет • Джо • Джой • Кейт • Кен • Кевин • Кид • Кайл • Кёко • Леон • Линда • Лиза • Мэйпл • Мейсон • Марк ( NES Open Tournament Golf ) • Марк ( Mario Tennis series) • Meg • Mel • Micki • Mynx • Napple • Neil • Nina ( Mario Tennis series) • Оскар • Пэм • Паула • Питер • Плам • Пауэрт • Путтс • Рой • Розари • Саманта • Сэмми • Саша • Сасс • Шон • Шэдоу Свинг Кинг • Шэдоу Свингстресс • Шон • Шери • Шерри • Шкипер • Сонни • София • Спайк • Стив • Сильвия • Тред • Крошка • Тони • Тори • Уискер • Вилли
Коз • Эйс • Алекс • Элли • Азалия • Б. Коз • Барб • Бин • Бет • Билли • Бёрд • Боб • Брайан • Базз • Чад • Чарли • Чес • Чет • Крис • Клэй • Курт • Дуизил • Элден • Элла • Элрой • Эми • Эмили • Фэй • Флит • Гэри • Джин • Грейс • Грэмми • Грэмпи • Гарри ( Марио Гольф ) • Гарри ( Марио Теннис серия) • Директор школы • Хелен • Джет • Джо • Джой • Кейт • Кен • Кевин • Кид • Кайл • Кёко • Леон • Линда • Лиза • Мэйпл • Мейсон • Марк ( NES Open Tournament Golf ) • Марк ( Mario Tennis series) • Meg • Mel • Micki • Mynx • Napple • Neil • Nina ( Mario Tennis series) • Оскар • Пэм • Паула • Питер • Плам • Пауэрт • Путтс • Рой • Розари • Саманта • Сэмми • Саша • Сасс • Шон • Шэдоу Свинг Кинг • Шэдоу Свингстресс • Шон • Шери • Шерри • Шкипер • Сонни • София • Спайк • Стив • Сильвия • Тред • Крошка • Тони • Тори • Уискер • Вилли Вашингтон • Кэтрин Диккенс • Чарльз Диккенс • Чарльз-Гаспар де ла Рив • Клеопатра • Констанция Моцарт • Дэвид Греневецки • Дебора Рид • Дон Ллойд • Герцог Алансонский • Эдмунд Галлей • Фердинанд Магеллан • Фрэнсис Дрейк • Фредерик Дуглас • Галилей Галилей • Джордж Вашингтон Карвер • Генри Форд • Хо Ти • Исаак Ньютон • Джефф Гриффит • Жанна д’Арк • Иоганн Гутенберг • Йозеф Гайдн • Хуан Себастьян Дель Кано • Юлий Цезарь • Хубилай Хан • Леонардо да Винчи • Луи Пастер • Людвиг ван Бетховен • Махатма Ганди • Марко Поло • Мэри Тодд Линкольн • Майкл Фарадей • Микеланджело Буонарроти • Минамото но Ёритомо • Пьер Поль Эмиль Ру • Платон • Королева Елизавета I • Рафаэль Санти • Ричард Бербедж • Королевское общество • Сара Барнард • Томас Эдисон • Томас Джефферсон • Цай Лунь • Уильям Шекспир • Вольфганг Амадей Моцарт
Вашингтон • Кэтрин Диккенс • Чарльз Диккенс • Чарльз-Гаспар де ла Рив • Клеопатра • Констанция Моцарт • Дэвид Греневецки • Дебора Рид • Дон Ллойд • Герцог Алансонский • Эдмунд Галлей • Фердинанд Магеллан • Фрэнсис Дрейк • Фредерик Дуглас • Галилей Галилей • Джордж Вашингтон Карвер • Генри Форд • Хо Ти • Исаак Ньютон • Джефф Гриффит • Жанна д’Арк • Иоганн Гутенберг • Йозеф Гайдн • Хуан Себастьян Дель Кано • Юлий Цезарь • Хубилай Хан • Леонардо да Винчи • Луи Пастер • Людвиг ван Бетховен • Махатма Ганди • Марко Поло • Мэри Тодд Линкольн • Майкл Фарадей • Микеланджело Буонарроти • Минамото но Ёритомо • Пьер Поль Эмиль Ру • Платон • Королева Елизавета I • Рафаэль Санти • Ричард Бербедж • Королевское общество • Сара Барнард • Томас Эдисон • Томас Джефферсон • Цай Лунь • Уильям Шекспир • Вольфганг Амадей Моцарт • Новый Донкер • Нина ( Super Mario Maker 2 ) • Оннаноко • Осама • Оязи • Папа Марио • Принц Пайн • Профессор Элвин Гэдд • Стэнли • Валентина
• Новый Донкер • Нина ( Super Mario Maker 2 ) • Оннаноко • Осама • Оязи • Папа Марио • Принц Пайн • Профессор Элвин Гэдд • Стэнли • Валентина С. • Полковник Калпеппер • Ковбой Джед • Краб • Криминальная волна Клайд • Каттер • Кибела • Синди Лаупер • Даниэлла • Дэвид Горовиц • Дилин Делберт • Дхалсим • Док Фрейд • Доктор Демис • Доктор Франкенштейн • Доктор Лайт • Доктор Нердник • Доктор Шелдон • Доктор Зигмунд Фруткейк • Доктор Т. Гарден • Доктор Тоби • Доктор Уолдо Блум • Доктор Вили • Клуб здоровья Дуга • Эдисон • Эгон • Эйнштейн • Элиана • Элвин Петрушка • Эльвира • Элвис Пресли • Эрик • Эрни Хадсон • Бог огня • Дряблые мальчики • Фред Ван Винкль • Дружелюбный Флойд • Джордж Вашингтон • Гондольер • Призрак гориллы • Бабушка Поганка • Бабушка Марио • Бабушка Мия • Дедушка • Элли Мэй • Гарри Блэкстоун мл. • Хару-дзи • Гельмут Коль • Hercufleas • Herlock Solmes • Herman • Herman Smirch • Hildy • Horace • Howard Stevens • Hugo • Imperial Poobah • Indiana Joe • Inspector Gadget • Inspector Klean • James • James Blond • Jason Bateman • Jean-Claude Truchet • Jenny • Отец Jenny • Jim Ланге • Джоди • Джо • Джолиет • Джонатан • Отец Джолиет • Джуниор • Мама Джуниора и папа • Каору • Кенворт • Кид Динамо • Кид Клоун • Король • Король Джеймс • Кинг Грибной Хамен • Кинг Ветряк • Клёсн • Маленький Роберт • Лиз • Лонг Джон • Лу Альбано • Люси Белль • Луиджина • Подруга Луиджи • Луиджи Марио • Лайл Альзадо • Мак • Мадам АГоГо • Безумная Донна • Махго • Сантехники Марко Поло • Марианна • Мэрилин • Марио Марио • Марио Джо и Луиджи Боб • Марк Тванг • Макс Миллиплатт • Мэр Нью-Йорка • Михаил Сергеевич Горбачев • Милли Ванилли • Мисаки • Мисс Эндлесс • Мисс Хурма О’Хара • Мисси • Мервин • Могучий сантехник • Мона • Устье реки • Мистер Бэнкрофт • Мистер Баркли • Мистер Гиббел • Мистер Левисон • Мистер Петров • Мистер Президент • Мистер X • Миссис Гаммлисс • Миссис Барвинок • Миссис Президент • Мугга • Грибной Король • Нетти • Николь • Николь Эггерт • Норман • Оби-Ван Канноли • ОМ • Угтар • Олаф • Пэм Маттесон • Пэтти ( Суббота Supercade ) • Пэтти ( Супершоу Super Mario Bros.
С. • Полковник Калпеппер • Ковбой Джед • Краб • Криминальная волна Клайд • Каттер • Кибела • Синди Лаупер • Даниэлла • Дэвид Горовиц • Дилин Делберт • Дхалсим • Док Фрейд • Доктор Демис • Доктор Франкенштейн • Доктор Лайт • Доктор Нердник • Доктор Шелдон • Доктор Зигмунд Фруткейк • Доктор Т. Гарден • Доктор Тоби • Доктор Уолдо Блум • Доктор Вили • Клуб здоровья Дуга • Эдисон • Эгон • Эйнштейн • Элиана • Элвин Петрушка • Эльвира • Элвис Пресли • Эрик • Эрни Хадсон • Бог огня • Дряблые мальчики • Фред Ван Винкль • Дружелюбный Флойд • Джордж Вашингтон • Гондольер • Призрак гориллы • Бабушка Поганка • Бабушка Марио • Бабушка Мия • Дедушка • Элли Мэй • Гарри Блэкстоун мл. • Хару-дзи • Гельмут Коль • Hercufleas • Herlock Solmes • Herman • Herman Smirch • Hildy • Horace • Howard Stevens • Hugo • Imperial Poobah • Indiana Joe • Inspector Gadget • Inspector Klean • James • James Blond • Jason Bateman • Jean-Claude Truchet • Jenny • Отец Jenny • Jim Ланге • Джоди • Джо • Джолиет • Джонатан • Отец Джолиет • Джуниор • Мама Джуниора и папа • Каору • Кенворт • Кид Динамо • Кид Клоун • Король • Король Джеймс • Кинг Грибной Хамен • Кинг Ветряк • Клёсн • Маленький Роберт • Лиз • Лонг Джон • Лу Альбано • Люси Белль • Луиджина • Подруга Луиджи • Луиджи Марио • Лайл Альзадо • Мак • Мадам АГоГо • Безумная Донна • Махго • Сантехники Марко Поло • Марианна • Мэрилин • Марио Марио • Марио Джо и Луиджи Боб • Марк Тванг • Макс Миллиплатт • Мэр Нью-Йорка • Михаил Сергеевич Горбачев • Милли Ванилли • Мисаки • Мисс Эндлесс • Мисс Хурма О’Хара • Мисси • Мервин • Могучий сантехник • Мона • Устье реки • Мистер Бэнкрофт • Мистер Баркли • Мистер Гиббел • Мистер Левисон • Мистер Петров • Мистер Президент • Мистер X • Миссис Гаммлисс • Миссис Барвинок • Миссис Президент • Мугга • Грибной Король • Нетти • Николь • Николь Эггерт • Норман • Оби-Ван Канноли • ОМ • Угтар • Олаф • Пэм Маттесон • Пэтти ( Суббота Supercade ) • Пэтти ( Супершоу Super Mario Bros. ! ) • Мать и отец Пэтти • Пиа • Пьетро • Принц Грибной Хамон • Принц Помпадур • Королева Грибной Хамен • Королева Ротонда • Ральф Вашингтон • Ребекка Роудс • Роб Стоун • Roller Stars • Романо • Отец Романо • Роуди Родди Пайпер • Роксана • Сальвадор Драйнотто • Сэм Шалам • Санта-Клаус • Секретный агент N • Сержант Куперман • Сержант. Бойня • Шабба-Ду • Угонщики овец • Сольмес • Капитан подводной лодки • Султан Пасба • Сюзанна Росс • Тэмми Трихаггер • Тони Тайлер • Тед Булл • Старая ясновидящая дама со злым глазом, которая предсказывает судьбу и знает все до того, как это произойдет • Томми Лазанья • Tommy Treehugger • Trapper Jack • Trucknappers • Vampa White • Vic Video • Vincent Van Gook • Waldo the Wizard • Willy White • Wizard King of the West • Young McDonald • Zangief • Zero
! ) • Мать и отец Пэтти • Пиа • Пьетро • Принц Грибной Хамон • Принц Помпадур • Королева Грибной Хамен • Королева Ротонда • Ральф Вашингтон • Ребекка Роудс • Роб Стоун • Roller Stars • Романо • Отец Романо • Роуди Родди Пайпер • Роксана • Сальвадор Драйнотто • Сэм Шалам • Санта-Клаус • Секретный агент N • Сержант Куперман • Сержант. Бойня • Шабба-Ду • Угонщики овец • Сольмес • Капитан подводной лодки • Султан Пасба • Сюзанна Росс • Тэмми Трихаггер • Тони Тайлер • Тед Булл • Старая ясновидящая дама со злым глазом, которая предсказывает судьбу и знает все до того, как это произойдет • Томми Лазанья • Tommy Treehugger • Trapper Jack • Trucknappers • Vampa White • Vic Video • Vincent Van Gook • Waldo the Wizard • Willy White • Wizard King of the West • Young McDonald • Zangief • Zero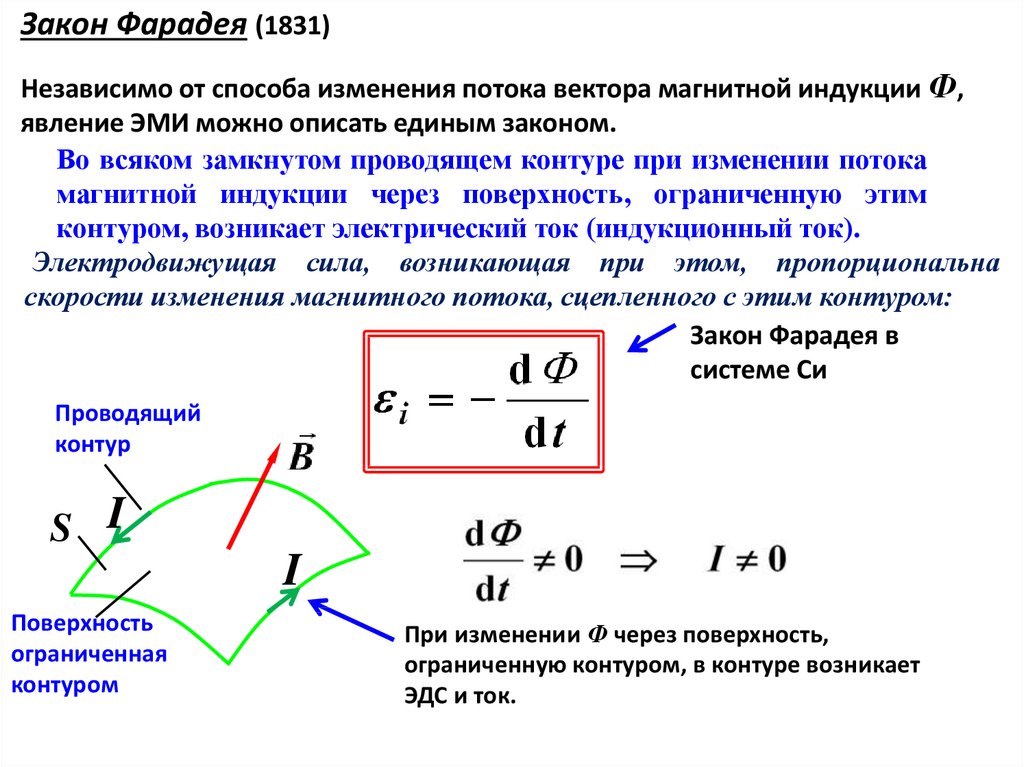 Голдфарб • Марк Грау • Тодд Хаберкорн • Дин Харрингтон • Кит Харрис • Кайл Хеберт • Кейт Хиггинс • Райан Хиггинс • Мишель Хиппе • Хитоми Хиросе • Нобуюки Хияма • Джон Хулатон • Келси Хатчисон • Мелисса Хатчисон • Эрико Ибэ • Кеннет В. Джеймс • Керри Кейн • Саманта Келли • Грант Киркхоп • Юки Кодаира • Шохей Комацу • Асако Кодзуки • Эрика Линдбек • Декс Мэнли • Джефф Мэннинг • Исаак Маршалл • Чарльз Мартине • Томоко Маруно • Ацуши Масаки • Карли МакМанус • Николь Миллс • Лани Минелла • Масато Мизута • Цугуо Могами • Тадд Морган • Шо Мурата • Дина Мастард • Такаси Нагасако • Зои Нельсон • Эрик Ньюсом • Кристин Пейсер • Гриффин Пуату • Долорес Роджерс • Мерседес Роуз • Рональд Б. Рубен • Кейти Сагоян • Масахир о Сакураи • Кахору Сасаджима • Тайлер Шами • Стефани Шех • Го Шиномия • Лаура Фэй Смит • Томас Спиндлер • Крис Сазерленд • Санаэ Сузаки • Катсуми Сузуки • Лесли Свон • Мотоки Такаги • Джен Тейлор • Оуэн Томас • Ребека Томас • Кадзуми Тотака • Вегас Поездка • Тосихидэ Цучия • Сацуки Цузуми • Майк Вон • Кристина Ви • Фрида Вольф • Нацуко Ёкояма
Голдфарб • Марк Грау • Тодд Хаберкорн • Дин Харрингтон • Кит Харрис • Кайл Хеберт • Кейт Хиггинс • Райан Хиггинс • Мишель Хиппе • Хитоми Хиросе • Нобуюки Хияма • Джон Хулатон • Келси Хатчисон • Мелисса Хатчисон • Эрико Ибэ • Кеннет В. Джеймс • Керри Кейн • Саманта Келли • Грант Киркхоп • Юки Кодаира • Шохей Комацу • Асако Кодзуки • Эрика Линдбек • Декс Мэнли • Джефф Мэннинг • Исаак Маршалл • Чарльз Мартине • Томоко Маруно • Ацуши Масаки • Карли МакМанус • Николь Миллс • Лани Минелла • Масато Мизута • Цугуо Могами • Тадд Морган • Шо Мурата • Дина Мастард • Такаси Нагасако • Зои Нельсон • Эрик Ньюсом • Кристин Пейсер • Гриффин Пуату • Долорес Роджерс • Мерседес Роуз • Рональд Б. Рубен • Кейти Сагоян • Масахир о Сакураи • Кахору Сасаджима • Тайлер Шами • Стефани Шех • Го Шиномия • Лаура Фэй Смит • Томас Спиндлер • Крис Сазерленд • Санаэ Сузаки • Катсуми Сузуки • Лесли Свон • Мотоки Такаги • Джен Тейлор • Оуэн Томас • Ребека Томас • Кадзуми Тотака • Вегас Поездка • Тосихидэ Цучия • Сацуки Цузуми • Майк Вон • Кристина Ви • Фрида Вольф • Нацуко Ёкояма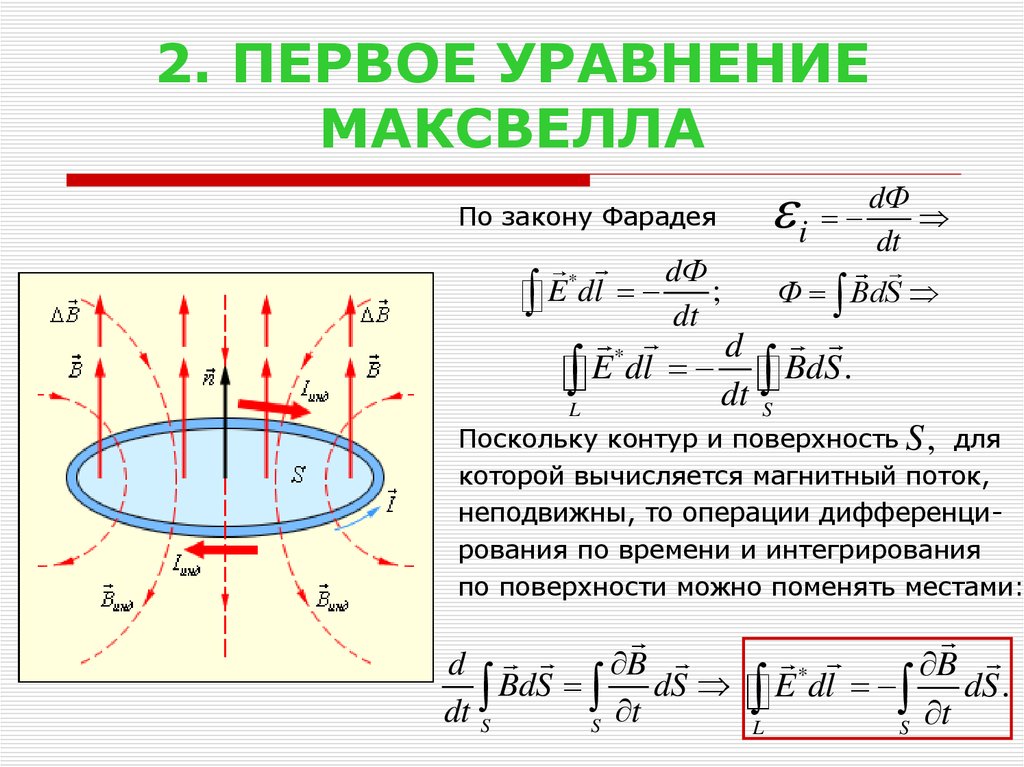 • Брайан Бонсолл • Кристофер Коллинз • Николь Эггерт • Деннис Хоппер • Дэвид Горовиц • Боб Хоскинс • Эрни Хадсон • Мэджик Джонсон • Джим Лэнг • Синди Лаупер • Джон Легуизамо • Пэм Маттесон • Алисса Милано • Моджо Никсон • Патрик Пинни • Роуди Родди Пайпер • Сержант. Слотер • Шабба-Ду • Роб Стоун • Эндрю Трего • Дэнни Уэллс
• Брайан Бонсолл • Кристофер Коллинз • Николь Эггерт • Деннис Хоппер • Дэвид Горовиц • Боб Хоскинс • Эрни Хадсон • Мэджик Джонсон • Джим Лэнг • Синди Лаупер • Джон Легуизамо • Пэм Маттесон • Алисса Милано • Моджо Никсон • Патрик Пинни • Роуди Родди Пайпер • Сержант. Слотер • Шабба-Ду • Роб Стоун • Эндрю Трего • Дэнни Уэллс Дж. Ходжсон • Эндрю Айверсон • Ли Лавдей • Перри Мартин • Клод Мойс • Питер Содер • Эд Соломон • Эрика Стробель • Майкл Тейтельбаум • Трейси Уэст • Тед Вулси
Дж. Ходжсон • Эндрю Айверсон • Ли Лавдей • Перри Мартин • Клод Мойс • Питер Содер • Эд Соломон • Эрика Стробель • Майкл Тейтельбаум • Трейси Уэст • Тед Вулси Вашингтон* • Кэтрин Диккенс* • Чарльз Диккенс* • Шарль-Гаспар де ла Рив* • Клеопатра • Констанция Моцарт* • Дэвид Греневецки* • Дебора Рид* • Дон Ллойд* • Герцог Алансонский • Эдмунд Галлей • Фердинанд Магеллан • Фрэнсис Дрейк • Фредерик Дуглас* • Галилео Галилей* • Джордж Вашингтон Карвер* • Генри Форд* • Хо Ти* • Исаак Ньютон • Джефф Гриффит * • Жанна д’Арк • Иоганн Гутенберг • Йозеф Гайдн* • Хуан Себастьян Дель Кано • Юлий Цезарь • Хубилай Хан • Леонардо да Винчи • Луи Пастер* • Людвиг ван Бетховен • Махатма Ганди • Марко Поло • Мэри Тодд Линкольн* • Майкл Фарадей* • Микеланджело Буонарроти • Минамото но Ёритомо† • Пьер Поль Эмиль Ру* • Платон • Королева Елизавета I • Рафаэль Санцио • Ричард Бербедж • Королевское общество • Сара Барнард* • Томас Эдисон • Томас Джефферсон • Цай Лунь* • Уильям Шекспир • Вольфганг Амадей Моцарт*
Вашингтон* • Кэтрин Диккенс* • Чарльз Диккенс* • Шарль-Гаспар де ла Рив* • Клеопатра • Констанция Моцарт* • Дэвид Греневецки* • Дебора Рид* • Дон Ллойд* • Герцог Алансонский • Эдмунд Галлей • Фердинанд Магеллан • Фрэнсис Дрейк • Фредерик Дуглас* • Галилео Галилей* • Джордж Вашингтон Карвер* • Генри Форд* • Хо Ти* • Исаак Ньютон • Джефф Гриффит * • Жанна д’Арк • Иоганн Гутенберг • Йозеф Гайдн* • Хуан Себастьян Дель Кано • Юлий Цезарь • Хубилай Хан • Леонардо да Винчи • Луи Пастер* • Людвиг ван Бетховен • Махатма Ганди • Марко Поло • Мэри Тодд Линкольн* • Майкл Фарадей* • Микеланджело Буонарроти • Минамото но Ёритомо† • Пьер Поль Эмиль Ру* • Платон • Королева Елизавета I • Рафаэль Санцио • Ричард Бербедж • Королевское общество • Сара Барнард* • Томас Эдисон • Томас Джефферсон • Цай Лунь* • Уильям Шекспир • Вольфганг Амадей Моцарт* / ** Эксклюзивно для версии Deluxe . / † Эксклюзивно для версии NES. / †† Не в версии для SNES.
/ ** Эксклюзивно для версии Deluxe . / † Эксклюзивно для версии NES. / †† Не в версии для SNES.