Лабораторная работа № 6 изучение электростатического поля

Цели и задачи работы: изучение электростатического поля; построение эквипотенциальных поверхностей поля.

Содержание работы:

Известно, что вокруг любого заряда или заряженного тела существует электрическое поле. В этом поле на внесенный в него другой заряд действует кулоновская сила. Электрическое поле характеризуется в каждой точке величинами: силовой – вектором электрической напряженности , и энергетической – скалярной величиной – потенциалом.

Напряженностью электрического поля называется физическая величина, численно равная и совпадющая по направлению с силой , действующей со стороны поля на единичный положительный точечный заряд, помещенный в рассматриваемую точку:

(1.1)

Потенциалом электрического поля в данной точке называется скалярная величина, численно равная потенциальной энергии U единичного положительного точечного заряда , помещенного в эту точку

(1. 2)

Потенциал и напряженность электрического поля связаны соотношением

(1.3)

Напомним, что градиентом любой скалярной величины называют вектор, направление которого совпадает с направлением быстрейшего увеличения величины, а модуль равен изменениюпри перемещении на единицу длины в направлении быстрейшего изменения. Знак «минус» в формуле (1.3) показывает, что напряженность полянаправлена в сторону убывания потенциала.

Направление вектора напряженности электрического поля в каждой точке поля и распределение потенциалов поля можно сделать особенно наглядным, если воспользоваться понятиями о силовых линиях и о поверхностях равного потенциала, так называемых эквипотенциальных поверхностях.

Силовыми линиями называются линии, касательные в каждой точке которых определяют направление векторов напряженностей электрического поля. Число же силовых линий проходящих через единицу площади, нормальной к этим линиям, определяет величину вектора напряженности электрического поля в центре этой площади. Линии напряженности электрического поля незамкнуты, они начинаются из положительного заряда и заканчиваются на оторицательном заряде.

Геометрическое место точек электрического поля, потенциалы которых одинаковы, называется эквипотенциальной поверхностью. Эквипотенциальные поверхности проводят таким образом, что разность потенциалов для двух соседних поверхностей всюду одна и та же. Это позволяет по густоте эквипотенциальных поверхностей судить о величине напряженности поля.

Векторы напряженности электрического поля и, следовательно, силовые линии поля нормальны к эквипотенциальным поверхностям. На рис.1.1 силовые линии некоторого поля проведены сплошной линией, а эквипотенциальные поверхности-штриховой.

рис. 1

Известно, что экспериментальное и теоретическое изучение распределения потенциалов электрического поля проще, чем определение напряженностей поля. Поэтому в данной работе экспериментально определяется распределение потенциалов электростатического, т.

е. не изменяющегося со временем электрического поля. Силовые линии изучаемого поля можно построить потом, как кривые, ортогональные к экспериментально найденным поверхностям равного потенциала.

Распределение потенциалов электростатического поля можно изучать методом зондов, заключающемся в следующем: в исследуемую точку поля вводится дополнительный электрод – зонд, устроенный так, чтобы он минимально нарушал своим присутствием исследуемое поле и принимал потенциал той точки поля, в которую он помещен. При этих условиях показания прибора, с которым зонд соединяется проводником, будут давать правильную картину распределения потенциалов в исследуемом поле.

Сложности работы с зондами и, вообще, трудности электростатических измерений привели к разработке особого метода изучения электростатических полей – путем искусственного воспроизведения их структуры в проводящих средах, по которым пропускается постоянный ток. Таким путем прямое изучение электростатического поля заменяется изучением его точной и более удобной модели.

Оказывается, что при некоторых условиях распределение потенциалов в среде, по которой течет ток между установленными в ней электродами, может быть сделано тождественным с распределением потенциалов между теми же электродами, когда между ними имеется электростатическое поле в вакууме или в однородном диэлектрике. Тогда изучение электростатического поля между системой заряженных проводников можно заменить изучением электростатического поля постоянного тока между той же системой проводников.

Описанный метод исследования, который называется моделированием электростатического поля, имеет широкое применение на практике. Этот метод полезен для изучения сложных электростатических полей, точный расчет которых затруднителен из-за сложности граничных условий (многоэлектродные радиолампы, электростатические линзы, фотоэлектронные умножители и т.д.).

Схема экспериментальной установки представлена на рис. 2.

рис.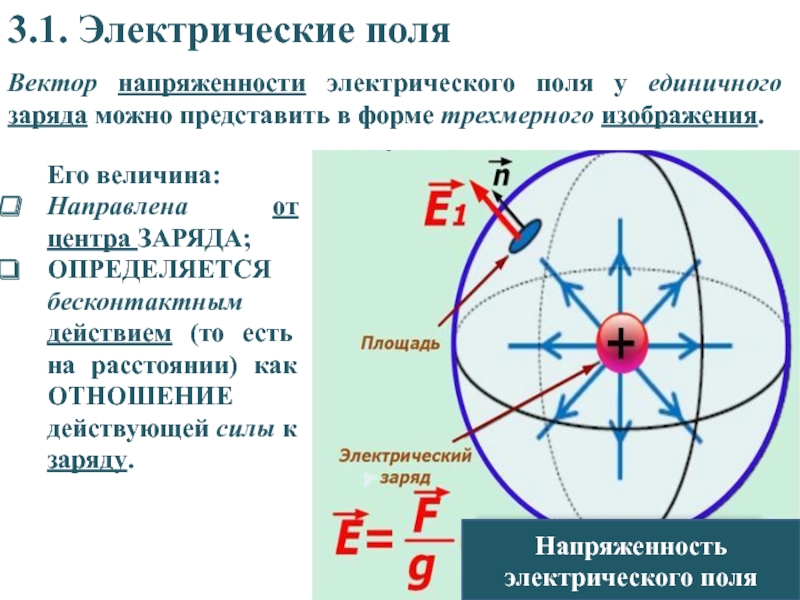 2

Она представляет собой мостовую схему, состоящую из электродов А и С, поле между которыми изучается, реохорды Р, нуль-гальванометра G, соединенного с зондом z, и источника питания – выпрямителя

В. Напряжение на электроды А и С подается с реохорды Р, подключенной на выход выпрямителя В. Средой, позволяющей моделировать электростатическое поле, служит токопроводящая бумага, контуры которой показаны на рис. 1.2. штриховыми линиями.

Принцип работы установки можно понять из следующего. Перемещая движок реохорды, этому движку можно придавать различные значения потенциала относительно электродов. Наличие или отсутствие тока в цепи зависит при этом от того, в какой точке поля находится зонд. Если он находится в такой точке поля, потенциал которой равен потенциалу, установленному на движке реохорды, то тока в цепи гальванометра не будет.

Геометрическое место точек поля, для которых ток в цепи гальванометра будет равен нулю, образует эквипотенциальную поверхность в исследуемом поле. Потенциал φ этой поверхности относительно электрода С можно найти как

(1.4)

где U – напряжение на выходе выпрямителя, N – число делений шкалы реохорды, n – деление шкалы, на который установлен движок.

Установка снабжена специальным приспособлением – координатником, позволяющим вращением ручек координатника перемещать зонд, а также отсчитывать координаты найденных точек эквипотенциальной поверхности.

Оборудование: специальная установка; гальванометр; источник тока.

Порядок выполнения работы:

1. Проверить схему экспериментальной установки.

2. Включить выпрямитель в сеть 220 В.

3. Установить движок реохорды на растоянии 8-10 см от одного из клемм реохорды. Определить потенциал движка по формуле (1.4).

4. Перемещая зонд вращением ручек координатника, находить такие точки, для которых ток гальванометра равен нулю.

   Количество этих точек должно быть достаточно для построения линии эквипотенциальной поверхности (7-10 точек). Координаты точек отсчитывать по линейкам координатника.

5. Нанести на миллиметровую бумагу найденные точки и соединить их плавной линией. На линии написать его потенциал.

6. Изменив положение реохорды повторить пп.4, 5. число повторений опыта 4-5 раз.

7. Используя найденные линии эквипотенциальных поверхностей, построить силовые линии поля. При этом надо иметь в виду, что в точках пересечения линии эквопотенциальных поверхностей и силовые линии должны быть нормальны друг к другу.

Контрольные вопросы:

1. Какими величинами характеризуется электрическое поле? Дайте определение этих величин и напишите единицы их измерения.

2. Какова связь между напряженностью и потенциалом электростатического поля в общем случае и в случае однородного поля?

3. Какими понятиями пользуются для наглядного представления электрического поля?

4. Нарисуйте силовые линии и эквипотенциальные поверхности поля точечного заряда, двух разноименных зарядов.

5. Какие экспериментальные методы используют для изучения электростатического поля?

Литература:

1. Савельев И.В. Курс общей физики. Электричество и магнетизм. Волны. Оптика. — М.: Наука, 1989.

2. Абдикасова А.А., Ниязова Ш.В., Утеулина К.А. и др. Электричество и магнетизм. Методическое указание к лабораторным работам. – Уральск: ТОО «Наука», 1996.

3. Матвеев А.Н. Электричество и магнетизм. Физический практикум. – М.: Высшая школа, 1983.

Исследование электростатического поля тока на электропроводной бумаге методом зондов (Лабораторная работа № 1э)

Лабораторная  работа №1э

ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ ТОКА НА ЭЛЕКТРОПРОВОДНОЙ БУМАГЕ МЕТОДОМ ЗОНДОВ

Краткая теория

Электростатическим полем в веществе называется поле, порождён­ное неподвижными электрическими зарядами и энергия которого не под­вержена превращениям.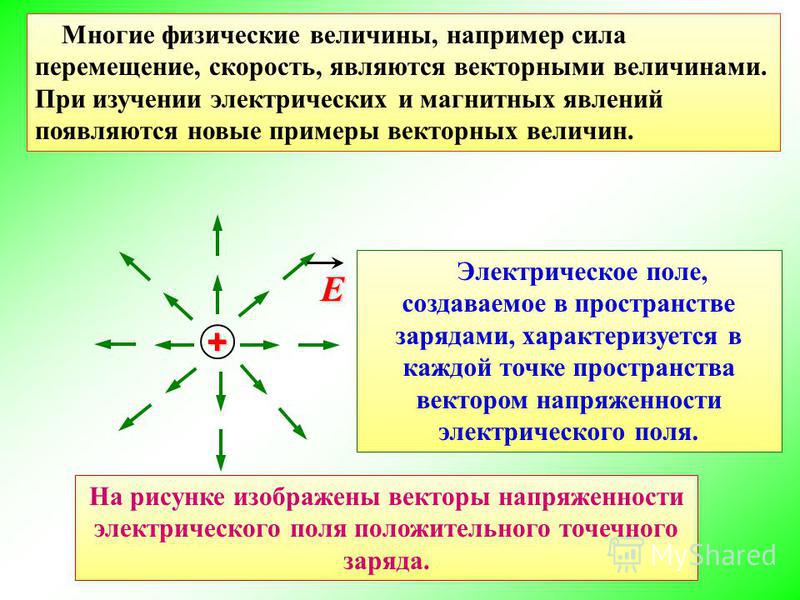 Поэтому структура электростатического поля зависит от величины и распределения электрических зарядов в прост­ранстве (среде).

Электростатическое поле характеризуется в каждой точке прост­ранства значением вектора напряжённости поля Е и значением потенциала U . Для наглядного изображения направления вектора напряжён­ности поля в каждой точке пространства и распределения потенциала пользуются понятиями о силовых линиях и о поверхностях равного по­тенциала, называемых эквипотенциальными поверхностями.

Силовой линией или линией напряжённости электростатического поля называется такая линия, в каждой точке которой касательная совпадает по направлению с вектором напряжённости поля в этой  точке пространства.

Поверхность равного потенциала или эквипотенциальная поверх­ность есть геометрическое место точек поля с одинаковыми значе­ниями потенциала.

Рассмотрим электрическое поле, создаваемое поло­жительным точечным зарядом q, находящимся в однородной сред». В этом случае силовые линии представляют собой прямые (радиус-векто­ры), исходящие из точки, в которую помещён заряд положительный q. На рис. 1 представлено сечение картины поля точечного отрицательного заряда плоскостью чертеже.

 Сплошные прямые — силовые линии, пунктирные окружности — следы пересечения эквипотенциальных поверхностей с плоскостью чертежа.

Силовые линии всегда совпадают по направлению с нормалями к экви­потенциальным поверхностям. Эта связь между силовыми линиями и экви­потенциальными поверхностями, пока­занная нами для частного случая поля точечного заряда, имеет место и в случае произвольного электростати­ческого поля.

Действительно, рассмотрим работу перемещения точечного электрического заряда q на малое расстояние l, вдоль какой-либо эквипо­тенциальной поверхности. Работа А перемещения заряда на данном пути будет равна:

                            (1)

С другой стороны, эта же работа может быть выражена как произведе­ние величины заряда q на разность потенциалов в начальном и конечном положениях заряда:

A = q×DU.                                                                                  (2)

Но так как перемещение происходит вдоль эквипотенциальной поверхности, очевидно, DU = 0. Таким образом, мы получаем:

Ввиду того, что ни заряд q, ни напряжённость поля Е, ни переме­щение l не равны нулю, очевидно, равен нулю косинус угла между направлением напряжённости поля Е и перемещениемl . Отсюда сле­дует, что направление вектора напряжённости электростатического поля E нормально к эквипотенциальным поверхностям в каждой данной точке поля.

Однако вектор напряжённости поля Е и вектор нормали к экви­потенциальным поверхностям, совпадающие по направлению, противопо­ложны по знаку: нормаль считается положительной в сторону возраста­ния потенциала, а вектор Е направлен в сторону действия поля на положительный заряд, то есть в сторону убывания потенциала.

Найдём соотношение между величиной напряжённости поля Еи потенциалом U поля в данной точке. Для этого будем перемещать точечный электрический заряд q в произвольном электростатическом поле из точки О с потенциалом j в точку O’ с потенциалом j + Dj (см. рис. 2).

Пусть расстояние между этими точками столь мало, что значение напряженности поля E между ними можно считать неизменным. Проведём эквипотенциальные поверхности j и j + Dj  и восстановим нормаль к эквипотенциальной поверхности в точке O. Очевидно, работа переме­щения заряда q из точки О в точку О’ равна:

С другой стороны, эта же работа может быть выражена через разность потенциалов точек O и О’ как 

           

Приравнивая два выражения для работы А, найдём:

           

или напряженность электростатического поля численно равна изме­нению потенциала на единицу длины нормали к эквипотенциальной по­верхности, взятому с обратным знаком. Величина   характеризует быстроту возрастания потенциала в направлении, перпендикуляр

ном эквипотенциальной поверхности, и называется градиентом потенциа­ла.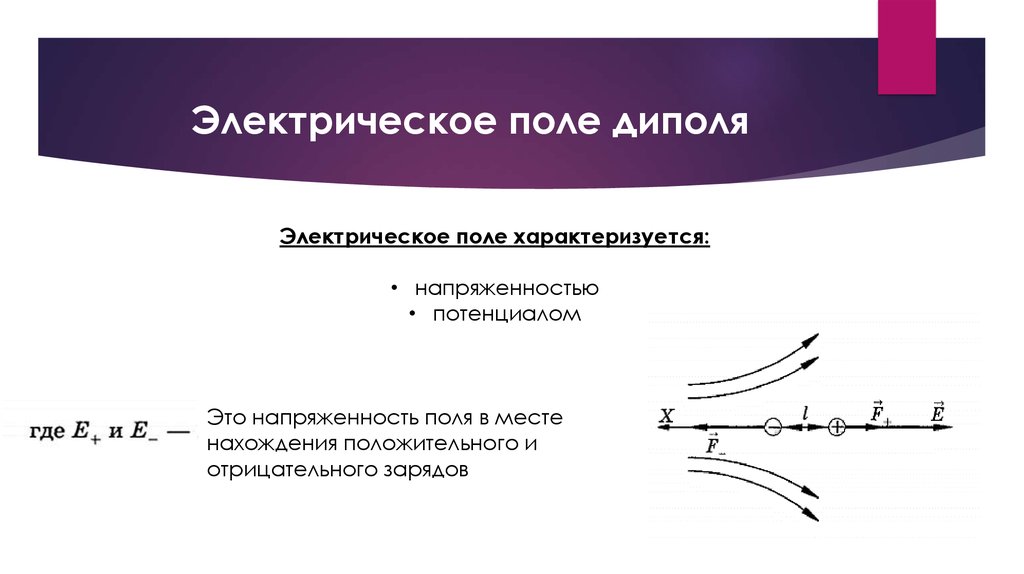 Однозначная связь между Е   и  j и ортогональность силовых линий и эквипотенциальных поверхностей позволяют легко перейти от изображения поля с помощью эквипотенциальных поверхностей к его изображению с помощью силовых линий и наоборот.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Постановка задачи

Целью работы является изучение различных электростатических полей, моделируемых с помощью стационарных электрических полей тока в электропроводной бумаге.

В качестве электродов предлагается использовать любые комби­нации имеющихся электродов:

1. Две плоские параллельные пластины.

2. Два коаксиальных кольца.

3. Два точечных электрода.

4. Кольцо и плоский электрод.

5. Полуэллипс и плоский электрод и т.д.

Теория измерений

В основу изучения распределения потенциалов в электростатичес­ком поле часто кладётся так называемый метод зондов. Его сущность заключается в следующем: в исследуемую точку поля вводится специаль­ный дополнительный электрод-зонд, по возможности так устроенный, чтобы он минимально нарушал своим присутствием исследуемое поле. Этот зонд соединяется проводником с прибором, измеряющий приобре­тенный зондом в поле потенциал по отношению к какой-нибудь избран­ной за начало отсчёта точке поля.

Но изучение электростатического поля зарядов, например, при помощи зондов, затруднено, поэтому в условиях задачи изучение электростатического поля между системой заряженных проводников можно заменить изучением его менее точней, но более удобной моделью — электростатического поля постоянного тока между той же системой проводников, если потенциалы проводников поддерживаются постоянными, а проводимость среды, в которой исследуется распределение потенциалов, намного меньше, чем проводимость данных проводников. Плохо проводящей средой может быть обыкновенная вода, влажный песок, электропроводная бумага и т.п.

Электростатика в ферментативном катализе | Boxer Lab

О рисунке: Используя хорошо откалиброванный вибрационный зонд, можно количественно оценить многие разнообразные межмолекулярные взаимодействия в унифицированной физической метрике электрических полей, включая как общие, так и специфические взаимодействия, например.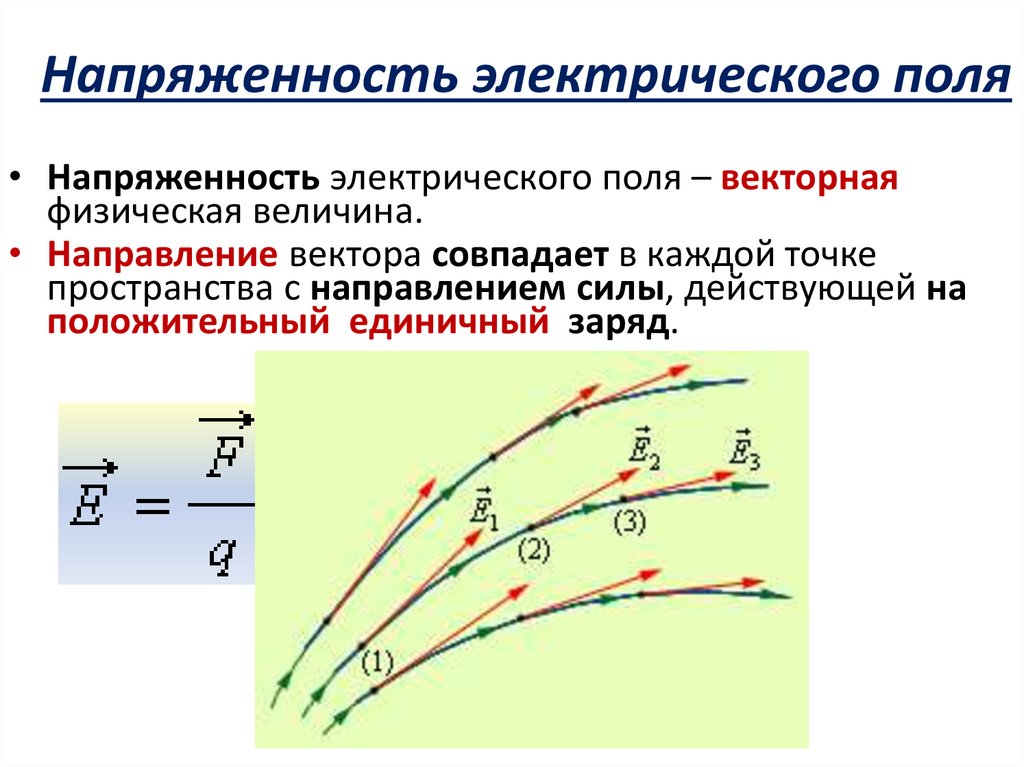 Н-связи.

Лаборатория Боксера установила и использовала эффект Штарка и спектроскопию Штарка для количественного определения электрических полей, характеризующих нековалентные межмолекулярные взаимодействия, как показано на рисунке слева. Благодаря длительной работе над электронной штарковской спектроскопией мы впервые разработали вибрационную штарковскую спектроскопию (VSS) [122], которая позволяет создать количественную модель, позволяющую интерпретировать ИК-частотные сдвиги как изменения физической силы, электрического поля окружающей среды, воздействующей на связь [176].

Используя эту схему, лаборатория Boxer применила колебательный эффект Штарка (VSE) для количественной оценки функционально значимых электрических полей в белках, например, в активном центре фермента кетостероидизомеразы (KSI) [303]. Посредством измерений барьера свободной энергии активации (из теории переходного состояния) и электрического поля, испытываемого при функционально значимом C = O на TS-подобном ингибиторе, впервые был измерен вклад электрических полей в каталитическую эффективность KSI. время. Последующие исследования с использованием Amber-супрессии путем введения неестественных производных Cl-Y показали, что как тонкие, так и пертурбативные мутации могут быть объяснены с помощью VSE [310]. Дальнейшая работа в лаборатории показала, что зонды C=O являются хорошо охарактеризованными и функционально значимыми зондами для изучения многих ферментативных систем [316]. Текущая работа расширяется в отношении того, как электрические поля связаны с ферментативной функцией и эволюцией ферментов, дизайном ферментов, сольватацией, фотоизомеризацией и небиологическим катализом.

О рисунке: (Вверху) Общий механизм реакции изомеризации, катализируемой KSI, при котором функционально значимый карбонил претерпевает значительную перегруппировку заряда в ходе реакции. (Внизу слева) Калибровочная кривая частоты электрического поля для зонда C=O как в органических, так и в водных растворителях, которая обеспечивает отображение между наблюдаемой частотой ИК-излучения и электрическим полем. (Внизу посередине) Общая модель электростатического катализа, согласно которой электрическое поле может оказывать благотворное влияние на катализ только за счет преимущественной стабилизации диполя переходного состояния (TS) по сравнению с основным состоянием (GS). (Внизу справа) Количественная оценка вклада электрического поля в каталитическую скорость KSI с использованием как традиционного мутагенеза, так и включения неканонических аминокислот, при этом наблюдается линейная зависимость между барьером свободной энергии и электрическим полем активного центра. Наклон и пересечение линии наилучшего соответствия относятся к степени переноса заряда между TS и GS и активационным барьером в отсутствие электрического поля, соответственно, последний обеспечивает электростатический вклад в катализ.

[316] «Электрические поля и ферментативный катализ», Стивен Д. Фрид и Стивен Г. Боксер, Ежегодные обзоры биохимии, 86, 387–415 (2017). [pdf]

​

[315] «Независимый от растворителя ангармонизм для карбонильных осцилляторов», Samuel H. Schneider, Huong T. Kratochvil, Martin T. Zanni и Steven G. Boxer, J. Phys. хим. Б, 121, 2331–2338 (2017). [pdf]

​

[311] «Вибрационные эффекты Штарка карбонильных зондов, применяемые для повторной интерпретации данных ИК и КР для ингибиторов ферментов с точки зрения электрических полей в активном центре», Сэмюэл Хейс Шнайдер и Стивен Г. Боксер. , J. Phys. хим. Б, 120, 9672-9684 (2016). [pdf]

 

[310] «Критический тест электростатического вклада в катализ с неканоническими аминокислотами в кетостероид-изомеразе», Юфан Ву и Стивен Г. Боксер, J. Am. хим. Soc., 138, 11890-11895 (2016). [pdf]

[303] «Катализ экстремальных электрических полей в активном центре кетостероид-изомеразы», ​​Стивен Д. Фрид, Саян Багчи, Стивен Г. Боксер, Наука, 346, 1510-1514 (2014). [pdf] [Перспектива]

Последние публикации:

Использование электрических полей в тканевой инженерии

1. Pethig R, Kell DB. Пассивные электрические свойства биологических систем: их значение в физиологии, биофизике и биотехнологии. физ.-мед. биол. 1987; 32: 933–970. [PubMed] [Google Scholar]

2. Габриэль С., Лау Р.В., Габриэль С. Диэлектрические свойства биологических тканей. 2. Измерения в диапазоне частот от 10 Гц до 20 ГГц. физ.-мед. биол. 1996;41:2251–2269. [PubMed] [Google Scholar]

3. Фостер К.Р., Шван Х.П. Диэлектрические свойства тканей и биологических материалов: критический обзор. CRC Crit Rev Biomed Eng. 1989;17:25–104. [PubMed] [Google Scholar]

4. Аланен Э., Лахтинен Т., Нуутинен Дж. Измерение диэлектрических свойств подкожной жировой клетчатки с помощью коаксиальных датчиков с открытым концом. физ.-мед. биол. 1998; 43: 475–485. [PubMed] [Google Scholar]

5. Райку В., Сайбара Т., Иримаджири А. Многочастотный метод диэлектрического мониторинга холодноконсервированных органов. физ.-мед. биол. 2000;45:1397–1407. [PubMed] [Google Scholar]

6. Керидо Д. Температурная коррекция абдоминального импеданса: улучшенная взаимосвязь между импедансом и посмертным интервалом. Международная криминалистика. 2000;109: 39–50. [PubMed] [Google Scholar]

7. Присоединяйтесь к WT, Zhang Y, Li CX, Jirtle RL. Измерены электрические свойства нормальных и злокачественных тканей человека в диапазоне частот от 50 до 900 МГц. Медицинская физика. 1994; 21: 547–550. [PubMed] [Google Scholar]

8. Кайл А.Х., технический директор Чан, А.И. Минчинтон. Характеристика трехмерных культур тканей с помощью электроимпедансной спектроскопии. Биофиз Дж. 1999; 76: 2640–2648. [Бесплатная статья PMC] [PubMed] [Google Scholar]

9. Harris CM, Todd RW, Bungard SJ, Lovitt RW, Morris JG, Kell DB. Диэлектрическая проницаемость микробных суспензий на радиочастотах: новый метод оценки микробной биомассы в реальном времени. Ферментная микробная технология. 1987;9:181–186. [Google Scholar]

10. Boudriot U, Dersch R, Greiner A, Wendorff JH. Подходы электропрядения к созданию строительных лесов — краткий обзор. Искусственные органы. 2006; 30: 785–792. [PubMed] [Google Scholar]

11. Wegener J, Keese CR, Giaever I. Электрическое определение импеданса клеток и субстрата (ECIS) как неинвазивное средство для мониторинга кинетики распространения клеток на искусственные поверхности. Разрешение ячейки опыта. 2000; 259: 158–166. [PubMed] [Google Scholar]

12. Ozkan M, Pisanic T, Scheel J, Barlow C, Esener S, Bhatia SN. Электрооптическая платформа для манипулирования живыми клетками. Ленгмюр. 2003;19: 1532–1538. [Google Scholar]

13. Ozkan M, Ozkan CS, Kibar O, Wang MM, Bhatia S, Esener SC. Гетерогенная интеграция посредством электрокинетической миграции. IEEE Eng Med Biol. 2001; 20: 144–151. [PubMed] [Google Scholar]

14. Хьюз, член парламента. Наноэлектромеханика в технике и биологии. Бока-Ратон: CRC Press; 2003. [Google Scholar]

15. Markx GH, Davey CL. Диэлектрические свойства биологических клеток на радиочастотах: приложения в биотехнологии. Ферментная микробная технология. 1999;25:161–171. [Google Scholar]

16. Джонс Т.Б. Электромеханика частиц. Кембридж: Издательство Кембриджского университета; 1995. Кембридж. [Google Scholar]

17. Миллер Р.Д., Джонс Т.Б. Электроориентация эллипсоидных эритроцитов. Биофиз Дж. 1993; 64: 1588–1595. [Бесплатная статья PMC] [PubMed] [Google Scholar]

18. Markx GH, Alp B, McGilchrist A. Электроориентация Schizosaccharomyces pombe в средах с высокой проводимостью. J Микробные методы. 2002; 50:55–62. [PubMed] [Академия Google]

19. Yang M, Zhang X. Электрическое моделирование сердечных миоцитов с контролируемой макроскопической анизотропией с использованием микрожидкостного диэлектрофореза. Приводы датчиков А. 2007; 35:73–79. [Google Scholar]

20. Арнольд В.М., Циммерманн Ю. Электровращение — разработка метода диэлектрических измерений на отдельных ячейках и частицах. J Электростат. 1988; 21: 151–191. [Google Scholar]

21. Wang XB, Huang Y, Gascoyne PRC, Becker FF, Hoelzel R, Pethig R. Изменения в клеточных мембранах мышиной эритролейкемии Friend во время индуцированной дифференцировки, определяемые электровращением. Биохим Биофиз Акта. 1994;1193:330–344. [PubMed] [Google Scholar]

22. Pohl HA. Диэлектрофорез. Кембридж: Издательство Кембриджского университета; 1978. [Google Scholar]

23. Pohl HA. Электрическое формирование масс живых клеток. J Коллоидный интерфейс Sci. 1972; 39: 437–438. [Google Scholar]

24. Markx GH, Buckle AM. Энциклопедия биоматериалов и биомедицинской инженерии. Нью-Йорк: Тейлор и Фрэнсис; 2005. Тканевая инженерия: электрокинетика переменного тока. [Google Scholar]

25. Мацуэ Т., Мацумото Н., Учида И. Быстрое микроструктурирование живых клеток с помощью силы отталкивания при диэлектрофорезе. Электрохим Акта. 1997;42:3251–3256. [Google Scholar]

26. Alp B, Stephens GM, Markx GH. Формирование искусственных структурированных микробных консорциумов (ИСМК) методом диэлектрофореза. Ферментная микробная технология. 2002; 31:35–43. [Google Scholar]

27. Alp B, Andrews JS, Mason VP, Wolowacz R, Markx GH. Создание структурированных биоматериалов с использованием электрокинетики переменного тока. IEEE Eng Med Biol. 2003; 22:91–97. [PubMed] [Google Scholar]

28. Альбрехт Д.Р., Сах Р.Л., Бхатия С.Н. Геометрические и материальные детерминанты эффективности формирования рисунка с помощью диэлектрофореза. Биофиз Дж. 2004; 87: 2131–2147. [Бесплатная статья PMC] [PubMed] [Google Scholar]

29. Verduzco Luque CE, Alp B, Stephens GM, Markx GH. Создание биопленок с определенной внутренней архитектурой с использованием диэлектрофореза и флокуляции. Биотехнология Биоинж. 2003; 83: 39–44. [PubMed] [Google Scholar]

30. Pethig R, Markx GH. Применение диэлектрофореза в биотехнологии. Тенденции биотехнологии. 1997; 15: 426–432. [PubMed] [Google Scholar]

31. Велев О.Д., Бхатт К.Х. Микроманипуляция на чипе и сборка коллоидных частиц электрическими полями. Мягкая материя. 2006; 2: 738–750. [Академия Google]

32. Петик Р., Хуанг И., Ван С.Б., Берт Дж.П.Х. Положительный и отрицательный диэлектрофоретический сбор коллоидных частиц с использованием встречно-штыревых зубчатых электродов. J Phys D: Appl Phys. 1992; 25:881–888. [Google Scholar]

33. Wang XB, Huang Y, Burt JPH, Markx GH, Pethig R. Избирательное диэлектрофоретическое удержание биочастиц в ямах потенциальной энергии. J Phys D: Appl Phys. 1993; 26: 1278–1285. [Google Scholar]

34. Мюллер Т., Пфенниг А., Кляйн П., Градл Г., Ягер М., Шнелле Т. Возможности диэлектрофореза для экспериментов с отдельными клетками. IEEE Eng Med Biol Mag. 2003: 51–61. [PubMed] [Академия Google]

35. Manaresi N, Romani A, Medoro G, Altomare L, Leonardi A, Tartagni M, Guerrieri R. Чип CMOS для манипулирования и обнаружения отдельных клеток. Журнал IEEE твердотельных схем. 2003; 38: 2297–2305. [Google Scholar]

36. Грей Д.С., Тан Дж.Л., Волдман Дж., Чен С.С. Диэлектрофоретическая регистрация живых клеток на микроэлектродной матрице. Биосенс ​​Биоэлектрон. 2004; 19: 1765–1774. [PubMed] [Google Scholar]

37. Розенталь А., Волдман Дж. Диэлектрофоретические ловушки для формирования паттерна одиночных частиц. Биофиз Дж. 2005; 88:2193–2205. [Бесплатная статья PMC] [PubMed] [Google Scholar]

38. Миттал Н., Розенталь А., Волдман Дж. Микролунки NDEP для формирования паттерна одиночных клеток в физиологических средах. Лабораторный чип. 2007; 7: 1146–1153. [PubMed] [Google Scholar]

39. Себастьян А., Пряжка А.М., Марккс Г.Х. Формирование многослойных агрегатов клеток млекопитающих методом диэлектрофореза. J Micromech Microeng. 2006; 16: 1769–1777. [Google Scholar]

40. Себастьян А., Венкатеш А.Г., Марккс Г.Х. Тканевая инженерия с электрическими полями: исследование формы агрегатов клеток млекопитающих, образованных на встречно-штыревых противоположно зубчатых электродах. Электрофорез. 2007; 28:3821–3828. [PubMed] [Академия Google]

41. Венкатеш А.Г., Марккс Г.Х. По высоте клеточные агрегаты образуются при положительном диэлектрофорезе. J Phys D: Appl Phys. 2007; 40:106–113. [Google Scholar]

42. Себастьян А., Бакл А.М., Марккс Г.Х. Тканевая инженерия с электрическими полями: иммобилизация клеток млекопитающих в многослойных агрегатах с помощью диэлектрофореза. Биотехнология Биоинж. 2007; 98: 694–700. [PubMed] [Google Scholar]

43. Альбрехт Д.Р., Цанг В.Л., Сах Р.Л., Бхатия С.Н. Фото- и электропаттерн массивов живых клеток, инкапсулированных в гидрогель. Лабораторный чип. 2005; 5:111–118. [PubMed] [Академия Google]

44. Альбрехт Д.Р., Андерхилл Г.Х., Вассерманн Т.Б., Сах Р.Л., Бхатия С.Н. Исследование роли многоклеточной организации в трехмерных микросредах. Природные методы. 2006; 3: 369–375. [PubMed] [Google Scholar]

45. Heida T, Rutten WLC, Marani E. Диэлектрофоретическое улавливание диссоциированных нейронов коры головного мозга крыс. IEEE Trans Biomed Eng. 2001; 48: 921–930. [PubMed] [Google Scholar]

46. Heida T, Vulto P, Rutten WL, Marani E. Жизнеспособность диэлектрофоретически захваченных клеток нервной коры в культуре. J Neurosci Методы. 2001; 110:37–44. [PubMed] [Академия Google]

47. Prasad S, Yang M, Zhang X, Ozkan CS, Ozkan M. Формирование нейронных сетей с помощью электрического поля для изучения функций мозга. Биомед микроприборы. 2003; 5: 125–137. [Google Scholar]

48. Yu Z, Xiang G, Pan L, Huang L, Yu Z, Xing W, Cheng J. Отрицательная диэлектрофоретическая сила помогла построить упорядоченные нейронные сети на биоэлектронных чипах, позиционирующих клетки. Биомед Микродев. 2004; 6: 311–324. [PubMed] [Google Scholar]

49. Ho CT, Lin RZ, Chang WY, Chang HY, Liu CH. Быстрое формирование гетерогенного паттерна клеток печени на чипе с помощью улучшенной ловушки диэлектрофореза, индуцированной полем. Лабораторный чип. 2006; 6: 724–734. [PubMed] [Академия Google]

50. Альбрехт Д.Р., Андерхилл Г.Х., Мендельсон А., Бхатия С.Н. Многофазное электропаттернирование клеток и биоматериалов. Лабораторный чип. 2007; 7: 702–709. [PubMed] [Google Scholar]

51. Yin T, Li L. Ниши стволовых клеток в костях. Журнал клинических исследований. 2006; 116:1195–1201. [Бесплатная статья PMC] [PubMed] [Google Scholar]

52. Markx GH, Andrews JS, Mason VP. К микробной тканевой инженерии? Тенденции биотехнологии. 2004; 22: 417–422. [PubMed] [Google Scholar]

53. Mason VP, Markx GH, Thompson IP, Andrews JS, Manefield M. Колониальная архитектура в сообществах смешанных видов влияет на экспрессию генов, опосредованную AHL. Письма по микробиологии FEMS. 2005; 244:121–127. [PubMed] [Академия Google]

54. Эндрюс Дж.С., Мейсон В.П., Томпсон И.П., Стивенс Г.М., Марккс Г.Х. Создание искусственно структурированных микробных консорциумов (ASMC) с использованием диэлектрофореза: изучение взаимодействия бактерий через метаболические промежуточные продукты в биопленках окружающей среды. J Микробные методы. 2006; 64: 96–106. [PubMed] [Google Scholar]

55. Абидин З.З., Даунс Л., Марккс Г.Х. Крупномасштабное диэлектрофоретическое конструирование биопленок с использованием текстильной технологии. Биотехнология Биоинж. 2007; 96: 1222–1225. [PubMed] [Академия Google]

56. Сухоруков В.Л., Муссауэр Х., Циммерманн Ю. Влияние сил электрической деформации на электропроницаемость мембран эритроцитов в средах с низкой и высокой проводимостью. J Мембранная биология. 1998; 163: 235–245. [PubMed] [Google Scholar]

57. McCaig CD, Rajnicek AM, Song B, Zhao M. Электрическое управление поведением клеток: текущие взгляды и будущий потенциал. Physiol Rev. 2005; 85: 943–978. [PubMed] [Google Scholar]

58. Чжао М., Сонг Б., Пу Дж., Вада Т., Реди Б., Тай Г.П., Ван Ф., Го А.Х., Вальчиско П., Гу Ю., Сасаки Т., Судзуки А., Форрестер Дж.В., Bourne HR, Devreotes PN, McCaig CD, Penninger JM. Электрические сигналы контролируют заживление ран посредством фосфатидилинозитол-3-ОН киназы-гамма и PTEN. Природа. 2006; 442: 457–460. [PubMed] [Академия Google]

59. Sun S, Wise J, Cho M. Миграция фибробластов человека в трехмерном коллагеновом геле в ответ на неинвазивный электрический раздражитель — I. Характеристика индуцированного трехмерного движения клеток. Тканевая инженерия. 2004; 10: 1548–1557. [PubMed] [Google Scholar]

60. Сун С., Титушкин И., Чо М. Регуляция адгезии и ориентации меземхимальных стволовых клеток в трехмерном коллагеновом каркасе с помощью электрического стимула. Биоэлектрохимия. 2006; 69: 133–141. [PubMed] [Google Scholar]

61. Джеямкондан С., Джаяс Д.С., Холли Р.А. Импульсная обработка пищевых продуктов электрическим полем: обзор. J Защита пищевых продуктов. 1999;62:1088–1096. [PubMed] [Google Scholar]

62. Нил Г.А., Циммерманн У. Электрофузия. Методы в энзимологии. 1993; 221:171–196. [PubMed] [Google Scholar]

63. Ho SY, Mittal GS. Электропорация клеточных мембран: обзор. Критический обзор биотехнологий. 1996; 16: 349–362. [PubMed] [Google Scholar]

64. Menachery A, Pethig R. Контроль разрушения клеток с помощью диэлектрофоретических сил. IEE Proc Nanobiotechnol. 2005; 152:145–149. [PubMed] [Google Scholar]

65. Fuhr G, Glasser H, Müller T, Schnelle T. Манипуляции с клетками и их культивирование под воздействием переменного электрического поля в культуральных средах с высокой проводимостью. Биохим Биофиз Акта. 1994;1201:353–360. [PubMed] [Google Scholar]

66. Арчер С., Ли Т.Т., Эванс А.Т., Бритланд С. Т., Морган Х. Клеточные реакции на диэлектрофоретические манипуляции. Biochem Biophys Res Comm. 1999; 257: 687–698. [PubMed] [Google Scholar]

67. Khademhosseini A, Langer R, Borenstein J, Vacanti JP. Микромасштабные технологии для тканевой инженерии и биологии. Proc Natl Acad Sci USA. 2006; 103: 2480–2487. [Бесплатная статья PMC] [PubMed] [Google Scholar]

68. Park H, Cannizzaro C, Vunjak-Novakovic G, Langer R, Vacanti CA, Farokhzad OC. Нанофабрикация и микрофабрикация функциональных материалов для тканевой инженерии. Тканевая инженерия. 2007; 13: 1867–1877. [PubMed] [Академия Google]

69. Волдман Дж. Электрические силы для микроманипуляций с клетками. Энн Рев Биомед Инж. 2006; 8: 425–454. [PubMed] [Google Scholar]

70. Гриер Д.Г. Революция в оптических манипуляциях. Природа. 2003; 424:810–816. [PubMed] [Google Scholar]

71. Биркбек А.Л., Флинн Р.А., Озкан М., Сонг Д.К., Гросс М., Эзенер С.К. Массивы VCSEL как микроманипуляторы в биосистемах на основе чипов.