«Что такое потенциал, какой его смысл? И что такое разность потенциалов?» — Яндекс Кью
ПопулярноеСообщества
Стать экспертом Кью
ТехнологииФизика+2
Просто Илья
·
22,2 K
ОтветитьУточнитьAsutpp
1,2 K
⚡Информационный сайт «ASUTPP». Статьи и рекомендации по ремонту электрооборудования… · 1 мар 2020 · asutpp.ru
Отвечает
Юрий Макаров
Если вы ведете речь о потенциале, как о разновидности электрической величины и как о характеристике, определяющей функцию напряжения, то это мера количества энергии. Все предметы вокруг нас состоят из атомов, молекул, электронов и других частиц, которые постоянно взаимодействуют между собой посредством электромагнитных сил.
Если рассмотреть суть электрического потенциала не с электрической стороны, а на более понятном примере, можете представить себе рогатку, в которую вы заряжаете шарик. Если оттянуть резинку на полметра и зафиксировать шар в этом положении, то он получит количество энергии, которая при освобождении запустит шар на 10 метров. Если тот же шар в резинке отвести на метр и зафиксировать в таком положении, то он будет обладать потенциалом энергии, которая сможет запустить его на 20 метров. Так вот потенциал представляет собой невидимую энергию, которая до возникновения определенных условий не может реализоваться или расходоваться.
Под разностью потенциалов понимается ситуация, когда в двух точках присутствует разное количество энергии. Классическим вариантом разности потенциалов является пальчиковая батарейка, на концах которой присутствует разность потенциалов в 1,5В – это означает, что потенциал плюсового полюса больше потенциала минусового полюса на 1,5В.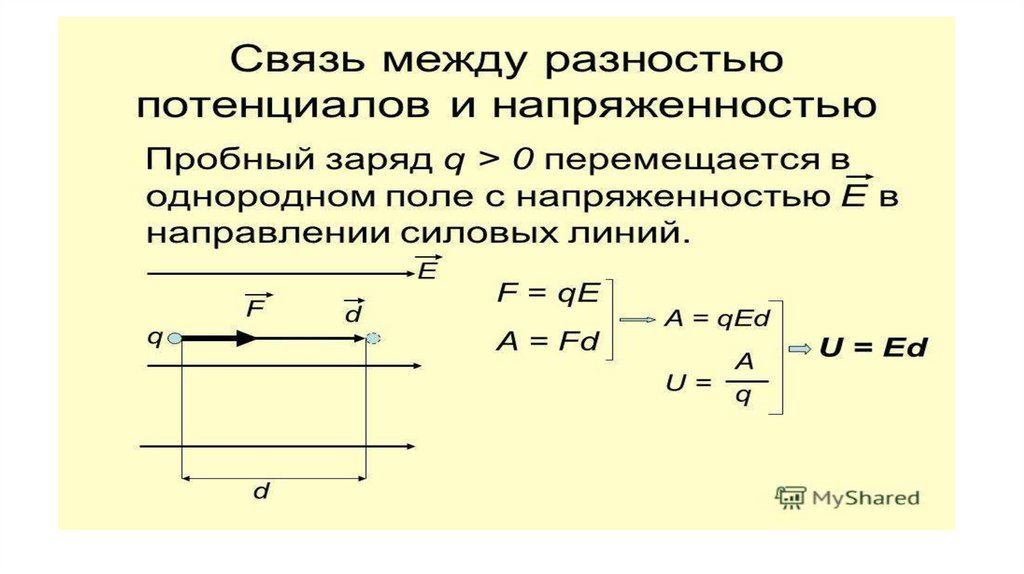 Если рассмотреть напряжение в розетке, то разность потенциалов в ней составит 220В, но в отличии от батарейки, величина потенциала в каждой точке постоянно меняется, однако их разность остается постоянной – 220В.
Если рассмотреть напряжение в розетке, то разность потенциалов в ней составит 220В, но в отличии от батарейки, величина потенциала в каждой точке постоянно меняется, однако их разность остается постоянной – 220В.
Больше полезной информации по электрике вы можете найти на нашем сайте:
Перейти на asutpp.ru1 эксперт согласен
12,8 K
Andrei Novikov
подтверждает
30 мая 2021
В целом так и есть.
Комментировать ответ…Комментировать…
Владимир Яшагин
Технологии
173
Инженер путей сообщения электромеханик. Электро и теплоэнергетика ,электрические машины. э… · 3 нояб 2020
Потенциал -это энергетическая характеристика электрического поля.
Потенциалом в данной точке поля называется скалярная величина ,
численно равная потенциальной энергии единичного положительного
заряда, помещенного в эту точку поля. Разность потенциалов между двумя точками электростатического
поля или электрической цепи это электрическое напряжение ,численно
равное… Читать далее
Разность потенциалов между двумя точками электростатического
поля или электрической цепи это электрическое напряжение ,численно
равное… Читать далее
1 эксперт согласен
Комментировать ответ…Комментировать…
Антон Климов
выпускник НГУ · 15 окт 2016
Я попробую объяснить на примере условной аналогии из механики. Представьте себе шарик, массы m, который находится на высоте h2, и вам надо переместить его на большую высоту h3. Для того, чтобы это сделать нужно совершить работу против сил поля тяжести. Тогда, работа по перемещению шарика из точки h2 в точку h3 есть разность потенциалов гравитационного поля в точках h2 и… Читать далее
1 эксперт согласен
Андрей О. Федотов
подтверждает
14 августа
Хотя не спрашивали, продолжу аналогию. Если потенциал высота горки, то напряженность Е — её наклон.
Комментировать ответ…Комментировать…
Powered House
64
Полезные советы и рекомендации в области строительства, ремонт и благоустройства… · 13 авг · poweredhouse.ru
Отвечает
PH
Объясню на примере генератора переменного тока состоящего из проводника (рамки), вращающегося в магнитном поле. Вращаясь, проводник пересекает линии магнитного поля (с разной скоростью и в разных направлениях, что дает синусоиду — но сейчас не об этом). В результате сила Лоренца перемещает электроны периодически то к одному концу проводника (рамки) то к другому. Это пере… Читать далее
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Разность потенциалов — это разность потенциалов.
 Что такое разность потенциалов?
Что такое разность потенциалов?”””””Предполагаетсячтопереносзарядаобразцанеменяетсяраспределениезарядависточникеполя
Альтернативноеопределениедляэлектростатическогополятаково
”””””нарасстояниемеждуиполюбомупутиизв
ЕдиницейизмерениянапряжениявСИявляетсявольт
РазностьпотенциаловсуществующаявдвухразныхточкахполяобозначаетсятерминомнапряжениеизмеряемоеввольтахВоднородномэлектрическомполесвязьмеждуэлектрическимнапряжениеминапряженностьюэлектрическогополяоченьчеткая
Потенциальнаяразницавпрактике
РазностьпотенциаловсуществующаявдвухразныхточкахполяназываетсянапряжениемиизмеряетсяввольтахВоднородномэлектрическомполесвязьмеждуэлектрическимнапряжениеминапряженностьюэлектрическогополяоченьхорошоопределена
ТочкисодинаковымпотенциаломвокругзаряженнойповерхностипроводникаполностьюзависятотформыэтойповерхностиВэтомслучаеразностьпотенциаловдляотдельныхточеклежащихнаоднойитойжеповерхностиравнанулюТакаяповерхностьпроводникагдекаждаяточкаимеетодинаковыйпотенциалназываетсяэквипотенциальнойповерхностью
ПриприближениикзаряженномутелупроисходитрезкоеувеличениепотенциалаирасположениеэквипотенциальныхповерхностейсближаетсяПомереудаленияотзаряженноготеларасположениеэквипотенциальныхповерхностейстановитсяболеедиффузнымПоложениелинийэлектрическихсилвсегдаперпендикулярноэквипотенциальнойповерхностивкаждойточке
ЧтобыразинавсегдаизбавитьсяотпутаницыдавайтеразберемсявразличияхмеждуэтимитремяпонятиямиДляэтогодавайтеподробнеерассмотримкаждыйизнихвотдельности
ЭДСразностьпотенциаловинапряжение–чтоэтотакоеивчемразницамеждунимиВучебникахпоэлектротехникеиэлектроникечастовстречаютсятрифизическиевеличиныимеющиеоднуитужеединицуизмерения–вольтразностьэлектрическихпотенциаловэлектрическоенапряжениеиэлектродвижущаясилаЭДС
ЧтобыразинавсегдаустранитьпутаницусвязаннуюсэтимитерминамидавайтеразберемсявразличияхмеждунимиДляэтогодавайтеподробнеерассмотримкаждыйизнихвотдельности
Разностьэлектрическихпотенциалов
ВнастоящеевремяфизикизнаютчтоисточникамиэлектрическогополяявляютсяэлектрическиезарядыилипеременныемагнитныеполяКогдамырассматриваемопределенныеточкиивэлектростатическомполеизвестнойнапряженностимыможемсразуговоритьоразностиэлектростатическихпотенциаловмеждуэтимидвумяточкамивданныймоментвремени
Разностьпотенциаловрассчитываетсякакинтегралэлектрическойнапряженностимеждуточкамиирасположеннымивэлектрическомполенаопределенномрасстояниидруготдруга
Практическитакаяхарактеристикакакпотенциалотноситсякединичномуэлектрическомузарядукоторыйтеоретическиможнозафиксироватьвданнойточкеэлектростатическогополяитогдазначениеэлектрическогопотенциаладляэтогозарядабудетравноотношениюпотенциальнойэнергиивзаимодействияэтогозарядасданнымполемквеличинеэтогозаряда
Изэтогоследуетчторазностьпотенциаловоказываетсячисленноравнымотношениюработыработапосути–изменениепотенциальнойэнергиизарядасовершаемойданнымэлектростатическимполемприпереноседанногозарядаизточкиполявточкуполяквеличинеданногопробногозаряда
Таковопрактическоезначениетермина“разностьпотенциалов”используемоговэлектротехникеэлектроникеиэлектрическихявленияхвцелом
Еслимыговоримобэлектрическойцепимытакжеможемоценитьразностьпотенциаловмеждудвумяточкамицепиесливданныймоментсуществуетэлектростатическоеполеименнопотомучтоточкицепитакжебудутнаходитьсявэлектростатическомполеданнойнапряженности
КакупоминалосьвышеразностьэлектрическихпотенциаловизмеряетсяввольтахвольтДжК
Электростатическоеполе–ЭлектрическоеполесоздаваемоенеподвижнымиэлектрическимизарядамиДлятогочтобыэлектрическиезарядыбылинеподвижнынанихнедолжныдействоватьсилыподдействиемкоторыхзарядымоглибыдвигатьсяНовнутрипроводниковзарядымогутсвободноперемещатьсяпоэтомуесливнутрипроводниковсуществуетэлектрическоеполетовпроводникахбудетпроисходитьдвижениезарядовэлектрическийток
Следовательнозарядымогутоставатьсянеподвижнымитолькоеслионисоздаютполеравноенулювездевнутрипроводниковиперпендикулярноеихповерхностипотомучтовпротивномслучаезарядыдвигалисьбывдольповерхности
Дляэтогонеподвижныезарядыдолжныбытьразмещенытольконаповерхностипроводниковитакимобразомчтобыэлектрическоеполевнутрипроводниковбылоравнонулюанаповерхностиперпендикулярноему
ВышеизложенноеотноситсякстационарнымзарядамДлямобильныхсборовтеПриналичиитоковвпроводникахвнихдолжносуществоватьэлектрическоеполеиначетокинемоглибытечьипоэтомудвижущиесязарядырасполагаютсявпроводникахвообщеговоряиначечемнеподвижныезарядыисоздаютэлектрическиеполяотличныепосвоейконфигурацииотэлектростатическогополяОднакопосвоимсвойствамэлектростатическоеполенеотличаетсяотэлектрическогополядвижущихсязарядов
Электрическоенапряжение
ТеперьрассмотримтакоепонятиекакэлектрическоенапряжениемеждуточкамиивэлектрическомполеиливэлектрическойцепиЭлектрическоенапряжение–этоскалярнаяфизическаявеличиначисленноравнаяработесовершаемойэффективнымэлектрическимполемвключаявнешниеполяприпереносеединичногоэлектрическогозарядаизточкивточку
ЭлектрическоенапряжениеизмеряетсяввольтахкакиразностьэлектрическихпотенциаловВслучаенапряженияпредполагаетсячтопереносзаряданеизменитраспределениезарядовкоторыеявляютсяисточникамиэффективногоэлектростатическогополяАнапряжениевэтомслучаебудетсуммойработыэлектрическихсилиработывнешнихсил
ЕслинетвнешнихсилтотолькопотенциальноеэлектрическоеполеВэтомслучаеэлектрическоенапряжениемеждуточкамиицепибудетчисленноточноравноразностипотенциаловмеждуэтимиточкамитеотношениюработыпопереносузарядаизточкивточкуквеличинезаряда
Вобщемслучаеоднаконапряжениемеждуточкамииотличаетсяотразностипотенциаловмеждуэтимиточкаминавеличинуработывнешнихсилпоперемещениюединичногоположительногозаряда
ЭтопроизведениевнешнихсилназываетсяэлектродвижущейсилойвданнойточкецеписокращенноЭДС
Электродвижущаясила–ЭДС
Электродвижущаясила–ЭДСравнанапряжениювМеждународнойсистемеединицСИизмеряетсяввольтах
ЭДС–этоскалярнаяфизическаявеличинакотораяописываетработунепосредственнодействующихвнешнихсиллюбыхсилкромеэлектростатическихвцепяхпостоянногоилипеременноготокаВчастностивзамкнутойпроводящейцепиЭДСравнаработеэтихсилпоперемещениюединичногоположительногозарядавдольцепи
ЗдесьпринеобходимостиврассмотрениевводитсяэлектрическаянапряженностьвнешнихсилкотораяявляетсявекторнойфизическойвеличинойравнойотношениювнешнейсилыдействующейнаэлектрическийзарядквеличинеэтогозарядаТогдавзамкнутомконтуреЭДСбудетравна
МыможемговоритьобэлектродвижущейсилевлюбойточкеэлектрическойцепиФактическиэтоудельнаяработавнешнейсилытольконаданнойчастиЭДСгальваническогоэлементаэтонапримернечтоиноекакработавнешнихсилпоперемещениюединичногоположительногозарядатольковнутриданногогальваническогоэлементааименноотодногополюсаэлементакдругому
РаботавнешнихсилнеможетбытьвыраженачерезразностьпотенциаловпотомучтовнешниесилынепотенциальныиихработазависитотформытраекторииТакнапримерработавнешнихсилпоперемещениюзарядамеждуклеммамиисточникатоказапределыэтогоисточникаравнанулю
ЭМПможетгенерироватьсяразличнымиспособамисредикоторыхможноупомянутьследующие
СпомощьюисточниковЭМПиспользующиххимическиепроцессыгальваническиеэлементыбатареи–химическиеисточникитока
источникамиЭМПиспользующимисвойствамагнитногополяэлектрическиемашины–генераторы
источникамиЭМПвкоторыхтепловаяэнергияпреобразуетсявэлектрическуютермоэлектрическиепреобразователи
СпомощьюисточниковЭМПвкоторыхэнергиясветовогоизлученияпреобразуетсявэлектрическуюэнергиюфотоприемникисолнечныебатареи
Задание№ВточкеполяточечногоисточниказарядапотенциалφВавточкеφВНайдитепотенциалφвточкеМлежащийнаполпутимеждуточкамииРисунок
ПотенциалРазницапотенциаловПроблемысрешениями
Формулыдляиспользованиянауроках“РешениезадачпотемеРаботасмещениязарядавэлектрическомполе”ПотенциалРазницапотенциалов”приподготовкекЕГЭ
ПРИМЕРЫЗАДАЧ
Задача№МеталлическаясферадиаметромзаряженповерхностнойплотностьюзарядаσНайдитепотенциалφсферыеслионаокруженазаземленнойпроводящейсферойимеющейснейобщийцентрДиаметрсферысоставляетЖидкость–этовоздух
Проблема№ПотенциалзаряженнойсферыφВКаковпотенциалφэлектрическоеполесферывточкерасположеннойнарасстояниисмотегоповерхностиеслирадиуссферысм
ПроблемаОпределитепотенциалφточкиполярасположеннойнарасстоянииасмотповерхностизаряженнойсферырадиусасмеслиплотностьповерхностногозаряданасфересоставляетσ–КельсмСреда–этовоздух
ПроблемаВточкеполяточечногоисточникапотенциалφВавточкеφВНайдитепотенциалφвточкеМлежащаяпосерединемеждуточкамииРисунок
ПроблемаВтрехвершинахквадратасосторонойасм–этозаряды–Кл–Кли––рисОпределитепотенциалφэлектрическогополясоздаваемогоэтимизарядамивчетвертойвершине
ЗаданиеЧетыреравныхточечныхзарядарасположенынаоднойпрямойнарасстояниидруготдругаЧтотакоеработаАчтонужносделатьчтобыперенестиэтизарядынавершиныправильноготетраэдрасосторонойСреда–вакуум
Проблема№ДвеодинаковозаряженныесферыдиаметромсмкаждыйрасположенынарасстояниисммеждуихповерхностямиРисунокДокакогопотенциалаφонизаряженыеслиихотталкивающаясиланаправленадругпротивдругаμСреда–этовоздух
ПроблемаВоднородномэлектрическомполенапряженностьюЕкВсмсместилзаряднКлвнаправлениилинииполянарасстояниисмНайтиработуполяАизменениепотенциальнойэнергииполяΔпинапряжениеразностьпотенциаловмеждуначальнойиконечнойточкамиперемещения
ПроблемаМеждудвумягоризонтальнымиплоскостямидиаметральнозаряженнымиирасположенныминарасстоянииммдруготдругавравновесиикаплимасламассойнгнанограммрисНайтичислоизбыточныхэлектроновнаэтойкаплеСреда–этовоздухРазностьпотенциаловмеждуплоскостямикВ
Проблема№НатарелкеМподдерживаетсяпотенциаломφВинапластине–φВрисаРасстояниемеждупластинамисмВдалисмотпластиныМпоместитезаземленнуюпластинуРрисбНайдитеизменениеинтенсивностиΔЕполявиизменениенапряженностиполяΔЕвокрестностяхводноитожевремяПостройтеграфикзависимостимеждунапряженностьюполяипотенциалаφφнарасстоянииточекполяотпластин
Этократкоеизложениетемы“Потенциал”РазницапотенциаловПроблемыирешения”Выберитеследующиешаги
Рис
Чтотакоеразностьпотенциалов
ТерминынапряжениеразностьпотенциаловиэдсотносятсякработесовершаемойсиламиэлектрическогополяприперемещениизарядавпространствеВчастностикогдазаряддвижетсявдольучасткацепиЭтооченьважныепонятияширокоиспользуемыекаквтеориитакинапрактикеидажечастовстречающиесявповседневнойжизниКазалосьбыдлянихсуществуютточныеобщепринятыеопределенияиониимеюточеньчеткийфизическийсмыслОднакоприближайшемрассмотренииоказываетсячтоделообстоитнетакпростоЕслисразностьюпотенциаловвсеболееилименеевпорядкетоснапряжениемиЭДСповезломеньшевэлектродинамикегдеэтипонятиябыливведеныизначальноинапрактикеатакжевтеориицепейгдеониособенноактивноиспользуютсядаютсясовершенноразныеопределенияэтихпонятий
Болеетоговрамкаходногоитогожекурсаэлектродинамикимогутпредлагатьсяразличныенеэквивалентныеверсииопределенийчтоделаетсмыслэтихважныхпонятийещеболеедвусмысленныминеопределенным
Врезультатеиногдадажеоченьавторитетныеавторысерьезныхкнигиспытываютзатрудненияприобращениикэтойтемесм“Авторитетныеисточникиистандартыпонапряженности”
Введение
Рис
ВэлектродинамикепонятиянапряженияразностипотенциаловииндукцииобычновводятсяследующимобразомПримерзарядапомещенныйвэлектрическоеполерисНаполевуюсторонузарядадействуетсилаТакимобразомеслизаряддвижетсятосиласовершаетработуРаботазатраченнаянаперемещениеединичногозарядапозаданномупутиявляетсянапряжениемВобщемслучаеработаинапряжениезависятоттраекториипокоторойдвижетсязарядНовслучаепотенциальногоэлектрическогополянапримерэлектростатическогоработазависиттолькоотначальногоиконечногоположенийзарядаинезависитотформытраекториипоэтомутожесамоеможносказатьионапряженииПоэтомулюбойточкевпространствеможносопоставитьскалярнуювеличину–потенциалАразностьпотенциаловмеждудвумяточкамибудетравнаработезатраченнойнапереносединичногозарядаизпервойточкивовторуюлюбымпутемТакимобразомнапряжениеиразностьпотенциаловвслучаепотенциальногополяравныВобщемслучаеэлектрическоеполеимеетпотенциальнуюинепотенциальнуюсоставляющиевихревоеэлектрическоеполекрометоговопределенныхобластяхпространствамогутсуществоватьтакназываемыевнешниеполяНапряжениеопределяетработупоперемещениюединичногозарядасовершаемуюсиламидействующиминазарядсостороныэлектрическогополявцеломвключаяпосторонниеполяВкладэлектростатическойпотенциальнойсоставляющейполявэтуработухарактеризуетсяразностьюпотенциаловкотораязависиттолькоотначальнойиконечнойточекВкладпостороннихиспиновыхполейназываетсяэдсэдскакинапряжениеобычнозависитотлиниивдолькоторойдвижетсязаряд
ТакимобразомтипичныйкурсэлектродинамикизнакомитспервойверсиейэтихпонятийСамоеинтересноечтообычнопослеэтогодаетсясовершенноновоеопределениенапряженияИтакимобразомонбезжалостноразрушаеттолькочтовыстроеннуюсистемупонятийКакипочемуэтопроисходитбудетрассмотренониже
ВтеориицепейвсегораздопрощеВопервыхизучаемыетамсистемырассматриваютсянаболеевысокомуровнечемвэлектродинамикеВтеориицепейнаснеинтересуетструктураполейвэлементахцепииокружающемпространствемыневдаемсявподробностипроцессовпроисходящихвотдельныхэлементахцепиВовторыхесливыполняютсяопределенныенеслишкомстрогиетребованияможнопредположитьчтоэлектрическоеполеявляетсяпотенциальнымвездевнеэлементовцепиипонятиепотенциаламожетбытьиспользованодляописаниясостоянияцепиТермины“напряжение”и“разностьпотенциалов”считаютсясинонимамивтеориицепейЭдсиногдавводитсяновцеломвтеориицепейможнообойтисьибезнееЭтодажеспособствуетболеечеткойпрезентации
Напряжениевэлектродинамике
ПриначислениивэлектрическомполесиласуществуетрисравноЗдесьмысчитаемчтоэлектрическоеполетакжевключаетвнешниеполяеслитаковыеимеютсявнешниесиловыеполятесилыдействующиеназаряднеэлектромагнитнойприродывмакроскопическомвыражениивозникающиеврезультатехимическихреакцийтепловыхпроцессовитд
Рис
Еслиполезнаянагрузкадвижетсяпоопределеннойтраекториирисизоднойточкипространствавдругуюточкусиласостороныполясовершаетработукотораяможетбытьвычисленаинтегрированиемпопути¯¯Линейныйинтегралвекторанапряженностиэлектрическогополявычисленныйвдольлиниисмещениязаряданазываетсянапряженностьюнапряженностьвыражаетработуполяпоперемещениюединичногозарядавдольэтойлинии
Рисунок
ВобщемслучаеработазатраченнаянаперемещениезарядаизоднойточкипространствавдругуюазначитинапряжениезависитотпутиинтегрированиятраекториидвижениязарядаПоэтомуеслимыговоримонапряжениинеобходимоуказатьккакомупутиинтегрированияоноотносится
ПутьинтеграцииневсегдауказаноднозначноНапримердляэлектрическойцепиэтоудобнееделатькосвенноуказываяэлементрисилиучастокцепирисккоторомуотноситсянапряжениеилиэдсоэдссмнижеПоэтомумычастоуказываемпутьинтеграциидаженезадумываясьобэтом
Рис
Рис
Напряжениеиразностьпотенциалов
ВнекоторыхслучаяхнапряжениезависиттолькоотначальнойиконечнойточекЭтопроисходитвтомслучаееслиполеявляетсяпотенциальнымтекогдаследовательнопотеоремеСтоксагде–этолюбойзамкнутыйконтурПримеромпотенциальногополяявляетсяэлектростатическоеполе
Такнарисработасовершаемаяприсмещениизарядаотввпотенциальномэлектрическомполевдольтраекторииодинаковы
Рис
ИзтогочтоинтегралполюбомузамкнутомуконтуруравеннулюследуетчтолинейныйинтегралнезависитотпутиинтегрированиямеждудвумяточкамилинейныйинтегралзависиттолькоотначальнойиконечнойточекчтолегкодоказатьПредположимчтосуществуютдветочкиипусть–некоторуюлиниюсоединяющуюэтиточкирисунокДокажемчторезультатинтегрированияполюбомудругомупутиравенинтегралупопути
Рисунок
Докажитеобратнымметодомпредположимчто¤точкаточкаточкарезультат–результатИзменитенаправлениеинтегрированиявовторомчленечтотакжеизменитрезультатинтегрирования■■Линиии–образуютзамкнутыйконтуррисобозначаемыйТогдаНомызнаемчтоинтегралпозамкнутомуконтуруравенМыполучилипротиворечиезначитсделанноепредположениебылоневернымидлякаждогопутимеждуточками
Рисунок
Приусловиинезависимостиполевыхработприперемещениигрузамеждудвумяточкамипоформетраекториимыможемприписатькаждойточкепространстватакуювеличинуназовемеепотенциаломчтобыразностьпотенциаловбыларавнаработесилполяпоперемещениюединичногогрузаизточкивточку–где–этолюбаяпрямаялиниясоединяющаяточкии
РазностьпотенциаловмеждудвумяточкамиопределяетсяоднозначноасампотенциалопределяетсякакпостояннаявеличинаеслимыизменимпотенциалывсехточекпространстванаоднуитужепроизвольнуювеличинуторазностьпотенциаловмеждулюбымидвумязаданнымиточкамиостанетсянеизменнойОднакоеслимыопределяемпотенциалдлялюбойточкипространстватопотенциалывсехостальныхточекопределяютсяоднозначноМыможемнапримеропределитьточкупотенциалкотороймыпримемзанульВэлектростатикезанулевойпотенциалчастопринимаютпотенциалбесконечноудаленнойточкиВтеориицепейпотенциалодногоузла“общегопровода”принимаетсязанулевойпотенциалотносительнокоторогоудобноотсчитыватьпотенциалыдругихузловцепи
НапряжениеиэлектродвижущаясилаЭДС
Рис
ТеперьрассмотримболеесложныйслучайПустьунасестьэлектрохимическаяячейкарисвкоторойсуществуютвнешниесилывозникающиеврезультатепроисходящиххимическихпроцессовВрезультатедействиявнешнихсилнапротивоположныхполюсахклеткинакапливаетсяизбыточныйположительныйиотрицательныйзарядсоответственносоздаетсяразностьпотенциаловмеждуполюсамиклеткиВотсутствиенагрузкитокнетечетзарядобразцапомещенныйвклеткунаходитсявравновесииэлектростатическиеипосторонниесилыкомпенсируются∗ПроинтегрируемэторавенствовдольлюбогопутипроходящийотполюсакполюсувнутриэлементаΔИзопределенияследуетчтозначениенапряжениенаэлементеИнтегралпотенциальнойсоставляющейэлектростатическогополя–эторазностьпотенциаловмеждуполюсамиэлемента–■¯ИнтегралотнеэлектростатическойвнешнейсоставляющейполяназываетсяэлектродвижущейсилойэдсТакимобразомполучаемчто–Напряжениенаненагруженномэнергоэлементеравноаразностьпотенциаловравнакорнюэдсспротивоположнымзнаком––Весьмапримечательныйрезультатспрактическойточкизрениянапрактикеоченьмалолюдейпридерживаютсямнениячтонапряжениевсетиравнонулю
Рисунок
Еслимырассмотримлюбойпроизвольныйпутьработающиевнеклеткитетамгдесуществуеттолькоэлектростатическоеполенетпостороннихполучаем–ОказываетсячтонапряжениеналюбойлиниивнеэлементаравноразностипотенциаловнаполюсахэлементарисЭтоужевполнесоответствуетраспространеннымнапрактикеинтуитивнымпредставлениямонапряжениииразностипотенциалов
Рис
РассмотримтеперьзаряженнуюячейкукогдапоцепитечеттоктепроисходитнаправленноедвижениезарядарисЗарядобразцапомещенныйвнутрьячейкитакжедолженприйтивдвижениеДляобеспеченияустановившегосятоказаданнойвеличинысучетомпотерьвовнутреннемсопротивленииисточникавнешнееполедолжнобытьбольшечемэлектростатическоепоабсолютнойвеличинеВэтомслучае–Вчастностивнаправлениивекторовпоказанныхнарисункекогдаклеткапереключенавэтойполярности–
Еслимысоединимклеммыэлементатакчторазностьпотенциаловмеждуполюсамистанетравнойтонапряжениеналиниипроходящейчерезэлементстанетравныминдукции
Выбираялюбуюлиниюпроходящуювненагруженногоэлементасноваполучаемчтонапряжениеравноразностипотенциаловнаполюсахэлемента–ἀ
Ещеразонапряжениивэлектродинамике
ИспользуяопределениепредложенноевышедлянапряжениямыпонимаемнапряжениенаучасткецеписпадениемнапряжениянасопротивленииэтогоучасткаВчастностиоказываетсячтоподнапряжениемнасиловомэлементеследуетпониматьпадениенапряжениянавнутреннемсопротивленииэлемента
СогласноэтомуопределениюнапряжениенаненагруженномэлементеследуетпринятьравнымнулюКакупоминалосьвышеэтотподходнеполучилпризнаниянапрактикеВэтомлегкоубедитьсяесливыдадитесвоемудругуисточникдостаточновысокогонапряженияэдсискажетеемучтонапряжениенанемравноонскореевсегонеоценитшуткуиувасстанетнаодногодругаменьше
Рисунок
Типичныекурсыэлектродинамикипризнаюттакоеположениеделипослевведениятрадиционногоопределениядаютобъяснениепосхеме
ТакоезамечаниенесколькоозадачиваетособенноеслиучестьчторанеекогдаприводилсяпервыйвариантопределенияакцентделалсяназависимостинапряженияотпутипокоторомуоноизмеряетсяВтораяверсияопределенияпредписываетпутьвнеустройстваноэтоможетбытьсделанонесколькимиспособамииеслиэлектрическоеполевнеустройстванепотенциальноемыкакправилополучимдругиерезультатыВеличинанапряжениявсоответствиистакимопределениемоказываетсянеоднозначнойАсамопонятиенапряжениякотороеказалосьбыдолжноиметьточноеистрогоеопределениестановитсядвусмысленныминеясным
КсожалениюлегкихпутейисправленияэтойситуациинесуществуетСоднойсторонынельзятребоватьоттеорииэлектродинамикиотказаотклассическогоопределениянапряженияТемболеечтосуществуетобширнаялитературавкоторойэтоопределениеужеустоялосьСдругойстороныдовольносложнодобитьсяотказаотобщепринятогоиспользованияизвестноготермина“напряжение”изаменыегоболеегромоздкимтермином“разностьпотенциалов”тамгдеговоритьонапряжениинесовсемкорректно
ТемнеменеевтеорииэлектрическихцепейэтапроблемауспешнорешенаиснекоторойосторожностьювполнеправомерноиспользоватьпонятиенапряжениявовторомсмыслекотороестановитсяэквивалентнымпонятиюразностипотенциаловЭтотакжеотноситсякцепямпеременноготока
Напряжениевцепяхпеременноготока
Внешниесилы–неединственнаяпричинапокоторойнапряжениевпервомопределениистановитсязависимымотпутиКрометогоналичиевихревойсоставляющейэлектрическогополявозникающейотпеременногомагнитногополяможетпривестикзависимостинапряженияотпутиобычноэлектрическоеполесоздаваемоепеременныммагнитнымполемнепринятоназыватьвнешнимполемавключаетсяврасчеткакиндукцияэдсПеременныемагнитныеполяобязательноприсутствуютвцепяхпеременноготокапосколькуонинеизбежновозникаютприпротеканиипеременноготокачерезпроводникиикомпонентыцепи
Рисунок
КакотмечалосьвышеэтосоздаетдополнительныепроблемысовторымспособомопределениякогдаполярноенапряжениеустройстваилиэлементацепиопределяетсявдольпутивнеэлементанобезуказаниявдолькакогопутиИдляразныхпутейрезультатымогутбытьоченьразнымиНапримервситуациипоказаннойнанетгарантиичтоустройстваипокажеттежезначения
СогласноуравнениюМаксвеллаΔ–fiиливинтегральнойформе––этолюбойзамкнутыйконтури–этопроизвольнаяповерхностькоторая“опирается”наданныйконтур
Рис
КаквидитеинтегралнапряженностиполярассчитанныйпозамкнутомуконтуруоказываетсяненулевымприизменениимагнитногопотокачерезконтуримеетсяввидумагнитныйпотокчерезлюбуюповерхностьграницейкоторойявляетсяданныйконтурДругимисловаминапряжениезависитотформыпутииизмерениеразностипотенциаловвольтметромстановитсяневозможнымрезультатизмерениязависитотположениясоединительныхпроводовПоэтомувольтметрыинарисункевольтметрыдляизмеренийвцепяхпеременноготокабудутпоказыватьразныезначенияЦепьобразованнаядвумявольтметрамиисоединяющимиихпроводамипронизанапеременныммагнитнымпотокомтрансформатораиливнашемслучаедросселя–этотконтурфактическипредставляетсобойкатушкутрансформаторавкоторойиндуцируетсяэлектрическийтокчтоприводиткразличнымпоказаниям
СдругойстороныесливнекоторойобластипространстваотсутствуетпеременноемагнитноеполеатакжепосторонниеполятоэлектрическоеполеоказываетсявэтойобластипотенциальнымнапряжениевдольлюбогозамкнутогоконтуравэтойобластиравнонулюаразностьпотенциаловмеждуточкамиможноизмеритьвольтметромирезультатизмерениянебудетзависетьоттогокакрасположенысоединительныепроводаДействительноеслинетпеременногомагнитногополятоΔидлялюбогоконтуразамкнутоговэтойобласти∗∗ИзэтогоследуетчтопоказаниявсехвольтметровсоединенныхмеждудвумязаданнымиточкамиконтурабудутодинаковыминезависимоотположениясоединительныхпроводовдотехпорпокаконтурыобразованныесоединениемвольтметровостаютсявобластипотенциальногополяТакнарисункевольтметрыпоказываютодинаковыйрезультатизмеренияпотомучтомагнитноеполечерезконтуркоторыйониобразуютравнопоэтомунаведеннаяЭДСвконтуреотвольтметровтакжеравнанулюконтурполностьюнаходитсявпотенциальномэлектрическомполеХотярядоммывидимдроссельвключенныйвцепьпеременноготоканокакмыустановилимагнитноеполеневыходитзапределыэтихэлементоввданномслучаеонососредоточеновмагнитопроводеизматериаласвысокоймагнитнойпроницаемостью
Рис
Напряжениеразностьпотенциаловиэлектрическийтоквтеориицепей
Втеориицепейнапряжениеопределяетсякакнапряжениеопределяемоепопутивнеэлементовцепи“второйвариантопределения”вэлектродинамикерисЭтопредполагаетчтовсемагнитныеполяипосторонниеэлектрическиеполяеслитаковыеимеютсясосредоточенывсоответствующихэлементахинесуществуютвнеихНуилипочтинетнасколько“почти”–зависитотточноститребуемоймоделиКакпоказановышеприуказанныхусловияхэлектрическоеполевнеэлементовявляетсяпотенциальныманапряжениемеждулюбымидвумяточкамивцепиравноразностипотенциаловмеждуэтимиточками
Рис
ОтсутствиемагнитногополявнеэлементовсхемыможетбытьдостигнуторазличнымиконструктивнымимерамиДляэтогостараютсясконцентрироватьмагнитныеполякатушекитрансформатороввнутриэтихустройствнапримериспользуязамкнутыемагнитопроводыизферромагнитныхматериаловпринеобходимостивыполняютэкранированиестараютсявыполнитьсоединениятакимобразомчтобырезультирующиецепиимелиминимальнуюплощадьповерхностипространственноотделяютисточникисильныхмагнитныхполейтакиекакмощныетрансформаторыисиловыецепиотчувствительныхцепейитд
ВлюбомслучаепредпринимаютсяпопыткиминимизироватьпетлиобразуемыеучасткамиконтураособенноподверженнымииндукциипосколькууменьшаяплощадьпетлипритойжемагнитнойиндукциимыуменьшаеммагнитныйпотокчерезпетлюУпрощенныйпримерпоказаннарисункегдеизображенучастоксхемысостоящийиздвухэлементовобразующихцепьИзменяяконфигурациюсхемымыуменьшаемплощадьограниченнуюсхемойиисвязимеждунимиПрипрочихравныхусловияхэтоуменьшитмагнитныйпотокчерезконтурииндукциювнем
Рис
ИлиесливамнужнопередатьсигналпоотносительнодлиннойлиниивыможетеуменьшитьперекрестныепомехивызванныеизменениеммагнитногополяиспользуявитуюпаруимпульсыиндуцированныевразныхчастяхвитойпарыимеютпротивоположныйзнакичастичнокомпенсируютсяИдеальнаякомпенсациянеможетбытьдостигнутаиззанеоднородностивнешнегополяинеидеальнойскруткипроводниковпарыновсежеможноожидатьзначительногоуменьшенияпомехсм
Рис
ЧтокасаетсятовтеориицепейэтопонятиемалокомунужноиегоможносмелоотброситькакизлишнееОнаслишкомтесносвязанаспроцессамивнутриэлементакоторыенеинтересуютнасврамкахтеориицепейНасамомделенеимеетзначенияестьлиЭДСвнутриклеткиилинетЕслиэтотактоэтоавтоматическиотразитсяввольттоковойхарактеристикеэлементакотораяотноситсякразностипотенциаловнаконтактахэлементаипротекающемучерезнеготоку
ИногдаЭДСопределяетсякакнапряжениенаконтактахненагруженногоисточникачто“примерно”соответствует“классическомуопределению”еслинеучитыватьзнаквеличиныобаопределениядаютпротивоположныйзнакдляЭДС
Авторитетныеисточникиистандартыпонапряжению
ДавайтепосмотримкакиеопределенияособеннодлянапряженияпредлагаютсявнекоторыхавторитетныхзаслуживающихдоверияисточникахЧтокасаетсяразностипотенциаловтоподходкэтомупонятиювразныхисточникахнесильнорасходитсяпоэтомувопроснетакинтересенАчтокасаетсятоэтопонятиедлянасвторостепенноинетребуетособоговнимания
БольшаяРоссийскаяэнциклопедия
Вкачествеотправнойточкидляданногообзорамывыбираем“Большуюроссийскуюэнциклопедию”доступнуювнастоящеевремявИнтернетеВстатье“Электрическоенапряжение”мыможемпрочитатьпредлагаемоеопределениенапряжения
Казалосьбывсевпорядкевседостаточнохорошосформулированоеслиупуститьизвидутотфактчтовеличиныиспользуемыеввыражениинасамомделедолжныобозначатьсякаквекторы
Однакозаэтимследуетобъяснениеиспользуемойнотациичтовызываетнекотороенедоумение
написанонастольконепонятночтобезобъясненийнеобойтисьОчевидночтоавторстатьиимелввидучтотовродеследующего“–бесконечномалыйэлементпутиинтегрированиябесконечномноговекторовнаправленныхвкаждуюточкукасательногопути”
ДалееотметимчтопосколькуэлектростатическоеполеявляетсяпотенциальнымпервыйинтегралвформуленезависитотпутиинтегрированияиравенразностипотенциаловвточкахиВторойинтегралназываетсяэлектродвижущейсилойЭДСпритогда–ÙЕслиучастокцепинесодержитэдстонапряжениеравноразностипотенциалов
Затемследуеттрадиционныйпереходкпрактическойверсииопределения
ФормулировкадовольноспорнаяВопервыхудобнорассматриватьнапряжениекакалгебраическуювеличинувеличинусознакомкотораяможетприниматьиотрицательныезначенияТоестькакразностьпотенциалованекакмодульэтойразностиВовторыхЭДСможетиметьотрицательноезначениеИдажееслизначениеЭДСположительноизменениенаправленияинтегрированияизточкивточкуизменитзнакЭДСнапротивоположныйПоэтомунесовсемкорректноговоритьчтомодульразностипотенциаловравенэдсэдсможетприниматьотрицательныезначениямодуль–нет
ВцеломстатьяявляетсяскорееподготовкойкхорошейстатьеМеждутемдляуровняэнциклопедиидаещероссийскойдаещеибольшойонаоткровеннослаба
Физическаяэнциклопедия
ТеперьобратимсякболееспециализированнымисточникамДлянапряжениявстатье“Электрическоенапряжение”в“Физическойэнциклопедии”даноследующееопределение
Далеевстатьеговоритсяобэлектродвижущейсиле
ЕстьдажехорошаястатьяооченьдлиннаяивитиеватаяснесколькоинымвзглядомнаконцепциюНомынебудемздесьостанавливатьсянаэтомвопросе
Нуадальшеестьтотзамечательныйпереходкоторыйпозволяетлюбоенапряжениепреобразоватьпростовразностьпотенциаловатакжевводитещеоднопонятие–“падениенапряжения”
Энциклопедическийсловарьпофизике
Естественно“базовое”определениевсловаренесильноотличаетсяотопределениявэнциклопедии
Вопределениинесказанопрямочтовнешниеполядолжныприниматьсявовниманиенодалеевтекстеэтообъясняетсясначаларассматриваетсяслучайпотенциальногоэлектростатическогополявкоторомнапряжениемеждудвумяточкамисовпадаетсразностьюпотенциаловмеждунимизатемрассматриваетсяслучайнепотенциальногополявкоторомнапряжениезависитотпутикоторыйпроходитзарядмеждуточками
ЗатемпредставленоопределениеиспользуемоенапрактикеОднаковотличиеотэнциклопедииздесьнетчеткогоразграничениямеждудвумя“вариантаминапряжения”Врезультатеэтапопыткаскрытьпротиворечиемеждупервоначальнымопределениемиопределениемиспользуемымнапрактикетолькоещебольшезапутываетэтотибезтогосложныйвопрос
новоеопределениенапряженияраспространяетсятакженаисточникиииндуктивностивцепяхпеременноготока
СоздаетсявпечатлениечтоэтотвариантданнекакотдельноеопределениеакакдополнениекосновномуопределениюНотогдасмыслпервоначальногоопределенияполностьюменяетсявкаждомслучаенапряжениепросторавноразностипотенциаловЕслимырассматриваемучастокцепибезЭДСтонапряжениенанемравноразностипотенциаловеслиучастокцеписодержитЭДСтомыдолжныизмеритьеенапутивнеэтогоучасткаиснованапряжениебудетравноразностипотенциаловИлижепозамыслуавторовнекаждыйэлементилиучастокцеписЭДСможетсчитаться“источником”Нозатемвсестановитсяещеболеезапутанным
ОсновытеорииэлектричестваИЕТамм
НельзяпройтимимоэтойоднойизсамыхизвестныхиклассическихкнигширокоупоминаемойвсерьезнойлитературеВчастностинаэтукнигучастоссылаютсяприобсуждениивопросовнапряжения
ДействительноматериалвкнигеоченьтщательныйиподробныйНокогдаделодоходитдонапряженияавторкажетсянестремитсявывестиэтуконцепциюнапервыйпланОноупоминаетсяемудаетсяопределениенесколькоразныхвразныхместахноонопочтинеиспользуетсявизложенииболееактивноиспользуютсяпонятияэдсразностьпотенциалов
НапряжениепервоначальновводитсявглавеопостоянномтокекогдамырассматриваемзаконОмадлячастицепибезЭДСтедляпроводникаДаетсяследующееопределение
Деноминациибылиизмененычтобысохранитьпоследовательностьденоминацийвэтойстатье
ПозженапряжениесноваупоминаетсяприрассмотрениизаконаОмадлячастицеписодержащейЭДС–обобщенныйзаконОмаЭтоделаетсявпроцессепереходаотдифференциальнойформызаконакинтегральной
Затемрассмотримучастокцепирасположенныймеждуучасткамиииинтегрируяэтовыражениеполучимгде–сопротивлениеданногоучасткацепи–токпротекающийвнемЗапишемэтовыражениеввидесобъяснением
Чтонесоответствуетопределениювдругихисточникахгденапряжениепонимаетсяименнокаксуммадвухчленоввправойчастипервыйизкоторыхвданномслучаепросторазностьпотенциаловавторой–МожносчитатьчтоэтоточкапереходаотклассическоготеоретическогоопределениякпрактическомуДалеемычитаемточтоследуетвподтверждениеэтогопредположения
Затемавторвозвращаетсякпонятиюнапряжениявглаве“Квазистационарноеэлектромагнитноеполе”гдеприводитсязависимостьнапряженияотвыборапутиинтегрированиявслучаепеременногополя
Опечаткавкниге■–■поэтому––––ине–
Наконецмырассмотримпростуюэлектрическуюцепьсостоящуюиз“генерирующейцепи”линиипередачии“потребляющейцепи”НапримереэтойсхемывпроцессесложныхрасчетовещеразвводитсяпонятиенапряженияНасамомделеоказываетсячтоэтоэквивалентноопределениюнапряжениякакразностипотенциалов
Международныйэлектротехническийсловарь–ЧастьЭлектромагнетизм
ТеперьобратимсякстандартамСсылкунанапряжениеможнонайтивразличныхдокументахвкачествепримерарассмотримопределениеданноевМЭКиГОСТРониопределяютнапряжение“классическим”способомвэлектродинамикеВМЭКмычитаем
Этоозначаетчтонапряжениеявляетсяскалярнойвеличинойравнойлинейномуинтегралунапряженностиэлектрическогополявдользаданногопутимеждудвумяточкамиивслучаеполябезвихрейнапряжениенезависитотпутииравноразностипотенциаловмеждудвумяточкамивзятымиспротивоположнымизнаками
Внашемслучаеразностьпотенциаловпринимаетсяравной–противоположноезначение–логичнееназыватьизменениемпотенциала
Этоопределениевполнесоответствует“классической”версииОднаковнемнесказанопрямоучитываетсяливнешнееполеОднакоэтоможнопрояснитьпроверивопределениенапряженностиэлектрическогополя
напряженностьвекторногополякотораядействуетнакаждуюзаряженнуюнеподвижнуючастицуссилойравнапроизведениюивзиматьплатучастицыСогласноэтомуопределениюполучаетсячтовнешнеесиловоеполесодержитсявэлектрическомполе
ГОСТРЭлектротехнологииТерминыиопределенияосновныхпонятий
Даетсяследующееопределениеэлектрическогонапряжения
Поэтомуздесьтакжеприводится“классическая”версияопределения
Литература
ФизическаяэнциклопедияАМПрохоровМБольшаяРоссийскаяэнциклопедия
ЭнциклопедическийсловарьпофизикеАВПрохоровМСоветскаяэнциклопедия
ТаммИЕОсновытеорииэлектричестваМОСКВАФИЗМАТЛИТ
Международныйэлектротехническийсловарь–ЧастьЭлектромагнетизм
Международныйэлектротехническийсловарь–ЧастьТеорияцепей
ГОСУДАРСТВЕННЫЙСТАНДАРТРЭлектротехнологияТерминыиопределенияключевыхтерминов
ϕАϕВВ
Потенциальнаяразницавпрактике
Вобычномупотребленииразностьпотенциалов–этонапряжениемеждудвумявыбраннымиточкамивцепиВтожевремянапряжениемеждукаждойизэтихточекитретьейточкойбудетразнымвточностикакопределено
Иллюстративныйпример
- ВточкецепинапряжениеотносительнозаземляющегопроводасоставляетВ
- ВточкенапряжениенатомжепроводникесоставляетВ
Найдитенапряжениемеждуточкамии
Вэтомслучаетребуемаяразницасоставляет
ϕϕВ
ОбсуждаемыеконцепциинеобходимыдляполученияминимальныхзнанийвобластиэлектротехникииэлектроникипосколькувсерасчетыипрактическиерешенияоснованынанихБезэтихосновуглубленноеизучениеэлектротехническихдисциплинневозможно
стр
Асламазов Л.
 Г. Напряженность, напряжение, потенциал // Квант
Г. Напряженность, напряжение, потенциал // КвантПо специальной договоренности с редколлегией и редакцией журнала «Квант»
Каждая точка электрического поля характеризуется векторной величиной – напряженностью поля. Напряженность поля в данной точке равна силе, действующей на положительный пробный заряд, помещенный в эту точку, и отнесенной к единице заряда. Это – силовая характеристика электрического поля.
При перемещении электрического заряда в поле совершается работа. Электростатическое поле обладает очень важным свойством потенциальностью: работа по перемещению заряда из одной точки поля в другую не зависит от формы траектории. Это позволяет ввести понятие напряжения (или разности потенциалов). Напряжение U между двумя точками поля (*Под словами «пояс», «электрическое поле» здесь и в дальнейшем мы будем понимать электростатическое поле, то есть поле, созданное неподвижными зарядами.) равно работе, совершаемой электрическим полем по перемещению единицы положительного заряда из одной точки в другую.
В отличие от напряженности, определенной в отдельно взятой точке, напряжение характеризует две точки ноля. Если зафиксировать одну точку, выбрав ее за начало отсчета, то любая точка поля будет иметь определенное напряжение по отношению к выбранной точке. Это напряжение называют потенциалом φ. Очевидно, что началу отсчета соответствует нулевой потенциал. Чаще всего нулевой потенциал приписывается точке, бесконечно удаленной от заряда, создающего поле. В этом случае потенциал φ некоторой точки поля равен работе, совершаемой электрическим полем по перемещению единицы положительного заряда из этой точки в бесконечность. Это – энергетическая характеристика электрического поля.
Иногда задавать в каждой точке скалярную величину – потенциал φ – удобнее, чем векторную величину напряженность . Естественно, что эти две величины должны быть связаны друг с другом.
Рассмотрим вначале однородное электрическое поле. Его напряженность одинакова во всех точках; силовые линии такого поля – параллельные прямые (рис. 1).
1).
Рис. 1
Найдем разность потенциалов между точками B и D. Потенциал φB точки B равен работе по перемещению единицы заряда из этой точки в бесконечность. Форма траектории при подсчете работы не имеет значения, поэтому будем перемещать заряд сначала по отрезку BC потом по отрезку CD а затем из точки D в бесконечность. Сила, действующая на единицу заряда со стороны электрического поля, равна напряженности. На отрезке ВС работа этой силы равна E·l, где E – проекция вектора напряженности на силовую линию, a l – длина отрезка ВС. На отрезке CD сила работы не совершает, так как она перпендикулярна перемещению. Наконец, работа по перемещению единицы заряда из точки D в бесконечность равна потенциалу φD. Поэтому: или для разности потенциалов:
(1)
Для того чтобы формула (1) давала правильный знак разности потенциалов, величине l надо приписывать определенный знак в зависимости от расположения точек B и C на силовой линии. Будем считать, что l – это проекция вектора BD на направление силовой линии. Тогда знак положителен, если точка C лежит «ниже» по силовой линии, чем точка B и отрицателен в противоположном случае. Для случая, изображенного на рисунке 1, l > 0, и разность потенциалов , что соответствует убыванию потенциала вдоль силовой линии .
Будем считать, что l – это проекция вектора BD на направление силовой линии. Тогда знак положителен, если точка C лежит «ниже» по силовой линии, чем точка B и отрицателен в противоположном случае. Для случая, изображенного на рисунке 1, l > 0, и разность потенциалов , что соответствует убыванию потенциала вдоль силовой линии .
Итак, в однородном электрическом иоле между напряженностью и разностью потенциалов имеется простая связь, даваемая формулой (1).
Какова связь между потенциалом и напряженностью в случае неоднородного электрического поля? В таком поле напряженность меняется от точки к точке. Пусть, для простоты рассуждений, изменение напряженности происходит только в одном направлении, которое примем за ось ОХ (рис. 2).
Рис. 2
Тогда напряженность поля зависит только от координаты x: . Ясно, что в небольших участках пространства напряженность меняется мало, и электрическое поле там можно приближенно считать однородным. Возьмем близкие точки B и D и найдем разность потенциалов между ними. Воспользуемся формулой (1). Потенциал так же, как и напряженность, зависит только от координаты x (*Плоскость x = const эквипотенциальна, так как при перемещении единицы заряда в этой плоскости электрическое поле работы не совершает.):
Возьмем близкие точки B и D и найдем разность потенциалов между ними. Воспользуемся формулой (1). Потенциал так же, как и напряженность, зависит только от координаты x (*Плоскость x = const эквипотенциальна, так как при перемещении единицы заряда в этой плоскости электрическое поле работы не совершает.):
Проекция вектора на ось ОХ равна разности координат точек D и B:
Таким образом, для близких точек B и D получаем:
или
(2)
Чтобы формула (2) стала точной, надо устремить точку B к точке D и найти предел, к которому стремится правая часть при неограниченном сближении точек:
(3)
Легко увидеть, что правая часть формулы (3) – это производная потенциала, взятая с обратным знаком. Таким образом, в неоднородном электрическом поле связь между потенциалом и напряженностью в каждой точке следующая:
Таким образом, в неоднородном электрическом поле связь между потенциалом и напряженностью в каждой точке следующая:
(4)
Знак минус в формуле (4) означает, что потенциал убывает вдоль силовой линии: поскольку проекция напряженности на силовую линию , что и означает убывание потенциала.
Если нарисовать график зависимости φ от x, то тангенс угла наклона α касательной к графику в каждой его точке равен производной в этой точке (рис. 3). Поэтому можно сказать, что напряженность электрического поля определяет наклон касательной к графику потенциала.
Рис. 3
Рассмотрим теперь несколько конкретных задач.
Задача 1. Сфера радиуса R имеет заряд Q. Найти зависимость напряженности и потенциала от расстояния r от центра сферы. Нарисовать графики.
Найдем вначале напряженность поля. Внутри сферы электрического поля нет: при r < RE = 0. Вне сферы напряженность поля такая же, как у точечного заряда Q помешенного в центр сферы: при r> R проекция напряженности на выбранное направление от центра , где ε0 – электрическая постоянная. На поверхности сферы, при r = R электрическое поле испытывает скачок . Зависимость E от r графически показана на рисунке 4, а.
а
б
Рис. 4
Величину скачка ΔE можно выразить через поверхностную плотность заряда (равную заряду, приходящемуся на единицу площади поверхности сферы):
Заметим, что это общее свойство электростатического поля: на заряженной поверхности его проекция на направление нормали всегда испытывает скачок независимо от формы поверхности.
Выясним теперь, как меняется потенциал φ в зависимости от r. Мы уже знаем, что в любой точке тангенс угла наклона касательной к графику потенциала должен совпадать со значением проекции напряженности (взятой с противоположным знаком). При 0 < r < RE = 0, и, следовательно, во всех этих точках касательная к графику потенциала должна быть горизонтальной. Это означает, что на участке 0 < r < R потенциал не меняется: φ = const.
Вне сферы, при r > R производная отрицательна и величина ее убывает с расстоянием r. Поэтому и потенциал должен убывать с расстоянием, стремясь к нулю при . Действительно, чем дальше расположена точка, в которой мы ищем потенциал, тем меньшую работу надо совершать при перемещении единицы заряда из этой точки в бесконечность. Величина потенциала φ при r > R такая же, как у точечного заряда, помещенного в центр сферы:
Может ли потенциал испытать скачок на поверхности сферы, то есть при r = R? Очевидно, что нет. Скачок потенциала означал бы, что при перемещении единичного заряда между двумя очень близкими точками 1 и 2 электрическое поле совершало бы конечную работу:
Скачок потенциала означал бы, что при перемещении единичного заряда между двумя очень близкими точками 1 и 2 электрическое поле совершало бы конечную работу:
должно оставаться конечным при что невозможно. Таким образом, потенциал не испытывает скачков.
График зависимости φ от r изображен на рисунке 4, б.
Задача 2. Шар радиуса R равномерно заряжен по всему объему. Полный заряд тара Q. Нарисуйте графики зависимости напряженности и потенциала от расстояния r от центра шара.
Такой шар можно представить себе состоящим из большого числа тонких заряженных сфер, вложенных одна в другую. Каждая сфера внутри себя поля не создает, а вне создает поле такое же, как точечный заряд, помещенный в ее центр. Поэтому вне шара, при r > R напряженность такая же, как напряженность поля точечного заряда Q помещенного в центр шара:
Внутри шара, на расстоянии R поле создают только сферы с радиусами от 0 до r (для сфер большего радиуса рассматриваемая точка находится внутри них). Следовательно, напряженность на расстоянии s от центра шара такая же, как напряженность поля точечного заряда Qr. помещенного в центр шара, где Qr– суммарный заряд всех сфер с радиусами от 0 до r, то есть заряд шара радиуса r. Если на шар радиуса R приходится заряд Q, то на шар радиуса r будет приходиться заряд
Следовательно, напряженность на расстоянии s от центра шара такая же, как напряженность поля точечного заряда Qr. помещенного в центр шара, где Qr– суммарный заряд всех сфер с радиусами от 0 до r, то есть заряд шара радиуса r. Если на шар радиуса R приходится заряд Q, то на шар радиуса r будет приходиться заряд
Таким образом, внутри шара напряженность поля – она линейно растет с расстоянием.
На поверхности шара, в точке r = R напряженность скачка не испытывает. Это находится в соответствии с общим правилом, так как поверхностная плотность заряда в данном случае равна нулю: шар заряжен однородно, и на бесконечно тонкий поверхностный слой приходится бесконечно малый заряд.
График зависимости E от r показан на рисунке 5, a.
а
б
Рис. 5
5
Нарисуем теперь график потенциала. Производная от потенциала
всегда отрицательна (E ≥ 0). Поэтому с увеличением r потенциал должен монотонно убывать. В точке r = 0 производная потенциала равна нулю. Следовательно, касательная к графику в. этой точке горизонтальна: в точке r = 0 потенциал имеет максимум. В точке r = R ни потенциал, ни его производная скачков не испытывают. Первое следует из общего правила для потенциала, о втором мы уже говорили выше. Поэтому кривые, изображающие зависимость потенциала от расстояния при r < R и r > R в точке r = R должны сопрягаться – гладко без излома переходить одна в другую. При потенциал . График зависимости φ от r представлен на рисунке 5, б.
Задача 3. Две плоскости расположены параллельно друг другу на расстоянии d и заряжены с поверхностной плотностью заряда σ1 и σ2 соответственно. Нарисовать графики зависимости напряженности поля и потенциала от координаты x (ось ОХ перпендикулярна пластинам). Рассмотреть случаи одноименных (рис. 6, а) и разноименных (рис. 7, а) зарядов на пластинах.
Нарисовать графики зависимости напряженности поля и потенциала от координаты x (ось ОХ перпендикулярна пластинам). Рассмотреть случаи одноименных (рис. 6, а) и разноименных (рис. 7, а) зарядов на пластинах.
Рис. 6 Рис. 7
Каждая плоскость создает по обе стороны от себя однородное электрическое поле, напряженность которого
Воспользовавшись принципом суперпозиции, для случая одноименных зарядов приходим к графику, показанному на рисунке 6, б, а для разноименных – к графику на рисунке 7, б. Скачки напряженности опять соответствуют общему правилу:
Соответствующие графики для потенциалов показаны на рисунках 6, в и 7, в. На отдельных участках зависимость потенциала от координаты – линейная, так как напряженность поля постоянна. Изломы происходят в тех местах, где напряженность поля испытывает скачок.
Заметим, что в данной задаче потенциал не стремится к нулю при . Это, очевидно, связано с тем, что плоскость бесконечна. В действительности размеры реальных пластин всегда ограничены; это приводит к тому, что потенциал падает с увеличением расстояния от пластин.
Задача 4. Две одинаковые параллельные пластины имеют заряды +q и –q. Как меняется разность потенциалов U между пластинами при увеличении расстояния d между ними? Нарисуйте график зависимости U от d.
Пока расстояние между пластинами значительно меньше их размеров, такую систему можно считать плоским конденсатором. Тогда – напряжение линейно растет с расстоянием (начальный участок на рисунке 8).
Рис. 8
Это соответствует тому, что напряженность поля . Как только расстояние между пластинами становится сравнимым с размерами пластин, электрическое поле появляется и вне пространства между пластинами. Тогда становятся существенными так называемые краевые эффекты, и зависимость потенциала от расстояния – довольно сложная. Однако качественно ясно, что, вследствие ослабления поля в области между пластинами, напряжение будет расти медленнее, чем по линейному закону (средний участок на рисунке 8). При дальнейшем увеличении расстояния между пластинами оно станет много больше их размеров. Тогда каждую пластину уже можно считать изолированным телом, и ее потенциал где C0 – емкость уединенной пластины. Таким образом, при очень больших расстояниях разность потенциалов перестает зависеть от расстояния между пластинами (график зависимости U от d. на рисунке 8 имеет горизонтальную асимптоту).
Тогда становятся существенными так называемые краевые эффекты, и зависимость потенциала от расстояния – довольно сложная. Однако качественно ясно, что, вследствие ослабления поля в области между пластинами, напряжение будет расти медленнее, чем по линейному закону (средний участок на рисунке 8). При дальнейшем увеличении расстояния между пластинами оно станет много больше их размеров. Тогда каждую пластину уже можно считать изолированным телом, и ее потенциал где C0 – емкость уединенной пластины. Таким образом, при очень больших расстояниях разность потенциалов перестает зависеть от расстояния между пластинами (график зависимости U от d. на рисунке 8 имеет горизонтальную асимптоту).
Краевые эффекты часто оказываются существенными при решении электростатических задач, связанных с законом сохранения энергии, рассмотрим, например, такой вариант ускорителя электронов.
Задача 5. В пластинах плоского конденсатора, заряженного до разности потенциалов U сделано сквозное отверстие. Конденсатор помещен в постоянное магнитное поле, направленное перпендикулярно электрическому полю в конденсаторе (рис. 9). Электрон влетает в пространство между пластинами конденсатора, ускоряется, приобретая энергию e·U вылетает через отверстие и. двигаясь в магнитном поле по окружности, возвращается в конденсатор. Затем он снова ускоряется, движется по окружности большего радиуса, опять входит в конденсатор и т.д. На первый взгляд кажется, что таким образом можно разогнать электрон до больших энергий, то есть создать ускоритель. Так ли это?
Конденсатор помещен в постоянное магнитное поле, направленное перпендикулярно электрическому полю в конденсаторе (рис. 9). Электрон влетает в пространство между пластинами конденсатора, ускоряется, приобретая энергию e·U вылетает через отверстие и. двигаясь в магнитном поле по окружности, возвращается в конденсатор. Затем он снова ускоряется, движется по окружности большего радиуса, опять входит в конденсатор и т.д. На первый взгляд кажется, что таким образом можно разогнать электрон до больших энергий, то есть создать ускоритель. Так ли это?
Рис. 9
Оказывается, такой ускоритель работать не будет – не учтен краевой эффект. Вне конденсатора всегда существует слабое электрическое поле, которое тормозит электрон при егодвижении по окружности. Отрицательная работа поля при этом в точности равна положительной работе при разгоне электрона в конденсаторе: работа в электростатическом поле не зависит от формы траектории. Магнитное поле работы не совершает (сила Лоренца перпендикулярна скорости движения электрона). Поэтому полная работа всех сил, действующих на электрон, при его возвращении в начальную точку будет равна нулю, и кинетическая энергия электрона не изменится. Ускоритель работать не будет.
Магнитное поле работы не совершает (сила Лоренца перпендикулярна скорости движения электрона). Поэтому полная работа всех сил, действующих на электрон, при его возвращении в начальную точку будет равна нулю, и кинетическая энергия электрона не изменится. Ускоритель работать не будет.
Упражнения
1. Может ли существовать электростатическое поле, у которого силовые линии – параллельные прямые, а абсолютная величина напряженности меняется только в направлении, перпендикулярном силовым линиям (рис. 10)?
Рис. 10
2. Две концентрические металлические сферы радиусов R1 и R2 имеют заряды Q1 и Q2 соответственно. Найдите напряженность и потенциал электрического поля на произвольном расстоянии r от центра сфер. Нарисуйте графики зависимости E от r и φ от r.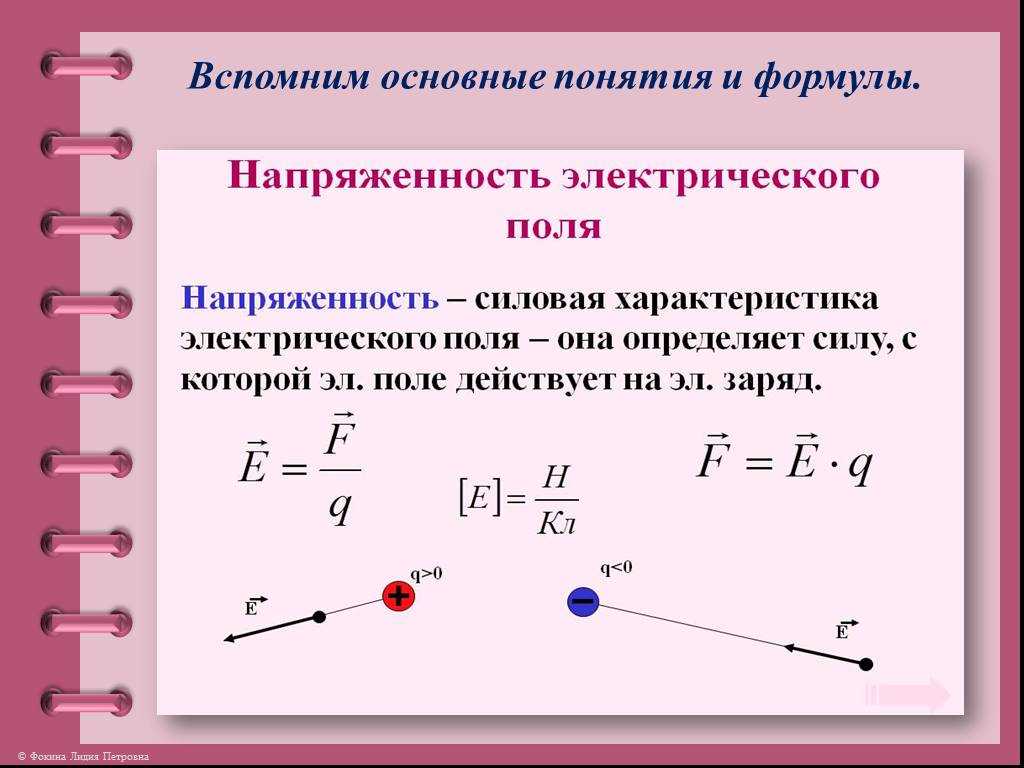 Рассмотрите случаи одноименных и разноименных зарядов. Как выглядят графики для случая Q1 = –Q2 (сферический конденсатор)?
Рассмотрите случаи одноименных и разноименных зарядов. Как выглядят графики для случая Q1 = –Q2 (сферический конденсатор)?
3. Точечный заряд q окружен металлической сферой радиуса R с зарядом Q. Найдите напряженность поля и потенциал на произвольном расстоянии r от заряда q если он находится в центре сферы; нарисуйте графики зависимости E от r и φ от r. Как изменятся графики, если заряд сместить из центра сферы? Решите ту же задачу для случая, когда металлическая сфера заземлена.
4. Электрон влетает в пространство между пластинами плоского конденсатора так, что его скорость составляет острый угол с направлением силовых линий. Тогда при движении в конденсаторе он будет тормозиться и вылетит с меньшей скоростью; его кинетическая энергии уменьшится. Увеличится ли при этом энергия конденсатора?
5. Два одинаковых конденсатора емкостью C каждый, один из которых заряжен до напряжения U а второй – не заряжен, соединяют параллельно. Найти энергию системы до и после соединения конденсаторов. Почему эти энергии не равны?
Найти энергию системы до и после соединения конденсаторов. Почему эти энергии не равны?
6. Точечный заряд q находится вне незаряженной металлической сферы радиуса R на расстоянии d от ее центра. Найти потенциал сферы.
Ответы.
1. Не может, иначе работа по перемещению заряда по замкнутому контуру была бы отлична от нуля.
2. При R1 > r > 0 напряженность E = 0 и ; при R2 > r > R и ; при r > R2 и (рис. 11).
а
б
Рис. 11
3. При R > r > 0 напряженность и ; при r > R и (рис. 12).
а
б
Рис. 12
12
4. Энергия конденсатора не изменяется; изменяется энергия взаимодействия электрона и конденсатора (работа по перемещению электрона в бесконечность из начальной и конечной точек не одна и та же).
5. ровно половина энергии перешло в тепло (независимо от сопротивления подводящих проводов).
6. (потенциал сферы такой же, как в ее центре, а там суммарный потенциал поля индуцированных на сфере зарядов равен нулю).
|
Заглавная страница
КАТЕГОРИИ: Археология Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 17Следующая ⇒ Физическая природа электрического поля и его графическое изображение.В пространстве вокруг электрически заряженного тела существует электрическое поле, представляющее собой один из видов материи. Электрическое поле обладает запасом электрической энергии, которая проявляется в виде электрических сил, действующих на находящиеся в поле заряженные тела. Электрическое поле условно изображают в виде электрических силовых линий, которые показывают направления действия электрических сил, создаваемых полем. Принято направлять силовые линии в ту сторону, в которую двигалась бы в электрическом поле положительно заряженная частица. Как показано на рис. 4, электрические силовые линии расходятся в разные стороны от положительно заряженных тел и сходятся у тел, обладающих отрицательным зарядом. Поле, созданное двумя плоскими разноименно заряженными параллельными пластинами (рис. Электрическое поле можно сделать видимым, если поместить в него взвешенные в жидком масле частички гипса: они поворачиваются вдоль поля, располагаясь по его силовым линиям (рис. 5). Напряженность поля.Электрическое поле действует на внесенный в него заряд ц (рис. 6) с некоторой силой Р. Следовательно, об интенсивности электрического поля можно судить по значению силы, с которой притягивается или отталкивается некоторый электрический заряд, принятый за единицу. В электротехнике интенсивность поля характеризуют напряженностью электрического поля Е. Под напряженностью понимают отношение силы Рис. 6. Схема действия электрического поля на внесенный в него электрический заряд ц ностью Е изображается графически силовыми линиями большой густоты; поле с малой напряженностью — редко расположенными силовыми линиями. Электрический потенциал.Электрическое поле обладает определенным запасом энергии, т. е. способностью совершать работу. Как известно, энергию можно также накопить в пружине, для чего ее нужно сжать или растянуть. За счет этой энергии можно получить определенную работу. Если освободить один из концов пружины, то он сможет переместить на некоторое расстояние связанное с этим концом тело. Точно так же энергия электрического поля может быть реализована, если внести в него какой-либо заряд. Под действием сил поля этот заряд будет перемещаться по направлению силовых линий, совершая определенную работу. Для характеристики энергии, запасенной в каждой точке электрического поля, введено специальное понятие — электрический потенциал. Понятие электрического потенциала аналогично понятию уровня для различных точек земной поверхности. Очевидно, что для подъема локомотива в точку Б (рис. 7) нужно затратить большую работу, чем для подъема его в точку А. Поэтому локомотив, поднятый на уровень #2, при спуске сможет совершить большую работу, чем локомотив, поднятый на уровень Н\. За нулевой уровень, от которого производится отсчет высоты, принимают обычно уровень моря. Точно так же за нулевой потенциал условно принимают потенциал, который имеет поверхность земли. Электрическое напряжение.Различные точки электрического поля обладают разными потенциалами. Обычно нас мало интересует абсолютная величина потенциалов отдельных точек электрического поля, но нам весьма важно знать разность потенциалов ф1—фг между двумя точками поля А и Б (рис. Следовательно, напряжение (У, действующее между различными точками электрического поля, характеризует запасенную в этом поле энергию, которая может быть отдана путем перемещения между этими точками электрических зарядов. Электрическое напряжение — важнейшая электрическая величина, позволяющая вычислять работу и мощность, развиваемую при перемещении зарядов в электрическом поле. Единицей электрического напряжения служит вольт (В). В технике напряжение иногда измеряют в тысячных долях вольта — милливольтах (мВ) и миллионных долях вольта — микровольтах (мкВ). Для измерения высоких напряжений пользуются более крупными единицами — киловольтами (кВ) — тысячами вольт. Напряженность электрического поля при однородном поле представляет собой отношение электрического напряжения, дейст-12 вующего между двумя точками поля, к расстоянию / между этими точками: Напряженность электрического поля измеряют в вольтах на метр (В/м). Электрический ток ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Связь между потенциалом и напряженностью электрического поля
Связь между потенциалом и напряженностью электрического поля
Какие две характеристики электростатического поля вы уже знаете? Как они определяются?
Для чего электрическое поле изображают силовыми линиями?
Каждой точке электрического поля соответствуют определённые значения потенциала и напряжённости. Найдём связь напряжённости электрического поля с разностью потенциалов.
Пусть заряд q перемещается в направлении вектора напряжённости однородного электрического поля Е из точки 1 в точку 2, находящуюся на расстоянии Δd от точки 1 (рис. 14.33). Электрическое поле совершает работу
Эту работу согласно формуле (14.19) можно выразить через разность потенциалов между точками 1 и 2:
А = g(φ 1 — φ 2) = -qΔφ = qU. (14.20)
(14.20)
Приравнивая выражения для работы, найдём модуль вектора напряжённости поля:
В этой формуле U — разность потенциалов между точками 1 и 2, лежащими на одной силовой линии поля (см. рис. 14.33).
Формула (14.21) показывает: чем меньше меняется потенциал на расстоянии Δd, тем меньше напряжённость электростатического поля. Если потенциал не меняется совсем, то напряжённость поля равна нулю.
Так как при перемещении положительного заряда в направлении вектора напряжённости электростатическое поле совершает положительную работу
А = q(φ 1 — φ 2) > 0,
то потенциал φ 1 больше потенциала φ 2 .
Любое электростатическое поле в достаточно малой области пространства можно считать однородным.
Формула (14.21) справедлива для произвольного электростатического поля, если только расстояние Δd настолько мало, что изменением напряжённости поля на этом расстоянии можно пренебречь.
Единица напряжённости электрического поля. Единицу напряжённости электрического поля в СИ устанавливают, используя формулу (14. 21).
21).
Единица напряжённости — вольт на метр (В/м).
Напряжённость, как мы уже знаем, можно также выражать в ньютонах на кулон. Действительно,
Эквипотенциальные поверхности. При перемещении заряда под углом 90° к силовым линиям электрическое поле не совершает работу, так как электростатическая сила перпендикулярна перемещению. Значит, если провести поверхность, перпендикулярную в каждой её точке силовым линиям, то при перемещении заряда вдоль этой поверхности работа не совершается. А это означает, что все точки поверхности, перпендикулярной силовым линиям, имеют один и тот же потенциал.
Эквипотенциальные поверхности однородного поля представляют собой плоскости (рис. 14.34, а), а поля точечного заряда — концентрические сферы (рис. 14.34, б).
Эквипотенциальные поверхности качественно характеризуют распределение поля в пространстве подобно тому, как линии уровня отражают рельеф поверхности на географических картах. Вектор напряжённости перпендикулярен эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала.
Эквипотенциальные поверхности строятся обычно так, что разность потенциалов между двумя соседними поверхностями постоянна. Поэтому согласно формуле (14.21) расстояния между соседними эквипотенциальными поверхностями увеличиваются по мере удаления от точечного заряда, так как напряжённость поля уменьшается.
Эквипотенциальные поверхности однородного поля расположены на равных расстояниях друг от друга.
Вопросы к параграфу
1. Чему равна разность потенциалов между двумя точками заряженного проводника?
2. Как связана разность потенциалов с напряжённостью электрического поля?
3. Потенциал электростатического поля возрастает в направлении снизу вверх. Куда направлен вектор напряжённости поля?
4. Как строятся эквипотенциальные поверхности?
5. Как по картине эквипотенциальных поверхностей поля можно судить о значении напряжённости в различных его точках?
Разность потенциалов или электрическое напряжение это отношение той работы, которую совершают силы электрического поля на перемещение заряда из одной точки поля в другую к величине этого заряда. При этом совершенно неважно, по какому пути будет перемещаться заряд. Важно лишь начало и конец пути. Траектория при этом не имеет никакого значения. Так как электрическое поле является потенциальным.
При этом совершенно неважно, по какому пути будет перемещаться заряд. Важно лишь начало и конец пути. Траектория при этом не имеет никакого значения. Так как электрическое поле является потенциальным.
Для упрощения понимания приведем аналогию с гравитационным полем. Представим себе лестницу, груз лежит на последней ступени при этом он обладает потенциальной энергией. То есть если его уронить с этой высоты, скажем на ногу, то предположительно будет больно. Если бы груз лежал на первой ступени, было бы не так больно, так как он обладал бы значительно меньшей потенциальной энергией.
Теперь представим, что груз лежал на первой ступени и вдруг появился злодей. Он взял этот груз и долго ходил с ним по городу, потом подумал, а зачем он мне. И в итоге принес назад, но положил уже на последнюю ступень лестницы. Потенциальная энергия этого груза изменилась пропорционально высоте, а не как не тому расстоянию, которое прошёл злодей с этим грузом. И совершенно все равно, куда он успел его сводить в ресторан там или в кино, а может и в темную подворотню.
Если вы еще не поняли все это захватывающее повествование было для того чтобы пояснить тот факт что траектория перемещения заряда не имеет значение.
Представим поле, создаваемое двумя зарядами одинаковыми по величине и противоположными по знаку. Поле является электростатическим, так как заряды неподвижны. В этом поле перемещается еще один заряд из точки 1 в точку 2. При этом заряд может совершать перемещение по произвольной траектории.
Рисунок 1 — заряд в электростатическом поле
Для любого поля величина разности потенциалов для всех рассматриваемых зарядов будет постоянной. Так как величина силы действующей со стороны поля на этот заряд пропорциональна заряду. Работа, затрачиваемая на перемещение заряда, имеет вид
Разность потенциалов не имеет направления как напряжённость электрического поля или индукция магнитного. Потому что она является скалярной величиной. Единицей измерения в международной системе единиц СИ для разности потенциалов принят единица в один вольт.
Один вольт это разность потенциалов между двумя точками при условии, что заряд величиной в один кулон перемещается между этими точками, на что поле затрачивает работу в один джоуль.
Из определения следует, что разность потенциалов определяется между двумя точками. В каждой из которых значение потенциала известно. Иногда можно встретить вычисление напряжения из одного значения потенциала при этом подразумевается, что значение второго потенциала равно нулю.
Можно заметить некоторую особенность разности потенциалов. Она заключается в том, что на эквипотенциальной поверхности, в каких бы точках не производилось бы измерение, разность потенциалов будет равна нулю. Казалось бы, точки берутся в разных участках поля, но напряжения между ними нет. Это происходит по тому, что на эквипотенциальной поверхности значение потенциала постоянно и не меняется при движении вдоль нее.
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду:
Энергетическая характеристика поля в
данной точке. Потенциал
не зависит от величины заряда, помещенного
в это поле.
Потенциал
не зависит от величины заряда, помещенного
в это поле.
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной.
Следствие принципа суперпозиции полей (потенциалы складываются алгебраически ).
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.
В СИ потенциал измеряется в вольтах:
Разность потенциалов
Напряжение — разность значений потенциала в начальной и конечной точках траектории.
Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.
Разность потенциалов (напряжение) не зависит от выбора
системы координат!
Единица разности потенциалов
напряженность
равна градиенту потенциала (скорости
изменения потенциала вдоль направления
d).
Из этого соотношения видно:
1. Вектор напряженности направлен в сторону уменьшения потенциала.
2. Электрическое поле существует, если существует разность потенциалов.
3. Единица напряженности: —Напряженность поля равна
Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля.
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная
Поток вектора магнитной индукции Ф в через произвольную поверхность S равен
Теорема Гаусса для поля В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,
Проводники в электростатическом поле. Электроемкость уединенного проводника.
Если
поместить проводник во внешнее
электростатическое поле или его зарядить,
то на заряды проводника будет действовать
электростатическое поле, в результате
чего они начнут перемещаться. Перемещение
зарядов (ток) продолжается до тех пор,
пока не установится равновесное
распределение зарядов, при котором
электростатическое поле внутри
проводника обращается в нуль. Это
происходит в течение очень короткого
времени. В самом деле, если бы поле не
было равно нулю, то в проводнике возникло
бы упорядоченное движение зарядов без
затраты энергии от внешнего источника,
что противоречит закону сохранения
энергии. Итак, напряженность поля во
всех точках внутри проводника равна
нулю:
Перемещение
зарядов (ток) продолжается до тех пор,
пока не установится равновесное
распределение зарядов, при котором
электростатическое поле внутри
проводника обращается в нуль. Это
происходит в течение очень короткого
времени. В самом деле, если бы поле не
было равно нулю, то в проводнике возникло
бы упорядоченное движение зарядов без
затраты энергии от внешнего источника,
что противоречит закону сохранения
энергии. Итак, напряженность поля во
всех точках внутри проводника равна
нулю:
По гауссу
Величину
называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Емкость
проводника зависит от его размеров и
формы, но не зависит от материала,
агрегатного состояния, формы и размеров
полостей внутри проводника. Это связано
с тем, что избыточные заряды распределяются
на внешней поверхности проводника.
Емкость не зависит также ни от заряда
проводника, ни от его потенциала. Сказанное не противоречит формуле, так
как она лишь показывает, что емкость
уединенного проводника прямо
пропорциональна его заряду и обратно
пропорциональна потенциалу.
Сказанное не противоречит формуле, так
как она лишь показывает, что емкость
уединенного проводника прямо
пропорциональна его заряду и обратно
пропорциональна потенциалу.
Единица электроемкости — фарад (Ф): 1Ф
Между напряженностью электрического поля и разностью потенциалов существует определенная зависимость. Пусть заряд перемещается в направлении напряженности однородного поля из точки в точку 2, находящуюся на расстоянии от точки (рис. 125). Электрическое поле совершает работу
Эту работу согласно формуле (8.24) можно выразить через разность потенциалов в точках и 2:
Приравнивая выражения для работы, найдем модуль вектора напряженности поля:
В этой формуле — разность потенциалов между точками 1 и 2, которые связаны вектором перемещения совпадающим по направлению с вектором Е (рис. 125).
Формула (8.28) показывает, что, чем меньше меняется потенциал на расстоянии тем меньше напряженность электрического поля. Если потенциал не меняется совсем, то напряженность поля равна нулю.
Так как при перемещении положительного заряда в направлении вектора Е электрическое поле совершает положительную работу то потенциал больше
потенциала Следовательно, напряженность электрического поля направлена в сторону убывания потенциала.
Любое электрическое поле в малой области пространства можно считать однородным. Поэтому формула (8.28) справедлива для произвольного электрического поля, если только расстояние настолько мало, что изменением напряженности поля на этом расстоянии можно пренебречь.
Единица напряженности электрического поля Единицу напряженности электрического поля в единицах СИ устанавливают на основе единицы разности потенциалов, используя формулу (8.28). Напряженность электрического поля равна единице, если разность потенциалов между двумя точками на расстоянии в однородном поле равна 1 В Наименование этой единицы вольт на метр
Как уже говорилось, напряженность можно также выражать в ньютонах на кулон. Действительно,
Эквипотенциальные поверхности. При перемещении заряда под углом 90° к силовым линиям поле не совершает работы, так как сила перпендикулярна перемещению. Значит, если провести поверхность, перпендикулярную в каждой точке силовым линиям, то при перемещении заряда вдоль этой поверхности работа не совершается. А это, в свою очередь, означает, что все точки поверхности, перпендикулярной силовым линиям, имеют один и тот же потенциал. Поверхности равного потенциала называют эквипотенциальными.
При перемещении заряда под углом 90° к силовым линиям поле не совершает работы, так как сила перпендикулярна перемещению. Значит, если провести поверхность, перпендикулярную в каждой точке силовым линиям, то при перемещении заряда вдоль этой поверхности работа не совершается. А это, в свою очередь, означает, что все точки поверхности, перпендикулярной силовым линиям, имеют один и тот же потенциал. Поверхности равного потенциала называют эквипотенциальными.
Эквипотенциальные поверхности однородного поля представляют собой плоскости (рис. 126), а поля точечного заряда — концентрические сферы (рис. 127). Эквипотенциальные поверхности поля диполя изображены на рисунке 128
Подобно силовым линиям, эквипотенциальные поверхности качественно характеризуют распределение поля в пространству.
Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала. Так, например, потенциал поля точечного положительного заряда убывает по мере удаления от заряда, и напряженность поля направлена от заряда вдоль радиусов концентрических сфер (рис.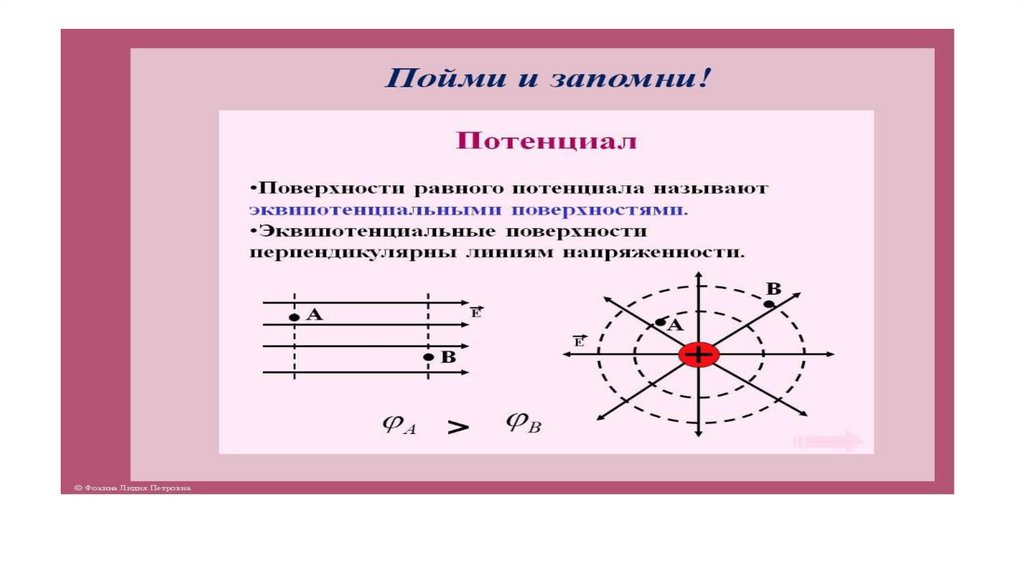 127).
127).
Эквипотенциальной является поверхность любого проводника в электростатическом поле. Ведь силовые линии поля перпендикулярны поверхности проводника. Причем не только поверхность, но и все точки внутри проводника имеют один и тот же потенциал. Напряженность поля внутри проводника равна нулю, а значит, равна нулю и разность потенциалов между любыми точками проводника.
Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.
Из этой формулы разность потенциалов
Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.
В СИ единицей разности потенциалов является вольт (В).
1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.
Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов часто называют электрическим напряжением между данными точками поля:
Разность потенциалов часто называют электрическим напряжением между данными точками поля:
Напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.
Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах. 1 эВ равен работе, совершаемой силами поля при перемещении электрона (е = 1,6·10 -19 Кл) между двумя точками, напряжение между которыми равно 1 В.
1 эВ = 1,6·10 -19 Кл·1 В = 1,6·10 -19 Дж.
1 МэВ = 10 6 эВ = 1,6·10 -13 Дж.
Электрическое поле графически можно изобразить не только с помощью линий напряженности, но и с помощью эквипотенциальных поверхностей.
Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков. Разность потенциалов между двумя любыми точками эквипотенциальной поверхности равна нулю.
Следовательно, работа по перемещению заряда вдоль эквипотенциальной поверхности равна 0. Но работа рассчитывается по формуле
Но работа рассчитывается по формуле
Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям. Первая эквипотенциальная поверхность металлического проводника — это поверхность самого заряженного проводника, что легко проверить электрометром. Остальные эквипотенциальные поверхности проводятся так, чтобы разность потенциалов между двумя соседними поверхностями была постоянной.
Картины эквипотенциальных поверхностей некоторых заряженных тел приведены на рис. 1.
Эквипотенциальными поверхностями однородного электростатического поля являются плоскости, перпендикулярные линиям напряженности (рис. 1, а).
Эквипотенциальные поверхности поля точечного заряда представляют собой сферы, в центре которых расположен заряд q (рис. 1, б).
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие. Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Интересное: Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны… Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 14 из 16Следующая ⇒ В пространстве вокруг заряженного тела существует электрическое поле, обладающее запасом электрической энергии, которая проявляется в виде электрических сил, действующих на находящиеся в поле заряженные частицы. Напряженность поля (Е) — характеризует интенсивность электрического поля, т.е. его способность притягивать или отталкивать некоторый электрический заряд принятый за единицу. Численно напряженность поля определяется как отношение силы, действующей на заряженное тело, к заряду этого тела. Электрический потенциал (φ) характеризует энергию, запасенную в каждой точке поля. Электрический потенциал поля в данной точке равен работе, которую могут совершить силы этого поля при перемещении единицы положительного заряда из этой точки за пределы поля. За нулевой потенциал условно принят потенциал поверхности земли. Разность потенциалов двух точек поля характеризует собой работу, затрачиваемую силами поля на перемещение единичного положительного заряда из одной точки поля с большим потенциалом в другую точку с меньшим потенциалом, и называется электрическим напряжением (U)U=φ1— φ2 [В] Электрический ток и электропроводность вещества. Согласно электронной теории одни атомы могут терять электроны, другие же приобретать их, в результате чего превращаются в положительные и отрицательные ионы. Этот процесс называется ионизацией. Ионизация может возникнуть только при сообщении атому определенного количества энергии: в виде тепла, облучения и т.д. Электроны, потерявшие связь с атомами и перемещающиеся в пространстве между ними, называются свободными. Если в каком-либо теле накопятся электроны или ионы, то говорят, что в теле накопилось электричество или они несут электрический заряд. Единицей электрического заряда принято считать заряд электрона. В веществе, помещенном в электрическое поле, под действием сил поля возникает процесс движения элементарных носителей электричества – ионов и электронов. Направленное движение электрически заряженных частиц под действием электрического поля называется электрическим током (I). За единицу силы тока принят ампер [A]: это такой ток, при котором через поперечное сечение проводника каждую секунду проходит 1 кулон электричества. Постоянным называется ток, значение и направление которого в любой момент времени остаются неизменными. Токи, значение и (или) направление которых не остаются постоянными, называются переменными. Свойство вещества проводить электрический ток под действием электрического поля называется электропроводностью. Существует два рода проводников, которые различаются физической природой протекания электрического тока. Это металлы – ток в них обусловлен движением свободных электронов (электронная проводимость) и электролиты – прохождение тока в них связано с движением ионов (ионная проводимость). Электрическое сопротивление и проводимость. При движении свободных электронов в проводнике они сталкиваются с ионами и атомами вещества, из которого сделан проводник и передают им часть своей энергии, которая выделяется в виде тепла, нагревающего проводник. Противодействие проводника прохождению электрического тока называется электрическим сопротивлением (R) [Ом]. Сопротивление прямолинейного проводника зависит не только от материала проводника, но и его длины и площади поперечного сечения. Электрическая цепь Электрическую цепь образуют источники электрической энергии (источники питания), ее приемники (электродвигатели, электронагревательные приборы, лампы) и соединительные провода, а также вспомогательное оборудование (для включения и выключения электроустановок), электроизмерительные приборы, защитные устройства. Электрическую цепь можно разделить на два участка: внутреннюю цепь (сам источник) и внешнюю цепь (линейные провода и приемники). Чертеж, на котором на котором изображены электрические цепи с помощью условных графических обозначений, называют электрической схемой (Рис.11). Для того чтобы обеспечить непрерывное прохождение тока по электрической цепи, цепь должна быть замкнутой, а на зажимах источника питания необходимо поддерживать разность потенциалов. Во внешней цепи ток направлен от плюса к минусу, внутри источника наоборот. Э.д.с. поддерживает разность потенциалов на зажимах источника и определяет собой напряжение источника питания. Э.д.с. обозначается Е и численно, равна работе, которую необходимо затратить на перемещение единичного положительного заряда от одного зажима к другому. Направления тока, напряжения и э.д.с. на схемах изображают стрелками, за положительное направление тока принимают движение положительных зарядов, т.е. от плюса к минусу. Положительное направление напряжения и э.д.с. совпадает с направлением тока. Закон Ома для электрической цепи: сила тока в электрической цепи равна э.д.с. источника поделенного на полное сопротивление цепи, которое можно представить виде суммы сопротивления приемника и внутреннего сопротивления источника питания. I=E/R I=E/R+R0 Закон Омаможет быть применен не ко всей цепи, но к любому ее участку (например аб): сила тока на данном участке цепи равна напряжению, приложенному к участку, поделенному на сопротивление этого участка. Закон Ома применим только к линейным цепям. Способы соединения потребителей. При последовательном соединении (рис.12)по всем элементам цепи протекает один и тот же ток. E=IR1+IR2 = I(R1+R2)=IRЭ.
RЭ=R1+R2+… U1:U2 =R1:R2 Если последовательно включеноnрезисторов с одинаковыми сопротивлениями R, то RЭ=nR При параллельном соединении (рис. I=I1+I2+… I=U/R1+U/R2 =U/(1/R1+1/R2)
I1:I2 =1/R1+1/R2 Для двух резисторов
При параллельном включении n одинаковых резисторов RЭ= R/n. При смешанном соединении резисторовэквивалентное сопротивление определяют методом преобразования. Понятие о магнитном поле При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды и на их потоки, т. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю. Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Интенсивность магнитного поля, т.е. его способность производить работу определяется магнитной индукцией (В). Магнитный поток (Ф), проходящий через какую-либо поверхность, определяется общим числом м.с.л. пронизывающих эту поверхность Ф=BS, B=Ф/S, где S поперечное сечение магнитопровода. Магнитная индукция зависит не только от тока, возбуждающего магнитное поле, но и от среды, в которой оно существует. Относительная магнитная проницаемость µотн=µа/µ0, где µ0-магнитная проницаемость вакуума = 4π*10-7(Гн/м). Напряженность магнитного поля Н не зависит от магнитных свойств среды, но учитывает влияние силы тока и формы проводника на интенсивность магнитного поля в данной точке. H=B/µа (А/м) ⇐ Предыдущая78910111213141516Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
Действительно ли напряжение и электрический потенциал — это одно и то же? Если нет, то почему?
Прежде, чем меня поджарят в комментариях, позвольте мне сказать, что я недавно получил степень бакалавра в области электротехники, так что я не новичок в этих концепциях. Я изучал электрическую потенциальную энергию, электрический потенциал, напряжение (также известное как разность электрических потенциалов, электрическое напряжение, электрическое давление), изменяющиеся во времени/неконсервативные электромагнитные поля, уравнения Максвелла и т. д. Я читал учебники по университетской физике, по электромагнитная теория, анализ цепей/теория. (Но я не изучал квантовую механику или теорию относительности.)
Прежде чем объяснить, почему я думаю, что напряжение и электрический потенциал на самом деле описывают одни и те же физические явления/процессы, сначала я кратко напомню некоторые факты об этих двух явлениях, чтобы вы могли убедиться, что у меня есть некоторое стандартное понимание этих концепций.
Электрический потенциал
Электрический потенциал – это электрическая потенциальная энергия на единицу заряда в точке пространства. Напомним, что электрическая потенциальная энергия — это вид потенциальной энергии ( т. е. энергия, которой обладает частица в силу своего положения в пространстве или в поле, это энергия, которая может быть использована для совершения работы), связанная с положением заряженных частиц.
Электрический потенциал определяется в точке пространства при условии, что мы предварительно определили точку нулевого электрического потенциала (обычно Земля или точка, бесконечно удаленная от исследуемой области пространства). Поскольку потенциал определен в любой точке пространства (по крайней мере, для консервативных электрических полей) и поскольку он является скалярной величиной в каждой точке, мы говорим, что электрический потенциал является скалярным полем. Это имеет смысл. Я могу сказать, что «электрический потенциал в точке $P_0$ равен $\phi_0$».

Мы иногда используем электрический потенциал (скалярное поле) для расчета статического электрического поля (векторного поля) как отрицательное значение градиента электрического потенциала, поскольку первое вычисляется легче, чем второе.
Электрический потенциал – это величина, которой описываются уравнение Лапласа и уравнение Пуассона.
Электрический потенциал можно изобразить как двумерное или трехмерное скалярное поле.
Мы можем записать уравнения Максвелла в терминах электрического потенциала и магнитного векторного потенциала.
Физики используют термин электрический потенциал чаще, чем напряжение .
И т. д.
Напряжение или разность электрических потенциалов
Напряжение определяется как работа, которую необходимо совершить (или передать энергию) на единицу заряда для перемещения заряженной частицы с единичным зарядом из одной точки пространства в другую точку пространстве, по некоторому пути или траектории.
 Итак, напряжение — это величина между двумя точками, а электрический потенциал — это величина в одной точке.
Итак, напряжение — это величина между двумя точками, а электрический потенциал — это величина в одной точке.Только при наличии консервативных электрических полей напряжение также можно рассчитать как разность электрических потенциалов в двух точках, отсюда и название разность электрических потенциалов .
Напряжение обычно рассматривается как скаляр, но не как (скалярное) поле , подобное электрическому потенциалу. Это имеет смысл. Я могу сказать, что «напряжение между точкой (или узлом в контексте цепей) $a$ и точкой $b$ равно $V_{ab}$». Но не имеет смысла говорить, что «напряжение в точке $c$ равно $V_c$», потому что мы не указываем, относительно какой другой точки мы его измеряем, если только это не очевидно.
Напряжение (и ток), а не электрический потенциал, является величиной, в которой записывается закон Ома, соотношение между напряжением и током для катушек индуктивности, конденсаторов и диодов.

Напряжение, а не электрический потенциал, является величиной, в которой описывается закон напряжения Кирхгофа.
Только в присутствии консервативных электромагнитных полей (нулевые токи [электростатика] или постоянные токи [магнитостатика]) работа, совершаемая между двумя точками, не зависит ни от одного из возможных путей, соединяющих эти две точки, и поэтому работа по быть выполненным при перемещении заряда по замкнутому контуру, равно нулю, а поскольку напряжение — это работа на заряд, то в таком случае напряжение также не зависит от пути. Но в присутствии неконсервативных электромагнитных полей (изменяющиеся во времени токи [электродинамика], например, цепи переменного тока, с незначительными электромагнитными полями рассеяния вне элементов цепи/устройств, таких как катушки индуктивности), работа, которую необходимо выполнить при перемещении заряда от одной точки к другой зависит от пути, и поэтому работа, которую необходимо совершить при перемещении заряда по замкнутому контуру, вообще говоря, не равна нулю, и поэтому напряжение также зависит от пути.

Инженеры-электрики/электронщики используют термин напряжение чаще, чем электрический потенциал .
И т. д.
Почему я думаю, что напряжение и электрический потенциал одинаковы
Хорошо, теперь к моему вопросу. Недавно у меня была онлайн-дискуссия с кем-то, где я сказал, что напряжение и электрический потенциал не совпадают, в то время как человек сказал, что это не так. Я объяснил их так же, как только что сделал выше. Но после разговора и размышлений я думаю, что эти две величины на самом деле описывают одно и то же. Ниже я постараюсь вас переубедить или хотя бы объяснить, почему мне эти величины кажутся одинаковыми.
Предположим, я выбираю одну точку в пространстве, которую я назову опорной точкой , относительно которой я измеряю напряжение во всех других точках пространства. Разве это не то же самое, что и электрический потенциал? Например, я мог бы выбрать в качестве точки отсчета землю или точку, бесконечно далекую от нас, таким образом, напряжение имело бы то же значение, что и электрический потенциал.
А так как я выбрал одну опорную точку для измерения напряжения, то в каждой точке пространства напряжение имеет определенную скалярную величину. Таким образом, напряжение теперь является скалярным полем, подобно электрическому потенциалу. Таким образом, мы также можем вычислить консервативное электрическое поле из этого «поля» напряжения, и мы можем написать уравнения Максвелла в терминах этого «поля» напряжения (и магнитного векторного потенциала), точно так же, как мы могли бы это сделать с электрическим потенциалом.
И эта идея выбора точки отсчета для измерения напряжения не является редкостью. Он широко используется в методе анализа цепей, известном как узловой анализ ; все или большинство симуляторов цепей используют этот метод; он также используется при анализе энергосистем для получения матрицы полной проводимости, которая математически описывает электрические характеристики энергосистемы; даже использование осциллографов в реальных электронных схемах то же самое, потому что мы присоединяем отрицательный щуп к одному узлу (обычно называемому заземление в электронике) цепи, а затем переместите только положительный контакт для измерения напряжения.
Итак, как вы можете видеть, электрический потенциал в точке — это напряжение, измеренное в этой точке относительно точки отсчета с нулевым потенциалом, поэтому потенциал — это то же самое, что и напряжение. Или, что то же самое, напряжение, измеренное между любыми двумя точками $a$ и $b$, является электрическим потенциалом в точке $a$ путем выбора точки отсчета с нулевым потенциалом в качестве точки $b$ (другими словами, чтобы получить напряжение из потенциального , точка нулевого потенциала не является фиксированной для измерения всех потенциалов), поэтому напряжение совпадает с потенциалом.
Обратите внимание: я предполагаю, что напряжение (электрическое напряжение, электрическое давление, разность электрических потенциалов) и электрический потенциал — это одно и то же, а не то, что любой из них совпадает с электрической потенциальной энергией. Я знаю, что первые два не то же самое, что последний.
Я искал, если этот вопрос уже задавался, но не нашел. Я нашел следующие, которые задают разные вопросы:
Разница между напряжением, электрическим потенциалом и разностью потенциалов
Электрический потенциал и напряжение
Почему напряжение описывается как потенциальная энергия на заряд?
В чем разница между электрическим потенциалом, разностью потенциалов (PD), напряжением и электродвижущей силой (ЭДС)?
Напряжение и потенциал
Разность потенциалов и напряжение
Является ли напряжение электрическим потенциалом или разностью электрических потенциалов?
Напряжение относительно разности потенциалов
Изменить после принятого ответа: дальнейшее разъяснение того, почему я говорю, что напряжение и потенциал одинаковы верно), другими словами, это напряжение находится между двумя точками (что верно), а потенциал находится только в одной точке (что не совсем верно).
 Позволь мне объяснить. Вы можете сказать, что потенциал — это количество, не более того? Что ж, посмотрите, пожалуйста, на уравнения (2.21) (для электрического потенциала) и (2.22) (для разности электрических потенциалов, также называемые напряжением) Дэвида Гриффитса.{\mathbf b} {\mathbf E} \cdot {\mathrm d} {\mathbf l} \tag {2.22}$
Позволь мне объяснить. Вы можете сказать, что потенциал — это количество, не более того? Что ж, посмотрите, пожалуйста, на уравнения (2.21) (для электрического потенциала) и (2.22) (для разности электрических потенциалов, также называемые напряжением) Дэвида Гриффитса.{\mathbf b} {\mathbf E} \cdot {\mathrm d} {\mathbf l} \tag {2.22}$Теперь посмотрим на правую часть обоих уравнений. Оба они представляют собой линейный интеграл вектора электрического поля из одной точки в другую по некоторому пути или траектории. Ага! Итак, электрический потенциал — это вообще величина между двумя точками, как и напряжение!
Да, я знаю, что для электрического потенциала (уравнение 2.21) мы обычно выбираем точку отсчета с нулевым потенциалом $\mathcal O$ на бесконечность, так что потенциал тогда является величиной в точке. Но мы также можем выбрать опорную точку $\mathbf b$ в напряжении (уравнение 2.22) также на бесконечности (если вы не согласны, поясните), так что напряжение теперь также является величиной в точке. И, как я уже говорил ранее, в электротехнике на самом деле очень часто говорят о напряжении в точке электрических цепей, потому что мы выбираем один узел в качестве эталонного узла (он же земля), относительно которого мы измеряем все напряжения в точке. другие нереферентные узлы.
И, как я уже говорил ранее, в электротехнике на самом деле очень часто говорят о напряжении в точке электрических цепей, потому что мы выбираем один узел в качестве эталонного узла (он же земля), относительно которого мы измеряем все напряжения в точке. другие нереферентные узлы.
После обсуждения с Роджером в комментариях к его ответу, похоже, что напряжение и электрический потенциал действительно одно и то же, но просто разные названия для одного и того же в зависимости от контекста (инженерия или физика соответственно), с единственной крошечной разницей заключается в том, что все потенциалы измеряются относительно фиксированной точки отсчета, тогда как напряжение может быть измерено относительно произвольной точки (хотя в узловом анализе мы также фиксируем такую точку отсчета как узел, аналогичный потенциалу).
Редактировать 2: Почему мой вопрос не является этим вопросом
У меня есть два предложения, в которых говорится, что мой вопрос совпадает со связанным вопросом в подзаголовке, поэтому я объясню, почему это не тот же самый вопрос. Я сошлюсь на ответ пользователя 11266.
Я сошлюсь на ответ пользователя 11266.
Первый и третий абзацы ответа пользователя 11266 говорят только о причине путаницы в двух терминах и о том, что следует делать вместо этого, поэтому эти абзацы не имеют отношения к моему вопросу.
Во втором абзаце ответа пользователя 11266 говорится о потенциале и разности потенциалов (также известном как напряжение). Он/она говорит: «Каждой точке пространства присвоено значение электрического потенциала», что верно, поскольку из уравнения Гриффитса (2.21) ясно, что для фиксированной точки отсчета $\mathcal O$ потенциал зависит на $\mathbfr$. Но знаете что? Вы также можете зафиксировать $\mathbf b$ в уравнении Гриффитса (2.22) (разность потенциалов, она же напряжение), и теперь у вас будет то же самое, что и потенциал: скалярное значение в каждой точке пространства. И если вы скажете «никто не фиксирует точку для измерения напряжения», то позвольте мне сказать вам, что это на самом деле чрезвычайно распространено: 1) мы используем его для узлового анализа, наиболее распространенного метода решения цепей; 2) его используют все симуляторы цепей; и 3) осциллографы считывают напряжения, фиксируя контрольную точку.
И да, я знаю, что в уравнении потенциала (2.21) точка отсчета $\mathcal O$ обычно находится на бесконечности, а в моем примере схем точка отсчета $\mathbf b$ для уравнения напряжения (2.22) есть не на бесконечности, а вместо узла цепи. Но, насколько я знаю, ничто не запрещает нам выбрать $\mathbf b$ также и на бесконечность, в этом случае уравнения (2.21) и (2.22) становятся одинаковыми, а значит, напряжение и потенциал — одно и то же.
И если вы скажете, что «потенциал более общий, чем напряжение, потому что напряжение применимо только к цепям, поэтому ваш пример схемы недействителен», мой ответ будет таким: просто игнорируйте мои примеры и вместо этого сосредоточьтесь на уравнении (2.22) Гриффитса и установите $\mathbf b = \mathcal O$ и $\mathbf a = \mathbf r$, затем поменяйте местами границы/пределы интеграла, добавив знак минус перед интегралом, и теперь вы получаете $V_{ab} = \phi$ . Et voilà , напряжение равно потенциалу или потенциал равен напряжению, так что это одно и то же. Таким образом, мои утверждения в предыдущем абзаце остаются в силе.
Таким образом, мои утверждения в предыдущем абзаце остаются в силе.
Разность между напряжением, электрическим потенциалом и разностью потенциалов
Спросил
Изменено 3 года, 6 месяцев назад
Просмотрено 1к раз
$\begingroup$
Мне трудно представить себе эти две концепции всерьез.
Сначала эта путаница возникла из-за двух параллельных пластин, которые были подключены к источнику питания, заряжались, затем отключались от источника питания, а затем отделялись друг от друга, странно увеличивалась разность потенциалов, но почему? Я узнал, что электрический потенциал равен $$ V= k \frac{q}{d} $$, и когда расстояние увеличивается, потенциал точки должен падать, но почему, когда мы говорим о разности потенциалов, она увеличивается, этого не происходит. Каждая точка между этими пластинами испытывает меньшее напряжение, когда пластины раздвигаются, и не означает ли это, что потенциал падает, а значит, и разность потенциалов?
Каждая точка между этими пластинами испытывает меньшее напряжение, когда пластины раздвигаются, и не означает ли это, что потенциал падает, а значит, и разность потенциалов?
- потенциал
- потенциал-энергия
- емкость
- напряжение
- определение
$\endgroup$
1
$\begingroup$
На самом деле в вашем рассуждении ошибка. Это ошибка, которую, как мне кажется, совершают любознательные студенты, и она помогает студентам лучше изучить электростатику. Я рад, что вы спросили об этом. V = kq/d применимо не везде. Это применимо только к статическому точечному заряду или за пределами однородной сферы. Но это верно не для всех ситуаций. Примером может служить система параллельных пластин.
Вместо этого верно то, что V является интегралом электрического поля по малому расстоянию. Это всегда верно, поскольку это определение V.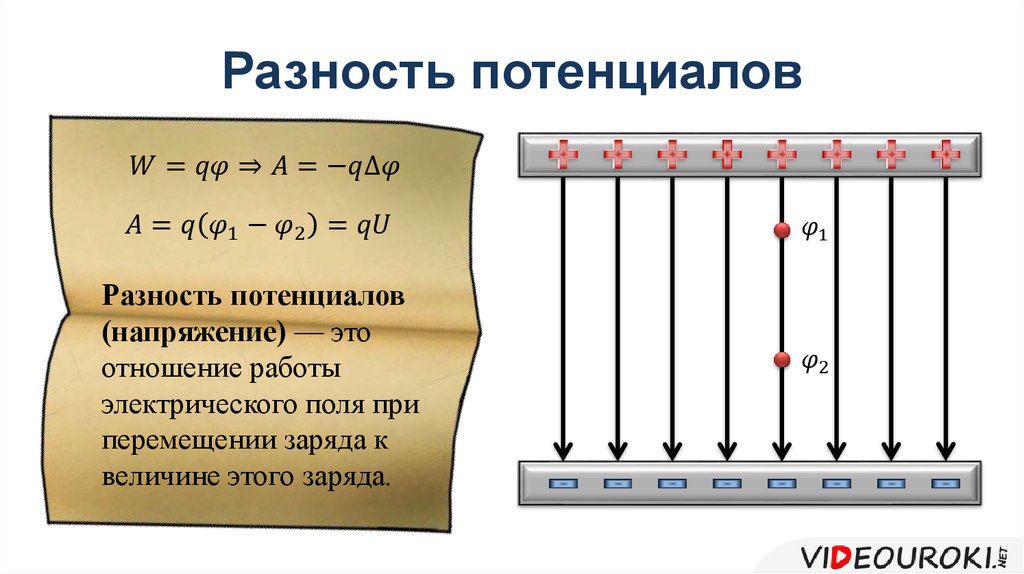 Проще говоря, V — это работа, необходимая для перемещения единичного положительного заряда из бесконечности в положение, в котором он находится в настоящее время.
Проще говоря, V — это работа, необходимая для перемещения единичного положительного заряда из бесконечности в положение, в котором он находится в настоящее время.
Теперь, если у вас есть система конденсаторов, Q = CV. Это следует из самого определения емкости. Теперь для конденсатора с параллельными пластинами C пропорциональна площади пластин и обратно пропорциональна расстоянию между пластинами. Когда вы разъединяете две пластины, площадь пластин остается неизменной. Поскольку заряду некуда деваться, заряд на каждой пластине также остается постоянным. Меняется только расстояние. Поскольку V = Q/C, это будет означать, что, поскольку 1/C пропорциональна расстоянию, V также пропорционально расстоянию между пластинами. Таким образом, когда вы увеличиваете расстояние, вы фактически увеличиваете разность потенциалов. Надеюсь, мне удалось это объяснить. Получайте удовольствие от обучения!
$\endgroup$
$\begingroup$
Я дам простое объяснение.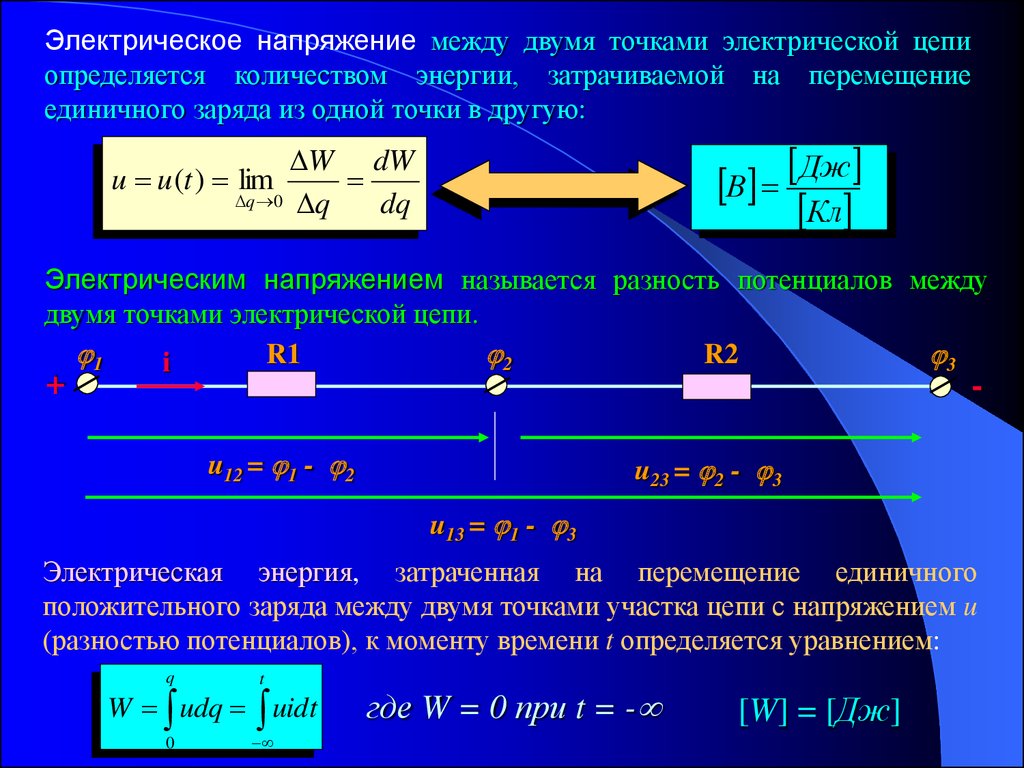 Разность потенциалов — это разность потенциалов между двумя точками (скажем, А и В).
Потенциал любой точки будет разностью потенциалов между этой точкой и другой точкой C, особенность C в том, что ее потенциал считается равным 0. Обычно мы держим C на бесконечности.
Разность потенциалов — это разность потенциалов между двумя точками (скажем, А и В).
Потенциал любой точки будет разностью потенциалов между этой точкой и другой точкой C, особенность C в том, что ее потенциал считается равным 0. Обычно мы держим C на бесконечности.
В вашем вопросе у нас есть конденсатор, мы заряжаем его, отключаем его, теперь заряд остается прежним, то есть электрическое поле между ними такое же, как и раньше. Вы знаете, что $V=E*d$, где V — разность потенциалов, E — электрическое поле, d — расстояние. Дано, что d увеличивается, следовательно, V увеличивается.
$V=\frac{Kq}{d}$ есть потенциал точки на расстоянии d от точечного заряда, на самом деле даже здесь мы делаем просто V=Ed но так как электрическое поле меняется по времени интегрируем($\int E.dx$) и получаем соотношение $V=\frac{Kq}{d}$. В заключение, $V=\frac{Kq}{d}$ применимо только для точечных зарядов/сфер (если d >радиус), а V=$\int E.dx$ выполняется везде.
$\endgroup$
$\begingroup$
Вы смешиваете свойства точечного заряда и конденсатора.
Формула, которую вы написали, отлично работает для точечных начислений, а интуитивно для двух сущностей, имеющих одинаковую природу заряда, и, чтобы быть очень точным, вы должны использовать $r$ вместо $d$ при работе с точечными начислениями в качестве электрическое поле от точечного заряда имеет сферическую симметрию. Обратите внимание, что эта формула не работает для заряженных пластин. Имеет смысл, что когда два положительных точечных заряда одинаковой полярности (не обязательно одинаковой величины) удаляются друг от друга, потенциальная энергия системы уменьшается. Но в своем вопросе вы говорите о том, что в бизнесе известно как конденсаторы. Возможно, вы знаете, что когда две противоположно заряженные пластины удаляются друг от друга, потенциальная энергия системы увеличивается, поскольку вы совершаете работу против электрического поля, а конденсатор состоит из двух пластин, расположенных в непосредственной близости, которые содержат одинаковые и противоположные заряды. Итак, здесь разность потенциалов между пластинами определяется выражением $$E=\frac{V}{d}$$
Как вы, возможно, знаете, электрическое поле в области между двумя пластинами всегда постоянно, независимо от того, как далеко вы перемещаете пластины, при условии, что пластины параллельны друг другу, и одна должна полностью закрывать обзор другой. Таким образом, отношение $$\frac{V}{d}$$ всегда будет постоянным. Таким образом, вы можете заключить, что при увеличении расстояния между пластинами увеличивается и потенциальная энергия системы.
Итак, здесь разность потенциалов между пластинами определяется выражением $$E=\frac{V}{d}$$
Как вы, возможно, знаете, электрическое поле в области между двумя пластинами всегда постоянно, независимо от того, как далеко вы перемещаете пластины, при условии, что пластины параллельны друг другу, и одна должна полностью закрывать обзор другой. Таким образом, отношение $$\frac{V}{d}$$ всегда будет постоянным. Таким образом, вы можете заключить, что при увеличении расстояния между пластинами увеличивается и потенциальная энергия системы.
$\endgroup$
2
$\begingroup$
В конденсаторе с параллельными пластинами электрическое поле однородно между пластинами (здесь мы пренебрегаем граничными эффектами) и определяется выражением
$$ E = \frac{\sigma}{\epsilon\epsilon_0},$$
где $\epsilon$ — относительная диэлектрическая проницаемость среды между пластинами, а $\sigma$ — плотность заряда на одной пластине. Направление вектора электрического поля нормально к поверхности пластин. Формула следует из прямого применения закона электростатики Гаусса.
Направление вектора электрического поля нормально к поверхности пластин. Формула следует из прямого применения закона электростатики Гаусса.
Разность потенциалов между пластинами представляет собой линейный интеграл от $E$ вдоль линии, соединяющей две пластины, что дает $$ \Delta V = \frac{\sigma}{\epsilon\epsilon_0}\times d.\quad (1)$$ Здесь $d$ — расстояние между двумя пластинами.
Если зарядить пластины, подключив их к источнику напряжения, подающему напряжение $\Delta V$, то получится плотность поверхностного заряда величины $$ \sigma = \frac{\epsilon\epsilon_0}{d}\Delta V$$ на каждой пластине (знак плотности заряда на двух пластинах будет разным).
Отключение пластин от источника напряжения оставляет заряды на пластинах без изменений. Точно так же плотность заряда $\sigma$ не изменится, если еще больше увеличить расстояние $d$ обкладок. Напряжение будет увеличиваться с $d$ согласно уравнению. (1).
Фактически величина $\epsilon\epsilon_0/d$ называется емкостью на единицу площади системы параллельных пластин.
$\endgroup$
$\begingroup$
Для параллельных пластин, где расстояние $d$ намного меньше размеров пластин (диаметр для круглых пластин), а разность потенциалов между пластинами $V$, электрическое поле $E$ определяется выражением
$$E=\frac{V}{d}$$
Где электрическое поле $E$ направлено от + пластины к – пластине.
Емкость, $C$, электрически определяется как количество заряда $q$ на пластинах на вольт между пластинами, или
$$C=\frac{q}{V}$$
физические характеристики конденсатора, емкость определяется выражением $$C=\frac{εA}{d}$$
Приравнивание двух последних уравнений дает нам
$$V=\frac{qd}{εA}$$
Где $ε$ — электрическая проницаемость среды между пластинами.
Подставив $V$ из последнего уравнения вместо $V$ в первое уравнение, мы получим
$$E=\frac{q}{εA}$$
Последнее уравнение показывает, что напряженность электрического поля между пластинами не зависит от расстояния между пластинами. Теперь, возвращаясь к первому уравнению, выраженному через разность потенциалов, мы имеем
Теперь, возвращаясь к первому уравнению, выраженному через разность потенциалов, мы имеем
$$V=Ed$$
Поскольку $E$ постоянна, увеличение расстояния увеличивает разность электрических потенциалов. Это имеет смысл, если принять во внимание следующее определение разности потенциалов или напряжения:
Разность потенциалов $V$ определяется как работа (джоули) на единицу заряда $q$ (кулон), необходимая для перемещения заряда между точками.
Сила, действующая на заряд $q$ между пластинами, равна $qE$. Работа, необходимая для перемещения заряда с одной пластины на другую, равна
$$W=qEd$$ Работа на единицу заряда равна $$\frac{W}{q}=Ed=V$$
Надеюсь, это поможет.
$\endgroup$
3
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
электростатика — Является ли напряжение электрическим потенциалом или разностью электрических потенциалов?
Спросил
Изменено 9 лет, 7 месяцев назад
Просмотрено 9000 раз
$\begingroup$
В Википедии напряжение определяется как разность электрических потенциалов. Однако я до сих пор не уверен, является ли напряжение электрическим потенциалом ($PE/q$) или изменением электрического потенциала ($\Delta PE/q$).
Меня частично смущает разговор о цепях и определение количества вольт в точке цепи.
Итак, напряжение — это электрический потенциал или его изменение? Если напряжение есть изменение электрического потенциала, то как можно измерить одну точку цепи в вольтах?
- электростатика
- потенциал
- напряжение
- электрический ток
$\endgroup$
2
$\begingroup$
Это может сбить с толку и является отличным примером небрежной терминологии, увековеченной небрежными авторами учебников. Никогда не следует заменять единицу измерения на название этого количества. Мы никогда не спрашиваем людей об их «годе», когда мы имеем в виду возраст, или «метрах», когда мы имеем в виду рост. Однако мы часто используем «пробег» вместо эффективности использования топлива, что также неверно. Добавьте к этому, что слишком много авторов используют один и тот же символ как для электрического потенциала, так и для разности электрических потенциалов.
Никогда не следует заменять единицу измерения на название этого количества. Мы никогда не спрашиваем людей об их «годе», когда мы имеем в виду возраст, или «метрах», когда мы имеем в виду рост. Однако мы часто используем «пробег» вместо эффективности использования топлива, что также неверно. Добавьте к этому, что слишком много авторов используют один и тот же символ как для электрического потенциала, так и для разности электрических потенциалов.
Физической величиной здесь является электрический потенциал, представляющий собой сравнение потенциальной электрической энергии и электрического заряда и представленный символом $V$. Эта величина составляет скалярное поле вокруг заряженных частиц. Каждой точке пространства присвоено значение электрического потенциала. Разность электрических потенциалов между любыми двумя точками называется разностью электрических потенциалов и обозначается символом $\Delta V$. Слишком много авторов используют $V$ для обозначения обеих величин, но это ошибочно, потому что это разные величины и они не взаимозаменяемы, несмотря на то, что имеют одну и ту же единицу измерения, вольт. Чтобы еще больше запутать ситуацию, вольт обозначается символом $\mathrm{V}$, который слишком похож на символ, используемый для обозначения электрического потенциала. Разность электрических потенциалов можно измерить непосредственно мультиметром, а электрический потенциал — нет.
Чтобы еще больше запутать ситуацию, вольт обозначается символом $\mathrm{V}$, который слишком похож на символ, используемый для обозначения электрического потенциала. Разность электрических потенциалов можно измерить непосредственно мультиметром, а электрический потенциал — нет.
Суть в том, что никогда не следует заменять это количество единицей измерения. Назовите величину тем, чем она является, электрическим потенциалом или разностью электрических потенциалов, и используйте четкие и недвусмысленные символы.
$\endgroup$
1
$\begingroup$
вы никогда не сможете измерить абсолютный электрический потенциал в любой точке. это просто невозможно. вот почему мы говорим о разнице потенциалов. аналогичное понятие идет к понятию внутренней энергии газа. разница измерима, но не является абсолютной величиной.
теперь, если вы хотите строго определить «вольт», это будет выглядеть так:
количество работы, совершаемой для перемещения единичного положительного заряда из бесконечности в желаемую точку. так что количество проделанной работы равно потенциалу в этой точке ИЛИ разности потенциалов между этой точкой и точкой в бесконечности (то есть любой точкой вне электрического поля).
так что количество проделанной работы равно потенциалу в этой точке ИЛИ разности потенциалов между этой точкой и точкой в бесконечности (то есть любой точкой вне электрического поля).
Итак, суть в том, что когда мы говорим о разности потенциалов, мы имеем в виду, что у нас есть две указанные точки. и когда это просто потенциал в точке, то на самом деле это разность потенциалов между этой указанной точкой и точкой в бесконечности (вне поля).
$\endgroup$
$\begingroup$
Электрический потенциал, который я буду обозначать как $\Phi$, изначально определяется следующим отношением к электрическому полю (если математика вам незнакома, не беспокойтесь, я просто включил ее для полноты картины) $$ \mathbf E = -\nabla \Phi $$ Одним из следствий этого является то, что
Электрический потенциал определяется только с точностью до аддитивной константы
Это означает, в частности, что можно свободно выбирать любую точку пространства, обычно называемую точкой отсчета, в которой потенциал равен нулю. Как только вы выберете эту точку, значение потенциала $\Phi$ в любой другой точке будет полностью определяться приведенным выше определением.
Как только вы выберете эту точку, значение потенциала $\Phi$ в любой другой точке будет полностью определяться приведенным выше определением.
Однако, если вы не выберете такую точку, то аддитивная неоднозначность в определении потенциала приведет к тому, что будет иметь смысл только вычисление разности потенциалов. В этом случае не имеет смысла говорить, что «такая-то точка схемы имеет такое-то значение».
Изюминка. Электрический потенциал определяется таким образом, что имеют смысл только различия в потенциале, если не выбрана контрольная точка, в которой указано значение потенциала.
Кроме того, термин «напряжение» обычно используется как термин, обозначающий разность электрических потенциалов между двумя точками, поэтому он не страдает такой же двусмысленностью, как термин «электрический потенциал». Таким образом, на стандартном языке было бы уместно сказать «потенциал в точке А» (при условии, что была выбрана контрольная точка), но было бы неуместно говорить «напряжение в точке А».
$\endgroup$
$\begingroup$
Для непрофессионала… Напряжение измеряется между двумя или более точками. Итак, разница потенциалов. Если у вас есть вольтовая батарея и 6-вольтовая батарея, соединенные своими отрицательными клеммами, каждая из них покажет правильное напряжение, если измерять его от земли, но если вы измерите напряжение на их положительных клеммах, вольтметр покажет 3 вольта, потому что он измеряет разность потенциалов между этими двумя точками.
$\endgroup$
$\begingroup$
Поначалу термин «напряжение» может сбивать с толку, я был довольно сбит с толку, когда узнал его впервые.
Это относится (как вы сказали) к электрическому потенциалу разности между двумя точками цепи. Если у вас есть кусок провода, вы бы определили напряжение на проводе как разность потенциалов между двумя концами провода.
Теперь, чтобы применить это к цепям, вы можете использовать удобный инструмент, называемый законами цепей Кирхгофа, который объясняет, как рассчитывать напряжения и токи. По сути, в цепи нельзя определить «потенциал», если у вас нет источника разности потенциалов (например, батареи). Напряжение определяется для каждого источника напряжения (аккумулятор, заряженный конденсатор), а затем добавляется в соответствии с законами схемы для элемента (последовательно, параллельно и т. д.). Затем 9{[1]}$ напряжение в любой точке провода является напряжением батареи. Вот как вы определяете напряжение в одной точке.
$[1]$ — Пожалуйста, никогда не пытайтесь делать это на самом деле. Это вызовет короткое замыкание в аккумуляторе и произойдет что-то плохое.
$\endgroup$
$\begingroup$
Напряжение всегда разница. ОДНАКО у вас обычно есть некоторая обозначенная точка * на принципиальной схеме, относительно которой вы измеряете напряжения, т. е. напряжение в точке P на принципиальной схеме дается разностью $$V_P-V_*$$ Обычно это точка ( любое) заземление в вашей цепи (предполагается, что они соединены друг с другом, поэтому имеют одинаковый потенциал).
е. напряжение в точке P на принципиальной схеме дается разностью $$V_P-V_*$$ Обычно это точка ( любое) заземление в вашей цепи (предполагается, что они соединены друг с другом, поэтому имеют одинаковый потенциал).
Например, посмотрите на http://www.hoodcomputing.com/blog/HeadlightCircuit.gif, странные черные параллельные линии в левом нижнем углу обозначают землю, поэтому все напряжения измеряются относительно этой точки. Иногда говорят: «мы устанавливаем напряжение в точке X равным нулю», что сводится к измерению напряжений относительно $V_X$, поскольку точка X явно имеет напряжение 0 относительно самой себя.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.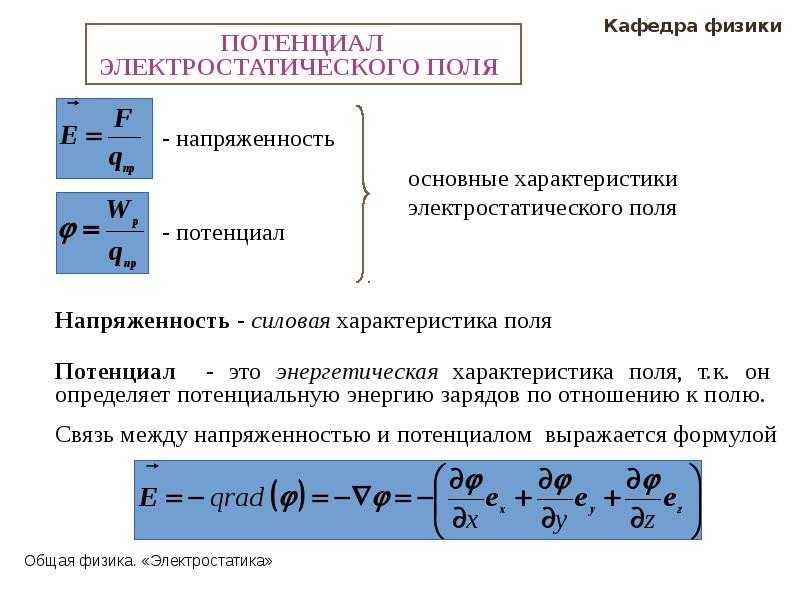
Напряжение и разность электрических потенциалов
Термин «напряжение» используется для обозначения разности потенциалов. Каждый материал в этом мире состоит из атомов. Каждый атом состоит из протонов, электронов и нейтронов, которые соответственно заряжены положительно, отрицательно и электрически нейтральны. Как мы знаем, между этими положительно заряженными протонами и отрицательно заряженными нейтронами существует сила притяжения. Для их разделения необходимо совершить определенную работу.
Электрический потенциал
Электрический потенциал — это количество работы, совершаемой при перемещении заряженных частиц, таких как электроны, между двумя точками. Всякий раз, когда мы хотим разделить две противоположно заряженные (положительную и отрицательную) частицы, между которыми существуют сильные силы связи, удерживающие их вместе, нам нужно проделать определенную работу по преодолению силы притяжения между ними. Работа, проделанная при их разделении, хранится в виде потенциальной энергии в каждой из этих заряженных частиц.
Работа, проделанная при их разделении, хранится в виде потенциальной энергии в каждой из этих заряженных частиц.
Обычно заряды имеют свойство растекаться, если они не ограничены внешней силой. Скопление одинаково заряженных частиц в точке создает напряжение в этой точке. При соединении этих частиц совершается определенная работа, и эта работа сохраняется в виде потенциальной энергии внутри этих частиц. Эта накопленная энергия известна как электрический потенциал.
Разность электрических потенциалов
Разность электрических потенциалов между двумя точками в электрическом поле, вызывающая движение заряженных частиц, таких как электроны, из точки с более высоким потенциалом в точку с более низким потенциалом, называется разностью потенциалов. Когда мы подключаем лампу к батарее, разница потенциалов между ее положительной и отрицательной клеммой заставляет электроны течь, и лампа светится. Здесь положительная клемма батареи имеет более высокий потенциал, а отрицательная клемма имеет более низкий потенциал. Разность потенциалов измеряется в вольтах.
Разность потенциалов измеряется в вольтах.
Что такое напряжение?
Напряжение — это общий термин, используемый для описания разности потенциалов. Нет разницы между разностью потенциалов и напряжением. Оба одинаковые. Иногда его также называют электродвижущей силой. Обозначается буквой V. Напряжение может быть как постоянным, как в случае питания постоянного тока, так и переменным, как в случае питания переменным током.
Единица разности потенциалов
Единица разности электрических потенциалов – вольт. Один вольт можно определить как разность потенциалов между двумя точками, когда один джоуль энергии используется для передачи одного кулона заряда из одной точки в другую.
Согласно «Hughes Electrical and Electronic Technology» , Один вольт можно также определить как разность потенциалов, измеренную между двумя точками проводника, по которому течет ток силой 1 ампер, когда мощность, рассеиваемая между этими точками, равна 1 ватту. . Он назван в честь итальянского физика и пионера электричества и энергии Алессандро Вольта (1745–1827). Он изобретатель электрической батареи. Источники электрического напряжения
. Он назван в честь итальянского физика и пионера электричества и энергии Алессандро Вольта (1745–1827). Он изобретатель электрической батареи. Источники электрического напряжения
Обычная батарея размера АА, которую вы можете найти в своем доме, имеет разность потенциалов в 1 вольт между положительной и отрицательной клеммами. Точно так же разность потенциалов, измеренная между линией и нейтралью настенной розетки, может составлять 230 В или 110 В. Разница в том, что батарея подает напряжение постоянного тока, а настенная розетка подает напряжение переменного тока. Напряжение переменного и постоянного тока кратко описано в следующих разделах.
Разница между однофазными и трехфазными источниками питания переменного тока
Математическое представление напряжения или разности потенциалов
Разность электрических потенциалов или напряжение V= Вт / Q или v= dw / dq
Где,
Вт – работа, выполненная при перемещении этих зарядов.
Q- Кулоны заряда.
Пример:
30 джоулей энергии расходуется на разделение двух зарядов по 10
кулонов каждый на расстоянии. Какое напряжение будет развиваться?
Решение:
Напряжение В= Вт / Q = 30/10 = 3 В
Мощность постоянного тока
Мощность постоянного тока заставляет все заряженные частицы двигаться в одном направлении. Наиболее распространенным источником постоянного тока является бытовая батарея. Электроны с отрицательной клеммы батареи перетекают на ее отрицательную клемму при подключении к нагрузке. Направление потока электронов никогда не меняется.
Мощность переменного тока
Направление движения заряженных частиц постоянно меняется при изменении мощности переменного тока. Электроэнергия, поставляемая энергоснабжающей компанией, является переменным током. Величина и направление питания переменного тока постоянно меняются с положительного на отрицательное и обычно носят синусоидальный характер. На электростанциях для преобразования механической энергии в электрическую используются огромные генераторы переменного тока. Изображение, показывающее разницу между напряжением переменного и постоянного тока Источник: http://www.acsolarwarehouse.com
На электростанциях для преобразования механической энергии в электрическую используются огромные генераторы переменного тока. Изображение, показывающее разницу между напряжением переменного и постоянного тока Источник: http://www.acsolarwarehouse.com
Как мы можем измерить напряжение?
Разность электрических потенциалов измеряется с помощью устройства, называемого вольтметром. Он подключается к двум точкам, между которыми измеряется напряжение. Вольтметр может быть аналоговым или цифровым. Аналоговые вольтметры состоят из высокого сопротивления, последовательно соединенного с гальванометром с подвижной катушкой. На рынке доступны различные типы аналоговых вольтметров. Цифровой вольтметр работает путем преобразования напряжения в цифровую форму и отображения его на цифровом дисплее.
Источник изображения: Taj Scientificсообщите об этом объявленииЭлектрический потенциал и напряжение | Вращающиеся числа
Мы исследуем, что происходит, когда заряды перемещаются (медленно) в электрическом поле. Мы узнаем об электрической форме потенциальной энергии и о том, что значит выполнять работу над зарядом.
Мы узнаем об электрической форме потенциальной энергии и о том, что значит выполнять работу над зарядом.
Определены некоторые новые термины со схожим звучанием — электрическая потенциальная энергия, электрический потенциал и разность электрических потенциалов. Мы заканчиваем формальным определением напряжения .
Это техническая статья. Если вы плохо знакомы с напряжением или только начинаете, посмотрите это видео и статью для ознакомления с напряжением.
Автор Вилли Макаллистер.
Содержимое
- Сила, работа и потенциальная энергия
- Что такое электрическая потенциальная энергия?
- Выполнение работ в электрическом поле
- Электрическая потенциальная энергия
- Электрический потенциал
- Электрический потенциал вблизи точечного заряда
- Визуализация электрического потенциала
- Разность электрических потенциалов
- Напряжение
- Напряжение вблизи точечного заряда
- Проверка концепции
- Дополнение (расширенное)
- Абсолютное напряжение
- Сколько стоит вольт?
Куда мы направляемся
Мы запускаем тестовый заряд в электрическом поле, чтобы посмотреть, что произойдет с его потенциальной энергией.
Если мы нормализуем тестовый заряд до значения $1$, его потенциальная энергия будет называться потенциальной . Потенциал — это свойство места, даже если там нет заряженной частицы.
Если мы перемещаем единичный тестовый заряд между двумя точками в электрическом поле, его потенциал изменяется. Специальное почетное название для разности потенциалов — напряжение .
Сила, работа и потенциальная энергия
Мы начнем с краткого обзора физических понятий силы, работы и энергии. Здесь тоже можно освежиться.
Сила
Сила — это толчок или притяжение, любое взаимодействие, изменяющее движение объекта. $\vec F = m\,\vec a$.
Работа
Работа в физике — это «сила, действующая на расстоянии». Запишем это с помощью векторного уравнения:
$W = \vec F \cdot \vec d$
Точечный оператор $\cdot$ в векторном уравнении указывает на скалярное произведение. Мы также можем написать это, используя определение скалярного произведения,
$W = |\vec F| \, |\vec д| \, \cos\тета$
$\theta$ — это угол между вектором $\vec F$ и направлением движения объекта, представленным $\vec d$.
Когда вы берете скалярное произведение двух векторов, вы получаете скалярное число. Это означает, что работа является скаляром. У него есть величина, но нет направления.
Энергия
Энергия — это «способность выполнять работу». Когда у объекта есть энергия, это означает, что он способен совершать работу.
Кинетическая энергия — это энергия, которой объект обладает благодаря своей скорости. Яблоко обладает кинетической энергией при падении. У него есть возможность работать. Когда он бьет вас по голове, он создает силу на расстоянии.
Потенциальная энергия — это энергия, которой обладает объект благодаря своему расположению в поле. Яблоко, висящее на дереве, может совершить работу, если упадет. (Сейчас оно не работает, но у него есть потенциал.)
Что такое поле? Поле — это физическая величина, имеющая значение повсюду в пространстве. Например, температура — это поле. Каждая точка пространства имеет температуру. Поскольку температура является скалярной величиной (имеющей величину, но не имеющей направления), она называется скалярное поле .
Поскольку температура является скалярной величиной (имеющей величину, но не имеющей направления), она называется скалярное поле .
Ветер — еще один тип поля. В каждой точке атмосферы воздух движется с некоторой скоростью в каком-то направлении. Это означает, что каждая точка в пространстве связана с векторной величиной. Это делает ветер векторным полем . Гравитация и магнетизм являются другими примерами векторных полей, как и электрические поля.
Когда вы работаете с объектом, перемещая его с силой, потенциальная энергия накапливается в объекте. Увеличение потенциальной энергии равно работе, совершаемой при перемещении тела на новое место.
Трудно вычислить потенциальную энергию чего-либо, если оно просто находится на одном месте. Если мы перемещаем объект (совершаем над ним работу), это позволяет нам обнаружить его потенциальную энергию.
Что такое электрическая потенциальная энергия?
Электрический заряд, находящийся в электрическом поле, обладает электрической потенциальной энергией . Вот наша стратегия для обнаружения того, что это такое:
Вот наша стратегия для обнаружения того, что это такое:
- Мы помещаем заряженный объект в электрическое поле.
- Мы немного поработали, чтобы заставить его двигаться.
- Изменяет потенциальную энергию объекта на равную величину. (Джоули работы становятся джоулями потенциальной энергии объекта.)
- Разница в потенциальной энергии дает нам подсказку, необходимую для определения потенциальной энергии объекта, когда он стоит на месте.
Давайте создадим простую схему оплаты и зададим несколько вопросов.
Начните с двух положительных зарядов, отстоящих друг от друга на некоторое расстояние $a$.
$Q$ и $q$ положительны, поэтому они отталкивают $q$ с силой, описываемой законом Кулона, 92}\hat r$
$\hat r$ («r-шляпа») — вектор величиной $1$, указывающий в интересующем направлении. $\hat r$ необходим, чтобы правая часть стала векторным выражением. В этом примере мы знаем вектор силы для $q$ точек сразу из $Q$.
Мы также можем описать силу, действующую на $q$, через электрическое поле, создаваемое $Q$. Сила, действующая на $q$, равна электрическому полю $Q$, умноженному на размер $q$,
$\vec F_q = q\,\vec E_Q$
Электрическое поле повсюду в пространстве, окружающем точечный заряд $Q $ есть, 92}\hat r$
Выполнение работы в электрическом поле
Предположим, что большой $Q$ приклеен к странице или удерживается на месте с помощью кнопки, чтобы он не мог двигаться. Маленький $q$ — это наш тестовый заряд. Мы медленно подталкиваем $q$ к $Q$ и думаем о его потенциальной электрической энергии.
Что значит совершать работу в электрическом поле? Вы совершаете работу, когда приближаете один заряд к отталкивающему заряду (или оттягиваете его от притягивающего заряда).
Мы наняли маленького чувака, чтобы подчеркнуть, что что-то должно удерживать $q$ на месте, чтобы он не сдвинулся влево. Маленький чувак отталкивает $q$ с той же силой, что и $Q$.
Теперь заставим чувака работать .
Если маленький чувак нажмет чуть сильнее, $q$ приблизится к $Q$. Это движение требует работы . Эта работа запасается в виде дополнительной потенциальной энергии в $q$.
Насколько сложно немного сложнее?
Для задач электростатики нам нужно квазистатическое движение . Таким образом, нам не нужно беспокоиться о кинетической энергии массы или магнитном поле движущегося заряда.
Сила едва превышает $q \vec E$, поэтому $\vec F_{ext} — q \vec E$ исчезающе мала.
$q$ движется без ускорения, поэтому ускорение и кинетическая энергия отсутствуют. Если двигаться так медленно, перемещение $q$ на новое место займет бесконечное время. Нас это не беспокоит, потому что мы просто говорим об этом, не дожидаясь, пока это произойдет на самом деле.
Давайте узнаем, что происходит в деталях.
Какова работа по перемещению $q$ из точки $a$ в точку $b$ в электрическом поле?
По определению, количество выполненной работы равно силе, умноженной на расстояние,
$W = \vec F \cdot \vec d$
Электрическое поле от $Q$ создает силу, $\vec F = q \ ,\vec E$.
$W = q \vec E \cdot \vec d$
Если мы расширим скалярное произведение, оно станет
$W = q\,|\vec E|\, |\vec d|\, \cos \ theta$
Какой угол между вектором силы и направлением движения? Силовые линии электрического поля от $Q$ направлены прямо наружу, и нам сказали, что маленький чувак толкает $q$ прямо в $Q$. Движение прямо связано с электрическим полем, поэтому угол $\theta$ равен $0$, а $\cos 0 = 1$. Работа есть просто произведение величин,
$W = q\,|\vec E|\,|\vec d|$
Пройденное расстояние равно $|\vec d| = |\,а — Ь\,|$.
Какова напряженность электрического поля? Это немного сложнее, потому что напряженность поля в каждой точке пути разная. Чем ближе $q$ подходит к $Q$, тем больше отталкивание и тем сильнее должен давить маленький чувак, чтобы заставить $q$ двигаться.
Узнаем, сколько работы требуется в каждой точке пути, и сложим все это под интеграл.
Давайте создадим две новые переменные, $r$ и $dr$, чтобы рассказать о путешествии из $a$ в $b$. 92}\hat r$
92}\hat r$
Это также сила, необходимая для перемещения $q$ в квазистатическом движении . (На самом деле маленький чувак толкает с чуть большей силой, но дополнительный толчок практически равен нулю.)
Сила различна для каждого значения $r$, что означает, что работа, необходимая для перемещения $q$, изменяется при каждом значении $ р$. Давайте сделаем это по одному шагу за раз. Рассмотрите путешествие из $a$ в $b$ как последовательность крошечных шагов размером $dr$.
На крошечном расстоянии $dr$ сила почти не меняется. На самом деле $dr$ настолько мала, что мы считаем силу постоянной от начала до конца движения. 9
$Работа, необходимая для перемещения заряда $q$ из положения $a$ в положение $b$ вблизи точечного заряда $Q$, равна
$\displaystyle W_{ab} = \dfrac{q\,Q}{4\ pi\epsilon_0} \left ( \frac{1}{b} — \frac{1}{a}\right )$
Если точка $b$ ближе к $Q$, чем $a$, работа положительна . Маленький чувак работает над $q$. Если $b$ находится дальше, работа отрицательна, то есть $q$ действует на маленького чувака.
Электрическая потенциальная энергия
До сих пор мы говорили о 9b -q \vec E \cdot dr$
$\displaystyle \text{изменение электрической потенциальной энергии}_{ab} = \dfrac{q\,Q}{4\pi\epsilon_0} \left ( \frac{1 }{b} — \frac{1}{a}\right )$
Мы можем поиграть с этим выражением, и получится что-то особенное.
Умножьте члены,
$\displaystyle \text{изменение электрической потенциальной энергии}_{ab} = \left (\dfrac{q\,Q}{4\pi\epsilon_0} \frac{1}{b } \right ) — \left (\dfrac{q\,Q}{4\pi\epsilon_0} \frac{1}{a} \right )$
Если все уравнение есть изменение потенциальной энергии, то два отдельных члена представляют полную потенциальную энергию $q$, когда он сидит неподвижно в каждом месте.
$\dfrac{q\,Q}{4\pi\epsilon_0} \dfrac{1}{a}$ — начальная потенциальная энергия $q$, когда он находится в точке $a$.
$\dfrac{q\,Q}{4\pi\epsilon_0} \dfrac{1}{b}$ — конечная потенциальная энергия $q$, когда он находится в точке $b$.
Дайте двум терминам имя переменной, чтобы мы могли о них поговорить. Пусть
Пусть
$U_r = \dfrac{q\,Q}{4\pi\epsilon_0} \dfrac{1}{r}$
И запишем изменение потенциальной энергии как
$\text{electric изменение потенциальной энергии}_{ab} = U_b — U_a$
$U_r$ представляет собой электрическую потенциальную энергию заряда $q$, когда он находится на расстоянии $r$ от $Q$.
На что следует обратить внимание
В выражении для изменения потенциальной энергии упоминаются только конечные точки. Неважно, какой маршрут вы выберете из $a$ в $b$. Изменение потенциальной энергии зависит только от того, где вы начинаете и где заканчиваете. Это все равно, что совершить прогулку по склону горы. Ваше общее изменение высоты зависит только от того, где вы начали и где закончили.
Электрический потенциал
Помните, как мы определяли электрическое поле, «нормируя» электрическую силу?
$\vec E = \dfrac{\vec F}{q}$
Вы представляете себе электрическое поле как
- силу на кулон
- сила при тестовом заряде $1$
Аналогичным образом мы определяем новый термин, электрический потенциал , нормализованную версию электрической потенциальной энергии,
$\text{электрический потенциал} = \dfrac{U_r}{q}$
Вы можете представить электрический потенциал как
- потенциальную энергию на кулон
- потенциальная энергия при испытательном заряде 1$
Мы взяли слово «потенциал» и превратили его в существительное вместо прилагательного.
Электрическая Потенциальная энергия измеряется в джоулях.
Электрический потенциал измеряется в джоулях/кулонах.
Электрический потенциал можно рассматривать как свойство пространства. Даже если вы уберете $q$, в этом месте все еще существует потенциал. Электрический потенциал — это скалярное поле, окружающее $Q$.
Электрический потенциал вблизи точечного заряда
Что такое электрический потенциал вблизи точечного заряда?
Ранее мы определили потенциальную энергию вблизи точечного заряда,
$U_r = \dfrac{q\,Q}{4\pi\epsilon_0} \dfrac{1}{r}$
Чтобы найти потенциал, нормируем деля обе части на $q$,
$\dfrac{U_r}{q} = \dfrac{Q}{4\pi\epsilon_0} \dfrac{1}{r}$
Это определение электрического потенциала вблизи точечного заряда. Потенциал зависит только от $Q$, ($q$ в правой части нет). Вы можете думать о потенциале как о свойстве пространства, окружающего $Q$.
Визуализация электрического потенциала
Давайте представим, как выглядит потенциал. Потенциал является скаляром, поэтому в этой визуализации нет векторных стрелок. На любом заданном радиусе от $Q$ потенциал один и тот же. Неважно, какое направление. Представьте себе сферу с $Q$ в центре. Везде на сфере потенциал одинаков. Сфера представляет собой «эквипотенциальный» контур ( экви = равный, потенциал = потенциал). На плоской странице рисуем эквипотенциальные контуры в виде окружностей.
Потенциал является скаляром, поэтому в этой визуализации нет векторных стрелок. На любом заданном радиусе от $Q$ потенциал один и тот же. Неважно, какое направление. Представьте себе сферу с $Q$ в центре. Везде на сфере потенциал одинаков. Сфера представляет собой «эквипотенциальный» контур ( экви = равный, потенциал = потенциал). На плоской странице рисуем эквипотенциальные контуры в виде окружностей.
Стоимость в центре $Q$. Окружности – это «эквипотенциальные контуры». Тестовый заряд $q$ показан на двух разных расстояниях: $a$ и $b$. Если $q$ нет, потенциал все еще существует.
Изображения, подобные этому, не очень хорошо показывают падение магнитуды как $1/r$. Вы должны представить это в своей голове.
Разность электрических потенциалов
Как и раньше, мы перемещаем тестовый заряд из $a$ в $b$, но на этот раз мы делаем $q$ единицей тестовый заряд и мы измеряем разность потенциала вместо потенциальной энергии.
Вычислить потенциал в начальной и конечной точках. Затем вычтите начало из конца,
$\text{разность электрических потенциалов}_{ab} = \dfrac{U_b}{q} — \dfrac{U_a}{q}$
Напряжение
Разность электрических потенциалов очень особенное имя.
Разность электрических потенциалов называется напряжением .
Напряжение между точками $a$ и $b$ равно,
$V_{ab} = \text{разность электрических потенциалов}_{ab} =\dfrac{U_b}{q} — \dfrac{U_a}{q}$
Это формальное определение напряжения.
Напряжение измеряется в единицах вольт , в честь изобретателя батареи.
Напряжение вблизи точечного заряда
Если потенциальное поле создается точечным зарядом, напряжение между точками $a$ и $b$ равно,
$V_{ab} = \dfrac{U_b}{q} — \dfrac{U_a}{q}$
$V_{ab} = \dfrac{Q}{4\pi\epsilon_0} \dfrac{1}{b} — \dfrac{Q}{4\pi\epsilon_0} \dfrac{1}{a}$
$V_{ab} = \dfrac{Q}{4\pi\epsilon_0} \left (\dfrac{1}{b} — \dfrac{1}{a} \right )$
Это одно и то же уравнения как потенциальная энергия, но $q$ не появляется в правой части. 2) \cdot \left (\dfrac{1}{\text m} — \dfrac {1}{\текст м} \справа )$ 9{\cancel 2}) \cdot \left (\dfrac{1}{\cancel{\text m}} — \dfrac{1}{\cancel{\text m}} \right )$
2) \cdot \left (\dfrac{1}{\text m} — \dfrac {1}{\текст м} \справа )$ 9{\cancel 2}) \cdot \left (\dfrac{1}{\cancel{\text m}} — \dfrac{1}{\cancel{\text m}} \right )$
$\text{volts} = \dfrac{\text{nm}}{\text C}$ или $\dfrac{\text J}{\text C}$
Задача 3. Работа вблизи точечного заряда
Если вам известен электрический потенциал в некоторой области пространства и вас просят найти работу, необходимую для перемещения заряженного объекта между двумя точками,
- Найдите потенциал в начале и конечные положения.
- Вычтите начальный потенциал из конечного, чтобы получить разницу. 9{-6} \,\текст J$
Резюме
Все термины, которые мы использовали, вероятно, звучат одинаково. Трудно держать его прямо, и это сводит большинство из нас с ума.
- Электрическая потенциальная энергия является свойством заряженного объекта в силу его положения в электрическом поле. Потенциальная энергия зависит как от $Q$, так и от $q$.
 Электрическая потенциальная энергия существует только в том случае, если это место занимает заряженный объект.
Электрическая потенциальная энергия существует только в том случае, если это место занимает заряженный объект. - Электрический потенциал – нормированная потенциальная энергия. Предполагается, что тестовый заряд $q$ имеет значение $1$. Потенциал есть свойство пространства. Место обладает электрическим потенциалом, даже если там нет заряженных частиц.
- Разность электрических потенциалов — это работа, необходимая для перемещения единичного пробного заряда из одного места в другое в электрическом поле. Разность электрических потенциалов — это изменение потенциальной энергии, испытываемое единичным испытательным зарядом.
- Напряжение — другое название разности электрических потенциалов.
Напряжение вблизи точечного заряда $Q$ равно,
$V_{ab} = \dfrac{Q}{4\pi\epsilon_0} \left (\dfrac{1}{b} — \dfrac{1} {а} \справа )$
В этой статье электрическое поле создается точечным зарядом, но определения действительны для любого электрического поля.

Ссылки
Кип, А. Х. (1969), Основы электричества и магнетизма (2-е издание, McGraw-Hill)
Дополнение (расширенное)
Абсолютное напряжение
Мы определили напряжение в разности электрических потенциалов в двух местах, разница потенциалов между здесь и там. Напряжение – это разность потенциалов между двумя точками.
Существует ли понятие абсолютной разности потенциалов (абсолютное напряжение)? Есть ли ответ на вопрос «Назовите мне напряжение здесь без привязки к какой-то другой точке»? Да есть, в каком-то смысле.
По соглашению $v=0$ на бесконечности. При таком соглашении появляется значение абсолютного напряжения. Начиная с точки $a = \infty$, напряжение в точке $r$ вдали от точечного заряда становится равным
$\text{V}_{r} = \left (\dfrac{Q}{4\pi \epsilon_0} \dfrac{1}{r} \right ) — \cancel{\left (\dfrac{Q}{4\pi\epsilon_0} \dfrac{1}{\infty} \right )}$
Второй член равен нулю. Таким образом, абсолютное напряжение в определенном месте представляет собой внешнюю работу, необходимую для перемещения единичного тестового заряда «из» бесконечности в положение $r$,
$\text{V}_{r} = \dfrac{Q}{4\ pi\epsilon_0} \dfrac{1}{r}$
Это не волшебство.
 Это просто оборот речи или словесная ловкость рук. Абсолютное напряжение — это то же самое, что сказать, что напряжение в точке $r$ — это разность потенциалов между $r$ и бесконечностью. Это работает до тех пор, пока все в разговоре разделяют предположение, что точка отсчета для нулевого напряжения находится за пределами бесконечности. Всегда безопасно придерживаться определения: напряжение — это разность потенциалов.
Это просто оборот речи или словесная ловкость рук. Абсолютное напряжение — это то же самое, что сказать, что напряжение в точке $r$ — это разность потенциалов между $r$ и бесконечностью. Это работает до тех пор, пока все в разговоре разделяют предположение, что точка отсчета для нулевого напряжения находится за пределами бесконечности. Всегда безопасно придерживаться определения: напряжение — это разность потенциалов.Внимание! Понятие абсолютного напряжения используется редко. Вы измеряете напряжение вольтметром. Вероятно, он не поставлялся с черным кабелем зонда, уходящим в бесконечность. Говоря о напряжении, лучше иметь в виду два момента.
Сколько стоит вольт?
В этой статье чего-то не хватает. Подробностей о величине вольта нет. вольт является «производной единицей СИ». Размер вольта получен из определений ампера и ватта. См. статью Определение стандартных электрических единиц.
19.3 Электрический потенциал, обусловленный точечным зарядом – College Physics
Резюме
- Объясните точечные заряды и составьте уравнение для электрического потенциала точечного заряда.

- Различать электрический потенциал и электрическое поле.
- Определите электрический потенциал точечного заряда при заданном заряде и расстоянии.
Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи. Кроме того, сферические распределения заряда (как на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть. Использование вычислений для определения работы, необходимой для перемещения пробного заряда [латекс]\boldsymbol{q}[/латекс] с большого расстояния на расстояние [латекс]\boldsymbol{r}[/латекс] от точечного заряда [ латекс]\boldsymbol{Q}[/latex], и учитывая связь между работой и потенциалом [латекс]\boldsymbol{(W = -q \Delta V)}[/latex], можно показать, что 92 .}[/латекс]
Электрический потенциал
В точечного зарядаЭлектрический потенциал [латекс]\boldsymbol{V}[/latex] точечного заряда определяется выражением
[латекс]\boldsymbol{V =}[/latex] [ латекс]\boldsymbol{\frac{kQ}{r}}[/latex] [латекс]\boldsymbol{( \textbf{Point Charge}),}[/latex]
Потенциал на бесконечности выбран равным нулю.
 Таким образом, [латекс]\boldsymbol{V}[/latex] для точечного заряда уменьшается с расстоянием, тогда как [латекс]\boldsymbol{E}[/латекс] для точечного заряда уменьшается с квадратом расстояния: 92}}.[/латекс]
Таким образом, [латекс]\boldsymbol{V}[/latex] для точечного заряда уменьшается с расстоянием, тогда как [латекс]\boldsymbol{E}[/латекс] для точечного заряда уменьшается с квадратом расстояния: 92}}.[/латекс]Напомним, что электрический потенциал [latex]\boldsymbol{V}[/latex] является скаляром и не имеет направления, тогда как электрическое поле [latex]\textbf{E}[/latex] является вектором. Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов , принимая во внимание величину и направление. Это согласуется с тем фактом, что [latex]\boldsymbol{V}[/latex] тесно связан с энергией, скаляром, тогда как [latex]\textbf{E}[/latex] тесно связан с силой, то есть вектором.
Пример 1. Какое напряжение создает небольшой заряд на металлическом шаре?
Заряды статического электричества обычно находятся в диапазоне от нанокулонов (нКл) до микрокулонов [латекс]\boldsymbol{( \mu \textbf{C})}[/latex].
 Чему равно напряжение на расстоянии 5,00 см от центра металлического шара диаметром 1 см, имеющего статический заряд -3,00 нКл?
Чему равно напряжение на расстоянии 5,00 см от центра металлического шара диаметром 1 см, имеющего статический заряд -3,00 нКл?Стратегия
Как мы обсуждали в главе 18 Электрический заряд и электрическое поле, заряд на металлическом шаре распространяется равномерно и создает поле, похожее на поле точечного заряда, расположенного в его центре. Таким образом, мы можем найти напряжение, используя уравнение [латекс]\boldsymbol{V = kQ/r}[/латекс] . 9{2} \;\textbf{m}})} \\[1em] & \boldsymbol{-539 \;\textbf{V}}. \end{array}[/latex]
Обсуждение
Отрицательное значение напряжения означает, что положительный заряд будет притягиваться с большего расстояния, поскольку потенциал ниже (отрицательнее), чем на больших расстояниях. И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.
Пример 2. Что такое избыточный заряд генератора Ван-де-Граафа
Демонстрационный генератор Ван-де-Граафа имеет металлическую сферу диаметром 25,0 см, которая создает напряжение 100 кВ вблизи своей поверхности.
Рисунок 1. Напряжение этого демонстрационного генератора Ван де Граафа измеряется между заряженной сферой и землей. Потенциал Земли принимается равным нулю в качестве эталона. Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре. (См. рис. 1.) Какой избыточный заряд находится на сфере? (Предположим, что каждое числовое значение здесь показано тремя значащими цифрами.)
(См. рис. 1.) Какой избыточный заряд находится на сфере? (Предположим, что каждое числовое значение здесь показано тремя значащими цифрами.)Стратегия
Потенциал на поверхности будет таким же, как у точечного заряда в центре сферы на расстоянии 12,5 см. (Радиус сферы равен 12,5 см.) Таким образом, мы можем определить избыточный заряд, используя уравнение 9{-6} \;\textbf{C} = 1,39 \;\mu \textbf{C}}. \end{array}[/latex]
Обсуждение
Это относительно небольшой заряд, но он производит довольно большое напряжение. У нас есть еще одно указание на то, что трудно хранить изолированные заряды.
Напряжения в обоих этих примерах можно измерить с помощью измерителя, который сравнивает измеренный потенциал с потенциалом земли.
 Потенциал земли часто принимается равным нулю (вместо того, чтобы принимать потенциал на бесконечности равным нулю). Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечалось в главе 19.1 Электрическая потенциальная энергия: разность потенциалов. Это аналогично тому, как уровень моря принимается за [латекс]\boldsymbol{h = 0}[/latex] при рассмотрении гравитационной потенциальной энергии, [латекс]\boldsymbol{\textbf{PE}_g = мгх}[/латекс].
Потенциал земли часто принимается равным нулю (вместо того, чтобы принимать потенциал на бесконечности равным нулю). Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечалось в главе 19.1 Электрическая потенциальная энергия: разность потенциалов. Это аналогично тому, как уровень моря принимается за [латекс]\boldsymbol{h = 0}[/latex] при рассмотрении гравитационной потенциальной энергии, [латекс]\boldsymbol{\textbf{PE}_g = мгх}[/латекс].- Электрический потенциал точечного заряда [латекс]\boldsymbol{V = kQ/r}[/латекс].
- Электрический потенциал — это скаляр, а электрическое поле — это вектор. Сложение напряжений в виде чисел дает напряжение, обусловленное комбинацией точечных зарядов, тогда как сложение отдельных полей в виде векторов дает общее электрическое поле. 9{-10} \;\textbf{m}}[/latex] от протона (среднее расстояние между протоном и электроном в атоме водорода)?
3: (a) Шар имеет поверхность, равномерно заряженную 1,00 Кл.
 2 \;\textbf{V}}[/latex]? 9{-14} \;\textbf{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?
2 \;\textbf{V}}[/latex]? 9{-14} \;\textbf{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?8: Исследовательский генератор Ван де Граафа имеет металлический шар диаметром 2,00 м с зарядом 5,00 мКл. а) Каков потенциал вблизи его поверхности? б) На каком расстоянии от его центра находится потенциал 1,00 МВ? (в) Атом кислорода с тремя недостающими электронами высвобождается вблизи генератора Ван де Граафа. Какова его энергия в МэВ на этом расстоянии?
9: Электростатический распылитель краски представляет собой металлическую сферу диаметром 0,200 м с потенциалом 25,0 кВ, которая отбрасывает капли краски на заземленный объект. а) Какой заряд находится на шаре? б) Какой заряд должен иметь капля краски массой 0,100 мг, чтобы достичь предмета со скоростью 10,0 м/с?
10: В одном из классических экспериментов по ядерной физике в начале ХХ века альфа-частица была ускорена к ядру золота, и ее траектория была существенно отклонена кулоновским взаимодействием.

- Электрическая потенциальная энергия является свойством заряженного объекта в силу его положения в электрическом поле. Потенциальная энергия зависит как от $Q$, так и от $q$.


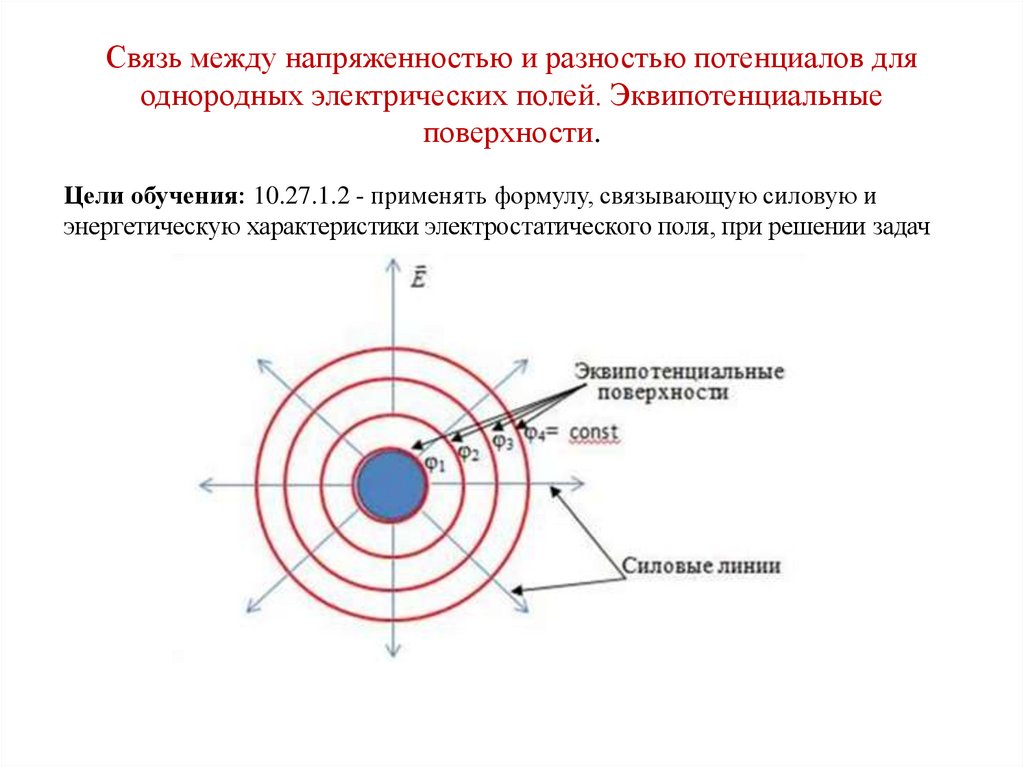
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

 По мере удаления от заряженного тела силовые линии электрического поля располагаются реже, т. е. напряженность поля уменьшается (см. рис. 4, а, б и в). Только в однородном электрическом поле (см. рис. А, г) напряженность одинакова во всех его точках.
По мере удаления от заряженного тела силовые линии электрического поля располагаются реже, т. е. напряженность поля уменьшается (см. рис. 4, а, б и в). Только в однородном электрическом поле (см. рис. А, г) напряженность одинакова во всех его точках. Электрический потенциал ср поля в данной точке равен работе, которую могут совершить силы этого поля при перемещении единицы положительного заряда из этой точки за пределы поля.
Электрический потенциал ср поля в данной точке равен работе, которую могут совершить силы этого поля при перемещении единицы положительного заряда из этой точки за пределы поля. , которую нужно затратить на перемещение положительного заряда ц из одной точки поля в другую, к этому заряду, т. е.
, которую нужно затратить на перемещение положительного заряда ц из одной точки поля в другую, к этому заряду, т. е. При напряженности поля в 1 В/м на заряд в 1 Кл действует сила, равная 1 ньютону (1 Н). В некоторых случаях применяют более крупные единицы измерения напряженности поля В/см (100 В/м) и В/мм (1000 В/м).
При напряженности поля в 1 В/м на заряд в 1 Кл действует сила, равная 1 ньютону (1 Н). В некоторых случаях применяют более крупные единицы измерения напряженности поля В/см (100 В/м) и В/мм (1000 В/м). su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.) ..
.. Условно электрическое поле изображают в виде электрических силовых линий, которые показывают направление действия электрических сил, создаваемых полем (рис.10). Принято направлять силовые линии в ту сторону, в которую бы двигалась в поле положительно заряженная частица.
Условно электрическое поле изображают в виде электрических силовых линий, которые показывают направление действия электрических сил, создаваемых полем (рис.10). Принято направлять силовые линии в ту сторону, в которую бы двигалась в поле положительно заряженная частица.
 В системе СИ количество электричества измеряют в кулонах 1Кл=6,29*1018 электронов.
В системе СИ количество электричества измеряют в кулонах 1Кл=6,29*1018 электронов. Электропроводность веществ зависит от концентрации свободных электрически заряженных частиц. Все вещества в зависимости от электропроводности делятся на проводники, полупроводники и диэлектрики.
Электропроводность веществ зависит от концентрации свободных электрически заряженных частиц. Все вещества в зависимости от электропроводности делятся на проводники, полупроводники и диэлектрики. R= ρl/s; ρ [Ом/м/мм2]
R= ρl/s; ρ [Ом/м/мм2] Такое перемещение зарядов внутри источника совершается благодаря э.д.с., которая возбуждается внутри источника.
Такое перемещение зарядов внутри источника совершается благодаря э.д.с., которая возбуждается внутри источника. I=U/R; U=IR; R=U/I
I=U/R; U=IR; R=U/I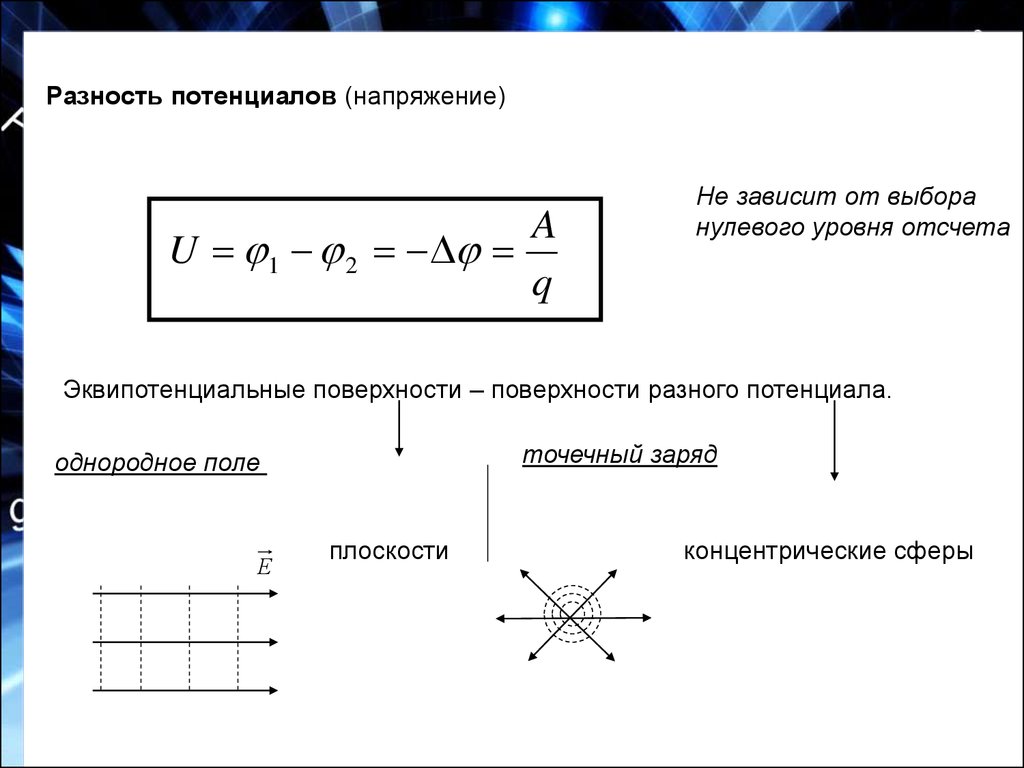 13) нескольких приемников ко всем резисторам приложено одинаковое напряжение
13) нескольких приемников ко всем резисторам приложено одинаковое напряжение е. электрический ток.
е. электрический ток. Влияние среды на магнитное поле характеризуется абсолютной магнитной проницаемостью среды µа (Гн/м)
Влияние среды на магнитное поле характеризуется абсолютной магнитной проницаемостью среды µа (Гн/м) ..
..
 Итак, напряжение — это величина между двумя точками, а электрический потенциал — это величина в одной точке.
Итак, напряжение — это величина между двумя точками, а электрический потенциал — это величина в одной точке.

 Электрическая потенциальная энергия существует только в том случае, если это место занимает заряженный объект.
Электрическая потенциальная энергия существует только в том случае, если это место занимает заряженный объект.
 Это просто оборот речи или словесная ловкость рук. Абсолютное напряжение — это то же самое, что сказать, что напряжение в точке $r$ — это разность потенциалов между $r$ и бесконечностью. Это работает до тех пор, пока все в разговоре разделяют предположение, что точка отсчета для нулевого напряжения находится за пределами бесконечности. Всегда безопасно придерживаться определения: напряжение — это разность потенциалов.
Это просто оборот речи или словесная ловкость рук. Абсолютное напряжение — это то же самое, что сказать, что напряжение в точке $r$ — это разность потенциалов между $r$ и бесконечностью. Это работает до тех пор, пока все в разговоре разделяют предположение, что точка отсчета для нулевого напряжения находится за пределами бесконечности. Всегда безопасно придерживаться определения: напряжение — это разность потенциалов.
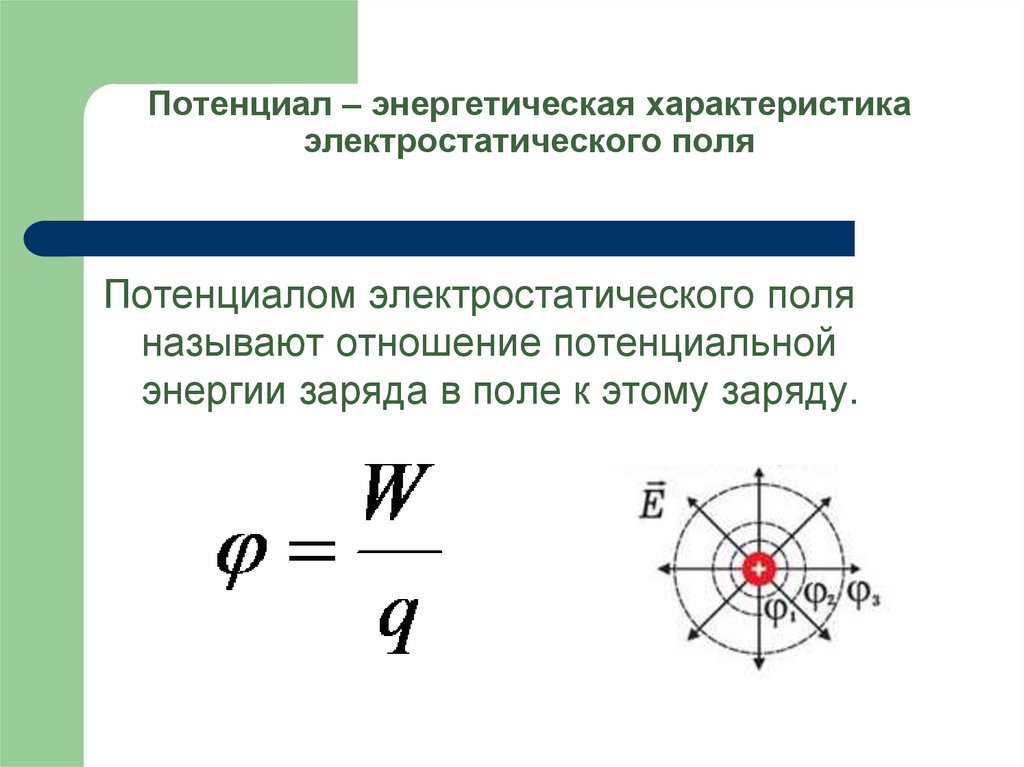 Таким образом, [латекс]\boldsymbol{V}[/latex] для точечного заряда уменьшается с расстоянием, тогда как [латекс]\boldsymbol{E}[/латекс] для точечного заряда уменьшается с квадратом расстояния: 92}}.[/латекс]
Таким образом, [латекс]\boldsymbol{V}[/latex] для точечного заряда уменьшается с расстоянием, тогда как [латекс]\boldsymbol{E}[/латекс] для точечного заряда уменьшается с квадратом расстояния: 92}}.[/латекс] Чему равно напряжение на расстоянии 5,00 см от центра металлического шара диаметром 1 см, имеющего статический заряд -3,00 нКл?
Чему равно напряжение на расстоянии 5,00 см от центра металлического шара диаметром 1 см, имеющего статический заряд -3,00 нКл? (См. рис. 1.) Какой избыточный заряд находится на сфере? (Предположим, что каждое числовое значение здесь показано тремя значащими цифрами.)
(См. рис. 1.) Какой избыточный заряд находится на сфере? (Предположим, что каждое числовое значение здесь показано тремя значащими цифрами.) Потенциал земли часто принимается равным нулю (вместо того, чтобы принимать потенциал на бесконечности равным нулю). Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечалось в главе 19.1 Электрическая потенциальная энергия: разность потенциалов. Это аналогично тому, как уровень моря принимается за [латекс]\boldsymbol{h = 0}[/latex] при рассмотрении гравитационной потенциальной энергии, [латекс]\boldsymbol{\textbf{PE}_g = мгх}[/латекс].
Потенциал земли часто принимается равным нулю (вместо того, чтобы принимать потенциал на бесконечности равным нулю). Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечалось в главе 19.1 Электрическая потенциальная энергия: разность потенциалов. Это аналогично тому, как уровень моря принимается за [латекс]\boldsymbol{h = 0}[/latex] при рассмотрении гравитационной потенциальной энергии, [латекс]\boldsymbol{\textbf{PE}_g = мгх}[/латекс]. 2 \;\textbf{V}}[/latex]? 9{-14} \;\textbf{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?
2 \;\textbf{V}}[/latex]? 9{-14} \;\textbf{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?