9. Электрическое поле в веществе.

Микро- и макрополе. Истинное электрическое поле в любом веществе — его называют микрополем — меняется весьма резко как в пространстве, так и во времени. Оно различно в разных точках атомов и промежутках между ними. Чтобы найти напряженность Е истинного поля в некоторой точке в данный момент, нужно было бы сложить напряженности полей всех отдельных заряженных частиц вещества — электронов и ядер. Решение этой задачи, очевидно, является совершенно нереальным. Да и сам результат оказался бы настолько сложным, что его просто нельзя было бы использовать.

Более того, для решения макроскопических задач такое поле и вовсе не нужно. для многих целей достаточно более простое и несравненно более грубое описание, которым мы и будем пользоваться в дальнейшем. Под электрическим полем Е в веществе его называют макрополем мы будем понимать пространственно-усредненное микрополе (после пространственного усреднения временное усреднение уже не требуется). Это усреднение проводится по так называемому физически бесконечно малому объему – объему, содержащему большое число атомов, но имеющему размеры во много раз меньше, чем те расстояния, на которых макрополе меняется заметно.

усреднение по таким объемам сглаживает все нерегулярные и быстро меняющиеся вариации микрополя на расстояниях поряд-ка атомных, но сохраняет плавные изменения макрополя на макроскопических расстояниях. Итак, поле в веществе

Влияние вещества на поле. При внесении любого Вещества в электрическое поле в веществе происходит смещение положительных и отрицательных зарядов (ядер и электронов) . что в свою очередь приводит к частичному разделению этих зарядов. В тех или иных местах вещества появляются нескомпенсированные заряды различного знака. Это явление называют электро-статической индукцией, а появившиеся

в результате разделения заряды – индуцированными зарядами. Индуцированные заряды создают дополнительное электрическое поле, которое вместе с исходным (внешним) электрическим полем образует результирующее поле. Зная внешнее поле и распределение индуцированных зарядов, можно при нахождении результирующего воля уже не обращать внимание на наличие самого вещества его роль уже учтена с помощью индуцированных зарядов.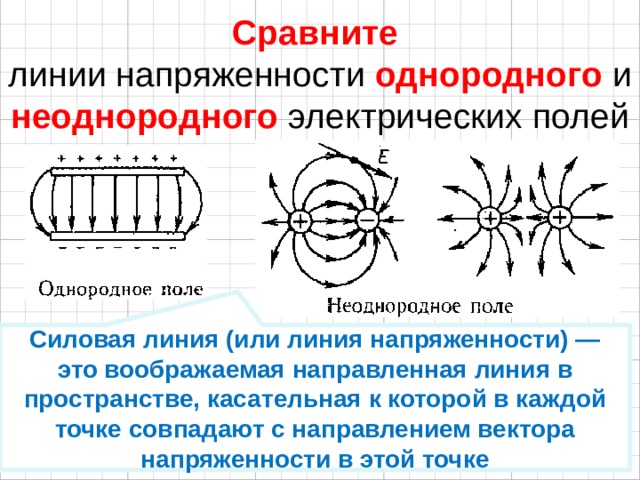 Таким образом, результирующее поле при наличии вещества, определяется просто как суперпозиция внешнего поля и поля индуцированных зарядов. однако во многих случаях дело усложняется тем, что мы заранее не знаем, как распределяются в пространстве все эти заряды – задача оказывается далеко не такой простой, как могло бы показаться вначале.

Поляризация – ограниченное смещение связанных зарядов или ориентация дипольных молекул.

О явлениях, обусловленных поляризацией диэлектрика, можно судить по значению диэлектрической проницаемости, а также угла диэлектрических потерь, если поляризация сопровождается рассеянием энергии, вызывающим нагрев диэлектрика.

В чем же заключается принцип поляризации: Под влиянием электрического поля связанные электрические заряды диэлектрика смещаются в направлении действующих на них сил и тем больше, чем выше напряженность поля. При снятии электрического поля заряды возвращаются в исходное состояние. В полярных диэлектриках, содержащих дипольные молекулы, воздействие электрического поля вызывает еще и ориентацию диполей в направлении поля.

При отсутствии поля диполи дезориентируются вследствие теплового движения.

Большинство диэлектриков характеризуются линейной зависимостью электрического смещения, т.е. поляризации от напряженности электрического поля, созданного в диэлектрике. Особую группу составляют диэлектрики, в которых с изменением напряженности поля смещение меняется нелинейно, обнаруживая насыщение при некотором значении напряженности поля. Такие диэлектрики называются сегнетоэлектриками. Наименование «сегнетоэлектрик» связано с тем, что нелинейность поляризации впервые была обнаружена у сегнетовой соли. Именно с помощью данного вещества в 1855 французский аптекарь открыл явление электрического старения, выражающееся в уменьшении диэлектрической проницаемости со временем.

11. Поверхностная плотность индуцированных зарядов.

12. Теорема Гаусса для электростатического поля в среде.

т. е. поток вектора смещения электростатического поля в диэлектрике сквозь любую замкнутую поверхность равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности.

В такой форме теорема Гаусса верна для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.

Для вакуума Dn = ε0En (ε=1), и поток вектора напряженности Е сквозь произвольно выбранную замкнутую поверхность равен

Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля Е в самом общем виде можно записать как

где ∑Qi и ∑Qsv— соответственно алгебраические суммы свободных и связанных зарядов, которые охватываются замкнутой поверхностью S. Но эта формула неприменима для описания поля Е в диэлектрике, поскольку она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз показывает целесообразность введения вектора электрического смещения.

Напряженность электростатического поля, как следует из ранее полученной формулы E=E0/ε , зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна ε.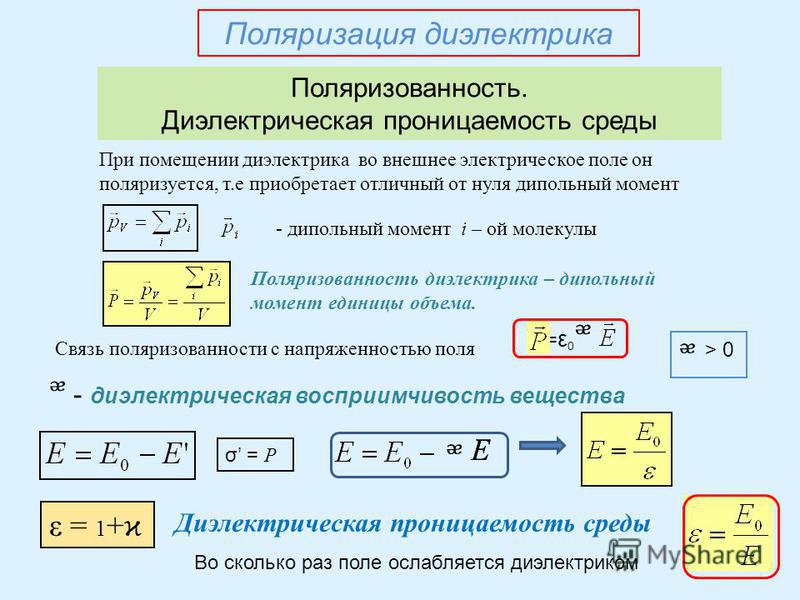 Вектор напряженности Е, при переходе через границу диэлектриков, испытывает скачкообразное изменение, тем самым делая неудобства при расчетах электростатических полей. Поэтому необходимо помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для электрически изотропной среды, по определению, равен

Поскольку ε=1+θ и P=θε0E , вектор электрического смещения равен

Единица электрического смещения — кулон на метр в квадрате (Кл/м2)

Электрическое поле в веществе. Лекция 16

ЭЛЕКТРОСТАТИКА
Лекция 16.
Тема: Электрическое поле в веществе.
Учебник:
Трофимова Т.И. Курс физики : учеб. пособ. для вузов / Т. И.
Трофимова. — М.: Академия, 2007.- с. 160-167.
к.ф.-м.н.
Курочкин А.Р.
Электрический диполь
Электрический диполь – электронейтральная система из двух
точечных одинаковых по модулю и противоположных по знаку
зарядов, находящихся друг от друга на расстоянии l, очень малом
по сравнению с расстоянием r до точки наблюдения.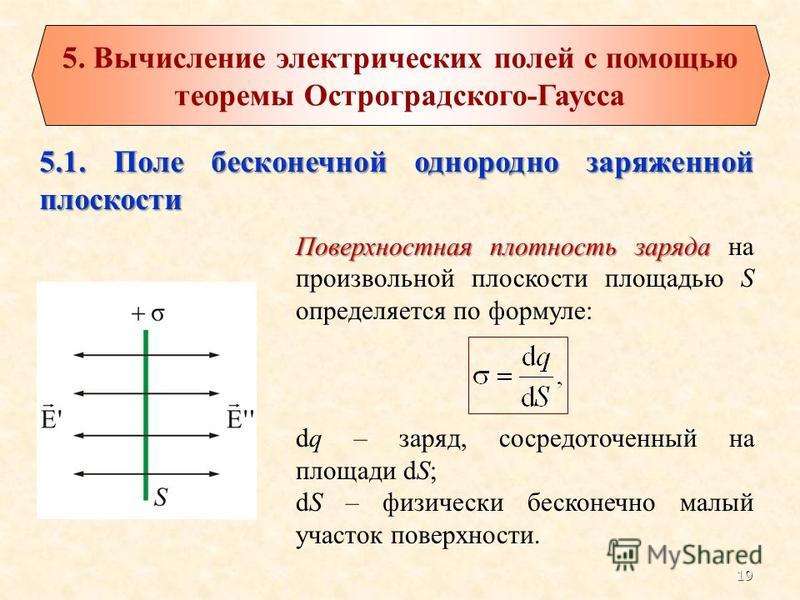 l r
Электрический дипольный момент pe –
ВФВ,
характеризующая
способность
диполя создавать электрическое поле,
равная произведению модуля одного из
q
зарядов диполя q на вектор l , проведенный
от центра отрицательного заряда к центру
положительного
pe q l ,
1
p
l
q
pe Кл м.
где l – плечо диполя.
2
Поляризация диэлектриков в электрическом поле
Диэлектрик – вещество,
• не способное проводить электрический ток;
• в котором нет свободных носителей электрического заряда. Все
заряды в таких диэлектриках связанные: принадлежат отдельным
атомам и молекулам.
1) Связанные заряды – заряды, совершающие микроскопические
движения в веществе и не способные перемещаться на значительные
расстояния.
Примеры связанных зарядов: заряженные микрочастицы, входящие
в состав атомов, молекул, ионов.
2) Свободные заряды – заряды, способные перемещаться в веществе
на значительные расстояния.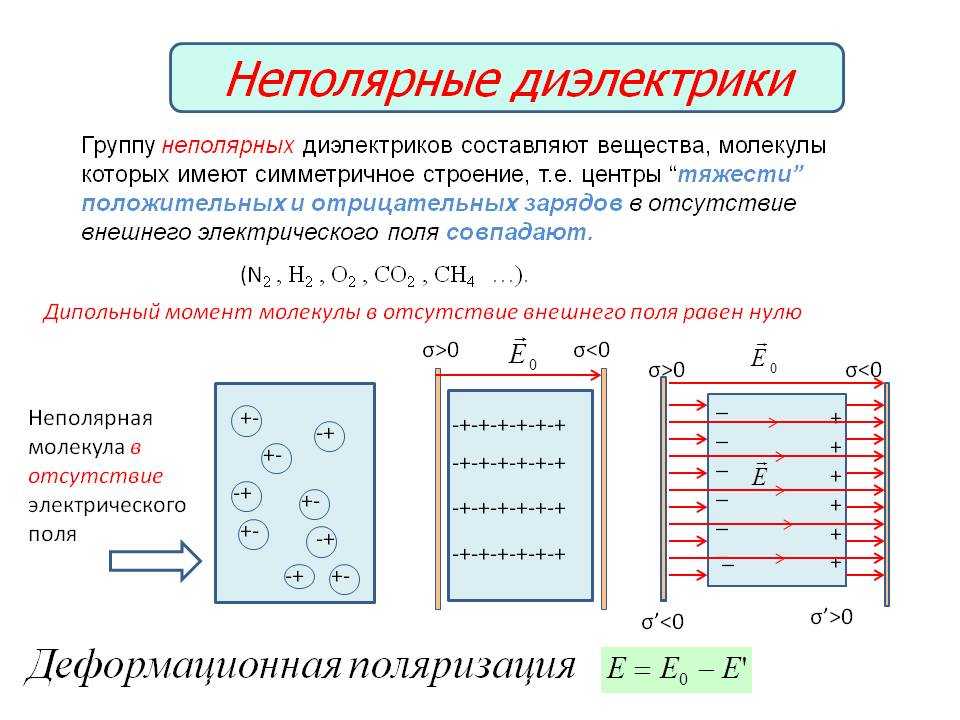
3
Поляризация диэлектриков
Поляризация – смещение связанных зарядов из свих положений
равновесия порядка атомных при внесении диэлектрика во
внешнее электрическое поле.
В соответствии с механизмом поляризации диэлектрики делятся
на III класса:
Диэлектрики
Неполярные
Механизм поляризации
Электронный
Полярные
Ионные кристаллы
Ориентационный
Ионный
4
Полярные и неполярные молекулы
1. В неполярных молекулах в отсутствие внешнего
электрического
поля
центры
положительного
и
отрицательного
зарядов
совпадают;
молекула
электронейтральна и не имеет дипольного момента.
2. Полярные
молекулы
в
отсутствие
внешнего
электрического поля являются диполями, поскольку
центры положительного и отрицательного зарядов у них
смещены.
+
5
I. Неполярные диэлектрики
Примеры неполярных молекул: N2, h3, O2, CO2, Ch5.
Электронный (деформационный) механизм поляризации
диэлектрика, состоящий из неполярных молекул.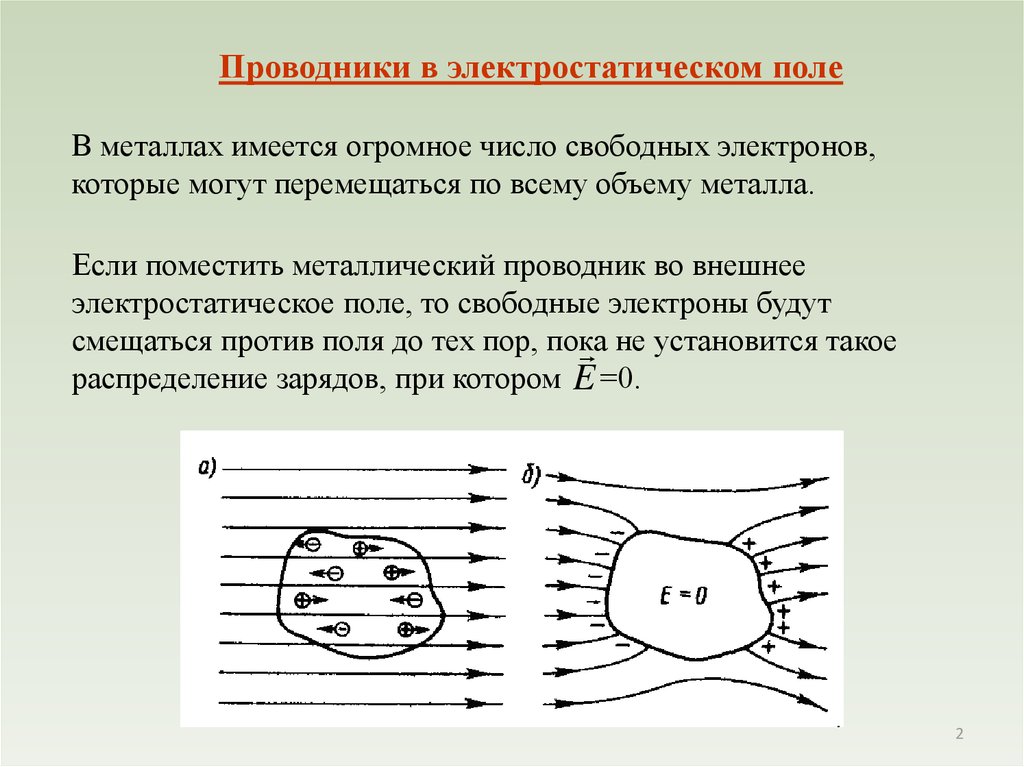
а
В отсутствии внешнего поля Е0 сторонних
зарядов
электронное облако молекулы
сферически
симметрично
и
центр
отрицательного заряда совпадает с положительно
заряженным ядром.
При включении внешнего поля Е0 электронное
облако деформируется (центр отрицательного
заряда перестает совпадать с ядром), и
образуется диполь.
Е0 0,
p
ei
0.
i
Е0
б
pei
Рис. 1
6
Механизм поляризации неполярных диэлектриков
1. При E0 0 диполей нет, поляризация отсутствует (рис. 2, а).
E0 0
Рис. 2а
2. При наличии внешнего поля E0 положительные и
отрицательные заряды в пределах каждой молекулы
смещаются, молекулы превращаются в диполи, диэлектрик
становится поляризованным (рис. 2, б).
E0
Рис. 2б
Поляризация
диэлектрика
–
явление
превращения
электрически нейтральной системы связанных зарядов
вещества в систему ориентированных по полю диполей.
7
II. Полярные диэлектрики
Примеры полярных молекул: h3O, Nh4, SO2, CO.
Механизм поляризации полярных диэлектриков.
1. Полярные молекулы являются диполями
p 0 , однако в
отсутствие внешнего электрического поля из-за хаотической
ориентации молекул суммарный дипольный момент всего вещества
равен нулю (рис. 3а).
E0 0,
Рис. 3a
pei 0.
i
2. Во внешнем поле полярные молекулы ориентируются так, что их
дипольные моменты стремятся выстроиться по полю (этому
препятствует тепловое движение), вследствие чего pei 0 (рис. 3б).
E0
p
ei
i
0.
i
Рис. 3б
III. Ионный механизм поляризации
Примеры ионных кристаллов: NaCl – поваренная соль, KCL, KBr.
Ионные кристаллы – кристаллы Включение
стороннего
поля
состоящие из чередующихся ионов приводит к относительному сдвигу
противоположного знака.
подрешеток,
образованных
положительно
и
отрицательно
Если стороннее поле отсутствует, то заряженными ионами (подрешетка
на каждой поверхности кристалла положительно
заряженных
ионов
имеется одинаковое количество смещается по полю).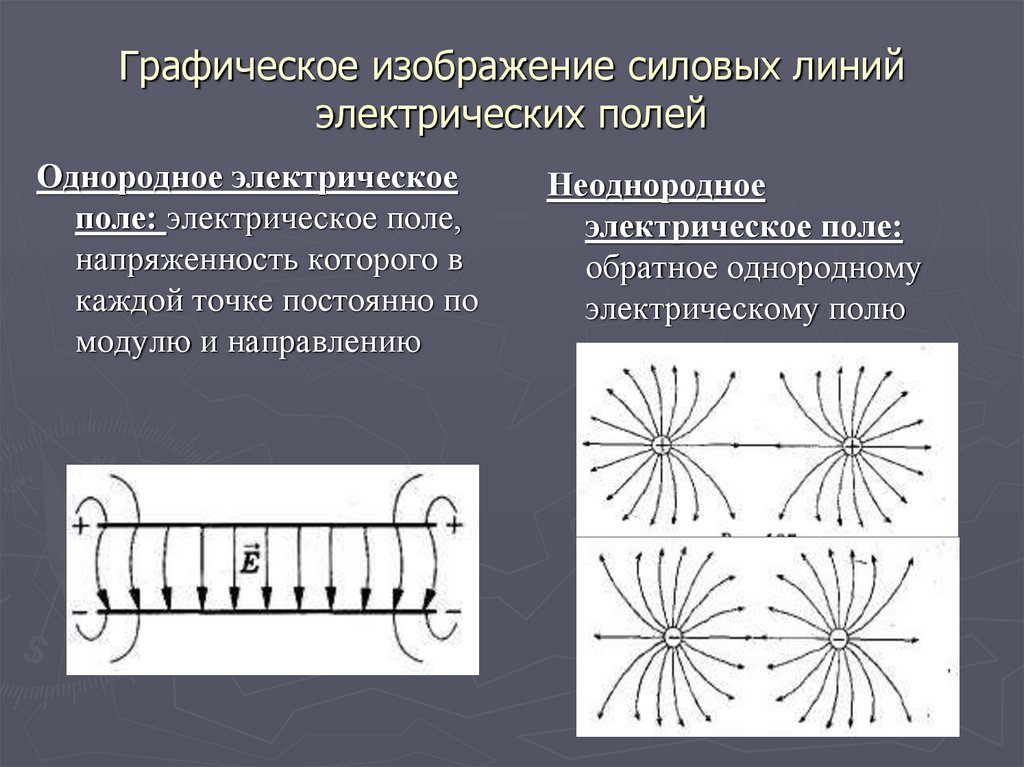
положительных (ионов натрия В результате на одной из граней
Na+) и отрицательных (ионов (левой)
сосредоточивается
хлора Cl-) зарядов, из-за чего нескомпенсированный положительный
вещество в целом неполяризовано. заряд, а на противоположный –
отрицательный.
Е0 0,
E0
p
pei 0.
ei
0.
i
i
a)
б)
9
1. Электронная — смещение электронных оболочек атомов под
действием внешнего электрического поля. Самая быстрая
поляризация (до 10-15с). Потери энергии отсутствуют.
2. Ионная — смещение узлов кристаллической структуры под
действием внешнего электрического поля, причем смещение на
величину, меньшую, чем величина постоянной решетки. Время
протекания 10-13с, без потерь.
3. Дипольная (ориентационная) — связана с ориентацией диполей во
внешнем электрическом поле. Протекает с потерями энергии на
преодоление сил связи и внутреннего трения.
10
Поляризованность
Количественной мерой степени поляризации диэлектрика во
внешнем поле является поляризованность P.
Поляризованность
P–
векторная величина, определяемая как
дипольный момент единицы объема диэлектрика:
n
P
где
p
i 1
V
ei
Кл
м 2
2
pei – дипольный момент i-й молекулы.
11
Поле внутри диэлектрика
• Внесем в однородное внешнее электрическое поле E0 (создается
двумя бесконечными параллельными разноименно заряженными
плоскостями) пластинку из однородного диэлектрика.
• Под действием поля диэлектрик поляризуется,
т.е.
происходит
смещение
зарядов;
положительные смещаются по полю,
отрицательные – против поля.
• В результате этого на правой грани
диэлектрика, обращенного к отрицательной
плоскости, будет избыток положительного
заряда с поверхностной плотностью +σʹ, на
левой
–
отрицательного
заряда
с
поверхностной плотностью -σʹ.
• Эти
нескомпенсированные
заряды,
появляющиеся в результате поляризации
диэлектрика, называются связанными.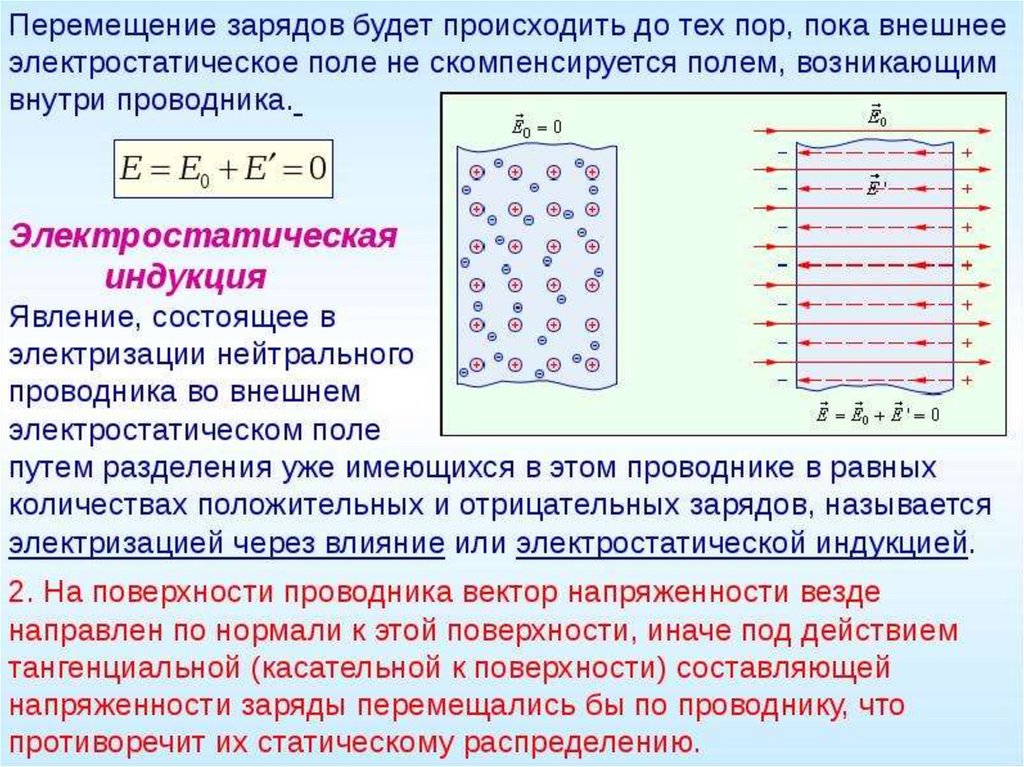
12
E0
q
_
_
_
_
+
+
+
+
_
_
_
_
+
+
+
+
_
_
_
_
+
+
+
+
_
_
_
_
+
+
+
+
q
S
q
Во внешнем поле молекулы диэлектрика поляризуются.
На торцевых поверхностях появляются связанные заряды.
13
Появление связанных зарядов приводит к возникновению
дополнительного электрического поля E ‘
(поля, создаваемого связанными зарядами),
которое направлено против внешнего поля E0
(поля, создаваемого свободными зарядами) и ослабляет его.
Результирующее поле внутри диэлектрика
E E0 E ‘,
E E0 E ‘
Мы уже знаем, что поле (напряжённость) в
вакууме, созданное между двумя бесконечными
заряженными плоскостями, равно
поэтому
‘
E’ ,
0
‘
E E0 .
0
E’
4
E0
14
Отступление.
Поверхностная плотность связанных зарядов σ’
Суммарный дипольный момент пластинки диэлектрика
p
ei
PV PSd ,
5
i
где S – площадь грани пластинки, d – её толщина.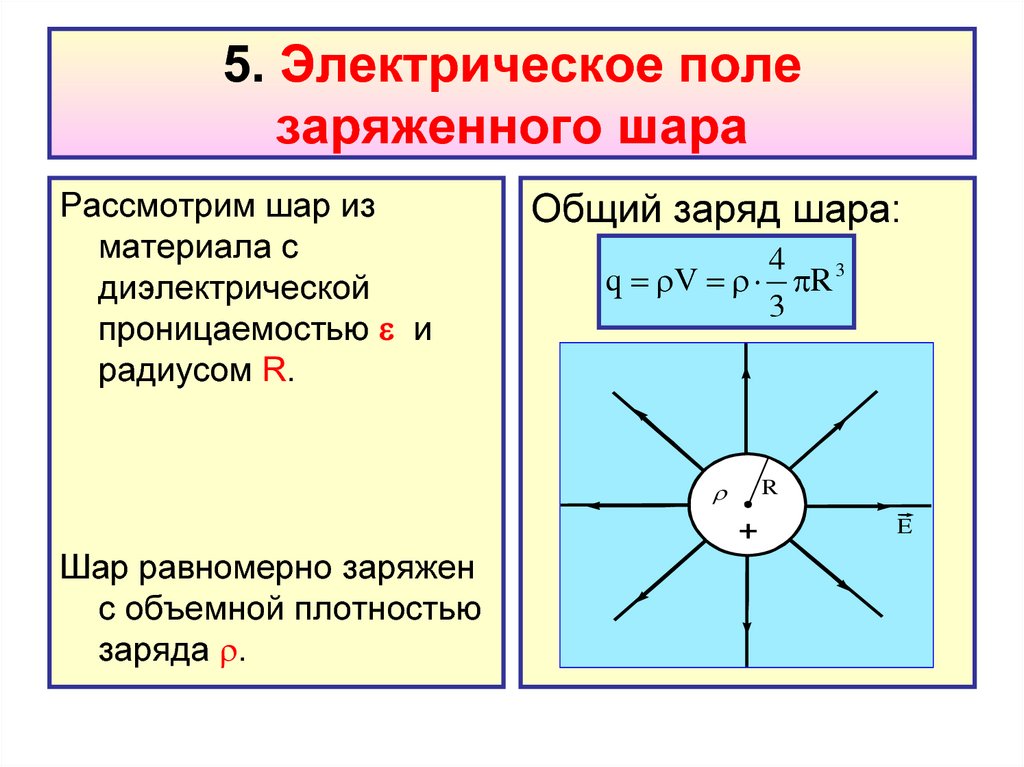
С другой стороны, суммарный
момент, равен
p
ei
дипольный
q ‘ d ‘ Sd .
6
i
Поэтому, приравняв (5) и (6), получим
PSd ‘ Sd
или
‘ P,
7
т.е. поверхностная плотность σʹ связанных зарядов равна модулю
вектора поляризованности P.
15
Для большого числа диэлектриков
(за исключением сегнетоэлектриков и некоторых ионных
кристаллов)
поляризованность P линейно зависит от напряжённости
поля E . Если диэлектрик изотропный и E не слишком велико,
то
P 0 E
3
где χ – диэлектрическая восприимчивость
характеризующая свойства диэлектрика.
вещества,
Важные нюансы
1. χ – величина безразмерная;
2. Всегда χ>0 и для большинства диэлектриков (твёрдых и
жидких) составляет несколько единиц.
16
Получаем
‘
0 E
P
‘
E0 E ,
E E0 E E0 E0 E0
0
0
0
откуда напряженность результирующего поля внутри диэлектрика
равна
E0
E0
E
.
1
7
Безразмерная величина
1
8
называется диэлектрической проницаемостью среды.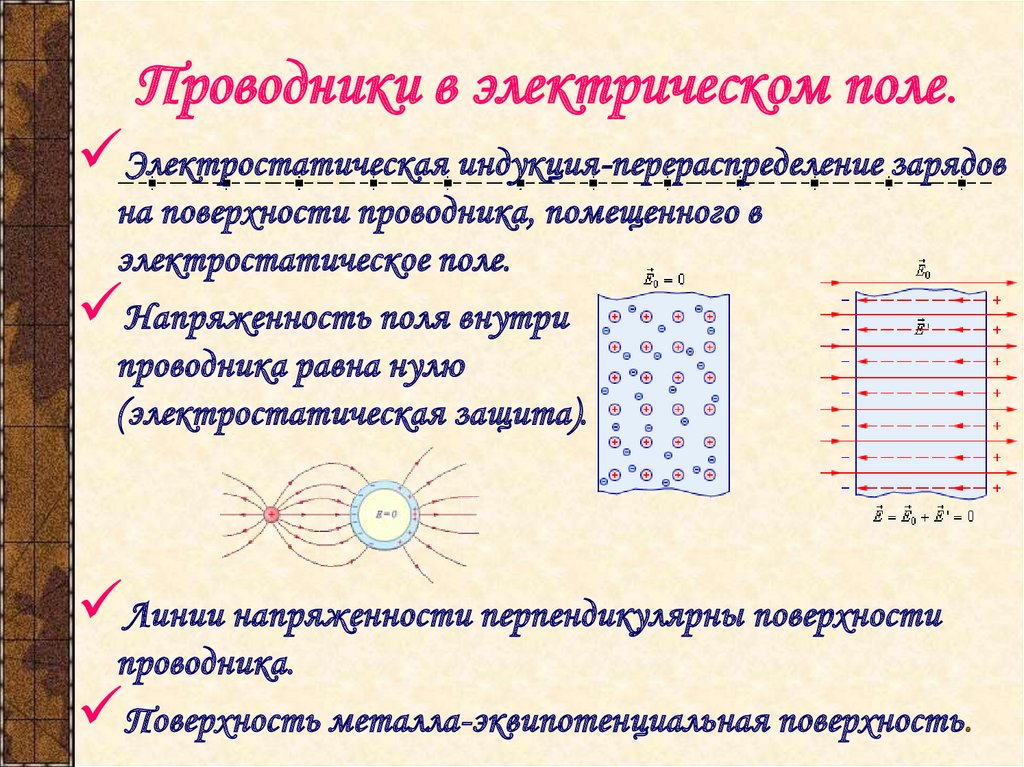
ε показывает, во сколько раз поле ослабляется диэлектриком, и
характеризует количественно свойство диэлектрика поляризоваться в
электрическом поле.
17
Вектор электрического смещения
D
Вектор напряжённости, переходя через границу диэлектриков,
претерпевает скачкообразное изменение, создавая тем самым
неудобства при расчётах электростатических полей. Поэтому удобно
ввести величину, учитывающую свойства среды, на которую действует
внешнее электростатическое поле.
D
Вектор электрического смещения
– ВФВ, являющаяся
вспомогательной характеристикой электрического поля, определяемая
соотношением
Кл
D 0 E P. 2
м
Вектор электрического смещения можно выразить следующим
образом:
D 0 E P 0 E 0 E 1 0 E 0 E.
D 0 E.
18
Возвращаясь к напряженности
диэлектрика равна
Умножим на
0
результирующего
поля
внутри
E0
E0
E
0
1
0 E 0 E0
D
D0
D D0
или
D D0
ВАЖНО! Электрическое смещение внутри пластины D совпадает
с электрическим смещением внешнего поля D0 при условии, что
однородный и изотропный диэлектрик заполняет объём,
ограниченный эквипотенциальными поверхностями.
E
E0
0 0
E0
0 E
D
т.е.
поверхностная
плотность
σ
свободных зарядов равна модулю
вектора электрического смещения D.
D
19
ВЫВОД
Если однородный и изотропный диэлектрик полностью
заполняет
объём,
ограниченный
эквипотенциальными
поверхностями
поля
сторонних
зарядов,
то
вектор
электрического смещения совпадает с вектором напряжённости
поля сторонних зарядов, умноженным на 0 ,
D 0 E0 .
и, следовательно, напряжённость поля внутри диэлектрика в
раз меньше, чем напряжённость поля сторонних зарядов.
E
E0
20
ФИЗИЧЕСКИЙ СМЫСЛ ВЕКТОРА
ЭЛЕКТРИЧЕСКОГО СМЕЩЕНИЯ
Вектор D
характеризует электростатическое поле, создаваемое
свободными зарядами (т.е. в вакууме), но при таком их распределении
в пространстве, какое имеется при наличии диэлектрика.
ВАЖНЫЕ НЮАНСЫ
E , изображается с помощью линий
1. Поле D , как и поле
электрического смещения, направление и густота которых
определяются точно так же, как и для линий напряженности.
2. Линии вектора E могут начинаться и заканчиваться на любых
зарядах – свободных и связанных, в то время как линии вектора D –
только на свободных зарядах.
21
Теорема Гаусса для электростатического поля
в диэлектрике
Поток вектора электрического смещения электростатического поля в
диэлектрике сквозь произвольную замкнутую поверхность равен
алгебраической сумме заключенных внутри этой поверхности
сторонних электрических зарядов.
n
DdS q
S
i 1
i стор
.
N
S
EdS
q
i 1
i всех
0
n
q
i 1
k
i стор
qi связ
0
i 1
Эта формула неприемлема для
описания поля в диэлектрике, так как
она выражает свойства неизвестного
поля через связанные заряды, которые,
в свою очередь, определяются им же.
22
Условия на границе раздела
двух диэлектрических сред
2
Пусть
в
диэлектриках
создано
поле,
напряженность которого в первом диэлектрике
равна E1 , а во втором — E2 .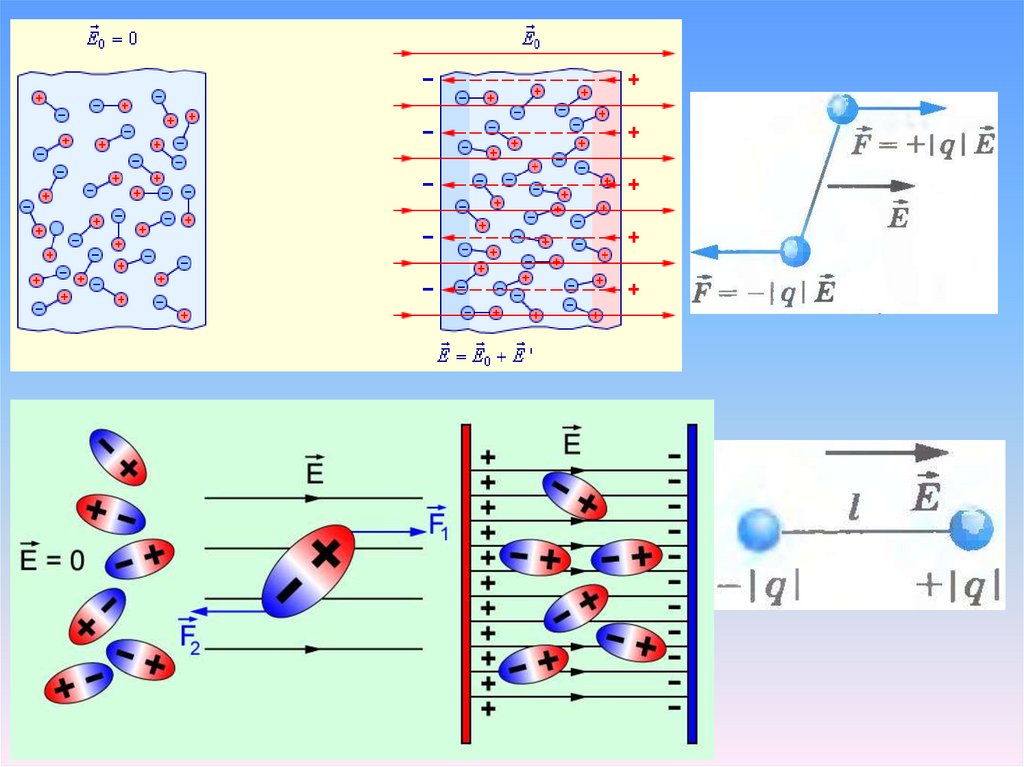
1
При отсутствии на границе свободных зарядов.
1
l
2
1
A
2
AB
CD
E
2l
AB
dl
AB
E
1l
CD
2
cos 2 dl
E2 l
C
D
E2l E1l
1
E2
2
E cos
1
CD
1
dl
l
E1l
E1
dl E2l l E1l l 0
E2l l E1l l 0
2
E
ABCDA
2
B
x
Edl 0
E dl E dl E
2
E1
Построим вблизи границы раздела диэлектриков
1 и 2 замкнутый прямоугольный контур ABCDA
длиной l. BC и DA ничтожно малы.
Согласно теореме о циркуляции вектора
E2
l
1
180 1
23
Представим каждый из векторов
составляющих:
E1 и E2 в виде суммы нормальной и тангенциальной
E1 E1n E1
E2 E2 n E2
Тогда
E1 E2
1.
D1 1 0 E1
D1
1 0
D2 2 0 E2
2
2 En1
E1
E 2 1
E 1
D2
2 0
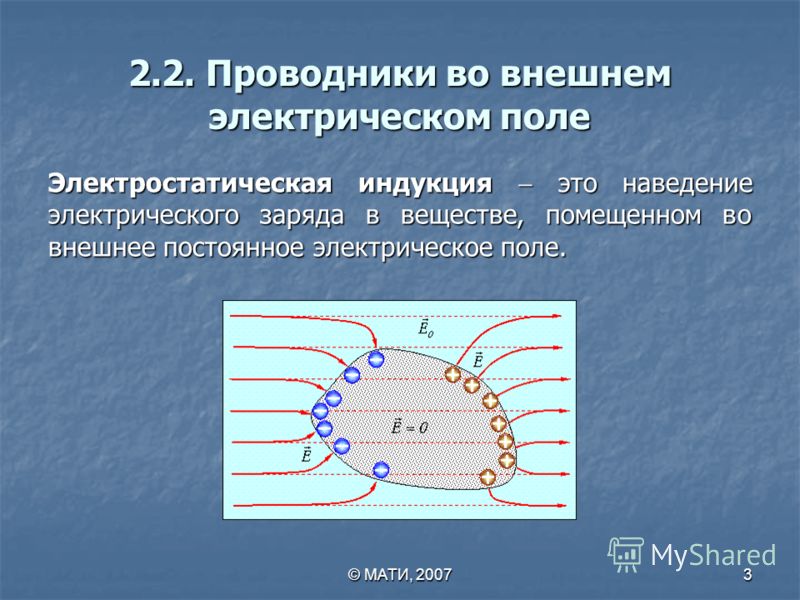
На границе раздела построим прямой цилиндр ничтожно
малой высоты h.
Согласно теореме Гаусса для вектора D
n
DdS q
i 1
1
D1 1
D2 2
2.
S
E2
En 2
i стор
2
n2
2
1
1
n1
24
n
DdS q
i стор
i 1
S
0
Dn1S Dn 2 S D Sбок 0
Dn1 Dn 2 0
Если проецировать
D1 и D2 на одну и туже нормаль, получится условие
1.
D1n 1 0 E1n
D2 n 2 0 E2 n
Dn1 Dn 2
1 0 E1n 2 0 E2 n
E1n 2
2.
E2 n 1
ВЫВОД:
При переходе через границу раздела двух диэлектриков нормальная составляющая
вектора электрического смещения и тангенциальная составляющая вектора
напряжённости электрического поля изменяются непрерывно.
E1 E2 , Dn1 Dn 2
Тангенциальная составляющая вектора электрического смещения и нормальная
составляющая вектора напряжённости электрического поля претерпевают скачок.
D1 1
,
D2 2
E1n 2
E2 n 1
25
Поле внутри диэлектрика
E E0 E ‘
Линии поля
связанных
зарядов
1
‘
E
E
E0
E0
2
‘
E
‘
E
3
E
E0
E
Линии внешнего
поля E0
‘
Поле E создается связанными зарядами диэлектрика. Оно ослабляет
поле E0 внутри диэлектрика (точка 1). За пределами диэлектрика
суммарное поле увеличивается (точка 2) или уменьшается (точка 3).
Сегнетоэлектрики
Формулировка. Сегнетоэлектрики — диэлектрики, обладающие в
определенном интервале температур спонтанной (самопроизвольной)
поляризованностью, т.е. поляризованностью в отсутствие
внешнего электрического поля. К таким материалам относится
сегнетова соль NaKC4h5O6∙4h3O и титанат бария BaTiO3.
Обычно сегнетоэлектрик не является однородно поляризованным,
а представляет собой совокупность доменов – малых областей,
поляризованных практически до точки насыщения. Векторы
поляризации соседних доменов ориентированы в разные стороны,
так что в целом макроскопический объем вещества оказывается
неполяризованным.
Pдомена 0,
Pсегнетоэл 0
27
Во внешнем электрическом поле происходит рост тех доменов,
векторы поляризации которых ориентированы по полю, вследствие
чего растёт поляризация вещества.
По мере увеличения стороннего поля весь сегнетоэлектрик
превращается в один домен, вектор поляризации которого
ориентирован по полю. При этом поляризация вещества достигает
насыщения. Этот рост незначителен, вследствие чего диэлектрическая
проницаемость сегнетоэлектроников в больших полях снижается и
стремится к значениям, типичным для твердых диэлектриков с
деформационным механизмом поляризации.
28
E 0
Р
2
1
0
а
Состояние 0
Е
Состояние 1
б
Состояние 2
Основная кривая поляризации (а) и схема состояния доменов
при увеличении внешнего поля (б).
29
Диэлектрический гистерезис
С
увеличением
напряжённости
электрического
поля
поляризованность P растёт, достигая
насыщения (кривая 1). Уменьшение P
с уменьшением E происходит по
кривой 2, и при E=0 сегнетоэлектрик
сохраняет
остаточную
поляризованность
Pос,
т.е.
сегнетоэлектрик
остаётся
поляризованным
в
отсутствие
внешнего электрического поля.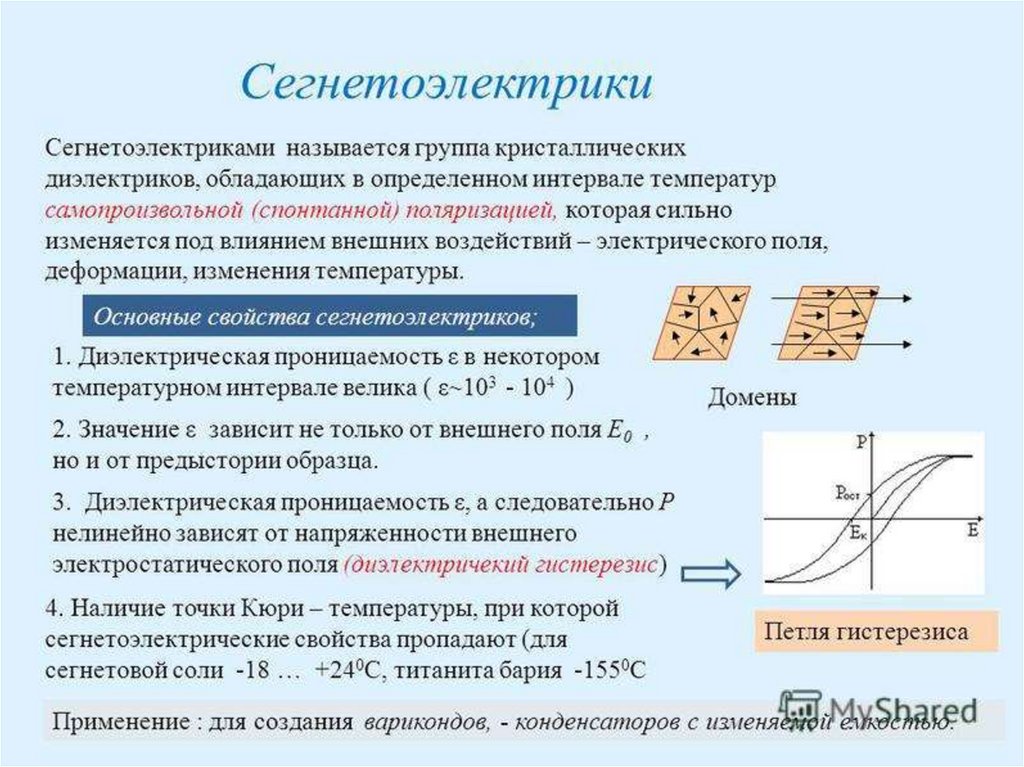
Для уничтожения остаточной поляризованности необходимо
приложит электрическое поле обратного направления (-Ec). Величина
Ec называется коэрцитивной силой. Если далее изменять E, то P
изменяется по кривой 3 петли гистерезиса.
30

Электрические поля в материи — Nexus Wiki

Что мы подразумеваем под «полями в материи»?

В наших предыдущих обсуждениях мы определили электрическое поле и электрический потенциал, ощущаемый пробным зарядом, рассматривая все другие заряды и суммируя их влияние на пробный заряд. Это требует идентификации всех заряженных частиц. Но на самом деле это взгляд на «частицы и заряды в вакууме», потому что если поблизости есть какая-либо другая материя (под материей мы подразумеваем любой вид атомов или молекул), она содержит как положительные заряды, так и отрицательные заряды (электроны), которые будут влиять на электрическое поле. и электрический потенциал, ощущаемый пробным зарядом. Большая часть биологии происходит внутри сложной материи, часто в жидкости, поэтому очень важно узнать, как окружающая материя и ее положительные и отрицательные заряды влияют на электрические поля и потенциалы, воспринимаемые пробным зарядом.

Давайте начнем с одного важного предостережения относительно полей и потенциалов в материи: электрическое поле и потенциал становятся действительно сложными, когда мы приближаемся к атомному масштабу! Поскольку силы и поля увеличиваются с уменьшением расстояния между зарядами, очень близко к любому заряду в материале поле становится огромным и сложным. Эта трудность определения свойства не нова при нашем подходе к электрическим силам и энергиям. У нас есть аналогичный опыт с такими величинами, как температура, pH и химическая концентрация. На молекулярном уровне (в нанометровом масштабе) эти величины сильно колеблются в зависимости от того, попадает ли молекула в крошечный объем, который мы рассматриваем. Но если мы говорим не об отдельных молекулах, а о более крупных структурах, таких как, например, мембран в масштабе сотен нанометров или pH митохондрий, объем, который мы могли бы рассмотреть, будет содержать тысячи атомов. В этом масштабе мы можем легко определить температуру или концентрацию. И в этом масштабе мы также условимся определять электрическое поле и электрический потенциал. Но то, что мы подразумеваем под ними, является своего рода сглаженным средним. Истинное электрическое поле или потенциал в молекулярном масштабе так же трудно описать, как и температуру в этом масштабе.

Используя нашу игрушечную модель

В некоторых из наших предыдущих чтений (   Простая электрическая модель: слой заряда, конденсатор) мы сделали «игрушечную модель» системы множества электрических зарядов, разбросанных по поверхность. Учитывая эффект каждого отдельного заряда, это был бы ужасный беспорядок. Нам пришлось бы сложить огромное количество отдельных векторов, каждый со своей величиной и направлением, и у нас действительно не было бы возможности говорить о результате.

Вместо этого мы рассмотрели простую модель, в которой наши заряды считались не отдельными частицами, а гладким распределением, равномерно распределенным по бесконечному плоскому листу.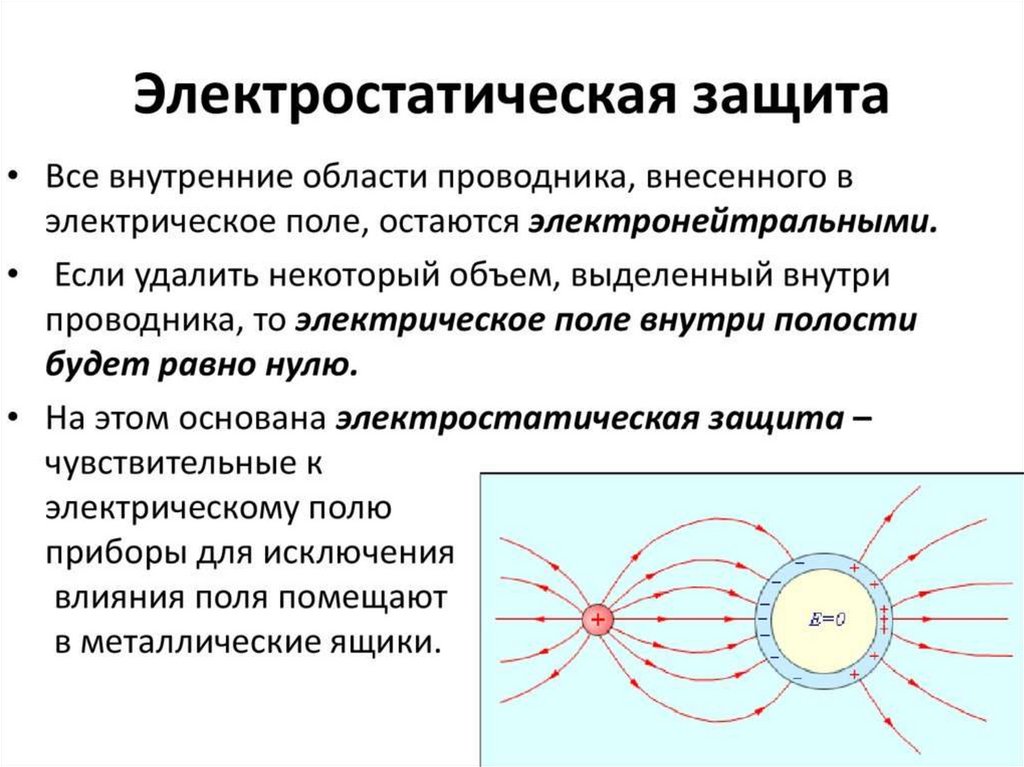 Мы могли бы (достаточно) легко показать, что поле вблизи такого листа было постоянным и перпендикулярным этому листу, и, немного вычислив, мы могли вычислить напряженность поля, которая, как оказалось, зависела только от плотности заряда на листе. Кроме того, мы вычислили как раз вместо , такая игрушечная модель была бы разумной: если бы рядом не было края слишком близко и пока мы не были бы так близко к листу, что мы могли бы видеть эффект отдельных дискретные заряды.

Эта модель идеально подходит для того, чтобы помочь нам понять общее влияние электрического поля на материю, увидеть среднее воздействие и определить параметры для его описания. Начнем с простейшего случая: что произойдет, если мы поместим проводник (скажем, кусок металла) в электрическое поле.

Поля в проводнике

В материи вообще заряды могут или не могут свободно перемещаться. (Обсуждение см. в разделе « Поляризация» .) Если в материи есть заряды, которые могут достаточно свободно перемещаться через все тело материала, это называется 9. 0012 проводник . Два примера: (1) металл, в котором подвижными зарядами являются электроны, распределенные между плотной упаковкой ионов (2) ионная жидкость, в которой подвижными зарядами являются ионы, например Na ⁺ и Cl ^— в виде солевого раствора. В «нейтральном» металле или жидкости баланс положительных и отрицательных зарядов.

Рассмотрите вариант размещения блока проводящего вещества между пластинами конденсатора, состоящего из двух бесконечных пластин с одинаковой и противоположной поверхностной плотностью заряда (внимание, игрушечная модель!), как показано на рисунках ниже. Слева мы показываем конденсатор до того, как в него вставили блок, и справа, как он выглядит через мгновение после этого.

Когда мы поместим проводник между пластинами, электрическое поле от двух пластин будет присутствовать повсюду внутри проводника. В частности, он будет присутствовать в местах расположения подвижных зарядов внутри проводника. Предположительно, до того, как он был помещен между пластинами, силы на каждом из подвижных зарядов в проводнике были уравновешены.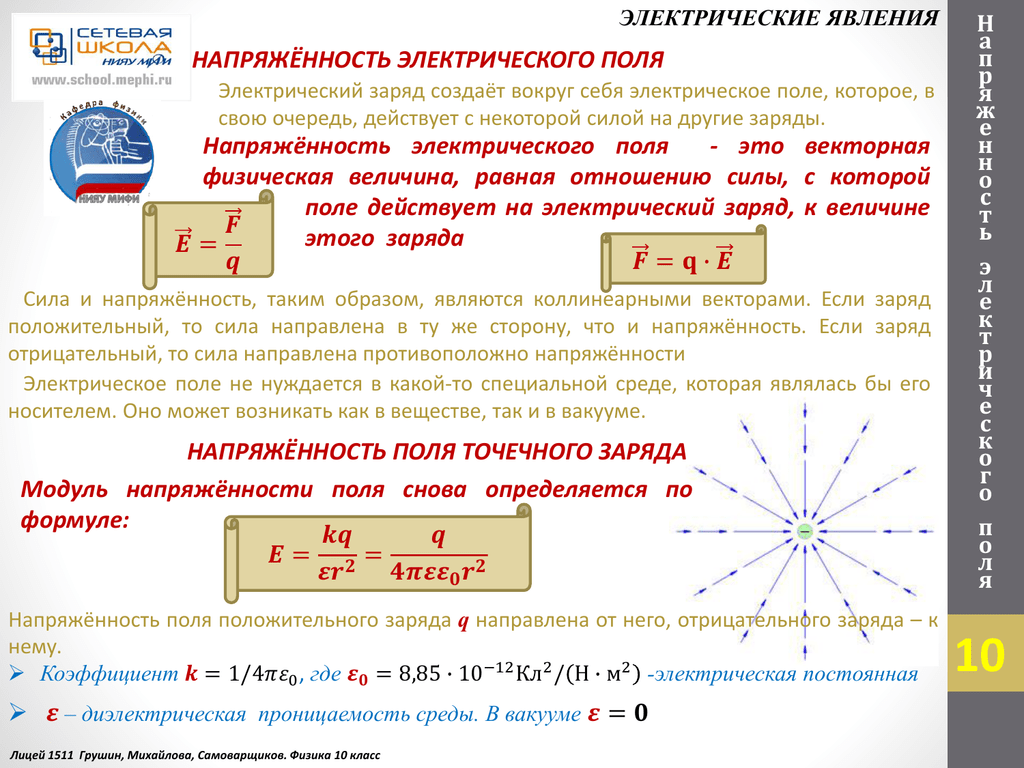 Теперь, с добавлением полей от обкладок конденсатора, силы больше не уравновешиваются. Электроны (при условии, что это металлический блок) будут двигаться против электрического поля, притягиваясь к положительной пластине конденсатора и отталкиваясь от отрицательной пластины конденсатора.

В результате слой электронов начнет формироваться на стороне проводника, ближайшей к положительной пластине, оставив слой несбалансированных ионов на стороне проводника, ближайшей к отрицательной пластине: что-то вроде того, как показано на рисунке право.

Обратите внимание на слабые красные (розовые) заряды, формирующиеся слева от проводника, и слабые синие (бирюзовые) заряды, формирующиеся справа от проводника. Они создают два новых слоя заряда, противоположных слоям конденсатора.

Эти листы также будут создавать электрическое поле в проводнике, но в направлении, противоположном исходным листам. Это уменьшит общее поле внутри проводника, но пластины конденсатора все равно будут побеждать и по-прежнему будут перемещать заряды до тех пор, пока слои неуравновешенного заряда, накопившиеся на поверхности проводника, не будут РАВНЫ по плотности заряда зарядам на обкладках конденсатора как показано справа.

Тогда поле внутри проводника уменьшится до нуля и движение зарядов прекратится. Внутри проводника поля не будет. Это дает нам наш первый опорный результат:

Электрическое поле внутри тела статического проводника (без движущихся зарядов) равно нулю.

Мы включаем ограничение «статический», поскольку, если заряды движутся по проводнику — например, когда электрический ток все еще течет, у нас может быть электрическое поле.

Поскольку изменение потенциала между двумя точками представляет собой интеграл электрического поля, умноженный на расстояние, если внутри проводника нет поля, не может быть изменения потенциала от одной точки проводника к другой. Это дает нам второй важный результат:

Все тело статического проводника (по нему не проходят заряды) имеет одинаковый потенциал.

Мы можем увидеть, что произойдет с емкостью конденсатора, если мы поместим в него блок проводника. Поскольку разность потенциалов является интегралом поля E, умноженного на расстояние ($ΔV = E \times d$, если поле постоянно, как в нашей игрушечной модели), если часть расстояния теперь имеет нулевое электрическое поле, это больше не вносит вклад в разность потенциалов. Если наш проводник имеет толщину $d_c$, то поле E будет только на расстоянии $d — d_c$, поэтому емкость теперь станет больше — мы можем хранить больше разделения зарядов при меньших затратах напряжения:

$$C= \frac{k_CA}{d-d_c}$$

Поля в изоляторе: диэлектрическая проницаемость немного, но не свободно — по сути (еще одно предупреждение об игрушечной модели!) мы можем думать о зарядах как о привязанных к своим контрзарядам. Полярная молекула может быть переориентирована, или заряды на молекуле могут немного разойтись. Эффект заключается в уменьшении среднего поля E в материале, поскольку заряды могут немного двигаться, противодействуя электрическому полю, но они больше не могут двигаться, противодействуя электрическому полю, до тех пор, пока поле не станет равным 0. какое электрическое поле может быть уменьшено, зависит от деталей свойств материала. Уменьшение поля можно измерить, определив, насколько падает напряжение в конденсаторе, когда вы вставляете в него блок материала.

Подобно обсуждению выше, уменьшение электрического поля в материале приводит к увеличению емкости конденсатора. конденсатор, заполненный материалом.

Мы определяем коэффициент, на который среднее поле уменьшается в данном материале, как диэлектрическую проницаемость этого материала, $κ$ (каппа).

$$E_{\mathrm{внутри\;материал}} = \frac{1}{\kappa} E_{\mathrm{если\;никакого\;материала\;не было\;там}}$$

Из Конечно, это относится к среднему полю E, измеренному путем рассмотрения полного изменения разности потенциалов. «Настоящее» поле E будет сильно колебаться в атомном масштабе.

Подробнее см. на страницах конденсатор и диэлектрическая проницаемость

Условное предупреждение! Постоянная Кулона $k_C$ иногда записывается как $k_C=1/4πε_0$. Тогда комбинация $κε_0$ иногда определяется как $ε=κε_0$. Закон Кулона для электрического поля внешнего заряда внутри вещества можно записать так же, как и в свободном пространстве, но с ε в константе Кулона вместо $ε_0$.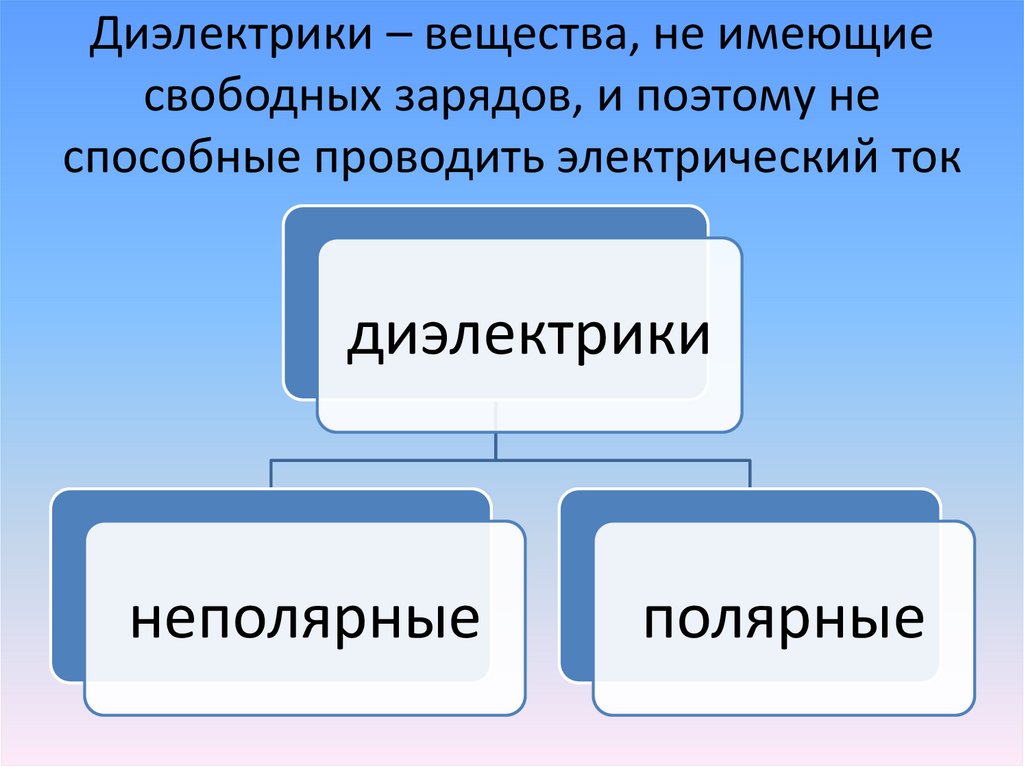 Эта форма включает эффекты поляризации среды. Однако обратите внимание, что в некоторых учебниках по химии и биологии «$ε$» используется для обозначения «$κ$». Это вводит в заблуждение, поскольку символы «$ε$» и «$ε_0$», которые появляются в одном и том же контексте, имеют разные единицы измерения. Вы часто видите, что такие вещи, как $εε_0$ в одном уравнении, означают $κε_0$. Тогда очень трудно держать юниты прямо.

Стоимость игрушечной модели

Что мы узнаем из нашей игрушечной модели? Глядя на все выводы, выделенные курсивом выше, совсем немного. Самое главное, мы узнали вещи, которые верны во многих случаях, например тот факт, что поле внутри проводника исчезает, как только заряды перестают течь. В то время как анализ применяет нашу игрушечную модель как способ мышления об однородном поле, определения, которые мы разработали, например, для диэлектрическая проницаемость будет работать даже на коротких расстояниях, когда силы НЕ однородны (во всяком случае, до микрометров).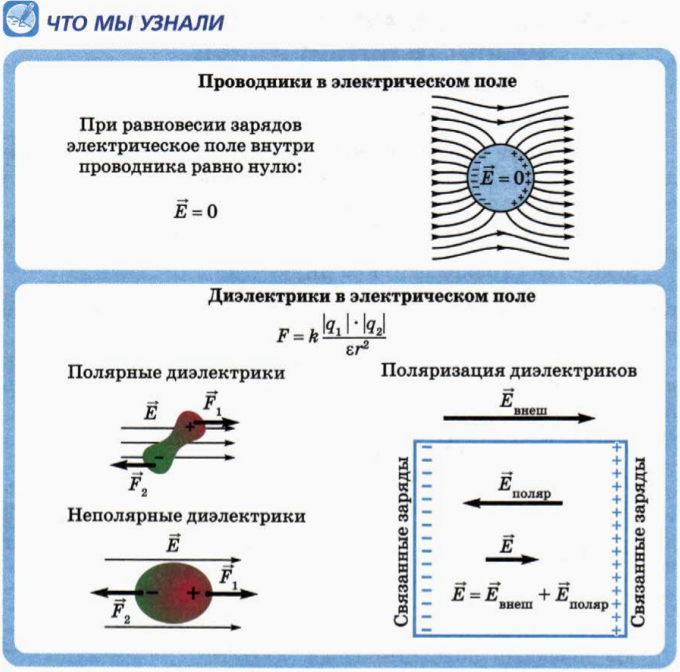

Принцип, согласно которому проводник находится под постоянным потенциалом, оказывается верным, даже если в проводнике есть ток, если проводник имеет сопротивление 0. Это очень ценный инструмент (эвристика) при решении задач с электрическими цепями . (См. принципы Кирхгофа и последующие примеры.) Проект Технологии РобоСпатиум Способствовать Предметный указатель Скачать Ответы Игры Советы по покупкам Контакт

---

<<< Баланс мощности         Напряжение >>>

Видео про электростатические поля

Терминология

Электромагнитная сила является одной из четырех фундаментальных сил в физике. Электромагнитная сила вызвана электрическим зарядом.
Квантование заряда — это принцип, согласно которому заряд любого отдельно стоящего объекта является целым числом, кратным элементарный заряд . По соглашению электрический заряд одного электрона равен -1e, что составляет минус 1,602 * 10 ^-19 кулонов. Это наименьшая единица измерения отрицательного заряда, переносимого изолированной частицей.
Заряд частицы заметен только в присутствии второй заряженной частицы, поэтому электрические поля обычно определяются с использованием другого положительного заряда, называемого пробным зарядом .

Кулоновская сила

Рис. 1:

Около 1785 года Шарль Огюстен де Кулон проанализировал взаимодействие между заряженными объектами и опубликовал свои выводы, которые сегодня известны как Закон Кулона

.
«Величина электростатической силы взаимодействия между двумя точечными зарядами прямо пропорциональна скалярному произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними. Если два заряда имеют одинаковый знак, электростатическая сила между они отталкивают; если они имеют разный знак, то сила между ними притягивает».

Таким образом, сила, действующая между заряженными частицами, зависит от величины зарядов, их знака и расстояния между ними. Заряд может быть как положительным, так и отрицательным. Объект заряжен отрицательно, если он имеет избыток электронов, и в противном случае он заряжен положительно или не заряжен. Производной единицей электрического заряда в системе СИ является кулон (C) или ампер-секунда (As), символ q или Q обычно используется для обозначения заряда.

Заряд проявляет электростатическое притяжение или отталкивание в присутствии другого вещества. Математически мы получаем закон кулона:

[3.1]    

Где находится:
F — сила Кулона
q _1,2 — зарядка
г — расстояние
k — постоянная Кулона = 8,987551787 * 10 ⁹ Вм/Ас

Векторная запись

Используя векторную запись, получаем:

. [3.1a]    

Где находится:
F — Результирующая сила
q _1,2 — Зарядка
k — постоянная Кулона = 8,987551787 * 10 ⁹ Вм/Ас
R ₁ , R ₂ — векторы положения Q ₁ и Q ₂

Для векторов положения есть:

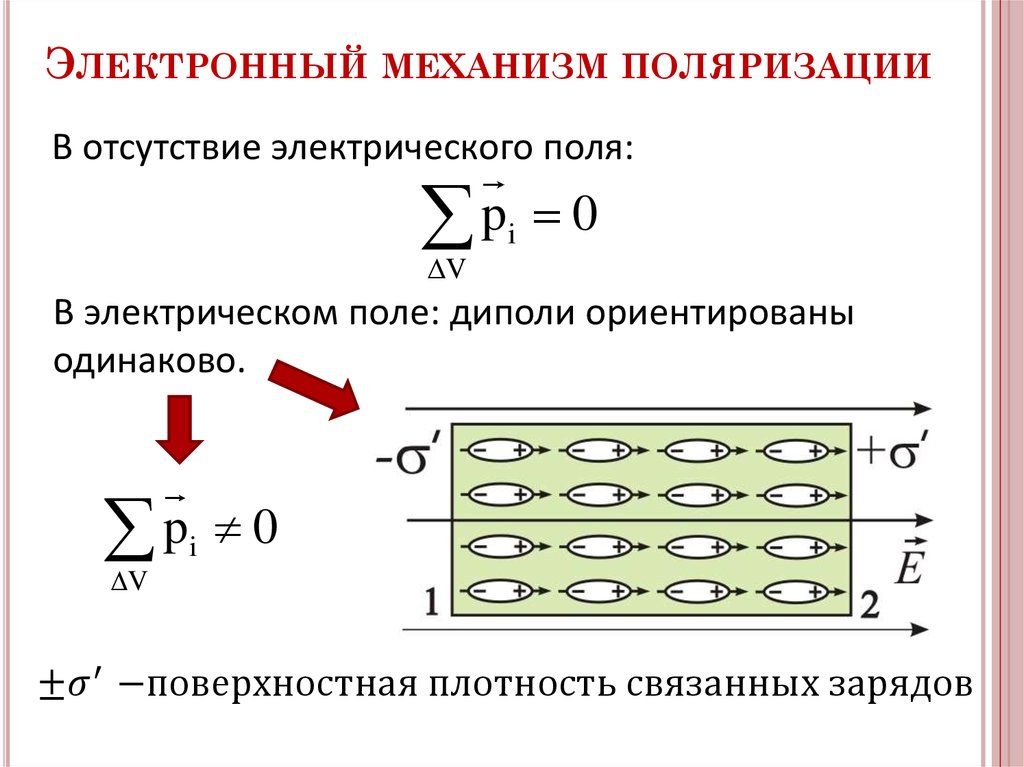. Когда размещение Q ₁ в точке происхождения, x ₁ 130130130130130 1 . и y ₁ равны нулю, поэтому разность векторов положения идентична r ₂ . Получаем более простое уравнение закона Кулона:

Рисунок 2:
Сила между двумя заряженными частицами в плоскости X/Y:

При x = 2, y = 1 мы получаем для величины (= длины) r ​​ ₂ значение √(2 ² + 1 ² ) = 2,24 м. Для кулоновской силы в этой точке мы получаем 1,80 мН, учитывая заряд +1 мкКл для q ₁ соответственно q ₂ . Для координат вектора силы получаем:
х _F = k * (q ₁ * q ₂ )/|r ₂ | ³ * х ₂ = 1,60
и
у _F = k * (q ₁ * q ₂ )/|r ₂ | ³ * у ₂ = 0,80

Рисунок 3:
Реакция на заряд, помещенный в исходную точку:

Чтобы получить силу, действующую на заряд 1, вектор положения 2 необходимо вычесть из вектора положения 1.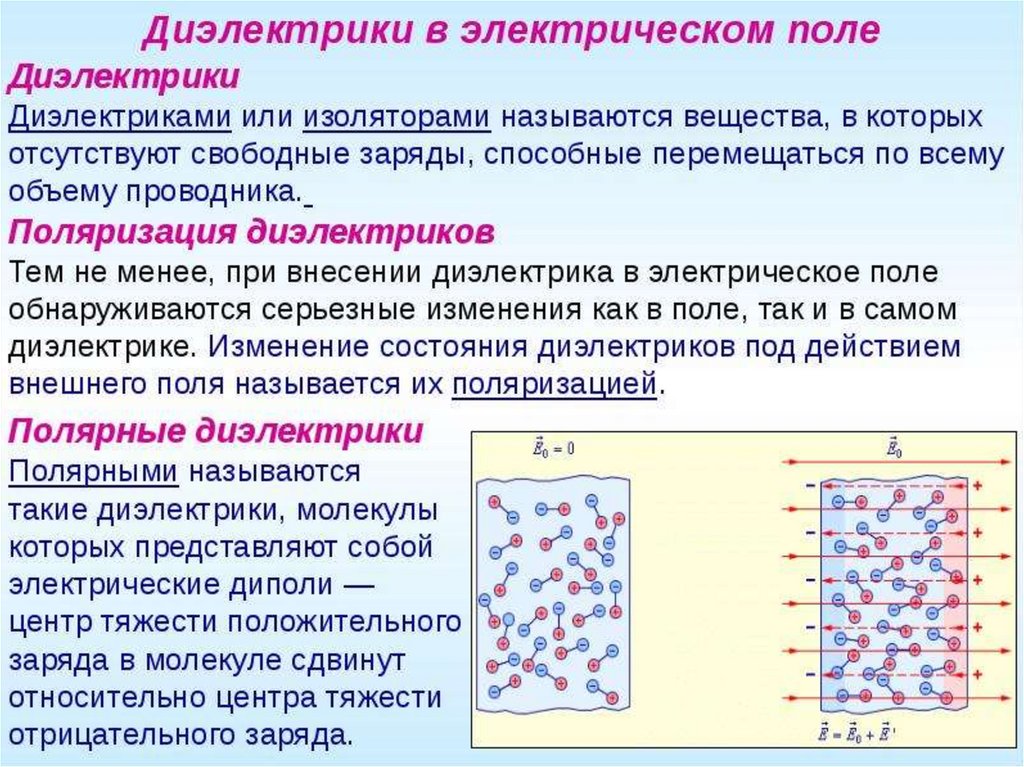 Учитывая, что r ₁ по-прежнему равен нулю, мы получаем -r ₂ для вектора расстояния между обоими зарядами. Мы получаем вектор силы с той же величиной, но противоположным направлением, начиная с исходной точки.
При x = -2,8, y = 1 величина r ₂ равна √(2,80 ² + 1 ² ) = 2,97 м. Учитывая +1 мкКл для каждого заряда, мы получаем силу 1,02 мН. Используя векторную запись закона Кулона, вектор силы равен:
. х _F = k * (q ₁ * q ₂ )/|r ₂ | ³ * (-х ₂ ) = 0,96
и
у _F = k * (q ₁ * q ₂ )/|r ₂ | ³ * (-y ₂ ) = -0,34

Электрическое поле

По закону Кулона сила, действующая на пробный заряд за счет поля другого заряда, определена во всех точках пространства. Величина результирующей силы зависит от заряда q ₁ , а также заряда q ₂ . При делении кулоновской силы на величину пробного заряда получим электрическое поле, обусловленное точечным зарядом:

Величина электрического поля в точке пространства эквивалентна силе, действующей на вторую частицу с зарядом одного кулона, поэтому размерность электрического поля равна силе на заряд, таким образом, Ньютон на кулон. Электрическое поле можно рассматривать как функцию, которая связывает вектор с каждой точкой пространства, учитывая величину и направление.

Рисунок 4:
Величина электрического поля постоянна во всех точках с постоянной длиной вектора расстояния:

При x = -0,5, y = 2 для величины r получаем: √((-0,5) ² + 2 ² ) = 2,06 м. Электрическое поле с учетом заряда +1 мкКл составляет 2,12 кН/Кл. Получаем координаты, используя векторную запись электрического поля:
х _E = k * (q ₁ )/|r| ³ * х ₂ = -1,53
и
y _E = k * (q ₁ )/|r| ³ * у ₂ = 2,06

Рисунок 5:
Сила, действующая на пробный заряд из-за системы точечных зарядов, представляет собой просто векторное сложение отдельных сил, действующих в одиночку на этот пробный заряд из-за каждого из зарядов. Учитывая, что вектор электрического поля представляет собой вектор силы, деленный на величину пробного заряда, мы получаем два вектора поля, каждый из которых вызван одним из двух исходных зарядов на рисунке, показанном здесь (красная и синяя стрелки). Два вектора могут быть сложены «голова к хвосту», чтобы определить результирующий или результирующий вектор электрического поля в этом месте (голубая стрелка). Используя этот принцип, известный как закон суперпозиции мы получаем вектор электрического поля в любом заданном месте, окружающем заряды.

Однородное поле

Рисунок 6:
Электрическое поле, все векторы которого имеют одинаковую величину и указывают в одном направлении, называется однородным полем . Следовательно, величина и направление силы, действующей на пробный заряд, помещенный в однородное поле, постоянны во всех точках пространства. Идеальное однородное электрическое поле создается между двумя параллельными пластинами бесконечных размеров, которые заряжены противоположно друг другу и несут одинаковый заряд на единицу площади. 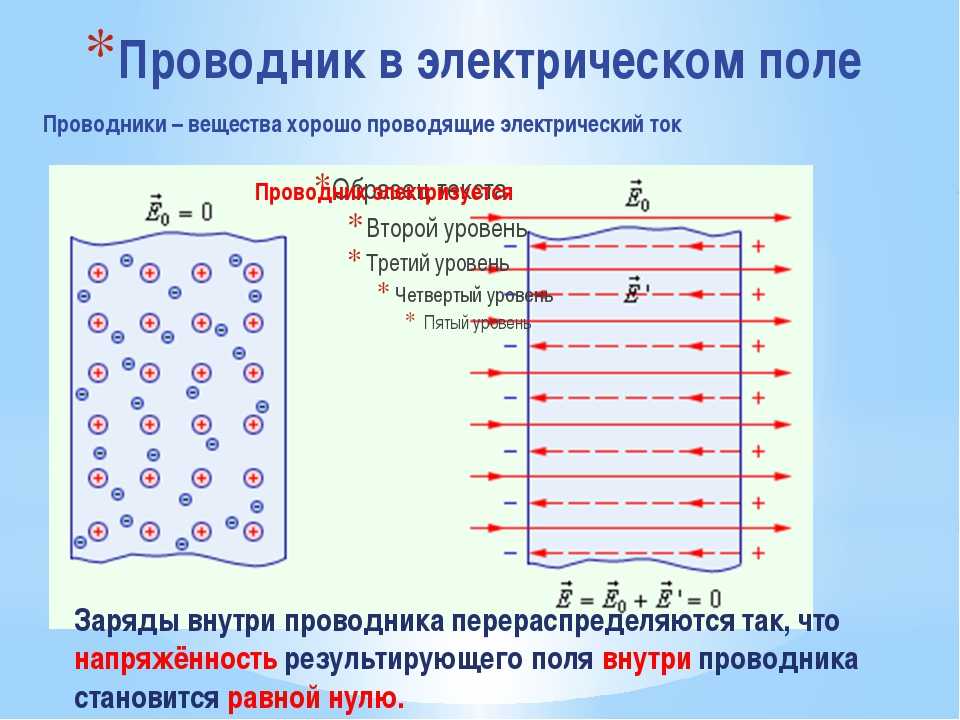Как показано на видео, электрическое поле почти однородно между двумя пластинами конечных размеров. Просто держите расстояние между пластинами небольшим по сравнению с их размером.

Линии поля

Линии поля часто используются для визуализации направления силы, действующей на пробный заряд из-за электрического поля. Единственная силовая линия иллюстрирует путь положительного пробного заряда без массы, движущейся в электрическом поле.

Рисунок 7:
Чтобы получить картину силовых линий, сначала вычисляется сила, действующая на пробный заряд. Затем положение пробного заряда немного смещается в направлении результирующего вектора, и сила вычисляется в соответствии с новым положением. Мы получаем очень грубое приближение при использовании большой ширины шага для каждой итерации, как показано на этом рисунке.

Рисунок 8:
Чем меньше ширина шага, тем ближе моделирование к реальному пути безмассового пробного заряда.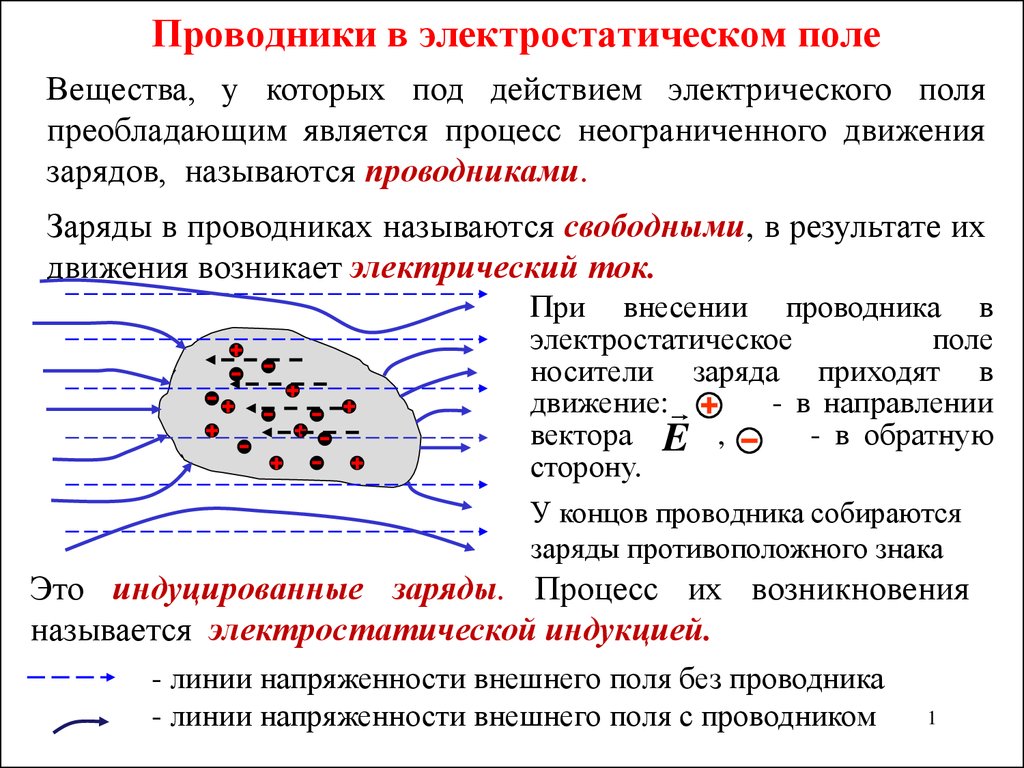
Рисунок 9:
Направление линии поля определяется движением положительного пробного заряда, поэтому линии направлены в сторону от положительных зарядов…
Рисунок 10:
…и вплоть до отрицательных зарядов.

Электрический диполь

Рисунок 11:
В простом случае двух точечных зарядов с фиксированным расстоянием, один с зарядом -q, а другой с зарядом +q, на пласт действует электрический дипольный момент. Устройство называется электрическим диполем, где d — вектор смещения, направленный от отрицательного заряда к положительному. Электрический дипольный момент увеличивается с увеличением величины зарядов, а также с увеличением расстояния между частицами. Единицей электрического дипольного момента является Кулон, умноженный на метр, или короткий кулон-метр.

Рисунок 12:
Объект с электрическим дипольным моментом подвергается крутящему моменту при помещении во внешнее электрическое поле. Диполь вращается так, что вектор смещения указывает направление векторов электрического поля. Крутящий момент максимален, если ось диполя перпендикулярна направлению электрического поля, и становится равным нулю, если ось параллельна этим векторам.

Постоянная Кулона

Влияние вещества, подобного воздуху, на электрическое поле и, следовательно, на силу, действующую между зарядами, связано с постоянной Кулона. Эта постоянная состоит из Pi и относительной диэлектрической проницаемости материала, то есть сопротивления, возникающего при формировании электрического поля в среде:

[3.1b]    

Где находится:
Π — 3.1415927
ε — Диэлектрическая проницаемость

Диэлектрическая проницаемость вакуума не равна нулю, а составляет 8,854 умножить на 10 до -12 Ас/Вм, таким образом, мы получаем для постоянной Кулона:

Где находится:
Π — 3. 1415927
ε ₀ — Диэлектрическая проницаемость вакуума = 8,854188*10 ^-12 As/Vm

Относительная диэлектрическая проницаемость отражает влияние материала на электрическое поле по сравнению с полем в вакууме:

Где находится:
ε _r — Относительная диэлектрическая проницаемость материала
ε — Абсолютная диэлектрическая проницаемость материала
ε ₀ — Диэлектрическая проницаемость вакуума

Получаем ε _r = 1,00059 для газообразного воздуха и обусловленное дипольным моментом и более высокой плотностью ε _r = 80 для жидкой воды.

Для закона Кулона получаем:

Рисунок 13:
Материал с ε _r > 1, таким образом, с высокой диэлектрической проницаемостью находится между положительным и отрицательным зарядом. Сила притяжения между обеими частицами усиливается материалом.
Рисунок 14:
Сила отталкивания между двумя положительными зарядами снижается тем же самым матриалом. Диполи расположены параллельно векторам поля, поэтому они касаются силовых линий.

электростатическая индукция

Рисунок 15:
Если положительный заряд приблизить к атому или молекуле, образуется диполь из-за поляризации искажения . Центр отрицательного заряда диполя смещен вправо, где находится положительно заряженная частица; В сумме есть сила, действующая на молекулу, направленную на вторую частицу. Чем меньше расстояние между обоими объектами, тем больше эффект. Перераспределение электрического заряда в объекте, вызванное влиянием близлежащих зарядов, называется электростатическая индукция .
Рисунок 16:
Этот эффект вызывает притяжение между легкими непроводящими объектами, такими как обрезки пенополистирола, и заряженными объектами, такими как электрически заряженный стеклянный стержень.