Почему электростатическое поле является потенциальным?

Содержание

• — Что означает что электростатическое поле потенциально?
• — Что называют силовыми линиями электрического поля?
• — Какое поле является электростатическим почему электростатическое поле потенциально?
• — Что называют напряжённость электрического поля?
• — Что такое потенциальное поле?
• — Что называется электрическим полем?
• — Какие линии называются силовыми линиями напряженности?
• — Как называется электрическое поле с замкнутыми силовыми линиями?
• — Каковы свойство и направление силовых линий электрического поля?
• — Какое поле не является потенциальным?
• — В чем разница между электрическим и электростатическим полем?
• — Как определяется работа поля по перемещению заряда из одной точки поля в другую?
• — Чему равна сила электрического поля?
• — Чему равна энергия электрического поля?
• — Как найти модуль напряженности электрического поля?

Работа электростатического поля не зависит от формы траектории, по которой пере- мещается заряд, и определяется лишь начальным и конечным положениями заряда. Работа поля по замкнутому пути равна нулю. Этот факт называется также потенциальностью электростатического поля.

Что означает что электростатическое поле потенциально?

Потенциальное (консервативное) поле − это поле, в котором работа при перемещении зависит только лишь от конечной и начальной точки пути и не зависит от траектории движения тела.

Что называют силовыми линиями электрического поля?

Силовая линия, или интегральная кривая, — это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой же точке.

Какое поле является электростатическим почему электростатическое поле потенциально?

Получили, что работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной точек перемещения. … Тогда работа по замкнутому пути: Поле, обладающее такими свойствами, называется потенциальным. Любое электростатическое поле является потенциальным.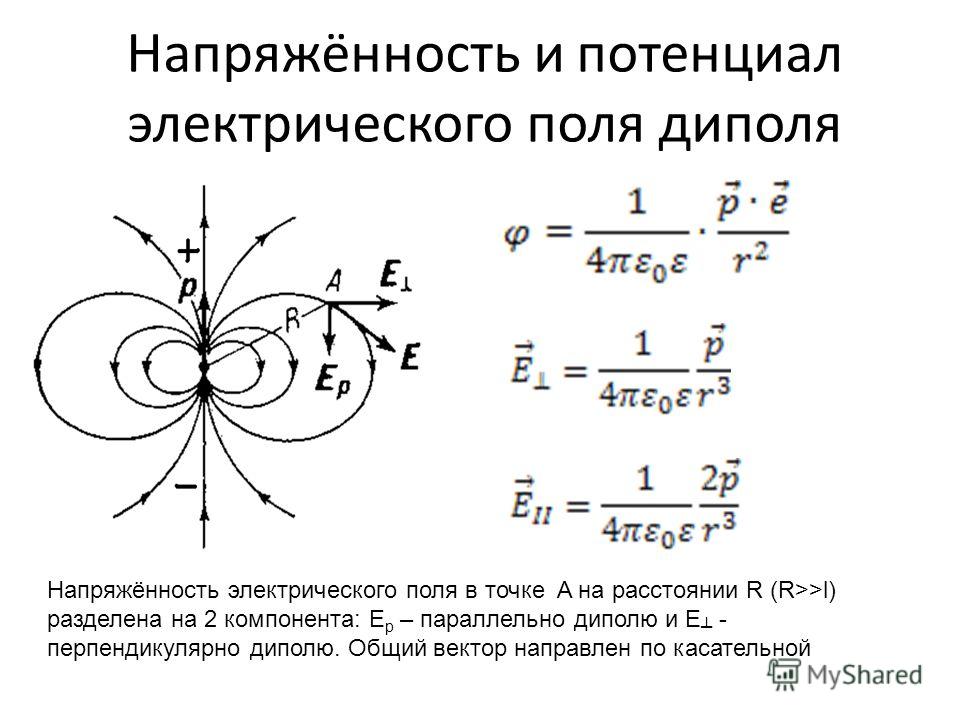

Что называют напряжённость электрического поля?

Напряжённость электрического поля Напряжённость электрического поля иногда называют силовой характеристикой электрического поля, так как всё отличие от вектора силы, действующей на заряженную частицу, состоит в постоянном множителе. может меняться со временем).

Что такое потенциальное поле?

Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат. Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля.

Что называется электрическим полем?

Электрическое поле (иногда E-field) — это физическое поле, которое окружает каждый электрический заряд и оказывает силовое воздействие на все другие заряды, притягивая или отталкивая их.

… Электрические поля возникают из-за электрических зарядов или из изменяющихся во времени магнитных полей.

Какие линии называются силовыми линиями напряженности?

Линии, касательные к которым совпадают с направлением вектора напряженности электрического поля, называются линиями напряженности электрического поля, или силовыми линиями.

Как называется электрическое поле с замкнутыми силовыми линиями?

Такое поле называется — визревым полем.

Каковы свойство и направление силовых линий электрического поля?

Силовые линии электростатического поля имеют следующие свойства: Всегда незамкнуты: начинаются на положительных зарядах (или на бесконечности) и заканчиваются на отрицательных зарядах (или на бесконечности). Не пересекаются и не касаются друг друга.

Какое поле не является потенциальным?

В стационарном силовом поле сила зависит только от положения частицы. Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от пути. … Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными.

В чем разница между электрическим и электростатическим полем?

Электростатическое поле также как и электрическое поле является особой формой материи, которая окружает тела, имеющие электрический заряд. Но в отличие от последнего, электростатическое поле создается только вокруг неподвижных заряженных тел, то есть, когда нет условий для создания электрического тока.

Как определяется работа поля по перемещению заряда из одной точки поля в другую?

Электростатическое поле обладает важным свойством: Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Чему равна сила электрического поля?

Формула напряжённости электрического поля

Напряжённость электрического поля равна отношению силы, действующей на помещённый в поле точечный заряд к величине этого заряда. – величина заряда. Единица измерения напряжённости электрического поля – В/м (вольт на метр) или Н/Кл (ньютон на кулон).

Чему равна энергия электрического поля?

Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.

Как найти модуль напряженности электрического поля?

Для нахождения модуля напряженности электрического поля в точке А разделим модуль силы на модуль заряда q1: Напряженность электрического поля точечного заряда прямо пропорциональна заряду q и обратно пропорциональна квадрату расстояния r от заряда до данной точки поля.

Интересные материалы:

Какая зарплата у пилота в Украине?
Какая зарплата у SMM?
Какая звезда самая маленькая какая самая горячая?
Какие акции дает Тинькофф за друга?
Какие акулы боятся дельфинов?
Какие анализы на бесплодие у женщин?
Какие ароматы любит сазан?

Какие атласы бывают по назначению?
Какие автомобили попадают под программу первый автомобиль?
Какие авторы и произведения относятся к литературе потерянного поколения?

Электростатическое поле потенциальное или вихревое. Вихревое электрическое поле — Гипермаркет знаний. Дидактические особенности компьютера

В соответствии с законом Фарадея для электромагнитной индукции в контуре, который движется в магнитном поле, возникает ЭДС, пропорциональная скорости изменения магнитного потока в этом контуре

Опытами Фарадея также установлено, что ЭДС электромагнитной индукции, определяемая выражением (67), возникает и тогда, когда неподвижный контур пронизывает изменяющееся магнитное поле (рисунок 48).

Если в движущемся контуре причиной возникновения ЭДС является сила Лоренца, томеханизм ее возникновения в неподвижном контуре (проводнике) становится неясным. Очевидно, сторонняя сила, разделяющая заряды в контуре, не может иметь электростатическое происхождение, поскольку кулоновские силы приводят не к возрастанию разности потенциалов, к ее выравниванию.

Рисунок 48

По общему определению ЭДС источника ε , (68)

где — напряженность поля сторонних сил.

С другой стороны . (69)

Символ частной производной в выражении (69) указывает на то, что в общем случае индукция магнитного поля зависит не только от времени, но и от координат.

С учетом формул (69) и (68) закон Фарадея для электромагнитной индукции преобразуется к виду . (70)

В соответствии с полученным выражением (70), любое изменение магнитного поля, пронизывающего контур, приводит к появлению напряженности поля сторонних сил и. как следствие, к возникновению в контуре ЭДС электромагнитной индукции. При этом изменение магнитного поля не сопровождается механическими, химическими, тепловыми и другими изменениями в контуре. Английский физик Дж. Максвелл предложил гипотезу, согласно которой сторонние силы, разделяющие заряды в контуре, имеют электрическую природу. Тогда и соотношение (70) можно записать в виде . (71)

Согласно формуле (71), в изменяющемся магнитном поле циркуляция вектора напряженности электрического поля не равна нулю, то есть электрическое поле является вихревым (рисунок 49).

Важно отметить, что вихревое электрическое поле возникает в любом пространстве, то есть для его существования наличие проводящего контура необязательно. Но если это поле возникло в проводящей среде, то оно приводит к появлению вихревых токов или токов Фуко (рисунок 50).

В проводниках, обладающих малым удельным сопротивлением, эти токи могут достигать больших величин. В связи с этим их часто используют для индукционного нагрева металлических деталей при закаливании, обезгаживают арматуры электронных приборов и т.

д.

Рисунок 49 Рисунок 50

При работе электрических машин (электродвигателей, электрогенераторов, трансформаторов) эти токи приводят к нежелательным тепловым потерям в металлических магнитопроводах. Для уменьшения потерь сердечники трансформаторов, статоры и роторы электрических машин набирают из тонких, изолированных друг от друга пластин из электротехнической стали. В других случаях в качестве магнитопроводов применяют высокоомные магнитные материалы – ферриты.

Конец работы —

Эта тема принадлежит разделу:

Электростатическое поле

Физические и химические свойства вещества от атома до живой клетки в значительной степени объясняются электрическими силами электрические.. электростатическое.. пример среда e вакуум воздух керосин вода..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Твитнуть

Все темы данного раздела:

Неоднородные цепи
Электрическая цепь, в которой непрерывное протекание тока обеспечивается за счет сторонних сил, называется н

Магнитное поле в вакууме
Вблизи неподвижных зарядов возникает электростатическое поле. Движение зарядов (протекание электрического тока) приводит к появлению новой формы материи – магнитного поля. Это особа

Циркуляция вектора магнитной индукции
По аналогии с электростатикой определяется понятие циркуляции вектора по замкнутому контуру

Контур с током в однородном магнитном поле
Применим закон Ампера к прямоугольному контуру с током в однородном магнитном поле. На ребра “a” действует сила

Контур с током в неоднородном магнитном поле
Если контур с током находится в неоднородном магнитном поле, то на разные его участки действуют неодинаковые силы

Контур с током в радиальном магнитном поле
Из формул (37) и (38) следует, что в однородном магнитном поле вращающий момент, действующий на контур с током максимален, если

Электродвигатели
Из рисунка 23 следует, что при выбранной ориентации полюсов магнита и направления тока а контуре вращающий момент направлен «на нас», то есть стремится повернуть контур против часов

Работа магнитного поля
Если действующая на проводник с током со стороны магнитного поля сила ампера вызывает его перемещение, то о

Намагниченность веществ
Различные вещества в магнитном поле намагничиваются, то есть приобретают магнитный момент и сами становятся источниками магнитных полей. Результирующее магнитное поле в среде является суммой полей,

Диа-, пара- и ферромагнетики и их применение
Магнитный момент атома включает несколько составляющих, где

Диамагнетики
У некоторых атомов (Cu, Au, Zn и др.) электронные оболочки имеют такое строение, что орбитальный и спиновый моменты взаимно скомпенсированы, и в целом магнитный момент атома равен н

Парамагнетики
У атомов таких веществ, как Al, Mn, Os и др. нескомпенсирован суммарный орбитальный момент, то есть в отсутствие внешнего поля у них имеются собственные магнитные моменты. Тепловое

Ферромагнетики и их применение
Вещества, у которых магнитная проницаемость достигает сотен и даже миллионов единиц, выделе

Электромагнитная индукция
В основе современного способа производства электроэнергии лежит физическое явление электромагнитной индукции, открытое Фарадеем в 1831 г. Современная энергетика все больше

Явление электромагнитной индукции
Рассмотрим сущность электромагнитной индукции и принципы, которые приводят к этому явлению. Предположим, что проводник 1-2 перемещается в магнитном поле со скоростью

Электрогенератор
Закон Фарадея относится к фундаментальным законам природы, и является следствием закона сохранения энергии. Он широко применяется в технике, в частности, в генераторах. Основная час

Самоиндукция
Явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток, пронизывающий контур. В частности, магнитный поток создается и током, текущим в самом контуре. Поэто

Переходные процессы в цепях с индуктивностью
Рассмотрим цепь, содержащую индуктивность и активное сопротивление (рисунок 44). В исходном состоянии ключ S находился в нейтральном положении. Пусть в момент времени t

Взаимная индукция. Трансформатор
Явление взаимной индукции – это частный случай явления электромагнитной индукции. Поместим два кон

Уравнения максвелла
К середине XIX века было накоплено большое количество экспериментальных фактов по электричеству и магнетизму. Неоценимый вклад в это внес М. Фарадей, венцом творческих успехов котор

Энергия магнитного поля
Рассчитаем энергию магнитного поля. Для этого вычислим работу источника тока в цепи с индуктивностью. При установлении тока в такой цепи по закону Ома имеем iR = ε

Ток смещения
В соответствии с прямой гипотезой Дж. Максвелла изменяющееся магнитное поле порождает переменное электрическое поле. Обратная гипотеза Максвелла утверждает, что переменное электриче

Уравнения Максвелла
В 1860-65 гг. Максвелл развил теорию единого электромагнитного поля, которое описывается системой уравнений Максвелла

ЭДС индукции возникает либо в неподвижном проводнике, помещенном в изменяющееся во времени поле, либо в проводнике, движущемся в магнитном поле, которое может не меняться со временем. Значение ЭДС в обоих случаях определяется законом (12.2), но происхождение ЭДС различно. Рассмотрим сначала первый случай.

Пусть перед нами стоит трансформатор — две катушки, надетые на сердечник. Включив первичную обмотку в сеть, мы получим ток во вторичной обмотке (рис. 246), если она замкнута. Электроны в проводах вторичной обмотки придут в движение. Но какие силы заставляют их двигаться? Само магнитное поле, пронизывающее катушку, этого сделать не может, так как магнитное поле действует исключительно на движущиеся заряды (этим-то оно и отличается от электрического), а проводник с находящимися в нем электронами неподвижен.

Кроме магнитного поля, на заряды действует еще поле электрическое. Причем оно-то может действовать и на неподвижные заряды. Но ведь то поле, о котором пока шла речь (электростатическое и стационарное поле), создается электрическими зарядами, а индукционный ток появляется под действием переменного магнитного поля. Это заставляет предположить, что электроны в неподвижном проводнике приводятся в движение электрическим полем и это поле непосредственно порождается переменным магнитным полем. Тем самым утверждается новое фундаментальное свойство поля: изменяясь во времени, магнитное поле порождает электрическое поле. К этому выводу впервые пришел Максвелл.

Теперь явление электромагнитной индукции предстает перед нами в новом свете. Главное в нем — это процесс порождения магнитным полем поля электрического. При этом наличие прово дящего контура, например катушки, не меняет существа дела. Проводник с запасом свободных электронов (или других частиц) лишь позволяет обнаружить возникающее электрическое поле. Поле приводит в движение электроны в проводнике и тем самым обнаруживает себя. Сущность явления электромагнитной индукции в неподвижном проводнике состоит не столько в появлении индукционного тока, сколько в возникновении электрического поля, которое приводит в движение электрические заряды.

Возникающее при изменении магнитного поля электрическое поле имеет совсем другую структуру, чем электростатическое. Оно не связано непосредственно с электрическими зарядами, и его линии напряженности не могут на них начинаться и кончаться. Они вообще нигде не начинаются и не кончаются, а представляют собой замкнутые линии, подобные линиям индукции магнитного поля. Это так называемое вихревое электрическое поле (рис. 247).

Направление его силовых линий совпадает с направлением индукционного тока. Сила, действующая со стороны вихревого электрического поля на заряд по-прежнему равна: Но в отличие от стационарного электрического поля работа вихревого поля на замкнутом пути не равна нулю. Ведь при перемещении заряда вдоль замкнутой линии напряженности

электрического поля (рис. 247) работа на всех участках пути будет иметь один и тот же знак, так как сила и перемещение совпадают по направлению. Работа вихревого электрического поля по перемещению единичного положительного заряда на замкнутом пути представляет собой ЭДС индукции в неподвижном проводнике.

Бетатрон. При быстром изменении магнитного поля сильного электромагнита появляются мощные вихри электрического поля, которые можно использовать для ускорения электронов до скоростей, близких к скорости света. На этом принципе основано устройство ускорителя электронов — бетатрона. Электроны в бетатроне ускоряются вихревым электрическим полем внутри кольцевой вакуумной камеры К, помещенной в зазоре электромагнита М (рис. 248).

Переменное магнитное поле порождает инду­цированное электрическое поле . Если магнитное поле постоянно, то индуциро­ванного электрического поля не возникнет. Следовательно, индуцированное электрическое поле не связано с зарядами , как это имеет место в случае элект­ростатического поля; его силовые линии не начинаются и не заканчиваются на зарядах, а замкнуты сами на себя , подобно силовым линиям магнитного поля. Это означает, что индуцированное электрическое поле , подобно магнитному, является вихревым.

Если неподвижный проводник поместить в переменное магнитное поле, то в нем индуцируется э. д. с. Электроны приводятся в направленное движение электрическим полем, индуцированным переменным магнитном полем; возни­кает индуцированный электрический ток. В этом случае проводник является лишь индикатором индуцированного электрического поля. Поле приводит в движение свободные электроны в проводнике и тем самым обнаруживает себя. Теперь можно утверждать, что и без проводника это поле существует, обладая запасом энергии.

Сущность явления электромагнитной индукции заключается не столько в появлении индуцированного тока, сколько в возникновении вихревого электрического поля.

Это фундаментальное положение электродинамики установлено Максвел­лом как обобщение закона электромагнитной индукции Фарадея.

В отличие от электростатического поля индуцированное электрическое поле является непотенциальным, так как работа, совершаемая в индуцированном электрическом поле, при перемещении единичного положительного заряда по замкнутому контуру равна э. д. с. индукции, а не нулю.

Направление вектора напряженности вихревого электрического поля уста­навливается в соответствии с законом электромагнитной индукции Фарадея и правилом Ленца. Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока.

Так как вихревое электрическое поле существует и в отсутствие проводника, то его можно применять для ускорения заряженных частиц до скоростей, со­измеримых со скоростью света. Именно на использовании этого принципа основано действие ускорителей электронов — бетатронов.

Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.

Отличие вихревого электрического поля от электростатического

1) Оно не связано с электрическими зарядами;
2) Силовые линии этого поля всегда замкнуты;
3) Работа сил вихревого поля по перемещению зарядов на замкнутой траектории не равна нулю.

электростатическое поле	индукционное электрическое поле (вихревое электр. поле)
1. создается неподвижными электр. зарядами	1. вызывается изменениями магнитного поля
2. силовые линии поля разомкнуты — потенциальное поле	2. силовые линии замкнуты — вихревое поле
3. источниками поля являются электр. заряды	3. источники поля указать нельзя
4. работа сил поля по перемещению пробного заряда по замкнутому пути = 0.	4. работа сил поля по перемещению пробного заряда по замкнутому пути = ЭДС индукции

Если замкнутый проводник, находящийся в магнитном поле, неподвижен, то объяснить возникновение ЭДС индукции действием силы Лоренца нельзя, так как она действует только на движущиеся заряды.

Известно, что движение зарядов может происходить также под действием электрического поля Следовательно, можно предположить, что электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле непосредственно порождается переменным магнитным полем. К этому выводу впервые пришел Дж. Максвелл.

Электрическое поле, создаваемое переменным магнитным полем, называется индуцированным электрическим полем . Оно создается в любой точке пространства, где имеется переменное магнитное поле, независимо от того, имеется ли там проводящий контур или нет. Контур позволяет лишь обнаружить возникающее электрическое поле. Тем самым Дж. Максвелл обобщил представления М. Фарадея о явлении электромагнитной индукции, показав, что именно в возникновении индуцированного электрического поля, вызванного изменением магнитного поля, состоит физический смысл явления электромагнитной индукции.

Индуцированное электрическое поле отличается от известных электростатического и стационарного электрического полей.

1. Оно вызвано не каким-то распределением зарядов, а переменным магнитным полем.

2. В отличие от линий напряженности электростатического и стационарного электрического полей, которые начинаются на положительных зарядах и заканчиваются на отрицательных зарядах, линии напряженности индуцированного поля — замкнутые линии . Поэтому это поле — вихревое поле .

Исследования показали, что линии индукции магнитного поля и линии напряженности вихревого электрического поля расположены во взаимно перпендикулярных плоскостях. Вихревое электрическое поле связано с наводящим его переменным магнитным полем правилом левого винта :

если острие левого винта поступательно движется по направлению ΔΒ , то поворот головки винта укажет направление линий напряженности индуцированного электрического поля (рис. 1).

3. Индуцированное электрическое поле не является потенциальным . Разность потенциалов между любыми двумя точками проводника, по которому проходит индукционный ток, равна 0. Работа, совершаемая этим полем при перемещении заряда по замкнутой траектории, не равна нулю. ЭДС индукции и есть работа индуцированного электрического поля по перемещению единичного заряда по рассматриваемому замкнутому контуру, т.е. не потенциал, а ЭДС индукции является энергетической характеристикой индуцированного поля.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н. Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 350-351.

Помимо потенциального кулоновского электрического, существует вихревое поле, в котором имеются замкнутые линии напряженности. Зная общие свойства электрического поля, легче понять природу вихревого. Оно порождается изменяющимся магнитным полем.

Что вызывает индукционный ток проводника, находящегося в неподвижном состоянии? Что такое индукция электрического поля? Ответ на эти вопросы, а также об отличии вихревого от электростатического и стационарного, токах Фуко, ферритах и другом вы узнаете из следующей статьи.

Как меняется магнитный поток

Вихревое электрическое поле, появившееся вслед за магнитным, совсем иного рода, нежели электростатическое. Оно не имеет прямой связи с зарядами, и напряженности на его линиях не начинаются и не заканчиваются. Это замкнутые линии, как у магнитного поля. Поэтому оно и называется вихревое электрическое поле.

Магнитная индукция

Магнитная индукция будет меняться тем быстрее, чем больше напряженность. Правило Ленца гласит: при увеличении магнитной индукции направление вектора напряженности электрополя создает левый винт с направлением другого вектора. То есть при вращении левого винта по направлению с линиями напряженности его поступательное перемещение станет таким же, как и у вектора магнитной индукции.

Если же магнитная индукция будет убывать, то направление вектора напряженности создаст правый винт с направлением другого вектора.

Силовые линии напряженности имеют то же направление, что и индукционный ток. Вихревое электрическое поле действует на заряд с той же силой, что и до него. Однако в данном случае его работа по перемещению заряда является отличной от нуля, как в стационарном электрическом поле. Так как сила и перемещение имеют одно направление, то и работа на всем протяжении пути по замкнутой линии напряженности будет прежней. Работа положительного единичного заряда здесь будет равна электродвижущей силе индукции в проводнике.

Токи индукции в массивных проводниках

В массивных проводниках индукционные токи получают максимальные значения. Это происходит потому, что они имеют малое сопротивление.

Называются такие токи токами Фуко (это французский физик, исследовавший их). Их можно применять для изменения температуры проводников. Именно этот принцип заложен в индукционных печах, к примеру, бытовых СВЧ. Он же применяется для плавления металлов. Электромагнитная индукция используется и в металлических детекторах, расположенных в аэровокзалах, театрах и других общественных местах со скоплением большого количества людей.

Но токи Фуко приводят к потерям энергии для получения тепла. Поэтому сердечники трансформаторов, электрических двигателей, генераторов и других устройств из железа изготавливают не сплошными, а из разных пластин, которые друг от друга изолированы. Пластины должны находиться строго в перпендикулярном положении относительно вектора напряженности, который имеет вихревое электрическое поле. Пластины тогда будут иметь максимальное сопротивление току, а тепла будет выделяться минимальное количество.

Ферриты

Радиоаппаратура функционирует на высочайших частотах, где число достигает миллионов колебаний в секунду. Катушки сердечников здесь не будут эффективны, так как токи Фуко появятся в каждой пластине.

Существуют изоляторы магнитов под названием ферриты. Вихревые токи в них не появятся при перемагничивании. Поэтому потери энергии для тепла сводятся к минимальным. Из них изготавливают сердечники, используемые для высокочастотных трансформаторов, транзисторные антенны и так далее. Их получают из смеси первоначальных веществ, которую прессуют и обрабатывают термическим путем.

Если магнитное поле в ферромагнетике быстро изменяется, это ведет к появлению индукционных токов. Их магнитное поле будет препятствовать изменению магнитного потока в сердечнике. Поэтому поток не будет меняться, а сердечник — перемагничиваться. Вихревые токи в ферритах так малы, что могут быстро перемагничиваться.

Курс по математическому анализу

• 1. Предел числовой последовательности.

• 2. Методы вычисления пределов последовательностей.

• 3. Предел функции в точке.

• 4. Бесконечно малые функции. Сравнение бесконечно малых функций.

• 5. Методы вычисления пределов функций.

• 6. Непрерывность функции в точке, на отрезке.

• 7. Классификация точек разрыва

• 8. Производная, ее вычисление, геометрический смысл.

• 9. Производные сложных, обратных функций.

• 10. Дифференцируемость, дифференциал.

• 11. Производные и дифференциалы высших порядков.

• 12. Исследование функций и построение графиков.

• 13. Кривые на плоскости.

• 14. Формула Тейлора.

• 15. Неопределенный интеграл, простейшие методы интегрирования.

• 16. Интегрирование некоторых классов функций.

• 17. Определенный интеграл. Формула Ньютона-Лейбница.

• 18. Применение определенного интеграла для площадей и длин дуг.

• 19. Несобственные интегралы.

• 20. Числовые ряды.

• 21. Сходимость знакоположительных рядов.

• 22. Сходимость знакопеременных рядов.

• 23. Функциональные ряды, равномерная сходимость.

• 24. Ряд Тейлора.

• 25. Ряд Фурье.

• 26. Сходимость ряда Фурье.

• 27. Функции многих переменных.

• 28. Частные производные, градиент.

• 29. Неявные функции.

• 30. Формула Тейлора для многих переменных.

• 31. Исследование на экстремум.

• 32. Условный экстремум.

• 33. Двойной и тройной интегралы.

• 34. Замена переменных в кратных интегралах.

• 35. Сферические и цилиндрические координаты.

• 36. Поверхностный интеграл по площади поверхности.

• 37. Криволинейный интеграл по длине дуги.

• 38. Скалярное поле.

• 39. Векторное поле.

• 40. Поток векторного поля.

• 41. Формула Остроградского.

• 42. Криволинейный интеграл в векторном поле.

• 43. Формула Стокса.

• 44. Потенциальное поле.

 

 

Наверх

1. Предел числовой последовательности.

Последовательность  — это функция, заданная на множестве натуральных чисел . Число  называется пределом последовательности , если для любого положительного числа , как бы мало оно ни было, существует такой номер, что для всех  c номерами  справедливо неравенство . Неравенство , эквивалентное неравенству , означает, что для любого существует такой номер , что все  c номерами расположены между и . Последовательность, предел которой — конечное число , называется сходящейся, и ее предел обозначают. Если изобразить элементы последовательности на плоскости точками с координатами  , то неравенства означают, что все точки  с номерами расположены между параллельными оси абсцисс прямыми и .

 

Бесконечно малая последовательность. Последовательность  , предел которой равен нулю , называется бесконечно малой.   

Бесконечно большая последовательность. Последовательность называется бесконечно большой, если для любого положительного числа  , как бы велико оно ни было, существует такой номер  , что для всех с номерамисправедливо неравенство  , записываем .

 

 

Наверх

2. Методы вычисления пределов последовательностей.

Пусть заданы две последовательности  и . Если существуют  и , то существуют и пределы суммы и произведения последовательностей, а при и предел частного, причем   ,        ,  . Для правильного применения этих теорем очень важно существование пределов каждой последовательности.

Неопределенности и их раскрытие.

Если    и  , то может существовать  . В этом случае говорят, что имеем неопределенность типа  . Также может существовать   , в этом случае имеем неопределенность типа  . Если   и  , то может существовать . В этом случае говорят, что имеем неопределенность типа   . Поскольку в перечисленных случаях не применимы теоремы о пределе суммы, произведения и частного, используют другие способы вычисления, которые называют методами раскрытия неопределенностей. Это, как правило, алгебраические преобразования, приводящие выражения к виду, при котором можно пользоваться упомянутыми теоремами.

 

 

Наверх

3. Предел функции в точке.

 

Рассмотрим функцию , определенную в некоторой окрестности точки  , , , за исключением, быть может, самой точки  . Число  называется пределом функции  при , стремящемся к , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число  , что для всех   , удовлетворяющих неравенству  , справедливо неравенство . Говорят “предел функции  в точке  ” и обозначают  . Неравенство  для всех , эквивалентное неравенствам , , означают, что для любого существует такое , что для  график функции   расположен на плоскости в прямоугольнике . При вычислениях на компьютере мы имеем дело с дискретными значениями переменных. Поэтому удобнее пользоваться другим, эквивалентным приведенному, определением предела. А именно:  , если для любой, сходящейся к  последовательности значений аргумента , соответствующая последовательность значений функции  сходится к числу . Отсюда следует, в частности, что для любого существует такое , что для любой последовательности , сходящейся к , точки с координатами  находятся на плоскости внутри прямоугольника   . 

Бесконечно большие функции.

Если для любой последовательности  значений аргумента соответствующая последовательность значений функции бесконечно большая, то функция называется бесконечно большой в точке . Если  бесконечно большая в точке , то для любого положительного числа , как бы велико оно ни было, существует такое число , что для всех , удовлетворяющих неравенству , справедливо неравенство ; обозначают  .

 

 

Наверх

4. Бесконечно малые функции. Сравнение бесконечно малых функций.

Рассмотрим функцию, определенную в некоторой окрестности точки , ,  за исключением, быть может, самой точки . Функция  называется бесконечно малой при , стремящемся к , если . Если — бесконечно малая в точке , то для любого положительного числа , как бы мало оно ни было, существует такое положительное число  , что для всех , удовлетворяющих неравенству , справедливо неравенство . Неравенства  для всех , эквивалентные неравенствам , , означают, что для любого существует такое , что для график функции расположен на плоскости в прямоугольнике . Важно, что слова “за исключением, быть может, самой точки ” означают, что нас не интересует сама эта точка. Это можно понять, если рассмотреть функцию.  При x, стремящемся к нулю, функция-таки стремится к нулю, независимо от того, какое значение она принимает в точке x=0. Следовательно, предел равен нулю и функция является бесконечно малой.   

Сравнение бесконечно малых функций.

Пусть и  — две функции, бесконечно малые в точке . Если , то говорят, что  более высокого порядка малости, чем и обозначают . Если же , то  более высокого порядка малости, чем ; обозначают . Бесконечно малые функции  и называются бесконечно малыми одного порядка малости, если  , обозначают  .  И, наконец, если   не существует, то бесконечно малые функции и  несравнимы.   

Эквивалентные бесконечно малые функции.

Если , то бесконечно малые функции и  называются эквивалентными, обозначают ~ .

 

 

Наверх

5. Методы вычисления пределов функций.

Пусть заданы две функции и . Если существуют  и  , то существуют и пределы суммы и произведения этих функций, а при и предел частного, причем        

,

,      

 .

Для правильного применения этих теорем очень важно существование пределов каждой функции. Не трудно доказать, что предел постоянной функции равен этой постоянной, то есть   . Из приведенных формул следует полезное утверждение: 

 , то есть постоянный множитель можно выносить за знак предела. Если сделать замену переменной , то вычисление предела при  всегда можно свести к вычислению предела при . Из определения непрерывной функции следует, что ее предел совпадает со значением функции в этой точке. Доказывают, что все элементарные функции непрерывны в области определения, поэтому, если функция определена, то вычисление предела сводится к применению указанных теорем и подстановке  в выражение для функции. 

 

Неопределенности и их раскрытие.

Существуют случаи, когда не применимы теоремы о пределах суммы, произведения, частного, но предел существует и может быть вычислен. Если  и   , то может существовать . В этом случае говорят, что имеем неопределенность типа . Также может существовать   , в этом случае имеем неопределенность типа   . Если   и   , то может существовать  .   В этом случае говорят, что имеем неопределенность типа . Если     и   , то может существовать  — неопределенность типа  . Рассматривают также неопределенности типа , и т. д. Основным признаком неопределенности является невозможность корректного вычисления функции простой подстановкой в выражение для функции. Полезно запомнить замечательные пределы: 

      (е = 2.71828… — основание натуральных логарифмов) — неопределенность типа .

       — неопределенность типа .

Использование эквивалентных бесконечно малых.

Если мы имеем неопределенность типа    , то это означает, что мы вычисляем предел отношения двух бесконечно малых функций. Напомним, что функция называется бесконечно малой, если ее предел в точке  равен нулю. Пусть, , ,  — бесконечно малые функции при  , причем эквивалентна  , т.е. ~ , ~ (напомним, что две бесконечно малых называются эквивалентными, если предел их отношения равен 1). Тогда, т.е. при вычислении пределов отношений бесконечно малых любую из них можно заменять на эквивалентную. 

Правило Лопиталя.

Неопределенности типа  или удобно раскрывать с помощью правила Лопиталя. Пусть  и  две бесконечно малые или бесконечно большие функции при  и существует предел отношения их производных при . Тогда  . Если в результате применения правила Лопиталя снова получится неопределенность, то его можно применить еще раз. 

 

Формула Тейлора.

Пусть функция имеет в точке  производные всех порядков до -го включительно. Тогда для    справедлива формула Тейлора:

где  называется остаточным членом формулы Тейлора.

 

 

Наверх

6. Непрерывность функции в точке, на отрезке.

Рассмотрим функцию , определенную на некотором промежутке . Функция  непрерывна в точке , если предел функции в точке  равен значению функции в этой точке,. 

Свойства функций, непрерывных на отрезке.

Функция, непрерывная в каждой точке промежутка , называется непрерывной на промежутке. Для функции, непрерывной на отрезке , справедливы следующие утверждения. 

Функция, непрерывная на отрезке  , достигает на нем своих наибольшего и наименьшего значений, т.е. на отрезке  существуют точки  такие, что

. 

Если функция  непрерывна на отрезке  и принимает на концах значения разных знаков, то на интервале  существует точка   , в которой функция обращается в нуль, т.е.   . Это утверждение применяют для отделения корней уравнений  с непрерывной левой частью — если найден отрезок, на концах которого функция принимает значения разных знаков, то можно утверждать, что на этом отрезке есть хотя бы один корень уравнения.

Если функция   непрерывна на отрезке    , дифференцируема хотя бы на интервале  , то на интервале  существует точка , такая, что  . Это свойство называют формулой Лагранжа или формулой конечных приращений.

 

 

Наверх

7. Классификация точек разрыва

Рассмотрим функцию  , определенную на некотором промежутке . Функция непрерывна в точке , если предел функции в точке  равен значению функции в этой точке, . 

Односторонние пределы функции в точке.

Функция, непрерывная в каждой точке промежутка , называется непрерывной на промежутке. Если функция определена на промежутке , , то при исследовании поведения функции в окрестности точки  имеет смысл говорить о пределе функции  в точке  справа, а при исследовании в окрестности точки — о пределе функции в точке  слева. Число называется пределом справа функции при , стремящемся к , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число  , что для всех  , удовлетворяющих неравенству , справедливо неравенство  . Говорят “предел справа функции в точке ” и обозначают . Аналогично говорят “предел слева функции в точке ” и обозначают , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число , что для всех , удовлетворяющих неравенству , справедливо неравенство  . Для существования предела функции в точке, необходимо и достаточно, чтобы существовали и совпадали односторонние пределы функции в этой точке. По той же схеме вводится понятие непрерывности слева и непрерывности справа. Функция, определенная на отрезке , , непрерывна справа в точке , если и непрерывна слева в точке  , если. Для того чтобы функция была непрерывна в точке  необходимо и достаточно, чтобы односторонние пределы функции в точке совпадали со значением функции в этой точке:. Если хотя бы одно из равенств нарушается, говорят о разрыве в точке . 

Классификация разрывов.

Если хотя бы одно из равенств  нарушается, говорят о разрыве в точке . Если  и односторонние пределы конечны, то разрыв в точке называется устранимым. Если и оба односторонние пределы конечны, то говорят о скачке функции в точке . Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.

 

 

Наверх

8. Производная, ее вычисление, геометрический смысл.

Производная функции в точке — Пусть функция  определена на промежутке . Точка — произвольная точка из области определения функции,   — приращение функции в точке , вызванное приращением независимой переменной .  Производной функции по независимой переменной  в точке ,  называется предел отношения приращения функции к приращению  при стремлении  к нулю, т.е.   

,  

— производная функции в точке . 

Односторонние производные — Если определена при , то можно определить правую производную функции в точке :

Аналогично, если  определена при , определяется левая производная функции в точке :

 Функция  имеет в точке  производную тогда и только тогда, когда в точкесовпадают ее левая и правая производные:  .  

Секущая графика функции — Пусть — функция, определенная на промежутке . Прямая, проходящая через точки , , ,  называется секущей графика функции  . Угловой коэффициент  секущей равен   и ее уравнение имеет вид  . 

Касательная и нормаль к графику функции — Касательной к графику функции  в точке  называется предельное положение секущей, проходящей через точки  , , когда . Угловой коэффициент касательной равен значению производной в точке и ее уравнение имеет вид . Нормалью к графику функции  в точке называется прямая , проходящая через эту точку перпендикулярно касательной. Угловой коэффициент нормали равен    и ее уравнение имеет вид  .

 

 

Наверх

9. Производные сложных, обратных функций.

Пусть    — функция, дифференцируемая в точке  ,   — функция, дифференцируемая в точке   , причем  . Тогда   — сложная функция независимого переменного , дифференцируема в точке    и ее производная в этой точке вычисляется по формуле   .

Обычно    называют внешней функцией, а — внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции. 

Производная обратной функции.

Пусть функция дифференцируема и строго монотонна на . Пусть также в точке производная . Тогда в точке   определена дифференцируемая функция , которую называют обратной к  , а ее производная вычисляется по формуле .

 

 

Наверх

10. Дифференцируемость, дифференциал.

Дифференцируемость функции в точке.

Пусть функция  определена в некоторой окрестности точки  . Рассмотрим приращение функции в этой точке:  . Функция называется дифференцируемой в точке , если ее приращение можно записать в виде , где — приращение независимой переменной, А – постоянная, не зависящая от , — бесконечно малая функция при . 

Дифференциал функции.

Дифференциалом функции  в точке называется линейная по  часть приращения . Дифференциал обозначается   , то есть  . Рассматривая функцию , нетрудно убедиться, что  , если  — независимая переменная. 

Связь дифференциала и производной.

Воспользуемся определением производной для дифференцируемой функции в точке : . Таким образом, дифференциал функции выражается формулой  , то есть для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на  . Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке существовала конечная производная. 

 

 

Наверх

11. Производные и дифференциалы высших порядков.

Производные высших порядков.

Рассмотрим функцию  , определенную на некотором промежутке   . Вычислим производную , которая также является функцией на . Производной второго порядка от функции  называется производная от ее производной:   . Аналогично определяют производную любого порядка:  .  

Дифференциалы высших порядков.

Рассмотрим дифференциал функции  в произвольной точке промежутка : . Здесь  — приращение независимой переменной, которое является числом и не зависит от . Сам же дифференциал есть функция от , и можно вычислить дифференциал от этой функции:   При  этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле Аналогично вычисляется дифференциал любого порядка .

Понятие инвариантности формы дифференциала.

Рассмотрим дифференциал функции  в произвольной точке промежутка : . Здесь — приращение независимой переменной, которое является числом и не зависит от . Пусть теперь   — функция независимого переменного , определенная на промежутке  . Тогда  — сложная функция переменного . Вычислим ее дифференциал, используя формулу для производной сложной функции: . Заметим, что и выражение для дифференциала принимает ту же форму , хотя здесь  уже функция переменного  . Это свойство дифференциала первого порядка называется инвариантностью (т. е. неизменностью) его формы. При вычислении дифференциала второго порядка придется учитывать, что  — функция переменного  . Поэтому и форма второго (а также и всех следующих) дифференциала неинвариантна.

 

 

Наверх

12. Исследование функций и построение графиков.

Рассмотрим функцию , определенную на промежутке (возможно,  ) . Характер поведения функции в области определения можно исследовать, опираясь на следующие утверждения. 

Если , то график функции пересекает ось абсцисс в точке  . 

Если , то график функции пересекает ось ординат в точке  .

Если в точке  функция имеет бесконечный разрыв, то график функции имеет вертикальную асимптоту  (Если расстояние от точки кривой до некоторой определенной прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой. В случае бесконечного разрыва расстояние от кривой до вертикальной асимптоты стремится к нулю при справа, слева или с обеих сторон). 

Если , или , существуют и конечны пределы и , то прямая — асимптота графика функции.  

Если , то график функции имеет на левой границе области сходимости вертикальную асимптоту  ; аналогично, если , то график функции имеет на правой границе области сходимости вертикальную асимптоту . 

Если и существует такое число , что для любого , то исследуемая функция периодична с периодом ; в этом случае достаточно построить график функции на промежутке  и доопределить его по периодичности на всю числовую ось.

Если , то исследуемая функция четная; этом случае график симметричен относительно оси ординат; достаточно построить график функции на промежутке и отобразить его симметрично относительно оси ординат на . 

Если  , то исследуемая функция нечетная; этом случае график симметричен относительно начала координат; достаточно построить график функции на промежутке  и отобразить его симметрично относительно начала координат на . 

Исследование функций с помощью производной.

Если функция дифференцируема на промежутке , за исключением, быть может, конечного числа точек этого промежутка, то можно дополнить изучение поведения функции исследованием на экстремум (точки максимума и точки минимума функции имеют общее название — точки экстремума), используя следующие утверждения.  

Для того, чтобы дифференцируемая на функция не убывала (не возрастала) на этом промежутке, необходимо и достаточно, чтобы () на . 

Пусть в точке  производная  или не существует. Если существует окрестность точки , такая, что для  из этой окрестности при  и при , то функция имеет в точке максимум. Если же при  и  при  , то функция имеет в точке  минимум (в этом случае говорят, что “производная меняет знак при переходе через точку ”).

Если непрерывная в точке функция дифференцируема на , при этом на  и на , то функция имеет в точке максимум; если же при  и  при , то функция имеет в точке  минимум.   

Исследование функций с помощью второй производной.

Если функция дважды дифференцируема на промежутке , за исключением, быть может, конечного числа точек этого промежутка, то исследование поведения функции можно дополнить исследованием выпуклости и вогнутости.

График функции называется выпуклым (выпуклым вниз) на промежутке , если он расположен выше касательной, проведенной в любой точке , . Если же график функции лежит ниже касательной, — то он называется вогнутым (выпуклым вверх). 

Если дважды дифференцируемая на промежутке  функция имеет на нем положительную вторую производную, то функция выпуклая на . Если же вторая производная отрицательна на промежутке , то функция на нем вогнута. 

Если вторая производная равна нулю в точке , а слева и справа от нее имеет значения разных знаков, точка  — точка перегиба.

 

 

Наверх

13. Кривые на плоскости.

Кривые на плоскости в декартовых координатах.

Кривая на плоскости в прямоугольных (декартовых) координатах — это множество точек, координаты которых связаны соотношениями , , , или ; первые два соотношения задают кривую явно, последнее — неявно. Кривая, заданная уравнением  , , называется гладкой, если функция дифференцируема на промежутке . В каждой точкегладкой кривой можно провести касательную , уравнение которой . Уравнение нормали в той же точке имеет вид  или  . Кривая, заданная неявно уравнением , называется гладкой, если на ней нет особых точек (точка линии называется особой, если в ней одновременно обращаются в нуль обе частные производные функции : ). Уравнения касательной и нормали к такой кривой, проходящих через точку , , имеют соответственно вид   и

Кривые, заданные параметрически.

Уравнения , , устанавливающие зависимость декартовых координат точки плоскости от значения параметра , определяют на плоскости кривую, заданную в параметрической форме (говорят еще — заданную параметрически). Поскольку производная функции , заданной параметрически уравнениями , в точке, которая не является особой точкой кривой, вычисляется по формуле , то уравнения касательной и нормали к кривой, проходящих через точку , имеют соответственно вид: .   

Кривые в полярных координатах.

Декартовы координаты точки  на плоскости связаны с полярными координатамисоотношениями . Многие кривые на плоскости удобно описывать как функции радиуса-вектора и полярного угла — в полярных координатах. Так, уравнение единичной окружности в полярных координатах имеет вид  . Уравнение кривой в полярных координатахобычно имеет вид . Угловой коэффициент касательной к графику функции, заданной уравнением , в точке   равен   , а декартовы координаты точки равны соответственно  и   .

 

 

Наверх

14. Формула Тейлора.

Остаточный член формулы Тейлора — Пусть функция имеет в точке  производные всех порядков до -го включительно. Тогда для справедлива формула Тейлора:

 ,

где ,  называется остаточным членом формулы Тейлора в форме Пеано; — бесконечно малая более высокого порядка малости, чем . Если отбросить остаточный член, то получится приближенная формула Тейлора

 

,

правая часть которой называется многочленом Тейлора функции ; его обозначают . Приближенная формула позволяет заменять в различных математических расчетах (аналитических и численных) произвольную функцию ее многочленом Тейлора. 

Из формулы Тейлора видно, что чем точка  ближе к точке , тем выше точность такой аппроксимации и эта точность растет с ростом степени многочлена. Это означает, в свою очередь, что чем больше производных имеет функция в некоторой окрестности точки , тем выше точность, с которой многочлен Тейлора аппроксимирует функцию в этой окрестности.  

Разложение основных элементарных функций — Положив  и вычислив соответствующие производные в нуле, получим формулы Тейлора для основных элементарных функций: 

• ; 

• ;

• ;

• ;

• ; 

•  ; 

• .

Разложение функций с использованием стандартных разложений — Для разложения по формуле Тейлора функции в окрестности произвольной точки необходимо сделать замену переменной , то есть  , и воспользоваться одним из приведенных выше разложений основных функций в окрестности точки  .

 

 

Наверх

15. Неопределенный интеграл, простейшие методы интегрирования.

Первообразная и неопределенный интеграл — Рассмотрим функцию , определенную на промежутке (здесь возможно ). Дифференцируемая на промежутке     функция , производная которой в каждой точке равна , называется первообразной функции  : . Поскольку  , то можно говорить о семействе первообразных — множестве функций вида  , . Семейство первообразных   функции называется неопределенным интегралом функции  и обозначается символом : для всех . Здесь    — знак интеграла, — подынтегральное выражение,  — подынтегральная функция,  — переменная интегрирования, — значение неопределенного интеграла, семейство первообразных функции , . То есть производнаянеопределенного интеграла равна подынтегральной функции. Наоборот,    , следовательно, дифференцирование и вычисление неопределенного интеграла, – взаимно обратные операции. Не представляет труда с помощью таблицы производных составить таблицу неопределенных интегралов. Важным свойством неопределенного интеграла является линейность: , здесь    — постоянные. Вычисление неопределенного интеграла обычно сводится к преобразованию подынтегрального выражения так, чтобы можно было воспользоваться таблицей интегралов. 

Интегрирование заменой переменной — Если — непрерывно дифференцируемая функция, то, полагая   , получим формулу интегрирования заменой переменной    . Если замена переменной выбрана правильно, то интеграл в правой части должен легко вычисляться. Для некоторых классов функций существуют стандартные замены, сводящие интеграл к табличному. 

Интегрирование по частям — Пусть   — непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям . Название “по частям” связано с тем, что для записи интеграла в правой части нужно проинтегрировать “часть”     подынтегрального выражения в левой части. Метод интегрирования по частям используется для интегралов вида   ,  ,  ,  и некоторых других.

 

 

Наверх

16. Интегрирование некоторых классов функций.

Интегрирование рациональных функций — Функция называется рациональной, если она вычисляется с помощью четырех арифметических действий, то есть в общем случае является частным от деления двух многочленов: . Если , рациональная дробь называется правильной. Неопределенный интеграл от рациональной функции всегда можно вычислить. Для этого: 

Если , выделяем целую часть рациональной дроби с помощью деления многочлена на многочлен. Правильную рациональную дробь (или правильный остаток от деления) раскладываем на простейшие дроби. Вид разложения определяется корнями многочлена   , а именно: 

Каждому действительному корню кратности 1 в разложении соответствует член   . 

Каждому действительному корню  кратности  в разложении соответствует набор из  членов     . 

Каждой паре комплексно сопряженных корней   кратности 1 в разложении соответствует член    ( — корни уравнения ).

Каждой паре комплексно сопряженных корней кратности  в разложении соответствует набор из членов       . 

В приведенных выражениях — неопределенные коэффициенты, которые можно найти, приводя разложение обратно к общему знаменателю , приравнивая полученные коэффициенты при степенях   к соответствующим коэффициентам  и решая систему относительно  . 

Наконец, полученное разложение интегрируем почленно. 

Интегрирование тригонометрических функций — Интегралы вида , где  — рациональная функция своих аргументов, вычисляются с помощью универсальной замены переменной  . При этом . Однако универсальная замена обычно связана с большими вычислениями, поэтому в некоторых случаях можно ее избежать.  

Интегралы вида   вычисляются с помощью замены  . Интегралы вида  вычисляются с помощью замены  . Интегралы вида  , если , то есть четная рациональная функция своих аргументов вычисляются с помощью замены    . 

Интегралы вида  вычисляются с помощью формул понижения степени  . 

Интегрирование иррациональных функций — Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен. 

Интегралы вида , где  — рациональная функция своих аргументов, вычисляются заменой . 

Интегралы вида   вычисляются заменой или . 

Интегралы вида   вычисляются заменой   или . Интегралы вида вычисляются заменой или .

 

 

Наверх

17. Определенный интеграл. Формула Ньютона-Лейбница.

Определенный интеграл, его геометрический смысл.

Рассмотрим функцию , определенную на промежутке . Разобьем промежуток на  произвольных частей точками   и обозначим , , . На каждом промежутке    возьмем произвольную точку  и вычислим в ней значение функции. Выражение   называется интегральной суммой функции на  .Если при  существует и конечен предел последовательности частичных сумм  , не зависящий ни от способа разбиения промежутка  точками  , ни от выбора , то этот предел называют определенным интегралом от функции по промежутку , а саму функцию — интегрируемой на . Обозначают    . 

Из приведенного определения естественно следует геометрический смысл определенного интеграла: если , то   равен площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми . 

Формула Ньютона-Лейбница.

Значение определенного интеграла может быть вычислено по формуле Ньютона-Лейбница =, здесь символ  означает, что из значения  при верхнем пределе b нужно вычесть значение при нижнем пределе a , — первообразная функция для . Таким образом, вычисление определенного интеграла сводится к нахождению первообразной, то есть неопределенного интеграла.  

Методы вычисления определенного интеграла.

Если — непрерывно дифференцируемая на отрезке  функция, , и , когда  изменяется на  , то, положив  , получим формулу замены переменной в определенном интеграле  .

Пусть  — непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям   . Эта формула применяется для тех же классов функций, что и при вычислении неопределенного интеграла.

 

 

Наверх

18. Применение определенного интеграла для площадей и длин дуг.

Вычисление площадей и длин дуг кривых в декартовых координатах.

Пусть на плоскости задана область, ограниченная снизу кривой  , заданной в декартовых координатах, сверху – кривой  , слева – прямой   (ее может и не быть, если  ), справа – прямой  . Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле   . Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например, , то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия. 

Пусть на отрезке  уравнением  задана плоская кривая. Ее длина вычисляется по формуле  

Вычисление площадей и длин дуг при параметрическом задании кривых.

Если область на плоскости снизу ограничена кривой, заданной параметрически, то есть   , при этом  , а сверху – кривой   . Тогда площадь такой плоской фигуры вычисляем по формуле . Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что  . 

Пусть кривая на плоскости задана параметрически   . Тогда длина этой кривой вычисляется по формуле  .

Вычисление площадей и длин дуг кривых в полярных координатах.

Когда кривая, ограничивающая область, задана в полярных координатах , то площадь этой области вычисляем по формуле  . Основная трудность в использовании этой формулы заключается в определении пределов интегрирования  . Здесь нужно понимать, что кривая  определена только, если . Поскольку в формуле присутствует , то она учтет и не существующую площадь, когда  . Решив уравнение , найдем пределы интегрирования. 

Если кривая, ограничивающая область, задана в полярных координатах  , то ее длина вычисляется по формуле . Пределы интегрирования определяются из тех же соображений, что и при вычислении площади.

 

 

Наверх

19. Несобственные интегралы.

Интеграл как функция верхнего предела.

Для функции , интегрируемой для всех  , значение интеграла  зависит от значения верхнего предела ; можно рассмотреть функцию переменной : каждому значению ставится в соответствие число, равное значению интеграла  . Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела: ; функция определена в области интегрируемости подынтегральной функции . Если — первообразная для , то значение можно вычислить по формуле Ньютона—Лейбница: . Функцию можно исследовать, не вычисляя первообразной. Для интегрируемой при функции справедливы следующие утверждения:   непрерывна на промежутке , причем ; если при , то     монотонно возрастает на промежутке ; если непрерывна при , то дифференцируема на промежутке , причем .  

Несобственные интегралы по неограниченному промежутку.

Пусть функция  интегрируема для всех  и   . Если существует предел , то этот предел называют несобственным интегралом по неограниченному промежутку и обозначают его  . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле . Аналогично определен интеграл для интегрируемой при  функции  и интеграл для функции , интегрируемой на . Если рассмотренные пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится. 

Несобственные интегралы от неограниченных функций.

Пусть функция  интегрируема на любом отрезке, целиком содержащемся в промежутке, и бесконечно большая в точке . Если существует предел , то этот предел называют несобственным интегралом от неограниченной функции по и обозначают его . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле . Аналогично определен интеграл от интегрируемой на любом конечном отрезке, содержащемся в , бесконечно большой в точке  функции . Если пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится. 

Исследование несобственных интегралов на сходимость.

Вычисление несобственных интегралов сводится к вычислению первообразной, использованию формулы Ньютона-Лейбница и вычислению предела. Каждый из этапов сам по себе достаточно сложен, и разумно приступать к ним, если есть уверенность, что интеграл сходится, то есть предел конечен. Поэтому, в конечном счете, самым важным в теории несобственных интегралов является исследование их на сходимость: если интеграл расходится, то его и вычислять не надо. Одним из главных инструментов исследования несобственных интегралов на сходимость являются теоремы сравнения.

Рассмотрим две неотрицательные функции  и , определенные при . Пусть  для всех  , начиная с некоторого числа . Тогда, если сходится интеграл от большей функции , то сходится и интеграл от меньшей, то есть. Если расходится интеграл от меньшей функции  ,то расходится и интеграл от большей — .  

Если   , то несобственные интегралы от этих функций или оба сходятся или оба расходятся. 

Аналогичные утверждения, которые называют признаками сравнения, имеют место и для интегралов по конечному промежутку от неограниченных функций.

 

 

Наверх

20. Числовые ряды.

Числовой ряд. Рассмотрим произвольную числовую последовательность и формально составим сумму ее членов    Это выражение называют числовым рядом, или просто рядом. Члены последовательности называют членами ряда. Конечно, невозможно вычислить сумму бесконечного числа слагаемых, но легко вычислить сумму первых n членов ряда . Эта сумма называется n-ой частичной суммой. 

 

Сходимость числового ряда. Ряд    называют сходящимся, если существует и конечен предел последовательности     частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают   , . Если предел частичных сумм не существует или бесконечен, то ряд расходится. Разность  называется остатком ряда. Очевидно, что для сходящегося ряда    . Это означает, что сумму сходящегося ряда можно вычислить с любой точностью, заменяя ее частичной суммой соответствующего порядка. Для расходящегося ряда это не так. Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования. Если ряд сходится, то  (необходимое условие сходимости ряда). Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом может расходиться. 

 

 

Суммирование числовых рядов. Если возможно найти общий член последовательности    , то по определению можно найти и сумму ряда, вычисляя предел этой последовательности.

 

 

Наверх

21. Сходимость знакоположительных рядов.

Теоремы сравнения.

1. Рассмотрим два числовых ряда с неотрицательными членами   и  , . Если при всех n, начиная с некоторого номера,  , то из сходимости ряда  следует сходимость ряда. Наоборот, из расходимости ряда следует расходимость ряда. 

2. Если для таких же двух рядов   , то оба ряда или сходятся или расходятся одновременно. При использовании теорем сравнения нужно иметь ряд-эталон, с которым сравнивать и про сходимость которого известно заранее. В качестве таких рядов чаще всего берут обобщенный гармонический ряд   , который сходится при и расходится при , или геометрический ряд , который сходится при  и расходится при  . 

Признаки сходимости. Признаки сходимости Даламбера. Для ряда с положительными членами , вычислим   . Если , то ряд сходится, — расходится. При признак Даламбера ответа не дает: ряд может как сходиться, так и расходиться. 

Признак сходимости Коши. Для ряда с неотрицательными членами   , вычислим . Если   , то ряд сходится, — расходится. При    признак Коши ответа не дает: ряд может как сходиться, так и расходиться.

 

 

Наверх

22. Сходимость знакопеременных рядов.

Абсолютная и условная сходимость. Если в последовательности  бесконечно много положительных и отрицательных членов, то ряд называется знакопеременным. Ряд   называется знакочередующимся. Знакопеременный ряд   называется абсолютно сходящимся, если сходится ряд   . Если ряд из модулей расходится, а сам ряд сходится, то его называют условно сходящимся. Исследование знакопеременного ряда   начинают с исследования на сходимость ряда из модулей  методами для рядов с неотрицательными членами. Если такой ряд сходится, то получен ответ: ряд сходится абсолютно. 

 

Исследование знакочередующихся рядов. Если ряд из модулей расходится, то для знакочередующегося ряда можно применить признак Лейбница: если последовательность   стремится к нулю, монотонно убывая,   , то ряд    сходится, по крайней мере, условно. Для знакочередующегося ряда очень просто оценивается остаток ряда: .

 

 

Наверх

23. Функциональные ряды, равномерная сходимость.

Функциональный ряд, его сходимость. Рассмотрим ряд,   , членами которого являются функции, определенные на промежутке   . При каждом фиксированном   имеем числовой ряд, сходимость которого может быть исследована рассмотренными ранее методами. Сумма функционального ряда   также является функцией от х:   . По определению предела последовательности: если для   можно указать номер  ( что интересно, для каждого фиксированного   — свой номер, т.е.  ), такой, что для    выполняется неравенство  , то это и означает, что функциональный ряд сходится к функции. Множество , для которого это выполняется, называется областью сходимости функционального ряда. 

 

Равномерная сходимость функционального ряда. Пусть   , т.е. функциональный ряд сходится. Если для   можно указать номер  независимо от  , такой, что для выполняется неравенство  , то говорят, что функциональный ряд сходится равномерно на множестве .   

  

Исследование на равномерную сходимость. Признак Вейерштрасса равномерной сходимости функционального ряда: если существует сходящийся числовой ряд   с положительными членами, такой, что для всех  , начиная с некоторого номера и всех  выполняется неравенство , то функциональный ряд   сходится на равномерно. Числовой ряд   в этом случае называют мажорантой для функционального ряда.

 

 

Наверх

24. Ряд Тейлора.

Степенные ряды. Функциональный ряд     , где — числовая последовательность, называется степенным рядом. Степенной ряд сходится на интервале   с центром в точке   . Число  — радиус сходимости степенного ряда может быть вычислено по формулам , или     . Степенной ряд сходится равномерно на любом отрезке, целиком лежащем внутри интервала сходимости. Сходимость степенного ряда на границах интервала сходимости необходимо исследовать специально для конкретного ряда. 

 

Разложение функций в ряд Тейлора. При исследовании свойств бесконечно дифференцируемых функций изучают их степенные ряды ряды Тейлора. Пусть функция   определена в некоторой окрестности точки   и имеет в этой точке производные всех порядков. Ряд 

называется рядом Тейлора для функции    в точке . При такой ряд называют также рядом Маклорена:    . Функция  может быть разложена в степенной ряд на интервале , если существует степенной ряд, сходящийся к  на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки , то это ряд Тейлора. Пусть функция   бесконечно дифференцируема на интервале и все ее производные ограничены в совокупности на этом интервале, то есть существует число   , такое, что для всех    и для всех   справедливо неравенство . Тогда ряд Тейлора сходится к   для всех   . Приведем разложения в ряд Тейлора для основных элементарных функций. 

 

 

Наверх

25. Ряд Фурье.

Ряд Фурье, его сходимость. Пусть функция  абсолютно интегрируема на отрезке  , то есть существует   . Тогда ей можно поставить в соответствие ее тригонометрический ряд Фурье: . Коэффициенты тригонометрического ряда Фурье называют коэффициентами Фурье и вычисляют по формулам Эйлера-Фурье: . Если функция  кусочно-гладкая на отрезке , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если   — сумма ряда Фурье, то для любого        . То есть, если   непрерывна в точке  , то   . Если в точке   у   разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке . 

  

Разложение в ряд Фурье на произвольном отрезке. Для кусочно-гладкой на отрезке  функции задача о разложении в ряд Фурье на этом отрезке линейной заменой сводится к задаче о разложении функции на отрезке  :   , .

 

 

Наверх

26. Сходимость ряда Фурье.

Сходимость ряда Фурье, явление Гиббса. Если функция  кусочно-гладкая на отрезке , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если — сумма ряда Фурье, то для любого  . То есть, если  непрерывна в точке  , то  . Если в точке  у     разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке  . В окрестности точек непрерывности функции   разность между значением функции в точке и значением частичной суммы ряда в этой точке стремится к нулю при  , что полностью соответствует теории, поскольку в этом случае   . В окрестности точек разрыва   частичные суммы ряда Фурье ведут себя иначе. Эта особенность поведения частичных сумм Фурье в окрестности точек разрыва называется явлением Гиббса. Оно состоит в том, что для некоторых функций в точке ее скачка      существуют такие значения    , что

Это не противоречит теории, поскольку у Гиббса рассмотрен предел  , а в теории v     . 

Приближение функций, минимальное свойство коэффициентов Фурье. Функция , где    — произвольные числа, называется тригонометрическим многочленом. Тригонометрическим многочленом наилучшего приближения n-ой степени для функции     на отрезке   называется такой многочлен , среднеквадратичное отклонение  которого от функции  минимально:    . Для любой ограниченной интегрируемой на    функции частичная сумма   ее ряда Фурье является тригонометрическим многочленом наилучшего приближения n-ой степени. 

 

Зависимость скорости сходимости от гладкости функций. Скорость сходимости ряда Фурье функции зависит от ее гладкости (количества непрерывных производных). Если   непрерывно дифференцируема r раз на отрезке   , то справедливо неравенство , где  . Для среднеквадратичного отклонения справедлива оценка   , где  .

 

 

Наверх

27. Функции многих переменных.

Функция двух переменных. Переменная  (с областью изменения  ) называется функцией независимых переменных  в множестве  , если каждой паре их значений из   по некоторому правилу или закону ставится в соответствие одно определенное значение   из множества . Множество v область определения функции, множество   v область ее значений. Функциональная зависимость   от обозначается так:  и т.п. Выберем в пространстве систему координат  , изобразим на плоскости   множество  ; в каждой точке этого множества восстановим перпендикуляр к плоскости и отложим на нем значение . Геометрическое место полученных таким образом точек и является пространственным графиком функции двух переменных. 

Линии и поверхности уровня. Линией уровня функции двух переменных   называется геометрическое место точек на плоскости   , в которых функция    принимает одно и то же значение. Линии уровня функции определяются уравнением  , где . Изучая линии уровня функции, можно исследовать характер ее изменения, не прибегая к пространственному графику. Поверхностью уровня функции трех переменных    называется геометрическое место точек в пространстве, в которых функция  принимает одно и то же значение. Уравнение поверхностей уровня имеет вид:  . Поскольку график функции трех переменных нам недоступен, поверхности уровня являются единственным средством изучения таких функций. 

  

Локальные экстремумы. Точка называется точкой локального минимума (максимума) функции , определенной в области , если существует окрестность этой точки, такая, что  для всех точек этой окрестности, отличных от . Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства.

 

 

Наверх

28. Частные производные, градиент.

Частные производные. Пусть  — функция двух переменных, определенная в некоторой окрестности точки . Если существует конечный предел   , то говорят, что функция   имеет в точке частную производную по переменной   . Аналогично определяется частная производная по    . Обозначают:

 . 

Пусть — функция n переменных, определенная в области   n-мерного пространства. Частной производной функции по переменной  называется предел 

. 

Из определения частной производной следует правило: при вычислении производной по одной из переменных все остальные переменные считаем постоянными, учитывая, что производная постоянной равна нулю и постоянную можно выносить за знак производной.  

Производная по направлению. Если в n-мерном пространстве задан единичный вектор , то изменение дифференцируемой функции в направлении этого вектора характеризуется производной по направлению: . В частности, для функции трех переменных   ,  — направляющие косинусы вектора  . 

Градиент. Производная по направлению представляет собой скалярное произведение вектора   и вектора с координатами   , который называется градиентом функции    и обозначается    . Поскольку   , где   — угол между   и   , то вектор указывает направление скорейшего возрастания функции   , а его модуль равен производной по этому направлению. 

Полный дифференцал. Для приращения дифференцируемой функции   справедливо равенство    . Линейная по приращениям аргументов часть приращения функции называется полным дифференциалом функции и обозначается    . 

Производные и дифференциалы высших порядков. Дифференцируя частную производную как функцию нескольких переменных по одной из переменных, получим производные второго порядка. Например, для функции двух переменных: . Если смешанные производные     и     непрерывны, то они равны, то есть не зависят от порядка дифференцирования. Аналогично определяются, например,     . Если при вычислении полного дифференциала от дифференциала первого порядка учесть, что приращения аргументов есть числа и оставить их неизменными, то получим дифференциал второго порядка. Например, для функции двух переменных:    . Здесь учтено равенство смешанных производных второго порядка и принято    . При этих допущениях формулу дифференциала любого порядка можно получить из символического выражения:   .

 

 

Наверх

29. Неявные функции.

Неявная функция одной переменной. Пусть в некоторой области   плоскости задана функция , и пусть линия уровня этой функции , определяемая уравнением   , является графиком некоторой функции   , определяемой уравнением    . В этом случае говорят, что функция    задана неявно уравнением   . Для существования неявной функции требуется выполнение следующих условий: функция   и ее частная производная по    непрерывны в     , . Тогда в некоторой окрестности точки   существует единственная непрерывная функция     , задаваемая уравнением   , так, что в этой окрестности   . 

  

Неявная функция многих переменных. Аналогично рассматривают функции многих переменных, заданные неявно. Например, при выполнении соответствующих условий, уравнение     задает неявно функцию   . Это же уравнение может задавать неявно функцию или      .  

 

Производная неявной функции. При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение  : . Отсюда получим формулу для производной функции    , заданной неявно:   . Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением   : , .

 

 

Наверх

30. Формула Тейлора для многих переменных.

Формулы Тейлора и Маклорена. Если функция   имеет в некоторой окрестности точки непрерывные частные производные до (n+1)-го порядка включительно, то для любой точки из этой окрестности справедлива формула Тейлора n-го порядка:  , где ,

 ,

 

и т.д. Формула Тейлора, записанная в окрестности точки (0,0) называется формулой Маклорена. Например, для функции двух переменных при n=2: . 

 

Аппроксимация функции многочленом. Выражение

называется многочленом Тейлора n-го порядка. Поскольку , то в окрестности точки функцию можно приближенно заменить, или, как говорят, аппроксимировать, ее многочленом Тейлора, т. е.  . Чем ближе точка  к точке , тем выше точность такой аппроксимации; кроме того, точность возрастает с ростом n. Это означает, что, чем больше непрерывных производных имеет функция  , тем точнее представляет ее многочлен Тейлора.

 

 

Наверх

31. Исследование на экстремум.

Локальные экстремумы. Точка   называется точкой локального минимума (максимума) функции , определенной в области , если существует окрестность этой точки, такая, что   для всех точек этой окрестности, отличных от . Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства. 

 

Исследование на экстремум функции двух переменных. Обозначим через приращение функции   в точке  . Если — точка локального минимума функции  , то существует окрестность   , в которой   (обратное неравенство в случае максимума). Из формулы Тейлора первого порядка   следует, что приращение   дважды непрерывно дифференцируемой функции   может сохранять знак, если главная линейная часть приращения функции в точке экстремума (максимума или минимума) равна нулю, т. е. выполнено необходимое условие экстремума: если точка   — точка экстремума, то   . Такая точка называется стационарной точкой функции. Приращение функции в стационарной точке имеет вид . Обозначим . Справедливо следующее достаточное условие экстремума. Пусть функция    дважды непрерывно дифференцируема в окрестности точки   и  . Если   , то в точке  функция достигает экстремума. Если при этом , то этот экстремум v минимум, при — максимум. Если же    , то в точке   экстремума нет. Геометрически достаточное условие означает, что в окрестности экстремума график функции   близок к поверхности . Если    , то для определения знака приращения   необходимо изучить члены формулы Тейлора более высокого порядка.

 

 

Наверх

32. Условный экстремум.

Условные экстремумы. Пусть функция  определена в некоторой области  и в этой области задана кривая уравнением . Условным экстремумом функции двух переменных  называют ее экстремум при условии, что точки берутся на заданной кривой. Если из уравнения кривой можно, например, выразить , то задача о нахождении условного экстремума сводится к исследованию на экстремум функции одной переменной . 

 

Метод множителей Лагранжа. Если уравнение  не разрешимо ни относительно  , ни относительно , то рассматривают функцию Лагранжа. Необходимым условием существования условного экстремума функции  при условии  является равенство нулю всех частных производных функции Лагранжа:   . 

  

Наибольшее и наименьшее значение функции в области. Поскольку функция  , непрерывная в ограниченной замкнутой области достигает в ней своего наибольшего и наименьшего значений, задача об их нахождении разделяется на две части: найти экстремумы функции двух переменных внутри области, найти ее условные экстремумы на границе области, при условии, что граница задана уравнением .

 

 

Наверх

33. Двойной и тройной интегралы.

Двойной интеграл в декартовых координатах. Пусть   ограниченная замкнутая область плоскости с кусочно-гладкой границей и пусть функция определена и ограничена на  . Посредством сетки кусочно-гладких кривых разобьем на конечное число элементарных областей с площадями  (разбиение ). Пусть — наибольший из диаметров областей , получающийся при разбиении . В каждой из элементарных областей выберем произвольную точку . Число    называется интегральной суммой и ставится в соответствие каждому разбиению и каждому выбору точек . Если существует    и он не зависит от выбора разбиения  и точек , то функция называется интегрируемой по Риману в области , а сам предел называется двойным интегралом от функции  по области и обозначается    или   . Двойной интеграл существует, если  непрерывна на . Допустимы точки разрыва первого рода, лежащие на конечном числе гладких кривых в . 

 

Свойства двойного интеграла. Свойства двойного интеграла аналогичны свойствам определенного интеграла: 

Линейность:  

. Аддитивность: 

, если S1 и S2 две области без общих внутренних точек. 

Если для каждой точки  выполнено неравенство  , то . 

Если  интегрируема на , то функция   также интегрируема, причем .  

Если  и  наименьшее и наибольшее значения функции в области, а ее  площадь, то . 

Теорема о среднем значении: если  непрерывна в связной области , то существует, по крайней мере, одна точка такая, что   . 

Вычисление двойного интеграла. 

Если  , где —    непрерывные на функции, то двойной интеграл может быть вычислен двумя последовательными интегрированиями: . Аналогично, если , то     . 

Тройной интеграл и его свойства. Пусть — ограниченная замкнутая пространственная область, границей которой является кусочно-гладкая поверхность, и пусть функция  определена и ограничена в  . Посредством сетки кусочно-гладких поверхностей разобьем на конечное число элементарных областей   с объемами  (разбиение). Пусть . наибольший из диаметров областей  , получающийся при разбиении . В каждой из элементарных областей выберем произвольную точку . Число ставится в соответствие каждому разбиению  и каждому выбору точек и называется интегральной суммой. Если существует   и он не зависит от выбора разбиения и точек,  то функция называется интегрируемой по Риману в области  , а сам предел называется тройным интегралом от функции   по области  и обозначается  . Свойства тройных интегралов такие же, как и у двойных интегралов. 

Вычисление тройного интеграла в декартовых координатах. Пусть  является цилиндрическим телом, проекция которого на плоскость  есть область  и которое ограничено снизу поверхностью , а сверху v поверхностью , где   — непрерывные функции в . Тогда , то есть интегрированием по z тройной интеграл сводится к двойному интегралу по области . Для областей более сложной формы вычисление двойных и тройных интегралов производится разбиением областей на конечное число простых областей с уже рассмотренными свойствами.

 

 

Наверх

34. Замена переменных в кратных интегралах.

Замена переменных в двойном интеграле. Пусть функции взаимно однозначно отображают открытое множество, содержащее область плоскости на открытое множество, содержащее область , и пусть является образом . Если и их частные производные непрерывны, а определитель   , то . Выражение  называется элементом площади в криволинейных координатах, функциональный определитель — якобианом.  

 

Вычисление площади.

Замена переменных в тройном интеграле. Пусть посредством функций производится взаимно однозначное отображение открытого множества, содержащего область пространства на открытое множество, содержащее область пространства и  есть образ . Если эти три функции непрерывны вместе со своими первыми частными производными в области и якобиан, то . Выражение  называется элементом объема в криволинейных координатах . 

 

Вычисление объема.

Двойной интеграл в полярных координатах. Введем на плоскости полярные координаты. Пусть — область, полученная взаимно однозначным отображением области плоскости , определяемым функциями . Тогда , а двойной интеграл в полярных координатах вычисляется по формуле: .Элемент площади в полярных координатах есть .

 

 

Наверх

35. Сферические и цилиндрические координаты.

Тройной интеграл в цилиндрических координатах. Введем в пространстве цилиндрические координаты. Для этого на плоскости используем полярные координаты, а третья координата произвольной точки остается . Учитывая связь полярных координат с декартовыми, получим выражение декартовых координат через цилиндрические:  . Тогда  и тройной интеграл в цилиндрических координатах вычисляется по формуле: . Элемент объема в цилиндрической системе координат есть  . 

  

Тройной интеграл в сферических координатах. Введем в пространстве сферическую систему координат. Для этого рассмотрим произвольную точку  в декартовой системе координат. Спроектируем ее на плоскость , получив точку  . Положение точки в пространстве будем характеризовать ее расстоянием от начала координат , углом между отрезком и положительной полуосью , углом между отрезком и положительной полуосью . Декартовы координаты точки выражаются через сферические по формулам: . В этом случае    . Тогда тройной интеграл в сферических координатах вычисляется по формуле: 

.

Элемент объема в сферической системе координат есть  .

 

 

Наверх

36. Поверхностный интеграл по площади поверхности.

Площадь гладкой поверхности. Рассмотрим кусок поверхности  , заданной уравнением . Пусть выполняется условие , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором . Разобьем поверхность сеткой гладких кривых на элементарные области ( разбиение ). Пусть   — наибольший из диаметров элементарных областей. Если независимо от разбиения  существует , то он и называется площадью данной поверхности. Пусть    однозначно проектируется на плоскость и  — эта проекция. Элементу площади области на плоскости  соответствует элемент площади поверхности , равный , где — угол между нормалью к поверхности и осью . Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла  по проекции поверхности на плоскость. Если поверхность задана уравнением , то     и площадь поверхности вычисляется по формуле   , здесь — проекция поверхности на плоскость . Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности.  

 

Поверхностный интеграл 1-го рода. Пусть некоторая функция определена и ограничена на гладкой поверхности . Выберем разбиение поверхности и точки на каждой элементарной области   и составим интегральную сумму . Если независимо от выбора разбиения и точек существует , то он называется поверхностным интегралом по площади поверхности (1-го рода) от функции и обозначается    . 

 

Свойства и вычисление поверхностного интеграла по площади поверхности. Если поверхность задана уравнением  и однозначно проектируется на плоскость , то поверхностный интеграл 1-го рода вычисляется по формуле . Нетрудно получить аналогичные формулы, если поверхность однозначно проектируется на другие координатные плоскости. Поскольку вычисление поверхностного интеграла сводится к двойному интегралу, то, естественно, все свойства поверхностного интеграла 1-го рода такие же, как и у двойного.

 

 

Наверх

37. Криволинейный интеграл по длине дуги.

Криволинейный интеграл 1-го рода. Пусть — отрезок кусочно-гладкой кривой с началом в точке и концом в точке и — ограниченная функция, определенная в некоторой области, содержащей кривую . Выберем на кривой произвольные точки , разбивая ее на элементарные отрезки (разбиение ), длина каждого  . Обозначим . Пусть  — произвольная точка на элементарном отрезке . Составим интегральную сумму . Если независимо от разбиения и выбора точек существует    , то он называется криволинейным интегралом по длине кривой (1-го рода) и обозначается  . Аналогично определяется криволинейный интеграл 1-го рода      от функции трех переменных   по отрезку пространственной кривой. 

 

Свойства и вычисление криволинейного интеграла по длине дуги. Криволинейный интеграл 1-го рода не зависит от направления движения по кривой , то есть. Это единственное свойство, которое не совпадает с обычными свойствами интегралов, определеямых через предел интегральной суммы. Если — отрезок кусочно-гладкой кривой, заданной параметрически:

 , то криволинейный интеграл вычисляется по формуле:

. Если плоская кривая задана в явном виде, то криволинейный интеграл вычисляется по формуле: .

 

 

Наверх

38. Скалярное поле.

Скалярное поле. Если каждой точке пространства ставится в соответствие скалярная величина , то возникает скалярное поле (например, поле температуры, поле электрического потенциала). Если введены декартовы координаты, то обозначают также

 или      . Поле может быть плоским, если   , центральным (сферическим), если   , цилиндрическим, если .

 

Поверхности и линии уровня. Свойства скалярных полей можно наглядно изучать с помощью поверхностей уровня. Это поверхности в пространстве, на которых   принимает постоянное значение. Их уравнение:  . В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение:   . В отдельных случаях линии уровня могут вырождаться в точки, а поверхности уровня в точки и кривые. 

 

Производная по направлению и градиент скалярного поля. Пусть   — единичный вектор с координатами  ,  — скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле  . Производная по направлению представляет собой скалярное произведение вектора   и вектора с координатами  , который называется градиентом функции  и обозначается  . Поскольку  , где  — угол между   и  , то вектор  указывает   направление скорейшего возрастания поля , а его модуль равен производной по этому направлению. Так как компоненты градиента являются частными производными, нетрудно получить следующие свойства градиента: 

 

 

Наверх

39. Векторное поле.

Векторное поле. Если каждой точке пространства ставится в соответствие вектор , то говорят, что задано векторное поле (поле скоростей частиц движущейся жидкости, силовое поле, поле электрической напряженности). В декартовой системе координат векторное поле можно записать в виде: . Скалярные функции однозначно определяют векторное поле. Векторное поле может быть плоским, если , сферическим, когда , , цилиндрическим, когда , .  

 Векторные линии (линии тока). Для наглядного представления векторных полей используют векторные линии (линии тока). Это кривые, в каждой точке которых вектор является касательным вектором. Через каждую точку проходит одна линия тока. За исключением точек, где поле не определено или , линии тока никогда не пересекаются. В декартовых координатах дифференциальные уравнения линий тока имеют вид:

 

 

Наверх

40. Поток векторного поля.

Поток векторного поля. Рассмотрим кусок поверхности , заданной уравнением . Пусть выполняется условие  , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором . Выберем одну из сторон поверхности следующим образом: построим на поверхности достаточно малый замкнутый контур, на котором задано направление обхода. Построим вектор нормали в точке поверхности, лежащей внутри контура. Если из конца вектора нормали обход контура кажется происходящим против часовой стрелки, то будем называть сторону поверхности, обращенную к вектору нормали положительной стороной. Таким образом, будем рассматривать ориентированную двухстороннюю поверхность, а односторонние поверхности лист Мебиуса, бутылку Клейна оставим в покое. Потоком векторного поля   через ориентированную поверхность называется поверхностный интеграл по площади поверхности (1-го рода)  , где —     единичный вектор нормали, направленный в положительную сторону. Выбор положительной стороны обычно диктуется физическими условиями задачи. 

 

Непосредственное вычисление потока. Поскольку поток векторного поля определен с помощью поверхностного интеграла, вычисление потока сводится к вычислению такого интеграла от функции , где  — компоненты векторного поля,  — направляющие косинусы вектора нормали.

 

 

Наверх

41. Формула Остроградского.

Поток векторного поля через замкнутую поверхность. Рассмотрим кусочно-гладкую двухстороннюю замкнутую ориентированную поверхность  . Поток векторного поля   через замкнутую поверхность является важной характеристикой поля и позволяет судить о наличии источников и стоков поля. При непосредственном вычислении потока через замкнутую поверхность приходится разбивать ее на части, однозначно проектируемые на координатные плоскости. 

Формула Остроградского. Пусть замкнутая поверхность ограничивает некоторый объем  . Тогда в декартовых координатах справедлива формула Остроградского: , где  — компоненты векторного поля. 

 

 

Дивергенция векторного поля. Дивергенцией   векторного поля  называется . Точка  находится внутри замкнутой поверхности , ограничивающей объем   , который при вычислении предела стягивается в эту точку.  является скалярной величиной и служит мерой источников поля. Если в некоторой области поля  , то источников поля в этой области нет. Такое поле называют соленоидальным. Используя формулу Остроградского, нетрудно получить выражение для вычисления дивергенции в декартовых координатах: . Из свойств частных производных следуют свойства дивергенции векторного поля: 

 

 

Наверх

42.

Криволинейный интеграл в векторном поле.

Криволинейный интеграл в векторном поле. Пусть заданы некоторое векторное поле  и кривая АВ (А — начальная точка, В — конечная). Криволинейный интеграл в векторном поле     есть скаляр, полученный следующим образом: 

Разобьем кривую точками А=А0, А1, А2-Аn=В на n частей, приближенно изображаемых векторами  (разбиение ). 

Обозначим  . 

На границе или внутри каждой элементарной дуги Аi-1Ai выберем точку, которой соответствует радиус-вектор   и составим интегральную сумму   . 

Если существует     и он не зависит от разбиения  и выбора точек, то этот предел называется криволинейным интегралом в векторном поле. В декартовой системе координат:, где — компоненты векторного поля.

Если кривая задана в параметрической форме:

, то вычисление криволинейного интеграла сводится к определенному интегралу: 

. Используя определение и формулу для вычисления нетрудно получить свойства криволинейного интеграла: 

Подчеркнем, что, в отличие от криволинейного интеграла по длине дуги, криволинейный интеграл в векторном поле меняет знак при изменении направления интегрирования.  

Если   векторное поле, описывающее физическое силовое поле, то криволинейный интеграл выражает работу, которую совершает   сила при переносе материальной точки из пункта А в пункт В вдоль кривой АВ. 

 

Циркуляция векторного поля. Важной характеристикой векторного поля является циркуляция векторного поля, которая равна криволинейному интегралу по замкнутой кривой в области поля, или, как говорят, по замкнутому контуру:   . Циркуляция векторного поля является скалярной величиной и характеризует вихревые свойства поля. Если в некоторой области поля циркуляция равна нулю, то поле называют безвихревым.

 

 

Наверх

43. Формула Стокса.

Формула Стокса. Рассмотрим в пространстве кусок двухсторонней кусочно-гладкой поверхности , край которой образуется кусочно-гладкой кривой . Выберем положительную сторону поверхности (из конца единичного вектора нормали      обход границы представляется против часовой стрелки). Для циркуляции векторного поля     вдоль контура границы имеет место формула Стокса: , где   — компоненты векторного поля,   — направляющие косинусы вектора нормали.  

  

Ротор векторного поля. Рассмотрим в пространстве замкнутый контур  с выбранным направлением обхода, лежащий в ориентированной плоскости на ее положительной стороне (из конца единичного вектора нормали   обход контура представляется против часовой стрелки). Ротором    (или вихрем) векторного поля в точке  называется вектор, проекция которого на направление вектора нормали есть    . Точка лежит  на плоскости внутри контура  , который стягивается в эту точку при вычислении предела. Поскольку ротор поля определяется через циркуляцию, то он тоже является мерой завихренности поля. Найдем компоненты ротора в декартовой системе координат, воспользовавшись формулой Стокса. Для этого выберем сначала координатную плоскость y0z с нормальным вектором   , затем x0z,     , затем x0y,   . Применяя каждый раз теорему о среднем для интеграла, получим:    

Теперь теорема Стокса может быть сформулирована следующим образом: циркуляция векторного поля вдоль контура равна потоку ротора поля через поверхность, натянутую на этот контур. Выражение для ротора поля проще запомнить, если записать его в виде определителя:. Используя свойства частных производных и определителей, получим следующие свойства ротора векторного поля:

 

 

 

Наверх

44. Потенциальное поле.

Потенциальное поле. Если векторное поле  , то оно называется потенциальным, а скалярное поле , соответственно, его потенциалом. Самым известным примером такого соответствия является электрическое поле, напряженность которого  , где — потенциал электрического поля. Минус в формуле связан с историческим выбором направления вектора напряженности от плюса к минусу, когда уже умели тереть шерсть об янтарь, но не знали, как это описывать математически. 

  

Условие потенциальности поля. Пусть задано скалярное поле  , причем данная функция дважды непрерывно дифференцируема. Напомним, что в этом случае смешанные частные производные второго порядка не зависят от порядка дифференцирования. Вычислим  . 

Нетрудно видеть, что при этих условиях получается тождественный ноль. То есть, если поле потенциальное, то его  . 

 

 

Вычисление потенциала векторного поля. Если мы убедились, что поле  является потенциальным, то есть его ротор равен нулю, то представляет интерес вычислить потенциал этого поля. Для этого рассмотрим криволинейный интеграл в данном векторном поле:  , где точки А и В — начальная и конечная точки кривой. Поскольку  , то скалярное произведение векторов     и      является полным дифференциалом функции  : . Поэтому из свойств криволинейного интеграла следует, что . Смысл полученной формулы состоит в том, что работа поля по перемещению материальной точки из А в В не зависит от пути интегрирования, а только от конечной и начальной точек, точнее, от разности потенциалов в этих точках. Понятие разности потенциалов хорошо известно из физики. Для вычисления потенциала поля в произвольной точке В выберем начальную точку А, от которой начнем отсчет (в физике часто это — бесконечно удаленная точка). Тогда . Поскольку интеграл не зависит от пути интегрирования, то выберем его так, как нам удобно: сначала параллельно оси 0х, потом параллельно 0у, наконец, параллельно 0z. Обозначая , получим: 

.

Здесь    — компоненты векторного поля    . Поскольку выбор начальной точки произволен, потенциал поля определяется с точностью до произвольной постоянной, которая определяется физическими соображениями.

Потенциал электрического поля. Разность потенциалов 10 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

Электрическое поле действует на помещенный в него заряд с силой, которая определяется величиной заряда и напряженностью поля в данной точке.

 

Если эта сила перемещает заряд – то она совершает работу. Даже если заряда в поле нет, то потенциально эта работа все равно может быть совершена, как только он там окажется. Из опыта других разделов физики мы знаем, что работа связана с энергией.

Для решения некоторых задач удобно использовать энергетическую модель описания электрического поля. Проведем аналогию с гравитационным полем.

 

Понятие потенциала

 

 

Если мы поднимем тело массы , лежащее на земле на высоту  (см. рис. 1), мы изменим его потенциальную энергию на величину . Именно такую работу  и необходимо совершить для этого подъема.

 

Рис. 1. Изменение потенциальной энергии

Для любой массы  разница энергий на высоте 0 и  будет равна  (см. рис. 2).

Рис. 2. Разница потенциальных энергий

Если разделить значение потенциальной энергии  на массу, мы получим величину, характеризующую гравитационное поле в данной точке. Выражение  уже не зависит от массы, оно показывает работу, которую необходимо совершить для переноса тела, с некоторой массой, на высоту , деленную на эту массу.

Теперь посмотрим, как ввести аналог потенциальной энергии приведенной на единицу массы в электрическом поле.

На заряд , находящийся в поле другого заряда , закрепленного в некоторой точке пространства, действует сила Кулона . Эта сила может переместить заряд , совершив при этом работу. Значит, система двух зарядов, находящихся на определенном расстоянии, обладает потенциальной энергией, зависящей от величины зарядов и расстояния между ними.

Если по аналогии с гравитационным полем рассмотреть величину, равную этой энергии, деленной на заряд , то она уже не будет зависеть от заряда  и охарактеризует только поле заряда  в данной точке. То есть будет являться функцией заряда  и расстояния между зарядами. Эта величина и называется потенциалом электрического поля.

Разность потенциалов двух точек, умноженная на величину заряда , равна работе, необходимой для перемещения этого заряда между этими точками. То есть разность потенциалов двух точек поля – это работа по перемещению между ними единичного заряда.

Как и в поле сил тяжести, эта работа не зависит от траектории  и определяется только положением точек, между которыми перемещается единичный заряд. Такие поля называют консервативными. В разделе «Механика» мы уже говорили, что энергия – величина, требующая для измерения задания «начала отсчета». Например, в гравитационном поле мы можем считать нулевой потенциальную энергию тела, находящегося на уровне земли. В случае электростатического поля, создаваемого зарядом, естественно считать нулевой потенциальной энергией некоторого заряда, находящегося в поле, его энергию на бесконечном удалении от заряда, в поле которого он находится. Это и есть «точка отсчета» для потенциальной энергии поля заряда.

Потенциал поля в некоторой точке равен работе по перемещению единичного заряда из этой точки на бесконечность.

 

Выражение для потенциала поля точечного заряда

 

 

Пусть положительный заряд  находится на расстоянии  от положительного заряда  (см. рис. 3).

 

Рис. 3. Изначальное положение заряда

Какую работу совершит электрическое поле при перемещении заряда  вдоль радиуса в точку, отдаленную на  от ? (см. рис. 4)

Рис. 4. Конечное положение заряда

По определению работа силы равна этой силе, умноженной на перемещение:

В данном случае действует сила электрического взаимодействия (см. рис. 5), по закону Кулона .

Рис. 5. Действие силы электрического взаимодействия

Сила и перемещение в нашем случае сонаправлены,  и . Так мы можем находить работу для случая, когда сила постоянна на всей траектории. Здесь же сила изменяется по мере отдаления зарядов друг от друга.

Обозначим перемещение заряда (см. рис. 6).

Рис. 6. Перемещение заряда

По мере перемещения заряда  сила изменяется, но на малом (в сравнении с расстоянием до заряда ) отрезке можем считать ее постоянной и находить работу по определению, которое мы привели выше.

Работа, совершаемая силой Кулона на таком малом отрезке  равна , где силу  можно считать постоянной на всем отрезке . Тогда работа при перемещении на расстояние  будет равна сумме работ на  участках (), на каждом из которых сила Кулона постоянна и равна .

Эта сумма будет равна 

Подробный вывод этой формулы вы можете проследить в ответвлении.

 

---

Работа при перемещении электрического заряда

Работа по перемещению заряда на малом участке  равна:

Работа на участке  равна сумме работ на каждом участке :

Воспользуемся приближенным равенством:

Прежде чем его применить, покажем, что равенство справедливо. Приведем правую часть к общему знаменателю:

Раскроем скобки:

Заметим, что  – пренебрежимо малая по сравнению с  величина,  не может считаться пренебрежимо малой, т. к. количество  участков  велико. Поэтому в знаменателе можем пренебречь членами  и .

Вернемся к нахождению работы. Распишем выражение по полученной формуле:

Распишем сумму:

---

 

Мы знаем, что работа связана с энергией. Система обладает энергией, если силы, возникающие в системе, могут выполнить работу (в нашем случае это сила электростатического взаимодействия зарядов). Работа равна уменьшению потенциальной энергии:

Сравнив с выражением , делаем вывод, что  – это потенциальная энергия взаимодействия двух зарядов. Ранее мы приняли, что потенциальная энергия заряда, отдаленного от источника электрического поля на бесконечность, равна нулю. Посмотрим, как с этим согласуется полученная формула:

Действительно,  будет равна нулю на бесконечном отдалении от заряда , т. к.  при .

Теперь проверим, как полученный результат соотносится с моделью, в которой разноименные заряды обозначены знаками плюс и минус. Если заряды одноименные, то потенциальная энергия взаимодействия положительна . Система стремится к состоянию с наименьшей потенциальной энергией (как и, например, камень на некоторой высоте  над поверхностью земли, предоставленный сам себе, будет падать вниз, т. е. уменьшать высоту и с ней потенциальную энергию )

Действительно, заряды будут отталкиваться и сила электрического взаимодействия будет вызывать перемещение заряда на большее расстояние, потенциальная энергия  будет уменьшаться.

Если заряды разноименные, то потенциальная энергия взаимодействия  имеет знак минус. Заряды притягиваются, и сила их взаимодействия вызывает перемещение заряда на меньшее расстояние , потенциальная энергия  уменьшается.

 

Потенциал электрического поля

 

 

Энергия заряда  в поле заряда , равная , зависит от величин обоих зарядов. Характеристика поля, созданного зарядом , естественно, не должна зависеть от величины помещенного в него заряда. Разделим  на  и получим . Эта величина называется потенциалом электрического поля и обозначается буквой . Эта характеристика поля показывает, какой энергией обладает положительный заряд, помещенный в данную точку поля. Как и энергия, потенциал – скалярная величина, измеряется в вольтах.

 

В нашем случае  – потенциал поля точечного заряда. Точка отсчета потенциалов в нашем случае естественным образом является бесконечно отдаленной точкой (см. рис. 7).

Рис. 7. Точка отсчета потенциалов

В зависимости от задачи точкой отсчета выбирают потенциал поверхности Земли, потенциал отрицательно заряженной пластины конденсатора или потенциал любой другой точки, удобной для решения задачи.

Таким образом, пользуясь определением потенциала, можно вычислить потенциальную энергию заряда, находящегося в электростатическом поле:

и работу поля по перемещению заряда из точки с потенциалом  в точку с потенциалом :

Электрическое поле является консервативным, его работа не зависит от траектории движения заряда, а зависит только от перемещения.

Заряд всегда распределен на каком-то теле, имеющем геометрические размеры. На расстояниях, много больших размеров тела, поле слабо зависит от объема и формы этого тела, и потому модели точечного заряда достаточно. Например, потенциал поля заряженного металлического шара при  эквивалентен потенциалу поля точечного заряда (см. рис. 8):

Рис. 8. Потенциал поля при

.

Внутри шара потенциал во всех точках одинаков и равен потенциалу на поверхности шара (см. рис. 9):

Рис. 9. Потенциал внутри шара

.

Если бы это было не так, то потенциальная энергия в разных точках внутри шара отличалась бы, а, так как внутри металла есть свободные носители заряда, поле выполняло бы работу по перемещению зарядов. В итоге электроны переместились бы в область большего потенциала, тем самым уменьшив его. Таким образом, потенциал во всех точках приравнивается.

Потенциал подчиняется принципу суперпозиции. При наличии нескольких источников поля складываются как векторы напряженности поля, так и потенциалы:

 

Задача 1

 

 

При перемещении заряда между точками с разностью потенциалов 1 кВ электрическое поле совершило работу 40 мкДж. Чему равен заряд?

 

Это простая задача на понимание смысла величины разности потенциалов.

Разность потенциалов равна работе по переносу заряда, деленной на величину этого заряда.

Выразим значение заряда:

И вычислим ответ:

Ответ: 

 

Задача 2

 

 

Какую работу надо совершить, чтобы перенести заряд 5 мкКл из бесконечности в точку поля, удаленную от центра заряженного шара на 18 см? Заряд шара – 20 мкКл.

 

Порассуждаем.

• Потенциал поля заряженного шара на бесконечности равен нулю. Следовательно, приближая заряд от бесконечности к шару, внешней силе нужно совершать работу для преодоления силы электростатического взаимодействия. Численно эта работа будет равна работе электрического поля заряженного шара по перемещения заряда с расстояния 18 см на бесконечность.
• Работа по переносу заряда в электрическом поле связана с разностью потенциалов между начальной и конечной точками траектории и величиной заряда 
• Величина переносимого заряда у нас есть.
• Потенциал поля заряженного шара на бесконечности, как мы уже отметили, равен нулю. А в конечной точке траектории мы сможем его вычислить, пользуясь формулой для потенциала поля точечного заряда, которая справедлива и для поля вне заряженного шара.

Приступим к решению.

Найдем потенциал электрического поля заряженного шара в конечной точке траектории.

Потенциал электрического поля заряженного шара на бесконечности равен нулю.

Разность потенциалов электрического поля по переносу заряда из точки с потенциалом  в точку с потенциалом  будет равна:

В то же время она будет равна работе электрического поля по переносу заряда, деленной на заряд:

Величина работы внешних сил, которую надо совершить, чтобы перенести заряд из точки с меньшим потенциалом в точку с большим потенциалом, равна работе электрического поля по переносу такого же заряда в обратном направлении.

Таким образом, мы получили систему из пяти уравнений, решив которую найдем искомую величину. Пронаблюдать математическую часть решения задачи вы можете в свертке.

Ответ: .

---

Математическая часть решения задачи 2

Подставим выражения для потенциалов из первого и второго уравнений в третье:

Подставим полученную разность потенциалов в четвертое уравнение.

И выразим работу электрического поля:

Согласно пятому уравнению это и есть искомая работа .

Подставим данные из условия и рассчитаем ответ:

Задача решена.

---

 

На этом наш урок закончен. Спасибо за внимание.

 

Список литературы

1. Соколович Ю. А., Богданова Г. С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
2. Мякишев Г. Я., Буховцев Б. Б., Сотский Н. Н. Физика: Учеб. для общеобразоват. учреждений. Базовый и профильный уровни. 19-е издание – М.: Просвещение, 2010. 

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт «phyzika. ru» (Источник)
2. Интернет-сайт «physics.ru» (Источник)
3. Интернет-сайт «knowlegeport.narod.ru» (Источник)

 

Домашнее задание

1. Какой вид имеет формула для работы электрического поля?
2. Что такое потенциал электрического поля?
3. Решите задачу: точечный заряд , находясь в некоторой точке поля, обладает потенциальной энергией 1 мкДж. Найдите потенциал этой точки поля.

 

Физика Потенциал электростатического поля, разность потенциалов

Материалы к уроку

• 50. Потенциал электростатического поля, разность потенциалов.doc

  44.5 KBСкачать

• ppt»>50. Потенциал электростатического поля, разность потенциалов.ppt

  9.93 MBСкачать

Конспект урока

В механике взаимное действие тел друг на друга характеризуют силой или потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряженность поля – это силовая характеристика.
Теперь введем энергетическую характеристику – потенциал. На замкнутой траектории работа электростатического поля равна нулю. Поля, обладающие таким свойством, называются потенциальными. Потенциальный характер, в частности, имеет электростатическое поле точечного заряда. Работу потенциального поля можно выразить через изменение потенциальной энергии. Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля, так и для любого другого. Следовательно, отношение потенциальной энергии к заряду не зависит от помещенного в поле заряда. Это позволяет ввести новую количественную характеристику поля —  потенциал, не зависящую от заряда, помещенного в поле.  
Потенциалом электростатического поля называют отношение потенциальной энергии заряда в поле к этому заряду. Согласно данному определению введем формулу. Потенциал (фи) φ  — скалярная величина, это энергетическая характеристика поля; потенциал определяет потенциальную энергию заряда (ку) q  в данной точке поля.
Если в качестве нулевого уровня потенциальной энергии, а, значит, и потенциала принять отрицательно заряженную пластину, то потенциал однородного поля равен произведению напряженности поля на перемещение заряда.
Работа перемещения заряда в однородном электростатическом поле не зависит от формы траектории заряда, а зависит от положения в этом поле начальной и конечной точек перемещения.
Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Практическое значение имеет не сам потенциал в точке, а изменение потенциала, которое не зависит от выбора нулевого уровня отсчета потенциала. Разность потенциалов называют также напряжением. Разность потенциалов оказывается равной отношению работы поля к величине заряда. Иначе работу по перемещению единичного заряда называют напряжением электрического поля. В Международной системе единиц работу выражают в джоулях, а заряд – в кулонах. Поэтому разность потенциалов между двумя точками равна единице, если при перемещении заряда в один кулон из одной точки в другую электрическое поле совершает работу в один джоуль. Эту единицу называют вольтом.
Охарактеризуем электростатическое поле.
Напряженность электрического поля – силовая характеристика поля, физическая векторная величина, численно равная силе, действующей на единичный положительный заряд. Единицы измерения: 1Н/Кл (ньютон на кулон) =1В/м (вольт на метр).
Работа перемещения заряда по замкнутой траектории, совершаемая силами электростатического поля, равна нулю. Силы, работа которых на замкнутой траектории равна нулю и не зависит от формы траектории, называются консервативными силами. Потенциальное поле — силовое поле, в котором на тела действуют консервативные силы.
Потенциал электростатического поля заряженного шара прямо пропорционален величине заряда и обратно пропорционален радиусу шара. 
Также, исходя из принципа суперпозиции электрического поля, мы приходим к выводу о том, что потенциал поля, созданного в данной точке множеством зарядов-источников, равен алгебраической сумме потенциалов полей, созданных в этой точке каждым зарядом в отдельности.
Решим задачу.
Металлический шар укреплен на изолированной подставке и соединен с источником тока постоянного напряжения. Второй полюс источника тока заземлен.
1) Определите значение потенциала в точке А, если расстояние от центра шара до точки А составляет 8 см, а радиус шара равен 2 с половиной см.
2) Определите потенциал поверхности шара.
3) Чему равен потенциал внутри шара, если он сплошной?
4) Определите напряженность электрического поля у поверхности шара.
1)    Отношение потенциала в точке А к потенциалу шара, который измеряет вольтметр, равен отношению радиуса шара к расстоянию от шара до точки А. Вычисления по этой формуле дают результат в 190 вольт.
2)    Потенциал поверхности шара такой же как у точечного заряда, он измерен прибором вольтметр. Показания в 600 вольт.
3)    В сплошном шаре потенциал внутри шара равен потенциалу на его поверхности.
4)    Напряженность поля на поверхности шара определим, как отношение потенциала шара к радиусу шара. Радиус шара в данном случае рассматривается как расстояние от точки на поверхности шара до точки в центре шара. Получаем результат в 24000 вольт на метр.
Для измерения разности потенциалов между каким-нибудь изолированным металлическим проводником и Землей достаточно присоединить стержень электрометра металлической проволокой к проводнику, а корпус — к Земле. После такого присоединения листочки электрометра принимают тот же потенциал, что и наш проводник, так как в металлах имеются свободные электроны, которые будут перемещаться, пока разность потенциалов между стержнем электрометра и проводником не сделается равной нулю. Таким образом, электрометр, показывающий разность потенциалов между стержнем и корпусом, одновременно будет показывать разность потенциалов между изучаемым проводником и Землей.
Рассмотрим электрический прибор для измерения разности потенциалов. Этот прибор, используемый для измерения напряжения в электрических цепях, называют вольтметром.
Чтобы разрядить заряженное тело его соединяют с Землей. Потенциал тела сравнивается с потенциалом Земли, которое условно принимается за нуль.
По мере подъема над земной поверхностью потенциал электрического поля земли увеличивается примерно по 100 вольт на 1 метр. При указанной напряженности, казалось бы, разность потенциалов между головой человека среднего роста (170 см) и его подошвами составляет почти 220 вольт. На самом деле, человек является довольно хорошим проводником с сопротивлением около 1 килоОм, и является эквипотенциальным объемом. С Земли на человека переходит часть заряда. Поле вокруг человека искажается примерно так, как показано на рисунке и потенциал человека по-прежнему 0 В.
Примеры: при влажности воздуха 65-90% человек, идущий по ковровому покрытию, генерирует потенциал до 1000 В, сидящий на стуле с полиэтиленовым покрытием — 1500 В, а поднимающий со стола портфель из синтетического материала — до 1200 В. При влажности 10-20% значения напряжений составляют соответственно 35000 В, 18000 В и 20000 В, в то время как для некоторых изделий микроэлектроники потенциал в сотни вольт уже фатален.
Приведем значения некоторых напряжений, которые мы замечаем в жизни.
ЭЛЕКТРОСТАТИЧЕСКИЙ ГЕНЕРАТОР — устройство, в котором напряжение создается при помощи механического переноса электрических зарядов механическим транспортером. Генератор с гибким транспортером из диэлектрической ленты называется генератором Ван-де-Граафа. Наибольшее напряжение электростатического генератора около 20 МВ (мегавольт) (строятся электростатические генераторы на напряжение до 30 МВ). На базе генераторов Ван-де-Граафа строятся ускорители заряженных частиц (электронов, протонов).
Генератор Ван-де-Граафа — устройство, генерирующее высокое напряжение с помощью концентрации электрических зарядов на внешней стороне полого проводника. Построенный Джоном Кокрофтом и Эрнестом Уолтоном ускоритель Кокрофта-Уолтона вырабатывал высокое напряжение с помощью группы заряженных конденсаторов, соединенных последовательно. Американский физик Роберт Ван де Грааф (1901-67) усовершенствовал эту конструкцию, распыляя положительные или отрицательные заряды по непрерывно движущейся ленте, которая переносила их в большую полую металлическую сферу, где накапливалось напряжение. Таким образом, задействованное напряжение около 50 000 вольт вырастало до 1 млн электрон-вольт. Сегодня генератор Ван де Граафа используется в основном для «впрыскивания» частиц в более мощные линейные ускорители.
Катушка Румкорфа — устройство для получения импульсов высокого напряжения. Состоит из цилиндрической части, с центральным железным стержнем внутри, на которую намотана первичная обмотка из толстой проволоки. Поверх первичной обмотки наматывается несколько тысяч витков вторичной обмотки из очень тонкой проволоки. Первичная обмотка подсоединена к батарее химических элементов и конденсатору. В эту же цепь вводится прерыватель (зуммер) и коммутатор. Назначение прерывателя состоит в быстром попеременном замыкании и размыкании цепи. Результатом этого является то, что при каждом замыкании и размыкании в первичной цепи во вторичной обмотке появляются сильные мгновенные токи: при прерывании — прямого (одинакового направления с током первичной обмотки) и при замыкании обратного.
 

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

Урок 27. Напряженность и потенциал электростатического поля. разность потенциалов — физика — 10 класс — Российская электронная школа

Теоретический материал для самостоятельного изучения

Содержание

Напряжение – это отношение силы, действующей на точку в поле, к точечному заряду.

Потенциал точки в электростатическом поле – отношение потенциальной энергии заряда, помещенного в точку, к этому заряду.

Напряжение – разность потенциалов.

Потенциальное поле – поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю.

Интенсивность в направлении уменьшения потенциала.

Эквипотенциальные поверхности – поверхности равного потенциала.

Бесплатные сборы – Заряженные частицы, которые могут свободно перемещаться в проводнике под воздействием электрического поля.

Электростатическая индукция – это явление разделения зарядов и их распределения по поверхности проводника во внешнем электрическом поле.

Ссылки и дополнительное чтение

Г. Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика. 10 класс. Учебник для общеобразовательных школ М.: Просвещение, 2014 – С. 290 – 320.

Рымкевич А.П. Сборник задач по физике. 9 – 11 класс. Дрофа Москва, 1999 – стр. 93 – 102

Теоретический материал для самостоятельного изучения

Идея Фарадея заключается в том, что электрические заряды не взаимодействуют друг с другом напрямую. Каждый из них создает электрическое поле в окружающем пространстве.

Электрическое поле – это особый вид материи, в которой заряды взаимодействуют друг с другом. Скорость электрического поля в вакууме составляет 300000 км/с.

Напряженность E – это сила, характерная для электрического поля.

Электрическое поле, напряженность которого одинакова во всех точках, называется однородным. Поле между параллельными пластинами является однородным

Основное свойство электрического поля заключается в том, что оно действует на электрические заряды с определенной силой.

Напряженность – это отношение силы, действующей на точечный заряд, помещенный в данную точку поля, к величине этого заряда.

Если в данной точке пространства различные заряженные частицы создают поля с напряженностью E₁, Е₂то результирующая напряженность поля в этой точке равна геометрической сумме этих напряженностей поля. Это принцип суперпозиции полей.

Заряд, помещенный в электрическое поле, обладает потенциальной энергией.

Потенциал φ точки в электростатическом поле представляет собой отношение потенциальной энергии Wn заряда, помещенного в данную точку, к этому заряду q.

Потенциал – это работа, совершаемая полем для перемещения заряда массой 1Кл.

Примеры и решения

1. Для каждого элемента в первом столбце добавьте соответствующий элемент во втором столбце

Потенциальная энергия заряда в однородном электростатическом поле

Решение: Вспомним формулы для величин

Потенциальная энергия заряда в однородном электростатическом поле

2. В однородном электрическом поле 1 В/м заряд -25 нКл переместился на 2 см к линии поля. Найдите работу поля, изменение потенциальной энергии заряда и напряжение между начальной и конечной точками смещения.

Работа электрического поля при движении заряда вдоль линий поля:

Изменение потенциальной энергии равно:

Напряжение между начальной и конечной точками смещения равно:

ΔA = -25 – 10 -9 Cl – 10 3 B/м – 0,02 м = -0,5 мкДж;

Ответ:

Поскольку, когда положительный заряд движется в направлении вектора напряженности, электрическое поле совершает положительную работу A = q (φ₁ – φ₂ )> 0, потенциал φ₁ больше, чем потенциал φ₂ . Поэтому напряженность электрического поля направлена в сторону уменьшения потенциала.

Разница потенциалов

Практическое значение имеет не сам потенциал в данной точке, а изменение (разность) потенциала φ₁ – φ₂ который не зависит от выбора нулевого опорного потенциала. Разность потенциалов φ₁ – φ₂ также называется напряжением и обозначается латинской буквой U. Формула для работы, необходимой для перемещения заряда, становится следующей

Напряжение U — физическая величина, которая определяется работой, совершаемой электрическим полем для перемещения единичного положительного заряда между двумя точками поля.,

Единицей разности потенциалов (напряжения), как и потенциала, является вольт,

Поскольку работа сил поля по перемещению заряда зависит только от разности потенциалов, то при перемещении заряда от первой эквипотенциальной поверхности ко второй поверхности (потенциалы которых равны φ₁ и φ₂ ) работа, совершаемая полем, не зависит от траектории этого движения.

Теперь попробуем внести единичный заряд в другое поле, созданное вдвое большим электрическим зарядом. Очевидно, что придется проделать больше работы, чем в первом случае. Поэтому потенциальная энергия поля увеличится больше, чем в первом случае.

Потенциал электрического поля

В зависимости от количества зарядов и их размера меняется энергия электрического поля, создаваемого зарядами. Очевидно, что энергия электрического поля, создаваемая одним “зарядом”, будет отличаться от энергии, создаваемой двумя или тремя одинаковыми зарядами.

На практике очень часто необходимо сравнивать различные напряженности поля. Такое сравнение проводится при взаимодействии полей на одном положительном заряде (так называемом зондовом заряде). Давайте объясним.

Определение: Единичный заряд – это заряд, стоимость которого равна одному единичному заряду.

Например, предположим, что поле образовано определенным положительным зарядом. Чтобы ввести единичный положительный заряд в точку поля, необходимо совершить определенную работу, чтобы преодолеть силу отталкивания между основным зарядом и единичным зарядом. Потенциальная энергия поля увеличивается.

Теперь попробуем внести единичный заряд в другое поле, созданное вдвое большим электрическим зарядом. Очевидно, что придется проделать больше работы, чем в первом случае. Поэтому потенциальная энергия поля увеличится больше, чем в первом случае.

В электротехнике для характеристики поля вводится специальное понятие – электрический потенциал.

Определение; Электрический потенциал некоторой точки поля численно равен работе, совершаемой при поднесении к этой точке единичного положительного заряда извне поля.

Потенциал электрического поля измеряется в вольтах. Эта единица потенциала названа в честь итальянского физика Алессандро Вольта (1745-1827), который открыл закон взаимодействия электрических токов и предложил первую гипотезу для объяснения магнитных свойств материи.

Характеристика поля с помощью электрического потенциала очень удобна. Это позволяет сравнивать не только различные электрические поля, но и отдельные точки одного и того же поля. Например, вместо того, чтобы сказать “шар A сильнее наэлектризован, чем шар B”, мы можем сказать “потенциал шара A выше, чем потенциал шара B”. Потенциал точки в поле обычно обозначается через φ.

Электрическое поле может быть создано не только положительным или отрицательным зарядом, но и их комбинацией. В таком поле отдельные точки могут иметь как отрицательные, так и положительные потенциалы. Чтобы иметь возможность сравнивать потенциалы различных точек в этом случае, вводится условное понятие точки с нулевым потенциалом, т.е. потенциалы остальной части поля определяются относительно точки с нулевым потенциалом. Потенциалы остальных точек поля определяются относительно нулевого потенциала. Этот метод аналогичен методу измерения температуры. Там также определенная температура (температура тающего льда) принимается за нулевую точку, и температура других тел определяется по отношению к ней.

В электротехнике принято считать, что поверхность земли имеет нулевой потенциал.

Если потенциал в точке выше, чем потенциал Земли, мы говорим, что эта точка имеет положительный потенциал. Если, наоборот, потенциал точки ниже потенциала земли, то точка имеет отрицательный потенциал.

Измеряя потенциалы различных точек электрического поля относительно Земли, мы можем увидеть, что они не одинаковы. Поэтому между точками может существовать некоторая разность потенциалов.

Определение: Разность потенциалов между двумя точками в электрическом поле называется напряжением. Напряжение, как и потенциал, измеряется в вольтах.

Поясним сказанное на примере.

На рисунке 1 мы условно показали четыре точки: A с потенциалом + 20 В, B с потенциалом + 40 В, C с нулевым потенциалом (земля) и D с потенциалом 15 В.

Рисунок 1. Разность потенциалов между различными точками в электрическом поле

Разность потенциалов между точками В и А =40-20=20В;

Разность потенциалов между точками А и В =20- 0=20В;

Разность потенциалов между точками B и C =40- 0=40В;

Разность потенциалов между точками A и D =20-(-15) =35 в.

Потенциал точки B выше, чем потенциалы точек A, C и D. Потенциал точки A выше, чем потенциалы точек C и D, но ниже, чем потенциал точки B. Потенциал точки B ниже, чем потенциалы точек A и B, но выше, чем потенциал точки D.

Обратите внимание, что точки с отрицательным потенциалом имеют более низкий потенциал, чем точки с нулевым потенциалом.

Определить напряжение между двумя точками можно и другим способом. Для этого рассмотрим две точки A и B электрического поля.

Предположим, что потенциал точки A равен φ_А потенциал точки B равен φ_Б. Потенциал точки A (или B) определяется работой, необходимой для переноса единичного положительного заряда извне поля в точку A (или B). Если для перемещения единичного положительного заряда от границы поля в точку A и в точку B требуется разное количество работы, то φ_А не равна φ_Б и между точками A и B существует некоторая разность потенциалов, или напряжение. Это напряжение определяется разностью φ_А – φ_БТ.е. Работа, совершаемая силами поля при переносе единичного положительного заряда из точки A в точку B.

ПОНРАВИЛАСЬ ЛИ ВАМ СТАТЬЯ? ПОДЕЛИТЕСЬ СО СВОИМИ ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Напряженность электрического поля в этой точке всегда имеет отдачу в направлении силы, действующей на положительный пробный заряд.

Потенциальная энергия

Чтобы вычислить потенциальную энергию пробного заряда в данной точке поля, воспользуемся свойством, согласно которому разность потенциальной энергии в двух точках равна работе, затраченной на перенос этой величины из одной точки в другую (то же самое мы делали, рассматривая энергию в гравитационном поле).

Чтобы рассчитать потенциальную энергию в этой точке, нам нужно переместить пробный заряд в место, где потенциал равен нулю. Такое место находится в точке, бесконечно удаленной от источника. Положительный или отрицательный знак потенциала выбирается в зависимости от того, отталкивается ли заряд от источника или притягивается. Если заряд источника отрицательный, то нахождение электростатического потенциала будет таким же. Когда источник положителен, потенциал также положителен.

Электрическое поле считается потенциалом, что означает, что работа по перемещению заряда через него не зависит от траектории и определяется исключительно потенциалом. Потенциал – это универсальное физическое понятие, которое часто используется. Например, для гравитационного поля Земли, происхождение которого до сих пор не объяснено. Известно, что массы притягиваются друг к другу по закону, аналогичному тому, который вывел Шарль Кулон.

Нулевой потенциал и потенциальное поле

Электрическое поле считается потенциальным полем, поэтому работа, необходимая для перемещения заряда в нем, не зависит от траектории и определяется самим потенциалом. Потенциал – это универсальное физическое понятие, которое часто используется. Например, для гравитационного поля Земли, происхождение которого до сих пор не объяснено. Известно, что массы притягиваются друг к другу по закону, аналогичному тому, который вывел Шарль Кулон.

Эскиз напряженности поля

В электрическом поле начальная точка становится шаром. Нет разницы, по отношению к чему рассчитывается потенциал, но вскоре люди поняли, что ток смолы бьет током, ток стекла кусает, а ток земли не причиняет вреда. Следовательно, в полном соответствии с логикой, принимается как ноль. Это плюс: Земля имеет огромный объем, огромные токи, статические и переменные токи обтекают планету без труда. Доказано, что на теле заряды стараются разнести друг друга на максимальное расстояние. Что соответствует поверхности планеты. В этом случае плотность заряда ничтожно мала, гораздо меньше, чем на любом наэлектризованном теле.

На Земле потенциал, за редким исключением, измеряется относительно земли, эта величина называется электрическим напряжением. Из контекста ясно, что напряжение бывает положительным и отрицательным. Однако это не всегда так. В линиях электропередачи иногда считается выгодным использование изолированных нейтральных цепей. Тогда потенциал любой точки не рассматривается относительно земли, нет нейтральности. Это становится возможным в трехфазных цепях.

На местной трансформаторной подстанции устанавливается разделительный трансформатор, заземление нейтрали вторичной обмотки которого позволяет подавать потребителям фазное напряжение 220 В, а не сетевое. Иногда люди наивно полагают, что планета едина, поэтому нейтраль не нужна, ток будет течь в любом случае. Однако он будет проходить через землю, нанося значительный экономический ущерб и подвергая опасности людей, создавая шаговое напряжение. Медный нейтральный проводник – в первой половине 19 века его называли обратным проводником – имеет низкое сопротивление и гарантированно не причинит никакого вреда.

В цепях с изолированным нейтральным проводником потенциал не рассчитывается относительно уровня земли, а напряжение измеряется между двумя точками. Стоит отметить, что согласно закону Ома, ток, протекающий через проводник, вызывает разность потенциалов. По этой причине в случае аварии нельзя прикасаться к контуру заземления. Низкое сопротивление может вызвать высокую разность потенциалов в этой точке. Человек должен знать об опасности напряжения прикосновения.

Однако в целях безопасности также используются цепи с изолированной нейтральной точкой. Если между двумя точками вторичной обмотки разделительного трансформатора есть напряжение, ток не потечет на землю через случайно оголенный провод – разность потенциалов на земле меньше. Поэтому разделительный трансформатор становится защитной мерой и часто используется на практике.

Потенциальная энергия взаимодействия двух зарядов равна:

Теорема Гаусса для магнитного поля

Электрическое поле – что это такое, понятие в физике

Теорема Гаусса – один из самых фундаментальных законов электродинамики. Существуют теоремы Гаусса для электрического и магнитного полей, которые являются частью уравнений Максвелла. Используя этот закон, можно установить зависимость между напряженностью электрического поля и зарядом для любой поверхности. Теорема (закон) Гаусса гласит, что на любой замкнутой поверхности поток вектора электрического поля пропорционален заряду, содержащемуся в этой поверхности. Для магнитного поля теорема Гаусса гласит, что поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

электричество | Определение, факты и типы

электрическая сила между двумя зарядами

Смотреть все СМИ

Ключевые люди:

Томас Эдисон Рукс Эвелин Белл Кромптон Эдвард Уэстон Чарльз Фрэнсис Браш Флиминг Дженкин

Похожие темы:

биоэлектричество термоэлектричество электрический потенциал электролиз электрофорез

Просмотреть весь соответствующий контент →

Резюме

Прочтите краткий обзор этой темы

электричество , явление, связанное с неподвижными или движущимися электрическими зарядами. Электрический заряд является фундаментальным свойством материи и переносится элементарными частицами. В электричестве задействованной частицей является электрон, несущий заряд, условно обозначаемый как отрицательный. Таким образом, различные проявления электричества являются результатом накопления или движения множества электронов.

Электростатика — это изучение электромагнитных явлений, происходящих при отсутствии движущихся зарядов, т. е. после установления статического равновесия. Заряды быстро достигают своего положения равновесия, потому что электрическая сила чрезвычайно велика. Математические методы электростатики позволяют рассчитывать распределения электрического поля и электрического потенциала по известной конфигурации зарядов, проводников и изоляторов. И наоборот, по набору проводников с известными потенциалами можно рассчитать электрические поля в областях между проводниками и определить распределение заряда на поверхности проводников. Электрическую энергию набора зарядов в состоянии покоя можно рассматривать с точки зрения работы, необходимой для сборки зарядов; в качестве альтернативы можно также считать, что энергия находится в электрическом поле, создаваемом этим набором зарядов. Наконец, энергию можно хранить в конденсаторе; энергия, необходимая для зарядки такого устройства, запасается в нем в виде электростатической энергии электрического поля.

Изучите, что происходит с электронами двух нейтральных объектов, потертых друг о друга в сухой среде

Просмотреть все видео к этой статье

Статическое электричество — это известное электрическое явление, при котором заряженные частицы переходят от одного тела к другому. Например, если два предмета потереть друг о друга, особенно если эти предметы являются изоляторами, а окружающий воздух сухой, предметы приобретают равные и противоположные заряды, и между ними возникает сила притяжения. Объект, потерявший электроны, становится положительно заряженным, а другой — отрицательно заряженным. Сила — это просто притяжение между зарядами противоположного знака. Свойства этой силы были описаны выше; они включены в математическое соотношение, известное как закон Кулона. Электрическая сила на заряде Q ₁ при этих условиях за счет заряда Q ₂ на расстоянии r дается законом Кулона,

Жирные буквы в уравнении указывают на векторный характер силы, а единичный вектор r̂ — это вектор размера 1, который указывает от заряда Q ₂ до заряда Q ₁ . Константа пропорциональности k равна 10 ⁻⁷ c ² , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10 ⁹ ньютонов-квадратный метр на кулон в квадрате (Нм ² /C ² ). На рисунке 1 показано усилие на Q ₁ из-за Q ₂ . Числовой пример поможет проиллюстрировать эту силу. Оба Q ₁ и Q ₂ выбраны произвольно как положительные заряды, каждый с величиной 10 ⁻⁶ кулонов. Заряд Q ₁ расположен по координатам x , y , z со значениями 0.03, 0, 0 соответственно, а Q ₂ имеет координаты все.0.0, 0.0.0.0. координаты даны в метрах. Таким образом, расстояние между Q ₁ и Q ₂ составляет 0,05 метра.

Викторина «Британника»

Электричество: короткие замыкания и постоянные токи

В чем разница между электрическим проводником и изолятором? Кто изобрел аккумулятор? Почувствуйте, как ваши клетки горят, пока вы перезаряжаете свою умственную батарею, отвечая на вопросы этой викторины.

Величина силы F на заряде Q ₁ , рассчитанная по уравнению (1), составляет 3,6 ньютона; его направление показано на рис. 1. Сила, действующая на Q ₂ со стороны Q ₁ , равна − F , которая также имеет величину 3,6 ньютона; однако его направление противоположно направлению F . Сила F может быть выражена через ее компоненты вдоль x и y осей, так как вектор силы лежит в плоскости x y . Это делается с помощью элементарной тригонометрии из геометрии рисунка 1, а результаты показаны на рисунке 2. Таким образом, в ньютонах. Закон Кулона математически описывает свойства электрического взаимодействия между покоящимися зарядами. Если бы заряды имели противоположные знаки, сила была бы притягивающей; притяжение будет указано в уравнении (1) отрицательным коэффициентом единичного вектора руб. Таким образом, электрическая сила, действующая на Q ₁ , будет иметь направление, противоположное единичному вектору r̂ , и будет указывать от Q ₁ до 6 . В декартовых координатах это привело бы к изменению знаков обеих составляющих силы x и y силы в уравнении (2).

Как можно понять эту электрическую силу на Q ₁ ? Принципиально сила обусловлена ​​наличием электрического поля в положении Q ₁ . Поле создается вторым зарядом Q ₂ и имеет величину, пропорциональную размеру Q ₂ . При взаимодействии с этим полем первый заряд, находящийся на некотором расстоянии, либо притягивается, либо отталкивается от второго заряда в зависимости от знака первого заряда.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас

электростатика — Связь между электрическим полем и потенциалом

спросил 6 лет, 5 месяцев назад

Изменено 11 месяцев назад

Просмотрено 167 тысяч раз

$\begingroup$

Я не могу понять из этого — приходит знак. Какой шаг я сделал неправильно?

электростатика электрические поля потенциал потенциальная энергия условности

$\endgroup$

6

$\begingroup$

Связь между электрическим полем и потенциалом

Связь между электрическим полем $\bf E$ и скалярным потенциалом $\varphi$ задается как $$\mathbf E= -\mathbf \nabla\,\varphi$$, где $\mathbf \nabla \equiv \textrm{ оператор градиента}\;.$

Я не могу понять из этого — приходит знак.

Стоит процитировать Перселла:

Знак минус появился потому, что электрическое поле указывает из в область положительного вывода в сторону в область отрицательного вывода, тогда как вектор $\mathbf \nabla \varphi$ определен так, что он указывает в направлении увеличение $\varphi\;. $

Суть этой цитаты в том, что электрическое поле $\bf E$ указывает в направлении, противоположном направлению возрастания скалярного потенциала $\varphi\;.$ 9x \,\mathbf F(x)\,\mathrm dx\;.$$

Итак, ваш подход должен быть равен работе, выполненной против электрического поля внешним агентом при переносе заряда из точки $\rm от A$ до $\rm B$ , а это означало бы, что работа будет производиться отрицательной составляющей электрического поля в направлении движения .

$\endgroup$

$\begingroup$

$W = q(V_{\rm окончательная} — V_{\rm начальная}) = q((V+dV) -V)=q\, dV$

Пусть $\vec E = E\,\hat i$ и $d\vec r = dr \hat i$, где $E$ и $dr$ — компоненты в направлении $\hat i$.

$\vec F_{\rm external} = -qE\, \hat i$ и, следовательно, $W = \vec F_{\rm external} \cdot d \vec r = -qE\, \hat i \cdot dr \hat i = -qE \, dr$

Что дает $E = — \dfrac{dV}{dr }$

Поскольку $dr$ является компонентой $d\vec r$ в направлении $\hat i$, $dr$ может быть как положительным, так и отрицательным в зависимости от того, в какую сторону смещена внешняя сила. Как только это выражение становится интегралом, знак $dr$ определяется пределами интегрирования.

Возвращаясь к $W = -q E \, dr$ и предположим, что $E$ положительно, а если $dr$ положительно, то работа $W$ отрицательна, т.е. работа совершается электрическим полем и потенциал уменьшился.

Если $dr$ отрицательно (как у вас на диаграмме), то работа $W$ отрицательна, т.е. работа выполняется внешней силой и потенциал увеличился.

$\endgroup$

$\begingroup$

Чтобы поместить заряд вблизи электрического поля, необходимо совершить работу против электростатической силы, действующей на заряд. Эта работа, совершаемая для переноса заряда $q$ в электрическое поле другой конфигурации заряда от бесконечности на расстояние $r$, в поле называется потенциалом в точке $r$.

Чтобы совершить работу по перемещению заряда $q$ из потенциала $V$ на бесконечно малое расстояние, где потенциал равен $V+dV$, необходимо совершить работу против электрического поля.

Сила, действующая на заряд $q$, равна

$$F = qE$$

Таким образом, работа, совершаемая для перемещения заряда через разность потенциалов $dV$, равна:

$$dW = -F.dr $$

отрицательный знак означает, что необходимо совершить работу против электростатической силы.

Эта работа равна разности потенциалов заряда, умноженной на точки a и b (разделенные расстоянием $dr$)

$$dW = -F.dr = -q(E.dr) = qdV$$

$$or$$

$$ — E.dr = dV$$

$$or$$

$$E = -\frac{dV}{dr}$$

$\frac{dV}{dr}$ называется градиентом скаляра потенциальный $V$.

Следовательно, электрическое поле есть отрицательный градиент скалярного потенциала. В результате появился отрицательный знак, потому что разность потенциалов — это работа, совершаемая на единицу заряда против электростатической силы для перемещения заряда из a в b.

Однако это уравнение справедливо только для статических электростатических полей.

Ошибка в ваших вычислениях заключалась в том, что для расчета проделанной работы перемещение должно быть направлено против силы. Поэтому вы должны поставить знак минус, как я:

$$dW = -F.dr$$

$\endgroup$

2

$\begingroup$

Что вы сделали неправильно, так это непоследовательное определение положительного направления!
В EQ1 вы определяете направление + к левому $(V_B > V_A)$.
На EQ2 вы определяете направление + к вправо (-qE).
Если вы сохраните левое обозначение на EQ2, вы «освободите» член (cos 180) (поскольку -qE уже указывает влево), и знак —, а не , будет отменен.

$\endgroup$

Определения электрического потенциала и электрической потенциальной энергии

спросил 4 года 4 месяца назад

Изменено 1 год, 9 месяцев назад

Просмотрено 853 раза

$\begingroup$

Я думал об определении этих двух понятий и не знаю, правильно ли я понимаю, что они означают. Электрический потенциал — это просто работа, которую необходимо совершить, чтобы доставить заряд из бесконечности в область пространства с электрическим полем, создаваемым любым способом (например, точечным зарядом), а электрическая потенциальная энергия — это энергия, которую заряд имеет только потому, что он выход в этом электрическом поле. Верны ли эти 2 определения?

потенциальная энергия электрических полей

$\endgroup$

$\begingroup$

ЭЛЕКТРИЧЕСКАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ

Когда заряженная частица движется в электрическом поле, поле оказывает силу, которая может совершить работу над частицей. Эту работу можно выразить через потенциальную энергию. Подобно тому, как гравитационная энергия зависит от высоты массы над земной поверхностью, электрическая потенциальная энергия зависит от положения заряженной частицы в электрическом поле, когда на частицу, движущуюся из точки а в точку, действует сила $\vec F$. точка b, работа $W_{a\rightarrow b}$, совершаемая силой, равна, 9b F \cos\theta \mathrm{d}s$$

где $\vec{\mathrm{d}s}$ — бесконечно малое смещение вдоль пути частицы, а $\theta$ — угол между $\vec F $ и $\vec{\mathrm{d}s}$ в каждой точке пути.

Во-вторых, если сила $\vec F$ консервативна, то выполненную работу можно выразить через потенциальную энергию. Когда частица движется из точки, где потенциальная энергия равна $U_a$, в точку, где она равна $U_b$, изменение потенциальной энергии равно $\Delta U$=$U_b$-$U_a$. Это связано работой $ W_ {a\rightarrow b}$ as

$$ W_ {a\rightarrow b} = U_a- U_b = -\Delta U\tag{1}$$

Здесь $ W_{a\rightarrow b}$ — работа, совершаемая при перемещении частицы из точки a в б консервативной (здесь электростатической) силой, а не нами. Более того, из уравнения (1) видно, что если $W_{a\rightarrow b}$ положительна, $\Delta U$ отрицательна и потенциальная энергия уменьшается. Таким образом, всякий раз, когда работа консервативных сил положительна, потенциальная энергия системы уменьшается, и наоборот. Вот что происходит, когда частица подбрасывается вверх, работа силы тяжести отрицательна, а потенциальная энергия увеличивается.

ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ

Потенциал определяется как потенциальная энергия на единицу заряда.

Электрический потенциал – это энергия на единицу заряда, полученная или потерянная при перемещении единичного положительного заряда из некоторой контрольной точки, в которой потенциал равен нулю.

Таким образом,

$$V=U/q$$

Подытожим:

Электрическая потенциальная энергия – это энергия, которой тело обладает благодаря своему положению в электрическом поле (способность выполнять работу, возникающая из положения или конфигурации, если вы хотите получить конкретную информацию). То есть, если у вас есть, скажем, положительный заряд (+ заряд) и вы перемещаете его рядом с другим положительным зарядом, он захочет отклониться. Если вы подтолкнете его ближе к положительному заряду, он захочет отклониться сильнее. Единицей электрической потенциальной энергии является джоуль.

Электрический потенциал — это значение, которое мы получаем, когда мы смещаем единицу заряда из точки отсчета (с потенциалом $0$) в определенную точку. Это единица Джоуль/заряд.

Надеюсь, это поможет вам.

$\endgroup$

1

$\begingroup$

Прежде чем определить электрический потенциал, позвольте мне описать электрическое поле . Любая область пространства, на которую помещен статический заряд и на которую действует сила, рассматривается как электрическое поле. Представьте, что у нас есть 3 разных платежа: $q_{1}, q_{2}$ и $q_{3}$ в регионе. Если в эту область поместить заряд $q$, сила, действующая на $q$, равна сумме: $F= F_{1}+F_{2}+F_{3}$

Поскольку сила, с которой каждый $q_{i}$ действует на $q$, пропорциональна $q$, $F$ будет пропорциональна $q$. Следовательно:

$$F=qE$$

Обратите внимание, что если заряд $q$ положительный, то электрическое поле и электрическая сила имеют одинаковое направление. Если заряд $q$ отрицателен, то и электрическое поле, и электрическая сила имеют противоположные направления. Этот факт объясняет, почему при приложении электрического поля к электролиту как положительные, так и отрицательные ионы имеют противоположные направления. 9{f} Fdr = U_{p}(i) — U_{p}(f)$$

Тогда электрический потенциал можно определить в любой точке электрического поля как:

$$V=\frac{ U_{p}}{q}$$

$\endgroup$

0

$\begingroup$

Ваши определения не совсем точны.

Вы можете думать о потенциальной энергии как об энергии, необходимой для того, чтобы обрести определенный заряд из бесконечности.

Вы можете думать о потенциале как об энергии, необходимой для переноса единиц заряда из бесконечности.

Потенциал является более гибким в том смысле, что, как только он получен за единицу заряда, его можно использовать для расчета энергии, необходимой для получения определенного заряда. Этот процесс проводится знакомым $$U=qV$$

$\endgroup$

$\begingroup$

Согласно Википедии, электрический потенциал — это «количество работы, необходимое для перемещения единица положительного заряда от контрольной точки до определенной точки внутри поля без какого-либо ускорения .Обычно контрольной точкой является Земля или точка в Бесконечности, хотя любая точка вне влияния электрического поля

В этом определении стоит упомянуть пару точек (npi). Во-первых, потенциал определяется для положительного единичного заряда, а не только заряда. Во-вторых, потенциал в контрольной точке определяется как ноль, что является лишь условностью. Учитывая эти моменты, мы можем однозначно определить абсолютный потенциал Φ и его знак в любой точке пространства и абсолютную потенциальную энергию и ее знак заряда q, приведенного в эту точку, как U =qΦ.

Таким образом, если поле создано положительным зарядом, работа по внесению положительного единичного заряда в это поле положительна (т. е. фактическая работа должна быть выполнена против поля), и, следовательно, потенциал в любой точке этого поля будет быть положительным, как это отражено в формуле для потенциала, создаваемого зарядом Q, Φ=kQ/r, которая говорит, что положительный заряд создаст положительный потенциал.

Если в это поле внести положительный заряд q, то оно приобретет положительную потенциальную энергию U=qΦ.

Если к такому полю поднести отрицательный заряд -q («минус» здесь использован явно в иллюстративных целях), оно захочет двигаться само (уступить в поле), так что, собственно, отрицательная работа необходимо было бы сделать, чтобы удержать его от ускорения и, следовательно, по определению его приобретенная потенциальная энергия была бы отрицательной, что отразится в формуле: U=-qΦ. Или мы можем сказать, что заряд потеряет часть потенциальной энергии, работая против силы, удерживающей его от ускорения.

Аналогично можно рассматривать потенциал электрического поля, создаваемого отрицательным зарядом.

Это соглашение не нарушает того принципа, что система, предоставленная самой себе, будет пытаться уменьшить свою потенциальную энергию. Если в поле высвобождается заряд с положительной потенциальной энергией, он возвращается к исходной точке или к нулевому потенциалу. Если его потенциальная энергия отрицательна, он будет двигаться к заряду, создающему поле, делая потенциальную энергию еще более отрицательной.

Таким образом, оба ваших определения точны, но я был бы немного осторожнее с фразой «уступает электрическому полю», потому что, как мы видели, в зависимости от знаков вовлеченных зарядов заряд может либо уступить место электрическое поле или быть принудительно помещенным в электрическое поле.

$\endgroup$

$\begingroup$

Электрический потенциал — это работа, совершаемая на единицу заряда для переноса некоторого заряда из бесконечности в некоторую область рядом с источником электрического поля. Важной здесь является эта часть на единицу заряда. Электрическая потенциальная энергия — это просто работа, совершаемая для переноса некоторого заряда из бесконечности в область рядом с источником. Итак, если q — это заряд, а U — это работа, то потенциал — это просто U/q.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Электрический потенциал: определение, энергия, единицы измерения, формула

Электрический потенциал является скалярной величиной; он описывает работу, которую совершает каждая заряженная частица, чтобы переместить ее из одной точки в другую. В то время как электрический потенциал является скалярным и не имеет направления, электрический заряд имеет знак, который относится к заряду интересующей частицы.

Характеристики электрического потенциала

• Электрический потенциал положителен вокруг изолированного положительного заряда.

• Электрический потенциал вокруг изолированного отрицательного заряда отрицательный.

• Электрический потенциал равен нулю на бесконечном расстоянии от исследуемого заряда.

Электрический потенциал в поле

Электрический потенциал точечного заряда (q) в поле пропорционален заряду, создающему потенциал, и обратно пропорционален диэлектрической проницаемости и расстоянию от точечного заряда. Математически это выражается в приведенном ниже уравнении, где V — электрический потенциал в вольтах, Q — точечный заряд, r — расстояние, измеренное в метрах, а εo — диэлектрическая проницаемость вакуума, измеренная в фарадах на метр, равная 8,85 ⋅ 10 ^-12 Ф/м.

Из уравнения можно сделать вывод, что для положительного заряда q электрический потенциал увеличивается при уменьшении расстояния r, так как для перемещения положительного заряда потребуется больше работы из-за силы отталкивания. Точно так же для отрицательного заряда q расстояние от заряда уменьшается, так как положительный пробный заряд будет двигаться легче из-за силы притяжения. Это показано ниже, где показано взаимодействие между положительным и отрицательным зарядом.

Электрическое поле, Джорджия Панаги — StudySmarter Originals

Чтобы найти потенциал в точке, вызванный несколькими зарядами, вы должны найти сумму потенциалов от каждого заряда.

Что такое электрическая потенциальная энергия?

Электрическая потенциальная энергия — это энергия, необходимая для перемещения заряда (q) из одной точки в другую в электрическом поле.

Например, чтобы переместить положительный заряд ближе к другому положительному заряду, необходима работа по преодолению силы отталкивания. Точно так же, когда положительный заряд удаляется от отрицательного заряда, также необходима работа для преодоления силы притяжения.

Энергия, передаваемая движущемуся заряду, называется потенциальной электрической энергией. Чем сильнее электрическое поле, тем больше потенциальной энергии требуется для перемещения заряда через поле.

Электрическая потенциальная энергия двух точечных зарядов

Электрический потенциал пары точечных зарядов прямо пропорционален величине произведения двух зарядов, как показано в приведенном ниже уравнении.

Диэлектрическая проницаемость вакуума ε ₀ — константа, представляющая тенденцию электрического поля проникать в вакуум. Его значение приведено ниже и измеряется в Ф/м.

Изменение потенциальной электрической энергии можно найти, используя соответствующее расстояние каждой единицы заряда.

Электрический потенциал и работа

Электрический потенциал также может быть выражен математически через работу; помните, это работа, необходимая для перемещения заряда через электрическое поле. Работа равна произведению электрического потенциала на заряд, вызывающий электрический потенциал. Это показано ниже, где ΔV — изменение электрического потенциала, измеренное в вольтах, а Q — заряд, измеренный в кулонах.

Что такое градиент электрического потенциала?

Градиент электрического потенциала — это изменение электрического потенциала в электрическом поле. Электрическое поле в любой точке равно отрицательному градиенту потенциального расстояния в этой точке. Разность потенциалов показана ниже.

Градиент определяется эквипотенциальными линиями, которые представлены оранжевыми пунктирными круговыми линиями и показывают электрический потенциал в электрическом поле. Они всегда перпендикулярны линиям электрического поля, которые показаны синими линиями. Эквипотенциальные линии выражают силу электрического потенциала. Чем плотнее эквипотенциальные линии, тем сильнее потенциал.

Электрическое поле и эквипотенциальные линии, Study Smarter

Что такое разность электрических потенциалов?

Разность электрических потенциалов — это работа, необходимая для перемещения заряженной частицы в электрическом поле из точки A в точку B. Это выражается в приведенном ниже уравнении, где E — напряженность электрического поля, V — электрический потенциал в вольтах, r — расстояние между двумя интересующими точками в метрах.

Отрицательный знак, показанный ниже, выражает направление электрического поля. Он всегда направлен наружу от положительного заряда и внутрь к отрицательному (взгляните на первое изображение).

Электрический генератор сферической формы имеет радиус 10 см и генерирует потенциал 150 кВ. Найти электрический потенциал на расстоянии 25 см от генератора.

Решение:

Начнем с нахождения заряда с помощью уравнения потенциала и перегруппировки, чтобы сделать Q субъектом, а затем подставить заданные значения.

Затем мы переходим к нахождению потенциала, используя уравнение потенциала. Но теперь мы используем общее расстояние в 25 см от генератора, которое равно расстоянию радиуса плюс расстояние от генератора.

Электрический потенциал — основные выводы

• Электрический потенциал — это работа, необходимая для перемещения заряда из одной точки в другую.

• Разность электрических потенциалов — это изменение напряженности электрического поля между двумя точками электрического поля.

• Электрический потенциал (В) уменьшается по мере увеличения расстояния между исследуемой точкой и источником электрического потенциала.

Калькулятор электрического потенциала

Автор Purnima Singh, PhD

Отзыв Стивена Вудинга

Последнее обновление: 24 ноября 2021 г.

Содержание:

• Разность электрических потенциалов
• Что такое электрический потенциал? – Определение электрического потенциала
• Формула электрического потенциала
• Как рассчитать электрический потенциал?
• Как пользоваться калькулятором электрического потенциала
• Единицы электрического потенциала
• Размерная формула электрического потенциала
• Часто задаваемые вопросы

Используйте калькулятор электрического потенциала, чтобы определить электрический потенциал в точке либо за счет одиночного точечного заряда, либо за счет системы точечных зарядов. Вы также можете использовать этот инструмент для определения разности электрических потенциалов между двумя точками.

Продолжайте читать эту статью, чтобы узнать:

• Что такое электрический потенциал?
• Какая связь между электрическим потенциалом и электрической потенциальной энергией?
• Как рассчитать электрический потенциал?
• Что такое единица электрического потенциала?

Разность электрических потенциалов

Чтобы понять идею разности электрических потенциалов, рассмотрим некоторое распределение заряда. Это распределение заряда создаст электрическое поле. Теперь, если мы хотим переместить небольшой заряд q между любыми двумя точками в этом поле, необходимо совершить некоторую работу против кулоновской силы. Эта проделанная работа сохраняется в заряде в виде его потенциальной электрической энергии.

Если мы рассмотрим две произвольные точки, скажем A и B, то выполненная работа ( Вт AB ) и изменение потенциальной энергии ( ∆U ) при перемещении заряда ( q ) из точки A в B можно записать как:

• W AB = ∆U = (V A - V B ) * q . ….. (1)

, где В А и В В — электрические потенциалы в точках А и В соответственно (мы объясним, что это значит, в следующем разделе).

Если величина q равна единице (мы называем положительный заряд единичной величины пробным зарядом), уравнение меняется на: AB / Q …… (2)

Используя приведенное выше уравнение, мы можем определить разность электрических потенциалов ( ∆V ) между двумя точками (B и A) как работу, выполненную для перемещения пробного заряда из A в B против электростатической силы .

Помните, что потенциальную электрическую энергию нельзя рассчитать по стандартной формуле потенциальной энергии E = mgh .

Что такое электрический потенциал? – Определение электрического потенциала

Если мы возьмем одну из точек в предыдущем разделе, скажем, точку A, находящуюся на бесконечности, и выберем потенциал на бесконечности равным нулю, мы можем изменить формулу разности электрических потенциалов (уравнение 2) следующим образом:

• В В = Ш ∞В / q

Следовательно, мы можем определить электрический потенциал в любой точке как количество работы, выполненной при перемещении пробного заряда из бесконечности в эту точку .

Мы также можем определить электрический потенциал как электрическую потенциальную энергию на единицу заряда, то есть:

• В = ∆U / q

Итак, вы видите, что электрический потенциал и электрическая потенциальная энергия — это не одно и то же.

Формула электрического потенциала

Для расчета электрического потенциала в любой точке А за счет одного точечного заряда (см. рис. 1), воспользуемся формулой:

• В = k * q/r

где:

• q — электростатический заряд;
• r — Расстояние между А и точечным зарядом; и
• k = 1/4 * π * ϵ 0 — постоянная Кулона.

Рис. 1: Электрический потенциал точечного заряда.

Заметим, что когда заряд q положительный, электрический потенциал положительный. Когда заряд q отрицателен, электрический потенциал отрицателен.

Теперь мы рассмотрим случай, когда есть четыре очка, Q 1 , Q 2 , Q 3 и Q 4 (см. Потенциал в точке А от заряда q 1 равен:

• В 1 = k * q 1 / r 1

Рис. 2: Электрический потенциал, обусловленный системой точечных зарядов.

Аналогичные выражения можно написать для потенциала в точке А от других зарядов:

В 3 = k * q 3 / r 3

В 4 = k * q 4 / р 4

Чтобы получить результирующий потенциал в точке А, воспользуемся принципом суперпозиции, т. е. сложим отдельные потенциалы:
V = k * [(q ₁ / r ₁ ) + (q ₂ / r ₂ ) + (q ₃ / r ₃ ) + (q 4 0 3 _{) + (q 4 0 3 035 ) 4} )]

Для системы n точечных зарядов, результирующий потенциал можно записать в виде: 1 / r ₁ ) + (q ₂ / r ₂ ) + (q ₃ / r ₃ ) + . … + (q _{n 6 n 3 n 9003]
В = k * ∑(q i / r i )}

В следующем разделе мы увидим, как рассчитать электрический потенциал на простом примере.

Как рассчитать электрический потенциал?

Рассчитаем электростатический потенциал в точке, обусловленной зарядом 4 × 10 -7 Кл , находящимся на расстоянии 10 см .

1. Нам дано:

   q = 4 × 10 -7 C и r = 10 см = 0,1 м .

2. Подставив эти значения в формулу электрического потенциала от точечного заряда, получим:

В = q / (4 * π * ϵ 0 * r)

В = [8,99 × 10 9 Н·м 2 /C 2 * 4 × 10 -7 C] / 0,1 м

В = 3,6 × 10 4 В

3. Следовательно, электрический потенциал в точке, обусловленной зарядом 4 × 10 -7 Кл , находящимся на расстоянии 10 см , равен 3,6 × 10 4 В .

Как пользоваться калькулятором электрического потенциала

Теперь посмотрим, как можно решить ту же задачу с помощью нашего калькулятора электрического потенциала:

1. В раскрывающемся меню выберите электрический потенциал за счет точечного заряда .

2. Введите значение электрического заряда , т. е. 4e-07 и расстояние между точечным зарядом и точкой наблюдения ( 10 см ).

3. Вы также можете изменить значение относительной диэлектрической проницаемости , используя Расширенный режим .

4. Калькулятор отобразит значение электрического потенциала в точке наблюдения, т. е. 3,595 × 10 4 В .

Единицы электрического потенциала

Единицей электрического потенциала СИ является вольт (В) . Можно сказать, что электрический потенциал в точке равен 1 В , если 1 Дж работы совершается при переносе положительного заряда 1 Кл из бесконечности в эту точку против электростатической силы.

Единицей измерения разности потенциалов также является вольт. Возможно, вы более знакомы с напряжением, а не с термином «разность потенциалов». Например, когда мы говорим о батарее 3 В , мы просто имеем в виду, что разность потенциалов между двумя ее выводами составляет 3 В .

Размерная формула электрического потенциала

Чтобы написать размерную формулу для электрического потенциала (или разности электрических потенциалов), мы сначала напишем уравнение для электрического потенциала:

• В = Вт / кв

Теперь подставив размерную формулу для работы/энергии и заряда, мы получим размерную формулу для электрического потенциала как: [M ¹ L ² T ^-3 A ^-1 ]

Часто задаваемые вопросы

Как рассчитать электрический потенциал точечного заряда?

Для расчета электрического потенциала точечного заряда (q) на расстоянии (r) следуйте приведенным инструкциям:

1. Умножьте заряд q на постоянную Кулона .

2. Разделить значение из шаг 1 на расстояние r.

3. Поздравляем! Вы вычислили электрический потенциал точечного заряда.

Может ли электрический потенциал быть отрицательным?

Да , электрический потенциал может быть отрицательным. Электростатический потенциал в точке из-за положительного заряда положителен. Если заряд отрицательный, электрический потенциал также отрицательный.

Что такое разность электрических потенциалов?

Разность электрических потенциалов между двумя точками A и B определяется как работа, совершаемая для перемещения единичного положительного заряда из A в B . Единицей разности потенциалов в системе СИ является вольт (В).

Является ли электрический потенциал скалярной или векторной величиной?

Электрический потенциал является скалярной величиной , так как он не имеет направления.

Какова единица измерения электрического потенциала?

Электрический потенциал – электрическая потенциальная энергия на единицу заряда. Единицей электрической потенциальной энергии в системе СИ является джоуль (Дж), а единицы заряда — кулон (Кл). Следовательно, единицей электрического потенциала в СИ является Дж/Кл, т. е. вольт (В) .

Чему равен электрический потенциал заряда в точке, удаленной на бесконечность?

Ноль . Электрический потенциал в точке P , обусловленный зарядом q , обратно пропорционален расстоянию между ними. Следовательно, когда расстояние бесконечно, электрический потенциал равен нулю.

Purnima Singh, PhD

Я хочу вычислить…..

Электрический потенциал

Заряд (q)

Расстояние (r)

Электрический потенциал (V)

Ознакомиться с 83 похожими калькуляторами электромагнетизма 🲧9 🲧

Ускорение частицы в электрическом полеМощность переменного тока Размер прерывателя… Еще 80

14.

3 Электрический потенциал, обусловленный точечным зарядом – Физика Колледжа Дугласа 1104 Пользовательский учебник – Зима и лето 2020

Глава 14 Электрический потенциал и электрическое поле

Резюме

• Объясните точечные заряды и составьте уравнение для электрического потенциала точечного заряда.
• Различать электрический потенциал и электрическое поле.
• Определите электрический потенциал точечного заряда при заданном заряде и расстоянии.

Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи. Кроме того, сферические распределения заряда (как на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть. Использование вычислений для определения работы, необходимой для перемещения пробного заряда [латекс]\boldsymbol{q}[/латекс] с большого расстояния на расстояние [латекс]\boldsymbol{r}[/латекс] от точечного заряда [ латекс]\boldsymbol{Q}[/latex], и учитывая связь между работой и потенциалом [латекс]\boldsymbol{(W = -q \Delta V)}[/latex], можно показать, что 92 . }[/латекс]

Электрический потенциал

В точечного заряда

Электрический потенциал [латекс]\boldsymbol{V}[/latex] точечного заряда определяется выражением

[латекс]\boldsymbol{V =}[/latex] [ латекс]\boldsymbol{\frac{kQ}{r}}[/latex] [латекс]\boldsymbol{( \textbf{Point Charge}),}[/latex]

Потенциал на бесконечности выбран равным нулю. Таким образом, [латекс]\boldsymbol{V}[/latex] для точечного заряда уменьшается с расстоянием, тогда как [латекс]\boldsymbol{E}[/латекс] для точечного заряда уменьшается с квадратом расстояния: 92}}.[/латекс]

Напомним, что электрический потенциал [latex]\boldsymbol{V}[/latex] является скаляром и не имеет направления, тогда как электрическое поле [latex]\textbf{E}[/latex] является вектором. Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов , принимая во внимание величину и направление. Это согласуется с тем фактом, что [latex]\boldsymbol{V}[/latex] тесно связан с энергией, скаляром, тогда как [latex]\textbf{E}[/latex] тесно связан с силой, то есть вектором.

Пример 1. Какое напряжение создает небольшой заряд на металлическом шаре?

Заряды статического электричества обычно находятся в диапазоне от нанокулонов (нКл) до микрокулонов [латекс]\boldsymbol{( \mu \textbf{C})}[/latex]. Чему равно напряжение на расстоянии 5,00 см от центра металлического шара диаметром 1 см, имеющего статический заряд -3,00 нКл?

Стратегия

Как мы обсуждали в главе 18 Электрический заряд и электрическое поле, заряд на металлическом шаре распространяется равномерно и создает поле, похожее на поле точечного заряда, расположенного в его центре. Таким образом, мы можем найти напряжение, используя уравнение [латекс]\boldsymbol{V = kQ/r}[/латекс] . 9{2} \;\textbf{m}})} \\[1em] & \boldsymbol{-539 \;\textbf{V}}. \end{array}[/latex]

Обсуждение

Отрицательное значение напряжения означает, что положительный заряд будет притягиваться с большего расстояния, поскольку потенциал ниже (более отрицательный), чем на больших расстояниях. И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.

Пример 2. Что такое избыточный заряд генератора Ван де Граафа

Демонстрационный генератор Ван де Граафа имеет металлическую сферу диаметром 25,0 см, которая производит напряжение 100 кВ вблизи своей поверхности. (См. рис. 1.) Какой избыточный заряд находится на сфере? (Предположим, что каждое числовое значение здесь показано тремя значащими цифрами.)

Рисунок 1. Напряжение этого демонстрационного генератора Ван де Граафа измеряется между заряженной сферой и землей. Потенциал Земли принимается равным нулю в качестве эталона. Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре.

Стратегия

Потенциал на поверхности будет таким же, как у точечного заряда в центре сферы на расстоянии 12,5 см. (Радиус сферы равен 12,5 см.) Таким образом, мы можем определить избыточный заряд, используя уравнение 9{-6} \;\textbf{C} = 1,39 \;\mu \textbf{C}}. \end{array}[/latex]

Обсуждение

Это относительно небольшой заряд, но он производит довольно большое напряжение. У нас есть еще одно указание на то, что трудно хранить изолированные заряды.

Напряжения в обоих этих примерах можно измерить с помощью измерителя, который сравнивает измеренный потенциал с потенциалом земли. Потенциал земли часто принимается равным нулю (вместо того, чтобы принимать потенциал на бесконечности равным нулю). Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечалось в главе 19.1 Электрическая потенциальная энергия: разность потенциалов. Это аналогично тому, как уровень моря принимается за [латекс]\boldsymbol{h = 0}[/latex] при рассмотрении гравитационной потенциальной энергии, [латекс]\boldsymbol{\textbf{PE}_g = мгх}[/латекс].

• Электрический потенциал точечного заряда равен [латекс]\boldsymbol{V = kQ/r}[/латекс]. 2 \;\textbf{V}}[/latex]? 9{-14} \;\textbf{m}}[/latex] из фрагмента, содержащего 46 протонов? б) Какова потенциальная энергия в МэВ одноименно заряженного фрагмента на этом расстоянии?

  8: Исследовательский генератор Ван де Граафа имеет металлический шар диаметром 2,00 м с зарядом 5,00 мКл. а) Каков потенциал вблизи его поверхности? б) На каком расстоянии от его центра находится потенциал 1,00 МВ? (в) Атом кислорода с тремя недостающими электронами высвобождается вблизи генератора Ван де Граафа. Какова его энергия в МэВ на этом расстоянии?

  9: Электростатический распылитель краски представляет собой металлическую сферу диаметром 0,200 м с потенциалом 25,0 кВ, которая отбрасывает капли краски на заземленный объект. а) Какой заряд находится на шаре? б) Какой заряд должен иметь капля краски массой 0,100 мг, чтобы достичь предмета со скоростью 10,0 м/с?

  10: В одном из классических экспериментов по ядерной физике в начале ХХ века альфа-частица была ускорена к ядру золота, и ее траектория была существенно отклонена кулоновским взаимодействием.