магнитное поле. однородное и неоднородное магнитное поле. | План-конспект урока по физике (8 класс) на тему:
Тема урока: Магнитное поле. Однородное и неоднородное магнитное поле.
Тип урока: изучение нового материала.
Цель урока:
- Образовательная
закрепить понятие постоянного и электрического магнита, магнитного поля; исследовать зависимость величины магнитного поля магнита от расстояния до него; исследовать взаимодействие полюсов двух магнитов; исследовать взаимодействие соленоида и постоянного магнита; познакомиться со свойствами магнитного поля.
- Воспитательная
формировать навыки работы в группах; прививать интерес к предмету через различные компоненты воспитательного процесса.
- Развивающая
развивать умение анализировать, сравнивать, систематизировать информацию; устанавливать причинно – следственные связи; делать выводы.
Литература:
- Физика.
 9 класс. Учебник. Перышкин А.В., Гутник Е.М.
9 класс. Учебник. Перышкин А.В., Гутник Е.М. - Физика (Физикон). 7-11 класс (CD), Библиотека наглядных пособий (CD).
Оборудование:
Компьютер, экран, мультимедийный проектор, магниты полосовые и дугообразные (по кол-ву детей в классе), железные опилки, магнитная стрелка, источник тока, соленоид, соединительные провода.
План урока:
- Организационный момент.
2. Историческая справка.
3. Изучение нового материала.
4. Практическое применение магнитного поля тока (презентация + видеоматериал).
5. Закрепление материала
6. Итог урока.
7.Задание на дом.
Ход урока:
- Организационный момент.
Приветствие учащихся. Проверка отсутствующих.
- Историческая справка.
Учитель: Магнетизм, как явление, известен, по крайней мере, с пятого века до нашей эры, но изучение его сущности продвигалось очень медленно. Еще древние греки знали, что существует особый минерал — камень из Магнесии (область в древнегреческой Фессалии), способный притягивать небольшие железные предметы.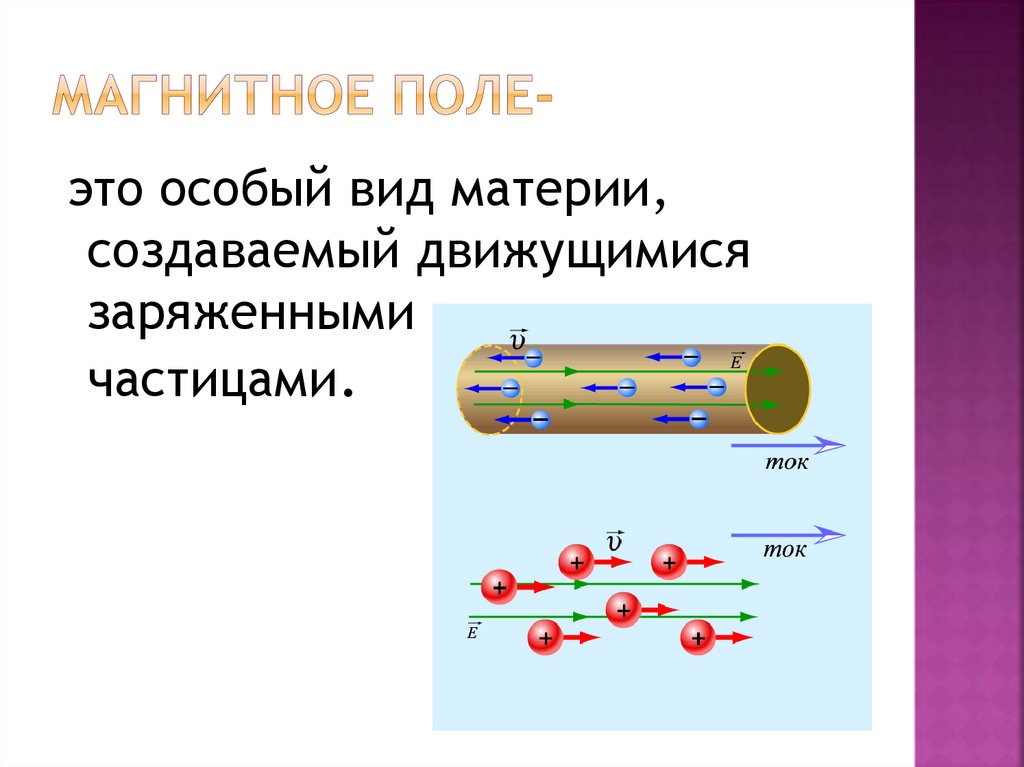
Однако впервые свойства магнита были описаны лишь в 1269 году. А первой крупной работой, посвященной исследованию магнитных явлений, является книга Вильяма Гильберта «О магните», вышедшая в 1600 году.
В древние времена свойства магнита пытались объяснить приписыванием ему «живой души». Теперь мы знаем, что все дело в особом поле, создаваемом магнитом – магнитном поле.
- Изучение нового материала. Опыт Эрстеда.
Учитель: Магнитное поле создается не только постоянными магнитами, но и проводниками с током. Убедится в этом нам поможет опыт, проведенный датским физиком Эрстедом.
Сообщение ученика: ЭРСТЕД Ганс Христиан (1777 — 1851) — датский физик, непременный секретарь Датского королевского общества (с 1815). Окончил Копенгагенский университет (1797). С 1806 года — профессор этого университета, с 1829 года одновременно директор Копенгагенской политехнической школы.
Работы Эрстеда посвящены электричеству, акустике, молекулярной физике. В 1820 году он обнаружил действие электрического тока на магнитную стрелку. Это привело к возникновению новой области физики — электромагнетизма. Идея взаимосвязи между различными явлениями природы характерна для научного творчества Эрстеда. Эрстед был блестящим лектором и популяризатором, организовал в 1824 году Общество по распространению естествознания, создал первую в Дании физическую лабораторию, способствовал улучшению преподавания физики в учебных заведениях страны.
В 1820 году он обнаружил действие электрического тока на магнитную стрелку. Это привело к возникновению новой области физики — электромагнетизма. Идея взаимосвязи между различными явлениями природы характерна для научного творчества Эрстеда. Эрстед был блестящим лектором и популяризатором, организовал в 1824 году Общество по распространению естествознания, создал первую в Дании физическую лабораторию, способствовал улучшению преподавания физики в учебных заведениях страны.
Эрстед почетный член многих академий наук, в частности, Петербургской АН (1830).
Учитель демонстрирует опыт:
Отклонение магнитной стрелки при прохождении тока через проводник.
Учитель: Этот опыт позволил другому физику, французу Амперу, сформулировать гипотезу о природе возникновения магнитного поля.
Гипотеза Ампера. Природа возникновения и свойства магнитного поля.
Сообщение ученика: Андре Мари Ампер(1775-1836) –французский физик и математик, родился в г. Лионе. Под руководством отца он получил домашнее образование.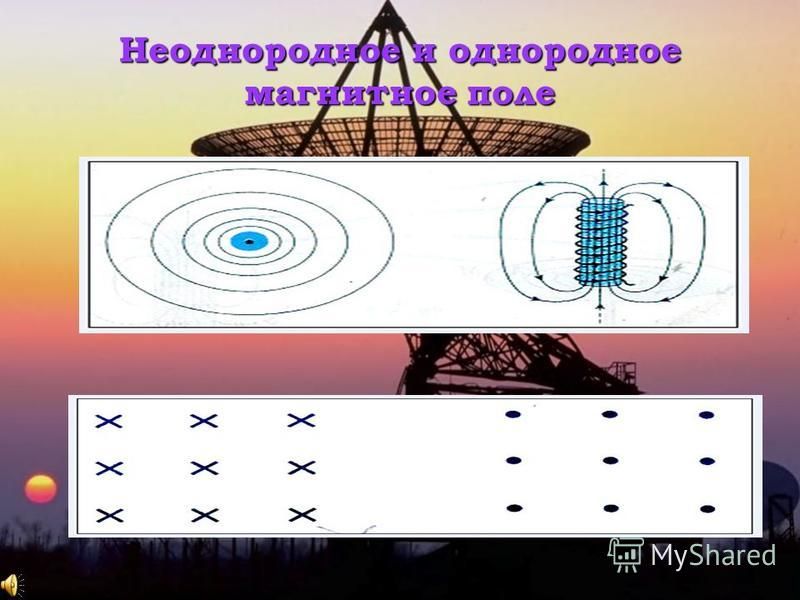 Амперу было 14 лет, когда он прочитал 20 томов «Энциклопедии». Трудовая деятельность Ампер начал в качестве домашнего учителя математики, физики и химии. В 1801 г. он был принят на должность учителя физики и химии в Центральную школу в Бурк-ан-Брес. В 1805 г. Ампер занимает место преподавателя математики в Политехнической школе в Париже. В 1814 г. Ампера избирают членом Парижской академии наук. В 1824 г. занимает должность профессора физики Нормальной школы в Париже.
Амперу было 14 лет, когда он прочитал 20 томов «Энциклопедии». Трудовая деятельность Ампер начал в качестве домашнего учителя математики, физики и химии. В 1801 г. он был принят на должность учителя физики и химии в Центральную школу в Бурк-ан-Брес. В 1805 г. Ампер занимает место преподавателя математики в Политехнической школе в Париже. В 1814 г. Ампера избирают членом Парижской академии наук. В 1824 г. занимает должность профессора физики Нормальной школы в Париже.
Ампер открыл механическое взаимодействие токов и на основании гипотезы о существовании молекулярных токов построил первую теорию магнетизма.
В 1826 г. Ампер подготовил и издал свой основной труд – «Теория электродинамических явлений, выведенная исключительно из опыта».
В честь Ампера названа единица силы тока – ампер.
Учитель: В 1820 г. Ампер предположил, что магнитные свойства постоянных магнитов обусловлены множеством круговых токов, циркулирующих внутри молекул этих тел в результате движения электронов. В подтверждении своей теории Ампер провел ряд опытов, один из которых, «Взаимодействие параллельных токов», мы сейчас посмотрим.
В подтверждении своей теории Ампер провел ряд опытов, один из которых, «Взаимодействие параллельных токов», мы сейчас посмотрим.
Видеоматериал «Взаимодействие параллельных токов» — 1,5 минуты — экран.
Учитель: Ампер сформулировал основные свойства магнитного поля:
Магнитное поле порождается только движущимися зарядами, в частности электрическим током.
В отличие от электрического поля магнитное поле обнаруживается по его действию на движущиеся заряды (движущиеся заряженные тела).
Магнитное поле, как и электрическое поле, материально, т.к. оно действует на тела, и следовательно, обладает энергией. Магнитное поле обнаруживается по действию на магнитную стрелку. Силовой характеристикой магнитного поля является векторная физическая величина – магнитная индукция В. Направление в котором устанавливается северный полюс магнитной стрелки, совпадает с направлением индукции магнитного поля в этой точке.
Графическое изображение силовых линий магнитного поля (работа в группах).
Учитель: Для наглядного представления магнитного поля будем пользоваться магнитными линиями. Получить эти линии нам поможет постоянный магнит и железные опилки.
Железные опилки – это маленькие магнитные стрелки. Линии, вдоль которых располагаются железные опилки, называются силовыми линиями магнитного поля.
Силовые линии всегда имеют форму замкнутых, закругленных линий.
Ход работы:
Учащимся раздаются листы для исследования:
№ опыта | Объект эксперимента | Результат – графическое изображение линий магнитного поля |
1 | Полосовой магнит | |
2 | Дугообразный магнит | |
3 | Соленоид | |
4 | Круговой проводник с током |
- Положите магнит на стол.

- Поднесите к нему другой магнит сначала одним полюсом, а затем другим.
- Соедините два магнита противоположными полюсами.
- Поместите на получившийся магнит кусок плотной бумаги.
- Сверху аккуратно насыпьте металлические опилки.
- Подключите соленоид к источнику тока, аккуратно насыпьте металлические опилки.
- Проделайте аналогичные действия с круговым проводником.
Ответьте на вопросы:
1. Как взаимодействуют два магнита?
- Как зависит густота силовых линий от расстояния до магнита?
- Какую форму имеют силовые линии магнитного поля?
Вывод: 1. Одноименные полюса магнитов отталкиваются, а разноименные притягиваются.
2. Чем ближе к полюсам магнита, тем силовые линии гуще.
3. Силовые линии всегда имеют форму замкнутых, закругленных линий.
Магнитное поле прямого тока (видеоматериал – 2 минуты – компьютер).
Учитель: Вы выяснили, как располагается магнитное поле рядом с постоянным магнитом, а теперь посмотрим как оно проявляет себя вокруг проводника с током (видео).
Правило буравчика (презентация + учебник).
Учитель: Как мы только что убедились, магнитные стрелки устанавливаются вокруг проводника в зависимости от направления тока в нем. Эту зависимость можно описать простым правилом – «правилом буравчика». Откройте страницу 147 учебника и прочитайте определение. Обратите внимание на обозначения силы тока в проводнике и линий магнитного поля.
Магнитное поле соленоида.
Учитель (рассказывает и показывает опыт, подтверждающий, что соленоид с током – это магнит): Магнитное поле обнаруживается не только вокруг проводника с током. Если проводник свернуть в кольцо в нём также порождается магнитное поле. Возьмём катушку с множеством витков и подключим её к источнику тока. В катушке возникнет магнитное поле, которое можно наблюдать, поднося магнитную стрелку к концу соленоида. Для определения направления силовых линий в катушке используют «правило буравчика» в несколько измененной форме. (страница 148 учебника – прочитать).
4. Практическое применение магнитного поля тока (презентация).
Учитель: Магнитное действие тока широко применяют в промышленности(вилеоматериал)
Грузоподъемные магниты – наиболее мощные из широко применяемых в промышленности. Как правило, они представляют собой катушку, охватывающую железный сердечник большого сечения. Хотя электромагнит подключается к сети переменного тока, он снабжен мощным выпрямителем, так что через катушку может течь постоянный ток, достигающий 50 ампер. Это позволяет электромагниту весом 1–2 тонны поднимать груз весом 10–15 тонн, если он допускает максимальную площадь контакта с сердечником. Электромагнит удобен также для перемещения металлического лома и уборки стружки. Кроме того, иногда грузоподъемные электромагниты могут применяться для отделения железной фракции из сыпучего вещества, например, угля или руды перед переработкой или транспортировкой.
5. Закрепление материала.
Вопросы:
- Как можно объяснить отклонение магнитной стрелки около проводника с током?
- Какое магнитное поле – однородное или неоднородное — образуется вокруг магнита, проводника с током, внутри соленоида?
- Перечислите основные свойства магнитного поля.

- Какое правило используют для определения направления линий магнитного поля?
- Применение электромагнитов.
- Обозначьте неизвестные полюса взаимодействующих магнитов:
- На рисунке указан проводник с током, расположенный перпендикулярно плоскости рисунка и одна магнитная линия. Укажите полюса магнитных стрелок, расположенных в точках А, В, С, Д.
- На рисунке указан проводник с током, расположенный перпендикулярно плоскости рисунка и одна магнитная линия. В точках А, В, С, Д магнитной линии расположены магнитные стрелки. Укажите направление электрического тока в проводнике.
- Изобразите с помощью линий магнитной индукции магнитное поле катушки с током:
6. Что собой представляют линии магнитного поля?
6. Итог урока.
Учитель: Давайте подведем итоги сегодняшнего урока (учащиеся сами формулируют вопросы и дают ответы на них):
Ответы:
1. Вокруг постоянного магнита, а также вокруг проводника с током существует магнитное поле, действующее на любой магнит, который в нем находится.
Вокруг постоянного магнита, а также вокруг проводника с током существует магнитное поле, действующее на любой магнит, который в нем находится.
2. Линии магнитного поля замкнуты. Там, где они выходят из магнита, — его северный полюс, там, где они входят в магнит, — южный.
3. «Правило буравчика» — если поступательное движение буравчика сонаправлено с током в проводнике, то направление вращения буравчика совпадает с направлением магнитных линий.
4. Устройство, состоящее из железного сердечника, обмотанного изолированным проводом, по которому течет ток, называют электромагнитом.
7. Задание на дом.
§ 44 упражнение 35 (повторить). § 49,50, ответить на вопросы.
Урок по физике в 9 классе на тему «Магнитное поле. Однородное и неоднородное магнитное поле»
МБОУ «Ромодановская средняя общеобразовательная школа №2»
Открытый урок по физике в 9 классе
Магнитное
поле.
Однородное и неоднородное
магнитное поле
Подготовила и провела: Ладикова М.А.
учитель физики
Ромоданово, 2016
Тема урока: Магнитное поле. Однородное и неоднородное магнитное поле.
Тип урока: изучение нового материала.
Цель урока:
1. Образовательная
закрепить понятие постоянного и электрического магнита, магнитного поля; исследовать зависимость величины магнитного поля магнита от расстояния до него; исследовать взаимодействие полюсов двух магнитов; исследовать взаимодействие соленоида и постоянного магнита; познакомиться со свойствами магнитного поля.
2. Воспитательная
формировать навыки работы в
группах; прививать интерес к предмету через различные компоненты
воспитательного процесса.
3. Развивающая
развивать умение анализировать, сравнивать, систематизировать информацию; устанавливать причинно – следственные связи; делать выводы.
Литература:
1. Физика. 9 класс. Учебник. Перышкин А.В., Гутник Е.М.
2. Физика (Физикон). 7-11 класс (CD), Библиотека наглядных пособий (CD).
Оборудование:
Компьютер, экран, мультимедийный проектор, магниты полосовые и дугообразные (по кол-ву детей в классе), железные опилки, магнитная стрелка, источник тока, соленоид, соединительные провода.
План урока:
1. Организационный момент.
2. Историческая справка.
3. Изучение нового материала.
4. Практическое применение магнитного поля тока.
5. Закрепление материала
6. Итог урока.
7.Задание на дом.
Ход урока:
1. Организационный момент.
Приветствие учащихся. Проверка
отсутствующих.
2. Историческая справка.
Учитель: Магнетизм, как явление, известен, по крайней мере, с пятого века до нашей эры, но изучение его сущности продвигалось очень медленно. Еще древние греки знали, что существует особый минерал — камень из Магнесии (область в древнегреческой Фессалии), способный притягивать небольшие железные предметы.
Однако впервые свойства магнита были описаны лишь в 1269 году. А первой крупной работой, посвященной исследованию магнитных явлений, является книга Вильяма Гильберта «О магните», вышедшая в 1600 году.
В древние времена свойства магнита пытались объяснить приписыванием ему «живой души». Теперь мы знаем, что все дело в особом поле, создаваемом магнитом – магнитном поле.
3. Изучение нового материала. Опыт Эрстеда.
Учитель: Магнитное
поле создается не только постоянными магнитами, но и проводниками с током.
ЭРСТЕД Ганс Христиан (1777 — 1851) — датский физик, непременный секретарь Датского королевского общества (с 1815). Работы Эрстеда посвящены электричеству, акустике, молекулярной физике. В 1820 году он обнаружил действие электрического тока на магнитную стрелку. Это привело к возникновению новой области физики — электромагнетизма.
Группа учеников демонстрирует опыт:
· Исследовательская работа учащихся (работа в группах)
1.Обнаружение магнитного поля прямолинейного проводника с током по его действию на магнитную стрелку.
Приборы и материалы:
Источник питания лабораторный, амперметр лабораторный, реостат ползунковый, ключ замыкания тока, компас, соединительные провода.
Порядок выполнения работы:
1.
Соберите
электрическую цепь как показано на рисунке. Один из соединительных проводов
расположите точно над стрелкой компаса в направлении север — юг. При этом
амперметр и реостат удалите от компаса как можно дальше.
При этом
амперметр и реостат удалите от компаса как можно дальше.
2. Замкните цепь и заметьте, в каком направлении отклоняется северный полюс магнитной стрелки относительно проводника.
3. Измените направление тока в проводнике и снова наблюдайте за стрелкой компаса.
4. Сделайте вывод.
Учитель: Этот опыт позволил другому физику, французу Амперу, сформулировать гипотезу о природе возникновения магнитного поля.
Гипотеза Ампера. Природа возникновения и свойства магнитного поля.
Андре Мари Ампер(1775-1836) –французский физик и математик, родился в г. Лионе. Ампер открыл механическое взаимодействие токов и на основании гипотезы о существовании молекулярных токов построил первую теорию магнетизма.
В честь Ампера названа единица силы тока – ампер.
Учитель: В 1820 г.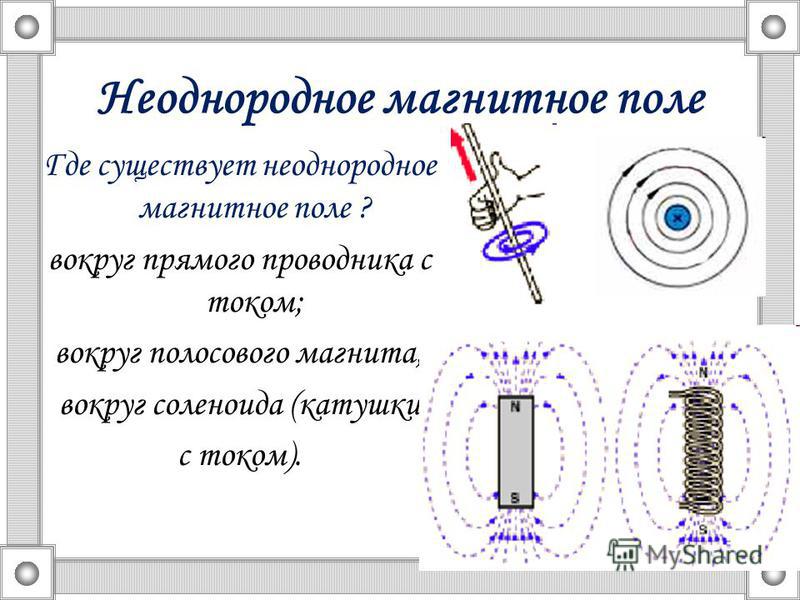 Ампер предположил, что магнитные свойства
постоянных магнитов обусловлены множеством круговых токов, циркулирующих
внутри молекул этих тел в результате движения электронов. В подтверждении
своей теории Ампер провел ряд опытов, один из которых, «Взаимодействие
параллельных токов».
Ампер предположил, что магнитные свойства
постоянных магнитов обусловлены множеством круговых токов, циркулирующих
внутри молекул этих тел в результате движения электронов. В подтверждении
своей теории Ампер провел ряд опытов, один из которых, «Взаимодействие
параллельных токов».
Взаимодействие двух проводников с током:
Каждый проводник с током имеет вокруг себя собственное магнитное поле, которое с некоторой силой действует на соседний проводник. В зависимости от направления токов проводники могут притягиваться или отталкиваться друг от друга.
Учитель: Ампер сформулировал основные свойства магнитного поля:
Магнитное поле порождается только движущимися зарядами, в частности электрическим током.
Магнитное поле, как и электрическое поле, материально, т.к. оно действует на тела, и следовательно, обладает энергией. Магнитное поле обнаруживается по действию на магнитную стрелку.
Силовой характеристикой
магнитного поля является векторная физическая величина – магнитная индукция В.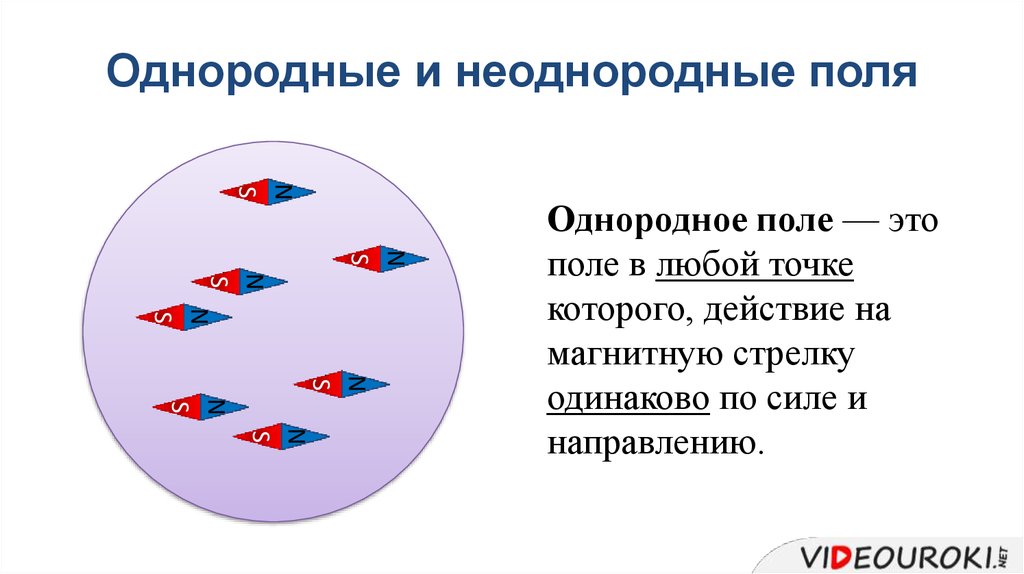 Направление, в котором устанавливается северный полюс магнитной стрелки,
совпадает с направлением индукции
Направление, в котором устанавливается северный полюс магнитной стрелки,
совпадает с направлением индукции
· Исследовательская работа учащихся (работа в группах)
2.Обнаружение магнитного поля катушки с током по его действию на магнитную стрелку.
Приборы и материалы:
Источник питания лабораторный, катушка — моток, реостат ползунковый, ключ замыкания тока, компас, соединительные провода.
Порядок выполнения работы:
1. Соберите электрическую цепь как показано на рисунке, катушку-моток вставьте в вырез бумажного экрана.
2. Замкните цепь. Перемещая компас вокруг катушки с током, определите, в каком направлении отклоняется северный полюс магнитной стрелки в различных точках поля.
3. Измените направление тока в катушке и снова наблюдайте за стрелкой компаса.
4.
Сделайте
вывод.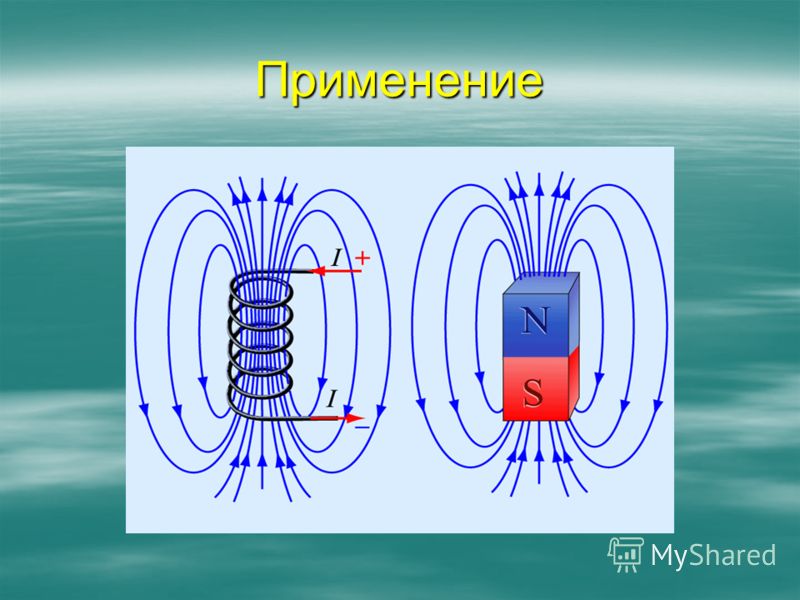
Графическое изображение силовых линий магнитного поля (работа в группах).
Учитель: Для наглядного представления магнитного поля будем пользоваться магнитными линиями. Получить эти линии нам поможет постоянный магнит и железные опилки.
Железные опилки – это маленькие магнитные стрелки. Линии, вдоль которых располагаются железные опилки, называются силовыми линиями магнитного поля.
Силовые линии всегда имеют форму замкнутых, закругленных линий.
· Исследовательская работа учащихся (работа в группах)
3.Обнаружение магнитного поля, используя мелкие железные опилки.
Приборы и материалы:
Полосовой магнит, лист бумаги, коробочка с железными опилками.
Порядок выполнения работы:
1. Положите на стол полосовой магнит, как показано на рисунке. Сверху на него положите лист бумаги.
2.
Осторожно
насыпьте на бумагу ровным слоем железные опилки и слегка встряхните бумагу.
3. Внимательно рассмотрите полученную картину.
4. В магнитном поле железные опилки намагничиваются и становятся маленькими магнитными стрелочками. Ось каждой стрелочки в магнитном поле устанавливается вдоль магнитных линий магнитного поля.
5. Сделайте вывод.
Магнитные линии (или иначе линии магнитной индукции)
— это воображаемые линии , вдоль которых располагаются магнитные стрелки, помещенные в магнитное поле. Магнитные линии можно провести через любую точку магнитного поля, они имеют направление и всегда замкнуты.
Виды магнитного поля прямого тока.
Учитель: Вы выяснили, как располагается магнитное поле рядом с постоянным магнитом, а теперь посмотрим какие виды магнитных полей бывают.
НЕОДНОРОДНОЕ МАГНИТНОЕ ПОЛЕ
Характеристика неоднородного магнитного
поля: магнитные линии искривлены;густота магнитных линий различна;сила, с
которой магнитное поле действует на магнитную стрелку, различна в разных точках
этого поля по величине и направлению.
— вокруг прямого проводника с током;
— вокруг полосового магнита;
— вокруг соленоида (катушки с током).
ОДНОРОДНОЕ МАГНИТНОЕ ПОЛЕ
Характеристика однородного магнитного поля: магнитные линии параллельные прямые;густота магнитных линий везде одинакова; сила, с которой магнитное поле действует на магнитную стрелку, одинакова во всех точках этого поля по величине и направлению.
Где существует однородное магнитное поле?
— внутри полосового магнита и внутри соленоида , если его длина много больше, чем диаметр.
4. Практическое применение магнитного поля тока (презентация).
Учитель: Магнитное действие тока широко применяют в промышленности(вилеоматериал)
Грузоподъемные магниты – наиболее мощные из широко применяемых в промышленности. Как правило,
они представляют собой катушку, охватывающую железный сердечник большого
сечения. Хотя электромагнит подключается к сети переменного тока, он снабжен
мощным выпрямителем, так что через катушку может течь постоянный ток,
достигающий 50 ампер.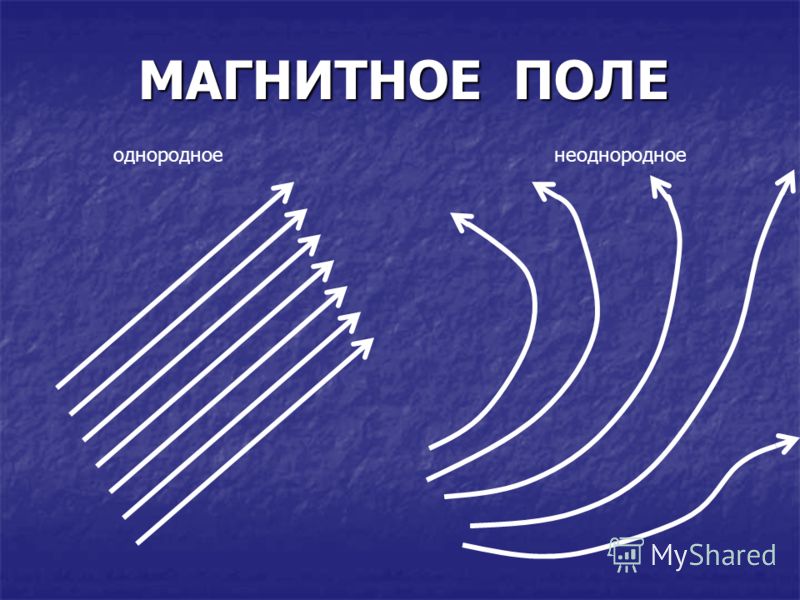 Это позволяет электромагниту весом 1–2 тонны
поднимать груз весом 10–15 тонн, если он допускает максимальную площадь
контакта с сердечником. Электромагнит удобен также для перемещения
металлического лома и уборки стружки. Кроме того, иногда грузоподъемные
электромагниты могут применяться для отделения железной фракции из сыпучего
вещества, например, угля или руды перед переработкой или транспортировкой.
Это позволяет электромагниту весом 1–2 тонны
поднимать груз весом 10–15 тонн, если он допускает максимальную площадь
контакта с сердечником. Электромагнит удобен также для перемещения
металлического лома и уборки стружки. Кроме того, иногда грузоподъемные
электромагниты могут применяться для отделения железной фракции из сыпучего
вещества, например, угля или руды перед переработкой или транспортировкой.
5. Закрепление материала.
Вопросы:
1. Как можно объяснить отклонение магнитной стрелки около проводника с током?
2. Какое магнитное поле – однородное или неоднородное — образуется вокруг магнита, проводника с током, внутри соленоида?
3. Перечислите основные свойства магнитного поля.
4. Какое правило используют для определения направления линий магнитного поля?
5. Применение электромагнитов.
6. Обозначьте неизвестные полюса взаимодействующих магнитов:
7.
На
рисунке указан проводник с током, расположенный перпендикулярно плоскости
рисунка и одна магнитная линия.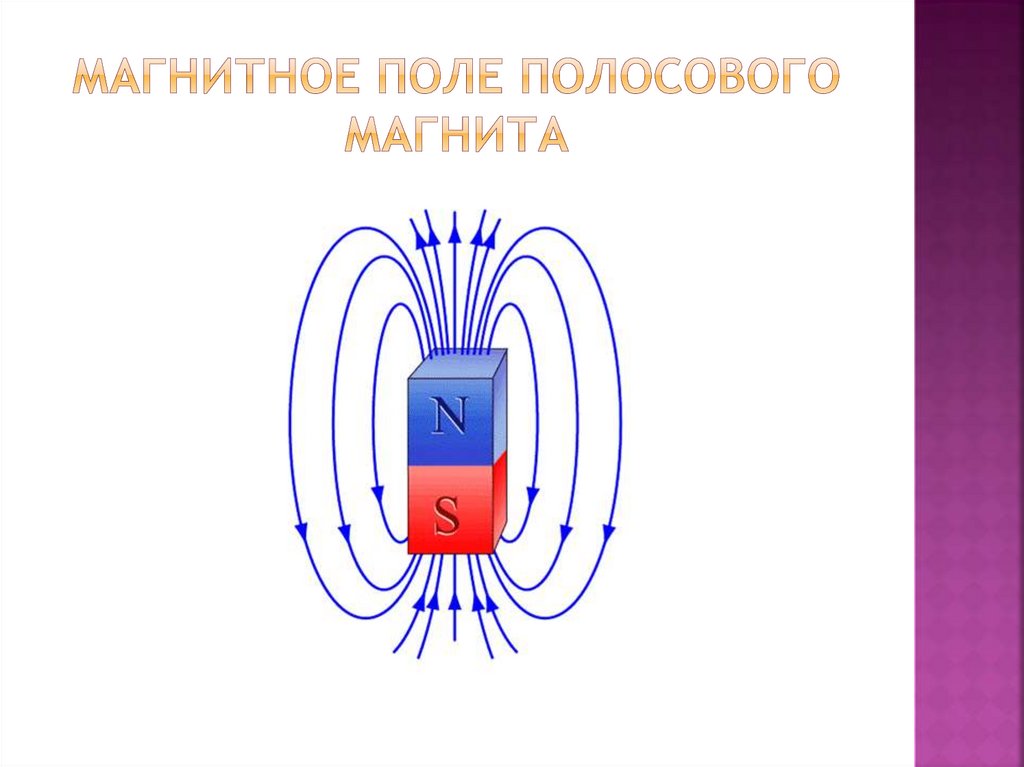 Укажите полюса магнитных стрелок, расположенных
в точках А, В, С, Д.
Укажите полюса магнитных стрелок, расположенных
в точках А, В, С, Д.
8. На рисунке указан проводник с током, расположенный перпендикулярно плоскости рисунка и одна магнитная линия. В точках А, В, С, Д магнитной линии расположены магнитные стрелки. Укажите направление электрического тока в проводнике.
9. Изобразите с помощью линий магнитной индукции магнитное поле катушки с током:
6. Что собой представляют линии магнитного поля?
6. Итог урока.
Учитель: Давайте подведем итоги сегодняшнего урока (учащиеся сами формулируют вопросы и дают ответы на них):
Ответы:
1. Вокруг постоянного магнита, а также вокруг проводника с током существует магнитное поле, действующее на любой магнит, который в нем находится.
2. Линии магнитного
поля замкнуты. Там, где они выходят из магнита, — его северный полюс, там, где
они входят в магнит, — южный.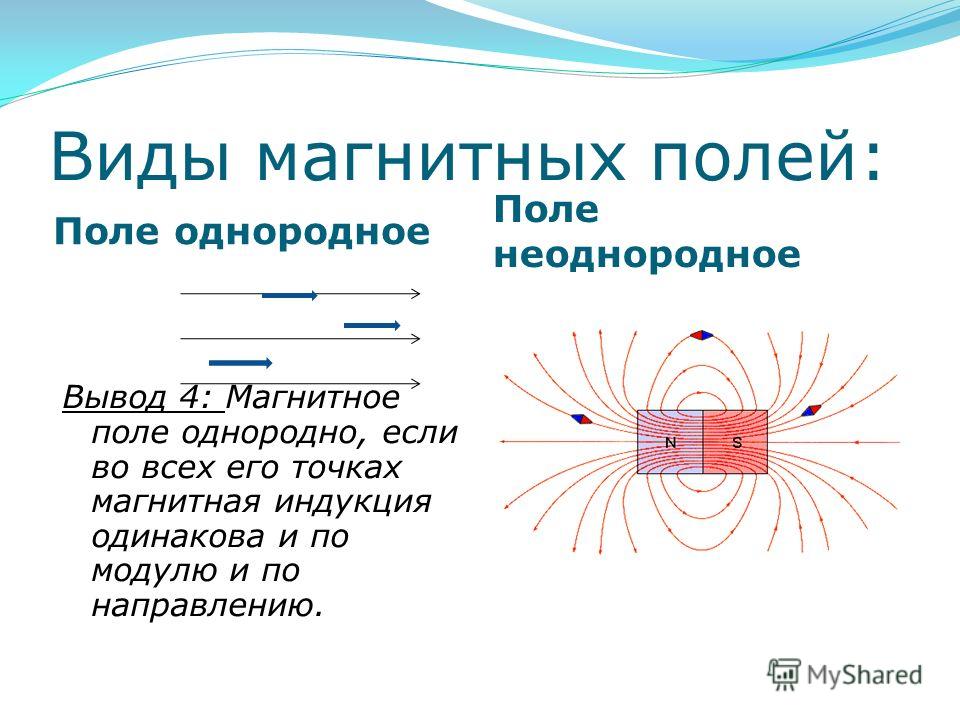
3. «Правило буравчика» — если поступательное движение буравчика сонаправлено с током в проводнике, то направление вращения буравчика совпадает с направлением магнитных линий.
4. Устройство, состоящее из железного сердечника, обмотанного изолированным проводом, по которому течет ток, называют электромагнитом.
7. Задание на дом.
§ 34 ,ответить на вопросы.
Physics for Science & Engineering II
от Office of Academic Technologies на Vimeo.
Пример 6. Электрическое поле с неоднородным распределением заряда
До сих пор мы изучали примеры распределений с равномерным распределением заряда. Другими словами, плотность заряда была постоянной на всем протяжении распределения.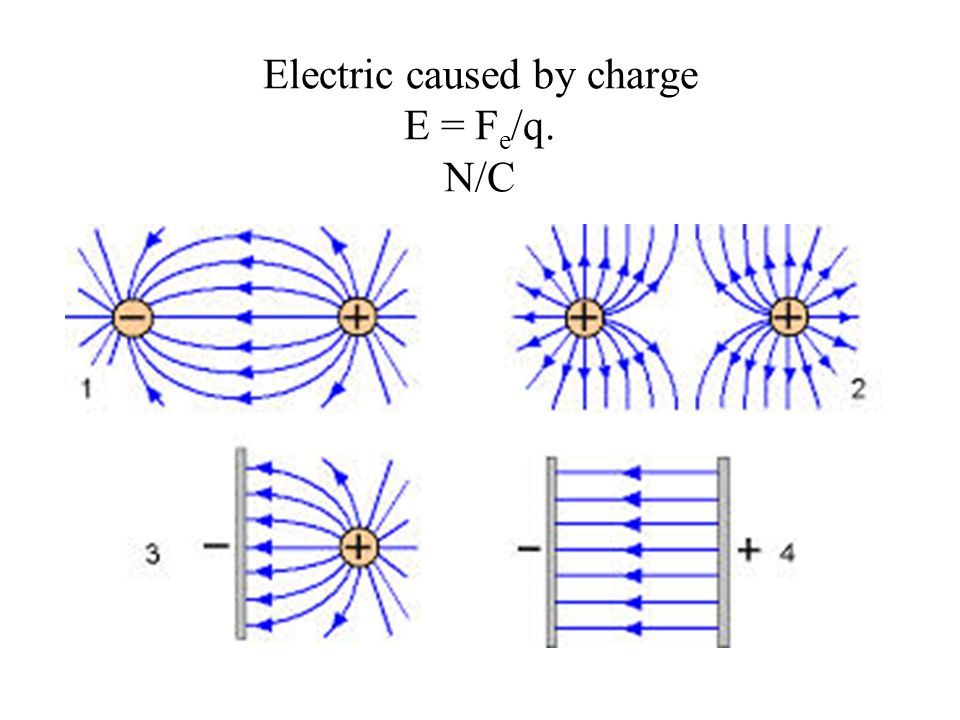 Теперь мы рассмотрим пример, в котором плотность заряда непостоянна. Для этого рассмотрим сплошную непроводящую сферу радиусом R , который имеет неравномерное распределение заряда по объемной плотности заряда. ρ равно некоторой константе ρ s умножить на малое r над большим R , скажем, где ρ s — это константа, а маленькое r — это центр r сферу до точки интереса.
Теперь мы рассмотрим пример, в котором плотность заряда непостоянна. Для этого рассмотрим сплошную непроводящую сферу радиусом R , который имеет неравномерное распределение заряда по объемной плотности заряда. ρ равно некоторой константе ρ s умножить на малое r над большим R , скажем, где ρ s — это константа, а маленькое r — это центр r сферу до точки интереса.
Что мы хотели бы сделать, так это рассчитать электрическое поле такого распределения в разных областях. Для начала попробуем вычислить общий заряд раздачи в виде знака вопроса. У нас твердое сферическое распределение заряда — заряд не распределен равномерно по всему объему этого объекта — так что его объемная плотность заряда изменяется в 9 раз.0011 ρ равно ρ s умножить на r свыше R . Таким образом, другими словами, когда мы удаляемся от центра распределения, имеющего радиус R , когда мы удаляемся радиально от центра распределения, плотность заряда увеличивается. На самом деле, когда маленькое r становится большим R на поверхности распределения, то оно достигает своего максимального значения, которое будет равно этой константе, ρ s кулонов на кубический метр.
На самом деле, когда маленькое r становится большим R на поверхности распределения, то оно достигает своего максимального значения, которое будет равно этой константе, ρ s кулонов на кубический метр.
Ну, конечно, если бы заряд был распределен равномерно и, следовательно, заряд на единицу объема был бы одинаковым в каждой точке внутри этой области, и чтобы иметь возможность получить общий заряд распределения, мы бы прямо взяли произведение объемной плотности заряда на объем всего распределения, что дало бы нам общий заряд. В данном случае мы не можем этого сделать, мы не можем взять произведение плотности заряда на объем всего распределения, чтобы получить полный заряд, потому что ρ не является одним и тем же в каждой точке внутри этой области. Как мало r изменится, так и ρ изменится.
Чтобы иметь возможность вычислить общую плотность заряда, мы смотрим на плотность, мы видим, что она меняется в зависимости от радиального расстояния R , поэтому мы собираемся предположить, что все это распределение состоит из концентрических сферических оболочек добавочная толщина. Если выбрать одну из этих оболочек в произвольном месте внутри раздачи, то примерно так, что она имеет очень-очень маленькую толщину оболочки, и радиус у нее r и толщина dr , а этот dr настолько мал, что при переходе от внутренней поверхности к внешней поверхности этой сферической оболочки изменение плотности незначительно. Другими словами, изменение этой величины настолько мало, малое r , что можно предположить, что на всей этой толщине ρ остается постоянным. Если это так, то это позволит нам рассчитать количество заряда, связанного с этой дополнительной оболочкой.
Если выбрать одну из этих оболочек в произвольном месте внутри раздачи, то примерно так, что она имеет очень-очень маленькую толщину оболочки, и радиус у нее r и толщина dr , а этот dr настолько мал, что при переходе от внутренней поверхности к внешней поверхности этой сферической оболочки изменение плотности незначительно. Другими словами, изменение этой величины настолько мало, малое r , что можно предположить, что на всей этой толщине ρ остается постоянным. Если это так, то это позволит нам рассчитать количество заряда, связанного с этой дополнительной оболочкой.
Поэтому нас интересует количество заряда по всему объему этой оболочки. Как только мы вычислим этот заряд, который мы назовем dq , мы сможем продолжить и вычислить сумму дополнительного заряда в следующей дополнительной оболочке, а затем в следующей дополнительной оболочке, и так далее и тому подобное. В конце концов мы суммируем все эти дополнительные расходы друг с другом по всему объему всего этого распределения и получаем общий заряд.
Дополнительное количество заряда, распределенного по этой дополнительной сферической оболочке, будет равно ρ -кратный объем добавочной оболочки. Следовательно, она будет равна плотности заряда, которая, как мы предполагаем, остается постоянной на всей этой очень малой толщине, ρ s r на протяжении R . Теперь объем инкрементной оболочки. Это будет произведение площади поверхности сферы на ее толщину. Другими словами, оно будет равно 4 πr 2 умножить на dr . Таким образом, это выражение дает нам ρ s умножить на 4 π разделить на большие R и r умножить на r 2 даст нам r 3 dr . Это количество заряда, распределенного через эту возрастающую сферическую оболочку. Используя ту же самую процедуру, мы вычисляем количество зарядов в следующей оболочке, а затем в следующей оболочке, а затем складываем все эти заряды друг с другом.
Процесс добавления здесь — это интеграция. Поэтому мы берем интеграл от обеих сторон, так что мы получим полный заряд в левой части. Если мы проинтегрируем эту величину здесь, ρ s 4 π и большой R , все они константы, мы можем взять их вне интеграла. Таким образом, Q становится равным ρ s 4 π над R , умноженным на r 3 dr . По мере сложения всех этих добавочных сферических оболочек друг к другу по всему объему всего распределения связанные с ними радиусы этих оболочек будут изменяться от 0, начиная с самой внутренней, и, выходя к самой внешней, от 0 до больших Р .
Поэтому мы берем интеграл от обеих сторон, так что мы получим полный заряд в левой части. Если мы проинтегрируем эту величину здесь, ρ s 4 π и большой R , все они константы, мы можем взять их вне интеграла. Таким образом, Q становится равным ρ s 4 π над R , умноженным на r 3 dr . По мере сложения всех этих добавочных сферических оболочек друг к другу по всему объему всего распределения связанные с ними радиусы этих оболочек будут изменяться от 0, начиная с самой внутренней, и, выходя к самой внешней, от 0 до больших Р .
Q будет равно ρ s время 4 π свыше R , интеграл от r 3 равен 1 большому по r 4, который будет оцениваться как 1 большой по r 4 . Здесь мы можем сократить эту 4 в числителе на единицу в знаменателе, оставив нам Q равным ρ s , и подставив большие R вместо маленьких r , мы получим R 4 здесь, R в знаменателе, а также π в числителе. Это R 4 и это R сокращаются, оставляя в числителе R 3, поэтому чистый заряд этого распределения будет равен ρ s πR 3. Теперь
Это R 4 и это R сокращаются, оставляя в числителе R 3, поэтому чистый заряд этого распределения будет равен ρ s πR 3. Теперь
5
45
12 3. , рассмотрим то же распределение и попробуем вычислить электрическое поле внутри произвольной точки этого распределения. Давайте перерисуем распределение здесь, наше сферическое распределение. Заряд распределяется неравномерно по всему объему распределения, имеющему радиус большой R , а плотность заряда была задана как постоянная ρ s умноженная на малое r над большим R , а маленькое r является местоположением точки интереса. Предположим, что наша точка интереса, P , находится где-то здесь. Опять же, мы собираемся применить закон Гаусса и, используя сферическую симметрию, выберем сферическую гауссову поверхность так, чтобы она проходила через интересующую точку. Естественно, он будет иметь радиус р . Закон Гаусса гласит, что E dot d A , интегрированное по этой поверхности s , равно суммарному заряду, заключенному внутри области, окруженной этой гауссовой сферой, деленной на ε 0. Как мы видели в В случае предыдущих примеров для сферической симметрии электрическое поле или распределение положительного заряда будет направлено радиально наружу повсюду вдоль поверхности этой гауссовой сферы, и вектор приращения площади поверхности, который также будет в радиальном направлении, как будучи перпендикулярным поверхности, он также будет направлен радиально во все стороны. Следовательно, угол между вектором электрического поля и вектором площади поверхности будет равен 0,9.0005
Как мы видели в В случае предыдущих примеров для сферической симметрии электрическое поле или распределение положительного заряда будет направлено радиально наружу повсюду вдоль поверхности этой гауссовой сферы, и вектор приращения площади поверхности, который также будет в радиальном направлении, как будучи перпендикулярным поверхности, он также будет направлен радиально во все стороны. Следовательно, угол между вектором электрического поля и вектором площади поверхности будет равен 0,9.0005
Тогда мы можем выразить левую часть в явном виде для как E dA косинус 0. Поскольку мы будем находиться на одном и том же расстоянии от заряда, пока мы находимся на поверхности этой гауссовой сферы, величина электрического поля будет постоянной на этой поверхности, поэтому мы можем взять ее за пределы интеграла, и правая часть снова будет q -заключенной над ε 0,
. есть E раз целое от dA по гауссовой поверхности s , так как косинус 0 равен 1. Следовательно, E , умноженный на интеграл dA по замкнутой поверхности s , будет равен q -заключено по , Складывая все возрастающие векторы площадей вдоль этой поверхности, мы в конечном итоге получим площадь поверхности этой сферы, которая будет равна 4 πr 2. В правой части у нас будет q -замкнутый над ε 0. Таким образом, левая часть закона Гаусса идентична предыдущим задачам о сферической симметрии.
Следовательно, E , умноженный на интеграл dA по замкнутой поверхности s , будет равен q -заключено по , Складывая все возрастающие векторы площадей вдоль этой поверхности, мы в конечном итоге получим площадь поверхности этой сферы, которая будет равна 4 πr 2. В правой части у нас будет q -замкнутый над ε 0. Таким образом, левая часть закона Гаусса идентична предыдущим задачам о сферической симметрии.
Теперь посмотрим на правую сторону. Если бы у нас было равномерное распределение заряда по всему объему этого распределения, как мы сделали в одном из предыдущих примеров, мы бы выразили объемную плотность заряда распределения, и просто взяв произведение этой плотности на объем этого области, которая нас интересует, которая является областью внутри гауссовой сферы, мы бы получили q -enclosed, чистый заряд внутри этой области. Мы не можем этого сделать, потому что плотность заряда непостоянна. Другими словами, он меняется от точки к точке.
Для того, чтобы получить q -включенный во всей этой области, которая является областью, окруженной гауссовой сферой, как и в предыдущей части этой задачи, мы собираемся выбрать инкрементную сферическую оболочку в произвольном месте, скажем что-то вроде этого. Толщина этой оболочки настолько мала, что можно предположить, что по мере продвижения по этой толщине изменение плотности заряда можно считать постоянным. Итак, мы рассчитаем количество заряда внутри сферической оболочки и обозначим его как dq , а затем мы собираемся вычислить количество заряда в следующей концентрической сферической оболочке, и так далее и тому подобное. Затем мы добавим все эти dq друг к другу по всей области внутри этой гауссовой сферы. Другими словами, мы применим ту же процедуру, что и в предыдущей части, за исключением того, что вместо интегрирования и добавления dq от 0 до большого R теперь мы собираемся добавить их от 0 до маленького . р . Это область наших интересов.
Чтобы избежать путаницы с маленькой переменной r и переменной радиуса этих концентрических оболочек, мы назовем радиус этой оболочки как s , новая переменная, а толщина как дс . С точки зрения этого, тогда мы можем выразить плотность как ρ s , мы заменим маленькое r на s , деленное теперь на радиус всего распределения, которое равно большому R .
Тогда q -enclosed будет суммой всех dq , связанных с этими концентрическими сферическими оболочками, что в конечном итоге делает всю область занятой гауссовой сферой, и добавление всех этих dq ‘ s, добавление здесь, опять же, интеграция, где у нас будет q -enclosed. Поэтому в явной форме это будет равно плотности заряда, ρ с , умноженное на с на R . Это плата за единицу объема, умноженная на объем интересующей нас области. Для dq , который связан с объемом этой добавочной сферической оболочки, и объем которого равен площади поверхности, 4 πs 2 , умноженной на ее толщину, ds . Здесь мы будем интегрировать это от 0 до маленького r . Это область нашего интереса, чтобы иметь возможность получить q -вложенный, чистый заряд внутри объема, окруженного гауссовой сферой.
Здесь мы будем интегрировать это от 0 до маленького r . Это область нашего интереса, чтобы иметь возможность получить q -вложенный, чистый заряд внутри объема, окруженного гауссовой сферой.
Здесь снова 4 π и R и ρ s , все они постоянны, поэтому мы можем взять их за пределы интеграла. Затем Q -Cenclosed становится равным ρ S Times 4 π над Big R Интеграл S Times S 2 IS S 3 DS , интегрированный от R . Двигаясь дальше, q -enclosed будет равно ρ s 4 π сверх R , интеграл от s 3 равен s 4 более 4, что мы немного оценим 1 при 4, что р . q -enclosed будет ρ s , мы можем сократить это 4 и это 4, и у нас будет π вместо R и сначала мы заменим r на s , так что у нас будет r на 4, и мы подставим 0 минус 0, что даст нам 0. Итак, q -enclosed будет равно ρ s π на R умножить на r 4-й.
Итак, q -enclosed будет равно ρ s π на R умножить на r 4-й.
Теперь вернемся к нашему выражению закона Гаусса и заменим его на q -прилагается. Если мы это сделаем, то получим E умножить на 4 πr 2 равно ρ s π больше большого R умножить на маленькое r 4 справа на
1 1-ε
1 стороны выражения закона Гаусса. Здесь мы можем сделать некоторые сокращения, разделив обе части на r 2, мы получим r 2 в правой части, и мы можем сократить π здесь. Если выразить то E , что будет равно ρ s разделить на 4 ε 0 R .
Теперь мы можем попытаться выразить это через общий заряд распределения. Помните, что мы нашли в предыдущей части, что Q равно ρ s πR 3. Чтобы получить то же соотношение, давайте умножим и числитель, и знаменатель этого выражения на πR 3. При этом у нас будет E равно ρ s πR 3, умножив их на πR 3, а также умножив знаменатель на эту же величину, чтобы сохранить соотношение неизменным. Итак, у нас будет 4 πε 0, R 3 умножить на R даст нам R 4. Тогда в этих обозначениях в числителе мы будем иметь общий заряд распределения.
При этом у нас будет E равно ρ s πR 3, умножив их на πR 3, а также умножив знаменатель на эту же величину, чтобы сохранить соотношение неизменным. Итак, у нас будет 4 πε 0, R 3 умножить на R даст нам R 4. Тогда в этих обозначениях в числителе мы будем иметь общий заряд распределения.
Не забудем терм r 2, который мы оставили на этом шаге, так что у нас будет р 2 сюда. Тогда окончательное выражение для электрического поля будет в терминах общего заряда, распределенного внутри сферы, как Q более 4 πε 0 R 4 умножить на r 2. Это в радиальном направлении , поэтому мы можем умножить это на единичный вектор, указывающий в радиальном направлении, чтобы выразить электрическое поле в векторной форме. Этот результат относится к случаю, когда точка интереса находится внутри распределения.
Теперь посмотрим на электрическое поле вне этого распределения для r больше, чем R . Простейший способ решения такой проблемы состоит в том, что, поскольку мы имеем дело со сферическим распределением заряда с радиусом R и нас интересует электрическое поле в точке вне распределения, снова применяя закон Гаусса, мы просто помещаем гауссову сфере, используя сферическую симметрию, проходящую через интересующую точку.
Простейший способ решения такой проблемы состоит в том, что, поскольку мы имеем дело со сферическим распределением заряда с радиусом R и нас интересует электрическое поле в точке вне распределения, снова применяя закон Гаусса, мы просто помещаем гауссову сфере, используя сферическую симметрию, проходящую через интересующую точку.
В данном случае E точка d A над этой закрытой поверхностью s будет равно q — заключено в ε 0. Левая часть будет идентична предыдущей части, что в конечном итоге даст нам электрическое поле, умноженное на площадь поверхности сферы, которая равна 4 πr 2, а заключенное в этом случае q — это суммарный заряд внутри области, окруженной этой гауссовой сферой. Когда мы смотрим на эту область, мы видим, что она заключает в себе весь заряд, распределенный по сфере. Если вы назовете его Q , q -enclosed будет равен большому Q . Следовательно, в правой части мы будем иметь Q на ε 0, и, решая для электрического поля, мы получим Q на 4 πε 0 r 2. Это снова знакомый результат, который идентично электрическому полю точечного заряда.
Это снова знакомый результат, который идентично электрическому полю точечного заряда.
Кроме того, если вы помните, мы говорили, что всякий раз, когда мы имеем дело со сферическими распределениями заряда, то для всех внешних точек система ведет себя так, как будто весь заряд сосредоточен в ее центре, и она ведет себя как точечный заряд для всех внешних точек. внешние точки, поэтому задача сводится к задаче о точечном заряде, так что мы вычисляем электрическое поле, которое он генерирует в точке P , который находится на расстоянии r от заряда, создавая электрическое поле в радиальном направлении наружу точно так же, как в этом случае. Другими словами, еще до того, как мы применим эти шаги, мы можем сказать, что система будет вести себя как точечный заряд, и полное электрическое поле будет равно этой величине.
В более явной форме, или с точки зрения плотности заряда, поскольку Q , полный заряд, был равен ρ s πR 3, мы также можем выразить это как ρ s πR 3 более 4 πε 0 r 2. Оба ответа являются правильными для данного случая. Опять же, это в радиальном направлении, поэтому мы можем выразить это в векторной форме следующим образом. Это электрическое поле, создаваемое этим распределением заряда в точке снаружи, на расстоянии r от центра распределения.
Оба ответа являются правильными для данного случая. Опять же, это в радиальном направлении, поэтому мы можем выразить это в векторной форме следующим образом. Это электрическое поле, создаваемое этим распределением заряда в точке снаружи, на расстоянии r от центра распределения.
Контроль электрического стресса | Однородные и неоднородные электрические поля
Распределение контроля электрического напряжения обычно регулируется уравнением Пуассона:
, где φ — потенциал в данной точке, ρ — плотность объемного заряда в области, а ε 0 — электрическая диэлектрическая проницаемость свободного пространства (вакуума). Однако в большинстве высоковольтных аппаратов пространственные заряды обычно отсутствуют, поэтому распределение потенциала определяется уравнением Лапласа:
Лапласиан и является вектором со свойствами
Существует множество методов определения распределения потенциала. Наиболее часто используемые методы
- метод электролитического бака и
- численные методы
Распределение потенциалов также можно рассчитать напрямую. Однако это очень сложно, за исключением простых геометрий. Во многих практических случаях хорошее понимание проблемы возможно при использовании некоторых простых правил для построения силовых линий и эквипотенциалов. Важные правила:
Однако это очень сложно, за исключением простых геометрий. Во многих практических случаях хорошее понимание проблемы возможно при использовании некоторых простых правил для построения силовых линий и эквипотенциалов. Важные правила:
- эквипотенциалы пересекают силовые линии под прямым углом,
- , когда эквипотенциалы и силовые линии нарисованы в форме криволинейных квадратов, плотность силовых линий является показателем контроля электрического напряжения в данной области, и
- в любой области максимальное электрическое поле определяется как dv∕dx, где dv – разность напряжений между двумя последовательными эквипотенциалами, отстоящими друг от друга на dx.
Значительное количество труда и времени можно сэкономить за счет правильного выбора плоскостей симметрии и соответствующей формы электродов. Как только распределение напряжения заданной геометрии установлено, можно легко переделать или изменить конструкцию электродов, чтобы свести к минимуму напряжения и предотвратить возникновение коронного разряда. Это случай, обычно встречающийся в высоковольтных электродах проходных изоляторов, стандартных конденсаторах и т. д. Когда два диэлектрика с очень разной диэлектрической проницаемостью соединены последовательно, контроль электрического напряжения намного выше в среде с более низкой диэлектрической проницаемостью. С учетом твердой изоляции в газовой среде напряжение в газе становится равным ε r раз больше, чем в твердом диэлектрике, где ε r – относительная диэлектрическая проницаемость твердого диэлектрика. Это повышенное напряжение возникает на краях электродов, и одним из способов преодоления этого является увеличение диаметра электрода. Другие методы контроля электрического напряжения показаны на рис. 1.1.
Это случай, обычно встречающийся в высоковольтных электродах проходных изоляторов, стандартных конденсаторах и т. д. Когда два диэлектрика с очень разной диэлектрической проницаемостью соединены последовательно, контроль электрического напряжения намного выше в среде с более низкой диэлектрической проницаемостью. С учетом твердой изоляции в газовой среде напряжение в газе становится равным ε r раз больше, чем в твердом диэлектрике, где ε r – относительная диэлектрическая проницаемость твердого диэлектрика. Это повышенное напряжение возникает на краях электродов, и одним из способов преодоления этого является увеличение диаметра электрода. Другие методы контроля электрического напряжения показаны на рис. 1.1.
При проектировании высоковольтного оборудования необходимо контролировать напряженность электрического поля, в противном случае более высокие напряжения вызовут или ускорят старение изоляции, что приведет к ее выходу из строя. За прошедшие годы было разработано множество методов управления и оптимизации электрических полей для получения наиболее экономичных конструкций. Методы управления электрическим полем составляют важный компонент общей конструкции оборудования.
Методы управления электрическим полем составляют важный компонент общей конструкции оборудования.
1.Электрическое поле Представлен краткий обзор представлений об электрических полях, так как для инженеров по высокому напряжению важно знать напряженность поля в различных средах под действием электрических напряжений. Это также помогает в выборе надлежащих конфигураций электродов и экономичных размеров изоляции, чтобы не образовывались области с высоким напряжением, а надежная работа оборудования приводила к ожидаемому сроку службы.
Напряженность поля E в любом месте электростатического поля представляет собой отношение силы, действующей на бесконечно малый заряд в этом месте, к самому заряду, когда заряд уменьшается до нуля. Сила F, действующая на любой заряд q в этой точке поля, равна
Плотность электрического потока D, связанная с напряженностью поля E, составляет
, где E — диэлектрическая проницаемость среды, в которой существует электрическое поле. Работа, совершаемая зарядом при его перемещении в электрическом поле, называется потенциалом. Потенциал φ равен
Работа, совершаемая зарядом при его перемещении в электрическом поле, называется потенциалом. Потенциал φ равен
, где l — путь, по которому движется заряд.
Несколько взаимосвязей между различными величинами электрического поля можно обобщить следующим образом:
где F — сила, действующая на заряд q в электрическом поле E, а S — замкнутая поверхность, содержащая заряд q.
2. Однородные и неоднородные электрические поля В общем случае электрические поля между любыми двумя электродами могут быть как однородными, так и неоднородными. В однородном зазоре среднее поле E одинаково во всей области поля, тогда как в неоднородном зазоре E различно в разных точках области поля.
Однородное или приблизительно однородное распределение поля существует между двумя бесконечными параллельными пластинами или двумя сферами одинакового диаметра, когда зазор меньше диаметра сферы. Сферические электроды часто используются для измерения высокого напряжения и для запуска в цепях генерации импульсного напряжения.
 Как мы видели в В случае предыдущих примеров для сферической симметрии электрическое поле или распределение положительного заряда будет направлено радиально наружу повсюду вдоль поверхности этой гауссовой сферы, и вектор приращения площади поверхности, который также будет в радиальном направлении, как будучи перпендикулярным поверхности, он также будет направлен радиально во все стороны. Следовательно, угол между вектором электрического поля и вектором площади поверхности будет равен 0,9.0005
Как мы видели в В случае предыдущих примеров для сферической симметрии электрическое поле или распределение положительного заряда будет направлено радиально наружу повсюду вдоль поверхности этой гауссовой сферы, и вектор приращения площади поверхности, который также будет в радиальном направлении, как будучи перпендикулярным поверхности, он также будет направлен радиально во все стороны. Следовательно, угол между вектором электрического поля и вектором площади поверхности будет равен 0,9.0005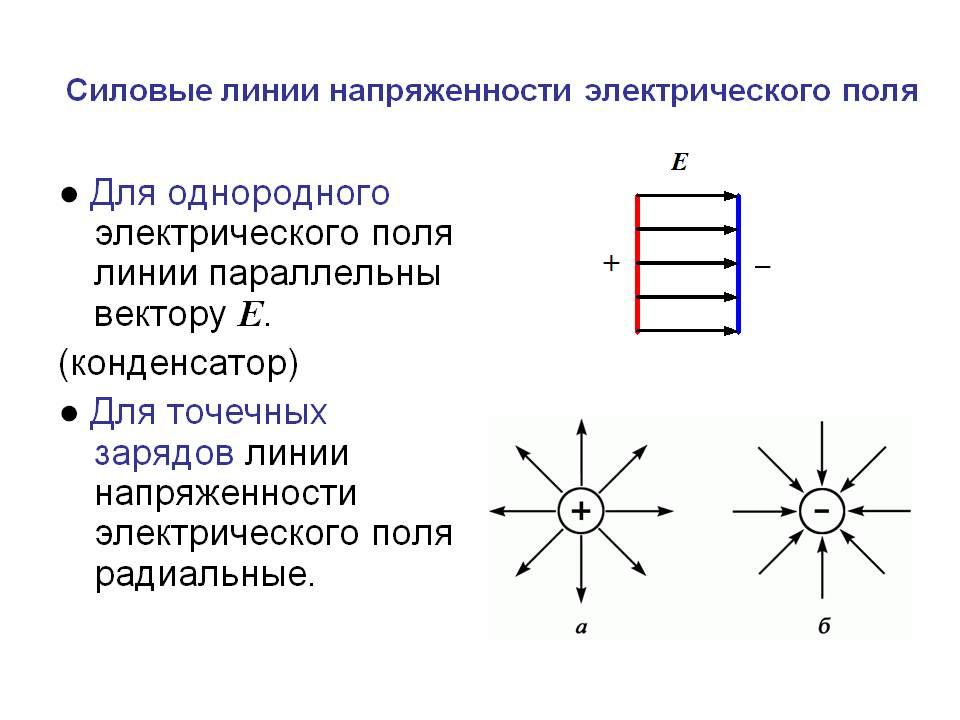 Следовательно, E , умноженный на интеграл dA по замкнутой поверхности s , будет равен q -заключено по , Складывая все возрастающие векторы площадей вдоль этой поверхности, мы в конечном итоге получим площадь поверхности этой сферы, которая будет равна 4 πr 2. В правой части у нас будет q -замкнутый над ε 0. Таким образом, левая часть закона Гаусса идентична предыдущим задачам о сферической симметрии.
Следовательно, E , умноженный на интеграл dA по замкнутой поверхности s , будет равен q -заключено по , Складывая все возрастающие векторы площадей вдоль этой поверхности, мы в конечном итоге получим площадь поверхности этой сферы, которая будет равна 4 πr 2. В правой части у нас будет q -замкнутый над ε 0. Таким образом, левая часть закона Гаусса идентична предыдущим задачам о сферической симметрии.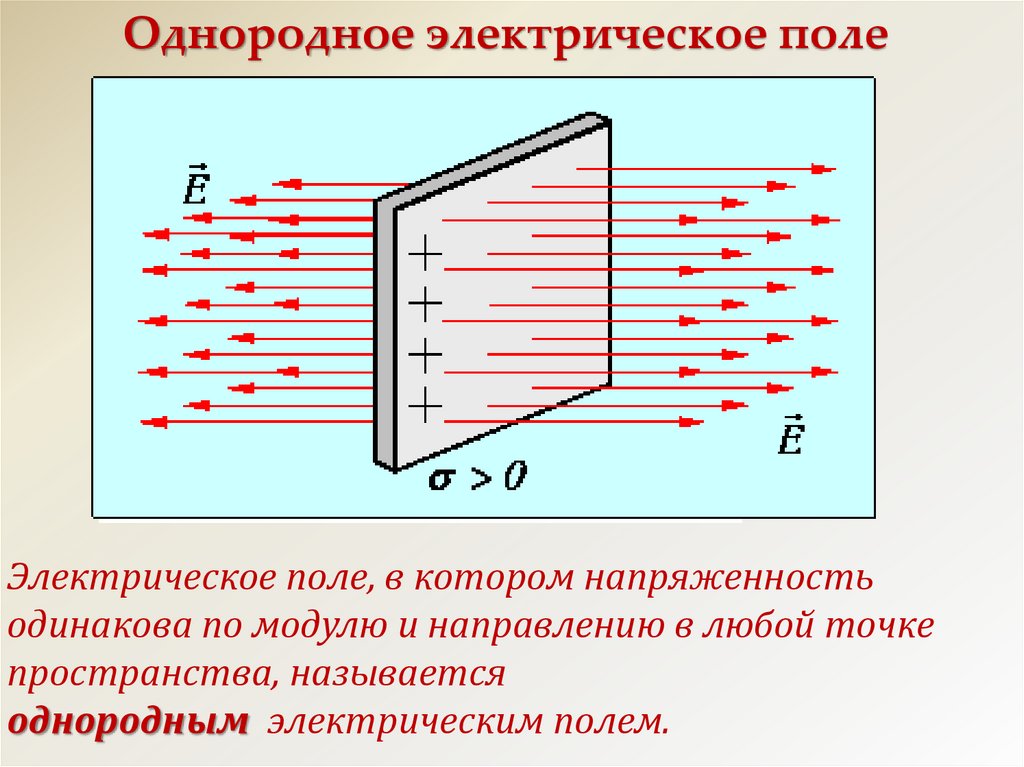

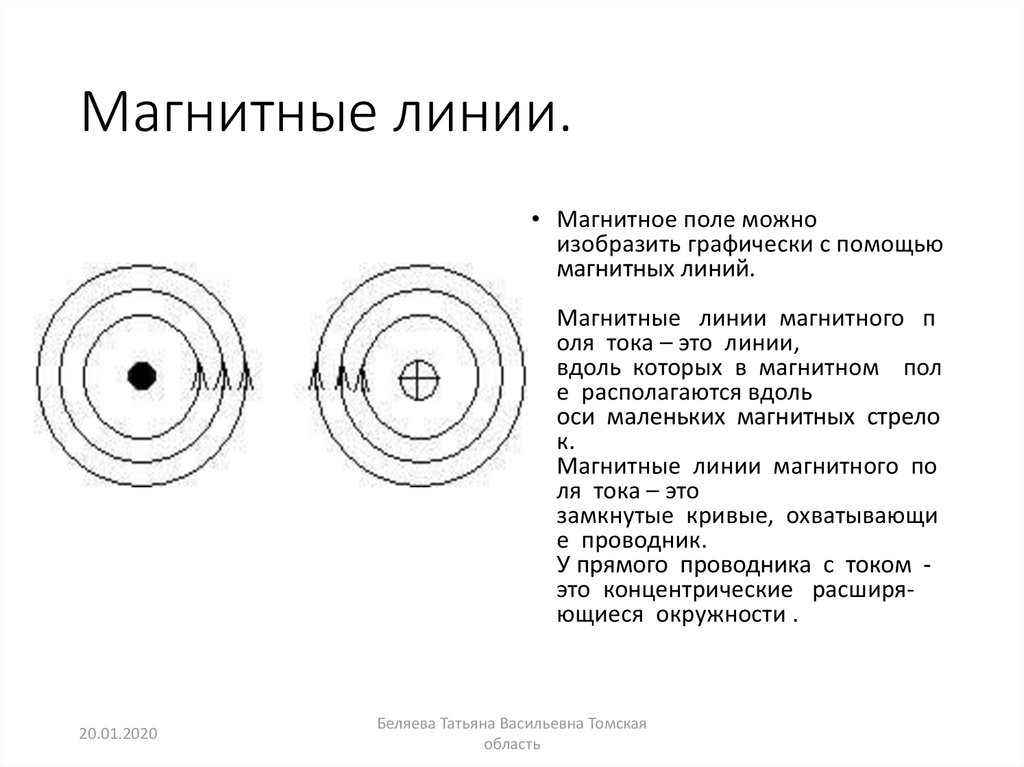 Здесь мы будем интегрировать это от 0 до маленького r . Это область нашего интереса, чтобы иметь возможность получить q -вложенный, чистый заряд внутри объема, окруженного гауссовой сферой.
Здесь мы будем интегрировать это от 0 до маленького r . Это область нашего интереса, чтобы иметь возможность получить q -вложенный, чистый заряд внутри объема, окруженного гауссовой сферой. Итак, q -enclosed будет равно ρ s π на R умножить на r 4-й.
Итак, q -enclosed будет равно ρ s π на R умножить на r 4-й. При этом у нас будет E равно ρ s πR 3, умножив их на πR 3, а также умножив знаменатель на эту же величину, чтобы сохранить соотношение неизменным. Итак, у нас будет 4 πε 0, R 3 умножить на R даст нам R 4. Тогда в этих обозначениях в числителе мы будем иметь общий заряд распределения.
При этом у нас будет E равно ρ s πR 3, умножив их на πR 3, а также умножив знаменатель на эту же величину, чтобы сохранить соотношение неизменным. Итак, у нас будет 4 πε 0, R 3 умножить на R даст нам R 4. Тогда в этих обозначениях в числителе мы будем иметь общий заряд распределения. Простейший способ решения такой проблемы состоит в том, что, поскольку мы имеем дело со сферическим распределением заряда с радиусом R и нас интересует электрическое поле в точке вне распределения, снова применяя закон Гаусса, мы просто помещаем гауссову сфере, используя сферическую симметрию, проходящую через интересующую точку.
Простейший способ решения такой проблемы состоит в том, что, поскольку мы имеем дело со сферическим распределением заряда с радиусом R и нас интересует электрическое поле в точке вне распределения, снова применяя закон Гаусса, мы просто помещаем гауссову сфере, используя сферическую симметрию, проходящую через интересующую точку. Это снова знакомый результат, который идентично электрическому полю точечного заряда.
Это снова знакомый результат, который идентично электрическому полю точечного заряда.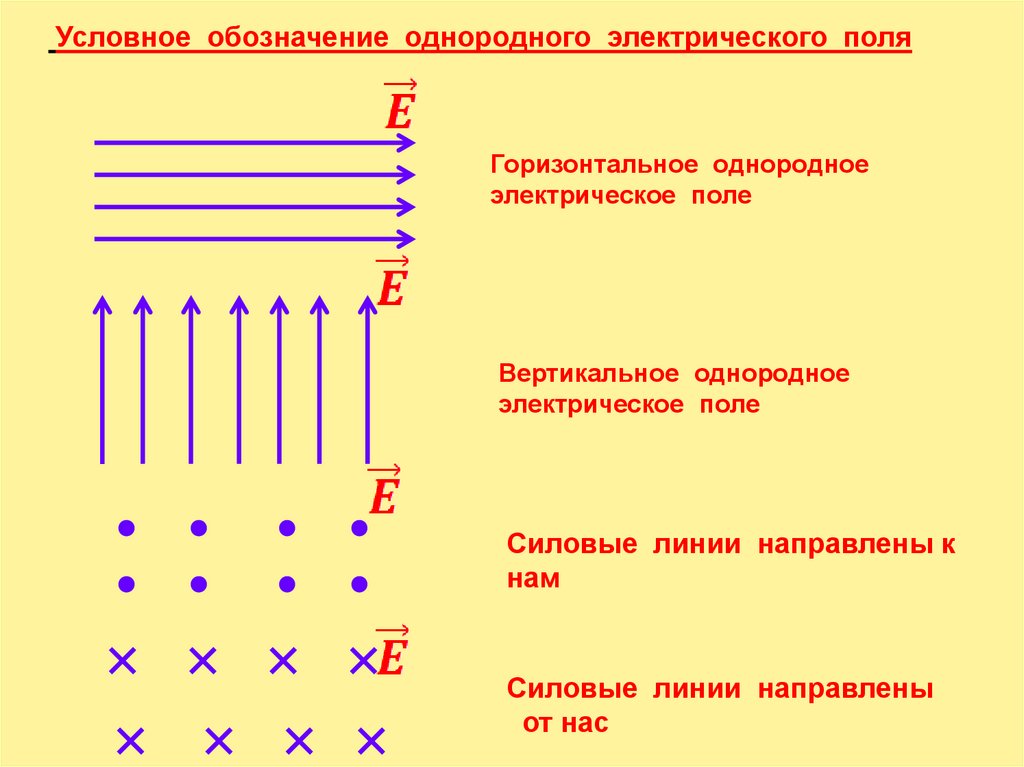 Оба ответа являются правильными для данного случая. Опять же, это в радиальном направлении, поэтому мы можем выразить это в векторной форме следующим образом. Это электрическое поле, создаваемое этим распределением заряда в точке снаружи, на расстоянии r от центра распределения.
Оба ответа являются правильными для данного случая. Опять же, это в радиальном направлении, поэтому мы можем выразить это в векторной форме следующим образом. Это электрическое поле, создаваемое этим распределением заряда в точке снаружи, на расстоянии r от центра распределения. Однако это очень сложно, за исключением простых геометрий. Во многих практических случаях хорошее понимание проблемы возможно при использовании некоторых простых правил для построения силовых линий и эквипотенциалов. Важные правила:
Однако это очень сложно, за исключением простых геометрий. Во многих практических случаях хорошее понимание проблемы возможно при использовании некоторых простых правил для построения силовых линий и эквипотенциалов. Важные правила: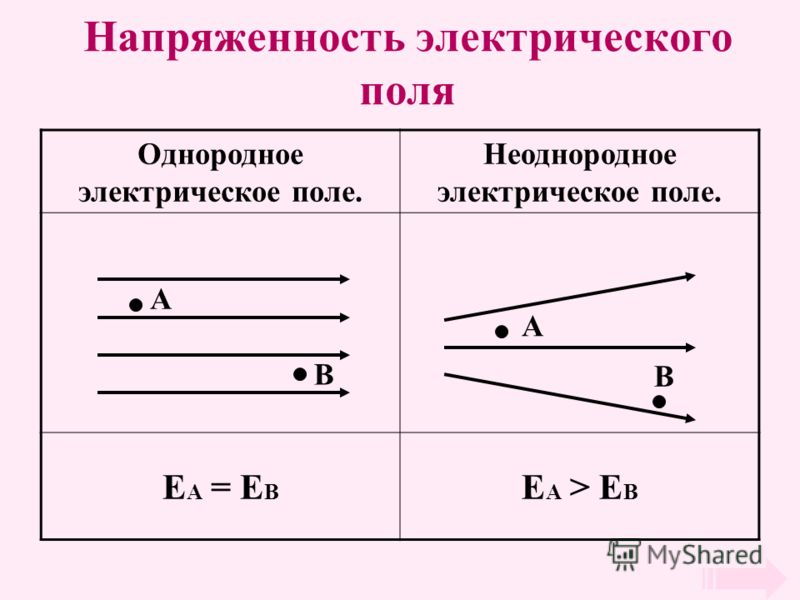 Это случай, обычно встречающийся в высоковольтных электродах проходных изоляторов, стандартных конденсаторах и т. д. Когда два диэлектрика с очень разной диэлектрической проницаемостью соединены последовательно, контроль электрического напряжения намного выше в среде с более низкой диэлектрической проницаемостью. С учетом твердой изоляции в газовой среде напряжение в газе становится равным ε r раз больше, чем в твердом диэлектрике, где ε r – относительная диэлектрическая проницаемость твердого диэлектрика. Это повышенное напряжение возникает на краях электродов, и одним из способов преодоления этого является увеличение диаметра электрода. Другие методы контроля электрического напряжения показаны на рис. 1.1.
Это случай, обычно встречающийся в высоковольтных электродах проходных изоляторов, стандартных конденсаторах и т. д. Когда два диэлектрика с очень разной диэлектрической проницаемостью соединены последовательно, контроль электрического напряжения намного выше в среде с более низкой диэлектрической проницаемостью. С учетом твердой изоляции в газовой среде напряжение в газе становится равным ε r раз больше, чем в твердом диэлектрике, где ε r – относительная диэлектрическая проницаемость твердого диэлектрика. Это повышенное напряжение возникает на краях электродов, и одним из способов преодоления этого является увеличение диаметра электрода. Другие методы контроля электрического напряжения показаны на рис. 1.1. Методы управления электрическим полем составляют важный компонент общей конструкции оборудования.
Методы управления электрическим полем составляют важный компонент общей конструкции оборудования. Работа, совершаемая зарядом при его перемещении в электрическом поле, называется потенциалом. Потенциал φ равен
Работа, совершаемая зарядом при его перемещении в электрическом поле, называется потенциалом. Потенциал φ равен


 9 класс. Учебник. Перышкин А.В., Гутник Е.М.
9 класс. Учебник. Перышкин А.В., Гутник Е.М.
