Электрические цепи. Последовательное и параллельное соединения проводников
Электрические цепи. Последовательное и параллельное соединения проводников
«Физика — 10 класс»
Как выглядит зависимость силы тока в проводнике от напряжения на нём?
Как выглядит зависимость силы тока в проводнике от его сопротивления?
От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию: электрической лампе, радиоприёмнику и др. Для этого составляют электрические цепи различной сложности.
К наиболее простым и часто встречающимся соединениям проводников относятся последовательное и параллельное соединения.
Последовательное соединение проводников.
При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочерёдно друг за другом. На рисунке (15.5, а) показано последовательное соединение двух проводников 1 и 2, имеющих сопротивления R1
Сила тока в обоих проводниках одинакова, т. е.
I1 = I2 = I. (15.5)
В проводниках электрический заряд в случае постоянного тока не накапливается, и через любое поперечное сечение проводника за определённое время проходит один и тот же заряд.
Напряжение на концах рассматриваемого участка цепи складывается из напряжений на первом и втором проводниках:
U = U1 + U2.
Применяя закон Ома для всего участка в целом и для участков с сопротивлениями проводников R1 и R2, можно доказать, что полное сопротивление всего участка цепи при последовательном соединении равно:
R = R1 + R2. (15.6)
Это правило можно применить для любого числа последовательно соединённых проводников.
Напряжения на проводниках и их сопротивления при последовательном соединении связаны соотношением
Параллельное соединение проводников.
На рисунке (15.5, б) показано параллельное соединение двух проводников 1 и 2 сопротивлениями R1 и R2. В этом случае электрический ток I разветвляется на две части. Силу тока в первом и втором проводниках обозначим через I1 и I2.
Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не накапливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время. Следовательно,
I = I1 + I2. (15.8)
Напряжение U на концах проводников, соединённых параллельно, одинаково, так как они присоединены к одним и тем же точкам цепи.
В осветительной сети обычно поддерживается напряжение 220 В. На это напряжение рассчитаны приборы, потребляющие электрическую энергию. Поэтому параллельное соединение — самый распространённый способ соединения различных потребителей. В этом случае выход из строя одного прибора не отражается на работе остальных, тогда как при последовательном соединении выход из строя одного прибора размыкает цепь. Применяя закон Ома для всего участка в целом и для участков проводников сопротивлениями R
Отсюда следует, что для двух проводников
Напряжения на параллельно соединённых проводниках равны: I1R1 = I2R2. Следовательно,
Обратим внимание на то, что если в какой-то из участков цепи, по которой идёт постоянный ток, параллельно к одному из резисторов подключить конденсатор, то ток через конденсатор не будет идти, цепь на участке с конденсатором будет разомкнута. Однако между обкладками конденсатора будет напряжение, равное напряжению на резисторе, и на обкладках накопится заряд q = CU.
Рассмотрим цепочку сопротивлений R — 2R, называемую матрицей (рис. 15.6).
На последнем (правом) звене матрицы напряжение делится пополам из-за равенства сопротивлений, на предыдущем звене напряжение тоже делится пополам, поскольку оно распределяется между резистором сопротивлением R и двумя параллельными резисторами сопротивлениями 2R и т. д. Эта идея — деления напряжения — лежит в основе преобразования двоичного кода в постоянное напряжение, что необходимо для работы компьютеров.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика
Электрический ток. Сила тока — Закон Ома для участка цепи. Сопротивление — Электрические цепи. Последовательное и параллельное соединения проводников — Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» — Работа и мощность постоянного тока — Электродвижущая сила — Закон Ома для полной цепи — Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»
Соединения проводников — материалы для подготовки к ЕГЭ по Физике
Темы кодификатора ЕГЭ: параллельное и последовательное соединение проводников, смешанное соединение проводников.
Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.
Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.
Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1):

Рис. 1. Резистор
Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2):

Рис. 2.
Стационарное поле совершает при этом положительную работу .
Так как и , то и , т. е. .
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3):

Рис. 3.
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.
1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике
Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть — сопротивление участка . По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).

Рис. 5. Параллельное соединение
Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от к (по направлению тока) называется неразветвлённой частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.
1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .
Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:
Сокращая на , получим:
(1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти :
(2)
К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
(3)
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:

откуда
Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис. 6).

Рис. 6. Смешанное соединение
Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :
Ом.
Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:
Ом.
Сопротивление цепи:
Ом.
Теперь находим силу тока в цепи:
A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
B;
B.
(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора и находятся под напряжением , поэтому:
A;
A.
(В сумме имеем А, как и должно быть при параллельном соединении.)
Сила тока в резисторах и одинакова, так как они соединены последовательно:
А.
Стало быть, через резистор течёт ток A.
Физика Электрические цепи. Последовательное и параллельное соединение проводников
Описание видеоурока
Изучая тему «Электрический ток», мы встречались с целым рядом физических величин:
— Сила тока; единица измерения — 1А; прибор для определения силы тока – амперметр, он характеризует электрический ток.
— Напряжение; единица измерения — 1В; прибор для определения – вольтметр, он характеризует электрическое поле.
— Сопротивление; единица измерения – 1Ом; прибор для определения сопротивления — омметр, он характеризует проводник.
Мы изучаем электрический ток, величины, которые характеризуют его действия. Но порой незнание, пренебрежение законами физики, к действиям электрического тока, ведет к трагедиям. Кто-то оставил без присмотра включенные электроприборы, кого –то убило током, об этом часто сообщают СМИ.
От чего может резко увеличиться сила тока? Почему загорается электропроводка?
Рассмотрим условное обозначение на схемах электрических приборов.
От источника тока энергия может быть передана по проводам и устройствам, потребляющим энергию: электрической лампе, радиоприемнику и др. Для этого составляют электрические цепи различной сложности. Электрическая цепь состоит из источника энергии, устройств, потребляющих электрическую энергию, соединительных проводов и выключателей для замыкания цепи. Часто в электрическую цепь включают приборы, контролирующие силу тока и напряжение на различных участках цепи, — амперметры и вольтметры. К наиболее простым и часто встречающимся соединениям проводников относятся последовательное и параллельное соединения.
При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включаются в цепь поочередно друг за другом.
Сила тока во всех проводниках одинакова, так как в проводниках электрический заряд в случае постоянного тока не накапливается и через любое поперечное сечение проводника за определенное время проходит один и тот же заряд.
Напряжение на концах рассматриваемого участка цепи складывается из напряжений на каждом из проводников.
Применяя закон Ома для всего участка в целом и для составляющих участков цепи, можно доказать, что полное сопротивление всего участка цепи при последовательном соединении равно сумме сопротивлений каждого из участков.
При параллельном соединении проводников электрический ток разветвляется на части. Точку разветвления проводников называют узлом. В узле электрический заряд не накапливается, следовательно, сила тока всей цепи равна сумме токов проходящих по каждому из ветвей цепи.
Напряжение на концах проводников, соединенных параллельно одно и то же.
Величина, обратная полному сопротивлению участка, равна сумме величин, обратных сопротивлениям отдельных проводников.
Решим задачи.
Вольтметр №1 показывает 12 Вольт. Каковы показания амперметра и вольтметра №2?
Запишем данные: сопротивление резистора №1 равно 6 Ом, резистора №2 – 2 Ом. На первый резистор подают напряжение в 12 вольт. Нужно определить силу тока во всей цепи и напряжение, поданное на второй резистор.
Ток во всей цепи равен току, проходящему через первый резистор, который можно определить по закону Ома как отношение напряжения на сопротивление первого резистора. Он равен двум амперам.
Теперь найдем напряжение на втором резисторе, умножив силу тока на сопротивление этого резистора. Получим 4 вольт.
Амперметр А показывает силу тока равную 1,6 (одной целой шести десятым) ампер при напряжении 120 вольт. Сопротивление резистора №1 равно 100 Ом. Определите сопротивление резистора №2 и показания амперметров А1 и А2.
По законам параллельного соединения напряжение на обоих резисторах будет по 120 вольт.
Ток в первом потребителе найдем по закону Ома, он равен 1,2 ампер.
Значит, во втором потребителе проходит ток в 0,4 ампер.
Снова воспользуемся законом Ома и определим, что второй резистор имеет сопротивление 300 Ом.
На рисунке изображена схема смешанного соединения проводников, сопротивления которых следующие: R1=3 Ом, R2=4 Ом, R3=5 Ом, R4=10 Ом, R5=5 Ом. Определить общее сопротивление на участке цепи.
Резисторы 1 и 2 соединены последовательно, поэтому применяем закон последовательного соединения для определения общего сопротивления на участке1-2.
Резисторы 3, 4, 5 соединены параллельно, поэтому применяем закон параллельного соединения для определения общего сопротивления на участке 3-5.
Участки1 -2 и 3- 5 соединены последовательно, опять применяем закон последовательного соединения для определения общего сопротивления всей цепи.
Различные проводники в цепи соединяются друг с другом последовательно и параллельно. В первом случае сила тока одинакова во всех проводниках, во втором случае одинаковы напряжения на проводниках. Чаще всего к осветительной сети различные потребители тока подключаются параллельно.
Основным недостатком последовательного соединения проводников является то, что при выходе из строя одного из элементов соединения отключаются и остальные. Так, например, если перегорит одна из ламп елочной гирлянды, то погаснут и все другие. Указанный недостаток может обернуться и достоинством. Представьте себе, что некоторую цепь нужно защитить от перегрузки: при увеличении силы тока цепь должна автоматически отключаться. Как это сделать? Например, использовать предохранитель.
Шунт — сопротивление, подключаемое параллельно к амперметру (гальванометру), для расширения его шкалы при измерении силы тока.
Если амперметр рассчитан на силу тока I0 (и нулевое), а с помощью него необходимо измерить силу тока, превышающую в n раз допустимое значение, то сопротивление, подключаемого шунта должно удовлетворять следующему условию.
добавочное сопротивление — сопротивление, подключаемое последовательно с вольтметром (гальванометром), для расширения его шкалы при измерении напряжения.
Если вольтметр рассчитан на напряжение U0 , а с помощью него необходимо измерить напряжение, превышающее в n раз допустимое значение, то добавочное сопротивление должно удовлетворять следующему условию.
Решим задачу. На фотографии – электрическая цепь. Показания включенного в цепь амперметра даны в амперах. Какое напряжение покажет идеальный вольтметр, если его подключить параллельно резистору 3 Ом?
Так как соединение в цепи – параллельное, то по третьему резистору будет проходить сила тока равная 0,8 ампер.
По закону Ома напряжение вычислим, умножив значения сопротивления и силы тока. Напряжение на третьем резисторе равно 2,4 вольт.
Действие электрического тока на живые организмы было открыто итальянским ученым Луиджи ГальвАни. Ноябрьским днем 1770 г. он был поражен странным явлением: находившиеся на столе обезглавленные лягушки, над которыми профессор производил опыты, вздрагивали. Их лапки судорожно сокращались всякий раз, когда из стоявшей в кабинете электростатической машины извлекали яркие искры. Особенно сильными были содрогания лапок, когда к ним были присоединены проволоки, свисавшие до земли. Гальвани провел несколько опытов: в одном из них прикрепил к нерву лапки свежепрепарированной лягушки медный крючок, после чего подвесил лапку к железной решетке, окружавшей висячий садик его дома. Однако никакого действия атмосферы не последовало. И лишь тогда, когда под порывами ветра лапка случайно коснулась решетки забора, ее мускулы резко согнулись. В другом опыте он один проводник, соединенный с крышей дома, подключал к нервам задних конечностей лягушки, другой присоединенный к мускулам соединял с колодцем, т.е. опускал в воду.
«Дело пошло совершенно по нашему желанию, как и в случае искусственного электричества,- писал Гальвани,- именно сколько раз вспыхивала молния, столько раз все мышцы в тот же момент впадали в сильнейшие и многократные сокращения, и как это обыкновенно происходит при вспышке молнии и мышечные движения, и сокращения этих животных предшествовали ударам грома и как бы возвещали о них». Гальвани решил, что в мускулах лягушки заключается «животное» электричество, поэтому при соединении проводниками (медные крючки и железная решетка балкона) нерва с мускулами происходит разряд.
Тело человека является проводником. Проходя по нему, электрический ток может вызвать повреждение жизненно важных органов, а иногда и смерть человека.
Тяжесть поражения током зависит от силы тока, прошедшего через человека, характера тока (является ли он постоянным или переменным, т.е. изменяющимся по величине и направлению), продолжительности его действия, а также от того, по какому пути внутри человека он шел.
Наибольшую опасность представляет прохождение тока через мозг и те нервные центры, которые контролируют дыхание и сердце человека. Сопротивление человеческого тела не имеет постоянного значения. Оно зависит от состояния человека, его кожи, наличия на ее поверхности пота, содержание алкоголя в крови и т. д. Сухая, огрубевшая кожа имеет высокое сопротивление, а тонкая, нежная и влажная — низкое. Наиболее чувствительными к току являются такие участки тела, как кожа лица, шеи и тыльной стороны ладоней. Их сопротивление существенно меньше, чем у остальных частей тела. Но самым уязвимыми у человека являются так называемые акупунктурные точки на шее и мочках ушей: при ударе током в эти точки смертельным может оказаться даже напряжение 10-15 В.
Наше здоровье, наша жизнь, жизнь и здоровье близких в наших руках — электробезопасности первоочередное внимание.
Последовательное и параллельное соединения проводников
От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию: электрической лампе, радиоприёмнику и так далее.
Совокупность устройств и элементов, предназначенных для протекания электрического тока, называют электрической цепью.
Любая электрическая цепь содержит, во-первых, источник тока, создающий необходимое напряжение, а во-вторых, нагрузку, то есть то устройство, в котором нужно создать ток и использовать одно из его действий. Нагрузкой может быть нагреватель или лампа накаливания (здесь используют тепловое действие тока), электродвигатель или звонок (используется магнитное действие тока), аккумулятор (это проявление химического действия тока). Звеньями же цепи являются соединительные провода и ключ, служащий для удобства и безопасности работы.
Рисунки, на которых изображены способы соединения электрических приборов в цепь, называются электрическими схемами.
Приборы на схемах принято обозначать условными знаками, часть из которых представлена на экране в виде таблицы.

Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного проводника, а из системы различных проводников, которые могут быть соединены между собой по-разному.
Рассмотрим простую цепь, составленную из источника ток, ключа и двух проводников. Обратите внимание на то, что в представленной цепи конец одного проводника соединяется с началом другого, его конец — с началом третьего и так далее. Проще говоря, проводники имеют по одной общей точке. Такое соединение проводников принято называть последовательным соединением.

Как вы уже знаете, в проводниках, по которым течёт постоянный ток, электрический заряд не накапливается, и через любое поперечное сечение проводника за определённое время протекает один и тот же заряд. Следовательно, ток во всех частях последовательно соединённой цепи в каждый данный момент времени одинаков:

Напряжение же на концах каждого из проводников будет различно. Покажем это. Пусть I — это сила тока в цепи, R1 и R2 — сопротивления проводников, a U1 и U2 — напряжения на концах этих проводников.
На основании закона Ома мы с вами можем записать, что напряжения на концах проводников пропорциональны силе тока в цепи и их сопротивлениям:

Разделив первое равенство на второе, получим, что при последовательном соединении напряжения на проводниках пропорциональны их сопротивлениям:

Только при таком распределении напряжений и становится возможным один и тот же ток во всех участках цепи.
А полное напряжение на обоих проводниках (или напряжение на полюсах источника тока) равно сумме напряжений на отдельных проводниках:

Это легко проверить, если измерить напряжение на концах обоих проводников и на двух проводниках одновременно.
Также записанное нами равенство вытекает из того, что напряжение есть величина, измеряемая работой, совершаемой при перемещении единицы заряда на данном участке цепи:

Работа же по перемещению заряда во всех последовательно соединённых проводниках равна сумме работ на отдельных проводниках.
Применяя закон Ома для всего участка цепи с последовательным соединением и для каждого проводника в отдельности, нетрудно показать, что полное сопротивление участка цепи равно сумме сопротивлений отдельных проводников:

Совершенно аналогично можно показать, что в случае п последовательно соединённых проводников общее сопротивление участка цепи, состоящей из нескольких последовательно соединённых проводников, равно сумме сопротивлений отдельных проводников:

Рост сопротивления цепи при добавлении в неё новых проводников объясняется увеличением длины проводящей части. Поэтому сопротивление цепи становится больше сопротивления одного проводника.
На практике последовательное соединение нескольких проводников используется очень редко, например, в ёлочной гирлянде. Дело в том, что недостатком такого соединения является то, что в такую цепь можно подключать только тех потребителей, которые рассчитаны на одинаковую силу тока. Кроме того, если в такой цепи выключить ток в одном звене (например, перегорит одна из лампочек в гирлянде), то разрывается вся цепь.
Этих недостатков лишена цепь, в которой потребители соединены параллельно.
Параллельное соединение — это такое соединение проводников, при котором одни их концы соединены в один узел, другие концы — в другой узел.
Узлом принято называть точку разветвлённой цепи, в которой сходятся более двух проводников.

Следствием этого является то, что напряжение на каждом параллельно соединённом проводнике одинаково и равно напряжению на всём участке параллельно соединённых проводников:

При параллельном соединении ток распределяется по проводникам так же, как поток воды, разветвляющийся на два параллельных канала. Количество воды, протекающее ежесекундно через неразвтвлённую часть потока воды, равно сумме количеств воды, протекающих ежесекундно через каждый из каналов.
Аналогично обстоит дело и с прохождением электрических зарядов через параллельно соединённые проводники. Включив амперметры в цепь до разветвления и в каждую ветвь разветвления, можно убедиться, что ток в неразветвлённой части цепи равен сумме токов, текущих в отдельных параллельно соединённых проводниках:

Этот опыт служит лишь подтверждением того, что в случае установившегося тока электрические заряды не скопляются в точках разветвления, а сколько их подходит к точкам разветвления, столько же и уходит.
Обозначим сопротивление каждого из разветвлённых участков цепи через R1 и R2, a напряжение во всей цепи через U. Теперь применим к каждой ветви закона Ома для участка цепи:

И выразим из этих формул напряжение.

Так как напряжение на каждом параллельно соединённом проводнике одинаково, то давайте приравняем правые части последних двух равенств:

Отсюда находим, что токи в отдельных ветвях разветвлённой части цепи обратно пропорциональны их сопротивлениям:

Третья закономерность параллельного соединения определяет общее сопротивление разветвлённого участка. Учтём, что сила тока в цепи равна сумме сил токов в ветвях, а напряжение везде одинаково. Тогда, на основании закона Ома, получим, что величина, обратная сопротивлению участка параллельно соединённых проводников, равна сумме величин, обратных сопротивлению отдельных проводников:

При этом общее сопротивление разветвлённой части цепи меньше наименьшего из сопротивлений её ветвей.
Нетрудно показать, что если в разветвление будет включено не два, а несколько проводников, то данная закономерность также будет выполняться:

Из этого равенства следует, что общее сопротивление участка цепи, состоящего из п параллельно соединённых проводников с одинаковым сопротивлением, в п раз меньше сопротивления одного из них:

Параллельное соединение — это основной способ включения в электрическую цепь различных потребителей, так как в одну и ту же электрическую цепь могут быть включены самые различные потребители. Однако следует иметь в виду, что параллельно включаемые в данную цепь потребители должны быть рассчитаны на одно и то же напряжение, соответствующее напряжению в цепи.
Большинство задач на расчёт цепи сводится к определению токов, текущих в отдельных её участках, по заданному напряжению и по сопротивлениям отдельных проводников.
Для примера рассмотрим цепь, представленную на рисунке.

Пусть нам известно общее напряжение, питающее цепь, и сопротивления включённых в цепь резисторов (сопротивлением амперметра мы пренебрегаем, так как оно очень мало). Пусть нам надо найти силу тока, протекающего по каждому из резисторов.
Прежде всего мы должны установить, из скольких последовательных участков состоит наша цепь. Легко видеть, что таких участков три, причём второй и третий участки представляют собой разветвления. Обозначим сопротивления трёх последовательных участков нашей цепи через RI, RII, RIII.
Тогда всё сопротивление цепи выразится как сумма сопротивлений этих участков:

Общее сопротивление цепи необходимо знать, так как заданное общее напряжение можно отнести только к полному общему сопротивлению цепи. Применяя закон Ома, мы найдём полный ток, текущий в нашей цепи:

Нетрудно увидеть, что сила тока на первом резисторе равна силе тока во всей цепи:

Для того чтобы найти токи в отдельных ветвях, надо предварительно найти напряжение на отдельных участках последовательных цепей. А поможет нам это сделать закон Ома:

Незабываем о том, что RII и RIII — это эквивалентные сопротивления разветвлённых участков. Эти сопротивления мы с вами можем легко найти по закону параллельного соединения
Ну а дальше, зная напряжения на отдельных разветвлениях, найдём и токи в отдельных ветвях используя всё тот же закон Ома (при этом не забываем, что напряжение на концах всех параллельно соединённых проводников одно и то же):

Таким образом, задача, поставленная перед нами, полностью решена.
Мощность тока при параллельном и последовательном соединении
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
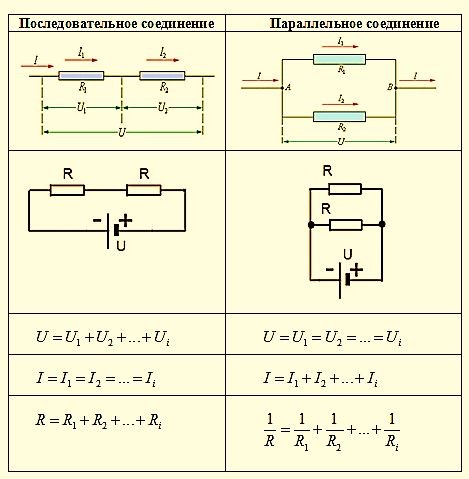
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
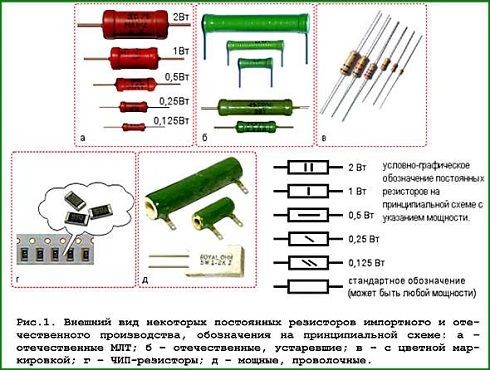
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
- P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
- P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
- P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
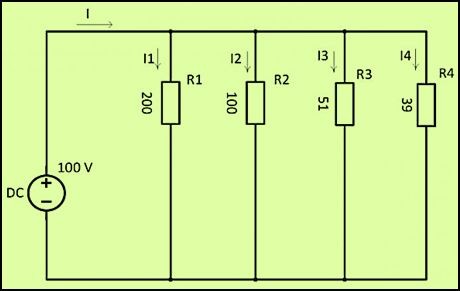
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P1 = U 2 /R1 = 100 2 /200 = 50 Вт; P2 = U 2 /R2 = 100 2 /100 = 100 Вт; P3 = U 2 /R3 = 100 2 /51 = 195,9 Вт; P4 = U 2 /R4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединение
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
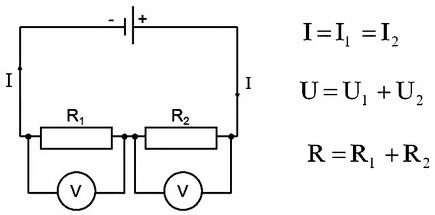
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Применение
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединение
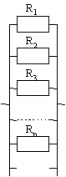
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
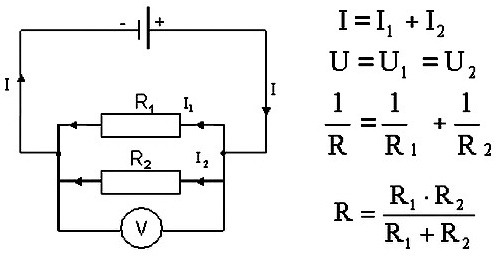
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
Применение
Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Работа тока
Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность тока
При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Р=U х I
После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:
Р=Р1 + Р2
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Влияние схемы соединения на новогоднюю гирлянду
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
Последовательное и параллельное соединение для конденсаторов
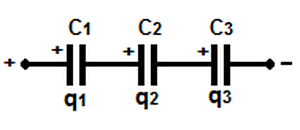
При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.
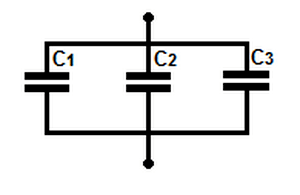
Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводников
В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
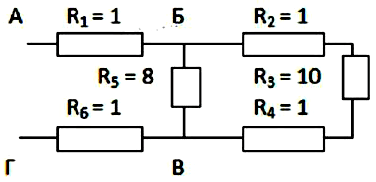
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
Параллельное соединение — урок. Физика, 8 класс.
При параллельном соединении все потребители подключены к источнику тока независимо друг от друга и образуют разветвлённую цепь.

При параллельном соединении все потребители подключены к одному источнику тока, между клеммами которого имеется определённое напряжение.
Каждый потребитель получает полное напряжение цепи.
U=U1=U2=U3=…

При параллельном соединении общий ток является суммой токов, протекающих через отдельные потребители.
I=I1+I2+I3+…
Общее сопротивление потребителей, находящихся в параллельном соединении, будет наименьшим (меньше, чем наименьшее из сопротивлений параллельно подключённых потребителей).
Если параллельно соединены \(n\) потребителей, а сопротивление каждого из них одинаково и равно \(R\), тогда общее сопротивление цепи будет равно \(R : n\).
Можно сделать вывод о том, что при увеличении числа потребителей общая сила тока неограниченно возрастает, что может привести к пожару.
Обрати внимание!
В одну розетку нельзя включать несколько мощных потребителей, так как перенагруженные провода нагреваются и могут загореться.
Электрический кабель, который используется в электрической цепи квартиры, имеет три провода. Третий провод является заземлением.
Преимуществом параллельного соединения является то, что при отключении одного из потребителей, остальные продолжают работать.
Источники:
Fizika 9. klasei/Ilgonis Vilks. — Rīga: Zvaigzne ABC, 2008. — 159 lpp.: izmantotā literatūra: 117, lpp.
(Физика для 9 класса// Илгонис Вилкс. — Рига: Zvaigzne ABC, 2008. — 159 стр.: использованная литература: 117. стр.)
Fizika pamatskolai 2. daļa// V. Rasmane, A. Vītols, Ā. Cacāne. — Rīga: RAKA, 2006. — 136 lpp.: il.-izmantotā literatūra: 84, lpp.
(Физика для начальной школы, 2 часть// Расмане В., Витолс А., Цацане А. — Рига: RAKA, 2006. — 136 стр.: ил.-использованная литература: 84. стр.)
http://www.ndg.lv/latvian/Macibas/FizInter/b2.2.4.htm
http://www.goerudio.com/demo/paralelais_slegums
http://www.ndg.lv/latvian/Macibas/FizInter/b2.2.4.htm


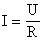
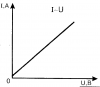

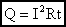
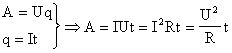
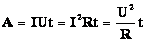
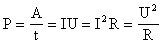
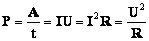

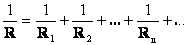
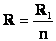
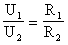 — чем больше сопротивление, тем больше напряжение.
— чем больше сопротивление, тем больше напряжение.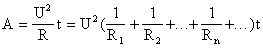 .
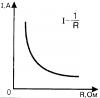
.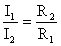 — чем больше сопротивление, тем меньше сила тока.
— чем больше сопротивление, тем меньше сила тока.